Systematic Literature Review on An Integrated Generalized Space Time Autoregressive Integrated Moving Average (GSTARIMA) Model with Heteroscedastic Error and Kriging Method for Forecasting Climate

Rapid climate change requires more powerful and precise modeling methods to forecast future climate variability. The GSTARIMA Model is efficient, combining space-time analysis with the Autoregressive Moving Average (ARIMA) Model. The integration of heteroscedasticity error and the Kriging method can strengthen the Model's ability to handle the problem of non-constant error variance in the GSTARIMA Model and forecast at unobserved locations of climate observations. This paper's Systematics Literature Review (SLR) is presented comprehensively with the principal aim of developing a thorough understanding of applying the GSTARIMA Model with heteroskedasticity error and the Kriging Method in climate forecasting following the Data Analytics Lifecycle methodology. The Systematic Literature Review (SLR) process consists of three main stages. We sourced the articles from databases such as Scopus, Dimensions, and EBSCO-Host The subsequent stage involved conducting a comprehensive literature review using the PRISMA method to ensure rigor and depth. Additionally, we performed bibliometric analysis to enhance rigor. Lastly, we conducted a gap analysis session to scrutinize existing research on the GSTARIMA Model and identify new opportunities. This literature review reveals that integrating GSTARIMA Model with heteroscedasticity errors and the Kriging method is suitable for climate forecasting. This research inspires researchers to contribute to the improvement and refinement of the Model, making it a more potent and valuable tool in climate forecasting.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

MSC: 62M10; 62H11

1. Introduction

Climate is a statistical description of the average variability of the relevant quantities over months to years, referred to as average weather [1]. In addition, it includes several interrelated elements, such as temperature, rainfall, humidity, atmospheric conditions, and wind patterns [2]. Climate change is a pressing global issue of paramount importance that demands comprehensive research. The Intergovernmental Panel on Climate Change (IPCC) is an organization founded by scientists worldwide to research the concept. The sixth assessment report of the IPCC explains that climate change affects ecosystem conditions, human activities, the global water cycle, infrastructure, health, and others [3].

The handling of climate change is in the world's spotlight, which is included in the pillars of SDGs [4,5]. Meanwhile, climate management is the 13^th goal in the SDGs, with the mission statement "Take urgent action to combat climate change and its impacts by regulating emissions and promoting developments in renewable energy” [6]. One of the climate changes very important to study is rainfall patterns [7,8]. Based on NASA's Global Precipitation Measurement, the Indonesian region has high rainfall around 1000-4000 mm per year. This is because Indonesia is located on the equator, and it is vulnerable to natural disasters such as floods and landslides. Based on data from the West Java Regional Disaster Management Agency (known as BPBD), which can be accessed on the website https://opendata.jabarprov.go.id/id/ (accessed on 01/04/2023), there were 1954 and 5,662 flood and landslide events in 2012-2021. The number of flood and landslide events for each district and city in West Java is presented in Figure 1.a and 1.b.

Natural disasters due to extreme rainfall have a significant impact and cause damage to community settlements. Based on data from the West Java BPBD report, settlement damage totaled 943,160 units from 2012-2021. Damage is categorized into destroyed, heavily damaged, slightly damaged, moderately damaged, threatened, and submerged/buried, as presented in Table 1.

Climate change is very detrimental regarding materials, infrastructure, and people's lives. Therefore, it is essential to forecast future climate conditions to take preventive, mitigation, and adaptation actions.

Climate forecasting can also be conducted using the Spatio-Temporal Model. The Spatio-Temporal Model combines location and time to model a phenomenon to understand the relationship between changes in spatial and time. The Generalized Space-Time Autoregressive (GSTAR) Model assumes heterogeneous characteristics between locations and stationary data. Furthermore, it has different autoregressive and Space-Time parameters for each location. The Model was studied using stationary data by Borovkova et al.[9]. Giacinto developed the Model into the Generalized Space-Time ARMA (GSTARMA) Model [10]. In addition, the GSTARMA Model adds the effect of an error element with a Moving Average (MA) and is applied to stationary data. The Model Estimation uses the Maximum Likelihood Estimation (MLE) method and is applied to forecast the unemployment rate in each region of Italy based on historical data. The Model of non-stationary data is called the GSTARIMA Model, developed by Min et al., 2010 [11].

The GSTAR Model has a non-constant error variance (heteroscedastic error) for climate data. The GSTAR-ARCH Model is an extension of the Spatio-Temporal Model, which considers the heteroscedasticity of variance that depends on previous information in an autoregressive manner by Nainggolan et al [12]. The Model is applied to stationary data as an extension of the GSTAR-ARCH model for non-stationary data by Bonar et al. [13]. The GSTARI-ARCH model also overcomes the non-constant error variance. Bonar et al. used the concept to model and forecast the Consumer Price Index (CPI) in North Sumatra. In forecasting Spatio Temporal Model, the respon variable is influenced by exogenous variables. For example, in climate data, rainfall is affected by humidity and temperature. The Spatio-Temporal model with the addition of exogenous variables is known as the GSTARI-X Model by Elfiyan et al. [14]. Ditago et al. (2016) used the GSTARX-GLS model, with the exogenous variable being calendar variation[15]. Monika et al. (2022) developed the GSTARI-X-ARCH model to forecast rainfall with exogenous variables in humidity [16].

In previous research, the Kriging Method was used to predict phenomena at unobserved locations. Kriging method is used for interpolation and forecasting Temperature in Mosul and Baghdad City [17]. Kriging method, land-use regression (LUR), and LightGBM (light gradient boosting machine) methods were combined to predict PM2.5 concentrations [18]. In Spatio-Temporal modeling, the GSTAR Model is integrated with the Kriging method to forecast rainfall at unobserved locations in West Java [19].

This study aims to summarize previous research on Spatio Temporal forecasting models with heteroskedastic errors and the Kriging method applied to climate data. This research attempts to cover several areas, such as Spatio Temporal models for stationary and non-stationary data, methods for parameter estimation in the models, forecasting at unsampled locations, and the potential to integrate Spatio Temporal models with Heteroskedastic errors and Kriging for climate forecasting. Ultimately, this review contributes to a broader understanding of integrated Spatio Temporal Models with Heteroskedastic errors and the Kriging Method for climate and highlights avenues for further research and innovation in this critical area. To facilitate the analysis process, we formulate the following research questions (RQs):

RQ1:: How to integrate GSTARIMA model with heteroskedastic errors using Kriging method?
RQ2:: How to forecast climate phenomena using the integration of GSTARIMA and Kriging models through a data analysis life cycle approach?

RQs were examined and explored by reviewing previous results carried out by searching literature on databases. The results were filtered and selected using the Preferred Reporting Items for Systematic Review and Meta-Analyses (PRISMA) method. Furthermore, relevant articles are presented in a state of the art to obtain research gaps. A bibliometric method was also used to show the linkage of keywords for each article. The review stage was performed to analyze search results and discuss new research. Potential new research was provided to be studied and developed on the GSTARIMA Model and its application.

2. Materials and Methods

2.1. Theoritical Background

2.1.1. The Generalized Space Time Autoregressive Integrated Moving Average (GSTARIMA)Model

In 1980, Pfeifer and Deutch introduced the Space-Time Autoregressive (STAR) Model, assuming each location has the same characteristics [20,21]. In 2002, Ruchjana developed the STAR model into the Generalized Space-Time Autoregressive (GSTAR) model. This is because the assumptions in the STAR model do not match the reality in the field, where there is a diversity of characteristics at each location. The GSTAR model introduced by Ruchjana assumes that the characteristics of each location are heterogeneous. The GSTAR

(p, λ_{k})

model has a time order of

p

and a spatial order of

λ_{k}

expressed in matrix form through equation (1)[9]

z (t) = \sum_{k = 1}^{p} \sum_{l = 0}^{λ_{k}} [Φ_{k l} W^{(l)} z (t - k)] + e (t)

(1)

where,

$Z (t)$: : the value of the observation at time $t$ ,
$Z (t - 1)$: : the value of the observation at time $t - 1$ ,
$ϕ$: : a parameter that indicates the influence of the value of $Z (t - 1)$ on the value of $Z (t),$
$e (t)$: : the value of error.

The GSTARMA model expands the GSTAR model by adding MA error elements. The GSTARMA model is applied to stationary data [10]. The GSTARMA model developed on nonstationary data is called the GSTARIMA model. Min et al. (2010) first introduced the GSTARIMA model with application to urban traffic network modeling and short-term traffic flow forecasting. The GSTARIMA model

(p_{λ_{k}}, d, q_{v_{k}})

with

d

being the differencing order is expressed in Equation (2) [11]

y (t) = \sum_{k = 1}^{p} \sum_{l = 0}^{λ_{k}} [Φ_{k l} W^{(l)} y (t - k)] - \sum_{k = 1}^{q} \sum_{l = 0}^{v_{k}} [Θ_{k l} W^{(l)} e (t - k)] + e (t),

(2)

where,

y (t) = z (t) - z (t - 1), y (t - 1) = z (t - 1) - z (t - 2), \dots, y (t - k) = z (t - k) - z (t - k - 1)

(3)

$z (t)$: : a vector of variables of size $(N \times 1)$ at time $t$ ,
$z (t - k)$: : vector of variables of size $(N \times 1)$ at time $(t - k),$
$λ_{k}$: : spatial order in the $k$ ^th autoregressive,
$v_{k}$: : spatial order of the $k$ ^th moving average,
$Φ_{k l}$: : autoregressive and space time parameters at time order $k$ and spatial order $l$ of size $(N \times N)$ in the form of diagonal matrix $(Φ_{k l}^{(1)}, Φ_{k l}^{(2)}, Φ_{k l}^{(3)}, \dots, Φ_{k l}^{(N)})$ ,
$Θ_{k l}$: : MA parameters at time order $k$ and spatial order $l$ of size $(N \times N)$ in the form of diagonal matrix $(Θ_{k l}^{(1)}, Θ_{k l}^{(2)}, Θ_{k l}^{(3)}, \dots, Θ_{k l}^{(N)}),$
$W^{(l)}$: : weight matrix of size $(N \times N)$ at spatial order $l, l = 0,1, 2, \dots, λ_{k}$ containing $w_{i i} = 0$ and $\sum_{i \neq j} w_{i j} = 1$ ,
$e (t)$: : error vector of size $(N \times 1)$ at time $t$ , assuming ${e (t)}_{~}^{i i d} N (0, σ^{2} I) .$

2.1.2. Autoregressive Conditional Heteroscedasticity (ARCH) Model

Although the GSTARIMA model assumes constant error variance, applying climate data often shows non-constant error variance. The GSTARIMA model is integrated with the Autoregressive Conditional Heteroscedasticity (ARCH) Model to overcome this. This time series model detects variance heteroscedasticity using historical data [22]. Describing the ARCH(

p

) model, researchers use the following expression [22]

h_{t} = σ_{t}^{2} = α_{0} + \sum_{i = 1}^{p} α_{i} e_{t - i}^{2}; i = 1,2, 3, \dots, p,

(4)

In Equation (4), the variables represented include:

$h_{t}$: : the conditional variance at time $t,$
$α_{0}$: : the intercept or constant error,
$α_{1}, α_{2}, \dots, α_{p}$: : ARCH model parameters,
$α_{0} > 0$ dan $α_{i} \geq 0$ .

2.1.3. Kriging Method

The Kriging method is a geostatistical interpolation technique used to predict variable values at unobserved locations based on variable values observed at other locations. This method assumes that variable values have a spatial structure related to the distance and direction between observation locations. In the calculation of the Kriging Method, a Semivariogram is required. An experimental semivariogram is calculated based on measurement data collected from the field or observations at a particular location. The formula for calculating the experimental semivariogram is as follows [23]:

\hat{ψ} (h) = \frac{1}{2 N (h)} \sum_{i = 1}^{N (h)} [Z (x_{i} + h) - Z (x_{i})]^{2}

(5)

where,

$\hat{ψ} (h)$: : semivariogram value at distance $h$ ,
$Z (x_{i})$: : observation value at location $x_{i,}$
$Z (x_{i} + h)$: : observation value at location $x_{i} + h,$
$N (h)$: : many pairs of data that have distance $h$ ,
$h$: : distance between 2 locations.

Theoretical semivariograms can be divided into Spherical, Gaussian, and Exponential Models. The Spherical Model is a model that assumes that spatial dependence has a certain maximum distance or radius. This Model is used if the spatial dependence decreases with distance and reaches a threshold value at a specific radius, after which the semivariogram value becomes constant. The semivariogram function of the Spherical Model can be expressed as [23]:

ψ (h) = \{\begin{matrix} c [(\frac{3 h}{2 a}) - {(\frac{h}{2 a})}^{3}], h \leq a \\ c, h > a \end{matrix}

(6)

The Exponential Model is a model that assumes that spatial dependence decreases exponentially with distance between locations. The semivariogram function of the Exponential Model can be expressed as [23]:

ψ (h) = \{\begin{matrix} c [1 - e x p (\frac{- h}{a})], h \leq a \\ c, h > a \end{matrix}

(7)

The Gaussian Model is a model that assumes that spatial dependence has a symmetric pattern and decreases exponentially with distance between locations. The semivariogram function of the Gaussian Model can be expressed as [23]:

ψ (h) = \{\begin{matrix} c [1 - e x p {(\frac{- h}{a})}^{2}], h \leq a \\ c, h > a \end{matrix}

(8)

where,

$h$: : distance between sample locations,
$c$: : sill value,
$a$: : range.

The semivariogram also provides the weights used in interpolation. The Kriging method aims to determine the value of the Kriging weight

θ_{i}

, which minimizes the estimator's variance so that a BLUE (Best Linear Unbiased Estimator) estimator is obtained. The Kriging estimator

\hat{Z} (x_{0})

can be written as follows [23]:

\hat{Z} (x_{0}) - ξ (x_{0}) = \sum_{i = 1}^{n} θ_{i} [Z (x_{i}) - ξ (x_{i})],

(8)

where,

$\hat{Z} (x_{0})$: : Kriging estimator at unobserved location $x$ ,
$x_{i}$: : the i^th data location adjacent to the unsampled location $x$ ,
$ξ (x_{0})$: : expectation value of $Z (x_{0})$ ,
$ξ (x_{i})$: : expectation value of $Z (x_{i})$
$n$: : many sample data used for estimation,
$θ_{i}$: : weight value at location $i$ .

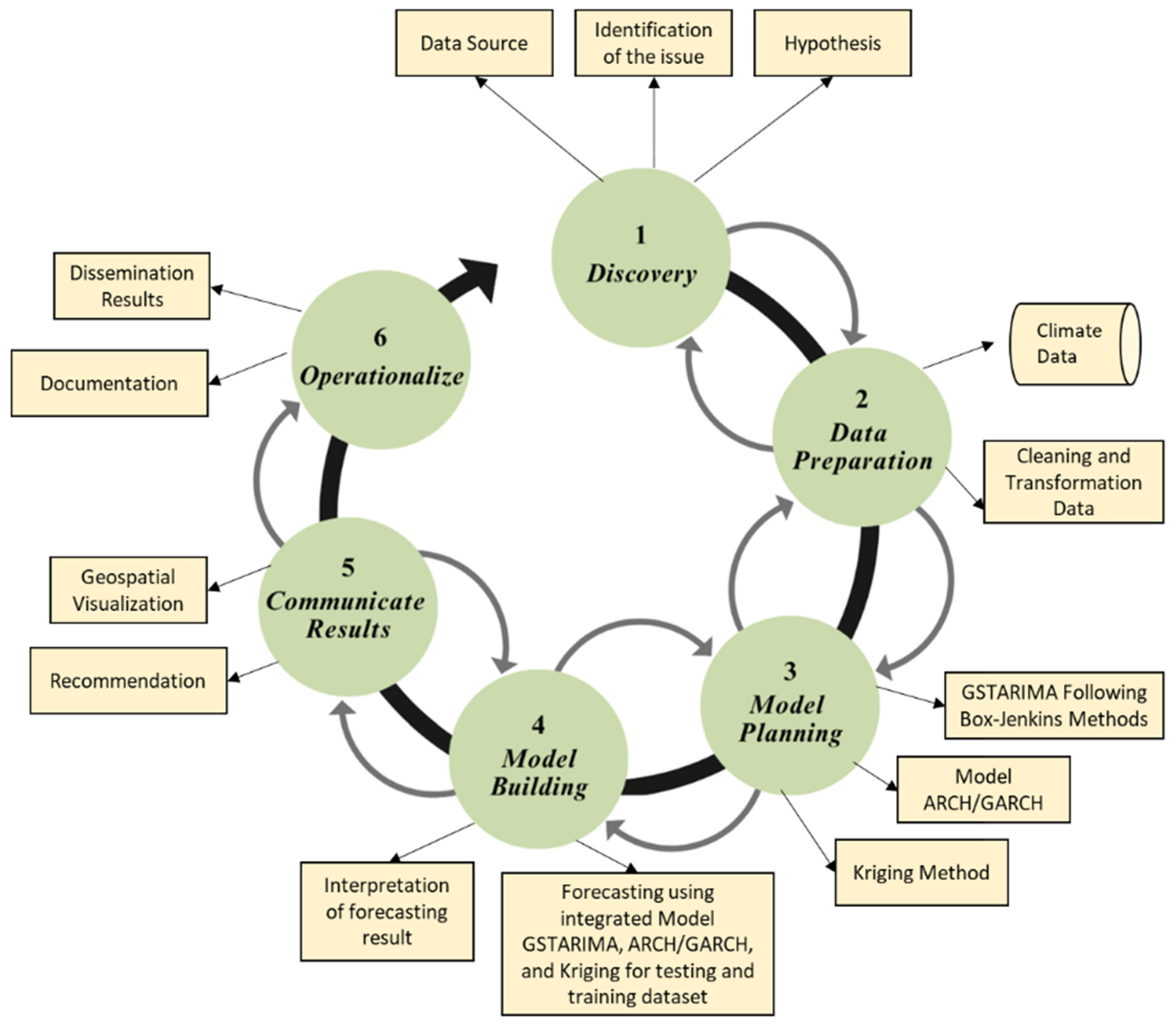
2.1.4. Data Analytics Life Cycle

Climate data has the Big Data criteria of volume, variety, and velocity. Big Data could be more efficient when analyzed using traditional methods. The Data Analytics Life Cycle methodology is specifically designed to handle Big Data problems and data science projects. The Data Analytics Life Cycle consists of six phases, including [24]:

Discovery -> At this stage, researchers must study, search and investigate facts, identify problems, and develop context and understanding of the data sources needed to support research.
Data Preparation -> Next, data is cleaned to identify missing values or noisy data. The results of data cleaning are transformed by aggregating daily data into monthly or according to the needs of the analysis. In this case, pre-processing data is obtained and ready for processing and analysis.
Model Planning -> At this stage, the model planning that will be used for analysis is carried out.
Model Building -> Researchers divide the results of data preparation into in-sample data (training) and out-sample data (testing) to do forecasting.
Communicate Results -> Researchers present forecasting results using visualizations in the form of time series plots, choropleth maps, diagrams, and others.
Operationalize -> The final stage is operationalized, and researchers provide final reports, recommendations, scripts, and technical documents. In addition, researchers can also apply the Model to the appropriate environment.

2.2. Collected Article

The PRISMA method is a widely used guide and methodological framework for conducting and presenting systematic reviews and meta-analyses [25]. The method provides the results of a systematic review, including completeness and clarity in reporting. The PRISMA method is supported by flowcharts in selecting articles [26,27].

The first stage in the PRISMA method is a literature search. Meanwhile, literature search through keywords was carried out in this research in four databases, namely Google Scholar, Dimensions, Science Direct, and Scopus. The keywords entered in the database consist of four codes connected with "OR" and "AND." The criteria selected in the collection of articles include:

The publication type selected is article research and conference paper.
Written in English
The range of article publications is 2000-2023.
The title, abstract, or keywords contain the words presented in Table 2.

The keywords provided in Table 2 are input into the database, followed by pressing the enter key to initiate a search. After displaying the search results, criteria 1-3, which pertain to the publication type, language selection, and publication year range, are configured to filter articles under the specified parameters. Subsequently, eligible articles are downloaded in .bib, .csv, and .ris formats. The number of article findings in each database is recorded for utilization as reference material in the subsequent stage.

The second stage involves the selection of articles, which is carried out through a manual process to ensure relevance. Specifically, the criteria for selecting relevant articles are those that explore the GSTAR model and its application. The articles included at this stage comprise both the ones obtained from the initial database search and the ones found manually through citation searching. The stages in article selection are explained as follows [28,29,30]:

(a): Duplicate selection aims to remove duplicate articles found. Duplication can be found in databases or literature sources with almost the same or similar structure. Duplication selection stage can be conducted with special software such as Jabref and Mendeley reference managers to compare titles, abstracts, and content.
(b): The relevance of the title and abstract is selected by assessing and ensuring that it matches the topic criteria. Titles and abstracts of selected articles are read in their entirety and irrelevant ones are excluded at this stage.
(c): The full selection aims to determine whether the discussion and content in the article are relevant to the topic. All articles are accessed and read manually to ensure their appropriateness. Articles that fail to meet the established criteria or do not pertain to the subject matter under investigation are hereby excluded from the subsequent phases of the process.

The final stage in the PRISMA method is the articles review, explaining, and answering the RQs presented in Section 1.

3. Results

3.1. Results of Literature Search and Dataset Analysis

The results of the literature search are presented in Table 3, where code A produces 213,557 articles, code B produces 1,121,262, code C produces 7,525,693, and code D is searched by combining code A, B, and C the "AND" connector to produce 286 articles.

The manual selection stage of the article is carried out as follows:

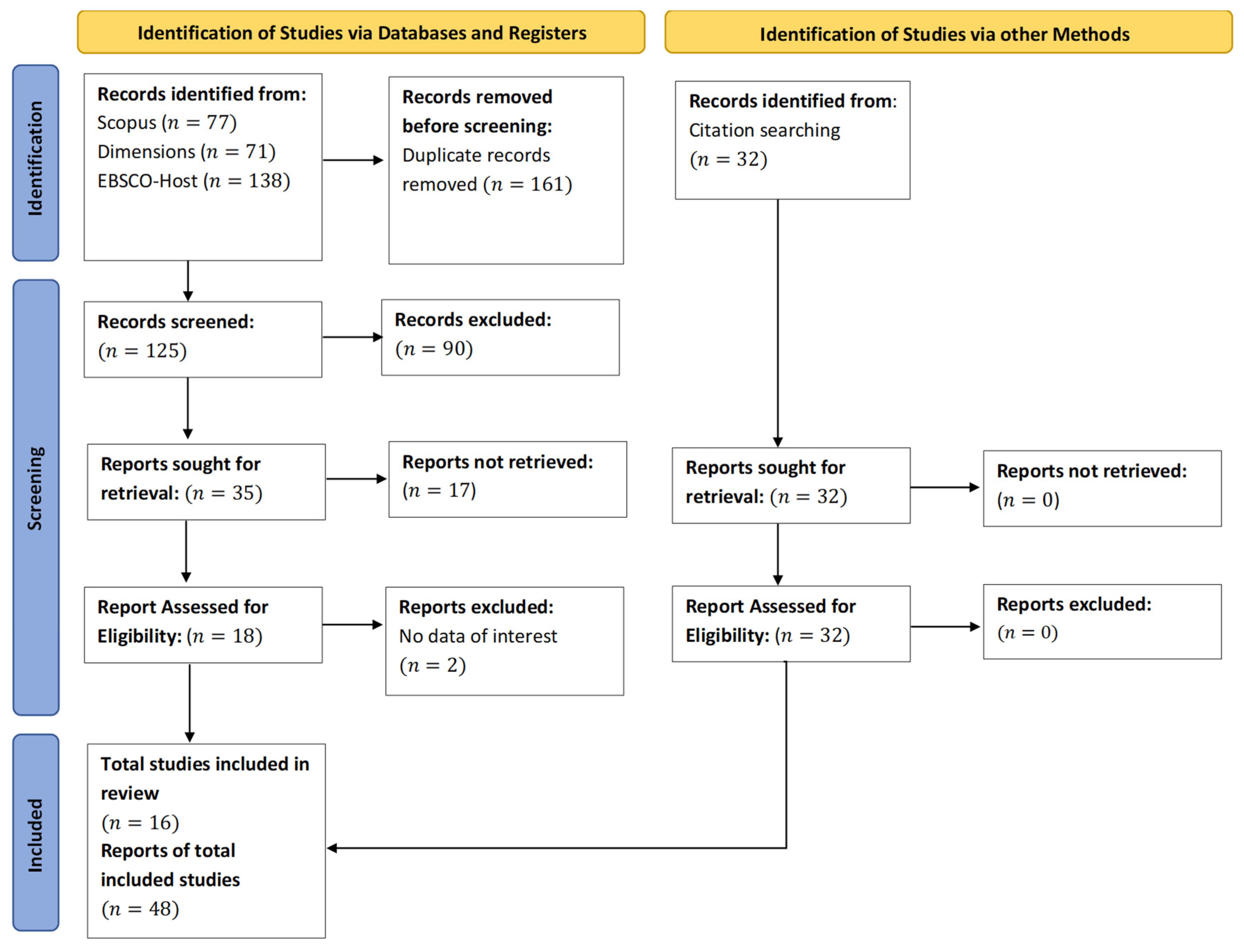
(a): At the initial stage, duplicate selection is conducted to identify 161 articles as duplicates and removed from the study.
(b): The selection stage is based on the relevance of the title and abstract, where 35 articles are selected as relevant and considered for further research.
(c): In the full paper accessibility selection stage, a total of 60 articles can be accessed and downloaded for further selection.
(d): In the full paper relevance selection stage, the entire contents of the 18 articles are read and analyzed to determine their relevance. Relevant papers were also added from another method with citation search, resulting in 32 relevant articles. So that a total of 48 review articles are obtained that are relevant to the topic discussed.

These stages are presented visually in the PRISMA diagram in Figure 2 with three stages, namely identification, screening, and inclusion. Identification includes the duplication selection stage in stage (a). Screening consists of stages (b) and (c) for selecting title-abstract and full paper. Finally, inclusion explains the number of research articles relevant to the topic.

3.2 Bibliometric Analysis

The next stage describes the selected articles in bibliometric mapping used as a visualization method to analyze the pattern of relationships between scientific articles [31,32,33]. This paper uses bibliometric maps to visualize scientific networks involving keywords in 48 articles. The visualization results are in the form of circles and clusters distinguished by different colors. The circles on the bibliometric map represent the number of related publications by keyword. A circle with a large size indicates several keywords with similar relationships between scientific articles. Clusters in a bibliometric map show connected circles and represent scientific articles with similarities in context, such as topics [34]. Furthermore, bibliometric mapping keyword analysis is obtained using VOSviewer to understand the structure, patterns, and relationships between scientific articles [35]. VOSviewer analyzes keywords that frequently appear in articles and identifies the relevant ones. The results of the bibliometric mapping for keyword analysis with VOSviewer are presented in Figure 3.

Figure 3 was created using the VosViewer software, and a total of 48 relevant articles are saved in .ris format. Article files are inputted into VOSviewer, which is a mapping selected for co-occurrence words. The bibliometric mapping in Figure 3 shows that the co-occurrence of keywords consists of five clusters. These clusters indicate the link between "Spatio-Temporal Models" and "Climate." Forecasting climate is done chiefly with Spatio-Temporal Models and Time Series Models. In Figure 3, it can be seen that there are clusters that show climate variables that are often used by researchers, such as rainfall, Pacific Decadal Oscillation (PDO), atmospheric pressure, etc.

As revealed by an analysis of 48 relevant articles, the state-of-the-art in this field highlights significant progress in several key topics shown in Table 4. First, "GSTARIMA models" are emerging as a prominent approach to analyzing Spatio-Temporal data. This cutting-edge model combines the capabilities of time series analysis and spatial relationships, enabling a comprehensive understanding of complex interactions. Secondly, the exploration of "Heteroscedastic Error" in this study is in terms of overcoming the non-constant variance of errors in the GSTARIMA Model. By addressing these heteroscedastic errors, researchers aim to improve the accuracy and reliability of their forecasts, ultimately leading to more robust modeling results. In addition, "Kriging," a geostatistical interpolation technique, plays an essential role in spatial analysis. This method incorporates the estimation of unknown values based on observed values in the vicinity, incorporating spatial correlation. Collectively, these advances show the evolving research landscape in spatial-temporal analysis, featuring the integration of cutting-edge methodologies such as the GSTARIMA Model, the consideration of heteroscedastic errors, and the application of techniques such as Kriging to unravel complex spatial patterns and relationships.

Table 4 provides a comprehensive overview of the research developments related to the GSTARIMA/Spatio-Temporal model. Several studies have been conducted in Spatio-Temporal modeling while considering heteroscedastic errors. Kumar et al. (2022) used a STARMA-GARCH model to forecast monthly temperatures, resulting in minimal Mean Absolute Percentage Error (MAPE) values in their predictions [36]. Similarly, Monika et al. (2022) used the GSTARI-X-ARCH model to forecast rainfall influenced by humidity, showing favorable forecast accuracy [16]. In a different context, Akbar et al. (2020) introduced the GSTARMAX model to forecast air pollutants in Surabaya, achieving low Root Mean Square Error (RMSE) values [51]. Furthermore, the integration of Spatio-Temporal and Kriging models is seen in several articles. Dhaher et al. (2023) applied the Spatio-Temporal-Kriging model for temperature interpolation and prediction in Baghdad and Mosul cities [17]. Dai et al. (2022) used four methods, including LUR, LightGBM, ML, and Kriging, to forecast PM2.5 concentrations, which resulted in satisfactory R² accuracy [18]. Pramoedyo et al. (2020) adopted the GSTARX-SUR-Kriging model to forecast cocoa plant diseases affected by rainfall with reasonably accurate forecast results [54]. However, Abdullah et al. (2018) used the GSTAR-Kriging model to forecast rainfall in unobserved locations and produced fairly reliable prediction results [19]. Shu-qin et al. (2014) explored two different approaches, namely GWR and Kriging methods [69].

4. Discussion

4.1. GAP Analysis

Conducting a GAP analysis based on relevant articles illustrates the evolving research landscape in Spatio-Temporal modeling, heteroscedastic errors, and Kriging methodologies for forecasting climate and environmental data. These articles collectively represent vital insights and areas that need further exploration. The research that has been evaluated demonstrates a high propensity to use GSTARIMA models' capacity to forecast climate-related variables like temperature, precipitation, and air pollutants [19,37,40,49,50,51,64]. A common thread is the evaluation of model performance metrics, especially MAPE, RMSE, R², and MSE. However, the gap lies in comprehensively exploring complex parameter configurations in the GSTARIMA framework, especially in dynamic Spatio-Temporal systems. In addition, progress still needs to be made in validating these models using more sophisticated techniques, especially in handling larger and higher-dimensional data sets.

It is clear that heteroskedastic errors are critical to climate prediction, and special attention has been paid to using ARCH and GARCH models to address this issue [16,36,57]. Researchers concentrate on achieving higher prediction accuracy, indicated by lower RMSE and MSE values. However, there are differences in research in dealing with complex and non-linear forms of heteroscedasticity, which can arise from complex climate datasets. Identifying more flexible methods to handle this complexity could be an interesting subject of investigation. By incorporating Kriging into a spatiotemporal model, discernible trends can be identified, especially in interpolation and forecasting climate variables [17,18,19,47,58]. This study relies heavily on RMSE and MAE as tools to assess prediction accuracy. However, areas still need to be addressed in creating an adaptive Kriging method that can capture the temporal and spatial changes present in complex climate data. Due to these limitations, there is a possibility for more complex techniques that are adapted to changing trends and non-stationary data.

4.2. The Framework for model integration for climate forecast

4.2.1. The Integration of GSTARIMA Model with Heteroskedastic error and Kriging Method for forecasting

After the review of previous researchers and gap analysis, a conceptual integration model of GSTARIMA with Heteroskedastic error and the Kriging method is made to answer RQ1. The GSTARIMA model is processed following the Box-Jenkins method, including identification, parameter estimation, and diagnostic checking. The initial identification of the GSTARIMA model is to determine the stationarity of the data. If the stationary test results show that the data is not stationary, then a differencing process is carried out until stationary data is obtained. Next, check the order of the model univariately with the ARIMA Model. The model order is received from the results of the Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF) plots. Models with the same order are selected for further multivariate and Spatio-Temporal modeling. In terms of Spatio-Temporal modeling, a weight matrix is used that shows the diversity in locations. The order of the Spatio-Temporal Model is obtained based on the calculation of the Space-Time Autocorrelation Function (STACF) and Partial Space-Time Autocorrelation Function (STPACF).

Furthermore, parameter estimation for the GSTARI Model is carried out using the Ordinary Least Square (OLS) method. The error generated by the GSTARI Model is re-modeled to obtain the GSTIMA Model using the Maximum Likelihood (MLE) method. The GSTARI Model and GSTIMA Model are combined to produce the GSTARIMA Model. On the other hand, if exogenous variables influence the response variable, it becomes the GSTARIMA-X Model. Furthermore, predictions are made on the testing data for the GSTARIMA Model. The last stage of the model diagnostic check to determine the model error is white noise and homoscedasticity.

The GSTARIMA Model errors with heteroscedasticity errors are re-estimated following the ARCH/GARCH Model to overcome the non-constant variance of the errors. GSTARIMA Model errors are divided into mean equations and variance equations. The mean equation of the GSTARIMA Model error is estimated using the MLE method, and the variance equation is estimated using the GLS method. Integrating the GSTARIMA Model with the ARCH/GARCH Model can minimize the model error. This model is only able to do forecasting at locations that have observed values.

Regarding climate data, some areas do not have observation stations. The GSTARIMA and ARCH/GARCH models are then integrated with the Kriging method. The Kriging method is proven to forecast phenomena at unobserved locations. Estimated parameters in the GSTARIMA-ARCH Model are input to obtain parameters at unobserved locations. Furthermore, experimental and theoretical semivariogram calculations are carried out to obtain Kriging weights from unobserved locations. The estimated parameters for the unobserved locations are simulated to get the data at the unsampled locations. Finally, the data at unsampled locations are forecasted with the GSTARI-MA-ARCH Model. The integration of the GSTARIMA Model, ARCH/GARCH Model, and Kriging Method can forecast the phenomenon at unobserved locations in the future.

4.2.2. Data Analytics Life Cycle for Climate Forecasting

The conceptual Integrated Model of GSTARIMA, ARCH/GARCH, and Kriging Method is then used in forecasting climate that meets the criteria of Big Data. Regarding answering RQ2, the modeling flow follows the data analytics life cycle methodology presented in Figure 4. The initial stage begins with discovery, problem identification, determination of data sources to be processed, and hypotheses that are proven using theorems and mathematical formulas. The next step involves data preparation, inputting climate data into the process. Raw climate data is taken at a daily interval and cleaned to eliminate missing value data. Daily data is transformed by aggregating daily data into monthly data. In model planning, mathematical model integration is carried out. At this stage, the theorem that answers the research hypothesis is created. The GSTARIMA model is developed following the Box-Jenkins method. Integrating the GSTARIMA model, ARCH/GARCH, and Kriging method requires complex mathematical reasoning, especially in estimating model parameters. The integrated model is used in the Model Building stage with the input of data preparation results. Climate data is divided into training data and testing data. The results of forecasting are interpreted by the model obtained. Furthermore, visualization is carried out at the communication results stage, and recommendations are obtained. The last step is to operationalize the results of discoveries in Model development with theorems on mathematical modeling and dissemination.

5. Conclusions

In conclusion, a systematic literature review was conducted in developing the Integration GSTARIMA model with heteroscedastic error and the Kriging method for climate forecasting. A comprehensive search and analysis of the literature was performed to provide a clear understanding of the latest research. This research uses the PRISMA and bibliometric methods in analyzing the developments on this topic. In this paper, the results of the study in integrating the GSTARIMA Model with the ARCH/GARCH Model can overcome the problem of non-constant error variance. The GSTARIMA and ARCH models provide an overview of multivariate modeling affected by time, location, and non-stationary data. On the other hand, the GSTARIMA/Spatio-Temporal Model can only forecast at the observed location. Through the integration of the GSTARIMA Model with the Kriging Method, it has been discovered that the prediction of Spatio-Temporal phenomena becomes feasible for unobserved locations in the future. The development of the GSTARIMA Model, ARCH/GARCH, and Kriging Method allows the discovery of theorems in mathematical modeling. The application of this model to climate data uses the data analytics life cycle methodology for more detailed processing and more accurate information.

Author Contributions

Conceptualization, P.M. and B.N.R.; methodology, P.M.; software, P.M., A.S.A. and R.B.; validation, P.M., B.N.R., A.S.A. and R.B.; formal analysis, B.N.R. and R.B.; investigation, A.S.A. and R.B.; resources, B.N.R.; data curation, P.M.; writing—original draft preparation, P.M.; writing—review and editing, P.M., B.N.R., A.S.A. and R.B.; visualization, P.M., A.S.A. and R.B.; supervision, B.N.R.; project administration, P.M. and B.N.R.; funding acquisition, B.N.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Padjadjaran Excellence Fastrack Scholarship (BUPP) and Academic Leadership Grant (ALG) with contract number 1549/UN6.3.1/PT.00/2023.

Data Availability Statement

Data are contained within the article.

Acknowledgments

The authors are grateful to the Rector and the Directorate of Research and Community Service (DRPM) of Universitas Padjadjaran for the Article Processing Charge (APC) support. This research is supported by 487 International Consortium RISE_SMA project 2019-2024.

Conflicts of Interest

The authors declare no conflict of interest.

References

Werndl, C. On Defining Climate and Climate Change. In Proceedings of the British Journal for the Philosophy of Science; Oxford University Press, July 1 2016; Vol. 67, pp. 337–364.
Nunes, L.J.R. Analysis of the Temporal Evolution of Climate Variables Such as Air Temperature and Precipitation at a Local Level: Impacts on the Definition of Strategies for Adaptation to Climate Change. Climate 2022, 10. [Google Scholar] [CrossRef]
Pörtner, H.O.; Roberts, D.C.; Adams, H.; Adler, C.; Aldunce, P.; Ali, E.; Ibrahim, Z.Z. Climate Change 2022: Impacts, Adaptation and Vulnerability; IPCC: Switzerland, 2022. [Google Scholar]
Alfarizi, M. Yuniarty Literature Review of Climate Change and Indonesia’s SDGs Strategic Issues in a Multidisciplinary Perspective. In Proceedings of the IOP Conference Series: Earth and Environmental Science; Institute of Physics, 2022; Vol. 1105. [CrossRef]
Kelman, I. Linking Disaster Risk Reduction, Climate Change, and the Sustainable Development Goals. Disaster Prev Manag 2017, 26, 254–258. [Google Scholar] [CrossRef]
Nerini, F.; Francesco; Sovacool; Benjamin; Hughes; Cozzi Connecting Climate Action with Other Sustainable Development Goals. Nat Sustain 2019, 2. [CrossRef]
Sipayung, S.B.; Nurlatifah, A.; Siswanto, B.; Slamet, L.S. Analysis of Climate Change Impact on Rainfall Pattern of Sambas District, West Kalimantan. In Proceedings of the IOP Conference Series: Earth and Environmental Science; Institute of Physics Publishing, May 16 2018; Vol. 149. [CrossRef]
Medeiros, E.S. de; Lima, R.R. de; Santos, C.A.C. dos Spatiotemporal Kriging for Days without Rainfall in a Region of Northeastern Brazil. Climate 2023, 11. [Google Scholar] [CrossRef]
Borovkova, S.A.; Lopuhaä, H.P.; Nurani, B. Generalized STAR Model with Experimental Weights. In Proceedings of the Proceedings of the 17th International Workshop on Statistical Modelling; 2002; pp. 139–147. [Google Scholar]
Di Giacinto, V. A Generalized Space-Time ARMA Model with an Application to Regional Unemployment Analysis in Italy. Int Reg Sci Rev 2006, 29, 159–198. [Google Scholar] [CrossRef]
Min, X.; Hu, J.; Zhang, Z. Urban Traffic Network Modeling and Short-Term Traffic Flow Forecasting Based on GSTARIMA Model. 13th International IEEE Annual Conference on Intelligent Transportation Systems 2010, 1535–1540. [Google Scholar] [CrossRef]
Nainggolan, N.; Ruchjana, B.N.; Darwis, S.; Siregar, R.E. GSTAR Models with ARCH Errors and The Simulation. Third International Conference on Mathematics and Natural Sciences 2010, 1075–1084. [Google Scholar]
Bonar, H.; Ruchjana, B.N.; Darmawan, G. Development of Generalized Space Time Autoregressive Integrated with ARCH Error (GSTARI – ARCH) Model Based on Consumer Price Index Phenomenon at Several Cities in North Sumatera Province. In Proceedings of the AIP Conference Proceedings; 2017; p. 20009. [Google Scholar] [CrossRef]
Elfiyan, I.; Ruchjana, B.N.; Bachrudin, A. GSTARI Model Approach By Involving Exogenous Variables To Predict Active Family Planning Participants. Proceedings of the Unpad Statistics National Seminar 2015, 5, 410–423. [Google Scholar]
Ditago, A.P.; Suhartono, S. Simulation Study of Parameter Estimation Two-Level GSTARX-GLS Model. IPTEK Journal of Proceedings Series 2016. [Google Scholar] [CrossRef]
Monika, P.; Ruchjana, B.N.; Abdullah, A.S. GSTARI-X-ARCH Model with Data Mining Approach for Forecasting Climate in West Java. Computation 2022, 10, 204. [Google Scholar] [CrossRef]
Dhaher, G.; Shexo, A. Using Kriging Technique to Interpolate and Forecasting Temperatures Spatio-Temporal Data. European Journal of Pure and Applied Mathematics 2023, 16, 373–385. [Google Scholar] [CrossRef]
Dai, H.; Huang, G.; Wang, J.; Zeng, H.; Zhou, F. Spatio-Temporal Characteristics of PM2.5 Concentrations in China Based on Multiple Sources of Data and LUR-GBM during 2016–2021. Int J Environ Res Public Health 2022, 19, 6292. [Google Scholar] [CrossRef] [PubMed]
Abdullah, A.S.; Matoha, S.; Lubis, D.A.; Falah, A.N.; Jaya, I.G.N.M.; Hermawan, E.; Ruchjana, B.N. Implementation of Generalized Space Time Autoregressive (GSTAR)-Kriging Model for Predicting Rainfall Data at Unobserved Locations in West Java. Applied Mathematics and Information Sciences 2018, 12, 607–615. [Google Scholar] [CrossRef]
Pfeifer, P.E.; Deutsch, S.J. A STARIMA Model-Building Procedure with Application to Description and Regional Forecasting. Transactions, Institute of British Geographers 1980, 5, 330–349. [Google Scholar] [CrossRef]
Pfeifer, P.E.; Deutsch, S.J. A Three-Stage Iterative Procedure for Space-Time Modeling A Three-Stage Iterative Procedure for Space-Time Modeling Space-Time Modeling STARIMA STAR STMA Time Series Modeling Three-Stage Model Building Procedure. Technometrics 1980, 22, 35–47. [Google Scholar] [CrossRef]
Engle, R.F. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 987. [Google Scholar] [CrossRef]
Montero, J.-M.; Fernandez-Aviles, G.; Mateu, J. Spatial and Spatio-Temporal Geostatistical Modeling and Kriging; First Edition.; John Wiley & Sons, Ltd. 2015. [Google Scholar]
Dietrich, D.; Heller, B.; Yang, B. Data Science & Big Data Analytics; John Wiley & Sons, Inc., 2015; ISBN 978-1-118-87613-8. [Google Scholar] [CrossRef]
Matthew J Page; Joanne E McKenzie; Patrick M Bossuyt; Isabelle Boutron; Tammy C Hoffmann; Cynthia D Mulrow The PRISMA 2020 Statement: An Updated Guideline for Reporting Systematic Reviews. [CrossRef]
Osayande, I.; Ogunyemi, O.; Gwacham-Anisiobi, U.; Olaniran, A.; Yaya, S.; Banke-Thomas, A. Prevalence, Indications, and Complications of Caesarean Section in Health Facilities across Nigeria: A Systematic Review and Meta-Analysis. Reprod Health 2023, 20. [Google Scholar] [CrossRef]
Saboyá Acosta, L.P.; Urbina-Cardona, J.N. Current State of Knowledge of Páramo Amphibians in Colombia: Spatio Temporal Trends and Information Gaps to Be Strengthened for Effective Conservation. Trop Conserv Sci 2023, 16. [Google Scholar] [CrossRef]
Sukono; Juahir, H.; Ibrahim, R.A.; Saputra, M.P.A.; Hidayat, Y.; Prihanto, I.G. Application of Compound Poisson Process in Pricing Catastrophe Bonds: A Systematic Literature Review. Mathematics 2022, 10. [Google Scholar] [CrossRef]
Ibrahim, R.A.; Sukono; Napitupulu, H.; Ibrahim, R.I. How to Price Catastrophe Bonds for Sustainable Earthquake Funding? A Systematic Review of the Pricing Framework. Sustainability (Switzerland) 2023, 15. [CrossRef]
Firdaniza, F.; Ruchjana, B.N.; Chaerani, D.; Radianti, J. Information Diffusion Model in Twitter: A Systematic Literature Review. Information (Switzerland) 2022, 13. [Google Scholar] [CrossRef]
Gil, M.; Wróbel, K.; Montewka, J.; Goerlandt, F. A Bibliometric Analysis and Systematic Review of Shipboard Decision Support Systems for Accident Prevention. Saf Sci 2020, 128. [Google Scholar] [CrossRef]
Li, J.; Jiang, Y. The Research Trend of Big Data in Education and the Impact of Teacher Psychology on Educational Development During COVID-19: A Systematic Review and Future Perspective. Front Psychol 2021, 12. [Google Scholar] [CrossRef]
Bravo-Toledo, L.; Barreto-Pio, C.; López-Herrera, J.; Milla-Figueroa, C.; Pilco-Nuñez, A.; Virú-Vásquez, P. Global Research Trends in Emergy and Wastewater Treatment: A Bibliometric Analysis. Environmental Research, Engineering and Management 2023, 79, 16–36. [Google Scholar] [CrossRef]
Tian, H.; Chen, J. A Bibliometric Analysis on Global EHealth. Digit Health 2022, 8. [Google Scholar] [CrossRef] [PubMed]
Mohamed, B.; Marzouk, M. Bibliometric Analysis and Visualisation of Heritage Buildings Preservation. Herit Sci 2023, 11. [Google Scholar] [CrossRef]
Kumar, R.R.; Sarkar, K.A.; Dhakre, D.S.; Bhattacharya, D. A Hybrid Space–Time Modelling Approach for Forecasting Monthly Temperature. Environmental Modeling & Assessment 2022, 28, 317–330. [Google Scholar] [CrossRef]
Mukhaiyar, U.; Ramadhani, S. The Generalized STAR Modeling with Heteroscedastic Effects. CAUCHY: Jurnal Matematika Murni dan Aplikasi 2022, 7, 158–172. [Google Scholar] [CrossRef]
Permatasari, N.P.; Chotimah, H.; Permana, P.; Tarigan, W.S.; Toharudin, T.; Ruchjana, B.N. Application of GSTARI (1, 1, 1) Model for Forecasting the Consumer Price Index (CPI) in Three Cities in Central Java. Jurnal Teori dan Aplikasi Matematika 2022, 6, 134–143. [Google Scholar] [CrossRef]
Kuo, P.-F.; Huang, T.-E.; Putra, I.G.B. Comparing Kriging Estimators Using Weather Station Data and Local Greenhouse Sensors. Sensors 2021, 21, 1853. [Google Scholar] [CrossRef]
Iriany, A.; Rosyida, D.; Arifin, A. A Comparison of GSTAR-SUR Models and a Hybrid GSTAR-SUR/Neural Network Model on Residuals of Precipitation Forecasting. Commun Stat Simul Comput 2021, 50, 2782–2792. [Google Scholar] [CrossRef]
Prastuti, M.; Aridinanti, L.; Dwiningtyas, W.P. Spatio-Temporal Models with Intervention Effect for Modelling the Impact of Covid-19 on the Tourism Sector in Indonesia. J Phys Conf Ser 2021, 1821, 12044. [Google Scholar] [CrossRef]
Alawiyah, M.; Kusuma, D.A.; Ruchjana, B.N. Application of Generalized Space Time Autoregressive Integrated (GSTARI) Model in the Phenomenon of Covid-19. J Phys Conf Ser 2021, 1722, 12035. [Google Scholar] [CrossRef]
Iriany, A.; Aini, N.N.; Sulistyono, A.D. Spatio Temporal Modelling for Government Policy the COVID-19 Pandemic in East Java. CAUCHY 2021, 6, 218–226. [Google Scholar] [CrossRef]
Yundari, Y.; Rizki, S.W. Invertibility of Generalized Space-Time Autoregressive Model with Random Weight. CAUCHY 2021, 6, 246–259. [Google Scholar] [CrossRef]
Alawiyah, M.; Kusuma, D.A.; Ruchjana, B.N. GSTARI-ARCH Model and Application on Positive Confirmed Data for COVID-19 in West Java. Media Statistika 2021, 14, 146–157. [Google Scholar] [CrossRef]
Primageza, H.; Vinarti, R.A.; Tyasnurita, R.; Riksakomara, E.; Muklason, A. Comparison of NNs-ARIMAX and NNs-GSTARIMAX on Rice Price Forecasting in Indonesia. In Proceedings of the 2021 International Conference on Advanced Computer Science and Information Systems (ICACSIS); 2021; pp. 1–8. [Google Scholar] [CrossRef]
Zhang, R.; Yang, S.; Wang, Y.; Wang, S.; Gao, Z.; Luo, C. Three-Dimensional Regional Oceanic Element Field Reconstruction with Multiple Underwater Gliders in the Northern South China Sea. Applied Ocean Research 2020, 105, 102405. [Google Scholar] [CrossRef]
Su, H.; Shen, W.; Wang, J.; Ali, A.; Li, M. Machine Learning and Geostatistical Approaches for Estimating Aboveground Biomass in Chinese Subtropical Forests. For Ecosyst 2020, 7, 64. [Google Scholar] [CrossRef]
Iriany, A.; Rosyida, D.; Sulistyono, A.D.; Ruchjana, B.N. Precipitation Forecasting Using Neural Network Model Approach. In Proceedings of the IOP Conference Series: Earth and Environmental Science; Institute of Physics Publishing, 2020; Vol. 458. [CrossRef]
Sulistyono, A.D.; Hartawati; Iriany, A.; Suryawardhani, N.W.; Iriany, A. Rainfall Forecasting in Agricultural Areas Using GSTAR-SUR Model. In Proceedings of the IOP Conference Series: Earth and Environmental Science; Institute of Physics Publishing, 2020; Vol. 458. [CrossRef]
Akbar, M.S.; Setiawan; Suhartono; Ruchjana, B.N.; Prastyo, D.D.; Muhaimin, A.; Setyowati, E. A Generalized Space-Time Autoregressive Moving Average (GSTARMA) Model for Forecasting Air Pollutant in Surabaya. J Phys Conf Ser 2020, 1490, 12022. [Google Scholar] [CrossRef]
Pramoedyo, H.; Ashari, A.; Fadliana, A. Application of GSTAR Kriging Model in Forecasting and Mapping Coffee Berry Borer Attack in Probolinggo District. J Phys Conf Ser 2020, 1563, 12005. [Google Scholar] [CrossRef]
Ashari, A.; Efendi, A.; Pramoedyo, H. GSTARX-SUR Modeling Using Inverse Distance Weighted Matrix and Queen Contiguity Weighted Matrix for Forecasting Cocoa Black Pod Attack in Trenggalek. Conference: Proceedings of the 13th International Interdisciplinary Studies Seminar 2020. [CrossRef]
Pramoedyo, H.; Ashari, A.; Fadliana, A. Forecasting and Mapping Coffee Borer Beetle Attacks Using GSTAR-SUR Kriging and GSTARX-SUR Kriging Models. ComTech: Computer, Mathematics and Engineering Applications 2020, 11, 65–73. [Google Scholar] [CrossRef]
Ji, S.; Dong, J.; Wang, Y.; Liu, Y. Research on CPI Prediction Based on Space-Time Model. Proceedings - 2019 6th International Conference on Dependable Systems and Their Applications, DSA 2019 2020. [CrossRef]
Sjahid, M.; Akbar; Setiawan; Suhartono; Ruchjana, B.N.; Prastyo, D.D. Prediction of PM10 Pollutant in Surabaya Using Generalized Space-Time Autoregressive Moving Average. Investigacion Operacional 2020, 41, 990–998. [Google Scholar]
Hølleland, S.; Karlsen, H.A. A Stationary Spatio-Temporal GARCH Model. J Time Ser Anal 2019, 41, 177–209. [Google Scholar] [CrossRef]
Venetsanou, P.; Anagnostopoulou, C.; Loukas, A.; Lazoglou, G.; Voudouris, P. Minimizing the Uncertainties of RCMs Climate Data by Using Spatio-Temporal Geostatistical Modeling. Earth Sci Inform 2018, 12, 183–196. [Google Scholar] [CrossRef]
Novianto, M.A.; Suhartono; Prastyo, D.D.; Suharsono, A.; Setiawan GSTARIX Model for Forecasting Spatio-Temporal Data with Trend, Seasonal and Intervention. J Phys Conf Ser 2018, 1097, 12076. [CrossRef]
Akbar, M.S.; Setiawan; Suhartono; Ruchjana, B.N.; Riyadi, M.A.A. GSTAR-SUR Modeling With Calendar Variations And Intervention To Forecast Outflow Of Currencies In Java Indonesia. J Phys Conf Ser 2018, 974, 12060. [Google Scholar] [CrossRef]
Jamilatuzzahro; Caraka, R.E.; Herliansyah, R.; Asmawati, S.; Sari, D.M.; Pardamean, B. Generalized Space Time Autoregressive of Chili Prices. In Proceedings of the 2018 International Conference on Information Management and Technology (ICIMTech); 2018; pp. 1–9. [CrossRef]
Yundari, Y.; Pasaribu, U.S.; Mukhaiyar, U. Error Assumptions on Generalized STAR Model. Journal of Mathematical and Fundamental Sciences 2017, 49, 136–155. [Google Scholar] [CrossRef]
Nainggolan, N.; Titaley, J. Development of Generalized Space Time Autoregressive (GSTAR) Model. In Proceedings of the AIP Conference Proceedings; 2017; p. 20034. [Google Scholar]
Nisak, S.C. Seemingly Unrelated Regression Approach for GSTARIMA Model to Forecast Rain Fall Data in Malang Southern Region Districts. CAUCHY 2016, 4, 57–64. [Google Scholar] [CrossRef]
Setiawan, S.; Prastuti, M. S-GSTAR-SUR Model for Seasonal Spatio Temporal Data Forecasting. Malaysian Journal of Mathematical Sciences 2016, 10, 53–65. [Google Scholar]
Suhartono; Wahyuningrum, S.R.; Setiawan; Akbar, M.S. GSTARX-GLS Model for Spatio-Temporal Data Forecasting. Malaysian Journal of Mathematical Sciences 2016, 10, 91–103. [Google Scholar]
Mukhaiyar, U. The Goodness of Generalized STAR in Spatial Dependency Observations Modeling. In Proceedings of the AIP Conference Proceedings; 2015; p. 20008. [Google Scholar] [CrossRef]
Setiawan, A.; Aidi, M.N.; Sumertajaya, I.M. Modelling of Forecasting Monthly Inflation By Using Varima and Gstarima Models. Forum Statistika Dan Komputasi 2015, 20. [Google Scholar]
Shu-qin, S.; Qi-wen, C.; Yan-min, Y.; Hua-jun, T.; Peng, Y.; Wen-bin, W.; Heng-zhou, X.; Jia, L.I.U.; Zheng-guo, L. Influence of Climate and Socio-Economic Factors on the Spatio-Temporal Variability of Soil Organic Matter: A Case Study of Central Heilongjiang Province, China. J Integr Agric 2014, 13, 1486–1500. [Google Scholar] [CrossRef]

Figure 1. Natural disasters caused by rainfall in West Java (a) Flood Disaster; (b) Landslide.

Figure 2. PRISMA Diagram for Relevant Article Selection.

Figure 3. Bibliometric mapping of keywords contained in 48 relevant articles.

Figure 4. Data Analytics Life Cycle for Integrated GSTARIMA, ARCH, and Kriging.

Table 1. Damage Due to Floods and Landslides in West Java in 2012-2021.

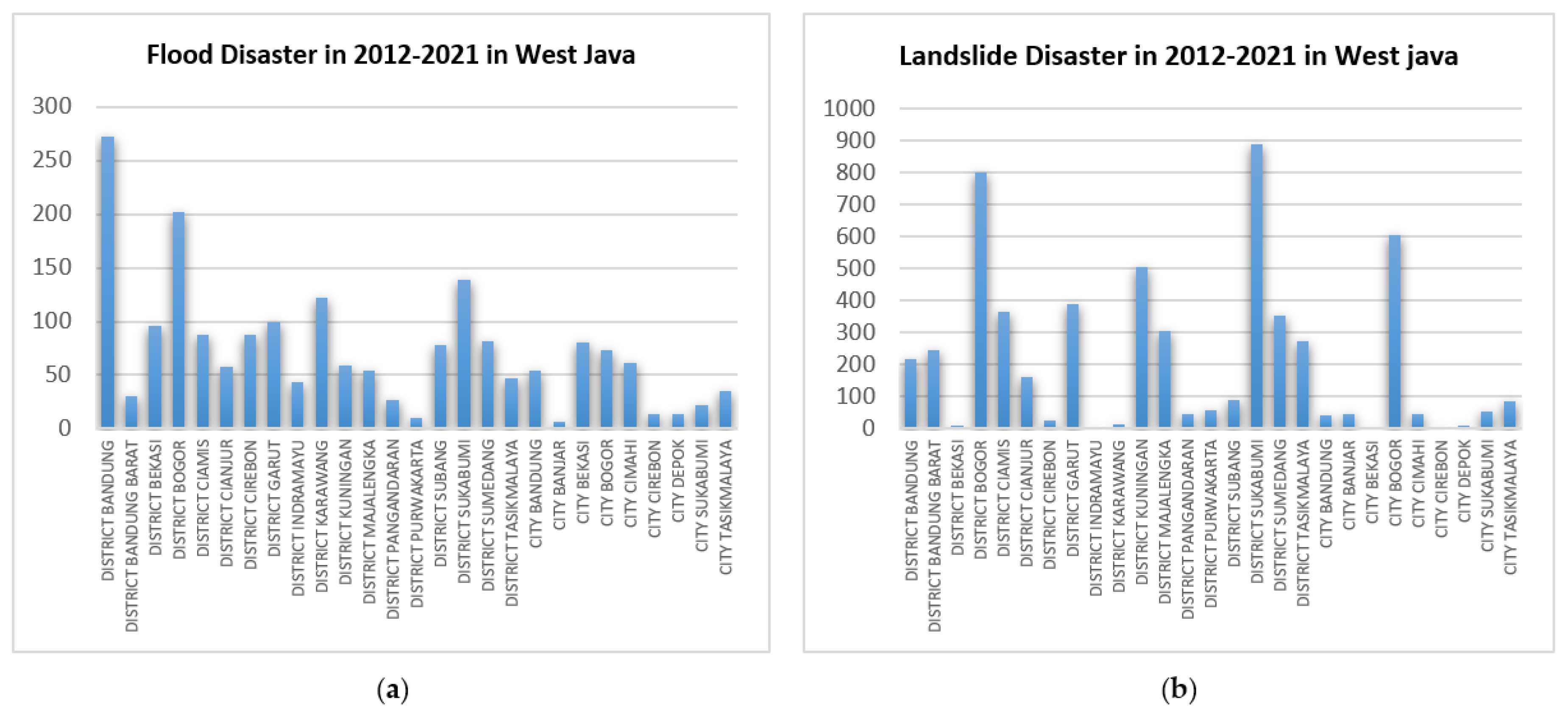
Damage Category	Number of units
Destroyed	607
Heavily Damaged	13.776
Light Damage	50.699
Moderate Damage	22.167
Threatened	27.459
Submerged/Buried	828.452
Total	943.160

Table 2. Keywords used for literature search.

Codes	Keywords
A	("Spatio Temporal" OR "GSTAR" OR "GSTARIMA" OR "Generalized Space Time Autoregressive")
B	(“Heteroscedasticity” OR “ARCH” OR “GARCH” OR “Seemingly Unrelated Regression” OR “SUR” OR “Kriging Method”)
C	(“Data Analytics Life Cycle” OR “Data Mining” OR “Big Data Approach” OR “Climate Change” OR “Extreme Rainfall” OR “Weather” OR “Temperature”)
D	A AND B AND C

Table 3. Keyword search results in the database.

Codes	Scopus	Dimensions	EBSCO-Host	Total
A	101,483	69,050	34,024	213,557
B	339,122	515,898	266,242	1,121,262
C	1,381,753	4,046,170	2,097,770	7,525,693
D	77	71	138	286

Table 4. State-of-the-art from 48 relevant articles.

References

Model(s)

Dataset

Application

Model Assumptions

Model Performance Analysis

MA Component

Exogenous Variable

Hetero. Error

Kriging Method

MAPE

RMSE

MSE

Accuracy

Dhaher et al. (2023)

[17]

Kriging, Spatio-Temporal

Temperature Data in Mosul and Baghdad city

Interpolate and Forecasting Temperatures

✓

A) Mosul = 0.16
B) Baghdad= 1.05
C) A+B=0.61

Dai et al. (2022)

[18]

LUR, LightGBM, ML, Kriging

PM_2.5 site
monitoring data (http://106.37.208.233:20035/)

Spatio-Temporal Characteristics of PM_2.5 Concentrations

✓

R²= 0.976 (average for 2016–2021)

Kumar et al. (2022)

[36]

STARMA, GARCH

Temperature Data (https://power.larc.nasa.gov/data-accessviewer/)

Forecasting Monthly Temperature

✓

MAPE for Max. Temperature 2-4% and MAPE for Temperature Range 10-12%

Monika et al. (2022)

[16]

GSTARI-X-ARCH

Climate Data (https://power.larc.nasa.gov/data-accessviewer/)

Forecasting Climate in West Java

✓

MAPE In-Sample= 20%, MAPE Outsample= 19%

Mukhaiyar et al. (2022)

[37]

GSTAR

The average daily wind speed from NOAA

Predict the occurrence of Hurricane Katrina

✓

MAPE= 6.86

MSE=0.86

MAD=0.70

Permatasi et al. (2022)

[38]

GSTARI

The Consumer Price Index (CPI) data

Forecasting the CPI in Three Cities in Central Java

MAPE <10%

Kuo et al. (2021)

[39]

Kriging

The sensors and the weather stations (http://e-service.cwb.gov.tw)

Comparing Kriging Estimators

✓

RMSE<3

MAE<3

Iriany et al. (2021)

[40]

GSTAR, SUR, NN

Precipitation data

Comparison GSTAR-SUR-NN for precipitation forecasting

✓

RMSE=5.8684

MAD=3.8917

Prastuti et al. (2021)

[41]

GSTARX

The number
of foreign tourist arrivals to Indonesia

Forecasting the number of foreign tourist arrivals to
Indonesia during COVID-19

✓

RMSE Jakarta= 21039, Bali= 32687, Surabaya=2228

Alawiyah et al. (2021)

[42]

GSTARI

The daily positive covid-19 positive patients

Forecasting Covid-19 in West Java

Iriany et al. (2021)

[43]

GSTAR

The daily data of the cumulative
number of COVID-19 cases(www.covid19.go.id)

Forecasting Covid-19 in East Java

MAPE=1.43

RMSE=0.005

Yundari et al. (2021)

[44]

GSTAR, Kernel Weight

The tea production data

Forecasting tea production

RMSE= 10-20

Alawiyah et al. (2021)

[45]

GSTARI-ARCH

Positive confirmed data for Covid-19

Forecasting Covid-19 in West Java

✓

RMSE=1.24356

Primageza et al. (2021)

[46]

NNs-GSTARIMAX

Historical data on the average price of rice in the period January 1,2008, to December 31,2019 (weekly)

Rice Price Forecasting in Indonesia

✓

NNs-GSTARIMAX= 1.09%

Zhang et al. (2020)

[47]

Spatio-Temporal, Kriging

Data for three
fixed locations from APDRC (Asia-Pacific Data Research Center)

✓

MSE=0.744

MAE=0.751

Su et al. (2020)

[48]

ML, Kriging

NFI datasets

Estimating aboveground
biomass

✓

RF=52.08%
RFOK=52.05%
RFCK=51.60%

RF=24.56
RFOK=23.47
RFCK=22.14

Iriany et al. (2020)

[49]

GSTAR, SUR, NN

Precipitation Data in Malang

Precipitation Forecasting

✓

General= 5.3131

R²= 0.6177

Sulistyono et al. (2020)

[50]

GSTAR, SUR

Rainfall Data

Rainfall forecasting in agricultural areas

✓

Training=5.779
Testing=10.433

Akbar et al. (2020)

[51]

GSTARMAX

Air Pollutant Data

Forecasting Air Pollutant in
Surabaya

✓

A smaller RMSE Value

Pramoedyo et al. (2020)

[52]

GSTAR Kriging

The percentage of coffee berry borer infestation and monthly rainfall

Forecasting and
mapping coffee berry borer attack

✓

GSTAR-SUR=5.04
GSTAR-Kriging=5.11

GSTAR-SUR=0.03
GSTAR-Kriging=0.04

Ashari et al. (2020)

[53]

GSTARX-SUR

The percentage of coffee berry borer infestation and monthly rainfall

Forecasting and
mapping coffee berry borer attack

✓

MAPE<15%

Pramoedyo et al. (2020)

[54]

GSTARX-SUR-Kriging

The percentage of coffee berry borer infestation and monthly rainfall

Forecasting and
mapping coffee berry borer attack

✓

GSTAR-Kriging=6.63%
GSTARX-Kriging=6.18%

GSTAR-Kriging=0.0434
GSTARX-Kriging=0.0423

Ji et al. (2020)

[55]

GSTARI

The montly CPI data

CPI Prediction

Dalian=38.29%
Shenyang=7.71%
Changchun=17.49%

Sjahid et al. (2020)

[56]

GSTARMA

The concentration of PM₁₀ pollutants

Prediction of PM₁₀ pollutant in surabaya

✓

Hølleland et al. (2019)

[57]

ST-GARCH

Dataset of sea surface temperature anomalies

✓

Venetsanou et al. (2018)

[58]

ST-Kriging

Precipitation and temperature dataset

Prediction precipitation and tem-perature

✓

Prec. MPI=25.7 and 0.3
Prec.HadGEM2=30.3 and 304.8
Temp. MPI=8.9 and 2.5
Temp. HadGEM2=6.6 and 14.7

Novianto et al. (2018)

[59]

GSTARIX

Tourist
arrival data in Indonesia

Prediction tourist arrival

✓

Jakarta=40.41
Denpasar=44.89
Surabaya=2.761
Surakarta=398

Akbar et al. (2018)

[60]

GSTARX-SUR

Rupiah outflow data in Java, Indonesia

Forecast Outflow Of Currencies

✓

MAPE<10%

Jamilatuzzahro et al. (2018)

[61]

GSTAR

The Weekly Progress of Retail Prices

Prediction Chili Prices

Jakarta=17406,22
Bandung=15830,43
Semarang=15754,02
D.I Yogyakarta=15103,99

Abdullah et al. (2018)

[19]

GSTAR-Kriging

Rainfall Data

Predicting
Rainfall Data at Unobserved Locations in West Java

✓

Model 1=8.97%
Model II=12.51%
Model III=7.72%

Bonar et al. (2017)

[13]

GSTARI-ARCH

CPI data in North Sumaterat, Indonesia

Forecasting CPI

✓

Yundari et al. (2017)

[62]

GSTAR

The
monthly tea production

Forecasting tea production

Parakan Salah=1.16
Sinumbra=1.70
Rancabali=5.15
Rancabolang=9.94
Panyairan=7.28

Nainggolan et al. (2017)

[63]

GSTAR-ARCH

Nisak (2016)

[64]

GSTARIMA-SUR

Rain Fall
Data in Malang Southern Region Districts

Forecasting rainfall

✓

Tangkilsari=5.263

R²=0.6481

Setiawan et al. (2016)

[65]

S-GSTAR-SUR

The number of tourist arrivals

Forecasting tourist arrivals

✓

GSTAR-SUR=13,60

Ditago et al. (2016)

[15]

GSTARX-GLS

The impact of Ramadhan effect

Adding a predictor of calendar variation model

✓

NRMSE closed to 0

Suhartono et al. (2016)

[66]

GSTARX-GLS

Inflation Data

Inflation forecasting

✓

GSTARX-OLS=0.801
GSTARX-GLS=0.826

Mukhaiyar (2015)

[67]

GSTAR-Kriging

The monthly tea production

Forecasting tea production

✓

SSR

Setiawan et al. (2015)

[68]

GSTARIMA

Inflation Data

Inflation forecasting

✓

RMSE=0.9199

Shu-qin et al. (2014)

[69]

GWR, Kriging

Climate and Socio-economic variable

Variability of Soil Organic Matter influenced by climate and socio-economic

✓

Nainggolan et al. (2010)

[12]

GSTAR-ARCH

Simulation data

✓

Min et al. (2010)

[11]

GSTARIMA

The traffic flow data

Short-term traffic flow forecasting

✓

MSE=7246

Giacinto (2006)

[10]

GSTARMA

Unemployment data

Regional Unemployment Analysis in Italia

✓

Borovkova et al. (2002)

[9]

GSTAR

Montly oil production

Forecasting oil production

R²=0.9227

Note: LUR: land-use regression, LightGBM: light gradient boosting machine, ML: Machine Learning, NN: Neural Network, GWR: Geographically Weighted Regression.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Systematic Literature Review on An Integrated Generalized Space Time Autoregressive Integrated Moving Average (GSTARIMA) Model with Heteroscedastic Error and Kriging Method for Forecasting Climate

Abstract

1. Introduction

2. Materials and Methods

2.1. Theoritical Background

2.1.1. The Generalized Space Time Autoregressive Integrated Moving Average (GSTARIMA)Model

2.1.2. Autoregressive Conditional Heteroscedasticity (ARCH) Model

2.1.3. Kriging Method

2.1.4. Data Analytics Life Cycle

2.2. Collected Article

3. Results

3.1. Results of Literature Search and Dataset Analysis

4. Discussion

4.1. GAP Analysis

4.2. The Framework for model integration for climate forecast

4.2.1. The Integration of GSTARIMA Model with Heteroskedastic error and Kriging Method for forecasting

4.2.2. Data Analytics Life Cycle for Climate Forecasting

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe