Submitted:
22 August 2023
Posted:
24 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
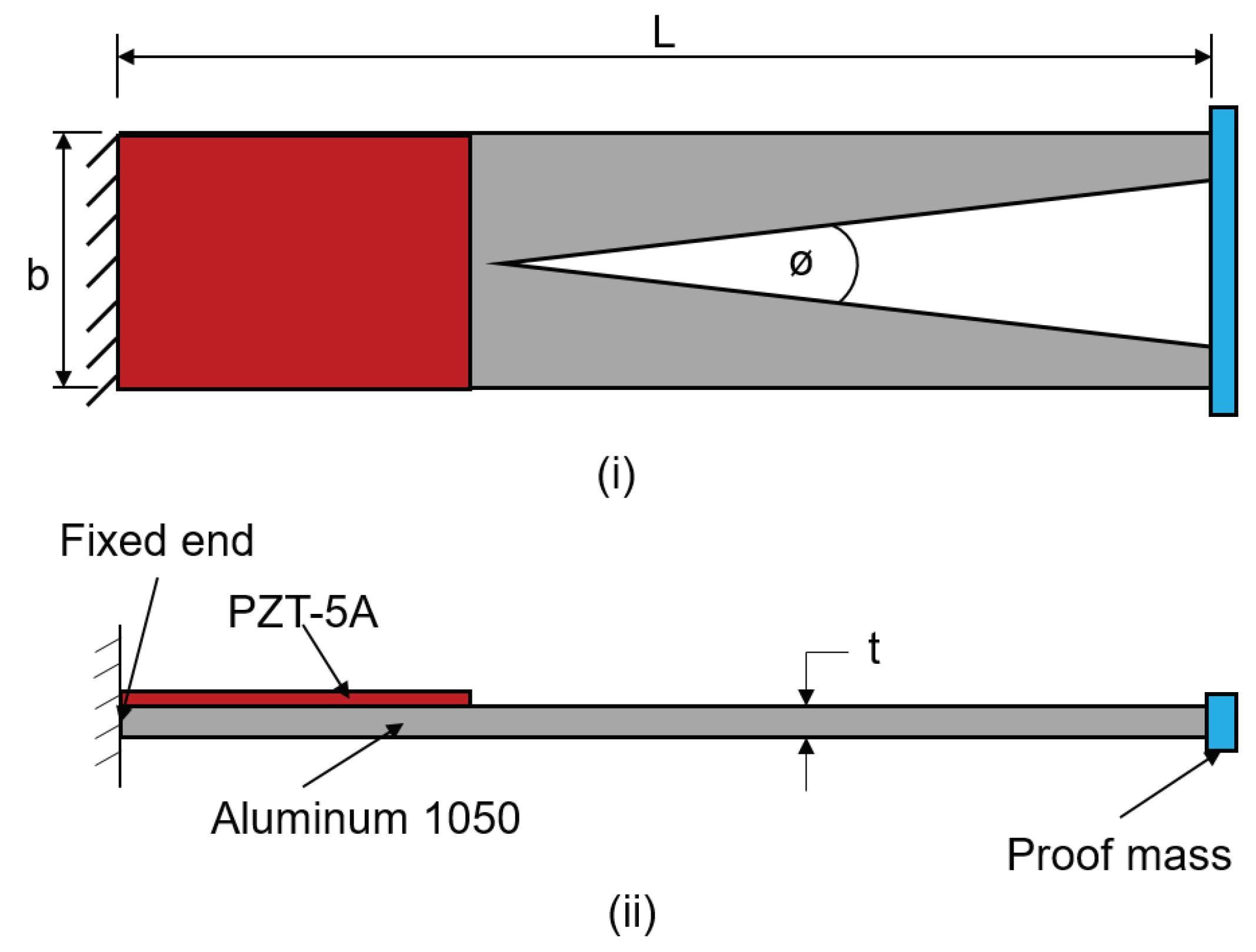
2. Design and Procedure of Analysis
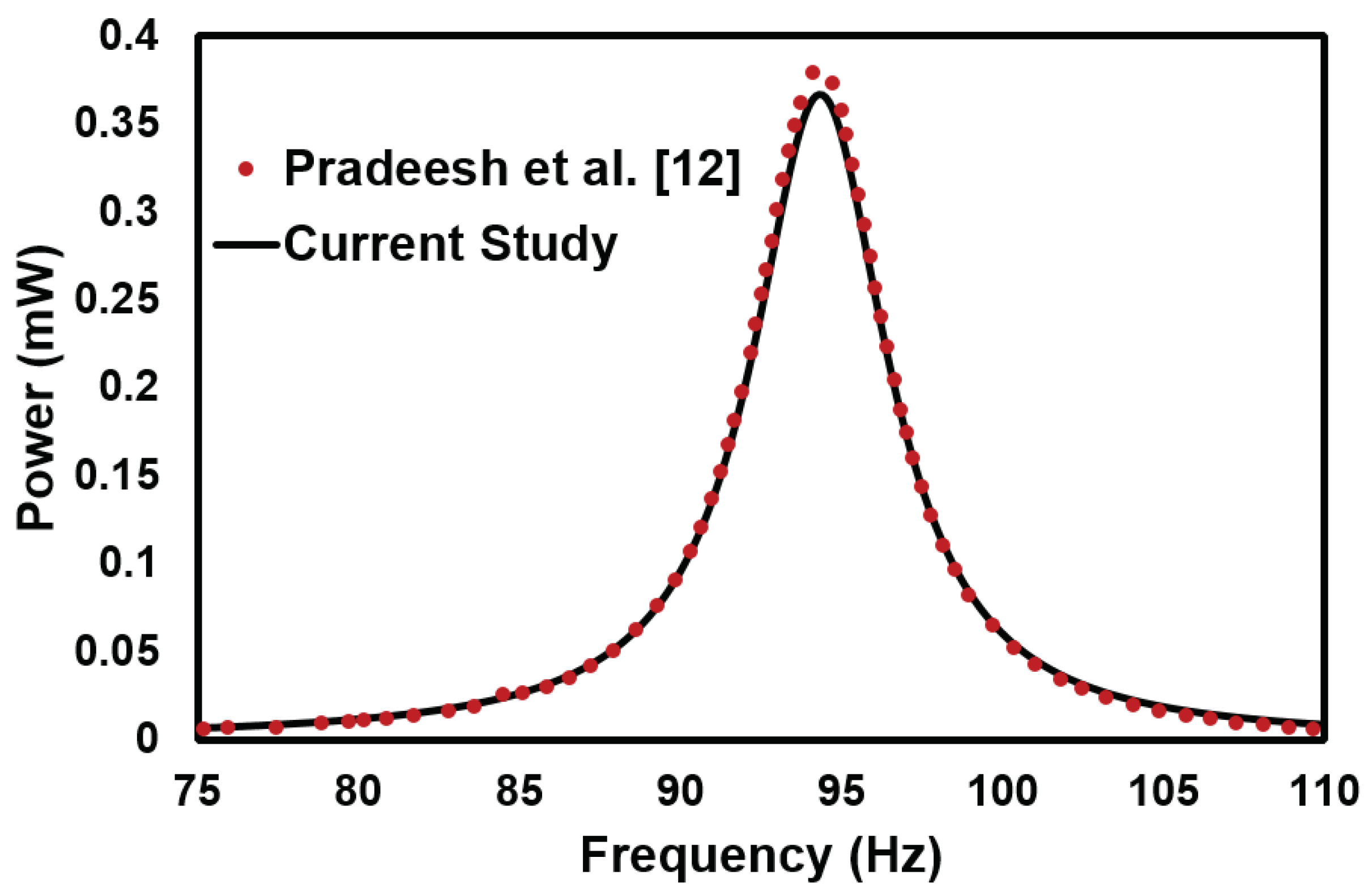
3. Validation of Procedure Analysis
4. Results and Discussions
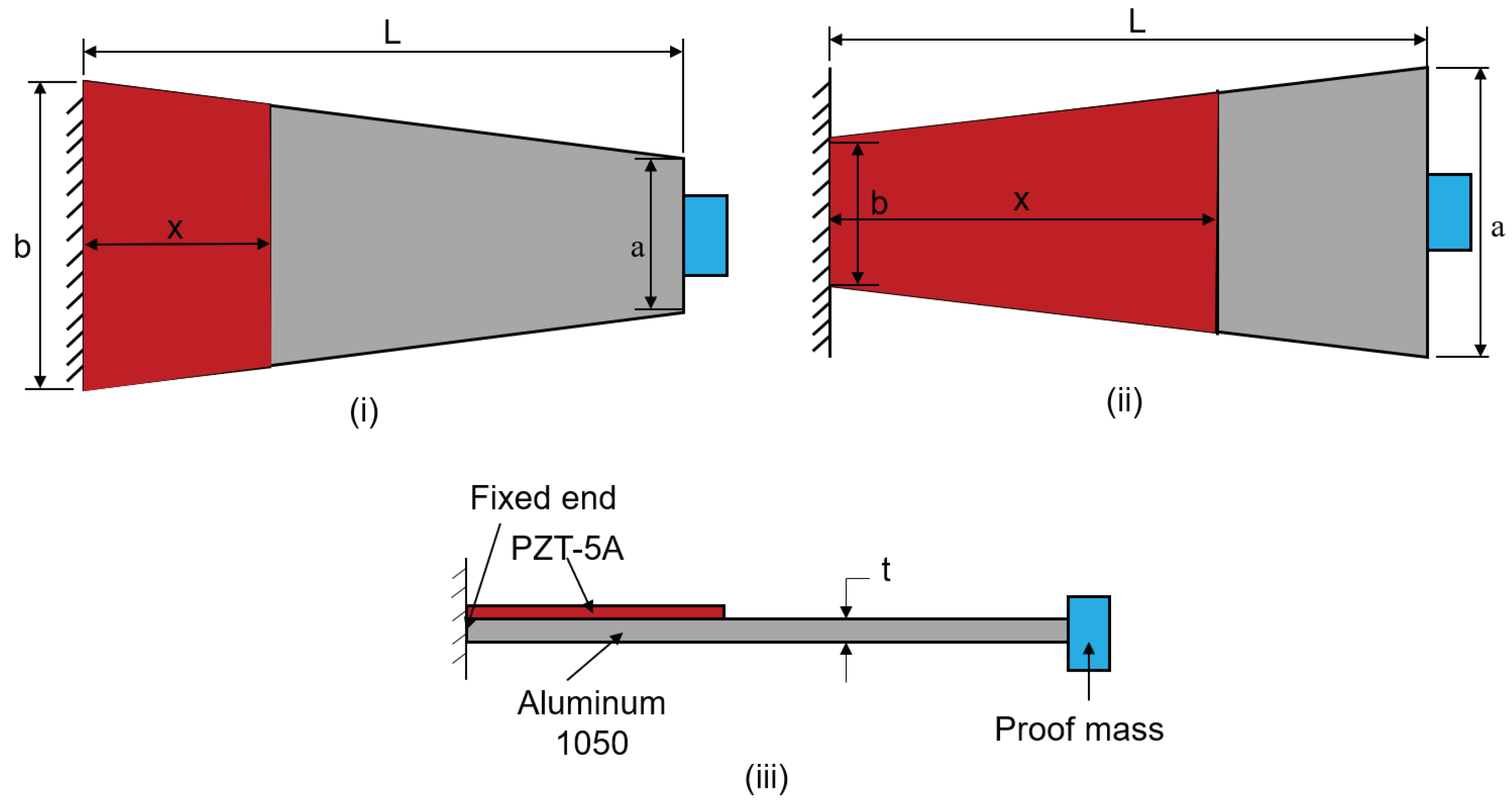
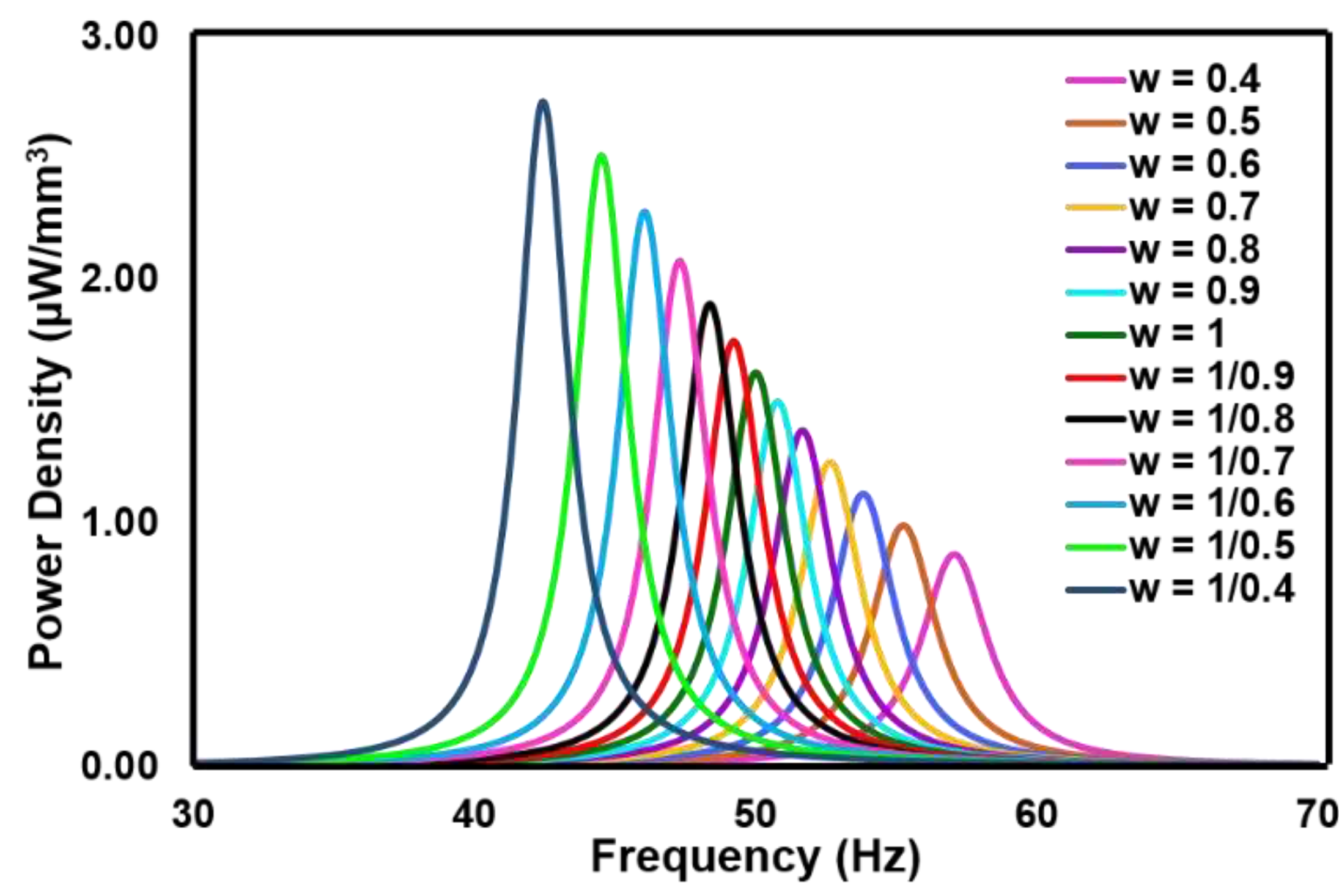
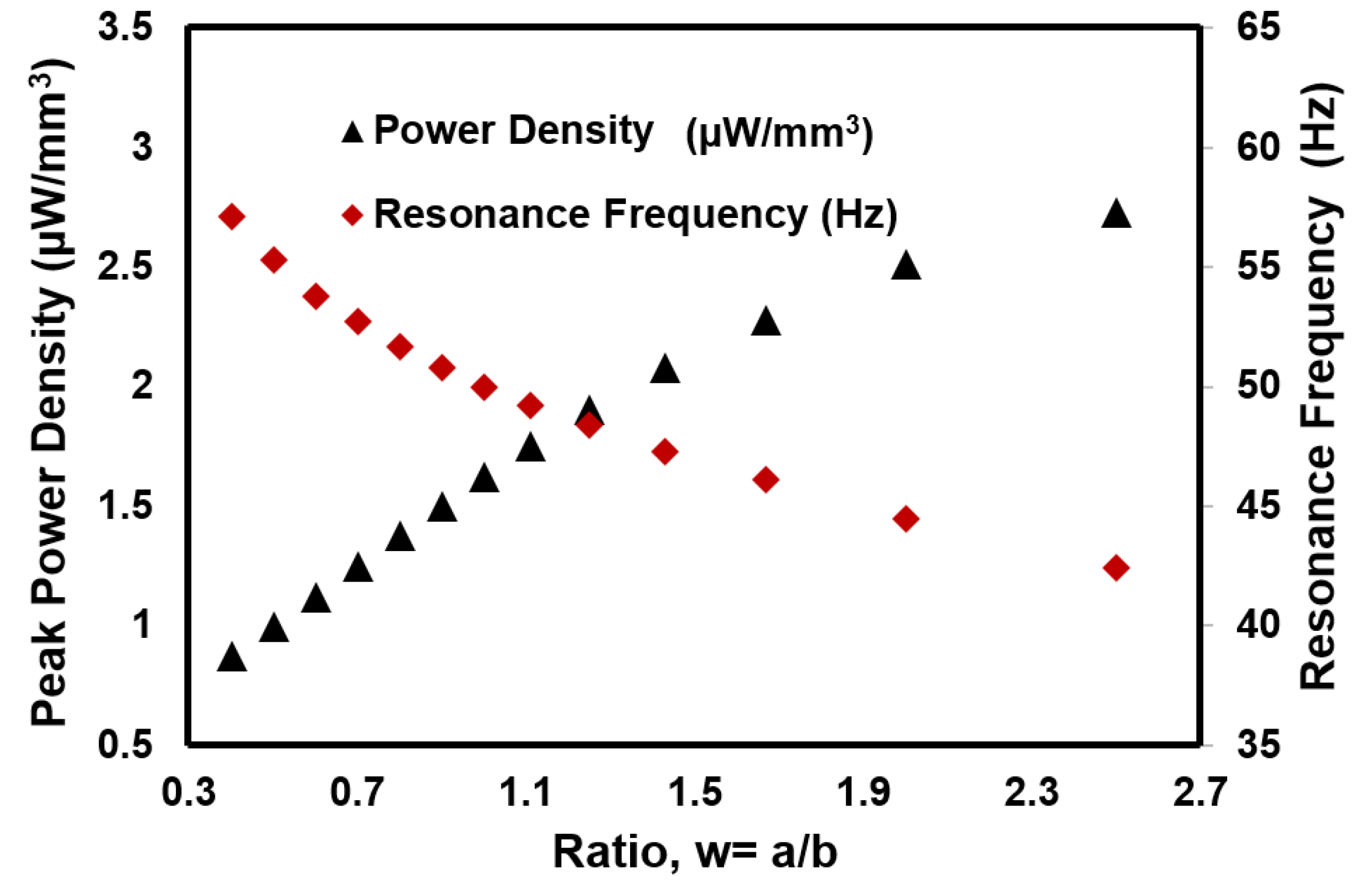
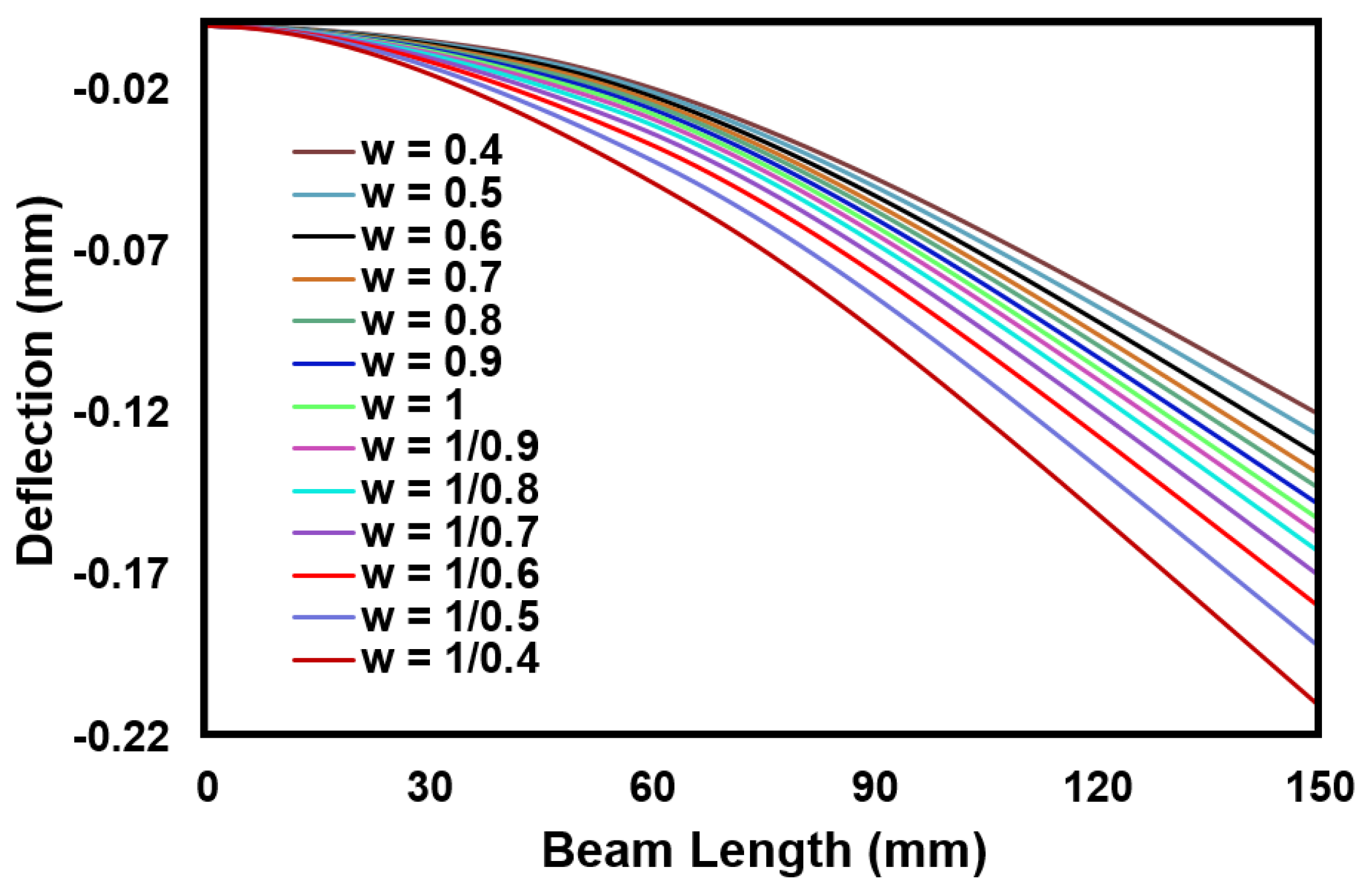
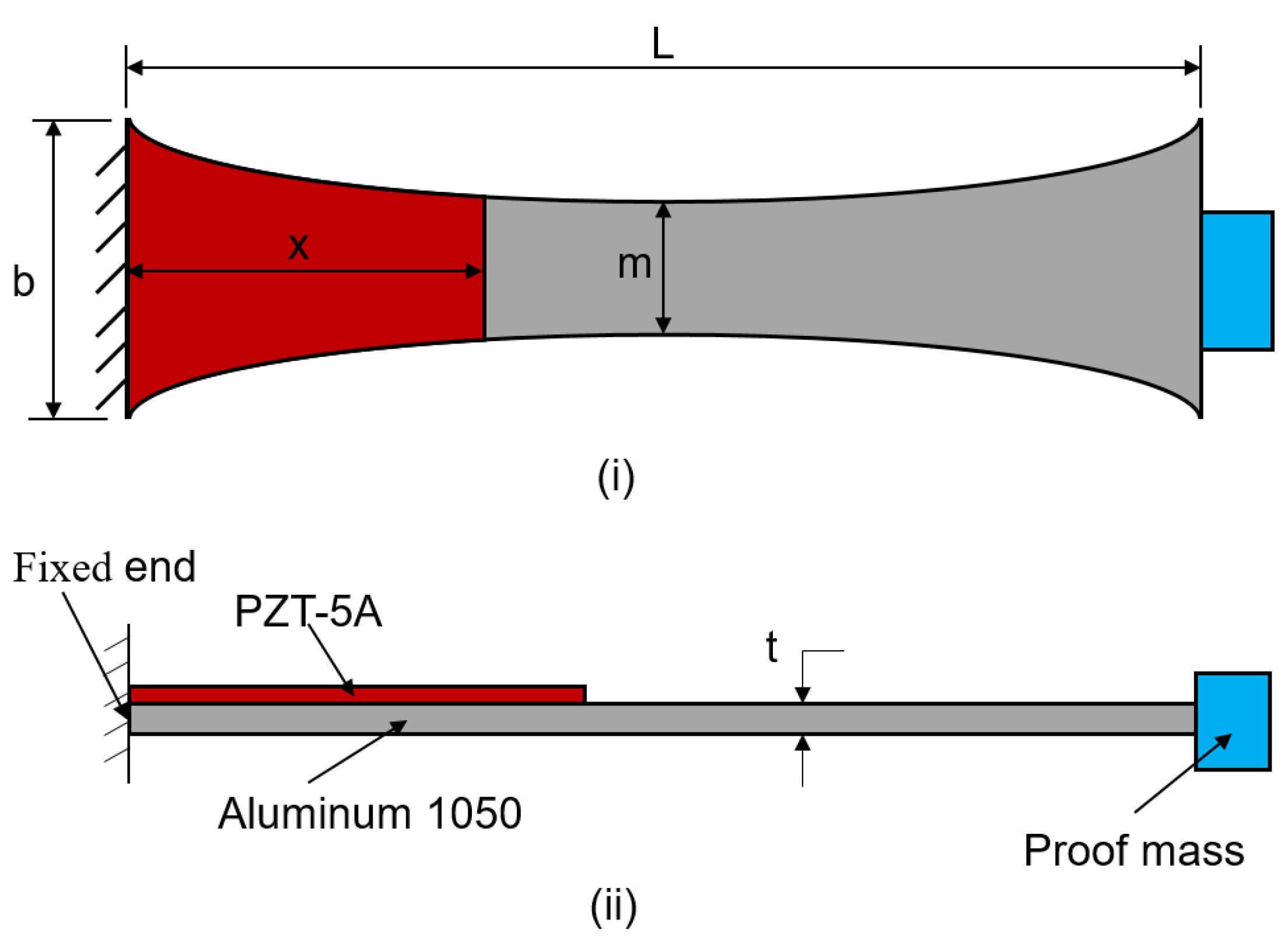
4.1. Analysis of Trapezoidal Beam
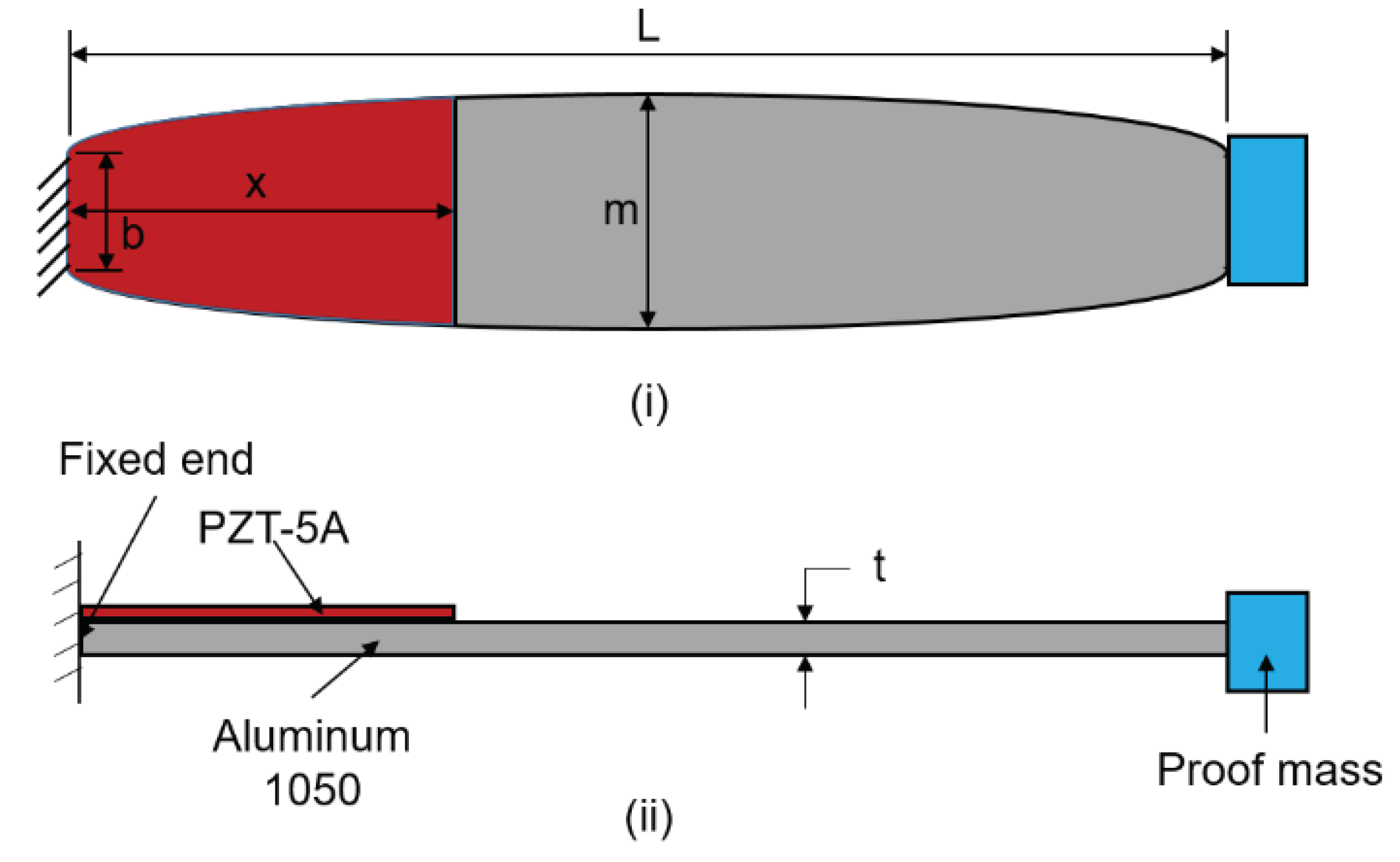
4.2. Analysis of Concave Beam
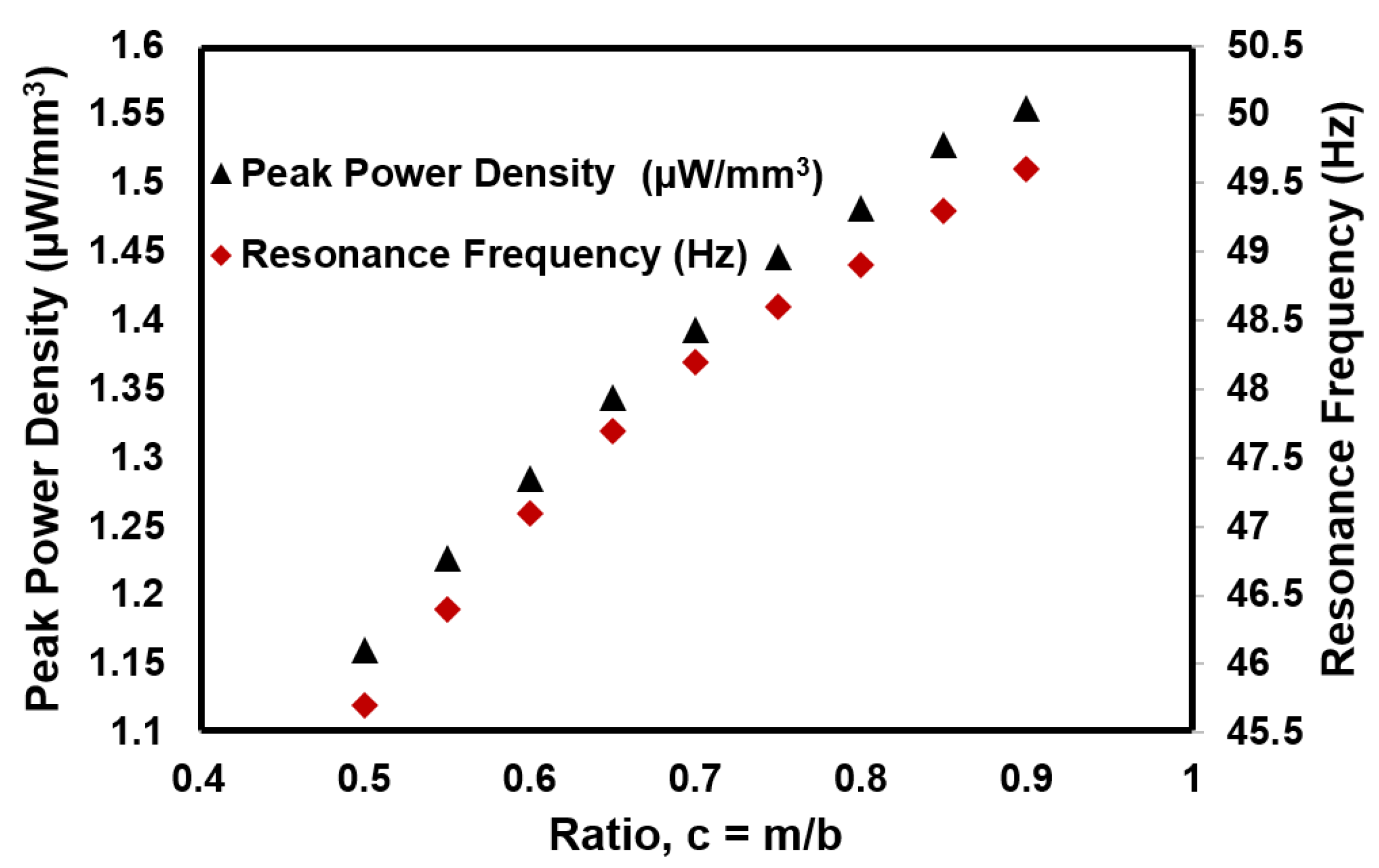
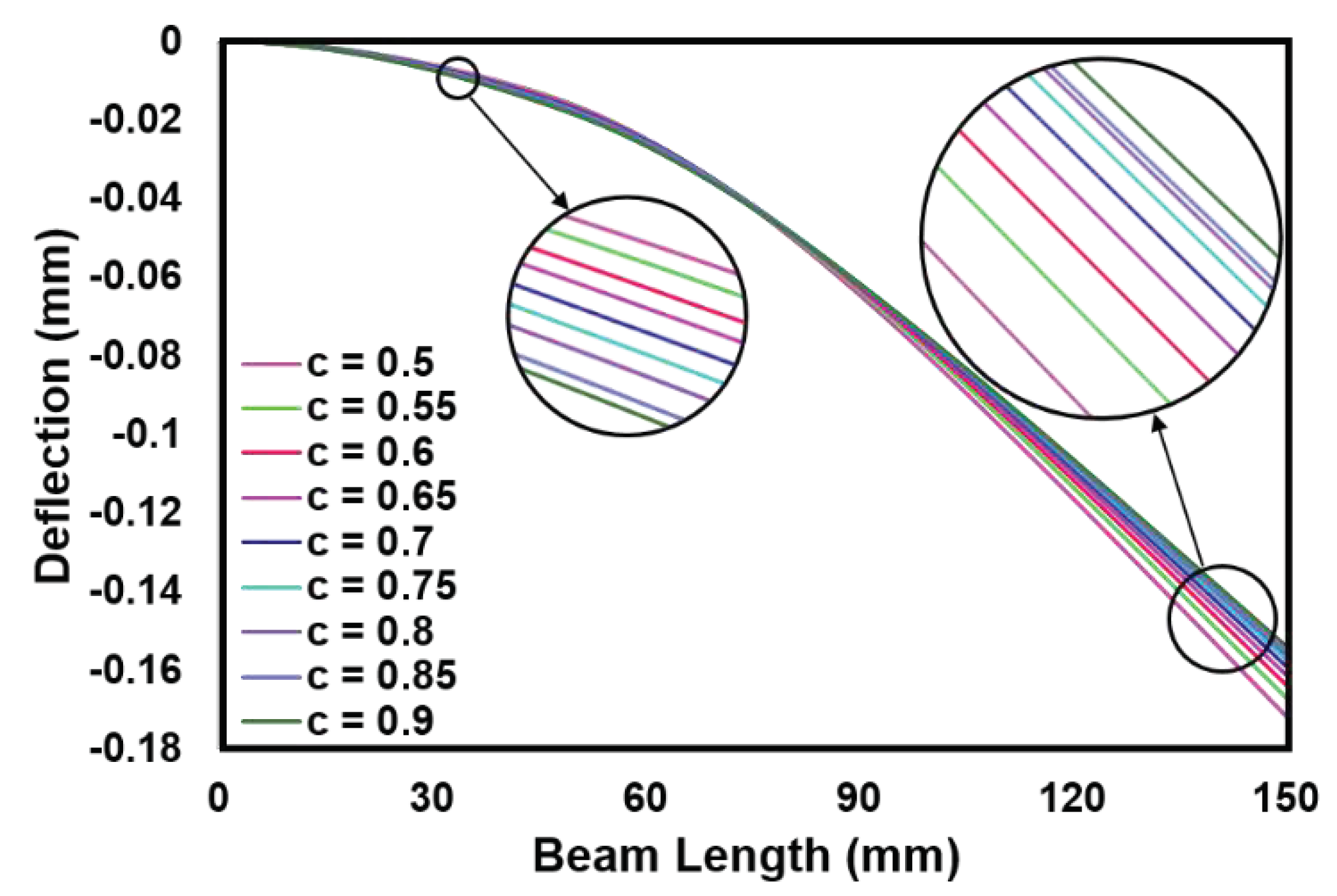
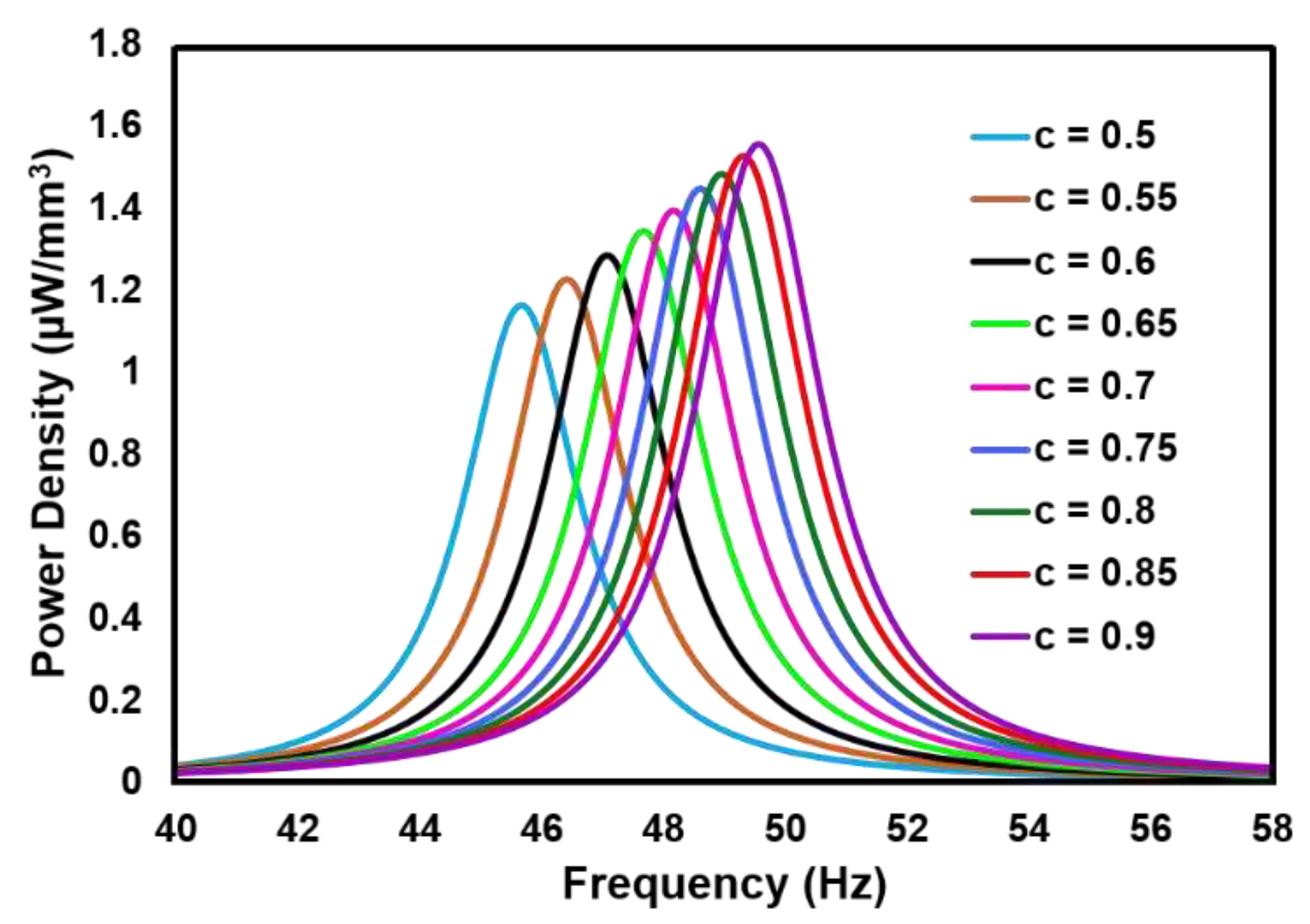
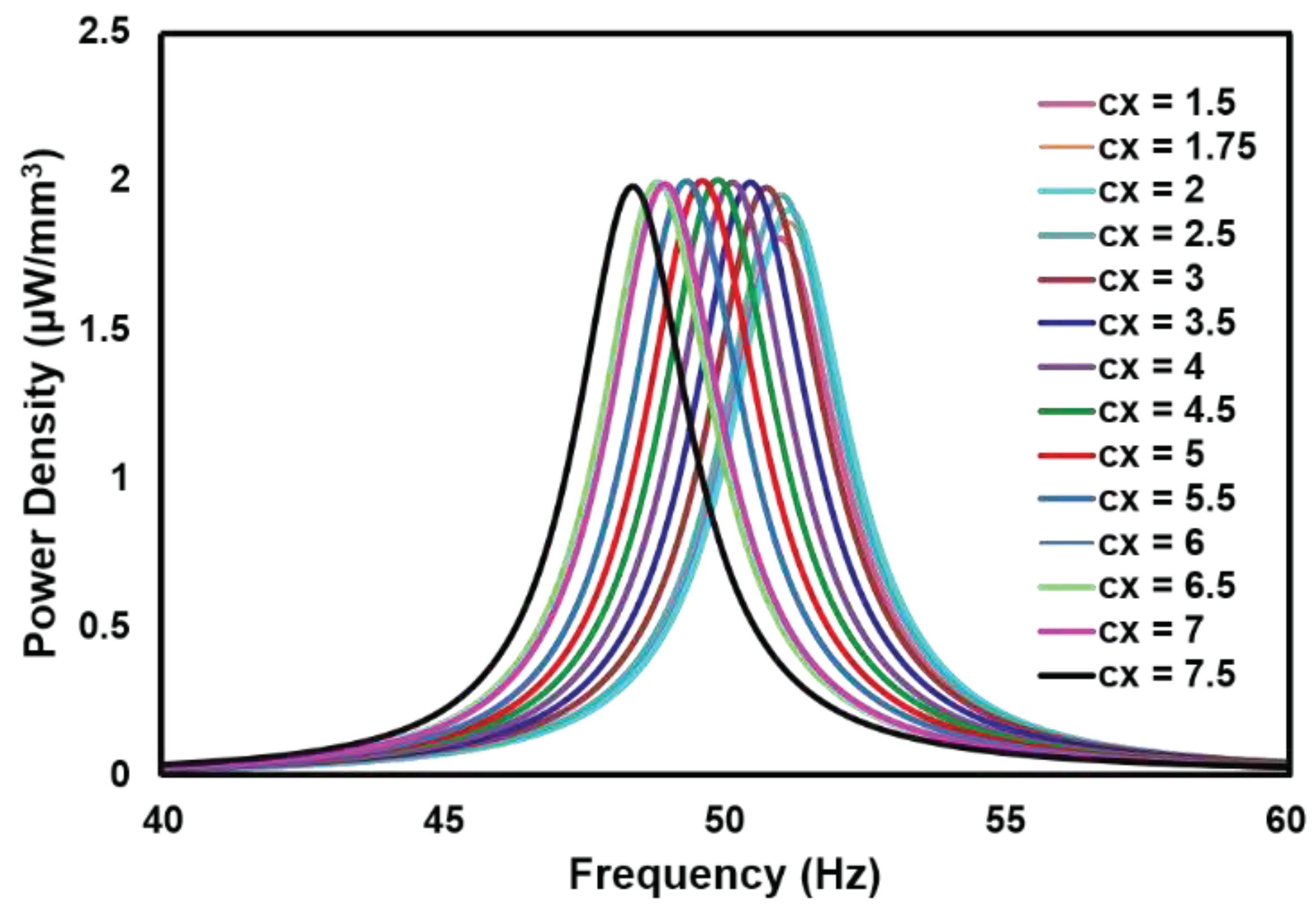
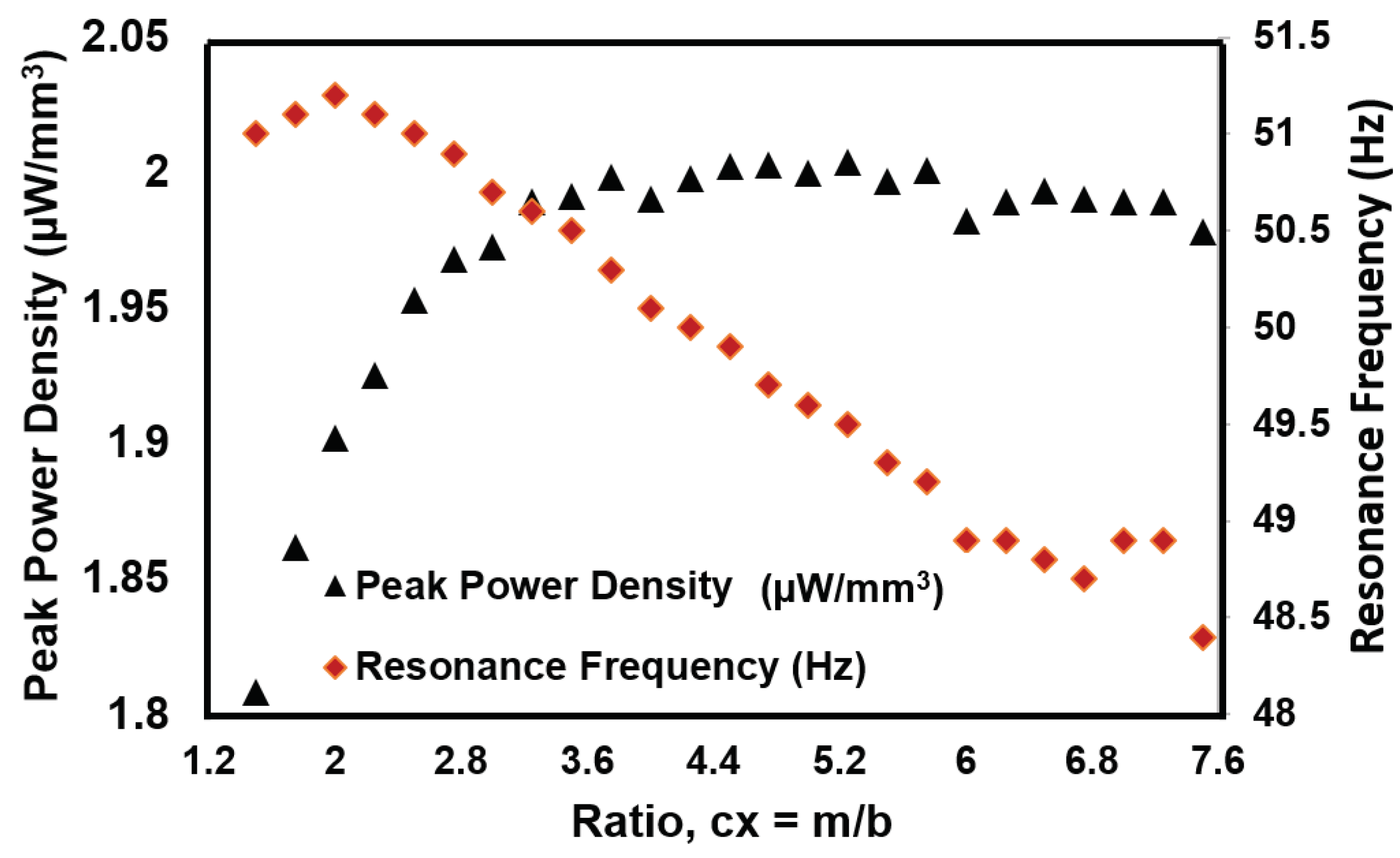
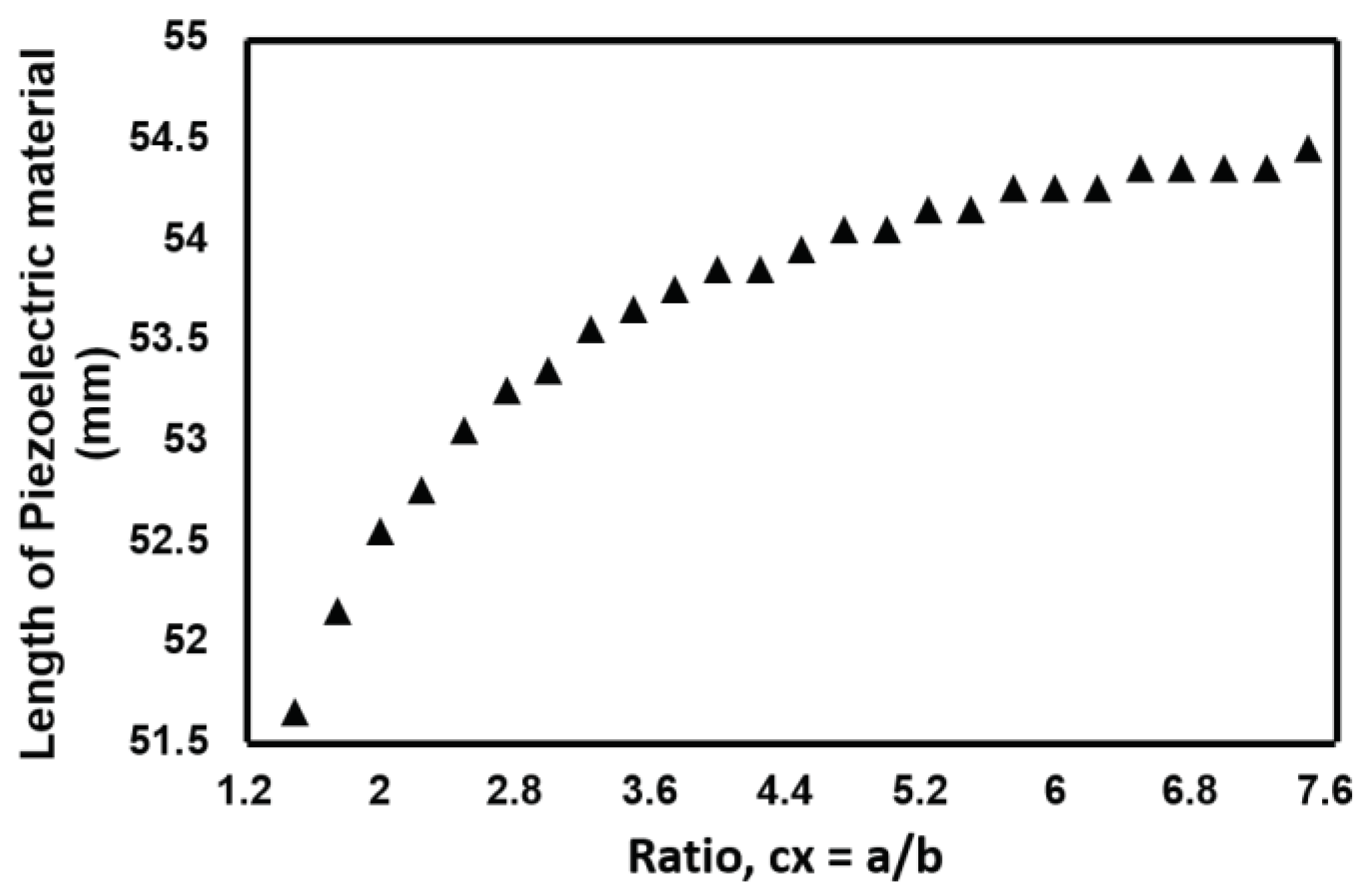
4.3. Analysis of Convex Beam
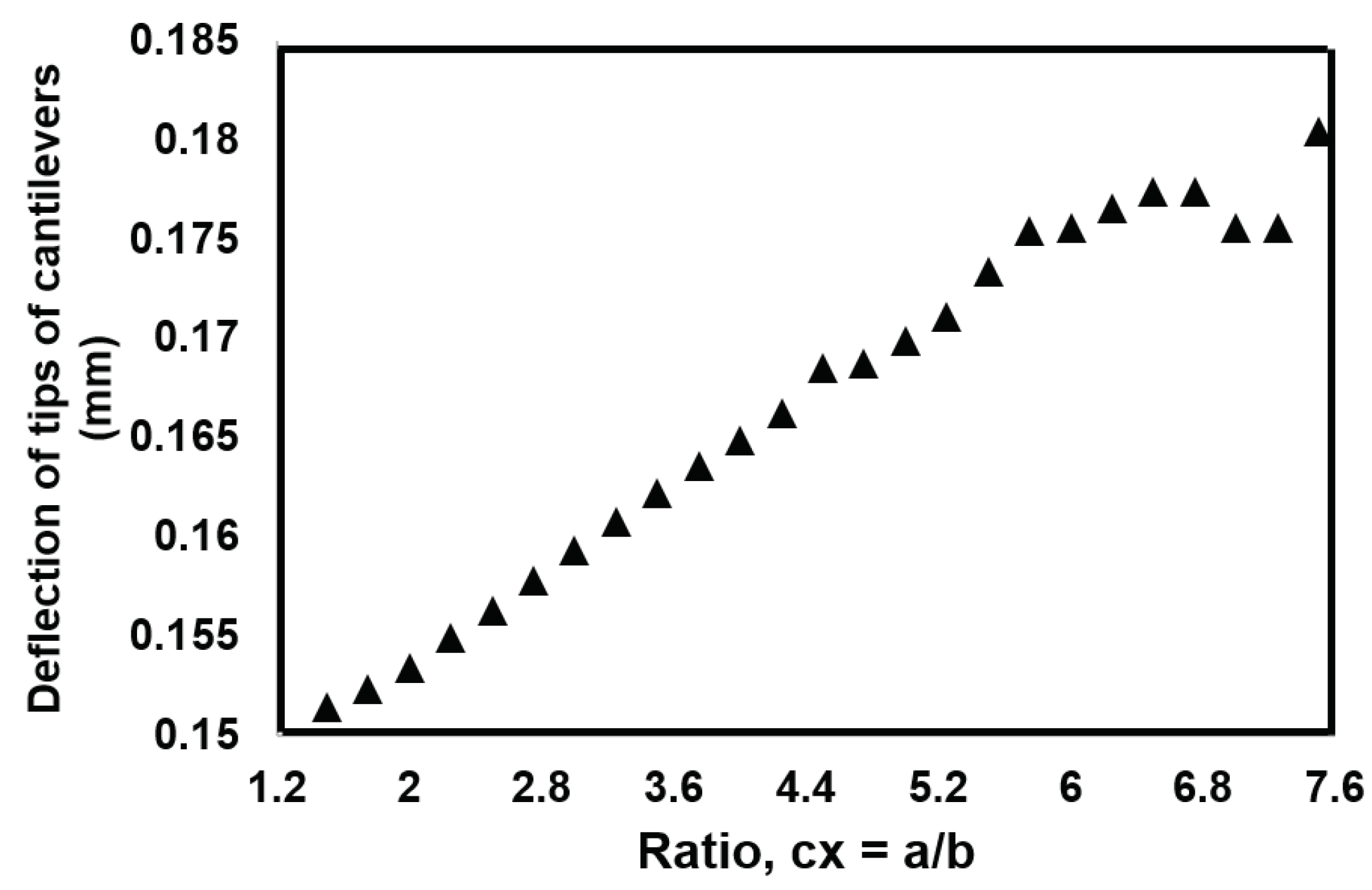
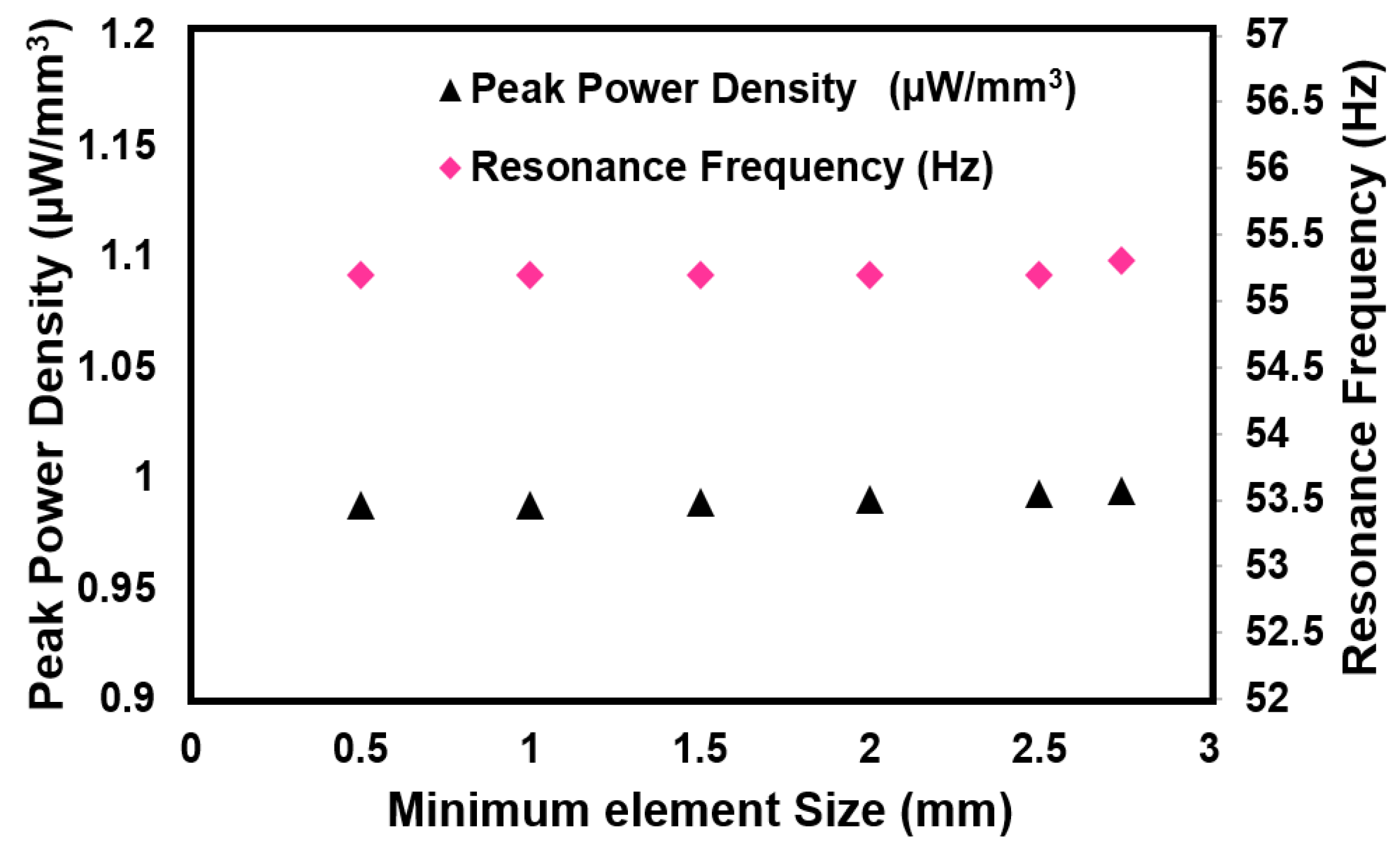
4.4. Analysis of V-cut Beam
4.5. Analysis of Triangular Beam
5. Comparison Among Beam Types
6. Conclusion
Conflicts of Interest
References
- Liu, H.; Zhong, J.; Lee, C.; Lee, S.W.; Lin, L. A Comprehensive Review on Piezoelectric Energy Harvesting Technology: Materials, Mechanisms, and Applications. Appl. Phys. Rev. 2018, 5, 041306. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K.; Rabaey, J. A Study of Low Level Vibrations as a Power Source for Wireless Sensor Nodes. Comput. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
- Baker, J.; Roundy, S.; Wright, P. Alternative Geometries for Increasing Power Density in Vibration Energy Scavenging for Wireless Sensor Networks. Collect. Tech. Pap. - 3rd Int. Energy Convers. Eng. Conf. 2005, 2, 959–970. [Google Scholar] [CrossRef]
- Zhang, G.; Gao, S.; Liu, H.; Niu, S. A Low Frequency Piezoelectric Energy Harvester with Trapezoidal Cantilever Beam: Theory and Experiment. Microsyst. Technol. 2017, 23, 3457–3466. [Google Scholar] [CrossRef]
- Rosmi, A.S.; Isa, M.; Ismail, B.; Rohani, M.N.K.H.; Wahab, Y. An Optimization of Electrical Output Power for Piezoelectric Energy Harvester Using Different Micro-Cantilever Beam Geometries. J. Phys. Conf. Ser. 2018, 1019, 012033. [Google Scholar] [CrossRef]
- Hosseini, R.; Hamedi, M. Improvements in Energy Harvesting Capabilities by Using Different Shapes of Piezoelectric Bimorphs. J. Micromechanics Microengineering 2015, 25, 125008. [Google Scholar] [CrossRef]
- Jin, L.; Gao, S.; Zhou, X.; Zhang, G. The Effect of Different Shapes of Cantilever Beam in Piezoelectric Energy Harvesters on Their Electrical Output. Microsyst. Technol. 2017, 23, 4805–4814. [Google Scholar] [CrossRef]
- Chen, Z.S.; Yang, Y.M.; Deng, G.Q. Analytical and Experimental Study on Vibration Energy Harvesting Behaviors of Piezoelectric Cantilevers with Different Geometries. 1st Int. Conf. Sustain. Power Gener. Supply, SUPERGEN ’09 2009. [Google Scholar] [CrossRef]
- Alameh, A.H.; Gratuze, M.; Nabki, F. Impact of Geometry on the Performance of Cantilever-Based Piezoelectric Vibration Energy Harvesters. IEEE Sens. J. 2019, 19, 10316–10326. [Google Scholar] [CrossRef]
- Patel, R.; McWilliam, S.; Popov, A.A. A Geometric Parameter Study of Piezoelectric Coverage on a Rectangular Cantilever Energy. Smart Mater. Struct. 2011, 20, 085004. [Google Scholar] [CrossRef]
- Salem, M.S.; Ahmed, S.; Shaker, A.; Alshammari, M.T.; Al-Dhlan, K.A.; Alanazi, A.; Saeed, A.; Abouelatta, M. Bandwidth Broadening of Piezoelectric Energy Harvesters Using Arrays of a Proposed Piezoelectric Cantilever Structure. Micromachines 2021, Vol. 12, Page 973 2021, 12, 973. [Google Scholar] [CrossRef] [PubMed]
- Pradeesh, E.L.; Udhayakumar, S. Effect of Placement of Piezoelectric Material and Proof Mass on the Performance of Piezoelectric Energy Harvester. Mech. Syst. Signal Process. 2019, 130, 664–676. [Google Scholar] [CrossRef]
- Pradeesh, E.L.; Udhayakumar, S. Investigation on the Geometry of Beams for Piezoelectric Energy Harvester. Microsyst. Technol. 2019, 25, 3463–3475. [Google Scholar] [CrossRef]
- Ibrahim, D.S.; Beibei, S.; Oluseyi, O.A.; Sharif, U. Performance Analysis of Width and Thickness Tapered Geometries on Electrical Power Harvested from a Unimorph Piezoelectric Cantilever Beam. 2020 IEEE 3rd Int. Conf. Electron. Technol. ICET 2020 2020, 100–104. [Google Scholar] [CrossRef]
- Tang, L.; Wang, J. Size Effect of Tip Mass on Performance of Cantilevered Piezoelectric Energy Harvester with a Dynamic Magnifier. Acta Mech. 2017, 228, 3997–4015. [Google Scholar] [CrossRef]
- Alameh, A.H.; Gratuze, M.; Elsayed, M.Y.; Nabki, F. Effects of Proof Mass Geometry on Piezoelectric Vibration Energy Harvesters. Sensors 2018, Vol. 18, Page 1584 2018, 18, 1584. [Google Scholar] [CrossRef]
- Satyanarayana, T.; Nikhitha, Y.; Neeraj Kumar, C.; Jeevan Naga Sai, K.; Lohitha, V. Optimization of Bimorph Cantilever Based Piezoelectric Energy Harvester for High Efficiency. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Li, W.G.; He, S.; Yu, S. Improving Power Density of a Cantilever Piezoelectric Power Harvester through a Curved L-Shaped Proof Mass. IEEE Trans. Ind. Electron. 2010, 57, 868–876. [Google Scholar] [CrossRef]
- Palosaari, J.; Leinonen, M.; Juuti, J.; Jantunen, H. The Effects of Substrate Layer Thickness on Piezoelectric Vibration Energy Harvesting with a Bimorph Type Cantilever. Mech. Syst. Signal Process. 2018, 106, 114–118. [Google Scholar] [CrossRef]
- Kim, G.Y.; Peddigari, M.; Lim, K.W.; Hwang, G.T.; Yoon, W.H.; Choi, H.S.; Lee, J.W.; Ryu, J. Effect of Thickness Ratio in Piezoelectric/Elastic Cantilever Structure on the Piezoelectric Energy Harvesting Performance. Electron. Mater. Lett. 2019, 15, 61–69. [Google Scholar] [CrossRef]
- Sunithamani, S.; Lakshmi, P. Experimental Study and Analysis of Unimorph Piezoelectric Energy Harvester with Different Substrate Thickness and Different Proof Mass Shapes. Microsyst. Technol. 2017, 23, 2421–2430. [Google Scholar] [CrossRef]
- Matova, S.P.; Renaud, M.; Jambunathan, M.; Goedbloed, M.; Van Schaijk, R. Effect of Length/Width Ratio of Tapered Beams on the Performance of Piezoelectric Energy Harvesters. Smart Mater. Struct. 2013, 22, 075015. [Google Scholar] [CrossRef]
- Paquin, S.; St-Amant, Y. Improving the Performance of a Piezoelectric Energy Harvester Using a Variable Thickness. Smart Mater. Struct. 2010, 19, 105020. [Google Scholar] [CrossRef]
- Reddy, A.R.; Umapathy, M.; Ezhilarasi, D.; Gandhi, U. Improved Energy Harvesting from Vibration by Introducing Cavity in a Cantilever Beam. J. Vib. Control. 2014, 22, 3057–3066. [Google Scholar] [CrossRef]
- Reddy, A.R.; Umapathy, M.; Ezhilarasi, D.; Uma, G. Cantilever Beam with Trapezoidal Cavity for Improved Energy Harvesting. Int. J. Precis. Eng. Manuf. 2015, 16, 1875–1881. [Google Scholar] [CrossRef]
- Srinivasulu Raju, S.; Umapathy, M.; Uma, G. Cantilever Piezoelectric Energy Harvester with Multiple Cavities. Smart Mater. Struct. 2015, 24, 115023. [Google Scholar] [CrossRef]
- Usharani, R.; Uma, G.; Umapathy, M. Design of High Output Broadband Piezoelectric Energy Harvester with Double Tapered Cavity Beam. Int. J. Precis. Eng. Manuf. Technol. 2016 34 2016, 3, 343–351. [Google Scholar] [CrossRef]
- Raju, S.S.; Umapathy, M.; Uma, G. High-Output Piezoelectric Energy Harvester Using Tapered Beam with Cavity. J. Intell. Mater. Syst. Struct. 2018, 29, 800–815. [Google Scholar] [CrossRef]
- Damya, A.; Abbaspour Sani, E.; Rezazadeh, G. An Innovative Piezoelectric Energy Harvester Using Clamped–Clamped Beam with Proof Mass for WSN Applications. Microsyst. Technol. 2020, 26, 3203–3211. [Google Scholar] [CrossRef]
- Lihua, C.; Jiangtao, X.; Shiqing, P.; Liqi, C. Study on Cantilever Piezoelectric Energy Harvester with Tunable Function. Smart Mater. Struct. 2020, 29, 075001. [Google Scholar] [CrossRef]
- Gao, X.; Shih, W.-H.; Shih, W.Y. Induced Voltage of Piezoelectric Unimorph Cantilevers of Different Nonpiezoelectric/Piezoelectric Length Ratios. Smart Mater. Struct. 2009, 18, 125018. [Google Scholar] [CrossRef]
- Wang, Q.; Dai, W.; Li, S.; Oh, J.A.S.; Wu, T. Modelling and Analysis of a Piezoelectric Unimorph Cantilever for Energy Harvesting Application. Mater. Technol. 2020, 35, 675–681. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, S.; Jin, L.; Liu, H.; Li, P. Effects of Changing PZT Length on the Performance of Doubly-Clamped Piezoelectric Energy Harvester with Different Beam Shapes under Stochastic Excitation. Microsyst. Technol. 2018, 24, 3799–3813. [Google Scholar] [CrossRef]
- Izadgoshasb, I.; Lim, Y.Y.; Lake, N.; Tang, L.; Padilla, R.V.; Kashiwao, T. Optimizing Orientation of Piezoelectric Cantilever Beam for Harvesting Energy from Human Walking. Energy Convers. Manag. 2018, 161, 66–73. [Google Scholar] [CrossRef]
- Gao, X.; Shih, W.H.; Shih, W.Y. Flow Energy Harvesting Using Piezoelectric Cantilevers with Cylindrical Extension. IEEE Trans. Ind. Electron. 2013, 60, 1116–1118. [Google Scholar] [CrossRef]
- McMaster-Carr. Available online: https://www.mcmaster.com/products/aluminum/shape~sheet-and-bar/system-of measurement~metric/thickness~2mm/width~10-mm/ (accessed on 8 August 2023).
- Piezoelectric Sheets & Plates | PIEZO.COM. Available online: https://piezo.com/collections/piezo-sheets-plates?_=pf&pf_t_quantity=Quantity__1&pf_t_piezo_material=Piezo Material__PZT 5A&pf_t_thickness=Thickness (in.)__0.0200 (accessed on 8 August 2023).
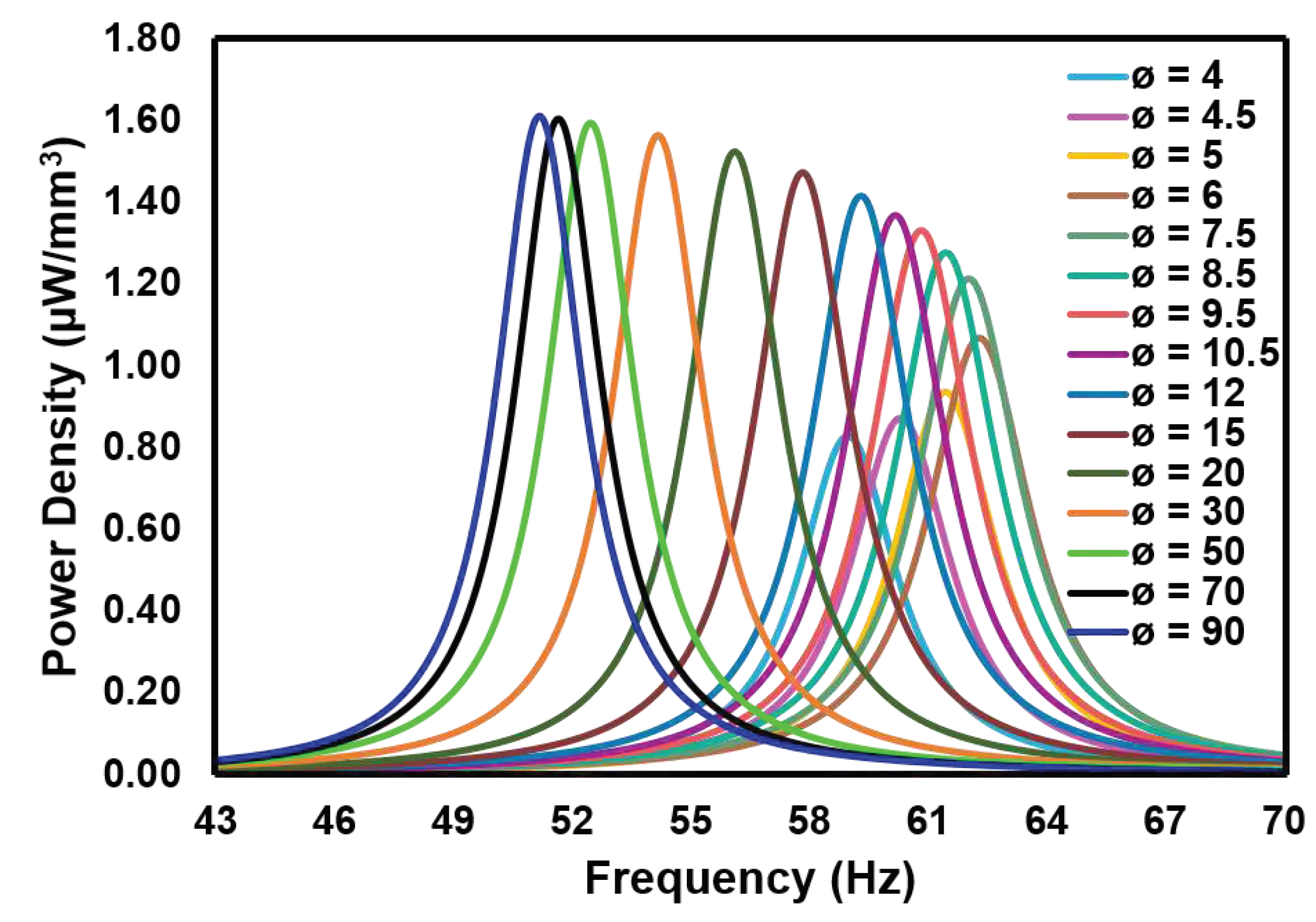
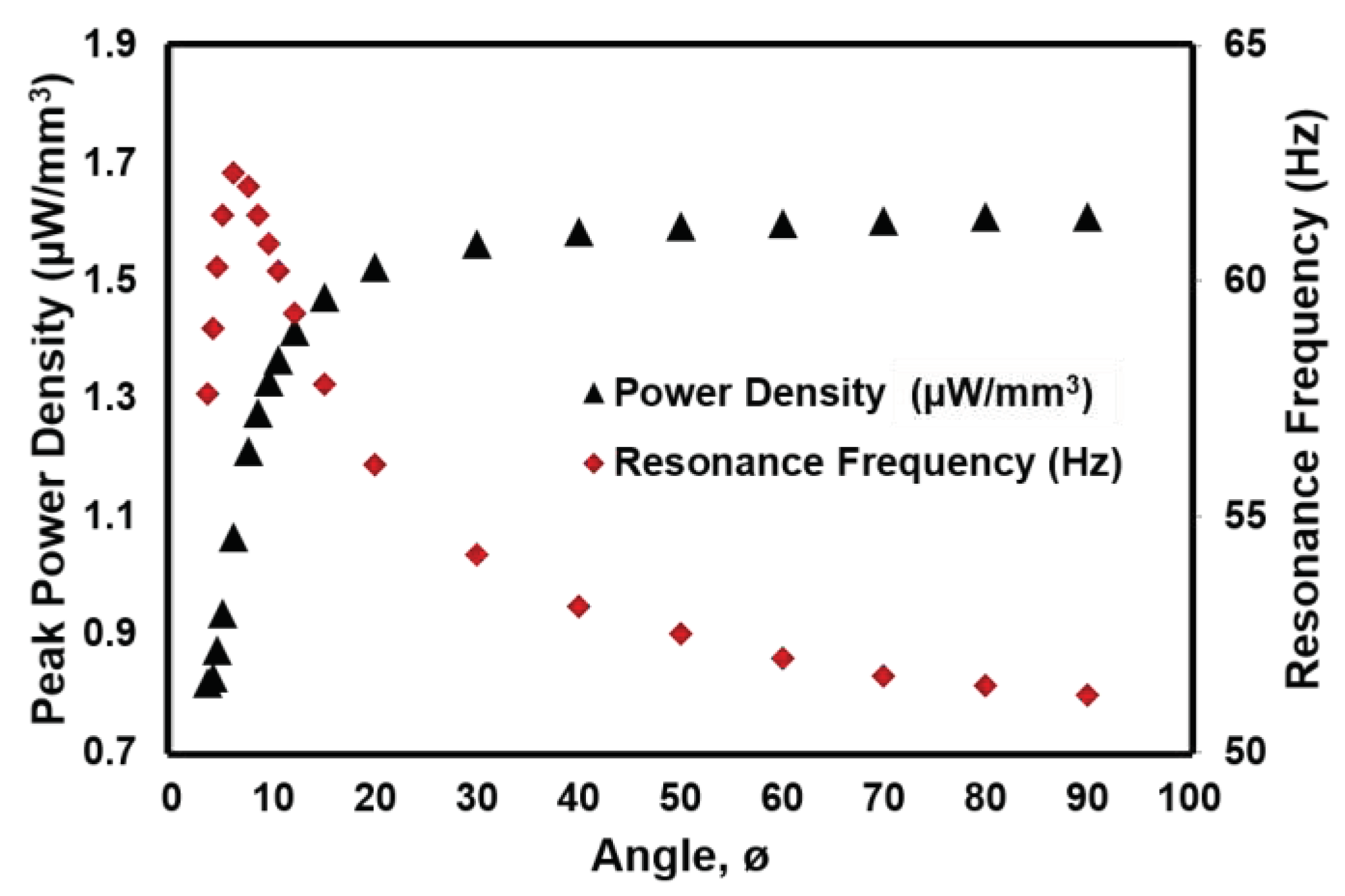
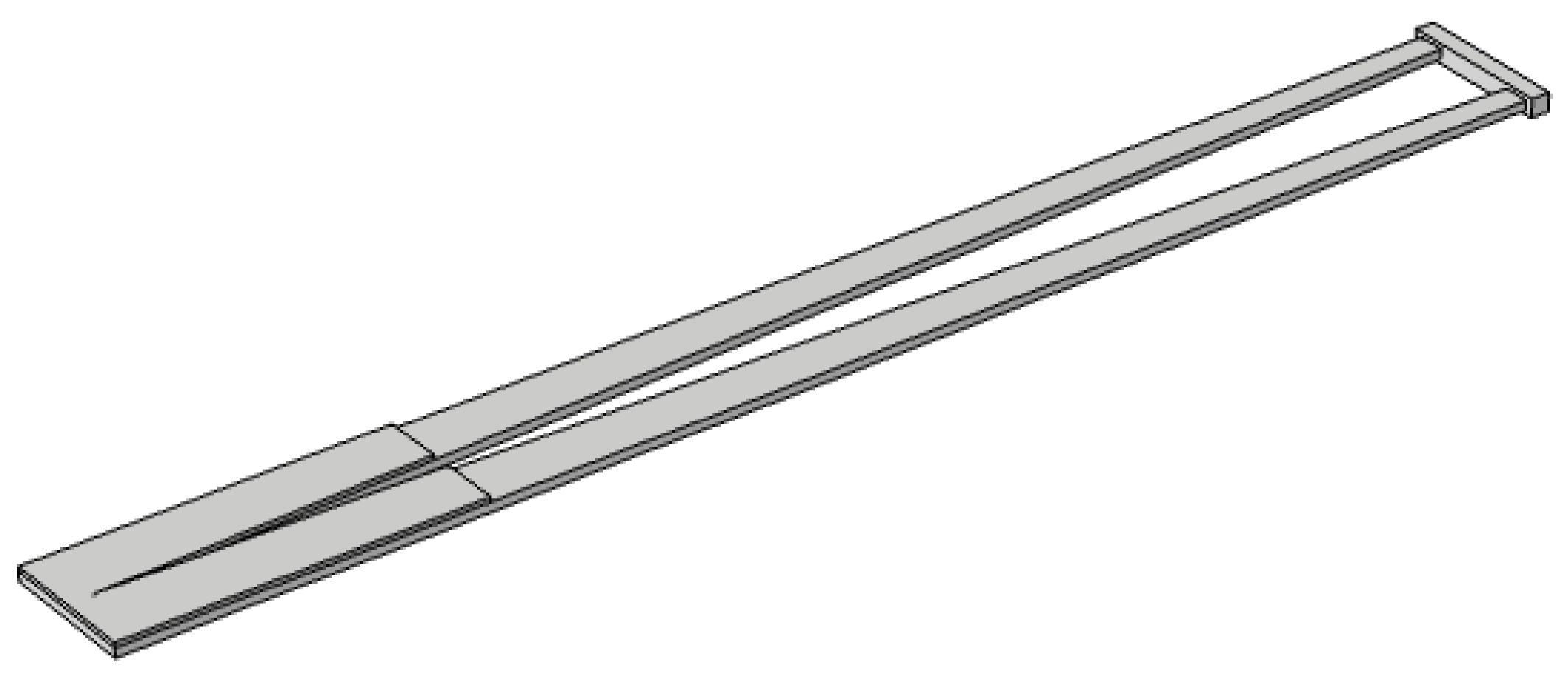
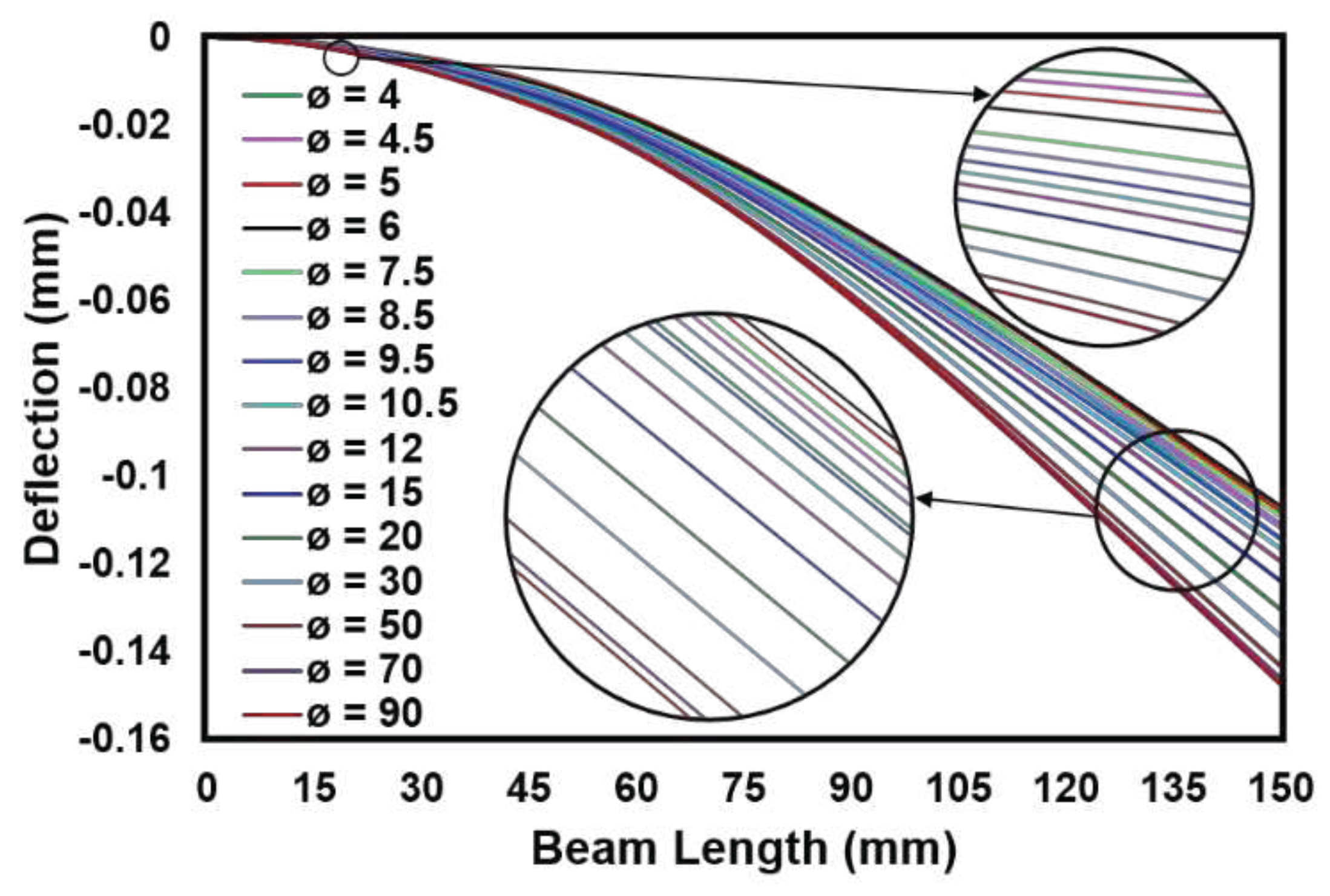
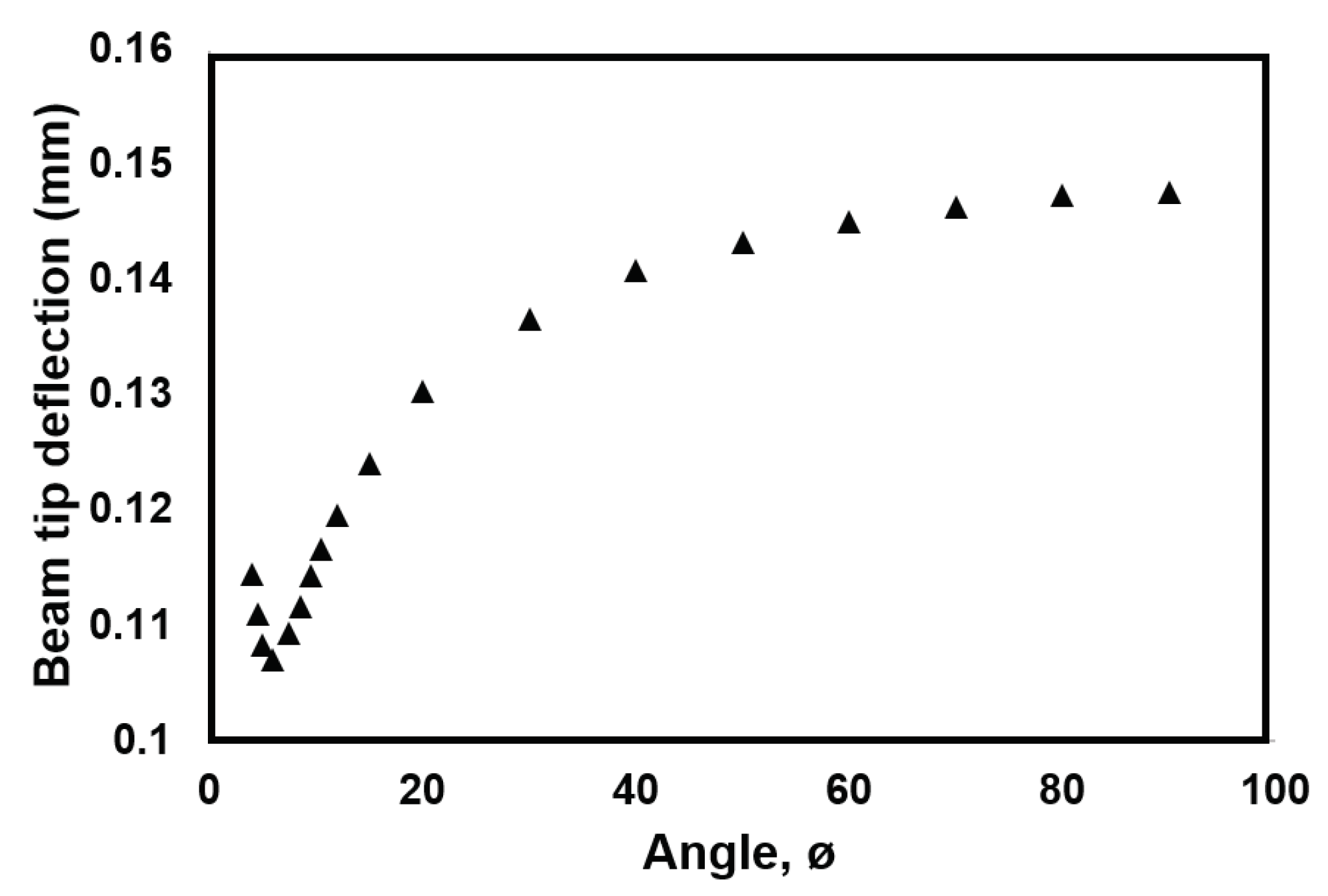
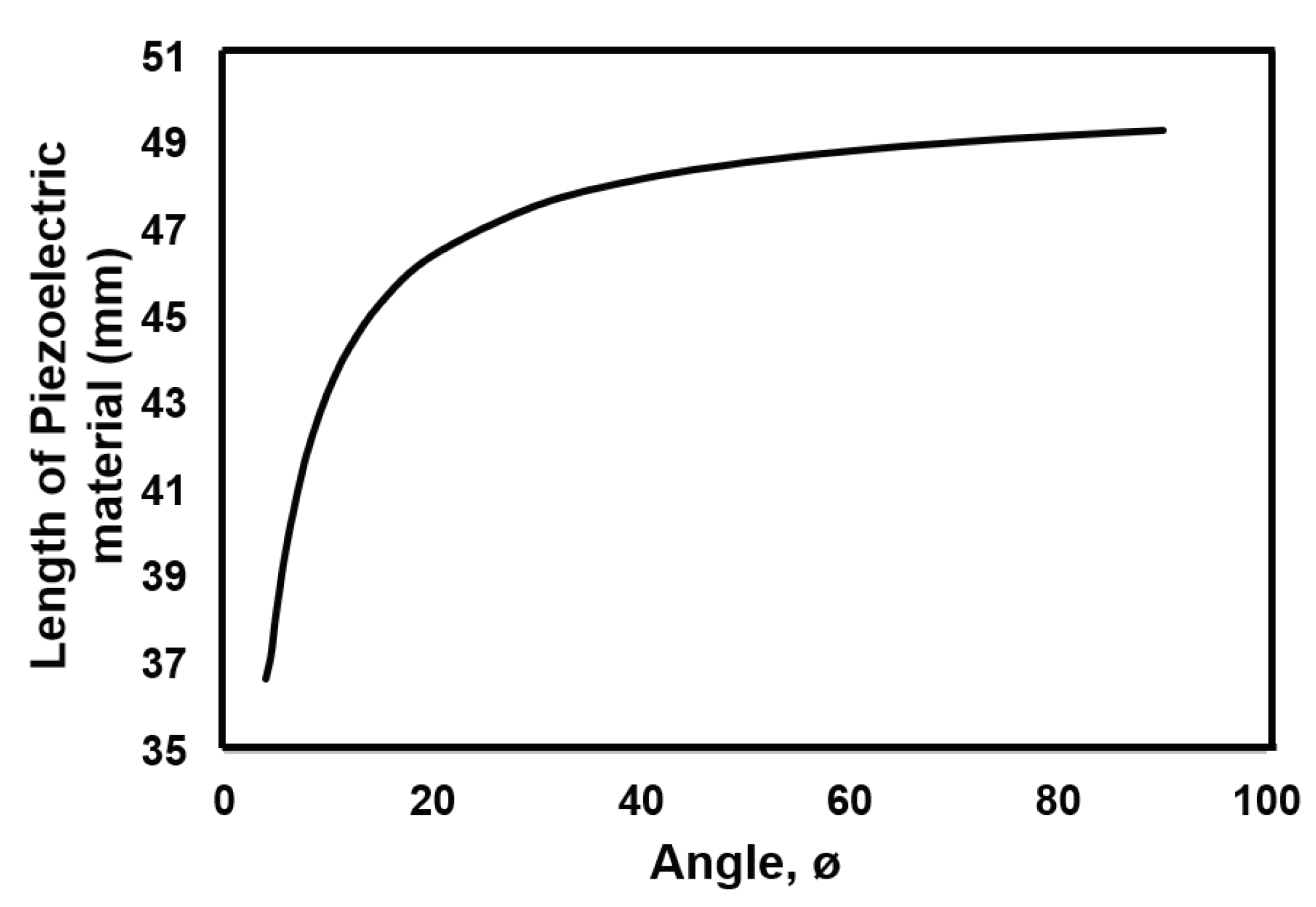
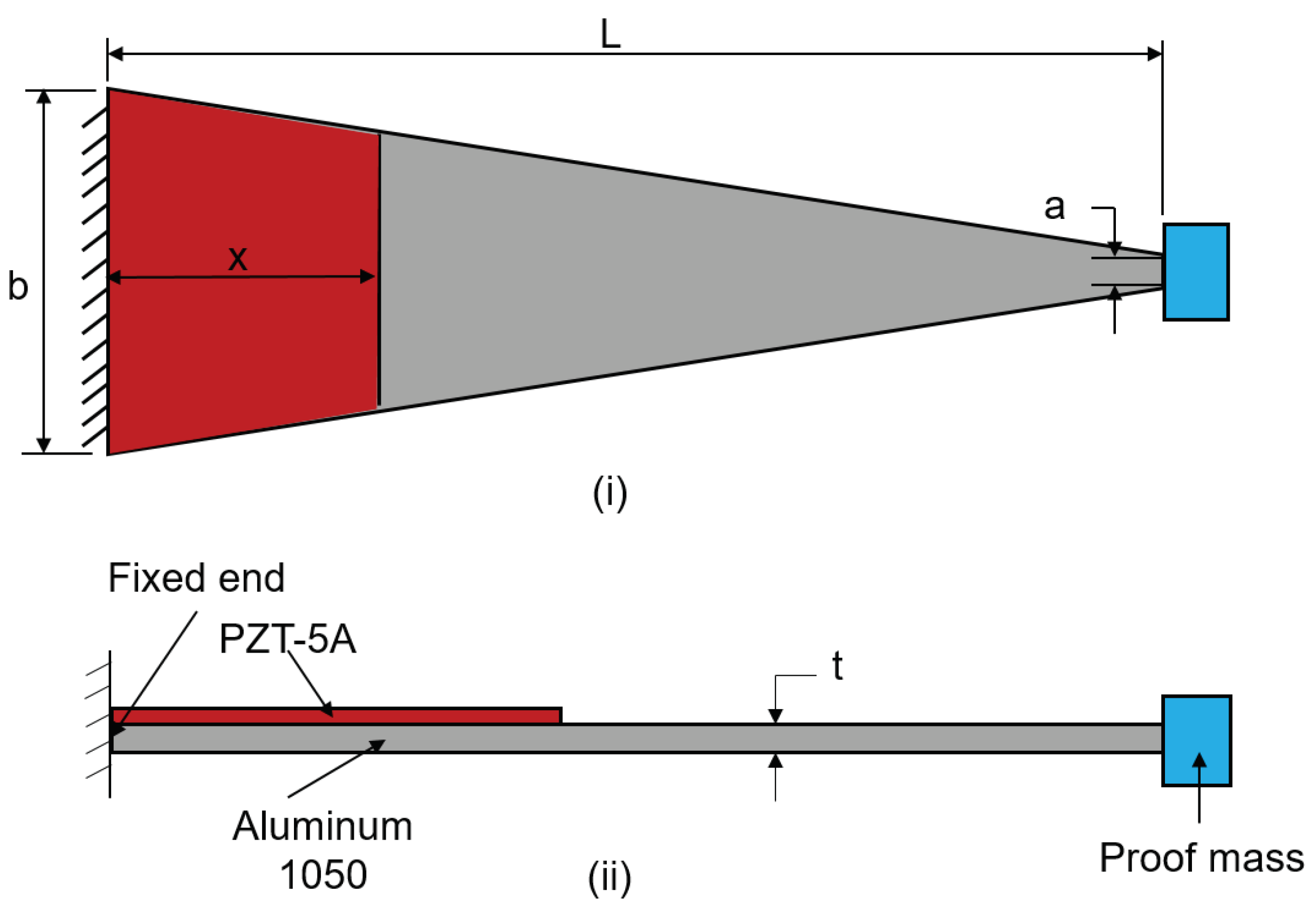
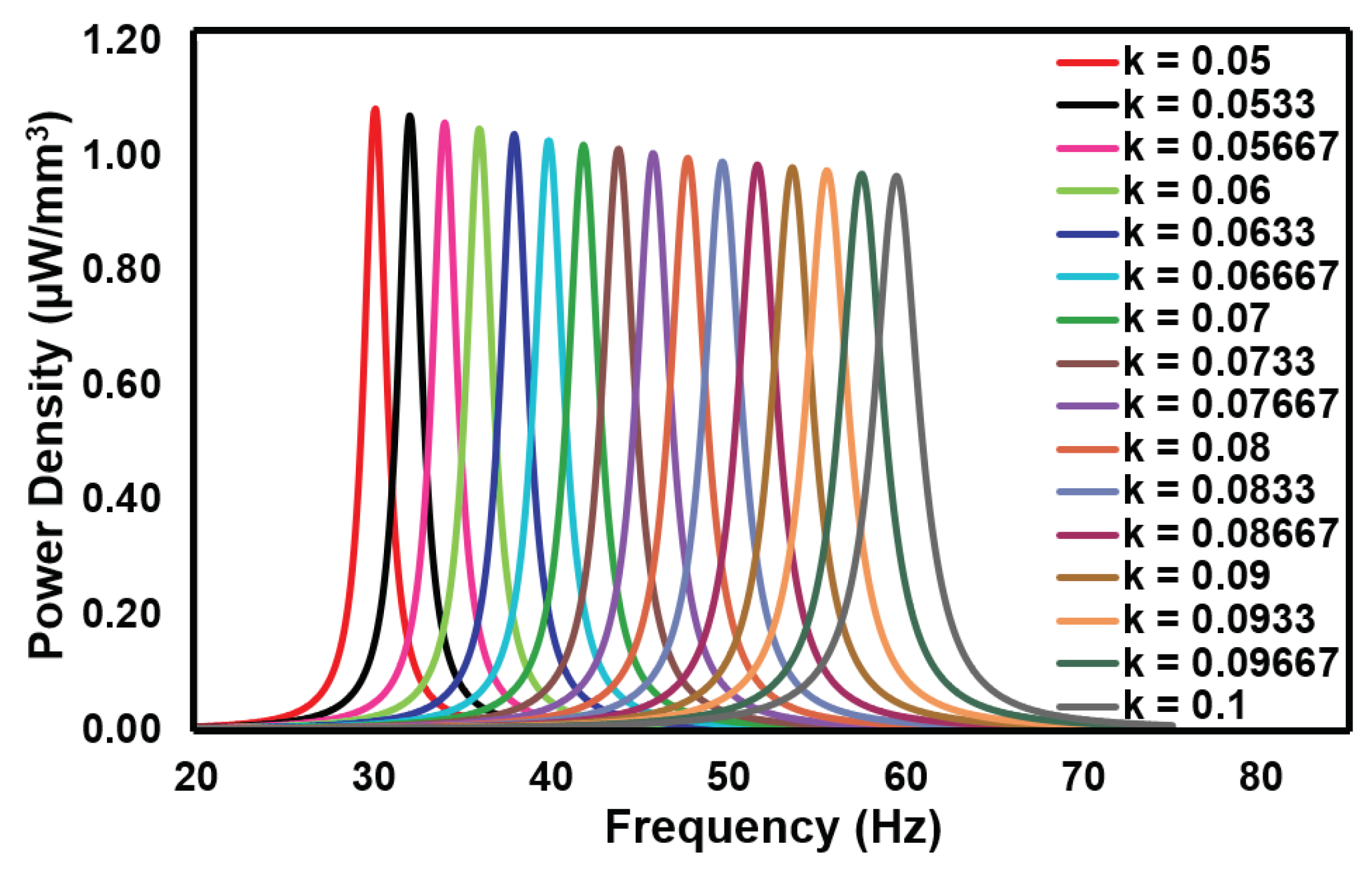
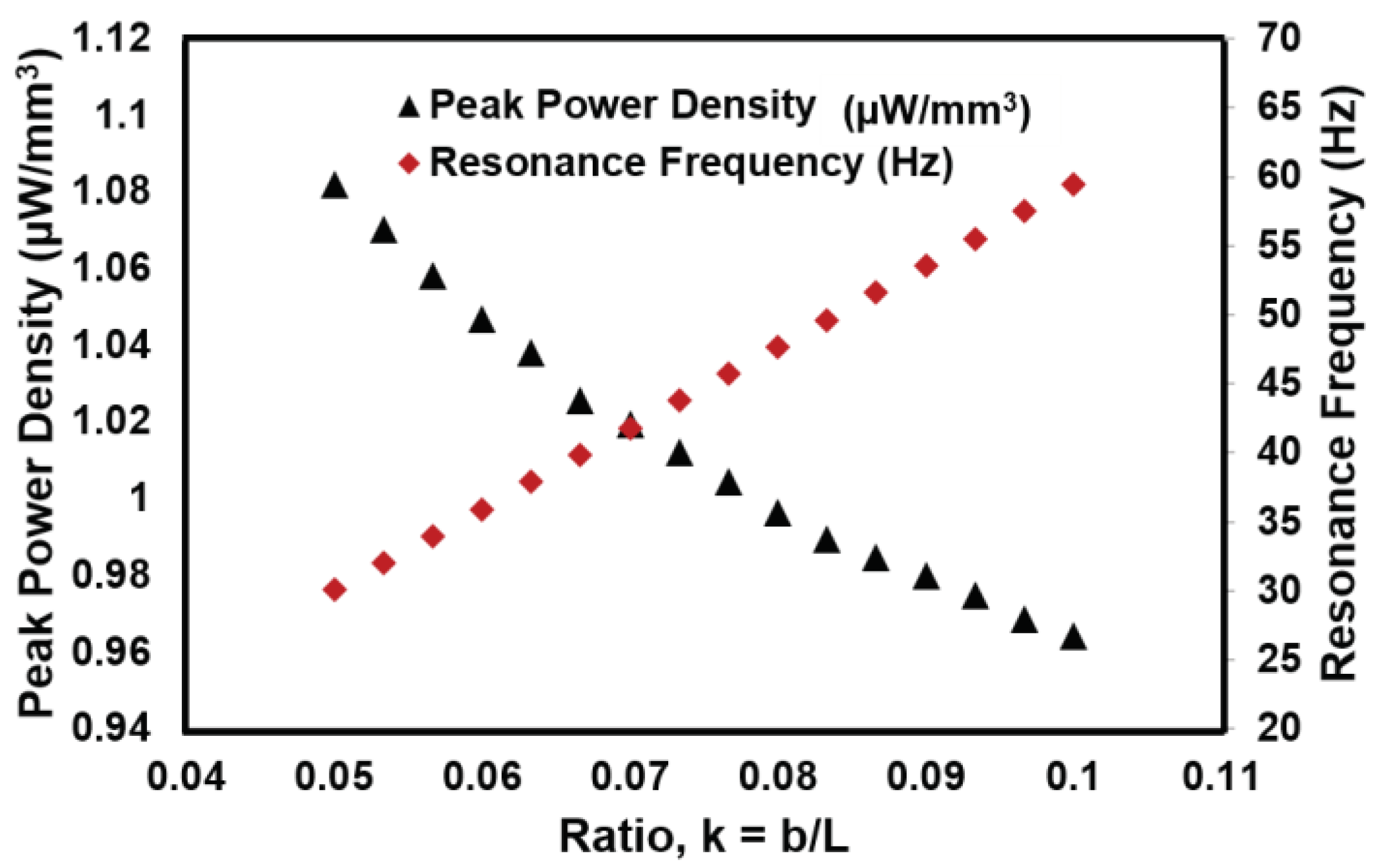
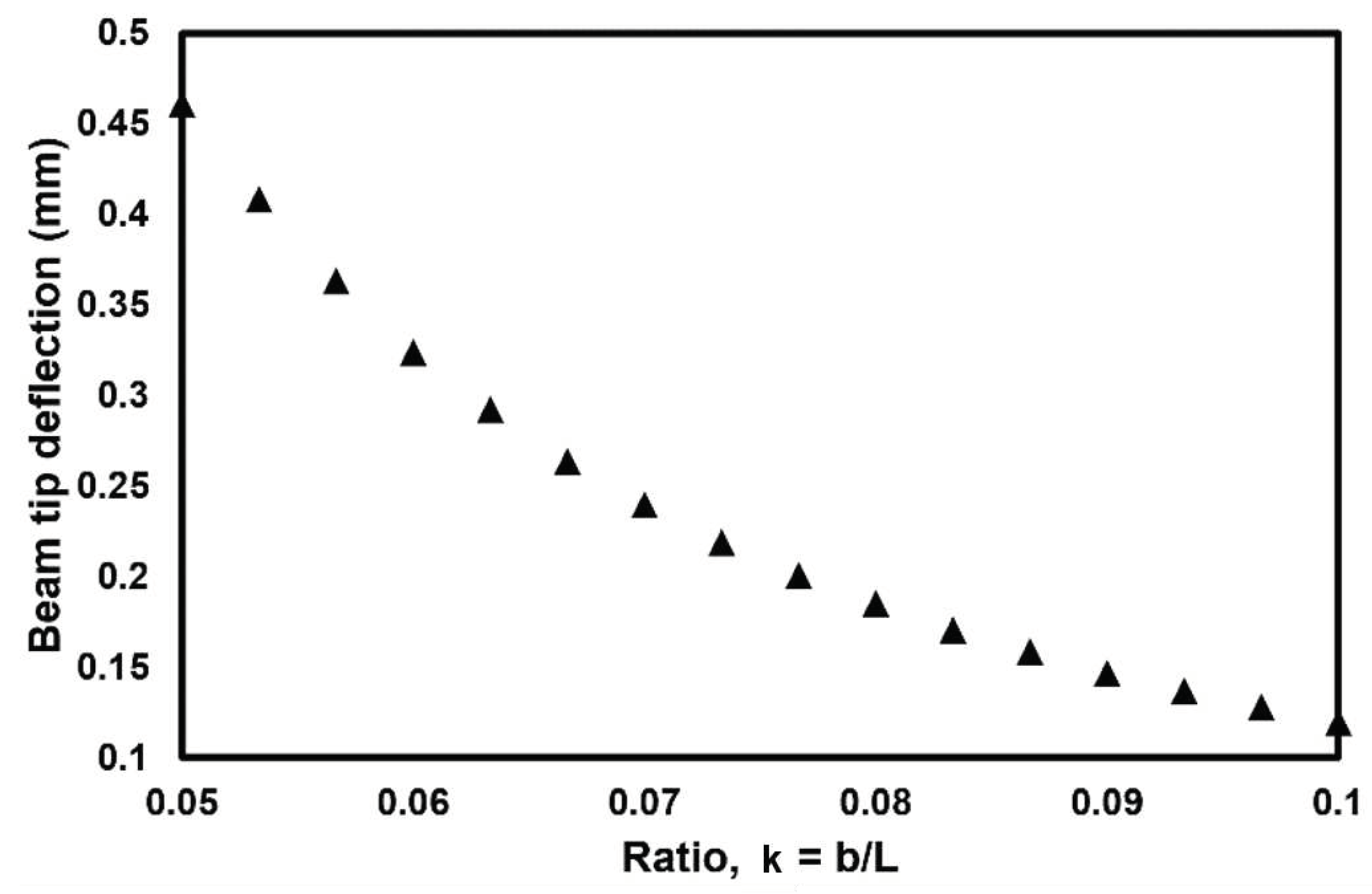
| Shape | Resonance frequency (Hz) |
Maximum output power density (µW/mm3) | Base width (mm) |
| Trapezoid | 42.4 | 2.73 | 5.71 |
| Concave | 49.6 | 1.55 | 10.85 |
| Convex | 49.7 | 2.003 | 2.53 |
| V-Cut | 51.2 | 1.61 | 10.13 |
| Triangular | 30.1 | 1.08 | 11.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




