Minimum Cost Design for Rectangular Isolated Footings Taking into Account That the Column Is Located in Any Part of the Footing

Preprint

Article

Minimum Cost Design for Rectangular Isolated Footings Taking into Account That the Column Is Located in Any Part of the Footing

Altmetrics

Downloads

142

Views

Comments

A peer-reviewed article of this preprint also exists.

Arnulfo Luévanos-Rojas^*

This version is not peer-reviewed

Submitted:

24 August 2023

Posted:

25 August 2023

You are already at the latest version

Alerts

Abstract

This work presents a new model to obtain the minimum cost design for a rectangular isolated footing, taking into account that the column is located in any part of the footing. The methodology is developed by integration to obtain the moments, bending shear and punching shear according to the American Concrete Institute ACI 318-14. This document presents the simplified and precise equations of the four moments, four bending shears and one punching shear acting on the footing. Some designs have been developed by the trial and error method to determine the footing dimensions, and later the thickness and steel area of the footing are obtained. Some authors present the minimum cost design for a rectangular isolated footing taking into account that the column is located in the center of gravity of the footing, and other authors present very complex algorithm. Numerical examples are presented to obtain the minimum cost design of rectangular isolated footings under biaxial bending, and some results are compared with those of other authors considering the same conditions. The new model presents a smaller contact area with the soil and a lower design cost than those presented by other authors.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

Footing or foundation is the structural member (sub-structure) that transfers the loads of the superstructure to the soil. Footings are used in various types of construction in structural engineering, such as buildings and bridges.

The main object of geotechnical and structural engineers is to obtain the smallest area and the minimum cost of the footing to support the loads imposed by the superstructure.

Optimization techniques have been successfully used in various foundation problems such as: Hannan et al. [1] showed a strategy to obtain minimum volume for reinforced concrete footing that support a wind load on the superstructure. Basudhar et al. [2, 3] investigated the optimal cost design for rigid raft foundation and circular isolated footings taking into account the cost of concrete, cost of excavations, cost of backfilling works and cost of steel reinforcement based in the mathematical programming problem using Powell's conjugate direction search method. Al-Douri [4] proposed an optimal model for the design of trapezoidal combined footings taking into account the cost of concrete, cost of excavations, cost of backfilling works and cost of steel reinforcement. Wang and Kulhawy [5] proposed the minimum construction cost as objective function for a foundation considering the serviceability limit state (SLS), ultimate limit state (ULS), and economics. Rizwan et al. [6] developed an optimal design of reinforced concrete combined footings using computational procedure, and objective function includes cost of excavation, filling, concrete and reinforcement for the footings. Jelušič and Žlender [7-8] developed an optimal design for reinforced pad and strip foundations based on optimizations as are: multiparametric, mixed-integer, and nonlinear programming (MINLP). Velázquez-Santillán et al. [9] presented the optimal design for reinforced concrete rectangular combined to obtain the minimum cost design, the radius, the thickness, and the reinforced steel areas in both directions. López-Chavarría et al. [10] designed an optimal model for circular isolated footings to obtain the minimum cost design, the radius, the thickness, and the reinforced steel areas in both directions. Khajuria and Singh [11] proposed a metaheuristic optimization for the design of reinforced concrete footings supporting a column based of the gravitational search algorithm (GSA). Al-Ansari and Afzal [12] presented a simplified analysis for the design of irregularly shaped reinforced concrete footings with an eccentric load subject to biaxial bending that support a square column, the shapes of the footings studied are: square, triangular, circular, and trapezoidal. Kashani et al. [13] studied the optimal design of reinforced concrete combined footings according to the American Concrete Institute ACI 318-05, using five swarm intelligence algorithms such as: particle swarm optimization (PSO), accelerated particle swarm optimization (APSO), whale optimization algorithm (WOA), ant lion optimizer (ALO), and moth flame optimization (MFO). Nigdeli and Bekdas [14] investigated the orientation of the column mounted on the footings using the optimal design based harmony search algorithm. Kamal et al. [15] presented a study on the optimal design of footing systems applied in the prefabricated industrial buildings, and the concrete bracket system using as the connection type in the reinforced concrete frames.

The main contributions through optimization techniques in the design of rectangular isolated footings are: Camp and Assadollahi [16] presented the optimal design of reinforced concrete footings according to the American Concrete Institute ACI 318-11 subjected to vertical load using a hybrid Big Bang-Big Crunch (BB-BC) algorithm. Luévanos-Rojas et al. [17] developed an optimal model for the design of rectangular isolated footings using computation to solve various integrals according to the American Concrete Institute ACI 318-13. Galvis and Smith-Pardo [18] presented design aids and simplified closed form equations to obtain the coupled axial load and biaxial moment capacity of hollow and solid circular and rectangular shallow foundations. Rawat and Mittal, Rawat et al. [19, 20] developed a simplified approach for the design of reinforced concrete rectangular isolated footings with eccentric load according to the American Concrete Institute ACI 318-14. Solorzano and Plevris [21] studied genetic algorithms (GA) with a selection technique applied to the optimal design of reinforced concrete rectangular isolated footings according to the American Concrete Institute ACI 318-19. Chaudhuri and Maity [22] investigated the optimal design of reinforced concrete isolated footings according to the Indian Standard (IS) 4568:2000, using two swarm intelligence algorithms such as: genetic algorithms (GA) and unified particle swarm optimization (UPSO). Also, metaheuristic optimization has been enthusiastically applied in the design of reinforced concrete rectangular isolated footings as a practical tool in parametric research used different algorithms, such as Harmony Search (HS), Teaching Learning Based Optimization (TLBO) algorithm and Flower Pollination Algorithm (FPA) [23], and Evolutionary Algorithm (EA) and the Genetic Algorithm (GA) [24].

This study shows a new model to obtain the minimum cost design for a rectangular isolated footing subjected to biaxial bending by the application of the load and moments of the column and also the column is located in any part of the footing. The least cost design is carried out in two stages: First stage: the objective function is the minimum area of contact with the soil; the known or constant parameters (independent variables) are σ_max, P, e_x. e_y, M_x and M_y; the unknown or decision variables (dependent variables) are: A_min, h_x and h_y. Second stage: the objective function is the minimum cost; the known or constant parameters (independent variables) are σ_max, P_u, M_ux and M_uy, h_x and h_y; the unknown or decision variables (dependent variables) are: C_min, d, A_sx and A_sy. Numerical examples are shown to find the minimum cost design of rectangular isolated footings subjected to biaxial bending for four example: Example 1: When the column is located at the center of gravity of the footing. Example 2: When the column is located at the limit of the footing in the Y direction. Example 3: When the column is located at the limit of the footing in the X direction. Example 4: When the column is located at the limit of the footing in the X and Y directions or at a corner. Also, some results are compared with those of other authors considering the same conditions to observe the differences.

2. Formulation of the Model

The loads and moments are obtained from a structural analysis, where the analysis of the structural framework is developed by any of the known methods (stiffness method, slope-deflection method and Hardy Cross method) that include dead, live, wind, and earthquake loads.

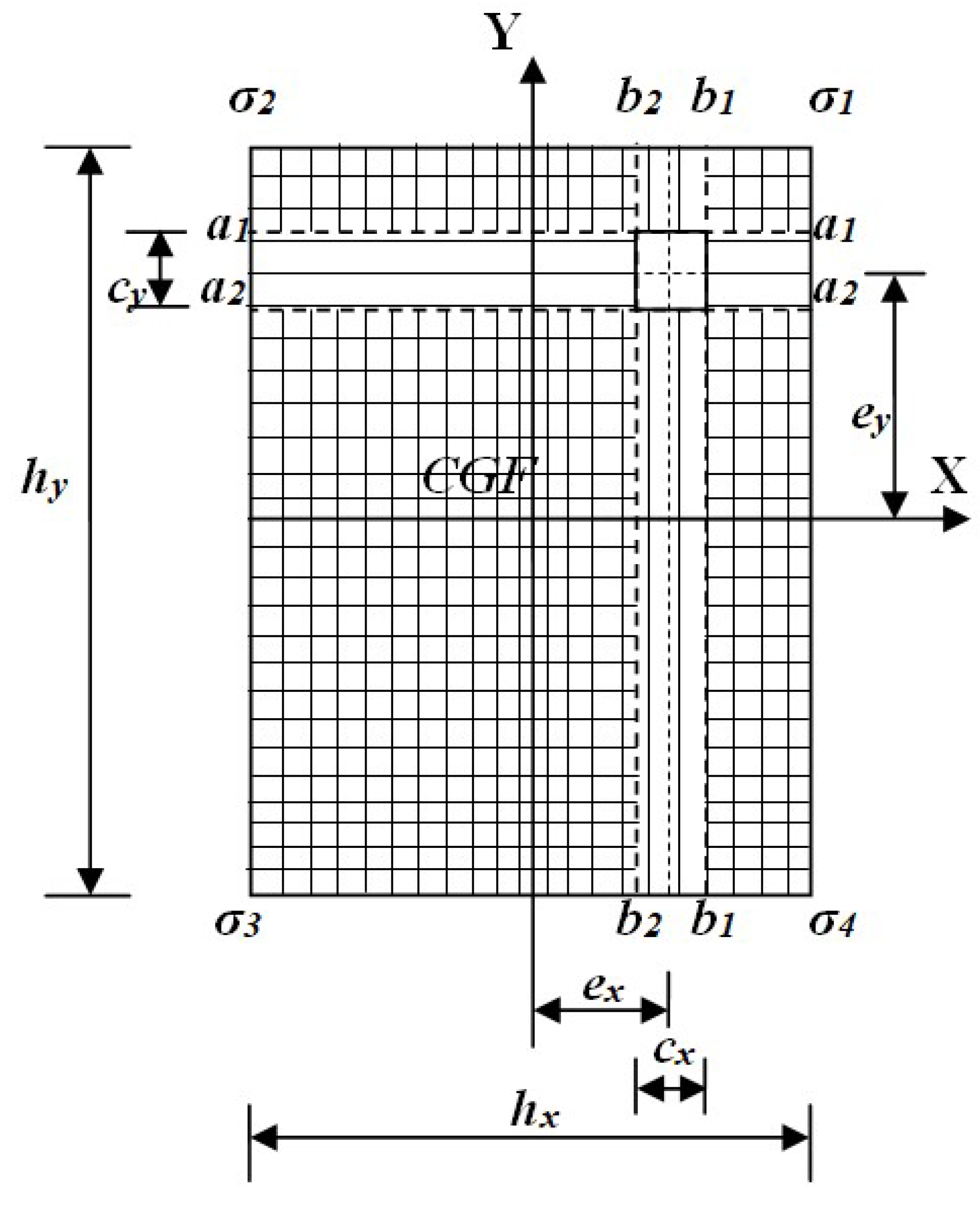
Figure 1 shows a rectangular isolated footing subjected to biaxial bending and the column located in any part of the footing on elastic soils, and assuming a linear distribution of soil pressure.

General equation for any type of footing subjected to biaxial bending is:

σ = \frac{P}{A} + \frac{M_{x T} y}{I_{x}} + \frac{M_{y T} x}{I_{y}},

(1)

where: σ is the pressure of the soil in any part of the footing, P is the axial load, M_xT and M_yT are the total moments on the X and Y axes, A is the area or surface of contact of the footing with the soil, I_x and I_y are the moments of inertia of the footing on the X and Y axes, x and y are the coordinates where it is desired to find the soil pressure on the footing.

Equation (1) assumes that the contact area of the footing with the soil works totally under compression.

Now, substituting A = h_xh_y, I_x = h_xh_y³/12, I_y = h_yh_x³/12, M_xT = M_x + Pe_y, M_yT = M_y + Pe_x, and the corresponding coordinates at each corner of the rectangular isolated footing, the pressures are obtained:

σ_{1} = \frac{P}{h_{x} h_{y}} + \frac{6 (M_{x} + P e_{y})}{h_{x} {h_{y}}^{2}} + \frac{6 (M_{y} + P e_{x})}{{h_{x}}^{2} h_{y}},

(2)

σ_{2} = \frac{P}{h_{x} h_{y}} + \frac{6 (M_{x} + P e_{y})}{h_{x} {h_{y}}^{2}} - \frac{6 (M_{y} + P e_{x})}{{h_{x}}^{2} h_{y}},

(3)

σ_{3} = \frac{P}{h_{x} h_{y}} - \frac{6 (M_{x} + P e_{y})}{h_{x} {h_{y}}^{2}} - \frac{6 (M_{y} + P e_{x})}{{h_{x}}^{2} h_{y}},

(4)

σ_{4} = \frac{P}{h_{x} h_{y}} - \frac{6 (M_{x} + P e_{y})}{h_{x} {h_{y}}^{2}} + \frac{6 (M_{y} + P e_{x})}{{h_{x}}^{2} h_{y}},

(5)

where: h_x and h_y are the sides of the footing in the directions X and Y.

2.1. Optimal Area for Rectangular Isolated Footing

The objective function for the minimum area “A_min” is obtained:

A_{m i n} = h_{x} h_{y},

(6)

The constraint functions are: the equations (2) to (5), 0 ≤ σ₁, σ₂, σ₃, σ₄ ≤ σ_max (allowable bearing capacity of the soil).

Note: The base area of the footing will be determined from unfactored load P, the unfactored moments M_x and M_y transmitted by footing to the soil.

2.2. Optimal Cost for Rectangular Isolated Footing

Substituting A = h_xh_y, I_x = h_xh_y³/12, I_y = h_yh_x³/12, M_xT = M_ux + P_ue_y, M_yT = M_uy + P_ue_x into Equation (1) to obtain the pressure in function of the coordinates for a rectangular isolated footing. The pressure equation is:

σ_{u} (x, y) = \frac{P_{u}}{h_{x} h_{y}} + \frac{12 (M_{u x} + P_{u} e_{y}) y}{h_{x} {h_{y}}^{3}} + \frac{12 (M_{u y} + P_{u} e_{x}) x}{h_{y} {h_{x}}^{3}} .

(7)

where: P_u is the factored load; M_ux and M_uy are the factored moments on the X and Y axes.

2.2.1. Equations for Moments

Figure 2 shows the critical sections for moments of a rectangular isolated footing subjected to biaxial bending and the column located in any part of the footing. The critical sections for moments are presented on the faces of the columns.

General equation for the moment on the a₁ axis “M_ua1” is obtained as follows:

M_{u a 1} = - \int_{e_{y} + \frac{c_{y}}{2}}^{\frac{h_{y}}{2}} \int_{- \frac{h_{x}}{2}}^{\frac{h_{x}}{2}} σ_{u} (x, y) (y - e_{y} - \frac{c_{y}}{2}) d x d y .

(8)

Substituting the Equation (7) into Equation (8) M_ua1 is obtained:

M_{u a 1} = - \frac{\{P_{u} {h_{y}}^{2} [{(h_{y} - c_{y})}^{2} - 4 e_{y} (h_{y} - e_{y} - c_{y})] + 2 (P_{u} e_{y} + M_{u x}) [2 {h_{y}}^{3} - 3 {h_{y}}^{2} (2 e_{y} + c_{y}) + {(2 e_{y} + c_{y})}^{3}]\}}{8 {h_{y}}^{3}} .

(9)

where: c_x and c_y are the sides of the column in the directions X and Y.

General equation for the moment on the a₂ axis “M_ua2” is obtained as follows:

M_{u a 2} = \frac{P_{u} c_{y}}{2} + M_{u x} - \int_{e_{y} - \frac{c_{y}}{2}}^{\frac{h_{y}}{2}} \int_{- \frac{h_{x}}{2}}^{\frac{h_{x}}{2}} σ_{u} (x, y) (y - e_{y} + \frac{c_{y}}{2}) d x d y .

(10)

Substituting the Equation (7) into Equation (10) M_ua2 is obtained:

M_{u a 2} = - \frac{\{P_{u} {h_{y}}^{2} [{(h_{y} - c_{y})}^{2} + 4 e_{y} (h_{y} + e_{y} - c_{y})] - 2 (P_{u} e_{y} + M_{u x}) [2 {h_{y}}^{3} + 3 {h_{y}}^{2} (2 e_{y} - c_{y}) - {(2 e_{y} - c_{y})}^{3}]\}}{8 {h_{y}}^{3}} .

(11)

General equation for the moment on the b₁ axis “M_ub1” is obtained as follows:

M_{u b 1} = - \int_{- \frac{h_{y}}{2}}^{\frac{h_{y}}{2}} \int_{e_{x} + \frac{c_{x}}{2}}^{\frac{h_{x}}{2}} σ_{u} (x, y) (x - e_{x} - \frac{c_{x}}{2}) d x d y .

(12)

Substituting the Equation (7) into Equation (12) M_ub1 is obtained:

M_{u b 1} = - \frac{\{P_{u} {h_{x}}^{2} [{(h_{x} - c_{x})}^{2} - 4 e_{x} (h_{x} - e_{x} - c_{x})] + 2 (P_{u} e_{x} + M_{u y}) [2 {h_{x}}^{3} - 3 {h_{x}}^{2} (2 e_{x} + c_{x}) + {(2 e_{x} + c_{x})}^{3}]\}}{8 {h_{x}}^{3}} .

(13)

General equation for the moment on the b₂ axis “M_ub2” is obtained as follows:

M_{u b 2} = \frac{P_{u} c_{x}}{2} + M_{u y} - \int_{- \frac{h_{y}}{2}}^{\frac{h_{y}}{2}} \int_{e_{x} - \frac{c_{x}}{2}}^{\frac{h_{x}}{2}} σ_{u} (x, y) (x - e_{x} + \frac{c_{x}}{2}) d x d y .

(14)

Substituting the Equation (7) into Equation (14) M_ub2 is obtained:

M_{u b 1} = - \frac{\{P_{u} {h_{x}}^{2} [{(h_{x} - c_{x})}^{2} - 4 e_{x} (h_{x} - e_{x} - c_{x})] + 2 (P_{u} e_{x} + M_{u y}) [2 {h_{x}}^{3} - 3 {h_{x}}^{2} (2 e_{x} + c_{x}) + {(2 e_{x} + c_{x})}^{3}]\}}{8 {h_{x}}^{3}} .

(15)

2.2.2. Equations for Bending Shear

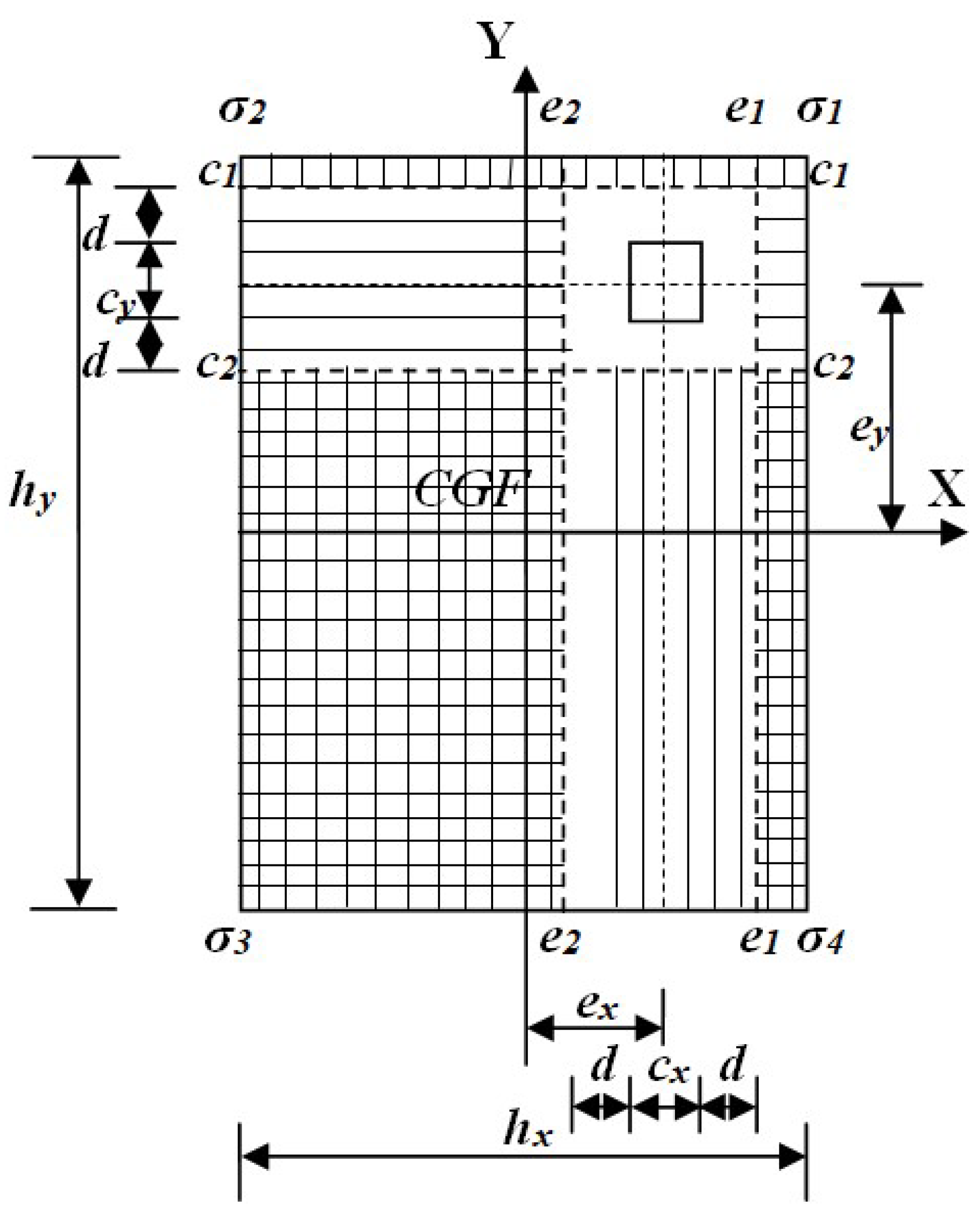
Figure 3 shows the critical sections for bending shear of a rectangular isolated footing subjected to biaxial bending and the column located in any part of the footing. The critical sections for bending shear occur at a distance d (effective depth of footing) from the column faces.

General equation for the bending shear on the c₁ axis “V_ufc1” is obtained as follows:

V_{u f c 1} = - \int_{e_{y} + \frac{c_{y}}{2} + d}^{\frac{h_{y}}{2}} \int_{- \frac{h_{x}}{2}}^{\frac{h_{x}}{2}} σ_{u} (x, y) d x d y .

(16)

Substituting the Equation (7) into Equation (16) V_fc1 is obtained:

V_{u f c 1} = - \frac{\{P_{u} {h_{y}}^{2} [h_{y} - c_{y} - 2 (e_{y} + d)] + 3 (P_{u} e_{y} + M_{u x}) [{h_{y}}^{2} - {(2 e_{y} + c_{y} + 2 d)}^{2}]\}}{2 {h_{y}}^{3}} .

(17)

General equation for the bending shear on the c₂ axis “V_ufc2” is obtained as follows:

V_{u f c 2} = P_{u} - \int_{e_{y} - \frac{c_{y}}{2} - d}^{\frac{h_{y}}{2}} \int_{- \frac{h_{x}}{2}}^{\frac{h_{x}}{2}} σ_{u} (x, y) d x d y .

(18)

Substituting the Equation (7) into Equation (18) V_ufc2 is obtained:

V_{u f c 2} = \frac{\{P_{u} {h_{y}}^{2} [h_{y} - c_{y} + 2 (e_{y} - d)] - 3 (P_{u} e_{y} + M_{u x}) [{h_{y}}^{2} - {(2 e_{y} - c_{y} - 2 d)}^{2}]\}}{2 {h_{y}}^{3}} .

(19)

General equation for the bending shear on the e₁ axis “V_ufe1” is obtained as follows:

V_{u f e 1} = - \int_{- \frac{h_{y}}{2}}^{\frac{h_{y}}{2}} \int_{e_{x} + \frac{c_{x}}{2} + d}^{\frac{h_{x}}{2}} σ_{u} (x, y) d x d y .

(20)

Substituting the Equation (7) into Equation (20) V_ufe1 is obtained:

V_{u f e 1} = - \frac{\{P_{u} {h_{x}}^{2} [h_{x} - c_{x} - 2 (e_{x} + d)] + 3 (P_{u} e_{x} + M_{u y}) [{h_{x}}^{2} - {(2 e_{x} + c_{x} + 2 d)}^{2}]\}}{2 {h_{x}}^{3}} .

(21)

General equation for the bending shear on the e₂ axis “V_ufe2” is obtained as follows:

V_{u f e 2} = P_{u} - \int_{- \frac{h_{y}}{2}}^{\frac{h_{y}}{2}} \int_{e_{x} - \frac{c_{x}}{2} - d}^{\frac{h_{x}}{2}} σ_{u} (x, y) d x d y .

(22)

Substituting the Equation (7) into Equation (22) V_ufe2 is obtained:

V_{u f e 2} = \frac{\{P_{u} {h_{x}}^{2} [h_{x} - c_{x} + 2 (e_{x} - d)] - 3 (P_{u} e_{x} + M_{u y}) [{h_{x}}^{2} - {(2 e_{x} - c_{x} - 2 d)}^{2}]\}}{2 {h_{x}}^{3}} .

(23)

2.2.3. Equations for Punching Shear

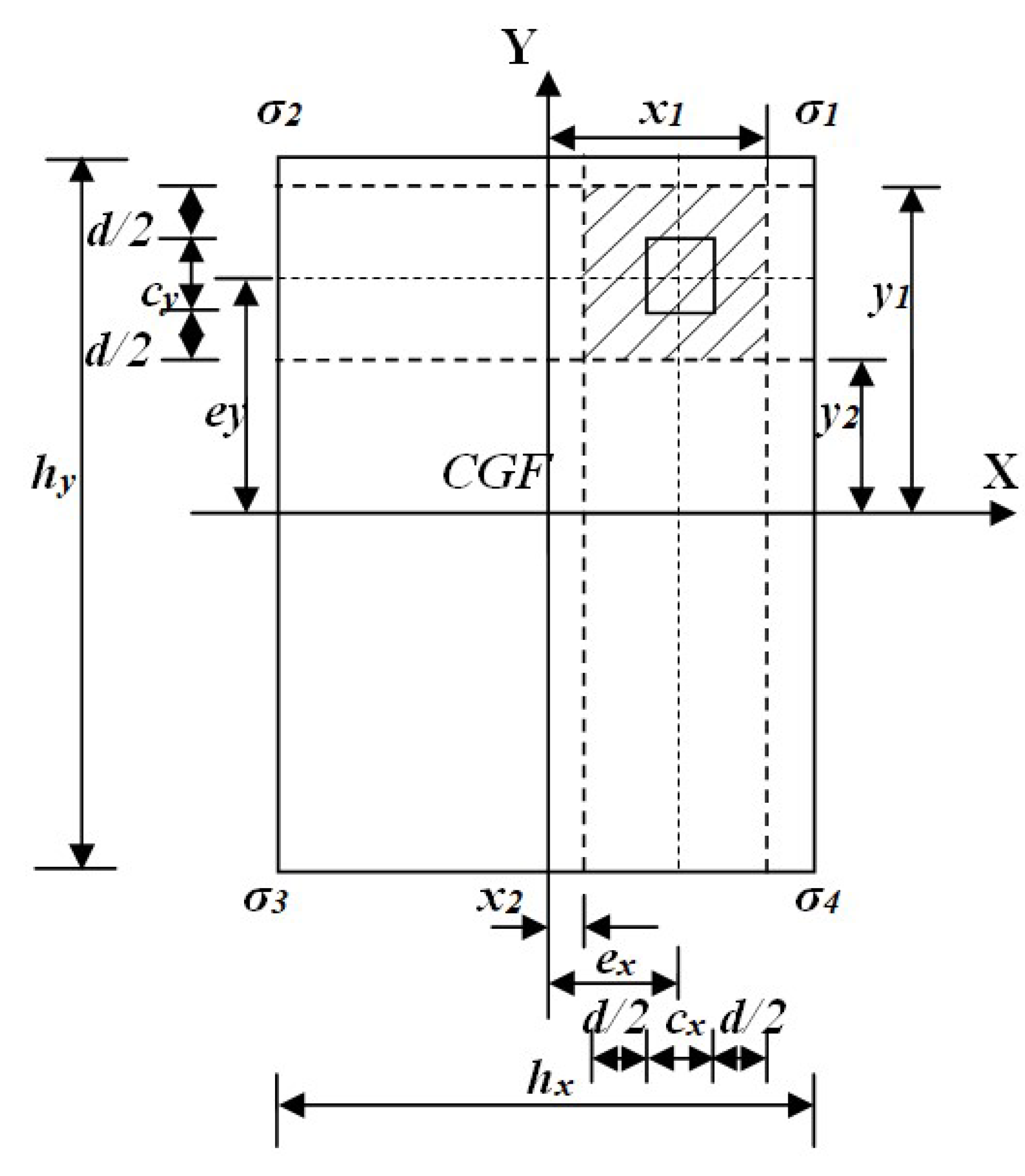
Figure 4 shows the critical section for punching shear of a rectangular isolated footing subjected to biaxial bending and the column located in any part of the footing. The critical section for punching shear occurs at a perimeter formed at a distance d/2 from the column faces in two directions.

General equation for the punching shear “V_p” is obtained as follows:

V_{u p} = P_{u} - \int_{y_{2}}^{y_{1}} \int_{x_{2}}^{x_{1}} σ_{u} (x, y) d x d y .

(24)

Substituting the Equation (7) into Equation (24) V_p is obtained:

V_{u p} = \frac{P_{u} {h_{x}}^{3} {h_{y}}^{3} - (x_{1} - x_{2}) (y_{1} - y_{2}) \{P_{u} {h_{x}}^{2} {h_{y}}^{2} - 6 [(P_{u} e_{y} + M_{u x}) {h_{x}}^{2} (y_{1} + y_{2}) + (P_{u} e_{x} + M_{u y}) {h_{y}}^{2} (x_{1} + x_{2})]\}}{{h_{x}}^{3} {h_{y}}^{3}} .

(25)

where: x₁, x₂, y₁ and y₂ are the coordinates of the corners of the critical perimeter in the directions X and Y.

2.2.4. Objective Function to Minimize the Cost

The minimum cost “C_min” is equal to steel cost more the concrete cost (The cost includes materials and manpower). The minimum cost of a rectangular isolated footing is:

C_{m i n} = V_{c} C_{c} + {V_{s} γ}_{s} C_{s},

(26)

where: C_min = Minimum cost in Dollars, C_c = Ready mix concrete cost in Dollars/m³, C_s = Steel cost in Dollars/kN, V_c = Concrete volume in m³, V_s = Steel volume in m³, γ_s = Concrete density is 24 kN/m³, γ_s = Steel density is 78 kN/m³.

The volumes for a rectangular isolated footing are:

V_{s} = A_{s x} h_{x} + A_{s y} h_{y},

(27)

V_{c} = h_{x} h_{y} (d + r),

(28)

where: r is concrete cover.

Substituting the γ_sC_s = αC_c (where α = γ_sC_s/C_c), and Equations (27) and (28) into Equation (26) to find “C_min”. Equation is obtained:

C_{m i n} = C_{c} [h_{x} h_{y} (d + r) + (α - 1) (A_{s x} h_{x} + A_{s y} h_{y})],

(29)

2.2.5. Constraint Functions

Equations for the design of a rectangular isolated footing are [25]:

Equations for the moments are:

|M_{u a 1}|, |M_{u a 2}| \leq Ø_{f} f_{y} d A_{s y} (1 - \frac{A_{s y} f_{y}}{1.7 h_{x} d {f^{'}}_{c}}),

(30)

|M_{u b 1}|, |M_{u b 2}| \leq Ø_{f} f_{y} d A_{s x} (1 - \frac{A_{s x} f_{y}}{1.7 h_{y} d {f^{'}}_{c}}),

(31)

where: f_y = Specified yield strength of reinforcement of steel (MPa), f’_c = Specified compressive strength of the concrete at 28 days (MPa) A_sy = Steel area in the Y direction, A_sx = Steel area in the X direction, Ø_f = Bending strength reduction factor is 0.90.

Equations for the bending shear are:

|V_{u f c 1}|, |V_{u f c 2}| \leq 0.17 \emptyset_{v} \sqrt{{f'}_{c}} h_{x} d,

(32)

|V_{u f e 1}|, |V_{u f e 2}| \leq 0.17 \emptyset_{v} \sqrt{{f'}_{c}} h_{y} d .

(33)

where: Ø_v = Shear strength reduction factor is 0.85.

Equation for the punching shear is:

|V_{u p}| \leq \{\begin{matrix} 0.17 \emptyset_{v} (1 + \frac{2}{β_{c}}) \sqrt{{f'}_{c}} b_{0} d \\ 0.083 \emptyset_{v} (\frac{α_{s} d}{b_{0}} + 2) \sqrt{{f'}_{c}} b_{0} d \\ 0.33 \emptyset_{v} \sqrt{{f'}_{c}} b_{0} d \end{matrix},

(34)

where: β_c = Relationship of the long side between the short side of the column; b₀ = Perimeter for the punching shear (m); α_s = 20 for corner columns, α_s = 30 for edge columns, and α_s = 40 for interior columns.

Equations for the percentage of reinforcing steel are:

ρ_{x}, ρ_{y} \leq 0.75 [\frac{0.85 β_{1} {f'}_{c}}{f_{y}} (\frac{600}{600 + f_{y}})],

(35)

ρ_{x}, ρ_{y} \geq \{\begin{matrix} \frac{0.25 \sqrt{{f^{'}}_{c}}}{f_{y}} \\ \frac{1.4}{f_{y}} \end{matrix},

(36)

0.65 \leq β_{1} = (1.05 - \frac{{f^{'}}_{c}}{140}) \leq 0.85,

(37)

where: ρ_x and ρ_y = Percentage of reinforcing steel in the X and Y directions, β₁ is the factor relating depth of equivalent rectangular compressive stress block to neutral axis depth.

Equations for the reinforcing steel are:

A_{s y} = ρ_{y} h_{x} d,

(38)

A_{s x} = ρ_{x} h_{y} d .

(39)

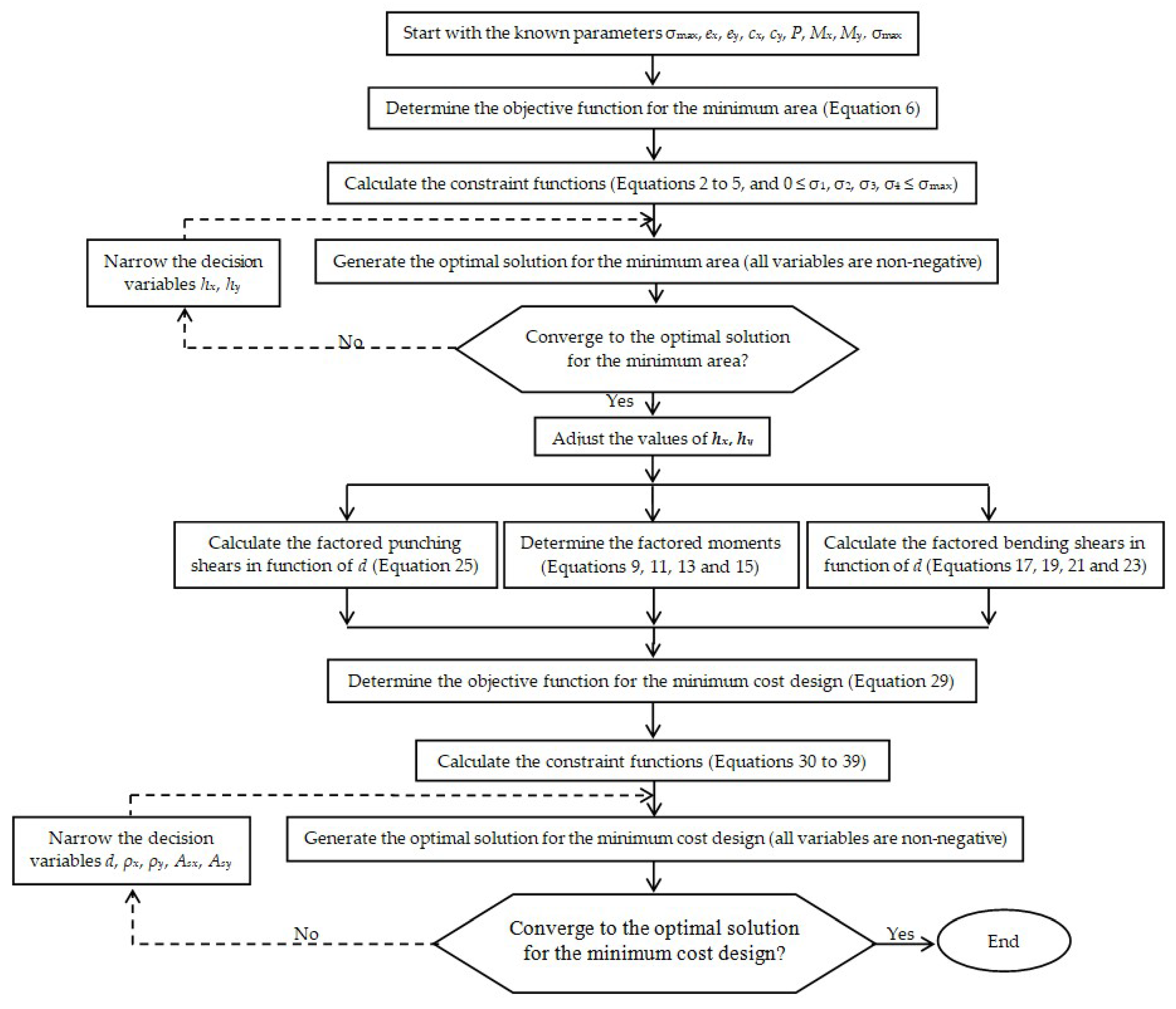
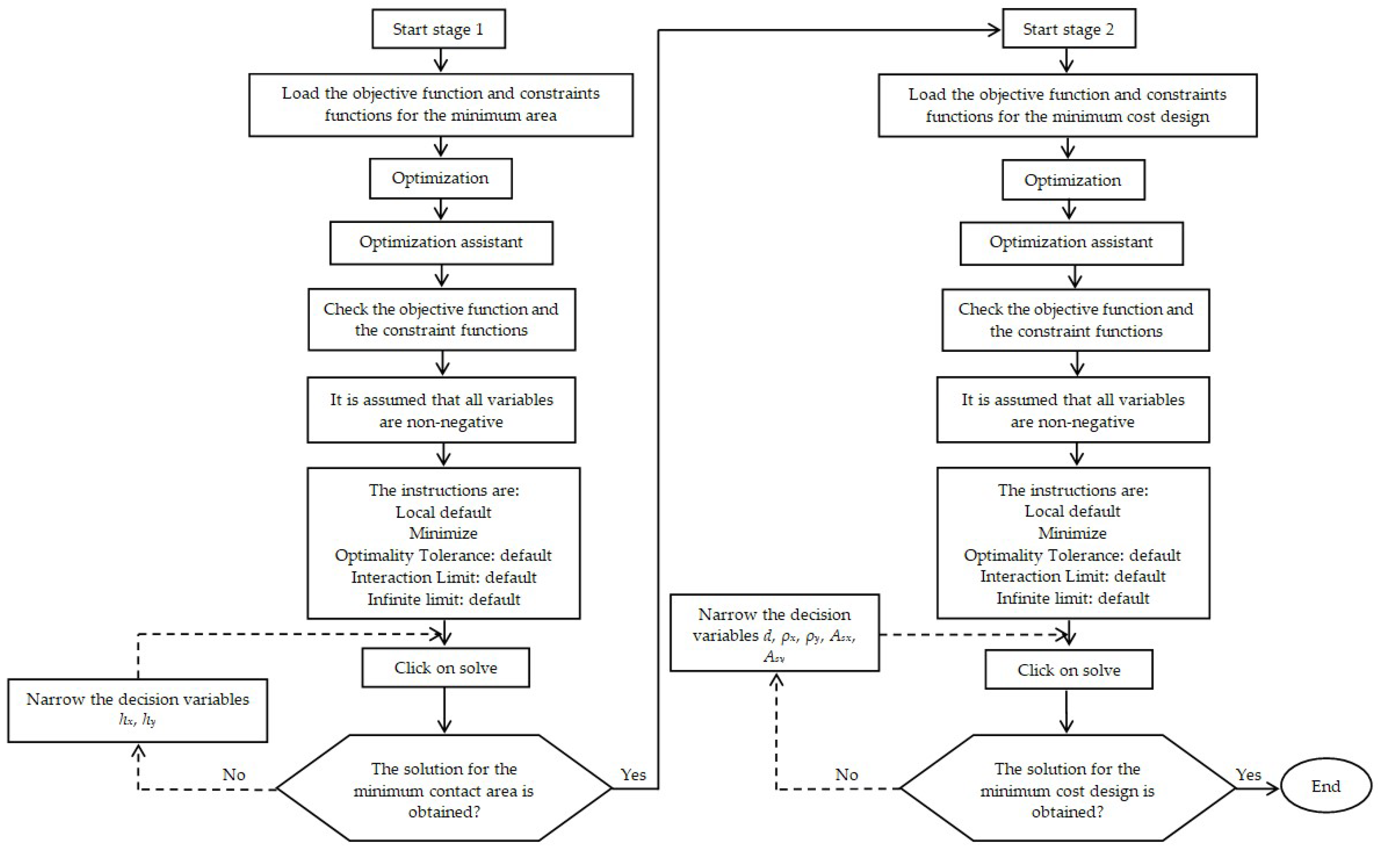
Figure 5 shows the flowchart of the algorithm for the optimal design procedure of reinforced concrete rectangular isolated footing.

Figure 6 shows the flowchart for the use of Maple software for the reinforced concrete rectangular isolated footing optimal design.

3. Numerical Problems

Table 1, Table 2, Table 3 and Table 4 present the four examples to obtain the rectangular isolated footing optimal design subjected to biaxial bending (An axial load, a moment on the X axis and a moment on the Y axis). Example 1: When the column is located at the center of gravity of the footing. Example 2: When the column is located at the limit of the footing in the Y direction. Example 3: When the column is located at the limit of the footing in the X direction. Example 4: When the column is located at the limit of the footing in the X and Y directions or at a corner. The general data for all footings are: c_x = c_y = 0.40 m, r = 0.08 m, σ_max = 180 kN/m², f´_c = 21 Mpa, f_y = 420 Mpa and α = 90.

Table 1 shows the results for P_D = 500 kN and P_L = 500 kN (Example 1.1), P_D = 400 kN and P_L = 450 kN (Example 1.2), P_D = 500 kN and P_L = 250 kN (Example 1.3), P_D = 400 kN and P_L = 200 kN (Example 1.4), M_xD = 150 kN-m, M_xL = 75 kN-m, M_yD = 100 kN-m, M_yL = 50 kN-m, e_x = 0, e_y = 0 (The column is located at the center of gravity of the footing). Therefore the unfactored loads and moments are: P = 1000 kN, M_x = 225 kN-m, M_y = 150 kN-m (Example 1.1); P = 850 kN, M_x = 225 kN-m, M_y = 150 kN-m (Example 1.2); P = 750 kN, M_x = 225 kN-m, M_y = 150 kN-m (Example 1.3); P = 600 kN, M_x = 225 kN-m, M_y = 150 kN-m (Example 1.4).

Table 2 shows the results for P_D = 600 kN and P_L = 425 kN (Example 2.1), P_D = 520 kN and P_L = 360 kN (Example 2.2), P_D = 500 kN and P_L = 250 kN (Example 2.3), P_D = 400 kN and P_L = 200 kN (Example 2.4), M_xD = -150 kN-m, M_xL = -75 kN-m, M_yD = 100 kN-m, M_yL = 50 kN-m, e_x = 0, e_y = h_y/2 – c_y/2 (The column is located at the limit of the footing in the Y direction). Therefore the unfactored loads and moments are: P = 1025 kN, M_x = -225 kN-m, M_y = 150 kN-m (Example 2.1); P = 880 kN, M_x = -225 kN-m, M_y = 150 kN-m (Example 2.2); P = 750 kN, M_x = -225 kN-m, M_y = 150 kN-m (Example 2.3); P = 600 kN, M_x = -225 kN-m, M_y = 150 kN-m (Example 2.4).

Table 3 shows the results for P_D = 600 kN and P_L = 425 kN (Example 3.1), P_D = 520 kN and P_L = 360 kN (Example 3.2), P_D = 500 kN and P_L = 250 kN (Example 3.3), P_D = 400 kN and P_L = 200 kN (Example 3.4), M_xD = 100 kN-m, M_xL = 50 kN-m, M_yD = -150 kN-m, M_yL = -75 kN-m, e_x = h_x/2 – c_x/2, e_y = 0 (The column is located at the limit of the footing in the X direction). Therefore the unfactored loads and moments are: P = 1025 kN, M_x = 150 kN-m, M_y = -225 kN-m (Example 3.1); P = 880 kN, M_x = 150 kN-m, M_y = -225 kN-m (Example 3.2); P = 750 kN, M_x = 150 kN-m, M_y = -225 kN-m (Example 3.3); P = 600 kN, M_x = 150 kN-m, M_y = -225 kN-m (Example 3.4).

Table 4 shows the results for P_D = 500 kN and P_L = 250 kN (Example 4.1), P_D = 420 kN and P_L = 185 kN (Example 4.2), P_D = 300 kN and P_L = 150 kN (Example 4.3), P_D = 200 kN and P_L = 100 kN (Example 4.4), M_xD = -500 kN-m, M_xL = -250 kN-m, M_yD = -400 kN-m, M_yL = -200 kN-m, e_x = h_x/2 – c_x/2, e_y = h_y/2 – c_y/2 (The column is located at the limit of the footing in the X and Y directions or at a corner). Therefore the unfactored loads and moments are: P = 750 kN, M_x = -750 kN-m, M_y = -600 kN-m (Example 4.1); P = 605 kN, M_x = -750 kN-m, M_y = -600 kN-m (Example 4.2); P = 450 kN, M_x = -750 kN-m, M_y = -600 kN-m (Example 4.3); P = 300 kN, M_x = -750 kN-m, M_y = -600 kN-m (Example 4.4).

4. Results

The way to verify the new model is as follows:

1.- For moments

a. When the column is located at the end of the footing in the positive Y direction and on the Y axis, then e_x = 0 and e_y = h_y/2 – c_y/2 are substituted into Equation (9) and M_ua1 = 0 is obtained.

b. When the column is located at the end of the footing in the negative Y direction and on the Y axis, then e_x = 0 and e_y = – h_y/2 + c_y/2 are substituted into Equation (11) and M_ua2 = 0 is obtained.

c. When the column is located in the center of the footing, then ex = 0 and ey = 0 are substituted into Equation (9) and

M_{u a 1} = - [P_{u} {h_{y}}^{2} + 2 M_{u x} (2 h_{y} + c_{y})] {(h_{y} - c_{y})}^{2} / 8 {h_{y}}^{2}

is obtained. When the column is located in the center of the footing, then e_x = 0 and e_y = 0 are substituted into Equation (11) and

M_{u a 2} = - [P_{u} {h_{y}}^{2} - 2 M_{u x} (2 h_{y} - c_{y})] {(h_{y} - c_{y})}^{2} / 8 {h_{y}}^{2}

is obtained. Now, if c_y = 0 is substituted and M_ua1 – M_ua2 is performed, the following result is obtained: – M_ux. This means that it is in equilibrium.

d. When the column is located at the end of the footing in the positive X direction and on the X axis, then e_x = h_x/2 – c_x/2 and e_y = 0 are substituted into Equation (13) and M_ub1 = 0 is obtained.

e. When the column is located at the end of the footing in the negative X direction and on the X axis, then e_x = – h_x/2 + c_x/2 and e_y = 0 are substituted into Equation (15) and M_ub2 = 0 is obtained.

f. When the column is located in the center of the footing, then e_x = 0 and e_y = 0 are substituted into Equation (13) and

M_{u b 1} = - [P_{u} {h_{x}}^{2} + 2 M_{u y} (2 h_{x} + c_{x})] {(h_{x} - c_{x})}^{2} / 8 {h_{x}}^{2}

is obtained. When the column is located in the center of the footing, then e_x = 0 and e_y = 0 are substituted into Equation (15) and

M_{u b 2} = - [P_{u} {h_{x}}^{2} - 2 M_{u y} (2 h_{x} - c_{x})] {(h_{x} - c_{x})}^{2} / 8 {h_{x}}^{2}

is obtained. Now, if c_x = 0 is substituted and M_ub1 – M_ub2 is performed, the following result is obtained: – M_uy. This means that it is in equilibrium.

2.- For bending shear

a. When the column is located at a distance h_y/2 – c_y/2 – d from the center of the footing in the positive Y direction and on the Y axis, then e_x = 0 and e_y = h_y/2 – c_y/2 – d are substituted into Equation (17) and V_ufc1 = 0 is obtained.

b. When the column is located at a distance – h_y/2 + c_y/2 + d from the center of the footing in the negative Y direction and on the Y axis, then e_x = 0 and e_y = – h_y/2 + c_y/2 + d are substituted into Equation (19) and V_ufc2 = 0 is obtained.

c. When the column is located in the center of the footing, then e_x = 0 and e_y = 0 are substituted into Equation (15) and

V_{u f c 1} = - [P_{u} {h_{y}}^{2} + 3 M_{u x} (h_{y} + c_{y} + 2 d)] (h_{y} - c_{y} - 2 d) / 2 {h_{y}}^{3}

is obtained. When the column is located in the center of the footing, then e_x = 0 and e_y = 0 are substituted into Equation (11) and

V_{u f c 2} = [P_{u} {h_{y}}^{2} - 3 M_{u x} (h_{y} + c_{y} + 2 d)] (h_{y} - c_{y} - 2 d) / 2 {h_{y}}^{2}

is obtained. Now, if c_y = 0 and d = 0 are substituted and V_ufc1 – V_ufc2 is performed, the following result is obtained: – P. This means that it is in equilibrium.

d. When the column is located at a distance h_x/2 – c_x/2 – d from the center of the footing in the positive X direction and on the X axis, then e_x = h_x/2 – c_x/2 – d and e_y = 0 are substituted into Equation (21) and V_ufe1 = 0 is obtained.

e. When the column is located at a distance – h_x/2 + c_x/2 + d from the center of the footing in the negative X direction and on the X axis, then e_x = – h_x/2 + c_x/2 + d and e_y = 0 are substituted into Equation (23) and V_ufe2 = 0 is obtained.

f. When the column is located in the center of the footing, then e_x = 0 and e_y = 0 are substituted into Equation (21) and

V_{u f e 1} = - [P_{u} {h_{x}}^{2} + 3 M_{u y} (h_{x} + c_{x} + 2 d)] (h_{x} - c_{x} - 2 d) / 2 {h_{x}}^{3}

is obtained. When the column is located in the center of the footing, then e_x = 0 and e_y = 0 are substituted into Equation (23) and

V_{u f e 2} = [P_{u} {h_{x}}^{2} - 3 M_{u y} (h_{x} + c_{x} + 2 d)] (h_{x} - c_{x} - 2 d) / 2 {h_{x}}^{2}

is obtained. Now, if c_x = 0 and d = 0 are substituted and V_ufe1 – V_ufe2 is performed, the following result is obtained: – P. This means that it is in equilibrium.

3.- For punching shear

a. When the column is located in the center of the footing, then x₁ = c_x/2 + d/2, x₂ = – c_x/2 – d/2, y₁ = c_y/2 + d/2, and y₂ = – c_y/2 – d/2 are substituted into Equation (25) and

V_{u p} = [P_{u} h_{x} h_{y} - (c_{x} + d) (c_{y} + d)] / h_{x} h_{y}

Tables 1 to 4 show the minimum cost design for the rectangular isolated footings subjected to an axial load and two bending moments in X and Y directions.

Table 1 presents the following: when the axial load P decreases; d and A_sx decrease for all the examples; A_min, A_sy, C_min decrease until P_u = 1000 kN and then it increases; ρ_x is the same for all the examples; ρ_y decreases until P_u = 1200 kN and then it increases.

Table 2 shows the following: when the axial load P decreases; d, A_sx, A_min, A_sy, C_min decrease for all the examples; ρ_x decreases until P_u = 1000 kN and then it increases; ρ_y is the same for all the examples.

Table 3 presents the following: when the axial load P decreases; d, A_sx, A_min, A_sy, C_min decrease for all the examples; ρ_x is the same for all the examples; ρ_y decreases until P_u = 1000 kN and then it increases.

Table 4 shows the following: when the axial load P decreases; A_min, A_sy, ρ_y, C_min increase for all the examples; d decreases; ρ_x is the same until P_u = 800 kN; A_sx decreases until P_u = 800 kN and then it increases.

Also, a comparison is made with the results of Solorzano and Plevris (2022) to show the advantages of the new model according to the American Concrete Institute ACI 318-19 [26].

Table 5 shows the results of the example 1 of Solorzano and Plevris (2022) for P_D = 1500 kN, P_L = 850 kN, e_x = 0.20 m, e_y = 0 m, c_x = c_y = 0.50 m, r = 0.05 m, σ_max = 400 kN/m², f´_c = 35 Mpa, f_y = 410 Mpa and C_s = 15C_c. Therefore the unfactored loads and moments are: P = 2350 kN, M_x = 0 kN-m, M_y = 470 kN-m.

Table 6 shows the results of the example 2 of Solorzano and Plevris (2022) for P_D = 1600 kN, P_L = 900 kN, e_x = 0 m, e_y = 0 m, c_x = 0.50 m, c_y = 0.80 m, r = 0.05 m, σ_max = 400 kN/m², f´_c = 35 Mpa, f_y = 410 Mpa and C_s = 15C_c. Therefore the unfactored loads and moments are: P = 2500 kN, M_x = 0 kN-m, M_y = 0 kN-m.

Table 5 presents the following: A_min, ρ_x, ρ_y, A_sy and C_min are smaller, and A_sx is greater in the new model compared to the one presented by Solorzano and Plevris, and d is the same for both models. The new model shows a saving of 12.75% in contact area with soil and of 24.86% in cost with respect to the model proposed by Solorzano and Plevris.

Table 6 shows the following: d, ρ_x, ρ_y, A_sx, A_sy and C_min are smaller, and A_min is greater in the new model compared to the one presented by Solorzano and Plevris. The new model shows a saving of 0.15% in contact area with soil and of 13.32% in cost with respect to the model proposed by Solorzano and Plevris.

Note: In the new model, the footing dimensions in Table 5 and Table 6 were not adjusted to observe the differences between the two models.

5. Conclusions

In this paper, a mathematical model is presented to determine the minimum cost design of a rectangular isolated footing subjected to an axial load and two moments due to a column located in any part of the footing on elastic soils, and assuming a linear distribution of soil pressure.

The new model is presented in two stages. The first stage is to obtain the minimum area, and the second is to find the minimum cost design once the dimensions of the footing are known. The first stage (minimum area), the known or constant parameters (independent variables) are: σ_max, P, M_x and M_y, and the unknown or decision variables (dependent variables) are: A_min, h_x, h_y. The second stage (minimum cost design), the known or constant parameters (independent variables) are: h_x, h_y, P_u, M_ux and M_uy, and the unknown or decision variables (dependent variables) are: d, ρ_x, ρ_y, A_sx, A_sy and C_min.

The main contributions showed in this paper are:

1.- Some engineers use the trial and error method to determine the dimensions for rectangular isolated footings subjected to biaxial bending, and later the design is obtained considering the maximum and uniform pressure along the underside of the footing.

2.- Other authors present the minimum cost design for rectangular isolated footings subjected to biaxial bending rested on elastic soils, but only consider the column located at the center of gravity of the footing.

3.- Some authors present very complex algorithm to obtain the minimum cost design for rectangular isolated footings subjected to biaxial bending rested on elastic soils.

4.- The new model presents a significant reduction in design costs for rectangular isolated footings (see Table 5 and Table 6).

5.- Equations for moments, bending shear and punching shear are verified by equilibrium.

6.- The new model can be used for any other building code, taking into account the equations that resist the moments, the bending shear and the punching shear. Also, equation of the reinforcing steel areas proposed for any other building code.

The main advantage of this work over other works is that the moment, bending shear and punching shear equations are presented in detail, as well as the optimization algorithm and its equations.

Future works may be:

Minimum cost design of a rectangular isolated footing subjected to an axial load and two moments due to a column located in any part of the footing, assuming that the contact area of the footing with the soil works partially under compression.

Funding

This research received no external funding.

Acknowledgments

The research described in this work was funded by the Multidisciplinary Research Institute of the Faculty of Accounting and Administration of the Autonomous University of Coahuila, Torreón, State of Coahuila, Mexico.

Conflicts of Interest

Declare conflicts of interest or state “The author declares no conflict of interest.”.

References

Hannan, M.R.; Johnson, G.E.; Hammond, C.R. A General Strategy for the Optimal Design of Reinforced Concrete Footings to Support Wind Loaded Structures. J. Mech. Des. 1993, 115, 751–756. [Google Scholar] [CrossRef]
Basudhar, P.K.; Das, A.; Das, S.K.; Dey, A.; Deb, K.; De, S. Optimal cost design of rigid raft foundation. In Proceedings of the 10th East Asia-Pacific Conference on Structural Engineering and Construction (EASEC-10), Bangkok, Thailand, 3–5 August 2006; pp. 39–44. [Google Scholar]
Basudhar, P.K.; Dey, A.; Mondal, A.S. Optimal Cost-Analysis and Design of Circular Footings. Int. J. Eng. Technol. Innov. 2012, 2, 243–264. [Google Scholar]
Al-Douri, E.M.F. Optimum design of trapezoidal combined footings. Tikrit J. Eng. Sci. 2007, 14, 85–115. [Google Scholar] [CrossRef]
Wang, Y.; Kulhawy, F.H. Economic design optimization of foundations. J. Geotech. Geoenviron. Eng. 2008, 134, 1097–1105. [Google Scholar] [CrossRef]
Rizwan, M.; Alam, B.; Rehman, F.U.; Masud, N.; Shahzada, K.; Masud, T. Cost Optimization of Combined Footings Using Modified Complex Method of Box. Int. J. Adv. Struct. Geotech. Eng. 2012, 1, 24–28. [Google Scholar]
Jelušič, P.; Žlender, B. Optimal Design of Reinforced Pad Foundation and Strip Foundation. Int. J. Geomech. 2018, 18. [Google Scholar] [CrossRef]
Jelušič, P.; Žlender, B. Optimal design of pad footing based on MINLP optimization. Soils Found. 2018, 58, 277–289. [Google Scholar] [CrossRef]
Velázquez-Santillán, F.; Luévanos-Rojas, A.; López-Chavarría, S.; Medina-Elizondo, M.; Sandoval-Rivas, R. Numerical experimentation for the optimal design for reinforced concrete rectangular combined footings. Adv. Comput. Des. 2018, 3, 49–69. [Google Scholar] [CrossRef]
López-Chavarría, S.; Luévanos-Rojas, A.; Medina-Elizondo, M.; Sandoval-Rivas, R.; Velázquez-Santillán, F. Optimal design for the reinforced concrete circular isolated footings. Adv. Comput. Des. 2019, 4, 273–294. [Google Scholar] [CrossRef]
Khajuria, K.; Singh, E.B.; Sandeep Singla, S. Design Optimization of RC Column Footings under Axial Load of Beam and Rooftop Surfaces. Int. J. Sci. Technol. Res. 2020, 9, 5683–5688. [Google Scholar]
Al-Ansari, M.S.; Afzal, M.S. Structural analysis and design of irregular shaped footings subjected to eccentric loading. Eng. Rep. 2021, 3, e12283. [Google Scholar] [CrossRef]
Kashani, A.R.; Camp, C.V.; Akhani, M.; Ebrahimi, S. Optimum design of combined footings using swarm intelligence-based algorithms. Adv. Eng. Soft. 2022, 169, 103140. [Google Scholar] [CrossRef]
Nigdeli, S.M.; Bekdas, G. The Investigation of Optimization of Eccentricity in Reinforced Concrete Footings. Proc. Int. Conf. Harmon. Search Soft Comput. Appl. 2022, 140, 207–215. [Google Scholar]
Kamal, M.; Mortazavi, A.; Cakici, Z. Optimal Design of RC Bracket and Footing Systems of Precast Industrial Buildings Using Fuzzy Differential Evolution Incorporated Virtual Mutant. Arab. J. Sci. Eng. 2023. [Google Scholar] [CrossRef]
Camp, C.V.; Assadollahi, A. CO2 and cost optimization of reinforced concrete footings using a hybrid big bang-big crunch algorithm. Struct. Multidiscip. Optim. 2013, 48, 411–426. [Google Scholar] [CrossRef]
Luévanos-Rojas, A.; López-Chavarría, S.; Medina-Elizondo, M. Optimal design for rectangular isolated footings using the real soil pressure. Ing. Investig. 2017, 37, 25–33. [Google Scholar] [CrossRef]
Galvis, F.A.; Smith-Pardo, P.J. Axial load biaxial moment interaction (PMM) diagrams for shallow foundations: Design aids, experimental verification, and examples. Eng. Struct. 2020, 213, 110582. [Google Scholar] [CrossRef]
Rawat, S.; Mittal, R.K. Optimization of eccentrically loaded reinforced-concrete isolated footings. Pract. Period. Struct. Des. Constr. 2018, 23. [Google Scholar] [CrossRef]
Rawat, S.; Mittal, R.K.; Muthukumar, G. Isolated Rectangular Footings under Biaxial Bending: A Critical Appraisal and Simplified Analysis Methodology. Pract. Period. Struct. Des. Const. 2020, 25. [Google Scholar] [CrossRef]
Chaudhuri, P.; Maity, D. Cost optimization of rectangular RC footing using GA and UPSO. Soft Comput. 2020, 24, 709–721. [Google Scholar] [CrossRef]
Solorzano, G.; Plevris, V. Optimum Design of RC Footings with Genetic Algorithms According to ACI 318-19. Buildings 2022, 10, 110. [Google Scholar] [CrossRef]
Nigdeli, S.M.; Bekdaş, G.; Yang, X.-S. Metaheuristic Optimization of Reinforced Concrete Footings. KSCE J. Civ. Eng. 2018, 22, 4555–4563. [Google Scholar] [CrossRef]
Waheed, J.; Azam, R.; Riaz, M.R.; Shakeel, M.; Mohamed, A.; Ali, E. Metaheuristic-Based Practical Tool for Optimal Design of Reinforced Concrete Isolated Footings: Development and Application for Parametric Investigation. Buildings 2022, 12, 471. [Google Scholar] [CrossRef]
ACI 318-14. Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
ACI 318-19. Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]

Figure 1. Rectangular isolated footing subjected to biaxial bending. Where: e_x and e_y are the location coordinates of the column.

Figure 2. Critical sections for moments.

Figure 3. Critical sections for bending shear.

Figure 4. Critical sections for punching shear.

Figure 5. Flowchart for the procedure of rectangular isolated footing optimal design.

Figure 6. Flowchart for the use of Maple software for the rectangular isolated footing optimal design.

Table 1. Optimal cost design of rectangular isolated footing (e_x = 0 and e_y = 0).

Example	h_x (m)	h_y (m)	σ₁ (kN/m²)	σ₂ (kN/m²)	σ₃ (kN/m²)	σ₄ (kN/m²)	A_min (m²)	P_u (kN)	M_ux (kN-m)	M_uy (kN-m)	A_sx (cm²)	A_sy (cm²)	d (m)	ρ_x	ρ_y	C_min ($)
1.1	2.55	3.80	176.29	103.44	30.11	102.96	9.69	1400	300	200	45.19	52.36	0.36	0.00333	0.00575	7.03C_c
1.2	2.45	3.65	177.49	95.33	12.61	94.77	8.94	1200	300	200	41.90	45.88	0.34	0.00333	0.00543	6.20C_c
1.3	2.40	3.60	173.61	86.81	0	86.81	8.64	1000	300	200	35.94	45.86	0.30	0.00333	0.00637	5.52C_c
1.4	3.00	4.50	88.89	44.44	0	44.44	13.50	800	300	200	35.51	62.77	0.24	0.00333	0.00883	7.74C_c

where: h_x and h_y are the fitted sides; σ₁, σ₂, σ₃ and σ₄ are the pressures at each corner of the footing due to the fitted sides; A_min is the minimum area; P_u, M_ux and M_uy are the factored load and moments; A_sx and A_sy are the steel areas in the X and Y directions; d is the effective depth of footing; ρ_x and ρ_y are the percentage of reinforcing steel in the X and Y directions; C_min is the minimum cost.

Table 2. Optimal cost design of rectangular isolated (e_x = 0 and e_y = h_y/2 – c_y/2).

Example	h_x (m)	h_y (m)	σ₁ (kN/m²)	σ₂ (kN/m²)	σ₃ (kN/m²)	σ₄ (kN/m²)	A_min (m²)	P_u (kN)	M_ux (kN-m)	M_uy (kN-m)	A_sx (cm²)	A_sy (cm²)	d (m)	ρ_x	ρ_y	C_min ($)
2.1	9.05	1.00	178.94	156.97	47.57	69.55	9.05	1400	-300	200	51.12	258.39	0.86	0.00596	0.00333	14.90C_c
2.2	6.95	1.00	178.92	141.66	74.32	111.58	6.95	1200	-300	200	39.66	167.88	0.73	0.00547	0.00333	9.54C_c
2.3	5.15	1.00	179.56	111.70	111.70	179.56	5.15	1000	-300	200	29.79	102.89	0.60	0.00496	0.00333	5.78C_c
2.4	4.00	1.15	179.35	81.52	81.52	179.35	4.60	800	-300	200	25.90	59.18	0.44	0.00507	0.00333	3.94C_c

Table 3. Optimal cost design of rectangular isolated (e_x = h_x/2 – c_x/2, e_y = 0).

Example	h_x (m)	h_y (m)	σ₁ (kN/m²)	σ₂ (kN/m²)	σ₃ (kN/m²)	σ₄ (kN/m²)	A_min (m²)	P_u (kN)	M_ux (kN-m)	M_uy (kN-m)	A_sx (cm²)	A_sy (cm²)	d (m)	ρ_x	ρ_y	C_min ($)
3.1	1.00	9.05	178.94	69.55	47.57	156.97	9.05	1400	200	-300	258.39	51.12	0.86	0.00333	0.00596	14.90C_c
3.2	1.00	6.95	178.92	111.58	74.32	141.66	6.95	1200	200	-300	167.88	39.66	0.73	0.00333	0.00547	9.54C_c
3.3	1.00	5.15	179.56	179.56	111.70	111.70	5.15	1000	200	-300	102.89	29.79	0.60	0.00333	0.00496	5.78C_c
3.4	1.15	4.00	179.35	179.35	81.52	81.52	4.60	800	200	-300	59.18	25.90	0.44	0.00333	0.00507	3.94C_c

Table 4. Optimal cost design of rectangular isolated (e_x = h_x/2 – c_x/2, e_y = h_y/2 – c_y/2).

Example	h_x (m)	h_y (m)	σ₁ (kN/m²)	σ₂ (kN/m²)	σ₃ (kN/m²)	σ₄ (kN/m²)	A_min (m²)	P_u (kN)	M_ux (kN-m)	M_uy (kN-m)	A_sx (cm²)	A_sy (cm²)	d (m)	ρ_x	ρ_y	C_min ($)
4.1	2.00	2.35	149.39	149.39	169.76	169.76	4.70	1000	-1000	-800	41.60	43.51	0.53	0.00333	0.00409	4.53C_c
4.2	2.15	2.60	38.09	108.60	178.37	107.85	5.59	800	-1000	-800	40.86	51.08	0.47	0.00333	0.00503	5.05C_c
4.3	2.65	3.20	1.50	51.56	104.63	54.57	8.48	600	-1000	-800	48.17	63.75	0.40	0.00379	0.00606	7.00C_c
4.4	3.80	4.65	0.72	16.80	33.24	17.15	17.67	400	-1000	-800	59.40	77.92	0.34	0.00378	0.00607	12.62C_c

Table 5. Comparison of the model proposed by Solorzano and Plevris (Example 1) against the new model.

Model	h_x (m)	h_y (m)	σ₁ (kN/m²)	σ₂ (kN/m²)	σ₃ (kN/m²)	σ₄ (kN/m²)	A_min (m²)	P_u (kN)	M_ux (kN-m)	M_uy (kN-m)	A_sx (cm²)	A_sy (cm²)	d (m)	t (m)	ρ_x	ρ_y	C_min ($)
Solorzano and Plevris	3.49	2.34	400.00	201.72	201.72	400.00	8.16	3160	0	632	153.20	122.90	0.48	0.53	0.01364	0.00734	5.55C_c
New model	1.00	7.12	400.00	288.97	288.97	400.00	7.12	3160	0	632	159.47	17.21	0.48	0.53	0.00470	0.00361	4.17C_c

where: t is the total thickness of the footing.

Table 6. Comparison of the model proposed by Solorzano and Plevris (Example 2) against the new model.

Model	h_x (m)	h_y (m)	σ₁ (kN/m²)	σ₂ (kN/m²)	σ₃ (kN/m²)	σ₄ (kN/m²)	A_min (m²)	P_u (kN)	M_ux (kN-m)	M_uy (kN-m)	A_sx (cm²)	A_sy (cm²)	d (m)	t (m)	ρ_x	ρ_y	C_min ($)
Solorzano and Plevris	2.14	3.02	399.29	399.29	399.29	399.29	6.46	3360	0	632	106.10	103.40	0.44	0.49	0.00798	0.01098	3.98C_c
New model	2.54	2.54	399.93	399.93	399.93	399.93	6.45	3360	0	632	44.14	39.83	0.43	0.48	0.00400	0.00361	3.45C_c

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Minimum Cost Design for Rectangular Isolated Footings Taking into Account That the Column Is Located in Any Part of the Footing

Abstract

1. Introduction

2. Formulation of the Model

2.1. Optimal Area for Rectangular Isolated Footing

2.2. Optimal Cost for Rectangular Isolated Footing

2.2.1. Equations for Moments

2.2.2. Equations for Bending Shear

2.2.3. Equations for Punching Shear

2.2.4. Objective Function to Minimize the Cost

2.2.5. Constraint Functions

3. Numerical Problems

4. Results

5. Conclusions

Funding

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe