Prerpints.org logo
Preprint
Article

Using Machine Learning to Identify the Risk Factors of Pancreatic Cancer from the NIH PLCO Dataset

Altmetrics

Downloads

191

Views

168

Comments

0

This version is not peer-reviewed

Machine Learning for Pharmacogenomics and Precision Medicine

Submitted:

26 August 2023

Posted:

29 August 2023

You are already at the latest version

Alerts
Abstract
Background: Pancreatic cancer (PC) is a disease with poor prognosis and survival rate. There is a pertinent need to identify the risk factors of this disease. The purpose of this study is to identify a subset of factors (a.k.a. features) as predictors of PC from the Prostate, Lung, Colorectal and Ovarian (PLCO) cancer dataset consisting of responses to 65 questions about demographics, cancer and health history, medication usage, and smoking habits from 154,897 participants. Method: There are two challenges to selecting the subset of features that predict PC with highest probability: the problem is computationally intractable, and the PLCO dataset is highly imbalanced. We use an innovative method to use the dataset in a balanced way, without involving up- or down-sampling. We use nine feature selection methods to select the optimal subset of features from the preprocessed and balanced dataset. Results: Our preprocessed dataset consists of 32 risk factors (8 demographics, 5 cancer history, 13 health history, 2 medication usage, 4 smoking habits). Risk factors belonging to cancer and health history, followed by smoking habits, were consistently chosen by the feature selection methods. We also discuss findings in the medical sciences literature that corroborate our findings. Conclusions: The study found that risk factors belonging to cancer and health history are the most prominent ones for PC. In particular, previously diagnosed with PC is chosen as the most prominent risk factor by majority of methods. While most of our findings are consistent with the literature, some of our findings shed light on novel factors that may not have received their due attention by the research community.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Pancreatic cancer (PC) is a disease with poor prognosis and survival rate. About 95% of people who contract PC would not make it to the five-year survival period [1]. Pancreas is an inner organ of the human body, surrounded by the duodenum and the small intestine; hence early symptoms are hard to detect [2]. Malicious cells in the pancreas are typically detected at a very advanced stage when it is impossible to save the patient. There is a pertinent need for a prediction model that can lead to early detection of this disease.
Biomarkers for early diagnosis of PC have been investigated (see for example, [3,4,5,6,7,8]). However, evidence for identified biomarkers has not been very conclusive. Image analysis and machine learning algorithms have been used for distinguishing between benign and malignant tissues in endoscopic ultrasound and computed tomography images (see for example, [9,10,11,12]). However, these models can detect PC only at an advanced stage and hence are not very useful.
The purpose of this study is to identify a set of factors as predictors of PC. We use a cancer dataset collected from 154,897 participants, each responding to 65 questions (or factors) about demographics, cancer and health history, medication usage, and smoking habits. There are two challenges to selecting the subset of 65 factors that predict PC with highest probability: the problem is computationally intractable, and the dataset is highly imbalanced. Our approach consists of balancing and preprocessing the dataset, and rank the risk factors based on their ability to predict PC.
Our study found that risk factors belonging to cancer and health history are the most prominent ones for PC. In particular, previously diagnosed with PC is chosen as the most prominent risk factor by majority of methods. We also discuss findings in the medical sciences literature that corroborate our findings. Some of our findings shed light on novel factors that may not have received their due attention by the research community.

2. Models and Methods

2.1. Problem Statement

Our problem is to predict whether a subject is diagnosed with PC or not, given information about his demographic characteristics, health history, medication usage, smoking habits, and his and his family’s cancer diagnosis history. This information is encoded as a vector of predictor variables where each predictor represents a risk factor (a.k.a. feature). The predictors are discrete and finite random variables.
Formally, given a set of data points X = [ x 1 , . . . , x N ] ∈ N d × N , N = { 0 , 1 , 2 , . . . } , and a set of labels { T r u e , F a l s e } , the task is to map each data point x i ∈ N d into one of the labels, where d is the dimension of each data point, and N is the number of data points in the dataset. This is a binary classification problem. Our goal is to select a subset of predictors such that classification using the subset is at least as accurate as that using the entire set. It has been shown that the accuracy does not always improve with increase in number of variables [13], hence choosing the optimal subset of predictors is imperative for accurate prediction of PC.

2.2. Materials

The Prostate, Lung, Colorectal and Ovarian (PLCO) cancer dataset [14] is collected by the National Cancer Institute from 154,897 participants. Among them, 76,678 or 49.5% were males, and 132,572 or 85.6% were non-Hispanic White. The participants, randomly selected based on a set of criteria from different parts of United States, were between 55-74 years of age with no history of prostate, lung, colorectal or ovarian cancer. Each participant filled out three questionnaires, thereby responding to 65 questions about demographics, cancer and health history, medication usage, and smoking habits. Therefore, N = 154 , 897 and d = 65 for our problem. The dataset is highly imbalanced; only 749 or 0.48% of the participants were diagnosed with pancreatic cancer. Visualizations of the PLCO dataset in two-dimensional (2D) space are shown in Figure 1. Table 1 lists the 65 risk factors.

2.3. Dataset Balancing

A balanced dataset contains equal number of data points in all classes. Usually, an imbalanced dataset is balanced using methods such as fixed-rate downsampling or clustering that downsample the majority subset, or using methods such as the SMOTE algorithm [17] that upsample the minority subset. Both approaches inherit drawbacks unless the true distribution generating the data is known. The true distribution is unknown for the current problem.
We use a balancing method, similar to that proposed in [18], whereby the majority subset is iteratively and randomly subsampled such that in each iteration, the sampled subset is balanced. This method refrains from eliminating any data point from or introducing any new data point into the given dataset. A feature selection method is applied independently on each subset. The final result is obtained by computing the mean over all the subsets.

2.4. Data Preprocessing

The PLCO dataset has a number of missing values. We employ two steps iteratively to obtain a less incomplete dataset. First, we eliminate factors that are either missing responses from more than 10% of the participants, or responses from all participants are same. Next, we eliminate participants who did not respond to more than 10% of the remaining factors. The two steps are again applied to the resulting dataset. Application of the two steps continues until there is no change in the dataset between two consecutive iterations.
Each feature is standardized by subtracting its mean and dividing by its standard deviation. The missing values in the resulting dataset are filled in. The j th element of the i th data point, if missing, is filled by:
x ^ i j = ∑ k = 1 k ≠ i N x k j d i s t ( x i , x k ) / ∑ k = 1 k ≠ i N d i s t ( x i , x k ) where d i s t ( x i , x k ) = | x i · x k | ∥ x i ∥ ∥ x k ∥ , x i · x k = ∑ m = 1 m not missing d x i m x k m , ∥ x i ∥ = ∑ m = 1 m not missing d x i m 2 ,
| . | denotes the absolute value, “ m not missing ” refers to the m th element of a data point that is not missing, and d i s t is the absolute of the cosine similarity (or normalized dot product) of two data points. Therefore, 0 ≤ d i s t ≤ 1 ; as two data points get closer, their d i s t increases. In Eq. 1, a missing element of a given data point is computed as the weighted mean of that element from all data points in which values of all elements are present, and the weights are proportional to the absolute cosine similarity. After filling in all missing values, each feature is standardized again.

2.5. Variable or Feature Selection

Our problem of selecting the optimal subset of features is intractable as a total of ∑ n = 1 d d n ∈ O ( 2 d ) subsets are possible. Computing O ( 2 d ) subsets to determine the optimal one is impractical for the PLCO dataset with d = 65 . Hence we resort to variable or feature selection methods [19,20].
We used several feature selection algorithms suitable for categorical and continuous features and classification task [21,22,23,24,25,26,27,28,29,30,31], implemented in MATLAB, to rank the features, such as rank features using chi-square tests (`fscchi2’ in MATLAB), rank features for classification using minimum redundancy maximum relevance (MRMR) algorithm (`fscmrmr’ in MATLAB), estimate predictor importance for classification using ensemble of decision trees (`fitcensemble’ in MATLAB), estimate predictor importance for classification using a binary decision tree (`fitctree’ in MATLAB), estimate predictor importance for classification with an ensemble of bagged decision trees (e.g., random forest) which assigns positive and negative scores to the predictors (`fitcensemble’ with method `bag’, and `oobPermutedPredictorImportance’ in MATLAB), rank key features by class separability criteria (`rankfeatures’ with criteria `ttest’, `entropy’, `bhattacharyya’, `roc’, and `wilcoxon’ in MATLAB), and Pearson correlation between each feature/predictor variable and response variable (`corrcoef’ in MATLAB) with correlation set to zero if not significant (i.e. p > 0.01 ). Figure 2, Figure 2 show the ranking of the features by each of these algorithms for males and females respectively. A brief description of each of these algorithms is presented in Appendix.

3. Experimental Results

Our analysis is done on the entire dataset as well as separately on the male and female participants. After preprocessing (ref. Section 2.4), the PLCO dataset containing 65 features and 154897 points (76682 male, 749 T r u e , 430 male T r u e ) reduces to 32 features and 148315 points (73162 male, 706 T r u e , 405 male T r u e ). For balancing (ref. Section 2.3), we randomly sample ⌊ 148315 / 706 ⌋ = 210 non-overlapping subsets for PC= F a l s e , each containing 706 or 707 data points. Thus after balancing, each subset contains a total of 1412 or 1413 points. Similarly, for male only analysis, we obtain ⌊ 73162 / 405 ⌋ = 180 balanced subsets, each containing 810 or 811 points. For female only analysis, we obtain ⌊ 75153 / 301 ⌋ = 249 balanced subsets, each containing 602 or 603 points.

3.1. Classification

Twenty four machine learning algorithms, briefly described in Section 6.4 were used and their statistical parameters are reported.
Using classification ensemble. In this ensemble algorithm, the weights or costs can be modified to correctly train the algorithm to predict PC. The weights are normalized to add unity, depicting the prior probabilities. Suppose ∈ i j ( i , j ∈ 1 . . . c , ∈ i i = 0 ) is the cost of misclassification of the example of the i t h class to the j t h class, where c is the number of classes. Then, the weight assigned to the i t h class after rescaling is given as [32]:
w i = n x ∈ i ∑ k = 1 c ( n k x ∈ k )
where n is the number of training samples, ∈ i = ∑ j = 1 c ∈ i j .
It uses the algorithms as described in [32,33,34]. For example, we can say the weight of predicting no PC for subjects with PC(False positive) is 1000 times more serious than predicting PC for subjects with no PC (False negative). Accordingly, we can change the weights to get a confusion matrix as per our need.

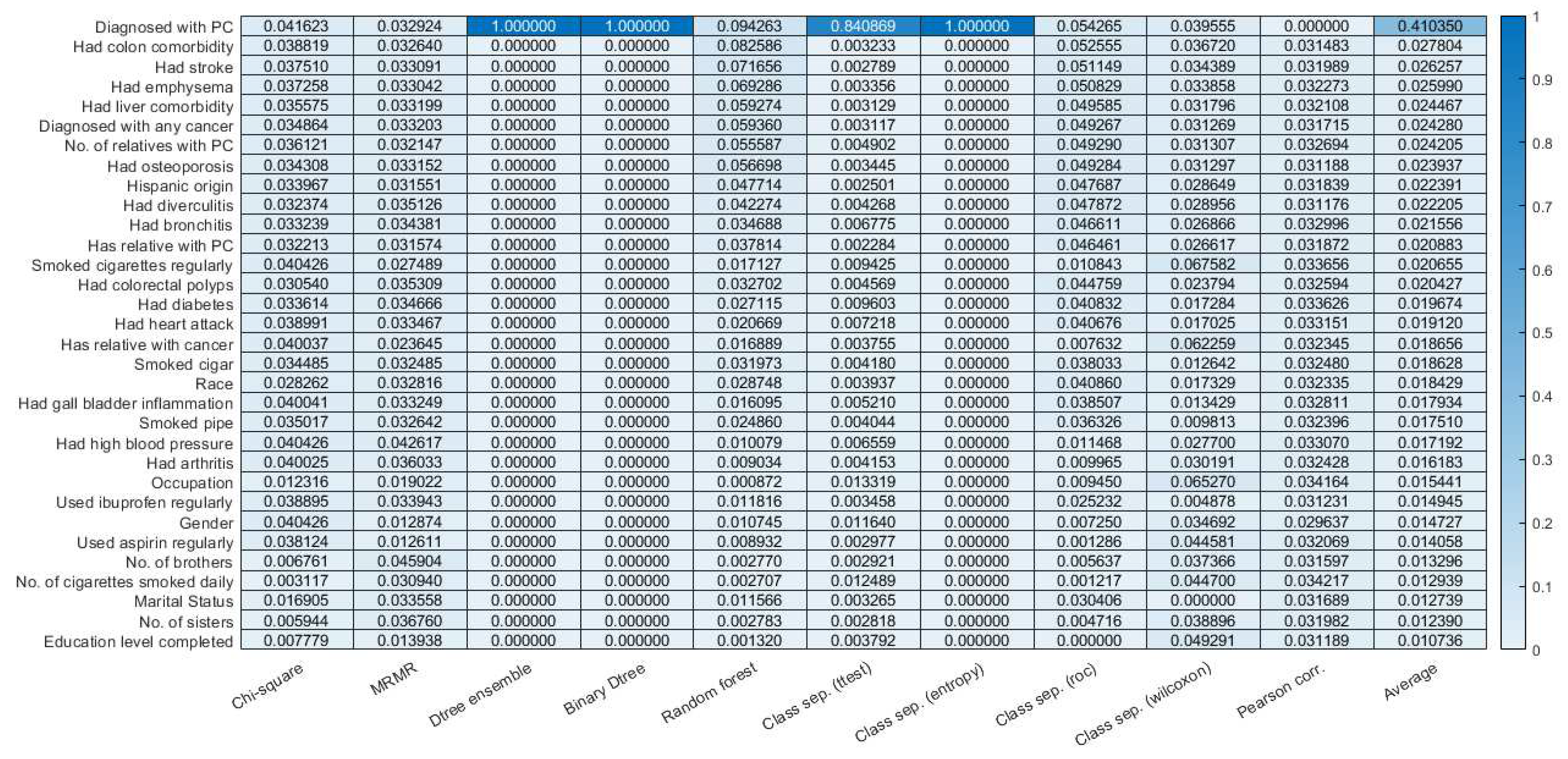
3.2. Feature selection.

We used several feature selection algorithms [21,22,23,24,25,26,27,28,29,30,31], implemented in MATLAB, to rank the features. Figure 2, Figure 2 show the ranking of the features by each of these algorithms for males and females respectively.

3.3. Finding probability feature combination using a Bayesian Network

Russell and Norvig in their book, Artificial Intelligence: A Modern Approach [35] have illustrated about Bayes Theorem and joint probability. Consider that the symptoms E 1 , E 2 are conditionally independent. Then their co-occurrence is as follows:
P ( E 1 , E 2 | C ) = P ( E 1 | C ) P ( E 2 | C )
Using the above equation,
P ( C | E 1 , E 2 ) = P ( C ) P ( E 1 , E 2 | C ) P ( E 1 Δ E 2 )
As any individual will either have PC or not have PC with the given symptoms, considering a universal set , P ( E 1 Δ E 2 ) can be resolved using normalization as follows:
P ( C | E 1 , E 2 ) + P ( C ¯ | E 1 , E 2 ) = 1
P ( C ¯ ) is the probability of non-occurrence of PC. Hence,
P ( E 1 Δ E 2 ) = P ( C ) P ( E 1 , E 2 | C ) + P ( C ¯ ) P ( E 1 , E 2 | C ¯ )
Substituting equation 3 in equation 6
P ( E 1 Δ E 2 ) = P ( C ) P ( E 1 | C ) P ( E 2 | C ) + P ( C ¯ ) P ( E 1 | C ¯ ) P ( E 2 | C ¯ )
Substituting equation 4 in equation 7,
P ( C | E 1 , E 2 ) = P ( C ) P ( E 1 , E 2 | C ) P ( C ) P ( E 1 , E 2 | C ) + P ( C ¯ ) P ( E 1 , E 2 | C ¯ )
Substituting equation 3 in equation 8,
P ( C | E 1 , E 2 ) = P ( C ) P ( E 1 | C ) P ( E 2 | C ) P ( C ) P ( E 1 | C ) P ( E 2 | C ) + P ( C ¯ ) P ( E 1 | C ¯ ) P ( E 2 | C ¯ )

4. Discussions

A number of risk factors of PC have been identified [36,37,38], such as, smoking, obesity, exposure to certain chemicals (e.g., pesticides, benzene, certain dyes, petrochemicals), age (older than 55 years), gender (male), race/ethnicity (Blacks, Ashkenazi Jewish heritage), family history (two or more first-degree relatives with PC), inherited genetic syndromes, diabetes, pancreatic cysts and chronic pancreatitis. Several different genes are associated with increased risk of PC. However, genetic risk factors are beyond the scope of this work as our dataset does not contain genetic information. Table 3 shows the ratio in which each symptom was distributed in the HPT(high probability table) chosen by selecting top percentage values of probability for that feature combination and in the LPT(low probability table) chosen by selecting bottom percentage values of probability for that feature combination.
Factors with unclear effect on risk include nature of diet, lack of physical activity, coffee and alcohol consumption, and certain infections (see for example, [38]) .
Smoking. Several studies have shown that smoking has a significant relationship with PC (see for example [39,40,41,42,43,44]). Yadav et al. [43] found that smoking cessation can significantly reduce risk of PC. Raimondi et al. [44] argue that smoking is the most common risk factor and accounts for 20-25% of all pancreatic tumors.
Diabetes. Diabetes also has a positive correlation with PC [45]. Huxley et al. [3] shows that individuals who have had type-II diabetes for less than four years were at a 50% higher risk of contracting PC than individuals who have had type-II diabetes for more than four years. Everhart et al. [4] have concluded that subjects with long standing diabetes have a higher relative risk of PC. Ben et al. [5] have also found similar relationship between diabetes and PC. Liao et al [46] shows that subjects in Taiwan who have had diabetes for less than 2 years are at elevated risk of PC. Long standing diabetes did not pose a strong risk. Also concurrent occurrence of diabetes and chronic pancreatitis puts subjects at a higher risk.
Reproductive history in women. Lo et al. [47] have shown that women with 7 or more live births had a lower risk of PC. Lactation period also had a significant effect on the possibility of PC. This study shows that women who lactated for 144 months or more had a one-fifth the risk of PC than women who lactated only for 89 months or less. Kreiger et al. [48] have shown that PC is an estrogen-dependent disease and aspects of reproductive history and hormone replacement are associated with a greater risk of this disease. Reduced risks were observed with 3 or more pregnancies and with the use of oral contraceptives.
Marriage. Baine et al. [31] shows marriages improves the survival rate and longevity of patients with PC. This paper also shows using Kaplan-Meier analysis, that patients who were married had a median survival rate of 4 months in comparison to unmarried patients who had a survival rate of 3 months. Aizer et al. [49] have shown that marriage has a beneficial effect on any cancer with regards to detection, treatment and survival. This improvement was observed more in males than females, highlighting the socio-economic elevation that a married person could have. The paper concluded that ”married people were less likely to present metastatic disease, more likely to receive definitive therapy, and less likely to die as a result of their cancer after adjusting for demographics, stage, and treatment than unmarried patients.” Multivariate logistic and Cox regression were used to analyze the patients.
Occupation. Logan et al. [50] shows how specific types of occupation pose higher risk to exposure to carcinogenic substances.In 1961 and 1971, for men, occupation categories of clothing, food, drink and tobacco and armed forces had higher standardised mortality rates(SMR) and relative standardised mortality rates(RSMR) whereas people in the clerical and leather industry saw low SMR and RSMR. For men in the occupation categories of mining, labourers and service, sport and recreation saw elevated but reduced RSMR. For men in administrative and managerial, and professional and technical disciplines, the trend was reduced SMR and elevated RSMR.In case of married women, if husbands worked in engineering, leather, wood, sales, clothing, construction work, both SMR and RSMR were high. For wives of husbands working in farm, gas, coke and chemicals industry, glass and ceramics and warehouse, both SMR and RSMR were low. In 1961, wives of husband in food, drink and tobacco had high SMR and RSMR and values were low for husbands in painting and decoration industry, and the trend was reversed in 1971.
Family composition. Gharidian et al. [51] have found an interesting relationship wherein there is the occurrence of this disease in two brothers and one sister in all the seventh decade of their life. This study was based in Montreal and there was no pancreatitis history between the patients or their relatives.
Use of certain medications. Tan et al. [52] have shown that aspirin use decreases risk of procuring PC. Aspirin use for 1day/month or greater was associated with a lower risk of PC than subjects who had aspirin for less than 1day/month. According to this study, there is no relationships between non-aspirin non-steroidal anti-inflammatory drugs (NSAID) and PC. Larsson et al. [53] have provided a doubtful evidence that regular use of aspirin over longer duration increases risk of PC. No relationship was found between use of frequent aspirin (7 tablets or more/week) or prolonged use of aspirin (more than 20 years) and the increase/decrease in PC. Harris et al. [54] have found a relationship between aspirin, ibuprofen, and other non-steroidal anti-inflammatory drugs (NSAID) and cancer prevention. However, results varied for different types of cancer.
Surgical history. Rosenberg et al. [55] have shown a positive correlation in increase in risk of PC by 1.8% because of vasectomy.
Inherited genetic syndrome. Certain rare genetic conditions causes almost 10 percent of all PCs. In our investigation, it can be found under family history of PC , that have been chosen by two of the feature-selection algorithms, viz, Relieff and Lasso in Table 3. Also, no of relatives with PC has been chosen by 4 of the feature selection algorithms, viz, ECFS, UDFS, LLCFS and CFS. From the graphs in Figure 3, it can be seen that if subject has family history of PC or any form of cancer, there is increase in probability of PC. Further the trend of increase is almost exponential as no. of relatives with PC increases, which strongly suggests that genetics play an important role in determination of possibility of PC. Such rare genetic conditions include [36]:
  • Hereditary breast and ovarian cancer syndrome, caused by mutations in the BRCA1 or BRCA2 genes,
  • Hereditary breast cancer, caused by mutations in the PALB2 gene,
  • Familial atypical multiple mole melanoma (FAMMM) syndrome, caused by mutations in the p16/CDKN2A gene and associated with skin and eye melanomas,
  • Familial pancreatitis, usually caused by mutations in the PRSS1 gene,
  • Lynch syndrome, also known as hereditary non-polyposis colorectal cancer (HNPCC), most often caused by a defect in the MLH1 or MSH2 genes,
  • Peutz-Jeghers syndrome, caused by defects in the STK11 gene. This syndrome is also linked with polyps in the digestive tract and several other cancers.
Race. Race has been a predominant factor in the determination of the risk of PC [36,37,38]. According to literature, blacks or African American people have a higher risk of contracting PC. This could be attributed to their dietary habits or smoking history. Race has been chosen as one of the features by 3 of our feature-selection algorithms, viz, Laplacian, FSASL and LLCFS in Table 2 and also Black race has been chosen as one of the highest probability of PC causing feature in Table 2.
Gender. Literature has shown that men are more likely to contract PC than women [36,37,38]. This could be because men are more likely to smoke than women and smoking has a significant effect on PC. Gender has been chosen as one of the features by 3 of our feature-selection algorithms, viz, Laplacian, CFS and ECFS in Table 2 and also gender is male in the highest probability of PC in Table 2.
Female hormones. Experimental findings from this article by [56] on use of affect of female hormones suggest that female hormones have a protective role towards incidence of PC.
Bronchitis. Although there is no direct evidence between bronchitis and PC risk, [57] is a study conducted on male smokers in Finland that suggests that bronchial asthma predict the subsequent risk of developing PC in male smokers and that greater physical activity may decrease the risk. Also bronchial asthma can increase chances of developing bronchitis.
Heart attack.Many references suggest the increased association between heart attack and stroke with any type of cancer (not necessarily PC). [58] shows the increased risk of heart attack and stroke in the months leading up to cancer diagnosis. In another article [59], it shows that recent epidemiological analyses suggest that cancer incidence is more common among subjects with a history of heart failure versus subjects with no history of heart failure.
Hypertension. Some references, for example [60] suggest that hypertension at baseline was associated with an increased risk of PC incidence.
Although the above factors-inherited genetic syndrome, race, diabetes history and gender have a strong relationship with PC, yet they were not one of the highly selected features by our algorithms, probably because other features have a stronger dependence when considered in unison.
Most of the remaining features as seen in Table 2 do not have a strong evidence yet to their dependency with PC, however they can act as a guide to biologists and researchers to delve into possible correlation between these symptoms.
Table 4. Table containing 2 features combinations from PLCO dataset that produces highest risk of PC for female.
Table 4. Table containing 2 features combinations from PLCO dataset that produces highest risk of PC for female.
Symptom 1 Symptom 2 Probability
No of cigarettes smoked daily= 61-80 No of relatives with PC=2+ 0.156
No of tubal/ectopic pregnancies=2+ No of relatives with PC=2+ 0.137
Usually filtered or not filtered?=Both No of relatives with PC=2+ 0.115
No of cigarettes smoked daily= 61-80 No of relatives with PC=2+ 0.095
No of tubal/ectopic pregnancies=1 No of relatives with PC=2+ 0.084
Heart attack history?=yes No of relatives with PC=2+ 0.08
No of cigarettes smoked daily=21-30 No of relatives with PC=2+ 0.077
No of relatives with PC=2+ Race=Asian 0.076
No of relatives with PC=2+ No of still births=1 0.074
No of relatives with PC=2+ Diabetes history?=Yes 0.0737
No of relatives with PC=2+ Race=American Indian 0.0737
No of relatives with PC=2+ Emphysema history?=Yes 0.0737
No of relatives with PC=2+ No of cigarettes smoked daily=31-40 0.0708
No of relatives with PC=2+ Colorectal Polyps history?=Yes 0.0708
No of relatives with PC=2+ Stroke history?=Yes 0.0704
No of relatives with PC=2+ Age at hysterectomy=40-44 0.0686
No of relatives with PC=2+ No. of brothers=7+ 0.0645
No of relatives with PC=2+ Bronchitis history?=2+ 0.064
No of relatives with PC=2+ Liver comorbidities history?=Yes 0.063
No of relatives with PC=2+ No of cigarettes smoked daily=11-20 0.063
Table 5. Table containing 3 features combinations from PLCO dataset that produces highest risk of PC for male and female.
Table 5. Table containing 3 features combinations from PLCO dataset that produces highest risk of PC for male and female.
Male
Symptom 1 conditional probability Symptom 2 conditional probability Symptom 3 conditional probability Total probability
No of cigarettes smoked daily is 61-80=0.005 Age when told had enlarged prostate is 70+ =0.0175 prior history of cancer is yes=0.05 0.00521
No of cigarettes smoked daily is 61-80=0.005 Age when told had enlarged prostate is 70+ =0.0175 family history of PC=yes=0.533 0.002368
No of cigarettes smoked daily is 61-80=0.005 Age when told had enlarged prostate is 70+ =0.0175 no. of relatives with PC is 1=0.04 0.004593
prior history of cancer is yes=0.05 Age when told had enlarged prostate is 70+ =0.0175 family history of PC is yes=0.533 0.002153
prior history of cancer is yes=0.05 Age when told had enlarged prostate is 70+ =0.0175 no. of relatives with PC is 1=0.04 0.004177
Age when told had enlarged prostate is 70+ =0.0175 family history of PC is yes=0.533 no. of relatives with PC is 1=0.04 0.00189
No of cigarettes smoked daily is 61-80=0.005 prior history of cancer is yes=0.05 family history of PC=yes=0.533 0.02742
No of cigarettes smoked daily is 61-80=0.005 prior history of cancer is yes=0.05 no. of relatives with PC is 1=0.04 0.05197055
No of cigarettes smoked daily is 61-80=0.005 family history of PC is yes=0.533 no. of relatives with PC is 1=0.04 0.024218
prior history of cancer is yes=0.05 family history of PC is yes=0.533 no. of relatives with PC is 1=0.04 0.02206
Female
No of tubal/ectopic pregnancies is 1=0.003 No. of relatives with PC is 2+=0.011 no. of cigarettes smoked is 61-80=0.007 0.3578

5. Conclusion

We have used widely used algorithms for our prediction for PC. Since the exact relationship between features and the cause of PC cannot be ascertained for sure, for example, some factors like education, marital status and several others could have an indirect causal relationship with this disease, hence these factors were not excluded from our prediction study. After running all the above algorithms, it is observed that k-means clustering and SMOTE method of oversampling are some of the superior algorithms for PC prediction. The artificial intelligence based Bayesian network prediction model can signify which individuals are at an elevated risk for PC.
Until now, very limited work has been done in PC prediction, so the accuracy obtained by our research is significant. Lack of online available datasets for PC have limited the work that can be done in this field. Still the PLCO dataset by NIH has been a very valuable resource. Future improvements can be made based on taking into account other features that would have been found as a possible precursor to PC, based on further research and availability of more datasets.

6. Appendix

To make this paper self-contained, here we briefly describe methods used in the paper for data visualization, data balancing, feature selection, and classification, as well as evaluation metrics.

6.1. Data Visualization Methods

t-distributed stochastic neighbor embedding (t-SNE) algorithm. [61]The t-SNE method is a non-linear dimensionality reduction method, particularly well-suited for projecting high dimensional data onto low dimensional space for analysis and visualization purpose. Distinguished from other dimensionality reduction methods, the t-SNE method was designed to project high-dimensional data onto low-dimensional space with minimum structural information loss. So that the points close to each other on the low-dimensional surface represent states that are similar in the high-dimensional space.
As Van der Maaten and Hinton explained [16] “The similarity of datapoint x j to datapoint x i is the conditional probability p j | i , that x i would pick as its neighbor x j if neighbors were picked in proportion to their probability density under a Gaussian centered at x i .”
This method [61] starts with converting the high-dimensional Euclidean distance between data points (the Cartesian coordinates of each frame in the simulation) into the conditional probability p j | i . Given x i and x j as two data points representing two structures in Cartesian coordinate, the probability density distribution of its neighboring data points for x i is assumed as a Gaussian function centered at x i with variance σ i . The probability of x j to be selected as the neighbor of x i is a conditional probability calculated as
p j | i = e x p ( − x i − x j 2 2 σ 2 ) ∑ k ≠ i e x p ( − x i − x k 2 2 σ 2 )
Adaptive Synthetic (ADASYN) algorithm. ADASYN is a method of generating synthetic examples for minority classes using a weighted distribution as shown in Figure 1a. The algorithm flowchart is described in detail in [15].

6.2. Data Balancing Methods

K-means clustering.k-means clustering performed on the majority class of the dataset yielded 743 cluster centers. The value of k is based on idea of equalizing minority class with majority class and generating 743 clusters for majority class. These points were mixed were the datapoints of the minority class to remove bias, and generate a total of 1486 datapoints. The 24 prediction algorithms were run on this new dataset and the results were validated using 5-fold cross validation.
Suppose we are given a dataset X = x 1 , . . . , x N , x n ∈ R d as stated in [62]. The M-clustering problem aims at partitioning this data set into M disjoint subsets (clusters) C 1 , . . . , C M , such that a clustering criterion is optimized. The most widely used clustering criterion is the sum of the squared Euclidean distances between each data point x i and the centroid m k (cluster center) of the subset C k which contains x i . This criterion is called clustering error and depends on the cluster centers m 1 , . . . , m M :
E ( m 1 , . . . , m M ) = ∑ i = 1 N ∑ k = 1 M I ( x i ∈ C k ) | x i − m k | 2
where I(X)=1 if X is true and 0 otherwise
SMOTE method of oversampling.[17] The SMOTE (Synthetic Minority Over-Sampling Technique) function takes the feature vectors with dimension (r,n) and the target class with dimension (r,1) as the input and returns final features vectors with dimension (r’,n) and the target class with dimension (r’,1) as the output. The minority class was oversampled and the new dataset was run through the algorithms. The highest accuracy was given by Fine Decision Tree of 95.4%.
Downsampling method. [63] The majority class dataset can be downsampled by an integer sampling factor, n. It samples the dataset by keeping the first sample and then every nth sample after that. In case of several columns in the dataset, each column will be treated as a separate sequence. After feeding the downsampled dataset into 24 algorithms, the highest accuracy was reported by Quadratic SVM of 56.4% only.
y = downsample(x,n) [63] decreases the sample rate of x by keeping the first sample and then every nth sample after the first. If x is a matrix, the function treats each column as a separate sequence.

6.3. Feature Selection Methods

Chi-square tests(fscchi2). [63] fscchi2(Tbl,ResponseVarName) ranks features (predictors) using chi-square tests. The table Tbl contains predictor variables and a response variable , and ResponseVarName is the name of the response variable in Tbl. The function returns idx, which contains the indices of predictors ordered by predictor importance, meaning idx(1) is the index of the most important predictor. You can use idx to select important predictors for classification problems
As stated in [64], the χ2 test is applied to test the independence of two events, where two events A and B are defined to be independent if P ( A B ) = P ( A ) P ( B ) or, equivalently, P ( A | B ) = P ( A ) and P ( B | A ) = P ( B ) . In feature selection, the two events are occurrence of the term and occurrence of the class. We then rank terms with respect to the following quantity:
χ 2 ( D , t , c ) = ∑ e t ∈ ( 0 , 1 ) ∑ e c ∈ ( 0 , 1 ) ( N e t e c − E e t e c ) 2 E e t e c
where,
N =observed frequency in D,
E=expected frequency,
e t = 1 (the document contains term t) and e t = 0 (the document does not contain term t),
C is a random variable that takes values e c = 1 (the document is in class C) and e c = 0 (the document is not in class c)
Minimum redundancy maximum relevance (MRMR)(fscmrmr) [65] This algorithm tends to select a subset of features having the most correlation with the class (output) and the least correlation between themselves. It ranks features according to the minimal-redundancy-maximal-relevance criterion which is based on mutual information. Minimal redundancy as stated in [66] will make the feature set a better representation of the entire dataset. Let S denote the subset of features we are seeking. The minimum redundancy condition is:
m i n W I , W I = 1 | S | 2 ∑ i , j ∈ S I ( i , j )
where, | S | is the number of features in S
Fitcensemble [63] fitcensemble(Tbl,ResponseVarName) returns the trained classification ensemble model object (Mdl) that contains the results of boosting 100 classification trees and the predictor and response data in the table Tbl. ResponseVarName is the name of the response variable in Tbl. By default, fitcensemble uses LogitBoost for binary classification and AdaBoostM2 for multiclass classification.
As stated in [67], let each (y, x) case in L be independently drawn from the probability distribution P. Suppose Y is numerical and ϕ ( x , L ) the predictor. Then the aggregated predictor is the average over L of ϕ ( x , L ) , i.e.
ϕ A ( x ) = E L ϕ ( x . L )
Fitctree [63,68] Estimate predictor importance for classification using a binary decision tree. fitctree(Tbl,VarName) returns a fitted binary classification decision tree based on the input variables (also known as predictors, features, or attributes) contained in the table Tbl and output (response or labels) contained in Tbl.VarName. The returned binary tree splits branching nodes based on the values of a column of Tbl.
We consider the problem of finding the best test for a nominal attribute with n values in a k-class L-ary decision tree as stated in [69]. We are particularly concerned with cases in which n or k, or both, are quite large; this situation arises in many pattern recognition problems and in some large real data mining applications. The problem is to find the optimal partition of n elements into L bins. A partition of the n distinct values of the attribute induces a partition of the examples: each example is put into the branch corresponding to the value that the given attribute takes for that example. The class impurity of the examples in each branch is computed, weighted, summed and assigned to the given partition. An n by k contingency matrix, computed at the start of the procedure, can be used to compute the impurity measure for each partition that is considered. The number of distinct partitions of n elements is exponential in n: for example, if L = 2, a binary tree, there are 2 n − 1 − 1 two-way partitions [69].
Rank key features by class separability criteria (rankfeatures)IDX = rankfeatures(X,GROUP) ranks the features in X using an independent evaluation criterion for binary classification. X is a matrix where every column is an observed vector and the number of rows corresponds to the original number of features. GROUP contains the class labels. IDX is a list of indices to the rows of X with the most significant features
The Bhattacharyya distance [70] is a common method for measuring the separation between two multivariate gaussians. Therefore, we will have to use this method based on the assumption that data is drawn from a Gaussian distribution. Because we have five classes in our data, we first estimate a Gaussian distribution from which the data is drawn, then we calculate all the possible combinations among the classes. Finally we add all this distances to produce a ranking for each feature. The Bhattacharyya distance for two multivariate distributions P1 and P2 can be calculated as follows:
B h a t D i s t a n c e ( P 1 , P 2 ) = = ( 1 / 8 ) ( m 1 − m 2 ) T P − 1 ( m 1 − m 2 ) + 0.5 l n d e t P d e t P 1 d e t P 2
P = P 1 P 1 + P 2
The Wilcoxon signed rank test as stated in [71]is used to test that a distribution is symmetric about some hypothesized value, which is equivalent to the test for location. We illustrate with a test of a hypothesized median, which is performed as follows:
  • Rank the magnitudes (absolute values) of the deviations of the observed values from the hypothesized median, adjusting for ties if they exist.
  • Assign to each rank the sign (+ or - ) of the deviation (thus, the name “signed rank”).
  • Compute the sum of positive ranks,T(+) , or negative ranks,T(-) , the choice depending on which is easier to calculate. The sum of T(+) and T(-) is n(n+1)/2, so either can be calculated from the other.
  • Choose the smaller of T(+) and T(-), and call this T.
  • Since the test statistic is the minimum of T(+) and T(-), the critical region consists of the left tail of the distribution, containing a probability of at most α / 2 . If n is large, the sampling distribution of T is approximately normal with
    μ = n ( n + 1 ) / 4 , a n d σ 2 = n ( n + 1 ) ( 2 n + 1 ) / 24
    which can be used to compute a z-statistic for the hypothesis test.
In case ofentropy criterion, atypical [72] ranking process consists of four steps:
  • Initialize set F to the whole set of p features. S is an empty set.
  • For all features f ∈ F compute J(f) coefficient.
  • Find feature f that maximizes J(f) and move it to S ← S ∪ { f } , F ∈ F { f }
  • Repeat until the cardinal of S is p
where J(f) is a criterion function (specific for a given algorithm) which gives a measure of dependency between features (f) and classes (C). Feature (variable) selection problems can be formulated into a [73] cardinality optimization (In general, it is NP hard)
β = a r g m i n β ∈ R p Q ( β ) = ∑ i = 1 n q ( X i T β , y i ) s . t . β 0 ≤ s
p is the number of features,
X i , β ∈ R p ,
n is the number of training samples,
X ∈ R n × p , y ∈ R n denotes training data;
s is the given sparsity level,
Q(·) is convex and smooth[74].
PredictorImportance [63] Imp = oobPermutedPredictorImportance(Mdl) returns a vector of out-of-bag, predictor importance estimates by permutation using the random forest of regression trees Mdl.
A classification tree [75] is a rule for predicting the class of an object from the values of its predictor variables. The tree is constructed by recursively partitioning a learning sample of data in which the class label and the values of the predictor variables for each case are known. Each partition is represented by a node in the tree.
If X is an ordered variable, this approach searches over all possible values c for splits of the form X ≤ c . A case is sent to the left subnode if the inequality is satisfied and to the right subnode otherwise. The values of c are usually restricted to mid-points between consecutively ordered data values. If X is a categorical predictor (i.e., a predictor variable that takes values in an unordered set), the search is over all splits of the form X ∈ A where A is a non-empty subset of the set of values taken by X.
predictorImportance [63] estimates predictor importance of the predictors for each tree learner in the ensemble ens and returns the weighted average imp computed using ens.TrainedWeight. The output imp has one element for each predictor. predictorImportance computes importance measures of the predictors in a tree by summing changes in the node risk due to splits on every predictor, and then dividing the sum by the total number of branch nodes. The change in the node risk is the difference between the risk for the parent node and the total risk for the two children. For example, if a tree splits a parent node (for example, node 1) into two child nodes (for example, nodes 2 and 3), then predictorImportance increases the importance of the split predictor by [63]:
( R 1 – R 2 – R 3 ) / N b
where R i is node risk of node i, and N b is the total number of branch nodes. A node risk is defined as a node error weighted by the node probability:
R i = P i E i ,
where P i is the node probability of node i, and E i is the mean squared error of node i.
Corrcoef [63] corrcoef(A) returns the matrix of correlation coefficients for A, where the columns of A represent random variables and the rows represent observations Correlation as stated in [76]is a measure of a monotonic association between 2 variables. A monotonic relationship between 2 variables is a one in which either (1) as the value of 1 variable increases, so does the value of the other variable; or (2) as the value of 1 variable increases, the other variable value decreases. In correlated data, therefore, the change in the magnitude of 1 variable is associated with a change in the magnitude of another variable, either in the same or in the opposite direction. In other words, higher values of 1 variable tend to be associated with either higher (positive correlation) or lower (negative correlation) values of the other variable, and vice versa. Assumptions of a Pearson correlation are as follows:
  • As is actually true for any statistical inference, the data are derived from a random, or at least representative, sample. If the data are not representative of the population of interest, one cannot draw meaningful conclusions about that population.
  • Both variables are continuous, jointly normally distributed, random variables. They follow a bivariate normal distribution in the population from which they were sampled. The bivariate normal distribution is beyond the scope of this tutorial but need not be fully understood to use a Pearson coefficient. The equation for correlation coefficent is represented as follows [77]:
ρ x y = c o v ( X , Y ) σ x σ y
where,
cov is the covariance,
σ x is the standard deviation of X,
σ y is the standard deviation of Y
Infinite Latent Feature Selection (ILFS). [78]: Consider a training set X = { x 1 → , . . . , x n → } , such that the distribution of the values assumed by the i t h features is given by m × 1 vector x l → , taking into account m samples. An undirected graph G is formed so that the features are represented by the nodes and the inter-node relationships are represented by the edges. If a i j is an element of the adjacency matrix, A associated with G, that represents the pairwise relationship between the features x i and x j ( 1 ≤ i , j ≤ n ) . G can be represented by the binary function [78]:
a i j = ϕ ( x i , x j )
where ϕ is a real valued potential function. The probability of each co-occurrence in x i and x j is framed as a mixture of conditionally independent multinomial distribution, where parameters are learned using Expectation Maximization(EM) algorithm.
Feature selection via Eigenvector Centrality (ECFS). The adjacency matrix of the above graph G can be written as [21]:
A = α k + ( 1 − α ) ∑ ( i , j )
where α ∈ 0 , 1 is a loading coefficient. In Eigenvector Centrality measure (EC), v o is calculated as the eigen vector of A associated with the largest eigen value. If e is any vector,
lim l → L A l e = v o
Relieff. Relieff is an algorithm developed by Kira and Rendell [79,80] in 1992 that uses filter-method approach for feature selection. If a dataset consists of n instances of p features, belonging to two classes. At each iteration, X is a feature vector belonging to one random instance and the feature vectors of the instances closest to X from each class using Manhattan L1 norm are chosen. ’Near hit’ is the closest instance of the same class and ’Near miss’ is the closest instance of different class. The weight vector is updated as follows [81]:
W i = W i − ( x i − n e a r H i t i ) 2 − ( x i − n e a r M i s s i ) 2
Feature Selection Concave (FSV). If matrices A ∈ R m x n and B ∈ R k x n are two point sets, then they can be discriminated by a separating plane, P as in [22]:
P = x | x ∈ R n , x T w = γ
where normal w ∈ R n and 1-norm distance to the origin is defined as γ w i n f .
Laplacian. A parameter used in this algorithm is the Laplacian Score(LS) which means that two points are related to the same topic if they are close to each other. Laplacian score of the r t h feature is calculated as follows [23]:
L r = f r ˜ T L f r ˜ f r ˜ T D f r ˜
Unsupervised Discriminative Feature Selection (UDFS). UDFS aims to select the most discriminative features for data representation, where manifold structure is considered. X = x 1 , x 2 , . . . , x n is the training set, x i ∈ R d ( 1 < i < n ) is the i t h datum and n is the number of data points in the training set. The objective function of this algorithm is: For an arbitrary matrix, A ∈ R r x p , its l 2 , 1 -norm [24] is:
A 2 , 1 = ∑ i = 1 R ∑ j = 1 p A i j 2
Local Learning Clustering based Feature Selection (LLCFS). This algorithm constructs the k-nearest neighbor graph in the weighted feature space. It performs joint clustering and feature weight learning [25].
Correlation based Feature Selection(CFS). This algorithm [26] performs feature selection on the basis of the hypothesis,“good feature subsets contain features highly correlated with the classification, yet uncorrelated to each other”. A merit function is a function that measures the agreement between data and the fitting model, for a particular choice of parameters. By definition, the merit function is small when the agreement is good. The merit function of a feature subset S consisting of k features is given as [82]:
M e r i t S k = k r c f ¯ k + k ( k − 1 ) r f f ¯ )
where r c f ¯ is the mean of all feature-classification correlations, and
r f f ¯ is the mean of all feature-feature correlations.

6.4. Classification Methods

Bayesian network. A Bayesian network is a directed acyclic graph with some quantitative probability information assigned to each node that corresponds to a random variable. It has many other synonyms, viz, belief networks, probabilistic network, causal network and knowledge map [35]. A conditional probability distribution P ( x i | p a r e n t s ( X i ) ) defines the relationship between each node and its parents. It is defined by the following equation [35]:
P ( x 1 , . . . . . , x n ) = ∏ i = 1 n P ( x i | p a r e n t s ( X i ) )
where P ( x 1 , . . . . . , x n ) = probability of joint conjunction of events x 1 , x 2 , ..... x n .
Decision tree. The goal attribute is true if and only if the input attributes follow the paths towards a leaf with value true. This assertion gives a decision tree and its propositional logic can be written as follows [35],
G o a l ⇔ P a t h 1 V P a t h 2 V . . .
In MATLAB definition, fine trees have the highest model flexibility [63] as they have many leaves to make many fine distinctions between classes. They allow a maximum of 100 splits. In case of medium trees, the model flexibility is medium. They allow a maximum of 20 splits. In case of coarse trees, the model flexibility is low and they allow a maximum of 4 splits.
Logistic regression. The logistic function is given by the following equation [35]:
L o g i s t i c ( z ) = 1 1 + e − z
It gives the probability of belonging to the class labeled 1. The process of fitting the weights of this model to minimize loss on a data set is called logistic regression.
RUS boosted trees. Random under-sampling (RUS) is used to balance an imbalanced class that is a common problem for any datasets having rare occurrences of a particular event, the algorithm of which can be found in [83].
Bagged trees. “Bagging predictors [67] is a method for generating multiple versions of a predictor and using these to get an aggregated predicton”- Breiman. Consider data ( y n , x n ) , n = 1 . . . , N in a learning set, where the y’s are either class labels or a numerical response. If the input is x we predict y by ϕ ( x , L ) , taking repeated bootstrap samples L B from L, and forming ϕ ( x , L B ) and if y is numerical
ϕ B ( x ) = a v b ϕ ( x , L ( B ) )
If y is a class label, let the ϕ ( x , L B ) vote to form ϕ B ( x ) . This is called “bootstrap aggregating” or bagging.
k-means clustering.k-means clustering performed on the majority class of the dataset yielded 743 cluster centers. The value of k is based on idea of equalizing minority class with majority class and generating 743 clusters for majority class. These points were mixed were the datapoints of the minority class to remove bias, and generate a total of 1486 datapoints. The 24 prediction algorithms were run on this new dataset and the results were validated using 5-fold cross validation.
Suppose we are given a dataset X = x 1 , . . . , x N , x n ∈ R d as stated in [62]. The M-clustering problem aims at partitioning this data set into M disjoint subsets (clusters) C 1 , . . . , C M , such that a clustering criterion is optimized. The most widely used clustering criterion is the sum of the squared Euclidean distances between each data point x i and the centroid m k (cluster center) of the subset C k which contains x i . This criterion is called clustering error and depends on the cluster centers m 1 , . . . , m M :
E ( m 1 , . . . , m M ) = ∑ i = 1 N ∑ k = 1 M I ( x i ∈ C k ) | x i − m k | 2
where I(X)=1 if X is true and 0 otherwise
where μ i is the centroid of cluster S i imbalanced dataset by increasing the number of samples of the minority class. The algorithm flowchart is described in detail in [17].
Support Vector Machine. SVM is a type of supervised learning, where data that is not linearly separable can be easily separated by mapping them into higher dimensional space. The optimal SVM separator is found by solving the following [35] :
arg m a x a ∑ j α j − 1 2 ∑ j , k α j α j y j y k ( x j . x k ) )
where α j ≥ 0 and ∑ j α j y j = 0 . Solution of this equation is done using software called as quadratic programming.
K-nearest neighbor KNN algorithm classification is a type of clustering where the nearest k datapoints NN(k, x q ) are considered. The distance metric is measured using Minkowski distance as follows [35]:
L p ( x j , x q ) = ( ∑ i x j , i − x q , i p ) 1 p
When p = 2 , it is called Euclidean distance and if p = 1 , it is Manhattan distance.

6.5. Evaluation Matrices

The statistical parameters calculated are as follows [84]:
A c c u r a c y = t p + t n t o t a l
P r e c i s i o n = t p t p + f p
R e c a l l = t p t p + f n
F 1 − S c o r e = 2 x P r e c i s i o n x R e c a l l P r e c i s i o n + R e c a l l
where t p , t n , f p , f n are the number of true positives, true negatives, false positives, false negatives respectively.

References

  1. Wikipedia contributors. Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/ (accessed on 25 August 2019).
  2. Ik-Gyu, J. Method of providing information for the diagnosis of pancreatic cancer using bayesian network based on artificial intelligence, computer program, and computer-readable recording media using the same, 2019. US Patent App. 15/833,828.
  3. Huxley, R.; Ansary-Moghaddam, A.; De González, A.B.; Barzi, F.; Woodward, M. Type-II diabetes and pancreatic cancer: a meta-analysis of 36 studies. British journal of cancer 2005, 92, 2076. [Google Scholar] [CrossRef] [PubMed]
  4. Everhart, J.; Wright, D. Diabetes mellitus as a risk factor for pancreatic cancer: a meta-analysis. Jama 1995, 273, 1605–1609. [Google Scholar] [CrossRef] [PubMed]
  5. Ben, Q.; Xu, M.; Ning, X.; Liu, J.; Hong, S.; Huang, W.; Zhang, H.; Li, Z. Diabetes mellitus and risk of pancreatic cancer: a meta-analysis of cohort studies. European journal of cancer 2011, 47, 1928–1937. [Google Scholar] [CrossRef] [PubMed]
  6. Jones, S.; Hruban, R.H.; Kamiyama, M.; Borges, M.; Zhang, X.; Parsons, D.W.; Lin, J.C.H.; Palmisano, E.; Brune, K.; Jaffee, E.M.; others. Exomic sequencing identifies PALB2 as a pancreatic cancer susceptibility gene. Science 2009, 324, 217–217. [Google Scholar] [CrossRef]
  7. Barton, C.; Staddon, S.; Hughes, C.; Hall, P.; O’sullivan, C.; Klöppel, G.; Theis, B.; Russell, R.; Neoptolemos, J.; Williamson, R.; others. Abnormalities of the p53 tumour suppressor gene in human pancreatic cancer. British journal of cancer 1991, 64, 1076. [Google Scholar] [CrossRef]
  8. Iacobuzio-Donahue, C.A.; Fu, B.; Yachida, S.; Luo, M.; Abe, H.; Henderson, C.M.; Vilardell, F.; Wang, Z.; Keller, J.W.; Banerjee, P.; others. DPC4 gene status of the primary carcinoma correlates with patterns of failure in patients with pancreatic cancer. Journal of clinical oncology 2009, 27, 1806. [Google Scholar] [CrossRef]
  9. Das, A.; Nguyen, C.C.; Li, F.; Li, B. Digital image analysis of EUS images accurately differentiates pancreatic cancer from chronic pancreatitis and normal tissue. Gastrointestinal endoscopy 2008, 67, 861–867. [Google Scholar] [CrossRef]
  10. Ge, G.; Wong, G.W. Classification of premalignant pancreatic cancer mass-spectrometry data using decision tree ensembles. BMC bioinformatics 2008, 9, 275. [Google Scholar] [CrossRef]
  11. Săftoiu, A.; Vilmann, P.; Gorunescu, F.; Gheonea, D.I.; Gorunescu, M.; Ciurea, T.; Popescu, G.L.; Iordache, A.; Hassan, H.; Iordache, S. Neural network analysis of dynamic sequences of EUS elastography used for the differential diagnosis of chronic pancreatitis and pancreatic cancer. Gastrointestinal endoscopy 2008, 68, 1086–1094. [Google Scholar] [CrossRef]
  12. Zhang, M.M.; Yang, H.; Jin, Z.D.; Yu, J.G.; Cai, Z.Y.; Li, Z.S. Differential diagnosis of pancreatic cancer from normal tissue with digital imaging processing and pattern recognition based on a support vector machine of EUS images. Gastrointestinal endoscopy 2010, 72, 978–985. [Google Scholar] [CrossRef]
  13. Baruah, M.; Banerjee, B. Modality selection for classification on time-series data. MileTS 2020, 20, 6th. [Google Scholar]
  14. Biometry.nci.nih.gov. (2019). Pancreas-Datasets-PLCO-The Cancer Data Access System. Available online: https://biometry.nci.nih.gov/cdas/datasets/plco/10/ (accessed on 25 August 2019).
  15. He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence). IEEE, 2008, pp. 1322–1328.
  16. Maaten, L.v.d.; Hinton, G. Visualizing data using t-SNE. Journal of machine learning research 2008, 9, 2579–2605. [Google Scholar]
  17. Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: synthetic minority over-sampling technique. Journal of artificial intelligence research 2002, 16, 321–357. [Google Scholar] [CrossRef]
  18. Khalilia, M.; Chakraborty, S.; Popescu, M. Predicting disease risks from highly imbalanced data using random forest. BMC medical informatics and decision making 2011, 11, 1–13. [Google Scholar] [CrossRef]
  19. Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. Journal of machine learning research 2003, 3, 1157–1182. [Google Scholar]
  20. Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. Data classification: Algorithms and applications 2014, 37. [Google Scholar]
  21. Roffo, G.; Melzi, S. Ranking to Learn. International Workshop on New Frontiers in Mining Complex Patterns. Springer, 2016, pp. 19–35.
  22. Mangasarian, O.; Bradley, P. Feature Selection via Concave Minimization and Support Vector Machines. Technical report, 1998.
  23. He, X.; Cai, D.; Niyogi, P. Laplacian score for feature selection. Advances in neural information processing systems, 2006, pp. 507–514.
  24. Yang, Y.; Shen, H.T.; Ma, Z.; Huang, Z.; Zhou, X. L2, 1-Norm Regularized Discriminative Feature Selection for Unsupervised. Twenty-Second International Joint Conference on Artificial Intelligence, 2011.
  25. Du, L.; Shen, Y.D. Unsupervised feature selection with adaptive structure learning. Proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining. ACM, 2015, pp. 209–218.
  26. Hall, M.A. Correlation-based feature selection for machine learning 1999.
  27. Fonti, V.; Belitser, E. Feature selection using lasso. VU Amsterdam Research Paper in Business Analytics 2017. [Google Scholar]
  28. Guo, J.; Zhu, W. Dependence guided unsupervised feature selection. Thirty-Second AAAI Conference on Artificial Intelligence, 2018.
  29. Roffo, G. Ranking to learn and learning to rank: On the role of ranking in pattern recognition applications. arXiv 2017, arXiv:1706.05933 2017. [Google Scholar]
  30. Roffo, G.; Melzi, S.; Castellani, U.; Vinciarelli, A. Infinite latent feature selection: A probabilistic latent graph-based ranking approach. Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 1398–1406.
  31. Baine, M.; Sahak, F.; Lin, C.; Chakraborty, S.; Lyden, E.; Batra, S.K. Marital status and survival in pancreatic cancer patients: a SEER based analysis. PloS one 2011, 6, e21052. [Google Scholar] [CrossRef]
  32. Zhou, Z.H.; Liu, X.Y. On multi-class cost-sensitive learning. Computational Intelligence 2010, 26, 232–257. [Google Scholar] [CrossRef]
  33. Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and regression trees. Belmont, CA: Wadsworth. International Group 1984, 432, 151–166. [Google Scholar]
  34. Zadrozny, B.; Langford, J.; Abe, N. Cost-Sensitive Learning by Cost-Proportionate Example Weighting. ICDM, 2003, Vol. 3, p. 435.
  35. Russell, S.J.; Norvig, P. Artificial intelligence: a modern approach; Malaysia; Pearson Education Limited, 2016.
  36. ”What are risk factors for Pancreatic Cancer?” The Sol Goldman Pancreatic Cancer Research Center, JHU. Available online: https://pathology.jhu.edu/pancreas/BasicRisk.php?area=ba.
  37. Pancreatic Cancer: Risk Factors Approved by the Cancer.Net Editorial Board, 05/2018. Available online: https://www.cancer.net/cancer-types/pancreatic-cancer/risk-factors.
  38. Pancreatic Cancer Risk Factors. 2019. Available online: https://www.cancer.org/cancer/pancreatic-cancer/causes-risks-prevention/risk-factors.html.
  39. Li, D.; Xie, K.; Wolff, R.; Abbruzzese, J.L. Pancreatic cancer. The Lancet 2004, 363, 1049–1057. [Google Scholar] [CrossRef] [PubMed]
  40. Lynch, S.M.; Vrieling, A.; Lubin, J.H.; Kraft, P.; Mendelsohn, J.B.; Hartge, P.; Canzian, F.; Steplowski, E.; Arslan, A.A.; Gross, M.; others. Cigarette smoking and pancreatic cancer: a pooled analysis from the pancreatic cancer cohort consortium. American journal of epidemiology 2009, 170, 403–413. [Google Scholar] [CrossRef] [PubMed]
  41. Louizos, C.; Welling, M.; Kingma, D.P. Learning Sparse Neural Networks through L_0 Regularization. arXiv 2017, arXiv:1712.01312 2017. [Google Scholar]
  42. Muscat, J.E.; Stellman, S.D.; Hoffmann, D.; Wynder, E.L. Smoking and pancreatic cancer in men and women. Cancer Epidemiology and Prevention Biomarkers 1997, 6, 15–19. [Google Scholar]
  43. Yadav, D.; Lowenfels, A.B. The epidemiology of pancreatitis and pancreatic cancer. Gastroenterology 2013, 144, 1252–1261. [Google Scholar] [CrossRef]
  44. Raimondi, S.; Maisonneuve, P.; Lowenfels, A.B. Epidemiology of pancreatic cancer: an overview. Nature reviews Gastroenterology & hepatology 2009, 6, 699. [Google Scholar]
  45. Silverman, D.; Schiffman, M.; Everhart, J.; Goldstein, A.; Lillemoe, K.; Swanson, G.; Schwartz, A.; Brown, L.; Greenberg, R.; Schoenberg, J.; others. Diabetes mellitus, other medical conditions and familial history of cancer as risk factors for pancreatic cancer. British journal of cancer 1999, 80, 1830. [Google Scholar] [CrossRef]
  46. Liao, K.F.; Lai, S.W.; Li, C.I.; Chen, W.C. Diabetes mellitus correlates with increased risk of pancreatic cancer: a population-based cohort study in Taiwan. Journal of gastroenterology and hepatology 2012, 27, 709–713. [Google Scholar] [CrossRef]
  47. Lo, A.C.; Soliman, A.S.; El-Ghawalby, N.; Abdel-Wahab, M.; Fathy, O.; Khaled, H.M.; Omar, S.; Hamilton, S.R.; Greenson, J.K.; Abbruzzese, J.L. Lifestyle, occupational, and reproductive factors in relation to pancreatic cancer risk. Pancreas 2007, 35, 120–129. [Google Scholar] [CrossRef]
  48. Kreiger, N.; Lacroix, J.; Sloan, M. Hormonal factors and pancreatic cancer in women. Annals of epidemiology 2001, 11, 563–567. [Google Scholar] [CrossRef]
  49. Aizer, A.A.; Chen, M.H.; McCarthy, E.P.; Mendu, M.L.; Koo, S.; Wilhite, T.J.; Graham, P.L.; Choueiri, T.K.; Hoffman, K.E.; Martin, N.E.; others. Marital status and survival in patients with cancer. Journal of clinical oncology 2013, 31, 3869. [Google Scholar] [CrossRef] [PubMed]
  50. Logan, W. Cancer mortality by occupation and social class 1851-1971 1982.
  51. Ghadirian, P.; Simard, A.; Baillargeon, J. Cancer of the pancreas in two brothers and one sister. International journal of pancreatology 1987, 2, 383–391. [Google Scholar] [CrossRef] [PubMed]
  52. Tan, X.L.; Lombardo, K.M.R.; Bamlet, W.R.; Oberg, A.L.; Robinson, D.P.; Anderson, K.E.; Petersen, G.M. Aspirin, nonsteroidal anti-inflammatory drugs, acetaminophen, and pancreatic cancer risk: a clinic-based case–control study. Cancer prevention research 2011, 4, 1835–1841. [Google Scholar] [CrossRef] [PubMed]
  53. Larsson, S.C.; Giovannucci, E.; Bergkvist, L.; Wolk, A. Aspirin and nonsteroidal anti-inflammatory drug use and risk of pancreatic cancer: a meta-analysis. Cancer Epidemiology and Prevention Biomarkers 2006, 15, 2561–2564. [Google Scholar] [CrossRef] [PubMed]
  54. Harris, R.E.; Beebe-Donk, J.; Doss, H.; Doss, D.B. Aspirin, ibuprofen, and other non-steroidal anti-inflammatory drugs in cancer prevention: a critical review of non-selective COX-2 blockade. Oncology reports 2005, 13, 559–583. [Google Scholar] [CrossRef] [PubMed]
  55. Rosenberg, L.; Palmer, J.R.; Zauber, A.G.; Warshauer, M.E.; Strom, B.L.; Harlap, S.; Shapiro, S. The relation of vasectomy to the risk of cancer. American journal of epidemiology 1994, 140, 431–438. [Google Scholar] [CrossRef]
  56. Andersson, G.; Borgquist, S.; Jirstrom, K. Hormonal factors and pancreatic cancer risk in women: The Malmo Diet and Cancer Study. International Journal of Cancer 2018, 143, 52–62. [Google Scholar] [CrossRef]
  57. Stolzenberg-Solomon, R.Z.; Pietinen, P.; Taylor, P.R.; Virtamo, J.; Albanes, D. A prospective study of medical conditions, anthropometry, physical activity, and pancreatic cancer in male smokers (Finland). Cancer causes and control 13.
  58. Navi, B.B.; Reiner, A.S.; Kamel, H.; Ladecola, C.; Okin, P.M.; Tagawa, S.T.; Panageas, K.S.; DeAngelis, L.M. Arterial thromboembolic events preceding the diagnosis of cancer in older persons. Clinical trials and observations 2019, 133, 781–789. [Google Scholar] [CrossRef]
  59. Bertero, E.; Canepa, M.; Maack, C.; Ameri, P. Linking heart failure to cancer. Circulations 2018, 138, 735–742. [Google Scholar] [CrossRef] [PubMed]
  60. Wang, Z.; White, D.L.; Hoogeveen, R.; Chen, L.; Whitsel, E.A.; Richardson, P.A.; Virani, S.S.; Garcia, J.M.; El-Serag, H.B.; Jiao, L. Anti-Hypertensive Medication Use, Soluble Receptor for Glycation End Products and Risk of Pancreatic Cancer in the Women’s Health Initiative Study. Journal of clinical medicine 197. [CrossRef] [PubMed]
  61. Zhou, H.; Wang, F.; Tao, P. t-Distributed stochastic neighbor embedding method with the least information loss for macromolecular simulations. Journal of chemical theory and computation 2018, 14, 5499–5510. [Google Scholar] [CrossRef] [PubMed]
  62. Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern recognition 2003, 36, 451–461. [Google Scholar] [CrossRef]
  63. Mathworks.com. Train models to classify data using supervised machine learning - MATLAB. Available online: https://www.mathworks.com/help/stats/classificationlearner-app.html (accessed on 25 August 2019).
  64. Manning, C.; Raghavan, P.; Schütze, H. Introduction to Information Retrieval; Vol. 39, Cambridge University Press, 2008.
  65. Radovic, M.; Ghalwash, M.; Filipovic, N.; Obradovic, Z. Minimum redundancy maximum relevance feature selection approach for temporal gene expression data. BMC bioinformatics 2017, 18, 1–14. [Google Scholar] [CrossRef]
  66. Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. Journal of bioinformatics and computational biology 2005, 3, 185–205. [Google Scholar] [CrossRef]
  67. Breiman, L. Bagging predictors. Machine learning 1996, 24, 123–140. [Google Scholar] [CrossRef]
  68. Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and regression trees 2017.
  69. Coppersmith, D.; Hong, S.J.; Hosking, J.R. Partitioning nominal attributes in decision trees. Data Mining and Knowledge Discovery 1999, 3, 197–217. [Google Scholar] [CrossRef]
  70. Rugeles, D. Study of feature ranking using Bhattacharyya distance 2012. 1, 1.
  71. King, A.P.; Eckersley, R. Statistics for biomedical engineers and scientists: How to visualize and analyze data; Academic Press, 2019.
  72. Biesiada, J.; Duch, W.; Kachel, A.; Maczka, K.; Palucha, S. Feature ranking methods based on information entropy with parzen windows 2005. 1, 1.
  73. Liu, H.; Motoda, H. Feature selection for knowledge discovery and data mining 2012. 454.
  74. Wikipedia contributors. Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/Wilcoxon_signed-rank_test (accessed on 5 June 2022).
  75. Loh, W.; Shih, Y. Split selection methods for classification trees. Statistica sinica.
  76. Schober, P.; Boer, C.; Schwarte, L.A. Correlation coefficients: appropriate use and interpretation. Anesthesia & Analgesia 2018, 126, 1763–1768. [Google Scholar]
  77. Wikipedia contributors. Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/Pearson_correlation_coefficient (accessed on 26 June 2022).
  78. Roffo, G.; Melzi, S.; Cristani, M. Infinite feature selection. Proceedings of the IEEE International Conference on Computer Vision, 2015, pp. 4202–4210.
  79. Kira, K.; Rendell, L.A. ; others. The feature selection problem: Traditional methods and a new algorithm. 1992, 2, 129–134. [Google Scholar]
  80. Kira, K.; Rendell, L.A. A practical approach to feature selection 1992. pp. 249–256.
  81. Wikipedia contributors. Wikipedia, The Free Encyclopedia. 2022. Available online: https://en.wikipedia.org/Relief_(feature_selection) (accessed on 5 June 2022).
  82. Wikipedia contributors. Wikipedia, The Free Encyclopedia 2022. [Online; accessed 5-Jun-2022].
  83. Seiffert, C.; Khoshgoftaar, T.M.; Van Hulse, J.; Napolitano, A. RUSBoost: A hybrid approach to alleviating class imbalance. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans 2009, 40, 185–197. [Google Scholar] [CrossRef]
  84. Wikipedia contributors. Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/Precision_and_recall) (accessed on 5 June 2022).
Preprints 83368 g001
Figure 1. PLCO dataset visualized in 2D using (a) ADASYN algorithm [15] and (b) t-SNE algorithm [16]. Data points corresponding to PC= T r u e and PC= F a l s e are shown in black and gray respectively.
Figure 1. PLCO dataset visualized in 2D using (a) ADASYN algorithm [15] and (b) t-SNE algorithm [16]. Data points corresponding to PC= T r u e and PC= F a l s e are shown in black and gray respectively.
Preprints 83368 g001
Preprints 83368 g002
Figure 2. Weights assigned by 9 feature selection algorithms (columns 1–9) to risk factors in the PLCO dataset.
Figure 2. Weights assigned by 9 feature selection algorithms (columns 1–9) to risk factors in the PLCO dataset.
Preprints 83368 g002
Preprints 83368 g003
Figure 3. Weights assigned by 9 feature selection algorithms (columns 1–9) to risk factors in the PLCO dataset.
Figure 3. Weights assigned by 9 feature selection algorithms (columns 1–9) to risk factors in the PLCO dataset.
Preprints 83368 g003
Table 1. The risk factors considered in the PLCO dataset. The ones marked “removed” are not considered in our analysis as there are not enough responses from the participants on these questions.
Table 1. The risk factors considered in the PLCO dataset. The ones marked “removed” are not considered in our analysis as there are not enough responses from the participants on these questions.
Risk factor categories Risk factors(values) Male risk factors (total 47, removed 15) Female risk factors (total 52, removed 20)
Cancer history 59. Has relative with cancer (yes, no)
60. Has relative with PC (yes, no)
61. No. of relatives with PC (0, 1, 2, 3, ...)
62. Diagnosed with any cancer (yes, no)
63. Diagnosed with PC (yes, no)
Demo- graphics 64. Gender (male, female)
38. Race (White, Black, Asian, Pacific Islander, American Indian/Alaskan Native)
39. Hispanic origin (yes, no)
1. Education level completed (<8 yrs, 8-11 yrs, 12 yrs, 12 yrs + some college, college grad, post grad)
2. Marital status (married, widowed, divorced, separated, never married)
3. Occupation (homemaker, working, unemployed, retired, extended sick leave, disabled, other)
6. No. of sisters (0, 1, 2, 3, 4, 5, 6, ≥7)
7. No. of brothers (0, 1, 2, 3, 4, 5, 6, ≥7)
Medi- cation usage 8. Used aspirin regularly (yes, no)
9. Used ibuprofen regularly (yes, no)
52. Taken birth control pills (yes, no) (removed)
20. Age started taking birth control pills (<30 yrs, 30-39 yrs, 40-49 yrs, 50-59 yrs, ≥60 yrs) (removed)
21. Currently taking female hormones (yes, no) (removed)
22. No. of years taking female hormones (≤1, 2-3, 4-5, 6-9, ≥10) (removed)
53. Taken female hormones (yes, no, don’t know) (removed)
Health history 27. Had high blood pressure (yes, no)
28. Had heart attack (yes, no)
29. Had stroke (yes, no)
30. Had emphysema (yes, no)
31. Had bronchitis (yes, no)
32. Had diabetes (yes, no)
33. Had colorectal polyps (yes, no)
34. Had arthritis (yes, no)
35. Had osteoporosis (yes, no)
36. Had diverculitis (yes, no)
37. Had gall bladder inflammation (yes, no)
57. Had colon comorbidity (yes, no)
58. Had liver comorbidity (yes, no)
40. Had biopsy of prostrate (yes, no) (removed)
41. Had transurethral resection of prostate (yes, no) (removed)
42. Had prostatetomy of benign disease (yes, no) (removed)
43. Had prostate surgery (yes, no) (removed)
47. Had enlarged prostate (yes, no) (removed)
48. Had inflamed prostate (yes, no) (removed)
49. Had prostate problem (yes, no) (removed)
50. No. of times wakes up to urinate at night (0, 1, 2, 3, >3) (removed)
23. Age started to urinate more than once at night (<30 yrs, 30-39 yrs, 40-49 yrs, 50-59 yrs, 60-69 yrs, ≥70 yrs) (removed)
24. Age when told had enlarged prostate (<30 yrs, 30-39 yrs, 40-49 yrs, 50-59 yrs, 60-69 yrs, ≥70 yrs) (removed)
25. Age when told had inflammed prostate (<30 yrs, 30-39 yrs, 40-49 yrs, 50-59 yrs, 60-69 yrs, ≥70 yrs) (removed)
26. Age at vasectomy (<25 yrs, 25-34 yrs, 35-44 yrs, ≥45 yrs) (removed)
51. Had vasectomy (yes, no) (removed)
44. Been pregnant (yes, no, don’t know) (removed)
45. Had hysterectomy (yes, no) (removed)
46. Had ovaries removed (yes, no) (removed)
10. No. of tubal pregnancies (0, 1, ≥2) (removed)
11. Had tubal ligation (yes, no, don’t know) (removed)
12. Had benign ovarian tumor (yes, no) (removed)
13. Had benign breast disease (yes, no) (removed)
14. Had endometriosis (yes, no) (removed)
15. Had uterine fibroid tumors (yes, no) (removed)
16. Tried to become pregnant without success (yes, no) (removed)
17. No. of pregnancies (0, 1, 2, 3, 4-9, ≥10) (removed)
18. No. of stillbirth pregnancies (0, 1, ≥2) (removed)
19. Age at hysterectomy (<40 yrs, 40-44 yrs, 45-49 yrs, 50-54 yrs, ≥55 yrs) (removed)
Smoking habits 4. Smoked pipe (never, currently, formerly)
5. Smoked cigar (never, currently, formerly)
54. Smoked cigarettes regularly (yes, no)
55. Smoke regularly now (yes, no) (removed) (removed)
56. Usually filtered or not filtered (filter more often, non-filter more often, both about equally) (removed) (removed)
65. No. of cigarettes smoked daily (0, 1-10, 11-20, 21-30, 31-40, 41-60, 61-80, >80)
Table 2. Table containing features from PLCO dataset that are plausible to being indicators of risk of PC.
Table 2. Table containing features from PLCO dataset that are plausible to being indicators of risk of PC.
Symptoms Results Conclusion
Occupation All subjects in HPT were retired(category 4) and in LPT, they were extended sick leave(category 5) Older people have a greater risk of PC
Smoked pipe Subjects in HPT were in ratio 0.22(never smoked):0.5(current smoker):0.28(past smoker) whereas subjects in LPT were in ratio 0.37(never smoked):0.27(current smoker):0.36(past smoker) Subjects who never smoked have a lesser risk than past smokers and risk for current smokers was doubled
Heart Attack Subjects in HPT were in ratio 0.23(never had heart attack):0.77(had heart attack) whereas subjects in LPT were in ratio 0.8(never had heart attack):0.2(had heart attack) Subjects who had heart attack at least once have a greater risk for PC
Hypertension Subjects in HPT were in ratio 0.36 (not diagnosed with hypertension):0.63(diagnosed with hypertension) whereas subjects in LPT were in ratio 0.68 (not diagnosed with hypertension):0.32(diagnosed with hypertension) Stress(or hypertension) is directly proportional to risk for PC
Taken female hormones Subjects in HPT were in ratio 0.7(never taken):0.3(taken) whereas subjects in LPT were in ratio 0.23(never taken):0.77(taken) Somehow female hormones reduces risk of PC
Race Subjects in HPT were mostly Asian(0.38) and only 0.3 were Pacific Islander whereas subjects in LPT were mostly American Indian(0.85) Clearly shows that Asians are at a higher risk of PC while Pacific Islander and American Indian were at lower risk.
Diabetes Subjects in HPT were in ratio 0.17(never had diabetes):0.83(had diabetes) whereas subjects in LPT were in ratio 0.75(never had diabetes):0.25(had diabetes) Diabetes is a clear risk factor for PC
Bronchitis Subjects in HPT were in ratio 0.27(never had):0.73(had) whereas subjects in LPT were in ratio 0.68(never had ):0.32(had) Bronchitis is a risk factor for PC
Liver comorbidities Subjects in HPT were in ratio 0.39(never had):0.61(had) whereas subjects in LPT were in ratio 0.62(never had ):0.38(had) Liver comorbidities is a risk factor for PC
Colorectal Polyps Subjects in HPT were in ratio 0.36(never had):0.64(had) whereas subjects in LPT were in ratio 0.62(never had ):0.38(had) Colorectal Polyps is a risk factor for PC
Gender Subjects in HPT were in ratio 0.53(male):0.47(female) whereas subjects in LPT were in ratio 0.35(male):0.65(female) Male were at higher risk of PC than female
No of relatives with pancreatic cancer Subjects in HPT were in ratio 0.02(no relative):0.1(1 relative):0.88(2 relatives) whereas subjects in LPT were in ratio 0.71(no relative:0.29(1 relative) Risk of PC increases as incidence of PC on family members increases.
Ever take birth control pills? Subjects in HPT were in ratio 0.76(no history):0.24(has history) whereas subjects in LPT were in ratio 0.17(no history):0.83(has history) birth control pills may lower risk of PC
Smoke regularly now? Subjects in HPT were in ratio 0.12(no history):0.88(has history) whereas subjects in LPT were in ratio 0.95(no history):0.05(has history) Current smokers have higher risk of PC
Ever smoke regularly more than 6 months? Subjects in HPT were in ratio 0.22(no history):0.78(has history) whereas subjects in LPT were in ratio 0.85(no history):0.15(has history) Smoking in excess of 6 months also poses higher risk of PC
Table 3. Table containing 2 features combinations from PLCO dataset that produces highest risk of PC for male.
Table 3. Table containing 2 features combinations from PLCO dataset that produces highest risk of PC for male.
Symptom 1 Symptom 2 Probability
Age when told had inflamed prostate= 70+ No of cigarettes smoked daily=80+ 0.032
Age when told had inflamed prostate= 70+ Prior history of any cancer?= Yes 0.03
Prior history of any cancer?= Yes No of cigarettes smoked daily=80+ 0.026
Age when told had inflamed prostate= 70+ Age when told had enlarged prostate= 70+ 0.026
Age when told had inflamed prostate= 70+ Family history of PC?=Yes 0.026
Age when told had inflamed prostate= 70+ No of relatives with PC=1 0.026
Age when told had enlarged prostate= 70+ No of cigarettes smoked daily=80+ 0.024
Family history of PC=Yes No of cigarettes smoked daily=80+ 0.024
No of relatives with PC=1 No of cigarettes smoked daily=80+ 0.024
Age when told had inflamed prostate= 70+ Bronchitis history?=Yes 0.022
Age when told had enlarged prostate= 70+ Prior history of any cancer?=Yes 0.022
Prior history of any cance?r=Yes Family history of PC=Yes 0.022
Prior history of any cancer?=Yes No of relatives with PC=1 0.021
Age when told had inflamed prostate= 70+ Gall bladder stone or inflammation=Yes 0.021
Age when told had inflamed prostate= 70+ Smoke regularly now?=Yes 0.021
No of cigarettes smoked daily=80+ Bronchitis history?=Yes 0.021
Age when told had inflamed prostate= 70+ During past year, how many times wake up in the night to urinate?=Thrice 0.021
Age when told had inflamed prostate= 70+ Smoked pipe=current smoker 0.021
Age when told had inflamed prostate= 70+ Diabetes history=yes 0.02
Age when told had inflamed prostate= 70+ No. of brother=7+ 0.02
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated