Prerpints.org logo
Preprint
Article

Caloric Effect Due to the Aharonov-Bohm Flux in an Antidot

This version is not peer-reviewed.

Submitted:

24 August 2023

Posted:

29 August 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
In this work, we report the caloric effect for an electronic system of the antidot type, modeled by combining a repulsive and attractive potential (parabolic confinement). In this system, we consider the action of a perpendicular external magnetic field and the possibility of having an Aharonov-Bohm flux (AB-flux) generated by a current passing through a solenoid placed inside the forbidden zone for the electron. The energy levels are obtained analytically, and the model is known as the Bogachek and Landman model. We propose to control the caloric response of the system by varying only the AB-flux, finding that in the absence of an external magnetic field, the maximization of the effect always occurs at the same AB-flux intensity independent of the temperature while fixing the external magnetic field at a non-zero value breaks this symmetry and changes the point where the caloric phenomenon is maximized and is different depending on the temperature to which the process is carried. Due to the great diversity in technological applications that have antidots in electronics, the possibility of controlling their thermal response just by varying the intensity of the internal current inside the solenoid can be a platform of interest for experimental studies.
Keywords: 
Subject: 
Physical Sciences  -   Thermodynamics

1. Introduction

Innovation in refrigeration systems represents a current research topic due to our planet’s deep climate crisis [1]. The search for materials to replace the compression gases usually used in such techniques is a focus of interest in the industry [2,3]. Within this framework, a topic strongly linked to the study of materials has been developed during the last time and corresponds to the so-called caloric effects. These effects have a straightforward concept: if a substance has a control parameter that governs a thermodynamic process, the variation of this parameter will generate a change in the entropy of the system, and this change will be proportional to the heat that could be used to cool or heat another technological device according to the second law of thermodynamics. That is why systems with controllable phase transitions are (in most cases) the most studied, since in general, in this type of transition, the entropy variation of the system is maximized, which results in an increase of heat and consequently the possibility of further heating or cooling an external system more intensively [3,4]. Among these phenomena, the following effects stand out: magnetocaloric (MC) [5,6,7,8,9,10,11,12,13], electrocaloric (ELC) [14,15,16], elastocaloric (EC) [17,18], and barocaloric (BC) [19,20,21,22]. The first of these effects is due to changes in the external magnetic field on the system, the second due to changes in the electric field, the third due to changes in stress, and the last due to changes in pressure.
The most widely studied caloric effect is the magnetocaloric effect (MCE), which corresponds fundamentally to the temperature variation of a magnetic material due to the change in the external magnetic field applied over the system. It has aroused great interest in the scientific community due to its potential applicability and versatility in its use and the great study of the magnetic properties of different types of materials at present [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. We highlight the works associated with high-temperature caloric materials [36], antiferromagnetic and ferromagnetic interactions [23,30,44,45,46], heavy lanthanides [47], Fe-Rh alloys [48] and diamagnetic systems [49,50,51,52,53,54].
The MCE has been studied in a quantum dot array where the material temperature variation due to the external magnetic field change has been analyzed for controllable additional effects: geometric confinement, Zeeman, spin-orbit coupling, electric field, and Rashba effect [55,56]. These effects either enhance the thermal effect or make the system respond directly or inversely, making it an ideal platform for technological sensors [57]. A less explored material for caloric effects corresponds to antidots, structures with significant potential for high-density data storage due to the possibility of controlling the domain walls of the system. In simple words, an antidot is a potential hill inaccessible to 2D electrons [58,59,60,61,62,63]. Technological advances allow these systems to work even below T = 1 K in temperature [64,65,66,67]. On simple model to characterize an antidot is the one proposed by Bogachek and Landman model [68], which constitutes a combination of repulsive potential ( U ( r ) ∝ r − 2 ) and attractive potential ( U ( r ) ∝ r 2 ) leaving the electron confined in a finite region of space. In addition to these potentials of a purely geometrical nature, this model contemplates the action of an external magnetic field perpendicular to the ring-like structure where the electron is located and considers the possibility of having an Aharonov-Bohm flux (AB-flux) in space, which is generated by a current passing through a solenoid located in the center of the system. In previous work, we found that AB-flux strongly controls the oscillatory behavior of the MCE, thus acting as a control parameter for the cooling or heating of the MCE. Given this previous analysis, a valid question is whether a caloric effect is associated with AB-flux control. That is, even in the absence of an external magnetic field, what would be the thermal response of this system to changes in the current inside the solenoid? In this paper, we answer this question and additionally see the effects on this response that have the controllable parameters in the model: the size of the antidot, the parabolic trap intensity, and the intensity of the external magnetic field (fixed in this study). The paper is organized as follows: first, there will be an introduction to the energy model presented in Section 2, then a discussion of the thermodynamics obtained from the canonical partition function and the physical definitions to quantify the caloric effect shown in Section 3 to finally show the results and discussions for the case without external field and with external field present on the material in Section 4.

2. Energy Model for the Confined Electron

Let us consider the model described by Bogachek and Landman, which corresponds to the description of a system given by an electron in the presence of a repulsive potential U A D ( r ) , an AB-flux ( Φ A B ) , an external magnetic field B and finally a parabolic potential U D ( r ) . The total Hamiltonian, which describes the system, is given by
H ^ = 1 2 m * p + e A 2 + U A D ( r ) + U D ( r ) .
Here, m * is the effective electron mass, A is the total vector potential, and the terms U A D ( r ) and U D ( r ) are given by
U A D ( r ) = ζ r 2 , U D ( r ) = 1 2 m * ω 0 2 r 2 ,
where the constant ζ is related to the chemical potential μ and the effective radius of the antidot r 0 given by the relation μ = ζ r 0 2 and where ω 0 is the parabolic trap frequency. The total vector potential involves two terms, A = A 1 + A 2 , where A 1 is related to the external magnetic field B = ∇ × A 1 , and A 2 describes the additional magnetic flux Φ A B inside the antidot. For the case of an external perpendicular magnetic field along the z direction, B = z ^ B , leads to energy levels for the confined electron
E n m a d = ℏ Ω 2 n + m + α 2 + a 2 1 / 2 + 1 + 1 2 ℏ ω c m + α ,
where, ω c = e B m * is the cyclotron frequency, Ω = ω 0 1 + ω c 2 ω 0 2 1 2 is the effective frequency of the trap, n, m are the radial and magnetic quantum numbers and a 2 = 2 m * ζ ℏ 2 = 2 m * μ ℏ 2 r 0 2 = k F 2 r 0 2 , is a constant proportional to antidot radius ( r 0 ) , in which k F is the Fermi wave vector of the electron. The values reported for a are located in the region of 0 ≤ a ≤ 10 in the original research [68]. The parameter α is defined in the form α = Φ A B Φ 0 , where Φ 0 = h 2 e is the magnetic flux quantum. The connection between the α parameter with the AB-flux is given by [69]
α = Φ A B Φ 0 = A H Φ 0 = π r s 2 H Φ 0 ,
where r s correspond to the radius of the solenoid, H the value of the magnetic field generated by the current inside the same, and A = π r s 2 is the solenoid section area, whose normal vector is parallel to the magnetic field H . We recall that the field H only exists for 0 < r ≤ r s and is zero outside of the solenoid (i.e., for r > r c ) . Thus, for given α , the intensity of the magnetic field inside the solenoid has the form of H = α Φ 0 / π r s 2 . Recent technological advances allow fabricating nano-solenoids with a radius of r s = 35 nm, made by graphene [70].

3. Calculation of Partition Function and Thermodynamic Functions

We can calculate the partition Z a d function, using the general solution of Equation (3), and summing over n ( n = 0 , 1 , 2 , . . . ) and m = 0 , ± 1 , ± 2 , . . .
Z a d = ∑ n , m e − β E n m a d .
Unfortunately, the structure of the energy levels of Equation (3) does not allow a full analytical solution, so we use numerical calculations to obtain the canonical partition function of Equation (5). We separate the contributions of antidot energy ( E n m a d ) in the form
Z = ∑ n e − 2 β ℏ Ω n + 1 2 ∑ m e − β ℏ Ω ( m + α ) 2 + a 2 1 2 − β ℏ ω B 2 m + α = 1 2 csch β ℏ Ω ∑ m e − β ℏ Ω ( m + α ) 2 + a 2 1 2 − β ℏ ω B 2 m + α .
The values that α can take are not priori-restricted. However, there is a particularity in the energy spectrum given by Equation (3) that has repercussions on the partition function and, therefore, in the thermodynamic quantities. If α takes integer values N , the partition function will take the same values as α = 0 . This is because it is always possible (if α is an integer) to write a new quantum number of the form m ˜ = m + α and make the sum of different energy levels of the partition function with the new quantum number. Concerning the range of temperature in our calculations, we work in the range from 0.5 K to 2 K, allowing us to consider the quantum number m = − 70 to m = 30 , which is sufficient to guarantee a good convergence in the thermodynamic calculations that will be presented in this work.

3.1. Entropy of the System and Caloric Response

In our thermodynamic analysis, it is important to recall that the electronic entropy is derived from the partition function Z . In the generic form:
S e ( T , B , α ) = k B T ∂ ln Z ∂ T B , α + k B ln Z .
On the other hand, the total entropy for this model can be written as
S t = S e ( T , B , α ) + S l ( T ) ,
where S l ( T ) is the entropy of the lattice related to the contribution of phonons in the system. Equation (8) assumes the following approximations: The entropy of phonons relies solely on temperature, thus neglecting the influence of phonon coupling with external magnetic fields. Furthermore, for the comprehensive assessment of entropy, distinctly for electrons and phonons, the discussion within this study excludes the consideration of electron-phonon interactions. Thus, the total entropy variation resulting from the change in the AB-flux in a process at constant temperature and a constant external magnetic field will be given by the expression:
− Δ S t = S e ( T , B , α 0 ) − S e ( T , B , α ) ,
where α 0 corresponds to the initial value of the AB-flux.
Another way to quantify this effect is to obtain the temperature variation directly when performing an adiabatic process, thus obtaining the so-called Δ T a d . This temperature variation can be visualized in a contour plot by applying the condition:
S e ( T , B , α ) = S e ( T 0 , B 0 , α 0 ) = cnt .
It is important to note that when you have a case in which − Δ S e > 0 , let’s call this kind of response of direct type. The system will heat up, while when the response is of the − Δ S e < 0 type, we call this inverse type response, and consequently, the system will cool down. Therefore, we expect for direct response a Δ T a d > 0 , and for the case of an inverse response, we expect a Δ T a d < 0 for the final result of the caloric phenomena.
We must note the differences concerning our previous work in Ref. [69]. In that work, a study of the MCE of this model is performed so that the reported temperature variations can be obtained directly through integration over the specific heat at a constant magnetic field and the derivative of magnetization of the system [69]. In our case, the correct expression to determine the temperature variation can be calculated from the total derivative of the entropy function S ≡ S ( T , α ) (with a fixed value of the external magnetic field) given by
d S = ∂ S ∂ T α d T + ∂ S ∂ α T d α .
In an isentropic trajectory, the total derivative of Equation (11) is zero, so by direct integration, Δ T a d of the proposed caloric phenomenon corresponds to the following expression:
Δ T a d = − ∫ α i α f T C α ∂ S ∂ α T d α ,
where C α = T ∂ S ∂ T α corresponds to specific heat at constant α parameter. We, therefore, emphasize that in this work, the expression for the Δ T a d presented in Equation (12) is a caloric effect purely related to the change of AB-flux. That is why we can not qualify this study as an MCE type.

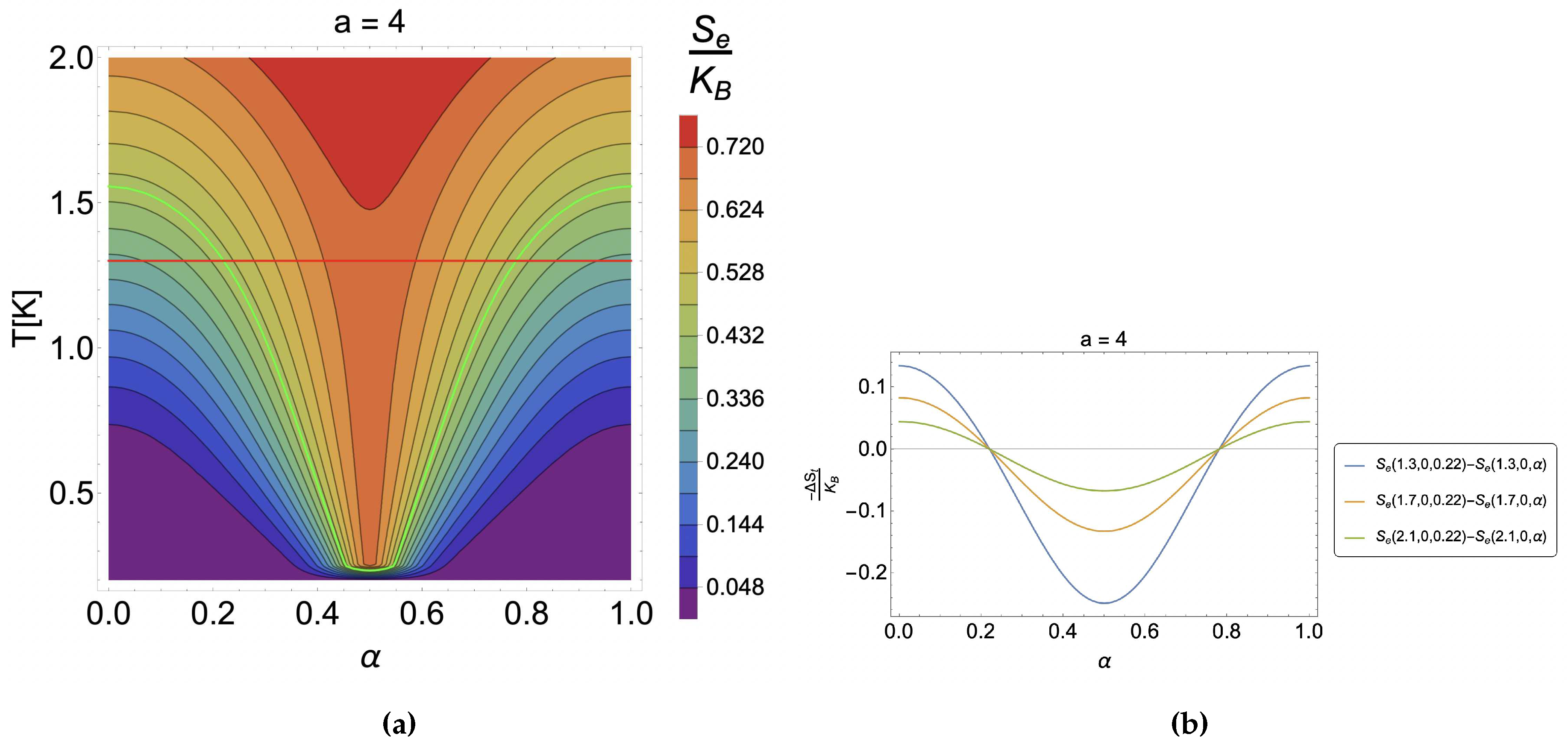
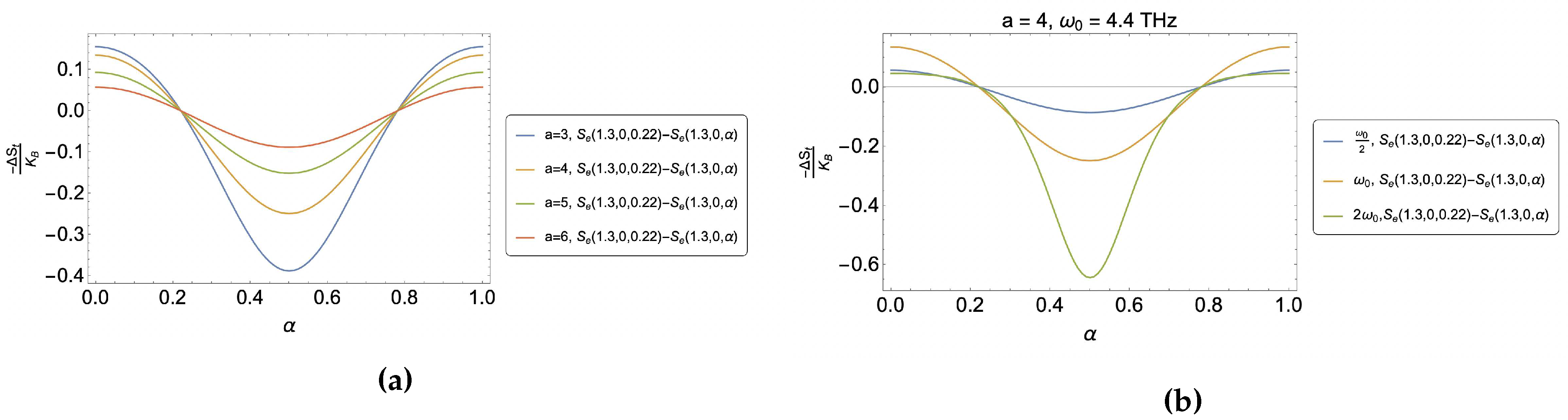
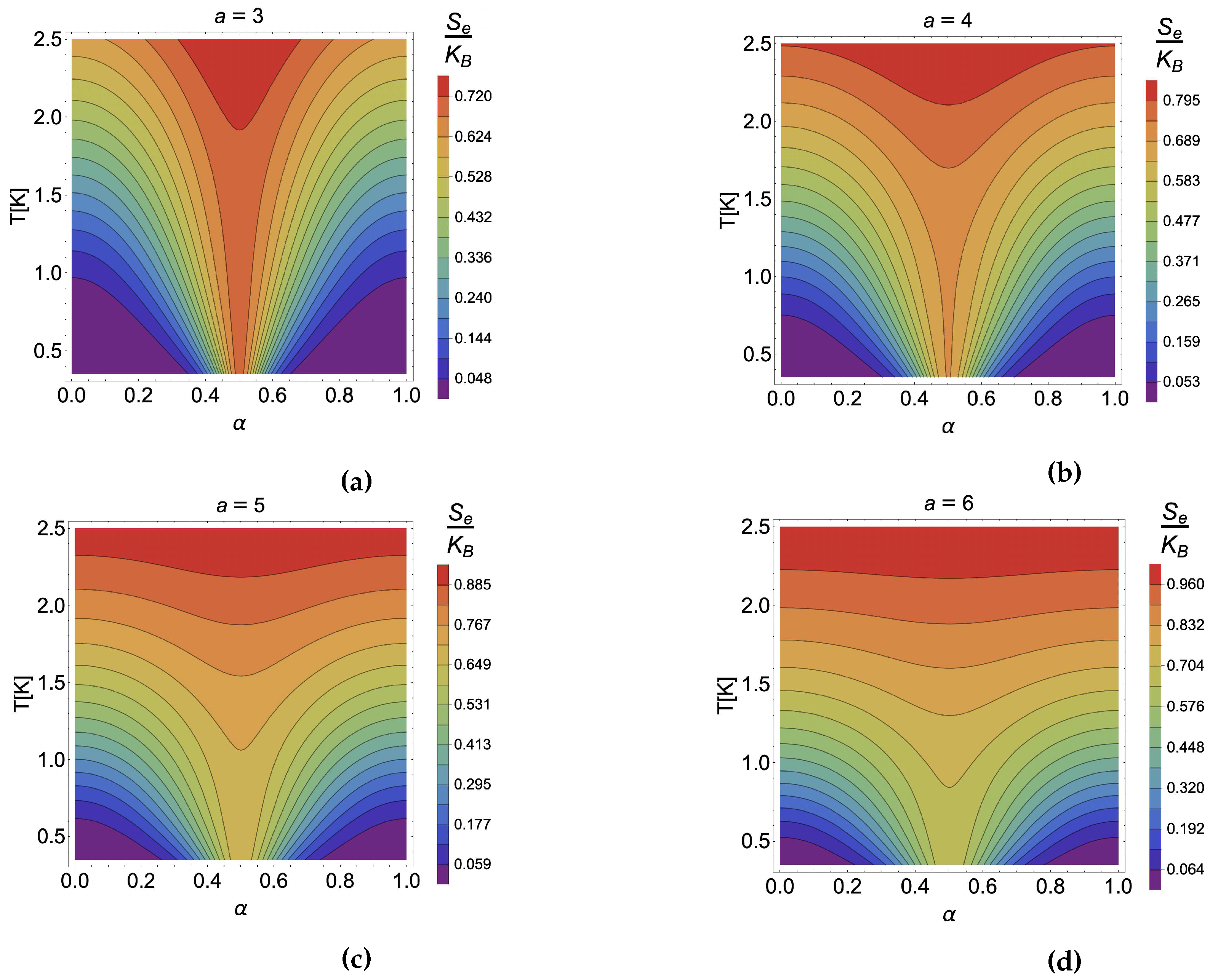
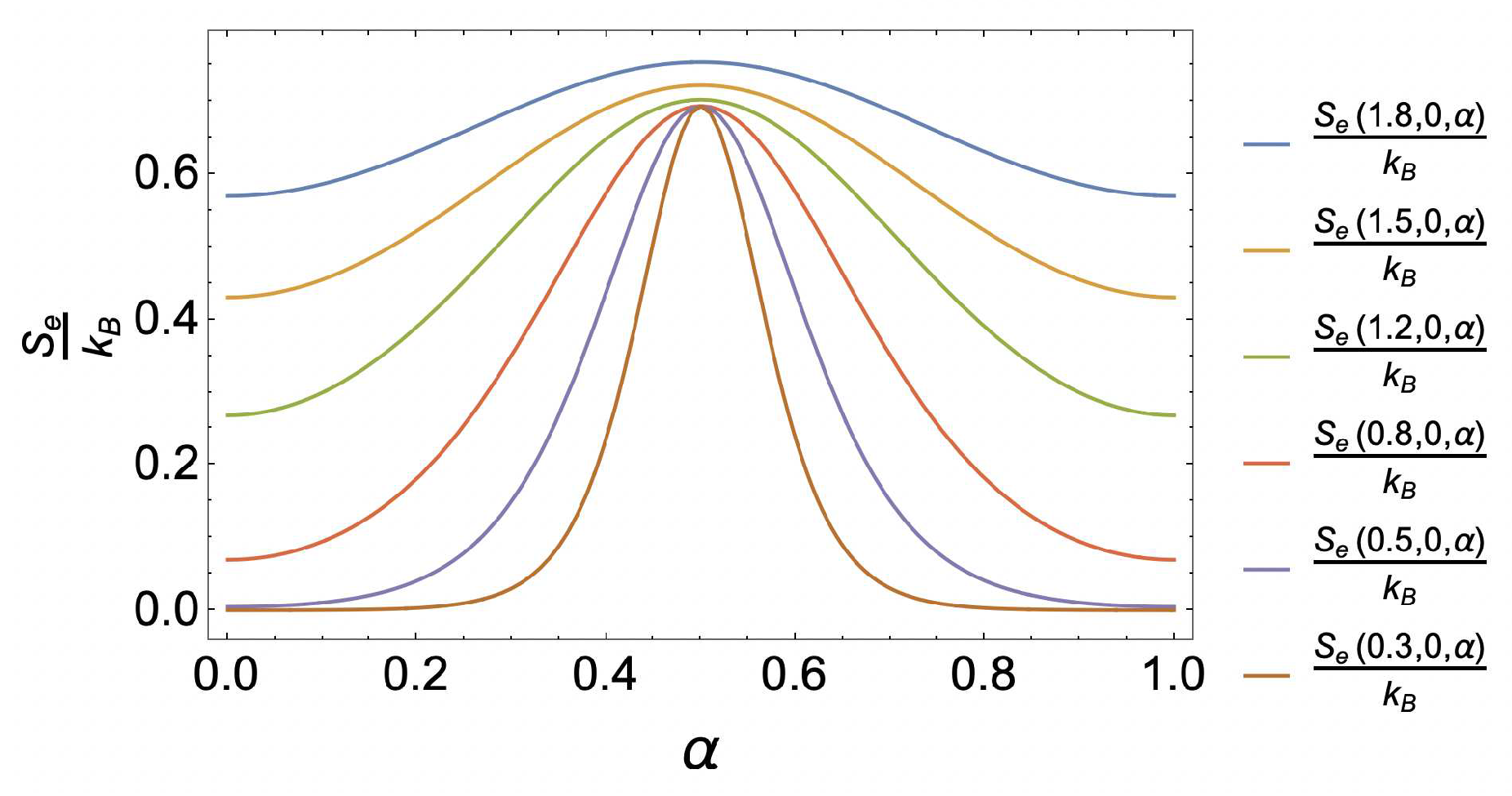
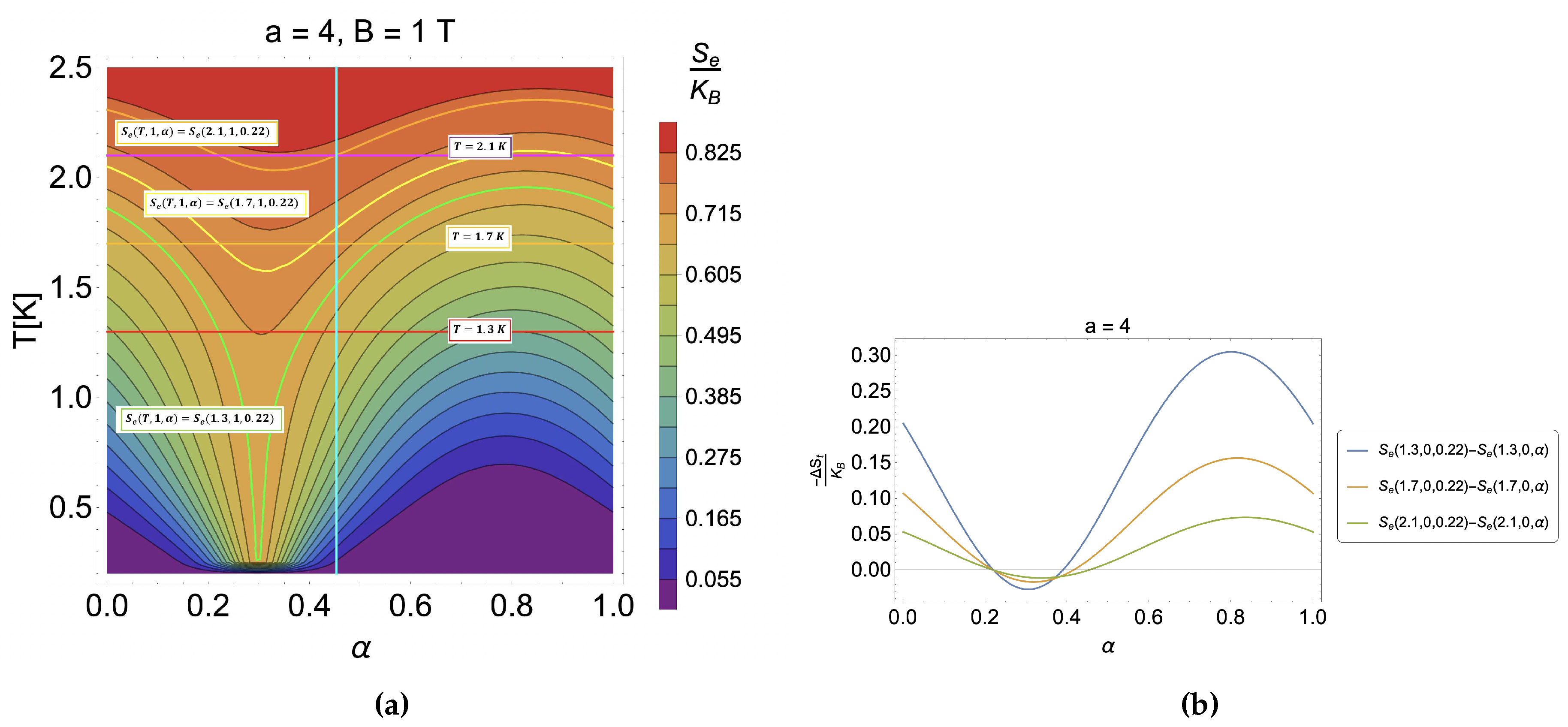
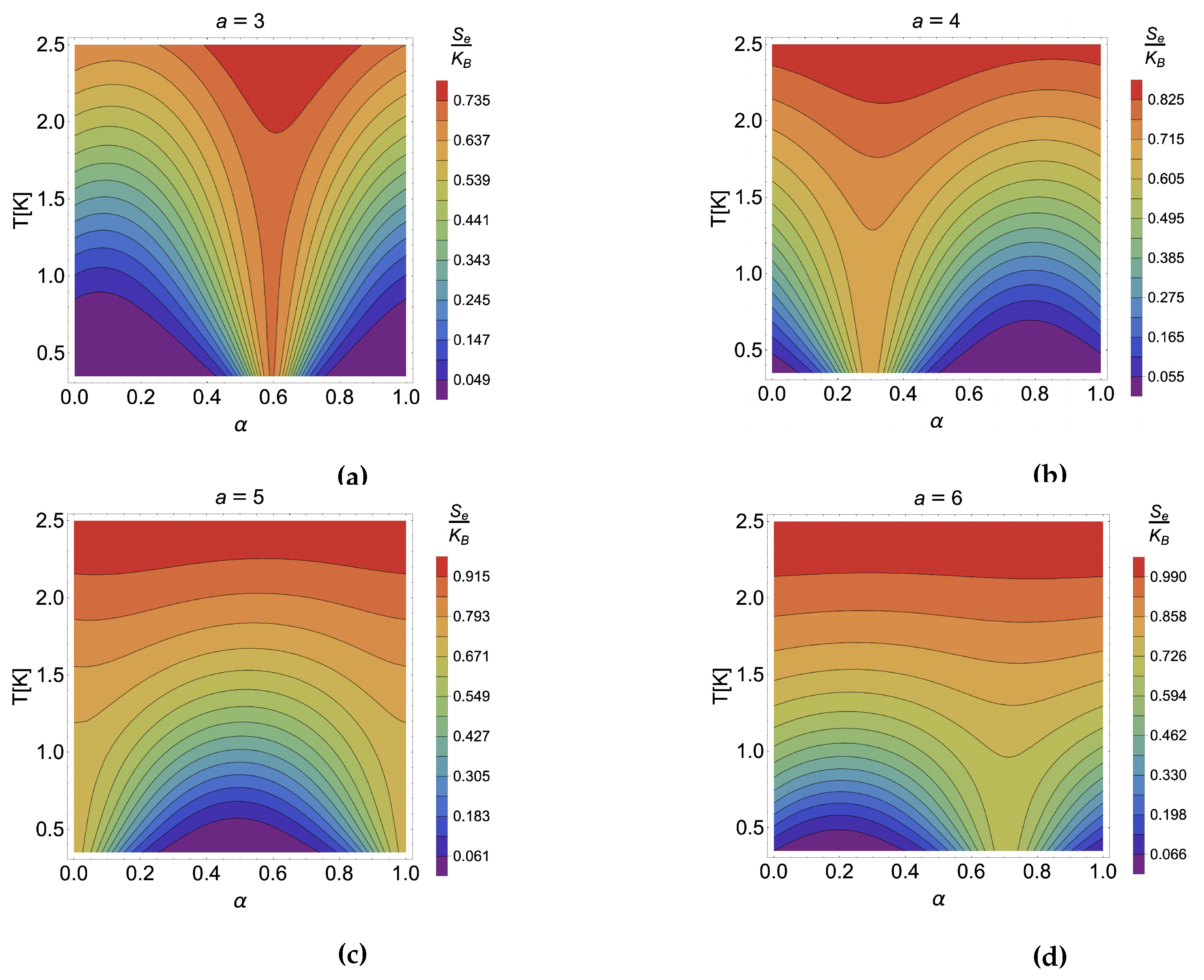
4. Results and discussion

4.1. Caloric effect without external magnetic field

We will begin the discussion of results in the absence of an external magnetic field with parameters given by: ω d = 4.4 THz, a = 4 , and m * = 0.067 m e (GaAs) [71,72]. In Figure 1, we can observe in panel (a) the contour plot for an isentropic process of the form S e ( T , 0 , α ) = cnt., where we can directly obtain the relation between temperature and AB-flux. We note from there that the temperature has a decreasing and then increasing behavior, which means that depending on the initial value we take as a reference to start the process, the system can be cooled or heated. To visualize this, on the contour plot, we have drawn a trajectory at a constant temperature given by T = 1.3 K (red horizontal line in Figure 1(a)), and we have marked the process of constant entropy in green color corresponding to S e ( 1.3 , 0 , 0.22 ) (Figure 1(a)). It can be seen that depending on the α region, the initial temperature of the system can be lower or higher depending on the final value that the control parameter will take. All points on the green line above the red line will be points where the temperature will always be higher than the initial temperature. In contrast, points on the green line below will result in final temperatures lower than the initial reference temperature given for the substance. Additionally, we find that the maximum effect for this case occurs for α = 0.5 . We will see later if this holds for all ranges of model parameters. The maximum temperature variation observed for this case is about ∼ 1 K (in absolute value) since the temperature at the minimum point of the contour marked by the green line at α = 0.5 is T = 0.34 K, thus Δ T = T − 1.3 K = − 0.96 K.
The temperature variation results discussed from Figure 1(a) should be consistent with the results that would be obtained for the − Δ S t . Therefore there should be regions where this result is positive and in others negative. This can be visualized in Figure 1(b), where we observe an oscillatory behavior for the entropy variation at a constant temperature as a function of α obtaining the minimum for all temperatures shown there, at α = 0.5 . It is also observed that the temperature increase decreases the effect considerably for the same initial conditions. For the variation of the antidot size associated with the value of the parameter a, we can appreciate from Figure 2(a) the variation of the entropy as a function of α for equal parameters of initial temperature, fixed external field and AB-flux where it is observed that as the size of the antidot increases, the heating effect decreases. This is because if we look at the energy spectrum given by Equation (3), α (contained between 0 and 1 in this study) becomes very small compared to the values of a presented. Consequently, small variations of α 2 will not compensate for the quadratic order in the energy of a 2 , thus making the thermal changes less noticeable when using the AB-flux as a control parameter of the model.
Another adjustable parameter corresponds to the frequency of the parabolic trap, ω 0 . Figure 2(b) shows the entropy variation as a function of α for different coupling frequencies for the same process parameters in temperature, external field, and initial value of α . As ω 0 increases, the proposed caloric effect also increases. This is consistent with the a parameter, where we discussed that as a decreases, the caloric effect increases. Consequently, increasing the value of the trap intensity further confines the electrons, and thus both effects, that of decreasing a and increasing ω 0 , lead to analogous results in this model.
To verify that the point where the caloric effect is maximized for the case in the absence of an external magnetic field is independent of the parameter a, we have plotted in Figure 3 the contours for the cases of constant entropy for a = 3 (a), a = 4 (b), a = 5 (c) and a = 6 (d). It is observed that independent of the value of the antidot size, the effect is maximized at the same value given by α = 0.5 . Of course, the intensity of each is different, the most remarkable being that of a = 3 presented in panel (a) of Figure 3. Also, it reinforces the results discussed above regarding the decrease of the heating effect as a increases where we see that the effect decreases strongly, finding, for example, for the case of a = 6 (panel (d) of the Figure 3), contour plots where almost horizontal curves are appreciated, which would mean that there is no temperature variation with changes in the α parameter and therefore the loss of the caloric phenomenon.
This exciting result about the location of the maximum caloric effect in the absence of an external magnetic field can be understood from the entropy plot as a function of the parameter α presented in Figure 4 for different temperatures between 1.8 K and 0.3 K. The entropy for any value of T clearly shows a maximum at α = 0.5 for all values of T. Consequently, the maximum in the caloric phenomenon will always be located at the same point. Of course, the most abrupt change is given for smaller and smaller temperatures. In contrast, the entropy will not show substantial variations around the α parameter as the temperature increases. It will generate horizontal curves, and no caloric effect associated with the deviation of the AB-flux will be reported.

4.2. Caloric effect in the presence of external magnetic field

In this subsection, we will analyze where a (constant) perpendicular magnetic field is present while thermodynamic processes are performed by varying the parameter α . To do so, we will first analyze the case of constant entropy contours for a = 4 of S e ( T , 1 , 0.22 ) . That is, we will fix the external field at 1 T. This case can be observed in Figure 5(a), where we appreciate that the maximum effect is now produced at another point different from 0.5. A symmetry breaking was observed for the caloric phenomenon when no external field was present. Moreover, let’s look at Figure 5(b). We see that the temperature now affects the maximum point of the effect, and again, contrary to the case without a field, the maximum for a fixed temperature is not seen for all cases at the same point. That is, the magnetic field generates a shift in the thermal response and windows of direct and inverse non-symmetrical heating effects to the variation of the proposed control parameter. In addition, not only the location of the maximum is modified, but also the passage from an inverse to a direct response for the caloric effect. Let’s compare Figure 2(b) with Figure 5(b), for a = 4 . The transfer from an inverse to a direct response type for the case without an external field co-occurs for any temperature at the same α parameter space point (with the same initial condition). In contrast, for the case with a magnetic field, this varies depending on the temperature at which the isothermal process occurs. As the temperature increases, the transfer from a direct to an inverse effect requires a more considerable change in the α parameter when the external field is applied. The different points where the heating effect changes can be seen in Figure 5(a), where the cases of S e ( T , 1 , α ) = S e ( 1.3 , 1 , 0.22 ) (green curve), S e ( T , 1 , α ) = S e ( 1.7 , 1 , 0.22 ) (yellow curve), and S e ( T , 1 , α ) = S e ( 2.1 , 1 , 0.22 ) (orange curve) and their respective horizontal curves at a constant temperature at T = 1.3 K (red line), T = 1.7 K (orange line) and T = 2.1 K (purple line) are plotted. For example, we have devised the vertical (light blue curve) at α ∼ 0.45 , which is the intersection point of the effect for the T = 2.1 K case. All the other transition points occur before that value in coherence with those presented in Figure 5(b).
Finally, we have plotted the different contour lines for the case of S ( T , 1 , α ) = cnt. in the Figure 6 for a = 3 (panel (a)), a = 4 (panel (b)), a = 5 (panel (c)) and a = 6 (panel (d)). The symmetry breaking in the caloric effect produced by the external field for different values of the antidot size can be seen. It is also corroborated that the effect decreases as the value of a increases in the same way as in the case without an external magnetic field. Regarding the intensity of the effect, there is no increase or decrease in the caloric phenomenon due to the presence of the external field. Therefore the net effect of a constant magnetic field perpendicular to the material generates a displacement in the space of the α parameter where the change from a direct response to an inverse type and from inverse to a direct one occurs.

5. Conclusions

In this work, we have presented the possibility of observing a caloric effect associated with the Aharonov- Bohm flux variation in an antidot-type system in a fixed magnetic field perpendicular to the system. In the absence of this external field, we have found that the effect is maximized for all cases treated in the same value of the Aharonov- Bohm flux independent of the temperature that follows the process. In contrast, the presence of the external field substantially modifies the location where the effect is maximized. We additionally report that the temperature variation associated with the entropy change at small antidot sizes is much more significant than at larger ones. We also studied the effect of the intensity of the parabolic trap on the system, showing that the higher the value of the trap we have, the more significant the caloric response is. Finally, we highlight that what is interesting in this work is that in the absence of an external magnetic field in the presence of changes in the intensity of the parameter associated with the Aharonov-Bohm flux, we found temperature variations (around ∼ 1 K). Aharonov- Bohm flux does not enter the phonon entropy of the system (or couples weakly) compared to how an external magnetic field would couple with the phonons. This is an advantage since the phonon entropy is usually dominant in the caloric phenomena compared to the other entropies of the system. Although it is generally modeled as a function that depends only on T, it may depend on the parameter that controls the caloric phenomenon. Therefore, it could not be compensated and canceled in an isothermal path hindering the pure measurement of the entropy temperature variation of the substance due to changes in its control parameter. Based on the discussion above, this proposal can be interesting from the experimental point of view regarding caloric effects and their possible technological applications.

Author Contributions

P. M and P. V. conceived the idea and made the numerical calculations. M. B. contributed to discussions and analysis of results. F. J. P has contributed to the numerical calculations, with the graphs of the manuscript and the analysis of results. F. J. P wrote the first version of the manuscript.

Acknowledgments

P.M-R. acknowledges support from ANID Fondecyt grant no. 1210312 and ANID PIA/Basal grant no. AFB 220001. M.E.B-V. acknowledges financial support from ANID Fondecyt, Iniciación en Investigación 2020 grant no. 11200032, ANID Fondecyt grant no. 1210312, “Millennium Nucleus in NanoBioPhysics” project NNBP NCN2021 _021. F.J.P. acknowledges financial support from ANID Fondecyt, Iniciación en Investigación 2020 grant no. 11200032, ANID Fondecyt grant no. 1210312, “Millennium Nucleus in NanoBioPhysics” project NNBP NCN2021 _021. P.V. acknowledges support from ANID Fondecyt grant no. 1210312 and ANID PIA/Basal grant no. AFB 220001.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Reis, M.S. Magnetocaloric and barocaloric effects of metal complexes for solid state cooling: Review, trends and perspectives. Coordination Chemistry Reviews 2020, 417, 213357. [Google Scholar] [CrossRef]
  2. Gschneidner, K. A., Jr.; Pecharsky, V. K. Magnetocaloric materials. Annual review of materials science 2020, 30, 387–429. [Google Scholar] [CrossRef]
  3. Franco, V.; Blázquez, J. S.; Ipus, J. J.; Law, J. Y.; Moreno-Ramírez, L. M.; Conde, A. Magnetocaloric effect: From materials research to refrigeration devices. Progress in Materials Science 2020, 93, 112–232. [Google Scholar] [CrossRef]
  4. Fishin, A. M.; Spichkin, Y. I. The magnetocaloric effect and its applications. PCRC Press.
  5. Warburg, E. Magnetische Untersuchungen. Ueber einige Wirkungen der Coërcitivkraft. Ann. Phys. (Leipzig) 1881, 249, 141–164. [Google Scholar] [CrossRef]
  6. Weiss, P.; Piccard, A. Le pheénoméne magnétocalorique. J. Phys. (Paris) 1917, 7, 103–109. [Google Scholar]
  7. Weiss, P.; Piccard, A. Sur un nouveau phénoméne magnétocalorique. Comptes Rendus 1918, 166, 352–354. [Google Scholar]
  8. Debye, P. Einige Bemerkungen zur Magnetisierung bei tiefer Temperatur. Annals of Physics 1926, 81, 1154–60. [Google Scholar] [CrossRef]
  9. Giauque, W. F.; Macdougall, D. P. The Production of Temperatures below One Degree Absolute by Adiabatic Demagnetization of Gadolinium Sulfate. Journal of the American Chemical Society 1935, 57, 1175–1185. [Google Scholar] [CrossRef]
  10. Brown, G. V. Magnetic heat pumping near room temperature. Journal of Applied Physics 1976, 47, 3673–3680. [Google Scholar] [CrossRef]
  11. Pecharsky, V. K.; Gschneidner, K. A. Jr. Giant Magnetocaloric Effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494–4497. [Google Scholar] [CrossRef]
  12. Reis, M. S. Oscillating magnetocaloric effect. Appl. Phys. Lett. 2011, 99, 052511. [Google Scholar] [CrossRef]
  13. Tarasenko, R.; Tkáč, V.; Orendáčová, A.; Orendáč, M.; Valentab, V.; Sechovský, V.; Feher, A. Experimental study of magnetocaloric effect in the two-level quantum system KTm(MoO4)2. Physica B: Condensed Matter 2018, 536, 450–453. [Google Scholar] [CrossRef]
  14. Shao, C.; Amirov, A. A.; Huang, H. A review on different theoretical models of electrocaloric effect for refrigeration. Frontiers in Energy 2023, 1–26. [Google Scholar] [CrossRef]
  15. Scott, J. F. Electrocaloric materials. Annual Review of Materials Research 2011, 41, 229–240. [Google Scholar] [CrossRef]
  16. Jia, Y.; Sungtaek Ju, Y. A solid-state refrigerator based on the electrocaloric effect. Applied Physics Letters 2012, 100. [Google Scholar] [CrossRef]
  17. Jia, Y.; Sungtaek Ju, Y.; Qian, S.; Geng, Y.; Wang, Y.; Ling, J.; Hwang, Y.; Radermacher, R.; Cui, J. A review of elastocaloric cooling: Materials, cycles and system integrations. International journal of refrigeration 2016, 64, 101380. [Google Scholar]
  18. Chen, J.; Lei, L.; Fang, G. Elastocaloric cooling of shape memory alloys: A review. Materials Today Communications 2021, 28, 102706. [Google Scholar] [CrossRef]
  19. Lloveras, P.; Tamarit, J. L. Advances and obstacles in pressure-driven solid-state cooling: A review of barocaloric materials. MRS Energy Sustainability 2021, 8, 3–15. [Google Scholar] [CrossRef]
  20. Cirillo, L.; Greco, A.; Masselli, C. Cooling through barocaloric effect: A review of the state of the art up to 2022. Thermal Science and Engineering Progress 2022, 33, 101380. [Google Scholar] [CrossRef]
  21. Lloveras, P.; Stern-Taulats, E.; Barrio, M.; Tamarit, J. L.; Crossley, S.; Li, W.; Moya, X. Giant barocaloric effects at low pressure in ferrielectric ammonium sulphate. Nature communications 2015, 6, 8801. [Google Scholar] [CrossRef]
  22. Lloveras, P.; Aznar, A.; Barrio, M.; Negrier, P.; Popescu, C.; Planes, A.; Tamarit, J. L. Colossal barocaloric effects near room temperature in plastic crystals of neopentylglycol. Nature communications 2019, 10, 1803. [Google Scholar] [CrossRef] [PubMed]
  23. Pathak, A.; K., *!!! REPLACE !!!*; Gschneidner, K. A.; Pecharsky, V. K. Negative to positive magnetoresistance and magnetocaloric effect in Pr0.6Er0.4Al2. Journal of Alloys and Compounds 2015, 621, 411–414. [Google Scholar] [CrossRef]
  24. Florez, J. M.; Vargas, P.; Garcia, C.; Ross, C. A. J. Phys. Condens. Matter 2013, 25, 226004. [CrossRef] [PubMed]
  25. Hudl, M.; Campanini, D.; Caron, L.; Hoglin, V.; Sahlberg, M.; Nordblad, P.; Rydh, A. Thermodynamics around the first-order ferromagnetic phase transition of Fe2P single crystals. Phys. Rev. B 2014, 90, 144432. [Google Scholar] [CrossRef]
  26. Miao, X. F.; Caron, L.; Roy, P.; Dung, N. H.; Zhang, L.; Kockelmann, W. A.; et al. Tuning the phase transition in transition-metal-based magnetocaloric compounds. Phys. Rev. B 2014, 89, 174429–6. [Google Scholar] [CrossRef]
  27. Sosin, S.; Prozorova, L.; Smirnov, A.; Golov, A.; Berkutov, I.; Petrenko, O.; et al. Magnetocaloric effect in pyrochlore antiferromagnet Gd2Ti2O7. Phys. Rev. B 2005, 71, 2005094413. [Google Scholar] [CrossRef]
  28. Wang, F.; Yuan, F.-Y.; Wang, J.-Z.; Feng, T.-F.; Hu, G.-Q. Conventional and inverse magnetocaloric effect in Pr2CuSi3 and Gd2CuSi3 compounds. Journal of Alloys and Compounds 2014, 592, 63–66. [Google Scholar] [CrossRef]
  29. Du, Q.; Chen, G.; Yang, W.; Wei, J.; Hua, M.; Du, H.; et al. Magnetic frustration and magnetocaloric effect in AlFe2-x Mn x B2 (x = 0-0.5) ribbons. Journal of Physics D-Applied Physics 2015, 48, 335001. [Google Scholar] [CrossRef]
  30. Balli, M.; Fruchart, D.; Zach, R. Negative and conventional magneto- caloric effects of a MnRhAs single crystal. Journal of Applied Physics 2014, 115, 203909. [Google Scholar] [CrossRef]
  31. Kolat, V. S.; Izgi, T.; Kaya, A. O.; Bayri, N.; Gencer, H.; Atalay, S. Metamagnetic transition and magnetocaloric effect in charge-ordered Pr0.68Ca0.32- xSrxMnO3 (x=0, 0.1, 0.18, 0.26 and 0.32) compounds. Journal of Magnetism and Magnetic Materials 2010, 322, 427433. [Google Scholar] [CrossRef]
  32. Phan, M. H.; Morales, M. B.; Bingham, N. S.; Srikanth, H.; Zhang, C. L.; Cheong, S.-W. Phase coexistence and magnetocaloric effect in La5/8-y Pry Ca3/8MnO3(y= 0.275). Phys. Rev. B 2010, 81, 094413. [Google Scholar] [CrossRef]
  33. Patra, M.; Majumdar, S.; Giri, S.; Iles, G. N.; Chatterji, T. Anomalous magnetic field dependence of magnetocaloric effect at low temperature in Pr0.52Sr0.48MnO3 single crystal. Journal of Applied Physics 2010, 107, 076101. [Google Scholar] [CrossRef]
  34. Szalowski, K.; Balcerzak, T. Normal and inverse magnetocaloric effect in magnetic multilayers with antiferromagnetic interlayer coupling. Journal of Physics Condensed Matter 2014, 26(38), 386003. [Google Scholar] [CrossRef] [PubMed]
  35. Midya, A.; Khan, N.; Bhoi, D.; Mandal, P. Giant magnetocaloric effect in magnetically frustrated EuHo2O4 and EuDy2O4 compounds. Applied Physics Letters 2012, 101, 132415. [Google Scholar] [CrossRef]
  36. Moya, X.; Kar-Narayan, S.; Mathur, N. D. Caloric materials near ferroic phase transitions. Nature Materials 2014, 13, 439–450. [Google Scholar] [CrossRef]
  37. Guillou, F.; Porcari, G.; Yibole, H.; van Dijk, N.; Bruck, E. Taming the First-Order Transition in Giant Magnetocaloric Materials. Advanced Materials 2014, 26, 2671–2675. [Google Scholar] [CrossRef] [PubMed]
  38. Gong, Y.-Y.; Wang, D.-H.; Cao, Q.-Q.; Liu, E.-K.; Liu, J.; Du, Y.-W. Electric Field Control of the Magnetocaloric Effect. Advanced Materials 2014, 27, 801–805. [Google Scholar] [CrossRef]
  39. Nalbandyan, V. B.; Zvereva, E. A.; Nikulin, A. Y.; Shukaev, I. L.; Whangbo, M.- H.; Koo, H.-J.; et al. New Phase of MnSb2O6 Prepared by Ion Exchange: Structural, Magnetic, and Thermodynamic Properties. Inorganic Chemistry 2015, 54, 1705–1711. [Google Scholar] [CrossRef] [PubMed]
  40. Tkac, V.; Orendacova, A.; Cizmar, E.; Orendac, M.; Feher, A.; Anders, A. G. Giant reversible rotating cryomagnetocaloric effect in KEr(MoO4)2 induced by a crystal-field anisotropy. Phys. Rev. B 2015, 92, 024406–5. [Google Scholar] [CrossRef]
  41. Tamura, R.; Ohno, T.; Kitazawa, H. A generalized magnetic refrigeration scheme. Applied Physics Letters 2014, 104, 052415–5. [Google Scholar] [CrossRef]
  42. Tamura, R.; Tanaka, S.; Ohno, T.; Kitazawa, H. Magnetic ordered structure dependence of magnetic refrigeration efficiency. Journal of Applied Physics 2014, 116, 053908-13. [Google Scholar] [CrossRef]
  43. Li, G.; Wang, J.; Cheng, Z.; Ren, Q.; Fang, C.; Dou, S. Large entropy change accompanying two successive magnetic phase transitions in TbMn2Si2 for magnetic refrigeration. Applied Physics Letters 2015, 106, 182405. [Google Scholar] [CrossRef]
  44. Szałowski, K.; Balcerzak, T. Normal and inverse magnetocaloric effect in magnetic multilayers with antiferromagnetic interlayer coupling. J. Phys.: Condens. Matter 2014, 26, 386003. [Google Scholar] [CrossRef] [PubMed]
  45. von Ranke, J. P.; Alho, B. P.; Nóbrega, B.P.; de Oliveira, N. A. Understanding the inverse magnetocaloric effect through a simple theoretical model. Physica B 2009, 404, 056004. [Google Scholar] [CrossRef]
  46. von Ranke, J. P.; de Oliveira, N. A.; Alho, B. P.; Plaza, E. J. R.; de Sousa, V.S. R.; Caron, L.; Reis, M. S. Understanding the inverse magnetocaloric effect in antiferro- and ferrimagnetic arrangements. J. Phys.: Condens. Matter 2009, 21, 3045–3047. [Google Scholar] [CrossRef]
  47. Zverev, V. I.; Tishin, A. M.; Min, Z.; Mudryk, Y.; Gschneidner Jr, K. A.; Pecharsky, V.K. Magnetic and magnetothermal properties, and the magnetic phase diagram of single-crystal holmium along the easy magnetization direction. J. Phys.: Condens. Matter 2015, 27, 146002. [Google Scholar] [CrossRef]
  48. Zverev, V. I.; Saletsky, A. M.; Gimaev, R. R.; Tishin, A. M.; Miyanaga, T.; and Staunton, J. B. Influence of structural defects on the magnetocaloric effect in the vicinity of the first order magnetic transition in Fe50.4 Rh49.6. Applied Physics Letters 2016, 108, 192405. [Google Scholar] [CrossRef]
  49. Reis, M. S. Oscillating adiabatic temperature change of diamagnetic materials. Solid State Communications 2012, 152, 921–923. [Google Scholar] [CrossRef]
  50. Reis, M. S. Oscillating magnetocaloric effect on graphenes. Appl. Phys. Lett. 2012, 101, 222405. [Google Scholar] [CrossRef]
  51. Reis, M. S. Step-like features on caloric effects of graphenes. Physics Letters A 2014, 378, 918–921. [Google Scholar] [CrossRef]
  52. Reis, M. S. Magnetocaloric cycle with six stages: Possible application of graphene at low temperature. Appl. Phys. Lett. 2015, 107, 102401. [Google Scholar] [CrossRef]
  53. Alisultanov, Z.Z.; Reis, M. S. Oscillating magneto - and electrocaloric effects on bilayer graphenes. Solid State Communications 2015, 206, 17–21. [Google Scholar] [CrossRef]
  54. Ma, N.; Reis, M.S. Barocaloric effect on graphene. Scientific Reports 2017, 7, 13257. [Google Scholar] [CrossRef]
  55. Sedehi, H. R.; Khordad, R. Magnetocaloric effect, magnetic susceptibility and specific heat of tuned quantum dot/ring systems. Physica E: Low-dimensional Systems and Nanostructures 2021, 134, 114886. [Google Scholar] [CrossRef]
  56. Rastegar-Sedehi, H. R. Magnetocaloric effect in Rashba spin-orbit coupling and Zeeman splitting of a narrow nanowire quantum dot. The European Physical Journal Plus 2021, 136, 1–8. [Google Scholar] [CrossRef]
  57. Negrete, O.A.; Peña, F. J.; Florez, J. M.; Vargas, P. Magnetocaloric Effect in Non-Interactive Electron Systems: “The Landau Problem” and Its Extension to Quantum Dots Entropy 2018, 20, 557. [PubMed]
  58. Kato, M.; Endo, A.; Katsumoto, S.; and Iye, Y. Aharonov-Bohm-type oscillations in antidot lattices in the quantum Hall regime. Phys. Rev. B 2008, 77, 155318. [Google Scholar] [CrossRef]
  59. Gräfe, J.; Weigand, M.; Stahl, C.; Träger, N.; Kopp, M.; Schütz, G.; Goering, E.; Haering, F.; Ziemann, P.; Wiedwald, U. Combined first-order reversal curve and x-ray microscopy investigation of magnetization reversal mechanisms in hexagonal antidot lattices. Phys. Rev. B 2016, 93, 014406. [Google Scholar] [CrossRef]
  60. Gräfe, J.; Weigand, M.; Stahl, C.; Träger, N.; Schütz, G.; Goering, E.; Skripnik, M.; Nowak, U.; Haering, F.; Ziemann, P.; Wiedwald, U. Geometric control of the magnetization reversal in antidot lattices with perpendicular magnetic anisotropy. Phys. Rev. B 2016, 93, 104421. [Google Scholar] [CrossRef]
  61. Weiss, D.; Richter, K.; Menschig, A.; Bergmann, R.; Schweizer, H.; von Klitzing, K.; Weimann, G. Quantized Periodic Orbits in Large Antidot Arrays. Phys. Rev. Lett. 1993, 70, 4118. [Google Scholar] [CrossRef]
  62. Vukmirović, N.; Stojanović, V.; and Vanević, M. Electron-phonon coupling in graphene antidot lattices: An indication of polaronic behavior. Phys. Rev. B 2010, 81, 041408. [Google Scholar] [CrossRef]
  63. Tornow, M.; Weiss, D.; Klitzing, K.; Eberl, K.; Bergman, E.; and Strelniker, Y. Anisotropic Magnetoresistance of a Classical Antidot Array. Phys. Rev. Lett. 1996, 77, 147. [Google Scholar] [CrossRef]
  64. Prance, J. R.; Smith, C. G.; Griffiths, J. P.; Chorley, S. J.; Anderson, D.; Jones, G. A. C.; Farrer, I.; Ritchie, D. A. Electronic Refrigeration of a Two-Dimensional Electron Gas. PRL 2009, 102, 146602. [Google Scholar] [CrossRef] [PubMed]
  65. Hübel, A.; Held, K.; Weis, J.; Klitzing, K. v. Correlated Electron Tunneling through Two Separate Quantum Dot Systems with Strong Capacitive Interdot Coupling. Phys. Rev. Lett. 2008, 101, 186804. [Google Scholar] [CrossRef] [PubMed]
  66. Hübel, A.; Weis, J.; Dietsche, W.; Klitzing, K. v. Two laterally arranged quantum dot systems with strong capacitive interdot coupling. Appl. Phys. Lett. 2007, 91, 102101. [Google Scholar] [CrossRef]
  67. Donsa, S.; Andergassen, S.; Held, K. Double quantum dot as a minimal thermoelectric generator. Phys. Rev. B 2014, 89, 125103. [Google Scholar] [CrossRef]
  68. Bogachek, E.N.; Landman, U. Edge states, Aharonov-Bohm oscillations, and thermodynamic and spectral properties in a two-dimensional electron gas with an antidot Phys. Rev. B 1995, 52, 14067. [Google Scholar] [CrossRef]
  69. Negrete, O. A.; Peña, F. J.; Vargas, P. Magnetocaloric effect in an antidot: The effect of the Aharonov-Bohm flux and antidot radius. Entropy 2018, 20, 888. [Google Scholar] [CrossRef]
  70. Xu, F.; Yu, H.; Sadrzadeh, A.; Yakobson, B. Riemann Surfaces of Carbon as Graphene Nanosolenoids. Nano Lett. 2016, 16, 34–39. [Google Scholar] [CrossRef] [PubMed]
  71. Jacak, L.; Hawrylak, P.; Wójs, A. Quantum Dots; Springer-Verlag, 1998. [Google Scholar]
  72. Muñoz, E.; Barticevic, Z.; Pacheco, M. Electronic spectrum of a two-dimensional quantum dot array in the presence of electric and magnetic fields in the Hall configuration. Phys. Rev. B 2005, 2005 71, 165301. [Google Scholar] [CrossRef]
Preprints 83253 g001
Figure 1. (a) Contour plots for the case of S ( T , 0 , α ) = cnt. The green line corresponds to the contour of S e ( 1.3 , 0 , 0.22 ) , and the red horizontal line fixes a temperature of 1.3 K as a reference to quantify the effect. (b) − Δ S e for the case of different temperatures, T = 1.3 K (blue line), T = 1.7 K (orange line), and T = 2.1 K (green line). Here, we have selected the initial value of α parameter to be 0.22.
Figure 1. (a) Contour plots for the case of S ( T , 0 , α ) = cnt. The green line corresponds to the contour of S e ( 1.3 , 0 , 0.22 ) , and the red horizontal line fixes a temperature of 1.3 K as a reference to quantify the effect. (b) − Δ S e for the case of different temperatures, T = 1.3 K (blue line), T = 1.7 K (orange line), and T = 2.1 K (green line). Here, we have selected the initial value of α parameter to be 0.22.
Preprints 83253 g001
Preprints 83253 g002
Figure 2. (a) − Δ S t in units of k B for the case of S ( 1.3 , 0 , 0.22 ) − S ( 1.3 , 0 , α ) for different values of a, corresponding to a = 3 (blue line), a = 4 (yellow line), a = 5 (green line) and a = 6 (red line). (b) − Δ S t
Figure 2. (a) − Δ S t in units of k B for the case of S ( 1.3 , 0 , 0.22 ) − S ( 1.3 , 0 , α ) for different values of a, corresponding to a = 3 (blue line), a = 4 (yellow line), a = 5 (green line) and a = 6 (red line). (b) − Δ S t
Preprints 83253 g002
Preprints 83253 g003
Figure 3. S e ( T , 0 , α ) = cnt. in units of k B for the case of (a) a = 3 , (b) a = 4 , (c) a = 5 and (d) a = 6 .
Figure 3. S e ( T , 0 , α ) = cnt. in units of k B for the case of (a) a = 3 , (b) a = 4 , (c) a = 5 and (d) a = 6 .
Preprints 83253 g003
Preprints 83253 g004
Figure 4. Caption
Figure 4. Caption
Preprints 83253 g004
Preprints 83253 g005
Figure 5. (a) Constant entropy contours in the presence of an external magnetic field S ( T , 1 , 0.22 ) = cnt. for the case of a = 4 . We have marked the cases S ( T , 1 , α ) = S ( 1.3 , 1 , 0.22 ) (green contour line), S ( T , 1 , α ) = S ( 1.7 , 1 , 0.22 ) (yellow contour line) and S ( T , 1 , α ) = S ( 2.1 , 1 , 0.22 ) (orange contour line). We also plotted the horizontal line of the isothermal process located in T = 1.3 K (red horizontal line), T = 1.7 K) (orange horizontal line), and T = 2.1 K (purple horizontal line). (b) Entropy differences for the case of a = 4 for T = 1.3 K (blue line), T = 1.7 K (orange line), and T = 2.1 K (green line).
Figure 5. (a) Constant entropy contours in the presence of an external magnetic field S ( T , 1 , 0.22 ) = cnt. for the case of a = 4 . We have marked the cases S ( T , 1 , α ) = S ( 1.3 , 1 , 0.22 ) (green contour line), S ( T , 1 , α ) = S ( 1.7 , 1 , 0.22 ) (yellow contour line) and S ( T , 1 , α ) = S ( 2.1 , 1 , 0.22 ) (orange contour line). We also plotted the horizontal line of the isothermal process located in T = 1.3 K (red horizontal line), T = 1.7 K) (orange horizontal line), and T = 2.1 K (purple horizontal line). (b) Entropy differences for the case of a = 4 for T = 1.3 K (blue line), T = 1.7 K (orange line), and T = 2.1 K (green line).
Preprints 83253 g005
Preprints 83253 g006
Figure 6. Constant entropy curves in the presence of an external magnetic field S ( T , 1 , α ) = cnt. for the case of (a) a = 3 , (b) a = 4 , (c) a = 5 and (d) a = 6 .
Figure 6. Constant entropy curves in the presence of an external magnetic field S ( T , 1 , α ) = cnt. for the case of (a) a = 3 , (b) a = 4 , (c) a = 5 and (d) a = 6 .
Preprints 83253 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated