Preprint

Article

Medium Rock-Soil Temperature Distribution Characteristics in Different Time Scales and New-Type Well Layout Form in Application of Medium-Deep Borehole Heat Exchanger

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Jun Liu^*

Yuping Zhang,

Zeyuan Wang,Cong Zhou,Boyang Liu,

Fenghao Wang^*

Jun Liu^*

Yuping Zhang,

Zeyuan Wang,Cong Zhou,Boyang Liu,

Fenghao Wang^*

This version is not peer-reviewed

Submitted:

30 August 2023

Posted:

31 August 2023

You are already at the latest version

Alerts

Abstract

Medium-deep Borehole Heat exchanger (MBHE) has been widely paid attention for building heating. In order to avoid the thermal interference of adjacent MBHEs, temperature distribution characteristics of medium-deep rock-soil was investigated in this work. The evolution on maximum rock-soil thermal affected radius (MTAR) in full life cycle was further analyzed. The results showed that the rock-soil thermal affected area (RTAA) continuously expands in both radial and vertical directions during a heating season. Several factors of thermal extraction load, fluid velocity, geothermal gradient and pipe length have main impacts on the RTAA in vertical direction. Rock-soil thermal conductivity affects the RTAA in both radial and vertical directions. In non-heating season, temperature difference of rock-soil in radial direction dominates the temperature recovery in the first year while geothermal flow nearly dominates temperature recovery after 20 years. The thermal affected radius (TAR) in the 30 th year could be determined as an effective MTAR in full life cycle. In order to decrease installed distance of adjacent MBHEs, a new well layout form by deflecting borehole was proposed. The recommended deflection angle is equal to or larger than 4 times TAR angle. This work provides scientific reference for promoting application of multiple MBHE arrays.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

With energy and environmental issues become increasingly prominent, the aim of carbon peak and carbon neutralization has been established by many countries in the world [1]. Energy structure adjustment is coming through various walks of life. There is a trend to exploit renewable energy sources instead of traditional fossil fuels energy. Spaceheating is traditionally sourced by coal, natural gas but nowadays the use of geothermal energy gradually plays an important role in order to depollute atomosphere and decarbonize [2-4].

According to ground layer depth, geothermal energy resources could be classified into shallow geothermal energy (<200 m), medium-deep geothermal energy (200~3000 m) and deep geothermal energy (>3000 m). The shallow and medium-deep geothermal energy have been successfully applied in spaceheating [5-10] whereas the deep geothermal energy was more used for power generation due to its high energy grade [11-13]. With a growing awareness of underground environment protection, the geothermal heating technique of indirect heat transfer has been widely promoted especially in the form of shallow borehole heat exchanger (SBHE) [6-7]. However, SBHE system needs a large amount of ground occupation area, which is not preferred in densely populated area. Hereto the medium-deep borehole heat exchanger (MBHE) usually with the depth of greater than or equal to 2000 m was proposed due to its less land demand and used into heating demonstration projects [8-10]. In view of advantages of environmental friendliness and high heating energy efficiency, multiple MBHE arrays have been applied in some heating projects [14-15].

In earlier studies, some field tests [16-18] and numerical simulations were carried out for a single MBHE in order to ensure its thermal extraction capacity. Due to the difference from the field test results, for example, that the measured thermal extraction capacity of single MBHE was ranging from 158~288 kW[17], the effects of the influencing factors including operating parameters (such as inlet temperature [19-20], flow velocity [21-23]), geological parameters (such as rock-soil thermal conductivity [24-25], rock-soil heat capacity [26] and geothermal gradient [27-28] and design parameters (such as pipe depth [29], pipe diameter [30], inner pipe thermal conductivity [31] on the thermal extraction capacity of MBHE were investigated by numerical analysis, which contributes to accurately evaluating the thermal extraction capacity. However, the relevant studies found that thermal interference exists in MBHE arrays [15, 32-33]. Cai [15] initially analyzed the thermal performance of 5 MBHEs with the maximum adjacent spacing of 30 m according to a practical heating engineering and found the thermal interactions do exist among MBHEs which have about 12 % shifted thermal load during 20-year operations. Based on this research [15], Cai [32] investigated the effects of soil thermal properties on the thermal performance of multiple MBHE arrays and optimized the system layouts. Zhang [33] proposed a superposition dimension reduction algorithm to fast calculate the fluid temperature of multiple MBHE arrays. By continuously computing the fluid temperatures in the conditions of various spacing and comparing their difference, the optimal design spacing of MBHE arrays can be ensured .

As mentioned above, the applied amount of MBHE developes from single to multiple arrays. The attendant problem is how to avoid the thermal interference between adjacent MBHEs to keep high energy efficiency and well stability of heating. In order to ensure a rational spacing distance, the key issues of demonstrating the temperature distribution characterisitics of medium-deep rock-soil needs to be solved, which helps to determine the maximum rock-soil thermal affected area (RTAA). According to the studies of single MBHE, it can be seen that many of the influencing factors highly impacts the thermal performance whereas there is a lack of related studies for their effects on the temperature distribution of medium-deep rock-soil. Thus, the temperature distribution characteristics of medium-deep rock-soil have not be fully clarified. Furthermore, the operation mode of MBHE is extracting the geothermal energy in heating season and stopping geothermal extraction in non-heating season. MBHE has a long thermal response period in heating season so that the analysis on rock-soil temperature distribution through a complete heating season is necessary. In non heating season, the rock-soil temperature starts to recover whereas how the RTAA is evoluting under the effects of both rock-soil temperature difference and geothermal flow has not been reported. Thus, the effect of the operation mode shoule be taken into account in analysis of rock-soil temperature distribution. At present, Cai [32] investigated the distribution patterns of maximum RTAA during 15-year operations but the thermal performance of MBHE has not come into a quasi-steady state according to Ref. [34], indicating the mentioned maximum RTAA may still changes with following operating years. Zhang [33] analyzed the evolution in 30-year operational fluid temperature of multiple MBHE arrays but did not payed attention to the RTAA. In order to determine a rational spacing distance, the most direct and effective method is to demonstrate the characteristics of medium-deep rock-soil temperature distribution and further analyze the maximum thermal affected area. It is necessary to carry out the studies on the effects of the various influencing factors on the maximum medium-deep RTAA in the full life cycle. Additionally, Zhang [33] concluded that the spacing between adjacent MBHEs comes to 50~60 m which is 10 times larger than spacing between adjacent SBHEs [7]. In this case, the multiple DBHE arrays will also occupy a large amount of ground area, which is detrimental to the application in densely populated area. Thus, how to decrease ground surface occupation of multiple MDBHE arrays is urgent to be solved.

Based on the analysis of previous studies, the medium-deep rock-soil temperature distribution characteristics in different time scales was investigated in this work. By proposing the numerical model of heat transfer between MBHE and surrounding rock-soil, the effects of influencing factors including thermal extraction load, operating parameters, geological parameters and design parameters on the medium-deep rock-soil temperature distribution were analyzed, whilst ensure the main factors which largely impact the maximum thermal affected radius (MTAR). Combining with the operation mode of extracting geothermal energy in heating season and stopping geothermal extraction in non-heating season, the effective MTAR in full life cycle was analyzed and determined. Last but not least, a new-type well layout was proposed to decrease ground surface occupation of mutiple MDBHE arrays. The conclusions of this work could guide the spacing design and optimize the well layout in the application of MBHEs.

2. Methodology

2.1. Heat Transfer between MBHE and Rock-soil

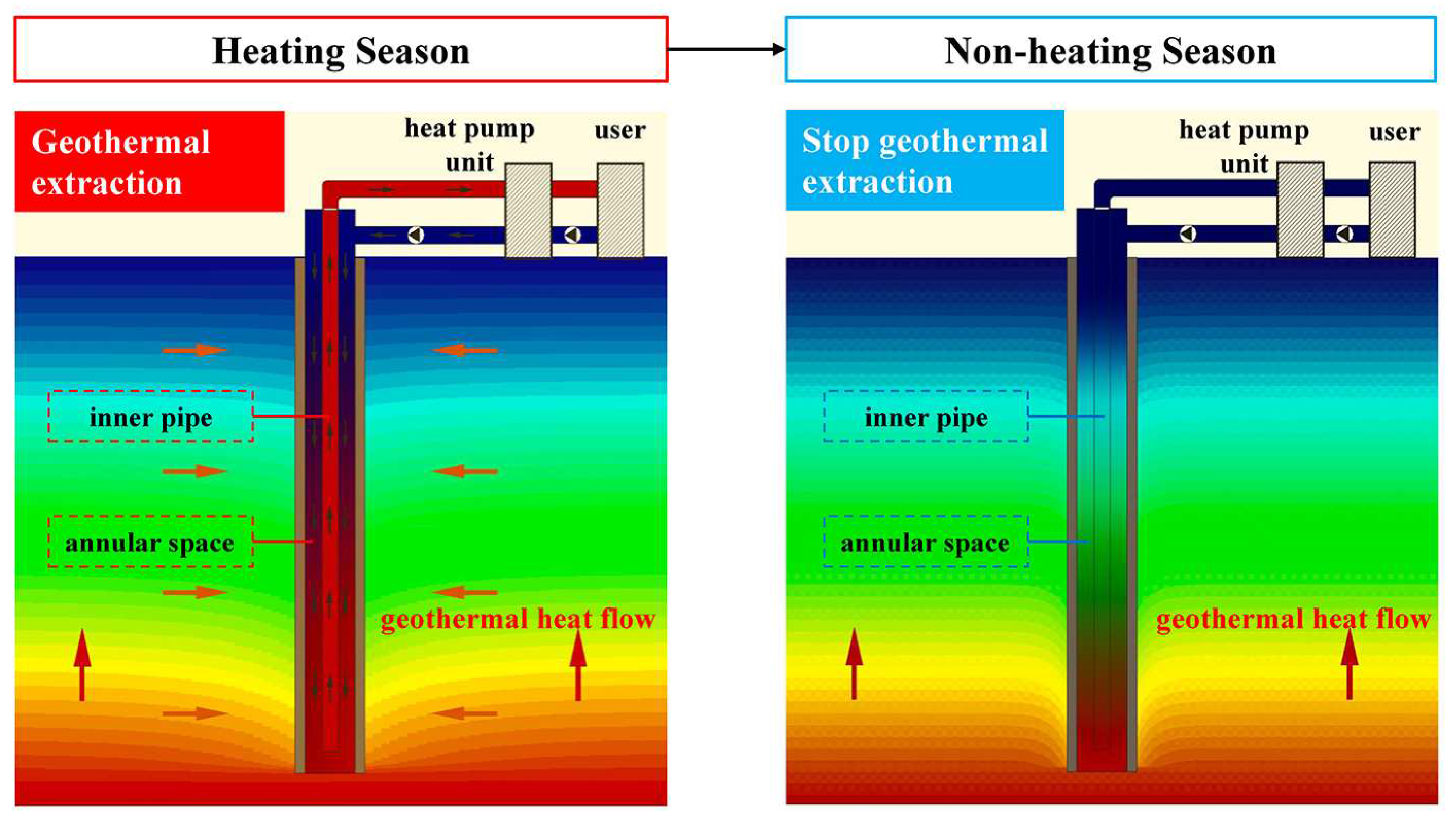
Due to high energy grade of medium-deep rock-soil, MBHE usually extracts the geothermal energy for building heating in the heating season and stop running in the non-heating season (Figure 1). During the heating season, the fluid with low temperature flows downstairs in annular space and absorbs the heat from surrounding rock-soil, where the fluid temperature increases but the rock-soil temperature decreases. Then, the heated fluid with high temperature is transported by inner pipe to ground surface. At the end, the energy contained in the high-temperature fluid is utilized by heat pump for building heating. During the non-heating season, the fluid keeps still in MBHE, thus there is no thermal extraction from medium-deep rock-soil. The rock-soil temperature recovers under the effect of heat supply from geothermal heat flow. Figure 2 shows the positional relationship between MBHE and surrounding rock-soil.

2.2. Numerical Simulation and Analysis Method

2.2.1. Balance Equations in Numerical Model

The numerical model is generated based on an 1D MBHE element coupled with a 2D rock-soil element. Four energy balance equations are needed as follows:

Energy equations of inner pipe fluid:

\frac{\partial T_{f_{r}}}{\partial t} + \frac{\partial (V_{f_{r}} \cdot T_{f_{r}})}{\partial z} = \frac{k_{ff} (T_{f_{an}} - T_{f_{r}})}{ρ_{f} A_{r} c_{pf}}

(1)

where T_fr, V_fr, T_fan, k_ff, ρ_f, A_r, c_pf are fluid temperature in inner pipe, fluid flow velocity in inner pipe, fluid temperature in annular space, heat transfer coefficient between fluids in inner pipe and annular space, fluid density, cross section area of inner pipe, fluid heat capacity, respectively.

Energy equations of annular space fluid:

\frac{\partial T_{f_{a n}}}{\partial t} + \frac{\partial (V_{f_{a n}} \cdot T_{f_{a n}})}{\partial z} = \frac{k_{f g} (T_{g} - T_{f_{a n}})}{ρ_{f} A_{a n} c_{p f}} - \frac{k_{f f} (T_{f_{a n}} - T_{f_{r}})}{ρ_{f} A_{a n} c_{p f}}

(2)

where V_fan, k_fg, T_g, A_an are fluid flow velocity in annular space, heat transfer coefficient between fluid in annular space and backfill material, backfill material temperature, cross section area of annular space, respectively.

Energy equations of backfill material:

\frac{\partial T_{g}}{\partial t} = \frac{k_{f g} (T_{f_{a n}} - T_{g})}{ρ_{g} A_{g} c_{p g}} + \frac{k_{g b} (T_{b} - T_{g})}{ρ_{g} A_{g} c_{p g}}

(3)

where ρ_g, A_g, c_pg, k_gb, T_b are backfill material density, cross section area of backfill material, backfill material heat capacity, heat transfer coefficient between backfill material and borehole wall, borehole wall temperature, respectively.

Energy equations of rock-soil:

ρ_{s} c_{p s} \frac{\partial T_{s}}{\partial t} = \frac{\partial}{\partial z} (λ_{s} \frac{\partial T_{s}}{\partial z}) + \frac{1}{r} \frac{\partial}{\partial r} (r λ_{s} \frac{\partial T_{s}}{\partial r})

(4)

where ρ_s, c_ps, T_s, λ_s are rock-soil density, rock-soil heat capacity, rock-soil temperature, rock-soil thermal conductivity, respectively.

2.2.2. Model Solving and Analysis Method

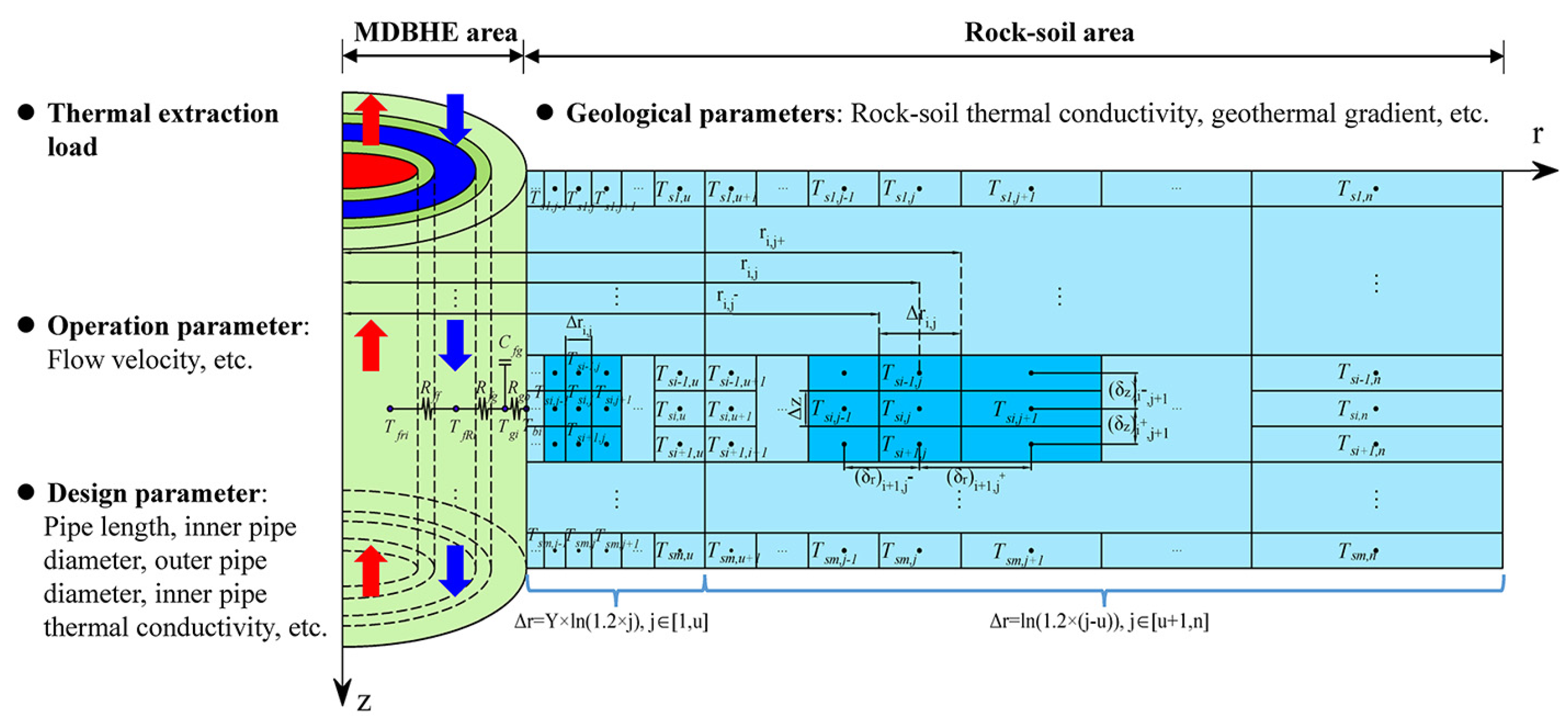
The numerical model is discretized by finite volume method (FVM) and solved by tridiagonal matrix algorithm, which has been validated in our previous work [34]. The same methodology of initial and boundary condition setting was also employed in this work. Figure 3 shows the discretized model which consists of MBHE area and rock-soil area. The temperatures of different elements in the numerical model could be computed so that the rock-soil temperature distribution characteristics could be analyzed.

The thermal performance of MBHE is affected by various influencing factors including geological parameters in rock-soil area, and thermal extraction load, operation parameter, design parameter in MBHE area (Figure 3). The rock-soil temperature distribution is also impacted by the above-mentioned factors which is taken into account in our numerical model. According to our previous work[34], the thermal extraction load of MBHE, the rock-soil thermal conductivity, geothermal gradient of geological parameters, the flow velocity of operation parameter, the pipe length, inner pipe diameter, outer pipe diameter, inner pipe thermal conductivity of design parameters have a larger impact on the thermal performance than other factors such as outer pipe thermal conductivity, backfill material thermal conductivity. Therefore, the effects of the 8 influencing factors (as shown in Figure 3) on the rock-soil temperature distribution characteristics were investigated in this work. Combining with the previous experimental and simulated work on MBHE, the analyzed parameters and benchmark parameter were listed in Table 1.

The aim of the analysis on medium-deep rock-soil temperature distribution is to ensure RTAA, which has a strong practical meaning to spacing design for MBHE arrays application. Unlike rock-soil temperature surrounding SBHE, the medium-deep rock-soil has characteristics of temperature gradient, i.e. a higher temperature with deeper position. Meanwhile, the heat transfer intensity along the MBHE varies from different depths according to our previous work [30]. It can be concluded that during a heating season, the change degree of rock-soil temperature along the depth direction is different. In order to determine the thermal affected radius (TAR) at different depths, the evolution of medium-deep rock-soil temperature in both radial and vertical directions during full life cycle was analyzed in this work. The temperature change compared with the undisturbed condition can be expressed as follow:

θ_{s} (z_{s}, r_{s}, t) = T_{s} (z_{s}, r_{s}, t) - T_{s 0} (z_{s}, r_{s}, 0)

(5)

where θ_s, T_s, T_s0 are rock-soil temperature change amount, rock-soil temperature at t time, undisturbed rock-soil temperature, respectively. z_s, r_s are depth and radial distance, respectively.

3. Results and discussion

3.1. Rock-soil Temperature Distribution in one Heating Season

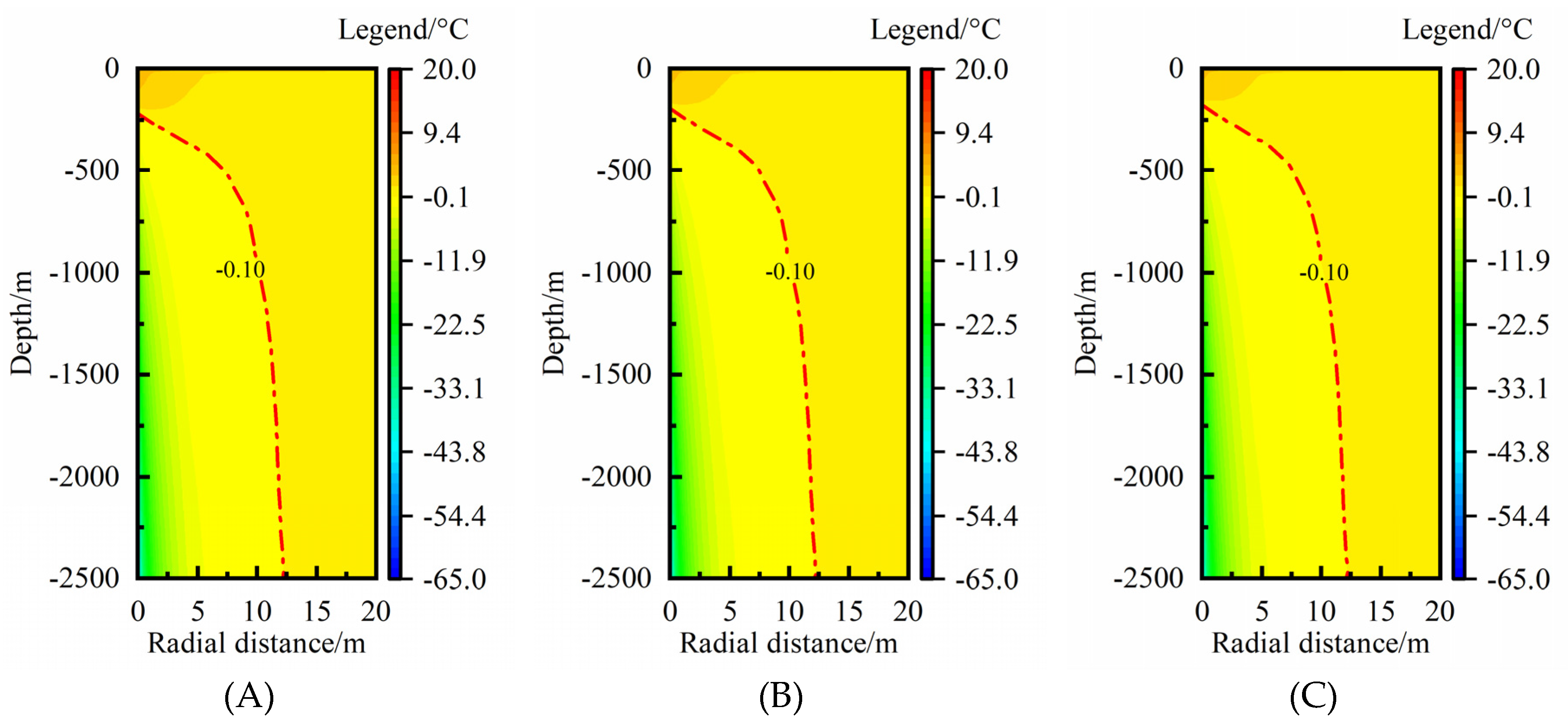
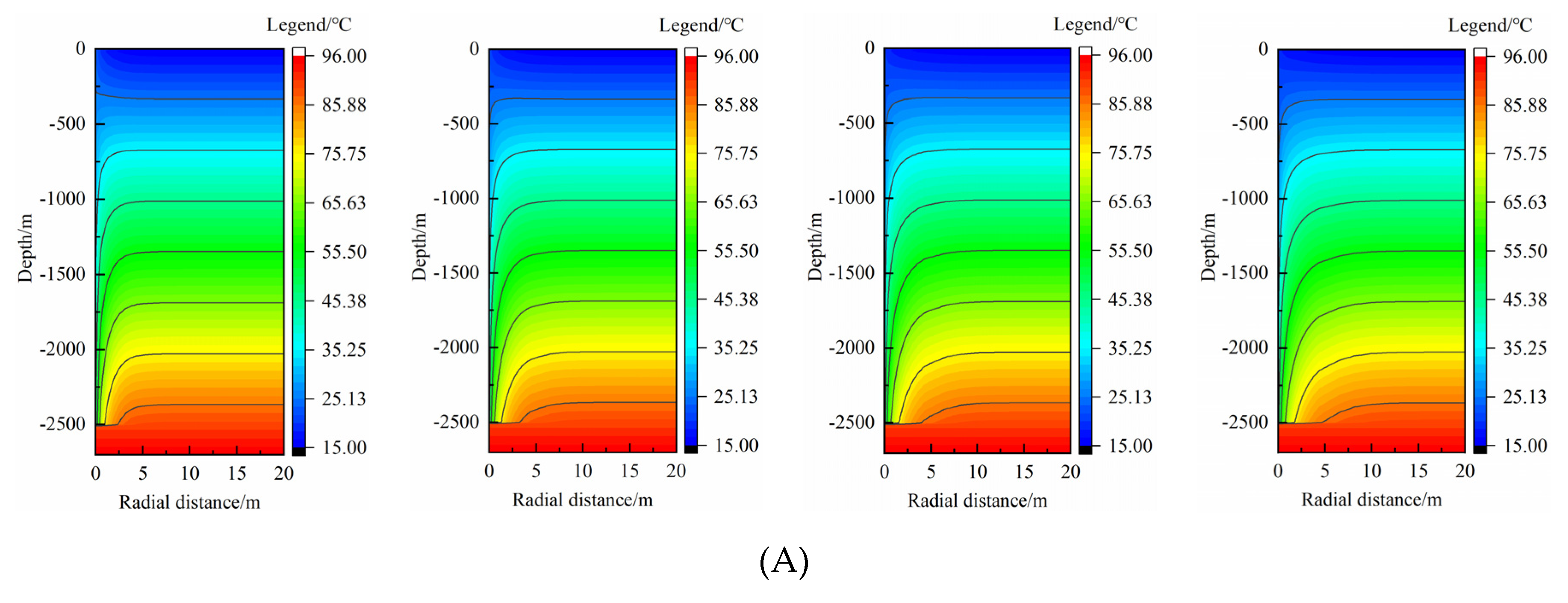
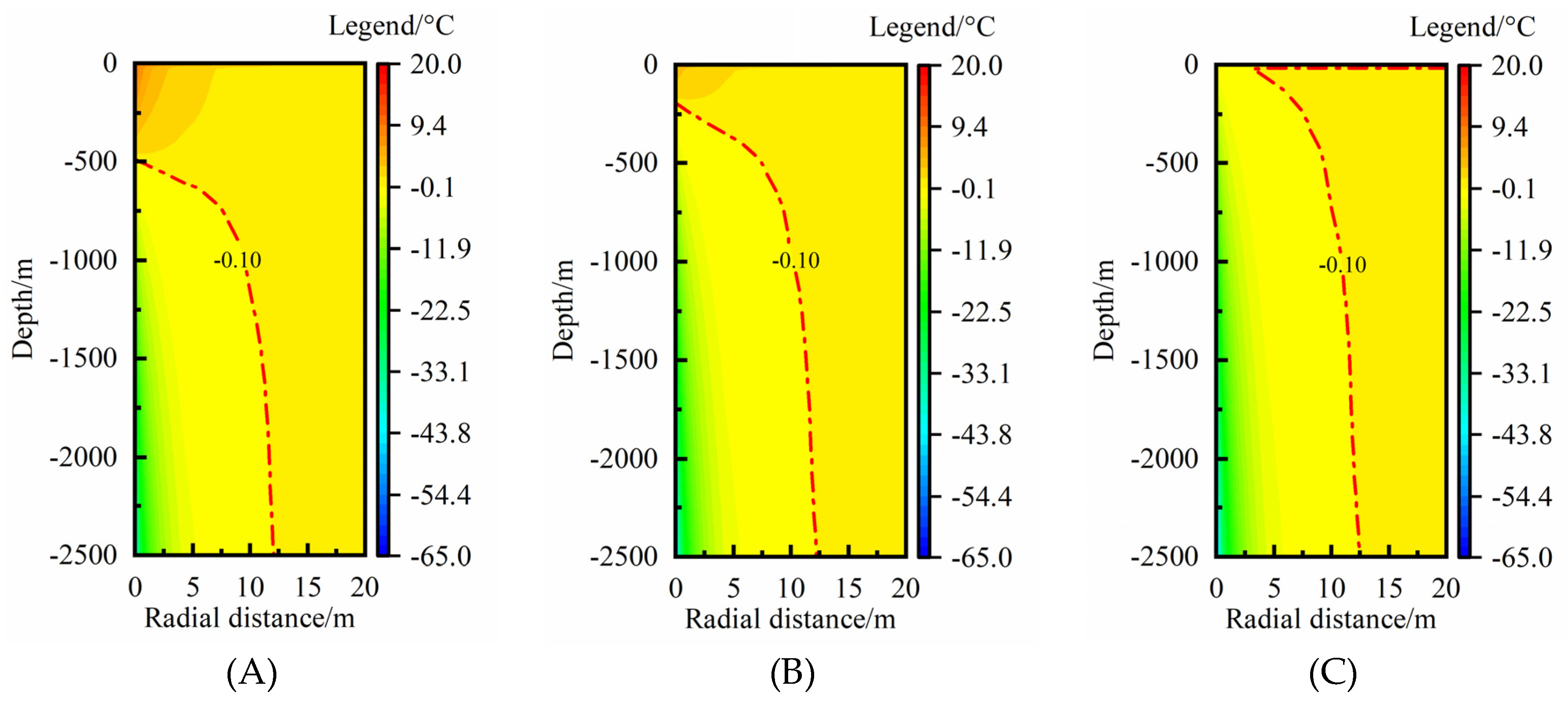
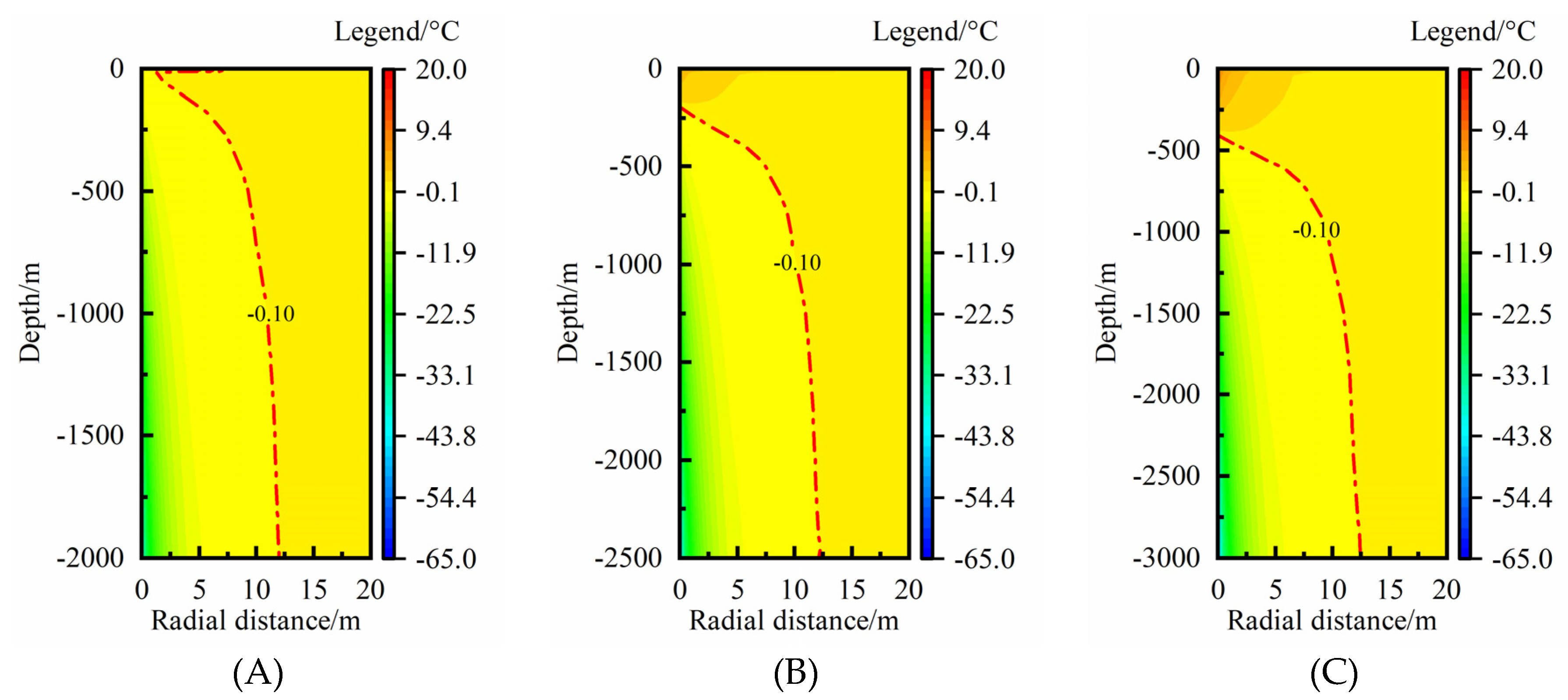
Figure 4 shows the rock-soil temperature distribution in a heating season (4 months). The longitudinal coordinate-axis represents rock-soil depth below the ground surface and the horizontal axis represents the radial distance between MBHE and rock-soil. A smaller radial distance means that rock-soil is closer to MBHE. In order to analyze the temperature distribution characteristics with thermal extraction time of MBHE, the calculated rock-soil temperature in typical time nodes of 30, 60, 90, 120 days were chosen. It can be seen the rock-soil temperature largely decreases at smaller radial distance. As the thermal extraction proceeds, the rock-soil temperature drop exists in both radial direction and vertical direction (Figure 4(A)). In general, the temperature change in radial direction is paid more attention because of its practical significance on spacing design. According to the change trend of the isotherm, it can be found the rock-soil temperature hardly changes beyond the radial distance of 6, 9, 11, 12 m at 30, 60, 90, 120 days, respectively. During a whole heating season, the TAR of medium-deep rock-soil gradually increases. At the end of the heating season, the TAR reaches maximum. 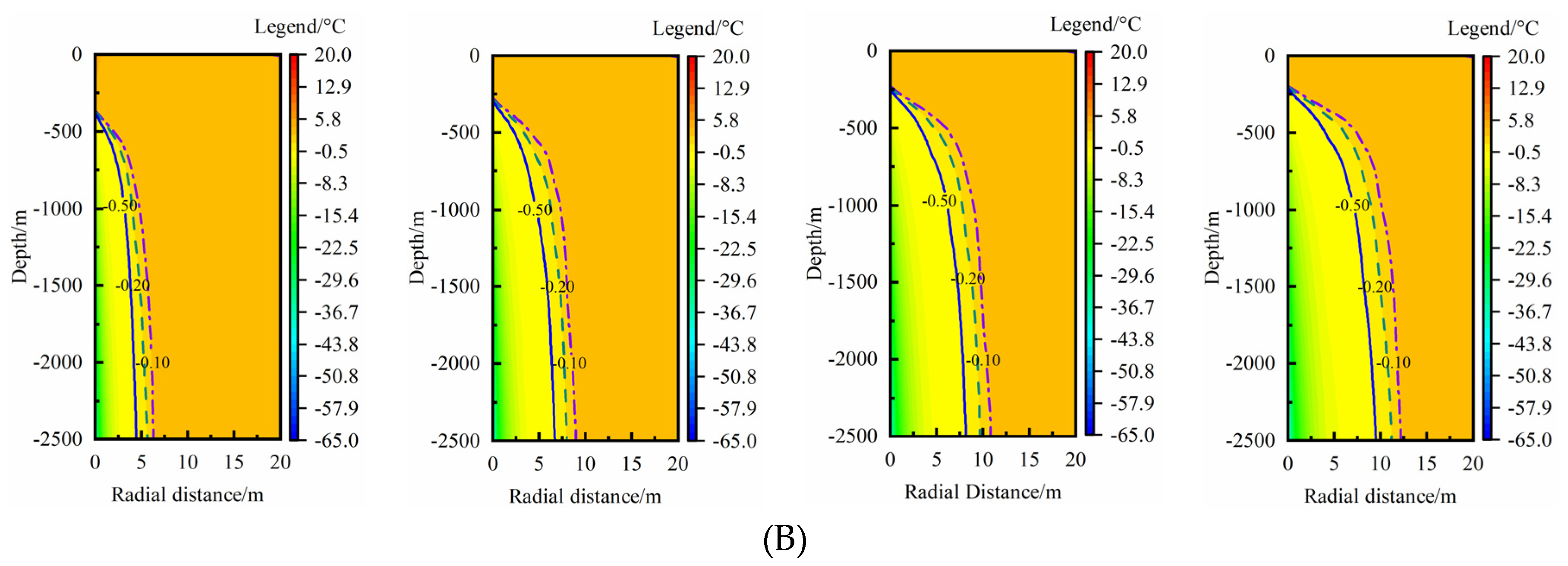Figure 4(B) shows the rock-soil temperature change compared with the undisturbed temperature. Three temperature drop isotherms of -0.5, -0.2 and -0.1 °C were chosen to analyze the RTAA. By comparison with Figure 4(A), Figure 4(B) reflects the RTAA more clearly. The larger temperature drop isotherm has a relatively smaller RTAA. According to statistics, the MTAR shown from the isotherm of -0.1 °C is 6.3, 9.0, 10.9, 12.2 m, which is nearly consistent to the fore-mentioned results from Figure 1(A). Thus, the isotherm of -0.1 °C is selected as a RTAA reference to analyze its characteristics in the following analysis.

3.2. Effects of Influencing Factors

The effects of the 8 influencing factors (as shown in Table 1) were investigated in this section. Because the RTAA continuously increases during a heating season, the rock-soil temperature distribution under various conditions at the end of heating season (120 days) were chosen to analyze.

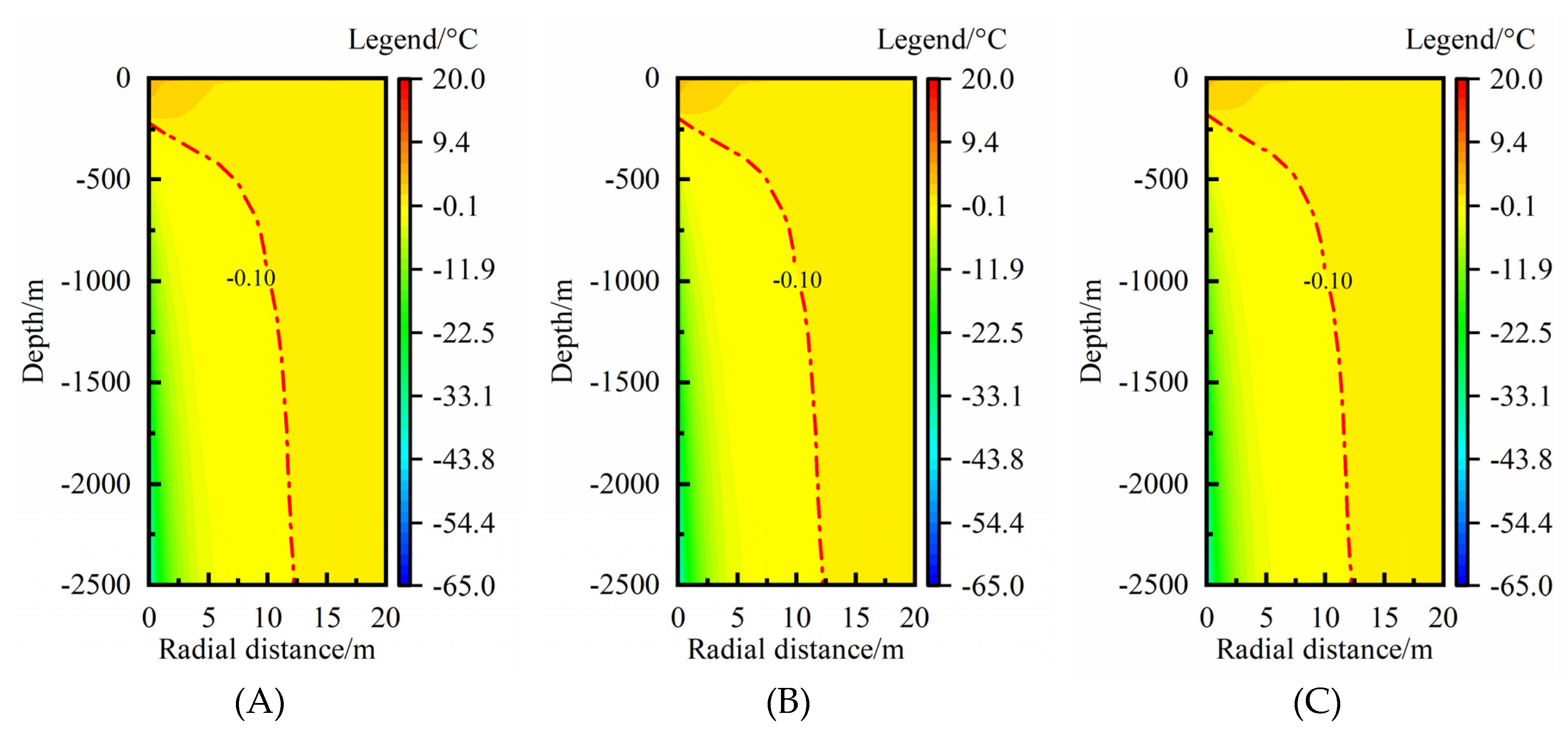
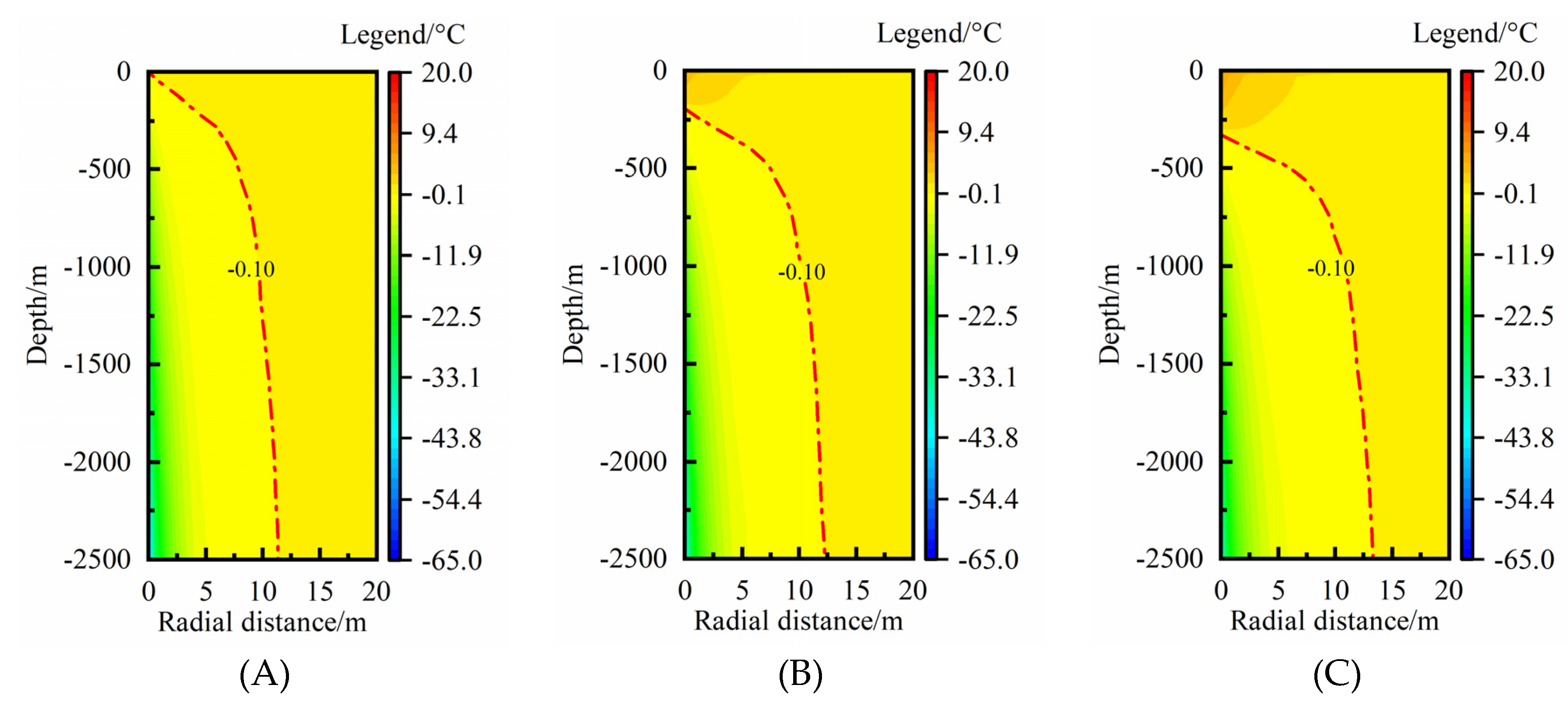
3.2.1. Thermal Extraction Load

Figure 5 shows the rock-soil temperature change in the condition of thermal extraction load of 75, 100, 125 W·m^-1. Under the lower thermal extraction load condition, the rock-soil temperature change in shallow depth is positive (Figure 5(A)), which means heat-transmission happens from MBHE to rock-soil. The length where MBHE dissipates heat to rock-soil gradually decreases with an increase of thermal extraction load. At the thermal extraction load of 75 W·m^-1, about 500 m length of MBHE is at condition of heat dissipation. When thermal extraction load increases to 125 W·m^-1, the heat dissipation length disappears and the whole length of MBHE extracts the geothermal energy from rock-soil (Figure 5(C)). In the radial direction, the maximum thermal affected radius (MTAR) increases by 0.38 m (from 12.00 to 12.38 m) when thermal extraction load increases from 75 to 125 W·m^-1, with an increase ratio of 3.2%. In a word, variation in thermal extraction load has an obvious effect on the RTAA in vertical direction but it slightly affects the MTAR.

3.2.2. Geological Parameters

Quality of geothermal condition could be indirectly evaluated by geothermal flow which is product of rock-soil thermal conductivity and geothermal gradient. In this section, the effects of these two geological parameters on rock-soil temperature distribution were analyzed.

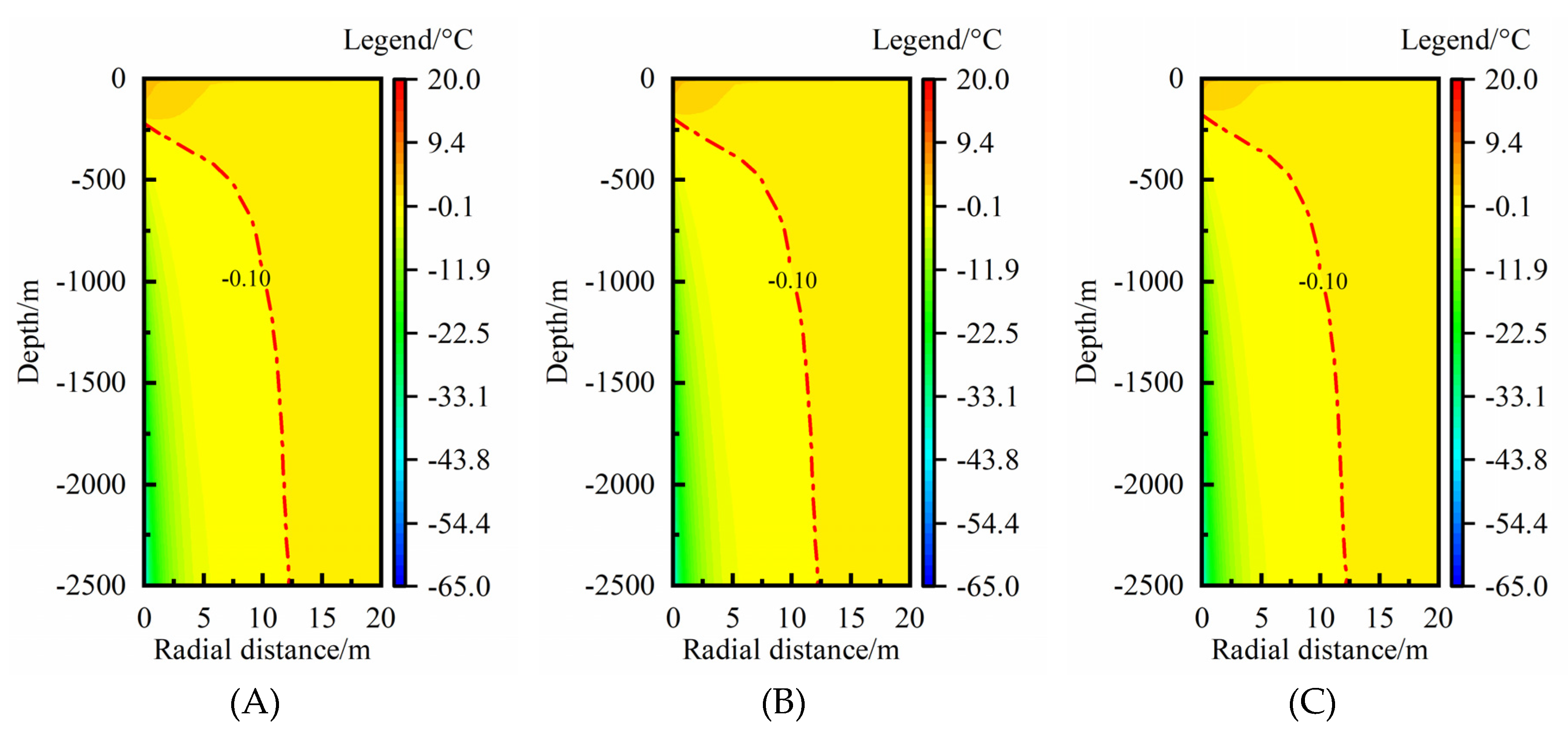
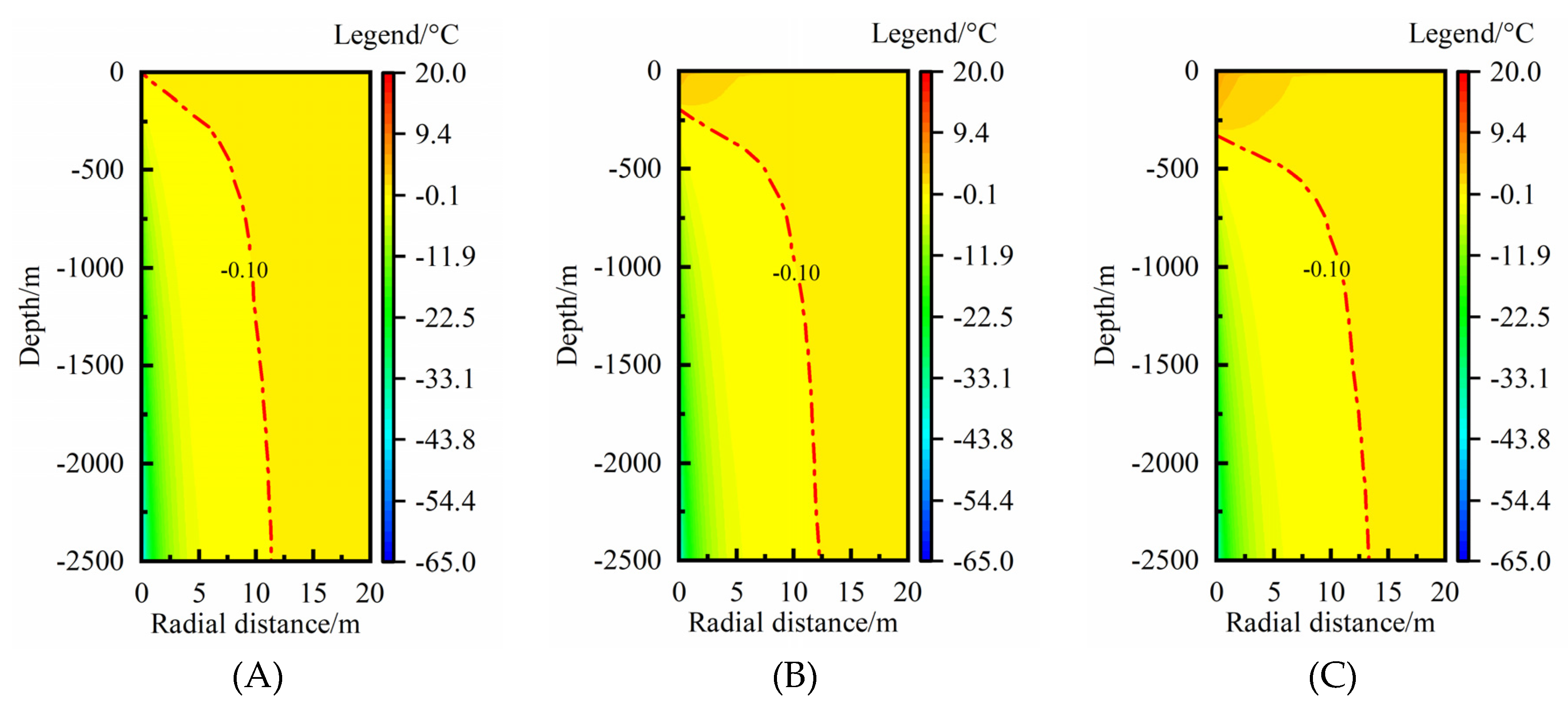
Figure 6 shows the rock-soil temperature change in the condition of rock-soil thermal conductivity of 2.0, 2.5, 3.0 W·m^-1·K^-1. In vertical direction, the geothermal energy was extracted from surrounding rock-soil at nearly the whole depth under a lower thermal conductivity condition (Figure 6(A)). With an increase of the thermal conductivity, the RTAA of thermal extraction moves along the deeper depth obviously (Figure 6(C)). As for the MTAR, it increases by 0.89 m and 1.06 m, respectively, when an increases of per 0.5 W·m^-1·K^-1 of thermal conductivity from 2.0 W·m^-1·K^-1 (Figure 6(A)) to 3.0 W·m^-1·K^-1 (Figure 6(C)). The MTAR increases by 17.2% when the thermal conductivity increases from 2.0 to 3.0 W·m^-1·K^-1 and the increase degree would further enlarge with the thermal conductivity increasing, which indicates that rock-soil thermal conductivity largely impacts the MTAR.

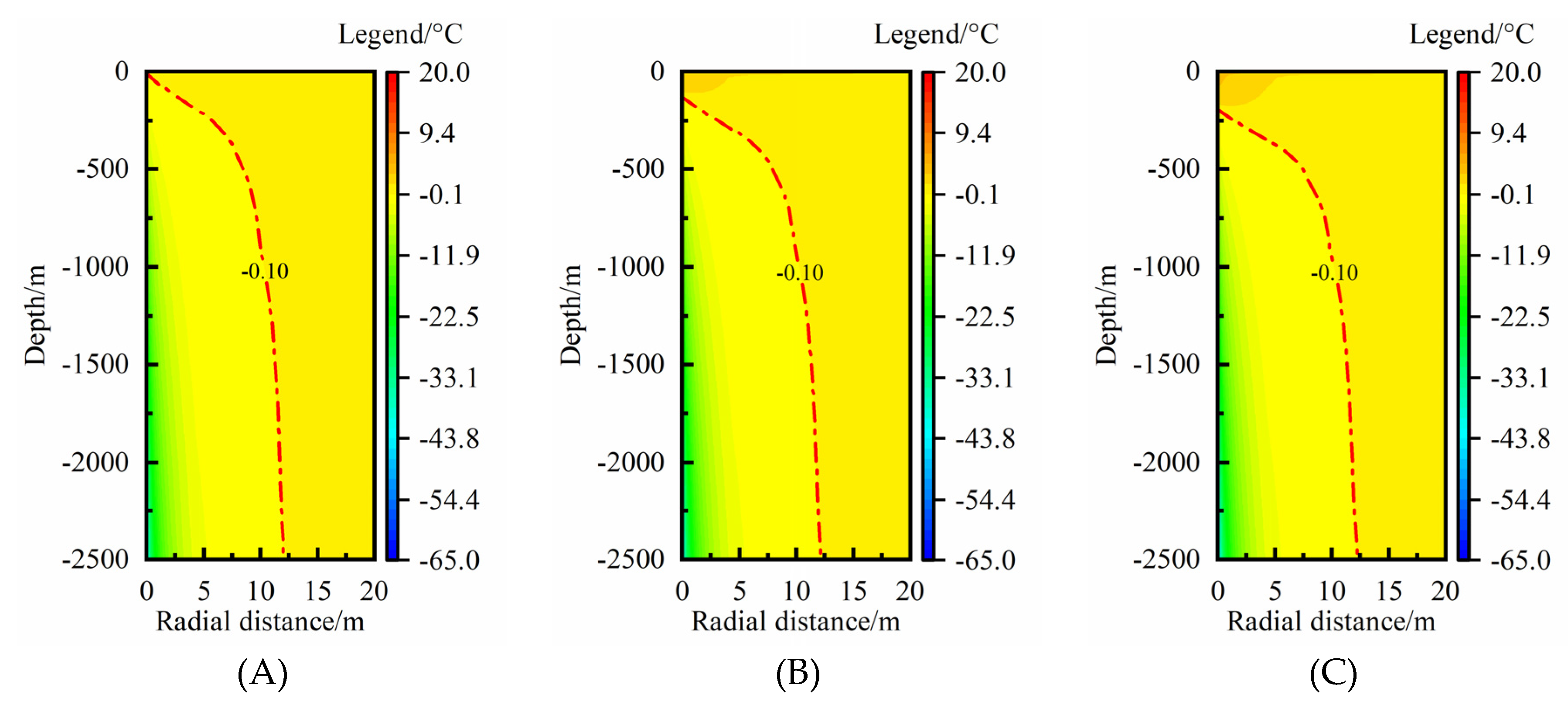
Figure 7 shows the rock-soil temperature change in the condition of geothermal gradient of 25, 30, 35 °C·km^-1. The same with the effect of rock-soil thermal conductivity, under lower geothermal gradient condition, the geothermal energy was extracted from surrounding rock-soil at nearly the whole depth (Figure 7(A)). Besides, the RTAA of thermal extraction moves along the deeper depth obviously with an increase of geothermal gradient. For the MTAR, it increases only by 0.26 m when an increases of per 5 °C·km^-1 of geothermal gradient from 25 °C·km^-1 (Figure 7(A) ) to 35 °C·km^-1 (Figure 7(C)). The MTAR increases by 4.4% when the geothermal gradient increases from 25 to 35 °C·km^-1, which indicates the variation in geothermal gradient slightly impacts the MTAR of medium-deep rock-soil.

3.2.3. Operation Parameter

Fluid velocity is one of the most important operation parameters for thermal extraction of MBHE. Elevating the fluid velocity contributes to improving the convective heat transfer coefficient between MBHE and surrounding rock-soil. Figure 8 shows the effects of fluid velocity on the rock-soil temperature change. It can be seen that the RTAA of thermal extraction mainly moves in the deeper depth direction with the fluid velocity increasing, whereas the MTAR increases only by 0.1, 0.1 m, respectively, when an increase of per 0.1 m·s^-1 of fluid velocity from 0.5 m·s^-1 (Figure 8(A)) to 0.7 m·s^-1 (Figure 8(C)). In general, the fluid velocity of 0.7 m·s^-1 has been at a relatively high level in the application of MBHE because the thermal extraction capacity of MBHE could not be effectively improved by continuously elevating fluid velocity. Based on the above analysis, it can be concluded that the fluid velocity hardly affects the MTAR.

3.2.4. Design Parameters

Design parameters of MBHE mainly involve pipe length and diameter. As is known to us, MBHE with a longer pipe length has a better thermal extraction capacity. Figure 9 shows the surrounding rock-soil temperature change of MBHEs with different pipe lengths. RTAA affected by different pipe lengths mainly varies in the vertical direction. The RTAA of thermal extraction moves along the deeper depth with the pipe length increasing (From Figure 9(A) to Figure 9(C)). In the radial direction, the MTAR increases only by 0.20 m when an increases of per 500 m of pipe length from 2000 m (Figure 9(A)) to 3000 m (Figure 9(C)). The MTAR increases by 3.6% when the pipe length increases from 2000 to 3000 m, which indicates the variation in pipe length slightly impacts the MTAR of medium-deep rock-soil.

Additionally, the effects of inner pipe diameter (Figure A1), outer pipe diameter (Figure A2), and inner pipe thermal conductivity (Figure A3) on the rock-soil temperature change were also analyzed. It can be found the variation in these three factors mainly affects the RTAA in the vertical direction. For MBHE with a smaller inner pipe diameter, larger outer pipe diameter, and/or lower inner pipe thermal conductivity, the RTAA of thermal extraction is positioned in a deeper depth. However, the MTAR hardly varies with pipe diameter and inner pipe thermal conductivity.

3.3. Rock-soil Temperature Distribution in Full Life Cycle

3.3.1. Rock-soil TAR

In full life cycle, MBHE extracts the geothermal energy in heating season and stops running in non-heating season. According to the study in Section 3.1, the TAR of medium-deep rock-soil reaches the maximum value at the end of heating season. During the non-heating season, rock-soil temperature begins to recover under the effect of the geothermal flow, which has a non-negligible impact on the TAR. In order to ensure the MTAR in full life cycle, the rock-soil temperature distribution change during the duration of 30-year thermal extraction was analyzed. In every year, the period of 4 months was set as heating season and the rest period is set as non-heating season, which is determined according to the building heating time in northern China.

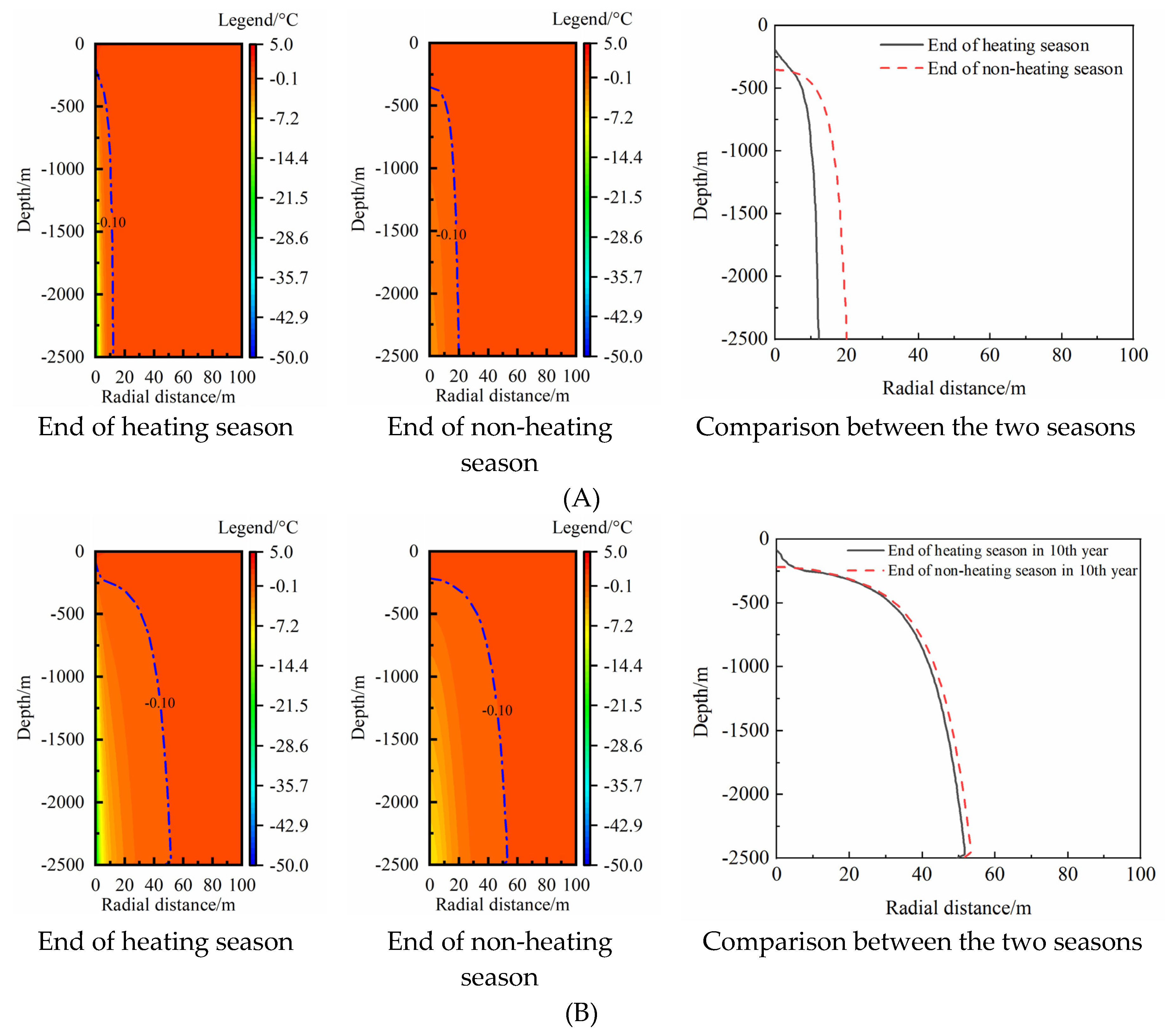
Figure 10 shows the TAR of medium-deep rock-soil at the end of heating season and non-heating season in different years. In the first year, the decline degree of rock-soil temperature closer to MBHE is larger with the maximum value of 50 °C and the MTAR is 12.2 m at the end of heating season. During the non-heating season, the rock-soil temperature surrounding MBHE obviously recovers but has not reached the undisturbed condition. The maximum temperature drop rises to 2.8 °C. 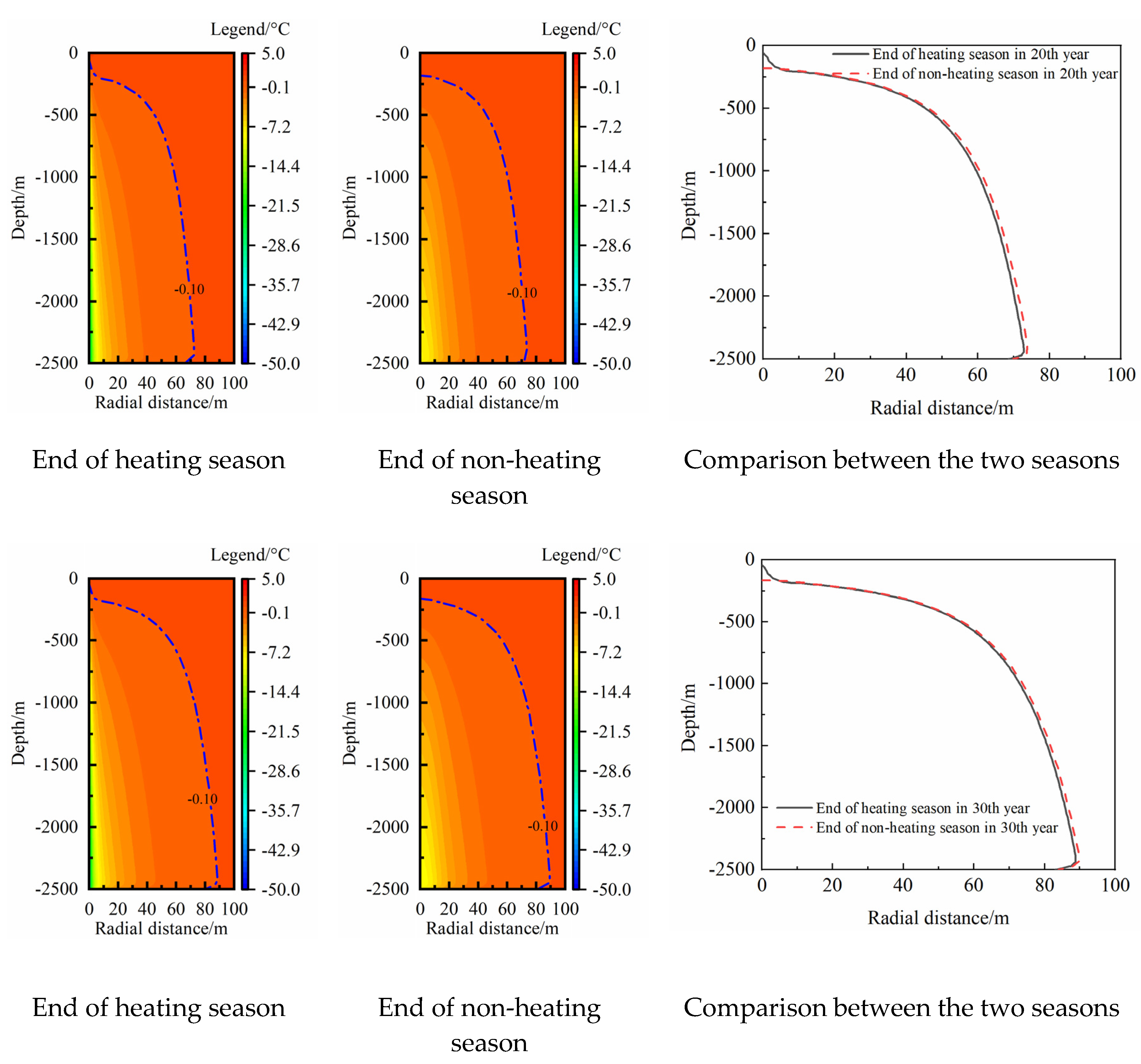It should be noted that the MTAR continues to increase during the non-heating season and expands to 20.0 m at the end of non-heating season which is nearly equal to the twice of the MTAR at the end of heating season (Figure 10(A)). It can be concluded that the temperature difference of medium-deep rock-soil in the radial direction dominates the temperature recovery of rock-soil surrounding MBHE in the first year. As the thermal extraction proceeds, the MTARs continuously increase to 51.4, 72.5, 89.9 m at the end of non-heating season in the 10 th, 20 th and 30 th year (Figure 10(B), Figure 10(C), and Figure 10(D)), respectively. The increase degree of MTAR with thermal extraction time gradually declines. Besides, by comparing the TAR at the end of heating season and non-heating season, their difference gradually reduces. After 20-year thermal extraction, the TAR at the end of heating season and non-heating season tend to be consistent (Figure 10(C)), which indicates that the geothermal flow nearly dominates the temperature recovery. In the 30 th year, the TAR at the end of heating season and non-heating season basically coincide (Figure 10(D)).

While the MTAR may still continue to extend after 30-year thermal extraction, a balance has basically reached between the thermal extraction of MBHE and the thermal recovery of medium-deep rock-soil at 30 th year. The thermal extraction capacity of MBHE would keep almost constant and comes into a quasi-steady state, which has been validated from our previous study [34]. To sum up, the MTAR in the 30 th year could be determined as an effective MTAR in full life cycle, which has reference value for borehole spacing design to ensure a sustainable thermal extraction of single MBHE.

3.3.2. Main Influencing Factors Analysis

According to the analysis in Section 3.2, the rock-soil thermal conductivity has an obvious effect on TAR. Besides, the thermal extraction loads of MBHE usually have a large fluctuation range in different engineering projects. Thus, the effects of the mentioned two factors on the MTAR in full life cycle were investigated. 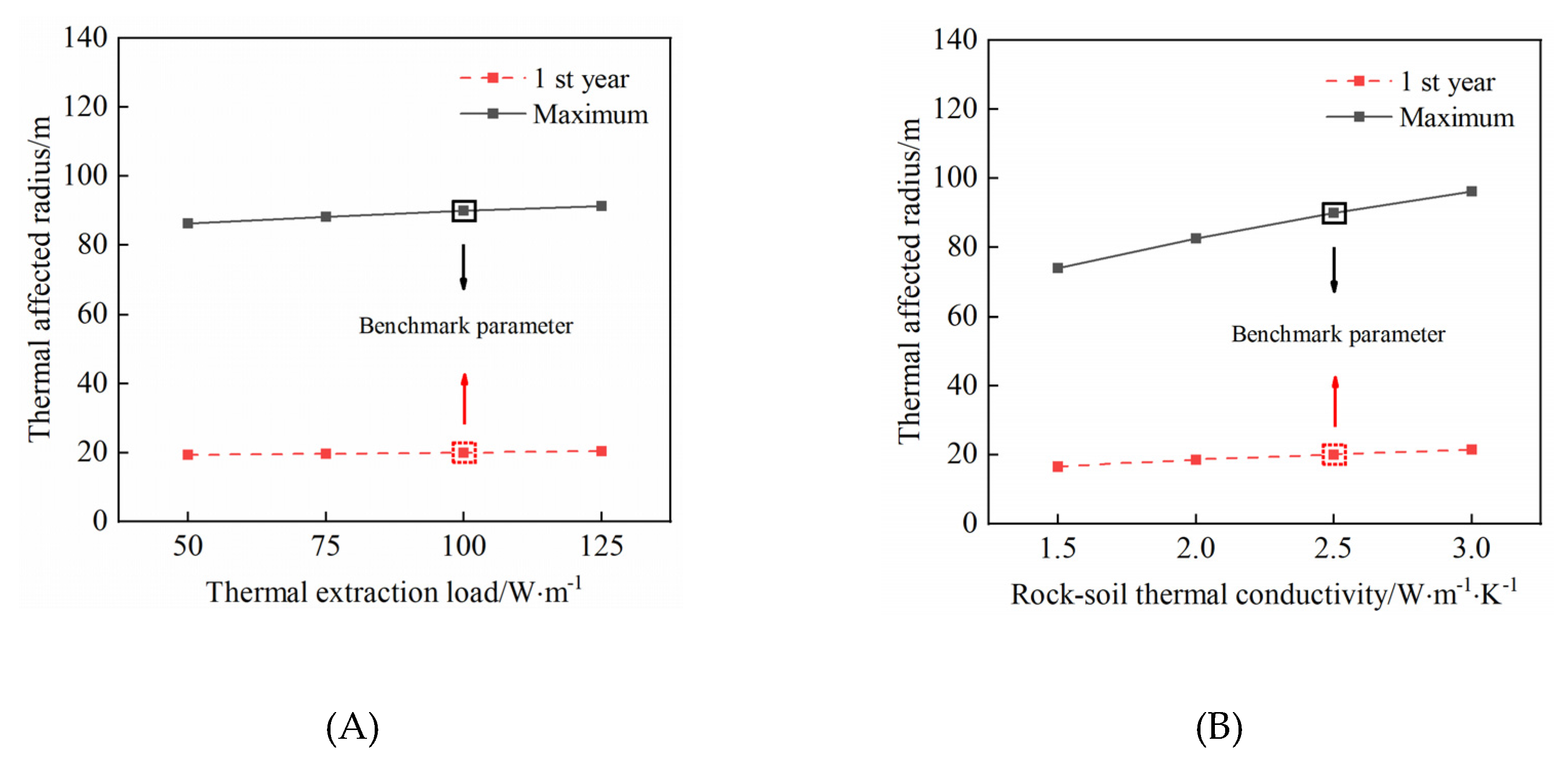Meanwhile, the maximum radius of full life cycle was compared with the MTAR in the first year in order to analyze the variation of TAR during full life cycle (Figure 11).

Figure 11 (A) shows the effects of thermal extraction load. Compared with the MTAR in the 1 st year, the maximum radius in full life cycle becomes significantly larger with over 80 m. However, the maximum radius only enlarges by nearly 5.0 m when the thermal extraction load increases from 50 W·m^-1 to 125 W·m^-1, indicating an slight effect on the variations in the maximum radius. Figure 11 (B) shows the effects of rock-soil thermal conductivity. In the first year, the MTAR at 3.0 W·m^-1·K^-1 is 5.0 m larger than that at 1.5 W·m^-1·K^-1. During full life cycle, the difference of maximum radius between the conditions of 3.0 W·m^-1·K^-1 and 1.5 W·m^-1·K^-1 increase to 22.3 m. In the condition of higher rock-soil thermal conductivity, the increase degree of MTAR with thermal extraction year is more obvious and the thermal interference between adjacent MBHEs should be paid attention.

3.4. New-type Well Layout Form

3.4.1. Well Layout Form Proposal

During full life cycle, the TAR significantly increases with thermal extraction year. The maximum radius in full life cycle analyzed in Section 3.3.2 reaches over 70 m at least, which means the spacing of more than 140 m between adjacent MBHEs should be designed. It is difficult to implement for heating application of multiple MBHE arrays because of the limitations on the project site area. Thus, optimizing the well layout form is urgent to be solved.

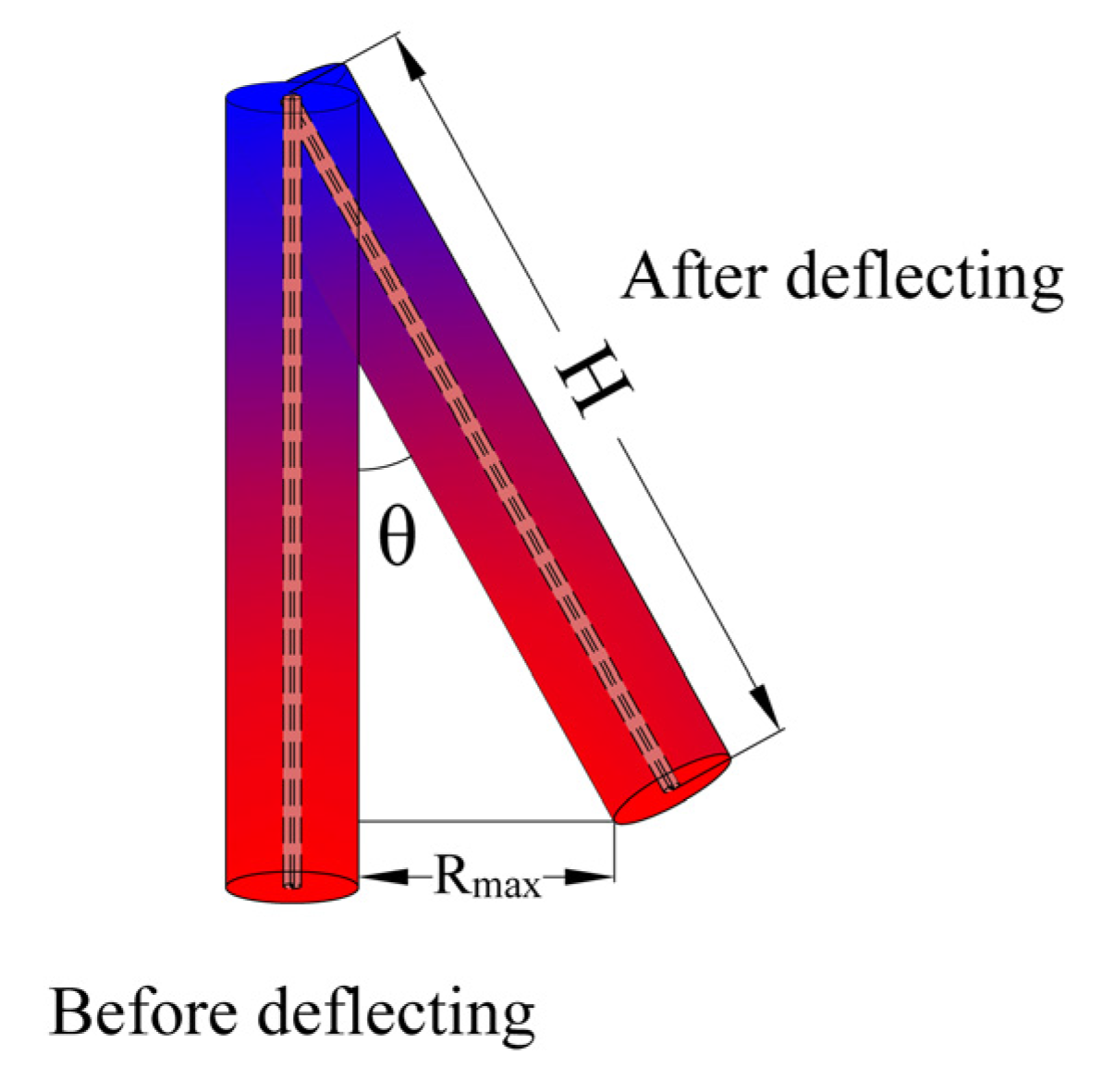
Based on the above analysis on the rock-soil temperature distribution characteristics, the main RTAA is focused on the deep part of rock-soil and the MTAR in full life cycle is positioned nearly at depth of pipe bottom. Hereto, a new-type well layout form of deflecting borehole was proposed in this study (Figure 12), the aim of which is saving ground surface occupation and avoiding the thermal interference between the adjacent MBHEs as much as possible. By deflecting the adjacent MBHEs in opposite directions, the overlapping RTAA would decrease even if the wellhead between adjacent MBHEs is close. The specific position relationship was shown in Figure 13. The normal MBHE is vertically installed and the new-type layout form is obliquely installed. There is an angle (θ) formed between the normal form and the new-type form. One benchmark angle was proposed as follow:

θ = \arcsin (\frac{R_{\max}}{H})

(6)

where θ, R_max, H are TAR angle, MTAR in full life cycle, and pipe length, respectively. Because the horizontal offset of MBHE bottom was determined as MTAR in full life cycle, the formed angle ( θ ) is named as TAR angle in this work.

3.4.2. Thermal Affected Area Analysis

MTAR in full life cycle is significantly affected by the rock-soil thermal conductivity but hardly affected by thermal extraction load, fluid velocity as well as design parameters. It could be concluded that the horizontal offset of MBHE after deflecting would only result in a position shift of RTAA rather than a variation in MTAR.

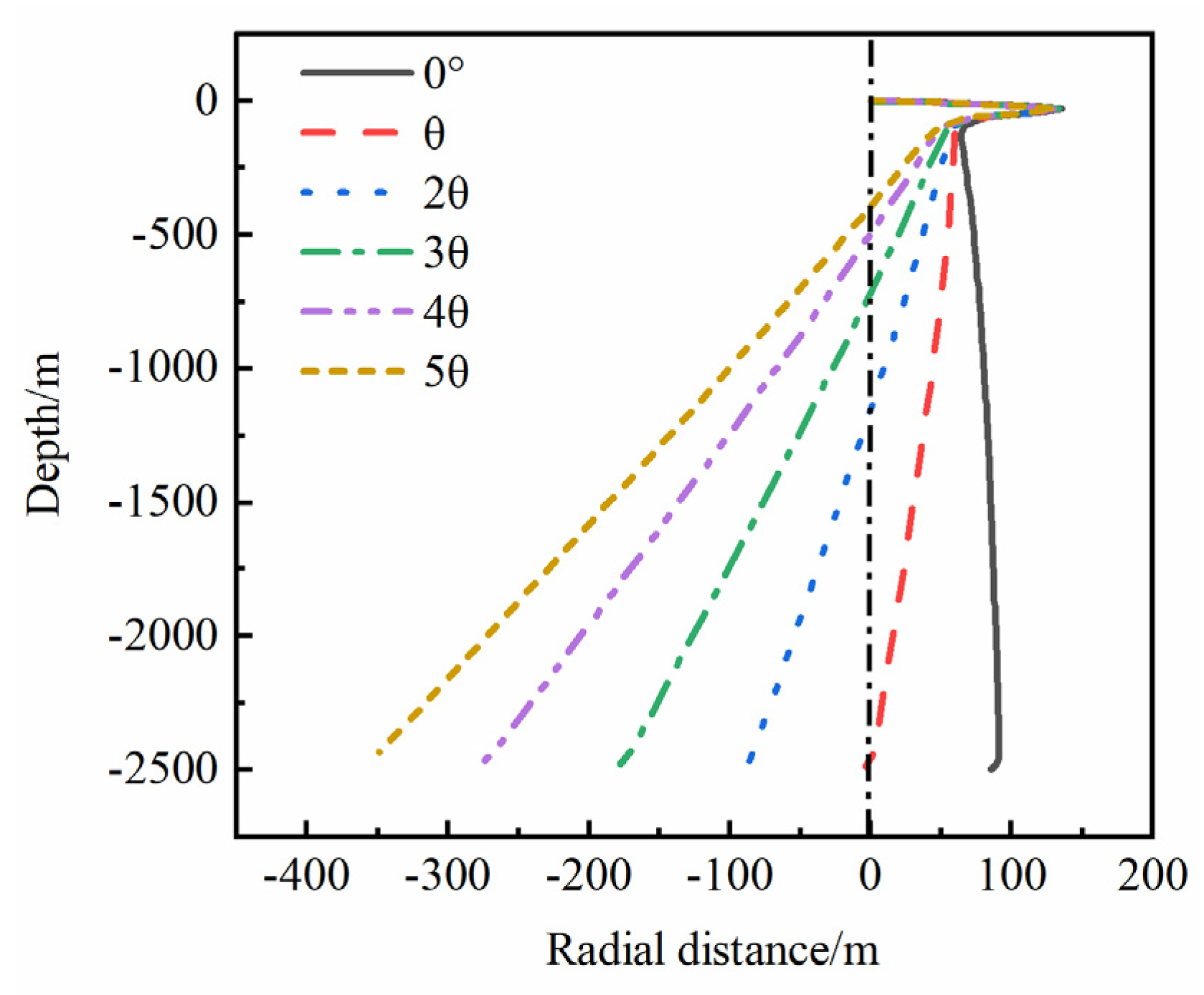
According to the optimal design method of thermal extraction capacity in our previous study [34], the recommended thermal extraction load and optimal operating parameter in the benchmark condition (shown in Table 1) could be determined. Then the MTAR in full life cycle obtained by rock-soil temperature distribution analysis was 91.3 m. Consequently, the TAR angle calculated by Eq. (5) is 2.1 °. Figure 14 shows the effects of TAR angle of different multiples on the MTAR in full life cycle. The position of MBHE before deflecting is at x = 0 m. The black solid line represents the TAR of different depths for MBHE without deflecting. In order to avoid the thermal interference in the right of the line x = 0 m, the MBHE would be deflected in the opposite x direction. It is noteworthy that after the deflection of one TAR angle, the thermal interference could only be avoided at the depth of MBHE bottom. A large amount of RTAA still exists in the right of line x = 0 m and may result in the thermal interference if the adjacent spacing is less than MTAR. Thus, the deflection angle needs to be further enlarged. When the deflection angle increases to 4 times TAR angle, about 80% of the whole depth could fully avoid the thermal interference, whilst the RTAA could not be efficiently reduced in the right of the line x = 0 m for over 4 times TAR angle. Therefore, the 4 times TAR angle was determined as the optimal deflection angle. Due to the deflection, the vertical depth of MBHE with 4 times TAR angle decreases by 26.6 m compared with the initial vertical depth of 2500 m, whereas the decreased depth hardly affects the thermal extraction of MBHE according to the previous study [34].

Furthermore, the optimal deflection angle of MBHE under different rock-soil thermal conductivities were also analyzed. The results show that the 4 times TAR angle could still avoid the thermal interference of adjacent MBHEs over 80% of the whole depth. Moreover, the thermal interference degree in the shallow depth is largely smaller than that in the deep depth [15], and the thermal extraction area of MBHE is mainly positioned in the deep depth [30]. In a word, 4 times TAR angle can be recommended as a optimal design inflection angle. The optimal TAR angles of MBHEs and corresponding vertical depths under various rock-soil thermal conductivities of 2.0-3.0 W·m^-1·K^-1 were tabulated in Table 2. The MBHE length ranges from 2000 to 3000 m. With the pipe length increasing, the optimal TAR angle becomes smaller. Additionally, while the vertical depth of MBHE after deflection declines, the decline degree hardly impacts the thermal extraction of MBHE. By the new-type well layout form, the spacing distance between the wellhead positions of adjacent MDBHEs could obviously reduced, which significantly contributes to save ground surface occupation.

4. Conclusions

In this work, the medium-deep rock-soil temperature characteristics under different time scales was investigated. By one single heating season analysis, the TAR distribution of medium-deep rock-soil at different depths was obtained so that the MTAR could be determined. Then the rounded parametric analysis including the effects of thermal extraction load, geological parameters, operating parameter and design parameters on the MTAR was carried out to demonstrate the evolution of MTAR. Next, combining with the MBHE operation feature of extracting geothermal energy in heating season and stopping geothermal extraction in non-heating season, the evolution mechanism of medium-deep rock-soil temperature in full life cycle was clarified and the effective MTAR was further discovered. Finally, based on above analysis, a new-type well layout form of MBHE was proposed, the advantage of which is effectively saving ground surface occupation and simultaneously avoiding the thermal interference between the adjacent MBHEs. The main results are as follows:

The results showed that the rock-soil thermal affected area (RTAA) continuously expands in both radial and vertical directions during a heating season. Several factors of thermal extraction load, fluid velocity, geothermal gradient and pipe parameters have main impacts on the RTAA in vertical direction. Rock-soil thermal conductivity affects the RTAA in both radial and vertical directions. In non-heating season, the temperature difference of medium-deep rock-soil in radial direction dominates the temperature recovery of rock-soil surrounding MBHE in the first year but after 20-year thermal extraction, the geothermal flow nearly dominates the temperature recovery. RTAA rapidly expands in the initial years. The thermal affected radius (TAR) in the 30 th year could be determined as a effective MTAR in full life cycle. In order to decrease the installed distance of adjacent MDBHEs on the surface, a new well layout form by deflecting borehole was proposed. When the deflection angle is equal to or larger than 4 times TAR angle, the thermal interference between the adjacent MDBHEs could be effectively avoided. This work provides the theoretical foundation and scientific reference for promoting the application of multiple MBHE arrays.

The RTAA continuously expands in both radial and vertical directions during a heating season. Among the analyzed influencing factors, only rock-soil thermal conductivity obviously affects the RTAA in both radial and vertical directions. The MTAR increases by 17.2% when the thermal conductivity increases from 2.0 to 3.0 W·m^-1·K^-1 and the increase degree would further enlarge with the thermal conductivity increasing. Other factors have main impacts on the RTAA only in vertical direction.
The temperature recovery mechanism in non-heating season of medium-deep rock-soil varies with thermal extraction year. In the first year, the temperature difference of medium-deep rock-soil in radial direction dominates the temperature recovery of rock-soil, whereas the geothermal flow nearly dominates the temperature recovery after 20-year thermal extraction. In the 30 th year, the TAR at the end of heating season and non-heating season basically coincide.
The TAR in the 30 th year could be determined as effective MTAR in full life cycle. According to rock-soil temperature distribution characteristics that main RTAA is focused on the deep part of rock-soil and MTAR in full life cycle is positioned nearly at depth of pipe bottom, a new-type well layout form by deflecting borehole was proposed. 4 times TAR angle was recommended as optimal deflection angle, which could effectively avoid the thermal interference between the adjacent MDBHEs.

Author Contributions

Conceptualization, J.L. and F.W.; Methodology, J.L and Z.W.; Software, Z.W.; validation, Y.Z, C.Z. and B.L.; Formal analysis, Z.W.; Investigation, B.L.; Resources, Y.Z.; Data curation, Z.W.; Writing—original draft preparation, J.L.; Writing—review and editing, F.W.; Visualization, F.W.; Supervision, F.W.; Project administration, Y.Z., C.Z., B.L.; funding acquisition, Y.Z.

Funding

This research was funded by Young Talent Fund of Shaanxi Association for Science and Technology (NYHB202218), Shaanxi Province Qin Chuangyuan "Scientist+Engineer" Team Construction (2022KXY-039), Shaanxi Province State-owned Assets Special Fund Project for Technological Innovation in Business Budget (2022-10).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Figure A1. Effects of inner pipe diameter on rock-soil temperature change compared with the undisturbed condition: (A) r=0.045 m, (B) r=0.055 m, (C) r=0.0625 m.

Figure A2. Effects of outer pipe diameter on rock-soil temperature change compared with the undisturbed condition: (A)R=0.0889 m, (B)R=0.1096 m, (C) R=0.1223 m.

Figure A3. Effects of inner pipe thermal conductivity on rock-soil temperature change compared with the undisturbed condition: (A) 0.45 W·m^-1·K^-1, (B) 0.20 W·m^-1·K^-1, (C) 0 W·m^-1·K^-1.

References

Wang, F.; Harindintwali, J.D.; Yuan, Z.Z; et al. Technologies and perspectives for achieving carbon neutrality. The Innovation 2021, 2, 100180. [Google Scholar] [CrossRef] [PubMed]
Chahartaghi, M.; Kalami, M.; Ahmadi, M.H.; et al. Energy and exergy analyses and thermo-economic optimization of geothermal heat pump for domestic water heating. International Journal of Low-Carbon Technologies 2019, 14, 108–121. [Google Scholar] [CrossRef]
Ghazvini, M.; Sadeghzadeh, M.; Ahmadi, M.H.; et al. Geothermal energy use in hydrogen production: A review. International Journal of Energy Research 2019, 43, 7823–7851. [Google Scholar] [CrossRef]
Lund, J.W.; Toth, A.N. Direct utilization of geothermal energy 2020 worldwide review. Geothermics 2020, 90, 101915. [Google Scholar] [CrossRef]
Tang, F.J.; Nowamooz, H. Long-term performance of a shallow borehole heat exchanger installed in a geothermal field of Alsace region. Renewable Energy 2018, 128, 210–222. [Google Scholar] [CrossRef]
Zhang, W.K.; Li, W.J.; Sørensen, B.R.; et al. Comparative analysis of heat transfer performance of coaxial pipe and U-type deep borehole heat exchangers. Geothermics 2021, 96, 102220. [Google Scholar] [CrossRef]
Chen, S.; Cai, W.L.; Witte, F.; et al. Long-term thermal imbalance in large borehole heat exchangers array - A numerical study based on the Leicester project. Energy and Buildings 2021, 231, 110518. [Google Scholar] [CrossRef]
Kohl, T.; Brenni, R.; Eugster, W. System performance of a deep borehole heat exchanger. Geothermics 2002, 31, 687–708. [Google Scholar] [CrossRef]
Śliwa, T.; Kotyza, J. Application of existing wells as ground heat source for heat pumps in Poland. Applied Energy 2003, 74, 3–8. [Google Scholar] [CrossRef]
Huchtemann, K.; Müller, D. Combined simulation of a deep ground source heat exchanger and an office building. Building and Environment 2014, 73, 97–105. [Google Scholar] [CrossRef]
Kelkar, S.; Wolde, G.G.; Rehfeldt, K. Lessons learned from the pioneering hot dry rock project at Fenton Hill, USA. Geothermics 2016, 63, 5–14. [Google Scholar] [CrossRef]
Ghavidel, A.; Gracie, R.; Dusseault, M.B. Design parameters impacting electricity generation from horizontal multilateral closed-loop geothermal systems in hot dry rock. Geothermics 2022, 105, 102469. [Google Scholar] [CrossRef]
Liu, D.X.; Zhang, W.; Lu, X.L.; et al. Research on a novel type of hot dry rock power generation system coupled with Kalina and ORC. Energy Reports 2022, 8, 65–76. [Google Scholar] [CrossRef]
Li, J.; Xu, W.; Li, J.F.; et al. Heat extraction model and characteristics of coaxial deep borehole heat exchanger. Renewable Energy 2021, 169, 738–751. [Google Scholar] [CrossRef]
Cai, W.L.; Wang, F.H.; Chen, S.; et al. Analysis of heat extraction performance and long-term sustainability for multiple deep borehole heat exchanger array: A project-based study. Applied Energy 2021, 289, 116590. [Google Scholar] [CrossRef]
Wang, Z.H.; Wang, F.H.; Liu, J.; et al. Field test and numerical investigation on the heat transfer characteristics and optimal design of the heat exchangers of a deep borehole ground source heat pump system. Energy Conversion and Management 2017, 153, 603–615. [Google Scholar] [CrossRef]
Deng, J.W.; Wei, Q.P.; Liang, M.; et al. Field test on energy performance of medium-depth geothermal heat pump systems (MD-GHPs). Energy and Buildings 2019, 184, 289–299. [Google Scholar] [CrossRef]
Deng, J.W.; He, S.; Wei, Q.P.; et al. Field test and optimization of heat pumps and water distribution systems in medium-depth geothermal heat pump systems. Energy and Buildings 2020, 209, 109724. [Google Scholar] [CrossRef]
Welsch, B.; Rühaak, W.; Schulte, D.O.; et al. Characteristics of medium deep borehole thermal energy storage. International Journal of Energy Research 2016, 40, 1855–1868. [Google Scholar] [CrossRef]
Hu, X.C.; Banks, J.; Wu, L.P.; et al. Numerical modeling of a coaxial borehole heat exchanger to exploit geothermal energy from abandoned petroleum wells in Hinton, Alberta. Renewable Energy 2020, 148, 1110–1123. [Google Scholar] [CrossRef]
Bu, X.B.; Ma, W.B.; Li, H.S. Geothermal energy production utilizing abandoned oil and gas wells. Renewable Energy 2012, 41, 80–85. [Google Scholar] [CrossRef]
He, Y.J.; Bu, X.B. A novel enhanced deep borehole heat exchanger for building heating. Applied Thermal Engineering 2020, 178, 115643. [Google Scholar] [CrossRef]
Song, X.Z.; Wang, G.S.; Shi, Y.; et al. Numerical analysis of heat extraction performance of a deep coaxial borehole heat exchanger geothermal system. Energy 2018, 164, 1298–1310. [Google Scholar] [CrossRef]
Fang, L.; Diao, N.R.; Shao, Z.K.; et al. A computationally efficient numerical model for heat transfer simulation of deep borehole heat exchangers. Energy and Buildings 2018, 167, 79–88. [Google Scholar] [CrossRef]
Chen, C.F.; Shao, H.B.; Naumov, D.; et al. Numerical investigation on the performance, sustainability, and efficiency of the deep borehole heat exchanger System for Building Heating. Geothermal Energy 2019, 7(1), 18. [Google Scholar] [CrossRef]
Le Lous, M.; Larroque, F.; Dupuy, A.; et al. Thermal performance of a deep borehole heat exchanger: insights from a synthetic coupled heat and flow model. Geothermics 2015, 57, 157–172. [Google Scholar] [CrossRef]
Holmberg, H.; Acuna, J.; Næss, E.; et al. Thermal evaluation of coaxial deep borehole heat exchangers. Renewable Energy 2016, 97, 65–76. [Google Scholar] [CrossRef]
Liu, J.; Wang, F.H.; Cai, W.L.; et al. Numerical investigation on the effects of geological parameters and layered subsurface on the thermal performance of medium-deep borehole heat exchanger. Renewable Energy 2020, 149, 384–399. [Google Scholar] [CrossRef]
Wang, Z.Y.; Wang, F.H.; Liu, J.; et al. Energy analysis and performance assessment of a hybrid deep borehole heat exchanger heating system with direct heating and coupled heat pump approaches. Energy Conversion and Management 2023, 276, 116484. [Google Scholar] [CrossRef]
Liu, J.; Wang, F.H.; Cai, W.L.; et al. Numerical study on the effects of design parameters on the heat transfer performance of coaxial deep borehole heat exchanger. International Journal of Energy Research 2019, 43, 6337–6352. [Google Scholar] [CrossRef]
Huang, Y.B.; Zhang, Y.J.; Xie, Y.Y.; et al. Thermal performance analysis on the composition attributes of deep coaxial borehole heat exchanger for building heating. Energy and Buildings 2020, 221, 110019. [Google Scholar] [CrossRef]
Cai, W.L.; Wang, F.H.; Chen, C.F.; et al. Long-term performance evaluation for deep borehole heat exchanger array under different soil thermal properties and system layouts. Energy 2022, 241, 122937. [Google Scholar] [CrossRef]
Zhang. F.F.; Fang, L.; Zhu, K.; et al. Long-term dynamic heat transfer analysis for the borehole spacing planning of multiple deep borehole heat exchanger. Case Studies in Thermal Engineering 2022, 38, 102373. [Google Scholar] [CrossRef]
Liu, J.; Wang, F.H.; Gao, Y.; et al. Influencing factors analysis and operation optimization for the long-term performance of medium-deep borehole heat exchanger coupled ground source heat pump system. Energy and Buildings 2020, 226, 110385. [Google Scholar] [CrossRef]

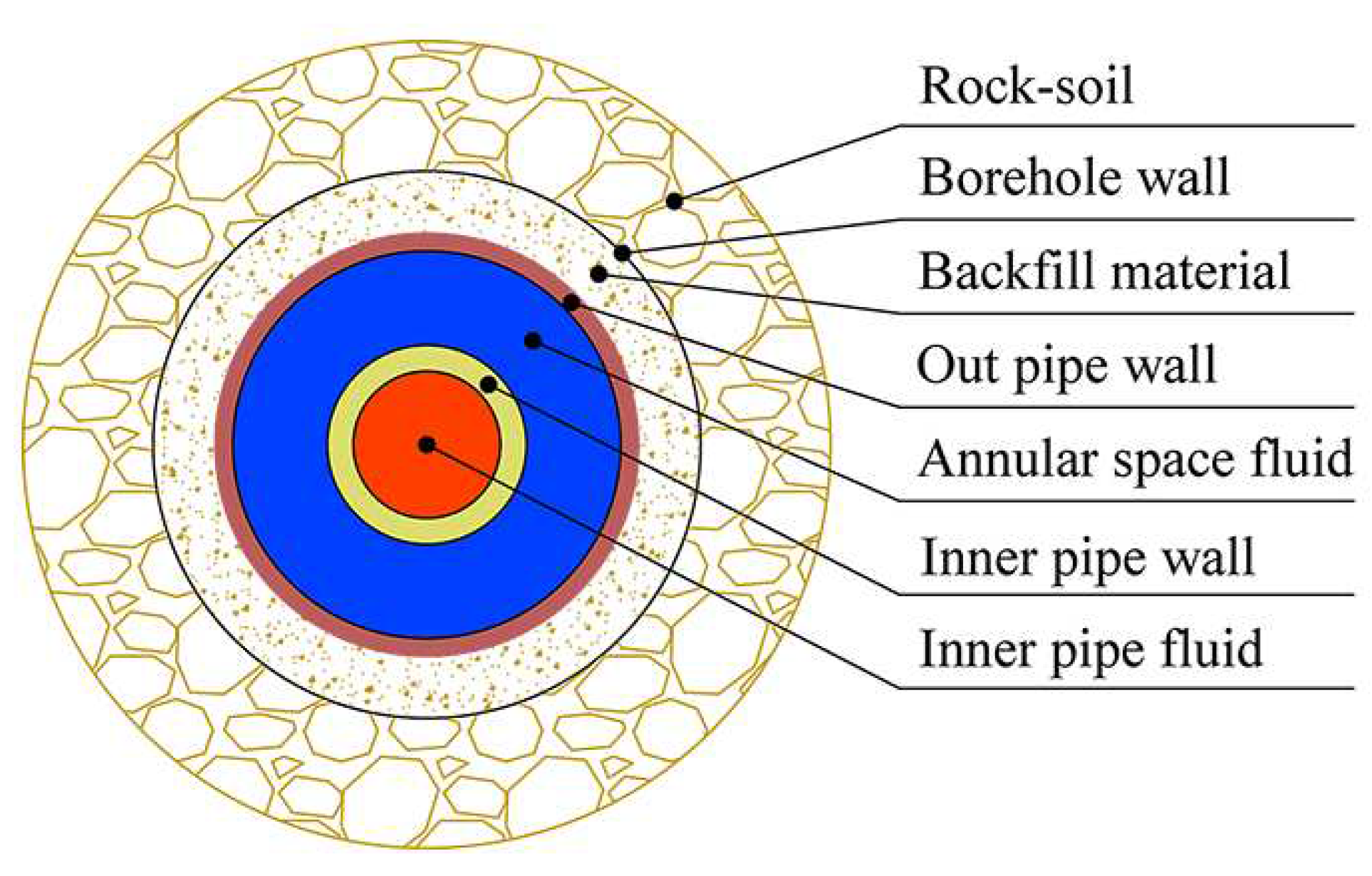
Figure 1. Periodic heat transfer process of MBHE.

Figure 2. Positional relationship between MBHE and rock-soil in cross section.

Figure 3. Discretized model and investigated influencing factors.

Figure 4. Rock-soil temperature distribution characteristics during a heating season: (A) rock-soil temperature distribution with thermal extraction time; (B) rock-soil temperature change compared with the undisturbed condition at different time.

Figure 5. Effects of thermal extraction load on rock-soil temperature change compared with the undisturbed condition:(A) 75 W·m^-1, (B) 100 W·m^-1, (C) 125 W·m^-1.

Figure 6. Effects of rock-soil thermal conductivity on rock-soil temperature change compared with the undisturbed condition: (A) 2.0 W·m^-1·K^-1, (B) 2.5 W·m^-1·K^-1, (C) 3.0 W·m^-1·K^-1.

Figure 7. Effects of geothermal gradient on rock-soil temperature change compared with the undisturbed condition: (A) 25 °C·km^-1, (B) 30 °C·km^-1 , (C) 35 °C·km^-1 .

Figure 8. Effects of fluid velocity on rock-soil temperature change compared with the undisturbed condition: (A) 0.5 m·s^-1, (B) 0.6 m·s^-1 , (C) 0.7 m·s^-1 .

Figure 9. Effects of pipe length on rock-soil temperature change compared with the undisturbed condition: (A) 2000 m, (B) 2500 m , (C) 3000 m.

Figure 10. TAR at the end of heating season and non-heating season: (A) 1st year, (B) 10 th year, (C) 20 th year, (D) 30 th year.

Figure 11. Comparisons between the 1 st-year TAR and the maximum radius in full life cycle: (A) effect of thermal extraction load, (B) effect of rock-soil thermal conductivity.

Figure 12. Proposed well layout form.

Figure 13. Positional relationship of adjacent MBHEs.

Figure 14. Analysis of RTAA in full life cycle for the proposed well layout form.

Table 1. Analyzed parameters and benchmark parameter.

No	Factor (unit)	Analyzed parameters	Benchmark parameter
(a)	Thermal extraction load (W·m^-1)	75, 100, 125	100
(b)	Rock-soil thermal conductivity (W·m^-1·K^-1)	2.0, 2.5, 3.0	2.5
(c)	Geothermal gradient (°C·km^-1)	25, 30, 35	30
(d)	Flow velocity (m·s^-1)	0.5, 0.6, 0.7	0.7
(e)	Pipe length (m)	2000, 2500, 3000	2500
(f)	Inner pipe diameter (m)	0.045, 0.055, 0.0625	0.055
(g)	Outer pipe diameter (m)	0.0889, 0.1096, 0.1223	0.0889
(h)	Inner pipe thermal conductivity (W·m^-1·K^-1)	0, 0.20, 0.45	0.45

Table 2. Deflection angle and vertical depth of MBHEs under various rock-soil thermal conductivities.

Pipe length/m	TAR angle/°	Vertical depth/m	Pipe length/m	Optimal TAR angle /°	Vertical depth /m
2000	2.1-2.9	1997.4-1998.6	2000	8.4-11.6	1958.6-1978.4
2500	1.8-2.4	2497.8-2498.8	2500	7.2-9.6	2464.4-2481.2
3000	1.5-2.1	2998.0-2999.0	3000	6.0-8.4	2968.6-2983.4

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer