Prerpints.org logo
Preprint
Article

Study on the Shear Resistance Performance of Grouped Stud Connectors

Altmetrics

Downloads

53

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

31 August 2023

Posted:

01 September 2023

You are already at the latest version

Alerts
Abstract
In order to further investigate the study of the effect of grouped stud effect on the force properties of stud connector, based on the premise that the correctness of the finite element simulation method in this paper, finite element modeling of grouped stud connectors was developed, the grouped stud effect and its sensitivity factors were analyzed, to validate the recommended formula for calculating the shear capacity of grouped stud connectors. Results show that the number of grouped stud rows and row spacing have a significant effect on the grouped stud effect, and the unevenness coefficient of grouped stud force Ⅰ is negatively correlated with the number of grouped stud rows as well as the grouped stud row spacing. For grouped stud connectors with commonly used concrete grades greater than C50 and height-to-diameter ratios greater than 4 in steel-concrete composite structural bridges, which is insensitive to changes in the concrete strength grades and the length of the studs. The direction of force transmission for the grouped stud changes with the change of loading angle, and the unevenness coefficient of force for the grouped stud will therefore be reduced. By comparing the results of the 62 existing groups of grouped stud connectors push-out tests, the mean value of the ratio of tested to calculated values is found to be 1.12, the variance is 0.023, the dispersion is small, it is shown that the recommended formula has a high degree of accuracy. The results of this paper can be used as a theoretical basis for the study of the shear stress performance of grouped stud connectors.
Keywords: 
Subject: Engineering  -   Civil Engineering

0. Introduction

As a key synergistic force-transferring member of steel-concrete composite structures, stud connectors are now widely used in steel-concrete composite beams, hybrid beams, composite columns and other structures [1,2,3]. The shear force between the steel member and concrete member is mainly borne by the connection, while resisting the role of lift-off, which is the key stress member of the steel-concrete composite structure [4,5,6]. Grouped stud connectors have the advantages of isotropy, high shear bearing capacity, good lifting resistance, easy construction, and so on, it is the most widely used shear connector [7,8,9,10].
The shear performance of stud connector has been of interest to scholars for decades, a large number of studies have been shown that the main forms of damage of stud connector under shear include: shear damage of studs, and compression damage of concrete [11]. The shear resistance of the studs is mainly affected by the stud material, stud body diameter, stud length, weld quality between the stud and steel plate, concrete strength, and hoop ratio [6,12,13,14]. The method of calculating the shear capacity of a single stud was creatively proposed by Viest, and is widely used in several national codes [15,16,17,18]. Wang et al. [19] analyzed the sensitivity of parameters such as stud diameter and concrete strength with the help of finite element modeling, and a new formula for calculating the shear capacity of stud connector was proposed. More and more novel stud connectors have been invented by research scholars and shear calculation methods were proposed, which are only applicable to the novel connectors [20,21,22], and are not generalizable.
With the continuous improvement of the road grade and the expansion of the construction scale, the application of cluster grouped stud connectors in steel-concrete composite structures is more widely used. For dense, large-sized grouped stud connectors under loads, the distribution of shear force across the studs was heterogeneous [23], the average shear capacity and shear stiffness of single stud of grouped stud connectors were significantly lower than that of single stud specimens [24,25,26]. With the increasing number of grouped stud rows in the direction of force, the degree of heterogeneity of the grouped stud shear would increase [24,26]. Through a parametric sensitivity analysis of the grouped stud connectors, it was found that grouped stud spacing, number of grouped stud rows in the loaded direction, concrete and stud material properties, and stud size are the main factors affecting the shear performance of grouped stud connectors [21,25,27]. For fiber-reinforced concrete grouped stud connectors, because the presence of fibers affects the ductility of the studs, the stress concentration at the interface between the studs and the concrete will be reduced [6,28]. Much scholarly attention has also been paid to the force properties of grouped stud in assembled composite beams [10,19,29]. Most current studies have concluded that the model provided in the Chinese design code for calculating shear capacity is conservative. On the basis of the analysis, new formulas or adjustment factors for calculating the shear capacity of grouped stud connectors in design codes are proposed [30,31]. In summary, the shear performance of single-row stud connector has been analyzed by previous literature, however, limited research has been conducted on the force behavior of grouped stud connectors, systematic analyses of the stress performance of grouped stud connectors are also rare.
The refined finite element analysis method was used to simulate the push-out test of existing single-row stud connector in this paper, based on the premise that the correctness of the finite element simulation method, multi-row stud finite element models were developed. In order to investigate the influence of grouped stud effect on the shear resistance performance of grouped stud connectors. By numerically analyzing the grouped stud effect and the main factors affecting it, the grouped stud effect of grouped stud connectors and the main factors affecting the grouped stud effect were numerically analyzed. On the basis of test data from the introduction of a total of 62 grouped stud connectors at home and abroad, the formula for calculating the shear capacity of grouped stud connectors is recommended.

1. Finite element simulation and verification

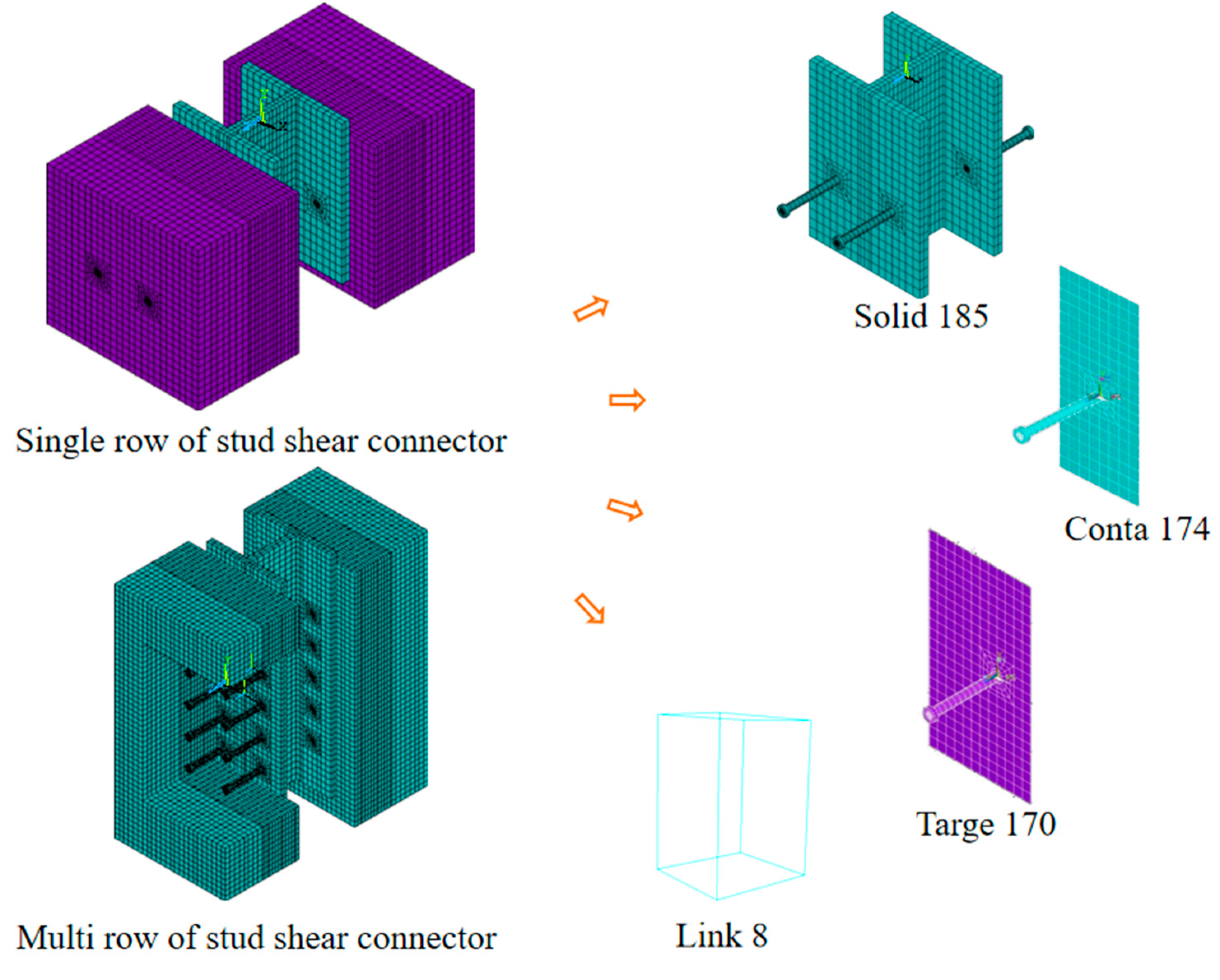
Considering steel and concrete material nonlinearities, to perform refined finite element simulations of the stud shear connector push-out test pieces, the large-scale general-purpose finite element analysis software ANSYS was employed. The finite element model is schematically shown in Figure 1. The stud shear connector is composed of 2 rows of φ22×200 studs with a spacing of 200mm horizontally on each side, the concrete material is C50, the stud material is ML15, and the steel plate material is Q345. The stud and steel plate were simulated using Solid185, a solid unit; the concrete was simulated using the tetrahedral solid unit Solid65; ordinary steel bars were simulated using the bar unit Link8, to achieve synergistic deformation of plain steel and concrete, three-way translational displacement degrees of freedom between ordinary steel nodes and corresponding concrete nodes were constrained. Both the steel plate-concrete block and the stud-concrete block were simulated using the face-to-face contact unit Conta174 and the target unit Targe170, respectively, and a friction coefficient of 0.4 was accounted [32]. The actual loading was simulated by applying a face load on the top surface of the steel plate, and the three-way translational displacement degrees of freedom of the bottom edge node of the concrete block were constrained [33].
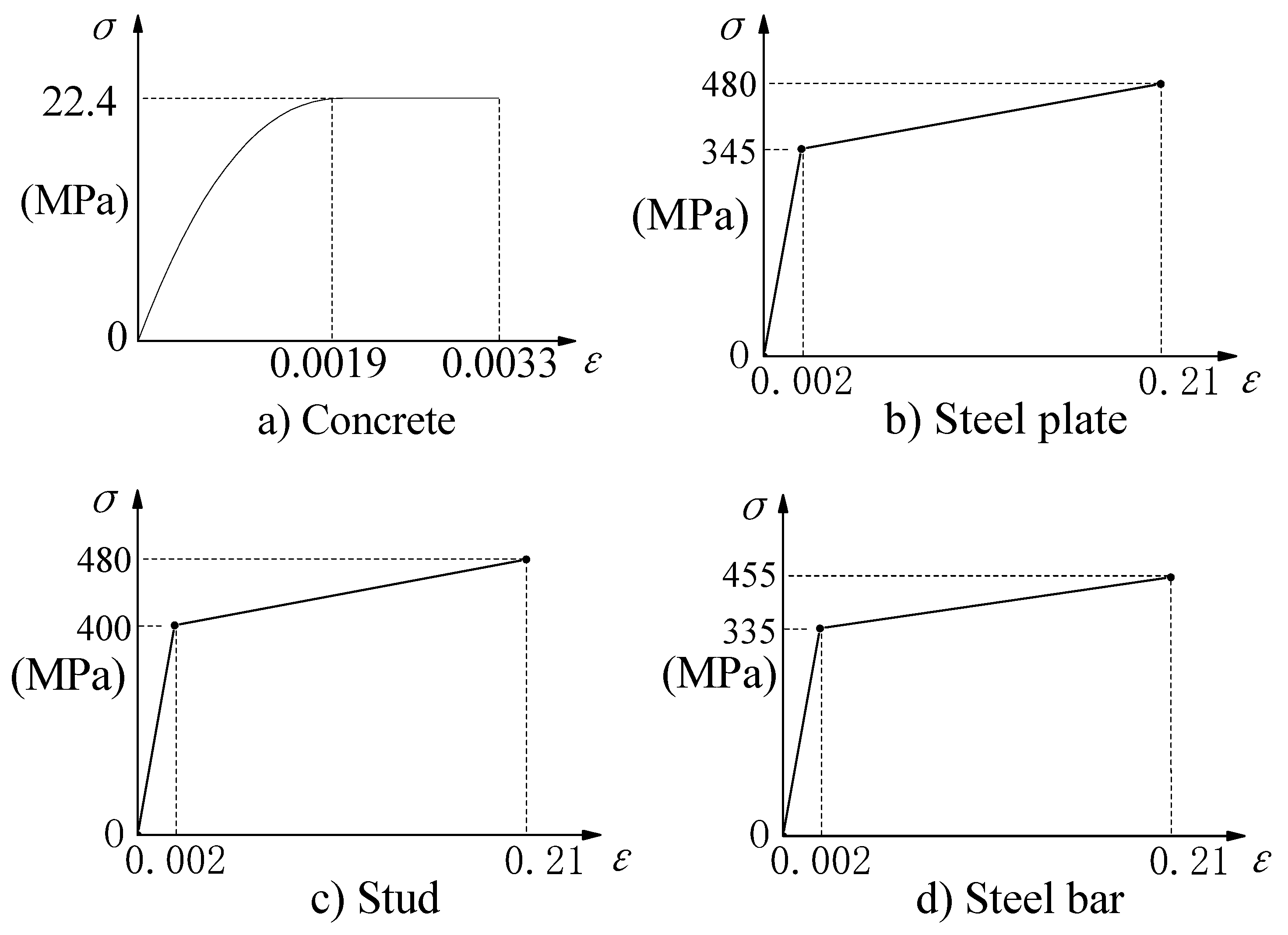
The materials in the model were defined using an elasto-plastic constitutive model, and their stress-strain relationship curves are shown in Figure 2.
In the literature [32] a push-out test was carried out on the single row of stud connector in Figure 1, the specimen eventually undergoes bending shear damage at the root of the studs, the average shear bearing capacity of 230kN for single stud was derived. According to the literature [34] method, the slope of the cut line at the 1/3 size of the shear capacity of the stud shear connection is taken as the shear stiffness of the connector, the average shear stiffness of the single stud was 206kN·mm-1. The results of finite element analysis of this single row of stud shear connector in this paper show that the average shear capacity and shear stiffness of single nails were 223kN and 217 kN·mm-1 respectively. The difference between simulated and experimental measured results is 3.0% and 5.4%, the reliability and computational accuracy of the finite element analysis method is thus confirmed in this paper.

2. Properties and damage mechanism

2.1. Critical stud spacing for the grouped stud effect

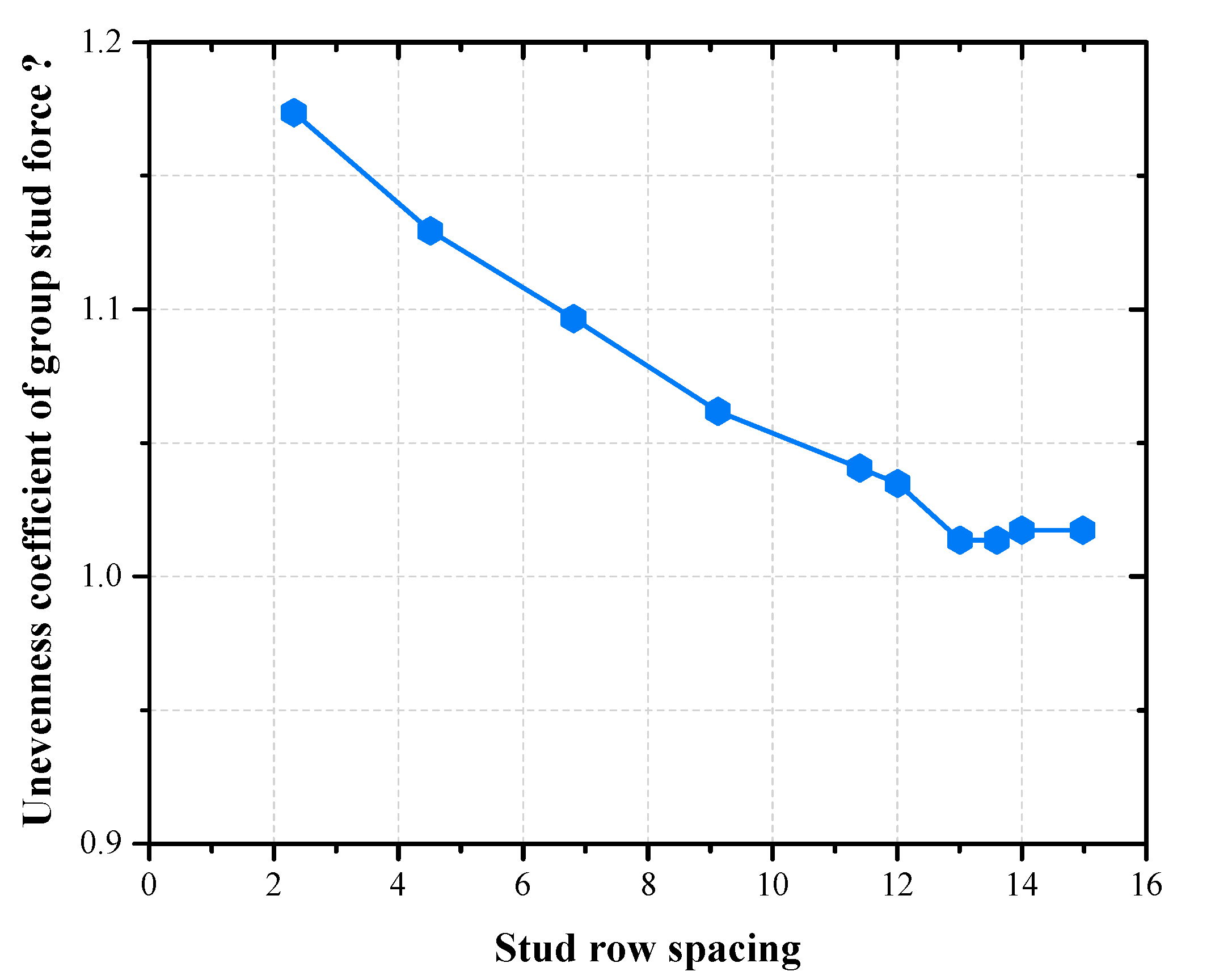
Stud connector are often employed in composite structures in the form of grouped stud. It is possible to follow the single stud design in some cases, but not in others, it depends on the magnitude of the concrete stresses in the surrounding studs. Within a certain range, its grouped stud effect diminishes with increasing grouped stud spacing, increases with increasing the shear force, and increases with increasing overlap of concrete pressure cracking zones. Generally, the grouped stud effect is more significant in shallow concrete than in deeper concrete; the grouped stud effect in the direction of load action is greater than that in the direction of perpendicular load action. Different stud spacings were analyzed by the authors, the results are shown in Figure 3, when the grouped stud spacing in the direction of load application is up to 13 times the stud diameter, the shear value of the grouped stud tends to be homogeneous, the effect of group stud effect on the shear force of the peg group can be neglected, at which time its grouped stud efficiency is close to 1.0, it can be considered as a single stud, and when it is less than 13 times the diameter of the stud body, the grouped stud effect should be taken into account, the values are taken to be consistent with the code. The findings of this study are in line with the literature [35]. Where the grouped stud efficiency is defined by the unevenness of force coefficient I, coefficient I is shown in Formula (1).
I = max . F 1 , F 2 , ⋯ , F i ∑ j = 1 n Q g u / n
Where: I is the unevenness coefficient of grouped stud force; Fi is the shear value of each stud in the grouped stud connectors; Qgu is the shear capacity of the grouped stud shear connector; n is the number of studs rows corresponding to the direction of the load.

2.2. Working properties and damage mechanism of grouped stud and influencing factors

2.2.1. Effect of grouped stud row spacing in the direction of shear action

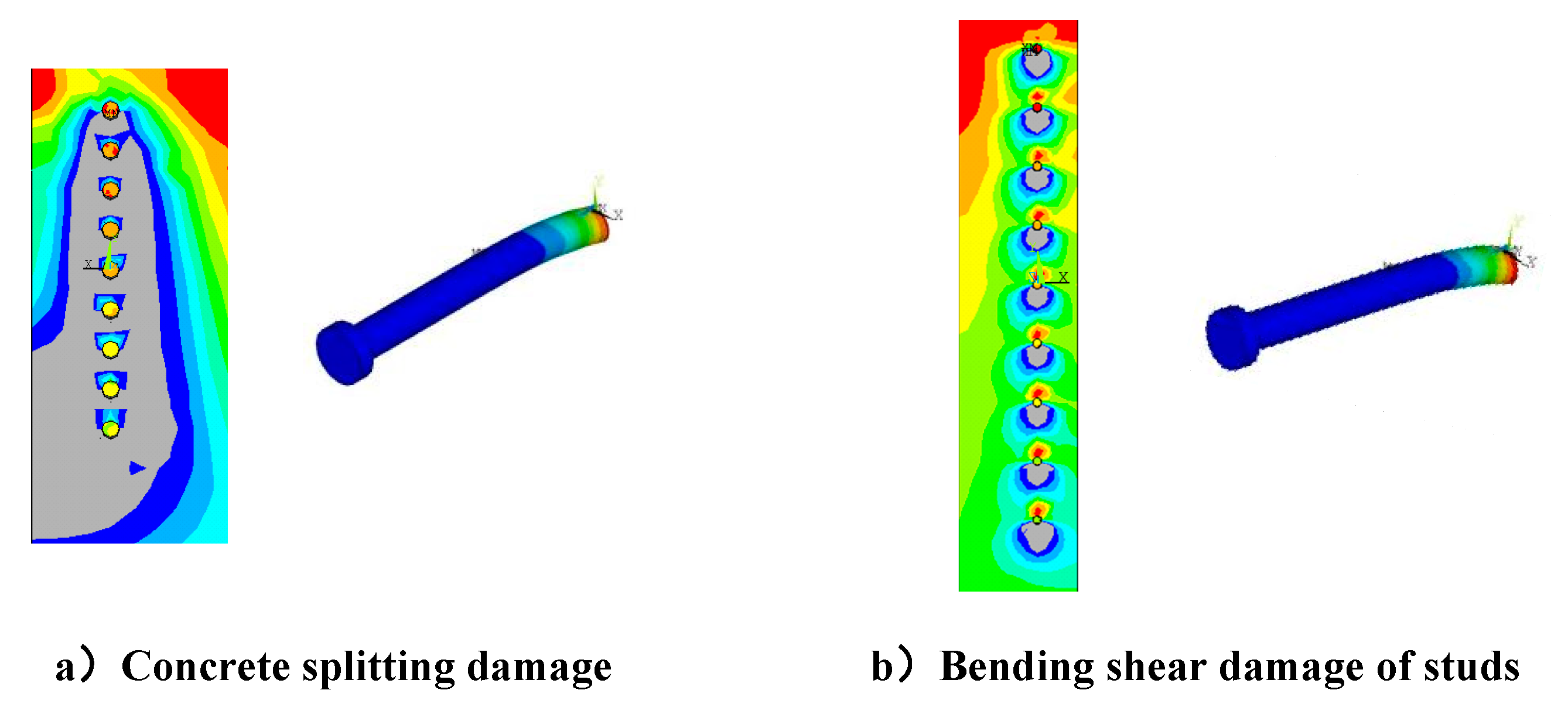
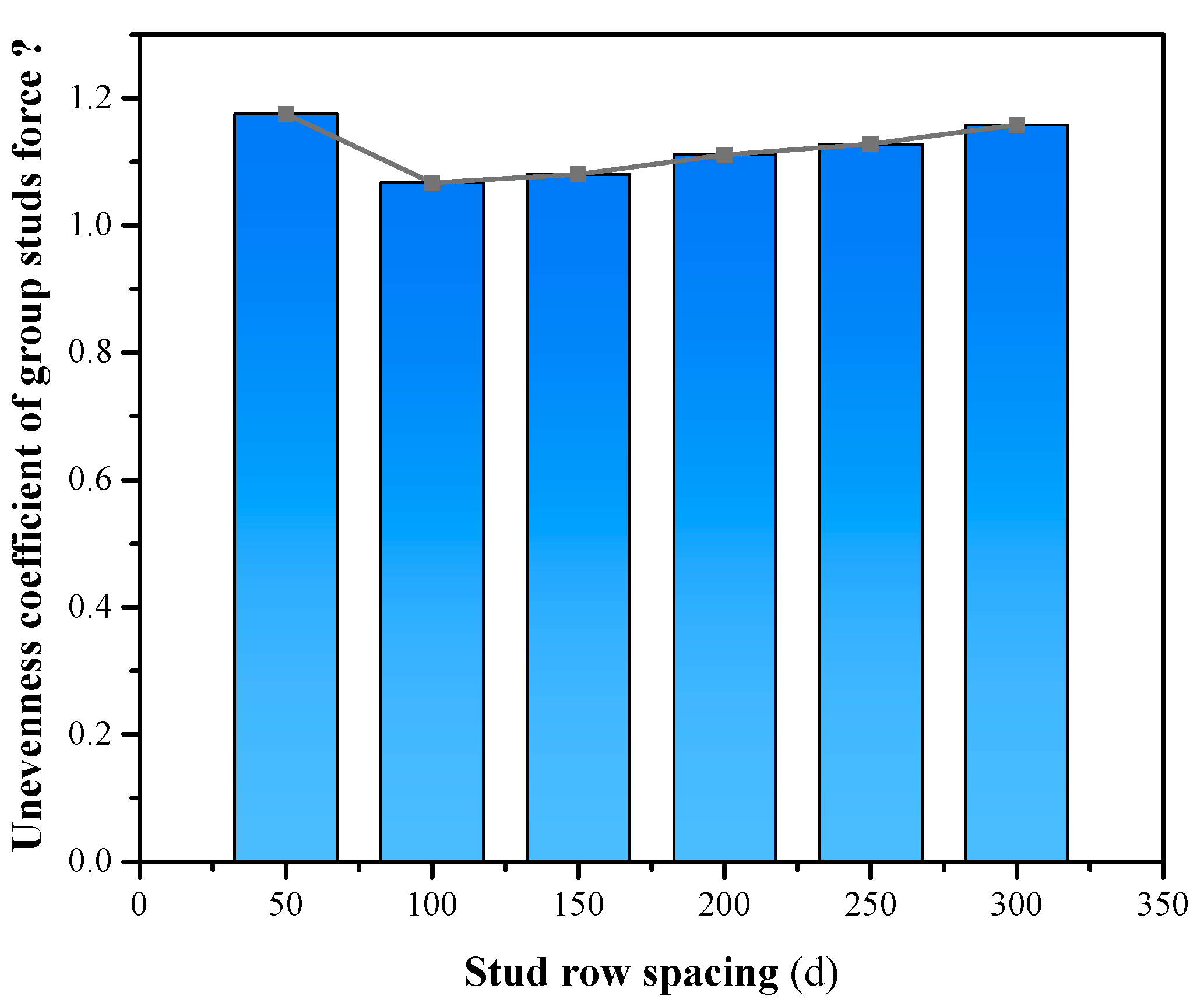
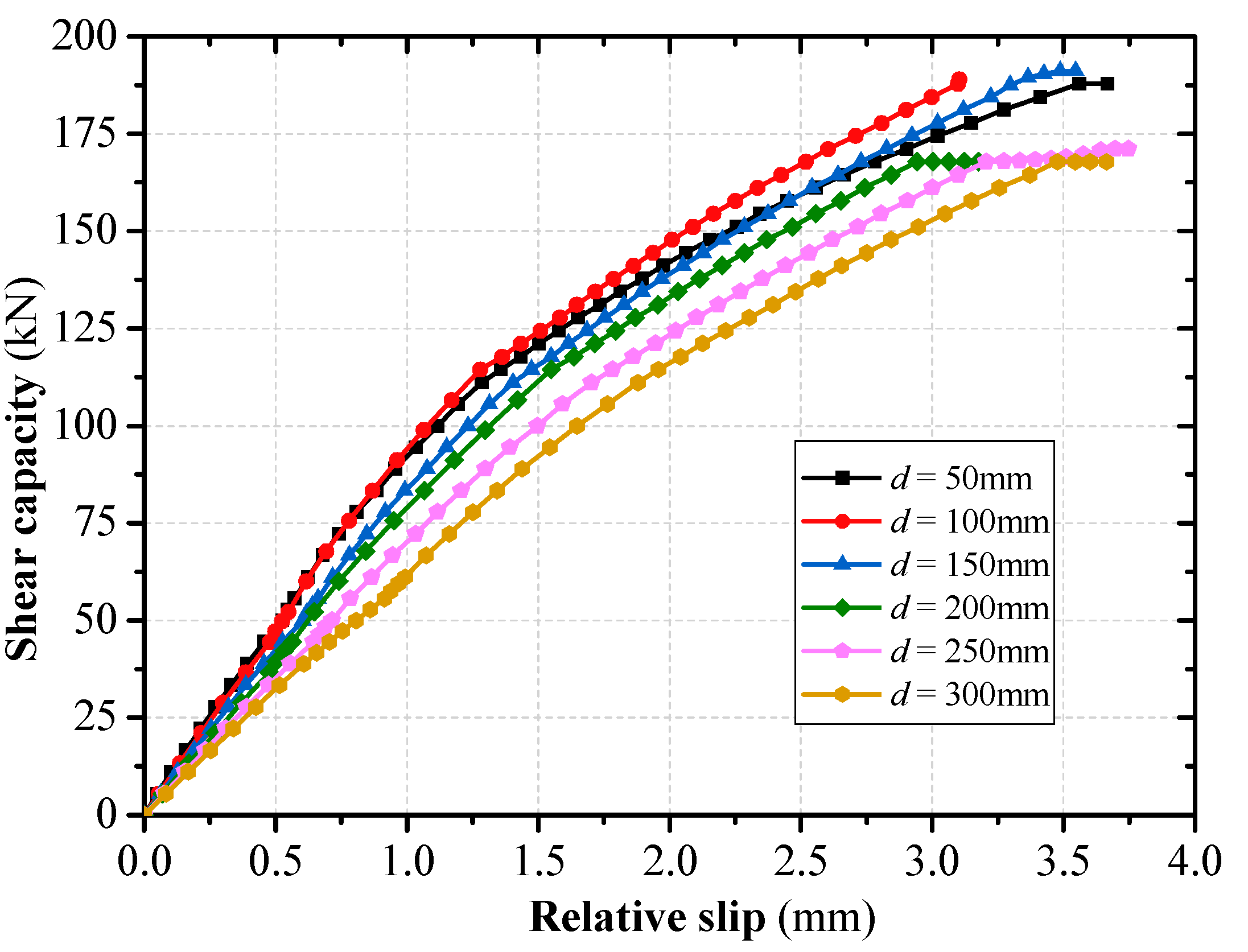
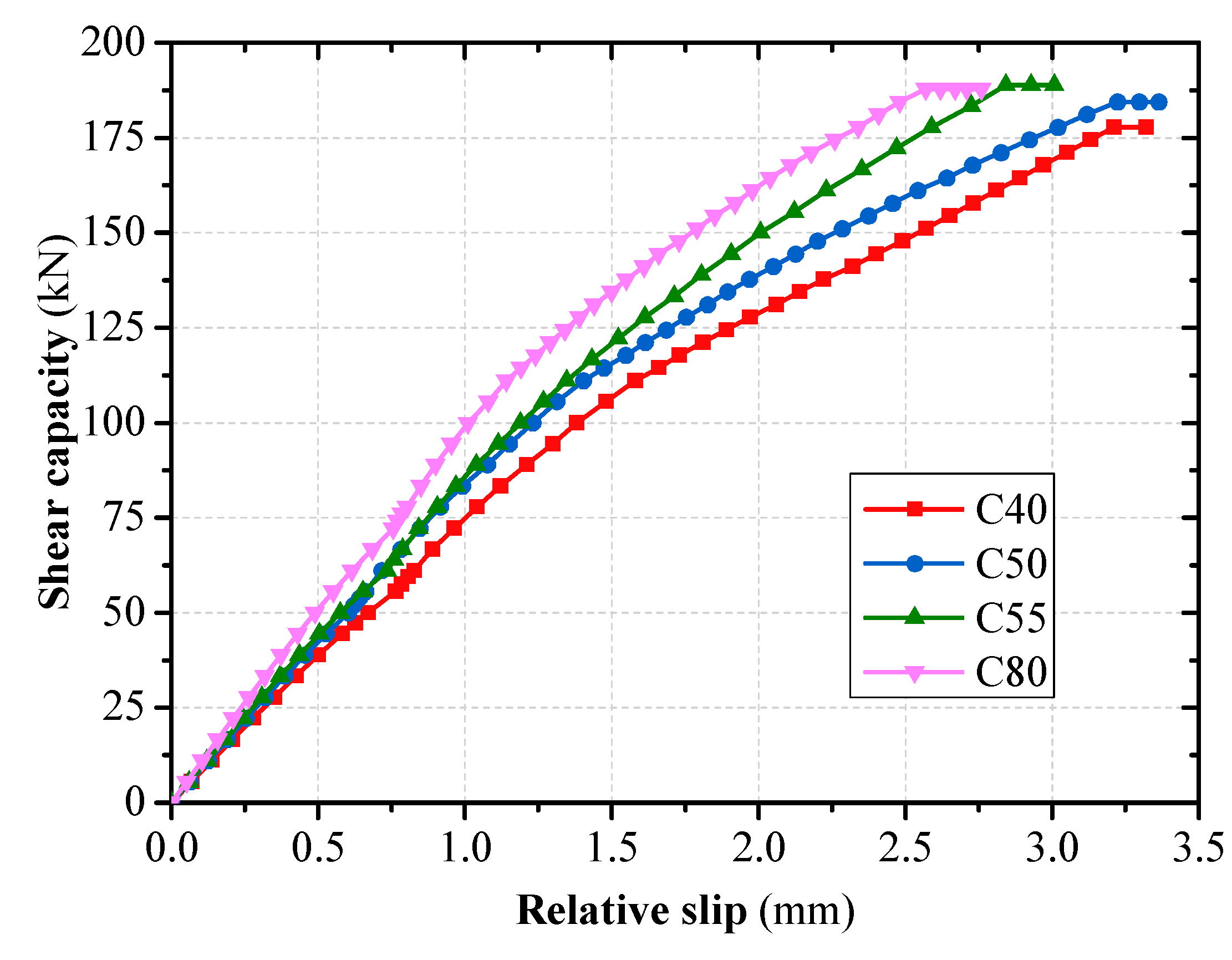
The spacing d between stud rows was set to 50mm (2.3d, d is the diameter of the stud body), 100mm (4.5d), 150mm (6.8d), 200mm (9.1d), 250mm (11.4d), 300mm (13.6d), respectively, the effect of row spacing on the force properties of grouped stud connectors was analyzed. The results show that splitting damage of the concrete occurred in the connector (Figure 4a) when the grouped stud spacing was 50mm, bending shear damage of the studs occurred in the remaining specimens (Figure 4b). This was caused by the interaction of concrete between grouped stud when the grouped stud is subjected to shear forces, overlapping stress distributions occur in the concrete between the grouped stud, and its overlap effect decreases with increasing stud spacing, and the unevenness of the grouped stud force decreases (Figure 5 and Figure 6). Consequently, when the studs spacing is small, the distribution of concrete stresses has a significant superposition effect, the connector may even undergo damage in the form of splitting damage of the concrete (e.g., d = 50 mm); when the stud row spacing is large, the distribution of concrete stresses has less overlapping effect, and when the stud spacing is more than 13 times the stud body diameter, the unevenness of the grouped stud force is close to 1, i.e., close to the same state of force as that of a single stud.

2.2.2. Effect of the grouped stud rows

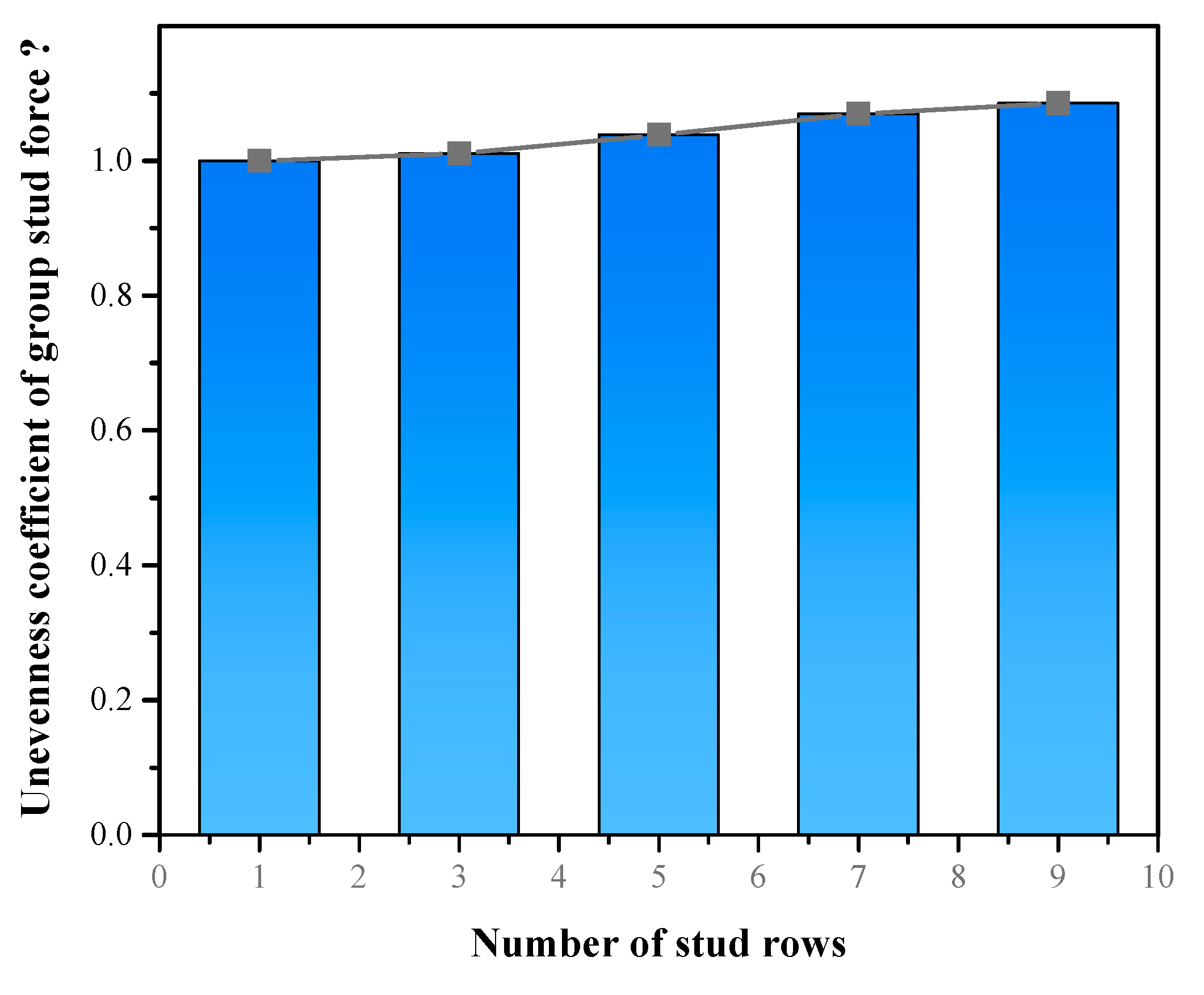
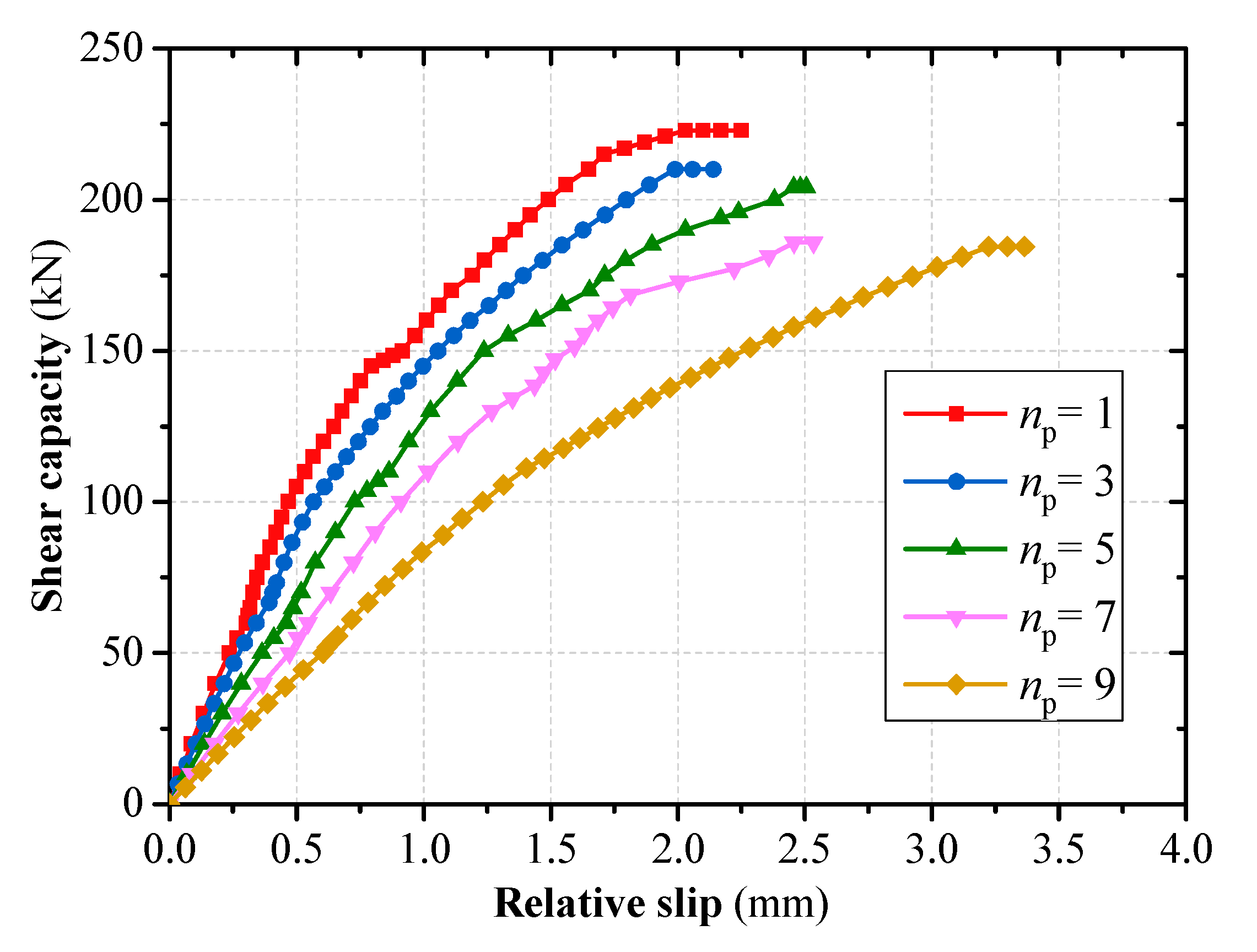
Keeping the grouped stud row spacing at 150 mm, and the number of grouped stud rows np was set as 1, 3, 5, 7, 9, the effect of row spacing on the force properties of grouped stud connectors was analyzed. The results show that bending shear damage of the studs occurred in all of these specimens; the unevenness coefficient of grouped stud force increases with the increase in the number of grouped stud rows (Figure 7); the shear capacity of the connector decreases with the increasing number of grouped stud rows, and the decreasing trend is significant. When the number of rows is increased from 1 to 9, the average shear capacity of single stud is reduced by 17.5% (Figure 8).

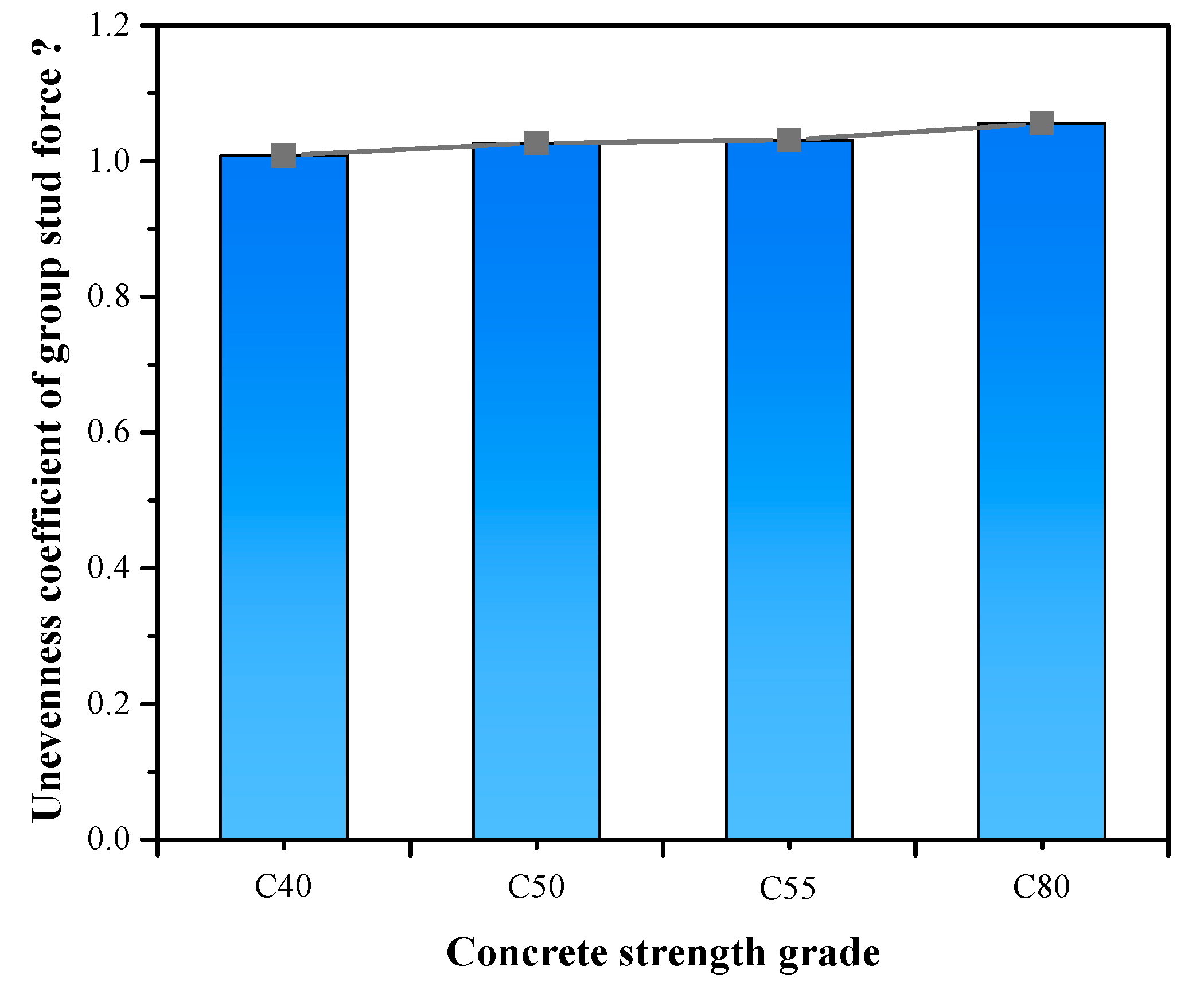
2.2.3. Effect of concrete strength grade

The deformation and force of the grouped stud will be restrained by the concrete, however, when the concrete strength exceeds C50, the shear capacity increase of the shear connector is relatively reduced, the unevenness coefficient of grouped stud force also varied less (Figure 9 and Figure 10). When the concrete strength grade is increased from C50 to C80, the average shear capacity of single stud is increased by only 0.53%, the unevenness coefficient of grouped stud force increased by only 2.36%, which is also consistent with the findings of the literature [10]. In combined structure bridges, concrete strength grade is normally C50 or higher. Therefore, the effect of concrete strength grade could be disregarded in the design of grouped stud for combination structure bridges.

2.2.4. Effect of stud body length

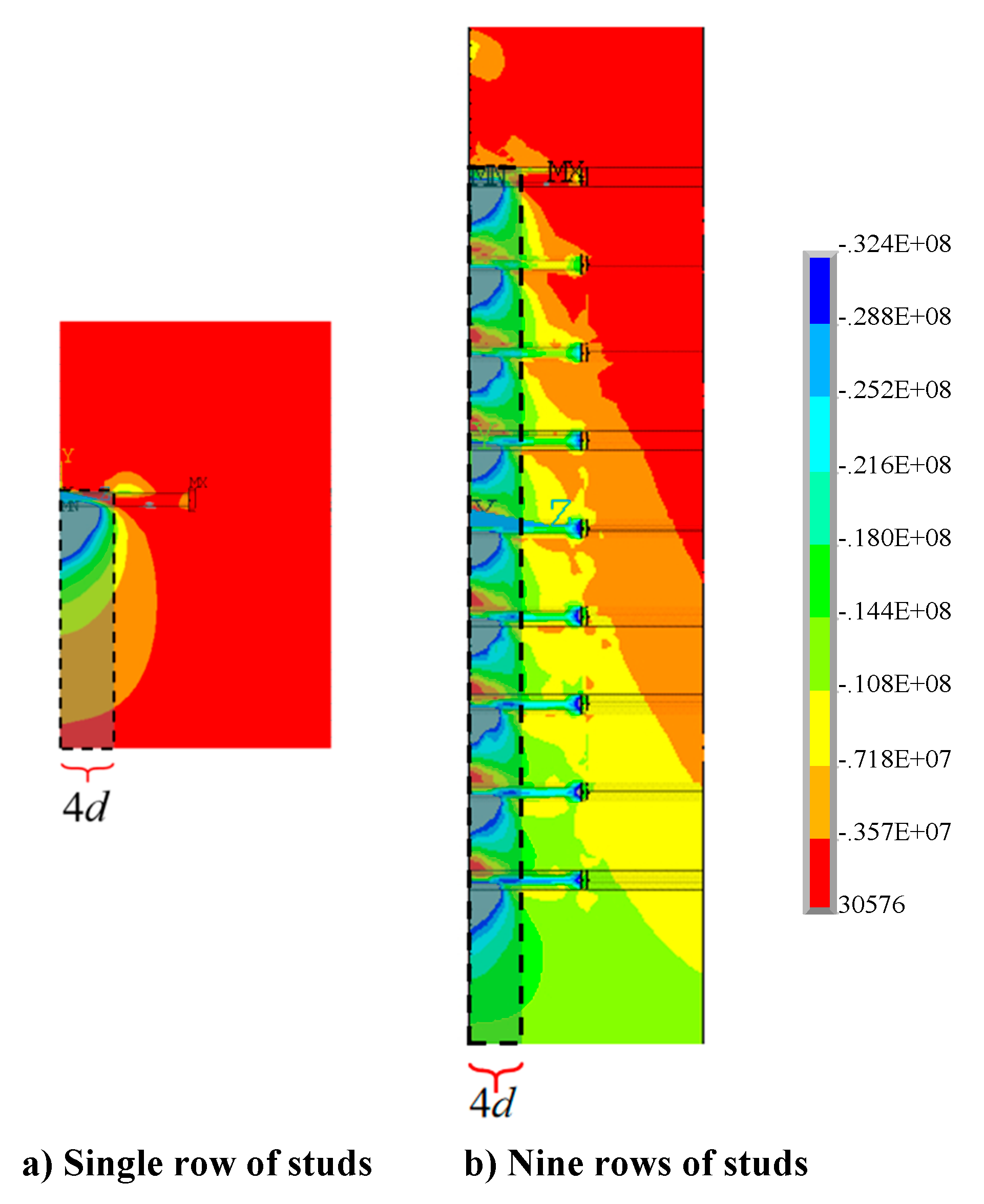
The stresses in the concrete are caused by the deformation of the studs in grouped stud connectors. The difference of stresses in the concrete around the weld end and the large head end of each stud is more pronounced, this is due to the cross-over of the areas of concrete stress change caused by the deformation of the studs. For grouped stud connectors under vertical shear, the more significant overlap of the concrete stress distribution is essentially located within 4 times the depth of the stud diameter inside the concrete (Figure 11), i.e., where the studs are more shallowly embedded. Chinese steel structure code states that when the ratio of the height and diameter of grouped stud is more than 4, the increase of the height to diameter ratio has less effect on the shear capacity of grouped stud [36]. Studs used in bridges are required to have a height-to-diameter ratio greater than 4, thus, the shear capacity of grouped stud is generally ignored in the calculation.

2.2.5. Effect of force angle

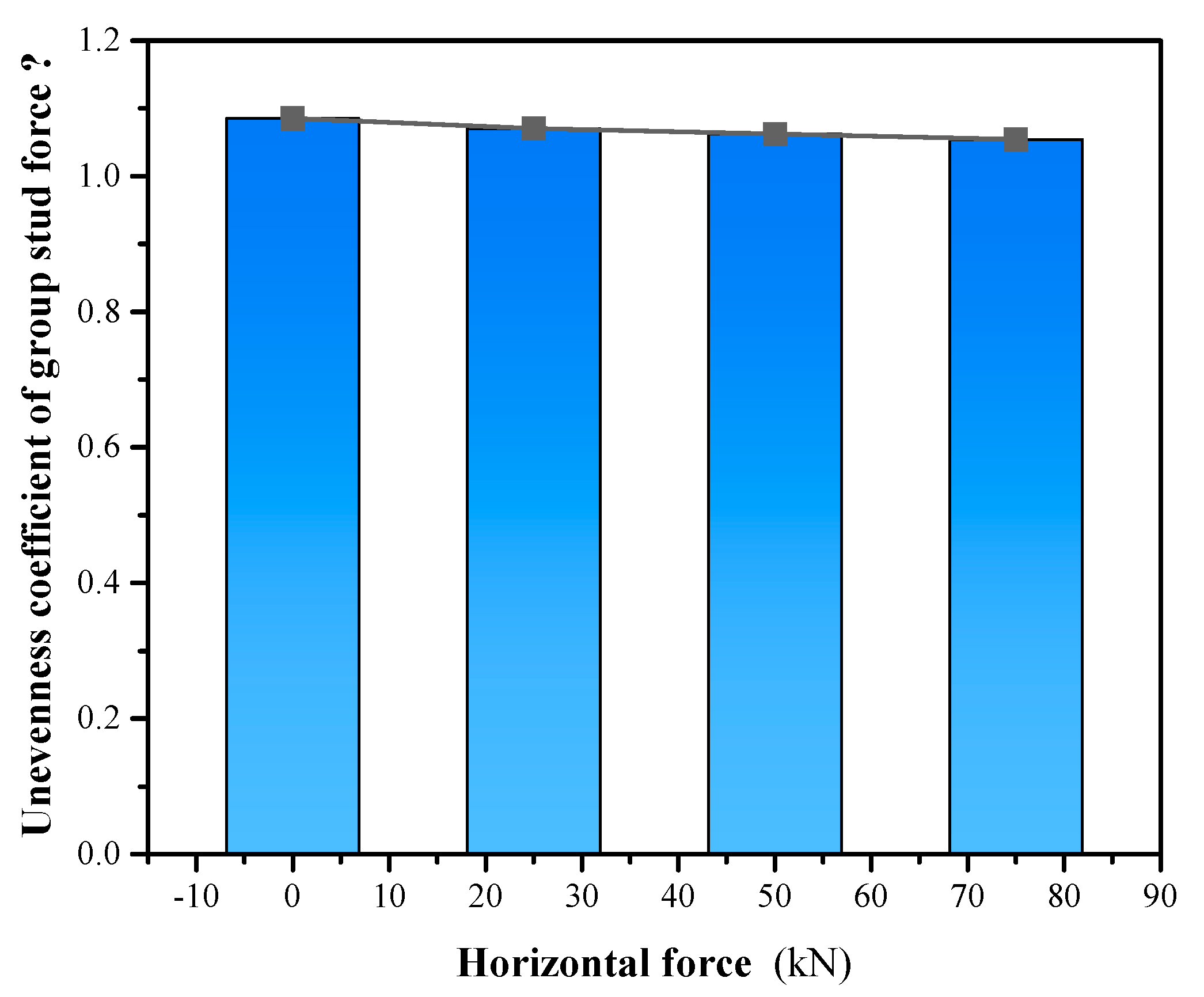
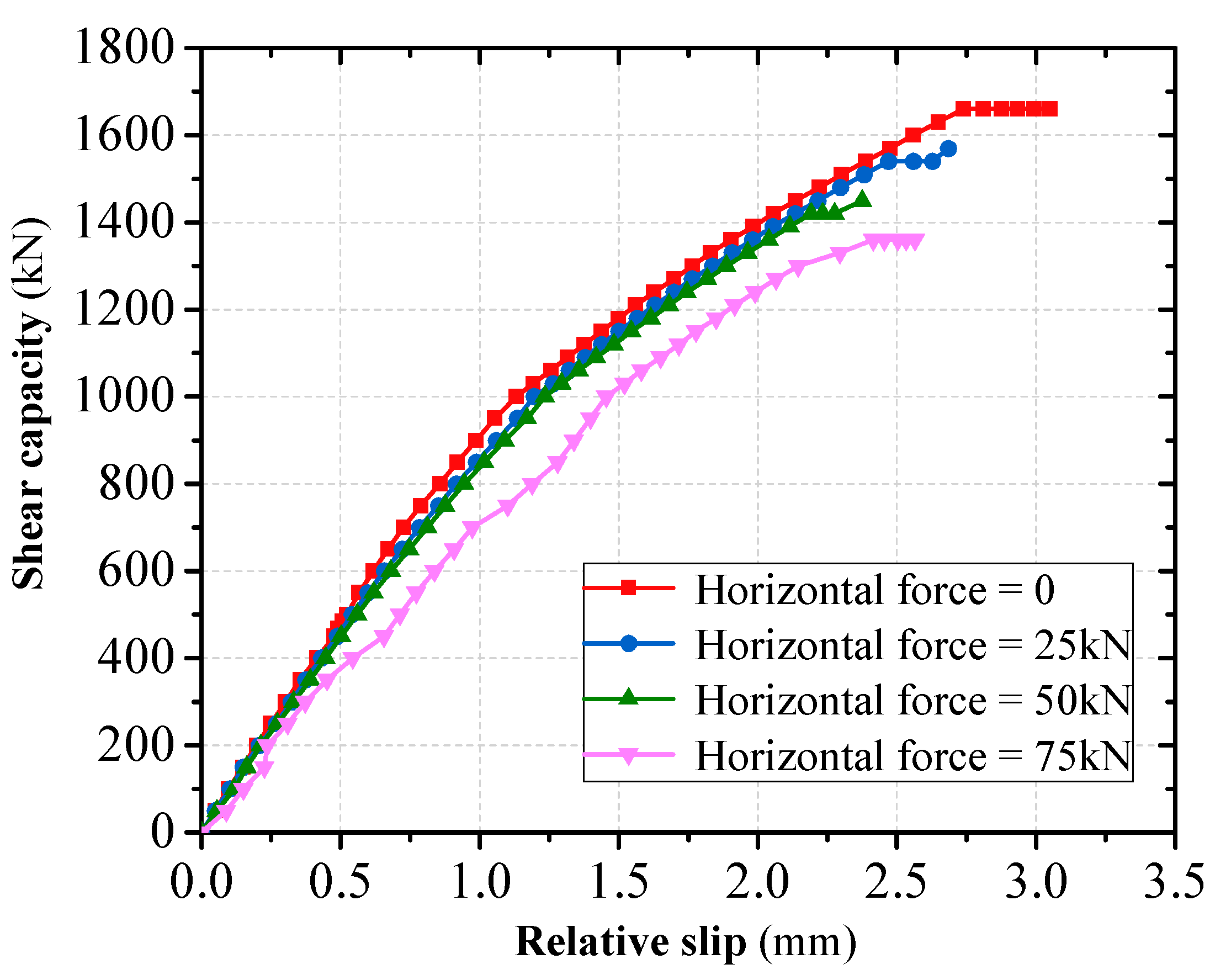
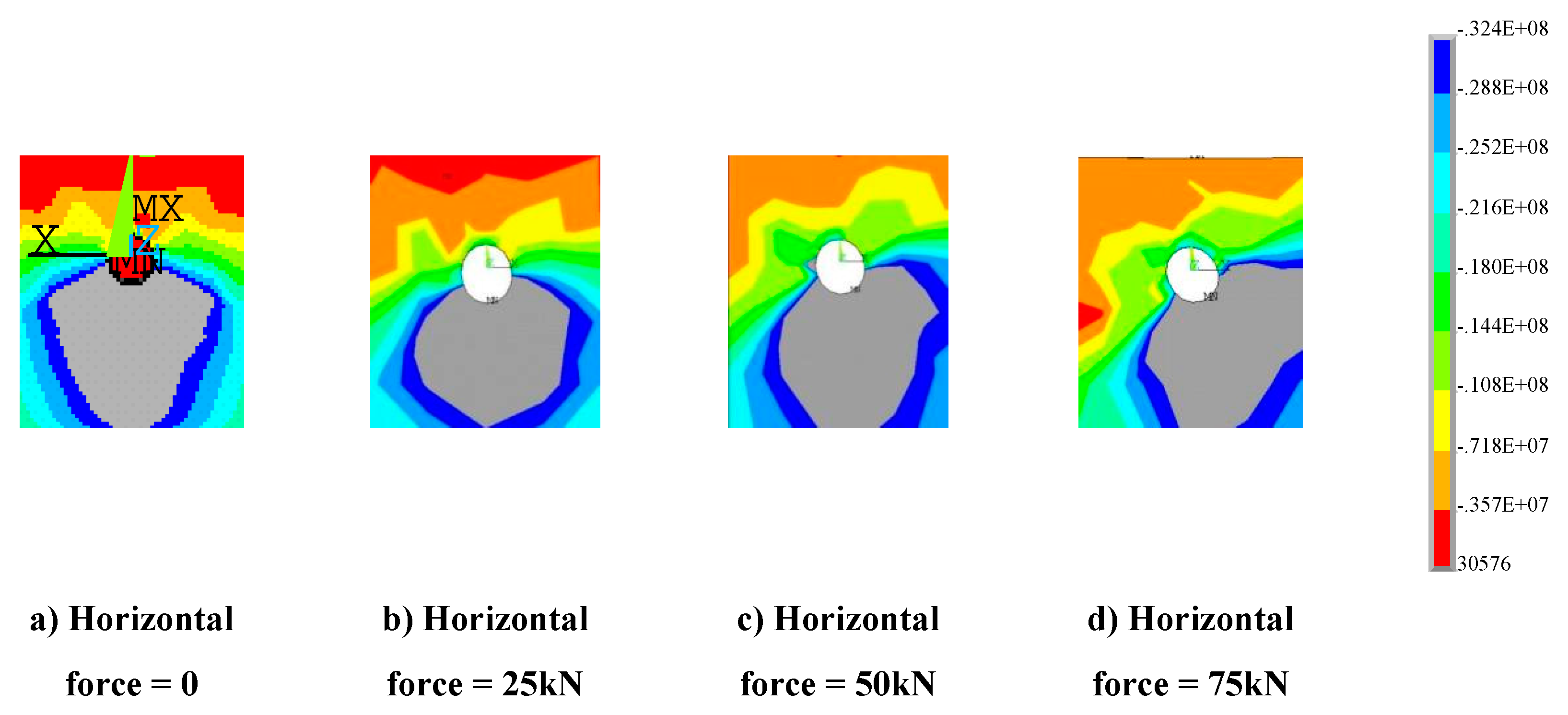
Through considering the vertical shear and diagonal shear, the shear resistance of grouped stud connectors was analyzed. When simulations in finite elements for oblique shear were performed, the simulations were performed using a certain horizontal force applied simultaneously with a varying vertical force. Where, when the calculated horizontal force is 0kN, 25kN, 50kN and 75kN respectively, the results of the ultimate vertical load bearing capacity assumed by the connector are shown in Figure 12 and Figure 13. The body of the single stud is round in cross-section, its forces are not affected by the loading angle of the load. However, for grouped stud connectors, when the loading angle is changed, the direction of force transmission of the grouped stud is altered (e.g., Figure 14 and Figure 15). When conducting force analysis of the grouped stud, the load can be decomposed into components that are aligned with the direction of the stud row and column according to the arrangement of the stud row and column. It is recommended that during design, the rows of grouped stud are arranged in the loading direction, to facilitate the analysis of the forces on the grouped stud.

3. Shear capacity of grouped stud connectors

According to the existing theories and data results, the formula for calculating the shear capacity Qgu of grouped stud connectors is recommended, as shown in Formulas (2) and (3) [37].
φ = 1 n p ≤ 3 φ = 0.9392 + 0.0423 n p − 0.0079 n p 2 3 < n p ≤ 5 φ = 0.9776 − 0.0034 n p − 0.0003 n p 2 5 < n p ≤ 15
Q gu = φ ⋅ n p 0.5 A s E c f ck A s E c f ck ≤ 344000 Q gu = φ ⋅ n p 0.26 A s E c f ck + 165 A s A s E c f ck > 344000
Where φ is the average shear capacity reduction coefficient of the single stud of the grouped stud shear connector; As is the cross-sectional area of the stud body (mm); Ec is the modulus of elasticity of concrete (MPa); fck is the axial compressive strength of concrete (MPa).
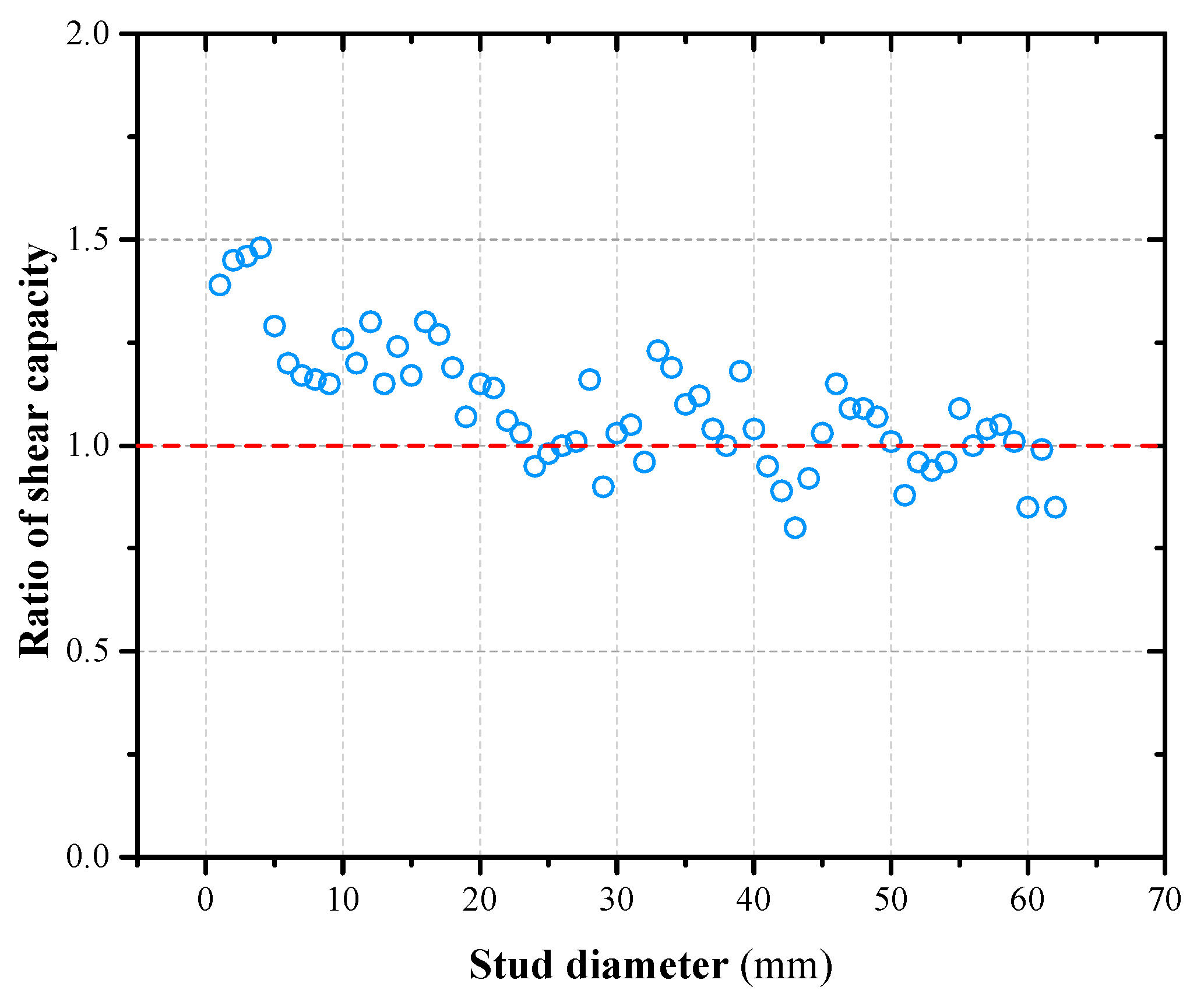
Push-out tests on the shear performance of grouped stud connectors have been carried out both at home and abroad, the test values of shear capacity for different number of studs and different specimen sizes were obtained [33,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60]. The design parameters of 62 specimens were referenced in this paper, the calculated values of shear capacity of grouped stud connectors were calculated according to Formulas (2) and (3), the ratios of the obtained test values to the calculated values are summarized in Figure 16. The average value of the ratio of the test and calculated shear capacity values of the grouped stud connectors is found to be 1.12 and the variance is found to be 0.023. It can be concluded that the dispersion of the calculated results of this method from the experimental values is small, which are in good agreement with the measured values, it can be used as a reference for shear force analysis of related grouped stud connectors.

4. Conclusion

To study the shear performance of the grouped stud connector, based on the push-out test, a refined finite element analysis method for grouped stud connectors has been developed, the grouped stud effect of the connectors and the main factors affecting the grouped stud effect have been numerically analyzed, and the formulae for calculating the shear capacity of grouped stud connectors are recommended, the main conclusions obtained are as follows:
(1) The shear performance of grouped stud connectors is affected by the grouped stud effect, this is related to the overlapping effect of the concrete compression cracking zones between the studs. When stud groups are densely arranged, the reduction in the average shear capacity of the single stud of the connector needs to be considered. When the stud spacing in the direction of load is less than 13 times the diameter of the stud body, the influence of the grouped stud effect needs to be taken into account in the design, considering the shear force reduction; otherwise, it is calculated as a single stud design.
(2) The inhomogeneity of the shear distribution of the stud group under load is presented, which is the most intuitive presentation of the grouped stud effect. At the same time, the average shear capacity of individual stud decreases as the shear inhomogeneity of the stud group increases. As the studs row spacing in the direction of load application becomes smaller or the number of rows increases, the more significant the superposition effect of the distribution of concrete stresses in the connectors, and the phenomenon of non-uniformity in the shear distribution of the stud group is also more significant. For grouped stud connectors with commonly used concrete grades greater than C50 and height-to-diameter ratios greater than 4 in steel-concrete composite structural bridges, which is insensitive to changes in the concrete strength grades and the length of the studs.
(3) The body of the single stud is round in cross-section, its forces are not affected by the loading angle of the load. However, for grouped stud connectors, when the loading angle is changed, the direction of force transmission of the grouped stud is altered. When conducting force analysis of the stud group, the load can be decomposed into components that are aligned with the direction of the stud row and column according to the arrangement of the stud row and column. It is recommended that during design, the rows of grouped stud are arranged in the loading direction, to facilitate the analysis of the forces on the grouped stud.
(4) Calculation of group stud connectors is not mentioned in the Chinese code. The recommended formula for calculating the shear capacity of group stud connectors is given in this paper, and the verification analysis was carried out by combining the results of 62 groups of existing group stud connector push-out tests. Results show that the mean value of the ratio of tested to calculated values is found to be 1.12, the variance is 0.023, the dispersion is small, the recommended formulas have high accuracy. The results of this paper are provided as a theoretical basis for the study of the shear performance of grouped stud connectors.

References

  1. Lee, P.G.; Shim, C.S.; Chang, S.P. Static and fatigue behavior of large stud shear connectors for steel–concrete composite bridges. Journal of Constructional Steel Research 2005, 61, 1270–1285. [Google Scholar] [CrossRef]
  2. Pallares, L.; Ramon-Llin, A.A.; Marti-Vargas, J.R.; Pallares, F.J. Behaviour of headed studs subjected to cyclic shear in steel frames with reinforced concrete infill walls. Construction Building Materials 2020, 262. [Google Scholar] [CrossRef]
  3. Liu, L.; Zhang, L.; Zhu, L.; Li, J.; Yang, Y.F.; Hao, L. Study on mechanical properties of stud connectors in steel-lightweight aggregate concrete composite structures. Structures 2023, 47, 1072–1085. [Google Scholar] [CrossRef]
  4. Chen, J.; Zhang, H.; Yu, Q.Q. Static and fatigue behavior of steel-concrete composite beams with corroded studs. Journal of Constructional Steel Research 2019, 156, 18–27. [Google Scholar] [CrossRef]
  5. Lowe, D.; Roy, K.; Das, R.; Clifton, G.C.; Lim, J.B.P. Full scale experiments on splitting behaviour of concrete slabs in steel concrete composite beams with shear stud connection. Structure 2019. [Google Scholar] [CrossRef]
  6. Zhang, Y.; Liu, A.; Chen, B.; Zhang, J.; Bradford, M.A. Experimental and numerical study of shear connection in composite beams of steel and steel-fibre reinforced concrete. Engineering Structures 2020, 215, 110707. [Google Scholar] [CrossRef]
  7. Viest, I.M. Investigation of Stud Shear Connectors for Composite Concrete and Steel T-Beams. Journal of American Concrete Institute 1956, 27, 875–891. [Google Scholar] [CrossRef]
  8. Slutter, R.G.; Driscoll, G.C. Flexural strength of steel-concrete composite beams. Journal of the Structural Division 1965, 91, 71–99. [Google Scholar] [CrossRef]
  9. Ding, F.X.; Yin, G.A.; Wang, H.B.; Wang, L.; Guo, Q. Static behavior of stud connectors in bi-direction push-off tests. Thin-Walled Structures 2017, 120, 307–318. [Google Scholar] [CrossRef]
  10. Wang, Y.; Yu, J.; Liu, J.; Chen, Y.F. Shear behavior of shear stud groups in precast concrete decks. Journal of Structural Engineering 2019, 187, 73–84. [Google Scholar] [CrossRef]
  11. Shariati, M.; Tahmasbi, F.; Mehrabi, P.; Bahadori, A.; Toghroli, A. Monotonic behavior of C and L shaped angle shear connectors within steel-concrete composite beams: an experimental investigation. Steel Composite Structures 2020, 35, 237–247. [Google Scholar] [CrossRef]
  12. Guezouli, S.; Lachal, A.; Nguyen, Q.H. Numerical investigation of internal force transfer mechanism in push-out tests. Engineering Structures 2013, 52, 140–152. [Google Scholar] [CrossRef]
  13. Han, Q.; Wang, Y.; Xu, J.; Xing, Y.; Yang, G. Numerical analysis on shear stud in push-out test with crumb rubber concrete. Journal of Constructional Steel Research 2017, 130, 148–158. [Google Scholar] [CrossRef]
  14. Xu, C.; Su, Q.; Sugiura, K. Mechanism study on the low cycle fatigue behavior of group studs shear connectors in steel-concrete composite bridges. Journal of Constructional Steel Research 2017, 138. [Google Scholar] [CrossRef]
  15. Brian D. Swartz, A.S., Andrea J. Schokker. AASHTO LRFD bridge design specifications. Available online: https://too.st/5Hg (accessed on 2012-07-09).
  16. CERI. GB 50017-2017 Code for design of steel structures. Available online: http://mtw.so/6nYYqL (accessed on 2018-08-01).
  17. Commission., E. Eurocode 4, Design of composite steel and concrete structures. Available online: http://mtw.so/6vvbjG (accessed on 2004-01).
  18. JCSE. Standard specification for steel and composite structures. Available online: http://mtw.so/69GICn (accessed on 2008-04-01).
  19. Wang, S.; Fang, Z.; Chen, G.; Jiang, H.; Teng, S. Numerical Analysis on Shear Behavior of Grouped Head Stud Shear Connectors between Steel Girders and Precast Concrete Slabs with High-Strength Concrete-Filled Shear Pockets. Journal of Bridge Engineering 2021, 26. [Google Scholar] [CrossRef]
  20. Ma, S.C.; Lou, Y.Y.; Bao, P. Experimental research and numerical analysis of shearing resistance in steel-concrete composite beam connectors. Case Studies in Construction Materials 2022, 17. [Google Scholar] [CrossRef]
  21. Patil, Y.D.; Singh, P.A.; Pardeshi, R.T. Experimental and analytical investigation of innovative wing plate headed stud shear connector in composite structures. Structures 2022, 46, 265–284. [Google Scholar] [CrossRef]
  22. Singh, P.A.; Patil, Y.D.; Pardeshi, R.T. Performance evaluation of triangular and circular bulged perforated headed stud shear connector in composite junction. Structures 2023, 53, 327–345. [Google Scholar] [CrossRef]
  23. Lebet, J.P.; Yoda, T.; Okada, J. A study of the grouped arrangements of stud connectors on shear strength behavior. Journal of Structural Mechanics Earthquake Engineering 2006, 23, 75S–89S. [Google Scholar] [CrossRef]
  24. Shim, C.S.; Lee, P.G.; Kim, D.W.; Chung, C.H. Effects of Group Arrangement on the Ultimate Strength of Stud Shear Connection. American Society of Civil Engineers 2011. [Google Scholar] [CrossRef]
  25. Xu, C.; Sugiura, K.; Wu, C.; Su, Q. Parametrical static analysis on group studs with typical push-out tests. Journal of Constructional Steel Research 2012, 72, 84–96. [Google Scholar] [CrossRef]
  26. Su, Q.; Yang, G.; Bradford, M.A. Static behaviour of multi-row stud shear connectors in high- strength concrete. Steel Composite Structures 2014, 17, 967–980. [Google Scholar] [CrossRef]
  27. An, L.; Cederwall, K. Push-out tests on studs in high strength and normal strength concrete. Journal of Constructional Steel Research 1996, 36, 15–29. [Google Scholar] [CrossRef]
  28. Yunbiao; Luo; Kazuaki; Hoki; Kazuhiro; Hayashi; Masayoshi; Nakashima. Behavior and Strength of Headed Stud-SFRCC Shear Connection. I: Experimental Study. Journal of Structural Engineering 2016, 142, 4015112–4015111-4015112-4015110. [CrossRef]
  29. Ding, J.; Zhu, J.; Kang, J.; Wang, X. Experimental study on grouped stud shear connectors in precast steel- UHPC composite bridge. Engineering Structures 2021, 242, 112479. [Google Scholar] [CrossRef]
  30. Dnmez, A.A. Size effect on the shear capacity of headed studs. Advances in Structural Engineering 2020, 24, 136943322096903. [Google Scholar] [CrossRef]
  31. Hu, Y.; Zhong, R.; Meloni, M.; Wang, J. A Novel Shear Strength Prediction Approach for Headed Shear Studs Embedded in Ultrahigh-Performance Concrete. Journal of Structural Engineering 2021, 147. [Google Scholar] [CrossRef]
  32. Zhang. X. G.; Q., L.Y. Cable-tower Composite Anchorage. Available online: https://too.st/5Hq (accessed on 2010-01-31).
  33. Xie, J.W.; Li, X. Research on the mechanical properties of shear connectors of large diameter stud in steel-concrete compositebridge decks. Engineering Construction 2020, 52, 18–23+29. [Google Scholar] [CrossRef]
  34. Liu. Y. Q. Steel-concrete Hybrid Bridge. Available online: https://too.st/5Hp (accessed on 2005-01-01).
  35. Jun, O.; Teruhiko, Y.; Jean-Paul, L. A study of the grouped arrangement of stud connectors on the shear strength behavior. Doboku Gakkai Ronbunshu 2004, 2004, 81–95. [Google Scholar] [CrossRef]
  36. CCCC HIGHWAY CONSULTANTS CO., L. Specifications for design of highway steel bridge. Available online: http://mtw.so/69GHnh (accessed on 2015-12-01).
  37. Lu, W.R. Study on mechanical behavior and design method of steel-concrete composite pylon anchorage system with steel anchor box. Doctor, Chang'an University, 2016.
  38. Chen, Z.Y.; Shi, J.J.; Li, B.S.; H., H.X. Experimental research on the load-bearing capacity of large diameter shear connector. China Civil Engineering Journal 1993, 67–74.
  39. Cao, J.A.; Ye, M.X. The ultimate load behavior of shear connectors of composite girders. Journal of Railway Science and Engineering 1999, 18–22. [Google Scholar] [CrossRef]
  40. Tang, J.; Ye, M.X. Load distribution state of crowded shear stud group. Journal of Railway Science and Engineering 1999, 68–73. [Google Scholar] [CrossRef]
  41. Ye, M.X.; Luo, R.D. Study of shear force of steel-concrete composite structures with a large number of closely arranged studs. Steel Construction 1999, 39–42. [Google Scholar]
  42. Ye, M.X.; Jiang, F. Study on the concrete slab-steel truss composite structures for Wuhu Yangtze River Bridge. Journal of the China Railway Society 2001, 65–69. [Google Scholar]
  43. Lin, C.J.; Zong, Z.H.; Tang, Z.Y. The experiment study on load-slip relationship of φ22 stud shear connectors. In Proceedings of the Sub-association for Steel-Concrete Composite Structures, Harbin, Heilongjiang, China; 2005; p. 6. [Google Scholar]
  44. Liao, Z.Q. Experimental study on the ultimate shear capacity of grouped stud connectors in continuous composite steel-concrete girder bridge. Master, Tongji University, 2007.
  45. Liu, Y.Q.; Wu, J.M.; Jiang, J.S. Experimental study of influence of service conditions on shearing behavior of welded stud connectors. Bridge Construction 2007, 23–25+64. [Google Scholar]
  46. Wu, C.; Liao, Z.Q.; Zeng, M.G.; Yu, G.J.; Zhu, H.L. Experimental study on ultimate shear capacity of studs group filled with high strength mortar in Continuous composite bridge. Building Structure 2008, 102–105. [Google Scholar] [CrossRef]
  47. Bai, G.L.; Tang, G.W.; Zhou, C.X. Test study of bearing capacity of shear connectors used for steel and concrete composite segment in bridge pylon. Bridge Construction 2010, 17–20. [Google Scholar]
  48. Chen, L.Z.; Jiang, S.C.; Zhang, J. The review on load-bearing capacity of stud shear connectors. Steel Construction 2010, 25, 5–10. [Google Scholar]
  49. Hou, W.Q.; Ye, M.X. Analysis on the ultimate bearing capacity and the statical behavior of the composite structures with grouped studs in railway bridge. China Railway Science 2011, 32, 55–61. [Google Scholar]
  50. Su, Q.T.; Han, X.; Ren, F. Static behavior of push-out specimen with multi-row stud connectors. Journal of Tongji University 2014, 42, 1011–1016. [Google Scholar]
  51. Huang, C.P.; Zhang, Z.X.; Zheng, Z.J.; Tan, Y. Force characteristics and failure mechanism experimental study of group-nail in steel-concrete composite structure. Journal of Wuhan University of Technology 2015, 37, 100–105. [Google Scholar]
  52. Li, C.J.; Zhou, Z.X.; Huang, Y.Y.; Fan, L. Research on shear resistance of shear studs in prefabricated composite beam. China Journal of Highway and Transport 2017, 30, 264–270. [Google Scholar] [CrossRef]
  53. Lin, B.Y. The research on load-bearing capacity of stud shear connectors. Master, South China University of Technology 2017.
  54. Xiang, Y.Q.; Guo, S.H. Parameter analysis of push-out specimens with different group studs in accelerated bridge construction steel-concrete composite beams under complicated stress condition. China Journal of Highway and Transport 2017, 30, 246–254. [Google Scholar] [CrossRef]
  55. Wang, W.H. Experimental and analytical study on shear properties of headed stud connector. Master, Zhejiang University, 2018.
  56. Li, C.J. Study on force transfer mechanism and computation method for shear connectorsof prefabricated composite beam. Doctor, Chongqing Jiaotong University, 2019.
  57. Wang, Y.; Zhang, Y.J.; Chen, B.C. Shear capacity study on stud shear connector of steel-concrete composite beams. Building Science 2019, 35, 20–24. [Google Scholar] [CrossRef]
  58. Yang, W.P.; Li, C.J.; Song, X.M.; Zhou, Z.X. Experimental study on shear capacity of prefabricated composite shear stud. Experimental study on shear capacity of prefabricated composite shear stud 2019, 59, 38–42. [Google Scholar]
  59. Chen, Y.C.; Liao, H.; Du, G.M.; Liao, L.S.; Liu, Y.Q. Research and finite element analysis of shearing performance testing of φ19 mm group nails. Engineering Construction 2020, 52, 6–12+54. [Google Scholar] [CrossRef]
  60. Zhou, D. Study on nonlinear mechanical behavior of assembled group studs. Master, Chongqing Jiaotong University, 2020.
Preprints 83859 g001
Figure 1. Finite element model of stud shear connector.
Figure 1. Finite element model of stud shear connector.
Preprints 83859 g001
Preprints 83859 g002
Figure 2. Constitutive relationship curves.
Figure 2. Constitutive relationship curves.
Preprints 83859 g002
Preprints 83859 g003
Figure 3. Stud row spacing and unevenness coefficient of grouped stud force.
Figure 3. Stud row spacing and unevenness coefficient of grouped stud force.
Preprints 83859 g003
Preprints 83859 g004
Figure 4. Connector damage pattern.
Figure 4. Connector damage pattern.
Preprints 83859 g004
Preprints 83859 g005
Figure 5. Studs row spacing and unevenness coefficient of force.
Figure 5. Studs row spacing and unevenness coefficient of force.
Preprints 83859 g005
Preprints 83859 g006
Figure 6. Effect of stud row spacing on load-slip curves.
Figure 6. Effect of stud row spacing on load-slip curves.
Preprints 83859 g006
Preprints 83859 g007
Figure 7. Number of stud rows and unevenness coefficient of force.
Figure 7. Number of stud rows and unevenness coefficient of force.
Preprints 83859 g007
Preprints 83859 g008
Figure 8. Effect of the number of stud rows on the load-slip curves.
Figure 8. Effect of the number of stud rows on the load-slip curves.
Preprints 83859 g008
Preprints 83859 g009
Figure 9. Concrete strength grade and unevenness coefficient of force.
Figure 9. Concrete strength grade and unevenness coefficient of force.
Preprints 83859 g009
Preprints 83859 g010
Figure 10. Effect of the number of stud rows on the load-slip curves.
Figure 10. Effect of the number of stud rows on the load-slip curves.
Preprints 83859 g010
Preprints 83859 g011
Figure 11. Concrete stress distribution in the length direction of the stud.
Figure 11. Concrete stress distribution in the length direction of the stud.
Preprints 83859 g011
Preprints 83859 g012
Figure 12. Force angle and unevenness coefficient of force.
Figure 12. Force angle and unevenness coefficient of force.
Preprints 83859 g012
Preprints 83859 g013
Figure 13. Effect of force angle on load-slip curves.
Figure 13. Effect of force angle on load-slip curves.
Preprints 83859 g013
Preprints 83859 g015
Figure 15. Concrete main compressive stress diagram for damage load of multi-row stud connector.
Figure 15. Concrete main compressive stress diagram for damage load of multi-row stud connector.
Preprints 83859 g015
Preprints 83859 g016
Figure 16. Comparison between the calculation formula of grouped stud and the actual push-out specimens.
Figure 16. Comparison between the calculation formula of grouped stud and the actual push-out specimens.
Preprints 83859 g016
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated