Preprint

Article

A Variety of Optical Wave Solutions to Space-Time Fractional Perturbed Kundu-Eckhaus Model with Full Non-Linearity

Altmetrics

Downloads

153

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 September 2023

Posted:

04 September 2023

You are already at the latest version

Alerts

Abstract

In this paper, the new optical wave solutions of truncated M-fractional perturbed Kundu-Eckhaus model with full non-linearity are obtained by utilizing the expa function technique and modified extended tanh expansion function technique. The solutions are in the form of dark soliton, bright soliton, singular solitons and other form of solutions. The gained solutions are helpful for the further development of concerned model. The obtained results have also been presented graphically in both two-dimensional and three-dimensional formats to discuss the dynamical features as well as the parametric dependence of the constructed solutions. The study offers a highly spectacular and acceptable techniques to combine various intriguing wave demonstrations for more sophisticated models of the modern day.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

Fractional Calculus (FC) is a generalization of classical calculus related with operations of integration and differentiation of non-integer (fractional) order. Since the 19th century, the theory of fractional calculus developed rapidly, mostly as a foundation for a number of applied disciplines, including fractional geometry, fractional differential equations (FDE) and fractional dynamics. The applications of FC are very wide nowadays. It is safe to say that almost no discipline of modern engineering, and science in general, remains untouched by the tools and techniques of fractional calculus. For example, wide and fruitful applications can be found in rheology, viscoelasticity, acoustics, optics, chemical and statistical physics, robotics, control theory, electrical and mechanical engineering, bio-engineering etc. In fact, one could argue that real world processes are fractional order systems in general. The main reason for the success of FC applications is that these new fractional-order models are often more accurate than integer-order ones, i.e., there are more degrees of freedom in the fractional order model than in the corresponding classical one. Fractional calculus is a field of mathematics study that grew out of the traditional definitions of calculus integral and derivative operators in much the same way fractional exponents are an outgrowth of exponents with integer values. A fractional equation (FE) is a differential equation that contains fractional derivatives or integrals. The awareness of the importance of this kind of equation has grown continually in the last decade. Fractional derivatives and integrals are used to better assess different physical phenomena, such as optics, fluid mechanics, electrochemistry, signal processing, control theory, population dynamics, and many other real-world issues. In recent years, the calculus of fractional differential equations (FDEs) has been one of the most concerning aspects in nonlinear dynamics. More comprehensive forms of differential equations (DEs) were defined as fractional differential equations that play a significant role in the thoughtful qualitative features of many nonlinear wave propagation phenomena.

There are many famous models to describe the dynamics of optical wave solutions perturbation in various types of waveguides [1,2,3,4]. While the very famous model is the non-linear Schrödinger’s equation and there are many others. Since these mathematical equations with exact solutions of the system have improved our understanding of their functioning, application and development [5,6,7]. Consequently, numerous researchers [8,9] have utilized a variety of analytical techniques to obtain precise solutions for nonlinear partial and fractional differential equations over the course of many years.

Our study model is the perturbed Kundu-Eckhaus model along full nonlinearity with truncated M-fractional derivative. Kundu-Eckhaus equation has been very famous recently, since the model would be useful for studying the dynamics of optical solitons in the nano-fibers and polarization preserving fibers. This model was independently introduced by Wiktor Eckhaus and by Anjan Kundu to model the propagation of waves in dispersive media. This model belongs to the class of non-linear Schrödinger’s equation which is more widely visible in the mathematical photonics area. Different types of exact wave solutions of this model have been obtained with the help of different methods in the literature. Instantly; dark soliton and singular soliton solutions have been achieved by using the modified simple equation scheme [10], the optical wave solutions in the form of dark, singular and dark-singular solitons have been gained with the use of

exp (- ϕ (ξ))

-expansion method and

(G^{'} / G^{2})

-expansion method [11], the bright and singular wave solutions have been attained by applying the extended trial function method [12].

In our research, we utilize the

{exp}_{a}

function technique and modified extended tanh expansion function technique. In the literature, there are many uses of these techniques. Instantly; optical wave solutions of perturbed Gerdjikov-Ivanov model by utilizing the

{exp}_{a}

function scheme [13], some new optical solitons of Sasa-Satsuma higher order equation in [14]. Similarly, different kinds of optical wave solutions of Triki-Biswas equation have been obtained by applying the modified extended tanh function expansion method [15], the dark, singular, dark-singular and periodic wave solutions of Biswas-Arshed equation have been achieved by this technique [16].

Main aim of this research is to investigate the new optical wave solutions to the truncated M-fractional perturbed Kundu-Eckhaus model along full non-linearity with the help of

{exp}_{a}

function technique and modified extended tanh expansion function technique.

The motivation of this paper is that for the first time truncated M-fractional derivative is used for our concerned model perturbed Kundu-Eckhaus as for as my knowledge. The importance of truncated M-fractional derivative is that it fulfill the both properties of integer and fractional order derivatives. The effect of fractional order derivative on the obtained solutions is also explained by graphically. The gained results are helpful for the ultrashort light pulses in optical fibers. Our study model has much importance in quantum optics and fluid mechanics, for explaining the optical characteristics of the femtosecond lasers and femtochemistry object. Optical soliton perturbation is the backbone of telecommunications industry. This industry stays in business because of the marvel of soliton transmission technology. One of the various models that govern these pulse transmission across inter–continental distances is the Kundu-Eckhaus (KE) equation.

Paper consists of different sections; In Section 2: we explain the our concerned model and it’s mathematical analysis. In Section 3: we describe the main steps of our concerned technique

{exp}_{a}

function technique and it’s application. In Section 4: we explain the modified extended tanh expansion function technique and it’s application to gain the new optical wave solutions of our concerned model. In Section 5: we give the conclusion of our research work.

2. The governing model

Let’s assume the truncated M-fractional perturbed Kundu-Eckhaus model given in [12].

ι D_{M, t}^{α, Υ} g + θ D_{M, 2 x}^{2 α, Υ} g + {ν | g |}^{4} g + τ D_{M, x}^{α, Υ} {(| g |}^{2}) g = ι [μ D_{M, x}^{α, Υ} g + Ω D_{M, x}^{α, Υ} {(| g |}^{2 n} g) + κ D_{M, x}^{α, Υ} {| g |}^{2 n} g] .

(1)

where

D_{M, t}^{α, Υ} u (t) = lim_{τ \to 0} \frac{u (t E_{Υ} (τ t^{1 - α})) - u (t)}{τ}, 0 < α \leq 1, Υ > 0,

(2)

here

E_{Υ} (.)

represents truncated Mittag-Leffler function of one parameter given in [17,18].

where

g = g (x, t)

represents the non-linear wave function while independent variables x and t are the spatial and temporal variables. First term denotes the evolution of the wave while the real-valued constants

θ

ν

and

τ

indicates the group velocity dispersion (GVD), quintic non-linearity and non-linear dispersion respectively. Parameters

μ

represents the inter-model dispersion,

Ω

denotes the co-efficient of self-steepening for short pulses and

κ

indicates the higher order dispersion co-efficient. The parameter n represents the full non-linearity. The perturbation terms are the Hamiltonian and appear with full non-linearity.

3. Methodology

3.1. The ${exp}_{a}$ function technique

We explain the main points of this technique.

Let’s take the non-linear partial differential equation (PDE);

G (q, q^{2} q_{t}, q_{x}, q_{t t}, q_{x x}, q_{x t}, . . .) = 0 .

(3)

Equation (3) changed into non-linear ordinary differential equation:

Λ (Q, Q^{^{'}}, Q^{^{″}}, . . .,) = 0 .

(4)

By applying the below transformations:

q (x, y, t) = Q (ζ), ζ = a x + b y + r t .

(5)

Assuming the solution of Equation (4) is given in [19,20,21,22]:

Q (ζ) = \frac{α_{0} + α_{1} d^{ζ} + . . . + α_{m} d^{m ζ}}{β_{0} + β_{1} d^{ζ} + . . . + β_{m} d^{m ζ}}, d \neq 0, 1 .

(6)

here

α_{j}

and

β_{j} (0 \leq j \leq m)

are unknowns. Natural number m is found with the use of homogeneous balance method into Equation (4). Inserting Equation (6) into Equation (4), yields

℘ (d^{ζ}) = ℓ_{0} + ℓ_{1} d^{ζ} + . . . + ℓ_{t} d^{t ζ} = 0 .

(7)

Putting

ℓ_{j} (0 \leq j \leq t)

in Equation (7) equal to 0, a system of algebraic equations is attained shown as

ℓ_{j} = 0, w h e r e j = 0, . . ., t .

(8)

exp (ι (- ρ x + λ t + ϑ))

With the help of attain results, we gain wave solutions of Equation (3).

3.2. The METhEF technique

We start with the fundamental steps of the modified extended tanh expansion function (METhEF) technique by assuming the following non-linear PDE:

Y (q, q^{2} q_{γ}, q_{θ}, q_{θ θ}, q_{γ γ}, q_{γ θ}, . . .) = 0

(9)

Here

q = q (γ, θ)

. Let us consider the following transformations:

q (γ, θ) = Q (ξ), ξ = γ - ν θ

(10)

the wave speed

ν

. Putting the Equation (10) into Equation (9), taking the following nonlinear ODE:

Z (Q (ξ), Q^{2} (ξ) Q^{^{'}} (ξ), Q^{^{'}} (ξ), Q^{^{″}} (ξ), . . .) = 0 .

(11)

Moreover, consider the solution of Equation (11) is of the shape:

Q (ξ) = α_{0} + \sum_{j = 1}^{m} α_{j} ϕ^{j} (ξ) + \sum_{j = 1}^{m} β_{j} ϕ^{- j} (ξ)

(12)

In Equation (12),

α_{0}, α_{j}, β_{j}, (j = 1, 2, 3, . . ., m)

are unknowns and to be find later. It is necessary that both

α_{j}

and

β_{j}

are not equal to simultaneously. By using the homogenous balance method into Equation (11), we get m. The function

ϕ (η)

fulfil the below Riccati differential equation:

ϕ^{'} (ξ) = ω + ϕ^{2} (ξ)

(13)

with

Ω

as a unknown parameter and the Equation (13) have the following form solutions [23]:

(i): if $Ω < 0$ , then

$ϕ (ξ) = - \sqrt{- ω} tanh (\sqrt{- ω} ξ),$

(14)

or

$ϕ (ξ) = - \sqrt{- ω} coth (\sqrt{- ω} ξ) .$

(15)
(ii): if $ω = 0$ , then

$ϕ (ξ) = \frac{- 1}{ξ}$

(16)
(iii): if $ω > 0$ , then

$ϕ (ξ) = \sqrt{ω} tan (\sqrt{ω} ξ) .$

(17)

or

$ϕ (ξ) = - \sqrt{ω} cot (\sqrt{ω} ξ) .$

(18)

Putting of the Equation (12) and it’s compulsory derivatives in the Equation (11) along Equation (13), give us the expressions in the form of polynomials in powers of

ϕ (ξ)

. By summing up the coefficients of

ϕ (η)

with the like order and taking each summation to zero, we achieve a system of algebraic expressions for

α_{0}, α_{j}, β_{j}, (j = 1, 2, 3, . . ., m)

and

ω

with the help of soft computation. Lastly, the unknown parameters are to be found. Putting the values of these parameter into Equation (12) along fixed value of m, provides the solutions to the Equation (9).

This method presents a wider applicability for handling many other nonlinear evolution equation in mathematical physics.

4. Mathematical analysis

Consider the following travelling wave transformations:

g (x, t) = G (ξ) \times exp (ι \frac{Γ (1 + Υ)}{α} ((- ρ x^{α} + λ t^{α}) + ϑ)),

(19)

and

ξ = \frac{Γ (1 + Υ)}{α} (x^{α} - ϖ t^{α}) .

(20)

here

G (ξ)

denotes the shape of the wave. Parameters

ϖ

represents the speed of the soliton,

ρ

denotes the frequency of soliton,

λ

stands the wave number and

ϑ

indicates the phase constant or the center of phase. Inserting Equation (20) into the Equation (1), we obtain the real and imaginary parts given as respectively:

\begin{matrix} θ G^{″} - (λ + θ ρ^{2} + μ ρ) G + 2 τ G^{2} G^{'} - ρ Ω G^{2 n + 1} + ν G^{5} & = & 0, \end{matrix}

(21)

\begin{matrix} ϖ + μ + 2 θ ρ + ((2 n + 1) Ω + 2 n κ) G^{2 n} & = & 0 . \end{matrix}

(22)

Taking the co-efficients of the linearly independent functions equal to zero.

ϖ = - (μ + 2 θ ρ) .

(23)

along with the constraint condition given as:

(2 n + 1) ρ + 2 n κ = 0 .

(24)

To gain the closed form exact wave solutions, we apply a transformation given as:

G (x, t) = V^{\frac{1}{2}} (x, t) .

(25)

that will transform Equation (21) into

4 ν V^{4} - 4 V^{3} ρ Ω - 4 V^{2} (θ ρ^{2} + λ + μ ρ) + θ (2 V V^{″} - {(V^{'})}^{2}) + 4 τ V^{2} V^{'} = 0 .

(26)

where V denotes the polynomial and prime

^{'}

represents the

\frac{d}{d ξ}

. By using homogenous balance scheme, we get m = 1. We will find the new soliton solutions of Equation (26) by using two different techniques in the following.

4.1. Applications of the ${exp}_{a}$ function technique

Equation (6) changes into the following for

m = 1

U (ζ) = \frac{α_{0} + α_{1} d^{ξ}}{β_{0} + β_{1} d^{ξ}},

(27)

inserting Equation (27) into Equation (26) along n = 1, a system of equations is achieved. By solving the system, we obtain different solution sets given as follows:

Set 1:

\begin{matrix} {λ = \frac{1}{4} θ {log}^{2} (d) - θ ρ^{2} - μ ρ, ρ = ρ, τ = \frac{- 2 \sqrt{θ ν Log {(d)}^{2} + ρ^{2} Ω^{2}} - ρ Ω}{log (d)}, \\ α_{0} = 0, α_{1} = α_{1}, β_{0} = β_{0}, β_{1} = - \frac{2 α_{1} (\sqrt{θ ν {log}^{2} (d) + ρ^{2} Ω^{2}} + ρ Ω)}{θ {log}^{2} (d)}} . \end{matrix}

(28)

\begin{matrix} g (x, t) = {\{\frac{α_{1} d^{(\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}))}}{β_{0} - \frac{(2 α_{1} (\sqrt{θ ν {log}^{2} (d) + ρ^{2} Ω^{2}} + ρ Ω)) d^{(\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}))}}{θ {log}^{2} (d)}}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- ρ x^{α} + (\frac{1}{4} θ {log}^{2} (d) - θ ρ^{2} - μ ρ) t^{α}) + ϑ)) . \end{matrix}

(29)

Set 2:

\begin{matrix} {λ = \frac{1}{4} θ {log}^{2} (d) - θ ρ^{2} - μ ρ, ρ = ρ, τ = \frac{2 \sqrt{θ ν {log}^{2} (d) + ρ^{2} Ω^{2}} - ρ Ω}{log (d)}, \\ α_{0} = 0, α_{1} = α_{1}, β_{0} = β_{0}, β_{1} = \frac{2 α_{1} (\sqrt{θ ν {log}^{2} (d) + ρ^{2} Ω^{2}} - ρ Ω)}{θ {log}^{2} (d)}} . \end{matrix}

(30)

\begin{matrix} g (x, t) = {\{\frac{α_{1} d^{(\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}))}}{β_{0} + \frac{(2 α_{1} (\sqrt{θ ν {log}^{2} (d) + ρ^{2} Ω^{2}} - ρ Ω)) d^{(\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}))}}{θ {log}^{2} (d)}}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- ρ x^{α} + (\frac{1}{4} θ {log}^{2} (d) - θ ρ^{2} - μ ρ) t^{α}) + ϑ)) . \end{matrix}

(31)

Set 3:

\begin{matrix} {λ = \frac{1}{4} θ {log}^{2} (d) - θ ρ^{2} - μ ρ, ρ = ρ, τ = \frac{2 \sqrt{θ ν {log}^{2} (d) + ρ^{2} Ω^{2}} + ρ Ω}{log (d)}, \\ α_{0} = α_{0}, α_{1} = 0, β_{0} = - \frac{2 α_{0} (\sqrt{θ ν {log}^{2} (d) + ρ^{2} Ω^{2}} + ρ Ω)}{θ {log}^{2} (d)}, β_{1} = β_{1}} . \end{matrix}

(32)

\begin{matrix} g (x, t) = {\{\frac{α_{0}}{β_{1} d^{(\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}))} - \frac{2 α_{0} (\sqrt{θ ν {log}^{2} (d) + ρ^{2} Ω^{2}} + ρ Ω)}{θ {log}^{2} (d)}}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- ρ x^{α} + (\frac{1}{4} θ {log}^{2} (d) - θ ρ^{2} - μ ρ) t^{α}) + ϑ)) . \end{matrix}

(33)

Set 4:

\begin{matrix} {λ = \frac{1}{4} θ {log}^{2} (d) - θ ρ^{2} - μ ρ, ρ = ρ, τ = \frac{ρ Ω - 2 \sqrt{θ ν {log}^{2} (d) + ρ^{2} Ω^{2}}}{log (d)}, \\ α_{0} = α_{0}, α_{1} = 0, β_{0} = \frac{2 α_{0} (\sqrt{θ ν {log}^{2} (d) + ρ^{2} Ω^{2}} - ρ Ω)}{θ {log}^{2} (d)}, β_{1} = β_{1}} . \end{matrix}

(34)

\begin{matrix} g (x, t) = {\{\frac{α_{0}}{β_{1} d^{(\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}))} + \frac{2 α_{0} (\sqrt{θ ν {log}^{2} (d) + ρ^{2} Ω^{2}} - ρ Ω)}{θ {log}^{2} (d)}}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- ρ x^{α} + (\frac{1}{4} θ {log}^{2} (d) - θ ρ^{2} - μ ρ) t^{α}) + ϑ)) . \end{matrix}

(35)

4.2. Applications of the METhEF technique

By applying the homogenous balance technique on Equation (26), we obtain

m = 1

. Then Equation (12) reduces into:

V (ξ) = α_{0} + α_{1} ψ (ξ) + β_{1} ψ {(ξ)}^{- 1},

(36)

substituting Equation (36) into Equation (26) along n = 1 and with the use of soft computations, we get the below sets of soliton solution:

Set 1:

\{λ = - \frac{4 a_{0} ν (\frac{4}{3} a_{0} θ ν - a_{0} Ω^{2} + μ Ω)}{3 Ω^{2}}, ω = - \frac{4 a_{0}^{2} ν}{3 θ}, ρ = \frac{4 a_{0} ν}{3 Ω}, τ = - \sqrt{3} \sqrt{θ ν}, a_{0} = a_{0}, a_{1} = 0, b_{1} = \frac{2 a_{0}^{2} \sqrt{θ ν}}{\sqrt{3} θ}\} .

(37)

ω < 0

\begin{matrix} g (x, t) = {\{a_{0} + \frac{2 a_{0}^{2} \sqrt{ν}}{\sqrt{3 θ} (- \sqrt{- ω} tanh (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{- ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} ν}{3 Ω}) x^{α} + (- \frac{4 a_{0} ν (\frac{4}{3} a_{0} θ ν - a_{0} Ω^{2} + μ Ω)}{3 Ω^{2}}) t^{α}) + ϑ)) . \end{matrix}

(38)

\begin{matrix} g (x, t) = {\{a_{0} + \frac{2 a_{0}^{2} \sqrt{ν}}{\sqrt{3 θ} (- \sqrt{- ω} coth (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{- ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} ν}{3 Ω}) x^{α} + (- \frac{4 a_{0} ν (\frac{4}{3} a_{0} θ ν - a_{0} Ω^{2} + μ Ω)}{3 Ω^{2}}) t^{α}) + ϑ)) . \end{matrix}

(39)

ω > 0

\begin{matrix} g (x, t) = {\{a_{0} + \frac{2 a_{0}^{2} \sqrt{ν}}{\sqrt{3 θ} (\sqrt{ω} tan (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} ν}{3 Ω}) x^{α} + (- \frac{4 a_{0} ν (\frac{4}{3} a_{0} θ ν - a_{0} Ω^{2} + μ Ω)}{3 Ω^{2}}) t^{α}) + ϑ)) . \end{matrix}

(40)

\begin{matrix} g (x, t) = {\{a_{0} + \frac{2 a_{0}^{2} \sqrt{ν}}{\sqrt{3 θ} (- \sqrt{ω} cot (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} ν}{3 Ω}) x^{α} + (- \frac{4 a_{0} ν (\frac{4}{3} a_{0} θ ν - a_{0} Ω^{2} + μ Ω)}{3 Ω^{2}}) t^{α}) + ϑ)) . \end{matrix}

(41)

Set 2:

\{λ = - \frac{4 a_{0} ν (\frac{4}{3} a_{0} θ ν - a_{0} Ω^{2} + μ Ω)}{3 Ω^{2}}, ω = - \frac{4 a_{0}^{2} ν}{3 θ}, ρ = \frac{4 a_{0} ν}{3 Ω}, τ = \sqrt{3} \sqrt{θ ν}, a_{0} = a_{0}, a_{1} = 0, b_{1} = - \frac{2 a_{0}^{2} \sqrt{θ ν}}{\sqrt{3} θ}\} .

(42)

ω < 0

\begin{matrix} g (x, t) = {\{a_{0} - \frac{2 a_{0}^{2} \sqrt{ν}}{\sqrt{3 θ} (- \sqrt{- ω} tanh (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{- ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} ν}{3 Ω}) x^{α} + (- \frac{4 a_{0} ν (\frac{4}{3} a_{0} θ ν - a_{0} Ω^{2} + μ Ω)}{3 Ω^{2}}) t^{α}) + ϑ)) . \end{matrix}

(43)

\begin{matrix} g (x, t) = {\{a_{0} - \frac{2 a_{0}^{2} \sqrt{ν}}{\sqrt{3 θ} (- \sqrt{- ω} coth (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{- ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} ν}{3 Ω}) x^{α} + (- \frac{4 a_{0} ν (\frac{4}{3} a_{0} θ ν - a_{0} Ω^{2} + μ Ω)}{3 Ω^{2}}) t^{α}) + ϑ)) . \end{matrix}

(44)

ω > 0

\begin{matrix} g (x, t) = {\{a_{0} - \frac{2 a_{0}^{2} \sqrt{ν}}{\sqrt{3 θ} (\sqrt{ω} tan (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} ν}{3 Ω}) x^{α} + (- \frac{4 a_{0} ν (\frac{4}{3} a_{0} θ ν - a_{0} Ω^{2} + μ Ω)}{3 Ω^{2}}) t^{α}) + ϑ)) . \end{matrix}

(45)

\begin{matrix} g (x, t) = {\{a_{0} - \frac{2 a_{0}^{2} \sqrt{ν}}{\sqrt{3 θ} (- \sqrt{ω} cot (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} ν}{3 Ω}) x^{α} + (- \frac{4 a_{0} ν (\frac{4}{3} a_{0} θ ν - a_{0} Ω^{2} + μ Ω)}{3 Ω^{2}}) t^{α}) + ϑ)) . \end{matrix}

(46)

Set 3:

\begin{matrix} {λ = - (8 a_{0} (a_{0} (\frac{8 θ^{2} ν^{2}}{3} + τ^{2} (- \frac{10 θ ν}{9} - \frac{Ω^{2}}{3}) + \frac{1}{2} θ ν Ω^{2} + \frac{4 τ^{4}}{27}) - \frac{1}{6} τ \sqrt{τ^{2} - 3 θ ν} (a_{0} (\frac{16 θ ν}{3} - \frac{8 τ^{2}}{9} + 2 Ω^{2}) \\ + μ Ω) + μ Ω (θ ν - \frac{τ^{2}}{6}))) / (3 θ Ω^{2}), ω = \frac{4 a_{0}^{2} (- 2 τ^{2} \sqrt{τ^{2} - 3 θ ν} + 3 θ ν \sqrt{τ^{2} - 3 θ ν} + 6 θ ν τ - 2 τ^{3})}{9 θ^{2} \sqrt{τ^{2} - 3 θ ν}}, \\ ρ = \frac{4 a_{0} (- τ^{2} \sqrt{τ^{2} - 3 θ ν} + 6 θ ν \sqrt{τ^{2} - 3 θ ν} + 3 θ ν τ - τ^{3})}{9 θ Ω \sqrt{τ^{2} - 3 θ ν}}, τ = τ, a_{0} = a_{0}, a_{1} = 0, b_{1} = - \frac{2 a_{0}^{2} (\sqrt{τ^{2} - 3 θ ν} + τ)}{3 θ}} . \end{matrix}

(47)

ω < 0

\begin{matrix} g (x, t) = {\{a_{0} - \frac{2 a_{0}^{2} (\sqrt{τ^{2} - 3 θ ν} + τ)}{3 θ (- \sqrt{- ω} tanh (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{- ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} (- τ^{2} \sqrt{τ^{2} - 3 θ ν} + 6 θ ν \sqrt{τ^{2} - 3 θ ν} + 3 θ ν τ - τ^{3})}{9 θ Ω \sqrt{τ^{2} - 3 θ ν}}) x^{α} + λ t^{α}) + ϑ)) . \end{matrix}

(48)

\begin{matrix} g (x, t) = {\{a_{0} - \frac{2 a_{0}^{2} (\sqrt{τ^{2} - 3 θ ν} + τ)}{3 θ (- \sqrt{- ω} coth (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{- ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} (- τ^{2} \sqrt{τ^{2} - 3 θ ν} + 6 θ ν \sqrt{τ^{2} - 3 θ ν} + 3 θ ν τ - τ^{3})}{9 θ Ω \sqrt{τ^{2} - 3 θ ν}}) x^{α} + λ t^{α}) + ϑ)) . \end{matrix}

(49)

ω > 0

\begin{matrix} g (x, t) = {\{a_{0} - \frac{2 a_{0}^{2} (\sqrt{τ^{2} - 3 θ ν} + τ)}{3 θ (\sqrt{ω} tan (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} (- τ^{2} \sqrt{τ^{2} - 3 θ ν} + 6 θ ν \sqrt{τ^{2} - 3 θ ν} + 3 θ ν τ - τ^{3})}{9 θ Ω \sqrt{τ^{2} - 3 θ ν}}) x^{α} + λ t^{α}) + ϑ)) . \end{matrix}

(50)

\begin{matrix} g (x, t) = {\{a_{0} - \frac{2 a_{0}^{2} (\sqrt{τ^{2} - 3 θ ν} + τ)}{3 θ (- \sqrt{ω} cot (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} (- τ^{2} \sqrt{τ^{2} - 3 θ ν} + 6 θ ν \sqrt{τ^{2} - 3 θ ν} + 3 θ ν τ - τ^{3})}{9 θ Ω \sqrt{τ^{2} - 3 θ ν}}) x^{α} + λ t^{α}) + ϑ)) . \end{matrix}

(51)

Set 4:

\begin{matrix} {λ = - (8 a_{0} (a_{0} (\frac{8 θ^{2} ν^{2}}{3} + τ^{2} (- \frac{10 θ ν}{9} - \frac{Ω^{2}}{3}) + \frac{1}{2} θ ν Ω^{2} + \frac{4 τ^{4}}{27}) + \frac{1}{6} τ \sqrt{τ^{2} - 3 θ ν} (a_{0} (\frac{16 θ ν}{3} - \frac{8 τ^{2}}{9} + 2 Ω^{2}) \\ + μ Ω) + μ Ω (θ ν - \frac{τ^{2}}{6}))) / (3 θ Ω^{2}), ω = \frac{4 a_{0}^{2} (- 2 τ^{2} \sqrt{τ^{2} - 3 θ ν} + 3 θ ν \sqrt{τ^{2} - 3 θ ν} - 6 θ ν τ + 2 τ^{3})}{9 θ^{2} \sqrt{τ^{2} - 3 θ ν}}, \\ ρ = \frac{4 a_{0} (- τ^{2} \sqrt{τ^{2} - 3 θ ν} + 6 θ ν \sqrt{τ^{2} - 3 θ ν} - 3 θ ν τ + τ^{3})}{9 θ Ω \sqrt{τ^{2} - 3 θ ν}}, τ = τ, a_{0} = a_{0}, a_{1} = 0, b_{1} = \frac{2 a_{0}^{2} (\sqrt{τ^{2} - 3 θ ν} - τ)}{3 θ}} . \end{matrix}

(52)

ω < 0

\begin{matrix} g (x, t) = {\{a_{0} + \frac{2 a_{0}^{2} (\sqrt{τ^{2} - 3 θ ν} - τ)}{3 θ (- \sqrt{- ω} tanh (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{- ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} (- τ^{2} \sqrt{τ^{2} - 3 θ ν} + 6 θ ν \sqrt{τ^{2} - 3 θ ν} - 3 θ ν τ + τ^{3})}{9 θ Ω \sqrt{τ^{2} - 3 θ ν}}) x^{α} + λ t^{α}) + ϑ)) . \end{matrix}

(53)

\begin{matrix} g (x, t) = {\{a_{0} + \frac{2 a_{0}^{2} (\sqrt{τ^{2} - 3 θ ν} - τ)}{3 θ (- \sqrt{- ω} coth (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{- ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} (- τ^{2} \sqrt{τ^{2} - 3 θ ν} + 6 θ ν \sqrt{τ^{2} - 3 θ ν} - 3 θ ν τ + τ^{3})}{9 θ Ω \sqrt{τ^{2} - 3 θ ν}}) x^{α} + λ t^{α}) + ϑ)) . \end{matrix}

(54)

ω > 0

\begin{matrix} g (x, t) = {\{a_{0} + \frac{2 a_{0}^{2} (\sqrt{τ^{2} - 3 θ ν} - τ)}{3 θ (\sqrt{ω} tan (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} (- τ^{2} \sqrt{τ^{2} - 3 θ ν} + 6 θ ν \sqrt{τ^{2} - 3 θ ν} - 3 θ ν τ + τ^{3})}{9 θ Ω \sqrt{τ^{2} - 3 θ ν}}) x^{α} + λ t^{α}) + ϑ)) . \end{matrix}

(55)

\begin{matrix} g (x, t) = {\{a_{0} + \frac{2 a_{0}^{2} (\sqrt{τ^{2} - 3 θ ν} - τ)}{3 θ (- \sqrt{ω} cot (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (- (\frac{4 a_{0} (- τ^{2} \sqrt{τ^{2} - 3 θ ν} + 6 θ ν \sqrt{τ^{2} - 3 θ ν} - 3 θ ν τ + τ^{3})}{9 θ Ω \sqrt{τ^{2} - 3 θ ν}}) x^{α} + λ t^{α}) + ϑ)) . \end{matrix}

(56)

Set 5:

\begin{matrix} {λ = - \frac{2 a_{0} (\frac{a_{0} θ^{3}}{8} - \frac{1}{4} a_{1}^{2} θ (a_{0} (4 θ ν + 2 Ω^{2}) + μ Ω) + a_{1}^{4} ν (2 a_{0} θ ν + μ Ω))}{a_{1}^{4} Ω^{2}}, \\ ω = - \frac{a_{0}^{2}}{a_{1}^{2}}, ρ = \frac{a_{0} (4 a_{1}^{2} ν - θ)}{2 a_{1}^{2} Ω}, τ = - \frac{4 a_{1}^{2} ν + 3 θ}{4 a_{1}}, a_{0} = a_{0}, a_{1} = a_{1}, b_{1} = 0} . \end{matrix}

(57)

ω < 0

\begin{matrix} g (x, t) = {\{a_{0} - a_{1} \sqrt{- ω} tanh (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{- ω})\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (\frac{- a_{0} (4 a_{1}^{2} ν - θ)}{2 a_{1}^{2} Ω} x^{α} - (\frac{2 a_{0} (\frac{a_{0} θ^{3}}{8} - \frac{1}{4} a_{1}^{2} θ (a_{0} (4 θ ν + 2 Ω^{2}) + μ Ω) + a_{1}^{4} ν (2 a_{0} θ ν + μ Ω))}{a_{1}^{4} Ω^{2}}) t^{α}) + ϑ)) . \end{matrix}

(58)

\begin{matrix} g (x, t) = {\{a_{0} - a_{1} \sqrt{- ω} coth (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{- ω})\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (\frac{- a_{0} (4 a_{1}^{2} ν - θ)}{2 a_{1}^{2} Ω} x^{α} - (\frac{2 a_{0} (\frac{a_{0} θ^{3}}{8} - \frac{1}{4} a_{1}^{2} θ (a_{0} (4 θ ν + 2 Ω^{2}) + μ Ω) + a_{1}^{4} ν (2 a_{0} θ ν + μ Ω))}{a_{1}^{4} Ω^{2}}) t^{α}) + ϑ)) . \end{matrix}

(59)

Set 6:

\begin{matrix} {λ = - \frac{2 a_{0} (\frac{a_{0} θ^{3}}{8} - \frac{1}{4} a_{1}^{2} θ (a_{0} (4 θ ν + 2 Ω^{2}) + μ Ω) + a_{1}^{4} ν (2 a_{0} θ ν + μ Ω))}{a_{1}^{4} Ω^{2}}, ω = - \frac{a_{0}^{2}}{4 a_{1}^{2}}, \\ ρ = \frac{a_{0} (4 a_{1}^{2} ν - θ)}{2 a_{1}^{2} Ω}, τ = - \frac{4 a_{1}^{2} ν + 3 θ}{4 a_{1}}, a_{0} = a_{0}, a_{1} = a_{1}, b_{1} = \frac{a_{0}^{2}}{4 a_{1}}} . \end{matrix}

(60)

ω < 0

\begin{matrix} g (x, t) = {\{a_{0} - a_{1} \sqrt{- ω} tanh (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{- ω}) + \frac{a_{0}^{2}}{4 a_{1} (- \sqrt{- ω} tanh (ξ \sqrt{- ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (\frac{- a_{0} (4 a_{1}^{2} ν - θ)}{2 a_{1}^{2} Ω} x^{α} - (\frac{2 a_{0} (\frac{a_{0} θ^{3}}{8} - \frac{1}{4} a_{1}^{2} θ (a_{0} (4 θ ν + 2 Ω^{2}) + μ Ω) + a_{1}^{4} ν (2 a_{0} θ ν + μ Ω))}{a_{1}^{4} Ω^{2}}) t^{α}) + ϑ)) . \end{matrix}

(61)

\begin{matrix} g (x, t) = {\{a_{0} - a_{1} \sqrt{- ω} coth (\frac{Γ (1 + Υ)}{α} (x^{α} + (μ + 2 θ ρ) t^{α}) \sqrt{- ω}) + \frac{a_{0}^{2}}{4 a_{1} (- \sqrt{- ω} coth (ξ \sqrt{- ω}))}\}}^{\frac{1}{2}} \\ \times exp (ι (\frac{Γ (1 + Υ)}{α} (\frac{- a_{0} (4 a_{1}^{2} ν - θ)}{2 a_{1}^{2} Ω} x^{α} - (\frac{2 a_{0} (\frac{a_{0} θ^{3}}{8} - \frac{1}{4} a_{1}^{2} θ (a_{0} (4 θ ν + 2 Ω^{2}) + μ Ω) + a_{1}^{4} ν (2 a_{0} θ ν + μ Ω))}{a_{1}^{4} Ω^{2}}) t^{α}) + ϑ)) . \end{matrix}

(62)

5. Stability analysis

Here, one study the Equation (1) stability for this we define the hamiltonian transformation as,

\begin{matrix} S = \frac{1}{2} \int_{- \infty}^{\infty} g^{2} d x, \end{matrix}

(63)

the momentum factor is delimited by

S

, while the possibility for power is expressed by

g (x, t)

. Following that, we describe the essential conditions for stable solitaires accordingly.

\begin{matrix} \frac{\partial S}{\partial ϖ} > 0, \end{matrix}

(64)

where

ϖ

is the wave solitons rate, then by substituting Equation (29) in Equation (63) from this we attain the outcome

\begin{matrix} S = \frac{1}{2} \int_{- 10}^{10} (\frac{d^{1.32934 (x + ϖ)}}{β_{0} - \frac{d^{1.32934 (x + ϖ)} (\sqrt{4 θ ν + ρ^{2} ϖ^{2}} + ρ ϖ)}{2 θ}}) d x, \end{matrix}

(65)

by applying the condition described in Equation (64)

\begin{matrix} \frac{β_{0} (2 . d^{26.5868} - 2 .) θ^{2} d^{1.32934 ϖ}}{(d^{1.32934 ϖ + 13.2934} (\sqrt{4 . θ ν + ρ^{2} ϖ^{2}} + ρ ϖ) - 2 . β_{0} θ) (d^{1.32934 ϖ} (1 . \sqrt{4 . θ ν + ρ^{2} ϖ^{2}} + 1 . ρ ϖ) - 2 . β_{0} d^{13.2934} θ)} > 0, \end{matrix}

(66)

so we can conclude that Equation (1) represents a stable nonlinear fractional model provided that the above condition is satisfied.

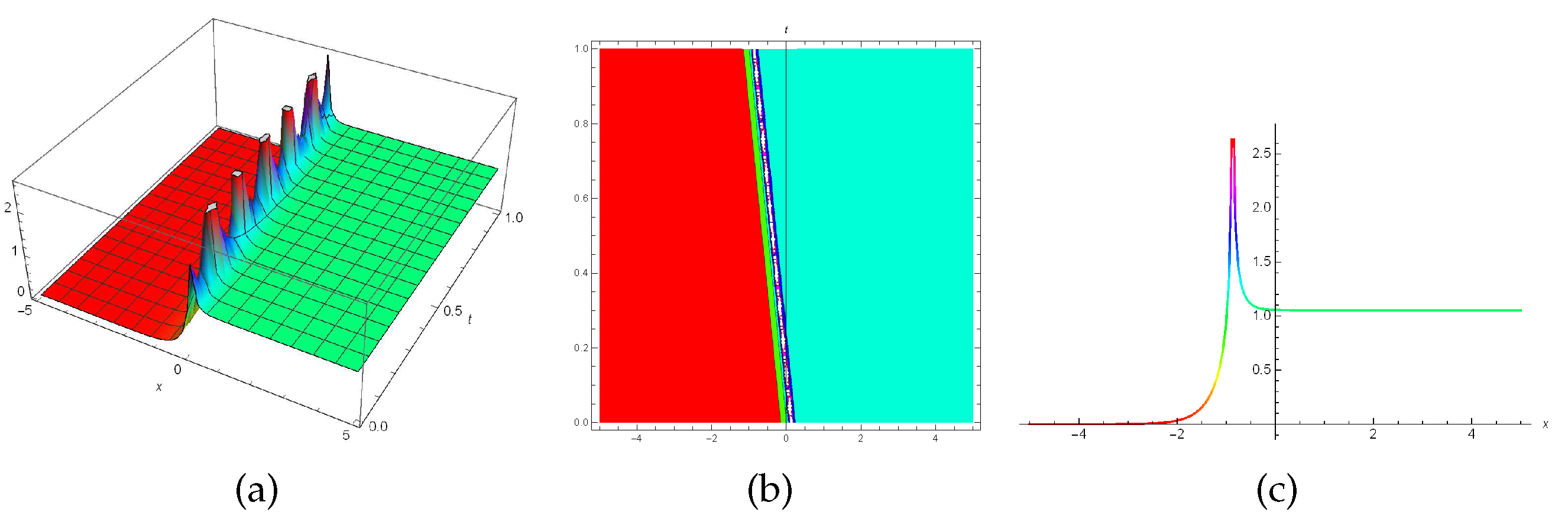
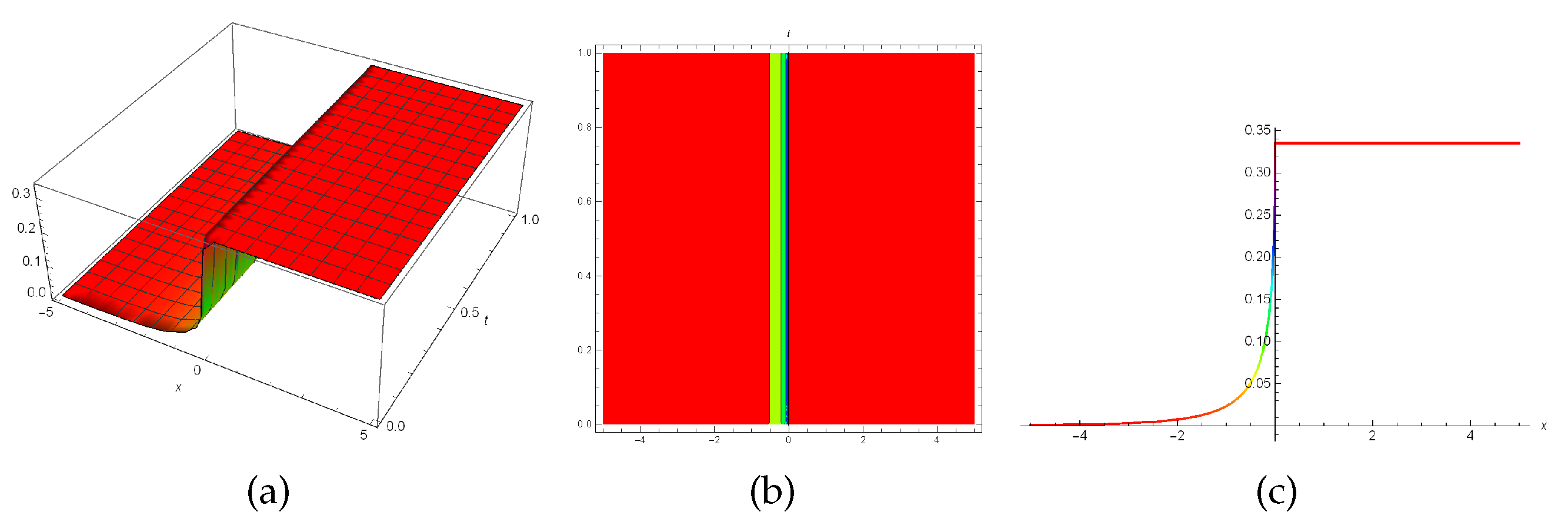
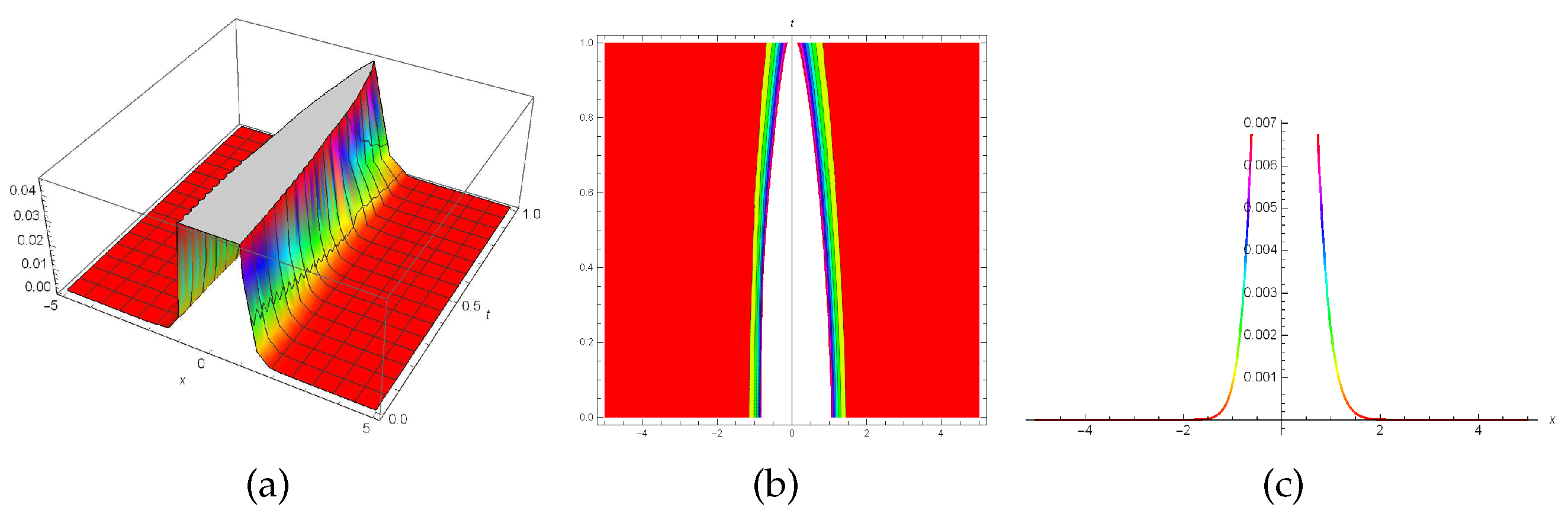
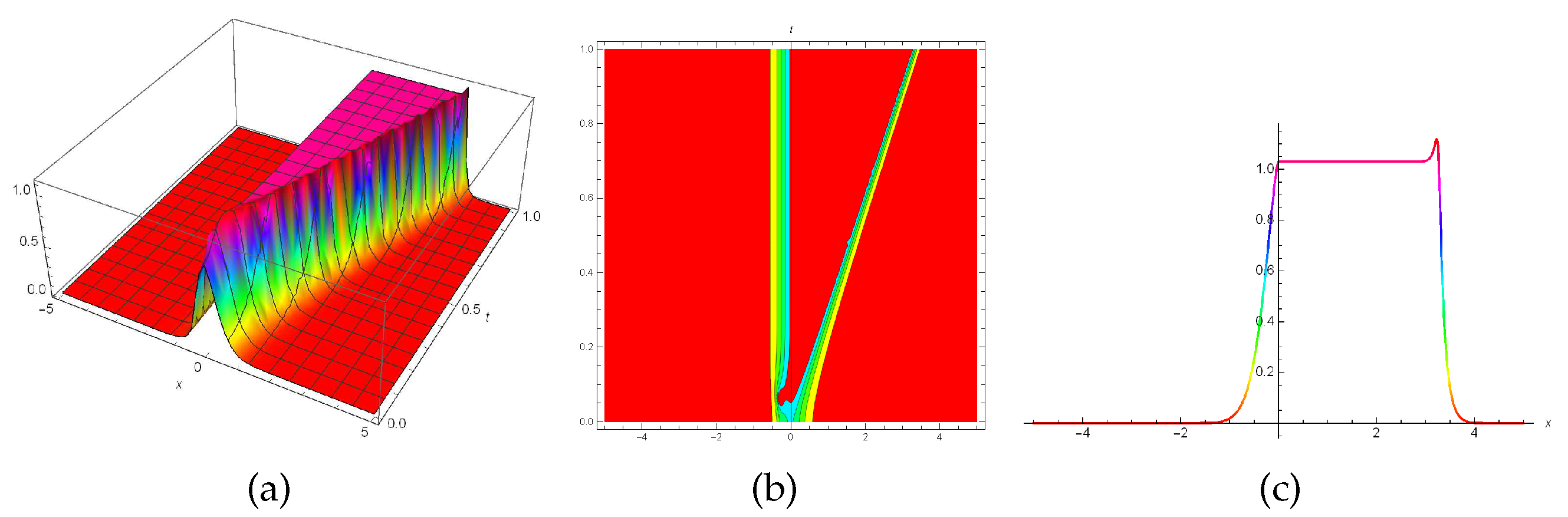
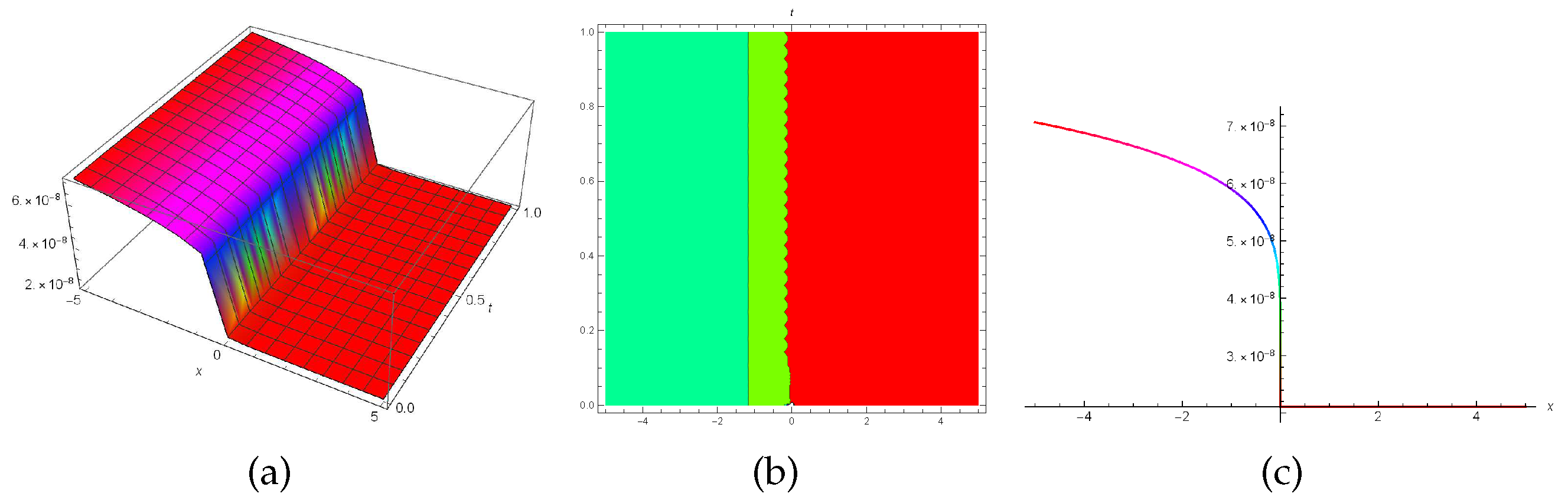
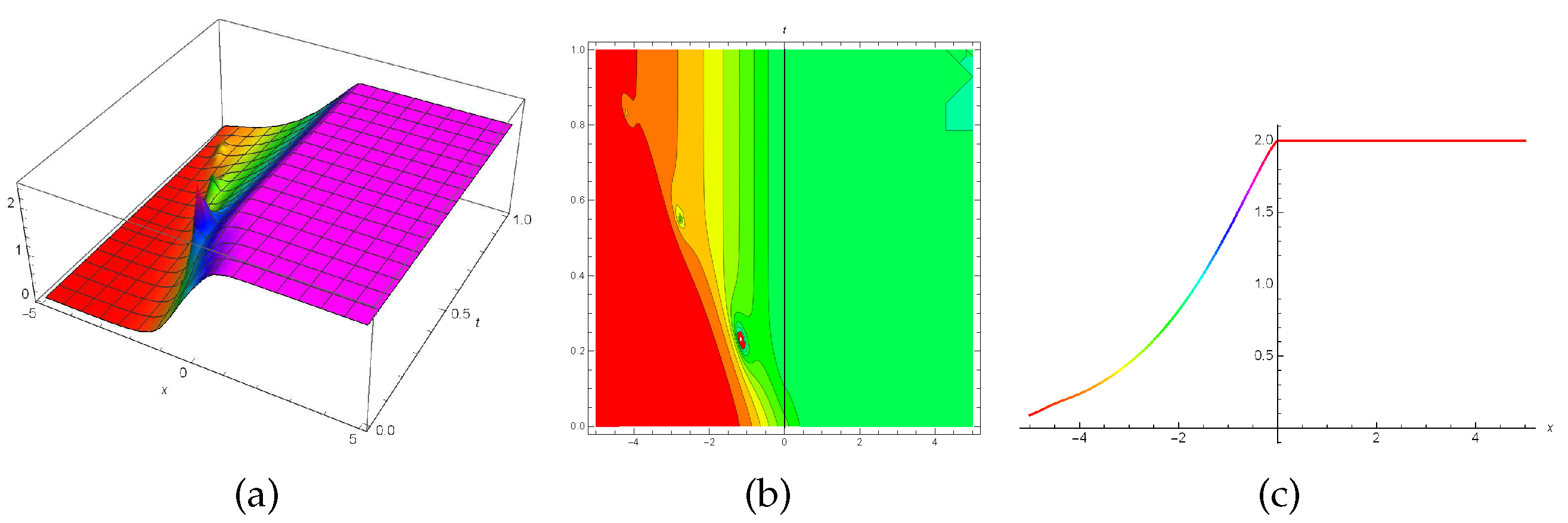
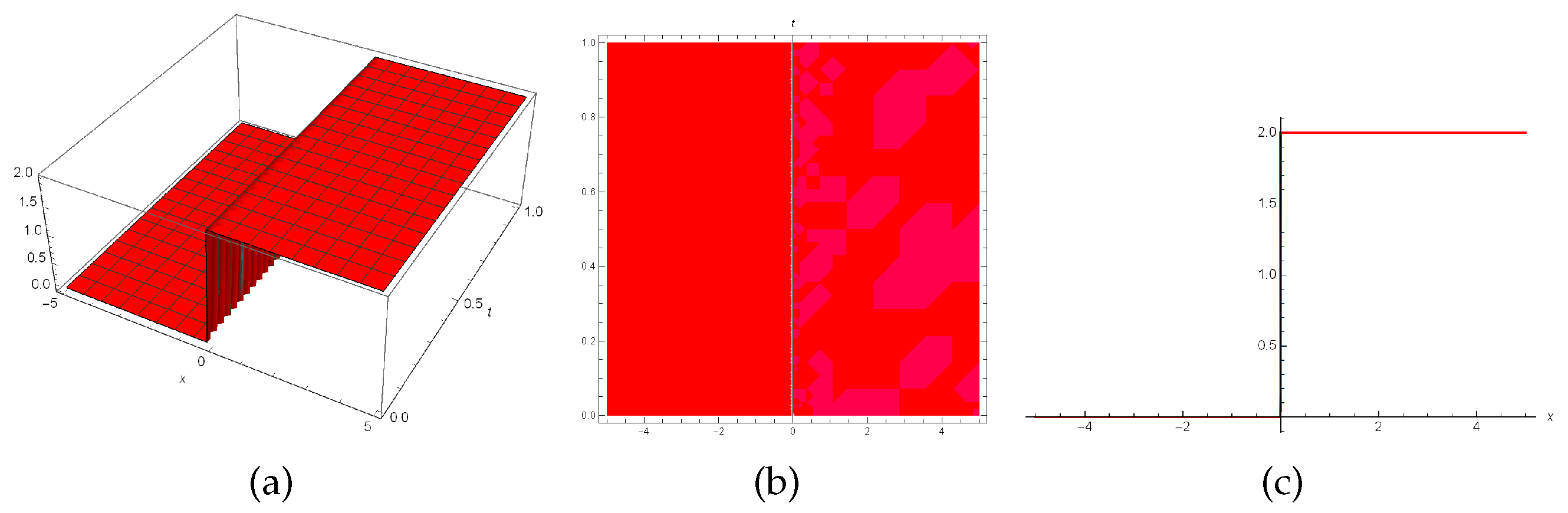
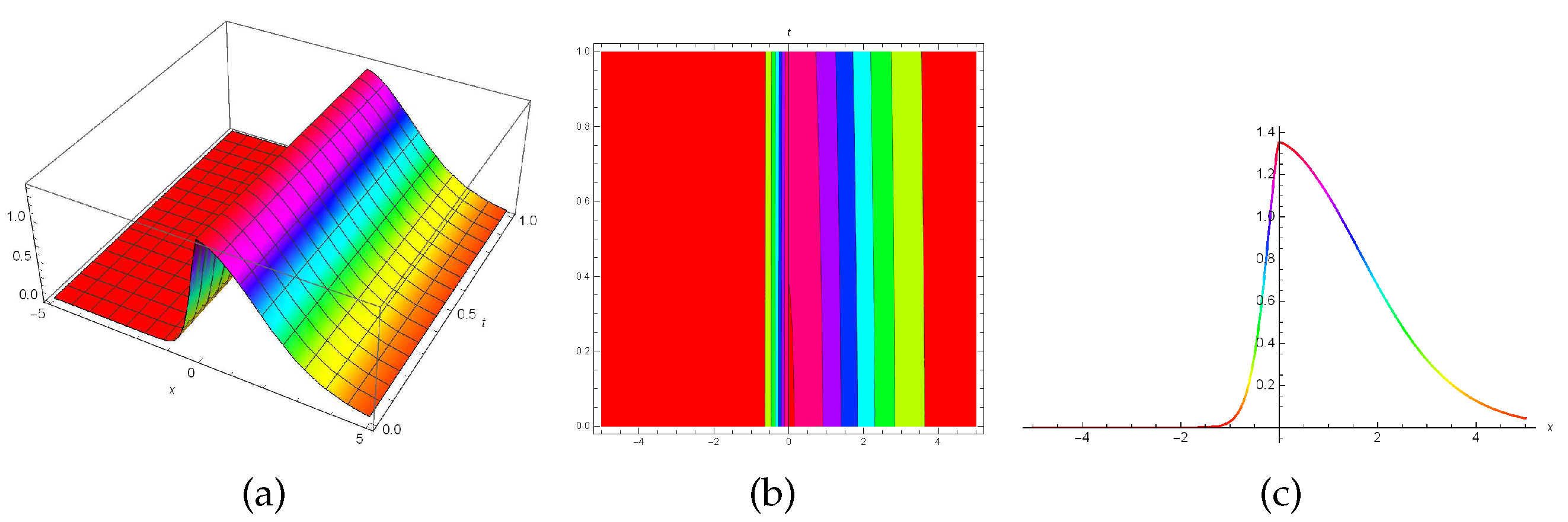
6. Discussion and results

In this section the graphical representations of the truncated M-fractional perturbed Kundu-Eckhaus model has been illustrated in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. The 3D, contour and 2D graphs visualize the nature of nonlinear waves constructed from Equation (1). A family of bright, dark, periodic and singular solitons are displayed for a set of values.

By employing the

e x p_{a}

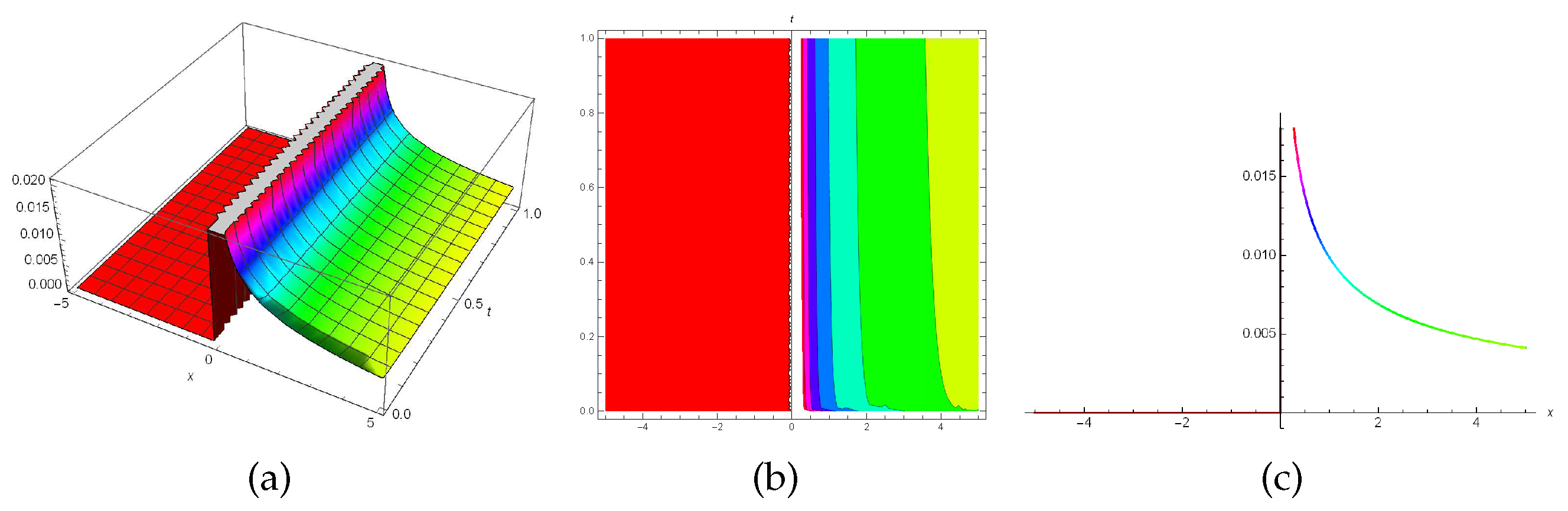
function approach: Figure 1 illustrates an bright singular wave soliton (29) when

α = 0.1, α_{1} = 1, β_{0} = 2, γ = 1.5, d = 100, θ = 0.25, μ = 2, ν = 2, ρ = - 1, Ω = 2

while Figure 2 demonstrates a solitary wave (33) when

α = 1.5, α_{1} = 1, β_{0} = - 0.5, γ = 2, d = 100, θ = 0.25, μ = 0.5, ν = 3, ρ = 3, Ω = - 1

whereas Figure 3 represents a optical soliton (33) when

α = 1.5, α_{1} = 1, β_{0} = - 0.5, γ = 2, d = 100, θ = 0.25, μ = 0.5, ν = 3, ρ = 3, Ω = - 1

and Figure 4 illustrates a bright solitary wave (35) when

α = 1.5, α_{1} = - 2, β_{0} = - 5, γ = 2, d = 100, θ = - 0.5, μ = - 5, ν = 1, ρ = 3, Ω = 0.25 .

Similarly, applying the modified extended tanh expansion function technique: Figure 5 depicts soliton (43) when

α = 0.1, a_{0} = 2, γ = 1, θ = 0.5, μ = 2, ν = 0.5, Ω = 4

while Figure 6 illustrates a travelling wave (45) when

α = 1.25, a_{0} = 2, γ = 1, θ = 0.5, μ = 2, ν = 0.5, Ω = 2

whereas Figure 7 displays a periodic wave (51) when

α = 0.5, a_{0} = 2, γ = 2, θ = 0.5, μ = 4, ν = 1, Ω = 2, τ = 3

then Figure 8 expresses a bright soliton (58) when

α = 1.5, a_{0} = 2, a_{1} = 4, γ = 1, θ = 5, μ = 2, ν = 3, Ω = 2, τ = 0.5

while Figure 9 expresses a singular optical wave (62) when

α = 1.5, a_{0} = 2, a_{1} = 4, γ = 1, θ = 5, μ = 2, ν = 3, Ω = 2, τ = 0.5 .

Figure 1. 3D, contour and 2D plots for the solution (29) when

α = 0.1, α_{1} = 1, β_{0} = 2, γ = 1.5, d = 100, θ = 0.25, μ = 2, ν = 2, ρ = - 1, Ω = 2 .

Figure 1. 3D, contour and 2D plots for the solution (29) when

α = 0.1, α_{1} = 1, β_{0} = 2, γ = 1.5, d = 100, θ = 0.25, μ = 2, ν = 2, ρ = - 1, Ω = 2 .

Figure 2. 3D, contour and 2D plots for the solution (31) when

α = 0.5, α_{1} = 1, β_{0} = 2, γ = 1.5, d = 100, θ = 0.25, μ = 4, ν = 2, ρ = - 1, Ω = 2 .

Figure 2. 3D, contour and 2D plots for the solution (31) when

α = 0.5, α_{1} = 1, β_{0} = 2, γ = 1.5, d = 100, θ = 0.25, μ = 4, ν = 2, ρ = - 1, Ω = 2 .

Figure 3. 3D, contour and 2D plots for the solution (33) when

α = 1.5, α_{1} = 1, β_{0} = - 0.5, γ = 2, d = 100, θ = 0.25, μ = 0.5, ν = 3, ρ = 3, Ω = - 1 .

Figure 3. 3D, contour and 2D plots for the solution (33) when

α = 1.5, α_{1} = 1, β_{0} = - 0.5, γ = 2, d = 100, θ = 0.25, μ = 0.5, ν = 3, ρ = 3, Ω = - 1 .

Figure 4. 3D, contour and 2D plots for the solution (35) when

α = 1.5, α_{1} = - 2, β_{0} = - 5, γ = 2, d = 100, θ = - 0.5, μ = - 5, ν = 1, ρ = 3, Ω = 0.25 .

Figure 4. 3D, contour and 2D plots for the solution (35) when

α = 1.5, α_{1} = - 2, β_{0} = - 5, γ = 2, d = 100, θ = - 0.5, μ = - 5, ν = 1, ρ = 3, Ω = 0.25 .

Figure 5. 3D, contour and 2D plots for the solution (43) when

α = 0.1, a_{0} = 2, γ = 1, θ = 0.5, μ = 2, ν = 0.5, Ω = 4 .

Figure 5. 3D, contour and 2D plots for the solution (43) when

α = 0.1, a_{0} = 2, γ = 1, θ = 0.5, μ = 2, ν = 0.5, Ω = 4 .

Figure 6. 3D, contour and 2D plots for the solution (45) when

α = 1.25, a_{0} = 2, γ = 1, θ = 0.5, μ = 2, ν = 0.5, Ω = 2 .

Figure 6. 3D, contour and 2D plots for the solution (45) when

α = 1.25, a_{0} = 2, γ = 1, θ = 0.5, μ = 2, ν = 0.5, Ω = 2 .

Figure 7. 3D, contour and 2D plots for the solution (51) when

α = 0.5, a_{0} = 2, γ = 2, θ = 0.5, μ = 4, ν = 1, Ω = 2, τ = 3 .

Figure 7. 3D, contour and 2D plots for the solution (51) when

α = 0.5, a_{0} = 2, γ = 2, θ = 0.5, μ = 4, ν = 1, Ω = 2, τ = 3 .

Figure 8. 3D, contour and 2D plots for the solution (58) when

α = 1.5, a_{0} = 2, a_{1} = 4, γ = 1, θ = 5, μ = 2, ν = 3, Ω = 2, τ = 0.5 .

Figure 8. 3D, contour and 2D plots for the solution (58) when

α = 1.5, a_{0} = 2, a_{1} = 4, γ = 1, θ = 5, μ = 2, ν = 3, Ω = 2, τ = 0.5 .

Figure 9. 3D, contour and 2D plots for the solution (62) when

α = 1.5, a_{0} = 2, a_{1} = 4, γ = 1, θ = 5, μ = 2, ν = 3, Ω = 2, τ = 0.5 .

Figure 9. 3D, contour and 2D plots for the solution (62) when

α = 1.5, a_{0} = 2, a_{1} = 4, γ = 1, θ = 5, μ = 2, ν = 3, Ω = 2, τ = 0.5 .

7. Conclusion

We are succeed to gain the new optical wave solutions of truncated M-fractional perturbed Kundu-Eckhaus model with full non-linearity by applying the

{exp}_{a}

function technique and modified extended tanh expansion function technique. The obtained solutions are in the form of dark soliton, bright soliton, singular solitons and other form of solutions. These results are very helpful in the further research in the field of non-linear optics. The attain solutions are helpful for the further development of concerned model. Finally, it is extended that the applied strategies are simple, fruitful and reliable to handle many nonlinear fractional models of contemporary era.

Author Contributions

Asim Zafar: Conceptualization, project administration. M. Raheel: Formal analysis and investigation, writing original draft. Kalim U. Tariq: Software, visualization. Ali M. Mahnashi: Scientific computing, review and editing. Emad H.M. Zahran: Formal analysis and investigation, methodology. Adem Cevikel: Validation, review and editing. Ahmet Bekir: Supervision, Conceptualization, methodology.

Funding

Not available.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Biswas, A.; Arshed, S. Optical solitons in presence of higher order dispersions and absence of selfphase modulation. Optik 2018, 174, 452–459. [Google Scholar] [CrossRef]
Biswas, A.; Ekici, M.; Sonmezoglu, A.; Alqahtani, R.T. Optical solitons with differential group delay for coupled FokasLenells equation by extended trial function scheme. Optik 2018, 165, 102–110. [Google Scholar] [CrossRef]
Biswas, A. Chirp-free bright optical soliton perturbation with Fokas Lenells equation by traveling wave hypothesis and semi-inverse variational principle. Optik 2018, 170, 431435. [Google Scholar] [CrossRef]
Zayed, E.M.E.; et al. Chirped and chirpfree solitons in optical fiber Bragg gratings with dispersive reflectivity having parabolic law nonlinearity by Jacobi’s elliptic function. Results in Physics 2019, 15, 102784. [Google Scholar] [CrossRef]
Mohammed, W.W.; El-Morshedy, M.; Cesarano, C.; Al-Askar, F.M. Soliton Solutions of Fractional Stochastic Kraenkel–Manna–Merle equations in Ferromagnetic Materials. Fractal Fract. 2023, 7, 328. [Google Scholar] [CrossRef]
Abdelwahed, H.G.; Alsarhana, A.F.; El-Shewy, E.K.; Abdelrahman, M.A.E. Characteristics of New Stochastic Solitonic Solutions for the Chiral Type of Nonlinear Schrödinger equation. Fractal Fract. 2023, 7, 461. [Google Scholar] [CrossRef]
Mohammed, W.W.; Al-Askar, F.M.; Cesarano, C.; El-Morshedy, M. The Optical Solutions of the Stochastic Fractional Kundu–Mukherjee–Naskar Model by Two Different Methods. Mathematics 2022, 10, 1465. [Google Scholar] [CrossRef]
Özkan, A.; Özkan, E.M.; Yildirim, O. On Exact Solutions of Some Space–Time Fractional Differential equations with M-truncated Derivative. Fractal Fract. 2023, 7, 255. [Google Scholar] [CrossRef]
Wu, G.; Guo, Y. New Complex Wave Solutions and Diverse Wave Structures of the (2+1)-Dimensional Asymmetric Nizhnik–Novikov–Veselov equation. Fractal Fract. 2023, 7, 170. [Google Scholar] [CrossRef]
Biswas, A.; Yildirim, Y.; Yasar, E.; Triki, H.; Alshomrani, A.S.; Ullah, M.Z.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Optical soliton perturbation with full nonlinearity for Kundu–Eckhaus equation by modified simple equation method. Optik 2018, 157, 1376–1380. [Google Scholar] [CrossRef]
Arshed, S.; Biswas, A.; Abdelaty, M.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Optical soliton perturbation with Kundu-Eckhaus equation by exp(-φ(ξ))-expansion scheme and (G^′/G²)-expansion method. Optik 2018, 172, 79–85. [Google Scholar] [CrossRef]
Biswas, A.; Ekici, M.; Sonmezoglu, A.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Optical soliton perturbation with full nonlinearity for Kundu-Eckhaus equation by extended trial function scheme. Optik 2018, 160, 17–23. [Google Scholar] [CrossRef]
Zafar, A.; Ali, K.K.; Raheel, M.; Nisar, K.S.; Bekir, A. Abundant M-fractional optical solitons to the pertubed Gerdjikov–Ivanov equation treating the mathematical nonlinear optics. Optical and Quantum Electronics 2022, 54, 25. [Google Scholar] [CrossRef]
Raheel, M.; Zafar, A.; Inc, M.; Tala-Tebue, E. Optical solitons to time-fractional Sasa-Satsuma higher-order non-linear Schrödinger equation via three analytical techniques. Optical and Quantum Electronics 2023, 55, 307. [Google Scholar] [CrossRef]
Zafar, A.; Bekir, A.; Raheel, M.; Nisar, K.S.; Mustafa, S. Dynamics of new optical solitons for the Triki–Biswas model using beta-time derivative. Modern Physics Letters B 2021, 35, 2150511. [Google Scholar] [CrossRef]
Zafar, A.; Raheel, M.; Bekir, A. Exploring the dark and singular soliton solutions of Biswas-Arshed model with full nonlinear form. Optik 2020, 204, 164133. [Google Scholar] [CrossRef]
Tukur, A.S.; Yel, G.; Bulut, H. M-fractional solitons and periodic wave solutions to the Hirota- Maccari system. Modern Physics Letters B 2019, 1950052. [Google Scholar]
Vanterler, J.; Sousa, D.A.C.; Capelas, E.; Oliveira, D.E. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. International Journal of Analysis and Applications 2018, 16, 83–96. [Google Scholar]
Ali, A.T.; Hassan, E.R. General Exp_a-function method for nonlinear evolution equations. Applied Mathematics and Computation 2010, 217, 451–459. [Google Scholar] [CrossRef]
Zayed, E.M.E.; Al-Nowehy, A.G. Generalized kudryashov method and general exp_a function method for solving a high order nonlinear schrödinger equation. J. Space Explor 2017, 6, 1–26. [Google Scholar]
Hosseini, K.; Ayati, Z.; Ansari, R. New exact solutions of the Tzitzéica-type equations in non-linear optics using the exp_a function method. Journal of Modern Optics 2018, 65, 847–851. [Google Scholar] [CrossRef]
Zafar, A. The exp_a function method and the conformable time-fractional KdV equations. Nonlinear Engineering 2019, 8, 728–732. [Google Scholar] [CrossRef]
Raslan, K.R.; Khalid, K.A.; Shallal, M.A. The modified extended tanh method with the Riccati equation for solving the space-time fractional EW and MEW equations. Chaos, Solitons and Fractals 2017, 103, 404–409. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Variety of Optical Wave Solutions to Space-Time Fractional Perturbed Kundu-Eckhaus Model with Full Non-Linearity

Abstract

1. Introduction

2. The governing model

3. Methodology

3.1. The exp a function technique

3.2. The METhEF technique

4. Mathematical analysis

4.1. Applications of the exp a function technique

4.2. Applications of the METhEF technique

5. Stability analysis

6. Discussion and results

7. Conclusion

Author Contributions

Funding

Institutional Review Board Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3.1. The ${exp}_{a}$ function technique

4.1. Applications of the ${exp}_{a}$ function technique