Prerpints.org logo
Preprint
Article

Empirical Discovery of Hyperspherical 5th Dimensionality by Application of Dirac Electron Hypertube Resonance to Kaluza-Klein Cyclicality

Altmetrics

Downloads

108

Views

26

Comments

0

This version is not peer-reviewed

Submitted:

02 September 2023

Posted:

05 September 2023

You are already at the latest version

Alerts
Abstract
Motivated by assumptions that Quantum Mechanics (QM) is not the basement of reality and that additional dimensionality (XD) is required to complete and extend the Standard Models (SM) of Particle Physics and Cosmology, experimental protocols utilizing putative properties of Kaluza-Klein-like (KK) cyclicality embedded within Dirac’s electron hypertube model in conjunction with a Dirac covariant polarized vacuum is developed to produce a new type of low-energy tabletop cross section based on topological phase transitions rather than high energy collision sprays as in the LHC. The model is presented in a highly theoretical axiomatic manner utilizing off-the-shelf parameters generally marginalized by the mainstream physics community. When successful the protocol leads to obsolescence of the highly efficacious 100-year supercollider run producing a paradigm shift with an inherent new set of Unified Field (UF) transformations beyond the Galilean Lorentz-Poincaré transformations of the SM to 3rd regime natural science: Classical – Quantum - UF.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

 

Some crazy experiment [1]

1. Introduction

A radical framework for a low energy table-top (sans supercollider) protocol for accessing M-theoretic-like Unified Field Mechanical (UFM) based Higher Dimensionality (XD) routinely violating the sacrosanct quantum uncertainty principle is proposed. The model is presented in an axiomatic conceptual manner since the mathematics is currently sufficiently opaque and will likely only be correctly established by experiment. Successful demonstration of the basic experiment outlined will produce additional spectral lines in hydrogen between .5Å and 2Å leading to a new set of transformations beyond the Galilean Lorentz-Poincairé ushering in the first stage of the long-anticipated paradigm shift to 3rd regime natural science: Classical, Quantum, Einstein-like Unified Field. Our UFM model requires utility of an inherent Dirac-Einstein-Rosen bridge to supervene QM.
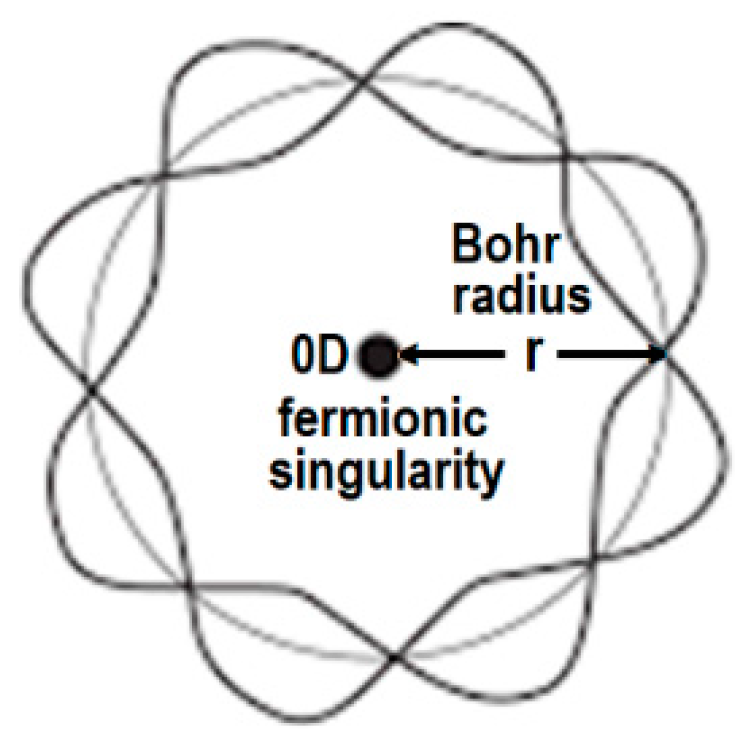
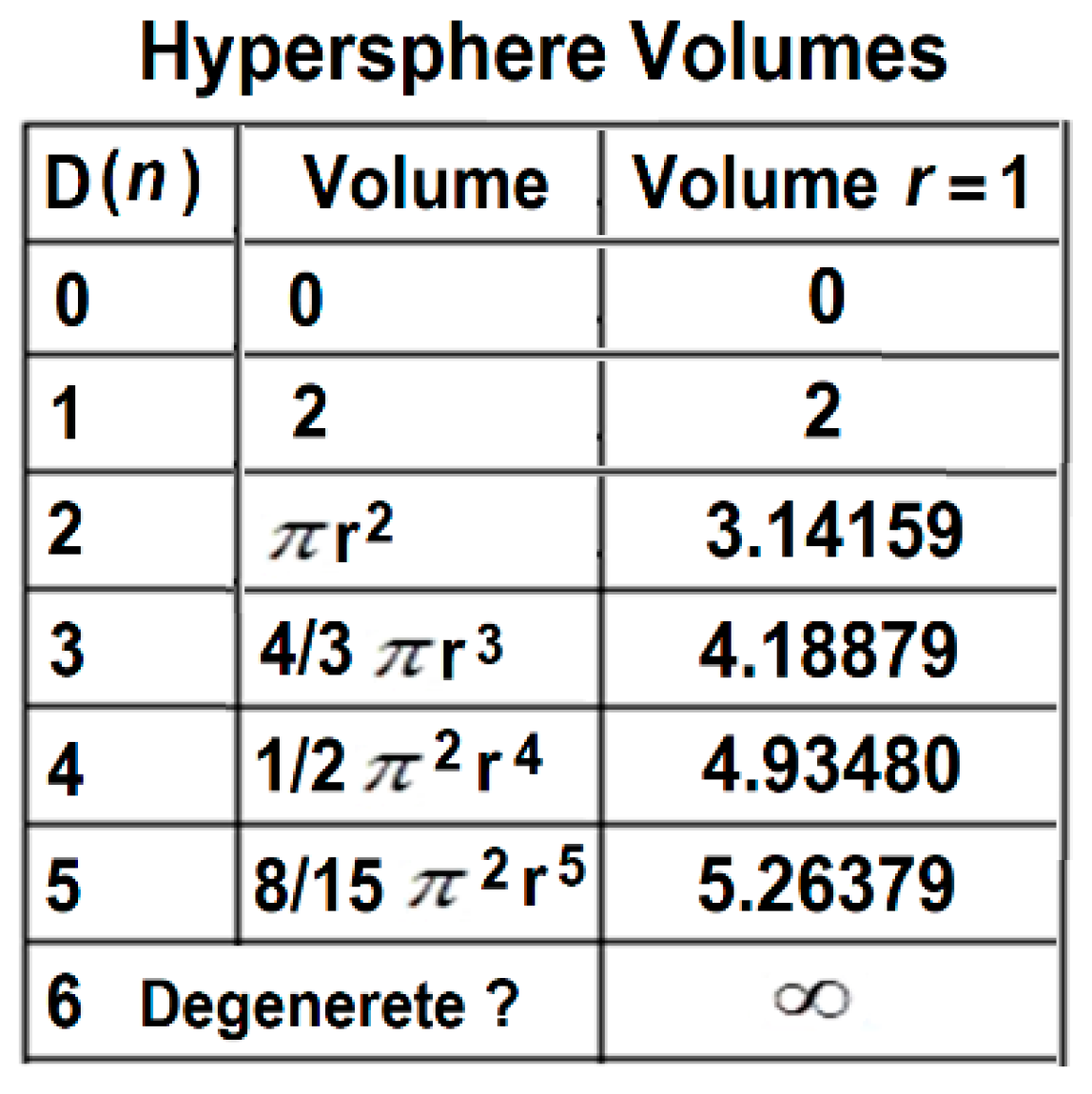
This model was originally inspired by work introduced by Vigier on Tight-Bound States (TBS) in the hydrogen atom [2,3,4] suggesting hidden energy levels below the lowest Bohr orbit. This suggestion was not accepted until twelve years later with the realization that TBS were likely hyperspherical XD cavities hidden behind the domain wall of the uncertainty principle (Figure 1). Insight occurred while contemplating a model for a continuous-state dimensional reduction compactification process where the Planck-scale was not the basement of reality but a virtual periodic asymptote never reached producing the first inkling for a Dirac hypertube incursive resonance oscillator supervening the sacrosanct ℏ -scale domain wall of the quantum uncertainty principle [5,6].
While challenging a priori to explain, and frustrating to comprehend as principles of quantum mechanics were historically reported by its founders; it is important to realize as a key element of this Noetic Unified Field Theory (NUFT) that the observed Planck-scale singularity or quantum zero-point stochastic field is not an absolute basement of reality. Rather the finite spacetime domain (Hubble radius to Planck scale) of observed reality is a dynamic subspace manifold of the 3rd regime (classical-quantum-unified) of NUFT. This is important because without a rudimentary understanding of the mechanisms involved, one cannot design or implement this experimental protocol properly.
To clarify, the usual QM Minkowski-Reimann 3(4D) + , + , + . − manifold (from within which our 3-space temporal reality is observed) is a submanifold of a XD-LSXD NUFT domain. Speaking cosmologically, the observed Hubble sphere, H R is a Universe of finite radius closed in time, beyond which as we hope to discover, exists an atemporal holographic Multiverse of infinite size. This is, contrary to current thinking, that XD must be curled up at the Planck-scale because they are unobserved. This is not the only interpretation. As shown in more detail in Sec. 2, in terms of a Wheeler-Feynman-Cramer present instant as a hyperspherical future-past standing-wave, the continuous-state dimensional reduction process and our view of Kaluza-Klein cyclicality, for an M-theoretic-like NUFT model, the Large-Scale XD (LSXD) complex manifold is annihilated and recreated within a semi-quantum spacetime domain limit. This structure suggests an inherent quantified nature for the arrow of time and a relation to KK-cyclicality.
An attempt will be made to introduce, summarize and clarify the at present hodgepodge of NUFT parameters as they relate to both the initial experimental elements and physical framework for the reality they correlate with. In way of introduction, we first mention the most important elements: A Dirac polarized vacuum [7], in conjunction with the Dirac electron hypertube [8,9], Kaluza-Klein Cyclicality [10,11], a finite radius Manifold of Uncertainty (MOU) [6] at the semi-quantum limit.
In Figure 1. hyperspherical cavity XD volume elements of the MOU can be used to postulate at least two and up to five new TBS spectral lines in hydrogen, D(n) 2 to 5 in Figure 1. If LSXD are discovered, degeneracy occurs at the MOU hypertube limit of r, suggesting in the same manner that the furthest energy level of an atom is detected when the outer electron achieves sufficient energy for escape to infinity. The initial experiment is designed to only access the 5th additional dimension (XD) opening the trap door of the DEH into the 1st rung or tiered hypercavity of the MOU.

2. Somewhat Detailed Description of Essential Parameters

In this section by way of introduction we make an attempt to define and describe the framework for essential protocol parameters and the physical background they relate to in terms of known theory and putative extended theory. It contains a Tinker Toy Cornucopia of key required parameters related to the background physical principles and their relation to the framework for setting up the experimental protocol.

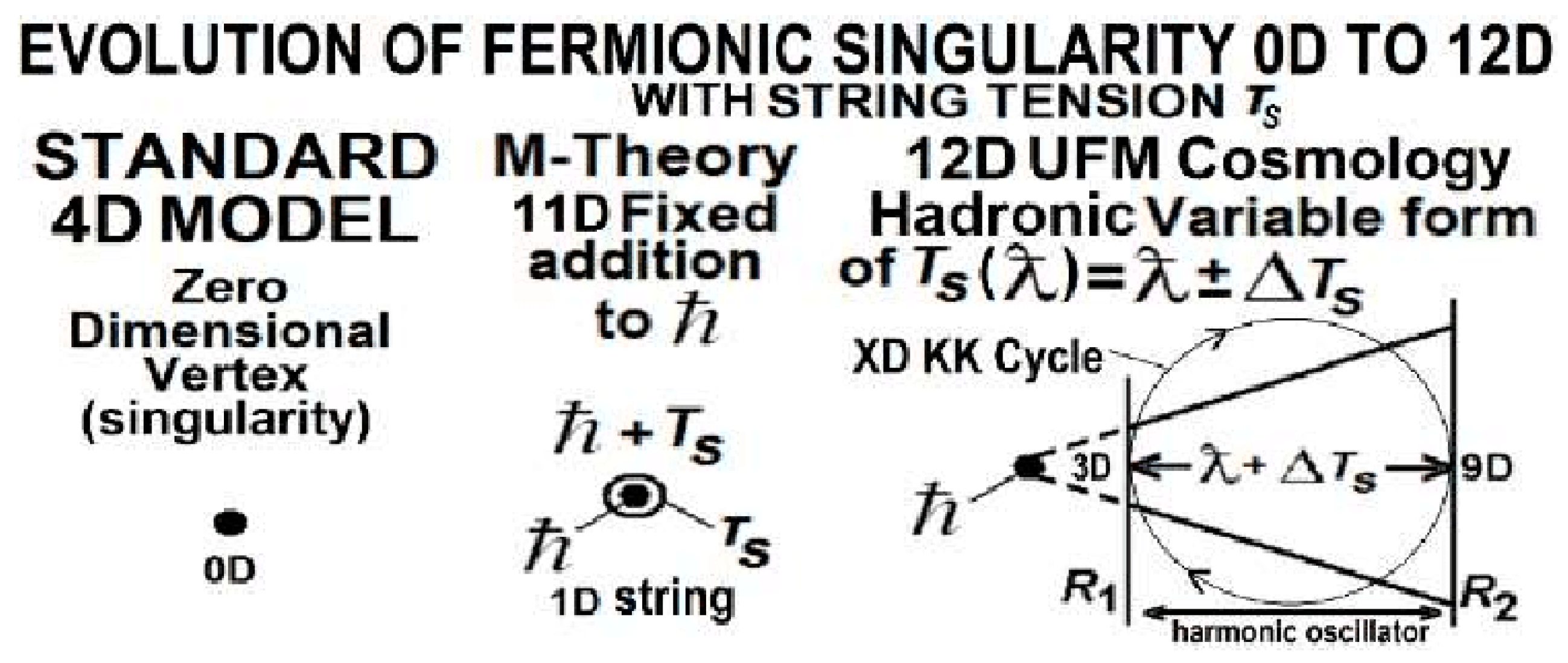
2.1. Extending the context of reality beyond the Standard Model (SM)

As generally accepted in terms of the standard models of cosmology and quantum mechanics, we live on the large-scale in what is often called the Hubble sphere or universe, generally believed to be of a finite Big Bang radius, recently called into question by observations of the James Webb Telescope. On the small-scale a zero-dimensional quantum mechanical singularity is observed currently called the basement of reality. This basement is the point of experimental attack by way of perceived properties of Diac’s electron hypertube. Destructive interference of the Planck-scale domain wall is applied in SM 4-space by the resultant action of the harmonic oscillator occurring in M-theoretic XD-space interrupting the temporal flow of cyclic Euclidean spacetime to uncover XD UF space.
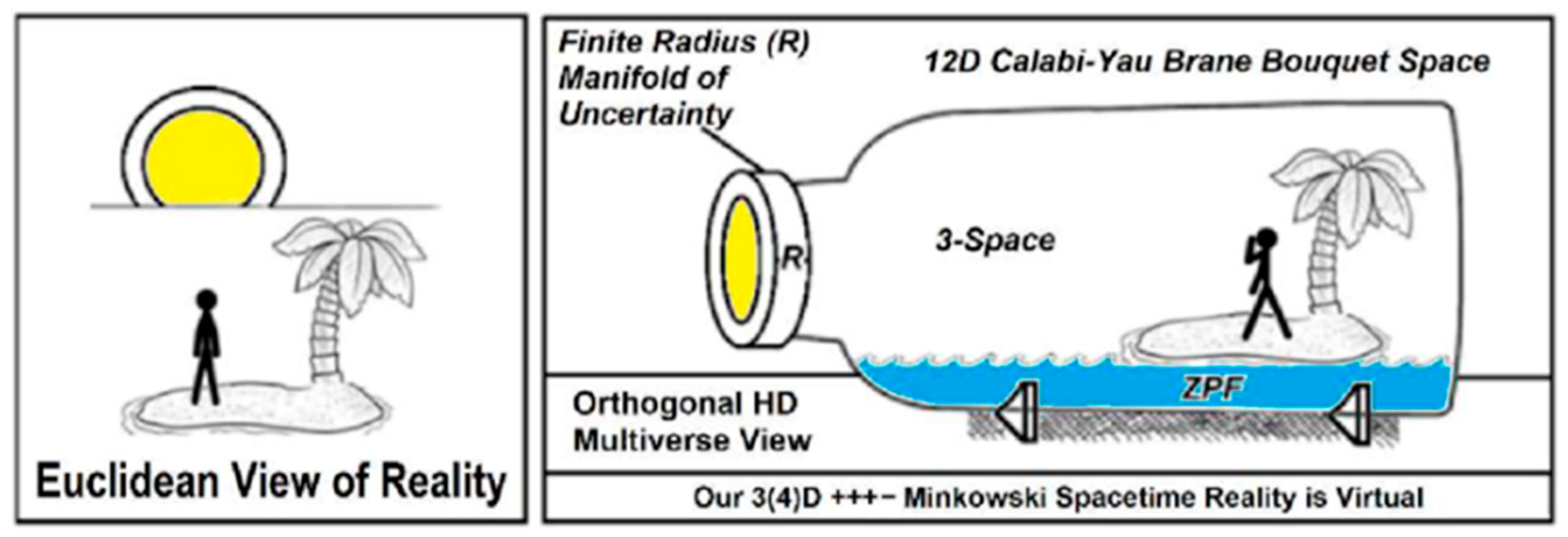
While conceptually Figure 2 has myriad shortcomings it is imperative to grasp that in contrast to the current view of existence, our perceived Minkowski-Riemann spacetime reality is the subspace not the other way around. This is an important realization for temporal aspects of living systems [12]. In general, current thinking claims, if XD exist, they are curled up microscopically at the Planck-scale because they are unobserved. This is not the only interpretation. There are two models of screen animation: 1) A figure appearing to walk to the right remains fixed at the center of the screen while the background appears to be in continuous motion to the left. 2) The background remains fixed while the figure appears to continuously move to the right off the edge of the screen and then reappears on the left starting a new cycle.
As in screen animation 2), when the figure gets to the end of the cycle at the domain wall at the right, it is annihilated and then recreated on the left in a continuous cycle. This cycle hints at the nature of the arrow of time especially as applied to our models of KK-cyclicality, continuous-state dimensional reduction compactification, within a Wheeler-Feynman-Cramer present instant as a future-past XD standing-wave LSXD cover.

2.2. The Dirac covariant polarized vacuum

In general, the Casimir, Zeeman and Aharonov-Bohm Effects would not be possible without a covariant, polarized Dirac vacuum. Vacuum polarization for our purposes allows the vacuum to be manipulated by applied electromagnetic field harmonic oscillators. According to quantum field theory (quantum electrodynamics), vacuum polarization is a process whereby a background electromagnetic field can produce virtual electron-positron pairs, or more generally, positive and negative electromagnetic field charges [7,9,13].

2.3. Extended electromagnetic theory

Extended Electromagnetic Theory, unpopular because it is erroneously believed to interfere with Gauge Theory and also allow photon mass anisotropy allows both transverse and longitudinal EM waves is described by the Proca equation with no vacuum cutoff [7,14,15].
A non-vanishing divergence of the electric field given below, can be added to Maxwell’s equations which results in space-charge distribution. A current density arises in vacuo and longitudinal electric non-transverse electromagnetic terms (i.e. magnetic field components) appears ( B ( 3 ) ) in the direction of propagation. Both sets of assumptions were anticipated by de Broglie and Dirac. They imply that the real zero-point (vacuum) electromagnetic distribution is not completely defined by F μ ν but by a four-vector field distribution given by a four-vector density A μ associated with a de Broglie-Proca equation
A μ ( x α ) = − m γ 2 c 2 ℏ 2 A μ ( x α )

2.4. Dirac Electron Hypertube (DEH)

Dirac proposed an electron hypertube model describing the interaction of electrons with radiation. Treating the electron as a point charge predicted infinite Coulomb energy. The electrons interior became a spatial region of superluminal transmission. Dirac thought the electrons interior was a region of failure, not of EM field equations, but of ultimate properties of spacetime [8]. Now we have learned spacetime is emergent not fundamental and is quantized. Interpreting Dirac’s theory, nonlocally, wave-particle constituents include extended MOU hypertubes which entails inherent clock-like unit cycles (arrow of time) carrying superluminal phase wave connections to the unified field.

2.5. Finite radius Manifold of Uncertainty (MOU)

The MOU gives a dynamic hierarchal structure to the Dirac Electron Hypertube (DEH). As in Figure 4b, the Dirac polarized vacuum is the local surface of the DEH in 4D spacetime. The 1st XD cavity is hyperspherical and periodic. It is postulated that there are several rungs on this see-saw ladder cavity controlled by the action of the uncertainty principle to remain a closed singularity to any local 4-space action. After 6D or 9D (to be experimentally determined); the TBS limit is reached and the DEW opens giving way to the LSXD 3rd regime of the nonlocal action of the unified field. Because of the nature of Self-Organized Living Systems (SOLS) residing in the subspace manifold of localized temporal reality, the LSXD of nonlocal instantaneous holographic entanglement cannot be directly observed by SOLS residing in the submanifold because of subtractive interferometry [16,17].

2.6. Kaluza-Klein (KK) cyclicality

The Kaluza-Klein hypotheses extend general relativity to 5D with the inclusion of a cylinder condition Klein explained Kaluza’s cylinder hypothesis as the condition that the fifth dimension is curled up microscopically and that geometrically the 5th XD too the form of a circle [10,11]. NUFT uses an alternate interpretation.

2.7. Unique string background

In reverting to the original Hadronic form of string theory with variable string tension, we were able to derive a unified field equation with a unique string vacuum [5,18].
Compactification plays an important role in string theory where compactified XD, is a generalization of Kaluza–Klein theory. It unifies the gap between our universe of four observable dimensions with the eleven, or twenty-six dimensions of M-theory. Current thinking assumes the XD are wrapped up on themselves, or curled up on Calabi–Yau manifolds. This is how string theory is described as compactified M-theory in 11XD.

2.8. Continuous-State cyclic dimensional reduction compactification

The NUFT Reality Universe - Multiverse model entails an observed temporal submanifold universe of observers embedded dynamically in a holographic multiverse which is the origin of matter and an anthropic principle.
The Continuous-State dimensional reduction compactification process cycles through the 12D M-theoretic unified field producing one unique compactification the SM Minkowski-Riemann 4-space manifold. This process has an inherent synchronization backbone which the proposed TBS protocol resonates in conjunction with [16,17].

2.9. Additional Dimensional (XD) - Large-scale (LSXD) duality

The structure of the XD system is one of the most elegant aspects of reality. On the one hand its wormhole structure maintains reality and its purpose of ordering complex SOLS by the power of the quantum uncertainty principle in tandem with the gating mechanism of the unified field. The XD-LSXD duality of the MOU is a profound mechanism of connectivity with the unified field Multiverse.

2.10. Additional Tight-Bound State (TBS) spectral lines in hydrogen

Finding additional TBS hyperspherical cavities below the lowest Bohr orbit provides an avenue of demonstrating the existence of XD.

2.11. Simplified initial experimental design to discover 1st TBS Bohr orbit

Historically we have made attempts to overview protocols for complete supervening of the uncertainty principle; but it is deemed too complicated to operate the Bessel function as an incursive harmonic oscillator with sufficient precision at this time to align the nodes of interference for full passage of the signal through the DPW MOU hierarchy to infinity. From 2D to a hyperspherical XD spacetime cavity an M-theoretic brane under string tension may contain transverse harmonic oscillations.
Preprints 84053 g006
Figure 6. The additional Bohr orbit spectral lines exist because of the hyperspherical structure of the DEH and the MOU cyclical dynamics of that structure for NUFT M-theory.
Figure 6. The additional Bohr orbit spectral lines exist because of the hyperspherical structure of the DEH and the MOU cyclical dynamics of that structure for NUFT M-theory.
Preprints 84053 g006
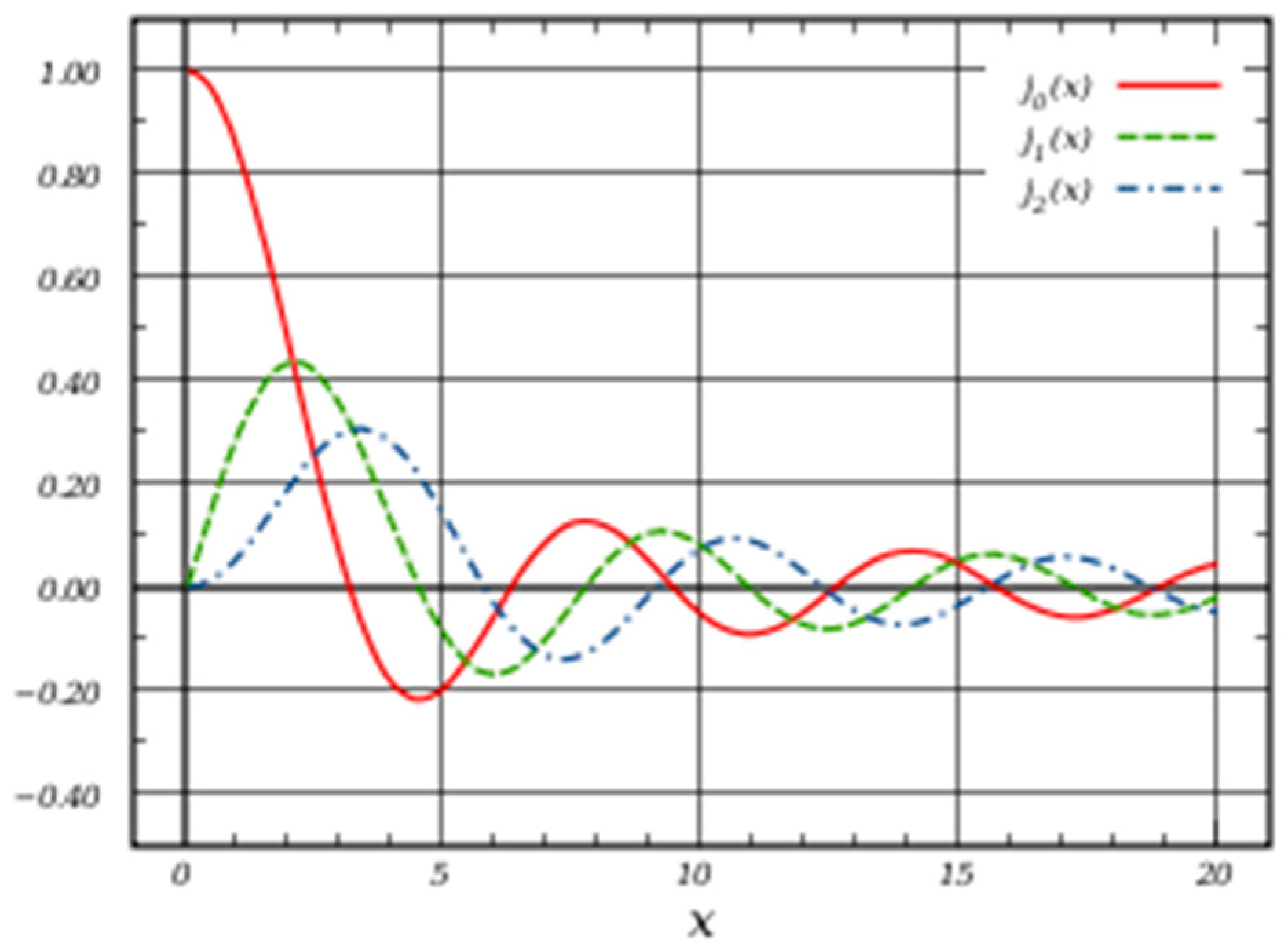
Bessel functions describe the radial component node shape vibrations of a circular or hyperspherical membrane. Generally, a Bessel function is a solution y(x) to the Bessel equation:
x 2 d 2 y d x 2 + d y d x + x 2 − α 2 y = 0
with a Bessel function ordered by complex number α . Since a Bessel function is a sine function it can be a standing wave correlated with harmonic oscillations on a string or M-brane of variable string tension in spherical or hyperspherical coordinates for wave propagation, static potentials or herein the hydrogen atom.
We arbitrarily illustrate the necessity of using the Bessel function for operating the MOU structure’s utility by embedding an incursive harmonic oscillator into the symmetry modes in order to control the timing nodes of annihilation and recreation synchronistically.
Preprints 84053 g007
Figure 7. An example of a spherical Bessel function of the 1st kind showing putative harmonic nodes for MOU oscillation.
Figure 7. An example of a spherical Bessel function of the 1st kind showing putative harmonic nodes for MOU oscillation.
Preprints 84053 g007

2.12. Definition of present instant

For NUFT a present instant or spacetime singularity is a dynamic hyperspherical line element of LCU complexes with M-theoretic-like dimensionality having a concatenation of properties described as a Wheeler-Feynman-Cramer standing wave [5,18]. This natural structure is aligned with the purported Feynman synchronization backbone for correlation with the harmonic oscillator.

2.13. Derivation of preliminary Einstein-like Unified Field (UF) Equation

Utilizing topological quantum field theory as a conceptual stepping stone we have offered in preliminary form an Ontological Phase Topological Field Theory as a stepping stone component to a unified field theory [16]. The action is an ontological phase transition because the field is not mediated by quanta, but rather by energyless topological switching. This may perhaps be understood by observing the vertices of an ambiguous Necker cube.

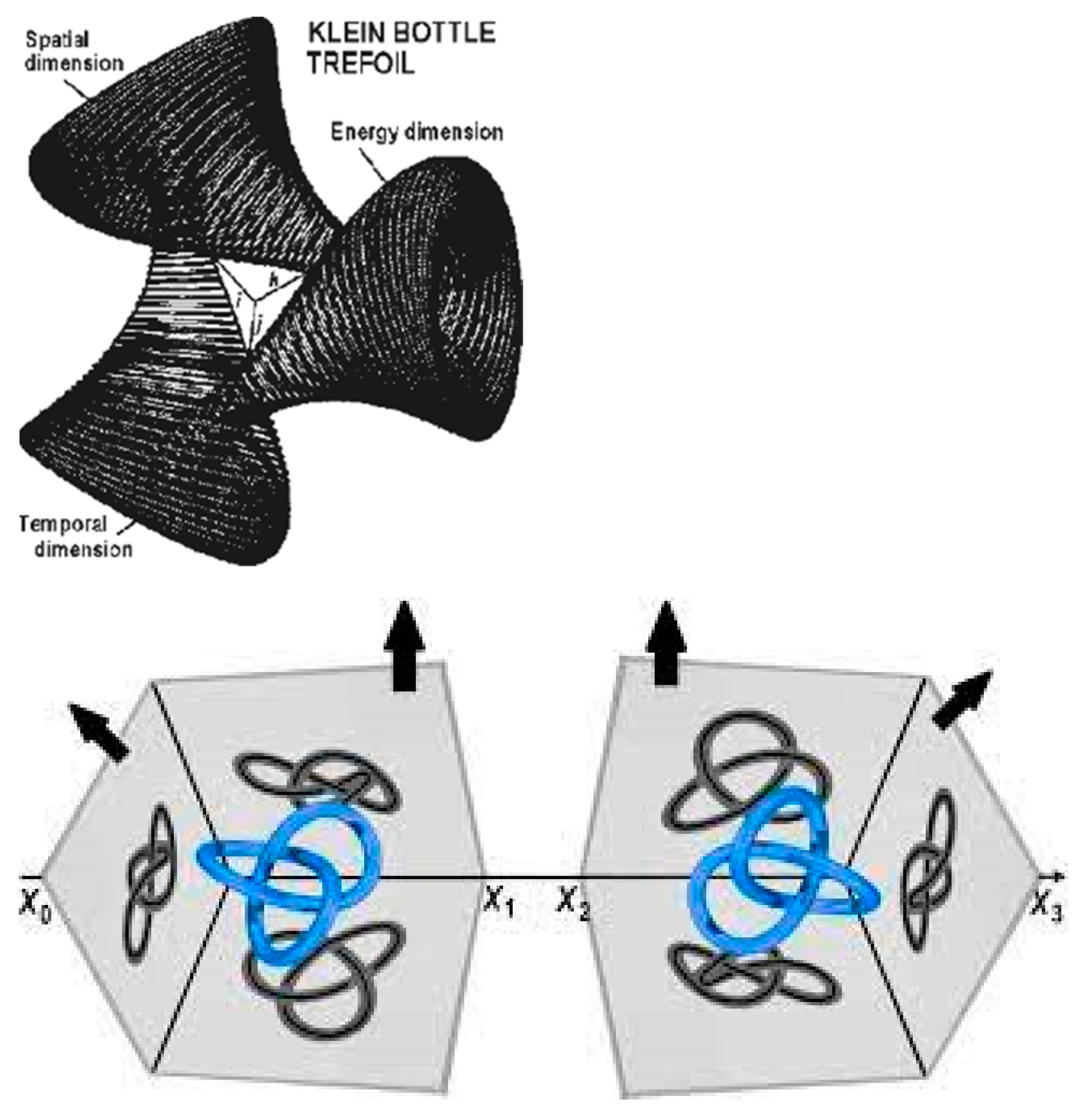
2.14. Spinor rotation (360 – 720) cycle handshakes in XD with two sets of three trefoils (hidden by the MOU at the semi-quantum limit)

The traditional model of a Dirac spinor is that rotation takes 720 rather than 360 degrees to return to the original orientation. This takes the form of a Mobius strip. We perceive this a limit hidden by the uncertainty principle at the semi-quantum limit. Instead in XD the spinor rotation continues as a Klein bottle topology with higher order XD cycles.
Preprints 84053 g008
Figure 8. Metaphorical suggestions that the common Dirac spinor undergoes additional XD rotations beyond the usual 360–720-degree rotations. a) Klein bottle suggestion. b) XD trefoil knots projected to 2D shadows. b) Adapted from [19].
Figure 8. Metaphorical suggestions that the common Dirac spinor undergoes additional XD rotations beyond the usual 360–720-degree rotations. a) Klein bottle suggestion. b) XD trefoil knots projected to 2D shadows. b) Adapted from [19].
Preprints 84053 g008

2.15. Feynman Synchronization Backbone

Feynman proposed utilization of what he termed a synchronization backbone as a substrate for developing bulk quantum computing [20]. He never defined what he actually meant beyond that comment, leaving that charge to others. Fruitless attempts were made, but as they were bi-local only they could not succeed [21].

4. The Experimental Protocol

Under the panoply of the theories two prime assumptions: 1) A Dirac polarized vacuum amenable to Extended Electromagnetic Theory [7], and 2) the existence of the Dirac electron hypertube [8,9] consisting of a hierarchical structured Manifold of Uncertainty (MOU) with a duality of local 4D Standard Model (SM) properties and putative nonlocal M-theoretic Unified Field-like parameters such as cyclical oscillating XD-LSXD hyperspherical dimensionality; some form of Bessel Function is deemed essential.
Simplistically, an incursive harmonic oscillator is applied to the Dirac polarized vacuum in conjunction with the nodes of the Bessel Function acting as points of destructive interference annihilating the inherent synchronization backbone KK cycle of local spacetime for signal entry into the 1st tier of the Bohr orbit TBS returning a new MOU spectral line (hidden behind the veil of uncertainty) between the usual .5Å and 2.0 Å lines of hydrogen.
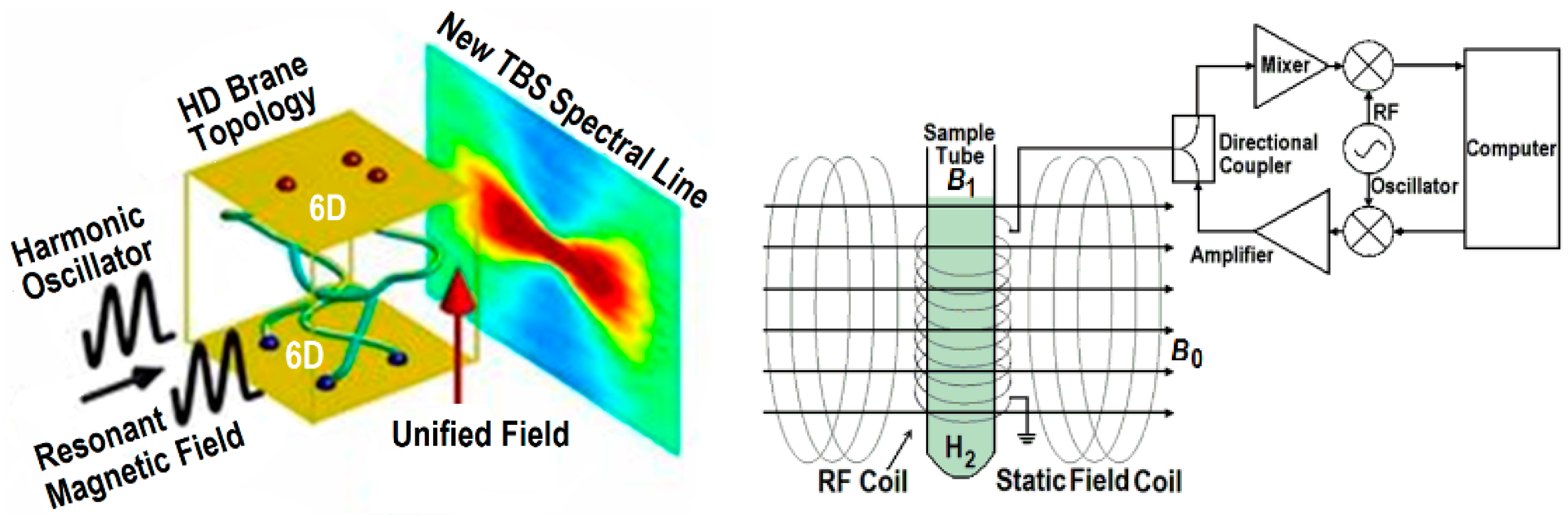
Preprints 84053 g009
Figure 9. Illustrations of basic TBS protocol. a) Through incursive resonance oscillator signal interferes with the 6D space-antispace MOU cavity. If the signal strikes the hyperspherical XD domain wall, as in usual spectroscopic analysis, the signal returns as a new TBS spectral line. b) Simplified experimental NMR-like resonance apparatus for putative LSXD C-QED ionization for hydrogen TBS. Only putative details for rf-modulation for QED resonant TBS are shown, not spectrographic recorders or analytical apparatus.
Figure 9. Illustrations of basic TBS protocol. a) Through incursive resonance oscillator signal interferes with the 6D space-antispace MOU cavity. If the signal strikes the hyperspherical XD domain wall, as in usual spectroscopic analysis, the signal returns as a new TBS spectral line. b) Simplified experimental NMR-like resonance apparatus for putative LSXD C-QED ionization for hydrogen TBS. Only putative details for rf-modulation for QED resonant TBS are shown, not spectrographic recorders or analytical apparatus.
Preprints 84053 g009

5. Afterward

At a point in life where I can still barely spell Octogenarian without the aid of the built in spell checker; it seems more and more unlikely that my team will be instrumental in performing the TBS experiment. Therefore, I bequeath my shoulders, such as they are, to whomever comes next. My journey in the Zeitgeist has been unusual in that there have been instants in similitude of the famed Jung-Pauli synchronicity messing with epistemology. For no apparent reason, other than in-my-face proximity initially, in the final decade of my 22-year chairmanship of the international symposium in honor of heretic J-P Vigier, a group of four congealed. The final compatriot had a dream of a wall of huge flaming letters – SPQR. Which upon Googling he found: Senatus Populus Que Romanus – interpreted to mean we would be the Emperors called to usher in 3rd regime natural science. SPQR is our given names in reverse alphabetical order of our surnames. This gave the team pause, but as yet no one believed I could be right about TBS. Several years later the SPQR group attended a PIRT conference in Moscow where Jung-Pauli synchronicity intervened again in numerous statistically unlikely occurrences. This was sufficient that the SPQRs, plus spouses if desired, agreed to meet for a 30-day retreat to develop the required TBS mathematics to operate the TBS experiment. Funding promises from several avenues were offered; but as yet I have not followed through.
The purpose of this article has been to divine and present how to open the 1st hyperspherical TBS cavity within the Dirac hypertube MOU of spacetime for utility of 3rd regime paradigm shift technological innovation. Actually, the MOU wormhole cavity opens and closes cyclically as a spacetime unit of the arrow of time within the inherent Feynman synchronization backbone of the NUFT XD-LSXD manifold. This complex structure cannot be touched or the uncertainty principle activates and firmly closes the MOU. The trick is to utilize a Bessel function coupled incursive harmonic oscillator to act when the wormhole is open in the cyclical fabric of the Dirac polarized vacuum.
It is assumed that the MOU is relatively complicated in order to hold temporal reality together and separate from the 3rd regime. However, we see two possibilities. Because of inherent Wheeler-Feynman-Cramer standing-wave dimensional reduction compactification cyclicality, there are either 2 XD before the experimental oscillator signal blows off to infinity (LSXD) or because of mirror symmetry within the LCU structure, there is likely 4 or 5 TBS spectral lines before the 3rd regime is routinely accessible.
The simple equations for the volume of hyperspherical cavities were formulated in 1895. It is possible to calculate the position of the expected new TBS spectral lines in the hierarchy of the MOU electron hypertube for the hydrogen atom. But we have not bothered to do so because Sommerfield-like precision corrections are likely; and this is why this effort confines itself to the 1st spectral line only suspected to be fairly easy to discover. Because of the elegance of the gating mechanism of the uncertainty principle, the action of the Bessel function must be discovered with precision in the synchronicity of the nodes of the incursive ordered Bessel function to fully open the Dirac hypertube in the bump-hole light house beacon-like cycle of the Dirac vacuum surface.
The NUFT cosmology is a beautiful model once one gets a glimpse of it; strikingly simple and complex at the same time. It is surprising that this will apply to the mathematics also; because the NUFT interaction with observed reality is a geometric topology, it could be modeled with a combined quaternion-octonion algebra. This is partly true because of the inherent Feynman synchronization backbone operating as an ontological topological phase transition mechanism within the XD-LSXD duality of the MOU. While mathematics needn’t have a basis in reality, quaternion-octonion algebras have a built it connection with reality. For this reason also, the forthcoming 3rd regime set of transformations can be created also with very simple trigonometric functions.
Essentially all of the dozens of new 3rd regime technologies will require true bulk Universal Quantum Computing (UQC) to operate or manipulate the Dirac polarized vacuum. The current qubit is not physically real, rather a mathematical object aiding design of algorithmic processes. What is required is a spacetime energy resonator that in the vernacular might be called a transistor of the vacuum. This requires the qubit to be formulated with a 12D basis allowing utility of NUFT transformations. This Laser Oscillated Vacuum Energy Resonator qubit, because it supervenes quantum uncertainty, will not be cryogenic, but rather tabletop and room temperature. This means of course that a quantum dot will be able to hold 1,000s of qubits, and a scalable array of quantum dots the size of a pin head to obtain virtually infinite computability [18,22,23]!
Why shouldn’t this paper be thrown in the trash bin? Looking over the landscape of published work and speculations, the author seems to be alone (momentarily) in postulating a complex unit of Dirac hypertubes are programmable vacuum transistors able to mediate the ontological phase transitions of the topology of the XD-LSXD of the unified field. What may be initially hard to embrace is that the Laser Oscillated Vacuum Energy Resonator (vacuum transiter) requires a 6D or 9D complex M-theoretic qubit to create UFM algorithms. Why is this so important? Because this paper is myopic, puerile and rigorless, completion of the TBS series will lead to at least 2-dozen multitrillion dollar industries almost overnight; among which are weather control, directed energy beams, fuelless rocket engines powered by vacuum energy, de Broglie matter-wave defense shields, incredible medical devices and psychology becoming a hard physical science to name a few.

5. Acknowledgements

Most credit for the Avant-garde insights introduced go to the unappreciated genius of heretical French physicist Jean-Pierre Vigier over the five-year period when he acted as my mentor, teacher, collaborator and indelible friend.
I would also like to thank Prof. Evgueni Oaks editor of the MDPI Foundations special issue for undue patience far beyond the call of duty over a nearly two-year period of procrastination enabling me to finally keep my promise to submit this paper. I pity the reviewers as it is certainly the worst paper I have ever written.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Nobel Laureate David Gross, comment to author during his presentation Yang-Mills Kaluza-Klein Equivalence: An Empirical Path Extending the Standard Model of Particle Physics at “60 Years of Yang–Mills Gauge Field Theories”, Singapore: NTU- Institute of Advanced Studies, 25--28 May 2015.
  2. Dragić, A; Marić, Z; Vigier, J. P. New quantum mechanical tight bound states and cold fusion experiments. Physics Letters A 2000, 265, 163–167. [Google Scholar] [CrossRef]
  3. Dragic, A.; Maric, Z.; Vigier, J.-P. On the Possible Existence of Tight Bound States in Quantum Mechanics. In: Amoroso, R.L., Hunter, G., Kafatos, M., Vigier, JP. (eds) Gravitation and Cosmology: From the Hubble Radius to the Planck Scale. Fundamental Theories of Physics, vol 126. Springer, Dordrecht. 2002. [CrossRef]
  4. Vigier, J.-P. New hydrogen (deuterium) Bohr orbits, 1993; Proceedings ICCF4, Hawaii, 4, 7.
  5. Amoroso, R.L.; Rauscher, E.A. The Holographic Anthropic Multiverse: Formalizing the Complex Geometry of Reality (Vol. 43). Singapore, World Scientific. 2009.
  6. Amoroso, R.L. Experimental Supersymmetry: Processing the Dimensional Barrier. Prespacetime Journal 2021, 12. [Google Scholar]
  7. Lehnert, B.; Roy, S. Extended Electromagnetic Theory, World Scientific, 2000.
  8. Dirac, P.A.M. Classical theory of radiating electrons. Proc. Roy. Soc. London A 1938, 167, 148–169. [Google Scholar]
  9. Amoroso, R.L.; Vigier, J.P. The Dirac electron hypertube revisited nonlocal parameters within extended particle elements. In Fundamental Physics at the Vigier Centenary: “L’Hérétique de la Physique” Lives On (pp. 1-69). 2022.
  10. Kaluza, T. "Zum Unitätsproblem in der Physik". Sitzungsber. Preuss. Akad. Wiss. Berlin. (Math. Phys.) 1921, 966–972. 1921. Available online: https://archive.org/details/sitzungsberichte1921preussi.
  11. Klein, O. Quantentheorie und fünfdimensionale Relativitätstheorie. Zeitschrift für Physik A. 1926, 37, 895–906. [Google Scholar] [CrossRef]
  12. Amoroso, R.L. Complementarity of mind and body: Realizing the dream of Descartes, Einstein and Eccles, New York, Nova Science Publishers. 2010.
  13. Dirac, P.A.M. Discussion of the infinite distribution of electrons in the theory of the positron. Mathematical Proceedings of the Cambridge Philosophical Society 1934, 30, 150–163. [Google Scholar] [CrossRef]
  14. Evans, M.W.; Vigier, J.-P. The Enigmatic Photon, Kluwer, 1996.
  15. Barrett, T.W. Electromagnetic Phenomena not Explained by Maxwell’s Equations: Essays on the Formal Aspects of Electromagnetic Theory, Singapore: World Scientific, 1993.
  16. Amoroso, R.L. Simple resonance hierarchy for surmounting quantum uncertainty, in Amoroso, R. L., Rowlands, P., and Jeffers, S. (eds.). AIP Conference Proceedings 2010, 1316, 185–193. [Google Scholar]
  17. Amoroso, R.L. Experimental Supersymmetry. Preprints 2020, 2020110172. [Google Scholar] [CrossRef]
  18. Amoroso, R.L. Universal Quantum Computing: Supervening Decoherence—Surmounting Uncertainty, 2017; World Scientific: London.
  19. Dabrowski-Tumanski, P. Knots, links, and lassos - Topological manifolds in biological objects. Thesis PhD, 2019. [Google Scholar] [CrossRef]
  20. Feynman, R.P. Quantum mechanical computers. Found Phys 1986, 116, 507. [Google Scholar] [CrossRef]
  21. Biafore, M. Can quantum computers have simple Hamiltonians? Proceedings Workshop on Physics and Computation. PhysComp 1994, 94, 63–68. [Google Scholar]
  22. Amoroso, R.L. Spacetime energy resonator: a transistor of complex Dirac polarized vacuum topology. US Patent US20120075682A1, 2012. Available online: https://patents.google.com/patent/US20120075682A1/en.
  23. Amoroso, R.L.; Vigier, J.-P. Evidencing tight bound states in the hydrogen atom Empirical manipulation of large-scale XD in violation of QED The Physics of Reality Space Time Matter Cosmos-Proc 8th Symp Honoring Math Physicist Jean-Pierre Vigier, R L Amoroso et al. Eds. 2013; World Sci: London. Available online: http://vixra.org/pdf/1305.0053v2.pdf.
Preprints 84053 g001
Figure 1. Hyperspherical volumes used to analyze additional TBS spectral lines. Hypervolume radii shown for increasing n-dimensionally as purported to exist in the MOU of a Dirac electron hypertube at the XD-LSXD semi-quantum limit; where r equals 1 for unit spheres (n-balls).
Figure 1. Hyperspherical volumes used to analyze additional TBS spectral lines. Hypervolume radii shown for increasing n-dimensionally as purported to exist in the MOU of a Dirac electron hypertube at the XD-LSXD semi-quantum limit; where r equals 1 for unit spheres (n-balls).
Preprints 84053 g001
Preprints 84053 g002
Figure 2. Extending the basis of reality to M-theoretic UFM XD-LSXD-space. The observer on the left perceives a 4D Planck-scale spacetime point as the fundamental quantum basement of SM reality. On the right the observer lives inside a temporal spacetime bubble.
Figure 2. Extending the basis of reality to M-theoretic UFM XD-LSXD-space. The observer on the left perceives a 4D Planck-scale spacetime point as the fundamental quantum basement of SM reality. On the right the observer lives inside a temporal spacetime bubble.
Preprints 84053 g002
Preprints 84053 g003
Figure 3. Conception of the Dirac covariant polarized vacuum model for extended electromagnetic theory, a line element of left-right standing-wave future-past symmetry. Bumps and holes needn’t be electron-positron pairs but rather for our experiment nodes of an applied EM harmonic oscillator acting on the topological surface of a DEW hypertube.
Figure 3. Conception of the Dirac covariant polarized vacuum model for extended electromagnetic theory, a line element of left-right standing-wave future-past symmetry. Bumps and holes needn’t be electron-positron pairs but rather for our experiment nodes of an applied EM harmonic oscillator acting on the topological surface of a DEW hypertube.
Preprints 84053 g003
Preprints 84053 g004
Figure 4. a) Dirac spacetime electron conceptual hypertube manifold model. The central point (black dot) is an SM ℏ asymptote (never reached). b) End view with polarized vacuum tessellated with Least Cosmological Units (LCU)s with a hysteresis loop suggesting precisely a timed applied rf-pulsed resonance incursive oscillator may open or close the hypertube cavity.
Figure 4. a) Dirac spacetime electron conceptual hypertube manifold model. The central point (black dot) is an SM ℏ asymptote (never reached). b) End view with polarized vacuum tessellated with Least Cosmological Units (LCU)s with a hysteresis loop suggesting precisely a timed applied rf-pulsed resonance incursive oscillator may open or close the hypertube cavity.
Preprints 84053 g004
Preprints 84053 g005
Figure 5. a) Standard Model 0D Planck scale singularity that represents a fermion as a fundamental physical object, b) The 1D parameter of current string theory, with the addition of a fixed length string tension at the Planck scale. c) M-theoretic / NUFT form containing variable or oscillating string tension with an inherent rotating KK cyclicality.
Figure 5. a) Standard Model 0D Planck scale singularity that represents a fermion as a fundamental physical object, b) The 1D parameter of current string theory, with the addition of a fixed length string tension at the Planck scale. c) M-theoretic / NUFT form containing variable or oscillating string tension with an inherent rotating KK cyclicality.
Preprints 84053 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated