Prerpints.org logo
Preprint
Article

Adsorption of the Low Density Lipoproteins on the Azobenzene-containing Polymer Brush: Modelling by the Coarse-grained Molecular Dynamics

Altmetrics

Downloads

81

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

04 September 2023

Posted:

06 September 2023

You are already at the latest version

Alerts
Abstract
One of the strategies to reduce the contents of the low density lipoproteins (LDLs) in a blood is a hemoperfusion, in which case they are selectively retracted from plasma by an adsorber located outside the patient body. Recently, a photo-controllable smart surface was developed for this purpose characterised by high selectivity and reusability [C.Guo et al., ACS Applied Materials & Interfaces 2022, DOI:10.1021/acsami.2c07193]. We present a mesoscopic model for such a setup involving the azobenzene-containing polymer brush and the model LDL particles. The latter comprise an uniform spherical core covered by a shell of elongated particles representing phospholipids. The system is studied using the coarse-grained molecular dynamics simulation. We examined the dependences of the binding energy on both the length of polymer chains and the grafting density of a brush, and established optimal conditions for the adsorption. These are explained by a competition between the concentration of azobenzenes and phospholipids in the same spatial region, flexibility of polymer chains, and excluded volume effects.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Lipoproteins are the major carriers of cholesterol within a human body and, therefore, are of great importance for metabolic processes. Low-density lipoproteins (LDL) bring cholesterol from liver to cells, whereas high-density lipoproteins (HDL) carry cholesterol from a heart and other organs back to liver, where it is removed out of the body. The LDL may cause cholesterol to build up within arteries and can eventually block arteries increasing risk for heart disease and stroke [1,2,3,4,5]. The indication of the increased risk of this scenario is an abnormally high level of LDL.
Two main strategies exist to reduce the risk of such a blockade: (i) by treating the blood vessels (stenting or stents implantation), or (ii) by reducing high concentration of LDL in a blood. The latter can be seen rather as the prevential approach with two ways of realisation: (a) in-body reduction by affecting liver activity (using statins) or digesting adsorbers, and (b) hemoperfusion approach when adsorbers are located outside the body [6].
In dealing with the atherosclerosis, which is characterised by an increased level of the total LDL cholesterol, pharmacological groups of drugs are widely and primarily used, with statins occupying the first place. The second- and third-line drugs used for this purpose are ezetimibe and fibrates. Currently, drugs combining statins and ezetimibe demonstrate particular effectiveness in this respect. Intolerance of hypolipidemic drugs manifests itself via (a) unwanted symptoms perceived by patients as unacceptable, and/or (b) abnormal laboratory results that indicate an excessive risk associated with the use of hypolipidemic drugs. In both cases such drugs are withdrawn. Such patients, characterised by either absolute or relative intolerance to this type of treatment, are the first candidates for a full or partial hemoperfusion therapy.
In a course of the adsorbent-based hemoperfusion, the patient’s blood is introduced into a container with the specific adsorbent. It binds LDL selectively and, at the same time, allows the HDL and other blood components to pass through and then be re-introduced into the patient’s body. There are several types of LDL hemoperfusion adsorbents that are widely used in clinical practice, including biomacromolecules, magnetic nanoparticles, carbon nanotubes, nanohydrogels, porous beads, see Ref. [1,2,6] for more details and references therein. The main aim of research in this area is to combine (i) high efficiency of LDL removal, (ii) high selectivity which prevents removal of HDL, and (iii) efficiency of usage in terms of high reusability.
We will mention just a few studies here that address one or more of these issues. In particular, an amphiphilic polymers were used by Cheng et al. [7], and these, at particular sulfonation rate and cholesterol grafting time, demonstrated high adsorption capacity for LDL without significantly adsorption of HDL. After 2 h hemoperfusion, the LDL levels decreased by fraction of five. To achieve binding of LDL with high affinity, the biomimetic adsorbent was developed by Yu et al. [6], which mimics the lipoprotein microemulsion present in the blood. In vitro studies revealed the LDL adsorption rate about twice as high as that of the HDL. In yet another work, the core-shell structured magnetic nanoparticles were embedded in an amphiphilic polymer layer to provide multifunctional highly selective binding for LDL particles [8]. Because of the electronegativity of the functional layer and charged surface of LDL, the nano-adsorbent demonstrated highly selective adsorption towards LDL, whereas chemical adsorption also plays a predominant role in binding of LDL. This nano-adsorbent possesses satisfactory recyclability, low cytotoxicity and hemolysis ratios [8].
An important aspect of the adsorption during hemoperfusion is the controllability of the adsorption, namely the ability to switch it “on” and “off” by means of some, preferably clean, external stimulus. This involves the concept of the so-called “smart surfaces”, i.e. the thermo- [9,10,11], magnetically- [12] and photo- [13] controllable surfaces, for more details see recent review [14]. For example, thermo-controllable surface based on PNIPAM polymer, already found numerous biomedical applications [9]. The photo-controllability of the surface properties can be achieved by incorporation some photosensitive group into it, with the azobenzene chromophore being the most widely used one [15]. Such “azobenzination” allows a number of features of the smart surface, to name: the control over adhesive properties of a surface [16], manipulation of nano objects on it [17], photo-controllable separation of a photoresponsive surfactant from the adsorbate [18], achieving photo-reversible surface polarity [19], photo-controllable orientational order affecting surface anchoring of liquid crytals [20], etc.
Recently, the advanced LDL adsorber in a form of a photo-controllable smart surface was developed characterised by high selectivity and reusability [21]. It exhibited excellent LDL adsorption capacity and could be regenerated by illumination with high efficiency, further verified by transmission electron microscopy and Fourier-transform infrared analysis. Green regeneration of the nanoadsorbent could be achieved completely through a simple photoregeneration process, and the recovery rate was still 97.9% after five regeneration experiments [21].
This experimental work sparkled our interest towards modelling the process of the LDL adsorption by such advanced photo-controllable adsorber by employing computer simulations. One should note that the native length scale of the problem, complexity and ambiguity of the LDL structure [2,22,23,24,25,26,27,28,29] prevent performing atomistic-scale simulation of such process in a foreseen future. There are a number of computer simulation studies performed mostly on a coarse-grained level that address the structure of LDL, lipid transport, receptor mutations, and other related topics [30,31,32,33,34,35,36,37,38,39].
We see the possibility to perform the coarse-grained simulations of the adsorption of the LDL particles explicitly if one uses:
  • minimalistic model containing only the elements directly involved in adsorption,
  • reduction of the length scale of a problem,
  • artificial speed-up of the system dynamics.
In doing this we follow our previous studies on modelling photo-sensitive polymers using coarse-grained simulations [40,41,42,43,44,45,46,47]. Modelling approach is covered in detail in Section 2. Ideally, the aim of performed simulations would provide important insights on the polymer architecture of the photo-controllable adsorber that are needed to improve its efficiency. These might be further used for refining synthesis protocols. On a minimalistic side, such simulations would validate suggested type of modelling, by comparing their results against observed experimental features.
The outline of this study is as follows. In the first part of Section 2 we review available experimental data on the overall shape and internal structure of LDL and on its photo-controllable adsorption. It sets the basis for constructing the coarse-grained model for the problem of interest, covered in detail in the second part of this section. Section 3 contains the results of the computer simulation of this model mimicking adsorption of LDL under visible light, whereas Section 4 focuses on the adsorber regeneration under ultraviolet light, followed by conclusions.

2. Experimental data on LDL Structure and the Modelling Details

Let us review first some available experimental data on the typical size of the LDLs. In general, plasma LDLs are heterogeneous in terms of their size, density and lipid content, varying from one individual to another. Two following types of LDL were identified: larger, pattern A type, of average dimension larger than 25.5 nm ; and pattern B of a smaller average dimension less than 25.5 nm [48]. The latter ones are found to be more prevalent in patients with coronary artery disease [49] with the higher risk of myocardial infarction [50] and of developing coronary disease [51,52]. The reason for this could be their reduced affinity for the respective receptor and, as the result, an increased residence time in plasma and higher probability to be oxidized at the artery walls, leading to atherosclerosis. For more detail see discussion in Ref. [53] and references therein. Therefore, the pattern B LDL of a smaller size is the main target for adsorption via hemoperfusion. The experimental measurements of their average dimensions provide the estimates from 20 to 23 nm [53].
In terms of their internal structure, the LDL particles can be interpreted as micellar complexes, macromolecular assemblies, self-organized nanoparticles or microemulsions [26,29]. A spherical three-layer model has been suggested based on the low-resolution data [24,25]. It assumes the presence of an internal core of LDL comprising cholesteryl ester and triglycerides. The core is enveloped by an outer shell of phospholipids, with their polar heads residing on the surface of LDL and their fatty acid ester tails pointing inward the LDL. About half of the external surface of the LDL is covered with apolipoprotein B-100, which form ligand recognition loops for various receptors [2,23]. In particular, the B-100 in a form of two ring-shaped structures were reported [22]. A liquid crystalline core model of LDL was also discussed, where cholesteryl ester molecules are arranged in stacks with their sterol moieties arranged side-by-side in the higher-density regions, while the fatty acyl chains extend from either side, and are found as parallel lower-density compartments [27].
Based on the complexity of their LDL internal structure, the question of the overall LDL shape turns to be rather controversial, as the spherical [25], discotic [22,26], as well full range of spherical, discotic and ellipsoidal [27] shapes all were reported. Possible explanation for these discrepancies may stem from the fact that the shape of the LDL particles is temperature-dependent due to the predominance of cholesteryl ester molecules in the particle core. As the result, at physiological temperatures the LDL appear more spherical, whereas at lower temperatures – discoidal [28]. In fact, the discotic shape indeed was predominantly found by means of cryo-electron microscopy [22,23,26,27], performed at low temperatures. One can conclude, that the exact structure of LDL is not quite exactly known in detail and it is still the matter of debates, see Ref. [29] and discussion therein.
These experimental findings lay out the basis for developing a range of moderately coarse-grained models of LDL. In general, this type of lipid simulations [31] can address main two issues. The first one is to improve one’s understanding of the internal LDL structure [30,32], addressing mutational space of the LDL receptor [37], etc. The other is to understand the physical chemistry mechanisms behind the lipid transfer [33,36,38,39]. On a more coarse-grained level, the interactions between oxidized LDL and scavenger receptors on the cell surfaces of macrophages, related to arterial stiffening, are addressed [34]. The smectic-isotropic transition inside the LDL core, related to the liquid crystalline order found there in Ref. [27], was modelled in Ref. [35]. In general, coarse-grained models allow to cover larger system sizes and longer simulation times, but at the expense of omitting some fine details of the initial system.
The modelling approach developed in this study follows the coarse-graining plan outlined in Section 1. According to statement (1.) there, the model contains only the elements directly involved in adsorption setup by Guo et al. [21]. They developed the nanoadsorbers consisting of a spherical support particle of diameter 200 nm which is functionalized by the side-chain polymers terminated by an azobenzene group. The ratio between the diameters of a nanoadsorber and that of LDL is about 10 : 1 . This results in relatively low curvature of a nanoadsorber comparing to the LDL size, and, therefore, one can approximate a surface of a former by a flat surface. This is done in our study. The model contains two adsorbing surfaces on both the bottom, z = 0 , and the top, z = L z , walls of the simulation box with dimensions L x , L y and L z . By using two walls instead on a single one, one (i) avoids possible artefacts at the top free wall, and (ii) improves statistics obtained in a course of a single simulation run. The polymers are of the side-chain architecture [6] with their side chains terminated by azobenzenes [21]. This setup is shown schematically in Figure 1 (a) with the arrangement of grafting points in the sites of a square lattice, all the details are provided in the figure caption.
In a similar way, only these structure elements of the LDL particles that are relevant to their adsorption are modelled explicitly. In the case of physiological temperature, one assumes a spherical shape for the LDL core [28] with its interior filled by cholesteryl esters and triglycerides. This part of LDL is believed not to be involved in adsorption in a direct way and can be treated as an uniform spherical object with a fixed diameter. However, the outer phospholipid shell is involved in adsorption explicitly, via the interaction with the azobenzenes of a brush and, therefore, is modelled as a collection of individual phospholipid spherocylinder particles. Such model for LDL is shown in Figure 1 (b) and (c), where a spherical core is shown in dark gray and spherocylinders representing phospholipids – in brown.
Similar coarse-grained building blocks are used and well tested in a set of our previous works involving polymer brushes and decorated nanoparticles [42,43,44,46,54,55]. The relation of their length scale to that for their real counterparts can be estimated from the diameter of the LDL spherical core. It is about 2.1 nm [54], which leads to the overall diameter of the LDL particle (core + shell) of about 5 nm (see estimates for the azobenzene unit length below). Therefore, we arrive at the scaling ratio about 1 : 5 between the model and the real life LDL, following the statement (2.) of the coarse-graining plan enlisted in Section 1.
The monomers of backbones and of side chains are represented by soft-core spherical beads of the diameter σ = 0.46 nm , mimicking approximately a group of three hydrocarbons each [56]. Each second bead of a backbone is as a branching point for a side chain of two spherical beads terminated by an azobenzene. The latter is modelled as a soft-core spherocylinder with the diameter of a spherical cap equal to D = 0.37 nm and the length-to-breadth radio of L / D = 3 , resulting in the total length of a spherocylinder of D / 2 + L + D / 2 = 4 D ≈ 1.5 nm . Phospholipids are modelled by the same type of prolate particles as the azobenzenes, to simplify modelling. An important question is the packing density of phospholipids in the outer shell, and there are some indications that it is not very high [32]. If we use 100 phospholipids per each LDL, the packing fraction of their ends on the core surface is about η = 0.77 . This value seems reasonable, e.g. it is close to the maximum packing fraction of discs arranged on a 2 D square lattice, η = π / 4 ≈ 0.79 . Due to finite curvature of a core, packing of phospholipids at the outer surface of their shell will be essentially lower, see Figure 1 (b) and (c).
After introducing main components of a model, one needs to define the effective interaction potentials between them. Two types of coarse-graining approaches can be employed here. In the bottom-up approach, one, typically, performs some pre-runs using atomic-scale model for particular chemical compound. Then, the model is coarse-grained by splitting the molecules into groups of atoms and the effective interactions between them are parametrised by matching the forces between these groups, radial distribution functions, radius of gyration, or transport coefficients. In this way, the initial chemical details of a particular compound of interest is, at least approximately, preserved, reflecting the idea of a multi-scale modelling [57,58]. The other approach focuses on universal, rather physical than chemical, aspects of the problem and employs some generic interaction potentials that are less related to a particular chemical compound, the potentials developed within the dissipative particle dynamics approach being a prominent example [59]. The approach used in the current study is some kind of mixture of the two. On one hand, we use the coarse-grained interaction potentials obtained from atomistic modelling [56,60], but their forms are rather generic and reflect the shape and the main features of interacting beads [61]. Therefore, these potentials are not specifically tuned to mimick a certain compound, but are aimed at description of universal physical features of a wider class of polymers. By using soft-core spherical and spherocylinder beads, one greatly speeds up the dynamics in a system, hence, implementing the statement (3.) of the coarse-graining plan enlisted in Section 1.
We will start from the non-bonded interactions. To simplify equations, each pair { i , j } of the particles is characterized by a shorthand containing a set of variables, q i j = { e ^ i , e ^ j , r i j } , where e ^ i and e ^ j are the unit vectors defining the orientation of the respective particles in space, and r i j is the vector that connects their centers of mass. For the case of spherical particles, their orientations are not defined. The Kihara type of potential, used here, implies evaluation of the closest distance, d ( q i j ) , between the internal cores of two interacting particles, where the core of a spherical particle is its center, and the core of a spherocylinder is the line connecting the centers of its two spherical caps. The scaling factor σ i j is evaluated for the pair, where σ i j = ( σ i + σ j ) / 2 for two spherical particles, σ i j = D for two spherocylinder particles, and σ i j = ( σ i + D ) / 2 for the mixed sphere-spherocylinder pair. The dimensionless closest distance between two interacting particles is defined then as d ′ ( q i j ) = d ( q i j ) / σ i j .
Using these notations, the general form of the pair interaction potential between ith and jth beads, that is of the soft attractive (SAP) type [61], can be written in a compact dimensionless form
V NB SAP [ d ′ ( q i j ) ] = U [ 1 − d ′ ( q i j ) ] 2 − ϵ ′ ( q i j ) , 0 ≤ d ′ ( q i j ) < 1 U { [ 1 − d ′ ( q i j ) ] 2 − ϵ ′ ( q i j ) . . − 1 4 ϵ ′ ( q i j ) [ 1 − d ′ ( q i j ) ] 4 } , 1 ≤ d ′ ( q i j ) ≤ d c ′ 0 , d ′ ( q i j ) > d c ′
where U defines repulsion strength. The dimensionless well depth of this potential
ϵ ′ ( q i j ) = 4 U a ′ − 5 ϵ 1 ′ P 2 ( e ^ i · e ^ j ) − 5 ϵ 2 ′ P 2 ( r ^ i j · e ^ i ) + P 2 ( r ^ i j · e ^ j ) − 1 ,
is obtained from the condition, that both the expression (1) and its first derivative on d ′ ( q i j ) turn to zero when d ′ ( q i j ) = d c ′ , where d c ′ = 1 + 2 ϵ ′ ( q i j ) is the cutoff separation for the potential [61]. Here r ^ i j = r i j / r i j is a unit vector along the line connecting the centers of two beads, U a ′ , ϵ 1 ′ , and ϵ 2 ′ are dimensionless parameters that define the shape of the interaction potential. These are chosen to represent the “model A” of Ref. [61]. P 2 ( x ) = ( 3 x 2 − 1 ) / 2 is the second Legendre polynomial.
The effective well depth, ϵ ′ ( q i j ) , influences both the shape of the attractive part and, via d c ′ , its range. When the parameters, contained in the expression for ϵ ′ ( q i j ) , are such, that it asymptotically reaches zero, the cutoff d c ′ approaches 1 and the interval for the second line in Eq. (1) shrinks to zero. As a result, in this limit, one retrieves the soft repulsive potential (SRP) of a quadratic form
V NB SRP [ d ′ ( q i j ) ] = U 1 − d ′ ( q i j ) 2 , 0 ≤ d ′ ( q i j ) ≤ 1 0 , d ′ ( q i j ) > 1 ,
that is used typically in the dissipative particle dynamics simulations [59]. This limit is illustrated in Figure 2 by the blue curve and is marked as ϵ ′ ( q i j ) → 0 .
Attractive potential (1) is used to model the interaction between the trans-azobenzene and a phospholipid only. The origin of their attraction in a water-like solvent lies in strong hydrophobicity of both groups, see, e.g. Ref. [62] for the estimates of a dipole moment of 4-substituted 4‘-(12-(dodecyldithio) dodecyloxy) azobenzene). For all other pair interactions, soft repulsive potential (3) is used, reflecting the nature of coarse-grained type of modelling. In this way we emphasize the role of the azobenzene-phospholipid interactions, as the key factor in the adsorption process. Other approach can also be employed, where the pairs of two trans-azobenzenes and of two phospholipids are interacting via the potential (1) as well. In this case, adsorption of LDL particles will compete against both the aggregation of LDL particles and the self-collapse of the brush. We might consider this case in the future. Strong repulsion, with the energy parameter U ′ = 2 U in Eq. (3), is introduced for the interaction of both trans-azobenzene and polymer beads with solvent, reflecting their poor solubility in water. Such type of modelling of azobenzenes has been already used in a number of previous studies [42,43,44,45,46,47].
The expressions for the total bonded interactions within the brush and within each LDL, respectively, are given as
V B BR = ∑ k = 1 N B R ∑ i = 1 n b ′ k b ( l i − l 0 ) 2 + ∑ i = 1 n a ′ k a ( θ i − θ 0 ) 2 + ∑ i = 1 n z ′ k z ( ζ i − ζ 0 ) 2 ,
V B LDL = ∑ k = 1 N L D L ∑ i = 1 n b ′ ′ k b ( l i − l 0 ) 2 + ∑ i = 1 n z ′ ′ k z ( ζ i − ζ 0 ) 2 ,
where N B R and N L D L are the total number of polymer chains in a brush and of LDL particles, respectively; n b ′ , n a ′ , and n z ′ are the numbers of bonds, branching angles, and terminal angles in a single polymer molecule, and n b ′ ′ and n z ′ ′ are the numbers of bonds and terminal angles in a single LDL particle. The purpose of bonds in LDL particles is to keep each phospholipid at a given separation from the center of a core, to form the outer spherical shell. The energy term involving branching angles, θ i , in Eq. (4) maintains certain level of perpendicularity of side chains to a local orientation of a backbone. Similarly, correct orientations ζ i of both the azobenzenes and phospholipids, with respect to the bond by which these are attached to a spherical bead, are ensured in Eqs. (4) and (5) by the energy term involving the terminal angle ζ i [60,63].
According to the model description provided above, the required numbers of beads and of various energy terms in a single polymer molecule can be derived from the chosen value for the backbone length, l b b . Namely, each polymer contains n s c = div ( l b b , 2 ) side chains (where div denotes division of two integers), in total n p = l b b + 2 n s c spherical and n a = n s c azobenzene beads. Therefore, the number of bonded interactions are given by: n b ′ = n p + n a − 1 , n a ′ = n s c , and n z ′ = n a . Each LDL particle consists of a spherical core particles and n p l = 100 phospholipids, therefore, n b ′ ′ = n z ′ ′ = n p l . All force field parameters are collected in Table 1 for the sake of convenience.
We will complete this section by specifying the parameters of the simulation runs. The simulation box of the dimensions L x = L y = L y = 20 nm is used, where both bottom, z = 0 , and top, z = L z , walls are functionalised by N B R polymers each, see Figure 1 (a). Polymers of five different backbone lengths, l b b = 5 , 6 , 10 , 16 and 22, are considered, as well as a range of brush grafting densities
ρ g = N B R σ 2 / ( L x L y ) .
Both characteristics affect adsorption scenario of macromolecules by a brush, e.g. for the case of peptides [64]. The arrangement of grafting points (shown in black in Figure 1 (a)) is in the sites of the square lattice to minimise inhomogeneities in the arrangement of polymers. The number of LDL particles is constant in all cases and is equal to N L D L = 25 . Box interior is filled by beads of the same dimensions as the monomers of a brush, these represent a water-like solvent. The simulations are carried out with the GBMOLDD [65,66] program generalised for the case of coarse-grained soft-core potentials [54], in the N V T ensemble at the bulk density ρ = 0.5 g / cm 3 and the temperature T = 480 K . This choice is based on the previous findings [54], where the melt involving the spherocylinders interacting via potential (1), exhibited the order-disorder transition at about T = 505 − 510 K . Therefore, at T = 480 K , we expect strong azobenzene-phospholipid interactions. Simulation runs of the duration of 40 ns were undertaken at each polymer length and grafting density, with the time step of Δ t ∼ 20 fs .

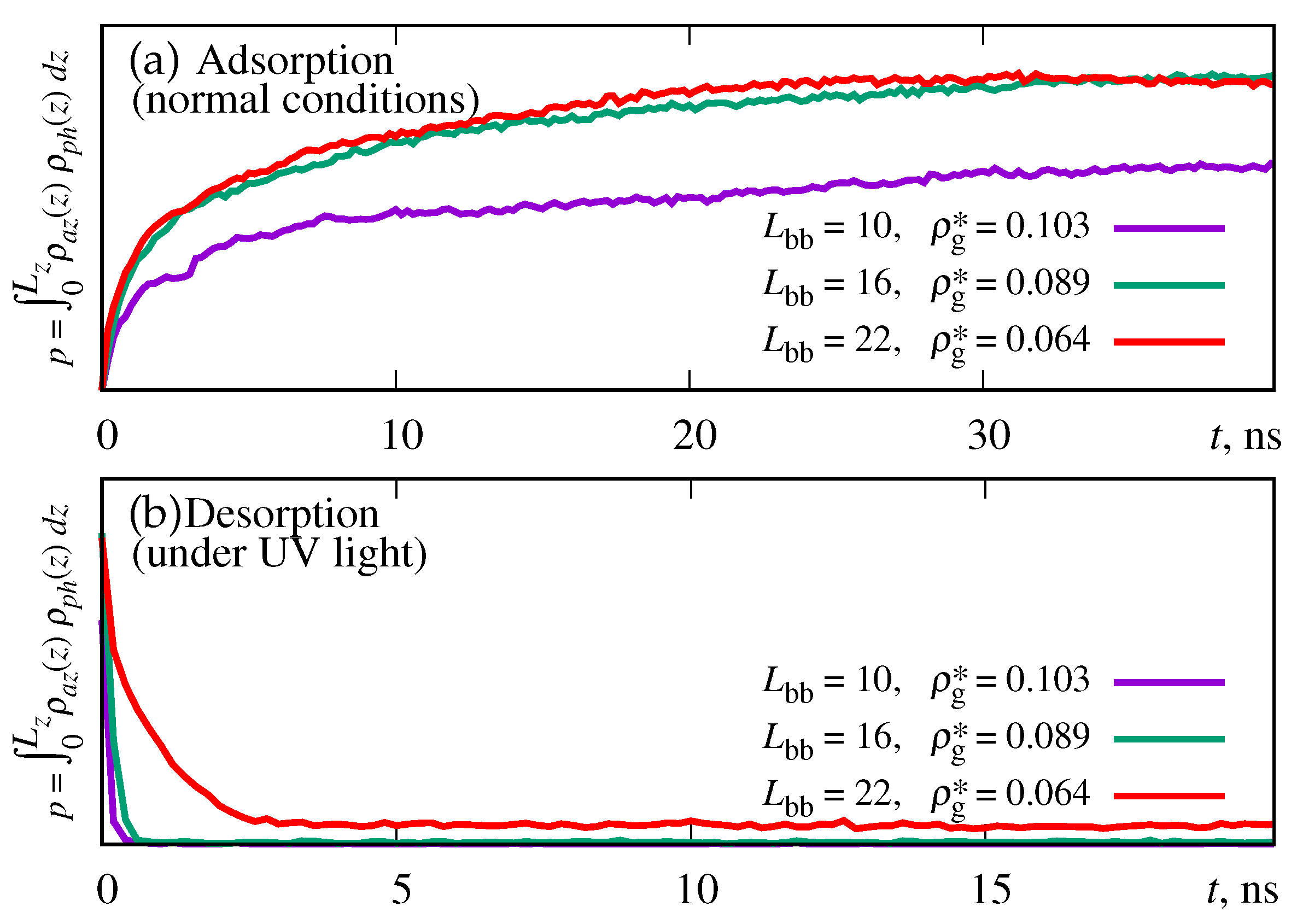
3. Adsorption of the LDL at Normal Conditions

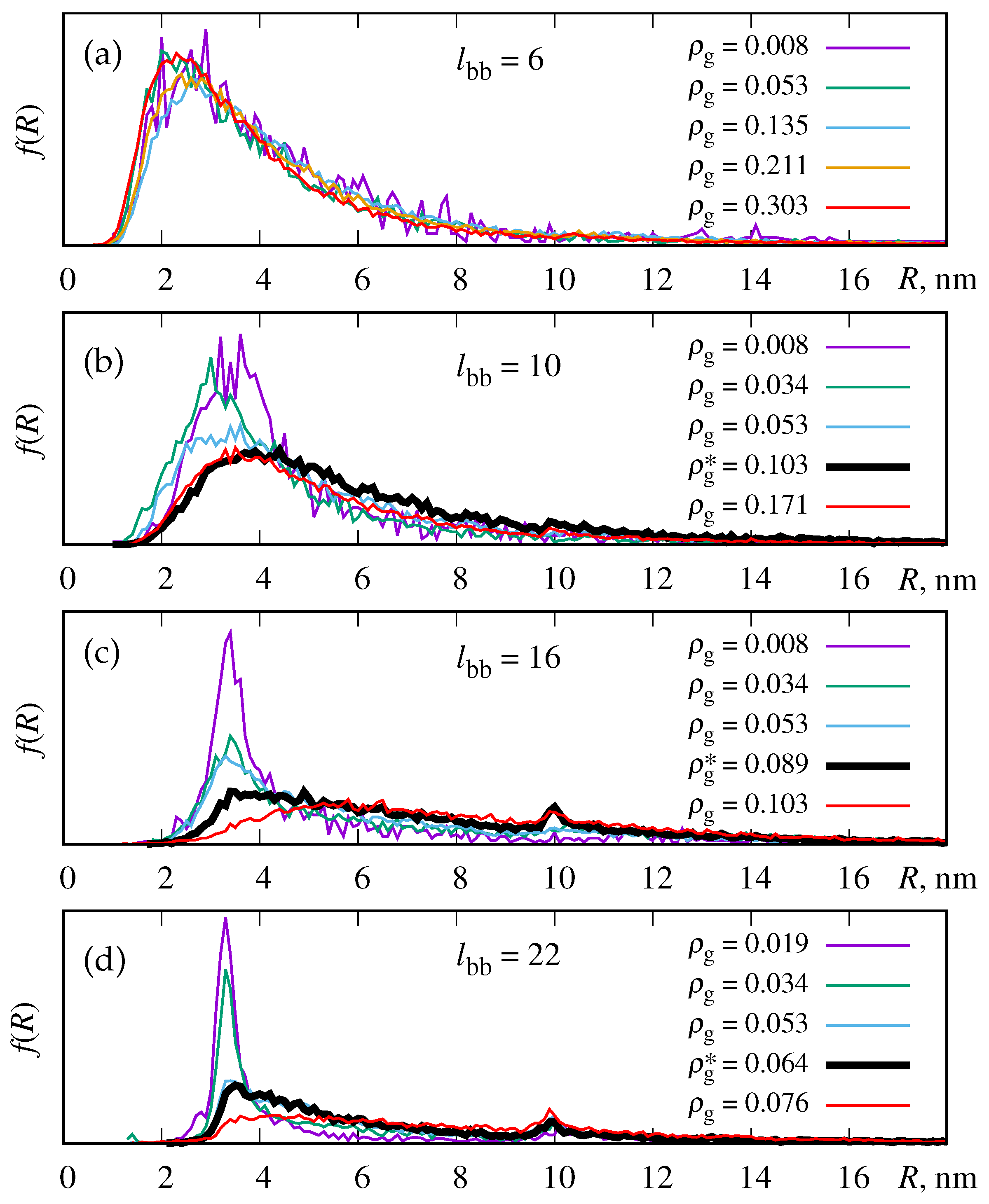
3.1. Density Profiles and the Probability for the Azobenzene-Phospholipid Contact

At normal conditions, under visible light, azobenzene chromophores are found in the trans isomeric state [67], and exhibit properties similar to ordinary mesogens, such as cyanobiphenyls [68]. In a water environment, trans-azobenzene is attracted to phospholipids from an outer shell of LDL due to strong hydrophobicity of both. This forms a basis for the adsorption of LDL onto azobenzene-containing ligands [21].
The process of gradual adsorption of LDL particles from the middle of channel onto the polymer brushes is illustrated by a series of snapshots given in Figure 3. The case of the polymer backbone length of l b b = 10 and the brush grafting density of ρ g = 0.02 is shown. Adsorption starts after about 1 ns , see frame (a), and partial adsorption is illustrated after 10 ns , see frame (b). After 40 ns , almost all available LDL particles are adsorbed on the walls, see frame (c). In general, similar scenario is found for all the backbone lengths, l b b = 5 − 22 , of brush polymers and within a broad range of their grafting densities, 0.008 < ρ g < 0.35 . As one can see in Figure 3 (c), in adsorbed state, azobenzenes (shown in blue) penetrate deeply into the outer layer of LDL particles (shown in brown), in a manner anticipated in Ref. [21].
To quantify the effects that both the backbone length, l b b , and the brush grafting density, ρ g , have on adsorption process, we introduce a set of relevant characteristics. The obvious prerequisite for the adsorption is a non-zero probability to find azobenzenes and phospholipids within the same region of space, hence we turn our attention to the spatial distributions of these beads. According to the setup symmetry, we consider a set of slabs spanning in both O X and O Y directions that are located at a certain distance z from the bottom wall. The density profiles, ρ a z ( z ) and ρ p h ( z ) are built, for azobenzenes and phospholipids, respectively. The histograms for these profiles are shown in Figure 4 for the case of l b b = 16 and three grafting densities ρ g , as indicated in the figure. Note that the area under the histogram ρ p h ( z ) is constant, as N L D L = 25 is the same in all cases. In contrary, the area under the histogram ρ a z ( z ) grows upon the increase of grafting density, ρ g , reflecting the increase of a number of azobenzene groups within a brush. The overlapping area between the histograms for ρ a z ( z ) and ρ p h ( z ) is proportional to the probability to find both types of beads in the same z-segment. As it is evident from the figure, with the raise of ρ g from 0.019 to 0.076 , the overlap area grows, the main effect being the increase of the number of azobenzenes in a brush. With the further raise of ρ g up to 0.135 , this area decays. The main effect here is the brush entering the regime of a dense brush with the consequence that the LDLs are expulsed from the brush because of the excluded volume effects.
Quantitatively, the probability of azobenzene to meet phospholipid at the same specified distance z from the bottom wall, is given by the joint probability, ρ a z ( z ) ρ a z ( z ) . It is displayed in Figure 5 (a) for the case of l b b = 16 and a range of grafting densities ρ g . The global probability for azobenzene and phospholipid to be found at the same z is given by
p = ∫ 0 L z ρ a z ( z ) ρ p h ( z ) d z .
Figure 5 (b) shows its dependence on the grafting density of a brush, ρ g , at various lengths of a polymer backbone, l b b . It is evident that at each backbone length l b b ≥ 10 , there is a specific value for the grafting density, ρ g * , at which p reaches its maximum value, as indicated in the figure Figure 5 (b). One, however, should take into account that the number of available azobenzenes per square area of a brush is proportional not only to the chains grafting density, ρ g , but also to their number in a single chain, n s c = div ( l b b , 2 ) . Therefore, it makes sense to express the probability p also in terms of the azobenzene surface density ρ a z
ρ a z = N a z D 2 / ( L x L y ) = ρ g n s c ( D / σ ) 2 ,
where N a z is the total number of azobenzenes on a single wall functionalized by a brush. The dependence p ( ρ a z ) , shown in Figure 5 (c), is practically the same and almost linear in ρ a z in the interval ρ a z < 0.3 for all backbone lengths. Therefore, in this interval of grafting densities, the probability p of azobenzene and phospholipid to meet at the same z is governed principally by the number of available azobenzenes. At ρ a z > 0.3 , the curves saturate indicating that the additional number of azobenzenes does not increase the probability p. This is attributed to a gradual expulsion of azobenzenes from the dense brush interior, see Figure 4 (c), and inaccessibility of azobenzenes adjacent to the wall for interacting with the LDL phospholipids. Therefore, for each given backbone length, l b b , there exists some optimal brush grafting density ρ g * , as specified in Figure 5 (b), and the further increase of ρ g beyond this value does not increase the probability for the azobenzene and phospholipid to meet at the same z.

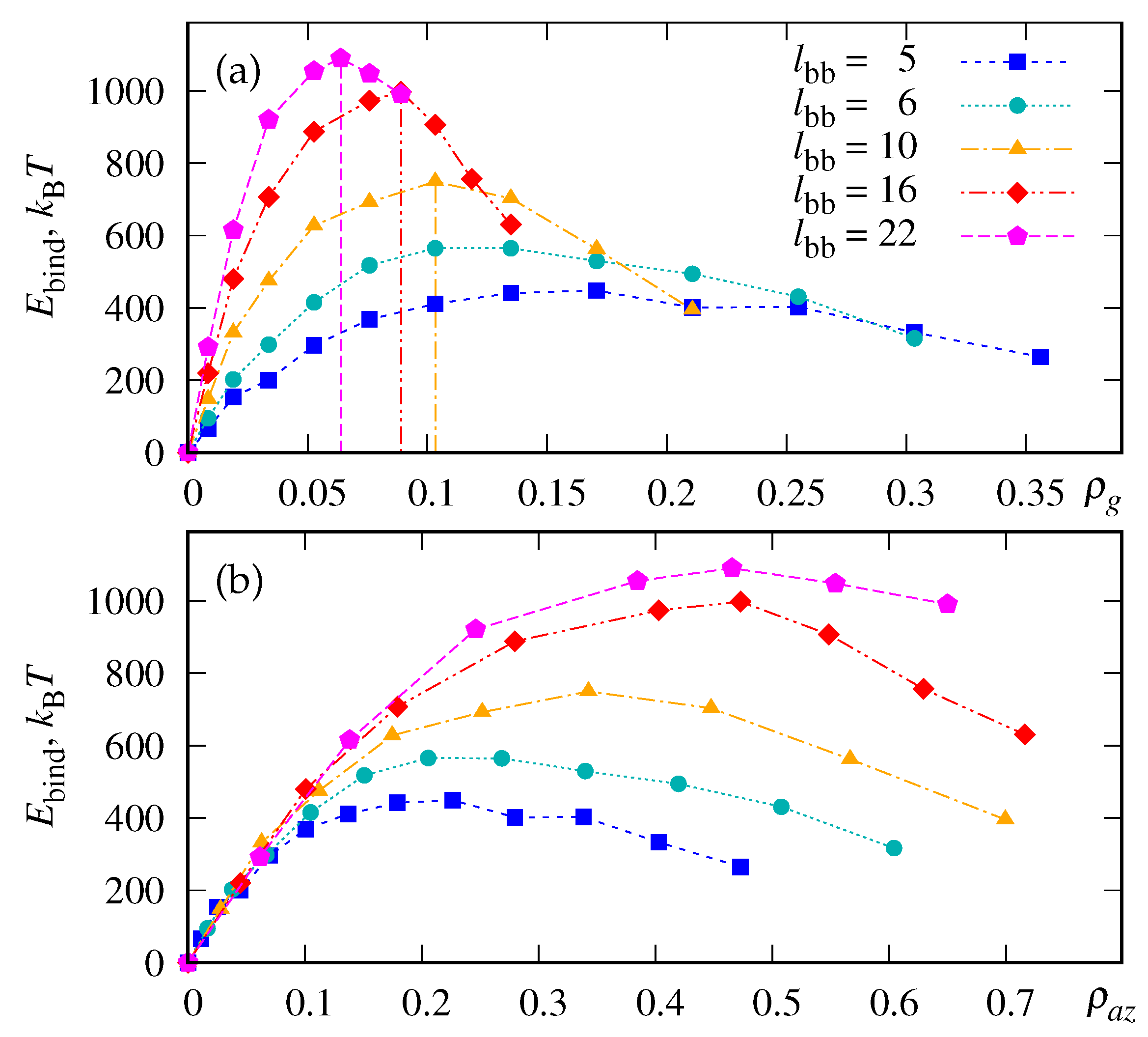
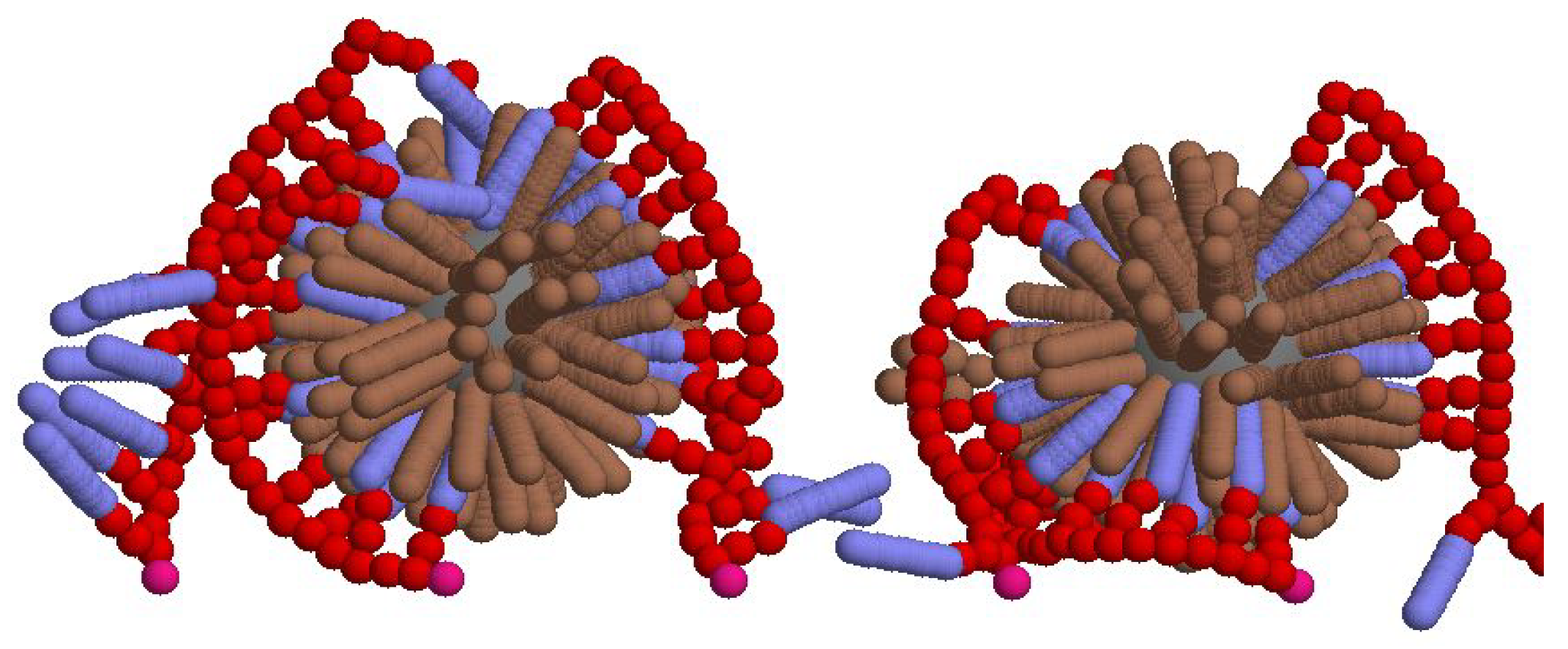
3.2. Binding Energy of LDLs

A more direct and standard measure of the adsorption efficiency is the the binding energy, E bind , evaluated per single LDL particle. In our simulations we define it as the magnitude of the sum of all negative pairwise interaction energies, V i j , between the azobenzene-phospholipid pairs 〈 i , j 〉 , divided by the number of the LDLs particles
E bind = 1 N L D L ∑ 〈 i , j 〉 V i j , if V i j = V NB SAP [ d ′ ( q i j ) ] < 0 .
The expression for the azobenzene-phospholipid interaction energy it is provided in Eq. (1). E bind is displayed, in k B T units, in Figure 9. Frame (a) shows it as the function of the grafting density ρ g , whereas frame (b) – as the function of azobenzene surface density ρ a z .
The first thing to note here is that the dependence of E bind has a similar shape to the probability p in Figure 5 (b), with the maximum reached at the very same characteristic respective values ρ g * . This indicates that that the magnitude of binding energy is essentially driven by a probability for azobenzenes and phospholipids to meet at the same z, given by p. On the other hand, comparing Figure 5 (c) and Figure 9 (b), one sees that E bind reaches progressively higher values with the increase of l b b at the same ρ a z for ρ a z > 0.1 . Hence, there is another additional factor that increases the number of azobenzene-phospholipid pairs upon the increase of the chain length which occurs at almost constant value of the probability p.

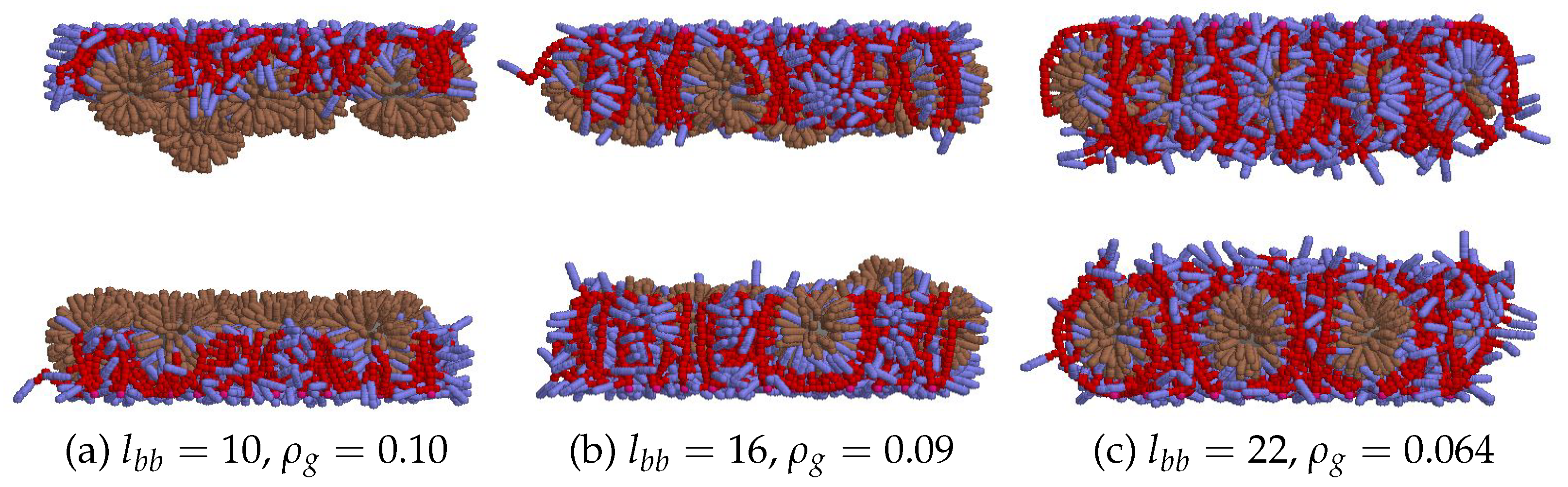
3.3. Polymer bending effect

This additional factor is the presence of specific conformations of polymer chains. It is quite obvious that, because of a finite curvature of the LDL particles, achieving the maximum number of the azobenzene-phospholipid contacts, and, thus, the largest magnitude for the binding energy, requires essential bending of the polymer chains. Such “wrap over” conformations of polymer chains are illustrated in the snapshot extracted from our simulations and shown in Figure 7.
The most probable radius of curvature R * for the backbone, in the case of an ideal wrap over scenario, can be estimated from the dimensions of all involved beads provided in Section 2. This results in R * ≈ 3.3 nm , the value is, of course, dependent on the diameter of the LDL particles. Such bend conformation demands, on one hand, sufficient flexibility of a polymer chain and, on another hand, conditions, that there is enough free volume around a chain to bend. Effective value of R * is expected to increase both at high brush grafting densities (because of straightening up of polymer chains), and at high concentration of adsorbed LDLs (in which case one chain may be in contact with two adjacent LDLs).
To examine the presence of bend conformations, we analyse each polymer of a brush separately. The beads comprising chosen backbone are fitted to the spherical surface using the algorithm that reduces this problem to the linear least squares problem [69]. The latter has been solved in Refs. [70,71,72] and is available in a form of an open source FORTRAN-90 package via GitHub [73]. The radius R of a spherical surface that fits the spatial distribution of backbone beads the best, provides the estimate for its radius of curvature.
We built the distributions, f ( R ) , of such radii of curvature, R, and these are shown in Figure 8 for four backbone lengths, l b b = 6 , 10, 16, and 22, and a set of characteristic grafting densities, ρ g , including optimal density ρ g * , in each case. Let us consider the case of a short backbone, l b b = 6 , first, shown in Figure 8 (a). It is evident that the distributions f ( R ) are very much the same within the broad interval of grafting densities, 0.008 < ρ g < 0.303 , with the maximum of the distribution positioned at R ≈ R * . It is so, because the chain length is much smaller than the diameter of LDL, and such chains follow easily the curvature of the LDL surface. For the case of a longer backbone, l b b = 10 , the increase of the grafting density leads to broadening of the f ( R ) distribution and shifting the maximum position to higher values, see frame (b) of the same figure. This reflects straightening of some polymers when the brush enters the dense brush regime. The same tendency is found upon a further increase of backbone length to l b b = 16 and l b b = 22 , see frames (c) and (d). Optimal densities, ρ g * , as found in Figure 5 (b) and 9 (a), are highlighted as thicker black curves. At these respective densities, a peak at R ≈ R * is still retained, indicating the presence of the wrap over conformations of chains around the LDL particles. Further increase of the density, ρ g ≥ 0.103 for l b b = 16 and ρ g ≥ 0.076 for l b b = 22 , eliminates this peak completely reflecting both straightening of polymer chains in the dense brush regime.

3.4. Concludings Remarks on Adsorption Efficiency

We can return now to the plots for the probability p, Figure 5 (b) and for the binding energy, Figure 9 (a), and relate these to the distributions for the radius of curvature, Figure 8 (b)-(d) at the same parameters of the chains. In particular, at ρ g < ρ g * , the distributions f ( R ) have well defined peaks at R = R * indicating perfect wrap over conformations, as shown in Figure 7. However, the density of azobenzenes in this case is low leading to smaller values for E bind (low adsorption efficiency). On the other hand, at ρ g > ρ g * , the density of azobenzenes is high, but the peak at R = R * in the distributions f ( R ) disappears, indicating relatively small amount of wrap over conformations of chains which, in turn, leads to the reduction of the value of E bind (low adsorption efficiency). Specific densities ρ g * are attributed to a good compromise between these two factors, when the density of azobenzenes is sufficiently high and, at the same time, there is abundance of wrap over conformations of polymer chains that ensure sufficient number of the azobenzne-phospholipid close contacts. As the result of this compromise, the binding energy reaches its maximum value (high adsorption efficiency).
Having this scenario in mind, one can suggest the reason why the maximum value for binding energy increases at the increase of chain length, l b b , see Figure 9. The shorter chains are able to wrap over the sides of LDLs only, whereas longer chains are able to wrap over the external poles of LDLs as well, thus increasing the number of interacting pairs. This is shown in a series of snapshots in Figure 9.
At ρ > ρ g * the excluded volume effects are brought into play and the brush expulses LDLs, and, thus, E bind decays because of reduced number of interacting azobenzene-phospholipid pairs. This arrangement of the brush and of the LDL particles is shown in Figure 10.
The findings presented in this section allow one to made following conclusions. Firstly, at each fixed length of polymer chains, given by its backbone length l b b , the grafting density ρ g * exists which is optimal for the LDL adsorption. The efficiency of the latter is characterised by the binding energy E bind per one LDL, as shown in Figure 9. The increase of adsorption efficiency at low ρ g should be attributed to the increase of azobenzenes density in the region accessible to LDLs, whereas the decrease of adsorption efficiency at higher ρ g is related both to straightening of chains reducing the azobenzene-phospholipid contacts and to the excluded volume effects in a regime of a dense brush, see Figure 10 (b). Secondly, with the increase of the backbone length, l b b , the adsorption efficiency increases until it starts to saturate, as seen in Figure 9. The initial increase is related to the growth of a number of available azobenzenes for binding, see Figure 9, whereas the saturation occurs when the brush height reaches the diameter of the LDL particle, see the same figure (c). Thirdly, an efficient adsorption requires the ability of polymer chains to bend and to wrap over the LDL particles, as shown in Figure 7 and Figure 8. However, in reality, this factor will depend strongly on the polymer chain flexibility and the relation between the chain length and the diameter of a LDL particle.

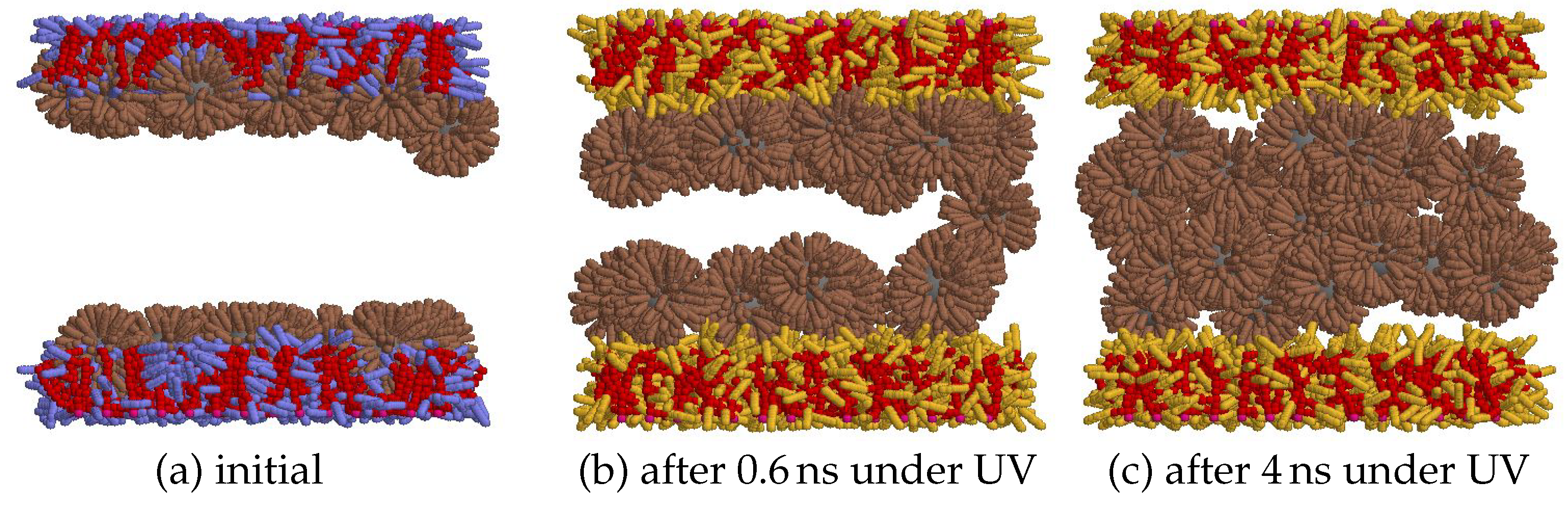
4. Adsorber Regeneration under Ultraviolet Light

Azobenzene-containing smart LDL adsorber, as suggested and tested in Ref. [21], allows its clean and efficient regeneration and reusage. This can be achieved by illumination of an adsorber by the UV light with a suitable wavelength. In this case, the azobenzenes in a polymer brush undergo the trans-to-cis photo-isomerization [74] and loose their liquid crystalline and apolar features. As the result, their interaction with phospholipids weakens and the LDL particles desorb from the polymer brush of an adsorber. The LDL particles can be washed out of the adsorber and the latter can be reused, with the reported recovery rate of 97.9 % after five regeneration cycles [21].
In terms of our modelling approach, described in detail in Section 2, the trans-to-cis photo-isomerization is mimicked via switching the interaction potential between the azobenzene and phospholipid spherocylinders from the attractive (1) to a repulsive (3) form.
Figure 11 shows a series of snapshots demonstrating gradual desorption of LDLs from a polymer brush of the backbone length l b b = 10 and with, optimal for adsorption, grafting density of ρ g * = 0.103 . Frame (a) shows the initial, adsorbed state, obtained after 40 ns under normal conditions, see Section 3. In this state the azobenzenes are in the trans-state indicated by their blue coloring. Upon switching on the UV light, azobenzenes photoisomerize into their cis-form indicated by yellow colouring, and the process of desorption starts. At its first stage, frame (b), both bottom and top layers of LDLs are pushed out of the brush but retain their layered structure. After some illumination time, indicated in the figure, the layers are destroyed and LDLs fill the bulk central region of a pore uniformly, see frame (c). Now they can be easily washed out the pore by a flow.
The issue of interest is the dynamics of desorption of LDLs under UV light, compared to their adsorption under normal conditions, covered in Section 3. For this purpose we cannot use the binding energy E bind (6), as it instantly drops to zero when all azobenzenes switch into a cis state. However, as it was shown in Section 3, its behaviour is very similar to that for p, the probability to find the azobenzene and phospholipid at the same distance from the bottom wall, see Figure 5. We used this probability as a rough estimate for the LDL adsorption and desorption dynamics. The results are shown in Figure 12 for three backbone lengths, l b b = 10 , 16 and 22 at their respective optimal brush densities, as obtained in Figure 6.
The first observation that stems from Figure 12 is that there is a saturation in the temporal behaviour of p at l b b ≥ 16 , see frame (a). The second thing to mention is that the desorption dynamics at l b b = 22 is essentially slower than for two other cases, l b b = 10 and 16, see frame (b). We explain this by essential reduction of the volume of a bulk region of a pore in the case of the longest chain and, as the result, slowing down its diffusion required for the desorption. Finally, perhaps, the main result is that the rate of desorption, shown in (a), is essentially higher that that for adsorption, shown in (b).

Conclusions

The study was motivated by the experimental results by Guo et al. [21], where the authors presented an advanced adsorber in a form of a photo-sensible smart surface, and examined its efficiency towards selective adsorption of the LDL particles in a course of a hemoperfusion protocol. Besides the definite success of these experimental findings, the question arises how the very details of the molecular architecture of such adsorber affect the efficiency of adsorption. The progress in this direction can be attempted by employing computer simulations.
The nature of the LDL adsorption is extremely complex and involves a range of relevant length and time scales. Indeed, microscopically, it is governed by highly specific atomic interactions between the functional groups of a brush and these of the LDL particle, particularly, the phospholipids. On the other hand, adsorption manifests itself in a statistical way, in a system with a considerable number of polymer chains and LDL particles, and is the result of the competition between various interactions effects being involved in this process. In this study we address the latter, statistical, aspect of the LDL adsorption, which inevitably leaves us with the only option to coarse-grain the principal interactions (i) within a polymer brush, (ii) within each LDL particle, and (iii) between relevant groups of both. This follows the philosophy of some of our previous studies, including azobenzene-containing polymeric systems [40,41,42,43,44,45,46,47].
The basic length scale ratio between the model and real systems is estimated from the dimensions of a model LDL particle vs its real counterpart, and it is about 1 : 5 . Other, geometry related, simplification is based on the fact that the diameter of spherical adsorbers used in Ref. [21] are ten times larger that the diameter of the LDL particle. Therefore, we replaced the curved surface of such adsorber by a flat surface. The polymer chains of a brush are of the side-chain architecture with their backbones and side chain made of soft-core repulsive spherical beads. A range of the backbone lengths, l b b = 5 − 22 spherical beads, are considered such that the longest polymer length does not exceed the diameter of the LDL particle. Their side chains are terminated by the azobenzene groups, represented by soft-core repulsive spherocylinders. The LDL particle comprises a spherical core which represents uniformly packed cholesteryl esters and triglycerides, surrounded by a shell of phospholipid groups modelled by the same spherocylinder beads. To simplify the description, only the azobenzene-phospholipid interaction is made attractive and it governs the adsorption process. Because of the nature of the soft-core interactions, the dynamics in the system is artificially speed-up and, therefore, does not reflect the dynamics in a real system.
Under normal conditions, LDLs are adsorbed by smart surface on both walls of a pore, this takes up to 40 ns in model time units. Assuming that the adsorption efficiency will depend on the probability for the azobezene and phospholipid beads to meet in the same segment of a pore, we evaluate the probability, p, of such event first. Its behaviour with the grafting density of a brush, ρ g , indicated the presence of some optimal value for ρ g * at which p reaches its maximum value. At ρ > ρ g * the value of p decreases, as the LDL particles are pushed out of a dense brush because of the excluded volume interactions. One, however, observes that if p is replotted in terms of the azobenzenes density, it shows weak or no dependence on a backbone length l b b .
More direct measure of the adsorption efficiency is provided by the magnitude of binding energy, E bind , which shows the similar dependence on ρ g to that for the probability p, but indicates higher adsorption efficiency with the increase of l b b until it saturates at l b b > 22 , when the chain length reaches the values comparable to the diameter of the LDL particle. The explanation of this dependence is found by analysing the curvature of chains in all cases being considered. In particular, at ρ g ≤ ρ g * , the longer chains are found to be able to bend over both the sides and the top of LDL particles, thus increasing E bind . At ρ g ≤ ρ g * , the radius of curvature is found to increase essentially indicating straightening of the chains, the effect characteristic for the dense brush regime. This factor, which prevents chains from bending over the LDL particles and, thus, reducing the number of azobenzene-phospholipid contacts, also contribute to the decrease of E bind , alongside with the excluded volume effect within the brush interior.
The results obtained here indicate that the optimal adsorption efficiency is achieved as the result of a compromise between several factors. The grafting density should be high enough to provide sufficiently high concentration of azobenzenes, but below the dense brush threshold to avoid expulsion of LDL from a brush due to strong excluded volume effects. Polymer chains of a brush should be flexible enough to allow polymer wrap over LDLs and their characteristic length be of the order of the half of the LDL circumference.
Under UV light, the model brush is found to clear up quickly, requiring up to 1 ns time in model time units. It occurs in two stages. At the first stage, LDLs desorb from both smart surfaces while preserving their layered structure, whereas at the second stage, they loose this structure and are distributed uniformly within a pore interior clear of brush regions. We found that dynamics of desorption is at least one order of magnitude faster that that for adsorption.
The study opens up future refinements and extensions. In particular, one can match parameters of a model more closely to that for a real systems, by incorporation of some variant of a multiscale approach. One also can consider the mixture of the LDL and HDL particles and model selective interaction between the brush and both types of lipoproteins. Various branched molecular architectures can be tested for the adsorption efficiency. Finally, one can study adsorption/desorption cycles under flow introduced within a pore, to mimic realistic situation found in the experimental setup. These cases are reserved for future studies.

Acknowledgments

DY acknowledges partial support from the NAS of Ukraine (the grant for research laboratories/groups of young scientists No 07/01-2022(4)). The authors are grateful to the Armed Forces of Ukraine for protection during the time this research was undertaken.

References

  1. Sacks, F.M.; Campos, H. Low-Density Lipoprotein Size and Cardiovascular Disease: A Reappraisal. The Journal of Clinical Endocrinology & Metabolism 2003, 88, 4525–4532. [Google Scholar] [CrossRef]
  2. Sikorski, J. Atherosclerosis/Lipoprotein/Cholesterol Metabolism. In Comprehensive Medicinal Chemistry II; Elsevier, 2007; pp. 459–494. [CrossRef]
  3. Mundi, S.; Massaro, M.; Scoditti, E.; Carluccio, M.A.; van Hinsbergh, V.W.M.; Iruela-Arispe, M.L.; Caterina, R.D. Endothelial permeability, LDL deposition, and cardiovascular risk factors—a review. Cardiovascular Research 2017, 114, 35–52. [Google Scholar] [CrossRef] [PubMed]
  4. Kiberstis, P.A. Fatty liver—too much of a bad thing? Science 2019, 364, 1044.6–1045. [Google Scholar] [CrossRef]
  5. Thierer, J.H.; Ekker, S.C.; Farber, S.A. The LipoGlo reporter system for sensitive and specific monitoring of atherogenic lipoproteins. Nature Communications 2019, 10. [Google Scholar] [CrossRef] [PubMed]
  6. Yu, Y.; Dong, J.; Ma, B.; Jiang, X.; Guo, C.; Liu, Z.; Chai, Y.; Wang, L.; Sun, L.; Ou, L.; et al. Bio-inspired dual-functional phospholipid–poly(acrylic acid) brushes grafted porous poly(vinyl alcohol) beads for selective adsorption of low-density lipoprotein. Journal of Materials Chemistry B 2021, 9, 6364–6376. [Google Scholar] [CrossRef]
  7. Cheng, Y.; Wang, S.; Yu, Y.; Yuan, Y. In vitro, in vivo studies of a new amphiphilic adsorbent for the removal of low-density lipoprotein. Biomaterials 2003, 24, 2189–2194. [Google Scholar] [CrossRef]
  8. Yu, Y.; Ma, B.; Jiang, X.; Guo, C.; Liu, Z.; Li, N.; Chai, Y.; Wang, L.; Du, Y.; Wang, B.; et al. Amphiphilic shell nanomagnetic adsorbents for selective and highly efficient capture of low-density lipoprotein from hyperlipidaemia serum. Journal of Materials Chemistry B 2022, 10, 4856–4866. [Google Scholar] [CrossRef]
  9. Lanzalaco, S.; Armelin, E. Poly(N-isopropylacrylamide) and Copolymers: A Review on Recent Progresses in Biomedical Applications. Gels 2017, 3, 36. [Google Scholar] [CrossRef]
  10. Sudre, G.; Siband, E.; Gallas, B.; Cousin, F.; Hourdet, D.; Tran, Y. Responsive Adsorption of N-Isopropylacrylamide Based Copolymers on Polymer Brushes. Polymers 2020, 12, 153. [Google Scholar] [CrossRef]
  11. Yaremchuk, D.; Kalyuzhnyi, O.; Ilnytskyi, J. Modelling thermoresponsive polymer brush by mesoscale computer simulations. Condensed Matter Physics 2023, 26, 33302. [Google Scholar] [CrossRef]
  12. Tian, L.; Dou, H.; Shao, Y.; Yi, Y.; Fu, X.; Zhao, J.; Fan, Y.; Ming, W.; Ren, L. Magnetically controlled super-wetting surface switching between ultra-low and ultra-high droplet adhesion. Chemical Engineering Journal 2023, 456, 141093. [Google Scholar] [CrossRef]
  13. Malm, J.; Sahramo, E.; Karppinen, M.; Ras, R.H.A. Photo-Controlled Wettability Switching by Conformal Coating of Nanoscale Topographies with Ultrathin Oxide Films. Chemistry of Materials 2010, 22, 3349–3352. [Google Scholar] [CrossRef]
  14. Bahl, S.; Nagar, H.; Singh, I.; Sehgal, S. Smart materials types, properties and applications: A review. Materials Today: Proceedings 2020, 28, 1302–1306. [Google Scholar] [CrossRef]
  15. Zhao, Y. Smart light-responsive materials; Wiley-Blackwell: Hoboken, NJ, 2009. [Google Scholar]
  16. Roling, O.; Stricker, L.; Voskuhl, J.; Lamping, S.; Ravoo, B.J. Supramolecular surface adhesion mediated by azobenzene polymer brushes. Chemical Communications 2016, 52, 1964–1966. [Google Scholar] [CrossRef] [PubMed]
  17. Santer, S. Remote control of soft nano-objects by light using azobenzene containing surfactants. Journal of Physics D: Applied Physics 2017, 51, 013002. [Google Scholar] [CrossRef]
  18. Wu, Z.; Li, X.; Jiang, X.; Xie, T.; Li, H.; Zhang, G.; Jiang, J. Photoswitchable de/adsorption of an azobenzene-derived surfactant on a silica surface. Physical Chemistry Chemical Physics 2019, 21, 21030–21037. [Google Scholar] [CrossRef] [PubMed]
  19. Hisham, S.; Sarih, N.M.; Tajuddin, H.A.; Abidin, Z.H.Z.; Abdullah, Z. Unraveling the surface properties of PMMA/azobenzene blends as coating films with photoreversible surface polarity. RSC Advances 2021, 11, 15428–15437. [Google Scholar] [CrossRef]
  20. Mukai, K.; Imai, K.; Hara, M.; Nagano, S.; Seki, T. A High-Density Azobenzene Side Chain Polymer Brush for Azimuthal and Zenithal Orientational Photoswitching of a Nematic Liquid Crystal. ChemPhotoChem 2019, 3, 495–500. [Google Scholar] [CrossRef]
  21. Guo, C.; Yu, Y.; Jiang, X.; Ma, B.; Liu, Z.; Chai, Y.; Wang, L.; Wang, B.; Du, Y.; Li, N.; et al. Photorenewable Azobenzene Polymer Brush-Modified Nanoadsorbent for Selective Adsorption of LDL in Serum. ACS Applied Materials & Interfaces 2022, 14, 34388–34399. [Google Scholar] [CrossRef]
  22. Antwerpen, R.V.; Gilkey, J.C. Cryo-electron microscopy reveals human low density lipoprotein substructure. Journal of Lipid Research 1994, 35, 2223–2231. [Google Scholar] [CrossRef]
  23. Orlova, E.V.; Sherman, M.B.; Chiu, W.; Mowri, H.; Smith, L.C.; Gotto, A.M. Three-dimensional structure of low density lipoproteins by electron cryomicroscopy. Proceedings of the National Academy of Sciences 1999, 96, 8420–8425. [Google Scholar] [CrossRef] [PubMed]
  24. Hevonoja, T.; Pentikäinen, M.O.; Hyvönen, M.T.; Kovanen, P.T.; Ala-Korpela, M. Structure of low density lipoprotein (LDL) particles: Basis for understanding molecular changes in modified LDL. Biochimica et Biophysica Acta (BBA) - Molecular and Cell Biology of Lipids 2000, 1488, 189–210. [Google Scholar] [CrossRef]
  25. Segrest, J.P.; Jones, M.K.; Loof, H.D.; Dashti, N. Structure of apolipoprotein B-100 in low density lipoproteins. Journal of Lipid Research 2001, 42, 1346–1367. [Google Scholar] [CrossRef] [PubMed]
  26. Teerlink, T.; Scheffer, P.G.; Bakker, S.J.; Heine, R.J. Combined data from LDL composition and size measurement are compatible with a discoid particle shape. Journal of Lipid Research 2004, 45, 954–966. [Google Scholar] [CrossRef] [PubMed]
  27. Ren, G.; Rudenko, G.; Ludtke, S.J.; Deisenhofer, J.; Chiu, W.; Pownall, H.J. Model of human low-density lipoprotein and bound receptor based on CryoEM. Proceedings of the National Academy of Sciences 2009, 107, 1059–1064. [Google Scholar] [CrossRef]
  28. Kumar, V.; Butcher, S.J.; Öörni, K.; Engelhardt, P.; Heikkonen, J.; Kaski, K.; Ala-Korpela, M.; Kovanen, P.T. Three-Dimensional cryoEM Reconstruction of Native LDL Particles to 16Å Resolution at Physiological Body Temperature. PLoS ONE 2011, 6, e18841. [Google Scholar] [CrossRef]
  29. Prassl, R.; Laggner, P. Lipoprotein Structure and Dynamics: Low Density Lipoprotein Viewed as a Highly Dynamic and Flexible Nanoparticle. In Lipoproteins - Role in Health and Diseases; InTech, 2012. [CrossRef]
  30. Heikelä, M.; Vattulainen, I.; Hyvönen, M.T. Atomistic Simulation Studies of Cholesteryl Oleates: Model for the Core of Lipoprotein Particles. Biophysical Journal 2006, 90, 2247–2257. [Google Scholar] [CrossRef]
  31. Vattulainen, I.; Rog, T. Lipid Simulations: A Perspective on Lipids in Action. Cold Spring Harbor Perspectives in Biology 2011, 3, a004655–a004655. [Google Scholar] [CrossRef]
  32. Murtola, T.; Vuorela, T.A.; Hyvönen, M.T.; Marrink, S.J.; Karttunen, M.; Vattulainen, I. Low density lipoprotein: structure, dynamics, and interactions of apoB-100 with lipids. Soft Matter 2011, 7, 8135. [Google Scholar] [CrossRef]
  33. Koivuniemi, A.; Vuorela, T.; Kovanen, P.T.; Vattulainen, I.; Hyvönen, M.T. Lipid Exchange Mechanism of the Cholesteryl Ester Transfer Protein Clarified by Atomistic and Coarse-grained Simulations. PLoS Computational Biology 2012, 8, e1002299. [Google Scholar] [CrossRef]
  34. Lewis, D.R.; Kholodovych, V.; Tomasini, M.D.; Abdelhamid, D.; Petersen, L.K.; Welsh, W.J.; Uhrich, K.E.; Moghe, P.V. In silico design of anti-atherogenic biomaterials. Biomaterials 2013, 34, 7950–7959. [Google Scholar] [CrossRef] [PubMed]
  35. Antonijevic, T.; Lancaster, J.L.; Starobin, J.M. Modeling order-disorder transition in Low-Density Lipoprotein. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE; 2014. [Google Scholar] [CrossRef]
  36. Cilpa-Karhu, G.; Jauhiainen, M.; Riekkola, M.L. Atomistic MD simulation reveals the mechanism by which CETP penetrates into HDL enabling lipid transfer from HDL to CETP. Journal of Lipid Research 2015, 56, 98–108. [Google Scholar] [CrossRef] [PubMed]
  37. Angarica, V.E.; Orozco, M.; Sancho, J. Exploring the complete mutational space of the LDL receptor LA5 domain using molecular dynamics: linking SNPs with disease phenotypes in familial hypercholesterolemia. Human Molecular Genetics 2016, 25, 1233–1246. [Google Scholar] [CrossRef] [PubMed]
  38. Lei, D.; Rames, M.; Zhang, X.; Zhang, L.; Zhang, S.; Ren, G. Insights into the Tunnel Mechanism of Cholesteryl Ester Transfer Protein through All-atom Molecular Dynamics Simulations. Journal of Biological Chemistry 2016, 291, 14034–14044. [Google Scholar] [CrossRef]
  39. Lauer, M.E.; Graff-Meyer, A.; Rufer, A.C.; Maugeais, C.; von der Mark, E.; Matile, H.; D’Arcy, B.; Magg, C.; Ringler, P.; Müller, S.A.; et al. Cholesteryl ester transfer between lipoproteins does not require a ternary tunnel complex with CETP. Journal of Structural Biology 2016, 194, 191–198. [Google Scholar] [CrossRef] [PubMed]
  40. Ilnytskyi, J.; Saphiannikova, M.; Neher, D. Photo-induced deformations in azobenzene-containing side-chain polymers: molecular dynamics study. Condensed Matter Physics 2006, 9, 87. [Google Scholar] [CrossRef]
  41. Ilnytskyi, J.M.; Neher, D.; Saphiannikova, M. Opposite photo-induced deformations in azobenzene-containing polymers with different molecular architecture: Molecular dynamics study. The Journal of Chemical Physics 2011, 135, 044901. [Google Scholar] [CrossRef]
  42. Ilnytskyi, J.M.; Saphiannikova, M. Reorientation Dynamics of Chromophores in Photosensitive Polymers by Means of Coarse-Grained Modeling. ChemPhysChem 2015, 16, 3180–3189. [Google Scholar] [CrossRef]
  43. Ilnytskyi, J.; Slyusarchuk, A.; Saphiannikova, M. Photo-controllable percolation of decorated nanoparticles in a nanopore: molecular dynamics simulation study. Mathematical Modeling and Computing 2016, 3, 33–42. [Google Scholar] [CrossRef]
  44. Ilnytskyi, J.M.; Slyusarchuk, A.; Saphiannikova, M. Photocontrollable Self-Assembly of Azobenzene-Decorated Nanoparticles in Bulk: Computer Simulation Study. Macromolecules 2016, 49, 9272–9282. [Google Scholar] [CrossRef]
  45. Ilnytskyi, J.M.; Toshchevikov, V.; Saphiannikova, M. Modeling of the photo-induced stress in azobenzene polymers by combining theory and computer simulations. Soft Matter 2019, 15, 9894–9908. [Google Scholar] [CrossRef] [PubMed]
  46. Slyusarchuk, A.Y. ; Yaremchuk, D.L.; Ilnytskyi, J.M.; and. Adsorption of decorated nanoparticles on a liquid crystalline polymer brush: molecular dynamics study. Mathematical Modeling and Computing 2020, 7, 207–218. [Google Scholar] [CrossRef]
  47. Yaremchuk, D.; Patsahan, T.; Ilnytskyi, J. Photo-switchable liquid crystalline brush as an aligning surface for liquid crystals: modelling via mesoscopic computer simulations. Condensed Matter Physics 2022, 25, 33601. [Google Scholar] [CrossRef]
  48. Austin, M.; Krauss, R. GENETIC CONTROL OF LOW-DENSITY-LIPOPROTEIN SUBCLASSES. The Lancet 1986, 328, 592–595. [Google Scholar] [CrossRef]
  49. Campos, H.; Genest, J.J.; Blijlevens, E.; McNamara, J.R.; Jenner, J.L.; Ordovas, J.M.; Wilson, P.W.; Schaefer, E.J. Low density lipoprotein particle size and coronary artery disease. Arteriosclerosis and Thrombosis: A Journal of Vascular Biology 1992, 12, 187–195. [Google Scholar] [CrossRef] [PubMed]
  50. Austin, M.A. Low-Density Lipoprotein Subclass Patterns and Risk of Myocardial Infarction. JAMA: The Journal of the American Medical Association 1988, 260, 1917. [Google Scholar] [CrossRef]
  51. Stampfer, M.J. A Prospective Study of Triglyceride Level, Low-Density Lipoprotein Particle Diameter, and Risk of Myocardial Infarction. JAMA: The Journal of the American Medical Association 1996, 276, 882. [Google Scholar] [CrossRef]
  52. Lamarche, B.; Tchernof, A.; Moorjani, S.; Cantin, B.; Dagenais, G.R.; Lupien, P.J.; Despre´s, J.P. Small, Dense Low-Density Lipoprotein Particles as a Predictor of the Risk of Ischemic Heart Disease in Men. Circulation 1997, 95, 69–75. [Google Scholar] [CrossRef]
  53. Scheffer, P.G.; Bakker, S.J.L.; Heine, R.J.; Teerlink, T. Measurement of low-density lipoprotein particle size by high-performance gel-filtration chromatography. Clinical Chemistry 1997, 43, 1904–1912. [Google Scholar] [CrossRef]
  54. Ilnytskyi. ; Lintuvuori.; Wilson. Simulation of bulk phases formed by polyphilic liquid crystal dendrimers. Condensed Matter Physics 2010, 13, 33001. [Google Scholar] [CrossRef]
  55. Ilnytskyi, J.M.; Slyusarchuk, A.; Sokołowski, S. Gelation of patchy ligand shell nanoparticles decorated by liquid-crystalline ligands: computer simulation study. Soft Matter 2018, 14, 3799–3810. [Google Scholar] [CrossRef] [PubMed]
  56. Hughes, Z.E.; Wilson, M.R.; Stimson, L.M. Coarse-grained simulation studies of a liquid crystal dendrimer: towards computational predictions of nanoscale structure through microphase separation. Soft Matter 2005, 1, 436. [Google Scholar] [CrossRef] [PubMed]
  57. Steinhauser, M.O. Computational Multiscale Modeling of Fluids and Solids; Springer Berlin Heidelberg, 2008. [CrossRef]
  58. Karplus, M. Development of Multiscale Models for Complex Chemical Systems: From 745 HHsub2/subto Biomolecules (Nobel Lecture). Angewandte Chemie International Edition 2014, 53, 9992–10005. [Google Scholar] [CrossRef] [PubMed]
  59. Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. The Journal of Chemical Physics 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
  60. Wilson, M.R.; Ilnytskyi, J.M.; Stimson, L.M. Computer simulations of a liquid crystalline dendrimer in liquid crystalline solvents. The Journal of Chemical Physics 2003, 119, 3509–3515. [Google Scholar] [CrossRef]
  61. Lintuvuori, J.S.; Wilson, M.R. A new anisotropic soft-core model for the simulation of liquid crystal mesophases. J Chem Phys 2008, 128, 044906. [Google Scholar] [CrossRef]
  62. Akiyama, H.; Tamada, K.; Nagasawa, J.; Abe, K.; Tamaki, T. Photoreactivity in Self-Assembled Monolayers Formed from Asymmetric Disulfides Having para-Substituted Azobenzenes. The Journal of Physical Chemistry B 2002, 107, 130–135. [Google Scholar] [CrossRef]
  63. Wilson, M.R. Molecular dynamics simulations of flexible liquid crystal molecules using a Gay-Berne/Lennard-Jones model. The Journal of Chemical Physics 1997, 107, 8654–8663. [Google Scholar] [CrossRef]
  64. Chen, Q.; Yu, S.; Zhang, D.; Zhang, W.; Zhang, H.; Zou, J.; Mao, Z.; Yuan, Y.; Gao, C.; Liu, R. Impact of Antifouling PEG Layer on the Performance of Functional Peptides in Regulating Cell Behaviors. Journal of the American Chemical Society 2019, 141, 16772–16780. [Google Scholar] [CrossRef]
  65. Ilnytskyi, J.; Wilson, M.R. A domain decomposition molecular dynamics program for the simulation of flexible molecules with an arbitrary topology of Lennard–Jones and/or Gay–Berne sites. Computer Physics Communications 2001, 134, 23–32. [Google Scholar] [CrossRef]
  66. Ilnytskyi, J.M.; Wilson, M.R. A domain decomposition molecular dynamics program for the simulation of flexible molecules of spherically-symmetrical and nonspherical sites. II. Extension to NVT and NPT ensembles. Computer Physics Communications 2002, 148, 43–58. [Google Scholar] [CrossRef]
  67. Jerca, F.A.; Jerca, V.V.; Hoogenboom, R. Advances and opportunities in the exciting world of azobenzenes. Nature Reviews Chemistry 2021, 6, 51–69. [Google Scholar] [CrossRef]
  68. Zannoni, C. Liquid Crystals and Their Computer Simulations; Cambridge University Press, 2022. [CrossRef]
  69. Jekel, C.F. Digital Image Correlation on Steel Ball; 2016; chapter Appendix A, pp. 83–87.
  70. Paige, C.C.; Saunders, M.A. LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares. ACM Transactions on Mathematical Software 1982, 8, 43–71. [Google Scholar] [CrossRef]
  71. Paige, C.C.; Saunders, M.A. Algorithm 583: LSQR: Sparse Linear Equations and Least Squares Problems. ACM Transactions on Mathematical Software 1982, 8, 195–209. [Google Scholar] [CrossRef]
  72. Saunders, M.A. Solution of sparse rectangular systems using LSQR and CRAIG. BIT Numerical Mathematics 1995, 35, 588–604. [Google Scholar] [CrossRef]
  73. LSQR. https://github.com/jacobwilliams/LSQR. Accessed: 2023-07-23.
  74. Todorov, T.; Nikolova, L.; Tomova, N. Polarization holography 1: A new high-efficiency organic material with reversible photoinduced birefringence. Applied Optics 1984, 23, 4309. [Google Scholar] [CrossRef]
Preprints 84158 g001
Figure 1. (a) Model adsorber comprising a double-wall azobenzene-containing polymer brush. The case of 16 polymers on each wall is shown, each polymer has backbone length of l b b = 10 and contains 5 azobenzene beads. Black spheres represent grafted monomers, red spheres represent polymer backbone and spacer beads, blue spherocylinders mimic trans-azobenzene units. (b) Model LDL particle: gray sphere represents central uniform core, brown spherocylinders mimic model phospholipid units. (c) The same but shown as being cut through the centre of a a core. Note that the scale in (a) is different of that in (b) and (c).
Figure 1. (a) Model adsorber comprising a double-wall azobenzene-containing polymer brush. The case of 16 polymers on each wall is shown, each polymer has backbone length of l b b = 10 and contains 5 azobenzene beads. Black spheres represent grafted monomers, red spheres represent polymer backbone and spacer beads, blue spherocylinders mimic trans-azobenzene units. (b) Model LDL particle: gray sphere represents central uniform core, brown spherocylinders mimic model phospholipid units. (c) The same but shown as being cut through the centre of a a core. Note that the scale in (a) is different of that in (b) and (c).
Preprints 84158 g001
Preprints 84158 g002
Figure 2. Illustration of the interaction potential V SAP [ d ′ ( q i j ) ] between two beads of any type shown for a range of effective dimensionless well depths ϵ ′ ( q i j ) (respective cutoffs d c ′ are indicated via vertical dashed lines). d ′ ( q i j ) is the minimum distance between the beads cores, which reduces to the dimensionless separation r i j ′ between the centers for the case of two interacting spherical beads. At the well depth approaching zero, ϵ ′ ( q i j ) → 0 , the potential V SAP [ d ′ ( q i j ) ] turns into a purely repulsive potential V SRP [ d ′ ( q i j ) ] , Eq. (3), see blue curve in the plot.
Figure 2. Illustration of the interaction potential V SAP [ d ′ ( q i j ) ] between two beads of any type shown for a range of effective dimensionless well depths ϵ ′ ( q i j ) (respective cutoffs d c ′ are indicated via vertical dashed lines). d ′ ( q i j ) is the minimum distance between the beads cores, which reduces to the dimensionless separation r i j ′ between the centers for the case of two interacting spherical beads. At the well depth approaching zero, ϵ ′ ( q i j ) → 0 , the potential V SAP [ d ′ ( q i j ) ] turns into a purely repulsive potential V SRP [ d ′ ( q i j ) ] , Eq. (3), see blue curve in the plot.
Preprints 84158 g002
Preprints 84158 g003
Figure 3. Snapshots showing the adsorption dynamics of LDLs on the double-wall brush composed of the side-chain polymers of the backbone length l b b = 10 (5 side chains in each chain terminated by the azobenzene bead) at grafting density ρ g = 0.02 under visible light. (a), (b), and (c) visualize the system after 1 ns , 10 ns , and 40 ns , respectively. Color coding of all beads is introduced in Figure 1.
Figure 3. Snapshots showing the adsorption dynamics of LDLs on the double-wall brush composed of the side-chain polymers of the backbone length l b b = 10 (5 side chains in each chain terminated by the azobenzene bead) at grafting density ρ g = 0.02 under visible light. (a), (b), and (c) visualize the system after 1 ns , 10 ns , and 40 ns , respectively. Color coding of all beads is introduced in Figure 1.
Preprints 84158 g003
Preprints 84158 g004
Figure 4. Density profiles for azobenzenes of a brush, ρ a z ( z ) , and for phospholipids of LDLs, ρ p h ( z ) , shown for the case of the backbone length l b b = 16 and three grafting densities: ρ g = 0.019 , 0.076 , and 0.135 . Note gradual expulsion of LDL phospholipids away from the brush-rich regions towards the center of a pore with the increase of ρ g .
Figure 4. Density profiles for azobenzenes of a brush, ρ a z ( z ) , and for phospholipids of LDLs, ρ p h ( z ) , shown for the case of the backbone length l b b = 16 and three grafting densities: ρ g = 0.019 , 0.076 , and 0.135 . Note gradual expulsion of LDL phospholipids away from the brush-rich regions towards the center of a pore with the increase of ρ g .
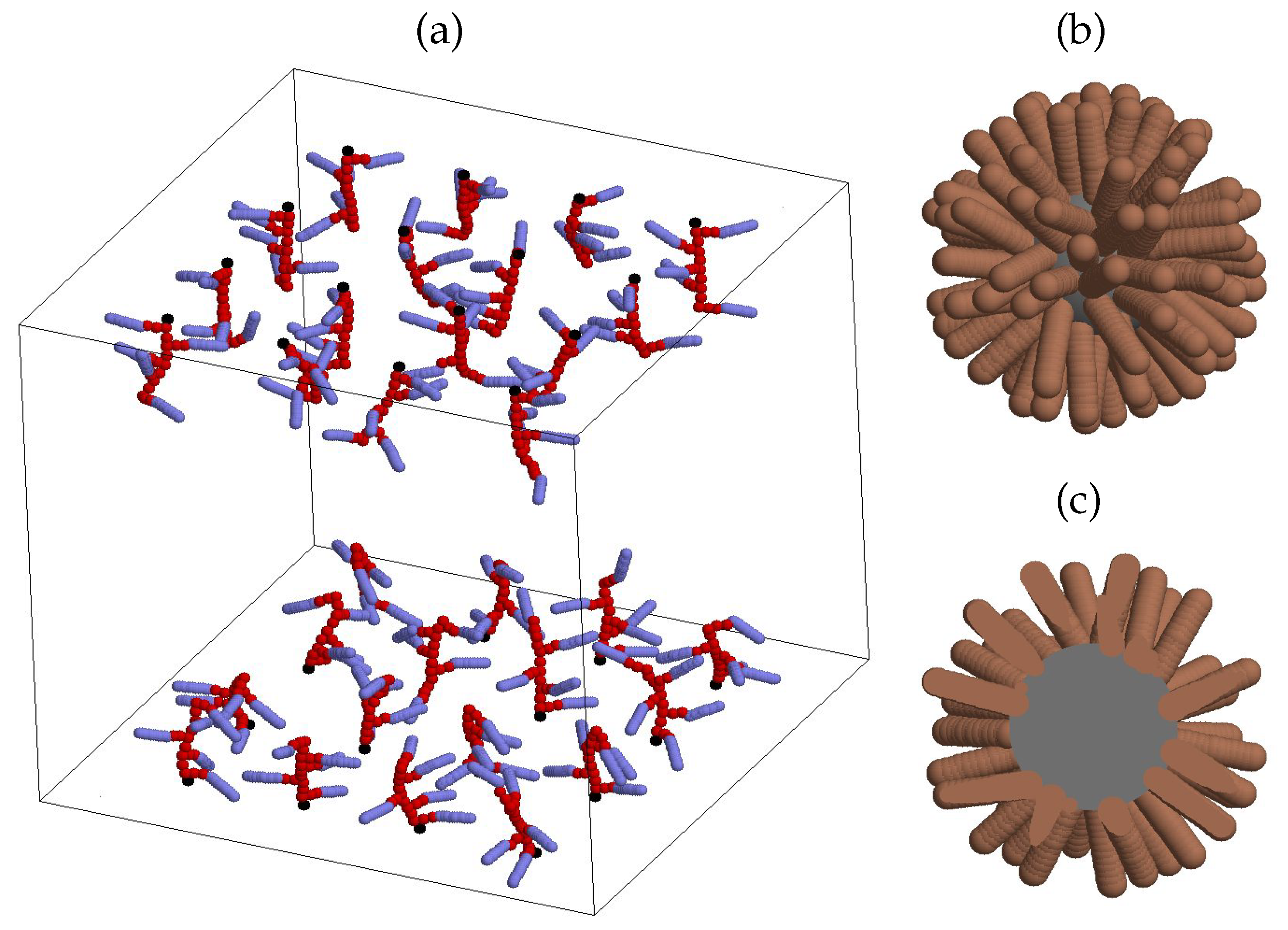
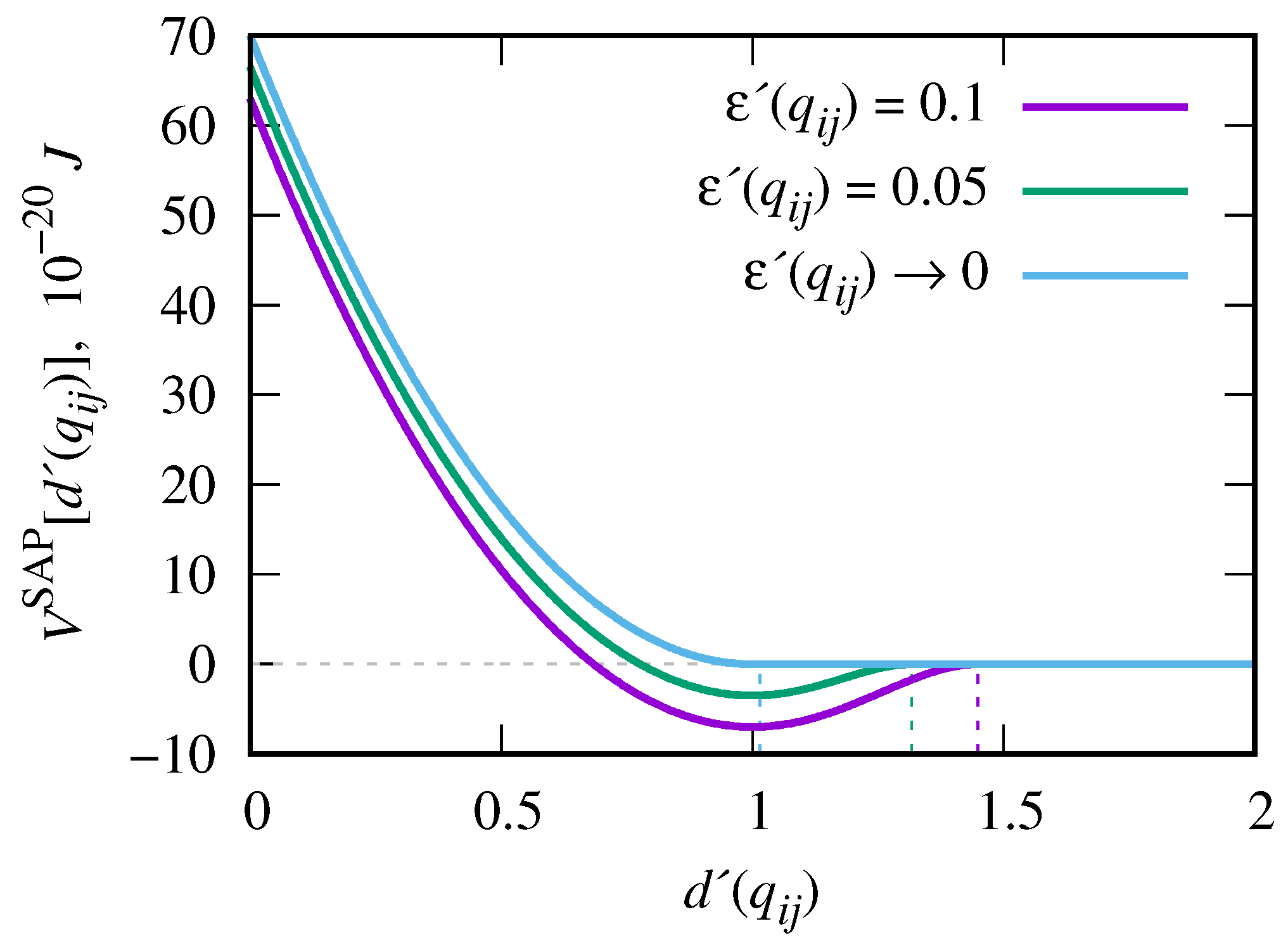
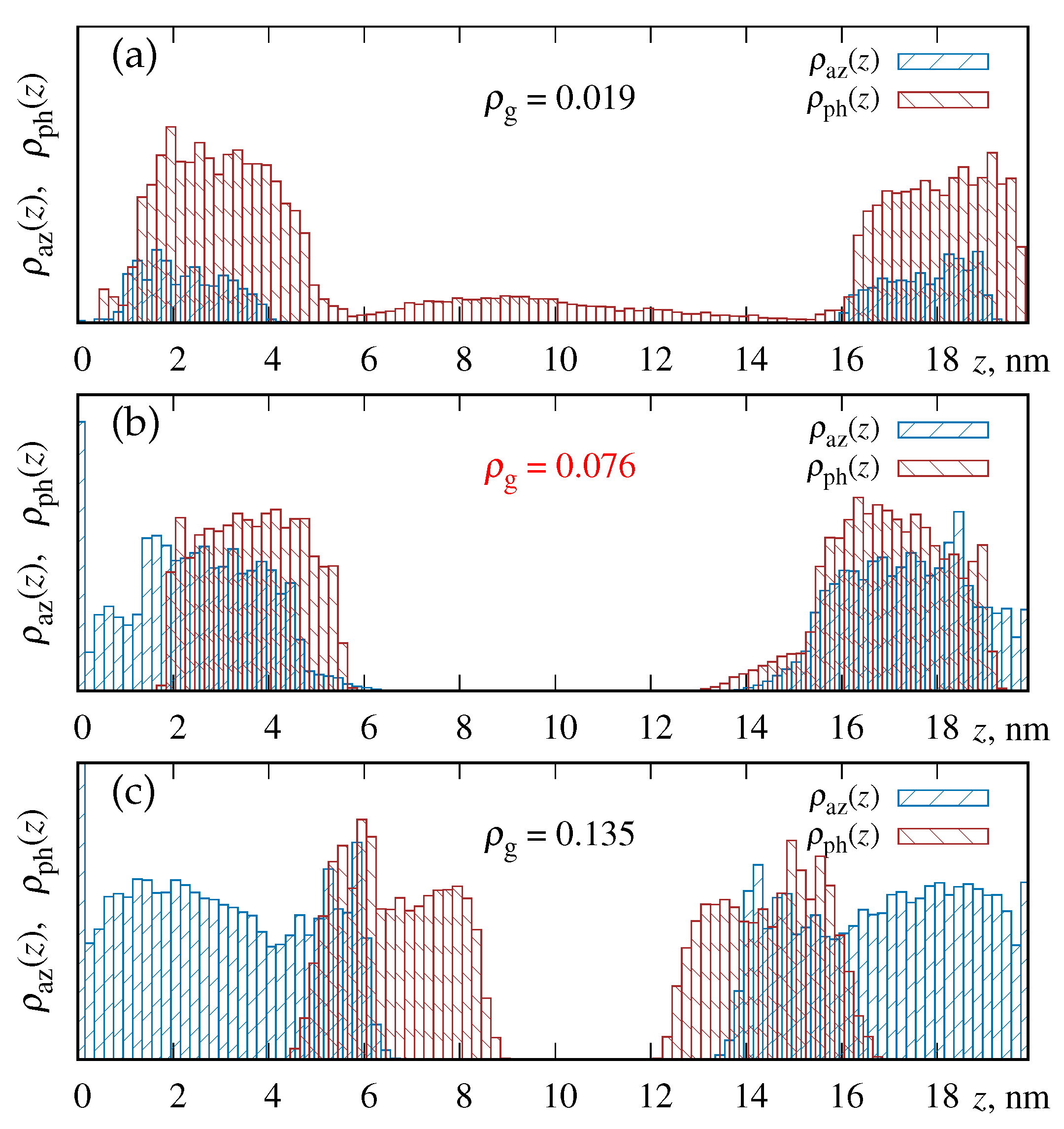
Preprints 84158 g004
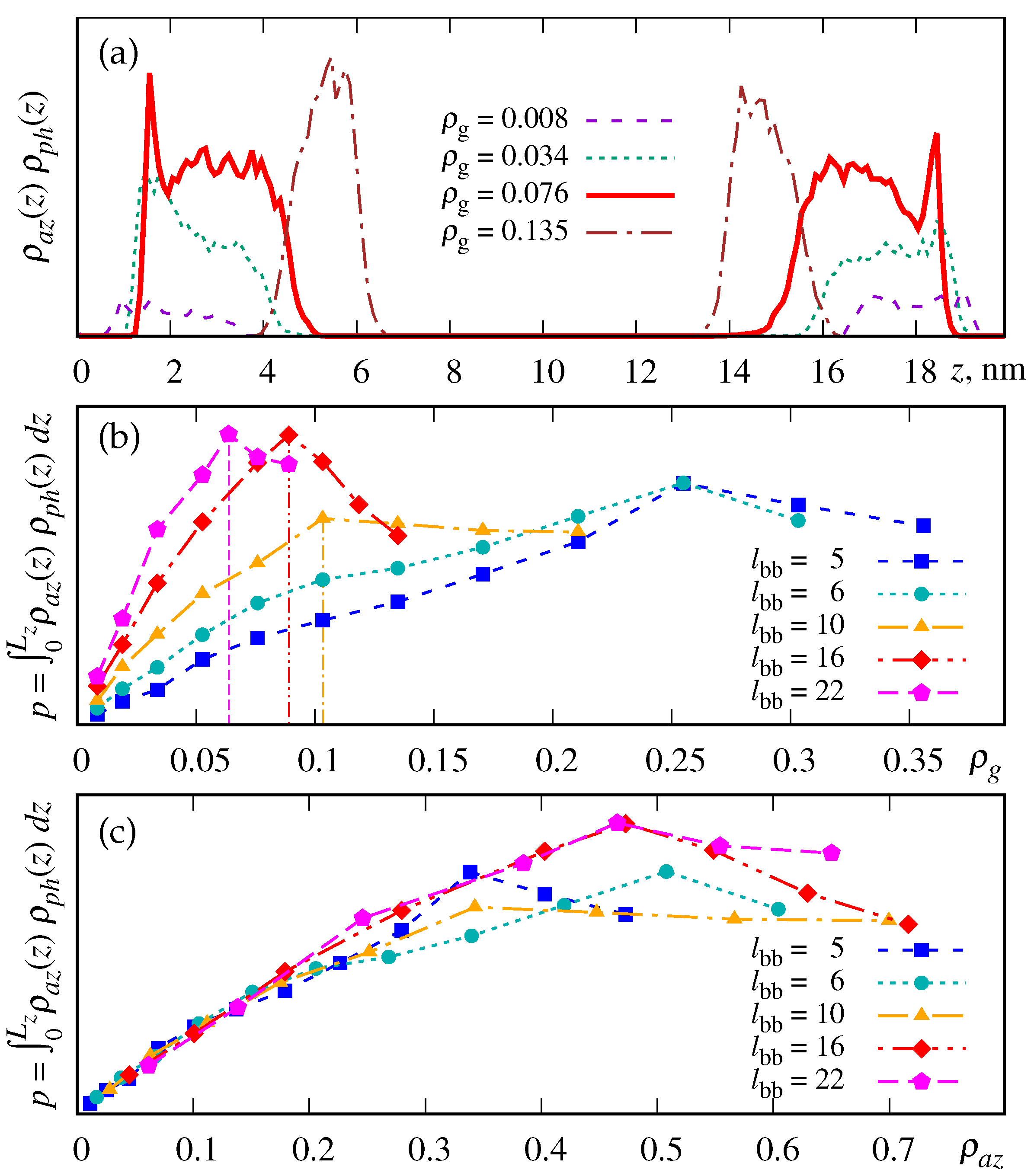
Preprints 84158 g005
Figure 5. (a) Joint probability ρ a z ( z ) ρ p h ( z ) profile for the backbone length l b b = 16 displayed at the set of grafting densities ρ g indicated in the plot. (b) The integral p of a joint probability defined in Eq. (7) as a function of grafting density ρ g at various backbone lengths l b b . Indicated maxima positions are: ρ g * = 0.103 , 0.089 , and 0.064 for the backbone lengths l b b = 10 , 16, and 22, respectively. (c) The same as in (b) expressed as the function of a surface number density of azobenzenes, ρ a z , in a brush.
Figure 5. (a) Joint probability ρ a z ( z ) ρ p h ( z ) profile for the backbone length l b b = 16 displayed at the set of grafting densities ρ g indicated in the plot. (b) The integral p of a joint probability defined in Eq. (7) as a function of grafting density ρ g at various backbone lengths l b b . Indicated maxima positions are: ρ g * = 0.103 , 0.089 , and 0.064 for the backbone lengths l b b = 10 , 16, and 22, respectively. (c) The same as in (b) expressed as the function of a surface number density of azobenzenes, ρ a z , in a brush.
Preprints 84158 g005
Preprints 84158 g006
Figure 6. (a) Binding energy per single LDL particle, E bind , in units of k B T , as the function of the grafting density ρ g . Indicated maxima positions, ρ g * = 0.103 , 0.089 , and 0.064 , for the backbone length l b b = 10 , 16, and 22, respectively, are the same as in Figure 5 (b). (b) the same expressed as the function of the azobenzene surface density ρ a z given by Eq. (8). Backbone lengths l b b are indicated in the figure.
Figure 6. (a) Binding energy per single LDL particle, E bind , in units of k B T , as the function of the grafting density ρ g . Indicated maxima positions, ρ g * = 0.103 , 0.089 , and 0.064 , for the backbone length l b b = 10 , 16, and 22, respectively, are the same as in Figure 5 (b). (b) the same expressed as the function of the azobenzene surface density ρ a z given by Eq. (8). Backbone lengths l b b are indicated in the figure.
Preprints 84158 g006
Preprints 84158 g007
Figure 7. A fragment of a snapshot with the focus on polymer bending in a form of “wrap over” the LDL particle during the adsorption of the latter. The case of l b b = 22 is shown.
Figure 7. A fragment of a snapshot with the focus on polymer bending in a form of “wrap over” the LDL particle during the adsorption of the latter. The case of l b b = 22 is shown.
Preprints 84158 g007
Preprints 84158 g008
Figure 8. Distributions f ( R ) for the radius of curvature, R, evaluated for each backbone by mapping its beads onto a spherical surface. (a), (b), (c), and (d) show the results for the backbone lengths l b b = 6 , 10, 16, and 22, respectively. Specific grafting densities, defined as the maxima positions in Figure 5 (b), are shown via thick black curves.
Figure 8. Distributions f ( R ) for the radius of curvature, R, evaluated for each backbone by mapping its beads onto a spherical surface. (a), (b), (c), and (d) show the results for the backbone lengths l b b = 6 , 10, 16, and 22, respectively. Specific grafting densities, defined as the maxima positions in Figure 5 (b), are shown via thick black curves.
Preprints 84158 g008
Preprints 84158 g009
Figure 9. Snapshots visualizing the role of a backbone length, l b b = 10 , 16, and 22, in adsorption of LDLs. In each case the respective optimal grafting density obtained in Figure 5 (c) and 6 (b) is used.
Figure 9. Snapshots visualizing the role of a backbone length, l b b = 10 , 16, and 22, in adsorption of LDLs. In each case the respective optimal grafting density obtained in Figure 5 (c) and 6 (b) is used.
Preprints 84158 g009
Preprints 84158 g010
Figure 10. Snapshots visualizing the role of grafting density in adsorption of LDLs at a fixed backbone length l b b = 16 . (a) optimal grafting density of ρ g = 0.089 , and (b) higher grafting density of ρ g = 0.135 .
Figure 10. Snapshots visualizing the role of grafting density in adsorption of LDLs at a fixed backbone length l b b = 16 . (a) optimal grafting density of ρ g = 0.089 , and (b) higher grafting density of ρ g = 0.135 .
Preprints 84158 g010
Preprints 84158 g011
Figure 11. Snapshots showing the desorption dynamics of LDLs on the double-wall brush composed of the side-chain polymers of the backbone length l b b = 10 (5 side chains in each chain terminated by the azobenzene bead) at grafting density ρ g * = 0.103 under UV light. (a) visualizes the initial system with adsorbed LDLs, (b) and (c) the system after illumination for 0.6 ns and 4 ns , respectively. Yellow scpherocylinders represent beads with the properties of cis-isomers of azobenzene.
Figure 11. Snapshots showing the desorption dynamics of LDLs on the double-wall brush composed of the side-chain polymers of the backbone length l b b = 10 (5 side chains in each chain terminated by the azobenzene bead) at grafting density ρ g * = 0.103 under UV light. (a) visualizes the initial system with adsorbed LDLs, (b) and (c) the system after illumination for 0.6 ns and 4 ns , respectively. Yellow scpherocylinders represent beads with the properties of cis-isomers of azobenzene.
Preprints 84158 g011
Preprints 84158 g012
Figure 12. (a) Time evolution of the global probability for azobenzene and phospholipid to be found at the same distance z from the bottom wall, p, see Eq. (7), during the process of adsorption under normal conditions. Three cases of the backbone length l b b are shown at their respective optimal densities, see Section 3. (b) the same during the process of desorption under UV light.
Figure 12. (a) Time evolution of the global probability for azobenzene and phospholipid to be found at the same distance z from the bottom wall, p, see Eq. (7), during the process of adsorption under normal conditions. Three cases of the backbone length l b b are shown at their respective optimal densities, see Section 3. (b) the same during the process of desorption under UV light.
Preprints 84158 g012
Table 1. Force field parameters, derived in Refs. [54,56]
Table 1. Force field parameters, derived in Refs. [54,56]
parameter description value
σ c core diameter 2.14 nm
σ monomer and solvent bead diameter 0.46 nm
D azobenzene and phospholipid cap diameter 0.37 nm
L / D azobenzene and phospholipid aspect ratio 3
U energy factor for regular repulsion 70 · 10 − 20 J
U ′ energy factor for strong repulsion 140 · 10 − 20 J
U a ′ attractive energy parameter 21.43
ϵ 1 ′ attractive energy parameter 1.714
ϵ 2 ′ attractive energy parameter − 1.714
m c core mass 62.44 · 10 − 25 k g
m monomer and solvent bead mass 0.70 · 10 − 25 k g
m a azobenzene and phospholipid mass 3.94 · 10 − 25 k g
I a azobenzene and phospholipid moment of inertia 6.00 · 10 − 24 k g
l c p bond length: core – phospholipid 1.82 nm
l bond length: monomer-monomer 0.36 nm
l a bond length: last spacer bead – azobenzene 0.3 nm
k b bond spring constant 5000 · 10 − 20 J / nm 2
θ pseudo-valent angle at branching points π / 2
k a pseudo-valent angle spring constant 20 · 10 − 20 J / r a d 2
ζ terminal angle for azobenzene and phospholipid 0
k z terminal angle for azobenzene and phospholipid spring constant 20 · 10 − 20 J / r a d 2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated