Submitted:
04 September 2023
Posted:
06 September 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
- We propose a deep learning method based on iterative dual-scale attentional fusion (iDAF), which complements the properties and complementarity of multimodal information with each other to achieve better recognition.
- We design two embedding layers to extract the local and global information, extracting information that promotes recognition from different-sized respective fields. The extracted features are sent into the iterative Dual-scale channel attention module (iDCAM), which consist of the local and global branch. The branches respectively focus on the details of the high-level features and the variability across modalities.
- Experiments on the RML2016.10A dataset demonstrate the validity and rationalization of iDAF. The highest accuracy amount of 93.5% is achieved at 10dB and the recognition accuracy is 0.6232 at full SNR.
2. Related works
2.1. Research on traditional AMR methods
2.2. Study of different inputs and DL-models
3. The Proposed Method
3.1. Data Preprocessing
- In-phase/orthogonal (IQ): Generally, the receiver stores the signal in the modality of I/Q to facilitate mathematical operation and hardware design, which is expressed as follows:where I and Q represent the in-phase and quadrature components, and refer to the real and imaginary parts of the signal, respectively.
- Amplitude/phase(AP): Calculate the instantaneous amplitude and phase of the signal, expressed as:where the values of n are .
- Spectrum (SP): The spectrum expresses the change of frequency over time, which is an important discrimination of different modulations. the calculation of the spectrum is expressed as:where n represents the n-th power of the spectrum, including 1, 2, 4 which are corresponding to the welch spectrum, square spectrum, and fourth power spectrum. Here, M1 and M2 represent signal waveform and frequency, and M3 refers to signal time-frequency characteristics. The feature vectors of the three modalities were normalized into (batchsize x 128).
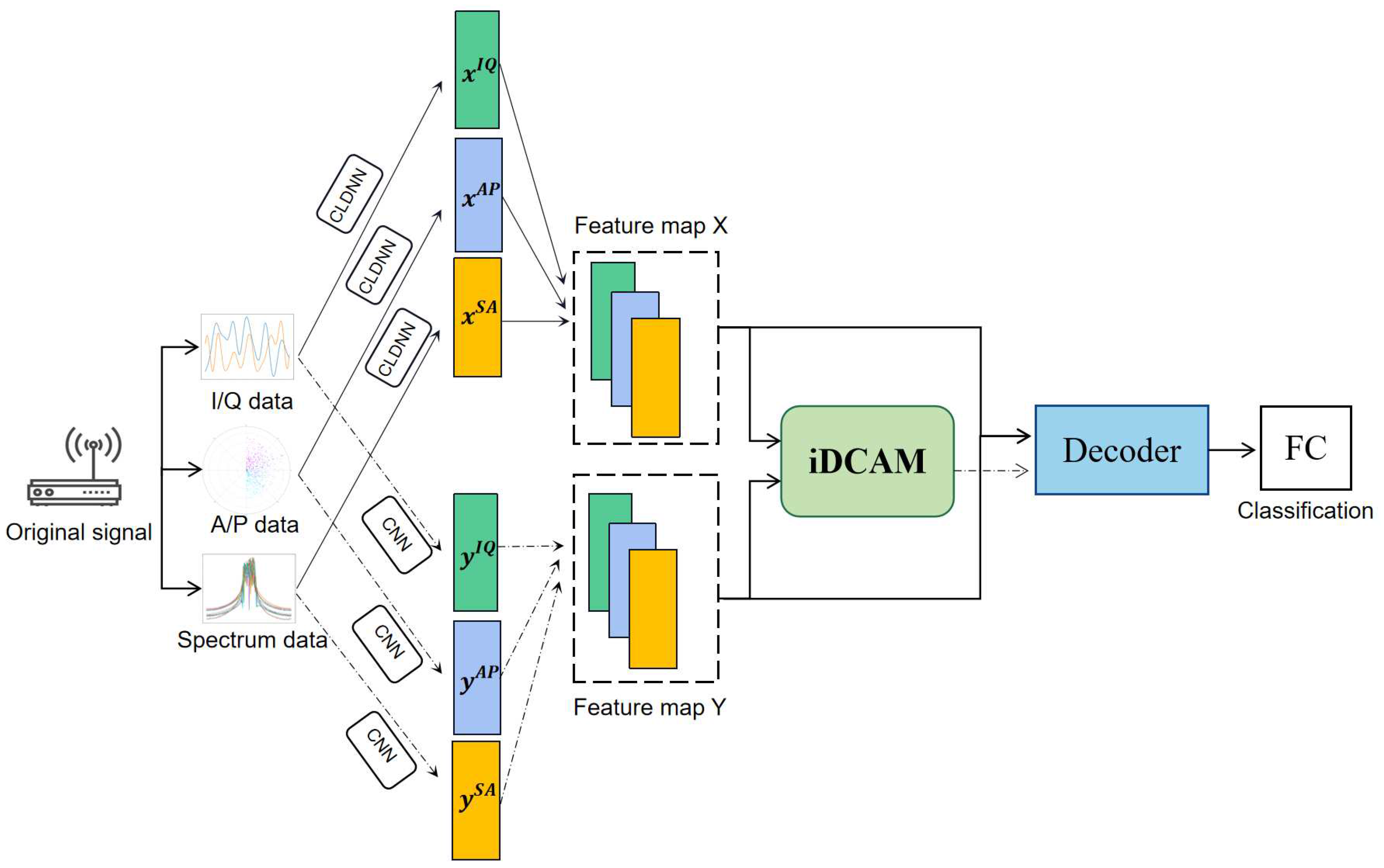
3.2. Iterative dual-channel attention fusion (iDAF)
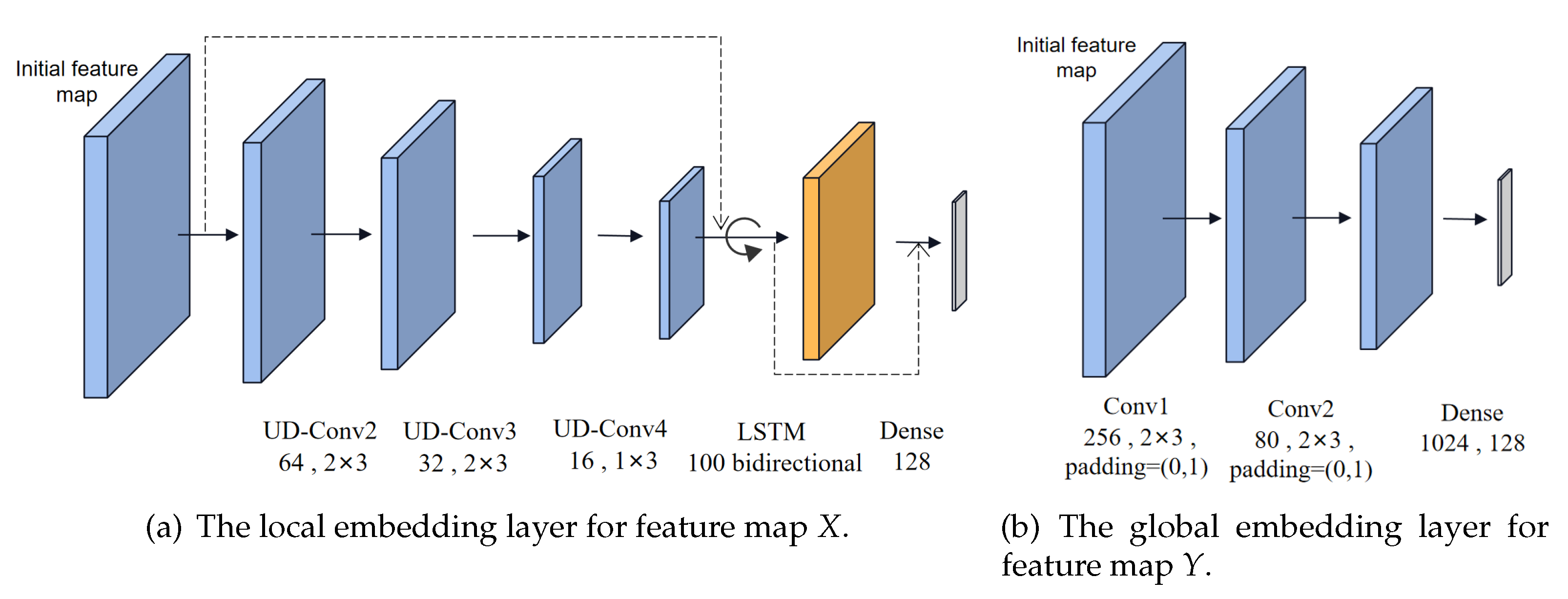
3.2.1. Data embedding

3.2.2. Dual-scale channel attention module
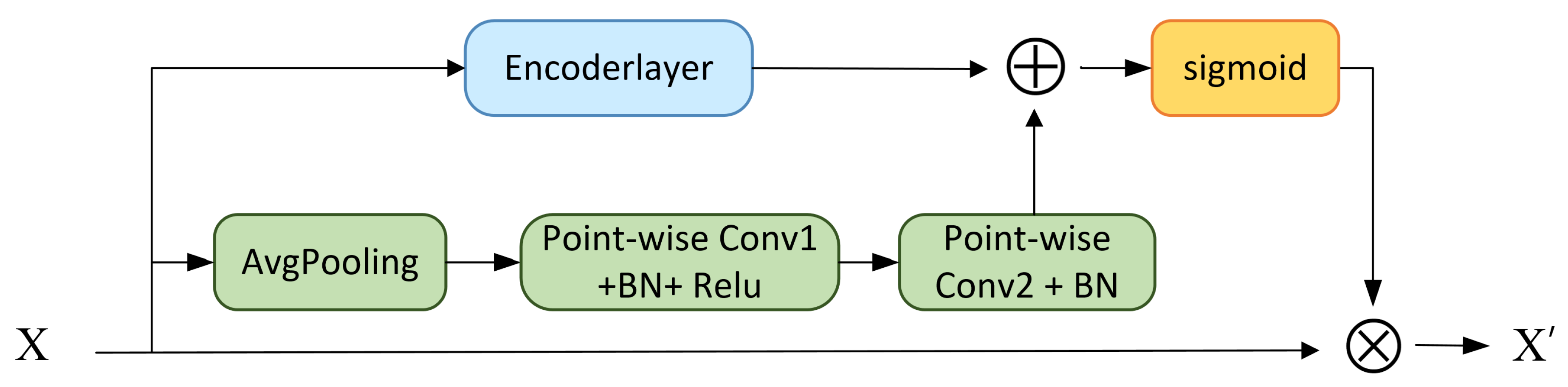
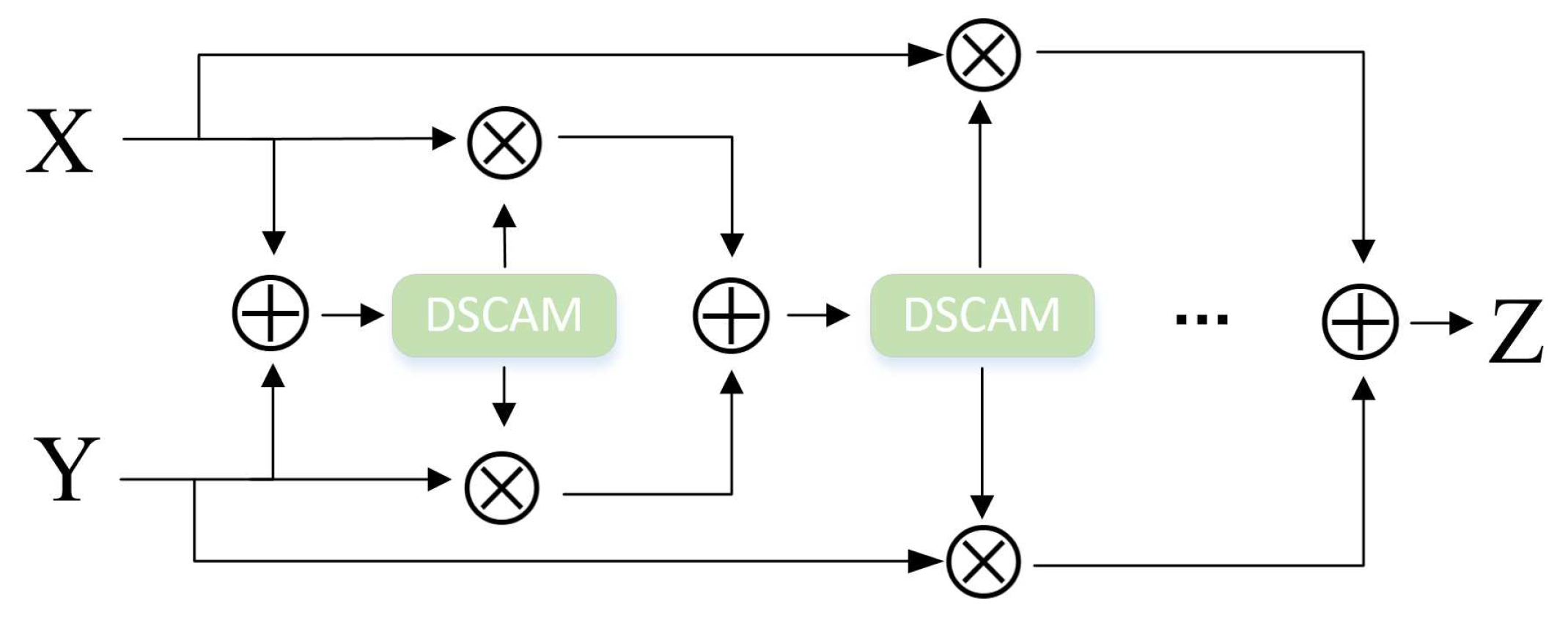
3.2.3. Iteritive dual-scale attentional module
3.2.4. Residual encoder
4. Experiment Results and Discussion
4.1. Datasets and implement details
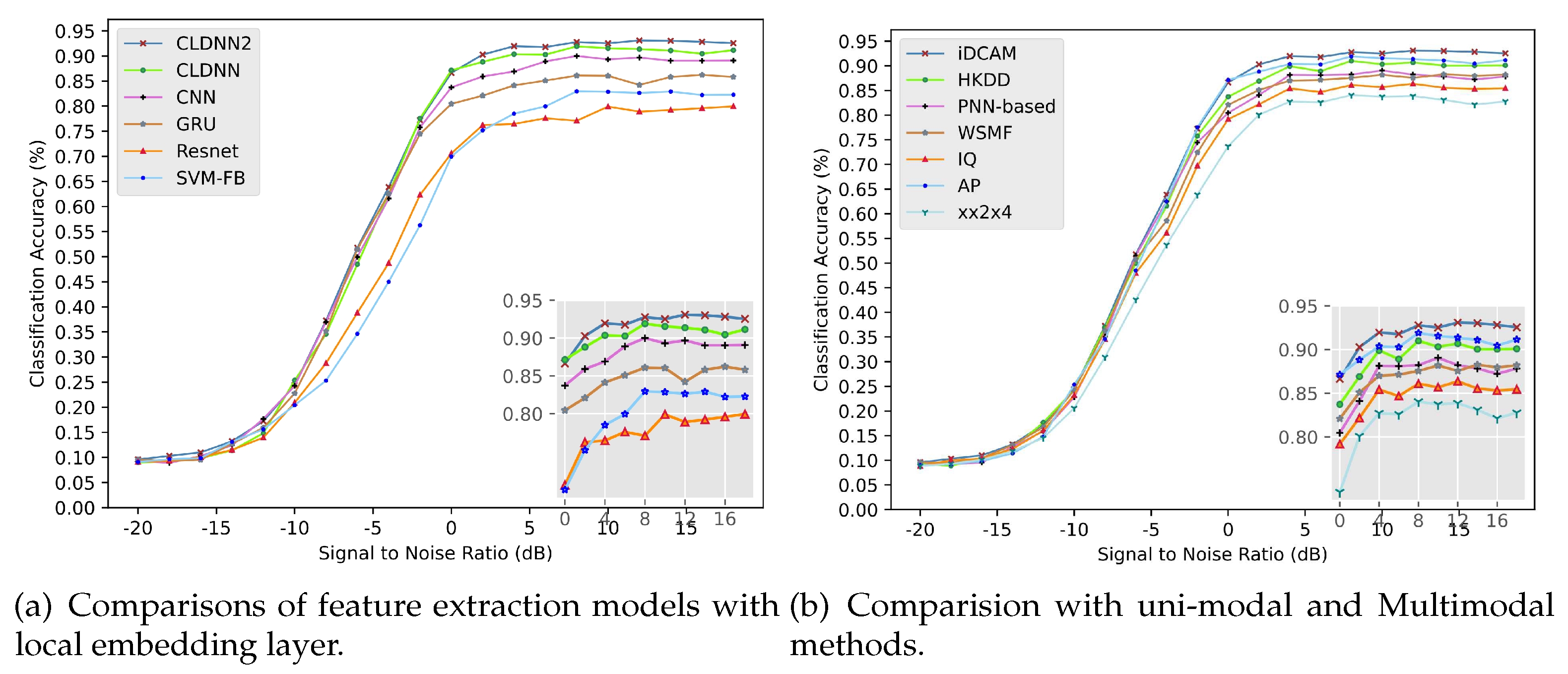
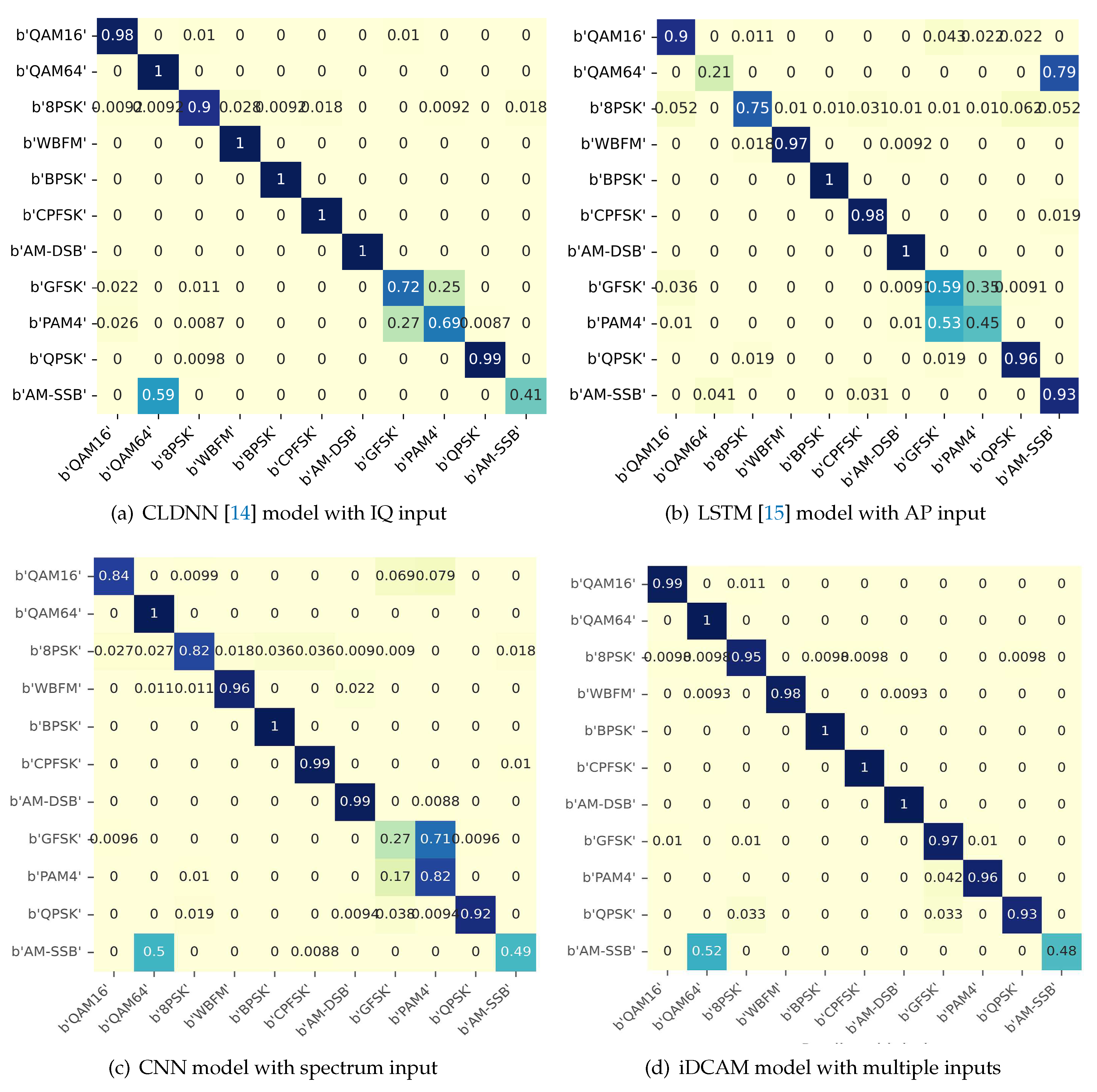
4.2. Comparative validity experiments
4.2.1. Compare local embedding layer with other feature extraction networks
4.2.2. Compare iDCAM and other attention mechanisms
4.2.3. Comparison with unimodal and multimodal methods
4.3. Abaltion studys
4.3.1. Ablation experiments at different scales with DCAM
4.3.2. Ablation experiments with iterative layers of iDSACM
5. Conclusion
Conflicts of Interest
References
- Dai, A.; Zhang, H.; Sun, H. Automatic modulation classification using stacked sparse auto-encoders. In Proceedings of the 2016 IEEE 13th international conference on signal processing (ICSP). IEEE; 2016; pp. 248–252. [Google Scholar]
- Al-Nuaimi, D.H.; Hashim, I.A.; Zainal Abidin, I.S.; Salman, L.B.; Mat Isa, N.A. Performance of feature-based techniques for automatic digital modulation recognition and classification—A review. Electronics 2019, 8, 1407. [Google Scholar] [CrossRef]
- Bhatti, F.A.; Khan, M.J.; Selim, A.; Paisana, F. Shared spectrum monitoring using deep learning. IEEE Transactions on Cognitive Communications and Networking 2021, 7, 1171–1185. [Google Scholar] [CrossRef]
- Richard, G.; Wiley, E. The interception and analysis of radar signals. Artech House, Boston 2006.
- Kim, K.; Spooner, C.M.; Akbar, I.; Reed, J.H. Specific emitter identification for cognitive radio with application to IEEE 802.11. In Proceedings of the IEEE GLOBECOM 2008-2008 IEEE Global Telecommunications Conference. IEEE, 2008, pp. 1–5.
- Wei, W.; Mendel, J.M. Maximum-likelihood classification for digital amplitude-phase modulations. IEEE transactions on Communications 2000, 48, 189–193. [Google Scholar] [CrossRef]
- Xu, J.L.; Su, W.; Zhou, M. Likelihood-ratio approaches to automatic modulation classification. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews) 2010, 41, 455–469. [Google Scholar] [CrossRef]
- Hazza, A.; Shoaib, M.; Alshebeili, S.A.; Fahad, A. An overview of feature-based methods for digital modulation classification. In Proceedings of the 2013 1st international conference on communications, signal processing, and their applications (ICCSPA). IEEE; 2013; pp. 1–6. [Google Scholar]
- Hao, Y.; Wang, X.; Lan, X. Frequency Domain Analysis and Convolutional Neural Network Based Modulation Signal Classification Method in OFDM System. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP). IEEE; 2021; pp. 1–5. [Google Scholar]
- Ali, A.; Yangyu, F. Unsupervised feature learning and automatic modulation classification using deep learning model. Physical Communication 2017, 25, 75–84. [Google Scholar] [CrossRef]
- Chang, S.; Huang, S.; Zhang, R.; Feng, Z.; Liu, L. Multitask-learning-based deep neural network for automatic modulation classification. IEEE internet of things journal 2021, 9, 2192–2206. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Corgan, J.; Clancy, T.C. Convolutional radio modulation recognition networks. In Proceedings of the Engineering Applications of Neural Networks: 17th International Conference, EANN 2016, Aberdeen, UK, September 2-5, 2016, Proceedings 17. Springer, 2016, pp. 213–226.
- Ke, Z.; Vikalo, H. Real-time radio technology and modulation classification via an LSTM auto-encoder. IEEE Transactions on Wireless Communications 2021, 21, 370–382. [Google Scholar] [CrossRef]
- Liu, X.; Yang, D.; El Gamal, A. Deep neural network architectures for modulation classification. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers. IEEE; 2017; pp. 915–919. [Google Scholar]
- Rajendran, S.; Meert, W.; Giustiniano, D.; Lenders, V.; Pollin, S. Deep learning models for wireless signal classification with distributed low-cost spectrum sensors. IEEE Transactions on Cognitive Communications and Networking 2018, 4, 433–445. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Gan, C.; Sun, S.; Wang, M. Automatic modulation classification using convolutional neural network with features fusion of SPWVD and BJD. IEEE Transactions on Signal and Information Processing over Networks 2019, 5, 469–478. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, M.; Han, F.; Gong, Y.; Zhang, J. Spectrum analysis and convolutional neural network for automatic modulation recognition. IEEE Wireless Communications Letters 2019, 8, 929–932. [Google Scholar] [CrossRef]
- Shi, F.; Hu, Z.; Yue, C.; Shen, Z. Combining neural networks for modulation recognition. Digital Signal Processing 2022, 120, 103264. [Google Scholar] [CrossRef]
- Fu-qing, H.; Zhi-ming, Z.; Yi-tao, X.; Guo-chun, R. Modulation recognition of symbol shaped digital signals. In Proceedings of the 2008 International Conference on Communications, Circuits and Systems. IEEE; 2008; pp. 328–332. [Google Scholar]
- Zhang, X.; Li, T.; Gong, P.; Liu, R.; Zha, X. Modulation recognition of communication signals based on multimodal feature fusion. Sensors 2022, 22, 6539. [Google Scholar] [CrossRef] [PubMed]
- Qi, P.; Zhou, X.; Zheng, S.; Li, Z. Automatic modulation classification based on deep residual networks with multimodal information. IEEE Transactions on Cognitive Communications and Networking 2020, 7, 21–33. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, H.; Wang, C.; Gan, C.; Xiang, Y. Automatic modulation classification using CNN-LSTM based dual-stream structure. IEEE Transactions on Vehicular Technology 2020, 69, 13521–13531. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 7132–7141.
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Vedaldi, A. Gather-excite: Exploiting feature context in convolutional neural networks. Advances in neural information processing systems 2018, 31. [Google Scholar]
- Gao, Z.; Xie, J.; Wang, Q.; Li, P. Global second-order pooling convolutional networks. In Proceedings of the Proceedings of the IEEE/CVF Conference on computer vision and pattern recognition, 2019, pp. 3024–3033.
- Lee, H.; Kim, H.E.; Nam, H. Srm: A style-based recalibration module for convolutional neural networks. In Proceedings of the Proceedings of the IEEE/CVF International conference on computer vision; 2019; pp. 1854–1862. [Google Scholar]
- Mnih, V.; Heess, N.; Graves, A.; et al. Recurrent models of visual attention. Advances in neural information processing systems 2014, 27. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition; 2018; pp. 7794–7803. [Google Scholar]
- Yang, F.; Yang, L.; Wang, D.; Qi, P.; Wang, H. Method of modulation recognition based on combination algorithm of K-means clustering and grading training SVM. China communications 2018, 15, 55–63. [Google Scholar]
- Hussain, A.; Sohail, M.; Alam, S.; Ghauri, S.A.; Qureshi, I.M. Classification of M-QAM and M-PSK signals using genetic programming (GP). Neural Computing and Applications 2019, 31, 6141–6149. [Google Scholar] [CrossRef]
- Das, D.; Bora, P.K.; Bhattacharjee, R. Blind modulation recognition of the lower order PSK signals under the MIMO keyhole channel. IEEE Communications Letters 2018, 22, 1834–1837. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, G.; Xu, X.; Li, X. The Methods of Recognition for Common Used M-ary Digital Modulations. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing; 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Benedetto, F.; Tedeschi, A.; Giunta, G. Automatic Blind Modulation Recognition of Analog and Digital Signals in Cognitive Radios. In Proceedings of the 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall); 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Jiang, K.; Zhang, J.; Wu, H.; Wang, A.; Iwahori, Y. A novel digital modulation recognition algorithm based on deep convolutional neural network. Applied Sciences 2020, 10, 1166. [Google Scholar] [CrossRef]
- Sainath, T.N.; Vinyals, O.; Senior, A.; Sak, H. Convolutional, Long Short-Term Memory, fully connected Deep Neural Networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2015; pp. 4580–4584. [Google Scholar] [CrossRef]
- Sermanet, P.; LeCun, Y. Traffic sign recognition with multi-scale convolutional networks. In Proceedings of the The 2011 international joint conference on neural networks. IEEE; 2011; pp. 2809–2813. [Google Scholar]
- Soltau, H.; Saon, G.; Sainath, T.N. Joint training of convolutional and non-convolutional neural networks. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE; 2014; pp. 5572–5576. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N. Kaiser, Ł.; Polosukhin, I. Attention is all you need. Advances in neural information processing systems 2017, 30. [Google Scholar]
- Park, J.; Woo, S.; Lee, J.Y.; Kweon, I.S. Bam: Bottleneck attention module. arXiv 2018, arXiv:1807.06514 2018. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the Proceedings of the European conference on computer vision (ECCV), 2018, pp. 3–19.
- Li, X.; Wang, W.; Hu, X.; Yang, J. Selective kernel networks. In Proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019, pp. 510–519.
| Feature domains | Models | Effects |
|---|---|---|
| I/Q | CNN combined with Deep Neural Networks (DNN)[12], a combined CNN scheme[18] | achieve high recognition of PAM4 in low signal-to-noise ratio (SNR) |
| A/P | Long Short Term Memory (LSTM) [15], a LSTM denoising auto-encoder [13] | well recognize AM-SSB, and distinguish between QAM16 and QAM64[19] |
| Spectrum | RSBU-CW with welch spectrum, square spectrum, and fourth power spectrum [20], SCNN [17] with the short-time Fourier transform(STFT), a fine-tuned CNN modelc̃itezhang2019automatic with smooth pseudo-wigner-ville distribution and Born-Jordan distribution | achieve high accuracy of PSK [20], recognize OFDM well which is revealed only in the spectrum domain due to its plentiful sub-carriers [16] |
| Model | Accuracy | Params(M) |
|---|---|---|
| SENet-ResNet18 | 0.6032 | 11.9 |
| SKNet-50 | 0.5994 | 27.6 |
| CBAM-ResNeXt50 | 0.6082 | 27.8 |
| Self-attention | 0.618 | 63.5 |
| BAM-Resnet-50 | 0.6038 | 24.7 |
| iDCAM | 0.6232 | 6.9 |
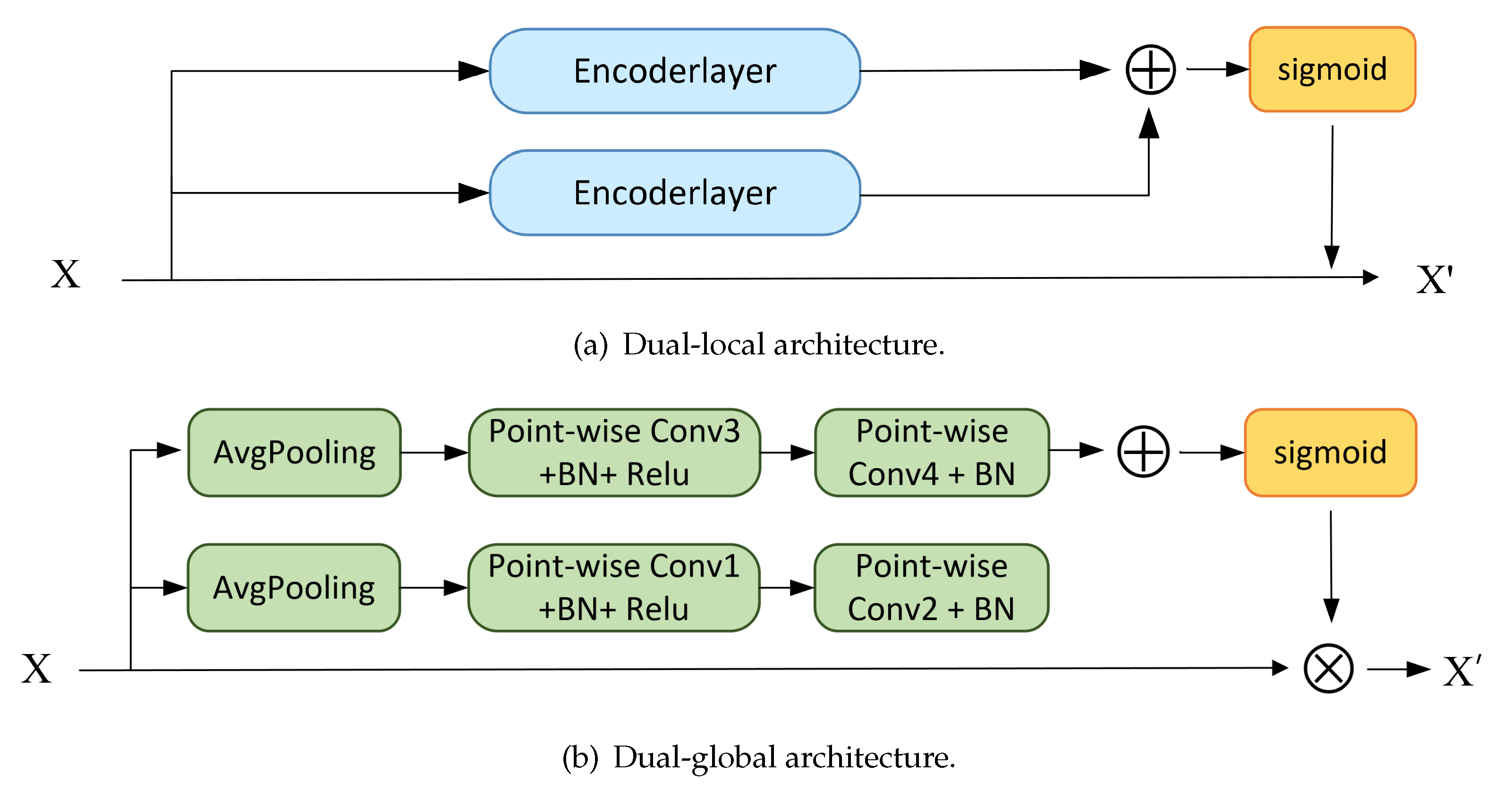
| Architectures | Recognition accuracy | FLOPs (G) |
|---|---|---|
| Local | 0.618 | 10.1 |
| Global | 0.6081 | / |
| Dual-local | 0.6192 | 20.2 |
| Dual-global | 0.6104 | / |
| Local-global | 0.6232 | 10.9 |
| Iterations K | one-layer | two-layer | three-layer | four-layer |
|---|---|---|---|---|
| Accuracy | 0.6194 | 0.6232 | 0.6204 | 0.6181 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





