Preprint

Article

Trajectory Tracking Predictive Control for Unmanned Surface Vehicles with Improved Nonlinear Disturbance Observer

Altmetrics

Downloads

120

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 September 2023

Posted:

05 September 2023

You are already at the latest version

Alerts

Abstract

The motion of Unmanned Surface Vehicles (USVs) is frequently disturbed by the ocean wind, wave and current. A poorly designed controller will lead to failures and even safety problems during actual navigation. In order to obtain satisfied control performance of the motion for the USVs, a Model Predictive Control (MPC) based on improved Nonlinear Disturbance Observer (NDO) is proposed. Firstly, the USV model is approximately linearized and MPC is designed for the multivariable system with constraints. In order to compensate the influence of disturbances, an improved NDO is designed, with which the calculation time for the MPC saved a lot. Finally, comparison experiments are conducted between the MPC with NDO and the MPC with improved NDO, and the results show that they have similar performance to the USVs. However, the proposed method has less parameter to be tuned and it is much more time-saving compared to the MPC with traditional NDO.

Keywords:

Subject: Engineering - Marine Engineering

1. Introduction

Recently, as the continuous development of technology, USVs have been extensive used in various fields. However, due to the disturbances from the sea wind, wave and current, the trajectory tracking control is one of the widespread concern topics. There are many researches about the control for the trajectory tracking technologies of USVs, including PID controller [1,2,3,4], sliding mode control [5,6,7,8], backstepping control [9,10,11,12], MPC [13,14,15,16], adaptive control [17,18,19,20] and intelligent control [21,22,23,24].

MPC has been developed as an advanced optimization control algorithm based on the superiorities of feedback correction and rolling optimization. Therefore, MPC can solve constrained and multivariable problems. Adaptive line-of-sight algorithm was developed to get the expected heading angle. And MPC was applied to reduce the lateral error, where the sideslip angle compensation was considered in [25]. In addition, in order to get accurate state variables in real time, a linear extended state observer was designed to overcome the influence of environment disturbances and the nonlinearity of the model. However, the linearization still caused certain deviation to the model disturbance estimation. In [26], to adjust the controller parameters, the MPC controller was used to carry out both control allocation and trajectory tracking in real-time. In addition, it concurrently optimized the closed loop performance with reinforcement learning-based and system identification methods. In [27], to convert the chance constraints into deterministic convex constraints, a convex conditional value at risk approximation was introduced. And the converted constraints were further transformed into the second order cone constraints. Then, to decline the external disturbances and fulfill the physical constraints, a stochastic model predictive control (SMPC) scheme was used to design the controller. In [28], the path planning and controller of the USVs was designed simultaneously to overcome the disadvantage of the “first planning then tracking” structure, and the artificial potential field and MPC was combined to solve the planning and tracking problem. In [29], finite control set model predictive control (FCS-MPC) was proposed. The more practical control commands formed a limited set of control: the thruster propulsion angle and speed about the USV. And a fast and safe collision avoidance system was designed according to the basic of FCS-MPC, which was applicable for varying environment.

The controllers are usually poorly tuned for the USV motion system and the disturbance rejection performance of controllers is not satisfactory due to the disturbances from the ocean wave, wind and current. Therefore, an improved NDO based MPC method for trajectory tracking control of USV is proposed in this paper. Firstly, the model predictive controller is designed for the USV trajectory tracking. Then, NDO is designed to estimate the disturbance of ocean wind, wave and current, which has less parameters. And, the Lyapunov stability is analyzed for the overall system. Finally, the proposed method is verified by simulation experiments. The main contributions of this work can be summarized as follows: the disturbances are compensated with an improved NDO, and better trajectory tracking performance are obtained for the USVs; also, with the improved NDO, the calculation time is saved compared with the traditional NDO.

The following of the paper is structured as follows: Section 2 introduces the USV kinematics model and dynamic model. In Section 3, the improved NDO based MPC is designed for the USV and Lyapunov stability is analyzed for the overall system. Comparison experiments and results discussion are performed in Section 4. Section 5 presents the conclusions.

2. State Space Model of Unmanned Surface Vehicle

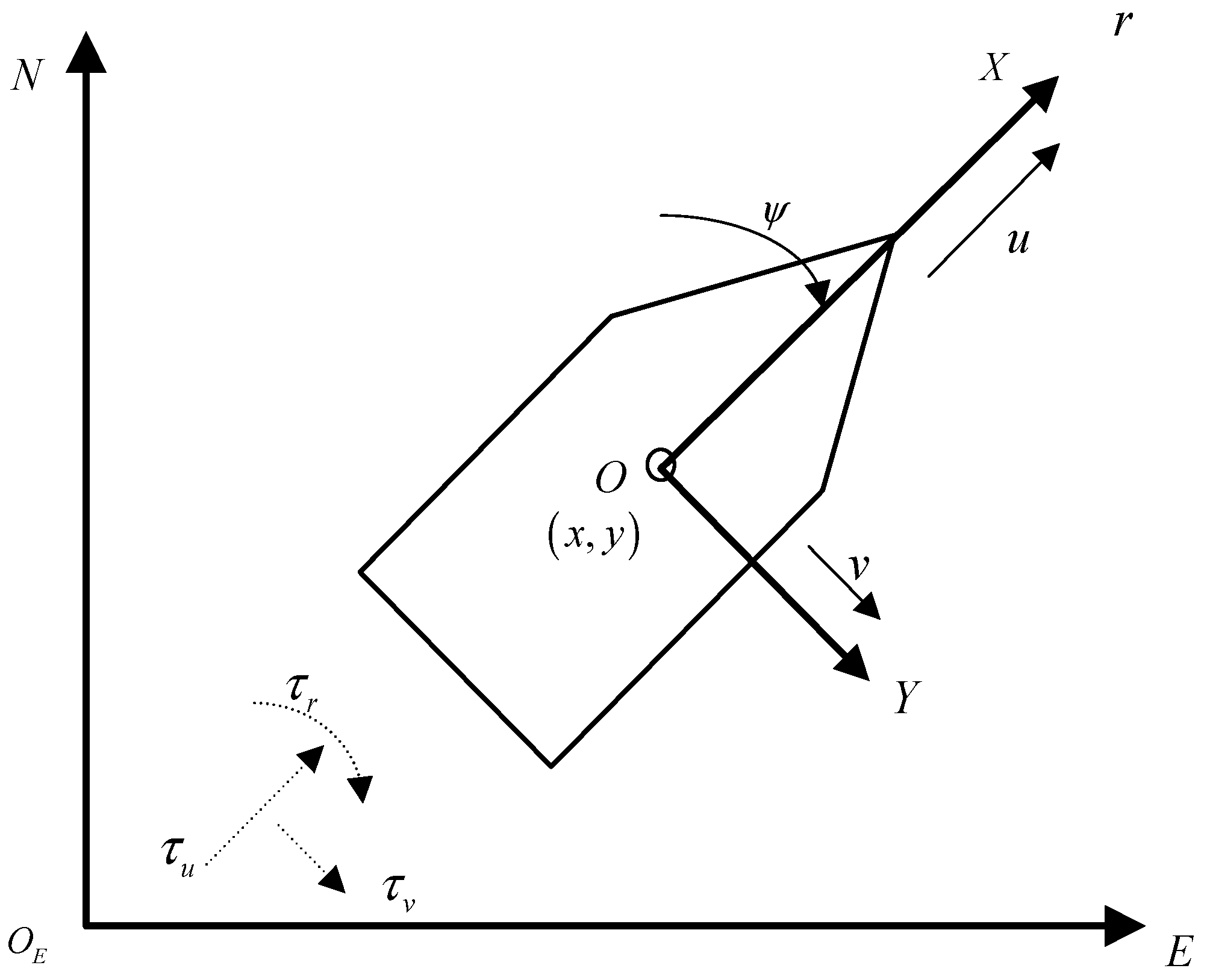
In general, the kinematics modeling of USV is represented in the North East Down coordinate system, while the dynamics model is built in the ship coordinate system. Among them, the North East Down coordinate system is also called the geodetic coordinate system or the inertial coordinate system. It is usually used as the reference system, and any point on the sea can be used as the origin of the geodetic coordinate system. The ship coordinate system changes with the motion of the ship and can describe the force, moment, linear velocity, and angular velocity of the unmanned ship in various degrees of freedom.

In order to simplify the model, a USV model is utilized with three degrees of freedom for trajectory tracking control. The motions of yaw, surge and sway are the most important for the trajectory tracking of the USVs, so the roll, pitch, and heave of the USVs are ignored. Thus, the USV model can be represented, in the ship coordinate system and the geodetic coordinate system, and it is shown in Figure 1.

In Figure 1, it can be seen the North East Down coordinate system is represented by

N O_{E} E

, and the coordinate system for the ship is described by

X O Y

. The kinematics and dynamics model of the ship can be obtained as:

\dot{η} = R (ψ) υ

(1)

M \dot{υ} + C (υ) υ + D (υ) υ = τ + τ_{d}

(2)

where

η = {[x, y, ψ]}^{T}

represents the

x

y

position and heading angle vector of USV in the inertial coordinate system;

x

and

y

represent the position of the ship with regard to the North East Down coordinate system,

ψ

represents the yaw angle information of USV;

υ = {[u, v, r]}^{T}

is the vector of the velocity and angular velocity for USV in the ship coordinate system,

u

v

and

r

are the surge velocity, sway velocity and yaw angular velocity of USV, respectively;

τ_{u}

τ_{v}

and

τ_{r}

represent the surge thrust, sway thrust and yaw moment, which are the control inputs of the system;

τ_{d} = {[τ_{u d}, τ_{v d}, τ_{r d}]}^{T}

is corresponding thrust and moment caused by the time-varying external disturbances.

R (ψ)

is the rotation matrix with the relationship of

R^{- 1} (ψ) = R^{T} (ψ)

;

M

represents the inertial matrix of USV, where

M = M^{T} > 0

;

C (υ)

represents the Coriolis centripetal force matrix, and

C (υ) = - C {(υ)}^{T}

;

D (υ)

is the nonlinear hydrodynamic damping matrix. The detailed information for the matrixes is shown as follows:

R (ψ) = [\begin{matrix} \cos ψ & - \sin ψ & 0 \\ \sin ψ & \cos ψ & 0 \\ 0 & 0 & 1 \end{matrix}] ， M = [\begin{matrix} m_{11} & 0 & 0 \\ 0 & m_{22} & m_{23} \\ 0 & m_{32} & m_{33} \end{matrix}]

(3)

C (υ) = [\begin{matrix} 0 & 0 & - m_{22} υ \\ 0 & 0 & m_{11} u \\ m_{22} υ & - m_{11} u & 0 \end{matrix}] ， D (υ) = - [\begin{matrix} d_{11} & 0 & 0 \\ 0 & d_{22} & d_{23} \\ 0 & d_{32} & d_{33} \end{matrix}]

(4)

According to equation (3) and (4), the reduced kinematics and dynamics equations can be obtained as:

\{\begin{cases} \dot{x} = u \cos ψ - v \sin ψ \\ \dot{y} = u \sin ψ + v \cos ψ \\ \dot{ψ} = r \end{cases}

(5)

\{\begin{cases} m_{11} \dot{u} - m_{22} v r + d_{11} u = τ_{u} + τ_{u d} \\ m_{22} \dot{v} + m_{23} \dot{r} + m_{11} u r + d_{22} v + d_{23} r = τ_{v} + τ_{v d} \\ m_{32} \dot{v} + m_{33} \dot{r} + (m_{22} - m_{11}) u v + d_{32} v + d_{33} r = τ_{r} + τ_{r d} \end{cases}

(6)

For the USVs, there are constraints for the actuators and the outputs. And they are described as follows.

The increment constraints for inputs can be represented as:

\begin{matrix} Δ u_{\min} (t + k) \leq Δ u (t + k) \leq Δ u_{\max} (t + k) \\ k = 0, 1, \dots, N_{c} - 1 \end{matrix}

(7)

where

N_{c}

denotes the control horizon.

The upper and lower limits constraints for inputs can be represented as:

\begin{matrix} u_{\min} (t + k) \leq u (t + k) \leq u_{\max} (t + k) \\ k = 0, 1, \dots, N_{c} - 1 \end{matrix}

(8)

The outputs of speed increment constraints can be represented as:

\begin{matrix} Δ υ_{\min} (t + k) \leq Δ υ (t + k) \leq Δ υ_{\max} (t + k) \\ k = 0, 1, \dots, N_{c} - 1 \end{matrix}

(9)

The outputs of speed upper and lower limit constraints can be represented as:

\begin{matrix} υ_{\min} (t + k) \leq υ (t + k) \leq υ_{\max} (t + k) \\ k = 0, 1, \dots, N_{c} - 1 \end{matrix}

(10)

The terminal equality constraint can be represented as:

{‖η (k + N |t) - η_{r} (k + N |t)‖}_{Q}^{2} = 0

(11)

where

η

denotes the vector to be controlled,

η_{r}

denotes the reference trajectory.

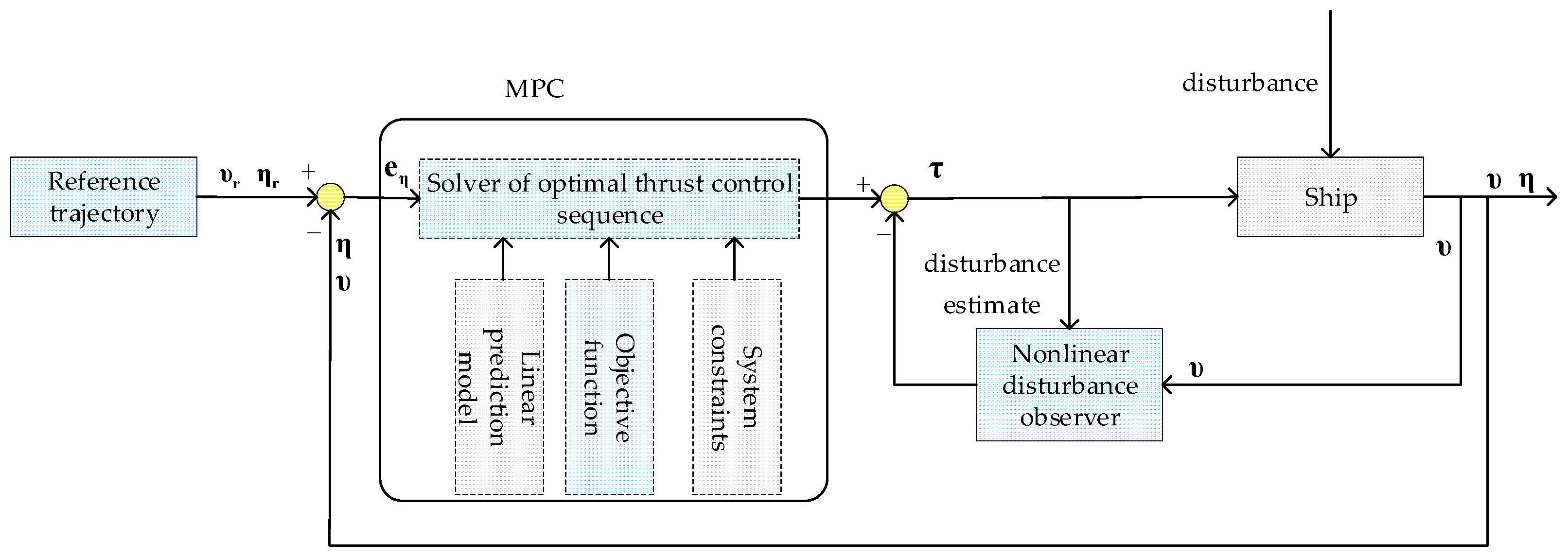
3. Nonlinear Disturbance Observer based Model Predictive Control

In this section, NDO based MPC is designed for the three degree of freedom kinematics and dynamics of USV with state space model. The design schematic diagram of NDO based MPC is shown in Figure 2.

According to equation (1) and (2), the state space equation for the ship is rewritten as as:

\{\begin{cases} \dot{η} = R (φ) υ \\ \dot{υ} = M^{- 1} (τ + τ_{d} - C (υ) υ - D (υ) υ) \end{cases}

(12)

3.1. Model Predictive Control Design of Unmanned Surface Vehicle

3.1.1. Discrete Linearization of Unmanned Surface Vehicle Model

In this paper, the NDO is designed to compensate the disturbance. Hence, a linear model of the USV is sufficient for the MPC design, where the uncertainty from the linearization of the USV model can be solved with NDO. So, the model is linearized firstly and then discretized. Finally, the optimal control sequence is obtained according to the linear model predictive control.

The linearization of a nonlinear system can be divided into approximate linearization and exact linearization. Among them, the approximate linearization method is relatively simple with lofty applicability, however low accuracy. The precision of the accurate linearization method is lofty, but it is essential that a special case analysis of a single system, which is tough and has poor universality.

The reference trajectory is represented in equation (13) with environmental disturbances. The first order Taylor expansion can be obtained at any point

(x_{r}, u_{r})

, then approximate linearization is achieved by leaving the higher order terms, it can be seen in equation (14).

{\dot{x}}_{r} = f (x_{r}, u_{r})

(13)

\dot{x} = f (x r, u r) + \frac{\partial f}{\partial x}| \begin{matrix} x = x r \\ u = u r \end{matrix} (x - x r) + \frac{\partial f}{\partial u}| \begin{matrix} x = x r \\ u = u r \end{matrix} (u - u r)

(14)

Subtract equation (13) from (14), the equation can be achieved.

\dot{\tilde{x}} = A \tilde{x} + B \tilde{u}

(15)

and

\tilde{x} = x - x_{r}

\tilde{u} = u - u_{r}

A = \frac{\partial f}{\partial x}| \begin{matrix} x = x r \\ u = u r \end{matrix}

B = \frac{\partial f}{\partial u}| \begin{matrix} x = x r \\ u = u r \end{matrix}

The discrete form for equation (15) is shown as follows:

\{\begin{cases} \tilde{x} (k + 1) = A_{d} \tilde{x} (k) + B_{d} \tilde{u} (k) \\ \tilde{y} (k) = C \tilde{x} (k) \end{cases}

(16)

where,

A_{d} = T A + I

B_{d} = T B

\tilde{y} (k) = y (k) - y_{r} (k)

T

is the discretization step.

3.1.2. Objective Function Design

In order to ensure that the surface unmanned ship can track the trajectory smoothly and quickly. The cost function shown in equation (17) is applied, which is about the increments of the control variables and the errors of the system states.

\min J = {\sum_{i = 1}^{N_{p}} ‖η (k + i) - η_{r} (k + i)‖}_{Q}^{2} + {\sum_{i = 1}^{N_{c} - 1} ‖Δ u (k + i)‖}_{R}^{2}

(17)

where,

Q

, and

R

are the weight matrixes for tracking errors and increments of the control variables, respectively; and

N_{p}

is the prediction horizon.

Δ u (k + i)

is the variable about the increments of the control variables, so it can be obtained as:

ξ (k) = [\begin{matrix} \tilde{x} (k) \\ \tilde{u} (k - 1) \end{matrix}]

(18)

The new state space equation is represented as:

\{\begin{cases} ξ (k + 1) = \tilde{A} ξ (k) + \tilde{B} Δ u (k) \\ \tilde{y} (k) = \tilde{C} ξ (k) \end{cases}

(19)

where

\tilde{A} = [\begin{matrix} A_{d} & B_{d} \\ 0 & I_{N u} \end{matrix}]

\tilde{B} = [\begin{matrix} B_{d} \\ I_{N u} \end{matrix}]

\tilde{C} = [\begin{matrix} I_{N x} & 0 \end{matrix}]

N_{u}

denotes the number of control variables,

N_{x}

denotes the number of state variables.

Hence, the system prediction outputs can be calculated as:

\begin{matrix} Y = Ψ ξ (k) + H \tilde{u} (k) \\ J = \frac{1}{2} △ u {(k)}^{T} H_{J} △ u (k) + f_{J} △ u (k) \end{matrix}

(20)

where

H_{J} = 2 (H^{T} Q_{c} H + R_{c})

f_{J} = 2 Ψ ξ (k) Q_{c} H

Q_{c} = {[\begin{matrix} Q \\ ⋱ \\ Q \end{matrix}]}_{N_{p} \times N_{p}}

R_{c} = {[\begin{matrix} R \\ ⋱ \\ R \end{matrix}]}_{N_{c} \times N_{c}}

3.2. Nonlinear Disturbance Observer Design of Unmanned Surface Vehicle

In order to make the MPC for the USV much more applicable, a nonlinear disturbance observer is designed. It can estimate and compensate the external environmental disturbance received by USV, so the stability and anti-disturbance performance is improved for the USV, while the rollover and unnecessary navigation accidents are avoided for the USV.

According to the mathematical model of the USV, the state equation is designed:

{\dot{\hat{τ}}}_{d} = K_{0} (τ_{d} - {\hat{τ}}_{d}) = - K_{0} {\hat{τ}}_{d} + K_{0} (M \dot{υ} + C (υ) υ + D (υ) υ - τ)

(21)

where

K_{0}

is a three-dimensional positive definite matrix; the estimated disturbance values

{\hat{τ}}_{d}

can be specifically written as

{\hat{τ}}_{d} = {[{\hat{τ}}_{u d}, {\hat{τ}}_{v d}, {\hat{τ}}_{r d}]}^{T}

, which are the estimated values of surge disturbance, sway disturbance and yaw direction disturbance.

It can be seen from equation (12) that

υ

of USV can be obtained directly, but the derivative term of the speed state variable

\dot{υ}

can not be obtained directly. Therefore, it is necessary to improve the disturbance observer. The variable

β

can be selected as the intermediate assignment variable of the observer, which is expressed as:

β = {\hat{τ}}_{d} - K_{0} M υ

(22)

Then,

\begin{matrix} \dot{β} = {\dot{\hat{τ}}}_{d} - K_{0} M \dot{υ} \\ = K_{0} (M \dot{υ} + C (υ) υ + D (υ) υ - τ) - K_{0} {\hat{τ}}_{d} - K_{0} M \dot{υ} \\ = - K_{0} (β + K_{0} M υ) + K_{0} (C (υ) υ + D (υ) υ - τ) \\ = - K_{0} β - K_{0} (K_{0} M υ - C (υ) υ - D (υ) υ + τ) \end{matrix}

(23)

So, the new equation of the improved NDO is:

\begin{matrix} {\hat{τ}}_{d} = β + K_{0} M υ \\ \dot{β} = - K_{0} β - K_{0} (K_{0} M υ - C (υ) υ - D (υ) υ + τ) \end{matrix}

(24)

The improved new equation avoids the calculation of

\dot{υ}

and simplifies the calculation process. Therefore, it can improve calculation efficiency and save calculation time.

The equation (24) is in a continuous form, and it can not be directly used for the MPC design, hence it is discretized with approximate discretization method:

\begin{matrix} τ_{d} (k + 1) = β_{d} + K_{d 1} M υ + τ_{d} (k) \\ β (k + 1) = - K_{d 2} β (k) - K_{d 1} (K_{0} M υ - C (υ) υ - D (υ) υ + τ) \end{matrix}

(25)

and

β_{d} = T β

K_{d 1} = T K_{0}

, and

K_{d 2} = T Κ_{0} - I

3.3. Stability Analysis of Unmanned Surface Vehicle

3.3.1. Stability Analysis of Model Predictive Control of Unmanned Surface Vehicle

In order to verify the stability of the USV control system under MPC, the Lyapunov function defined as

V^{0} (k)

is selected:

V^{0} (k) = \min_{Δ v} {\sum_{i = 1}^{N_{p}} ‖η (k + i |t) - η_{d} (k + i |t)‖}_{Q}^{2} + {\sum_{i = 1}^{N_{c} - 1} ‖Δ u (k + i |t)‖}_{R}^{2}

(26)

If the control horizon is defined to be equal the prediction horizon, the above equation can be simplified as:

V^{0} (k) = \min_{Δ v} \sum_{i = 1}^{N} {‖η (k + i |t) - η_{d} (k + i |t)‖}_{Q}^{2} + {‖Δ u (k + i |t)‖}_{R}^{2}

(27)

The quadratic function is always greater than 0, so its positive definiteness is proved:

{‖η (k + i |t) - η_{d} (k + i |t)‖}_{Q}^{2} + {‖Δ u (k + i |t)‖}_{R}^{2} = 0

(28)

Then, we only need to prove the

V^{0} (k)

is decreasing, then its stability is proved.

\begin{matrix} V^{0} (k + 1) = \min_{Δ υ} \{\sum_{i = 1}^{N} {‖η (k + i + 1 |t) - η_{d} (k + i + 1 |t)‖}_{Q}^{2} + {‖Δ u (k + i + 1 |t)‖}_{R}^{2}\} \\ = \underset{Δ v}{\min_{Δ υ} \{\begin{matrix} \sum_{i = 1}^{N} ({‖η (k + i |t) - η_{d} (k + i |t)‖}_{Q}^{2} + {‖Δ u (k + i |t)‖}_{R}^{2}) - \\ {‖η (k + 1 |t) - η_{d} (k + 1 |t)‖}_{Q}^{2} - {‖Δ u (k + 1 |t)‖}_{R}^{2} + \\ {‖η (k + 1 + N |t) - η_{d} (k + 1 + N |t)‖}_{Q}^{2} + {‖Δ u (k + 1 + N |t)‖}_{R}^{2} \end{matrix}\}} \\ = - {‖η (k + 1 |t) - η_{d} (k + 1 |t)‖}_{Q}^{2} - {‖Δ u (k + 1 |t)‖}_{R}^{2} + \\ \min_{Δ υ} \{\begin{array}{l} \sum_{i = 1}^{N} ({‖η (k + i |t) - η_{d} (k + i |t)‖}_{Q}^{2} + {‖Δ u (k + i |t)‖}_{R}^{2}) + \\ {‖η (k + 1 + N |t) - η_{d} (k + 1 + N |t)‖}_{Q}^{2} + {‖Δ u (k + 1 + N |t)‖}_{R}^{2} \end{array}\} \\ \leq - {‖η (k + 1 |t) - η_{d} (k + 1 |t)‖}_{Q}^{2} - {‖Δ u (k + 1 |t)‖}_{R}^{2} + V^{0} (k) + \\ \min_{Δ υ} \{{‖η (k + 1 + N |t) - η_{d} (k + 1 + N |t)‖}_{Q}^{2} + {‖Δ u (k + 1 + N |t)‖}_{R}^{2}\} \end{matrix}

(29)

The terminal equation constraint is:

{‖η (k + 1 + N |t) - η_{r} (k + 1 + N |t)‖}_{Q}^{2} = 0

(30)

And,

\min_{Δ υ} \{{‖η (k + 1 + N |t) - η_{d} (k + 1 + N |t)‖}_{Q}^{2} + {‖Δ u (k + 1 + N |t)‖}_{R}^{2}\} = 0

(31)

{‖η (k + i |t) - η_{r} (k + i |t)‖}_{Q}^{2} + {‖Δ u (k + i |t)‖}_{R}^{2} = 0

(32)

Therefore

V^{0} (k + 1) \leq V^{0} (k)

, and the stability of MPC is proved.

3.3.2. Stability Analysis of Nonlinear Disturbance Observer of Unmanned Surface Vehicle

In order to verify the stability of NDO and ensure that it can be applied to the trajectory tracking control system. Firstly, it is necessary to define the variable of the difference between the observer's estimated value and the actual value of the external disturbance to USV:

{\tilde{τ}}_{d} = τ_{d} - {\hat{τ}}_{d}

(33)

Considering the kinematic equation (2), (24) and (33) of USV, then calculating the derivative of time on both sides of equation (27), the formula is represented as:

\begin{matrix} {\dot{\hat{τ}}}_{d} = \dot{β} + K_{0} M \dot{υ} \\ = - K_{0} β - K_{0} (K_{0} M υ - C (υ) υ - D (υ) υ + τ) + K_{0} (- C (υ) υ - D (υ) υ + τ + τ_{d}) \\ = K_{0} (τ_{d} - (β + K_{0} M υ)) \\ = K_{0} {\tilde{τ}}_{d} \end{matrix}

(34)

From the equation (34), calculate the derivative of both sides of equation (33) with respect to time, and simplify it to get:

{\dot{\tilde{τ}}}_{d} = {\dot{τ}}_{d} - {\dot{\hat{τ}}}_{d} = {\dot{τ}}_{d} - K_{0} {\tilde{τ}}_{d}

(35)

The Lyapunov method is used to verify the stability of the disturbance observer, and the appropriate Lyapunov function is selected as:

V_{d} = \frac{1}{2} {\tilde{τ}}_{d}^{T} {\tilde{τ}}_{d}

(36)

According to equation (35), the derivative of both sides of equation (36) with respect to time can be obtained as:

{\dot{V}}_{d} = {\tilde{τ}}_{d}^{T} {\dot{\tilde{τ}}}_{d} = - {\tilde{τ}}^{T} K_{0} \tilde{τ} + {\tilde{τ}}^{T} {\dot{τ}}_{d}

(37)

According to Young's inequality theory, so:

{\tilde{τ}}_{d}^{T} {\dot{\tilde{τ}}}_{d} \leq a_{1} {\tilde{τ}}_{d}^{T} {\tilde{τ}}_{d} + \frac{C_{d}^{2}}{4 a_{1}}

(38)

and

a_{1} > 0

C_{d}

is the limit of disturbance change rate.

From equation (37) and (38), it can be written as inequality:

{\dot{V}}_{d} \leq - {\tilde{τ}}^{T} K_{0} \tilde{τ} + a_{1} {\tilde{τ}}^{T} {\dot{τ}}_{d} + \frac{C_{d}^{2}}{4 a_{1}} \leq - 2 (λ_{\min} (K_{0}) - a_{1}) V_{d} + \frac{C_{d}^{2}}{4 a_{1}}

(39)

Take,

\{\begin{cases} μ_{0} = 2 (λ_{\min} (K_{0}) - a_{1}) > 0 \\ C_{0} = \frac{C_{d}^{2}}{4 a_{1}} > 0 \end{cases}

(40)

Equation (39) can be abbreviated as:

{\dot{V}}_{d} \leq - μ_{0} V_{d} + C_{0}

(41)

The result can be obtained as:

0 \leq V_{d} \leq \frac{C_{0}}{μ_{0}} + (V_{d} (0) - \frac{C_{0}}{μ_{0}}) e^{- μ_{0} t}

(42)

According to equation (42), it shows that the Lyapunov function

V_{d}

stays in a closed ball of some radius whose origin is the center of the sphere. And it is uniformly ultimately bounded. In addition, the radius of the sphere is

R_{V_{d}} = \frac{C_{0}}{μ_{0}} = \frac{C_{d}^{2}}{8 a_{1} (λ_{\min} (K_{0}) - a_{1})}

. According to equation (36), it can be obtained that the disturbance estimation error variable

{\tilde{τ}}_{d}

also converges to the sphere radius

R_{{\tilde{τ}}_{d}} = \sqrt{2 \frac{C_{0}}{μ_{0}}} = \frac{C_{d}}{\sqrt{4 a_{1} (λ_{\min} (K_{0}) - a_{1})}}

with the origin as the center of the sphere. At the same time, it can also be known that if the external environmental disturbance value

τ_{d}

of USV is an arbitrary unknown constant value, the constant limit

C_{d}

is zero. According to equation (39), the observer estimation error value

{\tilde{τ}}_{d}

can converge to the origin.

According to equation (40), as long as the appropriate observer parameters

a_{1}

and

K_{0}

can be selected, an arbitrarily small error convergence radius

R_{{\tilde{τ}}_{d}}

can be obtained. In other words, NDO can estimate the external environmental disturbance suffered by the unmanned ship according to an arbitrarily small error, and the estimation accuracy depends on the selected parameters.

4. Results and Discussions

In order to verify the influence of the improved NDO based MPC, it is applied for trajectory tracking control of USV called CyberShip II. The tracking errors and performance of USV is shown in this part. In addition, the computational efficiency of the improved NDO is verified.

4.1. Model Parameters of Unmanned Surface Vehicle

In equations (3) and (4),

M = [\begin{matrix} 25.8 & 0 & 0 \\ 0 & 33.8 & 1 \\ 0 & 1 & 2.8 \end{matrix}]

D = [\begin{matrix} 0.72 & 0 & 0 \\ 0 & 0.86 & - 0.11 \\ 0 & - 0.11 & 1.90 \end{matrix}]

. In (16),

C = [\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}]

. In (17),

Q = [\begin{matrix} 10 & 0 & 0 & 0 & 0 & 0 \\ 0 & 10 & 0 & 0 & 0 & 0 \\ 0 & 0 & 10 & 0 & 0 & 0 \\ 0 & 0 & 0 & 10 & 0 & 0 \\ 0 & 0 & 0 & 0 & 10 & 0 \\ 0 & 0 & 0 & 0 & 0 & 10 \end{matrix}]

R = [\begin{matrix} 0.01 & 0 & 0 \\ 0 & 0.01 & 0 \\ 0 & 0 & 0.01 \end{matrix}]

In the simulation,

η = {[0 0 0^{\circ}]}^{T}

which is set as the initial state of USV;

υ = {[0 00]}^{T}

which is set as the initial speed of USV. And the reference trajectories of USV are shown as follows:

\{\begin{array}{l} x_{d} = 2 \sin (0.02 t), & 0 \leq t \leq 500 \\ y_{d} = 2 - 2 \cos (0.02 t), & 0 \leq t \leq 500 \\ ψ_{d} = \arctan ({\dot{x}}_{d} / {\dot{y}}_{d}), & 0 \leq t \leq 500 \end{array}

(43)

\{\begin{array}{l} x_{d} = 8 \sin (0.02 t), & 0 \leq t \leq 500 \\ y_{d} = t, & 0 \leq t \leq 500 \\ ψ_{d} = \arctan ({\dot{x}}_{d} / {\dot{y}}_{d}), & 0 \leq t \leq 500 \end{array}

(44)

T = 0.1

which is set as the simulation sampling time;

N_{x} = 6

which is set as the number of states;

N_{u} = 3

which is set as the number of control variables,

N_{p} = 20

which is set as the prediction horizon,

N_{c} = 10

which is set as the control horizon.

4.2. Experiments results and Analysis

NDO based MPC for trajectory tracking control of USV is compared with MPC without observer. Experiments with different disturbances are performed to verify the anti-disturbance and robustness performance. The performance of the improved NDO is discussed.

The composite model of external disturbances meets the requirements of Level 3 sea conditions. The specific external wind, wave, and current disturbances settings are:

\{\begin{matrix} τ_{d u} = m_{11} h (s) w_{u} (s) \\ τ_{d v} = m_{22} h (s) w_{v} (s) \\ τ_{d r} = m_{33} h (s) w_{r} (s) \end{matrix}

(45)

where wave transfer function

h (s) = \frac{K_{ω} s}{s^{2} + 2 ζ ω_{0} s + ω_{0}^{2}}

K_{ω} = 2 ζ ω_{0} σ_{0}

ω_{0}

ζ

and

σ_{0}

represent wave frequency, wave strength gain, and damping constant respectively;

K_{ω} = 0.255

ω_{0} = 0.808

w_{u} (s)

w_{v} (s)

and

w_{r} (s)

represent random white noise disturbances, then the noise power is set to 0.01, 0.005, and 0.1 respectively.

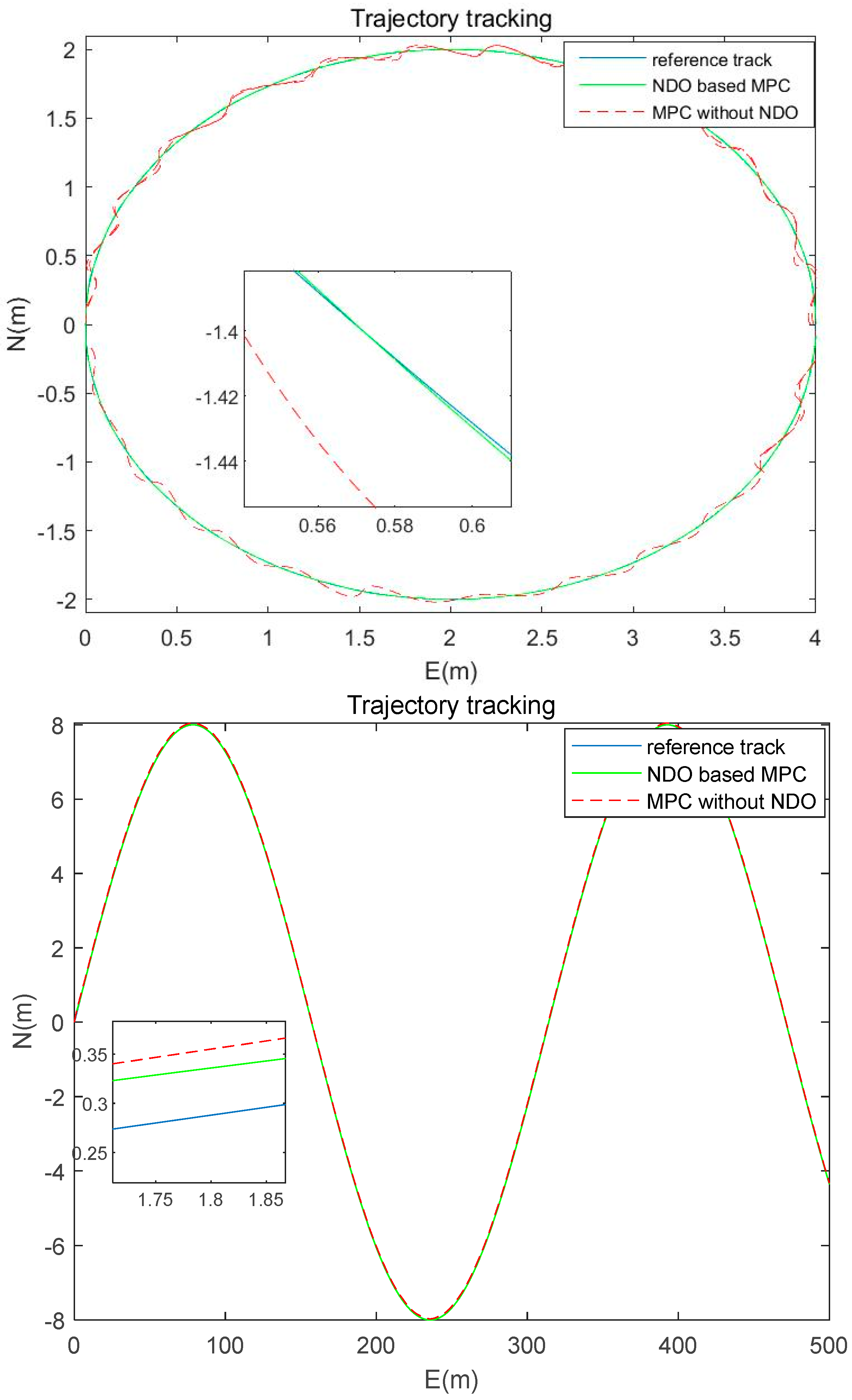
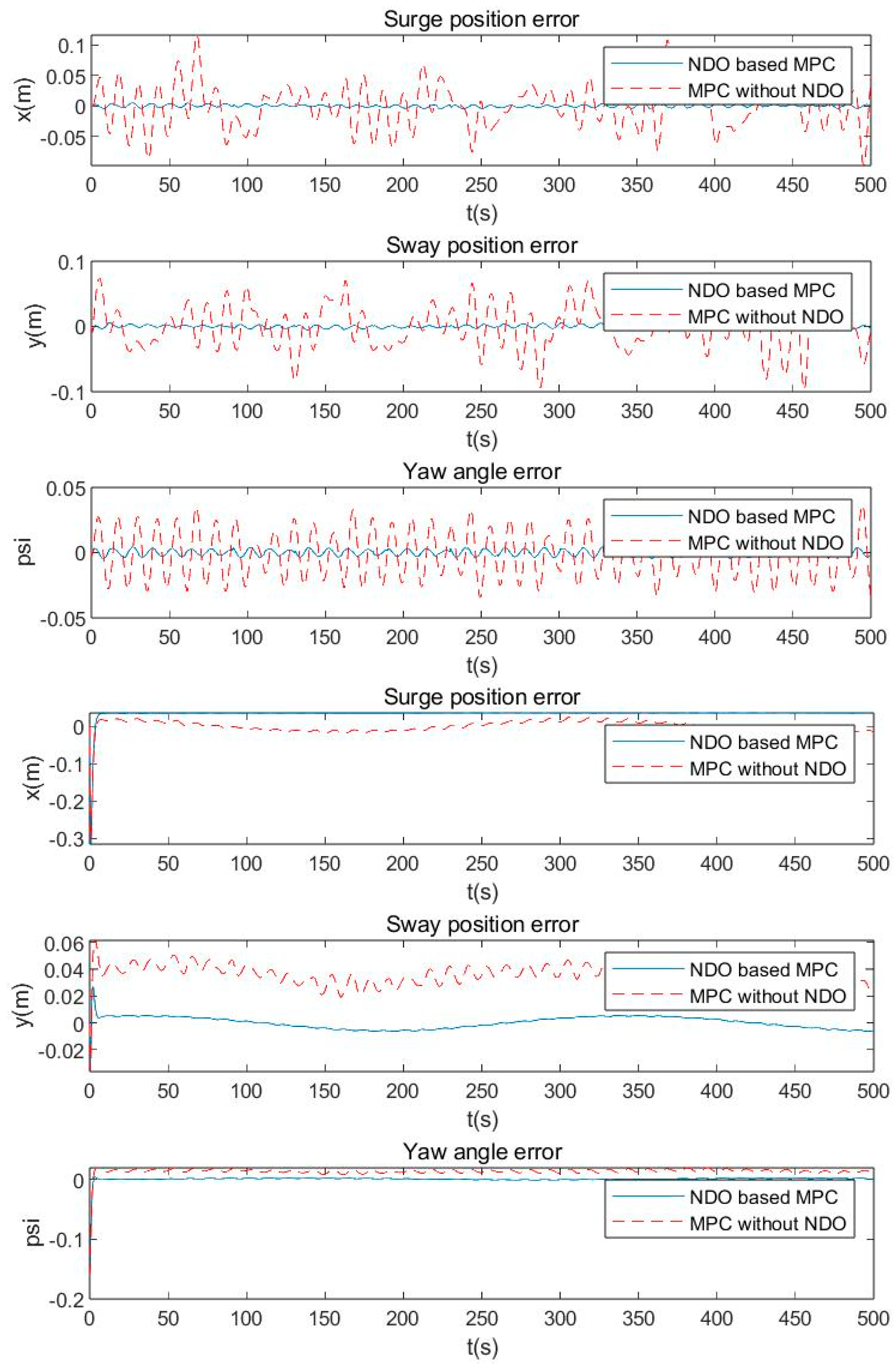
The experiments result of improved NDO based MPC for trajectory tracking control and traditional MPC with disturbances are shown in Figure 3. The tracking errors of the two control methods are shown in Figure 4. The calculation time between the two NDO methods with disturbances are shown in Figure 5. The trajectory tracking errors of three methods trajectory tracking with different parameters are shown in Figure 6.

In Figure 3, it shows that improved NDO based MPC has better disturbance rejection performance than MPC without observer. It also can be seen from the experiment that both methods can track the reference trajectory. But the former can track the reference trajectory stably, while the latter fluctuates a lot. In Figure 4, it shows the comparisons of the two trajectory tracking errors with disturbances. And the improved NDO based MPC has lower tracking errors than MPC without observer. The surge position error range of MPC without observer for trajectory tracking control is -0.1 to 0.1 meters, the sway position error range is -0.1 to 0.1 meters and the yaw angle error range is -0.05 to 0.05. While the surge position error range of NDO based MPC is -0.005 to 0.005 meters, the sway position error range is -0.005 to 0.005 meters and the yaw angle error range is -0.005 to 0.005. 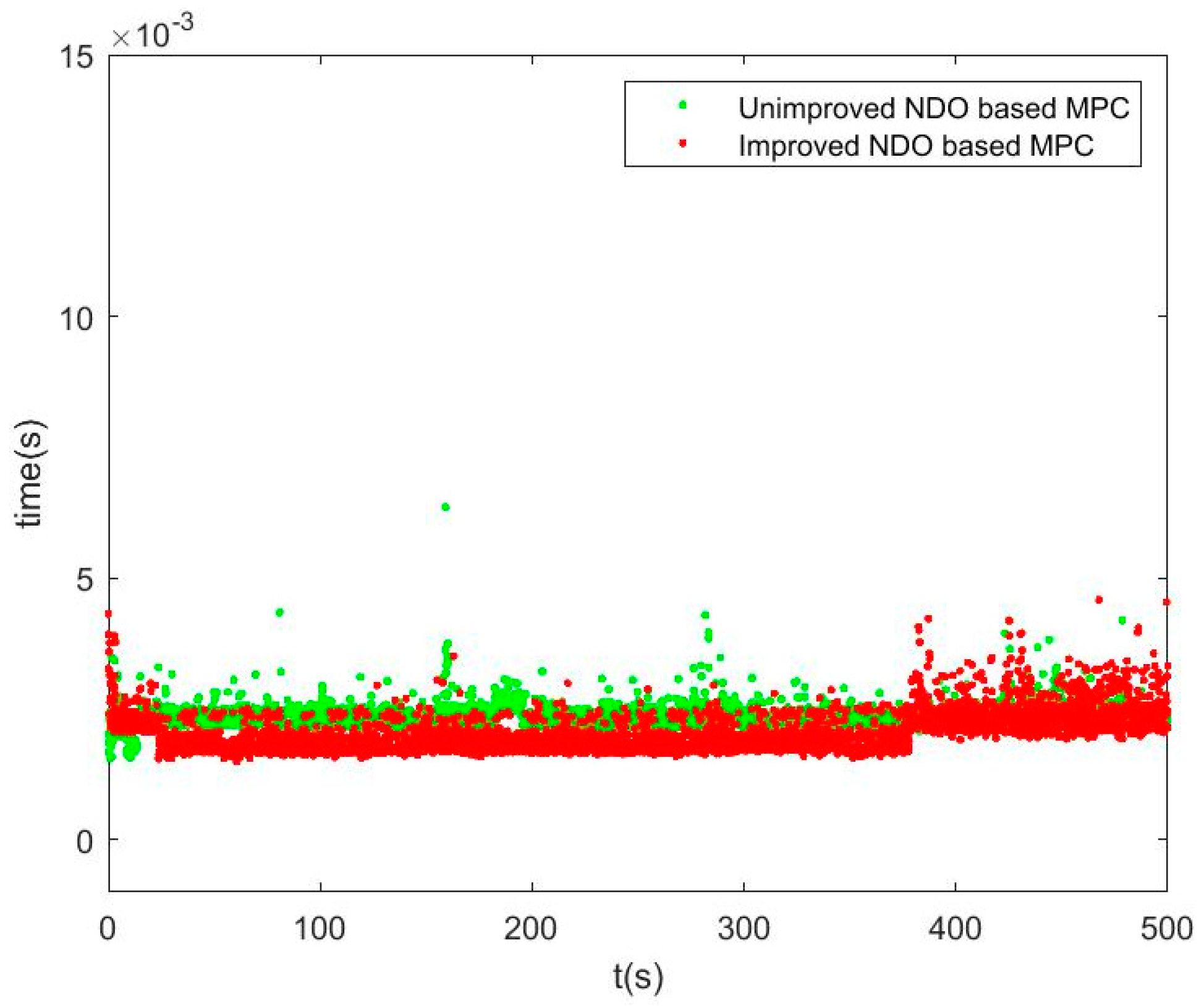In Figure 5, it shows that the improved NDO has better performance than unimproved NDO about the calculation time with disturbances.

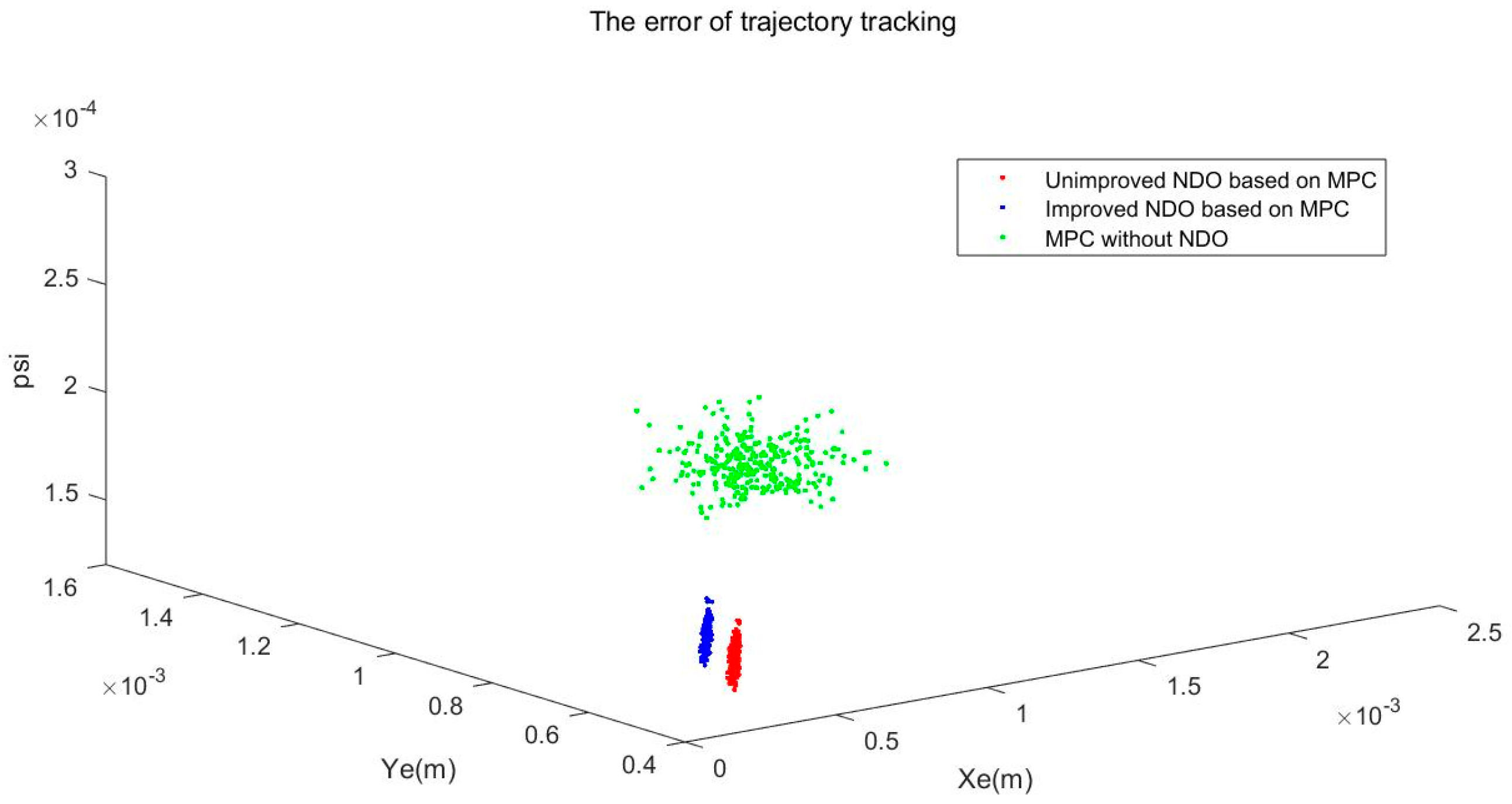
The USV model has uncertainty, so three methods were used for trajectory tracking for the USV with different model parameters. The three methods are unimproved NDO based MPC, improved NDO based MPC and MPC without NDO. In Figure 6, it shows that the improved NDO and unimproved NDO effectively reduce the instability caused by model uncertainty. And the unimproved NDO has similar perfomance of tracking errors with improved NDO based MPC.

In addition, the comparison of the calculation time of two NDOs with disturbances are shown in Table 1. It shows the average calculation time and maximum single calculation time of the two NDOs.

I A E = \int_{0}^{t} |e (ζ)| d ζ

and

R M S E = {(\frac{1}{t} \int_{0}^{t} e^{2} (ζ) d ζ)}^{1 / 2}

are used to evaluate the tracking effect and steady state performance. The smaller values of IAE and RMSE, the better control performance of the scheme applied. And the comprehensive performance comparisons of the position and speed tracking errors of two methods are shown in Table 2. It shows the

I A E

and

R M S E

of the two methods.

From Table 1, the calculation time of improved NDO is much lower than that of traditional NDO. The average calculation time of improved NDO is 0.0020, while it is 0.0024 of traditional NDO. The maximum single calculation time of improved NDO is 0.0046, while it is 0.0064 of the traditional NDO. The results show that compared with traditional NDO, the average calculation time of improved NDO is decreased by 16.67%, and the maximum individual calculation time is decreased by 28.13%.

From Table 2, the

I A E

and

R M S E

of NDO based MPC are lower than the MPC without observer. NDO based MPC effectively enhances the anti-disturbances performance of the system. MPC without observer trajectory tracking control has the characteristics of predictive model, rolling optimization and feedback correction, which can resist external disturbances and model mismatch to some extent.

With the data which are shown in Table 1 and Table 2, NDO based MPC is superior to MPC without observer for trajectory tracking control in terms of position and speed tracking errors.

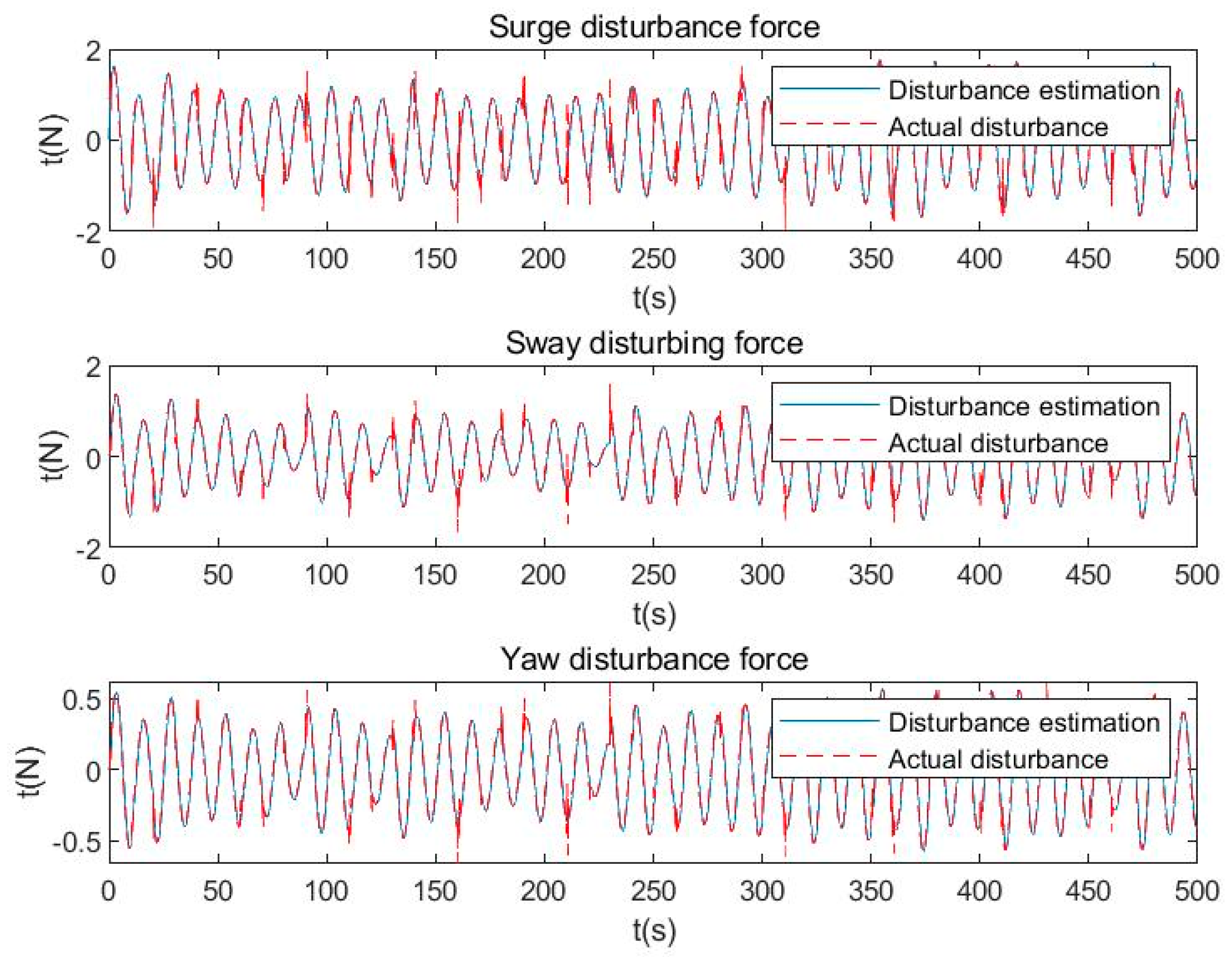
NDO is designed to estimate the external disturbances suffered, to improve the anti-disturbance performance of the USV. Thus, the comparison of estimated values of NDO and actual disturbances are shown in Figure 7.

In Figure 7, it shows the relationship between the estimated values of NDO and the actual values of the disturbances. NDO has good estimate performance about the disturbances, including surge disturbance force, sway disturbing force and yaw disturbance force.

5. Conclusions

An improved NDO based MPC for trajectory tracking is proposed to guarantee the stable motion of USV in this paper, which suffers various disturbances from the ocean wind, wave and current. The MPC is used to optimize the system torque based the measured position and speed state variables. Then, the NDO is designed to estimate the disturbances, and the estimated torque is compensated in the controller. The estimation errors can converge to zero in finite time. The experimental results show that NDO based MPC can effectively compensate external disturbances and obtain good tracking and disturbance rejection performance. The proposed method has similar tracking performance of the USVs with the MPC based on unimproved NDO, however, the improved NDO based MPC is much more time-saving.

Author Contributions

Conceptualization, H.F.; methodology, H.F. and S.Z.; software, Y.W.; validation, Y.W., R.C. and S.Z.; writing—original draft preparation, W.Y. and S.Z.; writing—review and editing, H.F., R.C. and S.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China, grant number 52271313; Innovative Research Foundation of Ship General Performance, grant number 21822216; Fundamental Research Funds for the Central Universities, grant number XK2040021004025.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study.

References

Miao, R.; Dong, Z.; Wan, L.; Zeng, J. Heading control system design for a micro-USV based on an adaptive expert S-PID algorithm. Polish Maritime Research 2018. [Google Scholar] [CrossRef]
Li, W.; Ge, Y.; Guan, Z.; Ye, G. Synchronized Motion-Based UAV–USV Cooperative Autonomous Landing. Journal of Marine Science and Engineering 2022, 10, 1214. [Google Scholar] [CrossRef]
Liao, Y.; Jia, Z.; Zhang, W.; Jia, Q.; Li, Y. Layered berthing method and experiment of unmanned surface vehicle based on multiple constraints analysis. Applied Ocean Research 2019, 86, 47–60. [Google Scholar] [CrossRef]
Jin, J.; Liu, D.; Wang, D.; Ma, Y. A Practical Trajectory Tracking Scheme for a Twin-Propeller Twin-Hull Unmanned Surface Vehicle. Journal of Marine Science and Engineering 2021, 9, 1070. [Google Scholar] [CrossRef]
Jiang, X.; Xia, G.; Feng, Z.; Wu, Z.G. Nonfragile Formation Seeking of Unmanned Surface Vehicles: A Sliding Mode Control Approach. IEEE Transactions on Network Science and Engineering 2021, 9, 431–444. [Google Scholar] [CrossRef]
Jiang, X.; Xia, G. Sliding mode formation control of leaderless unmanned surface vehicles with environmental disturbances. Ocean Engineering 2022, 244, 110301. [Google Scholar] [CrossRef]
Velueta, M.J.; Rullan, J.L.; Ruz-Hernandez, J.A.; Alazki, H. A Strategy of Robust Control for the Dynamics of an Unmanned Surface Vehicle under Marine Waves and Currents. Mathematical Problems in Engineering 2019, 2019. [Google Scholar] [CrossRef]
Wu, Y.; Yang, S.; Li, W.; Liu, D.; Hou, K. Dynamic Analysis and Motion Control of an Underactuated Unmanned Surface Vehicle (WL-II). Marine Technology Society Journal 2017, 51. [Google Scholar] [CrossRef]
Zhou, W.; Wang, Y.; Ahn, C.K.; Cheng, J.; Chen, C. Adaptive fuzzy backstepping-based formation control of unmanned surface vehicles with unknown model nonlinearity and actuator saturation. IEEE Transactions on Vehicular Technology 2020, 69, 14749–14764. [Google Scholar] [CrossRef]
Wang, C.; Xie, S.; Chen, H.; Peng, Y.; Zhang, D. A decoupling controller by hierarchical backstepping method for straight-line tracking of unmanned surface vehicle. Systems Science & Control Engineering 2019, 7, 379–388. [Google Scholar]
Jin, J.; Zhang, J.; Liu, D. Design and verification of heading and velocity coupled nonlinear controller for unmanned surface vehicle. Sensors 2018, 18, 3427. [Google Scholar] [CrossRef]
Weng, Y.; Wang, N. Data-driven robust backstepping control of unmanned surface vehicles. International Journal of Robust and Nonlinear Control 2020, 30, 3624–3638. [Google Scholar] [CrossRef]
Zhao, S.; Wang, S.; Cajo, R.; Ren, W.; Li, B. Power Tracking Control of Marine Boiler-Turbine System Based on Fractional Order Model Predictive Control Algorithm. Journal of Marine Science and Engineering 2022, 10, 1307. [Google Scholar] [CrossRef]
Feng, N.; Wu, D.; Yu, H.; Yamashita, A.S.; Huang, Y. Predictive compensator based event-triggered model predictive control with nonlinear disturbance observer for unmanned surface vehicle under cyber-attacks. Ocean Engineering 2022, 259, 111868. [Google Scholar] [CrossRef]
Zhao, S.; Cajo, R.; De Keyser, R.; Ionescu, C.M. The potential of fractional order distributed MPC applied to steam/water loop in large scale ships. Processes 2020, 8, 451. [Google Scholar] [CrossRef]
Han, X.; Zhang, X. Tracking control of ship at sea based on MPC with virtual ship bunch under Frenet frame. Ocean Engineering 2022, 247, 110737. [Google Scholar] [CrossRef]
Liu, Z.; Zhang, Y.; Yuan, C.; Luo, J. Adaptive path following control of unmanned surface vehicles considering environmental disturbances and system constraints. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2018, 51, 339–353. [Google Scholar] [CrossRef]
Liao, Y.; Du, T.; Jiang, Q. Model-free adaptive control method with variable forgetting factor for unmanned surface vehicle control. Applied Ocean Research 2019, 93, 101945. [Google Scholar] [CrossRef]
Liao, Y.; Jiang, Q.; Du, T.; Jiang, W. Redefined output model-free adaptive control method and unmanned surface vehicle heading control. IEEE Journal of Oceanic Engineering 2019, 45, 714–723. [Google Scholar] [CrossRef]
Li, Y.; Wang, L.; Liao, Y.; Jiang, Q.; Pan, K. Heading MFA control for unmanned surface vehicle with angular velocity guidance. Applied Ocean Research 2018, 80, 57–65. [Google Scholar] [CrossRef]
Huang, Z.; Liu, X.; Wen, J.; Zhang, G.; Liu, Y. Adaptive navigating control based on the parallel action-network ADHDP method for unmanned surface vessel. Advances in Materials Science and Engineering 2019, 2019. [Google Scholar] [CrossRef]
Wen, Y.; Tao, W.; Zhu, M.; Zhou, J.; Xiao, C. Characteristic model-based path following controller design for the unmanned surface vessel. Applied Ocean Research 2020, 101, 102293. [Google Scholar] [CrossRef]
Wang, R.; Li, D.; Miao, K. Optimized radial basis function neural network based intelligent control algorithm of unmanned surface vehicles. Journal of Marine Science and Engineering 2020, 8, 210. [Google Scholar] [CrossRef]
Zhou, Y.; Wu, N.; Yuan, H.; Pan, F.; Shan, Z.; Wu, C. PDE Formation and Iterative Docking Control of USVs for the Straight-Line-Shaped Mission. Journal of Marine Science and Engineering 2022, 10, 478. [Google Scholar] [CrossRef]
Liu, Z.; Song, S.; Yuan, S.; Ma, Y.; Yao, Z. ALOS-Based USV Path-Following Control with Obstacle Avoidance Strategy. Journal of Marine Science and Engineering 2022, 10, 1203. [Google Scholar] [CrossRef]
Martinsen, A.B.; Lekkas, A.M.; Gros, S. Reinforcement learning-based NMPC for tracking control of ASVs: Theory and experiments. Control Engineering Practice 2022, 120, 105024. [Google Scholar] [CrossRef]
Tan, Y.; Cai, G.; Li, B.; Teo, K.L.; Wang, S. Stochastic model predictive control for the set point tracking of unmanned surface vehicles. IEEE Access 2019, 8, 579–588. [Google Scholar] [CrossRef]
Wang, X.; Liu, J.; Peng, H.; Qie, X.; Zhao, X.; Lu, C. A Simultaneous Planning and Control Method Integrating APF and MPC to Solve Autonomous Navigation for USVs in Unknown Environments. Journal of Intelligent & Robotic Systems 2022, 105, 1–16. [Google Scholar]
Sun, X.; Wang, G.; Fan, Y.; Mu, D.; Qiu, B. Collision avoidance using finite control set model predictive control for unmanned surface vehicle. Applied Sciences 2018, 8, 926. [Google Scholar] [CrossRef]

Figure 1. Three degree of freedom motion model for USV.

Figure 2. Schematic diagram of MPC based on nonlinear observer.

Figure 3. Disturbance rejection results of the NDO based MPC and MPC without NDO.

Figure 4. Comparison of the tracking errors between the two trajectory tracking control methods with disturbances.

Figure 5. Comparison of the calculation time between the two NDO methods with disturbances.

Figure 6. Trajectory tracking errors of the three trajectory tracking methods with different parameters.

Figure 7. Comparison of estimated values of NDO and actual disturbances.

Table 1. Comparison of the calculation time of the two methods.

	Improved NDO based MPC	Unimproved NDO based MPC
Average calculation time(s)	0.0020	0.0024
Maximum single calculation time(s)	0.0046	0.0064

Table 2. Comparison of position and velocity errors of the two methods.

Tracking Error	Computing Method	Improved NDO Based MPC	Non Observer
$y_{e}$	$I A E$	9.3209	141.6562
$y_{e}$	$R M S E$	0.0072	0.1104
$x_{e}$	$I A E$	9.2273	135.6914
$x_{e}$	$R M S E$	0.0071	0.1061
$ψ_{e}$	$I A E$	10.7869	79.6175
$ψ_{e}$	$R M S E$	0.0077	0.0574
$‖u_{e}‖$	$I A E$	6.3167	55.5531
$‖u_{e}‖$	$R M S E$	0.0055	0.0435
$‖υ_{e}‖$	$I A E$	3.9132	58.2295
$‖υ_{e}‖$	$R M S E$	0.0030	0.0425
$‖r_{e}‖$	$I A E$	6.1470	40.2591
$‖r_{e}‖$	$R M S E$	0.0050	0.0290

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Trajectory Tracking Predictive Control for Unmanned Surface Vehicles with Improved Nonlinear Disturbance Observer

Abstract

1. Introduction

2. State Space Model of Unmanned Surface Vehicle

3. Nonlinear Disturbance Observer based Model Predictive Control

3.1. Model Predictive Control Design of Unmanned Surface Vehicle

3.1.1. Discrete Linearization of Unmanned Surface Vehicle Model

3.1.2. Objective Function Design

3.2. Nonlinear Disturbance Observer Design of Unmanned Surface Vehicle

3.3. Stability Analysis of Unmanned Surface Vehicle

3.3.1. Stability Analysis of Model Predictive Control of Unmanned Surface Vehicle

3.3.2. Stability Analysis of Nonlinear Disturbance Observer of Unmanned Surface Vehicle

4. Results and Discussions

4.1. Model Parameters of Unmanned Surface Vehicle

4.2. Experiments results and Analysis

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe