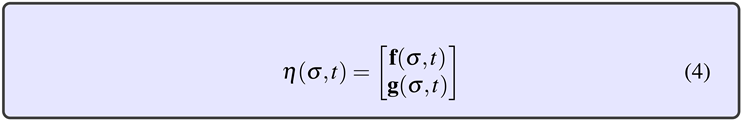Prerpints.org logo
Preprint
Short Note

Existence of Zeros for Holomorphic Complex Functions: A Dynamical Systems Approach

Altmetrics

Downloads

67

Views

619

Comments

0

This version is not peer-reviewed

Submitted:

05 September 2023

Posted:

06 September 2023

You are already at the latest version

Alerts
Abstract
This work introduces an approach to investigate the existence of zeros for holomorphic complex functions, defined on open and simply connected subdomains of C, in a systematic and direct way. This is achieved by means of the theory of dynamical systems (Poincar\'e index) and the perception that a zero of a specific complex function is an equilibtium for the associated dynamical system. The logical basis of proof is to find the mathematical expression for the Poincaré index of the vector field associated to the function under study, assuming the existence of a zero, and investigating the consequences. Depending on the value of the index, an inconsistency may occur, establishing a contradiction.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematics

1. Introduction

Oftentimes it is necessary to know whether a given function, η : C ⊇ A → C ≡ R 2 , has zeros in certain regions of the complex plane, here identified with R 2 . In general lines, the underlying idea in this work is to face the given function as a mapping, associating to each element of A, one vector in R 2 , that is to say, a 2-dimensional vector field usually referred to as the field associated to η [14], namely, η : A → R 2 , using the same designation for both objects. This atypical viewpoint gives rise to a nonlinear autonomous system [4,5].
X ˙ ( t ) = η ( X ( t ) ) X ( t ) ∈ A ⊆ R 2
which will be the basis for the development of the ideas to follow.
Obviously, the state space of system (1) can be extended to the full domain of η .

2. The function and its associated vector field

By identifying s = σ + i . t and ( σ , t ) , the function can be written
f ( σ , t ) = Δ R e ( η ( σ + i . t )
g ( σ , t ) = Δ I m ( η ( σ + i . t ) )
Preprints 84260 i001
viewed as a vector field with components given by its real and imaginary parts.
If η is holomorphic, its components are C ∞ and have partial derivatives of all orders. In addition, it satisfies Cauchy-Riemann equations [14].
The total differentials of f and g are given by
d f = ∂ f ∂ σ d σ + ∂ f ∂ t d t
d g = ∂ g ∂ σ d σ + ∂ g ∂ t d t
with
∂ g ∂ σ = − ∂ f ∂ t
∂ g ∂ t = ∂ f ∂ σ

3. Poincaré index for 2-dimensional dynamical systems

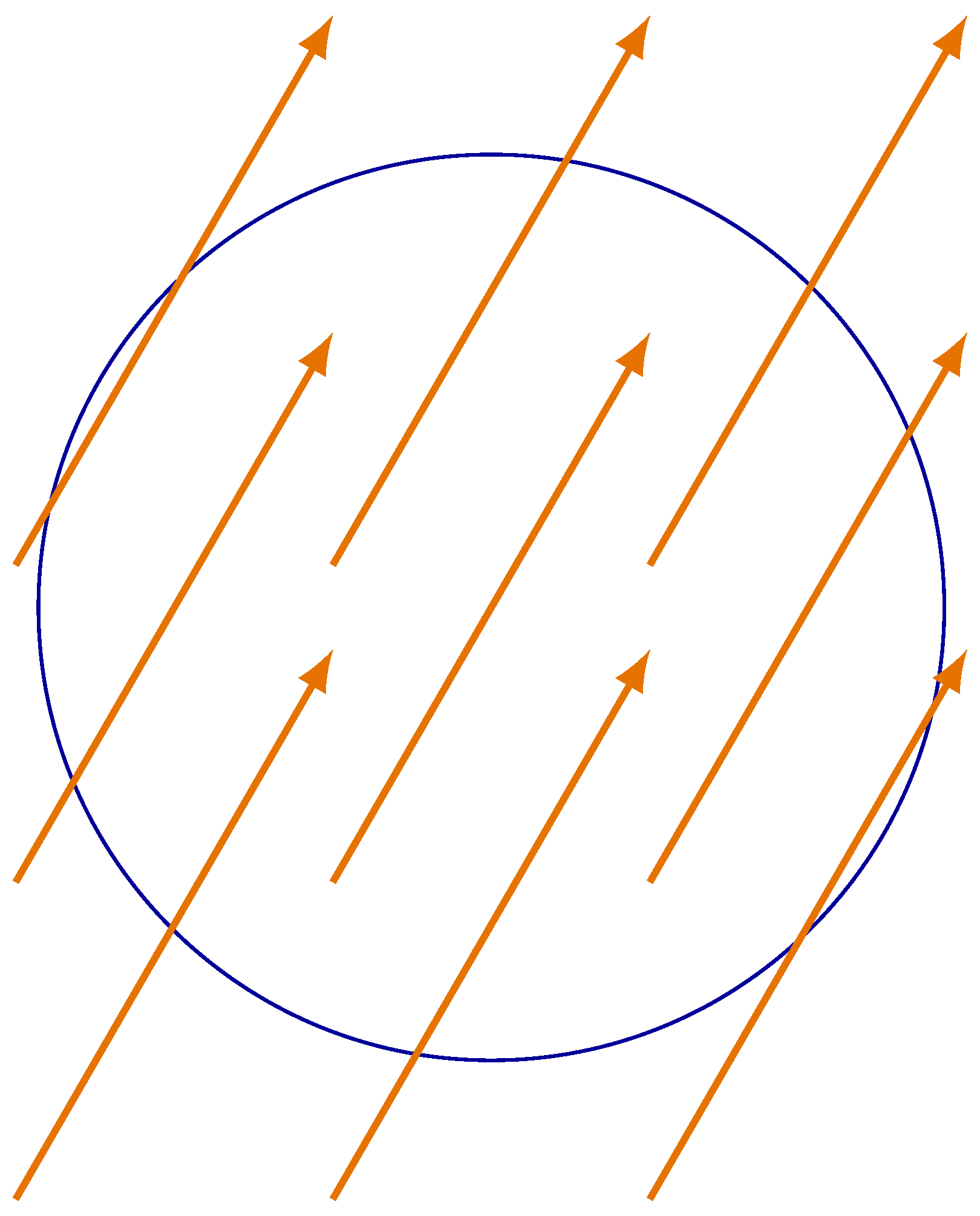
Given a 2-dimensional vector field V, defined in a simply connected region A ⊂ R 2 , consider any closed curve C fully contained in it and not enclosing any equilibrium points of the dynamical system originated by V in its interior.
X ˙ ( t ) = V ( X ( t ) ) X ( t ) ∈ A ⊆ R 2
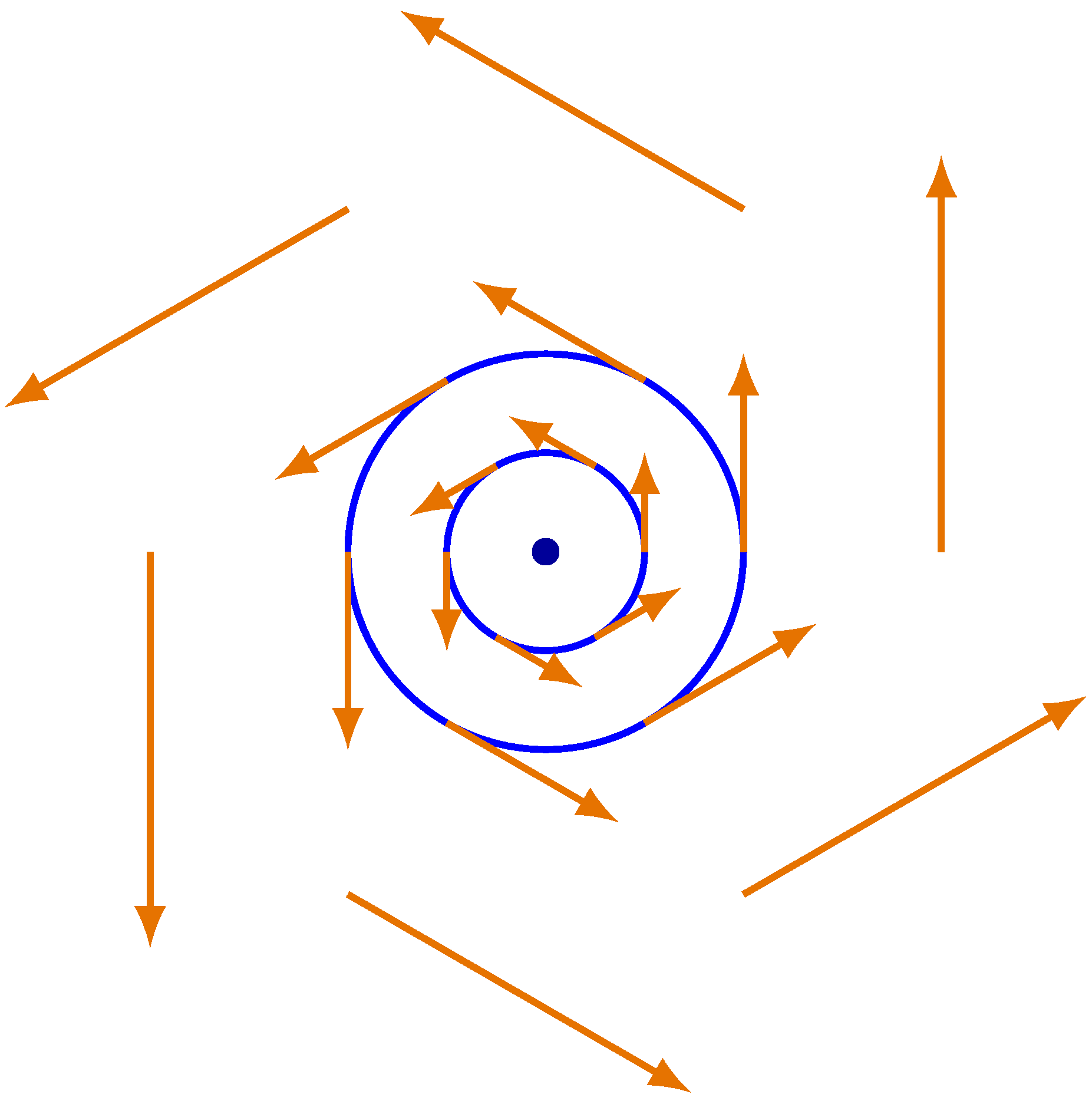
By restricting V to the closed curve C we obtain a vector field along it, as displayed in Figure 1.
By moving along C in the anti-clockwise, positive sense, the vectors with origin in C rotate and, after a full excursion, an angle 2 π k is traversed, where k ∈ Z - the integer k is called the Poincaré index of the curve C.
The index of a closed curve with no equilibria inside it can be obtained by integrating the change in the angle of the vectors at each point in C.
For a vector field given by
V ( σ , t ) = f ( σ , t ) g ( σ , t )
the index of C is
k = Δ 1 2 π ∮ C d ϕ = 1 2 π ∮ C d arctan ( g f ) = 1 2 π ∮ C f d g − g d f f 2 + g 2
The Poincaré index of a equilibrium point of V, ( x e , y e ) , is defined to be the index of a closed curve C which surrounds only this specific point, not existing equilibria on the closed curve.
The Poincaré index features some very significant properties [1,15,17,19]:
  • It is invariant under homotopical transformations of C, provided equilibria do not "clash" with curves.
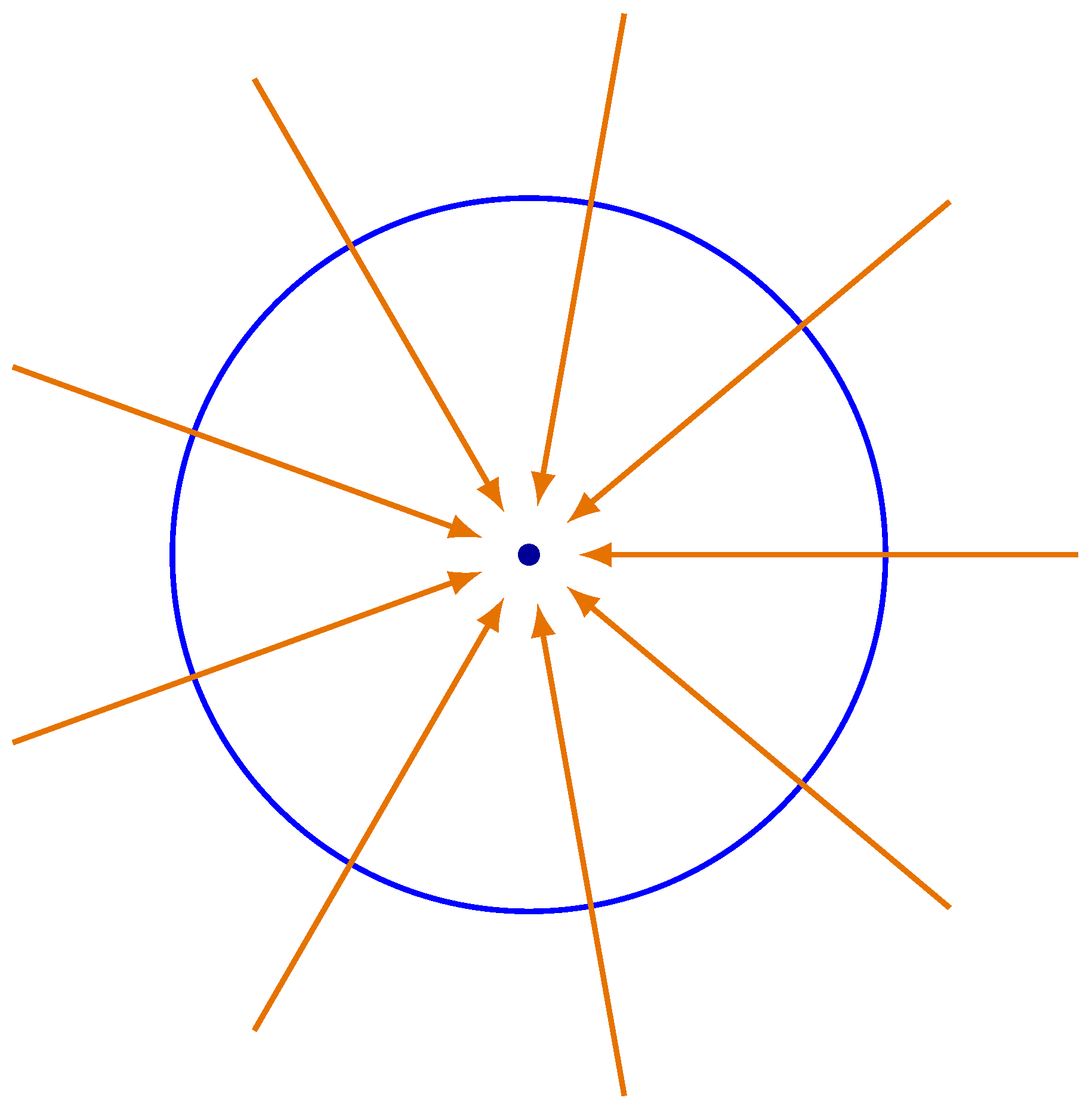
  • When C is a simple closed curve, V is a C 2 vector field defined on C and its interior, and there are no critical points of V inside C , the index of C relative to V is 0.
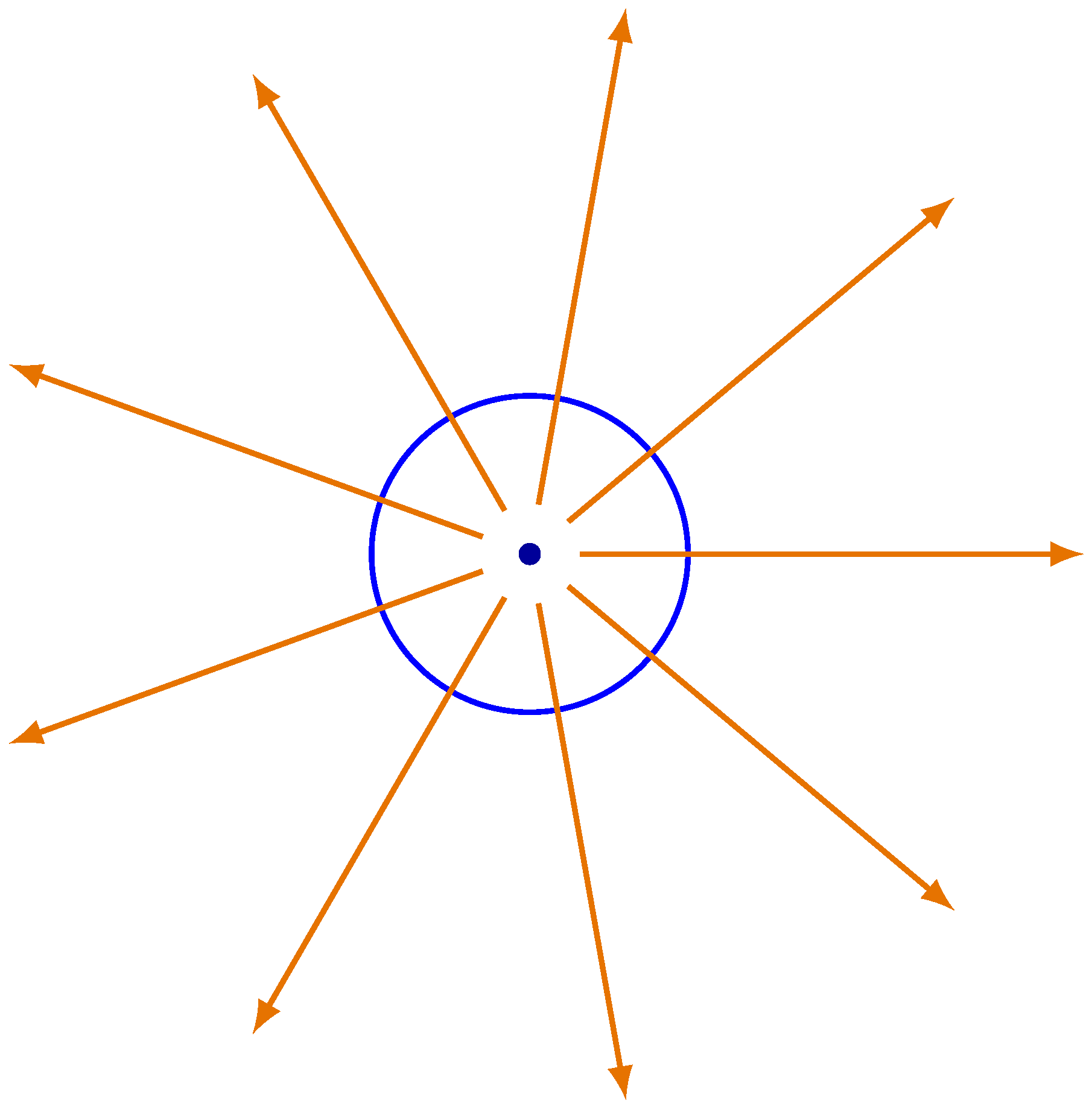
  • The index of a sink, a source, or a center is +1.
  • The index of a periodic orbit is +1.
  • The index of a hyperbolic saddle point is -1.
Preprints 84260 g002
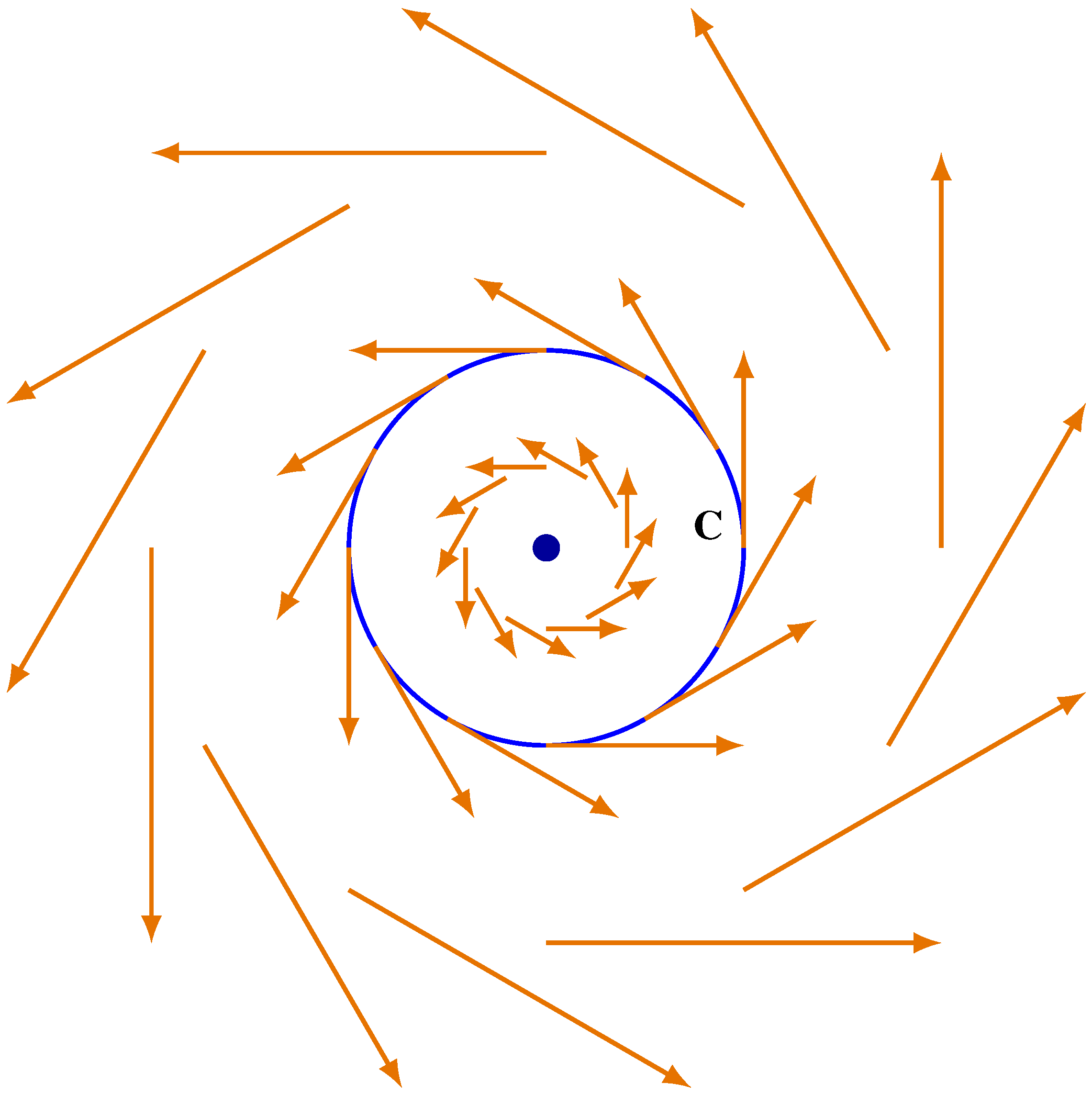
Figure 2. One isolated equilibrium (center) inside the closed curves ⇒ index = 1
Figure 2. One isolated equilibrium (center) inside the closed curves ⇒ index = 1
Preprints 84260 g002
Preprints 84260 g003
Figure 3. One isolated equilibrium (source) inside the closed curve ⇒ index = 1
Figure 3. One isolated equilibrium (source) inside the closed curve ⇒ index = 1
Preprints 84260 g003
Preprints 84260 g004
Figure 4. One isolated equilibrium (sink) inside the closed curve ⇒ index = 1
Figure 4. One isolated equilibrium (sink) inside the closed curve ⇒ index = 1
Preprints 84260 g004
Preprints 84260 g005
Figure 5. No equilibrium point inside the closed curve ⇒ index = 0
Figure 5. No equilibrium point inside the closed curve ⇒ index = 0
Preprints 84260 g005

4. Strategy of proof

The proposed method is very simple and consists of using the principle of non-contradiction. Supposing we want to prove the inexistence of roots for η in a particular region, it is assumed that there is at least one zero in the region at hand.
Departing from this scenario, and using particular aspects of the derived vector field and associated dynamical system, the objective is to find a logical inconsistency, leading to the conclusion that the initial premise is false, that is, there are no roots in the given subset.
On the other hand, if the objective is to prove the existence of roots, it is assumed they do not exist and the search is in the inverse path.

5. Conclusion

By leaving the complex numbers’ realm and entering the dynamical systems’ one it is feasible to obtain satisfactory conclusions about the existence of roots for complex functions - problems comparable to the generalized Riemann hypothesis may be investigated and possibly solved with the help of the proposed paradigm. It is amazing that one of the paths for the solution could take us so far and unveil the truth in such a harmonious way. By using concepts of the theory of dynamical systems and a specific vector field, associated to a complex function, the new context opens new paths which may be effective in the solution of so hard problems.
The underlying method described in this paper may be directed to any complex function, provided it satisfies certain (not very restrictive) regularity conditions, including Dirichlet L-functions [3] and so many others. Following this work, another publication will dive into a very significant example of application of the ideas here exposed.

References

  1. A. A. Andronov, E. A. Leontovich, I. I. Gordon and A. G. Maier, Qualitative Theory of Second-Order Dynamic Systems. Halsted Press, New York, 1973.
  2. A. A. Andronov, E. A. Leontovich, I. I. Gordon and A. G. Maier, Theory of Bifurcations of Dynamical Systems on a Plane. Wiley, New York, 1973.
  3. N. ARWASHAN, THE RIEMANN HYPOTHESIS AND THE DISTRIBUTION OF PRIME NUMBERS, Nova Science Publisher Inc, 2021.
  4. V. I. Arnold, Mathematical Methods of Classical Mechanics, Springer, New York, 1989.
  5. V. I. Arnold, Geometrical Methods in the Theory of Ordinary Differential Equations, Springer, New York, 1983.
  6. D. K. Arrowsmith and C. M. Place, Ordinary Differential Equations. A Qualitative Approach with Applications. Chapman & Hall, London, 1982.
  7. F. Brauer, J. A. Nohel, The Qualitative Theory of Ordinary Differential Equations: An Introduction. Courier Corporation, New York,1989.
  8. J. Derbyshire, Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York, Penguin, 2004.
  9. Edwards, H. M. Riemann’s Zeta Function. New York: Dover, 2001.
  10. J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer, New York, 2013.
  11. J. K. Hale, Ordinary Differential Equations. Robert E. Krieger Publishing Co. Inc., New York,1980.
  12. P. Hartman, Ordinary Differential Equations. John Wiley & Sons, New York, 1964.
  13. K. Knopp, Theory and Application of Infinite Series, Dover, 1990.
  14. S, Lang. Complex Analysis, 4th ed., Springer-Verlag, 1999.
  15. R. Marangell, Index Theory Lecture Notes, University of Sydney, 2017.
  16. Z. Nitecki, Differentiable Dynamics - An Introduction to the Orbit Structure of Diffeomorphisms. The MIT Press, New York, 1971.
  17. L. Perko, Differential Equations and Dynamical Systems. Springer Science & Business Media, New York, 2001.
  18. E. C. Titchmarsh.. The Theory of the Riemann Zeta Function, 2nd edition, Oxford University Press, 1986.
  19. S. Wiggins. An introduction to applied nonlinear dynamical systems and chaos 2nd ed., Springer, 2003.
Preprints 84260 g001
Figure 1. Vector field along closed curve
Figure 1. Vector field along closed curve
Preprints 84260 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated