Prerpints.org logo
Preprint
Article

Introduction to the E-Sense Artificial Intelligence System

Altmetrics

Downloads

182

Views

77

Comments

0

This version is not peer-reviewed

Submitted:

28 October 2024

Posted:

30 October 2024

You are already at the latest version

Alerts
Abstract
This paper describes the E-Sense Artificial Intelligence system. It comprises of a memory model with 2 levels of information and then a more neural layer above that. The lower memory level stores source data in a Markov (n-gram) structure that is unweighted. Then a middle ontology level is created from a further 3 phases of aggregating source information. Each phase re-structures from an ensemble to a tree, where the information transposition may be from horizontal set-based sequences into more vertical, typed-based clusters. The base memory is essentially neutral, where any weighted constraints or preferences should be stored in the calling module. The success of the ontology typing is open to question, but results produced answers based more on use and context. The third level is more functional, where each function can represent a subset of the base data and learn how to transpose across it. The functional structures are shown to be quite orthogonal, or separate and are made from nodes with a progressive type of capability, including unordered to ordered. Comparisons with the columnar structure of the neural cortex can be made and the idea of ordinal learning, or just learning relative positions, is introduced. While this is still a work in progress, it offers a different architecture to the current favourites and may be able to give different views of the data from what they can provide.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Artificial Intelligence is now at the apex of Computer Science. With advancements in pattern recognition and learning [25,30,35,42] and recently in prediction [40,41,46,58], the systems can perform many specific tasks as well as humans. Improvements in computing power and automated learning (for example, [14,32]) have also contributed. If the final bastions of reasoning and understanding can be mastered, then AI systems may well challenge humans in a general sense. However, the proponents are quick to point out that the systems are still mostly statistical, even though a new property of emergence has been realised in the very large distributed systems (Large Language Models [41]) that is not statistically predictable. While the path to success seems clear, there are still some hurdles and the problems that autonomous vehicles [11] have could be an example of this. Researchers are always inventing new ways to do things and this paper offers a different architecture to the established theory that may hopefully be able to complement the existing systems.
The new system is called E-Sense (Electronic Sense, or Essence). It comprises of a memory model with 2 levels of information and then a more neural layer above that. The lower memory level stores source data in a Markov [12] (n-gram) structure that is unweighted. In a spatial sense, this would still mean that similar patterns would be clustered together. Then a middle ontology level is created from a further 3 phases of aggregating source information. Each phase re-structures from an ensemble to a tree, where the information transposition may be from horizontal set-based sequences into more vertical, typed-based clusters [15]. The ontology is not critical to the results of this paper, but it may be useful in future, for suggesting alternative concepts during search processes. The success of the typing is open to question, but results produced answers, based more on use and context. For example, ‘linking’ with ‘structure’ or ‘provide’ with ‘web,’ for a document describing distributed service-based networks. The potential of it is described in section 4 and the Appendix A examples. The design and implementation of the model is strongly biased towards the author’s previous publications. For example, exactly how the information transposition for the ontology should be done is an open question. The base memory is essentially neutral, where any weighted constraints or preferences should be stored in the calling module. This would allow different weight sets to be imposed on the same linked structures, for example. The third level is more functional, where each function can represent a subset of the base data and learn how to transpose across it. The functional structures are shown to be quite orthogonal, or separate and are made from nodes with a progressive type of capability, from unordered to ordered. This was a surprising result that is described further in section 5. Comparisons with the columnar structure of the neural cortex can even be made. This is only a first implementation of the model and in fact, a use for its’ functionality is still not clear, when compared to what existing system can achieve. But it offers a different architecture to the current favourites and has some interesting biological comparisons that may be able to give different and new views of the data. Direct comparisons with the real human brain are made throughout the paper, where previous work by the author includes [15,16,17,22].
The rest of the paper is organised as follows: Section 2 briefly introduces the original model again, while section 3 gives some related work. Section 4 describes the new memory model that is the lower 2 levels, with some test results. Section 5 then introduces the new upper neural level and section 6 introduces the idea of ordinal learning, again with some test results. Section 7 makes comparisons with purely biological concepts, while section 8 gives some conclusions on the work.

2. The Original Cognitive Architecture

The original architecture [22] described 3 levels of increasing complexity. The lower-level optimised links locally, using stigmergy, for example. The middle-level aggregated the lower-level links and the upper-level aggregated those into more complex concepts. The original diagram is given in Figure 1.
Section 4 describes that these levels now form the basis for the new memory and neural models. An ontology [24] was also part of the original architecture and that is replaced by the new middle level. The memory model uses a statistical clustering process, rather than semantics and rules. The author supposes that this effect is covered in modern NLP programs by using Word Vector models [40] and Transformers [58], for example. Fully-connected neuron structures are central to some themes in the system, where this idea is quite common (for example, [1,27] and some of the author’s earlier papers). Gestalt theory has been mentioned before [21]. With Gestalt psychology, objects are seen independently of their separate pieces. They have an ‘other’ interpretation of the sub-features and not just a summed whole of them. Gestalt theory makes use of ideas like similarity and proximity (and good continuation) to group objects and it believes that the brain has an internal order and structure that it places external stimuli into. It does not simply copy the input exactly as it appears. The booklet [4] gives a formal description of the theory and a mathematical proof that links the psychology theories of memory span [5,39] and duality [48].

3. Related Work

There are a few notable AI systems that already produce human-like results, where most systems would claim to represent one or more parts of the human brain. In-line with the author’s theory, the review paper [47] describes that cognition calls for a mechanistic explanation, where intelligence may depend on specific structural and functional features in the brain. It gives an overview on what types of neural network are used to model which parts of the brain. For example, auto-associative networks have been used to model the cortical regions [55], while feedforward networks have modelled memory or vision. No network type has modelled the whole brain however, probably because of their fixed structures. The paper [38] also describes modular networks for modelling the human brain. For this task, ‘heavy-tailed’ connectivity becomes important and several papers have discovered this phenomenon when mathematically modelling the neural connectivity (for example, [37,49]). With heavy-tailed connectivity, synaptic connectivity is concentrated among a select few pairs of neurons that are attractors. This results in a sparse network of strong connections dominating over other interactions. The paper [37] has shown that they can occur simply through a mixture of Hebbian and random dynamics, or the preferential attachment model [2]. The paper [49] studied how different rewiring functions would affect the resulting structure that was generated. They observed that random structural connectivity was reshaped by ‘ordered’ functional connectivity towards a modular topology, which also indicates synchronous firing patterns. One example was that rewiring peripheral nodes inside a module was homogeneous, with high synchrony and low-dimensional chaotic dynamics. On the other hand, central hub nodes connected with other modules, exhibited unsynchronized, high-dimensional stochastic dynamics. To reduce chaotic activity and energy therefore, it makes sense that between-module interaction would occur through a select number of key nodes only.
The paper [52] describes a model of the Hippocampus that uses auto-associative networks with generative learning. It describes how episodic memory is constructive, rather than the retrieval of a copy. But it needs the resource of semantic memory, from the neocortex, which is factual knowledge. They used a modern Hopfield network, where feature units activated by an event were bound together by a memory unit. The two layers here, binding features, is considered in section 5, for example. The generative networks were implemented as variational autoencoders [32], which are autoencoders with special properties, so that the most compressed layer represents a set of latent variables. These variables can be thought of as hidden factors behind the observed data and can be used to re-create the data again. The paper [55] considered if an auto-associative network can accurately model the cortical region. It considered the different levels in the cortex [26,43] and the different types of connection and function in those levels. The conclusion was that an auto-associative network has sufficient capacity to be used as a memory model, but may require the addition of these other factors. Since then, the creation of modern Hopfield networks [33] has shown that this type of network can have sufficient capacity in general, but needs multi-dimensional functions.

3.1. Current State-Of-The-Art

Deep Neural Networks [30,35] probably kicked the current revolution off, but other notable successes would include Decision Trees [25], for example. Category Trees [18] might be an interesting alternative. Deep Learning [42] then combined Deep Neural Networks with Reinforcement Learning. It can automatically learn features from the data, which makes it well-suited for tasks like object classification and speech recognition. DeepMind (the company behind deep learning) introduced neural Turing machines (neural networks that can access external memory like a conventional Turing machine), resulting in a computer that loosely resembles short-term memory in the human brain. The model [42] used a convolutional neural network, which is organized similarly to the human visual cortex. The advantage of this kind of network is that the system can pick out particular features from the data, automatically. It is then able to comb through massive amounts of data and identify repeated patterns that can be used to create rules and processes. The general architecture means that DeepMind's algorithms have taught themselves to play Atari games and beat the best humans in Go or Chess. DeepMind has since moved on to tackling more and more real-world problems, such as unravelling the likely structures of Proteins. Then recently, Large Language Models [41], such as OpenAI’s ChatGPT and Chat-GPT4 [46] have advanced the state-of-the-art again. Some argue that GPT4 already exhibits a level of Artificial General Intelligence, maybe because of the emergence property. These systems can make use of Word Vector models [40] and Transformers [58], for example, to predict what comes next in a sequence, rather like an n-gram [3,12] for text. They can be trained on a large corpus of data but are then able to create answers for any type of question, even ones not known about. They can use the same process to manage images, mathematical equations and even computer code. The discovery of transformers allowed them to predict to a level not encountered before and together with deep learning, huge distributed models with billions of nodes can be built. But even with all the recent advances, some papers show that there can still be problems, even with benchmark datasets [9,31,45]. New solutions would also want to make the models more economic and reduce their reliability on data.

3.2. Alternative Models

Other designs are described in [36], where one option, used in SPAUN [10], was to transform an ensemble mass into a vector-style structure, with weighted sets of features. SPAUN is one of the most realistic brain model designs, but context is still a problem. This is also clear in one of the original designs called SOAR [34]. That system adhered strictly to Newell and Simon's physical symbol system hypothesis [44], which states that symbolic processing is a necessary and sufficient condition for intelligent behaviour. SOAR exploited symbolic representations of knowledge (called chunks) and used pattern matching to select relevant knowledge elements. Basically, where a production matched the contents of declarative (working) memory the rule fired and then the content from the declarative memory was retrieved. SOAR suffers from problems of memory size and heterogeneity. There is also the problem that production rules are not general knowledge but are specific and so there is still not a sufficient understanding at the symbolic level. IBM's Watson [28] is also declarative, using NLP and relies on the cross-referencing of many heuristic results (hyperheuristics) to obtain intelligent results. Context is a key feature of the Watson system however. A recent paper [59] describes a process for recognising ‘relation patterns’ between objects. Humans acquire abstract concepts from limited knowledge, not the massive databases that current systems use. Their relational bottleneck principle suggests that by restricting information processing to focus only on relations, it will encourage abstract symbol-like mechanisms to emerge in neural networks and they suggest a neuro-symbolic [50] approach. They argue that an inductive process can be used to learn a relation like ‘ABA’, where A or B can then be anything. The symbolic and connectionist approaches can be reconciled to focus on relations between objects rather than the attributes of individual objects. They propose to use inner products, which naturally capture a notion of relations in terms of similarity between learned attributes. A 'small changes' theory is part of this paper's model, described later in section 5.2. Also to be noted for the idea of massive overlap is the 'Thousand Brains Theory' in [26].
A good organisation ability may be an inherent property of humans, or even the animal kingdom and would be something that can be improved in the current systems. This is discussed further in section 6. The paper [29] suggests a theoretical framework that would try to convert the fixed neural network architecture into one that can represent images in more abstract part-whole hierarchies. The structure would not be so fixed, but neurons would be allocated to clusters dynamically. It is something that humans do, but neural networks currently cannot do. The paper is quoted in [13], which is interested in the mechanistic processes of human cognition. A section there on abstract encoding of sensory input used a vector format to encode data and create columns of vector sets. Similar columns can then be used to find parts of an object in a visual scene and the framework does not suffer from overfitting. The paper [53] used statistical mechanics to try to explain some of the mechanisms that occur in the biological brain. They then showed how their results suggest a thermodynamic limit to the neural activity, but have no definite explanation of why, and this limit suggests a boundary. They also noted that the brain is a nonequilibrium system and asked the question of how it then obtains equilibrium. Most of these papers consider the brain activity to be more entropic than local. The paper [8] is very mathematical, but it might give a solution to the problem of these looser constructs. It proposes to use sheaves and writes about unary and binary typing’s. Rather than global, they argue that time can be constructed, like local events, when it might also be thought of as an ordering and is entropic.

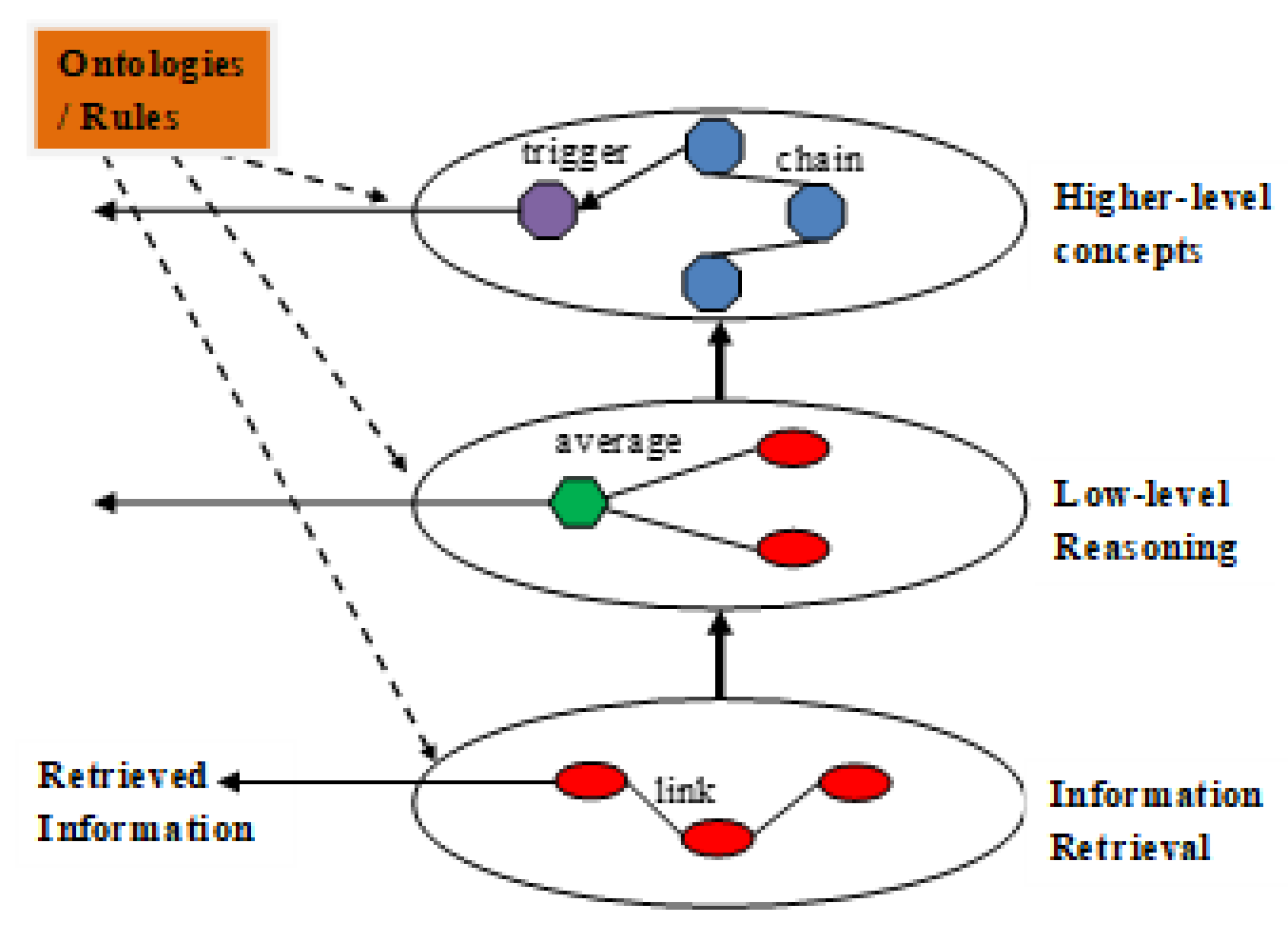
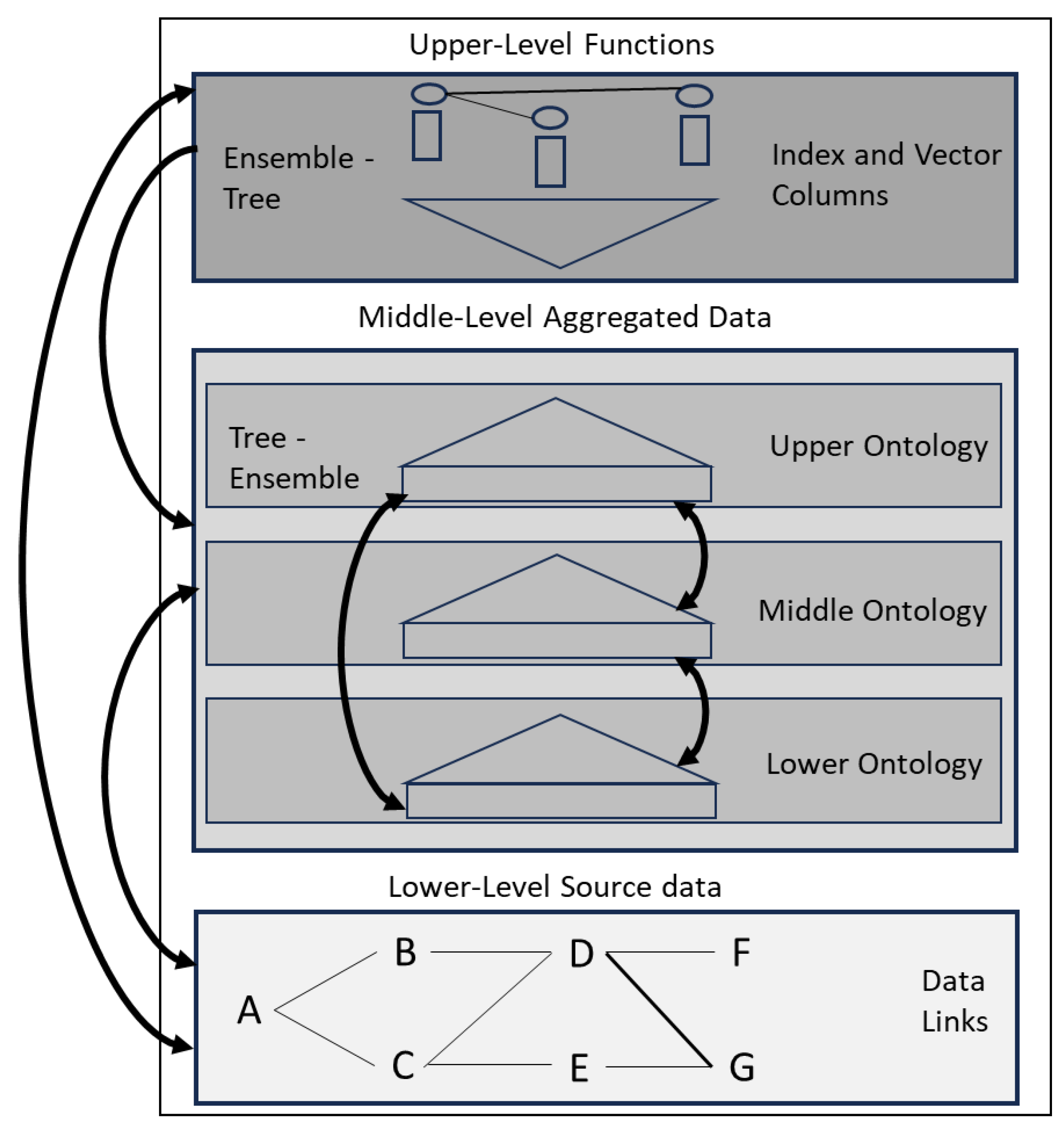
4. The Memory Model

The original cognitive model was based on a 3-level architecture of increasing complexity, which included an ontology that would be available to all the levels. Ontologies [24] describe the relations between concepts in a very structured and formal way. They are themselves high-level structures and it is not clear how they could be built simply from statistical processes. The ontology of this model is therefore not at that level, with sets of specific relations between concepts. Instead, it provides a loose clustering of concepts, but also a transition from context to type.

4.1. Memory Model Levels

Aligned with the cognitive model, the memory part is implemented in the two lower levels, with some referencing in the upper neural level. This is not surprising, as it is thought that memory is stored in all parts of the human brain. The 3 memory levels are therefore as follows, also shown in Figure 2:
(1)
The lowest level is an n-gram structure that is sets of links only, between every source concept that has been stored. The links describe any possible routes through the source concept sequences, but are unweighted.
(2)
The middle level is an ontology that aggregates the source data through 3 phases and this converts it from set-based sequences into type-based clusters.
(3)
The upper level is a combination of the functional properties of the brain, with whatever input and resulting conversions they produce, being stored in the same memory substrate.
It may be that the first 2 levels can be made from simpler structures, in the sense that it does not have to be functional. For example, the paper [15] describes that more recently, the perineuronal network [56] has received a lot of attention and may be a sort of simpler memory substrate. The paper [16] describes the types of knowledge transitions that may occur. If using a classification of experience-based or knowledge-based information, then experience-based information is dynamic and derived from the use of the system. Knowledge-based information is static and built from the experiences. The paper describes that the transitions may be:
  • Experience to knowledge.
  • Knowledge to knowledge.
  • Knowledge to experience.
If looking at Figure 2, then from the top level to the bottom level we get these transitions. The two outer-most layers would be the sensory input and the cortical columns, so they would be experience-based. Then between them are transitions into and out of knowledge. At least 1 time-based layer needs to be added to this region, which will be considered in future work. The paper [47] does not note auto-associative networks as being whole-brain models, but the new cognitive model could be seen as an auto-associative one, where the middle knowledge-based level would store compressed knowledge variables. The knowledge-to-knowledge transition would be between the middle and upper levels, but currently, there is no information flow here.

4.2. Lower Memory Level

The lowest level is an n-gram, where each node contains links to each possible next node. Thus, tracing through these links can return different sequences, but to provide some direction, possibly a 5-gram needs to be used. It is also possible to note start or end nodes in a sequence, to help with defining the sequences better. The database structure is appealing because it is very compact, but while it works well for most of the time, it may not always return every sequence, exactly as it was entered. Unlike neural representations however, this structure does not have to be weighted. A link between nodes in a region is noted only once, no matter how often it occurs during the input. The structure therefore only stores equal possibilities, where preferences or weighted choices would have to be transferred over to a calling module. If the n-gram is sufficient, then the theory would state that a Markov process may be sufficient to describe a Gestalt process. This is discussed further in section 7.

4.3. Middle Ontology Level

The idea of an ensemble-hierarchy [21] has not been discarded completely, but for the structure of this paper, it is an ensemble-tree, for filtering purposes only. The middle ontology level uses transitions from ensemble to tree, where the final trees look more like vector lists. While the ontology is still a low-level structure therefore, it may contain one important property in that it is able to convert set-based sequences into type-based clusters. This would introduce a small amount of knowledge into the ontology that a search process can make use of. The lower-level database can be described by an n-gram, but the middle ontology level is more complicated. It makes use of the Frequency Grid [21] to generate word clusters, but there would be more than 1 way to implement the aggregation process – from ensemble to tree, for example. The author has chosen a version that prunes the most nodes from the result, to save on time and resources, for running on a low power computer. This means that a text document the size of a book may return at the top ontology tree, only a few words clustered together (see Appendix A), but as the search could move back down the structure to the lower levels, it will be able to discover most of the text from matching there as well.

4.4. Ontology Tests

A computer program has been written in Java that implements the two memory-model levels for basic testing. The success of a test is measured rather arbitrarily, by judging if the words in a cluster have some relation and preferably, are not simply part of the same sentence. The author has judged that this is often the case. Each result is only from clustering on a single book however. It is even more difficult to judge how accurate the clusters are when texts are combined, where this is future work. One problem that has occurred with the frequency grid before is when 2 or more smaller clusters are joined together. This can result in a single cluster with apparently 2 or more meanings. This also occurs in some of the final upper ontology clusters, described in Appendix A. Rather than the program recognising associated antonyms, or something like that, it may have combined 2 lower and separate clusters somewhere. While the algorithms in this paper are different to what was used previously, this becomes an interesting feature when constructing the neural level, described in section 5, however.
Appendix A therefore lists some well-known texts [54], together with the final upper ontology sets that the program produced. The resulting structures were very narrow, where each value in each list was a child node of the one before. This would be consistent with a conversion from a horizontal set-based description to a vertical type-based one. However, the row ordering can change and so an ordered sequence might be an illusion. The results are very subjective, but the author hopes that it is possible to see how some level of real meaning in the words has been derived from the statistical process.

5. The Neural Level

The neural level is the top level of the design and contains more cognitive or functional units. There are to be 2 different types of neural level in the final model – one is interested in cognitive processes that may be described by a Cognitive Process Language [19], while the other is more interested in logical processes ([16] and the related papers). This paper deals only with the logical neural model, which comprises of functions that operate on the source data of the lower level. It does not follow-on from the middle ontology, but is separate from it, although it is able to query the ontology if needed. A typical definition of a function is something that maps a set of input values to a set of output values. It may do this by generating the output, or if the output already exists, then it is a selection process. If it can make use of existing output, then the function reduces to something more like a constraint, with a description like - a function in some cases, may be seen as something that reduces the possibilities for the next step. As the following sections describe, the neural level now looks quite a lot like the cortical regions in the human brain.

5.1. Function Identity

If there are lots of functions in the neural level, then they want to be recognised as separate units and be made distinct. One option is to consider every node in the function and comparing this amount would probably produce differences. Another option may be to consider only a set of base ‘marker’ nodes, when the rest of the function is built on-top of these. In fact, these key nodes can become an index set that should be found first in the source data and then a larger set of related vector values can be searched for. This is in fact what modern search engines do [7]. The index set could also help with maintenance. It could be checked for first, to see if some process returns the same function key. If not, then it is then likely that something has changed in the base data, where further reasoning processes would then need to determine what to do.

5.2. Function Structure

A function is therefore an ensemble of these index nodes, each with a set of index values. Each node then links to a larger set of vector values that represent a feature, or a set of vectors. Each index node matches with 1 or 2 sequences from the database and it also stores the relative position(s) of the sequence(s), so that the correct ordering can be re-constructed from values that may be in a different order. The operation might be like the relation patterns of [59], but potentially different because the relational patterns allow repeats. Each function part in fact resembles quite closely, the Symbolic Neural Network that was written about in [23]. The index values are quite orthogonal, or do not overlap very much. The features, as whole sets, are mostly unique as well, but some index nodes can share the same feature set. There could thus be closures at both the top and bottom of this structure. This type of structure was shown in [23] to be able to filter-out noise quite well, for example. Both the most commonly occurring terms and the least commonly occurring terms are stored in a feature for a sequence. The most common allow potential matches with the sequence to be found in a larger database. Then the least common allow this potential set to be sorted further, to match the feature more precisely. A group of the SNNs is stored in an ‘Ordinator,’ which is really the whole function for a particular operation. Because there is a lot of overlap in the results returned from each SNN, this produces only small changes in the statistical result, but usually, any changes then need to be included. When building the structure, some weighted components might be used, but when using the structure afterwards, it is mostly an un-weighted process. There might be some frequency counts, but not much else. It is probably the case that the orthogonal nature of the structure reduces the need for weights.

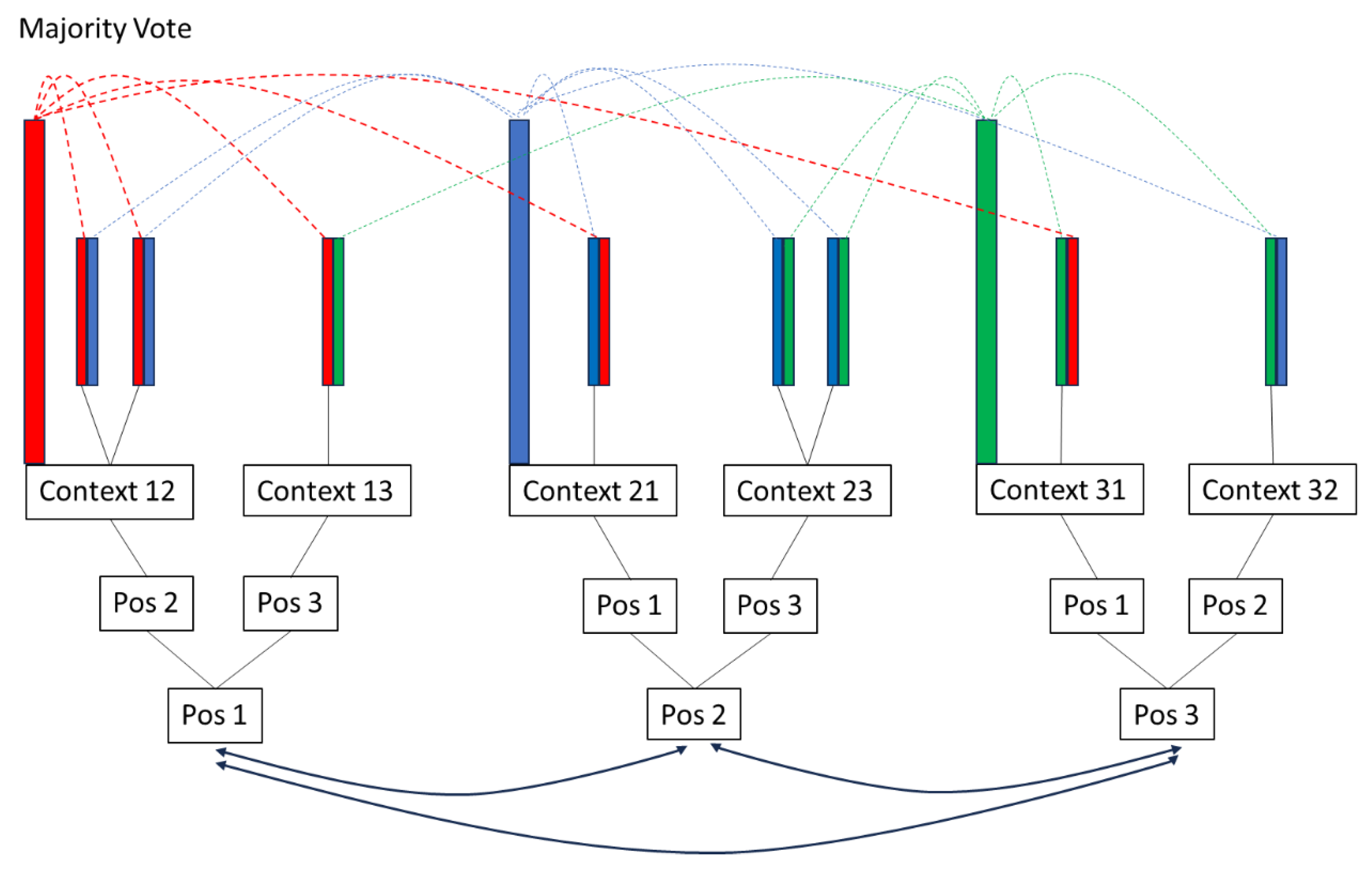
5.3. Index Types

The process of creating the index nodes and related vectors seemed to produce 3 different types. While it was not the case every time, a clear pattern of 3 distinct types emerged. One type may have a longer list of index terms but no related feature set. The other 2 had both index terms and related feature sets, but differ as explained next. These types map quite closely to known neuron types, as follows:
  • Unipolar Type: this has a list of index terms that is generally a bit longer and is unordered. It can be matched with any sequence in the input set, but to only 1 sequence.
  • Bipolar Type: this has a list of index terms and a related feature set. The index terms should be matched to only 1 sequence and some of the feature values should also match with that sequence. This matching should be in order however – the order in the feature should be repeated in the sequence. Then the rest of the feature values can match with any other sequence and in any order.
  • Pyramidal Type: this has a list of index terms and a related feature set. The index terms however are split over 2 specific sequences. Both the index terms and the related feature set should match with 2 specific sequences and the matching should be ordered in both.
There is thus a very interesting progression through the 3 types and suggests a progression in functionality as well. While the index structure maps to these neuron types, it could also be used to create more columnar structures. It would make quite a good basis for the neocortex columns [26,43], for example, with a columnar unit comprising an index node and feature set, and the index nodes would also have horizontal connections. This can be seen in Figure 2, in the top neural level.

6. Ordinal Learning

The author would like to introduce the idea of Ordinal Learning. It is being given a specific name, because current methods do not appear to do it. It is maybe more algorithmic than functional. Ordinal learning is concerned with re-creating the order of sequences it was trained with. But in this case, it can also interpret for previously unknown input that is statistically close to what it was trained with. Having a sense of order may be deeply inherent in animals, not just for the higher cognitive functions. The papers [37,38], for example, map the neural connectome for some animals and the heavy tails that separate the network into modules are described. The brain is also thought to have a scheduling functionality at the top of the cortex, probably to perform such tasks. Neural networks are able to interpret what a pattern is with some missing information, but do not typically re-order the information. Although, a second network or module might learn pattern ordering, for example. Large language models also predict across a known sequence but would not intuitively know how to change a faulty sequence order. A change in the sequence order would lead to a change in the question and thus prediction. But this is still a common algorithmic problem with many solutions already. It could probably be solved in a few lines of code in many cases, and so it remains to be seen if the much more complicated method of this paper is more useful.
The basis for the Ordinator that learns the ordering, is to have something like a heavy-tailed neuron at each ordinal position. Thus, while heavy-tailed neurons are due to a preferential attachment or rich-get-richer mechanism [37], they would now have a particular function as well, that is to order the surrounding neurons. The ordinator would have a heavy-tailed neuron that other neurons would link to, to place their sequence into that order position. There would then be a vote from the ordinator node for that position, where the most connections would dominate. But as a computer program, it is still a statistical process, where if the train example is missing, the sequence with the closest statistical match will be selected instead.
A schematic of the ordinator function is given in Figure 3. The system would store the feature network for the learned positions and then new input sets would match with it. There is a hierarchical path leading to each of the ordinator position nodes. It is not clear what exactly should be in the path, but the 2 positions from the neuron types and maybe the context of the query would be possible. Then, query answers that result in sequences being selected for either position 1 or 2 can be added, or in a simpler model, they could be simply linked with the position itself. A majority vote can then be done and would resemble the neurons competing for the position.

Ordinal Tests

The ordinal learning process has also been implemented in Java code, for basic testing purposes. The code is in no way optimised and it would take maybe 20 minutes to learn the ordering for a 3K document (40 sentences) on a standard laptop. The learned structures were also much larger in size, than the raw data. For the process to be useful therefore, it would be important that the information can be generalised and re-used in some way. But the amount of train data is quite small and so it appears to be able to use the data quite efficiently. It comprises lots of smaller separate algorithms, where it is likely that it could be parallelised.
A train text document can be read and stored in a source (lower level) database. It can then be queried for information about the main concepts in it. In fact, an ensemble approach is required, but the process is mostly automatic. A bag-of-words, for example, can determine the main terms in the document and so queries can be run to retrieve the related sequences and build the logic structures. But this process is also recursively repeated for each query, with results from that query. Thus, lots of the results are mostly the same. The index values are also part of the feature vectors, so a structure representing this would probably be quite self-contained. The paper [20] made use of the frequency grid to produce a self-organising system, but the problem of the order of the input data rows became clear and an ensemble solution was required to at least partly, overcome this problem. Some neural networks also have a problem when the input rows are presented in a different order, but this recursive method seems to solve that issue.
After the ordinator has been created, a different test document can be loaded, or the same train document can be used to test as well. There is no specific ordering in the base database, for example, and so the retrieval of sequences for any document will not be in order. The purpose of the function is to recognise itself in the source data again. It therefore tries to match with the source data and then sort that into the ordering that it has learnt. The ordering is only relative, where the number of sequences in the train and test documents can be different. Appendix B gives the results for some basic tests. Two cooking instruction documents were selected. The first train document described how to cook a hard-boiled egg and the second described how to make Panna Cotta. If the test document was the same, then the data would be returned correctly. However, an ordinator was generated for either train document and then the database was changed to the test one, which contained both - a different description of how to cook a hard-boiled egg and the Panna Cotta description. The egg ordinator was able to select the sequences relating to the second description and also place them in order, as shown. The Panna Cotta ordinator also performed, as shown. So, while this is still a work in progress, it did perform to 100% accuracy for these two small documents. The process is more entropic than local connections, however and so there would be a balancing act to adding specific rules about something. It is also slightly stochastic, but the ensemble training method helps to keep the results mostly the same. This is still a statistical process, where if the test document has other sequences that match better with the feature concepts, then they will get selected instead. The distinct concepts in a feature are thus very important. Results also showed however, that for larger documents, of even 40 lines or more, some sequences would typically be missed, or not even retrieved from the source database. It is therefore unlikely that the process can be used to simply rote learn a large corpus of information. But it could be a useful guide and along with search processes, sort through information and make some sense of it. There are still options to be tried, to make it more accurate.

7. Some Biological Comparisons

This section makes comparisons with some purely biological ideas.

7.1. Gestalt Psychology

With Gestalt psychology, objects have an ‘other’ interpretation of the sub-features and not just a summed whole of them. Gestalt theory could be realised in the lowest level of the memory structure. Because the links are unbiassed, one interesting aspect of the structure is that it may not return exactly what was input, thus satisfying the theory that the whole may be different to the parts. As part of the computer model, an n-gram depth can add accuracy, requiring that 2 or more previous concepts are present, where in fact a 5-gram is currently used. But even with this, sequences may get combined, even if they were added separately during input. Kolmogorov and Shannon were written about in [17], with regards to trying to measure intelligence. Shannon bases his Information Theory [51] on Entropy and a Markov model. Kolmogorov Complexity theory ([6], chapter 7) states that the shortest sequence is the most likely and also the best. This idea is also associated with Gestalt theory and would be compatible with the architecture. Because shorter sequences are likely to have fewer transitions they are likely to be more accurate, but they might also cause errors by terminating some sequences early.

7.1.1. Example of a Gestalt Process

Consider this example where the following 2 sentences are added to the lowest-level memory:
The cat sat on the mat and drank some milk.
The dog barked at the moon and chased its tail.
Start words would now include ‘the’ and end words would include ‘milk’ and ‘tail.’ Each word in the sequence also has a link to any words that immediately follow it. If, for example, the memory system is asked to retrieve a sequence that results in the ‘and’ word being considered, then there are two possibilities after that – ‘drank’ or ‘chased.’ Therefore, a question about a dog could retrieve either of the following two sentences:
The dog barked at the moon and chased its tail, or
The dog barked at the moon and drank some milk.
If the second sentence was returned, then it would not be violating the memory system and the person would probably not have a reason to disbelieve it. It could therefore be a legitimate answer, even though it is different to what was originally entered. It can also be argued that changing the information in this way is not a creative process, but simply taking a different route through the linked structure.

7.2. Brain Evolution

This section follows-on from ideas in [15] that describe how cells may have evolved from invertebrates to the human brain. Organisation was a key principle there, but also the conversion to types. The brain is typed, where even insects like ants can recognise types. Thus, if traversing through the new cognitive model of Figure 2, the middle ontology layer converts from the lower-level ensembles of set-based values to more type-based values. Then, between the middle and upper levels the types can be clustered back again into sequences, based on time and use. Possibly these new clusters however are missing some of the sensory information. If the cortex is mostly about actions, or how to do something, then it does not require all the extra ‘syntactic sugaring’ from the senses. It would want to know what the objects are and how to use them, but maybe not if it was nice or not. So possibly this type of information remains deeper in the brain, where it would also be closer to the senses themselves. The more functional upper cortex only learns how to manipulate it. Again, if thinking about a conscious experience, it would then require the sensory feedback from a whole-brain activation, not just local circuits in the cortex.

7.3. Small Changes

Thus, a constructive process can be seen in the building of brain structures. However, any new structure should not be so radical that it disturbs the mind. Thus, new structure should be added in small amounts each time. If we do not know about a subject for example, then the first structures for it should probably contain the basics or fundamentals for the subject. What this means is not clear, but possibly, what other concepts link with. If we already have some memory about a subject, then we can add to it instead, which can be new and richer information. This would also be the case when making a change to the existing structure. Turing [57] wrote about sub-critical and super-critical processes that a human brain would recognise more than an animal. But it suggested that single events were key and that maybe even the mind had some influence on what got stored. A mechanical process could simply make small changes until enough of them became critical and caused a change in thinking. But then the mechanical process should not try to store every piece of information that we receive. Therefore, some type of feedback from a more intelligent region that helps to reinforce the input and therefore preserve it could indeed happen. This might be from the sensory or the cortical regions, for example.

8. Conclusions and Future Work

This paper describes a first implementation stage for the 3-level cognitive model, now called E-Sense. While it is essentially a computer model, it is based strongly on our understanding of the human brain. Some direct comparisons with biological processes have been made and the fact that the model is mostly un-weighted should be an advantage. There are 2 memory levels that are economic in space and can transpose the information from set-based to types. This introduces new knowledge and the transition to types may in fact be helpful to an upper level that wants to know about objects and the technical ‘how‘. The upper level is more neural. Generating it produced a type of progressive functionality that could be loosely mapped to neuron types, or maybe just standard unary and binary operators. It might be convenient to look at the whole brain model as auto-associative. The bottom memory substrate / sensory level and the cortical levels map to each other through the middle-level transpositions. The two views are not exactly the same and so there is still an economy of storage, but the related parts in each map together. Then maybe, partial input in either can activate the related region in the other. The latent variables would be in the type-based layer between the middle and the upper levels. It is then convenient that the values here have been transposed into types, where combinations, maybe including time, can generate the required latent values.
There is still a lot of work to be done in all the levels. The results are not too bad and as the name suggests, they may be more about some type of general understanding, than the more direct results that the current systems provide. Some specifics probably need to be added, to increase the intelligence level. The number 3 has occurred in the paper. A value of 3 would allow something to be rooted (1), while two parts are being compared (2 and 3). If the brain likes to synchronise to balanced states, for example, then this might encourage the system to explore a step further, even when parts match. The model does push a lot of biological buttons however, including Gestalt, small changes and what heavy-tailed neurons might be for. The functional structure that maps to cortical columns is interesting and also the fact that a natural kind of ordering can be integrated into the structure. Considering future work, the source database does not always return exactly what was entered, so it would need to be determined if this is critical. Should it return everything exactly, or would that require reading the original source again? It is a very compact structure. Then, there is not a clear progression yet from the middle to the top level. The top level is currently created from accessing the source database directly, but middle to top could be included in a more dynamic system. Then also, making the system more accurate and useful.

Appendix A – Upper Ontology Trees for Book Texts

This appendix lists the upper-level ontology trees that were created for some well-known books. The clustering relates to the use of the word. Each row is a child node of the row immediately before it, but in fact the row ordering can change.
Romeo and Juilet, William Shakespeare [54].
Clusters
thou
love, o, thy
romeo, shall
death, eye, hath
day, give, lady, make, one, out, up, well
go, good, here, ill, night, now
come, thee
man, more, tybalt
The Wonderful Wizard of Oz, L. Frank Baum [54].
Clusters
dorothy
asked, came, see
city, emerald
great, oz
again, answered, away, before, down, made, now, shall, toto, up
scarecrow
lion, woodman
back, come, girl, go, green, head, heart, man, one, over, upon, very, witch
little, out, tin
The Adventures of Sherlock Holmes, Arthur Conan Doyle [54].
Clusters
back, before, came
down, know
more, room, think, well
day, eye, face, found, matter, tell
upon
holmes, very
little, man, now
one
away, case, good, heard, house, much, nothing, quite, street, such, through, two, ye
go, here
come, hand, over, shall, time
asked, never
door, saw
mr, see
out, up
made, way
Computing Machinery and Intelligence, A.M. Turing [57].
Clusters
answer, computer, man, question, think
machine
one
such

Appendix B – Documents and Test Results for the Neural-Level Sorting

This appendix lists the train and test files for testing the ordinal learning. The results of applying the ordering to the test files is also shown.
Train and Test Files
Train File – Hard-Boiled Egg
Place eggs at the bottom of a pot and cover them with cold water.
Bring the water to a boil, then remove the pot from the heat.
Let the eggs sit in the hot water until hard-boiled.
Remove the eggs from the pot and crack them against the counter and peel them with your fingers.
Train File – Panna Cotta
For the panna cotta, soak the gelatine leaves in a little cold water until soft.
Place the milk, cream, vanilla pod and seeds and sugar into a pan and bring to a simmer.
Remove the vanilla pod and discard.
Squeeze the water out of the gelatine leaves, then add to the pan and take off the heat.
Stir until the gelatine has dissolved.
Divide the mixture among four ramekins and leave to cool.
Place into the fridge for at least an hour, until set.
For the sauce, place the sugar, water and cherry liqueur into a pan and bring to the boil.
Reduce the heat and simmer until the sugar has dissolved.
Take the pan off the heat and add half the raspberries.
Using a hand blender, blend the sauce until smooth.
Pass the sauce through a sieve into a bowl and stir in the remaining fruit.
To serve, turn each panna cotta out onto a serving plate.
Spoon over the sauce and garnish with a sprig of mint.
Dust with icing sugar.
Test File – Hard-Boiled Egg and Panna Cotta
Remove the vanilla pod and discard.
For the panna cotta, soak the gelatine leaves in a little cold water until soft.
As soon as they are cooked drain off the hot water, then leave them in cold water until they are cool enough to handle.
Squeeze the water out of the gelatine leaves, then add to the pan and take off the heat.
Spoon over the sauce and garnish with a sprig of mint.
Stir until the gelatine has dissolved.
Place the eggs into a saucepan and add enough cold water to cover them by about 1cm.
Pass the sauce through a sieve into a bowl and stir in the remaining fruit.
Divide the mixture among four ramekins and leave to cool.
Place into the fridge for at least an hour, until set.
To peel them crack the shells all over on a hard surface, then peel the shell off starting at the wide end.
For the sauce, place the sugar, water and cherry liqueur into a pan and bring to the boil.
Place the milk, cream, vanilla pod and seeds and sugar into a pan and bring to a simmer.
Reduce the heat and simmer until the sugar has dissolved.
Take the pan off the heat and add half the raspberries.
Using a hand blender, blend the sauce until smooth.
Bring the water up to boil then turn to a simmer.
To serve, turn each panna cotta out onto a serving plate.
Dust with icing sugar.
Test Results
Selected Sequences from the Hard-Boiled Egg Function
[place, the, eggs, into, a, saucepan, and, add, enough, cold, water, to, cover, them, by, about]
[bring, the, water, up, to, boil, then, turn, to, a, simmer]
[as, soon, as, they, are, cooked, drain, off, the, hot, water, then, leave, them, in, cold, water, until, they, are, cool, enough, to, handle]
[to, peel, them, crack, the, shells, all, over, on, a, hard, surface, then, peel, the, shell, off, starting, at, the, wide, end]
Selected Sequences from the Panna Cotta Function
[for, the, panna, cotta, soak, the, gelatine, leaves, in, a, little, cold, water, until, soft]
[place, the, milk, cream, vanilla, pod, and, seeds, and, sugar, into, a, pan, and, bring, to, the, boil]
[remove, the, vanilla, pod, and, discard]
[squeeze, the, water, out, of, the, gelatine, leaves, then, add, to, the, pan, and, take, off, the, heat]
[stir, until, the, gelatine, has, dissolved]
[divide, the, mixture, among, four, ramekins, and, leave, to, cool]
[place, into, the, fridge, for, at, least, an, hour, until, set]
[for, the, sauce, place, the, sugar, water, and, cherry, liqueur, into, a, pan, and, bring, to, the, boil]
[reduce, the, heat, and, simmer, until, the, sugar, has, dissolved]
[take, the, pan, off, the, heat, and, add, half, the, raspberries]
[using, a, hand, blender, blend, the, sauce, until, smooth]
[pass, the, sauce, through, a, sieve, into, a, bowl, and, stir, in, the, remaining, fruit]
[to, serve, turn, each, panna, cotta, out, onto, a, serving, plate]
[spoon, over, the, sauce, and, garnish, with, a, sprig, of, mint]
[dust, with, icing, sugar]

References

  1. Anderson, J.A., Silverstein, J.W., Ritz, S.A. and Jones, R.A. (1977) Distinctive Features, Categorical Perception, and Probability Learning: Some Applications of a Neural Model, Psychological Review, Vol. 84, No. 5. [CrossRef]
  2. Barabasi A.L. and Albert R. (1999). Emergence of scaling in random networks, Science, 286:509-12. [CrossRef]
  3. Brown, P.F., Della Pietra, V.J., Desouza, P.V., Lai, J.C. and Mercer, R.L.. (1992). Class-based n-gram models of natural language. Computational linguistics, 18(4), pp.467-480.
  4. Buffart, H. (2017). A formal approach to Gestalt theory, Blurb, ISBN: 9781389505577.
  5. Cavanagh, J. P. (1972). Relation between the immediate memory span and the memory search rate. Psychological Review, 79, pp. 525 - 530. [CrossRef]
  6. Cover, T.M. and Joy, A.T. (1991). Elements of Information Theory, John Wiley & Sons, Inc. Print ISBN 0-471-06259-6 Online ISBN 0-471-20061-1.
  7. Dobrynin, V., Sherman, M., Abramovich, R., and Platonov, A. (2024). A Sparsifier Model for Efficient Information Retrieval, AICT’24.
  8. Dobson, S. and Fields, C. (2023). Constructing condensed memories in functorial time. Journal of Experimental & Theoretical Artificial Intelligence, pp.1-25. [CrossRef]
  9. Dong, M., Yao, L., Wang, X., Benatallah, B. and Zhang, S. (2018). GrCAN: Gradient Boost Convolutional Autoencoder with Neural Decision Forest. arXiv preprint arXiv:1806.08079.
  10. Eliasmith, C., Stewart, T.C., Choo, X., Bekolay, T. DeWolf, T., Tang, Y. and Rasmussen, D. (2012). A Large-Scale Model of the Functioning Brain, Science, 338(6111), pp. 1202 - 1205. [CrossRef]
  11. Feng, S., Sun, H., Yan, X., Zhu, H., Zou, Z., Shen, S. and Liu, H.X. (2023). Dense reinforcement learning for safety validation of autonomous vehicles. Nature, 615(7953), pp. 620 - 627.
  12. Fink, G.A. (2014). Markov models for pattern recognition: from theory to applications. Springer Science & Business Media.
  13. Friedman, R. (2021). Cognition as a Mechanical Process. NeuroSci, 2, 141–150. [CrossRef]
  14. Goodfellow, I.J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A. and Bengio, Y. (2014). Generative adversarial nets. Advances in neural information processing systems, 27.
  15. Greer, K. (2022). Neural Assemblies as Precursors for Brain Function, NeuroSci, 3(4), pp. 645 - 655. https://doi.org/10.3390/neurosci3040046. Also published in Eds. Parnetti, L., Paoletti, F.P. and Gallart-Palau, X., Feature Papers in NeuroSci : From Consciousness to Clinical Neurology, July 2023, pages 256. ISBN 978-3-0365-7846-0 (hardback); ISBN 978-3-0365-7847-7 (PDF). [CrossRef]
  16. Greer, K. (2021). New Ideas for Brain Modelling 7, International Journal of Computational and Applied Mathematics & Computer Science, Vol. 1, pp. 34-45.
  17. Greer, K. (2021). Is Intelligence Artificial? Euroasia Summit, Congress on Scientific Researches and Recent Trends-8, August 2-4, The Philippine Merchant Marine Academy, Philippines, pp. 307 - 324. Also available on arXiv at https://arxiv.org/abs/1403.1076.
  18. Greer, K. (2021). Category Trees - Classifiers that Branch on Category, International Journal of Artificial Intelligence & Applications (IJAIA), Vol. 12, No. 6, pp. 65 - 76.
  19. Greer, K. (2020). New Ideas for Brain Modelling 6, AIMS Biophysics, Vol. 7, Issue 4, pp. 308-322. [CrossRef]
  20. Greer, K. (2020). A Pattern-Hierarchy Classifier for Reduced Teaching, WSEAS Transactions on Computers, ISSN / E-ISSN: 1109-2750 / 2224-2872, Volume 19, Art. #23, pp. 183-193.
  21. Greer, K. (2019). New Ideas for Brain Modelling 3, Cognitive Systems Research, 55, pp. 1-13, Elsevier. [CrossRef]
  22. Greer, K. (2012). Turing: Then, Now and Still Key, in: X-S. Yang (eds.), Artificial Intelligence, Evolutionary Computation and Metaheuristics (AIECM) - Turing 2012, Studies in Computational Intelligence, 2013, Vol. 427/2013, pp. 43-62, Springer-Verlag Berlin Heidelberg. [CrossRef]
  23. Greer, K. (2011). Symbolic Neural Networks for Clustering Higher-Level Concepts, NAUN International Journal of Computers, Issue 3, Vol. 5, pp. 378 – 386, extended version of the WSEAS/EUROPMENT International Conference on Computers and Computing (ICCC’11).
  24. Gruber, T. (1993). A translation approach to portable ontology specifications. Knowledge Acquisition, 5, pp. 199 - 220.
  25. Gupta, B., Rawat, A., Jain, A., Arora, A. and Dhami, N. (2017). Analysis of various decision tree algorithms for classification in data mining. International Journal of Computer Applications, Vol. 163, No. 8, pp. 15 - 19.
  26. Hawkins, J., Lewis, M., Klukas, M., Purdy, S. and Ahmad, S. (2019). A Framework for Intelligence and Cortical Function Based on Grid Cells in the Neocortex, Frontiers in neural circuits, 12, p. 121.
  27. Hawkins, J. and Blakeslee, S. On Intelligence. Times Books, 2004.
  28. High, R., 2012. The era of cognitive systems: An inside look at IBM Watson and how it works. IBM Corporation, Redbooks, pp.1-16.
  29. Hinton, G., 2023. How to represent part-whole hierarchies in a neural network. Neural Computation, 35(3), pp.413-452.
  30. Hinton, G.E., Osindero, S. and Teh, Y.-W. (2006). A fast learning algorithm for deep belief nets, Neural computation, Vol. 18, No. 7, pp. 1527 - 1554.
  31. Katuwal, R., Suganthan, P.N. (2019). Stacked Autoencoder Based Deep Random Vector Functional Link Neural Network for Classification, accepted: Applied Soft Computing . [CrossRef]
  32. Kingma, D.P. and Welling, M., 2019. An introduction to variational autoencoders. Foundations and Trends in Machine Learning, 12(4), pp.307-392.
  33. Krotov, D. (2023). A new frontier for Hopfield networks. Nature Reviews Physics, 5(7), pp. 366 - 367.
  34. Laird, J. (2012). The Soar cognitive architecture, MIT Press.
  35. LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015). [CrossRef]
  36. Lieto, A., Lebiere, C. and Oltramari, A. (2017). The knowledge level in cognitive architectures: Current limitations and possible developments, Cognitive Systems Research.
  37. Lynn, C.W., Holmes, C.M. and Palmer, S.E. (2024). Heavy-tailed neuronal connectivity arises from Hebbian self-organization, Nature Physics, 20(3), pp.484-491.
  38. Meunier, D., Lambiotte, R. and Bullmore, E.T., 2010. Modular and hierarchically modular organization of brain networks. Frontiers in neuroscience, 4, p.200.
  39. Miller, G. A. (1956). The magical number seven, plus or minus two: some limits on our capacity for processing information. Psychological Review, 63, pp. 81 - 97.
  40. Mikolov, T., Sutskever, I., Chen, K., Corrado, G.S. and Dean, J. (2013). Distributed representations of words and phrases and their compositionality. Advances in neural information processing systems, 26.
  41. Minaee, S., Mikolov, T., Nikzad, N., Chenaghlu, M., Socher, R., Amatriain, X. and Gao, J., 2024. Large language models: A survey. arXiv preprint arXiv:2402.06196.
  42. Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A.A., Veness, J., Bellemare, M.G., Graves, A., Riedmiller, M., Fidjeland, A.K., Ostrovski, G., Petersen, S., Beattie, C., Sadik, A., Antonoglou, I., King, H., Kumaran, D., Wierstra, D., Legg, S. and Hassabis, D. (2015). Human-level control through deep reinforcement learning, Nature, Vol. 518, pp. 529-533.
  43. Mountcastle, V.B. (1997). The columnar organization of the neocortex, Brain: J Neurol, Vol. 120, pp. 701 - 722. [CrossRef]
  44. Newell, A. and Simon, H.A. (1976). Computer science as empirical inquiry: Symbols and search, Communications of the ACM, Vol.19, No. 3, pp. 113 - 126.
  45. Nguyen, T., Ye, N. and Bartlett, P.L. (2019). Learning Near-optimal Convex Combinations of Basis Models with Generalization Guarantees. arXiv preprint arXiv:1910.03742.
  46. OpenAI. 2023. GPT-4 Technical Report. (2023). arXiv:cs.CL/2303.08774.
  47. Pulvermüller, F., Tomasello, R., Henningsen-Schomers, M.R. and Wennekers, T. (2021). Biological constraints on neural network models of cognitive function, Nature Reviews Neuroscience, 22(8), pp. 488 - 502. [CrossRef]
  48. Rock, I. (1977). In defence of unconscious inference. In W. Epstein (Ed.), Stability and constancy in visual perception: mechanisms and processes. New York, N. Y.: John Wiley & Sons.
  49. Rubinov, M., Sporns, O., van Leeuwen, C., and Breakspear, M. (2009). Symbiotic relationship between brain structure and dynamics. BMC Neurosci. 10, 55. [CrossRef]
  50. Sarker, M.K., Zhou, L., Eberhart, A. and Hitzler, P. (2021). Neuro-symbolic artificial intelligence. AI Communications, 34(3), pp. 197 - 209. [CrossRef]
  51. Shannon, C.E. (1948). A Mathematical Theory of Communication, The Bell System Technical Journal, 27(3), pp. 379 - 423.
  52. Spens, E. and Burgess, N. (2024). A generative model of memory construction and consolidation, Nature Human Behaviour, 8(3), pp. 526 - 543. [CrossRef]
  53. Tkačik, G., Mora, T., Marre, O., Amodei, D., Palmer, S.E., Berry, M.J. and Bialek, W. (2015). Thermodynamics and signatures of criticality in a network of neurons, Proceedings of the National Academy of Sciences, Vol. 112, No. 37, pp. 11508 - 11513.
  54. The Gutenberg Project., https://www.gutenberg.org/browse/scores/top. (last downloaded 2/9/23).
  55. Treves, A. and Rolls, E.T. (1991). What determines the capacity of autoassociative memories in the brain?, Network: Computation in Neural Systems, 2(4), p.371.
  56. Tsien, R.Y. Very long-term memories may be stored in the pattern of holes in the perineuronal net. Proc. Natl. Acad. Sci. USA 2013, 110, 12456-12461. [CrossRef]
  57. Turing, A.M. (1950). Computing machinery and intelligence. Mind, 59, pp. 433 - 460.
  58. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, L. and Polosukhin, I. (2017). Attention is all you need. Advances in neural information processing systems, 30.
  59. Webb, T.W., Frankland, S.M., Altabaa, A., Segert, S., Krishnamurthy, K., Campbell, D., Russin, J., Giallanza, T., O’Reilly, R., Lafferty, J. and Cohen, J.D. (2024). The relational bottleneck as an inductive bias for efficient abstraction. Trends in Cognitive Sciences.
Preprints 137710 g001
Figure 1. The 3-Level Cognitive Model [22] with a related ontology.
Figure 1. The 3-Level Cognitive Model [22] with a related ontology.
Preprints 137710 g001
Preprints 137710 g002
Figure 2. The new 3-Level Cognitive Model.
Figure 2. The new 3-Level Cognitive Model.
Preprints 137710 g002
Preprints 137710 g003
Figure 3. Schematic of the Ordinator function with 3 positions (red, blue, green).
Figure 3. Schematic of the Ordinator function with 3 positions (red, blue, green).
Preprints 137710 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated