A Study of Urban Climate Resilience and Its Influencing Factors in China

Preprint

Article

A Study of Urban Climate Resilience and Its Influencing Factors in China

Altmetrics

Downloads

125

Views

Comments

He Jing^*

He Jing^*

This version is not peer-reviewed

Submitted:

07 September 2023

Posted:

07 September 2023

You are already at the latest version

Alerts

Abstract

Climate change represents a prevalent challenge confronted by humanity, and with cities being one of the regions most heavily impacted by such change, enhancing their climate resilience is paramount in adapting to and mitigating the associated risks and losses. This article evaluates the climate resilience of 270 major cities in China by creating an urban climate resilience indicator system centered on exposure, vulnerability, and resilience. The article analyses the spatial and temporal evolution trend of climate resilience in Chinese cities, as well as the source of regional differences using Kernel density analysis and the Dagum Gini coefficient decomposition. The article then explores the influence of financial investments on urban climate resilience, considering the moderating effect of urbanization rate.

Keywords:

Subject: Business, Economics and Management - Economics

1. Introduction

Climate change is a prevalent challenge for humankind. Continued climate change poses threats to both human and natural systems[1]. Cities, with their developed economies, high population density, critical infrastructure, industries and fragile ecosystems, are regions most affected by climate change[2]. Frequent severe weather and geological disasters resulting from climate change could lead to increased energy consumption in urban buildings, water shortages, frequent floods, accelerated depreciation of fixed assets such as buildings, reduced reliability and higher operating costs of key urban systems and increased damage to urban ecosystems. These threats jeopardize safe and stable urban operation, as well as the safety of people's lives and property. Therefore, urban officials ought to concentrate on sustaining the safety and stability of the municipality's operation. Therefore, city managers should strive to preserve the critical systems and functions of cities while also taking steps to mitigate and adapt to the hazards of climate change by modifying urban infrastructure and developing disaster prevention and mitigation strategies. This will enable urban planning, development, and management practices to adjust to evolving climatic conditions and improve the resilience of cities in the future. China is a large nation with cities spread out across various regions, each with their own unique climate and differing levels of infrastructure and urban development. This presents challenges in assessing the ability of cities to adapt to climate change. To address this issue, the development of an indicator system to measure the climate resilience of major Chinese cities would be highly practical. In this study, using pre-existing evaluation criteria for climate resilience, we shall assess the climate resilience of 270 large cities within China via the dimensions of exposure, vulnerability and resilience to climate change risks. Additionally, we will create an econometric model to investigate the factors that impact climate resilience in urban areas.

2. Literature review

Since the 1990s, scholarly research on the notion of "resilience" has steadily broadened from physics to ecological resilience, economic resilience, and other domains.[3] Holling initially introduced the concept of resilience in the field of ecological research and described it as "the capacity of ecosystems to absorb, adapt, and recover from external shocks."

The study of urban resilience dates back further in academic literature, with more extensive research available. Overall, scholars both domestically and internationally have progressed from qualitative to quantitative methods in researching urban resilience and have increasingly focused on subfields within this topic rather than a broad urban resilience index. Among them, the definition of urban resilience has long been vague in the academic community. Foreign scholars started studying urban resilience earlier, but consensus on the concept's connotation has yet to be reached. Campanella[4] analyzed the ability of New Orleans to recover from the destruction caused by Hurricane Katrina from the perspective of "urban resilience". He contends that urban resilience relies heavily on the size of the city's population as well as the sophistication and integrity of its social structure. Furthermore, urban resilience cannot be improved without corresponding enhancements to the social structure and public service system. Leichenko [5] defines urban resilience as the capacity of a city or urban system to withstand shocks and pressures. She attributes urban resilience to four key factors: ecological resilience, urban disaster prevention and reduction capacity, economic resilience, and resilience of governance systems and administrative institutions. Ernstson [6] proposed the theory of the "urban system", integrating relevant concepts from geography and arguing that transforming urban ecological governance is a crucial way to enhance cities' resilience to shocks and climate change. Liao's definition of urban resilience refers to a city's capacity to reorganize itself after facing physical damage due to natural disasters, as well as economic and social disruptions caused by floods[7]. Meerow[8], on the other hand, goes beyond a particular event and proposes a general urban resilience system applicable to all situations. Ribeiro[9] defines urban resilience as the ability of a city to withstand natural disasters and identifies five dimensions of this ability: natural, economic, social, physical and institutional. Foreign scholars have refined the connotation and analytical framework of urban resilience; however, the definition predominantly centers around the "resilience" of a city in response to external shocks, and requires further refinement in its evaluation system. Furthermore, qualitative research dominates the findings while the lack of quantifiable analyses hampers the formulation of convincing research conclusions. At the same time, the majority of research findings concentrate on qualitative research and are deficient in quantitative analyses, rendering it challenging to formulate persuasive research conclusions.

Domestic scholars in China have made significant advancements in the urban resilience evaluation index system, measuring urban resilience, and analyzing the factors that influence it. Zheng Yan [10] examined the resilient cities' connotation, theoretical foundation, and methods of evaluation. Zhang Mingshun [11] carried out an initial evaluation of domestic and foreign literature concerning the concept of resilience. They outlined an overall view of urban resilience research both nationally and internationally, and further established a framework for assessing urban resilience in the context of climate change, exploring possible quantitative research methods. Zheng Yan [12] selected 282 cities at prefecture level and above within the country and used rainstorms as the hazard factor. They developed a city resilience index that included urban development capacity, green infrastructure, and grey infrastructure capacity. Wang Xuan [13] employed kernel density analysis, ESDA, and spatiotemporal rearrangement scanning statistical analysis approaches to investigate the distribution pattern of resilience in urban agglomerations located in the Yellow River Basin between 2006 and 2018. Xuan observed that urban resilience demonstrated notable spatial clustering and correlation features. Similarly, Xu Hui [14] evaluated the resilience of the urban public space system by constructing a resilience function and conducting Monte Carlo simulations. Jiang Shuoliang [15] created a flood-based urban resilience indicator system and studied the resilience and hindrance factors of 18 cities in Henan province. He Guosheng[16] investigated the spatial influence and process of digital finance on urban economic resilience through the use of the spatial Durbin model and the mediation effect model. Wu Wenjie [17] analyzed the comprehensive resilience, sub resilience, and obstacle factors hindering the improvement of urban resilience of 9 national central cities from 2008 to 2020 using the entropy method, variance decomposition method, and obstacle factor diagnosis method. Zhang Sisi [18] investigated the dynamic changes and influencing factors of urban resilience in China systematically, employing methods such as improved entropy weight method and Dagum Gini coefficient. Generally, urban resilience research by domestic scholars focuses on the comprehensive evaluation of urban resilience, which favors quantitative research. Some have analyzed urban resilience specifically in response to natural disasters or events.

In conclusion, academic research into urban resilience remains in its early stages. Existing research results differ mainly due to the challenge of reaching consensus on the definition of urban resilience and the indicators required for coverage. Moreover, qualitative research findings outweigh those of empirical calculations, impacting the persuasiveness of the research. Moreover, the majority of literature on urban resilience concentrates solely on measuring the city's resilience as a whole or its key systems in a general sense. However, there are deficiencies in research on urban resilience when addressing particular adverse events or prolonged negative shocks, especially those resulting from climate change. There are certain limitations in the research on urban resilience in relation to certain adverse events, both short-term and long-term, and there is still a research gap in terms of urban resilience towards climate change specifically. Therefore, this paper aims to evaluate the climate resilience indices of 270 major cities in China. To achieve this, an urban climate resilience evaluation index system will be constructed. Additionally, the main influencing factors of the climate resilience indices will be analyzed through an econometric model, with the aim of providing policy recommendations for China to integrate development and security. Ultimately, this will comprehensively enhance the adaptive capacity to climate change and safeguard the safe and stable development of China's major cities. The paper's innovations lie in its synthesis of existing research results, proposal of the concept of urban climate resilience from the perspective of climate change adaptation, and measurement of urban climate resilience via the construction of an indicator system. Secondly, urban resilience to climate is further classified based on the occurrence of climate disasters in specific regions and the geographical location of the city. Regional climate differences are fully considered during the evaluation of climate resilience. Thirdly, the determinants of climate resilience in major cities of China are thoroughly investigated.

3. Measuring Climate Resilience in China's Major Cities

3.1. Theoretical foundations and research hypotheses

Research hypotheses Urban areas face a variety of climate change-related hazards, such as intensifying weather patterns and extreme weather events. These risks affect city systems through the exposure and vulnerability pathways. Exposure is a measure of a city's vulnerability to climate events, reflecting the adverse effects of climate change risks, including economic losses, and so on. It is widely acknowledged that higher exposure magnifies the magnitude of climate risk impacts on cities, underscoring the critical importance of this metric. The term "vulnerability" refers to a city's exposure to climate risk. A higher vulnerability can exacerbate loss in the event of a meteorological disaster, making it crucial to decrease vulnerability to climate change. This is an essential proactive adaptation measure for human society. Resilience assesses a city's capacity to recover to its previous state following a climate event. The fifth report of the IPCC highlights the efficacy of bolstering climate resilience and pursuing a route of green and sustainable development in order to adapt to and alleviate the threats of climate change while also diminishing its risk. Therefore, city managers must integrate climate change adaptation policies into the urban planning process and make reducing exposure and vulnerability to meteorological hazards along with enhancing urban resilience primary objectives in urban public infrastructure and social security systems.[19] This study merges current research with established urban planning policies to develop a framework for climate change adaptation. Based on this, the study combines existing research results to develop a climate resilience assessment system for 270 major cities in China, including exposure, vulnerability, and resilience indicators.

Fiscal policy is a crucial tool when it comes to enhancing the climate resilience of cities. Prevailing research findings generally concur that fiscal policy plays an indispensable role in tackling climate change. Governments across the globe face a shared challenge in how to optimize fiscal expenditures, foster positive collaboration between the government and market forces, and encourage mitigation and adaptation to the perils of climate change in urban areas[20]. Fiscal policy is commonly used worldwide as a crucial tool for mitigating and dispersing climate change risks through innovative fiscal policy[21]. It can help prevent climate change risks by offering incentives, synergies, and compensation mechanisms. Furthermore, it can contribute towards mitigating and adapting to climate change, enhancing the synergy between urban public policies and public service systems, effectively addressing the financial challenges of tackling climate change, reducing the costs associated with implementing public service policies, and strengthening the fundamental public service system in urban areas. The urban public service system comprises several key components. On one hand, fiscal policy incentivizes cities to lower pollutant emissions through taxation, transfer payments, and financial expenditures[22]. Additionally, it mitigates conversion costs for cities adapting to climate change, speeds up the green transformation of cities, and helps achieve regional ecological protection and green development. Furthermore, fiscal policy aims to reduce the physical risks stemming from regional climate change[23]. Below are some measures that may be taken to diminish the physical risks linked to regional climate change. On the contrary, financial outlays can lower city exposure to climate change hazards and limit economic, social, and environmental detriments by encouraging the creation of urban infrastructure and enhancing public amenities and social welfare schemes, thereby advancing the climate hardiness of cities.[24] Overall, fiscal policy forms a crucial component of urban climate resiliency. In conclusion, fiscal policy serves as a critical tool for developing urban climate resilience systems. Ensuring a reasonable and adequate budget allocation and optimizing financial resource allocation are vital factors for enhancing the climate resilience of cities. The preceding discussion gives rise to the following research hypotheses:

H1:Local government spending has a substantial impact on the resilience of cities to climate change, and increasing such spending can greatly enhance this resilience.

The degree of urbanization offers robust backing for urban development and the National Development and Reform Commission has highlighted the great influence urbanization has on economic, social, ecological and infrastructure resilience of cities. Although it is widely acknowledged that the urbanization rate contributes to the construction of an urban resilience system in a broader sense by improving urban infrastructure, optimizing the urban industrial structure and enhancing urban economic strength, in terms of climate resilience, the increase in the urbanization rate may also lead to the consequences of increasing urban population density, intensifying pressure on public infrastructure, and deteriorating the ecology of the urban area. This may make the city increasingly vulnerable in the process of adapting to climate change. The susceptibility of urban areas to the effects of climate change is on the rise. The 2020 United Nations World Social Development Report notes that uncontrolled urban growth can result in congestion, pollution, social inequality, and insufficient public services thereby failing to ensure a minimum quality of life for all citizens.[25] This phenomenon is partially explained by the inverted U-shaped relationship between urbanization rate and fiscal expenditure, suggesting that in later stages of urban development, with increasing income gaps amongst urban residents, the marginal effect of fiscal expenditure on urban GDP diminishes. Furthermore, the expansion of the urban population size adversely affects the living standards of urban residents instead. Based on the aforementioned conclusions, this paper aims to investigate the moderating impact of the urbanization rate on fiscal expenditure and its ability to boost urban climate resilience. This will be achieved through constructing a moderating effect model and proposing competing hypotheses as follows:

H2a: The urbanization rate positively moderates and strengthens the effect of fiscal expenditure on urban climate resilience.

H2b: The rate of urbanization has a moderating effect, which is negative, and counteracts the enhancing effect of fiscal expenditure on the resilience of urban climate.

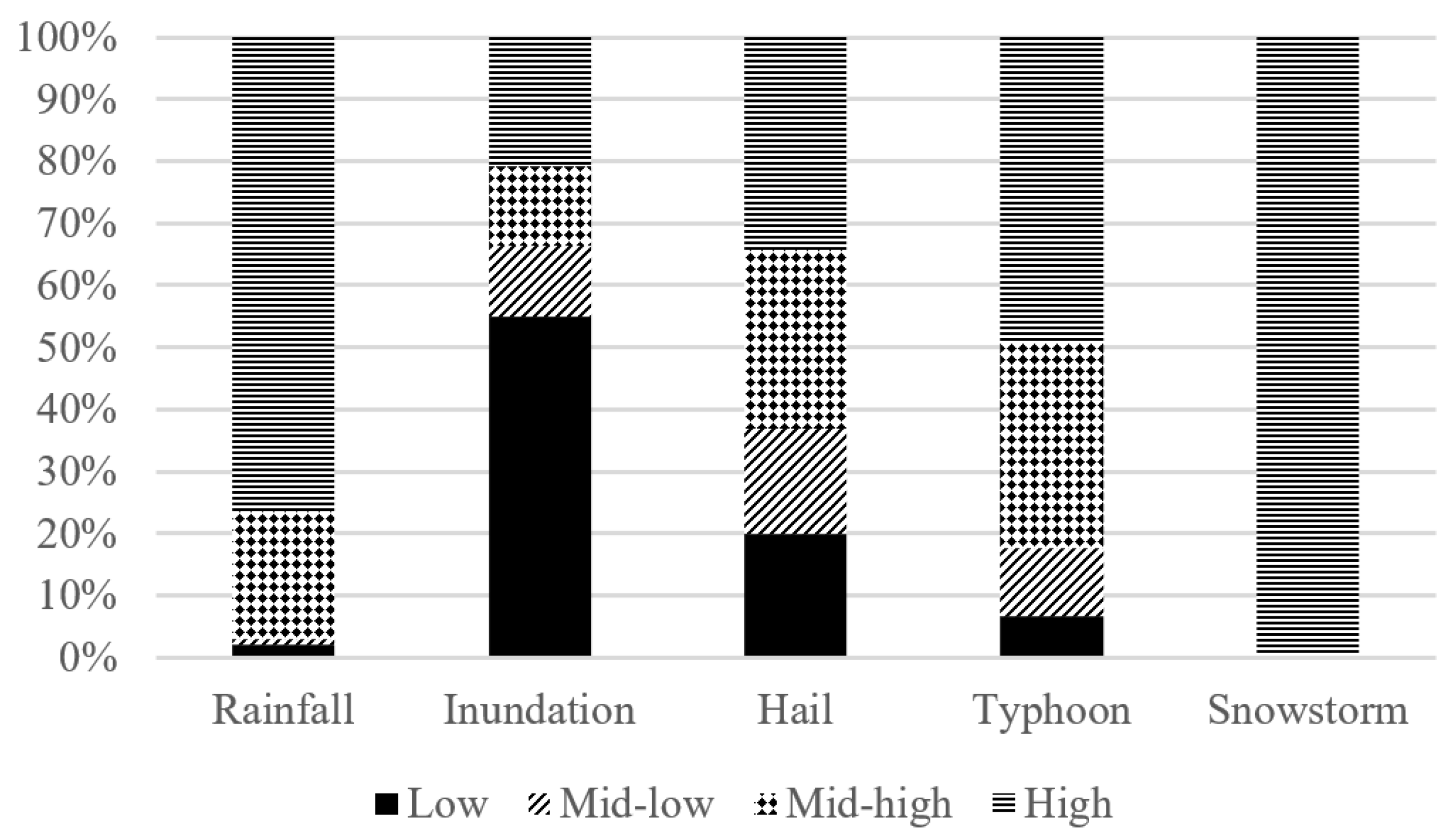
With China's extensive territory and the varied distribution of its cities, significant climatic and environmental differences exist between them. Moreover, the varying levels of economic development and sizes of urban populations necessitate the consideration of diverse levels of heterogeneity when measuring and analyzing urban climate resilience. Therefore, this paper aims to examine meteorological disaster data in various major cities throughout the country. It will analyze the dominant types of meteorological disasters in each city, based on their frequency and the resulting economic losses. This will serve as the foundation for assessing the climate resilience of 270 major cities in the country across five dimensions. Namely, the resilience of cities against rainfall, flooding, hail, typhoon, and snowstorm is evaluated. The climate resilience of the cities in each category is determined using the entropy weighting method.

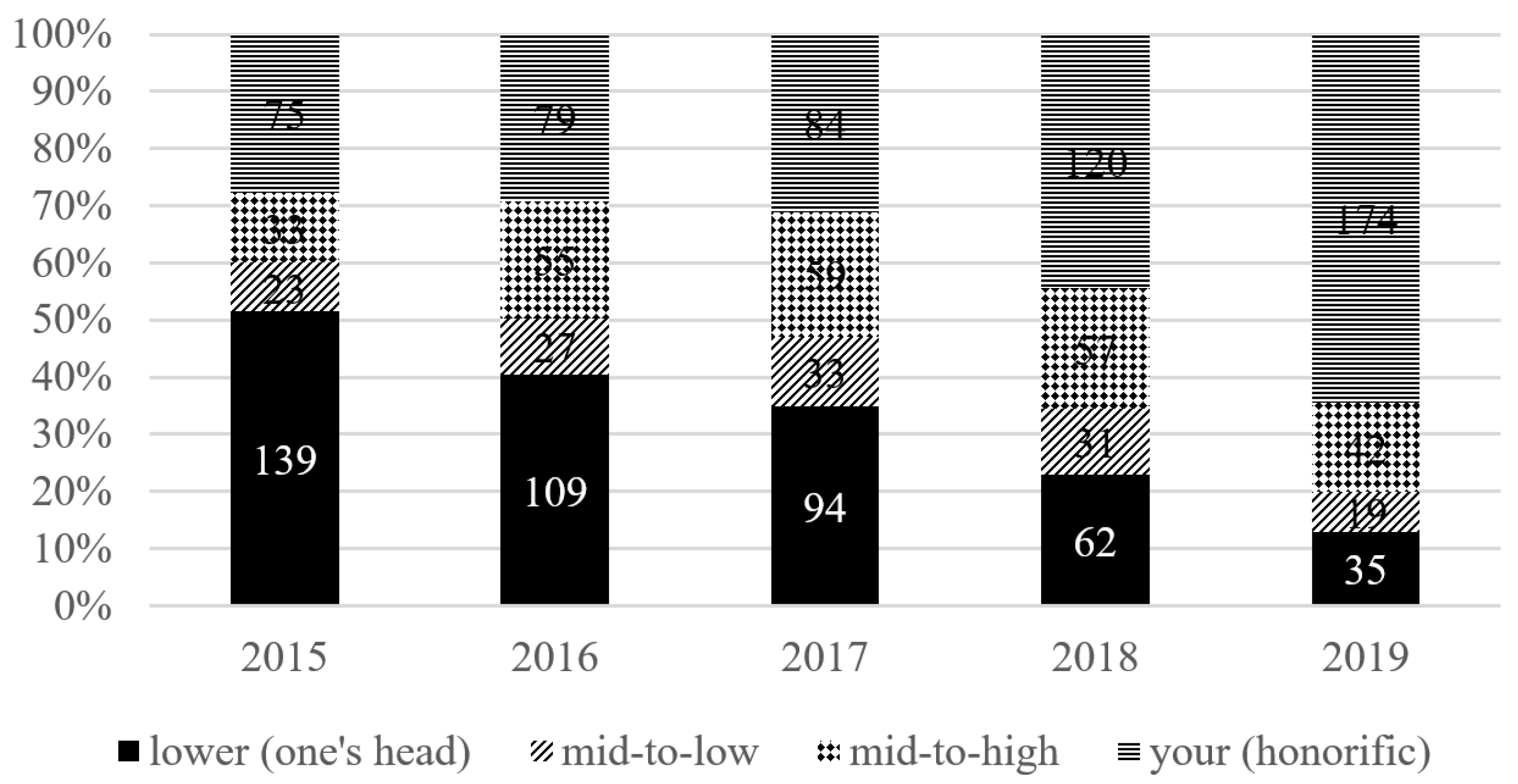
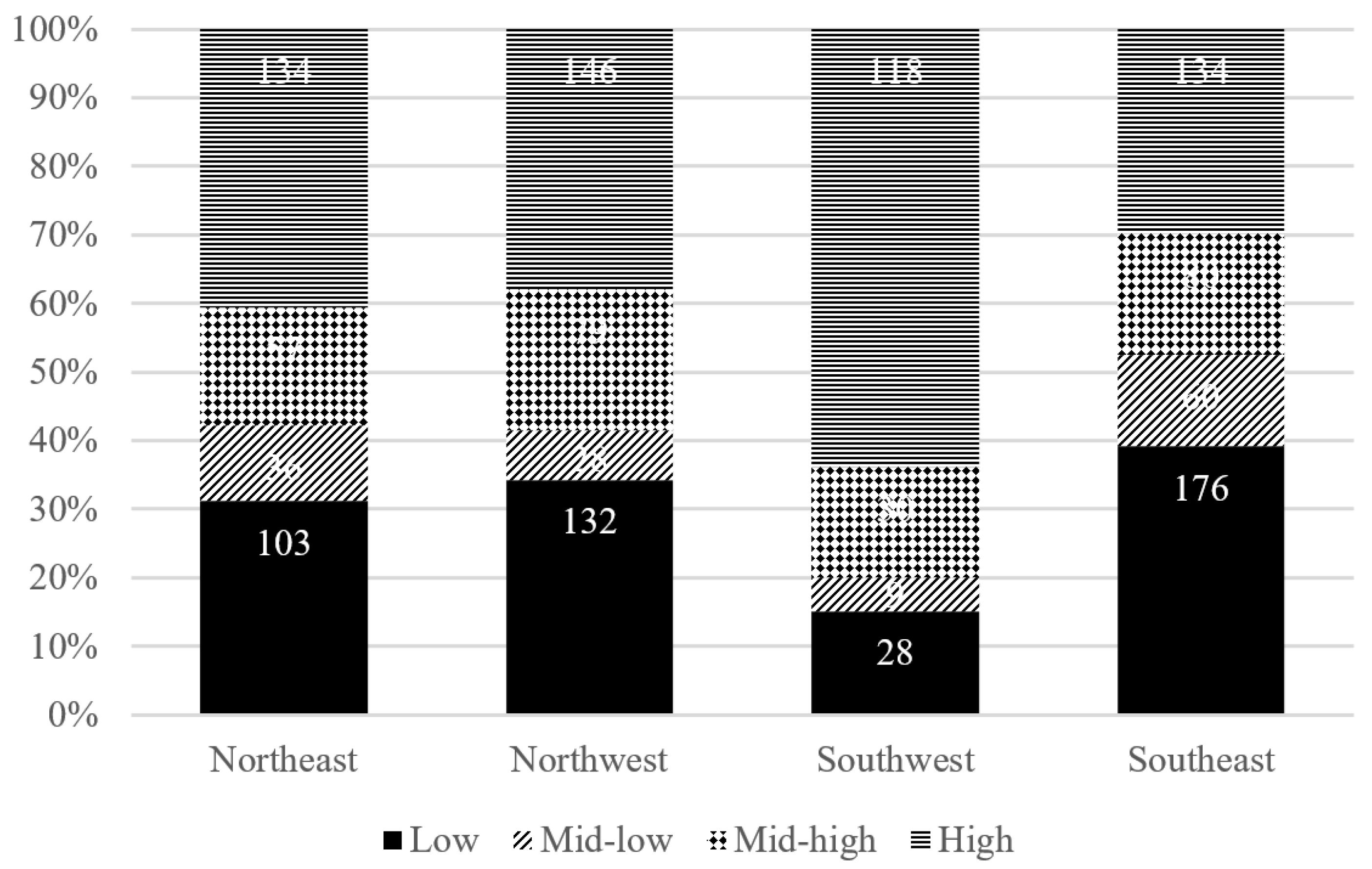
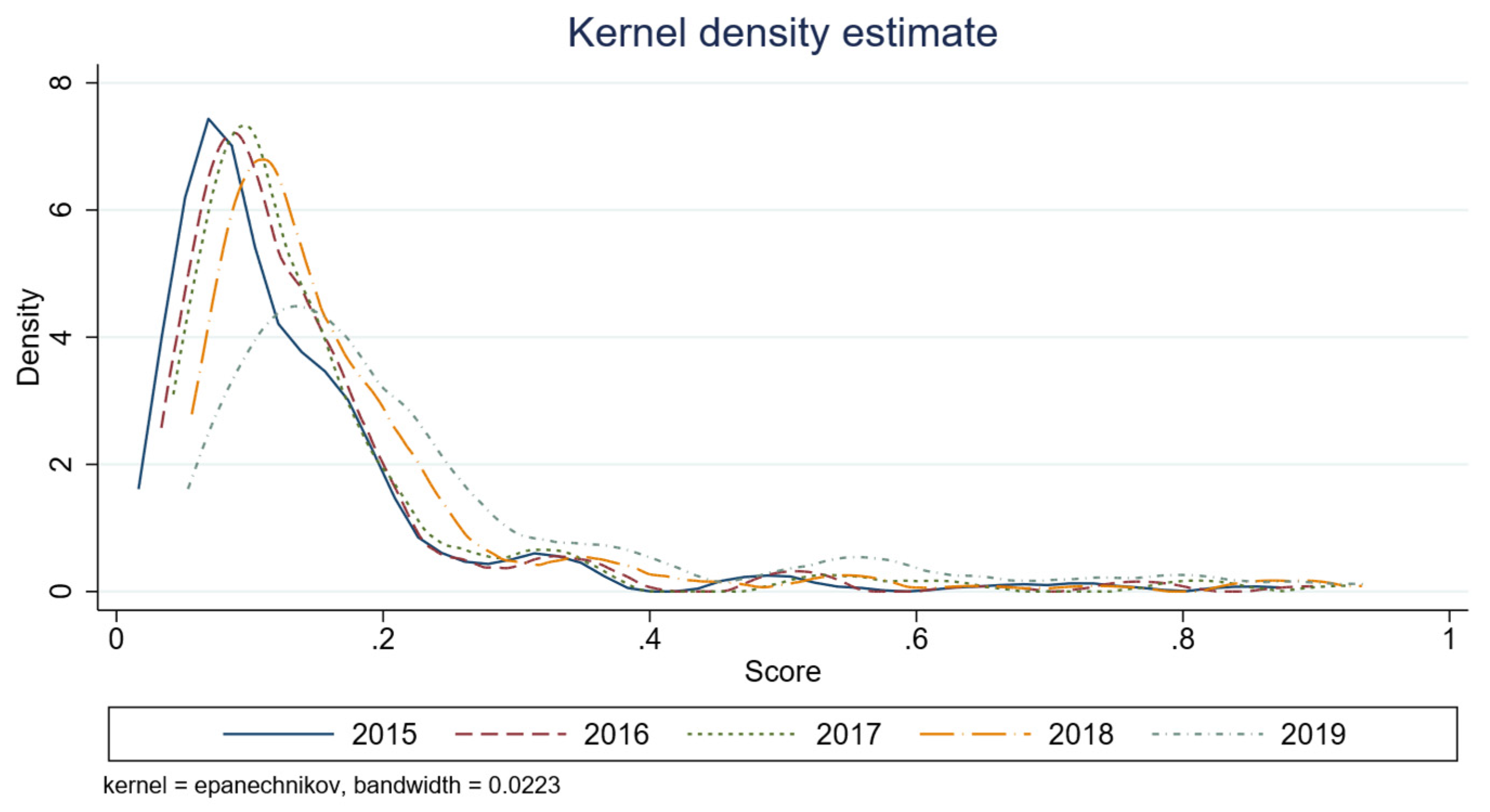
Urban climate resilience is a multifaceted concept that considers the geographical location, climatic conditions, and degree and characteristics of urban development. Its evaluative process involves assessing both the extent of damage to cities caused by climate-related hazards and the effectiveness of urban disaster prevention and mitigation measures. Therefore, when measuring variations in urban climate resilience, it is necessary to consider geographic location, regional climate fluctuations, as well as distinct factors such as the city's population and economic growth. Therefore, to analyses the regional variations in urban climate resilience, this study initially includes the cities' latitude and longitude in the samples and considers the latitude and longitude of China's population density demarcation line's midpoint west to east. "The Hu Huan Yong Line serves as the origin and divides major cities in China into four geographic quadrants: northeast, southeast, northwest and southwest. Additionally, the major cities in China are further described using Dagum's Gini coefficient test, which analyses the geographical distribution of climate resilience and its sources. This test provides insights into the variations in the resilience of major cities to climatic hazards." At the same time, this paper divides the urban climate resilience index into four quartiles representing low resilience, medium-low resilience, medium-high resilience and high resilience. It then divides the subsamples based on this and analyses the varied impacts of fiscal policies on the resilience intervals of different cities using the quartile regression model.

3.2. Methods and Models

3.2.1. Entropy weighting method

In this paper, the variable weights of the aforementioned indicators are obtained using the entropy weighting method and the final score of the city's climate resilience is obtained using the linear weighting method. The cities with a higher degree of data incompleteness are excluded from the process. The calculation process is as follows:

Data standardization:

For positive indicators:

$s_{i j} = \frac{v_{i j} - \min (v_{j})}{\max (v_{i j}) - \min (v_{i j})}$

(1)

For negative indicators:

$s_{i j} = \frac{\max (v_{j}) - v_{i j}}{\max (v_{i j}) - \min (v_{i j})}$

(2)
Calculate the weight in indicator j for the i_th evaluation object $p_{i j}$ :

$p_{i j} = \frac{s_{i j}}{\sum_{i = 1}^{m} s_{i j}}$

(3)
Calculate the information entropy of the indicator $e_{i j}$

$e_{i j} = - \frac{1}{\ln m} \sum_{i = 1}^{m} p_{i j} \times \ln p_{i j}$

(4)
Calculate the entropy weight of the indicator $ω_{i j}$

$ω_{j} = \frac{(1 - e_{j})}{\sum_{j = 1}^{n} (1 - e_{j})}$

(5)
Calculate the final score using a linear weighting method

$s c o r e = \sum_{j = 1}^{n} \sum_{i = 1}^{m} ω_{j} \times s_{i j}$

(6)

3.2.2. Kernel density estimation

Kernel density estimation is a non-parametric technique used for estimating the probability density function. It uses a kernel function K(u) as the weights, smoothed each data point, and produces a continuous density function. The method possesses the advantage of adaptively estimating the shape of the probability density function based on the data's characteristics without assuming a particular distribution. The equation for the kernel density estimation method follows:

\hat{f} (x) = \frac{1}{n h} \sum_{i = 1}^{n} K (\frac{x - x_{i}}{h})

(7)

where

x_{1}, x_{2}, \dots, x_{n}

represents an independent and identically distributed sample drawn from an unknown density function f, n denotes the number of cities, and k represents the kernel function, which is characterised by symmetry, normalisation, monotonically decreasing, and zero-mean. The smoothing parameter, also known as the bandwidth, is denoted by h.

3.2.3. Dagum Gini coefficient decomposition

The Dagum Gini coefficient decomposition, initially introduced by Dagum in 1997, examines the causes and magnitude of income inequality by dividing the Gini coefficient into three components: within-group inequality, between-group inequality, and overlapping inequality. Within-group inequality pertains to the income discrepancy within a subset, whereas overlapping inequality pertains to the section of the income distribution that intersects or overlays between different groups thereby creating more inequality. This paper discusses the application of Griffiths' formula [26] to assess variations in urban climate resilience and their origins across the four geographical regions: Northeast, Northwest, Southwest, and Southeast.

3.3. Samples and data

Construction of the indicator system

According to data on meteorological disasters released by the National Disaster Reduction Network, the most frequent and damaging meteorological disasters in China are rainstorms, floods, typhoons, hailstorms, and snowstorms. This paper initially gathers data on the frequency of meteorological disasters in 270 major cities throughout the nation. Afterwards, by focusing on the meteorological disasters with the highest incidence, a comprehensive evaluation of the climate resilience of all 193 major cities in China is conducted. The climate resilience of these cities is analyzed according to five dimensions. Rainfall climate resilience, flood climate resilience, typhoon climate resilience, hail climate resilience, and snowstorm climate resilience are evaluated based on the climate resilience system detailed in the fifth research report by the IPCC, as well as the research conducted by Zhao Chunli et al. [27]. In this paper, we have created an urban resilience indicator system that encompasses three dimensions: exposure, vulnerability, and resilience; with a total of 10 secondary indicators and 13 tertiary indicators. Among them, "exposure" quantifies the negative impacts of meteorological disasters on cities, which is the specific manifestation of climate change risks in urban environments. This paper employs four tertiary indicators, namely the economic losses caused by meteorological disasters, the number of individuals affected, the number of houses damaged and the affected crop area, to measure the losses incurred by meteorological disasters in cities. The data used in this study were sourced from the National Disaster Reduction Network's (NDRN) meteorological disaster report. Technical term abbreviations are explained when first used. The data is sourced from the meteorological hazard report of the National Disaster Reduction Network (NDRN). "Vulnerability" is a quantitative measure of a city's sensitivity to the risk of climate change. The impact of the climate change risk on the city is more significant if its vulnerability is higher. This paper measures the climate vulnerability indicators of a city using the following factors: the number of unemployed people registered at the end of the year, the population density of the urban area governed, per capita water consumption, per capita electricity consumption, and the number of doctors in the city. These factors are used to measure the city's vulnerability to climate change. Resilience refers to a city's capacity to reduce the impact of climate-related disasters and restore production and life to normalcy post-event. In this research, we measure resilience through indicators such as the length of drainage pipes, urban road area per person, citywide GDP, and green coverage of built-up areas. Vulnerability and resilience data are gleaned from the China Urban Statistical Yearbook and China Civil Affairs Statistical Yearbook. The specific set of indicators is detailed in Table 1.

4. Statistical results of urban climate resilience of major cities in China

4.1. Descriptive statistics of urban climate resilience

4.1.1. Overall descriptive statistics

Table 2 displays the descriptive statistical findings of urban climate resilience that were computed using the entropy weighting technique. In general, the urban climate resilience of the major cities of China saw a gradual improvement from 2015 to 2019, with the most significant enhancements taking place during 2018-2019. Furthermore, the sample cities were classified into four levels of resilience based on the quartiles of their climate resilience evaluation scores. These levels include low resilience cities, medium-low resilience cities, medium-high resilience cities, and high resilience cities. The results are presented below.

4.1.2. Sub-sample descriptive statistics

Due to significant geographic variation across Chinese cities, this paper adopts the midpoint of the Hu Huanyong line as the reference point, dividing cities into four geographic quadrants (northeast, northwest, southwest and southeast) based on latitude and longitude. It also categorizes the cities' climate resilience levels, determined by urban climate resilience criteria, according to year, climate resilience type and region of origin. From a regional distribution standpoint, evident spatial distribution differences in urban climate resilience levels exist; the average urban climate resilience value is relatively high in the northeast and southwest regions, while it is low in the northwest and southeast regions. Additional descriptive statistics can be found in Table 3.

As shown in Table 3, the average level of climate resilience in Chinese cities has steadily risen from 2015 to 2019, displaying a more noticeable increase in 2018 to 2019. Combined with the level of urban toughness and the corresponding number of cities, as depicted in Figure 1, the number of cities with low climate toughness has decreased from 2015 to 2019 along with a decline in their proportion each year. In contrast, the number of cities with high climate toughness has correspondingly increased, resulting in an expansion of the sample proportion for the corresponding years. This suggests that the number of cities transferring from low and medium-low climate toughness to high and medium-high climate toughness is on the rise. In addition, between 2015 and 2017 there was an increase in the number and proportion of cities classified as having either low or medium resilience. Furthermore, there was an increase in the number and proportion of cities classified as having either medium or high resilience, peaking in 2017, before a subsequent decrease. In general, there were more cities with medium or high resilience than with medium or low resilience. It is apparent from the aforementioned phenomenon that an increasing number of cities in China are transitioning from low to high climate resilience and enhancing their adaptive capacity towards climate change. This signifies the effective development of China's urban resilience system for coping with climate change. Furthermore, the major cities in China have demonstrated an overall upward trend in climate resilience.

There are notable regional disparities in urban climate resilience across distinct geographical quadrants. Table 4 displays the average values of urban climate resilience in conjunction with the level of urban resilience. It reveals that Northeast China boasts the highest average values of urban climate resilience, followed by Southwest China, whereas the levels of urban climate resilience in Southeast and Northwest China are comparatively lower. As illustrated in Figure 2, Northeast China has the highest number of cities with strong climate resilience amongst the four regions. Meanwhile, Southwest China has a higher proportion of cities with robust climate resilience, but also a higher proportion of cities with lower climate resilience. The number and proportion of cities with low climate resilience is at its lowest level among the four regions. Additionally, the southeast region of China exhibits a relatively small number of highly climate resilient cities, while the number of cities with low or medium climate resilience is comparatively large. This phenomenon highlights a severe regional imbalance in urban climate resilience across China. Compared to other regions, the level of urban climate resilience in Northeast China is generally higher due to its early urbanization, complete infrastructure construction, and lower frequency and intensity of extreme climate disasters. This has strengthened the region's ability to adapt to climate change. Due to the frequent occurrence of climate-related disasters, major cities in Southeast China have higher levels of both size and population density, making them more vulnerable to climate change risks. As a result, these cities exhibit greater levels of climate resilience compared to other regions, leading to a lower climate adaptability score.

In Table 5, cities with snow as their primary meteorological hazard exhibit greater climate resilience on average, in comparison to cities with rainfall hazards. Nonetheless, all cities in the sub-sample have a high level of climate resilience. In contrast, cities that face flooding as their primary meteorological threat exhibit weak climate resilience, with a considerable number and percentage of cities having low climate resilience. On the other hand, cities with weather hazards dominated by typhoons exhibit relatively high levels of resilience, with a substantial proportion of those cities scoring high on climate resilience. The mean climate resilience values for wind-hail dominated weather hazards lie in moderate territory. The above analyses reveal that major Chinese cities display greater resilience in managing meteorological disasters such as rainfall and snowstorms. Conversely, the capacity to cope with floods is deficient and exhibits certain limitations. Consequently, prioritizing the strengthening of urban infrastructure in flood-prone areas and improving the emergency management and response system are top priorities for major Chinese cities in mitigating climate change risks.

Figure 3. Urban climate resilience statistics by meteorological hazard category.

5. Dynamic Evolution and Regional Differences in Urban Climate Resilience in China

5.1. Dynamic evolution of urban climate resilience-Kernel kernel density analysis

Through examination of the Kernel density curves, the distribution pattern and dynamic evolution of urban climate resilience in major Chinese cities from 2015-2019 is clearly visible as shown in Figure 4

As demonstrated in Figure 4, the peak position of the distribution curve regarding climate resilience of major cities in China shifted to the right each year between 2015 and 2019. This verifies a year-on-year increase in climate resilience for cities in China. Meanwhile, the kernel density curve indicates an overall rightward bias, with a decreasing peak and increasing width, suggesting an increasing gap in the climate resilience of Chinese cities. This trend towards bifurcation is becoming increasingly pronounced. Furthermore, to illustrate the pattern of urban climate resilience across various geographic quadrants, we estimate kernel density and plot kernel density curves for the urban climate resilience subsamples in the Northeast, Northwest, Southwest, and Southeast regions. These results are presented in Figure 5.

As illustrated in Figure 5, the kernel density curves for subsamples of urban climate resilience in the four geographical quadrants exhibit a right-skew with evident tails to the right, implying that urban climate resilience is polarized across all geographical regions, demonstrating significant individual differences. Specifically for different geographical regions, the kernel density curves in the south-west and south-east regions demonstrate a rightward shift of the peak and a broadening of the shape as the number of years increases. This indicates that the urban climate resilience in these regions has been improved in recent years, but the differences have been increasing, and the synergistic enhancement of the urban climate resilience in this region has not been achieved at present. The highest point of the kernel density curve's main peak in the Northeast and Southeast regions decreased initially and then increased, continuously shifting towards the right since 2016. In 2015, the curve's peak in the Northeast region was to the right, and the pattern was broader than in other years. From 2016 onwards, the curve, as a whole, narrowed, and the peak kept moving towards the right. The urban climate resilience of the Northeast region exhibits significant variation across cities and multi-polar polarization in the initial stages of development. However, with the narrowing of the urban-rural development gap and consistent infrastructure development, the disparity in urban climate resilience within the region has decreased. Correspondingly, the adaptive capacity to climate change has improved overall. In brief, the kernel density curve confirms the trend of ongoing enhancement in urban climate resilience across China. However, it also highlights the unequal spatial distribution of resilience and significant regional, individual, and multilevel disparities. Therefore, to provide a more precise account of regional and inter-individual disparities in urban climate adaptability, this paper investigates the variations in urban climate adaptability and their origins using the Dagum Gini coefficient decomposition approach.

5.2. Sources of Variation in Urban Climate Resilience-Dagum Gini Coefficient Decomposition

As demonstrated in Table 6, apart from a small rise in 2019, the Gini coefficients regarding urban climate resilience in China display an overall decline from 2015 to 2019. This indicates that, as a whole, the differences in climate resilience between China's major cities have been decreasing during this period. Nevertheless, it does not eliminate the prospect of further expansion. Except for 2019, the intra-regional Gini uptake has consistently remained at a low level with a relatively low contribution rate. This suggests that intra-regional differences are not the primary source of differences in urban climate resilience. These findings align with the conclusions of Zhang[18]. In contrast, while certain regional differences in urban climate resilience are apparent in China, the primary reason for differentiation lies in the extreme highs or lows of climate resilience levels observed in some cities. Moreover, the contribution rate of inter-regional differences and hypervariable density is higher than the intra-regional rate, as shown in Kernel density estimation, underscoring the multipolar regional distribution of urban climate resilience.

Table 7 displays the inter-regional Gini coefficient values for urban climate resilience in China between 2015-2019. It is evident that the disparities in urban climate resilience among the four significant geographic regions gradually decreased between 2015-2018. However, in 2018-2019, some regional urban climate differences in urban climate resilience have increased. The urban climate resilience differences between the Northeast-Southwest and Southeast-Southwest regions are significant, with the highest Gini coefficient values appearing in 2015 as high as 0. Please note this text adheres to the given writing principles. 41973 and 0.42267, respectively, while the mean values were 0.37885 and 0.37858, respectively. In contrast, the cities in the Northeast-Southeast and Southeast-Northwest regions show less variation in climate resilience, with mean values of 0.34286 and 0.30472, respectively. In summary, China exhibits significant regional differences in urban climate resilience. The inter-regional Gini coefficients indicate a declining trend over time, with particularly notable differences between the Northeast and Southwest, and the Southeast and Southwest regions. These differences may be attributed to the influence of geographic environment and level of economic development, among other factors.

6. Analysis of factors influencing urban climate resilience

6.1. Variable Selection and Model Setting

6.1.1. Modelling

To investigate the factors that influence urban climate resilience, this paper aims to construct a statistical model examining the impact of local financial spending on urban climate resilience. The model is presented as follows:

{s c o r e}_{i t} = α_{0} + α_{1} {l g e x p}_{i t} + α_{j} X_{j i t} + μ_{τ i} + ϑ_{t} + ε_{i t}

(8)

where

{s c o r e}_{i t}

represents the level of urban climate resilience, and

{l g e x p}_{i t}

represents the logarithmised level of fiscal expenditure, and its regression coefficient. If the coefficient is significantly positive, it suggests that fiscal expenditure can effectively enhance urban climate resilience.

X_{j i t}

and

α_{j}

represent the control variables and their regression coefficients, including the number of urban resident population, etc., respectively. In order to address the endogeneity issue in the model, we added two sets of dummy variables, namely

μ_{τ i}

and

ϑ_{t}

. The

μ_{τ i}

variables represent province dummy variables to control province fixed effects, while

ϑ_{t}

represent time dummy variables for controlling year fixed effects.

6.1.2. Selection of indicators and data sources

In this article, we select city-level panel data from 2015-2019 encompassing seven indicators. The explanatory variable is the city's climate resilience score, while the core explanatory variable is the general public budget expenditure of the city. We obtained data from the National Bureau of Statistics (NBS) and the China Urban Statistical Yearbook. Meanwhile, in order to minimize the issue of omitted variables and eliminate the potential endogeneity of the model, control variables are incorporated into the model(8). The annual deposit balance of urban financial institutions, along with the number of urban resident population, urban hospital beds, urban education employees, water conservancy, environment and public facilities employees, as well as residents' services, repairs, and other services employees, are treated as core explanatory variables and control variables, and their natural logarithms are analyzed.

6.2. Epirical test

6.2.1. Benchmark regression results

To examine the effects of fiscal spending on urban climate resilience, we regressed model (8) and present the findings in Table 8. To ensure the reliability of the regression results, the baseline regression includes province fixed effects with time fixed effects. The regression results demonstrate that, while controlling the fixed effects, the regression coefficients of the core explanatory variables on the explanatory variables are all significantly positive. This suggests that urban fiscal expenditure can considerably strengthen urban climate resilience, and that augmenting fiscal expenditure can effectively increase the adaptability and resilience of cities in response to the risks brought about by climate change. Meanwhile, while controlling for double fixed effects, the impact of the yearly deposit balance of urban financial institutions on the level of urban climate resilience is remarkably positive. This, to some extent, highlights the significance of the security and stability of the urban financial system in boosting urban climate resilience. In addition, it appears that the climate resilience of a city decreases with an increasing number of residents. This implies that boosting urban education spending can, to some degree, bolster the city's resilience to the effects of climate change. This suggests that a greater populace contributes to higher vulnerability to climate change. On the other hand, the number of professionals dedicated to urban education has a positive impact on urban areas' climate resilience. In summary, the benchmark regression results confirm hypothesis 1 of this paper, which asserts that fiscal policy plays a significant role in improving urban resilience.

6.2.2. Moderated effects regression results

To investigate how urbanization rate affects the fiscal expenditure aimed at improving urban climate resilience, this paper establishes a moderating effect model that includes the interaction terms of urbanization rate, fiscal expenditure, and urbanization rate for regression. The model is set out below.

{S c o r e}_{i t} = β_{0} + β_{1} {l g e x p}_{i t} + β_{2} {l g e x p}_{i t} \times c z h l + β_{3} {c z h l + β}_{j} X_{j i t} + μ_{τ i} + ϑ_{t} + ε_{i t}

(9)

In model (9),

{l g e x p}_{i t}

denotes municipal fiscal expenditure,

c z h l

denotes urbanization rate, and the interaction term between the moderating variable of urbanisation rate and the core explanatory variable of fiscal expenditure is represented by

{l g e x p}_{i t} \times c z h l

indicating the regression coefficient. If the regression coefficient

β_{2}

is greater than 0, this indicates a positive moderating effect of urbanisation rate on urban climate resilience. In other words, the urbanisation rate enhances the enhancement effect of fiscal expenditure on urban climate resilience. Conversely, if the urbanization rate is negative, it shows a negative moderating effect on urban climate resilience, reducing the enhancement effect of fiscal expenditure on urban climate resilience. The regression results can be found in Table 9.

As shown in Table 9, the moderator term

{l g e x p}_{i t} \times c z h l

coefficient is significantly negative, indicating that the urbanization rate has a significant negative moderating effect on the upgrading effect of fiscal expenditure, which verifies the content of the competing hypothesis 2b, i.e., The relationship between the urbanization rate and the effectiveness of fiscal policy in enhancing the climate resilience of a city is weakened. There are two possible reasons for this: firstly, cities with higher urbanization rates tend to possess more advanced urban infrastructure and public service systems in order to combat "hard equipment" climate change risks. Firstly, the adequacy of urban equipment to manage climate change risks is dependent on the urbanization level of a city. More urbanized cities tend to have complete infrastructure and impeccable public service systems in place. Increasing fiscal expenditure for further developing climate resilience infrastructure shows a negative moderating effect due to a diminishing marginal increase. Secondly, China's increasing level of urbanization in recent years accompanies rapid economic growth. Secondly, in recent years, China has undergone rapid economic development, leading to an increase in urbanization and expansion in urban areas. However, this growth has resulted in a heightened urban population density, a concentration of high-pollution and high-emission industries, and subsequently, the fragility of the ecological environment and deterioration of the urban climate in some Chinese cities. The vulnerability and exposure of cities to climate change have been on the rise, which has weakened their climate resilience. Relying solely on financial expenditure to enhance this resilience is proving difficult. On this basis, it is challenging to attain the desired outcomes through merely increasing financial expenditures to amplify the climate resilience of cities. Thus, it is crucial to contemplate industry transformation, energy preservation, emission reduction, and green city development. Additionally, it is necessary to enhance the climate resilience of cities by reducing pollutant emissions and ameliorating the ecological environment.

6.3. Robustness test

6.3.1. Explanatory variables lagged by one period

To further demonstrate the robustness of the findings of the previous model, all explanatory variables were lagged by one period and regressed with the following results:

As shown in Table 10, after lagging the explanatory variables by one period and re-regressing them, the impact of fiscal revenues on the climate resilience of the city continues to be significantly positive and unaltered by time, which effectively demonstrates the robustness of the conclusion that fiscal expenditures improve China’s urban climate resilience.

6.3.2. Endogeneity test

In this paper, the two-stage least squares instrumental variable method is employed to address potential endogeneity issues. Specifically, the instrumental variable chosen is the urban general public budget expenditures from the previous period. The validity of the instrumental variables is then tested through weak instrumental variable and over-identification tests. The resulting regression is as follows.

Table 11 displays the outcomes of the baseline regression and the two-stage least squares regression's second stage using the instrumental variable method. The Anderson-Rubin-Wald F value of 43 signifies the strength of the results. The analysis shows that the instrumental variables in 81 meet the criteria for strength, and the Kleibergen-Paap rk Wald F, Kleibergen-Paap rk LM, and Cragg-Donald Wald F statistics fall within the critical value range. The one-period lagged instrumental variable for urban general public budget expenditures is highly significant in the first stage, and the effect of fiscal expenditures on urban climate resilience is still significantly positive in the second stage, which satisfies the significance test. Therefore, the conclusion that fiscal policy enhances urban climate resilience is robust.

6.3.3. Quantile regression

In order to ensure the model's robustness and explore the impact of fiscal expenditure on urban climate resilience at different development stages, this paper proposes regressing the urban sub-sample of four resilience levels: low, medium-low, medium-high, and high. The model is outlined below.

{S c o r e}_{i t} = β_{0} + β_{1} {l g e x p}_{i t} + β_{2} {l g e x p}_{i t} \times c z h l + β_{3} {c z h l + β}_{j} X_{j i t} + μ_{τ i} + ϑ_{t} + ε_{i t}

(10)

where.

{Q_{S c o r e}}_{i t}

is the conditional quantile of urban climate resilience as affected by fiscal expenditure, and the regression coefficient

β

can be described as a function of the quantile

φ

function, i.e., it varies with the change of quartile, and the results of the quartile regression are shown in Table 12.

As shown in Table 12, fiscal expenditure has a significant positive impact on cities with low to medium toughness, medium to high toughness, and high toughness grades, in which, from the regression coefficient, the ability of fiscal policy to enhance climate toughness in medium to high toughness and high toughness cities is higher than that of medium to low toughness cities, and it does not have a significant impact on climate toughness of low-toughness cities, which suggests that expansionary fiscal policy is not universally applicable to the development of city climate toughness This suggests that expansionary fiscal policies are not universally applicable to different stages of urban climate resilience development, and that differentiated policies need to be implemented based on different climate resilience benchmarks.

7. Conclusions and policy recommendations

7.1. Conclusions

The climate resilience of Chinese cities is generally high and has increased year-on-year from 2015 to 2019. In general, cities showed strong climate resilience.
There are apparent regional variations in the climate resistance of Chinese cities. On average, urban climate resistance is greater in the northeast and southwest, while it is lower in cities situated in the southeast and northwest.
There are distinct features of urban climate resilience for various climate hazard types. Cities vulnerable to snow and rainfall have high climate resilience, whereas cities prone to floods have low climate resilience.
Urban climate resilience displays an uneven spatial distribution, considerable disparities between regions and individuals, and multipolar dispersion.
Increased fiscal expenditure has a pronounced positive impact on the resilience of urban climate, and elevating fiscal expenditure can greatly improve urban climate resilience.
The rate of urbanization has a notable adverse moderating impact on urban climate resilience, reducing the efficacy of fiscal spending aimed at enhancing this resilience.

7.2. Policy recommendations

Based on the above findings, this paper makes the following policy recommendations:

Promote the enhancement of urban climate resilience by recognising the pivotal role of highly resilient cities.
Improve the urban climate adaptation system's deficiencies, reinforce the development of urban flood prevention and control facilities, and augment the city's overall ability to prevent floods.
Transform the conventional rough city constructions and encourage the greening of urban development, whilst enhancing the ecological state of urban areas.
Utilise fiscal policy to enhance the resilience of cities against climate change, optimising the fiscal toolbox and balancing the approaches of "open-source" and increased expenditure.

Author Contributions

Conceptualization, Li Cunpu and Pan Lishuo.; methodology, Li Cunpu; software, Pan Lishuo; validation, Li Cunpu, Pan Lishuo and He Jing; formal analysis, Li Cunpu; investigation, Pan Lishuo; resources, He Jing; data curation, Pan Lishuo; writing—original draft preparation, Pan Lishuo; writing—review and editing, Li Cunpu; visualization, Pan Lishuo; supervision, He Jing; project administration, Li Cunpu; funding acquisition, Li Cunpu. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by GENERAL PROJECT OF SHAANXI PROVINCIAL DEPARTMENT OF SCIENCE AND TECHNOLOGY, grant number 2022JM-432; KEY PROJECT OF SCIENTIFIC RESEARCH PROGRAMME OF SHAANXI PROVINCIAL DEPARTMENT OF EDUCATION, grant number 21JZ037; GENERAL PROJECT OF SHAANXI PROVINCIAL DEPARTMENT OF SCIENCE AND TECHNOLOGY, grant number S2023-ZC-RKXMS-0068

Conflicts of Interest

The authors declare no conflict of interest.

References

IPCC A. IPCC Fifth Assessment Report-Synthesis Report. 2014.
Feng, X.; Li, H.; Yang, X. International experience and insights of urban climate change adaptation actions. Ecological Economy 2016, 32(11), 120-124+135. [CrossRef]
Holling, C.S. Resilience and stability of ecological systems. Annual Review of Ecology and Systematics 1973, 4(4), 1-23. [CrossRef]
Campanella, T.J. Urban resilience and the recovery of New Orleans. Journal of the American Planning Association 2006, 72(2), 141-146. [CrossRef]
Leichenko, R. Climate change and urban resilience. Current Opinion in Environmental Sustainability 2011, 3(3), 164-168. [CrossRef]
Ernstson, H.; Van Der Leeuw, S.E.; Redman, C.L.; et al. Urban transitions: on urban resilience and human-dominated ecosystems. Ambio 2010, 39, 531-545. [CrossRef]
Liao, K.H. A theory on urban resilience to floods-a basis for alternative planning practices. Ecology and Society 2012, 17(4). [CrossRef]
Meerow, S.; Newell, J.P.; Stults, J.M. Defining Urban Resilience: a Review. Landscape and Urban Planning 2016, 147. [CrossRef]
Ribeiro, P.J.G.; Gonçalves, L.A.P.J. Urban resilience: a conceptual framework. Sustainable Cities and Society 2019, 50, 101625. [CrossRef]
Zheng, Y.; Lin, C. Theoretical foundation and assessment method of resilient cities. City 2017, (06), 22-28.
Zhang, M.; Li, H. Research progress on urban resilience assessment in the context of climate change. Ecological Economy 2018, 34(10), 154-161.
Zheng, Y.; Zhai, J.; Wu, Z.; Li, Y.; Shi, W. Classification evaluation of resilient cities based on adaptive cycle - an example of sponge city and climate-adapted city pilot in China. China Population-Resources and Environment 2018, 28(03), 31-38. [CrossRef]
Wang, X.; Shi, J.; Ci, F. Spatio-temporal evolution characteristics of the resilience degree of urban agglomerations in the Yellow River Basin. Statistics and Decision Making 2022, 38(05), 70-74. [CrossRef]
Xu, H.; Li, Y.; Deng, N.; Du, L. Resilience modelling of urban complex public space systems. Systems Engineering Theory and Practice 2022, 42(07), 1964-1978. [CrossRef]
Jiang, S.L.; Chen, X.S. Urban resilience assessment and analysis of obstacle factors under flood scenarios. Statistics and Decision Making 2022, 38(24), 63-67. [CrossRef]
He, G.; Yan, J. The impact of digital finance on the economic resilience of cities--an empirical analysis based on spatial econometric modelling. Exploration of Economic Issues 2023, (03), 97-110.
Wu, W.; Huang, H. Evaluation of comprehensive resilience of national central cities and analysis of obstacle factors. Ecological Economy 2023, 39(04), 89-94+102.
Zhang, S.; Ma, X.; Cui, Q. Spatio-temporal dynamic evolution of urban resilience in China and analysis of influencing factors. Statistics and Decision Making 2023, 39(03), 110-115. [CrossRef]
Jiang, T.; Li, X.; Chao, Q.; Yuan, J.; Lin, R. Key findings and new insights from Climate Change 2014: Impacts, Adaptation and Vulnerability. Advances in Climate Change Research 2014, 10(3), 157-166. [CrossRef]
Yang, J.; Chen, L. Fiscal policy and experience of foreign countries in coping with climate change. Environmental Economics 2010, (06), 32-43. [CrossRef]
Xu, S.; Zhang, L. International Experience and Implications of Fiscal Policy in Support of Climate Risk Response. Finance 2022, (02), 59-65.
Chen, S.; Qi, Y. A study on medium- and long-term fiscal policy to cope with climate change under the constraint of "dual-carbon" target. China Industrial Economy 2022, (05), 5-23. [CrossRef]
Pigato, M.A. Fiscal policies for development and climate action. World Bank: Washington, DC, 2019. [CrossRef]
Aligishiev, M.Z.; Massetti, E.; Bellon, M.M. Macro-Fiscal Implications of Adaptation to Climate Change. International Monetary Fund, 2022. [CrossRef]
Wan, G.; Zhang, X.; Zhao, M. Urbanisation can help reduce income inequality. Npj Urban Sustainability 2022, 2(1), 1. [CrossRef]
Griffiths, W.E. On Dagum's decomposition of the Gini coefficient. Department of Economics, University of Melbourne, 2008.
Zhao, C.; Yan, Y.; Lu, Y.; Ding, D.; Song, Y.; Wu, G. Assessment and characterisation of urban climate change adaptation capacity based on exposure-resilience-sensitivity. Journal of Ecology 2018, 38(09), 3238-3247. [CrossRef]

Figure 1. Urban climate resilience statistics by year.

Figure 2. Urban climate resilience statistics by region.

Figure 4. Kernel density curves for climate resilience for the full sample of cities.

Figure 5. Subregional urban climate resilience kernel density curves.

Table 1. Urban climate resilience evaluation system.

First indicators	Secondary indicators	Tertiary indicators	Unit of measure	Orientations
Exposure	Climate disaster losses	Economic loss	$10,000,000	-
		Affected population	-	-
		Number of houses damaged	-	-
		Crops affected	Hm²	-
Vulnerability	Low-income population	Number of registered unemployed persons in urban areas	-	-
	Population density	Population density in urban areas	Persons per Km²	-
	Water consumption	Water consumption per capita	T	-
	Level of energy consumption	Electricity consumption Per capita	Kw-h	-
	Medical ambulance capability	Number of doctors	-	+
Resilience	Drainage system	Length of drainage network	Km	+
	Transport capacity	Urban road space per capita	M²	+
	Economic aggregate	Citywide GDP	$10,000,000	+
	Natural ecosystem	Green coverage in built-up areas	%	+

Table 2. Overall descriptive statistics of urban climate resilience.

Statistical indicators	Value
Average value	0.1320598
Variance (statistics)	0.0841542
Low resilience cities	0.04371~0.09129
Low and medium resilience cities	0.09129~0.10523
Medium to high resilience cities	0.10523~0.13881
Highly resilient cities	0.13881~0.77065

Table 3. Descriptive statistics of annual urban climate resilience.

Year	Average	Minimum	Maximum	Climate resilience level/number of cities
Year	Average	Minimum	Maximum	Low	Mid-low	Mid-high	High
2015	0.136437	0.038786	0.850654	139	23	33	75
2016	0.145833	0.033613	0.897658	109	27	55	79
2017	0.148239	0.04264	0.92562	94	33	59	84
2018	0.17159	0.056453	0.934316	62	31	57	120
2019	0.228787	0.053595	0.937002	35	19	42	174

Table 4. Descriptive statistics of climate resilience by subregion.

Year	Average	Minimum	Maximum	Climate resilience level/number of cities
Year	Average	Minimum	Maximum	Low	Mid-low	Mid-high	High
Northeast	0.241219	0.049009	0.934316	103	36	57	134
Northwest	0.148007	0.040849	0.937002	132	28	79	146
Southwest	0.210615	0.042885	0.786491	28	9	30	118
Southeast	0.132027	0.033613	0.840705	176	60	80	134

Table 5. Descriptive statistics of urban climate resilience by category.

Year	Average	Minimum	Maximum	Climate resilience level/number of cities
Year	Average	Minimum	Maximum	Low	Mid-low	Mid-high	High
Rainfall	0.196458	0.072474	0.934316	4	2	41	153
Inundation	0.116598	0.033613	0.840705	390	82	90	148
Hail	0.179599	0.073441	0.937002	31	26	45	53
Typhoon	0.188894	0.078089	0.786491	14	23	70	103
Snowstorm	0.372754	0.185565	0.907432	0	0	0	75

Table 6. Decomposition of regional differences in urban climate resilience and their sources, 2015-2019.

Year	Full sample	Intraregional Gini coefficient				Contribution rate
Year	Full sample	Northeast	Southeast	Northwest	Southwest	Regional	Intra-regional	Hypervariable density
2015	0.37492	0.42281	0.28894	0.33944	0.35748	0.08846	0.12681	0.15965
2016	0.34681	0.38001	0.25766	0.32854	0.35783	0.08256	0.11584	0.14841
2017	0.32340	0.35759	0.23752	0.30123	0.35029	0.07705	0.10650	0.13985
2018	0.31420	0.35514	0.22915	0.29756	0.34053	0.07570	0.09216	0.14634
2019	0.34787	0.33281	0.36381	0.33401	0.34017	0.09251	0.04016	0.21519
average	0.34144	0.36967	0.27542	0.32016	0.34926	0.08326	0.09629	0.16189

Table 7. Inter-regional average Gini coefficient of urban climate resilience, 2015-2019.

Year	Northeast-southeast	Northeast-Northwest	Northeast-Southwest	Southeast-Northwest	Southeast-Southwest	Northwest-Southwest
2015	0.38612	0.39085	0.41973	0.32188	0.42267	0.40604
2016	0.34781	0.36230	0.38787	0.30069	0.39015	0.38801
2017	0.31872	0.33546	0.37613	0.27558	0.36979	0.36812
2018	0.31019	0.33185	0.36701	0.26883	0.34870	0.35581
2019	0.35145	0.33742	0.34354	0.35462	0.36160	0.33902
average	0.34286	0.35158	0.37885	0.30432	0.37858	0.37140

Table 8. Baseline regression results.

score	(1)	(2)	(3)	(4)	(5)	(6)	(7)
lexp	0.064^***	0.026^***	0.096^***	0.101^***	0.095^***	0.103^***	0.108^***
	(7.22)	(3.04)	(6.36)	(7.15)	(6.36)	(6.80)	(6.87)
ldepo		0.031^***	0.027^***	0.034^***	0.032^***	0.036^***	0.039^***
		(5.69)	(4.95)	(6.28)	(6.11)	(6.60)	(6.76)
lpeople			-0.073^***	-0.032^*	-0.069^***	-0.073^***	-0.072^***
			(-6.64)	(-1.68)	(-2.92)	(-3.05)	(-3.01)
lmedbed				-0.053^***	-0.064^***	-0.061^***	-0.067^***
				(-2.76)	(-3.28)	(-3.18)	(-3.43)
leduw					0.054^***	0.060^***	0.065^***
					(3.41)	(3.74)	(3.93)
lpubw						-0.019^***	-0.016^***
						(-3.29)	(-3.00)
lrepw							-0.006^**
							(-2.38)
Constant	-0.353^**	-0.280^*	-0.197	-0.524^***	-0.327^**	-0.554^***	-0.693^***
	(-2.21)	(-1.78)	(-1.40)	(-3.34)	(-1.98)	(-2.98)	(-3.37)
Year FE	YES	YES	YES	YES	YES	YES	YES
Province FE	YES	YES	YES	YES	YES	YES	YES
Observations	1,123	1,113	1,113	1,110	1,108	1,107	1,105
R-squared	0.551	0.564	0.581	0.569	0.575	0.579	0.583

Note: *, **, *** represent significant at the 10 per cent, 5 per cent and 1 per cent level of significance, respectively.

Table 9. Moderated effects regression results.

score	(1)	(2)
lgexp $\times$ czhl		-0.376^***
		(-4.66)
czhl		0.008^***
		(4.78)
lgexp	0.108^***	0.456^***
	(6.87)	(5.79)
ldepo	0.039^***	0.031^***
	(6.76)	(4.51)
lpeople	-0.072^***	-0.048^**
	(-3.01)	(-2.04)
lmedbed	-0.067^***	-0.061^***
	(-3.43)	(-3.11)
leduw	0.065^***	0.062^***
	(3.93)	(3.83)
lpubw	-0.016^***	-0.013^**
	(-3.00)	(-2.50)
lrepw	-0.006^**	-0.007^***
	(-2.38)	(-2.82)
cons	-0.693^***	0.541^*
	(-3.37)	(1.67)
Year FE	YES	YES
Province FE	YES	YES
Observations	1,105	1,105
R-squared	0.583	0.592

Note: *, **, *** represent significant at the 10 per cent, 5 per cent and 1 per cent level of significance, respectively.

Table 10. Robustness test results.

score	(1)	(2)
lgexp	0.108^***	0.125^***
	(6.87)	(7.31)
ldepo	0.039^***	0.041^***
	(6.76)	(6.16)
lpeople	-0.072^***	-0.075^***
	(-3.01)	(-2.87)
lmedbed	-0.067^***	-0.071^***
	(-3.43)	(-3.53)
leduw	0.065^***	0.060^***
	(3.93)	(3.45)
lpubw	-0.016^***	-0.010
	(-3.00)	(-1.23)
lrepw	-0.006^**	-0.009^***
	(-2.38)	(-2.79)
cons	-0.693^***	-0.854^***
	(-3.37)	(-4.19)
Year FE	YES	YES
Province FE	YES	YES
Observations	1,105	825
R²	0.583	0.572

Note: *, **, *** represent significant at the 10 per cent, 5 per cent and 1 per cent level of significance, respectively.

Table 11. Instrumental variable 2SLS regression results.

score	(1)	(2)	(3)
lexp	0.108^***		0.125^***
	(6.87)		(6.88)
IV_L.lexp		0.954845^***
		(0.01565)
ldepo	0.039^***	0.003177	0.038^***
	(6.76)	(0.0054)	(5.61)
lpeople	-0.072^***	0.020442	-0.120^***
	(-3.01)	(0.02014)	(-3.11)
lmedbed	-0.067^***	0.002577	-0.066^***
	(-3.43)	(0.01471)	(-2.87)
leduw	0.065^***	0.013163	0.103^***
	(3.93)	(0.0144)	(2.67)
lpubw	-0.016^***	-0.00116	-0.018^***
	(-3.00)	(0.00649)	(-2.68)
lrepw	-0.006^**	0.005285^*	-0.008^**
	(-2.38)	(0.00256)	(-2.40)
Constant	-0.693^***
	(-3.37)
Year FE	YES	YES	YES
Province FE	YES	YES	YES
Observations	1,105	827	827
R-squared	0.583	0.9927	0.228
Kleibergen-Paap rk LM			87.59
			{0.0000}
Kleibergen-Paap rk Wald F			3721.793
			{16.38}
Cragg-Donald Wald F			7319.235
			{16.38}

Note: *, **, *** represent significant at the 10 per cent, 5 per cent and 1 per cent level of significance, respectively.

Table 12. Quartile regression results.

score	(1)	(2)	(3)	(4)	(5)
score	.10	.25	.50	.75	.90
lexp	-0.011	-0.012	0.061^**	0.119^***	0.146^***
	(-1.31)	(-1.11)	(2.48)	(4.30)	(10.90)
ldepo	0.014^***	0.014^***	0.023^***	0.040^***	0.046^***
	(4.16)	(4.93)	(5.10)	(5.80)	(4.99)
lpeople	0.019	0.030^***	-0.010	-0.077^***	-0.144^***
	(1.59)	(3.40)	(-0.46)	(-2.61)	(-2.74)
lmedbed	-0.029^***	-0.028^***	-0.057^***	-0.050^***	0.002
	(-2.61)	(-3.49)	(-4.22)	(-2.68)	(0.09)
leduw	0.010	0.003	0.024	0.054^**	0.075^*
	(1.02)	(0.31)	(1.31)	(1.97)	(1.89)
lpubw	-0.005	-0.006	-0.008^*	-0.012^**	-0.017^**
	(-1.13)	(-1.25)	(-1.94)	(-2.32)	(-2.15)
lrepw	-0.001	-0.002^*	-0.005^***	-0.007	-0.007^*
	(-0.95)	(-1.94)	(-3.00)	(-1.58)	(-1.88)
Constant	0.535^***	0.470^***	-0.195	-0.836^***	-1.190^***
	(4.31)	(3.44)	(-0.77)	(-2.75)	(-4.49)
Observations	1,105	1,105	1,105	1,105	1,105
R²	0.2094	0.2536	0.3105	0.4102	0.5522
Year FE	YES	YES	YES	YES	YES
Province FE	YES	YES	YES	YES	YES

Note: *, **, *** represent significant at the 10 per cent, 5 per cent and 1 per cent level of significance, respectively.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Study of Urban Climate Resilience and Its Influencing Factors in China

Abstract

1. Introduction

2. Literature review

3. Measuring Climate Resilience in China's Major Cities

3.1. Theoretical foundations and research hypotheses

3.2. Methods and Models

3.2.1. Entropy weighting method

3.2.2. Kernel density estimation

3.2.3. Dagum Gini coefficient decomposition

3.3. Samples and data

Construction of the indicator system

4. Statistical results of urban climate resilience of major cities in China

4.1. Descriptive statistics of urban climate resilience

4.1.1. Overall descriptive statistics

4.1.2. Sub-sample descriptive statistics

5. Dynamic Evolution and Regional Differences in Urban Climate Resilience in China

5.1. Dynamic evolution of urban climate resilience-Kernel kernel density analysis

5.2. Sources of Variation in Urban Climate Resilience-Dagum Gini Coefficient Decomposition

6. Analysis of factors influencing urban climate resilience

6.1. Variable Selection and Model Setting

6.1.1. Modelling

6.1.2. Selection of indicators and data sources

6.2. Epirical test

6.2.1. Benchmark regression results

6.2.2. Moderated effects regression results

6.3. Robustness test

6.3.1. Explanatory variables lagged by one period

6.3.2. Endogeneity test

6.3.3. Quantile regression

7. Conclusions and policy recommendations

7.1. Conclusions

7.2. Policy recommendations

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe