Prerpints.org logo
Preprint
Review

Advances in Slime Mould Algorithm: A comprehensive Survey

Altmetrics

Downloads

202

Views

66

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 September 2023

Posted:

08 September 2023

You are already at the latest version

Alerts
Abstract
Slime Mould Algorithm (SMA) is a new swarm intelligence algorithm inspired by the oscillatory behavior of slime molds during foraging. Numerous researchers have widely applied SMA and its variants in various domains and proved its value by the experiments in literatures. In this paper a comprehensive survey on SMA is introduced, which is based on 130 articles visa Google-scholar between 2022 and July, 2023. Firstly, the theory of SMA is described. Secondly the improved SMA variants are provided and categorized according to the approach that they are applied with. Finally, it also discusses the main applications domains of SMA such as engineering optimization, energy optimization, machine learning, network, scheduling optimization, image segmentation and etc. This review presents some research suggestion for researcher who is interested in this algorithm.
Keywords: 
Subject: Computer Science and Mathematics  -   Data Structures, Algorithms and Complexity

1. Introduction

Optimization problem commonly exit in the real life and many of them are NP-hard problem, which is challenging for traditional optimization methods to solve. The researchers turn their attention to the meta-heuristic optimization algorithm for solving the optimization problem, special for complex, nonlinear and high-dimensional optimization problem. In recent years, meta-heuristic optimization algorithm has achieved great success in solving complex optimization problems. In general, the meta-heuristics algorithms are mainly divided into evolutionary algorithm, physics-based algorithm, swarm intelligence algorithm and human-based algorithm as shown in Figure 1.
Evolution-based algorithms are proposed to simulate Darwinian biological evolution and mainly include Genetic Algorithm (GA) [1] and Differential Evolution (DE) [2]. Physics-based algorithms are inspired by the laws of physics and mainly include Simulated Annealing (SA) [3], Gravitational Search Algorithm (GSA) [4], Multi-Verse Optimizer (MVO) [5], Atom Search Optimization (ASO) [6], and Equilibrium optimizer (EO) [7]. Swarm-based algorithms are derived from the collaborative behavior of mammals, insects, birds, fishes and other living creatures. Representative algorithms include Particle Swarm Optimization (PSO) [8], Artificial Bee Colony Algorithm (ABC) [9], Teaching Learning Optimization Algorithm (TLBO) [10], gray wolf optimizer (GWO) [11], Whale Optimization Algorithm (WOA) [12], Salp Swarm Algorithm (SSA) [13], Social Spider Optimization (SSO) [14], Seagull Optimization Algorithm (SOA) [15], Harris Hawks Optimization (HHO) [16], Aquila Optimizer (AO) [17], Bald Eagle Search (BES) [18], Slime Mould Algorithm (SMA) [19], Marine Predators Algorithm (MPA) [20], Chameleon Swarm Algorithm (CSA) [21] and so on. Finally, the human-based algorithms mimic the individual/collective interaction and behaviors, social activity or lifestyle and so on. Some of the most well-known methods found in the literature include Harmony Search(HS) [22], Firework Algorithm(FA) [23], Imperialist Competitive Algorithm (ICA)[24]and many more.
Slime mould algorithm (SMA) is a new swarm-based meta-heuristic algorithm proposed by Li et al. in 2020 [19], which mimics the oscillatory behavior of slime mould for finding the food. Due to the character of simple structure and good scalability that SMA own, many researchers applied it in many fields such as feature selection, energy, path finding, engineering and etc. In this paper, we propose a review of SMA with its variants and application domains. To collect the papers related to SMA, we conducted an extensive search in Google Scholar with key word of “Slime Mould Algorithm” or “SMA” since 2022. A total number of 130 papers are obtained from various well-known publishers like Springer, Elsevier, IEEE, Hindawi, MDPI, Taylor & Francis, Research square, ResearchGate and others. The statistics of survey are indicated in respectively Figures below. Figure 2 presents the number of SMA related papers from various scientific publishers since 2022. Table 1 lists 3 countries ranked in number of publications on SMA since 2022.
The sections are organized and detailed as: Section 2 first provides the SM’s concept and the SMA ‘s mathematic model, its pseudo-code and flowchart. Section 3 introduces the details on SMA's variants and improvements. In section 4, a wide range application domain of SMA and its variants is indicated. In section 5, the advantages and disadvantages of SMA are discussed respectively. Section 6 outlines conclusions and presents some possible future research directions.

2. Slime Mould Algorithm (SMA)

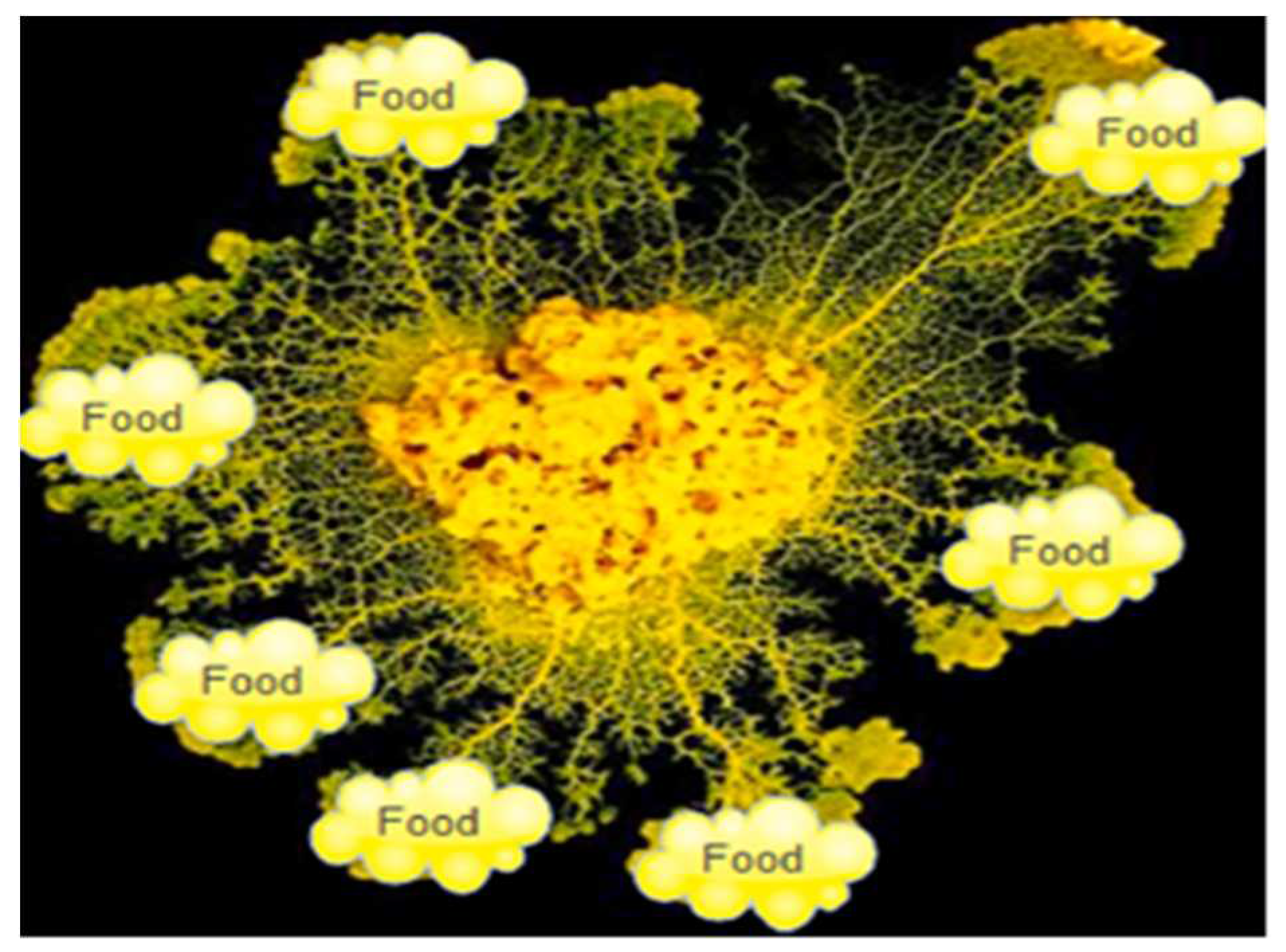
2.1. Concept of SMA

Slime mould algorithm (SMA) is proposed based on mathematical simulation of the oscillatory activity of slime molds during foraging. Slime mold has the property of oscillating and contracting when it finds food. The foraging behavior of slime molds is classified into three model: finding food, approaching food and digesting the food by enzymes [19]. In the process of the migration, the front end of slime mould disperses into fan-like shape and forms a network of veins with different thicknesses among multiple food sources, as shown in Figure 3.
The network’s thickness is proportional to the quality of food source to some extent. When the vein goes for the high-quality food, a biological oscillator generates stronger propagating wave that increase the flow of cytoplasmic, thus resulting into the wider thickness of the network. Therefore, the optimal path from slime mould to food source is established in this positive and negative feedback mechanism.
Slime mould also would likely search for other area for food sources. When the information is not enough and incomplete, following the heuristic or empirical rule that is based on the insufficient information would be best way for slime mound to evaluate current position and determined whether leave the current position or not [24]. The possibility of leaving area is decreased when slime mound finds high quality of food [26]. Slime mould still makes good use of various food sources at same time because of its unique biological characteristic.Even if the better food sources is found, slime mould allocate parts of its biomass to exploit both of food sources[27].
Slime mould also adjust the search pattern dynamically based on the food stuff provenience. When the high-quality food is attainable, slime mould would focus searching on the food available with region-limited search method [28]. If the original food deteriorates to low concentration, slime mould will leave it to explore a new high quality of food sources [29].

2.2. Mathematical model of SMA

The mathematical model to update the slime mould’s position is as Eq. (1).
X ( t + 1 ) → = r a n d ⋅ ( U B − L B ) + L B r a n d < z X b ( t ) → + v b → ⋅ W → ⋅ X A ( t ) → − X B ( t ) → r < p v c → ⋅ X ( t ) → r ≥ p
where L B and U B are the lower and upper boundary of the search scope, r a n d and r are random value taken within the range of [0,1], and z = 0.03 is a parameter, X b ( t ) → indicates the position that is found for the strongest food odor at present, v b → is a parameter taking values within [ − a , a ] , v c → is also a parameter fluctuating linearly from 1 to 0 with the number of iterations t , W → represents the slime mould’s weight determined by Eq. (4), X A ( t ) → and X B ( t ) → are two randomly selected agents positions in the population, X ( t ) → indicates the current position of the slime mould.
The value of p is calculated as Eq. (2).
p = tan h ⁡ | S ( i ) − D F |
where i ∈ 1,2 , . . . , n , S ( i ) denotes the fitness X → , D F stands for the best fitness obtained so far.
The value of a to determine the boundary of v b → is defined as Eq. (3).
a = arctan h ⁡ 1 − t max _ ⁡ t
where max _ ⁡ t indicates the maximum number of iterations.
The slime mould’s weight W → is calculated as Eq. (4).
W ( S m e l l I n d e x ( i ) ) → = 1 + r ⋅ log ⁡ b F − S ( i ) b F − w F + 1 c o n d i t i o n 1 − r ⋅ log ⁡ b F − S ( i ) b F − w F + 1 o t h e r s
S m e l l I n d e x → = s o r t ( S → )
where c o n d i t i o n represents that S ( i ) ranks first half of the population, r means a random number in [0, 1], b F represents the optimal fitness obtained in the current iteration, w F is the worst fitness obtained in the current iteration, S m e l l I n d e x → denotes the result of the ascending order of fitness values (in the minimization problem).

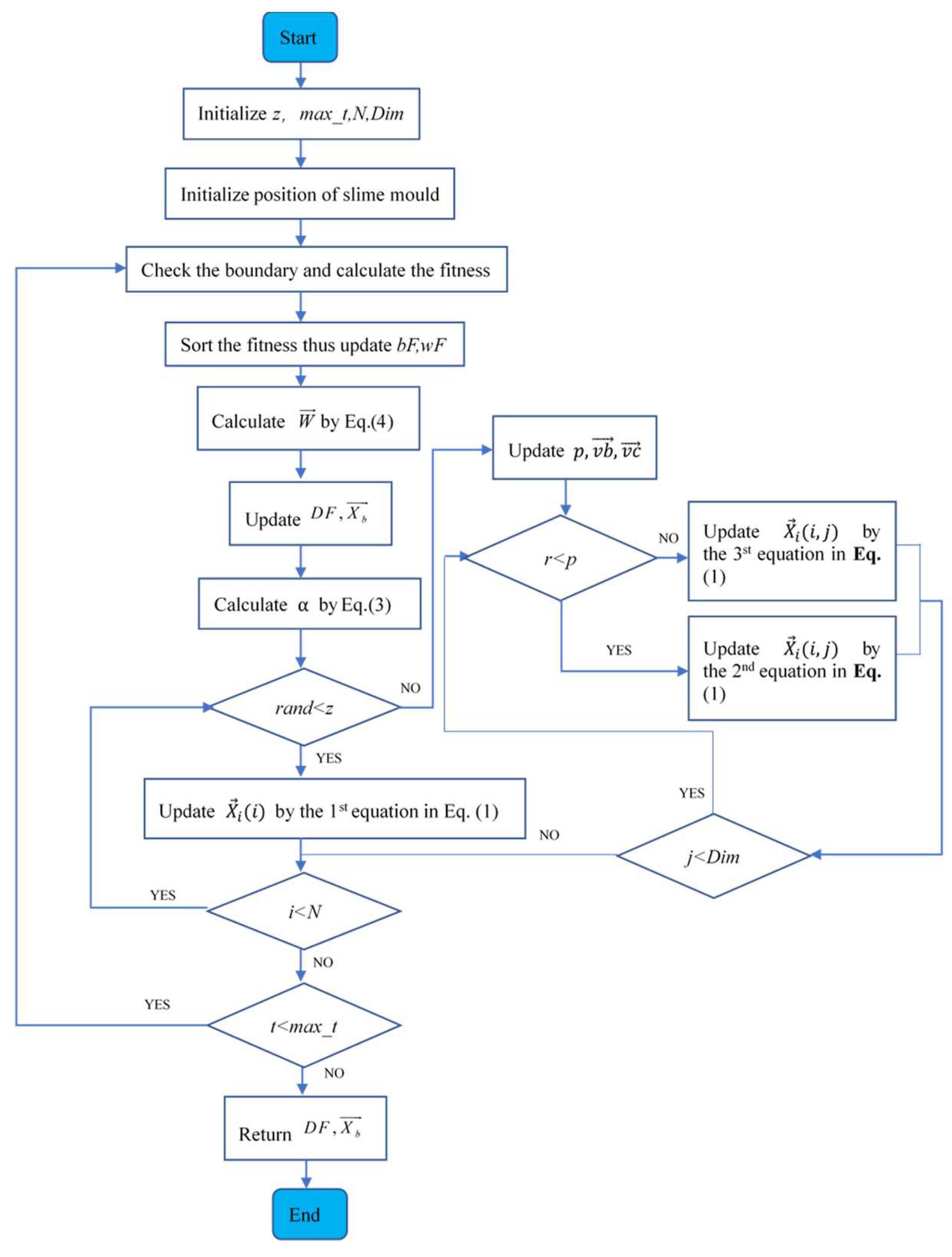
2.3. The pseudo-code and flow chart of SMA

The pseudo-code and flow chart of SMA are shown in Algorithm 1 and Figure 4 [27].
Algorithm 1: Pseudo-code of SMA
1. Initialize   the   parameters   z , m a x _ ⁡ t , N , D i m ;
2. Initialize slime mould’s random location X i → ( i = 1,2 , ⋯ , N ) ;
3. While ( t ≤ m a x _ ⁡ t )
4. Check the bound and determine the fitness S → ;
5.   Sort   the   fitness   S → ;
6.   Update   b F , w F , D F , X b → ;
7.   Calculate   W → as per Eq. (4);
8.   Update   p , v b → , v c → , A , B ;
9. For each search agents
10. Update location as per Eq. (1);
11. End For
12. t = t + 1 ;
13. End While
14. Return D F , X b → ;

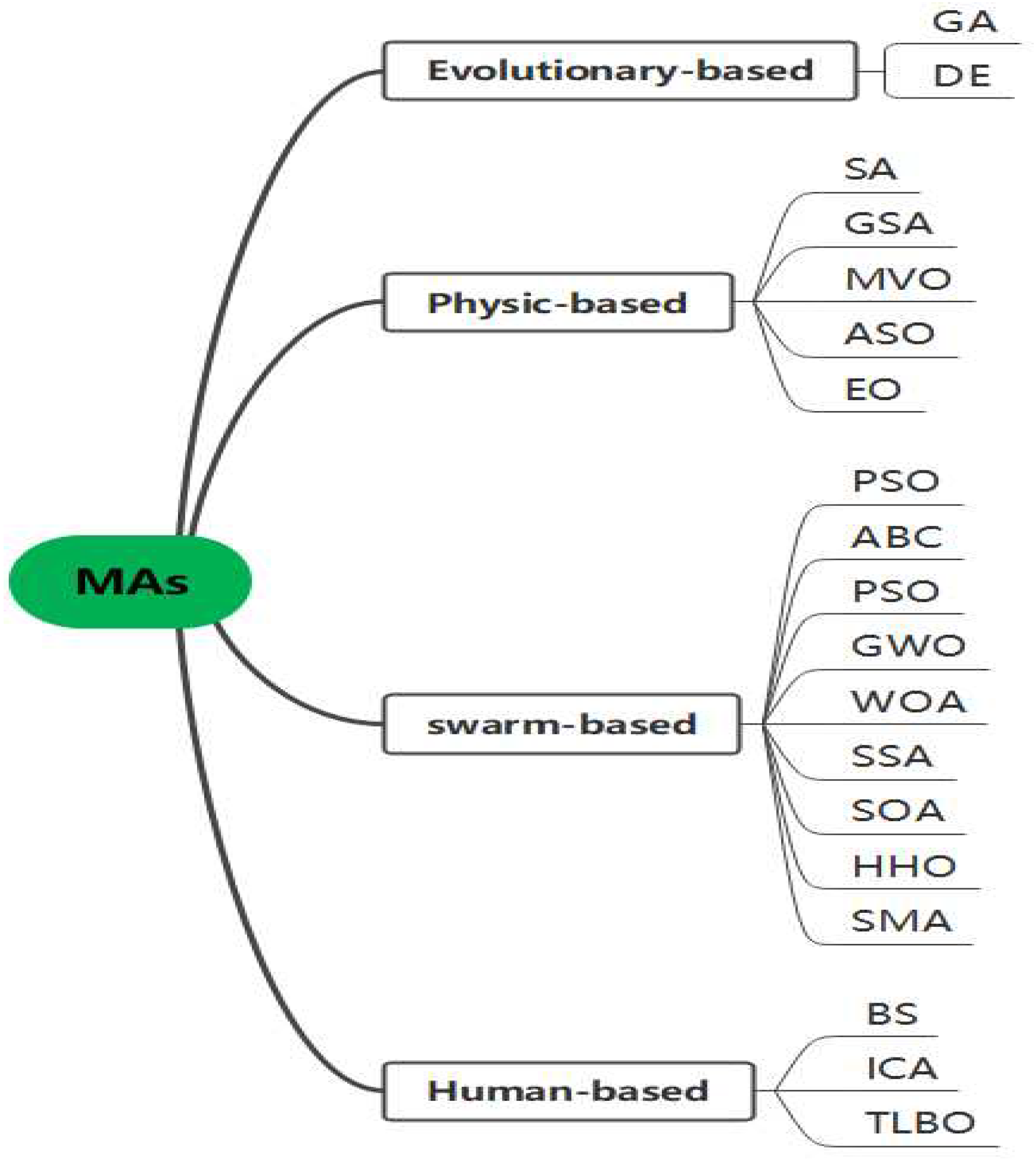
3. Recent variants of slime mould algorithm

The basic SMA is mainly aimed for solving continuous single-objective optimization problem when it is firstly proposed in 2020. SMA has been widely noticed by researchers and numerous SMA variants have been presented with improving techniques like strategies adding, hybridization with other algorithms for solving kinds of problems (single/multi-objective and continuous /discreate). According to 130 papers on SMA collected in well-known publishers between 2022 and July,2023, most of these SMA variants are applied for single and continuous problems , as indicated in Figure 5 and Figure 6. To our best knowledge, classification of SMA variants is not clearly defined and most of literatures classify them based on the methods and problem which they use and resolve. As shown in Figure 5 and Figure 6, 81% of surveyed papers belong to the category of single-objective version and 90% of surveyed papers belong to the category of continuous problems. So if not specially clarified, most of SMA variants are applied to solve single-objective and continuous optimization problem and it is not necessary to categorize them. Therefore, we classified these 130 papers into four categories: modified version, hybridized version, discrete version and multi-objective.

3.1. Modified version of SMA

Modified version of SMA variants refer to those which are employed the methods of simplifying, removing, replacing original operators or adding new operator while its framework remains unchanged. Take the SSMA [164] proposed by Yuanye Wei et al. as example. In the SSMA, the third equation in Eq. (1) was removed and the original oscillation factor was replaced by cosine function to form a simple version of SMA variants. We call those methods mentioned above as the strategy adding, which are often adopted by the researchers. The relevant SMA variants adding different strategies are shown in Table 2.

3.1.1. Opposition-based learning (OBL)

As shown in Table 2, opposition-based learning is the most popular strategy that researchers used for SMA variants. OBL was first proposed by Tizhoosh HR in 2005[87] and aimed at increasing the populational multiformity to jump out local optima.
In the literature of [30,32,35,37,41,42], researchers use the basic OBL to improve SMA variants’ exploration.
There are many modified version of OLB, namely adaptive OBL[39], Quasi Oppositional Optimization learning[84],random opposition-based learning[85],to further increase population diversity and improve populations' capacity to avoid local optimality. Izci D et al. [31] improved the original SMA’s exploration with a modified OBL. Houssein EH et al. [40]introduced a modified OBL that utilized Lévy flight distribution to SMA. In addition, Dipak Kumar Patra1 et al. [35] developed an enhanced SMA by incorporating the Quasi Opposition-based Learning (QOBL) mechanism in it. Krishna Gopal Dhal et al. [40]proposed an improved SMA (named as ISMA) based on random OBL and DE’s mutation strategy. Liang Xu et al.[38]presented an ISMA by imbedding an improved random OBL to increase convergence ability in the late iteration and prevent from local optimization. Sengathir J. et al. [39] utilized OBL strategy in the proposed AOLISMA to self-adjusting for exploration.

3.1.2. Chaotic strategy

The Chaotic strategy takes the second position but to OBL in the Table 2. Chaos, as a non-linear system common found in nature, is applied by many researchers to optimize search problem due to its randomness, traversal and regularity [90]. The researchers add the chaotic strategy to SMA for maintaining the population diversity, thus avoiding local stagnation.
Rizk-Allah RM et al. [33] proposed a version of CO-SMA by adding a chaotic strategy. The chaotic search strategy can enhance the neighborhood searching around the best position. Li YiFei et al. [43] imbeded polynomial chaos expansion (PCE)to SMA for multi-parameter identification of concrete dams. Yin Shihong et al. [44]sorted out a set of chaotic sequences by a chaotic grouping mechanism (CGM) to improve population diversity. Xuebing Cai et al. [45]proposed a multi-objective SMA,called asCRFSMA, which incorporated a chaotic mechanism to increase the search ability. Yuan L et al. [46]presented an enhanced algorithm of SMA called ECSMA, in which elite strategy and chaotic stochastic strategy were embedded into the structure to maintain well balance between the exploration and exploitation. Dhawale D et al. [47] used the chaotic SMA (named for CSMA) combined with tent chaotic function. Chen H et al. [48] replaced the original random initialization of SMA with chaotic maps in order to enhance the diversity of population. Zhong C et al. [49] employed an adaptive chaos control method to solve reliability-based design optimization (RBDO) problems. Miao H C et al. [51] presented a MSMA that adopted the elite chaotic search strategy (ECSS) to enhance exploration near elite individuals. Bhadoria A et al. [52] used a singer map chaotic search strategy to improve the local search during the exploitation phase. Sarhan S et al. [53] suggested an ESMO incorporating a chaotic strategy and an elitist group. Singh T et al. [54]proposed a chaotic slime mould algorithm (CSMA) with integration of chaotic sequences during the optimization process.

3.1.3. Mutation operator and crossover operator

The concept of mutation and crossover are derived from genetic algorithm (GA)[90] and differential evolution (DE)[91].Both algorithms conduct the process of mutation, crossover and selection to generate next generation of population. Researchers use mutation operator and crossover operator to increase the populational diversity, thus increasing exploration and exploitation.
Some researchers use both of mutation operator and crossover operator as multi-strategies for SMA. Ramin Ghiasi et al. [55] imbedded two operators of mutation and crossover to binary slime mould algorithm (ABSMA) to overcome the stagnation situation. Deng L et al. [57] presented a MSMA, in which a mutation operator was added to generate a new search equation to maintain the balance of exploitation and exploration, and an adaptive mutation probability was constructed to avoid premature convergence and maintain population diversity. Qiu F et al. [59] proposed an improved algorithm (ISMA) combining two strategies of Cauchy mutation and crossover mutation based on DE, to promote the coordination of global exploration and local exploitation.
There are also various SMA variants using the mutation operator and crossover operator respectively. Many versions of SMA variants with mutation mechanism adding have proposed and proved mutation was a useful method. Lin H et al. [32] developed an ASMA, in which a trigonometric-based mutation operator and a double-based best mutation operator were used to improve the convergence speed, and a binomial crossover operator also was used to increase the population diversity. Yin S et al. [56] added the random difference mutation strategy to the proposed EOSMA to help the algorithms jump out from the local stagnation. Pawani et al. [58]introduced a wavelet mutation into SMA to avoid local optimal. Zheng R et al. [60] integrated the multiple mutation operators and restart method into SMA. Yang H et al. [61]introduced the mutation mechanism and dynamic weight coefficient to the proposed SMA to solve problems of slow convergence and low optimization precision. Yang P et al. [62] added the mutation operation in SMA’s position update to improve the global optimization ability of SMA. The crossover operator adding method also has shown its advantages in many SMA variants. Rizk-Allah RM et al. [33] proposed a modified SMA added with a chaotic search strategy (CSS) and crossover opposition strategy (COS) to avoid trapping in local optima. Qi A et al. [66] presented a novel SMA variant, named SDSMA.In the SDSMA, the directional crossover mechanism was added to enhance the balance of exploration and exploitation, thus helping SDSMA to increase the convergence speed and accuracy. Ma TX et al. [70] introduced an improved crossover operator into the improved artificial bee colony slime mould algorithm to improve the convergence speed.

3.1.4. Lévy flight

Lévy flight is a probability distribution proposed by the Paul Pierre Lévy [92] , which specially enhances the global search capacity of SMA to prevent being stuck in local optimal. Lévy flight mechanism combines short-distance walking with long-distance jumping routes to search for space. Therefore researcher use it to improves the global search ability of the algorithm.
Ling Zheng et al. [63] proposed the Lévy flight-rotation SMA (LRSMA), in which utilized a variable neighborhood Lévy flight. He W et al. [64] sorted a Lévy flight sequences to increase the convergence speed of the SMA. Pan JS et al. [65] proposed a MFSMA, which was added with an adaptive Lévy flight. Qi A et al. [66] presented a SDSMA combining the adaptive Lévy diversity mechanism and directional crossover mechanism. Qiu F et al. [67] used Lévy flight to help SMA jump out the local optimum. Jui JJ et al. [68] integrated the Lévy distribution into SMA for solving the local optima problem. Kundu T et al. [69] introduced Lévy flight into SMA to improve the global search ability.

3.1.5. Elite strategy

The elite strategy is widely adopted by researcher in many SMA variants. The concept of elite strategy is to introduce elite individuals, which are used to generate the current solution corresponding to the elite solution. Then the elite solutions are compared to the current solutions for that the top individuals are chosen as the next generation. Therefore, the elite strategy not only increases the search scope of an algorithm but also improves the diversity of the population.
Yuan L et al. [46] proposed an enhanced SMA called ECSMA, in which the elite strategy was embedded into the structure. Miao H C et al. [51] added an elite chaotic search strategy (ECSS) to the proposed MSMA to enhance exploration around the elite individuals. Sarhan S et al. [53] incorporated an elitist group mechanism in ESMO. Kaveh A et al. [74] adopted an elitist strategy in replacement phase of SMA to increase convergence rate of the proposed ISMA. Luo Qifang et al. [80] proposed a MOEOSMA by adding elite archiving mechanism to promote the convergence speed.

3.1.6. Greedy selection (GS)

The greedy selection strategy is one of most wide-used strategies that is adopted by researchers for SMA variants. Liu J et al. [71] proposed a multi-strategy information interaction and optimally oriented initialization (MSII-SMA). The greedy selection strategy was employed for building the information exchange model to provide a better solution for the next iteration. Shubiao Wu et al. [72] adopted a greedy selection strategy to increase the convergence of proposed GBSMA. Yin S et al. [74] updated the individual and global historical optimal with the greedy strategy, resulting into acceleration of the convergence.

3.1.7. Fuzzy

Fuzzy strategy is commonly adopted in SMA variants. Prabhu, M et al.[75] proposed a fuzzy based Slime Mould optimization for Carrier Frequency Offset (FSM-CFO) . The fuzzy rules were designed and applied for the assignment of Resource Units (RU) to a certain job. Al-Kaabi M et al.[76] presented a Multi-Objective Slime Mould Algorithm (MOSMS), which fuzzy set theory was used to obtain the optimal solution. Yutong G et al. [77] present a fuzzy SMA(named as FSMA) whose control parameters was updated by a fuzzy system.

3.1.8. Neighborhood search (NS)

Neighborhood Search (NS) is a useful strategy to enhance the exploitation ability of algorithms. Yuanfei Wei et al. [78] added a variable NS strategy in the proposed EOSMA to increase the exploitation. Zhou X et al.[79] introduced an all-dimensional neighborhood search strategy for SMA(LASMA) to explore the search space more effectively.

3.1.9. Others

Besides of the strategies mentioned above, there are still many other strategies that researcher usually add to SMA, including Nelder–Mead simplex search[31],orthogonal learning[40], dynamic random search[57], sigmoid function[64] [81],Gaussian strategy [72] [82], dispersed foraging strategy[85], bee-foraging learning operator[84]and etc. These strategies have improved the SMA performance and is one of importance directions for researchers.

3.2. Hybridized version of SMA

Hybridization of SMA with other algorithms is one of importance method that researchers use to improve the performance of SMA. Because SMA have strong scalability, it is natural for SMA to hybridize other algorithms. Table 3 shows the relevant SMA variants hybridized with other algorithms based on 130 publications of the survey.
As conduct literature review on these 130 papers, we conclude two approaches that researchers generally use for algorithms hybridization: framework modification and operator fusion.
The framework modification approach is to modify the original SMA by adding the other algorithm’s strategy or combine both algorithms to solve the same optimization problem. For example, A. A. Ewees [108] combined the updating technique of Firefly algorithm (FA) into the structure of the SMA. The operators of SMA and FA were competed to update the solution, which maintained the balancing between the exploration and exploitation during the searching process. This approach allows the algorithms operate independently but they can exchange and modify inter-population information, taking advantage of multiple algorithms to complete the solution [93].
The operator fusion is to replace or modify the SMA operators with other algorithms or combine different operators from both algorithms to solve the drawbacks of original SMA. The operator fusion approach is mostly indicated in hybrid version of SMA with EO, EO and GA. As for hybridization of SMA and EQ in [56,73,78,80],the operators of best position found in SMA is replaced by the first solution in the equilibrium pool of EO. And the mutation operator and crossover operator of EO and GA are usually adopted to update the position during search solution for jumping out the local optimum.
Comparing with both approaches, the operator fusion is more popular than the framework modification. Because the it is relatively easy to modify and replace the original operator of SMA without changing the framework and structure, resulting into less computational time. But the full understanding of both algorithms’ mathematical model is a premise for the implementation of the operator fusion and a challenge task for the researchers.

3.2.1. Hybridization with equilibrium optimizer (EO)

Yin S et al. [56] [73]replaced the orignal search operator of SMA with concentration update operator of EO to improve the search efficiency of the algorithm. Yuanfei Wei et al. [78] changed the random search operator in SMA with EO strategy to enhance the population diversity. Luo Qifang et al. [80] integrated the equilibrium pool’s strategy to the proposed EOSMA at stage of population initialization, helping the proposed algorithm to improve the exploration.

3.2.2. Hybridization with differential evolution (DE)

Chen H et al. [48] proposed a CHDESMA which was added with the crossover and selection operators derived from DE to assist the algorithm step out of local optimal. Shubiao Wu et al. [72] proposed a GBSMA combined with DE’s position updating mechanism to enhance the exploration capability.

3.2.3. Hybridization with support vector machine (SVM)

Yuheng Guo et al. [94]employed SMA approach to optimize the parameters of SVM for ancient glass classification. Gao H et al. [95] proposed a prediction model on the basis of a modified SMA and SVM algorithm. Javidan SM et al. [96]combined SMA with SVM classifier to diagnose apple tress diseases. Shi B et al. [97] combined the proposed JASMA with the common kernel learning SVM for an analysis of recurrent spontaneous abortion (RSA).

3.2.3. Hybridization with whale optimization algorithm (WOA)

Anji Reddy Vaka et al. [98] proposed a hybrid SMA with WOA, which WOA technique performed exploration in the first half of the iteration and the SMA method performed exploitation in the second half of iterations. Bhandakkar AA et al. [99] improved the searching behavior of SMA by incorporated with WOA’s characters. Li X et al. [100] combined SMA and WOA with two fusion measure to enhance the global optimization ability: replacing the one parameter of WOA with a parameter in SMA and introducing the position updating strategy of WOA into each slime mould individual.

3.2.4. Hybridization with simulated annealing (SA) algorithm

Izci D et al. [30] proposed an opposition-based hybrid SMA with SA algorithm to improve the exploitation and exploration of original SMA. Leela Kumari Ch et al. [101] used SA algorithm to help SMA avoid trapping the local optimum.
3.2.5 Hybridization with teaching–learning based optimization (TLBO)
Zhong C et al. [49] suggested a hybrid SMA with TLBO, which can enhance the convergence speed of SMA. Kundu T et al. [69] utilized the character of SMA and TLBO to maintain a well-balance between the exploitation and exploration.
3.2.6 Hybridization with seagull optimization algorithm (SOA)
Bhadoria A et al. [52]enhanced the exploration and exploitation capability of SMA by sequentially hybridizing SMA and SOA. Das G et al. [102] hybridized SMA and SOA to improve the global and local search space.

3.2.7. Hybridization with artificial bee colony (ABC)

Ma TX et al. [70] introduced artificial bee colony (ABC) algorithm to hybridize SMA to improve the search ability and avoid local minima. Chen X et al. [103] added the position update mechanism of the artificial bee colony (ABC) into the SMA to jump off the local opima in the process of image segmentation.

3.2.8. Others

Moreover the researchers hybridize SMA with sine cosine algorithm(SCA) [81] , particle swarm optimization (PSO) [104], evolutionary algorithm(EA) [106], firefly algorithm(FA) [106],grey wolf optimization algorithm(GWOA) [107], marine predators algorithm(MPA) [108], gradient-based optimizer(GO) [109], quadratic approximation(QA) [110], tournament selection(TS) [111], artificial neural network(ANN) [112]],Moth-flame optimization algorithm(MFOA) [113], pattern search algorithm(PSA) [114], support vector regression(SVR) [115] and etc. These hybrid SMA variants have indicated their merits such as the well balance between exploration and exploitation, good convergence speed, avoiding premature convergence, less computation time and so on.

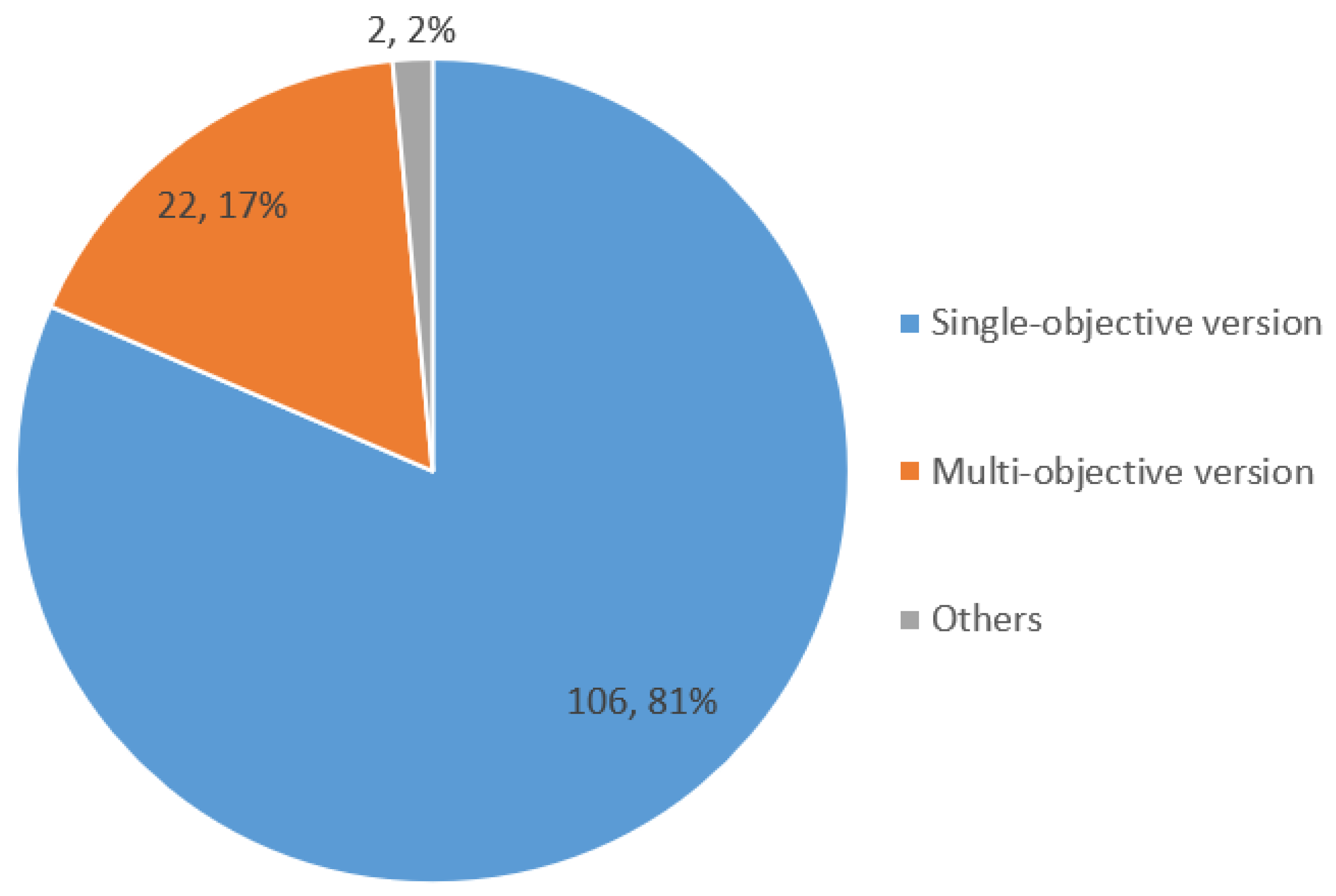
3.3. Multi-objective version of SMA

The multi-objective problems are the important branch of research in optimization problem. The general mathematical model of multi-objective optimization is shown in Eq.(6)
m i n m i z e y = f x = f 1 x , f 1 x , ⋯ , f k x s u b j e c t t o e ( x ) = e 1 x , e 1 x , ⋯ , e m x ≤ 0
Where x = ( x 1 , x 2 , ⋯ , x n ) ∈ X y = ( y 1 , y 2 , ⋯ , y n ) ∈ Y From Eq.(6), we know that multi-objective optimization has many functions and some of them conflict and compete with each other. The optimization of one function would be achieved at expense of others. It is impossible to attain the best solution for all function. The best solution can be attained from the coordination and compromise of various function. The multi-objective optimization is a challenge task for SMA.
Comparing with single-objective version of SMA, the multi-objective version of SMA take 17% of surveyed publication between 2022 and July of 2023, see Figure 5.Therefore multi-objective version of SMA need more researchers’ attention. Son, P. V. H. et al.[34] put forward an AOSMA to finding solution of construction project’s multi-objective optimization problem. Yin Shihong et al. [44]presented an multi-objective SMA(named IBMSMA) and applied it for the multi-objective truss optimization problem. Cai Xuebing et al. [45] also proposed a MOSMA and the simulation test demonstrated that the MOSMA attained the best convergence, accuracy and diversity among the compared multi-objective algorithms. Yin S et al. [73] applied the proposed multi-objective EOSMA (MOEOSMA) for the inverse kinematics of manipulators. Al-Kaabi M et al. [76] presented a MOSMA for attacking multi-objective optimal power flow problems. Luo Qifang et al. [80] proposed a MOEOSMA and assessed it in engineering problems, which indicated its efficiency from comparison. Pham Vu Hong Son et al. [111] applied the hybrid model adaptive selection slime mould algorithm (ASSMA) to address the project’s multi-objective of time, cost, quality, and environment trade-off problem, which outperformed other multi-objective algorithms through Pareto. Peng C et al. [115] proposed a MOSMA and optimized SVR parameters by MOSMA for global convergence. Sadasiva Behera et al.[119] used a MOISMA to solve a multi-renewable sources-based energy management and this MOISMA-based-energy management outperformed. Houssein EH et al. [116] proposed a MOSMA which proved its superiority with Pareto sets proximity by experiment. Yacoubi S et al. [117] introduced a MOOSMA for numerical association rule mining (NARM). Zhang Y et al. [118] proposed a process parameter optimization method for laser cladding combined MOSMA and support vector regression (SVR). Son PV et al. [120] employed a multi-objective version of SMA(ASSMA)to improve SMA’ performance via Pareto Front. From comparing result, the ASSMA model showed good diversification.

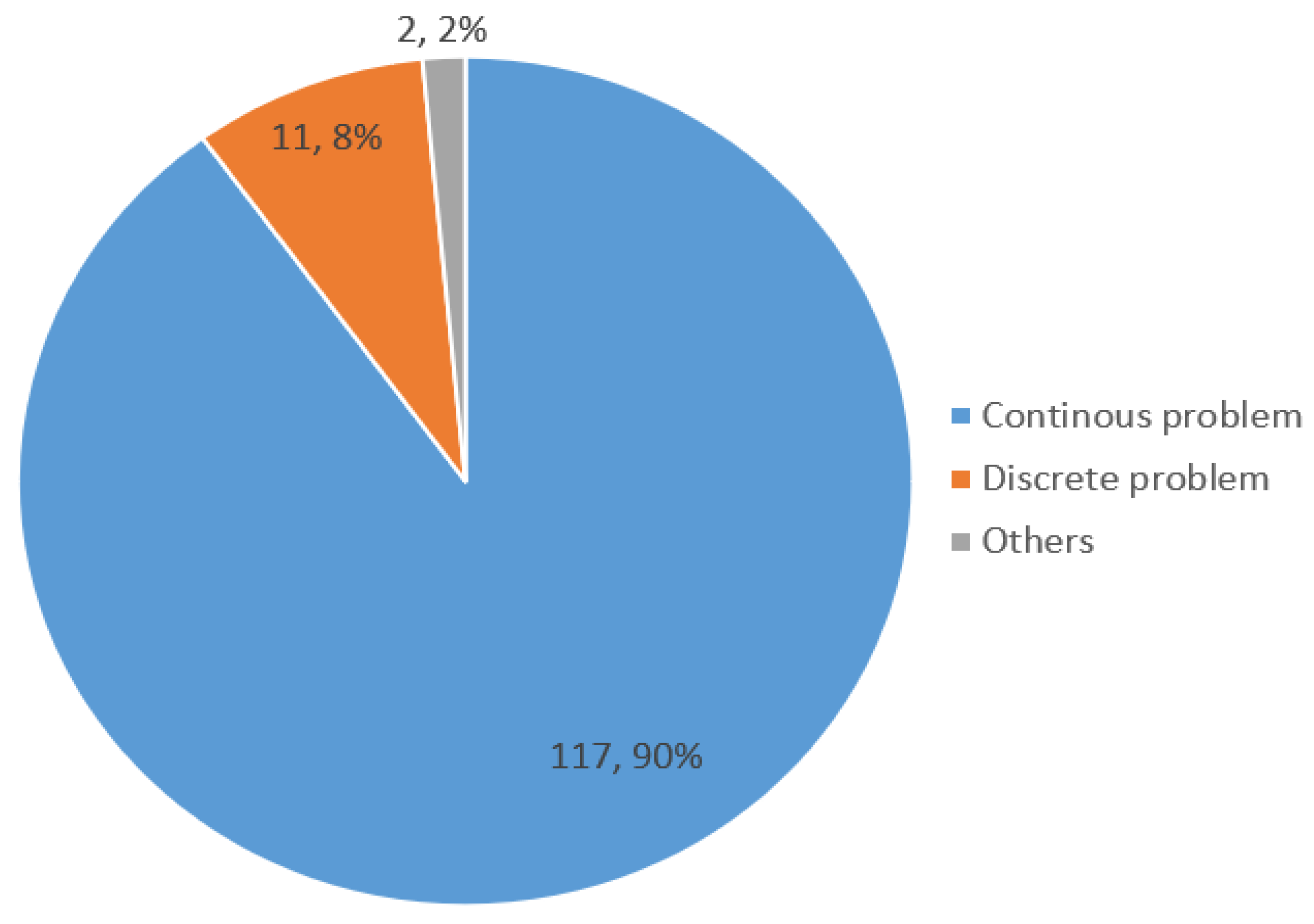
3.4. Discrete version of SMA

Discrete problem is an important domain of optimization problem, such as 0-1knasack problem, traveling salesman problem (TSP), job shop scheduling problem (JSSP) and etc. In this section, the discrete version of SMA refer to those SMA variants that researches use discrete mechanisms to discrete the original continuous SMA to solve discrete problems. In contrast to continuous version of SMA, the discrete version of SMA is only 8% of surveyed publications between 2022 and July,2023, as shown in Figure 6.Therefore it is one important of direction to further develop SMA variants.
Most of researchers discrete original SMA by encoding the continuous valve of solution into binary value without changing the framework of original SMA. Ghiasi Ramin et al. [55] introduced a binary SMA (ABSMA) to better classification of the structural damage. Feng Qiu et al. [59] converted SMA into the binary one with a transfer function and used it for the gene selection. Feng Qiu et al.[67] also mapped the proposed GLSMA to binary space via transformation function and applied for feature selection. Yuanfei Wei et al.[78] discreted the proposed EOSMA with a Sort-Order-Index (SOI)-based coding for Job Shop Scheduling Problem (JSSP).Zhou X et al.[79]used a V-shaped transfer function to convert proposed LASMA to binary algorithm. The experiments showed that bLASMA had better results in regarding to convergence speed and accuracy dealing with optimization problems and feature selection. Hu J et al.[85] proposed a binary dispersed foraging SMA (BDFSMA) ,which was promising in feature selection. H.S Hassan et al. [124] proposed a BSMA which converted the continuous space to discrete space with transformation function. Rifat Md Sayed Hasan et al. [125] employed a binary SMA to solve the unit commitment problem (UCP). Dan Li et al.[126] used the double-stranded chromosome encoding method and the solution space bisection decoding method to compose a model of GCSMA and applied it for the flexible job-shop scheduling problem(FJSP). MS K [128] proposed a discrete time-based slime mould optimization (SMO), providing an effective support to the buck converter based MPPT controller for SPV systems.

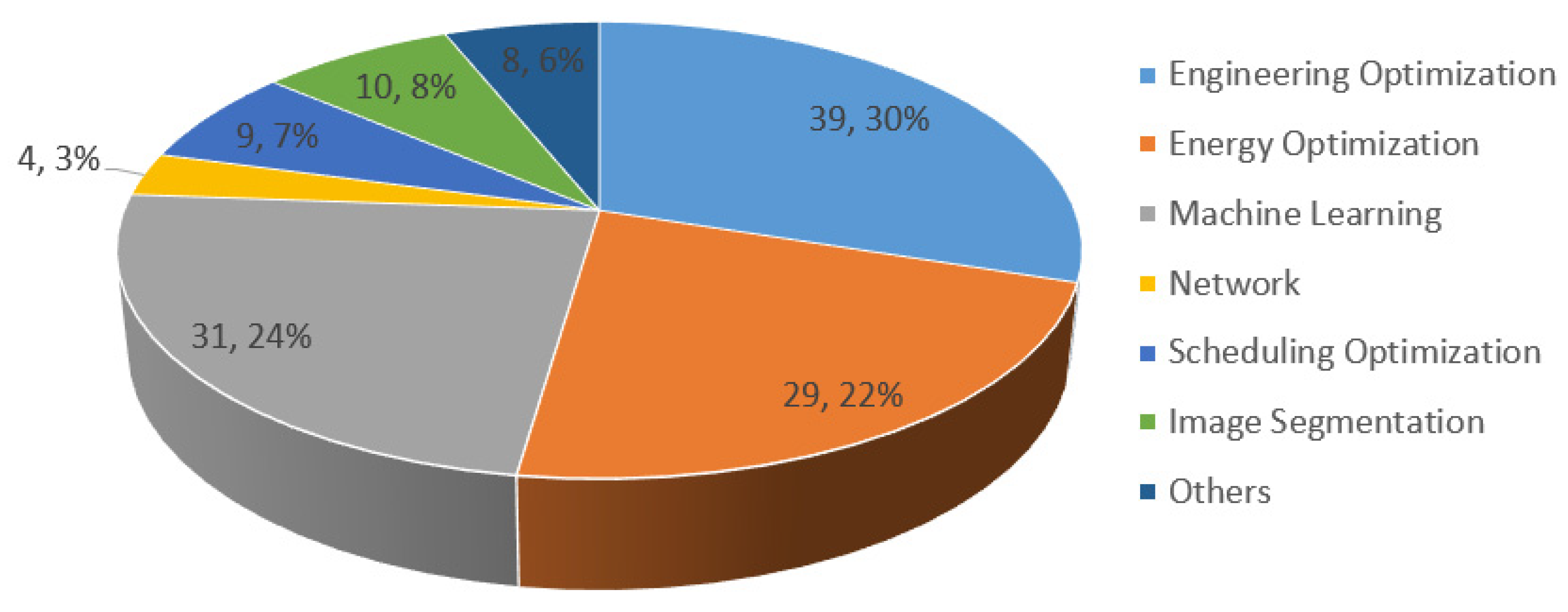
4. Applications of SMA

The SMA and its variants have been applied various fields of application and these fields cover the industry of energy, agriculture, forestry, medical and health, IT, manufacture, electronic and communication, education, finance and so on. In this section, we classified the 130 surveyed publications into seven categories: engineering optimization, energy optimization, machine learning, image segmentation, network, scheduling optimization and others, as shown in Figure 7.

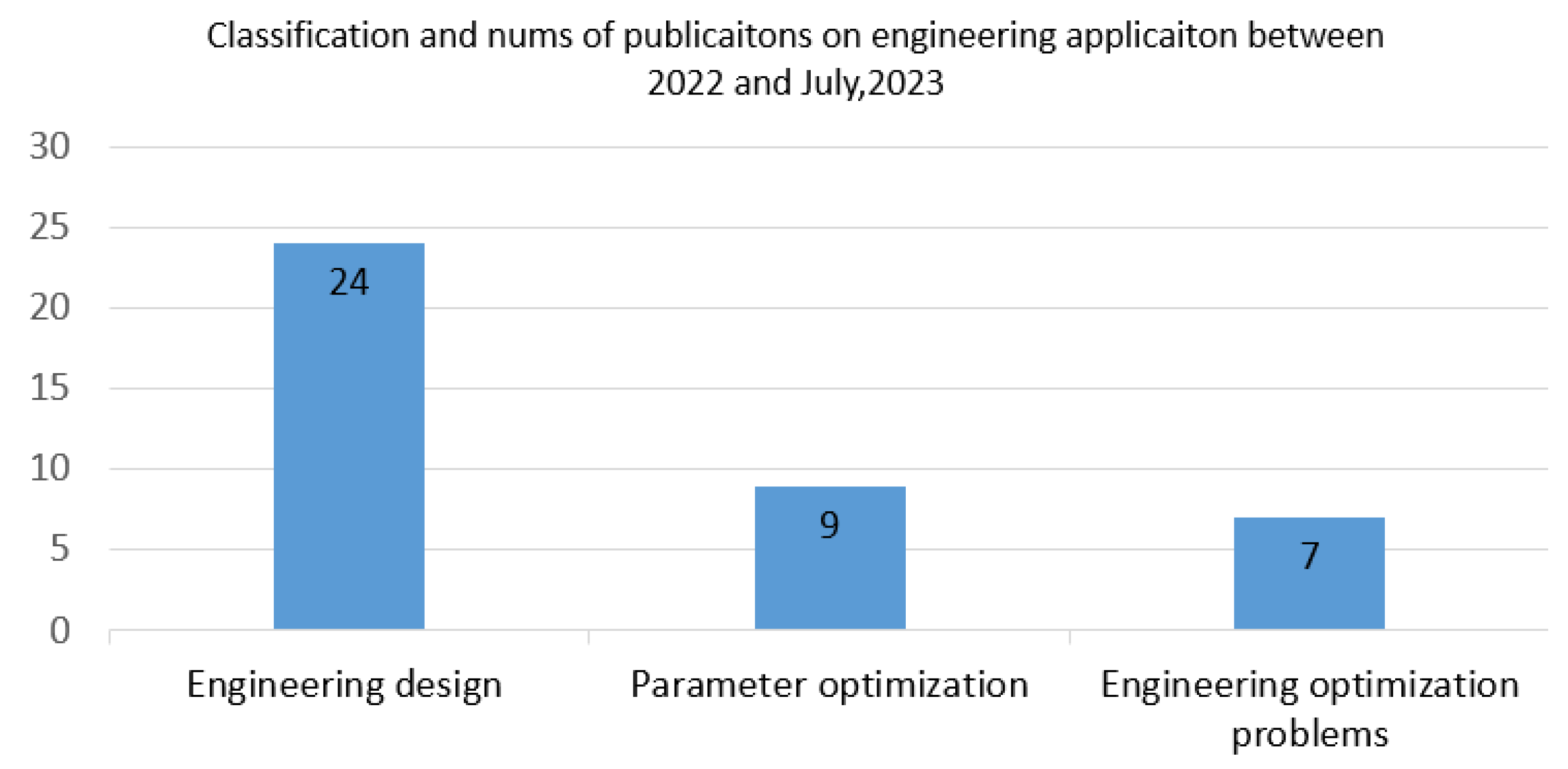
4.1. Enginnering optimization

Engineering optimization is on first position of application domains as indicated in Figure 7. We divide the engineering optimization into four categories: engineering design, engineering optimization problems and parameter optimization, as indicated in Figure 8.

4.1.1. Engineering design

Optimizing real-life engineering design problems are challenging and many applications have to deal with NP-hard problem. The real-world engineering design optimization problems is to achieve max or min objection under some predefined constraints. Usually a number of design constraints, like dimensions, strengthen, rigidity and so on, are nonlinear and complex, which lead to difficulty of finding solution. Because SMA has the advantages of simple structure and strong exploration ability, researchers developed various SMA for solving engineering design problem.
As SMA is proposed firstly to solve single-objective application problem, the SMA variants are mostly employed for the single-objective engineering design problem. Houssein EH et al. [40] evaluated the proposed SMA in three engineering design problems. Li Yuan et al. [46] applied the presented ECSMA for four structural design issues of the welded beam design problem, PV design problem, I-beam design problem, and cantilever beam design problem with excellent results. Chen H et al. [48] assessed the presented CHDESMA for four real world engineering problems, which indicate that CHDESMA had competitive performance. Yin S et al. [56] applied the proposed EOSMA for nine engineering design problems. Deng L et al. [57] evaluated the proposed MSMA using several practical engineering issues, which proved that the proposed algorithm was more efficient and robust than other algorithms. Zheng R et al. [61] employed three typical engineering design problems to verify the proposed ESMA’s performance. Jui JJ et al. [68] evaluated the proposed LSMA in 23 well-known benchmark test functions and the welded beam design problem. Kundu T et al. [69] evaluated the proposed LSMA-TLBO in I six engineering design problems. Liu J et al.[71]compared the proposed MSII-SMA with other algorithms for engineering design optimization problems and the experimental results demonstrated the universality, reliability and preponderance of MSII-SMA in dealing with engineering design constraint optimization problems. Örnek BN et al. [81] tested the performance of proposed SMA on designs’ optimization and the results demonstrated the proposed SMA had better ability of jumping out local optima. Leela Kumari Ch et al. [101] presented a hybrid version of SMA and assessed it in 11 kinds of interdisciplinary engineering design. Chauhan S et al. [107] tested the proposed PSEASMA and SSEASMA in classical engineering design problems to prove their superiority over other algorithms. Bala Krishna A et al.[114] proposed a hybrid SMA variants named as hSMA-PS and applied it for nine classical engineering. Yin S et al.[128] verified the performances of proposed DTSMA on nine engineering design problems. Qi A et al. [129] proposed a SDSMA and applied it to three real-world engineering design problems. Lingyun Deng et al. [130] presented an AGSMA for solving practical engineering problems, which demonstrated the AGSMA’s superiority over other compared algorithms.
SMA also has been further developed for multi-objective engineering design problems. Qifang Luo et al. [80] used the proposed MOEOSMA to solve eight real-world multi-objective constraint engineering problems. Houssein EH et al.[116] used a MOSMA for the real-world multi-objective optimization of helical coil spring and four multi-objective engineering design problems.
Many researchers focused on the structure optimization problems. Yin Shihong et al. [44] employed the proposed IBMSMA and evaluate it in multi-objective truss. Shubiao Wu et al. [72] proposed a GBSMA for solving truss structure optimization problems. Kaveh A et al. [74] used the proposed ISMA for three large-scale benchmark dome trusses. Qifang Luo et al. [80] used the proposed MOEOSMA to solve large-scale truss structure optimization problems.
In contrast to typical engineering design application described above, there is few SMA variants that is applied for the reliability-based design optimization (RBDO).Das G et al.[102] used the proposed TLSMA for solving five reliability-based design optimization problems.

4.1.2. Engineering optimization problem

Engineering optimization problem is always a hot research topic and SMA has been utilized in numerous applications, like the economics, combinational optimization, energy sector and etc. Shahenda Sarhan et al. [53] suggested the proposed ESMO for handling the optimal power flow (OPF). Wenhe He et al. [64] proposed an unresolved peaks analysis algorithm, which was based on the sigmoidal membership function, Lévy flight, and slime mould algorithm (SLSMA), for microchip electrophoresis (ME) signal detection. Chakraborty P et al. [110]proposed a hybrid SMA for three engineering optimization problems. From the evaluations, HSMA was an efficient algorithm for real-life problems. Rifat Md Sayed Hasan et al. [125]applied the presented BSMA for solving the unit commitment problem (UCP). Rizk-Allah RM et al. [132] employed the CO-SMA to optimize the wind turbines’ energy cost. Khelfa C et al. [133]used SMA to improve the response time for the ambulance dispatching problem. Mehrtash Eskandaripour et al. [167] proposed a SWMM-SMA model to design low-impact development (LID) approach for urban areas management. To assess this model, an Iranian urban area was used and the analyses showed that the proposed model was more effective.

4.1.3. Parameter optimization

Many researchers use SMA variants to optimize the process parameter of equipment, management system, projects and etc. Izci D et al. [30]proposed a hybrid SMA variants and evaluated it in the direct current motor and the automatic voltage regulator. Izci D et al. [31] also proposed an ISMA to adjust the parameters of DC motor speed and AVR control systems. Pham Vu Hong Son et al. [34] used a hybrid AOSMA to optimize the multi-parameters of planning time, cost, quality, and safety in the construction industry. Li YiFei et al. [43] used combined methods of polynomial chaos expansion and SMA for multi-parameter identification of concrete dams. Pham Vu Hong Son et al. [111,120]also used a hybrid ASSMA to obtain the project’s multi-objective time, cost, quality, and environment trade-off. Zhang Y et al. [118]used the proposed MOSMA for parameter optimization of laser cladding. F. Loucif et al. [134] presented a new application of SMA for the optimization of backstepping controller parameters for the tracking control and the perturbations rejection of the robot manipulator. Ding P et al. [135] proposed SMA to optimize the parameter of micro-milling, like the material removal rate, the processing cost and the processing time.

4.2. Machine learning

Machine learning is in the 2nd position in Figure 7. Due to successful application on the optimization problem, researchers have proposed SMA and its variants for i machine learning. We furtherly classify the machine learning into the five sub-categories: feature selection, data mining, prediction model, neural networks and deep learning. The details of publications are indicated in Figure 9.

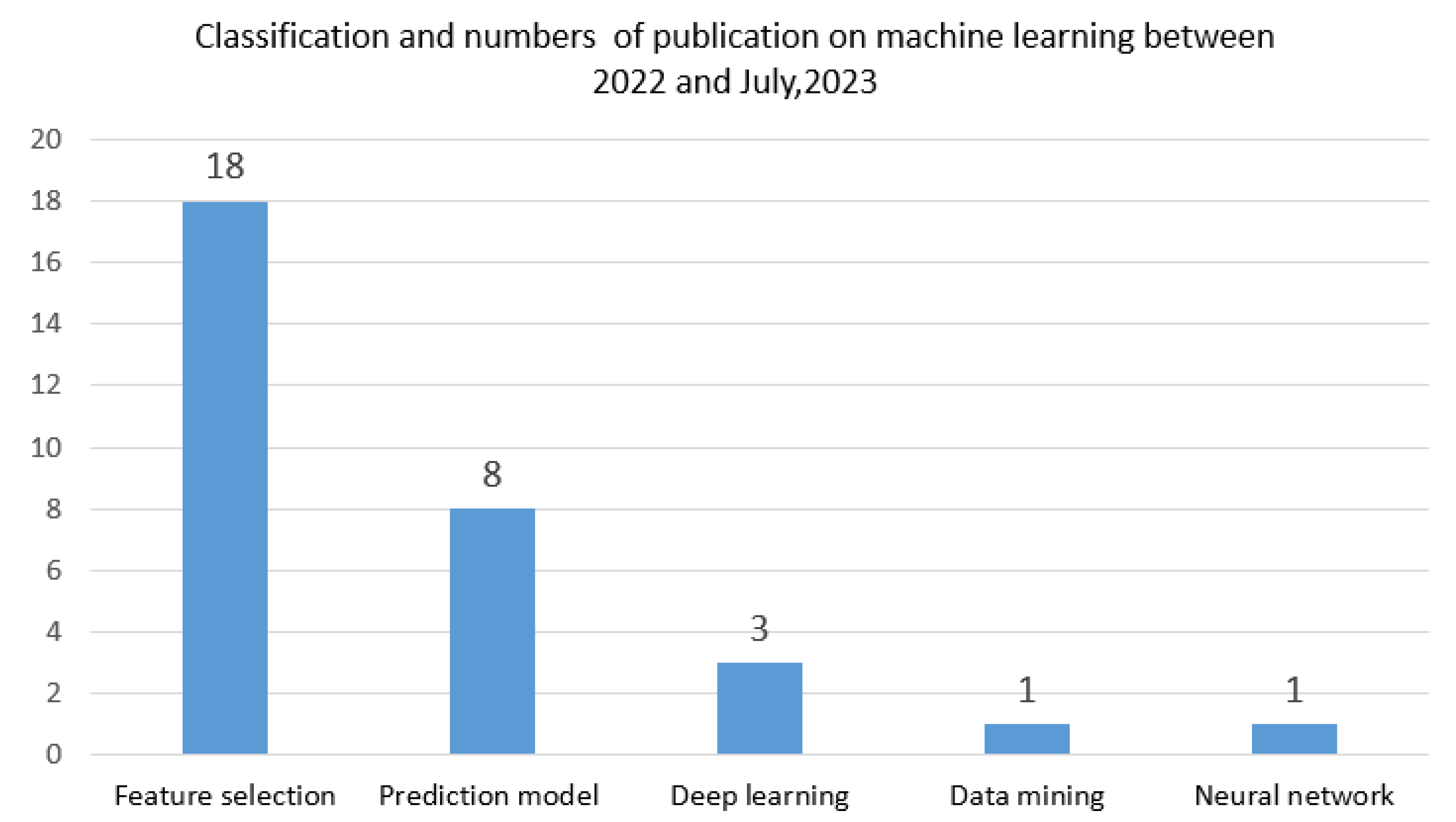
4.2.1. Feature selection (FS)

Feature selection (FS) are an effective method to enhance the performance of the machine learning algorithms by minimizing data features’ numbers and data preprocessing. Many researchers have applied SMA for feature selection. Ramin Ghiasi et al. [55] employed the binary SMA (BSMA) for feature subset selection to improve the performance of structural damage classification. Qiu F et al. [59] proposed a wrapper gene selection method based on BISMA and assessed it in 14 gene expression datasets. Yang P et al. [62] proposed a load identification method based on the improved slime mould algorithm-generalized regression neural network (ISMA-GRNN) and the ISMA-GRNN had hihger accuracy and precision of load identification from simulation results. Qiu F et al. [67] developed a BGLSMA for feature selection on 14 high-dimensional gene datasets and the experiments verified the discrete BGLSMA was promising approach for features selection. Zhou X et al. [79] proposed a binary SMA (bLASMA) and evaluated it in 18 datasets of varying dimensions from the UCI machine learning repository. From experiment results, the bLASMA outperformed other algorithms. Hu J et al. [85] presented a binary DFSMA (called BDFSMA) and evaluated it on 12 datasets in the UCI repository. The experiment demonstrated that the BDFSMA improved accuracy and decreased the number of features compared with other algorithms. Yuheng Guo et al.[95] employed SMA for the parameters optimization of SVM and examined a 69-group glass chemical composition dataset to classify ancient glass product. Javidan SM et al.[96] combined SM and SVM classifier to diagnose three apple tree diseases. Anji reddy Vaka et al. [98] proposed a hybrid WOA-SMA and applied in BreakHis and IDC datasets to evaluate breast cancer classification. Ahmed A Ewees et al. [108] developed a hybrid of SMA and MPA （SMAMPA）and evaluated it in UCI dataset and Quantitative structure-activity relationship (QSAR) models. Ewees AA et al. [109] also evaluated the performance of the proposed GBOSMA in several benchmark datasets to solves feature selection problems, which showed that the GBOSMA overcame others. H.S. Hassan et al. [124] proposed a binary SMA for feature selection. Mehwish Zafar et al. [149] used SMA to extract informative features and input them into to SVM and KNN classifiers to design a multi-classification of the skin lesions. Sayed GI et al. [154] introduced a pistachio species classification method on the basis of SMA. Khan AA et al. [156]presented a hybrid of SMA with GWO for feature selection and evaluated it in UCI repository datasets by comparing with other algorithms. Wei X et al. [157] proposed a SMA-VMD-WTD model to identify and eliminate the transient electromagnetic signal noise.

4.2.2. Prediction model

It is a popular way of utilizing SMA to make prediction model to improve the predication accuracy.
AlRassas AM et al. [41] used SMA to improve the developed timeseries forecasting model for oil production prediction. And the ANFIS-SMAOLB model was evaluated with oil production dataset. Nemani R et al. [84] introduced a statistical data mining for intelligent rainfall prediction using SMA and Deep Learning (SDMIRPSMODL) model and evaluated it in a rainfall dataset. Gao H et al. [95] proposed a prediction model based on modified SMA and SVM algorithm to predict employment stability of postgraduate. Shi B et al. [97] presented a framework where the JASMA was fused with the common kernel learning SVM for conducting an effective analysis of recurrent spontaneous abortion (RSA). The experimental results indicated that the proposed JASMA-SVM was a promising tool for RSA prediction. Samantaray S et al. [104] proposed an ANFIS-PSOSMA model to predict river flood discharge (QFD) considering data from four gauging stations of River Brahmani, Odisha India. From the evaluation, the proposed model had highest accuracy. Peng C et al. [115]optimized SVR’s hyperparameters with the MOSMA and two dataset of spindle vibration data and milling data were tested for evaluating the performance of MOSMA-SVR by comparing with other seven prediction models. Tiachacht S et al. [148] presented SMA-based method for structural damage detection, localization and quantification and competed to MPA-based method. The results showed that the proposed method can predict the location and level of damage with higher accuracy. Zhou J. et al. [150] introduced a COSMA-RF method for cutting force prediction of Since conical pick cutting. Zhang J. et al. [151] used six performance indicators including a SMA-ANN model to predict the settlements of a single footing on soft soil reinforced by rigid inclusions and the SMA-ANN outperformed other models according to experimental results.
4.2.3 Deep learning (DL)
SMA also has some advantages in optimizing deep learning frameworks. Shi B et al. [83] combined a multiple strategies SMA(MSSMA) with a kernel extreme learning machine, named as MSSMA-KELM. The MSSMA-KELM was applied for Pulmonary hypertension (PH) analysis from arterial blood gas. According to experiments, the MSSMA-KELM is a promising technology. Lan Ngoc-Nguyen et al. [153] introduced SMA to detect and monitor the suspension footbridge’s damage. The experimental results proved that SMA was more reliable at finding the damage location and determining damage’s degree than the CS and GA. Hamza MA et al. [155] introduced a SMO model with Bidirectional Gated Recurrent Unit (BiGRU) model to forecast traffic condition in smart cities. The simulation results proved the proposed model’s superiority.

4.3. Energy optimization

As indicate in Figure 7, the application of energy optimization takes 3th position. We further divide energy application into eight sub-categories. The clarification and numbers of publications on energy optimization’s application between 2022 and July,2023 is shown in Figure 10.

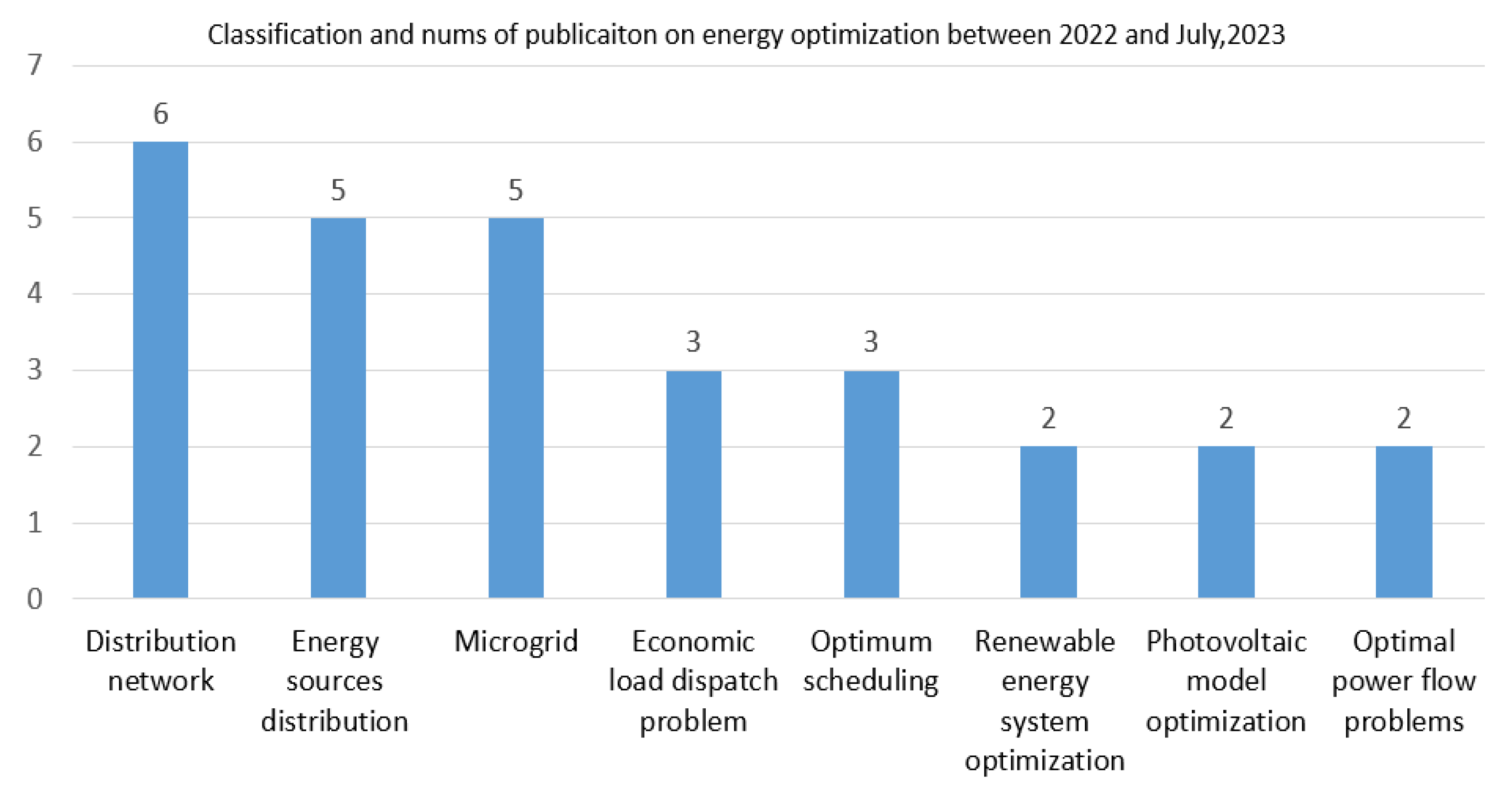
4.3.1. Distribution network

Ma TX et al. [70] employed an ISMA for DC distribution network fault location. Wang HJ et al. [136] applied the proposed PSMA for the distribution network reconfiguration (DNR) problem. And the experimental results showed that the PSMA was excellent method for DNR problem. Pan JS et al. [143] proposed a MFSMA for the dynamic distribution network reconfiguration problem.

4.3.2. Energy sources distribution

Abid MS et al.[50] used the proposed CSMA for the optimal load shedding technique of distribution system. Kanchan Pawani et al.[58] employed a comprehensive learning wavelet-mutated SMA to optimize the combined heat and power dispatch problem. Bhandakkar AA et al. [99] used an ISMA to optimize the layout of hybrid power flow controller. Behera et al. [119] induced a MOISMA to solve a multi-renewable sources-based energy management. Mohamed Zellagui et al. [122] used the SMA approach to determine the best simultaneous allocation of multiple Fault current limiters (FCL) units in the standard IEEE 69-bus test system. The simulation results demonstrated the efficiency and accuracy of the SMA to reduce the fault courant in the Electrical Distribution System (EDS). Ahmadianfar I et al.[137] proposed a MSMA to optimize operating strategies to problem forecast of complicated hydropower multiple reservoir. Wu X et al. [138] applied SMA to optimize the allocation of water resources in Wuzhi.

4.3.3. Microgrid (MG)

A Chakraborty et al. [139] proposed SMA to minimize the total operational cost via an energy management of a grid-connected low-voltage microgrid (MG), and SAM approach was a better EM with a lower operational cost of MG than other methods. Behera S et al. [144] employed SMA for the operation management of microgrids. Behera S et al. [146]also used the proposed MSMA to design an optimal battery management system in microgrid. Liu Z et al. [146] applied SMA algorithm for the power transaction of microgrid and grid master-slave game. Zare P et al. [147] suggested a novel control technique for frequency regulation in an Offshore Fixed Platforms Microgrid system based on fractional-order hybrid controllers which of coefficients adjusted by SMA.

4.3.4. Economic load dispatch (ELD) problem

Pawani K et al.[42] introduced a modified SMA for economic load dispatch problems and emission dispatch problems .Singh T et al.[54] suggested the proposed CSMA for economic load dispatch (ELD) problem. Kamboj VK et al. [142] applied SMA to solve an ELD in an electric power system.

4.3.5. Optimum scheduling

Dhawale D et al. [47] used the proposed CSMA to offer a solution to optimal generation scheduling of vehicle to grid (V2G) operation. Bhadoria A et al.[53] proposed a hybrid CSMA-SOA for solving the generation scheduling problem of realistic power system. Abid MS et al. [140] applied a SMA-based approach to identify the optimal charging strategies of electric vehicle (EV).

4.3.6. Renewable energy systems (HRES) optimization

Miao H et al.[51] proposed a MSMA and applied it for a Chinese cascade hydropower reservoirs system to optimize the annual power generation. Olalekan Kunle Ajiboye et al. [121] employed SMA for the optimization of hybrid renewable energy systems (HRES).

4.3.7. Photovoltaic model optimization

Lin H et al. [32] developed an ASMA and employed it to attain optimal parameters of PV models. K Padmanaban et al. [127] proposed a discrete time-based SMA to provide an effective support to the buck converter based Maximum Power Point Tracking (MPPT) controller for Solar PhotoVoltaic (SPV) systems.

4.3.8. Optimal power flow (OPF) problem

Al-Kaabi M et al.[76] employed MOSMA to solve multi-objective optimal power flow problems. Farhat M et al.[141] used the proposed ESMA for solving the Optimal power flow (OPF) problem.

4.4. Image segmentation

Image segmentation separates an image into sub-regions or objects depending on its components and it is useful method for various application, such as multi-threshold image segmentation, medical image processing, sonar image recognition, image compression, and others.
The multi-threshold image segmentation is a frequent method that scholars used in the domain of Image processing. Dipak Kumar Patra et al. [35] proposed a SMA-based multilevel thresholding technique for breast DCE-MRI segmentation and was evaluated in 200 DCE-MRI images of 40 patients. The simulation results indicated the proposed method outperformed other compared methods. Chen X et al. [103] proposed an improved SMA (called as ASMA) for a multilevel image segmentation (MLTIS) of Lupus Nephritis (LN) diagnosis, named as the ASMA-based MLTIS. The proposed approach was assessed and proved to be an efficient image segmentation method for LN images. Mehbodniya A et al. [152] used SMA to attain optimal threshold values on host image and experiments demonstrated the proposed approach was better than others. Yuanyuan Jiang et al. [158] presented an improved ISMA for a multi-level thresholding image segmentation and symmetric cross-entropy for image segmentation tasks. Shi M et al. [159] proposed a RWGSMA for multi-threshold image segmentation. To evaluate RWGSMA’s efficiency, the lupus nephritis’s instances were used and experiments demonstrated its superiority.
In additional to the multi-threshold image segmentation, researcher used image segmentation technology to assist the medical diagnosis[35] [103] [159].Krishna Gopal Dhal et al.[36] proposes an ISMA to perform illumination-free White Blood Cell (WBC) segmentation.
There is also other application of image segmentation. Yutong G et al. [77] designed a DCNN–ELM–FSMA model, in which a fuzzy SMA (FSMA)was applied. The DCNN–ELM–FSMA’s performance was evaluated in three sonar datasets and results indicated the proposed mode was more accurate in sonar image classification. Ren L et al. [82] developed an enhanced version of SMA called as MGSMA and applied it for a multi-level image segmentation (MLIS) model. The MGSMA-based MLIS method was compared with eight other peers at both high and low threshold levels using 10 images from BSDS500 and the results revealed that the suggested approach could deliver high-quality image segmentation results. Chavan PP et al. [105]suggested an image compression technique for Vector Quantization (VQ) with the K-means Linde–Buzo–Gary (KLBG) model. In the encoding stage, the hybrid GA and SMA was employed for generating optimal codebook. The comparation results revealed the proposed method performed better than others. Debnath A et al. [160] presented an improved image-denoising technique that is based on the combination of cascaded filters. SMA was used to combine different filters. From the visual and quantitative analysis, the proposed technique improved the quality of images.

4.5. Scheduling optimization

There are various SMA variants applied for scheduling optimization, including path finding, autonomous mobile robots, JSSP and others.
Path planning is to find an optimal route from the starting point to the targeted point under certain contains and is widely applied in various domains such as autonomous mobile robots (AMRs) logistics, safety evacuation and etc. Yang H et al. [61] proposed an improved SMA to find the optimal path of unmanned equipment in fire rescue. Ling Zheng et al. [63] proposed the Lévy flight-rotation SMA (LRSMA) for path planning of autonomous mobile robot (AMR). Experiments shows that the proposed approach was able to find out optimal path without obstruct and with higher accuracy and stability. Hu G et al. [161]proposed a HG-SMA to build a path planning model on the basis of Said-Ball curve. The HG-SMA approach was evaluated in three workplaces with rectangle, circle and mix obstacles and results revealed that suggested algorithm achieved the better value of path distance, smoothness and stability. Yueming Q et al. [163] developed both single/multi objective methods for the path planning of Automatic guided vehicle (AGV) based on SMA.
The motion control of autonomous mobile robots is also optimized with SMA and its variants. Yin S et al. [73]proposed both single-objective and multi-objective version of EOSMA and applied them to solve inverse kinematics (IK) of manipulators. The test indicated the proposed EOSMA had shorter computation time than compared algorithms. Li X et al. [100] developed a hybrid of SMA with WOS (SMWOA) for the joint trajectory planning of robot. 6-DOF UR5 manipulator was used to evaluated the SMWOA’s efficiency and the results showed that running time of the joints was less.
Job Shop Scheduling Problem (JSSP) play an important role in production process and many researchers applied SMA and its variants for JSSP. Dan Li et al. [126]introduced a multi-strategy SMA named GCSMA for flexible job-shop scheduling problem (FJSP).
In addition, Zheyuan Wang et al. [162] designed a SMA based energy-efficient traffic scheduling method (SMA-ETSM) for software defined network (SDN).

4.6. Network

Several papers composed the SMA and its variants for wireless sensor network (WSN).
J Sengathir et al. [39] proposed an adaptive opposition learning-improved SMA (AOLISMA)-based optimization routing to ensure reliable data dissemination among UAVs, extend network lifetime and minimize energy consumption. The experimental results demonstrated that the proposed AOLISMA can enhance the throughput and reduce the control overhead. Yuanye We et al. [164] proposed a SSMA for solving the WSN coverage problem. According to 13 groups of WSNs coverage optimization experiments, the SSMA outperformed other algorithm in regarding to the network nodes energy, the services quality and the network survival time. Alwan MH et al. [165] integrated SMA into the Intrusion Detection System (IDS) for wireless sensor networks for anomaly detection. SMA was used to decrease features’ quantity. From evaluation on the NSL-KDD dataset, the proposed method improved the value significantly.

4.7. Others

In this section, we sort out the SMA variants that only use the benchmark functions or is not applicable for the classification criterion described above as “other”.
Using the benchmark or basic function to evaluated the SMA variants are common methods for researchers. Xuebin Cai et al.[45,168] introduced a general multi-objective SMA and compared it with seven advanced multi-objective algorithms on 28 basis functions, which demonstrated that the proposed MSMA outperformed other algorithms. Alfadhli J et al. [166] proposed an adaptive fluctuant population size SMA (FP-SMA) and evaluated it in 13 standard and 30 IEEE CEC2014 benchmark functions. Bujok P et al. [170] compared 17 variants of the SMA algorithm with 16 other optimizers on CEC 2011. The result revealed that most of new SMA variants performed better than original SMA.
Singh CN et al. [170] applied the slime mould optimization algorithm (SMOA)to find the approximate value in the complex, large-scale continuous-time system.

5. Discussion

As discussed above, SMA is a new metaheuristic algorithms and researchers have developed numerous SMA variants by adding strategy or hybridizing other algorithms for various application domains. The advantages and disadvantages of SMA are summarized in Table 4.

5.1. Advantages of SMA

Firstly, SMA has fewer parameter to set and simpler structure comparing to other algorithms. As described in Section 2, there are only 3 parameters ( W → , v b → , v c → )that are adjusted adaptively with the number of iterations and the hyperparameter 𝑧 empirically is pre-set to 0.03. The SMA pseudo-code indicates that there are only double loop and the Eq. (1)conduct the exploration.
Secondly SMA has excellent scalability，which have been proved by various SMA variants based on the hybridization with other algorithms and adding strategies in this paper.
Because simple structure and good scalability mentioned above, SMA demonstrated its superiority for solving optimization problem. And the popularity of SMA is also indicated in recent publication, as see Figure 6.
Due to the feature that SMA have multi-points search ability, which conducted by position and negative feedback weights W → in Eq. (4), SMA can quickly find the optimal candidate solution from neighbor search region. Therefore, SMA has strong exploitation capability.
According to wall-clock time costs of SMA and other algorithms, the computational time of SMA process tremendous advantages over other algorithms [19].
Finally, SMA use a positive and negative feedback weight W → in Eq. (4) to regulate the individual’s position. The weight also is calculated according to the environment of the search individuals. When there is high quality food, the weight near the location become bigger. Otherwise the weight is reduced, turning to explore other location. The adaptive mechanism enables SMA adjust search pattern according to the environment change and location distribution of individuals, thus stepping out of local stagnation. Vibration parameter v b → ,which fluctuates at random between [−a , a] and finally approaches zero, ensure a quick convergent rate.

5.2. Disadvantages of SMA

SMA has gained significant popularity in solving a diverse range of problems since its proposal. However, it has some limitations and drawbacks.
The main problems of SMA are the local optimal stagnations, low convergent speed and low accuracy while handling the multimodal and high-dimensional problem, just like many meta-heuristic optimization algorithms. With increasing the problem size, algorithms' difficulty of finding solution also grows. Therefore, the algorithm would have difficulty for solving multimodal, high-dimension and nonlinear problems even if they get satisfactory result for unimodal difficulties. The basic version of SMA is designed to solve continuous single-objective optimization problems. It is inevitable for SMA to meet these problems of falling local optimum, slow convergent speed and low accuracy in face of high-dimensional and multimodal optimization problem.
Insufficient global exploration is another drawback of SMA. There are two reason for it. One is that the initial population of SMA is generated rather randomly, resulting in unstable and poor population quality. The poor population’s diversity would affect and weaken the search scope and convergent speed as the problem dimension increases and the search space expands. The other reason is due to the multi-point local search mechanism that SMA has. This mechanism can greatly improve the exploitation ability of SMA. However, the strong local search capability is achieved at cost of exploration, resulting imbalance exploitation and exploration.
Finally, according to the survey of publications on SMA between 2022 and July,2023, we find that there is small portion of multi-objective and discrete version of SMA variants, see the Figure 4 and Figure 5.That would be a research direction for researchers on SMA.

6. Conclusions and Future Work

This review paper intends to present the theory of SMA and recent develop of SMA variants. First of all, we introduce the concept and theory of SMA, including the mathematical model, the pseudo-code and flowchart. Then we collect 130 papers from various well-known publishers on SMA between 2020 and July 2023.Based on this collection of 130 papers, we classify the SMA variants by the method that they are employed to improve the performance: strategies embedding and hybridization of both algorithms. From the statistics analysis of survey, we find that the number of the multi-objective and discrete version of SMA variants are fewer than the compared single-objective and continuous version. Furthermore, the application of SMA and its variants are categorized into seven domains: engineering optimization, energy optimization, machine learning, network, scheduling optimization, image segmentation and others. The wide scape of application proves that SMA is promising algorithms for solving various real-world optimization problem, special in the fields of engineering and energy. Finally, we discuss the advantage and disadvantage of SMA. The advantage of SMA includes: few parameters to set, simple structure, excellent scalability, strong exploitation capability, less computational time, superiority for optimization problem, adaptive and vibration parameters and etc. In contrast to the advantage of SMA, SMA have several shortcomings. SMA have the same problems of easy trapping in local optima, slow convergent speed and low accuracy when handling high-dimensional and multimodal problem, which other metaheuristic algorithms commonly have. SMA also have drawbacks of insufficient global search capability, imbalance between exploration and exploitation, and few multi-objectives and discrete SMA variants.
Although the significant success of SMA research have been achieved, there are still some room for SMA’s improvement for future works. Firstly, the multi-objective and discrete SMA variants are worthy of further researching and focusing on. As shown in Figure 4 and Figure 5, there are only 22 papers of multi-objective version and 11 papers of discrete version, comparing to 106 papers of single-objective version and 117 papers of continuous version respectively. Secondly, the methods adopted for SMA and its variants can extend to neural networks, extreme learning machining and etc. Finally, it is promising direction to apply SMA and its variants to solve the real, complex, dynamic, and large-scale engineering optimization problems.

Author Contributions

Conceptualization, Z. Othman and K. M. Daud; methodology, Y.Z.; writing—original draft preparation, Y.W.; writing—review and editing, Y.Z. and Q.L.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Science Foundation of China, grant number 62066005 and Scientific Research project of Xiangsihu College of Guangxi Minzu University, grant number 2021XJKY21.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

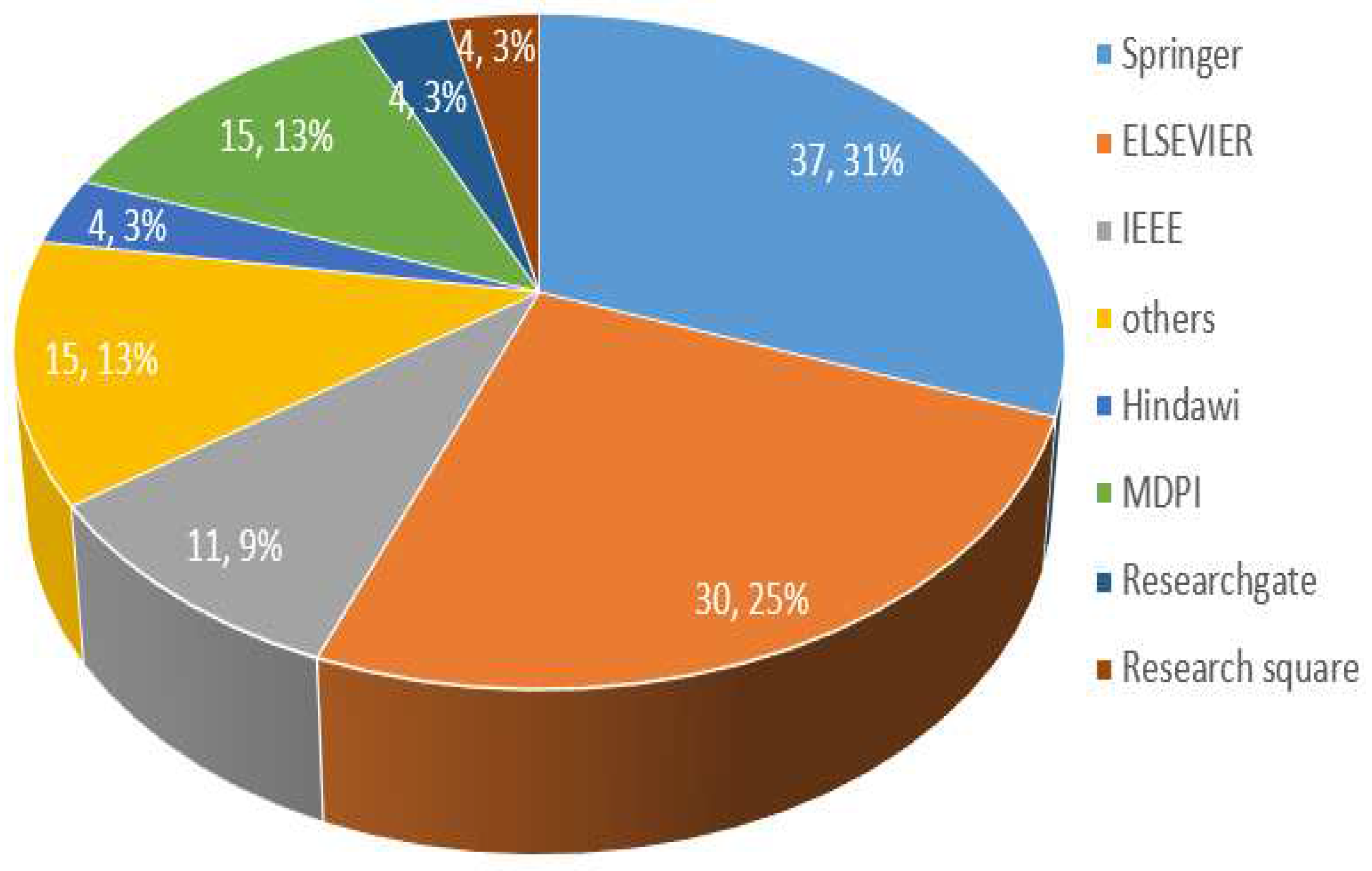
References

  1. Grefenstette, JJ. Genetic Algorithms and Machine Learning. In Proceedings of the sixth annual conference on Computational learning theory 1993; pp. 3–4.
  2. Storn R; Price K. Differential Evolution – A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Global Optim. [CrossRef]
  3. Kirkpatrick, S. Optimization by Simulated Annealing: Quantitative Studies. J. Stat. Phys. 1984, 34, 975–986. [Google Scholar] [CrossRef]
  4. Rashedi E; Nezamabadi-pour H. GSA: A Gravitational Search Algorithm. Inf. Sci. [CrossRef]
  5. Mirjalili S; Mirjalili SM. Multi-Verse Optimizer: a nature-inspired algorithm for global optimization. Neural. Comput.& Applic. [CrossRef]
  6. Zhao W; Wang L. A novel atom search optimization for dispersion coefficient estimation in groundwater. Future Gener. Comp. Sy. 2018, 91, 601–610. [Google Scholar] [CrossRef]
  7. Faramarzi A; Heidarinejad M. Equilibrium optimizer: A novel optimization algorithm. Knowl-Based Syst. [CrossRef]
  8. 06 October 1995, Eberhart R; Kennedy J. A new optimizer using particle swarm theory, MHS’95. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 04- ;IEEE,EDS(pp.39–43). [CrossRef]
  9. Karaboga D; Basturk B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. J. Glob. Optim. [CrossRef]
  10. Rao RV; Savsani VJ. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.Aided Design. [CrossRef]
  11. Mirjalili S; Mirjalili SM. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
  12. Mirjalili S; Lewis A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
  13. Mirjalili S; Gandomi AH. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. [CrossRef]
  14. Cuevas E; Cienfuegos M. A swarm optimization algorithm inspired in the behavior of the social-spider. Expert Syst. Appl. 6384. [CrossRef]
  15. Dhiman G; Kumar V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl-Based Syst. [CrossRef]
  16. Heidari AA; Mirjalili S. Harris hawks optimization: Algorithm and applications. Future Gener. Comp. Sy. [CrossRef]
  17. Abualigah L; Yousri D. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. [CrossRef]
  18. Alsattar HA; Zaidan AA. Novel meta-heuristic bald eagle search optimisation algorithm. Artif. Intell. Rev, 2264. [CrossRef]
  19. Li S; Chen H. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comp. Sy. [CrossRef]
  20. Faramarzi A; Heidarinejad M. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 3377. [CrossRef]
  21. Braik, MS. Chameleon Swarm Algorithm: A bio-inspired optimizer for solving engineering design problems. Expert Syst. Appl. 1146. [Google Scholar] [CrossRef]
  22. Geem ZW; Kim JH. A new heuristic optimization algorithm: harmony search. Simul. [CrossRef]
  23. Tan Y; Zhu Y. Fireworks algorithm for optimization. In Advances in Swarm Intelligence. Proceedings of first international conference (ICSI 2010), Beijing, China, June 2010. [CrossRef]
  24. 28 September 2007, Atashpaz-Gargari E; Lucas C. Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition. In Proceedings of 2007 IEEE congress on evolutionary computation, CEC 2007, Singapore, 25-. [CrossRef]
  25. Sharma AK;Saxena A. Oppositional Slime Mould Algorithm: Development and application for designing demand side management controller. Expert Syst. Appl. [CrossRef]
  26. Latty, T.; Beekman, M. Slime moulds use heuristics based on within-patch experience to decide when to leave. J. Exp. Biol. 2015, 218(8), 1175–1179. [Google Scholar] [CrossRef] [PubMed]
  27. Beekman, M.; Latty, T. Brainless but multi-headed: decision making by the acellular slime mould Physarum polycephalum. J. Mol. Biol. 2015, 427(23), 3734–3743. [Google Scholar] [CrossRef] [PubMed]
  28. Kareiva, P.; Odell, G. Swarms of predators exhibit ‘‘preytaxis’’ if individual predators use area-restricted search. Am. Nat. 1987, 130(2), 233–270. [Google Scholar] [CrossRef]
  29. Latty, T.; Beekman, M. Food quality affects search strategy in the acellular slime mould, Physarum polycephalum. Behav. Ecol. 2009, 20(6), 1160–1167. [Google Scholar] [CrossRef]
  30. Izci D; Ekinci S. Fractional order PID design based on novel improved slime mould algorithm. Electri. Pow. Compo. Sys. [CrossRef]
  31. Izci D; Ekinci S. Performance evaluation of a novel improved slime mould algorithm for direct current motor and automatic voltage regulator systems. T. I. Meas. Control. [CrossRef]
  32. Lin H; Ahmadianfar I. Adaptive slime mould algorithm for optimal design of photovoltaic models. Energy Sci. Eng, 2064. [CrossRef]
  33. Rizk-Allah RM; Hassanien AE. Chaos-opposition-enhanced slime mould algorithm for minimizing the cost of energy for the wind turbines on high-altitude sites. ISA T. [CrossRef]
  34. Son, P. V. H.; Khoi, L. N. Q. Optimization in construction management using adaptive opposition slime mould algorithm. Adv. Civ. Eng. 2023, 7228896. [Google Scholar] [CrossRef]
  35. Patra, Dipak Kumar; Si, T. Breast lesion detection from MRI images using quasi-oppositional slime mould algorithm. Multimed Tools App, 3064. [CrossRef]
  36. Krishna Gopal Dhal; Swarnajit Ray. Illumination-Free Clustering Using Improved Slime Mould Algorithm for Acute Lymphoblastic Leukemia Image Segmentation. 2023. [CrossRef]
  37. Sharma; Ankit Kumar. Oppositional Slime Mould Algorithm: Development and application for designing demand side management controller. Expert Syst. Appl. [CrossRef]
  38. Liang Xu; WANG Luyang. Elman neural network for predicting aero optical imaging deviation based on improved slime mould algorithm. Optoelectron. Lett. 2023, 19, 290–295. [Google Scholar] [CrossRef]
  39. Sengathir, J; M. Deva Priya. An Adaptive Opposition Learning-Improved Slime Mould Algorithm-Based Optimization Routing for Guaranteeing Reliable Data Dissemination in FANETs. In Micro-Electronics and Telecommunication Engineering. Proceedings of 6th ICMETE 2022, Singapore, 02 June 2023; Sharma, D.K., Peng, SL., Sharma, R., Jeon, G., Eds, *!!! REPLACE !!!*, Eds.; Sharma, D.K., Peng, SL., Sharma, R., Jeon, G.,Eds; Springer: Singapore, 2023; pp. 617153–166. [Google Scholar] [CrossRef]
  40. Houssein EH; Helmy BE. An efficient orthogonal opposition-based learning slime mould algorithm for maximum power point tracking. Neural Comput. & Applic. [CrossRef]
  41. AlRassas AM; Al-Qaness MA. Advance artificial time series forecasting model for oil production using neuro fuzzy-based slime mould algorithm. J. Petrol. Explor. Prod. Technol. [CrossRef]
  42. Pawani K; Singh M. Solving Economic Emission Load Dispatch Using Oppositional Slime Mould Algorithm with Wavelet Mutation. Electr. Pow. Compo. Sys. [CrossRef]
  43. Li YiFei; Cao MaoSen. Multi-parameter identification of concrete dam using polynomial chaos expansion and slime mould algorithm. Comput.Struct. [CrossRef]
  44. Yin Shihong; Qifang Luo. IBMSMA: An Indicator-based Multi-swarm Slime Mould Algorithm for Multi-objective Truss Optimization Problems. 2023; ,20. [CrossRef]
  45. Xuebing Cai; Zengyu He. Improved Slime mould algorithm using logical chaos perturbation and reference point non-dominated sorting for multi-objective optimization. IEEE Access, 7210. [CrossRef]
  46. Yuan L; Ji J. An Improved Elite Slime Mould Algorithm for Engineering Design. CMES. 2023, 137(1), 415–454. [Google Scholar]
  47. Dhawale D; Kamboj VK. An optimal solution to unit commitment problem of realistic integrated power system involving wind and electric vehicles using chaotic slime mould optimizer. Journal of Electrical Systems and Inf Technol 2023, 10(1), 1–21. [Google Scholar] [CrossRef]
  48. Chen H; Li X. Improved slime mould algorithm hybridizing chaotic maps and differential evolution strategy for global optimization. IEEE Access 2022, 10, 66811–30. [Google Scholar] [CrossRef]
  49. Zhong C;Li G. A hybrid teaching–learning slime mould algorithm for global optimization and reliability-based design optimization problems. Neural Comput. & Applic. 1664. [CrossRef]
  50. Abid MS; Apon HJ. Chaotic slime mould optimization algorithm for optimal load-shedding in distribution system. Ain Shams Eng. J. 0165. [CrossRef]
  51. Miao H; Qiu Z. Multi-strategy improved slime mould algorithm and its application in optimal operation of cascade reservoirs. Water Resour. Manage. [CrossRef]
  52. Bhadoria A; Marwaha S. Chaotic Slime Mould Inspired Hybrid Optimizer Approach for Day Ahead Generation Scheduling Problem, Research Square 2022, posted in 27 Oct. 2022. [CrossRef]
  53. Sarhan S; Shaheen AM. An enhanced slime mould optimizer that uses chaotic behavior and an elitist group for solving engineering problems. Mathematics 2022, 10(12), 1991. [Google Scholar] [CrossRef]
  54. Singh, T. Chaotic slime mould algorithm for economic load dispatch problems. Appl. Intell. 2022, 52(13), 15325–15344. [Google Scholar] [CrossRef]
  55. Ghiasi, Ramin; Abdollah Malekjafarian. Feature subset selection in structural health monitoring data using an advanced binary slime mould algorithm. J. Struct. Integ. & Maint. [CrossRef]
  56. Yin S; Luo Q. EOSMA: an equilibrium optimizer slime mould algorithm for engineering design problems. Arab. J. Sci. Eng. [CrossRef]
  57. Deng L; Liu S. A multi-strategy improved slime mould algorithm for global optimization and engineering design problems. Comput. Method. Appl. M. [CrossRef]
  58. Pawani, Kanchan; Manmohan Singh. Combined Heat and Power Dispatch Problem Using Comprehensive Learning Wavelet-Mutated Slime Mould Algorithm. Electr. Pow. Compo. Sys. [CrossRef]
  59. Qiu F; Zheng P. Mutational Slime Mould Algorithm for Gene Selection. Biomedicines 2022, 10(8), 2052. [Google Scholar] [CrossRef]
  60. Zheng R; Jia H. Enhanced slime mould algorithm with multiple mutation strategy and restart mechanism for global optimization. J. Intell. Fuzzy. Syst. 2022, 42(6), 2022,42(6),5069–83. [Google Scholar] [CrossRef]
  61. Yang H; Wang E; Z. Sun. Research on fire rescue path optimization of unmanned equipment based on improved Slime mould Algorithm. In Proceedings of 2022 IEEE Intl Conf on Dependable, Autonomic and Secure Computing, Intl Conf on Cloud and Big Data Computing, Intl Conf on Cyber Science and Technology Congress (DASC/PiCom/CBDCom/CyberSciTech), Falerna, Italy, 12-15 Sep 2022 ;IEEE:2022;pp. 1-6. [CrossRef]
  62. Yang P; Sun X. Load Identification Method Based on ISMA-GRNN. Math. Probl. in Eng. 8056. [CrossRef]
  63. Ling Zheng; Yan Tian. Path Planning of Autonomous Mobile Robots Based on an Improved Slime Mould Algorithm. Drones 2023, 7, 257. [Google Scholar] [CrossRef]
  64. He W; Liu Y. A Novel Unresolved Peaks Analysis Algorithm for ME Signal Detection Based on Improved SMA. IEEE T. MEAS 2023, 72, 1–9. [Google Scholar] [CrossRef]
  65. Pan JS;Wang HJ. Dynamic reconfiguration of distribution network based on dynamic optimal period division and multi-group flight slime mould algorithm. Electr. Pow. Sys. Res. [CrossRef]
  66. Qi A;Zhao D. Directional crossover slime mould algorithm with adaptive Lévy diversity for the optimal design of real-wo problems. J. Compu. Des. Eng. 2418. [CrossRef]
  67. Qiu F; Guo R. Boosting Slime Mould Algorithm for High-Dimensional Gene Data Mining: Diversity Analysis and Feature Selection. Comput. Math. Method. M. [CrossRef]
  68. Jui JJ; Ahmad MA. Lévy slime mould algorithm for solving numerical and engineering optimization problems. In Proceedings of the 6th International Conference on Electrical, Control and Computer Engineering; Kuantan, Pahang, Malaysia, 23rd 22; Md. Zain, Z., Sulaiman, Eds.; Springer: Singapore,2022; vol 842, pp. 381-394. 20 August. [CrossRef]
  69. Kundu T; Garg H. LSMA-TLBO: A hybrid SMA-TLBO algorithm with lévy flight-based mutation for numerical optimization and engineering design problems. Adv. Eng. Softw. [CrossRef]
  70. Ma TX; Duan X. Research on Fault Location in DC Distribution Network Based on Adaptive Artificial Bee Colony Slime Mould Algorithm. IEEE Access, 6263. [CrossRef]
  71. Liu J; Fu Y. A novel improved slime mould algorithm for engineering design. Soft Comput. 2023, 27, 12181–12210. [Google Scholar] [CrossRef]
  72. Shubiao Wu; Ali Asghar Heidari. Gaussian bare-bone slime mould algorithm: performance optimization and case studies on truss structures. Artif. Intell. Rev. [CrossRef]
  73. Yin S; Luo Q. An equilibrium optimizer slime mould algorithm for inverse kinematics of the 7-DOF robotic manipulator. Sci. Rep. [CrossRef]
  74. Kaveh A; Hamedani KB. Improved slime mould algorithm with elitist strategy and its application to structural optimization with natural frequency constraints. Comput. Struct. 2022, 264, 106760. [Google Scholar] [CrossRef]
  75. Prabhu, M. ; B. Muthu Kumar. Slime Mould Algorithm based Fuzzy Linear CFO Estimation in Wireless Sensor Networks. IETE J. Res. 2023, 1–11. [Google Scholar] [CrossRef]
  76. Al-Kaabi M; Dumbrava V. A slime mould algorithm programming for solving single and multi-objective optimal power flow problems with pareto front approach: A case study of the Iraqi super grid high voltage. Energies. [CrossRef]
  77. Yutong G; Khishe M. Evolving deep convolutional neural networks by extreme learning machine and fuzzy slime mould optimizer for real-time sonar image recognition. INT. J. FUZZY. SYST. 1389. [CrossRef]
  78. Yuanfei Wei; Othman Z. Equilibrium optimizer and slime mould algorithm with variable neighborhood search for job shop scheduling problem. Math. 2022, 10(21), 4063. [Google Scholar] [CrossRef]
  79. Zhou X; Chen Y. Boosted local dimensional mutation and all-dimensional neighborhood slime mould algorithm for feature selection. Neurocomputing. [CrossRef]
  80. Qifang, Luo; Yin, S. Qifang Luo; Yin, S. Multi-objective equilibrium optimizer slime mould algorithm and its application in solving engineering problems. Struct. Multidisc. Optim. [CrossRef]
  81. Örnek BN; Aydemir SB. A novel version of slime mould algorithm for global optimization and real world engineering problems: Enhanced slime mould algorithm. Math. Comput. Simulat. [CrossRef]
  82. Ren L; Heidari AA. Gaussian kernel probability-driven slime mould algorithm with new movement mechanism for multi-level image segmentation. Measurement. [CrossRef]
  83. Shi B; Zhou T. An evolutionary machine learning for pulmonary hypertension animal model from arterial blood gas analysis. Comput. Biol. Med. 2022, 146, 105529. [Google Scholar] [CrossRef]
  84. Nemani R; Moses GJ. Statistical Data Mining with Slime Mould Optimization for Intelligent Rainfall Classification. Comput. Syst. Sci.e Eng. 2023, 47(1), 919–935. [Google Scholar] [CrossRef]
  85. Hu J; Gui W. Dispersed foraging slime mould algorithm: Continuous and binary variants for global optimization and wrapper-based feature selection. Knowl-Based Syst. [CrossRef]
  86. Tizhoosh, HR. Opposition-based learning: a new scheme for machine intelligence. Proceedings of International conference on computational intelligence for modelling, control and automation and international conference on intelligent agents, web technologies and internet commerce (CIMCA-IAWTIC’06), Vienna,Austria, 28-30 November 2005. [Google Scholar]
  87. 28 September 2007, S. Rahnamayan; H. R. Tizhoosh; M. M. A. Salama. Quasi-oppositional Differential Evolution. In Proceedings of 2007 IEEE Congress on Evolutionary Computation, Singapore,25-; IEEE:2008; pp. 2229-2236. [CrossRef]
  88. LONG W;JIAO J J. A random opposition-based learning grey wolf optimizer. IEEE access, 1138. [CrossRef]
  89. C. Li; J. Li. A meta-heuristic-based approach for QoS-aware service composition. IEEE Access, 6959. [CrossRef]
  90. Sivanandam, S. N.; Deepa, S. N. Genetic algorithms. In Introduction to genetic algorithms; Springer: Berlin, Heidelberg, Germany, 2008; pp. 15–37. [Google Scholar] [CrossRef]
  91. Price K; Storn MR. A simple and efficient adaptive scheme for global optimization over continous space. Technical Report TR-95-012, ICSI,1995.
  92. P. Lévy. Théorie de L'Addition des Variables Aléatoires. Paris, France: Gauthier-Villars, 1937.
  93. Chen H; Li C. Slime mould algorithm: A comprehensive review of recent variants and applications. Int. J. Syst. Sci. [CrossRef]
  94. Yuheng Guo; Wei Zhan. Application of Support Vector Machine Algorithm Incorporating Slime Mould Algorithm Strategy in Ancient Glass Classification. Appl. Sci. 2023, 13, 3718. [Google Scholar] [CrossRef]
  95. Gao H; Liang G. Multi-population enhanced slime mould algorithm and with application to postgraduate employment stability prediction. Electronics. [CrossRef]
  96. Javidan SM; Banakar A; Keyvan Asefpour Vakilian. A feature selection method using slime mould optimization algorithm in order to diagnose plant leaf diseases. In Proceedings of 2022 8th Iranian Conference on Signal Processing and Intelligent Systems (ICSPIS), Behshahr, Iran, 28-29 Dec 2022; IEEE:2023; pp. 1-5. [CrossRef]
  97. Shi B;Chen J. Prediction of recurrent spontaneous abortion using evolutionary machine learning with joint self-adaptive sime mould algorithm. Comput. Biolo. Med. 2022. [CrossRef]
  98. ANJI REDDY VAKA;Anji Reddy Vaka. Breast Cancer Classification using Improved Hybrid Model by Leveraging Slime Mould Algorithm and Whale Optimization Algorithm. Soft Computing, 2023. [CrossRef]
  99. Bhandakkar AA; Mathew L. Merging slime mould with whale optimization algorithm for optimal allocation of hybrid power flow controller in power system. J. Exp.Theor. Artif. In. [CrossRef]
  100. Li X; Yang Q. Joints Trajectory Planning of Robot Based on Slime Mould Whale Optimization Algorithm. Algorithms 2022, 15(10), 363. [Google Scholar] [CrossRef]
  101. Leela Kumari Ch; Vikram Kumar Kamboj. Hybridizing slime mould algorithm with simulated annealing algorithm: a hybridized statistical approach for numerical and engineering design problems. Complex Intell. Syst. [CrossRef]
  102. Das G; Panda R; S. Agrawal. Slime Mould-Seagull optimizer. In Proceedings of 2022 IEEE 7th international conference for convergence in technology (I2CT),Mumbai, India, 07-09 Apr 2022;IEEE;2022；pp. 1-7. [CrossRef]
  103. Chen X; Huang H. An efficient multilevel thresholding image segmentation method based on the slime mould algorithm with bee foraging mechanism: A real case with lupus nephritis images. Comput. Biol. Med. [CrossRef]
  104. Samantaray S; Sahoo P. Flood discharge prediction using improved ANFIS model combined with hybrid particle swarm optimisation and slime mould algorithm. Environ. Sci. Pollut. Res. 2023, 30, 83845–83872. [Google Scholar] [CrossRef]
  105. Chavan PP; Rani BS. Image compression based on vector quantization and optimized code-book design using Genetic Mating Influenced Slime Mould (GMISM) algorithm. Web Intell.2023, Pre-press,1-20. DOI 10. 3233.
  106. Chauhan S; Vashishtha G. A synergy of an evolutionary algorithm with slime mould algorithm through series and parallel construction for improving global optimization and conventional design problem. Eng. Appl. Artif Intell. 2023, 118, 105650. [Google Scholar] [CrossRef]
  107. Khan AA;Nisha SS. Hybrid slime mould-Grey wolf optimization algorithm for efficient feature selection. Int. J. Health Sci. [CrossRef]
  108. Ewees, Ahmed A.; Mohammed A. A. Al-qaness. Enhanced feature selection technique using slime mould algorithm: a case study on chemical data. Neural Comput. & Applic. [CrossRef]
  109. Ewees AA; Ismail FH. Gradient-based optimizer improved by Slime Mould Algorithm for global optimization and feature selection for diverse computation problems. Expert Syst. Appl. [CrossRef]
  110. Chakraborty P; Nama S. A hybrid slime mould algorithm for global optimization. Multimed. Tools. Appl. [CrossRef]
  111. Son PV; Khoi LN. Optimization of Construction Projects Time-Cost-Quality-Environment Trade-off Problem Using Adaptive Selection Slime Mold Algorithm. J. Soft Comput. Civil Eng.
  112. Zhang J; Dias D. Applying a novel slime mould algorithm-based artificial neural network to predict the settlement of a single footing on a soft soil reinforced by rigid inclusions. Mech. Adv. Mater Struc. [CrossRef]
  113. Hussein SN; Hussein NK. Improving Moth-Flame Optimization Algorithm by using Slime-Mould Algorithm. Tikrit J. Pure Sci. 2022,27(1),99-109. [CrossRef]
  114. Bala Krishna A; Saxena S. hSMA-PS: a novel memetic approach for numerical and engineering design challenges. Eng. Comput. [CrossRef]
  115. Peng C; Che Z. Prediction using multi-objective slime mould algorithm optimized support vector regression model. Appl. Soft Comput. [CrossRef]
  116. Houssein EH; Mahdy MA. An efficient slime mould algorithm for solving multi-objective optimization problems. Expert Syst. Appl., 2022, 187, 115870. [Google Scholar] [CrossRef]
  117. Yacoubi S; Manita G. A modified multi-objective slime mould algorithm with orthogonal learning for numerical association rules mining. Neural Comput. & Applic. [CrossRef]
  118. Zhang Y; Gong B. Application of a bio-inspired algorithm in the process parameter optimization of laser cladding. Machines. [CrossRef]
  119. Behera, Sadasiva; Nalin B. Dev Choudhury. Adaptive optimal energy management in multi-distributed energy resources by using improved slime mould algorithm with considering demand side management. e-Prime-Advances in Electrical Engineering, Electronics and Energy,2023 (3),100108. [CrossRef]
  120. Hong Son PV; Khoi LN. Adaptive selection slime mould algorithm in time–cost–quality–environmental impact trade-off optimization. Can. J. Civil Eng. [CrossRef]
  121. Olalekan Kunle Ajiboye; Eric Antwi Ofosu1. Hybrid Renewable Energy System Optimization via Slime Mould Algorithm. Inter. J. Eng. Trends Tech. 2023, 6(71), (71),83–95. [Google Scholar] [CrossRef]
  122. Zellagui, Mohamed; Samir Settoul. Optimal Allocation of Multiple Hybrid Fault Current Limiter in Electrical Distribution System Using Slime Mould Algorithm. In Proceedings of Fourth International Conference on Technological Advances in Electrical Engineering (ICTAEE’23.)23-. 24 May.
  123. S. Mirjalili; A. Lewis. S-shaped versus V-shaped transfer functions for binary particle swarm optimization. Swarm Evol. Comput. [CrossRef]
  124. Hassan, H.S.; Hussein, N.K. A novel approach of features selection by using slime mould algorithm. In AIP Conference Proceedings, 1ST SAMARRA INTERNATIONAL CONFERENCE FOR PURE AND APPLIED SCIENCES (SICPS2021): SICPS2021, Samarra, Iraq, ;AIP:2022 ;Vol. 2394, No. 1, 070033. 23–24 March. [CrossRef]
  125. Rifat, Md Sayed Hasan; Md. Ashaduzzaman Niloy. Application of Binary Slime Mould Algorithm for Solving Unit Commitment Problem. IEEE Access 2023, 11, 45279–45300. [Google Scholar] [CrossRef]
  126. Dan Li ; Fei Gao. Improved slime mould algorithm based on Gompertz dynamic probability and Cauchy mutation with application in FJSP. J. Intell. Fuzzy. Syst. 1041. [CrossRef]
  127. MS, K. Experimental Investigation of efficiency enhancement in Solar Photovoltaic Systems under Partial Shading Conditions using Discrete Time Slime Mould Optimization. Research Square, 2023. [Google Scholar] [CrossRef]
  128. Yin S; Luo Q. DTSMA: Dominant swarm with adaptive t-distribution mutation-based slime mould algorithm. Math. Biosci Eng. 2022, 19(3), 2240–2285. [Google Scholar] [CrossRef]
  129. Qi A; Zhao D. Directional crossover slime mould algorithm with adaptive Lévy diversity for the optimal design of real-world problems. J. Comput. Des.Eng. [CrossRef]
  130. Deng, Lingyun; Sanyang Liu. An enhanced slime mould algorithm based on adaptive grouping technique for global optimization. Expert Syst. Appl. 2023, 222, 119877. [Google Scholar] [CrossRef]
  131. Celorrio L; Patelli E. Reliability-based design optimization under mixed aleatory/epistemic uncertainties: theory and application. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering. [CrossRef]
  132. Rizk-Allah RM; Hassanien AE. Chaos-opposition-enhanced slime mould algorithm for minimizing the cost of energy for the wind turbines on high-altitude sites. ISA T. [CrossRef]
  133. Khelfa C; Khennak I; Drias H. Slime Mould Algorithm for Solving Ambulance Dispatching Problem. In Proceedings of the 14th International Conference on Soft Computing and Pattern Recognition, 2022 Dec 14; Abraham, A., Hanne, T., Eds;. Springer: Cham Switzerland,2023; pp. 822-831. [CrossRef]
  134. Loucif, F. ; S. Kechida. Design of optimal backstepping controller for a robot manipulator using Slime Mould Algorithm.In Fourth International Conference on Technological Advances in Electrical Engineering (ICTAEE’23.), -24 2023. https://www.researchgate.net/publication/371038125. 23 May.
  135. Ding P; Huang X. Reliability optimization of micro-milling cutting parameters using slime mould sequence algorithm. Simul. Model. Prac. Th. [CrossRef]
  136. Wang HJ; Pan JS. Distribution network reconfiguration with distributed generation based on parallel slime mould algorithm. Energy 2022, 244, 123011. [Google Scholar] [CrossRef]
  137. Ahmadianfar I; Noori RM. Multi-strategy Slime Mould Algorithm for hydropower multi-reservoir systems optimization. Knowl-Based Syst. [CrossRef]
  138. Wu X; Wang Z. Multi-objective optimal allocation of regional water resources based on slime mould algorithm. J. Supercomput. 2022, 78(16), 18288–18317. [Google Scholar] [CrossRef]
  139. Chakraborty, A.; Ray, S. Operational cost minimization of a microgrid with optimum battery energy storage system and plug-in-hybrid electric vehicle charging impact using slime mould algorithm. Energy, 1278. [Google Scholar] [CrossRef]
  140. Abid MS; Apon HJ. Mitigating the Effect of Electric Vehicle integration in Distribution Grid using Slime Mould Algorithm. Alex. Eng. J. 2023, 64, 785–800. [Google Scholar] [CrossRef]
  141. Farhat M; Kamel S. ESMA-OPF: Enhanced slime mould algorithm for solving optimal power flow problem. Sus. 3586.
  142. Kamboj VK; Kumari CL. A cost-effective solution for non-convex economic load dispatch problems in power systems using slime mould algorithm. Sus. [CrossRef]
  143. Pan JS; Wang HJ. Dynamic reconfiguration of distribution network based on dynamic optimal period division and multi-group flight slime mould algorithm. Electr. Pow. Sys. Res. [CrossRef]
  144. Behera S; Dev Choudhury NB. Maiden Application of the Slime Mold Algorithm for Optimal Operation of Energy Management on a Microgrid Considering Demand Response Program. SN COMPUT. SCI. 2023, 4(5), 491. [Google Scholar] [CrossRef]
  145. Behera S; Choudhury NB. Modelling and simulations of modified slime mould algorithm based on fuzzy PID to design an optimal battery management system in microgrid. Cleaner Energy Sys. 2022, 3, 100029. [Google Scholar] [CrossRef]
  146. Liu Z; Tan Q; Rui J. Decentralized trading of high-proportion renewable energy microgrid based on master-slave game and slime mould algorithm (SMA). In Proceedings of the 16th Annual Conference of China Electrotechnical Society, He, J., Li, Y., Eds.; Springer: Singapore 2022; Volume 3, pp. 18-26; [CrossRef]
  147. Zare P; Davoudkhani IF; Mohajeri R. Performance Analysis and Design of FOPDF (1+ FOPI) Robust Controller Using Slim Mould Algorithm for Frequency Control in Offshore Fixed Platform Microgrid. In Proceedings of 2022 12th Smart Grid Conference (SGC), Kerman, Iran, 13-15 Dec 2022 ;IEEE:2023;pp. 1-7. [CrossRef]
  148. Tiachacht S; Khatir S. Inverse problem for dynamic structural health monitoring based on slime mould algorithm. Eng. Comput. 2228. [CrossRef]
  149. Mehwish Zafar; J Amin. DeepLabv3+-based segmentation and best features selection using slime mould algorithm for multi-class skin lesion classification. Math. [CrossRef]
  150. Zhou J; Dai Y. COSMA-RF: New intelligent model based on chaos optimized slime mould algorithm and random forest for estimating the peak cutting force of conical picks. Transp. Geotech. [CrossRef]
  151. Zhang J; Dias D. Applying a novel slime mould algorithm-based artificial neural network to predict the settlement of a single footing on a soft soil reinforced by rigid inclusions. Mech. Adv.Mater.Struc. [CrossRef]
  152. Mehbodniya A; Douraki BK. Multilayer reversible data hiding based on the difference expansion method using multilevel thresholding of host images based on the slime mould algorithm. Processes. [CrossRef]
  153. Ngoc-Nguyen L; Khatir S. Application of Slime Mould Optimization Algorithm on Structural Damage Identification of Suspension Footbridge. In Recent Advances in Structural Health Monitoring and Engineering Structures. Lecture Notes in Mechanical Engineering; Rao, R.V., Khatir, S., Eds.; Springer: Singapore, 2022; pp. 405–415. [Google Scholar] [CrossRef]
  154. Sayed GI; Hassanien AE. Explainable AI and Slime Mould Algorithm for Classification of Pistachio Species. In Artificial Intelligence: A Real Opportunity in the Food Industry; Hassanien, A.E., Soliman, M., Eds.; Springer: Cham, 2022 ; vol 1000; pp. 29–43. [Google Scholar] [CrossRef]
  155. Hamza MA;Alsolai H. Intelligent Slime Mould Optimization with Deep Learning Enabled Traffic Prediction in Smart Cities. Comput. Mater.Con. [CrossRef]
  156. Khan, A. A. R.; Nisha, S. S. Hybrid slime mould - Grey wolf optimization algorithm for efficient feature selection. Int. J. Health Sci. 2022, 6(S1), 7657–7663. [Google Scholar] [CrossRef]
  157. Wei X; Feng G. Reduce the noise of transient electromagnetic signal based on the method of SMA-VMD-WTD. IEEE Sens. J. [CrossRef]
  158. Yuanyuan Jiang; D Zhang. Multi-Level Thresholding Image Segmentation Based on Improved Slime Mould Algorithm and Symmetric Cross-Entropy. Entropy. [CrossRef]
  159. Shi M; Chen C. A grade-based search adaptive random slime mould optimizer for lupus nephritis image segmentation. Comput. Biol. Med. [CrossRef]
  160. Debnath A; Dhabal S;Chakrabarti R. An Improved Image Denoising Technique by designing Cascaded Filter using Slime Mould Algorithm. In Proceedings of 2022 IEEE Calcutta Conference (CALCON) , Kolkata, India, 10-11 Dec 2022; IEEE：2023; pp. 104-108. [CrossRef]
  161. Hu G; Du B. HG-SMA: hierarchical guided slime mould algorithm for smooth path planning. Artif. Intell. Rev. 2023, 56, 9267–9327. [Google Scholar] [CrossRef]
  162. 04 March 2023, Wang, Zheyuan; Junli Wang; Chungang Yan. An Energy-efficient Traffic Scheduling Method based on Slime Mould Algorithm for SDN. In Proceedings of 6th International Conference on Information Systems and Computer Networks (ISCON). Mathura, India, 03-; IEEE: 2023;pp.1-6. [CrossRef]
  163. Yueming Q;Xiangde L;Yi Z. Research on Scheduling Cooperation and Path Planning of Multi-AGV Based on Slime Moulds Algorithm. In Proceedings of the 2022 International Workshop on Control Sciences and Automation, Xiamen, China, 8 Apr. 2022 ; Association for Computing Machinery: New Youk,NY,USA,2022;pp. 66-71. [CrossRef]
  164. Yuanye Wei; Xiuxi Wei. SSMA: simplified slime mould algorithm for optimization wireless sensor network coverage problem. Syst. Sci. Control. Eng. [CrossRef]
  165. Alwan MH; Hammadi YI. High Density Sensor Networks Intrusion Detection System for Anomaly Intruders Using the Slime Mould Algorithm. Electronics 2022, 11(20), 3332. [Google Scholar] [CrossRef]
  166. Alfadhli J; Jaragh A. FP-SMA: an adaptive, fluctuant population strategy for slime mould algorithm. Neural Comput. & Applic. [CrossRef]
  167. Eskandaripour; Mehrtash. Optimization of low-impact development facilities in urban areas using slime mould algorithm. Sustain. Cities Soc. [CrossRef]
  168. Cai X; He Z. MOSMA: Multi-objective slime mold algorithm based on reference point non-dominated sorting. Research Square. [CrossRef]
  169. Singh CN; Kumar D. Slime mould optimization-based approximants of large-scale linear-time-invariant continuous-time systems with assured stability. Circuits Syst Signal Process. [CrossRef]
  170. Bujok P; Lacko M. Slime Mould Algorithm: An Experimental Study of Nature-Inspired Optimiser. In Bioinspired Optimization Methods and Their Applications, Lecture Notes in Computer Science, Mernik, M., Eftimov, T., Eds.; Springer: Cham, 2022 ; vol 13627. [Google Scholar] [CrossRef]
Preprints 84592 g001
Figure 1. Classification of meta-heuristic algorithms.
Figure 1. Classification of meta-heuristic algorithms.
Preprints 84592 g001
Preprints 84592 g002
Figure 2. The number of publications based on publishers since 2022.
Figure 2. The number of publications based on publishers since 2022.
Preprints 84592 g002
Preprints 84592 g003
Figure 3. Foraging morphology of slime mould [25].
Figure 3. Foraging morphology of slime mould [25].
Preprints 84592 g003
Preprints 84592 g004
Figure 4. Flowchart of SMA [27].
Figure 4. Flowchart of SMA [27].
Preprints 84592 g004
Preprints 84592 g005
Figure 5. Distribution of SMA publications based on single/multi objective since 2022
Figure 5. Distribution of SMA publications based on single/multi objective since 2022
Preprints 84592 g005
Preprints 84592 g006
Figure 6. Distribution of SMA publications based on continuous/discrete problem since 2022
Figure 6. Distribution of SMA publications based on continuous/discrete problem since 2022
Preprints 84592 g006
Preprints 84592 g007
Figure 7. Distribution of publications based on their application domains since 2022
Figure 7. Distribution of publications based on their application domains since 2022
Preprints 84592 g007
Preprints 84592 g008
Figure 8. Detailed classification and numbers of the survey literature in engineering optimization.
Figure 8. Detailed classification and numbers of the survey literature in engineering optimization.
Preprints 84592 g008
Preprints 84592 g009
Figure 9. Classification and numbs of publication on machine learning between 2022 and July,2023.
Figure 9. Classification and numbs of publication on machine learning between 2022 and July,2023.
Preprints 84592 g009
Preprints 84592 g010
Figure 10. Detailed classification and numbers of the survey literature in energy optimization.
Figure 10. Detailed classification and numbers of the survey literature in energy optimization.
Preprints 84592 g010
Table 1. Top 3 countries ranked by the number of SMA publications since 2022.
Table 1. Top 3 countries ranked by the number of SMA publications since 2022.
Country Rank Number of publications
China 1 56
India 2 30
Egypt 3 6
Iran 3 6
Table 2. Summary of SMA variants with different strategies
Table 2. Summary of SMA variants with different strategies
No Strategies References
1 Opposition-based learning Izci D et al.[30] [31], Lin H et al.[32], Son, P. V. H. et al.[34], Dipak Kumar Patra1 et al.[35], Krishna Gopal Dhal et al.[36], Sharma et al.[37], Liang Xu et al.[38], Sengathir J. et al.[39], Houssein EH et al.[40], AlRassas AM et al.[41], Pawani K et al.[42]
2 Chaotic strategy Rizk-Allah RM et al.[33], Li Yi Fei et al.[43], Yin Shihong et al.[44], Xuebing Cai et al.[45], Yuan L et al.[46], Dhawale D et al.[47], Chen H et al.[48], Zhong C et al.[49], Abid MS et al.[50] , Miao H C et al.[51], Bhadoria A et al.[52], Sarhan S et al.[53], Singh T[54]
3 Mutation operator Lin H et al. [32], Ramin Ghiasi et al.[55],Yin S et al.[56], Deng L et al.[57], Pawani et al.[58], Qiu F et al.[59], Zheng R et al.[60], H. Yang et al.[61], Yang P, et al.[62]
4 Lévy flight Ling Zheng et al.[63], He W et al.[64], Pan JS et al.[65], Qi A et al.[66], Qiu F et al.[67], Jui JJ et al.[68] , Kundu T et al.[69]
5 Crossover operator Rizk-Allah RM et al.[33], Ramin Ghiasi et al.[55], Qiu F et al.[59] , Qi A et al.[66], Ma TX et al. [70]
6 Elite strategy Yuan L et al.[46], Miao H C et al.[51], Sarhan S et al.[53], Kaveh A et al.[74] ,Luo Qifang et al.[80]
7 Greedy selection Liu J et al.[71] , Shubiao Wu et al.[72], Yin S et al.[73]
8 Fuzzy Prabhu, M et al.[75], Al-Kaabi M et al.[76], Yutong G et al.[77]
9 Neighborhood search Yuanfei Wei et al.[78], Zhou X et al.[79]
10 Sigmoid function He W et al.[64], Örnek BN et al.[81]
11 Gaussian strategy Shubiao Wu et al.[72], Ren L et al.[82]
Table 3. Summary of SMA variants hybridized with other algorithms.
Table 3. Summary of SMA variants hybridized with other algorithms.
No Hybrid algorithms References
1 Equilibrium optimizer (EO) Yin S et al.[56], Yin S et al.[73], Yuanfei Wei et al.[78], Luo Qifang et al.[80]
2 Differential evolution (DE) Krishna Gopal Dhal et al.[36], Chen H et al.[48], Qiu F et al.[59] , Shubiao Wu et al.[72]
3 Support vector machine (SVM) Yuheng Guo et al.[94], Gao H et al.[95], Javidan SM et al.[96], Shi B et al.[97]
4 Whale optimization algorithm (WOA) Anji Reddy Vaka et al.[98], Bhandakkar AA et al.[99], Li X et al.[100]
5 Simulated annealing (SA) algorithm Izci D et al. [30], Leela Kumari Ch et al.[101]
6 Teaching–learning based optimization (TLBO) Zhong C et al.[49], Kundu T et al.[69]
7 Seagull optimization algorithm (SOA) Bhadoria A et al.[52],Das G et al.[102],
8 Artificial bee colony (ABC) Ma TX et al. [70], Chen X et al. [103]
9 Particle swarm optimization (PSO) Samantaray S et al. [104]
10 Genetic algorithm (GA) P.P. Chavan et al. [105]
11 Evolutionary algorithm (EA) Chauhan S et al. [106]
12 Grey wolf optimization algorithm (GWOA) Khan AA et al. [107]
13 Sine cosine algorithm (SCA) Örnek BN et al. [81]
14 Marine predators algorithm (MPA) Ewees A.A. et al. [108]
15 Gradient-based optimizer (GO) Ewees A.A.et al. [109]
16 Quadratic approximation (QA) Chakraborty P et al. [110]
17 Tournament selection (TS) Son PV et al. [111]
18 Artificial neural network (ANN) Zhang J et al. [112]
19 Moth-flame optimization algorithm (MFOA) Hussein SN et al. [113]
20 Pattern search algorithm (PSA) Bala Krishna A et al. [114]
21 Support vector regression (SVR) Peng C et al. [115]
Table 4. Advantages and disadvantages of SMA.
Table 4. Advantages and disadvantages of SMA.
Advantages Disadvantages
-few parameters to set and simple structure
-excellent scalability
-superiority for optimization problem
-strong exploitation capability
-less computational time
- adaptive and vibration parameters		 -easily trap in local optimum, low convergent rate and accuracy in face of high-dimensional and multimodal problem
-insufficient global search capability
-imbalance between exploration and exploitation
-few multi-objectives and discrete SMA variants
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated