Prerpints.org logo
Preprint
Article

A Comprehensive Approach to LNOI Electro-Optic Modulator Design and Performances Optimizing

Altmetrics

Downloads

463

Views

106

Comments

0

This version is not peer-reviewed

Submitted:

08 September 2023

Posted:

11 September 2023

You are already at the latest version

Alerts
Abstract
Thin-film lithium niobate has gained significant attention in photonics due to its broad optical transparency, high refractive index, nonlinear coefficient, and substantial electro-optic coefficient. It holds great promise for developing electro-optic modulators with low loss, a compact size, and wide bandwidth. This study focuses on a meticulous investigation utilizing microwave photonics to establish a high-performance electro-optic modulator. Specifically, we analyze the optical mode field distribution and traveling wave electrode structure of lithium niobate thin-film materials. The proposed modulator achieves an impressive half-wave voltage-length product of 1.69 V·cm, a negligible metal loss of 0.01 dB/cm, and a substantial 3dB electro-optic bandwidth of 50 GHz. This research successfully realizes low-loss, high-efficiency LNOI electro-optical modulators, providing a strong foundation for large-scale integrated optoelectronic systems.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Electro-optic modulators (EOMs) translate electronic signals into the optical domain and are critical components in modern data communication, optical sensing, quantum optics, and photonic integrated circuits (PICs) [1,2,3,4]. As demands in these fields continue to rise, the performance requirements for EOMs are undergoing continual enhancement, necessitating attributes like low loss, low half-wave voltage, high bandwidth, and high linearity [5,6,7,8]. However, the present predominant materials for EOM fabrication include silicon-based, III–V, and bulk lithium niobate (LN) [9,10,11,12] yet struggle to simultaneously fulfill all the aforementioned demands. For silicon-based materials, due to inherent characteristics, the longer electron carrier transit time limits their bandwidth and extinction ratio. Although III-V materials effectively address bandwidth limitations and cater to the demands of high-speed communication and modulation, their performance are restricted by significant optical losses and high linearity requirements. By contrast, lithium niobate has garnered significant attention in photonics, owing to its broader optical transparency window, relatively higher refractive index, nonlinear coefficient, and substantial electro-optic coefficient [13,14]. For traditional bulk LN modulators, the relatively small refractive index difference between the core and cladding layers results in a weaker confinement of the optical mode field and higher power consumption, thereby constraining the performance of the modulator.
In recent years, thin-film lithium niobate (TFLN) manufactured through crystal ion slicing and chip bonding techniques [15] has provided a high-performance photonic waveguide platform for compact PICs [16,17]. EOMs based on the lithium niobate on insulator (LNOI) platform exhibit performance advantages such as compact size, low half-wave voltage, and high modulation bandwidth. In 2005, Rabiei et al. first proposed an LNOI-based EOM with a half-wave voltage-length product (VπL) of 15 V·cm and a waveguide transmission loss of 1.4 dB/cm [18]. In 2018, the Wang Cheng et al. achieved an ultra-compact, low propagation loss photonic waveguide through etching TFLN [19], reducing the VπL to 1.8 V·cm, with an achieved modulation bandwidth of 15 GHz. In the same year, they refined the fabrication process, significantly reducing the waveguide transmission loss of thin-film LN ridge waveguides to 0.3 dB/cm [20], establishing the foundation for large-scale applications of thin-film lithium niobate photonic integrated circuits. In 2021, the Liu Ye et al. utilized step-and-scan lithography to fabricate TFLN EOMs [21], further lowering the VπL to 1.75 V·cm while maintaining an electro-optic modulation bandwidth exceeding 40 GHz. Essentially, subsequent researches are based on the foundational structure designed by Wang Cheng’s team and are dedicated to improving the performance of the modulator unilaterally. For instance, to achieve a wider modulation bandwidth, one method is to reduce the electrode length, which sacrifices half-wave voltage performance and potentially increases power loss. However, a larger VπL is unfavorable for reducing the size of the modulator, decreasing energy consumption, and improving modulation efficiency. Therefore, while maintaining a lower VπL, increasing the bandwidth and reducing losses of the modulator is a reasonable design approach. Compared to existing research, this design approach has the potential to foster significant breakthrough advancements in the field of EOMs by enabling multifunctionality and high-performance attributes.
In order to achieve lower VπL and higher modulation bandwidth of EOMs, this work proposes a novel LNOI integrated Mach-Zehnder modulator (MZM) for electro-optic modulation. This modulator employs integrated optics technology to design optical waveguides, modulation electrodes and couplers on the surface of TFLN. Through meticulous design of optical transmission and microwave characteristics, a modulator with low VπL, low optical losses, and substantial modulation bandwidth is successfully engineered. The achieved VπL is 1.69 V·cm, with an impressive 3 dB EO bandwidth exceeding 50 GHz. This design establishes a high-performance platform meeting diverse criteria and provides valuable guidance for future high modulation efficiency, energy-efficient, and cost-effective optical communication networks.

2. Structure and Performance Parameters

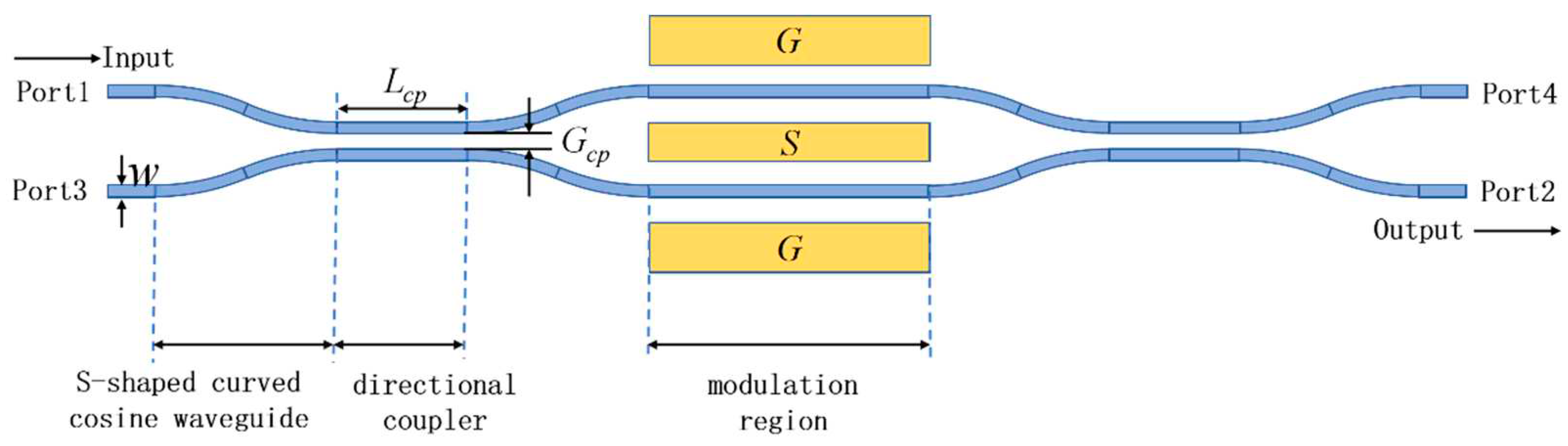
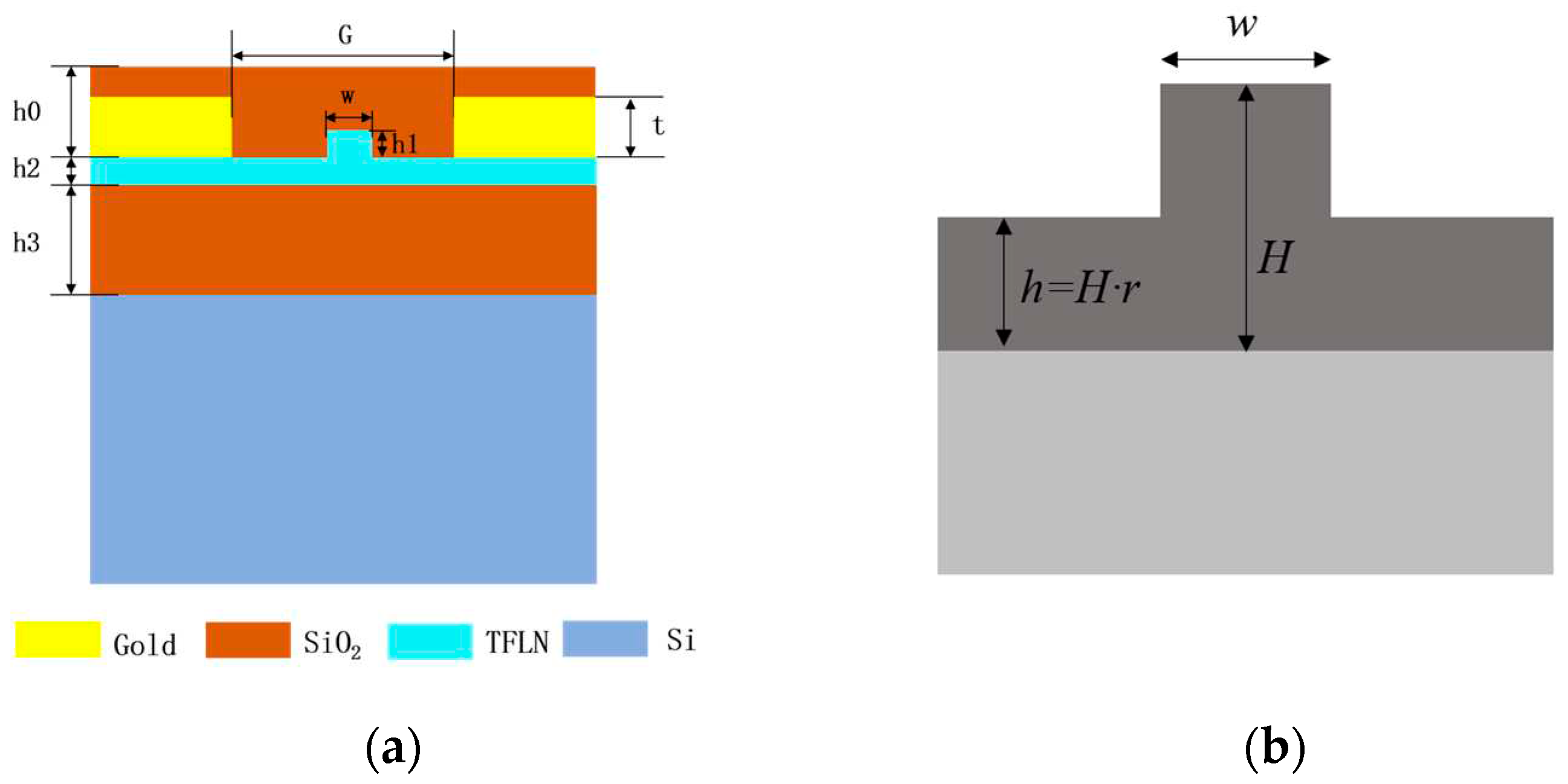
2.1. Modulator Structure

The MZM photonic modulator is an influential optical device that plays a crucial role in signal modulations and its primary function is to achieve variations in the amplitude, phase, or frequency of optical signals, making it a significant tool in the field of optics. This enables the conversion of electrical signals into optical signals or modulation of optical signals. As depicted in Figure 1, the overall structure consists of S-shaped curved cosine waveguide, directional coupler, and modulation region. In this work, it is utilized solely as an intensity modulator with Port 1 as the input and Port 2 as the output. The optical wave propagates through the curved waveguide and is directed to the directional coupler, where it is evenly split into two paths entering the modulation region. The modulation region, a vital part of lithium niobate electro-optic modulators, typically employs travelling waveguide structures, which significantly influence the device’s performance, including the half-wave voltage length product, modulation bandwidth, and loss. By fine-tuning the electrode voltage, we can skillfully modulate the refractive index and exercise control over the phase difference between the arms. This delicate adjustment allows us to achieve precise modulation of the optical signal. Subsequently, the optical signals from both paths are recombined, and modulation is achieved through interference.
By employing rational design and optimization techniques, the structure of the lithi-um niobate electro-optic modulator enables exceptional optical modulation performance and facilitates low-loss optical transmission. The structural parameters and performance of the modulation region, electrodes, splitter, and coupler should be designed and adjusted according to specific requirements. In the following sections, we will introduce the relevant performance parameters of the EOM and summarize a set of optimization strategies based on their structural parameters, for devices of similar types.

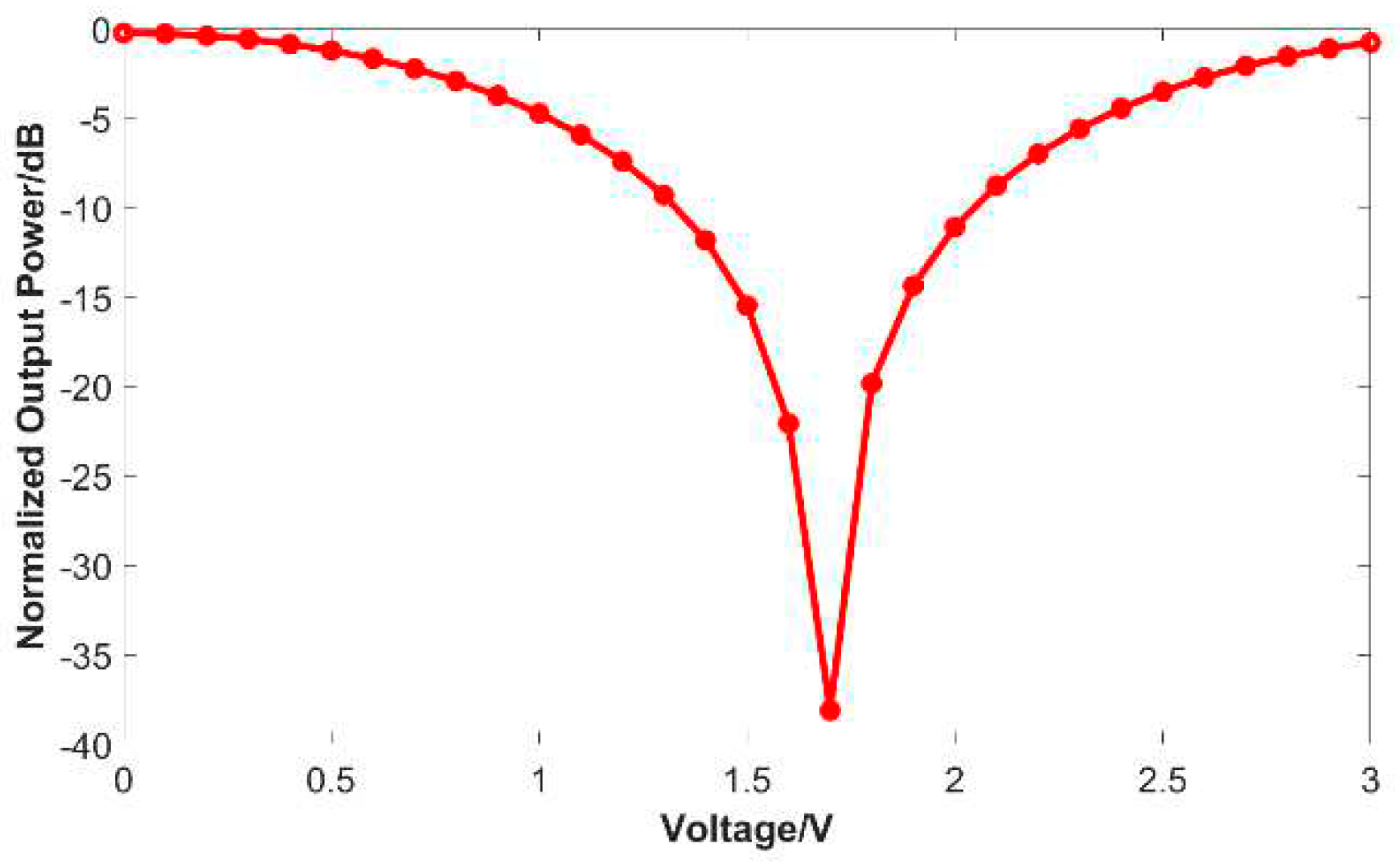
2.2. The half-wave voltage-length product

The principles of EOM in this paper are based on the effect of electric field-induced refractive index change. When a signal voltage is applied to the optical waveguide, the change in refractive index is proportional to the electric field E z , which is known as the Pockels effect. The relationship between them can be expressed as the following equation:
Δ n e f f = 1 n e f f ∬ ​ L N n ( x , z )   Δ n ( x , z ) | E 0 ( x , z ) | 2 d x d z ∬ ​ ∞ | E 0 ( x , z ) | 2 d x d z
where n ( x , z ) and Δ n ( x , z ) represent the material refractive index and the refractive index change at any position on the waveguide cross-section, respectively. And E 0 ( x , z ) is the optical signal in the modulation arm. The numerator in the equation is limited to the area of lithium niobate thin film where the refractive index change is generated by the Pockels effect, while the denominator covers the entire waveguide cross-section [22].
To maximize the linear electro-optic coefficient（ γ 33 = 30.8   p m / V for LN）, the waveguide is made from an x-cut lithium niobate crystal, with the TE fundamental mode polarized along the crystal z-axis, where the external electric field mainly induces the change in the extraordinary refractive index:
Δ n e = − 1 2 n e 3 γ 33 E z
here, E z represents the component of the external electric field along the crystal z-axis. In most practical cases, the well-designed mode is primarily polarized along the z-axis, with over 99% polarization efficiency. Hence, the refractive index changes induced by the electric field in the x and y directions can be neglected. By substituting the above equations into the variation of the mode refractive index and simplifying it, the normalized electro-optic overlap integral of the waveguide cross-section is obtained as:
Γ m o = G ∬ ​ L N | E 0 ( x , z ) | 2 E Z ( x , z ) d x d z V ∬ ​ ∞ | E 0 ( x , z ) | 2 d x d z
For an electro-optic modulator with a modulation arm length of L, the VπL of the lithium niobate push-pull type MZM is expressed as follows:
V π L = n e f f λ 0 G 2 n e 4 γ 33 Γ m o
A smaller VπL value indicates that lower voltage is required to achieve half-wave phase change in the same length of the modulating arm, leading to higher sensitivity of the modulator. Based on Equation (4), it is evident that reducing the VπL is mainly achieved through two methods: First, decreasing the electrode spacing G to generate a larger electric field under the same external voltage. Second, increasing the electro-optic overlap integral, which can be achieved by enlarging the optical mode field to enhance its sensitivity to the electric field.

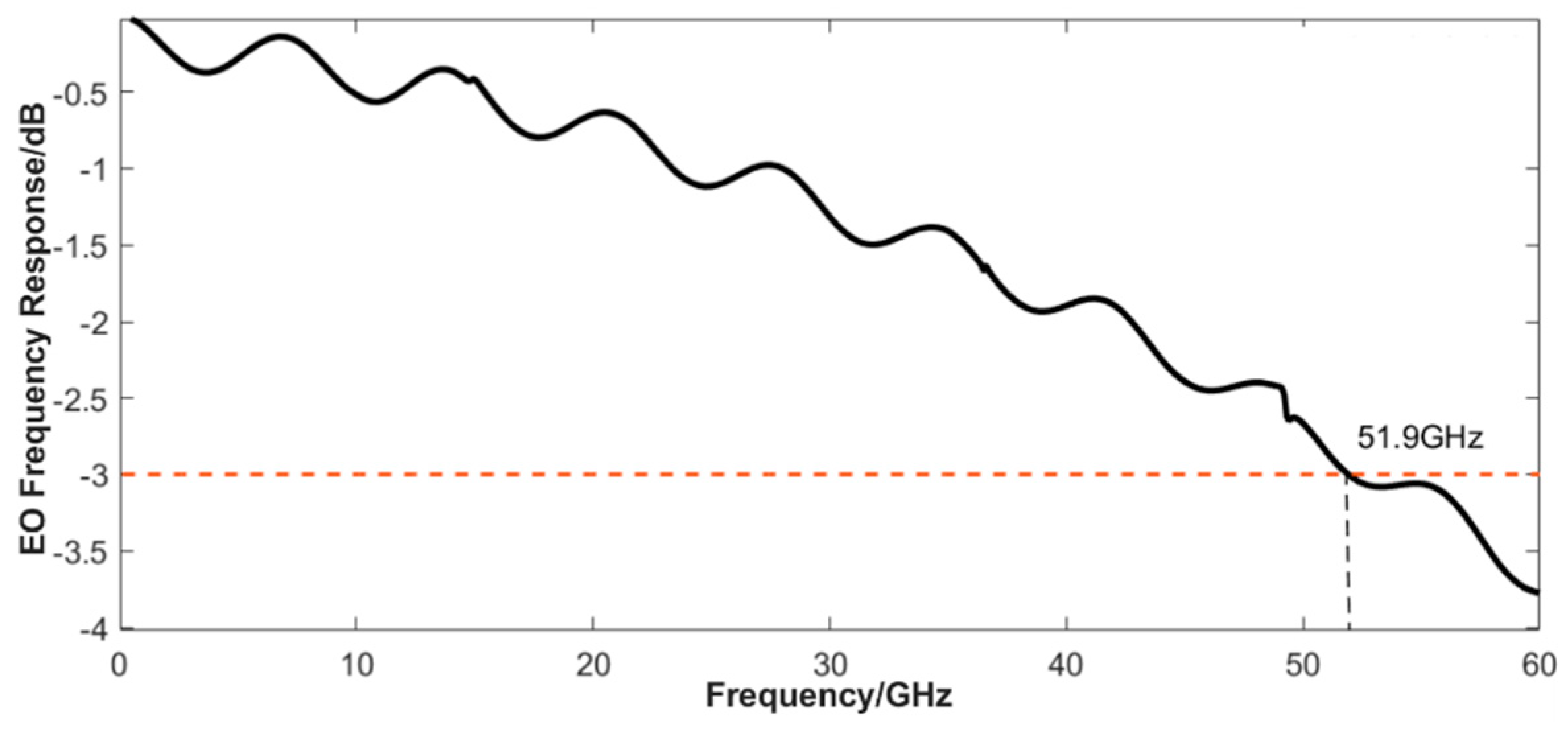
2.3. 3dB Modulation Bandwidth

Modulation bandwidth is another key performance metric for EOM. The traveling-wave electrode adopts a simple coplanar waveguide structure for microwave signal transmission, and impedance matching is the fundamental design consideration to avoid microwave reflection. Under the impedance matching condition, the frequency response function of the EOM can be represented by the following equation [23]:
H ( f ) = 20 l g { e α L 2 [ s i n h 2 ( α L / 2 ) + s i n 2 [ 2 π f ( η R F − η o p ) L / 2 c ] ( α L / 2 ) 2 + [ 2 π f ( η R F − η o p ) L / 2 c ] 2 ] 1 / 2 }
where α is the microwave attenuation coefficient of the traveling-wave electrode structure, which mainly includes conductor losses from the metal electrode and dielectric losses from materials such as lithium niobate and silicon dioxide that form the coplanar waveguide structure. Radiation losses caused by roughness of the metal electrode can be neglected. Both types of losses are inherent material properties, and their relationship with the microwave attenuation coefficient is given by the following equation [24]:
α = α c f + α d f
When the frequency response of the EOM decreases by 3 dB at lower frequencies, the corresponding range of microwave frequencies determines the 3 dB modulation bandwidth. To increase the modulation bandwidth, it is necessary to reduce microwave attenuation and achieve phase velocity matching between microwaves and optical waves. This involves minimizing the effective refractive index of microwaves η R F to approach the effective refractive index of optical modes η o p . The microwave refractive index in lithium niobate is much larger than the optical refractive index, which leads to phase velocity mismatch and limits the modulation bandwidth. To address this issue, two methods are primarily employed in this work to realize phase velocity matching: First, adding a buffer layer composed of low refractive index silicon dioxide to reduce the overall structure’s microwave refractive index. Second, appropriately increasing the electrode thickness to enable most of the microwave field to propagate in the low refractive index region between the electrodes.

2.4. Other Performance Metrics

The total power loss caused by inserting a modulator into an optical device is referred to as insertion loss. It encompasses both inter-device coupling loss and intra-chip propagation loss, quantifying the degree of optical power loss from the input to the output ports of the electro-optic modulator. The insertion loss is defined as the ratio of the output optical power P o u t to the input optical power P i n and can be expressed as follows:
I L = − 10 l g P o u t P i n  
Under the condition of constant input optical power to the EOM, the output optical power varies periodically as the voltage applied to the modulating arm increases from zero. The ratio of the maximum ( P m a x ) to the minimum ( P m i n ) output optical power is defined as the extinction ratio, also represented the modulation depth, and can be expressed as follows [25]:
E R = 10 l g P m a x P m i n
Through an analysis of the overall structure of the electro-optic modulator, the adoption of directional couplers for optical splitting allows for both beam splitting and extinction effects. In comparison to traditional Y-branch splitters, directional couplers can directly adjust the coupling length by tuning the coupling gap, thereby reducing the power difference between the two branches and promoting more uniform splitting of the optical power. This design approach is beneficial for enhancing the extinction ratio of the electro-optic modulator.

3. Design and Optimization of Traveling Wave Modulator Structure

3.1. Optical Modeling and performaces Optimizing of the Travelling Waveguide Structure

We constructed a 2D cross-sectional model of an EOM, as depicted in Figure 2a, utilizing Equations (6). By employing optical mode analysis, we obtained the optical mode field distribution of the waveguide cross-section. Through steady-state calculations, we determined the electric field distribution corresponding to the applied voltage, enabling us to evaluate the electro-optic overlap integral and the VπL. We further analyzed the impact of various structural parameters on the device performance, facilitating the design and optimization of the modulation region of the electro-optic modulator.

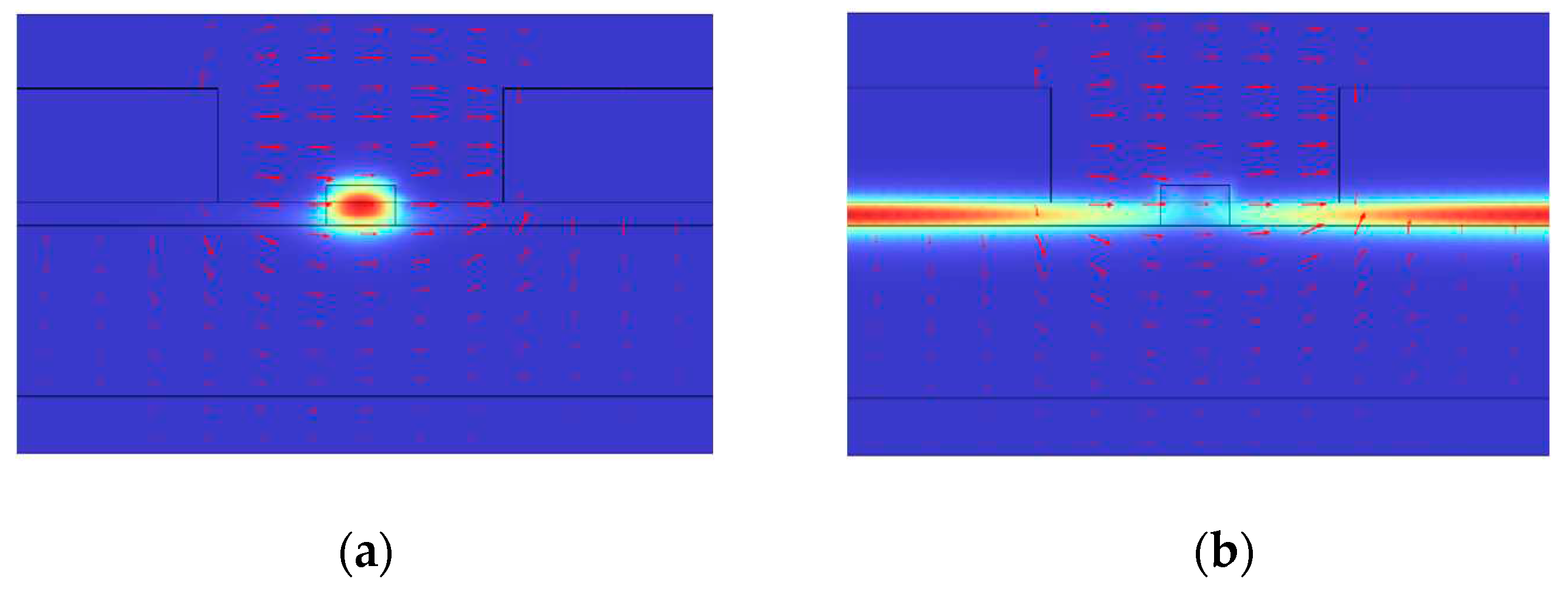
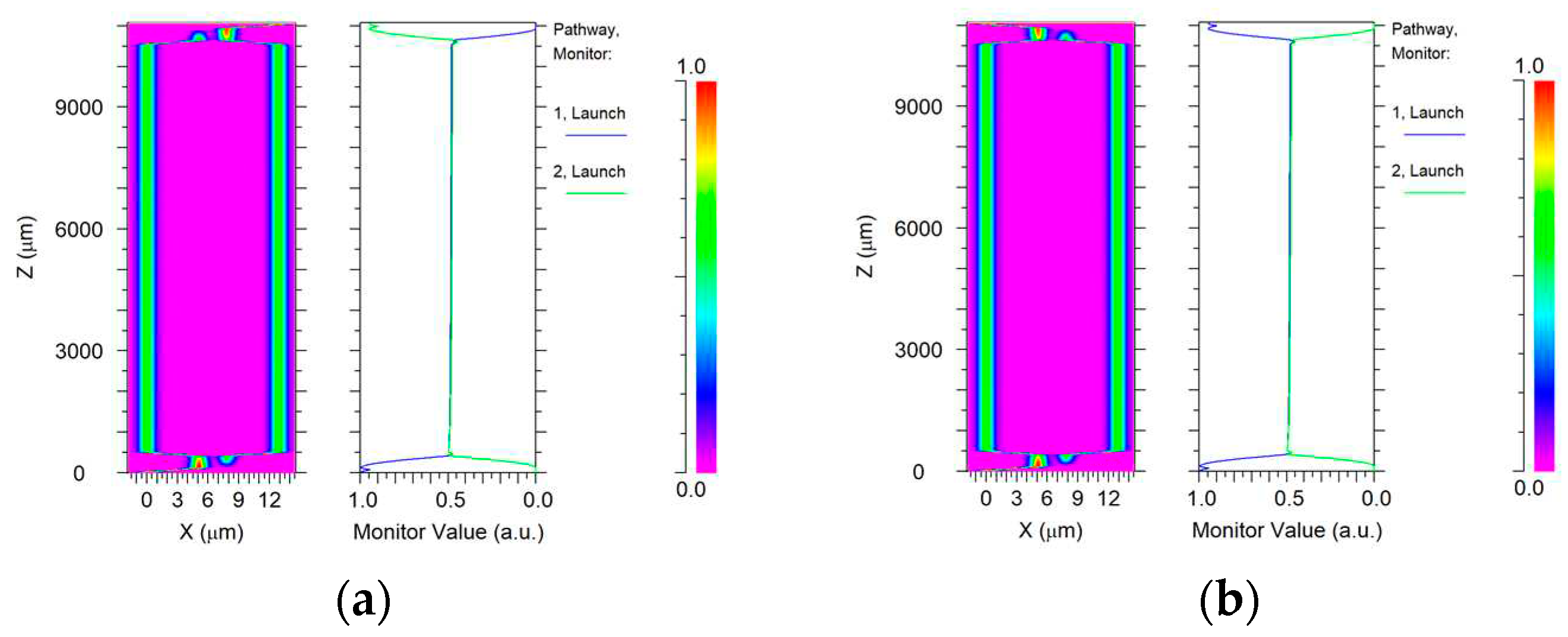
3.1.1. Design of steady-state distribution of optical mode field

Based on Wang et al.’s cross-sectional structure investigation [20], we undertook pertinent adjustments and comparisons to validate the optimization approach of the VπL. This optimization was achieved by augmenting the ridge width to enhance overlap integral, while keeping electrode spacing, lithium niobate film thickness, and ridge etching depth consistent. Nevertheless, the concomitant challenge involves the potential sustenance of higher-order modes due to the widened cross-section of the ridge waveguide. Hence, while guaranteeing single-mode propagation within the waveguide, a primary goal is to maximize the waveguide width. It depends on the geometric constraints of ridge width (w), inner ridge height (H), and rib height (2h) to achieve single-mode transmission with a certain ridge-type optical waveguide. The corresponding basic geometric model is illustrated in Figure 2b. R.A. Soref proposed the classical criterion for single-mode operation in ridge waveguides, which requires the ridge structure to satisfy the following relationship [26]:
t ≤ α + r 1 − r 2   0.5 ≤ r < 1
where, t = w / H ， r = h / H and α represent the normalized ridge width, normalized ridge height, and a constant value, respectively. α is determined experimentally by Soref using the beam propagation method. When the ridge width of the waveguide approaches the critical width, even slight variations in width can result in significant changes in the optical mode field distribution within the ridge waveguide. To ensure the stable existence of the desired mode, the ridge region must confine at least 5% of the mode’s energy. Therefore, in the design process, it is essential to employ more accurate and applicable single-mode conditions for the design of ridge-type optical waveguides using TFLN. It is crucial to maximize the ridge width while ensuring the stable transmission of the fundamental mode.
Due to the limitations of commercially available lithium niobate single-crystal thin films, this work chose a range of H=300~900 nm with a step size of 100 nm. Etching modeling was performed with r=0.4, 0.5, and 0.6, respectively. Considering the corresponding single-mode conditions provided in the reference [27], the model was established based on the initial theoretical maximum ridge width, and mode analysis was conducted to confirm the stable transmission of the TE fundamental mode within the ridge waveguide (Figure 3a). At the same time, it is demonstrated that only less than 5% of the first-order mode energy was confined within the ridge, that is, more than 95% of the energy was confined within the rib region, indicating that the first-order mode cannot be transmitted stably (Figure 3b). Therefore, the setting of the critical ridge width satisfies the single-mode transmission condition.
Upon preliminary analysis, it can be seen that when the film thickness is insufficient (H=300 nm), the leakage of the fundamental mode into the lower silica cladding is more pronounced. By setting different values of H and r and conducting mode analysis, the critical ridge width for each group was obtained, as shown in Table 1. With the determined critical ridge width for various etching conditions, the electro-optic overlap integral and VπL were calculated for electrode spacings of G=4 μm, 4.5 μm, and 5 μm, respectively. The thickness of the lower silica cladding was fixed at 4 μm (the maximum thickness of the commercial thin film’s silica buffer layer), the electrode height was fixed at 1 μm, and the thickness of the upper silica cladding was fixed at 1.8 μm. The variation of the VπL with respect to the structural parameters is shown in Figure 4.
Figure 4 illustrates a close correlation between the VπL and the ridge etching depth and electrode spacing G. Figures 4a-c correspond to fixed G of 4 μm, 4.5 μm, and 5 μm, respectively, showcasing the variation of the VπL with different etching depths as the film thickness( outer ridge height H) changes. The VπL varies with the increase of the film thickness H and the decrease of the etching depth (1-r). Specifically, at the same etching depth, there is a rapid reduction in the VπL as the H increases from 400 nm to 600 nm, followed by a flattening of the curve, indicating that further increasing H no longer significantly affects performance optimization. Additionally, when comparing the same H, transitioning from deep etching (r=0.4) to shallow etching (r=0.6) in the ridge waveguide can lead to a reduction in the VπL by up to 20%. Further verification was conducted to substantiate the assumption that the VπL is not governed by a linear relationship with rib height (determined jointly by thin-film thickness H and normalized etching depth r). Instead, it was established that the half-wave voltage is constrained by both H and r.
In order to investigate the impact of electrode spacing, we set r to 0.4, 0.5, and 0.6, respectively. Subsequently, we examined the variation of VπL at different electrode spacings G, while keeping H as a variable, as depicted in Figures 4d-f. It can be shown that the VπL decreases and gradually approaches a plateau as H increases. Under identical H values, a decrease in G from 5 μm to 4 μm results in a substantial reduction in VπL, with a maximum reduction exceeding 10% over a 0.5 μm range. Overall, a reduction in etching depth and electrode spacing contributes to the decrease in VπL. Decreasing the electrode spacing enhances the electric field, whereas a shallower etching depth weakens mode confinement, leading to an enlargement of the guided mode and a heightened influence of the electric field.

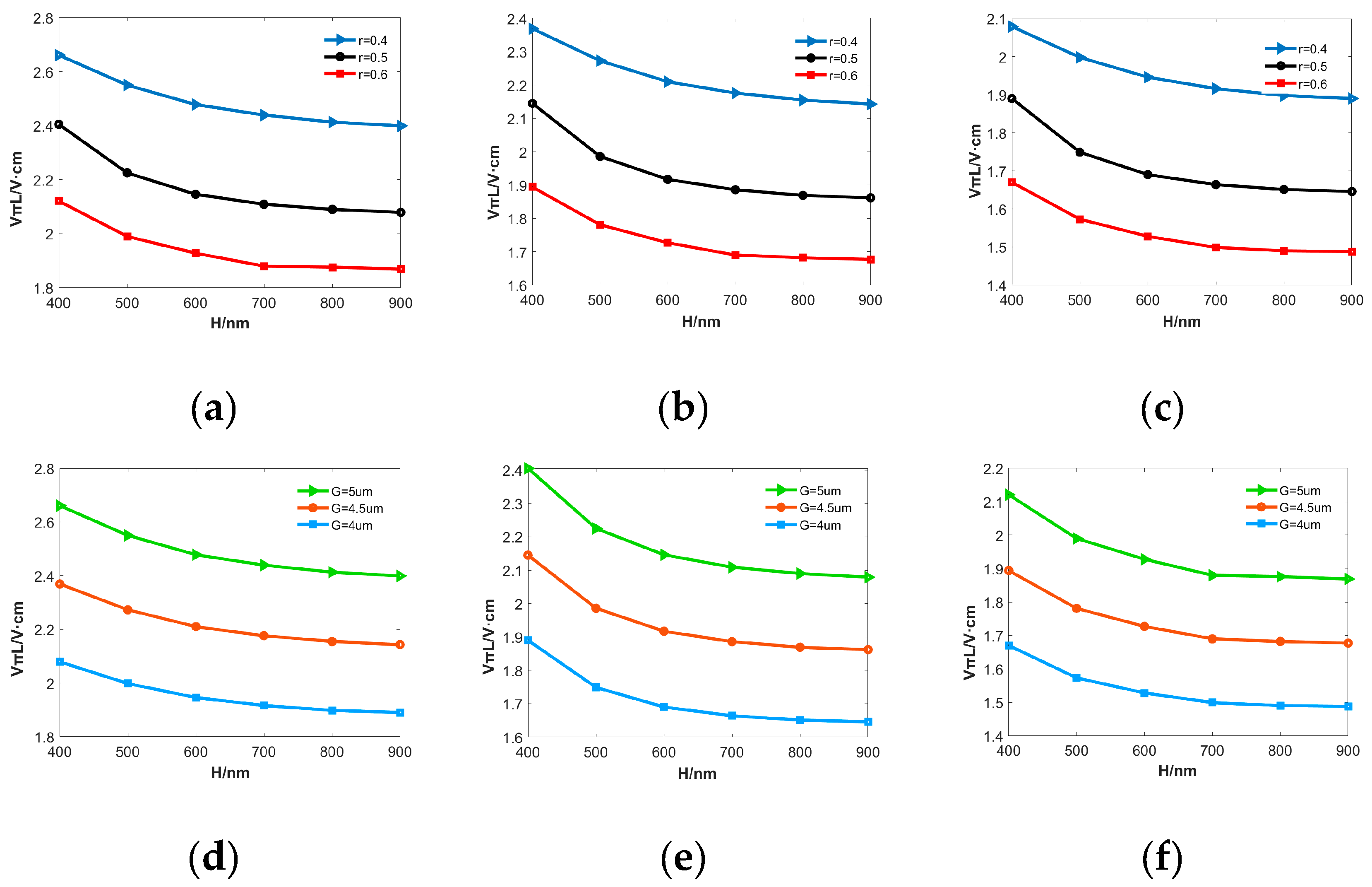
3.1.2. Trade-off between electrode spacing and waveguide losses

When the film thickness reaches 900 nm, and considering a shallower ridge etching (r=0.6) and reduced electrode spacing (4 μm), the simulated VπL can be reduced to 1.48 V·cm. This reduction is advantageous for achieving low-power on-chip integration of TFLN devices. However, when the electrode spacing decreases to 5 μm, the optical waveguide losses caused by metal electrode absorption become significant. Utilizing the configurations outlined in Figure 4, we conducted an analysis of the optical waveguide losses resulting from metal absorption during the transmission of the TE fundamental mode under corresponding parameter settings. The outcomes, excluding scattering losses related to fabrication, are presented in Figure 5.
The results indicate that the optical waveguide losses caused by metal electrode absorption are primarily influenced by G, but the relation between the loss and R and H is not obvious, except for the high metal absorption loss caused by special structure. The results from Figures 5a-c demonstrate that structures with H=700 nm and r=0.4, as well as H=900 nm and r=0.5, exhibit higher levels of metal absorption losses for various fixed values of G. Meanwhile, losses for other parameter configurations remain relatively consistent. Furthermore, Figure 5d-f reveal that, regardless of the chosen film thickness and etch depth for the ridge waveguide, the waveguide losses increase as the electrode spacing G decreases. Specifically, when G is 5 μm, losses are consistently below 0.01 dB/cm. Upon reducing the G to 4.5 μm, losses slightly increase, ranging from approximately 0.01 to 0.05 dB/cm. However, with a further reduction to 4 μm, waveguide losses may surpass 0.05 dB/cm and, in some instances, even exceed 0.1 dB/cm.
The comprehensive simulation results suggest that optimizing the waveguide structure for a lower VπL is favored through the utilization of a shallow-etched ridge and a smaller electrode spacing. Paradoxically, however, to reduce metal absorption losses, it is desirable to increase the electrode spacing. Therefore, a trade-off is necessary when determining the critical parameters of film thickness, etch depth, and electrode spacing to achieve a balance between low VπL and low losses for overall performance optimization.
Subsequently, we opted for four parameter sets exhibiting superior overall performance and conducted a detailed comparative analysis with those provided in reference [20]. The outcomes of this comparison are presented in Table 2. This investigation into waveguide structures has yielded significant improvements in VπL while maintaining comparable waveguide losses, with the highest reduction reaching 30%. By further optimization, the final design parameters are as follows: thin-film thickness (H) of 800 nm, ridge height of 350 nm, rib height of 450 nm, ridge width (w) of 1.2 μm, and electrode spacing (G) of 4.4 μm. This configuration yields a VπL of 1.7 V·cm, with waveguide losses measuring 0.01 dB/cm. This design not only ensures lower metal absorption losses, thereby mitigating the impact of metal electrodes on optical losses, but also effectively lowers the VπL.

3.1.3. Analysis of cladding structure

Once the key structural parameters of the waveguide were established, we proceeded with additional optimization by analyzing parameters that influence the electric field distribution, such as the electrode thickness and the thicknesses of the upper and lower silica cladding layers. The relationship between the VπL and the electrode thickness was simulated and analyzed by varying the thickness of the lower cladding layer. Figure 6a shows the variation curve of VπL as the electrode thickness increases while the lower cladding layer thickness remains constant. It can be observed that as the electrode thickness surpasses 2 μm, the curve becomes flattened, indicating that further increasing the electrode thickness has less significant impact on reducing VπL. Moreover, when comparing the curves associated with different lower cladding layer thicknesses in Figure 6a, it becomes apparent that, for a fixed electrode thickness, gradual increases in the lower cladding layer thickness from 1 μm to 4 μm result in a corresponding decrease in VπL.
The variation curve of VπL with the upper cladding layer thickness is shown in Figure 6b. The upper silica cladding layer plays a role in confining the inter-electrode electric field, resulting in an increased local electric field and effectively enhancing the electro-optic overlap integral, thereby reducing VπL. Analyzing the curve indicates that as the upper cladding layer thickness gradually increases and does not exceed approximately 1 μm, VπL decreases gradually. However, as the thickness of the upper cladding layer continues to increase, reaching a minimum value just slightly greater than the electrode thickness (approximately 1.2 μm), it ceases to decrease further and may even exhibit a slight increase. Furthermore, when assessing these parameters’ impact on waveguide losses, it is observed that increasing the electrode thickness slightly reduces the losses, while variations in the thicknesses of the upper and lower silica cladding layers have a minimal effect on losses. In conclusion, after establishing the fundamental structural parameters, it is advisable to maximize the electrode thickness to minimize VπL. The lower cladding layer thickness should be set at its maximum allowable value of 4 μm. When considering the upper silica cladding layer, its thickness should be marginally higher than the electrode thickness.

3.2. 3D microwave modeling and simulation of the modulation region

To save computational resources, a 2D cross-sectional modeling approach was employed to establish critical parameter configurations, including the ridge structure and electrode spacing of the waveguide. The primary objective was to achieve a low half-wave voltage and minimize metal absorption losses in the EOM. In this chapter, a 3D transmission line model was developed, specifically for traveling-wave electrodes. This model aimed at optimizing parameters such as electrode thickness, cladding thickness, and electrode width to achieve a characteristic impedance of 50 Ω for impedance matching. Additionally, the optimization process sought to minimize microwave attenuation and refractive index to maximize the electro-optic modulation bandwidth.
The cross-sectional structure of the transmission line and the simulated structural model are depicted in Figure 7, where the modulation section has a length of 10 mm. The accumulation of phase variation ( Δ φ ) in microwave signal transmission along the traveling wave electrode is derived from the interplay between the effective refractive index ( η R F ), microwave propagation constant ( β ), and wavenumber ( k ). Leveraging ( Δ φ ) and the electrode length ( L ), the ensuing formula facilitates the computation of the microwave’s effective refractive index for a specified frequency ( f ).
Furthermore, following the definition of the electrical conductivity of the metallic conductor and the dielectric loss tangent for each medium in the model [28,29,30], the determination of the conductor’s surface loss density and the dielectric’s volume loss density ensue. This process, in turn, allowed for the calculation of the microwave attenuation coefficient corresponding to the specific frequency of interest.
To delve further into the analysis, an investigation was carried out on the thick-ness of the lower cladding layer while maintaining other structural parameters constant. to examine the variation of microwave refractive index within the frequency range below 30 GHz, as illustrated in Figure 8a. Within this frequency range, the microwave refractive index exhibits slight fluctuations with frequency, which can be attributed to the interpolation algorithm used during the frequency point scan during simulations. Nonetheless, it remains stable overall within a narrow range. As the thickness of the lower cladding layer increases from 3 μm to 4 μm, the microwave refractive index demonstrates a decreasing trend. Generally, a wider electrode width corresponds to a larger cross-sectional area, resulting in a lower characteristic impedance. By performing a scan on the center electrode width at the same solving frequency, the variation of characteristic impedance with electrode width was obtained, as depicted in Figure 8b. The simulation results align with the theoretical expectations: as the center electrode width increases from 7 μm to 15 μm, the characteristic impedance gradually decreases from 55.7 Ω to 43.3 Ω, representing a reduction of 22%.
Building upon the initial simulation analysis as described earlier, the strategy to minimize the microwave refractive index, it is recommended to increase the thickness of the lower cladding layer, approaching the refractive index of light waves as closely as possible. Nevertheless, practical constraints stemming from commercial TFLN wafers impose a maximum thickness limit of 4 μm. This limitation, however, aligns harmoniously with the optimization criteria for achieving a favorable VπL. Similarly, according to the optimization principle of the VπL, it is advisable to maximize the electrode thickness. However, excessively large thickness would result in a larger electrode cross-sectional area, leading to a smaller characteristic impedance. Therefore, the initial value of the electrode thickness in the simulation is set to 2 μm. Furthermore, during the ongoing optimization process, if impedance matching is a desired objective, the center electrode width can be adjusted in accordance with the previously mentioned trend to closely approach a characteristic impedance of 50 Ω.
The influence of electrode width and upper cladding layer thickness on microwave attenuation, microwave refractive index, and characteristic impedance is intricate, rendering direct adjustments to optimize all performance metrics concurrently challenging. Consequently, the subsequent phase involves a coordinated scanning analysis aimed at approximating the microwave effective refractive index to 1.975, equivalent to the optical effective refractive index, and approaching a characteristic impedance of approximately 50 Ω. A comprehensive evaluation of performance metrics leads to a solution featuring a center electrode width of 10 μm, a ground electrode width of 17 μm, and an upper cladding layer thickness of t+0.3 μm. At a microwave frequency of 10GHz, the corresponding characteristic impedance is 47.9 Ω, the microwave effective refractive index is 2.197, the microwave attenuation is 7.4 dB/m, the return loss is below -20 dB, and the half-wave voltage is 1.69 V.
Indeed, the initial electrode thickness setting of 2 μm proves excessively large, rendering it inadequate to fulfill the impedance matching criterion of 47.9 Ω. Decreasing the electrode thickness, however, leads to a rise in the half-wave voltage. Consequently, while maintaining the other structural parameters constant, a meticulous scan of the electrode thickness is conducted in small 0.1 μm increments, closely monitoring the corresponding alterations in VπL.
According to the performance comparison results presented in Table 3, when the electrode thickness is reduced to 1.8 μm, the characteristic impedance increases to 49.3Ω, achieving a satisfactory impedance match. The microwave refractive index is 2.19, and the VπL experiences a slight increase, it still remains at approximately 1.69 V. With these optimized parameters, the various structural settings are defined, and a frequency scan is performed in the range of 0.1 to 60 GHz with a step size of 0.1 GHz. This process yields the S-parameters, characteristic impedance, and microwave refractive index of the traveling-wave electrode, as shown in Figure 9.
The performance parameters mentioned above reveal notable characteristics over the wide frequency range of 0-60 GHz. The 10 mm long traveling-wave electrode exhibits consistently demonstrates low insertion loss. However, with increasing frequency, there is a noticeable upward trend, indicating a rise in the microwave attenuation per unit length (i.e., microwave loss). This, in turn, restricts the upper limit of the modulation bandwidth. Nevertheless, the return loss remains below -20 dB throughout the operating frequency range, indicating a good impedance match with a characteristic impedance close to 50 Ω. The microwave refractive index remains stable at approximately 2.19, with slight fluctuations attributable to frequency variations.
By substituting the corresponding microwave attenuation, microwave refractive index, and optical refractive index (1.9747) into the theoretical Equation (9) for frequency response, the electro-optic frequency response curve of the designed modulator in this work can be obtained, as depicted in Figure 10. It is evident that the electro-optic frequency response gradually decreases with increasing microwave frequency. The corresponding 3dB modulation bandwidth is 51.9 GHz, which sufficiently meets the bandwidth requirements of this work.

3.3. Comprehensive Structure Design Optimizaiton and Comparation

The aforementioned work has optimized the key performance parameters of VπL and modulation bandwidth. Following the determination of the structural parameters in the modulation region, this section shifts its focus towards the comprehensive design of the electro-optical modulator, particularly emphasizing insertion loss and extinction ratio (i.e., modulation depth) as performance metrics. Given the computational complexity associated with 3D modeling and optical simulations of the entire structure, coupled with the limitation that 2D transmission models are only suitable for relatively simple waveguide structures lacking ridge features, they are not suitable for modeling ridge waveguides. Therefore, in this work, an optical simulation method based on the beam propagation method will be used for the analytical modeling.
The S-bend cosine structure consists of two identical concentric circular segments symmetrically distributed and connected by tangential straight lines. In the design of the modulation region, the values of electrode spacing and center electrode width have been determined. Analyzing the overall structure, the longitudinal displacement ( d y ) of the S-bend cosine structure is determined by the waveguide width w , electrode spacing ( G ), center electrode width ( w s ), and coupling spacing of the directional coupler ( G c p ):
d y = ( w s + G − w − G c p ) / 2
During the design process, it is also necessary to determine the bending radius ( r ) of the S-bend cosine structure to achieve sufficiently low transmission loss. Once the longitudinal displacement ( d y ) and bending radius ( r ) are determined, the lateral displacement ( d x ) and the maximum tilt angle of the transmission direction ( θ ) (angle with respect to the lateral direction) of the S-bend cosine structure are also determined by these two design parameters, as shown in the following relationship [31]:
θ = a r c o s [ ( r − d y / 2 ) / r ] 2
d x = 2 r s i n θ
By increasing r, the degree of curvature in the waveguide is reduced, allowing the optical waves to propagate stably along the curved cosine shape and significantly reducing scattering losses. When the bending radius in the model increases to 0.9 mm, the optical transmittance at the output port reaches 95.9%, with losses falling within an acceptable range.
To maximize the extinction ratio of the EOM, it is necessary to minimize the power difference between the two modulation arms, which can be achieved by adjusting the length of the directional coupler to a specific value. According to the coupling theory of the directional coupler, the power difference between the two modulation arms follows a sinusoidal distribution as the coupling length increases, which is consistent with the simulation results. To ensure good coupling efficiency and avoid waveguides being too close to each other, the waveguide spacing of the directional coupler ( G c p ) is set to 1.5 μm. By comparing the power differences between different coupling lengths ( L c p ), it can be determined that the length corresponding to the minimum power difference is a set of periodically distributed values, and when the minimum length is chosen L c p = 255   u m , the optical powers of the two modulation arms are 0.484 and 0.482 times the incident power, respectively, achieving a sufficiently close to 50:50 power split.
The overall structure is modeled based on the determined bending radius, coupling spacing, and coupling length. The simulation includes the intensity modulation of optical waves by applying a voltage, ensuring that the electric fields applied to the two modulation arms are equal in magnitude and opposite in direction. A voltage scan is performed across the range of 0 to 3 V. Additionally, within the interval of 1.6 to 1.7 V, an additional set of scan data points with a step size of 0.01 V is included. The resulting curve depicting the normalized output power variation concerning the applied voltage is illustrated in Figure 11.
When the applied voltage is zero, all optical wave energy is directed to Port 2 (the output port), representing the "on" state of intensity modulation. The transmission of the optical wave is illustrated in Figure 12a: the optical wave enters from Port 1 at the lower left position, divided by the directional coupler into the two modulation arms for transmission, and finally transferred to Port 2 at the upper right position through the directional coupler, with 95.9% of the optical wave energy being output. As the applied voltage reaches 1.69 V, the transmission of the optical wave is depicted in Figure 12b: the optical waves in the two modulation arms undergo opposite phase changes due to modulation. After passing through the directional coupler, the majority of the optical wave energy is directed to Port 3, while the output from Port 2 is close to zero, indicating the "off" state of intensity modulation. Through the simulations of the overall structure’s optical transmission and intensity modulation, it is determined that the insertion loss of the electro-optic modulator is 0.18 dB, and the extinction ratio is 46.81 dB.
The relevant design parameters are listed in Table 4. The designed EOM successfully meet its objectives, which include achieving a reduced half-wave voltage, a wide modulation bandwidth, and minimized losses. The final performance simulation results are summarized in Table 5. In comparison to reported designs, maintaining the electrode spacing at the typical value of 5 μm while adjusting the ridge etching structure enables a reduction in VπL to below 2 V·cm. Further reduction of the electrode spacing to 4.4 um, while maintaining low metal absorption losses of 0.01 dB, resulted in a further reduction of the VπL to 1.69 V·cm. This performance surpasses that of most TFLN electro-optic modulators of the same type and maintains a large modulation bandwidth of 51.9 GHz. Detailed performance comparisons with similar TFLN structures are provided in Table 5. In this work, has effectively achieved a well-balanced configuration between critical performance parameters, including half-wave voltage and modulation bandwidth. Notably, this structure type offers the advantage of low power consumption due to its low VπL, while still providing a modulation bandwidth exceeding 50 GHz at the 3 dB level. Furthermore, the designed structure ensures that optical losses attributed to metal absorption remain below 0.01 dB/cm, positioning it at the forefront among similar structures.

4. Conclusions

In conclusion, this study successfully optimized key parameters of TFLN electro-optic modulators, namely the VπL, modulation bandwidth, and overall transmission performance. The research focused on designing an optical waveguide structure that achieved the optimum VπL at the critical ridge width, resulting in minimal optical waveguide losses of approximately 0.01 dB/cm. Furthermore, the study addressed challenges related to microwave attenuation and phase velocity mismatch by incorporating a silica buffer layer to reduce the microwave refractive index and adjusting the electrode thickness to achieve phase velocity matching. These optimizations resulted in a significantly enhanced modulation bandwidth of 51.9 GHz. Additionally, the impact of parameters such as bend radius, coupling spacing, and coupling length on the modulator’s performance was investigated, leading to a low insertion loss of 0.18 dB and a high extinction ratio of 46.81 dB. By demonstrating a balanced approach between VπL and modulation bandwidth with a fixed electrode spacing of 5 μm, the study showed significant improvements while maintaining a low level of loss. Importantly, this research offers valuable insights into optimizing and enhancing the performance of TFLN electro-optic modulators, thereby contributing to the development of highly efficient and compact electro-optic devices for advanced photonic applications.

Author Contributions

Conceptualization, X.K. and Y.H.; methodology, X.K. and H.W.; simulations, X.K. and H.W.; validation, Y.H. and H.W.; formal analysis, H.W.; investigation, Y.H.; writing—original draft preparation, X.K.; writing—review and editing, Y.H. and H.W.; visualization, H.W.; supervision, Y.H.; project administration, Y.H.; funding acquisition, Y.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded in part by the National Natural Science Foundation of China under Grant 11673079 and the Hongque Innovation Center fund HQ202103002.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this work are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest

References

  1. Marpaung, D.; Yao, J.; Capmany, J. Integrated microwave photonics. Nat. Photon. 2019, 13, 80–90. [Google Scholar] [CrossRef]
  2. Yue, Y.; Wang, Q.; Anderson, J. Experimental investigation of 400 gb/s data center interconnect using unamplified high-baud-rate and high-order qam single-carrier signal. Appl. Sci. 2019, 9(12), 2455. [Google Scholar] [CrossRef]
  3. Zhu, D.; Shao, L.; Yu, M.; et al. Integrated photonics on thin-film lithium niobate. Adv. Opt. Photon. 2021, 13, 242–352. [Google Scholar] [CrossRef]
  4. Huang, X.; Liu, Y.; et al. Linearity-enhanced dual-parallel mach–zehnder modulators based on a thin-film lithium niobate platform. Photonics 2022, 9, 197. [Google Scholar] [CrossRef]
  5. Alloatti, L.; Palmer, R. ; Diebold, S; et al. 100 GHz silicon–organic hybrid modulator. Light Sci Appl. 2014, e173. [Google Scholar] [CrossRef]
  6. Liu, X.; Xiong, B.; Sun, C.; Wang, J.; et al. Sub-terahertz bandwidth capactively-loaded thin-film lithium niobate electro-optic modulators based on an undercut structure. Opt. Express 2021, 29, 41798. [Google Scholar] [CrossRef]
  7. Wu, Y. T.; Chiu; Lin, F. High-Speed (60 GHz) and Low-Voltage-Driving Electroabsorption Modulator Using Two-Consecutive-Steps Selective-Undercut-Wet-Etching Waveguide. IEEE Photon. Technol. Lett. 2008, 20, 1261. [Google Scholar] [CrossRef]
  8. Doi, M.; Sugiyama, M.; et al. Advanced LiNbO/sub 3/ optical modulators for broadband optical communications. IEEE J. Sel. Top. Quantum Electron 2006, 12, 745. [Google Scholar] [CrossRef]
  9. Khilo, A.; Sorace, C. M.; Kärtner, F. X. Broadband linearized silicon modulator. Opt. Express 2011, 19, 4485. [Google Scholar] [CrossRef]
  10. Li, E.; Wang, A. X. Theoretical Analysis of Energy Efficiency and Bandwidth Limit of Silicon Photonic Modulators. J. Lightwave Technol. 2019, 37, 5801. [Google Scholar] [CrossRef]
  11. Walker, R. G. High-speed III-V semiconductor intensity modulators. IEEE J. Quantum Electron 1991, 27, 654. [Google Scholar] [CrossRef]
  12. Bortz, M. L.; Fejer, M. M. Annealed proton-exchanged LiNbO3 waveguides. Opt. Lett. 1991, 16, 1844. [Google Scholar] [CrossRef] [PubMed]
  13. Weis, R. S.; Gaylord, T. K. Lithium niobate: summary of physical properties and crystal structure. Appl. Phys. A 1985, 37, 191–203. [Google Scholar] [CrossRef]
  14. Gaur, T.; Mishra, P.; Hegde, G.; Srinivas, T. Modeling and Analysis of Device Orientation, Analog and Digital Performance of Electrode Design for High Speed Electro-Optic Modulator. Photonics 2023, 10, 301. [Google Scholar] [CrossRef]
  15. Poberaj, G.; Hu, H.; et al. Lithium niobate on insulator (LNOI) for micro-photonic device. Laser Photon 2012, 6, 488. [Google Scholar] [CrossRef]
  16. Janner, D.; Tulli, D.; M. ; et al. Micro-structured integrated electro-optic LiNbO3 modulators. Laser Photon 2009, 3, 301. [Google Scholar] [CrossRef]
  17. Jin, M.; Chen, J.; Sua, Y.; et al. Efficient electro-optical modulation on thin-film lithium niobate. Opt. Lett. 2021, 46(18), 1884–1887. [Google Scholar] [CrossRef]
  18. Rabiei, P.; Steier, W. H. Lithium niobate ridge waveguides and modulators fabricated using smart guide. Appl. Phys. Lett. 2005, 86(16), 1–3. [Google Scholar] [CrossRef]
  19. Wang, C.; Zhang, M.; Stern, B.; et al. Nanophotonic lithium niobate electro-optic modulators. Opt. Express 2018, 26(2), 1547–1555. [Google Scholar] [CrossRef]
  20. Wang, C.; Zhang, M.; et al. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 2018, 562(7725), 101–104. [Google Scholar] [CrossRef]
  21. Liu, Y.; Li, H.; Liu, J.; et al. Low Vπ thin-film lithium niobate modulator fabricated with photolithography. Opti. Express 2021, 29(5), 6320–6329. [Google Scholar] [CrossRef] [PubMed]
  22. Weigel, P. O. High-Speed Hybrid Silicon-Lithium Niobate Electro-Optic Modulators & Related Technologies. San Diego:UC San Diego, 2018.
  23. Chung, H.; William, S.C.; Alder, E. L.; et al. Modeling and optimization of traveling-wave LiNbO3 interferometric modulators. IEEE J. Sel. Top. Quantum Electron 1991, 27(3), 608–617. [Google Scholar] [CrossRef]
  24. Honardoost, A.; Safian, R.; Rao, A.; et al. High-Speed Modeling of Ultracompact Electrooptic Modulators. J. Lightwave Technol 2018, 36, 5893–5902. [Google Scholar] [CrossRef]
  25. Tian, X.D. Research on Low Loss and Low Half Wave Voltage PLZT Thin Film Modulator. Diploma thesis, Southeast University, Nanjing China, 2020.
  26. Dai, D.; Sheng, Z. Numerical analysis of silicon-on-insulator ridge nanowires by using a full-vectorial finite-difference method mode solver. J. Opt. Soc. Am. B. 2007, 24, 2853–2859. [Google Scholar] [CrossRef]
  27. Soref, R.A.; Schmidtchen, J.; Peterman, K. Large single-mode rib waveguides in GeSi-Si and Si-on-SiO2. IEEE J. Sel. Top. Quantum Electron 1991, 27, 1971–1974. [Google Scholar] [CrossRef]
  28. Westphal, W. B.; Sils, A. Dielectric Constant and Loss Data. In Ohio:Technical Report AFML-TR-72-39; 1972. [Google Scholar]
  29. Krupka, J.; Kaminski, P.; Kozlowski, R. Dielectric properties of semi-insulating silicon at microwave frequencies. Appl. Phys. Lett. 2015, 107, 082105. [Google Scholar] [CrossRef]
  30. Lee, M. Dielectric constant and loss tangent in LiNbO3 crystals from 90 to 147 GHz. Appl. Phys. Lett. 2001, 79, 1342–1344. [Google Scholar] [CrossRef]
  31. Han, H.; Xiang, B. Integrated Electro-Optic Modulators in x-Cut Lithium Niobate Thin Film. Optik. 2020, 212, 164691. [Google Scholar] [CrossRef]
  32. Yang, D.; Chen, Y.; Wang, Y.; Xiang, M.; Chen, Z.; Liu, P.; Lan, T. Collaborative Simulation and Optimal Design of LiNbO3 Thin Film Modulator. Journal of Beijing University of Technology. 2021, 47, 565–572. [Google Scholar]
  33. Li, X.W. Research on Thin Film Lithium niobate Electro optic Modulator Based on Slit Waveguide. Diploma thesis, Jiangnan University, Wuxi China, 2022. [Google Scholar]
Preprints 84595 g001
Figure 1. Integrated structure of MZM electro-optic modulator.
Figure 1. Integrated structure of MZM electro-optic modulator.
Preprints 84595 g001
Preprints 84595 g002
Figure 2. (a) Schematic cross-section of the modulator structure. (b) Cross-section of the ridge waveguide.
Figure 2. (a) Schematic cross-section of the modulator structure. (b) Cross-section of the ridge waveguide.
Preprints 84595 g002
Preprints 84595 g003
Figure 3. (a) Distribution of optical mode and electric field under the substrate. (b) Optical mode distribution of the first order mode.
Figure 3. (a) Distribution of optical mode and electric field under the substrate. (b) Optical mode distribution of the first order mode.
Preprints 84595 g003
Preprints 84595 g004
Figure 4. Maintaining a consistent G, alterations in H and r induce variations in the VπL: (a) G = 5 μm; (b) G = 4.5 μm; (c) G = 4 μm. Maintaining a consistent r, alterations in H and G induce variations in the VπL: (d) r = 0.4; (e) r = 0.5; (f) r = 0.6.
Figure 4. Maintaining a consistent G, alterations in H and r induce variations in the VπL: (a) G = 5 μm; (b) G = 4.5 μm; (c) G = 4 μm. Maintaining a consistent r, alterations in H and G induce variations in the VπL: (d) r = 0.4; (e) r = 0.5; (f) r = 0.6.
Preprints 84595 g004
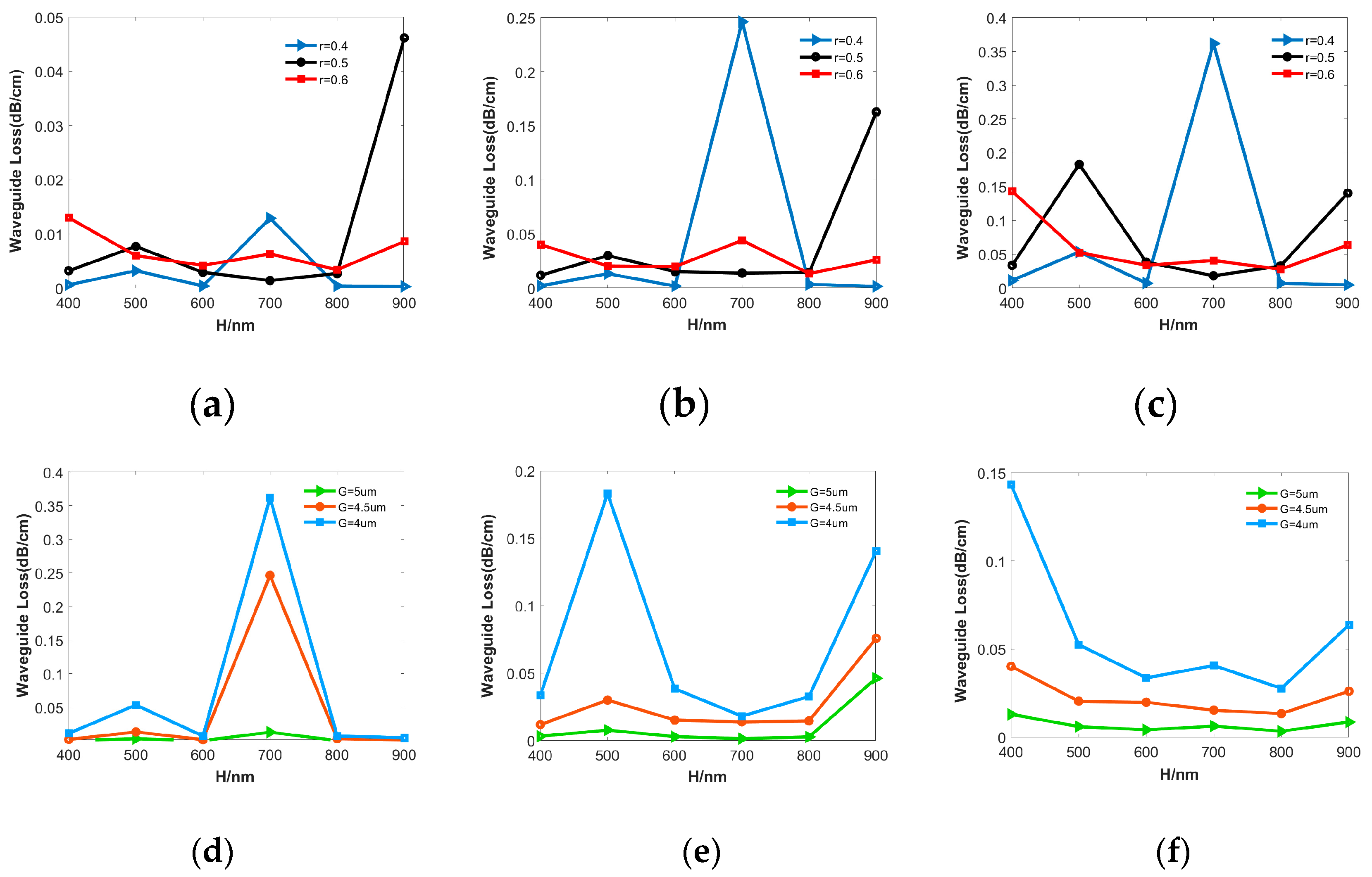
Preprints 84595 g005
Figure 5. Maintaining a consistent G, alterations in H and r induce variations in waveguide losses: (a) G = 5 μm; (b) G = 4.5 μm; (c) G = 4 μm. Maintaining a consistent r, alterations in H and G induce variations in the waveguide losses: (d) r = 0.4; (e) r = 0.5; (f) r = 0.6.
Figure 5. Maintaining a consistent G, alterations in H and r induce variations in waveguide losses: (a) G = 5 μm; (b) G = 4.5 μm; (c) G = 4 μm. Maintaining a consistent r, alterations in H and G induce variations in the waveguide losses: (d) r = 0.4; (e) r = 0.5; (f) r = 0.6.
Preprints 84595 g005
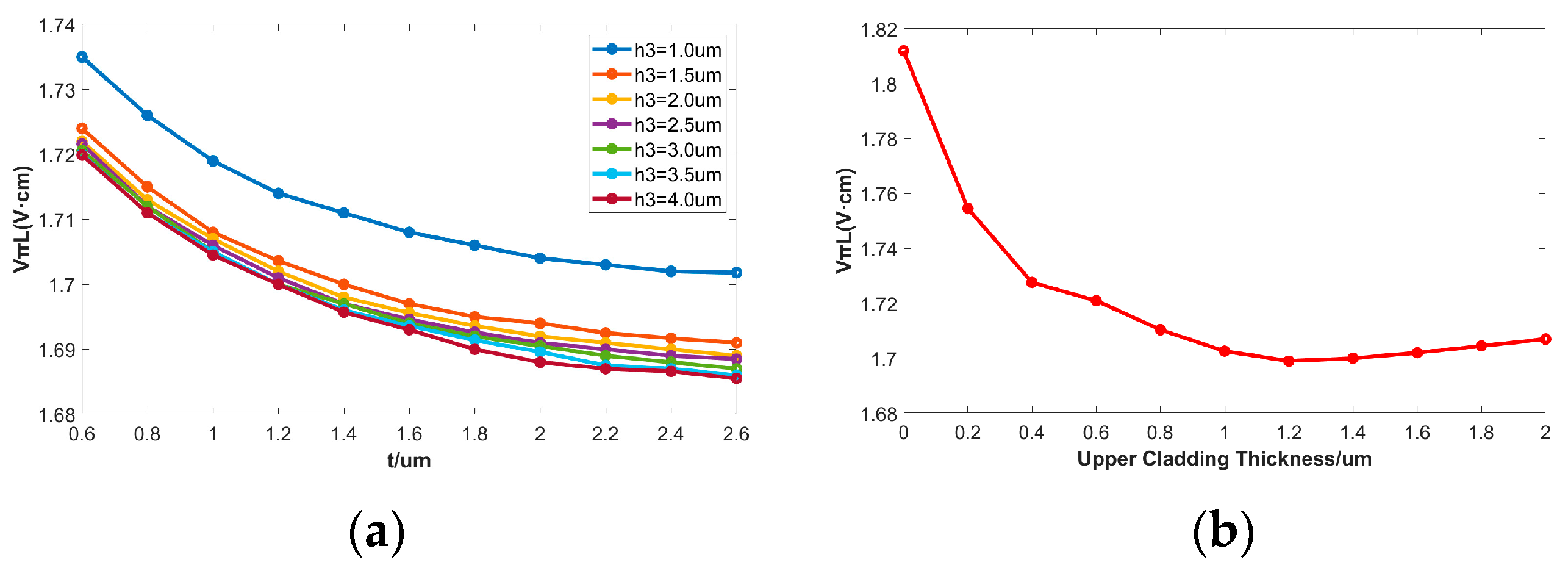
Preprints 84595 g006
Figure 6. (a) Variation of VπL with electrode thickness for different lower cladding thicknesses. (b) Variation of VπL with electrode thickness for different upper cladding thicknesses.
Figure 6. (a) Variation of VπL with electrode thickness for different lower cladding thicknesses. (b) Variation of VπL with electrode thickness for different upper cladding thicknesses.
Preprints 84595 g006
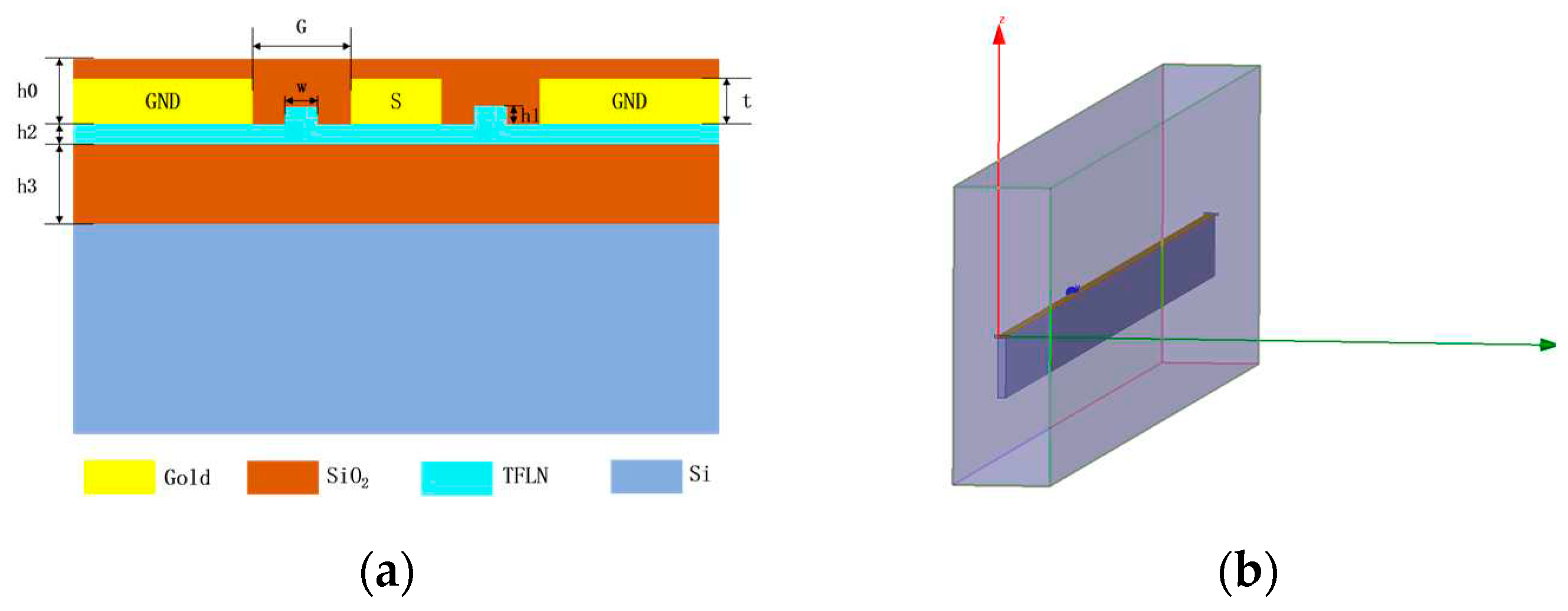
Preprints 84595 g007
Figure 7. Transmission line structure: (a) Cross-sectional structure; (b) 3D simulated structure.
Figure 7. Transmission line structure: (a) Cross-sectional structure; (b) 3D simulated structure.
Preprints 84595 g007
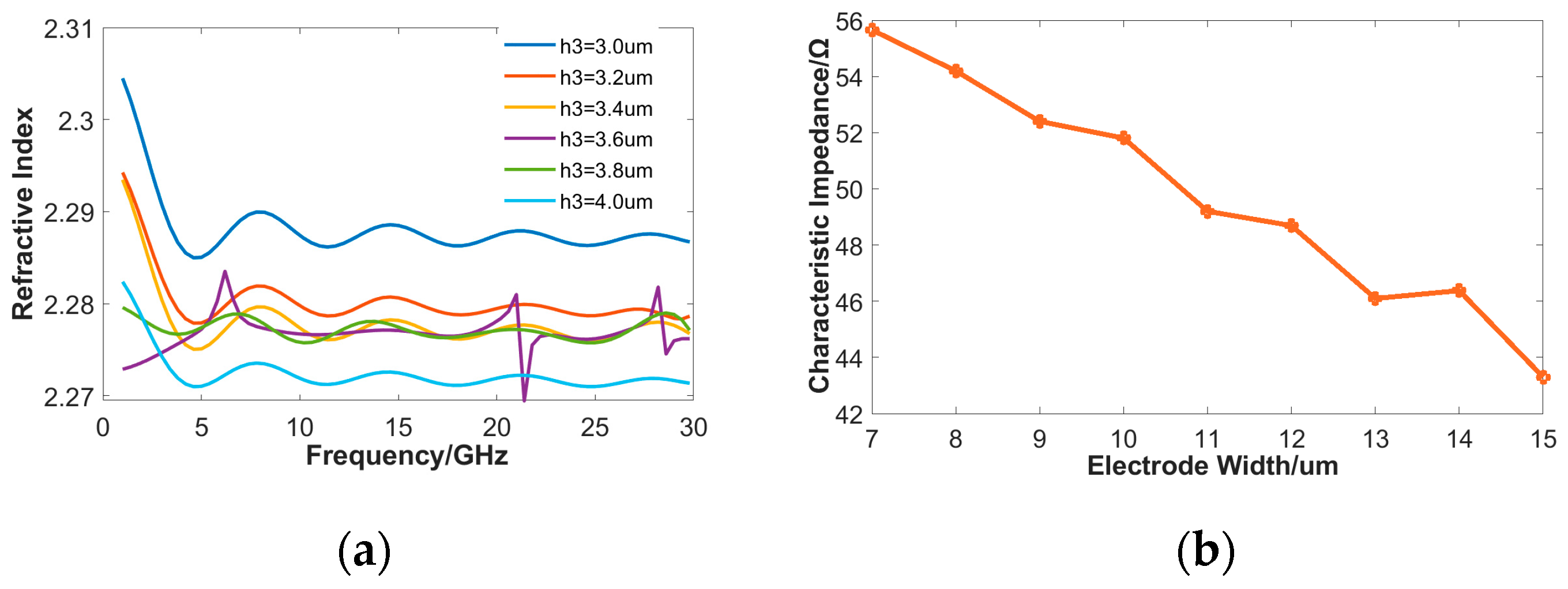
Preprints 84595 g008
Figure 8. (a) Microwave refractive index of the structure at different lower cladding thicknesses. (b) Variation of characteristic impedance with electrode width.
Figure 8. (a) Microwave refractive index of the structure at different lower cladding thicknesses. (b) Variation of characteristic impedance with electrode width.
Preprints 84595 g008
Preprints 84595 g009
Figure 9. Performance parameters of traveling wave electrodes: (a) S21; (b) S11; (c) characteristic impedance; (d) microwave refractive index.
Figure 9. Performance parameters of traveling wave electrodes: (a) S21; (b) S11; (c) characteristic impedance; (d) microwave refractive index.
Preprints 84595 g009
Preprints 84595 g010
Figure 10. Electro-optic frequency response curve.
Figure 10. Electro-optic frequency response curve.
Preprints 84595 g010
Preprints 84595 g011
Figure 11. Curve of normalized output power variation with voltage.
Figure 11. Curve of normalized output power variation with voltage.
Preprints 84595 g011
Preprints 84595 g012
Figure 12. Optical transmission results: (a) at zero applied voltage; (b) at half-wave voltage.
Figure 12. Optical transmission results: (a) at zero applied voltage; (b) at half-wave voltage.
Preprints 84595 g012
Table 1. Critical ridge widths (μm) for various etching depths.
Table 1. Critical ridge widths (μm) for various etching depths.
H/um 0.4 0.5 0.6 0.7 0.8 0.9
r/um
r=0.4 0.98 0.93 0.95 0.98 1.03 1.08
r=0.5 0.86 0.98 1.06 1.11 1.17 1.23
r=0.6 1.03 1.04 1.02 0.96 1.32 1.40
Table 2. Parameters and performance comparison.
Table 2. Parameters and performance comparison.
G/um H/nm r VπL(V·cm) waveguide loss (dB/cm)
4 800 0.6 1.49 0.028
4 700 0.5 1.664 0.018
4.5 800 0.6 1.682 0.013
5 800 0.6 1.876 0.003
5[20] 600 0.5 2.15 0.028
Table 3. Performance comparison for different electrode thicknesses.
Table 3. Performance comparison for different electrode thicknesses.
H/um impedance/Ω refractive index VπL(V·cm)
2 47.9 2.197 1.687
1.9 49 2.2 1.688
1.8 49.3 2.19 1.689
Table 4. Design parameters and performance of electro-optic modulator.
Table 4. Design parameters and performance of electro-optic modulator.
Parameter Value/um Parameter Value/um
w 1.2 G 4.4
h1 0.35 ws 10
h2 0.45 wg 17
h3 4 L 1×104
h0 2.1 r 9×103
h4 410 Gcp 1.5
t 1.8 Lcp 255
Table 5. Comparison of performance with similar TFLN electro-optic modulators.
Table 5. Comparison of performance with similar TFLN electro-optic modulators.
References VπL(V·cm) Vπ/V Modulation bandwidth (GHz) Metal loss (dB/cm)
[20] 2.2 4.4 100 <0.03
[20] 2.3 2.3 80 <0.03
[21] 1.75 3.5 >40 <0.1
[32] 2.17 2.17 >70 \
[33] 1.78 1.78 40 <0.01
This work 1.7 1.7 51.9 0.01
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated