Preprint

Article

Finite-Time Synchronization of Chaotic Systems using Fractional Order Nonlinear PID Adaptive Sliding Controller

Altmetrics

Downloads

119

Views

Comments

Mohammad Rasouli^*

Assef Zare^*

Roohallah Alizadehsani

Mohammad Rasouli^*

Assef Zare^*

Roohallah Alizadehsani

This version is not peer-reviewed

Submitted:

08 September 2023

Posted:

11 September 2023

You are already at the latest version

Alerts

Abstract

This study presents finite-time synchronization of chaotic fractional order systems with disturbance uncertainty and unknown time delay. First, a PID sliding surface is presented. Then, for the finite-time synchronization of the master and slave systems, a robust sliding-adaptive control method is provided. Update rules have been retrieved to estimate the system parameters by using the Lyapunov function while establishing the stability of the suggested mechanism and assuring the convergence of errors to zero. The proposed approach was used to solve the fractional order system of Gensou-Tsei with time-varying parameters, and the simulation results show that the presented approach performs well.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

One of the areas that has recently piqued the interest of many scientists is fractional calculus. More degrees of freedom are added in the model with fractional order systems. Furthermore, it has been demonstrated that fractional calculus can be a significant mathematical tool for precise modeling of practical systems. Medical sciences [1], zoological sciences [2], biological systems [3], viscoelastic materials [4], energy supply and demand system [5], nuclear cycle generating system [6], dynamo theory [7], multi-agent system [8], industrial automation system [9], and HIV immunity model [10] are some of the systems described using fractional differential equations. Because of its applications in secure communication, signal processing, encoding-decoding, and electronic circuits, the study of chaos, chaos synchronization, and control of fractional order systems has recently gained traction [7,11,12]. Researchers have proposed a variety of approaches to control and synchronize fractional order systems, including feedback control [13,14], nonlinear control technique [15], observation-based control [16], phase synchronization [17], impulse synchronization [18], multi-scale synchronization [19,20], sliding mode control technique [21,22,23], fault-tolerant control [24], and so on. Synchronization of chaotic systems has piqued the interest of scientists, with over 350,000 research papers listed in Google Scholar. Many studies have been conducted in this subject for the integer [25], fractional [26], and [(new article)] systems. Several control mechanisms have been presented thus far for this purpose. There are numerous synchronization strategies for the fractional order deterministic dynamic system. The time required for synchronization is not always restricted in all synchronization methods. However, in the actual world, synchronization must be completed in a timely manner. In finite-time stability, the system’s state variables converge to their equilibrium point more quickly and in a finite time. Because convergence time is critical, the time horizon is constrained, providing an effective foundation for faster synchronization in control systems and reducing convergence time.

Analyzing preset time synchronization for two chaotic systems of different dimensions, which can achieve the simultaneity of two chaotic systems of different dimensions in a predetermined time, employing adaptive control [27]. For synchronization between two separate chaotic systems with unknown parameters and disturbances, the fast non-singular terminal sliding mode adaptive control strategy has been examined [28]. For complex fractional-order laser synchronization in the presence of system uncertainties and external disturbances, a chatter-free finite-time SMC sliding surface approach has been suggested [29]. For a class of complex networks with fractional-order delays, delay-dependent finite-time synchronization has been investigated [30]. The finite-time synchronization problem for fractional order complex dynamical networks with intermittent control has been described in [31].

The finite-time synchronization problem of various systems with entirely unknown parameters has been investigated in this article. The synchronization error between the master and slave systems is defined first, and its finite time convergence to zero is demonstrated. The required adaptive rules are then derived to deal with the unknown characteristics of the systems, and the control law and update rules are built in such a way that the achievement condition is met. The next section introduces a mechanism for synchronizing fractional order systems with uncertainty, disturbance, and unknown time delay. The confirmation of its stability is examined in the following section. The proposed method was then applied to a system with time-varying characteristics, and a numerical simulation was provided at the end.

2. Definitions, Theorems, and Lemmas in Fractional Calculus

Definitions and lemmas for finite-time synchronization of fractional order chaotic systems with unknown uncertainty, disturbance, and time delay are given in this section.

Assume that the fractional order nonlinear system is defined as [32]:

D_{t}^{q} x (t) = f (x (t - τ), t)

(1)

In which

q ϵ (0,1), f = {(f_{1}, f_{2}, \dots, f_{n})}^{T}

, and the synchronization error is defined as follows:

\lim_{t \to T} |e_{i - 1} (t)| \to 0 i = 2,3, \dots, N

(2)

If for

t \geq T

, we have

|e (t)| \equiv 0

, system (1) is finite-time synchronized.

Lemma 1:

for each constant value,

α_{i} (i = 0,1, 2,3)

and

σ \in (0,1)

, the following relationships are established [33]:

{(| a_{1} | + | a_{2} | + \cdot \cdot \cdot + | a_{n} |)}^{σ} \leq {| a_{1} |}^{σ} + {| a_{2} |}^{σ} + \dots + {| a_{n} |}^{σ} {(| a_{1} | + | a_{2} | + \cdot \cdot \cdot + | a_{n} |)}^{2} \geq {| a_{1} |}^{2} + {| a_{2} |}^{2} + \dots + {| a_{n} |}^{2}

(3)

Theorem 1:

Assume that

x = 0

is the equilibrium point of the fractional order system (1), and that

f (x . t)

meets the Lipschitz condition with constant

l > 0

and

q \in (0,1)

. If the following equations are true for the Lyapunov function

v (t, x (t))

and the class

δ_{i}

k functions, then the Lyapunov function

v (t, x (t))

achieves zero in finite time T [34,35]:

δ_{1} (‖x‖) \leq v (t . x (t)) \leq δ_{2} (‖x‖)

(4)

D^{q} v (t . x (t)) \leq - δ_{3} (‖x‖)

(5)

D^{q} v (t . x (t)) \leq - α v (t . x (t)) + b v (t - τ_{i} (t) . x (t - τ_{i} (t))) - c v^{β} (t . x (t))

(6)

φ = {s u p}_{t_{0} - τ \leq s \leq t_{0}} v (t . x (t)) \in (0,1) ، β \in (0,1] ، τ_{i} (t) \leq τ ،

(7)

Such that

a > b > 0

and

c > 0

Thus,

v (t . x (t))

converges to zero in finite time T.

T \leq {[{v (0, x)}^{q - \frac{1}{β}} \frac{Γ (1 + \frac{1}{1 - β}) Γ (2 - α) Γ (1 + α)}{Γ (1 + \frac{1}{1 - β} - α) (a - b)} l n \frac{(a - b) φ^{1 - β} + c}{c}]}^{\frac{1}{q}}

(8)

Where

Γ

is the gamma function.

Lemma 2:

Assuming that

x (t) \in R^{n}

has continuous first order derivative, then [36]:

D_{t}^{q} (\frac{1}{2} x^{T} (t) Q x (t)) \leq x^{T} Q D_{t}^{q} x (t)

(9)

Where

q \in (0,1)

and the matrix is positive definite.

3. Dynamic of the Fractional Order System

The synchronization of a fractional order chaotic system in the face of disturbance, uncertainty, and unknown time delay is presented in this section. The saturation operator on the control signal is incorporated in the design process of this subject to facilitate implementation. The simulation findings indicate that the performance will be good and acceptable.

The sliding mode control strategy for the fractional order chaotic system is described, and the synchronization of the fractional order system is examined as a result.

Consider the fractional master and slave system shown below:

\{\begin{matrix} D^{q} x_{i} = x_{i + 1}, 1 \leq i \leq n - 1 \\ D^{q} x_{n} = σ_{0}^{T} x + f (x (t - τ_{1}), t) + ∆ f (x (t), t) + d_{1} (t) \end{matrix},

(10)

The fractional order slave system is as follows:

\{\begin{matrix} D^{q} y_{i} = y_{i + 1}, 1 \leq i \leq n - 1 \\ D^{q} y_{n} = σ_{0}^{T} y + g (y (t - τ_{2}), t) + ∆ g (y (t), t) + d_{2} (t) + φ (u (t)) \end{matrix}

(11)

In which

0 < q < 1

The fractional order error dynamic between the master (10) and slave (11) systems is given in (12).

\{\begin{matrix} D^{q} e_{i} = e_{i + 1}, 1 \leq i \leq n - 1 \\ D^{q} e_{n} = σ_{0}^{T} E + + g (y (t - τ_{2})) - f (x (t - τ_{1})) \\ + ∆ g (y (t), t) - ∆ f (x (t), t) + d_{2} (t) - d_{1} (t) + φ (u (t)) \end{matrix},

(12)

For system (11), Mittag-Leffler stability lemmas of fractional order type and asymptotic stability lemmas will be developed and proved, providing a theoretical foundation for demonstrating the performance of the suggested controllers.

Assumption 1:

In master and slave systems, uncertain external distortions

d_{1} (t) . d_{2} (t)

as well as unknown bounded nonlinear uncertainties

∆ f (x (t) . t)

and

∆ g (x (t) . t)

satisfy the following conditions:

‖∆ f (x (t) . t)‖ \leq β_{1} ω_{1} (x), ‖∆ g (y (t) . t)‖ \leq β_{2} ω_{2} (y), ‖d_{1} (t)‖ \leq ρ_{1} ‖d_{2} (t)‖ \leq ρ_{2} {\underline{τ}}_{1} \leq τ_{1} \leq {\bar{τ}}_{1} {\underline{τ}}_{2} \leq τ_{2} \leq {\bar{τ}}_{2}

(13)

So that

‖\cdot‖

indicates norm of

l_{1}

, and

β_{2} . β_{1} . γ_{2} . γ_{1}

are definite positive real values and

ω_{2} (\cdot) . ω_{1} (\cdot)

are definite functions in general.

Definition 1:

f (x, t)

is piecewise continuous at t and meets the Lipschitz condition, then [36]:

‖f (t . x) - f (t . z)‖ \leq γ_{f} ‖x - z‖ . \forall x, z \in R^{n}

(14)

Then,

f (x, t)

is Lipschitz at

x

and the positive constant,

γ_{f}

, is called the Lipschitz constant.

Assumption 2

: The unknown time delays presented by nonlinear functions

f (x (t - τ_{1}), t) . g (y (t - τ_{2}), t) \in R

and represented in general forms of (10) and (11) in the chaotic master and slave systems satisfy the Lipschitz conditions for each

x (t), y (t) \in R

and considering (14):

|f (x (t - τ_{1})) - f (x (t - {\hat{τ}}_{1}))| \leq m_{1} ‖x (t - τ_{1}) - x (t - {\hat{τ}}_{1})‖ \leq l_{1} |(t - τ_{1}) - (t - {\hat{τ}}_{1})| = l_{1} |τ_{1} - {\hat{τ}}_{1}| = l_{1} |{\tilde{τ}}_{1}| . |g (y (t - τ_{2})) - g (y (t - {\hat{τ}}_{2}))| \leq m_{2} ‖y (t - τ_{2}) - y (t - {\hat{τ}}_{2})‖ \leq l_{2} |(t - τ_{2}) - (t - {\hat{τ}}_{2})| = l_{2} |τ_{2} - {\hat{τ}}_{2}| = l_{2} |{\tilde{τ}}_{2}| .

(15)

Such that

τ_{1} . τ_{2} \in R

represents unknown time delays,

{\hat{τ}}_{1} . {\hat{τ}}_{2} \in R

represents estimate of unknown time delays, and

l_{1} . m_{1}

and

{l_{2} . m}_{2}

are unknown positive constants.

4. Calculating the Control Signal

If the system is in sliding mode, the following conditions should be met:

s (t) = 0, D^{q} s (t) = 0 s (t) = h (e) \cdot [k_{p} e_{n} (t) + T_{I} D^{- λ} \sum_{i = 1}^{n} k_{1 i} e_{i} + T_{d} D^{δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t)] = 0

(16)

Therefore, the sliding surface fractional order derivative in (16) is as follows.

D^{q} s (t) = k_{0} k_{p} D^{q} e_{n} (t) + k_{0} T_{i} D^{q - λ} \sum_{i = 1}^{n} k_{1 i} e_{i} (t) + k_{0} T_{d} D^{q + δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t) + (1 - k_{0}) k_{p} D^{q} (‖E (t)‖ e_{n} (t)) + (1 - k_{0}) T_{I} D^{q} (‖E (t)‖ D^{- λ} \sum_{i = 1}^{n} k_{1 i} e_{i} (t)) + (1 - k_{0}) T_{d} D^{q} (‖E (t)‖ D^{δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t)) = 0

(17)

In this case, the last dynamic of the fractional order system error, defined in (12) is substituted in (17):

D^{q} s (t) = k_{0} k_{p} (g (y (t - τ_{2}), t) + ∆ g (x (t), t) + d_{2} (t) - (f (x (t - τ_{1}), t) + ∆ f (x (t), t) + d_{1} (t)) + σ_{0}^{T} \cdot E (t) + u (t)) + k_{0} T_{i} D^{1 - λ} \sum_{i = 1}^{n} k_{1 i} e_{i} (t) + k_{0} T_{d} D^{1 + δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t) + (1 - k_{0}) k_{p} D^{q} (‖E (t)‖ e_{n} (t)) + (1 - k_{0}) T_{I} D^{q} (‖E (t)‖ D^{- λ} \sum_{i = 1}^{n} k_{1 i} e_{i} (t)) + (1 - k_{0}) T_{d} D^{q} (‖E (t)‖ D^{δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t)) = 0

(18)

Such that is defined as in (18):

u (t) = \frac{- 1}{k_{0} k_{p}} (k_{0} T_{i} D^{q - λ} \sum_{i = 1}^{n} k_{1 i} e_{i} (t) + k_{0} T_{d} D^{q + δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t) + (1 - k_{0}) k_{p} D^{q} (‖E (t)‖ e_{n} (t)) + (1 - k_{0}) T_{I} D^{q} (‖E (t)‖ D^{- λ} \sum_{i = 1}^{n} k_{1 i} e_{i} (t)) + (1 - k_{0}) T_{d} D^{q} (‖E (t)‖ D^{δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t))) + f (x (t - {\hat{τ}}_{1}), t) - g (y (t - {\hat{τ}}_{2}), t) - σ_{0}^{T} \cdot E (t) - b (s + s g n (s) {|s|}^{μ}) + \bar{u} (t), μ \in (0,1)

(19)

\bar{u} (t)

is defined as follows:

\bar{u} (t) = - s g n (s) [{\hat{β}}_{2} ω_{2} (y) + {\hat{β}}_{1} ω_{1} (x) + {\hat{ρ}}_{2} + {\hat{ρ}}_{1})] + u_{00} (t) u_{00} (t) = - \frac{b}{k_{0} k_{p} s} \sum_{i = 1}^{2} [{(|{\hat{ρ}}_{i}| + {\bar{ρ}}_{i})}^{2} + {(|{\hat{τ}}_{i}| + {\bar{τ}}_{i})}^{2} + {(|{\hat{β}}_{i}| + {\bar{β}}_{i})}^{2} + {(|{\hat{ρ}}_{i}| + {\bar{ρ}}_{i})}^{μ} + {(|{\hat{τ}}_{i}| + {\bar{τ}}_{i})}^{μ} + {(|{\hat{β}}_{i}| + {\bar{β}}_{i})}^{μ}],

(20)

(20) includes terms resulting from estimation of system uncertainties that are updated using the adaptive controller described in the next section. Thus, according to (13) in which the uncertainty bound is defined,

{\bar{β}}_{i}

{\bar{ρ}}_{i}

and

{\bar{τ}}_{i}

are the upper bound of uncertainty, disturbance, and time delay in master and slave systems.

5. Proof of Stability and Update Rules

In this section, we will develop a robust adaptive controller employing a non-linear fractional order PID-based sliding surface in such a way that the suggested control strategy ensures the stability of the synchronization process of the aforementioned chaotic systems.

Theorem 2-5:

Synchronization of the systems (10) and (11) is assured despite the disturbances

d_{1}

and

d_{2}

and the unknown uncertainties

∆ f

and

∆ g

, as well as the unknown time delay

τ_{1}

and

τ_{2}

with the controller definition

u (t)

as follows:

u (t) = - g (y (t - {\hat{τ}}_{1})) + f (x (t - {\hat{τ}}_{2})) - \frac{1}{k_{0} k_{p}} (k_{0} T_{l} D^{q - λ} \sum_{i = 1}^{n} k_{1 i} e_{i} (t) + k_{0} T_{d} D^{q + δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t) + (1 - k_{0}) k_{p} D^{q} (‖E (t)‖ e_{n} (t)) + (1 - k_{0}) T_{I} D^{q} (‖E (t)‖ D^{- λ} \sum_{i = 1}^{n} k_{1 i} e_{i} (t)) + (1 - k_{0}) T_{d} D^{q} (‖E (t)‖ D^{δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t))) - σ_{0}^{T} \cdot E (t) - b (s + s g n (s) {|s|}^{μ}) - s g n (s) ({\hat{β}}_{2} ω_{2} (y) + {\hat{β}}_{1} ω_{1} (x) + {\hat{ρ}}_{2} + {\hat{ρ}}_{1}) {+ u}_{00} (t)

(21)

where

{\hat{ρ}}_{1}

and

{\hat{ρ}}_{2}

are estimates of the input disturbance bounds,

{\hat{τ}}_{1}

and

{\hat{τ}}_{2}

are estimates of time delays, and

{\hat{β}}_{1}

and

{\hat{β}}_{2}

are estimates of the uncertainty bounds in the master and slave systems. Furthermore,

{\bar{ρ}}_{i}

{\bar{τ}}_{i}

, and

{\bar{β}}_{i}

represent the upper bounds of disturbance, time delay, and uncertainty, respectively. As a result, in order to ensure the system’s stability, we apply the update rules to estimate the mentioned parameters:

D^{q} {\hat{τ}}_{i} = {- D}^{q} {\tilde{τ}}_{i} = l_{i} |s| s g n ({\tilde{τ}}_{i}), {\hat{τ}}_{i} (0) = {\bar{τ}}_{i} D^{q} {\hat{ρ}}_{i} = {- D}^{q} {\tilde{ρ}}_{i} = k_{0} k_{p} |s| D^{q} {\hat{β}}_{1} = {- D}^{q} {\tilde{β}}_{1} = - k_{0} k_{p} |s| ω_{1} (x) D^{q} {\hat{β}}_{2} = {- D}^{q} {\tilde{β}}_{2} = - k_{0} k_{p} |s| ω_{2} (y)

(22)

l_{i}

is a positive constant number in the above relationship. Furthermore,

{\tilde{τ}}_{i}

{\tilde{ρ}}_{i}

, and

{\tilde{β}}_{i}

represent the estimation error of time delay, disturbance, and uncertainty, respectively. The update rules for delays are based on estimation errors, which are not available. You can overcome this problem by doing the following:

Given that:

0 < \underline{τ_{i}} < τ_{i} < \bar{τ_{i}}

such that

\bar{τ_{i}}

is the upper bound and

\underline{τ_{i}}

is the lower bound of the time delay. As a result of selecting

{\hat{τ}}_{i} (0) = \bar{τ_{i}}

), we have:

{\tilde{τ}}_{i} (0) = τ_{i} - {\hat{τ}}_{i} (0) = τ_{i} - \bar{τ} < 0 \Rightarrow s g n ({\tilde{τ}}_{i}) = - 1

By defining

v_{{\tilde{τ}}_{i}} = \frac{1}{2} {\tilde{τ}}_{i}^{2}

and calculating its derivative:

{D^{q} v}_{{\tilde{τ}}_{i}} \leq {\tilde{τ}}_{i} D^{q} {\tilde{τ}}_{i} = {\tilde{τ}}_{i} l_{i} |s| s g n ({\tilde{τ}}_{i}) = {- l}_{i} |{\tilde{τ}}_{i}| |s| < 0

(23)

Therefore,

v_{{\tilde{τ}}_{i}}

is a descending function that tends to zero, thus:

\forall t \geq 0 : {\tilde{τ}}_{i} < 0 \Rightarrow s g n ({\tilde{τ}}_{i}) = - 1

Thus, the update rules for time delays would be as follows:

D^{q} {\hat{τ}}_{i} = l_{i} |s| s g n ({\tilde{τ}}_{i}) = - l_{i} |s|, {\hat{τ}}_{i} (0) = \bar{τ_{i}}, i = 1.2

(24)

We will now investigate the stability of the controlled fractional order system by taking into account the sliding surface using nonlinear fractional order PID controllers. The following Lyapunov function is introduced for the sliding surface given in relation (5-9).

v (t) = \frac{1}{2} [s^{2} (t) + {\tilde{β}}_{1}^{2} + {\tilde{β}}_{2}^{2} + {\tilde{τ}}_{1}^{2} + {\tilde{τ}}_{2}^{2} + {\tilde{ρ}}_{1}^{2} + {\tilde{ρ}}_{2}^{2}]

(25)

According to (21), derivative of the Lyapunov function would be as follows:

\to D^{q} v (t) = \frac{1}{2} D^{q} (s^{2} + {\tilde{β}}_{1}^{2} + {\tilde{β}}_{2}^{2} + {\tilde{τ}}_{1}^{2} + {\tilde{τ}}_{2}^{2} + {\tilde{ρ}}_{1}^{2} + {\tilde{ρ}}_{2}^{2}) \leq s \cdot D^{q} s + \sum_{i = 1}^{2} ({\tilde{β}}_{i} D^{q} {\tilde{β}}_{i} + {\tilde{τ}}_{i} D^{q} {\tilde{τ}}_{i} + {\tilde{ρ}}_{i} D^{q} {\tilde{ρ}}_{i})

(26)

By applying (22) in (26), the above derivative is extended as follows:

D^{q} v (t) \leq s \cdot [k_{0} k_{p} (g (y (t - τ_{2}), t) + ∆ g (x (t), t) + d_{2} (t) - (f (x (t - τ_{1}), t) + ∆ f (x (t), t) + d_{1} (t)) + σ_{0}^{T} \cdot E (t) + u (t)) + k_{0} T_{i} D^{q - λ} \sum_{i = 1}^{n} k_{1 i} e_{i} (t) + k_{0} T_{d} D^{q + δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t) + (1 - k_{0}) k_{p} D^{q} (‖E (t)‖ e_{n} (t)) + (1 - k_{0}) T_{I} D^{q} (‖E (t)‖ D^{- λ} \sum_{i = 1}^{n} k_{1 i} e_{i} (t)) + (1 - k_{0}) T_{d} D^{q} (‖E (t)‖ D^{δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t)) + u_{00} (t)] + \sum_{i = 1}^{2} ({\tilde{β}}_{i} D^{q} {\tilde{β}}_{i} + {\tilde{τ}}_{i} D^{q} {\tilde{τ}}_{i} + {\tilde{ρ}}_{i} D^{q} {\tilde{ρ}}_{i})

(27)

In this case, the Lyapunov function derivative is as follows:

D^{q} v (t) \leq s \cdot [k_{0} k_{p} (g (y (t - τ_{2}), t) - g (y (t - {\hat{τ}}_{2}), t) + ∆ g (x (t), t) + d_{2} (t) + f (x (t - {\hat{τ}}_{1}), t) - f (x (t - τ_{1}), t) - ∆ f (x (t), t) - d_{1} (t) - \frac{b}{k_{0} k_{p}} (s + s g n (s) {|s|}^{μ}) - s g n (s) [{\hat{β}}_{2} ω_{2} (y) + {\hat{β}}_{1} ω_{1} (x) + {\hat{ρ}}_{2} + {\hat{ρ}}_{1})])] + s k_{0} k_{p} u_{00} (t) + \sum_{i = 1}^{2} ({\tilde{β}}_{i} D^{q} {\tilde{β}}_{i} + {\tilde{τ}}_{i} D^{q} {\tilde{τ}}_{i} + {\tilde{ρ}}_{i} D^{q} {\tilde{ρ}}_{i})

(28)

Thus, we have:

D^{q} v (t) \leq |s| \cdot [k_{0} k_{p} (|g (y (t - τ_{2}), t) - g (y (t - {\hat{τ}}_{2}), t)| + |∆ g (x (t), t)| + |f (x (t - {\hat{τ}}_{1}), t) - f (x (t - τ_{1}), t)| + |∆ f (x (t), t)| + |d_{2} (t) - d_{1} (t)|)] - b (s^{2} + {|s|}^{μ + 1}) + k_{0} k_{p} s (- s g n (s) [{\hat{β}}_{2} ω_{2} (y) + {\hat{β}}_{1} ω_{1} (x) + {\hat{ρ}}_{2} + {\hat{ρ}}_{1})]) - b (\sum_{i = 1}^{2} [{(|{\hat{ρ}}_{i}| + {\bar{ρ}}_{i})}^{2} + {(|{\hat{τ}}_{i}| + {\bar{τ}}_{i})}^{2} + {(|{\hat{β}}_{i}| + {\bar{β}}_{i})}^{2} + {(|{\hat{ρ}}_{i}| + {\bar{ρ}}_{i})}^{μ} + {(|{\hat{τ}}_{i}| + {\bar{τ}}_{i})}^{μ} + {(|{\hat{β}}_{i}| + {\bar{β}}_{i})}^{μ}]) + \sum_{i = 1}^{2} ({\tilde{β}}_{i} D^{q} {\tilde{β}}_{i} + {\tilde{τ}}_{i} D^{q} {\tilde{τ}}_{i} + {\tilde{ρ}}_{i} D^{q} {\tilde{ρ}}_{i})

(29)

Relationship (29) will be recast as follows, based on assumptions 1 and 2 stated in relations (14) and (15):

D^{q} v (t) \leq |s| \cdot [k_{0} k_{p} (l_{2} |τ_{2} - {\hat{τ}}_{2}| + β_{2} ω_{2} (y) + l_{1} |τ_{1} - {\hat{τ}}_{1}| - β_{1} ω_{1} (x) + ρ_{1} + ρ_{2})] - b (s^{2} + {|s|}^{μ + 1}) + k_{0} k_{p} s ((- s g n (s) [{\hat{β}}_{2} ω_{2} (y) + {\hat{β}}_{1} ω_{1} (x) + {\hat{ρ}}_{2} + {\hat{ρ}}_{1})])) - b (\sum_{i = 1}^{2} [{(|{\hat{ρ}}_{i}| + {\bar{ρ}}_{i})}^{2} + {(|{\hat{τ}}_{i}| + {\bar{τ}}_{i})}^{2} + {(|{\hat{β}}_{i}| + {\bar{β}}_{i})}^{2} + {(|{\hat{ρ}}_{i}| + {\bar{ρ}}_{i})}^{μ} + {(|{\hat{τ}}_{i}| + {\bar{τ}}_{i})}^{μ} + {(|{\hat{β}}_{i}| + {\bar{β}}_{i})}^{μ}]) + \sum_{i = 1}^{2} ({\tilde{β}}_{i} D^{q} {\tilde{β}}_{i} + l_{i} {\tilde{τ}}_{i} D^{q} {\tilde{τ}}_{i} + {\tilde{ρ}}_{i} D^{q} {\tilde{ρ}}_{i})

(30)

The derivative of the Lyapunov function would be as follows:

D^{q} v (t) \leq |s| [k_{0} k_{p} (l_{1} |{\tilde{τ}}_{1}| + {\tilde{β}}_{2} ω_{2} (y) + l_{2} |{\tilde{τ}}_{2}| + {\tilde{β}}_{1} ω_{1} (x) + {\hat{ρ}}_{2} + {\hat{ρ}}_{1})] - b (s^{2} + {|s|}^{μ + 1}) - b (\sum_{i = 1}^{2} [{(|{\hat{ρ}}_{i}| + {\bar{ρ}}_{i})}^{2} + {(|{\hat{τ}}_{i}| + {\bar{τ}}_{i})}^{2} + {(|{\hat{β}}_{i}| + {\bar{β}}_{i})}^{2} + {(|{\hat{ρ}}_{i}| + {\bar{ρ}}_{i})}^{μ} + {(|{\hat{τ}}_{i}| + {\bar{τ}}_{i})}^{μ} + {(|{\hat{β}}_{i}| + {\bar{β}}_{i})}^{μ}]) + \sum_{i = 1}^{2} ({\tilde{β}}_{i} D^{q} {\tilde{β}}_{i} + {\tilde{τ}}_{i} D^{q} {\tilde{τ}}_{i} + {\tilde{ρ}}_{i} D^{q} {\tilde{ρ}}_{i})

(31)

At this point, the update rules described in (22) are used to estimate the system parameters in relation (29). On the other hand:

|{\tilde{τ}}_{i}| = |τ_{i} - {\hat{τ}}_{i}| \leq |τ_{i}| + |{\hat{τ}}_{i}| \leq |{\hat{τ}}_{i}| + {\bar{τ}}_{i} \Rightarrow - {(|{\hat{τ}}_{i}| + {\bar{τ}}_{i})}^{2} \leq {- |{\tilde{τ}}_{i}|}^{2}

(32)

That relationship (32) can also be extended for

{\tilde{ρ}}_{i}

and

{\tilde{β}}_{i}

. In this case, the Lyapunov function derivative will be simplified as follows:

\Rightarrow D^{q} v (t) \leq - b ({|s|}^{2} + \sum_{i = 1}^{2} [{|{\tilde{β}}_{i}|}^{2} + {|{\tilde{τ}}_{i}|}^{2} + {|{\tilde{ρ}}_{i}|}^{2}]) - b ({|s|}^{1 + μ} + \sum_{i = 1}^{2} [{|{\tilde{β}}_{i}|}^{1 + μ} + {|{\tilde{τ}}_{i}|}^{1 + μ} + {|{\tilde{ρ}}_{i}|}^{1 + μ}])

(33)

\Rightarrow D^{q} v (t) \leq - b ({|s|}^{2} + \sum_{i = 1}^{2} [{|{\tilde{β}}_{i}|}^{2} + {|{\tilde{τ}}_{i}|}^{2} + {|{\tilde{ρ}}_{i}|}^{2}]) - b 2^{\frac{1 + μ}{2}} {(\frac{{|s|}^{2} + \sum_{i = 1}^{2} [{|{\tilde{β}}_{i}|}^{2} + {|{\tilde{τ}}_{i}|}^{2} + {|{\tilde{ρ}}_{i}|}^{2}] 1}{2})}^{\frac{1 + μ}{2}} \leq - b v - b 2^{\frac{1 + μ}{2}} v^{\frac{1 + μ}{2}}

(34)

Its finite-time stability is demonstrated for a chaotic considering the PID sliding surface and nonlinear fractional order derivative.

For boundedness, the control signal is modified as follows:

u (t) = - g (y (t - {\hat{τ}}_{1})) + f (x (t - {\hat{τ}}_{2})) - \frac{1}{k_{0} k_{p}} (k_{0} T_{l} D^{q - λ} \sum_{i = 1}^{n} k_{1 i} e_{i} (t) + k_{0} T_{d} D^{q + δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t) + (1 - k_{0}) k_{p} D^{q} (‖E (t)‖ e_{n} (t)) + (1 - k_{0}) T_{I} D^{q} (‖E (t)‖ D^{- λ} \sum_{i = 1}^{n} k_{1 i} e_{i} (t)) + (1 - k_{0}) T_{d} D^{q} (‖E (t)‖ D^{δ} \sum_{i = 1}^{n} k_{2 i} e_{i} (t))) - σ_{0}^{T} \cdot E (t) - b (s + s g n (s) {|s|}^{μ}) - s g n (s) ({\hat{β}}_{2} ω_{2} (y) + {\hat{β}}_{1} ω_{1} (x) + {\hat{ρ}}_{2} + {\hat{ρ}}_{1}) - \frac{b s}{k_{0} k_{p} (s^{2} + ϵ)} (\sum_{i = 1}^{2} [{(|{\hat{ρ}}_{i}| + {\bar{ρ}}_{i})}^{2} + {(|{\hat{τ}}_{i}| + {\bar{τ}}_{i})}^{2} + {(|{\hat{β}}_{i}| + {\bar{β}}_{i})}^{2} + {(|{\hat{ρ}}_{i}| + {\bar{ρ}}_{i})}^{μ} + {(|{\hat{τ}}_{i}| + {\bar{τ}}_{i})}^{μ} + {(|{\hat{β}}_{i}| + {\bar{β}}_{i})}^{μ}])

(35)

In which,

ϵ

is a small positive number.

Adaptive rules should be updated to increase their robustness to uncertainty and disturbance. These changes are possible in a variety of ways. The law of sigma correction is one of these ways.

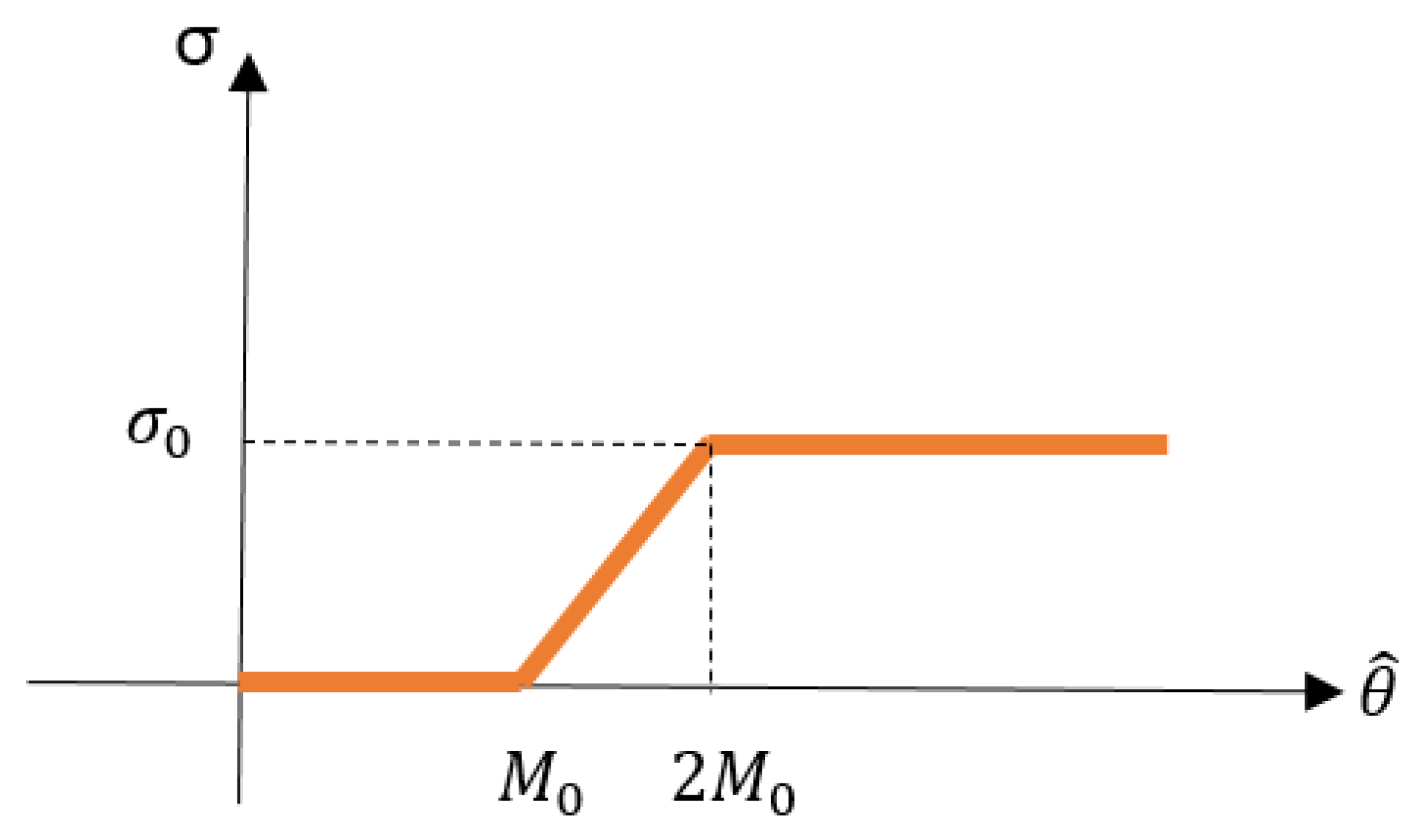
The Sigma function represented in Figure 1 is defined as follows:

σ (t) = \{\begin{matrix} 0 i f |\hat{θ} (t)| \leq M_{0} \\ {(|\hat{θ} (t)| / M_{0} - 1)}^{n} σ_{0} i f M_{0} < |\hat{θ} (t)| \leq {2 M}_{0} \\ σ_{0} i f |\hat{θ} (t)| \geq {2 M}_{0} \end{matrix}

(36)

The presence of uncertainty and disturbance in the system causes a mild increase in estimations in the controller under investigation, which can be dealt with utilizing the sigma correction approach. As a result, the following are the update rules of the estimation of delays and the disturbance and uncertainty bounds:

D^{q} {\hat{τ}}_{i} = - l_{i} |s| - σ_{0} (|{\hat{τ}}_{i}|) {\hat{τ}}_{i}, {\hat{τ}}_{i} (0) = \bar{τ_{i}}, i = 1.2 D^{q} {\hat{ρ}}_{i} = k_{0} k_{p} |s| - σ_{0} (|{\hat{ρ}}_{i}|) {\hat{ρ}}_{i}, i = 1.2 D^{q} {\hat{β}}_{1} = - k_{0} k_{p} |s| ω_{1} (x) - σ_{0} (|{\hat{β}}_{1}|) {\hat{β}}_{1}, D^{q} {\hat{β}}_{2} = - k_{0} k_{p} |s| ω_{2} (y) - σ_{0} (|{\hat{β}}_{2}|) {\hat{β}}_{2},

(37)

[] (new article going to be released) describes in full the proof of error convergence to zero in the condition that the sliding surface tends to zero.

6. Simulation Results

Consider the master and slave system with disturbance, uncertainty, unknown parameter and time delay for a fractional order Gensou-Tsei system as follows:

\begin{matrix} {{}_{0}D}_{t}^{q (t)} x_{1} (t) = x_{2} (t), \\ {{}_{0}D}_{t}^{q (t)} x_{2} (t) = x_{3} (t), \\ {{}_{0}D}_{t}^{q (t)} x_{3} (t) = - β_{1} x_{1} (t) - β_{2} (t) - β_{3} x_{3} (t) + f (x (t)), \end{matrix}

(38)

Such that

β_{1}, β_{2}, β_{3}, β_{4}

are system parameters, and

f (x (t)) = {β_{4} x}_{1}^{2} (t)

. In the presence of external disturbances, nonlinear uncertainties, parametric uncertainties, and unknown time delays, the above equations take the following form:

\begin{matrix} {{}_{0}D}_{t}^{q (t)} x_{1} (t) = x_{2} (t), \\ {{}_{0}D}_{t}^{q (t)} x_{2} (t) = x_{3} (t), \\ {{}_{0}D}_{t}^{q (t)} x_{3} (t) = - β_{1} (t) x_{1} (t) - β_{2} (t) (t) x_{2} (t) - β_{3} (t) x_{3} (t) \\ + f (x (t - τ_{1})) + ∆ f (x (t), t) + d_{1} (t), \end{matrix}

(39)

And

f (x (t - τ_{1})) = β_{4} {x_{1}}^{2} (t - τ_{1})

. Also, the slave system is presented as follows.

\begin{matrix} {{}_{0}D}_{t}^{q (t)} y_{1} (t) = y_{2} (t), \\ {{}_{0}D}_{t}^{q (t)} y_{2} (t) = y_{3} (t), \\ {{}_{0}D}_{t}^{q (t)} y_{3} (t) = - β_{1} (t) y_{1} (t) - β_{2} (t) (t) y_{2} (t) - β_{3} (t) y_{3} (t) \\ + g (y (t - τ_{2})) + ∆ g (y (t), t) + d_{2} (t) + u (t), \end{matrix}

(40)

β_{1} (t), β_{2} (t), β_{3} (t)

are parametric uncertainties, and

g (y (t - τ_{2})) = {β_{4} y_{1}}^{2} (t - τ_{2})

in the simulation process are considered as follows:

β_{i} (t) = β_{0 i} + ∆ β_{i} (t) β_{1} (t) = β_{1} + 0.3 \sin (t) \to β_{1} (t) \in [0.7 1.3], β_{2} (t) = β_{2} + 0.2 \cos (t) \to β_{2} (t) \in [0.9 1.3], β_{3} (t) = β_{3} + 0.6 \cos (t) \to β_{3} (t) \in [- 0.16 1.04] . β_{4} = 1 .

(41)

The following system disturbances and nonlinear uncertainties are considered during the simulation process:

d_{1} (t) = 0.6 \sin (t) c o s (π t), d_{2} (t) = \sin (π t) c o s (t) ∆ f (x (t), t) = 0.65 \sin (π x_{1} (t)) + 0.8 \sin (2 π x_{1} (t) x_{2} (t)) + 0.9 \sin (3 π x_{3} (t)), ∆ g (y (t), t) = 0.1 \cos (y_{1} (t) + y_{2} (t)) + 0.8 s i n (π y_{3} (t)),

(42)

The dynamic equations of the synchronization error of the fractional order chaotic system with uncertainty, unknown disturbance, and unknown time delay are defined using equations (10) and (11).

\begin{matrix} {{}_{0}D}_{t}^{q} e_{1} (t) = e_{2} (t), \\ {{}_{0}D}_{t}^{q} e_{2} (t) = e_{3} (t), \\ {{}_{0}D}_{t}^{q} e_{3} (t) = - β_{10} e_{1} (t) - β_{20} e_{2} (t) - β_{30} e_{3} (t) + g (y (t - τ_{2})) - f (x (t - τ_{1})) \\ + {∆ g}^{n e w} (y (t), t) - {∆ f}^{n e w} (x (t), t) + d_{2} (t) - d_{1} (t) + u (t) . \end{matrix}

(43)

Such that

β_{10} = 1, β_{20} = 1.1, β_{30} = 0.44

. Also:

{∆ f}^{n e w} (x (t), t) = ∆ f (x (t), t) - ∆ β_{1} (t) e_{1} (t) - ∆ β_{2} (t) e_{2} (t) - ∆ β_{3} (t) e_{3} (t)

{∆ g}^{n e w} (x (t), t) = ∆ g (x (t), t) - ∆ β_{1} (t) e_{1} (t) - ∆ β_{2} (t) e_{2} (t) - ∆ β_{3} (t) e_{3} (t)

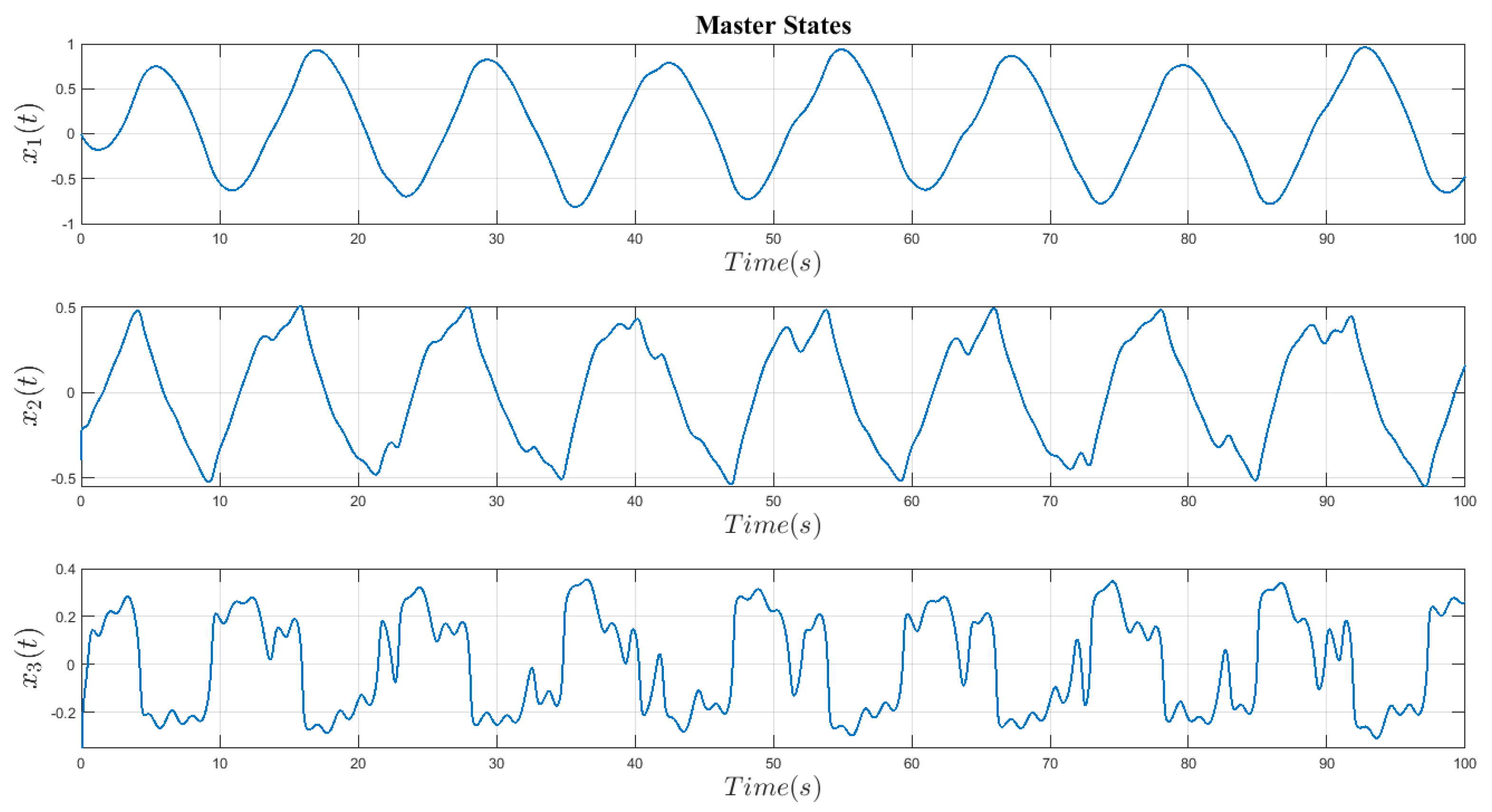
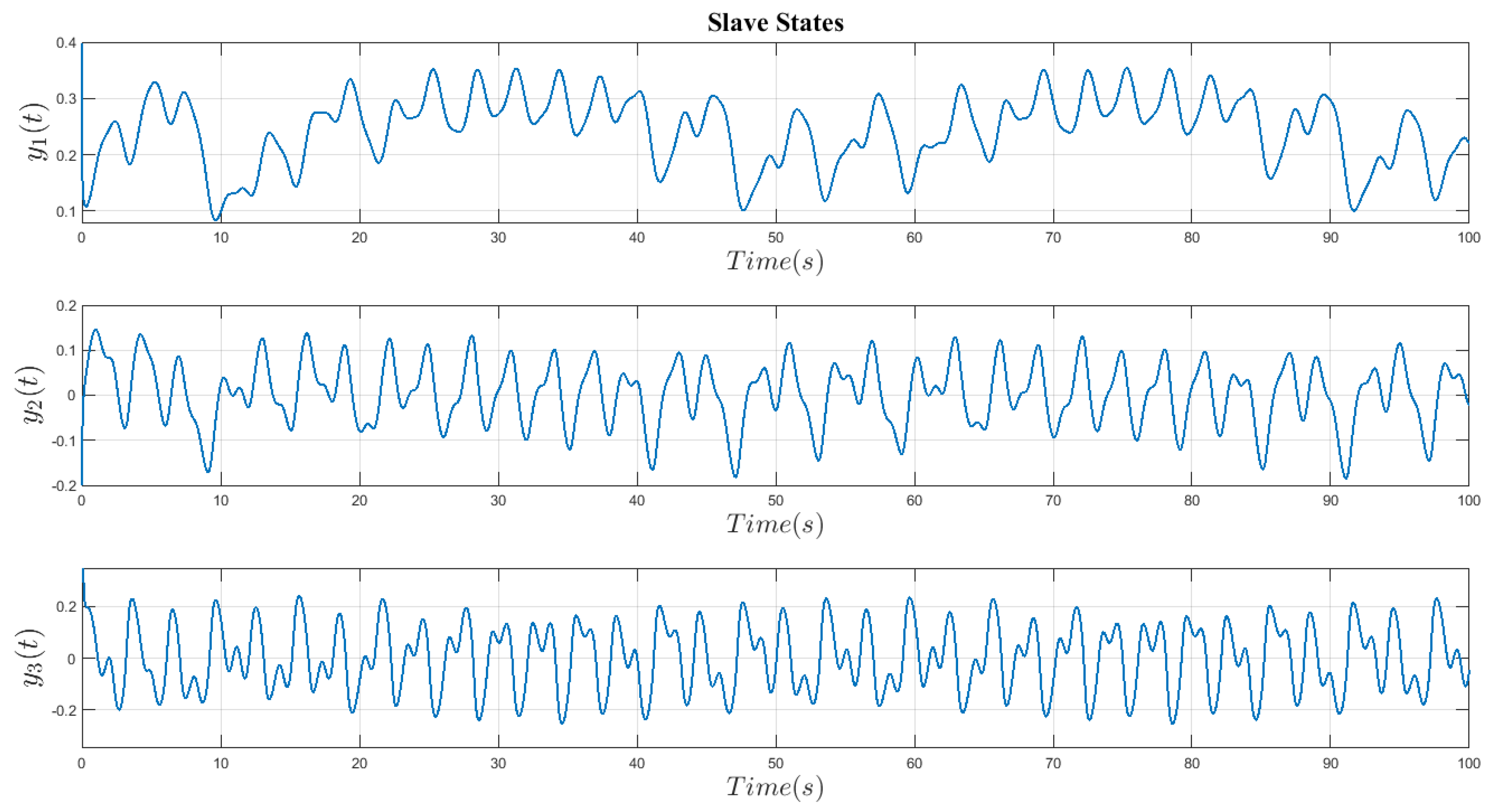
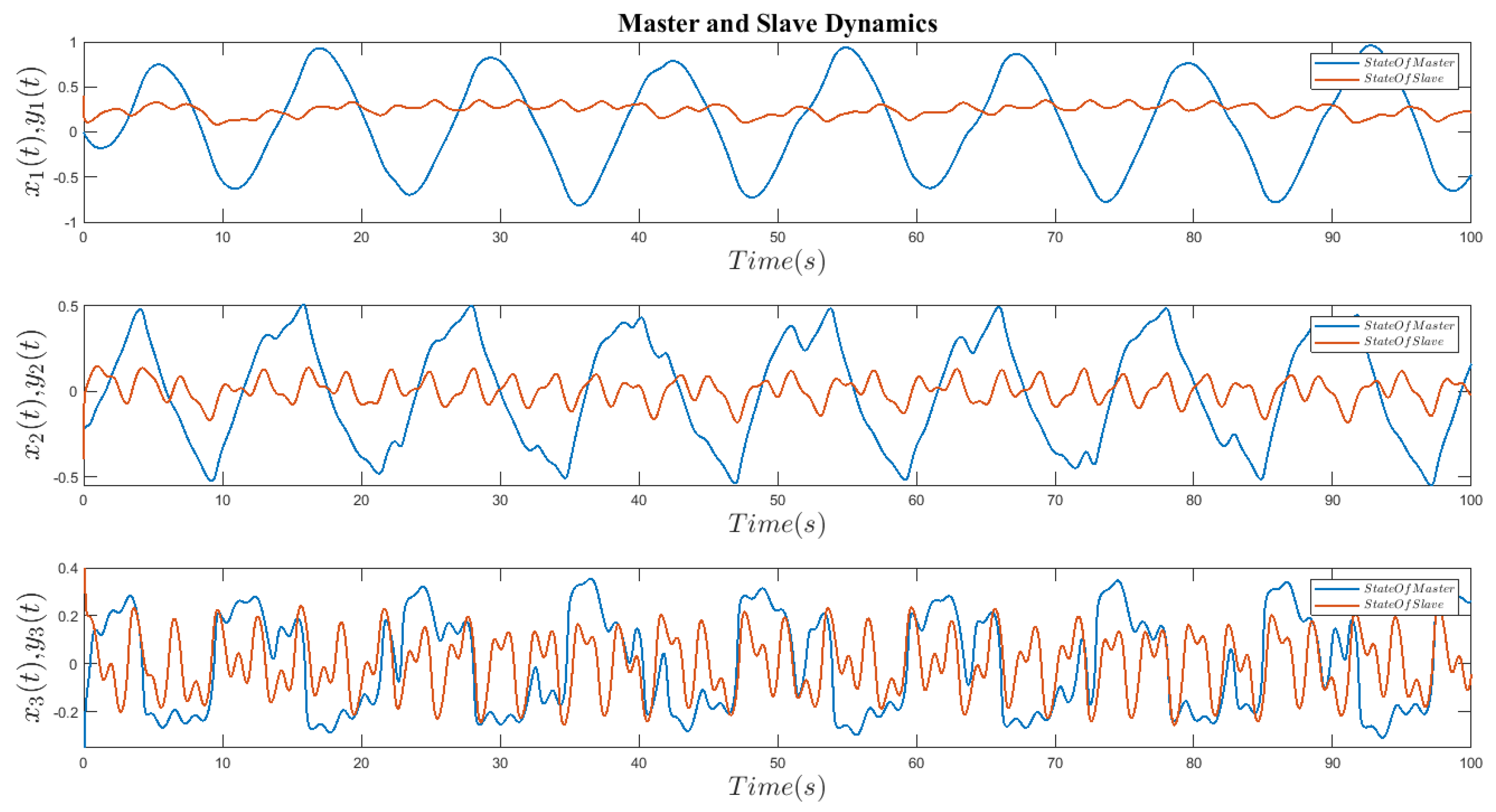
Figure 2 and Figure 3 depict the chaotic behavior of a fractional order master and slave system with time-varying parameters in the absence of controller operations.

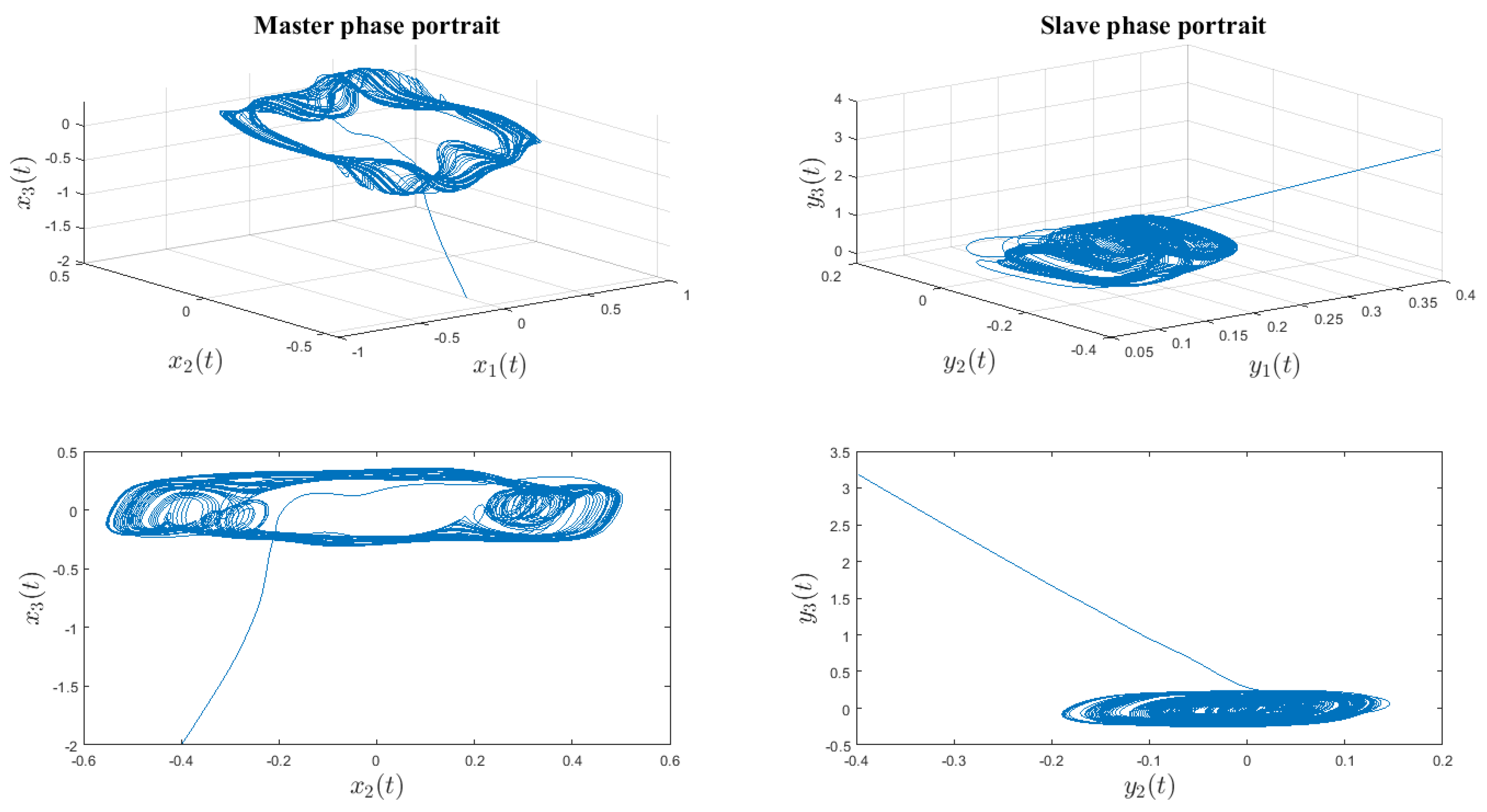
Figure 4 depicts the phase diagram of the fractional-order Gensou-Tsei system, and Figure 5 depicts the behavior of the master and slave system states separately and without controller actions. The behavior of both the master and slave systems is utterly chaotic, as demonstrated in the figures above.

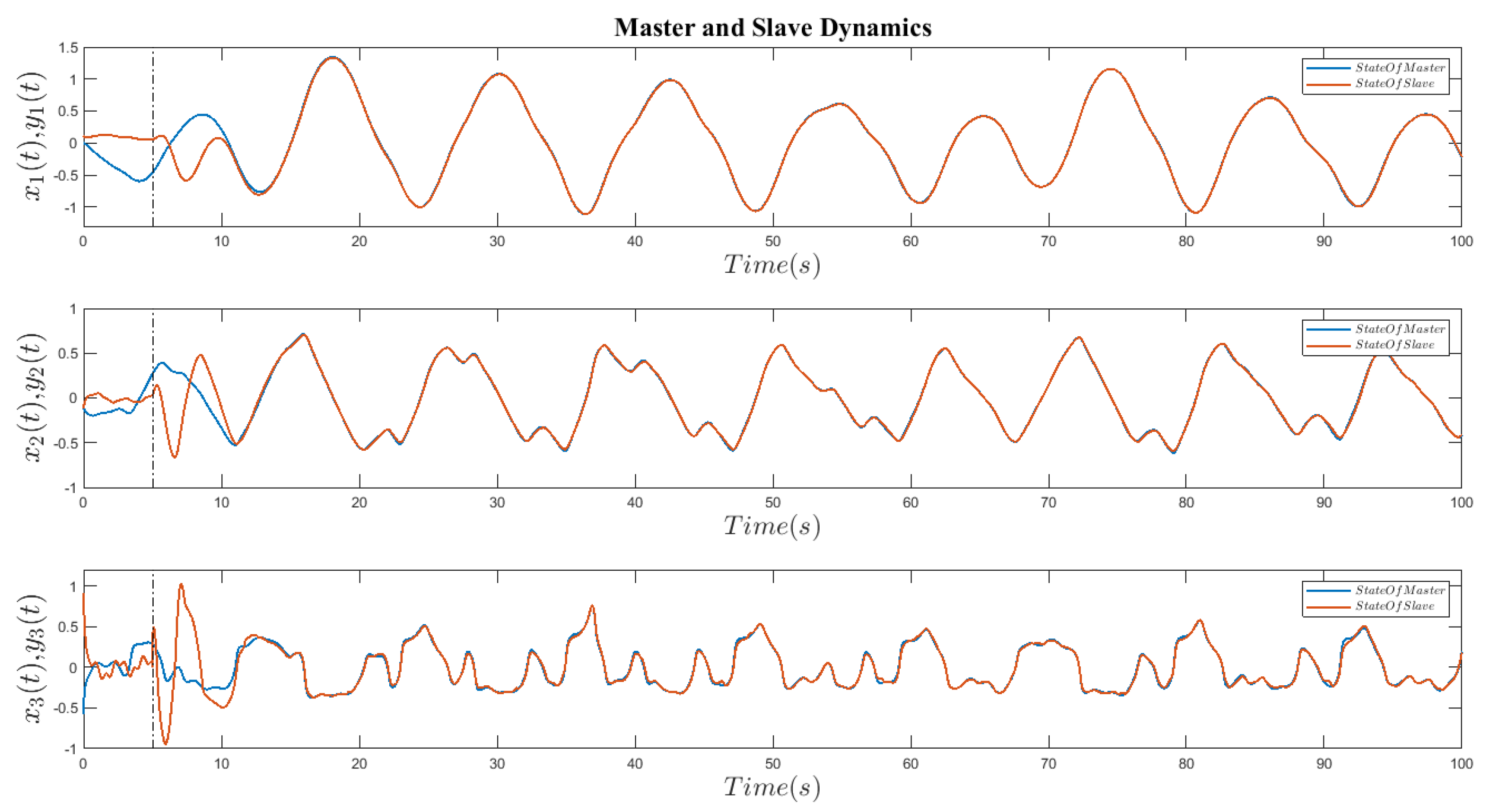
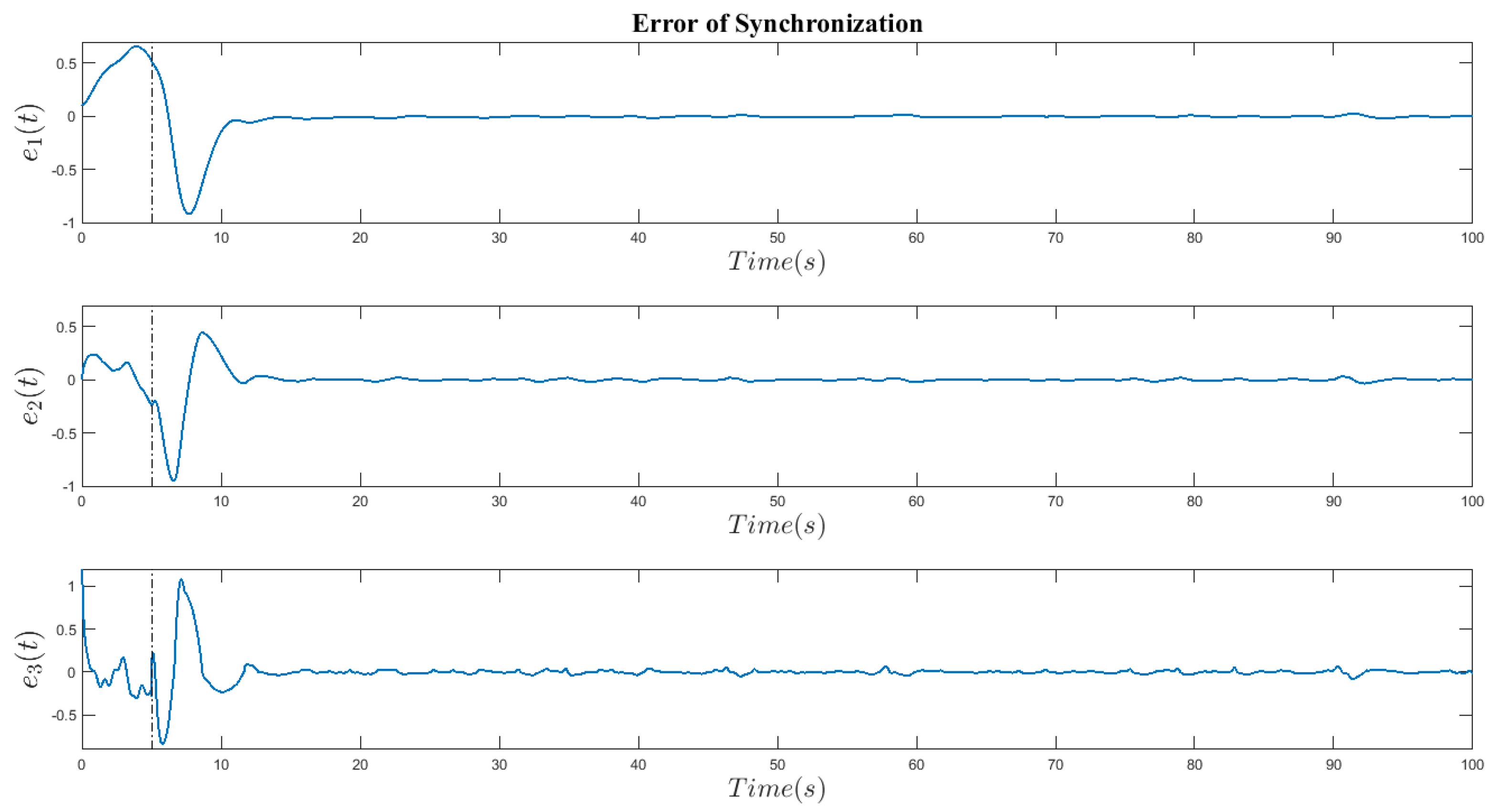
Figure 6 depicts the synchronization of the Gensou-Tsei chaotic system before and after the finite-time controller is applied. The suggested mechanism is based on adaptive sliding mode control, and its performance is such that after applying the controller, the synchronization error achieves zero at an acceptable speed, as illustrated in Figure 7.

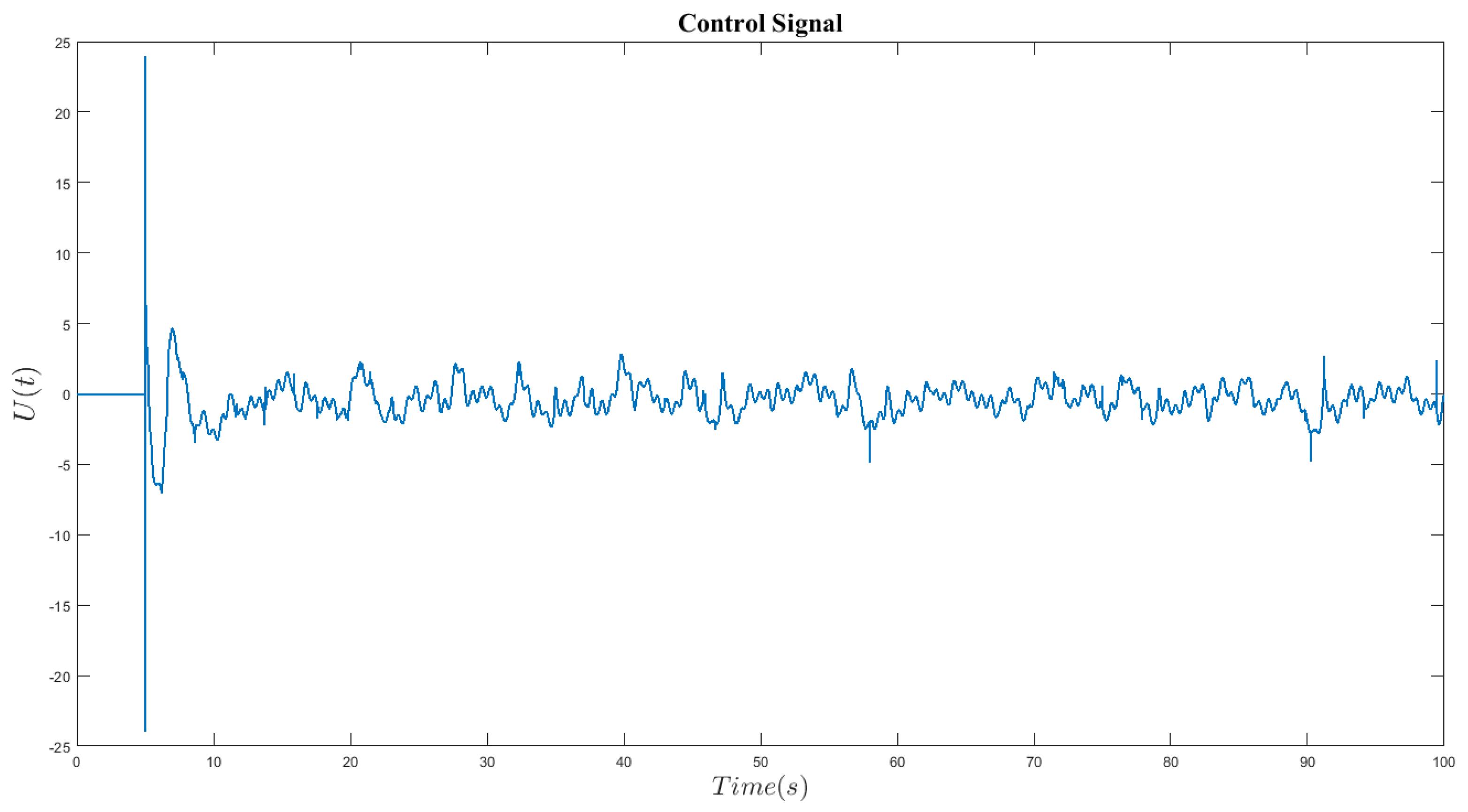
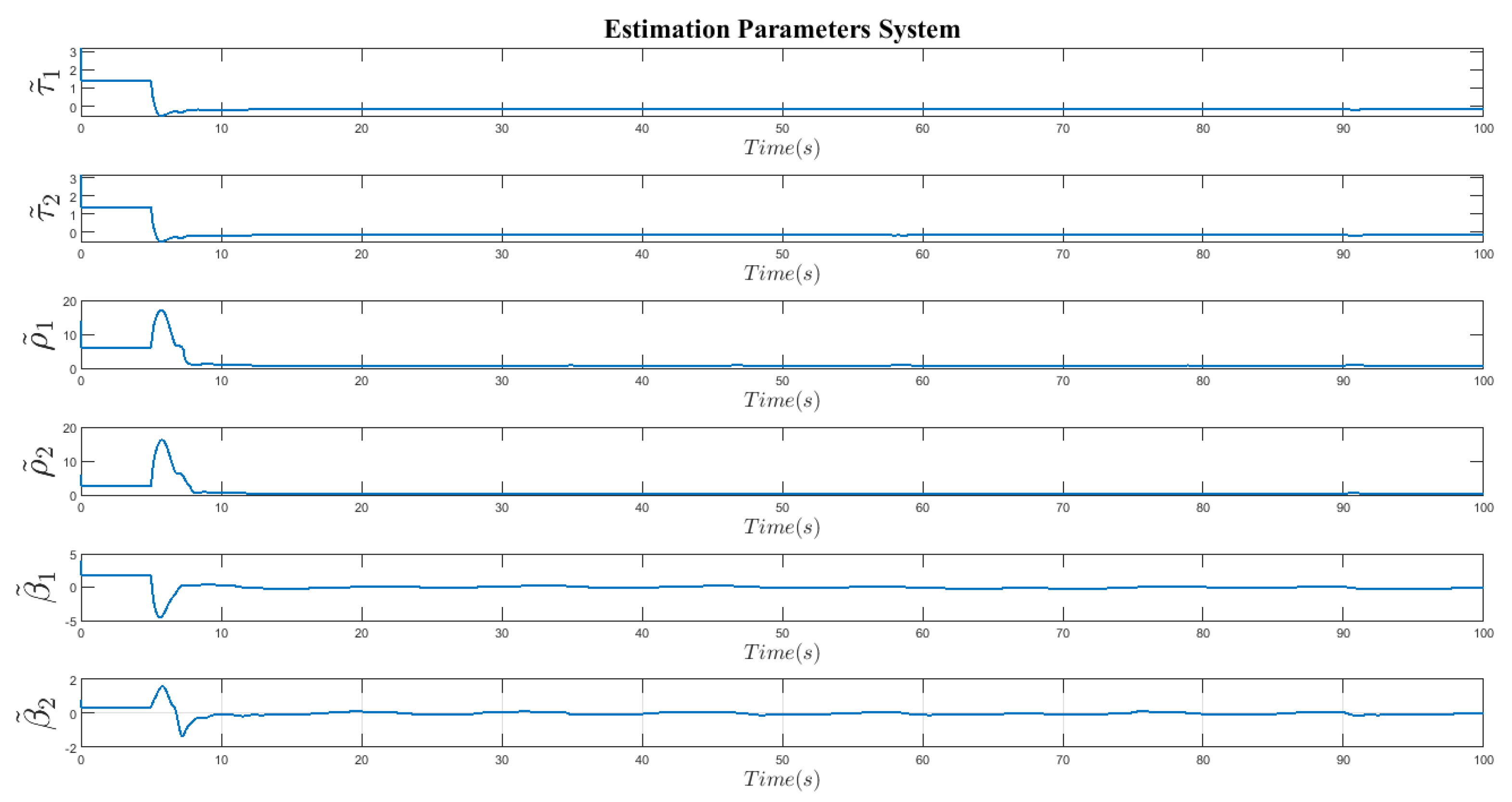
Figure 8 depicts the control signal obtained by employing the finite time scenario during the controller design process. Figure 9 depicts the estimation error of the system parameters, which has converged to zero well and rapidly, incorporating unknown uncertainties, time delays, and disturbances.

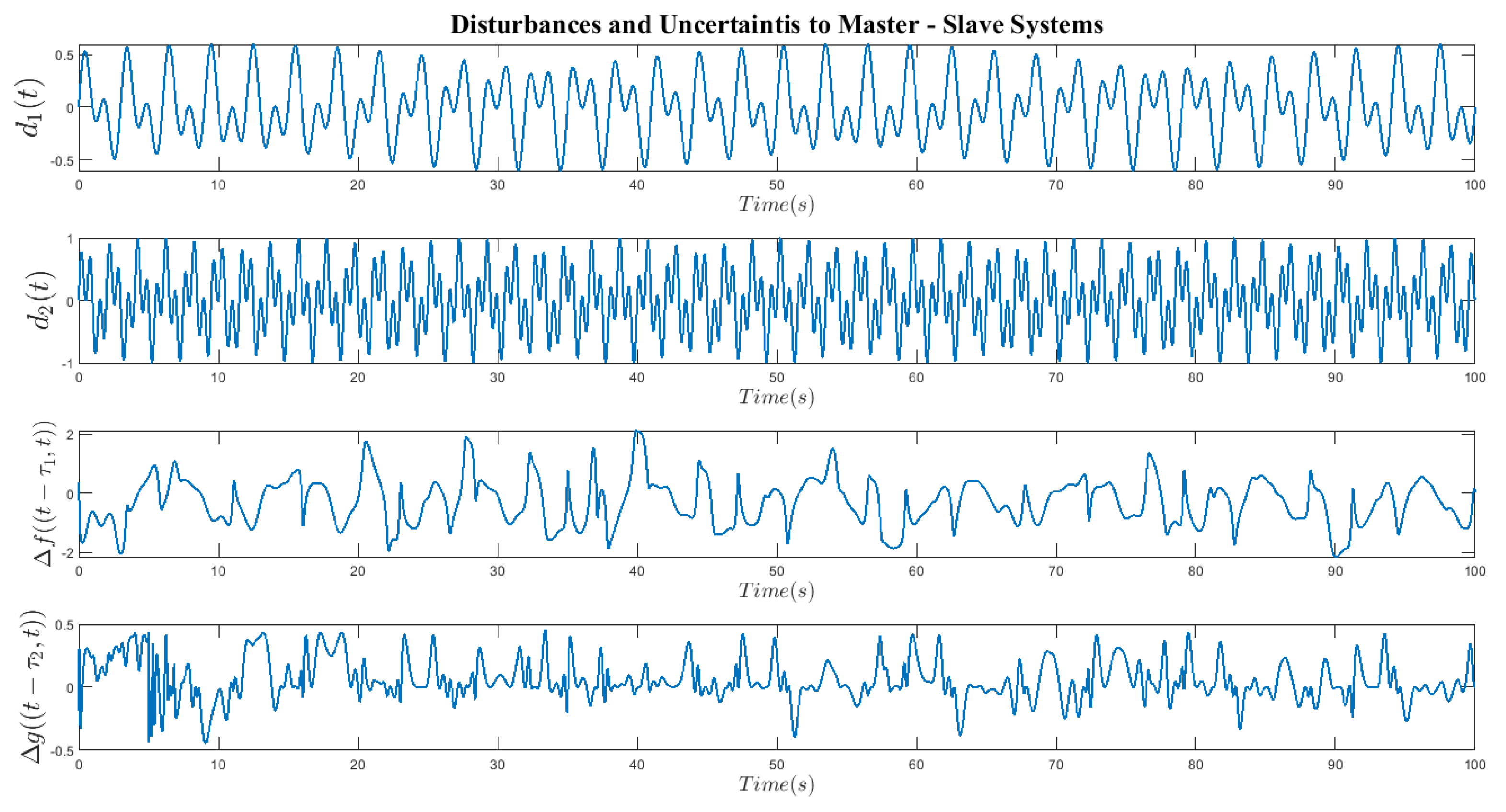
The uncertainties and disturbances in the master and slave systems are depicted in Figure 10. Despite the presence of undesired signals in Figure 10 and their imposition on the above system, the design mechanism of the above controller guarantees an effective synchronization process of the master and slave systems.

To evaluate the performance of the proposed adaptive control strategy for the robust synchronization of the systems (39) and (40), the initial conditions of the master and slave systems are set to

[0, - 0.1, - 0.5]

and

[0.1, - 0.1, 0.8],

, respectively, with time delays of

τ_{1} = 0.45 s

and

τ_{2} = 0.1 s

. At

t = 50 s

, the time delay of the master system changes to

τ_{1} = 0.3 s

, and the time delay of the slave system changes to

τ_{2} = 0.075 s

t = 60 s

. In addition, parameters

k_{3}, k_{2}, k_{1}

, and

k_{0}

are treated similarly to the preceding case. Furthermore, the upper bound. of disturbance is

{\bar{ρ}}_{1} = {\bar{ρ}}_{2} = 1

, the time delay is

{\bar{τ}}_{1} = 0.7

{\bar{τ}}_{2} = 0.5

, and the uncertainty bound of the slave system is

{\bar{β}}_{1} = 2

{\bar{β}}_{2} = 0.5

. Different simulation results are shown in (2) through (10).

Based on the simulation results in Figures 2 to 10, it is clear that using the proposed adaptive control strategy to synchronize uncertain chaotic systems with unknown time delays, disturbances, and parametric uncertainties leads to convergence of all synchronization errors. And this synchronization is of acceptable robustness. The quantity of chattering in the suggested control signal is low, indicating the optimal performance of the proposed controller. Furthermore, the error in predicting the unknown parameters of the systems depicted in Figure 9 demonstrates the efficacy of the proposed control mechanism in parameter estimation utilizing the proposed updating rules using equations (37).

References

K. Diethelm, “A fractional calculus based model for the simulation of an outbreak of dengue fever,” (in En;en), Nonlinear Dyn, vol. 71, no. 4, pp. 613–619, 2013. [CrossRef]
R. Caponetto, G. Di Pasquale, S. Graziani, E. Murgano, A. Pollicino, and C. Trigona, “Green Fractional Order Elements Based on Bacterial Cellulose and Ionic Liquids,” in 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), 2020. [Online]. [CrossRef]
“The role of fractional calculus in modeling biological phenomena: A review,” Communications in Nonlinear Science and Numerical Simulation, vol. 51, pp. 141–159, 2017. [CrossRef]
G. T. Oumbé Tékam, C. A. Kitio Kwuimy, and P. Woafo, “Analysis of tristable energy harvesting system having fractional order viscoelastic material,” Chaos, vol. 25, no. 1, p. 13112, 2015. [CrossRef]
Mohammad Pourmahmood Aghababa, “Fractional modeling and control of a complex nonlinear energy supply-demand system,” Complexity, vol. 20, no. 6, pp. 74–86, 2015. [CrossRef]
SH Hosseinnia, RL Magin, BM Vinagre, “Chaos in fractional and integer order NSG systems,” Signal Processing, vol. 107, pp. 302–311, 2015. [CrossRef]
Q Li, S Liu, Y Chen, “Combination event-triggered adaptive networked synchronization communication for nonlinear uncertain fractional-order chaotic systems,” Applied Mathematics and Computation, vol. 333, pp. 521–535, 2018. [CrossRef]
Xiuxia Yin, Dong Yue, and Songlin Hu, “Consensus of fractional-order heterogeneous multi-agent systems,” IET Control Theory & Applications, vol. 7, no. 2, pp. 314–322, 2013. [CrossRef]
M. Ö. Efe, “Fractional Order Systems in Industrial Automation—A Survey,” IEEE Trans. Ind. Inf., vol. 7, no. 4, pp. 582–591, 2011. [CrossRef]
Y. Ding, Z. Wang, and H. Ye, “Optimal Control of a Fractional-Order HIV-Immune System With Memory,” IEEE Trans. Contr. Syst. Technol., vol. 20, no. 3, pp. 763–769, 2012. [CrossRef]
Mouna Ben Smida, Anis Sakly, Sundarapandian Vaidyanathan, and Ahmad Taher Azar, “Control-Based Maximum Power Point Tracking for a Grid-Connected Hybrid Renewable Energy System Optimized by Particle Swarm Optimization,” in Research Anthology on Clean Energy Management and Solutions: IGI Global, pp. 353–384. [Online]. Available: https://www.igi-global.com/chapter/control-based-maximum-power-point-tracking-for-a-grid-connected-hybrid-renewable-energy-system-optimized-by-particle-swarm-optimization/286475.
W Cai, P Wang, J Fan, “A variable-order fractional model of tensile and shear behaviors for sintered nano-silver paste used in high power electronics,” Mechanics of Materials, vol. 145, p. 103391, 2020. [CrossRef]
P. B. P Muthukumar, Feedback synchronization of the fractional order reverse butterfly-shaped chaotic system and its application to digital cryptography‏, 2013. [Online]. Available: https://idp.springer.com/authorize/casa?redirect_uri=https://link.springer.com/article/10.1007/s11071-013-1032-3&casa_token=-sywiegxde0aaaaa:krtvcaerub3attgl0rjwjxoprgqsko6vhxzbibofx7ud70ypebvwyzxuzwfq0jmbshojx5bunb6an-q.
S. Balochian, A.K. Sedigh, A. Zare, “Variable structure control of linear time invariant fractional order systems using a finite number of state feedback law,” Communications in Nonlinear Science and Numerical Simulation, vol. 16, no. 3, pp. 1433–1442, 2011. [CrossRef]
A. E. AE Matouk, Achieving synchronization between the fractional-order hyperchaotic Novel and Chen systems via a new nonlinear control technique‏, 2014. [Online]. Available: https://www.sciencedirect.com/science/article/pii/s0893965913002954.
Chuang Li, Jingcheng Wang, Junguo Lu, and Yang Ge, “Observer-based stabilisation of a class of fractional order non-linear systems for 0 < α <2 case,” IET Control Theory & Applications, vol. 8, no. 13, pp. 1238–1246, 2014. [CrossRef]
Z Odibat, “A note on phase synchronization in coupled chaotic fractional order systems,” Nonlinear Analysis: Real World Applications, vol. 13, no. 2, pp. 779–789, 2012. [CrossRef]
JG Liu, “A novel study on the impulsive synchronization of fractional-order chaotic systems,” Chinese Phys. B, vol. 22, no. 6, p. 60510, 2013. [CrossRef]
P. Muthukumar, P. Balasubramaniam, and K. Ratnavelu, “Synchronization and an application of a novel fractional order King Cobra chaotic system,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 24, no. 3, 2014. [CrossRef]
L Pan, Z Guan, L Zhou, “CHAOS MULTISCALE-SYNCHRONIZATION BETWEEN TWO DIFFERENT FRACTIONAL-ORDER HYPERCHAOTIC SYSTEMS BASED ON FEEDBACK CONTROL,” International Journal of Bifurcation and Chaos, 2013. [CrossRef]
Mohammad Pourmahmood Aghababa, “Design of hierarchical terminal sliding mode control scheme for fractional-order systems,” IET Science, Measurement & Technology, vol. 9, no. 1, pp. 122–133, 2015. [CrossRef]
Z Wang, X Huang, J Lu, “Sliding mode synchronization of chaotic and hyperchaotic systems with mismatched fractional derivatives,” Transactions of the Institute of Measurement and Control, 2013. [CrossRef]
D. Chen, R. Zhang, J. C. Sprott, H. Chen, and X. Ma, “Synchronization between integer-order chaotic systems and a class of fractional-order chaotic systems via sliding mode control,” Chaos, vol. 22, no. 2, 2012. [CrossRef]
Hao Shen, Xiaona Song, and Zhen Wang, “Robust fault-tolerant control of uncertain fractional-order systems against actuator faults,” IET Control Theory & Applications, vol. 7, no. 9, pp. 1233–1241, 2013. [CrossRef]
M. Rasouli, A. Zare, M. Hallaji, and R. Alizadehsani, “The Synchronization of a Class of Time-Delayed Chaotic Systems Using Sliding Mode Control Based on a Fractional-Order Nonlinear PID Sliding Surface and Its Application in Secure Communication,” Axioms, vol. 11, no. 12, p. 738, 2022. [CrossRef]
A. A. Kekha Javan et al., “Design of Adaptive-Robust Controller for Multi-State Synchronization of Chaotic Systems with Unknown and Time-Varying Delays and Its Application in Secure Communication,” Sensors, vol. 21, no. 1, p. 254, 2021. [CrossRef]
El Abed Assali, “Predefined-time synchronization of chaotic systems with different dimensions and applications,” Chaos, Solitons & Fractals, vol. 147, p. 110988, 2021. [CrossRef]
N. Tino and P. Niamsup, “Finite-Time Synchronization Between Two Different Chaotic Systems by Adaptive Sliding Mode Control,” Front. Appl. Math. Stat., vol. 7, p. 589406, 2021. [CrossRef]
M. Taheri, Y. Chen, C. Zhang, Z.R. Berardehi, M. Roohi, “A finite-time sliding mode control technique for synchronization chaotic fractional-order laser systems with application on encryption of color images,” Optik, vol. 285, 2023.
F. Du, J.G. Lu, Q.H. Zhang, “Delay-dependent finite-time synchronization criterion of fractional-order delayed complex networks,” Communications in Nonlinear Science and Numerical Simulation, vol. 119, p. 107072, 2023. [CrossRef]
L. Zhang, J. Zhong, J. Lu, “Intermittent control for finite-time synchronization of fractional-order complex networks,” Neural Networks, vol. 144, pp. 11–20, 2021. [CrossRef]
S. K. MP Aghababa, “Finite-time synchronization of two different chaotic systems with unknown parameters via sliding mode technique,” Applied Mathematical Modelling, vol. 35, no. 6, pp. 3080–3091, 2011. [CrossRef]
L dos Santos Coelho, DL de Andrade Bernert, “A modified ant colony optimization algorithm based on differential evolution for chaotic synchronization,” Expert Systems with Applications, vol. 37, no. 6, pp. 4198–4203, 2010. [CrossRef]
M. Hui, C. Wei, J. Zhang, H. Ho-Ching Iu, R. Yao, L. Bai, “Finite-time synchronization of fractional-order memristive neural networks via feedback and periodically intermittent control,” Communications in Nonlinear Science and Numerical Simulation, vol. 116, p. 106822, 2023. [CrossRef]
W. Pan, T. Li, M. Sajid, S. Ali, and L. Pu, “Parameter Identification and the Finite-Time Combination–Combination Synchronization of Fractional-Order Chaotic Systems with Different Structures under Multiple Stochastic Disturbances,” Mathematics, vol. 10, no. 5, p. 712, 2022. [CrossRef]
J Jiang, D Cao, H Chen, “sliding mode control for a class of variable-order fractional chaotic systems,” Journal of the Franklin Institute, vol. 357, no. 15, pp. 10127–10158, 2020. [CrossRef]

Figure 1. Sigma Function Graph.

Figure 2. Chaotic behavior of the master Gensou-Tsei system.

Figure 3. Chaotic behavior of the slave Gensou-Tsei system.

Figure 4. The chaotic behavior of fractional order master and slave Gensou-Tsei in the absence of controller operations.

Figure 5. The behavior of the master and slave Gensou-Tsei system modes in the absence of a control signal.

Figure 6. Synchronization of chaotic Gensou-Tsei systems using the proposed adaptive sliding mode control and applying the control signal at t=5s.

Figure 7. Synchronization error of the master and slave system using the proposed adaptive sliding mode control mechanism.

Figure 8. The control signal based on the proposed adaptive sliding mode control mechanism.

Figure 9. Estimation error of the system parameters, including unknown uncertainties, time delays, and disturbances.

Figure 10. Representation of uncertainties and disturbances of the master and slave systems.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.