Constructing an Effective Field Theory to Recover MONDian Behaviour at Large Distances

Preprint

Article

Constructing an Effective Field Theory to Recover MONDian Behaviour at Large Distances

Altmetrics

Downloads

160

Views

106

Comments

Naman Kumar^*

This version is not peer-reviewed

Submitted:

18 August 2024

Posted:

19 August 2024

You are already at the latest version

Alerts

Abstract

In this letter, we construct an effective field theory of gravity at large distances. We obtain to the leading order for large distances: a cosmological constant term and a logarithmic term in addition to the usual General Relativistic terms. The novel logarithmic term has important implications in explaining phenomena such as flat galactic rotation curves and stronger gravitational lensing than predicted that are generally attributed to the presence of dark matter.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

General Relativity (GR) theory is a very successful and currently accepted description of the true nature of gravity. It explains a lot of phenomena, from solar system scales to the extreme objects of the universe: black holes. It can be inferred as a simplistic theory with the least free parameters compatible with observations. However, it faces challenges at large distances. Particularly, the problems of cosmological constant[1] and dark matter[2] are still not completely understood. To overcome these challenges, we can either introduce some new particles(dark matter), or we can modify the theory of gravity itself, called Modified Gravity theories(see [3] for a nice discussion on modified gravity theories). In[4], a new approach to describe gravity was proposed based on some assumptions such as analyticity and power counting renormalizability. The key concept was to impose spherical symmetry in addition to diffeomorphism invariance which is actually a good description in the IR. Setting the angular momentum and cosmological constant

Λ

to be zero, the modified potential in the IR was obtained as1

V = - \frac{M}{r} + a r

(1)

The second term is a Rindler term with the free parameter of the model a. It was then shown with the help of toy models that the potential given by (1) is a good fit for rotation curves. However, there is no evidence that such a term linear in r is indeed a good fit. A better fit was obtained in[5], where the authors reconstructed an effective field theory model for gravity at large distances. However, to achieve this, a new free parameter was introduced. In this letter, we propose a new model of gravity at large distances. This model like[4] is based on assumptions of analyticity and power counting renormalizability. The main feature of this model is that it has only one free parameter, there is no Rindler term and produces a very good fit to the data. Furthermore, this model is compatible with MOND[6]. All this points to the naturalness and robustness of our model.

2. Effective Field Theory

Similar to[4], we assume that the spacetime is described by a spherically symmetric metric in four dimensions

d s^{2} = - f (r) d t^{2} + f {(r)}^{- 1} d r^{2} + Φ^{2} (d θ^{2} + s i n^{2} θ d ϕ^{2})

(2)

where

Φ (r)

denotes the surface radius. The 2-dimensional Ricci scalar is given by

R = - \frac{d^{2} f}{d r^{2}}

(3)

This spherical reduction simplifies the

4 D

Einstein-Hilbert action to a

2 D

dilaton gravity model(see [7] for a nice review). Demanding the theory to be power counting renormalizable, we obtain the generalized action as[4]

S = - \frac{1}{κ^{2}} \int d^{2} x \sqrt{- g} [f (Φ) R + 2 {(\partial Φ)}^{2} - 2 V (Φ)]

(4)

where

f (Φ) - Φ^{2}

is required to produce Newtonian potential. We propose the following form of potential

V (Φ)

in the above action (4)

V (Φ) = 1 - 3 Λ Φ^{2} + a ln Φ

(5)

The main feature of potential given by Equation(5) is that it contains only those terms that dominate at large distances and are still free from curvature singularities since the Ricci scalar R given by (3) is finite. Furthermore, there is no Rindler term that has been dropped off on both theoretical and phenomenological grounds (see discussion section). Any term in

Φ

of order greater than 2 will give a curvature singularity in the IR and is thus not allowed in the model. Therefore, the action given by (4) becomes (with

κ = 1

)

S = - \int d^{2} x \sqrt{- g} [Φ^{2} R + 2 {(\partial Φ)}^{2} - 6 Λ Φ^{2} - 2 a ln Φ]

(6)

The solution of the metric function

f (r)

is obtained as[8]

f (r) = 1 - \frac{2 M}{r} - Λ r^{2} + a ln r

(7)

The 2-dimensional Ricci scalar

R = - d^{2} f / d r^{2} = 2 Λ + 2 a / r^{2} + 4 M / r^{3}

is well-behaved at large r. If

a = Λ = 0

, we recover the Schwarzschild black hole with mass M. The third term, which is interestingly logarithmic in nature, is novel and does not arise in the vacuum solution of Einstein’s gravity. As we will show, it is this term responsible for explaining the large-scale behavior of gravity.

3. Applications of the Model

3.1. Geodesics of Test Particles

We concentrate on the timelike geodesics in the equatorial plane (

θ = π / 2

) and follow the standard procedure(see for e.g., [9]) such that the conserved angular momentum is given by l and

{\dot{r}}^{2} / 2 + V^{e f f} = E

where E is a constant of motion, we obtain

V^{e f f} = - \frac{M}{r} + \frac{l^{2}}{2 r^{2}} - \frac{M l^{2}}{r^{3}} - \frac{Λ r^{2}}{2} + a ln r (1 + \frac{l^{2}}{r^{2}})

(8)

The first two are the usual terms, the third is the GR corrected term, the fourth is a cosmic acceleration term, and the last term is a logarithmic potential which is our novel result. For vanishing cosmological constant and angular acceleration, we have

F^{e f f} = - \frac{\partial V^{e f f}}{\partial r} = - \frac{M}{r^{2}} - \frac{a}{r}

(9)

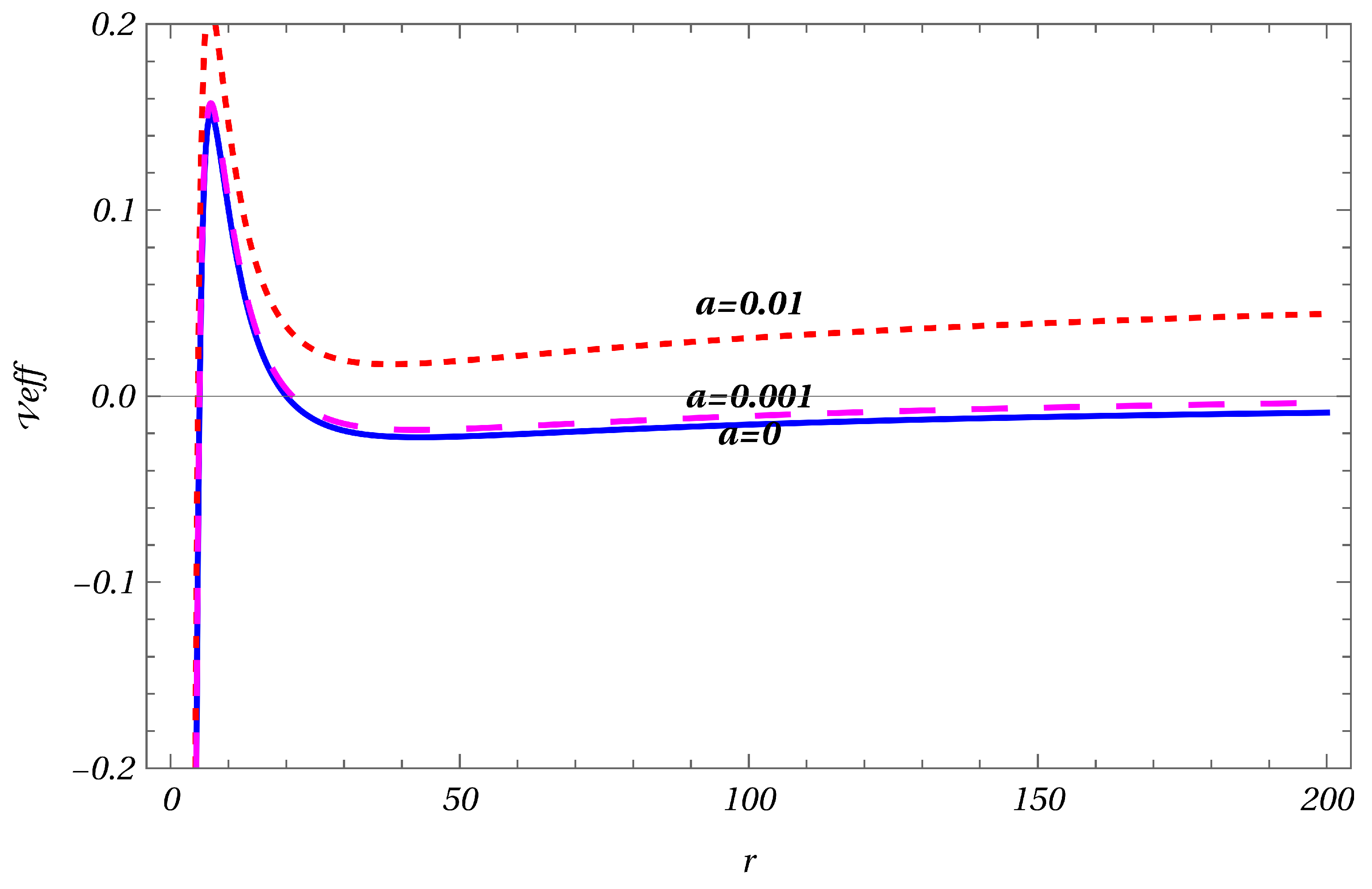
At sufficiently large distances, the second term becomes appreciable and dominates the dynamics. A plot of effective potential given by (8) for some values of a is shown below.

Figure 1. The red dotted curve is the plot of the effective modified potential for

a = 0.01

, the pink dotted curve is for

a = 0.001

and the blue curve is the effective GR potential.

Figure 1. The red dotted curve is the plot of the effective modified potential for

a = 0.01

, the pink dotted curve is for

a = 0.001

and the blue curve is the effective GR potential.

It is clear from the figure that the fall in the modified potential given by our effective field theory is lower than the GR case and increases with the increase in the value of a. This modified behaviour of the effective potential obtained with our effective field theory leads to a flat rotation curve of galaxies for large r, while for small r, their behaviour matches with that of GR as expected.

3.2. Galactic Rotation Curves

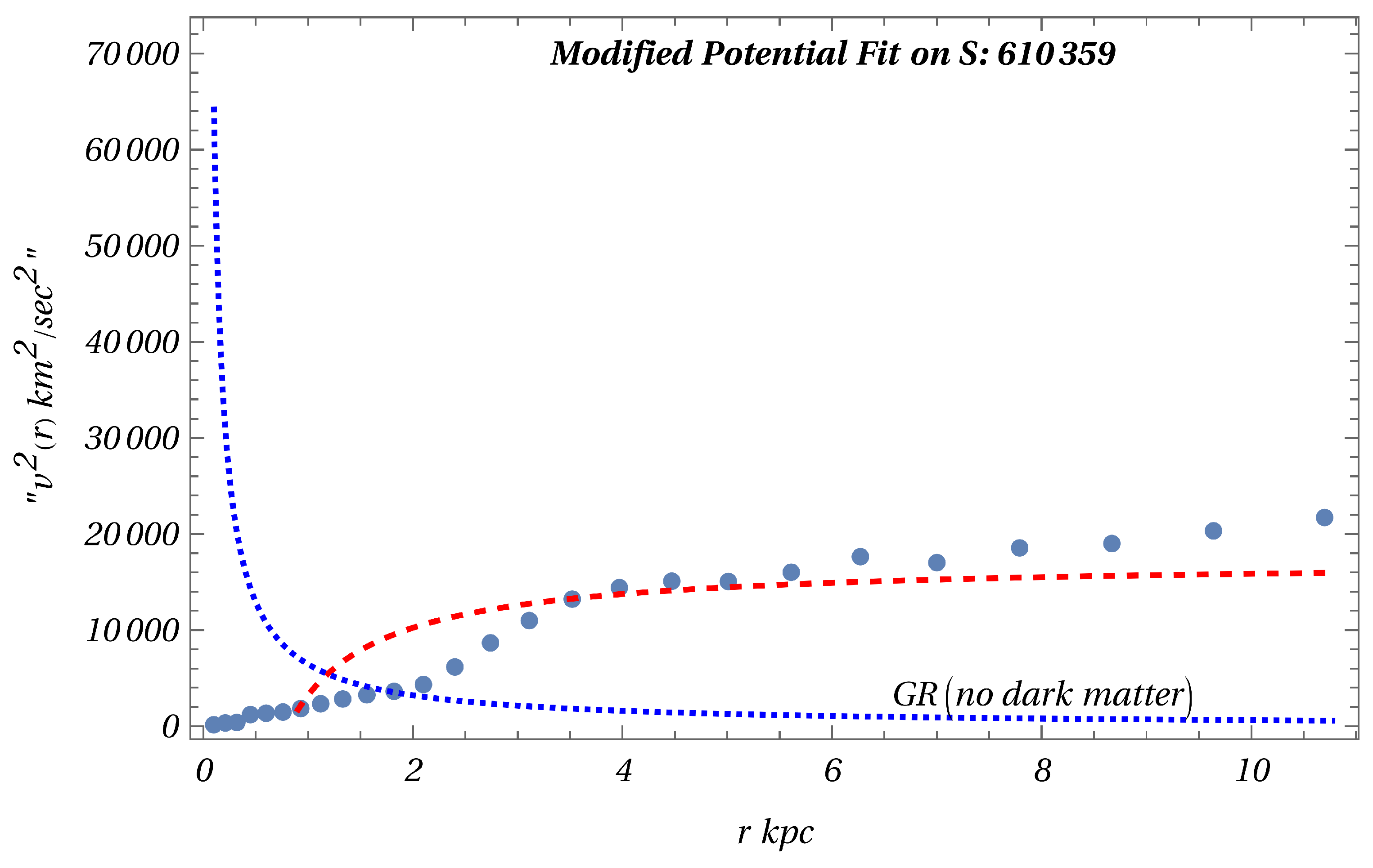
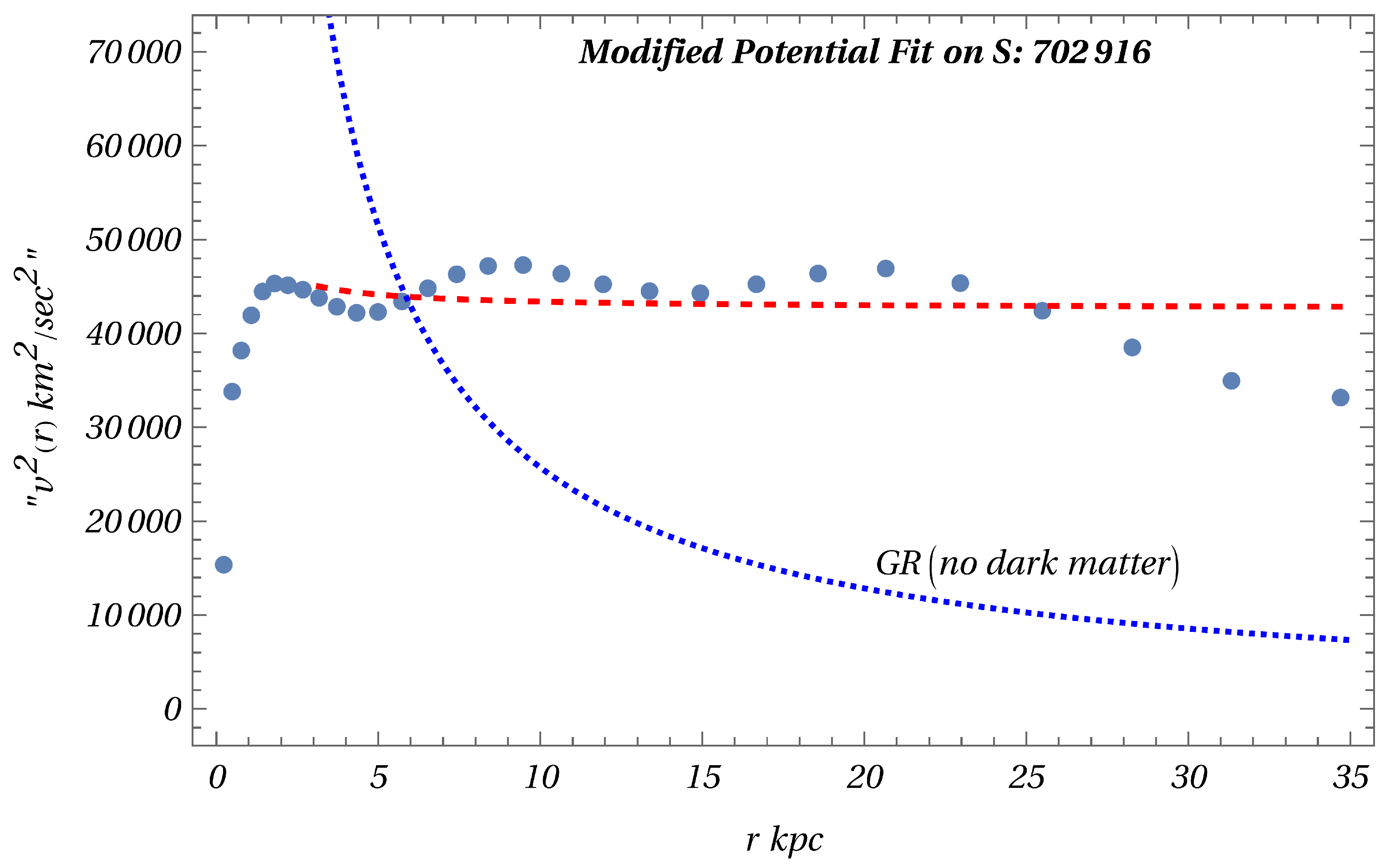
For a spherical galaxy, the modified radial velocity is obtained as

v (r) \approx \sqrt{\frac{M (r)}{r} + a}

(10)

The second term is constant, which dominates for a large distance. This is consistent with the MOND hypothesis. Obviously, MOND is more of an ad-hoc proposal and is not an effective field theory. Our result, which is valid for all r, is derived from an effective field theory proposed in section II. In Figure(Figure 2) and Figure(Figure 3) shown on the next page, we obtain the best fit for the velocity profile given by Equation(10). These plots are obtained following[5]. The red curve is the fit for the modified potential Equation(5) obtained from our model. Thick dots are data points obtained from[10]. The blue curve is the GR plot which is clearly poor. It is clear that the plots are in excellent agreement with the data. These two galaxies were chosen because of their different behaviour. S:610359 has a typical rising velocity profile, while the spiral galaxy S:702916 has a flat and slowly dropping velocity profile. Both behaviours are also reminiscent of the plots using the modified potential obtained from our effective field theory. It is amazing that our effective field theory with only one free parameter gives such an excellent fit with data.

3.3. Gravitational Lensing and The Value of Constant a

Following the standard procedures (outlined in for e.g.,[9]), the deflection angle of light due to a mass M in this case is given by

\begin{matrix} δ = \frac{2}{c^{2}} \int {\vec{\nabla}}_{⊥} (V_{N} + V) d s \end{matrix}

(11)

\begin{matrix} = δ_{1} + \frac{2 b a}{c^{2}} \int_{- \infty}^{\infty} \frac{d x}{(b^{2} + x^{2})} \end{matrix}

(12)

\begin{matrix} = \frac{4 G M}{b c^{2}} + \frac{2 π a}{c^{2}} \end{matrix}

(13)

\begin{matrix} \equiv \frac{4 G M^{'}}{b c^{2}} \end{matrix}

(14)

where b is the impact parameter and

M^{'} = M (1 + \frac{b π a}{2})

. Let us analyze this equation with a real example. For this, we take

M = 10^{13} M_{⊙} \approx 2 \times 10^{43} k g

b = 100 k p c \approx 3.1 \times 10^{21}

. This gives,

M^{'} \approx 7 M

with

a \approx 2 \times 10^{12}

. Thus, we find that the lensing is approximately 7 times larger in the case of dark matter-dominated galactic scales in agreement with[11]. Furthermore, from MOND theory, at galactic scales, we have the constant

\sqrt{G M a_{0}}

with

a_{0} = 1.2 \times 10^{- 10} m s^{- 2}

which is approximately equal to

1.67 \times 10^{12}

in close agreement to the value of a obtained above. This can solve the problem of a larger deflection angle of light around a lens than the standard case given simply by

δ_{1}

4. Discussion

In this letter, we presented a new model of gravity at large distances with the action (6). The solution to this action contains a novel logarithmic term that was shown to account for flat rotation curves and stronger lensing than predicted by GR. Although different modified potentials were obtained in[4,5] and the modifications in GR are based mainly on phenomenology or to fit with experimental data, our motivation mainly comes from our work[12] where we gave a possible "theoretical origin" of the modified gravity leading to dark matter. In[12], we argued that if we treat a gravitational system to be 1D in its entropy "flow" similar to that argued for black holes in[13], then for large distances, we obtain a logarithmic potential term. Furthermore, the authors of[14,15] also proposed a logarithmic potential as the solution of dark matter, but the origins of such a term were unknown. In this work, we presented an effective field theory leading toward such a modification. Our model accommodates the behaviour of gravity at all distances with great precision and is obtained from an action (6), which makes this model very natural and robust.

Funding

No funding was received to carry out this study.

Data Availability Statement

The data used in this study to plot figures are available in[10].

Conflicts of Interest

The author declares no conflict of interest.

References

Carroll, S.M. The cosmological constant. Living reviews in relativity 2001, 4, 1–56. [Google Scholar] [CrossRef]
Bertone, G.; Hooper, D. History of dark matter. Reviews of Modern Physics 2018, 90, 045002. [Google Scholar] [CrossRef]
Shankaranarayanan, S.; Johnson, J.P. Modified theories of gravity: Why, how and what? General Relativity and Gravitation 2022, 54, 44. [Google Scholar] [CrossRef]
Grumiller, D. Model for gravity at large distances. Physical review letters 2010, 105, 211303. [Google Scholar] [CrossRef]
Perivolaropoulos, L.; Skara, F. Reconstructing a model for gravity at large distances from dark matter density profiles. Physical Review D 2019, 99, 124006. [Google Scholar] [CrossRef]
Milgrom, M. A modification of the newtonian dynamics-implications for galaxies. The Astrophysical Journal 1983, 270, 371–383. [Google Scholar] [CrossRef]
Grumiller, D.; Kummer, W.; Vassilevich, D.V. Dilaton gravity in two dimensions. Physics Reports 2002, 369, 327–430. [Google Scholar] [CrossRef]
This follows from [5] where the general solution of the action (4) with f(ϕ)=ϕ² has been obtained.
Carroll, S.M. Spacetime and geometry; Cambridge University Press, 2019. [Google Scholar]
Available online: http://www.ioa.s.u-tokyo.ac.jp/∼sofue/smd2018/atlas_data_s-galaxies/.
Moffat, J.W. Scalar–tensor–vector gravity theory. Journal of Cosmology and Astroparticle Physics 2006, 2006, 004. [Google Scholar] [CrossRef]
Naman Kumar. 2d behavior of gravity at large distances. Preprints, August 2023.
Bekenstein, J.D.; Mayo, A.E. Black holes are one-dimensional. General Relativity and Gravitation 2001, 33, 2095–2099. [Google Scholar] [CrossRef]
Das, S.; Sur, S. Dark matter or strong gravity? International Journal of Modern Physics D 2022, 31, 2242020. [Google Scholar] [CrossRef]
Das, S.; Sur, S. Gravitational lensing and missing mass. Physics Open 2023, 15, 100150. [Google Scholar] [CrossRef]

1	We use natural units so that $G = c = 1$

Figure 2. The best-fit form of the velocity profile Equation(10) for S:610359. The red dashed curve is for the modified potential Equation(5) obtained from our model. The plot obtained from GR is obviously poor.

Figure 3. The best-fit form of the velocity profile Equation(10) for S:702916. The red dashed curve is for the modified potential Equation(5) obtained from our model. The plot obtained from GR is obviously poor.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Constructing an Effective Field Theory to Recover MONDian Behaviour at Large Distances

Abstract

1. Introduction

2. Effective Field Theory

3. Applications of the Model

3.1. Geodesics of Test Particles

3.2. Galactic Rotation Curves

3.3. Gravitational Lensing and The Value of Constant a

4. Discussion

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe