Prerpints.org logo
Preprint
Article

Magnetostriction of Amorphous Magnetic Microwires: Role of Local Atomic Environment and Internal Stresses Relaxation

Altmetrics

Downloads

105

Views

102

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.docx (16.95KB )

Submitted:

13 September 2023

Posted:

14 September 2023

You are already at the latest version

Alerts
Abstract
We studied the magnetostriction coefficients, λs, Curie temperature, Tc, and their dependence on annealing conditions in Fe47Ni27Si11B13C2 and Co67Fe3,9Ni1,5B11,5Si14,5Mo1,6 amorphous glass-coated microwires with rather different character of hysteresis loops. A positive λs≈20x10-6is observed in as-prepared Fe47Ni27Si11B13C2, while low and negative λs ≈-0.3x10-6 is ob-tained for Co67Fe3,9Ni1,5B11,5Si14,5Mo1,6 microwire. Annealing affects the magnetostriction coeffi-cients and Curie temperatures, Tc, of both Fe47Ni27Si11B13C2 and Co67Fe3,9Ni1,5B11,5Si14,5Mo1,6 glass-coated microwires in a similar way. Observed dependencies of hysteresis loops, λs and Tc on annealing conditions are discussed in terms of superposition of internal stresses relaxation and structural relaxation of studied microwires. We observed linear λs dependence on applied stress, σ, in both studied microwires. A decrease with applied stress is observed for Co-rich mi-crowires with negative magnetostriction coefficient. In contrast, a linear increase of the magne-tostriction coefficient with applied stress is observed for Fe-Ni- rich microwires with positive magnetostriction coefficient. Observed results are discussed in terms of influence of internal stresses and short range atomic rearrangements induced by annealing on hysteresis loops, magnetostriction coefficients and Curie temperatures of studied microwires.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

Magnetostriction, λs, refers to the behavior of a magnetic material that undergoes either expansion or contraction in the direction of magnetization when exposed to a magnetic field [1,2]. The λs can be either positive or negative, depending on whether the magnetostrictive effect leads to expansion or compression, respectively.
In amorphous alloys, magnetostriction is a phenomenon that relates to the deformation or change in shape of the material in response to an applied magnetic field. Unlike crystalline materials, amorphous alloys lack of long-range periodic atomic structure and instead have a disordered arrangement of atoms. In the absence of defects typical for crystalline materials (grain boundaries, dislocations, texture,…) the magnetoelastic anisotropy plays the determining role in magnetic softness of amorphous alloys [3-6]. The magnetoelastic anisotropy, Kme, is determined by the magnetostriction coefficient, λs, as well as by the stress, σ, [3,4]. It is commonly accepted that in amorphous alloys the λs is influenced by the chemical composition: for Fe-rich composition the λs is positive (up to 40x10-6) and large, while for Co-rich amorphous alloys λs is negative (up to -5 10-6). Consequently, nearly-zero λs values have been achieved in CoxFe1-x (0≤x ≤1) or CoxMn1-x (0≤x ≤1) alloys 0,03 ≤x≤ 0,08 [3-5]. In such amorphous alloys with vanishing λs values better magnetic softness is commonly reported [3-6].
However, magnetostriction of amorphous alloys is influenced by the local atomic environments, by the presence of clusters and even by stresses [7-9]. Thus, clusters are localized regions of atoms that exhibit different magnetic properties compared to the surrounding material. These clusters can arise due to variations in composition or local atomic arrangements within the amorphous structure. When an external mechanical stress is applied to an amorphous alloy with clusters, the magnetic moments within the clusters align with the stress direction, causing a local deformation or strain in the material. In the two-ion model, the strain experienced by one ion can affect the magnetic moment of the neighboring ion and vice versa. This coupling between strain and magnetism leads to changes in the magnetic properties of the material, including its magnetostriction [7].
Research on amorphous magnetic wires has attracted considerable attention owing to unusual magnetic properties, such as magnetic bistability related to fast magnetization switching through the fast domain wall (DW) propagation, superior magnetic softness or the giant magnetoimpedance (GMI) effect [4, 10-12]. Such magnetic properties have been proposed for numerous applications in magnetic and/or magnetoelastic sensors and devices [4,8-10]. While the better magnetic softness and the highest GMI effect are commonly reported in magnetic wires with vanishing λs, spontaneous magnetic bistability is usually reported for magnetostrictive compositions of amorphous wires [4, 10-12].
One of the recent tendencies in amorphous materials is the development of low dimensional amorphous materials with enhanced physical (mechanical, corrosion) properties and biocompatibility [4,6,11]. Therefore, studies of glass-coated microwires with unusual combination of physical properties, such as enhanced mechanical and corrosion properties, biocompatibility together with excellent magnetic softness with coercivities up to 2 A/m and high magnetoimpedance effect have attracted substantial attention [4,6,11].
The peculiarity of glass-coated microwires is the presence of the glass-coating intrinsically related to the fabrication method [4,6,11]. Such composite origin of glass-coated microwires is associated with high values of internal stresses in glass-coated microwires, discussed elsewhere [13-17]. Although there are several origins of the internal stresses in amorphous microwires, however the main contribution is related with the difference in thermal expansion coefficients of metallic alloy and glass coating [13-17].
The magnetostriction coefficient plays a significant role in determining the domain structure and hysteresis loop characteristics of glass-coated microwires. In compositions with low magnetostriction, the stress dependence of magnetostriction, whether applied or internal, becomes relevant. This stress dependence has been described as [8,9]:
λs (σ) = λs (0) – B σ
Here, λs(σ) represents the magnetostriction coefficient under stress, λs(0) is the magnetostriction coefficient at zero stress, B is a positive coefficient of the order 10-10 MPa, and σ represents the applied or internal stresses. The change in magnetostriction can be attributed to the presence of applied stresses (σappl), internal stresses (σi), or both (σ).
Mechanical stresses play a significant role in modifying the magnetic properties of ferromagnetic materials. Alongside magnetic field and temperature, they are a crucial factor influencing magnetic properties. This phenomenon is commonly employed in stress and torsion sensors, where the variation in the material's magnetic properties is utilized for sensing purposes [5-8, 18-22]. Magnetostriction also has an impact on various inductive or transport magnetic effects [20-22].
Recently, studies of glass-coated magnetic microwires have attracted growing attention. Among the principal advantages of glass-coated microwires are the most extended diameters range from 100 nm [13] up to 100 µm [23]. Additionally, the presence of flexible, insulating and thin glass-coating together with extended diameters are beneficial for several technical applications [4, 24,25].
Similarly to thicker amorphous magnetic wires prepared by in-rotating water technique, magnetic bistability related to remagnetization by fast DW propagation is observed in Fe-and Fe-Ni- rich glass-coated microwires [4,6]. While almost unhysteretic loops with vanishing coercivity and high GMI effect are reported in Co-rich glass-coated microwires [4, 6].
As mentioned above, the λs of amorphous alloys is principally affected by the chemical composition. Thus, in most commonly studied amorphous Co1-xFex alloys high and positive λs (up to 40x10-6) is reported for Fe-rich compositions, while negative (up to -5 10-6) λs is observed in Co-rich amorphous alloys. Therefore, observed dependence of magnetic properties on chemical composition is commonly attributed to compositional dependence of λs.
As discussed above, the λs in amorphous materials is affected by stress [8,9]. In the case of glass-coated microwires, the presence of a glass coating associated with a preparation method involving simultaneous solidification of a metallic alloy inside the glass coating leads to an elevated σi -value (up to hundreds of MPa) [13-17].
In the case of low-magnetostrictive compositions, where λs (0) is approximately 10-7, and internal stresses are on the order of hundreds of MPa, the second term in Equation (1) becomes comparable to the first term. Consequently, the magnetostriction value and even sign can be substantially different from that of conventional amorphous materials. Therefore, the correct evaluation of λs - magnitude in glass-coated microwires becomes a crucial factor for adjusting the magnetic properties of glass-coated microwires and it is relevant for technological applications.
One of the most commonly used methods for evaluation of the λs in amorphous materials, is so called small angle magnetization rotation (SAMR) [8,9, 18]. The magnetostriction of conventional (bulk) magnetic materials usually can be measured by direct methods, such as strain gauge method or the capacitance method [26,27]. However, direct methods require use of the strain gauge or the movable electrode. Therefore, use of such direct methods for λs measurements in low dimensional amorphous materials, like amorphous ribbons or wires seems to be difficult. Therefore, indirect methods, like the SAMR method, Villari effect of stress dependence of hysteresis loop have been proposed for studied of amorphous low dimensional materials since the 80s [8,9,18]. Some issues for use of indirect methods, like the stress dependence of the λs in amorphous materials and the influence of mechanical creep deformation of the sample can be successfully minimized using as short as possible keeping the sample under stress [8].
In the case of glass-coated magnetic microwires, the use of direct methods for λs evaluation is even more difficult owing to composite origin of glass-coated microwires and substantially lower dimensionality. Therefore, recently SAMR method has been successfully adapted for magnetic microwires by improved resolution obtained in new experimental set-up [28,29].
Consequently, for glass-coated microwires with elevated internal stresses, studies of the magnetostriction coefficient are essentially relevant both from the point of view of applications and for understanding of the intrinsic properties (the degree of internal stresses relaxation, short range atomic order) of amorphous microwires. Accordingly, this paper presents the experimental results on the magnetostriction coefficient of glass-coated microwires of two different chemical compositions.

2. Materials and Methods

We studied Fe47Ni27Si11B13C2 (metallic nucleus diameter, d =29 µm, total diameter, D=32.2 µm) and Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 (d =25.6 µm, D=26.6 µm) glass-coated microwires produced by Taylor-Ulitovsky technique [4,6,15,16,30]. The preparation method of glass-coated microwires consists by melting of the ingot using a high frequency inductor be heating above its melting temperature, and then drawing of a glass capillary filled with the molten metallic alloy. The composite microwire is then wound onto a rotating pick-up bobbin [4,6,30].
The metallic nucleus diameter, d, has been controlled by the impedance measurements during the preparation [4]. Additionally, an optical microscope Axio Scope A1 was used for the morphology analysis and evaluation of the d and D- values of prepared glass-coated microwires. From the images of prepared microwires (see Figure 1a,b) we can clearly see that the metallic nucleus are rather homogeneous and confirm the d and D- values.
The SAMR method was used to evaluate λs in both microwires. This method consists in saturating the sample with an axial magnetic field, while the transverse magnetic field created by AC electric current causes the small angle magnetization rotation [29,30]. When a tensile stress is applied, the magnetization rotation angle decreases due to an increase in the magnetic anisotropy field Hk, which leads to a decrease in the amplitude of the second harmonic of the electro-motive force, EMF, induced in the pick-up coil. Tensile stress, σ, is created by a weight attached to the end of the microwire. The magnetostriction coefficient, λs, is then estimated from the Hk(σ) dependence as:
λ s = µ 0 M s 3 d H k d σ k
where μοMs is the saturation magnetization
The SAMR method was also used for the evaluation of the λs (σ) dependence. The detailed description of the set-up developed for the λs evaluation in magnetic microwires is provided elsewhere [30].
Hysteresis loops were measured using the fluxmetric method, previously successfully employed for high resolution measurements of axial hysteresis loops of magnetically soft microwires [31]. The 5 cm long samples were placed inside a single layered pick-up coil located inside a 15 cm long solenoid producing an axial homogeneous magnetic field. For this geometry the influence of the demagnetizing field and hence shape magnetic anisotropy contribution or microwires are negligible. The hysteresis loops have been represented as the normalized magnetization, M/Mo versus magnetic field, H, being M– the magnetic moment at a given H and Mo -the magnetic moment at the maximum magnetic field amplitude, Ho. Such M/Mo(H) loops are useful for comparison of the soft magnetic properties of microwires with different chemical compositions and, therefore, with different saturation magnetization values.
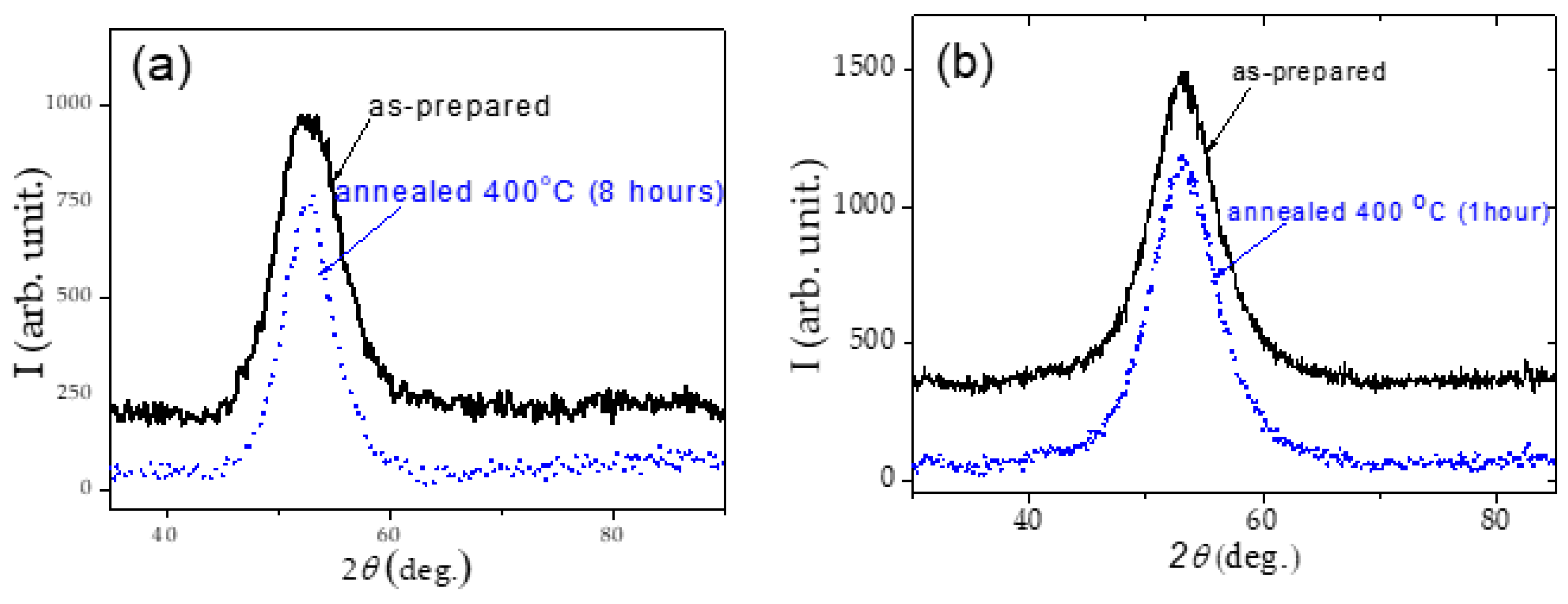
Amorphous structure of as-prepared and annealed samples have been proved by X-ray Diffraction (XRD) using a BRUKER (D8 Advance) X-ray diffractometer with Cu Kα (α=1.54 Å) radiation. XRD pattern of all the samples (as-prepared and annealed at 400 o C) present wide halo typical for amorphous alloys (see Figure 2).
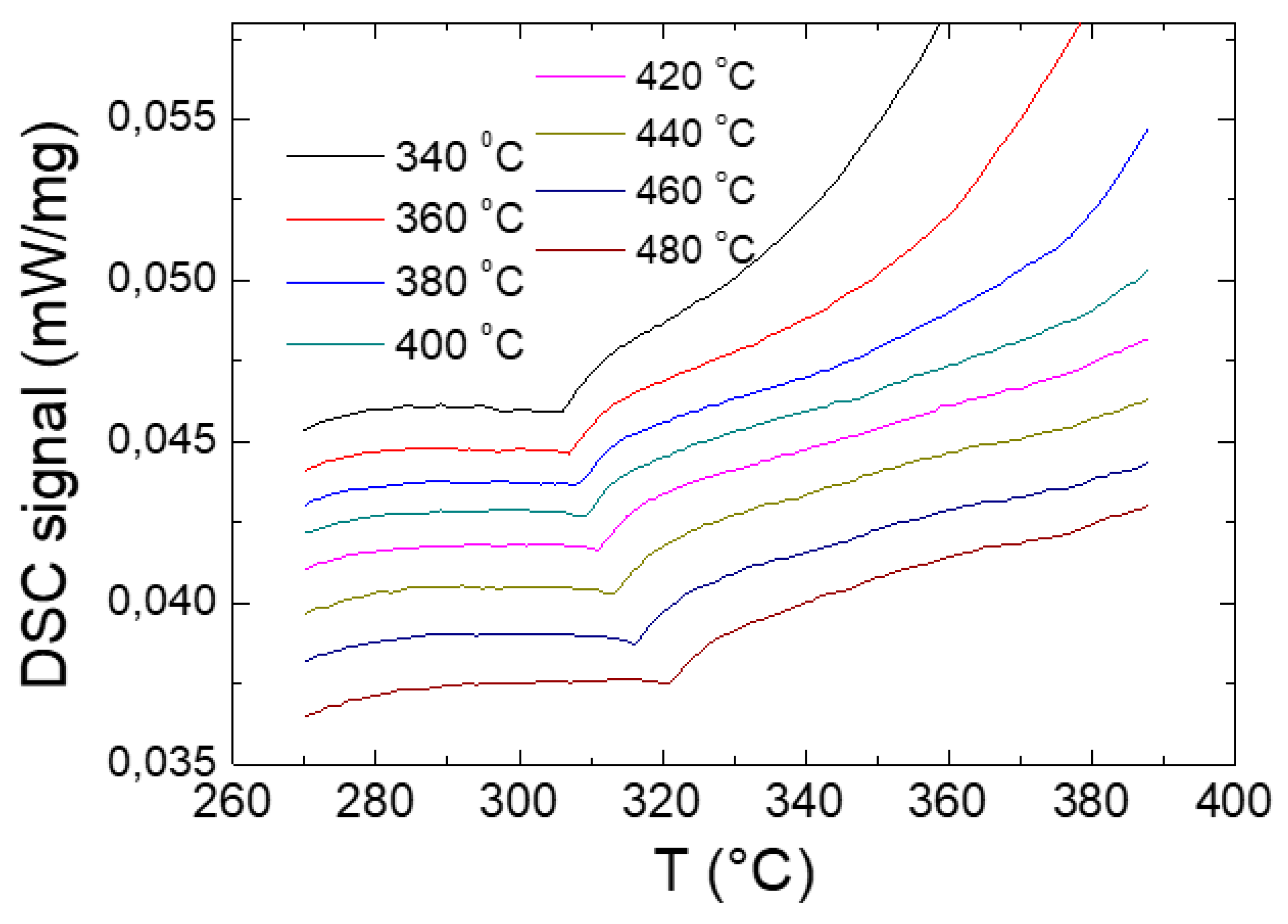
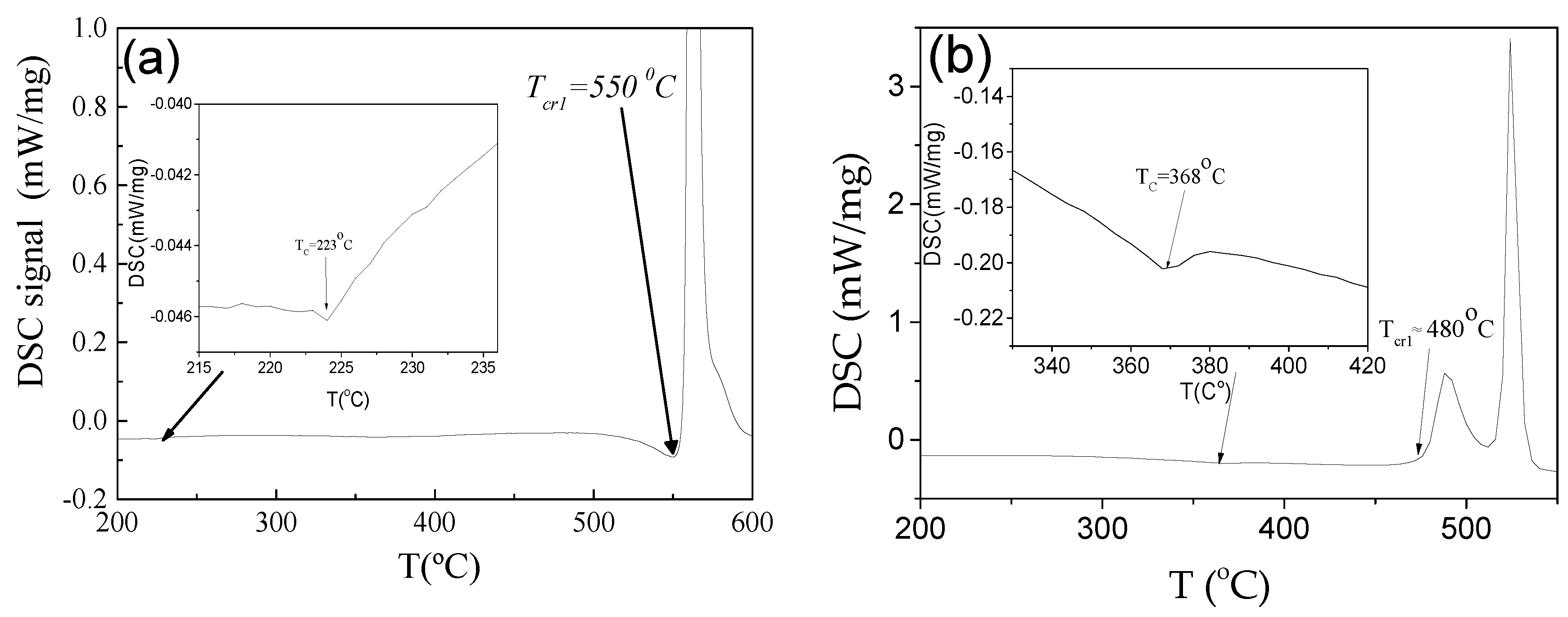
The crystallization and the Curie temperatures, Tc, of both microwires have been evaluated using the Differential Scanning Calorimetry, DSC, method [32]. We used DSC 204 F1 Netzsch calorimeter at a heating rate of 10 K/min (in Ar atmosphere).
The determination of the Curie temperature by the DSC method has been reported since more than 20 years [32]. In particular, comparison of the Tc –values obtained by the DSC with the Tc obtained by the other commonly accepted methods for Tc determination, such as temperature dependences of magnetization and electrical resistance, has proved that the turn on DSC curve actually corresponds to the Curie temperature Tc. One of the examples of the change in the DSC signal in the vicinity of Tc is provided in Figure 3.
In the provided example it is shown that annealing of microwires leads to a change of the position and the shape of DSC peak in the vicinity of the Tc: with increasing of the annealing temperature it shifts to higher temperatures. As- compared to the crystallization peak, the turn in the DSC curve in the vicinity of Tc looks smaller. However, the use of standard software and a big amount of glass-coated tiny microwires makes it possible to increase the scale of DSC curves and determine Tc quite accurately [32,33]. Thus, it was demonstrated that the accuracy of Tc determining from DSC curves is about ±0.5 K, which makes this method among the most precise for Tc determination [32].

3. Experimental Results and Discussion

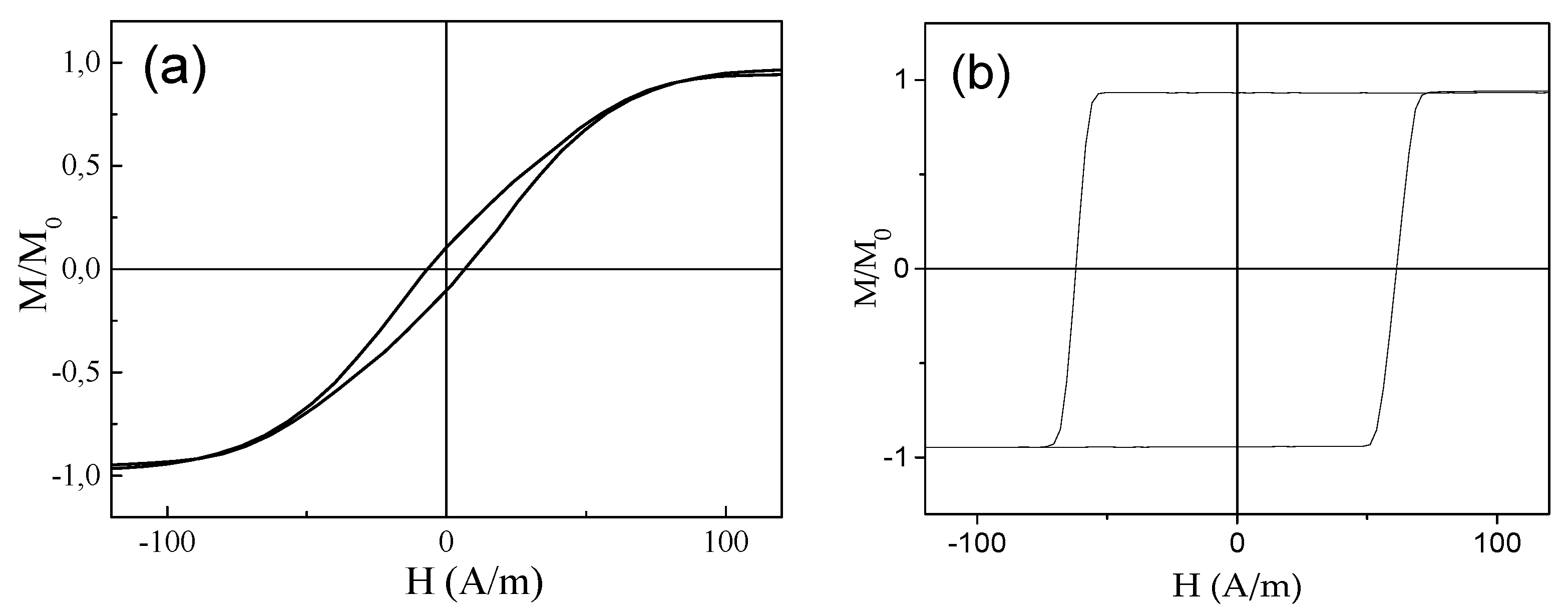
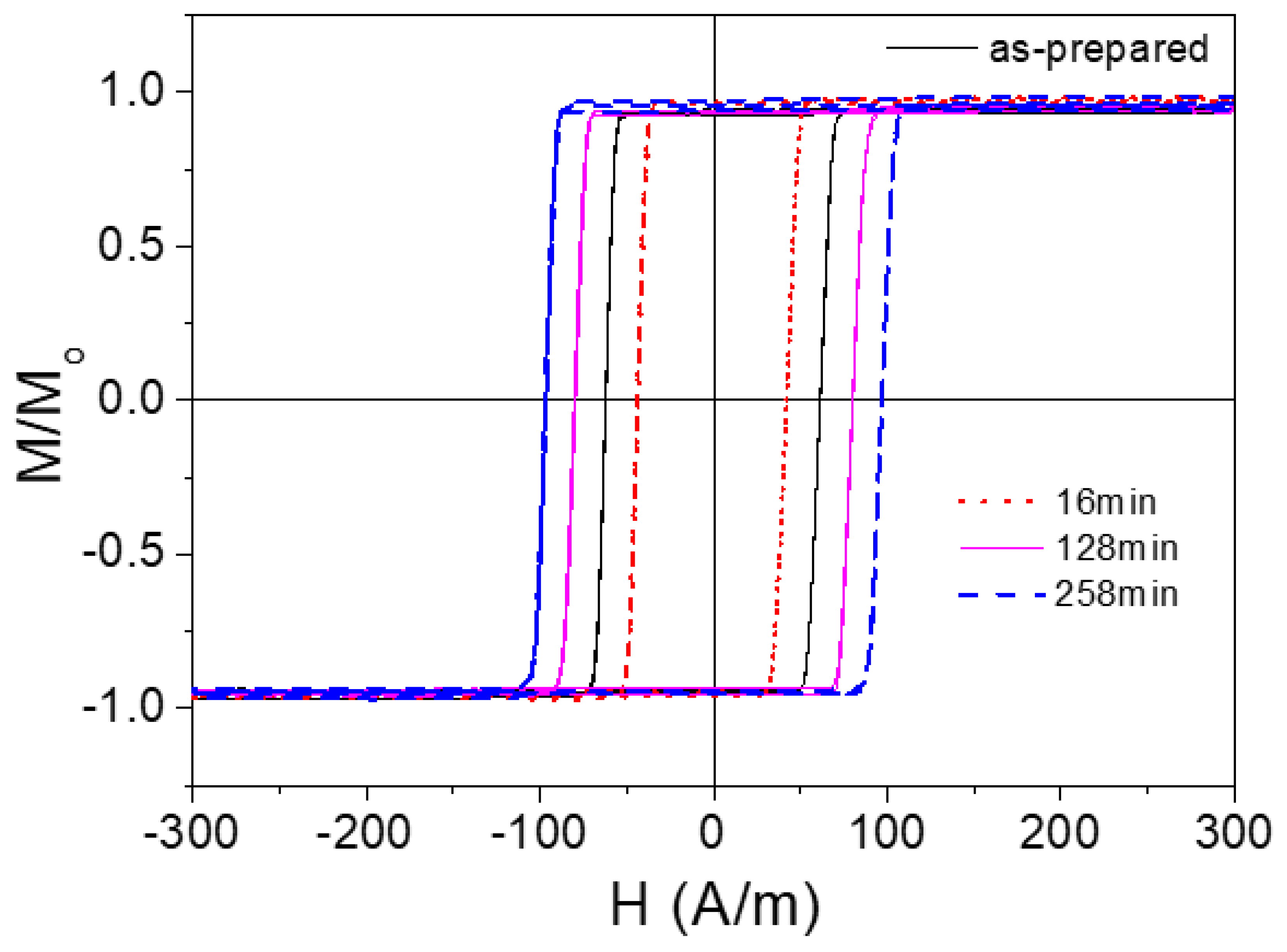
As can be observed from Figure 4, studied microwires present rather different hysteresis loops. A linear and almost unhysteretic loop is observed for Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 microwire (see Figure 4a), while a rectangular hysteresis loop is observed for Fe47Ni27Si11B13C2 microwire (see Figure 4b). The coercivity, Hc, of Fe47Ni27Si11B13C2 sample (Hc ≈61 A/m) is about, i.e., an order of magnitude higher than that for FeCo (Hc ≈6 A/m).
The coercivity, Hc, of Fe47Ni27Si11B13C2 sample is about, 61 A/m, i.e., an order of magnitude higher than that for Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 microwire (Hc ≈6 A/m).
The observed difference in the hysteresis loop of studied microwires can be explained in terms of core-shell domain structure model confirmed experimentally in magnetic microwires with different magnetostriction coefficients [10,21, 34-38]. The domain structure of both families (Co-rich and Fe-rich) microwires was extensively studied either by magneto-optical Kerr effect or magneto-optical indicator film methods [34-38]. The core-shell domain structure model describes the domain structure of amorphous magnetic wires as consisting of an inner axially magnetized core surrounded by an outer shell with transverse magnetization. The outer shell of Fe-rich wires has a radial magnetization orientation, while a bamboo domain structure with a circular magnetization orientation is proposed for Co-rich wires [10,21,38]. The difference in the outer shell domain structure is commonly explained considering the interplay of the magnetostriction and internal stresses and different λs sign of Fe- and Co-rich magnetic wires. As mentioned above, the axial component of internal stresses arising during the microwires preparation is the largest [14-17]. Consequently, such axial internal stresses produce the transverse magnetic anisotropy in as-prepared Co-rich glass-coated microwires with negative λs. In contrast, axial magnetic anisotropy with rectangular hysteresis loops internal stresses appears in Fe-rich microwires with positive λs.
From DSC curves both crystallization, Tcr1, and Curie, Tc, temperatures can be evaluated (see Figure 5).
Accordingly, increase in Hc –value of Fe47Ni27Si11B13C2 sample must be related to different magnetoelastic anisotropy or fine structural rearrangements associated to annealing.
As mentioned in the introduction, in amorphous materials with vanishing λs, λs(σ) dependence can be relevant [8]. Additionally, one of the main peculiarities of glass-coated microwires is the elevated magnetoelastic anisotropy, Kme, related to the presence of glass-coating [4,7]. As discussed elsewhere [4,7], Kme depends on the magnetostriction coefficient, λs, as well as on the total stresses, σ =σappl +σi, (being σappl and σi as applied and internal stresses, respectively) as [4,7]:
K me   ≈   3 2 λ s   σ ,
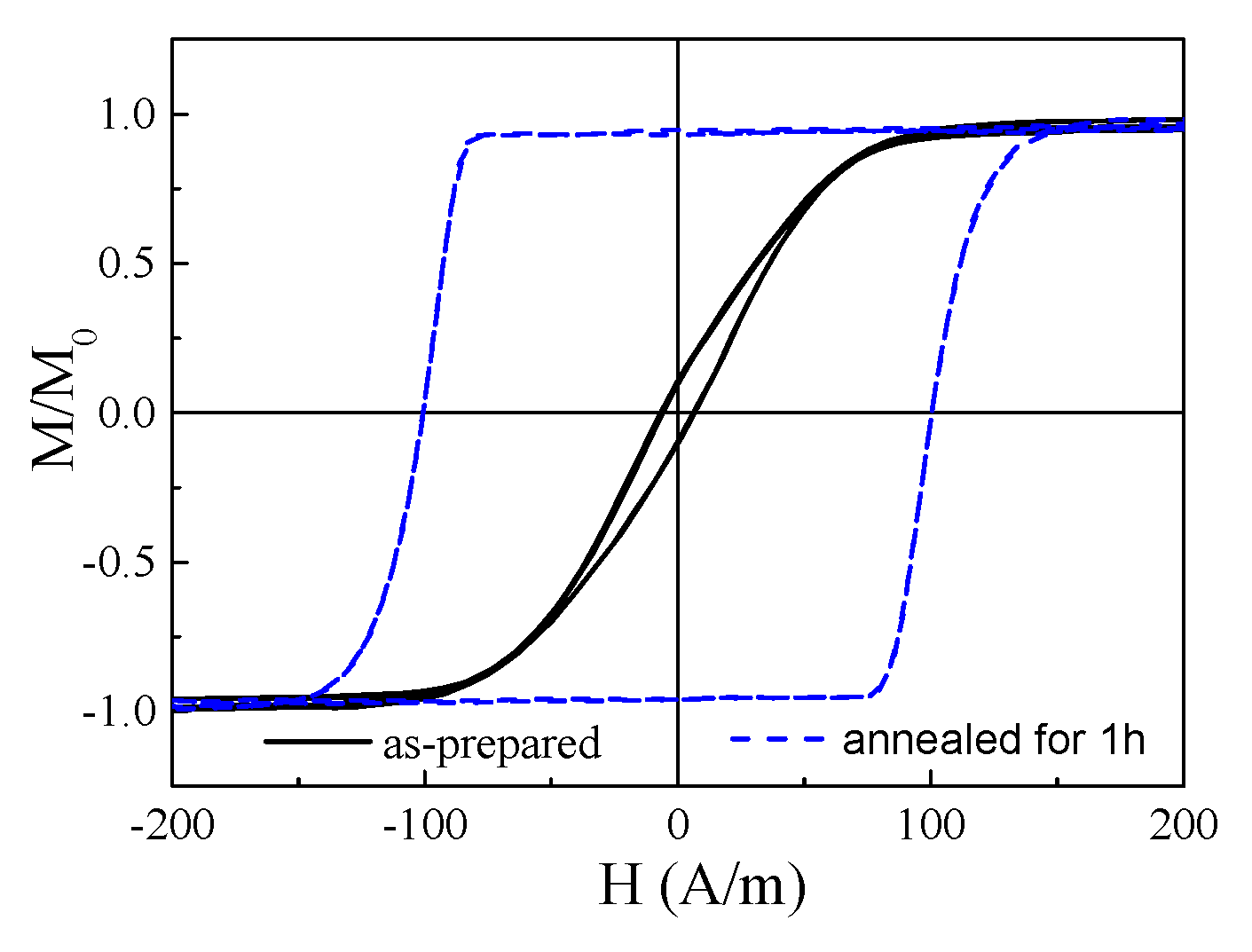
It is commonly assumed that λs -value and sign of amorphous materials are determined by the chemical composition of the alloys. Therefore, for the fixed composition of amorphous microwire it is expected that the annealing must be the common way allowing diminishing of Kme and hence magnetic softening. However, even for the Fe47Ni27Si11B13C2 microwire generally the opposite tendency is observed (see Figure 6): some coercivity, Hc, increasing is observed upon annealing at Tann =410 oC. Selected Tann is above Curie temperature, Tc (Tc ≈360 oC) and below the crystallization temperature, Tcr (Tcr ≈480 oC).
Similarly, substantial magnetic hardening is observed in Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 microwire after annealing (see Figure 7). Similarly to Fe47Ni27Si11B13C2 microwire, used Tann > Tc (Tc ≈223 oC) and Tann <T Tcr (Tcr ≈550 oC). The origin of magnetic hardening of amorphous materials upon annealing has been commonly discussed in terms of the directional ordering of atomic pairs or compositional and topological short- range ordering [39-43]. Accordingly, directional atomic pair ordering mechanism cannot explain observed magnetic hardening upon annealing of studied microwires.
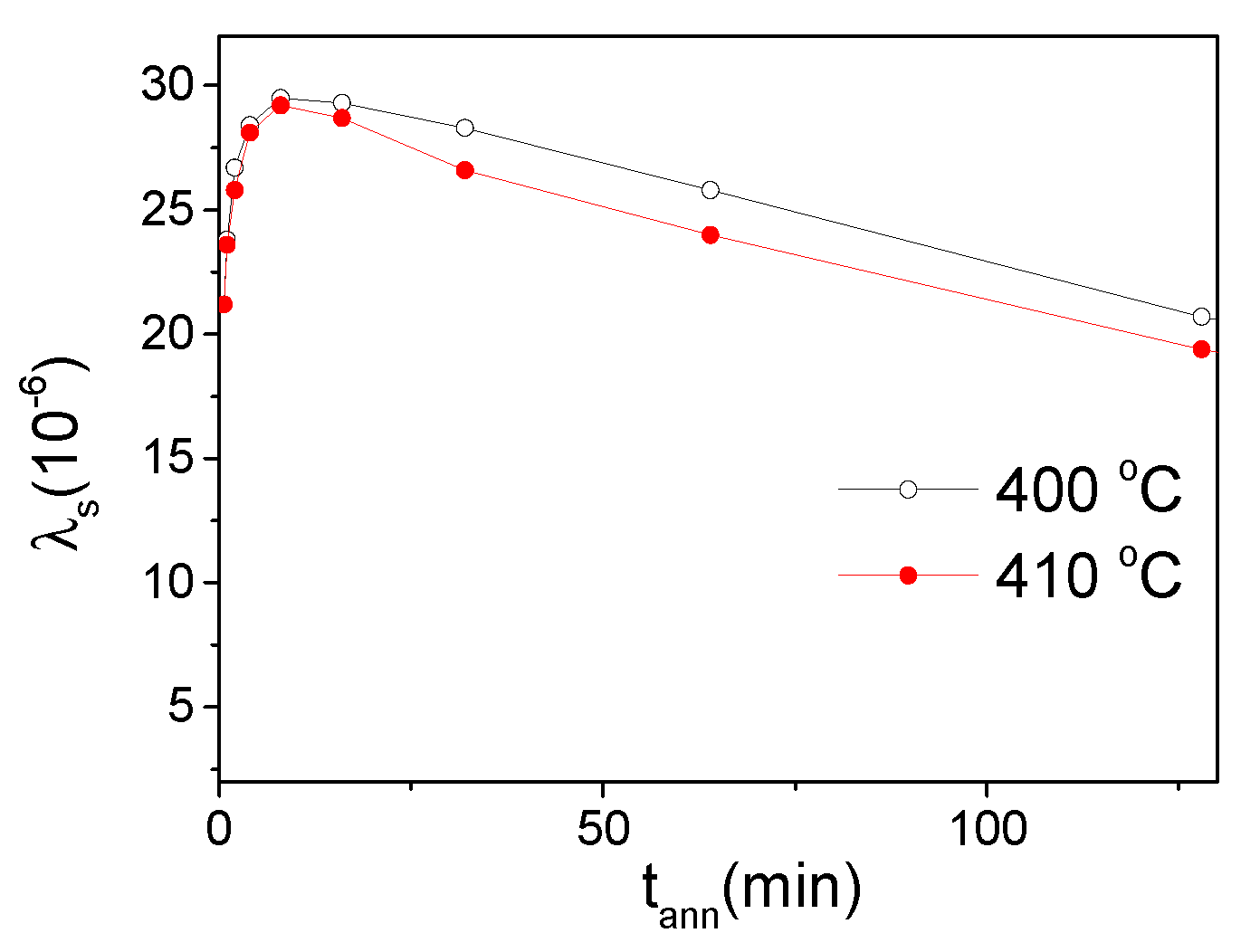
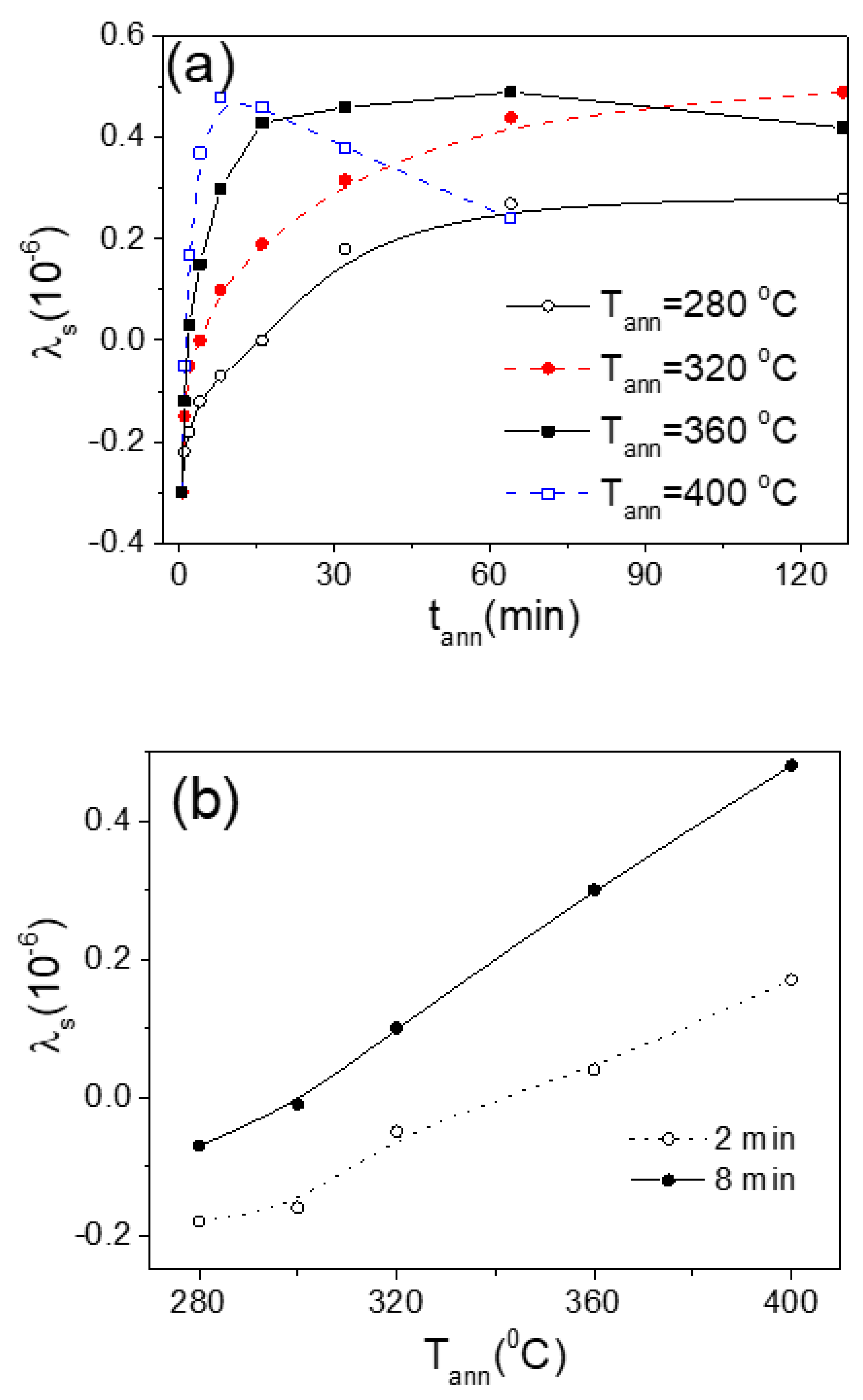
For better understanding of observed magnetic hardening of studied microwires upon annealing we analyzed the behaviour of λs -value upon annealing. As can be appreciated from Figure 8, an increase in λs is observed in Fe47Ni27Si11B13C2 microwire with annealing time, tann, at Tann>Tc (Tann =400 and 410 oC). Accordingly, some magnetic hardening of Fe47Ni27Si11B13C2 microwire can be attributed to observed increase in λs upon annealing.
Similar tendency: an increase in λs upon annealing is observed in Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 microwire (see Figure 9): an increase of λs –value is observed for all used Tann. The most remarkable feature is that change not only λs -value but also the sign upon annealing: after a few minutes of annealing λs becomes positive. Such modification of λs after annealing can explain the substantial change in the hysteresis loops of Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 microwire after annealing and magnetic hardening (see Figure 7). As previously shown experimentally, magnetic hardening of Co-rich microwires after annealing is related to the change in domain structure consisting of increase of the volume of the inner axially magnetized core [4, 35].
Additionally, λs is affected by both, Tann and tann (see Figure 9 a,b). Temperature- time dependencies of various structural and magnetic parameters were previously discussed in terms of structural relaxation involving changes in the atomic short-range order [39-43]. As shown in Figure 9b, an increase in λs is affected by both Tann and tann. For Tann <360 0C only an increase in λs is observed for the whole measured tann. However, for Tann ≥360 0C an increase in λs is followed by a decrease in λs (see Figure 9a). Similar influence of Tann and tann on λs was previously reported for Co-Fe rich amorphous ribbons [44] and quite recently in glass-coated microwires (but annealed at only one Tann) [45]. The appearance of the maximum on λs(tann) dependencies at elevated Tann was explained by the contribution of two different processes [44].
In the present case of glass-coated microwires, one of such processes must be associated with the internal stresses relaxation upon annealing. The other process must be related with aforementioned changes in in the atomic short-range order.
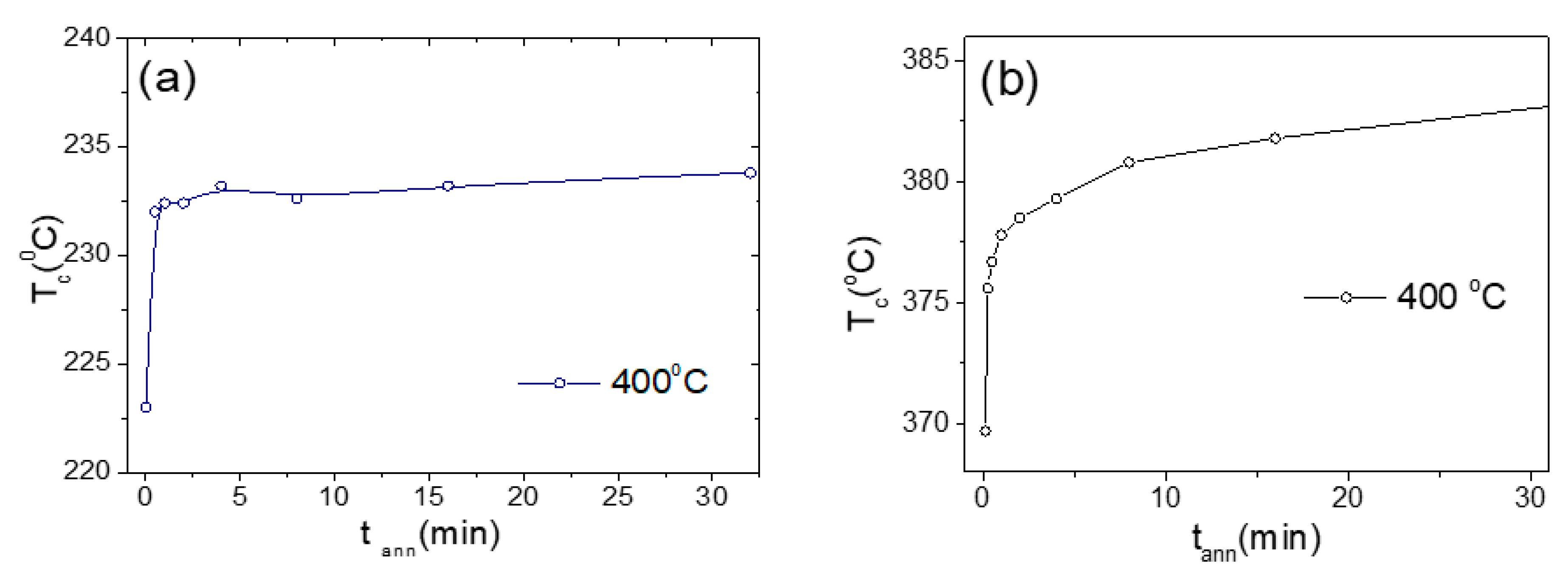
The Curie temperature, Tc, is one of the most sensitive magnetic parameters to local structural rearrangements [46-50]. As shown in Figure 10, substantial and monotonous increase in Tc is observed for both studied microwires after annealing. Similar dependencies of Tc upon annealing have been observed in various Fe-, Co- and Ni-rich amorphous alloys [46-48]. Such an increase in Tc of amorphous alloys upon annealing has been commonly attributed to structural relaxation of amorphous alloys [46-48]. Since, the magnetostriction of amorphous alloys is linked to the local atomic order, such structural relaxation can be one of the origins of observed λs evolution upon annealing.
From observed in Figure 10 substantial Tc(tann) dependence, observed for both studied microwires, we can deduce that structural relaxation processes upon annealing occur in both studied microwires. The detailed description of various atomic mechanisms responsible for the changes in Tc and other physical properties are provided elsewhere [41,42,49]. Such mechanisms include diffusion of structural defects, topological and compositional short range atomic ordering and clustering [42,43, 49,50]. However, the determination of the local atomic structure in amorphous materials by direct methods is a long-standing problem in materials science. Most of the methods allow only average structural information. There are only very few direct observations of local atomic configurations of amorphous materials interpreted as the presence of clusters [51,52].
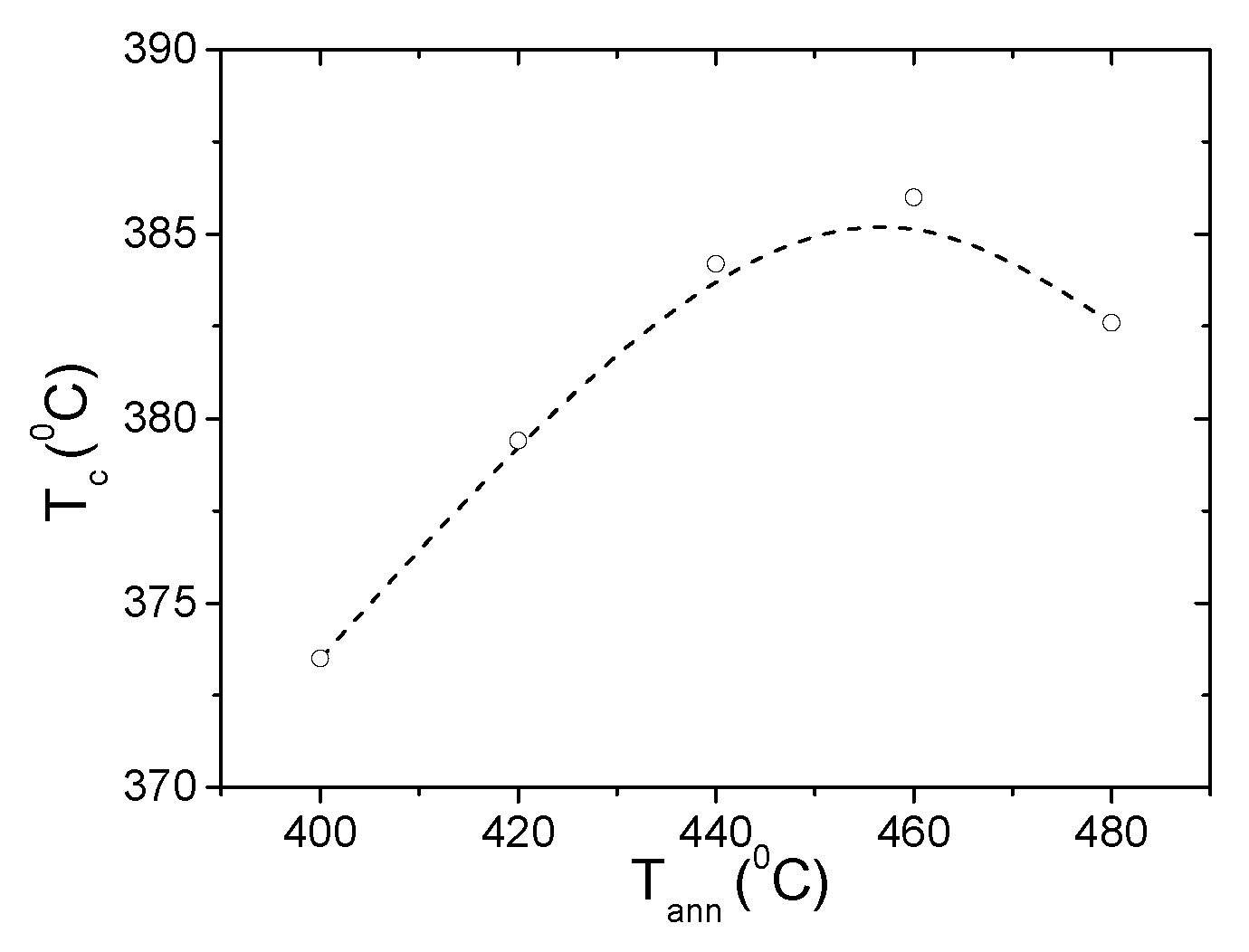
As mentioned above, one of the commonly involved mechanisms explaining magnetic hardening and magnetic field annealing induced anisotropy of amorphous materials with two or more ferromagnetic elements is atomic pairs ordering consisting of preferential reorientation of atomic pairs under the influence of the local magnetization [39-43,50]. Certainly, pair atomic ordering mechanism can be relevant for both studied microwires with the chemical composition consisting of more than two ferromagnetic elements. However, it is commonly assumed that such mechanism can be relevant for Tann < Tc. In the case of studied samples magnetic hardening is observed even upon annealing at Tann > Tc (see Figures 6,7). Provided in Figure 11 dependence of Tc on Tann measured in the Fe47Ni27Si11B13C2 microwire reflects the structural relaxation processes upon annealing at Tann > Tc and Tann < Tcr. Accordingly, various mechanisms previously discussed for amorphous alloys must be involved in observed dependencies of Tc and λs on annealing conditions.
On the other hand, structural relaxation should be also affected by the presence of mechanical stresses: transport processes including diffusion are affected by mechanical stresses [53]. Thus, previously was reported that the devitrification process (in particular the Tcr) and the structure of the crystalline phases are affected by the internal stresses produced by the glass-coating [54,55].
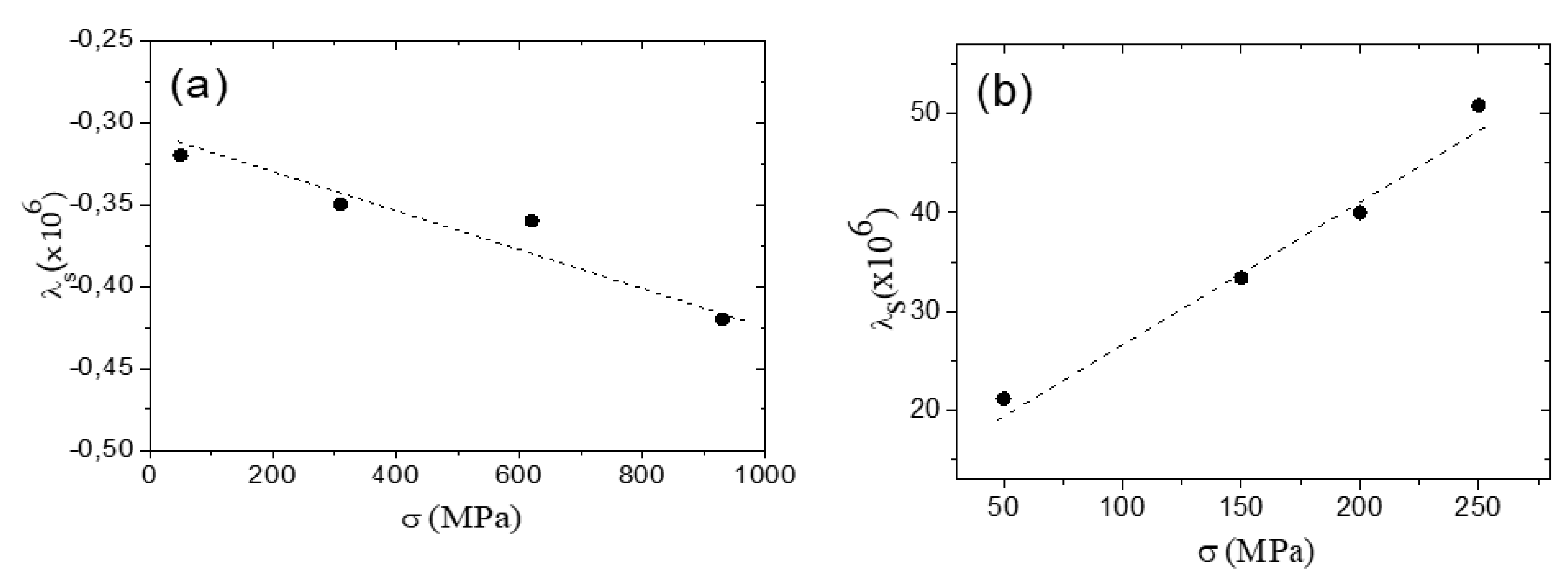
One of the peculiarities of glass-coated microwires is the composite structure and a higher level of internal stresses as-compared to the other amorphous materials associated with the presence of a glass-coating [6,13-17]. It is worth noting, that the internal stresses originated by the difference in the thermal expansion coefficients of metallic nucleus and the glass coating are the largest ones being an order of magnitude higher than the internal stresses related to the rapid melt quenching (typically present in conventional amorphous materials) [14-17]. Additionally, the internal stresses originated by the difference in the thermal expansion coefficients are mostly of tensile (axial) origin [14-17]. Therefore, the λs -value and stress-dependence can be rather different from conventional amorphous materials. Thus, one of the reasons for the λs modification upon annealing can be related to the internal stresses relaxation. Accordingly, we evaluated the stress dependence of λs in both studied microwires.
Similarly to Co-rich amorphous ribbons, a decrease in λs, well described as a linear λs(σ) dependence, is observed in Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 microwire (see Figure 12a). Phenomenologically, observed λs(σ) dependence can be described by eq. (1) with a slope, B≈ 1.25 x 10-7GPa, quite similar to the B-value, that was previously reported for Co-rich amorphous ribbons [9].
A linear λs(σ) dependence, is also observed in Fe47Ni27Si11B13C2 microwire, however an increase in λs is observed (see Figure 12b). The value of B- coefficient, B ≈ -1.2 x 10-5GPa is obtained for Fe47Ni27Si11B13C2 microwire. Previously, negative but rather lower B-coefficient values were observed for annealed Co-rich amorphous materials with positive λs – values [9]. However, recently an increase in λs upon application of tensile stress is also reported in Fe-Ni-rich microwires with positive λs [45].
From observed λs(σ) dependencies we can assume that the internal stresses relaxation can explain only an increase in λs for Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 microwire and a decrease in λs for Fe47Ni27Si11B13C2 sample. Therefore, the processes involved in dependence of λs on thermal treatment conditions (Tann or tann) and on applied stress cannot be explained considering only elevated magnitude of internal stresses for studied microwires.
As mentioned above, the role of local atomic environments is essential for understanding of the magnetostriction coefficient and Curie temperature behavior in glass-coated microwires. Therefore, both internal stresses relaxation and structural (topological or compositional) relaxation upon annealing must be taken into account for interpretation of evolution of magnetostriction upon annealing and applied stresses. One more possible origin of λs(σ) dependencies in amorphous materials is so-called “morphic” effect, related to the variation of a saturation elastic constants with the magnetization direction [56,57]. However, the existence of such “morphic” effect is predicted for amorphous materials with nearly-zero λs –values [56].
Most stress sensor applications ideally require materials that demonstrate significant reversible changes in magnetization when subjected to applied stress, while also exhibiting minimal magnetomechanical hysteresis. The dependence of magnetostriction on mechanical stress and annealing temperature can serve as a key starting point for determining the necessary treatment to use an adequate sensitive magneto-transport property, which is crucial for optimizing its sensitivity as a magnetostrictive stress sensor.

5. Conclusions

We evaluated the magnetostriction coefficients and Curie temperature and studied the influence of thermal treatment and applied stresses on magnetostriction coefficient values and the effect of annealing on Curie temperature. Annealing affects the magnetostriction coefficients and Curie temperature of both Fe47Ni27Si11B13C2 and Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 glass-coated microwires in a similar way. Observed influence of thermal treatment on magnetostriction coefficients and Curie temperature is discussed in terms of internal stresses relaxation and structural relaxation. We observed linear stress dependence of the magnetostriction coefficients in Fe47Ni27Si11B13C2 and Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 glass-coated microwires with different character of hysteresis loops and positive and low negative magnetostriction, respectively. A decrease with applied stress is observed in Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 microwire, while an increase of the magnetostriction coefficient is observed in Fe47Ni27Si11B13C2 microwire. Observed dependencies are discussed considering both internal stresses relaxation and short range atomic ordering. In summary, observed evolution of the magnetostriction upon applied stress and annealing confirms the importance of control of the magnetostriction coefficient for optimization of soft magnetic properties and understanding the origins of the influence of post-processing on magnetic softness in glass-coated microwires.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

Conceptualization, A.Z. and V.Z.; methodology, A.Z., M.C., P.C.L.,M.I. and V.Z,.; validation, S.K., A.Z, M.C., P.C.L., S.K., and V.Z.; formal analysis, A.Z. , S.K. and M.I.; investigation, A.Z, A.G., P.C.L., A.G.G, S.K., J.O..; resources, A.Z. and V.Z..; data curation, J.O, M.C. and M.I.; writing—original draft preparation, A.Z.; writing—review and editing, A.Z. and P.C.L.; visualization, M.C. and V.Z.; supervision, A.Z.; project administration, V.Z. and A.Z.; funding acquisition, A.Z. and V.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by EU under “INFINITE” (HORIZON-CL5-2021-D5-01-06) project, by the Spanish MICIN, under PID2022-141373NB-I00 project and by the Government of the Basque Country under PUE_2021_1_0009, Elkartek (MINERVA, MAGAF and ZE-KONP) projects and under the scheme of “Ayuda a Grupos Consolidados” (ref. IT1670-22). J.O. thanks the Ministry of Higher Education, Science and Technology (MESCYT) of the Dominican Republic.

Acknowledgments

The authors thank for technical and human support provided by SGIker of UPV/EHU (Medidas Magneticas Gipuzkoa) and European funding (ERDF and ESF). We wish to thank the administration of the University of the Basque Country, which not only provides very limited funding, but even expropriates the resources received by the research group from private companies for the research activities of the group. Such interference helps keep us on our toes.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hasegawa R., in: R. Hasegawa (Ed.), Glassy Metals: Magnetic Chemical and Structural Properties, CRC Press, Boca Raton, FL, 1983.
  2. Xing, Q.; Lograsso, T.A.; Ruffoni, M.P.; Azimonte, C.; Pascarelli, S.; Miller, D.J. Experimental exploration of the origin of magnetostriction in single crystalline iron. Appl. Phys. Lett. 2010, 072508. [Google Scholar] [CrossRef]
  3. Herzer, G. Amorphous and nanocrystalline soft magnets. In Proceedings of the NATO Advanced Study Institute on Magnetic Hysteresis in Novel Materials, Mykonos, Greece, 1–12 July 1996; NATO ASI Series (Series E: Applied Sciences); Volume 338, pp. 711–730.
  4. Zhukov, A.; Ipatov, M.; Corte-León, P.; Gonzalez-Legarreta, L.; Blanco, J.M.; Zhukova, V. Soft Magnetic Microwires for Sensor Applications. J. Magn. Magn. Mater. 2020, 498, 166180. [Google Scholar] [CrossRef]
  5. Herzer, G. Anisotropies in soft magnetic nanocrystalline alloys. J. Magn. Magn. Mater. 2005, 294, 99–106. [Google Scholar] [CrossRef]
  6. Zhukov, A.; Corte-Leon, P.; Gonzalez-Legarreta, L.; Ipatov, M.; Blanco, J.M.; Gonzalez, A.; Zhukova, V. Advanced Functional Magnetic Microwires for Technological Applications. J. Phys. D Appl. Phys. 2022, 55, 253003. [Google Scholar] [CrossRef]
  7. Du Tremolet de Lacheisserie E. Magnetostriction: Theory and Applications of Magnetoelasticity, CRC Press, Boca Raton, FL, 1994.
  8. Siemko, A.; Lachowicz, H.K. On the Origin of Stress-Dependent Saturation Magnetostriction in Metallic Glasses. J. Magn. Magn. Mater. 1990, 89, 21–25. [Google Scholar] [CrossRef]
  9. Barandiaran, M.; Hernando, A.; Madurga, V.; Nielsen, O.V.; Vazquez, M.; Vazquez-Lopez, M. Temperature, stress, and structural-relaxation dependence of the magnetostriction in (Co0.94Fe0.06)75Si15B10 glasses. Phys. Rev. B 1987, 35, 5066. [Google Scholar] [CrossRef] [PubMed]
  10. Vazquez, M.; Chen, D.-X. The magnetization reversal process in amorphous wires. IEEE Trans. Magn. 1995, 31, 1229–1238. [Google Scholar] [CrossRef]
  11. Sabol, R.; Klein, P.; Ryba, T.; Hvizdos, L.; Varga, R.; Rovnak, M.; Sulla, I.; Mudronova, D.; Galik, J.; Polacek, I.; et al. Novel Applications of Bistable Magnetic Microwires. Acta Phys. Pol. A 2017, 131, 1150–1152. [Google Scholar] [CrossRef]
  12. Mohri, K.; Uchiyama, T.; Panina, L.V.; Yamamoto, M.; Bushida, K. Recent Advances of Amorphous Wire CMOS IC Magneto-Impedance Sensors: Innovative High-Performance Micromagnetic Sensor Chip. J. Sens. 2015, 2015, 718069. [Google Scholar] [CrossRef]
  13. Chiriac, H.; Lupu, N.; Stoian, G.; Ababei, G.; Corodeanu, S.; Óvári, T.-A. Ultrathin Nanocrystalline Magnetic Wires. Crystals 2017, 7, 48. [Google Scholar] [CrossRef]
  14. Antonov, A.S.; Borisov, V.T.; Borisov, O.V.; Prokoshin, A.F.; Usov, N.A. Residual quenching stresses in glass-coated amorphous ferromagnetic microwires. J. Phys. D: Appl. Phys. 2000, 33, 1161–1168. [Google Scholar] [CrossRef]
  15. Chiriac, H.; Óvári, T.A.; Pop, G. Internal stress distribution in glass-covered amorphous magnetic wires. Phys. Rev. B 1995, 52, 10104–10113. [Google Scholar] [CrossRef] [PubMed]
  16. Zhukova, V.; Blanco, J.M.; Ipatov, M.; Zhukov, A. Magnetoelastic contribution in domain wall dynamics of amorphous microwires. Physica B 2012, 407, 1450–1454. [Google Scholar] [CrossRef]
  17. Torcunov, A.V.; Baranov, S.A.; Larin, V.S. The internal stresses dependence of the magnetic properties of cast amorphous microwires covered with glass insulation. J. Magn. Magn. Mater. 1999, 196–197. [Google Scholar] [CrossRef]
  18. Narita, K.; Yamasaki, J.; Fukunaga, H. Measurement of magnetostriction of a thin amorphous ribbon by means of small-angle magnetization rotation. IEEE Trans. Magn. 1980, 16, 435–439. [Google Scholar] [CrossRef]
  19. Zhukov, A.; Cobeño, A.F.; Gonzalez, J.; Blanco, J.M.; Aragoneses, P.; Dominguez, L. Magnetoelastic sensor of level of the liquid based on magnetoelastic properties of Co-rich microwires. Sens. Actuat. A Phys. 2000, 81, 129–133. [Google Scholar] [CrossRef]
  20. Praslička, D.; Blažek, J.; Šmelko, M.; Hudák, J.; Čverha, A.; Mikita, I.; Varga, R.; Zhukov, A. Possibilities of Measuring Stress and Health Monitoring in Materials Using Contact-Less Sensor Based on Magnetic Microwires. IEEE Trans. Magn. 2013, 49, 128–131. [Google Scholar] [CrossRef]
  21. Mohri, K.; Humphrey, F.B.; Kawashima, K.; Kimura, K.; Muzutani, M. Large Barkhausen and Matteucci effects in FeCoSiB, FeCrSiB, and FeNiSiB amorphous wires. IEEE Trans. Magn 1990, 26, 1781–1789. [Google Scholar] [CrossRef]
  22. Hristoforou, E.; Ktena, A. Magnetostriction and magnetostrictive materials for sensing applications. J. Magn. Magn. Mater. 2007, 316, 372–378. [Google Scholar] [CrossRef]
  23. Corte-Leon, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; González, J. Churyukanova, M.; Taskaev, S.; Zhukov, A. The effect of annealing on magnetic properties of “Thick” microwires. J. Alloys Compd. 2020, 831, 150992. [Google Scholar] [CrossRef]
  24. Zhukova, V.; Corte-Leon, P.; Blanco, J. M.; Ipatov, M.; Gonzalez, J.; Zhukov, A. Electronic Surveillance and Security Applications of Magnetic Microwires. Chemosensors 2021, 9, 100. [Google Scholar] [CrossRef]
  25. Kozejova, D.; Fecova, L.; Klein, P.; Sabol, R.; Hudak, R.; Sulla, I.; Mudronova, D.; Galik, J.; Varga, R. Biomedical applications of glass-coated microwires. J. Magn. Magn. Mater. 2019, 470, 2–5. [Google Scholar] [CrossRef]
  26. Brooks, H. A. Magnetostriction vs Co content in amorphous alloys of Fe-Co-P-B-AI. J. Appl. Phys. 1976, 47, 344–345. [Google Scholar] [CrossRef]
  27. Tsuya, N.; Arai, K. I.; Shiraga, Y.; Yamada, M.; Masumoto, T. Magnetostriction of amorphous Fe0.80PO.13C0.07 ribbon. Phys. Stat. Sol. A, 1975, 31, 557–561. [Google Scholar] [CrossRef]
  28. Churyukanova, M.; Semenkova, V.; Kaloshkin, S.; Shuvaeva, E.; Gudoshnikov, S.; Zhukova, V.; Shchetinin, I.; Zhukov, A. Magnetostriction investigation of soft magnetic microwires. Phys. Stat. Sol. A 2016, 213, 363–367. [Google Scholar] [CrossRef]
  29. Zhukov, A.; Churyukanova, M.; Kaloshkin, S.; Sudarchikova, V.; Gudoshnikov, S.; Ipatov, M.; Talaat, A.; Blanco, J.M.; Zhukova, V. Magnetostriction of Co-Fe-based amorphous soft magnetic microwires. J. Electr. Mater. 2016, 45, 226–234. [Google Scholar] [CrossRef]
  30. Baranov, S.A.; Larin, V.S.; Torcunov, A.V. Technology, Preparation and Properties of the Cast Glass-Coated Magnetic Microwires. Crystals 2017, 7, 136. [Google Scholar] [CrossRef]
  31. Gonzalez-Legarreta, L.; Corte-Leon, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Zhukov, A. Optimization of magnetic properties and GMI effect of Thin Co-rich Microwires for GMI Microsensors. Sensors 2020, 20, 1558. [Google Scholar] [CrossRef]
  32. Kaloshkin, S.; Churyukanova, M.; Zadorozhnyi, V.; Shchetinin, I.; Roy, R.- K. Curie temperature behaviour at relaxation and nanocrystallization of Finemet alloys. J. Alloys Compd. 2011, 509 (Suppl. 1), S400–S403. [Google Scholar] [CrossRef]
  33. Zhukova, V.; Kaloshkin, S.; Zhukov, A.; Gonzalez, J. DSC studies of Finemet-type glass-coated mictrowires. J. Magn. Magn. Mater. 2002, 249, 108–112. [Google Scholar] [CrossRef]
  34. Nderu, J. N.; Takajo, M.; Yamasaki, J.; Humphrey, F. B. Effect of stress on the bamboo domains and magnetization process of CoSiB amorphous wire. IEEE Trans. Magn. 1998, 34, 1312–1314. [Google Scholar] [CrossRef]
  35. Zhukov, A.; Chizhik, A.; Ipatov, M.; Talaat, A.; Blanco, J. M.; Stupakiewicz, A.; Zhukova, V. Giant magnetoimpedance effect and domain wall dynamics in Co-rich amorphous microwires. J. Appl. Phys. 2015, 117, 043904. [Google Scholar] [CrossRef]
  36. Soldatov, I.; Kolesnikova, V.; Rodionova, V.; Schäfer, R. Interpretation of Kerr Microscopic Domain Contrast on Curved Surfaces. IEEE Magn. Lett. 2021, 12, 7103804. [Google Scholar] [CrossRef]
  37. Kabanov, Y.; Zhukov, A.; Zhukova, V.; Gonzalez, J. Magnetic domain structure of microwires studied by using the magneto-optical indicator film method. Appl. Phys. Lett 2005, 87, 142507. [Google Scholar] [CrossRef]
  38. Orlova, N. N.; Gornakov, V. S.; Aronin, A. S. Role of internal stresses in the formation of magnetic structure and magnetic properties of iron-based glass coated microwires. J. Appl. Phys. 2017, 121, 205108. [Google Scholar] [CrossRef]
  39. Luborsky, F.E.; Walter, J.L. Magnetic Anneal Anisotropy in Amorphous Alloys. IEEE Trans. Magn. 1977, 13, 953–956. [Google Scholar] [CrossRef]
  40. Haimovich, J.; Jagielinski, T.; Egami, T. Magnetic and structural effects of anelastic deformation of an amorphous alloy. J. Appl. Phys. 1985, 57, 3581–3583. [Google Scholar] [CrossRef]
  41. Miyazaki, T.; Takahashi, M. Magnetic annealing effect of amorphous (Fe1- xCox)77Si10B13 alloys. J Appl. Phys. 1978, 17, 1755–1763. [Google Scholar] [CrossRef]
  42. Egami, T. Structural relaxation in amorphous Fe40Ni40P14B6 studied by energy dispersive X-ray diffraction. J. Mater. Sci. 1978, 13, 2587–2599. [Google Scholar] [CrossRef]
  43. Egami, T. Structural relaxation in amorphous alloys - compositional short range ordering. Mater. Res. Bull. 1978, 13, 557–562. [Google Scholar] [CrossRef]
  44. Hernando, A.; Madurga, V.; Núñez de Villavicencio, C.; Vázquez, M. Temperature dependence of the magnetostriction constant of nearly zero magnetostriction amorphous alloys. Appl. Phys. Lett. 1984, 45, 802–804. [Google Scholar] [CrossRef]
  45. Zhukova, V.; Churyukanova, M.; Kaloshkin, S.; Corte-Leon, P.; Ipatov, M.; Zhukov, A. Magnetostriction of amorphous Co-based and Fe-Ni-based magnetic microwires: Effect of stresses and annealing. J. Alloys Compd. 2023, 954, 170122. [Google Scholar] [CrossRef]
  46. Zhukova, V.; Blanco, J.M.; Ipatov, M.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Tailoring of magnetoimpedance effect and magnetic softness of Fe-rich glass-coated microwires by stress- annealing. Sci. Rep. 2018, 8, 1–14. [Google Scholar] [CrossRef] [PubMed]
  47. Chen, H.; Sherwood, R.; Leamy, H.; Gyorgy, E. The effect of structural relaxation on the Curie temperature of Fe based metallic glasses. IEEE Trans. Magn 1976, 12, 933–935. [Google Scholar] [CrossRef]
  48. Dzhumazoda, A.; Panina, L.V.; Nematov, M.G.; Tabarov, F.S.; Morchenko, A.T.; Bazlov, A.I.; Ukhasov, A.; Yudanov, N.A.; Podgornaya, S.V. Controlling the Curie temperature in amorphous glass coated microwires by heat treatment. J. Alloys Compd. 2019, 802, 36–40. [Google Scholar] [CrossRef]
  49. Serebryakov, A. V. Amorphization reactions and glass to crystal transformations in metallic materials. J. Non-Cryst. Solids 1993, 156-158, 594–597. [Google Scholar] [CrossRef]
  50. Becker, J.J. A new mechanism for magnetic annealing in amorphous metals. IEEE Tran. Magn. 1978, 14, 938–940. [Google Scholar] [CrossRef]
  51. Hirata, A.; Guan, P.; Fujita, T.; Hirotsu, Y.; Inoue, A.; Yavari1, A. R.; Sakurai, T.; Chen, M. Direct observation of local atomic order in a metallic glass. Nature Mater. 2011, 10, 28–33. [Google Scholar] [CrossRef]
  52. Hirotsu, Y.; Hanada, T.; Ohkubo, T.; Makino, A.; Yoshizawa, Y.; Nieh, T.G. Nanoscale phase separation in metallic glasses studied by advanced electron microscopy techniques. Intermetallics 2004, 12, 1081–1088. [Google Scholar] [CrossRef]
  53. Onsager, L. Reciprocal Relations in Irreversible Processes. II. Phys. Rev. 1931, 38, 2265–2279. [Google Scholar] [CrossRef]
  54. Zhukova, V.; Cobeño, A.F.; Zhukov, A.; Blanco, J.M.; Larin, V.; Gonzalez, J. Coercivity of glass-coated Fe73.4-xCu1Nb3.1Si13.4+xB9.1 (0≤x≤1.6) microwires. Nanostructured Materials 1999, 11, 1319–1327. [Google Scholar] [CrossRef]
  55. Aronin, A.S.; Abrosimova, G.E.; Kiselev, A.P.; Zhukova, V.; Varga, R.; Zhukov, A. The effect of mechanical stress on Ni63.8Mn11.1Ga25.1 microwire crystalline structure and properties. Intermetallics 2013, 43, 60–64. [Google Scholar] [CrossRef]
  56. Kraus, L. On the Stress Dependence of the Saturation Magnetostriction in Amorphous Alloys. Phys. Stat. Sol. (a) 1988, 109, K71–K74. [Google Scholar] [CrossRef]
  57. Masow, W. P. A Phenomenological Derivation of the First- and Second-Order Magnetostriction and Morphic Effects for a Nickel Crystal. Phys. Rev. 1951, 82, 715–723. [Google Scholar]
Preprints 84977 g001
Figure 1. Optical microscopy images of Fe47Ni27Si11B13C2 (a) and Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 (b) samples.
Figure 1. Optical microscopy images of Fe47Ni27Si11B13C2 (a) and Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 (b) samples.
Preprints 84977 g001
Preprints 84977 g002
Figure 2. XRD patterns of as-prepared and annealed at 400 oC Fe47Ni27Si11B13C2 (a) and Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 samples (b).
Figure 2. XRD patterns of as-prepared and annealed at 400 oC Fe47Ni27Si11B13C2 (a) and Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 samples (b).
Preprints 84977 g002
Preprints 84977 g003
Figure 3. Examples of a DSC curves in vicinity of Tc and their variation with annealing measured in Fe73.8Cu1Nb3.1Si13B9.1 microwire.
Figure 3. Examples of a DSC curves in vicinity of Tc and their variation with annealing measured in Fe73.8Cu1Nb3.1Si13B9.1 microwire.
Preprints 84977 g003
Preprints 84977 g004
Figure 4. Hysteresis loops of Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 (a) and Fe47Ni27Si11B13C2 (b) samples.
Figure 4. Hysteresis loops of Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 (a) and Fe47Ni27Si11B13C2 (b) samples.
Preprints 84977 g004
Preprints 84977 g005
Figure 5. DSC curves of Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 (a) and Fe47Ni27Si11B13C2 (b) samples.
Figure 5. DSC curves of Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 (a) and Fe47Ni27Si11B13C2 (b) samples.
Preprints 84977 g005
Preprints 84977 g006
Figure 6. Hysteresis loops measured in as-prepared Fe47Ni27Si11B13C2 microwires and annealed at 410oC for different time.
Figure 6. Hysteresis loops measured in as-prepared Fe47Ni27Si11B13C2 microwires and annealed at 410oC for different time.
Preprints 84977 g006
Preprints 84977 g007
Figure 7. Change of the hysteresis loops of Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 sample after annealing at 400 oC.
Figure 7. Change of the hysteresis loops of Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 sample after annealing at 400 oC.
Preprints 84977 g007
Preprints 84977 g008
Figure 8. Effect of annealing conditions on magnetostriction, λs of Fe47Ni27Si11B13C2 microwire.
Figure 8. Effect of annealing conditions on magnetostriction, λs of Fe47Ni27Si11B13C2 microwire.
Preprints 84977 g008
Preprints 84977 g009
Figure 9. Effect of annealing conditions on magnetostriction, λs, in Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 microwire: λs(tann) dependencies at different Tann (a) and λs(Tann) dependencies at tann =2 and 8 min (b).
Figure 9. Effect of annealing conditions on magnetostriction, λs, in Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 microwire: λs(tann) dependencies at different Tann (a) and λs(Tann) dependencies at tann =2 and 8 min (b).
Preprints 84977 g009
Preprints 84977 g010
Figure 10. Effect of annealing conditions on Tc of Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 (a) and Fe47Ni27Si11B13C2 (b) microwires.
Figure 10. Effect of annealing conditions on Tc of Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 (a) and Fe47Ni27Si11B13C2 (b) microwires.
Preprints 84977 g010
Preprints 84977 g011
Figure 11. Effect of annealing temperature on Tc of Fe47Ni27Si11B13C2 microwires.
Figure 11. Effect of annealing temperature on Tc of Fe47Ni27Si11B13C2 microwires.
Preprints 84977 g011
Preprints 84977 g012
Figure 12. λs(σ) dependence measured in Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 sample (a) and in Fe47Ni27Si11B13C2 sample (b).
Figure 12. λs(σ) dependence measured in Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 sample (a) and in Fe47Ni27Si11B13C2 sample (b).
Preprints 84977 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated