Categorical Join and Generating Families in Diffeological Spaces

Preprint

Article

Categorical Join and Generating Families in Diffeological Spaces

Altmetrics

Downloads

113

Views

Comments

A peer-reviewed article of this preprint also exists.

Enrique Macías -Virgós^*

,Reihaneh Mehrabi

Enrique Macías -Virgós^*

,Reihaneh Mehrabi

This version is not peer-reviewed

Submitted:

12 September 2023

Posted:

14 September 2023

You are already at the latest version

Alerts

Abstract

We prove that a diffeological space is diffeomorphic to the categorical join of any generating family of plots.

Keywords:

Subject: Computer Science and Mathematics - Geometry and Topology

MSC: 14F40

1. Introduction

Diffeological spaces were introduced by Souriau [5] as a generalization of differentiable manifolds. This setting includes not only finite-dimensional manifolds, but also manifolds with boundary, infinite-dimensional manifolds, leaf spaces of foliations or spaces of differentiable maps. The main reference is Iglesias-Zemmour’s book [1]. Many fundamental results are exposed in nLab [3] too.

A diffeological structure on a set X is given by declaring which maps from open subsets of Euclidean spaces into X are considered to be smooth. These maps are called the plots of the diffeology (Section 2). They can be seen as n-dimensional curves,

n \geq 0

, on X. This contravariant idea differs from the covariant classical one of declaring which real maps from a manifold X are smooth. On the other hand, the idea of an atlas on a manifold is generalized by the notion of a generating family of plots (Section 4).

Our main result (Theorem 6.1) will be to give a categorical interpretation of a generating family, namely by proving that the diffeological space is the join of the family, that is, the push-out of the pull-back.

Most examples will be related to finite-dimensional manifolds.

2. Diffeological Spaces

A diffeology on the set X is a family

D

of set maps

α : U \to X

called plots such that:

each plot $α$ is defined on an open subset $U \subset R^{n}$ of some Euclidean space $R^{n}$ , $n \geq 0$ ;
any constant map $α : U \subset R^{n} \to X$ belongs to $D$ ;
if $α : U \subset R^{n} \to X$ belongs to $D$ and if $h : V \subset R^{m} \to U \subset R^{n}$ is a $C^{\infty}$ -map, then the composition $α \circ h$ belongs to $D$ ;
the map $α : U \to X$ belongs to $D$ if and only if it locally belongs to $D$ , that is, for each $p \in U$ there exists some open subset $p \in V \subset U$ such that $α_{∣ V}$ belongs to $D$ .

Note that the domain U and the Euclidean space

R^{n}

n \geq 0

, depend on the plot

α

A diffeological space

(X, D)

is a set X endowed with a diffeology

D

Remark 2.1.

Diffeological spaces are considered to be of class

C^{\infty}

. By changing

C^{\infty}

C^{r}

in Axiom (3) for some

0 \leq r \leq ω

we could obtain a theory for diffeological spaces of class

C^{r}

Example 2.2.

Let M be a finite-dimensional manifold. The manifold diffeology

D_{M}

is the collection of all

C^{\infty}

-maps

U \subset R^{m} \to M

defined on open subsets of Euclidean spaces with values in M.

Example 2.3.

Let R be any equivalence relation on the manifold M and let

π : M \to M / R

be the quotient map. We endow

M / R

with the quotient diffeology

D_{M} / R

where the map

α : U \to M / R

belongs to

D_{M} / R

if it locally factors through some plot of the manifold diffeology

D_{M}

on M.

Example 2.4.

Let

N \subset M

be any subset of the manifold M. We endow N with the subspace diffeology formed by the plots

α : U \to M

in the manifold diffeology

D_{M}

such that

α (U) \subset N

The last two examples show that diffeology is a much more flexible setting than the classical one.

3. Smooth Maps

Definition 3.1.

Let

(X, D_{X})

(Y, D_{Y})

be two diffeological spaces. A set map

f : X \to Y

is smooth when

α \in D_{X}

implies

f \circ α \in D_{Y}

Example 3.2.

M, N

are

C^{\infty}

-manifolds endowed with the manifold diffeologies

D_{M}

D_{N}

, respectively, then the smooth maps between M and N as diffeological spaces are the

C^{\infty}

-maps as differentiable manifolds.

Proposition 3.3.

The composition of smooth maps is a smooth map.

Proposition 3.4.

The quotient map

π : M \to M / R

of Example 2.3 is smooth. Moreover, a map

f : M / R \to N

is smooth if and only if the composition

f \circ π : M \to N

is smooth.

Corollary 3.5.

A quotient map

α : U \to X

is a diffeomorphism if and only if it is bijective.

Proof.

Let

α^{- 1} : X \to U

be the inverse map. Since

α^{- 1} \circ α = {id}_{X}

is smooth,

α^{- 1}

is smooth. □

Example 3.6.

N \subset M

is a subset endowed with the subspace diffeology of Example 2.4 then the inclusion map

i_{N} : N \subset M

is smooth. Moreover, a map

f : P \to N

is smooth if and only if

i_{N} \circ f : P \to M

is smooth.

Example 3.7.

By Axiom 3 of diffeology, the plots

α : U \to X

of a diffeology are smooth maps.

Definition 3.8.

A diffeomorphism is a smooth map with a smooth inverse.

4. Generating Families

Definition 4.1.

It is easy to check that the intersection of diffeologies on a set X is a diffeology on X. Then if

F

is any family of set maps

α_{i} : U_{i} \subset R^{n_{i}} \to X

we can consider the smallest diffeology

D = 〈 F 〉

containing

F

. We will say that

F

is a generating family for the diffeology

D = 〈 F 〉

We will always assume that the family

F

contains all the constant plots on X.

Example 4.2.

Any atlas on a manifold M is a generating family of the manifold diffeology.

Example 4.3.

Let

(X, D_{X})

be a diffeological space and let

f : X \to Y

be a set map. The diffeology on Y generated by the maps

f \circ α

, with

α \in D_{X}

, is called the final diffeology. It is formed by the maps that locally are of the form

f \circ α

for some

α \in D_{X}

Example 4.4.

Let

(Y, D_{Y})

be a diffeological space and let

f : X \to Y

be a set map. The initial diffeology on X is the diffeology generated by the set maps

α : U \subset R^{n} \to X

such that

f \circ α \in D_{Y}

Example 4.5.

Let

(X, D_{X})

(Y, D_{Y})

be two diffeological spaces. The product diffeology on

X \times Y

is the intersection of the initial diffeologies for the projections

p_{X} : X \times Y \to X

and

p_{Y} : X \times Y \to Y

Example 4.6.

The coproduct diffeology on the disjoint union

X ⊔ Y

is the intersection of the final diffeologies for the inclusions

i_{X} : X ↪ X ⊔ Y

and

i_{Y} : Y ↪ X ⊔ Y

It is easy to check that the product and coproduct diffeologies verify the usual universal properties.

The following criterion of generation is very useful.

Theorem 4.7

([1] Art. 1.68). Let the diffeology

D = 〈 F 〉

be generated by the family

F

. A set map

α : U \subset R^{n} \to X

belongs to

D

if and only if it locally factors through some element of

F

(we assume that constant plots are all contained in

F

Moreover, a map

f : (X, D_{X}) \to (Y, D_{Y})

is smooth if and only if

f \circ α \in D_{Y}

for any

α \in F

in a generating family

F

D_{X}

5. Categorical Constructions

The category of diffeological spaces and smooth maps has limits and colimits. Here, we will show how to construct the pull-back, the push-out and the join of two smooth maps. Most times these maps will be plots of some diffeology on X.

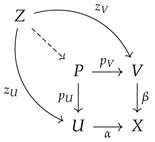
5.1. Pull-Back

Let

α : U \to X

β : V \to X

be two smooth maps with the same codomain. The pull-back of

α

and

β

is the set

P = {(u, v) \in U \times V : α (u) = β (v)}

endowed with the subspace diffeology of the product diffeology on

U \times V

The projections

p_{1} : U \times V \to U

and

p_{2} : U \times V \to V

induce smooth maps

p_{U} : P \to U, p_{V} : P \to V,

which verify

α \circ p_{U} = β \circ p_{V}

and the universal property of a pull-back:

5.2. Push-Out

Let

p_{U} : P \to U

p_{V} : P \to V

be two smooth maps with the same domain. The push-out of

p_{U}

and

p_{V}

is the quotient

J = (U ⊔ V) / R

of the coproduct

U ⊔ V

by the equivalence relation R generated by

u \in U, v \in V, u R v iff α (u) = β (v) .

The maps

j_{U} = π \circ i_{U}

and

j_{V} = π \circ i_{V}

verify

j_{U} \circ p_{U} = j_{V} \circ p_{V}

and the universal property of a push-out:

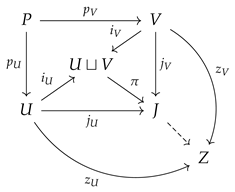
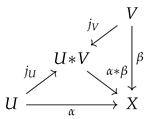
5.3. Join

Given two smooth maps

α : U \to X

and

β : V \to X

, it is an exercise to check that the push-out of the pull-back of

α

and

β

is diffeomorphic to the join

U * V

α

and

β

([4]), defined as follows: there is a well-defined smooth map

α * β : U * V \to X

and maps

j_{U} : U \to U * V

and

j_{V} : V \to U * V

such that

$(α * β) \circ j_{U} = α$ , $(α * β) \circ j_{V} = β$ ,
they verify the universal property

Analogously, given k maps

α_{i} : U_{i} \to X

, the join

U = U_{1} * \dots * U_{k}

and the universal map

α = α_{1} * \dots * α_{k} : U = U_{1} * \dots * U_{k} \to X

are defined by induction.

Remark 5.1.

It is possible to define the join of an infinite number of plots, but we will not develop this idea, for the sake of simplicity.

Lemma 5.2.

Let

F = {α_{i} : U_{i} \to X}

be a generating family. Then the universal map

α = *_{i} α_{i} : U = *_{i} U_{i} \to X

of the join is a quotient map.

Proof.

Let

γ : W \to X

be a plot on X. By Criterion 4.7, for each

p \in W

there exists a neighborhood

W_{p} \subset W

such that

γ

factors through some

α_{i}

. Hence it factors through the disjoint union and consequently through the join. □

6. Main Result

Next theorem is our main result.

Theorem 6.1.

Let

(X, D)

be a diffeological space. A family

F = {α_{i} : U_{i} \to X}

of plots is a generating family for

D

if and only if there is a diffeomorhism

α = α_{1} * \dots * α_{n} : U = U_{1} * \dots * U_{n} \to X

commuting with the maps

α_{i}

and the natural maps

j_{i} : U_{i} \to U

, that is

α \circ j_{i} = α_{i}

for all i.

Proof.

Let

F

be a generating family. The map

α

is surjective because generating families include all constant plots.

It is injective because

α ([u_{i}]) = α ([u_{j}])

means that either

u_{i} = u_{j}

u_{i} \in U_{i}

u_{j} \in U_{j}

and

α_{i} (u_{i}) = α_{j} (u_{j})

, that is

[u_{i}] = [u_{j}]

. Then

α

is bijective and Corollary 3.5 applies. Hence

α

is a diffeomorphism.

The converse statement follows from Lemma 5.2. □

Example 6.2.

Let X be the disjoint union of a line

X_{1} = R

and a point

X_{0} = {0}

, endowed with the diffeology generated by the constant plot

α_{0} : R^{0} \to X

α_{0} (0) = 0

, and the identity plot

α_{1} : R^{1} \to X_{1} \subset X

α_{1} (t) = t

, respectively. Clearly,

X ≅ U_{0} * U_{1} = U_{0} ⊔ U_{1}

Example 6.3.

Let X be the set

X = {(x, y) \in R^{2} : x y = 0} .

We consider the diffeology on X generated by the two plots

\begin{matrix} α_{1} & : U_{1} = R \to X, α_{1} (t) = (t, 0), \\ α_{2} & : U_{2} = R \to X, α_{2} (t) = (0, t) . \end{matrix}

Then

X ≅ U_{1} * U_{2}

As we pointed out in [2], this is not the cross diffeology on X induced by the manifold diffeology of

R^{2}

Example 6.4.

The manifold diffeology on a manifold M is the join of any atlas. More precisely, let

{α_{i} \subset R^{m} : U_{i} \to M}

be an atlas on the manifold

M^{m}

. Then

⋃_{i} α_{i} (U_{i}) = M ≅ *_{i} U_{i},

where the open subsets

U_{i} ≅ α (U_{i}) \subset M

are glued by inclusions.

References

Iglesias-Zemmour, Patrick. Diffeology. (Mathematical Surveys and Monographs 185. Providence, RI: American Mathematical Society (AMS) xxiii, 439 p. (2013).
Macías-Virgós, Enrique; Mehrabi, Reihaneh. Mayer-Vietoris sequence for generating families in diffeological spaces. Indag. Math., New Ser. 34, No. 4, 661-672 (2023).
nLab. Diffeological space. https://ncatlab.org/nlab/show/diffeological+space (viewed on August 28, 2023).
Rijke, Egbert. The join construction, arXiv:1701.07538 (2017).
Souriau, Jean-Marie. Groupes différentiels, in Differential Geometrical Methods in Mathematical Physics (Proc. Conf., Aix-en-Provence/Salamanca, 1979), Lecture Notes in Math. 836, Springer, Berlin, (1980), pp. 91–128.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Categorical Join and Generating Families in Diffeological Spaces

Abstract

1. Introduction

2. Diffeological Spaces

3. Smooth Maps

4. Generating Families

5. Categorical Constructions

5.1. Pull-Back

5.2. Push-Out

5.3. Join

6. Main Result

References

MDPI Initiatives

Important Links

Subscribe