Prerpints.org logo
Preprint
Article

Study on Extraction Method of Track Edge Acoustic Feature Based on Cyclic Stationary Analysis

Altmetrics

Downloads

55

Views

10

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 September 2023

Posted:

14 September 2023

You are already at the latest version

Alerts
Abstract
Due to the non-contact measurement characteristics of trackside acoustic technology, it is now utilized for train bearing fault diagnosis. However, the relative motion between the train and the trackside acoustic detection device introduces Doppler aberration in the collected acoustic signal, which affects bearing fault diagnosis. Moreover, when a fault occurs in the train bearing, its acoustic signal exhibits cyclic smoothness characteristics that can be effectively analyzed using the cyclic smoothness method for more accurate judgment. In order to minimize diagnostic errors and enhance accuracy in bearing fault diagnosis, this study integrates bearing fault characteristics with Doppler aberration correction methods and cyclic smoothness techniques for current-stage bearings diagnostics. The overall time-domain graph becomes more compact with an approximately 50% increase in amplitude after correction compared to pre-correction values; other parameters experience enhancements ranging from 20-60%. These results validate the feasibility of our proposed approach and establish a framework for conducting bearing fault diagnosis based on cyclically smoothed Doppler aberration correction.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

During train operation, the bearings, bogies, gearboxes, and other vehicle components are subjected to prolonged heavy load conditions. The structural integrity of these parts is susceptible to changes that can lead to fatigue, cracks, wear, indentation, and fractures on their surfaces. These failures pose a significant threat to long-term safety and stability while also triggering a series of safety accidents [1]. Amongst these numerous components, the bearing plays a crucial role; therefore, accurate identification of its condition and effective fault diagnosis become imperative [2].
In the 1980s, the United States initiated research on train fault detection and diagnosis systems. The team of technical experts developed a roadside acoustic diagnostic system [3], with a focus on train bearings. Initially, independent microphones were employed to collect signals from rolling bearings, which were then analyzed by a mainframe computer to derive corresponding diagnostic results [4]. In 1990, the research unit further optimized sensor equipment and implemented a microphone array system for high-precision signal acquisition. Subsequently, through optimization efforts, the system evolved into a practical Trackside Acoustic Detector System (TADS) for track acoustic detection. This upgraded version incorporated advanced algorithms like neural networks to significantly enhance the accuracy of diagnostic results, achieving an impressive precision rate of 97.0% [5,6]. In 1991, the Australian company Vipac Engineers Scientists Ltd. initiated a significant increase in resources dedicated to researching acoustic monitoring and judgment control systems for train bearings. Eventually, in the late 1990s, they successfully developed a bearing acoustic diagnostic system known as Railway Acoustic Monitoring System (Rail BAM). This system employs sensor arrays to effectively capture acoustic signals from moving trains. Subsequently, through computer-based logical analysis, early fault diagnosis reports of the trains can be generated. Furthermore, it possesses robust self-testing capabilities and has greatly enhanced stability [7,8].
Due to the non-contact measurement characteristics of rail-side acoustic technology, this technology is currently employed for fault diagnosis of train bearings [9]. However, the relative motion between the detection equipment and the fault sound source during the detection process leads to Doppler aberration phenomenon in acquired acoustic signals, which adversely affects bearing fault identification and diagnosis. Although various methods such as the energy center of gravity method [10], the adaptive correction method [11], and the Morse acoustic theory have been developed to correct the Doppler aberration phenomenon [12], they are unable to handle non-smooth characteristics exhibited by trackside acoustic signals from train bearings in complex fault situations. In such cases, analysis using the cyclic smoothing method becomes necessary for a more effective judgment [13]. The Cyclostationary signal analysis method is employed for analyzing signals exhibiting cyclostationary characteristics. W.R. Bennett introduced the concept of “Cyclostationary (CS: Cyclostationary)” [14], and since then, the theory of cyclostationarity has witnessed significant advancements. W.A. Gardner initially proposed the correlation properties of cyclostationary signals [15]. The advancement of research has led to the incorporation of spectral correlation theory into the analysis of cyclic smooth signals, thereby establishing detection techniques and theoretical foundations based on methods for cyclic smooth analysis [16].
Bonnardot Frédéric et al. decomposed the cyclic smooth characteristic of vibration signals into three components: periodic component [17], second-order cyclic smooth component, and noise. They proposed a set of filtering methods to decompose the second-order cyclic smooth component. Leonardi Riccardo et al. integrated the theories of cyclic smoothness and wavelet analysis [18], and introduced a 3D wavelet-based method for cyclic analysis.D.Hanson et al. combined cepstrum with the concept of cyclic cepstrum, applying it to modal analysis parameter identification through cyclic smooth analysis [19]. Roger Boustany presented a blind source separation method based on cyclically smooth signals [20]. P.Borghesani et al. incorporated envelopment spectral analysis to propose a method for analyzing envelopment signals based on second-order cyclical smoothing [21].Urbanek Jacek employed a time-frequency analysis method and effectively isolated the second-order cyclically smooth component in the domain of time-frequency analysis [22]. These approaches integrate the principles of cyclic smoothness with theories and analytical methods from diverse fields, thereby broadening the scope of application for cyclic smooth analysis in various domains.
The characteristics of bearing fault signals, the Doppler aberration correction algorithm, and the advantages of the cyclic smooth analysis method are re-deduced and calculated in this paper. They are then organically combined to propose a novel bearing fault diagnosis method: the fault diagnosis method based on cyclic smooth Doppler aberration correction.

2. Doppler distortion correction of rolling bearing fault signals

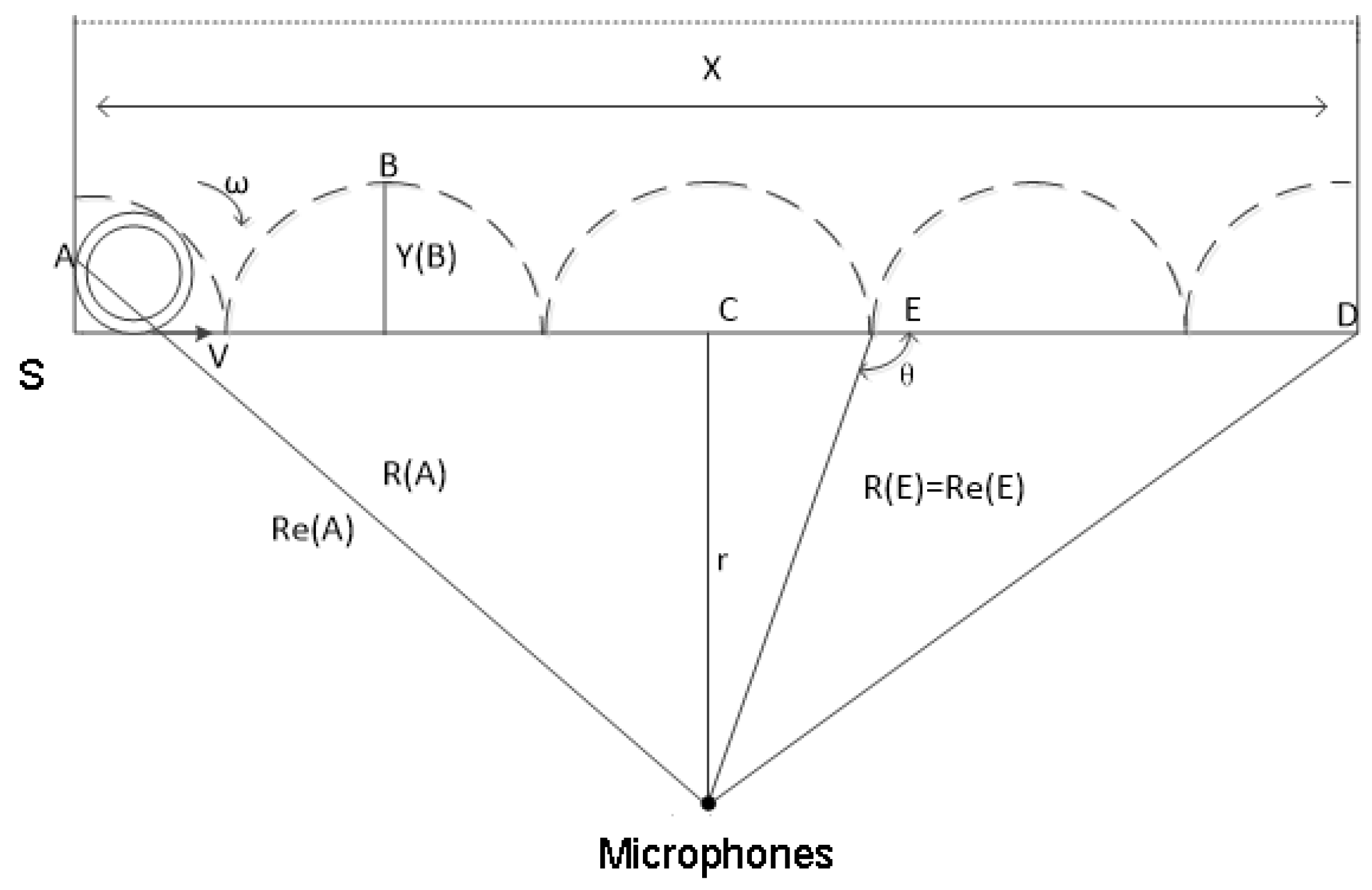
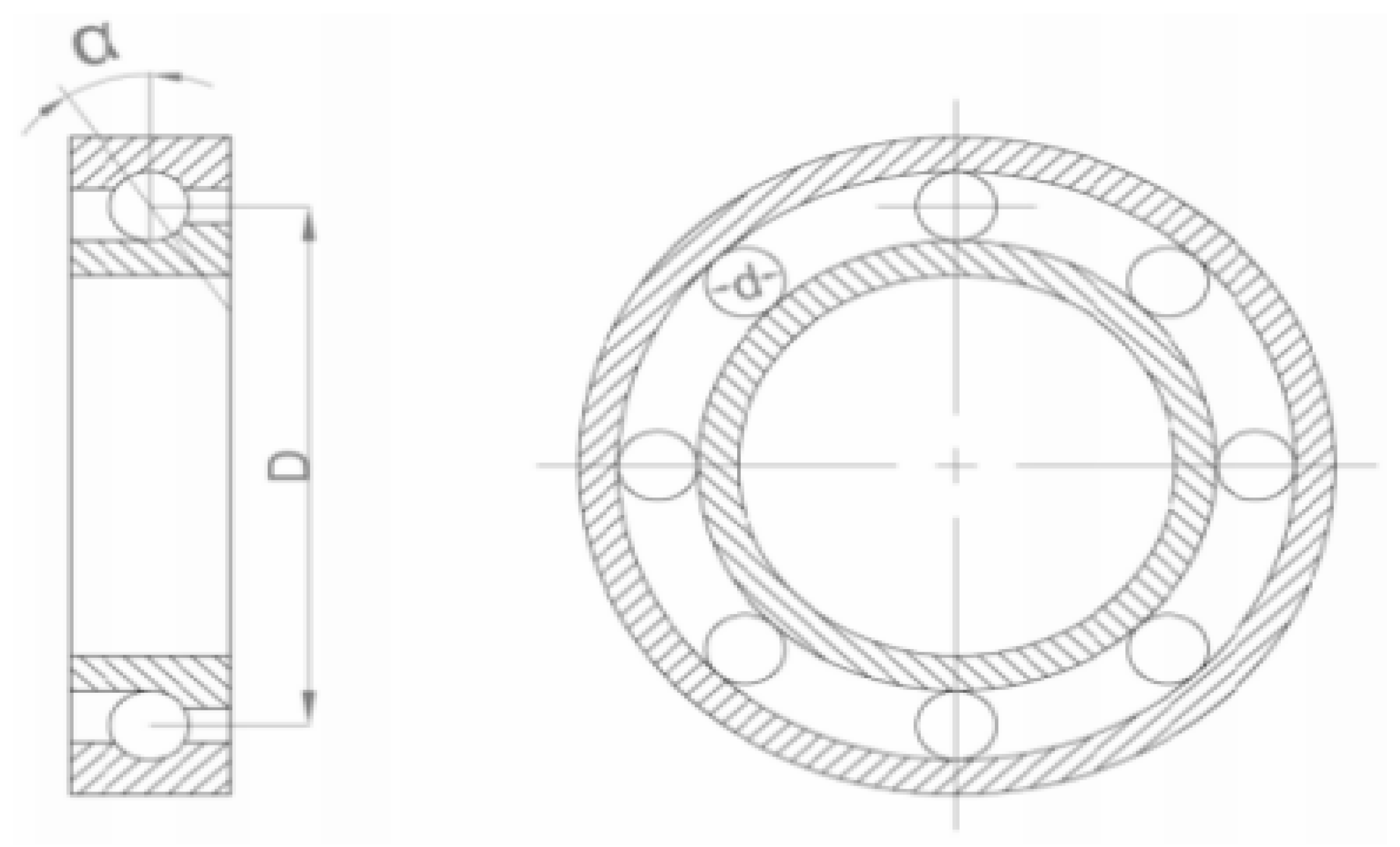
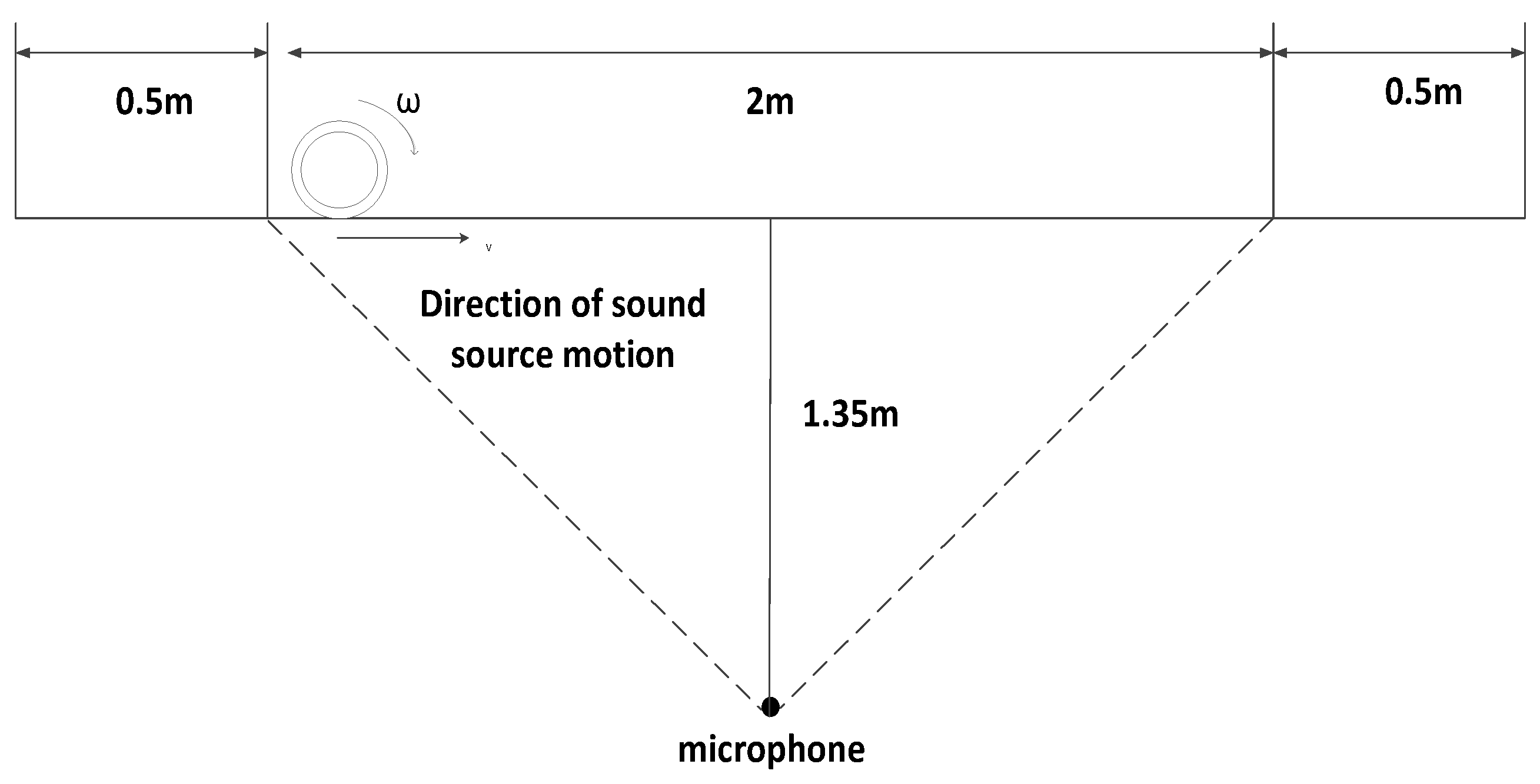
2.1. Rolling bearing failure sound source motion model

The bearing fault sound source motion model is established based on the positional relationship between the trackside bearing and the acquisition device, as depicted in Figure 1. The bearing fault sound source undergoes a uniform linear motion from left to right, while simultaneously performing rotational motion along the vertical horizontal plane. he motion trajectory of the faulty sound source S is depicted in the figure, where the horizontal distance of the motion path is X. The faulty bearing source moves with a uniform linear velocity v in the horizontal direction and rotates around the axis with an angular velocity w in the vertical-horizontal direction. Using point A as the initial reference, the motion is executed along the trajectory depicted in the diagram. Upon reaching point B, consider it as the precise location of the faulty sound source at a specific moment. Define Y(B) as the distance between the faulty sound source and the collecting device. Map this faulty sound source to point E on the horizontal plane, with Re(E) representing its distance from the collecting device. θ denotes the angle formed between Re(B), which represents horizontal motion trajectory, and Re(E). C refers to closest proximity of collecting device to faulty sound source, while r signifies their respective distance. When the faulty sound source reaches point D, the distance from the faulty sound source to the collecting device is denoted as Re(D), and c represents the speed of sound propagation in air (where M=v/c denotes Mach number). Given that the train’s velocity is significantly lower than the speed of sound propagation in air, this paper solely focuses on addressing issues related to subsonic motion of the faulty sound source, i.e., when M < 1 [23].
The faulty sound source undergoes circular motion around the axis of rotation. After a certain angle of rotation, the new coordinates of the faulty sound source (0,2R1) are represented as (x,y). The geometric relationship between the fault sound source and the acquisition device is derived from the following equation through relevant theoretical knowledge, calculation, and analysis.
x 1 = v ⋅ t
x = − R 1 ⋅ sin ω t
y = R 1 + R 1 ⋅ cos ω t
v x = R 1 ⋅ ω ⋅ cos ω t
R e = r 2 + [ ( x 1 + x ) − ( v + v x ) ⋅ ( i − 1 ) ⋅ t ] 2
R 1 = R e 2 + y 2

2.2. Analysis of the causes of Doppler aberrations in rolling bearings

The derived equation for the geometric relationship obtained from the above analysis leads to the conclusion that the distance between the acquisition device and the bearing fault sound source exhibits a non-linear variation over time. The signal received by the microphone from the bearing fault sound source undergoes nonlinear changes. Consequently, the acquisition device also captures the bearing fault sound source signal with non-linear variations. However, due to the equal time intervals at which the acquisition device collects the signal, a linear relationship is established during acquisition [24]. The sound source of the bearing fault undergoes a displacement in the vertical-horizontal plane during its propagation. Therefore, it is necessary to consider this displacement when determining the distance between the bearing fault sound source and the acquisition device. As a result, we express this distance as formula (6). The acquisition device captures the bearing fault signal with a time delay phenomenon, which is represented by equation (7), while equation (8) illustrates the temporal sequence of receiving this signal.
d t i = R 11 c
T i = ( i − 1 ) ⋅ i + d t i
The modeling process reveals a non-linear variation in the distance between the acquisition device and the bearing fault sound source, resulting in discrepancies in the sound pressure values of the acquired sound signals. Therefore, considering this as our theoretical foundation, we assume that the bearing fault sound source is a monopole point source, exhibiting uniform linear motion in the horizontal direction and rotational motion within its plane. Additionally, assuming an amplitude denoted by q representing the total mass flow rate emitted from the sound source s, we can express the distribution density of this point source as follows:
Q ( r → , t ) = q ( t ) δ ( x − v t ) δ ( y ) δ ( z )
The fluctuation equation for the sound field can be expressed as follows [25].
∇ 2 P − 1 c ∂ 2 P ∂ t 2 = ∂ ∂ t q ( t ) δ ( y ) ( z )
The equation for the sound pressure of a bearing fault source received by the collecting device is derived based on the aforementioned equations and geometric relationships:
P = q ' ( t − R c ) 4 π R ( 1 − M cos θ ) 2 + q [ t − R c ] ( cos θ − M ) 4 π R ( 1 − M cos θ ) 2
The equation (11) illustrates the variation in sound pressure of the bearing fault sound source during operation. This study focuses on trackside acoustic signals from wheel bearing faults, assuming that the train’s speed relative to the sound speed is negligible and thus does not affect it. Consequently, in the sound pressure formula, the second term can be disregarded as its impact on calculation results is minimal. For convenience, it is omitted here. By considering the correlation between the bearing fault sound source and collection device obtained from previous analysis, along with fluctuations in sound pressure. Equation (12) is derived to represent changes in sound pressure values of the bearing fault sound source during movement.
P = cos ( ω ⋅ ( t − R 22 c ) ) 4 π R 22 ( 1 − M ⋅ cos ( u ) ) 2
The sound pressure relationship of the bearing fault sound source can be derived from the aforementioned analysis. It is evident from the equation that the distance between the acquisition device and the bearing fault sound source exhibits non-linear variation, resulting in a corresponding non-linear change in sound pressure. Consequently, Doppler distortion primarily manifests as temporal and amplitude distortions in the acquired bearing fault signal. Therefore, it is necessary to correct for both time and amplitude aspects when addressing Doppler distortion.

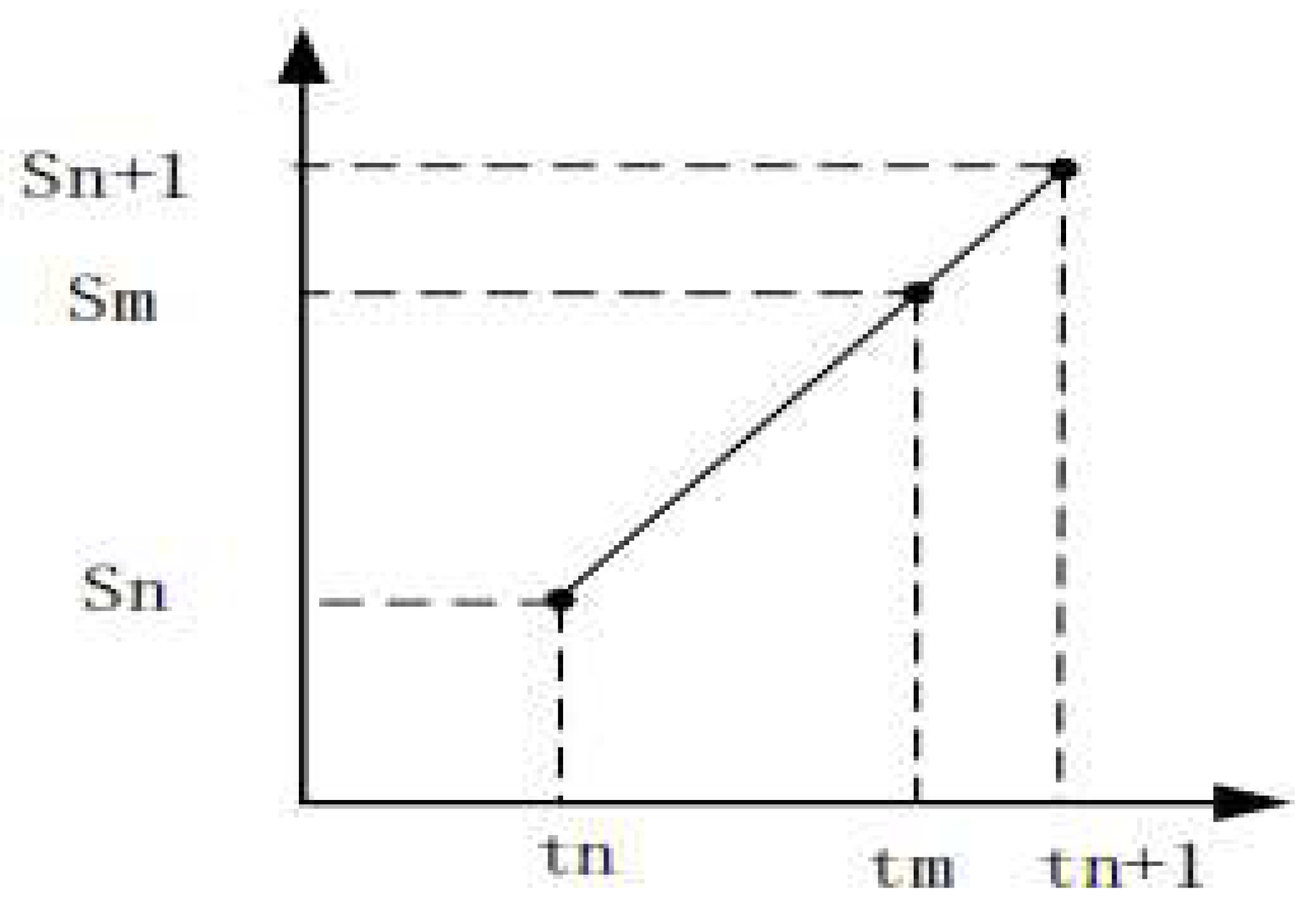
2.3. Time correction

According to the bearing motion model, the distance relationship and time sequence of the signal between the fault sound source and the acquisition device are obtained. The formula can be used to derive the time sequence of transmission from the fault sound source to the acquisition device. In practical detection processes, it is necessary for trains to continuously run. Consequently, during calculation of resampling time series, there will be constant changes in distance between the fault source and acquisition device. This dynamic aspect allows for more realistic and accurate time correction of distorted signals. Since signals are collected at equal time intervals while actual signal time series have unequal intervals, interpolation and resampling are required after collecting fault signals in order to obtain a more precise time series. The following presents delayed time series and resampling time series corresponding to each point in operation.
d t i 1 = R 22 c
T i 1 = ( i − 1 ) ⋅ t + R 22 c
The resampled time series is obtained by re-interpolating the faulty sound source’s time series Ti received by the acquisition device [26]. Interpolating and resampling a Doppler-distorted signal involves correcting the nonlinear variation of the acquired acoustic signal’s time series to a linear variation. In simpler terms, it means re-acquiring the acoustic signal using the same points and sampling frequency. Assuming that n and n+1 are adjacent acoustic signals captured by the acquisition device, with coordinates (tn, Sn) for point n and (tn+1, Sn+1) for point n+1, m represents an intermediate point between these two signal acquisition points. The schematic diagram can be seen in Figure 2.
The coordinates of point m are (tm, Sm), where the sampling frequency and sampling interval of the bearing fault sound source signal are known. The sampling interval is defined as 1/f, and a linear relationship is established between points n and n+1 [12]. Furthermore, the following relationship holds true.
S m − S n t m − t n = S n + 1 − S n t n + 1 − t n
S m = S n + 1 − S n t n + 1 − t n ( t m − t n ) + S n
The time series containing nonlinearity can be corrected through linear interpolation resampling, resulting in a new time series. At this stage, the signal has completed the process of interpolation resampling, indicating that the time correction of the acoustic signal has been accomplished.

2.4. Magnitude correction

The acoustic pressure of the signal received by the acquisition device varies with the changing location between the fault source and the acquisition device during train operation, resulting in amplitude distortion of the collected acoustic signal due to distance variation. In order to correct this Doppler-induced amplitude distortion in fault signals, a window function is created using the reference point closest to the acquisition device. The schematic is shown in Figure 3.
The equation (27) presents the derived sound pressure field of the bearing failure sound source in the derivation process of the bearing motion model equation.
P = cos [ ω ⋅ ( t − R 22 c ) ] 4 π R 22 [ 1 − M ⋅ cos ( u ) ] 2
The sound pressure at the minimum distance between the bearing fault source and the acquisition device is utilized as the reference signal after amplitude correction of the fault signal. Subsequently, this sound pressure becomes a modulation function of the sound pressure generated by the relative motion between the bearing fault source and the acquisition device. The amplitude-corrected signal [14] can be expressed as shown in equation (28). The acoustic signal obtained from equation (18) undergoes theoretical corrections in both time and amplitude, resulting in an acoustic signal free from Doppler distortion.
S f ( t ) = S 1 A
The distortion generated in time by the fault signal is corrected through a resampling algorithm. In terms of amplitude, the reference point closest to the acquisition device is utilized to create a window function, which compensates for the amplitude and restores its initial size. After both time and amplitude correction, the authentic fault sound source signal is ultimately obtained.

3. Cyclic and smooth characteristics of rolling bearing fault signals

3.1. Smooth second order cycle

The vibration signal of rotating machinery, characterized by its periodic rotation, not only contains numerous random components but also exhibits prominent periodic components. The second-order statistical characteristics of the signal are non-smooth, indicating a cyclic smoothness in the signal. Consequently, conventional signal processing methods fail to analyze and identify it effectively. Recognizing the significance of periodic changes in signal statistics for bearing fault diagnosis, it is essential to employ cyclic smoothing analysis method to extract crucial information for analysis [16].
The second-order cyclic statistics in the cyclic smooth analysis method provide a more accurate characterization of the cyclic smoothness of the signal. By analyzing these cyclic statistics, we can gain a comprehensive understanding of the characteristics and patterns of vibration fault signals, enabling us to make more precise diagnoses. Therefore, this paper primarily employs the second-order cyclic smooth statistic [24], specifically utilizing the cyclic autocorrelation function and the cyclic spectral correlation density function, to conduct thorough cyclic smooth analysis.

3.2. Cyclic smooth model for rolling bearings

The cyclic smooth model of rolling bearings is established to account for the cyclic smooth characteristics. It is assumed that pitting failure in rolling bearings occurs after T cycles, where s(t) represents a specific shock oscillation and Ai denotes the amplitude of the ith shock. Considering the complexity of the working environment, which includes various disturbances from environmental noise, a zero-mean smooth and randomized environmental noise n(t) is introduced. Based on this information, the pitting fault model can be formulated as follows:
x ( t ) = ∑ i = 1 A I s ( t − i T ) + n ( t )
The failure frequency of various components in rolling bearings is analyzed in conjunction with a pitting failure model.
The structure of the rolling bearing is illustrated in Figure 4, where D (mm) represents the raceway diameter, d (mm) denotes the rolling body diameter, and α indicates the bearing contact angle. Let N represent the number of rolling bodies, and N (r/min) denote the shaft speed.
The inherent frequency of the bearing when rotating is:
f r = N 60
Bearing inner ring failure, when the frequency of the rolling body passing a point on the inner ring (BPI) is:
B P I = 1 2 n ( 1 + d D cos α ) f r
Bearing outer ring failure, when the frequency of the rolling body passing a point on the outer ring (BPO) is:
B P O = 1 2 n ( 1 − d D cos α ) f r
Bearing rolling element failure, when the frequency of rolling elements through the inner or outer raceway (BS) is:
B S = 1 2 D d [ 1 − ( d D ) 2 cos 2 α ] f r
Bearing cage failure, at this time the rolling body of the common rotational frequency and cage speed frequency consistent (FT) for
F T = 1 2 ( 1 − d D cos α ) f r
The cyclic frequency characteristics of the cyclic smooth failure for each component of the bearing can be deduced by combining the specific features and theoretical knowledge of each component, as well as the characteristic frequencies associated with them, as presented in Table 1.

4. Experimentation and analysis

The fault diagnosis process, depicted in Figure 5, is established based on the theoretical knowledge presented in the preceding two sections. Firstly, a Doppler distortion correction algorithm is employed to rectify the time and amplitude of the fault signal, ensuring its freedom from any Doppler distortion. Subsequently, cyclic smooth autocorrelation and cyclic smooth density spectrum analysis are applied to process the signal. Finally, fault diagnosis is conducted.

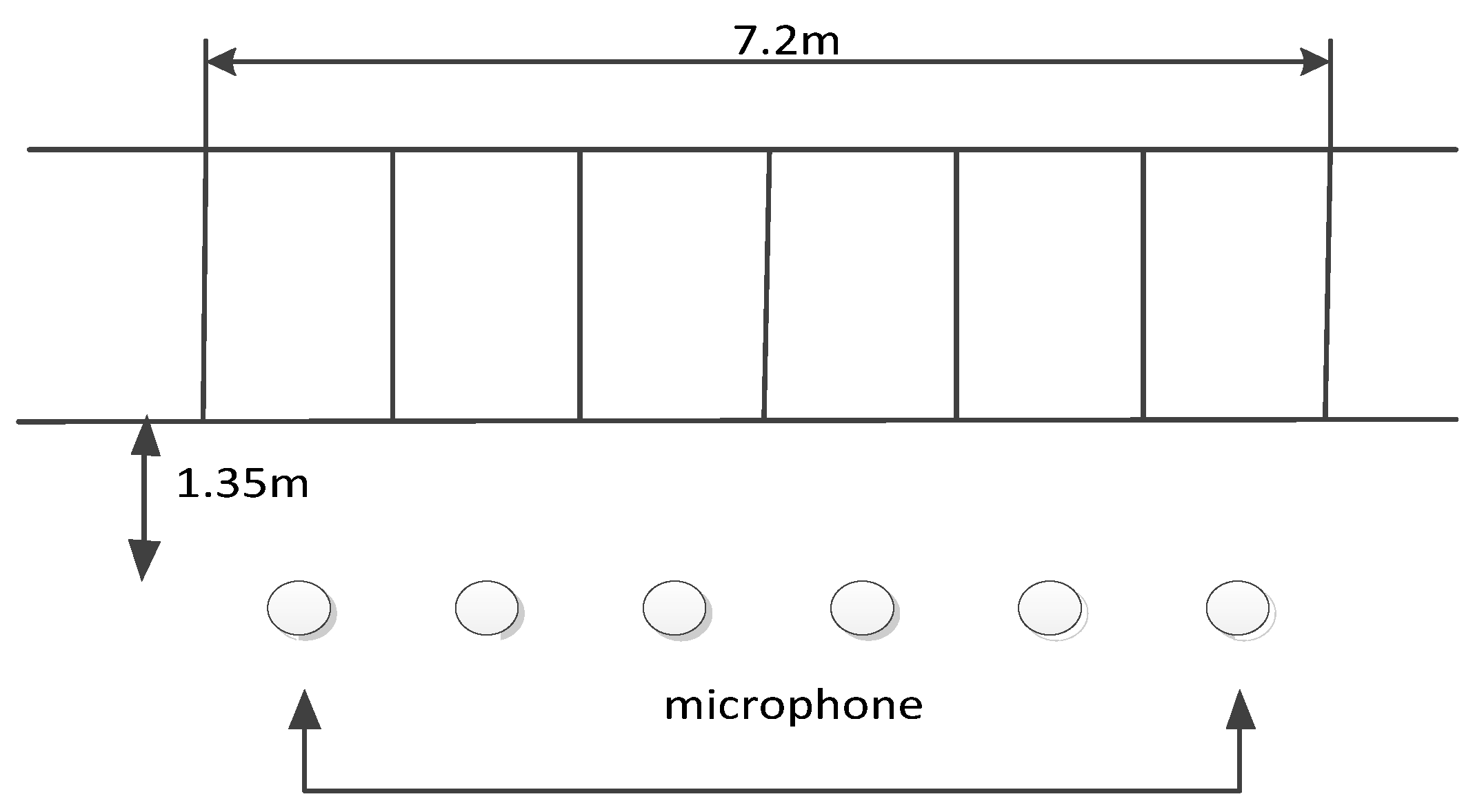
4.1. Trackside acoustic laboratory bench

The trackside acoustic test bench, depicted in Figure 6, comprises a servo motor, linear module, microphone, and acquisition card. This experimental setup emulates the motion of bearings in a tracksuit acoustic detection system and replicates the acoustic signals corresponding to various types of bearing faults [27]. It effectively simulates the actual operation of train bearings under simulated operating conditions while perceiving the bearing fault signals. In accordance with real wheel operations, this experiment equates to a stable running length of 2 meters within a 3-meter long module. Additionally, the speed of the guideway experimental table can be adjusted between 0-3m/s.

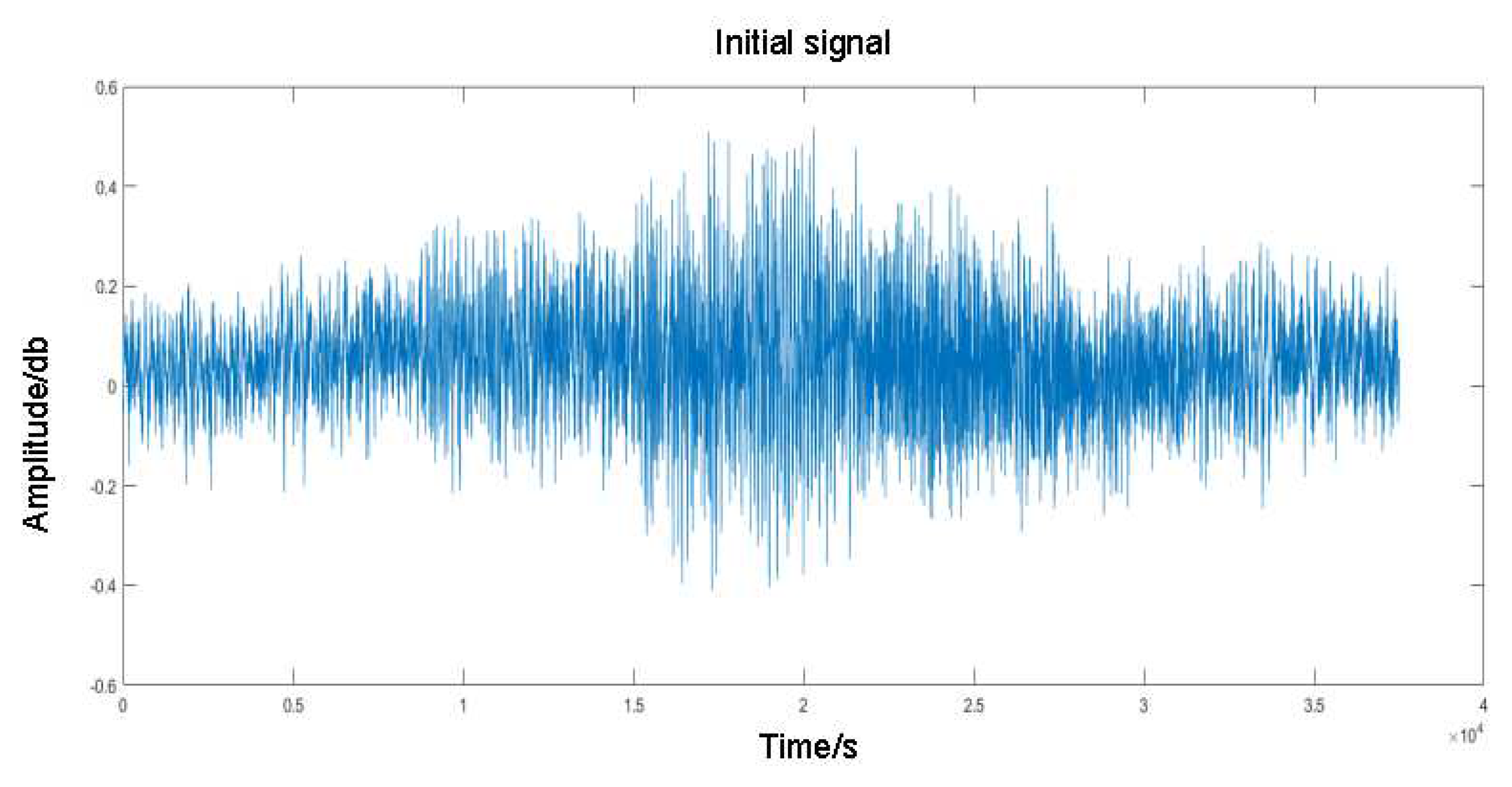
4.2. Rolling bearing experiments and data analysis

During the experiment, the bearing is loaded onto the slider and moves linearly in the horizontal direction. This means that the test bearing not only rotates perpendicular to the ground but also undergoes linear motion on a horizontally placed track. To accurately simulate the relationship between the bearing’s movement speed and its rotational speed in a train, it is necessary to set the horizontal speed of the slider to correspond with the vertical rotational speed of the bearing. In other words, the linear velocity of the test bearing during rotational motion is equivalent to that of the linear module slider. The calculation formula can be seen in equations (27) and (28).
v 1 = 2 π r n 1 60
n 2 = 60 v 2 s
The equation above defines v1 (m/s) as the equivalent horizontal linear speed of the test bearing, and v2 (m/s) as the speed of the linear module slider. It is important to note that v1 and v2 are numerically equal, i.e., v1 = v2. Additionally, n1 (rpm) represents the speed of the test bearing, while n2 (rpm) corresponds to the speed of the linear module AC motor. Furthermore, s (m) denotes the lead of the linear module, which refers to the displacement of the slider for one revolution of its drive motor. Please refer to your linear module manual for a specific value; in this case it is 0.165 m. Lastly, r (m) signifies the radius of the test bearing. The calculation results can be found in Table 2.
The linear module slider requires a certain amount of time and distance to accelerate to the target speed as it moves horizontally in a straight line, and the same applies to the deceleration process. The effective length of the linear module is 3m. To ensure that the slider does not collide with the edge block during movement, the first 0.5m of the linear module is designated for placement and acceleration, while the second 0.5m is used for deceleration. The middle 2m represents the effective distance for actual signal acquisition. Positioned at a vertical distance of 1.35m from the linear module, there is a microphone present in this experimental setup as depicted in Figure 7.
The trackside acoustic test bench is utilized to conduct bearing fault acquisition experiments, aiming to collect and analyze the acoustic signals of a wide range of experimental bearing faults. The known experimental bearing parameters are presented in Table 3:
The test bearing can be manipulated to achieve different states by combining a damaged component with other intact components during the experiment, thus simulating the actual fault conditions of a real test bearing. The various types of faulty test bearings are illustrated in Figure 8.
Combined with the actual working conditions and the bearing motion model, the effect of data collection becomes more pronounced as the speed increases. Therefore, in order to verify the feasibility of the Doppler correction algorithm, a comparative analysis is conducted on the time domain waveform and power spectrum of the signal before and after correcting for outer ring faults in bearings. As an example, a uniform speed of 1.6m/s at 600RPM is set for the bearing’s travel.
Comparing Figure 9 with Figure 10, it can be observed that the overall graph in Figure 10 becomes more condensed, indicating that the time domain correction has exerted an effect and there is a slight increase in amplitude compared to Figure 9. This suggests that the algorithmic processing of aberrations has somewhat improved the amplitude. The comparison reveals that both time domain and amplitude aberrations are partially eliminated after Doppler correction. To further evaluate the efficacy of the Doppler correction algorithm in rectifying Doppler-aberrated signals, power spectra of initial and corrected signals for outer ring faults were generated and compared, enabling clear visualization of changes. The power spectra for initial and corrected signals of outer ring faults are presented in Figure 11 and Figure 12.
Comparing the initial power spectrum in Figure 11 with the corrected power spectrum in Figure 12, it can be observed that the overall appearance of the corrected signal is more compact and dense compared to the initial signal, indicating successful time domain correction. In the initial power spectrum image, prominent amplitudes are concentrated between 200-300Hz, accompanied by sidebands around 100-200Hz and 400-700Hz. In contrast, the corrected power spectrum exhibits a significant increase in amplitude at 200-300Hz by approximately 50%, while the edge bands around 100-200Hz and 400-700Hz also experience an approximate growth of about 25%. These findings suggest that effective amplitude correction has been achieved to eliminate distortion. By comparing both time domain waveform and power spectrum of the outer ring fault signal, it can be concluded that the Doppler correction algorithm is feasible and yields satisfactory results.
The bearing fault signal, after undergoing Doppler correction, is subjected to cyclic smoothing analysis in order to validate the accuracy and reliability of the bearing fault diagnosis method based on cyclic smoothing analysis with Doppler aberration correction. The experimental verification is performed using the example of cyclic smoothing analysis applied to the bearing outer ring fault signal after Doppler aberration correction.
The cyclic characteristic frequency of the bearing outer ring fault was calculated to be 49.06Hz based on the previously established cyclic smooth model and specific experimental parameters. Subsequently, a cyclic smooth analysis of the fault signal after Doppler distortion correction for the bearing outer ring fault is conducted, and the resulting cyclic autocorrelation spectrum is presented in Figure 13.
The cyclic autocorrelation spectrum in Figure 13 reveals the presence of signals with prominent components. However, it is challenging to clearly observe the cyclic frequencies and frequency components at other locations during signal processing, particularly due to their small amplitudes. To achieve a more precise determination of the cyclic eigenfrequencies, an appropriate method of processing is necessary. Therefore, we will conduct a cyclic density spectrum analysis and utilize the cyclic density spectrum function to obtain the cyclic autocorrelation density spectrum as depicted in Figure 14.
The circular density spectrum in Figure 14 exhibits a distinct eigenfrequency component with prominent side bands near the circular eigenfrequencies. Notably, a cluster of signal-concentrated distribution of eigenfrequency points is observed in the figure. To assess the relationship among the remaining eigenfrequencies, refinement analysis is conducted on this concentrated distribution, resulting in a refined slice map as depicted in Figure 15.
The refined slice diagram reveals the main frequency components, with 98Hz corresponding to the 2x frequency of the characteristic frequency of the outer ring. This provides evidence that cyclic smoothing analysis accurately identifies and emphasizes the characteristic frequency of bearing outer ring faults. It demonstrates the feasibility of applying cyclic smoothing analysis to Doppler-corrected bearing fault signals and validates the accuracy of the bearing fault diagnosis method based on cyclic smoothing analysis with Doppler aberration correction. Additionally, although present in the refined slice diagram, the edge frequency band exhibits a small amplitude compared to that at the characteristic frequency and can be disregarded.
The method can be deemed correct and effective for bearing failure diagnosis, as it combines the bearing failure model and utilizes cyclic smooth analysis with Doppler aberration correction.

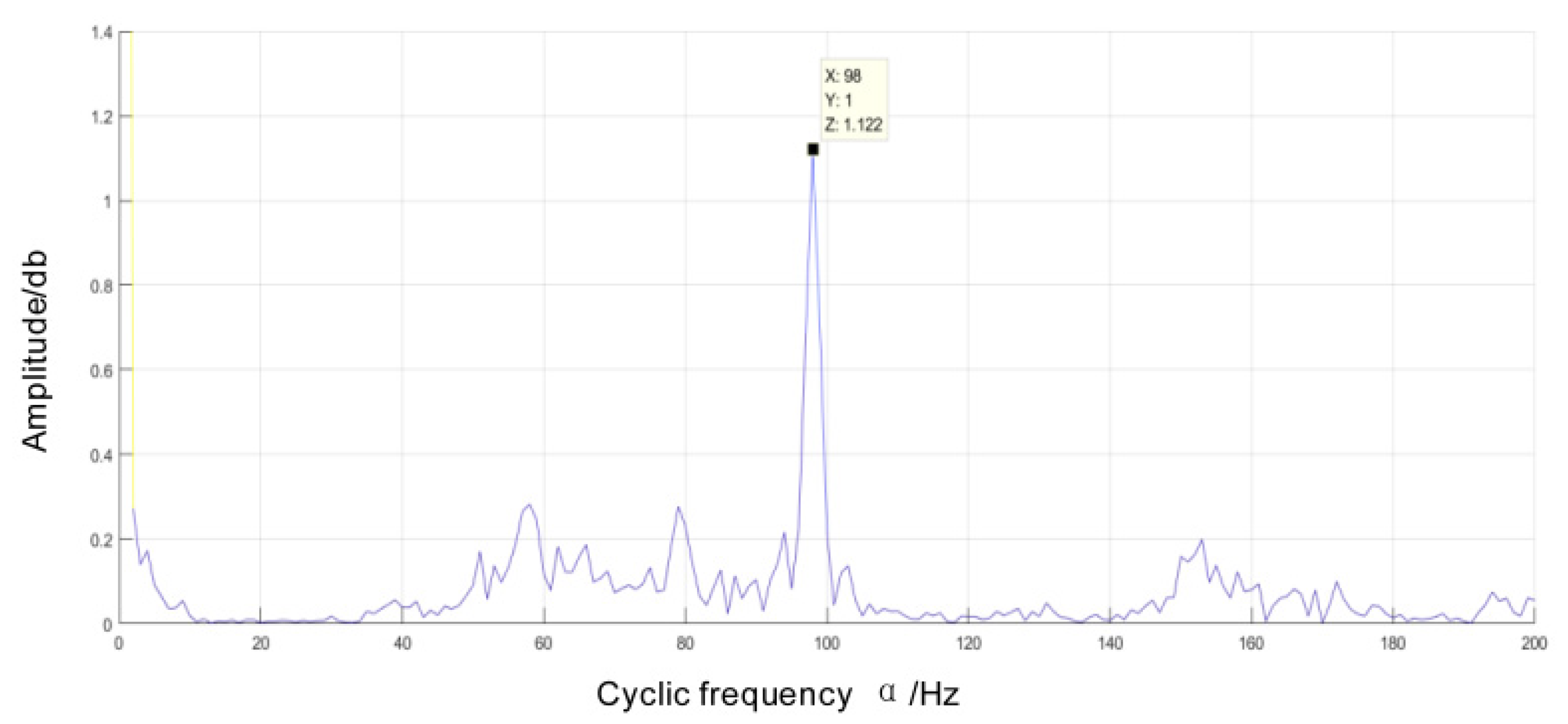
4.3. Project example analysis

To validate the efficacy of the proposed approach, a pre-existing TADS device was chosen within a vehicle section. The acquisition schematic of this device is depicted in Figure 25, featuring a linear array comprising six microphones evenly spaced at a distance of 1.35m from the track. With an acquisition range of 7.2m, it facilitates capturing acoustic signals emitted by train bearings during uniform speed operation for subsequent analysis and identification of bearing signal faults.
Preprints 84844 g016
Figure 16. Schematic diagram of equipment acquisition.
Figure 16. Schematic diagram of equipment acquisition.
Preprints 84844 g016
Test bearing parameters are shown in Table 4.
During the inspection of the TADS equipment, anomalies were detected in the bearings. Subsequently, a novel bearing fault detection method proposed in this paper, namely the Doppler distortion correction method based on cyclic smooth analysis, was employed to analyze and process the bearing signals. The acquired acoustic signals underwent Doppler distortion correction, and a comparison was made between the time domain maps before and after correction (refer to Figure 17 and Figure 18) for further evaluation.
A comparison between Figure 17 and Figure 18 reveals that the overall graph of Figure 18 exhibits a more compact form compared to Figure 17, indicating the successful correction in the time domain. Furthermore, the amplitude has increased by nearly 50% in comparison to Figure 17, suggesting that the algorithm has effectively corrected the amplitude to some extent after processing. The comparison of time domain waveforms demonstrates that both time domain and amplitude distortions have been partially rectified following Doppler correction. To further restore the bearing fault signal and evaluate the efficacy of the Doppler correction algorithm in addressing Doppler distortion signals, power spectra were generated for both initial and corrected signals of outer ring faults, facilitating a clear observation of changes.
Comparing the power spectrum of the fault signal in Figure 19 with that of the corrected signal in Figure 20, it can be observed that the overall distribution of amplitudes in the corrected signal is more densely concentrated compared to the initial signal. This indicates that the time domain correction has effectively addressed temporal distortion. In the power spectrum image of the initial signal, prominent amplitudes are mainly concentrated between 20-60Hz, with additional side bands around 100-120Hz and 160-200Hz. However, in the power spectrum image of the corrected signal, there is a significant increase (approximately 125%) in amplitude within the range of 20-60Hz, along with an additional increase (about 25%) in side bands around 100-120Hz and 160-200Hz. These findings suggest that effective amplitude correction has been achieved to rectify amplitude distortion. At this stage, through Doppler correction algorithm, bearing fault signals have been reduced to real fault signals. By comparing time domain waveforms and power spectra before and after bearing fault signal correction, it can be concluded that Doppler correction algorithm is feasible and yields satisfactory results.
The bearing fault signals, which have been corrected for Doppler aberration, were subjected to cyclic smoothing analysis in order to determine the type of bearing fault and verify the accuracy and feasibility of the diagnostic method based on cyclic smoothing analysis with Doppler correction. The resulting signal, after correcting for Doppler distortion, was then analyzed using cyclic smoothing techniques and the corresponding autocorrelation spectrum is presented in Figure 21.
The cyclic autocorrelation spectrum in Figure 21 reveals the presence of signals with prominent components. However, during the signal processing procedure, it is challenging to clearly observe the cyclic frequencies and frequency components at other locations due to their small amplitudes. To enhance our understanding of the cyclic characteristic frequency, we perform a thorough analysis using cyclic density spectrum and obtain the corresponding cyclic autocorrelation density spectrum as depicted in Figure 22.
The circular density spectrum in Figure 22 exhibits a distinct eigenfrequency component with prominent side bands near the circular eigenfrequencies. Additionally, a cluster of signal-concentrated distribution of eigenfrequency points is evident in the figure. To establish the relationship among the remaining eigenfrequencies, a refinement analysis was conducted at this concentrated distribution and yielded a refinement slice diagram, as depicted in Figure 23.
The refined slice diagram reveals that the dominant frequency component is 76Hz, accompanied by some minor frequency bands. However, their amplitudes are insignificant and can be disregarded. By integrating the cyclic smooth model of bearing failure established in Chapter 2 with the bearing speed of 396rpm obtained from the TADS system and specific parameters of the bearing, we calculated the cyclic characteristic frequencies for each component in case of failure. The corresponding data is presented in Table 5.
The comparison of characteristic frequencies in Table 5 revealed that the dominant frequency component of 76Hz on the refined slice diagram depicted in Figure 23 was five times higher than the outer ring failure frequency of 15.2Hz, leading to the deduction that the bearing failure occurred at the outer ring location. Subsequently, disassembly of the bearing was carried out, as illustrated in Figure 24.
It is evident from the bearing failure diagram that the bearing failure was caused by a scratch on the outer ring of the bearing, resulting in an abnormal bearing signal detected by the TADS equipment. This confirms the accuracy of our previous inference. Therefore, utilizing cyclic smoothing analysis can effectively determine the location of bearing failure by identifying its cyclic characteristic frequency (or multiples thereof). This demonstrates both feasibility and accuracy when applying cyclic smoothing analysis to Doppler-corrected bearing fault signals, thus validating the reliability of our diagnostic method based on cyclic smoothing analysis with Doppler distortion correction. Through analyzing and verifying experimental and engineering signals, this paper illustrates the practicality and effectiveness of our proposed Doppler aberration correction method based on cyclic smoothing analysis.

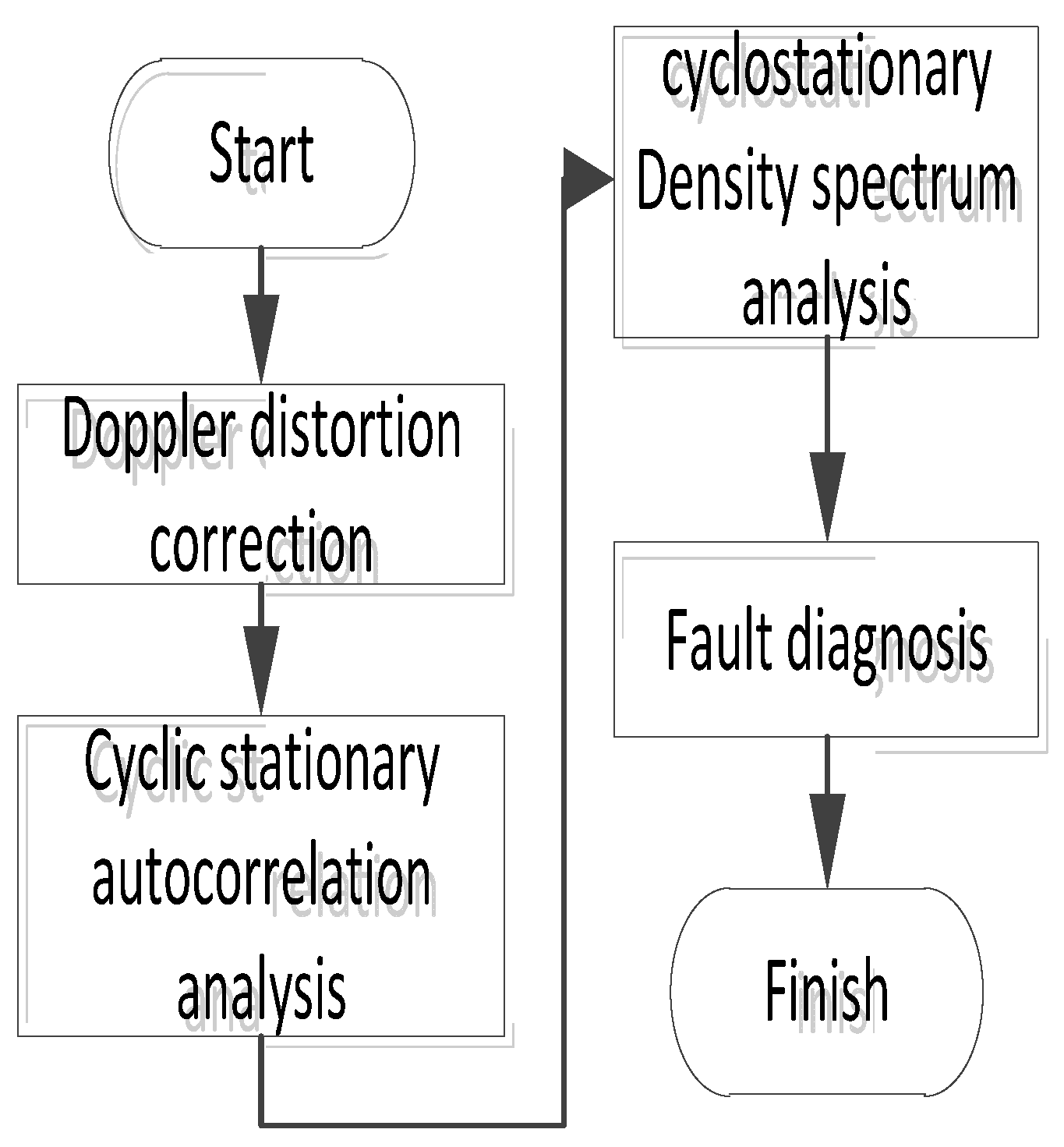
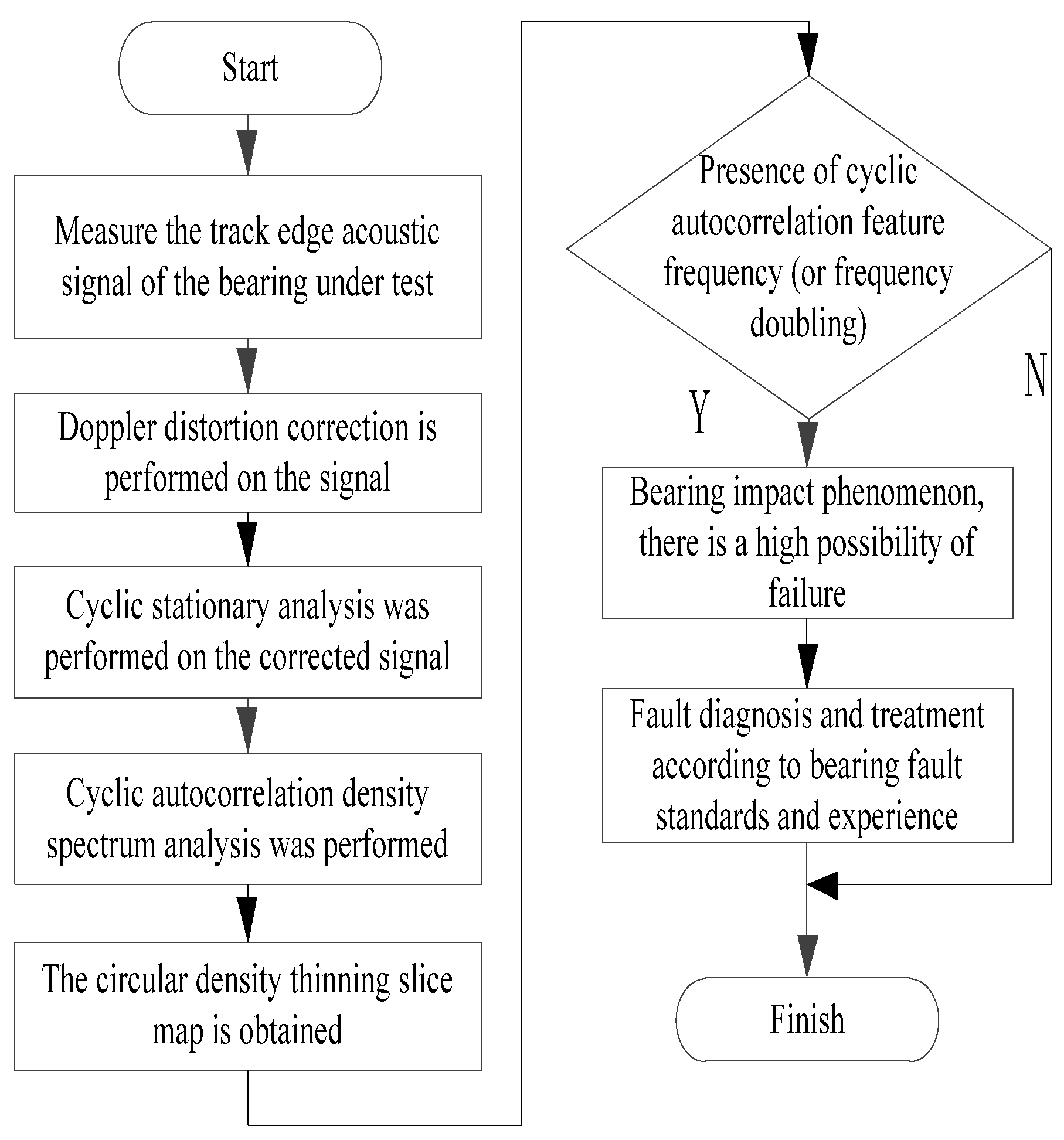
4.4. Bearing fault diagnosis step

The steps for diagnosing rolling bearing faults with the Doppler aberration correction method based on cyclic smooth analysis are summarized as follows by integrating the Doppler aberration correction algorithm, the cyclic smooth analysis method, and the rolling bearing model.
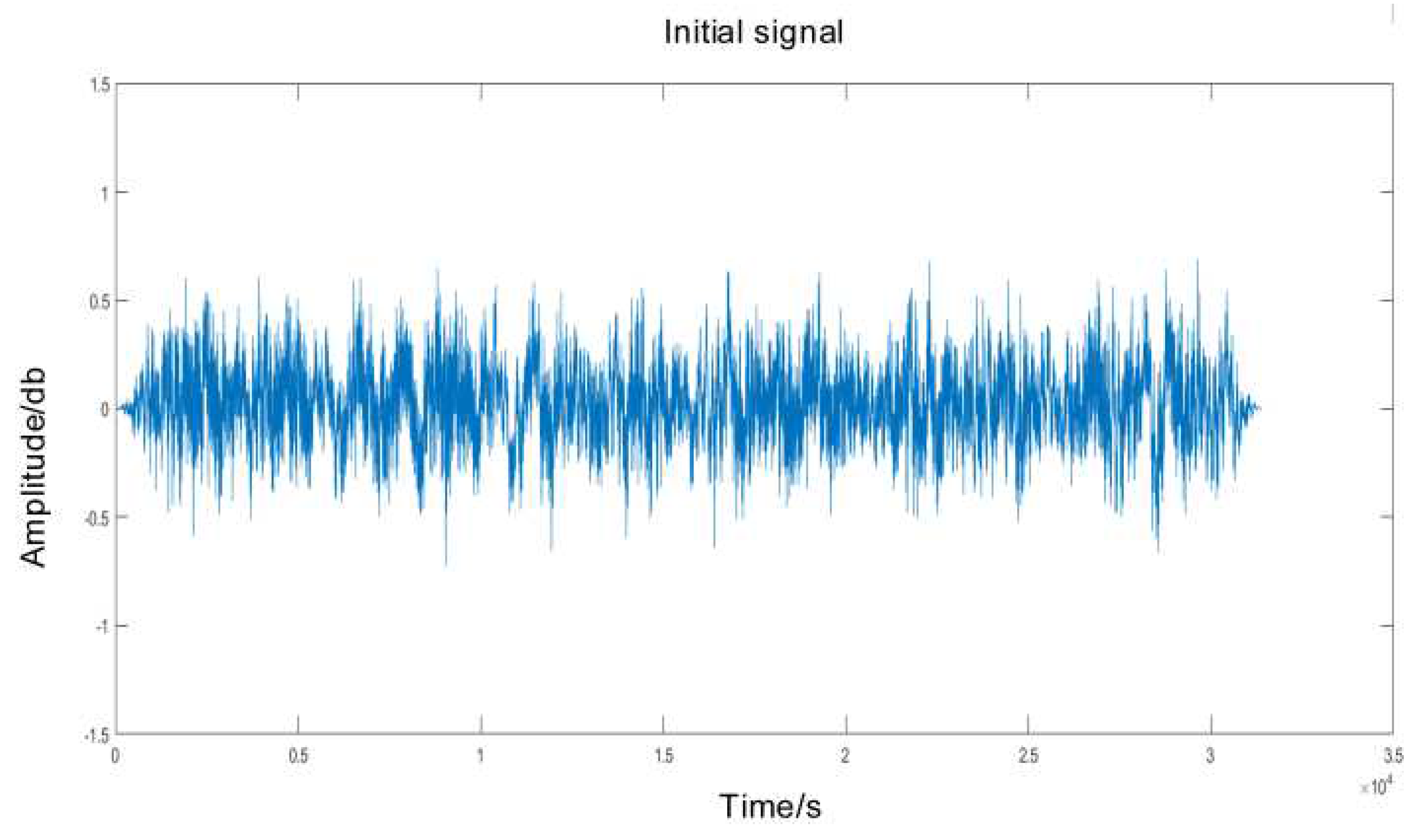
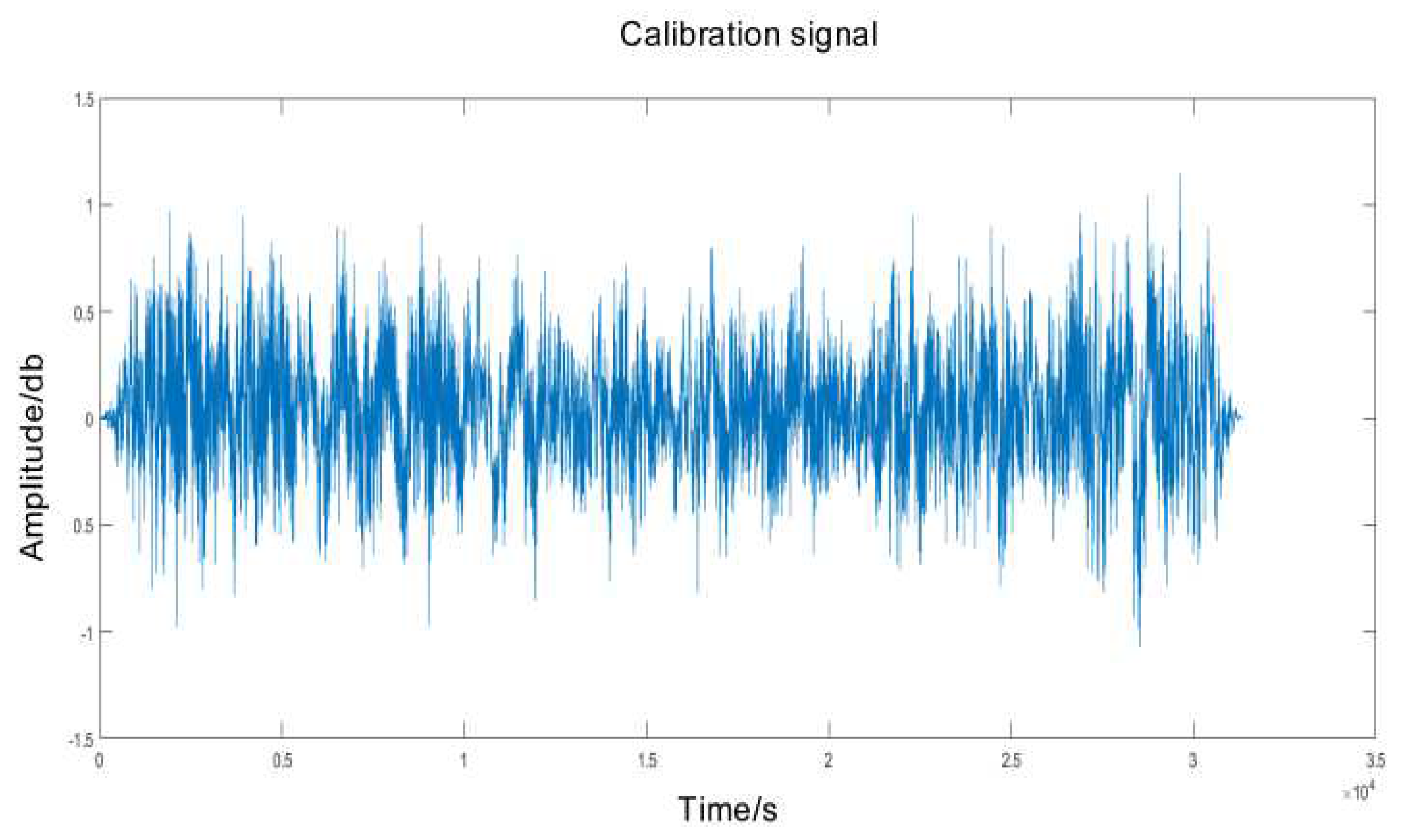
  • The trackside acoustic signal of the bearing to be measured, primarily consisting of vibration and speed signals, is subject to measurement.
  • The correction of Doppler distortion for acoustic signals received trackside.
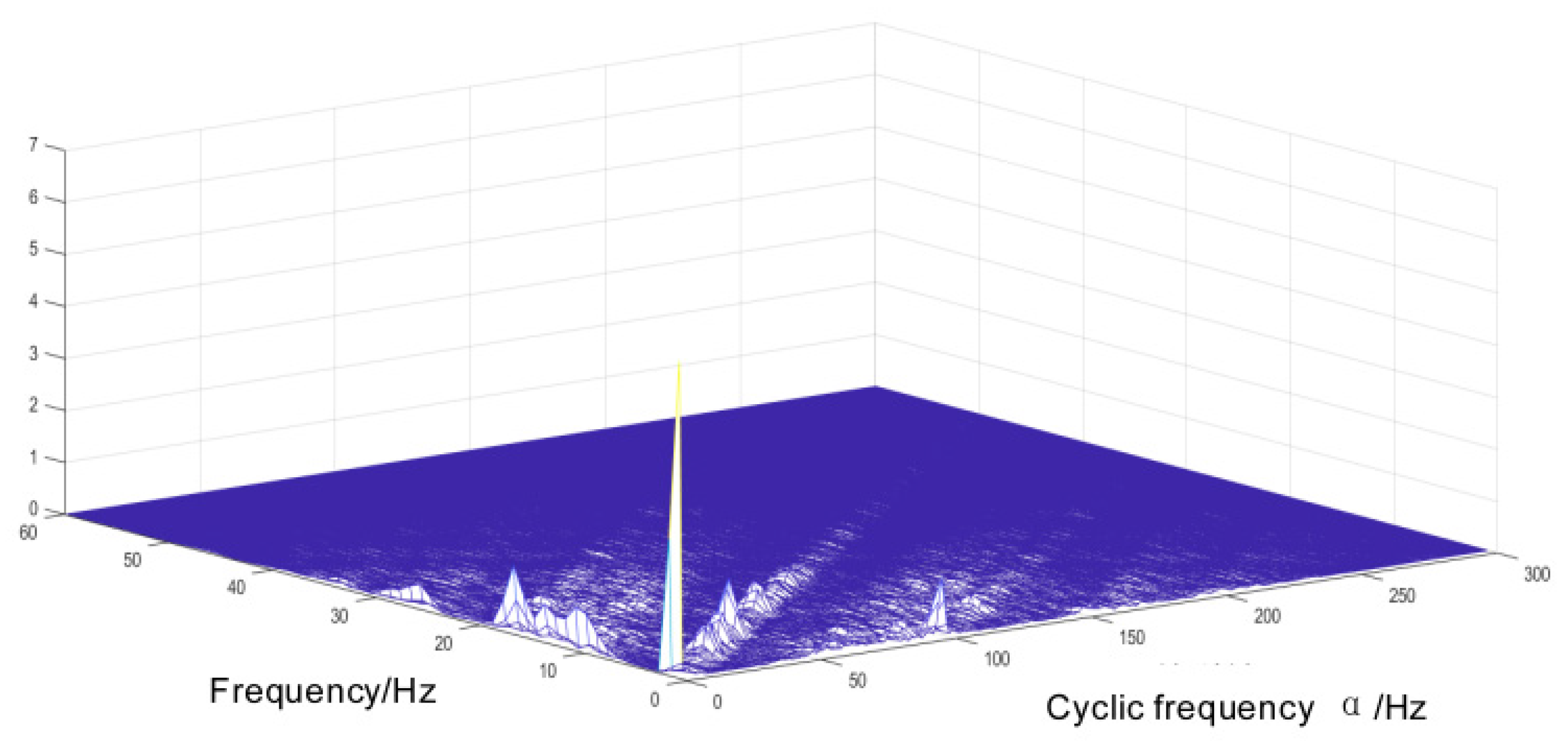
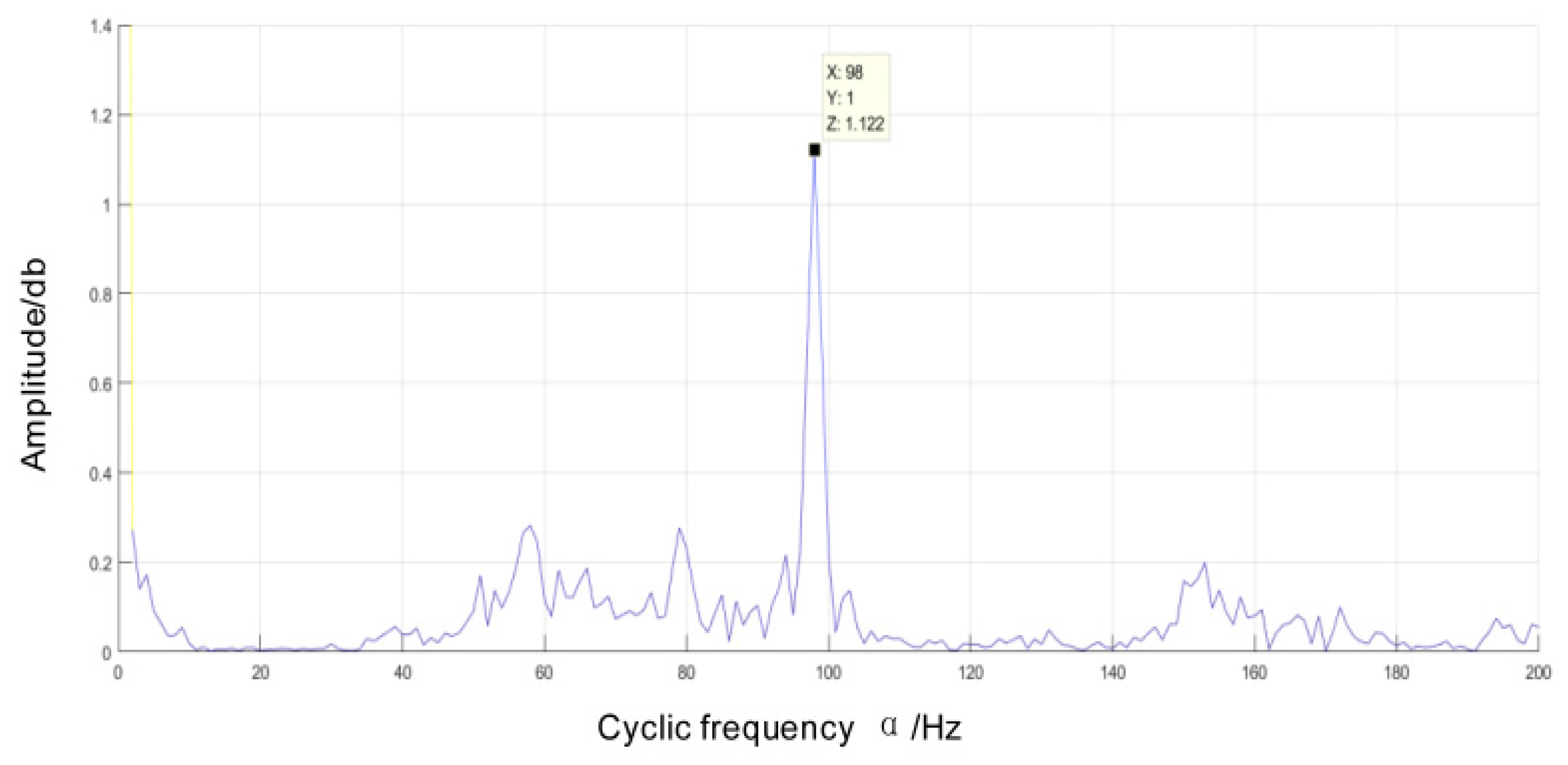
  • The Doppler-corrected signal underwent cyclic smoothing analysis. Firstly, a cyclic autocorrelation analysis was conducted to obtain a spectrum of cyclic autocorrelation. Secondly, the spectrum of cyclic autocorrelation density was examined to refine it into a slice of cyclic density refinement in order to determine the presence of a characteristic frequency or its multiple in the cyclic autocorrelation. If such frequency exists, it indicates the occurrence of shock phenomenon in the bearing at that time and suggests an impending failure.
  • The faults are assessed based on predetermined criteria for evaluating bearing faults and practical experience to determine their impact on the component’s operation. Subsequently, appropriate handling procedures are implemented.
The sequence of diagnostic procedures is illustrated in Figure 25.
The proposed diagnostic procedure for faulty bearings is based on the Doppler distortion correction algorithm and cyclostationary analysis method investigated in this study. In comparison to the conventional diagnostic procedure, it is anticipated that the diagnostic accuracy will be enhanced by approximately 50%, leading to a reduction in error rate

5. Summary

The present paper proposes a novel method for bearing fault diagnosis based on the fault characteristics of rolling bearings, utilizing Doppler aberration and cyclic smoothing techniques. Specifically, it introduces a fault diagnosis approach that incorporates cyclic smoothing with Doppler aberration correction, tailored to the current stage of bearing fault detection. Experimental validation through trackside acoustic experiments and engineering examples confirms the effectiveness and feasibility of the proposed method in diagnosing bearing faults. Consequently, this study presents a compilation of bearing fault diagnosis procedures based on the Doppler aberration correction method using cyclic smoothing analysis.

Author Contributions

Conceptualization, X.Z.; methodology, X.Z.; software, L.C.; validation, Y.L. and B.C.; formal analysis, L.C. and Y.L.; investigation, B.C.; resources, X.Z.; data curation, Y.L.; writing-original draft preparation, Y.L. and L.C.; writing-review and editing, B.C.; visualization, X.Z.; project administration, X.Z.; funding acquisition X.Z. All authors have read and agreed to the published version of the manuscript.

Funding

The National Science Foundation of China Youth Science Fund Project (62001079). Dalian High-level Talents Innovation Support Program (2021RQ134).

Data Availability Statement

The data presented in this study are available upon request from the corresponding author.

Acknowledgments

Then authors would like to thank the anonymous reviewers and editors for their valuable suggestions to improve the quality of this work.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Sun, Y. Research on key technology of rolling bearing fault detection. Master’s Thesis, Harbin Engineering University of China: Harbin, China, 2019. [Google Scholar]
  2. Ouyang, K. Research on circular array short-time technique for train bearing wayside acoustic signal separation and distortion correction. Ph.D Thesis, University of Science and Technology of China, Hefei, China, 2018. [Google Scholar]
  3. Xia, J.; Liang, G. Trackside acoustic detector system (TADS) for rolling bearing of train. Harbin Bearing. 2005, 6, 3–4. [Google Scholar]
  4. Barke, D. Structural Health Monitoring in the Railway Industry: A Review. Structural Health Monitoring. 2005, 4, 81–93. [Google Scholar] [CrossRef]
  5. Choe, H.; Wan, Y.; Chan, A. Neural pattern identification of railroad wheel-bearing faults from audible acoustic signals: Comparison of FFT, CWT,and DWT features. Texas A&M Univ. 1997, 30, 480–496. [Google Scholar]
  6. Sneed, W.H.; Smith, R.L. On-board real-time railroad bearing defect detection and monitoring.Proceedings of the 1998 ASME/IEEE Joint Railroad Conference. 1998; pp. 149–153.
  7. Southern, C.; Rennison, D.; Kopke, U. RailBAM: an advanced bearing acoustic monitor: Initial operational performance results. Core New Horizons for Rail. 2004, 23, 1–7. [Google Scholar]
  8. Snell; Nairne. Acoustic bearing monitoring, the future RCM 2008.4th IET International Conference on Railway Condition Monitoring. 2008; pp. 32–47.
  9. Zhang, S. Research on time-varying array analysis of fault spectrum identification in trackside acoustic diagnosis of train bearing. Ph.D Thesis, University of Science and Technology of China, Hefei, China, 2017. [Google Scholar]
  10. Zhang, A.; Hu, F.; Shen, C. Doppler distortion removal based on energy centrobaric method for wayside fault diagnosis of train bearings by acoustic signals. Vibration and Shock 2014, 33, 17–19. [Google Scholar]
  11. Liu, F.; Hou, C.; Zhai, T. An adaptive correction method for Doppler distorted signal of moving sound source. Journal of Acoustics. 2022, 47, 820–831. [Google Scholar]
  12. Zhang, H.; Lu, S.; He, Q. Fake time-frequency analysis of acoustic signals with Doppler distortion and its correction. Vibration and Shock 2016, 35, 14–20. [Google Scholar]
  13. Li, Q. Application research on new methods of non-stationary signal feature extraction and diagnosis techniques. Master’s Thesis, Tianjin University of China, Tianjin, China, 2005. [Google Scholar]
  14. Bennett, W.R. Statistics of Regenerative Digital Transmission. Bell System Technical Journal 1958, 37, 1501–1542. [Google Scholar] [CrossRef]
  15. Gardner, W.A.; Franks, L. Characterization of cyclostationary random signal processes. IEEE Transactions on Information Theory 1975, 21, 4–14. [Google Scholar] [CrossRef]
  16. Gardner, W.A. Signal interception: a unifying theoretical framework for feature detection. IEEE Transactions on Communications 1988, 36, 897–906. [Google Scholar] [CrossRef]
  17. Bonnardot, F.; Randall, R.B.; Guillet, F. Extractio of second-order cyclostationary sources—Application to vibration analysis. Mechanical Systems and Signal Processing 2005, 9, 1230–1244. [Google Scholar] [CrossRef]
  18. Leonardi, R.; Signoroni, A. Cyclostationary error analysis and filter properties in a 3D wavelet coding framework. Signal Processing: Image Communication 2006, 21, 653–675. [Google Scholar] [CrossRef]
  19. Hanson, D.; Randall, R.B.; Antoni, J.; Thompson, D.J.; Waters, T.P.; Ford, R.a.J. Cyclostationarity and the cepstrum for operational modal analysis of mimo systems—Part I: Modal parameter identification. Mechanical Systems and Signal Processing 2007, 21, 2441–2458. [Google Scholar] [CrossRef]
  20. Boustany, R.; Antoni, J. Blind extraction of a cyclostationary signal using reduced-rank cyclic regression—A unifying approach. Mechanical Systems and Signal Processing 2008, 22, 520–541. [Google Scholar] [CrossRef]
  21. Bouaynaya, N.; Schonfeld, D. Nonstationary Analysis of Coding and Noncoding Regions in Nucleotide. J. Sel. Topics Signal Processing 2008, 3. [Google Scholar] [CrossRef]
  22. Urbanek, J.; Barszcz, T.; Antoni, J. Time–frequency approach to extraction of selected second-order cyclostationary vibration components for varying operational conditions. Measurement 2013, 46, 1454–1463. [Google Scholar] [CrossRef]
  23. Guo, X. Trackside acoustic signal Doppler correction and acoustic detection platform system design. Master’s Thesis, Dalian Jiaotong University of China, Dalian, China, 2021. [Google Scholar]
  24. Zhao, X. Study on fault diagnosis of rolling bearing based on angle-domain cyclostationary. Ph.D Thesis, M Dalian Jiaotong University, Dalian, China, 2017. [Google Scholar]
  25. Liu, F. Research on wayside acoustical fault diagnosis for train-wheel bearings when the train is running at a non-uniform velocity. Ph.D Thesis, University of Science and Technology of China, Hefei, China, 2014. [Google Scholar]
  26. Wu, Q.; Kong, F.; He, Q. Doppler shift correction for acoustic signals using resampling technique. Signal Processing 2012, 28, 1308–1313. [Google Scholar]
  27. Han, Y. Design of experimental platform for trackside acoustic detection based on LabVIEW. Master’s Thesis, Dalian Jiaotong University of China, Dalian, China, 2022. [Google Scholar]
Preprints 84844 g001
Figure 1. Bearing failure sound source motion model.
Figure 1. Bearing failure sound source motion model.
Preprints 84844 g001
Preprints 84844 g002
Figure 2. Resampling schematic.
Figure 2. Resampling schematic.
Preprints 84844 g002
Preprints 84844 g003
Figure 3. Schematic diagram of amplitude correction.
Figure 3. Schematic diagram of amplitude correction.
Preprints 84844 g003
Preprints 84844 g004
Figure 4. Structure of rolling bearing.
Figure 4. Structure of rolling bearing.
Preprints 84844 g004
Preprints 84844 g005
Figure 5. Fault diagnosis process based on cyclic smoothing.
Figure 5. Fault diagnosis process based on cyclic smoothing.
Preprints 84844 g005
Preprints 84844 g006
Figure 6. Trackside acoustic testing experimental platform.
Figure 6. Trackside acoustic testing experimental platform.
Preprints 84844 g006
Preprints 84844 g007
Figure 7. Experimental schematic.
Figure 7. Experimental schematic.
Preprints 84844 g007
Preprints 84844 g008
Figure 8. (a) Test bearings outer ring failure; (b) Test bearing inner ring fault; (c) Test bearing rolling element fault.
Figure 8. (a) Test bearings outer ring failure; (b) Test bearing inner ring fault; (c) Test bearing rolling element fault.
Preprints 84844 g008
Preprints 84844 g009
Figure 9. Outer ring fault time domain waveform.
Figure 9. Outer ring fault time domain waveform.
Preprints 84844 g009
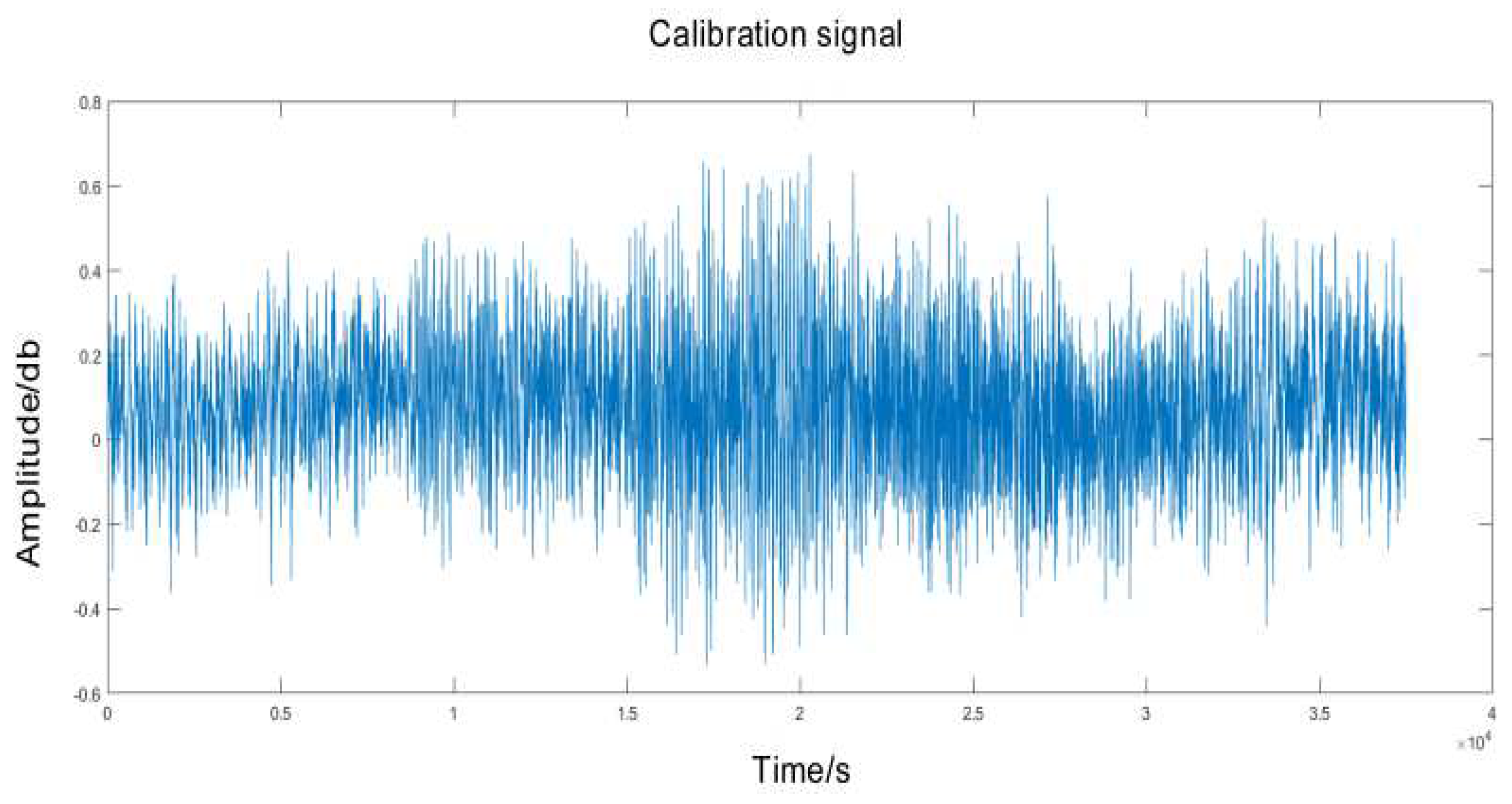
Preprints 84844 g010
Figure 10. Time domain waveform for outer ring correction.
Figure 10. Time domain waveform for outer ring correction.
Preprints 84844 g010
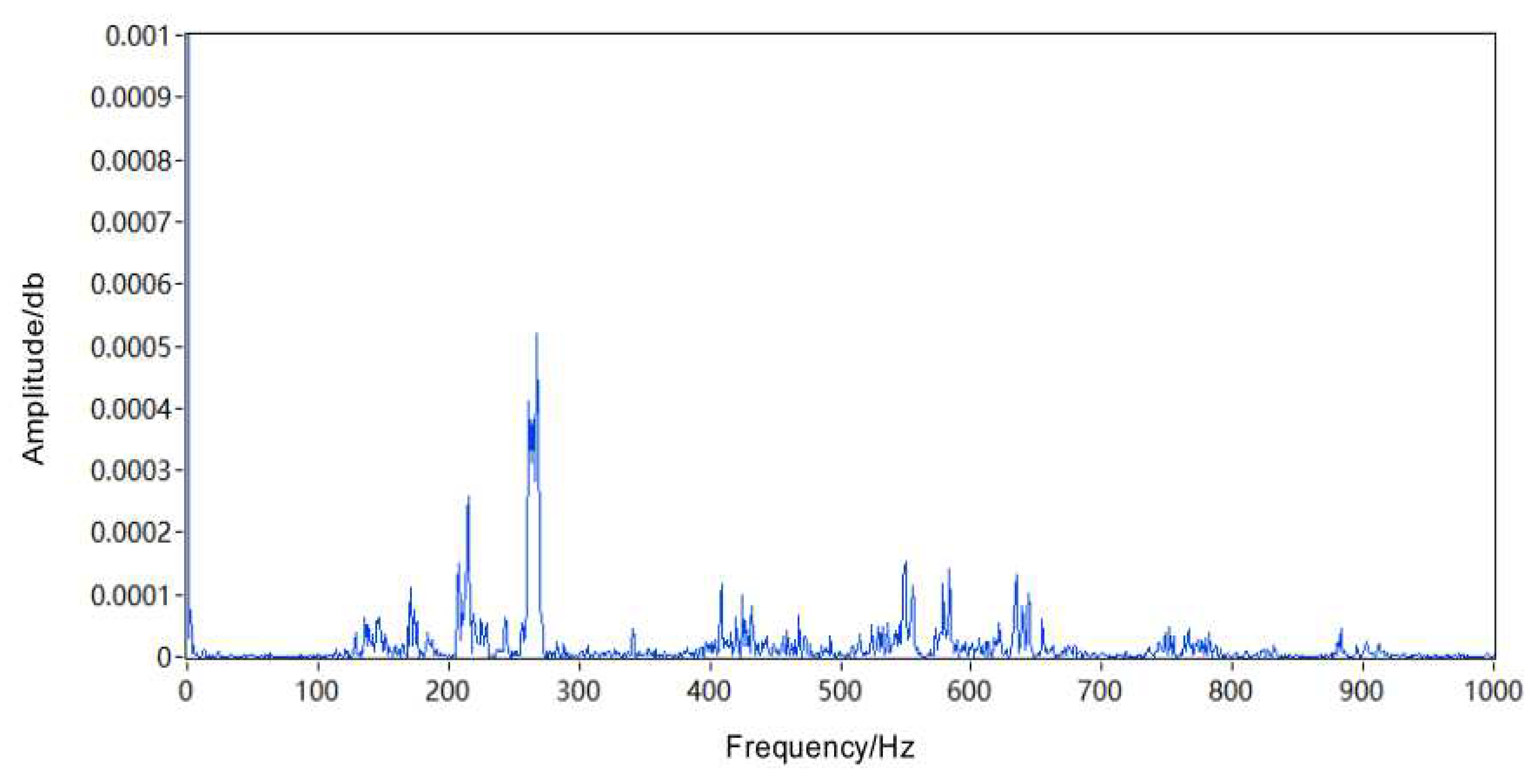
Preprints 84844 g011
Figure 11. Initial signal power spectrum of outer ring fault.
Figure 11. Initial signal power spectrum of outer ring fault.
Preprints 84844 g011
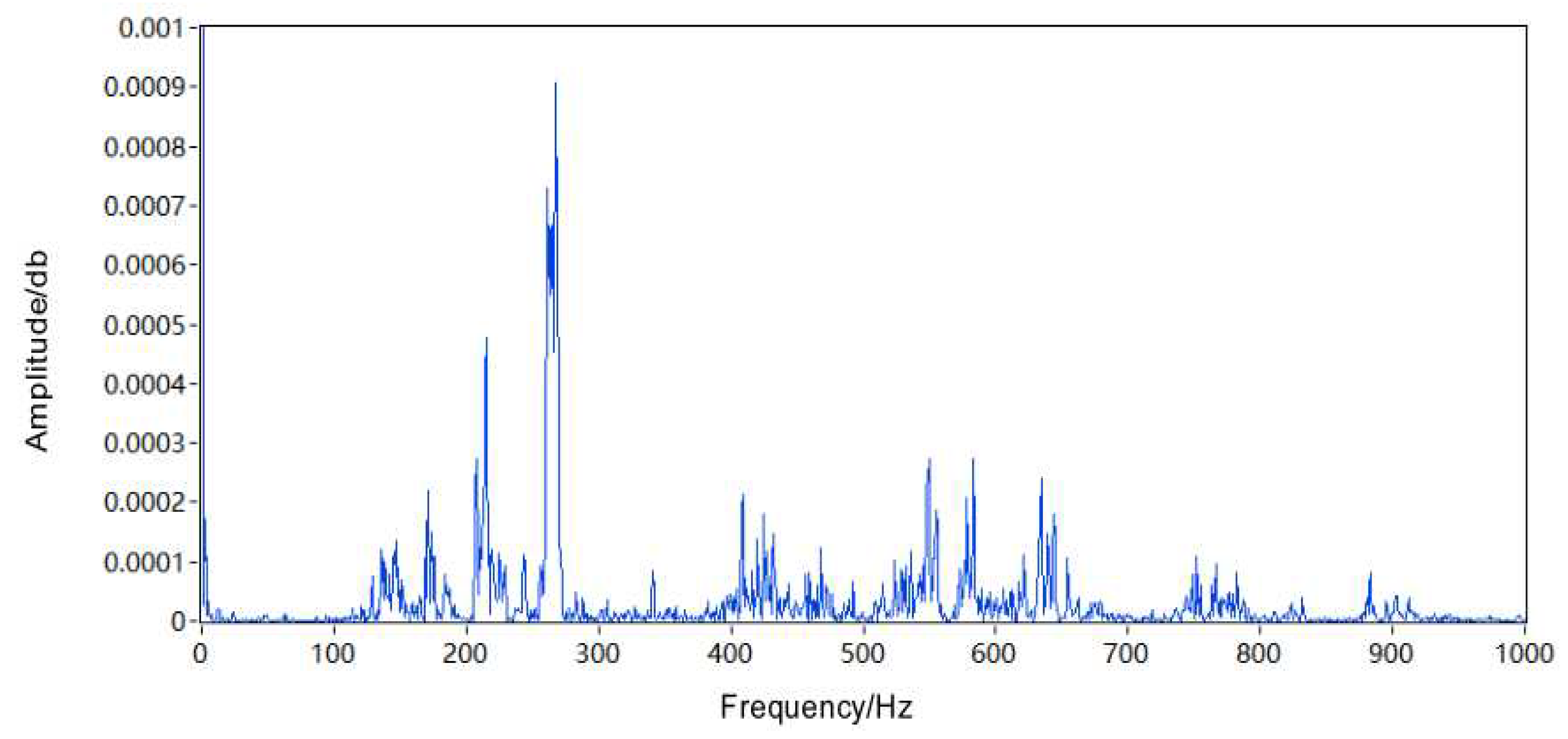
Preprints 84844 g012
Figure 12. Power spectrum of the outer ring fault correction signal.
Figure 12. Power spectrum of the outer ring fault correction signal.
Preprints 84844 g012
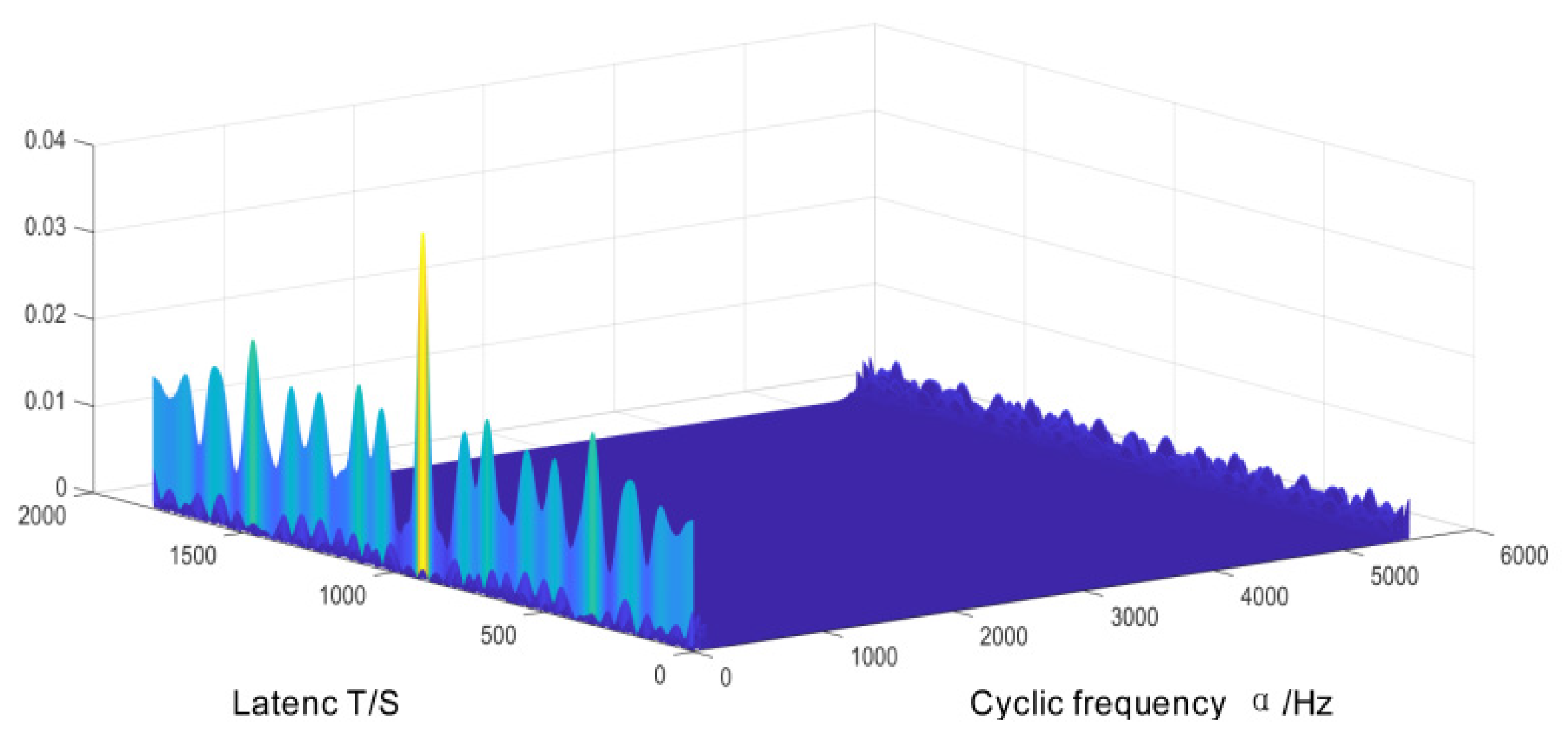
Preprints 84844 g013
Figure 13. Cyclic autocorrelation spectrum of outer ring fault correction signal.
Figure 13. Cyclic autocorrelation spectrum of outer ring fault correction signal.
Preprints 84844 g013
Preprints 84844 g014
Figure 14. Cyclic autocorrelation density spectrum of the outer ring fault correction signal.
Figure 14. Cyclic autocorrelation density spectrum of the outer ring fault correction signal.
Preprints 84844 g014
Preprints 84844 g015
Figure 15. Slices of the cyclic density refinement of the outer ring fault correction signal.
Figure 15. Slices of the cyclic density refinement of the outer ring fault correction signal.
Preprints 84844 g015
Preprints 84844 g017
Figure 17. Fault signal time domain waveform.
Figure 17. Fault signal time domain waveform.
Preprints 84844 g017
Preprints 84844 g018
Figure 18. Correction signal time domain waveform.
Figure 18. Correction signal time domain waveform.
Preprints 84844 g018
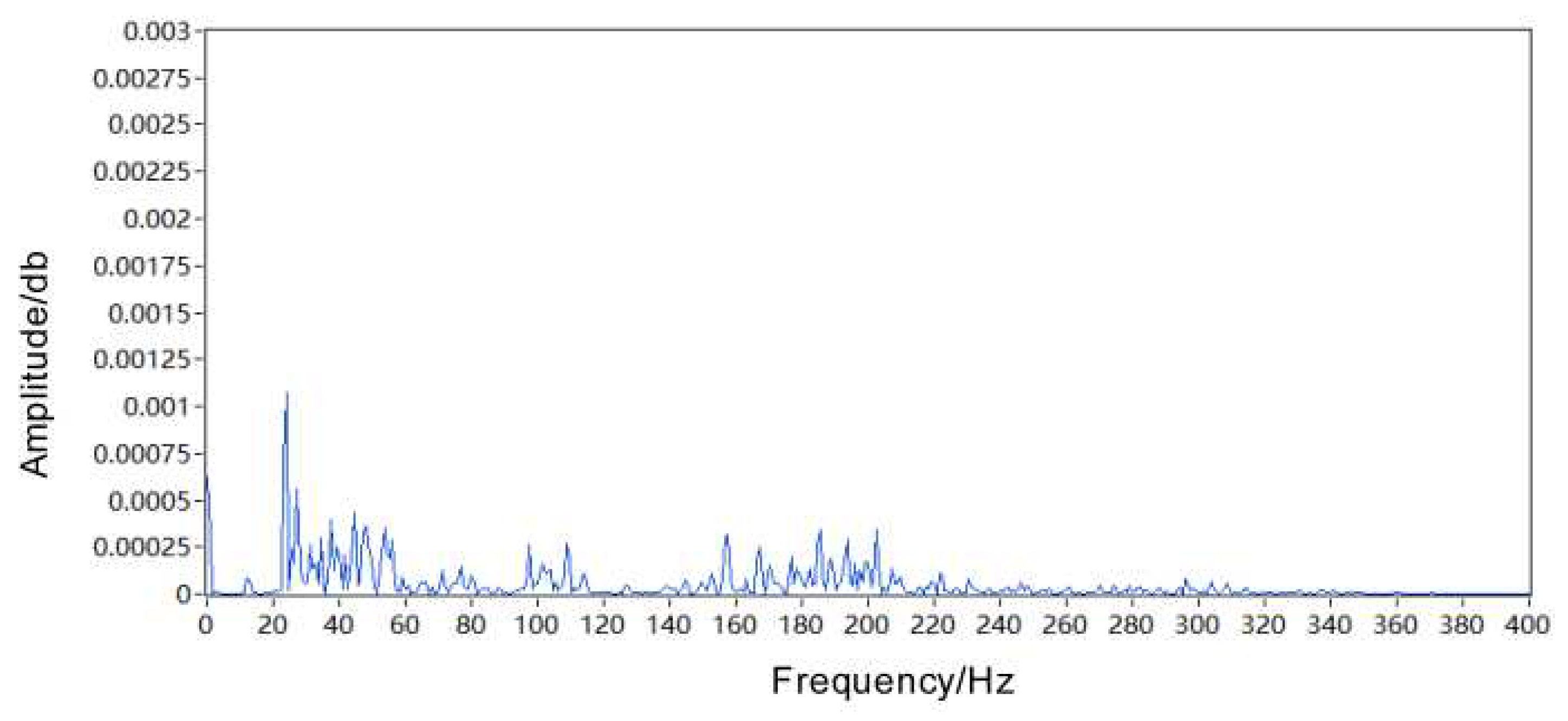
Preprints 84844 g019
Figure 19. Fault signal power spectrum.
Figure 19. Fault signal power spectrum.
Preprints 84844 g019
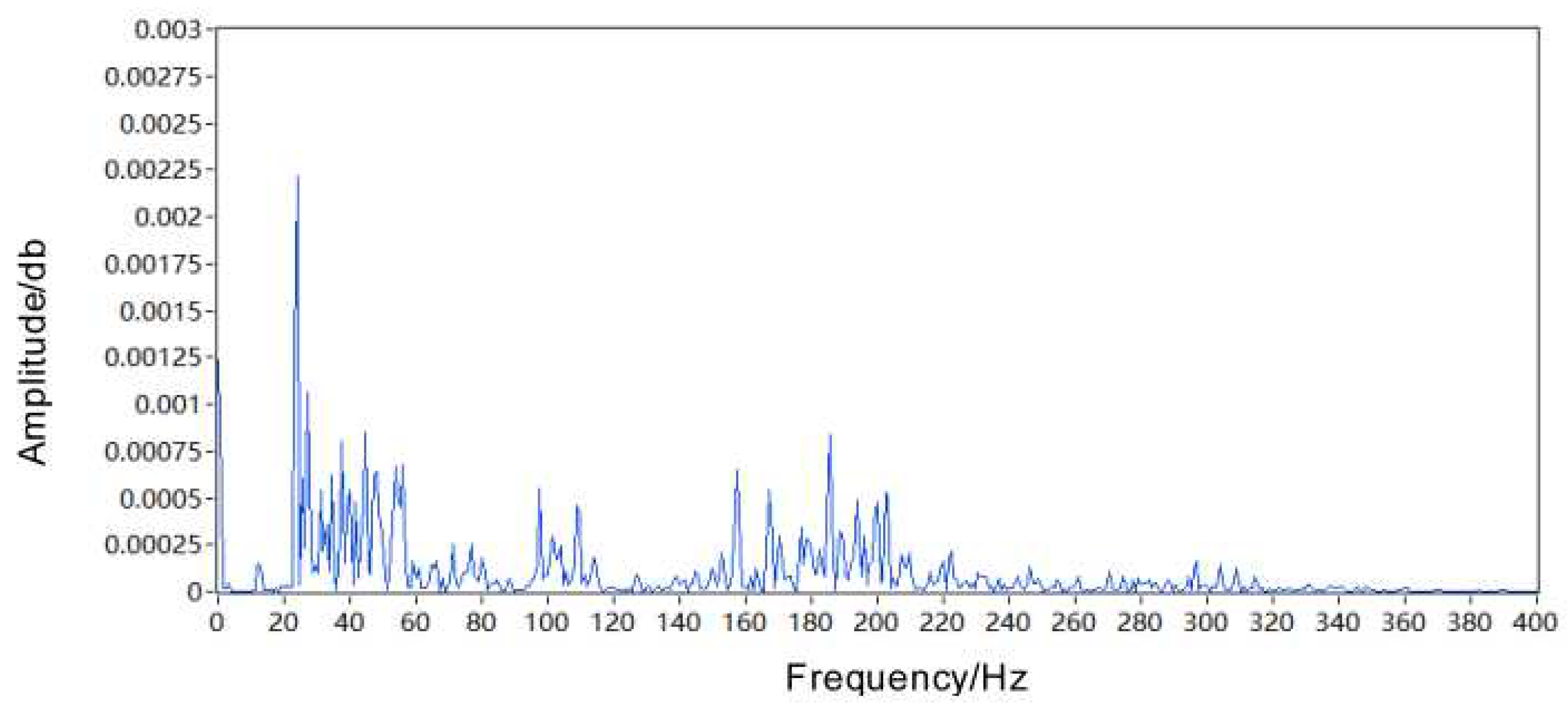
Preprints 84844 g020
Figure 20. Calibration signal power spectrum.
Figure 20. Calibration signal power spectrum.
Preprints 84844 g020
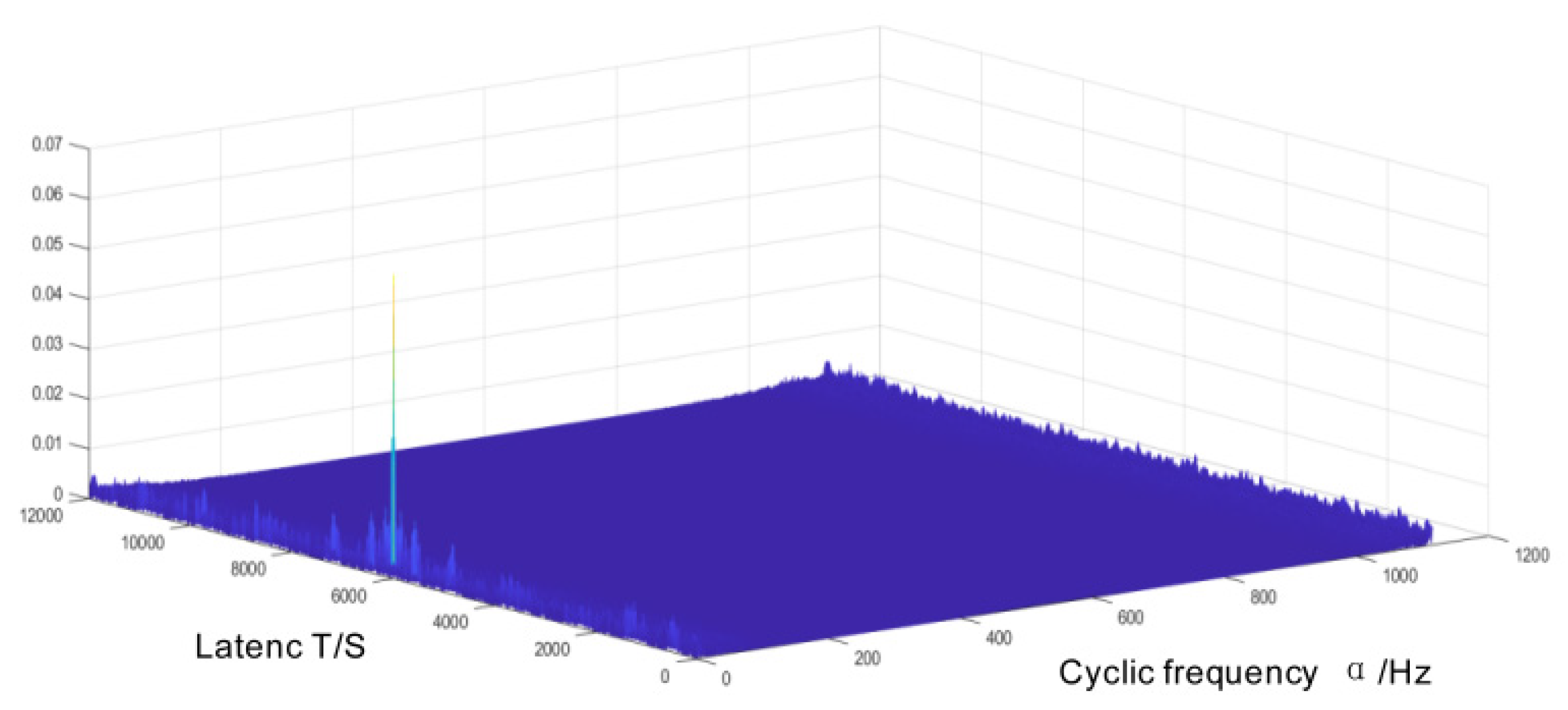
Preprints 84844 g021
Figure 21. Cyclic autocorrelation spectrum.
Figure 21. Cyclic autocorrelation spectrum.
Preprints 84844 g021
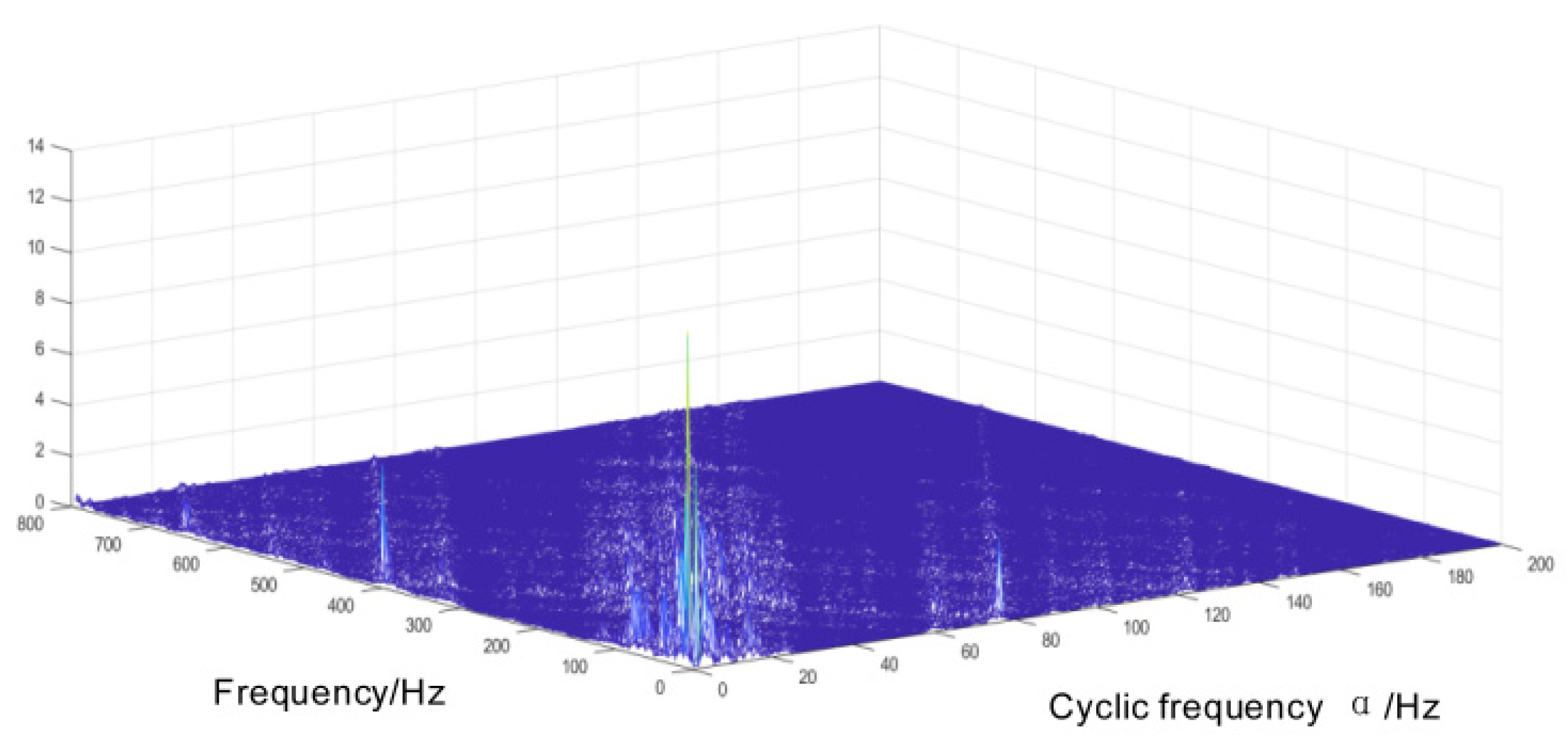
Preprints 84844 g022
Figure 22. Cyclic autocorrelation density spectrum.
Figure 22. Cyclic autocorrelation density spectrum.
Preprints 84844 g022
Preprints 84844 g023
Figure 23. Section of cyclic density refinement.
Figure 23. Section of cyclic density refinement.
Preprints 84844 g023
Preprints 84844 g024
Figure 24. Bearing failure diagram.
Figure 24. Bearing failure diagram.
Preprints 84844 g024
Preprints 84844 g025
Figure 25. Fault diagnosis steps for rolling bearings.
Figure 25. Fault diagnosis steps for rolling bearings.
Preprints 84844 g025
Table 1. Cycle frequency characteristics in the event of failure of individual rolling bearing components.
Table 1. Cycle frequency characteristics in the event of failure of individual rolling bearing components.
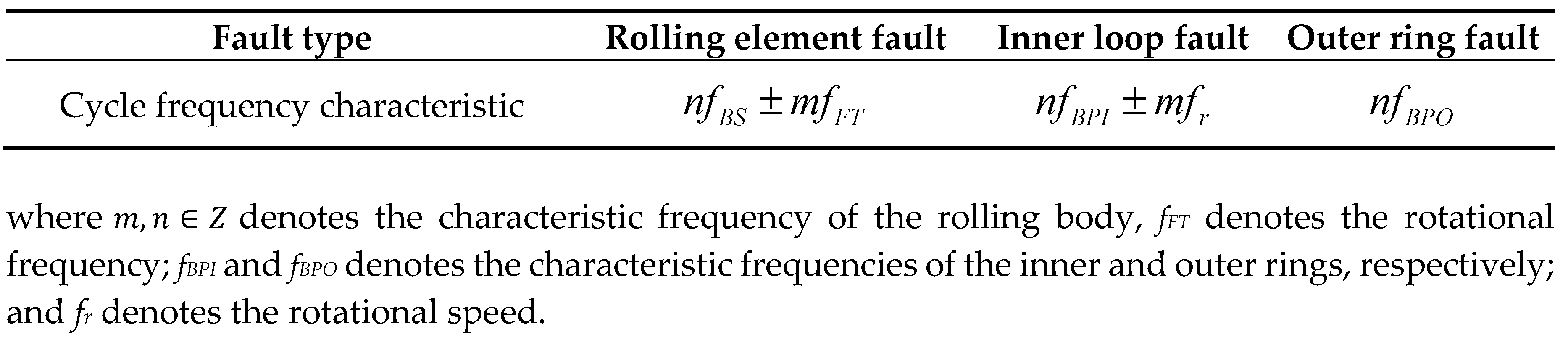
Preprints 84844 i001
Table 2. Calculation of rotational speed.
Table 2. Calculation of rotational speed.
Test bearing speed n1(rpm) Slider horizontal speed v2(m/s) Slider drive motor speed n2(rpm)
150 0.4 145
300 0.8 291
600 1.6 582
Table 3. Calculation of rotational speed.
Table 3. Calculation of rotational speed.
Bearing type Inside diameter (mm) Pitch diameter (mm) Outside diameter (mm) Rolling diameter (mm) Number of rolling elements
N205 25 38.5 52 7.5 12
Table 4. Calculation of rotational speed.
Table 4. Calculation of rotational speed.
Bearing type Inside diameter (mm) Pitch diameter (mm) Outside diameter (mm) Rolling diameter (mm) Number of rolling elements
353130B 150 200 250 22 23
Table 5. Frequency of cyclic failure characteristics of rolling bearings.
Table 5. Frequency of cyclic failure characteristics of rolling bearings.
Fault type Rolling element fault Inner loop fault Outer ring fault
Cycle frequency characteristic 23.1Hz 177.4Hz 15.2Hz
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated