Prerpints.org logo
Preprint
Article

Numerical Study on Seismic Behavior of Demountable Joints Consisting of RC Columns and Steel Beams

Altmetrics

Downloads

124

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 September 2023

Posted:

19 September 2023

You are already at the latest version

Alerts
Abstract
In this study, three new demountable joints consisting of reinforced concrete columns and steel beams were proposed and their seismic performance was investigated using cyclic loading tests. The test results demonstrated that the three demountable RCS joints had good seismic performance. Using the finite element software ABAQUS, the influence of parameters such as beam flange thickness, bolt strength, and connector steel strength on the seismic performance of each joint was analyzed, and the influence of different parameters on the seismic behavior of the joint was determined. The results also showed that the three demountable RCS joints were sensitive to changes in the thickness of the steel beam flange, while the connector steel strength and bolt type had little impact on the joint's capacity. Additionally, shear capacity calculation formulas for the joint core area provided by different codes and researchers were compared with test and finite element results. The results showed that the calculation results of the ASCE guidance method, the Nishiyama method, and the CECS 347-2013 method were higher than the test values, while the calculation results of the Para method were lower because it did not consider the contribution of the cylindrical steel plate to the shear capacity of the joint core area.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Construction and demolition waste (C&DW) constitutes around 30% of global waste production, resulting in diverse environmental impacts such as resource depletion, global warming, and land degradation [1,2,3,4,5]. While traditional buildings are usually designed as permanent structures, the disposal of demolition waste is a complex problem [6]. Using demountable structures in building construction can promote the reuse of building materials and decrease the amount of demolition waste [7]. However, the reuse of building components has not yet become a widely adopted practice [8]. Demountable building components that can be directly disassembled and reassembled in a new building at the end of their life cycle have exceptional environmental and economic advantages. Furthermore, demountable structural components can be manufactured in factories and assembled on-site, leading to a reduction in air pollution at construction sites to a certain degree.
The connections of prefabricated elements play a vital role in the performance of the complete demountable structure due to the stable quality of prefabricated components. Earlier research has indicated that the connections of prefabricated components tend to fail before the prefabricated components themselves during earthquakes. Demountable joints have been the subject of numerous studies exploring their behavior. For demountable steel structures, Uy et al. [7] carried out finite element simulations for connections between beams, columns, and plates, with parametric analysis included. Various novel methods for demountable beam-to-column connections were suggested. The calculation results indicate that, if the load does not exceed 50% of the calculated load, the beam-to-beam connection can detach the cover plate. To improve the stiffness and ultimate tensile strength of the demountable column-to-column joint nod, it is recommended to increase the length of the sleeve and the reinforcement ratio. Wang et al. [9] conducted experimental research on the static and hysteretic performance of a novel beam-to-column bolt joint that can be detached. A finite element model, which was verified through experimentation, was used for parametric analysis. The study results revealed that as long as the load does not exceed 40% of the ultimate load, the steel elements remain in the elastic stage, and all demountable components can be removed as intended. Ataei et al. [10,11] have performed experimental studies on the semi-rigid demountable joint of flat end plates between steel beams and steel pipe columns. The results indicate that the joint exhibits a remarkable capacity for bending and rotation. Moreover, the proposed structural system can be conveniently disassembled and reused in other buildings once its service life is completed. To investigate the seismic performance of the repaired demountable steel column-steel beam joint, Peng [12] initially conducted a quasi-static test on the joint. Afterward, the joint was repaired by removing and replacing the beam. A study of the repaired steel column-steel beam joint was then undertaken through low-cycle repeated load testing. The results of the experiment demonstrate that the seismic design requirements are met by the repaired joint and the seismic performance is good. There has been extensive research on demountable concrete connections in addition to demountable steel connections. Xiao et al. [13] carried out five full-scale experimental studies on the beam-to-beam connection of concrete frame exterior joints. The experimental findings indicate that the demountable concrete joints exhibit substantial ductility under static and seismic loads. Ding et al. [14] investigated seven full-scale demountable concrete beam-to-column joints through experimental research, which showed that the joint possesses commendable seismic performance but lacks ductility. Moreover, the demountable concrete structure's practicability was confirmed during the construction process. Huang et al. [15] suggest utilizing multi-slot devices to improve the seismic performance of demountable concrete beam-to-column joints. Furthermore, steel-concrete composite beams exhibit enhanced structural characteristics in terms of strength and stiffness when compared with traditional pure steel and reinforced concrete beams. In the past few years, the demountable connection between steel beams and concrete slabs has been a crucial area of research.
To enhance installation efficiency and simplify disassembly, the replacement of customary steel studs with steel-concrete composite slabs is recommended. Wang et al. [16] performed push-out experiments on multiple steel bolts joining fixed concrete slabs and steel beams and corroborated their numerical model through validation and parameter analysis. Malla et al. [17] carried out numerical studies on demountable links among concrete shear walls. The results indicate that the mode of failure in the connection is significantly influenced by the bolts. Scholars have come up with different types of shear bolts for the study, including demountable shear connecting bolts (LB-DSC and HTFGB) proposed by He [18] and Loqman et al. [19] for steel-concrete composite structures. The push-out experiment and finite element simulation results indicate that, in contrast to other shear connecting bolts, it exhibits high shear resistance and stiffness. Furthermore, a connecting formula for determining the ultimate bearing capacity of connecting pieces has been proposed.
On the other hand, the evolution of steel-concrete composite structures draws from traditional concrete and steel structures, yet boasts superior mechanical capabilities. For solid constructions, the inclusion of steel has the potential to decrease the weight of the structure, decrease the cross-sectional area of the components, conserve molds, and quicken the pace of construction. Conversely, in the case of steel frameworks, the inclusion of concrete can heighten the fire resilience and longevity of the structure, strengthen overall rigidity, decrease the quantity of steel needed, and lower expenses. [2]. Due to the advantages of both steel and concrete, the reinforced concrete column-steel beam (RCS) composite structure has garnered attention from scholars worldwide in recent years. When compared to steel structures, the RCS structure not only reduces construction costs but also improves damping and lateral stiffness [20]. Furthermore, the RCS structure is lighter in weight than concrete structures. A substantial body of research has been dedicated to assessing the effectiveness of RCS structures. Tests were conducted by Le et al. on steel beam-concrete column exterior joints featuring an integrated I-beam short steel [21]. An experiment on the steel-concrete composite beam-reinforced concrete column joint under monotonic load was carried out by Zhang et al. [22]. The seismic performance of RCS joints was experimentally explored by Fargier-Gabald 'on et al. who also examined the impact of column width [23]. Men et al. [24] investigated the impact of plate widths on RCS joints by testing three RCS sub-components. Previous studies primarily examined cast-in-place RCS joints, and as a result, there is a scarcity of research on demountable RCS joints.
To attain sustainability throughout the entire life cycle of composite structures consisting of reinforced concrete columns and steel beams, three novel demountable RCS joints have been proposed in this study. The safety of these joints under earthquake conditions was ensured through an experimental and numerical evaluation that compared their seismic performance to that of non-demountable RCS joints. In addition, a finite element model was created for the demountable RCS joint, considering parameters like beam flange thickness, bolt strength, and detailed connection steel strength. Various approaches were used, selected based on existing specifications and research findings, to determine the ratio between the theoretical and experimental results of the joint core shear bearing capacity.

2. Experiment investigation

2.1. Experimental design

This article has created four 1/2 scaled specimens of beam-column exterior joints for a prototype frame structure with multiple levels, boasting a floor height of 4 m and a beam span of 7.4 m. The specimens feature a column height of 2000mm and a beam height of 3700mm. The joint design is based on the design criteria "strong column, weak beam" and "strong shear, weak bending" in GB/T 50011-2010 "Code for Seismic Design of Buildings". To simplify the disassembly of the RCS joint, bolt connections are used. The specimens are categorized into four types based on the various forms of beam-column joint connections, namely RCS-0, RCS-1, RCS-2, and RCS-3. Figure 1 shows the detailed dimensions and overall size of the specimens.

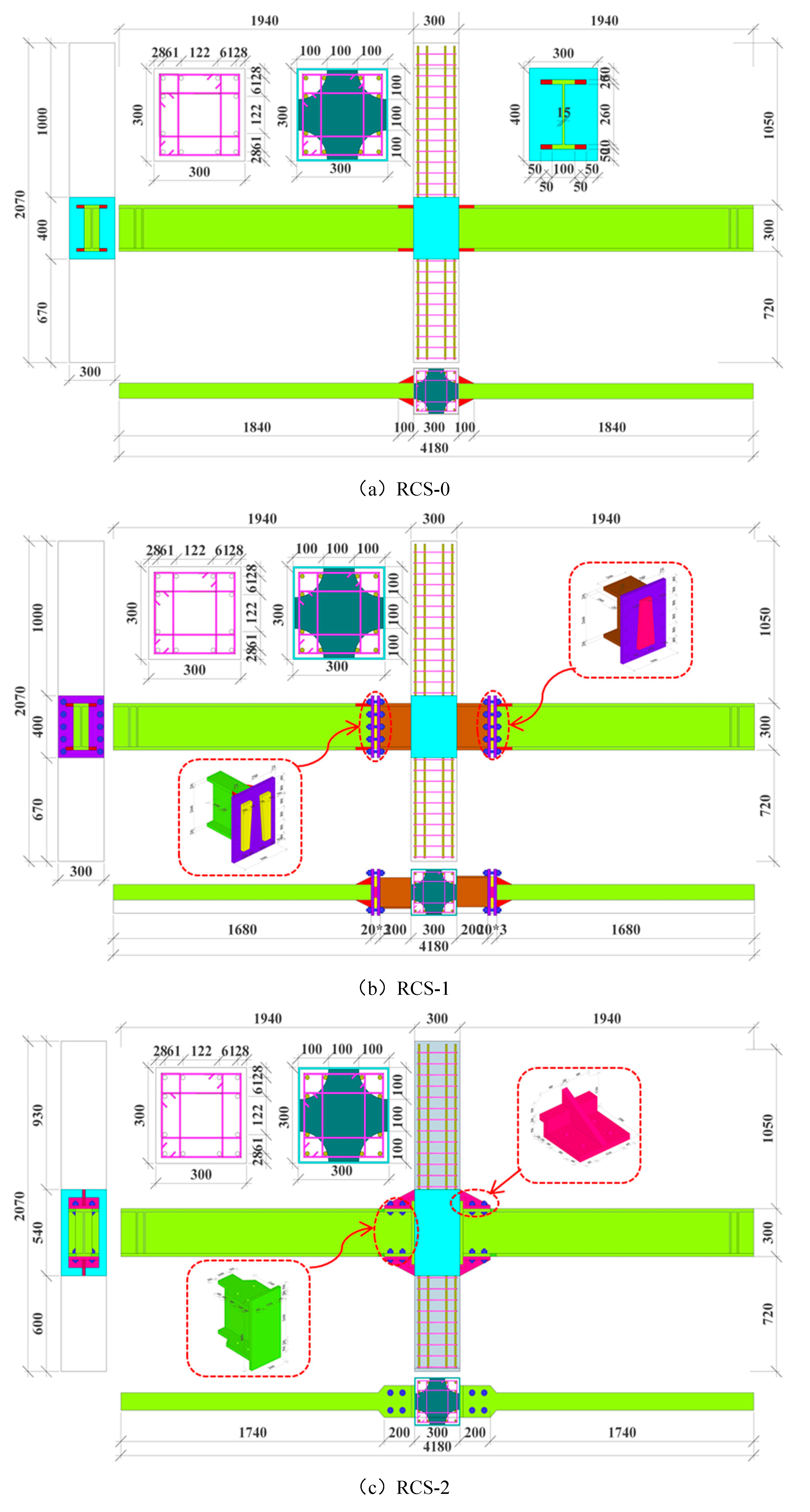
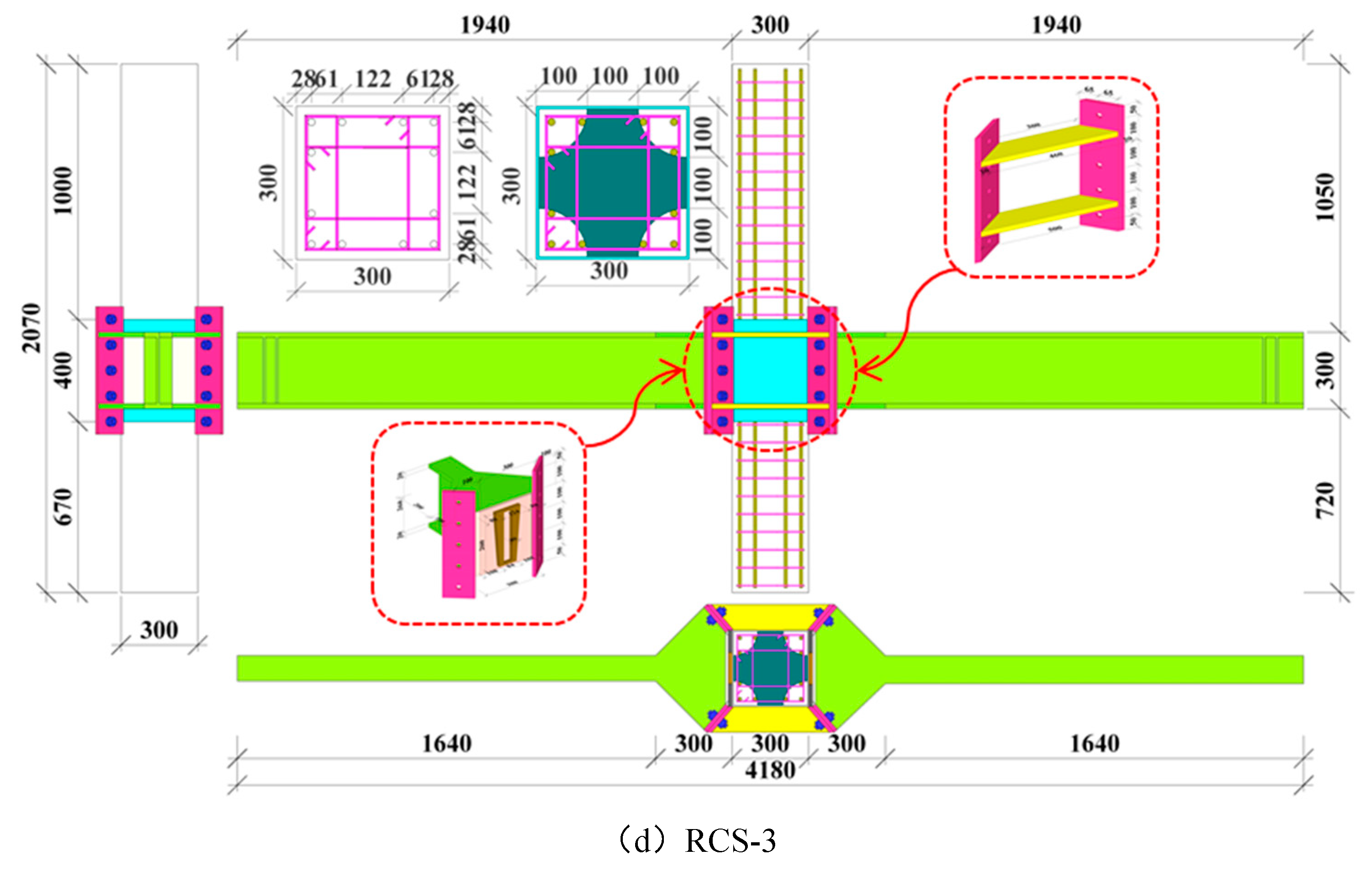
2.1.1. Specimen specification preparation

As depicted in the Figure 1, specimen RCS-0 is taken as a reference specimen. The H-section steel beam and reinforcing ribs are welded and fastened to a steel plate ring. A reinforcing plate is positioned in the central part where it meets the concrete column, augmenting the joint's stiffness and bending capacity. The triangular rib on the side of the beam can enhance the welding strength between the steel beam and the steel plate hoop, preventing joint failure resulting from weld cracking. For specimen RCS-1, the end plate with perforations is welded to the outer end of the flange at the column end and the steel beam, with a wedge plate placed between the end plates for transferring sheer force. Also, the two end plates are joined using high-strength bolts. Vertically distributed high-strength bolts link the connection piece of the RCS-2 sample to the steel beam. In addition, the upper and lower flanges are connected to the steel beam utilizing a groove to assemble, enabling them to transmit bending moment and shear force. To enhance the efficiency of on-site construction joints and facilitate speedy installation, we designed a demountable RCS-3 joint. Figure 1-(4) illustrates the connection structure. It is akin to the demountable RCS-2 joint and makes use of a wedge block to facilitate the transfer of shear force. An external beam and end plate, along with 4 sets of diagonal bolts, are employed to secure the concrete column and steel beam. This method of joint connection can decrease the necessary quantity of bolts, and the diagonal bolt group can withstand some shear force and transfer bending moment. Except for the separate energy-absorbing connections installed in the demountable RCS-1, RCS-2, and RCS-3 joints, the material selection, and dimensions of all other components remain consistent. These include square-sectioned concrete columns (mm), I-beam steel sections (mm), high-strength grade 8.8 friction bolts with a diameter of 20mm for longitudinal bars and hoops, longitudinal bars with diameters of 14mm spaced 61mm apart, and hoops with diameters of 6mm spaced 80mm apart. Technical abbreviations will be explained upon first use.

2.1.2. Material properties

Specimens were prepared using HPB300 steel bars, with a diameter of 6mm, and HRB400 steel bars, with a diameter of 14mm. Steel beams were fabricated by welding Q235 steel plates, with thicknesses of 10mm and 20mm. Material properties of the necessary steel and steel bars were assessed in accordance with the "Metal Materials Tensile Test Part 1: Room Temperature Test Methods" (GB/T 228.1-2010) [26] specifications. Table 1 presents a summary of the mechanical properties of steel, steel bars, and bolts, obtained by averaging test results derived from three material specimens. The concrete columns were mixed in the laboratory with a predetermined mixing ratio and then poured into forms. P. O 42.5R ordinary Portland cement was utilized, alongside medium sand as fine aggregate and a coarse aggregate that had a particle size range of 5-25mm. O 42.5R ordinary Portland cement was utilized, alongside medium sand as fine aggregate and a coarse aggregate that had a particle size range of 5-25mm. The concrete's average compressive strength was determined by creating cylindrical specimens that were 300mm in height and 150mm in diameter. Subsequently, static load compression strength tests were performed on each group of specimens to acquire the average compressive strength values, which are presented in Table 2.

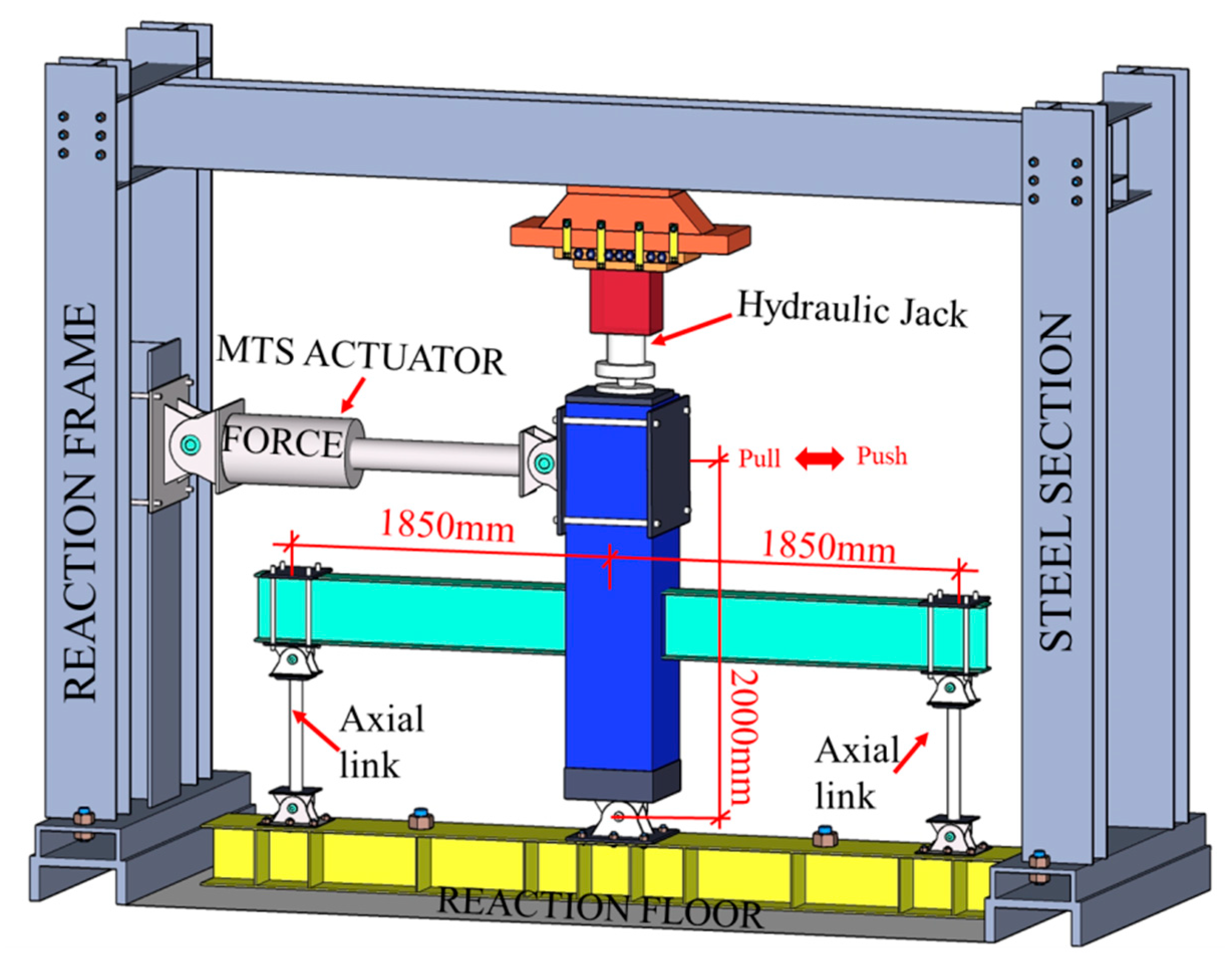
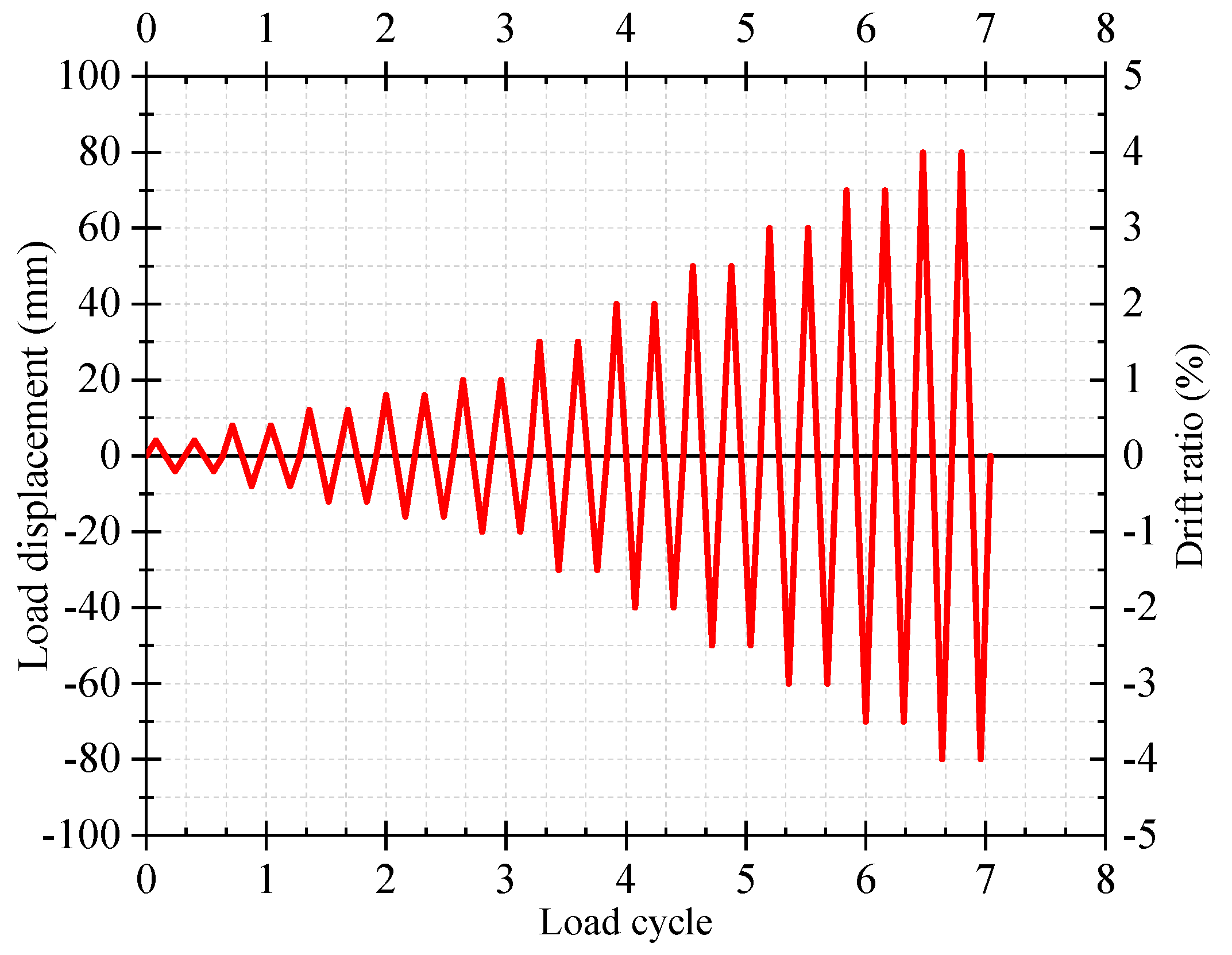
2.2. Test setup and loading condition

The experimental loading apparatus comprises a robust steel framework, a 500KN MTS hydraulic servo actuator, a vertical hydraulic jack, a firm steel beam, anchor bolts, and auxiliary loading devices such as beam end clamps and column bottom sleeve hinge bearings. Figure 2 shows the complete apparatus. The removable RCS joint sample is scheduled for static testing via the application of vertical loads to the column top through hydraulic jacks, controlling the axial stress ratio, followed by horizontal reciprocating loads at the end of the column. The loading protocol for this experiment conforms to the "Code for Seismic Testing Methods of Buildings" (JGJ101-2015) [27], and the loading regime for the planned static testing of the sample utilizes a full-stage displacement-controlled loading configuration. The loading displacement value is controlled by multiples of the interlayer displacement angle, and each loading is repeated twice. The loading system is depicted in Figure 3. In the later phase of the experiment, it is crucial to observe that loading ceases when the lateral load on the specimen decreases to 85% of the peak load or cannot be sustained any longer.

3. FEM simulation

3.1. Model description

Using the general finite element software ABAQUS, we modeled four beam-column joint specimens. Figure 1 shows the structural parameters and layout drawings of each specimen. The concrete constitutive input for the numerical model was calculated as per the Code for Design of Concrete Structures (GB 50010-2010) [28], based on the tensile and compressive constitutive relationship criterion. Additionally, the CDP plastic damage model in ABAQUS was employed to calculate the damage parameters. The isotropic Von Mises ideal bilinear constitutive model was adopted for the reinforcing steel, steel, and high-strength bolts, with specific input constitutive parameters calculated based on measured values. The concrete columns, steel beams, bolts, and connecting pieces were modeled using C3D8R solid elements, while the longitudinal bars and hoops were modeled using T3D2, which are three-dimensional two-node truss elements.
To replicate the experimental loading process, the control points were linked to the underside of the concrete column and the beam end section employing the “coupling” function. The displacement and rotational degrees of freedom for the control points, i.e., the six degrees of freedom, were then restricted in the X, Y, and Z planes to ensure comparable boundary conditions to the experimental loading process. The reinforcing steel of the concrete column was incorporated into the corresponding concrete components using the “Embedded Region” instruction to allow the steel and concrete to function together under load and deformation. The “Tie” directive was utilized to limit the welded connections between steel members. Surface-to-surface contact between steel components was established with contact pairs, which included bolt-plate and plate-plate contact. Technical term abbreviations have been explained upon first use. The language is clear and objective, and filler words have been avoided. The grammatical correctness has been ensured. Therefore, no further changes are required. A vertical constant uniformly distributed load of 8 MPa was applied at the top of the column to meet the 0.2 axial pressure ratio of the experimental frame column. Additionally, a cyclic horizontal load was applied at the column end as demonstrated in Figure 4.
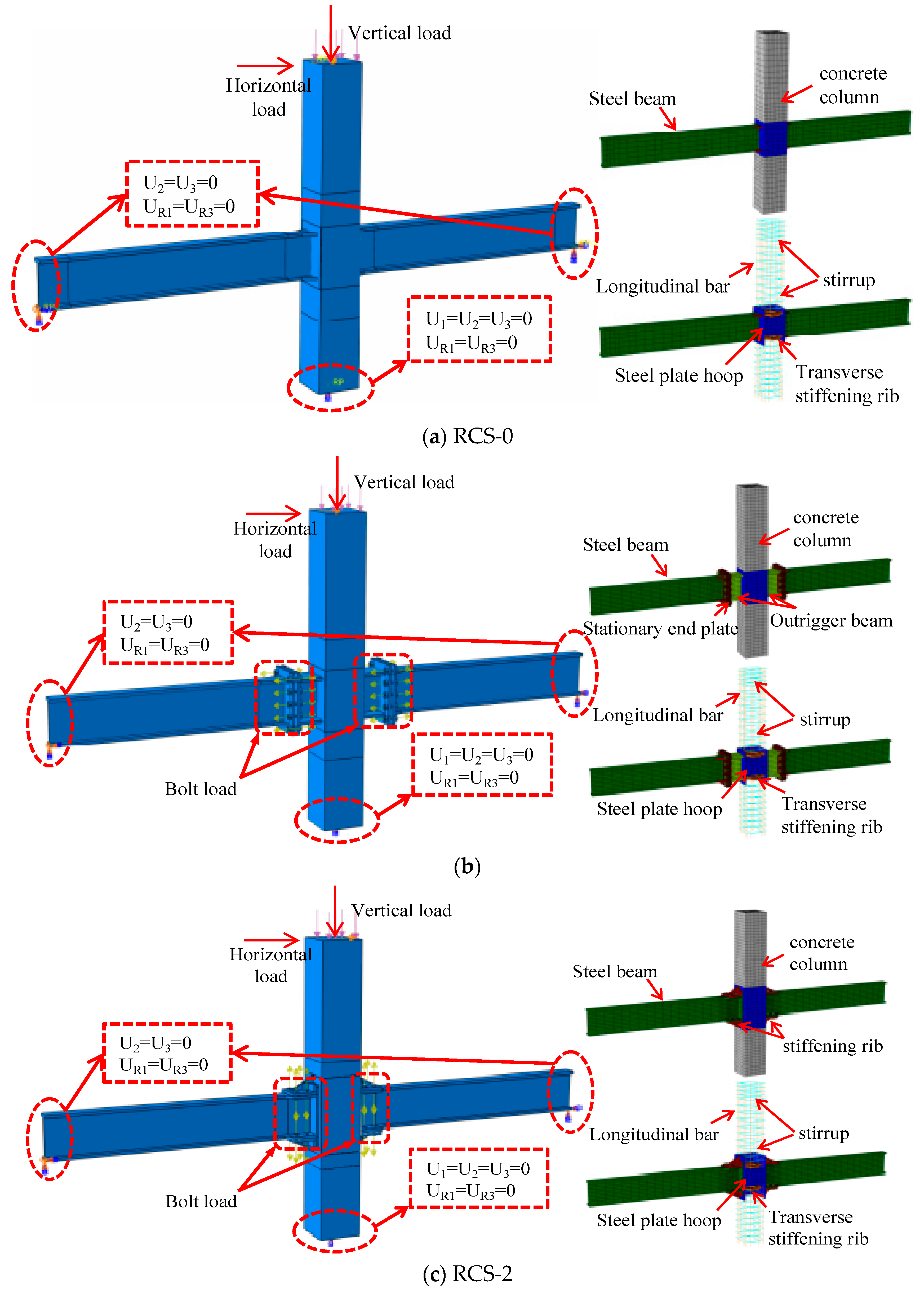
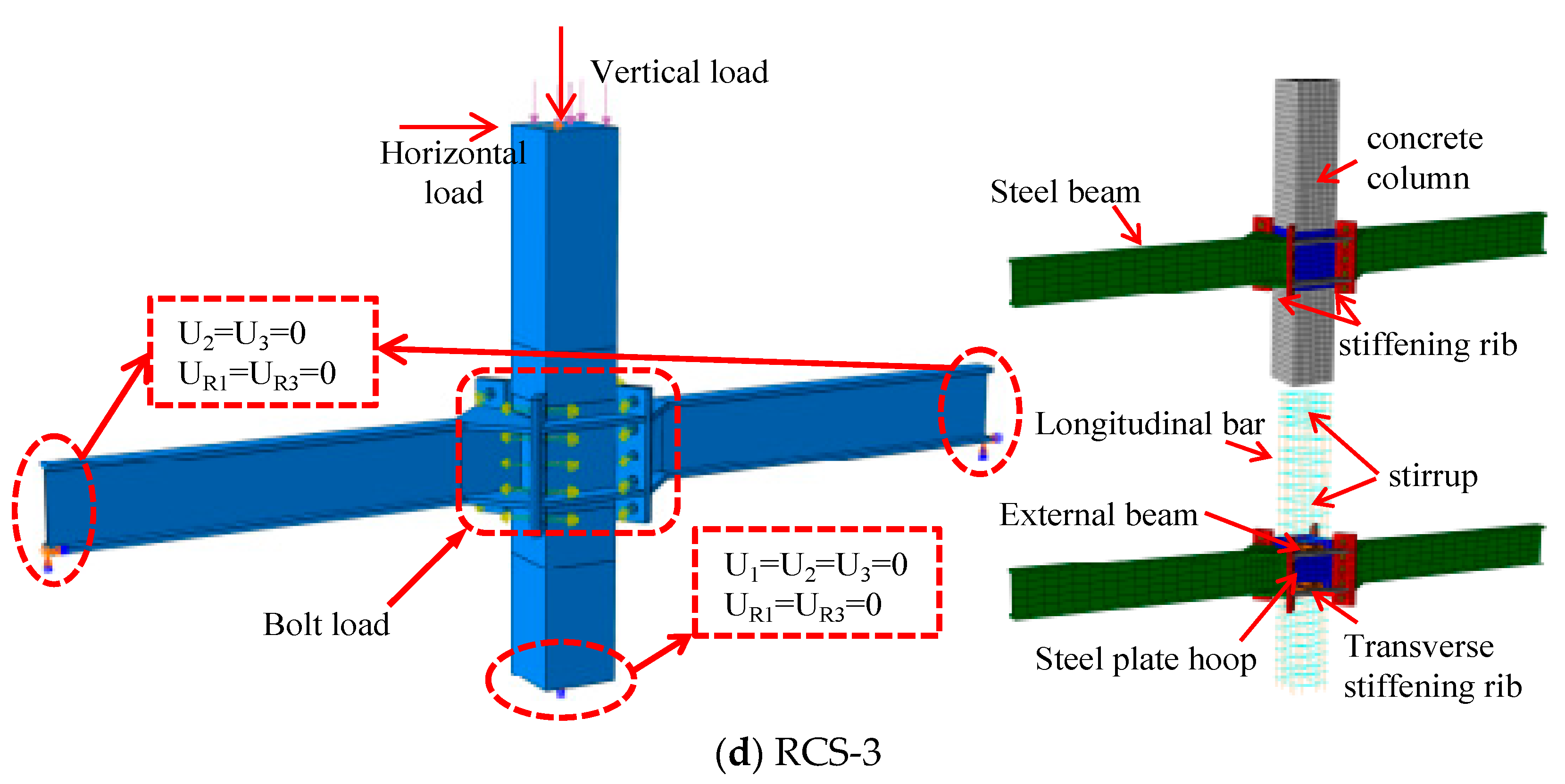
Preprints 85209 g004aPreprints 85209 g004b
Figure 4. Boundary conditions and meshing of finite element model.
Figure 4. Boundary conditions and meshing of finite element model.
Preprints 85209 g004aPreprints 85209 g004b

3.2. Model validation

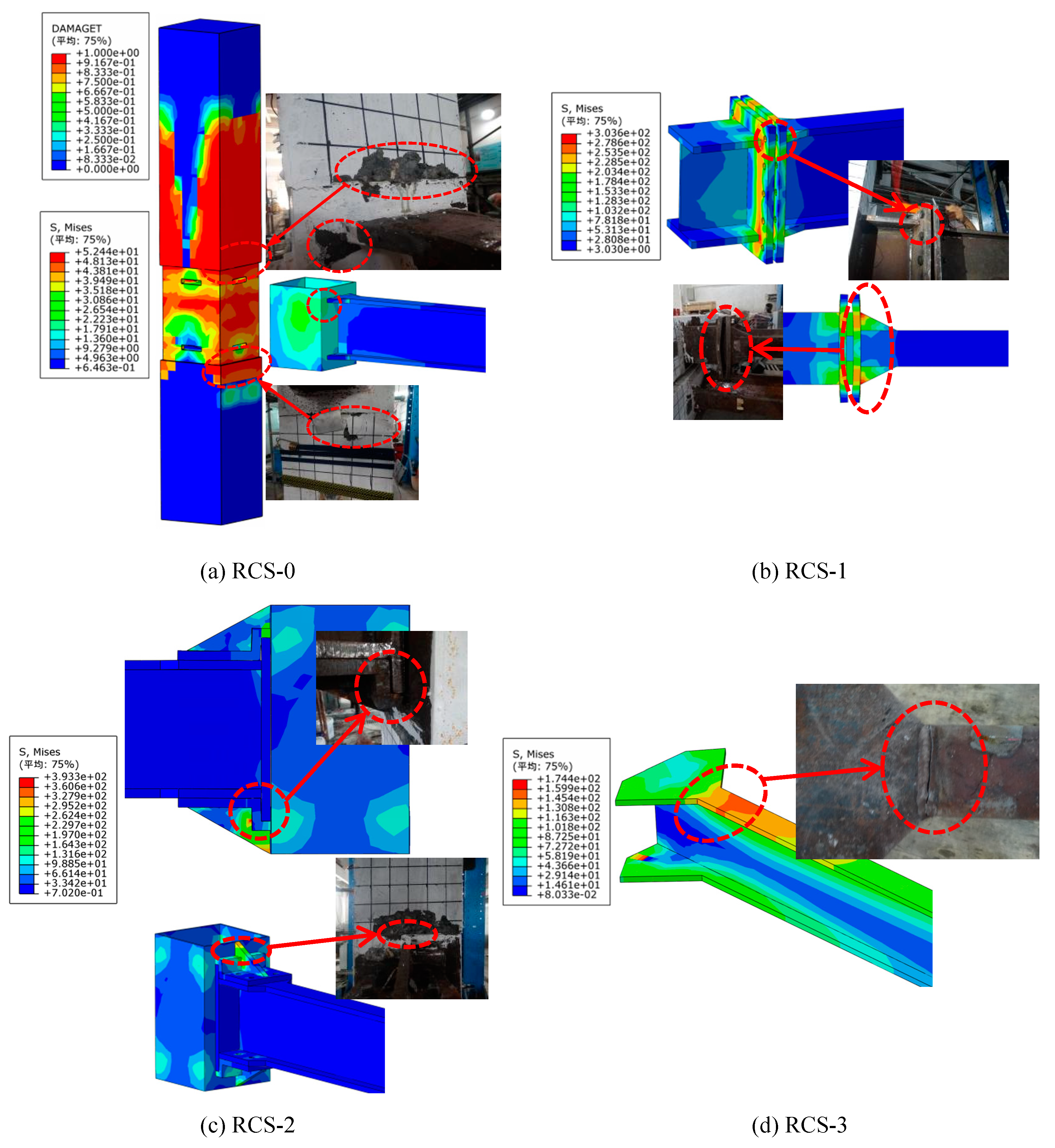
3.2.1. Failure pattern

During the loading process of the experiment, the four joints exhibited various failure modes. The specimen RCS-0 underwent failure during the second cycle, as the loading displacement at the column top reached 30mm. The concrete at the upper and lower joints of the steel plate hoops and the column was crushed, and cracks emerged in the welding seam between the steel beam and the steel plate hoop, signifying a substantial reduction in the lateral bearing capacity of the joint that is deemed as failure. When the loading displacement at the top of the column reached 50mm on the second cycle, the external hanging short beam welding seam area of the RCS-1 specimen cracked, and noticeable out-of-plane flexural deformation occurred on the two end boards. As the displacement was further loaded to 80mm, the welding seam cracks continued to widen, and the horizontal bearing capacity of the joint was less than 85% of the peak load, indicating that the specimen had failed and reached destruction. The steel beam and column of the RCS-2 specimen were fixed using a slot. During testing, audible friction was detected between the end board and slot. The slot connection was responsible for transmitting both bending moment and shear force. Beyond a loading displacement of 40mm, cracks emerged in the welding seam joining the slot and cover board. Continuing to load up to 50 mm in the second cycle resulted in crushing and serious spalling of the upper concrete of the steel plate hoop. Additionally, the welding seam between the slot and the cover board was fractured, which points towards joint failure and destruction. The beam-column connection of the RCS-3 specimen was established by means of an outer ring beam and lateral bolts, accompanied by a wedge plate at the end board to bear a portion of the shear force. When the interlayer displacement reached 50 mm during loading, the joint achieved its highest bearing capacity. As loading continued and reached 60 mm during the second cycle, a fracture became apparent in the welding seam of the left beam flange mutation, leading to the cessation of the loading process and indicating that the specimen had failed.
As demonstrated in Figure 5, a comparison of the failure modes of the experimental specimens and the instantaneous stress distribution of the FEM model suggests that numerical simulation can accurately predict and replicate the ultimate failure states observed in the experiment. These include concrete crushing and spalling, weld fracture, and steel bending deformation. Although there are slight disparities between the numerical and experimental outcomes, the numerical model still satisfies the precision criteria and adequately depicts the stress transfer and mechanical behavior of the joints during the loading process.

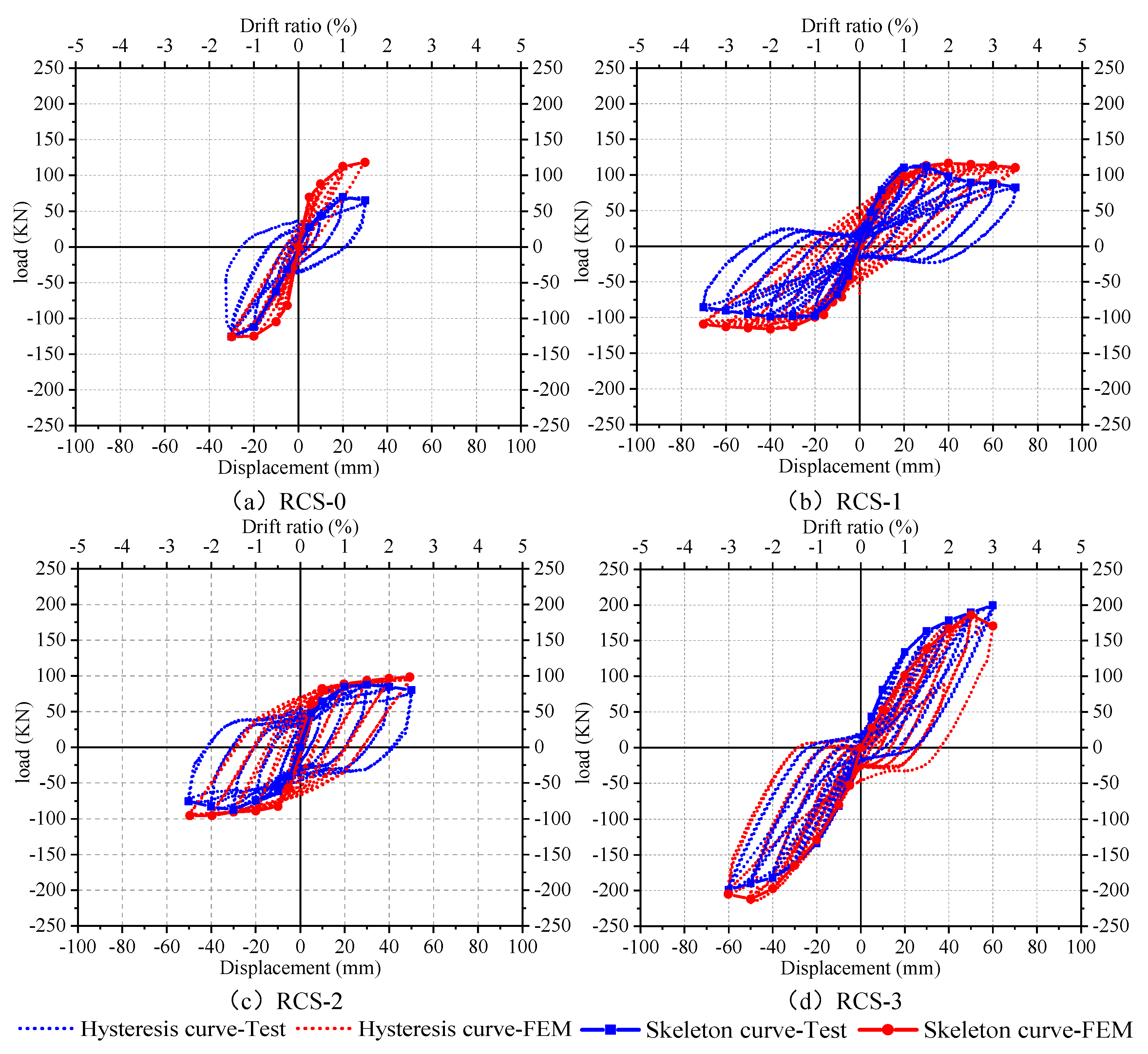
3.2.2. The hysteresis curves and skeleton curves

The hysteresis curve and skeleton curve, as obtained via finite element analysis, are presented in Figure 6. The numerical simulation can reasonably predict the overall trend of the hysteresis curves of the four joints in comparison to the experimental findings. However, RCS-1 did not exhibit significant necking effects in the final numerical results. The hysteresis loop envelopes for RCS-2 and RCS-3 are in good agreement, whereas the hysteresis loop envelopes obtained through numerical simulation for RCS-0 and RCS-1 are marginally smaller when compared to experimental results.
For the non-demountable RCS-0 specimen in the reference group, the negative loading skeleton curve corresponds to the experimental results, whereas the positive loading skeleton curve exceeds the experimental results. This phenomenon could be explained by the initial damage incurred in the positive direction during the experiment. The concrete was tensioned before being pushed, first in the negative direction and then in the positive direction, resulting in a substantially lower positive bearing capacity compared to the negative bearing capacity and numerical findings. On the contrary, regarding the separable RCS-1, RCS-2, and RCS-3 specimens, during the initial loading, as well as the elastic and plastic phases, the numerically estimated skeleton curves in the positive and negative directions correspond closely with the experimental outcomes. However, in the numerical simulation, welding is designated as a "tie" connection, and the concrete cannot reach the damaged state of crushing and spalling, hence the skeleton curve in the numerical simulation does not exhibit a noticeable descending section.

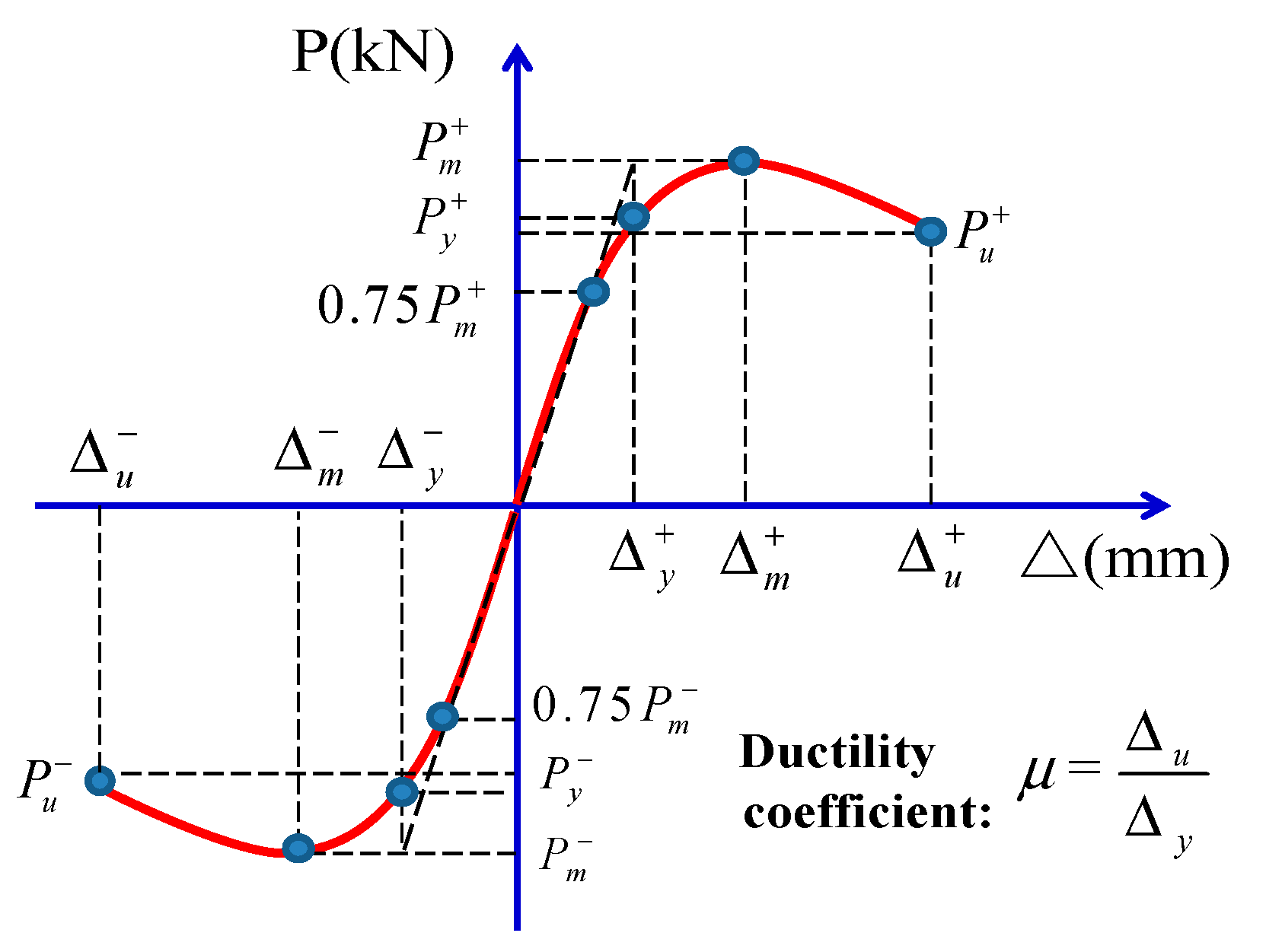
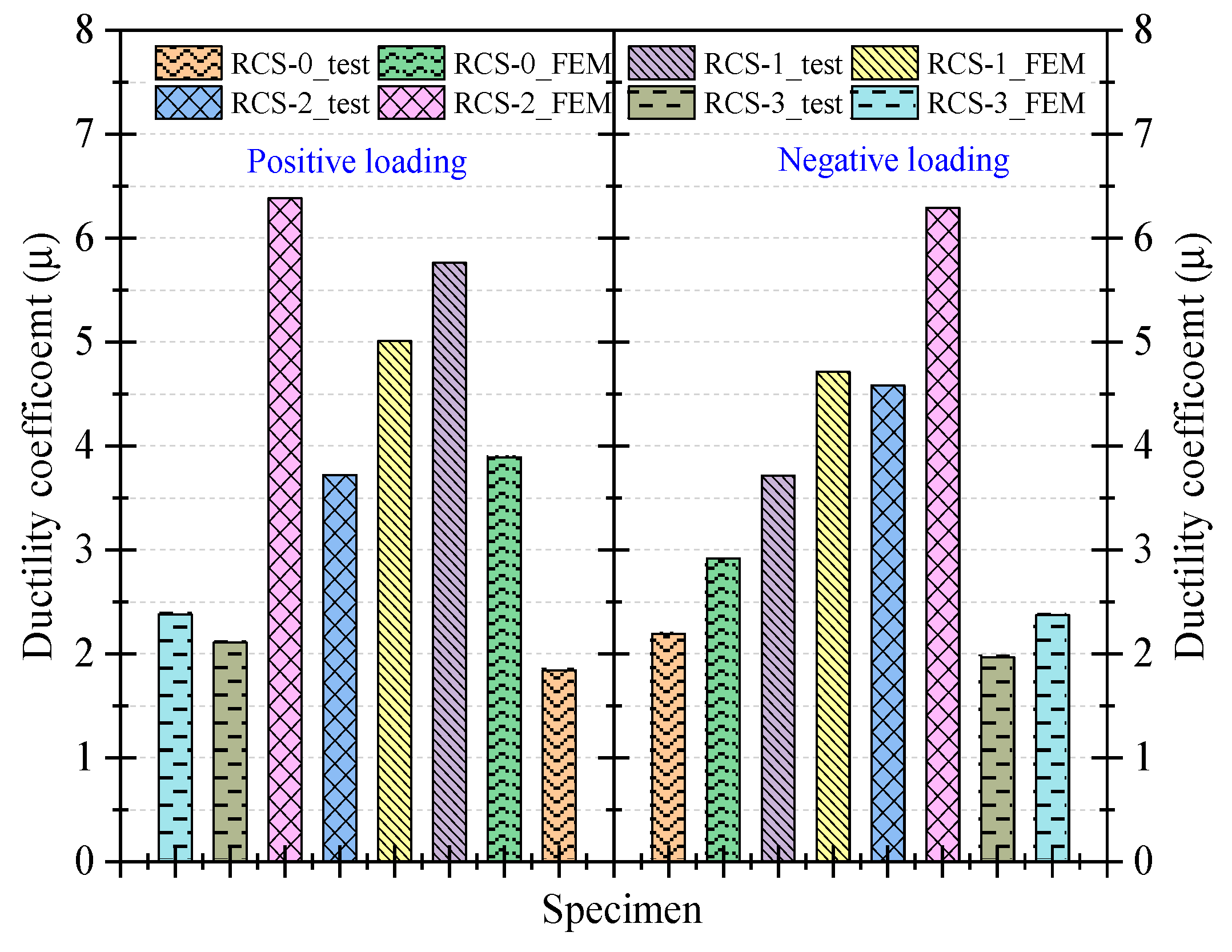
3.2.3. Ductility

As illustrated in Figure 7, the yield point and yield displacement can be determined from the ultimate bearing capacity of the skeleton curve. Table 3 presents the yield load, yield displacement, ultimate load, ultimate displacement, and ductility coefficient for specimens with four joints. From this data, Figure 8 is plotted. The ductility coefficient is defined as the ratio of the beam end displacement at joint failure to the beam end displacement. This can be computed using the below formula:
μ = δ u δ y
From Table 3 and Figure 8, it is evident that the ductility of the RCS-0 and RCS-3 specimens is poor, as indicated by the finite element results which reveal positive and negative direction ductility coefficients of 2.92 and 3.89, and 2.37 and 2.38, respectively. In contrast, the RCS-1 and RCS-2 specimens exhibited better ductility or deformation capacity, with positive and negative direction ductility coefficients of 4.71 and 5.01, and 6.29 and 6.38, respectively. The ductility coefficients obtained from the finite element analysis exceed the experimental values. The experiment applied negative loading, leading to a build-up of concrete damage in the positive direction. As a result, the positive direction demonstrates a higher level of yield point displacement and lower ductility coefficients than the negative direction.

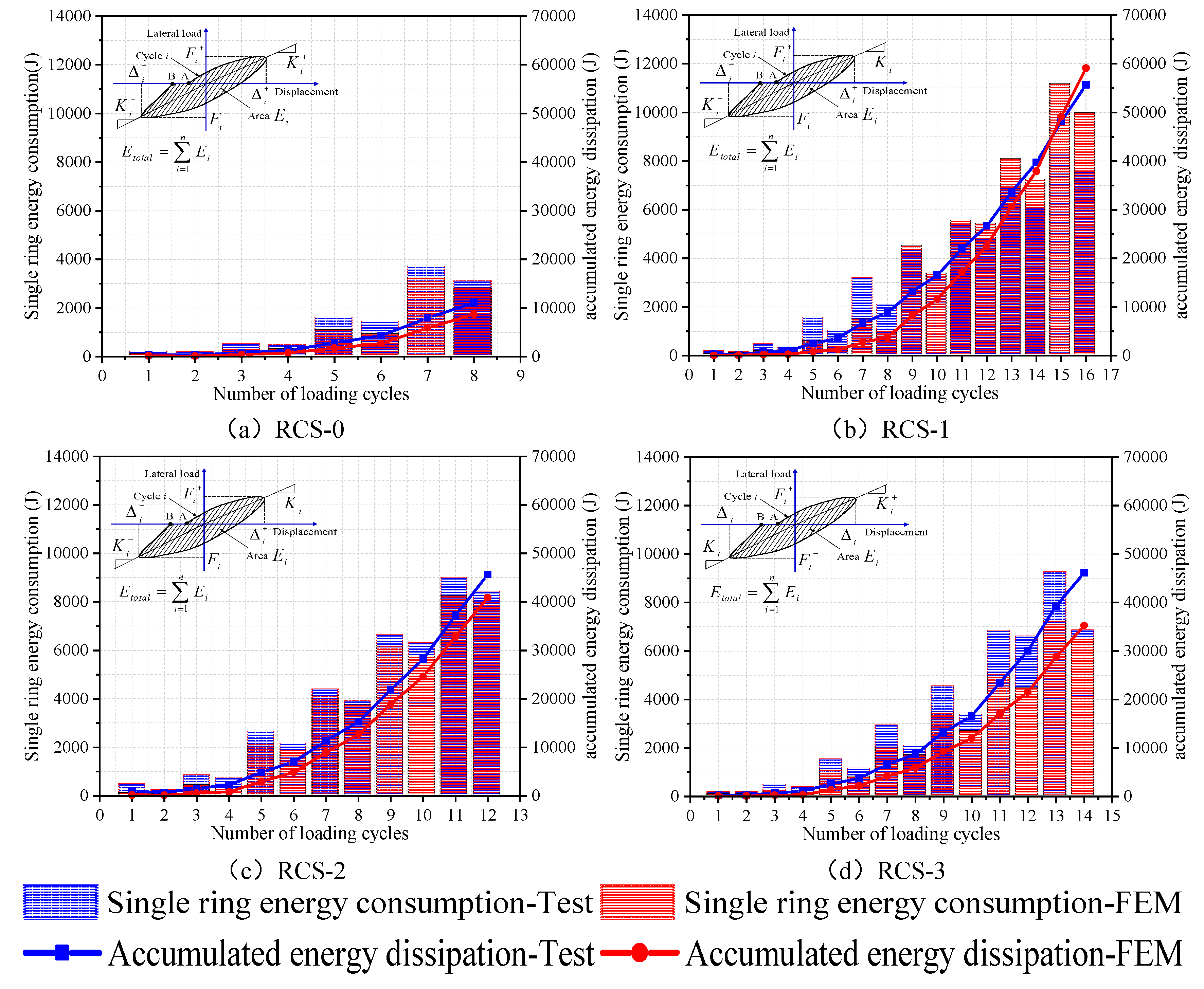
3.2.4. Energy dissipation

As illustrated in Figure 9, the single-cycle and cumulative energy absorption of each joint are displayed. Upon comparison, it is apparent that the non-demountable RCS-0 specimen exhibits lower single-cycle and cumulative energy absorption at each level of displacement compared to the other three demountable joints. Among them, the cumulative energy absorption of the RCS-1 specimen is the highest, with a 21.97% and 20.57% increase compared to the RCS-2 and RCS-3 specimens in the experimental results. Meanwhile, based on finite element analysis results, the cumulative energy absorption of the RCS-1 specimen is 44.58% and 67.52% greater than that of the RCS-2 and RCS-3 specimens, respectively. Compared to the experimental and finite element analysis outcomes, it is evident that they are in excellent accordance, confirming the precision of the finite element model.

4. FEM parameter analysis

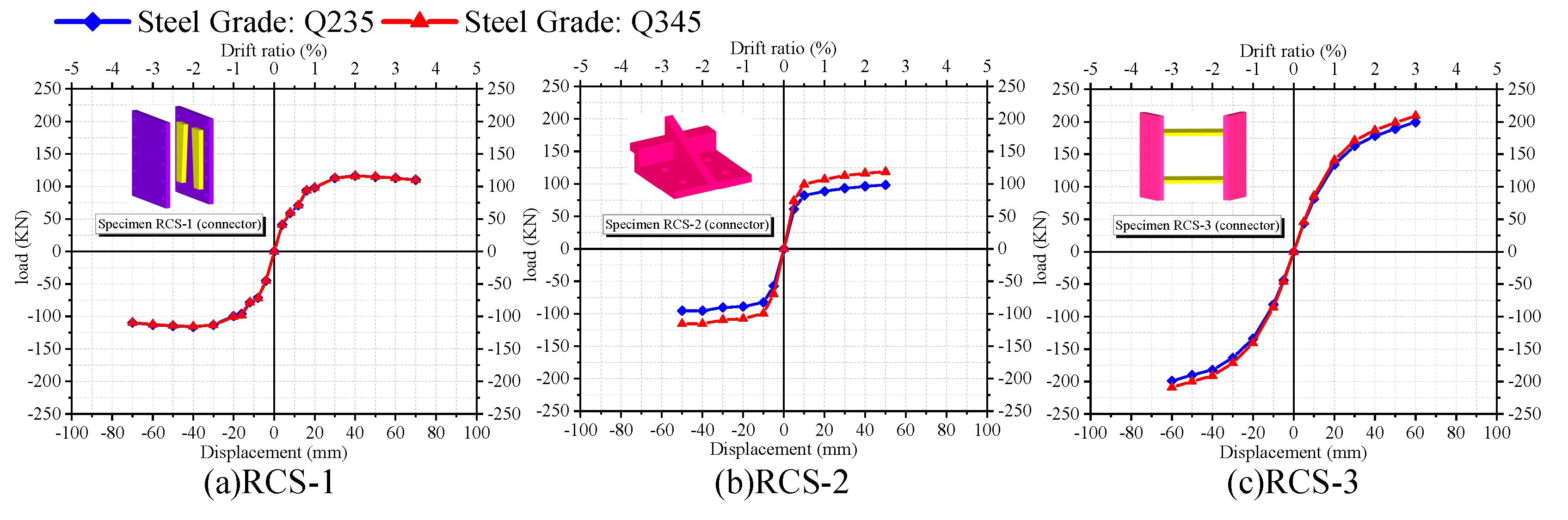
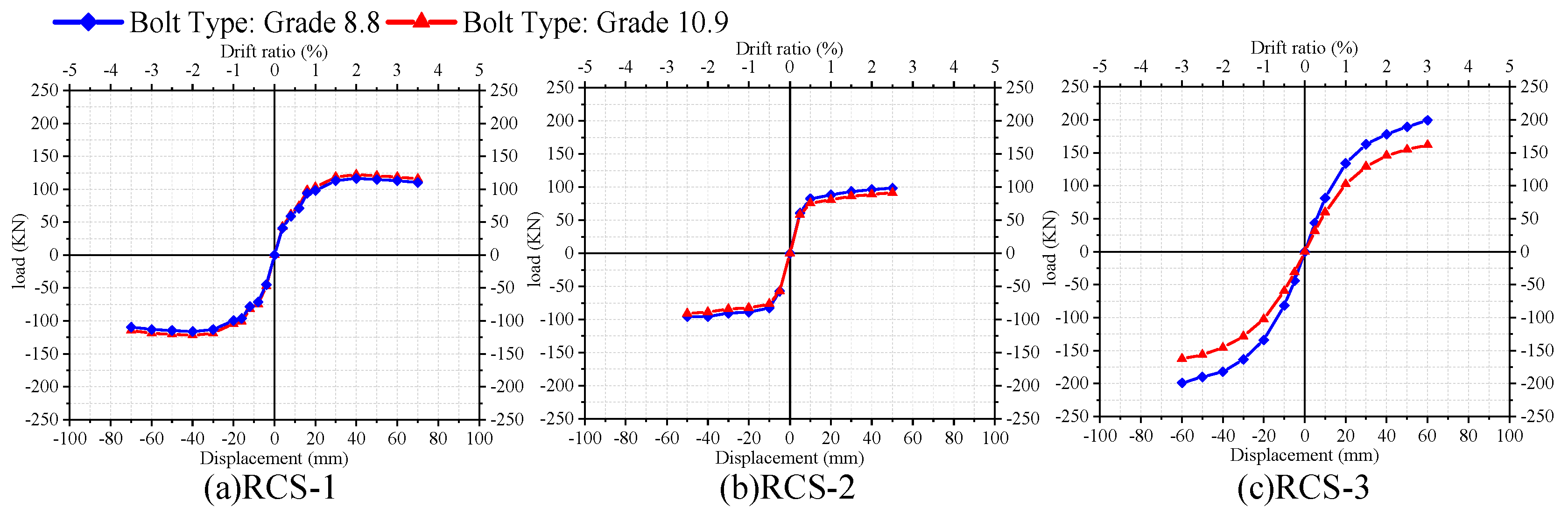
4.1. Steel strength of some connector

Given the structural variances in the beam-column connections between the three separate RCS joints, this section selects specific connecting components for each joint. One of the analysis parameters is the modification of their steel strength. Figure 10 exhibits the detailed connection components. The validated finite element model permits a comparison of the skeleton curve of the beam-column joint under reciprocating load. Keeping the dimensions of the specimens and all other conditions unchanged, only the steel grades of the key connecting components in the three demountable joints have been altered from the original Q235 steel to Q345 steel. The finite element analysis obtains the column load-displacement skeleton curves of the three demountable joints under different strength steel connection conditions, as demonstrated in Figure 10.
For the demountable RCS-1 and RCS-3 specimens, the strength of the steel connecting elements has no notable impact on the skeleton curve. However, the skeleton curve of the demountable RCS-2 specimen is considerably affected by it. As the RCS-2 sample depends on its connecting components to transfer both bending moments and shear forces between the beam and column, the vertical high-strength bolts that secure the connecting components to the beam also play a role in bend moment transfer. Thus, strengthening the steel of the connecting components can result in a corresponding increase in bending capacity. Therefore, switching the connecting components from Q235 steel to Q345 steel has no significant impact on the initial stiffness of the joint. However, the ultimate load-bearing capacity rises by 21.00%. Hence, the findings indicate that enhancing the steel strength of the connecting components in the demountable RCS-2 specimen can substantially upgrade the joint's bearing capacity.

4.2. Bolt strength

To examine the effect of bolt strength on the seismic behavior of RCS joints, the numerical models of three demountable beam-column joints have high-strength bolts upgraded from grade 8.8 to 10.9. Additionally, the bolts' pre-tightening force in the finite element model has been raised from 120kN to 150kN. The skeleton curves for each RCS joint with different bolt types are illustrated in Figure 11. It is evident from the diagram that the bolt type does not have a noteworthy impact on the load-carrying capacity of RCS-1 and RCS-2 specimens. In contrast, the removable RCS-3 joint specimen features a concrete column with a crossbeam that is connected to a steel beam using diagonal bolts. The diagonal bolts are responsible for the primary shear force and bending moment support. As such, bolstering the strength of the bolts could improve the joint's ability to withstand horizontal loads.

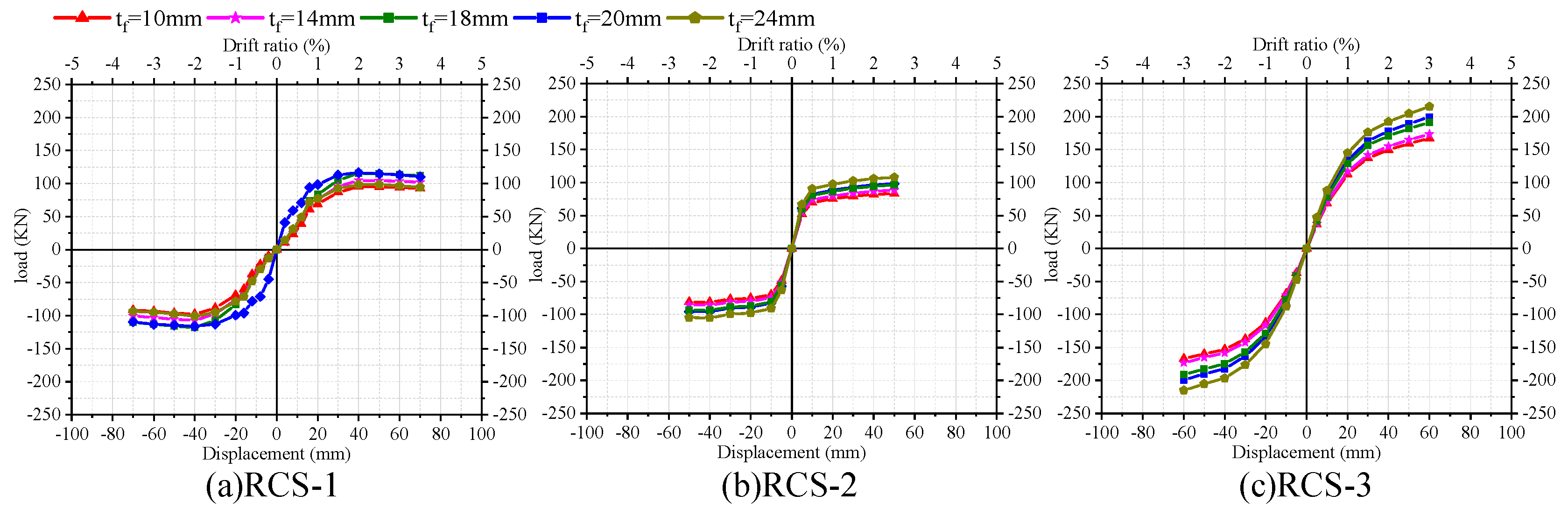
4.3. Steel beam flange thickness

Figure 12 demonstrates the vital impact of flange thickness on the mechanical behavior of the joint. For studying the effect of the flange thickness of pure steel beam segments on the seismic conduct of demountable RCS joints, five finite element models with varying flange thicknesses ( t f = 10 mm , 14 mm , 18 mm , 20 mm , 24 mm ) were developed. From the skeleton curves acquired through finite element analysis, it is evident that the RCS-2 and RCS-3 specimens' maximum bearing capacity improves as the flange thickness increases. The bearing capacity increases by 10.02% and 8.24%, respectively when the flange thickness increases from 10mm to 24mm. Concerning the RCS-1 specimen's skeleton curve, the joint's bearing capacity exhibits a continually increasing trend with an increase in the flange thickness. However, when the flange thickness continues to increase to 24mm, the joint's maximum bearing capacity diminishes. The results indicate that the design of the RCS-1 specimen's steel beam section is the most suitable, enabling the maximum bearing capacity of the joint.

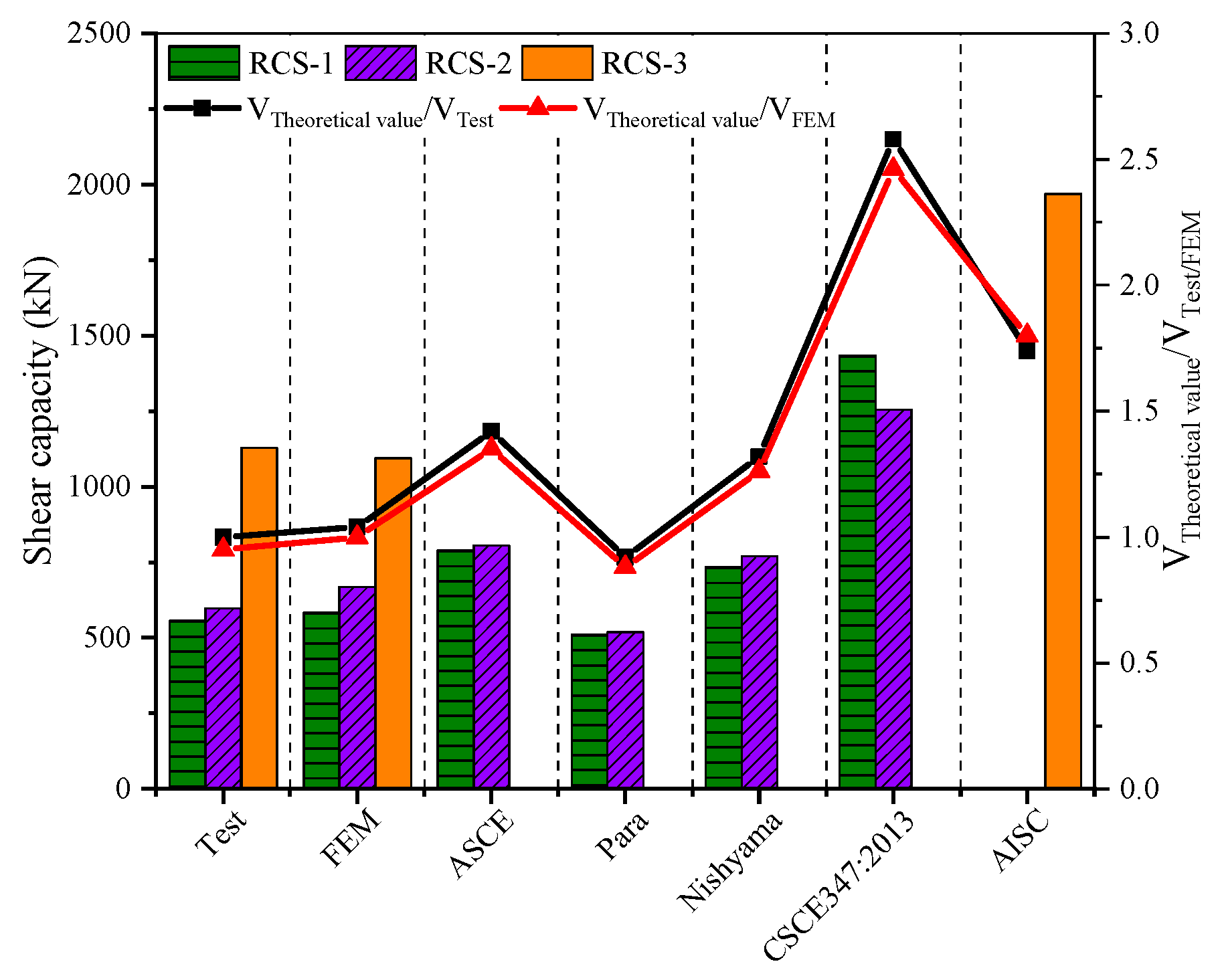
5. Shear capacity analysis

This article presents three novel varieties of demountable RCS joints, each designed as a "column through" joint. A steel plate hoop limits the central region of the joint, while transverse reinforcement ribs mounted inside transmit stress. The transverse reinforcement ribs significantly enhance the joint's stiffness. From the failure mode of the specimens, it is apparent that other components fail before the core area of the joint, demonstrating compliance with the design principle of "strong column, weak beam, and strong joint, weak member".
To investigate a more practical calculation approach for determining the shear bearing capacity of steel beam-reinforced concrete (RCS) composite joints, Tao et al. [29] compiled shear failure test data of RCS joints from recent years and compared the results with those gained from the Chinese code technique, Nishiyama method, Para method, and ASCE guideline method. The study examined the impact of various parameters on the shear-bearing capacity of the joints. The research findings demonstrate the practical engineering value of all four methods. Teaching assistants are reminded to explain abbreviations when first used to ensure comprehensibility. The Para method exhibits the least dispersion, while the ASCE method is overly conservative with perpendicular beam specimens and displays the greatest dispersion. The Chinese code and Nishiyama method yield similar results, both indicate a hazardous state for joints where the concrete strength exceeds 60 MPa. The Chinese code offers the most straightforward calculation method. Following the four distinct shear-bearing capacity calculation methods presented in the reference article, the shear-bearing capacity of each new demountable RCS joint's core area is computed separately.
According to ASCE guidelines [30] and literature [31], it is possible to calculate the ultimate shear strength of the core area of an RCS beam-column joint using the subsequent formula:
V j ≤ 0.85 ( 0.85 ∙ γ k 0 f c ' b 0 h + 0.75 ∙ 1 6 t c p b c p f y c p )
Where, V j is the shear strength of the beam-column panel region; γ is the strength factor, with internal seams taken as 1.0 and external seams taken as 0.6; k 0 is the restraint strength factor of external concrete columns: for joints with tension fasteners and steel straps, it is 2.5, and for other joints, it is 2.0; f c ' is the standard compressive strength of concrete (MPa); b 0 is the effective joint width; f is the thickness of the cover plate at the beam-column core region; t c p is the width of the cover plate along the shear direction; and f y c p is the standard yield strength of the cover plate.
To compensate for the shortcomings of the ASCE guideline calculation method, Para et al [32] proposed a method that can be used for the design of "through beam" joints with concrete strengths ranging from 21 MPa to 70 MPa in high seismic intensity areas. This method divides the shear capacity of the joint into three parts: steel beam webs, and internal and external concrete regions.
V j = 0.9 f w y 3 t w h c + 0.3 f c i ′ b i h c + 0.3 f c o ′ b o h c
f c i ' = V i b a s e ( − 0.0048 f c ' + 1.13 ) k 1 k 2
f c o ' = V o b a s e ( − 0.0048 f c ' + 1.13 ) k 1 k 2 k 3
Based on the experimental study, the concrete compressive strength is 48.2 MPa, and the concrete in the core area of the joint is not distinguished between the inner and outer areas. Considering the contribution of the added transverse reinforcement ribs to the shear capacity of the slab area, a modification of the Para method is made and the formula is as follows:
V j = 1 6 t c p b c p f y c p + 0.3 f c ' b c h c
f c ' = V b a s e ( − 0.0048 f c ' + 1.13 ) k 1 k 2 k 3
Where, b c is the width of the column section; h c is the height of the column section; V b a s e is the basic strength factor, which for RCS joints ARE approximately twice that of edge joints; and k 1 k 2 k 3 is the concrete restraint factor, which aims to consider the strength enhancement of construction elements such as stirrups, steel hoops, and column surface plates, and requires selecting corresponding values according to different constructions when calculating. For specific details, please refer to Table 1 in Literature [32].
Nishiyama et al [33] provided a design method for the seismic performance of RCS joints in their guidelines for the seismic design of concrete structures. This method applies to concrete strengths ranging from 21 to 60 MPa. Unlike the previous two methods, the concrete is no longer divided into inner and outer elements. Instead, the shear strengths of the concrete, beam webs, stirrups, and steel plates on the column surface are directly superimposed. Considering that all the specimens are 'column-through' joints, with no steel webs passing through the core area of the slab, the shear capacity of the joint can be calculated using the following formula:
V j = V f + V h + V c
V f = 0.5 A s 1 f s 2 / 3
V r = 1 6 t c p b c p f y c p
V c = 0.04 C 2 C 3 b c h c f c ' δ
where, V f , V h , V c represent the shear load-bearing capacity contributions of the column surface plate, transverse stiffeners, and concrete, respectively; A s 2 is the area of the steel hoops in the shear direction; f s 2 is the design value of the tensile strength of the steel hoops; δ is the influence coefficient of the joint location: for interior joints, exterior joints, and corner joints, the values are 3, 2, and 1, respectively; C 2 , C 3 are coefficients related to joint construction, which specifically consider the enhancement effects of extending surface plates, steel hoops, perpendicular beams, etc. on concrete strength. The specific values are shown in Table 2 of Reference [33].
China Code CECS347:2013 "Technical Specification for Confining Concrete Column-Composite Beam Frame Structure" [34] proposes two types of joints, beam through and column through, and provides corresponding formulas to calculate the bearing capacity. Like the calculation approach of the Nishiyama method, the shear strength of each component is directly superimposed to obtain the joint capacity. The nodal strength of the column consists of the concrete, the hoops, and the steel plate of the column surface. However, in the experimental specimens, there are no hoops in the slab area and horizontal reinforcing ribs are used instead. Therefore, the joint shear strength consists of concrete, column surface steel plate, and horizontal reinforcing ribs:
V i = 0.15 α b c h c f c + 0.4 ∑ A s 2 f s 2 + 1 6 t c p b c p f y c p
where,   α is the joint position influence coefficient, it has a value of 1 for interior joints, 0.7 for e exterior joints, and 0.4 for top corner joints. The remaining parameters are referenced to the above comments.
Unlike the RCS-1 and RCS-2 specimens, the RCS-3 specimens have wedge and corner plates welded to the outer ring of the steel plate hoops. These two detailed components contribute to the shear capacity of the joint. Referring to ANSI/AISC 358-16 [35], the formula for calculating the shear strength is as follows:
V j ≤ 0.6 f y c p A p z
A p z = 2 d c t c o l + 4 d l e g C C t l e g C C
where, d c is the depth of the concrete column section; t c o l is the thickness of the steel hoop; d l e g C C is the effective depth of the leg components, with a value of d l e g C C = 89 m m ; t l e g C C is the effective thickness of the leg components of the axial ring angle component, with a value of t l e g C C = 13 m m .
The following Figure 13 and Table 4 shows the theoretical shear strength calculation values obtained by four different shear strength methods for three demountable RCS joint specimens. The results show that, compared with the experimental results, except for the Para method which calculates a shear strength lower than the experimental result, the remaining formulae calculate shear strengths higher than the experimental results. This is because the RCS-1 and RCS-2 specimens did not reach yield throughout the loading process of the experiment, resulting in a relatively small contribution to the shear strength. The theoretical calculation formula uses the yield strength of the steel; therefore, the theoretical calculation value is greater than the experimental result. From the data in the table, the finite element analysis of RCS-1 and RCS-2 joint core regions has greater shear strength than the experimental results, while the finite element calculation result of RCS-3 is smaller than the experimental value. Therefore, the ratio of the theoretical calculation result to the finite element result is smaller than the ratio of the theoretical calculation result to the experimental result. Because the Para method does not consider the shear strength of the columnar steel plate, the calculated shear strengths of the RCS-1 and RCS-2 specimens are 8% and 13% less than the experimental results and 12% and 22% less than the FEM predicted values, respectively. The ASCE guide method calculates results that are 42% and 30% higher than the experimental values, which are 35% and 21% higher than the FEM predicted values. The method gives results that are 32% and 29% higher than the experimental values, which are 26% and 15% higher than the FEM predicted values. The calculated value using the national standard CSCE 347:2013 is 158% and 110% higher than the experimental values, which are 146% and 88% higher than the FEM predicted values. This is because the formula recommended in the CSCE standard for calculating the shear strength of the core region of the columnar through type joint also considers the influence of the end plate bolt connection, resulting in a greatly overestimated shear capacity of the joint. For the RCS-3 specimens, the calculated result using the AISC standard is 74% higher than the experimental value and 80% higher than the FEM predicted value. This is because the formula considers the influence of the welding of four corner plates on the side of the steel plate hoop, which improves the calculated value of the shear capacity of the joint core region.

6. Conclusions

This paper proposes three new demountable RCS joints with different connection structures and conducts cyclic loading tests to investigate the seismic performance of demountable RCS joints. In addition, three finite element models of the specimens are established and the accuracy of the finite element models is verified by the experimental results. Then, the influence of different design parameters (strength of the demountable steel connection, type of high-strength bolts, and thickness of the steel flange) on the seismic performance of the joints is analyzed. Based on the experimental and finite element results, the following conclusions are drawn:
(1)
From the experimental results, the bearing capacity and seismic performance of the three new demountable RCS joints are superior to the control group of non-demountable RCS joints. The RCS-1 and RCS-2 specimens have better deformation capabilities than the RCS-0 specimen, with ductility coefficients increased by 69% and 109%, respectively, while the difference in deformation capability between the RCS-3 specimen and the RCS-0 specimen is not significant, with positive and negative loading direction ductility coefficients differing by 14.68% and 10.04%, respectively. The same trend is observed in the energy dissipation capacity of the joints, as the deformability of the joints determines the cumulative energy dissipation of the joints.
(2)
The established finite element model can simulate the performance of non-demountable RCS joints (RCS-0) and demountable RCS joints (RCS-1, RCS-2, and RCS-3) under low cycle reciprocal loading. The finite element model can effectively reproduce the experimental results and meet the accuracy requirements in terms of joint failure mode, hysteresis behavior, ductility, and energy dissipation.
(3)
The finite element model validated by experimental results was further analyzed by parameter studies. The results showed that the hysteretic response of demountable joints RCS-1 and RCS-2 is not sensitive to the strength of the detailed connections, while the bolt strength has no significant influence on the hysteretic response of demountable joints RCS-1 and RCS-3.
(4)
The flange thickness of the steel beam has a significant effect on the bearing capacity of the demountable joints. As the flange thickness increases from 10 mm to 24 mm, the ultimate bearing capacity of each joint increases by 9.44%, 10.02%, and 8.24%, respectively. Compared with the skeleton curve, the cross-sectional design of the experimental steel beam is appropriate and can fully exert its flexural bearing capacity.
(5)
This study refers to four different calculation methods recommended in the literature to check whether the shear capacity of the nodal core area meets the requirements. By comparing the theoretical calculation results with the experimental and FEM predicted values, it is found that the calculation results for RCS-1 and RCS-2 specimens are higher than the experimental and predicted values because the cylindrical steel plates in these specimens have not yielded. On the other hand, the Para method does not consider the contribution of the cylindrical steel plate to the shear strength of the joint core area, so the calculated result obtained from the formula is underestimated. For the RCS-3 specimen, a four-sided plate is added to the outer ring of the steel plate hoop according to the calculation requirements of ANSI/AISC 358-16, and the calculated shear capacity of the joint core area is overestimated.

Author Contributions

Conceptualization,Li.W.; methodology, Cai.J.G.; software, Deng.Z. and Li.W.; investigation, Li, W.; resources,Li.W.; data curation, Deng.Z.; writing—review and editing, Cai, J.G.; visualization, Li, W.; project administration, Li.W.; All authors have read and agreed to the published version of the manuscript.

Funding

National Natural Science Foundation of China (NSFC) [Grant No. 51308419].

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Figueira D, Ashour A, Yıldırım G, et al. Demountable connections of reinforced concrete structures: Review and future developments[C]//Structures. Elsevier, 2021, 34: 3028-3039.
  2. Yang Y, Chen B, Su Y, et al. Concrete mix design for completely recycled fine aggregate by modified packing density method[J]. Materials, 2020, 13(16): 3535.
  3. Yang Y, Chen B, Zeng W, et al. Utilization of completely recycled fine aggregate for preparation of lightweight concrete partition panels[J]. International Journal of Concrete Structures and Materials, 2021, 15: 1-11.
  4. Uy B, Patel V, Li D, et al. Behaviour and design of connections for demountable steel and composite structures[C]//Structures. Elsevier, 2017, 9: 1-12.
  5. Han D, Kalantari M, Rajabifard A. Building information modeling (BIM) for construction and demolition waste management in Australia: A research agenda[J]. Sustainability, 2021, 13(23): 12983.
  6. van den Berg M, C. Managing circular building projects[J]. 2019.
  7. Tingley D D, Davison B. Design for deconstruction and material reuse[J]. Proceedings of the institution of civil engineers-energy, 2011, 164(4): 195-204.
  8. Rakhshan K, Morel J C, Alaka H, et al. Components reuse in the building sector–A systematic review[J]. Waste Management & Research, 2020, 38(4): 347-370.
  9. Wang J, Uy B, Thai H T, et al. Behaviour and design of demountable beam-to-column composite bolted joints with extended end-plates[J]. Journal of Constructional Steel Research, 2018, 144: 221-235.
  10. Ataei A, Bradford M A, Valipour H R. Experimental study of flush end plate beam-to-CFST column composite joints with deconstructable bolted shear connectors[J]. Engineering structures, 2015, 99: 616-630.
  11. Ataei A, Bradford M A, Valipour H R, et al. Experimental study of sustainable high strength steel flush end plate beam-to-column composite joints with deconstructable bolted shear connectors[J]. Engineering Structures, 2016, 123: 124-140.
  12. Peng L, F. Study on Hysteretic Behavior of a New Prefabricated Concrete Filled Square Steel Column-Steel Beam Joint，PhD dissertation, 2020.
  13. Xiao J, Ding T, Zhang Q. Structural behavior of a new moment-resisting DfD concrete connection[J]. Engineering Structures, 2017, 132: 1-13.
  14. Ding T, Xiao J, Chen E, et al. Experimental study of the seismic performance of concrete beam-column frame joints with DfD connections[J]. Journal of Structural Engineering, 2020, 146(4): 04020036.
  15. Huang W, Hu G, Miao X, et al. Seismic performance analysis of a novel demountable precast concrete beam-column connection with multi-slit devices[J]. Journal of Building Engineering, 2021, 44: 102663.
  16. Wang W, Zhang X D, Chen J, et al. Repetitive behavior of an advanced demountable bolted shear connection in push-off tests[J]. Construction and Building Materials, 2023, 362: 129656.
  17. Malla P, Xiong F, Cai G, et al. Numerical study on the behaviour of vertical bolted joints for precast concrete wall-based low-rise buildings[J]. Journal of Building Engineering, 2021, 33: 101529.
  18. He J, Suwaed A S H, Vasdravellis G, et al. Behaviour and design of the ‘lockbolt’demountable shear connector for sustainable steel-concrete structures[C]//Structures. Elsevier, 2022, 44: 988-1010.
  19. Loqman N, Safiee N A, Bakar N A, et al. Structural behavior of steel-concrete composite beam using bolted shear connectors: A review[C]//MATEC Web of Conferences. EDP Sciences, 2018, 203: 06010.
  20. Cheng C T, Chen C C. Seismic behavior of steel beam and reinforced concrete column connections[J]. Journal of constructional steel research, 2005, 61(5): 587-606.
  21. Dung Le D, Nguyen X H, Nguyen Q H. Cyclic testing of a composite joint between a reinforced concrete column and a steel beam[J]. Applied Sciences, 2020, 10(7): 2385.
  22. Zhang J, Hu X, Gong S, et al. Experimental investigation of steel-concrete composite beam to reinforced-concrete column joints with single plate shear connection[J]. Engineering Structures, 2021, 245: 112906.
  23. Fargier-Gabaldón L B, Parra-Montesinos G J, Wight J K. Seismic Behavior of Exterior Reinforced Concrete Wide-Column-to-Steel Beam Joints[J]. ACI Structural Journal, 2020, 117(2): 117-128.
  24. Men J, Xiong L, Wang J, et al. Effect of different RC slab widths on the behavior of reinforced concrete column and steel beam-slab subassemblies[J]. Engineering Structures, 2021, 229: 111639.
  25. Huang S-M, Wang Y-Y, Ding J-M, et al. National standard of the People's Republic of China.GB 50011-2010 Code for seismic design of buildings [S]. Beijing: China Construction Industry Press, 2010.
  26. Gao Yifei, Liang Xinbang, Dong Li, et al. National standard of the People's Republic of China.GB/T 228.1-2010 Tensile testing of metallic materials Part I: Room temperature test methods [S]. Beijing: China Construction Industry Press, 2010.
  27. Cheng Shaoge, Shi Tihua, Bai Xueshuang et al. National standard of the People's Republic of China. jgj/t 101-2015 specification for seismic testing of buildings [S]. Beijing: China Construction Industry Press, 2015.
  28. Zhao Kida, Xu Youyi, Huang Xiaokun et al. National standard of the People's Republic of China.GB 50010-2010 Design code for concrete structures [S]. Beijing: China Construction Industry Press, 2010.
  29. TAO Yuchen, XIAO Zhibin, ZHAO Weijian.Comparative study on calculation methods of shear capacity of RCS hybrid joints[J/OL]. Journal of Harbin Institute of Technology:1-16.
  30. P. Cordova, Validation of the Seismic Performance of Composite RCS Frames: Full-Scale Testing Analysis and Seismic Design, Stanford University, USA, 2005.PhD dissertation.
  31. H.W. Ma, Study on the Joints of Composite Beam and Continuous Compound Spiral Hoop Reinforced Concrete Column, PhD dissertation, Xi’an University of architecture and technology, Xi’an, P.R. China, 2003 [in Chinese].
  32. Parra-Montesinos G, Wight J K. Modeling shear behavior of hybrid RCS beam-column connections[J]. Journal of structural engineering, 2001, 127(1): 3-11.
  33. Nishiyama I, Kuramoto H, Noguchi H. Guidelines: seismic design of composite reinforced concrete and steel buildings[J]. Journal of structural engineering, 2004, 130(2): 336-342.
  34. Jiang Weishan, Yu Qingrong, Pan Shubin, et al. National Standard of the People's Republic of China.CECS 347-2013 Technical Specification for Constrained Concrete Column Combined Beam Frame Structures [S]. Beijing: China Construction Industry Press, 2013.
  35. AISC, Prequalified Connections for Special and Intermediate Steel Moment Frames for Seismic Applications, AISC, Chicago, 2016. ANSI/AISC 358-16.
Preprints 85209 g001aPreprints 85209 g001b
Figure 1. Demountable beam-column joints in the whole and connecting piece structure diagram.
Figure 1. Demountable beam-column joints in the whole and connecting piece structure diagram.
Preprints 85209 g001aPreprints 85209 g001b
Preprints 85209 g002
Figure 2. Laboratory specimen loading device.
Figure 2. Laboratory specimen loading device.
Preprints 85209 g002
Preprints 85209 g003
Figure 3. Loading system.
Figure 3. Loading system.
Preprints 85209 g003
Preprints 85209 g005
Figure 5. Comparison of stress distribution between test and finite element results.
Figure 5. Comparison of stress distribution between test and finite element results.
Preprints 85209 g005
Preprints 85209 g006
Figure 6. Comparison of hysteresis curve and skeleton curve between finite element simulation and test results.
Figure 6. Comparison of hysteresis curve and skeleton curve between finite element simulation and test results.
Preprints 85209 g006
Preprints 85209 g007
Figure 7. Ductility coefficient calculation diagram.
Figure 7. Ductility coefficient calculation diagram.
Preprints 85209 g007
Preprints 85209 g008
Figure 8. Ductility coefficient of each joint specimen.
Figure 8. Ductility coefficient of each joint specimen.
Preprints 85209 g008
Preprints 85209 g009
Figure 9. Single-ring energy dissipation and cumulative energy dissipation of each joint specimen.
Figure 9. Single-ring energy dissipation and cumulative energy dissipation of each joint specimen.
Preprints 85209 g009
Preprints 85209 g010
Figure 10. Effect of steel strength on the bearing capacity of demountable joint specimens.
Figure 10. Effect of steel strength on the bearing capacity of demountable joint specimens.
Preprints 85209 g010
Preprints 85209 g011
Figure 11. Effect of steel strength on the bearing capacity of demountable joint specimens.
Figure 11. Effect of steel strength on the bearing capacity of demountable joint specimens.
Preprints 85209 g011
Preprints 85209 g012
Figure 12. Effect of steel strength on the bearing capacity of demountable joint specimens.
Figure 12. Effect of steel strength on the bearing capacity of demountable joint specimens.
Preprints 85209 g012
Preprints 85209 g013
Figure 13. Comparison of shear strength of demountable RCS joints for different methods.
Figure 13. Comparison of shear strength of demountable RCS joints for different methods.
Preprints 85209 g013
Table 1. Material properties of steel, rebar, and bolt.
Table 1. Material properties of steel, rebar, and bolt.
Grade Sampling position E s /GPa f y / M P a ε y f u / M P a ε u
Q235 Web and cover plate 198 308.3 0.00206 450.5 0.1598
Flange and side plate 205 254.5 0.00217 423.2 0.1612
HRB400 Longitudinal bar 196 479.3 0.00213 631.2 0.1532
HPB300 Stirrup 201 342.7 0.00221 487.6 0.1956
8.8 Bolts 200 780 0.00202 900 0.1360
Table 2. Average compressive strength of concrete cylinder test block.
Table 2. Average compressive strength of concrete cylinder test block.
Specimen ID RCS-0 RCS-1 RCS-2 RCS-3
Average compressive strength（MPa） 38.50 42.52 30.95 39.24
V2b −787.1 −797.0 −620.2 −380.7 1.01 0.30
Table 3. Yield load, ultimate load, and ductility factor.
Table 3. Yield load, ultimate load, and ductility factor.
Specimen ID Load direction Yield load p y / k N Yield displacement △ y / m m Peak load △ u / k N Peak displacement p u / m m Ductility coefficient μ
Test RCS-0 Negative -94.20 -16.28 -125.6 -30.00 1.84
Positive 52.31 13.68 69.75 30.00 2.19
RCS-1 Negative -74.00 -12.15 -98.66 -70.00 5.76
Positive 83.93 11.67 111.9 43.29 3.71
RCS-2 Negative -65.64 -13.44 -87.52 -50.00 3.72
Positive 65.76 10.92 87.68 50.00 4.58
RCS-3 Negative -159.00 -28.37 -212 -60.00 2.11
Positive 139.36 30.46 185.81 60.00 1.97
FEM RCS-0 Negative -94.23 -7.71 -125.64 -30.00 3.89
Positive 88.58 10.29 118.10 30.00 2.92
RCS-1 Negative -87.04 -13.98 -116.06 -70.00 5.01
Positive 87.23 14.86 116.31 70.00 4.71
RCS-2 Negative -71.64 -7.84 -95.52 -50.00 6.38
Positive 73.64 7.95 95.19 50.00 6.29
RCS-3 Negative -149.30 -25.22 -199.06 -60.00 2.38
Positive 149.51 25.31 199.34 60.00 2.37
Table 4. Comparison of shear strength of demountable RCS joints.
Table 4. Comparison of shear strength of demountable RCS joints.
Joint types RCS-1 RCS-2 RCS-3
Test values 555.48 596.21 1128.32
FEM 583.25 667.76 1094.47
ASCE 788.78 804.88 -
V J A S C E / V J t e s t 1.42 1.30
V J A S C E / V J F E M 1.35 1.21
Para 511.04 518.70
V J P a r a / V J t e s t 0.92 0.87
V J P a r a / V J F E M 0.88 0.78
N i s h i y a m a 733.23 769.11
V J N i s h i y a m a / V J t e s t 1.32 1.29
V J N i s h i y a m a / V J F E M 1.26 1.15
CSCE 347:2013 1433.29 1254.84
V J C E C S / V J t e s t 2.58 2.10
V J C E C S / V J F E M 2.46 1.88
AISC - 1967.88
V J A I S C / V J t e s t 1.74
V J A I S C / V J F E M 1.80
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions, or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated