Numerical Aperture Dependent Spatial Scaling of Plasma Channels in HPHT Diamond

The investigation of plasma channels induced by focused ultra-short 1030-nm laser pulses in bulk of synthetic HPHT diamond revealed strong dependence of their size and shape on the used numerical aperture of the lens (NA=0.15-0.45). It was shown that at loose focusing conditions, it is possible to significantly increase the length of the plasma channel with a slight increase in pulse power, while tight focusing allows to obtain more compact structures in the same range of used powers. Such dependence paves the way to new possibilities in 3D processing of transparent dielectrics, allowing, for example, to vary the spatial parameters of modified regions without changing the setup, but only by controlling the lens aperture, which seems very promising for industrial applications.

Keywords:

Subject:

Physical Sciences - Optics and Photonics

1. Introduction

The investigation of ultrafast light-matter interactions, particularly those involving femtosecond laser pulses and dielectric materials, has ushered in a new era of advancements across multiple scientific and technological domains. Ultra-short pulse lasers, characterized by short pulse durations and high peak intensities, offer unprecedented precision and control for laser-induced modifications within materials, revolutionizing fields such as precise microfabrication [1,2], optical communication [3], and biomedical imaging [4]. During femtosecond laser irradiation of dielectric materials, multiphoton or tunnel ionization of the dielectric atoms takes place, leading to the generation of a plasma. In the presence of dense plasma, its properties are primarily governed by interactions between charged particles (electrons and ions), rather than neutral atoms and molecules. This dense plasma absorbs and scatters incident light, influencing the propagation of the laser pulses [5].The propagation of the femtosecond laser pulses in dielectrics is dependent on the nonlinear dynamical balance between self-focusing and defocusing phenomena.

The self-focusing effect is based on the optical Kerr effect, a third-order nonlinear optical phenomenon [6]. As femtosecond laser pulses propagate through a dielectric material, the electric field of these pulses induces a nonlinear polarization response within the material. This response leads to a change in the material's refractive index, which becomes intensity-dependent. Regions of the beam with higher intensity exhibit a greater refractive index, resulting in a focusing effect and eventual collapse of the beam known as catastrophic self-focusing [7].

On the other hand, defocusing is commonly associated with the formation of a plasma caused by the high pulse intensity. At increased laser intensities, ionization occurs in the dielectric material, giving rise to plasma, state consisting of free electrons and ions [8]. This phenomenon can be described by the Drude model [9] or the plasma critical density condition. The generation of a plasma involves a local reduction in the refraction index causing the beam to diverge and counteract the self-focusing effect, resulting in plasma defocusing. Plasma defocusing plays a crucial role in balancing the self-focusing effect, providing beam stability, and facilitating the formation of plasma channels [10]. The process of filamentation directly affects the energy deposition efficiency, which defines the trajectory and extent of laser-induced modifications. This complex nonlinear interaction leads to the formation of spatially confined regions with altered refractive indices known as "channels" caused by the light-matter interactions [11].

Interaction between intense femtosecond lasers and transparent media have been intensively studied, but the main focus was on discovering material damage thresholds and their practical applications [12,13,14]. One notable consequence of nonlinear laser-matter interaction is the formation of plasma channels. This process is influenced by various factors, including laser parameters (beam quality, pulse duration, wavelength, etc.) and medium properties (nonlinear refractive index (n₂), linear refractive index (n₀), and multi-photon absorption coefficient) [10,15,16]. Previous studies have examined the nonlinear optical effect of filamentation by analyzing plasma luminescent channels formed by ultrashort laser pulses in bulk of dielectric materials. Research conducted in [17] reported pulse-width dependent self-focusing critical powers for linearly- and circularly-polarized, focused 515-nm and 1030-nm laser pulses with varying pulse widths in fused silica, fluorite, natural diamond, and synthetic diamond. Furthermore, a study in [18] explored the polarization-dependent filamentation by analyzing the luminescence of plasma channels generated in HPHT diamond under the influence of focused ultrashort laser pulses. However, the role of focusing geometry, specifically the numerical aperture (NA) of the focusing lens, remains relatively unexplored, providing an open field for investigation, particularly considering the variation in plasma density under tight and loose focusing conditions. When the focusing is not excessively tight, the medium tends to remain relatively uniform, resulting in less dense plasma generation [19]. Additionally, in [20], the phenomenon of micro-explosions induced by ultrafast laser pulses in transparent materials was examined, demonstrating that the focusing geometry plays a significant role in determining the expansion and propagation of shockwaves. In [21], it was demonstrated that tightly focused femtosecond laser pulses can induce optical breakdown and structural changes in glass, even at low pulse energies achievable without amplification. Examining the formation of filaments and associated refractive index changes using focusing lenses with different NA, a study conducted in [22] observed that the length of the region exhibiting refractive index changes increased with decreasing NA, while the stability time of the refractive index was also influenced by the NA. Investigating the intricacies of femtosecond pulse propagation in fused silica under loose focused conditions, including the effects of self-focusing and defocusing due to the presence of a free electron plasma, [23] shed light on the role of NA in controlling the interaction of femtosecond laser pulses with transparent materials. Emphasizing the influence of NA on supercontinuum generation and damage thresholds, [24] confirmed bulk damage at all NA studied, with catastrophic damage occurring at high NA. Further exploration of the NA dependence of white-light continuum generation and material damage in different samples was conducted in [25]. As an independent linear optical parameter, NA plays a crucial role in controlling the interaction between femtosecond laser pulses and transparent materials, impacting the generation of supercontinuum and the occurrence of material damage. Through high-resolution three-dimensional simulations and analysis of filamentation under varying focusing conditions, it was revealed in [26] that the filamentation process is influenced by the interplay between geometric focusing and the nonlinear Kerr effect. [27,28] propose a transition from the linear focusing mechanism to the nonlinear focusing mechanism during filamentation in air, illustrating changes in physical equilibrium through the degree of focus. Under high-NA conditions, the Kerr self-focusing effect becomes negligible compared to plasma defocusing and geometric focusing. Despite these findings, the impact of NA on the filamentation threshold power remains largely unexplored, resulting in a knowledge gap regarding the dynamics of femtosecond laser propagation.

This research aims to investigate the relationship between the numerical aperture and filamentation threshold power. The selection of suitable materials plays a crucial role in these interactions. High-pressure, high-temperature (HPHT) diamond, renowned for its exceptional thermal and optical properties, serves as an intriguing platform for studying ultrafast laser-material interactions. The impressive attributes of HPHT diamond, including its high thermal conductivity, wide bandgap, and robust optical nonlinearity [29], position it as an outstanding candidate for advancing our comprehension of ultra-short pulse propagation and filamentation phenomena. Such insights hold the potential to contribute to more effective and precise utilization of femtosecond laser technology.

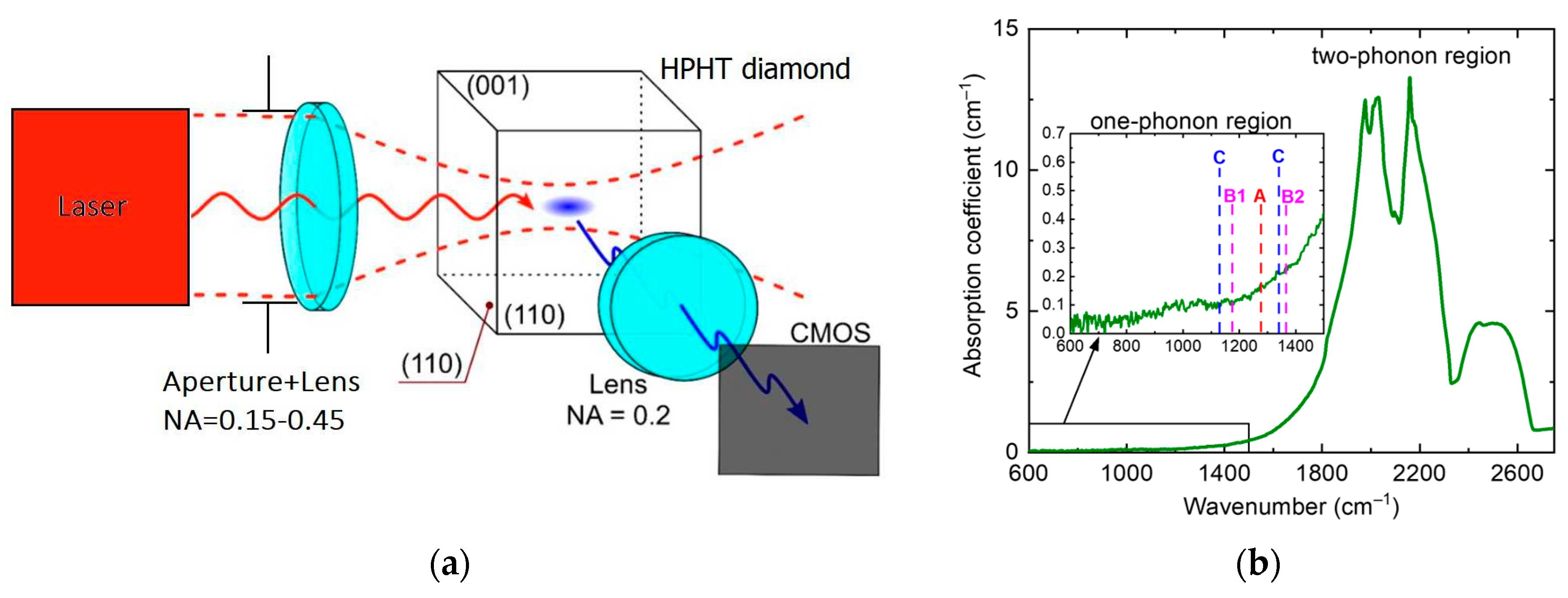
2. Materials and Methods

The femtosecond fiber Yb⁺³ ion laser Satsuma (Amplitude Systemes, France) with wavelength of 1030 nm was used as a source of linearly polarized radiation. The laser pulses were focused in bulk of the HPHT synthetic type IIA diamond with dimensions of 3×3×1,5 mm³ using quartz/fluorite microscope objective with varying numerical apertures NA=0.15–0.45 (focal spot with 1/e² radius w₀ ≈ 2.2–0.73 μm). During the multi-pulse exposure to ultrashort pulses with a duration of ~300 fs with a repetition rate of ν = 100 kHz, the formation of extended luminous channels was observed in the rear focal plane of the microscope objective. Micro-images of these luminous channels were captured at a right angle using a monochromatic CMOS-camera (see Figure 1a).

The irradiation was focused in the bulk of the sample via (110) face at a normal angle and the images of the luminous tracks were captured at a right angle via another (110) face. The optical absorption spectrum of the sample was obtained using an IR spectrometer VERTEX 70v (Bruker, Germany). The obtained spectral characteristic shown in the Figure 1b demonstrates the absence of the nitrogen impurity absorption bands (<1 ppm).

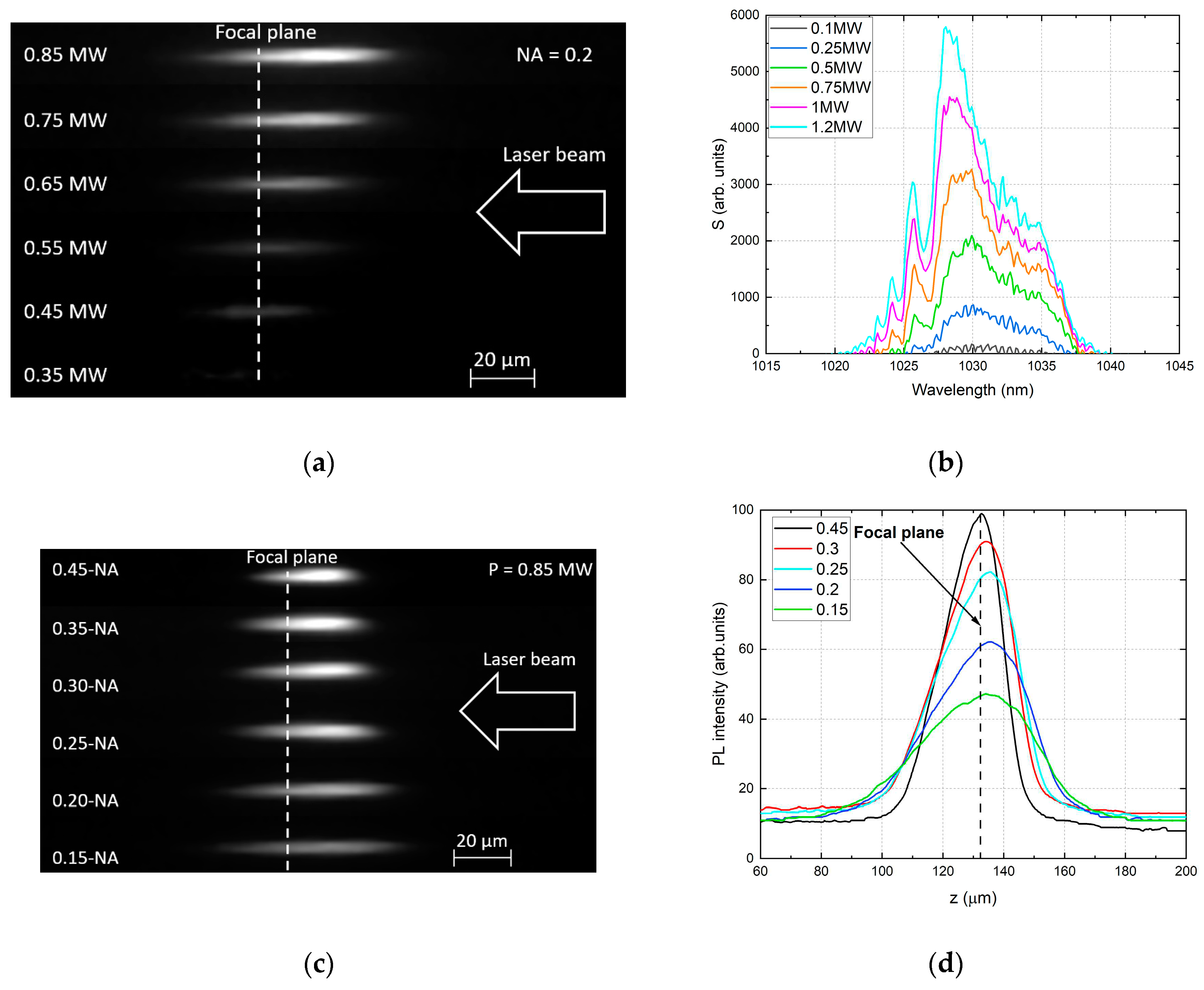
3. Experimental Results

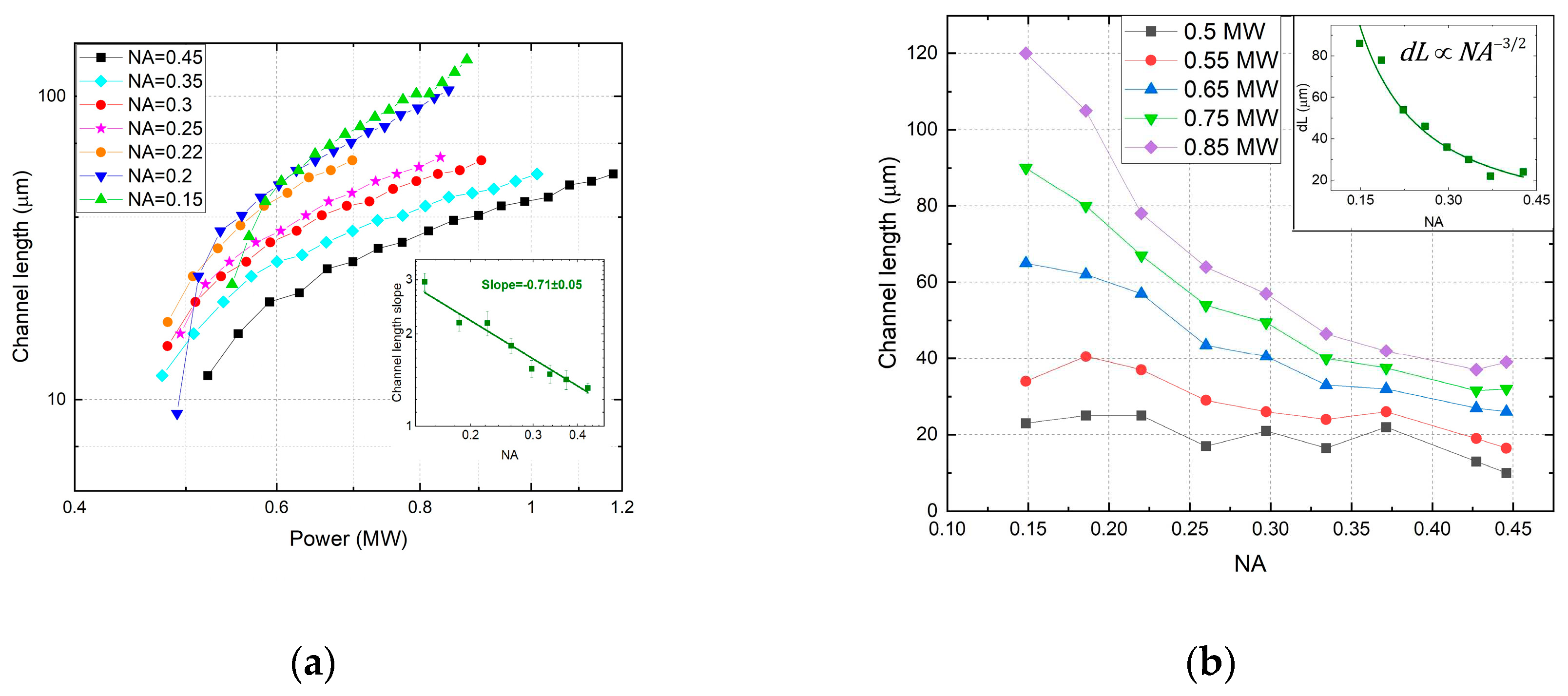
3.1. Dimensional parameters of luminous channels vs NA

The micro-images of the luminous spatial channels induced by the ultrashort laser pulses are shown in Fig 2. Firstly, the focusing conditions were determined using a NA=0.2 aperture microscope objective. The luminous channels appeared around the central position of the linear focus

z_{f} \approx 1300

μm at pulse energies E ≥ 100 nJ. With a further increase in energy, channels began to asymmetrically elongate from the geometric focus towards the incident radiation (Figure 2a). This is due to the increase in the contribution of nonlinear effects to the process of in-bulk laser-matter interaction. When the pulse power exceeds the critical power of a certain threshold value, the filamentation process begins, which leads to a nonlinear broadening of the spectrum of passing pulses, which is clearly demonstrated in the Figure 2b. The spectrum is symmetrical for pulses with a power of less than 0.5MW, but with a further increase in power, it widens and side peaks appear in the red and blue regions, which indicates the presence of self-focusing and the formation of dense defocusing plasma resulting from photoionization [10,27,30,31,32,33]. At the same time, its central maximum shifts toward the blue region with increasing power, which is consistent with the results obtained in [34]. To study the effect of focusing conditions on the filamentation process, we analyzed plasma channels induced at a fixed peak pulse energy P=0.85 MW while varying numerical aperture from 0.45 to 0.15 (Figure 2c,d).

The transition from long plasma channels for NA<0.2 to a compact structure for tighter focusing conditions is clearly demonstrated in Figure 2c,d. As we decrease the focal spot size by using higher NA, the filament length shortens, becoming a compact structure for tight focusing (NA=0.45, w₀ ≈ 0.73 μm). In can be also observed that for weak focusing, plasma creation begins sooner, before the geometrical focus, although the incident laser intensity is smaller for larger spot sizes (since the total peak power was kept constant) and luminous channels are elongated toward the upstream direction of the laser pulses with decreasing numerical aperture. This indicates that the nonlinear Kerr effect and self-focusing must play an important role in the regime with longer plasma channels. In contrast, for tighter focusing conditions, the position of the focus is very close to the geometrical focus, indicating a potentially smaller contribution of the nonlinear Kerr effect and domination of geometrical focusing.

The measured lengths of observed channels are presented in Figure 3a. The lengths varied from 5 to 120 μm, depending on the NA of the focusing lens and peak pulse power. As can be seen, the length enlarges nonlinearly with increasing pulse power and for lower apertures the length of the channels is significantly longer than for high ones. This is clearly demonstrated in Figure 3b where the dependence of the channels length on the numerical aperture is shown.

The range of the channels length changes nonlinearly decreases with the growth of the aperture

d L \propto N A^{- 3 / 2}

and at low apertures is several times greater than at low ones (see Figure 3b). That is, with weak focusing, it is possible to significantly increase the length of the plasma channel with a slight increase in pulse power. While with tight focusing, it is possible to obtain more compact structures in the same range of used powers.

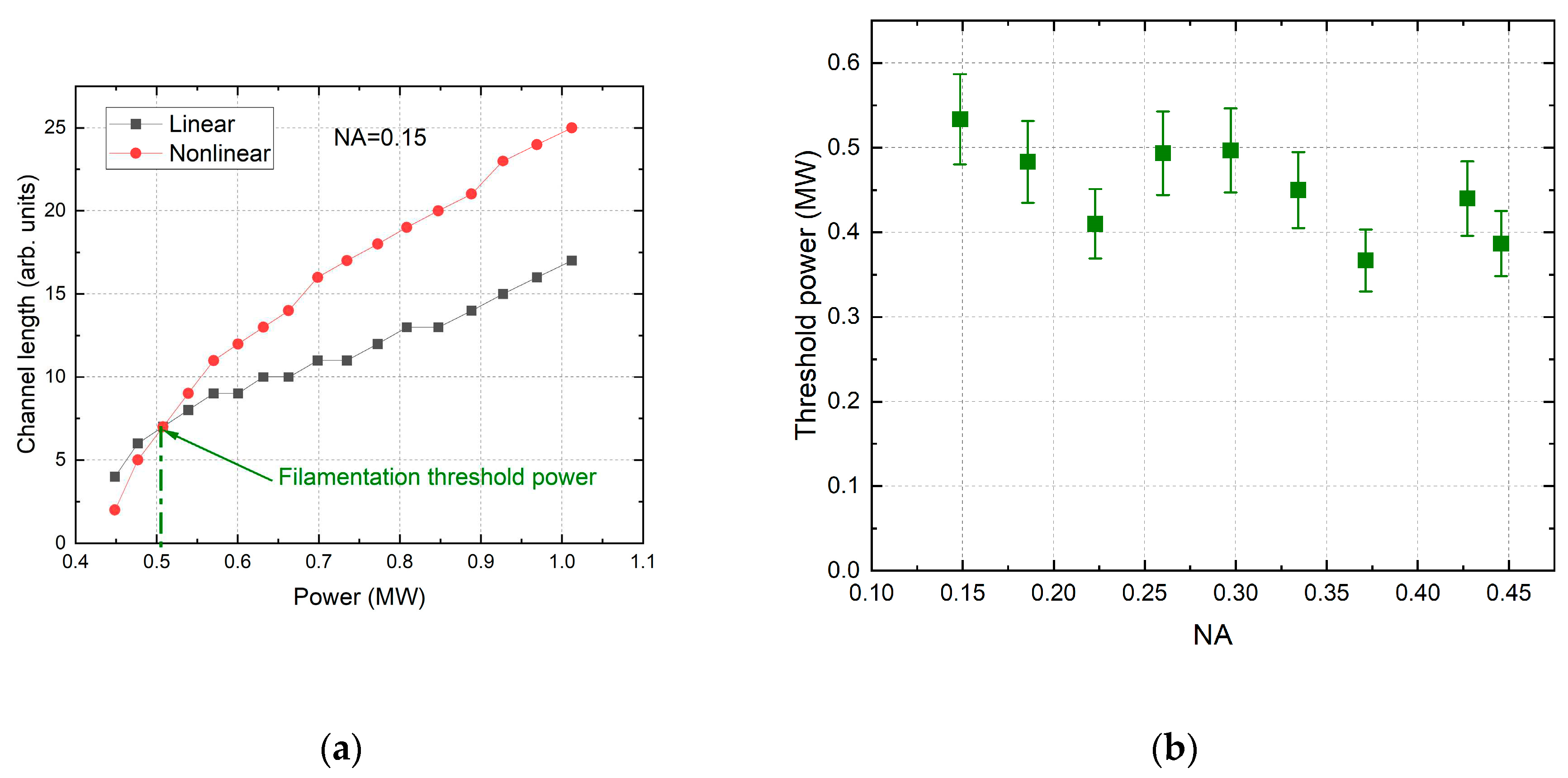
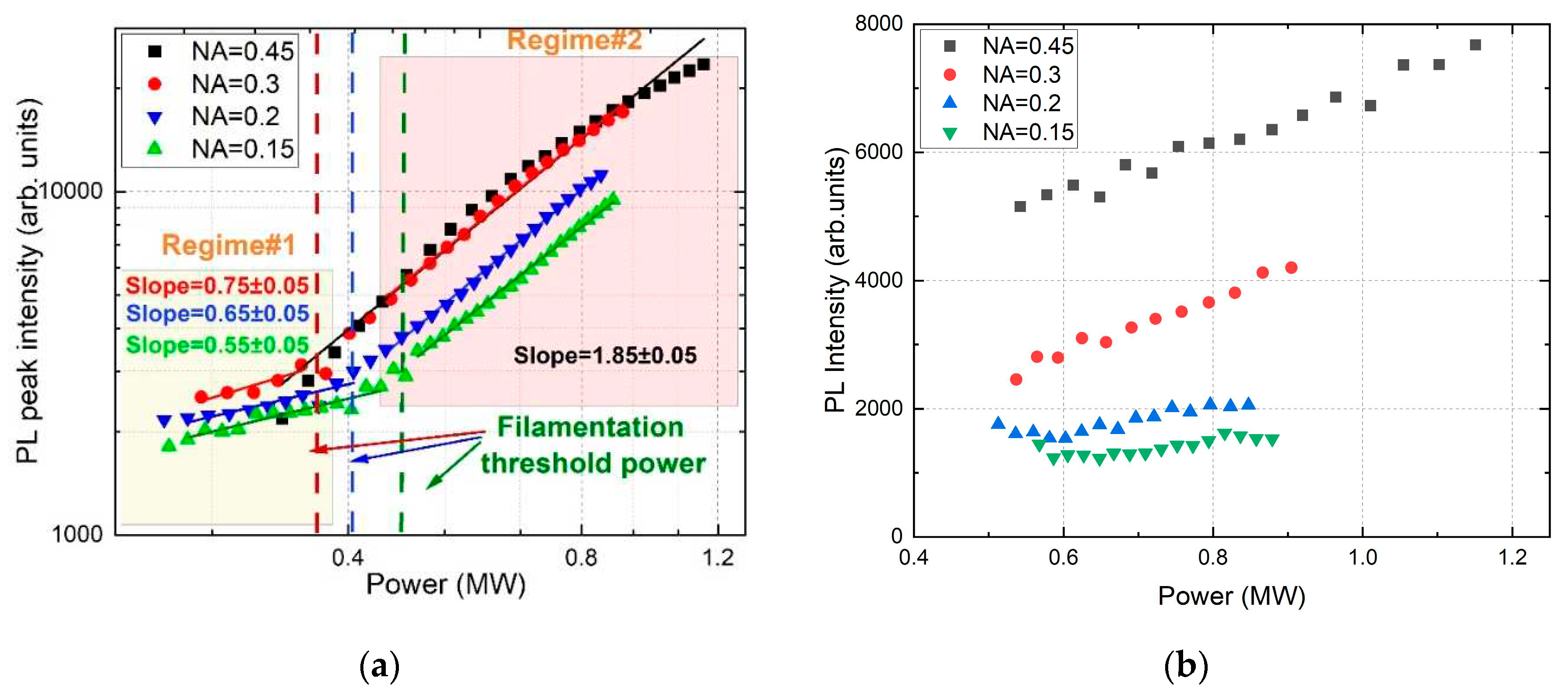
3.2. Filamentation threshold power vs NA

In our research, the onset of the filamentation process was identified as a visible asymmetric elongation of the luminous channels with increasing of peak pulse power. According to the technique outlined in [17], the threshold power of the filamentation onset was determined based on the analysis of the difference between the linear and nonlinear parts of the luminous channel length (see Figure 4a). Plot of the obtained dependence of the filamentation threshold power on NA is shown in Figure 4b.

Self-focusing does not depend on intensity, but only on the peak power [9,28] thus the critical self-focusing threshold does not depend on the focusing geometry determined by the aperture and is the same for tight and weak external focusing. However, contribution from plasma defocusing to filament formation strongly depends on focusing conditions [26]. When using high-NA focusing, the plasma density required to balance the Kerr nonlinearity can be obtained at lower pulse energies. Thus, the threshold for the filamentation onset with tighter focusing conditions will be lower than with weak focusing: the filamentation threshold power is equal to P_th≈0.55±0.05 MW for NA=0.15 and P_th≈0.38±0.05 MW for NA=0.45.

3.3. PL intensity vs NA

It is known, that bends in the slopes in the pump power-dependent stationary PL output can be identified as transition points between different characteristic regimes, apparently representing some features of ultrafast inter-band photoexcitation accompanying the dynamics of free charge carriers and the filamentation process [16,33,36]. The dependences of the peak photoluminescence (PL) intensity of the observed channels on the peak pulse power for different NA are shown in Figure 5a. With weak focusing geometry, there is a bend in the dependencies observed in the region of 0.5 MW, which corresponds to the estimated value of the threshold power of the filamentation onset. In the pre-filamentation mode (Regime #1), the slope of the curves increases with the growth of the numerical aperture from 0.55 to 0.75, which happens due to the dominance of geometric linear focusing over nonlinear. However, at higher energies in the filamentation regime (Regime #2), an increase in the slope of the curves is observed, which is due to an increase in the intensity in the near-axial region caused by the Kerr nonlinearity. At the same time, the angle of inclination of all curves becomes the same and does not depend on the aperture, which indicates the predominance of non-linear focusing. It should be noted that there is no change in the slope for tight focusing NA=0.45, due to the fact that geometric focusing is the determining factor in the entire studied energy range.

With an increase in the pulse energy, the size of the photoluminescence region begins to increase, therefore, to assess the effect of pulse power and NA on the PL due to nonlinear effects, we normalized the dependences of the integrated PL intensity on the channel length (Figure 5b). It was found that for weak focusing conditions (NA=0.15, 0.2) with an increase in the intensity of ultrashort laser pulses in the registered plasma channels, there is almost no increase in the PL yield and that pulse energy goes into the channel elongation, which is in good agreement with the well-known fact about the intensity clamping in the filamentation process [37,38]. However, with tight focusing (NA>0.3), there is a monotonous increase in the PL yield with increasing peak pulse power, which is due to the dominance of geometric linear focusing and the deposition of laser energy in the limited focal area accompanied by the generation of dense luminous plasma.

4. Discussion

The filamentation process is initiated by self-focusing of the laser pulse, which occurs when the input laser power exceeds the critical power and leads to the nonlinear shift of the focal area position towards the laser radiation. In general case in which the beam has arbitrary power and arbitrary beam-waist position, the distance from the entrance face of the sample to the position of the self-focus is given by the formula [30]

z_{s f} = \frac{\frac{1}{2} k w^{2}}{{(\frac{P}{P_{t h}} - 1)}^{\frac{1}{2}} + 2 z_{f} / k w_{0}^{2}},

(1)

where

k = 2 π n_{0} / λ

is the wavenumber in the medium,

n_{0}

is the linear refractive index of the medium, w is the 1/e² beam radius at the entrance face. Using the threshold value of the filamentation onset P_th determined from the experimental data, the dependencies of nonlinear focal shift

d f = z_{f} - z_{s f}

on the pulse peak power were calculated (Figure 6a, solid lines). For comparison, experimental shifts were also determined (symbols).

It can be seen that the theoretical calculations are several times lower than the experimental ones. Moreover, with a decrease in NA, the discrepancy in displacements also decreases. This effect may be associated with plasma shielding (that is not taken into account in the calculations) during tight focusing, which shows up in decreased length of “linear” part and as a consequence in an underestimation of the focal shift.

At Figure 6b (numerical calculation) it can be noticed that higher NAs are less subject to change and remain almost stable as power increases, whereas at low NA elongation reaches 2.5x. This opens up possibilities for controlling the size of the modifiable regions by varying the aperture of the focusing optics in a limited range of energies.

5. Conclusions

In conclusion, laser irradiation of HPHT diamond with ultra-short 1030-nm pulses at different NAs revealed strong dependence of the size and shape of the modified region on the used NA of the lens. Such dependence opens up another degree of freedom in 3D processing in transparent dielectrics, allowing, for example, to vary the cross-section of the waveguide without changing the recording setup, but only by controlling the lens aperture, which seems very promising for industrial applications.

Author Contributions

Conceptualization, Y.G. and S.K.; methodology, Y.G., G.K., and E.K; software, Y.G., G.K. and E.K.; validation, Y.G. and S.K.; formal analysis, J.Z., G.K., and E.K.; investigation, Y.G. and G.K.; resources, S.K.; data curation, G.K. and E.K.; writing—original draft preparation, Y.G. and J.Z.; writing—review and editing, Y.G., G.K., E.K. and S.K.; visualization, Y. G., G.K. and E.K.; supervision, S.K.; project administration, S.K.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Russian Science Foundation, grant number 21-79-30063.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

Sugioka, K.; Cheng, Y. Ultrafast Lasers—Reliable Tools for Advanced Materials Processing. Light: Science & Applications 2014, 3, e149–e149. [Google Scholar] [CrossRef]
Kudryashov, S.; Nastulyavichus, A.; Krasin, G.; Khamidullin, K.; Boldyrev, K.; Kirilenko, D.; Yachmenev, A.; Ponomarev, D.; Komandin, G.; Lebedev, S.; Prikhod'ko, D.; Kovalev, M. CMOS-compatible direct laser writing of sulfur-ultrahyperdoped silicon: Breakthrough pre-requisite for UV-THz optoelectronic nano/microintegration. Optics & Laser Technology 2023, 158, 108873. [Google Scholar] [CrossRef]
Temprana, E.; Myslivets, E.; Kuo, B.-P.; Liu, L.; Ataie, V.; Alic, N.; Radic, S. Overcoming Kerr-Induced Capacity Limit in Optical Fiber Transmission. Science 2015, 348, 1445–1448. [Google Scholar] [CrossRef]
Horton, N.G.; Wang, K.; Kobat, D.; Clark, C.G.; Wise, F.W.; Schaffer, C.B.; Xu, C. In Vivo Three-Photon Microscopy of Subcortical Structures within an Intact Mouse Brain. Nature photonics 2013, 7, 205–209. [Google Scholar] [CrossRef]
Chen, F.F. Introduction to Plasma Physics and Controlled Fusion; Springer, 1984; Vol. 1. [Google Scholar] [CrossRef]
Chekalin, S.V.; Kandidov, V.P. From Self-Focusing Light Beams to Femtosecond Laser Pulse Filamentation. Physics-Uspekhi 2013, 56, 123. [Google Scholar] [CrossRef]
Marburger, J.H. Self-Focusing: Theory. Progress in quantum electronics 1975, 4, 35–110. [Google Scholar] [CrossRef]
Mao, S.S.; Quéré, F.; Guizard, S.; Mao, X.; Russo, R.E.; Petite, G.; Martin, P. Dynamics of Femtosecond Laser Interactions with Dielectrics. Applied Physics A 2004, 79, 1695–1709. [Google Scholar] [CrossRef]
Mann, C.R. The Theory of Optics. By Paul Drude. Translated from the German by CR Mann and RA Millikan. New York, Longmans, Green & Co. 1902. Pp. Xxi+ 546. Science 1903, 18, 432–434. [Google Scholar] [CrossRef]
Couairon, A.; Mysyrowicz, A. Femtosecond Filamentation in Transparent Media. Physics reports 2007, 441, 47–189. [Google Scholar] [CrossRef]
Théberge, F.; Liu, W.; Simard, P.T.; Becker, A.; Chin, S.L. Plasma Density inside a Femtosecond Laser Filament in Air: Strong Dependence on External Focusing. Physical Review E 2006, 74, 036406. [Google Scholar] [CrossRef]
Stuart, B.C.; Feit, M.D.; Herman, S.; Rubenchik, A.M.; Shore, B.W.; Perry, M.D. Nanosecond-to-Femtosecond Laser-Induced Breakdown in Dielectrics. Physical review B 1996, 53, 1749. [Google Scholar] [CrossRef] [PubMed]
Neauport, J.; Lamaignere, L.; Bercegol, H.; Pilon, F.; Birolleau, J.-C. Polishing-Induced Contamination of Fused Silica Optics and Laser Induced Damage Density at 351 Nm. Optics express 2005, 13, 10163–10171. [Google Scholar] [CrossRef] [PubMed]
Couairon, A.; Sudrie, L.; Franco, M.; Prade, B.; Mysyrowicz, A. Filamentation and damage in fused silica induced by tightly focused femtosecond laser pulses. Physical Review B 2005, 71, 125435. [Google Scholar] [CrossRef]
Gattass, R.R.; Mazur, E. Femtosecond Laser Micromachining in Transparent Materials. Nature photonics 2008, 2, 219–225. [Google Scholar] [CrossRef]
Bergé, L.; Skupin, S.; Nuter, R.; Kasparian, J.; Wolf, J.-P. Ultrashort Filaments of Light in Weakly Ionized, Optically Transparent Media. Reports on progress in physics 2007, 70, 1633. [Google Scholar] [CrossRef]
Kudryashov, S.I.; Danilov, P.A.; Kuzmin, E.V.; Gulina, Y.S.; Rupasov, A.E.; Krasin, G.K.; Zubarev, I.G.; Levchenko, A.O.; Kovalev, M.S.; Pakholchuk, P.P. Pulse-Width-Dependent Critical Power for Self-Focusing of Ultrashort Laser Pulses in Bulk Dielectrics. Optics Letters 2022, 47, 3487–3490. [Google Scholar] [CrossRef] [PubMed]
Krasin, G.K.; Gulina, Y.S.; Kuzmin, E.V.; Martovitskii, V.P.; Kudryashov, S.I. Polarization-Sensitive Nonlinear Optical Interaction of Ultrashort Laser Pulses with HPHT Diamond. In Photonics; Multidisciplinary Digital Publishing Institute, 2023; Vol. 10. [Google Scholar] [CrossRef]
Dubietis, A.; Couairon, A. Ultrafast Supercontinuum Generation in Transparent Solid-State Media; Springer, 2019. [Google Scholar] [CrossRef]
Glezer, E.N.; Mazur, E. Ultrafast-Laser Driven Micro-Explosions in Transparent Materials. Applied physics letters 1997, 71, 882–884. [Google Scholar] [CrossRef]
Schaffer, C.B.; Brodeur, A.; García, J.F.; Mazur, E. Micromachining Bulk Glass by Use of Femtosecond Laser Pulses with Nanojoule Energy. Optics letters 2001, 26, 93–95. [Google Scholar] [CrossRef]
Yamada, K.; Watanabe, W.; Toma, T.; Itoh, K.; Nishii, J. In Situ Observation of Photoinduced Refractive-Index Changes in Filaments Formed in Glasses by Femtosecond Laser Pulses. Optics letters 2001, 26, 19–21. [Google Scholar] [CrossRef]
Wu, A.Q.; Chowdhury, I.H.; Xu, X. Plasma Formation in Fused Silica Induced by Loosely Focused Femtosecond Laser Pulse. Applied physics letters 2006, 88, 111502. [Google Scholar] [CrossRef]
Ashcom, J.B.; Gattass, R.R.; Schaffer, C.B.; Mazur, E. Numerical Aperture Dependence of Damage and Supercontinuum Generation from Femtosecond Laser Pulses in Bulk Fused Silica. JOSA B 2006, 23, 2317–2322. [Google Scholar] [CrossRef]
Poudel, M.P.; Chen, J. Nonlinear Optical Effects during Femtosecond Photodisruption. Optical Engineering 2009, 48, 114302–114302. [Google Scholar] [CrossRef]
Naseri, N.; Dupras, G.; Ramunno, L. Mechanism of Laser Induced Filamentation in Dielectrics. Optics Express 2020, 28, 26977–26988. [Google Scholar] [CrossRef] [PubMed]
Lim, K.; Durand, M.; Baudelet, M.; Richardson, M. Transition from Linear-to Nonlinear-Focusing Regime in Filamentation. Scientific reports 2014, 4, 7217. [Google Scholar] [CrossRef] [PubMed]
Lim, K. Laser Filamentation-beyond Self-Focusing and Plasma Defocusing. 2014.
Trojánek, F.; Zídek, K.; Dzurnák, B.; Kozák, M.; Malý, P. Nonlinear Optical Properties of Nanocrystalline Diamond. Optics Express 2010, 18, 1349–1357. [Google Scholar] [CrossRef]
Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic: Boston, USA, 1992. [Google Scholar]
Jukna, V.; Galinis, J.; Tamosauskas, G.; Majus, D.; Dubietis, A. Infrared extension of femtosecond supercontinuum generated by filamentation in solid-state media. Applied Physics B 2014, 116, 477–483. [Google Scholar] [CrossRef]
Fang, X.J.; Kobayashi, T. Evolution of a super-broadened spectrum in a filament generated by an ultrashort intense laser pulse in fused silica. Applied Physics B 2003, 77, 167–170. [Google Scholar] [CrossRef]
Chekalin, S.V.; Kandidov, V.P. From self-focusing light beams to femtosecond laser pulse filamentation. Physics-Uspekhi 2013, 56, 23. [Google Scholar] [CrossRef]
Heins, A.; Guo, C. Spectral investigation of higher-order Kerr effects in a tight-focusing geometry. Optics Express 2013, 21, 29401–29412. [Google Scholar] [CrossRef]
Kudryashov, S.; Danilov, P.; Smirnov, N.; Levchenko, A.; Kovalev, M.; Gulina, Yu.; Kovalchuk, O.; Ionin, A. Femtosecond-laser-excited luminescence of the A-band in natural diamond and its thermal control. Opt. Mater. Express 2021, 11, 2505–2513. [Google Scholar] [CrossRef]
Kudryashov, S.I.; Levchenko, A.O.; Danilov, P.A.; Smirnov, N.A.; Ionin, A.A. ; IR femtosecond laser micro-filaments in diamond visualized by inter-band UV photoluminescence. Opt. Lett. 2020, 45, 2026–2029. [Google Scholar] [CrossRef] [PubMed]
Liu, W.; Petit, S.; Becker, A.; Aközbek, N.; Bowden, C.M.; Chin, S.L. Intensity clamping of a femtosecond laser pulse in condensed matter. Opt. Commun. 2002, 202, 189–197. [Google Scholar] [CrossRef]
Kandidov, V.P.; Fedorov, V.Y.; Tverskoi, O.V.; Kosareva, O.G.; Chin, S.L. Intensity clamping in the filament of femtosecond laser radiation. Quant. Electron. 2011, 41, 382–386. [Google Scholar] [CrossRef]

Figure 1. (a) Experimental scheme for registering luminous tracks in the HPHT diamond, (b) optical absorption spectrum of the sample, inset shows the mid-IR absorption spectra with the main optical defects positions marked.

Figure 2. Micro-images of the luminous plasma channels for fixed NA=0.2 with varying peak pulse energy P=0.35-0.85 MW (a) and for fixed peak pulse power P=0.85MW and varying NA=0.15-0.45 (c); (b) spectra of laser pulse transmitted through sample at different incident pulse powers for NA=0.2; the cross-sections for few selected luminous channels for peak power P=0.85MW (d).

Figure 3. Dependence of the luminous channel length on pulse power (a) and on NA (b). Luminous channel length error bars: 10%. dL on the inset shows the range of the channels length change.

Figure 4. (a) Dependence of the luminous channel lengths on the peak pulse power; (b) dependence of the filamentation threshold power on NA.

Figure 5. Dependence of the PL peak intensity (a) and integrated PL intensity (b) on pulse power. PL intensity error bars: 10%.

Figure 6. Dependence of nonlinear focal shift on peak pulse power (a) and on NA (b). Focal shift error bars: 10%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer