Prerpints.org logo
Preprint
Article

Assessing Satellite-Based Products in Characterizing Flash Drought Under Climate Change in Northeastern South America

Altmetrics

Downloads

123

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

19 September 2023

Posted:

21 September 2023

You are already at the latest version

Alerts
Abstract
In a 1.5°C warmer world, the Northeastern (NE) South America’s ecosystems will experience more severe droughts, associated with decreasing rainfall. The severity of flash drought events based on vegetation and surface soil moisture has not been identified over the Caatinga ecosys-tem. This study aimed to characterize the impact of flash drought events on vegetation response via soil moisture over NE South America during the first two decades of the 2000s. Three drought indices were used to characterize flash droughts: the Standardized Difference Vegetation Index (SDVI) derived from Meteosat Second Generation (MSG), the Standardized Precipitation Index (SPI) from ground-data, and the Surface Soil Moisture (SSM) product-based Soil Moisture and Ocean Salinity (SMOS). Results revealed dramatic impacts of flash drought events on vegetation dynamics that caused abrupt changes in the regional vegetation phenology. The regional patterns of flash drought events in 2012 over NE South America were identified and had a severe impact on its Caatinga-like vegetation-dependent moisture response. In 2012, anomalously long dry spells with negative rainfall anomalies in the non-rainy season and persistent on vege-tation greenness and rapidly decreased soil moisture were prominent, thus identifying NE South America to the impacts of flash drought events. Additionally, the results from the trends analysis of radiance fluxes estimated from the MSG satellites over 18 years revealed that an overall drying trend in the NE South America semiarid ecosystem during the last two decades. Here, flash drought events were identified as the conse-quent rainfall deficiency at SPI-3< −1 for a period of five consecutive weeks or more, which the soil moisture content dropping from the 40th percentile to below the 20th percentile, with the NDVI lower than 0.30 unit. These results could be useful to guide flash-droughts early warning systems in NE South America.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

Drought has affected most regions of the globe in the 2000s [1]. It poses a significant global environmental challenge that carries with it profound environmental and socio-economic implications [1,2]. It refers to a period with anomalies from average moisture conditions during which limitations in water availability result in negative impacts for various components of natural systems and economic sectors. It can happen on a wide range of timescales from flash droughts on a scale of weeks [3,4] to multi-year or decadal rainfall deficits [5,6,7,8,9]. Droughts are often analyzed using indices, which are measures of drought severity, duration, and frequency, addressing different types of drought characteristics [1].
Severe droughts occur as a combination of thermodynamical and dynamical processes. Thermodynamical processes contributing to drought, which are mostly related to heat and moisture exchanges and in part modulated by plant coverage and physiology, can be affected by greenhouse gas forcing both at global and regional scale [2]. They affect for instance atmospheric humidity, temperature, radiation, which in turn lead to modified precipitation and/or evapotranspiration (ET) in some regions and time frames [1]. On the other hand, dynamical processes are particularly important to explain drought variability on several time scales, from flash droughts to decadal droughts [1]. Nevertheless, there is limited evidence of circulation changes attributable to greenhouse gas forcing that are affecting long-term changes in drought [2].
Many studies have focused on being to detect, monitor, and predict drought events. Historically, this has been accomplished through anomalies in single variables (e.g., rainfall, vegetation, soil moisture, runoff, evapotranspiration) to complex indices combining different drought aspects. These indices range from the Standardized Precipitation Evapotranspiration Index (SPI, SPEI; [3,8,9]), Soil moisture-based: Soil Moisture Stress (SMS; [4]), and Soil Moisture Volatility Index (SMVI; [11]), Relative Rate of Dry Down (RRD; [12]), Evaporative Stress Index (ESI; [13]), ET and Potential ET-based: EDDI [14], Atmospheric Evaporative Demand (AED)-based: Evaporative Stress Index (ESR; [15]),Vegetation indices-Vegetation Drought Response Index (VegDRI; [16]), Standardized Difference Vegetation Index (SDVI; [17]), Leaf Area Index (LAI; [15]), among others.
The impact of climate change on severe drought varies across regions. In South America, the recent severe drought, from 2012 to 2016, was the worst on record since 1900 for Northeastern (NE) South America [8,18]. This extreme event had significant impacts, including significant reduction in agricultural production, reduced water availability for industrial and consumptive use [19]. Total damage resulting from the 2012-2016 drought has been estimated at $125 billion [20]. Recent extreme drought, however, reduced surface vegetation cover over NE South America during the past decade [17]. Some studies suggest [8,21] that severe droughts in NE South America will become more frequent.
The NDVI (Normalized Difference Vegetation Index) is one of the most commonly used proxies to assess vegetative drought [17,22,23]. The rainfall – NDVI relationship varies across biomes, soil, and vegetation types. For example, xeric/herbaceous and annual/perennial, will response differently to rainfall [24,25,26]. However, there are often substantial time lags between rainfall anomalies and vegetation response [17,27,28]. In NE South America, vegetation phenology is highly variable and largely driven by interannual variations in rainfall at the landscape level. On a monthly timescale, Barbosa et al. [17] observed a lag between the NDVI and rainfall on the order of one and three months, which is dependent on the type of vegetation that dominates the area. Rainfall-driven phenological cycles over NE South America’s landscape are partially attributed to the fact that persistent drought conditions can lead to a gradual decrease in the soil moisture level, resulting in weaker-than-normal photosynthetic activity and a slow browning process [25]. In the study of trend analysis of vegetation dynamics over South America, Barbosa et al. [25] found the vegetation degradation is coupled to decline in amount of rainfall in some areas.
There are only a small number of studies evaluating the impacts of flash drought events over different ecosystems across the globe, but not over the Caatinga biome. While many conventional drought events (such as meteorological, agricultural, and hydrological) develop slowly over months or years, some special events, called flash droughts, can intensify over the course of days or weeks. These special events intensified suddenly and cause a quick reduction of soil moisture leading to vegetation stress conditions (i.e., the inability to photosynthesize because the atmosphere is too dry for stomata to open). The importance of flash drought within the scientific community in the last decade has received more attention. As such, flash drought events occupy a unique space within the framework of extreme climate and weather events, possessing no singular definition or criteria. Otkin et al. [4] have determined that flash drought is identified by a sudden decrease of soil moisture percentile from above 40% to below 20% within 20 days period. Therefore, this study aimed to characterize the impact of flash drought on vegetation response via soil moisture over NE South America during the first two decades of the 2000s. A variety of methods were applied, including three drought indices and remote sensing techniques to analyze the response of its ecosystems to flash drought events.
In the next section the data are presented and methos are applied. Section 3 shows both the spatial and temporal impacts of drought events on vegetation dynamics over NE South America using varying satellite-based surface soil moisture-vegetation thresholds and climatic data from ground-based station measurements. Section 4 discusses the derived modes of vegetation-rainfall activity and links these mains modes with the large-scale radiance fluxes and ends with some concluding remarks.

2. Datasets and Methods

2.1. Northeastern South America Study Area

Northeastern South America (NE South America) is taken to encompass mainland South America between the parallels 1° and 18°S and the meridians 35° and 47°W and spans a total area of 1.6 million km2 (see Figure 1). It is a home to around 53.1 million individuals [29]. NE South America represents a large geographical area covering semi-arid climate with low and irregular rainfall, high temperatures, and high evaporation rates [28]. Within the NE South America, other types of climates exist, depending on location, relief, and vegetation influences [28].
The climate pattern of NE South America is characterized by a transition in rainfall from the dry inland (Caatinga biome; Figure 1) to the humid Atlantic coast (Mata Atlântica biome). Mean annual rainfall increases steadily from less than 800 mm in the semi-arid interior to 1,800 mm at the coast (Figure 2b). The semi-arid area covers 60% of the region. Within the NE South America, the wettest season typically occurs from December to April, while the dry season extends from July to October [22]. The rainfall regime is mainly influenced by the seasonal migration of the Intertropical Convergence Zone (ITCZ), El Niño Southern Oscillation (ENSO) and the Tropical North Atlantic sea surface temperature. Severe droughts happened during El Niño events in 1983, 1998, and 2016, and due to warm surface waters in the Tropical North Atlantic between 2012 and 2018 [8,22].
Vegetation within NE South America was classified into four six land cover types, including both unmanaged native and managed agricultural vegetation (Figure 1; Figure 2a). The four most prevalent land cover types within NE South America are Caatinga, Cerrado, Atlantic Forest, and Amazon Forest, covering 52.5%, 29.4%, 10.7% and 7.4% of land area, respectively [30]. The Caatinga ecosystem (Figure 1) covers 735,000 km² of NE South America and is characterized by a mosaic of xerophytic vegetation [22]. The term “Caatinga” (Caa = forest, tinga = white) comes from the Tupi language, and is used synonymously with Steppe Savannah as defined by Trochain [17,22]. Typical Caatinga is composed of woody vegetation with discontinuous canopy (three to nine meters). Most Caatinga plants are formed with a fearsome array of thorns that emerge from microphyllous foliage - lost during the periodic droughts. The ground layer is rich in bromeliads, annual herbs, and geophytes. Typical species include Amburana cearensis, Anadenanthera colubrina, Aspidosperma pyrifolium, Poincianella pyramidalis and Cnidoscolus quercifolius [20].
One prominent feature observed in the Caatinga land cover during a prolonged period of drier-than-normal rainfall conditions is a gradual weakening in vegetative greenness [22]. The vulnerability of the Caatinga to periodic droughts is further exacerbated by high levels of habitat degradation [25]. Indeed, the biome is one of the most threatened in Brazil due to widespread deforestation for farming and mineral extraction [31]. Despite the fauna and flora of the Caatinga biome region being clearly adapted to periodic droughts, some scientists believe that they may already be operating at their physiological limits [20]. Prolonged and frequent occurrences of droughts present significant challenges to flora and fauna [18].

2.2. Datasets

2.2.1. Meteosat SEVIRI NDVI Data from EUMETCast Service

Meteosat Second Generation (MSG) Spinning Enhanced Visible and Infrared Imager (SEVIRI) NDVI-derived monthly NDVI data used in this study are composed of daily NDVI data [17,32]. These data are produced by the European Organization for the Exploitation of Meteorological Satellites in Darmstadt, Germany, which uses the processing method originally proposed by Ertürk et al. [33]. They are then uplinked to the SES-6 communication satellite in wavelet compressed format. The Laboratório de Análise e Processamento de Imagens de Satélites (LAPIS) of the Universidade Federal de Alagoas (UFAL) receives and archives these data in compressed form on drivers accessible through personal computers on the network (Figure 3).
MSG satellites have measured operationally shortwave and longwave radiation from the Earth and its atmosphere to eleven instrument channels with a time frequency of 15 minutes since 2003 [17,33]. Data from the operational missions of the MSG 1-4 satellites, located near 0° longitude (Gulf of Guinea), were used for the purpose of this study. A pentad data frequency (i.e., the mean over 5 days) was chosen for the correct sign of vegetation-precipitation relationship at regional scale to provide sufficient statistical significance with a moderate computational effort [17]. Over the entire study area and 18-year period, composited daily SEVIRI NDVI to monthly for comparison with drought index by computing average value of daily NDVI within a single month [23]. A pentad data frequency was also chosen for the correct sign of vegetation-precipitation relationship at regional scale to provide sufficient statistical significance with a moderate computational effort [23].
18 years of monthly-pentad MSG SEVIRI NDVI were obtained through the LAPIS/UFAL (https://lapismet.com.br/dados/). Operational NDVI product derived from the SEVIRI Level 1.5 image data for the VIS0.6 and the VIS0.8 data is part of an automatic processing approach developed by [33] and [17]. The original data were corrected: (1) for all data, (2) atmospheric correction performed, (3) Bidirectional Reflectance Distribution Function (BRDF), (4) adjacency correction performed, and (5) low or average aerosol quantities. The MSG SEVIRI NDVI was defined by Barbosa et al. [17].
The SEVIRI-NDVI dataset was initially gridded using the NE South America boundaries as a mask; a total of 18,399 grid cells were extracted and structured as a numerical matrix (number of grid cells versus one column for each monthly composite). The NDVI time series was denoted as NDVIijk, where i is the month (i = 1…12) or i is the five-days (pentad) (i = 1…73), j is the year (j = 2004…2022) and k is the grid cells (k = 1…18,399) and was transformed to a matrix of monthly NDVI anomalies (NDVIaijk) with respect to the 2004–2022 base period. NDVIa time series [17] were then scaled by the standard deviation, as follows:
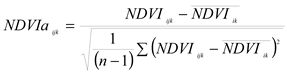
Preprints 85611 i001
The matrix of standardized NDVI anomalies (i.e., SDVI; [17]) was referred to as the NDVIa matrix (number of grid cells versus number of months, pentads or days). Because spatially complete information at high temporal resolution is of crucial importance to support the statistical analysis, the choice of SEVIRI-calculated grid size resolution is a compromise between achieving the highest possible at the daily timescale and still maintaining at regional to local scales to guarantee pixel information in almost all grid cells. Most importantly, however, a previous study by Barbosa et al. [17] showed that the SEVIRI NDVI derived from the daily 1.5-data serves as a good proxy for rainfall activity in NE South America during the rainy season months.

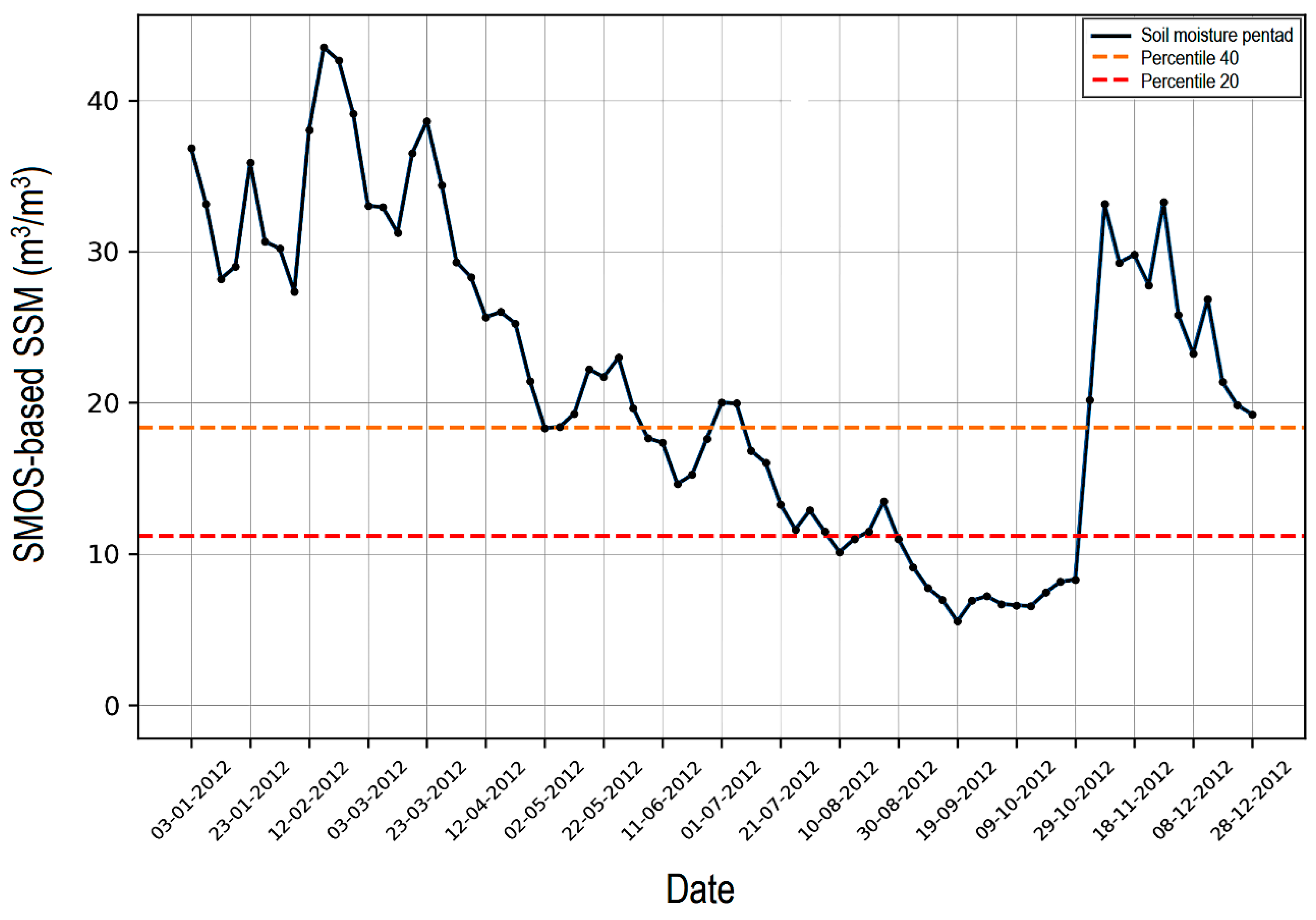
2.2.2. SMOS Surface Soil Moisture Data

SMOS is an L-band passive microwave satellite dedicated to global surface soil moisture (SSM, top 0-5 cm) monitoring [9]. For this study, the SSM estimates were extracted from the SMOS L3 SSM product (version 3.0) provided by the Barcelona Expert Center (https://bec.icm.csic.es/). This product was averaged considering its ascending and descending orbits to minimize the influence of the radio frequency interference (RFI) on retrieved SSM values [34]. The choice of this product was based on its acceptable performance in the identification of drought when compared to in situ measurements in the study area [8,35].

2.2.3. Rainfall and Air-Temperature Datasets

The climatic datasets were acquired from several hundred ground-based station measurements across NE South America, provided by the Brazilian Meteorological Institute (INMET: https://portal.inmet.gov.br). The accuracy of these climatic datasets had been assessed through a cross-validation procedure by Barbosa and Lakshmi Kumar [23]. To evaluate the dependency of vegetation response to hydroclimatic extremes on the degree of dryness (lack of rainfall) and wetness (humid) conditions at regional scale, the original ground-based station datasets were resampled for analysis with SEVIRI.

2.3. The Standardized Precipitation Index (SPI)

The SPI, proposed by McKee et al. [36], is an index that monitors drought conditions by exclusively considering rainfall data. It is commonly used to monitor meteorological drought. In this study, the SPI was calculated based on the quarterly scale (SPI-3), a common timescale used to assess the effects of meteorological drought [23]. The rainfall time series is initially fit to a gamma distribution, which is then transformed into a normal distribution using an equal probability transformation [36]. Daily rain gauge totals from the INMET’s network stations in Brazil from 2004–2022 were used for the calculation of the SPI [23]. In general, negative SPI values indicate a dry period, and positive values indicate a wet period. The SPI-3 time series were structured in one numerical matrix referred to as the SPI3 matrix, based on Barbosa et al. [17]. The probability density function for the gamma distribution is given by the expression:
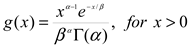
Preprints 85611 i002
where α > 0 is the shape parameter, β > 0 is the scale parameter, and x > 0 is the total accumulated precipitation over a three-month period (called the time scale). Γ(α) represents the gamma function, which is defined by the integral [37]:
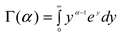
Preprints 85611 i003
The gamma function was evaluated either numerically or using tabulated values depending on the value of α. A maximum-likelihood estimation based on the method of L-moments was used to estimate parameters α and β [38]. The probability density function, g(x), is then integrated with respect to x to obtain an expression for the cumulative density function, G(x), which represents the accumulated rain that has been observed for a given month and time scale:
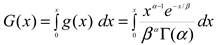
Preprints 85611 i004
Although negligible rainfall amounts are frequent in NE South America [22,39], G(x) is not defined at x = 0 [40]; therefore, G(x) was calculated following the approach of Stagge et al. [41]:
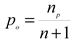
Preprints 85611 i005
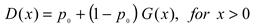
Preprints 85611 i006
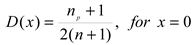
Preprints 85611 i007
where np refers to the number of zero-rainfall events, n is the sample size, po is the observed likelihood of zero-rainfall events, and D(x) is the cumulative density function for observed precipitation. Finally, D(x) is transformed into a normal standardized distribution using a zero mean and unit variance, from which the SPI drought index using the 3-month time scale (SPI3) was obtained.

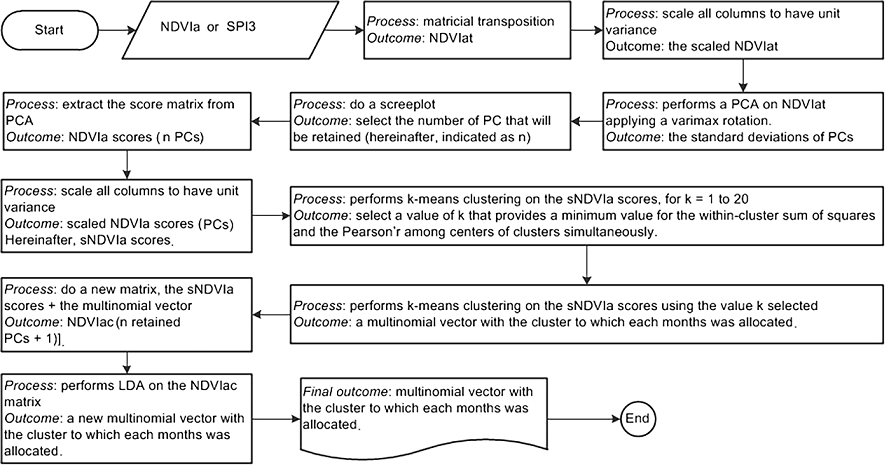
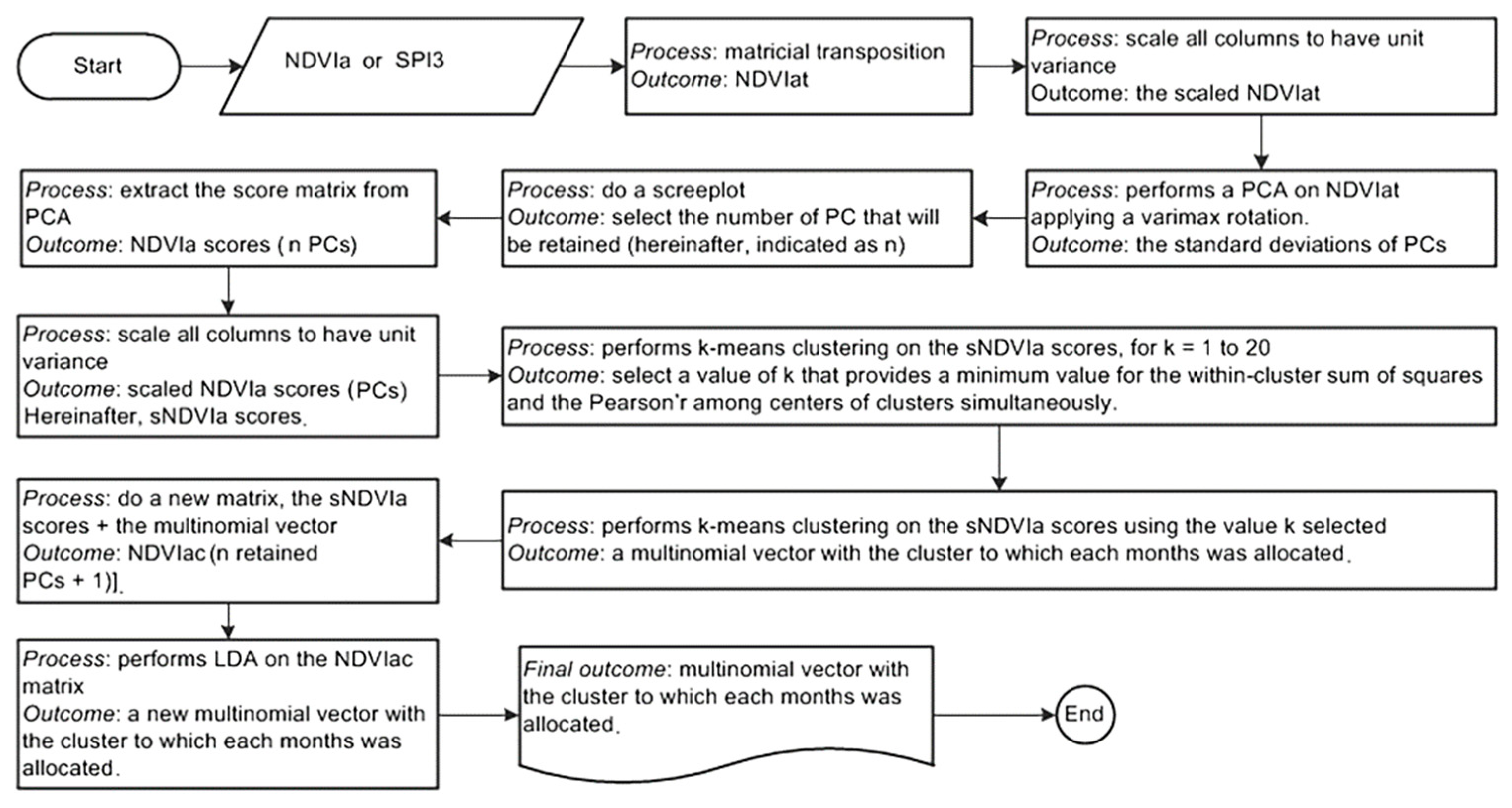
2.4. Statiscal Analyses

To understand the regional scale in vegetation response to rainfall extremes on the magnitude of anomalies in NDVI and SPI3, the statistical analyses over NE South America were computed using the 18-years NDVI-rainfall anomalies from 2004 to 2022. The approach was carried out in four main steps, as response to seasonal and interannual variations in hydroclimatic conditions across space. The first step involved rearranging the NDVIat and SPI3t matrices to obtain two matrices that are referred to as NDVIat and SPI3t, respectively. During the second step, a Principal Component Analysis (PCA) was applied to the NDVIat and SPI3t matrices [23]. PCA was performed by computing the eigenvectors of the covariance matrix, while the varimax method was used to provide an orthogonal rotation.
It is important to note that the original PCs are associated to an arbitrary coordinate system. The rotation procedure changes the PCs to another coordinate system that yields a better separation of the PCs in the spatial context [23]. Unlike other orthogonal rotations, the rotation maximizes the sum of the variances of the squared loadings (squared correlations between variables and PCs) [42]. The number of PCs retained was based on screen plots for NDVIa and SPI3, which show the variances for each against the number of PCs (criterion known as the Kaiser’s rule).
The principal component scores for the retained PCs were computed and resulted in two matrices, which are referred to here as NDVIat and SPI3t scores, respectively. Each score matrix has a dimension equal to rows × n PCs, where n is the number of retained PCs. The scores matrices were scaled by column during the third step of this approach by the mean and the standard deviation.
A Canonical Analysis (CA) was then performed on the NDVIat and SPI3t scores matrices. The k groups used is based on two criteria: a) minimization of the sum of squares of distances between each grid cell and the assigned cluster center, and b) verifying that the linear correlation coefficient between the centers of clusters is less than 0.36 [43]; if the algorithm did not converge based on this criterion, then the first relative minimum that was found was selected [44]. The algorithm of Hartigan and Wong [45] was used to perform the iterations, and the Euclidean distance was used as the distance measure.
The fourth and final step involved combining the NDVIat scores matrix (216 × n retained PCs) with the NDVIa clusters defined by the CA (represented by a row × 1 multinomial vector with), which result in a matrix that is referred to as NDVIac [column × (n retained PCs + 1)]. A discriminant model that considers the multinomial vector as a factor specifying the class for each observation and the scores of retained PCs as discriminators was then fit [46]. The moment method has been used to standardize estimators of the mean and variance. The clusters with different classifications were re-coded according to discrimination based on linear discriminant analysis (LDA). The LDA was then applied to the SPI3 score matrix as well. The final products of this approach were two multinomial vectors containing the classifications for NDVIa and SPI3 variables at monthly scales.
Overall, eight PCs retained 46 percent of the variance for NDVIa, while eight PCs retained 80 percent of the variance for SPI3. The clustering based on the k-means method identified eight similar groups for NDVIa and SPI3 variables. The LDA-based classifier improved the CA-based discrimination; e.g., the NDVIa variable has been structured in the groups N1, N2, N3, N4, N5, N6, N7 and N8, which contain 20, 55, 36, 40, 30, 15, 82 and 104 members, respectively, while the SPI3 variable has been reduced to the groups S1, S2, S3, S4, S5, S6, S7 and S8, which contain 44, 62, 56, 32, 49, 57, 49 and 33 members, respectively. Figure 4 shows a flowchart that illustrates the procedure described above.
It should be noted that the order of the identified clusters (N1 to N8) is not related to the spatial average of the NDVIa or SPI3 in NE South America; the order has been defined randomly by the applied algorithms used during the discrimination process while only considering the similarity between members as a criterion for clustering. Therefore, these clusters have been reclassified based on the median calculated from spatially averaged SPI3 and NDVIa values over the NE South America (Figure 5 and Figure 6) and will be referred to as patterns throughout the remainder of this study. The median was chosen for this purpose as it allows splitting the upper half of the NDVIa or SPI3 time series averaged over the entire NE South America area from the lower half.
This approach has linked the clusters N1, N2, N3, N4, N5, N6, N7 and N8 with the NDVIa patterns F5, F4, F7, F1, F6, F8, F2 and F3; and the clusters S1, S2, S3, S4, S5, S6, S7 and S8 with the SPI3 patterns F2, F6, F1, F8, F4, F7, F3 and F5. It is important to note that this new order provides information concerning the dominant process that is taking place, e.g., regarding the NDVIa patterns, F1 indicates the occurrence of a widespread greening over the entire NE South America (highest median), while F8 indicates the occurrence of a widespread browning in the entire study area (lowest median). Similarly, for the SPI3 patterns, F1 indicates the occurrence of widespread wet conditions over the NE South America (highest median), while F8 indicates the occurrence of widespread drought conditions over the NE South America (lowest median).

3. Results

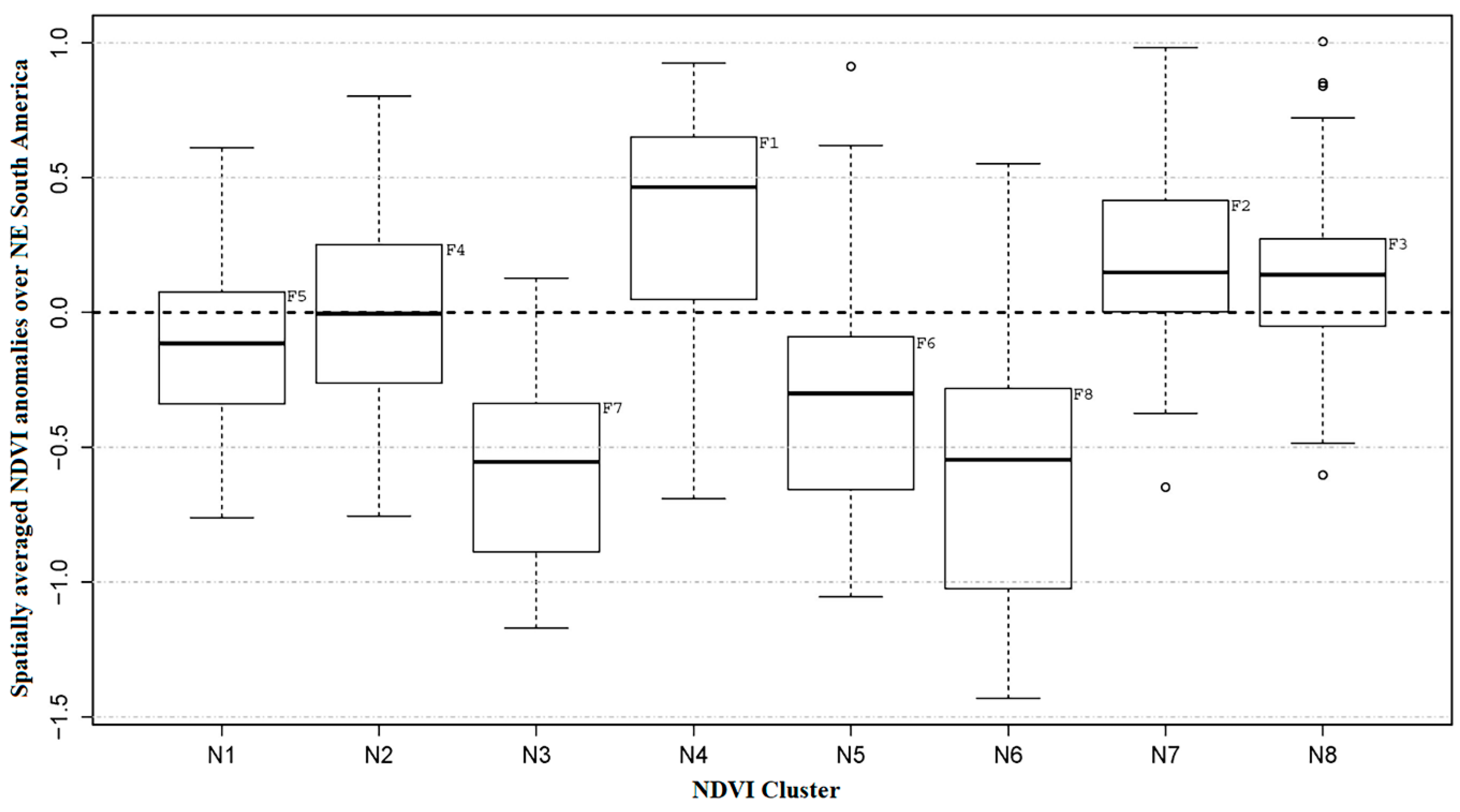
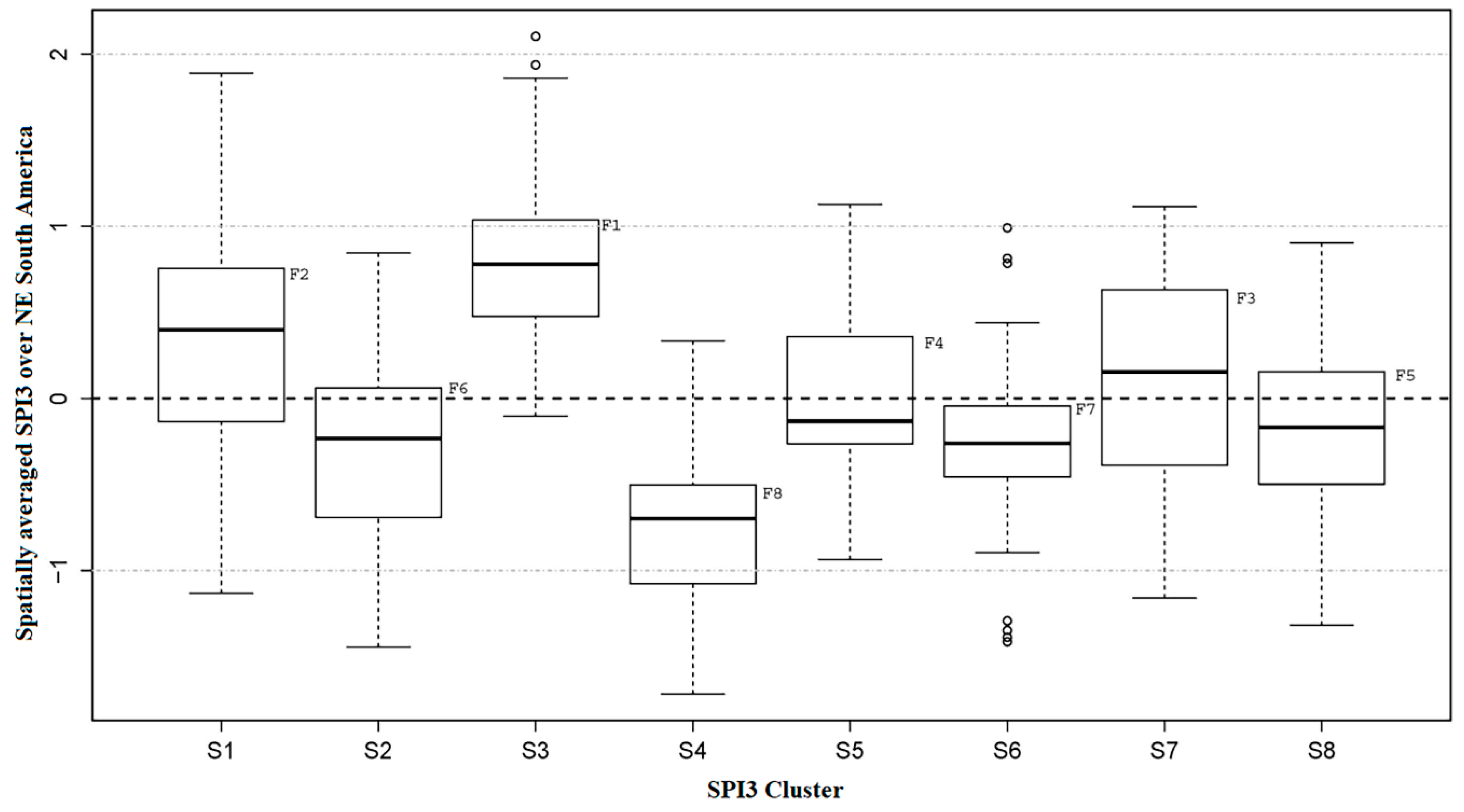
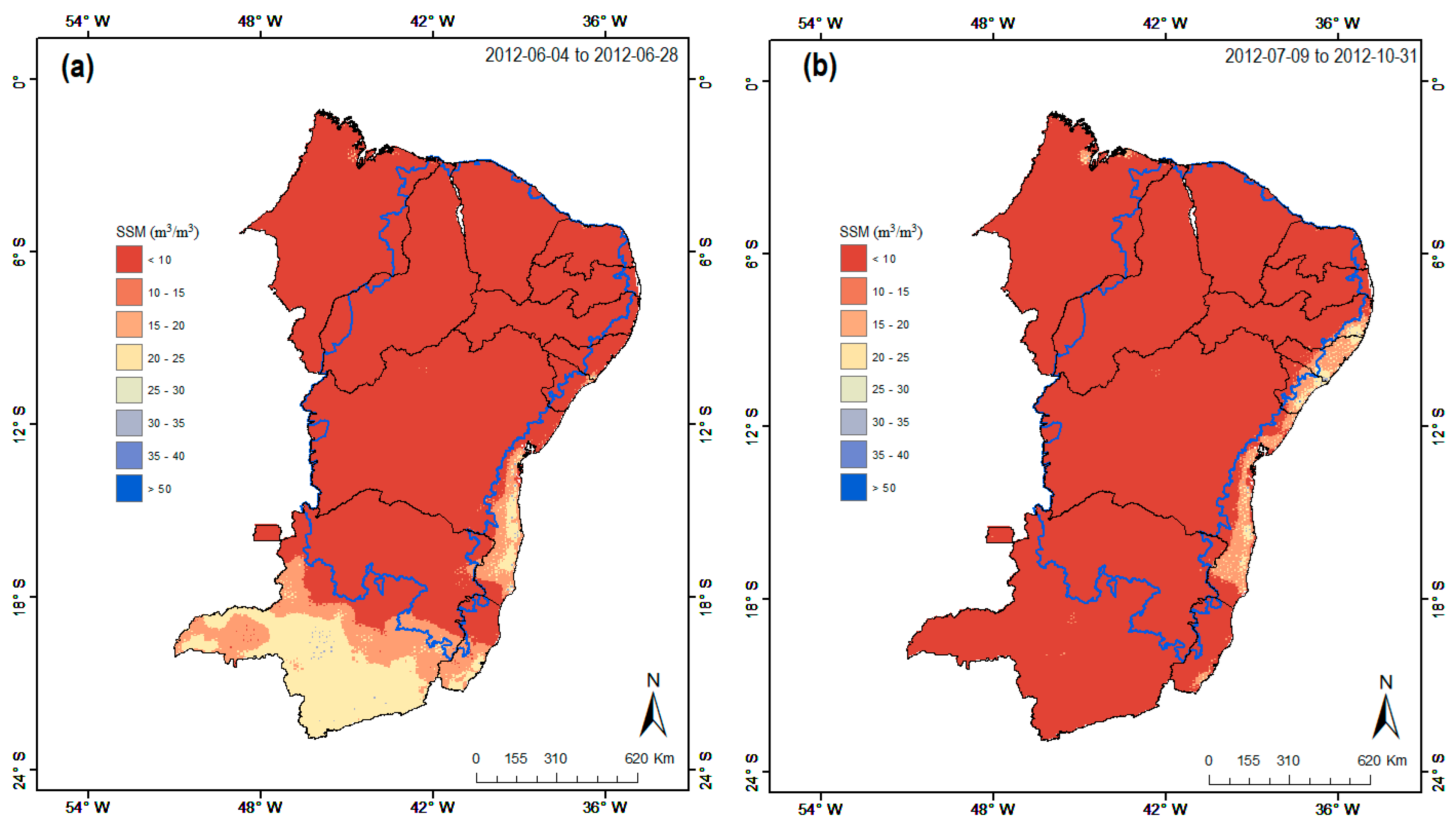
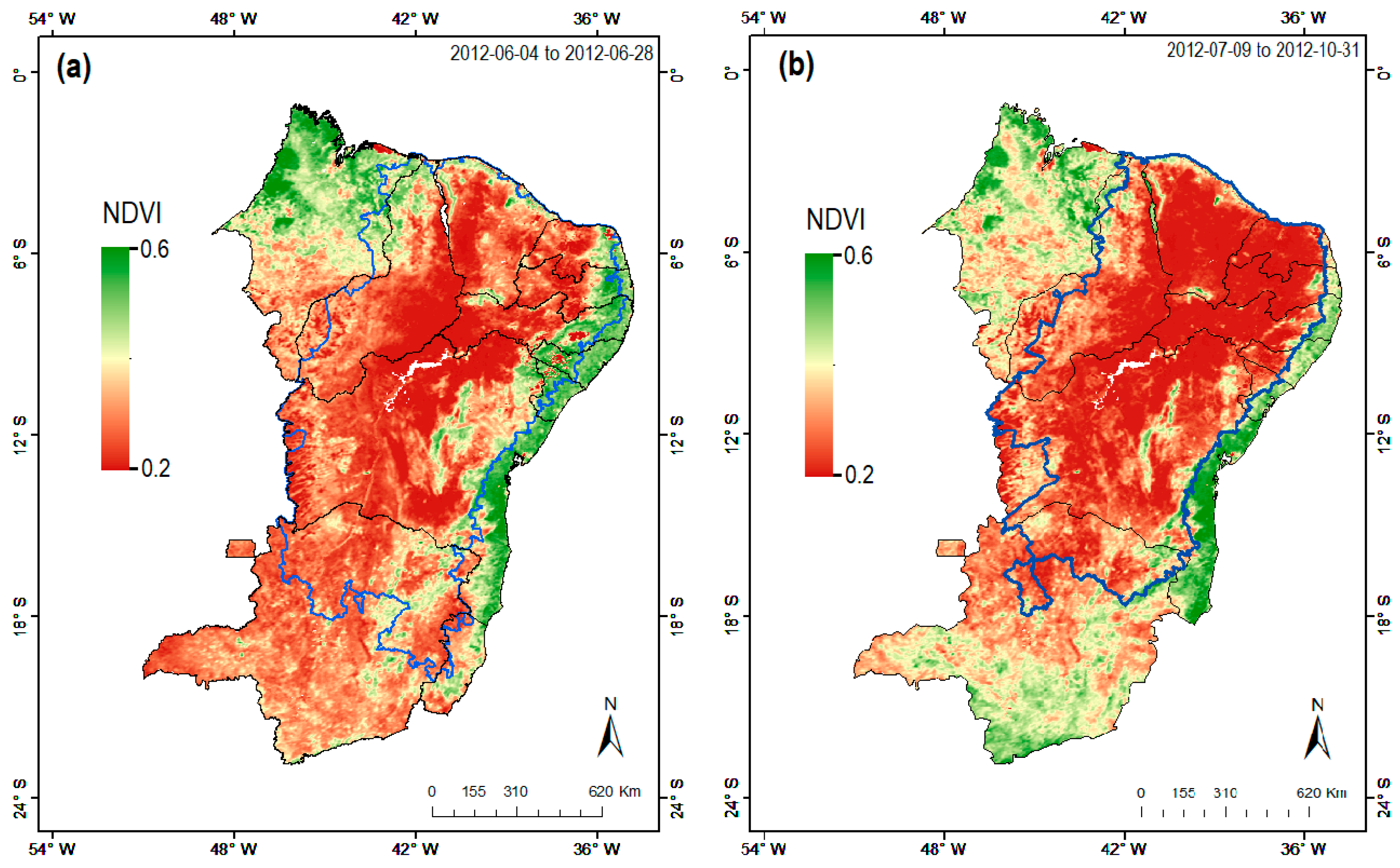
3.1. The Impacts of Flash Drought Events on Vegetation Dynamics over NE South America

A visual inspection of Figure 7d and Figure 7c shows the seasonal and interannual variations of NDVI and SPI-3 indices over the entire NE South America from 2004 to 2022. Regional analysis revealed that drought and wet cycles had considerable impacts on vegetation dynamics. The SPI-3 drought index shows that NE South America experienced intensified drought in the second decade of the 2000s, with 2012 and 2017 among two of the three worst droughts since 2004 (Figure 7). Annual rainfall was below the 18-year term average during the entire 2012–2017 period. This dry period was broken, dramatically, by a moderate La Niña event in 2020 with regional average annual rainfall surpassing the 18-year term average by nearly 190 mm. Although 2012 was the driest year in terms of annual rainfall within 2004–2022, both 0.6 µm (solar channel) and 10.8 µm (infrared radiation channel) decreased by -6% and -8K (see Appendix A), respectively, in the radiances measured by MSG satellites over NE South America. In addition, there was overall positive correlation of +0.51 between 0.6 µm and 10.8 µm, but it was also found many local of both positive and negative relationships. Increased radiative losses are clearly implicated in this enhanced drying, which enhanced atmospheric evaporative demand, coupled with below average rainfall in 2012 and 2017. Consistent with the results from the trends analysis of radiance fluxes estimated from the Meteosat Second Generation (MSG) satellites over 18 years (Appendix A) indicate that an overall drying trend in the NE South America semiarid ecosystem during the last two decades. This could explain vegetation stress or vegetative drought [17], mostly in Caatinga biome, induced by increased temperature and radiation and amplified by reduction in rainfall.
Overall, the second decade of the 2000s warm and dry periods spanning NE South America were characterized by below average rainfall and anomalously higher temperature, representing drought response to warming. Significant negative trend (P<0.05) in annual rainfall of -1,307 mm. year-1 and significant positive trend (>95th percentile) in annual air temperature of 0.762 °C. year-1 were identified for the period 2004-2022 (Figure 7a and Figure 7b).
There is ample evidence of differential responses of vegetation phenology to drought (i.e., SPI-3< −1) and wet extremes (i.e., SPI-3> +1) over NE South America – growth enhancement in vegetation is strongly controlled by water availability (Figure 7c). An overall reduced seasonality of vegetation phenology was detected from 2012–2017 (Figure 7c). In contrast, a general increase in vegetation seasonality, dominated by the wetter-than-average periods of 2004-2011 and 2018-2022, was identified. Additional changes in rainfall not only affect vegetation activity but also decreased vegetation phenology, as indicated in the shape and magnitude of seasonal NDVI profiles on the regional scale (Figure 7d). Yet evidence that there is some correspondence in the interannual variability of rainfall to noticeable seasonal differences in the NDVI extreme profiles. Over the entire study area and 18-year period, there were decreasing trend in NDVI over 17%.
The drought that affected this study area in 2012 was the most extreme in the period from 2004 to 2022, as indicated by consecutive negative SPI-3 lasting for 9–10 months (Figure 7c). Another way to look at the 2012 drought year is by computing soil moisture derived from remote sensing observations for describing the onset and termination time of this drought. The duration and interval of the data set processed is presented in Figure 8. Rapid and dramatic declines in soil moisture resulting from a period of abnormally warm-dry weather conditions over NE South America, with the peak of SPI-3 intensity of -2.50 (Figure 7b). A notable bimodal distribution was observed, with the dry-wet abrupt transition (i.e., nearly-flat line below the 20th percentile that is equivalent to NDVI ≈ 0.2). This is shown in Figure 8 for the timing when soil moisture reaches the value equal to the 20th percentile after drying of soil moisture (i.e., onset time of a drought event) and the increases in the soil moisture prior to the 20th percentile plus the 20th percentile amplitude during the wetting-up phase (i.e., end time of a drought event). Here the length of soil moisture deficit is calculated as the difference between end time and onset time of a drought event.
A more quantitative method to identify the timing, duration and intensification of the 2012 drought year can be computed through the rate of intensification using weekly soil moisture percentiles on the regional analysis [4,47]. This method may not analyze changes in drought per se, but changes in mean soil moisture that can be inferred to be related to the occurrence of events with high soil moisture deficits. Under conditions of critical soil moisture deficits, the threshold adopted here is twofold: 1) soil moisture is less than the 40th percentile, and 2) the peak drought intensity must fall below the 20th percentile. Two relevant flash droughts were identified, which occurred from June 04 to June 28 (duration = 24 days) and July 11 to October 31 (duration = 114 days). The two flash drought events were a subset of the 2012 drought year (the SPI = 303 days from January to October). The rate intensification for the short duration event (24 days) was relatively lower magnitude as compared to the high magnitude resulting from the long-duration event (114 days). In this analysis, flash droughts represented 46% of all droughts (SPI-3). A flash drought event was recognized when the absolute value of rate intensification of soil moisture retreated the 20th percentile per week. Of the flash droughts over the 2004–2022 period, 88.9% experienced rapid intensification within 4-weeks of drought onset (Figure 8).
Here SPI-3 variability is mostly driven by rainfall variability. SPI-3 is not intended to be a proxy of soil moisture, but rather a flexible metric of vegetation water stress. Regardless of the time scale of the SPI-3, a drought event begins when SPI-3 ≤ −1.00 and persists until SPI-3 > −1.00; the value of -1.00 is the threshold value that differentiates dry vs. non-dry. In general, the lower the time scale, the higher its capacity to identify short-term droughts [48]. When the soil moisture content dropping from the 40th percentile to below the 20th percentile is not shorter than 4 pentads (20 days), the NDVI exhibits values lower than 0.20. For example, if temperatures are abnormally high, evaporation increases, drying out soils beyond what would have occurred just from the lack of precipitation. This is particularly true for flash drought. Vegetation may play a critical role in flash drought self-intensification under dry conditions because it modulates soil moisture drying.
Spatial patterns in soil moisture and vegetation conditions are shown in Figure 9 and Figure 10, by the average pentad data of soil moisture content and values of NDVI over the two sub-seasonal changing periods in the 2012 flash-drought events. Resulting of the spatial analysis revealed differential impact of flash drought events on vegetation activity, primarily over the Caatinga vegetation (highlighted by red areas in Figure 10). The drought resulted in reduced vegetation activity across 88% of study area, which 96% areas showed soil moisture content below 10 (m3/m3). The persistence of low soil moisture content is still prominent, thus exposing NE South America to the strong effects of flash drought on vegetation activity, particularly over the Caatinga biome.
As shown in the Figure 9 and Figure 10, the values of NDVI are not changing uniformly over the study area, decreasing dramatically from the northwestern dry interior (where the vegetation was classified as xerophytic or Caatinga), to open savanna (the Cerrado vegetation). Overall, the contrast of NDVI values between the eastern-coastal-forested areas and the Caatinga has strong spatial variability. Different locations with the same value of NDVI are not necessarily have the same vegetation greenness. However, regional changes in NDVI are not only governed by changes in soil moisture, but also influenced by changes in land use (human signal). Yet, NDVI may be increased by irrigation, which can enhance vegetation activity in the short-medium term but may reduce resilience, by increasing risk of soil salinization. In much of NE South America, flash drought events were identified if the values of NDVI is less than 0.3 in which soil moisture becomes less than 10 (m3/m3) (i.e., the rate of soil drying). Robust declines in soil moisture occurred over Caatinga areas where the radiance in the solar measured by Meteosat decreased by about 0.608 W m-2 relative to the 2004-2022 period.

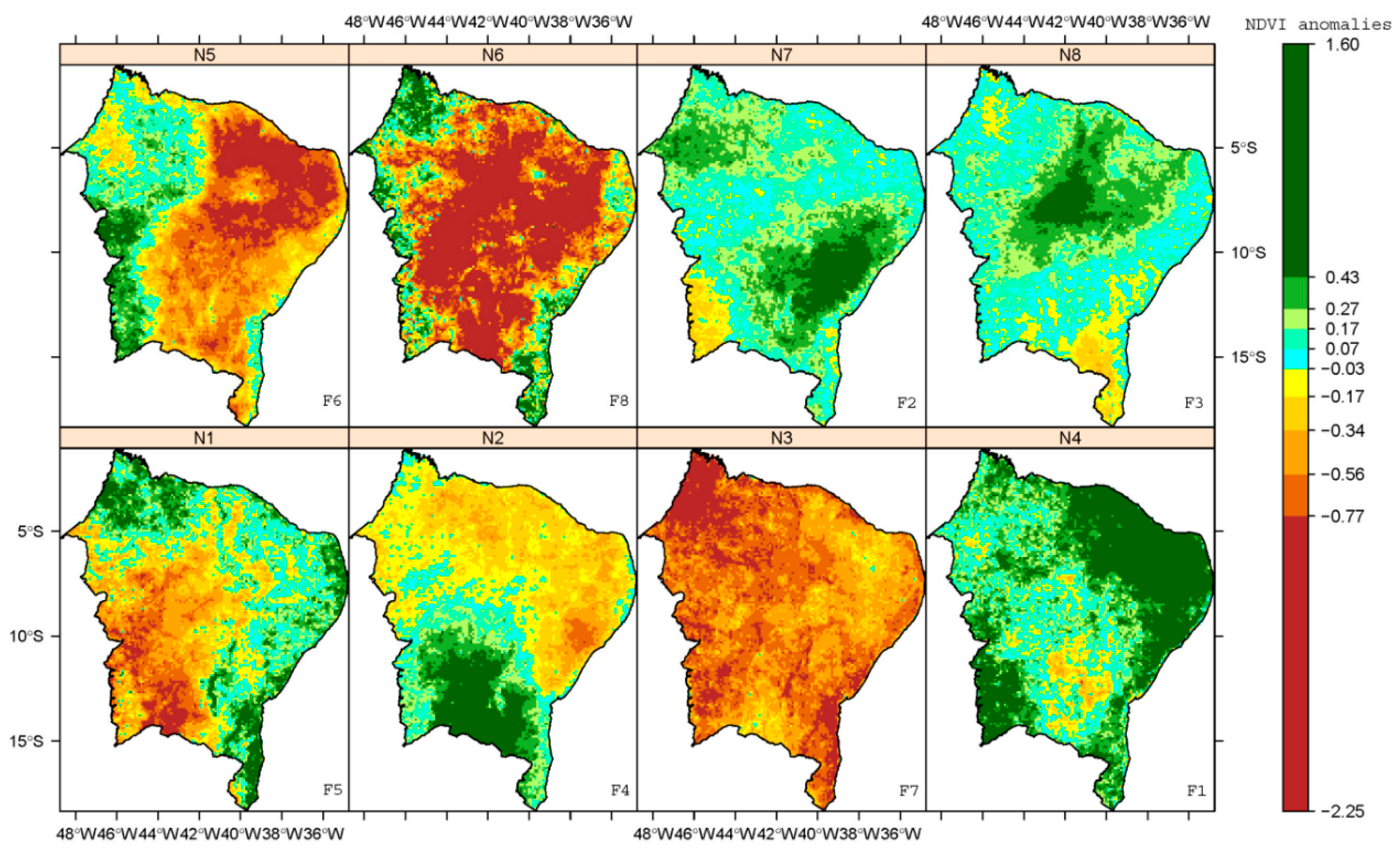
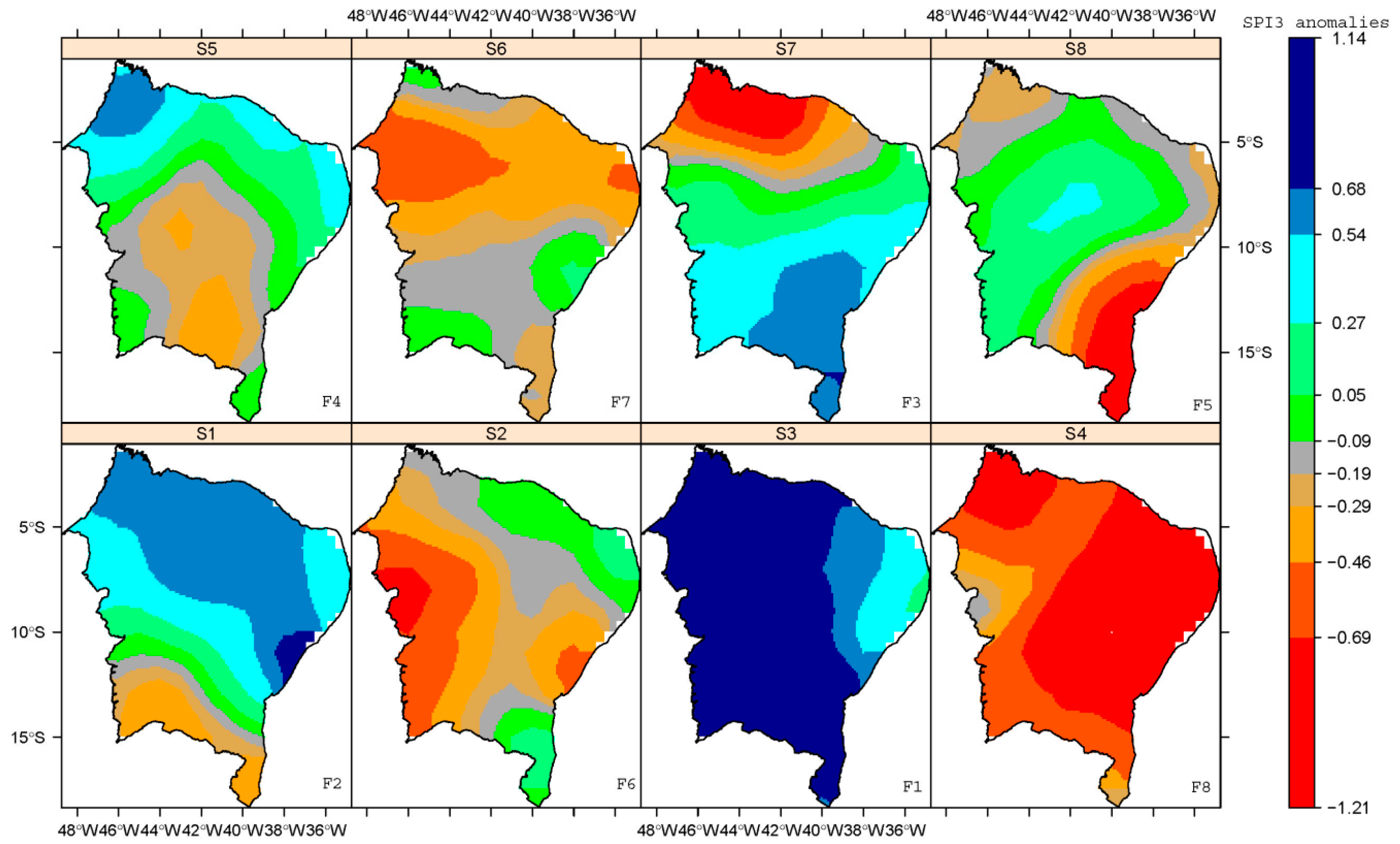
3.1. Ecogeographic Patterns in Vegetation Dynamics Across the NE South America

Regional maps were generated to assess large-scale ecogeographical patterns in vegetation growth (monthly averaged NDVI anomalies; see Section 2.4) over NE South America (Figure 11). Changes in large-scale clusters of vegetation activity are difficult to isolate from local scale based on the pixel, thus justifying the use of statistical method to capture the spatial and temporal features of gridded-NDVI anomalies. As a result, within the 2004–2022 period, eight sub-regions (N) were identified based on the cluster analysis. The regional centroids ranged from −0.55 to 0.47, whose seasonal domains (F) are defined in Figure 5. The corresponding maximum, median, and minimum area averaged-NDVI anomalies are shown in Figure 5. The regional response of the NDVI anomalies varies widely and is also dependent on its ecogeographical environment. The ecogeographical distribution of these sub-regions classified as N4, N7 or N8 (with positive centroids) for greening vegetation, and the distribution classified as N1 to N3, and N5 or N6 (with negative centroids) for browning vegetation.
Among the eight sub-regions through multivariate analyses, the sub-region where the average anomaly of NDVI is greater (cluster centroid) is N4, and it is associated with the green-up pattern (F1). Nonetheless, it is clear on Figure 5 and Figure 11 that N6 is characterized by the lowest anomaly of NDVI; it has the brown-down pattern (F8). Visually comparing variations of the NDVI anomalies (Figure 11) show that ecogeographical transition zones between green-up and brown-down environments are identified, which also exhibit differential responses of ecosystems to humid and drought conditions across space and among the main land cover types (Caatinga, Cerrado, Atlantic Forest, and Tropical Rainforest) of the study area. It is apparent that changes in the brown-down areas were dependent on land cover types, increasing dramatically from the northeastern dry interior (where the vegetation was classified as a xeric scrubland and open thorn forest), to open shrub woodland. Additionally, these brown-down areas are dominated by Caatinga’s species, which are highly sensitive to drought variability, land use, soil properties, and topography. For example, vegetation on loamy soils responded much more to drought conditions than other soils [8].
Given that NE South America’s ecosystems are affected by rainfall variability on the sub-regional level, it is natural to consider to which extent this variability can be attributed to either climatic variability or human induced environmental change. This variability was evaluated via a multivariate analysis of both the distribution (in %) and the spatial distribution for NDVI (Figure 11) and SPI-3 (Figure 12) anomalies. The size and magnitude of the different clustering groups did not differ much between the NDVI and SPI3 data analyses. The intra-regional variability (F1 and F8 ecogeographic patterns) between NDVI and SPI3 anomalies across extreme humid and drought conditions were very similar, as shown in Figure 7. However, the spatial distribution was not always the same. In all the F2, F3, F4, F5, F6 and F7 patterns for the NDVI and SPI3 anomalies were found to considerably differ among them. This is largely attributed to an increase in rainfall does not result in higher green-up because NE South America ecosystems are also covered with evergreen species or, the other way round, a decrease in rainfall does not result in further brown-down because these ecosystems are already covered with minimal vegetation growth. The influence of rainfall in the variations of NDVI was low and perhaps human factors (land use change and landscape disturbance) have stronger impact in all the patterns from F2 to F7.

4. Results and Final Remarks

To characterize flash drought events, this study assessed the rainfall deficits influence on vegetation activity over NE South America by combine time series of surface drought indicators with vegetation index based on satellite dataset, and to recognize to which extent the drought-vegetation relationship can be attributed to rainfall variability depletion of soil moisture resulting from dry weather conditions.
The NE South America region experienced the driest years (2012-2017) in the twentieth century. The observed changes in air temperature above normal for the climatic conditions, combined with a wet season rainfall marked by significant water deficiencies, may have contributed to a drier climate (Figure 7 and Appendix A). Periods of drought-breaks and the persistence of low vegetation growth were prominent, particularly after the onset, thus exposing the region to the impacts of flash drought events (Figure 8). For instance, soil moisture may play a role in drought self-intensification under dry conditions in which vegetation growth is dormant and leads to higher atmospheric evaporative demand, yet still maintain capability to contribute to the length of flash drought events [4,16,47].
Here, flash droughts were identified as the consequent rainfall deficiency at SPI-3< −1 for a period of five consecutive weeks or more, which the soil moisture content dropping from the 40th percentile to below the 20th percentile, with the NDVI lower than 0.30 unit. Soil moisture limitations is often more relevant than atmospheric dryness to explain vegetation stress, in semi-arid regions [49].
At regional scales and sub-regional scales, the results showed abrupt shifts in vegetation activity between dry and wet rainfall variations (Figure 7). Overall, the rainfall – NDVI relationship varied across eco-climatic zones (Figure 11 and Figure 12). Rainfall was a stronger driver of NDVI. It was found that negative NDVI anomaly pattern identified the influence of drought on vegetation because water scarcity can negatively affect vegetation growth and thus the corresponding the NDVI lower than 0.30 unit. It is important to emphasize that the NDVI lower than 0.30 unit does not always indicate vegetation stress condition in which atmospheric evaporative demand plays an important role (Appendix A). Examples of such impact is when declining agricultural productivity due to climate change drives an intensification of agriculture elsewhere, which may cause land degradation [25]. Distinction between the impacts of climate variation and land degradation/improvement is an important and contentious issue. There is no simple and straightforward way to disentangle these two effects. The interaction of different determinants of primary production is not well understood and a critical limitation to such disentangling is a lack of understanding of the inherent seasonal and inter-annual variability of vegetation dynamics [24,25,26].
Results from multivariate analysis indicate that the effect of soil moisture changes on vegetation-dependent rainfall varies across biomes, soil and vegetation types, involving a delayed response of vegetation to rainfall. The lagged SPI-NDVI correlation was regionally dependent, with the north and central areas of the study area having a rapid response to the lagged SPI-NDVI, while in eastern, western, and southern areas it was delayed by three months. For instance, grassland to xerophytic thorn savanna (shallowly rooted plants) and shrub woodland (deeply rooted plants), responded differently to drought conditions. Most of the studies based on rainfall-NDVI relationship are valid for woody vegetation, but also herbaceous vegetation composition seems to be responsive to drought conditions in a similar way [25]. As shown by several studies, NDVI might for some biomes (Floresta Amazônica e Mata Atlântica) be indirectly driven by rainfall anomalies [23] while the direct impacts on NDVI might be negligible [22,25]. Additionally, NDVI can be affected by land use changes and desertification [25]. This can cause problems for assessing how rainfall anomalies and NDVI response interact at the landscape level.
Due to lack of consistent definition and data on flash drought in NE South America, it is not straightforward to make a characterization of changes in flash drought using a single universal definition [50] or directly measured based on a single variable [51]. Ground-based soil moisture observations are available in some areas but still scarce [20]. However, flash drought variability as function of satellite-based vegetation indices has not been assessed in NE South America. A key advantage of satellite-based vegetative drought estimates is the temporal resolution of some products providing subdaily data for vegetation indices (e.g., Meteosat Second Generation; Barbosa et al. [17]). Thus, results confirmed the SEVIRI-derived vegetation index product (NDVI) has performed quite well. Furthermore, based on the SEVIRI estimates over its Mean Field of View (MFOV), the results revealed a negative trend in the evolution of the radiance in the solar (around -6%) and infrared radiation (around -8K) bands, over NE South America, for the 2004-2022 period. Overall, the results from this trend analysis indicated that in the NE South America’s Caatinga biome, there was an increase in dryness or aridity.
Since each satellite-based drought index has different strengths, weaknesses, and limitations, the drought early warning systems should be based on the combination of an ensemble of satellite-based drought indices. Nonetheless, whenever possible, in situ data should be added to improve forecast accuracy and reliability. Yet, there is no clear-cut distinction between a flash drought event and a dry spell event, although usage implies that they are of different space and time scales in general. Flash drought-based definitions also vary depending on the selection of the percentile-based sample of soil moisture, whether they are from the entire year or from only wet days [52]. Under conditions of critical soil moisture deficits, plant water deficits (low NDVI unit) are generally critically affected by high levels of atmospheric evaporative demand; however, the effects can be limited outside the vegetation growing season and under humid soil moisture but dry atmospheric conditions.
Future research will be oriented on the use of other types of drought indices and/or satellite vegetation indices to characterize the impact of flash droughts on vegetation response. Moreover, since NDVI is taken as rainfall proxy, it carries some limitations about the local rainfall variability. For instance, the NDVI- rainfall relationship depicts a quasi-linearity, without consideration of nonlinear factors (like in soil moisture and soil types), especially in tropical semi-arid areas where soil erosion is highly sensitive to vegetation cover and drought variability.

Supplementary Materials

Appendix A

Author Contributions

H.A.B wrote the paper.

Funding

This work was supported by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES 01/2022), Brazil, through PEPEEC (Programa Emergencial de Prevenção e Enfretamento de Desastres Relacionados a Emergências Climáticas, Eventos Extremos e Acidentes Ambientais), under the Grant/Award Number (88881.7050501/2022-01 to H.A.B).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

This study was undertaken as part of the PEPEEC project supported by CAPES (Grant # 88881.7050501/2022-01 to H.A.B). The author wishes to thank the EUMETSAT (European Organization for the Exploitation of Meteorological Satellites) and INMET (Brazilian Meteorological Institute) for making the SEVIRI NDVI-derived daily product and ground-data publicly available, respectively. Data generated as part of this study are available from the author upon request.

Conflicts of Interest

The author declares that he no conflict of interest.

Appendix A

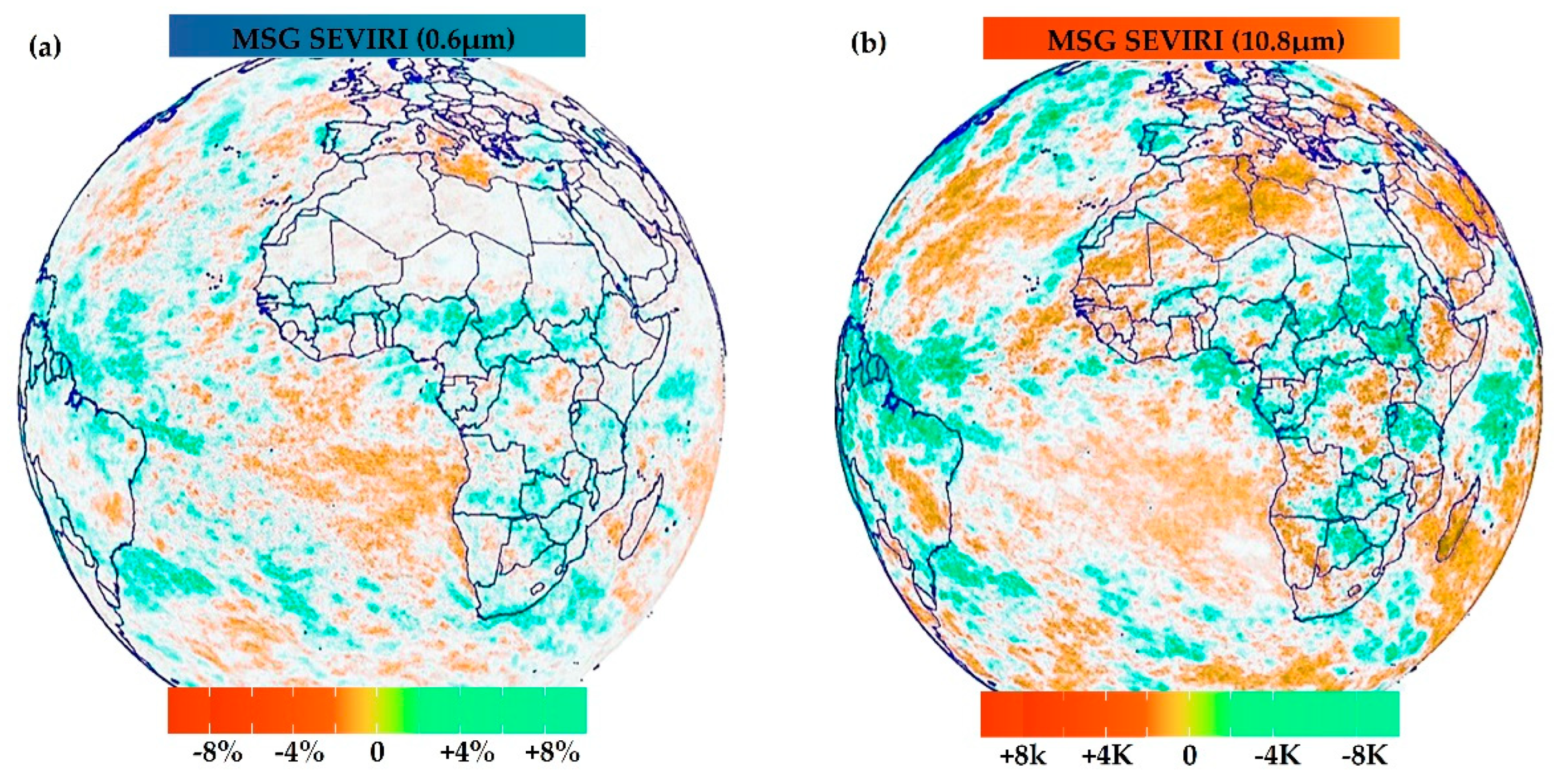
Preprints 85611 g0a1
Figure A1. Resulting of the trends analysis of radiance fluxes estimated from the Meteosat Second Generation (MSG) satellites over 18 years provide indication of the climate influence on surface soil moisture deficits caused by higher temperatures over NE South America. (a) The trend of solar radiation (channel at 0.6µm), with units of solar albedo (%) after comparison of the radiance with the solar constant. (b) (b) Trend of infrared thermal (IR) radiation (channel at 10.8 µm), in units of kelvin (K) after conversion of the radiance through the Planck function into a brightness temperature. Because regionally complete information at high tem-poral resolution is of crucial importance to the statistical analysis, the choice of pentad (i.e., the mean over 5 days) was a com-promise between achieving the highest possible temporal resolution and still maintaining a coarse enough resolution to guar-antee pixel information in almost all pixel cells (see Section 2.2.1). The calibrated and geolocated (level 1.5) radiance is a com-pressed version of the original data with a resolution of 3km under the nominal field of view of Meteosat at 0 degrees longitude, every 15 minutes for the 2004-2022 period. A few pentads are missing in the level 1.5 dataset, which together with the high-resolution resampling occasionally resulted in pixel cells without information. Daily 1.5-data for a full scan were only used at 1200 UTC (late morning), because it leads to near-polar orbiting time that crosses over the equator at approximately 1200UTC. A few pentads are missing in the level 1.5 dataset, which together with the high-resolution resampling occasionally resulted in cells without information. This should not affect the outcome of the results. Overall, the results from this trend analysis showed that in NE South America, there was an increase in dryness or aridity.
Figure A1. Resulting of the trends analysis of radiance fluxes estimated from the Meteosat Second Generation (MSG) satellites over 18 years provide indication of the climate influence on surface soil moisture deficits caused by higher temperatures over NE South America. (a) The trend of solar radiation (channel at 0.6µm), with units of solar albedo (%) after comparison of the radiance with the solar constant. (b) (b) Trend of infrared thermal (IR) radiation (channel at 10.8 µm), in units of kelvin (K) after conversion of the radiance through the Planck function into a brightness temperature. Because regionally complete information at high tem-poral resolution is of crucial importance to the statistical analysis, the choice of pentad (i.e., the mean over 5 days) was a com-promise between achieving the highest possible temporal resolution and still maintaining a coarse enough resolution to guar-antee pixel information in almost all pixel cells (see Section 2.2.1). The calibrated and geolocated (level 1.5) radiance is a com-pressed version of the original data with a resolution of 3km under the nominal field of view of Meteosat at 0 degrees longitude, every 15 minutes for the 2004-2022 period. A few pentads are missing in the level 1.5 dataset, which together with the high-resolution resampling occasionally resulted in pixel cells without information. Daily 1.5-data for a full scan were only used at 1200 UTC (late morning), because it leads to near-polar orbiting time that crosses over the equator at approximately 1200UTC. A few pentads are missing in the level 1.5 dataset, which together with the high-resolution resampling occasionally resulted in cells without information. This should not affect the outcome of the results. Overall, the results from this trend analysis showed that in NE South America, there was an increase in dryness or aridity.
Preprints 85611 g0a1

References

  1. IPCC: Summary for Policymakers. In: Climate Change and Land: an IPCC special report on climate change, desertification, land degradation, sustainable land management, food security, and greenhouse gas fluxes in terrestrial ecosystems [P.R. Shukla, J. Skea, E. Calvo Buendia, V. Masson-Delmotte, H.- O. Pörtner, D. C. Roberts, P. Zhai, R. Slade, S. Connors, R. van Diemen, M. Ferrat, E. Haughey, S. Luz, S. Neogi, M. Pathak, J. Petzold, J. Portugal Pereira, P. Vyas, E. Huntley, K. Kissick, M. Belkacemi, J. Malley, (eds.)]. 2019, In press.
  2. IPCC Summary for Policymakers. In: Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change [Masson-Delmotte, V., P. Zhai, A. Pirani, S.L. Connors, C. Péan, S. Berger, N. Caud, Y. Chen, L. Goldfarb, M.I. Gomis, M. Huang, K. Leitzell, E. Lonnoy, J.B.R. Matthews, T.K. Maycock, T. Waterfield, O. Yelekçi, R. Yu, and B. Zhou (eds.)]. 2021, In Press.
  3. Hunt, E.D.; Svoboda, M.; Wardlow, B.; Hubbard, K.; Hayes, M.; Arkebauer, T. Monitoring the effects of rapid onset of drought on non-irrigated maize with agronomic data and climate-based drought indices. Agric. For. 10 Meteorol. 2014, 191, 1–11. [Google Scholar] [CrossRef]
  4. Otkin, J.A.; Svoboda, M.; Hunt, E.D.; Ford, T.W.; Anderson, M.C.; Hain, C.; et al. Flash droughts: A review and assessment of the challenges imposed by rapid-onset droughts in the United States. Bull. Am. Meteorol. Soc. 2018, 99, 911–919. [Google Scholar] [CrossRef]
  5. Ault, T.R.; Cole, J.E.; Overpeck, J.T.; Pederson, G.T.; Meko, D.M. Assessing the Risk of Persistent Drought Using Climate Model Simulations and Paleoclimate Data. J. Clim. 2014, 27, 7529–7549. [Google Scholar] [CrossRef]
  6. Cook, B.I.; Cook, E.R.; Smerdon, J.E.; Seager, R.; Williams, A.P.; Coats, S.; et al. North American megadroughts in the Common Era: Reconstructions and simulations. Wiley Interdiscip. Rev. Clim. Chang. 2016, 7, 411–432. [Google Scholar] [CrossRef]
  7. Garreaud, R.D.; Alvarez-Garreton, C.; Barichivich, J.; Boisier, J.P.; Christie, D.; Galleguillos, M.; et al. The 2010–2015 megadrought in central Chile: impacts on regional hydroclimate and vegetation. Hydrol. Earth Syst. Sci. 2017, 21, 6307–6327. [Google Scholar] [CrossRef]
  8. Buriti, C.; Barbosa, H.A.; Paredes-Trejo, F.J.; Kumar, T.V.L.; Thakur, M.K.; Rao, K.K. Un Siglo de Sequías: ¿Por qué las Políticas de Agua no Desarrollaron la Región Semiárida Brasileña? Rev. Bras. Meteorol. 2020, 35, 683–688. [Google Scholar] [CrossRef]
  9. Paredes-Trejo, F.; Barbosa, H. Evaluation of the SMOS-Derived Soil Water Deficit Index as Agricultural Drought Index in Northeast of Brazil. Water 2017, 9, 377. [Google Scholar] [CrossRef]
  10. Devanand, A.; Huang, M.; Ashfaq, M.; Barik, B.; Ghosh, S. Choice of Irrigation Water Management Practice Affects Indian Summer Monsoon Rainfall and Its Extremes. Geophys. Res. Lett. 2019, 6, 9126–9135. [Google Scholar] [CrossRef]
  11. Osman, M.; Zaitchik, B.F.; Badr, H.S.; Christian, J.I.; Tadesse, T.; Otkin, J.A.; Anderson, M.C. mosman01/Flash_Droughts: Flash Droughts – SMVI (Version v1.0.0) [Data set], Flash drought onset over the Contiguous United States: Sensitivity of inventories and trends to quantitative definitions, Zenodo. 2021. [CrossRef]
  12. Sehgal, V.; Gaur, N.; Mohanty, B.P. Global surface soil moisture drydown patterns. Water Resources Research 1029, 57, 1. [Google Scholar] [CrossRef]
  13. Nguyen, H.; Wheeler, M.C.; Otkin, J.A.; Cowan, T.; Frost, A.; Stone, R. Using the evaporative stress index to monitor flash drought in Australia. Environ. Res. Lett. 2019, 14, 064016. [Google Scholar] [CrossRef]
  14. Noguera, I.; Domínguez-Castro, F.; Vicente-Serrano, S.M. Characteristics and trends of flash droughts in Spain, 1961–2018. Annals of the New York Academy of Sciences 2020, 1472, 155–172. [Google Scholar] [CrossRef] [PubMed]
  15. Lisonbee, J.; Woloszyn, M.; Skumanich, M. Making sense of flash drought: definitions, indicators, and where we go from here. Journal of Applied and Service Climatology 2021, 001. [Google Scholar] [CrossRef]
  16. Otkin, J.A.; Anderson, M.C.; Hain, C.; Svoboda, M.; Johnson, D.; Mueller, R.; et al. Assessing the evolution of soil moisture and vegetation conditions during the 2012 United States flash drought. Agric. For. Meteorol. 2016, 218, 230–242. [Google Scholar] [CrossRef]
  17. Barbosa, H.A.; Kumar, T.V.L.; Paredes, F.; Elliott, S.; Ayuga, J.G. Assessment of Caatinga response to drought using Meteosat SEVIRI Normalized Difference Vegetation Index (2008–2016). ISPRS Journal of Photogrammetry and Remote Sensing 2019, 148, 235–252. [Google Scholar] [CrossRef]
  18. Marengo, J.A.; Torres, R.R.; Alves, L.M. Drought in Northeast Brazil-past, present, and future. Theoretical and Applied Climatology 2017, 129, 1189–1200. [Google Scholar] [CrossRef]
  19. Novaes, R.L.M.; Felix, S.; Souza, R.F. Save Caatinga from drought disaster. Nature, 2013, 498, 170. [CrossRef]
  20. Buriti, C.O.; Barbosa, H.A. Um século de secas: por que as políticas hídricas não transformaram o Semiárido Brasileiro?. 1. ed. Lisboa-Portugal: Chiado Editora, 2018, 1, 305p.
  21. Marengo, J.A., Cunha, A.P.M.A., Nobre, C.A., Ribeiro Neto, G.G., Magalhaes, A.R., Torres, R.R., Sampaio, G., Alexandre, F., Alves, L.M., Cuartas, L.A., Deusdará, K.R.L., Álvala, R.C.S. Assessing drought in the drylands of northeast Brazil under regional warming exceeding 4 °C. Natural Hazards 2020, 102, 1−26. [CrossRef]
  22. Barbosa, H.A.; Huete, A.R.; Baethgen, W.E. A 20-year study of NDVI variability over the Northeast Region of Brazil. J. Arid Environ, 2006, 67, 288–307. [CrossRef]
  23. Barbosa, H.A.; Lakshmi Kumar, T.V. Influence of rainfall variability on the vegetation dynamics over Northeastern Brazil. Journal of Arid Environments, 2016, 124, 377-387. [CrossRef]
  24. Ruppert, J.C.; Holm, A.; Miehe, S.; Muldavin, E.; Snyman, H.A.; Wesche, K.; Linstädter, A. Meta-analysis of ANPP and rain-use efficiency confirms indicative value for degradation and supports non-linear response along precipitation gradients in drylands. J. Veg. Sci., 2012, 23, 1035–1050. [CrossRef]
  25. Barbosa, H.A.; Lakshmi Kumar, T.V.; Silva, L.R.M. Recent trends in vegetation dynamics in the South America and their relationship to rainfall. Natural Hazards (Dordrecht), 2015, 77, 883-899. [CrossRef]
  26. Huxman, T.E.; et al. Convergence across biomes to a common rain-use efficiency. Nature, 2004, 429, 651–654. [CrossRef]
  27. Santiago, D.B.; Barbosa, H.A.; Correia Filho, W.L.F.; Oliveira-Junior, J.F. Interactions of Environmental Variables and Water Use Efficiency in the Matopiba Region via Multivariate Analysis. Sustainability, 2022, 1, 1–13 doiorg/103390/su14148758. [Google Scholar] [CrossRef]
  28. Paredes-Trejo, F.; Barbosa, H.A.; Daldegan, G.A.; Teich, I.; García, C. L; Kumar, T. V. Lakshmi; Buriti, C.O. Impact of Drought on Land Productivity and Degradation in the Brazilian Semiarid Region. Land, 2023, 12, 954. [CrossRef]
  29. IBGE, Instituto Brasileiro de Geografia e Estatística (IBGE) Sinopse Do Censo Demográfico 2023.
  30. MAPBIOMAS O Projeto. [s. l.]. 2019. Available online: https://mapbiomas.org/o-projeto (accessed on 10 January 2022).
  31. Correia, W.L.; José, O.J.; Dimas, B.S.; Paulo, B.T.; Paulo, E.T.; Givanildo, D.G.; Claudio, C.B.; et al. Rainfall variability in the Brazilian Northeast Biomes and their interactions with meteorological systems and ENSO via CHELSA product. Big Earth Data 2019, 3, 315–37. [Google Scholar] [CrossRef]
  32. EUMETSAT A planned change to the MSG Level 1.5 image production radiance definition. EUMETSAT Sci. Rep. EUM/OPS-MSG/TEN/06/0519, 2007, 9. Available online: http://www.eumetsat.int/groups/ops/documents/document/ pdf_msg_planned_change_level15.pdf.
  33. Ertürk, A.G.; Elliott, S.; Barbosa, H.A.; Samain, O.; Heinemann, T.; Yıldırım, A.; van de Berg, L. Pre-operational NDVI Product Derived from MSG SEVIRI. 2014, 7p. Available online: https://www-cdn.eumetsat.int/files/2020-04/pdf_conf_p57_s1_05_erturk_p.pdf.
  34. González-Zamora, Á.; Sánchez, N.; Martínez-Fernández, J.; Gumuzzio, Á.; Piles, M.; Olmedo, E. Long-term SMOS soil moisture products: A comprehensive evaluation across scales and methods in the Duero Basin (Spain). Phys. Chem. Earth, Parts A/B/C 2015, 84–84, 123–136. [Google Scholar] [CrossRef]
  35. Spatafora, L.R.; Vall-llossera, M.; Camps, A.; Chaparro, D.; Alvalá, R.C. dos S.; Barbosa, H. Validation of SMOS L3 AND L4 Soil Moisture Products In The Remedhus (SPAIN) AND CEMADEN (BRAZIL) Networks. Rev. Bras. Geogr. Física 2020, 13, 691. [Google Scholar] [CrossRef]
  36. McKee, T.B.; Doesken, N.J.; Kleist, J. ; others. In The relationship of drought frequency and duration to time scales. In Proceedings of the Proceedings of the 8th Conference on Applied Climatology (17 - 22 January 1993); American Meteorological Society: Anaheim, California, 17, 179–183. 1993. [Google Scholar]
  37. Stacy, E.W. A generalization of the gamma distribution. The Annals of Mathematical Statistics 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
  38. Hosking, J.R.M.; Wallis, J.R. Regional frequency analysis: an approach based on L-moments. Cambridge University, 2005, Press.
  39. Rao, V.B.; Hada, K.; Herdies, D.L. On the severe drought of 1993 in northeast Brazil. International journal of climatology 1995, 15, 697–704. [Google Scholar] [CrossRef]
  40. Belayneh, A.; Adamowski, J. Standard precipitation index drought forecasting using neural networks, wavelet neural networks, and support vector regression. Applied Computational Intelligence and Soft Computing, 2012, 6, 1–13. [Google Scholar] [CrossRef]
  41. Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate distributions for climatological drought indices (SPI and SPEI). International Journal of Climatology 2015, 13, 4027–4040. [Google Scholar] [CrossRef]
  42. Jolliffe, I.T. Rotation of principal components: choice of normalization constraints. Journal of Applied Statistics, 1995, 22, 29-35. [CrossRef]
  43. Mo, K.; Ghil, M. Cluster analysis of multiple planetary flow regimes. Journal of Geophysical Research. 1988, 93, 10927–10952. [Google Scholar] [CrossRef]
  44. James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An introduction to statistical learning. New York: Springer, 2013.
  45. Hartigan, J.; Wong, M. A K-means clustering algorithm. Applied Statistics, 1979, 28, 100-108. [CrossRef]
  46. Kemp, F. Modern Applied Statistics with S. Journal of the Royal Statistical Society 2003, 52, 704–705. [Google Scholar] [CrossRef]
  47. Ford, T.W.; Labosier, C.F. Meteorological conditions associated with the onset of flash drought in the eastern United States. Agric. For. Meteor., 2017, 247, 414– 423. [CrossRef]
  48. Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
  49. Stocker, B.D.; Zscheischler, J.; Keenan, T.F.; Prentice, I.C.; Penuelas, J.; Seneviratne, S.I. Quantifying soil moisture impacts on light use efficiency across biomes. New Phytol., 2018, 218, 1430–1449. [Google Scholar] [CrossRef]
  50. Lloyd-Hughes, B. The impracticality of a universal drought definition. Theor. Appl. Climatol., 2014, 117, 607–611. [CrossRef]
  51. Wilhite, D.A. Integrated drought management: moving from managing disasters to managing risk in the Mediterranean region. Euro-Mediterr J. Environ. Integr., 2019, 4, 42. [Google Scholar] [CrossRef]
  52. Schär, C.; Ban, N.; Fischer, E.M.; Rajczak, J.; Schmidli, J.; Frei, C.; et al. Percentile indices for assessing 58 changes in heavy precipitation events. Clim. Change, 2016, 137, 201–216. [CrossRef]
Preprints 85611 g001
Figure 1. Location map of the Caatinga biome and its geographic features (topography) within NE South America. It covers approximately 735,000 km² and comprises the following states: Alagoas (AL), Bahia (BA), Ceará (CE), Maranhão (MA), Paraíba (PB), Piauí (PI), Pernambuco (PE), Rio Grande do Norte (RN) and Sergipe (SE).
Figure 1. Location map of the Caatinga biome and its geographic features (topography) within NE South America. It covers approximately 735,000 km² and comprises the following states: Alagoas (AL), Bahia (BA), Ceará (CE), Maranhão (MA), Paraíba (PB), Piauí (PI), Pernambuco (PE), Rio Grande do Norte (RN) and Sergipe (SE).
Preprints 85611 g001
Preprints 85611 g002
Figure 2. NE South America: (a) its nine states, including the Caatinga biome, along with the spatial distribution of temporary and permanent crops in 2006 [29]; (b) mean annual rainfall for the 2004-2022 period provided by the Brazilian Meteorological Institute (INMET: https://portal.inmet.gov.br).
Figure 2. NE South America: (a) its nine states, including the Caatinga biome, along with the spatial distribution of temporary and permanent crops in 2006 [29]; (b) mean annual rainfall for the 2004-2022 period provided by the Brazilian Meteorological Institute (INMET: https://portal.inmet.gov.br).
Preprints 85611 g002
Preprints 85611 g003
Figure 3. Near real-time SEVIRI data flow processing at Laboratório de Análise e Processamento de Imagens de Satélites (LAPIS: https://www.lapismet.com.br).
Figure 3. Near real-time SEVIRI data flow processing at Laboratório de Análise e Processamento de Imagens de Satélites (LAPIS: https://www.lapismet.com.br).
Preprints 85611 g003
Preprints 85611 g004
Figure 4. Procedure applied for reducing the high dimensionality of the NDVIa or SPI3 matrices.
Figure 4. Procedure applied for reducing the high dimensionality of the NDVIa or SPI3 matrices.
Preprints 85611 g004
Preprints 85611 g005
Figure 5. Spatially averaged NDVIa over the entire NE South America grouped by the NDVI clusters for the period 1982-2012. The labels F1 to F8 located in top-right of each box indicates the decreasing order each NDVI cluster according to median calculated from spatially averaged NDVIa over the entire NE South America. Each box shows the median and first and third quartiles, while the whiskers extend to the last values that are 1.5 times the inter-quartile range above or below the quartiles. The medians are equals to -0.115, -0.004, -0.554, 0.466, -0.301, -0.547, 0.149 and 0.140 by the clusters N1, N2, N3, N4, N5, N6, N7 and N8, respectively. .
Figure 5. Spatially averaged NDVIa over the entire NE South America grouped by the NDVI clusters for the period 1982-2012. The labels F1 to F8 located in top-right of each box indicates the decreasing order each NDVI cluster according to median calculated from spatially averaged NDVIa over the entire NE South America. Each box shows the median and first and third quartiles, while the whiskers extend to the last values that are 1.5 times the inter-quartile range above or below the quartiles. The medians are equals to -0.115, -0.004, -0.554, 0.466, -0.301, -0.547, 0.149 and 0.140 by the clusters N1, N2, N3, N4, N5, N6, N7 and N8, respectively. .
Preprints 85611 g005
Preprints 85611 g006
Figure 6. As in Figure 5, but here for the SPI clusters. The medians are equals to 0.400, -0.232, 0.781, -0.699, -0.132, -0.260, 0.155 and -0.169 by the clusters S1, S2, S3, S4, S5, S6, S7 and S8, respectively.
Figure 6. As in Figure 5, but here for the SPI clusters. The medians are equals to 0.400, -0.232, 0.781, -0.699, -0.132, -0.260, 0.155 and -0.169 by the clusters S1, S2, S3, S4, S5, S6, S7 and S8, respectively.
Preprints 85611 g006
Preprints 85611 g007
Figure 7. Regional mean changes in annual mean rainfall (mm), annual mean air temperature (0C), and the impact of rainfall anomaly on the vegetation greenness response for NE South America from 2004 to 2022. (a) Annual variability of mean rainfall amount (mm) over the 512 grid cells within NE South America. (b) Annual variability of mean air temperature (0C) over the 512 grid cells within NE South America. (c) Five-day averaged SEVIRI NDVI over the 512 grid cells within NE South America from 2004 to 2022. A drought pentad (5-day-mean) is defined as when SPI-3 was less than -1.0, and a wet week is defined as when SPI-3 was greater than 1.0. Mean drought severity, defined as the mean SPI of drought period (SPI-3 < -1.0). Each pentad SEVIRI NDVI is marked with a circle from 2004 to 2012. (d) Seasonal variations of SEVIRI NDVI profile during 2009 (wet year; the solid blue line) and 2012 (drought year; the solid yellow line) for NE South America for the entire period 2004-2022.
Figure 7. Regional mean changes in annual mean rainfall (mm), annual mean air temperature (0C), and the impact of rainfall anomaly on the vegetation greenness response for NE South America from 2004 to 2022. (a) Annual variability of mean rainfall amount (mm) over the 512 grid cells within NE South America. (b) Annual variability of mean air temperature (0C) over the 512 grid cells within NE South America. (c) Five-day averaged SEVIRI NDVI over the 512 grid cells within NE South America from 2004 to 2022. A drought pentad (5-day-mean) is defined as when SPI-3 was less than -1.0, and a wet week is defined as when SPI-3 was greater than 1.0. Mean drought severity, defined as the mean SPI of drought period (SPI-3 < -1.0). Each pentad SEVIRI NDVI is marked with a circle from 2004 to 2012. (d) Seasonal variations of SEVIRI NDVI profile during 2009 (wet year; the solid blue line) and 2012 (drought year; the solid yellow line) for NE South America for the entire period 2004-2022.
Preprints 85611 g007
Preprints 85611 g008
Figure 8. Time series of 5-day averaged soil moisture in 2012 from SMOS-based SSM (m3/m3) over NE South America. The pentad is the mean over 5 days of consecutive soil moisture. The orange and red dashed lines denote the 40th– 20th percentile range of soil moisture values.
Figure 8. Time series of 5-day averaged soil moisture in 2012 from SMOS-based SSM (m3/m3) over NE South America. The pentad is the mean over 5 days of consecutive soil moisture. The orange and red dashed lines denote the 40th– 20th percentile range of soil moisture values.
Preprints 85611 g008
Preprints 85611 g009
Figure 9. Regional comparison of (a) averaged soil moisture from 2012-06-04 to 2012-06-28 and (b) averaged soil moisture from 2012-07-09 to 2012-10-31 for major flash drought events. Blue line area within the NE South America highlights its semi-arid domain (Caatinga biome).
Figure 9. Regional comparison of (a) averaged soil moisture from 2012-06-04 to 2012-06-28 and (b) averaged soil moisture from 2012-07-09 to 2012-10-31 for major flash drought events. Blue line area within the NE South America highlights its semi-arid domain (Caatinga biome).
Preprints 85611 g009
Preprints 85611 g010
Figure 10. As in Figure 9, but here for the SEVIRI NDVI. Regional comparison of (a) averaged SEVIRI NDVI from 2012-06-04 to 2012-06-28 and (b) averaged SEVIRI NDVI from 2012-07-09 to 2012-10-31 for major flash drought events. Blue line area within the NE South America highlights (a) its semi-arid domain and (b) its Caatinga biome, respectively.
Figure 10. As in Figure 9, but here for the SEVIRI NDVI. Regional comparison of (a) averaged SEVIRI NDVI from 2012-06-04 to 2012-06-28 and (b) averaged SEVIRI NDVI from 2012-07-09 to 2012-10-31 for major flash drought events. Blue line area within the NE South America highlights (a) its semi-arid domain and (b) its Caatinga biome, respectively.
Preprints 85611 g010
Preprints 85611 g011
Figure 11. Monthly averaged SEVIRI NDVI anomalies for each NDVIa pattern during the 2004–2022 period. The N1 to N8 label located in top-center in each panel indicates the NDVI cluster. The F1 to F8 label located in bottom-right in each panel indicates the decreasing order each NDVI cluster according to median calculated from spatially averaged NDVIa over the entire NE South America.
Figure 11. Monthly averaged SEVIRI NDVI anomalies for each NDVIa pattern during the 2004–2022 period. The N1 to N8 label located in top-center in each panel indicates the NDVI cluster. The F1 to F8 label located in bottom-right in each panel indicates the decreasing order each NDVI cluster according to median calculated from spatially averaged NDVIa over the entire NE South America.
Preprints 85611 g011
Preprints 85611 g012
Figure 12. As in Figure 11, but here for the SPI3 patterns. The S1 to S8 label located in top-center in each panel indicates the SPI3 cluster.
Figure 12. As in Figure 11, but here for the SPI3 patterns. The S1 to S8 label located in top-center in each panel indicates the SPI3 cluster.
Preprints 85611 g012
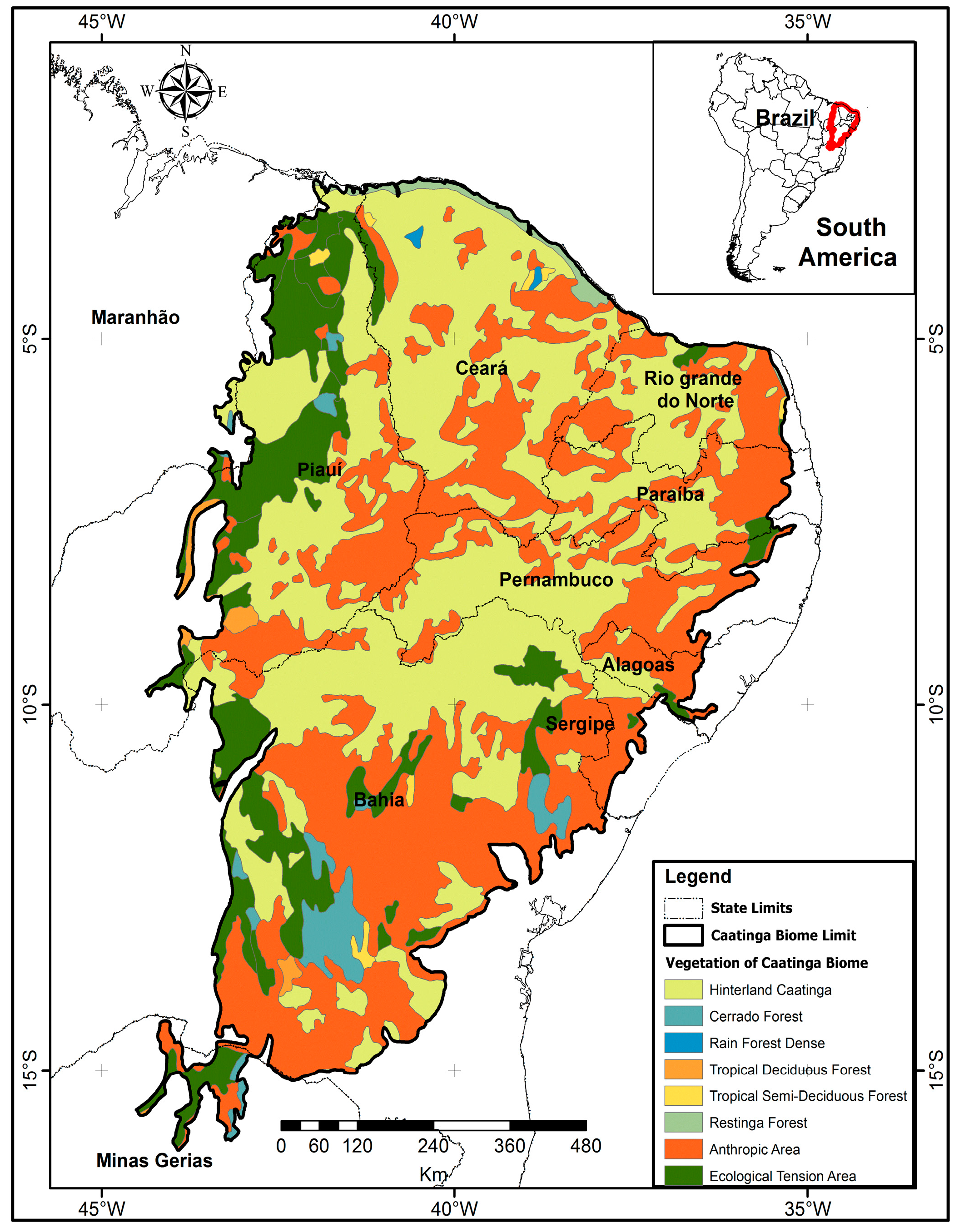
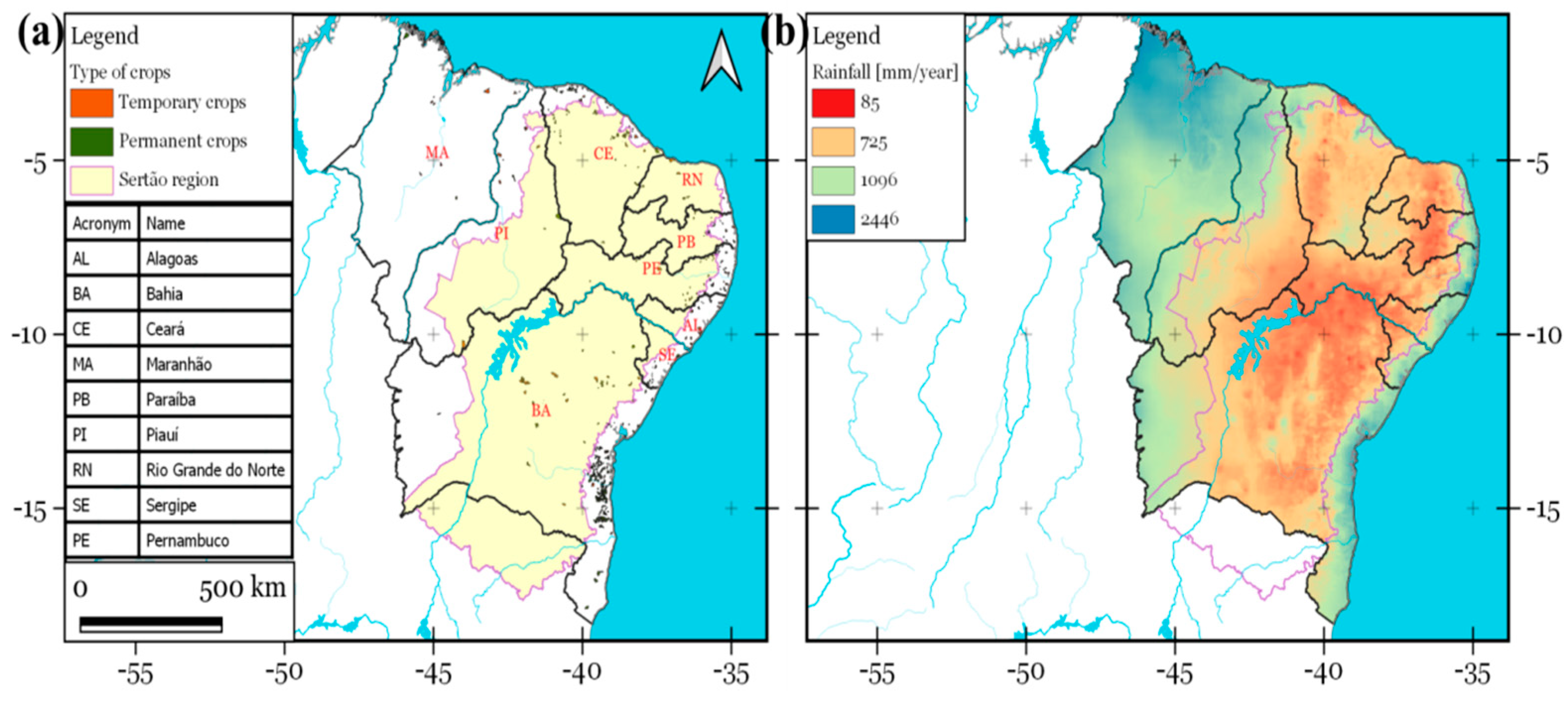
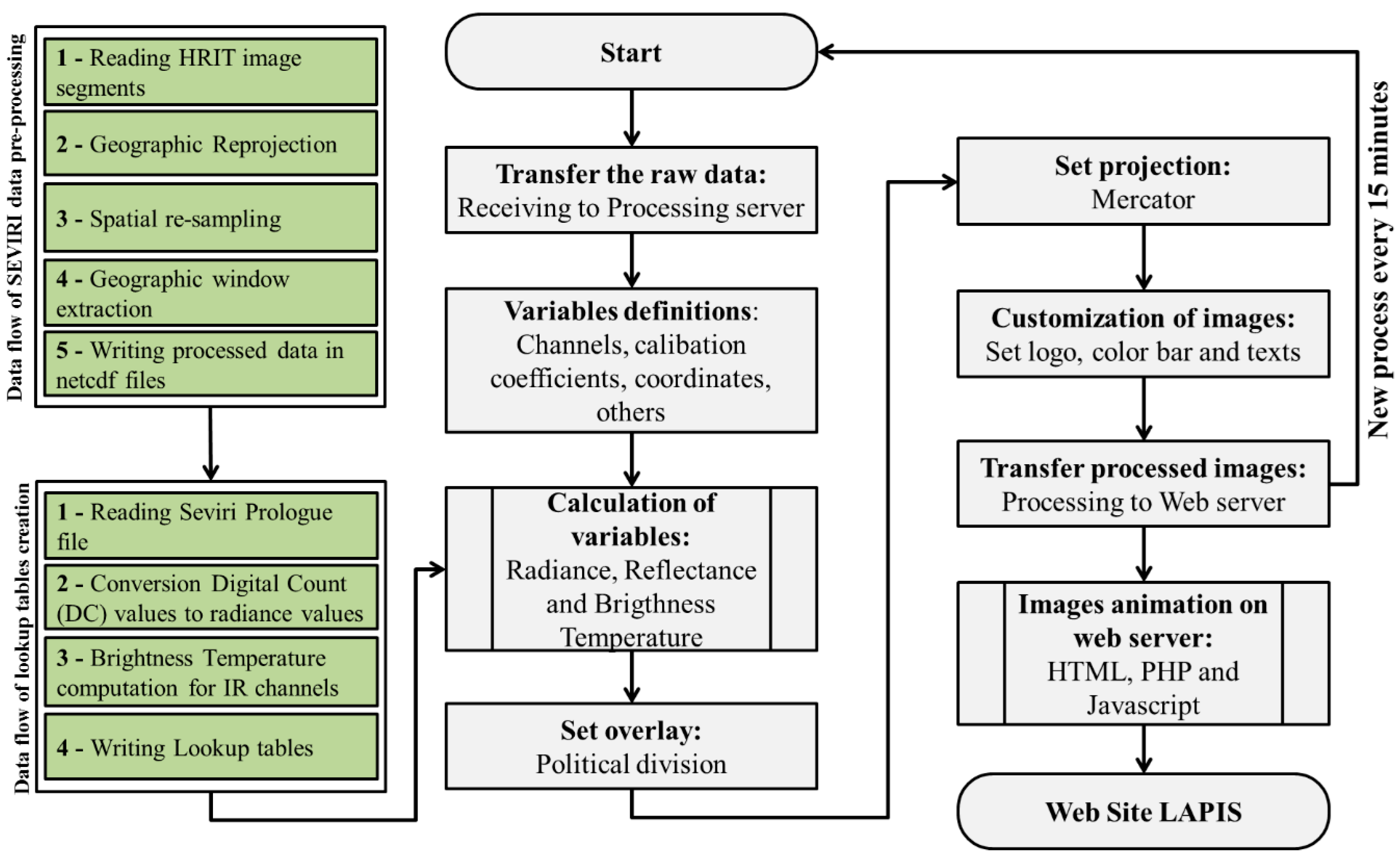
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated