Prerpints.org logo
Preprint
Article

Bi-Mirror Tunable Reflective Axicon-like Device for Broadband THz Applications

Altmetrics

Downloads

84

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.docx (175.85KB )

This version is not peer-reviewed

Submitted:

22 September 2023

Posted:

25 September 2023

You are already at the latest version

Alerts
Abstract
THz radiation has assumed a great importance thanks to the efforts in the development of technological tools used in this versatile band of the electromagnetic spectrum. Here we propose a reflecting bi-mirror axicon-like device with wavelength-independent long focusing performances in the THz band, by exploiting the high thermo-mechanical deformation of the elastomer polydimethylsiloxane (PDMS). This deformation permits to achieve significant optical path modulations in the THz band and effective focusing. The surface of a PDMS layer is covered with a gold thin film, acting as heater thanks to its absorption for wavelengths below ~500 nm . An invariance property of the Fresnel integral has been exploited to verify experimentally the THz performances of the device with an ordinary visible laser source, finding excellent agreement with the theoretical predictions at 1 and 3 THz. The same property allowed also to verify experimentally that the axicon focus has a longitudinal extension much greater than that one exhibited by a benchmark cylindrical mirror with the same optical power. The axicon is thermo-mechanically stable up to a heating power of 270 mW, although it might be potentially exploited at higher powers with a minor degradation of the optical performances.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

The radiation in the THz range (0.1 THz up to 10 THz) has demonstrated so far a high flexibility for the use in many different applications. Indeed, the implementation of tools for bio-medical [1,2,3,4,5], industrial [6,7], communications [8,9,10] or sensing [11,12] operating in this frequency range, has received great attention, together with the prerequisite of the proper managing of the THz radiation, and a lot of innovative solutions has been currently examined so far [13,14,15,16,17,18,19].
Among the different optical functions, the long focusing by means of the generation of Quasi Bessel Beams (QBBs) is one of the most studied because of the potential benefits in many field, like remote sensing, optical trapping and sensing [20]. Currently, the most performing approaches, like Computer Numerical Control, namely CNC , injection molding and milling [21,22,23], are still time and money consuming. Aiming to overcome these drawbacks, recent progresses in 3D printing have been successfully exploited to produce less expensive and still even exotic geometries for THz devices [24,25,26,27,28], but at the moment the resolution of conventional 3D printers (~100 μm) limits the quality of the finishing of the surfaces, and as a consequence 3D printed devices usually operate at wavelengths not lower than than 500 μm.
More sophisticated devices based on all-dielectric metasurfaces can be effective in generating QBBs [29], but the design tolerances limit the wavelength range of operation and the focus extension, and require sophisticated fabrication hardware. Good results have been achieved with the use of more conventional fabrication tools. For instance, traditional polymeric refractive conical axicons exhibited good long focusing properties in an extended THz range (0.1- 1 THz)[30], while axicons working at 0.55 THz formed by sedimentation of SiO2 particles have demonstrated to reduce the number of fabrication steps [31].
Apart the inherent drawbacks of complex technical implementation and the potential limitations in the exploitable frequency range, all the proposed devices lack an important feature, namely the tunability at different working wavelengths.
This latter problem has been partially resolved by the technology of Parallel Plate Waveguide Structures (PPWG) in the range 0.1- 1 THz [32,33], because the relatively long wavelength considerably relaxes the opto-mechanical tolerances and allows the mass production with minimal efforts. This technology has been proposed to fabricate axicons with an operating frequency in a restricted range, namely 0.35 THz -0.45 THz, that can be tuned by a simple repositioning of triangularly sagomated metal foils [34] . However, PPWG devices seem not suitable to operate in the range of higher THz frequencies, as the use of lower wavelengths, down to 30 μm, would strongly limit the mechanical design tolerances and the waveguide losses.
In this work, we report on a tunable metallic optical axicon-like system exploitable in the band 1-10 THz, by exploiting the potentials of such thermomechanical devices just demonstrated in [35].
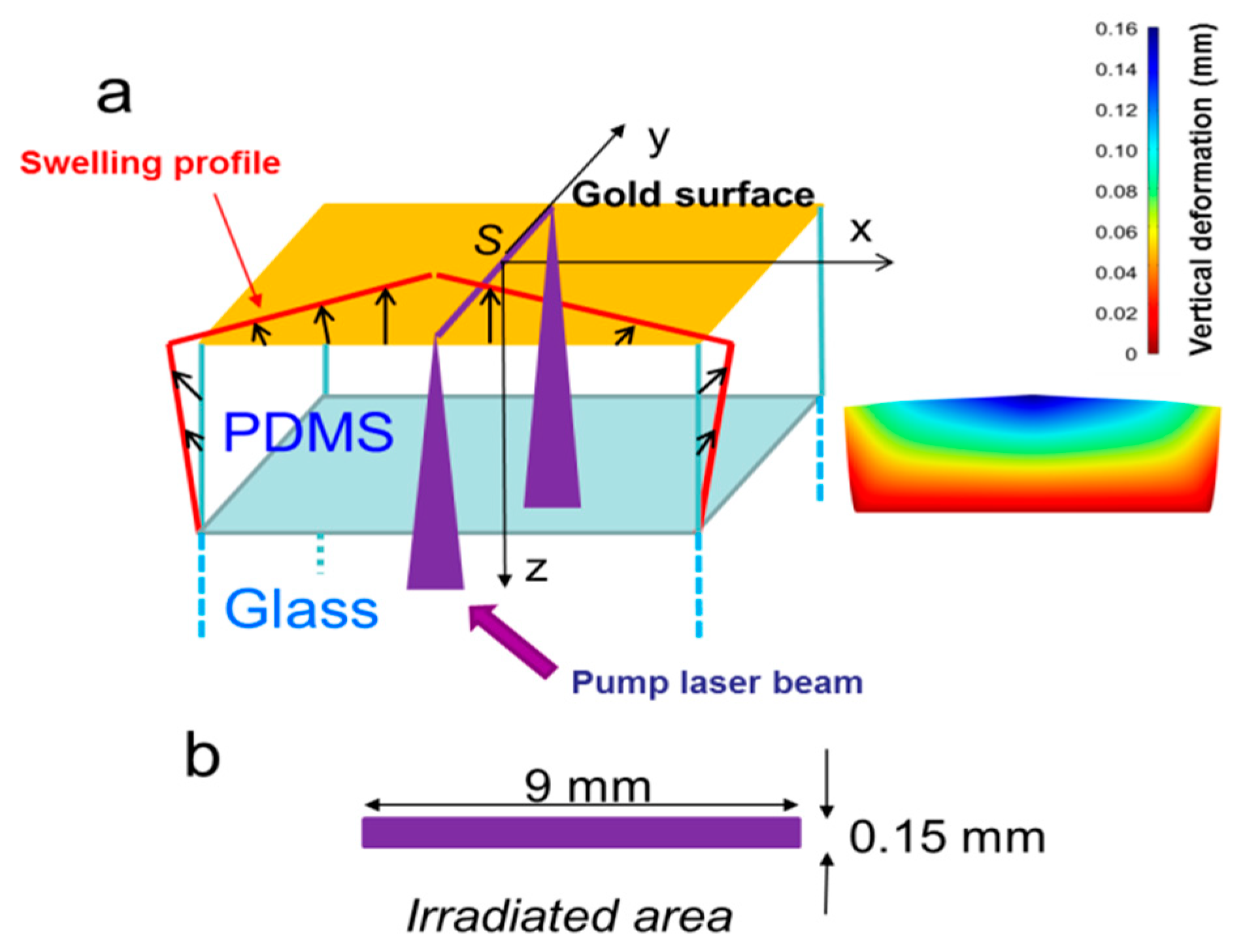
The core structure is a Fresnel- like bimirror axicon, generated by the modification of the profile of a gold-coated PDMS layer when a heating radiation is focused onto a line (1D). Due to the strong absorption of gold for wavelengths below ∼ 500 nm, PDMS expands and, thanks to its high dilatation coefficient, a two pitches roof-like reflective structure is generated. The maximum swelling amplitude is as high as 164 μm, so that under reflection a significant optical path difference (OPD) can be obtained, corresponding to the spectral region of THz wavelengths. Indeed, we demonstrate that when a Gaussian wave impinges on the device, the reflected light beam spreads in the far field, while a well resolved virtual focus is formed behind the reflecting surface. By exploiting an invariance property of the Fresnel diffraction integrals, we implemented a method to simulate experimentally the behavior of our device at 1 and 3 THz by using a visible radiation. The proposed axicon can be easily modulated by simply varying the pump power, operates with low power consumption and is not affected by chromatic dispersion in the whole THz band, which represents a common drawback in traditional THz radiation beam shaping systems.

2. Theoretical modeling

2.1. Thermomechanical model

In this section we present the modeling of the thermal-mechanical-optical behavior of the proposed device, at first inferring the maximum optical power allowing the safe use of the device, and then calculating the swelling profiles at different heating powers. These profiles have been used to evaluate the optical behavior, with both ray tracing and electromagnetic calculations.
The geometry used for the computations is illustrated in Figure 1(a), and considers three main regions. The lower one is a BK7 glass substrate (1 mm thickness), covered by a layer of PDMS with a thickness of 1.5 mm (second region), on which a gold thin film with a thickness of about 100 nm is deposited. The device is surrounded by the third medium, air in the present case.
The sample is illuminated with a pump beam (λ = 450 nm) from the air side and focused on a line (Figure 1(b)), where it has a uniform intensity. The heated area has a length of 9 mm, much higher than its transversal FWHM in the x direction (FWHMx) of 0.15 mm. Given the huge difference between the dimensions of the heated area, the thermomechanical behavior of the device can be modeled considering an indefinite 2D structure along the y-direction. Since gold has a strong absorption at the wavelength of 405 nm, it heatens efficiently the PDMS, provoking its huge swelling due to the high coefficient of linear thermal expansion of about 3·10−4 °C−1 [36].
The purpose of the thermo-mechanical study is to determine the swelling profile at increasing heating powers Ph, namely the fraction of the optical pump power converted into heat, and establish the power Ph that produces a temperature Tmax= 300 °C, that we consider the maximum temperature for the safe use of the device. At a first glance, this limit can seem excessive, as the data sheets report a temperature limit od PDMS of ~200°C. Nevertheless, it has been demonstrated that actually PDMS begins to degrade at temperatures around 300-350°C, at which the components of the polymer begins to decompose in volatile products [37].
The calculations have been performed with COMSOL 5.3a software in the 2D indefinite frame. The temperature Tmax= 300 °C is obtained at Phmax= 270 mW, corresponding to a power density of 2.0·105 W/m2. This condition gives rise to the spatial temperature distributions shown in Figure 2(a), (b) for surface and depth profiles, respectively. The surface temperature halves at a distance from the symmetry plane of 1.20 mm (x-direction), while this occurs at a depth of 1.08 mm from the PDMS surface (z-direction).
The temperature Tmax corresponds to the maximum swelling of 164 μm. The transverse profile of the deformation is reported in Figure 3(a). As shown, the profile is described by a y-invariant triangle-like function, with almost constant slopes at both sides up to an x-coordinate of about ± 2.5 mm.
Indeed, the root mean square (RMS) of the deviation with respect to a the best-fit linear function is 623 nm on 2 mm on the x-axis. This structure well resembles a 1D axicon working in reflecting mode. The effect of the increase of Ph is illustrated in the plot of Figure 3(b). Herein, we see that the top swelling increases linearly with Ph, with a rate A=0.61 μm/mW. Thus, the function representing the y-invariant swelling profile, namely f(x), can be obtained by multiplying an adimensional function g(x) by a factor H representing the maximum deformation for a given Ph, namely f(x)=H·g(x) , where H= A·Ph. The average slope of the flanks, namely β, increases linearly as well, with a rate of 9.3·10−5 rads/mW, reaching a value of 0.025 rads at Ph = Phmax. To summarize, the swelling induced in the PDMS layer can be very high, with protrusions that can push in a range corresponding to the THz wavelengths, where a significant spatial modulation of the light intensity is thus expected.
This statement was demonstrated in the subsequent optical modeling.

2.2. Optical modeling

A preliminary evaluation has been obtained with a 2D ray-tracing analysis by coupling three physics modules in Comsol: Heat Transfer, Solid Mechanics and Geometrical Optics . The input ray distribution is constituted by a bundle of rays with a full aperture of 2 mm, indefinite in the y-direction, impinging on the device parallel to the y-z symmetry plane (zero angle of incidence). The results are shown in Figure 4, in which the input rays (not reported in the figure for sake of clarity) is split into two separate bundles of rays, whose angular aperture is proportional to the impinging power, reaching ~ 0.1 rads at Ph=270 mW.
By prolonging the reflected rays in the region z < 0 , a virtual focus region is produced. Thus, a positive optical relay will be necessary to use effectively the THz probe radiation. In principle, one could produce also a real focus by launching the probe rays from the PDMS side, but in this way the radiation would experience a dispersive effect, leading to chromatic aberrations in the considered THz broad spectral window.
The light distribution in the virtual focus has been calculated with the Electromagnetic Beam Wave Envelope approximation implemented in the Comsol Wave Optics module, using a THz input field with Gaussian distribution invariant in the y-direction, with waist w0 = 1 mm and unit amplitude, namely Uin(x)= exp(-(x/w0)2).
In spite of the finite extension of the actual input field in the y-direction, we will demonstrate in the Experimental Section that this modeling assumption is well reproduced experimentally. With this hypothesis, we calculated the length (DOFax) and the minimum width (Dax) of the virtual line focus. Here, we adopt the usual definition of DOFax as the Full Width at Half Maximum (FWHM) extension of the axial light intensity distribution, and Dax as the minimum FWHM of the intensity distribution on to the x-y plane. The field output after the reflection by the axicon facets is calculated with the Fresnel diffraction formula for a cylindrical wave:
U ( x 0 , z ) = exp ( i k z ) λ z ∫ − ∞ ∞ U a x ( x ) exp ( i π x 2 + x 0 2 λ z ) exp ( − i k x 0 x λ z ) d x ,
where x is the transverse coordinate in the observation plane at z-coordinate, Uax(x) is the distribution of the field at the axicon output plane, obtained by multiplying Uin for a phase shift due to the axicon reflection Φ(x) . The field at the axicon plane output Uax(x) is given by:
U a x ( x o u t ) = exp ( i k Φ ( x o u t ) ) exp ( − ( x o u t w 0 ) 2 )
with:
Φ ( x ) = 4 π A P h g ( x ) λ .
In the hypothesis of thin optical element, we can assume xout ~ x obtaining:
U ( x 0 , z ) = exp ( i k z ) λ z ∫ − ∞ ∞ exp ( − ( x w 0 ) 2 ) exp ( 4 π i g ( x o u t ) A P h λ ) exp ( i π x 2 + x 0 2 λ z ) exp ( − i k x 0 x λ z ) d x
In this case, the intensity is given by:
I ( x 0 , z ) = | U ( x 0 , z ) | 2 λ z
where I(x0, z) is the power per linear unit in the x-z plane .
An inspection of Eq. 4 shows that the integrals depend on the product λz and the ratio A·Ph/λ , rather than on the wavelength alone. This fact suggests an interesting way to infer the light distribution at a given wavelength λ1 and using a heating power Ph1, if the behavior at another wavelength λ2 and heating power Ph2 are known.
We can indeed introduce the following scaling rules:
λ 1 z 1 = λ 2 z 2
P h 1 λ 1 = P h 2 λ 2
where λ1, and λ2 are two wavelengths of the probe beams impinging on the axicon, generated with top swellings A·Ph1 and A·Ph2 respectively, and z1, z2 are the corresponding z-coordinates at which the fields are calculated. It is easy to verify that under the conditions described by Eqs. 6-7, the integral of Eq.4 doesn`t change. This property will be used in the experimental section to retrieve the light distribution at THz frequencies from measurements performed at a visible frequency.
The modification of the light distribution due to the significant phase changes at THz frequencies, just previously anticipated, are clearly visible in the plots in the plots of Figure 5, reporting the focused intensity distributions at 1 and 3 THz radiations. The occurrence of the focusing effect is clearly visible. Indeed, the maximum intensity increases with respect to the maximum Gaussian input intensity I0 without pumping (blue lines) from approximately 30% at 1 THz to about 100% at 3 THz frequency (green lines). This focusing becomes rapidly less efficient at lower frequencies. For instance, at 0.6 THz (0.5 mm wavelength), the maximum intensity in the focus lowers to 16%. As well known, increasing the focus intensity for a fixed probe input w0 and optical power is feasible only by increasing the axicon base angle β [38] and thus cannot be accomplished if we want to risk the overheating of the device. However, we will show in the Experimental Section that this overheating can be actually not so detrimental for the device performances, provided that some minor degradations of the performances can be tolerated.
On the contrary, the focusing becomes more efficient at higher frequencies. In order to cover the higher THz band, we repeated the calculations for 5 THz and 10 THz. The minimum width Dax passes from 0.92 mm at 1 THz to 0.42 mm at 5 THz and 0.20 mm at 10 THz frequency, while the focus intensity increases to 257% (5 THz) and 370 % (10 THz) with respect to I0 . The DOFax becomes nearly constant, namely ~ 20 mm, at increasing frequency (see Tab.1). It is worth noticing that this last result is consistent with the geometrical optics predictions. Indeed, referring to the scheme in the left side of Figure 4, the geometrical depth of focus is approximately given by DOFgeom= w0/2β = 20 mm, that resembles the calculated DOFax with improved approximation at decreasing wavelengths, as expected in the geometrical optics limit.In order to assess the focusing advantages of this device, we can compare these results with those ones achievable by using conventional cylindrical optics. This comparison give meaningful information about the major differences, primarily the improved depth of focus of the axicon-like device we propose. To this aim, we considered a convex cylindrical mirror with focal length fmir equal to the coordinate of maximum intensity of the axicon (from here on the axicon focal length fax ) and the same Gaussian input, namely Uin(x)= exp(-(x/w0)2, and calculate the corresponding DOFG of the mirror with the well known relations of Gaussian optics.
In particular, the focused virtual beam waist w1 is calculated with the relationship w1= fmir λ/πw0, where fmir= fax, λ is the radiation wavelength, w0 is the waist of the field input (= 1 mm), and the depth of focus is DOFG=2πw12/λ, namely twice the Rayleigh range. The results have been enclosed in Table 1. At all frequencies, DOFax>DOFG , from 7-times to about 20 times at 1 and 10 THz respectively, demonstrating the advantage of the axicon in terms of long focusing with respect to an equivalent optic with the same focal length.

3. Experimental section

We simulated experimentally the optical performances of the thermally generated axicons at the frequencies of 1 and 3 THz, by using a probe laser light in the visible, namely the radiation of a He-Ne laser at the wavelength of λ2= 0.633 μm . The proposed approach is justified by the scaling property of the Fresnel integral as shown in the previous section and will be detailed later on.
The preparation of the sample was performed as follows. First, a conventional microscope glass slide was covered with a PDMS layer. We accurately mixed the monomer and the curing liquid in a 10:1 volume ratio, then a volume necessary to generate a 1 mm nominal thickness polymer was poured onto the glass surface. After degassing the liquid solution (about 0.5 hours), the monomer was let to polymerize overnight in air without any pre-heating. A thin gold layer (100 nm nominal thickness) was successively deposited at a rate of 0.5 nm/s onto PDMS by thermal evaporation under high vacuum conditions (pressure : 4 × 10−5 Torr).
Then, we measured the absorption of the gold layer at the pump radiation wavelength of 405 nm, that resulted 85%. This absorption value is different from 74%, calculated with WINSPALL 3.02 software for a bilayer structure composed by PDMS (refractive index: 1.46) and Au (refractive index: 1.47+1.95i [39]. However this difference can be attributable to a nanostructuration of the deposition of Au onto the porous PDMS surface that, as well known, can give rise to substantial differences in the optical properties with respect to a flat deposition [40]. At a given Pin pump power, the heating power Ph is thus given by Ph=Pin·0.85.
In a second step, we checked the behavior of the swelling vs. the heating power by analyzing the reflected beam pattern. The ray tracing analysis has shown (Figure 4) that the reflected rays forms two bundles separated by an angle that is directly proportional to the input power.
Thus, referring to the “Swelling” part of Figure 6, we generated the extrusion of the PDMS surface by using different heating powers, from the minimum required (Ph = 0.58 mW) up to the maximum theoretically allowable for a safe use (Ph= 270 mW). The impinging probe beam , coming from a He-Ne laser ( λ2 = 0.633 μm) is reflected towards the screen into two separate lobes. We recorded the intensity profiles at 500 mm distance from the sample on the transverse axis of the light distribution.
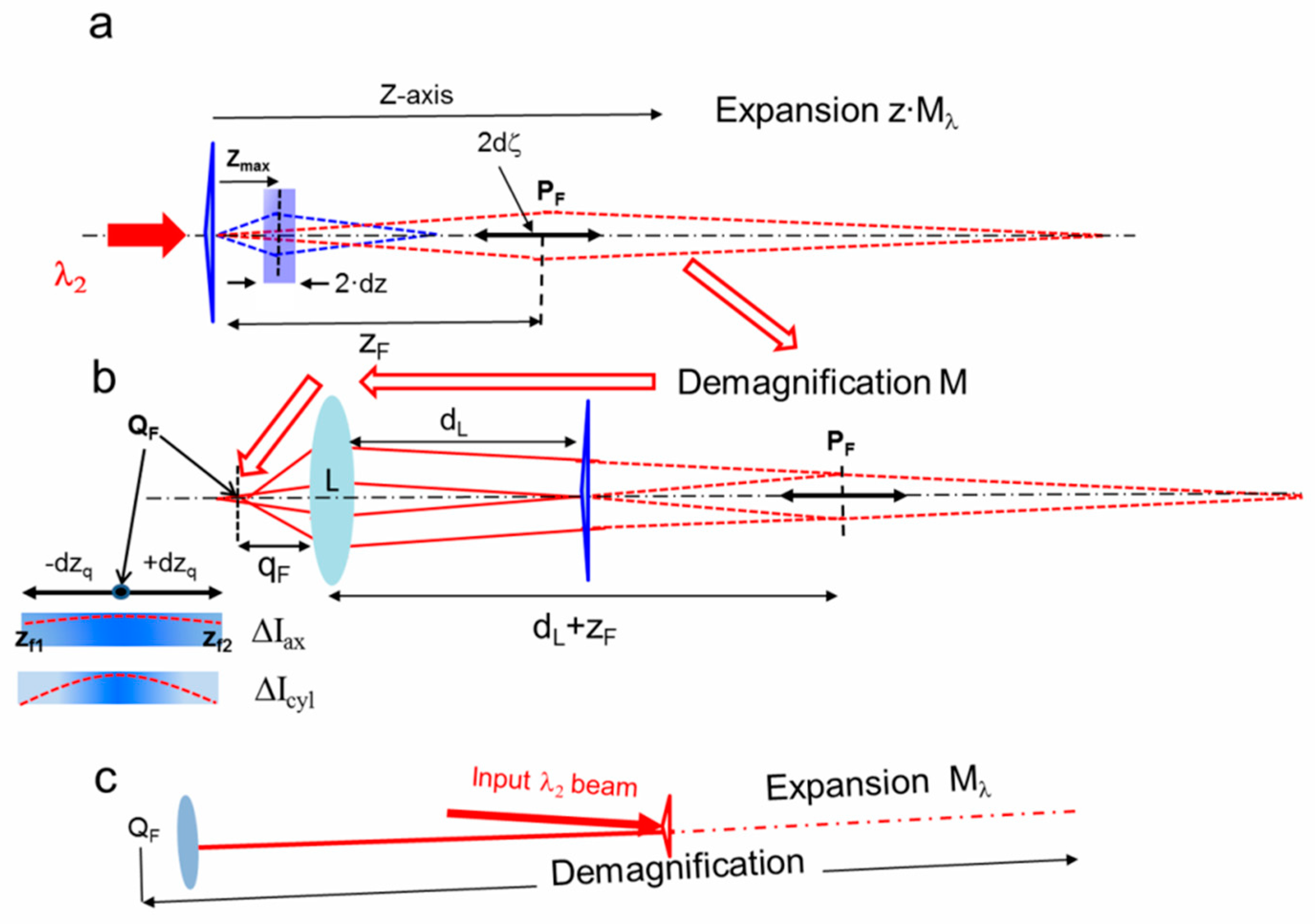
With the “Focus” part of the set up, we simulated, at the probe wavelength λ2 , the axicon by focusing the 1 THz and 3 THz radiations. By using the proper pump heating powers calculated from Eq.7, namely Ph= 0.58 mW and 1.74 mW for the simulation of 1 THz and 3 THz respectively, we generate the axicon-like devices, that correspond to swellings of 164 μm (1 THz) and 54.5 μm (3 THz). The probe beam waist is expanded from 0.55 mm to 1 mm, impinges on the device and, upon reflection, produces virtual focused fields that reproduce those ones at THz frequencies, but, following Eq.6, with the z-coordinates zz scaled with respect to that ones, z1 , at λ1 . These fields are demagnified by the lens L and transformed in real images, re-expanded by an objective (140X magnification) on a screen, recorded with a CCD camera and analyzed in real time with the image processing software IMAGE PRO. By moving axially the objective, we lock the position zmax of the focus when the maximum intensity is observed. The x- intensity distribution is recorded along a transversal line in the central part of the light pattern..The same set up was adopted to simulate the long focusing performance at 1 THz frequency. However, this is a priori a more difficult operation to perform. Indeed, the transformation of the axial virtual light distribution into the real one is not so direct, because the longitudinal de-magnification of the lens L is not uniform . This demands for more considerations to support the measurement strategy, that are detailed in the Appendix.
Experimentally, the objective is moved back and forth with respect to zmax of the amount dz =0.3 mm and measure the intensity fall with respect to the maximum by recording the transversal intensity along the same lines as before. This fall is compared with that one calculated when the axicon is changed with a fictitious cylindrical mirror with the same focal length, and this comparison will permit to establish the advantage of using the axicon with respect to the focusing of a conventional optic.

4. Results and discussion

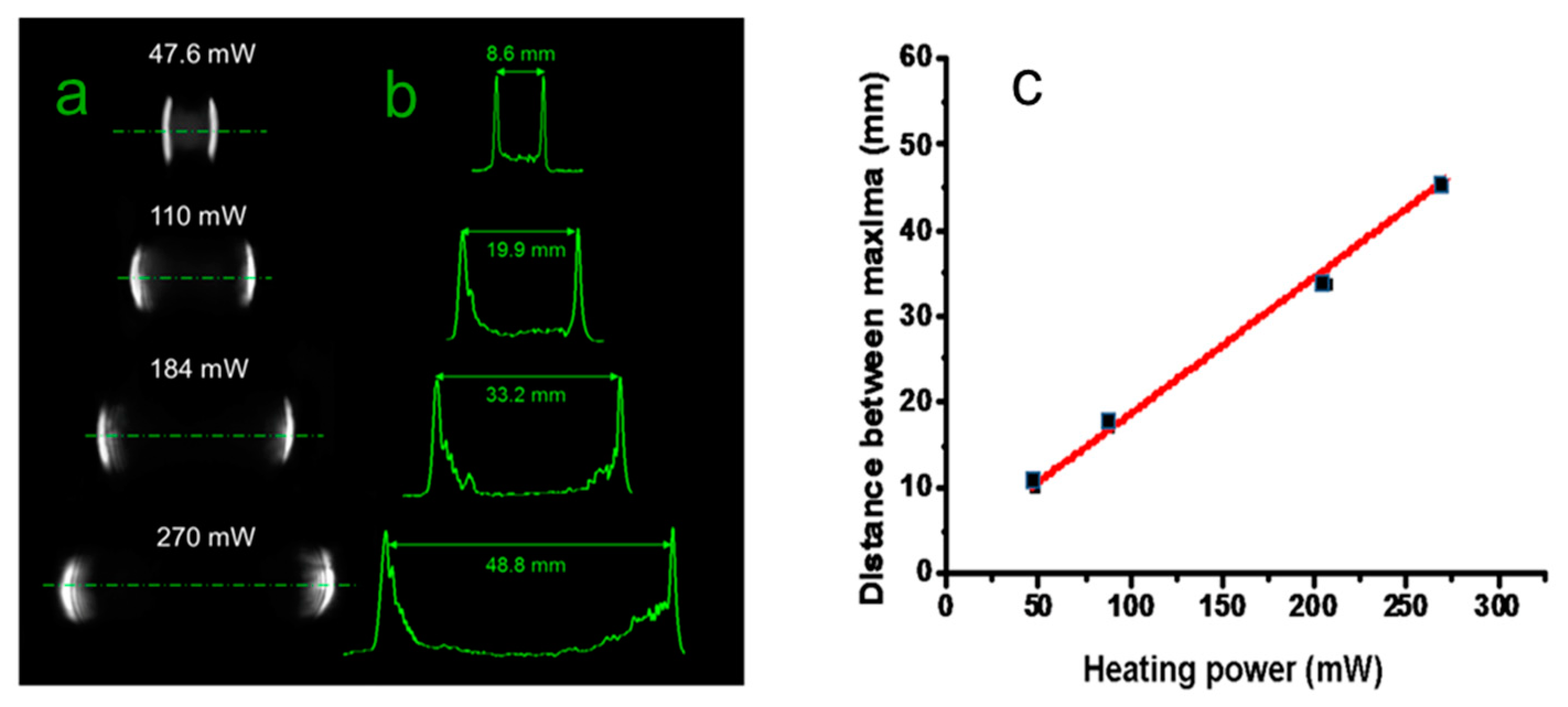
The photos of the far field intensity patterns and their transversal profiles reflected by the axicon-like device are reported in Figure 7a, b for various heating powers. .
They put in clear evidence the splitting of the input beam, that increases linearly with increasing Ph as reported in Figure 7c , as theoretically predicted. We raised the input power until an effect of surface cracking was evidenced by the upset of scattering light around the far field pattern, occurrence observed at Ph= 285 mW, not far from the theoretical maximum value of 270 mW.
The distance between the maxima at this heating power is 48.8 mm, corresponding to a full angle of 0.098 rads , with a rate of increase of 2.8x10−4 rads/mW. Repeating the measurements in different heating cycles at the same power we didn’t observe significant changes in the light distribution, indicating a substantial stability of the gold surface.To summarize, the maximum axicon base angle β experimentally found without surface damaging, is β ~ 0.098/4 = 0.0245 rads (1.4 deg.). The maximum phase change expected at the lower frequency of 1 THz (wavelength λ1= 300 μm) for a beam width w0 of 1 mm is 4πβw0/λ1~1 rad, and can thus produce significant focusing effects, as theoretically predicted by the electromagnetic calculations shown in the Modeling section. Considering the radiation at 1 THz, its simulation at λ2 requires a swelling of 344 nm, which is 476 times lower than that one generated by the highest pump power. In spite of this huge difference, the effect of the PDMS swelling is still wellresolved. Indeed, as shown in Figure 8, the two lobes are not completely separated in the far field , but nevertheless they are clearly formed. Thus, also in this case, a well defined focusing should be experimentally found.
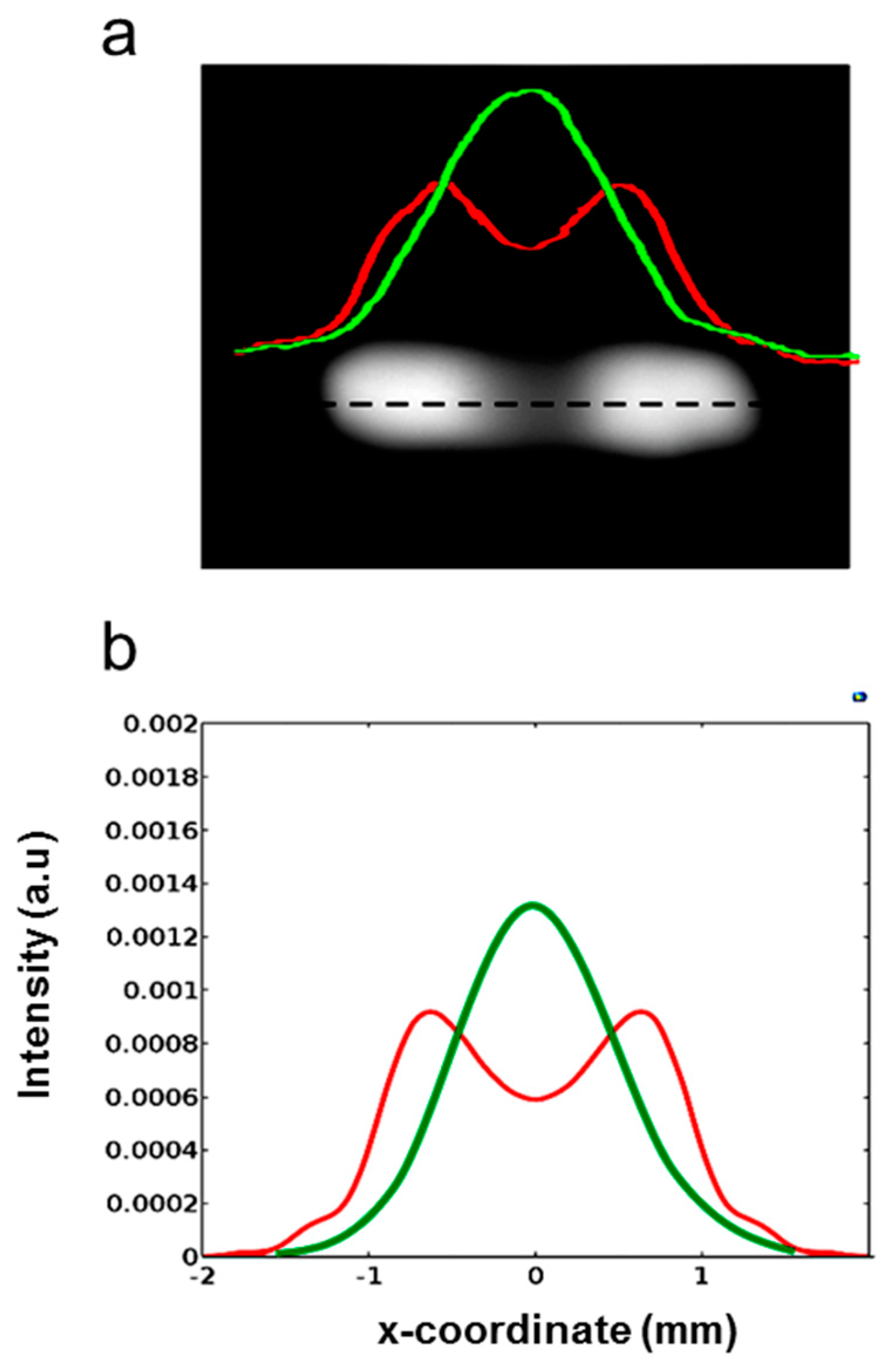
Preprints 85876 g008
Figure 8. (a) Photograph and far field intensity profiles, recorded on the dashed black line, of the probe beam (λ2 = 0.633 μm) reflected by the axicon-like device generated with a heating power Phvis= 0.58 mW, at a distance of 1280 mm from the sample. The 1D intensity pattern was recorded on the horizontal symmetry axis of the light distribution (dashed black line) with (red line) and without (green line) the pump light. (b) Calculated probe beam far field produced at the same distance by the axicon with a swelling of 344 nm (red line), or without pump power (green line).
Figure 8. (a) Photograph and far field intensity profiles, recorded on the dashed black line, of the probe beam (λ2 = 0.633 μm) reflected by the axicon-like device generated with a heating power Phvis= 0.58 mW, at a distance of 1280 mm from the sample. The 1D intensity pattern was recorded on the horizontal symmetry axis of the light distribution (dashed black line) with (red line) and without (green line) the pump light. (b) Calculated probe beam far field produced at the same distance by the axicon with a swelling of 344 nm (red line), or without pump power (green line).
Preprints 85876 g008
All the more so, the focusing of 3 THz radiation is expected to be effectively produced.
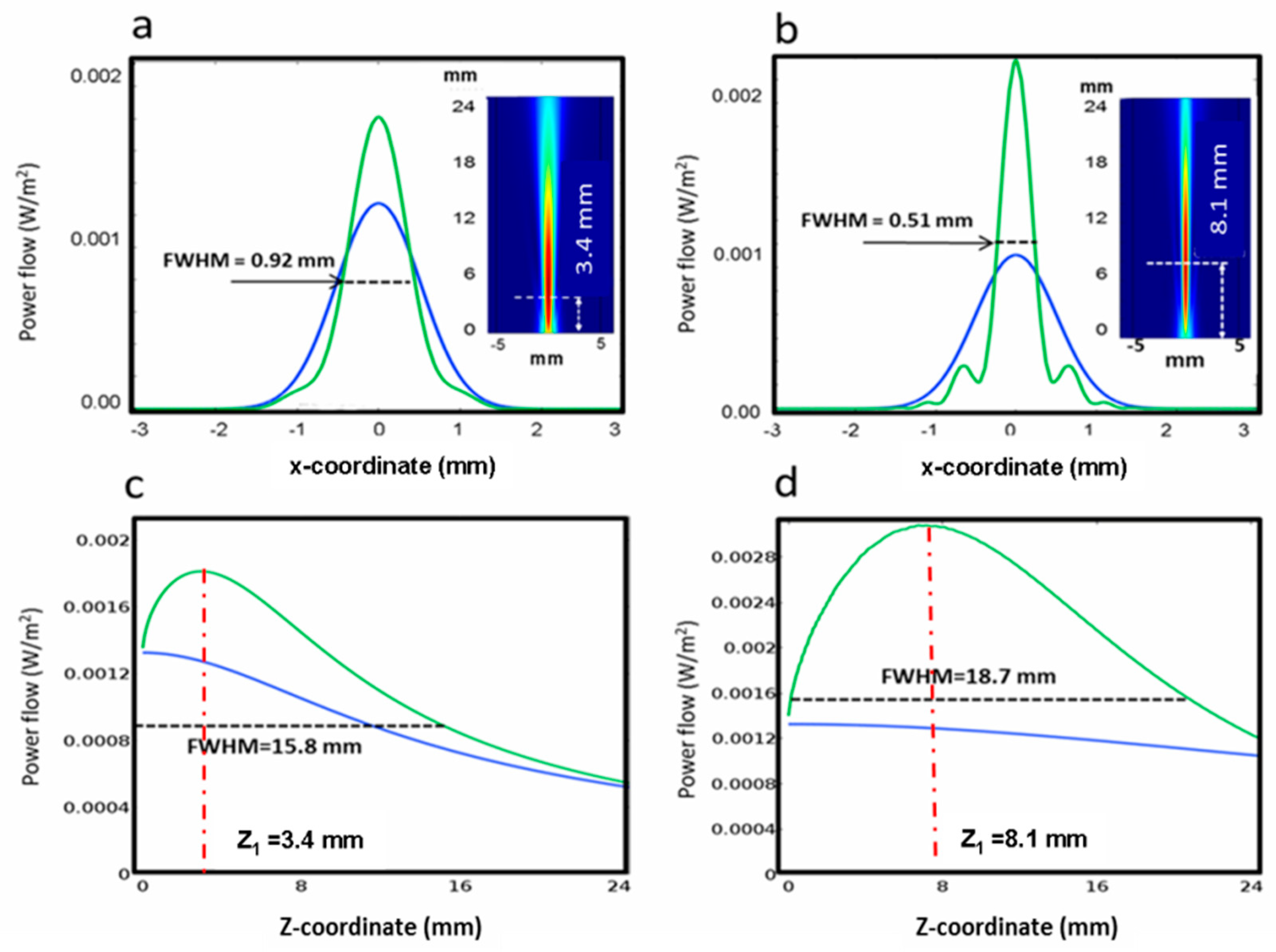
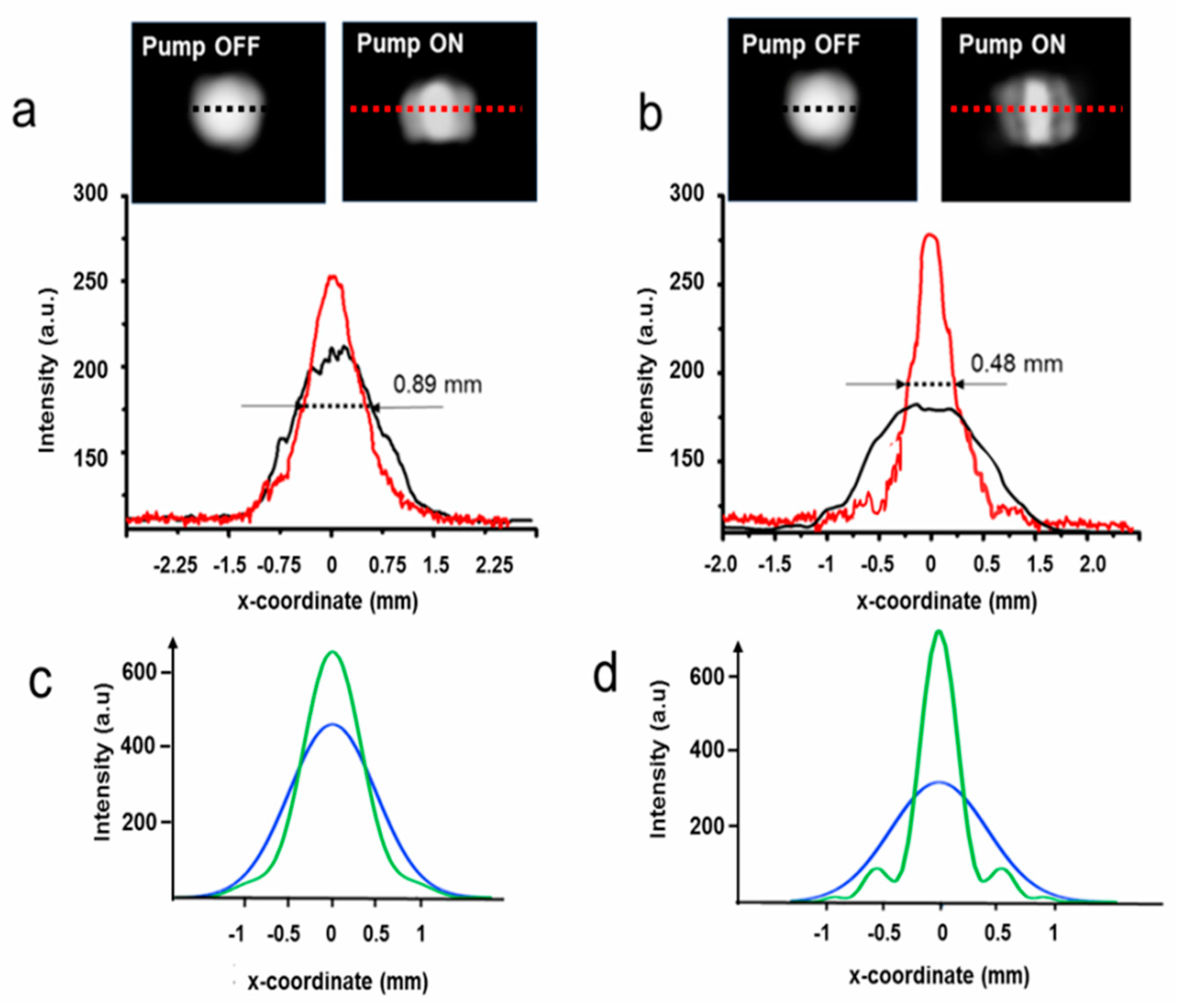
The focal transversal light distributions corresponding to the simulations of 1 and 3 THz radiations are reported in Figure 9 a, b together with those ones obtained without the optical pumping (black lines). The measured FWHM widths result in 0.89 mm and 0.48 mm for the experimental simulation of 1 THz and 3 THz, respectively. The results are in good agreement with the theoretical intensities calculated with the “true” THz radiations, considering the proper heating powers and swellings of the axicon, as the intensity plots reported in Figure 9 c, d show that their FWHMs are 0.92 mm (1 THz) and 0.51 mm (3 THz), very close to the theoretical predictions, giving an experimental evidence of the affordability of the simulation approach.
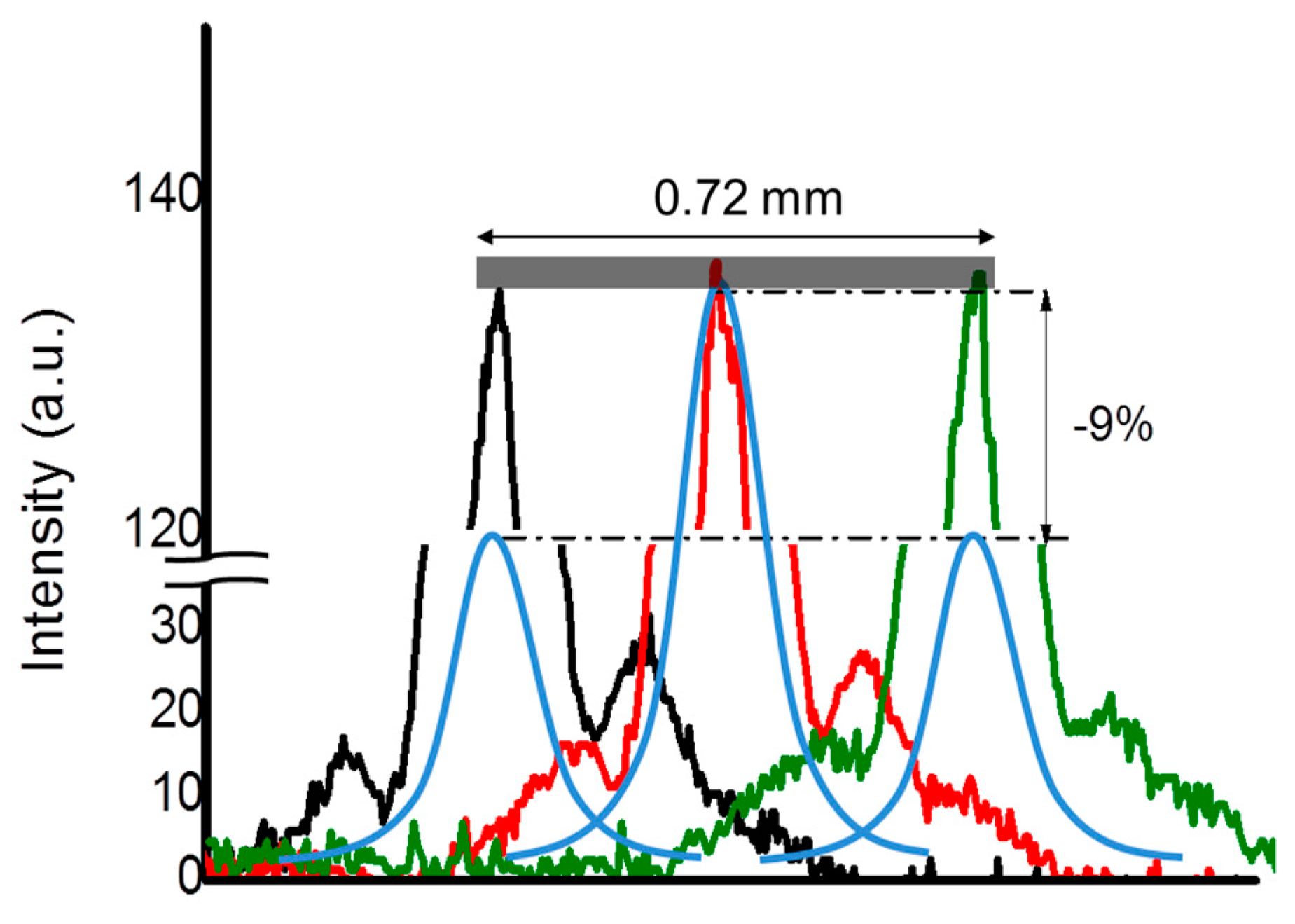
The results of the long focusing simulation are represented by the traces of Figure 10, reporting the transversal intensity profiles at the axial points zmax, zmax+dz, zmax-dz We found that axial intensity remains constant within 0.8%, that is the resolving power of the experimental detection system, and for this reason the predicted change of 0.2% couldn’t be put in clear evidence.
However, the experimental percentage is approximately one order of magnitude lower than the fall calculated in the Appendix for the focusing of an equi-focal cylindrical optic (-9%) . This occurrence demonstrates that the axicon focus the 1 THz beam is much more robust to diffraction with respect to that one calculated for the conventional focusing of a benchmark cylindrical mirror, indicating the presence of a much higher depth of focus
In order to assess the robustness of the device vs. heating, we checked the modifications induced on the gold surface using heating powers up to Phmax= 540 mW.
The reflected probe beam far field intensity at λ2 is still constituted by two separate lobes that increase their distance to 98 mm at Phmax but, as compared to the distributions in Figure 7, their light pattern suffers some broadening and smearing towards the center. Moreover, when the pump is switched OFF, the pattern no longer resembles that one of the initial Gaussian beam but, rather, it appears deformed in a fringed-like figure elongated in the horizontal direction, as visible in Figure 11(c).These observations indicate that a vertical crack of the surface has occurred, whose edges move apart from each other when the PDMS swells and re-shut at zero pump power. Surprisingly, we found that in 5 repeated cycles of heating, the far field intensity pattern developes only a slight intensity nuance towards the center, presumably due to the scattering and diffraction introduced by the crack, resembling the pattern reported in Figure 12(b). The stability in the pattern indirectly evidences that the surface crack reaches a steady shape, and that a base angle β as high as 0.05 rads (3 deg.) can be reversibly obtained using heating powers that overcomes the safe temperature of 300°C. A check of the gold surface after the thermal cycling actually confirmed the presence of that vertical crack (Figure 11(d)). As the optical path difference in the reflective axicon is proportional to β, significant phase changes in the lower THz band (0.1-1 THz) could still be obtained, guessly without major issues in the focusing performances. The verification of this claim is beyond the scope of the present work, and will be reported in future investigations. A possible drawback of this cracked axicon structure is that the underneath PDMS is no longer shielded from the external environment by the gold layer, so that degradation issues are more likely to occur [41].
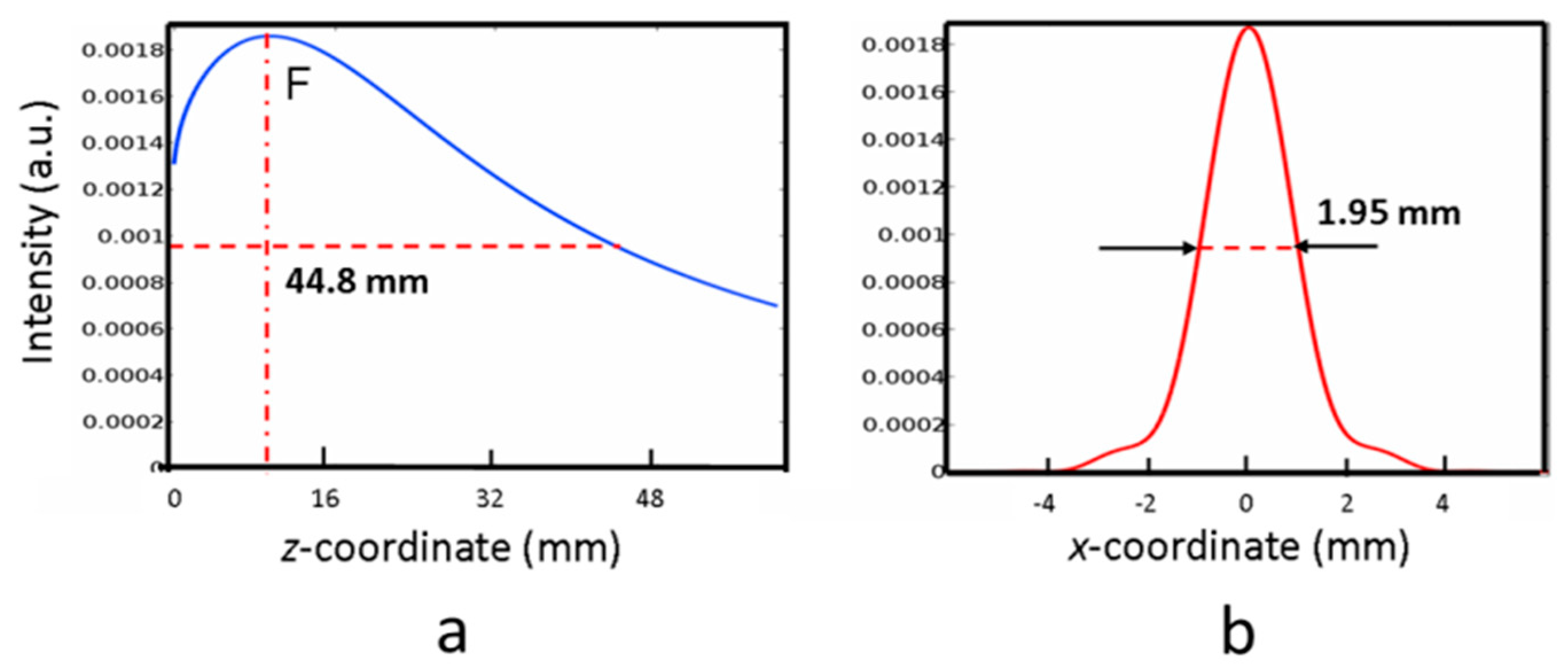
At the best of our knowledge, this is the first report on the performances of a bi-mirror Fresnel reflaxicon working in the THz range above 1 THz, so that a direct comparison with other reports was not possible. However, the concept of 1D long focusing in the THz range was successfully demonstrated by using PPWG axicons working below 1 THz frequency [34]. At a frequency of 0.45 THz , supposing w0=1 mm, our device reaches a theoretical DOFax ~ 30 mm, and the minimum measured Dax is approximately 1.88 mm. However, considering a higher w0 = 2.5 mm, that is approximately the limit of linearity of our reflaxicon (see Figure 3a), we found a DOFax = 44.8 mm against 46 mm reported in [34] , while the FWHM in the focus, 1.95 mm, is only slightly higher than that one of 1.85 mm, deducible from the data shown in Figure 3 of [34]
The interest in long focusing in the band 0.1-1 THz constantly receives noticeable attention. For instance, quite recently [30] the use of refractive conical axicons with base angles of 10° has allowed the generation of a focus spot 7 mm wide in a depth of focus exceeding 160 mm. A similar good performance can be reached with or axicon as well. Indeed, considering the simulation implemented for 0.45 THz, the spot width of 1.85 mm can be expanded with a positive relay optics with transverse magnification M=3.8. Following the magnification law of geometrical optics for axial magnification, its approximate value results M2=14.4 leading to a theoretical DOFax~460.8 mm. This value suggests that our device can reach, at least as order of magnitude, the high depth of focus reported in [30]

5. Conclusions

In this paper we have presented an Au-PDMS Fresnel-type bimirror axicon able to generate a virtual long focus using radiations in the frequency band 1-10 THz. The working principle of the device is based on the swelling of a PDMS layer provoked by a heating of the overneath gold layer generated by the absorption of focused violet laser light in a tight line. Thanks to the high expansion coefficient of PDMS, the deformed reflecting surface of the elastomer generates differences in the optical path of a probe beam that fall into the range of THz wavelengths. The corresponding phase changes are significant, and allow to shape efficiently the impinging probe beam in long foci. The axicon can be fabricated with cost-effective tools and is easily tunable, as its shape can be modified by simply varying the input heating power without any mechanical adjustment. Thanks to an invariance property of the Fresnel integral, scaling rules can be introduced that allow to simulate experimentally the behavior of the device at 1 and 3 THz frequencies with a probe red beam., thus avoiding the expensive labware necessary for generating the THz radiation and its managing. The experimental results are in good agreement with the theoretical predictions, and confirm the effectiveness of the device in the long focusing of THz radiation. As the axicon produces a virtual focus, a relay optic is necessary to use it in practice. If from one side this represent an obvious drawback, nevertheless it can be easily circumvented by coupling a conventional positive mirror to form a positive long focusing system. Thanks to the high wavelengths of the THz radiation that relaxes the requirements on the quality of the components, such an all-catoptric device would have minor concerns for optical aberrations, while chromatic aberrations are completely absent. As the current device has limited performances below 1 THz, our future research aims at investigating the improvement of the focusing performances in the band 0.1-1 THz by exploiting the experimentally observed reversible extra-swelling of the gold surface reflector beyond the cracking limit .

Author Contributions

Conceptualization: G. Margheri, T. Del Rosso; methodology : G.Margheri, T.Del Rosso; software: G.Margheri ; validation : G. Margheri, T.Del Rosso; resources: T. Del Rosso ; data curation : G.Margheri, T.Del Rosso ; writing-original draft preparation: G.Margheri; writing review and editing : G. Margheri, T.Del Rosso; supervision : G.Margheri, funding acquisition : T.Del Rosso. All authors have read and agreed to the published version of the manuscript.

Funding

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001. Funding from FAPERJ for processes E-26/010.000980/2019 , E-26/211.180/2019 and E-26/211.540/2021 is acknowledged. We acknowledge also CNPq and the Instituto Nacional de Engenharia de Superfícies (INCT-INES) (Processes 423349/2018-0 and 465423/2014-0).

Data Availability Statement

N/A.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

In this section we design a procedure based on the use of visible radiation (wavelength λ2 = 0. 633 μm), to simulate the longitudinal focusing performances of the axicon at 1THz frequency (wavelength λ1 =300 μm). Referring to the scheme of Figure A1 , the axicon produced with a heating power of 270 mW (swelling : 164 μm) , focuses virtually the radiation at 1 THz frequency with a maximum intensity Imax at a distance zmax= 3.4 mm from the surface, with a focus FWHMx = 0.92 mm.
Let’s consider a segment of length 2δz centered at zmax, at the ends of which the relative intensity reduction is ΔI/Imax . As explained in the Theoretical modeling section, by properly reducing the heating power we can generate an axicon that yields at a wavelength λ2 the same spatial field distribution produced at the wavelength λ1. Indeed, the field at coordinates zmax±δz is reproduced at unchanged transversal coordinates, but at expanded z-coordinates, namely Mλ (zmax±δz) = Mλ·zmax± δζ, where δζ = Mλ·δz =142.8 mm and Mλ=λ1/λ2= 476. The maximum intensity is transferred at the point PF whose z-coordinate is zF = zmaxMλ and here the FWHMx remains unchanged while its distance from L is pF = dL+ zF = 2218 mm and the overall Dax is enlarged to 7520 mm. This expanded virtual focal region at λ2 is imaged and demagnified in the real space by the positive lens L (Figure A1).
Preprints 85876 g0a1
Figure A1. (a) Schematic representation of the simulation at the wavelength λ2 = 0.633 μm of the focus region produced by the axicon at 1 THz frequency (flattened blue triangle). The length dz (= 0.30 mm) is an arbitrarily small width of the longitudinal region around the point of maximum intensity, placed at zmax= 3.4 mm (blue dashed quadrilateral). The virtual expanded simulation region is represented by the red dashed quadrilateral . (b) Transfer and demagnification in the real space by the lens L (focal length =100 mm) of the expanded virtual focal region. The variation ΔIax at the endpoints of the focal region is compared with that one, ΔIcyl, calculated when the axicon is changed with a cylindrical mirror with the same focal length. (c) In order to simplify the optical set-up, in the experimental layout the two sections (a) and (b) are collinear and tilted by a small angle with respect to the input light probe at wavelength λ2 . For the detailed description see the text of Appendix.
Figure A1. (a) Schematic representation of the simulation at the wavelength λ2 = 0.633 μm of the focus region produced by the axicon at 1 THz frequency (flattened blue triangle). The length dz (= 0.30 mm) is an arbitrarily small width of the longitudinal region around the point of maximum intensity, placed at zmax= 3.4 mm (blue dashed quadrilateral). The virtual expanded simulation region is represented by the red dashed quadrilateral . (b) Transfer and demagnification in the real space by the lens L (focal length =100 mm) of the expanded virtual focal region. The variation ΔIax at the endpoints of the focal region is compared with that one, ΔIcyl, calculated when the axicon is changed with a cylindrical mirror with the same focal length. (c) In order to simplify the optical set-up, in the experimental layout the two sections (a) and (b) are collinear and tilted by a small angle with respect to the input light probe at wavelength λ2 . For the detailed description see the text of Appendix.
Preprints 85876 g0a1
However , aiming to consider the imaging of the whole focus region, one should take into account that the demagnification suffers a strong change along the axis, and as a consequence the light intensity distribution downline of L would have strong distortions with respect that one in the axicon focus of 1 THz radiation. In order to avoid this complication and simplify the calculations, we will select δζ<< pF by choosing an arbitrarily low value of δz =0.3 mm << zmax in our case. By applying the law of conjugate points, PF is imaged in the point QF at a distance qF= pF/M=104.72 mm from L, with a transversal de-magnification M =22.2 . As it can be easily verified, M is uniform within ±3.5 % with respect to its average value (Mav =21.8) in the segment centered on PF, whose length is 2dζ . As δz/pF= 0.064<<1, the length δzq, longitudinal image of dζ, can be simply found by applying the approximate relationship of geometrical optics δzq~ δζ/M2 = 0.29 mm. The z-coordinates of the endpoints of the focal region, centered at distance qF, are thus zf1= (qF+δζ)/M2 , zf2 =(qF-δζ)/M2. As M is almost constant, the virtual field in the expanded focal region is transferred in the real focus with almost uniform M-scaling in the transversal coordinates and M2 -scaling in the axial coordinate. As a consequence, indicating with Imax the maximum intensity in the focus QF, the ratios of the intensities at its endpoints, I(zf1)/Imax and I(zf2)/Imax, reply with good approximation the ratios of the intensities at the virtual endpoints of the expanded focal line at λ2 and, for the scaling property of Eq.5, at the endpoints of the simulated focal line at 1 THz. To summarize, the axial intensity distribution generated by the axicon at 1 THz frequency can be reproduced with good fidelity by using the visible probe beam at λ2 , provided that only a small region around the focus is considered. It is transformed in a region close to the focus of the lens L that is demagnified M=22.2 in the cross section and M2=492 in the axial direction. The intensity fall at the endpoints ΔIax is ΔIax ~0.2% Imax, so the intensity is almost uniform in the considered width around the focal point. Even if we limited ourselves to examine the intensity variations in a small region around the focus, this is still enough to evaluate the long focusing performances if we compare this result to that one achieved if a conventional focusing optics would be used.
To demonstrate this statement, we replace the axicon with a fictitious convex cylindrical mirror that focuses virtually at the coordinate zmax the same Gaussian beam used as input for the axicon (beam waist w0= 1 mm) . The focal distance fTHz of the mirror is thus fTHz= zmax . The beam waist at focus is w1= λ1fTHζ/πw0 = 0.32 mm. Then, as for the axicon, we change the wavelength λ1 with the simulation wavelength λ2. The focused field is calculated with Eq.5 by simply substituting the phase factor corresponding to the axicon (Eq.3) with that one introduced by the fictitious optics, that is Φ(x)=πx2P1/λ1, where P1 =1/fTHz is the dioptric power of the mirror. This expression of Φ(x) has a form analogous to that one of Eq.3 that describes the phase variation introduced by the axicon, namely a constant multiplied for a function of x. Thus, the replication at λ2 of the field distribution produced at λ1 , is possible by expanding the z-coordinate to zMλ and changing the power of the mirror to P2=P1/Mλ. The focal length is enlarged to f2 = MλfTHz = zF , while the virtual focus waist w1 is simply translated to zF . The lens L provides to transfer this focus in the real space. The well known formulas of Gaussian optics permit to calculate the beam waist of the focused beam and its distance from L, that result wf= 0.0148 mm and 104.50 mm respectively. The corresponding Rayleigh range is zf= πwf2/λ2 = 0.98 mm. The relative intensity fall with respect to the maximum Imax expected at coordinates ±dzq from wf , namely ΔIcyl/Imax, can be approximately calculated by the formula ΔIcyl/Imax ~1-(1+ (dzq/zf )2 )−1 = 9%, to be compared with the observed constant trend of the axial intensity vs. distance.

References

  1. Sun, Q. , He Y., Liu K, Fan S, Parrott E.P.J., Pickwell-MacPherson E. Recent advances in terahertz technology for biomedical applications. Quant. Imaging Med. Surg. 2017, 7, 345–355. [Google Scholar] [CrossRef]
  2. Sung, S. , Selvin S., Bajwa N., Chantra S., Nowroozi B., Garritano J., aaGoell J., Li A., Deng S.X., Brown E., W. Grundfest S., Taylor Z.D. THz imaging system for in vivo human cornea. IEEE Trans Terahertz Sci Technol. 2018, 8, 27–37. [Google Scholar] [CrossRef]
  3. Smolyanskaya, O. , Chernomyrdin N., Konovko A., Zaytsev K., Ozheredov I., Cherkasova O., Nazarov M., Guillet J.P., Kozlov S., Kistenev V., Coutaz J.L., Mounaix P., Vaks V., Son J.H., Cheon H., Wallace V., Feldman Y., Popov I., Yaroslavsky A., Shkurinov A., Tuchin V.V. Terahertz biophotonics as a tool for studies of dielectric and spectral properties of biological tissues and liquids. Progress in Quantum Electronics 2018, 62, 1–77. [Google Scholar]
  4. Zaytsev, K. , Dolganova I., Chernomyrdin N., Katyba G., Gavdush A., Cherkasova O., Komandin G., Shchedrina M., Khodan A., Ponomarev D., Reshetov I., Karasik V., Skorobogatiy M., Kurlov V., Tuchin V. The progress and perspectives of terahertz technology for diagnosis of neoplasms: a review. Journal of Optics 2019, 22, 013001. [Google Scholar]
  5. Musina, G. , Dolganova I., Chernomyrdin N., Gavdush A., Ulitko V., Cherkasova O., Tuchina D., Nikitin P., Alekseeva A., Bal N., Komandin G., Kurlov V., Tuchin V., Zaytsev K. Optimal hyperosmotic agents for tissue immersion optical clearing in terahertz biophotonics. Journal of Biophotonics 2020, 13, e202000297. [Google Scholar]
  6. Ellrich, F. , Bauer M., Schreiner N., Keil A., Pfeiffer T., Klier J., Weber S., Jonuscheit J., Friederich F., Molter D., Ellrich F. Terahertz quality inspection for automotive and aviation industries. J. Infrared Millimeter Terahertz Waves 2020, 41, 470–489. [Google Scholar] [CrossRef]
  7. Hernandez-Serrano, A. , Corzo-Garcia S., Garcia-Sanchez E., Alfaro M., Castro-Camus E., Quality control of leather by terahertz time-domain spectroscopy, Appl. Opt. 2014, 20, 7872–7876. [Google Scholar]
  8. Headland, D. , Monnai Y., Abbott D., Fumeaux C., Withayachumnankul W., Tutorial: Terahertz beamforming, from concepts to realizations, Appl. Photon. 2018, 3, 051101. [Google Scholar]
  9. Ma, J. , Karl N.J., Bretin S., Ducournau G., Mittleman D.M., Frequency-division multiplexer and demultiplexer for terahertz wireless links, Nat. Commun. 2017, 8, 1–8. [Google Scholar]
  10. Ghasempour, Y. , Shrestha R., Charous A., Knightly E., Mittleman D.M., Single-shot link discovery for terahertz wireless networks, Nat. Commun. 2020, 11, 1–6. [Google Scholar]
  11. Cruz A., Cunha W., Del Rosso T., Dmitriev V., Costa K., Spectral Analysis of a SPR Sensor based on Multilayer Graphene in the Far Infrared Range. Journal of Microwaves, Optoelectronics and Electromagnetic Applications 2023, 22, 184–195. [CrossRef]
  12. Ming, Z. , Qian C., Baozhu W., Lin Y., Jianchao W., Ruihong W., Weimin H. Highly sensitive terahertz sensors based on polarization independent and multiple resonance. Optics Communications 2022, 507, 127519. [Google Scholar]
  13. Lepeshov, S. , Gorodetsky A., Krasnok A., Rafailov E., Belov P. Enhancement of terahertz photoconductive antenna operation by optical nanoantennas. Laser & Photonics Reviews 2017, 11, 1770001. [Google Scholar]
  14. Yachmenev, A. , Lavrukhin D., Glinskiy I., Zenchenko N., Goncharov Y., Spektor I., Khabibullin R., Otsuji T., Ponomarev D. Metallic and dielectric metasurfaces in photoconductive terahertz devices: a review. Optical Engineering 2019, 59, 061608. [Google Scholar] [CrossRef]
  15. Morozov, M. , Leiman V., Popov V., Mitin V., Shur M., Karasik V., Ryzhii M., Otsuji T., Ryzhii V. Optical pumping in graphene-based terahertz/far-infrared superluminescent and laser heterostructures with graded-gap black-PxAs1-x absorbing-cooling layers. Optical Engineering 2020, 59, 061606. [Google Scholar]
  16. Yachmenev, A.; Pushkarev, S.; Reznik, R.; Khabibullin, R. .; Ponomarev D.. Arsenides and related III{V materials-based multilayered structures for terahertz applications. Progress in Crystal Growth and Characterization of Materials 2020, 59, 100485. [Google Scholar] [CrossRef]
  17. Sun, Q.; Chen, X.; Liu, X.; Stantchev, R. .; Pickwell-MacPherson E. Exploiting total internal reection geometry for terahertz devices and enhanced sample characterization. Advanced Optical Materials 2020, 8, 1900535. [Google Scholar] [CrossRef]
  18. Manjappa, M.; Singh, R. Materials for terahertz optical science and technology. Advanced Optical Materials 2020, 8, 1901984. [Google Scholar] [CrossRef]
  19. Islam, M.; Cordeiro, C.; Franco, M.; Sultana, J.; Cruz, A.; Abbott, D. Terahertz optical fibers. Optics Express 2020, 28, 16089–16117. [Google Scholar] [CrossRef]
  20. Cabrini, S.; Liberale, C.; Cojoc, D.; Carpentiero, A.; Prasciolu, M.; Mora, S.; Degiorgio, V.; De Angelis, F.; Di Fabrizio, E. Axicon lens on optical fiber forming optical tweezers, made by focused ion beam milling. Microelectronic Engineering 2006, 83, 804–807. [Google Scholar] [CrossRef]
  21. Zhang, Z.; Buma, T. Terahertz imaging in dielectric media with quasi-Bessel beams. Proc. SPIE 2011, 7938, 793806. [Google Scholar]
  22. Trappe, N.; Mahon, R.; Lanigan, W.; Murphy J., A.; Withington, S. The quasi-optical analysis of Bessel beams in the far infrared. Infrared Phys. Technol. 2005, 46, 233–24. [Google Scholar] [CrossRef]
  23. Shaukat, M.; Dean, P.; Khanna, S.; Lachab, M.; Chakraborty, S.; Linfield, E.; Davies, A. Generation of Bessel beams using a terahertz quantum cascade laser. Opt. Lett. 2009, 34, 1030–1032. [Google Scholar] [CrossRef] [PubMed]
  24. Castro-Camus, E.; Koch, M.; Hernandez-Serrano, A.I. . Additive manufacture of photonic components for the terahertz band. Journal of Applied Physics 2020, 127, 210901. [Google Scholar] [CrossRef]
  25. Jeong, H.Y.; Lee, E.; An, S.C.; Lim, Y.; Jun, Y.C. 3D and 4D printing for optics and metaphotonics. Nanophotonics 2020, 9, 1139–1160. [Google Scholar] [CrossRef]
  26. Wei, X.; Liu, C.; Niu, L.; Zhang, Z.; Wang, K.; Yang, Z.; Liu, J. Generation of arbitrary order Bessel beams via 3D printed axicons at the terahertz frequency range. Appl. Opt. 2015, 54, 10641–10649. [Google Scholar] [CrossRef]
  27. Niu, L.T.; K. Wang J.; Yang Y.Q.; Wu Q.; Ye X.; Z. Yang G.; Liu J. S.; Yu H. Y.Diffractive elements for zero-order Bessel beam generation with application in the terahertz reflection imaging. IEEE Photonics J. 2018, 11, 5900212. [Google Scholar]
  28. Xiang, F.; Liu, D.; Xiao, L.; Shen, S.; Yang, Z.; Liu, J.; Wang, K. Generation of a meter-scale THz diffraction-free beam based on multiple cascaded lens-axicon doublets: detailed analysis and experimental demonstration. Optics Express 2020, 28, 36873–36883. [Google Scholar] [CrossRef]
  29. Ma, Z.; Hanham S., M.; Albella, P.; Ng, B.; H. Tzu Lu; Gong Y., Maier S. A., Hong Zhijie Ma M.. Terahertz All-Dielectric Magnetic Mirror Metasurfaces. ACS Photonics 2016, 3, 1010–1018. [Google Scholar] [CrossRef]
  30. Cui, Z.; Li, L.; Ren, J.; Zhang, D.; Gu, J.; Yu, J. Broadband THz Bessel beam generation based on axicon, Proc. SPIE 2022, 12555, 1255504–1255509. [Google Scholar]
  31. Ulitko, V.E.; Kurlova, V.N.; Masalova, V.M.; Dolganova, I.N.; Chernomyrdin, N.V.; Zaytsev, K.I.; Katyba, G.M. Terahertz axicon fabricated by direct sedimentation of SiO2 colloidal nanoparticles in a mold. Proc. SPIE 2021, 11827, 118270M. [Google Scholar]
  32. Karl, N.J.; McKinney, R.W.; Monnai, Y.; Mendis, R.L; Mittleman, D.M. Frequency-division multiplexing in the terahertz range using a leaky-wave antenna. Nat. Phot. 2015, 9, 717–720. [Google Scholar] [CrossRef]
  33. Matsumoto, H.; Watanabe, I.; Kasamatsu, A.; Monnai, Y. Integrated terahertz radar based on leaky-wave coherence tomography. Nat. Electron. 2020, 3, 122–129. [Google Scholar] [CrossRef]
  34. Hernandez-Serrano A., I.; Pickwell-MacPherson Emma. Low cost and long-focal-depth metallic axicon for terahertz frequencies based on parallel-plate-waveguides. Scientific Reports 2021, 11, 3005. [Google Scholar] [CrossRef] [PubMed]
  35. Margheri, G. Opto-Thermally Tunable Axicon-Like Device Based on PDMS-Au Bilayers. IEEE Phot.Tech.Lett. 2022, 34, 395–398. [Google Scholar] [CrossRef]
  36. C. -Sub Park; K.I. Joo; Kang S.W.; Kim H.-Rin. A PDMS-Coated Optical Fiber Bragg Grating Sensor for Enhancing Temperature Sensitivity. Journal of the Optical Society of Korea 2011, 15, 329–334. [Google Scholar] [CrossRef]
  37. Öm, A. Degradation studies of polydimethyl siloxane, Master Thesis, https://www.doria.fi/bitstream/handle/10024/169311/orn_anton.pdf?sequence=2.
  38. Wang, Y.; Yan, S.; Friberg A., T.; Kuebel, D.; Visser T., D. Electromagnetic diffraction theory of refractive axicon lenses. Journal of the Optical Society of America A 2017, 34, 1201–1211. [Google Scholar] [CrossRef] [PubMed]
  39. Johnson P., B. ; R Christy W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [CrossRef]
  40. Lee, C.; Robertson C., S.; Nguyen A., H.; Kahraman, M.; Wachsmann-Hogiu, S. Thickness of a metallic film, in addition to its roughness, plays a significant role in SERS activity. Scientific Reports 2015, 5, 11644. [Google Scholar] [CrossRef]
  41. Munaro A., P.; Da Cunha G., P.; Filgueiras J., G.; Pinto J., M.; Munaro, M.; De Azevedo E., R. , Akcelrud L. C. Ageing and structural changes in PDMS rubber investigated by time domain NMR. Polymer Degradation and Stability 2019, 166, 300–306. [Google Scholar] [CrossRef]
Preprints 85876 g001
Figure 1. (a) Geometry of the axicon-like device, assumed indefinite in the y-direction. (b) Dimensions of the area irradiated by the pump light.
Figure 1. (a) Geometry of the axicon-like device, assumed indefinite in the y-direction. (b) Dimensions of the area irradiated by the pump light.
Preprints 85876 g001
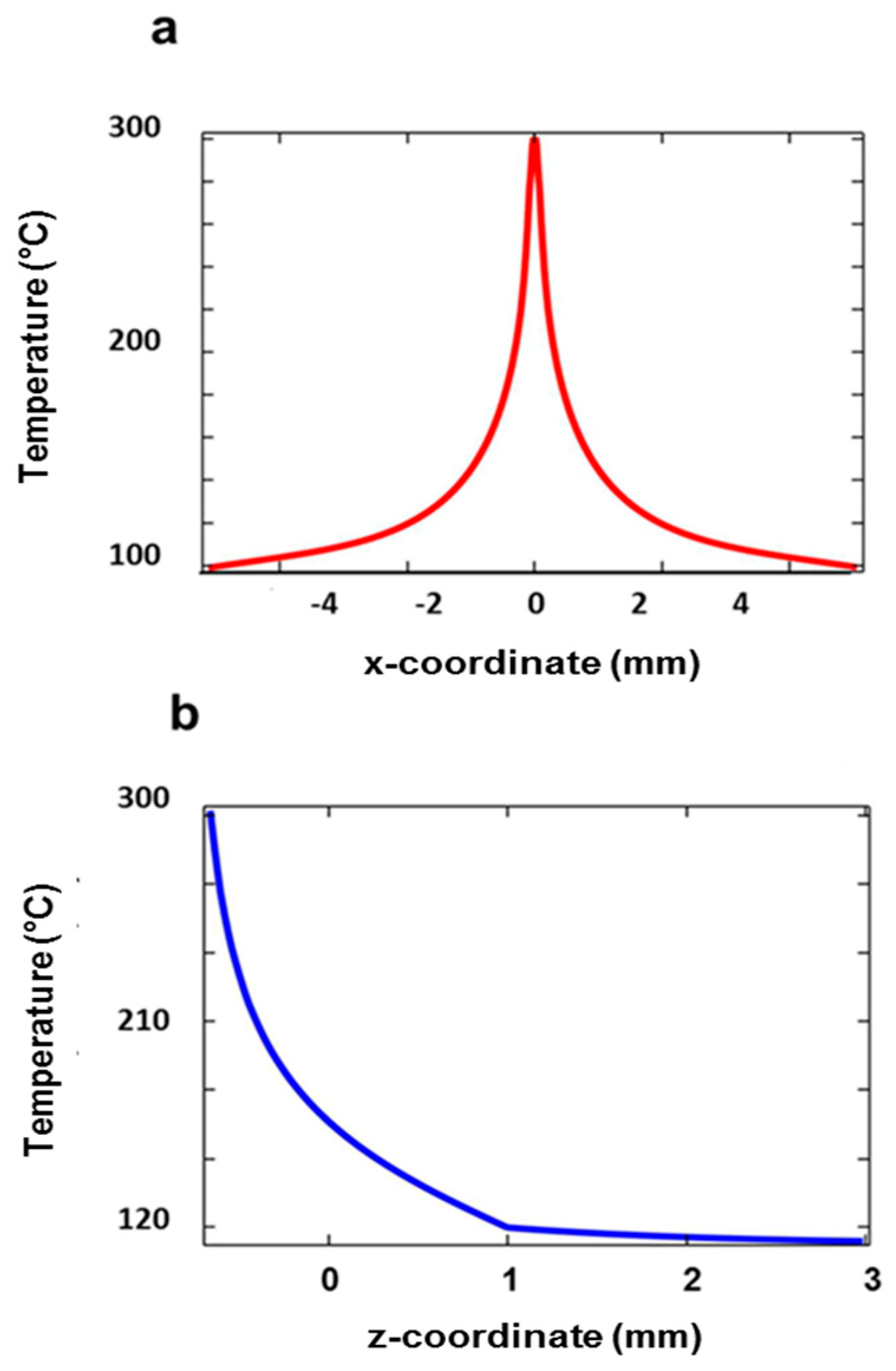
Preprints 85876 g002
Figure 2. Temperature distribution for the maximum heating power Phmax= 270 mW. (a) Surface profile in the x-y plane and (b) depth profile in the z-direction.
Figure 2. Temperature distribution for the maximum heating power Phmax= 270 mW. (a) Surface profile in the x-y plane and (b) depth profile in the z-direction.
Preprints 85876 g002
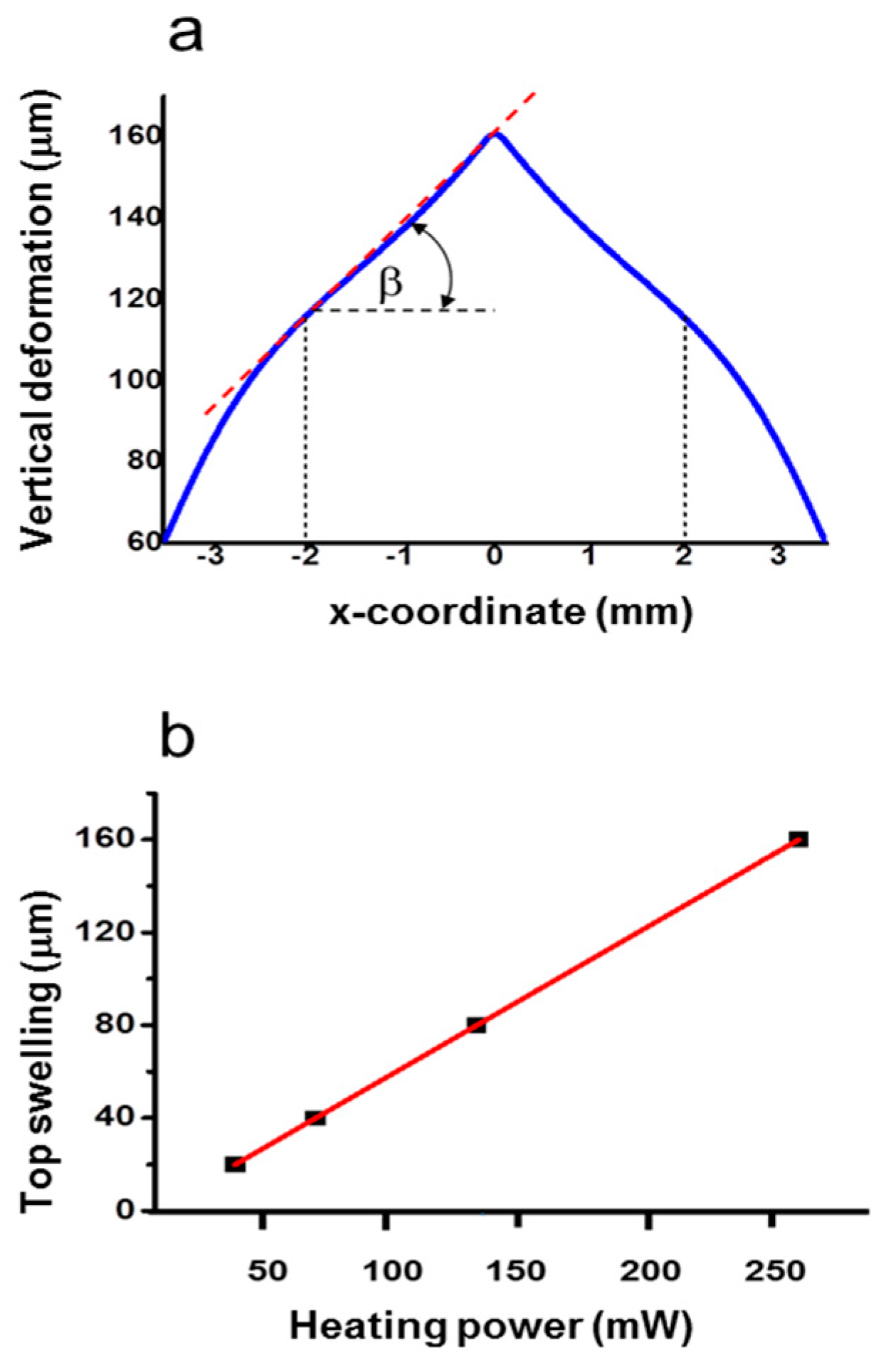
Preprints 85876 g003
Figure 3. (a) Swelling profile of PDMS in the z-direction for the heating power of 270 mW. (b) Linear trend of the maximum deformation at x = 0 mm vs. the heating power.
Figure 3. (a) Swelling profile of PDMS in the z-direction for the heating power of 270 mW. (b) Linear trend of the maximum deformation at x = 0 mm vs. the heating power.
Preprints 85876 g003
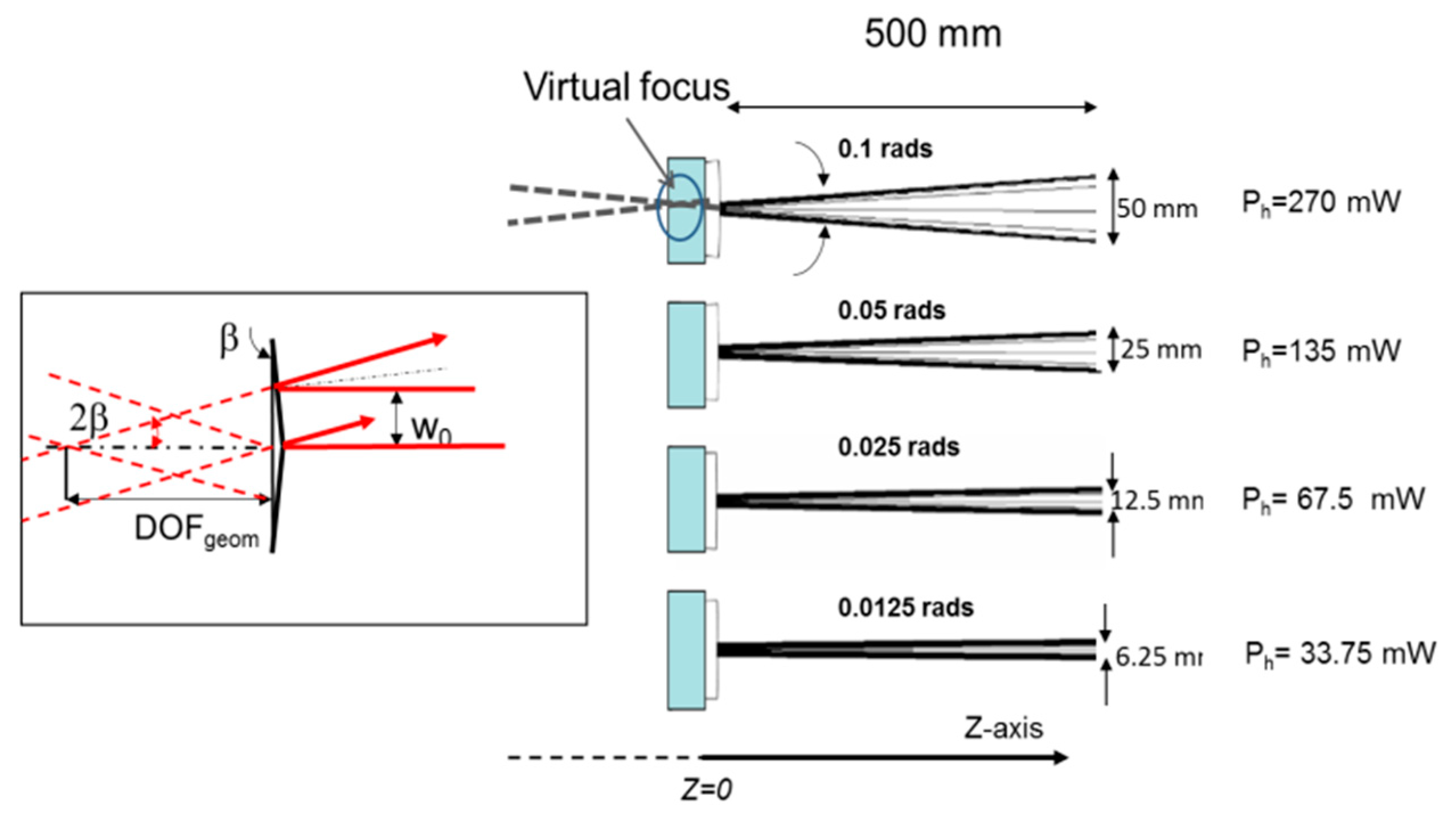
Preprints 85876 g004
Figure 4. Right side: ray-tracing simulations illustrating the splitting of the input ray distribution and the formation of the virtual focus behind (z<0) the deformed surface at different heating powers Ph. Left side: expanded view of the virtual focus region.β: base angle of the axicon, DOFgeom: geometrical optics definition of the axicon depth of focus, w0 is the beam waist of the impinging Gaussian beam (see text for the mathematical details).
Figure 4. Right side: ray-tracing simulations illustrating the splitting of the input ray distribution and the formation of the virtual focus behind (z<0) the deformed surface at different heating powers Ph. Left side: expanded view of the virtual focus region.β: base angle of the axicon, DOFgeom: geometrical optics definition of the axicon depth of focus, w0 is the beam waist of the impinging Gaussian beam (see text for the mathematical details).
Preprints 85876 g004
Preprints 85876 g005
Figure 5. Intensity profiles for Ph=270 mW (green curves) and Ph=0 mW (blue curves). (a), (b): calculated transverse intensities in the focal points at 1 THz (focus distance: 3.4 mm) and 3 THz frequency (focus distance: 8.1 mm), respectively. (c), (d): corresponding axial intensities.
Figure 5. Intensity profiles for Ph=270 mW (green curves) and Ph=0 mW (blue curves). (a), (b): calculated transverse intensities in the focal points at 1 THz (focus distance: 3.4 mm) and 3 THz frequency (focus distance: 8.1 mm), respectively. (c), (d): corresponding axial intensities.
Preprints 85876 g005
Preprints 85876 g006
Figure 6. Experimental set-up. In the lower part (“Swelling”) it is shown the optical layout used to measure indirectly the swelling of the thermally-generated Fresnel bi-mirror axicon. The focused pump beam (violet triangle) heatens the PDMS, that forms the axicon. The probe beam coming from a He-Ne laser (λ2 = 633 nm) is reflected by the Au-PDMS sample and let to propagate towards the observation screen. The input beam is divided into two main lobes in the far field, whose interdistance depends linearly on the heating power Ph (see Figure 8 in the main text). In the upper part (“Focus”) the virtual foci at 1 and 3 THz ( λ1=300 μm and λ1=100 μm respectively) , whose .coordinates are z1 = 3.4 mm (1 THz) and 8.1 mm (3 THz) are scaled τo λ2 following condition 2), These fields are reproduced at the same wavelength closely to the focus of a positive lens L ( focal length f=100 mm, distance dL from the sample= 600 mm) and magnified (140X) with an objective Obj (0.65 NA , 40X) .) to be properly visualized on a screen and recorded by a CCD camera.
Figure 6. Experimental set-up. In the lower part (“Swelling”) it is shown the optical layout used to measure indirectly the swelling of the thermally-generated Fresnel bi-mirror axicon. The focused pump beam (violet triangle) heatens the PDMS, that forms the axicon. The probe beam coming from a He-Ne laser (λ2 = 633 nm) is reflected by the Au-PDMS sample and let to propagate towards the observation screen. The input beam is divided into two main lobes in the far field, whose interdistance depends linearly on the heating power Ph (see Figure 8 in the main text). In the upper part (“Focus”) the virtual foci at 1 and 3 THz ( λ1=300 μm and λ1=100 μm respectively) , whose .coordinates are z1 = 3.4 mm (1 THz) and 8.1 mm (3 THz) are scaled τo λ2 following condition 2), These fields are reproduced at the same wavelength closely to the focus of a positive lens L ( focal length f=100 mm, distance dL from the sample= 600 mm) and magnified (140X) with an objective Obj (0.65 NA , 40X) .) to be properly visualized on a screen and recorded by a CCD camera.
Preprints 85876 g006
Preprints 85876 g007
Figure 7. Photographs (a) and traces (b) of the far field intensity recorded at 500 mm from the screen for various heating powers. (c) distance between intensity maxima vs. heating power Ph. The wavelength of the probe beam was λ2 = 633 nm.
Figure 7. Photographs (a) and traces (b) of the far field intensity recorded at 500 mm from the screen for various heating powers. (c) distance between intensity maxima vs. heating power Ph. The wavelength of the probe beam was λ2 = 633 nm.
Preprints 85876 g007
Preprints 85876 g009
Figure 9. Experimental intensity profiles of the reflected probe beam (λ2 = 633 nm) measured with the set-up of Figure 6. The results simulate the focusing of the axicon at λ1 = 300 μm (1 THz) and λ1 = 100 μm (3 THz), in (a) and (b) respectively. Insets : photos of the light distributions when the pump is Off or ON. The experimental light intensities are recorded on the horizontal black dotted lines (no pump power) and red dotted lines (pump power ON) (c, d).The same of Figure 5(c), (d), here reported for reader`s convenience.
Figure 9. Experimental intensity profiles of the reflected probe beam (λ2 = 633 nm) measured with the set-up of Figure 6. The results simulate the focusing of the axicon at λ1 = 300 μm (1 THz) and λ1 = 100 μm (3 THz), in (a) and (b) respectively. Insets : photos of the light distributions when the pump is Off or ON. The experimental light intensities are recorded on the horizontal black dotted lines (no pump power) and red dotted lines (pump power ON) (c, d).The same of Figure 5(c), (d), here reported for reader`s convenience.
Preprints 85876 g009
Preprints 85876 g010
Figure 10. Experimental intensity transversal profiles of the probe beam (λ2 = 633 nm) in the focal region of the axicon, simulating the 1 THz radiation (black, red and green traces). The intensity is constant within 1% (grey rectangle) in a range of 0.60 mm while it should decrease of 9 % if the focus would be produced by a cylindrical mirror with the same focal length of the axicon (3.4 mm) at 1 THz ( pale blue lines). The foci produced by the axicon and cylindrical mirror, that are calculated to be actually 0.22 mm apart, have been superimposed for sake of clarity.
Figure 10. Experimental intensity transversal profiles of the probe beam (λ2 = 633 nm) in the focal region of the axicon, simulating the 1 THz radiation (black, red and green traces). The intensity is constant within 1% (grey rectangle) in a range of 0.60 mm while it should decrease of 9 % if the focus would be produced by a cylindrical mirror with the same focal length of the axicon (3.4 mm) at 1 THz ( pale blue lines). The foci produced by the axicon and cylindrical mirror, that are calculated to be actually 0.22 mm apart, have been superimposed for sake of clarity.
Preprints 85876 g010
Preprints 85876 g011
Figure 11. Experimental 2D intensity profile of the reflected probe beam (λ2 = 633 nm): (a) before the optical pumping; (b) with optical pumping, after 5 heating cycles at Ph= 540 mW; (c) at zero pump power after 5 heating cycles. (d) Photo of the gold surface the after 5 heating cycles. The fracture line in correspondence to the focal pump irradiation is clearly evident.
Figure 11. Experimental 2D intensity profile of the reflected probe beam (λ2 = 633 nm): (a) before the optical pumping; (b) with optical pumping, after 5 heating cycles at Ph= 540 mW; (c) at zero pump power after 5 heating cycles. (d) Photo of the gold surface the after 5 heating cycles. The fracture line in correspondence to the focal pump irradiation is clearly evident.
Preprints 85876 g011
Preprints 85876 g012
Figure 12. Simulated behavior of the bi-mirror reflaxicon at 0.45 THz (wavelength: 0.667 mm). The waist of the input Gaussian beam is w0= 2.5 mm, the axicon angle is 0.025 rads. The dashed red lines represent the FWHM of the axial (a) and transversal (b) light intensities. The distance of the focus F from the surface is 11.8 mm. These theoretical results are comparable with those ones obtained in Ref.[34].See text for details.
Figure 12. Simulated behavior of the bi-mirror reflaxicon at 0.45 THz (wavelength: 0.667 mm). The waist of the input Gaussian beam is w0= 2.5 mm, the axicon angle is 0.025 rads. The dashed red lines represent the FWHM of the axial (a) and transversal (b) light intensities. The distance of the focus F from the surface is 11.8 mm. These theoretical results are comparable with those ones obtained in Ref.[34].See text for details.
Preprints 85876 g012
Table 1. Comparison between the theoretical focal depth of the axicon produced with a heating power Ph=270 mW, focal lenght fax, and a cylindrical mirror with focal length fmir = fax .
Table 1. Comparison between the theoretical focal depth of the axicon produced with a heating power Ph=270 mW, focal lenght fax, and a cylindrical mirror with focal length fmir = fax .
Frequency (THz) fax (mm) DOFax (mm) DOFG (mm)
1 3.4 15.8 2.2
3 7.1 18.7 3.1
5 8.0 19.0 2.44
10 6.1 19.2 0.94
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated