Prerpints.org logo
Preprint
Article

Determination of Significant 3D Hemodynamic Features for Post-Embolization Recanalization in Cerebral Aneurysms through Explainable Artificial Intelligence

This version is not peer-reviewed.

Submitted:

22 September 2023

Posted:

26 September 2023

You are already at the latest version

Abstract
Recanalization poses challenge in coil embolization for cerebral aneurysms. Establishing predictive models for post-embolization recanalization is important for clinical decision-making. However, conventional statistical and machine learning (ML) models may overlook critical parameters during the initial selection process. In this study, we automated the identification of significant hemodynamic parameters using a PointNet-based deep neural network (DNN), leveraging their inherent 3D features. Further feature analysis was conducted utilizing saliency mapping, an explainable artificial intelligence (XAI) technique. The study encompassed the analysis of velocity, pressure, and wall shear stress (WSS) in both pre- and post-coiling models derived from computational fluid dynamic (CFD) simulations for 59 aneurysms. Velocity was identified as the most pivotal parameter, supported by the lowest P-value from statistical analysis and the highest area under the curves (AUROC)/precision-recall curves (AUPRC) values from DNN model. Moreover, visual XAI analysis revealed robust injection flow zones with notable impingement points in pre-coiling models, as well as pronounced interplay between flow dynamics and the coiling plane were important 3D features in identifying the recanalized aneurysms. The combination of DNN and XAI was found to be an accurate and explainable approach not only at predicting post-embolization recanalization but also at discovering unknown features in the future.
Keywords: 
Subject: 
Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Cerebral aneurysms are abnormal focal outpouchings of cerebral arteries that are associated with significant morbidity and mortality [1]. They have a prevalence of 1-5% in the adult population, and rupture of an aneurysm can result in subarachnoid hemorrhage, a type of hemorrhagic stroke with a high mortality rate [2,3]. There are three options for treating intracranial aneurysms: observation, craniotomy with clip ligation (clipping), and endovascular occlusion using detachable coils (coiling) [1]. Coil embolization has been increasingly used due to its reduced physical burden on patients compared to clipping surgery [4]. Notwithstanding this advantage, recanalization, or the reopening of an aneurysm after coiling, is a significant challenge [5,6,7]. Therefore, the establishment of predictive models for the post-embolization recanalization in cerebral aneurysm is crucial for physicians in terms of surgery planning, decision-making and postoperative management.
Statistical analysis has shown that various morphological and hemodynamic features are significantly associated with recanalization in cerebral aneurysms. Morphological parameters, such as maximum size, neck width, height, area of aneurysm inlet, neck, posterior communicating (Pcom), as well as dimensionless parameters, such as aspect ratio, bottleneck, size ratio, area ratio and the ratio of the aneurysm volume to coil volume (VER), were identified as risk factors for recanalization [8,9,10,11,12,13,14]. Hemodynamic parameters acquired from computational fluid dynamics (CFD), such as velocity, pressure, wall shear stress (WSS) and shear rate, along with their related dimensionless parameters, including pressure difference (PD), aneurysmal residual flow volume and maximal force with porous media as coil, were also considered important risk factors [5,6,7,15,16,17,18,19,20,21]. In recent developments, machine learning (ML) models emerged as important tools for the prediction of cerebral aneurysm-related diseases. ML models, encompassing random forest, k-nearest neighbor, and support vector machines, were used to predict treatment outcomes with flow diverters, relying on predetermined hemodynamic parameters derived from CFD simulations [22]. However, both statistical and traditional ML models were notably constrained by their reliance on pre-defined input parameters. These parameters may be overlooked in the initial feature selection phase due to lack understanding of the pathology, or they may be difficult to determine accurately due to the complexity of in-vivo fluid dynamics [23,24]. Additionally, these parameters were typically spatiotemporally maximized or averaged zero-dimensional (0D) extracted from 3D or 4D CFD results (time plus 3D coordinates).
Recent advances in deep learning (DL) techniques were applied to the automated extraction of 3D morphological and hemodynamic features from CFD simulation results, albeit with certain limitations. The PointNet architecture was adopted upon its suitability for processing data from CFD simulation expressed as 3D point clouds, where each data point was described by its spatial coordinates (x, y, z) coupled with relevant hemodynamic attributes [25]. One instance developed an integrated model, employing PointNet to extract features for subsequent classification of aneurysm rupture status with traditional ML algorithm. Notably, impingement zones were predetermined in CFD simulation results for feature extraction [26]. An alternative instance used an End-to-End PointNet-based deep neural network (DNN) for the purpose of predicting aneurysm recanalization. This model extracted and determined automatically the key morphological and hemodynamic features, without the need for prior assumption or data processing. A notable drawback of this approach was the "black-box problem," which hindered its acceptance among medical experts and healthcare practitioners, who required transparency in model decision-making processes for making informed clinical inferences [27].
Recently, the technique of explainable artificial intelligence (XAI) garnered substantial attention in the field of medical diagnosis, providing insights into diagnoses and uncovering previously unknown information [28]. XAI techniques were distinguished based on three criteria [29,30]:
  • Model-based versus post hoc explanation: Model-based explanation entails the utilization of intelligible yet sufficiently sophisticated models, exemplified by linear regression, which effectively capture and elucidate the relationships between input and output variables. Conversely, post hoc explanation aims at analyzing a trained model to achieve insight into learned relationships. Saliency mapping, also called visual explanation, is the most common post hoc approach in medical image analysis [31].
  • Model-specific versus model-agnostic explanation: Model-specific explanation techniques are constrained to specific model categories, whereas model-agnostic explanation methods operate independently of the neural network's architectural choice, focusing solely on the input and output of the neural network.
  • Local versus global explanation: Global explanation offers overarching insights by delivering general relationships. In contrast, local explanation focuses on elucidating the rationale behind individual inputs, providing a detailed explanation for the certain dataset.
The objective of this study was twofold: first, to explore previously unknown hemodynamic features associated with aneurysm recanalization, and second, to develop a robust and interpretable predictive model. To achieve this, hemodynamic data were collected for 59 aneurysms through CFD simulations, and subsequently analyzed employing two distinct methodological approaches. Velocity, pressure and WSS simulated in both pre- and post-coiling models were analyzed. This involved the utilization of a PointNet-based DNN trained with the point-cloud-formatted data in 3D. Additionally, the conventional statistical analysis approach was applied, focusing on spatially averaged scalars in 0D. By comparing the results from two approaches, the significant parameters of post-embolization recanalization were determined. The 3D features of these parameters were further analyzed using saliency mapping, the post hoc, model-specific, and localized XAI technique.

2. Materials and Methods

2.1. Patients

Recanalized aneurysms were defined as aneurysms with an increase in the Raymond–Roy grade or enlargement within a grade resulting in retreatment, whereas the stable type was defined as aneurysms that showed no change or enlargement within a grade with no retreatment [32].
Clinical and radiological data of consecutive patients who underwent endovascular treatment for aneurysms between January 2007 and December 2020 were investigated. The inclusion criteria of this study were as follows: (1) saccular aneurysms; (2) coiling performed without stent placement; (3) class I or II initial aneurysm embolization results according to the Raymond–Roy classification; (4) volume embolization ratio (VER), the ratio of the aneurysm volume to the coil volume, over 20%; (5) a follow-up period of at least 1 year after endovascular coiling; and (6) pretreatment 3-dimensional rotational angiography (3D-RA) images available and of good quality for use in computational modeling [33].
A total of 58 intracranial aneurysms from 57 patients were included in the final analysis, including nine recanalized and 49 stable aneurysms. The included patients were regularly followed up with magnetic resonance angiography every six months after treatment. Digital subtraction angiography was performed when recanalization was suspected on magnetic resonance imaging and additional endovascular treatment was administered if needed.

2.2. Ethics approval

The protocol for this retrospective study was approved by the ethics committee of Kanazawa University (No. 1781). Written informed consent was waived due to the retrospective collection of clinical data; however, all patients had the right to opt-out of the study at any time.

2.3. Workflow

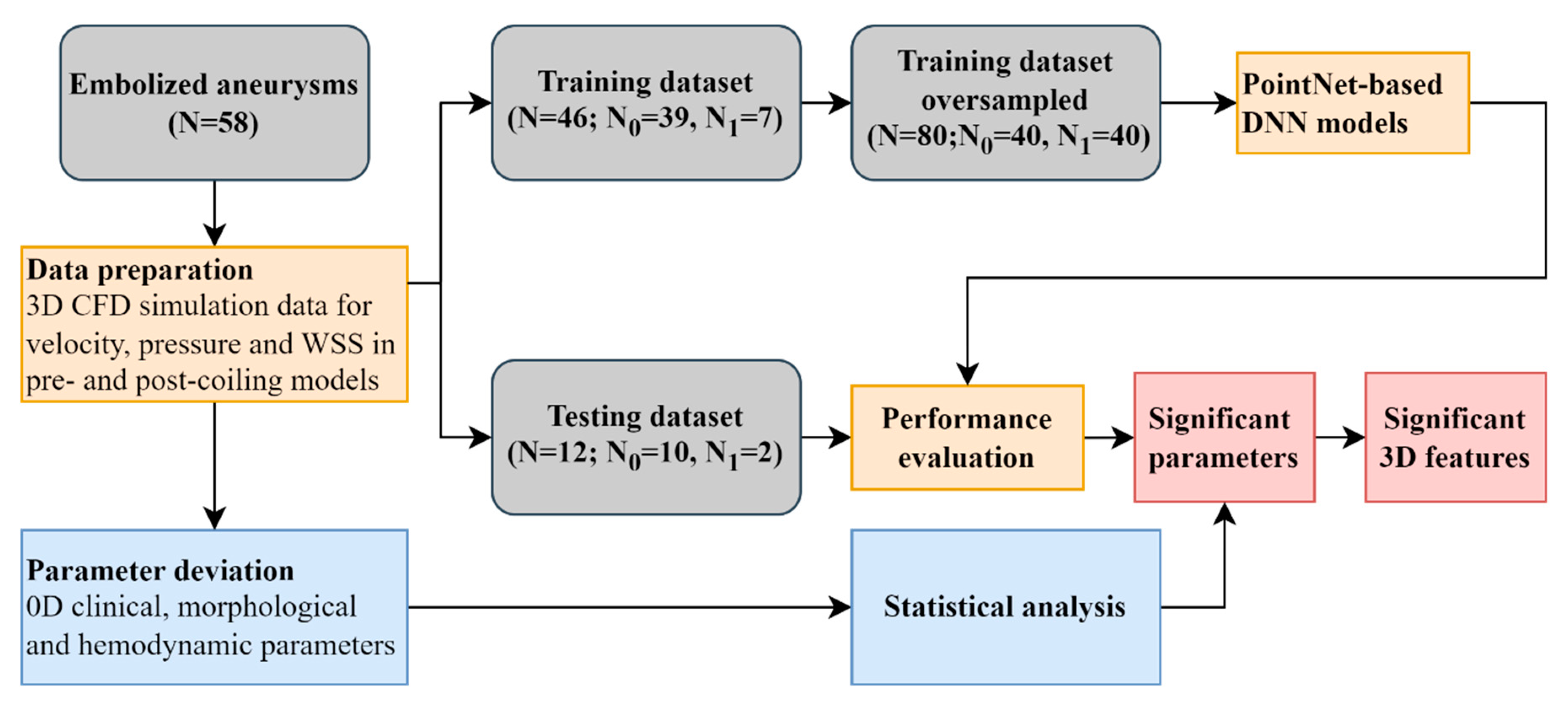
The workflow of this study was shown in Figure 1. Velocity, pressure, and wall shear stress (WSS) in both pre- and post-coiling models were derived from computational fluid dynamic (CFD) simulations for 59 aneurysms. Two approaches were utilized to identify the significant parameters for aneurysm recanalization. First, a PointNet-based DNN was used leveraging their inherent 3D features. Second, the conventional statistical analysis was conducted analyzing the spatially averaged parameters in 0D. Further 3D feature analysis was conducted utilizing the visual saliency mapping proposed in [34]. It assigns each point a saliency score to reflect its contribution to the output. A higher (positive) score was expected to indicate a more (positive) contribution. The scores were normalized to the range between 0 and 1 in this study.

2.4. CFD simulation

Digital Imaging for Communication in Medicine format was utilized for 3D-RA (Philips Healthcare, Best, Netherlands). Blood vessels were extracted and converted into standard triangulated language data via Amira (version 5.6, Maxnet Co, Ltd, Tokyo, Japan). Inlet and outlet extensions were performed to generate fully developed flow profiles. Hemodynamics in the pre-coiling and virtual post-coiling models were considered in this study. In the pre-coiling model, we defined the neck plane as the flat plane that divided the aneurysm and branching vessel (posterior communicating artery) or parent artery (internal carotid artery). Based on the pre-coiling model, the virtual post-coiling was created by removing the aneurysm dome, and we defined the coil plane as the surface of the coil mass in the same plane as the neck plane in the pre-coiling model. The inlet plane was defined as the section plane located 1 mm proximal to the aneurysm. For meshing, the 3D images were imported into ANSYS ICEM CFD software (version 16.2, ANSYS Inc., Canonsburg, Pennsylvania). To enhance the analytical precision of the boundary layer, seven prism element layers were created at the wall surface. We performed a steady-state simulation with ANSYS CFX (version 16.2, ANSYS Inc., Canonsburg, Pennsylvania) to acquire the patient-specific hemodynamic data. Blood was modeled as a Newtonian fluid with a density of 1100 kg/m3 and a viscosity of 0.0036 Pa·s. A no-slip boundary condition was applied to the rigid vessel walls. The outflow boundary condition was set as 0 Pa [5,6,7,27]. The inlet boundary condition was a mass flow rate of 0.003465 kg/s, which was the value at diastole end of pulsatile profile from literature [35].

2.5. Parameter deviation for statistical analysis

Morphological parameters were measured using 3D-RA, including the maximum size, neck width, height, area of aneurysm inlet, neck and posterior communicating (Pcom) [5,8]. Aspect ratio was defined as the ratio of the maximum perpendicular height to the neck diameter [9,10]. Bottleneck factor was defined as the ratio of the dome width to the neck diameter [11]. Size ratio was defined as the ratio of the maximum aneurysm height to the parent vessel diameter [12]. Area ratio was defined as the area ratio of the aneurysm neck to the aneurysm inlet in parent artery [13]. VER was the ratio of the aneurysm volume to the coil volume [14].
Dimensionless hemodynamic parameters were utilized for analyzing, building a model independent on patient-specific inflow rate [5,6,7,21]. Hemodynamic parameters in pre-coiling model included velocity in aneurysm dome (volvel), WSS, static pressure (P) and dynamic pressure (Pdyn) at aneurysm neck plane, which were normalized using surface-averaged velocity, WSS and P at aneurysm inlet in parent artery. Inflow rate ratio (FR) was defined as the ratio of the inflow rate at the neck plane to the flow rate at the inlet plane [5]. In the post-coiling model, PP was defined as pressure change between aneurysm neck and inlet, whereas pressure difference (PD) was defined as the ratio of PP to Pdyn at aneurysm inlet. All hemodynamic parameters were spatially averaged.

2.6. Statistical analysis

All continuous parameter values were subsequently expressed as mean ± standard deviation. Continuous variables were analyzed using the Levene test to determine the normality. The Levene test was employed to examine the equality of variances between two groups with continuous variables. Differences in variables between the two groups were tested using Welch’s t-test for data with unequal variance or t-test for data with equal variance. For categorical variables, a chi-square test was used to examine the significant differences between the groups. A P-value less than 0.05 was considered statistically significant. Statistical analyses were performed using Scipy (version 1.9.3) [36].

2.7. Data preparation and augmentation for DNN

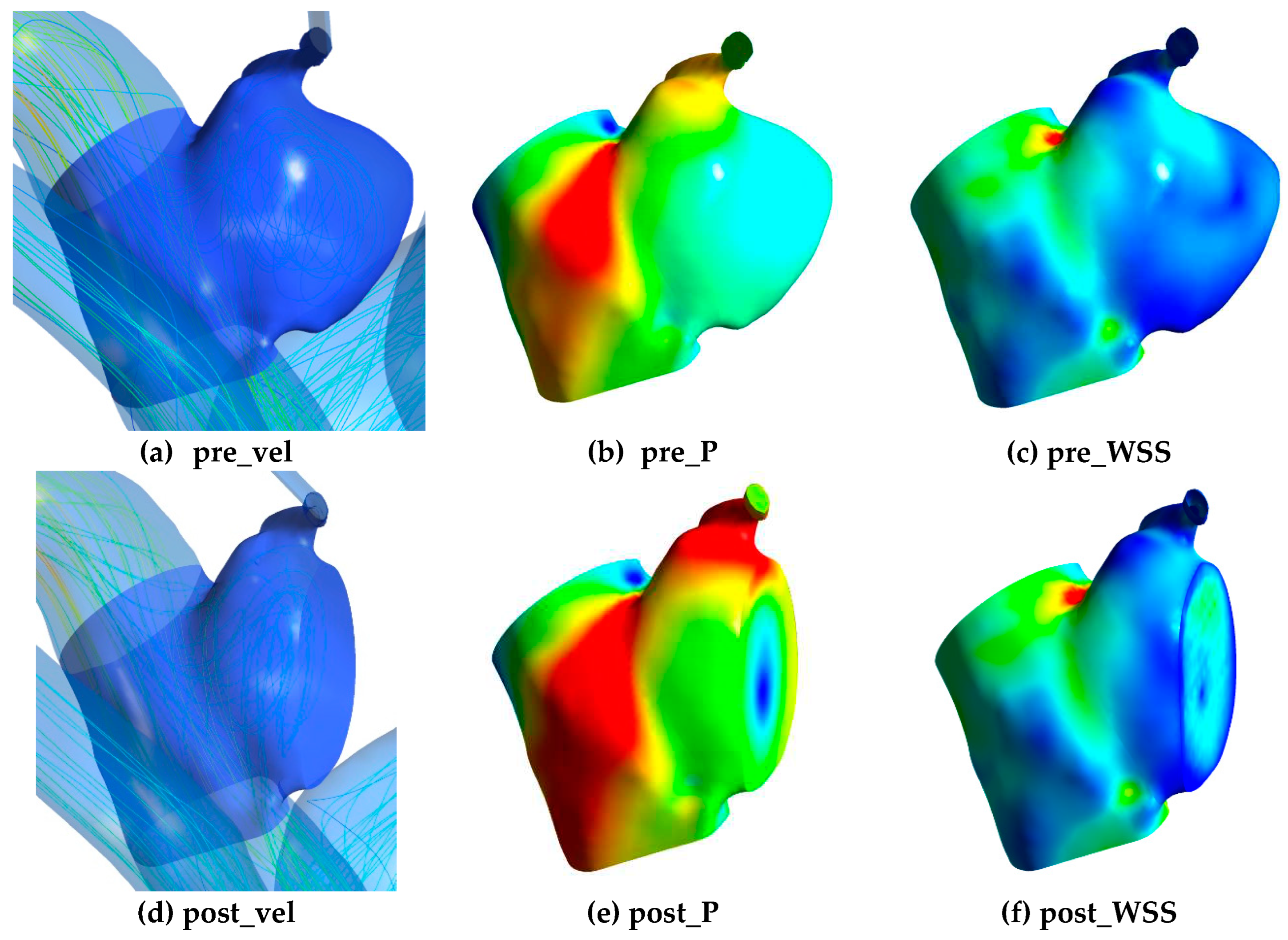
To train the DNN, 3D morphological data including x, y, z coordinates and the relevant hemodynamic data were exported from CFD simulation results. The hemodynamic data included velocity, pressure and WSS in pre-coiling (pre_vel, pre_P, pre_WSS) and post-coiling model (post_vel, post_P, post_WSS) as shown in Figure 2. For all the parameters, only data at the aneurysm part was considered. Velocity and pressure data were exported from the internal field of the aneurysm, whereas WSS data were obtained from surface nodes. Voxelization with a voxel size of 0.5mm was employed on velocity and pressure data to ensure uniform distribution in the dataset. Without this process, data points tended to cluster near the wall due to the presence of mesh wall layers in CFD simulations.
The DL algorithms have trouble learning when some classes dominate others [37]. The minority class within the training dataset was initially augmented through oversampling, involving the replication of instances. Subsequently, online augmentation techniques were applied during the training process. The morphological point cloud was augmented by randomly rotating the object along x, y, z axis in the range of [−180°, 180°] and by jittering its position by a Gaussian noise with a mean of 0 and standard deviation of 0.01 [25]. The hemodynamic data was augmented by adding a random type of noise (Gaussian or white noise) with a random level in the range of [0, 0.025] [27].

2.8. DNN model architecture and training

This study utilized a PointNet-based DNN to extract both 3D morphological and hemodynamic features to predict post-embolization recanalization in cerebral aneurysm [25,27]. It consumed the 3D point clouds with two feature channels (morphology and hemodynamics) as inputs and predicted recanalization probabilities as outputs. The DNN consisted of two key modules: feature extraction and classification. In the first module, we approximated the model by a convolutional network; then its output was aggregated in a latent global feature with a vector of size 1024 by the symmetric function, herein, max pooling was utilized. Based on the features from the first module, the probability of aneurysm recanalization was decoded in the second module. In this stage, multi-layer perceptron (MLP) mapped the output to probability of K classes, herein, 2 events (recanalized or stable) for each patient. The detailed description could be found in our previous work [27].
Before training, the input point clouds were normalized to within [0, 1] with each parameter’s maximum and minimum value. A batch size of 10 and batch-norm was used in this study. Dropout layers were utilized for the MLP. Stochastic gradient descent optimization was used to update the weights and biases, herein, adaptive moment estimation (ADAM). During training, an eight-fold cross validation and repetition of 2000 was used. Parameters of the best epoch with lowest loss on validation dataset were recorded. An adaptive learning rate with an exponential decay was adopted with an initial learning rate of 0.0001, decay step of 200000 and decay rate of 0.7. The technique was implemented using the TensorFlow DNN library and executed on a PC cluster with 32 cores of Intel(R) Xeon(R) Gold 6242 CPU @ 2.80GHz and 1.5T RAM in total. The operating system is CentOS 7.4.1708.

2.9. Evaluation of DNN model

The receiver-operating characteristic (ROC) curves were constructed after training and the area under the curves (AUROC) values were calculated to evaluate the predictive performance of DNN model. Furthermore, to address the imbalanced nature of the dataset, in which only 18% of the aneurysms exhibited recanalization, we utilized the area under the precision recall curve (AUPRC) together with AUROC as a metric for performance evaluation. This method is specially designed to detect rare events and are appropriate in these scenarios as they particularly show a classifier having a low performance if it is misclassifying most or all the minority class [38]. Results were further plotted in confusion matrix to analyze its performance for each class. Confusion matrix plots the number of correct and incorrect model-predicted outcomes (horizontal axis) against the actual outcomes (vertical axis). The performance examination was performed with Scikit-learn (version 1.0.2) [39].

2.10. Data and code availability

The datasets generated for this study are protected patient information. The code is available at https://github.com/saradeuJP/XAI_PointNet_CA.git.

3. Results

3.1. Patient characteristics

Characteristics of patients in each group are listed in Table 1. There was no significant difference in age, sex, rupture status and aneurysm locations between two groups. The recanalized group showed higher mean values for all morphological parameters except area ratio in comparison to the stable group. Max size, Height and Area Neck were significantly larger in the recanalized group. Within the hemodynamic features, volvel and PD demonstrated significant differences between the two groups, whereas P, PP, Pdyn, WSS and FR did not show significant differences.

3.2. Model training and performance

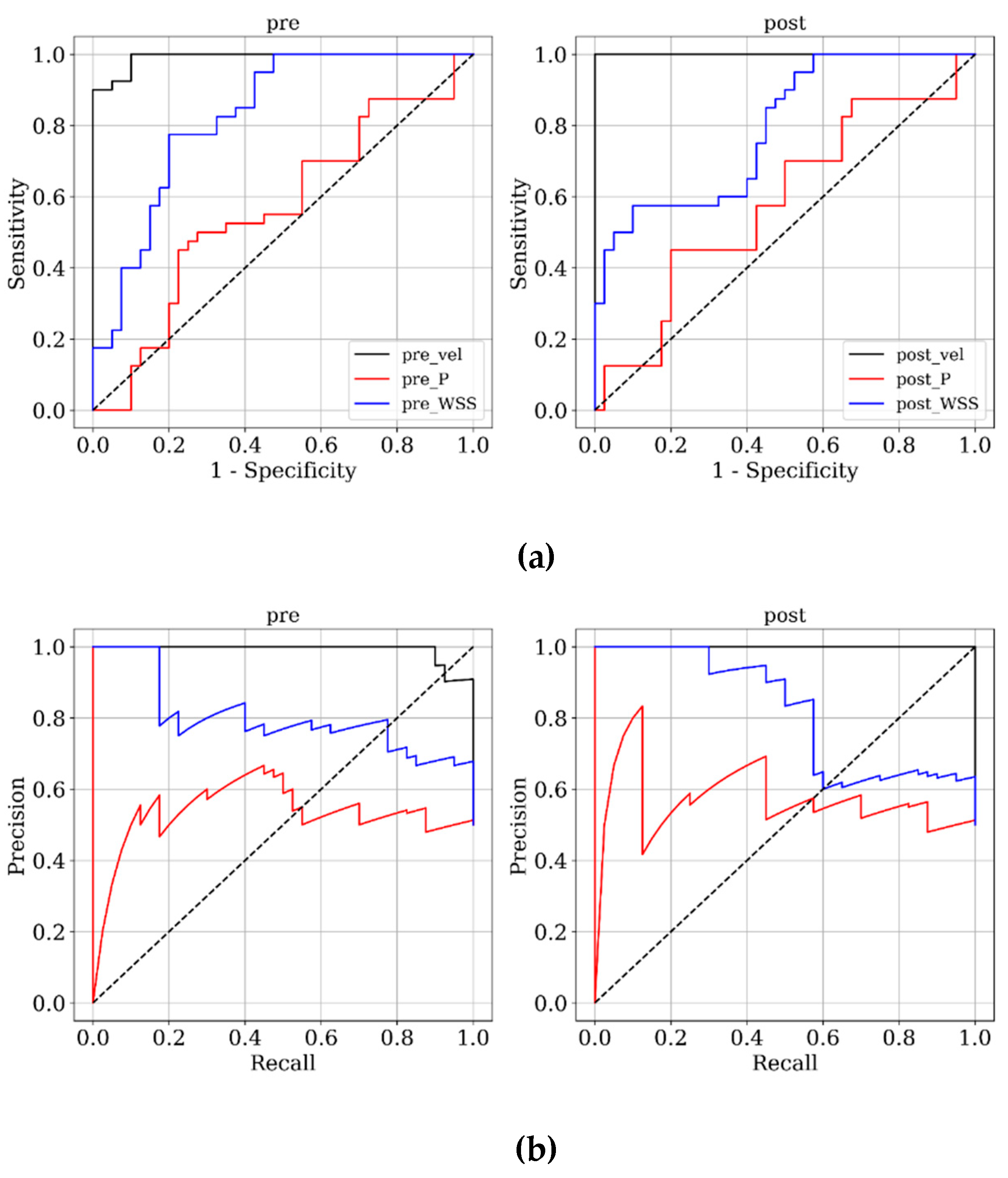
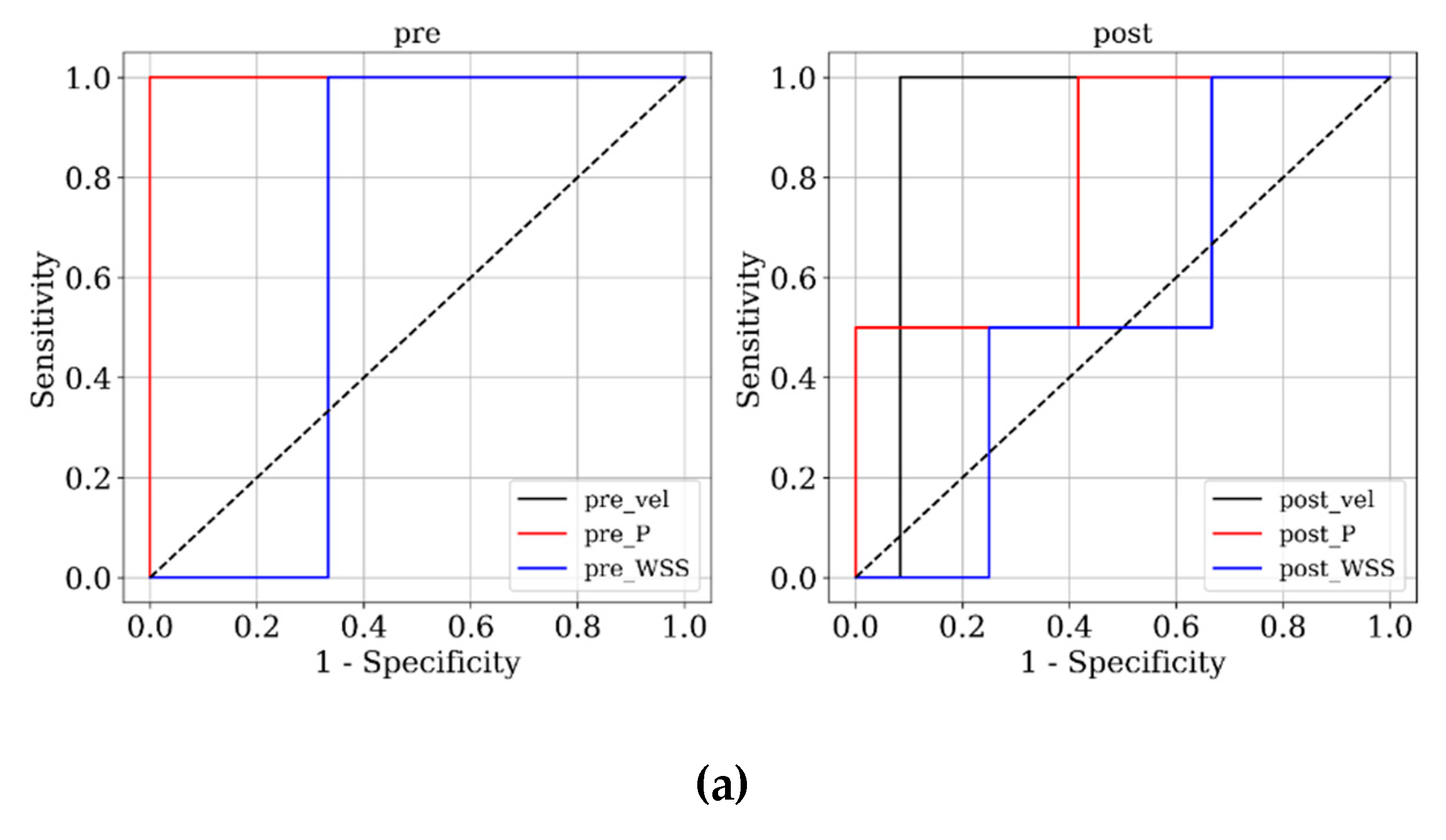
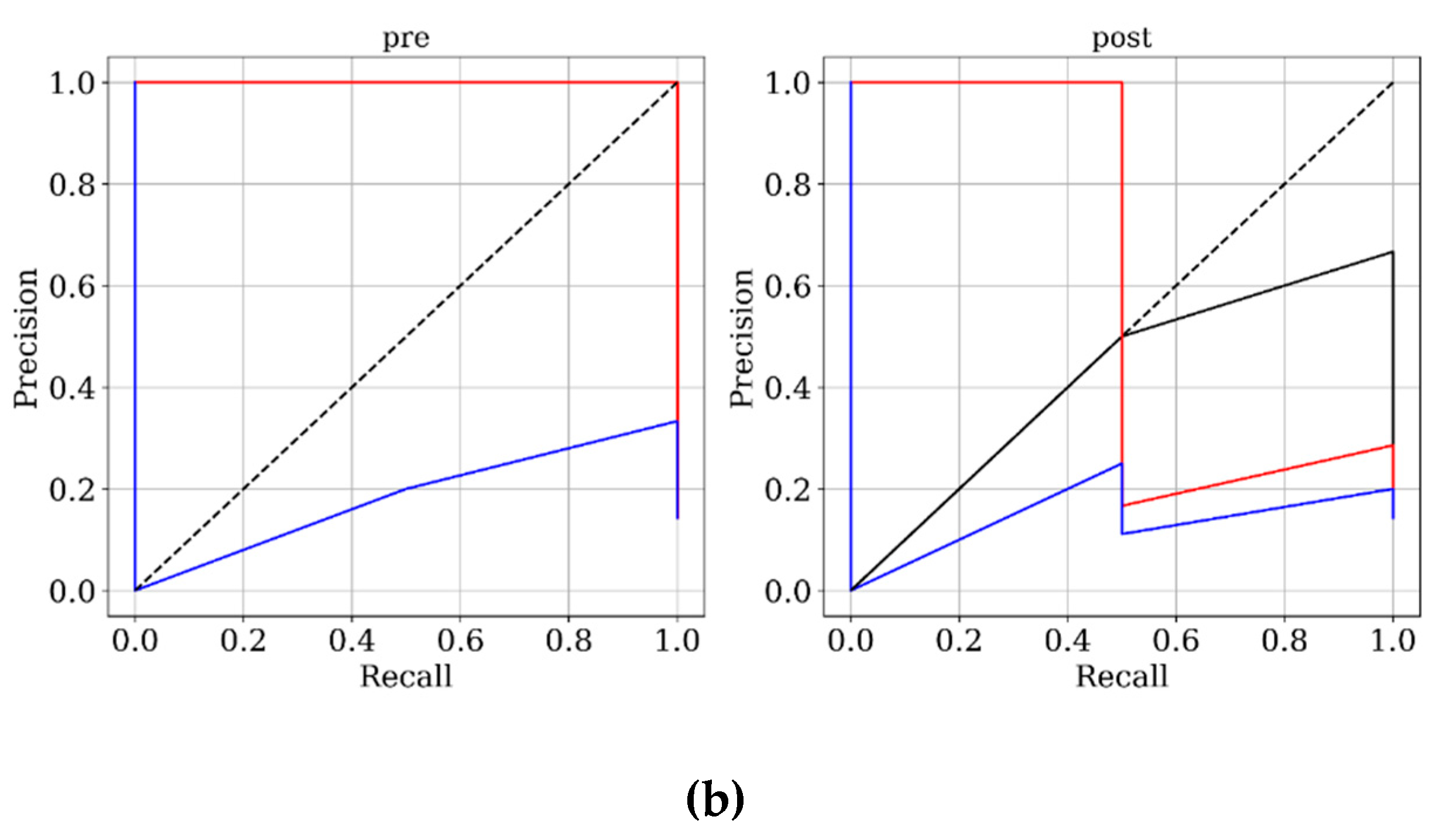
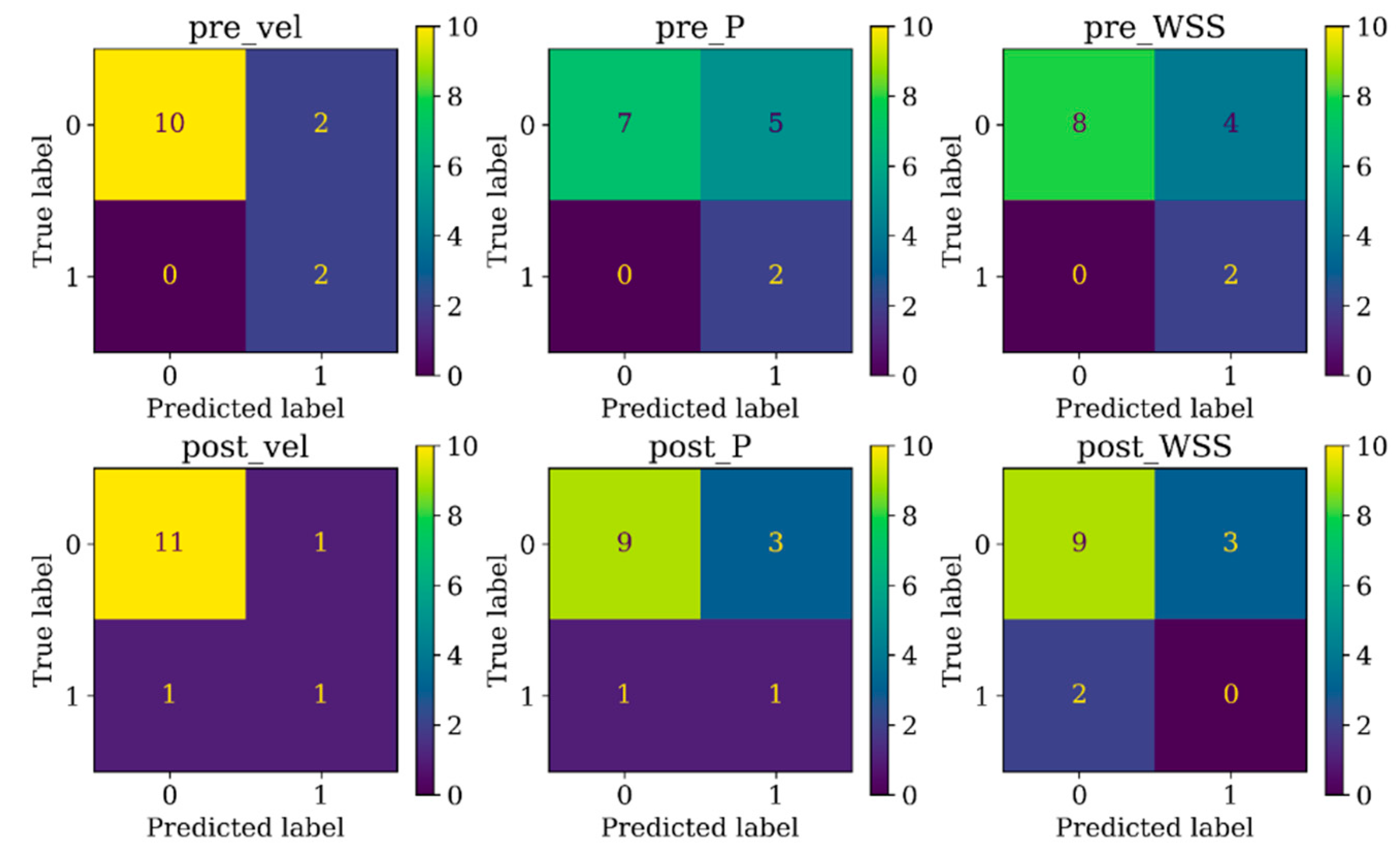
Figure 3 and Figure 4 present ROC and PRC analyses on the training and testing datasets, enabling a performance comparison of DNN models trained with 3D velocity, pressure, and WSS in both pre- and post-coiling models. On the training dataset, the model trained with velocity data from the post-coiling model demonstrated the highest performance with AUROC/AUPRC values of 1.000/1.000, a statistically significant improvement over the other five models (P < 0.05). The model trained with velocity data from the pre-coiling model achieved also commendable results with AUROC/AUPRC values of 0.991/0.992. Especially, it displayed its superior performance on the testing dataset, as detailed in Table 2, distinguishing the two recanalized aneurysms, as highlighted by confusion matrix in Fig. 5. In contrast, DNN models trained with pressure and WSS data exhibited less satisfactory performance on both training and testing dataset. Consequently, the subsequent section focused on elucidating the explainability of the DNN model trained with 3D velocity data.

3.3. Model explainability

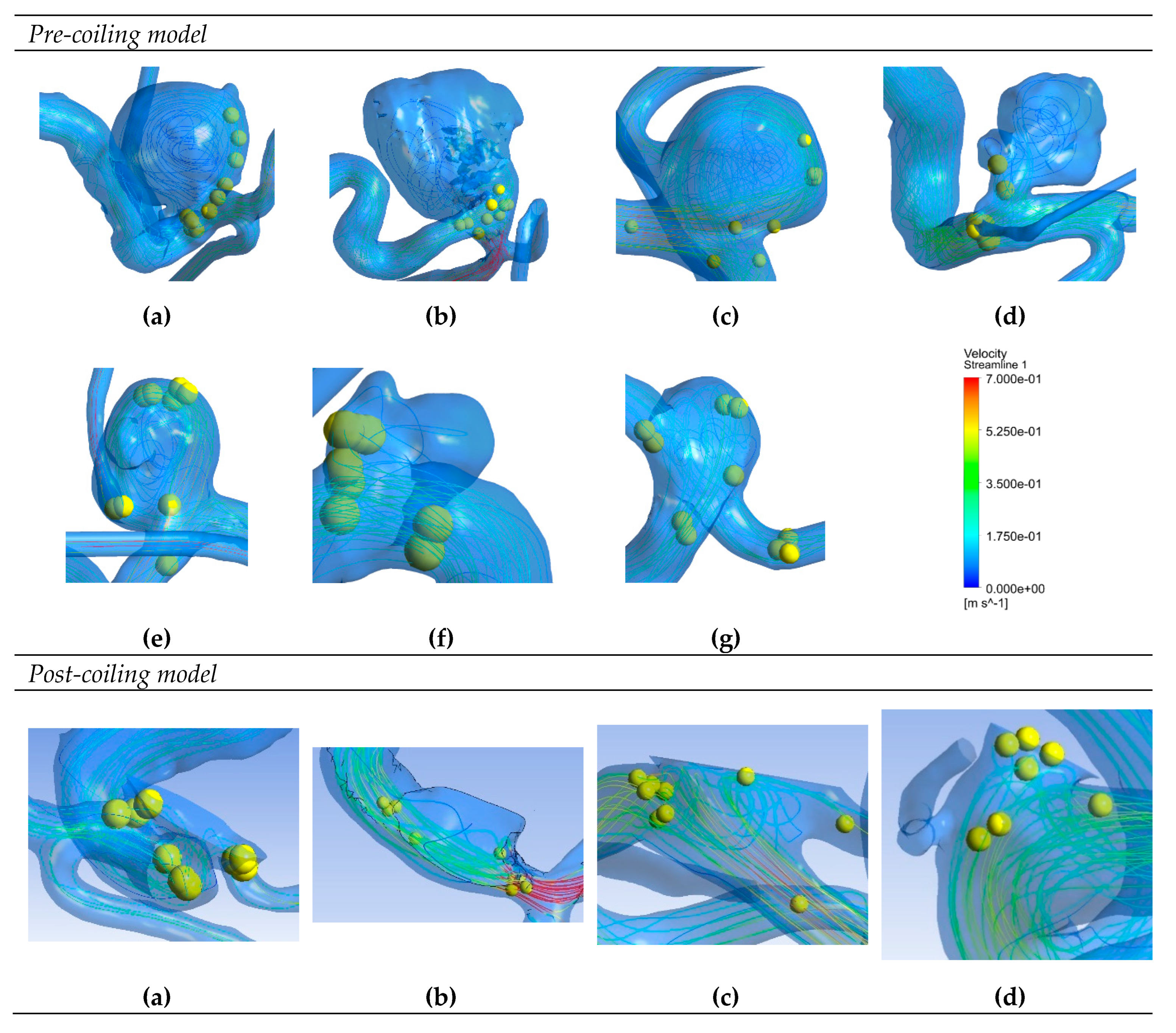
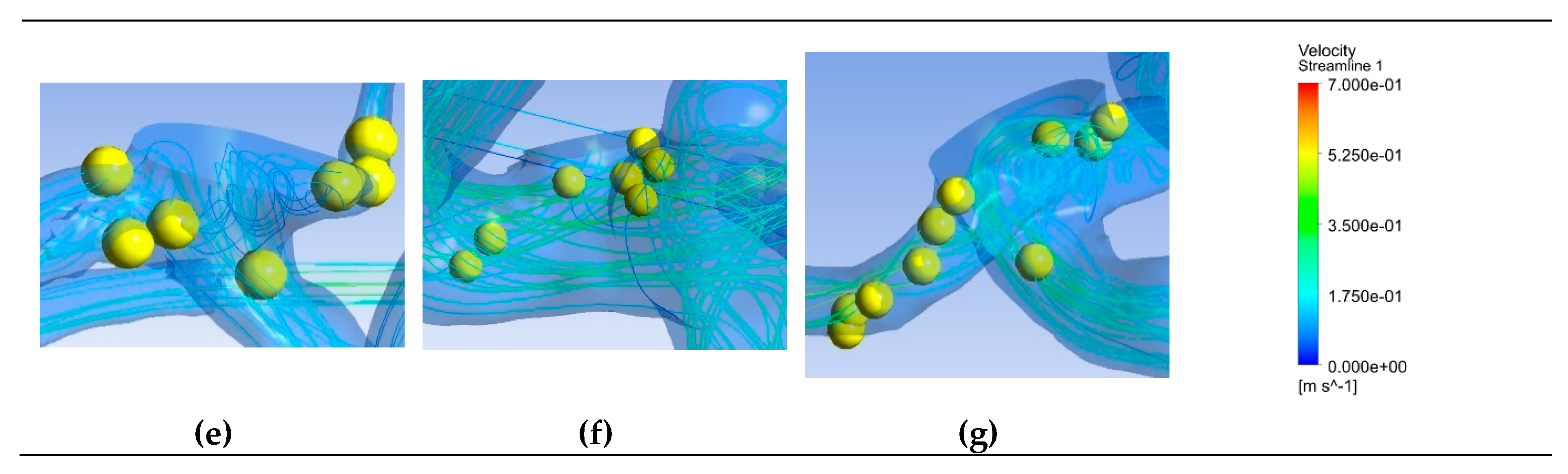
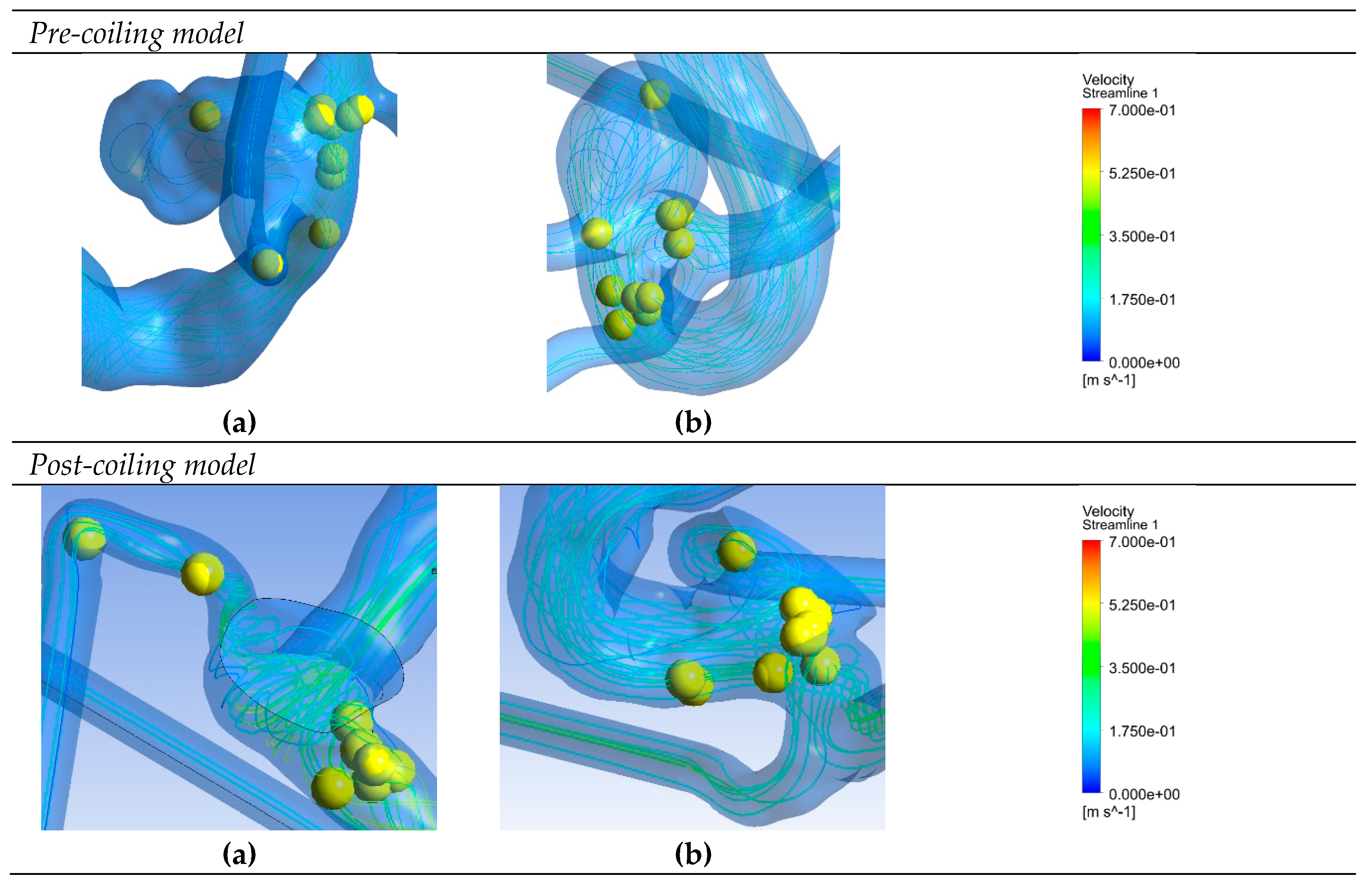
Figure 6 depicts saliency maps illustrating the top ten salient points within seven recanalized aneurysms from the training dataset in both pre- and post-coiling models. Within the pre-coiling models, the recanalized cases revealed robust injection flow zones with strong impingement impact points at walls. These points were observed within the aneurysms for cases (a), (c), (e), and (g). For cases (d) and (f), these impact points manifested in secondary aneurysms, whereas case (b) exhibited them at the aneurysm inlet. Within the post-coiling models, our observations revealed the presence of three interacting modes in recanalized aneurysms. These modes encompassed the presence of forceful impact points in cases (a), (c), (d), (e), (f), and (g), revealing the salient points on the aneurysm neck plane, as well as the existence of the Pcom within the flow direction in cases (a), (c) and (e), with salient points observed in this artery. Additionally, substantial contact areas in the direction parallel to the flow were also considered as important features, with salient points found at both aneurysm in- and outlet in case (b). In contrast, these influential effects were conspicuously absent in stable cases shown in Figure 7 within both pre- and post-coiling models.

4. Discussion

In this study, we identified the significant hemodynamic parameter using a DNN with PointNet architecture. Its important 3D features that significantly contributed to the DNN's decision-making process were further analyzed through XAI technique. Firstly, significant hemodynamic parameter, that were automatically determined by DNN, were in alignment with those identified through the conventional statistical analysis. DNN models trained with velocity data demonstrated superior performance, as evidenced by ROC and PRC curves, in both training and testing datasets compared to models trained with pressure and WSS data. The statistical analysis had the same conclusions, where velocity within the aneurysm dome in the pre-coiling model (volvel) yielded the lowest P-value, whereas pressure and WSS exhibited no significant differentiation between the two groups. Secondly, the saliency map visualization technique hinted at the existence of hitherto unknown 3D hemodynamic features associated with recanalization. In the pre-coiling models, it identified strong injection flow zones with impingement impact points in recanalized aneurysms as the important 3D features to classify aneurysm recanalization. While this represents a novel finding in the context of aneurysm recanalization, it aligns with prior research in aneurysm development and rupture emphasizing the significance of injection and impingement patterns [18,40]. In post-coiling models, the saliency map illuminated a pronounced interplay between the flow and coiling plane. The XAI technique effectively identified potential factors contributing to this interaction, including impingement points on the coiling plane, the presence of Pcom in the direction of the flow, and substantial contact areas. This discovery, to the best of our knowledge, marks the first report of such phenomena. However, it was noteworthy that the 0D parameters utilized in this study provided an incomplete representation of the complex 3D flow features. Future research endeavors will encompass a broader spectrum of 0D parameters, including flow jet angle and dispersion index, to corroborate the consistency between DNN and statistical analyses, as well as the features observed from XAI visualization [44]. Additionally, DNN models trained with velocity data from both pre- and post-coiling models exhibited no significant differences on the testing dataset, underscoring the necessity for a larger and external patient dataset for future analyses aimed at selecting the most effective model.
The complexity and inherent instability of flow patterns in cerebral aneurysm ranged from simplistic configurations with a singular recirculation region to intricate arrangements featuring multiple vortical structures that could be stable, dynamic, or intermittent throughout the cardiac cycle. These patterns were not solely contingent upon the size and shape of the aneurysm but were profoundly influenced by the manner in which blood flowed from the parent vessel into the aneurysm, a phenomenon intricately linked to the geometry of the parent artery [19]. One widely employed parameter for quantitatively assessing the impact of inflow impingement on the aneurysm wall was WSS. Locally elevated WSS characterized concentrated inflow jets, whereas a more uniform WSS distribution with lower magnitudes delineated areas of stagnation within the aneurysm [41]. However, the complex interplay between morphology and hemodynamics engendered a contentious debate regarding the role of high versus low WSS in cerebral aneurysm pathophysiology [42,43]. To further describe the inflow and impingement pattern, one categorized inject and impingement sizes manually, typically as small or large, the other determined the quantitative size through predefined thresholds such as exceeding 80% of the maximum WSS within the aneurysm sac [15,26]. In contrast, our approach leveraged automatic feature extraction and determination from raw 3D flow pattern data. This approach eliminated the constraints associated with manual preprocessing and prior assumptions or knowledge. Additionally, the flexibility of the DNN model allows for the incorporation of various 3D hemodynamic data inputs, thereby addressing the confounding factors contributing to recanalization. Furthermore, this framework can be readily extended to accommodate 4D input data, incorporating the temporal dimension to capture the temporal instability of flow patterns.
This study did not consider the coiling configuration. The coil surface was represented by a flat and rigid plane; whereas in clinical practice, the coil surface is typically rough and allows for blood penetration into the coil mass. Further investigation is needed to integrate the realistic coil surface obtained through advanced techniques such as silent magnetic resonance angiography into the analysis [45].
Other than saliency map, we also experimented with GradCAM heatmaps but found that the resolution of these is too coarse to capture the fine details that are important to understand the models [46]. For 1024 input points in this work, the GradCAM heatmap would be 170x coarser resolution than the input. In comparison, saliency map have the same resolution as the input image and allow us to examine the predictions at the pointwise level [47]. Other XAI methods are also planned to be used in the future to deepen our understanding of recanalization pathology [29,30].
There are also other limitations to this study. First, the analysis encompassed a total of 58 aneurysms in this study. To further evaluate the model, a larger cohort of cases will be analyzed as a future step. Second, this was a retrospective study. To validate the effectiveness of developed models as a predictive tool, a prospective study with a larger cohort involving all types of aneurysms is required. Third, the fluid-solid interaction between the vessel walls and blood was not considered. Finally, the boundary conditions were uniform for all the patients. To enhance accuracy, future investigations will explore the utilization of patient-specific boundary conditions derived from 4D-Flow MRI or Transcranial Doppler Ultrasonography, if feasible.

5. Conclusions

PointNet-based DNN model trained utilizing 3D velocity data exhibited significant potential in prognosticating post-embolization aneurysm recanalization. The integration of XAI methodologies provided insight into critical 3D features that played a pivotal role in the decision-making framework, holding the potential to unearth hitherto unexplored 3D hemodynamic characteristics in the future.

Author Contributions

Conceptualization, J.L.; methodology, J.L.; software, J.L., K.M. and J.S.; validation, J.L., K.M. and J.S.; formal analysis, J.L. and K.M.; investigation, J.L.; resources, K.M., T.U., M.N. and J.S.; data curation, K.M., T.U. and J.L.; writing—original draft preparation, J.L.; writing—review and editing, J.L. and K.M.; visualization, J.L.; supervision, J.S.; project administration, J.L. and J.S.; funding acquisition, J.L. and K.M.; All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Japan Science and Technology Agency Support for Pioneering Research Initiated by the Next Generation (JST SPRING), grant number JPMJSP2135 and The Japan Society for the Promotion of Science (JSPS) KAKENHI, grant number C-16K10783.

Institutional Review Board Statement

The protocol for this retrospective study was approved by the ethics committee of Kanazawa University (No. 1781).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Data is unavailable due to privacy or ethical restrictions. The code is available at https://github.com/saradeuJP/XAI_PointNet_CA.git.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Brisman, J.L.; Song, J.K.; Newell, D.W. Cerebral Aneurysms. N. Engl. J. Med. 2006, 355, 928–939. [Google Scholar] [CrossRef] [PubMed]
  2. Wiebers, D.O. Unruptured Intracranial Aneurysms: Natural History, Clinical Outcome, and Risks of Surgical and Endovascular Treatment. The Lancet 2003, 362, 103–110. [Google Scholar] [CrossRef] [PubMed]
  3. Le Roux, P.D.; Winn, H.R.; Newell, D.W. Management of Cerebral Aneurysms; WB Saunders Company, 2004.
  4. Hwang, J.S.; Hyun, M.K.; Lee, H.J.; Choi, J.E.; Kim, J.H.; Lee, N.R.; Kwon, J.-W.; Lee, E. Endovascular Coiling versus Neurosurgical Clipping in Patients with Unruptured Intracranial Aneurysm: A Systematic Review. BMC Neurol. 2012, 12, 99. [Google Scholar] [CrossRef] [PubMed]
  5. Nambu, I.; Misaki, K.; Uchiyama, N.; Mohri, M.; Suzuki, T.; Takao, H.; Murayama, Y.; Futami, K.; Kawamura, T.; Inoguchi, Y.; et al. High Pressure in Virtual Postcoiling Model Is a Predictor of Internal Carotid Artery Aneurysm Recurrence after Coiling. Neurosurgery 2019, 84, 607–615. [Google Scholar] [CrossRef]
  6. Misaki, K.; Uno, T.; Nambu, I.; Yoshikawa, A.; Kamide, T.; Uchiyama, N.; Nakada, M. Prediction of Post-Embolization Recurrence of Anterior Communicating Aneurysms with A1 Segment Asymmetry by Fluid Dynamic Analysis. J. Neuroendovascular Ther. 2021, 15, 71–76. [Google Scholar] [CrossRef]
  7. Uno, T.; Misaki, K.; Nambu, I.; Yoshikawa, A.; Kamide, T.; Uchiyama, N.; Nakada, M. Prediction of Internal Carotid Artery Aneurysm Recurrence by Pressure Difference at the Coil Mass Surface. Neuroradiology 2021, 63, 593–602. [Google Scholar] [CrossRef]
  8. Chen, Y.; Lin, B.; Zhou, J.; Chen, L.; Yang, Y.; Zhao, B. Morphological Predictors of Middle Cerebral Artery Bifurcation Aneurysm Rupture. Clin. Neurol. Neurosurg. 2020, 192, 105708. [Google Scholar] [CrossRef]
  9. Ujiie, H.; Tachi, H.; Hiramatsu, O.; Hazel, A.L.; Matsumoto, T.; Ogasawara, Y.; Nakajima, H.; Hori, T.; Takakura, K.; Kajiya, F. Effects of Size and Shape (Aspect Ratio) on the Hemodynamics of Saccular Aneurysms: A Possible Index for Surgical Treatment of Intracranial Aneurysms. Neurosurgery 1999, 45, 119–130. [Google Scholar]
  10. Ujiie, H.; Tamano, Y.; Sasaki, K.; Hori, T. Is the Aspect Ratio a Reliable Index for Predicting the Rupture of a Saccular Aneurysm? Neurosurgery 2001, 48, 495–503. [Google Scholar] [CrossRef]
  11. Hoh, B.L.; Sistrom, C.L.; Firment, C.S.; Fautheree, G.L.; Velat, G.J.; Whiting, J.H.; Reavey-Cantwell, J.F.; Lewis, S.B. Bottleneck Factor and Height-Width Ratio: Association with Ruptured Aneurysms in Patients with Multiple Cerebral Aneurysms. Neurosurgery 2007, 61, 716–723. [Google Scholar] [CrossRef]
  12. Dhar, S.; Tremmel, M.; Mocco, J.; Kim, M.; Yamamoto, J.; Siddiqui, A.H.; Hopkins, L.N.; Meng, H. Morphology Paramaters for Intracranial Aneurysm Rupture Risk Assessment. Neurosurgery 2008, 63, 185–197. [Google Scholar] [CrossRef] [PubMed]
  13. Huang, Z.-Q.; Meng, Z.-H.; Hou, Z.-J.; Huang, S.-Q.; Chen, J.-N.; Yu, H.; Feng, L.-J.; Wang, Q.-J.; Li, P.-A.; Wen, Z.-B. Geometric Parameter Analysis of Ruptured and Unruptured Aneurysms in Patients with Symmetric Bilateral Intracranial Aneurysms: A Multicenter CT Angiography Study. Am. J. Neuroradiol. 2016, 37, 1413–1417. [Google Scholar] [CrossRef] [PubMed]
  14. Neki, H.; Kohyama, S.; Otsuka, T.; Yonezawa, A.; Ishihara, S.; Yamane, F. Optimal First Coil Selection to Avoid Aneurysmal Recanalization in Endovascular Intracranial Aneurysmal Coiling. J. Neurointerventional Surg. 2018, 10, 50–54. [Google Scholar] [CrossRef] [PubMed]
  15. Cebral, J.R.; Castro, M.A.; Burgess, J.E.; Pergolizzi, R.S.; Sheridan, M.J.; Putman, C.M. Characterization of Cerebral Aneurysms for Assessing Risk of Rupture by Using Patient-Specific Computational Hemodynamics Models. Am. J. Neuroradiol. 2005, 26, 2550–2559. [Google Scholar]
  16. Cebral, J.R.; Mut, F.; Sforza, D.; Löhner, R.; Scrivano, E.; Lylyk, P.; Putman, C. Clinical Application of Image-Based CFD for Cerebral Aneurysms. Int. J. Numer. Methods Biomed. Eng. 2011, 27, 977–992. [Google Scholar] [CrossRef] [PubMed]
  17. Cebral, J.R.; Duan, X.; Gade, P.S.; Chung, B.J.; Mut, F.; Aziz, K.; Robertson, A.M. Regional Mapping of Flow and Wall Characteristics of Intracranial Aneurysms. Ann. Biomed. Eng. 2016, 44, 3553–3567. [Google Scholar] [CrossRef]
  18. Cebral, J.R.; Mut, F.; Gade, P.; Cheng, F.; Tobe, Y.; Frosen, J.; Robertson, A.M. Combining Data from Multiple Sources to Study Mechanisms of Aneurysm Disease: Tools and Techniques. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3133. [Google Scholar] [CrossRef]
  19. Sforza, D.M.; Putman, C.M.; Cebral, J.R. Hemodynamics of Cerebral Aneurysms. Annu. Rev. Fluid Mech. 2009, 41, 91–107. [Google Scholar] [CrossRef]
  20. Zhang, Q.; Jing, L.; Liu, J.; Wang, K.; Zhang, Y.; Paliwal, N.; Meng, H.; Wang, Y.; Wang, S.; Yang, X. Predisposing Factors for Recanalization of Cerebral Aneurysms after Endovascular Embolization: A Multivariate Study. J. NeuroInterventional Surg. 2018, 10, 252–257. [Google Scholar] [CrossRef]
  21. Fujimura, S.; Takao, H.; Suzuki, T.; Dahmani, C.; Ishibashi, T.; Mamori, H.; Yamamoto, M.; Murayama, Y. A New Combined Parameter Predicts Re-Treatment for Coil-Embolized Aneurysms: A Computational Fluid Dynamics Multivariable Analysis Study. J. NeuroInterventional Surg. 2018, 10, 791–796. [Google Scholar] [CrossRef]
  22. Paliwal, N.; Jaiswal, P.; Tutino, V.M.; Shallwani, H.; Davies, J.M.; Siddiqui, A.H.; Rai, R.; Meng, H. Outcome Prediction of Intracranial Aneurysm Treatment by Flow Diverters Using Machine Learning. Neurosurg. Focus 2018, 45, E7. [Google Scholar] [CrossRef]
  23. Kallmes, D.F. Point: CFD—Computational Fluid Dynamics or Confounding Factor Dissemination. Am. J. Neuroradiol. 2012, 33, 395–396. [Google Scholar] [CrossRef] [PubMed]
  24. Xiang, J.; Tutino, V.M.; Snyder, K.V.; Meng, H. CFD: Computational Fluid Dynamics or Confounding Factor Dissemination? The Role of Hemodynamics in Intracranial Aneurysm Rupture Risk Assessment. Am. J. Neuroradiol. 2014, 35, 1849–1857. [Google Scholar] [CrossRef] [PubMed]
  25. Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep Learning on Point Sets for 3d Classification and Segmentation. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition; pp. 2017652–660.
  26. Chen, R.; Mo, X.; Chen, Z.; Feng, P.; Li, H. An Integrated Model Combining Machine Learning and Deep Learning Algorithms for Classification of Rupture Status of IAs. Front. Neurol. 2022, 13, 868395. [Google Scholar] [CrossRef] [PubMed]
  27. LIAO, J.; SAKAMOTO, J.; MISAKI, K.; SIRITANAWAN, P.; KOTANI, K. Prediction of Post-Embolization Recurrence in Internal Carotid-Posterior Communicating Aneurysms with Vel-PointNet. J. Biomech. Sci. Eng. 2023, advpub, 22–00471. [Google Scholar] [CrossRef]
  28. Zhang, Y.; Weng, Y.; Lund, J. Applications of Explainable Artificial Intelligence in Diagnosis and Surgery. Diagnostics 2022, 12, 237. [Google Scholar] [CrossRef] [PubMed]
  29. Adadi, A.; Berrada, M. Peeking Inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
  30. Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Definitions, Methods, and Applications in Interpretable Machine Learning. Proc. Natl. Acad. Sci. 2019, 116, 22071–22080. [Google Scholar] [CrossRef]
  31. van der Velden, B.H.M.; Kuijf, H.J.; Gilhuijs, K.G.A.; Viergever, M.A. Explainable Artificial Intelligence (XAI) in Deep Learning-Based Medical Image Analysis. Med. Image Anal. 2022, 79, 102470. [Google Scholar] [CrossRef]
  32. Darflinger, R.; Thompson, L.A.; Zhang, Z.; Chao, K. Recurrence, Retreatment, and Rebleed Rates of Coiled Aneurysms with Respect to the Raymond–Roy Scale: A Meta-Analysis. J. NeuroInterventional Surg. 2016, 8, 507–511. [Google Scholar] [CrossRef]
  33. Roy, D.; Milot, G.; Raymond, J. Endovascular Treatment of Unruptured Aneurysms. Stroke 2001, 32, 1998–2004. [Google Scholar] [CrossRef] [PubMed]
  34. Zheng, T.; Chen, C.; Yuan, J.; Li, B.; Ren, K. PointCloud Saliency Maps.; 2019; pp. 1598–1606.
  35. Ford, M.D.; Alperin, N.; Lee, S.H.; Holdsworth, D.W.; Steinman, D.A. Characterization of Volumetric Flow Rate Waveforms in the Normal Internal Carotid and Vertebral Arteries. Physiol. Meas. 2005, 26, 477. [Google Scholar] [CrossRef] [PubMed]
  36. Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
  37. Johnson, J.M.; Khoshgoftaar, T.M. Survey on Deep Learning with Class Imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]
  38. Saito, T.; Rehmsmeier, M. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PloS One 2015, 10, e0118432. [Google Scholar] [CrossRef] [PubMed]
  39. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
  40. Cebral, X.J.R.; Detmer, X.F.; Chung, X.B.J.; Choque-Velasquez, X.J.; Rezai, X.B.; Lehto, X.H.; Tulamo, X.R.; Hernesniemi, X.J.; Niemela, X.M.; Yu, X.A.; et al. Local Hemodynamic Conditions Associated with Focal Changes in the Intracranial Aneurysm Wall. 7.
  41. Sadasivan, C.; Fiorella, D.J.; Woo, H.H.; Lieber, B.B. Physical Factors Effecting Cerebral Aneurysm Pathophysiology. Ann. Biomed. Eng. 2013, 41, 1347–1365. [Google Scholar] [CrossRef]
  42. Meng, H.; Tutino, V.M.; Xiang, J.; Siddiqui, A. High WSS or Low WSS? Complex Interactions of Hemodynamics with Intracranial Aneurysm Initiation, Growth, and Rupture: Toward a Unifying Hypothesis. Am. J. Neuroradiol. 2014, 35, 1254–1262. [Google Scholar] [CrossRef]
  43. Nixon, A.M.; Gunel, M.; Sumpio, B.E. The Critical Role of Hemodynamics in the Development of Cerebral Vascular Disease: A Review. J. Neurosurg. 2010, 112, 1240–1253. [Google Scholar] [CrossRef]
  44. Saitta, S.; Maga, L.; Armour, C.; Votta, E.; O’Regan, D.P.; Salmasi, M.Y.; Athanasiou, T.; Weinsaft, J.W.; Xu, X.Y.; Pirola, S.; et al. Data-Driven Generation of 4D Velocity Profiles in the Aneurysmal Ascending Aorta. Comput. Methods Programs Biomed. 2023, 233, 107468. [Google Scholar] [CrossRef]
  45. Suzuki, T.; Genkai, N.; Nomura, T.; Abe, H. Assessing the Hemodynamics in Residual Cavities of Intracranial Aneurysm after Coil Embolization with Combined Computational Flow Dynamics and Silent Magnetic Resonance Angiography. J. Stroke Cerebrovasc. Dis. 2020, 29, 105290. [Google Scholar] [CrossRef] [PubMed]
  46. Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. Int. J. Comput. Vis. 2020, 128, 336–359. [Google Scholar] [CrossRef]
  47. Schweizer, L.; Seegerer, P.; Kim, H.; Saitenmacher, R.; Muench, A.; Barnick, L.; Osterloh, A.; Dittmayer, C.; Jödicke, R.; Pehl, D.; et al. Analysing Cerebrospinal Fluid with Explainable Deep Learning: From Diagnostics to Insights. Neuropathol. Appl. Neurobiol. 2023, 49, e12866. [Google Scholar] [CrossRef] [PubMed]
Preprints 85917 g001
Figure 1. Figure 1. Workflow of this study. Grey rounded rectangles were patients’ number; orange and blue rectangles were DNN and statistical approach to determine the significant parameters for aneurysm recanalization, respectively; red rectangles were 3D features analysis.
Figure 1. Figure 1. Workflow of this study. Grey rounded rectangles were patients’ number; orange and blue rectangles were DNN and statistical approach to determine the significant parameters for aneurysm recanalization, respectively; red rectangles were 3D features analysis.
Preprints 85917 g001
Preprints 85917 g002
Figure 2. Hemodynamic training data for DNN, including velocity, pressure and WSS in (a-c) pre-coiling (pre_vel, pre_P, pre_WSS) and (d-f) post-coiling model (post_vel, post_P, post_WSS). Only data in aneurysm and connected parent artery part was considered (deep blue part in (a) and (d)).
Figure 2. Hemodynamic training data for DNN, including velocity, pressure and WSS in (a-c) pre-coiling (pre_vel, pre_P, pre_WSS) and (d-f) post-coiling model (post_vel, post_P, post_WSS). Only data in aneurysm and connected parent artery part was considered (deep blue part in (a) and (d)).
Preprints 85917 g002
Preprints 85917 g003
Figure 3. (a) ROC and (b) PRC curves on training dataset trained with velocity (black), pressure (red) and WSS (blue) from pre- (left) and post-coiling (right) model.
Figure 3. (a) ROC and (b) PRC curves on training dataset trained with velocity (black), pressure (red) and WSS (blue) from pre- (left) and post-coiling (right) model.
Preprints 85917 g003
Preprints 85917 g004aPreprints 85917 g004b
Figure 4. (a) ROC and (b) PRC curves on testing dataset.
Figure 4. (a) ROC and (b) PRC curves on testing dataset.
Preprints 85917 g004aPreprints 85917 g004b
Preprints 85917 g005
Figure 5. Confusion matrix on testing dataset.
Figure 5. Confusion matrix on testing dataset.
Preprints 85917 g005
Preprints 85917 g006aPreprints 85917 g006b
Figure 6. (a-g) Top 10 points in saliency map of seven recanalized aneurysms on the training dataset. DNN was trained with 3D velocity simulation results from pre- and post-coiling models.
Figure 6. (a-g) Top 10 points in saliency map of seven recanalized aneurysms on the training dataset. DNN was trained with 3D velocity simulation results from pre- and post-coiling models.
Preprints 85917 g006aPreprints 85917 g006b
Preprints 85917 g007
Figure 7. (a-b) Top 10 points in saliency map of two stable aneurysms on the training dataset.
Figure 7. (a-b) Top 10 points in saliency map of two stable aneurysms on the training dataset.
Preprints 85917 g007
Table 1. Comparison of clinical, morphological, and hemodynamic features between patients with stable and recanalized aneurysms.
Table 1. Comparison of clinical, morphological, and hemodynamic features between patients with stable and recanalized aneurysms.
Stable (N = 49) Recanalized (N = 9) P-value
Clinical features
Age 64±13 65±12 0.897
Sex | Female 44 7 0.645
Rupture status 8 4 0.142
Locations | ICPC 38 8 0.848
Locations | IC paraclinoid 8 1
Locations | IC-Oph 2 0
Locations | C1 1 0
Morphological features
Max size 8.241±3.250 11.344±4.330 0.018
Neck width 4.825±1.468 6.311±2.353 0.117
Aspect ratio 1.279±0.483 1.409±0.489 0.469
Bottleneck 1.630±0.655 1.731±0.564 0.673
Height 6.077±2.767 8.444±3.855 0.035
Size ratio 2.047±0.883 2.456±1.026 0.226
Diam Inflow 2.570±1.126 2.534±1.187 0.931
Area Inflow 9.517±4.235 11.848±6.148 0.174
Area Neck 22.616±14.350 34.336±19.490 0.042
Area Ratio 0.494±0.235 0.385±0.160 0.193
Pcom 1.071±0.826 1.672±1.246 0.219
Area Pcom 1.436±1.447 3.415±3.682 0.170
VER 24.188±4.914 20.967±7.970 0.118
Hemodynamic features
volvel 0.439±0.165 0.299±0.161 0.025
PD 0.404±0.631 0.903±0.765 0.043
P 1.031±0.049 1.046±0.047 0.401
PP 0.043±0.038 0.055±0.037 0.425
Pdyn 0.075±0.077 0.036±0.021 0.140
WSS 9.535±6.202 6.176±2.794 0.123
FR 0.001±0.001 0.002±0.004 0.060
Table 2. Table 2. Model performance on training and testing dataset trained with velocity, pressure and WSS from pre- and post-coiling model.
Table 2. Table 2. Model performance on training and testing dataset trained with velocity, pressure and WSS from pre- and post-coiling model.
AUROC Opt. cutoff Sensitivity Specificity AUPRC
On the training dataset
pre_vel 0.991 (0.980 - 0.999) 0.988 0.900 1.000 0.992 (0.976 - 0.999)
pre_P 0.564 (0.462 - 0.677) 0.833 0.450 0.775 0.526 (0.411 - 0.666)
pre_WSS 0.829 (0.748 - 0.904) 0.619 0.775 0.800 0.800 (0.692 - 0.890)
post_vel 1.000 (1.000 - 1.000) 0.999 1.000 1.000 1.000 (1.000 - 1.000)
post_P 0.586 (0.471 - 0.687) 0.319 0.450 0.800 0.564 (0.442 - 0.714)
post_WSS 0.791 (0.706 - 0.863) 0.452 0.575 0.900 0.817 (0.722 - 0.890)
On the testing dataset
pre_vel 1.000 (1.000 - 1.000) 4.457 1.000 1.000 1.000 (1.000 - 1.000)
pre_P 1.000 (1.000 - 1.000) -0.756 1.000 1.000 1.000 (1.000 - 1.000)
pre_WSS 0.667 (0.455 - 0.900) -0.049 1.000 0.667 0.183 (0.071 - 0.417)
post_vel 0.917 (0.769 - 1.000) -2.792 1.000 0.917 0.417 (0.167 - 1.000)
post_P 0.792 (0.462 - 1.000) 0.646 1.000 0.583 0.613 (0.071 - 1.000)
post_WSS 0.542 (0.231 - 0.846) -1.151 1.000 0.333 0.140 (0.045 - 0.352)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated