Prerpints.org logo
Preprint
Article

Evaluating the Sustainable Human Resource Management in Manufacturing Firms Using Single-Valued Neutrosophic Distance Measure-Based RANCOM-AROMAN Model

Altmetrics

Downloads

232

Views

125

Comments

0

Submitted:

23 September 2023

Posted:

26 September 2023

You are already at the latest version

Alerts
Abstract
Along with the economic growth, the companies must contribute to social progress and promote environmental sustainability in equal harmony. Sustainable human resource management (SHRM) strategies make it possible to attain the economic, social and environmental goals of a firm. In this regard, a survey method is discussed using the literature review and online questionnaire to identify the main factors/indicators during the SHRM evaluation of manufacturing firms in India. Uncertainty is commonly occurred in the assessment of SHRM factors. As a generalized version of fuzzy sets, single-valued neutrosophic set (SVNS) has been demonstrated as a valuable tool to illustrate the indeterminate, inconsistent and uncertain data of realistic decision-making problems. Considering the idea of SVNSs, this study develops a hybrid multi-criteria group decision-making (MCGDM) approach for assessing the SHRM of manufacturing firms under uncertainty settings. For this purpose, an SVN-alternative ranking order method accounting for two-step normalization (AROMAN) is proposed based on VIFI-score function-based decision experts’ (DEs’) weighting tool and integrated criteria weight-determining model to solve the MCGDM problems with fully unknown DEs and criteria weights. In this regard, we develop new SVN-distance measure to compute the degree of difference between SVNSs. Some examples are presented to demonstrate the efficacy of developed measure over the existing ones. In addition, new criteria weight-determination model is presented with the integration of objective weights through IVIF-distance measure-based model and subjective weights through ranking comparison (RANCOM) tool on SVNSs. The proposed ranking method is applied to an empirical study of SHRM assessment for manufacturing firms in India, which shows its applicability and feasibility. In this study, the evaluation criteria are characterized into social, environmental and economic aspects with DE’s opinions. Comparative and sensitivity analyses are made to show the strength and steadiness of presented approach. This study provides an innovative MCGDM analysis framework, which makes a significant contribution to the SHRM assessment problem under indeterminate, inconsistent and uncertain setting.
Keywords: 
Subject: Business, Economics and Management  -   Business and Management

1. Introduction

Sustainable development (SD) is one of vital topics in today's society considering several aspects of economic prosperity, social equality and environmental protection. It is defined as “the development that meets the need of the present generation without compromising the ability of the future generation to meet their own needs” (Piwowar-Sulej, 2021). The concept of SD is described as a process that incorporates the economic growth with ecological balance and environmental protection by considering social aspects (Saeidi et al., 2022). In the 2030 Plan for “sustainable development goals (SDGs)”, participant of “United Nations (UNs)” agreed on the significance of moving toward sustainable forms of consumption and creation, with the developed nations captivating the lead and with all nations profiting from the procedure (Glass & Newig, 2019; Shayan et al., 2022). Based on the UNs, corporate sustainability (CS) and triple bottom line (TBL) are guiding notions for the organizational achievement of SDGs. The concept of “CS” states to a business policy for long-term development that works in agreement with persons and the planet (de Oliveira et al., 2023), while the concept of “TBL” entails of the stability in identical harmony among the social, environmental and economic dimensions of firms (Ramalho & Martins, 2022).
Sustainable human resource management (SHRM) can be defined as “the pattern of planned or emerging human resource management (HRM) strategies and practices anticipated to enable the achievement of economic, social and ecological goals while simultaneously reproducing the human resource base over a long term” (Kramar, 2014; Macke & Genari, 2019). In actual fact, the reaction to the internal and external challenges including increasing work-related health problems (De Vos & Van der Heijden, 2017; Chams & García-Blandón, 2019), a lack of labour force (App & Büttgen, 2016), makes it essential to adapt the elegance towards the managing of people (Stankevičiūtė & Savanevičienė, 2018). SHRM has extensively applied for the HRM practices because it might lead to a “win–win” state for staffs and firms. Adoption of SHRM practices results in the better performance of the companies through improved employment relationships, long-term investment instead of just a financial assistance and employer branding (Sorribes et al., 2021; Martini et al., 2023).
The idea of SHRM is defined as the role of HRM in developing the organizational sustainability and the sustainability of HRM practices (Kramar, 2014; Macke & Genari, 2019). Tooranloo et al. (2017) identified the main indicators influencing SHRM in the manufacturing companies. Moreover, the authors have used fuzzy DEMATEL model to determine the weight of considered factors. Chams & García-Blandón (2019) presented the literature review to examine key role of SHRM and its impact on sustainability. They also investigated the relationship between SHRM and sustainable perspectives and identified the HRM processes that can contribute to attain the SDGs. Macke & Genari (2019) provided the comprehensive review on SHRM to recognize key features, developments and research challenges. In a study, Kainzbauer et al. (2021) presented a bibliometric study to cognize how SHRM contributes to CS. In addition, they highlighted that existing studies on SHRM are heavily weighted towards environmental issues. With the presence of the stakeholders in the supply chain, Ramalho & Martins (2022) presented a theoretical development of SHRM towards sustainability in the construction business. Cachon-Rodríguez et al. (2022) analyzed the result of SHRM with social capital activities on retention and loyalty of employees in higher education sector. Saeidi et al. (2022) used a survey approach to identify the main indicators of SHRM assessment and determined their weights through Pythagorean fuzzy SWARA model. In terms of the SHRM practices, the authors have ranked the manufacturing companies through Pythagorean fuzzy TOPSIS approach. Martini et al. (2023) presented the relationship between SHRM and organizational consequences. In this regard, they explored how corporate training designed at supportive employability influences the employee-employer association and worker retaining. Assessment of SHRM practices of any company depends on several factors including social, economic, environmental (SEE) dimensions of sustainability. Thus, the MCGDM models are more appropriate to deal such varieties of problems.
Due to the overwhelming vagueness and subjectivity of human’s cognizance, it is not always possible for decision experts (DEs) to express the assessment rating of an alternative in terms of crisp number. To express the uncertainty of realistic situations, Zadeh (1965) originated the idea of fuzzy sets (FSs), which has been implemented for diverse disciplines (Li & Zhang, 2023). As the FSs doctrine is described as “belongingness grade (BG)”, however, it may not continuously hold that the nonbelongningness grade (NG) of an object in FSs is equal to complement of BG. As an extension of FSs, Atanassov (1986) originated the notion of intuitionistic FSs (IFSs), which is regarded as BG, NG and indeterminacy grade (IG). Since the doctrine of IFSs can simply manage imprecise and uncertain information but it is not able to handle indeterminate and inconsistent data obtains in realistic concerns. To conquer these issues, Smarandache (1999) introduced the theory of neutrosophic sets (NSs), which is an extended version of FSs and IFSs. Further, Wang et al. (2010) developed the theory of single-valued neutrosophic sets (SVNSs), which overcomes the limitation of NSs in handling with the scientific and manufacturing problems. The SVNS theory provides a more useful and reasonable way to manage indeterminate, inconsistent and uncertain information. Due to its higher flexibility, the SVNS doctrine has been broadly explored from different perspectives.
Li et al. (2023) studied a novel MCDM approach that integrates the aspect-based sentiment analysis, TOPSIS model with SVNS doctrine and further applied for doctor selection. In the context of SVNS, Fetanat and Tayebi (2023) evaluated the hydrogen technologies using the combined CRITIC and CRADIS models. Meng et al. (2023) presented a novel SVNS and geographic information system based MCDM framework for prioritizing the sites for waste-to-energy plant development. Ye et al. (2023) proposed the SVN-score and SVN-accuracy functions for SVNSs and then developed a series of trigonometric “aggregation operators (AOs)” to combine the individual’s decision information in the context of SVNS. In addition, they presented MCGDM tool with combination of SVN-score/accuracy function and the proposed aggregation operators for solving MCGDM problems.
To derive the subjective weight of attributes, Więckowski et al. (2023) proposed the RANCOM tool. This model computes the criteria weight using DE’s knowledge. Its implementation is defined on attributes ranking order to derive the weight value. In the literature, there is no study which uses a weighting model based on SVN-RANCOM model.
To deal with the MCDM problems, several novel methods have been developed under the context of SVNSs (Mishra et al., 2021; Ridvan et al., 2021; Li et al., 2023; Luo et al., 2023; Fetanat & Tayebi, 2023). It is known that different normalization tools have different advantages and disadvantages, and different aggregation tools have different functions. Recently, Bošković et al. (2023a) developed AROMAN model to solve the decision-making problem with crisp number. In this model, two different normalization tools are included, and the gained normalized ratings are combined into averaged normalized decision-matrix. In a study, Bošković et al. (2023b) evaluated the cargo bike delivery concept selection using classical AROMAN model. Nikolic et al. (2023) presented interval type-2 fuzzy generalization of AROMAN tool and applied to enhance the sustainability of postal system in rural regions. There is no research which develops the AROMAN method from SVN information perspective.
In the following, we identify some issues in the existing studies:
  • Several existing SVN-distance measures (SVN-DMs) (Ye, 2014; Xu et al., 2020; Chai et al., 2021) generate some counter-intuitive results during the computation of degree of difference between SVNSs.
  • The AROMAN method has developed in the context of crisp set and interval type-2 FS (Bošković et al., 2023a,b; Nikolic et al., 2023). The methods presented by (Bošković et al., 2023a,b; Nikolic et al., 2023) ignores the significance of criteria and experts’ weights. In addition, their studies are not able to deal with SVN information.
  • Some authors (Tooranloo et al., 2017; Saeidi et al., 2022) have presented different ranking techniques to rank the manufacturing firms, but these studies are not able to illustrate the indeterminate, inconsistent and uncertain data in the assessment of SHRM practices of manufacturing firms.
The key contributions of the paper are listed as follows:
  • New SVN-DM is developed to avoid the limitations of extant SVN-DMs under the context of SVNSs.
  • A hybrid MCGDM model is proposed to deal with the single-valued neutrosophic MCDM problems in which the information about indicators and DEs are completely unknown.
  • To determine the DEs’ weight, a novel procedure is presented in the context of SVNSs.
  • To find the indicators’ weights, a weight-determination model is presented with the integration of objective weights using SVN-DM-based model and subjective weights using RANCOM model with SVNSs.
  • The presented SVN-DN-RANCOM-AROMAN method is applied on a case study of evaluation of SHRM of manufacturing firms in India, which illustrates its powerfulness and applicability.
The remaining part of this study is organized as follows: Section 2 confers the comprehensive literature review related to this work. Section 3 first discusses the basic concepts and then introduces a new DM for SVNSs. Section 4 develops a hybridized AROMAN method for assessing the MCDM problem from single-valued neutrosophic information perspective. Section 5 shows the introduced tool on a case study of SHRM assessment of manufacturing firms. Furthermore, this section confers the comparative and sensitivity analyses. Section 6 concludes the whole study and suggests for future researches.

2. Sustainable Human Resource Management (SHRM)

The purpose of SD is to define viable schemes considering the SEE aspects of human activity. It is the basis for today's leading global framework for international collaboration. It is a continuing process that responds to changing technology and capacity (Chams & García-Blandón, 2019). As per the SDGs, firms need to strategize about CS practices including worldwide climate change, CO2 and waste reduction, cleaner production, poverty reduction, education improvement, quality improvement in public health, human rights promotion in their business prototypes (Maunganidze, 2022). CS states to the attainment of sustainable earnings and capacity enrichment by means of economic, social and environmental, factors (Chen, 2023). According to Jiang et al. (2018), the notion of CS is a strategic procedure for firms to search for equilibrium between the stakeholders and the financial profit, social equity and environmental concern. SHRM is perceived as an extra dimension of strategic HRM that provides an up-to-date tool to the personnel management (Stankevičiūtė & Savanevičienė, 2018). It includes TBL concepts and attempts to flourish in equilibrium between each different region (Ehnert et al., 2012).
In the literature, the concept “SHRM” has been defined from various perspectives. According to Cohen et al. (2012), “SHRM highlights the role that HRM plays in supporting business sustainability by implementing practices. This concept can impact individuals and groups to develop behaviors and attitudes according to the sustainable perspective”. Kramar (2014) defined the SHRM as “the pattern of emerging human resource strategies and activities planned to enable the attainment of economic, social and environmental goals while simultaneously reproducing the human resource base over a long term”. Ehnert et al. (2016) described the SHRM as “the implementation of HRM strategies and practices that enable the attainment of economic, social and environmental goals, with impact inside and outside the organization and in the long term, while controlling unintended side effects and negative feedback”. According to Järlström et al. (2018), “SHRM encourages a more holistic view emphasizing the ability of HRM to involve with the sustainability agenda from multiple outlooks to meet the needs and interests of the organization’s numerous internal and external stakeholders”.
In the literature, several authors have considered numerous factors affecting the SHRM practices of the companies/organizations. Considering the TBL concept, Tooranloo considered the twenty six criteria to assess the SHRM practices of an organization. Stankevičiūtė & Savanevičienė (2018) identified several indicators to assess the SHRM assessment of the organizations. These indicators are objectivity and equality, amenability beyond guidelines, employee cooperation, flexibility, employee growth, external partnership, long-term coordination, care of staffs and environment, productivity and social discussion. According to Ogbeibu et al. (2020), environmental dynamic competence, product innovation, technological instability and green side creativeness are significant factors during the SHRM assessment of organizations. Further, Ramalho & Martins identified several criteria during the SHRM assessment in the supply chain. Saeidi et al. (2022) considered the three aspects of sustainability and recognized the twenty criteria including eight from social aspects, eight from environmental aspects and remaining four are from economic aspects.
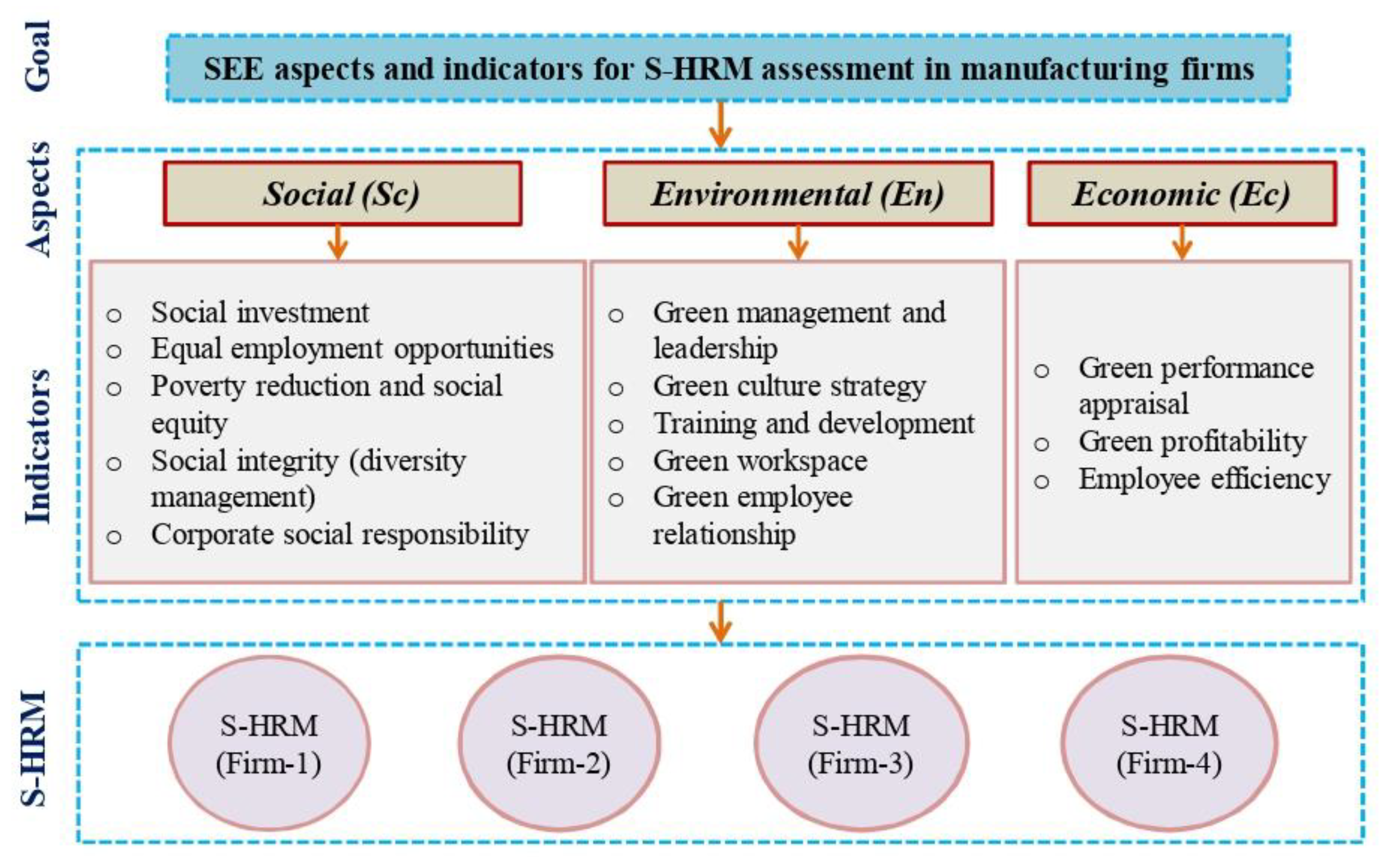
On the basis of literature review and questionnaire, we are considering the TBL concept and selecting 13 criteria. Out of which, 5 of the factors are listed as social aspect, another five factors are listed as environmental aspect and the last four factors are listed as economic aspect. Table 1 and Figure 1 provide the description of chosen criteria in the assessment of SHRM for a manufacturing company in India.

3. Proposed SVN-Distance Measure (SVN-DM) for SVNSs

This section proposes SVNSs notion and SVN-DM to avoid the limitations of extant SVN-DMs.

3.1. Basic Concepts

Definition 1 (Wang et al., 2010). 
Let  Ω = { x 1 , x 2 , ... , x n }  be a fixed set. A SVNS N on  Ω  is described in mathematical form as
N =   { 〈 x ,   T N ( x ) ,   I N ( x ) , F N ( x ) 〉 | x ∈   Ω } ,
where  T N ( u ) : Ω → [ 0 , 1 ] ,   I N ( u ) :   Ω → [ 0 , 1 ]  and  F N ( u ) : Ω → [ 0 , 1 ]  denote the truth BG, the indeterminacy BG and the falsity BG, respectively. For every  x   ∈   Ω ,   0 ≤   T N ( x ) +   I N ( x ) + F N ( x ) ≤ 3 .  For convenience, the SVNN can be presented as  κ = ( T N , I N , F N ) .
Definition 2 (Ye 2017). 
For any two SVNNs  κ 1 = ( T 1 ,   I 1 ,   F 1 )  and  κ 2 = ( T 2 ,   I 2 ,   F 2 ) ,  and  λ > 0 ,  the operations on SVNSs are presented as
  • κ i c = ( F i ,     1 −   I i ,     T i ) ,     i   = 1 ,   2 ,
  • κ 1 ⊆ κ 2       if       T 1 ≤   T 2 ,     I 1 ≥   I 2     and     F 1 ≥   F 2 ,
  • κ 1 = κ 2   ⇔     κ 1 ⊆ κ 2     and     κ 2 ⊆   κ 1 ,
  • κ 1 ∪ κ 2 = ( { T 1 ∨ T 2 } ,   { I 1 ∧ I 2 } ,     { F 1 ∧ F 2 } ) ,
  • κ 1 ∩ κ 2 = ( { T 1 ∨ T 2 } ,   { I 1 ∧ I 2 } ,   { F 1 ∧ F 2 } ) ,
  • κ 1 ⊕ κ 2 = ( T 1 +   T 2 − T 1   T 2 ,     I 1   I 2 ,     F 1   F 2 ) ,
  • κ 1 ⊗ κ 2 = ( T 1   T 2 ,     I 1 + I 2 − I 1   I 2 ,     F 1 + F 2 − F 1   F 2 ) ,
  • λ   κ i = ( 1 − ( 1 − T i ) λ ,   I i λ ,   F i λ ) ,     i   = 1 ,   2 ,
  • κ i λ = ( T i γ ,     1 − ( 1 − I i ) γ ,     1 − ( 1 − F i ) γ ) ,     i   = 1 ,   2 ,
  • κ 1 − κ 2 = ( T 1 − T 2 1 − T 2 ,     I 1 I 2 ,     F 1 F 2 ) ,  which is valid under the conditions  κ 1 ≥ κ 2 ,   T 2 ≠ 1 ,   I 2 ≠ 0  and  F 2 ≠ 0 .
Definition 3 (Smarandache, 2020). 
For a SVNN, the normalized SVN-score function is given by
S ( κ ) = 2 +   T −   I − F 3 ,     S ( κ ) ∈ [ 0 , 1 ] .
Definition 4 (Ye, 2014). 
Let  κ i = ( T i ,   I i ,   F i )  be SVNNs and  ϖ = ( ϖ 1 ,   ϖ 2 , ... , ϖ r ) T  be weight of  κ i ,  with  ϖ i ∈ [ 0 , 1 ]  and  ∑ i = 1 r ϖ i = 1 .  Then the SVNWA and SVNWG operators are defined as
S V N W A ( κ 1 , κ 2 , ... , κ r ) = ⊕ i = 1 r ( ϖ i   κ i ) = ( 1 − ∏ i = 1 r ( 1 − T i ) ϖ i ,   ∏ i = 1 r ( I i ) ϖ i ,   ∏ i = 1 r ( F i ) ϖ i   ) ,
S V N W G ( κ 1 , κ 2 , ... , κ r ) = ⊗ i = 1 r ( ϖ i   κ i ) = ( ∏ i = 1 r ( T i ) ϖ i ,   1 − ∏ i = 1 r ( 1 − I i ) ϖ i ,   1 − ∏ i = 1 r ( 1 − F i ) ϖ i   ) .
Definition 5 (Majumdar & Samanta, 2014). 
Let  M ,   N ,   P   ∈   S V N S s ( Ω ) .  A real-valued mapping  d   : S V N S s ( Ω ) × S V N S s ( Ω ) → [ 0 ,     1 ]  is called SVN-DM which holds the following axioms:
(a1)
0 ≤ d ( M ,   N ) ≤ 1 ,
(a2)
d ( M ,   N ) = d ( N ,   M ) ,
(a3)
d ( M ,   N ) = 0 ⇔ M =   N ,
(a4)
If M   ⊆   N ⊆   P ,  then  d ( M ,   P ) ≥ d ( M ,   N )  and  d ( M ,   P ) ≥ d ( N ,   P ) ,   ∀     M ,   N ,   P     ∈ S V N S s ( Ω ) .

3.2. SVN-DM and Its Effectiveness Over the Existing DMs

In the context of SVNSs, the concept of DM has widely used for medical diagnosis, cluster analysis etc. Ye (2014) proposed Hamming, Euclidean and generalized DMs for SVNSs and presented a clustering algorithm to cluster SVN data. Chai et al. (2021) suggested some SVN-DM and SVN-similarity measure (SVN-SM) with their application in medical diagnosis and pattern recognition. Based on matrix norm, Luo et al. (2022) presented a novel DM for SVNSs, which satisfies the axiomatic definition of the metric. Ali et al. (2023) introduced two schemes to compute the Hausdorff DM and its equivalent SVN-SM.
For M ,   N   ∈   S V N S s ( Ω ) , we propose new SVN-DM, given as
d ( M ,   N )     = 1 9   r ∑ i   = 1 r [ | T M ( x i ) −   T N ( x i ) | + | I M ( x i ) −   I N ( x i ) | +   | F M ( x i ) −   F N ( x i ) | + | T M ( x i )   I N ( x i ) − T N ( x i )   I M ( x i ) | +   | T M ( x i )   F N ( x i ) − T N ( x i )   F M ( x i ) | +   | I M ( x i )   F N ( x i ) − I N ( x i )   F M ( x i ) | + ( | min { T M ( x i ) ,     I N ( x i )   } −   min { T N ( x i ) ,     I M ( x i ) } | + | max { T M ( x i ) ,     I N ( x i )   } −   max { T N ( x i ) ,     I M ( x i ) } | ) + ( | min { T M ( x i )   ,   F N ( x i ) } −   min { T N ( x i ) ,     F M ( x i ) } | + | max { T M ( x i )   ,   F N ( x i )   } −   max { T N ( x i ) ,     F M ( x i ) } | ) + ( | min { F M ( x i ) ,     I N ( x i )   } −   min { F N ( x i ) ,     I M ( x i ) } | + | max { F M ( x i ) ,     I N ( x i )   } −   max { F N ( x i ) ,     I M ( x i ) } | ) ] .
The properties of d ( M ,   N ) are discussed as follows:
Property 3.1: 
For  M ,   N   ∈   S V N S s ( Ω ) ,   0 ≤   d ( M ,   N )     ≤ 1 .
Proof: 
Let M and N be SVNSs, then 0   ≤   T M ( x i ) ≤   1   0   ≤   I M ( x i ) ≤   1 and 0   ≤   F M ( x i ) ≤   1 , and 0   ≤   T M ( x i ) ,   I M ( x i ) ,   F M ( x i )   ≤   3 . Thus, it is obvious that d ( M ,   N )   ≥   0 . Also, d ( M ,   N ) is defined with its normalization, which implies d ( M ,   N )   ≤   1 . Hence, 0   ≤ d ( M ,   N )   ≤   1 .
Property 3.2: 
d ( M ,   N )   = 0 iff M = N.
Proof: 
For given two IVIFSs M and N, if M = N, then
d ( M ,   N )   =   1 9   r ∑ i   = 1 r [ | T M ( x i ) −   T M ( x i ) | + | I M ( x i ) −   I M ( x i ) | +   | F M ( x i ) −   F M ( x i ) | + | T M ( x i )   I M ( x i ) − T M ( x i )   I M ( x i ) | +   | T M ( x i )   F M ( x i ) − T M ( x i )   F M ( x i ) | +   | I M ( x i )   F M ( x i ) − I M ( x i )   F M ( x i ) | + ( | min { T M ( x i ) ,     I M ( x i )   } −   min { T M ( x i ) ,     I M ( x i ) } | + | max { T M ( x i ) ,     I M ( x i )   } −   max { T M ( x i ) ,     I M ( x i ) } | ) + ( | min { T M ( x i )   ,   F M ( x i ) } −   min { T M ( x i ) ,     F M ( x i ) } | + | max { T M ( x i )   ,   F M ( x i )   } −   max { T M ( x i ) ,     F M ( x i ) } | ) + ( | min { F M ( x i ) ,     I M ( x i )   } −   min { F M ( x i ) ,     I M ( x i ) } | + | max { F M ( x i ) ,     I M ( x i )   } −   max { F M ( x i ) ,     I M ( x i ) } | ) ]   =   0 .
Conversely, if d ( M ,   N )   = 0 , then
d ( M ,   N )     = 1 9   r ∑ i   = 1 r [ | T M ( x i ) −   T N ( x i ) | + | I M ( x i ) −   I N ( x i ) | +   | F M ( x i ) −   F N ( x i ) | + | T M ( x i )   I N ( x i ) − T N ( x i )   I M ( x i ) | +   | T M ( x i )   F N ( x i ) − T N ( x i )   F M ( x i ) | +   | I M ( x i )   F N ( x i ) − I N ( x i )   F M ( x i ) | + ( | min { T M ( x i ) ,     I N ( x i )   } −   min { T N ( x i ) ,     I M ( x i ) } | + | max { T M ( x i ) ,     I N ( x i )   } −   max { T N ( x i ) ,     I M ( x i ) } | ) + ( | min { T M ( x i )   ,   F N ( x i ) } −   min { T N ( x i ) ,     F M ( x i ) } | + | max { T M ( x i )   ,   F N ( x i )   } −   max { T N ( x i ) ,     F M ( x i ) } | ) + ( | min { F M ( x i ) ,     I N ( x i )   } −   min { F N ( x i ) ,     I M ( x i ) } | + | max { F M ( x i ) ,     I N ( x i )   } −   max { F N ( x i ) ,     I M ( x i ) } | ) ] =   0 .
Since every term of Eq. (5) is non-negative, then by d ( M ,   N )   =   0 , we can observe that every term of Eq. (5) should be equal to zero, it implies that we have T M ( x i ) =   T N ( x i ) ,   I M ( x i ) =   I N ( x i ) and F M ( x i ) =   F N ( x i ) . Thus, d ( M ,   N )   = 0 iff M = N .
Property 3.3: 
d ( M ,     N )   =   d ( N ,   M ) .
Proof: 
For given SVNSs M and N, we get
d ( N ,   M )   =     1 9   r ∑ i   = 1 r [ | T N ( x i ) −   T M ( x i ) | + | I N ( x i ) −   I M ( x i ) | +   | F N ( x i ) −   F M ( x i ) | + | T N ( x i )   I M ( x i ) − T M ( x i )   I N ( x i ) | +   | T N ( x i )   F M ( x i ) − T M ( x i )   F N ( x i ) | +   | I N ( x i )   F M ( x i ) − I M ( x i )   F N ( x i ) | + ( | min { T N ( x i ) ,     I M ( x i )   } −   min { T M ( x i ) ,     I N ( x i ) } | + | max { T N ( x i ) ,     I M ( x i )   } −   max { T M ( x i ) ,     I N ( x i ) } | ) + ( | min { T N ( x i )   ,   F M ( x i ) } −   min { T M ( x i ) ,     F N ( x i ) } | + | max { T N ( x i )   ,   F M ( x i )   } −   max { T M ( x i ) ,     F N ( x i ) } | ) + ( | min { F N ( x i ) ,     I M ( x i )   } −   min { F M ( x i ) ,     I N ( x i ) } | + | max { F N ( x i ) ,     I M ( x i )   } −   max { F M ( x i ) ,     I N ( x i ) } | ) ]
=     1 9   r ∑ i   = 1 r [ | T M ( x i ) −   T N ( x i ) | + | I M ( x i ) −   I N ( x i ) | +   | F M ( x i ) −   F N ( x i ) | + | T M ( x i )   I N ( x i ) − T N ( x i )   I M ( x i ) | +   | T M ( x i )   F N ( x i ) − T N ( x i )   F M ( x i ) | +   | I M ( x i )   F N ( x i ) − I N ( x i )   F M ( x i ) | + ( | min { T M ( x i ) ,     I N ( x i )   } −   min { T N ( x i ) ,     I M ( x i ) } | + | max { T M ( x i ) ,     I N ( x i )   } −   max { T N ( x i ) ,     I M ( x i ) } | ) + ( | min { T M ( x i )   ,   F N ( x i ) } −   min { T N ( x i ) ,     F M ( x i ) } | + | max { T M ( x i )   ,   F N ( x i )   } −   max { T N ( x i ) ,     F M ( x i ) } | ) + ( | min { F M ( x i ) ,     I N ( x i )   } −   min { F N ( x i ) ,     I M ( x i ) } | + | max { F M ( x i ) ,     I N ( x i )   } −   max { F N ( x i ) ,     I M ( x i ) } | ) ]   =   d ( M ,   N ) .
Hence, d ( M ,   N )   =   d ( N ,   M ) .
Property 3.4: 
If  M   ⊆   N ⊆   P ,  then  d ( M ,   P ) ≥ d ( M ,   N )  and  d ( M ,   P ) ≥ d ( N ,   P ) ,   ∀     M ,   N ,   P     ∈ S V N S s ( Ω ) .
Proof: 
For given three SVNSs M   =   { 〈 x i ,   T M ( x i ) ,   I M ( x i ) ,   F M ( x i ) 〉   :   x i ∈   Ω } ,   N   =   { 〈 x i ,   T N ( x i ) ,   I N ( x i ) ,   F N ( x i ) 〉   :   x i ∈   Ω } and P   =   { 〈 x i ,   T P ( x i ) ,   I P ( x i ) ,   F P ( x i ) 〉   :   x i ∈   Ω } , if M ⊆   N ⊆   P , then T M ( x i ) ≤   T N ( x i ) ≤   T P ( x i ) ,   I P ( x i ) ≤   I N ( x i ) ≤   I M ( x i ) and F P ( x i ) ≤   F N ( x i ) ≤   F M ( x i ) ,     ∀   x i   ∈   Ω . Therefore, we have | T M ( x i ) −   T P ( x i ) |   ≥   | T M ( x i ) −   T N ( x i ) | ,   | I M ( x i ) −   I P ( x i ) |   ≥   | I M ( x i ) −   I N ( x i ) | and | F M ( x i ) −   F P ( x i ) | ≥   | F M ( x i ) −   F N ( x i ) | ,   ∀   x i   ∈   Ω . It will also imply that 0   ≤   min { T M ( x i ) ,   I P ( x i ) }   ≤   min { T M ( x i ) ,   I N ( x i ) }   ≤   min { T N ( x i ) ,   I M ( x i ) } ≤   min { T P ( x i ) ,   I M ( x i ) }   ≤   1 ,   0   ≤   min { T M ( x i ) ,   F P ( x i ) }   ≤     min { T M ( x i ) ,   F N ( x i ) } ≤   min { T N ( x i ) ,   F M ( x i ) }   ≤   min { T P ( x i ) ,   I M ( x i ) }   ≤   1 ,   0   ≤   max { T M ( x i ) ,   I P ( x i ) }   ≤     max { T M ( x i ) ,   I N ( x i ) }   ≤   max { T N ( x i ) ,   I M ( x i ) }   ≤   max { T P ( x i ) ,   I M ( x i ) }   ≤   1 , and 0   ≤   max { T M ( x i ) ,   F P ( x i ) }   ≤   max { T M ( x i ) ,   F N ( x i ) }   ≤   max { T N ( x i ) ,   F M ( x i ) }     ≤   min { T P ( x i ) ,   I M ( x i ) }   ≤   1 ,   ∀   x i   ∈   Ω
Thus, it follows that
( | min { T M ( x i ) ,     I P ( x i )   } −   min { T P ( x i ) ,     I M ( x i ) } | ≥   ( | min { T M ( x i ) ,     I N ( x i )   } −   min { T N ( x i ) ,     I M ( x i ) } | + | max { T M ( x i ) ,     I P ( x i )   } −   max { T P ( x i ) ,     I M ( x i ) } | ) + | max { T M ( x i ) ,     I N ( x i )   } −   max { T N ( x i ) ,     I M ( x i ) } | ) ,
( | min { T M ( x i )   ,   F P ( x i ) } −   min { T P ( x i ) ,     F M ( x i ) } | ≥   ( | min { T M ( x i )   ,   F N ( x i ) } −   min { T N ( x i ) ,     F M ( x i ) } | + | max { T M ( x i )   ,   F P ( x i )   } −   max { T P ( x i ) ,     F M ( x i ) } | ) + | max { T M ( x i )   ,   F N ( x i )   } −   max { T N ( x i ) ,     F M ( x i ) } | ) ,
( | min { F M ( x i ) ,     I P ( x i )   } −   min { F P ( x i ) ,     I M ( x i ) } | + | max { F M ( x i ) ,     I P ( x i )   } −   max { F P ( x i ) ,     I M ( x i ) } | )
≥   ( | min { F M ( x i ) ,     I N ( x i )   } −   min { F N ( x i ) ,     I M ( x i ) } | + | max { F M ( x i ) ,     I N ( x i )   } −   max { F N ( x i ) ,     I M ( x i ) } | ) ,     ∀   x i   ∈   Ω .
In addition, we have
| T M ( x i )   I P ( x i ) − T P ( x i )   I M ( x i ) | ≥ | T M ( x i )   I N ( x i ) − T N ( x i )   I M ( x i ) | ,
| T M ( x i )   F P ( x i ) − T P ( x i )   F M ( x i ) | ≥ | T M ( x i )   F N ( x i ) − T N ( x i )   F M ( x i ) | ,
| I M ( x i )   F P ( x i ) − I P ( x i )   F M ( x i ) | ≥ | I M ( x i )   F N ( x i ) − I N ( x i )   F M ( x i ) | ,     ∀   x i   ∈ Ω .
It implies that d ( M ,   P ) ≥ d ( M ,   N ) ,   ∀     M ,   N ,   P     ∈ S V N S s ( Ω ) . Similarly, if M ⊆   N ⊆   P , then T M ( x i ) ≤   T N ( x i ) ≤   T P ( x i ) ,   I P ( x i ) ≤   I N ( x i ) ≤   I M ( x i ) and F P ( x i ) ≤   F N ( x i ) ≤   F M ( x i ) ,     ∀   x i   ∈   Ω , therefore, we can prove that d ( M ,   P )   ≤   d ( N ,   P ) .
Proposition 3.1: 
From the Properties 3.1-3.4, Eq. (4) holds all the necessary conditions of Definition

3.5. Hence, Eq. (4) is valid SVN-distance measure on S V N S s ( Ω ) .

To demonstrate the efficacy of developed SVN-DM, we compare it with some of the extant SVN-DMs given by (Ye, 2014; Xu et al., 2020; Chai et al., 2021), which are presented by Eqs. (6)-(10). The required results are presented in Table 2.
Normalized hamming distance (Ye, 2014)
d 1 ( M ,   N )   =     1 3   ( | T M ( x i ) −   T N ( x i ) | +   | I M ( x i ) −   I N ( x i ) | +   | F M ( x i ) −   F N ( x i ) | ) .
Hausdorff distance (Xu et al., 2020)
d 2 ( M ,   N )   =     max   ( | T M ( x i ) −   T N ( x i ) | ,     | I M ( x i ) −   I N ( x i ) | ,     | F M ( x i ) −   F N ( x i ) | ) .
SVN-distance measure by Chai et al. (2021)
d 3 ( M ,   N )   =     1 3   | Ω |   ∑ x i   ∈   Ω ( | T M 2 ( x i ) −   T N 2 ( x i ) | +   | I M 2 ( x i ) −   I N 2 ( x i ) | +   | F M 2 ( x i ) −   F N 2 ( x i ) | ) .
d 4 ( M ,   N )   =     1 3   | Ω |   ∑ x i   ∈   Ω | ( T M 2 ( x i ) −   T N 2 ( x i ) ) −   ( I M 2 ( x i ) −   I N 2 ( x i ) ) −   ( F M 2 ( x i ) −   F M 2 ( x i ) ) | .
d 5 ( M ,   N )   =   1 −     1 | Ω |   ∑ x i   ∈   Ω ( ( T M 2 ( x i ) ∧ T N 2 ( x i ) )   +   ( I M 2 ( x i ) ∧   I N 2 ( x i ) ) +   ( F M 2 ( x i ) ∧   F N 2 ( x i ) ) ( T M 2 ( x i ) ∨ T N 2 ( x i ) )   +   ( I M 2 ( x i ) ∨   I N 2 ( x i ) ) +   ( F M 2 ( x i ) ∨   F N 2 ( x i ) ) ) .
Based on the computational outcomes obtained in Table 2, we present the following results:
  • For two different sets (set-I and set-II), the measures d2(M,N) and d4(M,N) present the same results, which are 1 and 0.3333, respectively.
  • For two different sets (set-II and set-III), the Hamming measure d1(M,N) obtains the same value, which is 0.3333. For these two sets, d4(M,N) obtains the value, which dissatisfies the property (a1) of Definition 5.
  • For the set-IV and set-V, the Hausdroff distance measure d2(M,N) obtains the same value 0.1.
  • For all the sets, the proposed measure successfully describes the difference between SVNSs, which prove its effectiveness.

4. A hybrid SVN-RANCOM-AROMAN approach

This section firstly proposes hybrid SVN-DM-RANCOM-AROMAN approach to solve the MCDM problems under SVNSs setting. To determine the solution of MCGDM problems, the developed model involves the following steps:
  • Step 1: Let F =   { F 1 ,   F 2 ,   ... ,   F m } and H   =   { H 1 ,   H 2 ,   ... ,   H n } be the set of options and criteria, respectively. Let   E = { e 1 ,   e 2 ,   ... ,   e l } be DEs who offers their opinion for each option Fi over Hj in term of “linguistic ratings (LRs)”. Let R = ( ξ i j ( k ) ) m   ×   n be “linguistic assessment matrix (LAM)” presented by DEs, where ξ i j ( k ) denotes assessment information of an option Fi over a criterion Hj in the form of LRs and further changed into SVNNs.
  • Step 2: Compute the DEs’ significance values.
    Assume that e k = ( T k ,   I k ,   F k ) ,   k = 1 , 2 , ... , l be the performance of kth DE. Then the procedure for estimating the numeric significance value of kth DE is as follows:
  • Step 2a: Determine the matrix using score function.
    Each SVN e k is normalized and computed using SVN-score function as
    e ¯ k = ( 2 +   T κ −   I κ − F κ ) ∑ k = 1 l ( 2 + T κ −   I κ − F κ ) ,   ∀   k .
  • Step 2b: Determine the rank of DEs’ performances and compute the DE’s significance value l − ρ k + 1 , wherein ρ k denotes the priority of kth expert. The normalization process is used to normalize each significance value:
    e ¯ k r = l − ρ k + 1 ∑ k = 1 l ( l − ρ k + 1 ) , ∀   k .
  • Step 2c: Compute the numeric weights.
In accordance with the combination of Eq. (11) and Eq. (12), DE’s weighting formula is given as
ϑ k = 1 2 ( ( e ¯ k ) + ( e ¯ k r ) ) ,     ∀   k ,   wherein   ϑ k ≥   0   and   ∑ k = 1 l ϑ k =   1 .
  • Step 3: Create the “aggregated SVN decision matrix (A-SVNDM)”.
In the procedure of MCGDM, there is a need to aggregate the individual DEs’ opinions. We create the A-SVNDM Z = ( η i j ) m   ×   n , using SVNWA operator, where
η i j = ( T i j ,   I i j ,   F i j ) = ( 1 − ∏ k = 1 l ( 1 − T i j ( k ) ) ϑ k ,   ∏ k = 1 l ( I i j ( k ) ) ϑ k , ∏ k = 1 l ( F i j ( k ) ) ϑ k   ) .
  • Step 4: Estimation of weight of attributes
Let w = ( w 1 , w 2 , ... , w n ) T be the weight of attributes satisfying ∑ j = 1 n w j   = 1 and   w j ∈ [ 0 ,     1 ] . Next, we develop the SVN-DM-RANCOM tool to estimate the integrated weight of attribute.
  • Case I: Determine the objective weights using SVN-DM-based model given by Eq. (15).
    w j o = 1 m − 1 ∑ i = 1 m ∑ k = 1 m d ( η i j ,   η k j ) ∑ j = 1 n ( 1 m − 1 ∑ i = 1 m ∑ k = 1 m d ( η i j ,   η k j ) ) ,     ∀   j .
  • Case II: Determining of subjective weight through SVN-RANCOM model.
This method considers the following steps for computing the subjective criteria weighs:
  • Step 4a: Estimate the A-SVNDM based on the linguistic assessment degrees provided by the DEs through introduced SVNWA operator and obtained given as
    N = ( ξ j ) 1 ×   n = S V N W A ϑ k ( ξ j ( 1 ) , ξ j ( 2 ) , ... , ξ j ( l ) ) ,
    or
    N = ( ξ j ) 1 ×   n = S V N W G ϑ k ( ξ j ( 1 ) , ξ j ( 2 ) , ... , ξ j ( l ) ) .
  • Step 4b: Find the SVN-SM.
Next, compute the SVN-SM of A-SVN-DM based on Eq. (17).
η ¯ j = 1 2 ( S ( ξ j )   +   1 ) .
Step 4c: Determine the prioritization of attributes.
The minimum score value represents the most significant rank of the attribute. Some attributes may have equal score values, which reveals that ties are offered through the DEs’ result. Though, the changes that happened in prioritization would not influence the computed weight unless they comprise diverse attributes hierarchy.
Step 4d: Found the “matrix of ranking comparison (MRC)”.
The MRC is computed based on the pairwise comparison of prioritization of attributes by DEs ratings. The MRC is represented by Eq. (18), where φ i j =   1 , 0.5 and 0 for ρ ( η ¯ j ) < ρ ( η ¯ t ) ,   ρ ( η ¯ j ) = ρ ( η ¯ t ) and ρ ( η ¯ j ) > ρ ( η ¯ t ) , respectively and ρ ( η ¯ j ) is the rank of jth criterion.
                      r 1         r 2     ⋯     r n α t j = r 1 r 2 ⋮ r n [ φ 11 φ 11 ⋯ φ 1 n φ 21 φ 22 ⋯ φ 2 n ⋮ ⋮ ⋱ ⋮ φ n 1 φ n 2 ⋯ φ n n ] .
Step 4e: Compute the summed criteria weights (SCWs).
In accordance with previous step, the horizontal vector of the SCW is computed using Eq. (19).
S C W j = ∑ t = 1 n α t j ,   j = 1 , 2 , ... , n .
Step 4f: Derive the subjective weight of attribute.
Thus, the subjective weight of attributes is defined as
w j s = S C W j ∑ j = 1 n S C W j ,   j = 1 , 2 , ... , n .
Case III: Combined SVN-DM-RANCOM weight-determining tool.
In order to consider the benefits of objective and subjective weights of criteria through SVN-distance measure and SVN-RANCOM models, respectively, we present an integrated weighting model, given as
w j =   ζ w j o + ( 1 − ζ ) w j s ,
where ζ   ∈   [ 0 ,   1 ] represents the weighting precision parameter.
  • Step 5: Normalize the A-SVNDM.
In this step, the A-SVNDM Z = ( η i j ) m   ×   n is normalized A-SVNDM (NA-SVNDM) into ℕ = ( ε i j ) m   ×   n using the linear and vector normalization tools.
  • Step 5.1 (Linear normalization). It eliminates the dimensions of criteria using the doctrine of max-min operator. A linear NA-SVN-DM ℕ ( 1 )   =   ( ε i j ( 1 ) ) m × n is created using Eq. (22), where
    ε i j ( 1 ) = ( T i j ( 1 ) ,   I i j ( 1 ) ,   F i j ( 1 ) ) = η i j max i S ( η i j ) .
  • Step 5.2 (Vector normalization). A vector NA-SVN-DM ℕ ( 2 )   =   ( ε i j ( 2 ) ) m × n is constructed using Eq. (23), where
    ε i j ( 2 ) = ( T i j ( 2 ) ,   I i j ( 2 ) ,   F i j ( 2 ) ) = η i j ∑ i = 1 m ( S ( η i j ) ) 2 .
  • Step 5.3. Find the averaged NA-SVN-DM
    The averaged NA-SVN-DM ℕ = ( ε i j ) m   ×   n , where ε i j = ( T ¯ i j ,   I ¯ i j ,   F ¯ i j ) is done by applying the following expression as follows:
    ε i j = β ε i j ( 1 ) + ( 1 − β ) ε i j ( 2 ) ,
    where ε i j denotes the averaged NA-SVN-DM and β represents the normalization parameter changing from 0 to 1. Here, we take β= 0.5.
  • Step 6: Calculate the weighted averaged NA-SVN-DM.
    Corresponding to Eq. (25), the weighted NA-SVM-DM ℕ w = ( τ ⌢ i j ) m   ×   n , where τ ⌢ i j = ( T ⌢ i j ,   I ⌢ i j ,   F ⌢ i j ) is constructed, where
    τ ⌢ i j = ( T ⌢ i j ,   I ⌢ i j ,   F ⌢ i j ) = ( 1 − ∏ k = 1 l ( 1 − T ¯ i j ) w j ,   ∏ k = 1 l ( I ¯ i j ) w j , ∏ k = 1 l ( F ¯ i j ) w j   ) .
  • Step 7: Evaluate the SVN-score ratings of weighted NA-SVN-DM of each option.
    From weighted NA-SVN-DM, we find the weighted normalized rating (Li) for benefit-type attribute and the weighted normalized rating (Mi) for cost-type attribute as
    L i   =   ∑ j ∈ C b S ( τ ⌢ i j ) ,
    M i   =   ∑ j ∈ C c S ( τ ⌢ i j ) ,
    where S ( τ ⌢ i j ) symbolizes the SVN-score function of each rating of weighted averaged NA-SVN-DM.
  • Step 8: Calculate the “final utility degree (FUD)” of each option.
    The FUD (gi) of each option is obtained using Eq. (28) as
    s i   =   λ   L i   +   ( 1 −   λ )   M i ,
    wherein λ exemplifies the parameter of changing the attribute type. If we involve both types of criteria, then we take λ= 0.5. Though, there is a choice to change the parameter λ by taking the different criterion type.
  • Step 9: Based on the FUD (si), where i = 1, 2, …, m, prioritize the options.

5. Case Study: SHRM Assessment of Manufacturing Firms

HRM contributes considerably to manufacturing firms in India as each participant has an essential portion of firms, and their distinct features will reinforce the manufacturing procedures, attaining an growing in production (Saeidi et al., 2022). Thus, human resources are the main aspect for the affordability, efficacy, and expansion of manufacturing firms in India. This region being inside very competitive and dynamic market that needs continuous progress in all corporate regions, particularly paying better consideration to essential human resources, since they are persons that offer awareness, and capabilities to the firms and involve to the advance of innovative policies to attain continuous development and attainment of manufacturing firms. Additionally, the firms must distinguish the significance of the HRM to assurance its better management (Yánez Sarmiento et al., 2018). As whole, HRMs are vital for the appropriate working of a business, irrespective of its firm and size. Furthermore, the competitiveness of manufacturing firms is huge because of the feature of their HRM, so as to the abilities of staffs and their constant growth, in which training subjugates a vital place, is to become a stable aspect of competitive returns. Hence, committing time and resources to attain, sustain, and progress the capabilities of the firm's HRM becomes an essential strategic goal ( Saeidi et al., 2022).
Here, we use the proposed approach on an empirical study of manufacturing companies’ assessment from SVN information perspective. In this section, a panel of four DEs is created to identify the criteria and assess the alternatives based on considered criteria. Based on the literature review and online questionnaire, we have considered four companies alternatives and thirteen criteria. Details description of indicators is given in Table 1.
The required implementation procedure is presented in the following steps:
  • Steps 1-2: Table 3 presents the linguistic variables and the consequent SVNNs (Hezam et al., 2023). Using Table 3 and Eqs (11)-(13), the significance degree of each DE is derived and depicted in Table 4.
  • Step 3: Considering the LRs into mind, the DEs provide their opinions for each alternative with respect over indicators and required LAM is given in Table 5. To create the A-SVNDM, the SVNWA operator (14) is applied on Table 5 and required results are presented in Table 6.
  • Step 4: From Eq. (5) and Eq. (15), the objective weight of indicators for SHRM assessment in manufacturing firms are estimated and presented as w j o = {0.1003, 0.1015, 0.0654, 0.0883, 0.0855, 0.0926, 0.0807, 0.0307, 0.0852, 0.0613, 0.0296, 0.0867, 0.0922}.
Next, to determine indicators ranking for SHRM assessment in manufacturing firms, we compute the A-SVNDM and SVN-score value of indicators using Eq. (16)-Eq. (17) and given in Table 7. Based on the comparisons made by DEs, the MRC is determined using Eq. (18) and presented in Table 8. Based on the MRC, the SCWs are calculated using Eq. (19) and given in Table 8. From Eq. (20), we have calculated the subjective weights using the SVN-RANCOM tool of each indicator for SHRM assessment in manufacturing firms. The resultant values are shown in Figure 1 and presented as follows:
w j s = {0.1006, 0.0769, 0.0355, 0.1124, 0.0533, 0.1243, 0.0651, 0.0059, 0.0888, 0.1361, 0.1479, 0.0355, 0.0178}.
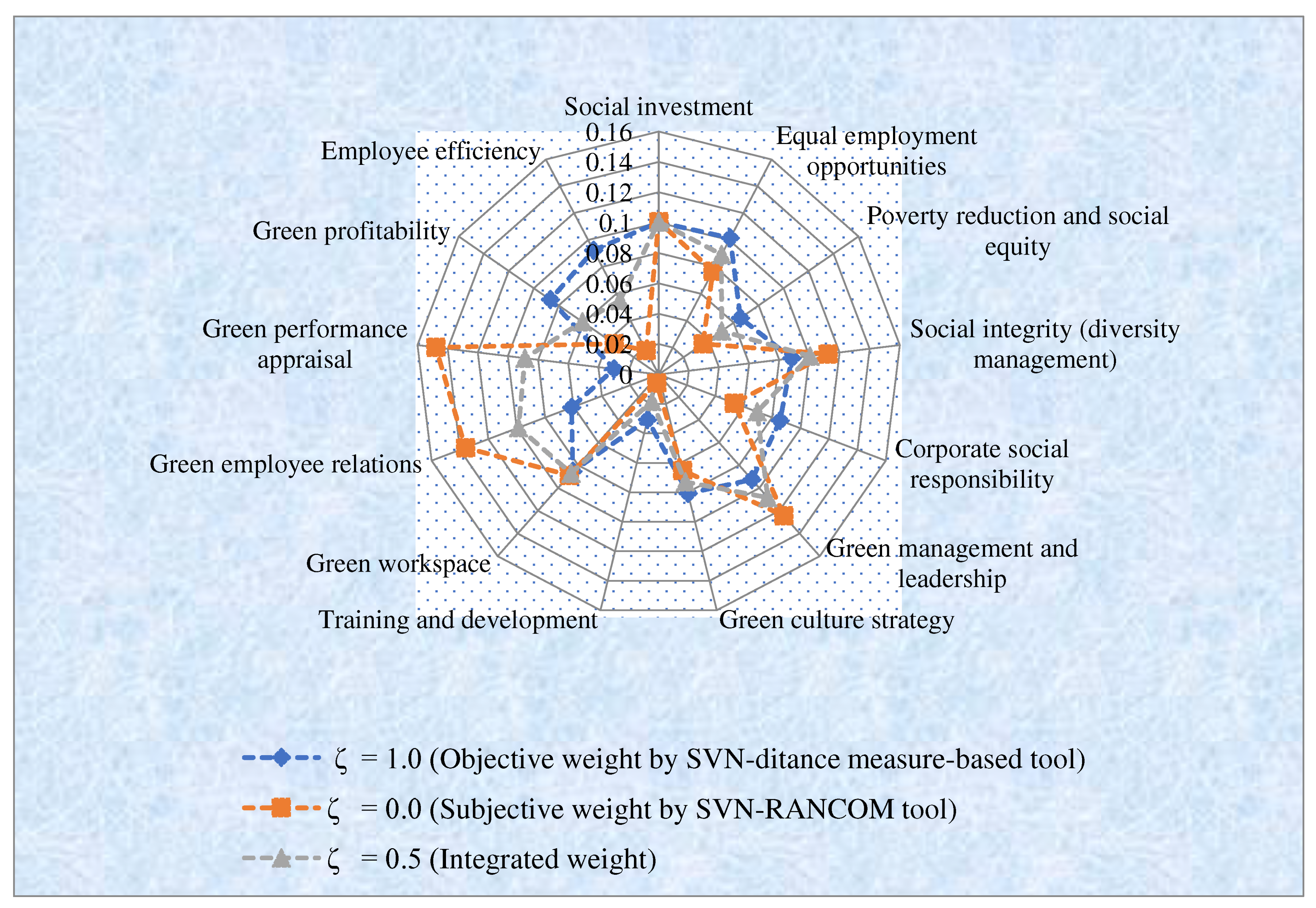
From Eq. (21), we integrate the SVN-DM-based tool and the SVN-RANCOM models. The integrated weight with the combination of the SVN-distance-RANCOM tool for τ = 0.5 for SHRM assessment in manufacturing firms is depicted in the Figure 3 and is given by wj = (0.1005, 0.0892, 0.0504, 0.1004, 0.0694, 0.1084, 0.0729, 0.0183, 0.087, 0.0987, 0.0887, 0.0611, 0.055).
Here, Figure 3 shows the variation of weight of diverse criteria for SHRM assessment in manufacturing firms. Green management and leadership (0.1084) is the most important indicators for SHRM assessment in manufacturing firms. Social investment (0.1005) is the second most criteria for SHRM assessment in manufacturing firms. Social integrity (diversity management) (0.1004) is third, Green employee relations (0.0987) is fourth, Equal employment opportunities (0.0892) is fifth most important criterion for SHRM assessment in manufacturing firms and remaining are measured crucial indicators for SHRM evaluation in manufacturing firms.
  • Step 5: From Table 5 and Eq. (22)-Eq. (23), linear normalization matrix and vector normalization matrix are constructed and presented in Table 9 and Table 10. The next step is to combine the linear and vector normalized A-SVN-DM using Eq. (24) to determine the averaged NA-SVN-DM and depicted in Table 11.
  • Step 6: From Eq. (25) and Table 11, we determine the weighted averaged normalized A-SVN-DM using SVNWAO or SVNWGO and criteria weights obtained in Eq. (21) and given in Table 12.
  • Step 7-9: The Li and Mi ratings are estimated using Eq. (26)-Eq. (27). The FUDs (si) value is calculated using Eq. (28). Here, we take λ = 0.5 as S1, S2, S3 and S4, are considered as cost-type and rest are benefit-type. Table 13 shows the SVN-score values of weighted averaged NA-SVN-DM to estimate the Li, Mi and OADs (gi). In this way, the following ranking order of manufacturing firms for SHRM assessment in manufacturing firms is obtained: F1 (0.4241) > F2 (0.3843) > F3(0.3742) > F4 (0.3672). Thus, the manufacturing firm-I (F1) is most suitable one with highest FUD (0.4241) for SHRM assessment in manufacturing firms.

5.1. Sensitivity Analysis

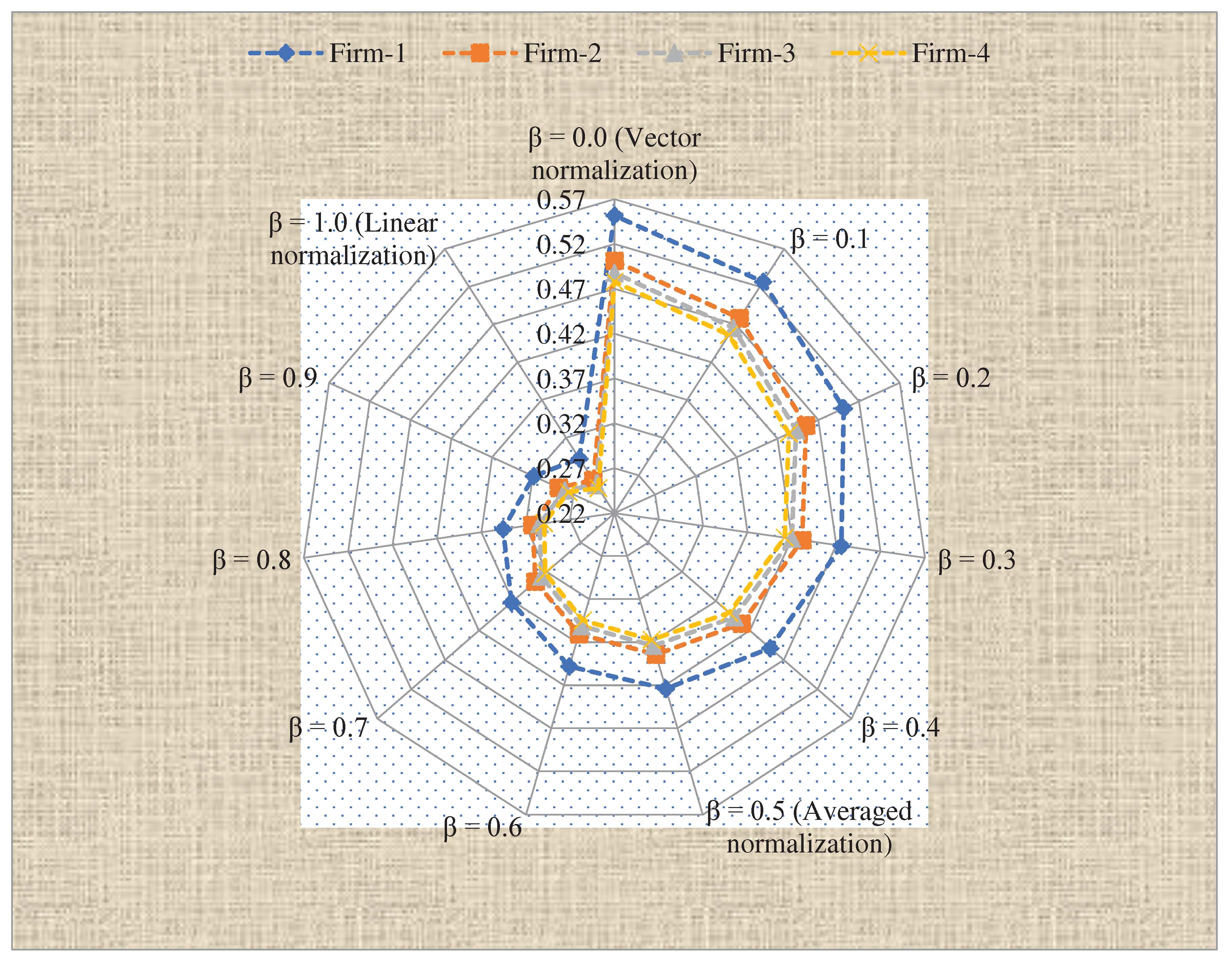
The variation of indicators’ weight to objective and subjective for different parameter (ζ) degrees in the proposed SVN-distance measure-RANCOM tool, changes in type of S-HRM indicators from benefit to cost with different parameter (λ) and varying the parameter β from linear to vector normalization to illustrate the FUDs of manufacturing firms for SHRM assessment in manufacturing firms. The investigations are performed by considering three cases.
  • Case I: When employing the normalization tool over diverse parameter (β) values. The changing in β from linear to vector normalization type is helping us to assess the sensitivity of the developed SVN-distance measure-RANCOM-AROMAN model to the prominence of normalization types. Table 14 and Figure 4 exemplify sensitivity of manufacturing firms for SHRM assessment in manufacturing firms over different normalization parameter β. According to the results, we find the same prioritizations F1 ≻ F2 ≻ F3 ≻ F4 for β = 0.0 to β = 1.0, which provides firm-I (S1) is the best choice, while firm-IV (F4) has the last rank for SHRM assessment in manufacturing firms. Thus, it is observed that the developed model holds suitable solidity with diverse parameter degrees.
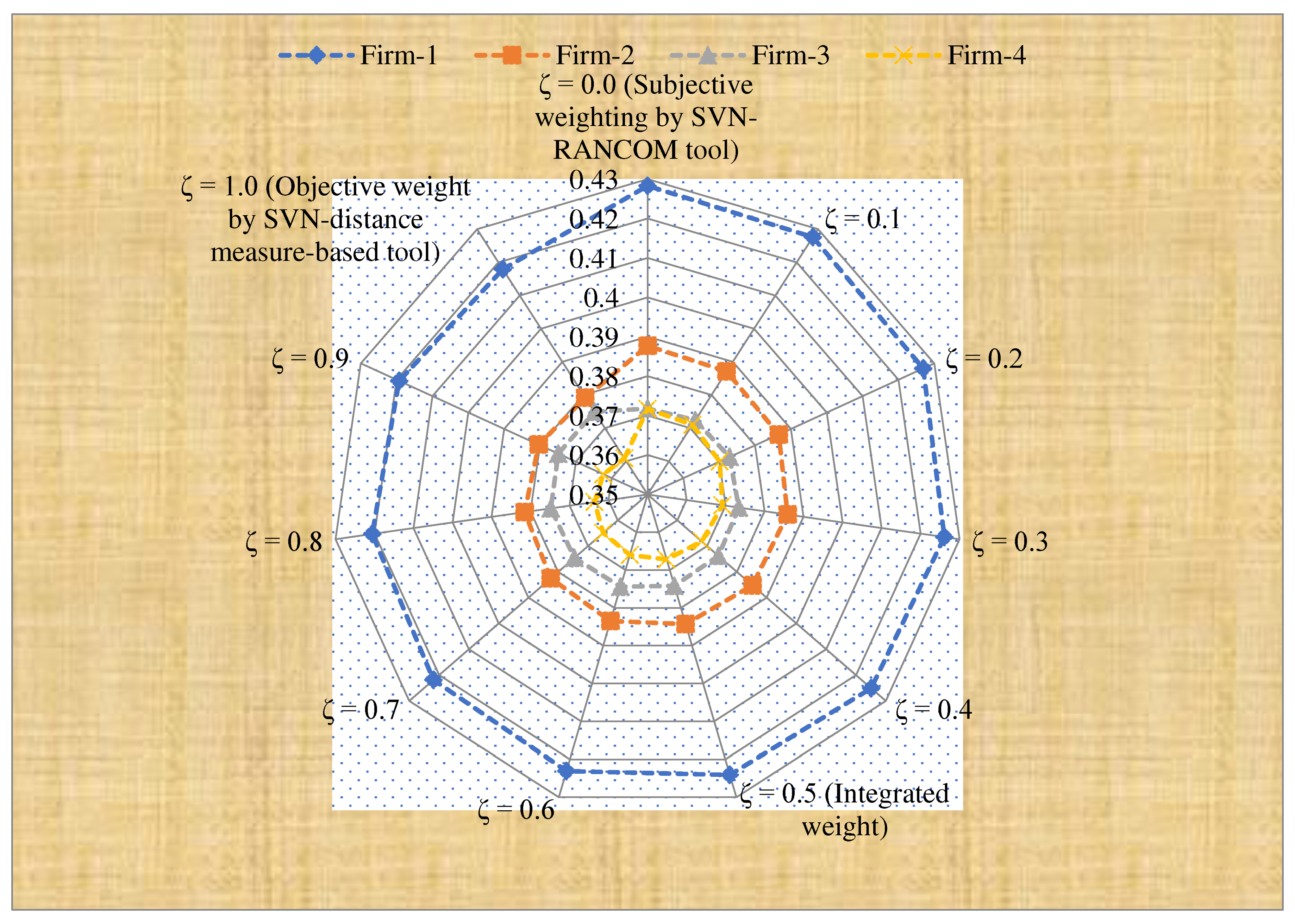
  • Case II: When considering weight-determining tool, objective (for ζ = 1.0) and subjective (for ζ = 0.0) weights are registered to offer enhanced weights for SHRM assessment in manufacturing firms. In this context, the weights of indicators are estimated by considering the objective and subjective weight separately in place of integrated weight of drivers. The prioritizations have been determined by changing the drivers’ weights from SVN-distance measure to SVN-RANCOM instead of SVN-distance measure-RANCOM weighting tool and depicted in Table 15 and Figure 5. Using SVN-distance measure (for ζ = 1.0), the FUD and preference of manufacturing firms are presented as follows: the FUD of option as F1= 0.4179, F2 = 0.3792, F3 = 0.3749 and F4 = 0.3609 and prioritization of firms is obtained as F1 ≻ F2 ≻ F3 ≻ F4. Applying the SVN-RANCOM (for ζ = 0.0) tool, the FUD and prioritization of manufacturing firm are estimated as follows: the FUD of options as F1 = 0.4283, F2 = 0.3877, F3 =0.3718, and F4 = 0.3717 and prioritization of manufacturing firms for S-HRM assessment in manufacturing firms is obtained as F1 ≻ F2 ≻ F3 ≻ F4. Based on aforesaid investigation, it is determined that by changing diverse parameter degrees will enhance the performance of developed SVN-distance measure-RANCOM-AROMAN method.
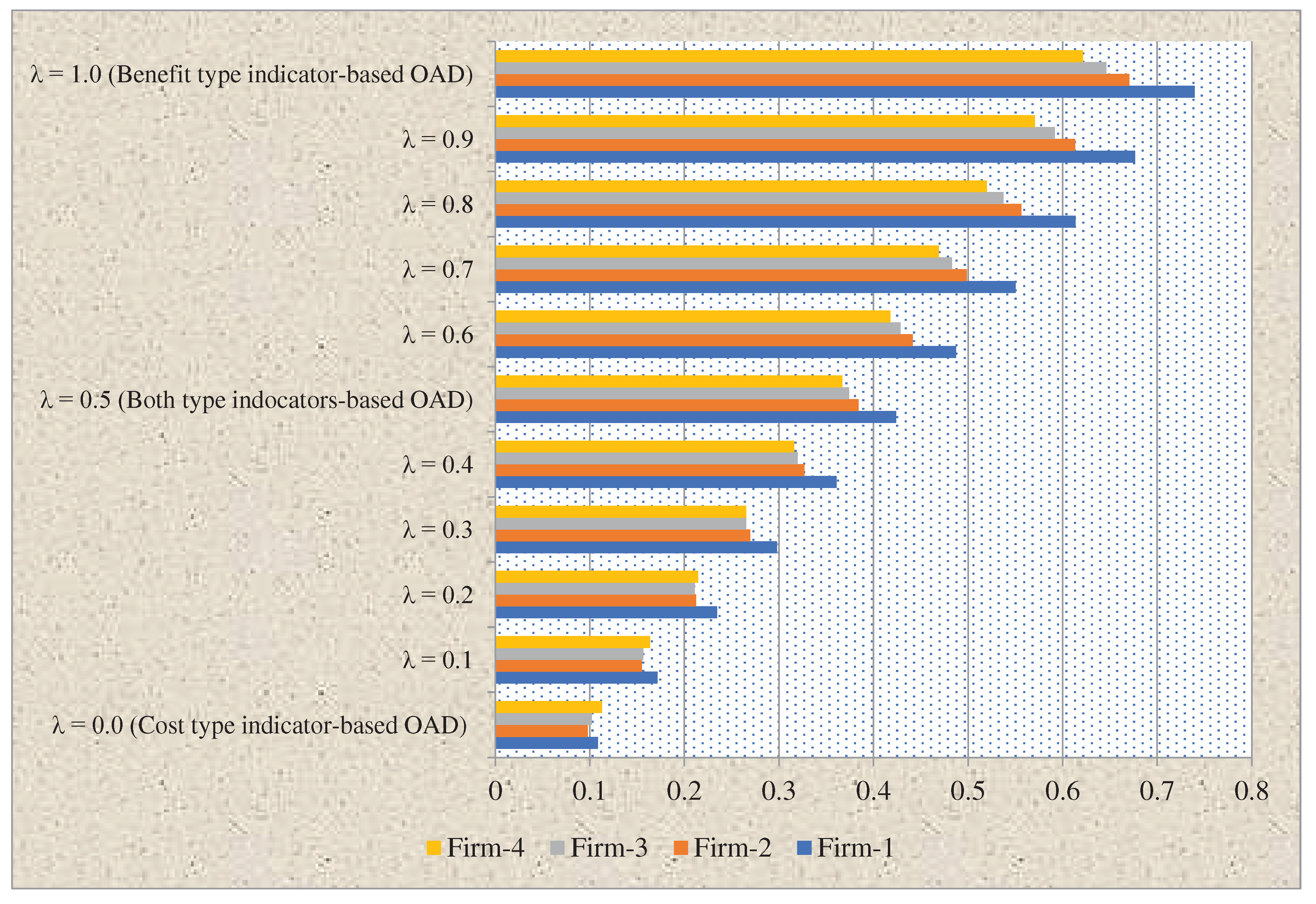
  • Case III: When considering attribute changing parameter, benefit (for λ= 1.0) and cost-type (for λ = 0.0) indicators for SHRM assessment in manufacturing firms are taken separately to show changes of prioritization of manufacturing firms for SHRM assessment in manufacturing firms. In this context, the FUD of firms are computed by considering the benefit and cost indicators separately in place of integrated FUD of manufacturing firms for SHRM assessment in manufacturing firms. The prioritizations have been determined by changing the indicators from benefit to cost for SHRM assessment in manufacturing firms and depicted in Table 16 and Figure 6. Considering only benefit indicators (for λ = 1.0), the FUD and preference of manufacturing firms are presented as follows: the FUD of option as F1=0.7398, F2 =0.6707, F3 =0.6461 and F4 =0.6216 and prioritization of manufacturing firms is obtained as F1 ≻ F2 ≻ F3 ≻ F4. Applying the cost indicators (for λ = 0.0) tool, the FUD and prioritization of manufacturing firms are estimated as follows: the FUD of manufacturing firms as F1 = 0.1085, F2 = 0.0980, F3 =0.1022, and F4 = 0.1128 and prioritization of firms for SHRM assessment in manufacturing firms is obtained as F4 ≻ F1 ≻ F3 ≻ F2. Based on aforesaid investigation, it is determined that by changing indicators type will enhance the performance of developed SVN-DM-RANCOM-AROMAN method.

5.2. Comparative Investigation

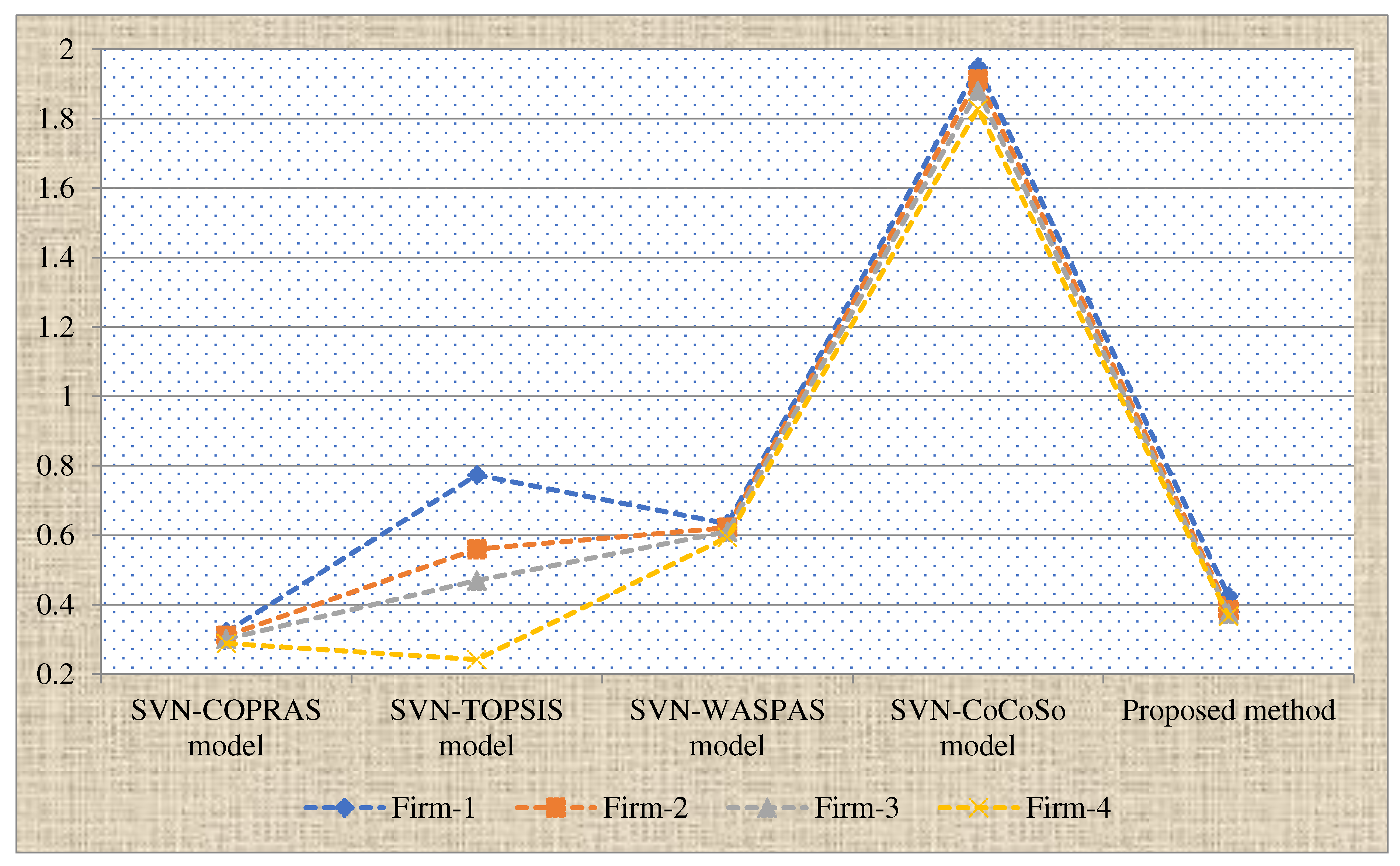
Here, we compare the results of proposed method and some of extant methods such as SVN-COPRAS (Hezam et al., 2022), SVN-WASPAS (Zavadskas et al., 2016), SVN-TOPSIS (Nancy and Garg, 2019) and SVN-CoCoSo (Rani and Mishra, 2020) tools.

5.2.1. SVN-COPRAS

The SVN-COPRAS model is applied on SHRM assessment problem of manufacturing firms. The sum of maximization criteria is obtained as ℘ 1 = (0.489, 0.443, 0.483), ℘ 2 = (0.466, 0.488, 0.519), ℘ 3 = (0.446, 0.497, 0.527) and ℘ 4 = (0.434, 0.511, 0.543) and the sum of minimization criteria is estimated as ℑ 1 = (0.127, 0.877, 0.864), ℑ 2 = (0.118, 0.891, 0.877), ℑ 3 = (0.120, 0.884, 0.869) and ℑ 4 = (0.133, 0.871, 0.861). The relative degree of each alternative is ℓ 1 = 0.3212, ℓ 2 = 0.3103, ℓ 3 = 0.3011 and ℓ 4 = 0.2885. Finally, the degree of utility of each option is obtained as α 1 = 100, α 2 = 96.61, α 3 = 93.73 and α 4 = 89.82. Then the ranking order of the firms is F 1 ≻ F 2 ≻ F 3 ≻ F 4 and the “firm-1 (F1)” is considered to be the best choice among the others for SHRM assessment in manufacturing firms.

5.2.2. SVN-WASPAS

The SVN-WASPAS model (Zavadskas et al., 2016) is implemented on aforesaid SHRM assessment problem. Using this model, the measures obtained through WSM are U 1 ( 1 )   = (0.633, 0.345, 0.391), U 2 ( 1 )   = (0.625, 0.353, 0.401), U 3 ( 1 )   = (0.605, 0.363, 0.418) and U 4 ( 1 )   = (0.590, 0.383, 0.418). In addition, the score values of WSM measures are S ( U 1 ( 1 ) ) = 0.632, S ( U 2 ( 1 ) ) = 0.624, S ( U 3 ( 1 ) ) = 0.608 and S ( U 4 ( 1 ) ) = 0.597. The measures obtained through WPM are U 1 ( 2 ) = (0.621, 0.322, 0.400), U 2 ( 2 )   = (0.616, 0.342, 0.416), U 3 ( 2 )   = (0.599, 0.346, 0.414) and U 4 ( 2 )   = (0.583, 0.368, 0.441). The score values of WPM measures are S ( U 1 ( 2 ) ) = 0.633, S ( U 2 ( 2 ) ) = 0.619, S ( U 3 ( 2 ) ) = 0.613 and S ( U 4 ( 2 ) ) = 0.591. Next, the UD of each firm is estimated as U 1 = 0.6327, U 2 = 0.6216, U 3 = 0.6106 and U 4 = 0.5939. Thus, the prioritization of manufacturing firm is F 1 ≻ F 2 ≻ F 3 ≻ F 4 and the most appropriate firm for SHRM assessment in manufacturing firms is manufacturing firm-1 (F1).

5.2.3. SVN-TOPSIS

The SVN-TOPSIS model (Nancy & Garg, 2019) is implemented on aforesaid SHRM assessment problem. Using this model, the SVN-IS and SVN-AIS of options are calculated as ϕ j + = {(0.294, 0.740, 0.690), (0.609, 0.357, 0.389), (0.666, 0.262, 0.315), (0.574, 0.356, 0.394), (0.778, 0.171, 0.201), (0.642, 0.286, 0.331), (0.628, 0.312, 0.356), (0.319, 0.697, 0.671), (0.660, 0.271, 0.320), (0.649, 0.273, 0.325), (0.304, 0.713, 0.673), (0.288, 0.752, 0.702), (0.249, 0.761, 0.734)} and ϕ j − = {(0.419, 0.569, 0.568), (0.456, 0.471, 0.483), (0.583, 0.360, 0.399), (0.461, 0.528, 0.522), (0.644, 0.296, 0.340), (0.525, 0.438, 0.455), (0.526, 0.428, 0.454), (0.358, 0.662, 0.621), (0.548, 0.396, 0.426), (0.572, 0.384, 0.409), (0.337, 0.672, 0.641), (0.396, 0.607, 0.577), (0.363, 0.597, 0.566)}. Next, the degrees of discrimination of each option from SVN-IS are 0.006, 0.010, 0.013 and 0.018 and the degrees of discrimination of each option from SVN-AIS are presented as 0.020, 0.012, 0.011 and 0.006. The “relative closeness coefficient (RCC)” of each firm over the SVN-IS is estimated as 0.7735, 0.5600, 0.4698 and 0.2415. Thus, prioritization firms is F 1 ≻   F 2 ≻   F 3 ≻   F 4 and the most appropriate firm for SHRM assessment in manufacturing firms is manufacturing firm-1 (F1).

5.2.4. SVN-CoCoSo

The SVN-CoCoSo model is applied on the SHRM assessment problem of manufacturing firms. In this model, the balanced compromise degrees of alternatives are determined as Q 1 ( 1 ) = 0.2573, Q 2 ( 1 ) = 0.2528, Q 3 ( 1 ) = 0.2483 and Q 4 ( 1 ) = 0.2415, Q 1 ( 2 ) = 2.1309, Q 2 ( 2 ) = 2.0932, Q 3 ( 2 ) = 2.0563 and Q 4 ( 2 ) = 2.0000, Q 1 ( 3 ) = 1.0000, Q 2 ( 3 ) = 0.9823, Q 3 ( 3 ) = 0.9650 and Q 4 ( 3 ) = 0.9386. Next, the OCDs of manufacturing firms are estimated as Q1 = 1.9479, Q2 = 1.9135, Q3 = 1.8797 and Q4 = 1.8283. Then the ranking order of manufacturing firms is F 1 ≻   F 2 ≻   F 3 ≻   F 4 and the most appropriate firm for SHRM assessment in manufacturing firms is manufacturing firm-1 (F1).
Preprints 85972 g007
Figure 7. Comparison of assessment degree of firms for SHRM assessment with various methods.
Figure 7. Comparison of assessment degree of firms for SHRM assessment with various methods.
Preprints 85972 g007

5.3. Discussion

At the present time, sustainability is the major apprehensions of administrations and society. Along with all sectors of each country’s business, organizations are considerably trying to achieve SDGs. In this way and to promote firm’s sustainability, various firms are trying to establish relation with sustainability to HRM, which is formed an innovative standard named as “sustainability human resource management (SHRM)”. Corresponding to Ehnert et al. (2016), SHRM is associated to those actions which lead to attaining the SEE sustainability dimensions objectives inside and outside of the manufacturing firms.
From Figure 7, it can effortlessly be seen that most suitable “manufacturing firm (F1)” is same for all the MCGDM approaches, namely SVN-COPRAS, SVN-WASPAS, SVN-TOPSIS and SVN-CoCoSo. The main advantages of the developed SVN-DM-RANCOM-AROMAN methodology are as follows:
  • The SVN-DM proposed in this study overcomes the limitations of existing measures in order to enumerate the amount of distance between SVNSs.
  • The developed tool uses weighting model using the combination of SVN-DM-based tool for objective weight and SVN-RANCOM model for subjective weight, which results in more accurate, optimal weights.
  • Existing SVN-WASPAS and SVN-TOPSIS models consider direct weight of criteria, while the proposed model has used a rank sum-based procedure to compute the DEs weights. Thus, the proposed model has good effectiveness through the evaluation of manufacturing firms for SHRM assessment.
  • The SVN-DM-RANCOM-AROMAN model uses the linear and vector normalization models to aggregate the indeterminate, inconsistent and uncertain information, therefore it provides more accurate decision than existing methods.
Preprints 85972 g008
Figure 7. Depiction of the Sustainability aspects weight of SEE analysis by SVN-DM-RANCOM.
Figure 7. Depiction of the Sustainability aspects weight of SEE analysis by SVN-DM-RANCOM.
Preprints 85972 g008
Based on the previous studies, organizations can do various activities in order to reach SHRM. In this study, in order to consider all earlier studies providing a systematic review and planning interviews, we have characterized aspects of SHRM into three SEE sustainability dimensions. This work has been documented five indicators to the social dimension: social investment, equal employment opportunities, poverty reduction and social equity, social integrity and corporate social responsibility, considered five indicators with the environmental dimension as green management and leadership, green culture strategy, training and development, green workspace, green employee relationship, and finally three indicators comprising of green performance appraisal, green profitability, employee efficiency, creating the economic dimension.
Moreover, in Figure 7, assessment outcomes of manufacturing firms for S-HRM assessment are prioritized as: Social (0.4099) ≻ Environmental (0.3853) ≻ Economic (0.2048), which means social dimension have highest impact on manufacturing firms for S-HRM assessment, followed by Environmental and Economic and risks. Aforementioned assessments, four manufacturing firms for S-HRM assessment continuously preserve the prioritization in spite of how indicators weight varies. It can be observed the firmness and practicality of SVN-DM-RANCOM-AROMAN model.

6. Conclusions

SHRM plays a crucial role in SEE sustainability dimensions management. In this work, we have introduced hybrid MCGDM model called “SVN-DM-RANCOM-AROMAN” to evaluate SHRM indicators in the manufacturing firms. For this purpose, new SVN-distance measure has been presented for SVNSs, which overcomes the limitations of extant SVN-DMs. In the developed model, the objective weight of indicators has been computed with the SVN-DM-based model, while the subjective weights of indicators have been derived through novel SVN-RANCOM model. Further, the integrated weight of indicators for SHRM assessment in manufacturing firms has been determined with SVN-DM-RANCOM tool. To rank the firms, the AROMAN method has been combined with the SVN-DM-RANCOM model from SVNNs perspectives. To validate the proposed method, we have executed it on a case study of SHRM assessment in manufacturing firms in India with multiple indicators and DEs. In this study, four manufacturing firms have been extensively assessed by means of 3 SEE dimensions and 13 indicators in the presence of four DEs. Furthermore, comparison with extant models has been presented to confirm the robustness of developed model. Moreover, sensitivity investigation has been made over diverse normalization and weighting parameters. The advantages of the developed approach include the development of new SVN-distance measure, linear and vector normalization tools and criteria weighting through SVN-distance measure-RANCOM model. Thus, the developed model is more capable and accurate while making decisions under SVNSs environment.
This study has some limitations such as it does not consider the interrelationships among the criteria. In addition, more decision experts should be considered during the assessment of SHRM factors in manufacturing firms. In future, we will try to evade the shortcomings of presented work by developing new model based on Shapley function, prospect theory and evidential reasoning under SVNSs environment. Moreover, we can extend the present study under the context of Plithogenic sets, linear Diophantine sets, hyperbolic sets and others.

Funding

This research was conducted under a project titled “Researchers Supporting Project”, funded by King Saud University, Riyadh, Saudi Arabia under grant number (RSP2023R323).

References

  1. Erdogan, N.; Pamucar, D.; Kucuksari, S.; Deveci, M. An integrated multi-objective optimization and multi-criteria decision-making model for optimal planning of workplace charging stations. Appl Energy 2021, 304, 117866. [Google Scholar] [CrossRef]
  2. Deveci, M.; Erdogan, N.; Pamucar, D.; Kucuksari, S.; Cali, U. A rough Dombi Bonferroni based approach for public charging station type selection. Applied Energy 2023, 345, 121258. [Google Scholar] [CrossRef]
  3. Charly, A.; Thomas, N.J. Aoife Foley, Brian Caulfield, Identifying optimal locations for community electric vehicle charging. Sustainable Cities and Society 2023, 94, 104573. [Google Scholar] [CrossRef]
  4. Saeidi, P.; Mardani, A.; Mishra, A.R.; Cajas, V.E.C.; Carvajal, M.G. Evaluate sustainable human resource management in the manufacturing companies using an extended Pythagorean fuzzy SWARA-TOPSIS method. Journal of Cleaner Production 2022, 370, 133380. [Google Scholar] [CrossRef]
  5. Piwowar-Sulej, K. Core functions of Sustainable Human Resource Management. A hybrid literature review with the use of H-Classics methodology. Sustainable Development 2021, 29, 671–693. [Google Scholar] [CrossRef]
  6. Więckowski, J.; Kizielewicz, B.; Shekhovtsov, A.; Sałabun, W. RANCOM: A novel approach to identifying criteria relevance based on inaccuracy expert judgments. Engineering Applications of Artificial Intelligence 2023, 122, 106114. [Google Scholar] [CrossRef]
  7. Ramalho, T.S.; Martins MD, F. Sustainable Human Resource Management in the Supply Chain: A new framework. Cleaner Logistics and Supply Chain 2022, 5, 100075. [Google Scholar] [CrossRef]
  8. Sayyadi Tooranloo, H.; Azadi, M.H.; Sayyahpoor, A. Analyzing factors affecting implementation success of sustainable human resource management (SHRM) using a hybrid approach of FAHP and Type-2 fuzzy DEMATEL. Journal of Cleaner Production 2017, 162, 1252–1265. [Google Scholar] [CrossRef]
  9. Ehnert, I. Sustainable human resource management; A Conceptual and Exploratory Analysis from a Paradox Perspective: Heidelberg, 2009. [Google Scholar]
  10. Bernstein, E. Making transparency transparent: the evolution of observation in management theory. Acad. Manag. Ann. 2017, 11, 217–266. [Google Scholar] [CrossRef]
  11. Chams, N.; García-Blandón, J. On the importance of sustainable human resource management for the adoption of sustainable development goals. Resources, Conservation and Recycling 2019, 141, 109–122. [Google Scholar] [CrossRef]
  12. Fetanat, A.; Tayebi, M. Sustainability and reliability-based hydrogen technologies prioritization for decarbonization in the oil refining industry: A decision support system under single-valued neutrosophic set. International Journal of Hydrogen Energy 2023. [CrossRef]
  13. Bošković, S.; Švadlenka, L.; Jovčić, S.; Dobrodolac, M.; Simić, V.; Bacanin, N. An Alternative Ranking Order Method Accounting for Two-Step Normalization (AROMAN)- A Case Study of the Electric Vehicle Selection Problem. IEEE Access 2023, 11, 39496–39507. [Google Scholar] [CrossRef]
  14. Nikolic, I.; Milutinovic, J.; Božanic, J.; Dobrodolac, M. Using an Interval Type-2 Fuzzy AROMAN Decision-Making Method to Improve the Sustainability of the Postal Network in Rural Areas. Mathematics 2023, 11, 01–26. [Google Scholar] [CrossRef]
  15. Mishra, A.R.; Rani, P.; Prajapati, R.S. Multi-criteria weighted aggregated sum product assessment method for sustainable biomass crop selection problem using single-valued neutrosophic sets. Applied Soft Computing 2021, 113. [Google Scholar] [CrossRef]
  16. Luo, X.; Wang, Z.; Yang, L.; Lu, L.; Hu, S. Sustainable supplier selection based on VIKOR with single-valued neutrosophic sets. PLoS ONE 2023. [CrossRef]
  17. Ridvan, S.; Fuat, A.; Dilek, K.G. A single-valued neutrosophic multicriteria group decision approach with DPL-TOPSIS method based on optimization. International Journal of Intelligent Systems 2021, 36, 3339–3366. [Google Scholar] [CrossRef]
  18. Meng, Q.; Pang, N.; Zhao, S.; Gao, J. Two-stage optimal site selection for waste-to-energy plant using single-valued neutrosophic sets and geographic information system based multi-criteria decision-making approach: A case study of Beijing, China. Waste Management 2023, 156, 283–296. [Google Scholar] [CrossRef]
  19. Li, X.; Luo, Y.; Wang, H.; Lin, J.; Deng, B. Doctor selection based on aspect-based sentiment analysis and neutrosophic TOPSIS method. Engineering Applications of Artificial Intelligence 2023, 124, 106599. [Google Scholar] [CrossRef]
  20. Ogbeibu, S.; Emelifeonwu, J.; Senadjki, A.; Gaskin, J.; Kaivo-oja, J. Technological turbulence and greening of team creativity, product innovation, and human resource management: Implications for sustainability. Journal of Cleaner Production 2020, 244, 118703. [Google Scholar] [CrossRef]
  21. Järlström, M.; Saru, E.; Vanhala, S. Sustainable Human Resource Management with Salience of Stakeholders: A Top Management Perspective. Journal of Business Ethics 2018, 152, 703–724. [Google Scholar] [CrossRef]
  22. Ye, J.; Du, S.; Yong, R. Multi-criteria decision-making model using trigonometric aggregation operators of single-valued neutrosophic credibility numbers. Information Sciences 2023, 644, 118968. [Google Scholar] [CrossRef]
  23. Smarandache, F. A unifying field in logics. Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press: Rehoboth, 1999. [Google Scholar]
  24. Ehnert, I.; Parsa, S.; Roper, I.; Wagner, M.; Muller-Camen, M. Reporting on sustainability and HRM: a comparative study of sustainability reporting practices by the world's largest companies. The International Journal of Human Resource Management 2016, 27, 88–108. [Google Scholar] [CrossRef]
  25. Smarandache, F. The score, accuracy, and certainty functions determine a total order on the set of neutrosophic triplets (T,I,F). Neutrosophic Sets and Systems 2020, 38, 1–14. [Google Scholar]
  26. Ye, J. Single Valued Neutrosophic Cross-Entropy for Multi-criteria Decision Making Problems. Applied Mathematical Modelling 2014, 38, 1170–1175. [Google Scholar] [CrossRef]
  27. Zadeh, L.A. Fuzzy sets. Information and Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
  28. Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets and Systems 1986, 20, 87–96. [Google Scholar] [CrossRef]
  29. Wang, H.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Single valued neutrosophic sets, Multispace and Multistructure. 2010, 4, 410–413. [Google Scholar]
  30. Ali, M.; Hussain, Z.; Yang, M.-S. Hausdorff Distance and Similarity Measures for Single-Valued Neutrosophic Sets with Application in Multi-Criteria Decision Making. Electronics Decision Making. Electronics 2022, 12, 1–16. [Google Scholar] [CrossRef]
  31. Chai, J.S.; Selvachandran, G.; Smarandache, F.; Gerogiannis, V.C.; Son, L.H.; Bui, Q.-T.; Vo, B. New similarity measures for single-valued neutrosophic sets with applications in pattern recognition and medical diagnosis problems. Complex & Intelligent Systems 2021, 7, 703–723. [Google Scholar] [CrossRef]
  32. Luo, M.; Zhang, G.; Wu, L. A novel distance between single valued neutrosophic sets and its application in pattern recognition. Soft Computing 2022, 26, 11129–11137. [Google Scholar] [CrossRef]
  33. Ye, J. Clustering Methods Using Distance-Based Similarity Measures of Single-Valued Neutrosophic Sets. Journal of Intelligent Systems 2014, 23, 379–389. [Google Scholar] [CrossRef]
  34. Xu, D.; Xian, H.; Cui, X.; Hong, Y. A new single-valued neutrosophic distance for TOPSIS, MABAC and new similarity measure in multi-attribute decision-Making. IAENG Int. J. Appl. Math. 2020, 50, 72–79. [Google Scholar]
  35. Tooranloo, H.S.; Azadi, M.H.; Sayyahpoor, A. Analyzing factors affecting implementation success of sustainable human resource management (SHRM) using a hybrid approach of FAHP and Type-2 fuzzy DEMATEL. Journal of Cleaner Production 2017, 162, 1252–1265. [Google Scholar] [CrossRef]
  36. Shayan, N.F.; Mohabbati-Kalejahi, N.; Alavi, S.; Zahed, M.A. Sustainable Development Goals (SDGs) as a Framework for Corporate Social Responsibility (CSR). Sustainability 2022, 14, 1222. [Google Scholar] [CrossRef]
  37. Stankevičiūtė, Ž.; Savanevičienė, A. Designing Sustainable HRM: The Core Characteristics of Emerging Field. Sustainability 2018, 10, 4798. [Google Scholar] [CrossRef]
  38. Jiang, Y.; Xue, X.; Xue, W. Proactive Corporate Environmental Responsibility and Financial Performance: Evidence from Chinese Energy Enterprises. Sustainability 2018, 10, 964. [Google Scholar] [CrossRef]
  39. Glass, L.-M.; Newig, J. Governance for achieving the Sustainable Development Goals: How important are participation, policy coherence, reflexivity, adaptation and democratic institutions? Earth System Governance 2019, 2, 100031. [Google Scholar] [CrossRef]
  40. de Oliveira, U.R.; Menezes, R.P.; Fernandes, V.A. A systematic literature review on corporate sustainability: contributions, barriers, innovations and future possibilities. Environ Dev Sustain 2023. [Google Scholar] [CrossRef]
  41. Kramar, R. Beyond strategic human resource management: Is sustainable human resource management the next approach? International Journal of Human Resource Management 2014, 25, 1069–1089. [Google Scholar] [CrossRef]
  42. Bošković, S.; Švadlenka, L.; Dobrodolac, M.; Jovčić, S.; Zanne, M. An Extended AROMAN Method for Cargo Bike Delivery Concept Selection. Decision Making Advances 2023, 1, 1–9. [Google Scholar] [CrossRef]
  43. Ehnert, I.; Harry, W. Recent developments and future prospects on sustainable human resource management: Introduction to the special issue. Manag. Rev. 2012, 23, 221–238. [Google Scholar] [CrossRef]
  44. Macke, J.; Genari, D. Systematic literature review on sustainable human resource management. Journal of Cleaner Production 2019, 208, 806–815. [Google Scholar] [CrossRef]
  45. De Vos, A.; Van der Heijden, B. Current thinking on contemporary careers: the key roles of sustainable HRM and sustainability of careers. Current Opinion in Environmental Sustainability 2017, 28, 41–50. [Google Scholar] [CrossRef]
  46. Maunganidze, L. Corporate social investment practices as ‘soft technology’: A case of selected Botswana firms. Journal of Cleaner Production 2022, 368, 132957. [Google Scholar] [CrossRef]
  47. Sorribes, J.; Celma, D.; Martínez–Garcia, E. Sustainable human resources management in crisis contexts: interaction of socially responsible labour practices for the well-being of employees. Corporate Social Responsibility and Environmental Management 2021, 28, 936–952. [Google Scholar] [CrossRef]
  48. Martini, M.; Riva, E.; Marafioti, E. Sustainable HRM, training for employability and organizational outcomes: the moderating role of competitive intensity. Employee Relations 2023, 45, 79–102. [Google Scholar] [CrossRef]
  49. Kainzbauer, A.; Rungruang, P.; Hallinger, P. How Does Research on Sustainable Human Resource Management Contribute to Corporate Sustainability: A Document Co-Citation Analysis, 1982–2021. Sustainability 2021, 13, 11745. [Google Scholar] [CrossRef]
  50. Cachon-Rodríguez, G.; Blanco-Gonzalez, A.; Prado-Roman, C.; Del-Castillo-Feito, C. How sustainable human resources management helps in the evaluation and planning of employee loyalty and retention: Can social capital make a difference? Evaluation and Program Planning 2022, 95. [Google Scholar] [CrossRef]
  51. Chen, P. Curse or blessing? The relationship between sustainable development plans for resource cities and corporate sustainability - Evidence from China. Journal of Environmental Management 2023, 341, 117988. [Google Scholar] [CrossRef]
  52. Yánez Sarmiento, M.M.; Yánez Sarmiento, J.R.; Morocho Espinoza, J.M. Importancia de los recursos humanos en las micro, pequeñas y medianas empresas del Ecuador. Revista Universidad y Sociedad 2018, 10, 89–93. [Google Scholar]
Preprints 85972 g001
Figure 1. Hierarchical structure of the SHRM assessment based on 13 criteria/indicators/factors.
Figure 1. Hierarchical structure of the SHRM assessment based on 13 criteria/indicators/factors.
Preprints 85972 g001
Preprints 85972 g002
Figure 2. Graphical framework of the proposed ranking approach.
Figure 2. Graphical framework of the proposed ranking approach.
Preprints 85972 g002
Preprints 85972 g003
Figure 3. Weights of indicators for SHRM assessment in manufacturing firms.
Figure 3. Weights of indicators for SHRM assessment in manufacturing firms.
Preprints 85972 g003
Preprints 85972 g004
Figure 4. Sensitivity test on normalization parameter (β) for assessing SHRM.
Figure 4. Sensitivity test on normalization parameter (β) for assessing SHRM.
Preprints 85972 g004
Preprints 85972 g005
Figure 5. Sensitivity test on weighting parameter (ζ) for SHRM assessment in manufacturing firms.
Figure 5. Sensitivity test on weighting parameter (ζ) for SHRM assessment in manufacturing firms.
Preprints 85972 g005
Preprints 85972 g006
Figure 6. Sensitivity test on attribute changing parameter (λ) for S-HRM assessment in manufacturing firms.
Figure 6. Sensitivity test on attribute changing parameter (λ) for S-HRM assessment in manufacturing firms.
Preprints 85972 g006
Table 1. Meaning of considered indicators for SHRM assessment.
Table 1. Meaning of considered indicators for SHRM assessment.
Dimension Indicators Type References
Social Social investment (H1) C Dempsey et al., 2011; Kramar, 2014; Zhang et al., 2019
Equal employment opportunities (H2) B Sharma, 2016; Stankevičiūtė & Savanevičienė, 2018
Poverty reduction and social equity (H3) B Saeidi et al., 2022
Social integrity (Diversity management) (H4) B Tooranloo et al., 2017
Corporate social responsibility (H5) B Jamali et al., 2015
Environmental Green management and leadership (H6) B Heizmann & Liu, 2018
Green culture strategy (H7) B Gehrels & Suleri, 2016; Järlström et al., 2018; Zhang et al., 2019
Training and development (H8) C Saeed et al., 2019; Zhang et al., 2019
Green workspace (H9) B Rayner & Morgan, 2018; Chams & García-Blandón, 2019
Green employee relationship (H10) B Ehnert et al., 2016
Economic Green performance appraisal (H11) C Chams & García-Blandón, 2019
Green profitability (H12) C Järlström et al., 2018; Saeidi et al., 2022
Employee efficiency (H13) C Tooranloo et al., 2017
Table 2. Comparative results of introduced and existing measures.
Table 2. Comparative results of introduced and existing measures.
Set-I Set-II Set-III Set-IV Set-V Set-VI
M (1,0,0) (1,0,0) (0.5,0,0) (0.3,0.2,0.4) (0.3,0.2,0.3) (0.4,0.2,0.3)
N (0,1,1) (0,0,0) (0,0,0.5) (0.4,0.2,0.3) (0.4,0.2,0.3) (0.8,0.4,0.6)
d1(M,N) 1 0.3333 0.3333 0.0667 0.0333 0.3
d2(M,N) 1 1 0.5 0.1 0.1 0.4
d3(M,N) 1 0.3333 0.1667 0.0467 0.0233 0.29
d4(M,N) 0.3333 0.3333 0 0 0.0233 0.29
d5(M,N) 0.6667 1 1 0.4138 0.2273 0.5735
d(M,N) 1 0.3333 0.3611 0.0789 0.0389 0.2111
Table 3. LRs into SVNNs for SHRM assessment in manufacturing firms.
Table 3. LRs into SVNNs for SHRM assessment in manufacturing firms.
LVs SVNNs
Extremely high (EH) (1, 0, 0)
Very very high (VVH) (0.9, 0.1, 0.1)
Very high (VH) (0.8, 0.15, 0.2)
High (H) (0.7, 0.25, 0.3)
Moderately high (MH) (0.6, 0.35, 0.4)
Fair (F) (0.5, 0.5, 0.5)
Moderately low (ML) (0.4, 0.65, 0.6)
Low (L) (0.3, 0.75, 0.7)
Very low (VL) (0.2, 0.85, 0.8)
Very very low (VVL) (0.1, 0.9, 0.9)
Extremely low (EL) (0, 1, 1)
Table 4. DEs’ weights for SHRM assessment in manufacturing firms.
Table 4. DEs’ weights for SHRM assessment in manufacturing firms.
DEe e1 e2 e3 e4
LRs VVH EH H VH
SVNNs (0.9, 0.1, 0.1) (1, 0, 0) (0.7, 0.25, 0.3) (0.8, 0.15, 0.2)
e ¯ k 0.2609 0.2899 0.2126 0.2367
l − ρ k + 1 3 4 1 2
e ¯ k r 0.3 0.4 0.1 0.2
λ k 0.2804 0.3449 0.1563 0.2183
Table 5. LAM for DEs’ opinions for SHRM assessment in manufacturing firms.
Table 5. LAM for DEs’ opinions for SHRM assessment in manufacturing firms.
F1 F2 F3 F4
H1 (ML,ML,F,L) (ML,L,VL,F) (ML,L,L,VL) (MH,L,F,L)
H2 (MH,F,ML,F) (VH,F,MH,ML) (VH,F,F,MH) (MH,F,F,MH)
H3 (VH,MH,MH,F) (VH,MH,H,MH) (VVH,F,MH,F) (H,F,MH,MH)
H4 (MH,H,F,F) (F,ML,ML,MH) (MH,MH,F,F) (H,MH,F,ML)
H5 (VVH,VH,MH,H) (VH,MH,F,H) (F,VH,F,H) (VH,F,H,MH)
H6 (F,H,MH,VH) (MH,F,H,VH) (MH,F,VH,ML) (ML,F,MH,H)
H7 (F,H,VH,F) (MH,F,MH,F) (VH,F,MH,MH) (F,F,MH,H)
H8 (F,VL,VVL,ML) (L,ML,F,VL) (VL,F,L,ML) (ML,ML,F,VL)
H9 (VH,MH,F,H) (MH,MH,F,VH) (F,MH,ML,H) (F,MH,MH,H)
H10 (MH,H,VH,MH) (MH,F,F,VVH) (F,F,F,VH) (F,H,MH,VH)
H11 (L,F,VVL,L) (F,VL,ML,VL) (L,ML,VVL,F) (VL,ML,F,VL)
H12 (ML,F,L,ML) (ML,VL,L,L) (ML,VL,F,L) (F,L,ML,VL)
H13 (VVL,L,F,VL) (VL,F,L,VL) (ML,F,VL,L) (ML,L,ML,L)
Table 6. A-SVNDM for SHRM assessment in manufacturing firms.
Table 6. A-SVNDM for SHRM assessment in manufacturing firms.
F1 F2 F3 F4
H1 (0.377, 0.644, 0.603) (0.349, 0.673, 0.636) (0.294, 0.740, 0.690) (0.419, 0.569, 0.568)
H2 (0.456, 0.471, 0.483) (0.609, 0.357, 0.389) (0.552, 0.330, 0.368) (0.471, 0.419, 0.447)
H3 (0.633, 0.298, 0.346) (0.666, 0.262, 0.315) (0.678, 0.301, 0.308) (0.583, 0.360, 0.399)
H4 (0.574, 0.356, 0.394) (0.461, 0.528, 0.522) (0.539, 0.400, 0.435) (0.557, 0.386, 0.417)
H5 (0.778, 0.171, 0.201) (0.660, 0.271, 0.320) (0.638, 0.284, 0.326) (0.644, 0.296, 0.340)
H6 (0.642, 0.286, 0.331) (0.629, 0.312, 0.355) (0.557, 0.397, 0.424) (0.525, 0.438, 0.455)
H7 (0.607, 0.326, 0.363) (0.526, 0.428, 0.454) (0.628, 0.312, 0.356) (0.548, 0.407, 0.432)
H8 (0.319, 0.697, 0.671) (0.330, 0.689, 0.648) (0.346, 0.655, 0.626) (0.358, 0.662, 0.621)
H9 (0.660, 0.271, 0.320) (0.622, 0.308, 0.356) (0.548, 0.396, 0.426) (0.576, 0.387, 0.426)
H10 (0.649, 0.273, 0.325) (0.654, 0.318, 0.331) (0.572, 0.384, 0.409) (0.642, 0.286, 0.331)
H11 (0.322, 0.671, 0.648) (0.320, 0.702, 0.670) (0.337, 0.672, 0.641) (0.304, 0.713, 0.673)
H12 (0.396, 0.607, 0.577) (0.288, 0.752, 0.702) (0.324, 0.706, 0.666) (0.345, 0.673, 0.640)
H13 (0.249, 0.761, 0.734) (0.303, 0.694, 0.666) (0.363, 0.597, 0.566) (0.330, 0.705, 0.654)
Table 7. Aggregated ratings for indicators and SVN-score for SHRM assessment in manufacturing firms.
Table 7. Aggregated ratings for indicators and SVN-score for SHRM assessment in manufacturing firms.
e1 e2 e3 e4 SVNNs S ( ξ j ) Rank of criteria
H1 MH F H VH (0.629, 0.312, 0.355) 0.654 5
H2 H MH F F (0.652, 0.364, 0.401) 0.629 7
H3 VH ML H L (0.577, 0.383, 0.409) 0.595 10.5
H4 F VVH ML L (0.631, 0.327, 0.318) 0.662 4
H5 H H ML ML (0.580, 0.358, 0.389) 0.611 9
H6 H VH F F (0.650, 0.272, 0.316) 0.687 3
H7 F H MH MH (0.583, 0.344, 0.386) 0.618 8
H8 MH ML H H (0.573, 0.382, 0.413) 0.593 13
H9 F H ML VH (0.618, 0.315, 0.353) 0.650 6
H10 H H ML VH (0.669, 0.260, 0.306) 0.701 2
H11 H VH F H (0.687, 0.234, 0.283) 0.723 1
H12 F H MH F (0.562, 0.372, 0.405) 0.595 10.5
H13 MH ML VH MH (0.573, 0.380, 0.413) 0.594 12
Table 8. Estimation of MRC and SCW of each criterion for SHRM assessment in manufacturing firms.
Table 8. Estimation of MRC and SCW of each criterion for SHRM assessment in manufacturing firms.
Criteria MRC SCW w j s
H1 H2 H3 H4 H5 H6 H7 H8 H9 H10 H11 H12 H13
H1 0.5 1 1 0 1 0 1 1 1 0 0 1 1 8.5 0.1006
H2 0 0.5 1 0 1 0 1 1 0 0 0 1 1 6.5 0.0769
H3 0 0 0.5 0 0 0 0 1 0 0 0 0.5 1 3 0.0355
H4 1 1 1 0.5 1 0 1 1 1 0 0 1 1 9.5 0.1124
H5 0 0 1 0 0.5 0 0 1 0 0 0 1 1 4.5 0.0533
H6 1 1 1 1 1 0.5 1 1 1 0 0 1 1 10.5 0.1243
H7 0 0 1 0 1 0 0.5 1 0 0 0 1 1 5.5 0.0651
H8 0 0 0 0 0 0 0 0.5 0 0 0 0 0 0.5 0.0059
H9 0 1 1 0 1 0 1 1 0.5 0 0 1 1 7.5 0.0888
H10 1 1 1 1 1 1 1 1 1 0.5 0 1 1 11.5 0.1361
H11 1 1 1 1 1 1 1 1 1 1 0.5 1 1 12.5 0.1479
H12 0 0 0.5 0 0 0 0 1 0 0 0 0.5 1 3 0.0355
H13 0 0 0 0 0 0 0 1 0 0 0 0 0.5 1.5 0.0178
Table 9. Linear normalization matrix for SHRM assessment in manufacturing firms.
Table 9. Linear normalization matrix for SHRM assessment in manufacturing firms.
F1 F2 F3 F4
H1 (0.266, 0.750, 0.718) (0.245, 0.772, 0.744) (0.203, 0.822, 0.785) (0.299, 0.691, 0.691)
H2 (0.318, 0.623, 0.633) (0.446, 0.524, 0.552) (0.396, 0.498, 0.534) (0.330, 0.578, 0.603)
H3 (0.503, 0.431, 0.477) (0.534, 0.393, 0.447) (0.546, 0.434, 0.440) (0.456, 0.491, 0.527)
H4 (0.432, 0.505, 0.540) (0.336, 0.655, 0.650) (0.401, 0.545, 0.576) (0.417, 0.532, 0.561)
H5 (0.700, 0.242, 0.276) (0.579, 0.351, 0.401) (0.558, 0.364, 0.407) (0.564, 0.377, 0.421)
H6 (0.506, 0.423, 0.468) (0.494, 0.449, 0.491) (0.429, 0.530, 0.554) (0.400, 0.567, 0.582)
H7 (0.457, 0.481, 0.516) (0.386, 0.574, 0.597) (0.476, 0.467, 0.509) (0.405, 0.555, 0.578)
H8 (0.204, 0.807, 0.789) (0.211, 0.802, 0.774) (0.222, 0.778, 0.757) (0.231, 0.783, 0.754)
H9 (0.525, 0.407, 0.456) (0.489, 0.444, 0.491) (0.422, 0.528, 0.555) (0.446, 0.519, 0.555)
H10 (0.520, 0.402, 0.455) (0.525, 0.448, 0.460) (0.448, 0.512, 0.535) (0.513, 0.416, 0.461)
H11 (0.245, 0.749, 0.731) (0.243, 0.775, 0.749) (0.257, 0.750, 0.725) (0.231, 0.783, 0.751)
H12 (0.259, 0.743, 0.721) (0.183, 0.844, 0.810) (0.208, 0.813, 0.785) (0.222, 0.790, 0.767)
H13 (0.156, 0.851, 0.832) (0.193, 0.805, 0.786) (0.235, 0.736, 0.714) (0.212, 0.812, 0.777)
Table 10. Vector normalization matrix for SHRM assessment in manufacturing firms.
Table 10. Vector normalization matrix for SHRM assessment in manufacturing firms.
F1 F2 F3 F4
H1 (0.370, 0.650, 0.610) (0.343, 0.679, 0.643) (0.288, 0.746, 0.696) (0.412, 0.576, 0.575)
H2 (0.548, 0.375, 0.388) (0.706, 0.261, 0.292) (0.649, 0.236, 0.272) (0.564, 0.321, 0.350)
H3 (0.768, 0.172, 0.213) (0.798, 0.142, 0.186) (0.809, 0.174, 0.179) (0.721, 0.226, 0.262)
H4 (0.671, 0.261, 0.297) (0.552, 0.435, 0.429) (0.635, 0.304, 0.338) (0.654, 0.289, 0.321)
H5 (0.902, 0.065, 0.083) (0.812, 0.133, 0.172) (0.793, 0.142, 0.176) (0.798, 0.152, 0.188)
H6 (0.765, 0.172, 0.211) (0.753, 0.194, 0.232) (0.683, 0.272, 0.298) (0.649, 0.312, 0.329)
H7 (0.719, 0.219, 0.253) (0.637, 0.316, 0.342) (0.739, 0.206, 0.246) (0.660, 0.295, 0.320)
H8 (0.294, 0.722, 0.697) (0.303, 0.714, 0.676) (0.318, 0.682, 0.655) (0.330, 0.688, 0.650)
H9 (0.783, 0.158, 0.200) (0.748, 0.189, 0.232) (0.675, 0.270, 0.299) (0.703, 0.261, 0.299)
H10 (0.789, 0.145, 0.188) (0.794, 0.182, 0.193) (0.717, 0.241, 0.265) (0.783, 0.156, 0.194)
H11 (0.315, 0.679, 0.656) (0.312, 0.709, 0.678) (0.329, 0.680, 0.650) (0.297, 0.720, 0.681)
H12 (0.366, 0.638, 0.609) (0.264, 0.774, 0.727) (0.298, 0.731, 0.693) (0.317, 0.699, 0.669)
H13 (0.224, 0.786, 0.761) (0.273, 0.725, 0.699) (0.328, 0.634, 0.605) (0.298, 0.734, 0.688)
Table 11. Averaged normalization matrix for SHRM assessment in manufacturing firms.
Table 11. Averaged normalization matrix for SHRM assessment in manufacturing firms.
F1 F2 F3 F4
H1 (0.320, 0.698, 0.662) (0.295, 0.724, 0.691) (0.247, 0.783, 0.739) (0.358, 0.631, 0.630)
H2 (0.445, 0.484, 0.495) (0.597, 0.370, 0.401) (0.540, 0.343, 0.381) (0.460, 0.431, 0.460)
H3 (0.660, 0.272, 0.319) (0.693, 0.236, 0.288) (0.705, 0.275, 0.281) (0.610, 0.333, 0.371)
H4 (0.568, 0.363, 0.401) (0.455, 0.534, 0.528) (0.532, 0.407, 0.442) (0.551, 0.392, 0.424)
H5 (0.829, 0.125, 0.151) (0.719, 0.216, 0.262) (0.697, 0.228, 0.268) (0.703, 0.239, 0.282)
H6 (0.659, 0.270, 0.314) (0.646, 0.295, 0.338) (0.574, 0.380, 0.406) (0.541, 0.420, 0.438)
H7 (0.609, 0.324, 0.361) (0.528, 0.426, 0.452) (0.630, 0.310, 0.354) (0.550, 0.405, 0.430)
H8 (0.250, 0.763, 0.742) (0.259, 0.756, 0.723) (0.272, 0.728, 0.704) (0.282, 0.734, 0.700)
H9 (0.679, 0.253, 0.302) (0.641, 0.289, 0.337) (0.566, 0.377, 0.408) (0.594, 0.368, 0.407)
H10 (0.682, 0.242, 0.292) (0.687, 0.286, 0.298) (0.605, 0.351, 0.376) (0.675, 0.254, 0.299)
H11 (0.281, 0.713, 0.693) (0.279, 0.741, 0.712) (0.294, 0.714, 0.686) (0.265, 0.751, 0.715)
H12 (0.315, 0.688, 0.663) (0.224, 0.808, 0.767) (0.254, 0.771, 0.738) (0.271, 0.743, 0.716)
H13 (0.191, 0.818, 0.796) (0.234, 0.764, 0.741) (0.283, 0.683, 0.657) (0.256, 0.772, 0.731)
Table 12. The weighted averaged NA-SVN-DM for S-HRM assessment in manufacturing firms.
Table 12. The weighted averaged NA-SVN-DM for S-HRM assessment in manufacturing firms.
F1 F2 F3 F4
H1 (0.038, 0.965, 0.959) (0.035, 0.968, 0.964) (0.028, 0.976, 0.970) (0.044, 0.955, 0.955)
H2 (0.051, 0.937, 0.939) (0.078, 0.915, 0.922) (0.067, 0.909, 0.918) (0.053, 0.928, 0.933)
H3 (0.053, 0.936, 0.944) (0.058, 0.930, 0.939) (0.060, 0.937, 0.938) (0.046, 0.946, 0.951)
H4 (0.081, 0.903, 0.912) (0.059, 0.939, 0.938) (0.073, 0.914, 0.921) (0.077, 0.910, 0.918)
H5 (0.115, 0.866, 0.877) (0.084, 0.899, 0.911) (0.080, 0.902, 0.913) (0.081, 0.906, 0.916)
H6 (0.110, 0.867, 0.882) (0.107, 0.876, 0.889) (0.088, 0.900, 0.907) (0.081, 0.910, 0.914)
H7 (0.066, 0.921, 0.928) (0.053, 0.940, 0.944) (0.070, 0.918, 0.927) (0.057, 0.936, 0.940)
H8 (0.005, 0.995, 0.995) (0.005, 0.995, 0.994) (0.006, 0.994, 0.994) (0.006, 0.994, 0.993)
H9 (0.094, 0.887, 0.901) (0.085, 0.898, 0.910) (0.070, 0.919, 0.925) (0.075, 0.917, 0.925)
H10 (0.107, 0.869, 0.886) (0.108, 0.884, 0.887) (0.088, 0.902, 0.908) (0.105, 0.874, 0.888)
H11 (0.029, 0.970, 0.968) (0.029, 0.974, 0.970) (0.030, 0.971, 0.967) (0.027, 0.975, 0.971)
H12 (0.023, 0.977, 0.975) (0.015, 0.987, 0.984) (0.018, 0.984, 0.982) (0.019, 0.982, 0.980)
H13 (0.012, 0.989, 0.988) (0.015, 0.985, 0.984) (0.018, 0.979, 0.977) (0.016, 0.986, 0.983)
Table 13. SVN-Score of weighted NA-SVNDM for SHRM assessment in manufacturing firms.
Table 13. SVN-Score of weighted NA-SVNDM for SHRM assessment in manufacturing firms.
F1 F2 F3 F4
H1 0.038 0.034 0.027 0.045
H2 0.058 0.080 0.080 0.064
H3 0.058 0.063 0.062 0.050
H4 0.088 0.061 0.079 0.083
H5 0.124 0.091 0.088 0.086
H6 0.120 0.114 0.094 0.085
H7 0.072 0.057 0.075 0.060
H8 0.005 0.005 0.006 0.006
H9 0.102 0.093 0.075 0.078
H10 0.117 0.112 0.093 0.115
H11 0.030 0.028 0.031 0.027
H12 0.023 0.015 0.017 0.019
H13 0.012 0.015 0.021 0.016
Li 0.740 0.671 0.646 0.622
Mi 0.108 0.098 0.102 0.113
gi 0.4241 0.3843 0.3742 0.3672
Table 14. The FUDs of manufacturing firms for SHRM assessment over normalization parameter (β).
Table 14. The FUDs of manufacturing firms for SHRM assessment over normalization parameter (β).
β 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
F1 0.5517 0.5266 0.5012 0.4757 0.4500 0.4241 0.3981 0.3719 0.3455 0.3189 0.2922
F2 0.5013 0.4782 0.4550 0.4316 0.4080 0.3843 0.3605 0.3365 0.3124 0.2882 0.2638
F3 0.4879 0.4654 0.4428 0.4200 0.3971 0.3742 0.3510 0.3278 0.3044 0.2809 0.2573
F4 0.478 0.4561 0.4340 0.4119 0.3896 0.3672 0.3446 0.322 0.2992 0.2763 0.2533
Table 15. The UDs of manufacturing firms for SHRM assessment over weighting parameter (ζ).
Table 15. The UDs of manufacturing firms for SHRM assessment over weighting parameter (ζ).
Firms ζ = 0.0 ζ = 0.1 ζ = 0.2 ζ = 0.3 ζ= 0.4 ζ = 0.5 ζ = 0.6 ζ = 0.7 ζ = 0.8 ζ = 0.9 ζ = 1.0
F1 0.4283 0.4276 0.4269 0.4261 0.4251 0.4241 0.4231 0.4219 0.4206 0.4193 0.4179
F2 0.3877 0.3871 0.3866 0.3859 0.3852 0.3843 0.3835 0.3825 0.3815 0.3804 0.3792
F3 0.3718 0.3724 0.3729 0.3734 0.3738 0.3742 0.3744 0.3746 0.3748 0.3749 0.3749
F4 0.3717 0.3710 0.3701 0.3692 0.3682 0.3672 0.366 0.3649 0.3636 0.3623 0.3609
Table 16. The UDs of manufacturing firms for SHRM assessment over AROMAN parameter (λ).
Table 16. The UDs of manufacturing firms for SHRM assessment over AROMAN parameter (λ).
λ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
F1 0.1085 0.1716 0.2347 0.2979 0.3610 0.4241 0.4873 0.5504 0.6136 0.6767 0.7398
F2 0.0980 0.1552 0.2125 0.2698 0.3271 0.3843 0.4416 0.4989 0.5562 0.6134 0.6707
F3 0.1022 0.1566 0.2110 0.2654 0.3198 0.3742 0.4285 0.4829 0.5373 0.5917 0.6461
F4 0.1128 0.1636 0.2145 0.2654 0.3163 0.3672 0.418 0.4689 0.5198 0.5707 0.6216
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated