1. Introduction
It is known that form factors are a substantial entity in all the phenomena that concern radiation. As this powerful and subtle kind of heat transfer does not imply any sort of proximity between the involved elements, sheer form and geometric approach turn paramount for the distribution of energies [
1]. However, the diffusion of radiative fields is heavily dependent on spatial configuration of surface sources [
2]. At the level of unit areas of no defined shape the issue may seem nugatory [
3,
4]; but when we arrive to definite widespread forms like the circle or the triangle it is frequently problematic to extend the well-known differential equations to concrete and finite forms arbitrarily displayed, as we need to manage two sets of different and often complex double integrals [
4]. It is evident that to achieve a manageable solution from quadruple integrands even of the most basic emitters implies a feat of calculus unsuitable for conventional engineering [
5], but it is substantially needed to ascertain the energy balance achieved in the said elements.
Even recent studies have failed to overcome this severe hindrance for the completion of important problems in radiative transfer [
6,
7]. Experts have too long resorted to numerical or statistical approaches like probabilistic methods, [
8] albeit they are inconsequential in most cases, not merely due to the many errors that arise in the lengthy process but also due to the unfeasibility to prove their results as they remained the sole procedure available to attempt to overcome such problem.
In this case the author has followed a special procedure of dummy variables to perform the inner part of the integral, that is, referred to the receiving source in an exact manner. Formerly only rectangles and parallel disks could have been submitted to total integration [
7]. It is paradoxical that the relatively simple form of the triangle could not have been included in the catalogue of solved form factors but we have to admit that some mathematical drawbacks impeded it for an undesirably long lapse of time [
9].
In this manner, the problem can be prepared for the final phase of integration as the dummy variables now take an active value in the third and fourth round of operation that is usually performed by numerical methods [
10]. We have to bear in mind that in the early part, the more feasible equation due only to the so-called configuration factor (an equation that reduces the interchange to just arbitrary points on the emitting surface) is treated and solved. [
8]. A considerable fraction of the difficulty of the problem lies in the three-dimensional nature of the elements under consideration. [
11].
Different approximations so far employed for the problem have shown increasing flaws [
12] as, being an elementary unit in itself the triangle is not apt for division into let us say square or round tiles for example. The accurate finding of such expressions can be considered a postulate in itself that can be added rightfully to the six principles of radiation exchanges that we have developed previously [
13]. Such algebraic expressions can be automatically computed with the software that we have created and a detailed explanation of the procedure segues out.
2. Materials and Methods. General Flux Expression.
As it has been enunciated several times since the last quarter of the 18
th century [
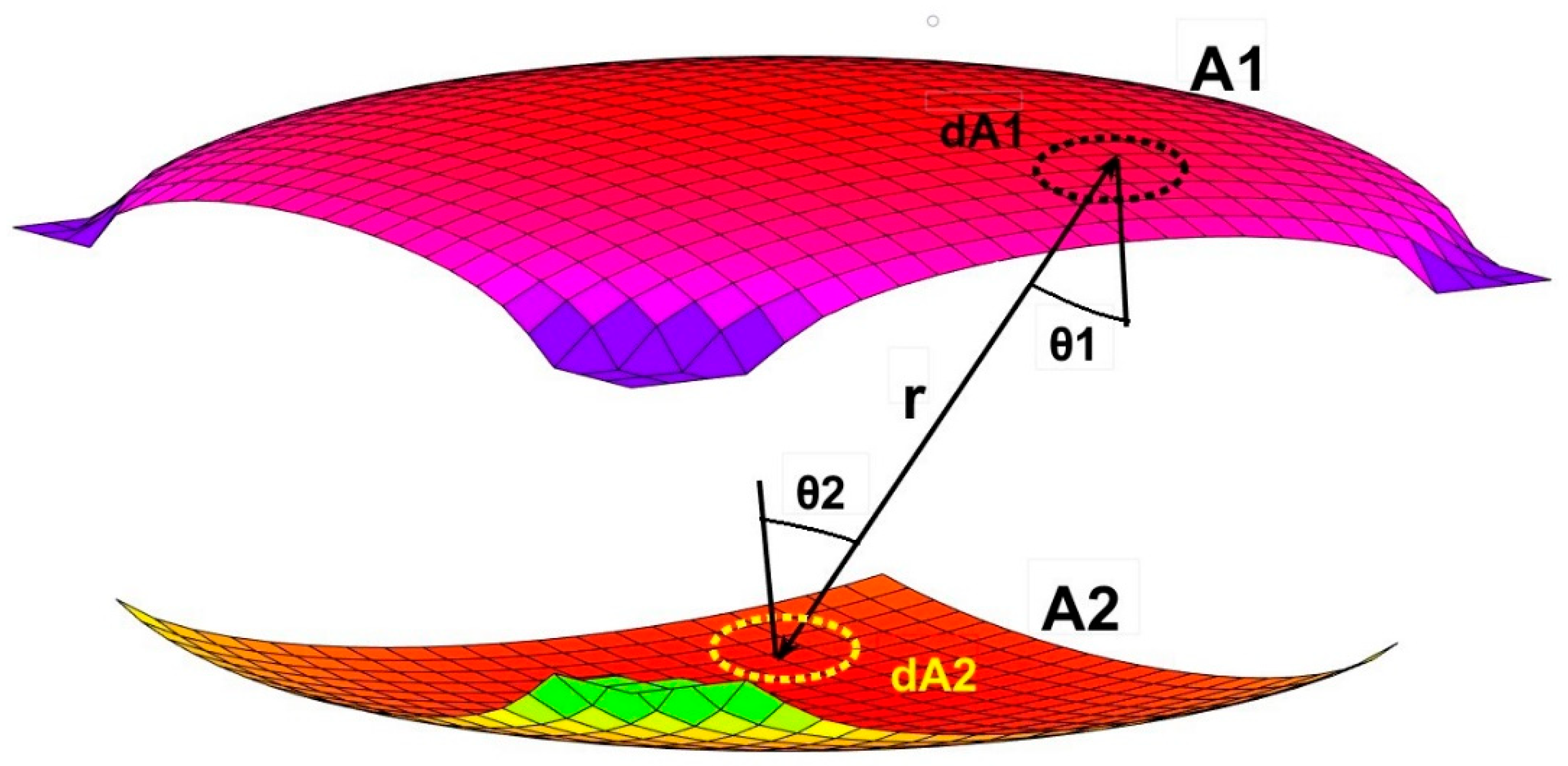
14] the most general expression that defines the probability of an arbitrary interchange of radiated flux for any kind of three-dimensional forms positioned in the manner illustrated in
Figure 1, follows the structure described as follows (Eq.1):
Equation 1 initiates in the reciprocal principle, originally enunciated by J. H. Lambert [15-17] and it yields the probable amount of radiation emitted by unit area that is transferred (W/m
2), from each surface defined as E
1 and E
2. The respective angles θ
1 and θ
2 that appear in the figure represent the deviation from the perpendicular that the vector r
ij encounters in its rectilinear way from a random point in surface 1 to its correspondent in surface 2 [
18].
The solution of Eq. 1, which renders the value of the form factor between the two surfaces, would normally involve four rounds of integration, following Eq. (2) [
15].
However, we have concentrated in this article in the first two stages (Eq. 3), which are also simpler, leaving a sort of harbinger for the next step which is a variable (x
0) that can be considered constant (dummy) in these early phases and will only become active for the third and fourth rounds of integrals.
The latter operation is usually performed by means of deterministic numerical methods through extension of the results to the whole emitting surface. With it, we can obtain the value of the form factor for the two complete surfaces in a more comfortable and accurate manner [
18]. Ensuing, we would use these form factors in various three-dimensional volumes that appear in the most shading devices, some kind of buildings affected by the triangle, like warehouses and gabled-ceiling spaces, and different industrial and aeronautical fixtures [
19,
20].
For other different positions of the surface sources, an exact solution has not been achieved yet [
5]. Neither for irregular fragments of triangles, rectangles and circles or even for the familiar form of the sphere [
20,
21].
Intermediate steps to proceed only with the first and the second round of integration have been proposed [
22]. They usually end at a particular point or elementary area that belongs to the receiving surface. Some of them are recorded under the inexact and cumbersome manner of copied nomograms at catalogues of radiation view factors [
23,
24]. Such results are somewhat indicative but they are by no means general and can be misleading in many situations.
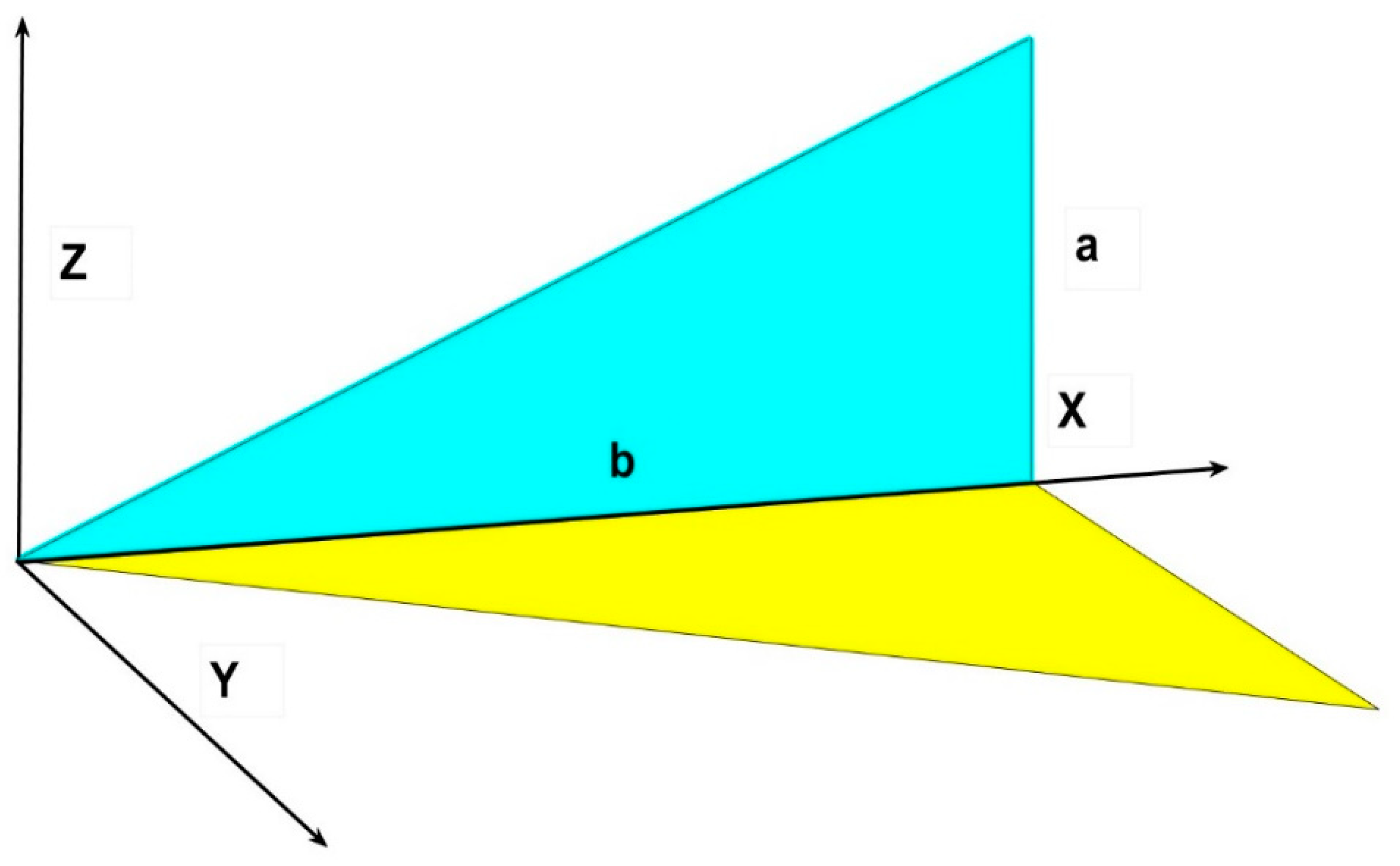
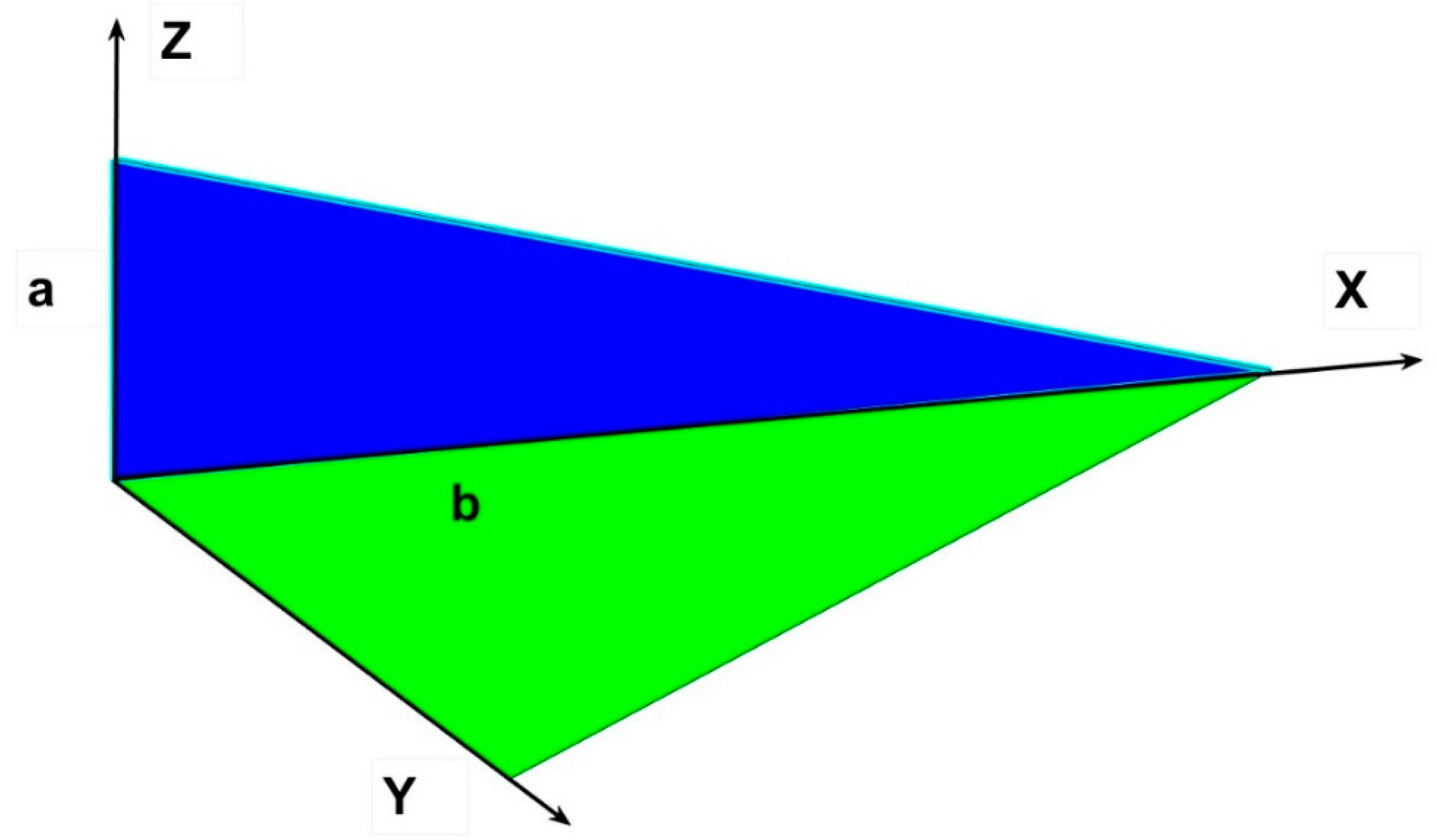
In order to proceed with the said method, we shall start with a general right triangle of sides a (vertical) and b (horizontal) located at the origin of coordinates (
Figure 2).
Under this disposition, the coordinate Z axis is vertical and X is horizontal and perpendicular, the sides of the triangle are, in Z equal to a, and in X to b as seen in
Figure 2
The tangent of the angle formed from the upper edge of the triangle to the horizontal equates tanα=a/b, therefore, the equation of the superior line of the triangle is,
The axis Y in the graph represents the free coordinate perpendicular to X.
Introducing the “dummy” variable x
0 , the squared distance (Eq.5) from one receiving point-source of the triangle to another emitting point moving freely over the plane XY, presented as r
12 in Eq. 2 above, would be:
The respective cosines β and γ, to the normal from Eqs. 1 to 3, would be accordingly y/r12 and z/r12
The integral to solve deriving from Eq.3, would then turn to (Eq. 6):
We need to solve the root equation for a generality of types of triangles in diverse positions [
25]. To avoid special difficulties we will provide the solution at the intermediate stage of configuration, that is the double integral firstly, obtained point by point over a rectangular emitting field. Once we have achieved this, to advance towards the complete form factor of Eq. 2, we need to apply another property previously enuntiated by the autor [
26]; namely the form factor is the average over the emitting surface of the configuration factor previously obtained on point basis. It is now feasible by numerical calculus alone to extract such mean value for any kind of planar figures contained in the said field. With a similar approach, the total form factors are found for the usual sets of precints, such as prisms or oblique cuboids. Inter-reflection within the so-generated space is also an issue that we have to foresee, in the case of triangular prisms we would require a set of five equations with five unknowns which is detailed at the appendix [
27].
For example, when designing and solving inclined slats, the triangles that appear are not right, but usually they come as obtuse or acute, in these situation we cannot employ the already solved form factor for perpendicular rectangles, instead we need to resort to the extended formulas developed by the author [
28] to take into account the exchanges between inclined rectangles.
3. Results. Solutions for various forms of triangles and trapezes
3.1. Right Triangle with minor vertex at the origin of coordinates
Consequently, let us advance towards the solution set above for the more representative triangles and rhomboids, beginning with the case depicted in
Figure 3,
In Eq. 6 we mentioned the integral to be solved as,
In this case, the primitive is the quotient of the denominator and integration with respect to z gives,
And regrouping, the result is
Now, we only need to integrate with respect to x,
The first part presents not much difficulty to identify,
The second part is slightly lengthier in calculation,
Arranging the two parts and multiplying by
y/2 which was outside of the integral in Eq. 8, we obtain:
Finally, we need to divide everything by π to keep the factor dimensionless in terms of radiant power,
If x
0=0, which means that we are calculating at the vertex point of the triangle,
Which was obtained previously by the author for the triangle at its minor vertex [
5],
If x
0=b, the end of the base, then,
This was the formula previously obtained for the horizontal extreme corresponding to the right angle, which coincides exactly with the former, (Eq. 17).
Finally, if we make x
0=x, igniting the dummy variable, the above expression compares well with the one used for the rectangle of vertical side
a and horizontal side
b when the study point moves freely on the horizontal plane (Eq. 18) [
7].
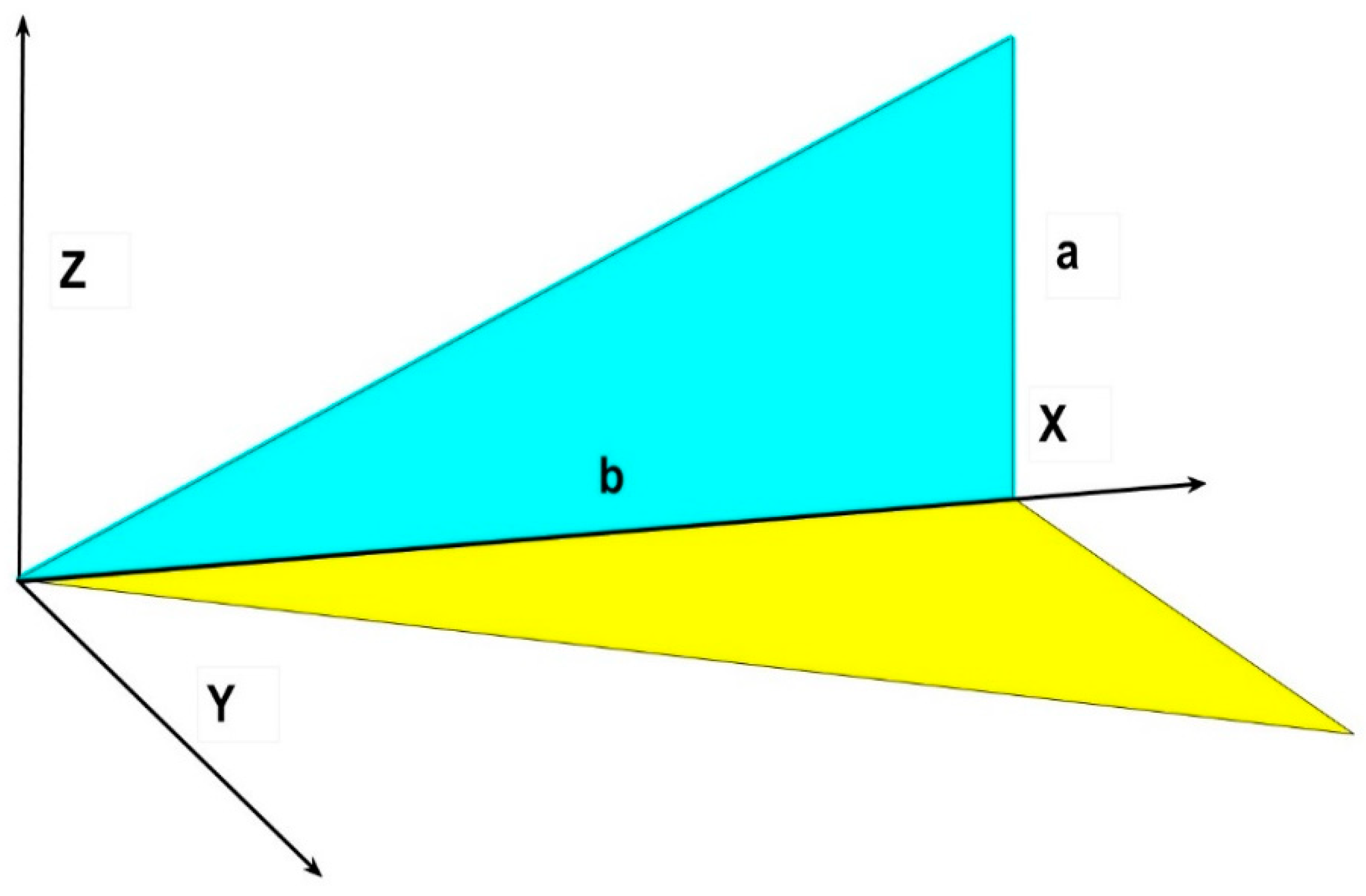
Let us now calculate, for the sake of generality, the same triangle in a more general position outside the origin of coordinates, see
Figure 4,
In this case, integration limits in z, would change between,
And regrouping, the partial result is
Which conveniently developed gives,
The first term of the integral is already solved in Eq. 10,
For the second part we need to integrate,
Developing all the terms in the denominator, we receive,
And grouping in terms of x,
The final integral to be solved is,
Arranging all the necessary terms and multiplying by y/2 we obtain,
By making m=0 we would find that,
Which is exactly the same as previously found in Eq.(13), which we now define as Cabeza-Lainez, seventh postulate, that is,
3.2. Right Triangle with minor vertex removed from the origin of coordinates
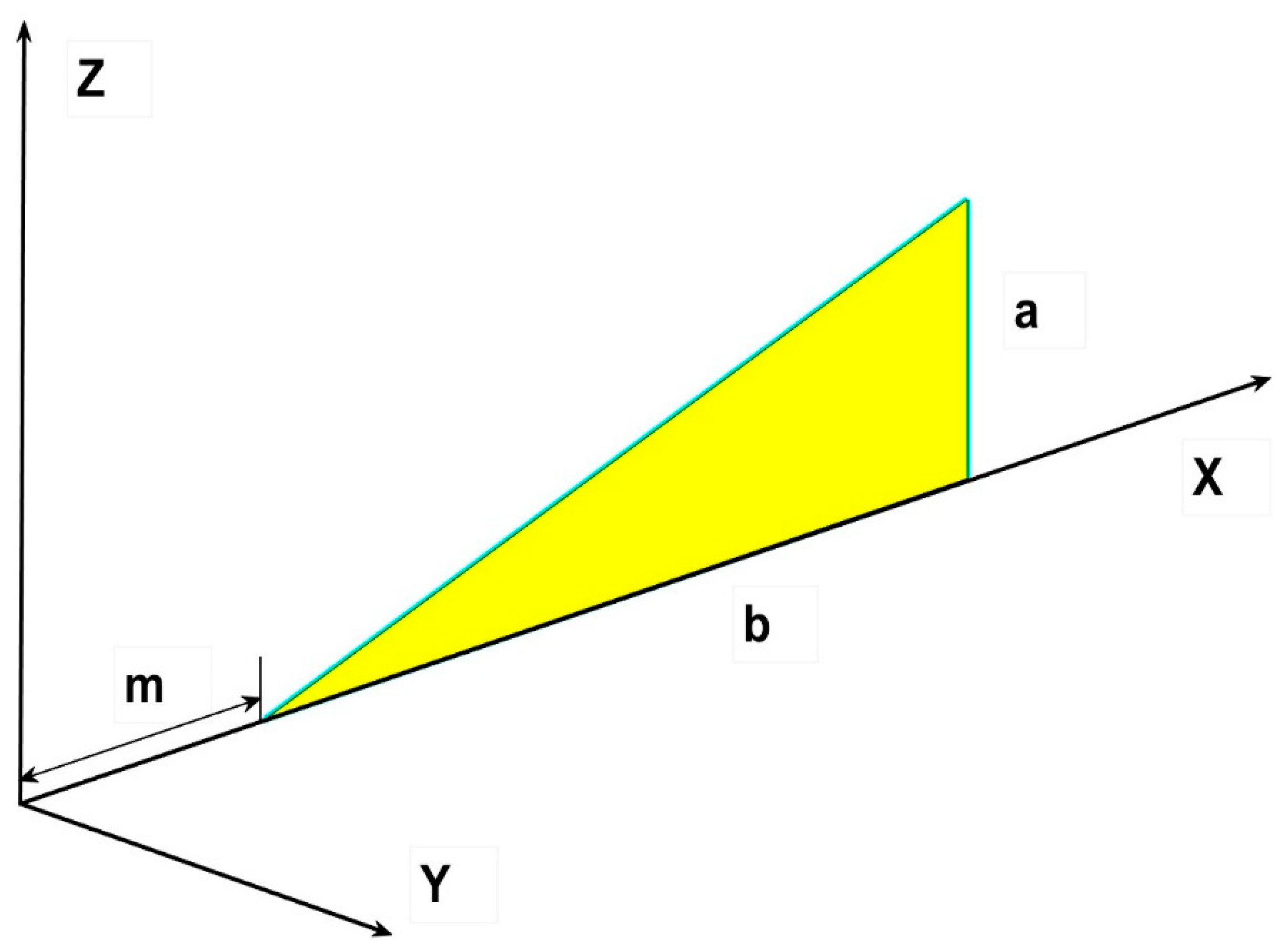
To continue with the former mathematical reasoning, we could apply the same kind of integration procedure to the triangle in the reverse position, referring to the X-axis (
Figure 5).
In this case, integration limits in z, would change to ,
And regrouping, the result of the first part amounts to,
The expression expanded gives,
The first term of the integral is already solved, as we know with,
For the second part we need to integrate,
Developing all the terms in the denominator, we find,
And grouping now in terms of x,
The final integral to be found would be,
Arranging all the necessary terms and multiplying by y/2 we finally reach,
Dividing by π the sought-for Factor, called the eight postulate of Cabeza-Lainez is,
In this new case, by making x
0 equal to zero we arrive to the more familiar formula below (Eq.16) attributed to the right triangle following
Figure 6
Which was obtained previously for the triangle at the minor vertex (Eq.15),
3.3. Trapeze at the origin of coordinates that includes the triangle in the upper part
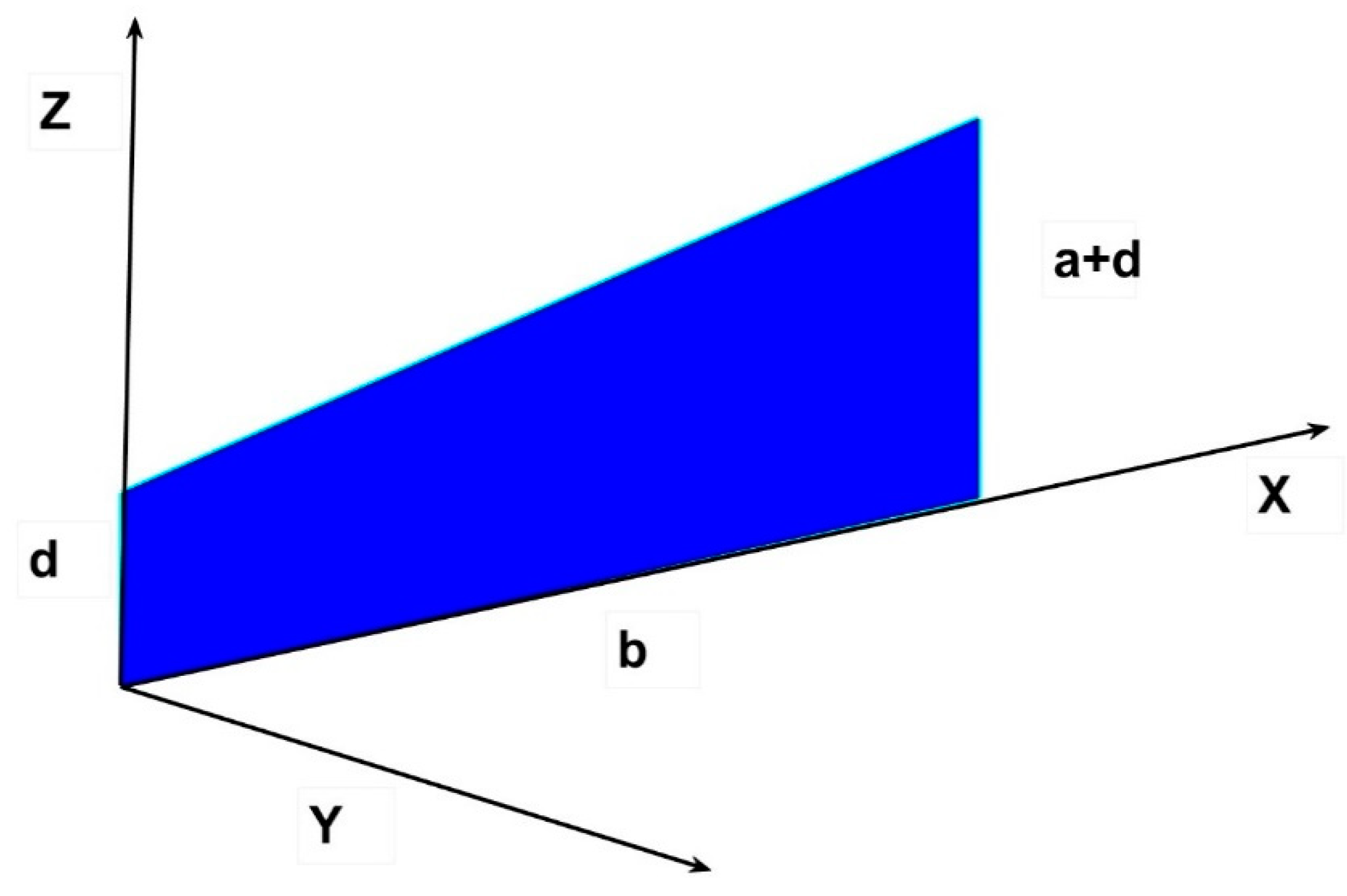
Following the relatively simple examples of common triangles, we could try now to integrate a kind of trapeze topped by the triangle, which is representative of many rooms with sloped ceilings at the lateral wall. From the mathematical point of view, it would be just a matter of changing the integration limits in z, taking the value of rectangular part of the trapeze as d (
Figure 7).
The limits of integration will be kept accordingly between,
The previous integral will be,
And the expression for the new binomial equals to,
And regrouping, the first part result is,
The final equation for these operations gives,
Th first term of the ensuing integral is as before,
For the second part we need of more integration in the same fashion,
Which seems correct because if d were zero, the trapeze turns into a triangle and we come back to the previous formula or the seventh postulate, Eq. (13). This new equation is called the ninth postulate of Cabeza-Lainez [
30].
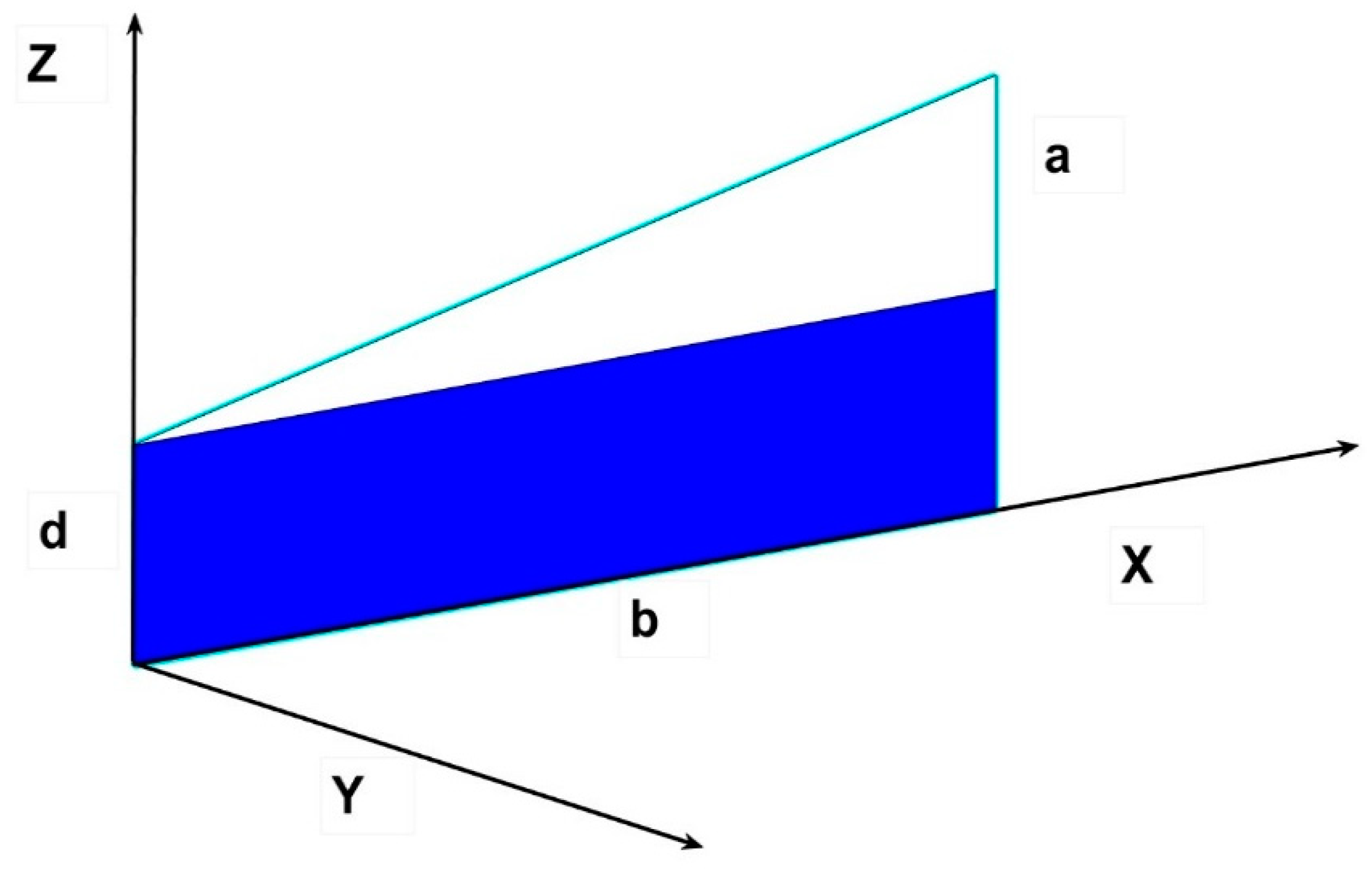
To calculate only the influence of the upper triangle (
Figure 8), which is especially interesting for windows in the lateral wall of a sloped ceiling room, the lower limit of integration in the first integral would be d instead of 0 and the result in that case, by the same procedures employed in the above chapters, is,
This innovative result will be the tenth postulate of Cabeza-Lainez. Once again if d were equal to zero and we were left with the triangle alone we would arrive to the previous formula in Eq.13.
It is interesting to notice that by virtue of deft additions or subtractions maintaning the same axis we can compose different sets of triangles as seen in
Figure 9, for a non-right triangle. It means that we can calculate the daylingting effects of many triangular windows as the ones presented in
Figure 10.
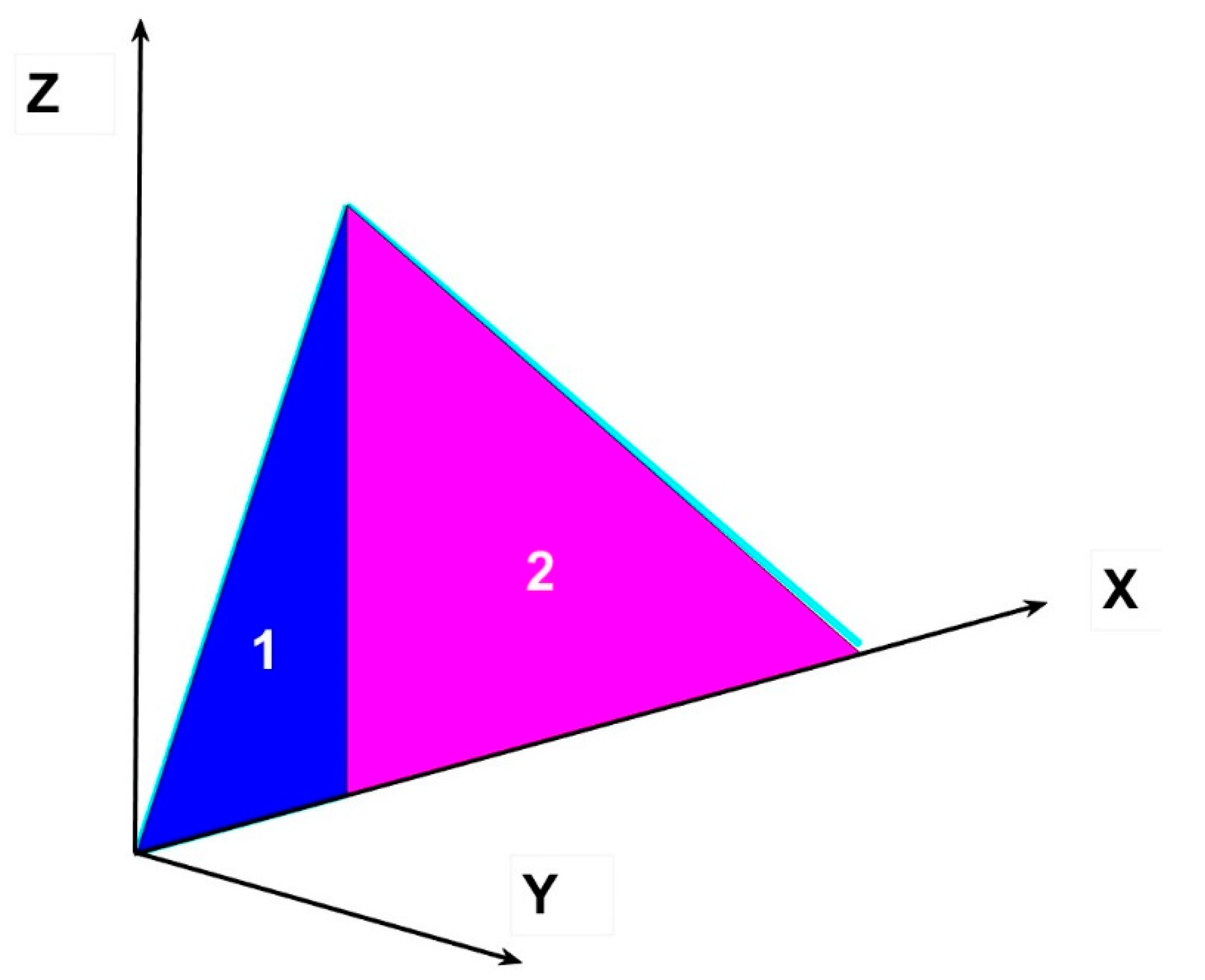
In turn, an obtuse triangle marked as 2 (
Figure 11), can be formed by subtraction of right triangle 1 from a larger right triangle.
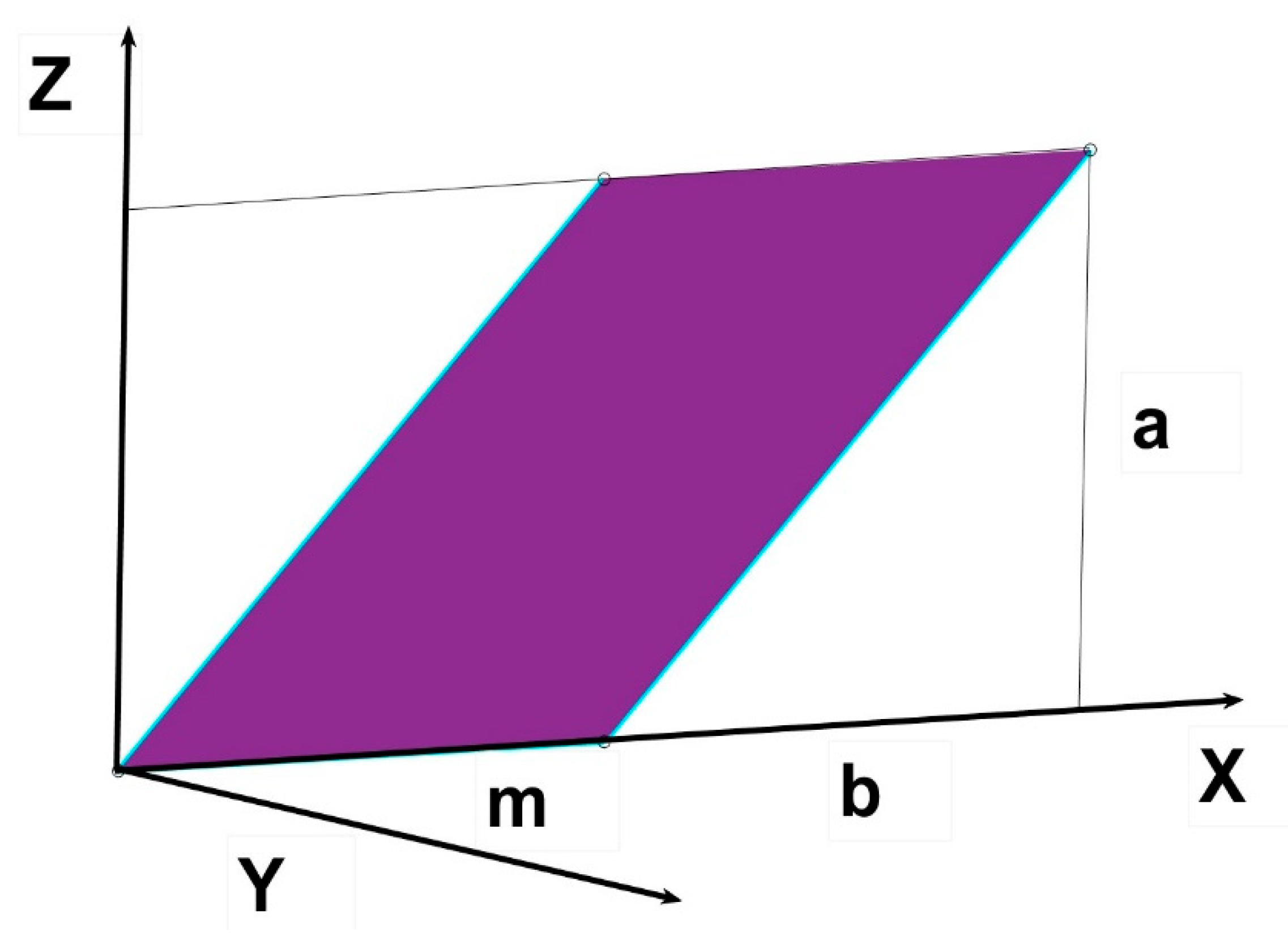
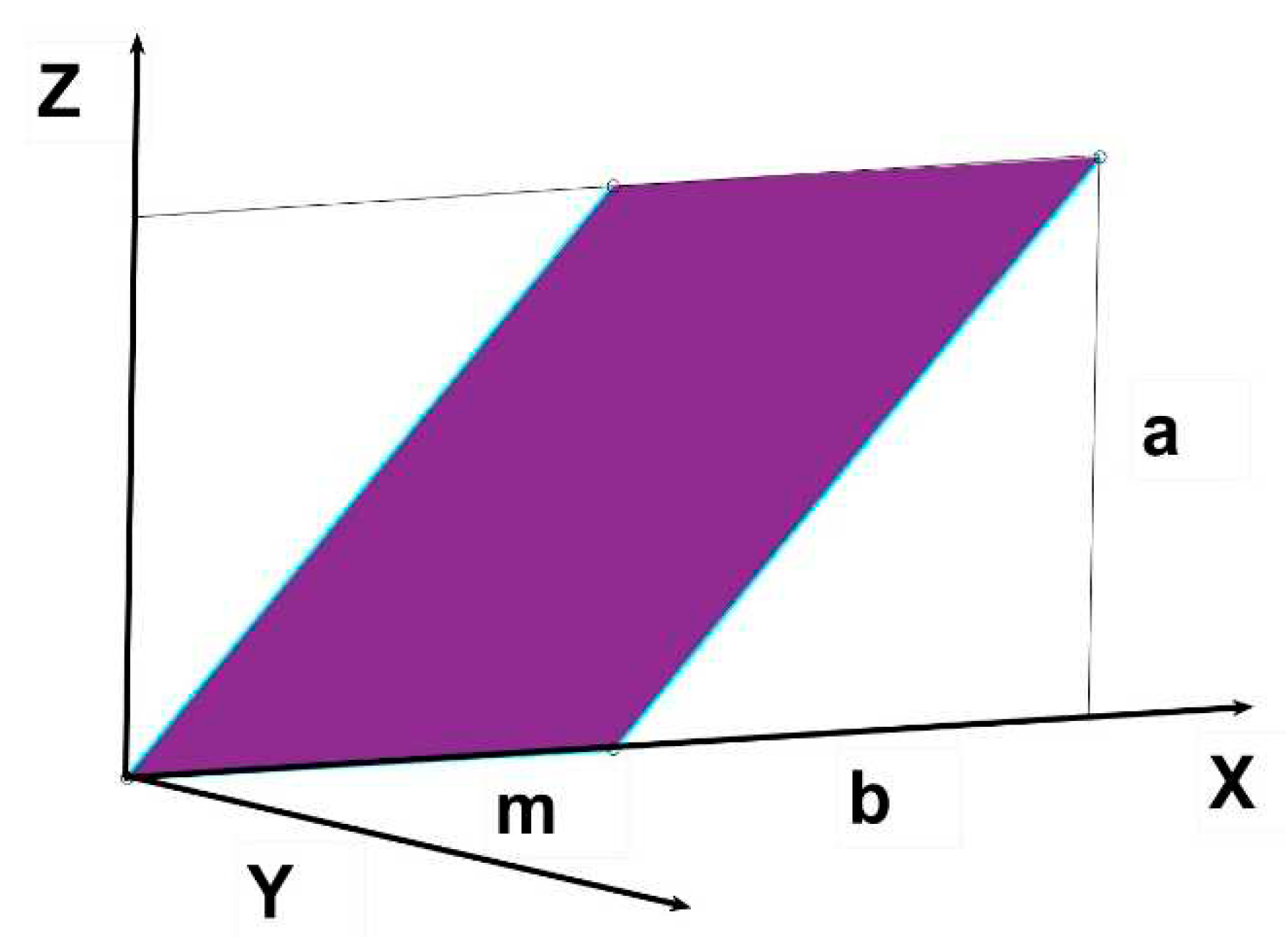
It is possible by combining rectangles and triangles to sculpt “diverse” polygons regular or irregular which would be the basis for the calculation of polygonal prisms. An important case for this article would be the rhomboid depicted in
Figure 12.
In this case its is clear that subtracting from a rectangle of base m+b and heigh a, the displaced triangle ab and the flipped triangle ma at the origin of coordinates we would find the configuration factor of the rhomboid over the horizontal plane.
The flipped triangle will come from the solution of the former integral,
Applying the same results obtained previoulsy we will find that,
Which gives the eleventh postulate of Cabeza-Lainez.
If now we subtract the latter expression to the general factor of the rectangle, which was given by Eq. 56 ( formerly 18), and also the one of the displaced triangle, Eq. 57,
Eq. 56 minus Eqs. 55 and 57 offer the result for the rhomboid,
The final result which becomes the twelfth postulate would be (Eq. 59),
These algorithms might seem complicated by they are easily programmed for simulation once the process is duly automated [
31].
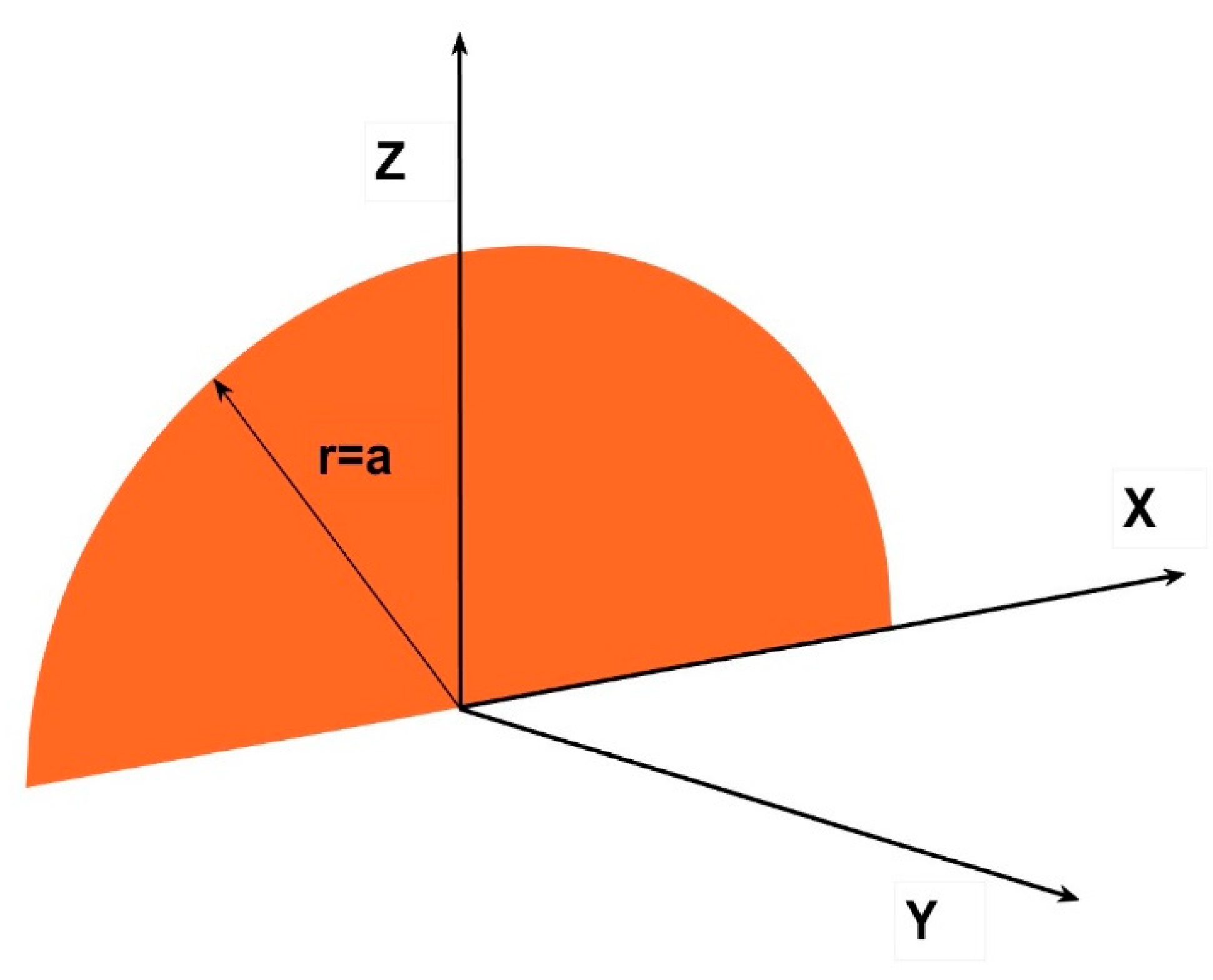
3.4. Vertical semicircle at the origin of coordinates
Although it is not related with the triangle and due to its singularity it has been the subject of study of other articles by the author [
32], it is interesting to remark that applying the same rationale of integration we could find the configuration factors for several curves and among them the circumference (
Figure 13).
In this case for the quarter of circle, in
Figure 13 the limits of integration for z would have been accordingly,
and 0,
And the first integral would have produced:
Since the second term in x is linear, the integration to perform is easier than before.
In fact the result of the integral would be,
Grouping all results again as the latter integral bears the minus sign in the preceding expression, we arrive to:
But as a=b, and represents the radius r of the quarter of circle,
Which coincides exactly with the factor found by other means by the author for the quarter of circle, (angle = π /2), [
32,
33]. There it was named Cabeza-Lainez eigth postulate, but now it must be renumbered in accordance as the thirteenth postulate. We must bear in mind that a=b=r and as previously x
0=x,
It is obvious that for the whole semicircle (angle= π), with the limits of the integral from b to –b instead of 0 we would receive, (fourteenth postulate),
For the quarter of circle (angle = π /2), as we had in Eq. 63, the same form factor is
If the semicircle were now displaced from the origin of coordinates we could just have the integral of the logarithm in the second term.
The first integral was solved previously with limits d+r and d-r respectively as,
The result of the second integral for the same limits is,
And the latter developed gives,
The total result would be,
The latter expression becomes the fifteenth postulate of Cabeza-Lainez.
A wide set of curves like ellipses and parabolas could be resolved with the same procedure.
For instance in the case of the semiellipse we only need to change the upper integral limif for ,
In such situation the first integral would have given,
Eq. 75 becomes the sixteenth postulate of Cabeza Lainez. That the former expression is greater than zero, seems likely once that in an ellipse a>b as the major semi-axis is larger than the minor one, but this must be checked against the x and y dimensions of the horizontal plane beforehand. For example in an elipse of major semiaxis = 4m. and minor=1m. for an x,y grid of 10 by 10 meters all values of Δ are positive and the result of Eq. 75 is valid.
This is a crucial development since many researchers have been so far unable to give a consistent expression for the form factor of elliptical shapes [
33].
4. Discussion. Finding of the global form factor
As previously explained we need to find the average over the chosen emitting surface (normally rectangular) of the previously found configuration factors for the triangles and other shapes identified in section 3.
4.1. Determination procedures
It has been proved by the author [
34,
35] that the form factor amounts to the average over the domain of the emitting surface of the configuration factor previously obtained on a point to point basis, as it precisely represents the integral extendend to this second area. It is affordable by any numerical automated procedure to obtain the mean value of all the point factors for any sort of figure contained in the said transferring field.
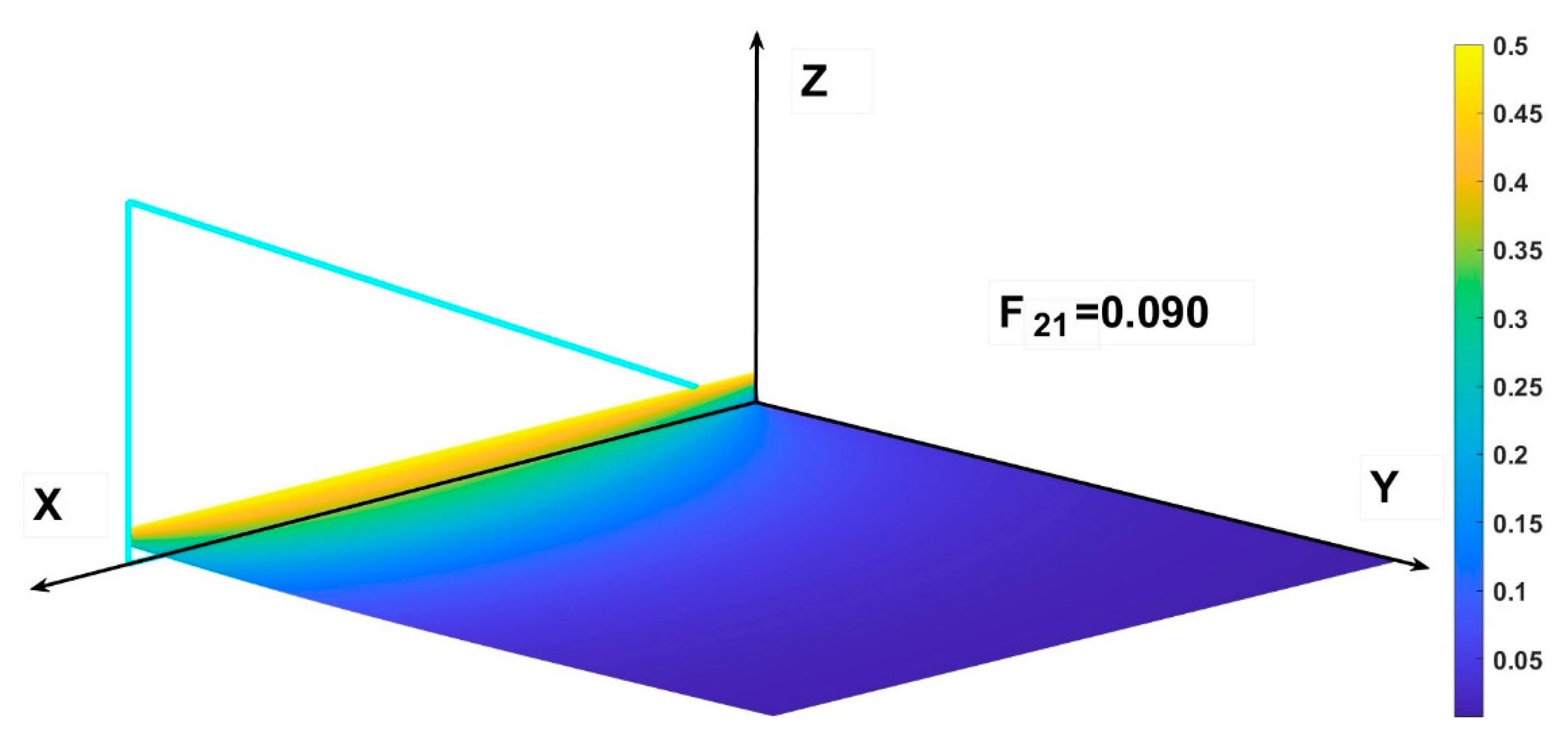
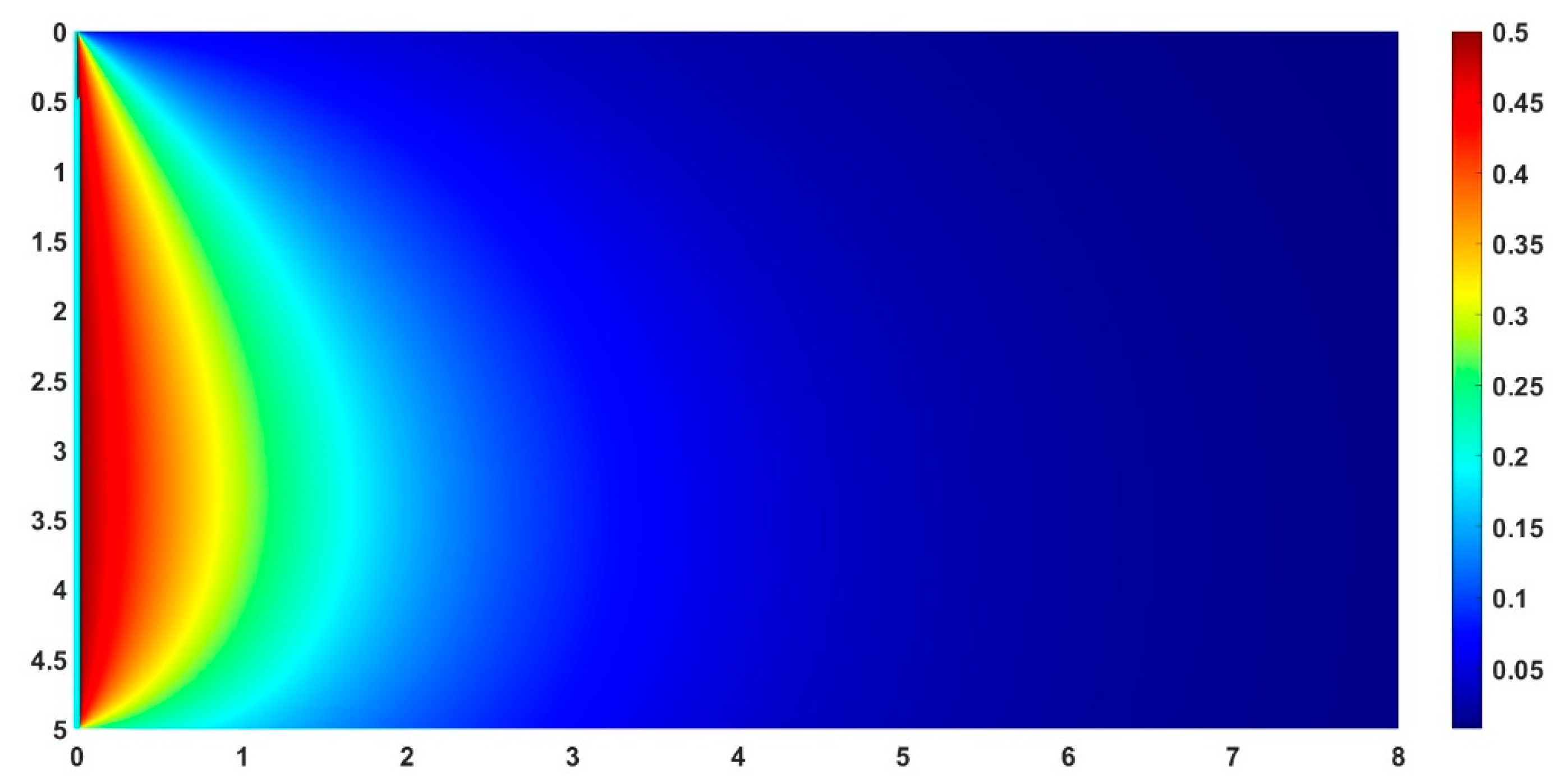
For instance in nephograph of
Figure 14 with the results of Eq. 13 by virtue of the seventh postulate, we have automatically calculated the form factor F
21 from a rectangle of 8m. by 5m. to a triangle of 5m. height by 5m. width, it amounts to 0.090.
In
Figure 15 we can see the radiative field in plan due to the triangle over the rectangle, the curves of received radiation are more pronounced in the left lower part of the nephograph due to to the higher altitude of the triangle in that area as it nears its upper vertex.
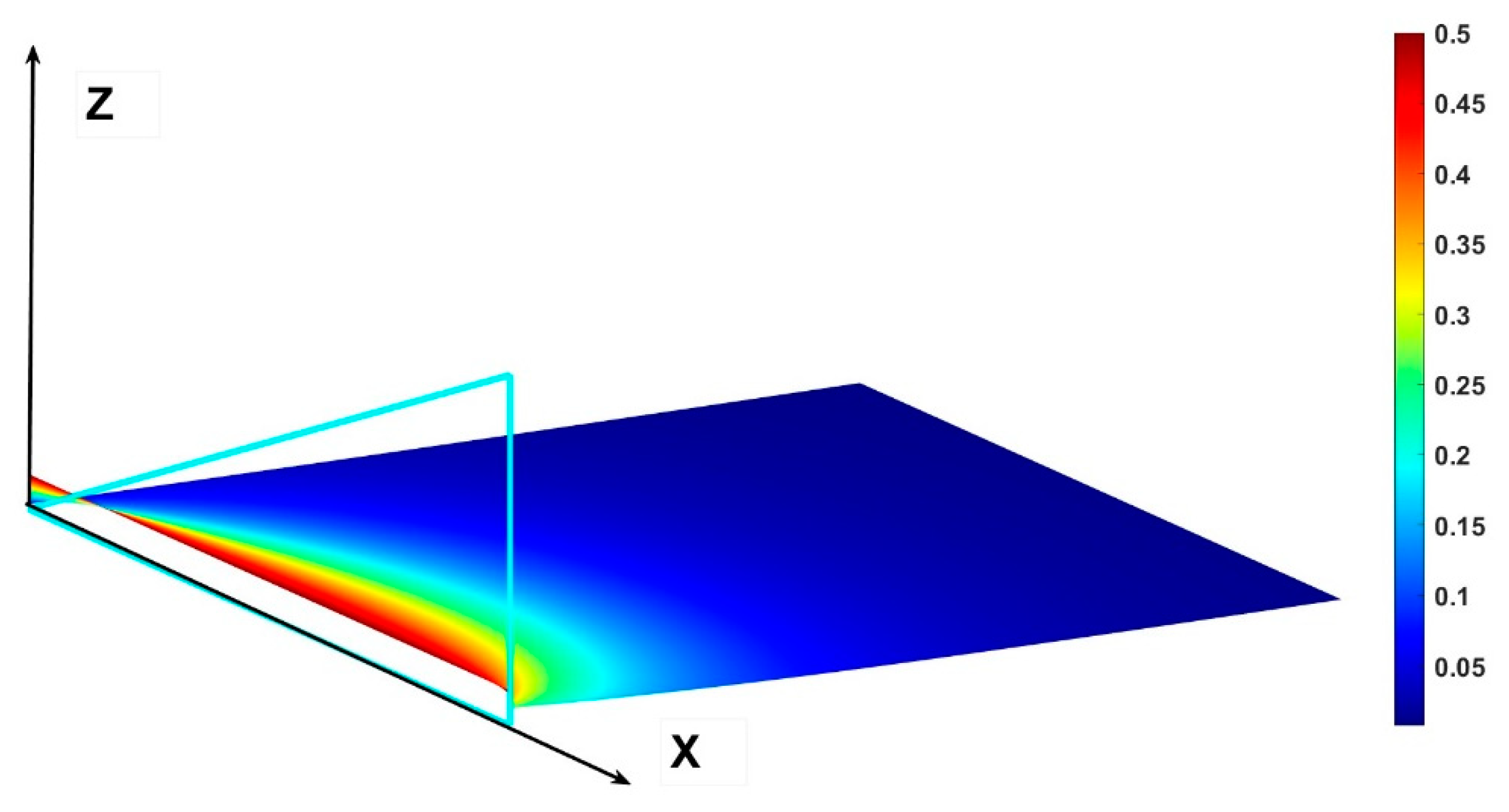
In
Figure 16 we have represented the same field in a three-dimensional view to understand better how the exchanges are manifest for example in luminous emissions such as windows or LED devices.
With a similar approach, the total form factors can be found for the usual sets of precints, such as prisms or oblique cuboids. Inter-reflection within the so-generated volumes is also an issue that we have to foresee, in the case of triangular prisms we would require a set of five equations with five unknowns which is detailed at the appendix [
36].
For example, when designing and solving inclined slats, the triangles that appear are not right, but usually they come as obtuse or acute angles, in these situation we cannot employ the already solved form factor for perpendicular rectangles [
5], instead we need to resort to different extended formulas developed by the author [
37] to take into account the exchanges between inclined rectangles.
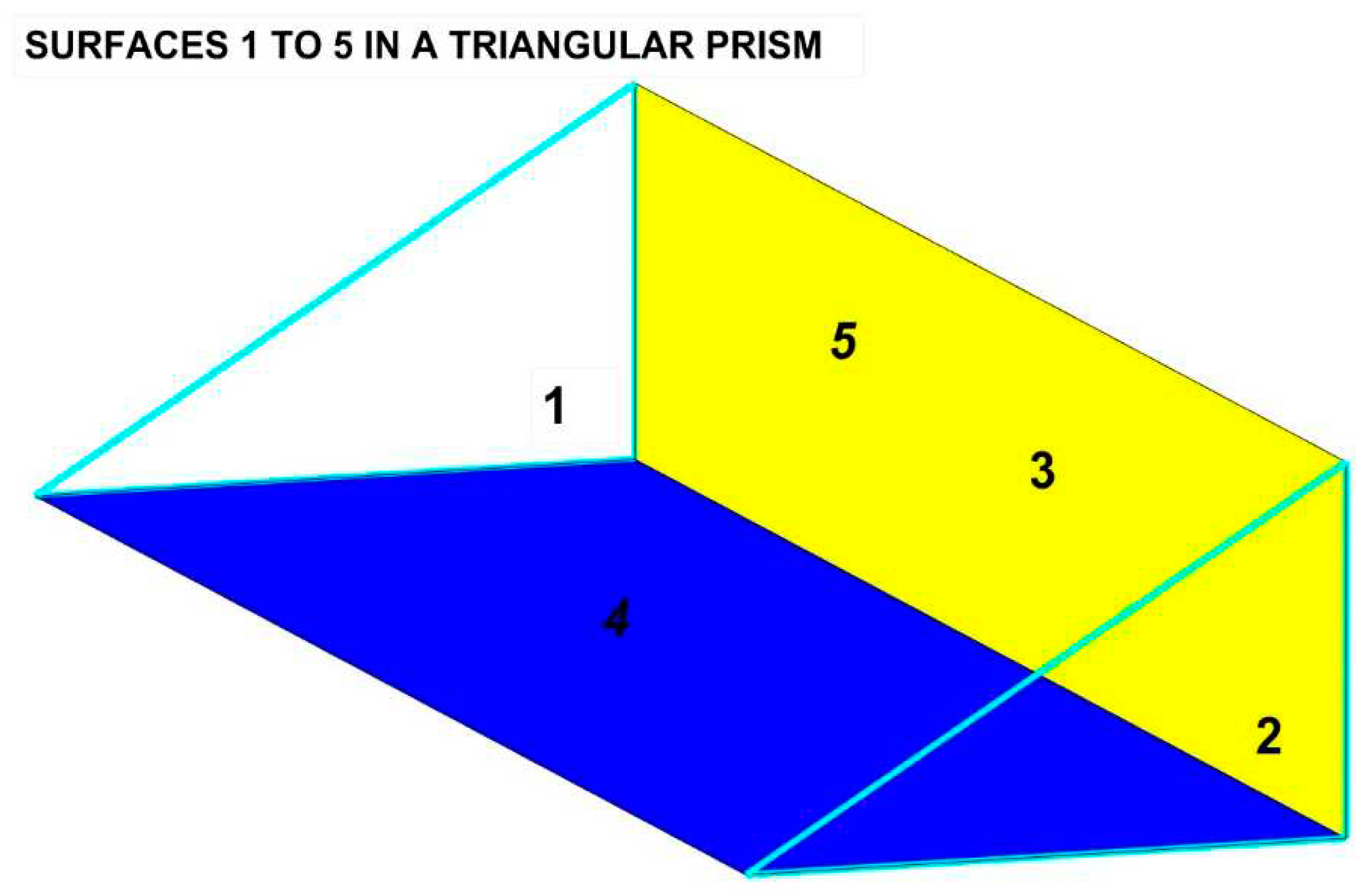
Let us proceed to explain how the twenty form factors Fij with i and j from 1 to 5 but excluding the dummy sub-indexes like F11, F12, as all surfaces are planar.
With the first direct integration using Eq. 13 and detailed in
Figure 14,
Figure 15 and
Figure 16, we obtain the exchange between the horizontal surface (4) and the side triangles (surfaces 1 and 2 in
Figure 17), by symmetry,
But by reciprocity (Eq.1)
F
43 and F
34 are known since we have deducted the expression for perpendicular rectangles with a common edge [
38].
The form factor algebra demonstrated elsewhere [
1,
5,
34,
35] states that,
Once we know F
54, we can write,
F
51 is unknown, but similarly to Eq. 76, rotating the triangles to the vertical side of the prism (Surf. 3) we would find,
And also we can deduct F
13 and F
23 as,
F
34 is already known as it was the perpendicular rectangle factor,
Knowing F
53 implies that,
With which, once we have F
51 = F
52 the problem is completely solved and the matrix of four by five elements is known, for,
Knowing for example F12 = F21 carries implicit the solution of a long unresolved problem, namely the rate of exchange between two parallel triangles which also opens the way for a wide set of forms that we are not in the position to detail in this article.
4.2. The case of inclined rectangles
With the former, we could consider now that all kind of polygonal prisms are completely solved. However, this is not the case since there are still some configurations in which the triangle is not right but obtuse or acute. Then the form factors for penpendicular or parallel rectangles cannot be applied. Therefore we have to employ other formulas apt for inclined rectangles, also developed by the author.
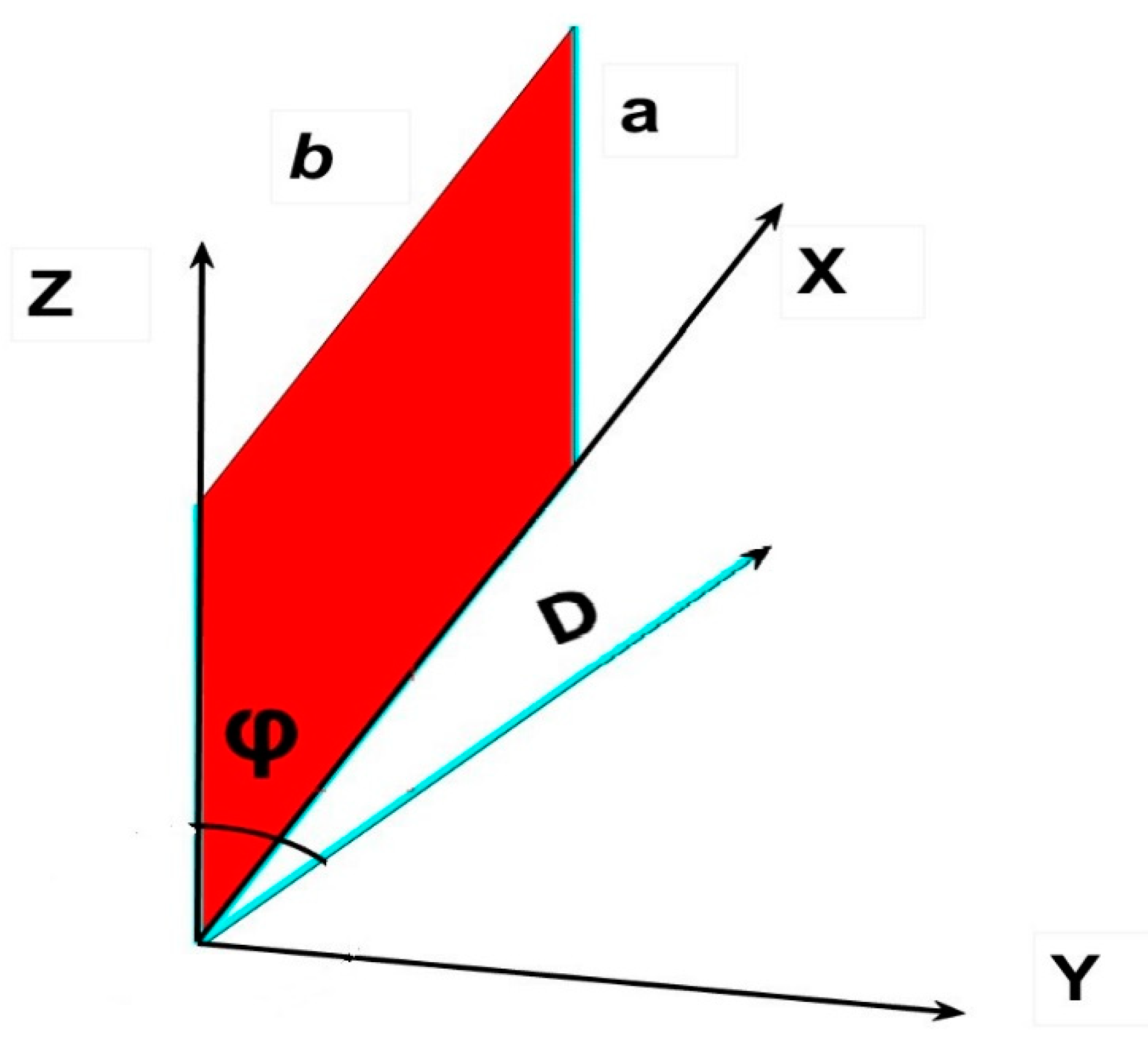
In order to tackle such a complex issue, let us consider a rectangle positioned in the form described in
Figure 18. As we already know, the general formula to apply for a particular point at an inclined distance D is:
This represents a logical evolution from the previously described formulas [
39]
The configuration factor
f, on the given point with angle φ is the sum of two integrals.
After considerable operations and adding all necessary terms we conclude that the equation governing the whole process is the following.
For a general position of the point on the XY plane we find,
In order this will be the seventeenth postulate of Cabeza-Lainez.
Thanks to this new property it is feasible to calculate the interchanges in the rhomboidal prism whose end section is presented in
Figure 19 and
Figure 20. Many other polygonal prisms can be solved in the same manner. We have to notice that beforehand, the parallel faces of the prism could be found using combinations of the equations for parallel rectangles but there was no exact way to find the exchanges between the inclined rectangles, only rough approximations or blurred tables [
40]. A singular advance has been produced in this fashion.
4.3. Examples and applications for shading devices
A great deal of shading devices, present this rhomboid configuration and their radiative performance could not be assessed in an accurate manner. In
Figure 21 and
Figure 22 we can find details of the brise-soleil for the Sri Aurobindo Ashram designed and built by the architect Antonin Raymond in Pondicherry in 1937 [
41].
Another famous shading device in architectural terms is the one employed around the same time in 1938 by architects Oscar Niemeyer and Lucio Costa in Rio de Janeiro (
Figure 23 and
Figure 24).
In this case the inclination degree is fixed by a lever gear, therefore it is more critical to determine the performance of the inclined blinds but so far the attempts to objectively assess the efficacy of the system have not been consequential in terms of for example finding which is the best angle for seasonal evolution of the sun-path.
The problem is also that such shading devices became popular as a cliché for architectural imagery and where imitated throughout the globe but lacking the tool that we now provide to attest to their validity. This produced more damage than good in the energy behavior of the buildings and especially in tropical developing countries where the brise-soleil turned from an audacious novelty into a sort of stifling petticoat [
42].
5. Conclusion
In this article we have identified at least nine innovative and significant postulates that resolve many of the issues of radiative heat transfer that arise in the interior of spaces when the triangular geometry is involved in the radiators. Strictly, it is not needed that the surfaces that produce the interchanges are pure triangles, they can be combinations of rectangles and triangles or polygons either regular or irregular. Some determinations for circles, ellipses and other curves have been described as well. The results of a first stage integration by a new procedure of mute variables subsequently activated in the later stages is deft for finding with perfect ease the desired form factor without resorting to quadruple integrals that are rather cumbersome and occasionally untreatable.
Triangular surfaces and their derivatives have been systematically used in all kind of building and industrial features since the beginning of mankind. Nonetheless, a systematic logic to address them in the heat transfer domain had not been possible as a consequence of the mathematical difficulties that we have now skipped with adroit manipulation. Statistical simulation methods were not of much avail in this situation since they cannot deal accurately with the singularity of triangular shapes. The expressions granted are particularly useful for the design of openings for daylighting in clerestories, lanterns and skylights but foremost in the design and construction of shading devices which have become an ever-present feature of buildings in warm climates but without real substance as of their efficacy and advantages. With this manuscript, we hope to have elucidated the greatest part of the issues in a definite manner. The paramount innovation that these postulates imply, reside in the circumstance that they have also been introduced into simulation algorithms apt for automated simulation. We are persuaded that they possess immediate applicability and in this fashion they will revolve the many activities and situations involving radiative transfer is in the field of lighting industries, aircraft manufacturing and building solutions. In this manner, pivotal themes of radiative heat transfer can be treated in an appropriate and positive manner to enhance sustainability. We expect that transcendental derivations should follow from this in due course of time.
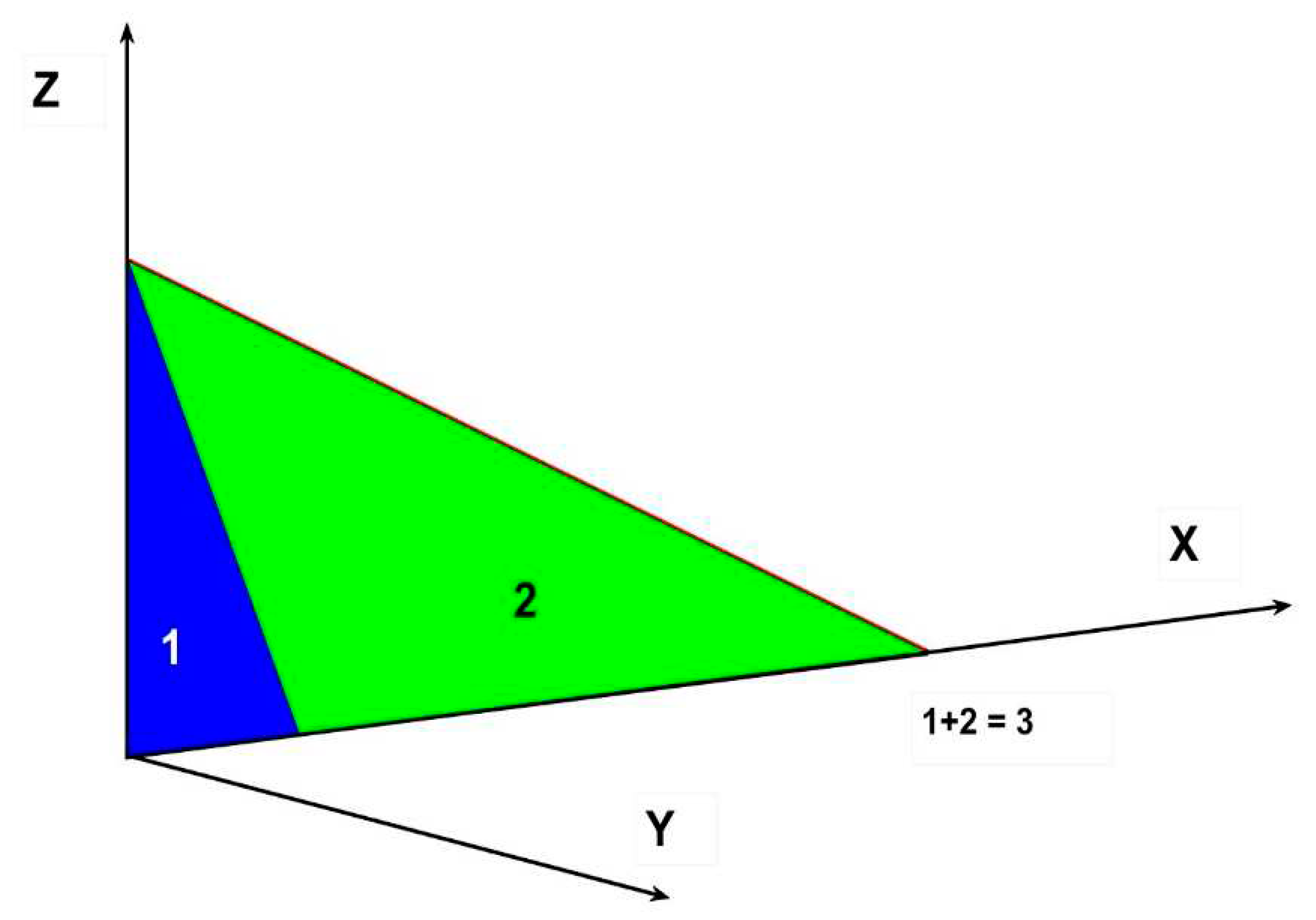
Figure 1.
Radiant interchanges for a couple of undefined surfaces, named A1 and A2.
Figure 1.
Radiant interchanges for a couple of undefined surfaces, named A1 and A2.
Figure 2.
Coordinates for the right triangle form factor determination over a horizontal plane.
Figure 2.
Coordinates for the right triangle form factor determination over a horizontal plane.
Figure 3.
Coordinates for the triangle form factor over a horizontal plane.
Figure 3.
Coordinates for the triangle form factor over a horizontal plane.
Figure 4.
Coordinates for the triangle form factor over a horizontal plane.
Figure 4.
Coordinates for the triangle form factor over a horizontal plane.
Figure 5.
The triangle in a reversed position with the rectangular angle at the origin of coordinates.
Figure 5.
The triangle in a reversed position with the rectangular angle at the origin of coordinates.
Figure 6.
Configuration factor between a right triangle and a point over the normal to the vertex at a perpendicular plane.
Figure 6.
Configuration factor between a right triangle and a point over the normal to the vertex at a perpendicular plane.
Figure 7.
Coordinates for the trapeze’s form factor over a horizontal plane.
Figure 7.
Coordinates for the trapeze’s form factor over a horizontal plane.
Figure 8.
Coordinates and dimensions for the triangular extension over a rectangle form factor over a horizontal plane.
Figure 8.
Coordinates and dimensions for the triangular extension over a rectangle form factor over a horizontal plane.
Figure 9.
Coordinates for the triangle form factor over a horizontal plane.
Figure 9.
Coordinates for the triangle form factor over a horizontal plane.
Figure 10.
Triangular windows and their reflections at the studio of the artist Sebastian García Garrido in Benalmadena (Malaga).
Figure 10.
Triangular windows and their reflections at the studio of the artist Sebastian García Garrido in Benalmadena (Malaga).
Figure 11.
Coordinates for the triangle obtained by subtraction to calculate form factor over a horizontal plane.
Figure 11.
Coordinates for the triangle obtained by subtraction to calculate form factor over a horizontal plane.
Figure 12.
Coordinates for the calculation of the form factor of a rhomboid over a horizontal plane.
Figure 12.
Coordinates for the calculation of the form factor of a rhomboid over a horizontal plane.
Figure 13.
Coordinates for the quarter-circle form factor over a horizontal plane.
Figure 13.
Coordinates for the quarter-circle form factor over a horizontal plane.
Figure 14.
Average for a triangle of 5m. by 5m. over a horizontal rectangle of length 8m. The form factor F21 from the rectangle (2) to the triangle (1) is equal in this case to 0.090.
Figure 14.
Average for a triangle of 5m. by 5m. over a horizontal rectangle of length 8m. The form factor F21 from the rectangle (2) to the triangle (1) is equal in this case to 0.090.
Figure 15.
Nephograph in plan of the radiative field from the triangle to the rectangle.
Figure 15.
Nephograph in plan of the radiative field from the triangle to the rectangle.
Figure 16.
Nephograph of radiative distribution for the same case in 3D.
Figure 16.
Nephograph of radiative distribution for the same case in 3D.
Figure 17.
The five surfaces of the volume of a triangular prism ending in right triangles.
Figure 17.
The five surfaces of the volume of a triangular prism ending in right triangles.
Figure 18.
Configuration factor between a rectangle and a point at an inclined plane forming an angle φ with respect to the lower vertex of the said rectangle and distanced D from it.
Figure 18.
Configuration factor between a rectangle and a point at an inclined plane forming an angle φ with respect to the lower vertex of the said rectangle and distanced D from it.
Figure 19.
Coordinates for the triangle form factor over a horizontal plane.
Figure 19.
Coordinates for the triangle form factor over a horizontal plane.
Figure 20.
Rhomboidal prism formed by two inclined slats that appear in many shading devices.
Figure 20.
Rhomboidal prism formed by two inclined slats that appear in many shading devices.
Figure 21.
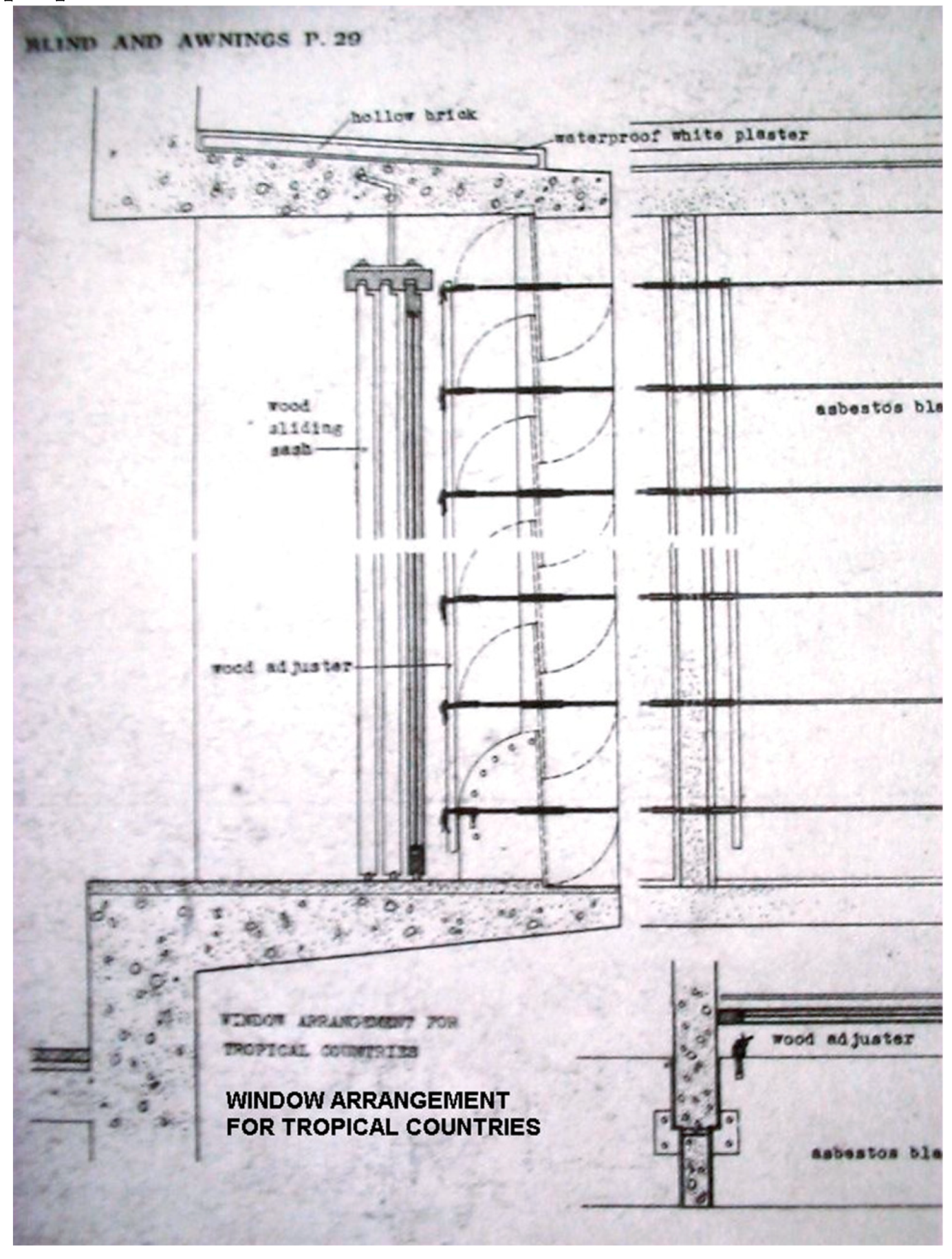
Section of the movable shading system where we can read “Window Arrangement for tropical countries”, notice that there is no glazing in such window arrangement.
Figure 21.
Section of the movable shading system where we can read “Window Arrangement for tropical countries”, notice that there is no glazing in such window arrangement.
Figure 22.
View from the outside of the same shading system in Pondicherry (India).
Figure 22.
View from the outside of the same shading system in Pondicherry (India).
Figure 23.
Rhomboidal prism in the louvers for the Ministry of Education in Rio de Janeiro (Brazil). Architect Oscar Niemeyer. Source (Author).
Figure 23.
Rhomboidal prism in the louvers for the Ministry of Education in Rio de Janeiro (Brazil). Architect Oscar Niemeyer. Source (Author).
Figure 24.
Interior view of the movable shading system of the Ministry of Education.
Figure 24.
Interior view of the movable shading system of the Ministry of Education.