Prerpints.org logo
Preprint
Article

Application of Physics-Informed Neural Networks for River Silting Simulation

Altmetrics

Downloads

142

Views

58

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 September 2023

Posted:

26 September 2023

You are already at the latest version

Alerts
Abstract
Water resource pollution, particularly in river channels, presents a grave environmental challenge that necessitates a comprehensive and systematic approach encompassing assessment, forecasting, and effective management. This article provides a comprehensive exploration of the methodology and modeling tools employed to scrutinize the process of river channel pollution due to silting, rooted in the fundamental principles of hydrodynamics and pollutant transport dynamics. The study's methodology seamlessly integrates numerical simulations with state-of-the-art neural network techniques, with a specific focus on the Physics-informed neural networks (PINN) method. This innovative approach represents a groundbreaking fusion of artificial neural networks (ANN) and physical equations, offering a more efficient and precise means of modeling a wide array of complex processes and phenomena. The proposed mathematical model, grounded in the Euler equation, has been meticulously implemented using the Ansys Fluent software package, ensuring accuracy and reliability in the computations. In a pivotal phase of the research, a thorough comparative analysis was conducted between the results derived from the PINN method and those obtained through conventional numerical approaches using the Ansys Fluent software package. The outcomes of this analysis revealed the superior performance of the PINN method, characterized by the generation of smoother pressure fluctuation profiles and significantly reduced computation time, underscoring its potential as a transformative modeling tool. The calculated data originating from this study assumes paramount significance in the ongoing battle against river sedimentation. Beyond this immediate application, these findings also serve as a valuable resource for creating predictive materials pertaining to river channel silting, thereby empowering decision-makers and environmental stakeholders with essential information. The utilization of modeling techniques to address pollution concerns in river channels holds the potential to revolutionize risk management and safeguard the integrity of our vital water resources. However, it is imperative to underscore that the effectiveness of such models hinges on ongoing monitoring and frequent data updates, ensuring that they remain aligned with real-world conditions. This research not only contributes to the enhanced understanding and proactive management of river channel pollution due to silting but also underscores the pivotal role of advanced modeling methodologies in the preservation of our invaluable water resources for present and future generations.
Keywords: 
Subject: Environmental and Earth Sciences  -   Space and Planetary Science

1. Introduction

One of the main causes of water pollution is the process of silting, or, in other words, segmentation. Otherwise, silting is water pollution caused by solid particles of clastic material dominated by particles or clays.
The silting process can also be formed as a result of erosion on land or human activities in the water (Wu et al., 2023, [26]). Erosion in rural areas is caused by poor agricultural practices, while in urban areas, erosion can be caused by construction activities such as clearing vegetation from the ground when buildings are erected. Constant climate change in residential areas increases the rate of erosion and, accordingly, siltation of river objects. In this regard, the prevention of erosion, the preservation of vegetation cover is the primary task in agriculture.
A river that is a naturally self-organizing system that is regulated through the accumulation and transport of sedimentary materials such as clay, sand, silt and gravel is called an alluvial river. The main sources of alluvial materials for the river are the erosion of soil, rock formations, and bank areas in the river basin. When the river carries these materials in water flows, they settle to the bottom of the channel and can change its shape and depth. However, these processes are directly or indirectly affected by anthropogenic disturbances caused by intensive dam construction, irrigation and land use chang (Best and Darby, 2020, [22]), causing the topographical evolution of the river to deviate from its natural course (Marren et al., 2014, [23]). This deviation can further affect the various socio-economic functions performed by rivers, such as navigation, flood mitigation, and water supply. It follows from this that the river system should be considered as a complex component of a single natural system. (Hawley, 2018, [24]; Merembayev, 2023, [25]).
River silting processes are extremely unstable (Constantine et al., 2014, [18]), they pose a serious threat to the life and property of people living in their floodplains, and can also harm infrastructure and the environment. The increased frequency of meteorological disasters leads to the fact that the risk of floods on these rivers may increase (Dottori et al., 2018, [19]). For example, severe silting of the Kosi and Indus rivers in South Asia led to the formation of ultra-high channels, resulting in a dam failure in 2008 and 2010, respectively, causing severe damage to downstream residential areas (Sinha et al., 2019, [20] ). For this reason, when modeling the prediction of the behavior of silty rivers, it is very important to take into account complex hydrodynamic processes (Philips et al., 2022, [21]). Thus, it is extremely important to be able to manage silty rivers, because this problem is relevant not only for researchers, but also for politicians and other stakeholders and requires careful further study and consideration.
For a more detailed study of the described problem, it is necessary to conduct full-scale experiments (Powledge et al., 1989, [3]; Schmocker and Hager 2009, [4]), which make it possible to study the nature of the movement of the water flow and the sedimentary layer under various conditions, as well as based on real observations (Froehlich 2008, [5]). While real-world observations clearly demonstrate the problem, they are often poorly documented. In contrast, conducting experiments in specially equipped laboratories makes it possible to observe the process of erosion and siltation with one's own eyes. Thus, numerous laboratory experiments were carried out to study the clogging of streams with silt particles (Fetzer et al., 2017, [12]; Yao et al., 2013, [13]; Kazidenov et al., 2023 [14]; Omirbekov et al. , 2023, [15]). However, large-scale real experiments on the silting process are not only extremely difficult to perform, they also require huge resource costs. The high cost of laboratory experiments makes it impossible to carry out this process with the required frequency. The closest and most accurate replacement for a full-scale experiment today is numerical simulation. Numerical simulation, although it requires high-performance computers, is generally less resource-intensive in contrast to laboratory experiments. Often, the developed numerical algorithm is tested on the basis of experimental data (Ecemis, 2021, [16]; Narbayev et al., 2022, [17]; Omarova, P., Merembayev, T. et. Al., 2023, [33]) . A study (Soares-Frazão et al., 2007, [1]) presents a laboratory experiment demonstrating morphological changes in a river channel and destruction of river banks. The bottom and banks of the river channel consisted of homogeneous sand, and the cross section of experimental setup has the shape of a rectangular trapezoid. The article (Goutiere et al., 2011, [2]) demonstrates the behavior of water flow in an expanding installation above a moving layer of homogeneous sand.
Most of the early research was based on numerical simulation methods, however, in the last decade, breakthroughs in computer vision (CV) (Buribayev et al., 2021, [34], Kenshimov et al., [35]) and natural language processing (NLP) have led to the rapid development of artificial neural networks (ANNs) (Yeleussinov et. al [36]). ANN takes input (eg a series of images) and outputs a prediction based on the task (eg image recognition). The quality of the prediction is based on the amount of information contained in the training data, which is usually the amount of different data, and the training of the neural network, which is the minimization of the objection function (i.e., the loss function). However, for problems of hydrodynamics, one often has to deal with the lack of access to experimental data, which is required by neural networks. Recently, Physics Based Neural Network (PINN) (Sukumar and Srivastava, 2022, [6]) has emerged as a neural network based technique that does not require observational data to model physics by training neural networks on random samples generated in a given areas.
In this study, the task is to assess the indicators of velocity, pressure, and density in the aquatic environment for subsequent modeling of silting of river channels. Indicators are predicted using the modern approach of physics-informed neural networks. A comparative analysis of the simulation results with ANSYS Fluent was also performed to determine the most optimal method in terms of computational speed and computational accuracy.
The methodology section elaborates on the utilization of physics-based neural networks and modeling techniques within the ANSYS Fluent software package, specifically addressing the Euler problem. Subsequently, the results section encompasses the presentation of simulation outcomes obtained using physics-based neural networks and numerical simulation techniques in ANSYS Fluent. The discussion section provides a concise summary of the methodologies employed and offers a brief examination of the findings..

2. Materials and Methods

Neural networks based on physics.
The Physics-informed neural networks (PINN) method is extremely popular in fluid flow simulation, and numerous studies demonstrate the success of using this method (Meng et al., 2020, [7]; Cheng et al., 2021, [8]; Huang et al., 2023, [9]). However, free surface problems are a major problem for the PINN method in its original formulation. So far, studies on solving free surface flow problems using the PINN method are limited, and free surface problems have been solved only in the shallow water approximation (Holland, 2011, [10]), where all calculations are performed on the free surface (Ardakani and Bridges, 2010, [11]), where the basic equations are simpler. Therefore, a PINN structure for solving the general problem of a free surface in rough water conditions is not available and, therefore, is very necessary.
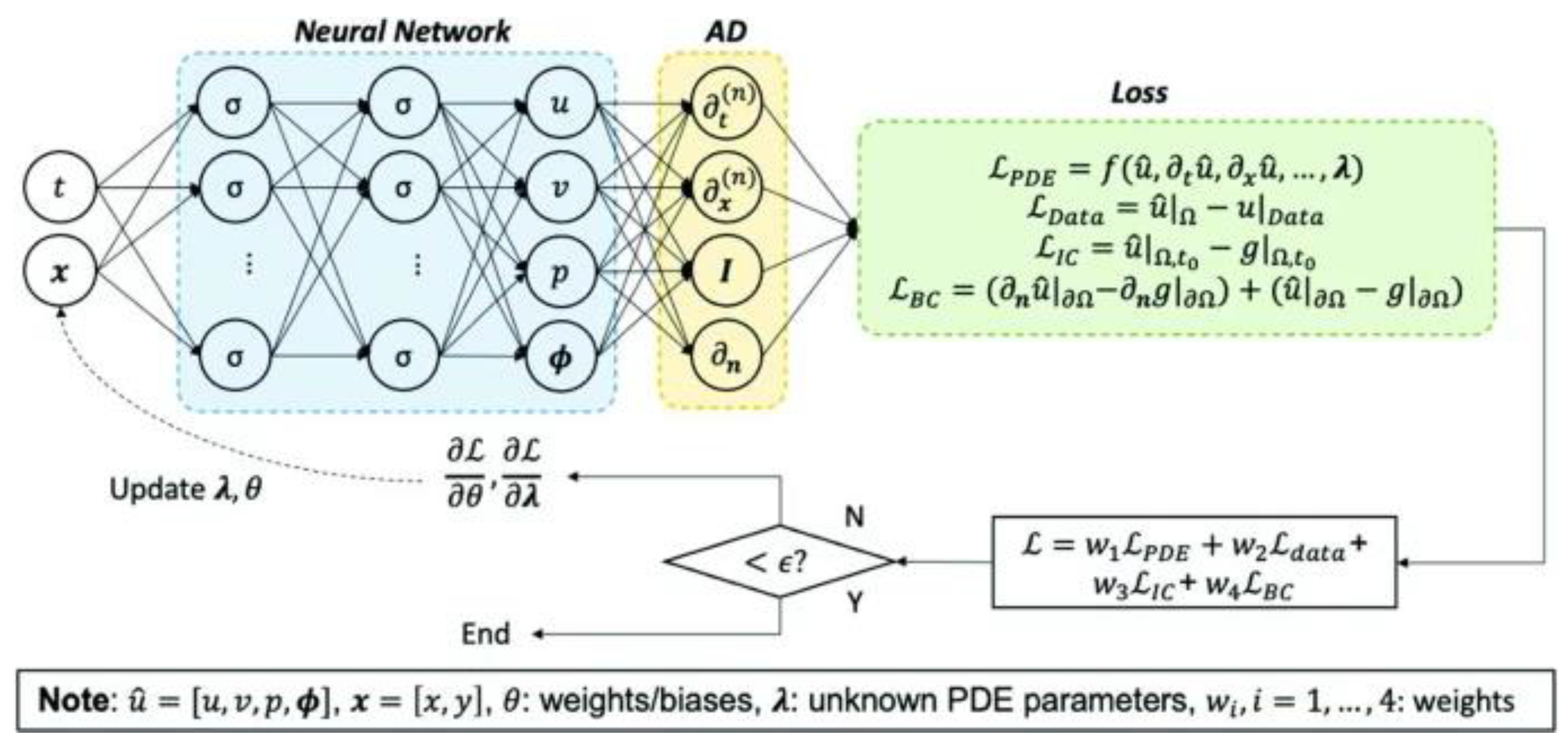
The PINN implementation approach is shown in Figure 1, which shows the concept scheme for solving the objective function optimization problem.
In our study, we will consider the problem of modeling the hydrodynamics of a shock wave. The Euler equation is considered as a mathematical model.
Consider one-dimensional compressible Euler equations in characteristic form, where Ω⸦R
d U d t + A d U d x = 0 , ( 3 )
where,
U = ρ , u , p T , A = u ρ 0 0 u 1 ρ 0 ρ a 2 u
where, a = γ p ρ - is the speed of sound, ρ - is the density, u - is the velocity, p - is the pressure, а γ - is the heat capacity coefficient. Usually, for a standard hydrodynamic problem about a shock tube, the initial condition has the form:
U x , 0 = U 0 = u L , x < x u R > x , u L = ρ L , u L , p L , , u R = ρ R , u R , p R ,
with Dirichlet boundary conditions taking on the boundaries the values of the initial condition.
Before modeling, we consider what the spatial domain Ω of the problem means. We increase Ω,
so that if u L ˃ u R , Ω expands such that the initial state leans to the left of the newly expanded spatial domain Ω e .
The second modification we make to PINN is to introduce weights into the loss function. To solve the Euler equations with PINN, we build a deep neural network, U x , t , 0 , where x , t - are the inputs to the network and U ¯ = ρ , u ¯ , p - are the outputs. Similarly, the standard loss is determined by the formula:
G θ = 1 N f ∂ U ¯ ∂ t x , t , θ + A ~ ∂ U ¯ ∂ t x , t , θ Ω × 0 , T , ν 1 2 + 1 N I C U ~ x , 0 , θ + U x , 0 Ω , ν 2 2 + 1 N B C U ~ x , t , θ + U x , t ∂ Ω × 0 , T , ν 3 2
We will denote the first, second and third components in (4) as G f θ , G I C θ and G B C θ respectively. Since the boundary conditions are determined by the initial conditions, we will omit the boundary condition term in (4). Hence,
G θ = G f θ + G I C θ
Mathematical model in ansys.
The mathematical model consists of a two-dimensional Euler equation that describes the wave propagation velocity, contact discontinuity and shock discontinuity. The shock tube problem has an analytical solution for the time before the impact of the shock wave on the edge of the tube (Jr. Anderson, J.D., 1989, [28]). The analytical solution to this problem Sod is often used as an example for compressible solvers. An analytical solution of this problem can also be obtained using exact Riemann solvers ([31], [32]). This paper demonstrates two-dimensional numerical simulation of the Sod problem in the ANSYS Fluent software package.
Numerical simulation algorithm in ansys.
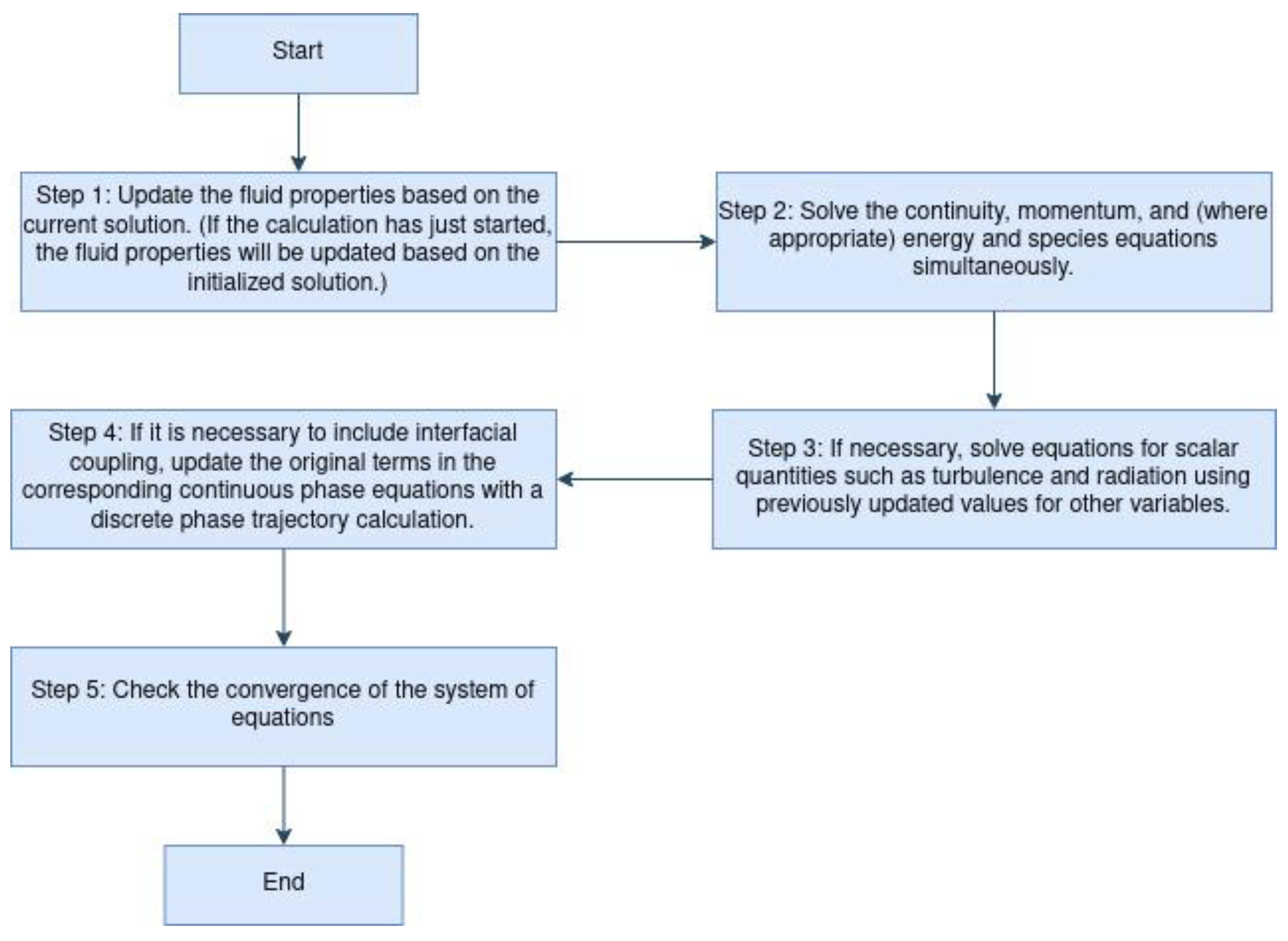
The density-based algorithm solves the basic equations of continuity, momentum, and (where appropriate) energy and matter transport simultaneously. The governing equations for additional scalars will be solved subsequently and sequentially (i.e. separately from each other and from the associated set). Since the governing equations are non-linear (and coupled), several iterations of the solve loop must be performed before a convergent solution is obtained. Each iteration consists of the steps described below in Figure 3.
These steps continue until the convergence criteria are met. In the density-based solution method, it is possible to solve a coupled system of equations (continuity, momentum, energy, and species equations, if available) using either the coupled explicit formulation or the coupled implicit formulation. The main difference between explicit and implicit density-based formulations are:
In density-based solution methods, discrete non-linear master equations are linearized to obtain a system of equations for the dependent variables in each computational cell. The resulting linear system is then solved to obtain an updated flow field solution. The method of linearizing the governing equations may take an "implicit" or "explicit" form with respect to the dependent variable (or set of variables) of interest. Implicit or explicit means the following:
- implicit: for a given variable, the unknown value in each cell is calculated using a ratio that includes both existing and unknown values from adjacent cells. Therefore, each unknown will appear in more than one equation of the system, and these equations must be solved simultaneously in order to obtain unknown quantities.
- Explicit: For a given variable, the unknown value in each cell is calculated using a relation that includes only existing values. Therefore, each unknown will only appear in one equation in the system, and the equations for the unknown value in each cell can be solved one at a time to get the unknowns.
In the density-based solution method, there is a choice of using implicit or explicit linearization of the governing equations. This selection only applies to the associated set of master equations. The transport equations for additional scalars are solved separately from the associated set (eg turbulence, radiation, etc.). The transport equations are linearized and solved implicitly. Regardless of the choice of implicit or explicit methods, the decision procedure described above is carried out.
If the explicit variant of the density solver is chosen, each equation in the associated set of master equations is linearized explicitly. This will result in a system of equations with N equations for each cell in the domain, and similarly, all dependent variables in the set will be updated at the same time. However, this system of equations is explicit with respect to unknown dependent variables. For example, the x-momentum equation is written such that the updated speed x is a function of the existing values of the field variables. Because of this, a linear equation solver is not needed. Instead, the solution is updated with a multi-stage (Runge-Kutta) solver. There is an additional option to use a multi-grid full approximation storage scheme (FAS) to speed up a multi-stage solver. Thus, the explicit density-based approach solves for all variables p , u , v , w , T one cell at a time.

3. Results

3.1. Numerical result from pinn

The problem of hydrodynamics with a shock tube is a standard hydrodynamic test problem. The problem is used as a test problem to test the ability of numerical methods to capture characteristics unique to solving conservation laws. The solution for each physical quantity gives a contact discontinuity and a shock wave. The numerical calculation of the shock wave and the contact discontinuity is difficult because the numerical scheme creates artificial dispersion or scattering near the discontinuity points.
In our study, we considered the following architecture of PINN, Figure 4. The input to this architecture is 2 vectors of values t and tix, and the result is 3 vectors of values u,p and ρ (velocity, pressure and density).
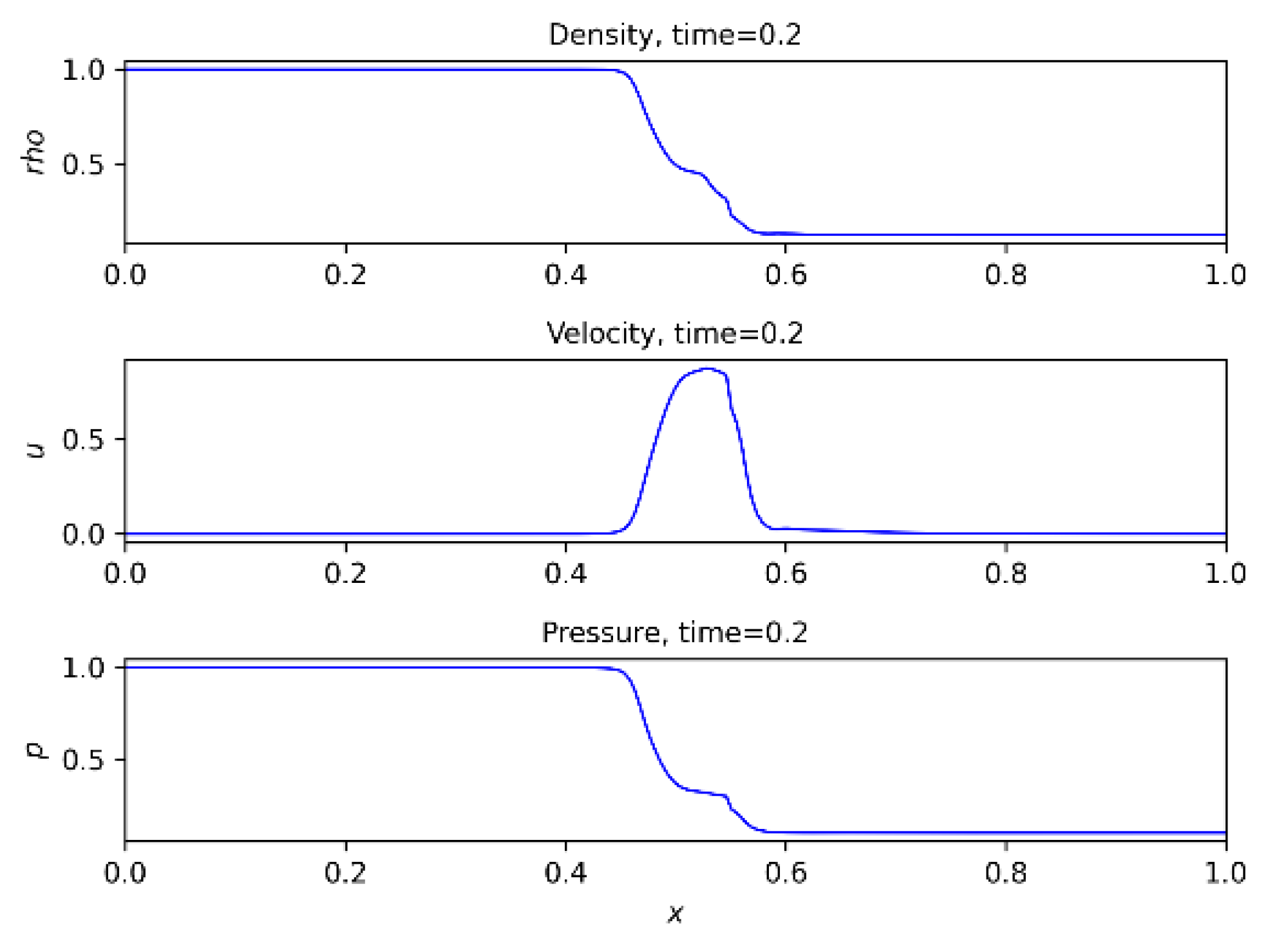
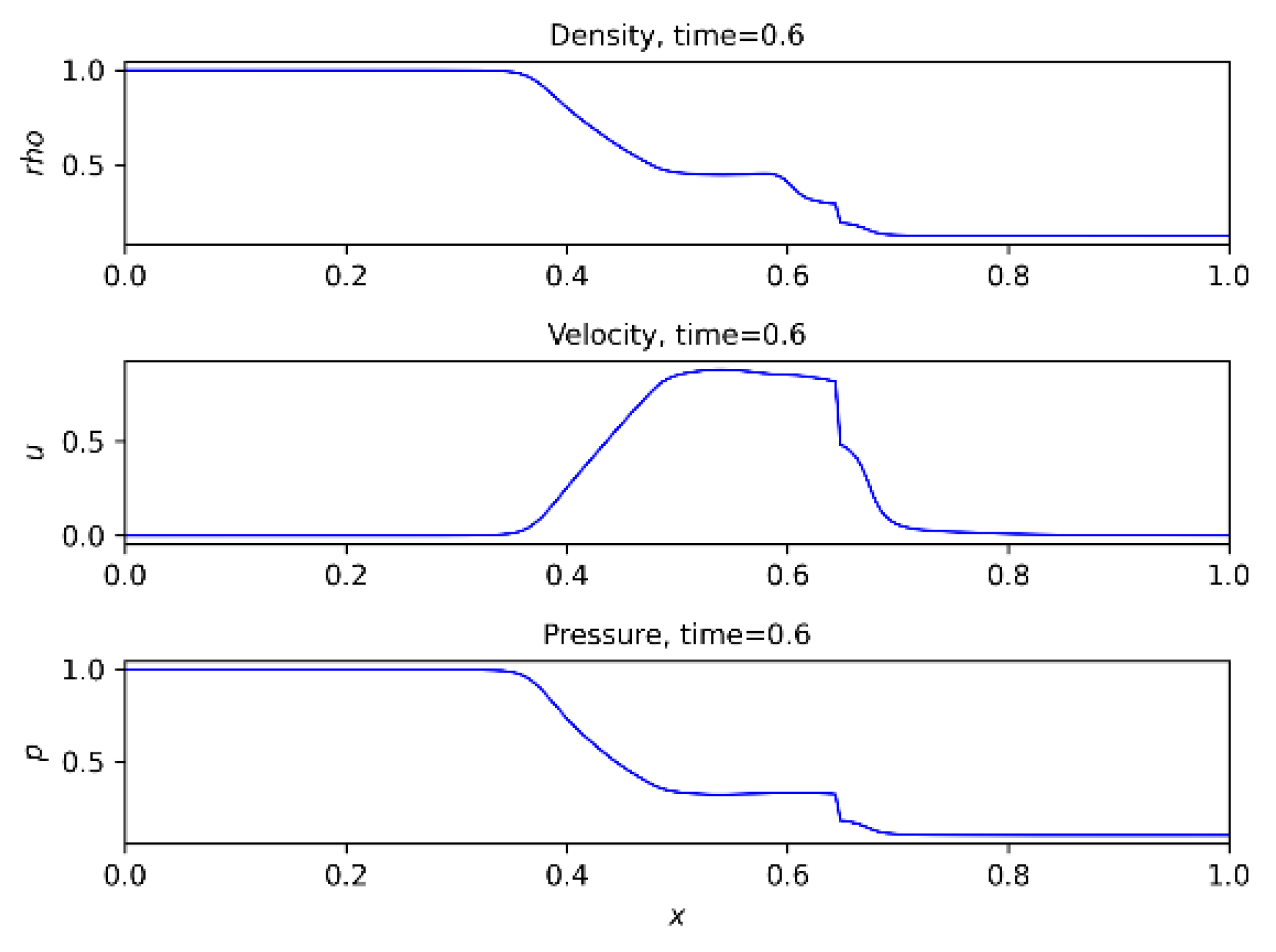
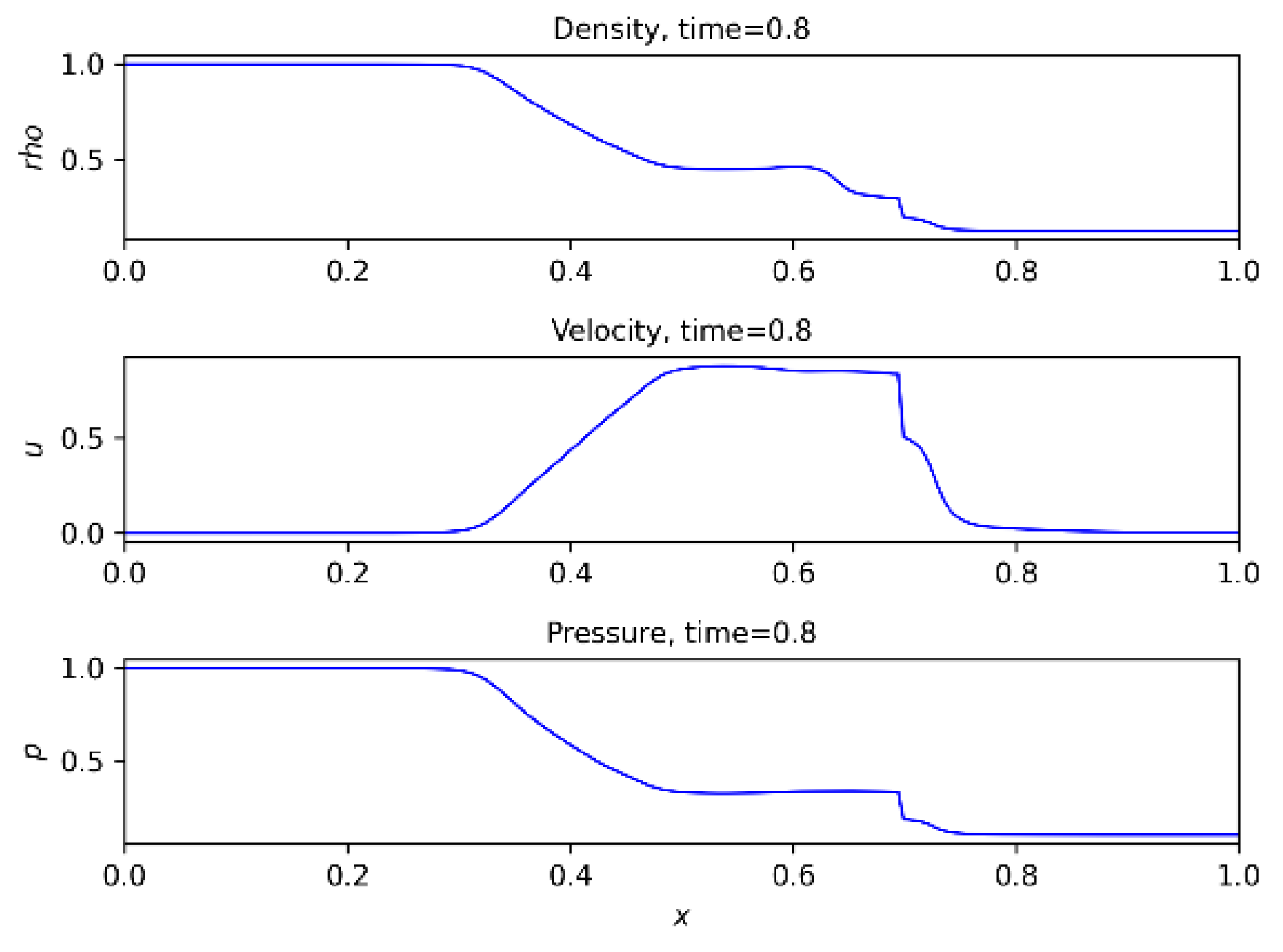
Figure 5, Figure 6 and Figure 7 show the prediction results using PINN for density, pressure and velocity over time = 0.2, 0.6, 0.8 respectively.
The use of the PINN approach opens up possibilities for solving a general class of discontinuous solutions of compressible Euler equations. This is achieved through the ability to capture physical phenomena such as impacts, contact breaks and rarefaction.
In Figure 5, Figure 6 and Figure 7, the velocity behavior shows scattering near impact angles. This allows for computational errors, and one of the goals of PINN is to find solutions that are as accurate as possible.

3.2. Numerical result from ansys

This study aims to model the problem of sod's shock tub. The task is to simulate the propagation of a normal shock wave inside a shock tube under experimental conditions. The obtained numerical results are compared with the results obtained using the PINN method, which is a widely popular method in fluid flow simulation.
To check the correctness and accuracy of the mathematical model used, the test problem was solved numerically, based on the research of other authors.
For this, a 2D Shock tube model was used, which is a long metal tube consisting of two chambers and separated by a diaphragm. The diaphragm separates the high-pressure area from the low-pressure area (Anderson Jr., J.D., 2003, [29]). 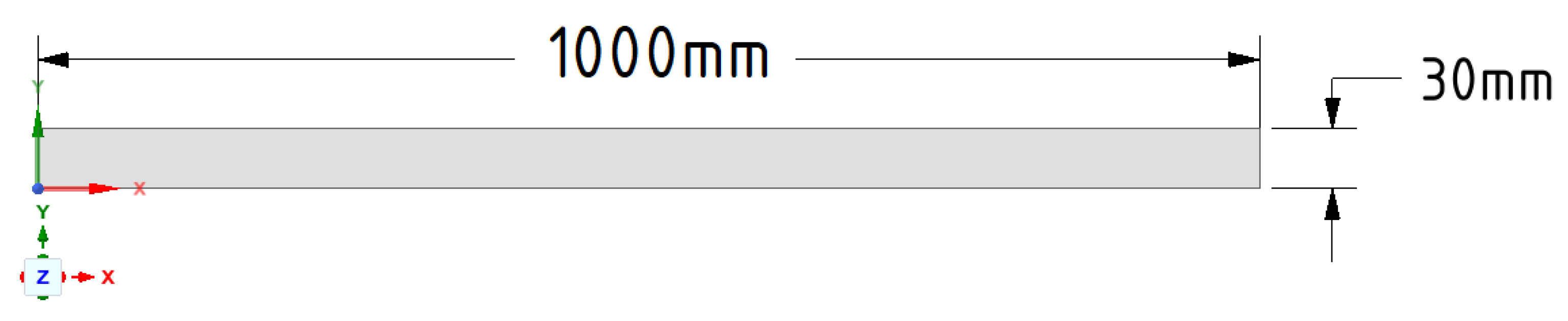After the diaphragm is removed, the shock wave and the contact discontinuity begin to move to the region of initially low pressure, and the rarefaction wave moves to the region of initially high pressure (Khodadadi Azadboni et al., 2013, [30]). Two different solvers were used in the problem: driver and driven. The chamber used consists of two gases with a high-pressure ratio. Thus, one chamber is filled with high-pressure ideal-gas, like a driver, and the other chamber, vice versa, is low-pressure, and is called driven. Schematic representation of the studied reservoir is shown in Figure 8. The length of this reservoir is Lb=1m and Hb=0.03m. When modeling, piercing mechanism was built into the diaphragm, which breaks the diaphragm under given conditions. When the contact is suddenly broken, a series of pressure waves are created that cause a shock wave.
For this task, a structured computational mesh was used, the total number of elements of which was 30,000, the number of nodes was 31,031. Face meshing=1e-03m. The computational grid for the study area is shown in Figure 9. The total duration of the task calculation is: Number of time steps=3000.
Figure 10 shows the initial conditions for the area under consideration at t=0. The diaphragm separates the ideal-gas with different pressures and densities, and the velocity on both sides is 0. All boundaries were set as walls.
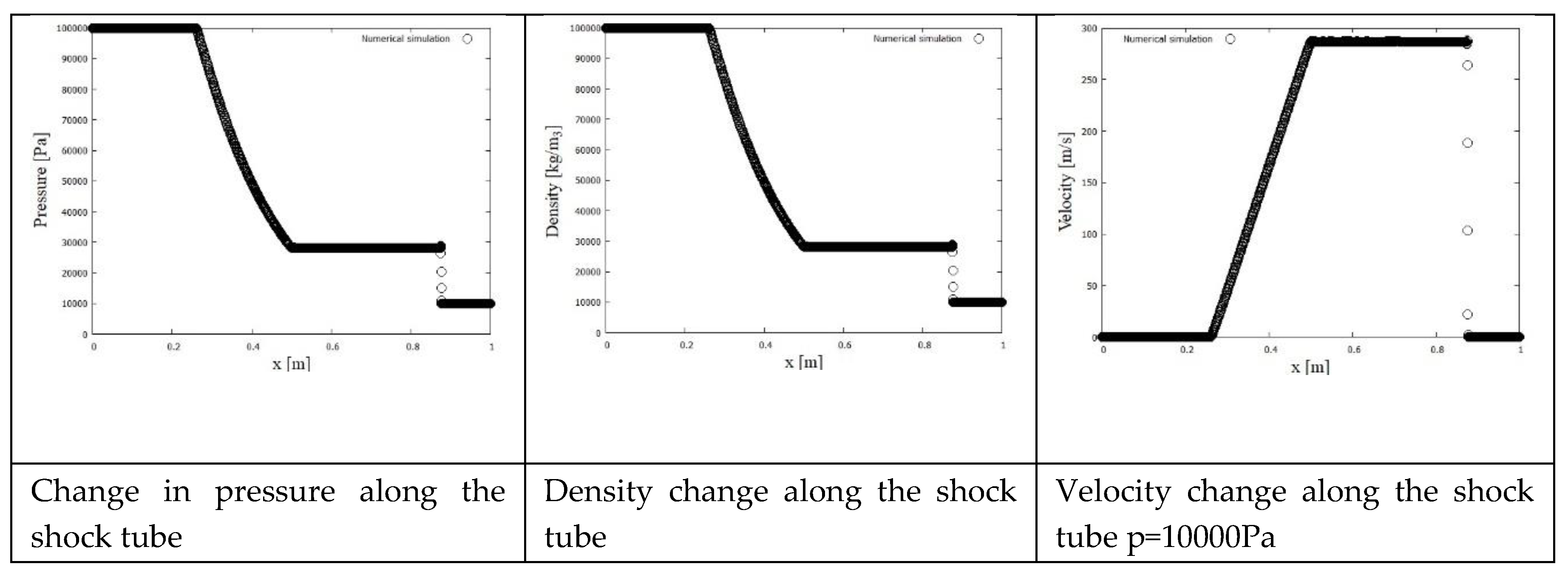
The obtained numerical results were compared with the results obtained by using the PINN method. As can be seen, the numerical simulation results show exact solutions to the problem with a
clear shock effect. In solving the problem using PINN, the shock effect is not explicitly shown. The results obtained are presented in Figure 11.
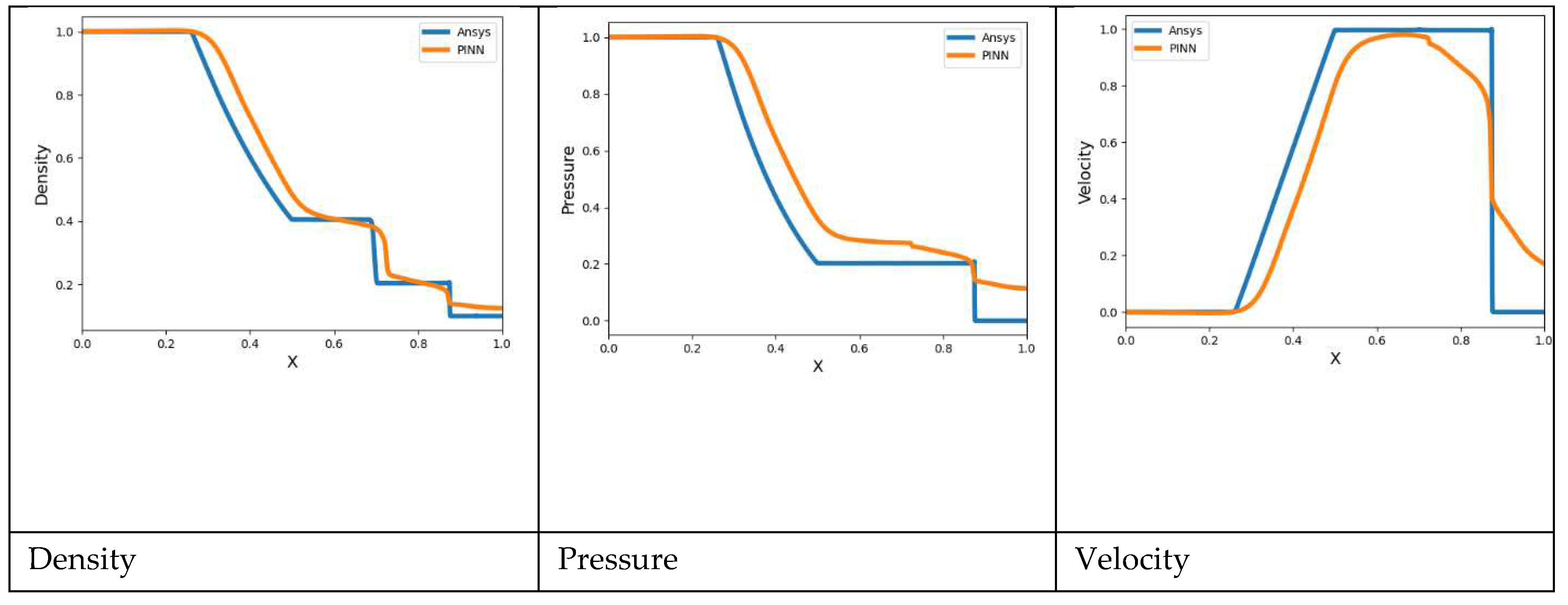
The Figure 12 shows the comparisons of PINN solutions with exact solutions from Ansys at various x locations.
We can observe that while we can achieve accurate results for density, our ability to make precise predictions for velocity and pressure is limited. This limitation arises from the fact that the flow has not yet reached the area between the shock and the right boundary. Thus, attempting to incorporate pressure information from this region into the available data and equations would not uncover the actual pressure and velocity fields within the desired domain.
As the results show, numerical simulation more clearly shows the shock effect, where are the boundaries of pressure, velocity, and density changes. And the obtained results of the PINN method are smoother, since using a neural network, training was carried out considering the physical constraints and conditions of the problem. However, the calculation time using the PINN method is much less than numerical simulation.

4. Discussion

In this discussion, we delve into the comparative analysis of the Physics-informed Neural Network (PINN) method and classical numerical simulation techniques for solving problems related to the simulation of physical processes. Both approaches have their advantages and limitations, and understanding their differences is crucial in selecting the most suitable method for a given problem.
The PINN method represents a novel approach to solving physical problems by incorporating neural networks into the learning process. This integration allows neural networks to assimilate the physical laws and constraints of the problem during training. Consequently, the neural network can make predictions while considering the problem's inherent physical conditions. Notably, the PINN method can offer computational advantages, particularly in scenarios where sufficient and accurate data are available. By learning from data, the PINN method can potentially reduce computational intensity.
In contrast, classical numerical simulation relies on solving differential equations that describe physical processes through numerical integration methods. This approach has a well-established foundation in scientific computing and is widely used in various fields. Numerical simulations are highly accurate when appropriate numerical methods and parameters are employed. However, they can be computationally intensive, especially for complex problems or high-resolution simulations.
Table 1 provides a comparative analysis of the time performance of the PINN method and numerical simulation, measured in seconds and the number of elements or parameters involved. The results demonstrate that the PINN method requires 1948 seconds with 4833 elements or parameters, while ANSYS simulation takes 1080 seconds with 50300 elements, 780 seconds with 30000 elements, and 240 seconds with 4800 elements. It is important to note that the PINN model was trained for 7500 epochs on a CPU resource, matching the computational platform used for ANSYS simulation.
The choice between the PINN method and numerical simulation depends on several factors, including the availability of data, problem complexity, and computational resources. While the PINN method may offer computational advantages, its accuracy may be compromised in cases with insufficient or inaccurate data. Additionally, training the neural network under certain physical conditions can be challenging. On the other hand, numerical simulation excels in accuracy but may require substantial computational resources, making it less efficient for some applications.
In conclusion, both the PINN method and numerical simulation play vital roles in simulating physical processes. Researchers and engineers must carefully evaluate the specific requirements and constraints of their problems to determine the most suitable approach. Furthermore, ongoing advancements in computational methods, including the integration of neural networks, continue to expand the possibilities for solving complex physical problems efficiently and accurately.

5. Conclusions

This paper proposes a comparative analysis of the PINN method and numerical simulation for estimating the indicators of velocity, pressure, and density in the aquatic environment. Thanks to the PINN method, numerical results obtained on time can be used for subsequent numerical modeling of silting of river channels and channels. Predicting the above indicators is important in preventing river pollution due to sedimentation. This method makes it possible to evaluate various fluid types (compressible, incompressible, Newtonian, non-Newtonian, etc.). Also, during the modeling process, accurate numerical results were obtained, demonstrating the behavior of the flow of compressible fluids.
Comparing the results of PINN and numerical simulations in Ansys, the profiles of the velocity, density and pressure indicators are the same, except for the areas where the shock effect occurs. Also, PINN simulation results can be obtained faster than Ansys numerical simulations, which is a clear advantage. It should be noted that numerical simulation for a natural area requires a lot of computational costs, depending on the area of calculation, since the number of elements in the construction of the grid plays an important role. For this reason, in some calculations to prevent pollution of rivers due to sedimentation for a real area, it is better to use the PINN method.
With the PINN method, it is possible to estimate different fluid types, for example, in terms of density, and further model the siltation of river channels for more complex conditions and measurements.
In future work, the PINN method will be extended to higher dimensions, and real problems in river silting will be modeled. In future works, the Euler and Navier-Stokes equations solved using the PINN method will be investigated, and we will also consider a comparative analysis of the PINN and FEM methods.

Author Contributions

“Conceptualization, P. Omarova and Ye. Amirgaliyev,; methodology, P. Omarova and Ye. Amirgaliyev; software, P. Omarova, A. Kozbakova, A. Ataniyazova; formal analysis, P. Omarova, A. Kozbakova, A. Ataniyazova; project administration, P. Omarova.; Supervision, P. Omarova, Ye. Amirgaliyev, A. Kozbakova, A. Ataniyazova. All authors have read and agreed to the published version of the manuscript.

Funding

Funding was supported by grant funding from the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (BR18574144).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The work was supported by grant funding from the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (BR18574144).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Soares-Frazão, S. , Le Grelle, N., Spinewine, B., & Zech, Y. (2007). Dam-break induced morphological changes in a channel with uniform sediments: measurements by a laser-sheet imaging technique. Journal of Hydraulic Research, 45(sup1), 87–95–87–95. [CrossRef]
  2. Goutiere, L. , Soares-Frazão, S., & Zech, Y. (2011). Dam-break flow on mobile bed in abruptly widening channel: experimental data. Journal of Hydraulic Research, 49(3), 367–371. [CrossRef]
  3. Powledge, G.R. , Ralston, D.C., Miller, P., Chen, Y.H., Clopper, P.E., Temple, D.M. (1989). Mechanics of overflow erosion on embankments. I: Research activities; II/hydraulic and design considerations. J. Hydraulic Eng. 115(8), 1040–1075.
  4. Schmocker, L. , Hager, W.H. (2009). Modelling dike breaching due to overtopping. J. Hydraulic Res. 47 (5), 585–597. [CrossRef]
  5. Froehlich, D.C. (2008). Embankment dam breach parameters and their uncertainties. J. Hydraulic Eng. 134(12), 1708–1721.
  6. Sukumar, N. , Srivastava, A. (2022). Exact imposition of boundary conditions with distance functions in physics-informed deep neural networks. Computer Methods in Applied Mechanics and Engineering, Volume 389, 114333, ISSN 0045-7825. [CrossRef]
  7. Meng, X. , Li, Z., Zhang, D., & Karniadakis, G. E. (2020). PPINN: Parareal physics-informed neural network for time-dependent PDEs. Computer Methods in Applied Mechanics and Engineering, 370, 113250. [CrossRef]
  8. Cheng, C. , Meng, H., Li, Y-Z., Zhang, G-T. (2021). Deep learning based on PINN for solving 2 DOF vortex induced vibration of cylinder. Ocean Engineering, Volume 240, 109932, ISSN 0029-8018. [CrossRef]
  9. Huang, Y.H. , Xu, Z., Qian, C., Liu, L. (2023). Solving free-surface problems for non-shallow water using boundary and initial conditions-free physics-informed neural network (bif-PINN). Journal of Computational Physics, Volume 479, 112003, ISSN 0021-9991. [CrossRef]
  10. Holland, P. (2011). Hydrodynamics, Particle Relabelling and Relativity. International Journal of Theoretical Physics, 51(3), 667–683. [CrossRef]
  11. ALEMI ARDAKANI, H. , & BRIDGES, T. J. (2010). Dynamic coupling between shallow-water sloshing and horizontal vehicle motion. European Journal of Applied Mathematics, 21(06), 479–517. [CrossRef]
  12. Fetzer, J. , Holzner, M., Plötze, M., & Furrer, G. (2017). Clogging of an Alpine streambed by silt-sized particles – Insights from laboratory and field experiments. Water Research, 126, 60–69. [CrossRef]
  13. Yao, P. , Su, M., Wang, Z., van Rijn, L. C., Zhang, C., Chen, Y., & Stive, M. J. F. (2015). Experiment inspired numerical modeling of sediment concentration over sand–silt mixtures. Coastal Engineering, 105, 75–89. [CrossRef]
  14. Kazidenov, D. , Khamitov, F., & Amanbek, Y. (2023). Coarse-graining of CFD-DEM for simulation of sand production in the modified cohesive contact model. Gas Science and Engineering, 113, 204976. [CrossRef]
  15. Omirbekov, S. , Colombano, S., Alamooti, A., Batikh, A., Cochennec, M., Amanbek, Y., ... & Davarzani, H. (2023). Experimental study of DNAPL displacement by a new densified polymer solution and upscaling problems of aqueous polymer flow in porous media. Journal of Contaminant Hydrology, 252, 104120. [CrossRef]
  16. Ecemis, N. (2021). Experimental and numerical modeling on the liquefaction potential and ground settlement of silt-interlayered stratified sands. Soil Dynamics and Earthquake Engineering, 144, 106691. [CrossRef]
  17. Narbayev, B. , & Amanbek, Y. (2022, July). Finite Element Model for Wind Comfort Around a Tall Building: A Case Study of Tower of Qazaqstan. In Computational Science and Its Applications–ICCSA 2022 Workshops: Malaga, Spain, July 4–7, 2022, Proceedings, Part IV (pp. 540-553). Cham: Springer International Publishing.
  18. Constantine, J. A. , Dunne, T., Ahmed, J., Legleiter, C., & Lazarus, E. D. (2014). Sediment supply as a driver of river meandering and floodplain evolution in the Amazon Basin. Nature Geoscience, 7(12), 899–903. [CrossRef]
  19. Dottori, F. , Szewczyk, W., Ciscar, J.-C., Zhao, F., Alfieri, L., Hirabayashi, Y., Feyen, L. (2018). Increased human and economic losses from river flooding with anthropogenic warming. Nature Climate Change. [CrossRef]
  20. Sinha, R. , Gupta, A., Mishra, K., Tripathi, S., Nepal, S., Wahid, S. M., & Swarnkar, S. (2019). Basin-scale hydrology and sediment dynamics of the Kosi River in the Himalayan foreland. Journal of Hydrology. [CrossRef]
  21. Phillips, C.B. , Masteller, C.C., Slater, L.J., Dunne, K.B.J., Francalanci, S., Lanzoni, S., et al., (2022). Threshold constraints on the size, shape and stability of alluvial rivers. Nat. Rev. Earth Environ. 3, 406–419. [CrossRef]
  22. Best, J. , & Darby, S. E. (2020). The Pace of Human-Induced Change in Large Rivers: Stresses, Resilience, and Vulnerability to Extreme Events. One Earth, 2(6), 510–514. [CrossRef]
  23. Marren, P. M. , Grove, J. R., Webb, J. A., & Stewardson, M. J. (2014). The Potential for Dams to Impact Lowland Meandering River Floodplain Geomorphology. The Scientific World Journal, 2014, 1–24. [CrossRef]
  24. Hawley, R. J. (2018). Making Stream Restoration More Sustainable: A Geomorphically, Ecologically, and Socioeconomically Principled Approach to Bridge the Practice with the Science. BioScience, 68(7), 517–528. [CrossRef]
  25. Merembayev, T. , Amirgaliyev, Y., Saurov, S., & Wójcik, W. (2022). Soil Salinity Classification Using Machine Learning Algorithms and Radar Data in the Case from the South of Kazakhstan. Journal of Ecological Engineering, 23(10), 61-67. [CrossRef]
  26. Wu, X. , Feng, X., Fu, B., Yin, S., He, C. (2023). Managing erosion and deposition to stabilize a silt-laden river. Science of The Total Environment, Volume 881, 163444, ISSN 0048-9697. [CrossRef]
  27. Cai, S. , Mao, Z., Wang, Z., Yin, M., & Karniadakis, G. E. (2021). Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mechanica Sinica, 37(12), 1727-1738.
  28. Anderson, Jr. J.D. Modern Compressible Flow with Historical Perspective, McGraw Hill Professional Publishing, 2nd ed., Oct. 1989.
  29. Anderson, Jr. J. D. Modern Compressible Flow: With Historical Perspective, 3rd ed. McGraw-Hill, New York, USA, 2003.
  30. Khodadadi Azadboni, R. , et al. (2013). Evaluate Shock Capturing Capability with the numerical method in OpenFOAM, Journal of THERMAL SCIENCE, Vol. 17, No. 4, pp. 1255-1260.
  31. Modern compressible flow: with historical perspective. Third edition. McGraw-Hill.
  32. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction. Third edition. Springer.
  33. Omarova, P. , Merembayev, T., & Amirgaliyev, Y.. (2023). Mathematical modeling of water movement during a dam break using the vof method. Scientific Journal of Astana IT University, 14(14). [CrossRef]
  34. Buribayev, Z. , Merembayev, T., Amirgaliyev, Y., & Miyachi, T. (2021, April). The Optimized Distance Calculation Method with Stereo Camera for an Autonomous Tomato Harvesting. In 2021 IEEE International Conference on Smart Information Systems and Technologies (SIST) (pp. 1-5). IEEE.
  35. Kenshimov, C. , Mukhanov, S., Merembayev, T., & Yedilkhan, D. (2021). A COMPARISON OF CONVOLUTIONAL NEURAL NETWORKS FOR KAZAKH SIGN LANGUAGE RECOGNITION. Eastern-European Journal of Enterprise Technologies, 113(2).
  36. Yeleussinov, A. , Amirgaliyev, Y., & Cherikbayeva, L. (2023). Improving OCR Accuracy for Kazakh Handwriting Recognition Using GAN Models. Applied Sciences, 13(9), 5677. [CrossRef]
Preprints 86084 g001
Figure 1. Concept implementation scheme PINN [27].
Figure 1. Concept implementation scheme PINN [27].
Preprints 86084 g001
Preprints 86084 g002
Figure 2. An example of domain extension in the Sod inverse problem in Section IV.C. This domain [0; 1] extended to [-2.625; 2.5].
Figure 2. An example of domain extension in the Sod inverse problem in Section IV.C. This domain [0; 1] extended to [-2.625; 2.5].
Preprints 86084 g002
Preprints 86084 g003
Figure 3. The flowchart of simulation in the Ansys.
Figure 3. The flowchart of simulation in the Ansys.
Preprints 86084 g003
Preprints 86084 g004
Figure 4. PINN architecture.
Figure 4. PINN architecture.
Preprints 86084 g004
Preprints 86084 g005
Figure 5. Solving the problem using PINN for a period of time = 0.2.
Figure 5. Solving the problem using PINN for a period of time = 0.2.
Preprints 86084 g005
Preprints 86084 g006
Figure 6. Solving the problem using PINN for a period of time = 0.6.
Figure 6. Solving the problem using PINN for a period of time = 0.6.
Preprints 86084 g006
Preprints 86084 g007
Figure 7. Solving the problem using PINN for a period of time = 0.8.
Figure 7. Solving the problem using PINN for a period of time = 0.8.
Preprints 86084 g007
Preprints 86084 g008
Figure 8. Geometry of the test problem.
Figure 8. Geometry of the test problem.
Preprints 86084 g008
Preprints 86084 g009
Figure 9. Computational grid for the test problem.
Figure 9. Computational grid for the test problem.
Preprints 86084 g009
Preprints 86084 g010
Figure 10. Initial conditions for the test problem.
Figure 10. Initial conditions for the test problem.
Preprints 86084 g010
Preprints 86084 g011
Figure 11. The result of ANSYS modeling.
Figure 11. The result of ANSYS modeling.
Preprints 86084 g011
Preprints 86084 g012
Figure 12. The comparison of density, pressure, and velocity with the exact solutions.
Figure 12. The comparison of density, pressure, and velocity with the exact solutions.
Preprints 86084 g012
Table 1. Time comparison of the PINN method and numerical simulation.
Table 1. Time comparison of the PINN method and numerical simulation.
Time (sec) Element numbers or parameters
PINN 1948 4833
ANSYS 1080 50300
780 30000
240 4800
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated