Prerpints.org logo
Preprint
Article

The Polarization and Heat Generation Characteristics of Lithium-ion Battery with Electric-thermal Coupled Modeling

Altmetrics

Downloads

231

Views

43

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 September 2023

Posted:

26 September 2023

You are already at the latest version

Alerts
Abstract
This paper investigates the polarization and heat generation characteristics of batteries under different ambient temperatures and discharge rates by means of using a coupled electric-thermal model. The study found that the largest percentage of polarization is ohmic polarization, followed by concentration polarization and electrochemical polarization. The values of the three types of polarization are generally small and stable under normal-temperature environments and low-discharge rates. However, they increase significantly in low-temperature environments and high-discharge rates and continue to rise during the discharge process. Additionally, ohmic heat generation and polarization generation also increase significantly under these conditions. Reversible entropy heat is less sensitive to ambient temperature but increases significantly with the increase of the discharge rate. Ohmic heat generation and polarization heat generation contribute to the total heat generation of the battery at any ambient temperature, while reversible entropy heat only contributes to the total heat generation of the battery at the end of discharge.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Currently, electric vehicles powered by lithium-ion batteries face several challenges including limited driving range [1], slow charging times [2,3], battery temperature inconsistencies [4,5,6], and the risk of thermal runaway [7,8,9]. To address the problem of limited range, researchers focused on improving the energy density of lithium-ion batteries. This is achieved through innovations in electrode materials, battery weight reduction, and pack optimization. The energy density of ternary system batteries has already reached 200-300 Wh/kg, and further developments such as high nickel ratio [10,11,12], silicon carbon cathodes [13,14,15,16], and CTP or CTC technology [17] promise even higher energy densities. Most electric vehicles rely on a 400 V voltage platform and increasing charging current to achieve faster charging, but this can exacerbate internal polarization effects leading to reduced chargeable and dischargeable capacity, substance decomposition, and lithium precipitation [18,19,20]. These effects are more pronounced at low temperatures and high charge or discharge rates, indicating a need for further research in these areas.
Polarization is the difference between the terminal voltage and the equilibrium potential, which is more evident at low temperatures and high currents. Lithium-ion batteries undergo complex electrochemical reactions during charging and discharging, and temperature plays a crucial role in their performance, as well as the risk of thermal runaway [21,22]. At low temperatures, the electrode polarization phenomenon intensifies due to the battery's lithium-ion diffusion velocity being lessened and the reaction rate at the electrode-electrolyte interface being slower. This causes the internal resistance to significantly rise, which lowers the ability to discharge energy. Charging or discharging the battery at a high rate at very low temperatures may cause lithium precipitation, and if the growing lithium dendrites pierce the battery separator, it might result in a thermal runaway and an internal short circuit [23,24]. The polarization phenomenon and heat production mechanism of the battery are complex and influenced by various factors such as battery characteristics (internal resistance and entropy thermal coefficient), operating conditions (ambient temperature and load current), and the scheme, structure, and control strategy of the battery thermal management system. Therefore, it is essential to investigate how changes in the battery's internal polarization and heat generation characteristics by using electrical and heat production models.
Polarization is a phenomenon where the terminal voltage of a lithium-ion battery deviates from the equilibrium potential when current passes through it. Regardless of the current load, the battery undergoes polarization, to a varying degree. There are three types of polarization: ohmic, electrochemical, and concentration polarization [25,26]. Ohmic polarization is due to ohmic resistance, electrochemical polarization is caused by the electrochemical reaction rate being lower than the electron transport rate, and concentration polarization is due to the lithium-ion diffusion rate being lower than the electrochemical reaction rate. Ohmic polarization occurs in conductive structures, such as electrode materials and collectors, while electrochemical polarization occurs at the electrode and electrolyte solid-liquid reaction interfaces, and concentration polarization occurs in electrode materials and electrolytes. The polarization phenomenon reduces the power density of the battery, which results in reduced energy conversion efficiency and more energy waste. It also reduces the cycle stability of the battery and affects the structural stability of the electrode material and SEI membranes. The polarization phenomenon is influenced by the temperature and charge-discharge rate of the battery, especially in low-temperature environments and at high-discharge rates, showing sudden changes in load current connection and disconnection instantaneous voltage, early termination of discharge, and reduction of discharge plateau period. Ohmic polarization and concentration polarization cause the largest polarization voltage drops, with electrochemical polarization causing smaller ones. In numerical models, the resistor-capacitance (RC) equivalent circuit model and the pseudo-two-dimensional (P2D) electrochemical model effectively demonstrate the battery polarization phenomenon. Researchers have also developed new models to study the polarization phenomenon and improve simulation accuracy. He analyzed both short-time-scale and long-time-scale polarization characteristics using an equivalent circuit model and explored different model parameters under various initial polarization conditions and current ratios [27]. The root-mean-square errors of the voltage and current simulations were reduced by 79.65 % and 79.27 %, respectively, compared to the conventional RC model. Lin employed the battery electrochemical mode to create a new polarization voltage model based on current and time [28]. Simulation results showed that when charging the battery from 0 % SOC (state of charge) to the cutoff voltage at a rate of 3 C, the errors in terminal voltage and polarization voltage at the cutoff voltage were 1.4 % and 4.9 %, respectively. The average errors for the entire process were 1.14 % and 4 %, respectively. Fan investigated the polarization characteristics of lithium-ion batteries under different charging methods [29]. They analyzed the time-varying characteristics of the three polarizations and the relationship between battery voltage, polarization voltage, and SOC at different constant current charging rates based on the spatial distribution of battery voltage and electrolyte salt concentration. The results indicated that polarization voltage was directly influenced by charge current and SOC, and in turn affected the battery voltage.
The temperature of a battery is influenced by several factors, such as heat generation, transfer, and dissipation. Therefore, accurately determining the heat generation characteristics of the battery is crucial for battery modeling and thermal management [30,31,32]. In 1958, JM Sherfey developed an isothermal calorimeter to measure the thermal effect of batteries [33]. Later, Bernardi derived the battery heat balance equation in 1985, which includes four main heat production components: reversible entropy heat, ohmic heat, polarization heat, and side reaction heat [34].
The battery heat production rate can be calculated by using the current, open circuit voltage, terminal voltage, temperature, and entropy heat coefficient. This equation is widely used to calculate the battery heat production rate. The heat generation characteristics of the battery can be measured by using equipment such as adiabatic accelerated calorimetry (ARC) and differential scanning calorimetry (DSC). The Bernardi battery heat generation rate calculation equation is commonly used in numerical models. However, to optimize the efficiency of the coupling calculation of the electric field and the thermal field, some researchers use the heat production power of a single battery as a fixed value. This approach can only reflect heat production under specific working conditions. To accurately model and manage the temperature of batteries, it is crucial to understand the combined effects of battery heat generation, transfer, and dissipation. Zhu compared theoretical calculation results of the Bernardi model with and without considering reversible entropy heat to experimental results obtained by ARC testing, showing better agreement when considering reversible entropy heat [35]. Chen [36] and Ren [37] both established electrochemical-thermal coupling models to analyze the effects of electrochemical parameters on heat generation, and proposed models to predict total heat production at various discharge rates.
The current research on battery polarization and heat generation characteristics has primarily focused on the influence of discharge rate, with less attention given to ambient temperature, different types of polarization, and quantitative analysis of heat generation. This paper aims to address this gap by using a coupled electric-thermal model that is both accurate and efficient. The key parameters of the model are obtained through testing the entropy heat coefficient and convective heat transfer coefficient, which enables investigation of the reversible entropy thermal effects under high-ambient temperature and low-discharge rate conditions. A pulse discharge test is conducted at different ambient temperatures to identify the offline parameters of the equivalent circuit model's resistance and capacitance. Using the established electric-thermal coupling model, this study quantitatively examines the polarization and heat production characteristics of the battery, analyzes the impact of ambient temperature and discharge rate on three types of polarization and three types of heat production, and explores the dominant types under different operating conditions.

2. Experiment Setup and Calibration Method

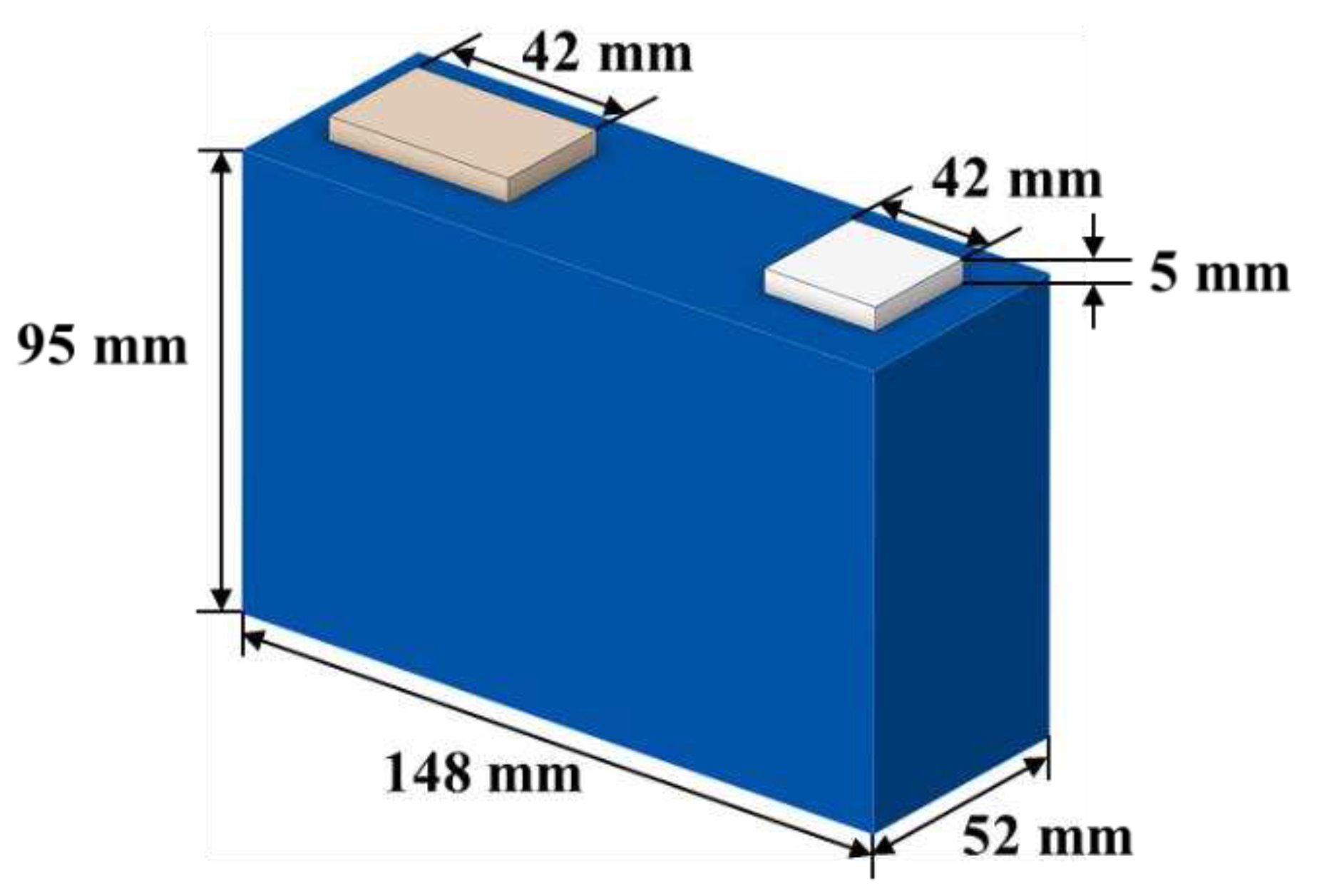
2.1. Specifications of Battery and Equipment

For this study, a commercial ternary square shell lithium-ion battery was used, with graphite as the negative electrode material and Li[Ni8/10CO1/10Mn1/10]O2 as the positive electrode material, and its key characteristics are presented in Table 1.
The equipment involved in the battery performance test process includes battery charge/discharge test system, high and low-temperature humidity test chamber, thermocouple, and other equipment. Figure 1 depicts the signal input and output relationship among the various devices, and Table 2 provides detailed information about the equipment. During the actual experiment, each condition will be repeated three times to ensure accuracy and consistency.

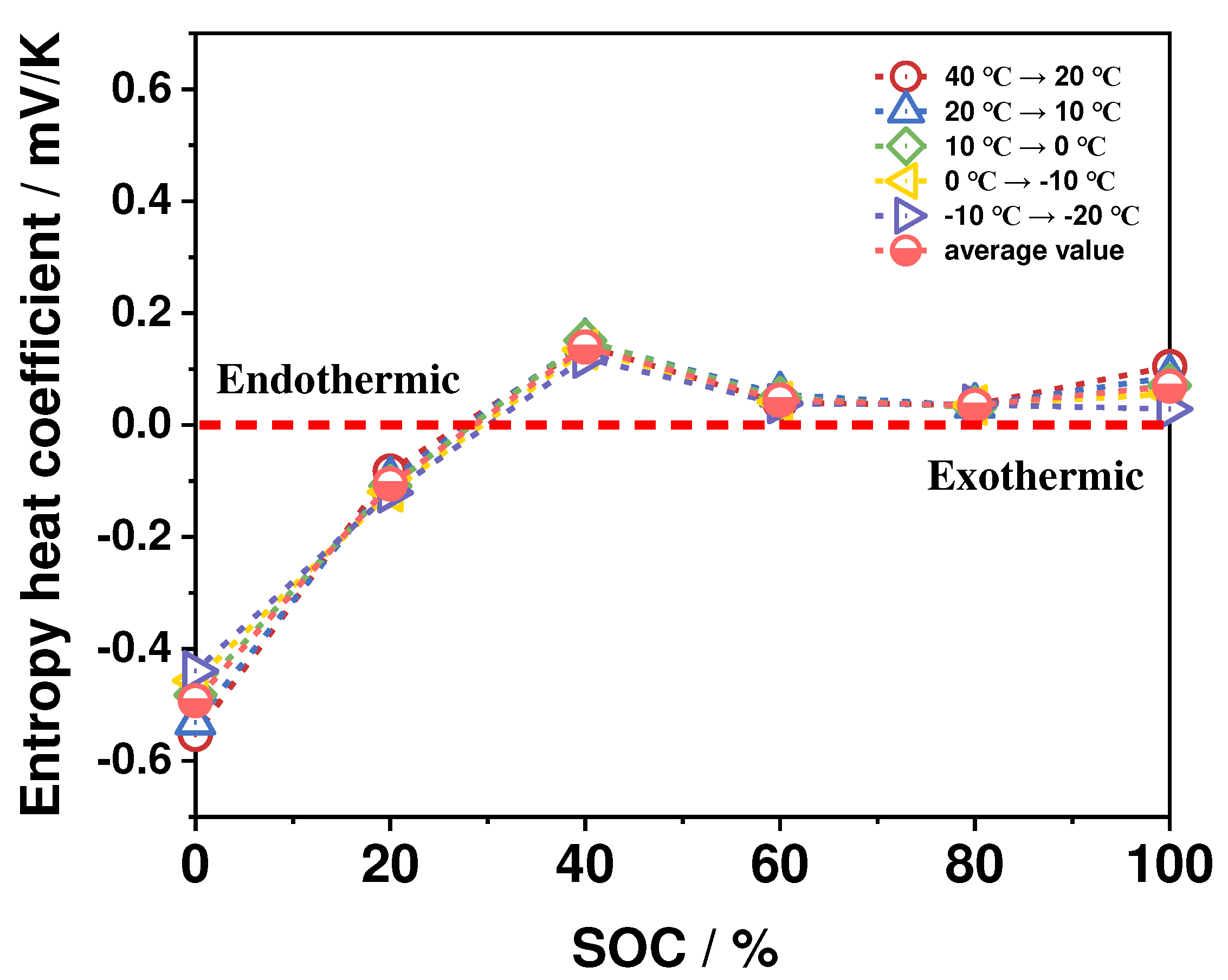
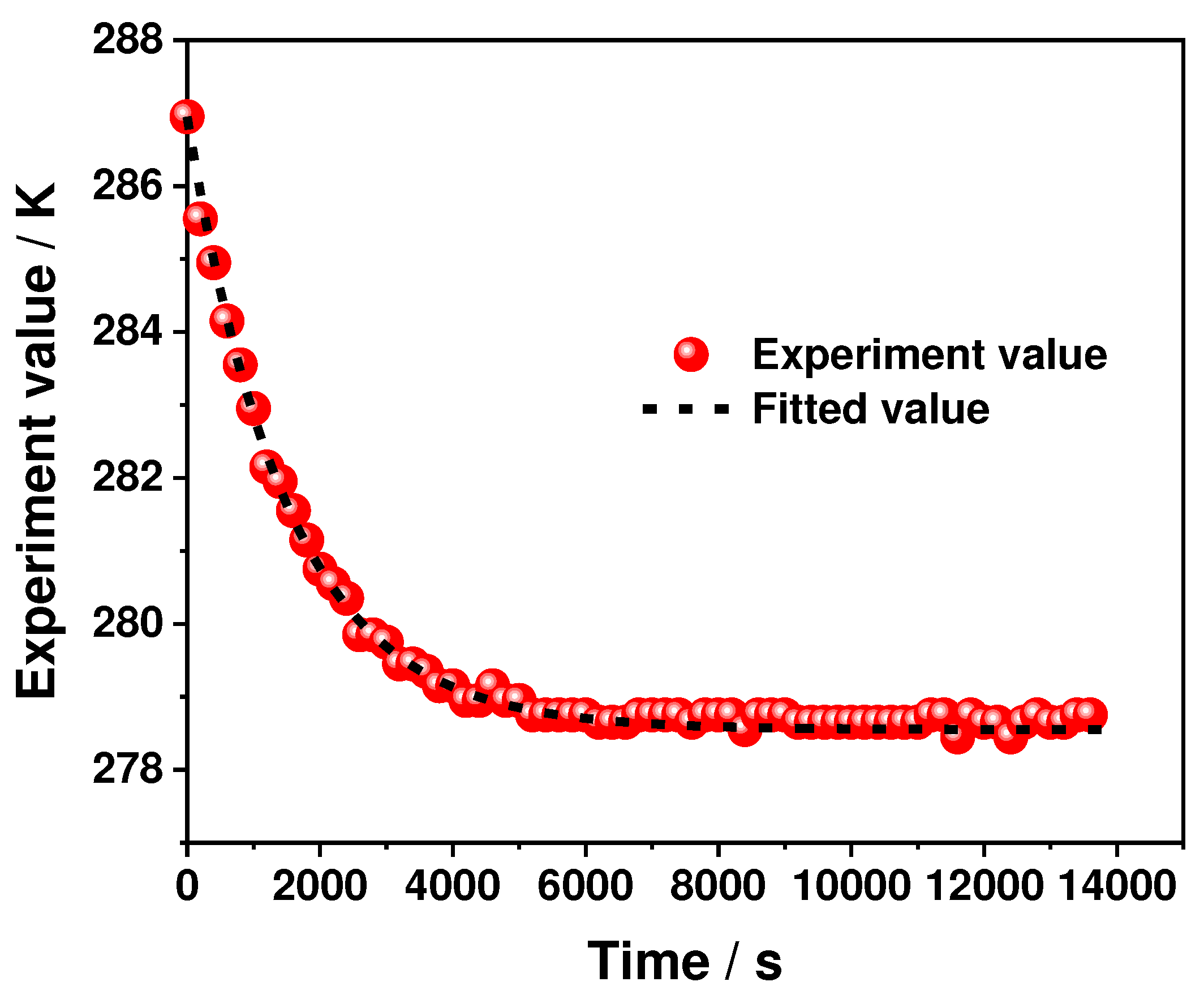
2.2. Determination of the Entropy Heat Coefficient

The reversible entropy heat of the battery varies with different SOC and may exhibit exothermic or endothermic reactions, and can cause a direct decrease in the battery temperature. Therefore, it has a significant impact on the accuracy of the battery thermal model. As the battery temperature and open circuit voltage directly affect the entropy heat coefficient, the open circuit voltage of the battery was measured at various ambient temperatures and different SOCs to determine the entropy heat coefficient. Figure 2 illustrates the relationship between voltage and ambient temperature over time during the entropy heat experiment.
After a long period of shelving state, the internal physicochemical properties of the battery can be assumed to reach a stable condition, and the voltage of the battery at this time can be treated as equivalent to the open-circuit voltage. The entropy heat coefficient of various SOCs can be calculated based on the open circuit voltage change caused by the ambient temperature change, as shown in Figure 3. The entropy heat coefficient displays an increase-decrease-increase trend, with a maximum value at approximately 40 % SOC. When the battery capacity is less than 30 % SOC, the entropy heat coefficient is negative, and the reversible entropy heat term promotes total heat production of the battery, resulting in an increase in battery heat production and temperature. When the entropy heat coefficient is positive, the irreversible entropy heat is negative, which inhibits total heat production of the battery, leading to an endothermic reaction and causing a drop in battery temperature. Thus, the entropy heat coefficient is of great significance for accurately modeling heat generation in power batteries.

2.3. Convective Heat Transfer Coefficient Test

The convective heat transfer coefficient is a critical parameter for accurately modeling the heat generation of the battery and reflects the battery's ability to exchange heat with its surroundings. To obtain this coefficient, the temperature change characteristics of the battery in an incubator are tested. The test involves two stages: a constant current discharge stage and a shelving stage. Firstly, the fully charged battery is discharged to the cut-off voltage under a constant current discharge mode. Then, it is shelved while the temperature of the incubator is adjusted to 5 ℃ until the battery temperature stabilizes at 5 ℃. The temperature change is recorded during the shelving process to obtain the convective heat transfer coefficient of the battery surface.
When the battery is stewing, the heat balance equation (1) is satisfied:
C p m d T d t + h A ( T − T ∞ ) = 0
where Cp represents the battery-specific heat capacity, J/ (kg·K); m represents the battery mass, kg; T is the battery temperature, K; t is the time, s; h is the convective heat transfer coefficient, W/ (m2·K); A is the battery surface area, m2; T∞ is the final stable battery temperature, K.
Equation (1) can be transformed to get equation (2):
h A − C p m = 1 T − T ∞ d T d t
Equation (3) will result from the simultaneous integration of both sides.
∫ 0 t h A − C p m d t = ∫ T 0 T ∞ 1 T − T ∞ d T
Equation (4) can be formulated as a result:
T = T ∞ + ( T 0 − T ∞ ) e − h A C p m t
Figure 4 shows the temperature change during the shelving stage after the battery is discharged at a rate of 1 C and a temperature of 25 °C. Equation (4)'s curve fitting technique can be used to determine the convective heat transfer coefficient, resulting in a value of h = 20.6 W/(m2·K).

2.4. Other Thermal and Physical Parameters

There are numerous components that make up the internal structure of lithium-ion batteries, including separators, current collectors, positive and negative electrode materials, and others, which can number in hundreds. However, current internal lithium-ion battery models do not consider the layers of these materials. Instead, it is assumed that the internal materials are homogeneous and that the physical properties of each layer remain constant. The average specific heat capacity and thermal conductivity of the battery are determined by using a weighted average approach. The necessary thermophysical parameter values are presented in Table 3.

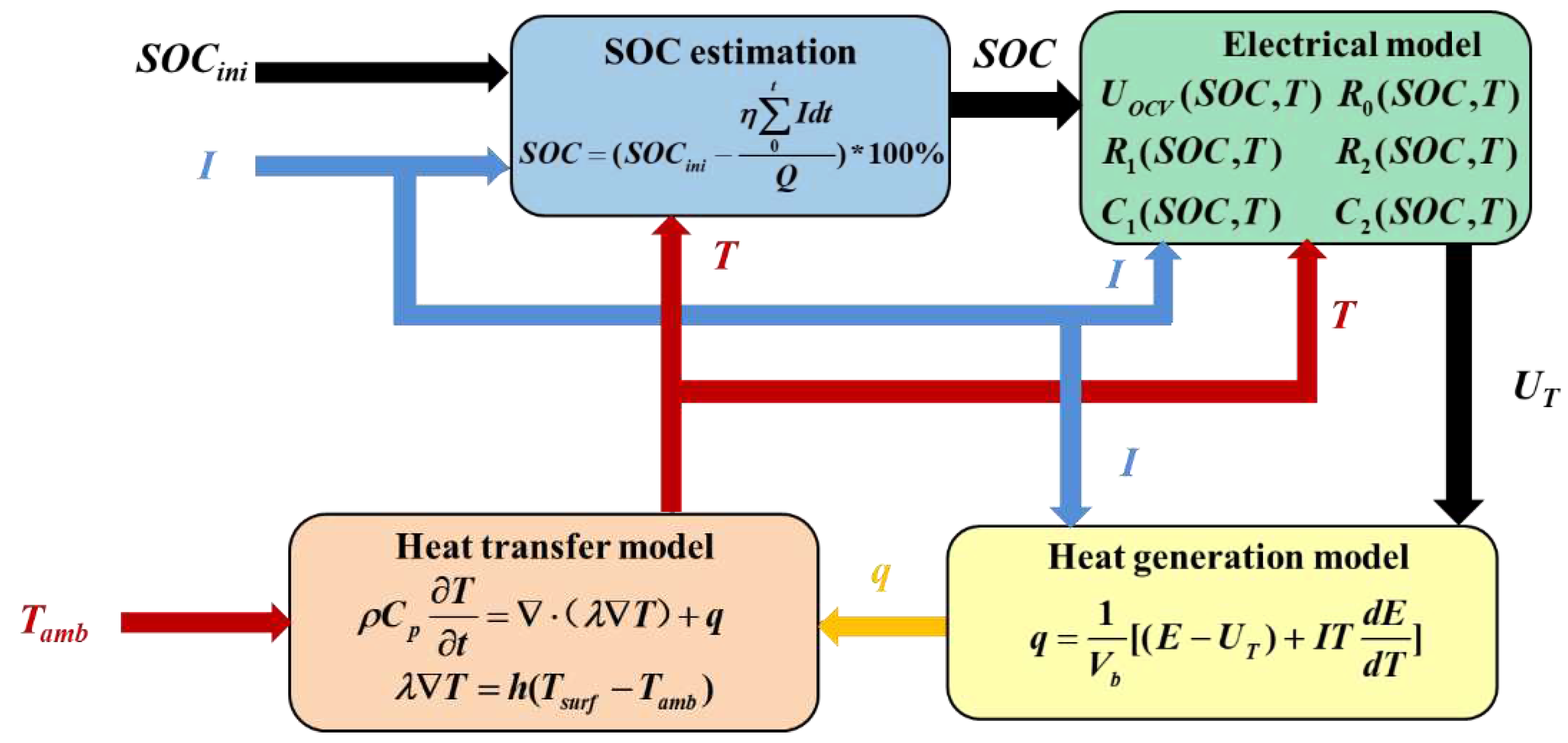
3. Construction of the Electric-Thermal Coupling Model

This part uses a pulse discharge test scheme to identify and collect the electrical parameters of the second-order RC model, which is based on the fundamental principles of the equivalent circuit model. The relationship between the SOC, ambient temperature, and the variation rules of open-circuit voltage, ohmic resistance, polarized internal resistance, and polarized capacitance are examined. Subsequently, a battery module's electric-thermal coupling model is established by using COMSOL software, and by contrasting it with the outcomes of the experiment, the simulation model is verified.

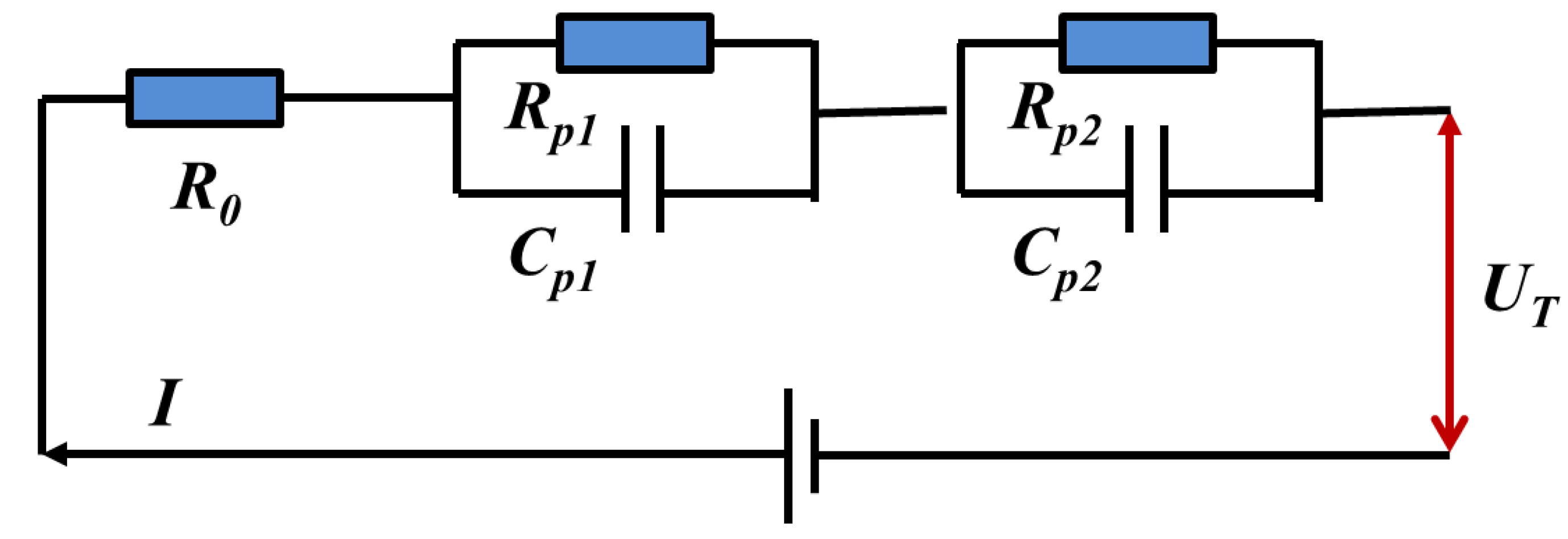
3.1. Electrical Model of the Battery

The equivalent circuit model that uses electrical components, such as resistance and capacitance, has better overall performance compared to the electrochemical model in terms of model complexity, prediction accuracy, and response time. Hence, it is widely employed in battery management systems. This paper adopts a second-order RC model to depict the battery's electrical features. The model has a simple structure and can accurately illustrate the battery’s polarization characteristics, demonstrating its nonlinear characteristics. The second-order RC equivalent circuit model comprises an ideal voltage source, an ohmic resistance, and two RC circuits, as illustrated in Figure 5.
The above electrical parameters are changing with the battery SOC, where SOC=0 % means fully discharged, and SOC=100 % means fully charged, which be calculated by equation (5):
SOC = ( 1 − η ∑ 0 t I d t Q ) * 100 %
where, η is the discharge efficiency of the battery, %; Q is the rated capacity of the battery, Ah. I is the current flowing through the battery, A, stipulating that charging is positive and discharging is negative.

3.1.1. Electrical Parameter Identification Method

  • Determination of the open circuit voltage in the initial shelving stage;
The battery terminal voltage response characteristics during a single-pulse discharge are analyzed, as shown in Figure 6. Since the battery has been left for a long time before the single-pulse discharge, it is generally assumed that the open circuit voltage of the battery is numerically equal to the terminal voltage of the battery. Therefore, according to the pulse discharge test results, the battery terminal voltage U(t0) is taken as the open circuit voltage UOCV.
2.
Calculation of the ohmic resistance by voltage mutation;
The value of the ohmic resistance in the state of charge can be calculated by the following equation (6):
R 0 = ( U ( t 0 ) − U ( t 1 ) ) + ( U ( t 3 ) − U ( t 2 ) ) 2 I
Among them, U(t0), U(t1), U(t2), and U(t3) are the battery terminal voltage at different times t. I represents the absolute value of the current during the pulse current application process, and the state of charge of the battery does not change at the instant the current is applied or withdrawn.
3.
Identification of RC parameters in the shelving stage;
From t3 to t4 is the shelving period, and the battery terminal voltage meets the zero-input response condition during this period, as shown in equation (7):
U T = U O C V − U 1 ( t 3 ) e − t τ 1 − U 2 ( t 3 ) e − t τ 2
Among them, U1(t3) and U2(t3) represent the voltages at both ends of the RC circuit corresponding to the moment when the current is removed. The expressions are equation (8) and (9):
U 1 ( t 3 ) = I R 1
U 2 ( t 3 ) = I R 2
In the period between t3 and t4 during a pulse discharge, the least square method is used to obtain the parameters U1(t3), U2(t3), t1, and t2 from the voltage-time relationship. C1 and C2 are determined from the relationship between the resistance and capacitance parameters and the time constant. Given the SOC remains unchanged before and after the pulse discharge, the open circuit voltage recorded before the discharge is taken as the SOC after the discharge, and the values of UOCV, R0, R1, R2, C1, and C2 can be obtained for that SOC. These parameters are crucial in accurately describing the battery's electrical characteristics by using the second-order equivalent circuit model. Among them, R0, R1, R2, C1, and C2 are closely related to the SOC and are affected by changes in ambient temperature. Thus, parameter identification is necessary under different SOCs and temperature conditions.

3.2. Thermal Model of the Battery

3.2.1. Heat Generation Model of the Battery

Most of the heat produced inside a lithium-ion battery comes from reversible entropy heat Qr, ohmic heat Qj, polarization heat Qp, and side reaction heat Qs. However, side reactions typically do not occur during normal charging or discharging under normal temperature conditions. Therefore, when calculating the total heat generation, only ohmic heat, polarization heat, and reversible entropy heat need to be taken into account, as shown in equation (10):
Q t o t a l = Q j + Q p + Q r
The calculating model that most frequently employed is the Bernardi battery heat generation rate model [34], which presupposes that the battery's internal heat supply is steady and uniform, as indicated by equation (11):
q = Q t o t a l V b = 1 V b [ ( I 2 R p + I 2 R j ) + I T d E d T ] = 1 V b [ ( E − U T ) + I T d E d T ]
where, I is the battery charge and discharge current, A; Vb is the battery volume, m3; E is the battery electromotive force whose value is equal to the open circuit voltage, V; UT is the battery operating voltage, V; T is the battery temperature, K.

3.2.2. Heat Transfer Model of the Battery

Heat conduction and heat convection are the primary modes of heat transfer for lithium-ion batteries during typical operation. However, heat radiation is typically negligible due to the low temperatures involved.
The interior of the battery follows the basic equation of solid heat transfer as equation (12):
ρ C p ∂ T ∂ t = ∇ ⋅ （ λ ∇ T ） + q
where, ρ is the battery density, kg/m3; Cp is the specific heat capacity of the battery, J/(kg·K); λ is the thermal conductivity of the battery, W/(m·K); q is the volumetric heat production rate of the battery, W/m3.
Equation (13) can be used to describe the convective heat transfer process on the exterior surface of the battery when the external medium is air, coolant, or other fluids:
λ ∇ T = h ( T s u r f − T a m b )
where, h is the surface convective heat transfer coefficient, W/(m2·K); Tamb is the temperature of the external heat transfer medium, K; Tsurf is the battery surface temperature, K.

3.3. Electric-Thermal Coupling Model

Figure 7 illustrates the schematic representation of the electric-thermal coupling approach. The heat generation model estimates the battery's volumetric heat production rate based on the difference between the battery's terminal voltage and open circuit voltage, current, and battery entropy heat coefficient. The electrical model predicts the battery's SOC and terminal voltage during charging and discharging by taking into account initial SOC, battery current, open circuit voltage, and ohmic resistance. The battery's volumetric heat production rate and the ambient temperature are utilized as inputs in the heat transfer model to forecast the battery temperature. To link the electrical and thermal models of the battery in the simulation, the battery temperature, combined with the SOC, adjusts the open circuit voltage, ohmic resistance, and other electrical model parameters related to temperature and SOC dynamically.

3.3.1. COMSOL Model Building

In this paper, the battery heat generation simulation is performed by using the COMSOL Multiphysics software. To avoid excessive consumption of computational resources, a reasonably simplified geometric model of the battery is used. The stacked pole pieces are considered as a non-layered structure, and the battery core, top cover, and shell are integrated. Additionally, small internal air spaces and safety valves, as well as the chamfering of the pole and the insulating cover, are ignored. Figure 8 depicts the final battery three-dimensional geometric model.

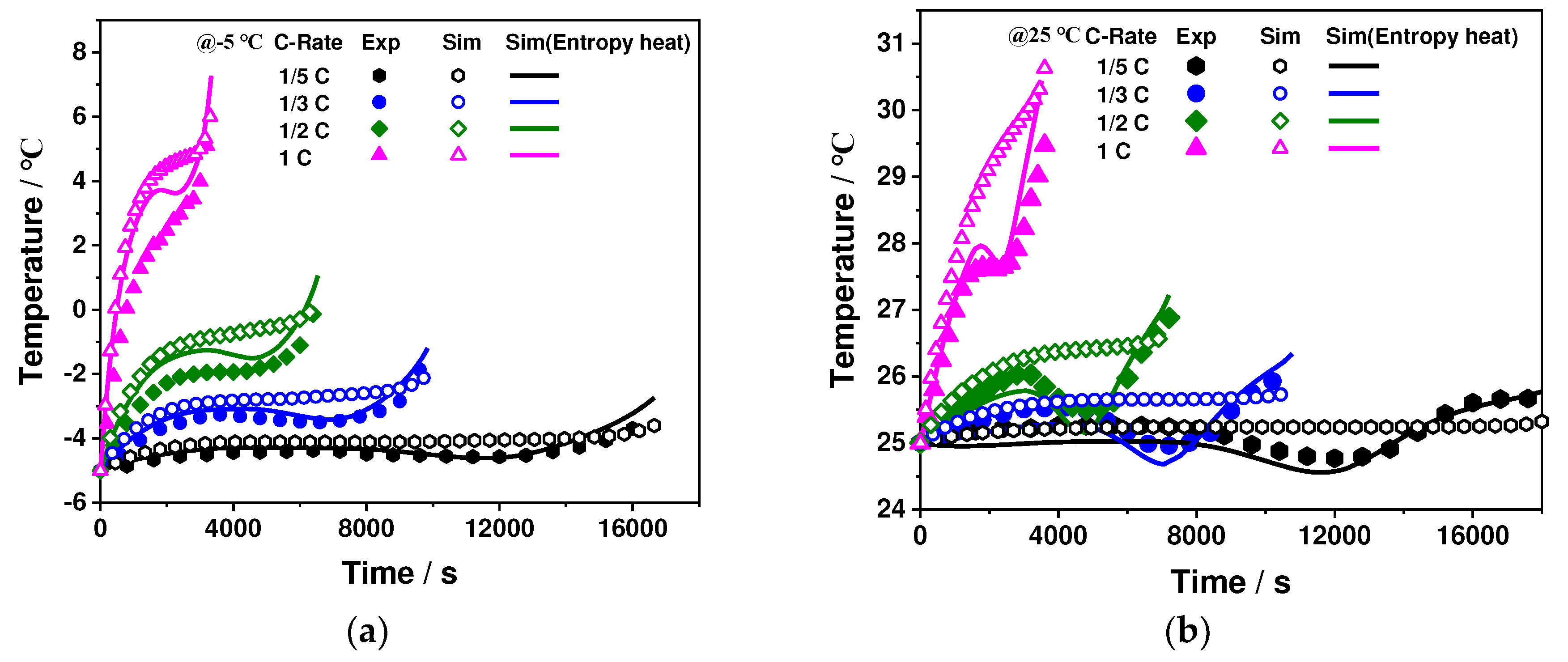
3.4. Battery Electrical and Thermal Performance Verification

3.4.1. Electrical Characteristics Verification

The voltage simulation data were compared and validated with the related test data obtained at various discharge rates and ambient temperatures, respectively, as shown in Figure 9. The voltage-changing trend observed in both the modeling and experimental results was similar, and the deviations were very small. Furthermore, it is believed that the impact of reversible entropy heat on the precision of the voltage simulation value was negligible.

3.4.2. Thermal Characteristics Validation

Figure 10 depicts the comparison and validation of the temperature simulation data with experimental data for various discharge rates and ambient temperatures. The results of both the experiment and simulation show excellent consistency in the battery temperature and its changing trend. The temperature initially increases, drops slightly, and then rises sharply during the discharge process. Furthermore, the reversible entropy heat in the simulation leads to more accurate results compared to those results by the simulation that ignore this factor.

4. Result and Discussion

4.1. Polarization Characteristics of the Battery

This section analyzes the effects of ambient temperature and discharge rate on the battery's ohmic polarization, concentration polarization, and electrochemical polarization. These effects are investigated under different temperature conditions, including -15 ℃, -5 ℃, 25 ℃, and 35 ℃, and various discharge rates, including 1/5 C, 1/2 C, 1 C, and 2 C. These conditions are selected to represent a range of realistic operating conditions.

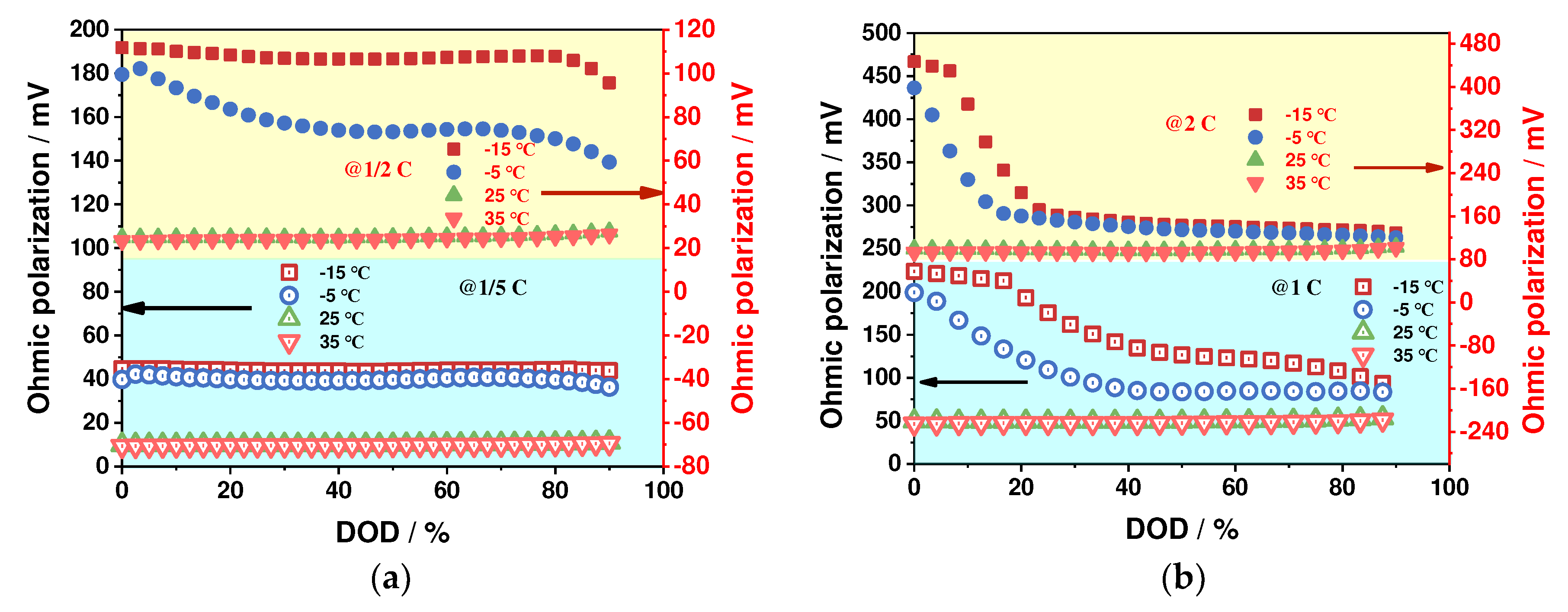
4.1.1. Ohmic Polarization Characteristics

Figure 11 illustrates the impact of ambient temperature and discharge rate on the ohmic polarization of the battery. At low temperatures, particularly below 0 ℃ (such as -15 ℃ and -5 ℃), the ohmic polarization increases significantly and decreases overall with an increase in DOD (depth of discharge). In contrast, the ohmic polarization is considerably low at high temperatures (25 ℃ and 35 ℃) and remains almost constant throughout the discharge. Since the battery temperature change during discharge is higher under low-temperature conditions than high-temperature conditions for the same discharge rate, the ohmic resistance change value is larger under low-temperature conditions than that at high-temperature conditions. Furthermore, since the battery temperature rises during discharge, the ohmic polarization decreases with discharge in low-temperature environments, however, with small or almost constant values observed in ambient and high-temperature environments. Moreover, as the discharge rate increases, the ohmic polarization rises significantly due to an increase in current. Under low-temperature conditions, it is affected by the change in ohmic resistance, while in ambient and high-temperature environments, it is proportional to the discharge rate change. Thus, if the discharge rate increases from 1/5 C to 2 C, the initial ohmic polarization increases by approximately ten times.

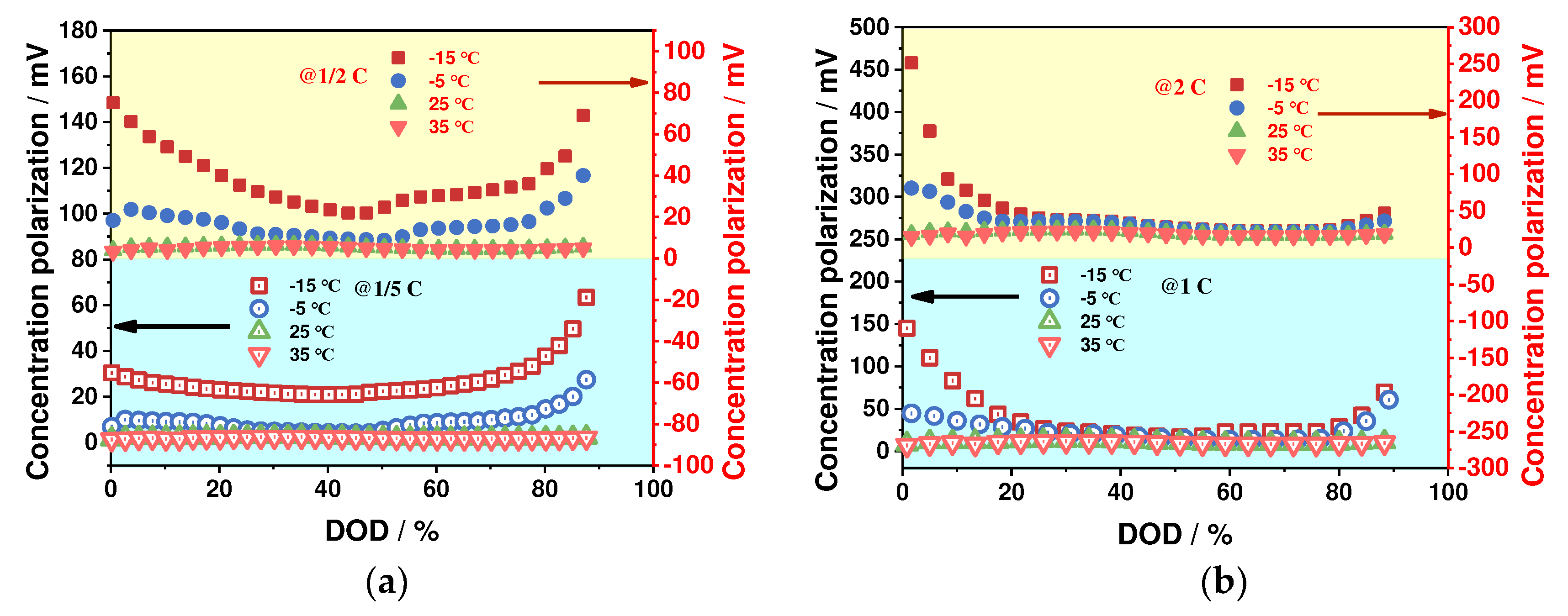
4.1.2. Concentration Polarization Characteristics

Figure 12 depicts the impact of ambient temperature and discharge rate on concentration polarization. The concentration polarization increases noticeably as the ambient temperature decreases. Moreover, it exhibits a “U” shape trend with the increase of DOD under low-temperature conditions, while remaining relatively stable under ambient and high-temperature conditions. The higher concentration polarization at the initial discharge stage may be due to the higher overpotential required to initiate the motion of lithium ions from a static state to a moving state when the current is connected. The high concentration polarization at the end of discharge may be attributed to the movement of lithium ions from the negative to the positive electrode inside the battery, where the lithium-ion concentration at the negative electrode is much lower than that at the positive electrode. Nevertheless, the lithium-ions still move towards the high-concentration areas, resulting in a reverse concentration gradient, which is unfavorable for the diffusion process according to Fick’s law. Therefore, a considerable overpotential is needed, causing a serious polarization phenomenon. The low-temperature environment severely exacerbates this physicochemical behavior, changing the motion state of lithium ions.
Additionally, concentration polarization increases with the increase of the discharge rate. This is because of the excessive accumulation of electrons at the positive electrode, which requires the transfer of more lithium ions from the negative electrode to the positive electrode per unit time. However, the diffusion rate of lithium ions is limited, which hinders the electrochemical reaction at the positive electrode, resulting in an increase in concentration polarization.

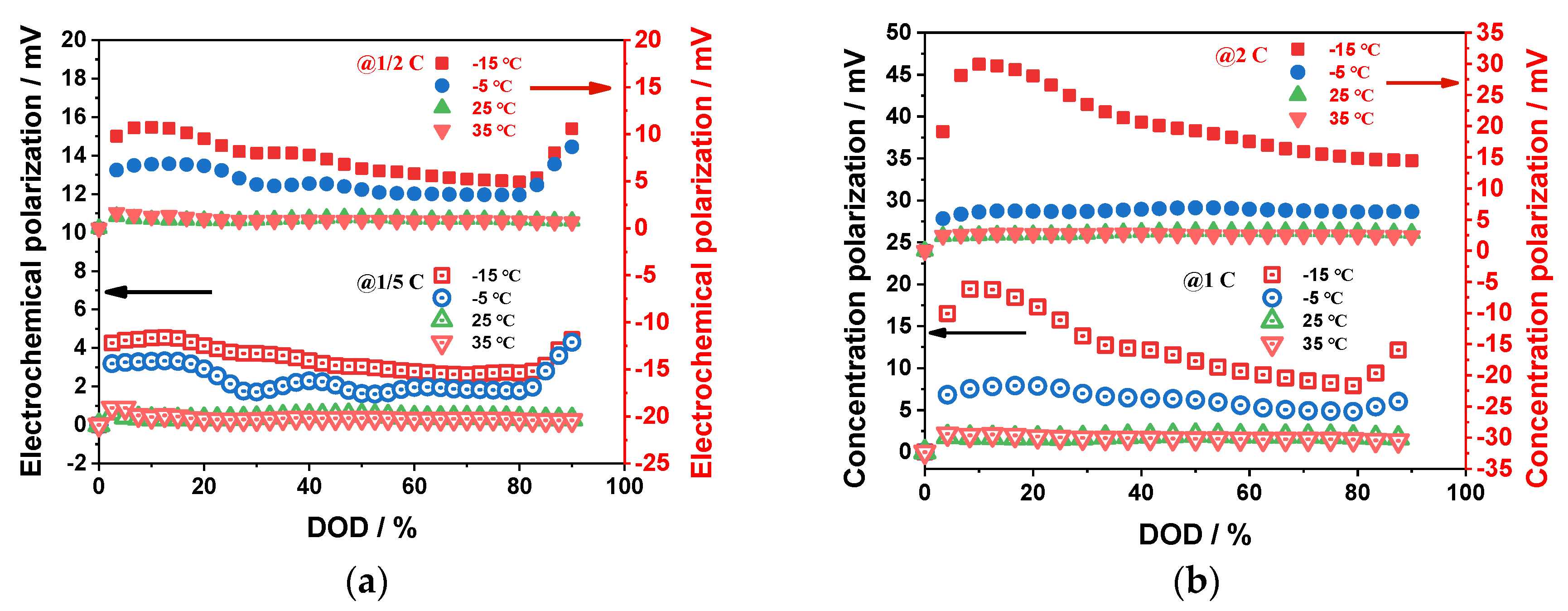
4.1.3. Electrochemical Polarization Characteristics

Figure 13 illustrates the impact of ambient temperature and discharge rate on electrochemical polarization. Electrochemical polarization increases with decreasing ambient temperature, and it rises sharply at the beginning of the discharge process, then gradually decreases and finally increases again at the end of the discharge process under low temperature condition. In contrast, electrochemical polarization is relatively stable and maintained at a low level at room-temperature and in high-temperature environments. This may be because the electron transport rate is significantly faster than the lithium-ion transport rate, and at the beginning of the discharge process, the electrons arrive at the anode before the lithium ions, leading to a slower electrochemical reaction and thus causing electrochemical polarization. As the discharge process proceeds, the lithium-ion concentration gradient between the negative and positive electrodes gradually decreases, which facilitates the lithium-ion transport process and thus reduces electrochemical polarization. However, at the end of the discharge process, when the concentration gradient is reversed, the reverse transport process of lithium ions becomes more difficult, resulting in a sharp increase in electrochemical polarization. Moreover, electrochemical polarization increases with increasing discharge rate.

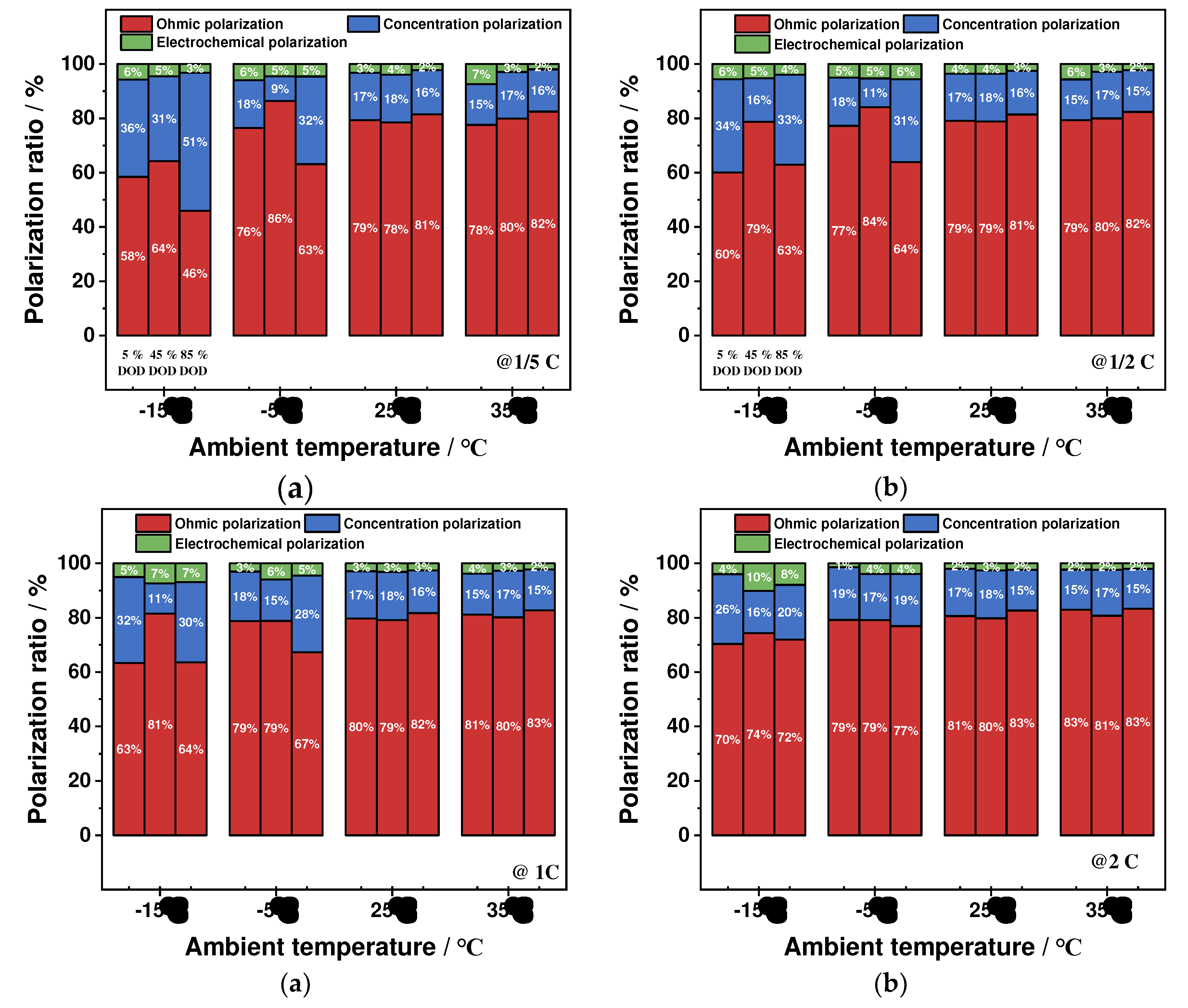
4.1.4. Proportion of Polarization Types

Figure 14 illustrates the impact of ambient temperature and discharge rate on the percentages of different polarizations. The results show that the ohmic polarization has the highest percentage, accounting for approximately 80 % in most cases, followed by concentration polarization at around 17 %, while electrochemical polarization has the lowest proportion, approximately 3 %. With an increase in the ambient temperature, the proportion of ohmic polarization gradually increases, while the percentage of concentration polarization and electrochemical polarization declines gradually.
Moreover, under the low-temperature environment of -15 ℃ and -5 ℃, the percentages of concentration polarization at 5 % and 85 % DOD are notably higher than those at 45 % DOD. This is because the concentration polarization is more pronounced at the beginning and end of discharge in low-temperature environment. Additionally, the proportion of ohmic polarization increases, and the proportion of the other two polarizations decreases with the increase of discharge rate under low-temperature conditions. In contrast, at room-temperature and high-temperature environments, the percentages of the three polarizations are relatively stable and less affected by the change in discharge rate.

4.2. The Heat Generation Characteristics of the Battery

In this section, the impact of ambient temperature and discharge rate on the production of ohmic heat, polarization heat, and reversible entropy heat in batteries are examined. Specifically, four representative ambient temperature conditions are considered: low temperature conditions of -15 ℃ and -5 ℃, room-temperature environment of 25 ℃, and high-temperature environment of 35 ℃. Additionally, four discharge rate conditions are investigated: lower discharge rates of 1/5 C and 1/2 C, and higher discharge rates of 1 C and 2 C.

4.2.1. Ohmic Heat Generation Characteristics

Figure 15 illustrates the effects of ambient temperature and discharge rate on the generation of ohmic heat. The trend of ohmic heat generation characteristics is similar to that of ohmic polarization characteristics. As the ambient temperature decreases, especially below 0 ℃, the ohmic heat generation increases significantly. Additionally, the ohmic heat generation decreases with an increase in the DOD. Furthermore, the ohmic heat production is significantly lower in ambient-temperature and high-temperature environments, and it remains stable throughout the discharge process.
As the discharge rate increases, the generation of ohmic heat significantly increases with the increased current. The generation of ohmic heat is more affected by the change in ohmic resistance under low-temperature conditions; nevertheless, it is basically proportional to the change in discharge rate under normal and high-temperature conditions. According to Ohm's law, if the discharge rate increases 10 times from 1/5 C to 2 C, the generation of ohmic heat will increase to approximately 100 times. The effect of the discharge rate on ohmic heat production is greater than its effect on ohmic polarization.

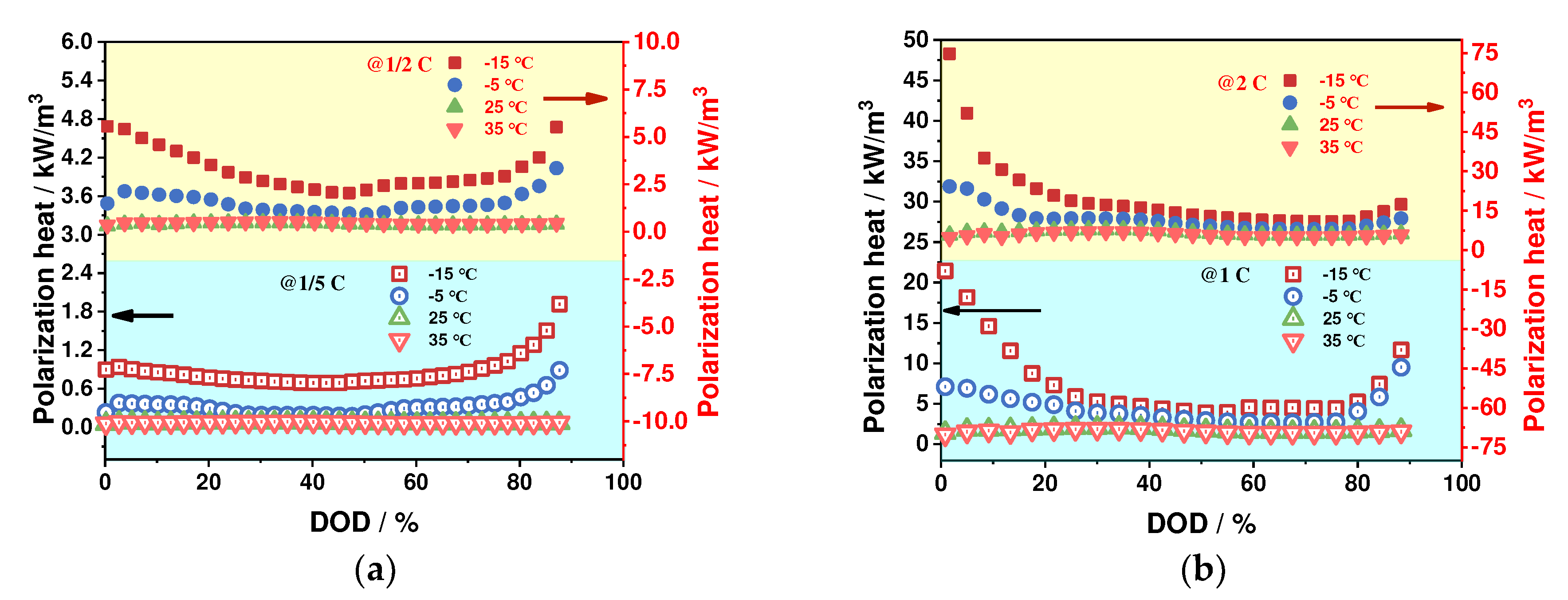
4.2.2. Polarization Heat Generation Characteristics

The effects of ambient temperature and discharge rate on the creation of polarization heat are depicted in Figure 16. Since the electrochemical polarization is smaller than the concentration polarization, the heat production of polarization is dominated by the concentration polarization, and the trend of the heat production of polarization is similar to that of the concentration polarization. As the ambient temperature decreases, the polarization heat production increases significantly. It shows a “U” shape change with the increase of DOD under low-temperature conditions, and it is more stable under room and high-temperature conditions. In addition, the heat production of polarization increases with the increase of the discharge rate.

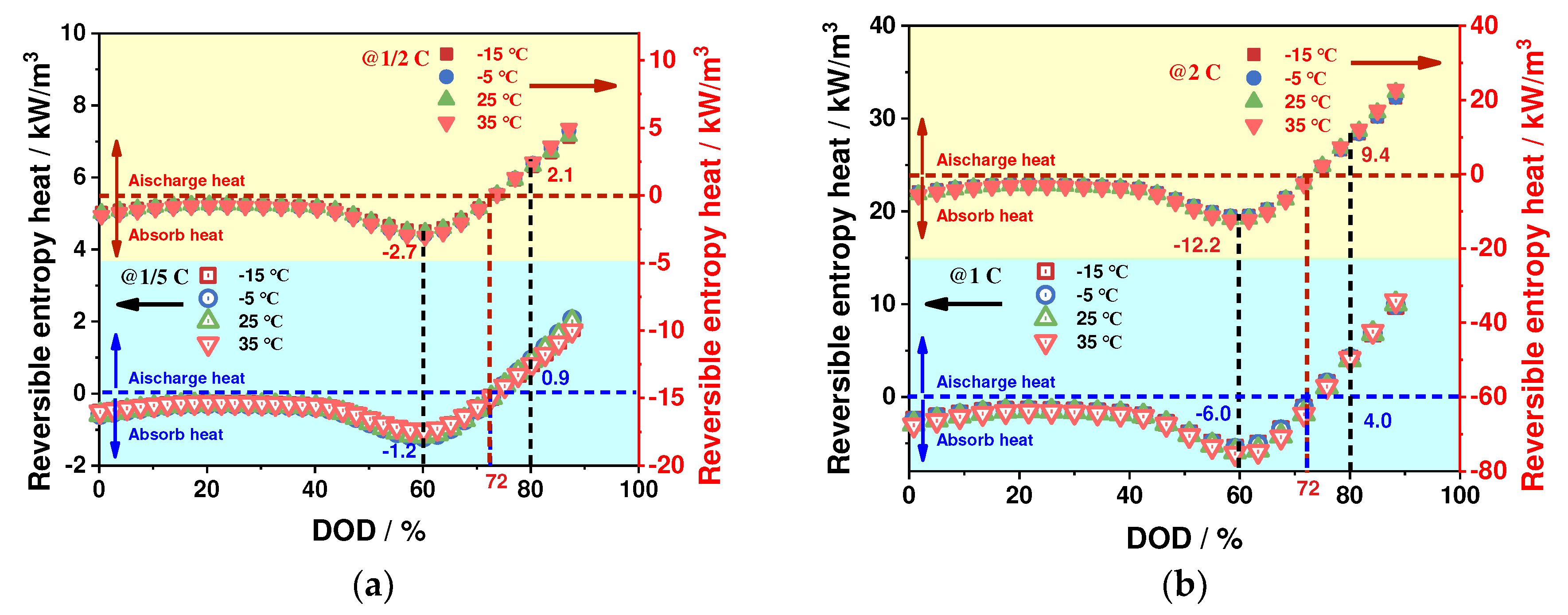
4.2.3. Reversible Entropy Heat Characteristics

In Figure 17, the effects of ambient temperature and discharge rate on reversible entropy heat are shown. The reversible entropy heat is mostly negative in the 0 % to 72 % DOD interval and positive in the 72 % to 90 % DOD interval, with a relatively small value throughout the discharge process. For consistency with other types of heat production, the reversible entropy heat is defined as positive when discharge heat and negative when absorb heat. Thus, the reversible entropy heat suppresses total heat production of the battery in the 0 % to 72 % DOD range and promotes it in the 72 % to 90 % DOD range. It is noteworthy that within the 40% to 60% DOD range, this inhibitory effect becomes increasingly pronounced with the escalation of DOD. Conversely, within the 72% to 90% DOD range, the enhancing influence of reversible entropy enthalpy on total heat production becomes more conspicuously evident as DOD rises.
Overall, the influence of ambient temperature on reversible entropy enthalpy appears relatively minor, whereas the discharge rate exhibits a more pronounced impact on reversible entropy enthalpy. Within the 0% to 72% discharge depth range, reversible entropy enthalpy increasingly restrains battery heat generation with rising discharge rates. Specifically, at 25°C and a 60% depth of discharge (DOD), the reversible entropy enthalpy values for 1/5 C, 1/2 C, 1 C, and 5 C are -1.2, -2.7, -6.0, and -12.2 kW/m³, respectively. However, within the 72% to 90% discharge depth range, reversible entropy enthalpy promotes battery heat generation with increasing discharge rates. For instance, at an 80% DOD, the reversible entropy enthalpy values for 1/5 C, 1/2 C, 1 C, and 5 C are 0.9, 2.1, 4.0, and 9.4 kW/m³, respectively.

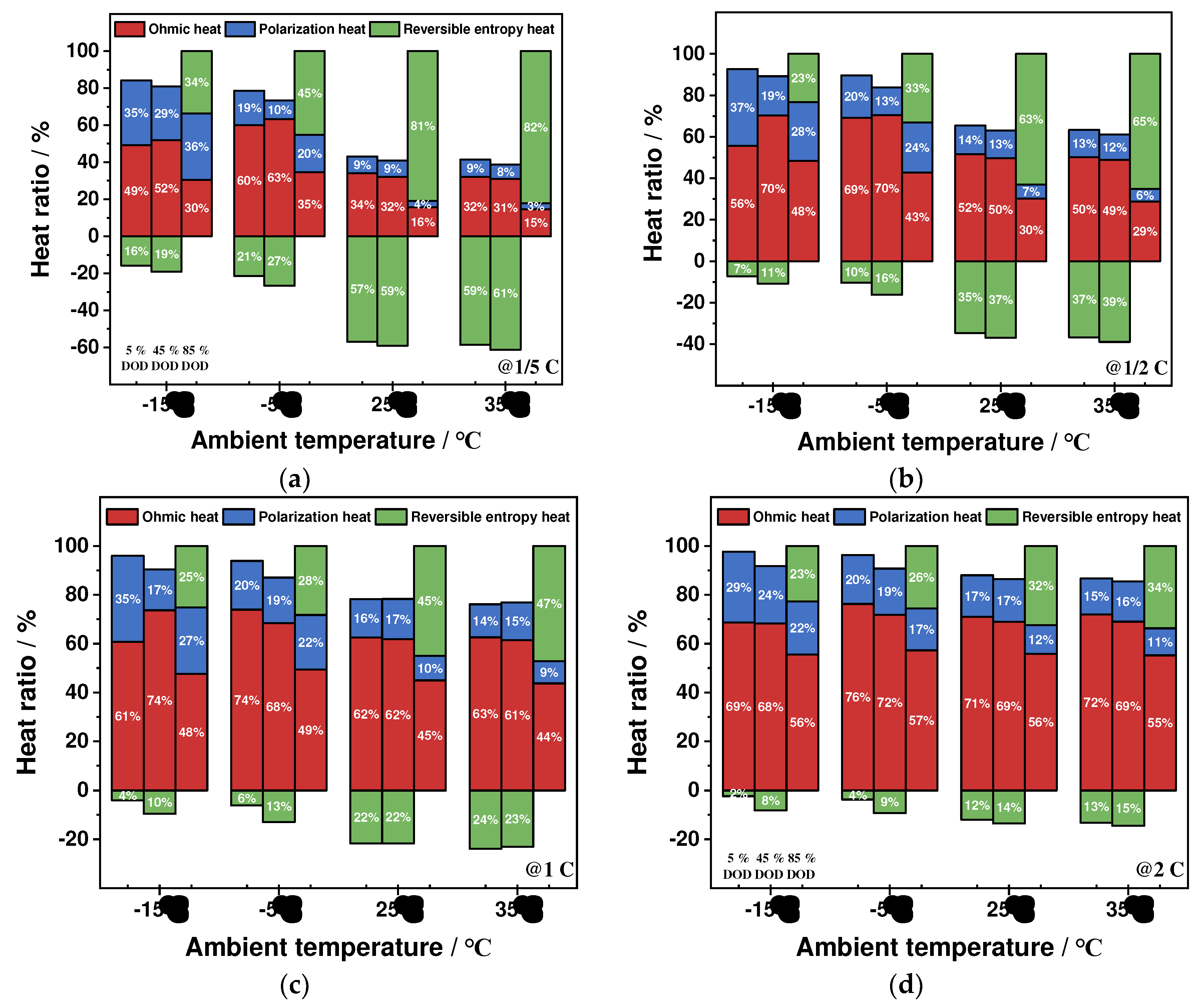
4.2.4. Proportion of Heat Production Types

Figure 18 illustrates the impact of ambient temperature and discharge rate on the proportion of various types of heat generation. Both ohmic heat production and polarization heat production contribute to the total heat production of the battery at any ambient temperature, while reversible entropy heat only promotes the total heat production of the battery at the end of discharge. As the ambient temperature increases, the proportion of ohmic heat generation and polarization heat generation gradually decreases, while the proportion of reversible entropy heat effect increases. Therefore, when simulating battery thermal behavior in a high-temperature environment, it is crucial to consider the entropy heat coefficient and reversible entropy heat to enhance simulation accuracy. As the discharge rate increases, the proportion of ohmic heat production gradually increases, and the proportion of polarization heat production decreases in low-temperature environments, but it increases in normal- and high-temperature environments. The concentration polarization heat generation is highly sensitive to ambient temperature. The proportion of reversible entropy heat effect decreases with the increase of discharge rate, as the ohmic heat production dominates under high-rate discharge since it is proportional to the square of the current, whereas the reversible entropy heat in the Bernardi heat production rate equation is proportional to the current.

5. Conclusions

This study aimed to investigate the electrical-thermal characteristics of batteries through the development of an electric-thermal coupling model. The polarization and heat generation characteristics of the battery were analyzed under various ambient temperatures and discharge rates. The main conclusions are as follows:
  • The electric-thermal coupling simulation model was validated by using experimental data under different ambient temperatures and discharge rates. The comparisons demonstrate that the developed model accurately simulates the electrical and thermal characteristics of the battery under various operating conditions.
  • The impact of ambient temperature and discharge rate on the battery's ohmic, electrochemical, and concentration polarizations is analyzed, revealing that these factors have a significant effect on these polarization types. Specifically, low-temperature environments and high-discharge rates resulted in a significant increase in these polarization values, with the greatest changes observed during the discharge process. In contrast, these values remained stable at ambient temperature and low-discharge rates. The proportion of ohmic polarization was found to be the highest among the three types, accounting for approximately 80 % of the total polarization, while electrochemical polarization was the least significant at about 3 %, and concentration polarization was about 17 %.
  • The ohmic heat production and polarization heat production increase significantly at low-ambient temperatures and high-discharge rates, while the reversible entropy heat is less affected by ambient temperatures and increases significantly with the increase of discharge rates The ohmic heat generation and polarization heat generation contribute to the total heat generation of the battery at any ambient temperature, and the reversible entropy heat contributes to the total heat generation of the battery only at the end of the discharge period. The entropy heat coefficient and reversible entropy heat play an important role in the thermal simulation of batteries at low discharge rates and high ambient temperatures.

Author Contributions

Conceptualization, Jie Liu; Data curation, Jiayong Guo; Supervision, Jie Liu; Writing – review & editing, Jiayong Guo, Qiang Guo, Jie Liu and Hewu Wang. All authors have read and agreed to the published version of the manuscript.

Funding

This study is supported by the National Key Research and Development Program of China (No.2022YFB2502304)

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Voskuijl, M. Cruise Range in Formation Flight. Journal of Aircraft 2017, 54, 2184–2191. [Google Scholar] [CrossRef]
  2. Xue, Q.; Li, J.; Chen, Z.; Zhang, Y.; Liu, Y. Shen, J. Online Capacity Estimation of Lithium-Ion Batteries Based on Deep Convolutional Time Memory Network and Partial Charging Profiles. IEEE Transactions on Vehicular Technology 2022, 72, 444–457. [Google Scholar] [CrossRef]
  3. Mathieu, R.; Briat, O.; Gyan, P. Vinassa, J.-M. Fast charging for electric vehicles applications: Numerical optimization of a multi-stage charging protocol for lithium-ion battery and impact on cycle life. Journal of Energy Storage 2021, 40, 102756. [Google Scholar] [CrossRef]
  4. Hales, A.; Prosser, R.; Diaz, L. B.; White, G.; Patel, Y. Offer, G. The Cell Cooling Coefficient as a design tool to optimise thermal management of lithium-ion cells in battery packs. Etransportation 2020, 6, 100089. [Google Scholar] [CrossRef]
  5. Hua, X.; Heckel, C.; Modrow, N.; Zhang, C.; Hales, A.; Holloway, J.; Jnawali, A.; Li, S.; Yu, Y. Loveridge, M. The prismatic surface cell cooling coefficient: A novel cell design optimisation tool & thermal parameterization method for a 3D discretised electro-thermal equivalent-circuit model. ETransportation 2021, 7, 100099. [Google Scholar]
  6. Qin, P.; Sun, J.; Yang, X. Wang, Q. Battery thermal management system based on the forced-air convection: A review. ETransportation 2021, 7, 100097. [Google Scholar] [CrossRef]
  7. Aiello, L.; Hanzu, I.; Gstrein, G.; Ewert, E.; Ellersdorfer, C. Sinz, W. Analysis and Investigation of Thermal Runaway Propagation for a Mechanically Constrained Lithium-Ion Pouch Cell Module. Batteries 2021, 7, 49. [Google Scholar] [CrossRef]
  8. Amano, K. O. A.; Hahn, S.-K.; Tschirschwitz, R.; Rappsilber, T. Krause, U. An Experimental Investigation of Thermal Runaway and Gas Release of NMC Lithium-Ion Pouch Batteries Depending on the State of Charge Level. Batteries 2022, 8, 41. [Google Scholar] [CrossRef]
  9. Koch, S.; Birke, K. Kuhn, R. Fast Thermal Runaway Detection for Lithium-Ion Cells in Large Scale Tractiones Batteri. Batteries 2018, 4, 16. [Google Scholar] [CrossRef]
  10. Du, M.; Li, Q. Pang, H. Oxalate-derived porous prismatic nickel/nickel oxide nanocomposites toward lithium-ion battery. Journal of Colloid and Interface Science 2020, 580, 614–622. [Google Scholar] [CrossRef]
  11. Xia, R.; Zhao, K.; Kuo, L. Y.; Zhang, L.; Cunha, D. M.; Wang, Y.; Huang, S.; Zheng, J.; Boukamp, B.; Kaghazchi, P.; Sun, C.; ten Elshof, J. E. Huijben, M. Nickel Niobate Anodes for High Rate Lithium-Ion Batteries. Advanced Energy Materials 2021, 12, 2102972. [Google Scholar] [CrossRef]
  12. Zheng, W.; Bi, W.; Gao, X.; Zhang, Z.; Yuan, W. Li, L. A nickel and cobalt bimetal organic framework with high capacity as an anode material for lithium-ion batteries. Sustainable Energy & Fuels 2020, 4, 5757–5764. [Google Scholar]
  13. Xiaomei, J.; Yanjun, C.; Xiaokai, M.; Weiguo, C.; Changcheng, L.; Que, H.; Nithesh, N.; Vignesh, M.; Mina, H. Zhanhu, G. The impact of electrode with carbon materials on safety performance of lithium-ion batteries: A review. Carbon 2022, 191, 448–470. [Google Scholar]
  14. Onishchenko, D. V.; Popovich, A. A. Boiko, Y. N. Carbon-silicon anode composites for lithium-ion (polymer) rechargeable batteries. Russian Journal of Non-Ferrous Metals 2010, 51, 169–172. [Google Scholar] [CrossRef]
  15. Wang, L.; Ding, C. X.; Zhang, L. C.; Xu, H. W.; Zhang, D. W.; Cheng, T. Chen, C. H. A novel carbon–silicon composite nanofiber prepared via electrospinning as anode material for high energy-density lithium ion batteries. Journal of Power Sources 2010, 195, 5052–5056. [Google Scholar] [CrossRef]
  16. Wenjie, T.; Shuai, L.; Sandile, F.; Jiangang, H.; Jiaxin, W.; Chen, W. Jianqiang, C. Ionic liquid-induced interfacially bonding of bio-based RH-Si/SiOx@C anodes for enhanced ultra-long cycling of Li-ion batteries. Materials Chemistry and Physics 2022, 291, 126671. [Google Scholar]
  17. Yang, X.-G.; Liu, T. Wang, C.-Y. Thermally modulated lithium iron phosphate batteries for mass-market electric vehicles. Nature Energy 2021, 6, 176–185. [Google Scholar] [CrossRef]
  18. Yue, M.; Lv, Z.; Zheng, Q.; Li, X. Zhang, H. Battery assembly optimization: Tailoring the electrode compression ratio based on the polarization analysis in vanadium flow batteries. Applied Energy 2018, 235, 495–508. [Google Scholar] [CrossRef]
  19. Haber, S. Leskes, M. Dynamic Nuclear Polarization in battery materials. Solid State Nuclear Magnetic Resonance 2021, 117, 101763. [Google Scholar] [CrossRef]
  20. Qiu, C.; He, G.; Shi, W.; Zou, M. Liu, C. The polarization characteristics of lithium-ion batteries under cyclic charge and discharge. Journal of Solid State Electrochemistry 2019, 23, 1887–1902. [Google Scholar] [CrossRef]
  21. Luyao, Z.; Minxue, Z.; Junming, Z.; Hong, L.; Wei, L. Mingyi, C. Numerical modeling of thermal runaway for low temperature cycling lithium-ion batteries. Journal of Energy Storage 2023, 63, 107053. [Google Scholar]
  22. Zhizuan, Z.; Xiaodong, Z.; Bei, C.; Lizhong, Y. Liew, K. M. Investigating the relationship between heating temperature and thermal runaway of prismatic lithium-ion battery with LiFePO4 as cathode. Energy 2022, 256, 124714. [Google Scholar]
  23. Kalaf, O.; Solyali, D.; Asmael, M.; Zeeshan, Q.; Safaei, B. Askir, A. Experimental and simulation study of liquid coolant battery thermal management system for electric vehicles: A review. International Journal of Energy Research 2021, 45, 6495–6517. [Google Scholar] [CrossRef]
  24. Jiang, Z.; Li, H.; Qu, Z. Zhang, J. Recent progress in lithium-ion battery thermal management for a wide range of temperature and abuse conditions. International Journal of Hydrogen Energy 2022, 47, 9428–9459. [Google Scholar] [CrossRef]
  25. Ji, H.; Luo, T.; Dai, L.; He, Z. Wang, Q. Numerical investigation on the polarization and thermal characteristics of LiFePO4-based batteries during charging process. Applied Thermal Engineering 2022, 214, 118709. [Google Scholar] [CrossRef]
  26. Yu, Z.; Yang, J.; Yuan, Y.; Zhang, H.; Tian, S.; Lu, X.; Zhang, X.; Jiang, F.; Liu, Z.; Zhang, J. Yuan, L. Distributed Measurement of Polarization Characteristics for a Multifunctional Integrated Optical Chip: A Review. IEEE Transactions on Instrumentation and Measurement 2018, 68, 1543–1553. [Google Scholar] [CrossRef]
  27. He, X.; Sun, B.; Zhang, W.; Fan, X.; Su, X. Ruan, H. Multi-time scale variable-order equivalent circuit model for virtual battery considering initial polarization condition of lithium-ion battery. Energy 2022, 244, 123084. [Google Scholar] [CrossRef]
  28. Lin, P.; Jin, P.; Hong, J. Wang, Z. Battery voltage and state of power prediction based on an improved novel polarization voltage model. Energy Reports 2020, 6, 2299–2308. [Google Scholar] [CrossRef]
  29. Fan, Y.; Yanlong, Q. Degang, G. Lithium-ion battery polarization characteristics at different charging modes. Trans China Electrotech Soc 2017, 32, 171. [Google Scholar]
  30. Renfeng, C.; Xingjuan, Z.; Han, Y. Chao, W. Experimental study on heat generation characteristics of lithium-ion batteries using a forced convection calorimetry method. Applied Thermal Engineering 2022, 219, 119559. [Google Scholar]
  31. Rui, H.; Yidan, X.; Qichao, W.; Junxuan, C.; Fenfang, C. Xiaoli, Y. Simulation Study on Heat Generation Characteristics of Lithium-Ion Battery Aging Process. Electronics 2023, 12, 1444. [Google Scholar]
  32. Xie, Y.; Shi, S.; Tang, J.; Wu, H. Yu, J. Experimental and analytical study on heat generation characteristics of a lithium-ion power battery. International Journal of Heat and Mass Transfer 2018, 122, 884–894. [Google Scholar] [CrossRef]
  33. Sherfey, J. Brenner, A. Electrochemical calorimetry. Journal of the Electrochemical Society 1958, 105, 665. [Google Scholar] [CrossRef]
  34. Bernardi, D.; Pawlikowski, E. Newman, J. A General Energy Balance for Battery Systems. Journal of The Electrochemical Society 1985, 132, 5. [Google Scholar] [CrossRef]
  35. Zhu, L.; Xiong, F.; Chen, H.; Wei, D.; Li, G. Ouyang, C. Thermal analysis and optimization of an EV battery pack for real applications. International Journal of Heat and Mass Transfer 2020, 163, 120384. [Google Scholar] [CrossRef]
  36. Chen, Z.; Qin, Y.; Dong, Z.; Zheng, J. Liu, Y. Numerical study on the heat generation and thermal control of lithium-ion battery. Applied Thermal Engineering 2023, 221, 119852. [Google Scholar] [CrossRef]
  37. Ren, H.; Jia, L.; Dang, C. Qi, Z. An electrochemical-thermal coupling model for heat generation analysis of prismatic lithium battery. Journal of Energy Storage 2022, 50, 104277. [Google Scholar] [CrossRef]
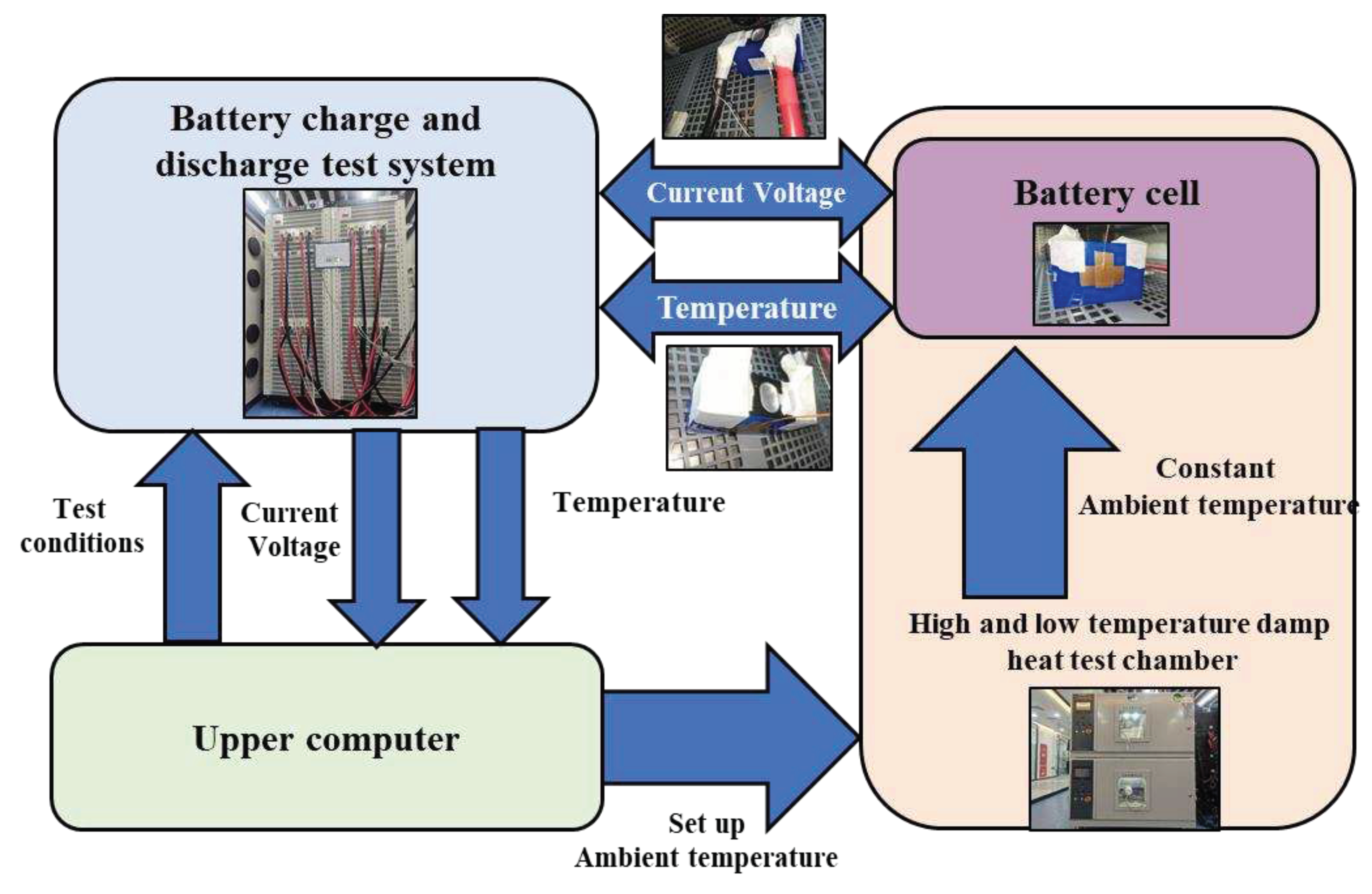
Preprints 86043 g001
Figure 1. Schematic diagram of the performance test platform.
Figure 1. Schematic diagram of the performance test platform.
Preprints 86043 g001
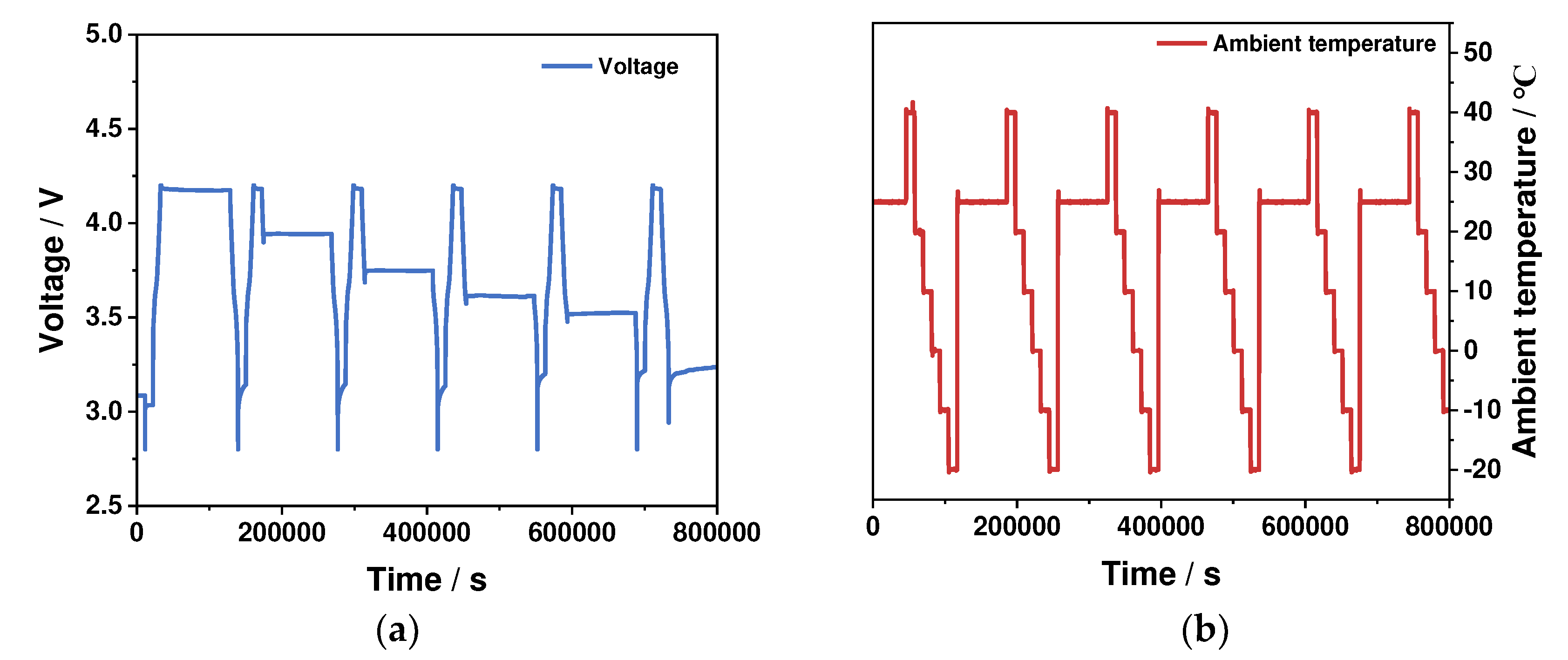
Preprints 86043 g002
Figure 2. Voltage and ambient temperature in entropy heat coefficient test: (a) Voltage; (b) Ambient temperature.
Figure 2. Voltage and ambient temperature in entropy heat coefficient test: (a) Voltage; (b) Ambient temperature.
Preprints 86043 g002
Preprints 86043 g003
Figure 3. Entropy heat coefficients at different ambient temperatures.
Figure 3. Entropy heat coefficients at different ambient temperatures.
Preprints 86043 g003
Preprints 86043 g004
Figure 4. Variations in temperature in the experiment on the convective heat transfer coefficient.
Figure 4. Variations in temperature in the experiment on the convective heat transfer coefficient.
Preprints 86043 g004
Preprints 86043 g005
Figure 5. Schematic diagram of Second-order RC model circuit structure.
Figure 5. Schematic diagram of Second-order RC model circuit structure.
Preprints 86043 g005
Preprints 86043 g006
Figure 6. The schematic diagram of pulse condition at a SOC point.
Figure 6. The schematic diagram of pulse condition at a SOC point.
Preprints 86043 g006
Preprints 86043 g007
Figure 7. The schematic diagram of the electro-thermal coupling mechanism.
Figure 7. The schematic diagram of the electro-thermal coupling mechanism.
Preprints 86043 g007
Preprints 86043 g008
Figure 8. The simplified geometric model diagram of a single battery.
Figure 8. The simplified geometric model diagram of a single battery.
Preprints 86043 g008
Preprints 86043 g009
Figure 9. Experiment and simulation voltage verification: (a) -5℃; (b) 25℃.
Figure 9. Experiment and simulation voltage verification: (a) -5℃; (b) 25℃.
Preprints 86043 g009
Preprints 86043 g010
Figure 10. Experiment and simulation temperature verification: (a) -5℃; (b) 25℃.
Figure 10. Experiment and simulation temperature verification: (a) -5℃; (b) 25℃.
Preprints 86043 g010
Preprints 86043 g011
Figure 11. The effects of ambient temperature on ohmic polarization: (a) -1/5 C and 1/2 C; (b) 1/ C and 2 C.
Figure 11. The effects of ambient temperature on ohmic polarization: (a) -1/5 C and 1/2 C; (b) 1/ C and 2 C.
Preprints 86043 g011
Preprints 86043 g012
Figure 12. The effects of ambient temperature on concentration polarization: (a) -1/5 C and 1/2 C; (b) 1/ C and 2 C.
Figure 12. The effects of ambient temperature on concentration polarization: (a) -1/5 C and 1/2 C; (b) 1/ C and 2 C.
Preprints 86043 g012
Preprints 86043 g013
Figure 13. The effects of ambient temperature on electrochemical polarization: (a) -1/5 C and 1/2 C; (b) 1/ C and 2 C.
Figure 13. The effects of ambient temperature on electrochemical polarization: (a) -1/5 C and 1/2 C; (b) 1/ C and 2 C.
Preprints 86043 g013
Preprints 86043 g014
Figure 14. The effects of ambient temperature on the proportion of polarization types: (a) -1/5 C; (b)1/2 C; (c) 1/ C; (d)and 2 C.
Figure 14. The effects of ambient temperature on the proportion of polarization types: (a) -1/5 C; (b)1/2 C; (c) 1/ C; (d)and 2 C.
Preprints 86043 g014
Preprints 86043 g015
Figure 15. The effects of ambient temperature on ohmic heat: (a) -1/5 C and 1/2 C; (b) 1/ C and 2 C.
Figure 15. The effects of ambient temperature on ohmic heat: (a) -1/5 C and 1/2 C; (b) 1/ C and 2 C.
Preprints 86043 g015
Preprints 86043 g016
Figure 16. The effects of ambient temperature on polarization heat: (a) -1/5 C and 1/2 C; (b) 1/ C and 2 C.
Figure 16. The effects of ambient temperature on polarization heat: (a) -1/5 C and 1/2 C; (b) 1/ C and 2 C.
Preprints 86043 g016
Preprints 86043 g017
Figure 17. The effects of ambient temperature on reversible entropy heat: (a) -1/5 C and 1/2 C; (b) 1/ C and 2 C.
Figure 17. The effects of ambient temperature on reversible entropy heat: (a) -1/5 C and 1/2 C; (b) 1/ C and 2 C.
Preprints 86043 g017
Preprints 86043 g018
Figure 18. Effect of ambient temperature on the proportion of heat types: (a) -1/5 C; (b)1/2 C; (c) 1/ C; (d)and 2 C.
Figure 18. Effect of ambient temperature on the proportion of heat types: (a) -1/5 C; (b)1/2 C; (c) 1/ C; (d)and 2 C.
Preprints 86043 g018
Table 1. The parameters of the battery.
Table 1. The parameters of the battery.
Parameter Unit Value
Nominal capacity Ah 104
Nominal voltage V 3.66
Working voltage V 2.8~4.2
Size mm 52*148*95
Weight kg 1.7
Energy density Wh/kg 220
State of charge window % 5~100
Table 2. Equipment specification.
Table 2. Equipment specification.
Equipment Type Manufacturer Range Accuracy
Battery charge/discharge test system CT-8008-5 V 300 A-NTFA Shenzhen Xinwei Electronics Co., Ltd 0 V~5 V
-200 A~ +200 A		 ±0.05 % FSR
High and low temperature-humidity test chamber SC2-400-SD-3 Guangdong Sanmu Technology Co., Ltd -70 ℃~180 ℃ ±1 °C
Thermocouple -200~260 °C ±1 °C
Table 3. Additional thermophysical variables.
Table 3. Additional thermophysical variables.
Parameter Unit Value
Average specific heat capacity of the battery J/(kg·K) 1020
Thermal conductivity
W/(m·K)
 17.8 (X direction)
8.8 (Y direction)
4.9 (Z direction)
Density kg/m3 2353
Surface convective heat transfer coefficient W/(m2·K) 20.6
Positive terminal material - Al
Negative terminal material - Cu
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated