Phase Transition and Atomic Distances Behavior of ZnO Rocksalt Structure under Extended Pressure: a Parallel and Equilibrium MD Computation

Yahia Chergui; Abd elaziz Ouatizerga; Essma Redouane Salah

doi:10.20944/preprints202309.1739.v1

Submitted:

25 September 2023

Posted:

27 September 2023

You are already at the latest version

Abstract

Zinc oxide (ZnO) as a semiconductor in its crystalline or amorphous form is still a promised material, especially under isobaric and isothermal ensembles. In this work, Parallel and Equilibrium Molecular Dynamics and DL_POLY_4 software are employed to predict the relationship between the behavior of ZnO chemical bonds and the phase transition literatures, using correlation function g(r) of Zn-Zn, Zn-O, and O-O pairs. Our system is composed of 5832 atoms of ZnO rocksalt structure (2916 atoms of Zn2+ and 2916 atoms of O2-), under the temperature of 300 (K) and the range of pressure 0-400 (GPa). The lengths of ZnO bonds, the standard error, standard deviation, the maximum of g(r), and the percentage of the variation of the bonds are analyzed. The interatomic interactions are modeled by the potential of Buckingham for short-range and Coulomb for long-range interactions. The calculations were run on the RAVEN Supercomputer of Cardiff University (UK). Our data are mostly in the vicinity of available information of bonds lengths; the rest can be deduced from the pressure of phase transition to use it as a new approach of phase transition confirmation. However, the rest of our results are still a prediction because of no results under extended pressure used in this work.

Keywords:

pressure temperature

;

ZnO

;

MD

;

Chemical Bonds

Subject:

Chemistry and Materials Science - Physical Chemistry

Introduction

Zinc oxide is used in everyday applications because it is listed as a safe material. It is an abundant material used in II-VI semiconductors, due to its optoelectronic properties [1,2,3,4,5,6,7,8,9,10]. It has a wide band gap of 3.37 (eV) and a high exciting binding energy of 60 meV. ZnO nanoparticles have various morphologies such as nanorods, tetrapods [11,12,13], nanowires [14,15], nanohelices [16], and microcheerois [17]) and have been synthesized and studied theoretically and experimentally [18,19,20]. Zinc oxide is stable under ambient conditions under the Wurtzite structure (B4), while Zinc blend (B2) and Rocksalt structures (B1) are metastables. The rocksalt type exists only at relatively high-pressure [21,22,23,24,25]. ZnO has a tetrahedral binding configuration, and it possesses large iconicity at the borderline between that of covalent and ionic semiconductors. The surface of ZnO (B1) is low at 0.63 (Jm^-2), which is lower than that of Wurtzite (B4) and Zinc blend (B2), and lower than that of rocksalt MgO, the crystalline form of ZnO has low hardness [26]. To obtain preferable conductivity; it is desired to dope it with high valence element [26]. The crystalline form of ZnO is utilized for ultraviolet light emitters [21], it has thermal stability, and it is anticipated also in charge coupled devices [27]. The amorphous form of ZnO is inspected for thermoelectric devices [28], it is also beneficial to appreciate the optical constant of ZnO thin films [29]. ZnO has been proposed as an alternative photo catalyst to TiO₂ as it possesses some bands gap energy that exhibits higher absorption efficiency across a large fraction of the solar spectrum when compared to TiO₂ [30,31]. The production of ZnO is up to 75% lower than that of TiO₂ and Al₂O₃ nanoparticles. ZnO nanostructures can be divided into zero-dimensional, one dimensional, two-dimensional and three-dimensional. Each nanostructure can be divided into quantum dots arrays. Note that the crystalline form of ZnO (used in this work) has a band gap bigger than that of its amorphous form [32].

In this paper, we have been dealt with ZnO rocksalt structure; we focused on the behavior of bonds lengths of ZnO (Zn-Zn, Zn-O, and O-O), standard error (SE), standard deviation (SD), the maximum of radial distribution function (RDF or g(r)), and the percentage of variation of each bond length under the effect of pressure (low and high) at ambient temperature (i.e., 300 (K)). The unit cell of ZnO rocksalt is cubic with the parameters a = b = c = 4.271 (Å) [21,33,34,35,36,37], the potential applied to model the inter-atomic interactions takes the Buckingham form [17]. The pressure changes the phase of rocksalt to other types of ZnO (as mentioned in Figure 6 and Figure 7) as stated by scientific research. The mechanization of phase transition under high-pressure is still a challenge and is under exploration. The starting transition pressure of Wurtzite to rocksalt phase is stable up to 50 (GPa) [38,39], for nano materials, the onset phase transition pressure from Wurtzite to Rocksalt is 10.5GPa, which is higher than that observed for bulk ZnO. Upon decompression, the Rocksalt structure is transmitted to the Wurtzite phase; both in ZnO bulk and nano materials. It is well known that numbers of new type structural materials with excellent mechanical and superconductivity properties were found under high-pressure; however, most of these structures recovered to their starting forms with losing the unique properties of their high-pressure phase. Rocksalt to Wurtzite phase transition occurred at 2 (GPa) that has a hysteresis effect during decompression [39,40,41,42]. Only a few works have paid special attention to application of Molecular Dynamics Technique and according to our knowledge; there is no available study concerning the effect of extended pressure on the ZnO bonds lengths, so this work is to fill that lack and to present a new approach to deduce the phase transition from the bond length value, which correspond the literature of the phase transition’s pressure.

Simulation Method

The unit cell of ZnO rocksalt structure (B1) contains eight atoms (four atoms of Zn²⁺ and four atoms of O^2-), our sample is composed of 5832 atoms, the matrix dimensions of our sample are 9a × 9a × 9a and the parameters of unit cell are a = b = c = 4.271 (Å) [21]. With a view to measure the length of Zn-Zn, Zn-O, and O-O of ZnO rocksalt type at temperature of 300 (K) and under the range of pressure 0-400 (GPa), the technique of Molecular Dynamics is used; the correlation function g(r) permits to describe the structure of materials like X-rays, also it specifies the probability to find a neighbor atom from the reference [43]. The distance between the reference atom and the nearest neighbor can be figured from the position of the first peak in the correlation function, which can be found also by X-ray spectra. Note that, far from the reference atom, individual peaks of RDF occasionally become Gaussian, which reduces the precision of calculations [30,31]. We concluded that the bond length could be determined by considering only the pairs of atoms that are neighbors, from the initial conditions of simulation, each atom saves its neighbors. To estimate the bond length, we obtain primarily the topmost value of g(r), where the probability to find a neighbor atom is upper [44], next the projection of that point on x axis will give the distance between a neighbor number and the reference atom. To simulate the unit cell over the matrix, the periodic boundary conditions are utilized, and Ewald sum is applied for long-range calculations [45,46]. Through the simulation, the ensemble of Nose-Hoover [47] is employed to fix the system temperature, where the initial temperature is 300 (K). The system is relaxed under each pressure for 10 (ps), for data calculations. The velocity Varlet algorithm is adopted, a time step of 0.001 (ps) is adjusted for integration of Newton’s equations, and the total time of simulation is 300000 steps. The MDs technique is inspected to check the equilibrium of the system, so as to achieve the structural configuration at the temperature of 300 (K).

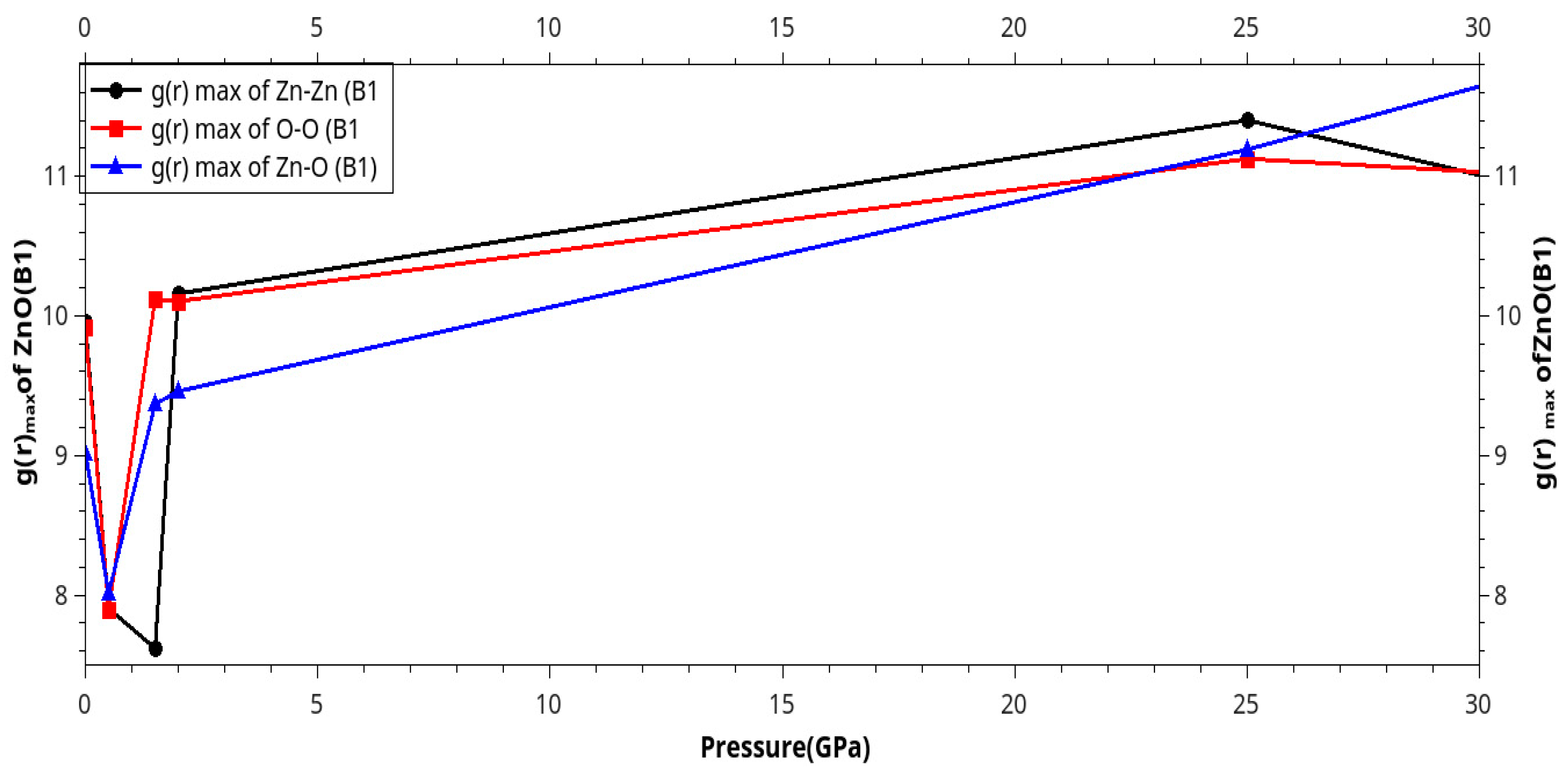
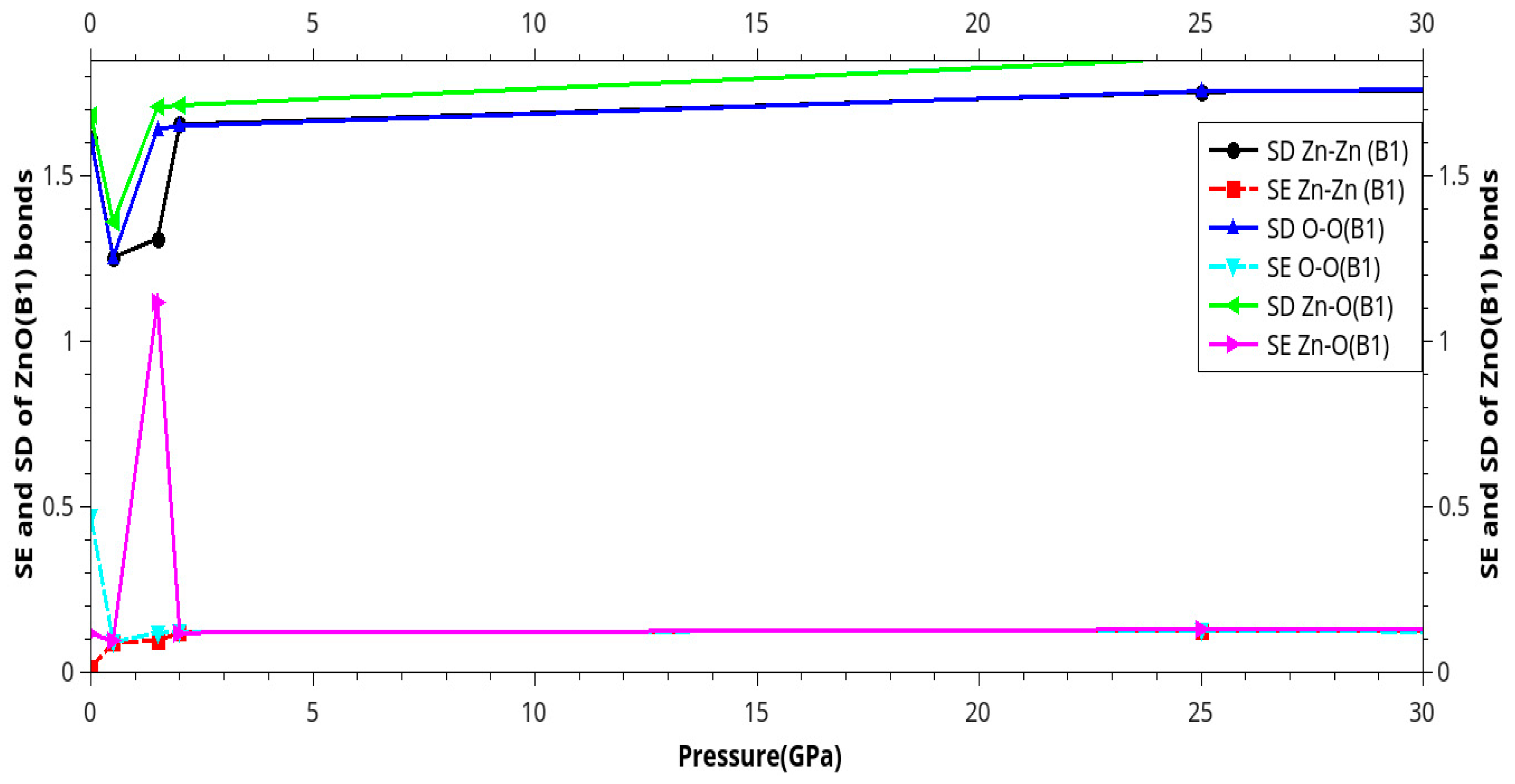
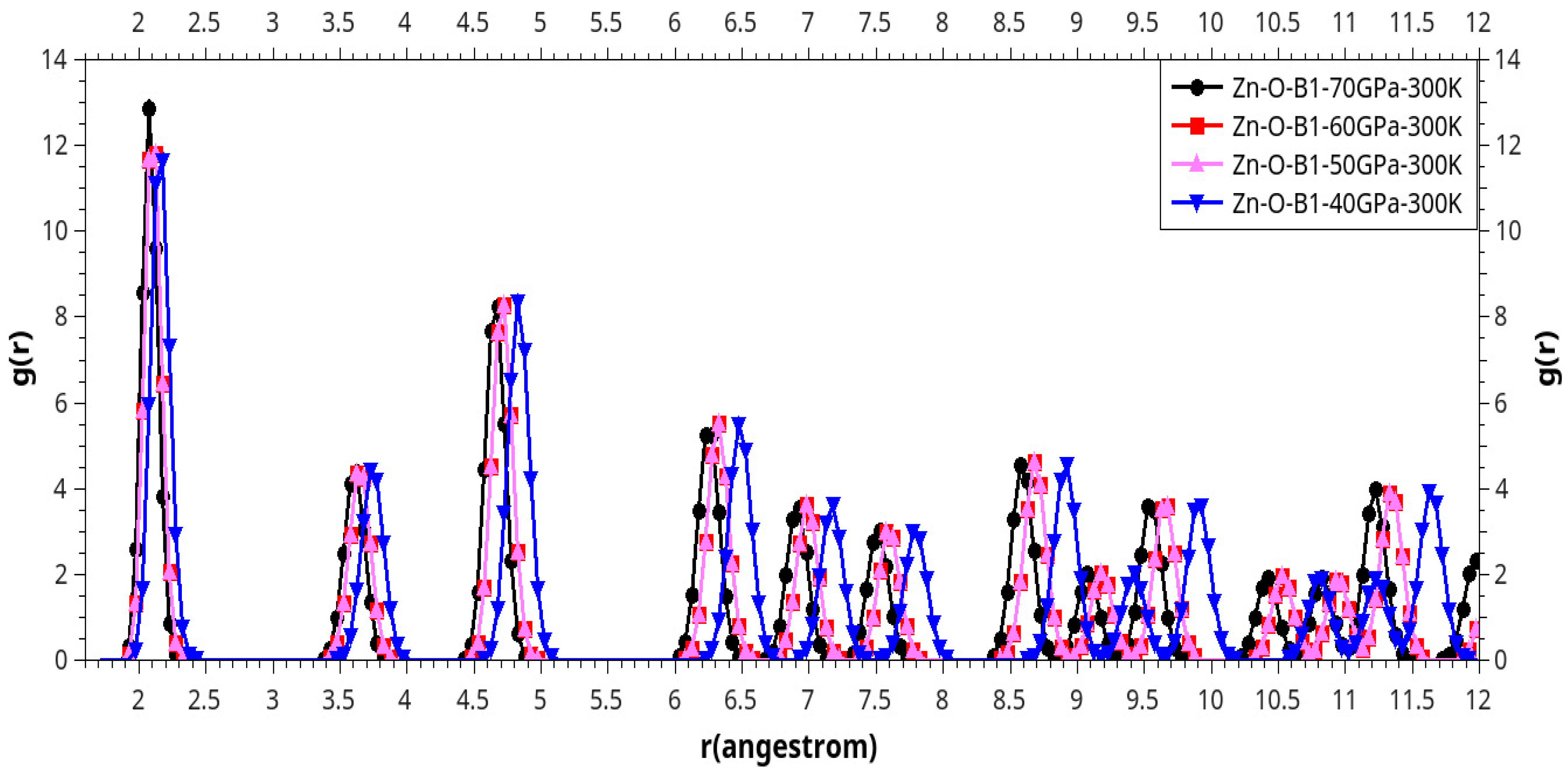
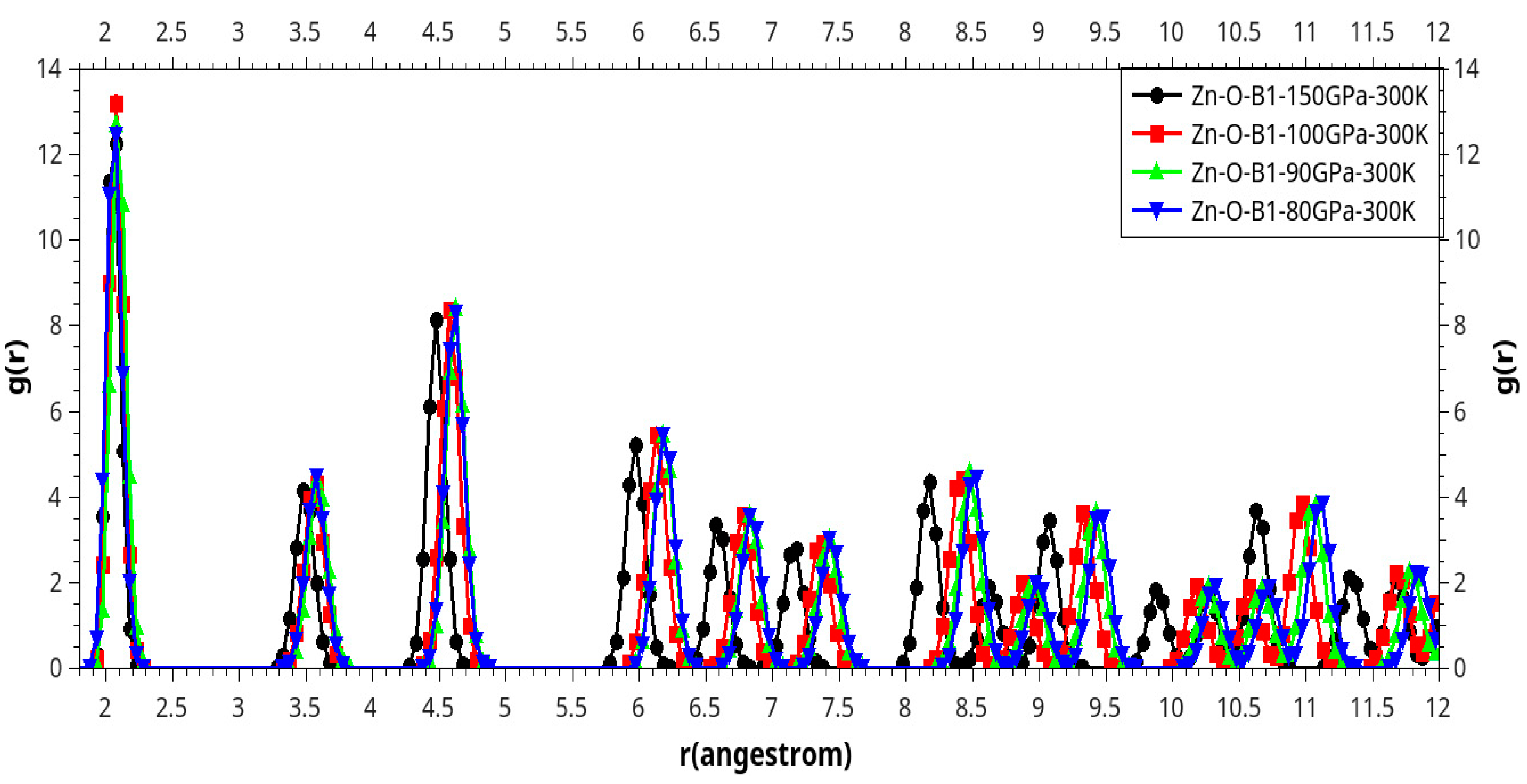
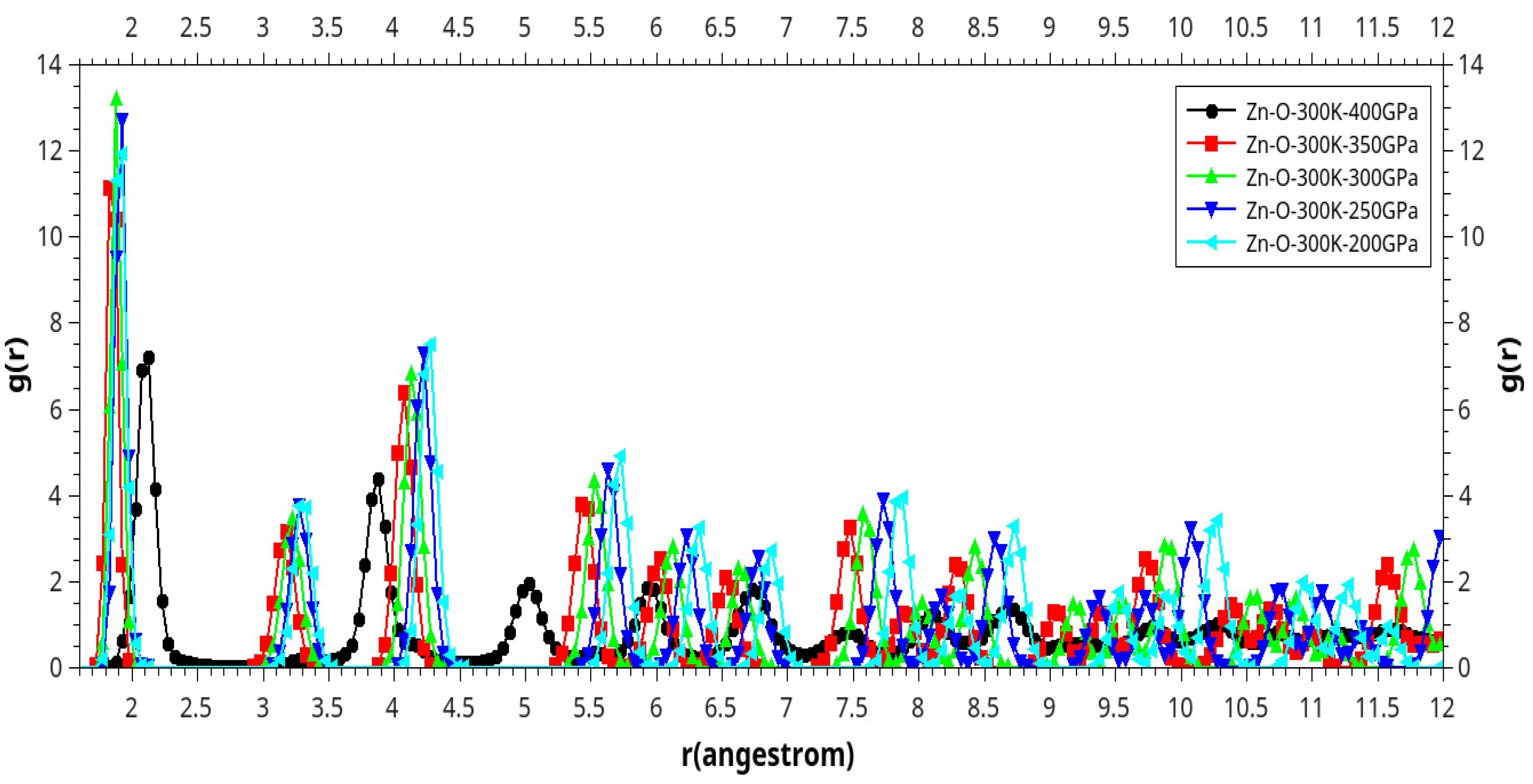
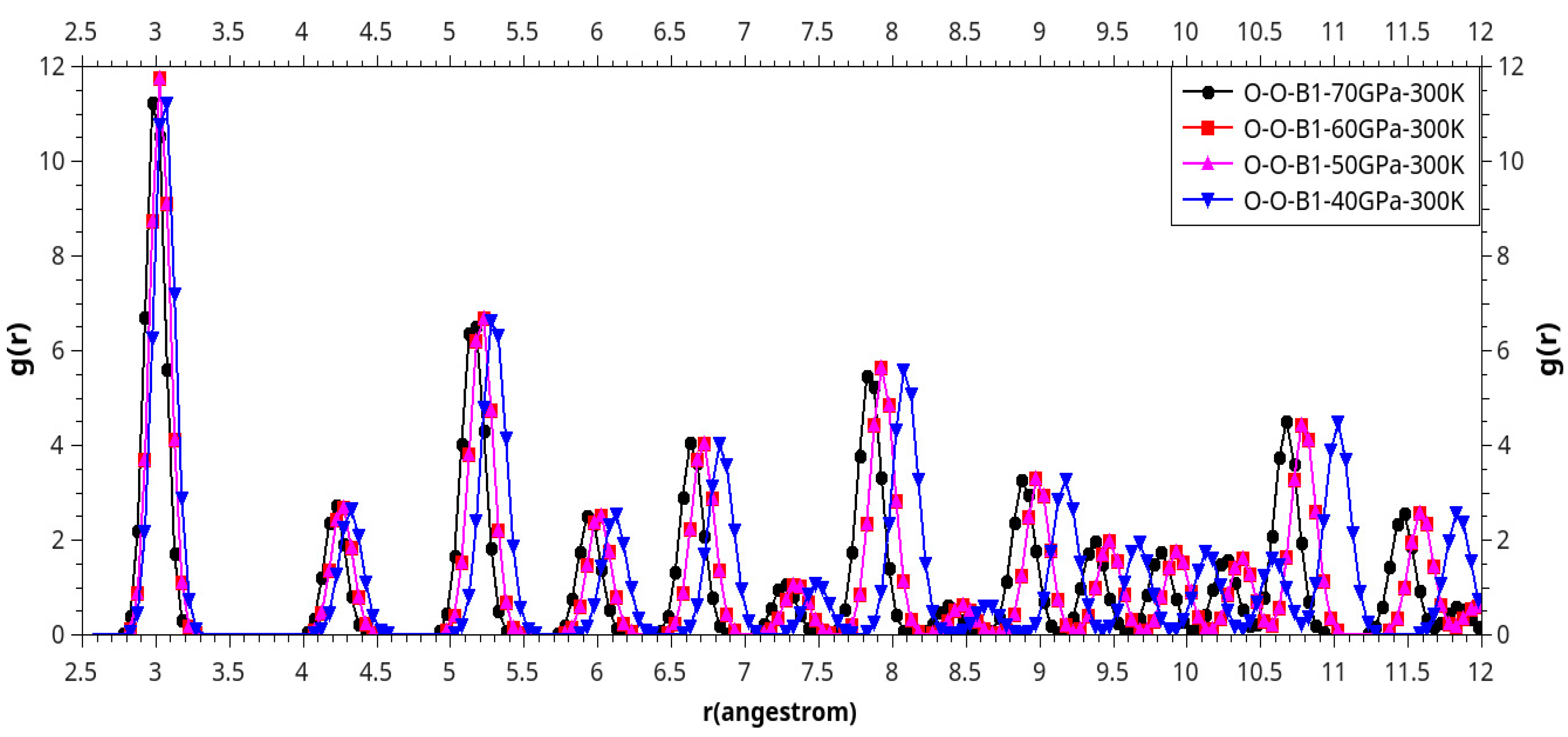
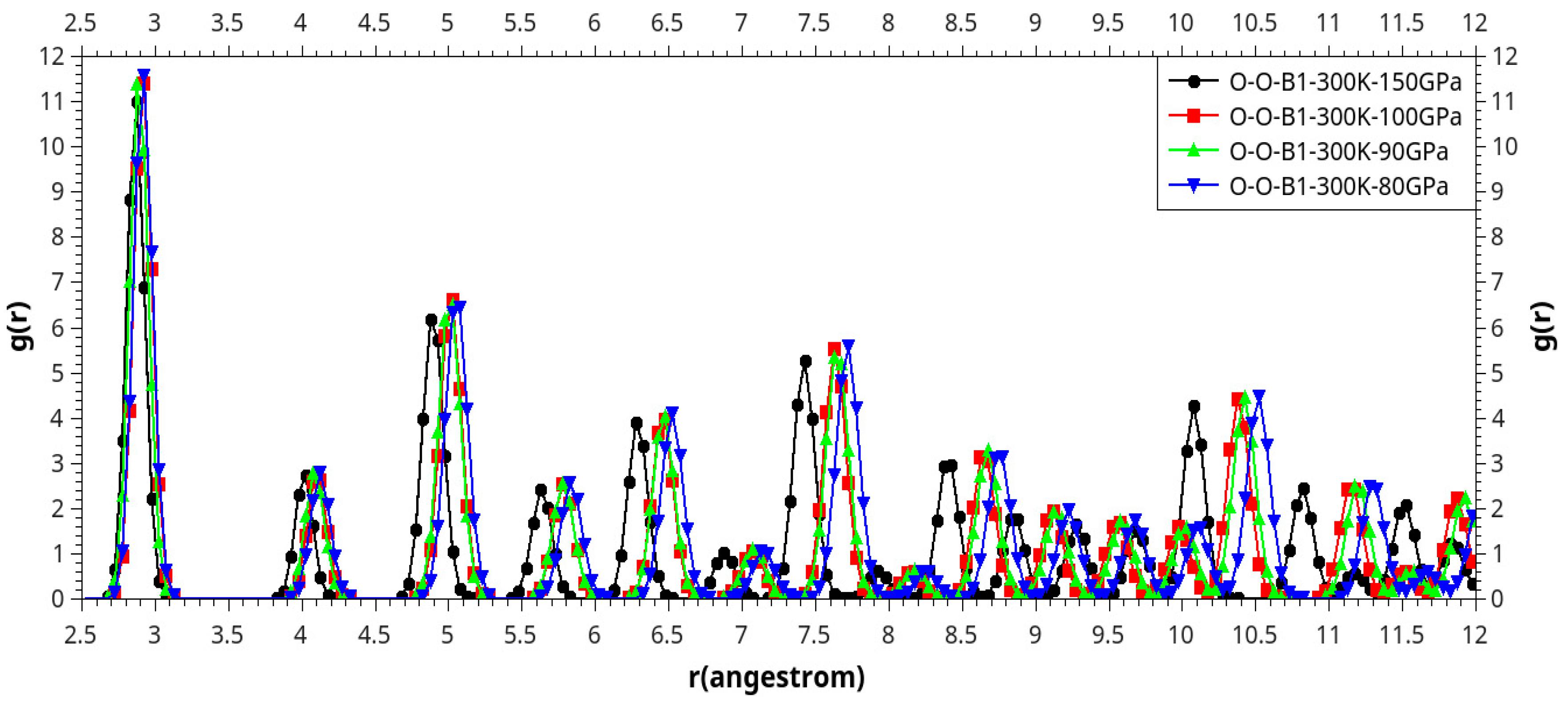
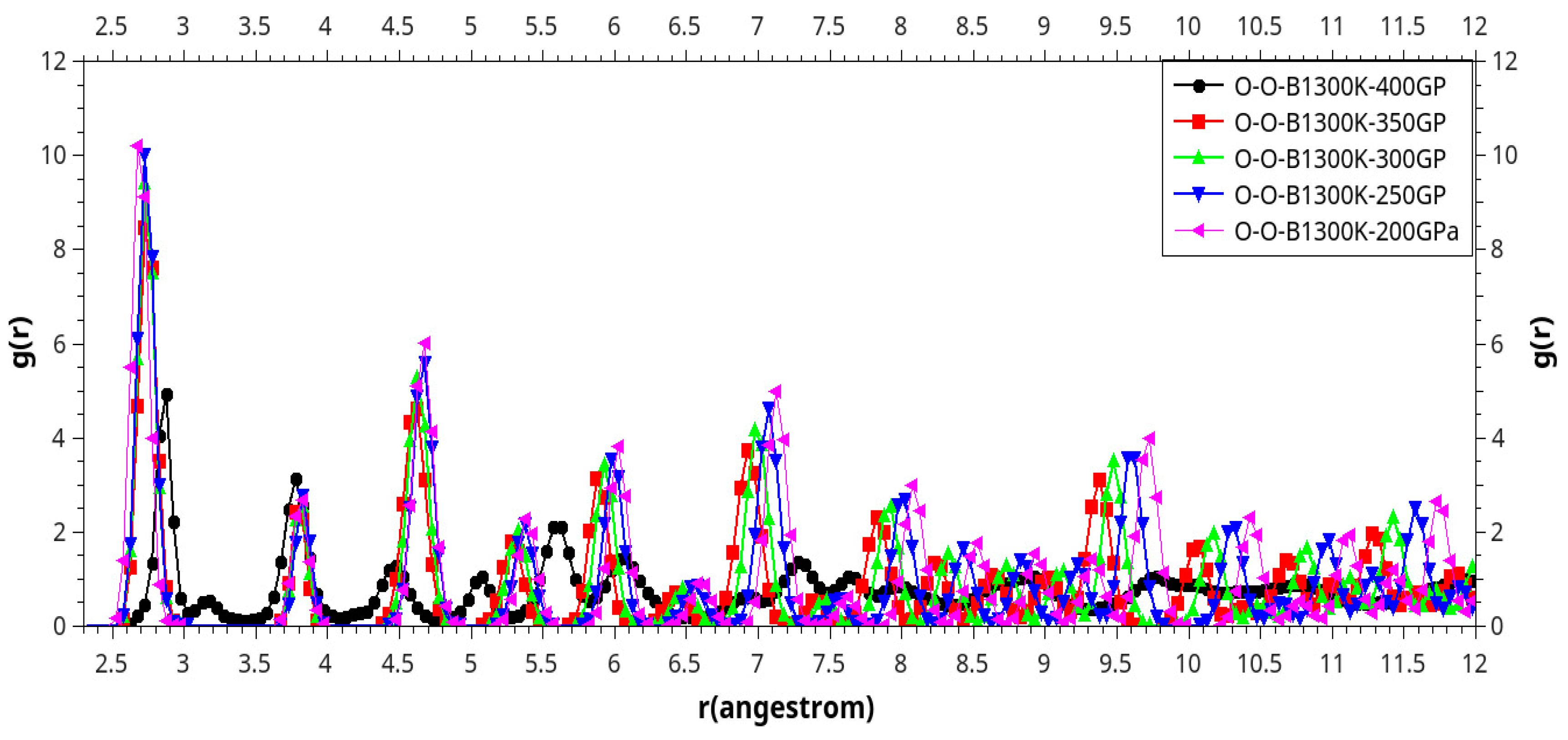
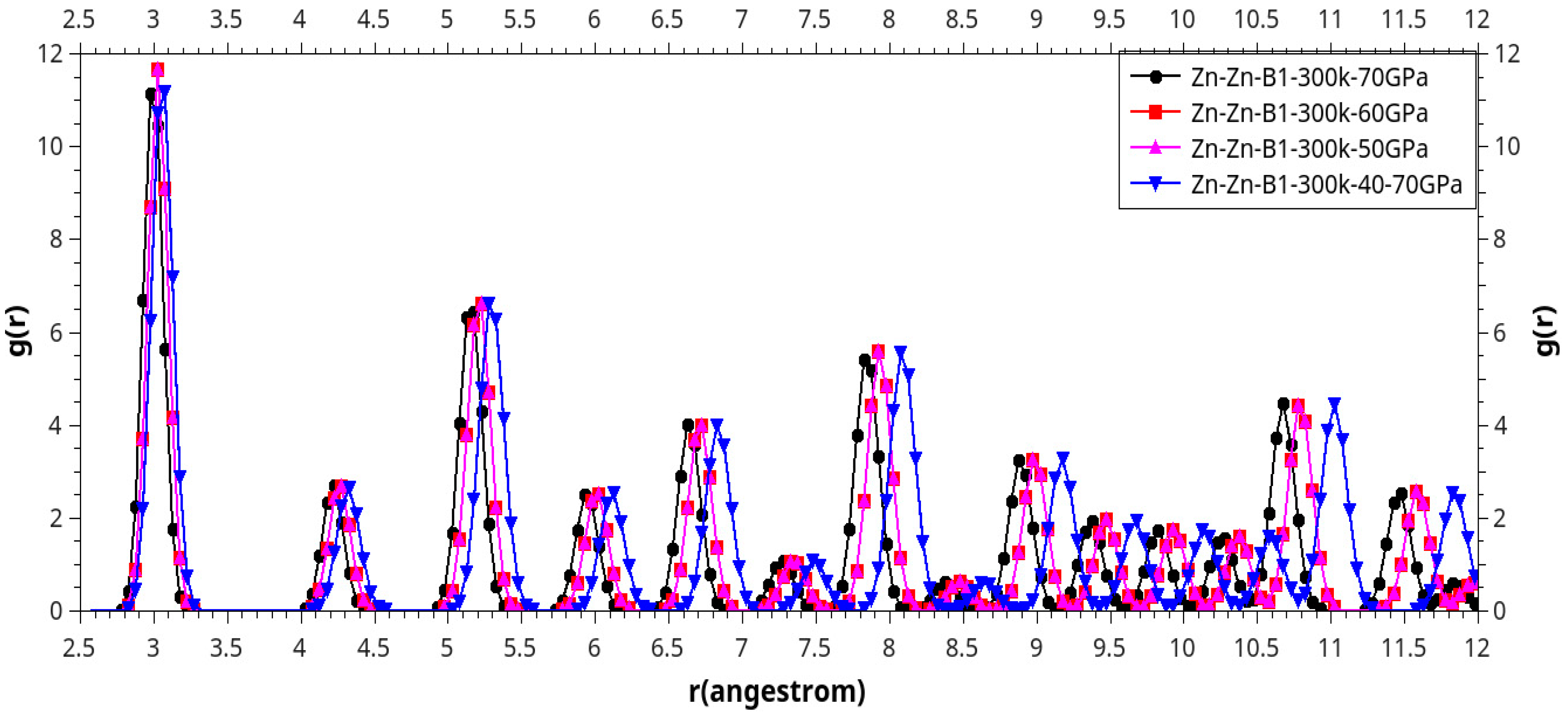
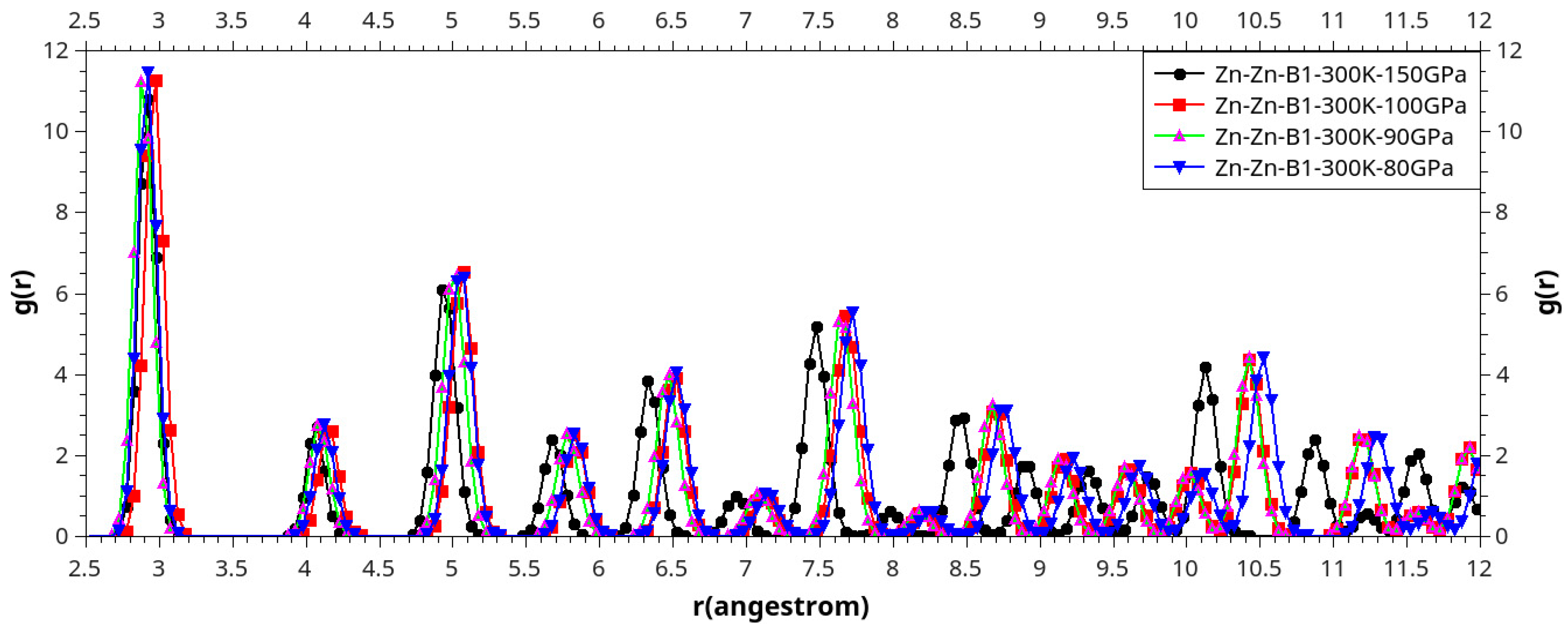
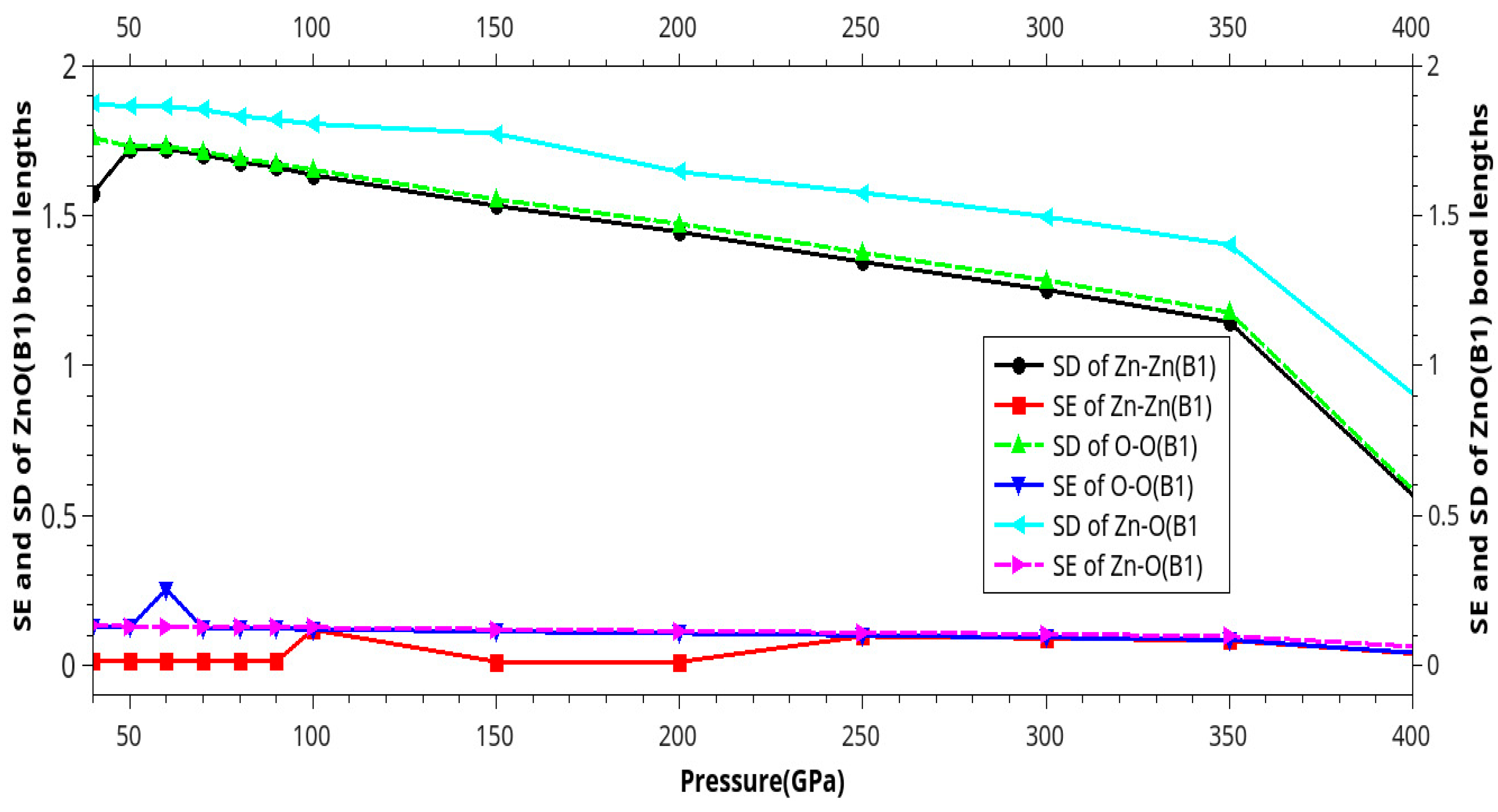
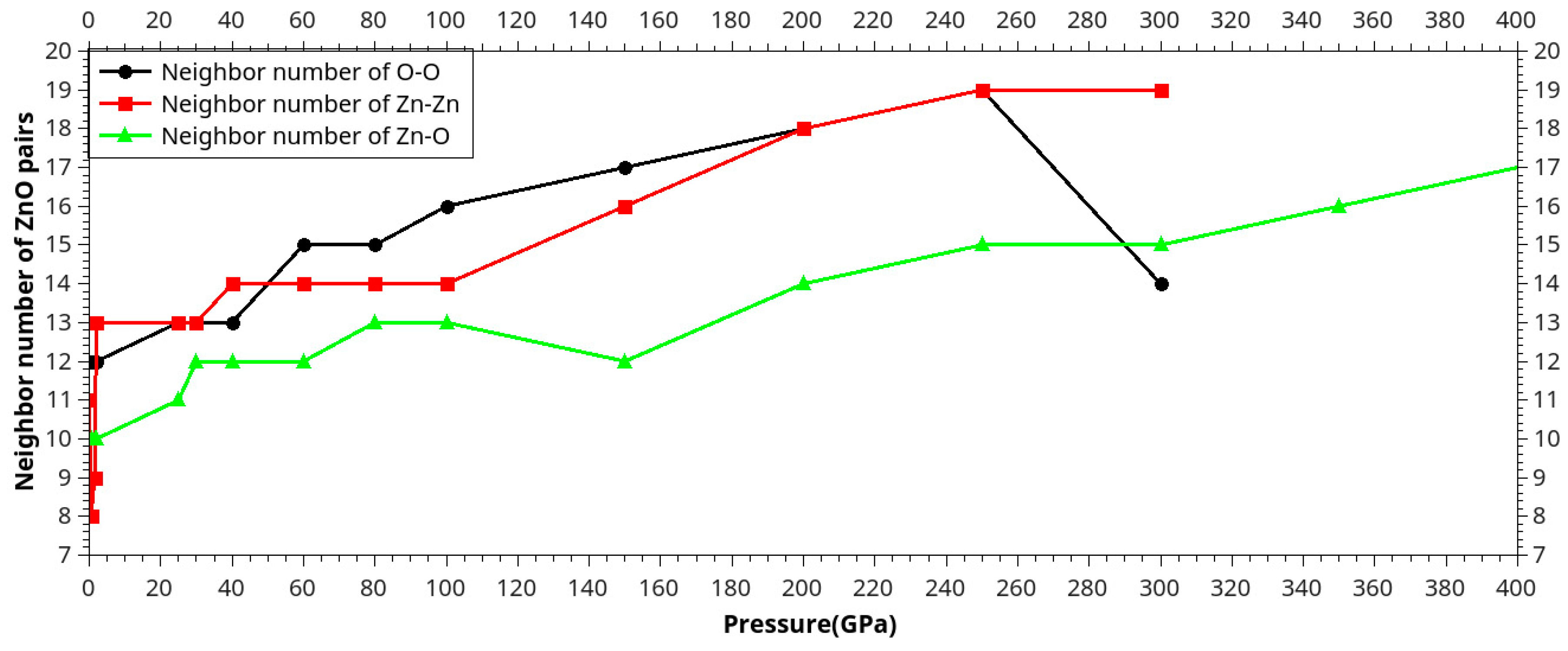
Results and Discussion

The situations of the peaks in the correlation function indicate the interatomic distance that is evidenced with high probability. It is similar to the X-ray diffraction (XRD) diagram. The edged peaks are for crystal type, while Gaussian shapes are for the amorphous form. In order to appreciate the bond lengths of Zn-Zn, Zn-O, and O-O, firstly, the effects of low pressure (0-30 (GPa)) secondly, the effect of high-pressure (40-400 (GPa)) on those bonds as mentioned in the following Sections, Part I and II; these bonds lengths also can be used as a new approach to deduce the phase transition comparing with the literature value of the phase transition’s pressure.

I. Under Low Pressure

Under the temperature of 300 K and the range of pressure 0-30 (GPa), we estimated the bond lengths, , SE, SD, the maximum of peaks and its relationship with the bond length of ZnO rocksalt type(B1), and the percentage of variation of those bonds Zn-Zn, Zn-O, and O-O from the RDF. Figure 1 shows the RDF of Zn-O of B1 type under the range of pressure 0-30 (GPa) and at 300 (K). Under 25 GPa and 30 (GPa), the probability to find an atom near the origin is more than that under the range of 0-2 (GPa). Higher peaks show higher probability, and low peaks show low probability. The original atom is at the origin, for a distance more than the cutoff of 12 (Å), there are no significant peaks due to neglected interatomic interactions; however, between 2 Å and 12 (Å), the probability is significant.

It is noted that under 25 (GPa) and 30 (GPa), there are similar values of g(r) and identical atomic distances because of the similar structure of rocksalt [30,31,43,44,45,46,47,48]. Further, under very low pressure 0-2 (GPa), there are similar values of g (r) and bonds lengths because the same type of Wurtzite (less than 2(GPa) there is a transition from rocksalt to wurtzite) [30,31,43,44,45,46,47,48]. Also, under both pressure of 25 (GPa) and 30G Pa, the probability to find an atom near from the origin is more than that under the range of 0-2 (GPa).

The correlation function of O-O bond under low pressure at the temperature of 300 (K) is displayed in Figure 2. It is noted that the peaks of g(r) under 25 (GPa) and 30 (GPa) are higher than those under the range of pressure 0-2 (GPa), which means more probability to find an atom near from the reference. Also, the length of the bond O-O is more than that of Zn-O, due to the weak potential and the difference in distance between two atoms of Oxygen in the unit cell. The peaks of both bonds are edged that traduce the crystal phase.

The effect of temperature (300 (K)) and the pressure (0-30 (GPa)) on the Zn-Zn bond are exhibited on RDF curves in Figure 3. The high and low peaks of the bond of Zn-Zn are similar to the bond of O-O because of no ionic and covalent liaison as Zn-O bond, also to nearby distance. It is observed that the structure in both figures is still crystalline since the peaks are sharped and not Gaussian.

From the previous curves presented in Figure 1, Figure 2 and Figure 3, we can depict the behavior of ZnO bonds lengths in Figure 4. The length of Zn-O bond under 0 (GPa) is around 2.23 (Å), which tends to be 2.2 (Å) under 30 (GPa). It is bit linear on account of the strong kind of this chemical bond. While for O-O and Zn-Zn bonds that are larger than Zn-O, they have the same variation with exception under 25 (GPa). Further, O-O bond is tended to around 3.125 (Å); however, Zn-Zn bond dropped to 2.22 (Å) under the effect of pressure on account of the big distance between the cations of Zn²⁺ and the weak potential. This diminution of length products a phase transition from Wurtzite to other structure of ZnO [47,48].

The effect of pressure on ZnO bonds lengths can be displayed better in Figure 5, where the percentages of variation for each bond of Zn-O, Zn-Zn, and O-O are shown.

These curves of Zn-O, Zn-Zn, and O-O bonds lengths and those percentages of variation are linear and bit neighbors (Figure 5); however, they are similar, only for Zn-Zn bond under 25 (GPa), which is jumped to around 35.2 %, while the rest of bonds tend to around 5.1 %, because of the phase transitions under low and high pressure [30,31,43,44,45,46,47,48]; wurtzite(B4), rocksalt (B1), zinc blend(B2), PbO(B10), ΝaTi(B32), WC(B_h), BΝ(B_k), ΝiAs(B8₁), and AsTi(Bi) are the different types of ZnO. The energy of these phases areaccording to the following order (LDA and GGA); EB4 ˂ EB3 ˂ EB_h˂ EB1˂ EB_i˂ EB81˂ EB1˂ EB10˂ EB2˂ EB32, with B4 is the most stable (under low-pressure) and B32 is less stable at equilibrium. While B2 is stable under high pressure (phase transitions B4 to B1 to B2 phase transition [47,48]. There are other intermediate phases from B4 to B2 phase with B_k, B_{h, ,} B10, and B8₁ structures [47,48,49,50] see Figure 6 and Figure 7; B_k phase is stable only under the range of 24.65-32.85GPa.there is another phase transition from B_k to B1 to B_i to B2 under the range of 16.56- 213.30(GPa). It is noted that B2 phases has never been observed experimentally, due to the challenging of high-pressure 250 (GPa) [51].

The bonds lengths of ZnO under different pressures can be used as a sign of phase transition; for each phase transition there is a known value of pressure (see Table 1), and for this value of pressure, there is a bond length, so from this length and the percentage of variation, the phase transition can be deduced.

In order to understand the relation between the bonds lengths and the probability to find an atom near the reference or the total neighbors, Figure 8 is presented.

The RDF dropped and raised under the range of pressure 0-5 (GPa). Indeed, the rocksalt is transferred to Wurtzite at less than 2 (GPa), and at more than 2 (GPa) the material is returned to rocksalt [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. The g(r) values of Zn-Zn and O-O are more important than that of Zn-O because they are affected by the pressure. This is due to the weak potential comparing with that of ionic –covalent of Zn-O; however, under 25 (GPa), there is another phase transition with different parameters of unit cell [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. The precision of these calculations can be extracted from the value of the SE and the SD (see Figure 9).

The SE of Zn-O, Zn-Zn, and O-O bonds are linear, similar, and minimum under the range of pressure 2-30 (GPa). However, in the area of phase transition from rocksalt to Wurtzite and under 0-2 (GPa), the SE increases from around 0.1 to 1.1 in the Wurtzite phase, and later it drops to the starting value for rocksalt phase; indeed, SE of O-O bond is decreased from 0.5 to 0.1, SE of Zn-Zn raises from 0 to 0.1, and for O-O bond it is bit straight on 0.1 value. However, the SD is more than SE for all ZnO bonds, as they are linear and bit increasing with augmenting the pressure, while for Zn-0 bond it is raised more. It is shown that under the range of 0-2 (GPa) the SD dropped and raised [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39].

II. Under high-pressure

The RDF of Zn-O bond under high-pressure (40-400 (GPa)) and the temperature of 300 (K) are shown in Figure 10, Figure 11 and Figure 12.

The peaks in Figure 10, Figure 11 and Figure 12 have approximately the same height; however, the distance from the origin atom is reduced. This means that the numbers of neighbor atoms are augmented, where the peaks are more condensed from far distance to the nearest one even if they are still edged as a crystal structure. Also, reducing the distance between the atoms of Zinc (Zn) and the atoms of oxygen (O), it increases the probability for finding neighbor atoms.

For the behavior of RDF of the bonds of O-O and Zn-Zn under the range of pressure 40-400 (GPa) and at 300 (K) is bit the similar but different than that of Zn-O because of the different potentials and distances between those atoms, see Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18.

For Zn-Zn bond under high-pressure of the range 40-400 (GPa) and at 300 (K), see Figure 16, Figure 17 and Figure 18.

For the first neighbor, we can summarize the RDF of ZnO (B1) versus distance of the cutoff in Figure 19 where the distance between the pairs of Zn-O, Zn-Zn, and O-O are calculated.

To determine the values of affected pressure on ZnO (B1) bonds lengths, Figure 20 shows the percentage of variation of each bond. The percentage of variation of Zn-O bond is less than that of Zn-Zn and O-O bonds due to the high chemical bonds, while the weak one between the other bonds make the percentage of variation bit similar. For Zn-O, it is started from around 6% and it is ended at around 26%, while that for Zn-Zn it is 7% and 32% under 400 (GPa), whereas it is 8% under 40 (GPa) and 33% for O-O bond.

In order to analyze the previous peaks of RDF, Figure 21 exhibited the maximum of the RDF versus the pressure (40-400 (GPa)). It is observed that in Figure 18 the black color of peak (400 (GPa)) and the red one (350 (GPa)) are reduced under high-pressure: that decreases the probability to find an atom near the reference one each time when the position of a neighbor atom becomes farther, which is clear in Figure 21. The maximum of RDF of O-O and Zn-Zn have the same variation due to approximately the same distance and the same potential, while the RDF of Zn-O pair is less reduced under high-pressure because of the strong liaison and the atoms become close to each other due to the high pressure. It is noted that the peaks in Figure 21 interpreted the phase transition existence [30,31,43,44,45,46,47,48]. Rocksalt phase is stable under high pressure up to 209 (GPa) at room temperature, Liu et al. [51]. At pressure around 260 (GPa) there is a phase transition from the B1 to the eight-fold- coordinated B2 structure [51,52,53,54], in other hand Zaoui and Sekkal [36] predicted the transition at 305 (GPa). However, most of theoretical studies did not consider any other intermediate structures of ZnO on high-pressure, except B4 (wurtzite), B3(Zinc blend), B1(rocksalt), and B2, while Azzaz et al. [53] predicted other types such as cinnabar, d-ß-tin and NiAs, also Li et al.[54] investigated a tetragonal PbO-type(B10) as intermediate phase. B2 (CsCl) phase has never been observed experimentally around 250 (GPa) [51].The knowledge of the bond length of ZnO or its percentage of variation for each pressure will be a tool of deducing each kind of phase transition, see Table 2.

Radial distribution function versus the pressure shows the probability to find an atom near from the reference; this probability is proportional with the RDF, increases and decreases with RDF as mentioned in Figure 21. However, the probability to find an atom of Zn (or Oxygen) near from Oxygen (or Zinc) is more than that of Oxygen-Oxygen and Zinc-Zinc, where the both last one are similar. The neighbors of Zn-O are more than that of Zn-Zn and O-O atoms.

As a general result, to evaluate the precision and accuracy of our calculations under high-pressure, Figure 22 offers the SE and SD of ZnO (B1) bonds; it seems that the SE of Zn-O, O-O ad Zn-Zn have the same values under the range of 250-400 (GPa), while there is it difference under the range of 40-250 (GPa), this due to the phase transitions. For the SD of Zn-Zn and O-O have the same behaviours, however Zn-O standard deviation is more than that of the rest of bonds but is similar. We can conclude that the SE of ZnO (B1) bonds are less than that of SD; this maybe due to the short distance of Zn-O bond. Also under low pressure there is a great gap between the value of SE ad SD, while under high pressure, they try to converge to the same value because of the deformation of the structure.

In order to understand the relation between the neighbors’ number of ZnO pairs and the pressure, Figure 23 clarifies that.

The number of neighbors of Zn-Zn bond is increased under the range of 0-5 (GPa) because of the reverse phase transition from rocksalt to wurtzite, so the parameters of unit cell will change; it is noted that the neighbors number are increased with pressure for all ZnO pairs, however, the Zn-Zn and O-O pairs have a bit the same behavior of neighbors number under 0 -25 (GPa) due to the same parameters of unit cell, while under 30-200 (GPa), O-O bond neighbors number are increased more than Zn-Zn neighbors because of the phase transition of ZnO structures [47,48]. Under the range of 200-260 (GPa) both ZnO pairs (Zn-Zn and O-O) have the same value because of the same structure, since that under 260-300 (GPa), the number of Zn-Zn neighbors is 19 atoms, while O-O pairs is dropped to 14 (another type of ZnO).

Conclusion

Parallel Equilibrium Molecular Dynamics (RAVEN Supercomputer) and DL_POLY_4 software are investigated to analyze the behavior of correlation function of ZnO rocksalt type, under low and high pressure; we estimated the bonds lengths and their percentage of variation for first neighbor of Zn-Zn, Zn-O, and O-O bonds, standard deviation, standard error, and the maximum of radial distribution function g (r).We found that the length of Zn-Zn, and O-O are bit similar but more than Zn-O length, also, the percentage of variation of Zn-O comparing with that of Zn-Zn, and O-O bonds have the same behavior of the bonds lengths; due to the strong potential of ionic-covalent chemical liaisons. The bonds lengths, standard error, standard deviation, and the maximum of g (r) of ZnO are decreased with rising of pressure; if there is no phase transition, which is not the case for the percentage of variation of the bonds lengths. The RDF curves becomes Gaussian with augmenting the pressure and the neighbors number due to phase transition from crystal form to amorphous one, that minimize the accuracy of calculations of bonds lengths outside the cutoff, there are no significant beaks because of the neglected interatomic interactions. The standard error and standard deviation gives an idea about the strength of the interatomic potential and the kind of phase transition. Finally, the correlation functions are a good tool to extract results for the structure of materials. The knowledge of the bond length under different pressure can be used like a tool to deduce the phase transition, although this will be a great challenge to find the interval of bond length variation for each phase transition. The results of this work are in the vicinity of available information under ambient conditions, the rest are a prediction, which need experimental confirmation.

Author Contributions

Y. Chergui did the ccalculations, analysed the results, wrote the manuscript; A. Ouatizerga checked the Figures and language, and E. . revised the manuscript as a reviewer.

Acknowledgments

This work is supported by the IGEE Institute, University M’Hamad Bougara, Boumerdes, Algeria. This work is financially supported by the dlpoly_4 software; calculations were performed at advanced research computing Cardiff, UK (ARCCA) using the RAVEN supercomputing. We thank D J Willock fromChemistry school Cardiff University, UK, for the help and the guidance during the work, to Christian Reece for hishelp. Also, we thank Martyn Guest, Thomas Green, and Christine A Kitchen, for training courses. Finally, we do not forget to thank Dr Clarence Matthai for his invitation to Physics department in Cardiff University, UK. We do not forget Dr. Adam Ralph, Computational Scientist at ICHEC in Ireland for his remarks and advice.

Conflicts of Interest

The authors declare that they have no conflict of interest.

References

Pearton S. Norton D. Ip, K. Heo, Y. Steiner, T. Recent progress in processing and properties of ZnO, 2005, Progress in Materials Science, 50: 293 - 340. [CrossRef]
Schmidt - Mende, L.; Mac Manus - Driscoll, J. L. ZnO nanostructure, decfets, and devices, 2007, Materials Today, 1: 40-48. [CrossRef]
ozgur ,U. Alivov,Y. I. Liu, C. Teke, et al. A comprehensive review of ZnO materials and devices. 2005, J. Appl. Phys., 98: 041301. [CrossRef]
Djurii A. Leung,Y. H. Optical Properties of ZnO Nanostructures. 2006, PubMed Small, 2: 944 - 961. [CrossRef]
Bagnall, D. M. Chen, Y. F. Zhu, Z. Et al. Optically pumped lasing of ZnO at room temperature. 1997, Applied Physics Letters, 70: 2230 - 2232. [CrossRef]
Fortunato,E, Barquinha,P, Pi-mentel, A. Et al. Fully transparent ZnO thin-film transistor produced at room temperature. Advanced Materials 2005, 17, 590 – 594. [CrossRef]
Zhang, Q. Dandeneau, C. S. Zhou,X. Cao, G. ZnO nanostructures for dye-sensitized solar cells. 2009, Advanced Materials, 21: 4087-4108. [CrossRef]
T. sukazaki, A. Ohtomo, A. Onuma, et al. Repeated temperature modulation epitaxy for p-type doping and light-emitting diode based on ZnO. 2005, Nature materials, 4: 42-46. [CrossRef]
Wan, Q. Li, Q.H. Chen,Y. J. Et al. Fabrication and ethanol sensing characteristics of ZnO nanowire gas sensors. 2004, Applied Physics Letters, 84:3654-3656. [CrossRef]
Soci, C. Zhang, A. Xiang, B. Et al. ZnO nanowire UV photodetectors with high internal gain. 2007, Nano Letters, 7:1003-1009. [CrossRef]
Dai, Y. Zhang, Y. Li, Q. Nan, C. Synthesis and optical properties of tetrapod like ZincOxide nanorods. 2002, Chemical Physics letters, 358;83-86. [CrossRef]
Yang, Y. Jin, Y. He, et al. Dopant - induced shape evolution of colloidal nanochrystals: The case of Zinc Oxide. 2010, J. Am. Chem. Soc., 132:13381-13394. [CrossRef]
Ding, Y. Wang, Z. L.; Sun, T. Qiu, J. Zinc-blende ZnO and its role in nucleating Wurtzite tetrapode and twinned nanowires. 2007, Applied Physics Letters, 90:15310. [CrossRef]
Heo, Y. W. Kaufman, M Pruessner, K. Seibeinet al. ZnO cubic (Mg.Zn) O radial nanowire heterostructure. 2005, Appl. Phys. A. Mater. Sci. Process, 80, 263-266. [CrossRef]
Rosenberg, R. A. Shenoy, G. K. Chisholm, M. F. Et al.. Getting to the core of the problem origin of the luminescence from (Mg. Zn) O heterostructured nanowires, 2007, Nan. Lett., 7:1521-1525. [CrossRef]
Kong X. Y., Wang Z. L., Spontaneouse polarization – induced nanohelixes, nanosprings and nanorings, of peizoelectronic nanobelts, 2003, Nano. Lett., 3;1625-1631. [CrossRef]
S. Li , Z. W. Li , Y. Y. Tay , et al., Growth Mechanism and Photonic behaviors of Nanoporous ZnO Microcheerios. 2008, Cryst. Groth. Des., 8:1623-1627. [CrossRef]
Jaffe, J.E. Snyder, J. A. Lin, Z. Hess, A. C. LDA and GGA Calculationsfor High-Pressure Phase Transitions in ZnO and MgO. 2000, Phys. Rev. B: Condens .Matter Mater. Phys., 62:1660-1665. [CrossRef]
Pu, C. Y. Tang, X. Zhang Q. Y. First Principles Study, on the Structural and Optical Properties of the High - Pressure ZnO Phases. 2011, Solid State Commun, 151:1533- 1536. [CrossRef]
Saeed, Y. Shaukat,A. kram,N. Tan-veer, M. Structural and Electronic Prop-ertiesof Rock Salt Phase of ZnO un-derCompression. 2008, J. Phys. Chem. Solids, 69:1676-1683. [CrossRef]
Decremps F.,Pellicer-Porres J.,Datchi F.,et al., Trapping of cubic ZnO nanocrystallites at ambient conditions, 2002, Appl.Phys.Lett.,81:4820-4822. [CrossRef]
Sokolov P. S., A. Baranov A. N., Dobrokhotov N. V., and Solozhenko V. L., Synthesis and thermal stability of cubic ZnO in the salt nanocomposites 2010, Russ. Chem.Bull., 59:325-328. [CrossRef]
Razavi-Khosroshahi H., Edalati K., Wu J., Nakashima Y., Arita M., Ikoma Y., Sadakiyo M., Inagaki Y., Staykov A., Yamauchi M., Horita Z., and Fuji M., High-pressure zinc oxide phase as visible-light-active photocatalyst with narrow band gap Mater J., Chem. A., 5, 20298- 20303 (2017). [CrossRef]
Kunisu M., Tanaka I, Yamamoto T., Suga T., andMizoguchi T., The formation of a rock-salt type ZnO thin film by low-level alloying with MgO J. Phys. Condens. Matter,, 16, 3801 (2004). [CrossRef]
Kashiwaba Y., HagaK,., Watanabe H., Zhang B. P., Segawa Y., and Wakatsuki K., Structures and Photoluminescence Properties of ZnO Films Epitaxially Grown by Atmospheric Pressure MOCVD, 2002, Phys. Status Solidi B, 229 (2): 921 - 924. [CrossRef]
Rozati S. M., and Akesteh Sh, Characterization of ZnO: Al Thin Films Obtained by Spray Pyrolysis Technique Mater. 2007, Charact.58:319-322. [CrossRef]
Gordon R. G., Transparent Conducting Oxides, 2000, MRS Bull. 25:52-27. [CrossRef]
Sierros K. A., Cairns D. R., Abell J. S., and Kukurek S. N., Pulsed laser deposition of indium tin oxide films on flexible polyethylene naphthalate display substrates at room temperature. 2010, Thin Solid Films, 518:2623. [CrossRef]
Khoshman J. M. And Kordesch M. E., Optical constants and band edge of amorphous zinc oxide thin films, 2007, Thin Solid Films, 515 18:7393-7399. [CrossRef]
Qiu R., Zhang D., Moy Y., et al. Photocatalytic activity of polymer- modified ZnO under visible light irradiation, 2008, J. Hazard Mater. 150:80-5. [CrossRef]
Yogendra K., Naik S., Mahadevan N., A comparative study of photocatalytic activities of two different synthesized ZnO composites against caralene red F₃BS dye in presence of natural solar light, 2011, J. Environ Sci. Res.1:11-5.
KimK. S., Lee, T. S., Lee, J. H., et al., Effect of fluorine addition on transparent and conducting Al doped ZnO films, 2006, J. Appl. Phys.,100: 063701. [CrossRef]
Horsfield A. P., A.M. Bratkovsky A. M., Fear M.,Pettifor D. G., and Aoki M., Bond-order potentials: Theory and implementation, 1996, Phys. Rev. B, 53:12694. [CrossRef]
Gerward L.andOlsen J. S., The High-Pressure Phase of Zincite, J.SynchrotronRadiat., 2233 (1995). [CrossRef]
Karzel H. et al., Lattice dynamics and hyperfine interactions in ZnO and ZnSe at high external pressures, 1996. Phys. Rev. B 5311425. [CrossRef]
Zaoui A. et al., Pressure-induced softening of shear modes in wurtzite ZnO: A theoretical study, Phys. Rev. B, 66174106 (2002). [CrossRef]
Wang J., Xiao P., Zhou M., Wang Z. R., and Ke F. J., Wurtzite – to - tetragonal structure phase transformation and size effect in ZnO nanorods, 2010, J. Appl. Phys.,107:023512.
J. P. Perdew, K. Burke, and M. Emzerhof, Generalized Gradient Approximation Made Simple 1996, Phys. Rev. Lett., 77:3865. [CrossRef]
Irfan Ayoub , Vijay Kumar , Reza Abolhassani, et al., Advances in ZnO: Manipulation of defects for enhancing their technological potentials, 2022, Nanotechnology Reviews;11:575-619. [CrossRef]
J. Wrobel and J. Piechot, Structural Properties of ZnO Polymorphs, 2007. Phys. Status Solide B. 244:1538. [CrossRef]
M. D. Seggal, P. L. D. Linda, M. J. Probert, et al. First-Principles Simulation: Ideas, Illustrations and the CASTEP Code. 2002, J. Phys. Condens. Matter, 14:2717. [CrossRef]
Molecular Dynamics simulation of diamond pyramid structure in electroless copper deposite Woodhead Publishing limited (2011). [CrossRef]
Tan J., Wang G., Liu Z. Y., et al., Correlation between atomic structure evolution and strength in a bulk metallic glass at cryogenic temperature, 2014, Sci., Rep., 4:3897. [CrossRef]
Kuzmin A., Timoshenko J., Kalinko A., Jonane I., Anspoks A., Treatment of disorder effects in X-ray absorption spectra beyond the conventional approach, 2020, Phys. Chem., 175. [CrossRef]
Bochara D., Krack M., Rafalskij Y., Kuzmin A., Purans J., Ab initio molecular dynamics simulations of negative thermal expansion in ScF₃: the effect of the supercell size, 2020, Compt. Matter Sci. 171:109198. [CrossRef]
Nose S., A unified formulation of the constant temperature molecular dynamics methods, 1984, J. Chem. Phys., 81:511-519. [CrossRef]
Mahlaga M. P., Computational study of the structural phase transitions and pressure dependent electronic structure ZnO, May 2, 2012, PhD thesis, University of Witwatersrand of Physics, Johansburg,.
J. Uddin, G. E. Scuseria, Theoretical study of ZnO phases using a screened hybrid density functional Phys. Rev. B 74, 245115 ( 2006 ). [CrossRef]
Y. Saeed, A. Shaukat, N. Ikram, M. Tanveer, 2008, J. Phys. Ghem. Solids 69 ( 7 ):1676-1683 ). [CrossRef]
H. Liu, et al., Magnetic-field-induced superconductivity in the antiferromagnetic organic superconductor κ−(BETS)₂FeBr₄, 2004, Phys. Rev.B 70:094114. [CrossRef]
H. Liu, J. Tse, H. Mao, Stability of rocksalt phase of zinc oxide under strong compression: Synchrotron x-ray diffraction experiments and first-principles calculation studies, 2006, J. Appl. Phys.100,093509. [CrossRef]
Abner Shimony (Editor), Herman Feshbach (Editor), Physics as Natural Philosophy: Essays in honor of Gasz lofiszaon 1982 (The MIT Press) 2nd Edition, ISBN-10: 0262693089, ISBN-13:978-0262693080.111.
Y. Azzaz, S. Kacimi, A. Zaoui, B. Bouhafs, Electronic properties and stability of ZnO from computational study, 2008, Physica B: Condensed Matter 403(18):3154-3158. [CrossRef]
Z. Li, Y. Xu, G. Gao, T. Cui, Y. Ma, Tetragonal high-pressure phase of ZnO predicted from first principles Physical Review B 79 (19):193201. [CrossRef]

Figure 1. The Radial distribution functions of Zn-O bonds of rocksalt structure at 300 (K) and under the range of pressure 0-30(GPa).

Figure 2. The Correlation functions of O-O pair of ZnO rocksalt type under the range of pressure 0-30 GPa and at 300 K.

Figure 3. TheRDF of Zn-Zn pair of ZnO rocksalt structure under the range of pressure 0-30 (GPa) and at the temperature of 300 (K).

Figure 4. Bonds lengths of ZnO (B1): Zn-O, Zn-Zn, and O-O under the pressure of 300 (K) and 0-30 (GPa).

Figure 5. Percentage of variation of ZnO (B1) bonds lengths under the range of pressure 0-30 (GPa) at ambient temperature (300 (K)).

Figure 6. the structure of ZnO; a)rocksalt, b) Zincblende, and c) Wurtzite.

Figure 7. ZnO structures; d) Cesium (B2), e) BN structure (B_k), f) NaTI(B32), g) PBO, and WC(B_h)[47].

Figure 8. Maximum of radial distribution function (RDF) of Zn-O, Zn-Zn, and O-O under the pressure of 0-30 (GPa) at the ambient temperature (300 (K)).

Figure 9. Standard error (SE), standard deviation (SD) of ZnO (B1) lengths measured under the range of 0-30(GPa) ad at 300(K).

Figure 10. the RDF of Zn-O bond (B1) under the range of 40-70 (GPa) and 300(K).

Figure 11. Radial distribution function (RDF) of Zn-O (B1) under the range of pressures 80-150 (GPa) and the temperature of 300 (K).

Figure 12. Radial distribution function (RDF) of Zn-O (B1) under the range of 80-150 (GPa) and the temperature of 300 K.

Figure 13. the RDF of O-O bond of ZnO (B1) under the range of 40-70 (GPa) and at 300(K).

Figure 14. The RDF of O-O bond of ZnO (B1) under the range of 80-150 (GPa) and at 300 (K).

Figure 15. The RDF of O-O bond of ZnO (B1) under the range of 200-400 (GPa) and at 300 (K).

Figure 16. the RDF of Zn-Zn bond of ZnO (B1) under the range of 40-70 (GPa) and at 300 (K).

Figure 17. the RDF of Zn-Zn bond of ZnO (B1) under the range of 80-150 (GPa) and at 300 (K).

Figure 18. the RDF of Zn-Zn bond of ZnO (B1) under 200-400 (GPa) and at 300 (K).

Figure 19. Length of ZnO (B1) bonds under the range of pressure 40-400 (GPa) and at 300 (K).

Figure 20. Percentage of variation of ZnO (B1) bonds under the ranges of 40-400 (GPa) and at 300 (K).

Figure 21. Maximum of radial distribution function (RDF) of ZnO (B1) pairs under high-pressure (40-400 (GPa)) at 300 (K).

Figure 22. Standard error (SE) and standard deviation (SD) of ZnO (B1) bonds under the range of pressure 40-400 (GPa) at 300 (K).

Figure 23. the Neighbors number of ZnO pairs under the range of pressure 0-400 (GPa) .

Table 1. Phase transition P_t (GP) of ZnO(LDA and GGA) correspondent bonds lengths and percentage of variation(this work) .

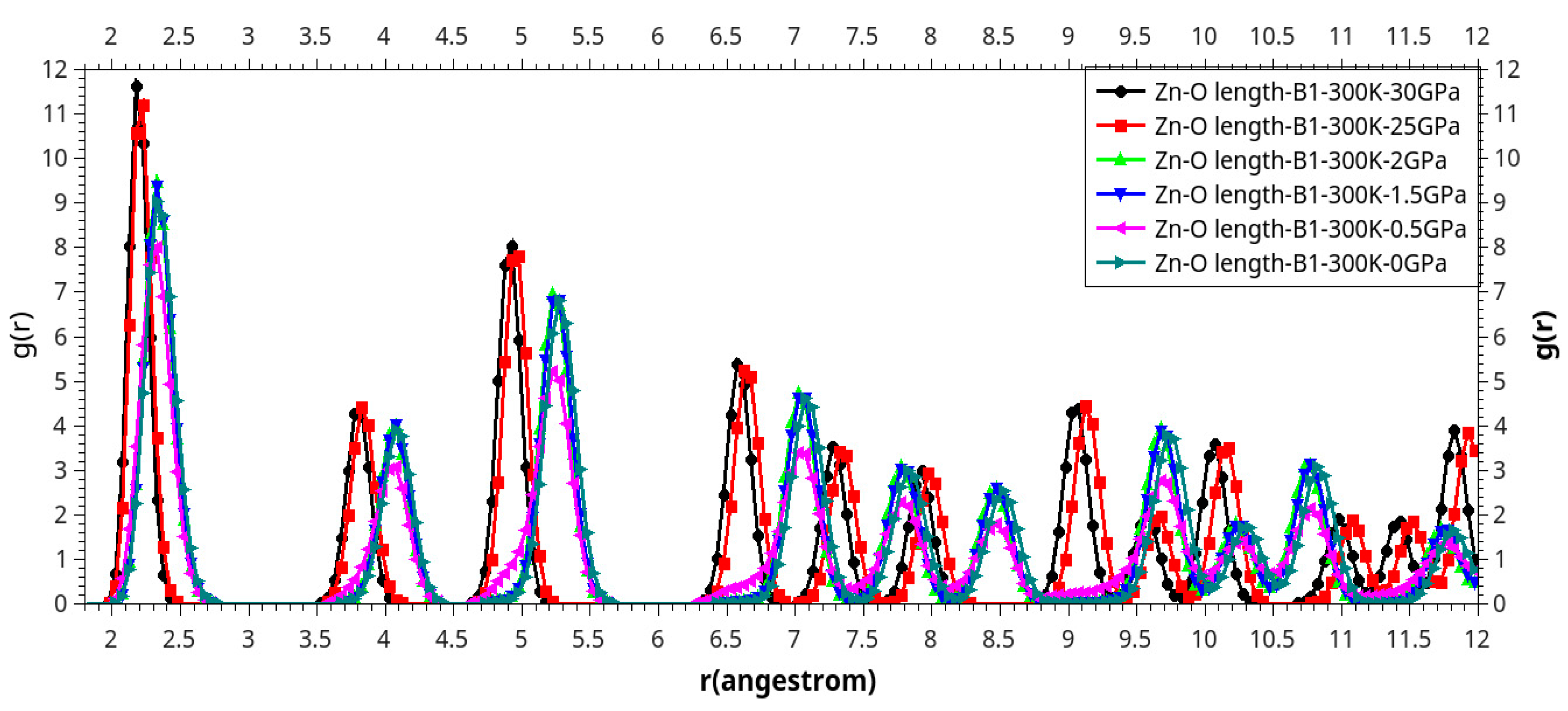
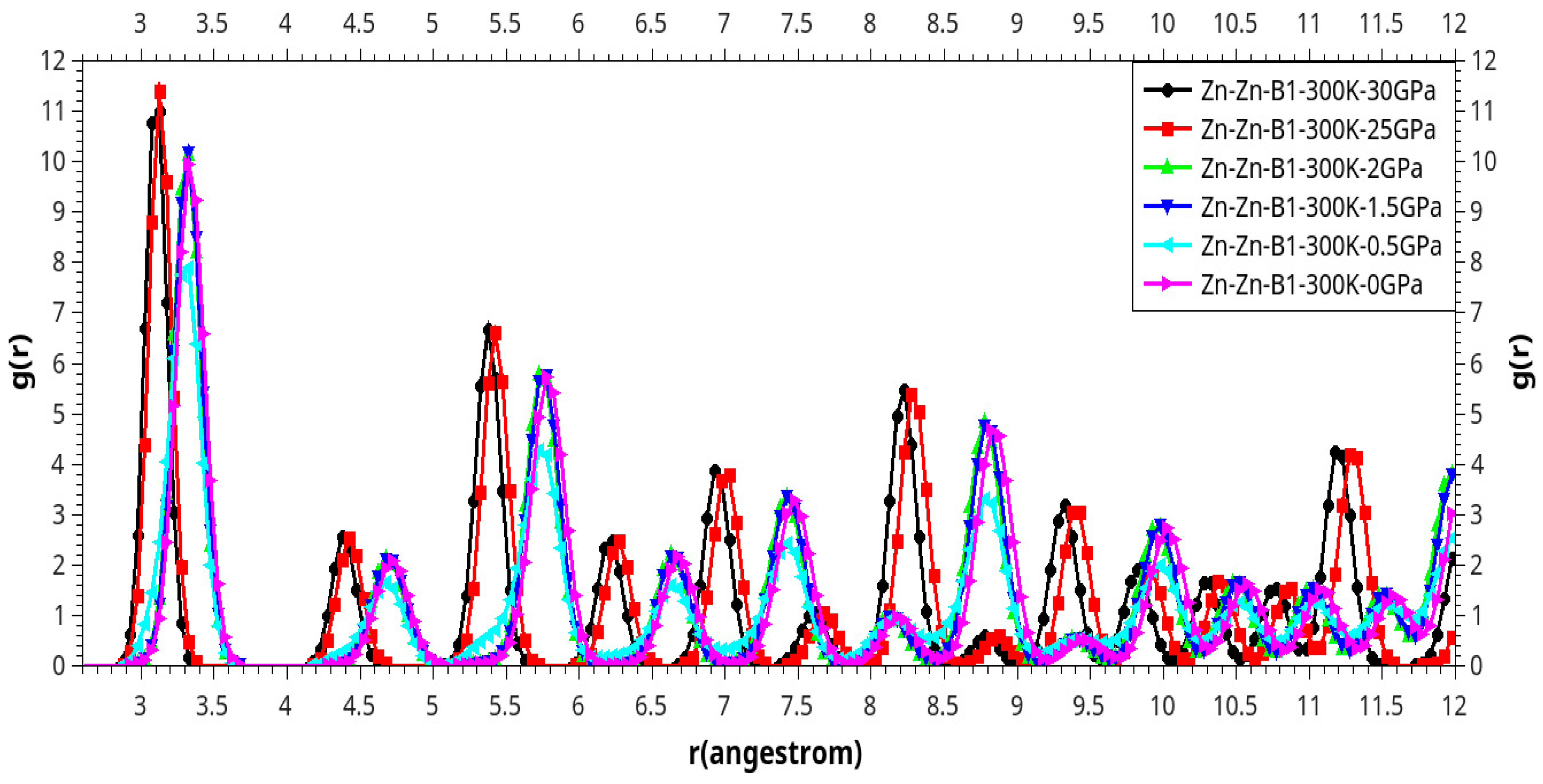
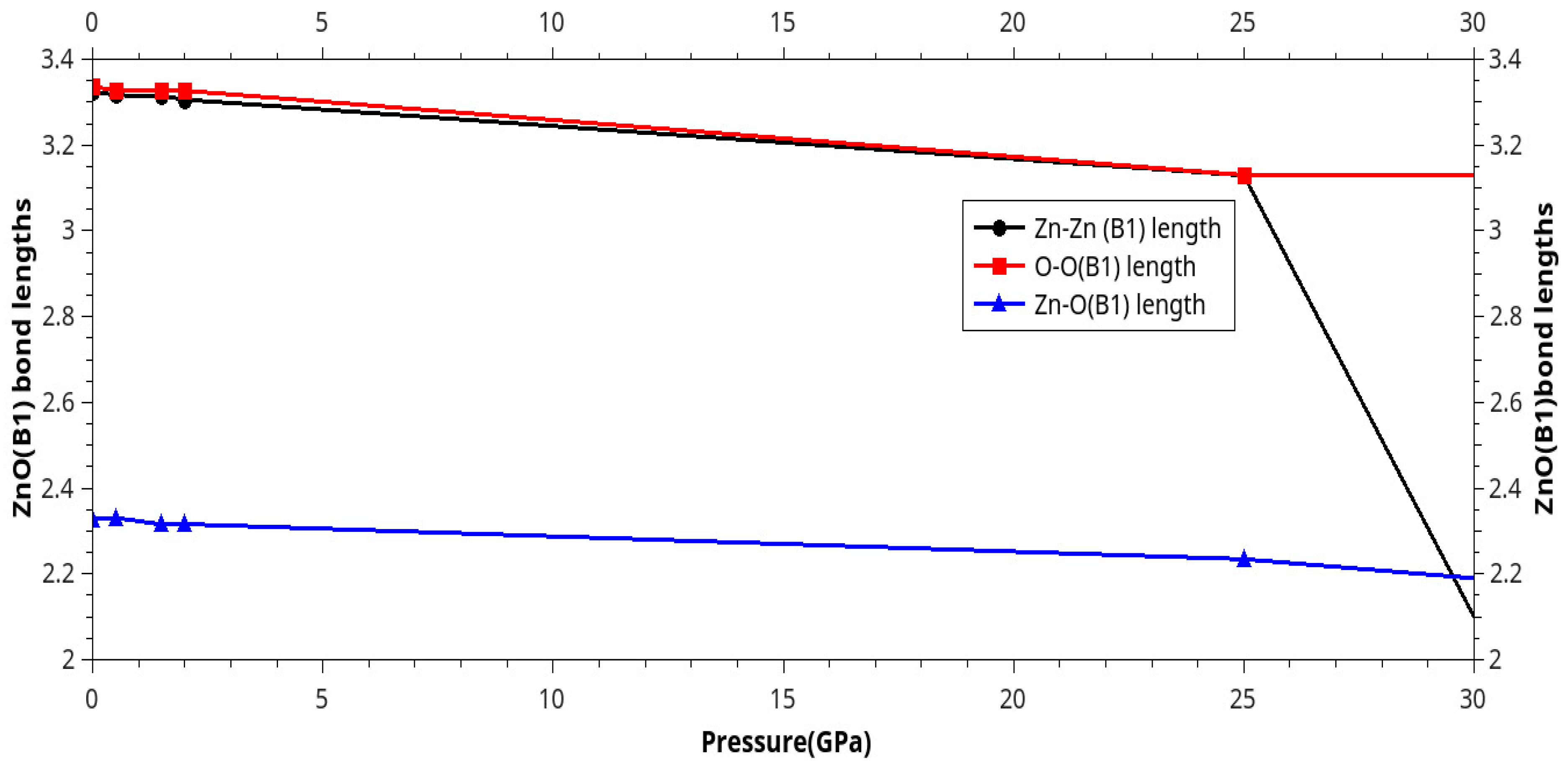
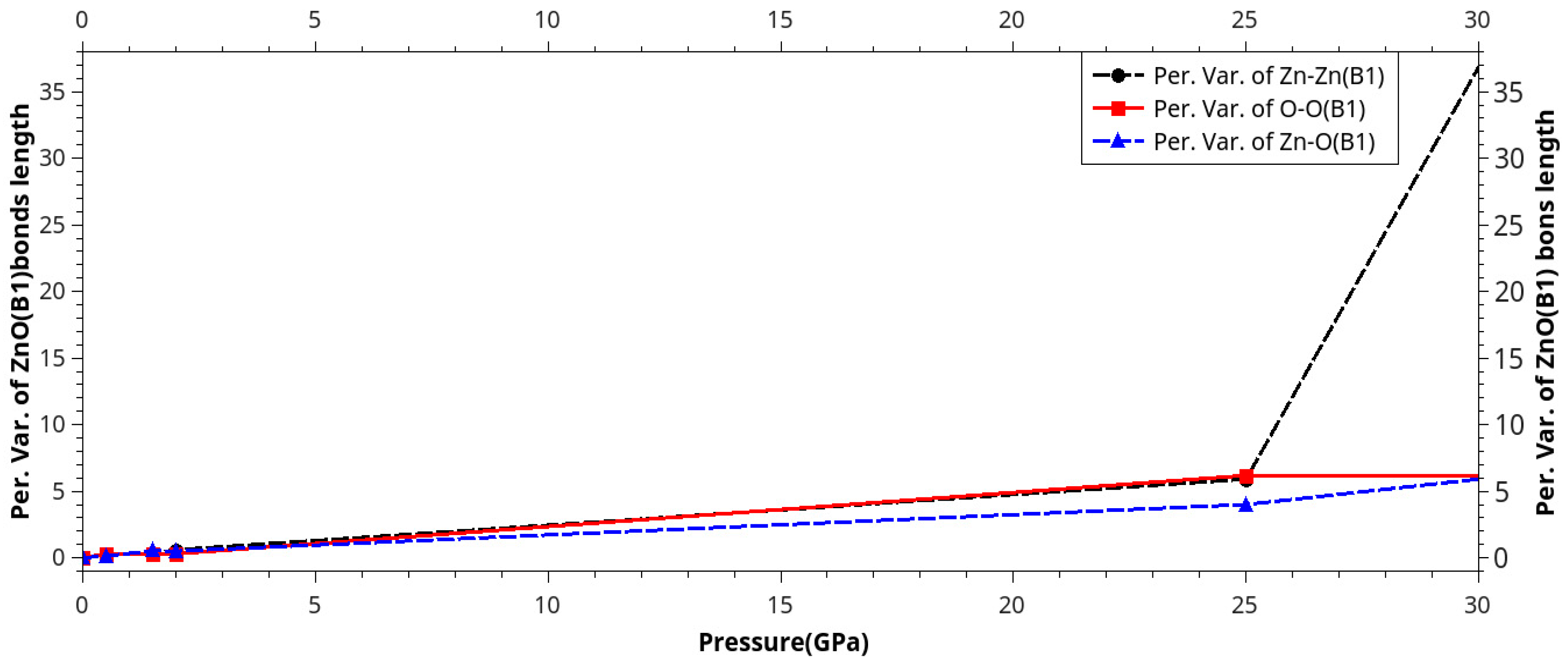
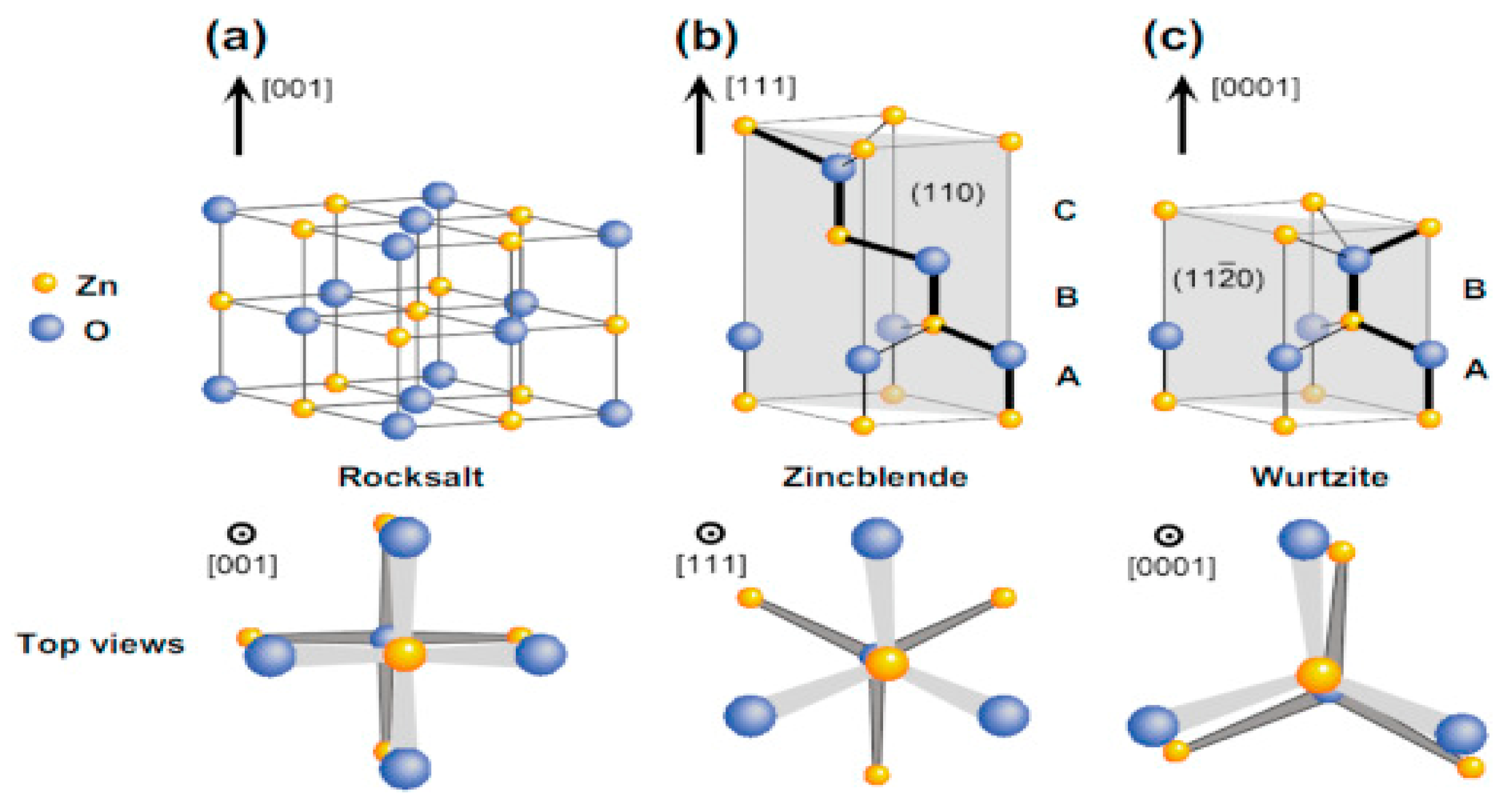
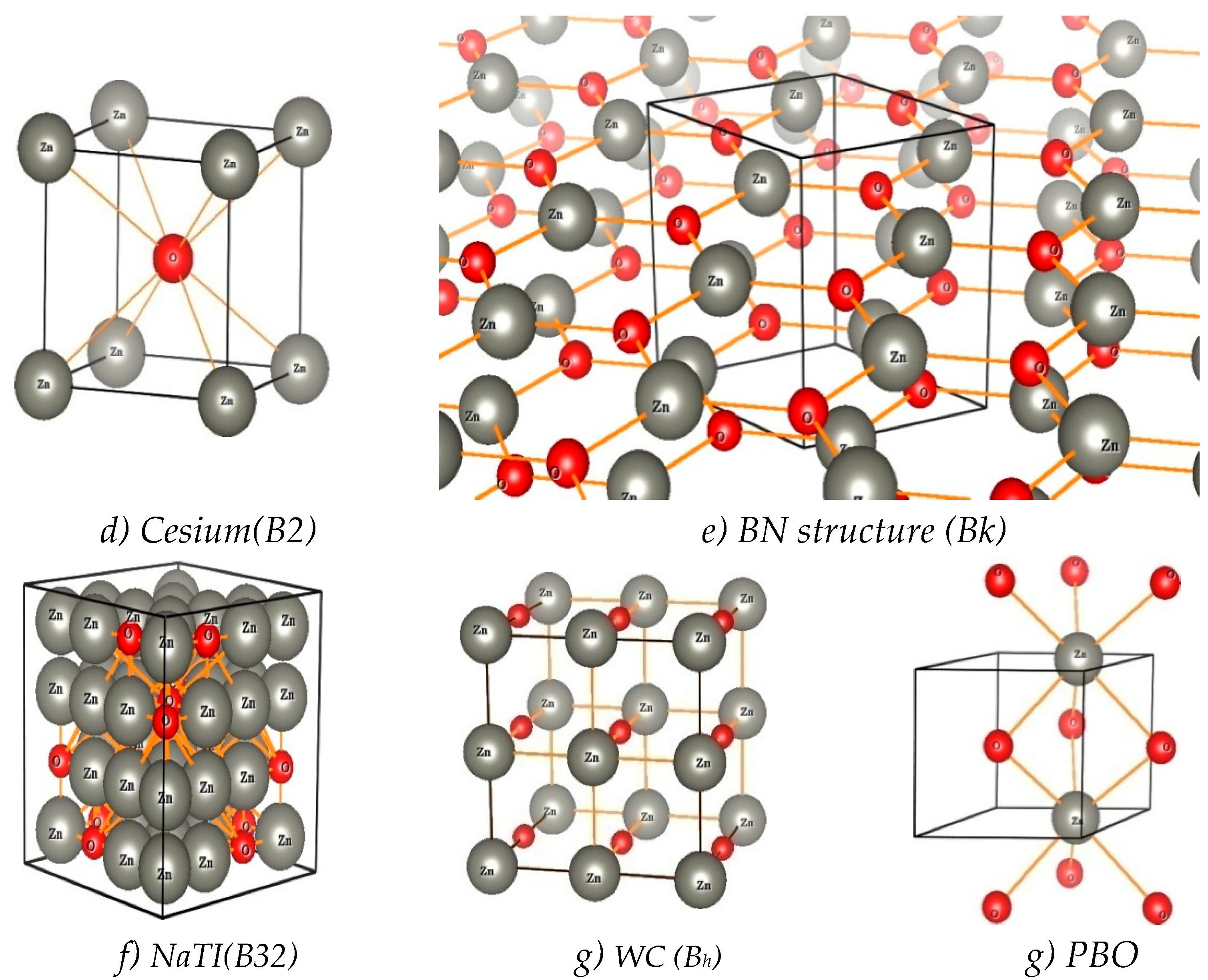
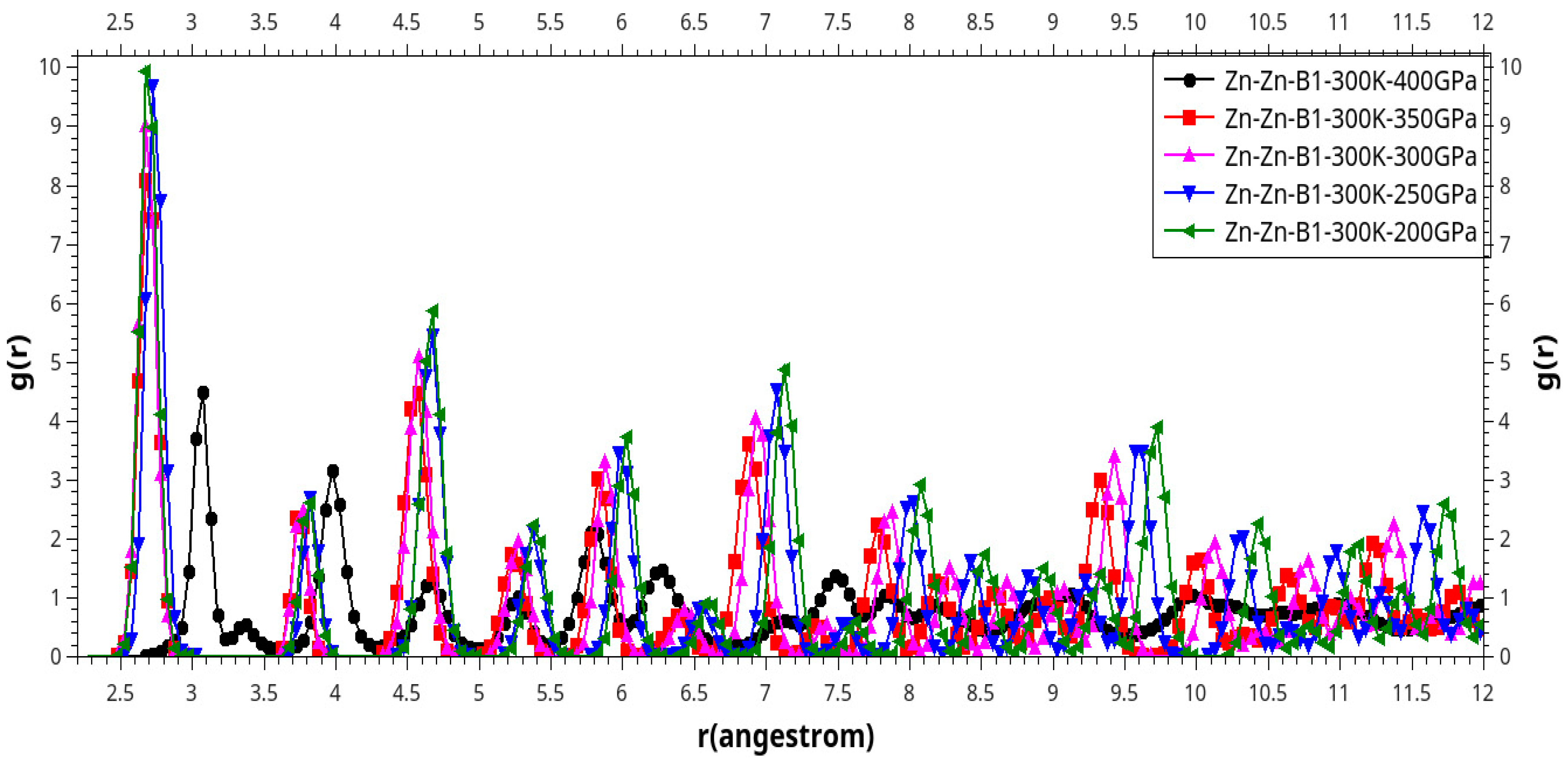
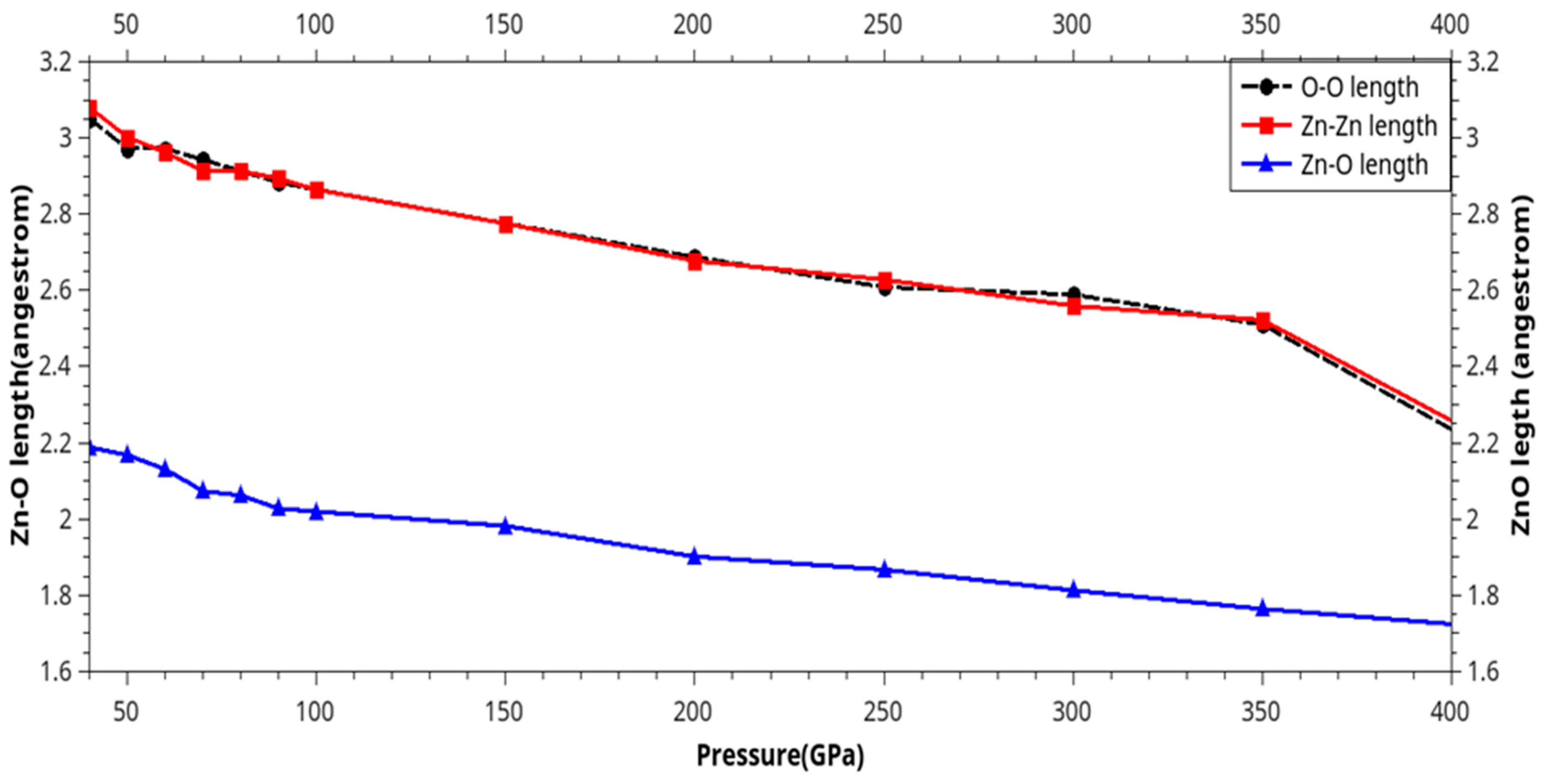
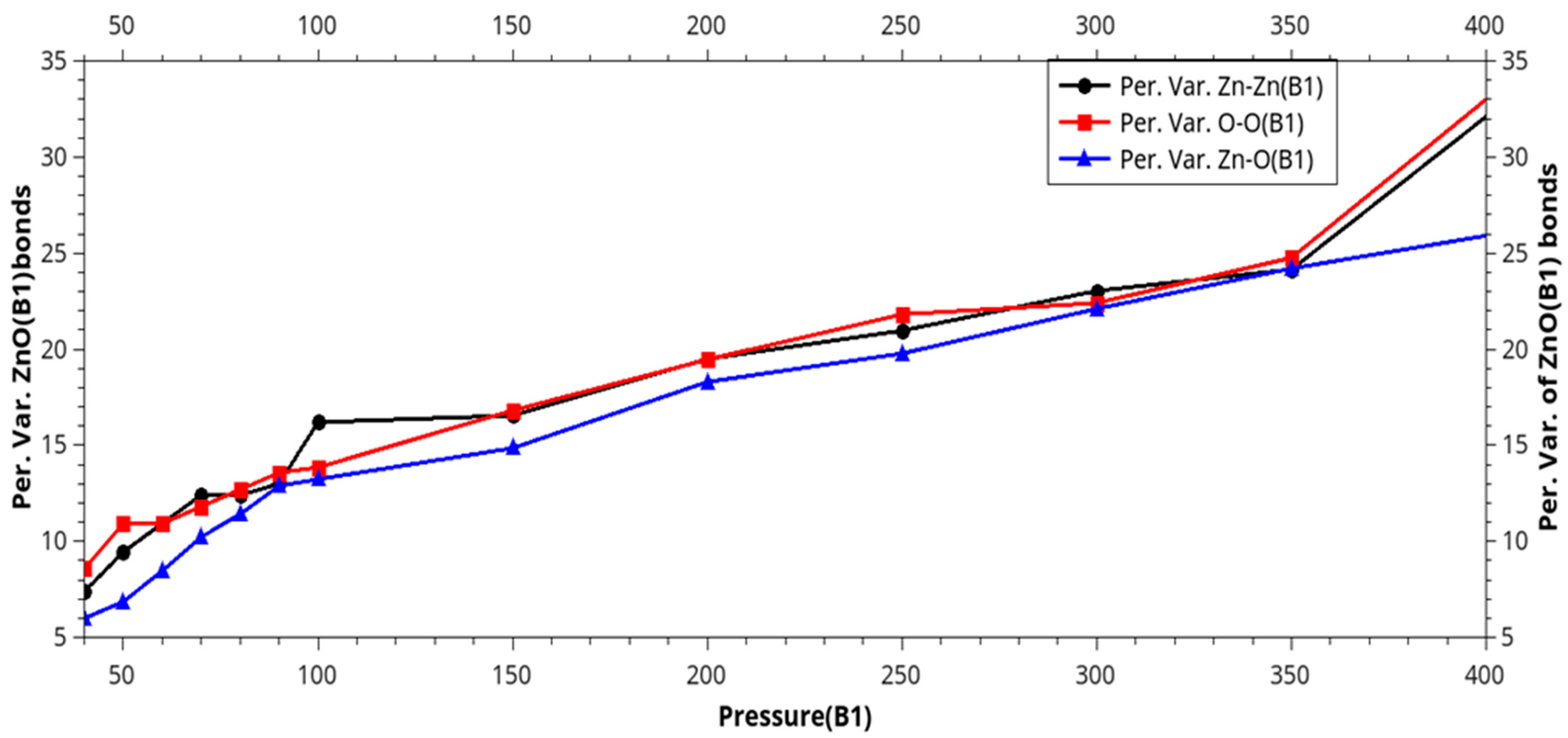
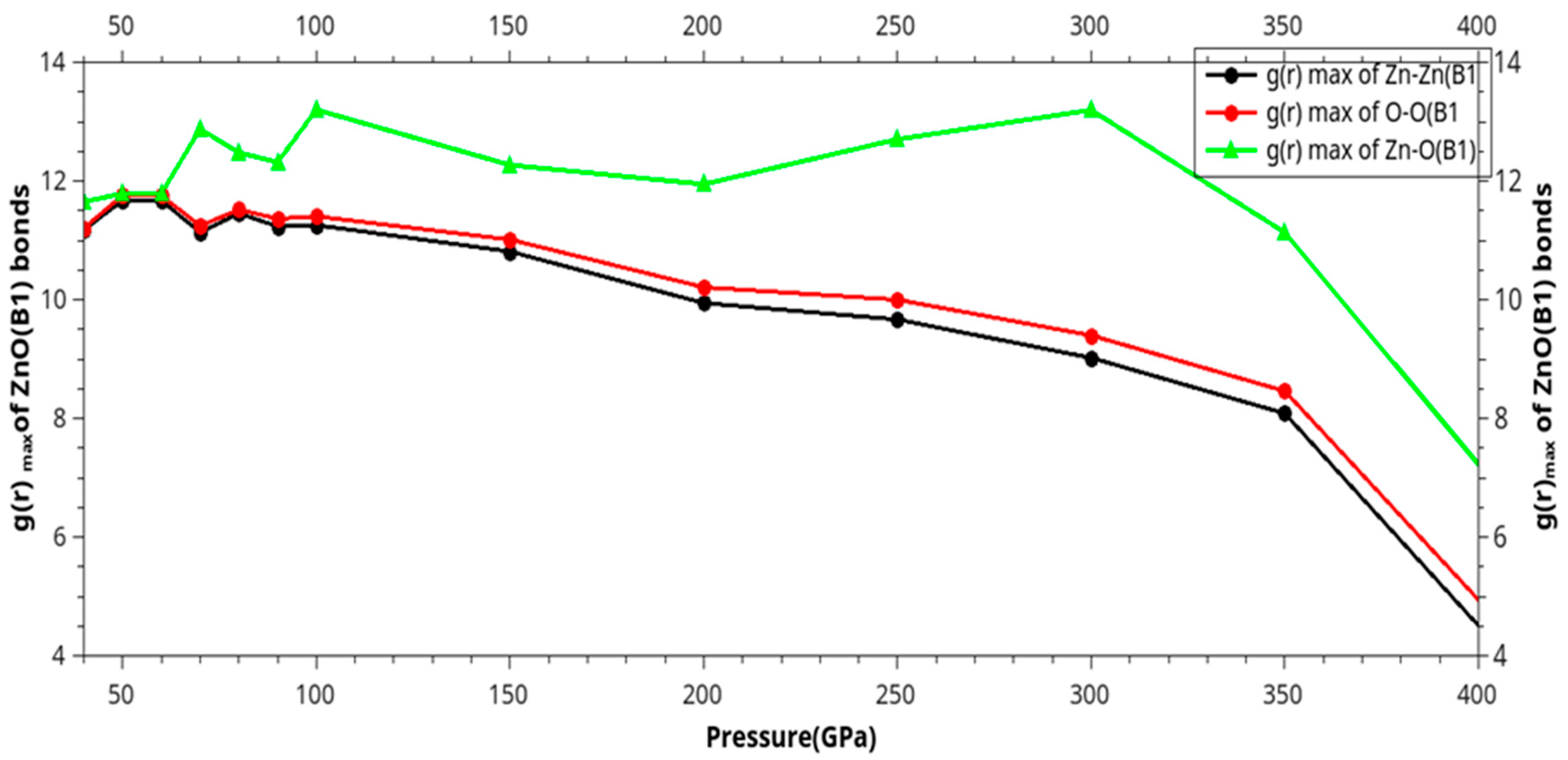
Phase transition	P_t (LDA)[47]	P_t( GGA)[47]	Zn-O length (other work)[47]	Zn-O length (this work)	(%) of variation
B4 to B1 B4 to B_k B_k to B_h B_k to B_i B4to B8₁	9.08(9.20) 27.66 30.6(30.2) 12.19 (12.13) 17.93(17.70)	11.59(11.51) 24.35(24.65) 32.36(32.85) 16.56(16.53) 19.60(19.52)	1.99-1.95 (B4)	2.2684(10GPa) 2.2262(25GPa) 2.1768(30GPa) 2.2667(15GPa) 2.2249(20GPa)	2.52 4.36 6.46 2.60 4.92

Table 2. The value of the phase transition’s pressure (LDA, GGA) comparing with the correspondent bonds lengths and the percentage of variation (of this work).

Phase transition	P_t (LDA)[47]	P_t( GGA)[47]	Zn-O length(Å)( this work)	(%) of variation This work
B1to B10 B10to B2 B1 to B2 B_h to B2 B_i to B2 B8₁toB32	261.5 296.5 268.3 156.9 248.2 230.20	- - - 144.4 213.5 218.9	1.849(260GPa) 1.8131(300GPa) - 1.9820(150GPa) 1.864(250GPa) 1.9018(200GPa)	20.56 22.30 - 14.85 19.922 18.29

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.