Prerpints.org logo
Preprint
Review

Magnetostructural D‐Correlations and Their Impact to Single‐Molecule Magnetism

This version is not peer-reviewed.

Submitted:

25 September 2023

Posted:

27 September 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Functional dependence of the axial zero-field splitting parameter D with respect to a properly chosen geometrical parameter (Dstr) in metal complexes is termed the Magnetostructural D-Correlation. In mononuclear hexacoordinate Ni(II) complexes with the ground electronic term 3B1g (3A2g in the regular octahedron) it proceeds along two intercepting straight lines allowing to predict the sign and magnitude of the D-parameter by knowing the X-ray structure alone; Dstr is constructed from the metal-ligand bond lengths. In hexacoordinate Co(II) complexes it is applicable only in the segment of the compressed bipyramid where the ground electronic term 4B1g is orbitally non-degenerate so that the spin Hamiltonian formalism holds true. The D vs Dstr correlation is strongly non-linear and it is represented by a set of decreasing exponentials. In tetracoordinate Co(II) complexes, on the contrary, the angular distortion from the regular tetrahedron is crucial so that the appropriate structural parameter Dstr is constructed of bond angles. All of these empirical correlations originate in the electronic structure of metal complexes that can be modelled by the generalized crystal-field theory. As the barrier to spin reversal in the single-molecule magnets is proportional to the D-value, for a rational tuning and/or prediction of the single-molecule magnetic behavior knowledge/prediction of the D-parameter is beneficial. In this review, we present the statistical processing of an extensive set of structural and magnetic data of Co(II) and Ni(II) complexes, which were published over the past 15 years. Magnetostructural D-correlations defined for this data set are reviewed in detail.
Keywords: 
Subject: 
Chemistry and Materials Science  -   Inorganic and Nuclear Chemistry

supplementary.docx (220.14KB )

1. Introduction

Though a dodecanuclear plaquette-type complex, [MnIII8MnIV4O12(ac)16(H2O)4] ·2Hac·4H2O, abbr. Mn12ac, was synthesized in 1980, its unusual magnetic properties were reported in 1991 and later termed as new class of magnetic materials–single molecule magnets [1,2,3,4]. These systems show quantum effects of which the most important is a slow magnetic relaxation. Slow means that the extrapolated relaxation time (time extrapolated to infinity temperature) is typically of the order τ0~10-6–10-8 s, unlike to spin glasses where τ0 < 10-20 s [4,5]. At temperature low enough the system retains its magnetization for a time long enough to find potential applications in recording technique. In course of time, a plethora 3d-metal complexes were identified as single-molecule magnets; for instance systems of different nuclearity cover Mn2, Mn3, Mn4, Mn6, Mn7, Mn8, Mn9, Mn10, Mn12, Mn16, Mn18, Mn21, Mn22, Mn25, Mn26, Mn30, Mn84, Fe4, Fe8, Fe9, Fe10, Fe11, Fe19, Co4, Co6, Ni4, Ni8, Ni12, Ni21, MnCu, V4, MnMo6, Mn2Cr, Mn2Fe, Mn2Ni2, Ni3Cr, Mn4Re4, Cu6Fe8, Co9W6, Co9Mo6, Mn8Fe4, etc. [6]. It can be concluded that high nuclearity is not an ultimate demand for single-molecule magnetic behaviour since many mononuclear complexes of Cr(III), Mn(III), Mn(II), Fe(III), Fe(II), Fe(I), Co(II) and Ni(II) possessing the spin S = 1 through 5/2 also show slow magnetic relaxation [7,8,9]. Moreover, some S = 1/2 spin systems, such as V(IV), low-spin Mn(IV), low-spin Co(II), low-spin Ni(III), Ni(I) and Cu(II), exhibit the slow magnetic relaxation as well [10,11,12,13]. Slow magnetic relaxation and single-molecule magnetism was identified among 4f-complexes (mononuclear and polynuclear) as well as heterometallic 4f-3d complexes; for instance, Tb1, Dy1, TbCu, Dy2, Dy4, Dy6Mn6, Dy4Mn11, and many others were classified as single-molecule magnets [6].
Unlike to classical magnetic materials (like ferrites widely used in daily recording technique and many useful tools) the single-molecule magnet retains its magnetization due to the magnetic anisotropy. The magnetic anisotropy in single crystals is defined through the non-isotropic magnetization tensor having at least two main-axes components different, or the non-isotropic susceptibility tensor. In molecules, the spin-spin interaction tensor, when rotated to its main axes, possesses the diagonal elements
H ^ ss = ℏ − 2 ( D x x S ^ x 2 + D y y S ^ y 2 + D z z S ^ z 2 )
that define two eccentricity parameters:
(a)
the axial zero-field splitting (ZFS) parameter D
D = ( − D x x − D y y + 2 D z z ) / 2 → ( 3 / 2 ) D z z
(b)
the (ortho)rhombic ZFS parameter E
E = ( D x x − D y y ) / 2
These two parameters modify (split) the ground-state energy levels in the absence of the magnetic field and they are responsible for the magnetic anisotropy. The magnetic anisotropy manifests itself in the way that with increasing magnetic field the magnetization components as well as the magnetic susceptibility (Cartesian) components develop differently.
Using the ZFS parameters, the spin-spin interaction can be rewritten to the form
H ^ ss = ℏ − 2 [ D ( S ^ z 2 − S ^ 2 / 3 ) + E ( S ^ x 2 − S ^ y 2 ) ]
and usually a constraint | D | ≥ 3 E ≥ 0 is maintained. For a uniaxial system (like D4h or C4v) the effective spin-Hamiltonian collapses to
H ^ aniso = ℏ − 2 D S S ^ z 2
giving rise to the energy levels depending upon the magnetic quantum number M
ε = D S M 2
(In these formulae it is emphasized that we are working in the strong exchange limit for polynuclear systems, so that the D-parameter depends upon the (good) total molecular spin quantum number S, hence DS). When DS > 0 (easy-plane anisotropy) a model of a particle in the potential box is appropriate: a fast relaxation from the state M = − S to M = 0 (or M = ± 1 / 2 ) proceeds and the magnetic record disappears. On the contrary, when DS < 0 (easy-axis anisotropy) a model of a particle in the double potential is applicable; the two minima are separated by a barrier to spin reversal Δ E = | D S | S 2 (or Δ E = | D S | S 2 − | D S | / 4 for the half-integral spin) and thermal activation mechanism of the relaxation, or tunnelling mechanism apply. For this reasoning a deep knowledge about the DS-parameter is a key factor for a rational synthesis of single-molecule magnets with aimed properties. The rhombic ZFS parameter ES is also in the play through the term E S ( S ^ x 2 − S ^ y 2 ) and it causes a further modification of the energy levels and consequently the single-molecule magnetic behavior.

2. Spin-Hamiltonian Formalism

The spin-Hamiltonian (SH) formalism is applicable when the ground electronic term is orbitally non-degenerate (e.g., 3A2g, 4B1g). In this model the electronic wave function is substituted by spin-only kets | S , M S 〉 . This very restricted basis set is under the action of operators covered by three leading terms: the spin Zeeman term, the orbital Zeeman term, and the spin-orbit interaction term
H ^ ′ = ℏ − 1 μ B g e ( S → ⋅ B → ) + ℏ − 1 μ B ( L → ⋅ B → ) + ℏ − 2 λ ( L → ⋅ S → )
Here ge is the spin-only magnetogyric factor and λ = ± ξ / 2 S is the spin-orbit splitting parameter within the ground electronic term dependent upon the spin-orbit coupling constant ξ (the minus sign applies for the configurations dn more than half-full). Then the second-order perturbation theory yields the contribution [14]
H ^ S = ℏ − 2 ( S → ⋅ D ¯ ¯ ⋅ S → ) + ℏ − 1 μ B ( B → ⋅ g ¯ ¯ ⋅ S → ) + ( B → ⋅ κ ¯ ¯ ⋅ B → )
To this end, three magnetic tensors contribute:
  • D–tensor (tensor of the spin-spin interaction)
D a b = λ 2 Λ a b   [ energy ]
  • g–tensor (tensor of the magnetogyric ratio)
g a b = g e δ a b + 2 λ Λ a b   [ dimensionless ]
  • κ−tensor (tensor of the temperature-independent paramagnetism)
κ a b = μ B 2 Λ a b   [ energy × induction – 2 ]
All of them are constituted of the Λ-tensor (tensor of the angular momentum unquenching)
Λ a b = − ℏ − 2 ∑ K ≠ 0 〈 0 | L ^ a | K 〉 〈 K | L ^ b | 0 〉 E K − E 0   [ energy – 1 ]
where the summation runs over all excited states (electronic terms). The scalar product of the vectors and tensors can be developed as follows
H ^ S = ∑ a x , y , z ∑ b x , y , z { ℏ − 2 λ 2 Λ a b S ^ a S ^ b + ℏ − 1 μ B B a ( g e δ a b + 2 λ Λ a b ) S ^ b + μ B 2 Λ a b B a B b }
In the zero magnetic field we arrive at the formulae (1) through (4) that are widely used in analysing the magnetic data (susceptibility and magnetization) as well as the spectroscopic data such as Electron-Spin-Resonance (ESR) or Far-Infra-Red (Far-IR) spectra referring to electronic transitions.
For degenerate ground electronic terms of the T-type the above formalism is inappropriate and one is left to pass beyond the spin-Hamiltonian formalism. In early stages it was covered by Griffith and Figgis theory, respectively, dealing with the ground T1(g) or T2(g) terms, eventually under the symmetry lowering and configuration interaction [15,16]. A more complete approach that involves all members of the dn-electron configuration has been outlined by König-Kremer theory [17]. This theory was reformulated and simplified elsewhere [18,19].

3. Electronic Structure of 3d-Complexes

Almost complete description of the energy levels in metal d- or f-complexes can be obtained by considering five operators acting to the basis set of free-atom terms | l n v L S M L M S 〉 with the seniority number v:
(a)
the interelectron repulsion
H I J ee = 〈 l n v L S M L M S | V ^ ee | l n v ′ L ′ S ′ M ′ L M ′ S 〉 = δ M L , M ′ L δ M S , M ′ S δ L , L ′ δ S , S ′ 〈 l n v L S ‖ ∑ i = 1 n ∑ j > i n ∑ k = 0 , 2 , 4 2 l F l l k ∑ q = − k + k ( − 1 ) q C ^ − q k ( i ) C ^ q k ( j ) ‖ l n v ′ L ′ S ′ 〉
(b)
the crystal-field potential
H I J cf = 〈 l n v L S M L M S | V ^ cf | l n v ′ L ′ S ′ M ′ L M ′ S 〉 = δ S , S ′ δ M S , M ′ S 〈 l n v L S M L M S | ∑ i = 1 n ∑ K = 1 N z K ∑ k = 0 , 2 , 4 2 l F k ( R K ) ∑ q = − k + k ( − 1 ) q C ^ − q k ( K ) C ^ q k ( i ) | l n v ′ L ′ S ′ M ′ L M ′ S 〉
(c)
the spin-orbit interaction
H I J so = 〈 l n v L S M L M S | V ^ so | l n v ′ L ′ S ′ M ′ L M ′ S 〉       = 〈 l n v L S M L M S | ℏ − 2 ∑ i = 1 n ξ i ( l → i ⋅ s → i ) | l n v ′ L ′ S ′ M ′ L M ′ S 〉
(d)
the orbital Zeeman term
H I J lB = 〈 l n v L S M L M S | V ^ lB | l n v ′ L ′ S ′ M ′ L M ′ S 〉       = δ v , v ′ δ L , L ′ δ S , S ′ δ M S , M ′ S 〈 l n v L S M L M S | ℏ − 1 μ B κ ( B → ⋅ L → ) | l n v ′ L ′ S ′ M ′ L M ′ S 〉
(e)
the spin Zeeman term
H I J sB = 〈 l n v L S M L M S | V ^ sB | l n v ′ L ′ S ′ M ′ L M ′ S 〉 = δ v , v ′ δ L , L ′ δ S , S ′ δ M L , M ′ L 〈 l n v L S M L M S | ℏ − 1 μ B g e ( B → ⋅ S → ) | l n v ′ L ′ S ′ M ′ L M ′ S 〉
Here, the Racah operator (rationalized spherical harmonics) C ^ q k ( i ) = ( 4 π / 2 k + 1 ) 1 / 2 Y q k ( i ) occurs; k–rank, q–component. The parameter
F k ( R K ) = ( e 2 / 4 π ε 0 ) 〈 r > − ( k + 1 ) ⋅ r < k 〉 ≈ ( e 2 / 4 π ε 0 ) R K − ( k + 1 ) ⋅ 〈 r k 〉
refers to the crystal-field strength of the K-th ligand; F l l k = ( e 2 / 4 π ε 0 ) 〈 r > − ( k + 1 ) ⋅ r < k 〉 are Slater-Condon parameters of rank k. The orbital Zeeman term includes κ–orbital reduction factor. The advantage of this approach is that all matrix elements can be expressed through closed formulae [18,19]. By selecting certain combination of operators/matrix elements, several cases can be mapped:
(i)
By diagonalizing the matrix
H I J = H I J ee + H I J cf
the resulting eigenvalues refer to the energies of crystal-field terms. No constrain to the crystal-field strength is needed (weak field, strong field, intermediate field) since the variation principle is applied. The resulting eigenvectors | l n ( v L ) S M S Γ γ a 〉 can be probed for symmetry operations of the respective point group of symmetry allowing a classification according to the irreducible representations Γγ (like A2g, T1g, T2g for the group Oh of the d8 system, Mulliken notation).
(ii)
By diagonalizing the matrix
H I J = H I J ee + H I J cf + H I J so
one gets the crystal-field multiplets. The eigenvectors | l n ( v L S ) J Γ ′ γ ′ b 〉 , when probed to symmetry operations of the respective double group, yield assignment of the Bethe symbols (Γ1 through Γ8 for the O’ double group) to the energy levels.
(iii)
By diagonalizing the matrix
H I J = H I J ee + H I J cf + H I J so + H I J lB ( B ) + H I J sB ( B )
the Zeeman levels dependent upon the magnetic field are obtained. They enter the partition function Z(B,T) from which the magnetization components Ma(B,T), the susceptibility components χab(B,T), and eventually the heat capacity cV(B,T) can be obtained by the apparatus of the statistical thermodynamics [18,19].
The above matrices, in general, are complex-Hermitian so that the programming requires complex*16 arithmetic. The size of the basis set for d5 through d9 systems is 256, 210, 120, 45, and 10 members, respectively. In this approach the configuration interaction is naturally involved and it is termed the Generalized Crystal-Field Theory (GCFT).

4. Zero-Field Splitting Parameters

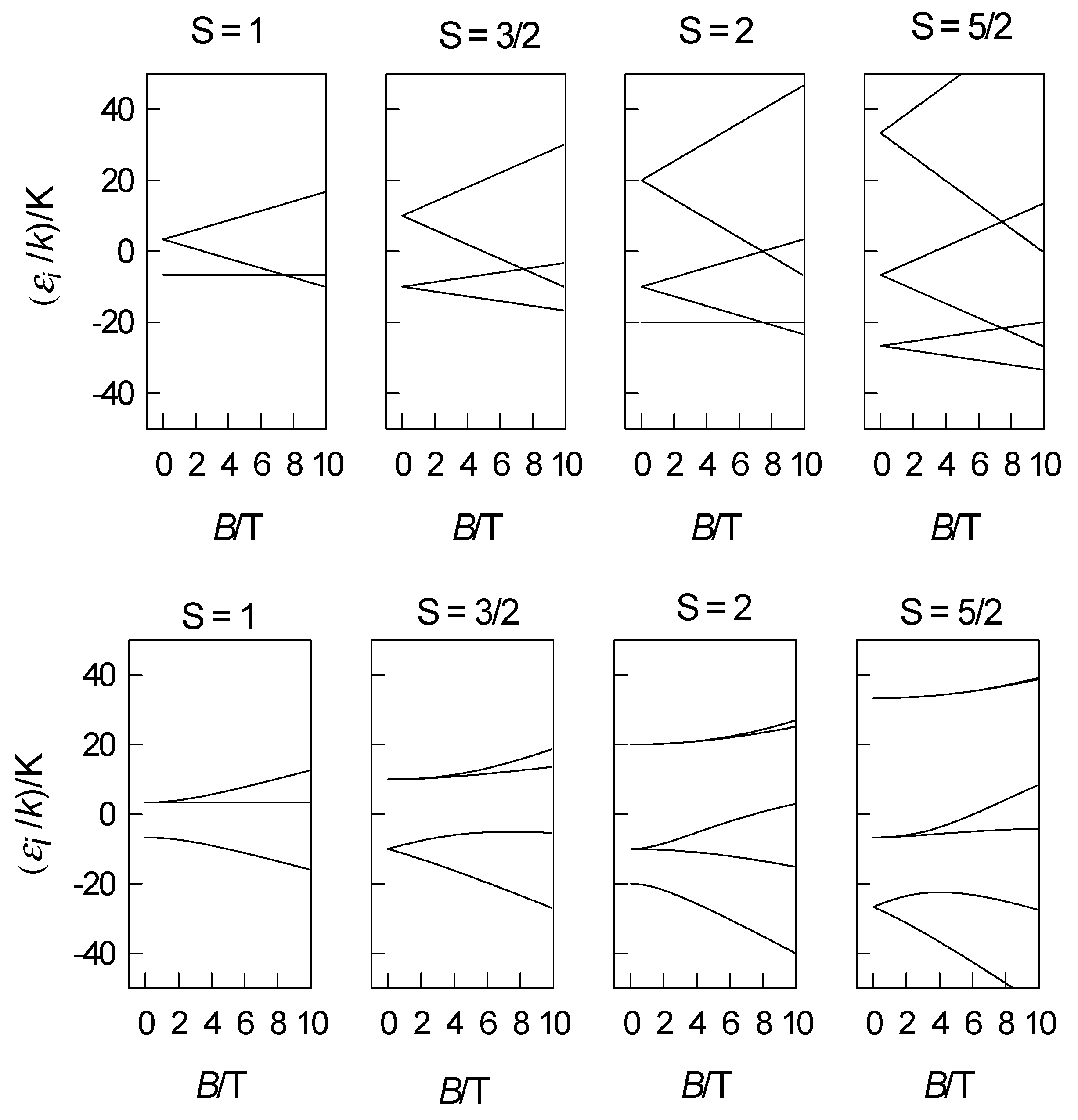
The application of the spin-Hamiltonian offers a modelling of the energy levels, magnetization, and magnetic susceptibility depending upon the spin quantum number S = 1, 3/2, 2, and 5/2. The corresponding spin matrices have dimension of 3, 4, 5, and 6 in the basis set of spin kets | S , M S 〉 . The members of the spin multiplets in the zero field are separated by amount D, 2D, (D, 3D) and (2D, 4D), respectively as shown in Figure 1.
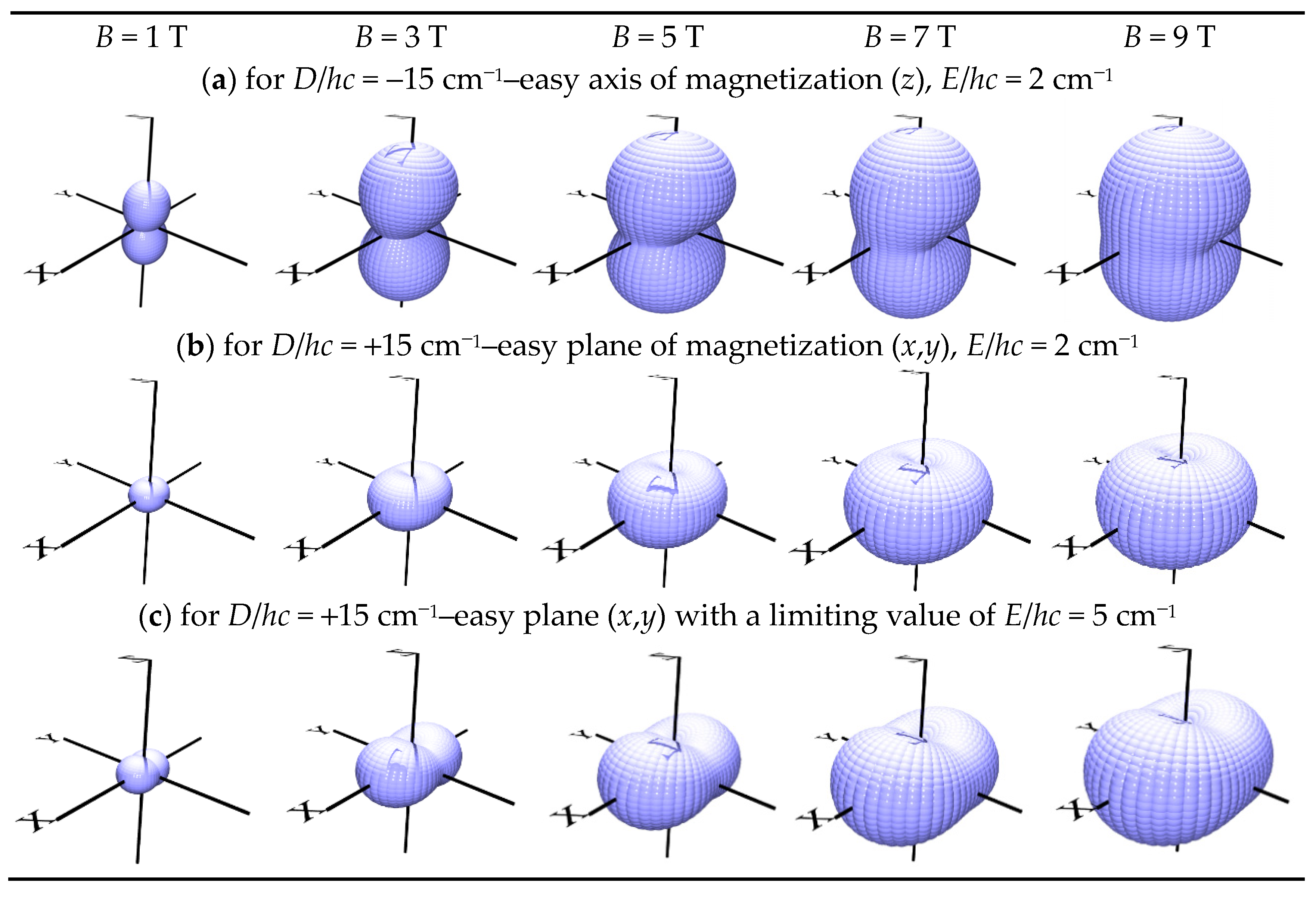
In general, the spin Zeeman term depends upon the polar coordinates ( ϑ , φ ) as follows
H ^ k l , m Z = μ B B m ( g x sin ϑ k cos φ l S ^ x + g y sin ϑ k sin φ l S ^ y + g z cos ϑ k S ^ z ) ℏ − 1
where (k, l) refer to grids distributed uniformly over a sphere. In this way the magnetization can be visualized via a 3D-diagram as shown in Figure 2. It must be noted that when |D| < 3E, a renumbering of the Cartesian axes results to the usual constraint |D| > 3E. In a very high field (50 T) the system becomes isotropic and its 3D-magnetization refers to a sphere.
At the higher level of the theory (GCFT), when all members of the dn configuration are considered, the D and E values are not rigorously defined. Figure 3 brings a modelling of the lowest energy gap between crystal-field multiplets beyond the SH formalism by using GCFT for a wide range of the crystal-field strengths; it is briefly discussed below.
The octahedral d3 and d8 systems are fortunate cases since the ground electronic term is nondegenerate (4A2g, 3A2g) and it stays nondegenerate for the whole array of compressed and elongated tetragonal bipyramids (4B1g, 3B1g). For Ni(II) complexes (S = 1) the lowest crystal-field multiplets, labelled in the D’4 double group by Bethe (Mulliken) symbols Γ4(B2) and Γ5(E1) are separated by the energy gap Δ = ε ( Γ 5 ) − ε ( Γ 4 ) ; this value adopts role of the D-parameter (the Γ5 level is doubly degenerate in the zero field). D > 0 applies for an elongated tetragonal bipyramid, and D < 0 holds true for the compressed bipyramid. For the octahedral geometry the energy gap collapses to the zero. The range of D-values for Cr(III) is by one order of magnitude lower relative to Ni(II); this is a consequence of much lower spin-orbit splitting parameter λ/hc = 92 vs 315 cm-1 (D ~ λ2).
The octahedral d7 system possesses the ground term 4T1g that is orbitally triply degenerate. On distortion to a compressed tetragonal bipyramid it is split into {4A2g, 4Eg} terms; on distortion to an elongated bipyramid the splitting is opposite {4Eg, 4A2g}. The spin-orbit coupling causes a further splitting to six Kramers doublets: 1Γ6, 1Γ7, 2Γ6, 3Γ6, 2Γ7, 3Γ7 for the compression and 1Γ6, 2Γ6, 1Γ7, 2Γ7, 3Γ6, 3Γ7 for the elongation. This means that only the first case is consistent with the SH formalism and, moreover, the crystal field asymmetry should be large (much stronger axial crystal field F4(z)); in such a case always Δ = 2D > 0 and it is very high (typically 200 cm-1).
The counter parting d2 system with the ground state 3T1g resembles the tetragonal splitting to {3A2g, 3Eg} on the compression and the spin-orbit coupling splits the ground term into Γ1(A1) and Γ5(E1) multiplets. In this case Δ = D > 0 holds true. For the elongated bipyramid the six-membered multiplet manifold is Γ3(B1), Γ4(B2), Γ5(E1), Γ1(A1), Γ2(A2) and it has no relationship to the SH approach.
For Mn(III) systems (d4, S = 2) the situation is more complex. The spin-Hamiltonian (SH) formalism predicts that for D > 0 (compressed tetragonal bipyramid) the ground state | S , M S 〉 is a singlet | 2 , 0 〉 ; the first excited Kramer doublet | 2 , ± 1 〉 is by the D-value higher, and the second excited Kramer doublet | 2 , ± 2 〉 lies by 4D amount above the ground state. The GCFT is consistent with SH-formalism only for the first three multiplets Γ1 and Γ5 (doubly degenerate). The remaining two excited states Γ3 and Γ4 are not exactly degenerate (they do not form a Kramer doublet) but they are split in the zero field by 0.2 cm-1. (Calculated energy levels are, for instance: Γ1(A1)×1 at 0; Γ5(E1)×2 at 5.1 cm-1; Γ3(B1)×1 at 19.8 cm-1; Γ4(B2)×1 at 20.0 cm-1. Thus, for D = 5.1 cm-1 is 4D = 20.4 cm-1, but the Γ4 level is by 0.4 cm-1 lower.) This demonstrates that we cannot rely to the spin-Hamiltonian formalism in all cases.
The d6 system, like high-spin Fe(II), again is a complex task. In the octahedral geometry the ground term is orbitally triply degenerate, 5T2g. On tetragonal elongation it is split to {5B2g, 5Eg} terms and five member of the ground term 5B2g are further split by the spin-orbit interaction into multiplets Γ4, Γ5, Γ1, Γ2. Then the SH formalism is approximately valid (the Γ1, Γ2 pair is quasi-degenerate and separated from the ground Γ4 by ca 4D); D-value is moderate: D/hc ~ 10 cm-1. On tetragonal compression the 10-membered manifold of the 5Eg term is split in the way having no relationship to the SH formalism, so that the D-parameter is undefined.
The electronic structure of tetrahedral dn systems matches complementary octahedral systems d10−n. For instance, tetrahedral Co(II)–d7 possesses the ground state 4A2, like octahedral Cr(III)–d3.

5. Magnetostructural J-Correlations

Before proceeding to the discussion of magnetostructural D-correlations, we briefly mention the original type of correlation analysis of structure-magnetism relations in transition metal complexes. Relationships between selected structural parameters and the magnetic properties of dinuclear (polynuclear) metal complexes were outlined by Hatfield [20,21], his co-workers and followers. In the [CuII-(OH)2-CuII] type complexes the isotropic exchange constant J correlates with the bond angle α = Cu-O-Cu along a straight line with negative slope
J[cm−1] = −74.53·α[°] + 7270, r = −0.99
Involvement of more data with greater structural diversity along the superexchange path led to the differentiation according to the alkoxido- or phenoxido- class [22]. Analogous linear correlations were developed for [CrIII-(OH)2-CrIII] and [MnIV-(O)2-MnIV] type complexes [23,24,25].
According to Gorun and Lippard the J-value correlates with the shortest Fe-O distance (abbr. P) along the superexchange path in the [FeIII-O-FeIII] type complexes [26]. The correlation was proposed along a decreasing exponential curve that is applicable only in the segment of negative J
−J[cm−1] = (2.360 × 1010 )⋅exp(−10.661 P[10−10 m]), r = −0.97
However, also a linear correlation is acceptable, hence [27]
J[cm−1] = 525.7⋅P[10−10 m] – 1055, r = 0.96
It must be critically said that any kind of magnetostructural relationship or correlation heavily depends upon the quality of structural and magnetic data. Another aspect is that almost all correlations are restricted to the linear relationships of J-α or J-P type. Nowadays, modern packages of statistical software (multivariate methods) are at the disposal: correlation analysis, Cluster Analysis, Principal Component Analysis, Factor Analysis, etc. can be applied to the carefully filtered datasets. An approach like this appeared very recently [28,29].

6. Magnetostructural D-Correlations

It is obvious that, the correlation D vs P (a geometrical parameter) is derived from the electronic structure of complexes. The problem of electronic structure, as well as magnetic properties, is solved mainly at the level of quantum-chemical (first principle) calculations [79,80,81]. Application of the partitioning technique and/or quasi-degenerate perturbation theory yields the matrix elements of the effective Hamiltonian spanned by the spin manifold of the orbitally non-degenerate ground electronic state | 0 S M 〉 as follows
〈 0 S M | H ^ eff | 0 S M ′ 〉 = E 0 δ M M ′ + 〈 0 S M | H ^ 1 | 0 S M ′ 〉 − ∑ b S ″ M ″ Δ b − 1 〈 0 S M | H ^ 1 | b S ″ M ″ 〉 ⋅ 〈 b S ″ M ″ | H ^ 1 | 0 S M ′ 〉
with the denominator defined by excitation energies
Δ b − 1 = ( E b − E 0 ) − 1 ,   E 0 = 〈 0 S M | H ^ 0 | 0 S M 〉
Then the D-tensor components (m, n = x, y, z) arising from the spin-orbit interaction are obtained in the form
D m n ( 0 ) = − 1 S 2 ∑ b ( S b = S ) Δ b − 1 〈 0 S S | ∑ i h ^ m ( i ) s ^ z ( i ) | b S S 〉 ⋅ 〈 b S S | ∑ i h ^ n ( i ) s ^ z ( i ) | 0 S S 〉
D m n ( − 1 ) = − 1 S ( 2 S − 1 ) ∑ b ( S b = S − 1 ) Δ b − 1 〈 0 S S | ∑ i h ^ m ( i ) s ^ + 1 ( i ) | b , S − 1 , S − 1 〉 ⋅ 〈 b , S − 1 , S − 1 | ∑ i h ^ n ( i ) s ^ − 1 ( i ) | 0 S S 〉
D m n ( + 1 ) = − 1 ( S + 1 ) ( 2 S + 1 ) ∑ b ( S b = S + 1 ) Δ b − 1 〈 0 S S | ∑ i h ^ m ( i ) s ^ − 1 ( i ) | b , S + 1 , S + 1 〉 ⋅ 〈 b , S + 1 , S + 1 | ∑ i h ^ n ( i ) s ^ + 1 ( i ) | 0 S S 〉
where the one-electron (i) orbital operator for the spin-orbit coupling is
h ^ m ( i ) = ∑ A ξ A ( i ) l ^ m A ( i )
A comparison with the simple perturbation theory applied to the crystal-field terms arising from d-electrons of the central atom [82,83,84]
D m n CFT = − 1 4 S 2 ∑ K ≠ 0 〈 0 | L ^ m ξ | K 〉 〈 K | L ^ n ξ | 0 〉 ℏ − 2 E K − E 0
shows that more contributions are in the play. Quantum-chemical calculations show that the individual contributions to the D-parameter are different in size and sign and a lot of terms approximately cancel. The dominating part arises from the spin-orbit coupling, however, the contributions from the spin-spin interaction also cannot be completely neglected in many cases [85].
A much simplified approach is GCFT. By inspecting Figure 4 it is possible to transform the 3D-graph D = f(F4(xy), F4(z)) into a 2D-diagram D = f(P). The crystal-field poles can be expressed through the fourth electronic moment < r 4 > common for the complex as follows
F 4 ( R K ) ≈ ( e 2 / 4 π ε 0 ) R K − 5 〈 r 4 〉
hence a relationship
( e 2 / 4 π ε 0 ) 〈 r 4 〉 = F 4 ( z ) R z 5 = F 4 ( x y ) R x y 5
holds true. This method enables relatively fast mapping of structural dependence of the D-parameter for a wide range of distortions.

6.1. Hexacoordinate Ni(II) Complexes

Magneto-structural relationships for the nearly-octahedral Ni(II) complexes was mapped along tetragonal distortion mode characterized by the difference between axial (Rz) and equatorial (Rxy) metal-ligand bond lengths. Thus, the structural D-parameter can be expressed by introducing the XF function as follows
D str = R z − R x y = R z [ 1 − ( F 4 ( z ) F 4 ( x y ) ) 1 / 5 ] = R z ⋅ X F
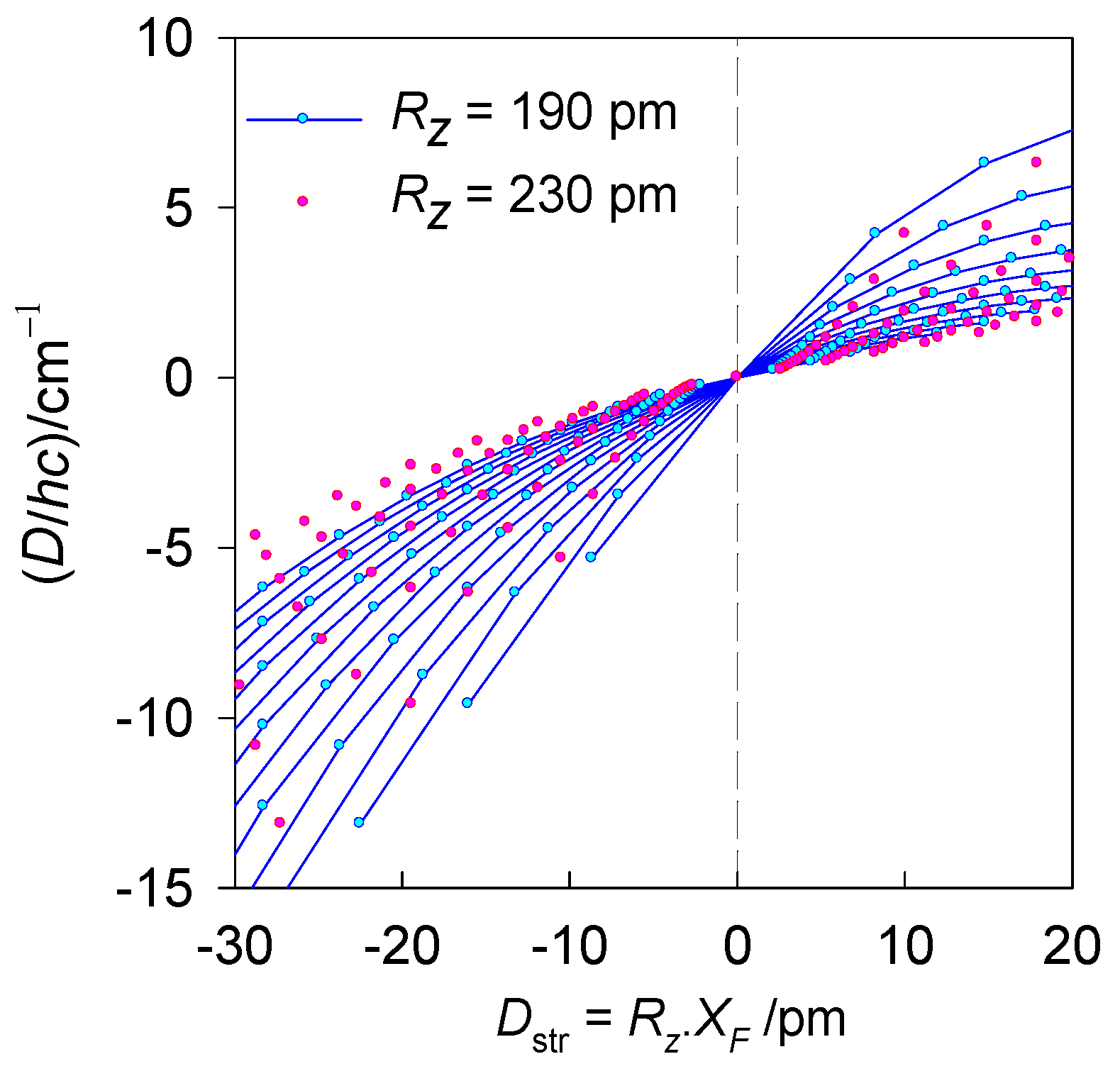
A modelling of the magnetic D-values (exact multiplet splitting) depending upon the transformed structural ordinate is shown in Figure 4. Important message is that such dependence is generally non-linear; however, within the relevant experimental range it follows a nearly linear relationship. In fact, the dependence–the correlation line of the magnetostructural D-correlation is represented by a pair of nearly collinear straight lines intercepting at the octahedral geometry where D and Dstr are zero. The calculations by GCFT were done for the nephelauxetic ratio β = 1, and the orbital reduction factors κz = κxy = 1; therefore, the results are tentative.
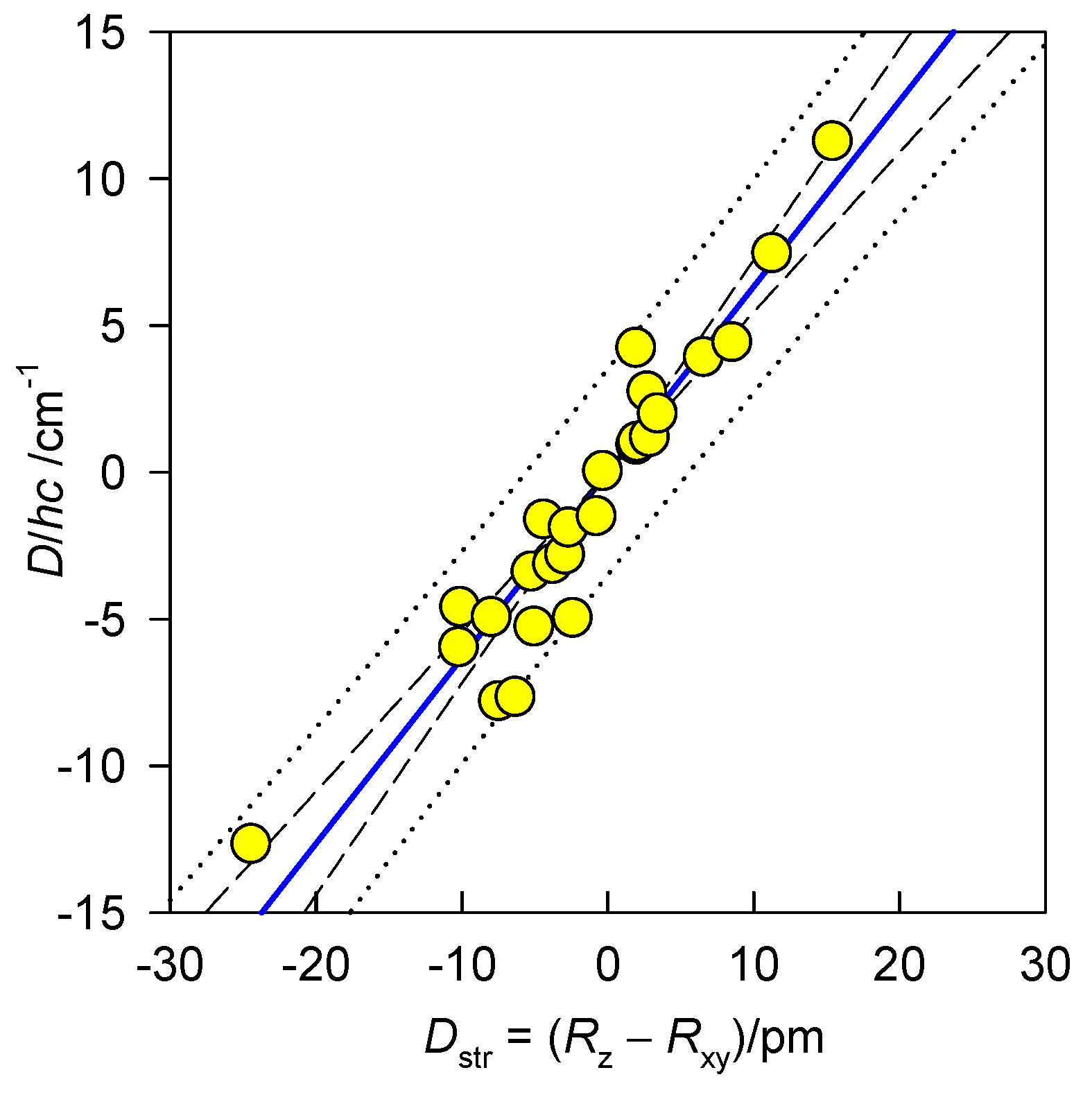
The magnetic data used hereafter were collected quite recently using the SQUID magnetometer. The magnetic susceptibility (χ) was taken at the applied field of BDC = 0.1 T between T = 1.9 and 300 K. The magnetization data (M) was taken at T = 2.0 and 4.6 K respectively, up to B = 5 or 7 T. Both datasets were fitted simultaneously by a numerical procedure that minimizes a joint functional F = R ( χ ) ⋅ R ( M ) . A collection of 25 data-points is displayed in Figure 5 along with a common (linear) correlation curve passing through the origin: D [ cm − 1 ] = 0.632 ⋅ D str [ pm ] . The list of the compounds and numerical data is collected in Supplementary Information [30,31,32,33,34,35,36,37]. The correlation predicts that with increasing structural tetragonality Dstr (in the direction compressed tetragonal bipyramid–octahedron–elongated tetragonal bipyramid) the axial zero-field splitting parameter D increases.
It must be mentioned that for the complexes with a heterogeneous coordination sphere, e.g., possessing {NiN4O2} chromophore, the evaluation of the experimental value of Dstr requires a correction taking into account the averaged bond lengths of the given donor atom. For instance
D str = Δ z − ( Δ y + Δ x ) / 2
where Δ a = ( R a − R ¯ a ) for a = x, y, z is a shift relative to the mean distance R ¯ a for a given bond. For the N- and O-donor ligands these values have been taken from complexes containing the [Ni(NH3)6]2+ and [Ni(H2O)6]2+ units, respectively: R ¯ ( Ni − N ) = 2.145 and R ¯ ( Ni − O ) = 2.055 Å. For a more ionic bond the value of R ¯ ( Ni − NCS ) = 2.070 Å was used.
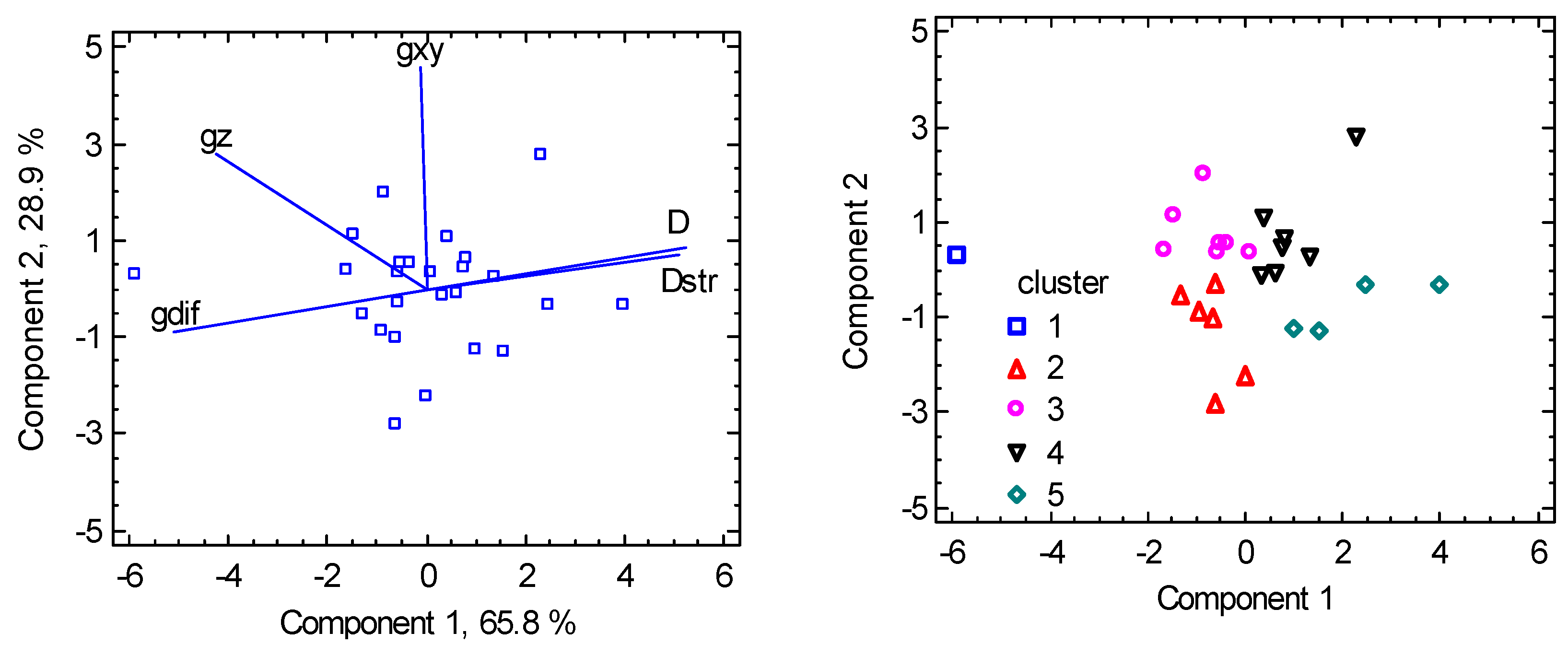
Another piece of information brings the Principal Component Analysis (PCA) which transforms the set of original variables to their linear combinations (principal components) bearing the maximum variability of the data. Two components bear 94.7 % of the variability in the present case. The biplot in Figure 6 shows how the individual variables are interrelated: the closest rays refer to a positive correlation, the farthest to a negative one (anticorrelation). The graph proves that the g-factor asymmetry (gdif = gz – gxy) anticorrelates with the D parameter in agreement with the spin-Hamiltonian formula D = − ( ξ / 2 S ) ( g z − g x y ) / 2 . Classification of the individual points according to the clusters allows us to visualize the clusters separation.
The Factor Analysis (FA) constructs a small number of new variables–common factors which represent a large percentage of the variability in the original variables. Factor loadings may be obtained from either the sample covariance or sample correlation matrix. The initial loadings may be rotated (e.g., by varimax rotation). Two factors cover 96.5 % of the variability of the original data (Dstr, D, gxy, and gz) in the present case (Figure S1). Again, the strong correlation of parameters D and Dstr is confirmed.

6.2. Hexacoordinate Co(II) Complexes

The above procedure outlined for Ni(II) complexes has been also applied to a set of hexacoordinate Co(II) complexes. As already mentioned, only the segment of the compressed tetragonal bipyramids matches the spin-Hamiltonian formalism and the D-values are expected to be very high [38,39,40,41,42,43,44,45,46,47,48].
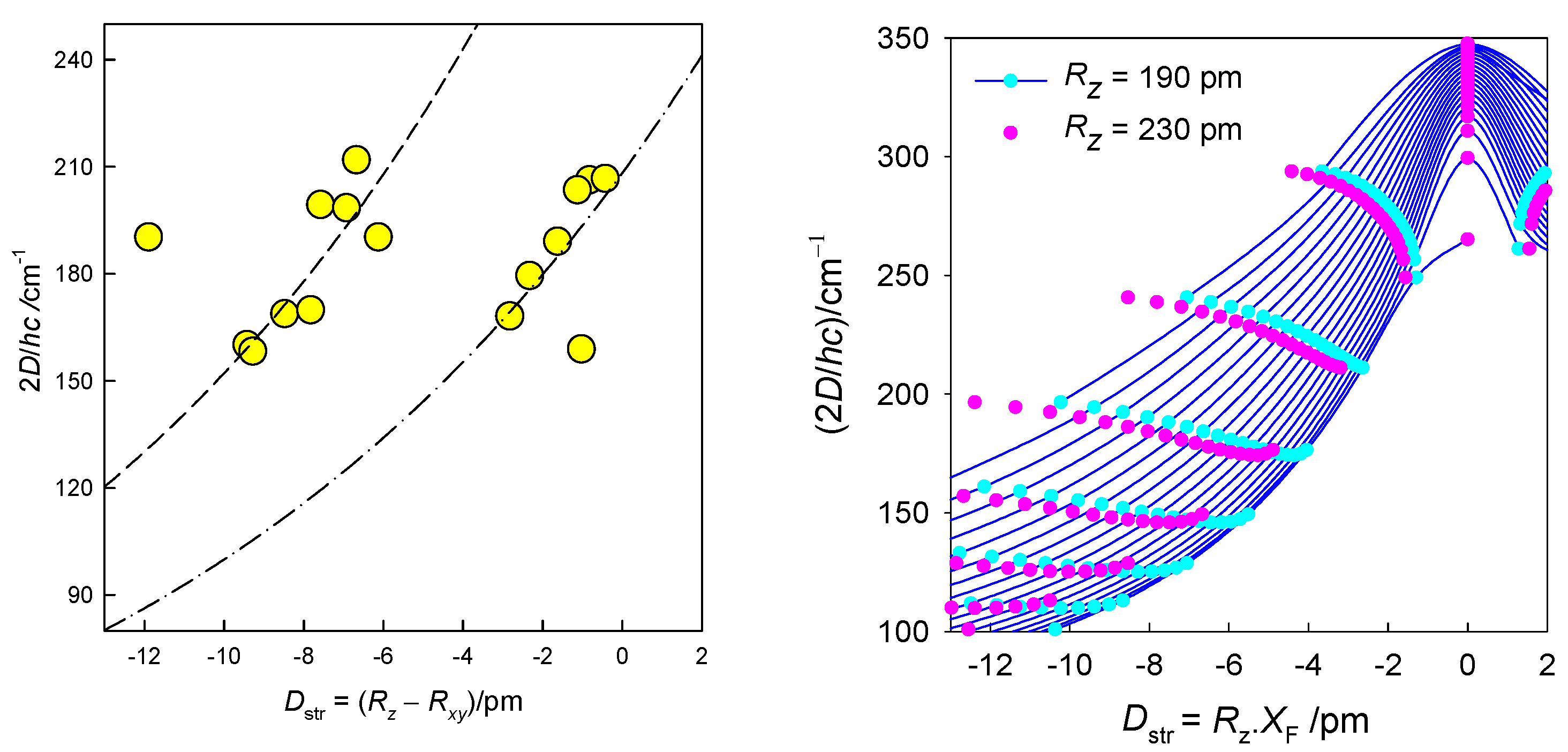
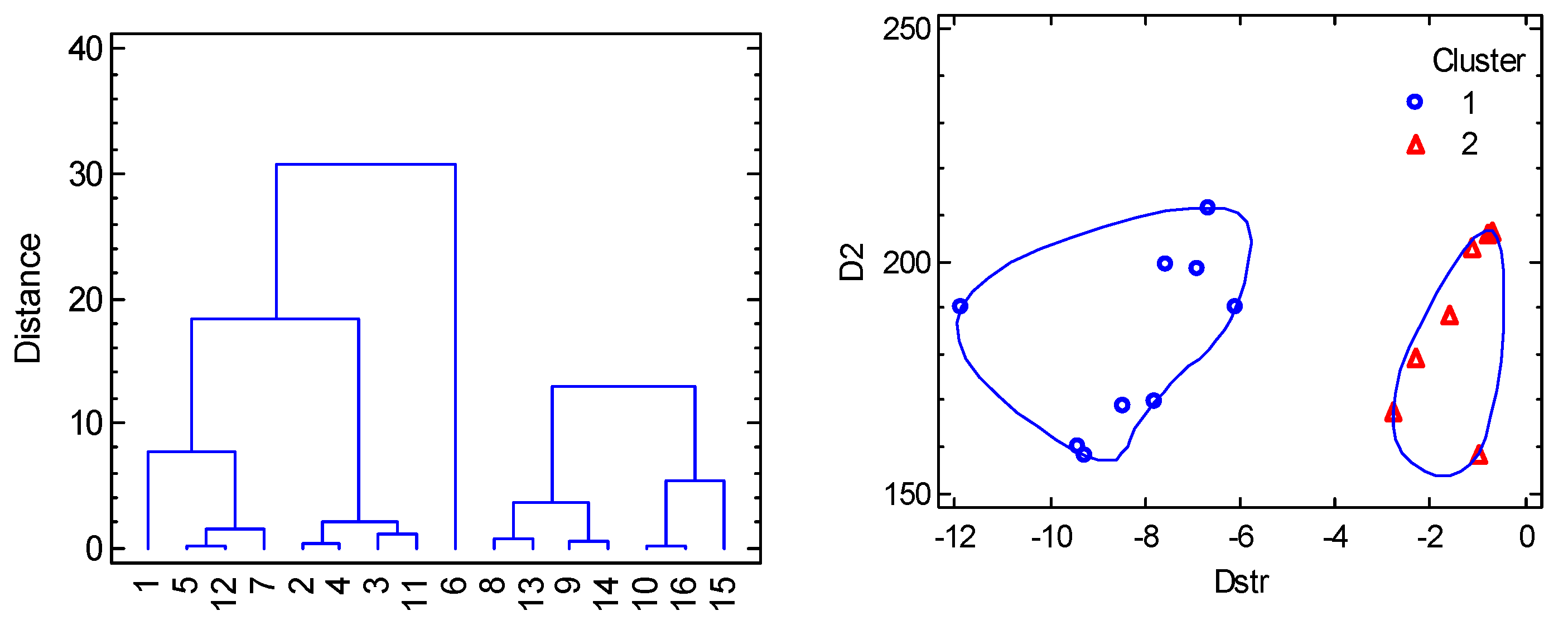
A collection of 16 data-points is displayed in Figure 7 (left) from which it is evident that a linear correlation does not apply in this case. This is understood from the transformed 3D-graph D = f(F4(xy), F4(z)) to a 2D-diagram D = f(Dstr) (Figure 7, right). For the complexes with a heterogeneous coordination sphere the mean distances R ¯ ( Co − N ) = 2.185, R ¯ ( Co − O ) = 2.085, and R ¯ ( Co − Cl ) = 2.475 Å were used in calculating experimental Dstr values. The data worksheet is listed in SI and processed by the multivariate statistical methods. The Cluster Analysis based upon three variables (labelled as Dstr, D2 = 2D and gxy) shows that the distance separates the objects into two principal clusters (Figure 8). Their separation is well seen also from the Principal Component Analysis (Figure S2). The assumption on which the correlation 2D vs Dstr is based is thus statistically confirmed.

6.3. Tetracoordinate Co(II) Complexes

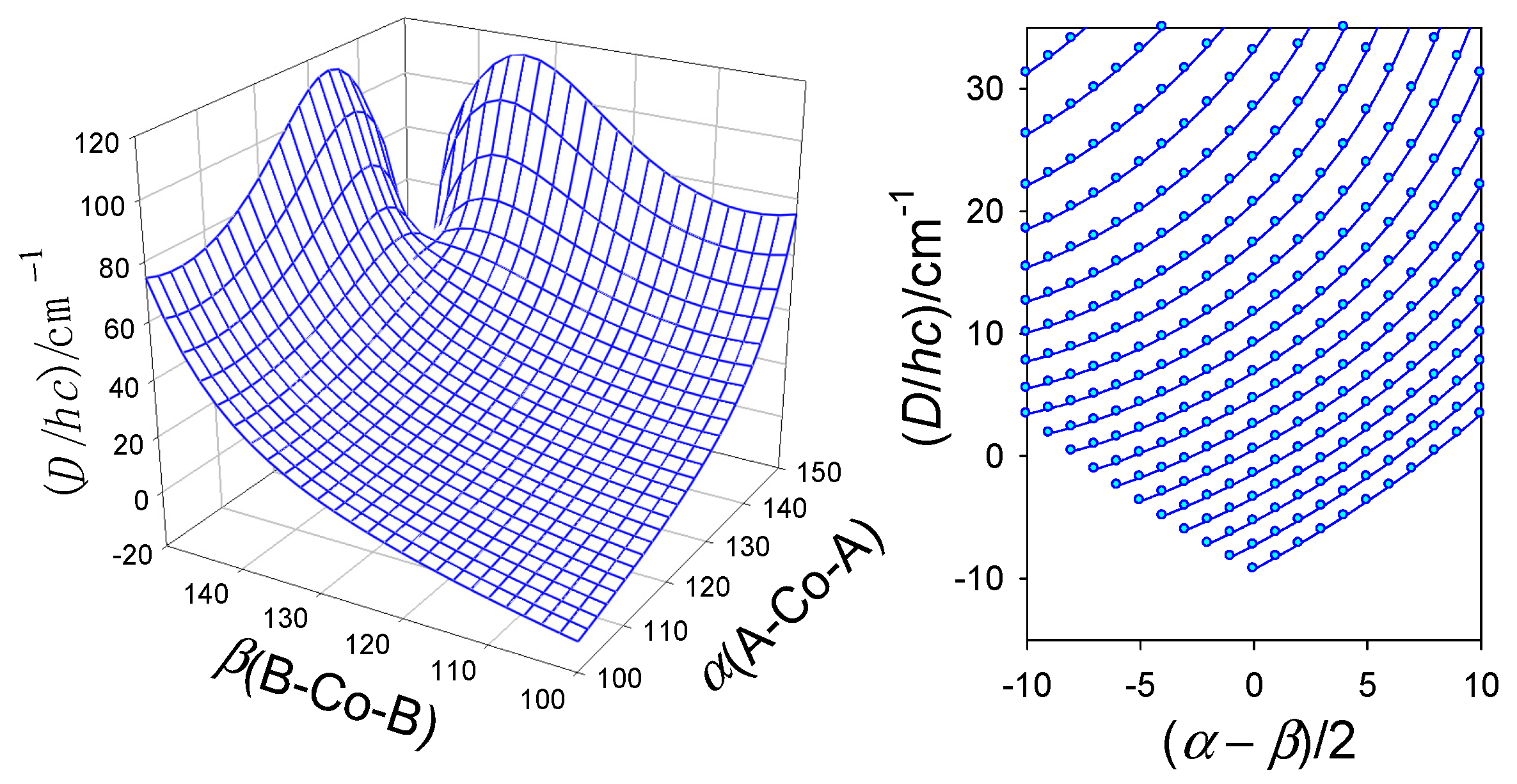
A collection of the spin-Hamiltonian parameters in this case is based upon High-Frequency/High-Field Electron Spin Resonance (syn. EPR, EMR)–10 datapoints, and completed by 5 results from a simultaneous fitting of the susceptibility/magnetization data for [CoA2B2] type complexes [49,50,51,52,53,54]. The basic problem arises from the fact that in addition to radial variations (bond lengths Co-A, Co-B) also the angular distortion (bond angles A-Co-A, B-Co-B) is substantial. Moreover, four twisting angles A-Co-B come into the play (in total, 9 coordinates are independent).
The importance of the angular distortion was proven by modelling using the GCFT that is shown in Figure 9; the energy gap between the lowest crystal-field multiplets refers to Δ = 2 ( D 2 + 3 E 2 ) 1 / 2 ≐ 2 D . On right, the transformed ordinate was used for the 2D plot giving rise to a general route to be followed by the magnetostructural D-correlation in tetracoordinate Co(II) complexes. It proceeds according to an increasing exponential. The correlation of D vs A− is shown in Figure 10 and it can be concluded that the experimental data matches the general course predicted by GCFT modelling. A fit to exponential curves D = a + b ⋅ exp ( c ⋅ A − ) is also shown by dashed lines.
For the multivariate methods, 7 variables were considered: R(Co-A), R(Co-B), α(A-Co-A), β(B-Co-B), gz, gxy, D abbreviated as RA, RB, alpha, beta, gz, gxy, D. Also, three transformed variables were added: Aplus = (alpha + beta)/2, Aminus = (alpha–beta)/2, gdif = gz–gxy. It must be mentioned that the data involve very different chromophores as follows: {CoN4}, {CoN2N2}, {CoCl4}, {CoBr4}, {CoCl2P2}, {CoBr2P2}, and the most numerous {CoCl2N2} one. 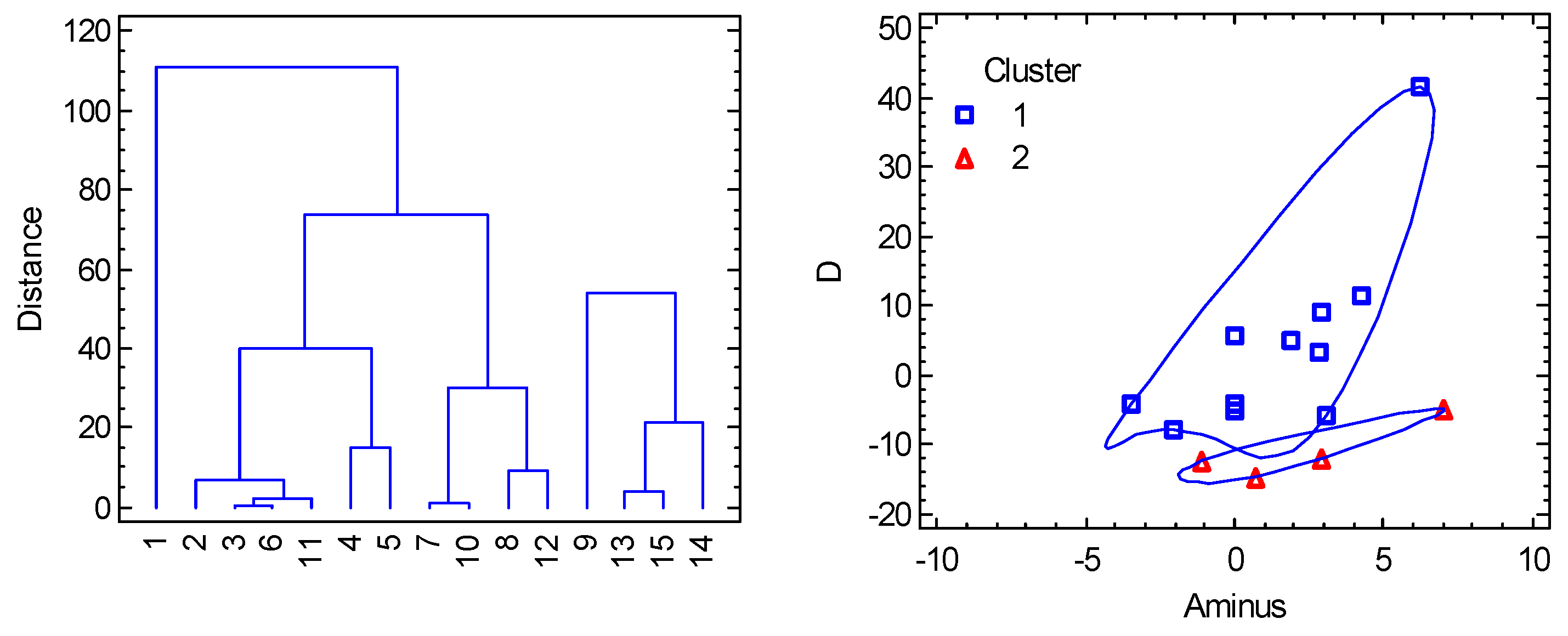(Two datapoints with {CoN2O2}, {CoO2S2} chromophores were deleted from consideration due to evident dissimilarity). The Cluster Analysis points to two principal clusters (Figure 11) containing 11 and 4 members, respectively. 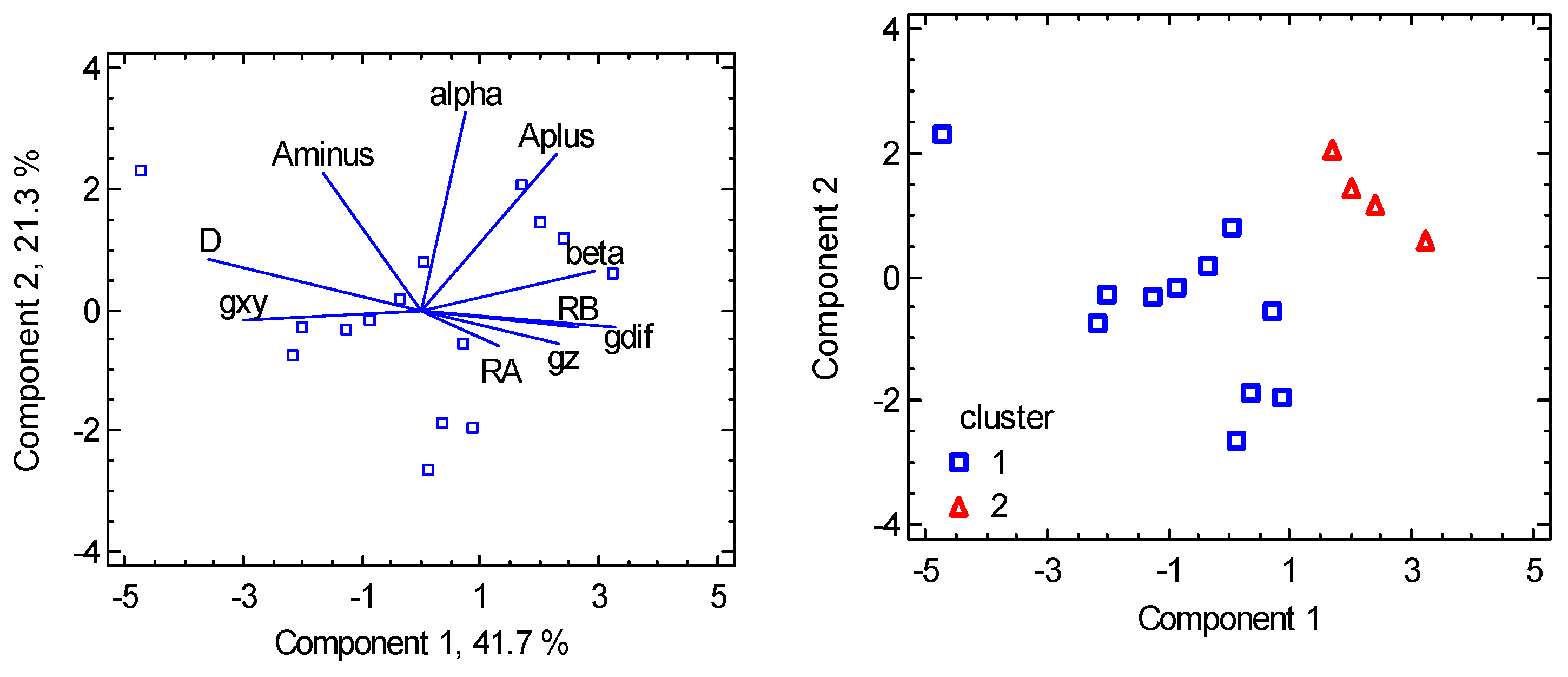Eventually, the compound with large D/hc = 41 cm-1 could be classified as a new cluster. The PCA method (Figure 12) shows a rather weak correlation of the D-values with individual geometric parameters; the best correlation is D vs Aminus. PCA also confirms an anticorrelation of D and gdif as expected by the spin-Hamiltonian formalism. On the other hand, the PCA analysis evidently separates the individual clusters.

6.4. Pentacoordinate Co(II) Complexes

For pentacoordinate complexes of the [CoXA2B2] type the basic obstacle arises from the fact that too many (12) geometrical parameter come into the play and the coordination polyhedron is often far from the ideal tetragonal pyramid and/or trigonal bipyramid. Also the description of the intermediate geometries through the angular distortion (trigonality) τ-parameter represents a strong idealization. Moreover, there are only a few reliable magnetic data based upon both, the susceptibility and magnetization measurements (HF/HF EPR cannot be used since D-values are too large).
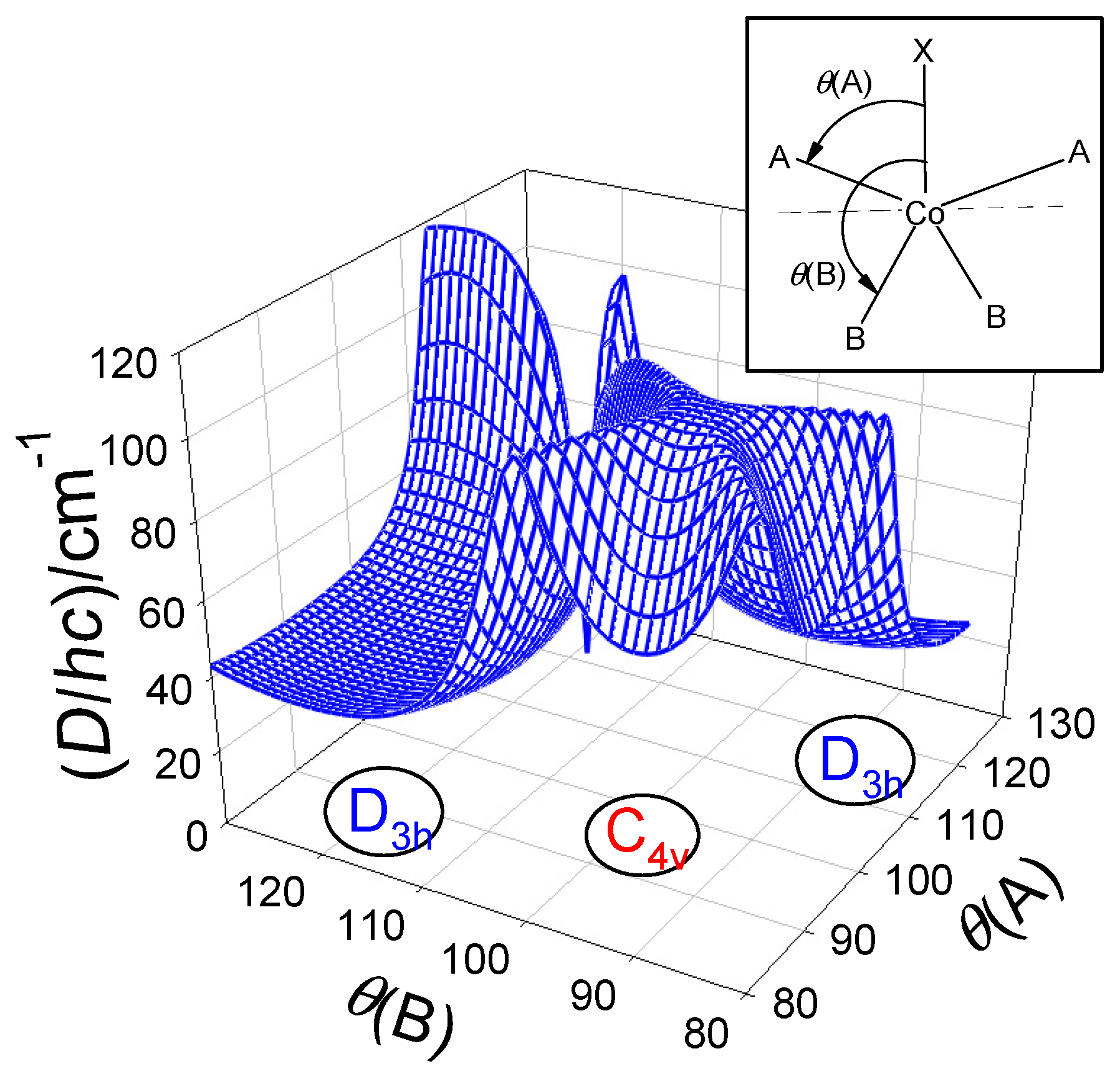
The angular dependence of the D-parameter with respect to two geometrical parameters is shown in Figure 13: polar angles θ(A) and θ(B) were used in mapping the Berry-kind of transformation between trigonal bipyramid and tetragonal pyramid using GCFT. Worth noting is the fact that majority of the complexes under study possess trigonality parameter τ > 1 due to a rigid tridentate ligand with the {XA2} donor set.
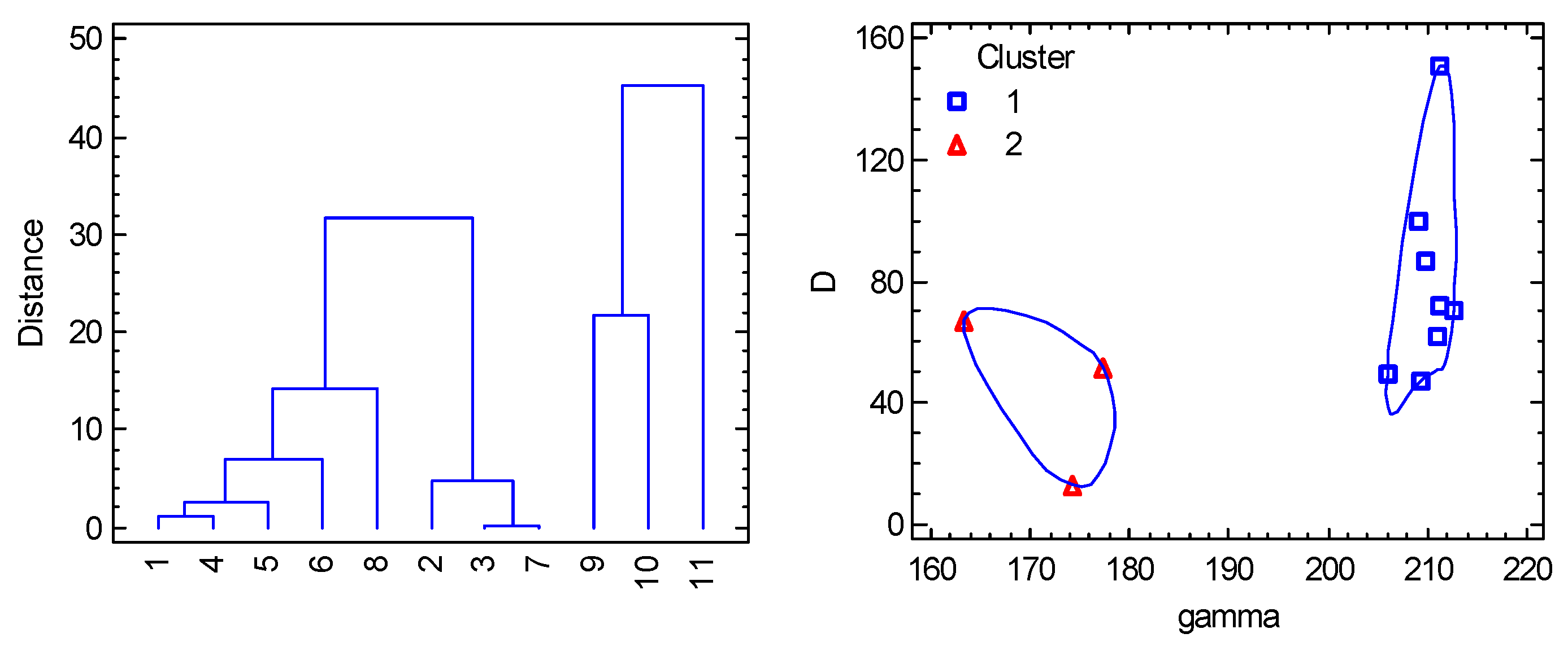
Eleven datapoints have been collected (see SI) [55–59] and the variables R(Co-X), R(Co-A), R(Co-B), α(A-Co-A), β(B-Co-B), θ(X-Co-A), θ(X-Co-B), D, gxy are abbreviated for statistical analysis as RX, RA, RB, alpha, beta, theta, thetaB, D, gxy. Moreover, three transformed variables were considered: γ = 360–2θ(A), τ = (α –β)/60 or τ = (γ–β)/60 when γ > 180 deg, and δ = (α–β)/2 abbreviated as gamma, tau and dis. The cluster analysis distinguishes two main clusters with 8 and 3 datapoints, respectively (Figure 14). For the first cluster γ > 180 deg and τ > 1 holds true; for the second cluster: γ < 180 deg, τ < 1. The PCA revealed a significant correlation of parameter D with parameters R(Co-X), R(Co-B), and gx, which, however, does not provide more fundamental information in this case. Rather, a weak positive correlation with the γ parameter and anticorrelation with α appear to be more significant. Moreover, PCA again separates visibly two clusters (Figure 15).
Preprints 86100 g014
Figure 14. Cluster analysis for pentacoordinate Co(II) complexes. Individual cluster areas are circled.
Figure 14. Cluster analysis for pentacoordinate Co(II) complexes. Individual cluster areas are circled.
Preprints 86100 g014
Preprints 86100 g015
Figure 15. PCA biplot for pentacoordinate Co(II) complexes. The points are the individual objects.
Figure 15. PCA biplot for pentacoordinate Co(II) complexes. The points are the individual objects.
Preprints 86100 g015
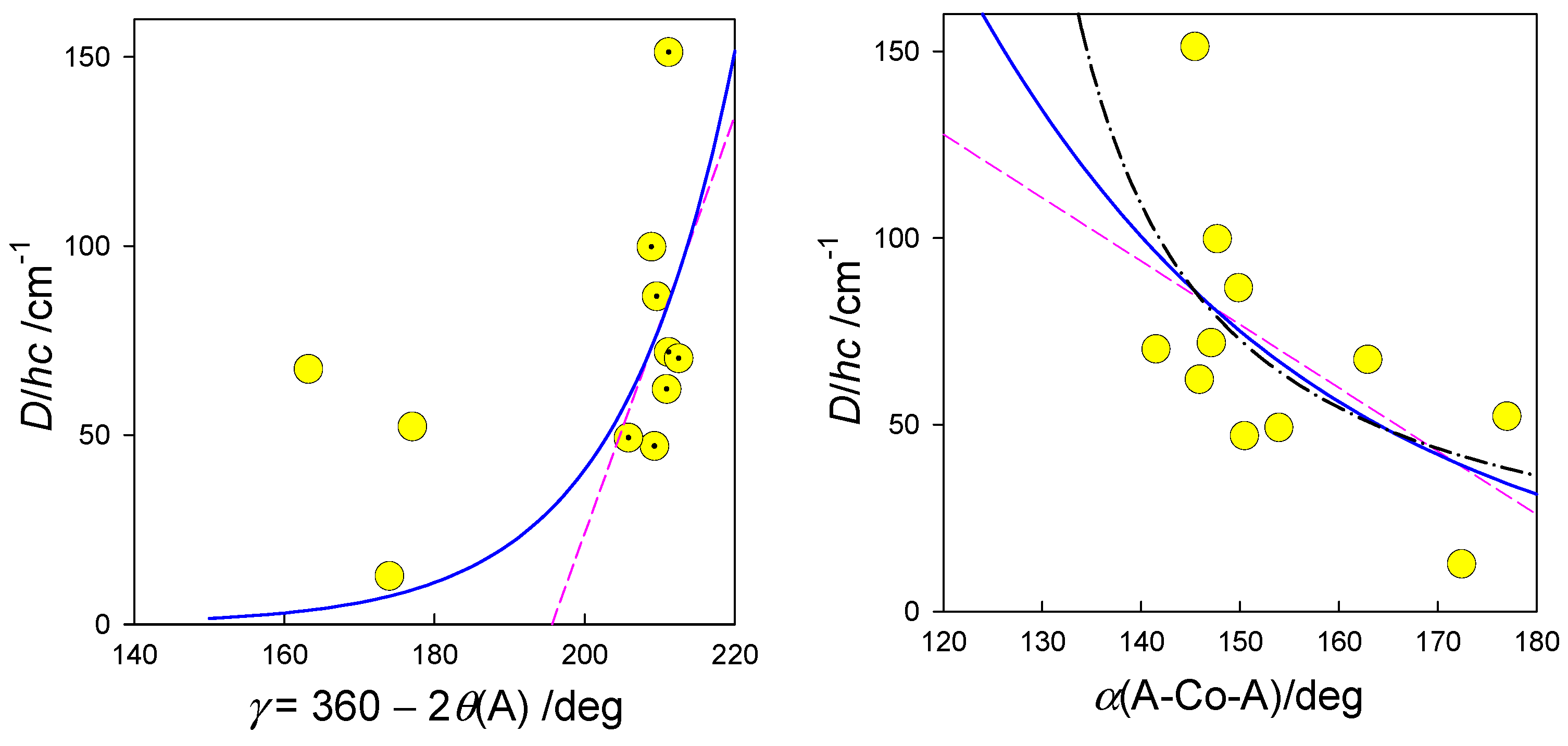
A trial set of functions to fit the observed D vs structural parameter relationships is probed in Figure 16. Notice, the actual geometry is far from an ideal polyhedron where a crude averaging of bond angles was applied. Moreover, some of the [Co(LCn)Cl2] systems form a supramolecular dimer with exchange interaction J > 0. In such a case the local D-tensors are not necessarily collinear and this circumstance affects the fitted D-values. The correlation coefficient between D and gx (r = 0.83) proves that the spin-Hamiltonian formula D = λ(gz–gx)/2 is fulfilled for pentacoordinate complexes. This conclusion matches the forecast that only D > 0 applies for pentacoordinate Co(II) complexes [18,78]. In this light the reported values of D/hc= –40 cm-1 in {CoN2N3} type complexes seem be problematic: the authors fail in fitting the magnetization data and, moreover, they used closed formula for addition of three Cartesian components and neither their average nor a correct powder average was applied [74].

7. Selected Single-Molecule Magnets

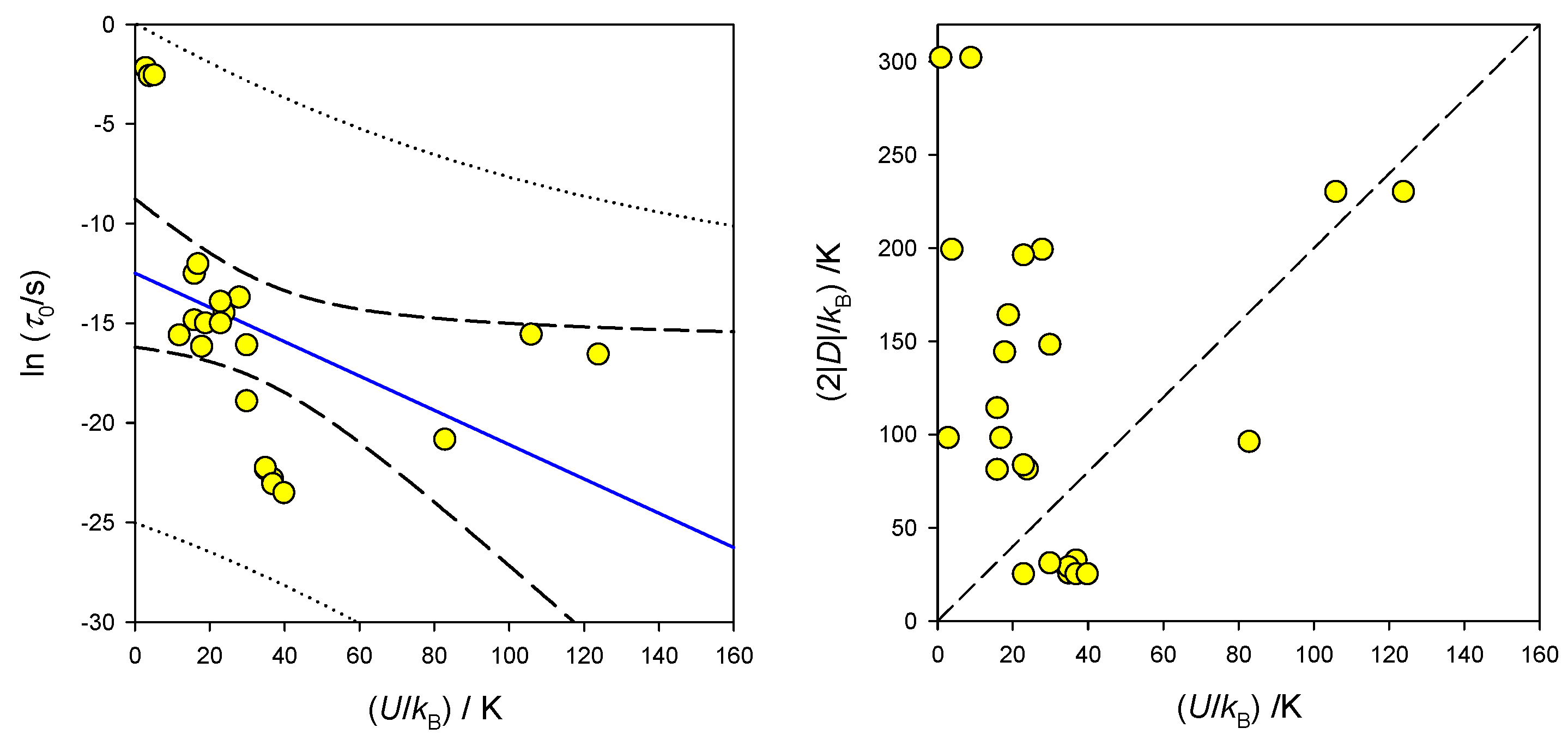
List of known single-molecule magnets based upon one metal centre (single-ion magnets, SIM) is rapidly increasing. They cover, for instance, Mn(III), Mn(II), Fe(III), Fe(II), Fe(I), Co(II), Ni(III) and Ni(II) complexes) [60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77]. Representative examples for Co(II) are presented in Table 1. Worth noting is also an inverse relationship between the extrapolated relaxation time lnτ0 and barrier to spin reversal U as shown in Figure 17.
The existence of the barrier to spin reversal is traditionally expected only for D < 0 (easy-axis of magnetization). However, SMM (SIM) behaviour was registered also in the case of D > 0; a presence of sufficient rhombic anisotropy (E > 0) rationalizes this observation. In this case, the easy-plane allowing unhindered relaxation no longer exists; small barrier to spin reversal is determined by the E parameter.
The above outlined magnetostructural correlations allows us to predict whether the system under study is a potential candidate for the single-molecule magnetism. For instance, observed value of D/hc = −12.5 cm-1 in [Co(PPh3)2Br2] complex from the DC magnetization studies motivated the AC susceptibility measurements and indeed, the SMM behaviour was confirmed [73].
The expected relationship for the half-integral spin S = 3/2 is U = 2 | D S | (in the zero field) and this is evidently not obeyed (Figure 17). Questionable is also the way of extracting the SMM parameters: usually they arise from the Arrhenius-like linear relationship ln τ = ln τ 0 + ( U / k B ) T − 1 applied to higher-temperature points. However, a more complex equation that involves also the Raman, direct and quantum tunnelling processes is available
τ − 1 = τ 0 − 1 exp ( − U / k B T ) + C T n + A B 2 T + D ( B )
This can be enriched by the phonon bottleneck effect F T 2 and the reciprocating thermal behaviour term G T − 1 .
Some samples exhibit multiple relaxation processes that vary with the applied magnetic field so that it is problematic to relate single D with different U-values. Presence of various relaxation processes is visible only if a search for them was applied, e.g., for low (ν < 1 Hz) or high (ν > 1500 Hz) frequencies of the AC field. Co(II) complexes represent a rich class of single-ion magnets. These exhibit large magnetic anisotropy that for compressed tetragonal bipyramid necessarily is positive. The Orbach relaxation mechanism, however, required D < 0. For (pseudo)octahedral systems we found that the ZFS parameter D, and thus magnetic anisotropy, strongly decreases with tetragonal distortion. For near-octahedral structures, the D-parameter achieves large positive values (up to 350 cm-1 for ideal Oh–Jahn-Teller systems). Hexacoordinate Co(II) complexes with markedly negative D values were also reported, such as e.g., (HNEt3)+(CoIICoIII3L6)-, D/hc = −115 cm-1. However, symmetry of this structure is D3 [86].

8. Summary

Magnetostructural D-correlations, i.e., dependence of the axial zero-field splitting parameter D vs the structural anisotropy parameter Dstr originate in the electronic structure of the central atom. They are tuned by the ligand diversity and structural variability of the individual metal complexes. Intuitive linear relationships (as in hexacoordinate Ni(II) systems) not always are supported by deep theoretical analysis which can rationalize various types of non-linear dependences. This is the case of the hexa-, penta- and tetracoordinate Co(II) complexes. Magnetostructural D-correlations represent an effective tool for the design of magnetically anisotropic molecules. Only from the knowledge of structural characteristics of the complexes can the magnitude and sign of the axial zero-field splitting parameter D be predicted, which enables the creation of relevant prediction models using contemporary machine learning methods [87].

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Figure S1: FA biplot after varimax rotation for hexacoordinate Ni(II) complexes; Figure S2: PCA biplot for hexacoordinate Co(II) complexes; Table S1: title; Table S1: Review of the matrix elements between the atomic-term kets; Table S2: Energy level diagrams for selected dn systems; Table S3: Hexacoordinate Ni(II) complexes-structural and magnetic parameters, statistics; Table S4: Hexcoordinate Co(II) complexes-structural and magnetic parameters, statistics; Table S5: Tetracoordinate Co(II) complexes-structural and magnetic parameters, statistics; Table S6: Pentacoordinate Co(II) complexes-structural and magnetic parameters, statistics; Data selections for multivariate methods.

Author Contributions

Conceptualization, J.T. and R.B.; methodology, J.T. and R.B.; validation, J.T., R.B. and C.R.; formal analysis, J.T., R.B. and C.R.; investigation, J.T., R.B. and C.R.; data curation, J.T., R.B. and C.R.; writing—original draft preparation, J.T., R.B. and C.R.; writing—review and editing, J.T., R.B. and C.R.; visualization, J.T., R.B. and C.R. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

Slovak grant agencies (APVV-19-0087 and VEGA 1/0086/21) are acknowledged for the financial support.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lis, T. Preparation, structure, and magnetic properties of a dodecanuclear mixed-valence manganese carboxylate. Acta Crystallogr. 1980, B36, 2042–2046. [Google Scholar] [CrossRef]
  2. Caneschi, A.; Gatteschi, D.; Sessoli, R.; Barra, A.L.; Brunel, L.C.; Guillot, L.C. Alternating current susceptibility, high field magnetization, and millimeter band EPR evidence for a ground S = 10 state in [Mn12O12(Ch3COO)16(H2O)4].2CH3COOH.4H2O. J. Am. Chem. Soc. 1991, 133, 5873–5874. [Google Scholar] [CrossRef]
  3. Aubin, S.M.J.; Wemple, M.W.; Adams, D.M.; Tsai, H.L.; Christou, G.; Hendrickson, D.N. Distorted MnIVMnIII3 Cubane Complexes as Single-Molecule Magnets. J. Am. Chem. Soc. 1996, 118, 7746–7754. [Google Scholar] [CrossRef]
  4. Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: 2006.
  5. Mydosh, J.A. Spin Glasses: An Experimental Introduction; Taylor and Francis: London, 1995. [Google Scholar]
  6. Winpenny, R. (Ed.) Single-Molecule Magnets and Related Phenomena. In Structure and Bonding; Springer: 2006; Volume 122.
  7. Boča, R.; Rajnák, C. Unexpected behavior of single ion magnets. Coord. Chem. Rev. 2021, 430, 213657. [Google Scholar] [CrossRef]
  8. Rajnák, C.; Boča, R. Reciprocating thermal behavior in the family of single ion magnets. Coord. Chem. Rev. 2021, 436, 213808. [Google Scholar] [CrossRef]
  9. Rajnák, C.; Titiš, J.; Boča, R. Reciprocating Thermal Behavior in Multichannel Relaxation of Cobalt(ii) Based Single Ion Magnets. Magnetochemistry 2021, 7, 76. [Google Scholar] [CrossRef]
  10. Atzori, M.; Tesi, L.; Morra, E.; Chiesa, M.; Sorace, L.; Sessoli, R. Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits, J. Am. Chem. Soc. 2016, 138, 2154–2157. [Google Scholar] [CrossRef]
  11. Ding, M.; Cutsail, G.E.I.; Aravena, D.; Amoza, M.; Rouzières, M.; Dechambenoit, P.; Losovyj, Y.; Pink, M.; Ruiz, E.; Clérac, R. A low spin manganese(iv) nitride single molecule magnet. Chem. Sci. 2016, 7, 6132–6140. [Google Scholar] [CrossRef]
  12. Bhowmick, I.; Shaffer, D.W.; Yang, J.Y.; Shores, M.P. Single molecule magnet behaviour in a square planar S = 1/2 Co(ii) complex and spin-state assignment of multiple relaxation modes. Chem. Commun. 2020, 56, 6711–6714. [Google Scholar] [CrossRef]
  13. Chen, L.; Song, J.; Zhao, W.; Yi, G.; Zhou, Z.; Yuan, A.; Song, Y.; Wang, Z.; Ouyang, Z.W. A mononuclear five-coordinate Co(ii) single molecule magnet with a spin crossover between the S = 1/2 and 3/2 states. Dalton Trans. 2018, 47, 16596–16602. [Google Scholar] [CrossRef]
  14. Boča, R.; Mingos, D.M.P. (Eds.) . Theoretical Foundations of Molecular Magnetism; Elsevier: Amsterdam, 1999. [Google Scholar]
  15. Griffith, J.S. The Theory of Transition Metal Ions; Cambridge University Press: 1964.
  16. Figgis, B.N. Introduction to Ligand Fields; Wiley: New York, 1966. [Google Scholar]
  17. König, E.; Kremer, S. Magnetism Diagrams for Transition Metal Ions; Plenum Press: New York, 1979. [Google Scholar]
  18. Boča, R. Magnetic Functions Beyond the Spin-Hamiltonian; Springer: 2006; Volume 117.
  19. Boča, R. A Handbook of Magnetochemical Formulae; Elsevier: Amsterdam, 2012. [Google Scholar]
  20. Crawford, V.H.; Richardson, H.W.; Wasson, J.R.; Hodgson, D.J.; Hatfield, W.E. Relation between the singlet-triplet splitting and the copper-oxygen-copper bridge angle in hydroxo-bridged copper dimers. Inorg. Chem. 1976, 15, 2107–2110. [Google Scholar] [CrossRef]
  21. Hatfield, W.E.; Willett, R.D.; Gatteschi, D.; Kahn, O. Magneto-Structural Correlations in Exchange Coupled Systems; NATO ASI Series Reidel: Dordrecht, 1985; p. 555. [Google Scholar]
  22. Thompson, L.K.; Mandal, S.K.; Tandon, S.S.; Bridson, J.N.; Park, M.K. Magnetostructural Correlations in Bis(μ2-phenoxide)-bridged Macrocyclic Dinuclear Copper(ii) Complexes. Influence of Electron-withdrawing Substituents on Exchange Coupling. Inorg. Chem. 1996, 35, 3117–3125. [Google Scholar] [CrossRef] [PubMed]
  23. Glerup, J.; Hodgson, D.J.; Pedersen, E. A Novel Correlation Between Magnetism and Structural Parameters in Superexchange Coupled Chromium(iii) Dimers. Acta. Chem. Scand. 1983, 37a, 161–164. [Google Scholar] [CrossRef]
  24. Hodgson, D.J.; Willet, R.D.; Gatteschi, D.; Kahn, O. Magneto-Structural Correlations in Exchange Coupled Systems; NATO ASI Series Reidel: Dordrecht, 1985; p. 501.
  25. Law, N.A.; Kampf, J.W.; Pecoraro, V.L. A magneto-structural correlation between the Heisenberg constant, J, and the Mn-O-Mn angle in [MnIV(μ-O)]2 dimers. Inorg. Chim. Acta 2000, 297, 252–264. [Google Scholar] [CrossRef]
  26. Gorun, S.M.; Lippard, S.J. Magnetostructural Correlations in Magnetically Coupled (.mu.-oxo)diiron(iii) Complexes. Inorg. Chem. 1991, 30, 1625–1630. [Google Scholar] [CrossRef]
  27. Vranovičová, B.; Boča, R. Magnetostructural J-Correlations in Fe(III) Complexes-A Revison. Nova Biotechnol. Chim. 2013, 12, 70–74. [Google Scholar] [CrossRef]
  28. Tokárová-Puterová, Z.; Mrázová, V.; Kožíšek, J.; Valentová, J.; Vranovičová, B.; Boča, R. Magnetostructural correlation in tetracopper(II) cubanes. Polyhedron 2014, 70, 52–58. [Google Scholar] [CrossRef]
  29. Makohusová, M.; Mrázová, V.; Haase, W.; Boča, R. Magnetostructural J-correlations in complexes with tetrahedro-{Cu4} core. Polyhedron 2014, 81, 572–582. [Google Scholar] [CrossRef]
  30. Baran, P.; Boča, M.; Boča, R.; Krutošíková, A.; Miklovič, J.; Pelikán, J.; Titiš, J. Structural characterization, spectral and magnetic properties of isothiocyanate nickel(II) complexes with furopyridine derivatives. Polyhedron 2005, 24, 1510–1516. [Google Scholar] [CrossRef]
  31. Mašlejová, A.; Ivaniková, R.; Svoboda, I.; Papánková, B.; Dlháň, L.; Mikloš, D.; Fuess, H.; Boča, R. Structural characterization and magnetic properties of hexakis(imidazole)nickel(II) bis(formate), bis(chloroacetate), bis(2-chloropropionate) and hexakis(1-methyl-imidazole)nickel(II) chloride dihydrate. Polyhedron 2006, 25, 1823–1830. [Google Scholar] [CrossRef]
  32. Ivaniková, R.; Boča, R.; Dlháň, L.; Fuess, H.; Mašlejová, A.; Mrázová, V.; Svoboda, I.; Titiš, J. Heteroleptic nickel(II) complexes formed from N-donor bases, carboxylic acids and water: Magnetostructural correlations. Polyhedron 2006, 25, 3261–3268. [Google Scholar] [CrossRef]
  33. Titiš, J.; Boča, R.; Dlháň, Ľ.; Ďurčeková, T.; Fuess, H.; Ivaniková, R.; Mrázová, V.; Papánková, B.; Svoboda, I. Magnetostructural correlations in heteroleptic nickel(II) complexes. Polyhedron 2007, 26, 1523–1530. [Google Scholar] [CrossRef]
  34. Boča, R.; Titiš, J. Coordination Chemistry Research Progress; Nova Science Publishers: New York, 2008; p. 247. [Google Scholar]
  35. Titiš, J.; Boča, R. Magnetostructural D Correlation in Nickel(II) Complexes: Reinvestigation of the Zero-Field Splitting. Inorg. Chem. 2010, 49, 3971–3973. [Google Scholar] [CrossRef] [PubMed]
  36. Packová, A.; Miklovič, J.; Titiš, J.; Koman, M.; Boča, R. Positive Zero-field Splitting in a Hexacoordinate Nickel(ii) Complex. Inorg. Chem. Commun. 2013, 32, 9–11. [Google Scholar] [CrossRef]
  37. Miklovič, J.; Packová, A.; Segľa, P.; Titiš, J.; Koman, M.; Moncoľ, J.; Boča, R.; Jorík, V.; Krekuska, H.; Valigura, D. Synthesis, Crystal Structures, Spectral and Magnetic Properties of Nickel(ii) Pyridinecarboxylates with N-heterocyclic Ligands. Inorg. Chim. Acta 2015, 429, 73–80. [Google Scholar] [CrossRef]
  38. Papánková, B.; Boča, R.; Dlháň, Ľ.; Nemec, I.; Titiš, J.; Svoboda, I.; Fuess, H. Magneto-structural relationships for a mononuclear Co(II) complex with large zero-field splitting. Inorg. Chim. Acta 2010, 363, 147–156. [Google Scholar] [CrossRef]
  39. Hudák, J.; Boča, R.; Dlháň, Ľ.; Kožíšek, J.; Moncoľ, J. Structure and Magnetism of Mono-, Di-, and Trinuclear Benzoato Cobalt(ii) Complexes. Polyhedron 2011, 30, 1367–1373. [Google Scholar] [CrossRef]
  40. Rajnák, C.; Titiš, J.; Boča, R.; Moncol’, J.; Padělková, Z. Self-assembled cobalt(II) Schiff base complex: synthesis, structure, and magnetic properties. Monatsh. Chem. 2011, 142, 789–795. [Google Scholar] [CrossRef]
  41. Miklovič, J.; Segľa, P.; Mikloš, D.; Titiš, J.; Herchel, R.; Melník, M. Copper(ii) and Cobalt(ii) Hydroxypyridinecarboxylates: Synthesis, Crystal Structures, Spectral and Magnetic Properties. Chem. Pap. 2008, 62, 464–471. [Google Scholar] [CrossRef]
  42. Segľa, P.; Miklovič, J.; Mikloš, D.; Titiš, J.; Herchel, R.; Moncoľ, J.; Kaliňáková, B.; Hudecová, D.; Mrázová, V.; Lis, T. Crystal structure, spectroscopic and magnetic properties, and antimicrobial activities of cobalt(II) 2-methylthionicotinate complexes with N-heterocyclic ligands. Trans. Met. Chem. 2008, 33, 967–974. [Google Scholar] [CrossRef]
  43. Titiš, J.; Hudák, J.; Kožíšek, J.; Krutošíková, A.; Moncoľ, J.; Tarabová, D.; Boča, R. Structural, Spectral and Magnetic Properties of Carboxylato Cobalt(ii) Complexes with Heterocyclic N-donor Ligands: Reconstruction of Magnetic Parameters from Electronic Spectra. Inorg. Chim. Acta 2012, 388, 106–113. [Google Scholar] [CrossRef]
  44. Šebová, M.; Boča, R.; Dlháň, Ľ.; Nemec, I.; Papánková, B.; Pavlik, J.; Fuess, H. Direct determination of zero-field splitting in Co(II) complexes by FAR infrared spectroscopy. Inorg. Chim. Acta 2012, 383, 143–151. [Google Scholar] [CrossRef]
  45. Titiš, J.; Boča, R. Magnetostructural D Correlations in Hexacoordinated Cobalt(ii) Complexes. Inorg. Chem. 2011, 50, 11838–11845. [Google Scholar] [CrossRef] [PubMed]
  46. Idešicová, M.; Boča, R. Magnetism, IR and Raman spectra of a tetracoordinate and hexacoordinate Co(II) complexes derived from aminopyrimidine. Inorg. Chim. Acta 2013, 408, 162–171. [Google Scholar] [CrossRef]
  47. Váhovská, L.; Potočňák, I.; Vitushkina, S.; Dušek, M.; Titiš, J.; Boča, R. Low-dimensional compounds containing cyanido groups. XXVI. Crystal structure, spectroscopic and magnetic properties of Co(II) complexes with non-linear pseudohalide ligands. Polyhedron 2014, 81, 396–408. [Google Scholar] [CrossRef]
  48. Herchel, R.; Váhovská, L.; Potočňák, I.; Trávníček, Z. Slow Magnetic Relaxation in Octahedral Cobalt(II) Field-Induced Single-Ion Magnet with Positive Axial and Large Rhombic Anisotropy. Inorg. Chem. 2014, 53, 5896–5898. [Google Scholar] [CrossRef]
  49. van Stapele, R.P.; Beljers, H.G.; Bongers, P.F.; Zijlstra, H. Ground State of Divalent Co Ions in Cs3CoCl5 and Cs3CoBr5. J. Chem. Phys. 1966, 44, 3719–3725. [Google Scholar] [CrossRef]
  50. Krzystek, J.; Zvyagin, S.A.; Ozarowski, A.; Fiedler, A.T.; Brunold, T.C.; Telser, J. Definitive Spectroscopic Determination of Zero-Field Splitting in High-Spin Cobalt(II). J. Am. Chem. Soc. 2004, 126, 2148–2155. [Google Scholar] [CrossRef]
  51. Idešicová, M.; Titiš, J.; Krzystek, J.; Boča, R. Zero-Field Splitting in Pseudotetrahedral Co(II) Complexes: A Magnetic, High-Frequency and -Field EPR, and Computational Study. Inorg. Chem. 2013, 52, 9409–9417. [Google Scholar] [CrossRef]
  52. Šebová, M.; Jorík, V.; Kožíšek, J.; Moncoľ, J.; Boča, R. Structure and Magnetism of Co(ii) Complexes with Bidentate Heterocyclic Ligand Hsalbim Derived from Benzimidazole. Polyhedron 2011, 30, 1163–1170. [Google Scholar] [CrossRef]
  53. Idešicová, M.; Dlháň, Ľ.; Moncoľ, J.; Titiš, J.; Boča, R. Zero-field Splitting in Tetracoordinate Co(ii) Complexes. Polyhedron 2012, 36, 79–84. [Google Scholar] [CrossRef]
  54. Titiš, J.; Miklovič, J.; Boča, R. Magnetostructural study of tetracoordinate cobalt(II) complexes. Inorg. Chem. Commun. 2013, 35, 72–75. [Google Scholar] [CrossRef]
  55. Rajnák, C.; Titiš, J.; Šalitroš, I.; Boča, R.; Fuhr, O.; Ruben, M. Zero-field splitting in pentacoordinate Co(II) complexes. Polyhedron 2013, 65, 122–128. [Google Scholar] [CrossRef]
  56. Rajnák, C. Cyril and Methodius. Ph.D. Thesis, University of SS, Trnava, 2014. [Google Scholar]
  57. Rajnák, C.; Titiš, J.; Miklovič, J.; Kostakis, G.E.; Fuhr, O.; Ruben, M.; Boča, R. Five Mononuclear Pentacoordinate Co(ii) Complexes with Field-induced Slow Magnetic Relaxation. Polyhedron 2017, 126, 174–183. [Google Scholar] [CrossRef]
  58. Rajnák, C.; Titiš, J.; Fuhr, O.; Ruben, M.; Boča, R. Single-Molecule Magnetism in a Pentacoordinate Cobalt(II) Complex Supported by an Antenna Ligand. Inorg. Chem. 2014, 53, 8200–8202. [Google Scholar] [CrossRef]
  59. Habib, F.; Luca, O.R.; Vieru, V.; Shiddiq, M.; Korobkov, I.; Gorelsky, S.I.; Takase, M.K.; Chibotaru, L.F.; Hill, S.; Crabtree, R.H.; et al. Influence of the Ligand Field on Slow Magnetization Relaxation versus Spin Crossover in Mononuclear Cobalt Complexes. Angew. Chem. Int. Ed. 2013, 52, 11290–11293. [Google Scholar] [CrossRef]
  60. Ishikawa, R.; Miyamoto, R.; Nojiri, H.; Breedlove, B.K.; Yamashita, M. Slow Relaxation of the Magnetization of an MnIII Single Ion. Inorg. Chem. 2013, 52, 8300–8302. [Google Scholar] [CrossRef]
  61. Grigoropoulous, A.; Pissas, M.; Rapatolis, P.; Psycharis, V.; Kyritsis, P.; Sanakis, Y. Spin-relaxation Properties of a High-spin Mononuclear Mniiio6-containing Complex. Spin-Relaxation Properties of a High-Spin Mononuclear MnIIIO6-Containing Complex. Inorg. Chem. 2013, 52, 12869–12871. [Google Scholar] [CrossRef]
  62. Vallejo, J.; Pascual-Alvarez, A.; Cano, J.; Castro, I.; Julve, M.; Lloret, F.; Krzystek, J.; De Munno, G.; Armentano, D.; Wernsdorfer, W.; Ruiz-Garcia, R.; Pardo, E. Field-induced Hysteresis and Quantum Tunneling of the Magnetization in a Mononuclear Manganese(iii) Complex. Field-Induced Hysteresis and Quantum Tunneling of the Magnetization in a Mononuclear Manganese(III) Complex. Angew. Chem. Int. Ed. 2013, 125, 14325–14329. [Google Scholar] [CrossRef]
  63. Mossin, S.; Tran, B.L.; Adhikari, D.; Pink, M.; Heinemann, F.W.; Sutter, J.; Szilagyi, R.K.; Meyer, K.; Mindiola, D.J. A Mononuclear Fe(III) Single Molecule Magnet with a 3/2↔5/2 Spin Crossover. J. Am. Chem. Soc. 2012, 134, 13651–13661. [Google Scholar] [CrossRef]
  64. Harman, W.H.; Harris, T.D.; Freedman, D.E.; Fong, H.; Chang, A.; Rinehart, J.D.; Ozarowski, A.; Sougrati, M.T.; Grandjean, F.; Long, G.J.; et al. Slow Magnetic Relaxation in a Family of Trigonal Pyramidal Iron(ii) Pyrrolide Complexes. Slow Magnetic Relaxation in a Family of Trigonal Pyramidal Iron(II) Pyrrolide Complexes. J. Am. Chem. Soc. 2010, 132, 18115–18126. [Google Scholar] [CrossRef] [PubMed]
  65. Freedman, D.E.; Harman, W.H.; Harris, T.D.; Long, G.J.; Chang, C.J.; Long, J.R. Slow Magnetic Relaxation in a High-spin Iron(ii) Complex. J. Am. Chem. Soc. 2010, 132, 1224–1225. [Google Scholar] [CrossRef]
  66. Weismann, D.; Sun, Y.; Lan, Y.; Wolmershauser, G.; Powell, A.K.; Sitzmann, H. High-Spin Cyclopentadienyl Complexes: A Single-Molecule Magnet Based on the Aryl-Iron(II) Cyclopentadienyl Type. Chem. Eur. J. 2011, 17, 4700–4704. [Google Scholar] [CrossRef] [PubMed]
  67. Lin, P.-H.; Smythe, N.C.; Gorelsky, S.J.; Maguire, S.; Henson, N.J.; Korobkov, I.; Scott, B.L.; Gordon, J.C.; Baker, R.T.; Murugesu, M. Importance of Out-of-state Spin–orbit Coupling for Slow Magnetic Relaxation in Mononuclear Feii Complexes. J. Am. Chem. Soc. 2011, 133, 15806–15809. [Google Scholar] [CrossRef]
  68. Zadrozny, J.M.; Xiao, D.J.; Atanasov, M.; Long, G.J.; Grandjean, F.; Neese, F.; Long, J.R. Magnetic Blocking in a Linear Iron(i) Complex. Nat. Chem. 2013, 5, 577–581. [Google Scholar] [CrossRef]
  69. Eichhofer, A.; Lan, Y.; Mereacre, V.; Bodenstein, T.; Weigend, F. Slow Magnetic Relaxation in Trigonal-planar Mononuclear Fe(ii) and Co(ii) Bis(trimethylsilyl)amido Complexes—A Comparative Study. Inorg. Chem. 2014, 55, 1962–1974. [Google Scholar] [CrossRef]
  70. Zadrozny, J.M.; Long, J.R. Slow Magnetic Relaxation at Zero Field in the Tetrahedral Complex [Co(SPh)4]2–. J. Am. Chem. Soc. 2011, 133, 20732–20734. [Google Scholar] [CrossRef] [PubMed]
  71. Zadrozny, J.M.; Liu, J.; Piro, N.A.; Chang, C.J.; Hill, S.; Long, J.R. Slow Magnetic Relaxation in a Pseudotetrahedral Cobalt(ii) Complex with Easy-plane Anisotropy. Chem. Commun. 2012, 48, 3927–3929. [Google Scholar] [CrossRef]
  72. Yang, F.; Zhou, Q.; Zhang, Y.; Zeng, G.; Li, G.; Shi, Z.; Wang, B.; Feng, S. Inspiration from Old Molecules: Field-induced Slow Magnetic Relaxation in Three Air-stable Tetrahedral Cobalt(ii) Compounds. Chem. Commun. 2013, 49, 5289–5291. [Google Scholar] [CrossRef]
  73. Boča, R.; Miklovič, J.; Titiš, J. Simple Mononuclear Cobalt(ii) Complex: A Single-molecule Magnet Showing Two Slow Relaxation Processes. Inorg. Chem. 2014, 53, 2367–2369. [Google Scholar] [CrossRef]
  74. Jurca, T.; Farghal, A.; Lin, P.-H.; Korobkov, I.; Murugesu, M.; Richeson, D.S. Single-Molecule Magnet Behavior with a Single Metal Center Enhanced through Peripheral Ligand Modifications. J. Am. Chem. Soc. 2011, 133, 15814–15817. [Google Scholar] [CrossRef] [PubMed]
  75. Vallejo, J.; Castro, I.; Ruiz-Garcia, J.; Cano, J.; Julve, M.; Lloret, F.; De Munno, G.; Wernsdorfer, W.; Pardo, E. Field-induced Slow Magnetic Relaxation in a Six-coordinate Mononuclear Cobalt(ii) Complex with a Positive Anisotropy. J. Am. Chem. Soc. 2012, 134, 15704–15707. [Google Scholar] [CrossRef] [PubMed]
  76. Colacio, E.; Ruiz, K.; Ruiz, E.; Cremades, E.; Krzystek, J.; Carretta, S.; Cano, J.; Guidi, T.; Wernsdorfer, W.; Brechin, E.K. Slow Magnetic Relaxation in a Coii–yiii Single-ion Magnet with Positive Axial Zero-field Splitting. Angew. Chem. Int. Ed. 2013, 125, 9300–9304. [Google Scholar] [CrossRef]
  77. Zhu, Y.-Y.; Cui, C.; Zhang, Y.-Q.; Jia, J.-H.; Guo, X.; Gao, C.; Qian, K.; Jiang, S.-D.; Wang, B.-W.; Wang, Z.-M. Zero-field slow magnetic relaxation from single Co(ii) ion: A transition metal single-molecule magnet with high anisotropy barrier. Chem. Sci. 2013, 4, 1802–1806. [Google Scholar] [CrossRef]
  78. Makinen, M.V.; Kuo, L.C.; Yim, M.B.; Wells, G.B.; Fukuyama, J.M.; Kim, J.E. Ground Term Splitting of High-spin Cobalt(2+) Ion as a Probe of Coordination Structure. 1. Dependence of the Splitting on Coordination Geometry. J. Am. Chem. Soc. 1985, 107, 5245–5255. [Google Scholar] [CrossRef]
  79. Neese, F.; Solomon, R.I. Calculation of Zero-Field Splittings, g-Values, and the Relativistic Nephelauxetic Effect in Transition Metal Complexes. Application to High-Spin Ferric Complexes. Inorg. Chem. 1998, 37, 6568–6582. [Google Scholar] [CrossRef]
  80. Maganas, D.; Krzystek, J.; Ferentinos, E.; Whyte, A.M.; Robertson, N.; Psycharis, V.; Terzis, A.; Neese, F.; Kyritsis, P. Investigating Magnetostructural Correlations in the Pseudooctahedral Trans-[niii{(opph2)(epph2)n}2(sol)2] Complexes (E = S, Se; Sol = DMF, THF) by Magnetometry, HFEPR, and Ab Initio Quantum Chemistry. Inorg. Chem. 2012, 51, 7218–7231. [Google Scholar] [CrossRef]
  81. Duboc, C.; Ganyushin, D.; Sivalingam, K.; Collomb, M.-N.; Neese, F. Systematic Theoretical Study of the Zero-field Splitting in Coordination Complexes of Mn(iii). Density Functional Theory Versus Multireference Wave Function Approaches. J. Phys. Chem. A 2010, 114, 10750–10758. [Google Scholar] [CrossRef]
  82. Carlin, R.L. Magnetochemistry; Springer: Berlin, 1986. [Google Scholar]
  83. Boča, R.; Dlháň, Ľ.; Haase, W.; Herchel, R.; Mašlejová, A.; Papánková, B. Limiting Negative Zero-field Splitting in Tetrakis(imidazole)bis(acetato) Nickel(ii) Complex. Chem. Phys. Lett. 2003, 373, 402–410. [Google Scholar] [CrossRef]
  84. Boča, R. Zero-field splitting in metal complexes. Coord. Chem. Rev. 2004, 248, 757–815. [Google Scholar] [CrossRef]
  85. Neese, F. Importance of Direct Spin−spin Coupling and Spin-flip Excitations for the Zero-field Splittings of Transition Metal Complexes: A Case Study. J. Am. Chem. Soc. 2006, 128, 10213–10222. [Google Scholar] [CrossRef] [PubMed]
  86. Zhu, Y.Y.; Cui, C.; Zhang, Y.Q.; Jia, J.H.; Guo, X.; Gao, C.; Qian, K.; Jiang, S.D.; Wang, B.W.; Wang, Z.M. Zero-field slow magnetic relaxation from single Co(ii) ion: a transition metal single-molecule magnet with high anisotropy barrier. Chem. Sci. 2013, 4, 1802–1806. [Google Scholar] [CrossRef]
  87. Kulik, H.J. Making machine learning a useful tool in the accelerated discovery of transition metal complexes. WIREs Comput. Mol. Sci. 2019, e1439. [Google Scholar] [CrossRef]
Preprints 86100 g001
Figure 1. Energy levels modelled by the spin-Hamiltonian formalism, D/k = 10 K; parallel direction (z)-upper panel, perpendicular direction (x)–bottom panel.
Figure 1. Energy levels modelled by the spin-Hamiltonian formalism, D/k = 10 K; parallel direction (z)-upper panel, perpendicular direction (x)–bottom panel.
Preprints 86100 g001
Preprints 86100 g002
Figure 2. 3D-view of the magnetization M(D,E) for different applied field, S = 1.
Figure 2. 3D-view of the magnetization M(D,E) for different applied field, S = 1.
Preprints 86100 g002
Preprints 86100 g003
Figure 3. Calculated lowest energy gap by the GCFT over a wide range of the crystal-field strengths between compressed and elongated tetragonal bipyramid (D4h) for the electron configurations d1 through d9. The D-parameter results from the splitting of a non-degenerate ground electronic term by the spin-orbit interaction.
Figure 3. Calculated lowest energy gap by the GCFT over a wide range of the crystal-field strengths between compressed and elongated tetragonal bipyramid (D4h) for the electron configurations d1 through d9. The D-parameter results from the splitting of a non-degenerate ground electronic term by the spin-orbit interaction.
Preprints 86100 g003
Preprints 86100 g004
Figure 4. Calculated magnetic D-values (exact multiplet splitting by GCFT) for different equatorial-axial crystal-field strengths vs the transformed structural ordinate Dstr for hexacoordinate Ni(II) complexes. Solid lines interpolate the points for common axial metal-ligand distance Rz = 190 pm. Red points bracket the second limiting case, Rz = 230 pm.
Figure 4. Calculated magnetic D-values (exact multiplet splitting by GCFT) for different equatorial-axial crystal-field strengths vs the transformed structural ordinate Dstr for hexacoordinate Ni(II) complexes. Solid lines interpolate the points for common axial metal-ligand distance Rz = 190 pm. Red points bracket the second limiting case, Rz = 230 pm.
Preprints 86100 g004
Preprints 86100 g005
Figure 5. Magnetostructural D-correlation for hexacoordinate Ni(II) complexes. Confidence and prediction intervals are shown at 95 % probability level.
Figure 5. Magnetostructural D-correlation for hexacoordinate Ni(II) complexes. Confidence and prediction intervals are shown at 95 % probability level.
Preprints 86100 g005
Preprints 86100 g006
Figure 6. PCA biplot for hexacoordinate Ni(II) complexes. The points are the individual objects.
Figure 6. PCA biplot for hexacoordinate Ni(II) complexes. The points are the individual objects.
Preprints 86100 g006
Preprints 86100 g007
Figure 7. Magnetostructural D-correlation for hexacoordinate Co(II) complexes. Lines–fitted with an exponential, 2 D = b ⋅ exp ( c ⋅ D str ) (left). Calculated magnetic D-values for different equatorial-axial crystal-field strengths vs the transformed structural ordinate Dstr for hexacoordinate Co(II) complexes. Solid lines interpolate the points for common axial metal-ligand distance Rz = 190 pm. Red points bracket the second limiting case, Rz = 230 pm (right).
Figure 7. Magnetostructural D-correlation for hexacoordinate Co(II) complexes. Lines–fitted with an exponential, 2 D = b ⋅ exp ( c ⋅ D str ) (left). Calculated magnetic D-values for different equatorial-axial crystal-field strengths vs the transformed structural ordinate Dstr for hexacoordinate Co(II) complexes. Solid lines interpolate the points for common axial metal-ligand distance Rz = 190 pm. Red points bracket the second limiting case, Rz = 230 pm (right).
Preprints 86100 g007
Preprints 86100 g008
Figure 8. Cluster analysis for hexacoordinate Co(II) complexes. Individual cluster areas are circled.
Figure 8. Cluster analysis for hexacoordinate Co(II) complexes. Individual cluster areas are circled.
Preprints 86100 g008
Preprints 86100 g009
Figure 9. Calculated magnetic D-values (exact multiplet splitting by GCFT) for different distortion angles α (A-Co-A) and β (B-Co-B) (in deg) with fixed crystal-field strengths F4® = 5000 cm-1. Right–transformed 2D graph for increasing angle α (from bottom to top).
Figure 9. Calculated magnetic D-values (exact multiplet splitting by GCFT) for different distortion angles α (A-Co-A) and β (B-Co-B) (in deg) with fixed crystal-field strengths F4® = 5000 cm-1. Right–transformed 2D graph for increasing angle α (from bottom to top).
Preprints 86100 g009
Preprints 86100 g010
Figure 10. Magnetostructural D-correlation for tetracoordinate Co(II) complexes.
Figure 10. Magnetostructural D-correlation for tetracoordinate Co(II) complexes.
Preprints 86100 g010
Preprints 86100 g011
Figure 11. Cluster analysis for tetracoordinate Co(II) complexes. Individual cluster areas are circled.
Figure 11. Cluster analysis for tetracoordinate Co(II) complexes. Individual cluster areas are circled.
Preprints 86100 g011
Preprints 86100 g012
Figure 12. PCA biplot for tetracoordinate Co(II) complexes. The points are the individual objects.
Figure 12. PCA biplot for tetracoordinate Co(II) complexes. The points are the individual objects.
Preprints 86100 g012
Preprints 86100 g013
Figure 13. Calculated magnetic D-values (exact multiplet splitting by GCFT) for polar angles θ(A) and θ(B) (in deg) with fixed crystal-field strengths F4R = 6000 cm-1.
Figure 13. Calculated magnetic D-values (exact multiplet splitting by GCFT) for polar angles θ(A) and θ(B) (in deg) with fixed crystal-field strengths F4R = 6000 cm-1.
Preprints 86100 g013
Preprints 86100 g016
Figure 16. Magnetostructural D-correlation for pentacoordinate Co(II) complexes. Trial correlation curves: dashed–linear, solid–exponential y = a ⋅ exp ( b x ) , dot-dashed y = y 0 + a / ( x − x 0 ) .
Figure 16. Magnetostructural D-correlation for pentacoordinate Co(II) complexes. Trial correlation curves: dashed–linear, solid–exponential y = a ⋅ exp ( b x ) , dot-dashed y = y 0 + a / ( x − x 0 ) .
Preprints 86100 g016
Preprints 86100 g017
Figure 17. A relationship between the barrier to spin reversal and the extrapolated relaxation time in SIM containing Co(II). Right–interrelation of D and U (dashed–expected U = 2|D|).
Figure 17. A relationship between the barrier to spin reversal and the extrapolated relaxation time in SIM containing Co(II). Right–interrelation of D and U (dashed–expected U = 2|D|).
Preprints 86100 g017
Table 1. List of single-molecule (single-ion) magnets containing Co(II).
Table 1. List of single-molecule (single-ion) magnets containing Co(II).
C.n. Chromophore Geometry a (D/hc)/cm-1 (E/hc)/cm-1 BDC/T (U/kB)/K τ0/s Ref.
3 {CoN3} -57 12.7 0.08 16 3.5 × 10-7 [69]
{CoN2O} -72 13.5 0.06 18 9.3 × 10-8 [69]
{CoN2P} -82 0.075 19 3.0 × 10-7 [69]
4 {CoS4} -74 0.10 30 1.0 × 10-7 [70]
{CoN3Cl} +12.7 1.2 0.15 35 2 × 10-10 [71]
{CoP2Cl2} -16.2 0.9 0.10 37 1.2 × 10-10 [72]
{CoP2Cl2} -14.4 1.7 0.10 35 2.1 × 10-10 [72]
{CoP2Cl2} -15.4 1.3 0.10 30 6.0 × 10-9 [72]
{CoP2Br2} -12.5 0.10 37 9.4 × 10-11 [73]
0.20 40 6.0 × 10-11 [73]
5 {CoN3N2} 4py -40.5 J > 0 0.20 16 3.6 × 10-6 [74]
{CoN3N2} 4py -40.6 0.20 24 5.1 × 10-7 [74]
{CoN3N2} 3bpy (+49.0), calc 0.06 17 5.85 × 10-6 [59]
0.56 3 0.110 [59]
{CoN3Cl2} 4py (+99.5), calc 0.06 28 1.1 × 10-6 [59]
0.56 4 0.074 [59]
{CoN3Cl2}2 4py 151 11.6, J > 0 0.20 9 3.1 × 10-7 [58]
0.20 1 0.27 [58]
6 {CoN4N2} +48 13.0 0.30 83 8.7 × 10-10 [48]
{CoN4N2} +98 8.4 0.10 23 3.0 × 10-7 [75]
{CoO3N3} +41.7 1.6 0.10 23 8.9 × 10-7 [76]
{CoO6} -115 2.8 0 106 1.7 × 10-7 [77]
0.15 124 6.3 × 10-8 [77]
a C.n.–coordination number; 4py–tetragonal pyramid, 3bpy–trigonal bipyramid; calc–estimate from the calculated energy gap between the lowest Kramers doublets as Δ = 2 ( D 2 + 3 E 2 ) 1 / 2 ~ 2 D .
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated