Time Series Homogenization with ACMANT: Comparative Testing of Two Recent Versions in Large-Size Synthetic Temperature Datasets

Preprint

Article

Time Series Homogenization with ACMANT: Comparative Testing of Two Recent Versions in Large-Size Synthetic Temperature Datasets

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Peter Domonkos^*

This version is not peer-reviewed

Submitted:

26 September 2023

Posted:

28 September 2023

You are already at the latest version

Alerts

Abstract

Homogenization of climatic time series aims to remove non-climatic biases which come from the technical changes of climate observations. The method comparison tests of the Spanish MULTITEST project (2015-2017) showed that ACMANT was likely the most accurate homogenization method available at that time, in spite of the tested ACMANTv4 version gave suboptimal results when the test data included synchronous breaks for several time series. The technique of combined time series comparison has been introduced to ACMANTv5 in order to treat better this specific problem. Tests confirm that ACMANTv5 treats adequately synchronous inhomogeneities, but the accuracy has slightly worsened in some other cases. Results for a known daily temperature test dataset for 4 U.S. regions show that the residual errors after homogenization may be larger with ACMANTv5 than with ACMANTv4. Further tests have been performed to learn more about the efficiencies of ACMANTv4 and ACMANTv5, and to find solutions for the appearing problems with the new version. Planned changes in ACMANTv5 are presented in the paper along with connecting test results. The overall results indicate that the combined time series comparison can be kept in ACMANT, but smaller networks should be generated by the automatic networking process of the method. For the further improvements of homogenization methods and for obtaining more reliable and more solid knowledge about their accuracies, more synthetic test datasets mimicking fairly the true spatio-temporal structures of real climatic data would be in need.

Keywords:

Subject: Environmental and Earth Sciences - Atmospheric Science and Meteorology

1. Introduction

The purpose of the homogenization of observed climatic time series is to remove possible non-climatic biases which often occur for changes in station location, instrumentation, instrument installation, station surrounding, or observing practices. The effects of such technical changes are referred to as inhomogeneities, and they usually manifest as sudden, non-climatic shifts (breaks) of the section mean values of the time series and in other properties of the probability distribution of the observed data, although sometimes gradually growing biases also occur. The homogenization of climatic time series (hereafter: homogenization) intends to separate non-climatic biases from true climate variation. In homogenization, a candidate series is usually compared to several neighbor series, and the differences are evaluated by appropriately designed statistical methods [1,2,3,4]. This procedure is named relative homogenization, and its advantage is that regionally common climatic variations are not present in the spatial difference series. So that the use of spatial difference series (they can be arithmetic differences or ratios according to climatic variables, and all of them can be referred to as relative time series) helps to separate non-climatic changes from true climate variation. Homogenization can be performed with the help of documents (so-called metadata) about the history of technical changes of the observations, but the inclusion of statistical homogenization is preferred even when metadata support homogenization. When insufficient station density limits or impedes the use of neighbor series, reanalysis data or other kinds of auxiliary climate series may help homogenization [5,6], and in some special cases absolute homogenization, i.e., homogenization of a candidate series without the use of any other time series, can be performed.

In this study the accuracy of some relative homogenization methods without metadata use will be analyzed in synthetically developed test datasets. For tests, the use of synthetically developed datasets are needed, since true inhomogeneity properties are known only in synthetic data.

A large number of statistical methods have been developed to provide accurate relative homogenization. Some important milestones of this development were the creation of the MASH [7], PRODIGE [8], PHA [9], HOMER [10], Climatol [11] and ACMANT [12] homogenization methods. In international method comparison tests, ACMANT was found to be the best performing method more frequently than any other tested method [13,14,15,16,17], although the rank order of efficiency depends on test dataset properties, efficiency measures and the tested method versions. Regarding recent developments, some promising novel techniques are included in ACMANTv5 [18], in Bart [19] and in MASHv4 [20], but in this study only some ACMANT versions are tested for limits of technical and working capacity.

Domonkos [18] reported that the method of “combined time series comparison”, including a break detection step with pairwise comparisons and another break detection step with composite reference series use, increases the efficiency of homogenization when time series are affected by synchronous or semi-synchronous breaks (they are referred also to as clustered breaks). That paper showed, using a test dataset [16] having been part of the Spanish MULTITEST project [17] and is referred to as MULTITEST dataset in this study, that the new method tends to give more accurate homogenization results even for datasets free of clustered breaks. However, newer tests with the synthetic daily temperature test dataset developed by Killick [13] (hereafter K2016 dataset) gave somewhat less favorable results, which inspired the author to perform even more tests and search possible refinements of the methodology. The objective of this paper is to share the results of the new tests with the research community, and discuss the knowledge provided by these tests.

The K2016 dataset is used throughout the paper, but in two different forms: it is used in its original form, but also in a modified form where subsets of 50 time series are selected from the original dataset. ACMANTv4 and two experimental versions of ACMANTv5 are tested. More detailed descriptions of the test datasets and homogenization methods are provided in Section 2 and 3, respectively. The used measures of homogenization accuracy are presented in Section 4. Finally, the presentation of the results, the discussion of the results and the main conclusions will be shown in the last three sections of the study.

2. Data

The study uses the synthetic daily temperature dataset of K2016 [13]. In the first part of this section (Section 2.1), some characteristics of the original dataset are presented, then the two ways how it is used in this study are described in Section 2.2 and Section 2.3. However, the description starts here with the definition of some terms.

“synthetic”, “surrogate” and “simplified” test data: During the European project HOME [21] the concept of surrogate data was introduced for those which mimic well most spatial and temporal variations of observed data in a given geographical area, while test data developed by simpler methods are called synthetic data. A drawback of this use of terms is that any artificially developed dataset can be called synthetic dataset. Using the term “simplified dataset” would likely be better for datasets excluding the reproduction of truly occurring low frequency changes of spatial climatic gradients.

In this study, term “network” is reserved for groups of time series whose data are homogenized together, and it is not used in other contexts, e.g., for sections of a dataset specific for a geographical region or for the way of the dataset generation.

2.1. Properties of the source dataset

The source dataset K2016 is a surrogate daily temperature dataset representing 4 U.S. regions of 2*10⁵ to 3*10⁵ km² size for each. They are referred to as Wyoming (WY), Northeastern (NE), Southeastern (SE) and Southwestern (SW) regions. The base of the dataset development was the 20^th Century Reanalysis dataset [22], but observed climatic data and large-scale circulation indices were also used in the formation of temporal and spatial structures of the data. The test dataset has a “clean” section which does not contain inhomogeneities or missing data, while its “corrupted” section includes both inhomogeneities and missing data. Three or four inhomogeneous sections were developed for each region, such sections sometimes differ also in station density. The overall number of inhomogeneous dataset sections is 13, and each of them includes 75 to 222 time series. All time series cover the 1970-2011 period with less than 25% missing data. The median spatial correlation is around 0.75, although it is only ~0.6 for the SW region (see Figure 3.6 of [13]). These correlations allow to use neighbor series to any candidate series from almost all parts of a region. However, the simulated climate and its temporal evolution are not constant spatially. Temporal changes of spatial climatic gradients might cause the detection of false breaks, since they cause the presence of some climate effects in relative time series. Killick [13] tested the frequency of false break detection with the PHA method in the homogeneous sections of the dataset. Domonkos et al. [23] performed the same kind tests with ACMANTv5. The results of these tests (Table 1) are important to the correct interpretation of the test results for the inhomogeneous sections of the dataset.

The frequency of time series with detected false breaks may be expected to do not exceed the 5-10% of the number of the tested time series. However, many false breaks were detected for the SW region by both tested methods, this is due to the complex geographical composition of that region [13]. Overall, ACMANT detected much more false breaks than PHA, but not in each region. Table 1 shows that the ratio of false breaks depends both on the spatio-temporal changes of climate and on homogenization methods. For instance, in the SE region only ACMANT detects more false breaks than expected. Fortunately, the magnitudes of these breaks are generally very small, hence their effect on the accuracy of inhomogeneity bias removal is minor [13,23].

2.2. Dense test dataset

The source K2016 dataset is used in its original form, and it is referred to as dense dataset. The mean distance between adjacent stations is about 40-50 km.

2.3. Moderately dense test dataset

The core operation is the random selection of 50 stations from a section of the source K2016 dataset. This operation was performed 10 times for each of the WY1, NE1, SE1 and SW1 sections of the K2016 dataset. In this way, the moderately dense test dataset has been generated, which includes 40 dataset sections. The mean distance between adjacent stations is ~80 km. The main goal of this dataset creation was to use a dataset with a higher number of dataset sections than the source dataset has, in order to reduce the random component of the estimated homogenization accuracies.

3. ACMANT homogenization method

The development of ACMANT started around 2010 on the base of the PRODIGE method (ACMANT = Adapted Caussinus-Mestre Algorithm for the homogenization of Networks of climatic Time series). The method contains modern and effective tools both for break detection and the calculation of adjustment terms. It approaches to the final solution with 3 homogenization cycles, and ensemble homogenization helps to attenuate random effects. A brief description of ACMANT is provided in a recent daily temperature and precipitation dataset development for Catalonia [24], while the full description of ACMANTv4 was published by Domonkos [12]. ACMANTv4 participated in the method comparison tests of the MULTITEST project. In those tests, ACMANTv4 often produced more accurate homogenization results than any other tested method [16,17], but a problem of ACMANTv4 was also revealed: the method cannot treat effectively inhomogneities of clustered breaks. To achieve advance in this issue, the combined time series comparison was introduced to ACMANTv5 [18]. The development of ACMANTv5 is continuous, and some of the recent developments have not been published in other documents. Here the differences from ACMANTv4 in three subversions of ACMANTv5 are presented. Note that from the three subversions only ACMANTv5.1 is available yet, the other subversions, referred to as A52 and A53, are under development.

3.1. ACMANTv5.1

The method of combined time series comparison has been introduced into the first homogenization cycle of the method, and it has exchanged the ensemble homogenization of that cycle in the earlier versions. The first step of combined time series comparison is a break detection with pairwise comparison of time series and optimal step function fitting with the Caussinus-Lyazrhi criterion [8]. Then, in the second step, the time series comparison is performed by using composite reference series, while the break detection method is the same as in the first step. In the second step, the timings of the detected breaks of the first step are introduced as obligatory break positions, so that the final set of detected breaks by the combined time series comparison contains the detected breaks of the first step together with the additionally detected breaks of the second step. Of course, the number of detected breaks can be zero in any step. Inhomogeneity bias removal is performed only after both steps of the combined time series comparison are finished, and it is done with the ANOVA correction model [25]. The full description of the combined time series comparison was presented by Domonkos [18].

Two more important novelties of ACMANTv5 are: (i) this method has both automatic and interactive versions [26], (ii) metadata can be treated in both of the automatic and interactive versions [27]. Details of these aspects are not provided here, since the present study examines only automatic homogenization without metadata.

In ACMANTv5.1 the parameterization of the final ensemble homogenization (at step 17.3.2 of ACMANTv4) is modified. There 9 linear combinations of the minimum of the ensemble results (z’) of the second homogenization cycle and the arithmetical average of the same ensemble results (z⁺) are used both in ACMANTv4 and ACMANTv5. In ACMANTv4 the weights of z’ (denotation of weight: c’) change from –3 to 4, while those of z⁺ (c⁺) decrease from 4 to –3. In ACMANTv5, weights c’ are increased with 0.5, while c⁺ are decreased with 0.5 (Table 2).

3.2. Version A52

The changes introduced by ACMANTv5.1 are kept, but further three kinds of modifications are applied.

(i): The length of the overlapping periods in the use of relative time series for break detection is changed. The concept and practice of using overlapping relative time series are presented at section B6 and step 10.1 of the ACMANTv4 description [12].

As a first approach, only one relative time series is used, always the one with the highest β score. This score is determined primarily by the number of neighbor series included in the composite reference series, but some other factors are also considered (see at Section B6 of the ACMANTv4 description). However, close to any endpoint of a relative time series (which can be different than the endpoints of the candidate series), the reliability of break detection is reduced. Therefore, overlapping of relative time series is applied when it helps to cease or reduce such edge effects. In ACMANTv4 the maximum length of the overlap is 9 years, while in ACMANTv5 it is increased to 15 years. However, when a detected break point is close to the endpoint of the previously used relative time series, the overlap by the lately used relative time series extends only to the timing of that detected break. This parameter change is applied in all break detection steps of A52 when multiple relative time series are used.

(ii): The creation of relative time series for break detection in the first homogenization cycle is modified. The applied modifications partly change the content of steps 9.1-9.3 of ACMANTv4. Note that in ACMANTv5, these steps are part of the combined time series comparison.

Networks are classified to be small networks or large networks. In the classification the mean number of time series with comparable observed data (N^*) is considered. For the calculation of N*, the period from the earliest staring year (Y_A ≥ 1) of all homogenized periods to the latest ending year (Y_B ≤ n) of all homogenized periods is used. n denotes the number of years in the study period defined by the user, while homogenized period defines the period of a time series, in which the ratio and compactness of observed data, as well as the availability of spatially comparable data of neighbor series make it possible to perform homogenization with ACMANT [26]. When the total number of time series in network is N, the number of truly comparable data N’ (N’ ≤ N) may vary in time (i), Equation (1).

N^{*} = \frac{1}{Y_{B} - Y_{A} + 1} \sum_{i = Y_{A}}^{Y_{B}} N' (i)

(1)

In method A52 a network is considered to be small network if N* ≤ 15, while it is considered to be large network in the opposite case.

In small networks 1 only relative time series is edited to each candidate series. It covers the whole homogenized period of the candidate series. The composite reference series includes all neighbor series which have homogenized period overlapping with the homogenized period of the candidate series. When the considered neighbor series have missing data, they are completed over the homogenized period of the candidate series, and the completed series are used in the creation of the relative time series. Neighbor series are equally weighted in small networks.

In large networks the neighbor series are weighted by their squared spatial correlations with the candidate series. There is no other change in the edition of multiple relative time series for large networks.

Note again that this methodology is used only at the second step of the combined time series comparison and is not used in other relative time series edition steps of A52.

(iii): In the gap filling steps of A52, the use of monthly data is preferred in several details of the procedure, even when daily data homogenization is performed. The earlier concept of always using daily data for gap filling in daily data homogenization was based on the fact that monthly values may have elevated uncertainty when some of their daily data are missing. However, tests proved (not shown) that the use of daily data in gap filling does not yield perceptible accuracy improvement of the final results, except in a few details of the procedure, which are presented here and still considered in A52. The motivation of these changes is that the reduction of using daily data in gap filling steps often significantly reduces the computational time consumption.

The gap filling for monthly temperatures is performed by Equations (2)-(5) according to Section B12 of the ACMANTv4 description:

{g c}_{h 0} = \frac{1}{W^{'}} \sum_{s = 1}^{N^{″}} w_{s} g_{s, h 0}^{'}

(2)

g_{s, h 0}^{'} = g_{s, h 0} + \frac{1}{H^{''}} \sum_{h = h_{1}}^{h_{2}} ({g c}_{h} - g_{s, h})

(3)

W^{'} = m a x (p_{4}, W)

(4)

W = \sum_{s = 1}^{N^{″}} w_{s}

(5)

Denotations: gc – candidate series, g_s – neighbor series s, h – serial number of month, h₀ – timing (month) of missing data in the candidate series, N’’ – number of used neighbor series, w_s – weight (depending most on the squared spatial correlation between gc and g_s), h₁ and h₂ are the applied time window around h₀, H’’ – number of months with observed data in both of gc and g_s within the time window, p₄ – parameter (usually 0.4).

When the time resolution is changed from monthly to daily, d (day) can be written instead of h in Equations (2) and (3), with which the formulas are converted to Equations (6) and (7).

{g c}_{d 0} = \frac{1}{W^{'}} \sum_{s = 1}^{N^{″}} w_{s} g_{s, d 0}^{'}

(6)

g_{s, d 0}^{'} = g_{s, d 0} + \frac{1}{D^{''}} \sum_{d = d_{1}}^{d_{2}} ({g c}_{d} - g_{s, d})

(7)

In ACMANTv4 and ACMANTv5.1, Equations (6) and (7) are applied in all gap filling steps of daily data homogenization. (Gap filling for precipitation data is somewhat different, but its presentation is excluded in this study.) However, Equation (7) is not used in A52, except for at the initial generation of monthly data (next paragraph). In the preliminary operations and within the first two homogenization cycles, only monthly data are used in gap filling, and Equations (2) and (3) are used there also in daily data homogenization. It is possible, because in the first two homogenization cycles the other steps of the homogenization are also done in monthly or annual resolution. In the last homogenization cycle and also in the final gap filling step, the daily values are determined by Equation(6), but still monthly data are used for calculating the differences between the averages of station series, as it is shown by Equation (8)

g_{s, d 0}^{'} = g_{s, d 0} + \frac{1}{H^{''}} \sum_{h = h_{1}}^{h_{2}} ({g c}_{h} - g_{s, h})

(8)

In the daily data homogenization with ACMANT, a monthly data is considered to be observed when at least 75% of the daily data in the month are observed. Differences between the mean climate anomaly of the observed data of a month and that of the other days of the month may cause biased estimations of monthly values. To reduce such biases, gap filling with daily data is performed in the initial generation of monthly data. In this step, only the data of the month including the target missing data (d₀) are used. Here, Equation (7) is used with d₁ = 1, and d₂ equals the number of days in the month.

3.3. Version A53

The changes introduced by A52 are kept, but further modifications are included. All the newly introduced changes are related to the automatic network construction. In A53 two networks are used when the input dataset contains more than 22 time series. One of the networks is constructed in exactly the same way as in the earlier method versions, while the other network is constructed with the modification of a few parameters. These new type networks are generally smaller than the networks of the earlier method versions, and to distinct the two network types easily, they will be referred to as large networks and small networks.

(iv)

Generation of large networks: Identical with the network construction of the earlier method versions (see step 3.6 of the ACMANTv4 description).

(v)

Generation of small networks:

a): First, the best correlating 20 neighbor series are selected;
b): When the first 20 neighbor series no cover sufficiently parts of the homogenized section of the candidate series, further neighbor series are selected when neighbor series s with index S > 0 can be found (Equation 9).

S (s) = S_{1} + S_{2} + S_{3}

(9)

S₁ is an empirically constructed index characterizing the frequency of those observed monthly values of the candidate series, which are paired with less than 10 synchronous observed data of the neighbor series. S₂ is also an empirically constructed index, with which the frequency of less than 20 synchronous observed data of neighbor series is considered in overlapping 10-year-long sections of the homogenized period of the candidate series. There is no change in the calculation of S₁ and S₂ relative to their use in large networks. Index S₃ is a penalty term for the excess in network size (N’, see Equation 10).

S_{3} = {- (N' - q)}^{2}

(10)

In the construction of large networks q = 31, while in that of the small networks, q = 21. When S is positive for more than one neighbor series, the one with the highest S is selected. The network construction is finished when no neighbor series with S > 0 can be found.

(c): Use of small networks and large networks in A53: In most part of A53 the small network is used. Exceptions are the second step of the combined time series comparison, i.e. the break detection with composite reference series in the first homogenization cycle, and the preparatory steps for that break detection step.

3.4. Selection of method versions

Here the reasoning of the actual method version selection is provided. As preliminary examinations indicated that the network size impacts more the test results than the applied other modifications, A52 and A53 are selected to compare two method versions differing only in the construction and use of networks. The results of these ACMANTv5 versions are contrasted with the results of ACMANTv4 to analyze the favorable and unfavorable features of the recent modifications in ACMANT.

4. Efficiency measures

The accuracy of homogenization results is evaluated by examining the differences between the homogenized series (U) and the perfectly homogeneous series (V). In this study, the centered root mean square error (RMSE) of daily values, the RMSE of annual means, the absolute value of linear trend bias for the whole period of individual time series and the absolute value of network mean linear trend bias are examined. Note that a particularity of the centered RMSE is that possible deviations in the overall mean values are not considered, but only the deviations in the temporal variation. The use of centered RMSE was introduced to the evaluation of homogenization accuracy during HOME [21].

(i): RMSE of daily values:

R M S E (d) = \sqrt{\frac{1}{M} \sum_{i = 1}^{M} {(u_{i} - v_{i} - \frac{1}{n} \sum_{j = 1}^{n} {(u}_{j} - v_{j}))}^{2}}

(11)

In Equation (11) M and n stand for the length of time series in days and years, respectively.

(ii): RMSE of annual values:

R M S E (y) = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(u_{i} - v_{i} - \frac{1}{n} \sum_{j = 1}^{n} {(u}_{j} - v_{j}))}^{2}}

(12)

(iii): Absolute value of linear trend bias (Trb) when trend slopes are denoted with α:

T r b = |α_{u} - α_{v}|

(13)

Equation (13) can be applied for the calculation of trend bias both in individual time series and in area mean series. In the calculation of regional mean trend bias, the regional mean annual values are calculated before the application of Equation (13). In this study, the default unit of Trb is °C per 100 years, but some exceptions will be indicated when another unit is applied for visualization purposes.

(iv): The improvement of ACMANTv5 in comparison with the ACMANTv4 results is characterized by the Z index (Domonkos, 2021a).

Z = \frac{E (A C M A N T v 5)}{E (A C M A N T v 4)} - 1

(14)

In Equation (14) E stands for the mean of a given kind of errors (RMSE or Trb) calculated by Equations (11)-(13). Negative (positive) values of Z indicate improvement (worsening) relative to ACMANTv4. When the absolute value of the denominator is small, Z-index might show unrealistic values, therefore Equation (14) is applied only to sufficiently large samples of homogenization results.

5. Results

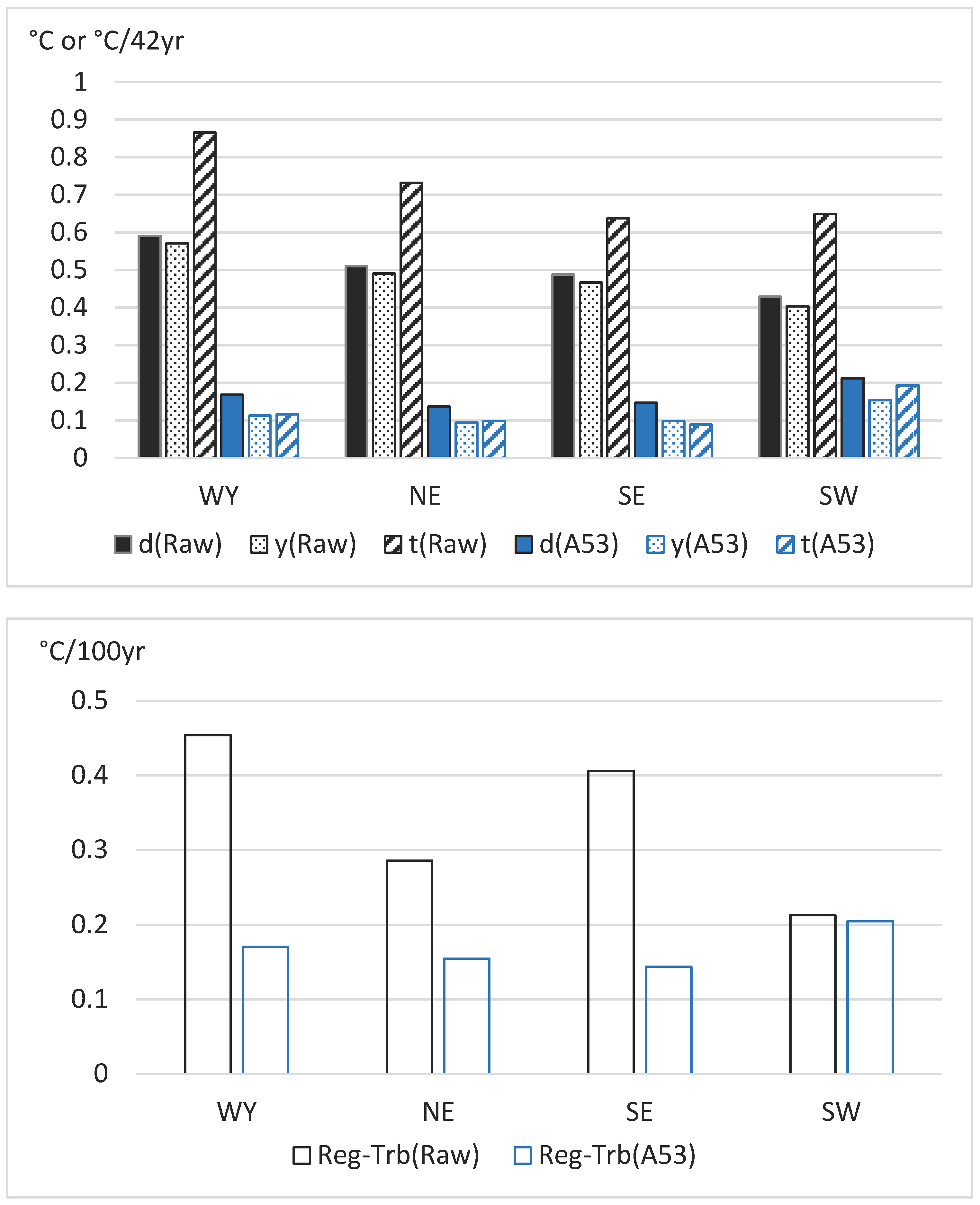
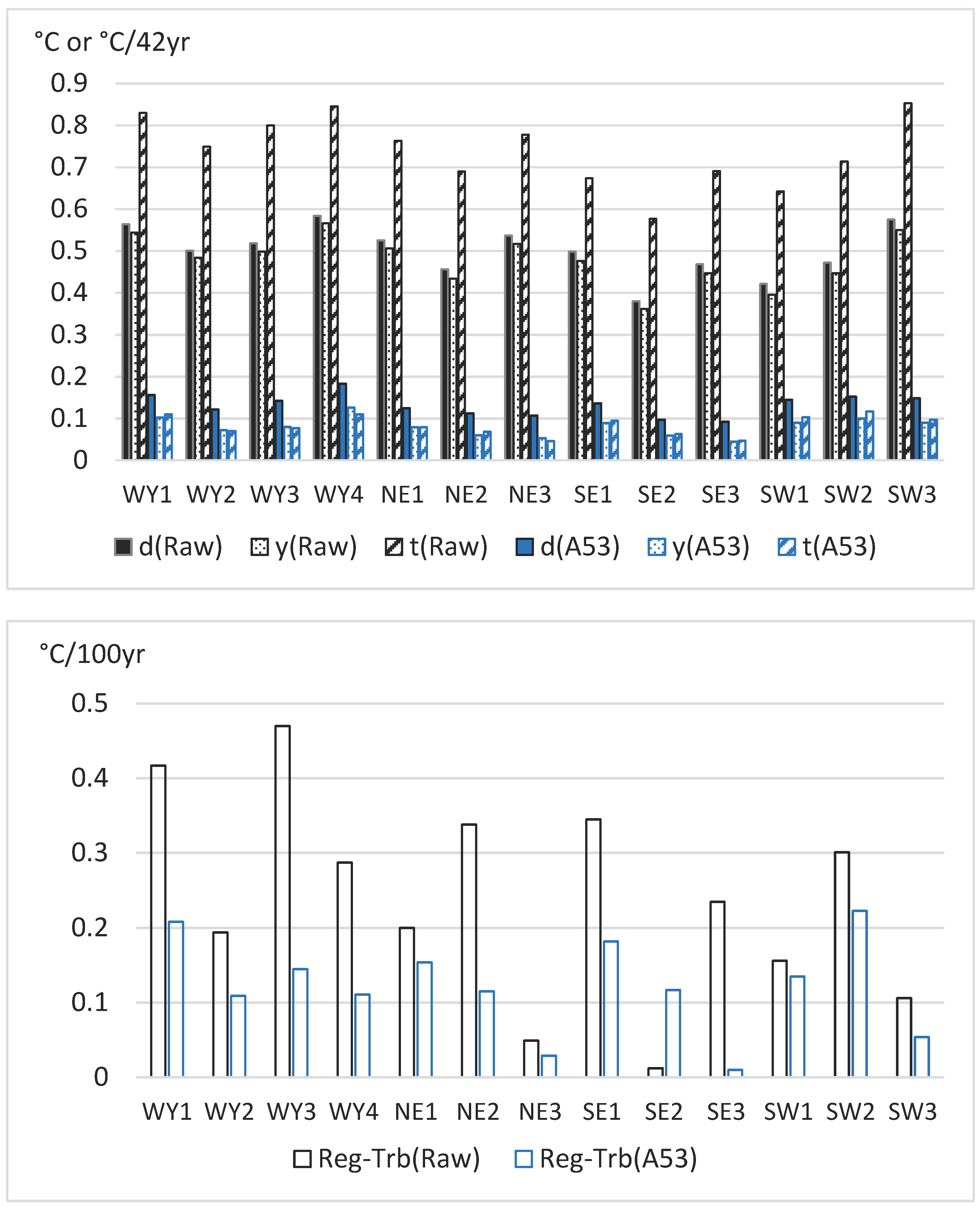
5.1. Results for the dense test dataset

Figure 1 shows the inhomogeneity bias reduction by A53 method in the 13 sections of the original, dense K2016 dataset.

Figure 1a shows that high ratios of the raw data errors are removed in all error types of daily RMSE, annual RMSE and trend bias for individual time series. The highest error reduction is achieved for the Trb of individual series. By contrast, the error reduction in regional mean trend bias (Figure 1b) is much smaller, but note that regional mean trend biases of the raw data are generally small, particularly if the shortness of time series (42 years) is also considered. When the found efficiencies according to error types are ranked from the highest to the lowest, the order is Trb for individual time series, annual RMSE, daily RMSE and Trb for regional mean series. This rank order is typical for homogenization results, and it was found in several other studies [16,21] with the only difference that monthly RMSE is tested instead of daily RMSE when the test data are of monthly resolution. In the present test results, the error reductions in RMSE and Trb for individual time series are higher than in many other tests, mainly for the high station density, high spatial correlations and generally high signal-to-noise ratio in the K2016 dataset.

In Figure 2 the residual homogenization errors are compared between different ACMANT versions. Figure 2a compares the results of A52 and ACMANTv4, while Figure 2b shows the same kind comparison for A53 and ACMANTv4.

Increasing (decreasing) errors relative to ACMANTv4 results are drawn with red (blue) color. Figure 2a shows that although the absolute values of differences are small, the sign of the changes is rather consequent, and the errors with A52 are mostly larger than with ACMANTv4. The typical magnitude of the difference is lower than 0.02°C RMSE or 0.02°C /100yr Trb. In the trend bias results, and particularly in the regional mean trend bias results, the differences between A52 and ACMANTv4 results are sometimes larger. Note, however, that this difference in the magnitude of differences is likely for the relatively large sampling errors of regional trend bias values (there are only 13 regions). The presence of sampling errors in the results explains that large error decrease from ACMANTv4 to A52 also occurred (in region SW1), which, however, does not change much on the generally unfavorably picture regarding the A52 results.

Figure 2b shows that the A53 results tend to be more accurate than the ACMANTv4 results, although the magnitudes of the differences are very small. The regional trend bias results are exceptions, no decreasing tendency can be found for them, i.e. in 6 regions the A53 results are the most accurate, in other 6 regions the ACMANTv4 results are the most accurate, while in 1 region the regional trend bias is exactly the same with any of the examined two methods.

5.2. Results for the moderately dense dataset

Figure 3 shows the residual errors of homogenization with A53 in comparison with the raw data errors.

Figure 3. Mean raw data errors and mean residual errors after homogenization with method A53 for the 4 main sections of the moderately dense dataset. Upper panel (a) d – RMSE of daily values, y – RMSE of annual means, t – mean absolute trend bias for station series; lower panel (b) Reg-Trb – regional mean absolute trend bias. Note: trend bias for station series is shown in °C per length of time series (42 years) unit for better visualization.

The results of Figure 3 show that the reduction of station density relative to that of the original dataset has little effect on the homogenization accuracy, except for in the SW region where the error increase relative to the errors of the dense dataset is notable.

In Figure 4 the residual homogenization errors of A52 and A53 are compared to those of the ACMANTv4 results in the same way as they were compared in Figure 2 for the dense test dataset.

In comparing the A52-ACMANTv4 differences between the results of Figure 4a and those of Figure 2a, one can find both similarities and notable differences. An important similarity between Figure 4a and 2a is the dominance of red color indicating generally poorer results for A52 than for ACMANTv4. However, an important difference is that the regional differences are generally larger in Figure 4a. There the difference between A52 and ACMANTv4 results is practically zero for the WY and NE regions, the differences are higher for the SE region and the highest for the SW region. These results indicate that false breaks for the complexity of spatial-temporal climatic structures (see Table 1 in Section 2.1) may affect more the homogenization results when the station density is moderated, and they affect more the accuracy of A52 than the accuracy of ACMANTv4.

In Figure 4b the regional differences are smaller than in Figure 4a, and most pieces of the A53 results indicate small improvement in comparison with the ACMANTv4 results. However, the regional trends are exceptions, there the ACMANTv4 results are the better. When the frequency of false breaks is low (Table 1), the reduction of network size between A52 and A53 caused improvement in the RMSE errors, but worsening in the regional trend estimations. These results are concordant with the results of an earlier study where the network size effect on the homogenization accuracy was examined [28] with ACMANTv3 and with large surrogate datasets based on a WY section of the K2016 dataset.

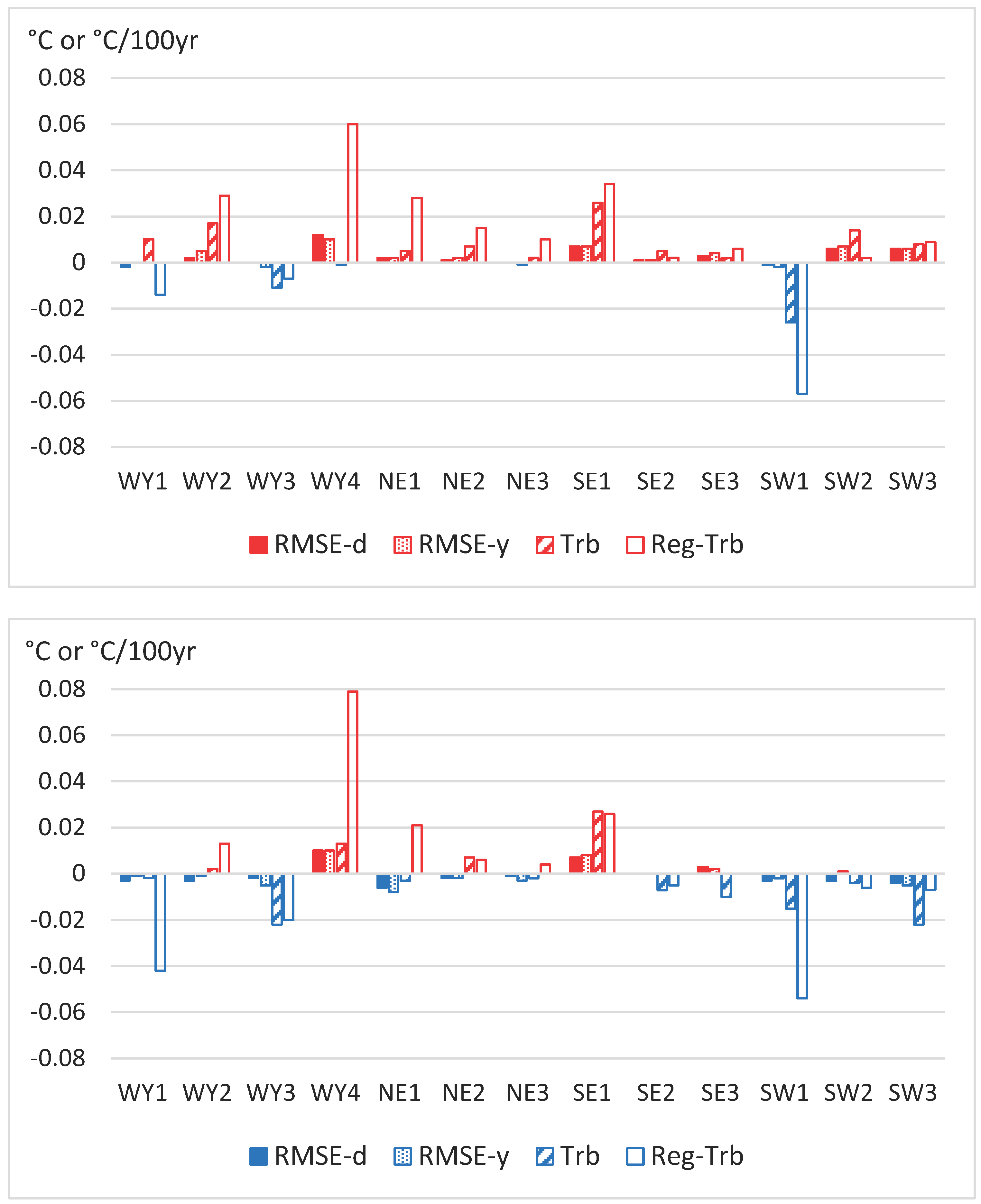
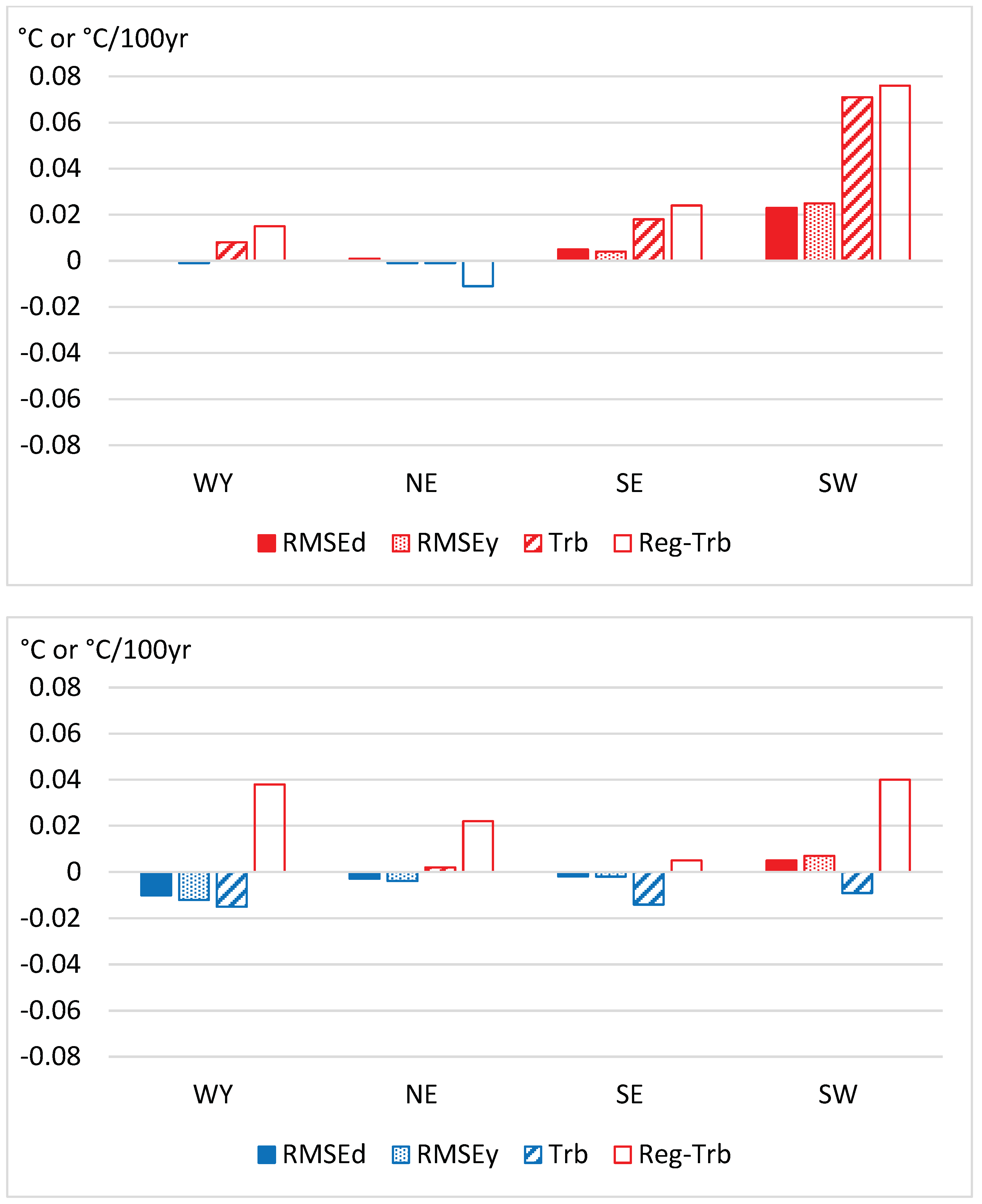
5.3. Z-index of accuracy improvement

Z-index values are examined for the averages of homogenization errors in the 13 (40) sections of the dense (moderately dense) datasets, Table 3 presents the results.

The reduction of network-size between A52 and A53 methods results in a small, but consequent accuracy improvement in the RMSE and station specific trend estimations. However, the results are less clear for the regional trend bias: in dense datasets the network size reduction improved the results, while in the moderately dense dataset the regional trend estimations are almost the same with A52 and A53, and they both poorer than with ACMANTv4. The advantage of ACMANTv4 in the regional trend estimations seems to be notable in the Z-index results, but note that the absolute differences are very small, as they were showen in Section 5.1 and Section 5.2.

6. Discussion

The results show generally small differences between the accuracies of the tested method versions, therefore one question is if such small differences merit attention. I think the correct answer is yes, for two main reasons.

(i): Homogenization methods are applied for several climate variables and for data observed under varied geographical conditions and by varied observation practices. Therefore, the found differences between homogenization efficiencies might be related to larger and more important absolute differences of climate characteristics than in case of the K2016 dataset.
(ii): Small differences of the mean errors often indicate more significant differences in the risk of committing large homogenization errors, this was demonstrated by the MULTITEST results [16,23].

The results with the K2016 dataset do not show any advantage of the pre-homogenization with combined time series comparisons, and the regional mean trend errors are found to be larger with the ACMANTv5 versions than with ACMANTv4. The likely reason of the disappointing weak results with methods including the combined time series comparison is that regional mean trend biases are generally very small in the K2016 dataset, which, however, is not rare in real observational datasets. The accuracy of regional mean trends has enhanced importance in climate science [23,29], therefore the found problems need further studies. Note here that although pairwise comparisons is often considered a modern and powerful homogenization tool [4,10,30], the method has both advantages and drawbacks in comparison with the use of composite reference series [23].

The differences in the two experimental versions of ACMANTv5 relative to ACMANTv5.1 influence most the homogenization of large datasets and the automatic networking procedure, while their effect is minor on previously defined small networks like most segments of the MULTITEST dataset. Therefore, the results of a comparison between ACMANTv4 accuracy and ACMANTv5 accuracy in an earlier study [18] in which the MULTITEST dataset and ACMANTv5.1 were used are considered to be usable for the joint analysis with the results of this study. Given that ACMANTv5 performed better than ACMANTv4 in most sections of the MULTITEST dataset, some slight advantage of the combined time series comparison can be concluded by the joint evaluation. The use of reduced network size in A53 is found to be more favorable than the former parameterization of automatic networking included in A52 and in previous ACMANT versions. Note, however, that these evaluations do not free from the subjectively judged importance dedicated to individual pieces of the results, and later tests might lead to other conclusions. One key issue of the further progress in relative homogenization is to learn more about the frequency and magnitude of low frequency changes in climatic gradients between time series with seemingly sufficient spatial correlations. To find reliable answers to these questions, the development of homogeneous surrogate datasets should be continued in the way started by the creation of the K2016 dataset, but further climatic zones and further climatic variables should be included.

A peculiarity of the automatic networking with A53 is that the old parameterization is used in one only break detection step of the procedure, i.e. in the second step of the combined time series comparison. There, the use of larger networks is advantageous, since only relatively large breaks are searched by using a stricter significance threshold than in the other break detection steps [12]. Stricter significance thresholds could also be used in the pairwise detection step of the combined comparisons, but experiments with them (not shown) did not yield better results than the originally set parameterization of ACMANTv5 [18].

Actually, the A53 version of ACMANT is selected as the base for further methodological developments, but later research results might modify this preference in three different ways: (i) May be that a more effective way of combining pairwise comparisons and the use of composite reference series will be found; (ii) Future test results might indicate the superiority of the ensemble pre-homogenization method of ACMANTv4; (iii) The way of pre-homogenization might depend on some parameters and/or previously calculated statistics of the input data. Concerning present day practical homogenization, any of the ACMANTv5 and ACMANTv4 methods can be recommended, since the inclusion of the ANOVA correction model, bivariate homogenization (when applicable) and ensemble homogenization provide the superior performance of the analyzed ACMANT versions in comparison with many other homogenization methods.

7. Conclusions

Some versions of the ACMANT homogenization method have been tested with the original dense version and with a derived moderately dense version of the synthetic daily temperature dataset developed for 4 U.S. regions (K2016 dataset) [13]. Two experimental versions of ACMANTv5, referred to as A52 and A53, were used, and the changes of homogenization accuracy relative to the ACMANTv4 accuracy have been analyzed. The main conclusions are summarized as follows:

The found differences between ACMANTv5 accuracy and ACMANTv4 accuracy are generally small, and ACMANTv5 often gave slightly worse results than ACMANTv4.
A reduction in network sizes reduced the RMSE and station specific trend errors of ACMANTv5, while it did not change significantly regional mean trend biases.
Regional mean trend biases are particularly sensitive both to the simulated climate properties of the test dataset and to the fine details of the applied homogenization method. Therefore, further improvements need the creation and use of more high quality homogenous test datasets.
The joint analysis of the results of this study and an earlier study indicates that the inclusion of combined time series comparison in ACMANT is likely favorable.

References

Moberg, A.; Alexandersson, H. Homogenization of Swedish temperature data. Part II: Homogenized gridded air temperature compared with a subset of global gridded air temperature since 1861. Int. J. Climatol. 1997, 17, 35-54.
Auer, I.; Böhm, R.; Jurkovic, A.; Orlik, A.; Potzmann, R.; Schöner, W.; Ungersböck, M.; Brunetti, M.; Nanni, T.; Maugeri, M.; Briffa, K.; Jones, P.; Efthymiadis, D.; Mestre, O.; Moisselin, J-M.; Begert, M.; Brazdil, R.; Bochnicek, O.; Cegnar, T.; Gajic-Capka, M.; Zaninovic, K.; Majstorovic, Z.; Szalai, S.; Szentimrey, T.; Mercalli, L. A new instrumental precipitation dataset for the Greater Alpine Region for the period 1800–2002. Int. J. Climatol. 2005, 25, 139–166. [CrossRef]
Begert, M.; Schlegel, T.; Kirchhofer, W. Homogeneous temperature and precipitation series of Switzerland from 1864 to 2000. Int. J. Climatol. 2005, 25, 65-80. [CrossRef]
Menne, M.J.; Williams, C.N.; Vose, R.S. The U.S. Historical Climatology Network Monthly Temperature Data, Version 2. Bull. Amer. Meteor. Soc. 2009, 90, 993–1008. [CrossRef]
Haimberger, L.; Tavolato, C.; Sperka, S. Homogenization of the global radiosonde temperature dataset through combined comparison with reanalysis background series and neighboring stations. J. Clim. 2012, 25, 8108–8131. [CrossRef]
Nguyen, K.N.; Quarello, A.; Bock, O.; Lebarbier, E. Sensitivity of change-point detection and trend estimates to GNSS IWV time series properties. Atmosphere 2021, 12(9), 1102. [CrossRef]
Szentimrey, T. Multiple Analysis of Series for Homogenization (MASH). 1999. In eds. Szalai, S.; Szentimrey, T.; Szinell, Cs. Second Seminar for Homogenization of Surface Climatological Data. WMO WCDMP-41, 27-46, Geneva, Switzerland.
Caussinus, H.; Mestre, O. Detection and correction of artificial shifts in climate series. JR Stat. Soc. Ser. C Appl. Stat. 2004, 53, 405–425. http://doi.org/10.1111/j.1467-9876.2004.05155.x.
Menne, M.J.; Williams Jr, C.N. Homogenization of temperature series via pairwise comparisons. J. Clim. 2009, 22, 1700–1717. [CrossRef]
Mestre, O.; Domonkos, P.; Picard, F.; Auer, I.; Robin, S.; Lebarbier, E.; Böhm, R.; Aguilar, E.; Guijarro, J.; Vertacnik, G.; Klancar, M.; Dubuisson, B.; Štěpánek, P. HOMER: homogenization software in R – methods and applications. Időjárás 2013, 117, 47-67.
Guijarro, J.A. Homogenization of climatic series with Climatol. 2018. http://www.climatol.eu/homog_climatol-en.pdf. (accessed: 25-09-2023).
Domonkos, P. ACMANTv4: Scientific content and operation of the software. 2020, 71pp. https://github.com/dpeterfree/ACMANT/blob/ACMANTv4.4/ACMANTv4_description.pdf (accessed: 25-09-2023).
Killick, R.E. Benchmarking the Performance of Homogenisation Algorithms on Daily Temperature Data. 2016, PhD thesis, University of Exeter, UK. https://ore.exeter.ac.uk/repository/handle/10871/23095.
Chimani, B.; Venema, V.; Lexer, A.; Andre, K.; Auer, I.; Nemec, J. Inter-comparison of methods to homogenize daily relative humidity. Int. J. Climatol. 2018, 38, 3106–3122. http:/doi.org/10.1002/joc.5488.
Guijarro, J.A. Recommended homogenization techniques based on benchmarking results. WP-3 report of INDECIS project. 2019. http://www.indecis.eu/docs/Deliverables/Deliverable_3.2.b.pdf (accessed: 25-09-2023).
Domonkos, P.; Guijarro, J.A.; Venema, V.; Brunet, M.; Sigró, J. Efficiency of time series homogenization: method comparison with 12 monthly temperature test datasets. J. Clim. 2021, 34, 2877-2891. [CrossRef]
Guijarro, J.A.; López, J.A.; Aguilar, E.; Domonkos, P.; Venema, V.K.C.; Sigró, J.; Brunet, M. Homogenization of monthly series of temperature and precipitation: Benchmarking results of the MULTITEST project. Int. J. Climatol, 2023, 43, 3994-4012. [CrossRef]
Domonkos, P. Combination of using pairwise comparisons and composite reference series: a new approach in the homogenization of climatic time series with ACMANT. Atmosphere 2021, 12(9), 1134. https:// doi.org/10.3390/atmos12091134.
Joelsson, L.M.T.; Sturm, C.; Södling, J.; Engström, E.; Kjellström, E. Automation and evaluation of the interactive homogenization tool HOMER. Int. J. Climatol. 2022, 42(5), 2861–2880. [CrossRef]
Szentimrey, T. Development of new version MASHv4.01 for homogenization of standard deviation. 2023. In: 11^th Seminar for Homogenization and Quality Control in Climatological Databases, 9-11 May 2023, Budapest, Hungary. https://www.met.hu/en/omsz/rendezvenyek/.
Venema, V.; Mestre, O.; Aguilar, E.; Auer, I.; Guijarro, J.A.; Domonkos, P.; Vertacnik, G.; Szentimrey, T.; Štěpánek, P.; Zahradníček, P.; Viarre, J.; Müller-Westermeier, G.; Lakatos, M.; Williams, C.N.; Menne, M.; Lindau, R.; Rasol, D.; Rustemeier, E.; Kolokythas, K.; Marinova, T.; Andresen, L.; Acquaotta, F.; Fratianni, S.; Cheval, S.; Klancar, M.; Brunetti, M.; Gruber, C., Duran, M.P.; Likso, T.; Esteban, P.; Brandsma, T. Benchmarking monthly homogenization algorithms. Clim. Past 2012, 8, 89-115. [CrossRef]
Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Matsui, N.; Allan, R.J.; Yin, X.; Gleason Jr., B.E.; Vose, R.S.; Rutledge, G.; Bessemoulin, P.; Brönnimann, S.; Brunet, M.; Crouthame, R.I.; Grant, A.N.; Groisman, P.Y.; Jones, P.D.; Kruk, M.C.; Kruger, A.C.; Marshall, G.J.; Maugeri, M.; Mok, H.Y.; Nordli, O.; Ross, T.F.; Trigo, R.M.; Wang, X.L.; Woodruff, S.D.; J.Worleyu, S. The twentieth century reanalysis project. Q. J. Roy. Meteor. Soc. 2011, 137, 1–28. [CrossRef]
Domonkos, P.; Tóth, R.; Nyitrai, L. Climate observations: Data quality control and time series homogenization. 2022, Elsevier, 302pp. https://www.elsevier.com/books/climate-observations/domonkos/978-0-323-90487-2.
Prohom, M.; Domonkos, P.; Cunillera, J.; Barrera-Escoda, A.; Busto, M.; Herrero-Anaya, M.; Aparicio, A.; Reynés, J. CADTEP: A new daily quality-controlled and homogenized climate database for Catalonia (1950–2021). Int. J. Climatol. 2023, 43, 4771-4789. [CrossRef]
Lindau, R.; Venema, V. On the reduction of trend errors by the ANOVA joint correction scheme used in homogenization of climate station records. Int. J. Climatol. 2018, 38, 5255–5271. http://doi.org/10.1002/joc.5728.
Domonkos, P. Manual of ACMANTv5. 2021. https://github.com/dpeterfree/ACMANT/tree/ACMANTv5_documents (accessed: 25-09-2023).
Domonkos, P. Automatic homogenization of time series: How to use metadata? Atmosphere 2022, 13(9), 1379. [CrossRef]
Domonkos, P.; Coll, J. Time series homogenisation of large observational datasets: The impact of the number of partner series on the efficiency. Clim. Res. 2017, 74, 31-42. [CrossRef]
Williams, C.N.; Menne, M.J.; Thorne, P. Benchmarking the performance of pairwise homogenization of surface temperatures in the United States. J. Geophys. Res. 2012, 117, D05116. [CrossRef]
Trewin, B. A daily homogenized temperature data set for Australia. Int. J. Climatol. 2013, 33, 1510–1529. [CrossRef]

Figure 1. Raw data errors and residual errors after homogenization with method A53 for the 13 sections of the original (dense) K2016 dataset [13]. Upper panel (a) d – RMSE of daily values, y – RMSE of annual means, t – mean absolute trend bias (Trb) for station series; lower panel (b) Reg-Trb – regional mean absolute trend bias. Note: trend bias for station series is shown in °C per length of time series (42 years) unit for better visualization.

Figure 2. Differences between homogenization errors in comparing ACMANTv5 versions to ACMANTv4 in using the dense dataset. Upper panel (a): comparison of A52 and ACMANTv4; lower panel (b): comparison of A53 and ACMANTv4. Trb – mean absolute trend bias for station series, Reg-Trb – regional mean absolute trend bias.

Figure 4. Differences between homogenization errors in comparing ACMANTv5 versions to ACMANTv4 in using the moderately dense test dataset. Each piece of the results is an average for 10 subsections of the test dataset. Upper panel (a): comparison of A52 and ACMANTv4; lower panel (b): comparison of A53 and ACMANTv4. Trb – mean absolute trend bias for station series, Reg-Trb – regional mean absolute trend bias.

Table 1. Number of detected breaks in the homogeneous section of the K2016 dataset. Mean magnitudes (°C) of ACMANT detected breaks are shown in brackets. Adopted from [23].

Data section	Number of series	Number of detected breaks in homogeneous data
Data section	Number of series	PHA	ACMANTv5
WY1	75	4	7 (0.15)
WY2	158	5	11 (0.12)
WY3	158	16	9 (0.18)
WY4	75	3	12 (0.61)
SE1	153	13	53 (0.09)
SE2	210	9	58 (0.10)
SE3	210	15	69 (0.10)
NE1	146	11	4 (0.09)
NE2	207	9	11 (0.09)
NE3	207	11	5 (0.06)
SW1	151	50	77 (0.16)
SW2	222	28	131 (0.15)
SW3	222	31	100 (0.18)

Table 2. Coefficients of adjustment terms z’ and z⁺ in the 9 ensemble members of the final homogenization cycle in ACMANTv5.

	c’	c⁺		c’	c⁺		c’	c⁺
1	–2.50	3.50	4	0.31	0.69	7	2.44	–1.44
2	–1.30	2.30	5	1.00	0.00	8	3.30	–2.30
3	–0.44	1.440	6	1.69	–0.69	9	4.50	–3.50

Table 3. Z index (percentage) of the change of homogenization errors in comparing versions A52 and A53 of ACMANTv5 to ACMANTv4. Mean results for entire datasets. RMSE-d – RMSE of daily values, RMSE-y – RMSE of annual values, Trb – mean absolute trend bias for station series, Reg-Trb – regional mean absolute trend bias for dataset sections.

		Z (%)
		RMSE-d	RMSE-y	Trb	Reg-Trb
Dense dataset	A52	2.1	3.7	2.2	7.4
Dense dataset	A53	–0.4	–0.6	–1.5	1.0
Moderately dense dataset	A52	4.3	5.7	7.9	18.2
Moderately dense dataset	A53	–1.5	–2.3	–3.0	18.4

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Time Series Homogenization with ACMANT: Comparative Testing of Two Recent Versions in Large-Size Synthetic Temperature Datasets

Abstract

1. Introduction

2. Data

2.1. Properties of the source dataset

2.2. Dense test dataset

2.3. Moderately dense test dataset

3. ACMANT homogenization method

3.1. ACMANTv5.1

3.2. Version A52

3.3. Version A53

3.4. Selection of method versions

4. Efficiency measures

5. Results

5.1. Results for the dense test dataset

5.2. Results for the moderately dense dataset

5.3. Z-index of accuracy improvement

6. Discussion

7. Conclusions

References

MDPI Initiatives

Important Links

Subscribe