Prerpints.org logo
Preprint
Article

Effect of Variation of Location of the Blowing on the Aerodynamic Characteristics over the Delta Wing

Altmetrics

Downloads

108

Views

46

Comments

0

This version is not peer-reviewed

Submitted:

26 September 2023

Posted:

28 September 2023

You are already at the latest version

Alerts
Abstract
The flow field around a delta wing is substantially altered by the impact of the active flow control technique. The present study involves the sharp-edged delta wing of 65 deg sweep angle with different active flow control configurations. The blowing was employed as an active flow control method on the top surface of the delta wing. The various configurations considered are the baseline delta wing, delta wing with blowing holes located at 1.62%, 3.24% and 4.86% of root chord from the leading edge to the centre of the blowing holes. The computation is performed using the commercial software ANSYS Fluent. Unsteady, incompressible Reynolds-averaged Navier-Stokes equation and the shear-stress transport k-ω turbulence model are employed. The angles of attack varied in the range of 0o < α < 35o and Reynolds number is 2.64 x106 and the jet momentum coefficient is fixed at 0.05. The blowing of air from the injection region enhances the strength of the leading-edge vortices resulting in the delay of the vortex breakdown. The performance of the delta wing is greatly improved while using the blowing method specifically for the blowing holes located at 3.24% of root chord from the leading edge as compared to without the blowing method.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

Introduction

Delta wings have been widely deployed on unmanned aerial vehicles and combat aircraft. The Aerodynamics of delta wings primarily deals with lift, which is made up of potential lift and vortex lift. The vortex lift has a very nonlinear structure and is heavily influenced by the angle of attack. With an increase in the angle of attack, the vortex lift above the delta wing grows until the wing stalls. Leading-edge vortex breakdown occurs over the delta wing at crucial angles of attack. The vortex collapse has a negative impact on the delta wing aerodynamics, causing the wing and fin to buffet and the lifting force to degrade. Because vortex disintegration is a severe issue, both active and passive flow control techniques can help.
A leading-edge sweep angle of less than 60 deg can be termed as a non-slender delta wing whereas, a delta wing with an above 65 deg leading-edge sweep angle can be termed a slender delta wing or highly swept delta wing. The analogy of the leading-edge suction was created by Polhamus et al. [1,2] The relation holds true for thin wings with no camber or twist. Furthermore, the strategy is applicable to wings with leading edges that are sharp enough that separation is fixed at the leading edge. Controlling vortex breakdown in the case of slender delta wings is a crucial problem, whereas, for non-slender delta wings, leading-edge vortex breakdown is noticed to be gradual [13]. Slender delta wings are suitable for high-speed fighter planes. Conversely, this wing at subsonic flight regime shows typically low aerodynamic performance. To augment the aerodynamic characteristics, especially at high angles of attack, a lot of research has been performed employing many devices which include active and passive flow control techniques. Mitchell et al. [3] used periodic tangential blowing at the leading edge to control the flow over a slender delta wing, finding that the aerodynamic performance was noticeably improved. In their investigation, Greenblatt et al. [4] performed an experimental study on a delta wing sweep angle of 60 deg with DBD plasma actuators with a direction perpendicular to the leading edge and reported a gradual increase in the normal force coefficient at post-stall angles. Numerous kinds of research have been conducted employing the DBD plasma actuator in controlling the flow. [5,6,7,8,9]
Yavuz et. al. [10] conducted an experimental study on a delta wing with a sweep angle of 38.7 deg to examine the flow characteristics of streamlines, velocity pattern and vorticity in the close vicinity of the delta wing surface using the particle image velocimetry based on laser technique. Yaniktepe and Rockwell [11] experimentally investigated the flow field pattern behaviour over the delta wings with varying leading-edge sweep angles in the close vicinity of the trailing edge on the lambda and diamond planforms. Ol and Gharib [12] experimentally studied the nature and intensity of the leading-edge shear layer and pair of vortical flow structures inside the shear layer in the crossflow plane over delta wings with a sweep angle of 50 deg and 65 deg.
Taylor and Gursul [13] performed a wind tunnel test to investigate the effect of the unstable vortex structures and reaction of buffeting phenomenon for a delta wing with a sweep angle of 50 deg. It was reported that at a small angle of attack, a dual vortex structures system was observed. Also, velocity fluctuations were abrupt near the line of reattachment. For a delta wing with a sweep angle of 50 deg, Chen et al. [14] numerically investigated the impact of the Reynolds number on the vortex flow. Sahin et. al. [15] performed the dye visualization and stereoscopic PIV method to investigate the flow behaviour on the delta wing with a wing sweep angle of 40 deg and concluded that the location of vortex breakdown mainly depends on the yaw angle. Gursul et. al., 2007 [16] reviewed many types of flow control devices to regulate the flow control parameters such as leading-edge vortex breakdown or formation, flow separation and attachment etc. Mitchell et al. [3] investigated at how core blowing affected the collapse of the vortex over a slender delta wing. By shifting the vortex collapse site downstream of the root chord by 20%, they were able to delay the vortex breakdown using this arrangement. Renac et al. [17] used fluidic blowing to try to regulate the vortical flow over a delta wing with a sweep angle of 60 degrees and rounded leading edges. The effect of lateral blowing on the delta wing to regulate vortex breakdown from extremely low to medium range of angle of attack was investigated by Hong et al. [18] They came to the conclusion that the jet momentum coefficient and angle of attack had a notable impact on the strength and location of vortex collapse. From a small to a large angle of attack, Wood and Roberts [19] examined the impact of tangential blowing at the leading edge on a delta wing with a sweep angle of 60 degrees. They demonstrated how managing the main separation allows one to regulate the vortex breakup. Experimentally, Greenwell and Wood [20] modified the flow by utilising the Coanda effect on the leading-edge blowing. It was noticed that the flow is attached at low angles of attack and the phenomenon of vortex formation was absent. Gu et al. [21] conducted research to investigate the influence of the blowing, suction and their combined effect on the rounded leading-edge delta wing.
Williams et al. [22] examined how flow structures behaved on a delta wing with a 50-degree sweep angle. They observed an appreciable lift force increase and stall delay. Cui et al. [23] executed the forebody slot blowing over a delta wing with a 60-degree sweep angle. Jiang et al. [24] carried out an experimental investigation on the effects of irregular blowing towards the trailing edge. over a delta wing with a sweep angle of 60o. Johari et al. [25] applied the blowing technique at various blowing angles with a spanwise direction. Lamar [26] performed an experiment using an aileron positioned near the trailing edge of a cropped delta wing. This arrangement induced a constant rolling moment. Rao and Campbell [27] investigated the effect of passive flow control techniques such as vortex generators, and leading-edge vortex flaps which can be mounted either on lower or upper surfaces.
Smith et al. [28] investigated the flow over slender and non-slender delta wings experimentally and compared the strength of the leading-edge vortices and identified the vortex using the Q, λ2 and λci criterion. Sedlacek et al. [29] performed an experimental study on a triple and a double delta wing design at high angles of attack and angles of sideslip. It was reported that for high angles of attack, lateral disturbances will be higher. Balogun et al. [30] experimentally studied the flow characteristics on slender delta wings using trailing edge jets mechanism and studied the effect of jet angle, Reynolds number and angle of attack on the flow behaviour.
The primary objective of the present study is mainly concerned with the formation and breakdown of the vortex over the delta wing adopting the active flow control technique to delay the vortex breakdown by shifting the location of vortex breakdown in downstream towards the trailing edge. The study is conducted using unsteady, incompressible, RANS simulations with the commercial flow solver ANSYS Fluent. In this paper, the aerodynamic characteristics of the delta wing with sweep angle, Λ = 65 deg using three different leading-edge blowing configurations for various angles of attack varying from 0o to 35o are estimated and compared.
Consequently, the study's initial goal was to successfully and consistently collect numerical data on the 65-degree delta's aerodynamic performance. These outcomes were then compared with previous numerical and experimental results that have been identified in the literature. After validating the results, the study can be extended to meet the present objectives of the study. In order to investigate how blowing affects the vortex breakdown process and greatly improves the vortex lift envelope, it will be useful to know where the best location for spanwise suction is for a given delta wing for various blowing configurations.

Numerical Methodology

Description of a Validation Model

The model was designed for validation purposes with the following specifications as shown in Table 1 [31].
Once the validation part was over, much attention was required to simulate the model with the key geometrical features as shown in Table 3. The flow conditions for the present study are shown in Table 4.
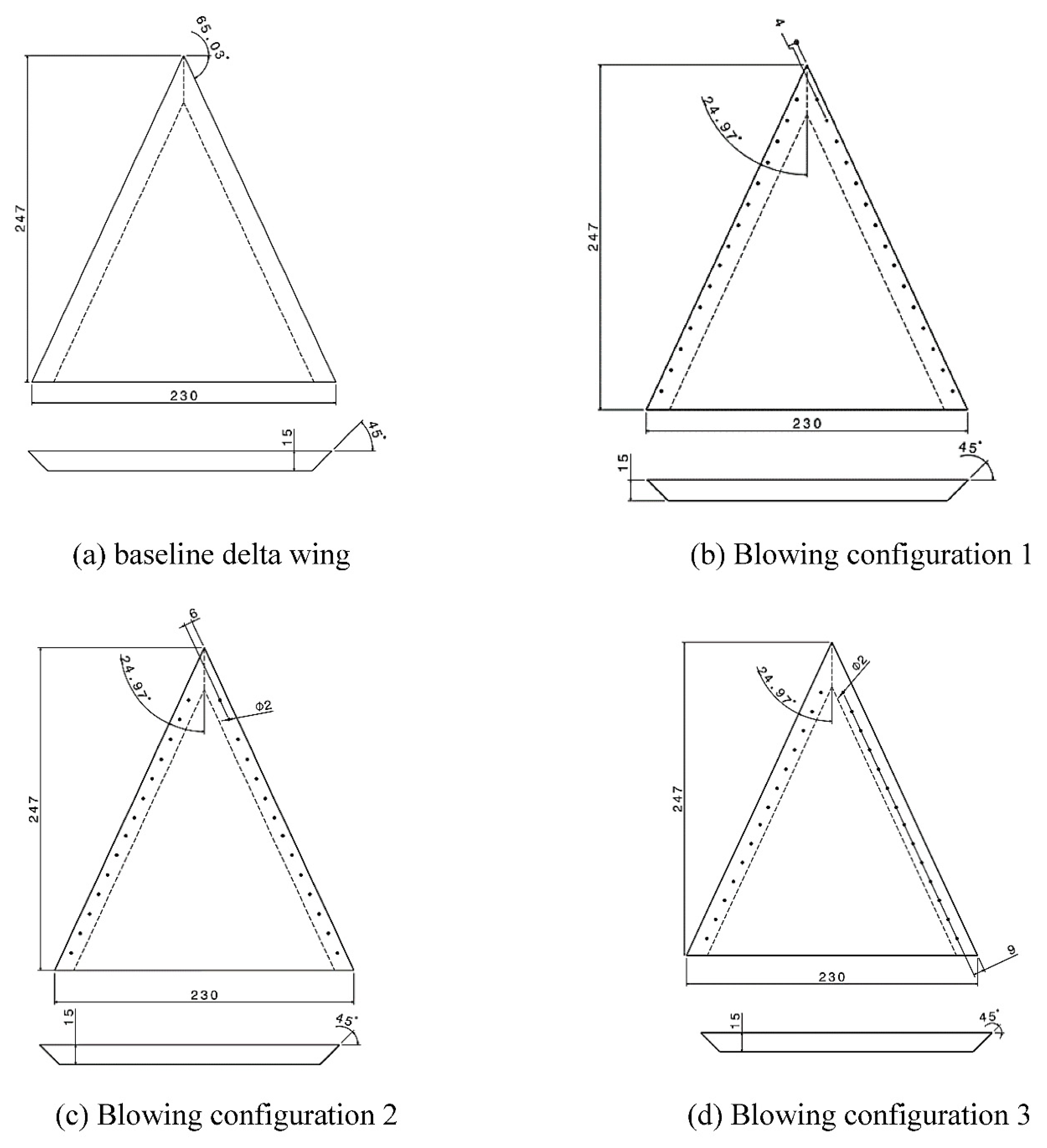
The delta wing without adopting the flow control technique was selected as a baseline delta wing with a root chord (Cr) of 0.247m and a sweep angle of 65o as shown in Figure 1 (a). The other three delta wing configurations utilized the blowing technique with different blowing locations over the suction surface of the delta wing. The different locations of blowing ports are made on the suction surface of the delta wing located at 1.62% (blowing configuration 1), 3.24% (blowing configuration 2) and 4.86% (blowing configuration 3) of the root chord from the centre of the blowing port to the leading edge as shown in Figure 1 (b), 1 (c) and 1 (d) respectively. The diameter of each of the blowing holes was 2 mm and a total of 14 blowing holes are located on the suction surface. The distance between the holes from centre to centre was 15 mm. The first blowing hole was located at a distance of 40 mm from the apex of the delta wing. The flow conditions for the present study are shown in Table 4. The Reynolds Number (Re) based on the mean aerodynamics chord (mac) was 2.64 x 105. The angle of attack (AoA) varied from 0o to 35o. For the non-dimensional jet momentum coefficient Cµ = 0.05, the ratio of the jet velocity to the freestream velocity value is 2.3. The jet momentum coefficient was calculated as
C μ = Q j V j U ∞ 2 S
where
Q j = volumetric flow rate of the jet; V j = mean velocity of the blowing at leading edge
U ∞ = freestream velocity; S= planform area
The port side of the delta wing is selected for the present investigation. This is because, the flow structure on the port side and starboard side of the delta wing has very little difference in their vortex strength. For 0o angle of attack, the upstream boundary was selected as the velocity inlet and the downstream wall as the pressure outlet. The Top and bottom wall was selected as a wall. The left boundary was selected as symmetry and the right boundary as the wall boundary. For the angles of attack other than 0o, velocity inlet boundary conditions were applied for the upstream as well as bottom boundary of the computational domain of the delta wing [35]. Downstream of the delta wing as well as the top boundary of the computational domain was selected as the pressure outlet boundary condition. The upstream boundary was placed at 10 Cr from the apex of the delta wing. The downstream location, top boundary, bottom boundary and left boundary were placed at 20 Cr.
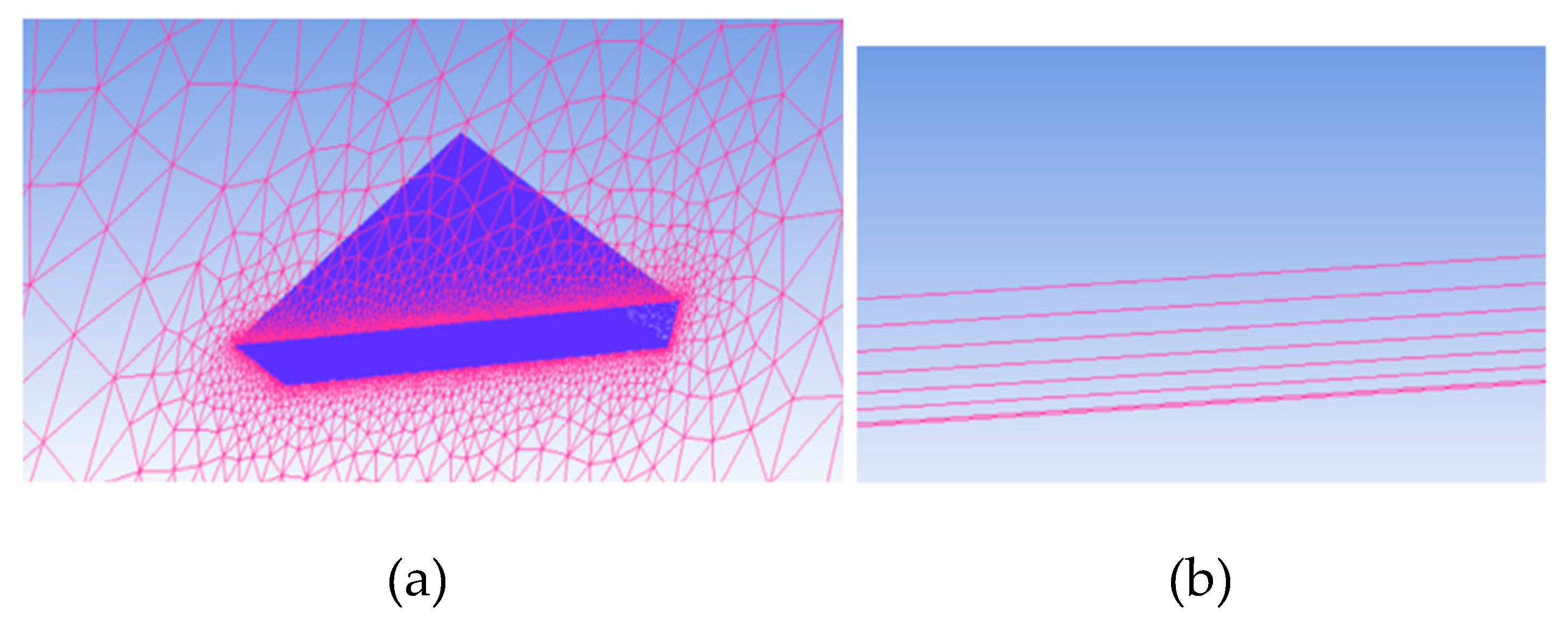
Mass flow inlet boundary conditions were applied at the blowing holes. The grid was generated for the half delta wing along with its domain using the commercial software ANSYS® ICEM CFD 19.1. The mesh was more refined close to the leading edge, trailing edge, the region near the leading-edge vortices and the blowing holes. The grid generated based on maximum y+ = 1 has 35 million cells. The grid generated inside the domain is shown in Figure 3.
Preprints 86170 g001
Figure 1. Geometry of the baseline delta wing and with different blowing configurations (units in mm).
Figure 1. Geometry of the baseline delta wing and with different blowing configurations (units in mm).
Preprints 86170 g001
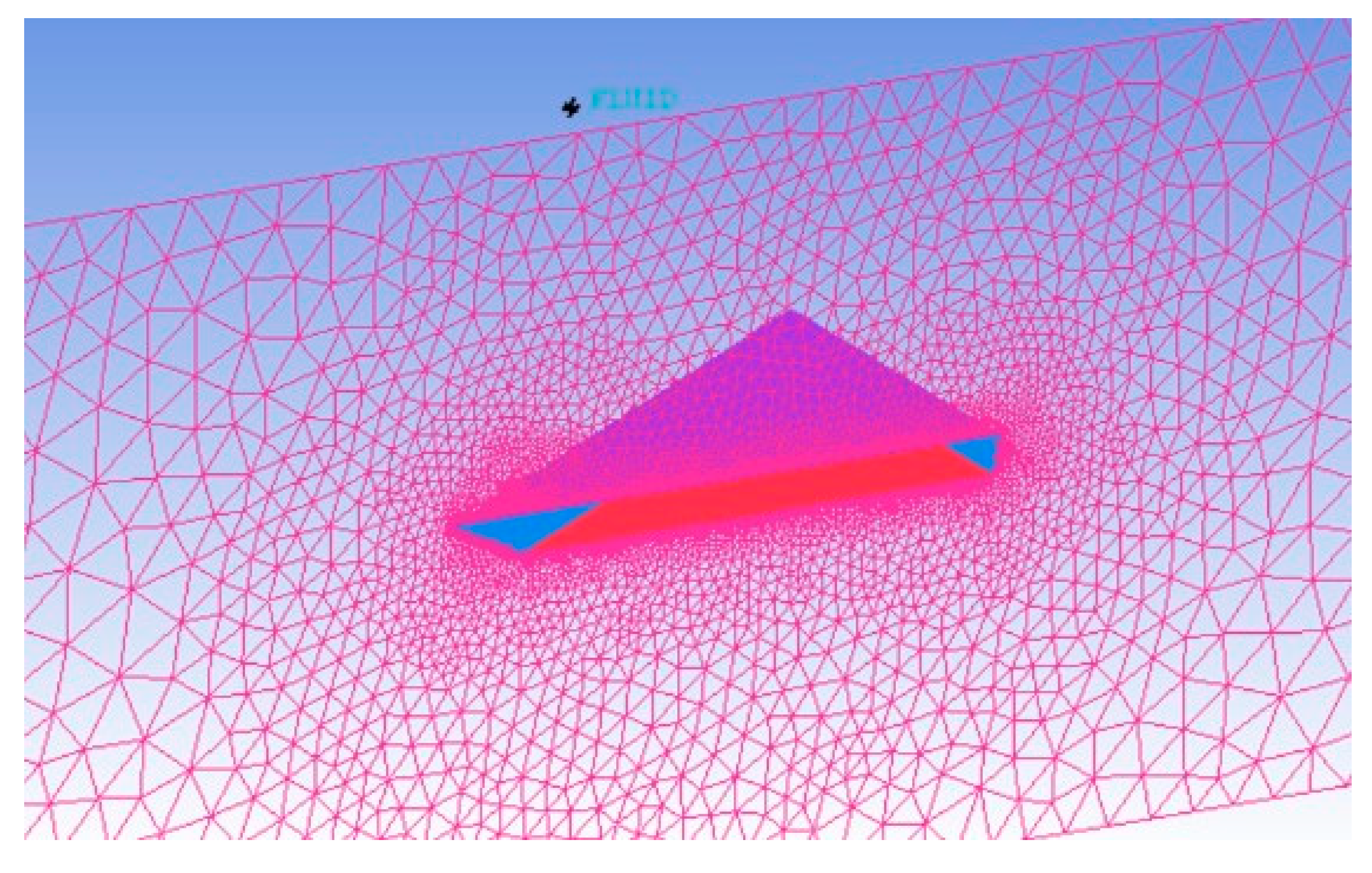
To capture the viscous effects inside the boundary layer, twenty prism layers are included inside the boundary layer. The details of the grid are shown in Table 5. The zoomed view of the grid around the delta wing with the prism layers is shown in Figure 4 a and b. Figure 5 shows the grid on the symmetry plane of the delta wing with configuration 1 and Figure 6 represents the zoomed view of the surface grid on the suction surface of the delta wing with configuration 1.
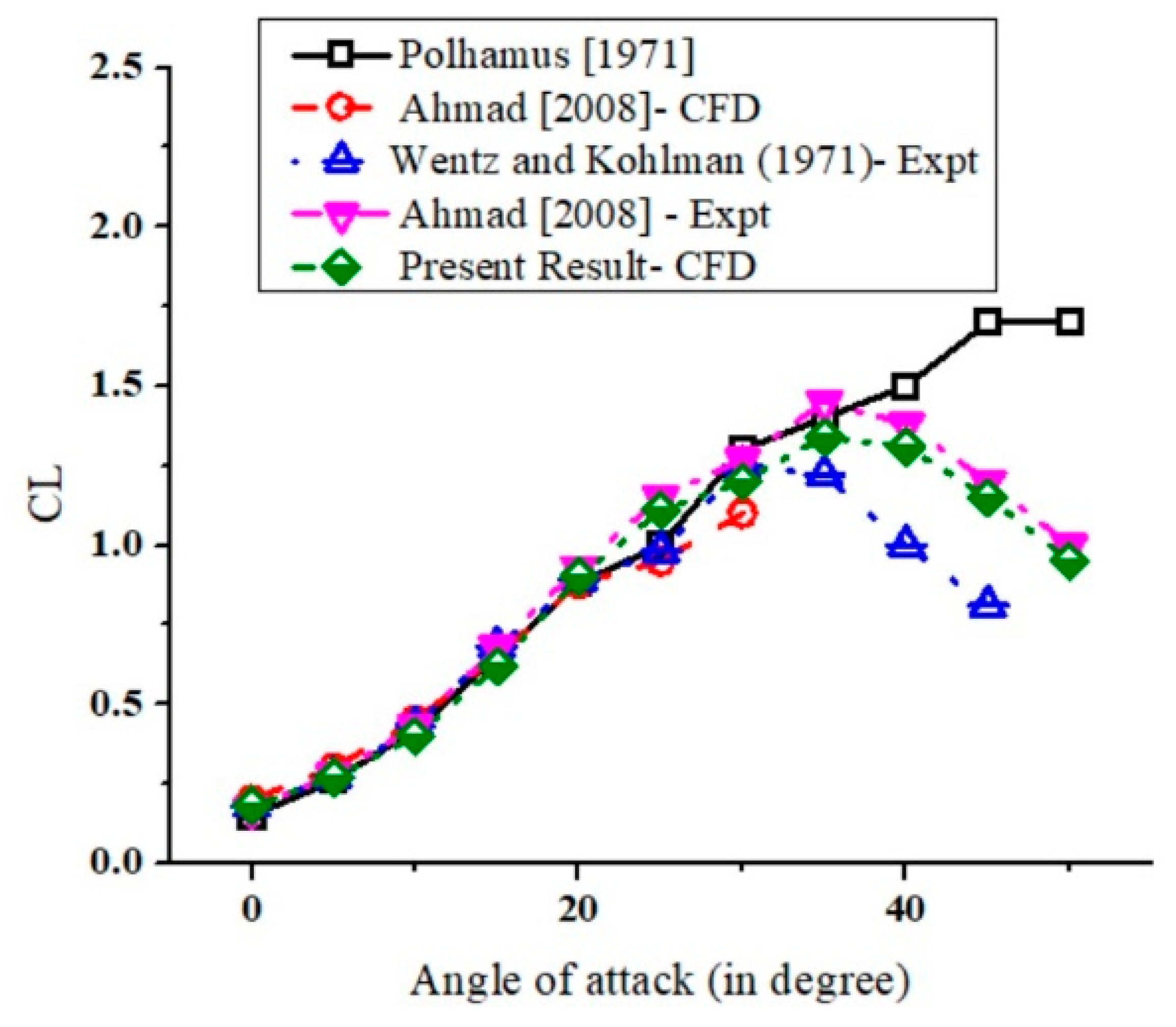
ANSYS® FLUENT® 19.1 software was employed as a solver to numerically simulate the prescribed problem. In the initial phase, the numerical model was validated using the results available in the literature for the baseline delta wing with the present numerical result as shown in Figure 2. The similar boundary conditions and solver set-up were adopted for the present study based on delta wings using an active flow control technique.
The Three-dimensional unsteady, pressure-based RANS equation and turbulence model adopted as SST-K-omega with both low Reynold’s number corrections and curvature corrections was selected for the numerical simulation. The SST-K-omega better predicts the leading-edge vortex breakdown location and its strength [31,33]. The Pressure-based solver along with the SIMPLEC (Semi-Implicit Method for Pressure-Linked Equations Consistent) scheme is used for the pressure-velocity coupling. For spatial discretization of the computational domain, the least square cell-based was chosen with second-order accuracy. The fixed time-stepping of 0.002s was chosen to capture the flow physics of leading-edge vortex breakdown. [34] The residual convergence criterion for all the variables was 1 x 10-5.
Preprints 86170 g002
Figure 2. Validation of the Lift Coefficient (CL) vs. angle of attack (α) [2,31,32].
Figure 2. Validation of the Lift Coefficient (CL) vs. angle of attack (α) [2,31,32].
Preprints 86170 g002
Preprints 86170 g003
Figure 3. Grid generated inside the computational domain.
Figure 3. Grid generated inside the computational domain.
Preprints 86170 g003
Preprints 86170 g004
Figure 4. Zoomed view of the grid around the baseline delta wing. a) Grid around the baseline delta wing with prism layers on the symmetry plane; b) close-up view of the grid representing the prism layers above the surface of the baseline delta wing.
Figure 4. Zoomed view of the grid around the baseline delta wing. a) Grid around the baseline delta wing with prism layers on the symmetry plane; b) close-up view of the grid representing the prism layers above the surface of the baseline delta wing.
Preprints 86170 g004
Preprints 86170 g005
Figure 5. Grid on the symmetry plane of the delta wing with blowing configuration 1.
Figure 5. Grid on the symmetry plane of the delta wing with blowing configuration 1.
Preprints 86170 g005
Preprints 86170 g006
Figure 6. Zoomed view of the surface grid on the suction surface of the delta wing with blowing configuration 1.
Figure 6. Zoomed view of the surface grid on the suction surface of the delta wing with blowing configuration 1.
Preprints 86170 g006

Results and Discussion

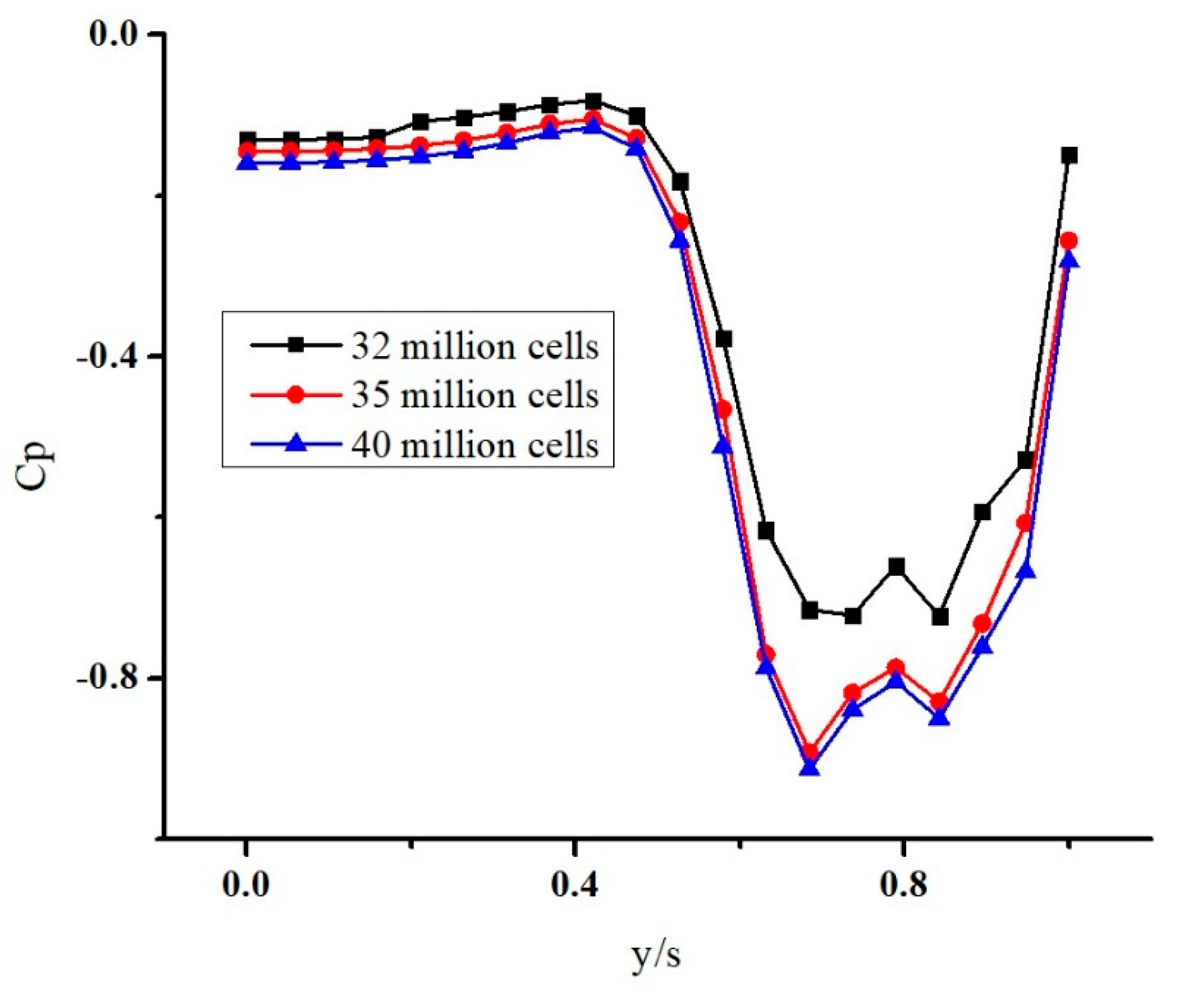
Grid Independent Test

A grid-independent test was performed to ensure that the computational results do not depend on the sensitivity of the grid size, indicating that the simulation has reached a level of mesh refinement where further grid refinement will not substantially alter the results. Three different grids of size 32 million cells, 35 million cells and 40 million cells were generated around the baseline delta wing to estimate the pressure distribution (Cp) with respect to the non-dimensional distance along the span (y/s) at a chord-wise distance of 25% of root chord as shown in Figure 7. Less difference in the results was obtained when compared to the simulation from the grid size of 35 million cells and 40 million cells. Therefore, a grid of 35 million cells was selected for the present case comprising the baseline and blowing configurations of the delta wing.
The different configurations of the delta wings are numerically simulated. The different cases considered are case 1: baseline delta wing without any flow control technique, case 2: delta wing with injection ports located at 1.62% of cr from its centre to the leading edge, case 3: delta wing with injection ports located at 3.24% of cr from its centre to the leading edge and case 4: delta wing with injection ports located at 4.86% of cr from its centre to the leading-edge. 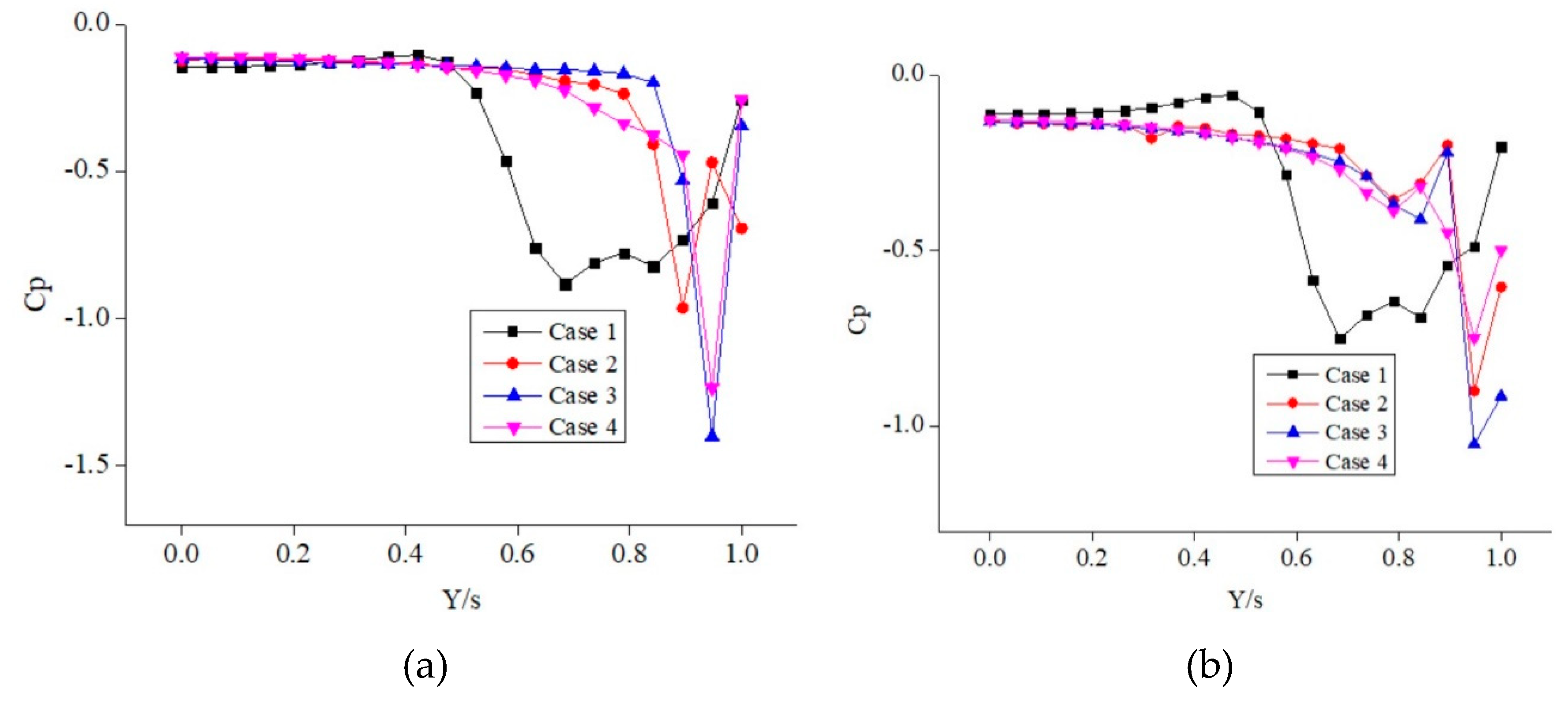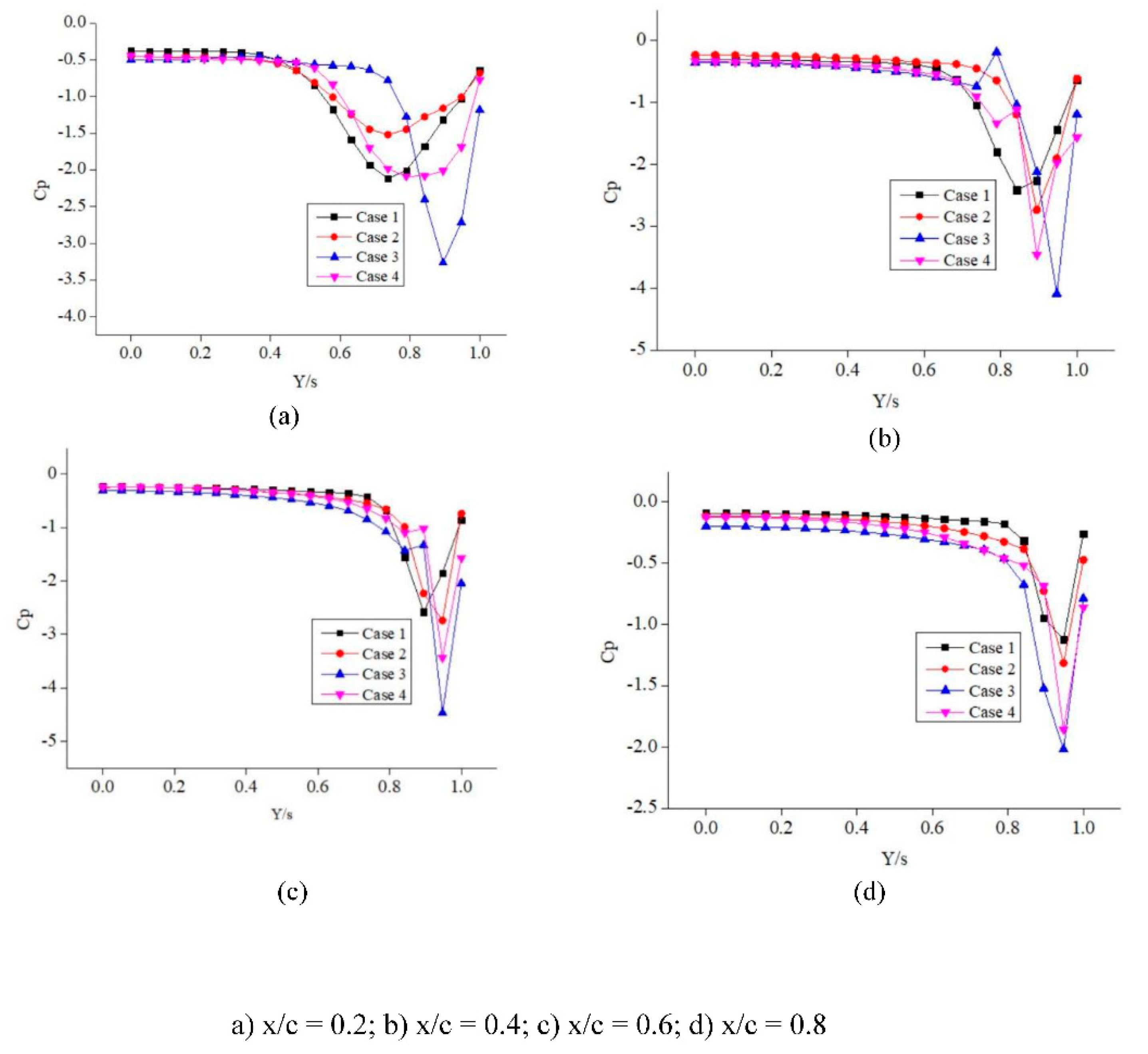In all the cases, the wing sweep angle of the delta wing is fixed at 65o. The Pressure coefficient plot versus the local Y/s location at the fixed chord station of x/c ranging from 0.2 to 0.8 with an interval of 0.2 is chosen. 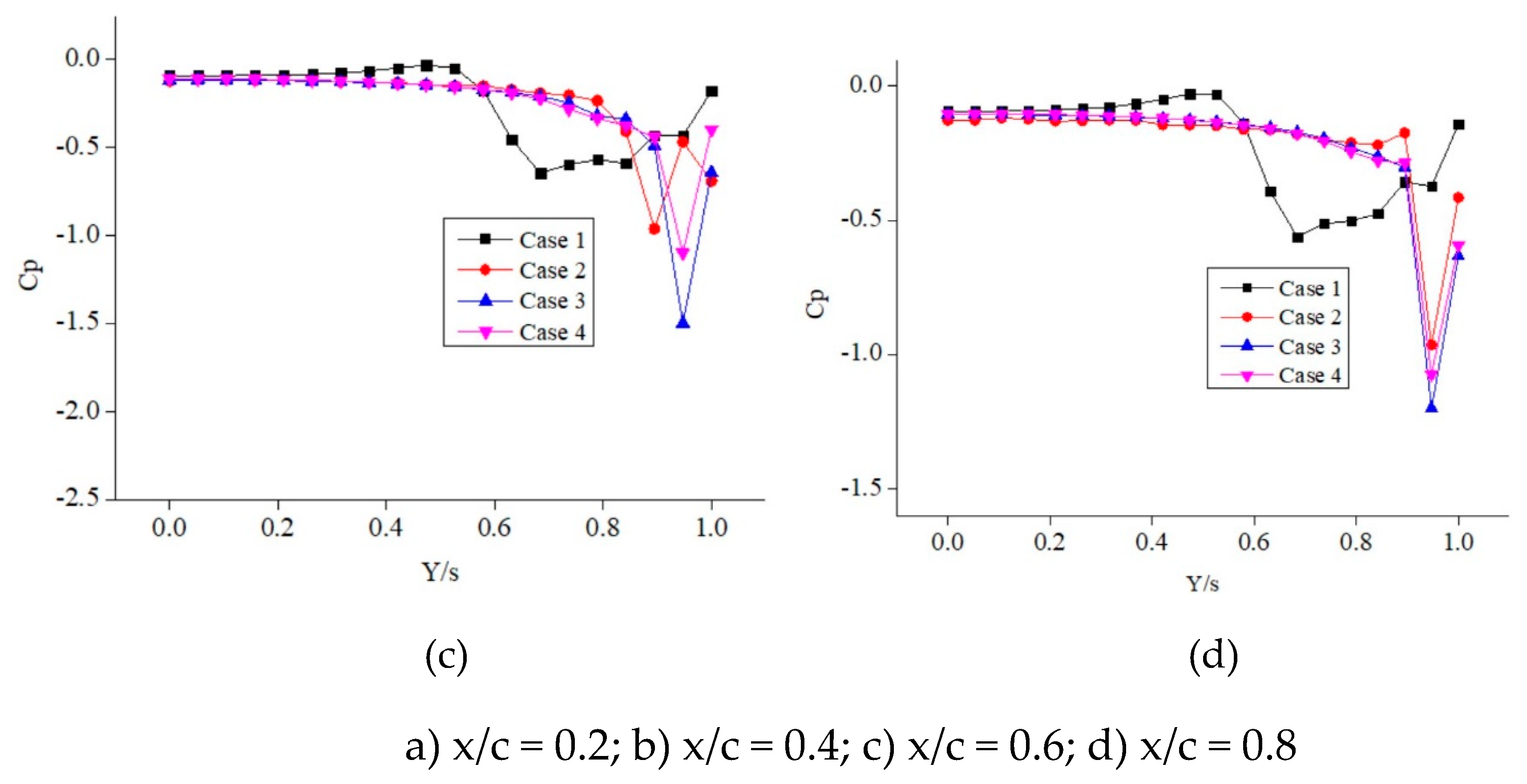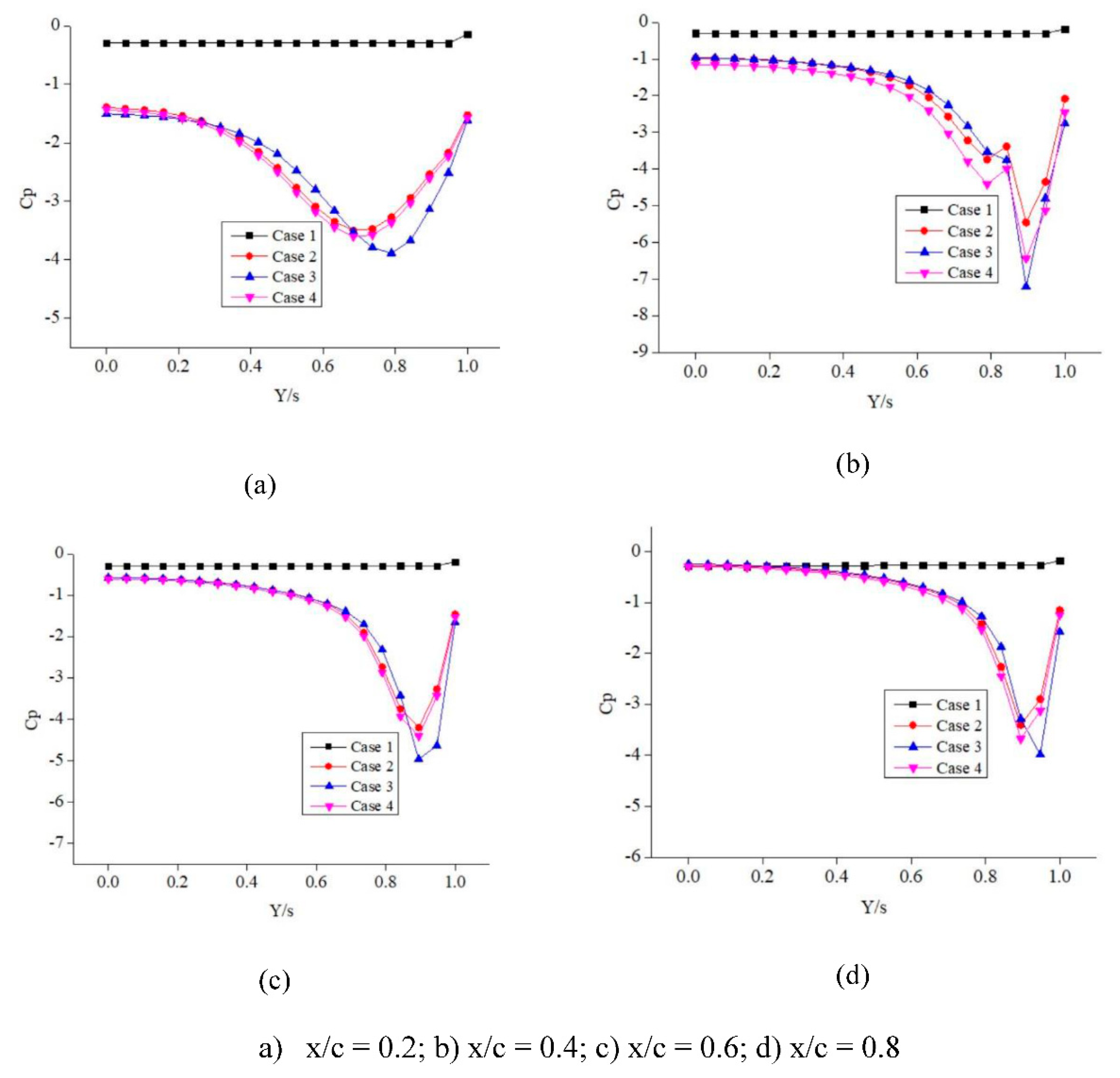The Cp distribution graph for the 5o angle of attack is shown in Figure 8. From these results, it can be clearly observed that the suction peak for case 3 is relatively higher than the other cases considered. This may be probably because the stagnant fluid flow at the separation zone interacts with the fluid flow blown on the upper surface effectively resulting in the momentum transfer and this mixing phenomenon increases the overall suction, the lift generated for case 3 will be higher due to the presence of the higher suction zone. The maximum suction peak is observed for case 3 at x/c = 0.6. As can be analysed clearly from Figure 9. Cp for case 3 attains the maximum value at x/c = 0.4 at 10o angle of attack. 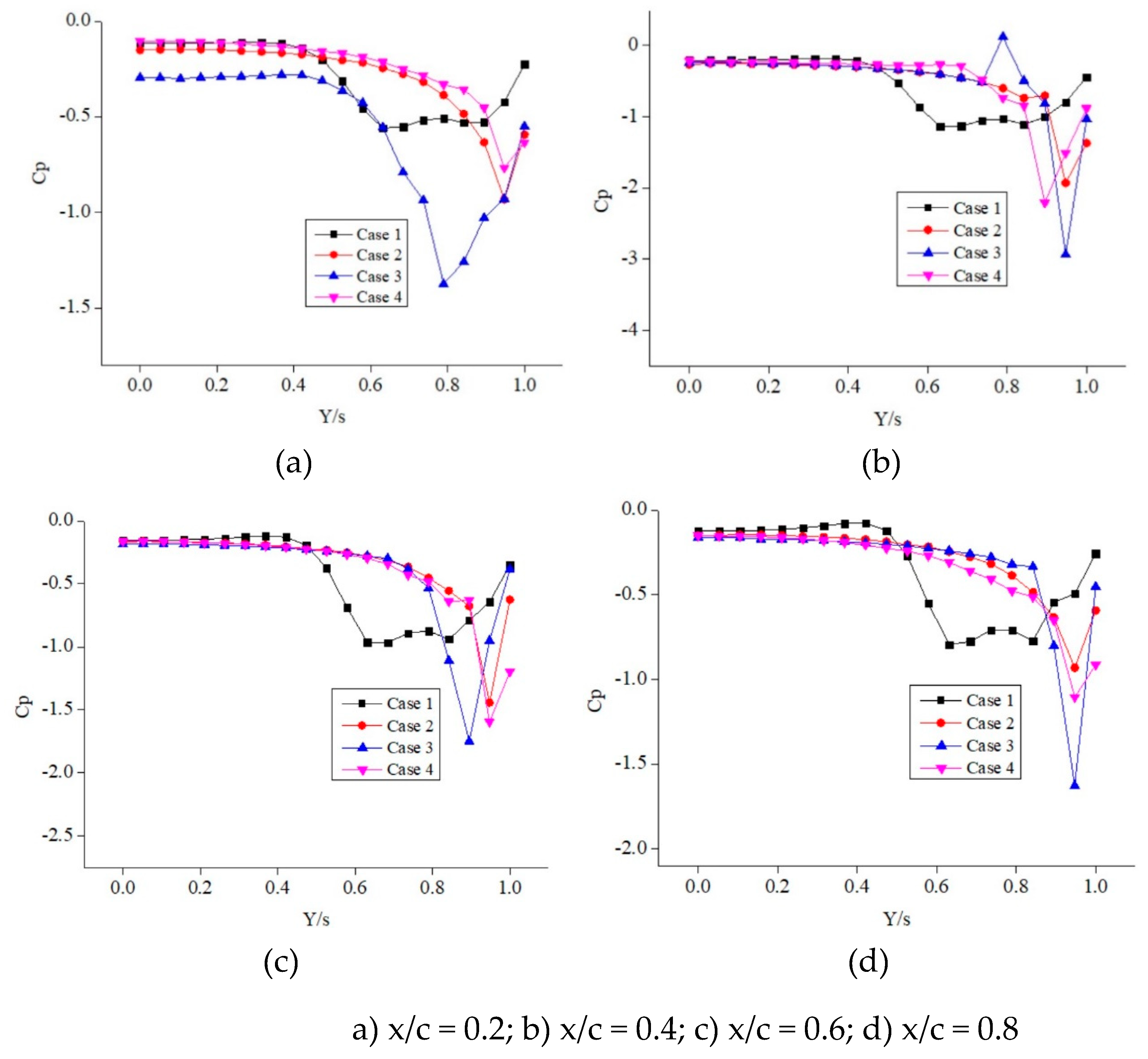For x/c = 0.8, the Cp for case 3 is considerably higher than the other cases. This shows that the phenomenon of flow separation is largely restricted and delayed. For a 15o angle of attack as shown in Figure 10, the Cp value has a maximum suction at x/c = 0.6. 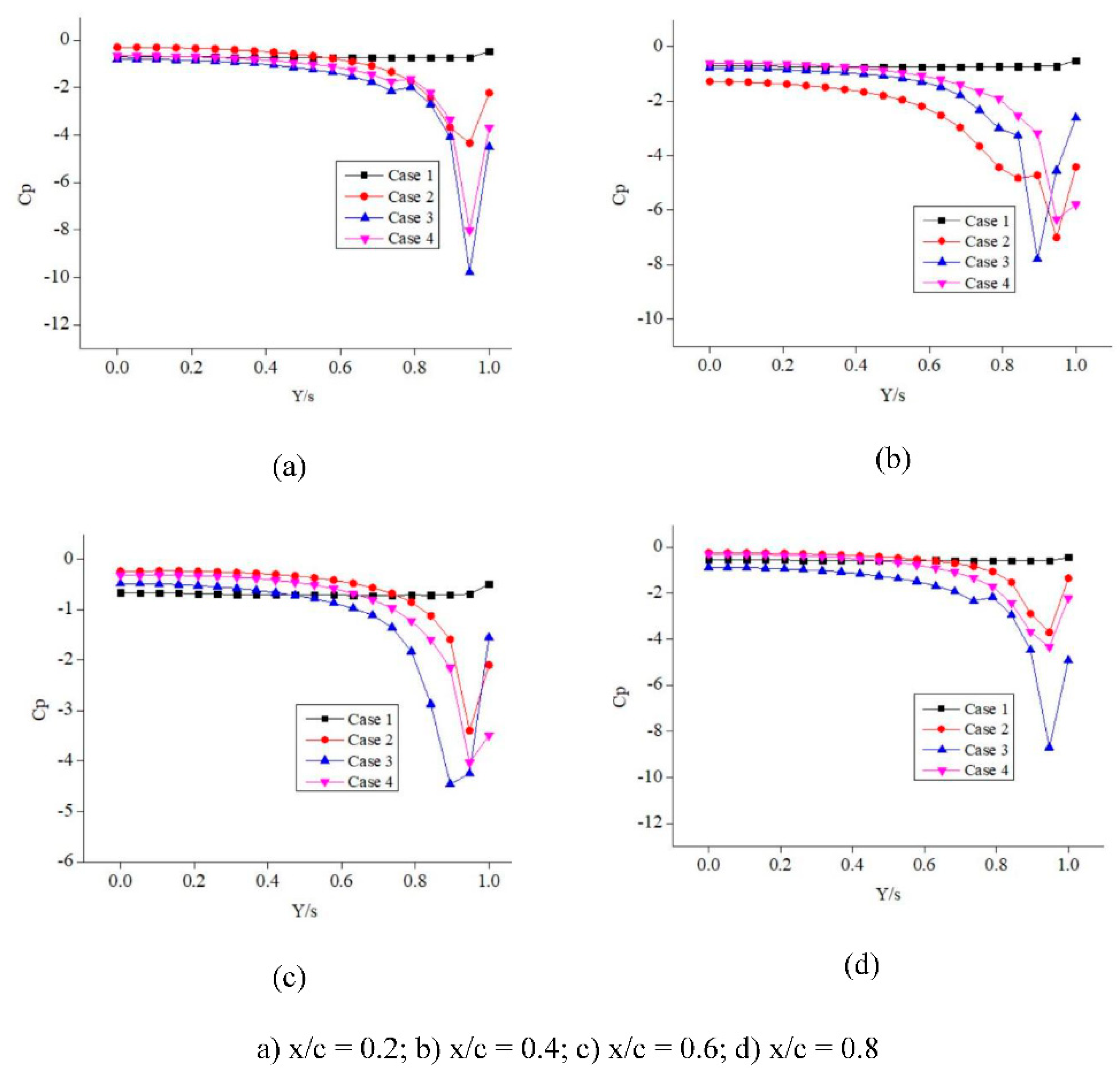The Cp difference between case 1 and case 2 is marginal and does not seem to have much impact on the delta wing aerodynamics. For 30o and 35o angles of attack as shown in Figure 11 and Figure 12 respectively, the Cp curve for case 1 becomes flattened and shows highly reduced suction and therefore the baseline delta wings tend to show stall behaviour. Case 3 proved to be more effective in delaying the flow separation. Therefore, the operating range of the angle of attack is increased. The blowing phenomenon of controlling the flow seems to be effective. The blowing near the flow separation zone effectively increases the aerodynamic efficiency.
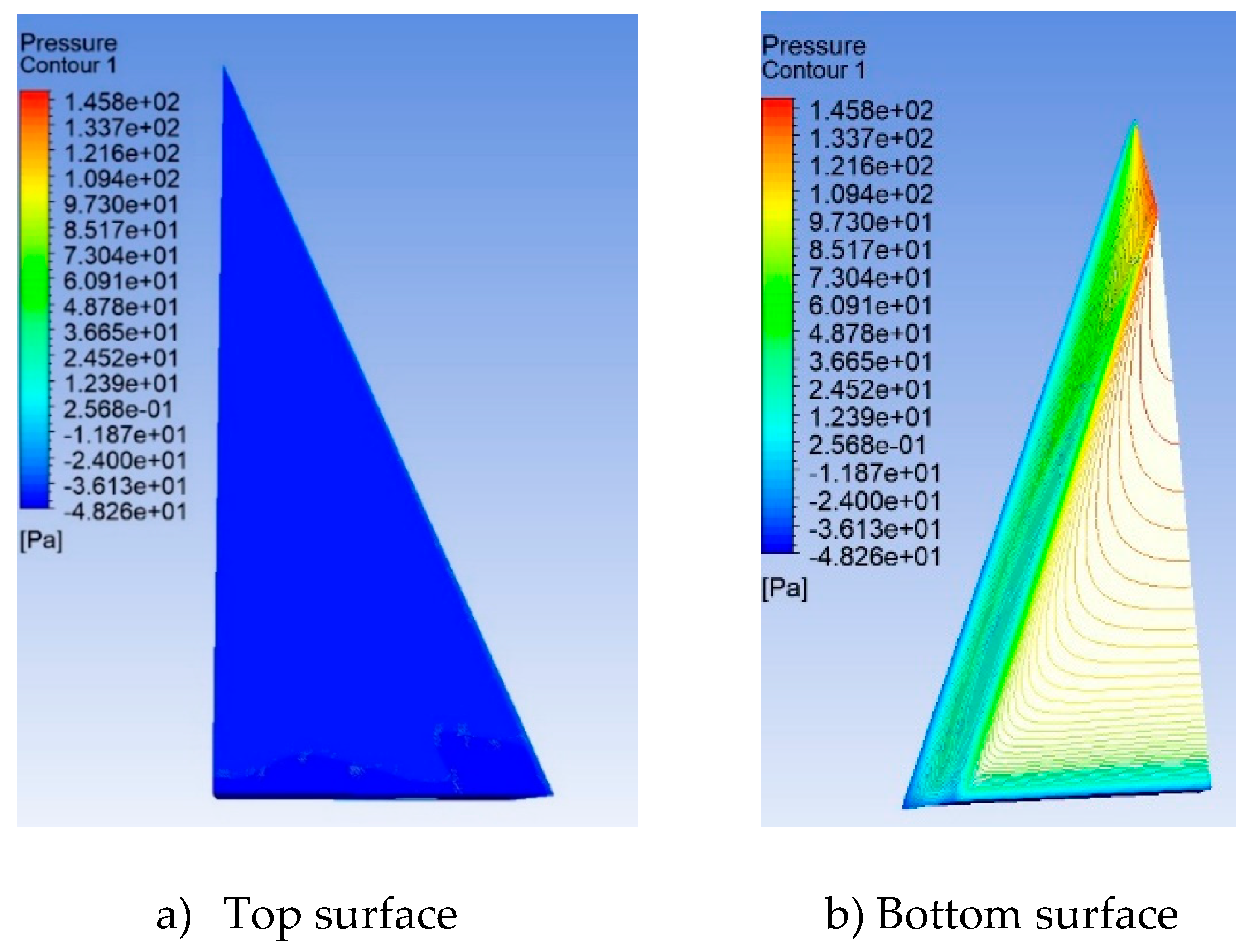
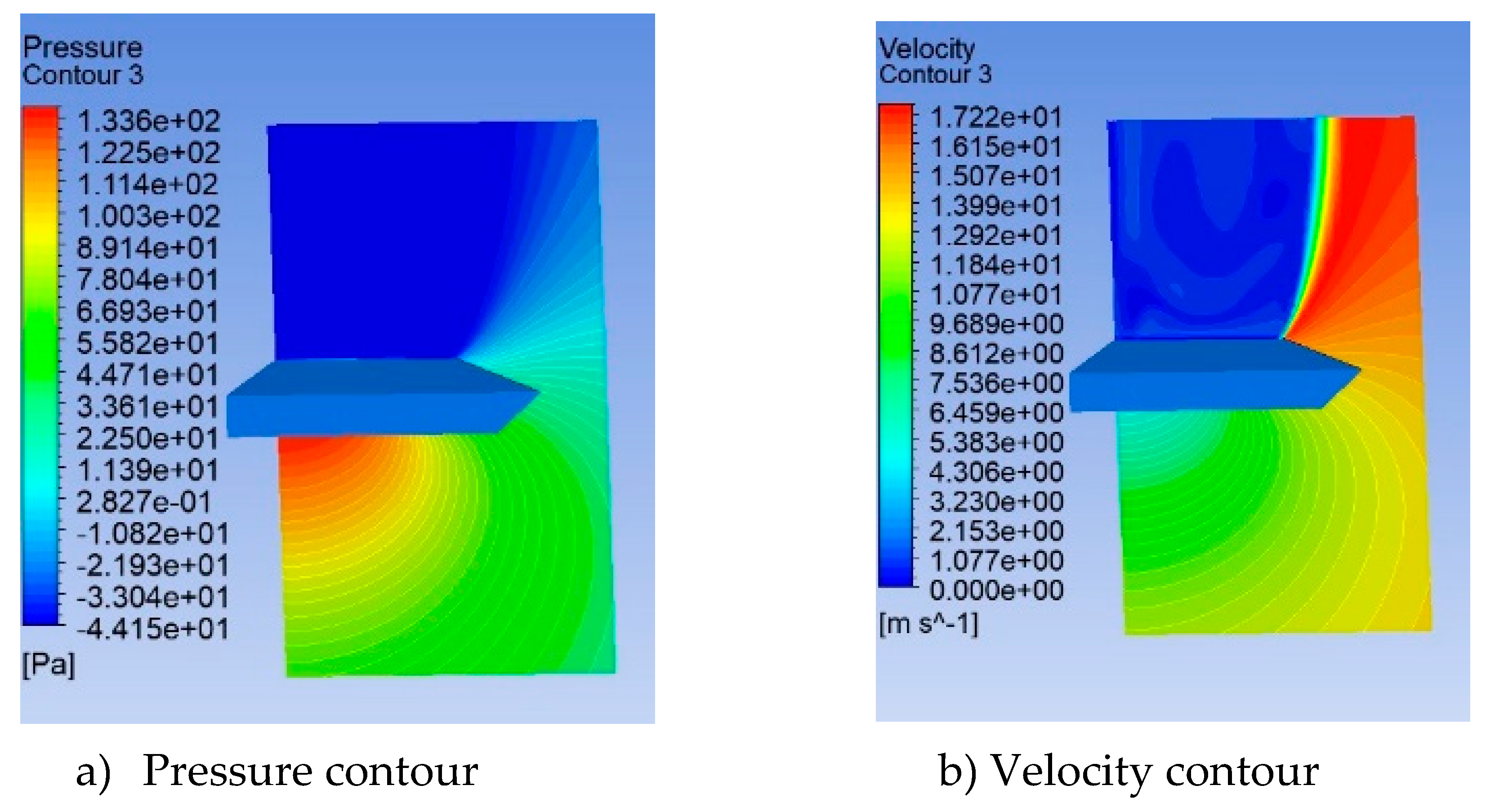
The Pressure contour for the baseline delta wing on the top and bottom surface at α = 35o is shown in Figure 13 a and b respectively. The peak pressure on the delta wing is located near the apex region and the bottom surface. The pressure contour plot and velocity plot for the baseline delta wing at α = 35o and x/c =0.6 are shown in Figure 14 a and b respectively. 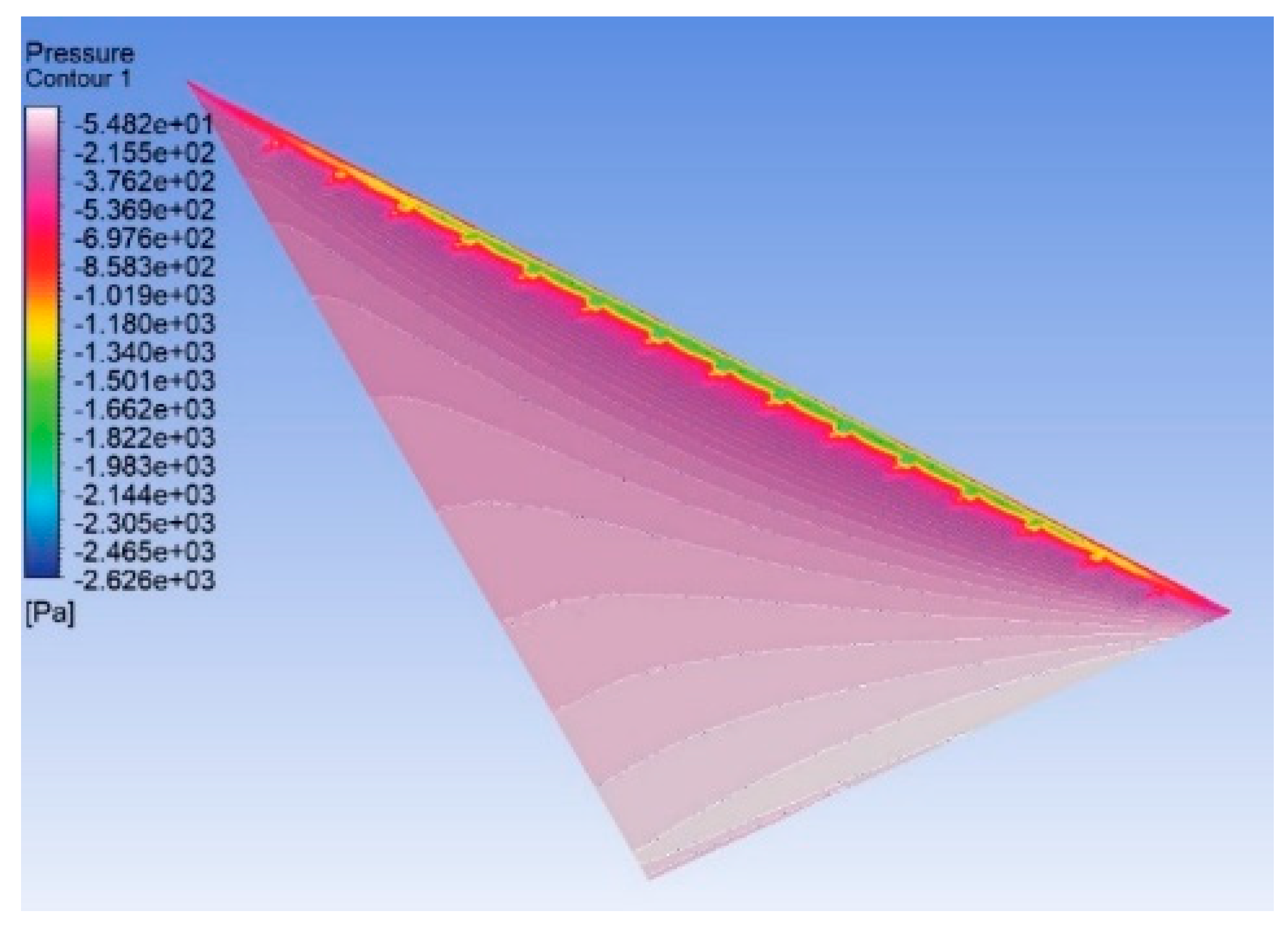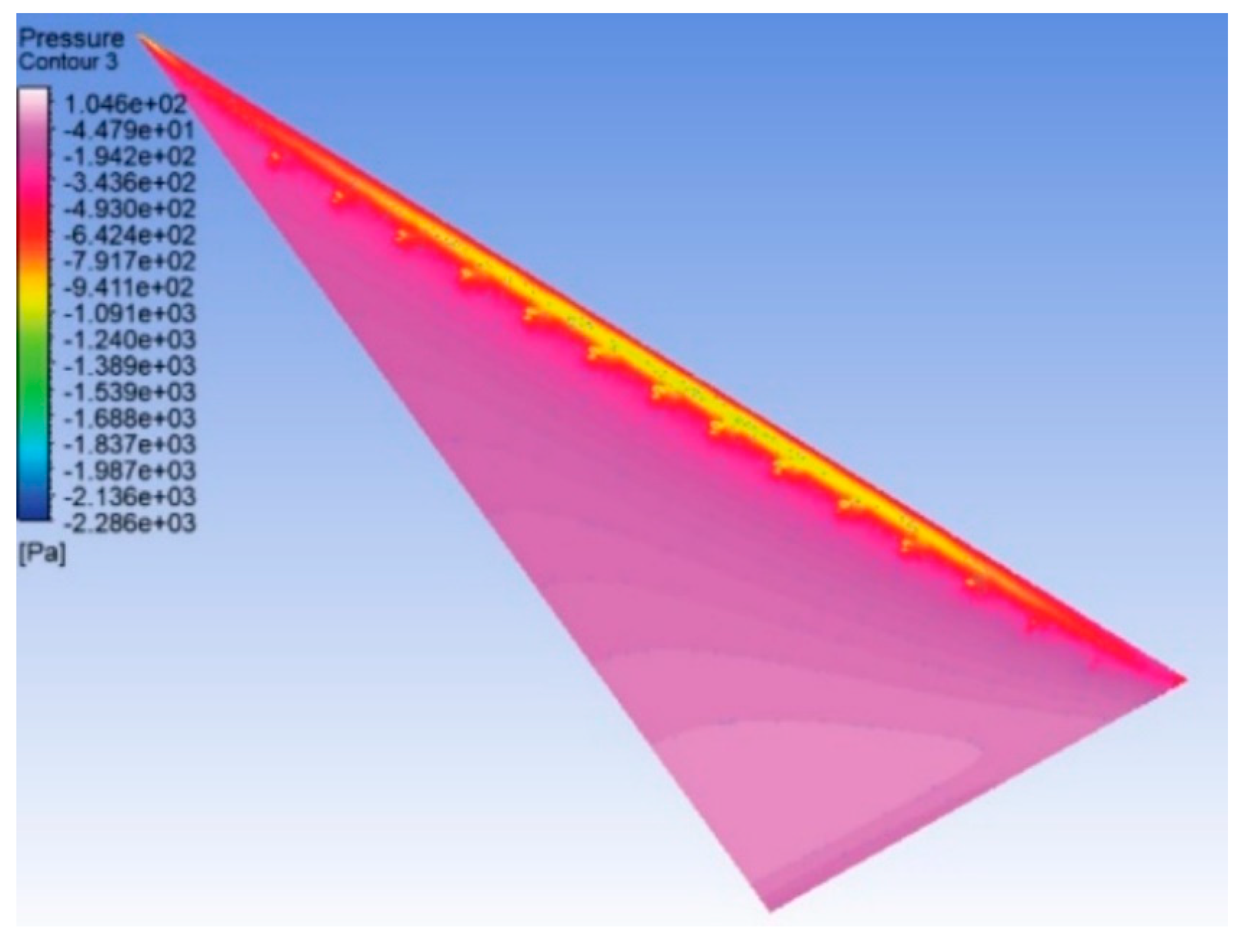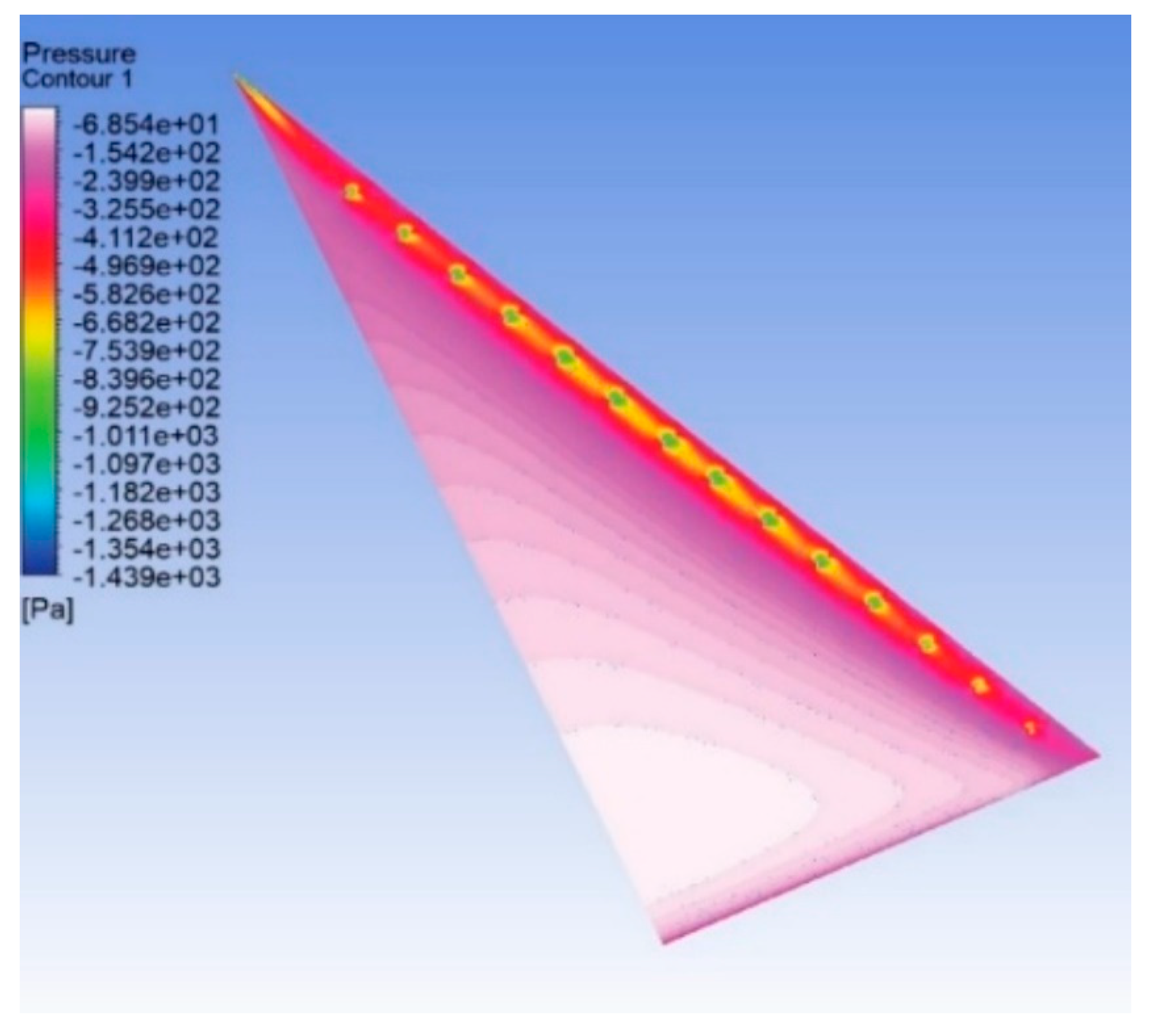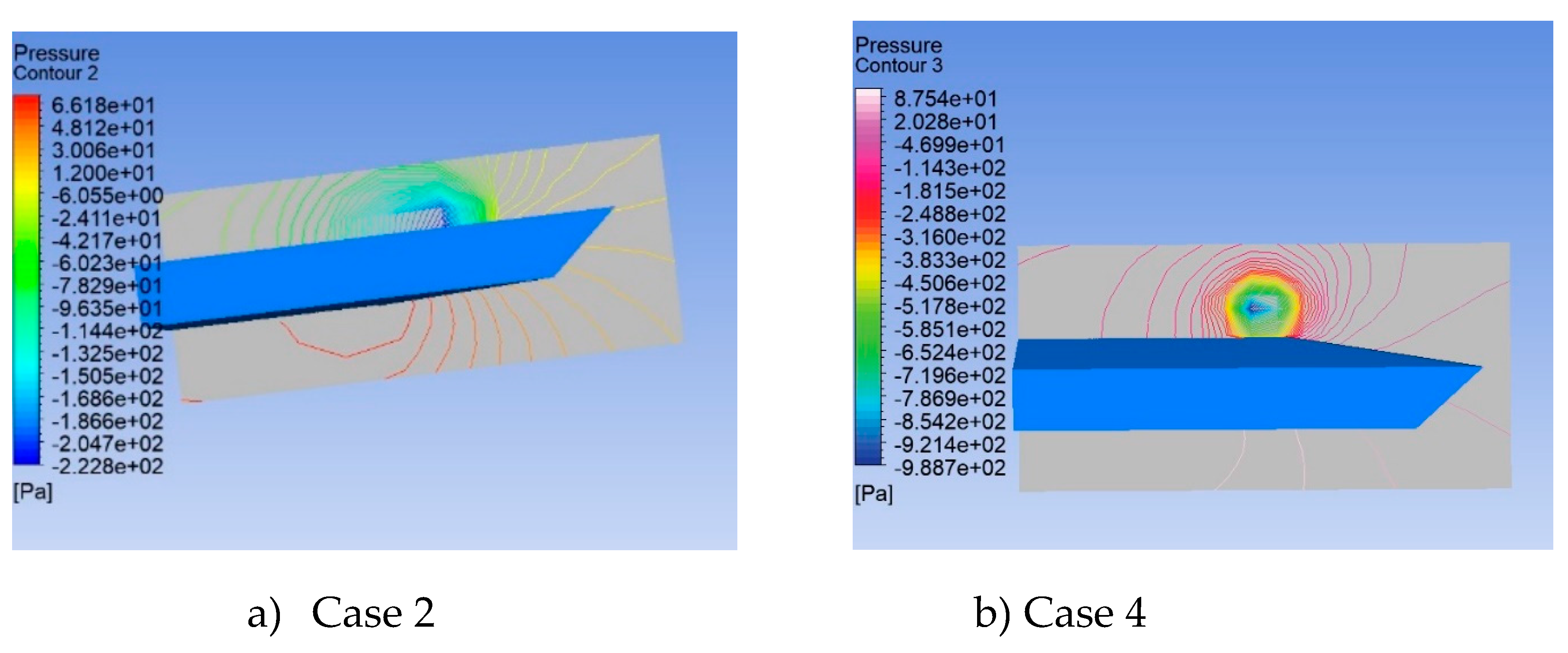The pressure contour on the top surface at α = 30o for case 2, case 3 and case 4 are shown in Figure 15, Figure 16 and Figure 17 respectively. The maximum peak suction pressure on the top surface can be observed for case 3. The maximum the suction on the top surface, the maximum will be the lift produced by the wing. Therefore, these results clearly depict the effectiveness of the active flow control technique for the case 3 delta wing. 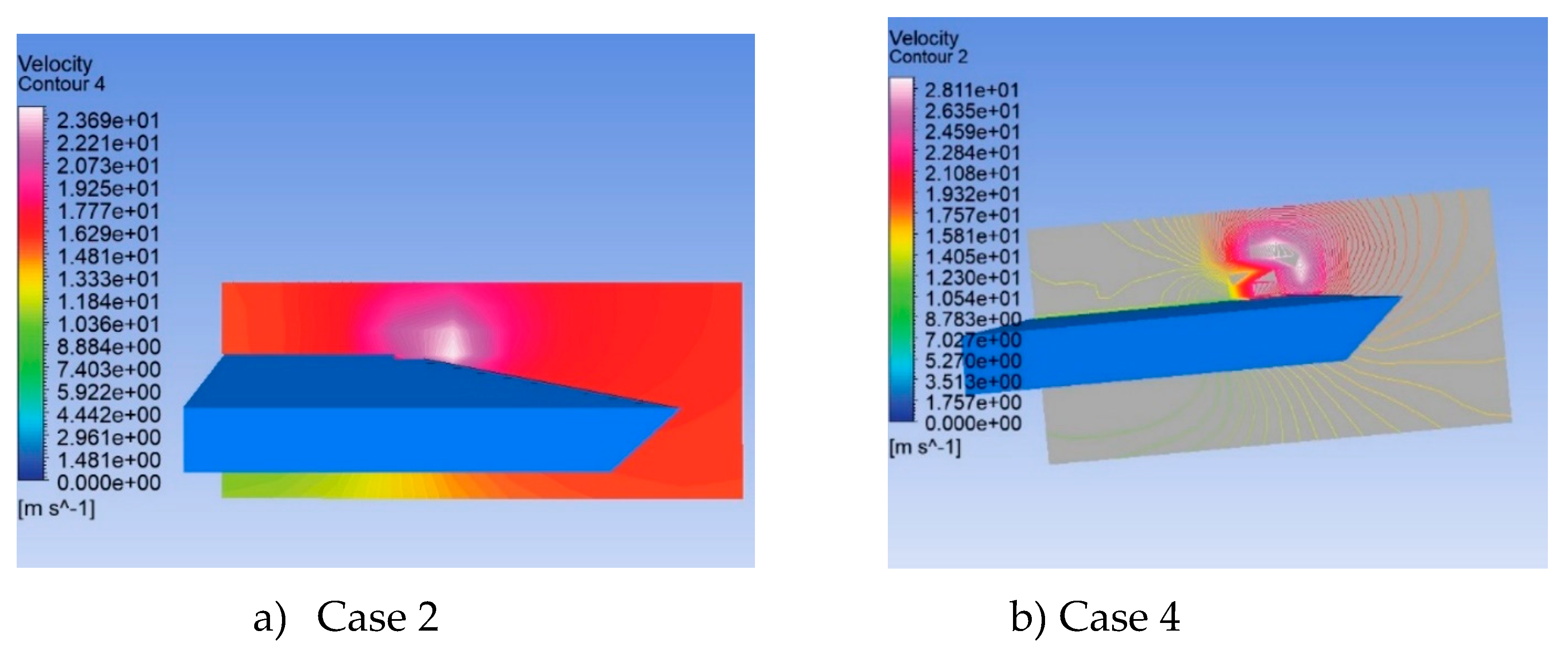Figure 18 a and b shows the pressure contours for the delta wing with case 2, and case 4 respectively at α = 30o & x/c = 0.6. Also, Figure 19 a and b shows the velocity contours for the delta wing with case 2, and case 4 respectively at α = 30o & x/c = 0.6. For Case 3 delta wing, the velocity contour plotted on the symmetry plane is shown in Figure 20.
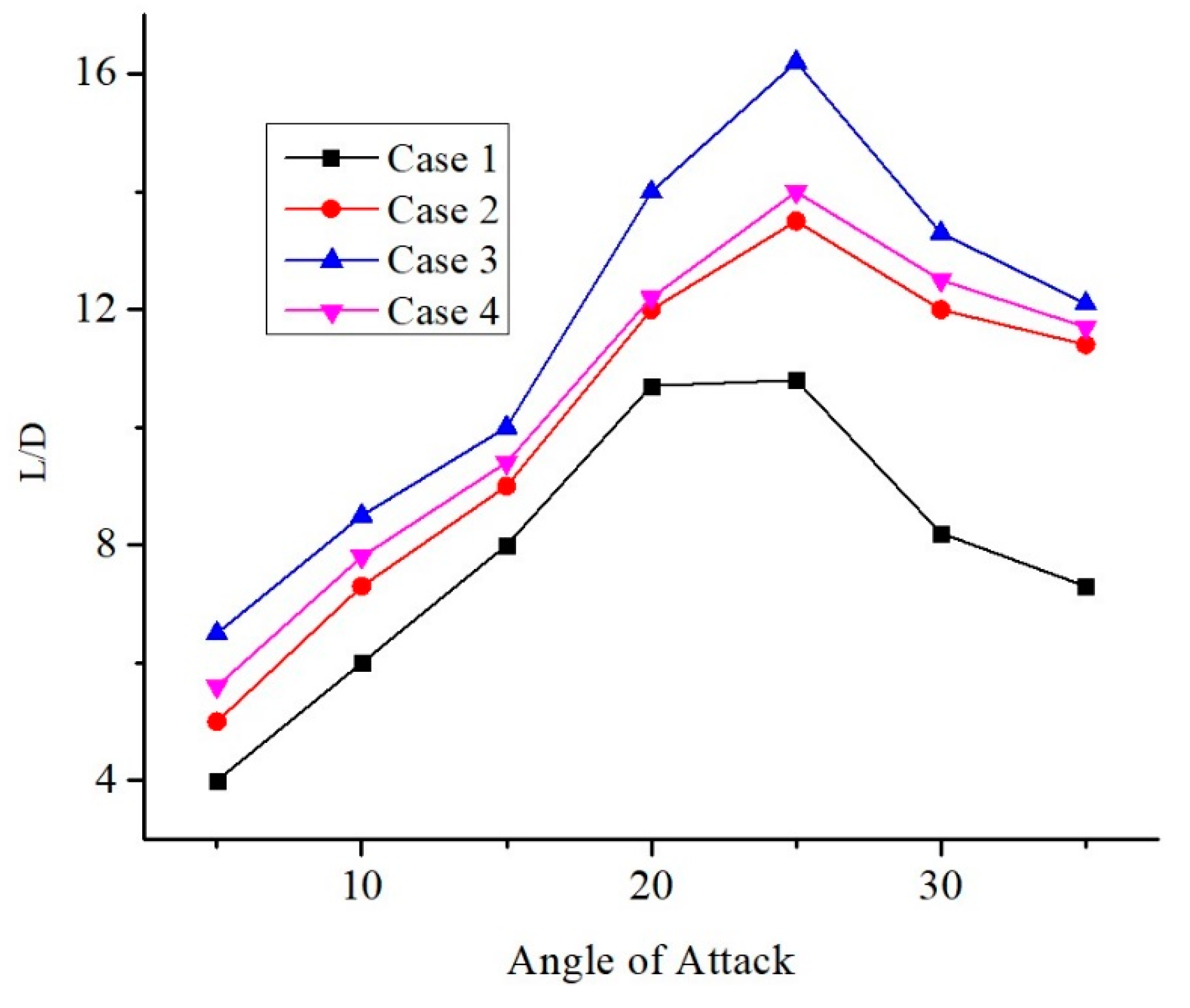
The lift-to-drag ratio (L/D) at various angles of attack was calculated for the baseline and the other blowing delta wing configurations. The plot comparison of L/D ratio vs. angle of attack is shown in Figure 21. which clearly shows the effectiveness and the aerodynamic efficiency. The L/D ratio for a delta wing of Case 3 proved to possess the highest aerodynamic efficiency.

Conclusions

The blowing flow control technique has been implemented for the case of delta wings. The location of the blowing location was varied. The three different configurations of blowing were identified. The blowing configuration shown in case 3 proved superior to the other configurations in delaying the vortex breakdown. The artificial jet generated by blowing the fluid in the delta wing configuration of case 3 provides an adequate amount of momentum and hence energy to the vortex core which upon the absence of blowing would have a breakdown. This transfer of energy from the jet to the vortex enables it to propagate downstream of the delta wing and hence the phenomenon of vortex breakdown completely disappears. Moreover, the operating range of the angle of attack is further increased. The most important point to be addressed while implementing the active flow control technique is that it involves additional subcomponents which in turn increases the overall weight of the aircraft and the drag will be certainly increased.

Future Work

Assessing the outcomes against a different kind of optimal control solver is the major recommended course of action for this research. This will enable the deployment of an increasingly complicated delta wing configuration while also enabling further testing of the veracity of the results. Delta wing configurations with a wide variety of flow control techniques will give new insights to classify the optimal technique in terms of energy management. Due to computational limitations, the use of flow control techniques on complex delta wing configurations is difficult to study.

Author Contributions

Conceptualization, Methodology, Software, Validation, Writing original Draft S.G; Supervision, S.K and R.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

The authors are thankful to the Department of Aerospace Engineering, Punjab Engineering College (Deemed to be University) for the Computational Fluid Dynamics Lab test facility.

Conflicts of Interest

No potential conflict of interest was reported by the authors.

References

  1. Polhamus, E.C. Predictions of Vortex-Lift Characteristics by a Leading Edge Suction Analogy. Journal of Aircraft 1971, 8, 193–199. [Google Scholar] [CrossRef]
  2. Polhamus, E.C. Charts for Predicting the Subsonic Vortex-Lift Characteristics of Arrow, Delta and Diamond Wings, NASA TN D6243, April 1971.
  3. Mitchell, A.M.; Barberis, D.; Délery, J. Oscillation of vortex breakdown location and its control by tangential blowing, 29th AIAA Fluid Dyn. Conf. 1998, vol. 38, 1–11. [CrossRef]
  4. Greenblatt, D.; Kastantin, Y.; Nayeri, C.N.; Paschereit, C.O. Delta-wing flow control using dielectric barrier discharge actuators. AIAA J. 2008, 46, 1554–1560. [Google Scholar] [CrossRef]
  5. Margalit, S.; Greenblatt, D.; Seifert, A.; Wygnanski, I. Delta wing stall and roll control using segmented piezoelectric fluidic actuators. J. Aircr. 2005, 42, 698–709. [Google Scholar] [CrossRef]
  6. Roupassov, D.V; Nikipelov, A.A.; Nudnova, M.M.; Starikovskii, A.Y. Flow separation control by plasma actuator with nanosecond pulsed-periodic discharge. AIAA J. 2009, 47, 168–185. [Google Scholar] [CrossRef]
  7. Nishihara,M. ; Takashima, K.; Rich, J.W.; Adamovich, I.V. Mach 5 bow shock control by a nanosecond pulse surface dielectric barrier discharge. Phys. Fluids 2011, 23. [Google Scholar] [CrossRef]
  8. Benard, N.; Zouzou, N.; Claverie, A.; Sotton, J.; Moreau, E. Optical visualization and electrical characterization of fast-rising pulsed dielectric barrier discharge for airflow control applications. J. Appl. Phys. 2012, 111. [Google Scholar] [CrossRef]
  9. Zhao, G.Y.; Li, Y.H.; Hua, W.Z.; Liang, H.; Han, M.H.; Niu, Z.G. Experimental study of flow control on delta wings with different sweep angles using pulsed nanosecond DBD plasma actuators. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 1966–1974. [Google Scholar] [CrossRef]
  10. Yavuz, M.M.; Rockwell, D. Identification and control of three-dimensional separation on low swept delta wing. AIAA J. 2006, 44, 2805–2811. [Google Scholar] [CrossRef]
  11. Yaniktepe, B.; Rockwell, D. Flow structure on diamond and lambda planforms: Trailing-edge region. AIAA J. 2005, 43, 1490–1500. [Google Scholar] [CrossRef]
  12. Ol, M.V.; Gharib, M. Leading-edge vortex structure of nonslender delta wings at low Reynolds number. AIAA J. 2003, 41, 16–26. [Google Scholar] [CrossRef]
  13. Taylor, G.S.; Gursul, I. Buffeting flows over a low-sweep delta wing. AIAA J. 2004, 42, 1737–1745. [Google Scholar] [CrossRef]
  14. Chen, L.; Wang, J.; Zuo, L.X.; Feng, L.H. Influence of Reynolds number on vortex flow over a non-slender delta wing. AIAA J. 2010, 48, 2831–2839. [Google Scholar] [CrossRef]
  15. Sahin, B.; Yayla, S.; Canpolat, C.; Akilli, H. Flow structure over the yawed non slender diamond wing. Aerosp. Sci. Technol. 2012, 23, 108–119. [Google Scholar] [CrossRef]
  16. Gursul, I.; Wang, Z.; Vardaki, E. Review of flow control mechanisms of leading-edge vortices. Prog. Aerosp. Sci. 2007, 43, 246–270. [Google Scholar] [CrossRef]
  17. Renac, F.; Barberis, D.; Molton, P. Control of vortical flow over a rounded leading-edge delta wing. AIAA J. 2005, 43, 1409–1418. [Google Scholar] [CrossRef]
  18. Hong, J.S.; Çelik, Z.Z.; Roberts, L. Effects of leading-edge lateral blowing on delta wing aerodynamics. AIAA J. 1996, 34, 2471–2478. [Google Scholar] [CrossRef]
  19. Wood, N.J.; Roberts, L. Control of vortical lift on delta wings by tangential leading-edge blowing. J. Aircr. 1988, 25, 236–243. [Google Scholar] [CrossRef]
  20. Greenwell, D.I.; Wood, N.J. , Roll moment characteristics of asymmetric tangential leading-edge blowing on a delta wing. J. Aircr. 1994, 31, 161–168. [Google Scholar] [CrossRef]
  21. Gu, W.; Robinson, O.; Rockwell, D. Control of Vortices on a Delta Wing by Leading-Edge Injection. AIAA J. 1993, 31. [Google Scholar] [CrossRef]
  22. Williams, N.M.; Wang, Z.; Gursul, I. Active flow control on a non-slender delta wing. J. Aircr. 2008, 45, 2100–2110. [Google Scholar] [CrossRef]
  23. Cui, Y.D.; Lim, T.T.; Tsai, H.M. Control of Vortex Breakdown over a Delta Wing Using Forebody Slot Blowing. AIAA J. 2007, 45. [Google Scholar] [CrossRef]
  24. Jiang, P.; Wang, Z.; Gursul, I. Effects of unsteady trailing-edge blowing on delta wing aerodynamics. J. Aircr. 2010, 47, 591–602. [Google Scholar] [CrossRef]
  25. Johari, H.; Olinger, D.J.; Fitzpatrick, K.C. Delta wing vortex control via recessed angled spanwise blowing. J. Aircr. 1995, 32, 804–810. [Google Scholar] [CrossRef]
  26. Lamar, J.E. Special Course on Fundamental of Fighter Aircraft Design, AGARD Report No. 740, 1988.
  27. Rao, D.M.; Campbell, J.F. Vortical flow management techniques. Prog. Aerosp. Sci. 1987, 24, 173–224. [Google Scholar] [CrossRef]
  28. =, *!!! REPLACE !!!*. Smith, A.; Balogun, H.; Khan, M.; Aji, C.; Salehian, S. Characterization of the Flow Field of Slender and Non-Slender Delta Wings using Volumetric PIV, AIAA 2022-1195. AIAA SCITECH 2022 Forum.
  29. Sedlacek, D.; Breitsamter, C., Aerodynamic Characteristics and Topology of Interfering Vortex Systems at Hybrid Delta Wings, AIAA 2022-0026. AIAA SCITECH Forum.
  30. Balogun, H.; Smith, A.; Khan, M.J.; Aji, C.A., Characterization of the Flow Field of Slender Delta Wings with Trailing Edge Jets Using Volumetric PIV, AIAA 2023-2300. AIAA SCITECH.
  31. Al-Garni Ahmad, Z.; Saeed, F.; Al-Garni Abdullah, M. Experimental and Numerical Investigation of 65 Degree Delta and 65/40 Degree Double-Delta Wings. J. Aircr. 2008, 45. [Google Scholar] [CrossRef]
  32. Wentz, W.H.; Kohlman, D.L. Vortex Breakdown on Slender Sharp-Edged Wings. J. Aircr. 1971, 8, 156–161. [Google Scholar] [CrossRef]
  33. Cummings, R.M.; Morton, S.A.; McDaniel, D.R. Experiences in Accurately Predicting Time-Dependent Flows. Prog. Aerosp. Sci. 2008, 44, 241–257. [Google Scholar] [CrossRef]
  34. Allan, M., “A CFD Investigation of Wind Tunnel Interference on Delta Wing Aerodynamics,” Ph.D. Thesis, Univ. of Glasgow, Glasgow, Scotland, U.K., 2002.
  35. Ramakrishna, M., S.K, C., and Venkatesh, B., “Influence of Leading Edge Shapes on Vortex Behaviour of Delta Wing. IOP Conf. Series, Journal of Physics, 2019, 1276, 012008. [CrossRef]
Preprints 86170 g007
Figure 7. Grid Independence Test: Plot of Cp vs. y/s at x/c = 0.2.
Figure 7. Grid Independence Test: Plot of Cp vs. y/s at x/c = 0.2.
Preprints 86170 g007
Preprints 86170 g008aPreprints 86170 g008b
Figure 8. Cp distribution versus Y/s for various x/c at 5o angle of attack.
Figure 8. Cp distribution versus Y/s for various x/c at 5o angle of attack.
Preprints 86170 g008aPreprints 86170 g008b
Preprints 86170 g009
Figure 9. Cp distribution versus Y/s for various x/c at 10o angle of attack.
Figure 9. Cp distribution versus Y/s for various x/c at 10o angle of attack.
Preprints 86170 g009
Preprints 86170 g010
Figure 10. Cp distribution versus Y/s for various x/c at 15o angle of attack.
Figure 10. Cp distribution versus Y/s for various x/c at 15o angle of attack.
Preprints 86170 g010
Preprints 86170 g011
Figure 11. Cp distribution versus Y/s for various x/c at 30o angle of attack.
Figure 11. Cp distribution versus Y/s for various x/c at 30o angle of attack.
Preprints 86170 g011
Preprints 86170 g012
Figure 12. Cp distribution versus Y/s for various x/c at 35o angle of attack.
Figure 12. Cp distribution versus Y/s for various x/c at 35o angle of attack.
Preprints 86170 g012
Preprints 86170 g013
Figure 13. Pressure contours for the baseline delta wing at α = 35o.
Figure 13. Pressure contours for the baseline delta wing at α = 35o.
Preprints 86170 g013
Preprints 86170 g014
Figure 14. Plot for the baseline delta wing at α = 35o and x/c =0.6.
Figure 14. Plot for the baseline delta wing at α = 35o and x/c =0.6.
Preprints 86170 g014
Preprints 86170 g015
Figure 15. Pressure contour for the delta wing with case 2 on the top surface at α = 30o.
Figure 15. Pressure contour for the delta wing with case 2 on the top surface at α = 30o.
Preprints 86170 g015
Preprints 86170 g016
Figure 16. Pressure contour for the delta wing with case 3 on the top surface at α = 30o.
Figure 16. Pressure contour for the delta wing with case 3 on the top surface at α = 30o.
Preprints 86170 g016
Preprints 86170 g017
Figure 17. Pressure contour for the delta wing with case 4 on the top surface at α = 30o.
Figure 17. Pressure contour for the delta wing with case 4 on the top surface at α = 30o.
Preprints 86170 g017
Preprints 86170 g018
Figure 18. Pressure contour at α = 30o & x/c = 0.6.
Figure 18. Pressure contour at α = 30o & x/c = 0.6.
Preprints 86170 g018
Preprints 86170 g019
Figure 19. Velocity contour for the delta wing with case 2 at α = 30o & x/c = 0.6.
Figure 19. Velocity contour for the delta wing with case 2 at α = 30o & x/c = 0.6.
Preprints 86170 g019
Preprints 86170 g020
Figure 20. Velocity contour on the symmetry plane for the delta wing with case 3 at α = 30o.
Figure 20. Velocity contour on the symmetry plane for the delta wing with case 3 at α = 30o.
Preprints 86170 g020
Preprints 86170 g021
Figure 21. Comparison of L/D Ratio versus Angle of Attack.
Figure 21. Comparison of L/D Ratio versus Angle of Attack.
Preprints 86170 g021
Table 1. Design parameters of the delta wing model.
Table 1. Design parameters of the delta wing model.
Design Parameters Specifications of Delta wing
Leading-edge sweep angle, Λ 65 deg
Root chord, cr 0.3 m
Wing span, b 0.2798 m
Wing area, S 0.04197 m
Aspect ratio, AR 1.865
Thickness 0.01 m
Bevel angle 8.5 deg
Table 2. Test Conditions for Validation.
Table 2. Test Conditions for Validation.
Flow conditions Value
Freestream velocity 13 m/s
Dynamic pressure 100 N/m2
Rec 2.67 x 105
Temperature 300 K
Atmospheric pressure 1.008 x 105 N/m2
Angle of attack range 0 – 35 deg
Table 3. Delta wing design with/without blowing.
Table 3. Delta wing design with/without blowing.
Design Parameters Specifications of Delta wing
Leading-edge sweep angle, Λ 65 deg
Root chord, cr 0.247 m
Wing span, b 0.230 m
Wing area, S 0.028405 m2
Aspect ratio, AR 1.862
Thickness 0.015 m
Bevel angle 45 deg
Blowing locations 1.62%, 3.24% & 4.86% of cr
Table 4. Flow conditions for the present study.
Table 4. Flow conditions for the present study.
Flow conditions Value
Freestream velocity 15.6 m/s
Dynamic pressure 148.8 N/m2
Rec 2.64 x 105
Temperature 300 K
Atmospheric pressure 1.008 x 105 N/m2
Angle of attack range 0 – 35 deg
Momentum coefficient 0.05
Table 5. Grid Details.
Table 5. Grid Details.
Parameter Value
Grid Size (number of cells) 35 million
Grid Type Tetrahedral
Number of Prism Layers 20
Reynold’s Number 2.64 x 105
Mach Number 0.06
Total memory consumed (MB) 2514
Processor Type Intel Xeon
Number of Cores 32
RAM (GB) 128
Average CPU time/iteration, s 8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated