1. Introduction
Cyber-physical systems (CPSs) are cyber systems consisting of cyber (computing and communication) and physical (sensors and actuators) components that interact in a feedback loop with the help of possible human intervention, interaction, and exploitation [
1]. Due to the tight integration of physical processes, networks, and computing, current CPSs are widely used in different fields, such as power transmission systems, healthcare, communication systems, military systems, transportation, automotive systems, entertainment, and many other areas directly related to people’s daily lives [
2,
3]. However, the interconnection of the cyber and physical worlds has brought new and dangerous security challenges. For example, in the information network area, in 2003, many websites and Internet services were rendered inaccessible because they were hit by the Sapphire worm [
4]. In the energy sector, in 2010, the Stuxnet virus attacked Iran’s nuclear power plant, destroying its centrifuges, and rendering the nuclear reactor inoperable for a long time [
5]. In the healthcare area, in 2017, WannaCry attacked the National Health Service, causing huge casualties and financial losses [
6]. These security incidents provide sufficient evidence that attacks on CPS, which eventually penetrate actual physical processes, can lead to significant losses of people’s livelihoods. Therefore, it is important to study the security of CPSs.
The security defense problem of CPS can be mainly divided into the cyber layer and the physical layer. The defense means of the cyber layer are mainly similar to the security defense methods of the information network, for example, the defense against network attacks is achieved by encryption keys[
7], watermark detection[
8], and restriction of access rights[
9]. However, the high coupling of CPS with real physical devices leads to the fact that some attacks against the cyber layer can also penetrate and affect the actual physical processes, especially some automatic control systems, resulting in reduced control performance. Therefore, defense against the physical layer is very important and necessary from the point of view of the last means of defense and brings worthwhile defense benefits.
The security defense problem for the physical layer of CPS can be divided into several stages: attack detection, secure state estimation, and secure control[
10]. Among them, each of them has a different and necessary function. However, most of the studies focus on one of these phases for analysis and discussion only. In terms of attack detection, a blended detection scheme that appropriately uses a combination of two existing detection methods is proposed to achieve the detection of a large class of false data injection attacks[
11]. In [
12] , a moving target defense that introduces random, time-varying parameters in the control system is proposed to inhibit the attacker’s ability to construct a stealthy attack sequence. Combining existing concepts of watermark signals and auxiliary systems, a novel control architecture capable of detecting spoofing attacks that affect the network control system without compromising control performance is proposed[
13]. In terms of secure state estimation, a Bayesian method based on random sets for switching signals and spurious measurement attacks is deployed to ensure resilient state estimation[
14]. In [
15] , a robust asymptotic fault estimation method is designed for CPS with sensor faults that can estimate the system state well. Considering a secure reconstruction problem for linear CPS with both sparse actuator and sensor attacks, a descriptor switched sliding mode observer that effectively reconstructs the sparse FDI attacks and the system state is constructed [
16]. In terms of secure control, an architectural framework for resilient CPS based on stochastic MPC is proposed to ensure robustness in the presence of stochastic uncertainty and to achieve resilient control against cyber-attacks[
17]. In [
18], by analyzing various cyber-attacks, a unified system model with uncertainty is developed and the robust control theory is applied to achieve secure control of the system after an attack. A model predictive switching control strategy based on attack perception is proposed to compensate for the untrusted sequences of data caused by false data injection attacks[
19].
From the above analysis, we can find that as the application of CPS expands, people pay more and more attention to the security of CPS. Although all the above studies have good results, they all focus on only one phase of CPS security defense, and rarely consider the complete security defense process. Therefore, in this paper, we consider the scenario that a CPS containing multiple sensors is subject to stealthy cyber-attacks (e.g., zero-dynamics attacks, covert attacks, and replay attacks), combine the attack detection method based on improved residuals [
20], propose an optimal state estimation based on improved Kalman filtering and a recovery control strategy based on the optimal state, and give a complete framework of security defense process from attack detection to recovery control. Finally, the theory is validated by design simulation, and the results prove the feasibility of the proposed method.
The main contributions of this paper can be summarized as follows.
1) By analyzing the structural characteristics of CPS, a system model containing the attacks is developed, and stealthy attacks (i.e., zero-dynamics attacks, covert attacks, and replay attacks) and the detection method based on improved residuals are described.
2) For the case of attacks on a CPS containing multiple sensors, an optimal state estimation method based on improved Kalman filtering is proposed, which can achieve the estimation of the actual state of the CPS after the attack.
3) Based on the estimated optimal state, a recovery control strategy is designed that can achieve recovery control of the system after identifying the attack. And at the end, a framework for the security defense process is given.
The rest of this paper is organized as follows. In Section II, the CPS structure and stealthy attacks are described, and the improved residual-based attack detection method is presented. In Section III, the optimal state estimation based on the improved Kalman filter and the recovery control strategy based on the optimal state are proposed, and a complete framework of the security defense process is given. Simulation experiments are designed in Section IV, and the results are analyzed and illustrated. Section V summarizes the full work and provides an outlook for future work.
3. State Estimation and Recovery Control
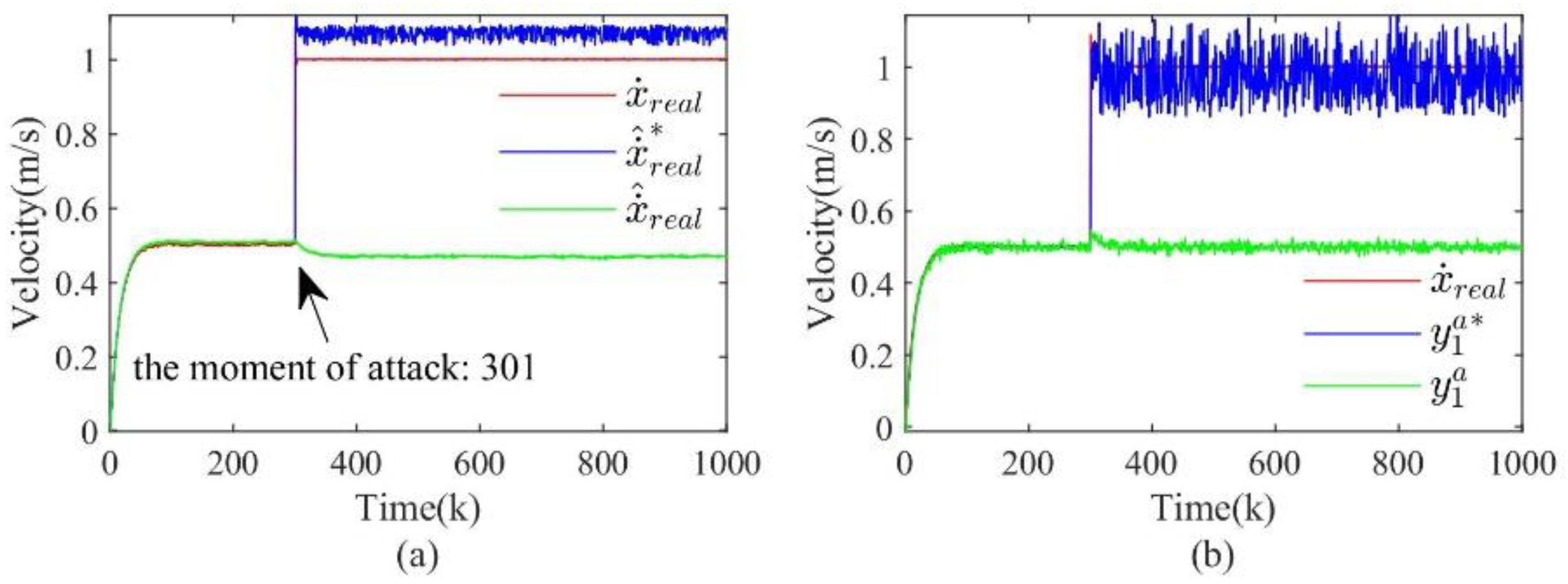
The CPS is subject to various stealthy cyber-attacks, and its control performance is significantly reduced. Obviously, the main concern of both attackers and defenders is how to influence or improve the control performance of the control system to achieve the attack and defense objectives. Therefore, a well-integrated controller design solution that can detect, isolate, and recover control from attacks is a must in the face of stealthy cyber-attacks.
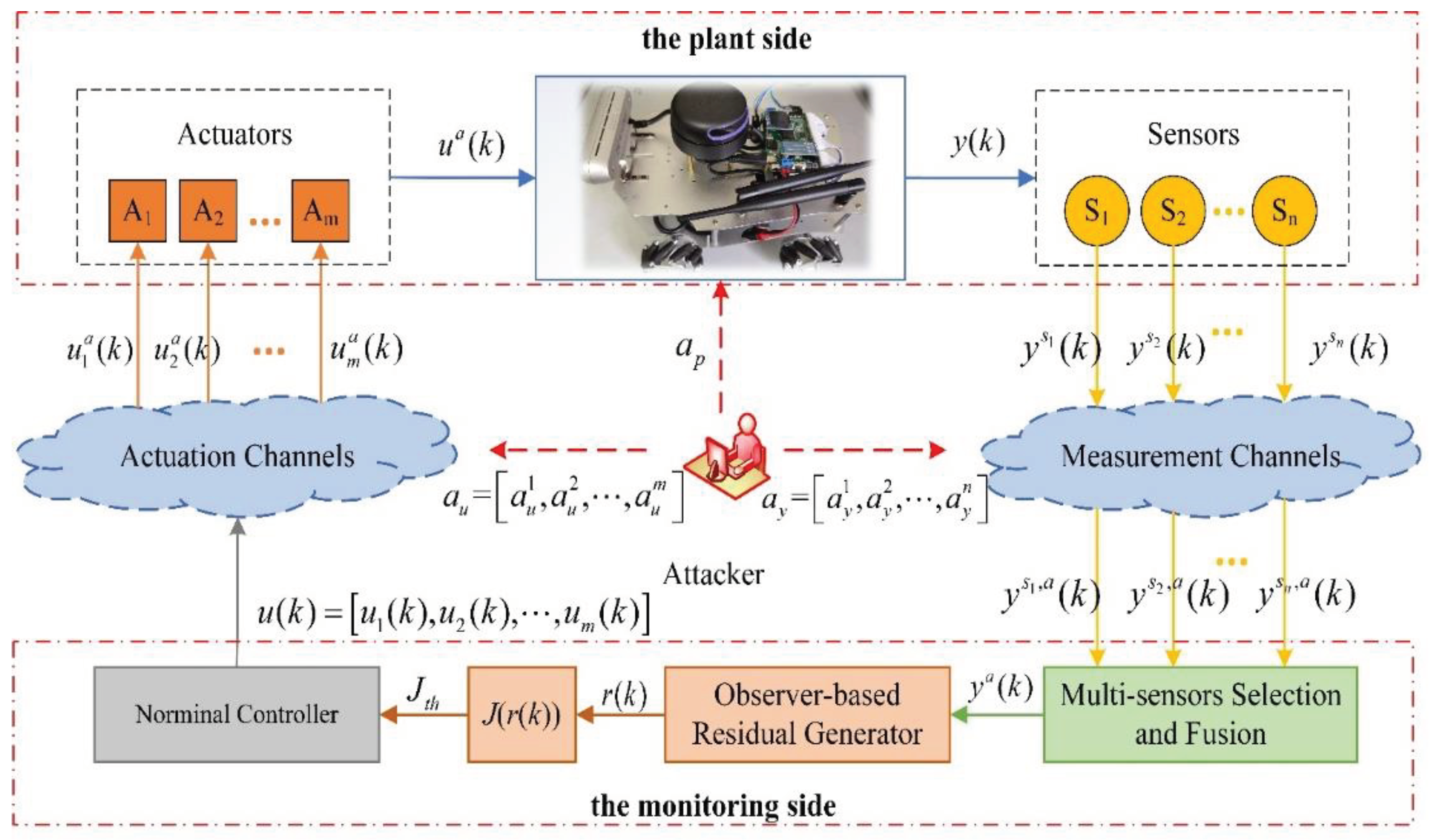
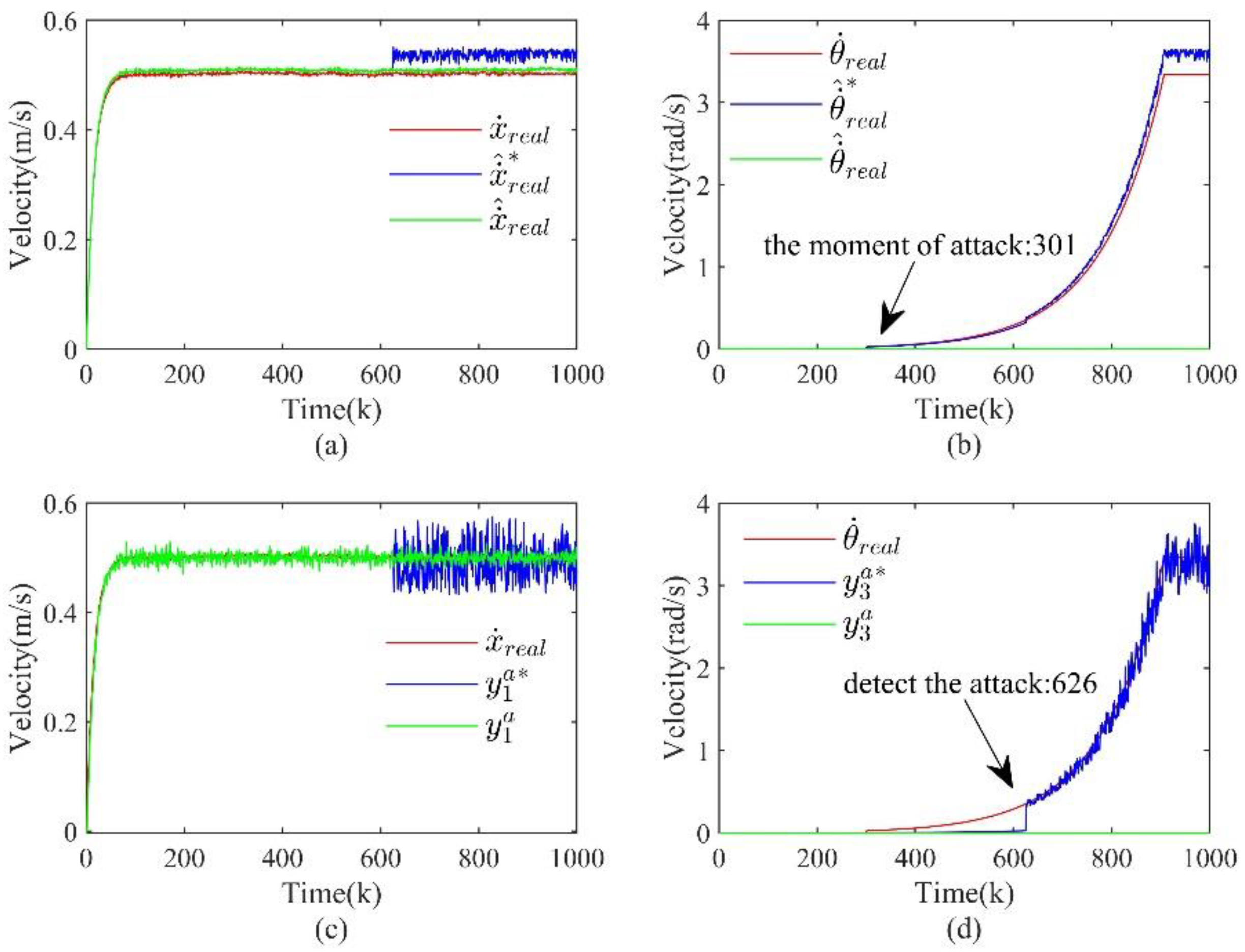
Consider a CPS as shown in
Figure 1, containing multiple actuators as well as multiple sensors that can be independently measured to obtain the complete system output. The analysis of stealthy attacks in Section II shows that the key to their stealthy implementation lies in the tampering with the sensor measurement output, while the attack on the actuators is only to achieve the purpose of the attack and control the specific actions of the system. Therefore, considering
sensors
there are unknown sensors suffered from the attack, the specific attacks are described as follows.
Without knowing which sensor is under attack, it is undesirable to directly fuse the sensor output data using the multi-sensor fusion method . Therefore, each sensor must be detected in advance and the sensor detected to be under attack must be isolated, and finally, the normal sensors are selected for fusion to obtain the correct system state for recovery control.
3.1. Optimal State Estimation Based on Improved Kalman Filtering
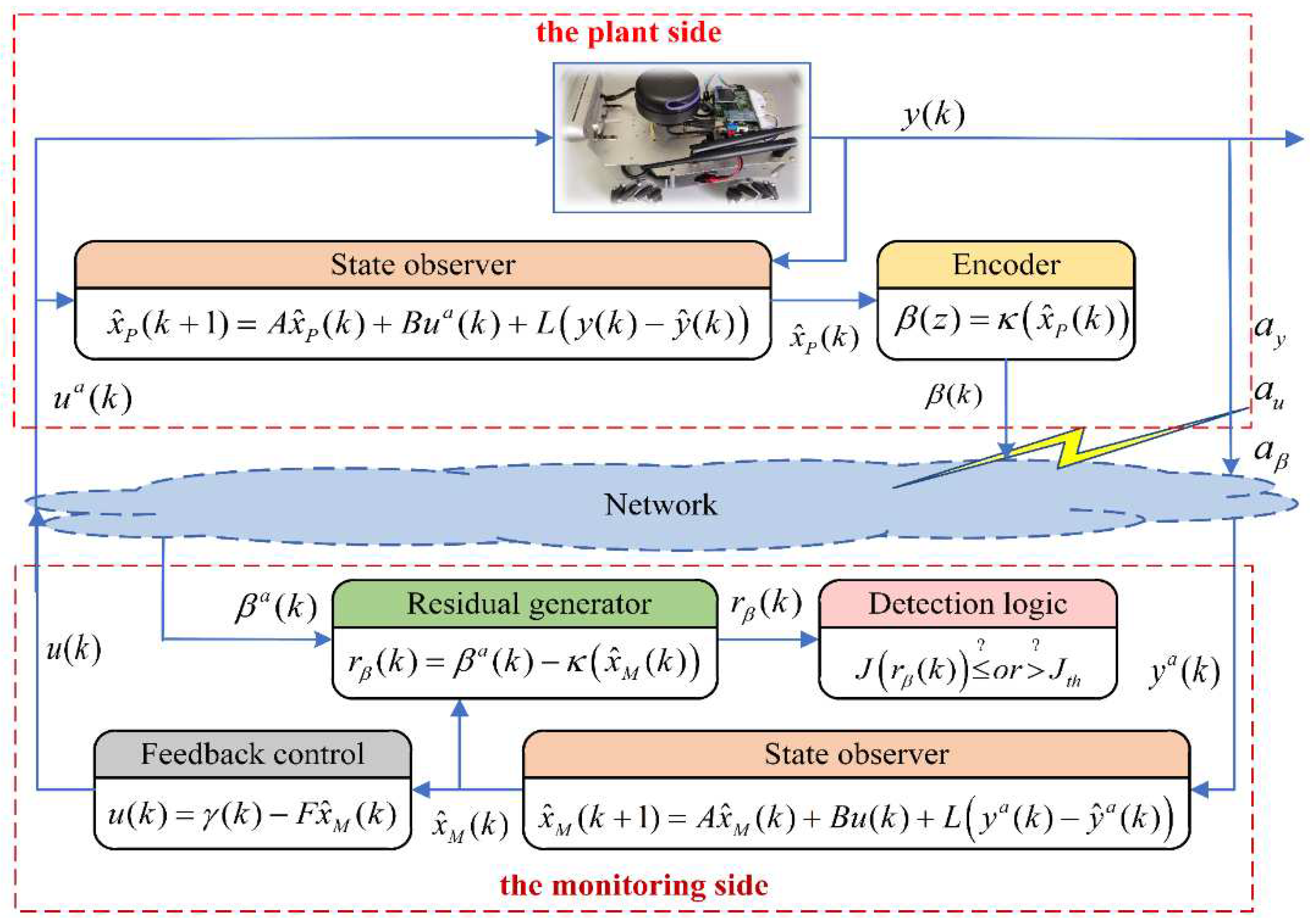
To detect whether each sensor is under attack, the detection method in Section II is used to calculate the residual signal for each sensor to detect stealthy attacks. Assume that the sequence of residual signals for all sensors is calculated as follows.
According to the
detection theory, drawing on the detection logic of (3) and (4), the detection of stealthy attacks can be achieved for each sensor.
Assume that the set of residual signals of the sensors that detected the attack is expressed as:
After detecting the sensors under attack, they need to be isolated and the remaining normal sensors are used to estimate the system state. Therefore, the weighting factors are introduced to achieve isolation and fusion according to (12) and (14). That is, the fusion function
in (1) is constructed in the following form.
where,
is the weight value corresponding to each sensor calculated from the residual signal
, calculated as shown below.
From (16), it can be found that whenever a sensor is detected an attack, its corresponding weighting factor is set to 0, while sensors that are not detected an attack are weighted and fused according to the corresponding residuals. Since the residuals reflect the degree of state deviation, the larger the residuals are when calculating the weighting factors, the smaller the weighting factors will be.
Then, according to the explanations in Remark 1 and Remark 2, the model of CPS shown in (1) can be simplified to the following form without considering process attacks.
where,
is the measurement output of the
sensor after attacking and
is the corresponding system output matrix.
Meanwhile, on the monitoring side, the state estimation equation, and the observation estimation equation for (17) are:
where,
is the value estimated at moment
for the measurement output of the
attacked sensor at moment
.
Then, the state error covariance matrix
can be calculated as follows.
where,
is the covariance matrix of the attack signal
and
is the covariance matrix of the process noise
.
Similarly, the observation error covariance matrix
can be calculated as follows.
where,
is the covariance matrix of the attack signal
and
is the covariance matrix of the measurement noise
.
The goal of Kalman filtering is for an iterative estimation expression based on errors that can be continuously corrected, in the form shown below.
where,
is the Kalman gain matrix and
is the observation estimation error, defined as:
The solution procedure for
is as follows.
Expanding (23) into the form of a trace:
to
by taking the partial derivative and making it equal to 0 to compute the optimal
:
Finally, we obtain the optimal
W:
Then, substituting (27) into (19) again, the iterative form of the state error covariance matrix can be obtained by simplification:
In conclusion, considering isolation and fusion of the attacked sensors, the optimal state estimation based on the improved Kalman filtering can be summarized as:
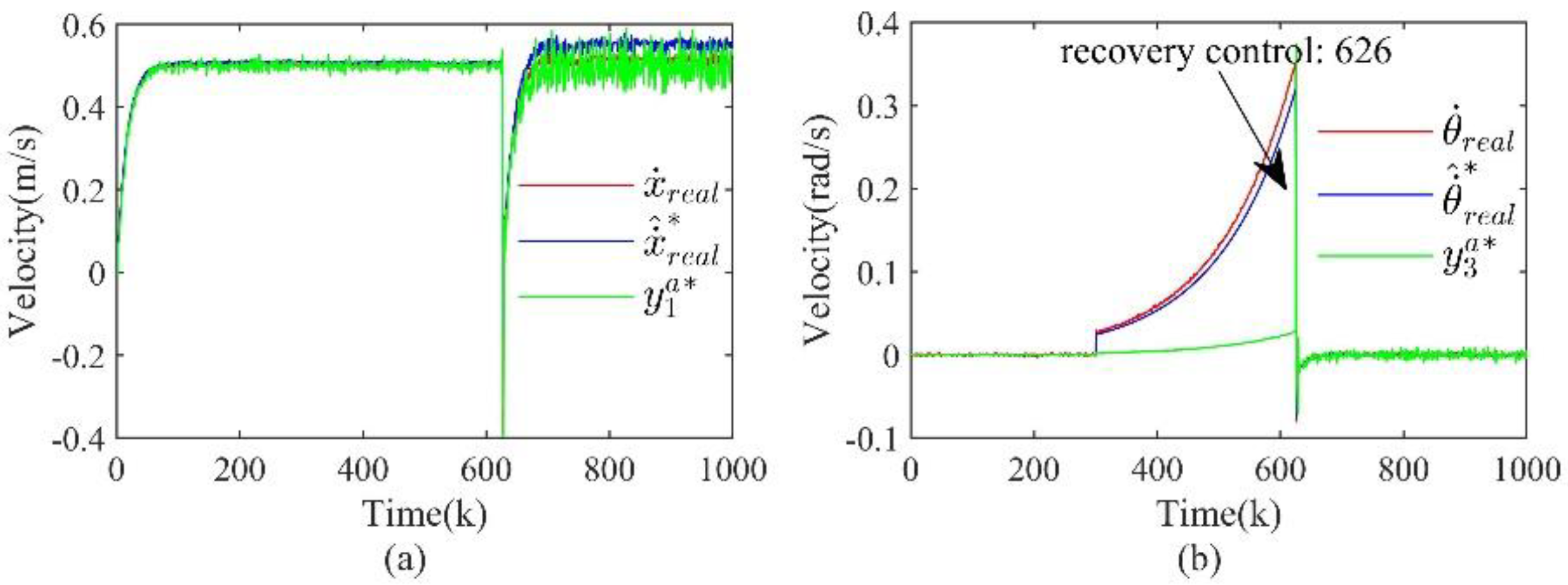
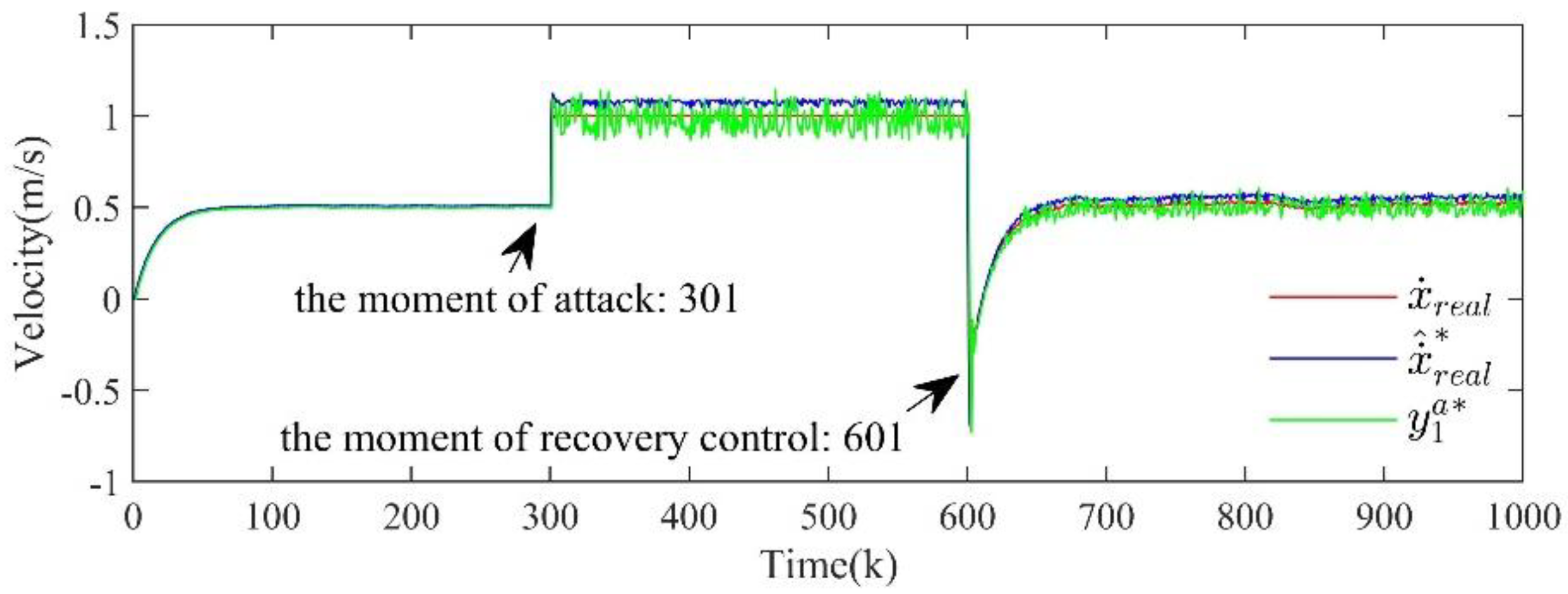
3.2. The Recovery Control Strategy Based on Optimal State
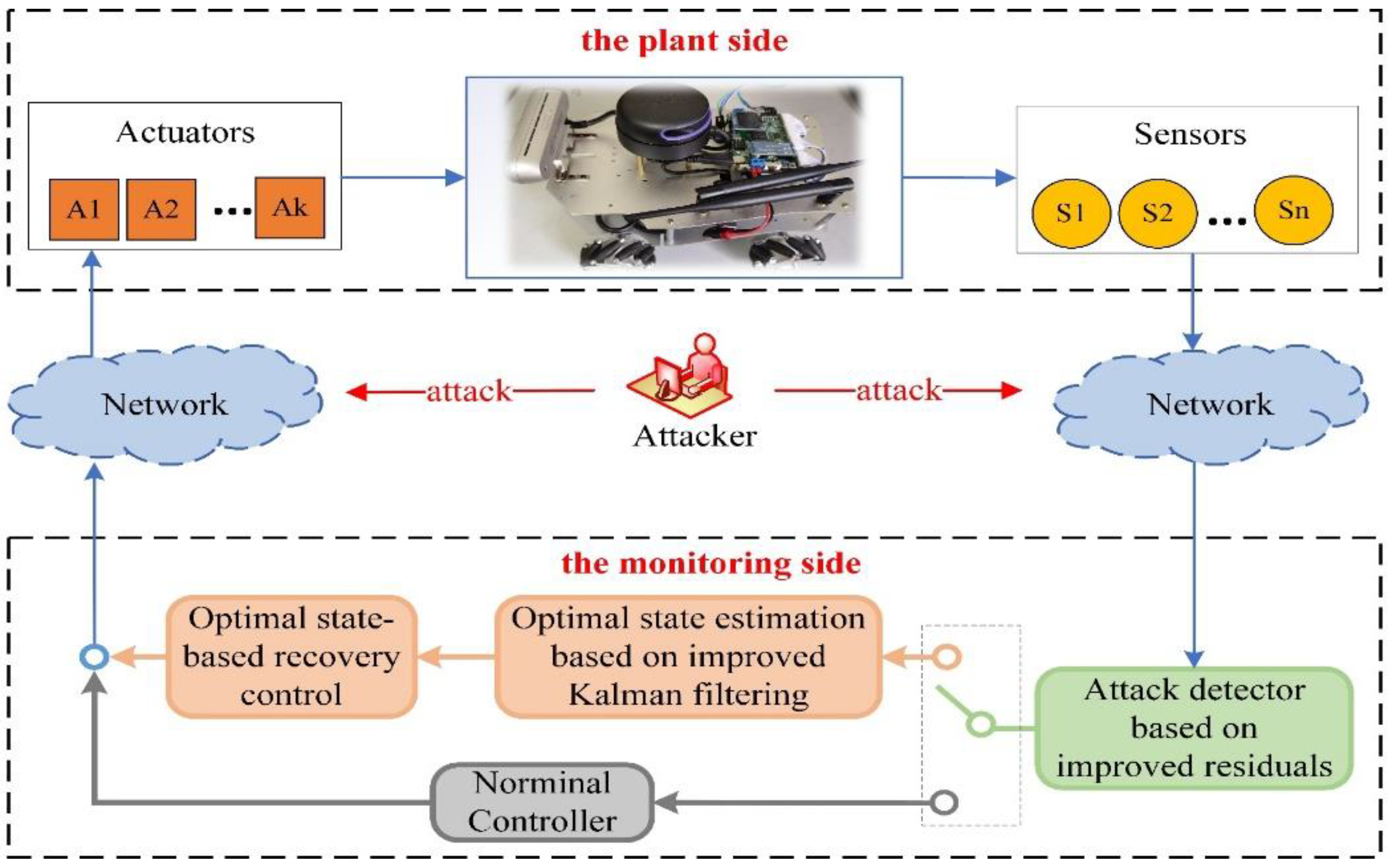
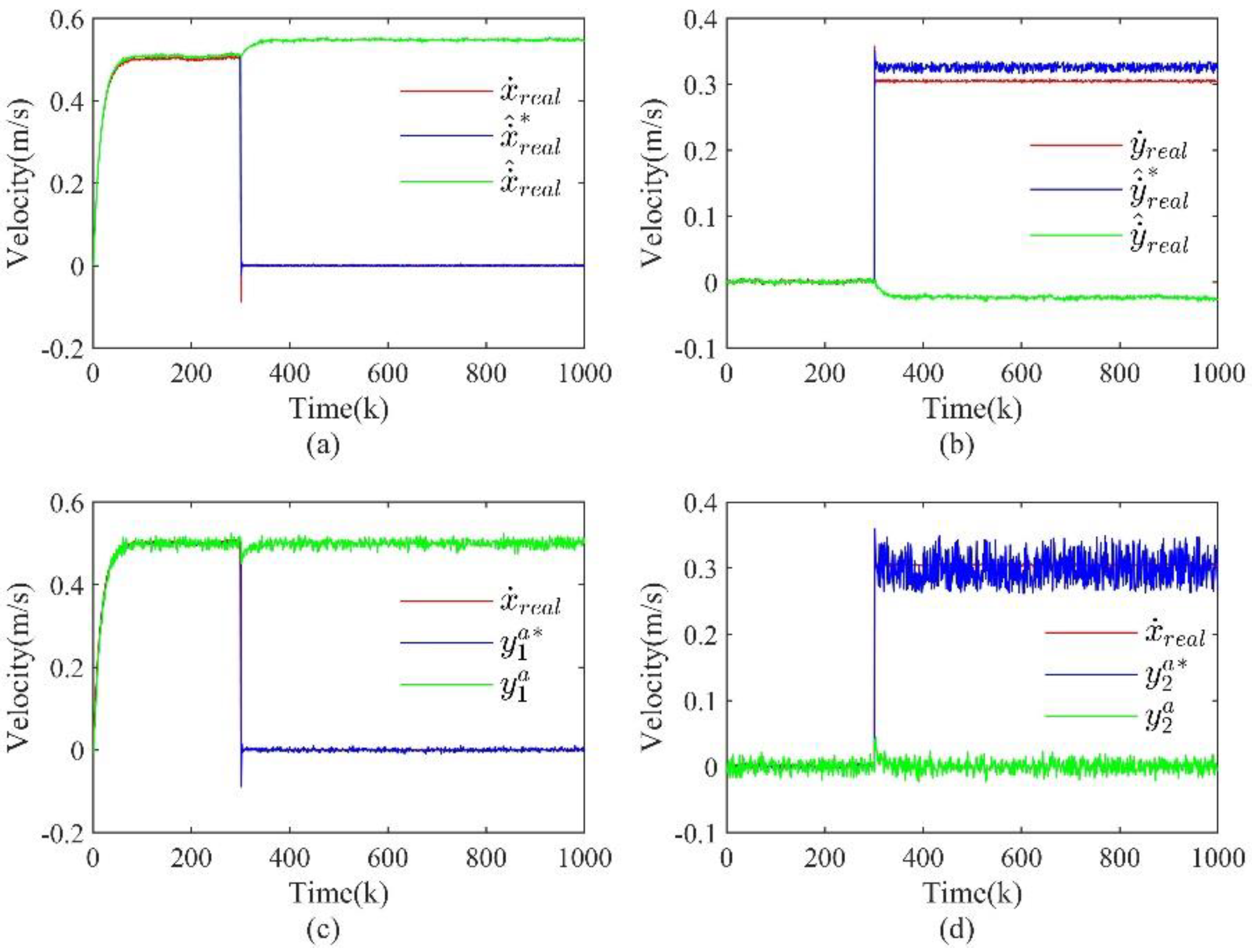
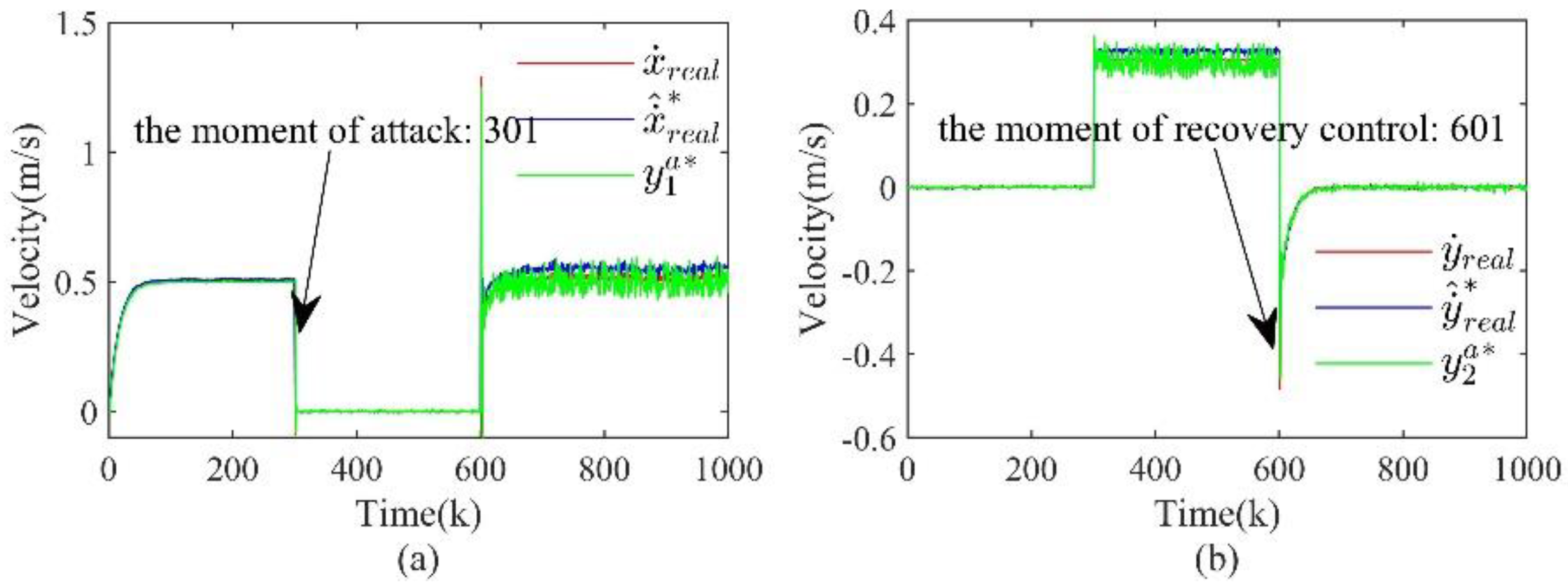
In the security defense problem of CPS, it is the goal to ensure that the system can continue to maintain the normal operation state even after an attack. Therefore, after detecting an attack using the detection method in Section II and performing attack isolation and system state estimation according to the method in Section III, the next step is to implement recovery control for the system based on the above results. This section introduces an optimal state-based recovery control strategy and summarizes the attack detection, attack isolation, state estimation and recovery control comprehensively to give a complete framework of the CPS security protection process, as shown in
Figure 3.
Figure 3.
The security defense process of CPS that includes attack detection, secure state estimation, and recovery control.
Figure 3.
The security defense process of CPS that includes attack detection, secure state estimation, and recovery control.
In control systems, many control objectives are to enable the system to stably track the reference input to achieve the control requirements. The internal model control (IMC) has a very wide range of applications in the control field as a way to enable the system to track the reference input asymptotically with zero steady-state error. For the recovery control problem of CPS under attacks, this paper introduces an integration link of the reference input signal by combining IMC with the optimal state to achieve the stable operation of the attacked system according to the target command.
Assume that the reference input signal
is generated by the following model.
Also, define the tracking error
:
Then, the state space can be extended as follows.
where,
denotes the difference of the state variable
, i.e.,
.
If the system shown in (32) is controllable, then a set of feedback control signals can be designed to make the system stable, i.e.
This means that the tracking error
is stable. Therefore, the system is then able to track the reference input signal with zero steady-state error. Integrating (33), the feedback control signal inside the system is obtained as:
Since the state of the system cannot be obtained directly, the optimal state estimate is obtained by an improved Kalman filtering method and used to replace the true state in (34).