Prerpints.org logo
Preprint
Article

Unveiling the Strain Rate Sensitivity of G18NiCrMo3-6 Cast Steel in Tension/Compression Asymmetry

Altmetrics

Downloads

77

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 September 2023

Posted:

29 September 2023

You are already at the latest version

Alerts
Abstract
This contribution was devoted to unveil the strain rate sensitivity (SRS) of G18NiCrMo3-6 cast steel in tension/compression asymmetry. For that purpose, detailed mechanical characterization tests were conducted providing a process window covering quasi-static and medium strain rate regimes (0.001, 0.1, 10 [ s¯¹]) in tension and compression states. By means of this experimental ef-fort, the SRS of the material could be extracted by a function of strain and strain rate which ena-bling to create a mathematical expression to easily be implemented as a state variable for constitu-tive material modeling. Finally, a pressure and rate dependent constitutive material model on the basis of Cocks'89 yield locus definition was created by a subroutine (UMAT) file and the material parameters were verified with respect to the experimental data. The UMAT file also takes into account the tension/compression asymmetry in yielding to handle the effect of porous media plas-ticity concept. The predictions of the proposed material model are quite in line with the experi-mental outputs.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Casting operation - even though it is probably the most ancient manufacturing process- is still needed and/or provide a powerful alternative in production of parts having complex geometries especially with large dimensions. By proper precautions, great dimensional variations in cross section or large internal cavities do not lead to compelling challenges as in the case of other manufacturing process alternatives. In this regard, cast steel materials are mostly good candidates for under-body system components of combat vehicles such as suspension arms, steering knuckles and etc. which often have large dimension with complex geometries. When the demanding design requirements of defense industry are taken into account, those aforementioned components should have significant mechanical properties and durability, either. Therefore, high strength structural steel castings could find reasonable area of applications in combat vehicle designs. In that sense, G18NiCrMo3-6 material (conforming to EN 10340:2007) having an ultimate tensile strength (UTS) nearly 1.0 GPa come to sight for certain engineering designs of under-body systems. While having superior mechanical properties, this material has some drawbacks in the meantime. A priori, G18NiCrMo3-6 is a cast steel, thus, should be treated by cast iron plasticity approach since it absolutely has certain amount of porosity to some extent. This fact, in turn, eliminates the possibility to model this material with J₂ plasticity theory where the hydrostatic stress does not contribute to yielding and hence there is not any volume change in plastic range (i.e., strain tensor is deviatoric by definition). In other words, hydrostatic stress dependent yield locus should be constructed with a proper flow rule to model the material behavior of G18NiCrMo3-6. Secondly, this type of cast steel may posses tension/compression asymmetry, i.e., the yield stress and strain hardening behavior differs with respect to tension/compression stress states. This point clearly has to be considered by keeping in mind the fact that some under-body component encounters moment loads in several directions which means for a specific spatial material point both tensile and compressive stress states may occur interchangeably. In addition, owing to the harsh service-life conditions, under-body components may experience road loads with a wide strain rate spectrum mostly caused by the off-road scenario. As in the case of strain hardening, strain rate dependency could also have an asymmetric character which dictates creating hydrostatic stress and rate dependent constitutive material models that also account for tension/compression asymmetry aiming to predict the real-life mechanical response of the designed components with high precision. Those aforementioned technical challenges deeply investigated by numerous researchers. Perhaps, the first attempt to construct a hydrostatic stress dependent yield function was performed by Drucker and Prager [1]. Drucker-Prager model has been still using at present, however it foresees a zero resistance in tension since it was proposed for soil mechanics. Then, Gurson at his pioneering work proposed a hydrostatic stress dependent yield locus definition which has still been working as a solid basis [2]. Apart from being hydrostatic stress dependent, Gurson model was also created through a damage-coupled manner which means that damage parameter also contributes to the plastic potential which makes it quite appropriate for porous materials [3]. In the specific subfield of cast iron plasticity, tension/compression asymmetric material modeling was also investigated in a deeply manner. The most common and appropriate way to handle this asymmetry is to use multiple yield surface definitions [4,5,6,7,8]. Similar and relatively straight-forward application of this kind of modeling strategy is also used by the commercial finite-element software ABAQUS/Standard. It uses a J₂ plasticity formulation in compression modes whereas regarding tensile stress states a Rankine-cube like yield function is defined [9]. In this regard, the studies of Josefson and Hjelm [10] and Metzger et al. [11] have a distinguishing character such that they performed benchmark analysis among existing possible multi-surface yield surface definitions. In particular, there also studies which were devoted to micro-mechanically motivated material models, either they were embedded with unit cell and homogenization or microstructural interactions are coupled with macro-mechanics [12]. Some of them clearly includes detailed microstructural analysis and quantitative metallography as in the studies of Pina et al. [13], Fernandino et al. [14] and Brauer et al. [15]. From this perspective, Cocks also have proposed a new hydrostatic yield locus definitions [16] which have certain advantages especially for industrial applications. The main advantage is that the yield locus definition does not depend on hardening of the matrix (defect-free portion of the material), thus the yield definition contains two specific void volume functions which acts on macro effective and (Von mises) hydrostatic stress separately. This type of yield expression provide significant ease in mathematical manipulations and especially in partial differentials. Indeed, the need for material parameter extraction is also limited. Therefore, this model (Cocks’89) and some of its derivations are studied by some following researches [17,18]. And recently Cocks’89 model was implemented to assess the mechanical performance of cast aluminum samples by our research group [19]. Moreover, determination of SRS was also performed for various type of materials. However, the SRS related researches generally focused on parameter extraction by experimental methods [20,21,22,23] or theoretical formulations [24,25]. The current contribution differs from those researches such a way that SRS was experimentally obtained as a function of strain and strain rate and this parameter was buried into the constitutive material model (UMAT file) as a state variable. For that purpose, uni-axial tension and compression tests were conducted for 0.001, 0.1 and 10 (s−1) strain rates at Gleeble thermo-psychical simulator machine. The necessary data processing procedures were performed aiming to detect the SRS parameter in an asymmetric and rate dependent fashion. And lastly, this valuable data was coupled with a modified Cocks’89 based formalism to account for rate dependency and tension/compression asymmetry. Although G18NiCrMo3-6 is widely used in engineering designs especially for structural purposes, there is very limited information in the literature especially regarding its material parameters. The existing literature data on G18NiCrMo3-6 is mostly related to empirical and/or theoretical relation between the process parameters and final mechanical properties [26,27]. This study intends to fill this technical gap which would probably assist any further constitutive modeling efforts regarding G18NiCrMo3-6 material henceforth.

2. Materials and Methods

2.1. Studied Material

As indicated in the previous section, the studied cast steel grade is G18NiCrMo3-6. In particular, the material was in QT-1 condition which means that it experienced a conventional quench and tempering QT-1 operation. (QT-1 condition corresponds to a 25 Joule of impact energy requirement in Charpy test at -20 °C in EN 10340 standard) The casting samples had a process route as like austenization at 920 °C which was followed by oil quenching operation. And as a last step, tempering process was carried out at 500 °C Chemical composition of the casting samples was also displayed in Table 1.
Two micrographs of the casted samples can be found in Figure 1, where the tempered martensite dominant micro-structure could easily be observed at ×5000 and ×50 magnification. For metallographic inspections, related sample preparations procedure was applied which consists of several grinding and polishing operations followed by etching with 5% nital solution.

2.2. Mechanical Testing

Mechanical tests were conducted in uni-axial tension and compression condition at 0.001, 0.1, 10 (s−1) strain rates through Gleeble-3500 thermo-mechanical simulator machine. For that purpose, cylindrical specimens (ϕ8*12 mm) were manufactured for the compression tests whereas dog-bone cylindrical specimens having an initial gauge length of 12 mm were used in tensile testing. The specimens were manufactured while having a good surface finish quality, especially the compression test specimens processed through grinding operations to assure the necessary parallelism between the frontal faces. The technical drawings and real pictures of the specimens were shown in Figure 2. Furthermore, aiming to increase the precision in strain measurement tactile extensometer was implemented to tensile tests at 0.001 and 0.1 (s−1) strain rates. Apart from those tests, the strain values were computed on the basis of conventional cross-head displacement data. A test set-up image with the extensometer installation was also given in Figure 2. All mechanical tests were performed 3 times to ensure the consistency of results. The whole data of mechanical tests were submitted at Section 4.1.
Thanks to the fully integrated digital closed-loop control system of the Gleeble-3500, strain rate during the whole deformation process could be monitored and controlled with high precision. The true stress vs. true strain data was able to be created by the test machine. As can be seen in Figure 3, the results were assessed as satisfactory.
Afterwards, a specific code was created in MATLAB® environment to compute the yield stresses for the whole tests. To do this, the conventional offset stress ( R p 0.2 ) method was used. A sample data regarding this computation method was illustrated and also the computed yield stress value was written in Figure 4.

2.3. Determination of SRS

After being obtained the strain-stress response at specific strain rates, this data was processed properly to obtain the SRS parameter (As a general convention of theory of plasticity, SRS parameter is often denoted as m parameter). When a power-law based strain rate effect (Equation (1)) is used, then automatically parameter m can be obtained by processing of two plastic response at distinct strain rates. (Readers should give attention to the fact that first component of Equation (1) is the rate-independent hardening functions, and the second term contributes the rate sensitivity effect). In other words, when two flow curves are present (in general one of them is the reference train rate data), it is possible the determine m by the help of Equation (2).
σ = γ   ε p * ε p ˙ ε 0 ˙ m
m ( ε 0 ,     ε p ˙ ) = ∂ ln ⁡ ( σ 1 σ 0 ) ∂ ln ⁡ ( ε 1 ˙ ε 0 ˙ )
In Equation (1), ε p   ˙ is the strain rate which is apart from the reference strain rate ε 0 ˙ . Within the scope of this contribution ε 0 ˙   was taken as 0.001 (s−1), as like the general rule-of-thumb of plasticity, which is based on the fact that beyond this limit materials do mostly not possess any rate dependency. Furthermore, in Equation (2), σ 0   and σ 1 are the true stress values which correspond to the same strain value at the strain rates of ε 0 ˙   and ε 1 ˙ , respectively.
As can be observed in Equation (2), m is not constant, and it is generally a function of plastic strain and strain rate. However, it is still possible to obtain it with proper data processing operations. This task also fulfilled by a specific MATLAB® code, either. Since the experimental data was obtained with high frequency (may reach up to 10⁵ Hz), linear interpolation approach was accepted as a proper solution. While using the above-mentioned formulation and the procedure, m was determined regarding tension and compression asymmetry as like Figure 5. The built-in function interp1 of MATLAB® and the above-mentioned formulation were used, for that purpose (In order to capture the asymmetry of SRS in tension and compression zones, m was computed separately for the designated stress states specifically). The obtained m parameter data was depicted as an advanced version (surface data) at Section 4 since it creates a 3D surface by having two independent variables).

3. Results

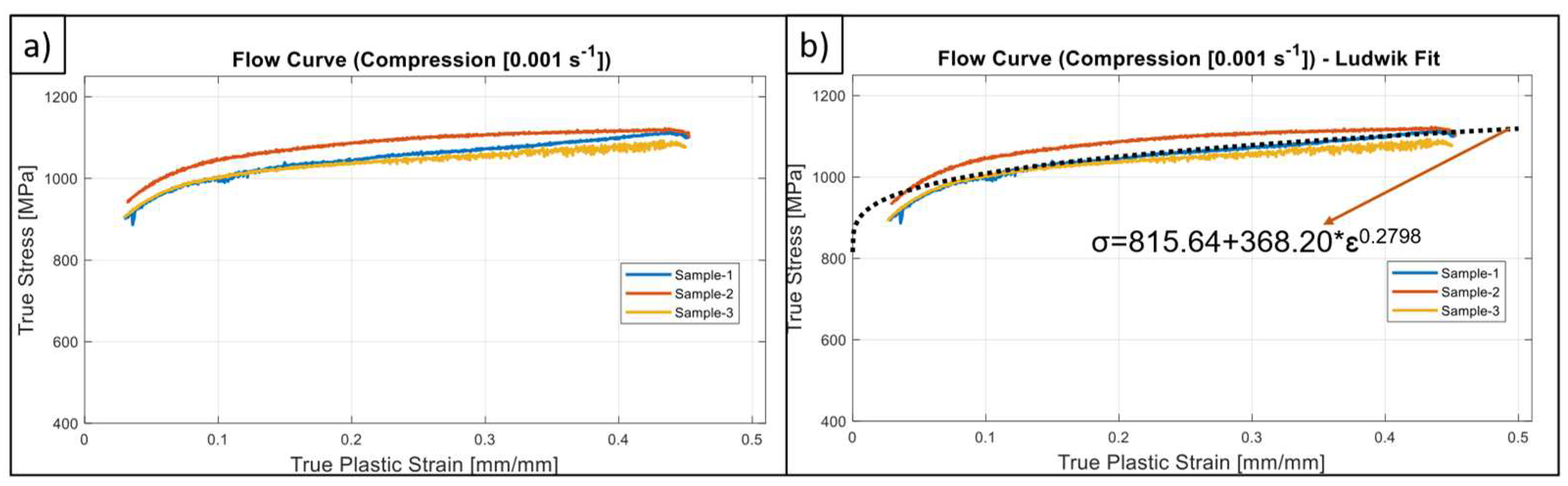
3.1. Basic Formulation

The yield locus was defined in Cocks’89 material model as in Equation (3).
ϕ = σ e q 2 g 1 ( f ) + σ m 2 g 2 ( f ) ⏟ σ ¯ − σ y = 0
In Equation (3), σ e q   is the equivalent Von Mises stress and σ m   is mean stress which were explicitly given in Equation (4), moreover g 1 and g 2 are functions of f which is nothing but the void volume fraction. In particular, σ   ¯ is the equivalent stress definition of Cocks’89 plasticity model.
σ e q = 3 2 S i j S i j   ,     σ m = σ k k 3
In Equation (4) σ is the (Cauchy) stress tensor and S i j is the deviatoric part of it (Please note that Einstein’s summation convention is in place for the formulation). Therefore, σ k k is actually a scalar value and equals to I 1 which is the first invariant of the stress tensor (Aiming to eliminate any possible confusions, the tensorial expressions were designated by bold character to be easily distinguished from scalar quantities). To clarify the yield locus definition in Cocks’89, the two separate function of f was also given in Equation 5 As expected, when → 0 , i.e., void volume fraction is zero (conventional metal plasticity approach), the yield locus definition turns out to the Von Mises yield criteria 3 J 2 − σ y = 0 .
g 1 = 1 − f 2 1 + 2 3 f ,   g 2 = 2 9 1 + f 1 − f 2 f
By assuming associative flow rule, the plastic strain rate equation can be written as Equation6. (Similar to the conventional computational plasticity approach, Equation (6) was constructed as a time rate of change form since the analysis are conducted via time integration scheme).
ε p ˙ = λ ˙   ∂ ϕ ∂ σ ⏟ N p
Equation (6), ε p is the plastic strain tensor, λ   is plastic multiplier and N p is the unit normal vector of the plastic flow, while dot operator denotes time derivative of the tensors (Unit normal vector was given with capital letter to eliminate the confusion with n and n+1 subscripts of time integration). By taking the partial derivative of Equation (4), reads as (Equation (7)):
N p = 3 2 S i j ( g 1   σ ¯ ) + 1 9 σ k k ( g 2   σ ¯ ) 1
In this study, Euler backward time integration scheme was used, then N p calculation (Equation (8)) dictates under Equation (7).
N n + 1 p = 3 2     S i j n + 1 ( g 1   σ ¯ n + 1 ) + 1 9   σ k k n + 1   ( g 2   σ ¯ n + 1 ) 1
By combining Equation (6) and Equation (8), one can obtain the plastic strain tensor at the end of time increment as (Equation (9)):
ε n + 1 p = Δ λ   ⏟ λ ˙ d t N n + 1 p
Equation (9) can also be written as a scalar form as Equation (10), where ε ¯   denotes equivalent plastic strain:
ε ¯   n + 1 p = Δ λ   N n + 1 p + ε ¯   n p
On the other hand, with the assumption of incompressible plastic flow of the defect-free matrix material (without any porosity), the only contribution to volume change is the change of porosity level. Then, the accumulation of porosity level can directly by linked to non-isochoric portion of strain tensor as indicated in Equation (11) (This assumption omits the contribution of elastic strains to volume change, but it is still a proper strategy since elastic strains are extremely small compared to plastic counterparts especially in moderate strain regime).
f ˙ = 1 − f * ε ˙ k k
Again, the similar convention of Equation (9), f was defined at the end of the time increment as Equation (12):
f n + 1 = f n + ( 1 − f n + 1 ) ( ε ˙ k k n + 1 ) Δ t = f n + ( 1 − f n + 1 ) ( Δ ε k k ) n + 1
By necessary mathematical manipulations finally Equation (12) converts to Equation (13)
f n + 1 = f n + ( Δ ε k k ) n + 1 1 + ( Δ ε k k ) n + 1
Combining Equation (12), Equation (13) and Equation (8) finally yields Equation (14) for f n + 1 .
f n + 1 = f n + Δ λ   1 3 σ k k n + 1   ( g 2 ) n   σ ¯ n + 1 1 + Δ λ   1 3 σ k k n + 1   ( g 2 ) n   σ ¯ n + 1
Equation (14) also means that at the end of time increment, when the stress and strain update is conducted, f can also be determined. Thus, f parameter was processed as like a state variable. Sticking to elastic predictor - plastic update methodology of computational plasticity, σ ¯ n + 1 can be written in an open form as (Equation (15)):
σ n + 1 = 2 G   d e v ε n + 1 − d e v ε n + 1 p   + κ     t r ε n + 1 − t r ε n + 1 p     1
In Equation (15), G is the shear and κ is the bulk modulus, in addition dev and tr represent the deviatoric part and trace of the tensors, respectively. Combining Equation (8), Equation (9) and Equation (15) yields (Equation (16)) for σ n + 1 .
σ n + 1 = 2 G   d e v ε n + 1 − d e v ε n p − Δ λ   3   2   d e v σ n + 1   g 1 n   σ ¯ n + 1   + κ   [   t r ε n + 1 − … … t r ε n p − 1 3   t r σ n + 1 )   Δ λ     g 2 n   σ ¯ n + 1 ]   1
By rearranging and conducting necessary mathematical manipulations, Equation 16, σ n + 1 can be decomposed as Equation (17) and Equation (18).
d e v ( σ n + 1 ) = 2 G   [   d e v ε n + 1 − d e v ε n p ] 1 + 3 G Δ λ   g 1 n   σ ¯ n + 1
t r ( σ n + 1 ) = 3 κ   [   t r ε n + 1 − t r ε n p ] 1 + κ Δ λ   g 2 n   σ ¯ n + 1
With the help of Equation (3) and Equation (18), the yield locus definition for the plastic increment can be formulated as Equation (19). For the simplicity of formulation, the nominators of Equation (17) and Equation (18) (expressions in blue color) were termed as P and Q, respectively.
ϕ n + 1 = 3   2   d e v ( σ n + 1   :   d e v ( σ n + 1 ) ]   g 1 n + 1   9   [ t r 2 ( σ n + 1 ) ]   g 2 n
The basic motivation behind Equation (19) is to formulate the yield locus as a function of incremental plastic multiplier ( Δ λ ). One can easily observe that in Equation (19) the first term was composed of all known quantities. In other words, the only unknown in Equation (19) is the incremental plastic multiplier (Please note that σ ¯ n + 1 = f ( Δ λ ) ) By means of the equilibrium condition ( ϕ n + 1 = 0 ) and the trial stress (elastic predictor) formulation (Equation (21)), Equation (19) can be reconstructed as Equation 20 by leaning to co-axiality principle (Equation (22)) meaning that trial and Cauchy stress tensors have the same unit outward normal direction.
ϕ n + 1 = S n + 1 t r i a l   :   S n + 1 t r i a l   g 1 n   P 2 + 1   9   [ σ n + 1 t r i a l ] 2   g 2 n   Q 2 − σ y n + 1 = 0
σ n + 1 t r i a l = 2 G     d e v ε n + 1 − d e v ε n p   + κ     t r ε n + 1 − t r ε n p 1
N n + 1 p = N t r i a l p
As the fact that Equation (20) is a non-linear equation of one unknown, it could be solved by means of numerical methods. In this contribution, Newton-Raphson method was engaged to solve Equation 20 with a convergence criteria of 10−6.
The details of the time integration scheme in UMAT subroutine was given in the following section.

3.2. Time Integration Procedure

The UMAT subroutine runs as follows:
  • Initialization: Uptake the material parameters, state variables and the deformation gradient (F) at beginning of the time increment.
  • Computation of strain tensor: Compute the Hencky strain tensor by use of F (Our code was constructed as finite-strain basis in such a way that free body translations were eliminated by means of Hencky strain measure [28], however Kroner decomposition [28] was discarded for the present study). Hencky strain measure is one of the most appropriate ways to deal with moderate deformations [30].
  • Check the plasticity criterion: Compute the trial stress (Equation (21)) and check for the yield locus definition (Equation (23)).
    ϕ t r i a l = S n + 1 t r i a l   :   S n + 1 t r i a l   g 1 n + 1   9   [ σ k k t r i a l ] 2   g 2 n   − σ y n ≤ 0
  • Update state variables:
    If φ t r i a l ≤ 0 → step is elastic (∆λ = 0) thus, conserve the state variables.
    If φ t r i a l > 0 → step is plastic, solve for ∆λ (Equation (20)). Update σ n + 1 , ε n + 1 p , f n , m n .
  • Finalization: Deliver the state variables and tangent modulus to Abaqus solver for the convergence check.

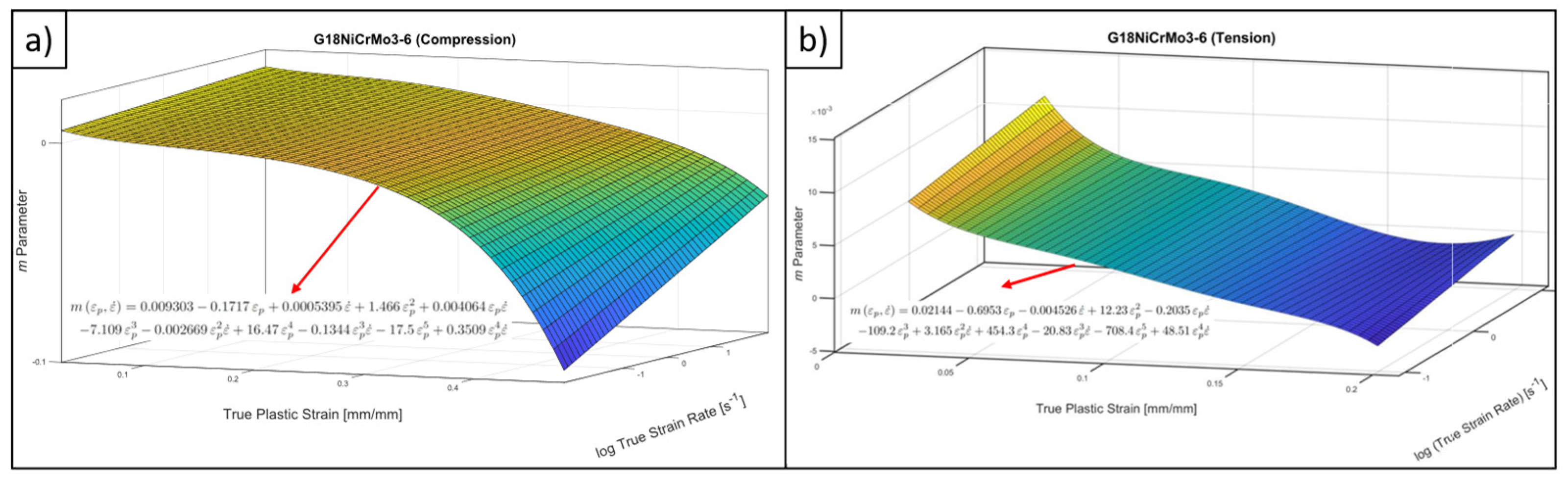
3.3. Imposing the Asymmetry and Rate Dependence

The tension/compression asymmetry and rate dependence contribute to the computation of flow through incremental plastic multiplier as Equation (20). In particular, the experimentally obtained material parameters differ where the state of stress behaves as a switching parameter. This fact explained through mathematical expressions as below Equation (24):
σ y = σ 0 + B   ε ¯ p r *   ε p ˙ ε 0 ˙ m *
where r *   is defined as like in Equation (25). Likewise, σ 0   and m * were determined separately regarding tension and compression conditions.
r * = r t                           f o r   t e n s i o n   r t   ∈   N r c     f o r   c o m p r e s s i o n   r c   ∈   N
Then, Equation (24) could be rewritten as Equation (26) (Please note that ∆ t is a known scalar quantity which is delivered by the Abaqus solver).
σ y = σ 0 + B   ε ¯ p n + Δ λ r *   Δ λ ∆ t   ε 0 ˙ m *

4. Results and Discussion

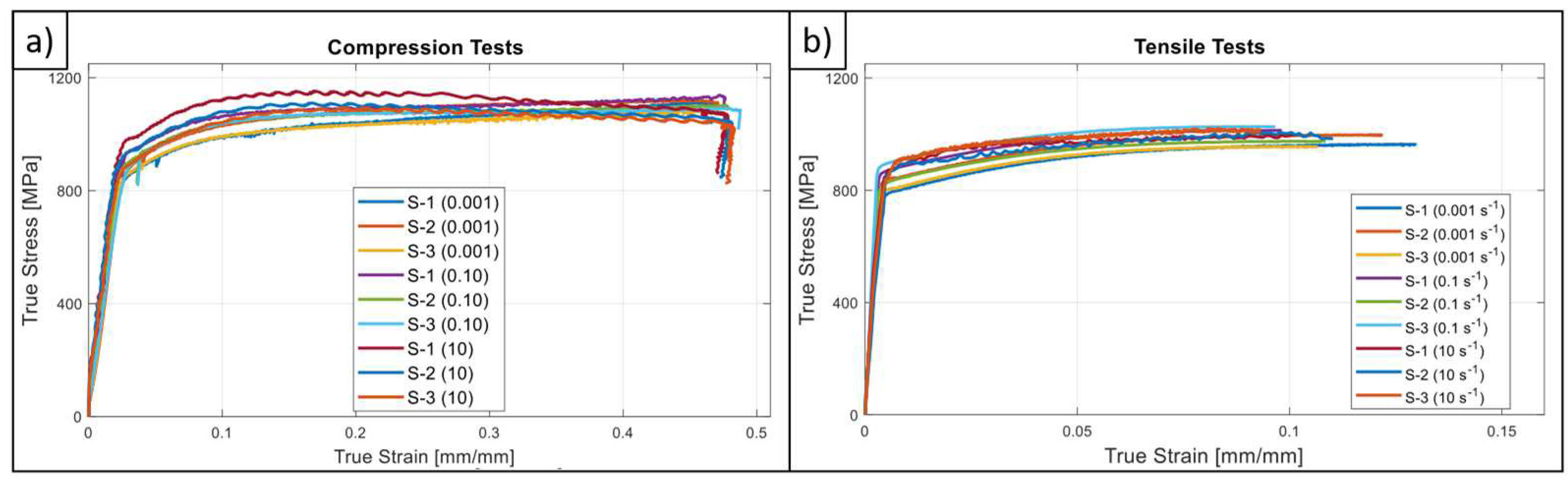
4.1. Mechanical Testing

The obtained Gleeble test results (whole set) were depicted in Figure 6.
Moreover, in order to perform the necessary curve fitting operation which was proposed in Equation (24), the flow curves (true plastic strain vs. true stress) at the reference strain rate were extracted with data processing. At a first glance, Ludwik equation [31] ( σ y = σ 0 + B ε p n ) suits quite well to the experimental data. Therefore, this formalism was used to model the flow curve behavior. The flow curves and fitted parameters of Ludwik equation were shown in Figure 7 for the compression mode. The explained data processing procedure was also conducted for tensile tests and computed parameter set was given in Table 2.
σ 0   ( 0.001   s − 1 ) σ 0   ( 0.1   s − 1 ) σ 0   ( 10 s − 1 )

4.2. Determination of SRS

After having being conducted the mechanical tests, SRS parameter was calculated with the aforementioned methodology. The obtained SRS behavior was constructed as a surface plot in Figure 8 aiming to display the distinct behavior in compression/tension asymmetry, The experimental results (only the mid-valued ones) were depicted in Figure 9.
In Figure 8 and Figure 9, as a first observation it could be stated that the studied material has a dominantly saturation type plastic response. This character is more dominant for moderate strain rates. Secondly, the strain rate dependence can also be detected in both stress states which is more effective in near-yielding zone. With the increasing plastic strain, the rate sensitivity diminishes and even turn out to be negative. In other words, G18NiCrMo-3-6 shows a strain softening effect at moderate strain rates compared to the quasi-static condition. This fact was interpreted as adiabatic heating induced thermal softening effect. This finding agrees well with the previous literature data [32,33,34]. Since the studied material could be accepted as high-strength metal by having a UTS nearly 1.0 GPa, there is a significant amount of inelastic energy introduced to the system during deformation process. In our view, this is the basic reason behind strain softening phenomena after moderate strain values (i.e., ε p ≥ 0.30 ). Since the obtainable strain values are much more higher for compression tests, this strain softening is modest in tension side. In addition, it is also worth to emphasize that, there is also a slight change in yield stress for tension/compression asymmetry, as expected. The compressive yield stress is bigger than the tensile one 4%. As a result, separate characters of SRS parameter were quantified and the analytical formulations were also given in Figure 8. The strain softening character in high strain value at compression tests yield a negative SRS phenomena. Therefore, in high strain rate in compression, material on the onset of plastic deformation exhibits rate sensitivity unlike the moderate strain values. This type of flow stress character cannot be precisely predicted by the conventional approach of Johnson-Cook plasticity [35] model where the flow curve is raised or lowered by a constant multiplier term.

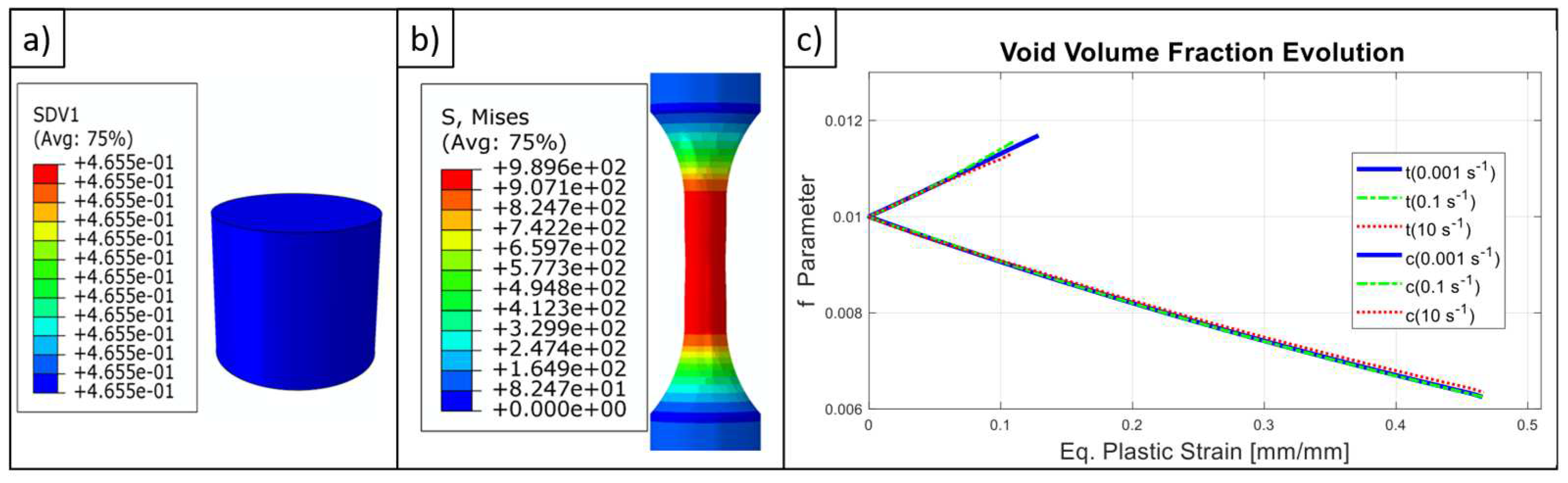
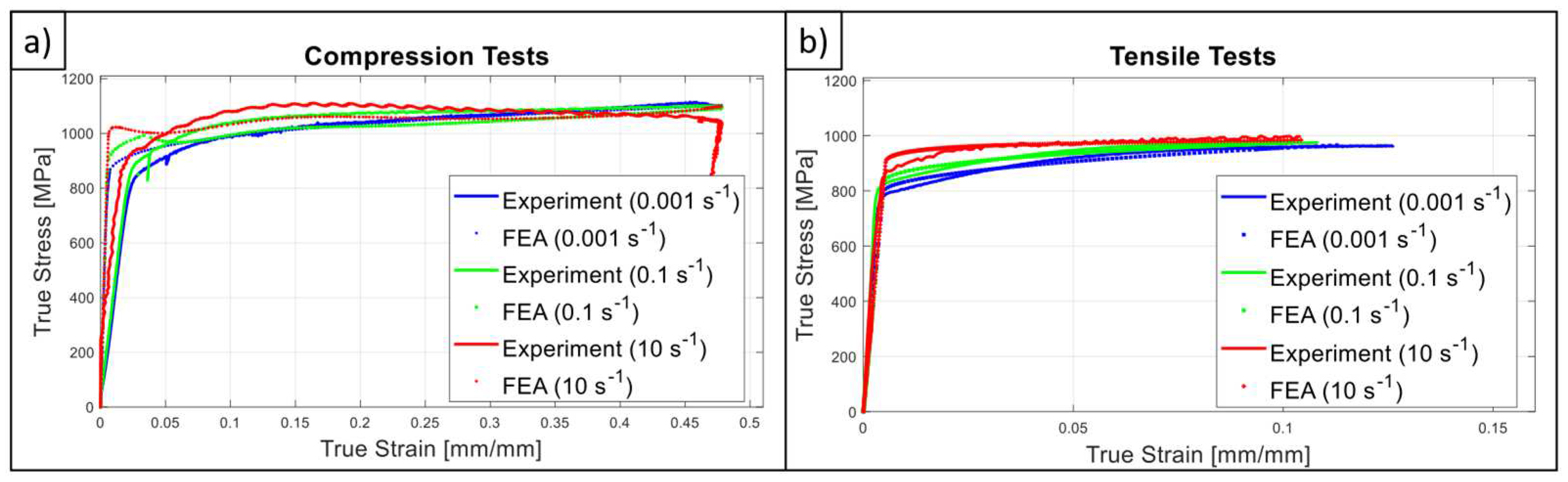
4.3. FEA Models

The experiments were reproduced in Abaqus environment with the created UMAT subroutine. Based on the axi-symmetric nature of the conducted mechanical tests, the FEA models were modeled by CAX8R elements (biquadratic, quadrilateral element with reduced integration) in 2D condition. The experimentally obtained time vs. displacement data was given as a boundary condition to the upper face while providing encastre (zero rotation and translation) condition at the lower face of the specimens. With this type of modeling, the rate effect can be introduced to the FEA model under the circumstance of sticking to SI unit system. In this perspective, the elasto-plastic behavior of the material is numerically obtained, and the results were compared with the experimental findings. Keeping in mind the condition that (i) tensile tests were modeled up to diffuse necking and in compression tests the barreling effect is neglected, the total deformations are both homogeneous in compression specimen and the gauge zone of the tensile specimen. In fact, the stress values and the evolution of porosity level (f) were able to be computed by the code (In that sense, the analysis can be modeled by one element test without sacrificing from the precision of results, however, a stable meshing was applied on the geometries to be ready for upcoming efforts regarding instable plastic flow region). This UMAT file intended to be modified and enhanced to capture the response in instability region or even in fracture by improving the formulation of void volume fraction and coupling it with any damage model approach. In Figure 10, some results in calculated stress, equivalent plastic strain and porosity evolution values were depicted, in a detailed manner. Furthermore, in Figure 11, the comparison of experimental and numerical results was given. Those reveals that, the proposed material constitutive model succeeds in capturing pressure, rate dependent and asymmetric plastic behavior of G18CrNiMo3-6 material. For FEA analysis, initial void volume fraction was taken as 0.010.
) (b) Eq. stress value at the end of FEA analysis (0.001 s − 1 ) (c) The evolution of void volume fraction regarding to FEA analysis.

5. Conclusions

In this study, the SRS of G18NiCrMo3-6 cast steel material was experimentally obtained including tension/compression asymmetry. For that purpose, a specific set of mechanical testing was carried out at distinct strain rate conditions. By means of this experimental effort, power-law based strain rate dependent flow behavior was determined and the necessary material parameters were extracted and shared with readers. To better capture SRS, m parameter was formulated as strain, strain rate and asymmetry dependent fashion. Finally aforementioned material model parameters were embedded to a pressure and rate dependent constitutive model by means of a UMAT file. The following outputs could be withdrawn from the current contribution:
  • G18NiCrMo3-6 material possess an asymmetric yielding character, in other words, yields stress in compression in 4% bigger than the tensile one.
  • Indeed, the strain hardening and SRS character is also quite asymmetric for the studied material. This fact was quantified with the help of power law-based flow stress formulation and determination of m parameter. From a general point-of-view, SRS is more dominant on tensile direction however, it has a decreasing tendency with increasing strain as like the compressive stress states. In the view of authors’, the shared material data within this study provides an important resource for the upcoming research activities on G18NiCrMo3-6 about which the existing literature data is extremely limited.
  • Unlike the tensile test in medium strain rate regime, strain softening phenomena was observed in compression tests which was interpreted as the effect of adiabatic heating. Owing to this finding in compression side the material exhibits rate sensitivity character up to certain strain value but then strain softening effect contributes to the plastic response. This fact can be handled by defining SRS parameters as a function of strain as in the proposed constitutive model. On the contrary, a conventional Johnson-Cook type formalism cannot catch up this phenomenon where the effect of rate contribution is formulated through a constant multiplier term.
  • The created constitutive model (UMAT file) run without any problem which was formulated on finite strain basis and uses implicit time integration scheme. This UMAT file could easily serve in inspecting the effect of material parameters (like initial void volume fraction and etc.) on the macro-mechanical performance of any design which is made up of G18NiCrMo3-6.
  • Our efforts will focus on creating proper coupling between the estimated void volume fraction and any appropriate damage rule to improve the proposed model which would account for both damage, void coalescence, and localization phenomena.

Author Contributions

Conceptualization, B.Ç. and O.A.; methodology, B.Ç. and O.A.; software, B.Ç.; validation, B.Ç.; writing—review and editing, B.Ç. and O.A and E.B.; All authors have read and agreed to the published version of the manuscript.

Funding

This contribution is a portion of an R&D project which was funded by FNSS Savunma Sistemleri A.Ş. and Turkish Defense Industry Agency.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

FEA Finite element analysis
SRS Strain rate sensitivity
UMAT User subroutine to define a material’s mechanical behavior
UTS Ultimate tensile strength

References

  1. Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Quarterly of Applied Mathematics 1952, 10, 157–165. [Google Scholar] [CrossRef]
  2. Gurson, A.L. Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I—Yield Criteria and Flow Rules for Porous Ductile Media. Journal of Engineering Materials and Technology 1977, 99, 2–15. [Google Scholar] [CrossRef]
  3. Trillat, M.; Pastor, J. Limit analysis and Gurson’s model. European Journal of Mechanics - A/Solids 2005, 24, 800–819. [Google Scholar] [CrossRef]
  4. Coffin, L. F., J. The Flow and Fracture of a Brittle Material. Journal of Applied Mechanics 2021, 17, 233–248. [Google Scholar] [CrossRef]
  5. WIESE, J.W.; DANTZIG, J.A. Modeling stress development during the solidification of gray iron castings. Metallurgical Transactions A 1990, 21, 489–497. [Google Scholar] [CrossRef]
  6. Hjelm, H.E. Yield Surface for Grey Cast Iron Under Biaxial Stress. Journal of Engineering Materials and Technology 1994, 116, 148–154. [Google Scholar] [CrossRef]
  7. Altenbach, H.; Stoychev, G.; Tushtev, K. On elastoplastic deformation of grey cast iron. International Journal of Plasticity 2001, 17, 719–736. [Google Scholar] [CrossRef]
  8. Hosseini, E.; Holdsworth, S.R.; Flueeler, U. A temperature-dependent asymmetric constitutive model for cast irons under cyclic loading conditions. The Journal of Strain Analysis for Engineering Design 2018, 53, 106–114. [Google Scholar] [CrossRef]
  9. Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp: United States, 2009. [Google Scholar]
  10. Josefson, B.L.; Hjelm, H.E. Modelling Elastoplastic Deformations in Grey Cast Iron. In Low Cycle Fatigue and Elasto-Plastic Behaviour of Materials—3; Springer Netherlands: Dordrecht, 1992; pp. 465–472. [Google Scholar] [CrossRef]
  11. Metzger, M.; Seifert, T. Computational assessment of the microstructure-dependent plasticity of lamellar gray cast iron – Part II: initial yield surfaces and directions. International Journal of Solids and Structures 2015, 66, 194–206. [Google Scholar] [CrossRef]
  12. Andriollo, T.; Thorborg, J.; Tiedje, N.S.; Hattel, J. Modeling of damage in ductile cast iron - The effect of including plasticity in the graphite nodules. IOP Conference Series: Materials Science and Engineering 2015, 84, 012027. [Google Scholar] [CrossRef]
  13. Pina, J.; Shafqat, S.; Kouznetsova, V.; Hoefnagels, J.; Geers, M. Microstructural study of the mechanical response of compacted graphite iron: An experimental and numerical approach. Materials Science and Engineering: A 2016, 658, 439–449. [Google Scholar] [CrossRef]
  14. Fernandino, D.O.; Cisilino, A.P.; Boeri, R.E. Determination of effective elastic properties of ferritic ductile cast iron by computational homogenization, micrographs, and microindentation tests. Mechanics of Materials 2015, 83, 110–121. [Google Scholar] [CrossRef]
  15. Brauer, S.A.; Whittington, W.R.; Johnson, K.L.; Li, B.; Rhee, H.; Allison, P.G.; Crane, C.K.; Horstemeyer, M.F. Strain Rate and Stress-State Dependence of Gray Cast Iron. Journal of Engineering Materials and Technology 2017, 139. [Google Scholar] [CrossRef]
  16. Cocks, A. Inelastic deformation of porous materials. Journal of the Mechanics and Physics of Solids 1989, 37, 693–715. [Google Scholar] [CrossRef]
  17. Yalçinkaya, T.; Erdoğan, C.; Tandoğan, I.T.; Cocks, A. Formulation and Implementation of a New Porous Plasticity Model. Procedia Structural Integrity 2019, 21, 46–51. [Google Scholar] [CrossRef]
  18. Erdoğan, Can. Numerical Implementation and Analysis of a Porousplasticity Model for Ductile Damage Prediciton, PhD., Middle East Technical University, Turkey, January 2021.
  19. Gul, A.; Aslan, O.; Kayali, E.S.; Bayraktar, E. Assessing Cast Aluminum Alloys with Computed Tomography Defect Metrics: A Gurson Porous Plasticity Approach. Metals 2023, 13. [Google Scholar] [CrossRef]
  20. Maier, V.; Durst, K.; Mueller, J.; Backes, B.; Höppel, H.W.; Göken, M. Nanoindentation strain-rate jump tests for determining the local strain-rate sensitivity in nanocrystalline Ni and ultrafine-grained Al. Journal of Materials Research 2011, 26, 1421–1430. [Google Scholar] [CrossRef]
  21. Ghosh, A. On the measurement of strain-rate sensitivity for deformation mechanism in conventional and ultra-fine grain alloys. Materials Science and Engineering: A 2007, 463, 36–40. [Google Scholar] [CrossRef]
  22. Acharya, S.; Gupta, R.; Ghosh, J.; Bysakh, S.; Ghosh, K.; Mondal, D.; Mukhopadhyay, A. High strain rate dynamic compressive behavior of Al6061-T6 alloys. Materials Characterization 2017, 127, 185–197. [Google Scholar] [CrossRef]
  23. Kumaresan, G.; Kalaichelvan, K. Multi-dome forming test for determining the strain rate sensitivity index of a superplastic 7075Al alloy sheet. Journal of Alloys and Compounds 2014, 583, 226–230. [Google Scholar] [CrossRef]
  24. Nemes, J.A.; Eftis, J.; Randles, P.W. Viscoplastic Constitutive Modeling of High Strain-Rate Deformation, Material Damage, and Spall Fracture. Journal of Applied Mechanics 1990, 57, 282–291. [Google Scholar] [CrossRef]
  25. Hao, S.; Brocks, W. The Gurson-Tvergaard-Needleman-model for rate and temperature-dependent materials with isotropic and kinematic hardening. Computational Mechanics 1997, 20, 34–40. [Google Scholar] [CrossRef]
  26. Fan, H.; Li, Y.; Jin, X.; Chen, B. Effect of tempering temperature on microstructure and mechanical properties of G18NiMoCr3-6. Jinshu Rechuli/Heat Treatment of Metals 2017, 42, 163–165. [Google Scholar] [CrossRef]
  27. Salemi, A.; Abdollah-zadeh, A. The effect of tempering temperature on the mechanical properties and fracture morphology of a NiCrMoV steel. Materials Characterization 2008, 59, 484–487. [Google Scholar] [CrossRef]
  28. Hencky, H. The Elastic Behavior of Vulcanized Rubber. Journal of Applied Mechanics 2021, 1, 45–48. [Google Scholar] [CrossRef]
  29. Kröner, E. Allgemeine Kontinuumstheorie der Versetzungen und Eigenspannungen. Archive for Rational Mechanics and Analysis 1959, 4, 273–334. [Google Scholar] [CrossRef]
  30. Anand, L. On H. Hencky’s Approximate Strain-Energy Function for Moderate Deformations. Journal of Applied Mechanics 1979, 46, 78–82. [Google Scholar] [CrossRef]
  31. Ludwik, P. Elemente der technologischen Mechanik; Springer Berlin, Heidelberg, 1909. [CrossRef]
  32. Sorini, C.; Chattopadhyay, A.; Goldberg, R.K. Micromechanical modeling of the effects of adiabatic heating on the high strain rate deformation of polymer matrix composites. Composite Structures 2019, 215, 377–384. [Google Scholar] [CrossRef]
  33. Soares, G.; Patnamsetty, M.; Peura, P.; Hokka, M. Effects of Adiabatic Heating and Strain Rate on the Dynamic Response of a CoCrFeMnNi High-Entropy Alloy. Journal of Dynamic Behavior of Materials 2019, 5. [Google Scholar] [CrossRef]
  34. Nasraoui, M.; Forquin, P.; Siad, L.; Rusinek, A. Influence of strain rate, temperature, and adiabatic heating on the mechanical behavior of poly-methyl-methacrylate: Experimental and modeling analyses. Materials and Design 2012, 37, 500–509. [Google Scholar] [CrossRef]
  35. Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates, and high temperatures. In Proceedings of the 7th International Symposium on Ballistics. The Netherlands, 1983, Vol. 21 (1), pp. 541–547.
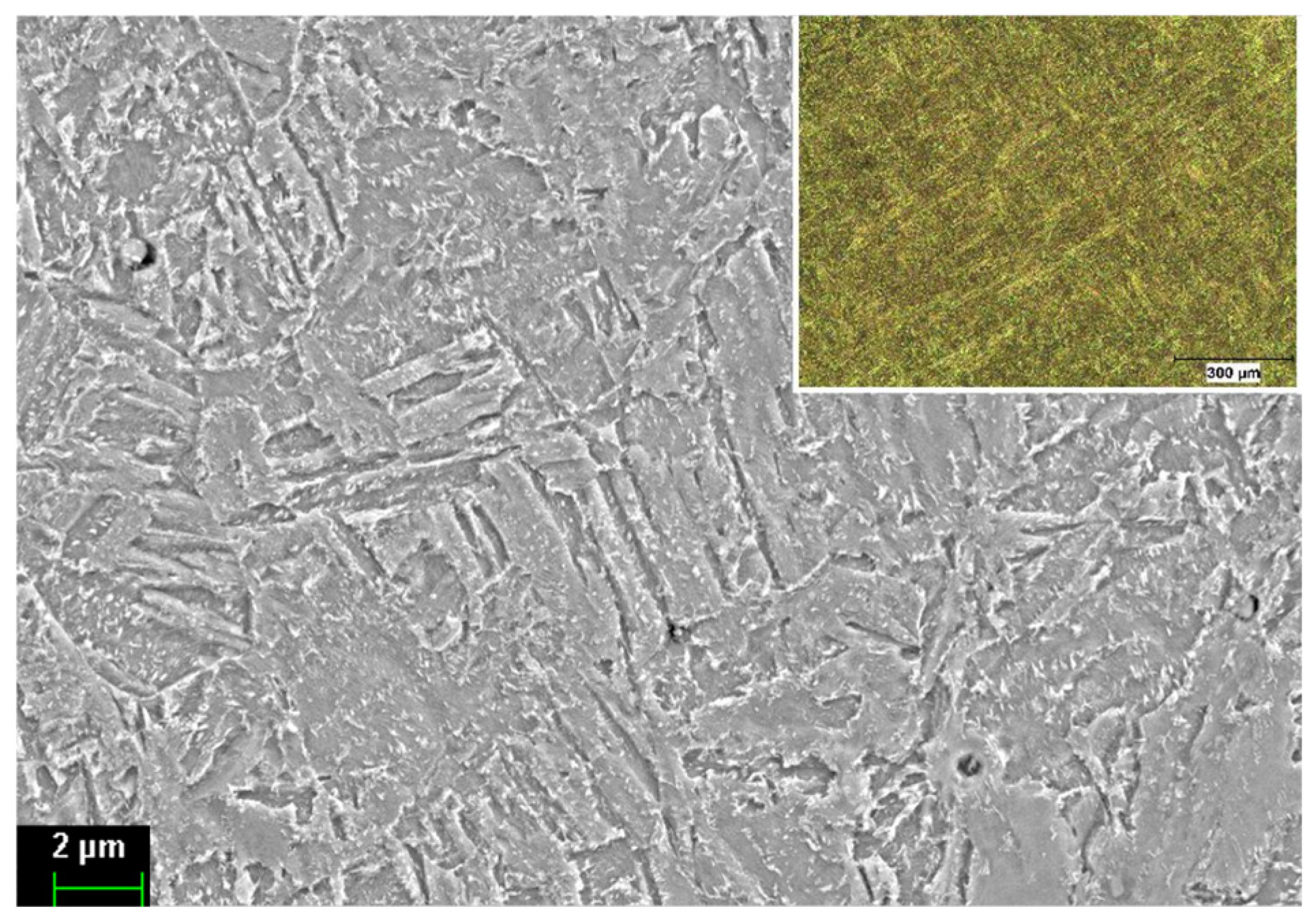
Preprints 86452 g001
Figure 1. SEM micro-graphs of the casted sample taken at 5000×; the inset is optical micro-graphs taken at 50× magnification.
Figure 1. SEM micro-graphs of the casted sample taken at 5000×; the inset is optical micro-graphs taken at 50× magnification.
Preprints 86452 g001
Preprints 86452 g002
Figure 2. (a) Pictures and technical drawings of the samples (b) Tensile test set-up with extensometer.
Figure 2. (a) Pictures and technical drawings of the samples (b) Tensile test set-up with extensometer.
Preprints 86452 g002
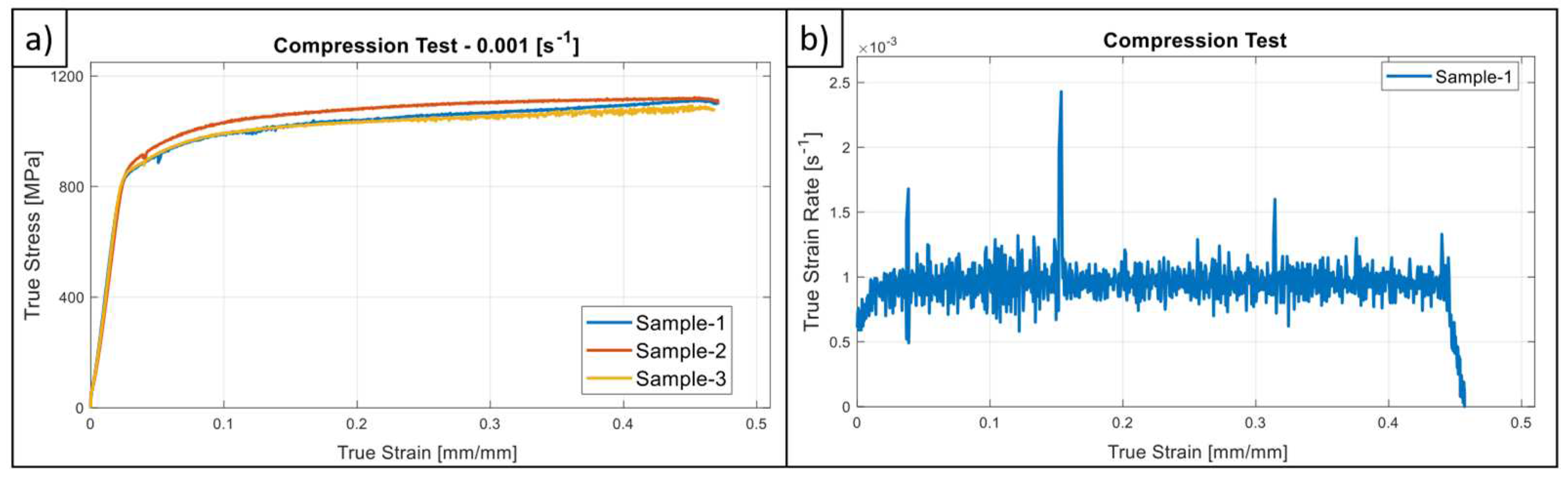
Preprints 86452 g003
Figure 3. (a) Test results for uni-axial compression test at 0.001 (s−1) (b) True strain vs. true strain rate data for Sample-1 at 0.001 (s−1).
Figure 3. (a) Test results for uni-axial compression test at 0.001 (s−1) (b) True strain vs. true strain rate data for Sample-1 at 0.001 (s−1).
Preprints 86452 g003
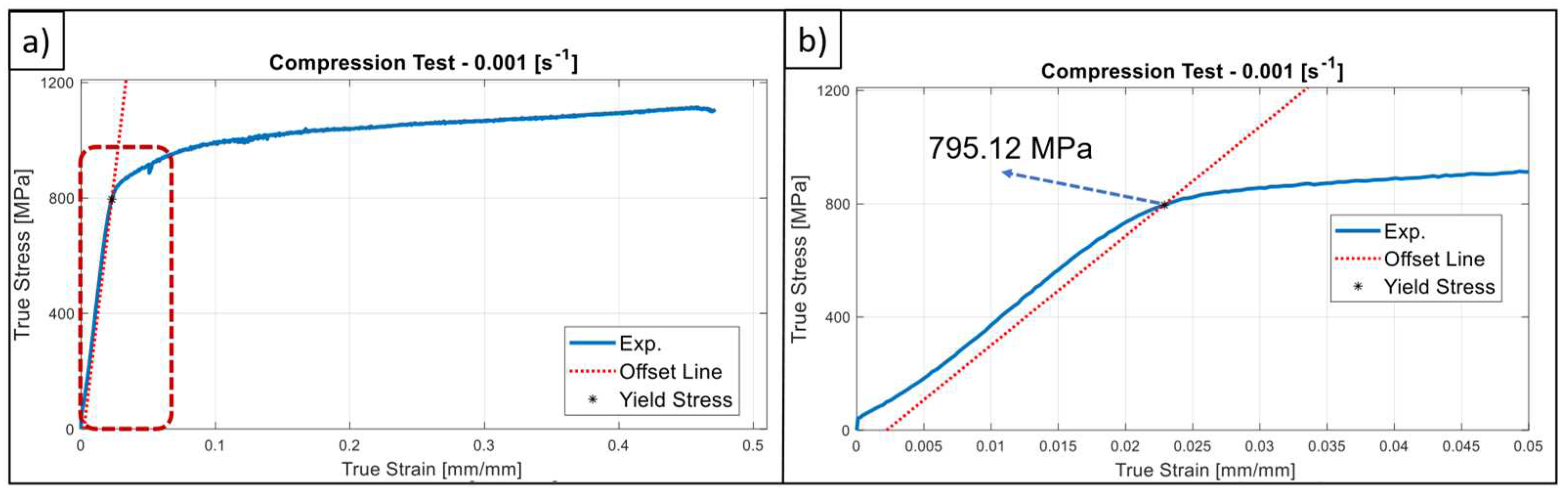
Preprints 86452 g004
Figure 4. (a) True strain vs. true stress data of Sample-1 (b) Detailed view of the designated (red dotted) area.
Figure 4. (a) True strain vs. true stress data of Sample-1 (b) Detailed view of the designated (red dotted) area.
Preprints 86452 g004
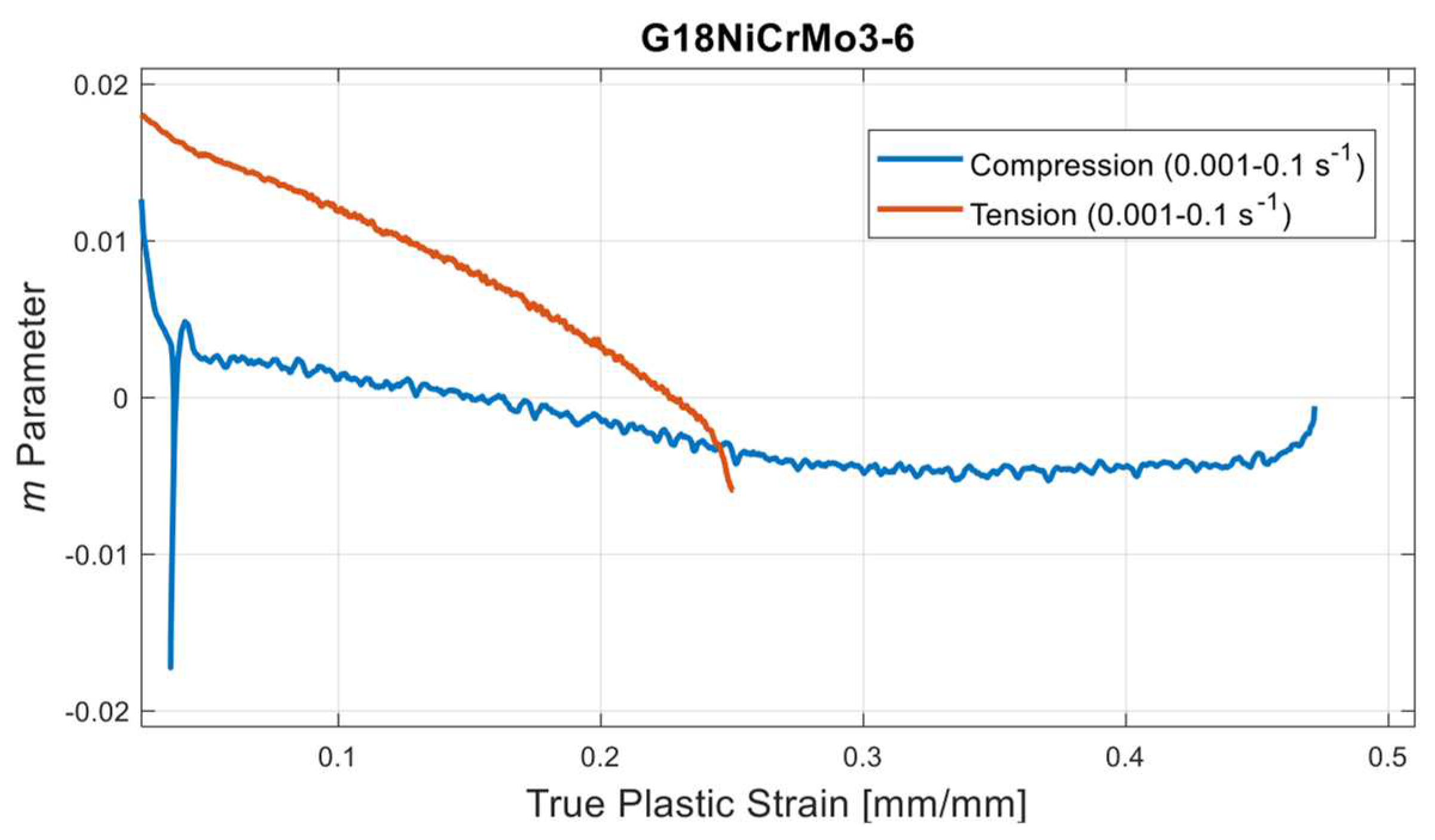
Preprints 86452 g005
Figure 5. SRS parameter for tension and compression modes.
Figure 5. SRS parameter for tension and compression modes.
Preprints 86452 g005
Preprints 86452 g006
Figure 6. (a) Test results of uni-axial compression tests (b) Test results of uni-axial tensile tests.
Figure 6. (a) Test results of uni-axial compression tests (b) Test results of uni-axial tensile tests.
Preprints 86452 g006
Preprints 86452 g007
Figure 7. (a) Test results of uni-axial compression tests (b) Test results of uni-axial tensile tests.
Figure 7. (a) Test results of uni-axial compression tests (b) Test results of uni-axial tensile tests.
Preprints 86452 g007
Preprints 86452 g008
Figure 8. (a) SRS parameter for compressive stress states (b) SRS parameter for tensile stress states
Figure 8. (a) SRS parameter for compressive stress states (b) SRS parameter for tensile stress states
Preprints 86452 g008
Preprints 86452 g009
Figure 9. (a) Compression tests of ADI with distinct strain rates (b) Compression tests of CS with distinct strain rates.
Figure 9. (a) Compression tests of ADI with distinct strain rates (b) Compression tests of CS with distinct strain rates.
Preprints 86452 g009
Preprints 86452 g010
Figure 10. (a) Eq. plastic strain value at the end of FEA analysis (0.001 s − 1
Figure 10. (a) Eq. plastic strain value at the end of FEA analysis (0.001 s − 1
Preprints 86452 g010
Preprints 86452 g011
Figure 11. (a) Comparison of FEA and experiment for tensile tests (b) Comparison of FEA and experiment for compression tests.
Figure 11. (a) Comparison of FEA and experiment for tensile tests (b) Comparison of FEA and experiment for compression tests.
Preprints 86452 g011
Table 1. Chemical composition of G18NiCrMo3-6 (%wt).
Table 1. Chemical composition of G18NiCrMo3-6 (%wt).
C Si Mn Ni Cr Mo Cu Fe
0.20 0.50 0.90 0.80 0.50 0.45 0.15 Balance
Table 2. Extracted parameters from curve fitting operations (Standard deviation values were indicated in parenthesis).
Table 2. Extracted parameters from curve fitting operations (Standard deviation values were indicated in parenthesis).
σ 0   ( 0.001   s − 1 ) σ 0   ( 0.1   s − 1 ) σ 0   ( 10 s − 1 ) B n
Compression 815.64 (±1.93%) 862.79 (±1.89%) 882.18 (±2.89%) 368.20 0.2798
Tension 808.65 (±2.70%) 858.73 (±2.84%) 876.80 (±1.36%) 551.30 0.5075
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated