Exact Similarity Solutions of Unsteady Laminar Boundary Layer Flows

Preprint

Article

Exact Similarity Solutions of Unsteady Laminar Boundary Layer Flows

Altmetrics

Downloads

225

Views

108

Comments

Bohua Sun^*

This version is not peer-reviewed

Submitted:

28 September 2023

Posted:

30 September 2023

Read the latest preprint version here

Alerts

Abstract

The studies of laminar unsteady boundary layer flows is crucial for understanding turbulence origins. However, the task of finding its solutions poses a significant challenge. In this paper, we propose a novel approach by introducing a similar transformation to convert the 2D unsteady laminar boundary layer equations into a single partial differential equation with constant coefficients. By applying this transformation, we are able to obtain the exact solution for the velocity field of the 2D unsteady laminar boundary layer equations, specifically for the case of flat plate boundary flow. Notably, this is the first time that such an exact solution has been obtained.

Keywords:

Subject: Physical Sciences - Fluids and Plasmas Physics

1. Introduction

The origins of turbulence are a widespread phenomenon and remain one of the most significant unsolved mysteries in classical physics [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. The study of unsteady flows is considered crucial for understanding the dynamics of laminar-turbulence transition, especially in cases involving accelerated flows, motions from rest, or transitions from one steady flow to another [12,16].

The Navier-Stokes equations, which govern fluid flow, are highly complex and pose significant challenges in obtaining exact solutions. Only a few one-dimensional non-steady problems have been able to achieve exact solutions, such as Stokes’ problem and the flow due to an oscillating infinite plane. The latter was the first exact solution in fluid dynamics.

One example of an exact solution is Rayleigh’s problem, which involves an infinite flat plate impulsively started into motion in its own plane with a velocity of U. The solution to this problem is given by the equation

u (y, t) = U erfc (y / (2 \sqrt{ν t}))

, where erfc is the complementary error function.

However, despite these achievements, no exact solutions have been obtained for the unsteady boundary layer equations of any two-dimensional problem. This lack of exact solutions has shattered our expectations of finding them based on historical exact solutions. As a result, we are left with no choice but to confront this challenge and strive to find new ideas and approaches to explore new frontiers in understanding unsteady flows.

After introduction in Section 1, the rest of this paper is organized as follows. In Section 2, we formulate the 2D turbulent boundary layers and introduce a similarity transformation. Under special conditions, the partial differential equations of the 2D turbulent boundary layers can be reduced to a single ordinary differential equation. In Section 3, Flow along a flat plate at zero incidence in a uniform stream is studied, whos exact solution is obtained for the first time. In Section 4, the convergent channel flows is investigated. In Section 5, the wedge flows is also studied. Finally, in Section 6, conclusions and perspectives are drawn.

2. Similarity transformations of 2D laminar boundary layers equations

A thin flat plate is immersed at zero incidence in a uniform stream, which flows with speed

U (x)

and is assumed not to be affected by the presence of the plate, except in the boundary layer. The fluid is supposed unlimited in extent, and the origin of coordinates is taken at the leading edge, with x measured downstream along the plate and y perpendicular to it.

The unsteady Navier-Stokes equations of the two dimensional boundary layers flow under gradient,

\frac{d p}{d x}

, are reduced to

\begin{matrix} \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} & = 0, \end{matrix}

(1)

\begin{matrix} - \frac{1}{ρ} \frac{\partial p}{\partial y} & = 0, \end{matrix}

(2)

\begin{matrix} \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} & = - \frac{1}{ρ} \frac{d p}{d x} + ν \frac{d^{2} u}{d y^{2}}, \end{matrix}

(3)

and initial-boundary conditions:

\begin{matrix} u (x, 0, t) = 0, & v (x, 0, t) = 0, \end{matrix}

(4)

\begin{matrix} u (x, \infty, t) = U (x), \end{matrix}

(5)

where

ν

is the kinematic viscosity,

ρ

is flow density, p is pressure,

U (x)

is outer of boundary layer potential flow velocity. The pressure gradient must be negative, namely

\frac{d p}{d x} < 0

, to maintain the flow motion. For a curved boundary layers, the coordinates

(x, y)

should be replaced by

(s, n)

, where s is arc length and n is normal to the curve layers.

Integration of Equation (2) yields

\frac{p}{ρ} = \frac{p_{e}}{ρ}

, where

p_{e}

is a function of x only [3], then

\frac{\partial p}{\partial x} \approx \frac{d p_{0}}{d x}

. From Bernoulli equation, we have relation:

p_{e} + \frac{1}{2} ρ U^{2} = c o n s t a n t .

, leads to

\frac{d p_{e}}{d x} = ρ U \frac{d U}{d x}

. The boundary equations are reduced to following:

\begin{matrix} \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} & = 0, \end{matrix}

(6)

\begin{matrix} \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} & = U \frac{d U}{d x} + ν \frac{d^{2} u}{d y^{2}}, \end{matrix}

(7)

Introducing a stream function

Ψ (x, y)

and express the velocity components as follows

u = \frac{\partial ψ}{\partial y}, v = - \frac{\partial ψ}{\partial x},

(8)

with the relation in Equation (8), the mass conservation Equation (refrans-4) is satisfied, and the momentum conservation Equation (7) becomes

\frac{\partial ψ}{\partial t \partial y} + \frac{\partial ψ}{\partial y} \frac{\partial ψ}{\partial x \partial y} - \frac{\partial ψ}{\partial x} \frac{\partial ψ}{\partial y^{2}} = U \frac{d U}{d x} + ν \frac{d^{3} ψ}{d y^{3}},

(9)

and corresponding boundary conditions.

A suitable scaling factor for u could be the free stream velocity

U (x)

, while for y, "boundary-layer thickness"

δ (x)

, which increases with distance x, could be used. The similarity law of the velocity profile can thus be written as

u / [δ (x) U] = f (η)

with

η = y / δ (x)

, where the function

f (η)

is independent of x.

Regarding the similarity of time t, it is known that the time for any bulk property of the fluid, such as vorticity or momentum, to diffuse through a distance

δ

is of the order of

δ^{2} / ν

(the "diffusion time") [6], hence, we can introduce a dimensionless time as

τ = t / (δ^{2} / ν)

Based on the above understanding, introducing following transformations

\begin{matrix} ψ & = U (x) δ (x) f (η, τ), \end{matrix}

(10)

\begin{matrix} η & = \frac{y}{δ (x)}, \end{matrix}

(11)

\begin{matrix} τ & = \frac{ν}{δ^{2}} t, \end{matrix}

(12)

where the dimensionless time transformation in Equation (12) is the key of success to solve the 2D unsteady laminar boundary layer flows and is introduced firstly in this Letter.

To formulate the Equation (9) in terms of

f (η, τ)

, we need to calculate some derivatives of function

ψ

respect to both x and y, for simplification, we denote

ψ_{, x} = \frac{\partial ψ}{\partial x}

and

f_{, η} = \frac{\partial f}{\partial η}

and so on. Noting the

η_{, x} = - η δ^{- 1} δ_{, x}

and

τ_{, x} = - 2 τ δ^{- 1} δ_{, x}

, and by chain rule of differential, we can get

\begin{matrix} ψ_{, x} & = {(U δ)}_{, x} f - U η δ_{, x} f_{, η} - 2 U τ δ_{, x} f_{, τ}, \end{matrix}

(13)

\begin{matrix} ψ_{, y} & = U f_{, η}, \end{matrix}

(14)

\begin{matrix} ψ_{x y} & = U_{, x} f_{, η} - η U δ^{- 1} δ_{, x} f_{, η η} - 2 U τ δ^{- 1} δ_{, x} f_{, η τ}, \end{matrix}

(15)

\begin{matrix} ψ_{, y y} & = U δ^{- 1} f_{, η η}, \end{matrix}

(16)

\begin{matrix} ψ_{, y y y} & = U δ^{- 2} f_{, η η η}, \end{matrix}

(17)

\begin{matrix} ψ_{t y} & = U ν δ^{- 2} f_{, τ η}, \end{matrix}

(18)

Thus the velocity components become

\begin{matrix} u & = U f_{, η}, \end{matrix}

(19)

\begin{matrix} v & = - [{(U δ)}_{, x} f - U η δ_{, x} f_{, η} - 2 U τ δ_{, x} f_{, τ}] . \end{matrix}

(20)

Substituting Equations (13)–(18) into Equation (9), we have a single partial differential equation as follows

\begin{matrix} f_{, η η η} & + α f f_{, η η} + β [1 - {(f_{, η})}^{2}] \\ = f_{, τ η} + γ τ (f_{, τ} f_{, η η} - f_{, η} f_{τ η}), \end{matrix}

(21)

where the coefficients are

α = \frac{δ}{ν} \frac{d U δ}{d x}

β = \frac{δ^{2}}{ν} \frac{d U}{d x}

, and

γ = \frac{U}{ν} \frac{d δ^{2}}{d x}

, and initial-boundary conditions become:

η = 0 : f = 0, \frac{\partial f}{\partial η} = 0

and

η = \infty : \frac{\partial f}{\partial η} = 1

If the coefficient

α

β

and

γ

were constants, the Equation (21) is solvable because it will get rid of the variable x. Following from the relation

\frac{d δ^{2} U}{d x} = (2 α - β) ν

, its integration leads to

δ^{2} U = (2 α - β) ν x

, canceling out

δ^{2}

β = \frac{δ^{2}}{ν} \frac{d U}{d x}

, we have

\frac{d U}{U} = \frac{β}{(2 α - β)} \frac{d x}{x}

, hence when

β \neq 2 α

, the general solution of this equation is of the form:

\begin{matrix} U (x) & = C x^{n}, \end{matrix}

(22)

\begin{matrix} δ (x) & = {[\frac{| (2 α - β) x | ν}{| U (x |)}]}^{1 / 2} . \end{matrix}

(23)

where the exponent

n = \frac{β}{2 α - β}

In the same way, we have

\frac{d δ^{2} U}{d x} = (β + γ) ν

, leads to a relation

2 α - β = β + γ

, namely

γ = 2 (α - β)

. It implies that

γ

is constant if both

α

and

β

were constants.

Regarding the solution of Equation (21), for constants

α, β

and

γ

, Equation (21) can be numerically solved.

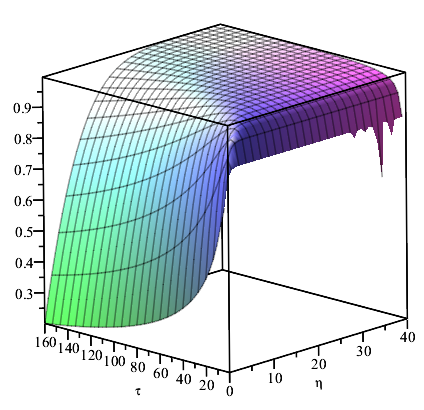
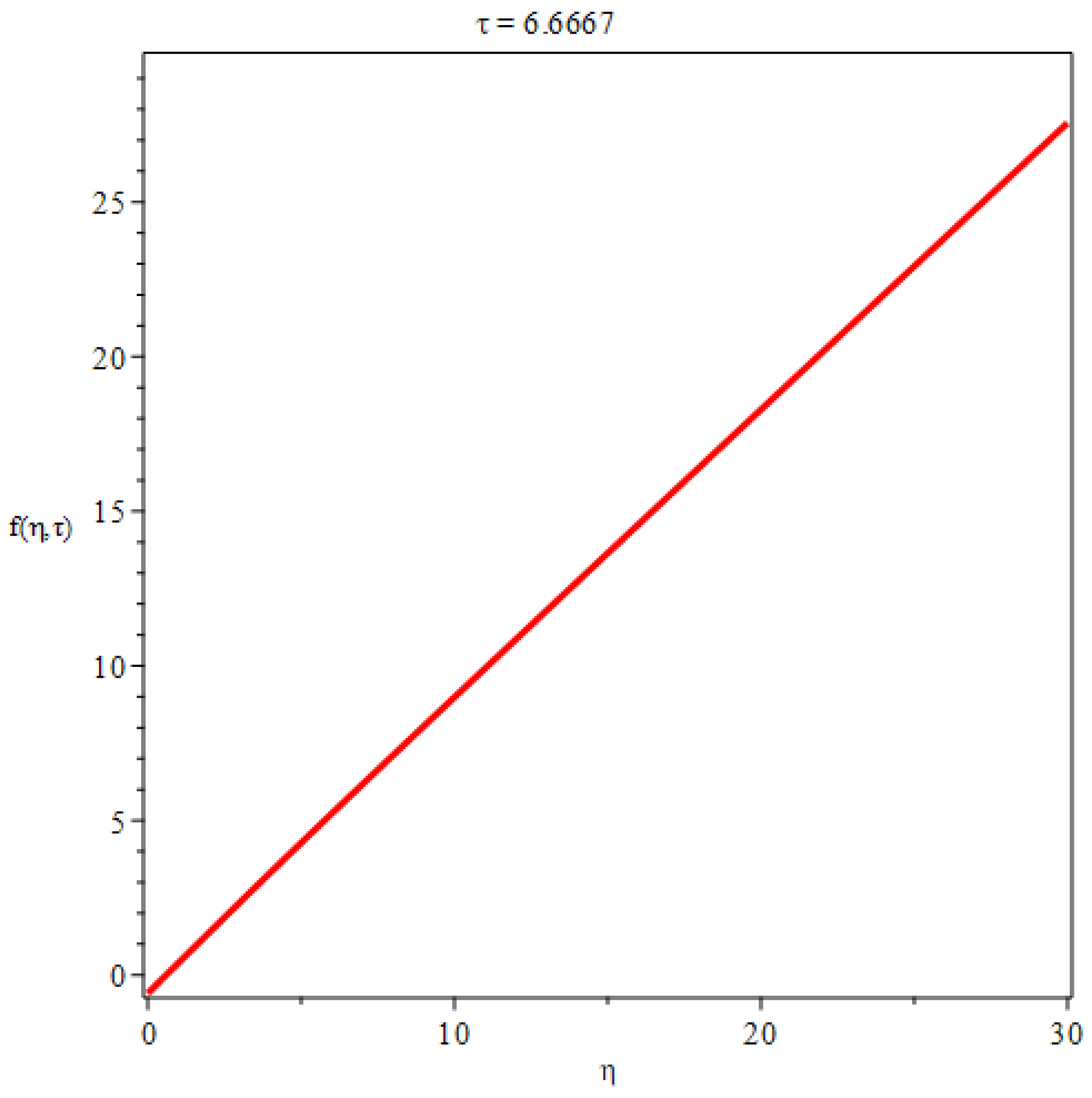
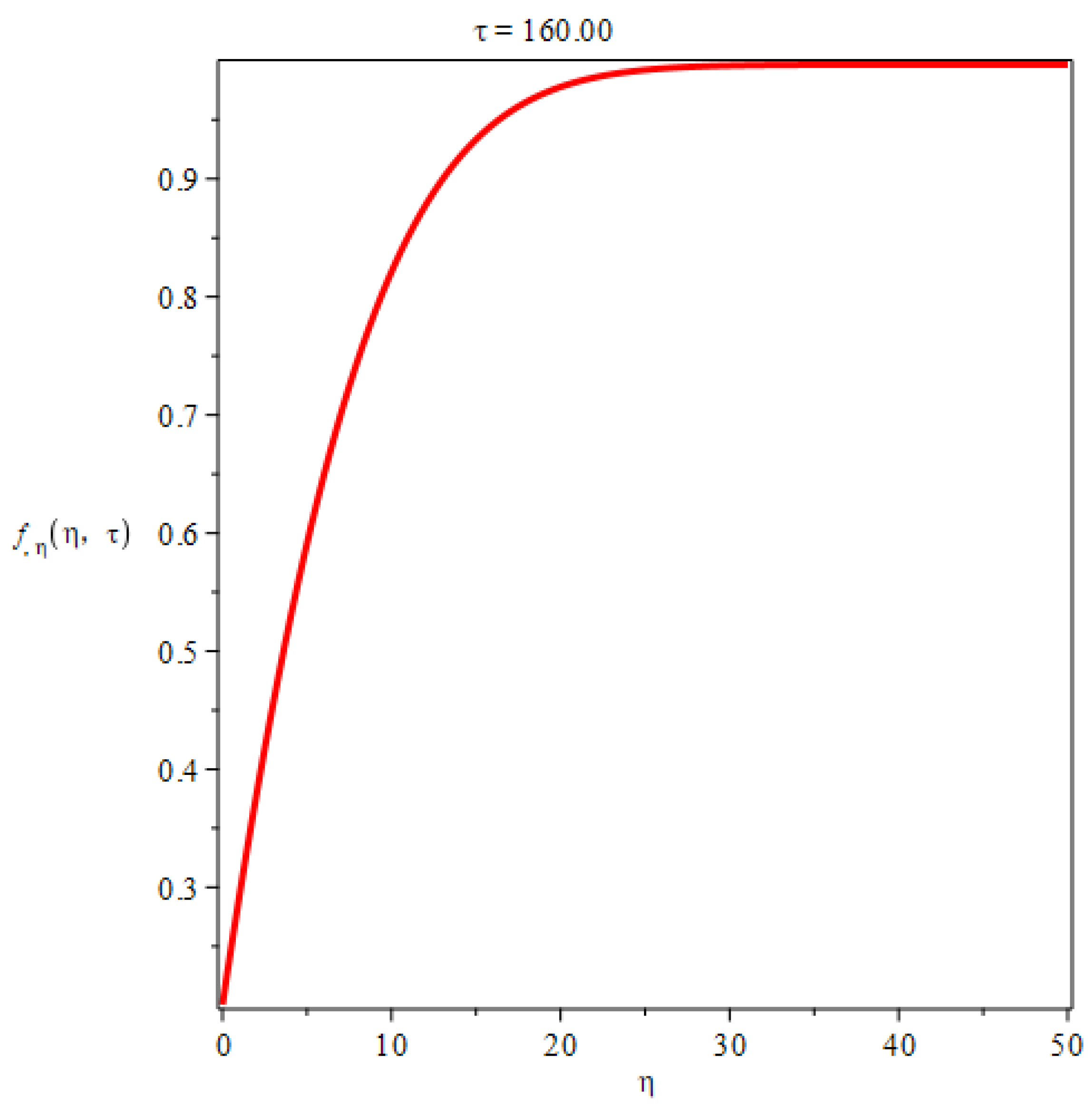
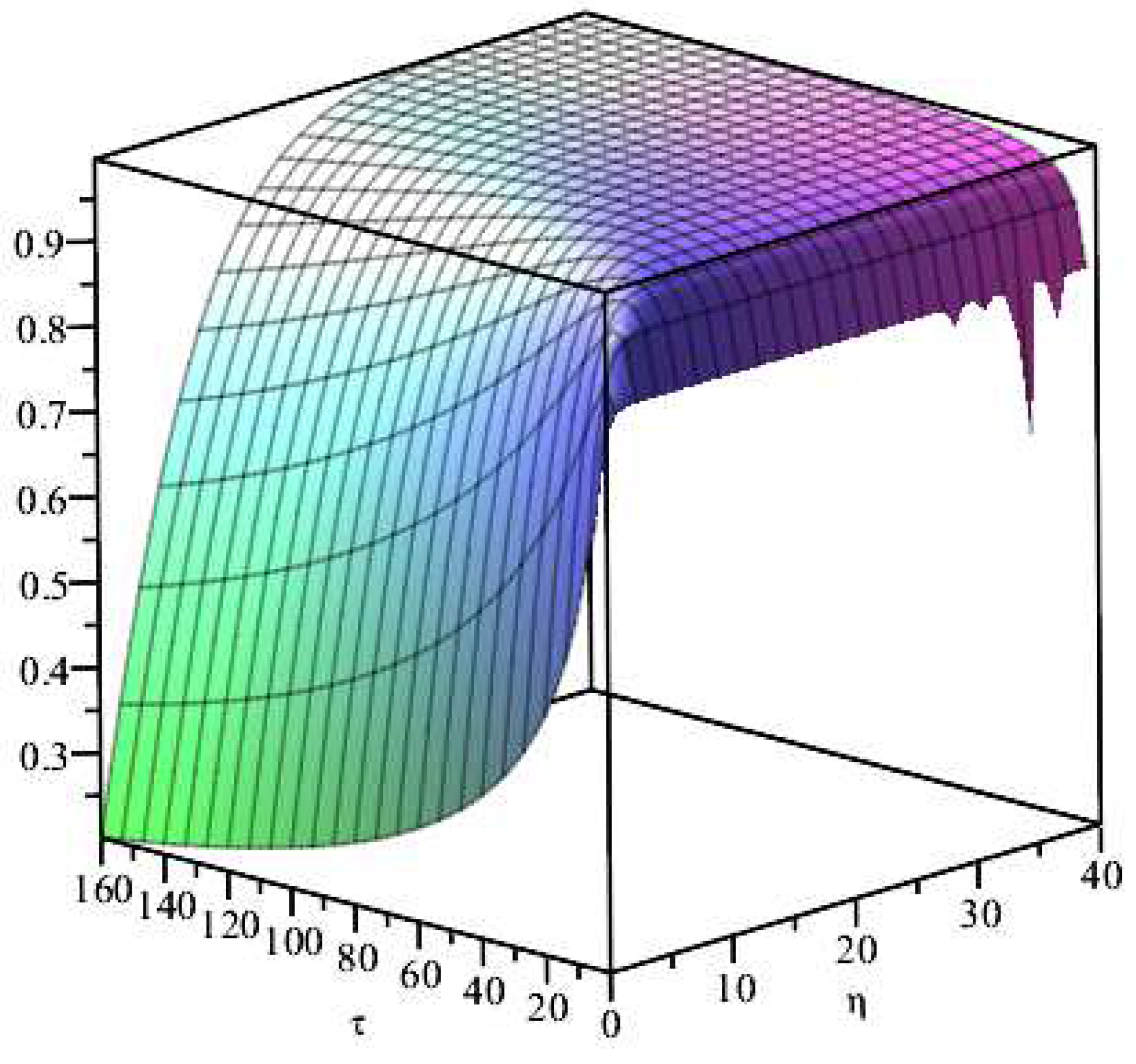
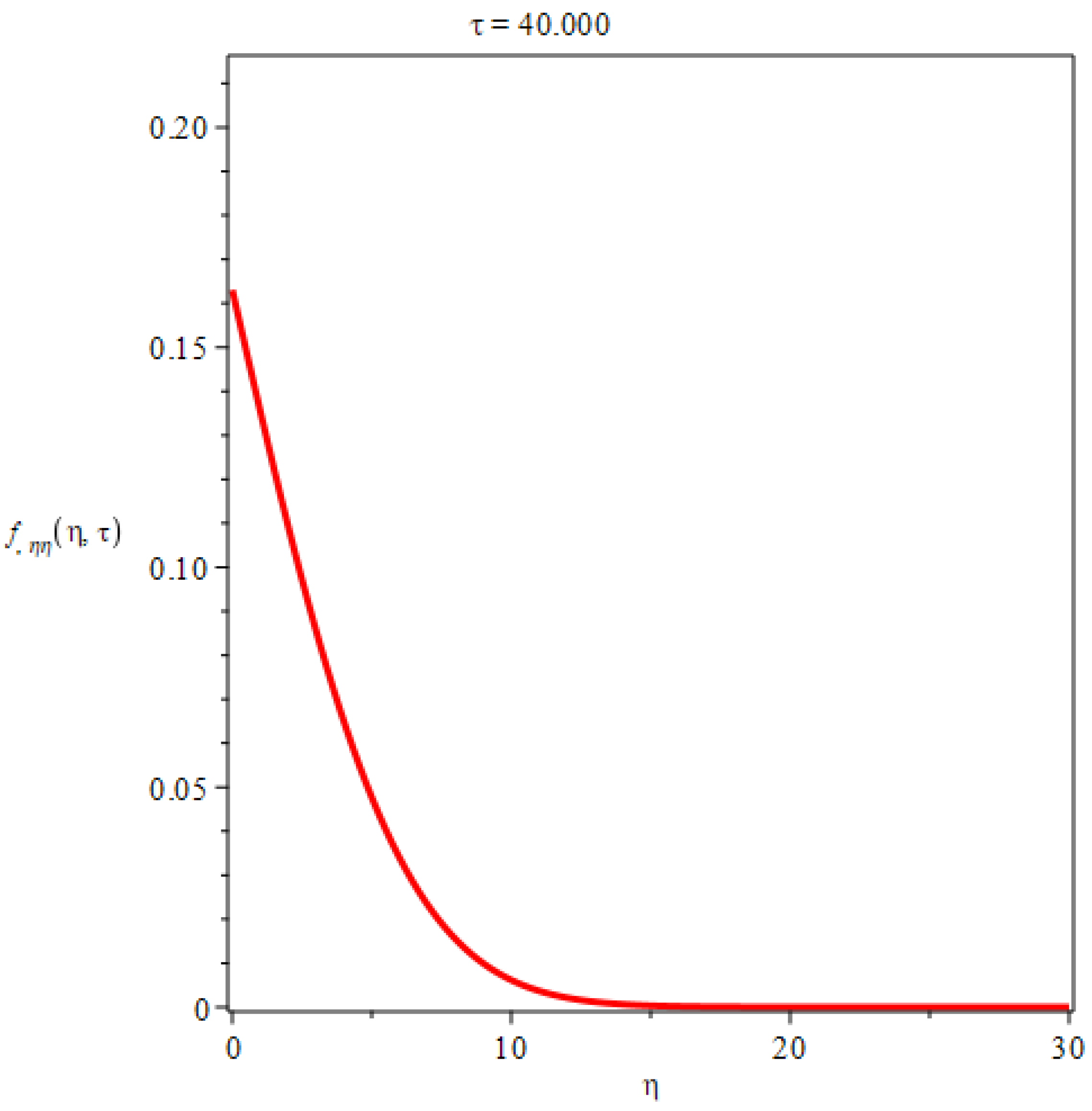
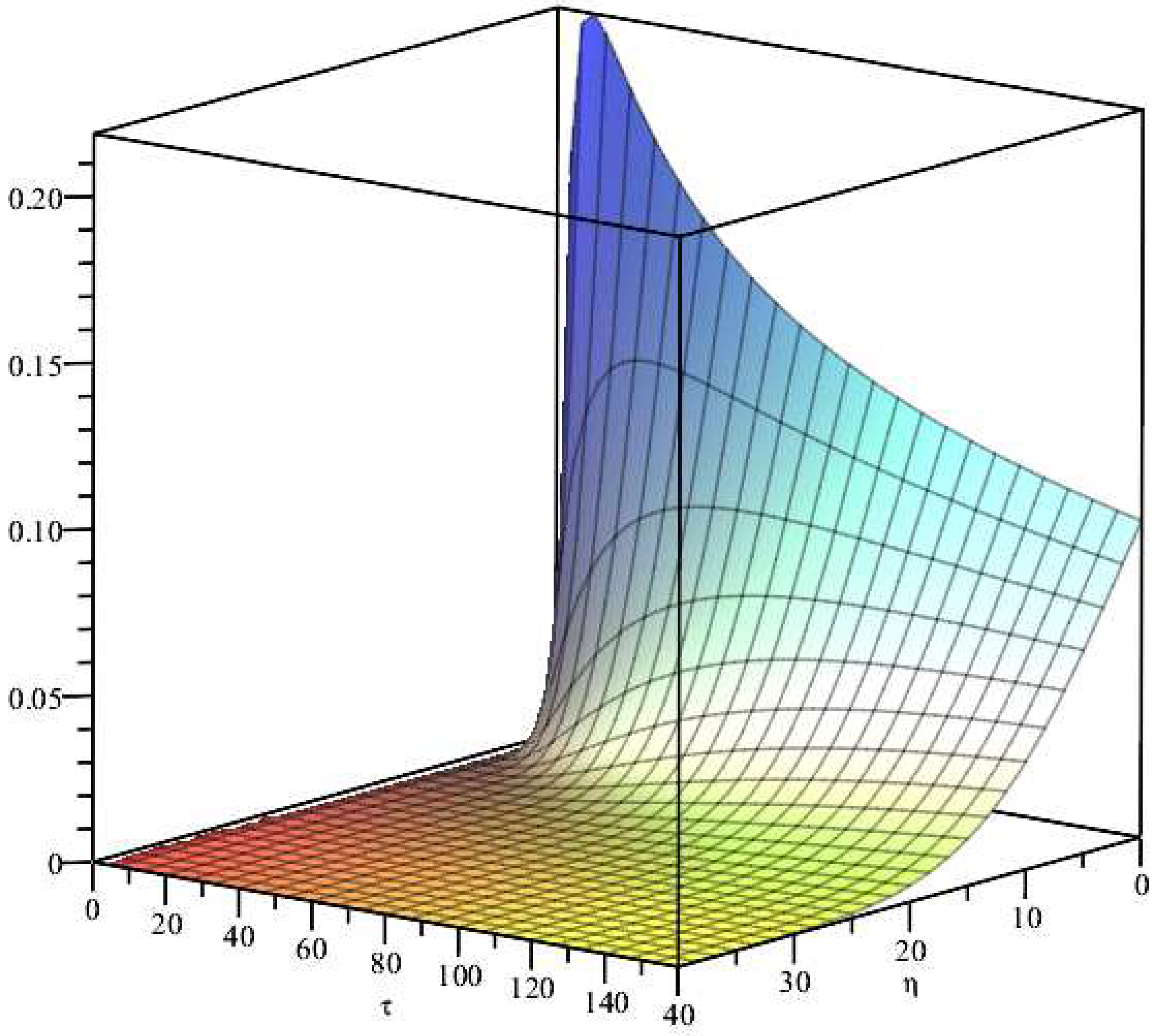
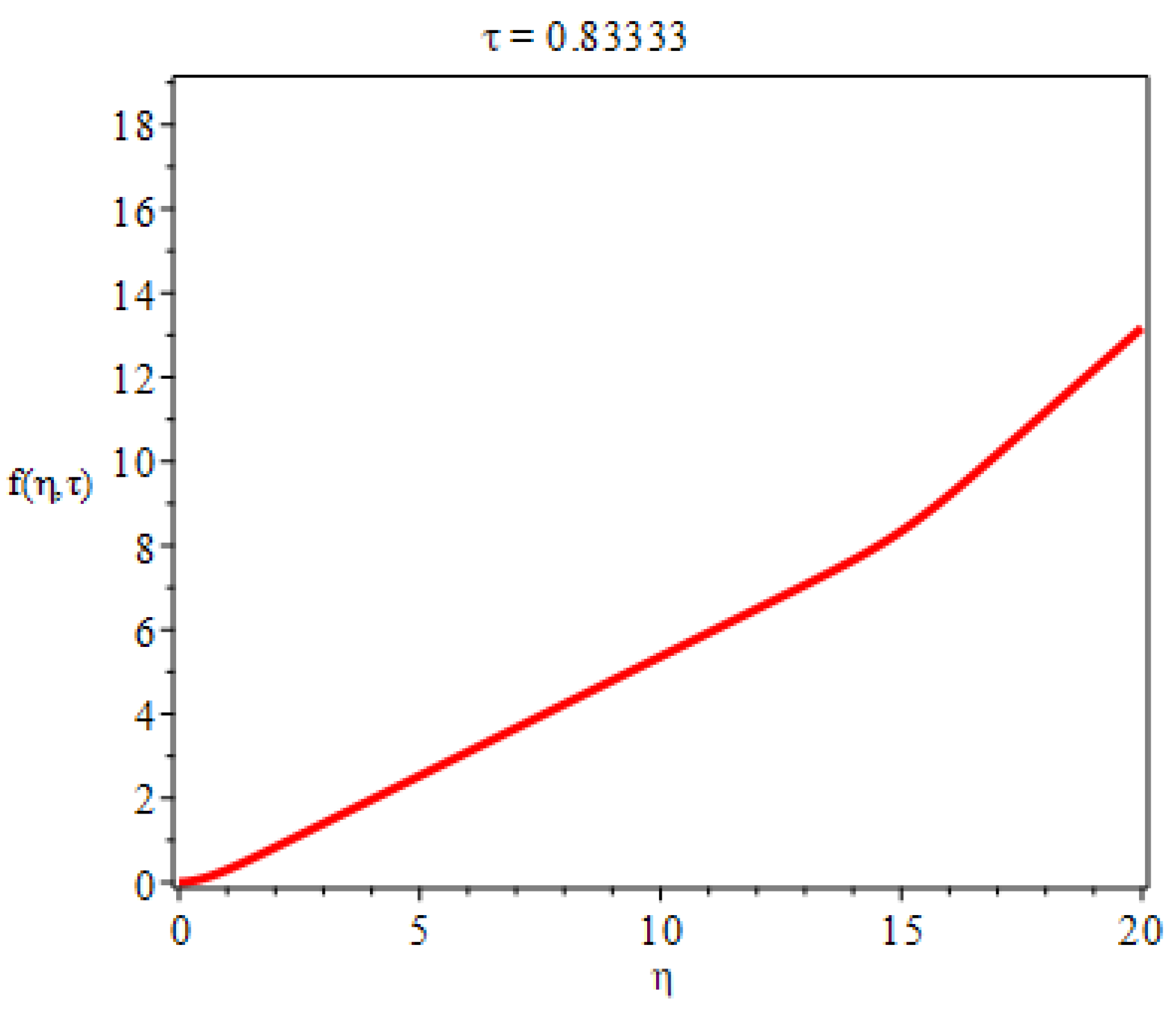
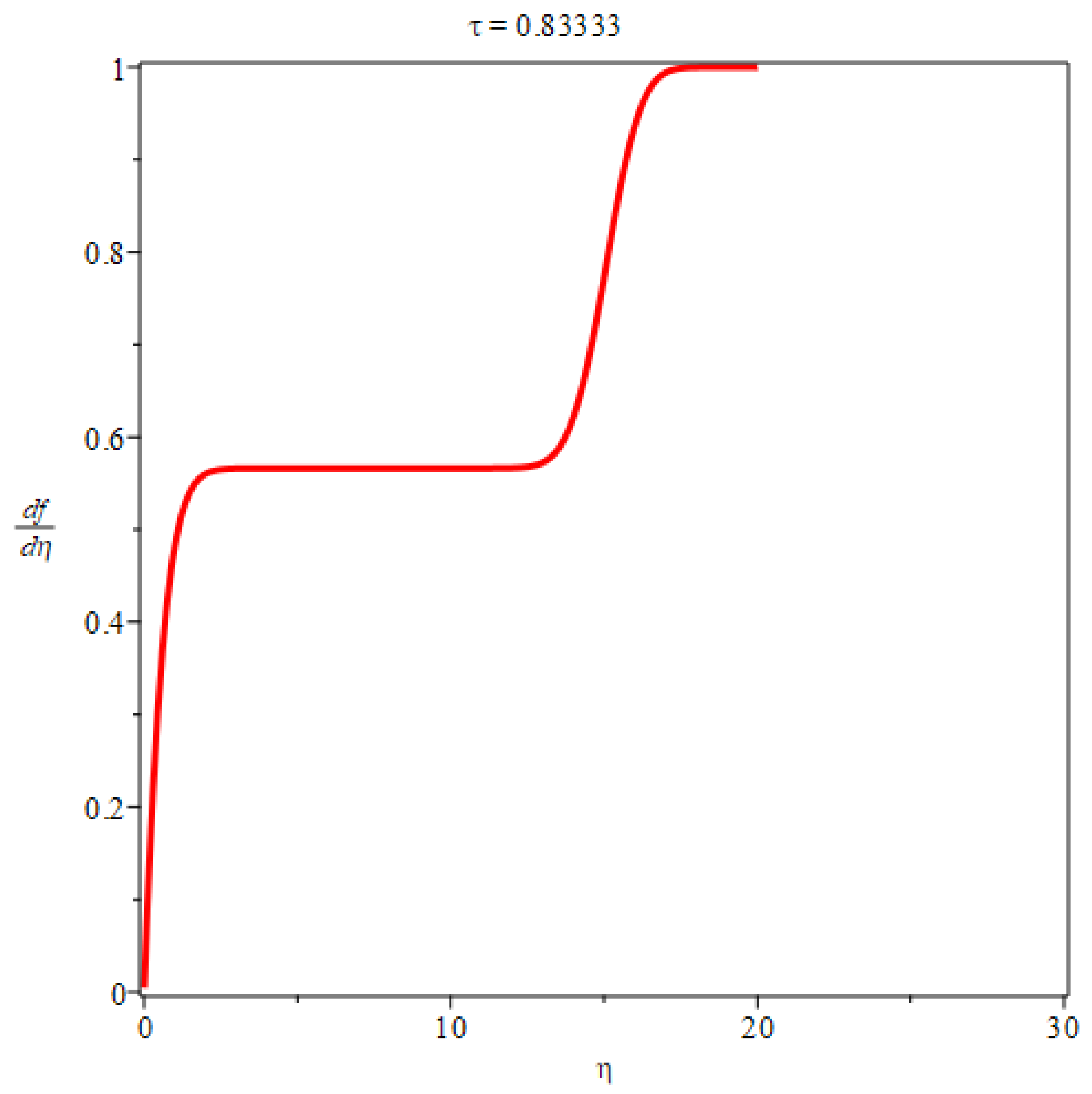
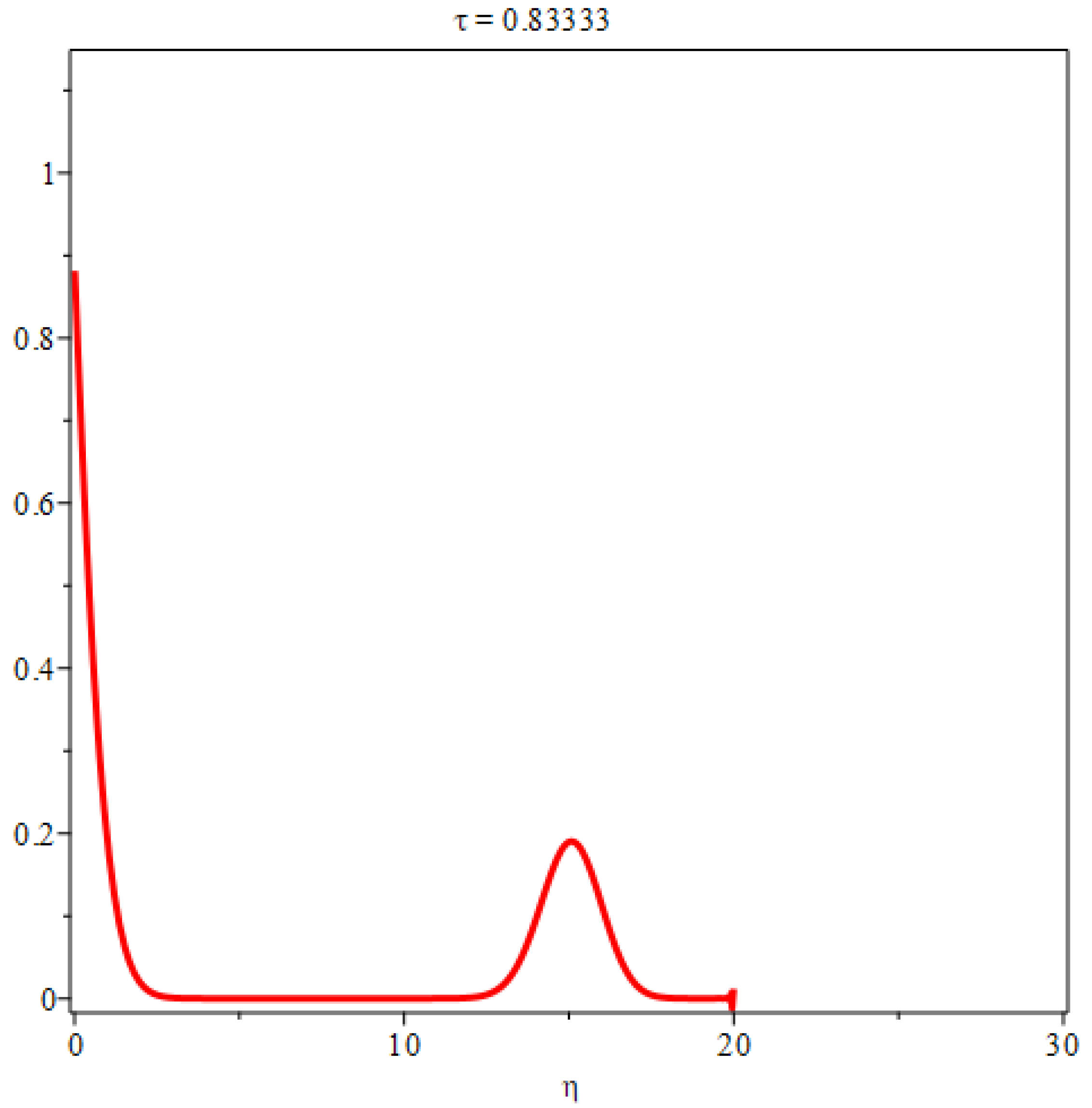
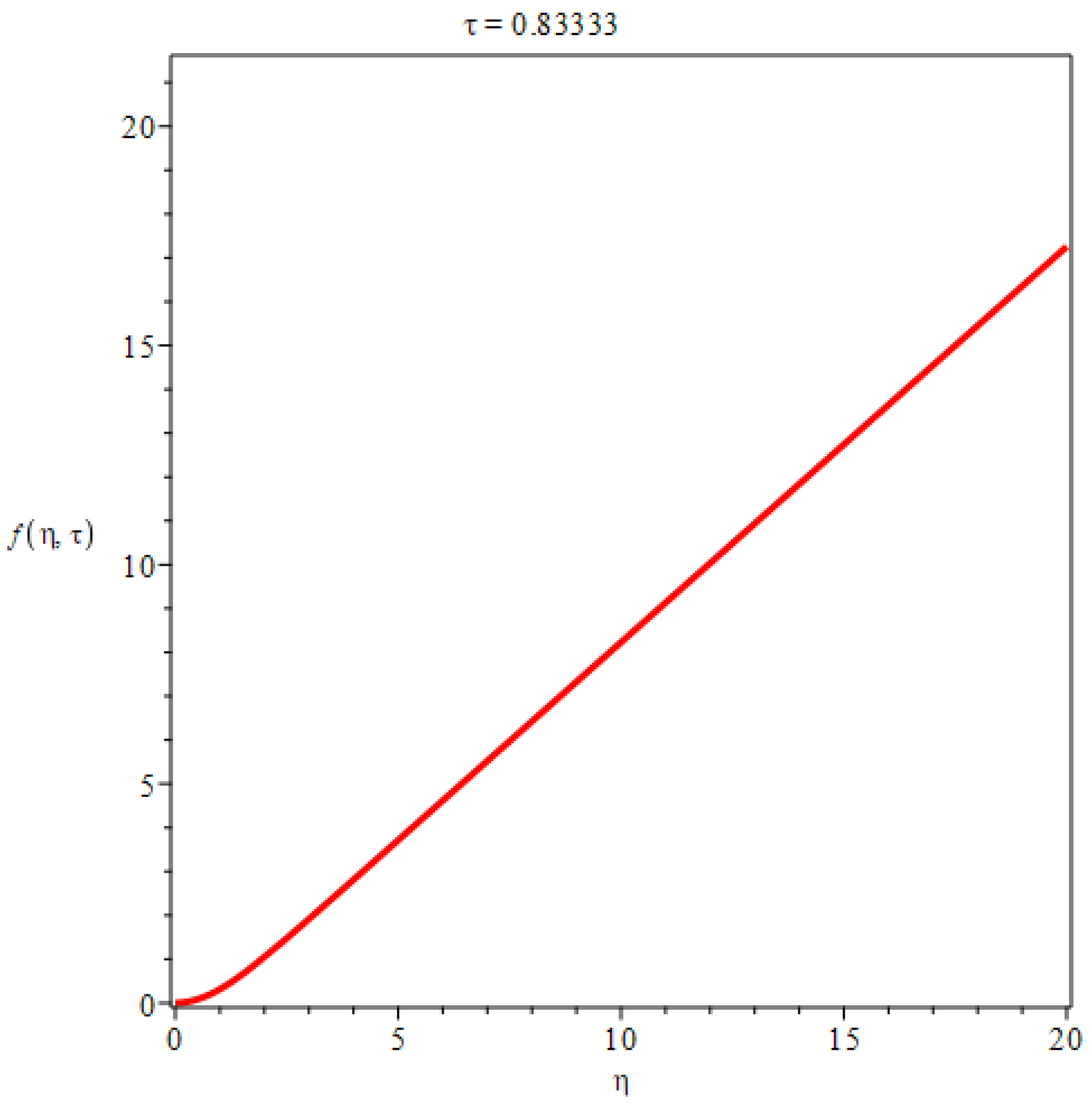
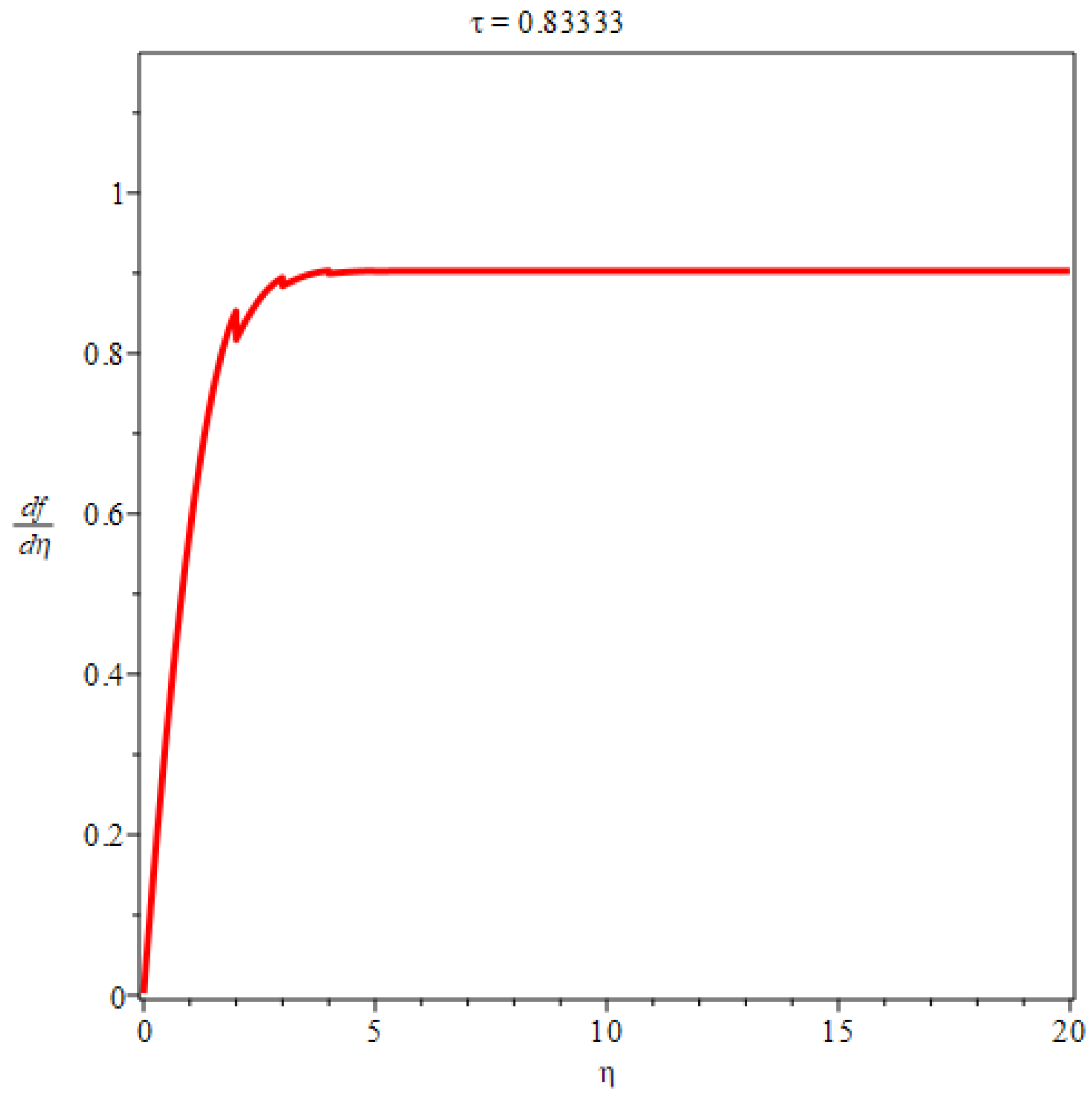
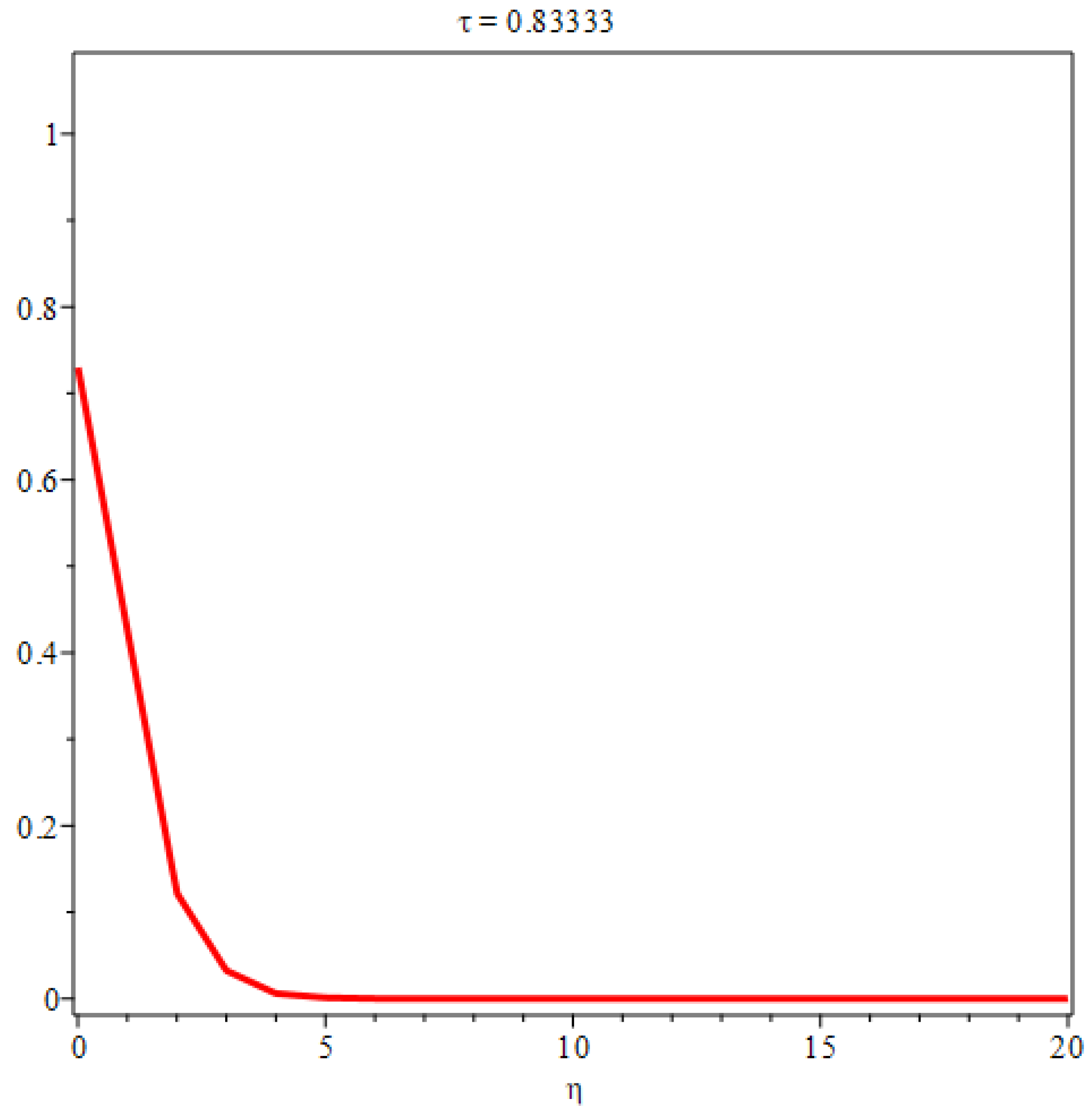
3. Flow along a flat plate at zero incidence in a uniform stream

In the case of two dimensional plate boundary layers, if

β = 0

then we have

n = 0

, flow velocity

U (x) = U_{\infty}

α

can be any real number, without loss of generality, we set

α = 1

, hence

γ = 2 (α - β) = 2

. The boundary thickness is

δ (x) = {(\frac{2 ν x}{U_{\infty}})}^{1 / 2}

The stream function is of the form

ψ = {(2 ν U_{\infty} x)}^{1 / 2} f (η, τ),

(24)

where

η = y {(\frac{U_{\infty}}{2 ν x})}^{1 / 2}

, and diffusion time

τ = \frac{U_{\infty}}{2} \frac{t}{x}

The equation Equation (21) can be reduced to the following:

f_{, η η η} - f f_{, η η} = f_{, τ η} + 2 τ (f_{, τ} f_{, η η} - f_{, η} f_{τ η}) .

(25)

With the help of Maple and initial-boundary conditions, we can find the similarity solution of Equation (25) as follows

\begin{matrix} f & = \frac{9}{τ} (2 + η) (η^{2} + 4 η + \frac{2}{9} τ + 4) exp (σ) (c_{2} A_{1} - C_{3} B_{1}) \\ + 3 (2 + η) exp (σ) (3 c_{3} A_{2} + 2 c_{2} B_{2}) + c_{1} \sqrt{τ} + \frac{2 + η}{2 τ}, \end{matrix}

(26)

where the integral constants

c_{1}, c_{2}, c_{3}

and notations

\begin{matrix} σ & = - \frac{3 {(2 + η)}^{2}}{4 τ}, \\ A_{1} & = K u m m e r M (\frac{5}{6}, \frac{3}{2}, σ), \\ B_{1} & = K u m m e r U (\frac{5}{6}, \frac{3}{2}, σ), \\ A_{2} & = K u m m e r M (- \frac{1}{6}, \frac{3}{2}, σ), \\ B_{2} & = K u m m e r U (- \frac{1}{6}, \frac{3}{2}, σ), \end{matrix}

(27)

in which,

KummerM

and

KummerU

are the Kummer function [24].

After applying initial-boundary conditions, we have

\begin{matrix} f & = η - \frac{2 + η}{2 τ} \\ + \frac{3 \sqrt{3 π} (2 + η)}{10 τ Γ (\frac{2}{3})}) (η^{2} + 4 η + \frac{2}{9} τ + 4) exp (σ) B_{1} \\ - \frac{2 \sqrt{3 π}}{5 Γ (\frac{2}{3})} (2 + η) exp (σ) B_{2} - \frac{4 π \sqrt{τ}}{15 Γ (\frac{2}{3}) Γ (\frac{5}{6})} \end{matrix}

(28)

From the solution in Equation (28), we can get some useful derivatives as follows

\begin{matrix} f_{, η} & = 1 + \frac{\sqrt{3 π}}{Γ (\frac{2}{3}) τ} exp (σ) B_{1} - \frac{2 \sqrt{3 π}}{3 Γ (\frac{2}{3})} B_{2} - \frac{1}{2 τ}, \end{matrix}

(29)

and

\begin{matrix} f_{, η η} & = \frac{\sqrt{3 π}}{3} (2 + η) exp (σ) B_{1}, \end{matrix}

(30)

and

\begin{matrix} f_{, τ} & = - \frac{\sqrt{3 π}}{10 τ^{2}} (η^{2} + 4 η - \frac{8}{9} τ + 4) exp (σ) B_{1} \\ \frac{2}{15 τ} exp (σ) B_{2} - \frac{1}{2 τ^{2}} - \frac{2 \sqrt{3} 2^{2 / 3} π^{3 / 2}}{45 {(Γ (\frac{2}{3}))}^{2}} \frac{1}{\sqrt{τ}} \end{matrix}

(31)

where

Γ (r)

is the Gamma function [24].

By differentiation, the flow velocity components are obtained as

\begin{matrix} u & = U_{\infty} f_{, η}, \end{matrix}

(32)

\begin{matrix} v & = {(\frac{ν U_{\infty}}{2 x})}^{1 / 2} (η f_{, η} - f + 2 τ f_{, τ}) . \end{matrix}

(33)

The shear stress is given by

\begin{matrix} τ_{x y} & = μ \frac{\partial u}{\partial y} = \frac{ρ ν}{δ} \frac{\partial u}{\partial η} = ρ {(\frac{ν U_{\infty}}{2 x})}^{1 / 2} f_{, η η} . \end{matrix}

(34)

The wall shear stress

τ_{w} = τ_{x y} |_{η = 0}

, we have

\begin{matrix} τ_{x y} & = ρ {(\frac{ν U_{\infty}}{2 x})}^{1 / 2} f_{, η η} |_{(0, τ)} . \end{matrix}

(35)

The function

f (η, τ)

, its derivatives are depicted in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, respectively.

4. The Main-Stream Convergent Channel Flow

In this case, the parameters

α = 0, β = 1

and

γ = - 2

, we have the convergent channel flow velocity function

U (x) = \frac{| Q |}{ρ θ x}

, which simply expresses the coacervation of the discharge

Q < 0

in the flow,

θ

being the angle between the planes. Now we have the boundary layer thickness

δ (x) = x {(\frac{ν ρ θ}{| Q |})}^{1 / 2}

, similarity variable

η = \frac{y}{δ} = \frac{y}{x} {(\frac{| Q |}{ν ρ θ})}^{1 / 2}

, and dimensionless diffusion time

τ = \frac{| Q |}{ρ θ} \frac{t}{x^{2}}

The Equation (21) can be reduced to the following:

\begin{matrix} f_{, η η η} + 1 - {(f_{, η})}^{2} = f_{, τ η} - 2 τ (f_{, τ} f_{, η η} - f_{, η} f_{τ η}) . \end{matrix}

(36)

Equation (36) can be solved numerically, some results are depicted in Figure 6, Figure 7 and Figure 8, respectively.

5. The mAin-Stream Wedge Flow

In this case wedge flows, the parameters

α = 1, 0 < β < 2

, here we set

β = 3 / 2

, thus we have

γ = 1

and

n = 1 / 2

, hence the wedge flows velocity function

U (x) = C x^{1 / 2}

, the boundary layer thickness

δ (x) = {(\frac{2 ν \sqrt{x}}{C})}^{1 / 2}

, similarity variable

η = \frac{C y}{2 ν \sqrt{x}}

, and dimensionless diffusion time

τ = t / (2 \sqrt{x})

The equation Equation (21) can be reduced to the following:

\begin{matrix} f_{, η η η} & + f f_{, η η} + \frac{3}{2} [1 - {(f_{, η})}^{2}] \\ = f_{, τ η} + τ (f_{, τ} f_{, η η} - f_{, η} f_{τ η}), \end{matrix}

(37)

Equation (37) can be solved numerically, some results are depicted in Figure 9, Figure 10 and Figure 11, respectively.

6. Conclusions and Perspectives

The transformation of the 2D unsteady laminar boundary layer equations into a single partial differential equation with constant coefficients is a clever approach that allows for the exact solution of the velocity field.

Overall, this theoretical studies contributes to the understanding the origins of turbulence from unsteady laminar boundary flows investigation.

Data Availability Statement

The data supporting the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

This work was supported by Xi’an University of Architecture and Technology (Grant No. 002/2040221134). The author would like to express his gratitude to Prof. Cunbiao Lee from Peking University for engaging and informative discussions. Special thanks are also extended to Academician Xiaogang DENG of the Chinese Academy of Sciences for identifying an error in the differential calculation of

ψ_{, x}

Conflicts of Interest

The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Schlichting, H. Boundary Layer Theory, McGraw-Hills, 1960 translated by J. Kestin.
Morkovin, M.V. On the many faces of transition, in Viscous Drag Reduction, edited by C. S. Wells (Springer, New York, 1969), pp. 1-C31Morkovin, M.V. On the many faces of transition, in Viscous Drag Reduction, edited by C. S. Wells (Springer, New York, 1969), pp. 1-C31.
Tennekes, H.; Lumley, J.L. A First Course of Turbulence, The MIT Press, Cambridge (1972).
Reshotko, E. Boundary-layer stability and transition. Annu. Rev. Fluid Mech. 8, 311–C349 (1976). [CrossRef]
Bayly, B.J.; Orszag, S.A.; Herbert, T. Instability mechanisms in shear-flow transition. Annu. Rev. Fluid Mech. 20, 359–C391 (1988). [CrossRef]
Rosenhead, L. Laminar Boundary Layers, Dover Publications, Inc. New York (1988).
Beckwith, I.E.; C.G.M., III. Aerothermodynamics and transition in high-speed wind tunnels at NASA Langley. Annu. Rev. Fluid Mech. 22, 419–C439 (1990). [CrossRef]
Kachanov, Y.S. Physical mechanisms of laminar-boundary-layer transition. Annu. Rev. Fluid Mech. 26, 411–C482 (1994). [CrossRef]
Frisch, U. Turbulence, Cambridge University Press, Cambridge (1995).
Reed, H.L.; Saric, W.S.; Arnal, D. Linear stability theory applied to boundary layers. Annu. Rev. Fluid Mech. 28, 389–C428 (1996). [CrossRef]
Herbert, T. Parabolized stability equation. Annu. Rev. Fluid Mech. 29, 245–C283 (1997). [CrossRef]
Lee, C.B. Possible universal transitional scenario in a flat plate boundary layer: Measurement and visualization. Phys. Rev. E 62, 3659 (2000). [CrossRef]
Saric, W.S.; Reed, H.L.; White, E.B. Stability and transition of threedimensional boundary layers. Annu. Rev. Fluid Mech. 35, 413–C440 (2003). [CrossRef]
Durbin, P.; Wu, X. Transition beneath vortical disturbances. Annu. Rev. Fluid Mech. 39, 107–C128 (2007). [CrossRef]
Eckhardt, B.; Schneider, T.M.; Hof, B.; Westerweel, J. Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–C468 (2007). [CrossRef]
Lee, C.B.; Wu, J.Z. Transition in wall-bounded flows. Appl. Mech. Rev. 61, 030802 (2008). [CrossRef]
Fedorov, A. Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 43, 79–C95 (2011). [CrossRef]
Zhong, X.; Wang, X. Direct numerical simulation on the receptivity, instability, and transition of hypersonic boundary layers. Annu. Rev. Fluid Mech.44, 527–C561 (2012). [CrossRef]
Jiménez, J. Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, 513–C531 (2018). [CrossRef]
Wu, X. Nonlinear theories for shear flow instabilities: Physical insights and practical implications. Annu. Rev. Fluid Mech. 51, 451–C485 (2019). [CrossRef]
Lee, C.B.; Jiang, X.Y. Flow structures in transitional and turbulent boundary layer. Phys. Fluids 31, 111301 (2019). [CrossRef]
Jiang, X.Y.; Lee, C.B.; Chen, X.; Smith, C.R.; Linden, P.F. Structure evolution at early stage of boundary layer transition: simulation and experiment. J. Fluid Mech. (2020), vol. 890.
Sun, B.H. Thirty years of turbulence study in China. Appl. Math. Mech. 40(2) (2019) 193-214. [CrossRef]
Abramowitz, M.; Stegun, I.; (Eds). Handbook of Mathematical Functions. New York: Dover, 1972.

Figure 1.

f (η, τ)

Figure 1.

f (η, τ)

Figure 2.

f_{, η}

Figure 2.

f_{, η}

Figure 3. 3D of

f_{, η}

Figure 3. 3D of

f_{, η}

Figure 4.

f_{, η η}

Figure 4.

f_{, η η}

Figure 5. 3D of

f_{, η η}

Figure 5. 3D of

f_{, η η}

Figure 6.

f (η, τ)

Figure 6.

f (η, τ)

Figure 7.

f_{, η}

Figure 7.

f_{, η}

Figure 8.

f_{, η η}

Figure 8.

f_{, η η}

Figure 9.

f (η, τ)

Figure 9.

f (η, τ)

Figure 10.

f_{, η}

Figure 10.

f_{, η}

Figure 11.

f_{, η η}

Figure 11.

f_{, η η}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Exact Similarity Solutions of Unsteady Laminar Boundary Layer Flows

Abstract

1. Introduction

2. Similarity transformations of 2D laminar boundary layers equations

3. Flow along a flat plate at zero incidence in a uniform stream

4. The Main-Stream Convergent Channel Flow

5. The mAin-Stream Wedge Flow

6. Conclusions and Perspectives

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe