Prerpints.org logo
Preprint
Article

The Classification for The Sources in SDSS DR18: Searching for QSOs by Machine Learning

Altmetrics

Downloads

131

Views

36

Comments

0

Submitted:

29 September 2023

Posted:

30 September 2023

You are already at the latest version

Alerts
Abstract
We tested selecting data randomly or proportionally in class imbalanced sample. Collecting data into the training and test set according to the initial ratio of QSOs, galaxies and stars were rec-ommended. We experimented using the original imbalanced data or introducing the class balance technologies: SMOTE, SMOTEENN, SMOTETomek, ADASYN, BorderlineSMOTE1, Border-lineSMOTE2, and RandomUndersampling. The SMOTEENN performed the best in the Sample 1. The LightGBM, CatBoost, XGBoost, and RF were compared when adopting the SMOTEENN using the petroMag_u, petroMag_g, petroMag_r, petroMag_i, petroMag_z, J, H, Ks, W1, W2, W3, W4 magnitudes as features. All of the precisions or recalls exceeded 0.94. The RF cost a little more time than the other three algorithms, but resulted in the best evaluating indicators. Utilizing the SMOTEENN +RF technology, the precision, recall and f1-score for QSOs (galaxies, stars) could achieve 0.98 (0.99, 0.98), 0.99 (0.96, 1.00), 0.98 (0.97, 0.99) respectively in Sample 1. Utilizing the SMOTEENN +RF technology, the precision, recall and f1-score for QSOs (galaxies, stars) could achieve 0.94 (0.96, 0.96), 0.98 (0.90, 0.97), 0.96 (0.93, 0.97) using the petroMag_u, petroMag_g, petroMag_r, petroMag_i, petroMag_z, W1, W2, W3, W4 magnitudes as features.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

The new era in modern astronomy is closely connected to using the big data by artificial intelligence. Broad band photometry from wide-field surveys has been our main source of information, and produces a large amount of data. Spectroscopy provides a more detailed and deeper understanding of individual objects, but yields less sample than photometry. It is possible to estimate the astronomical nature from the photometry, i.e., stars, galaxies, QSOs, planetary nebulae, or supernovae. The classification of objects in survey catalogues could speed up considerably studies focusing on a particular object. Many classification problems in astronomy have started to be approached using a machine learning (ML) algorithm, which is a purely data-driven methodology [1,2,3,4,5,6,7,8,9,10,11,12].
Brescis et al. 2015 [3] applied the MLPQNA (Multi Layer Perceptron with Quasi Newton Algorithm) method to the optical data of the Sloan Digital Sky Survey (SDSS)—Data Release 10, investigating whether photometric data alone sufficed to disentangle different classes of objects as they were defined in the SDSS spectroscopic classification. In disentangling quasars from stars and galaxies, their method achieved an overall efficiency of 91.31% and a QSO class purity of ∼ 95%. They used 5 psfMag and 5 modelMag magnitudes as input features.
Bai et al. 2018 [13] applied the random forest (RF) algorithm to class 85,613,922 objects in the Gaia Data Release 2, based on a combination of Pan-STARRS 1 and AllWISE data. The fraction of stars in their sample was 98%, and the fraction of galaxies was 2%. The total accuracy was 91.9%. Bai et al. 2019 [14] also applied the RF to the star/galaxy/QSO classification based on the combination of Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST) and SDSS spectroscopic data. Narrow line QSOs were classified as galaxies by both the SDSS and LAMOST pipelines. A QSO was referred to a theoretical one with broad emission lines. The training samples were built with a nine-color data set of about three million objects. They obtained classification accuracies higher than 99% for stars and galaxies, and higher than 94% for QSOs.
Costa-Duarte et al. 2019 [5] used the RF algorithm to a star/galaxy classification for the Southern Photometric Local Universe Survey. They trained the algorithm using the S-PLUS optical photometry up to r=21, matched to SDSS/DR13. The influence of the morphological parameters had been evaluated training the RF with and without the inclusion of morphological parameters, presenting accuracy values of 95.0% and 88.1%, respectively. The morphology could notably improve the classification of stars and galaxies. The classification of QSOs as extragalactic objects was slightly better using photometric-only case.
Nakoneczny et al. 2019 [15] trained the RF on SDSS DR14 spectroscopic data. They identified QSOs from broad-band photometric ugri data of the Kilo-Degree Survey Data Release 3 (KiDSDR3). They selected the 17 most useful features for the classification by a feature importance analysis, and limited the inference set to r < 22. Accuracy of 97% (percentage of correctly classified objects), purity of 91% (percentage of true quasars within the objects classified as such), and completeness of 87% (detection ratio of all true quasars), as derived from a test set extracted from SDSS were confirmed by comparison with external spectroscopic and photometric QSO catalogs overlapping with the KiDSDR3 footprint.
Logan et al. 2020 [6] presented an unsupervised machine learning method to separate stars, galaxies and QSOs using photometric data. Their work used Hierarchical Density-Based Spatial Clustering of Applications with Noise (hdbscan) to find the star, galaxy, and QSO clusters in a multidimensional color space. They obtained f1-scores of 98.9, 98.9, and 93.13 respectively for star, galaxy, and QSO selection in their 50 000 spectroscopically labelled sample. They created a multiwavelength catalogue of 2.7 million sources using the KiDS, VIKING, and ALLWISE surveys and published corresponding classifications.
Baqui et al. 2021 [16] cross-matched the mini Javalambre-Physics of the Accelerating Universe Astrophysical Survey (miniJPAS) dataset with SDSS and Hyper Suprime-Cam Subaru Strategic Program data, whose classification was trustworthy within the intervals 15 ≤ r ≤ 20 and 18.5 ≤ r ≤ 23.5. They used six different ML algorithms on the two cross-matched catalogs: K-nearest neighbors, decision trees, RF, artificial neural networks, extremely randomized trees (ERT), and an ensemble classifier. They used the magnitudes from the 60 filters together with their errors, with and without the morphological parameters as features. They found that, an area under the curve (Area Under Curve) AUC = 0.957 with RF when photometric information alone was used, and AUC = 0.986 with ERT when photometric and morphological information was used together, when 15 ≤ r ≤ 23.5. They observed that errors (the width of the distribution) were as important as the measurements (central value of the distribution).
Cunha & Humphrey 2022 [7] combined the outputs from the XGBoost, LightGBM, and CatBoost learning algorithms to create a stronger classifier named SHEEP, using the psfMag, petroMag, cModelMag, modelMag for the five optical bands (u, g, r, i, z) and the Wide-field Infrared Survey Explorer (WISE) magnitude W1, W2, W3, W4. The best results were in one vs all by LightGBM: the accuracy, precision, recall, f1-score for QSOs were 0.991, 0.985, 0.978, 0.982. The accuracy, precision, recall, f1-score for galaxies were 0.989, 0.989, 0.986, 0.987. The accuracy, precision, recall, f1-score for stars were 0.995, 0.993, 0.989, 0.991, respectively.
Martínez-Solaeche et al. 2023 [9] developed two algorithms based on artificial neural networks (ANN) to classify objects into four categories: stars, galaxies, quasars at low redshift (z < 2.1), and quasars at high redshift (z ≥ 2.1) in miniJPAS. In the mock test set, the f1-score for quasars at high redshift with the ANN1 (ANN2) were 0.99 (0.99), 0.93 (0.92), and 0.63 (0.57) for 17 < r ≤ 20, 20 < r ≤ 22.5, and 22.5<r≤23.6. In the case of low-redshift quasars, galaxies, and stars, the f1-scores reached 0.97 (0.97), 0.82 (0.79), and 0.61 (0.58); 0.94 (0.94), 0.90 (0.89), and 0.81 (0.80); and 1.0 (1.0), 0.96 (0.94), and 0.70 (0.52) in the same r bins. In the SDSS DR12Q superset miniJPAS sample, the weighted f1-score reached 0.87(0.88) for objects that were mostly within 20<r≤22.5.
All these studies were not focus on the unbalanced classification of categories. Classification of imbalanced dataset was necessary to study carefully in machine learning. Our paper used different sampling methods to redress disequilibrium, including Synthetic Minority Over-sampling Technique + Edited Nearest Neighbor (SMOTEENN), BorderlineSMOTE, Synthetic Minority Over-sampling Technique (SMOTE), Adaptive synthetic sampling (ADASYN), random undersampling, random oversampling, and so on. We employed the following classification methodologies: LightGBM, CatBoost, XGBoost, RF, which were the most popular ones.
The paper was organized as follows: in Sect.2, we described the data we employed and how we preprocessed the data. In Sect.3, we introduced the class balance technologies and the classification algorithms. We did the classifications using the original data or different class balance technologies. We did experiments using 4 different ML methodologies, and stated the evaluating indicators respectively. We compared the efficiency and effect of these methodologies. In Sect.4, we gave our summary and discussion.

2. Data and Preprocessing

2.1. Data

The SDSS has created the most detailed three-dimensional maps of the Universe ever made, with deep multi-color images of one third of the sky, and spectra for more than three million astronomical objects. It has progressed through several phases, SDSS-I (2000-2005), SDSS-II (2005-2008), SDSS-III (2008-2014), SDSS-IV (2014-2020) and SDSS-V (2020-). Data Rease 18 (DR18) is the first data release for the SDSS-V [17]. The AllWISE Data Release [18] gave the WISE [19] W1 magnitude (3.35𝞵m), W2 magnitude (4.6𝞵m), W3 magnitude (11.6𝞵m), W4 magnitude (22.1𝞵m) joint with the Two Micron All Sky Survey (2MASS) J magnitude (1.25𝞵m), 2MASS H magnitude (1.65𝞵m) and 2MASS Ks magnitude (2.17𝞵m). This ALLWISE catalog was a subset of the full AllWISE catalog available from NASA/IPAC Infrared Science Archive with a selection of the columns of the full catalog. The 2MASS magnitudes were from the 2MASS All-Sky Catalog of Point Sources [20]. Some sources were short of J, H, Ks magnitudes in the catalog since the limit of WISE was higher and deeper than 2MASS.
The ra, dec, redshifts, class, petroMag_u, petroMag_g, petroMag_r, petroMag_i, petroMag_z and errors of the five bands, were downloaded from the SpecPhoto Catalog of SDSS DR18 through https://skyserver.sdss.org/CasJobs/. The class labels were from the spectral information and were regarded as true. We sorted on the ra, dec and deduplicated the coordinates. 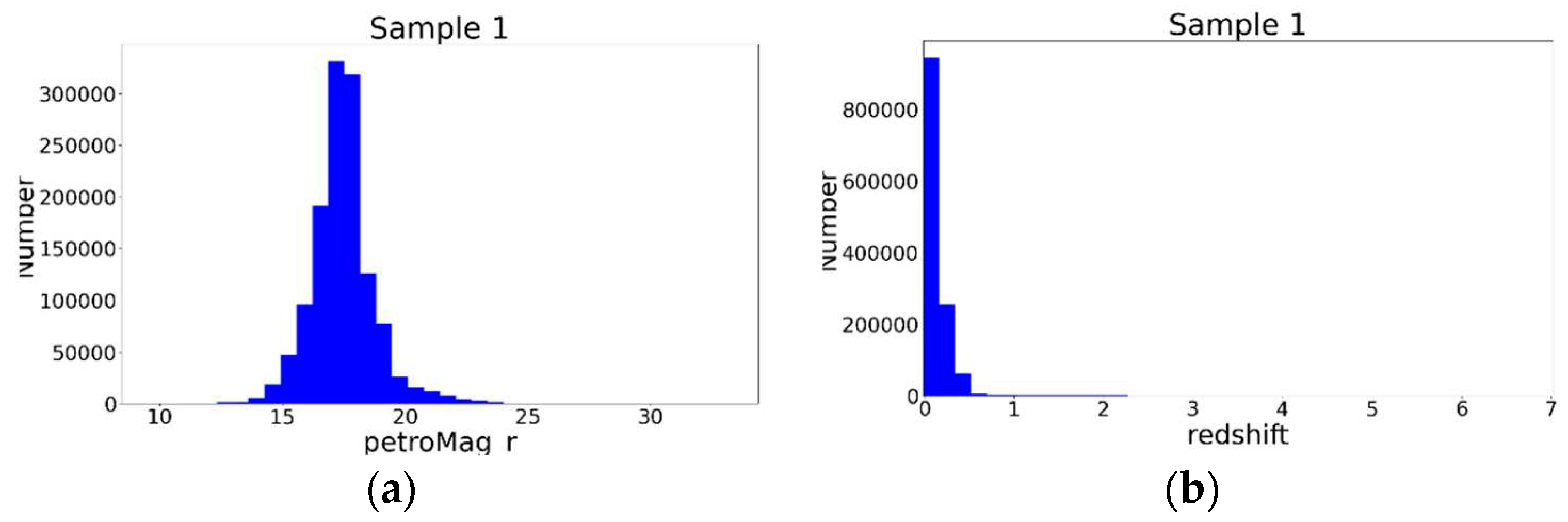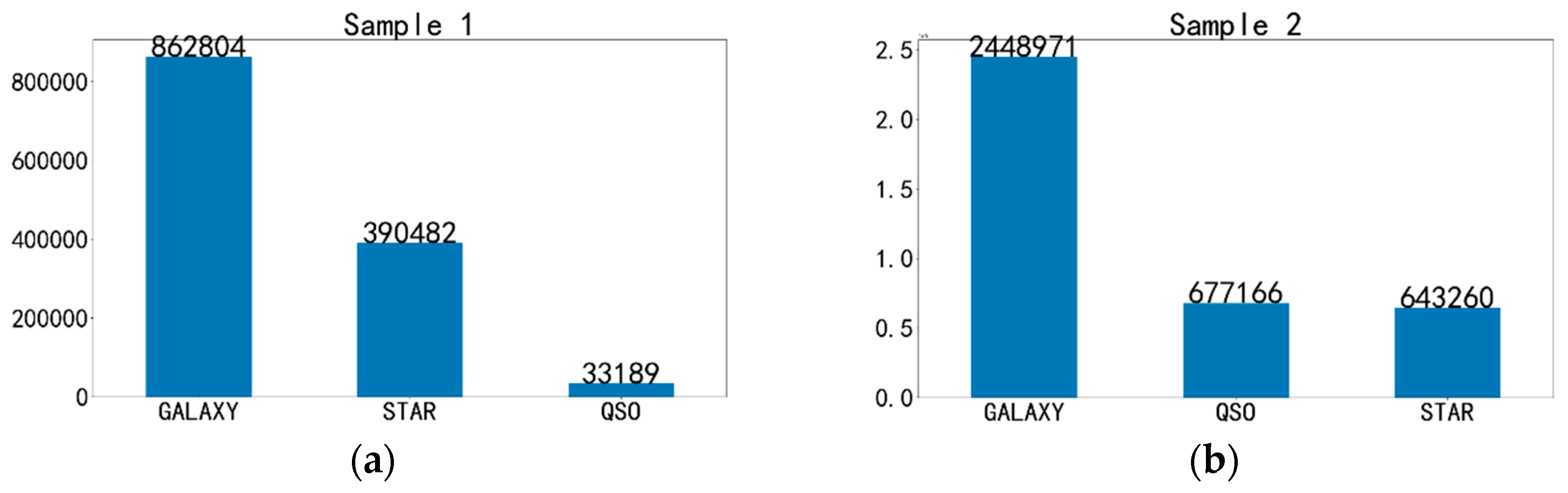We crossmatched these coordinates to ALLWISE in CDS Xmatch1. We chose the nearest match when one SDSS source corresponding to muti-ALLWISE sources or one ALLWISE source corresponding to muti-SDSS sources. Those sources without accurate measurements were discarded. We found some sources with the spectroscopic redshift equal to integer 0 and deleted those sources. Those sources with |zerr| >=1 were deleted. All the errors in ALLWISE magnitudes were lower than 1, but some errors in SDSS magnitudes were large. Those sources with either |petroMagErr_u| > 5, |petroMagErr_g| > 5, |petroMagErr_r| > 5, |petroMagErr_i| > 5, or |petroMagErr_z| > 5 were deleted. There were some null values in the J, H, Ks, W2, W3, W4 magnitudes, which were filled with blank spaces. The reason was that these sources could be collected into the catalog when their SDSS and W1 bands were observed. However, the J, H, Ks, W2, W3, W4 magnitudes might be too weak to be determined. In Sample 1, we deleted those sources with any of the 12 bands equal to the ‘nan’. Sample 1 contained 1286475 sources with the petroMag_u, petroMag_g, petroMag_r, petroMag_i, petroMag_z, J, H, Ks, W1, W2, W3, W4 magnitudes, including 33189 QSOs, 862804 galaxies, and 390482 stars. Sample 1 was composed of many bright sources, the peak of petroMag_r ~ 17. It consisted of many nearby sources, although the redshift of QSOs could reach 7. The distributions were shown in Figure 1.
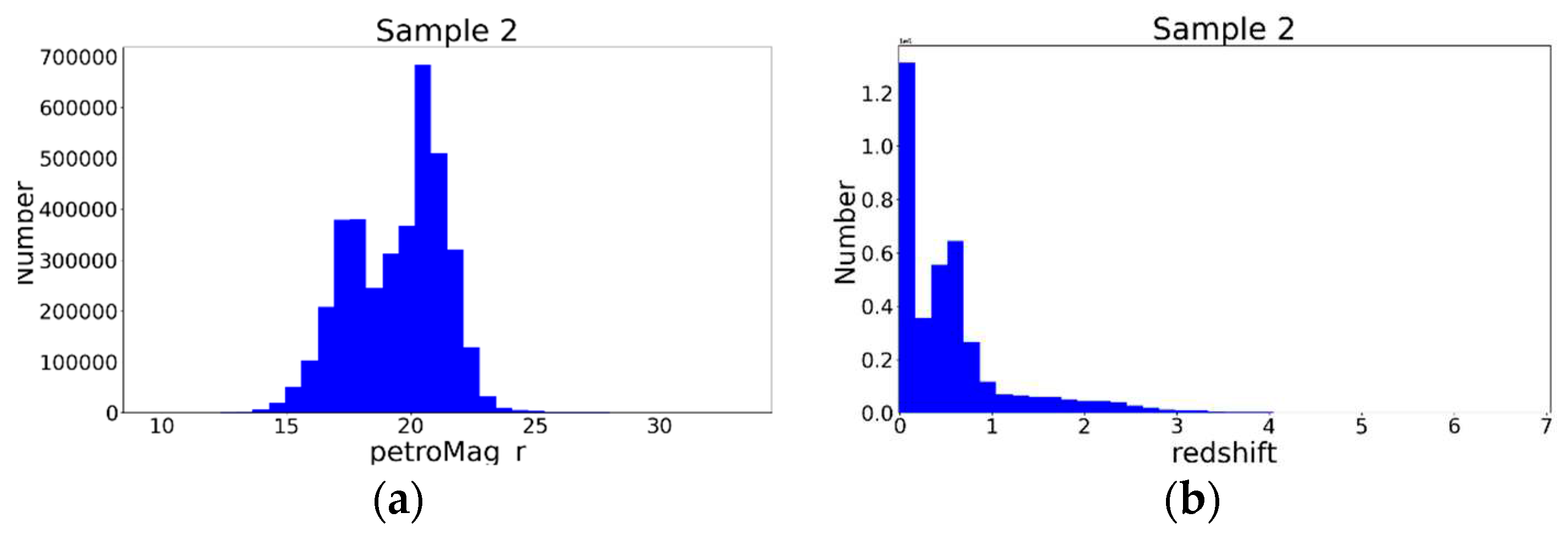
Instead, we did not consider the J, H, Ks observations and deleted the sources with any of the 9 bands being the ‘nan’. If we unused the features of the J, H, Ks, the sample should be larger, which were called Sample 2. Sample 2 contained 3769397 sources with the petroMag_u, petroMag_g, petroMag_r, petroMag_i, petroMag_z, W1, W2, W3, W4 magnitudes, including 677166 QSOs, 2448971 galaxies, and 643260 stars. Sample 2 was comprised of two parts: the nearby sources and the intermediary redshifts sources, or the bright sources and the dim sources. The distance and brightness were not the one-to-one correspondence. The distributions were shown in Figure 2.
In Costa-Duarte et al. 2019, the optical photometry was up to r=21. In Nakoneczny et al. 2019, the inference was set to r < 22. In Baqui et al. 2021, the photometry was up to r ≤ 23.5. In Martínez-Solaeche et al. 2023, the photometry was up to r ≤ 23.6. In our Sample 1 and Sample 2, the optical photometry up to r ~ 30. It seemed to be larger and deeper. Our two samples were very imbalanced. The imbalance of Sampe 1 and Sample 2 were shown in Figure 3.

2.2. Preprocessing

We adopted the RobustScaler from sklearn.preprocessing to do the standardization of the features. The RobustScaler calculation method was as follows:
v i ’ = v i − m e d i a n I Q R = v i − m e d i a n Q 3 − Q 1
v i was any value in one feature, v i ’ was the rescaled values, Q 1 was the first Quartile, Q 3 was the first Quartile, and IQR was InterQuartile Range.
The RobustScaler was a data standardization tool based on statistical methods, which was used to eliminate scales and biases in data. It could reduce the distance between features by comparing the scale differences between different features. It could ensure that the algorithm could better handle features of different scales during training. This preprocessing made the algorithm more accurate.

3. Experiments

The StratifiedKFold from sklearn.model_selection was a good tool to collect samples according to the primary proportion of different categories. We tested selecting data randomly or proportionally in class imbalanced sample. Also, the experiment was tried without any data balancing technology according to the initial ratio of QSOs, galaxies and stars as a comparison. The sample, no matter the original sample or the resampled sample were divided into the train set (4/5) and the test set (1/5) at random. The test set was not used in training the classifier, but in testing the classifier. The class labels of the training objects were from spectroscopy and were regarded as true.

3.1. Class Balance Technologies

random undersampling: For example, QSO was the fewest category in the Sample 1. The number of the QSOs was 33189. We picked up 33189 galaxies and 33189 stars at random, and combined a new sample with the same ratio of different types. The disadvantage of undersampling was that it might lead to losing some information. We could use the new sample to train the machine learning model, and retrained the model using the original imbalanced data to reduce the loss of information.
random oversampling: It copied minority class samples to make the number of categories in the dataset more balanced. It was easy to implement. Its disadvantage was that it might lead to overfitting. We did not employ this method.
Synthetic Minority Oversampling Technique (SMOTE) [21]: (1) For each sample x in the minority class, this method calculated distances from all samples in the minority class sample using Euclidean distance as the standard, and obtained the k-nearest neighbor. (2) It set a sampling ratio based on the sample imbalance ratio to determine the sampling rate. For each minority sample x, it randomly selected several samples from its k-nearest neighbors, assuming the selected nearest neighbor was x ~ . (3) For each randomly selected nearest neighbor x ~ , it constructed a new sample with the original sample according to the following formula:
x n e w = x + r a n d ( 0,1 ) × ( x ~ − x )
Adaptive Synthetic Sampling (ADASYN) [22]: It was based on SMOTE with some improvement. It adaptively generated new samples based on the distribution differences between different categories. It calculated the distance between each minority class sample and its neighboring samples, and then calculated the distribution density of each sample based on the distance. In areas with low distribution density, ADASYN generated more composite samples to increase the number of minority class samples, which avoided generating too many synthesized samples in areas with high distribution density.
Borderline-SMOTE [23]: Boundary and nearby examples were more likely to be misclassified than examples far from the boundary, making classification more important. Examples that were far from the boundary might not be helpful for classification. In order to achieve better prediction, most classification algorithms attempted to learn the boundaries of each class as accurately as possible during the training process. When generating new samples from boundary sample points, Borderline-SMOTE 1 chose the minority samples randomly in the k-neighbour, but Borderline-SMOTE 2 chose any samples in the k-neighbour.
SMOTEENN [24]: The minority class samples generated by the ordinary SMOTE method were obtained through linear interpolation, which expanded the sample space of the minority class. The problem was that the space originally belonging to the majority class samples might be “invaded” by the minority class, which could easily cause overfitting of the model. This method generated new minority class samples using the SMOTE method to obtain the expanded dataset. Then it used K-NearestNeighbor (usually 3 out of K) method to predict each sample in the expanded dataset. If the predicted result did not match the actual category label, this sample point would be removed.
SMOTETomek [24]: It also generated new minority class samples using the SMOTE method to obtain the expanded dataset. Tomek links should remove noise points or boundary points to avoid SMOTE causing the space that originally belonged to the majority class sample to be “invaded” by the minority class. When dealing with the noise or boundary points, it could effectively solve the problem of “intrusion”.

3.2. Classification Algorithms

Ensemble learning could effectively solve the problem of class imbalance by combining the prediction results of multiple base learners for decision-making. The ensemble learning included Bagging, Boosting, and Stacking. Boosting trained multiple base learners through serialization. Each base learner focused on the wrongly predicted samples from the previous base learner to improve the recognition ability of the model to classify samples.
Light Gradient Boosting Machine (LightGBM) [25] was a gradient boosting framework that used tree based learning algorithms. It was designed to be distributed and efficient with the following advantages: faster training speed and higher efficiency, lower memory usage, better accuracy, support of parallel, distributed, GPU learning, and capable of handling large-scale data. LightGBM adopted a leaf growth strategy to optimize this issue. The specific rule was to select the leaf that could bring the maximum gain during each split. Under the same number of divisions, it was evident that leaf growth could reduce the loss function even more.
CatBoost [26] was a high-performance open source library for gradient boosting on decision trees. The advantages lay in its ability to efficiently handle categorical variables, effectively prevent overfitting, and high model training accuracy. It also combined existing category-based features based on their inherent connections in modeling, enriching the feature dimension and improving the accuracy of prediction results. It was based on a random sorting of samples, processing and calculating the samples to obtain unbiased estimates of target variable statistics and model gradient values, effectively avoiding prediction shift.
XGBoost [27] was an end-to-end gradient lifting tree system proposed by Chen Tianqi. It directly added the loss function and regularization term to form a global loss function. The second derivative of this loss function was got to obtain the final obj, and a score was calculated using obj. The smaller the score, the better. Finally, the score calculated using obj determined the structure of the tree and the score of the entire strong learner. So XGBoost was not achieved by fitting residuals, but by directly calculating the obj function to obtain the tree structure.
RF [28] was to establish a forest in a random manner, where there were many decision trees, and there was no correlation between each decision tree in a random forest. After obtaining the forest, when a new input sample entered, each decision tree in the forest was asked to make a judgment separately to see which class the sample should belong to (for classification algorithms), and then to see which class was selected the most, to predict which class the sample belonged to.
LightGBM, CatBoost, XGBoost belonged to the Boosting algorithms. RF belonged to the Bagging algorithms. All the four algorithms could prevent overfitting in some way.

3.3. Results

There were some definitions. The True Positive (TP) were the number of the predicted positive classes when they were true positive classes. The False Positive (FP) were the number of the predicted positive classes when they were true negative classes. The False Negative (FN) were the number of the predicted negative classes when they were true positive classes. The True Negative (TN) were the number of the predicted negative classes when they were true negative classes. The precision was equal to TP/(TP+FP). The recall was equal to TP/(TP+FN). The accuracy was equal to (TP+TN)/(TP+FP+TN+FN). The f1-score was equal to 2*(precision* recall)/(precision + recall). If the micro avg was adopted, the accuracy was equal to the precision, the recall, or the f1-score. All of them were equal.

3.3.1. Comparing Class Balance Technologies

The accuracy was meaningless in extreme imbalance data. For example, there were 100 samples, including 1 female and 99 males. When the model predicting everyone as males, the accuracy could reach 99%. The precision and recall were recommended. The experiments was once tested using the original imbalanced data. When considering putting the data into the training and test set, we used two ways: selecting randomly or selecting proportionally. When selecting data randomly, the train_test_split from sklearn.model_selection was used, which was the most popular way as we guessed. However, selecting randomly would lead to inaccurate precision in unbalanced data.
The StratifiedKFold was used to collect samples according to the initial ratio of QSOs, galaxies and stars. The ratio of the training set and the test set that we used was 4:1. Then we used the 7 class balance technologies to do the experiments. The LightGBM algorithm was adopted when comparing the class balance technologies or nonuse them. The results of the test set were given in Table 1. When putting the data into the training and test set randomly not proportionally, the accuracy was a little high but unbelievable. There were some overfitting more or less. When putting the data into the training and test set proportionally, the evaluation indicators were really low.
When using random-undersampling for the Sample 1, we picked up 33189 galaxies, and 33189 stars randomly to match the number of QSOs, and combined them into a new sample. The random-undersampling method lost some information and produced poor effects not even retraining the model by original data again. It was hard to predict the minority class QSOs, while searching for QSOs was the potential demand in some surveys.
For example, GALAXY was the most category in the Sample 1 with the number of 862804. When using all the oversampling for the Sample 1, we resampled the QSO and STAR to the number of 862804. Among the 7 class balance technologies, the SMOTE, SMOTEENN, SMOTETomek outperformed the other 4 technologies in our Sample 1 data. The improved versions of SMOTE such as ADASYN, BorderlineSMOTE1, BorderlineSMOTE2 had poor performances. The SMOTEENN was the best method especially for QSOs, in which the precision ~ 0.94, recall ~ 0.96, f1-score ~ 0.95. There was a method called SVMSMOTE, which could result in better recall but worse precision than the SMOTEENN. However, it cost a lot of time and was not illuminated in Table 1.

3.3.2. Comparing Classification Algorithms

When comparing different classification algorithms, we employed the SMOTEENN in our following tests. The most popular algorithms were the LightGBM, CatBoost, XGBoost, and RF at present. The comparison was elaborated in Table 2. The bagging algorithm—RF outperformed the boosting algorithm: LightGBM, CatBoost, and XGBoost. Actually all of them were really good. For all of the algorithms, the precision or recall exceeded 0.94. CatBoost produced the same indicators as XGBoost. RF cost a little more time than the other three algorithms, although all of them were not time-consuming as the other algorithms, such as the Support Vector Machine.
In the RF algorithm, the precision, recall and f1-score for QSOs were 0.98, 0.99 and 0.98 separately. That meant 99% of QSOs in the sample could be found. It was very useful in the following photometry surveys searching for more QSOs candidates. The precision, recall and f1-score for galaxies were 0.99, 0.96 and 0.97. The precision, recall and f1-score for stars were 0.98, 1.00 and 0.99 respectively.

3.3.3. Comparing Different Samples

Sample 1 and Sample 2 had different depth of redshift and different imbalance. The SMOTEENN could perform well in extreme imbalance data, for example the Sample 1. The SMOTEENN +RF was performed in different samples. The precision and recall in the Sample 2 were a little lower than those in the Sample 1. It demonstrated that the J, H, K magnitudes were important than the number of the samples. Nonetheless, the SMOTEENN +RF algorithm could still give good search for the QSOs in Sample 2. The 98% of all QSOs could be picked out. Any precision or recall reached 0.90 of any categories. The prediction was still good until the redshift to 7, and r magnitudes to 30. The results were described in Table 3.
Table 2. Sample 1, using 12 features by 4 different classification algorithms.
Table 2. Sample 1, using 12 features by 4 different classification algorithms.
Sample 1 - 12 features
SMOTEENN
precision recall f1-score support
LightGBM QSO 0.94 0.96 0.95 172125
GALAXY 0.97 0.93 0.95 165234
STAR 0.97 0.99 0.98 169550
accuracy 0.96 506909
macro avg 0.96 0.96 0.96 506909
weighted avg 0.96 0.96 0.96 506909
run_time: 1118.32(s)
CatBoost QSO 0.96 0.97 0.96 172136
GALAXY 0.98 0.94 0.96 165206
STAR 0.97 0.99 0.98 169560
accuracy 0.97 506902
macro avg 0.97 0.97 0.97 506902
weighted avg 0.97 0.97 0.97 506902
run_time: 1466.98(s)
XGBoost QSO 0.96 0.97 0.96 172126
GALAXY 0.98 0.94 0.96 165211
STAR 0.97 0.99 0.98 169526
accuracy 0.97 506863
macro avg 0.97 0.97 0.97 506863
weighted avg 0.97 0.97 0.97 506863
run_time: 1776.15(s)
RF QSO 0.98 0.99 0.98 172122
GALAXY 0.99 0.96 0.97 165232
STAR 0.98 1.00 0.99 169562
accuracy 0.98 506916
macro avg 0.98 0.98 0.98 506916
weighted avg 0.98 0.98 0.98 506916
run_time: 2260.97(s)

4. Summary and Discussion

When putting data into the training and test set, it was not good to use selecting data randomly in class imbalanced sample. Selecting data proportionally to make the training set, the test set and the original data consisting of the same proportion of categories was important. We tested the class balance technologies: SMOTE, SMOTEENN, SMOTETomek, ADASYN, BorderlineSMOTE1, BorderlineSMOTE2, and RandomUndersampling. The contrast of class balance technologies was executed in the LightGBM algorithm. The former three outperformed the other 4 technologies in our Sample 1 data. The improved versions of SMOTE such as ADASYN, BorderlineSMOTE1, BorderlineSMOTE2 had poor performances. The SMOTEENN was the best method especially for QSOs, in which the precision ~ 0.94, recall ~ 0.96, f1-score ~ 0.95.
The LightGBM, CatBoost, XGBoost, and RF were compared when adopting the SMOTEENN class balance technologies in Sample 1. For all of the algorithms, the precision or recall exceeded 0.94. The RF cost a little more time than the other three algorithms, but yielded the best evaluating indicators.
Utilizing the SMOTEENN + RF technology, we obtained excellent classifiers. Adopting the simple features of petroMag_u, petroMag_g, petroMag_r, petroMag_i, petroMag_z, J, H, Ks, W1, W2, W3, W4 magnitudes, not including any morphological parameters, the precision, recall and f1-score for QSOs could achieve 0.98, 0.99, 0.98. The precision, recall and f1-score for galaxies could achieve 0.99, 0.96, 0.97. The precision, recall and f1-score for stars could achieve 0.98, 1.00, 0.99 respectively. That meant if a study focused on QSOs, only 1% of the supposed QSOs had been missed. Among the found QSOs, the purity was 98%. The SMOTEENN +RF technology was very kind to those projects searching for QSOs, since QSO was a minority class among the sources in the sky.
Adopting the simple features of petroMag_u, petroMag_g, petroMag_r, petroMag_i, petroMag_z, W1, W2, W3, W4 magnitudes, not including any morphological parameters, the precision, recall and f1-score for QSOs could achieve 0.94, 0.98, 0.96. The precision, recall and f1-score for galaxies could achieve 0.96, 0.90, 0.93. The precision, recall and f1-score for galaxies could achieve 0.96, 0.97, 0.97.
Our study had the similar precision, recall, f1-score, and accuracy as Cunha & Humphrey 2022. The results seemed better than the others’ results introduced in Section 1. If we demanding no omissions, we needed the higher recall. If we demanding the purity, we needed the higher precision. Paying the close attention to the f1-score or AUC was not recommended. When we focused on the QSOs study which was the minority class, the accuracy for the whole sample would not work.
In the former studies, such as Costa-Duarte et al. 2019, Baqui et al. 2021, the morphologies were used as input features. However, excluding the morphological parameters were important. In many of the following photometry surveys, there were no any morphological parameters included, providing just different kinds of photometry. One could match the photometry of surveys to ALLWISE or Simbad to get a labeled training set, and adopted the SMOTEENN to enlarge the training set. They could train their own RF classifiers, and applied the models to their whole surveys to get a clear classification of the sources. The SMOTEENN technology was necessary to search the QSOs in the surveys.

Author Contributions

Wen, Xiao-Qing designed the research, interpreted and analyzed the results. The authors declare no competing interests.

Funding

This research was funded by by the National Natural Science Foundation of China, grant number 62066026.

Acknowledgments

Funding for the Sloan Digital Sky Survey V has been provided by the Alfred P. Sloan Foundation, the Heising-Simons Foundation, the National Science Foundation, and the Participating Institutions. SDSS acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org. SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration, including the Carnegie Institution for Science, Chilean National Time Allocation Committee (CNTAC) ratified researchers, the Gotham Participation Group, Harvard University, Heidelberg University, The Johns Hopkins University, L’Ecole polytechnique fédérale de Lausanne (EPFL), Leibniz-Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Extraterrestrische Physik (MPE), Nanjing University, National Astronomical Observatories of China (NAOC), New Mexico State University, The Ohio State University, Pennsylvania State University, Smithsonian Astrophysical Observatory, Space Telescope Science Institute (STScI), the Stellar Astrophysics Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Illinois at Urbana-Champaign, University of Toronto, University of Utah, University of Virginia, and Yale University. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration.

Conflicts of Interest

The authors declare no conflict of interest.

Notes

1
http://cdsxmatch.u-strasbg.fr

References

  1. Ball, N.M.; Brunner, R.J.; Myers, A.D.; Tcheng, D. Robust Machine Learning Applied to Astronomical Data Sets. I. Star-Galaxy Classification of the Sloan Digital Sky Survey DR3 Using Decision Trees. Astrophys. J. 2006, 650, 497–509. [Google Scholar] [CrossRef]
  2. Salvato, M.; Hasinger, G.; Ilbert, O.; Zamorani, G.; Brusa, M.; Scoville, N.Z.; Rau, A.; Capak, P.; Arnouts, S.; Aussel, H.; et al. PHOTOMETRIC REDSHIFT AND CLASSIFICATION FOR THEXMM-COSMOS SOURCES. Astrophys. J. 2008, 690, 1250–1263. [Google Scholar] [CrossRef]
  3. Brescia, M.; Cavuoti, S.; Longo, G. Automated physical classification in the SDSS DR10. A catalogue of candidate quasars. Mon. Not. R. Astron. Soc. 2015, 450, 3893–3903. [Google Scholar] [CrossRef]
  4. Fotopoulou, S.; Paltani, S. CPz: Classification-aided photometric-redshift estimation. Astron. Astrophys. 2018, 619, A14. [Google Scholar] [CrossRef]
  5. M. V. Costa-Duarte, L. Sampedro, A. Molino, H. S. Xavier, F. R. Herpich, A. L. Chies-Santos, C. E. Barbosa, A. Cortesi, W. Schoenell, A. Kanaan, T. Ribeiro, C. Mendes de Oliveira, S. Akras, A. Alvarez-Candal, C. L. Barbosa, J. L. N. Castell’on, P., Coelho, M. L. L. Dantas, R. Dupke, A. Ederoclite, A. Galarza, T. S. Gon¸calves, J. A. Hernandez-Jimenez, Y. Jim´enez-Teja, A. Lopes, P. A. A. Lopes, R. Lopes de Oliveira1, J. L. Melo de Azevedo, L. M. Nakazono, H. D. Perottoni, C. Queiroz, K. Saha, L. Sodr´e Jr.1 , E. Telles, R. C. Thom de Souza, The S-PLUS: a star/galaxy classification based on a Machine Learning approach. [CrossRef]
  6. Logan, C.H.A.; Fotopoulou, S. Unsupervised star, galaxy, QSO classification. Astron. Astrophys. 2020, 633, A154. [Google Scholar] [CrossRef]
  7. Cunha, P.A.C.; Humphrey, A. Photometric redshift-aided classification using ensemble learning. Astron. Astrophys. 2022, 666, A87. [Google Scholar] [CrossRef]
  8. Queiroz, C.; Abramo, L.R.; Rodrigues, N.V.N.; Pérez-Ràfols, I.; Martínez-Solaeche, G.; Hernán-Caballero, A.; Hernández-Monteagudo, C.; Lumbreras-Calle, A.; Pieri, M.M.; Morrison, S.S.; et al. The miniJPAS survey quasar selection – I. Mock catalogues for classification. Mon. Not. R. Astron. Soc. 2023, 520, 3476–3493. [Google Scholar] [CrossRef]
  9. Martínez-Solaeche, G.; Queiroz, C.; Delgado, R.M.G.; Rodrigues, N.V.N.; García-Benito, R.; Pérez-Ràfols, I.; Abramo, L.R.; Díaz-García, L.; Pieri, M.M.; Chaves-Montero, J.; et al. The miniJPAS survey quasar selection. Astron. Astrophys. 2023, 673, A103. [Google Scholar] [CrossRef]
  10. Ignasi Pérez-Ràfols1,2,3,⋆ , L. Raul Abramo4 , Ginés Martínez-Solaeche5 , Matthew M. Pieri6 , Carolina Queiroz4 , Natália V.N. Rodrigues4 , Silvia Bonoli7,8 , Jonás Chaves-Montero2,7 , Sean S. Morrison6,9 , Jailson Alcaniz10, Narciso Benitez11, Saulo Carneiro12, Javier Cenarro13, David Cristóbal-Hornillos14, Renato Dupke10, Alessandro Ederoclite13, Rosa M. González Delgado11, Antonio Hernán-Caballero13, Carlos López-Sanjuan13, Antonio Marín-Franch13, Valerio Marra15,16,17, Claudia Mendes de Oliveira18, Mariano Moles14, Laerte Sodré Jr.18, Keith Taylor19, Jesús Varela14, and Héctor Vázquez Ramió, The miniJPAS survey quasar selection IV: Classification and redshift estimation with SQUEzE, arXiv:2309.00461. [CrossRef]
  11. Karsten, J.; Wang, L.; Margalef-Bentabol, B.; Best, P.N.; Kondapally, R.; La Marca, A.; Morganti, R.; Röttgering, H.J.A.; Vaccari, M.; Sabater, J. A multi-band AGN-SFG classifier for extragalactic radio surveys using machine learning. Astron. Astrophys. 2023, 675, A159. [Google Scholar] [CrossRef]
  12. Rodrigues, N.V.N.; Abramo, L.R.; Queiroz, C.; Martínez-Solaeche, G.; Pérez-Ràfols, I.; Bonoli, S.; Chaves-Montero, J.; Pieri, M.M.; Delgado, R.M.G.; Morrison, S.S.; et al. The miniJPAS survey quasar selection – II. Machine learning classification with photometric measurements and uncertainties. Mon. Not. R. Astron. Soc. 2023, 520, 3494–3509. [Google Scholar] [CrossRef]
  13. Bai, Y.; Liu, J.; Wang, S.; Yang, F. Machine Learning Applied to Star–Galaxy–QSO Classification and Stellar Effective Temperature Regression. Astron. J. 2019, 157. [Google Scholar] [CrossRef]
  14. Bai, Y.; Liu, J.-F.; Wang, S. Machine learning classification of Gaia Data Release 2. Res. Astron. Astrophys. 2018, 18. [Google Scholar] [CrossRef]
  15. Nakoneczny, S.; Bilicki, M.; Solarz, A.; Pollo, A.; Maddox, N.; Spiniello, C.; Brescia, M.; Napolitano, N.R. Catalog of quasars from the Kilo-Degree Survey Data Release 3. Astron. Astrophys. 2019, 624, A13. [Google Scholar] [CrossRef]
  16. Baqui, P.O.; Marra, V.; Casarini, L.; Angulo, R.; Díaz-García, L.A.; Hernández-Monteagudo, C.; Lopes, P.A.A.; López-Sanjuan, C.; Muniesa, D.; Placco, V.M.; et al. The miniJPAS survey: star-galaxy classification using machine learning. Astron. Astrophys. 2021, 645, A87. [Google Scholar] [CrossRef]
  17. Almeida, A.; Anderson, S.F.; Argudo-Fernández, M.; Badenes, C.; Barger, K.; Barrera-Ballesteros, J.K.; Bender, C.F.; Benitez, E.; Besser, F.; Bird, J.C.; et al. The Eighteenth Data Release of the Sloan Digital Sky Surveys: Targeting and First Spectra from SDSS-V. Astrophys. J. Suppl. Ser. 2023, 267, 44. [Google Scholar] [CrossRef]
  18. R. M. Cutri, E. L. Wright, T. Conrow, J. Bauer, D. Benford, H. Brandenburg, J. Dailey, P. R. M. Eisenhardt, T. Evans, S. Fajardo-Acosta, J. Fowler, C. Gelino, C. Grillmair, M. Harbut, D. Hoffman, T. Jarrett, J. D. Kirkpatrick, D. Leisawitz, W. Liu, A. Mainzer, K. Marsh, F. Masci, H. McCallon, D. Padgett, M. E. Ressler, D. Royer, M. F. Skrutskie, S. A. Stanford, P. L. Wyatt, D. Tholen, C. W. Tsai, S. Wachter, S. L. Wheelock, L. Yan, R. Alles, R. Beck, T. Grav, J. Masiero, B. McCollum, P. McGehee, M. Papin, M. Wittman, Explanatory Supplement to the WISE All-Sky Data Release Products, 2014yCat.2328....0C. [CrossRef]
  19. Wright, E.L.; Eisenhardt, P.R.M.; Mainzer, A.K.; Ressler, M.E.; Cutri, R.M.; Jarrett, T.; Kirkpatrick, J.D.; Padgett, D.; McMillan, R.S.; Skrutskie, M.; et al. The Wide-Field Infrared Survey Explorer (WISE): Mission Description And Initial On-Orbit Performance. Astron. J. 2010, 140, 1868–1881. [Google Scholar] [CrossRef]
  20. R. M. Cutri, M. F. Skrutskie, S. van Dyk, C. A. Beichman, J. M. Carpenter, T. Chester, L. Cambresy, T. Evans, J. Fowler, J. Gizis, E. Howard, J. Huchra, T. Jarrett, E. L. Kopan, J. D. Kirkpatrick, R. M. Light, K. A. Marsh, H. McCallon, S. Schneider, R. Stiening, M. Sykes, M. Weinberg, W. A. Wheaton, S. Wheelock, N. Zacarias, 2MASS All Sky Catalog of point sources, 2003tmc..book.....C. Available online: http://irsa.ipac.caltech.edu/applications/Gator/.
  21. Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
  22. He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceeding of the IEEE International Joint Conference on Neural Networks, Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef]
  23. Hui Han, Wen-Yuan Wang & Bing-Huan Mao, Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning, International Conference on Intelligent Computing: 2005: Advances in Intelligent Computing pp 878–887.
  24. BATISTA G E A P A, PRATI R C, MONARD M C. A study of the behavior of several methods for balancing machine learning training data[J]. ACM SIGKDD Explorations Newsletter, 2004, 6 (1): 20-29.
  25. G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye, T.-Y. Liu, LightGBM: A Highly Efficient Gradient Boosting Decision Tree, Advances in Neural Information Processing Systems 30 (2017) 3146-3154.
  26. L Prokhorenkova, G Gusev, A Vorobev, AV Dorogush, A Gulin, CatBoost: unbiased boosting with categorical features, Advances in Neural Information Processing Systems (2018) 6638-6648. [CrossRef]
  27. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD ’16: 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
  28. L. Breiman, Random forests, Machine learning 45 (2001) 5-32.
Preprints 86549 g001
Figure 1. the distributions of the Sample 1 (a) the petroMag_r; (b) the redshift.
Figure 1. the distributions of the Sample 1 (a) the petroMag_r; (b) the redshift.
Preprints 86549 g001
Preprints 86549 g002
Figure 2. the distributions of the Sample 2 (a) the petroMag_r; (b) the redshift.
Figure 2. the distributions of the Sample 2 (a) the petroMag_r; (b) the redshift.
Preprints 86549 g002
Preprints 86549 g003
Figure 3. (a) the imbalance of Sampe 1: 33189 QSOs, 862804 galaxies, and 390482 stars; (b) the imbalance of Sampe 2: 677166 QSOs, 2448971 galaxies, and 643260 stars.
Figure 3. (a) the imbalance of Sampe 1: 33189 QSOs, 862804 galaxies, and 390482 stars; (b) the imbalance of Sampe 2: 677166 QSOs, 2448971 galaxies, and 643260 stars.
Preprints 86549 g003
Table 1. Sample 1, using 12 features by LightGBM algorithm. We compared using different class balance technologies or original data.
Table 1. Sample 1, using 12 features by LightGBM algorithm. We compared using different class balance technologies or original data.
Sample 1 - 12 features
LightGBM
precision recall f1-score support
original data, selected randomly QSO 0.86 0.81 0.83 6690
GALAXY 0.99 0.99 0.99 172353
STAR 0.98 0.98 0.98 78252
accuracy 0.98 257295
macro avg 0.94 0.93 0.93 257295
weighted avg 0.98 0.98 0.98 257295
precision recall f1-score support
original data, select proportionally QSO 0.40 0.22 0.28 6638
GALAXY 0.96 0.94 0.95 172560
STAR 0.84 0.91 0.87 78097
accuracy 0.91 257295
macro avg 0.73 0.69 0.70 257295
weighted avg 0.91 0.91 0.91 257295
precision recall f1-score support
Random
Undersampling, select proportionally		 QSO 0.3 0.96 0.46 6638
GALAXY 0.98 0.91 0.94 172560
STAR 0.93 0.9 0.92 78097
accuracy 0.91 257295
macro avg 0.74 0.92 0.77 257295
weighted avg 0.95 0.91 0.92 257295
precision recall f1-score support
Random
undersampling
train the model
by original data (select proportionally) again		 QSO 0.49 0.28 0.35 6638
GALAXY 0.96 0.94 0.95 172560
STAR 0.84 0.91 0.87 78097
accuracy 0.91 257295
macro avg 0.76 0.71 0.72 257295
weighted avg 0.91 0.91 0.91 257295
precision recall f1-score support
SMOTE, select proportionally QSO 0.92 0.96 0.94 172561
GALAXY 0.96 0.88 0.92 172560
STAR 0.94 0.98 0.96 172561
accuracy 0.94 517682
macro avg 0.94 0.94 0.94 517682
weighted avg 0.94 0.94 0.94 517682
precision recall f1-score support
ADASYN, select proportionally QSO 0.63 0.75 0.69 172535
GALAXY 0.95 0.77 0.85 172560
STAR 0.63 0.63 0.63 173007
accuracy 0.72 518102
macro avg 0.74 0.72 0.72 518102
weighted avg 0.74 0.72 0.72 518102
precision recall f1-score support
BorderlineSMOTE1 select proportionally QSO 0.82 0.97 0.89 172561
GALAXY 0.95 0.84 0.89 172560
STAR 0.87 0.82 0.84 172561
accuracy 0.87 517682
macro avg 0.88 0.87 0.87 517682
weighted avg 0.88 0.87 0.87 517682
precision recall f1-score support
BorderlineSMOTE2 select proportionally QSO 0.7 0.88 0.78 172561
GALAXY 0.78 0.82 0.8 172560
STAR 0.76 0.53 0.63 172561
accuracy 0.74 517682
macro avg 0.75 0.74 0.74 517682
weighted avg 0.75 0.74 0.74 517682
precision recall f1-score support
SMOTEENN, select proportionally QSO 0.94 0.96 0.95 172125
GALAXY 0.97 0.93 0.95 165234
STAR 0.97 0.99 0.98 169550
accuracy 0.96 506909
macro avg 0.96 0.96 0.96 506909
weighted avg 0.96 0.96 0.96 506909
precision recall f1-score support
SMOTETomek, select proportionally QSO 0.92 0.96 0.94 172541
GALAXY 0.96 0.88 0.92 172414
STAR 0.94 0.98 0.96 172426
accuracy 0.94 517381
macro avg 0.94 0.94 0.94 517381
weighted avg 0.94 0.94 0.94 517381
Table 3. Sample 1 and Sample 2 using SMOTEENN+RF algorithms.
Table 3. Sample 1 and Sample 2 using SMOTEENN+RF algorithms.
SMOTEENN+RF
precision recall f1-score support
Sample 1 QSO 0.98 0.99 0.98 172122
GALAXY 0.99 0.96 0.97 165232
STAR 0.98 1.00 0.99 169562
accuracy 0.98 506916
macro avg 0.98 0.98 0.98 506916
weighted avg 0.98 0.98 0.98 506916
run_time: 2260.97(s)
Sample 2 QSO 0.94 0.98 0.96 469389
GALAXY 0.96 0.90 0.93 380337
STAR 0.96 0.97 0.97 462677
accuracy 0.95 1312403
macro avg 0.96 0.95 0.95 1312403
weighted avg 0.95 0.95 0.95 1312403
run_time: 6659.07(s)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated