Prerpints.org logo
Preprint
Article

Modeling the Grinding Process of the Cereal Grains as a Result of Friction in the Millstones

Altmetrics

Downloads

90

Views

27

Comments

0

Submitted:

03 October 2023

Posted:

04 October 2023

You are already at the latest version

Alerts
Abstract
The grinding process by friction at the micro-scale in a mill with stones is considered a variable combination of contacts: with two-body (the asperities of lower millstone in direct contact with the asperities of upper millstone) and the three-body (micro-particles of ground seeds trapped between the asperities of lower and the upper stones of the mill). Three elements are described: (1) the mechanic contact of the asperities of the lower and upper millstone, to predict pressures on asperities, by modeling; (2) tests on a millstone sample covered with grinding particles, and (3) tests on a wafer sample formed by the millstones with the grinding particles between them. The paper highlights the combined effects of the micro-scale friction by individual measurements and to sum these effects an analytical model was used, and to validate the model, several experiments were performed. A suitable grind by friction assumes the grain’s movement and the interaction between the seeds and solid surfaces and is highlighted through theoretical and experimental studies. Topography analysis of the surface of the millstones revealed the model of microscopic frictional force. Endpoint measurements (the traces of the surface topography evolution), enable model verification in the grinding process.
Keywords: 
Subject: Engineering  -   Industrial and Manufacturing Engineering

1. Introduction

In the grinding process, the interaction between the seeds and solid surfaces as well as the movement of the grain is very important to obtain an appropriate grind. This movement and interaction between and with solid surfaces of the seeds occur through friction that in the grinding process helps to obtain the desired grist. The very fine grind is achieved at the micro-scale level, as a result of the friction activity combined with the mechanical one.
Past research shows that friction at the micro-scale mainly depends on the molecular adhesion of two contacting bodies [1,2,3,4,5,6,7]. Thus, Li et al. [1] presents and brings clarifications to the rice grinding process respectively it offers indications for the design of friction rice mills. At the same time, using the discrete element method they numerically simulated the rice motion in the friction mill and introduced a method for quantification of the grinding uniformity. The moisture effect cereal seeds on the grinding process by friction, respectively the grind powder properties are presented of Jung et al. [2]. On the other hand, Zeng et al. [3], have simulated the motion of particles (considered spherical) with different static friction coefficients in a rice mill, to clarify the asperities influence of the rice surface on the grinding process. Li et al. [4] shows that the filling level (examined experimentally and numerically) of rice in a friction rice mill determines and improves rice milling quality (as an effect on grinding degree and uniformity). The authors established and applied a method that can quantify grinding uniformity, affected directly by particle rotational kinetic energy. Regarding obtaining the degree and uniformity of grinding, it is necessary to solve optimization problems. Almessiere et al. [5] describes a concrete example of optimization by investigating the exchange and properties of the hard/soft nanocomposites.
Other researchers have evaluated the friction plates’ hardness effect and the orientation of its surfaces on the static friction coefficient and of cereal seeds’ angle [5,6]. The study of the external friction coefficients of grain agricultural products, in static and dynamic friction conditions, was studied by Khozyaev [7] as being the physical and mechanical characteristics of bulk seeds, the most important. Then, Savenkov et al. [8] have highlighted aspects related to these characteristics study of bulk cereal seeds by the internal friction coefficients in static and dynamic regimes. Also, they have presented a carousel-type device and the methodology for determining the internal friction dynamic coefficients, as well as the program and research results of practical use of these coefficients for the cereal agricultural products in bulk, by layers linear displacement, in a speeds range. Kozlovskiy & Zdorovets [9] a concrete example of promising materials for practical applications, with an effect on the research results of the practical use of dynamic coefficients of internal friction, for bulk cereal agricultural products is presented.
The question is asked: What will happen when micro/nanoparticles collide with a solid surface? Thus, for the milling industry (the present case), it becomes an important problem, like in the powders manufacturing industry, the ultra-smooth surface manufacturing industry, etc. Also, it offers important information for a general understanding of micro/nanoparticle collision, essential for controlling and preventing solid surface damage, in micro/nano-modification. In order to evaluate compliance with a specification, the properties of a material, components, structure, or system for different characteristics or defects, without causing damage to the original element, respectively for the control and prevention of damage to the solid surface, in micro/nano-modification, foam testing is necessary for to determine its properties [10], or non-destructive testing [11]. However, they are quite rare, in the research on micro/nanoparticles collision on a solid surface.
To investigate the interactions/collisions between the solid surfaces and energetic clusters was performed more tests and simulations in the last decades [12,13,14,15,16]. The energetics clusters are atomic and molecular groups connecting both individual atoms and solids. They can be used both as models for the fundamental research of the physical aspects transition from the atomic scale to bulk material and as versatile and controllable tools for the surface modification of superficial layers on the micro/nanometer scale [12]. The interaction with small energetic clusters of metallic atoms at the surface was investigated, by molecular dynamics simulations computerized. In order to elucidate the cluster and substrate relative elastic properties, as well as the effects of incidence angle, size, and cluster energy studied cluster-solid combinations in a wide variety [13]. Additionally, Afify et al. [14] have studied by molecular dynamics simulations at a large scale the impact of a single cluster on a hardened surface with the aim to investigate cluster-surface interactions, the highly energetic. Then, Ilie [15] are presented the experimental and theoretical studies on the movement and collision between micro/nanoparticles in the chemical-mechanical polishing/planarization process slurry, as well as between solid surfaces and these, using a friction model microscopic on the basis of the surface topography. Also, Ilie [16] analyzes the impact of chemical-mechanical interactions/collisions, inter-micro/nanoparticles, and between the polishing/planarization head - micro/nanoparticles - polishing/planarization platen on the chemical-mechanical polishing/planarization performance, by measuring the friction force at the interface. By extrapolation, such phenomena (interactions and collisions between energetic clusters) take place also in the case of cereal agricultural products.
Therefore, the paper presents theoretical and experimental seeds movement, the collision between seeds and between the seeds and solid surfaces during the grinding process, using the frictional force model microscopic on the basis of the surface topography.

2. Materials and Methods

In the work process, the upper millstone is maintained on position pressed against the lower millstone with a normal load and which is fixed on a rotating turntable. This trains the mechanical entry of seeds between the upper millstone and lower millstone (even seeds dispersed), provides the grinding activity, and contains a flooded surface with grind material. Very fine grind is realized at the micro-scale as a result of the combined mechanical and friction activity.
Past research demonstrated that in friction mills, friction predominates depending on the molecular adhesion of two contacting bodies, at the micro-scale. Then, we suggested that the grinding process as a result of the pressing and sliding movement is accompanied by friction at the micro-scale and can be dependent on three bodies in contact: between seeds (micro-particles of grind), respectively the seeds (micro-particles of grind) caught between the asperities of the lower millstone and of the upper one. Therefore, the authors propose total friction to be the sum of the friction of individual three-body contacts of seeds trapped between the asperities of the lower millstone and of the upper one (2 contacts), and individual contacts between the asperities of the lower millstone and of the upper one (3rd contact). This is schematically shown in Figure 1.
At the base of this understanding stayed the experimental micro-indenter adhesion measurements both of seeds and of the asperities of the lower millstone and the upper one. Micro-identification was carried out with Micro-scratch Testing from Ebatco, USA with the following key specifications: the maximum load of up to 30 N; load resolution of 0.3 mN; maximum depth of 1 mm; depth resolution of 0.3 nm; maximum scratch length of 120 mm; the scratch speed of 0.4 - 600 mm/min. To measure the material’s asperities an Atomic Force Microscope (AFM) was used. A pin/disk tribometer was used to perform the friction measurements. The tribometer disk is rotating at a speed of 60 rpm, on which are fixed samples of a lower millstone with flour particles. The pin/disc tribometer is also provided with an articulated arm in which the upper millstone samples are fixed (in the form of cylindrical pins with a diameter of 10 mm) and maintained in contact with the other samples in the circular plate form with a diameter of 80 mm, fixed on the tribometer disk. It is mentioned that the material from which the millstones are made – can be granite or ceramic, and in this paper, ceramic was used, as the best naturally transparent material (a rock-forming mineral in the crystalline form of aluminum oxide (Al2O3) typically containing traces of iron, titanium, vanadium, and chromium). Therefore, the samples meter is made of the same material as the millstones (corundum ceramic). .
In accordance with the micro-scale adhesion measurements, each contact between seeds and/or asperities will generate a friction force suitable. For this, a profilometer (ST 400 Nanovea, Switzerland) was needed, which measures the replicas of the asperities of the lower millstone in order to develop a contact model, as well as a virtual micro-tribometer to simulate the contact under the effect of the contact pressure on the asperity. Based on an analytical model the total friction will be determined as a multiplication of the individual friction forces of the contacts with the contacts' total number. The bench-scale experiments will be done to guide the research and validate the model.

3. Results and Discussion

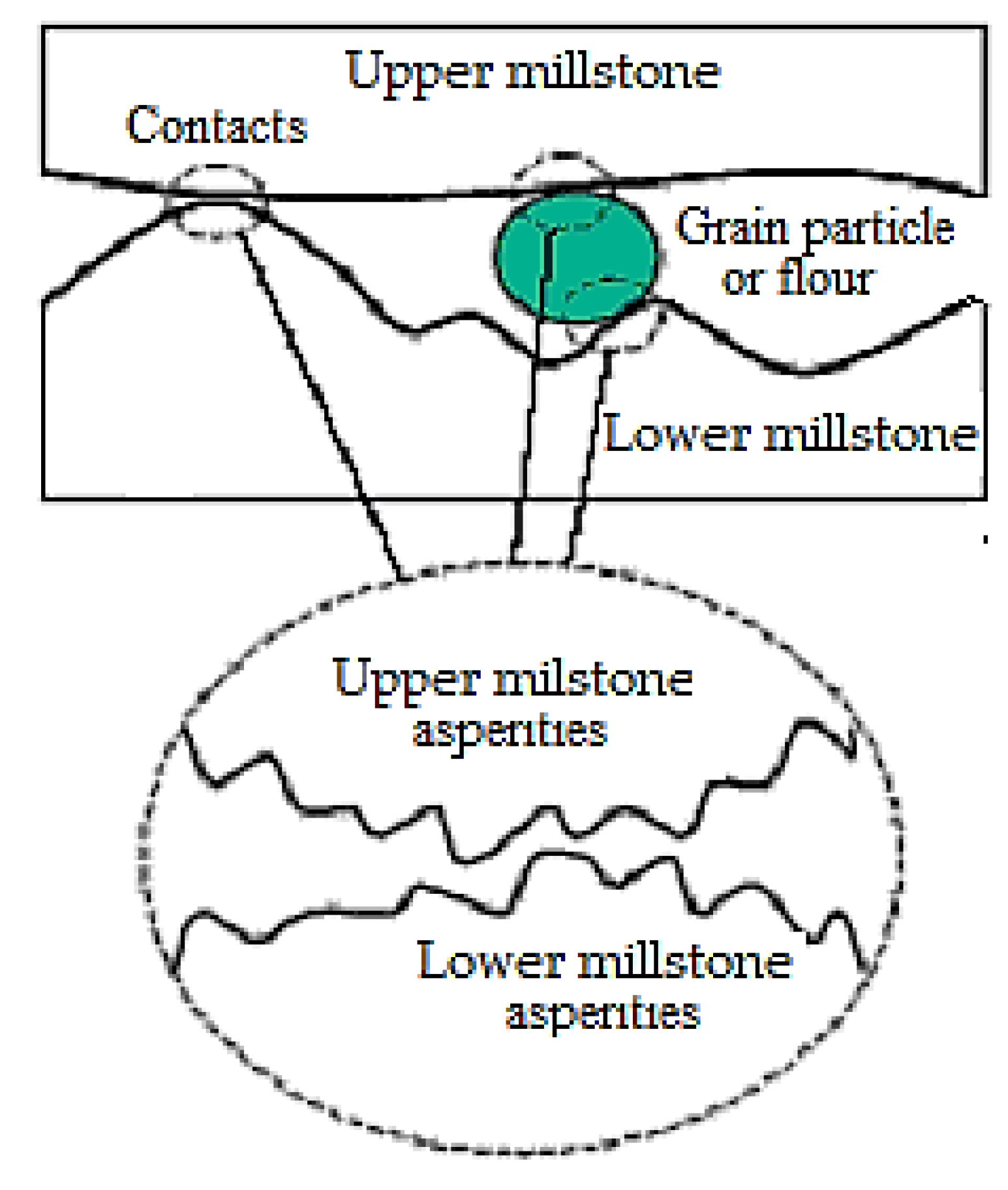
3.1. Friction Modeling

The development of a friction model was necessary considering that the total friction between the lower millstone, seeds, and upper millstone in the grinding process has three distinct friction force components [15,17].
The development of a friction model was necessary considering that the total friction between the lower millstone, seeds, and upper millstone in the grinding process has three distinct friction force components [15,17].
Thus, the frictional force between the lower millstone and the upper millstone, Ffl-u is the first component, the frictional force between grain and upper millstone, Ffg-u is the second component, and the frictional force between seeds and lower millstone, Ffg-l is the third component. Each component of the friction force has an associated friction coefficient μl-u, μg-u, and μg-l), which are corresponding molecular and mechanical adhesion components, [18].
The friction force components cumulated represent the friction force, Ff, and can be written in the form:
F f = [ C 1 μ l − u + C 2 μ g − u − μ g − l ] F n ,
where: Ff – is the total friction force by sliding; Fn – is the applied normal force; C1 and C2 – are constants which consider the contact’s number.
Through seeds density, the asperities distribution of the lower millstone, respectively of upper millstone, and rough contact modeling, the number of contacts can be evaluated [19]. Also, for evaluation of the contacts, the lower millstone porosity is considered. Figure 2 illustrates a schematic of the typical tool setup to measure friction between the upper millstone and grain (flour, which is on the pad), and between the lower millstone and grain (flour, which flows from the upper millstone) and below has a short presentation.
Experiments using different samples of lower millstones show distinctive endpoint traces, while the upper millstone gives unusable results.
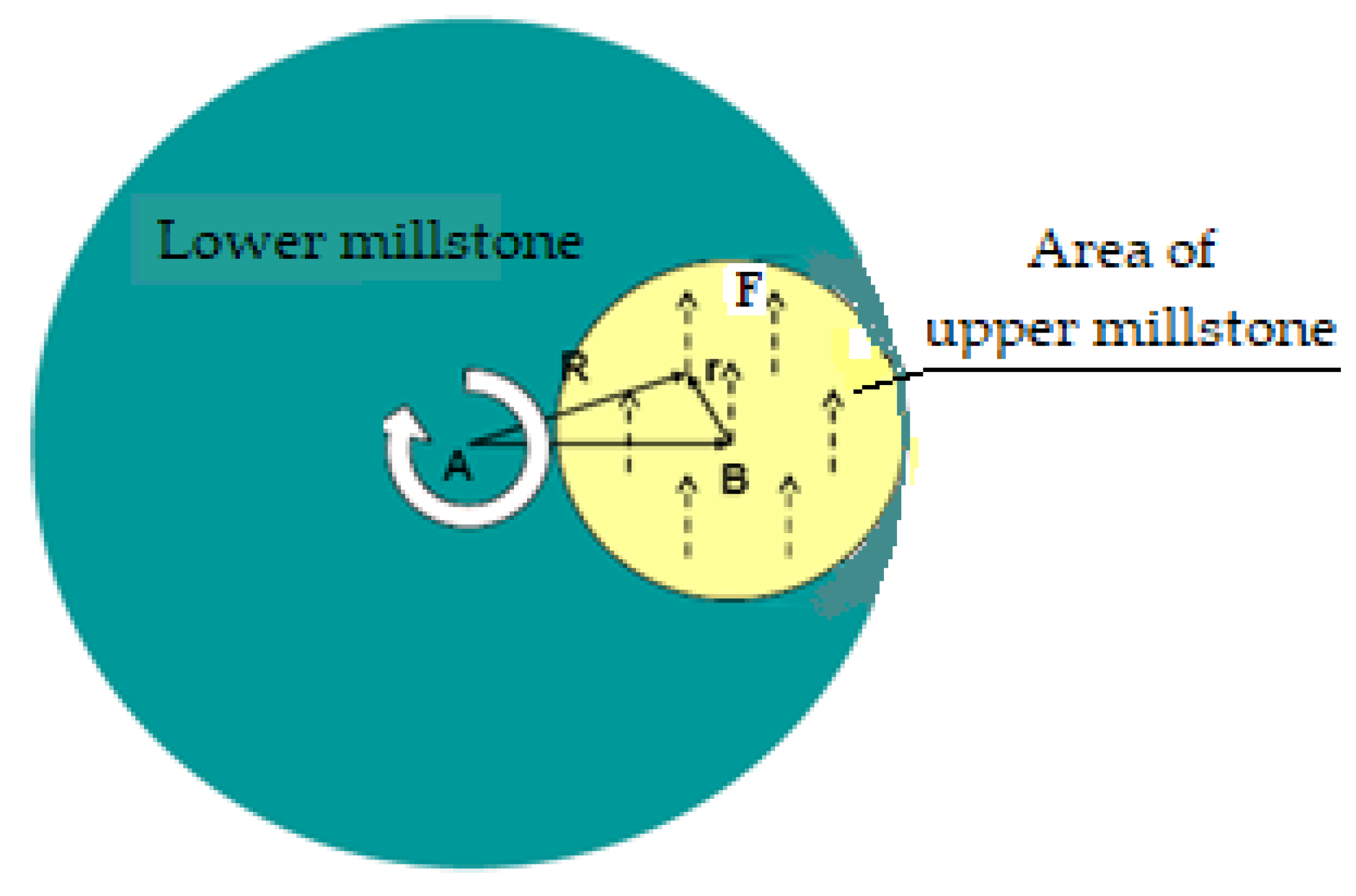
If it is assumed that all the necessary energy for grinding is consumed by the friction between the upper millstone and lower millstone, then it can consider that this is roughly proportional linearly to the average Ff. A way to highlight Ff exerted by the upper millstone on the lower one is shown in Figure 3 (considering an area (the yellow one, for visualization) from the upper millstone in contact with the lower millstone, something that can be generalized over the entire surface of the upper millstone).
The Ff is periodically distributed on the contact surfaces of the upper millstone and of the lower one because the small flour particles are anchored and symmetrically distributed on each surface and the relative velocity between the two surfaces is constant. As a result, it is expected that the net torque of friction forces in ratio with the upper millstone is almost zero, while the net torque in relation to the lower millstone contributes and are added the small torques of these forces. This explains that lower millstone presents distinctive traces of endpoint and those from upper millstone are not useable.
Therefore, the traces during the grinding process provide us the information on friction evolution. To better understand the grinding process and to improve the endpoint monitoring of it, a model for evaluating friction is needed.
Below, is presented a friction model with two-factor (the standard deviation of the highest areas, σsd, and averaged material friction coefficient, μav), relatively simple, although can be considered more friction models. The goal is to understand the interactions between lower millstone with the physics model of the wafer (lower millstone with flour particle) in more detail, and on the basis of the experimental data, also additional factors will be considered.
The model admits that two factors are the cause change of Ff, during the grinding process, namely: adherence of flour layer and surface topography variation (surface heights) [20]. To characterize the Ff between lower millstone and upper millstone, it is assumed as the Ff is proportional linearly with the multiplication between the μav and the σsd, and the Ff relation becomes:
F f ~ μ a v 1 + β ⋅ σ s d ,
where: μav - it is obtained by averaging a weighted friction coefficient of material from friction exposed area; β - empirical parameter dependent on the friction coefficients sensitive to the flour blanket and the materials used for the lower millstone and upper one.
For the σsd determination first, the lower millstone was discredited into cells on friction length size and was calculated as the average of the highest heights of each cell.

3.2. Experimental Procedure

At the beginning was performed a series of experiments to isolate the friction effects between the lower millstone material and the upper millstone. It is important to mention, that and here the frictional forces may be affected by individual flour particles in contact with the lower millstone asperities and of upper millstone.
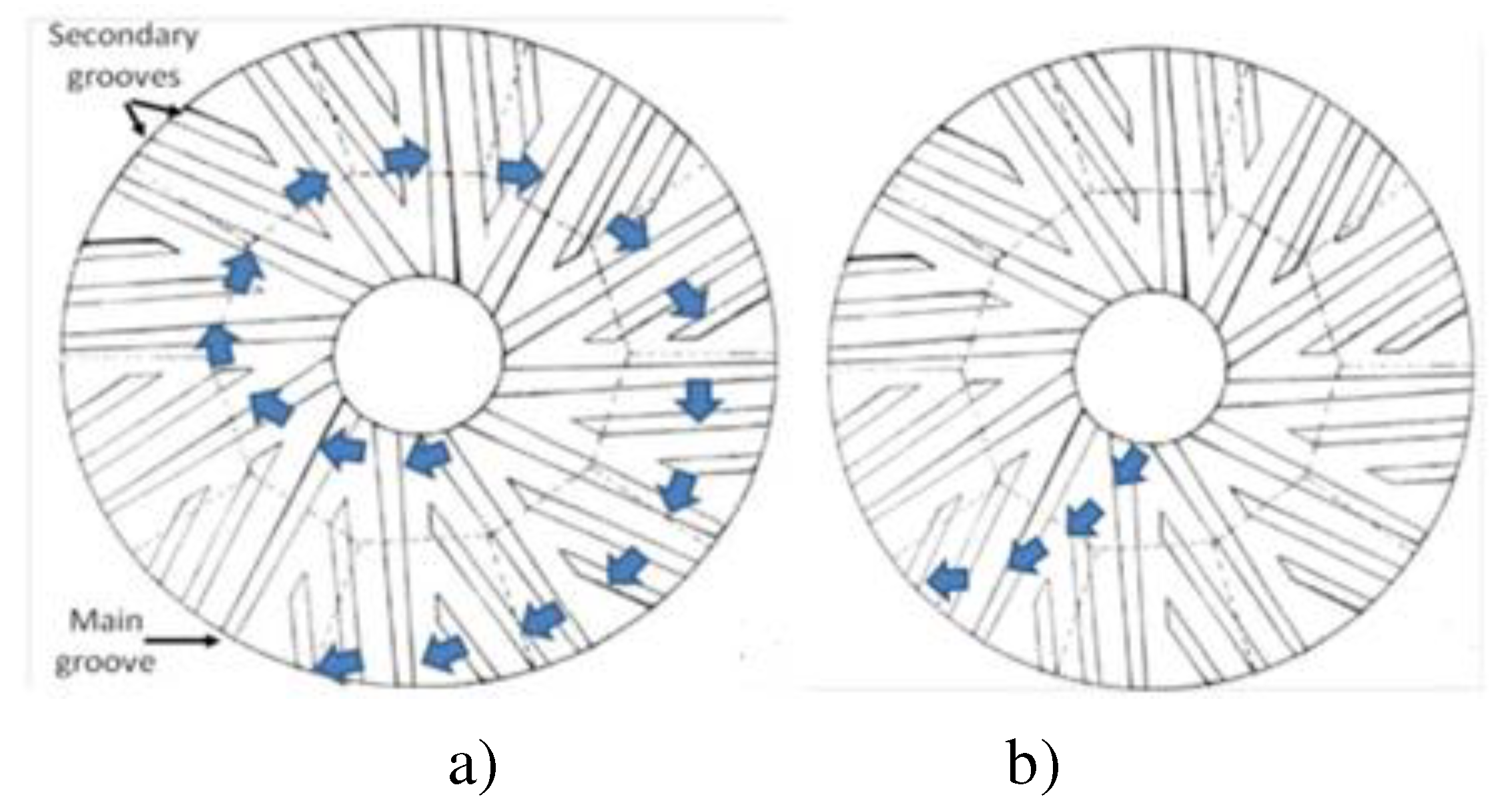
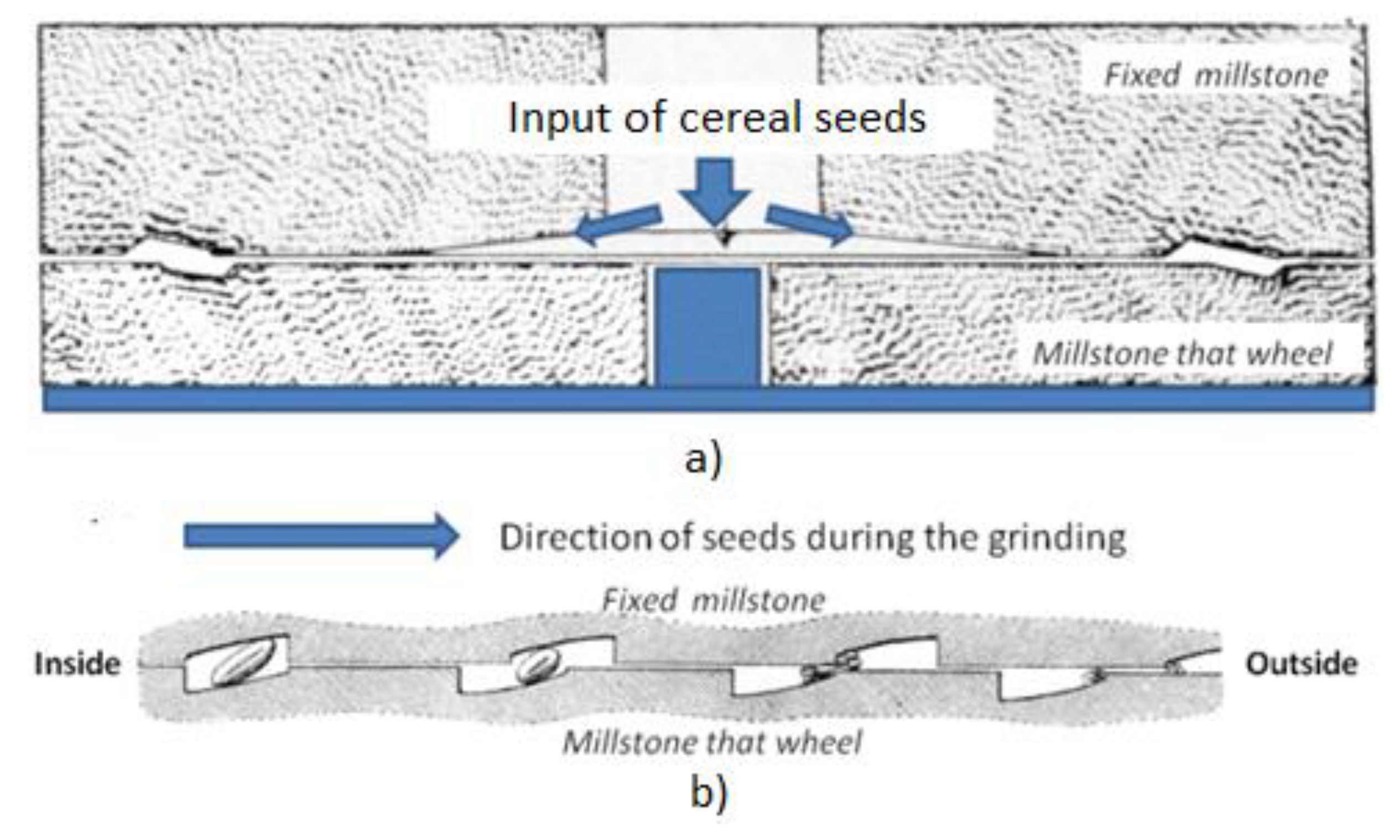
For this, the surface of the millstones must be foreseen by grooves organized radially to allow both the correct friction between the stone’s asperities and seeds (see Figure 1) and the movement of seeds (Figure 4). In particular, the main grooves that begin from the hole until the border of the millstone have the main function of cooling the stone, whereas the secondary grooves contribute to uniform distribute the product on the stone and help to eliminate the flour. As shown in Figure 4, the movement of the seeds on every stone is different between the stones. On the upper millstone (Figure 4a), in fact, seeds are inserted by the hole in the middle of this and move after a spiral path, whereas on the lower stone (Figure 4b) they follow a route after a curve.
Moreover, the hole has a trapezoidal section to allow a regular and uniform distribution of the seeds (Figure 5a) on the one hand, and on the other hand because there is a distance between the two stones of about 10 mm in the center and much less at border (endpoint). Then, grains are grounded (by grain crushing and breaking) and displaced by the millstone until border and collected in externally, along the border (endpoint), in form of flour (Figure 5b).
The grinding and movement of the grains towards the border, takes place by friction, according to the presentation above (see Figure 1), which was analyzed by modeling, simulation and experimentally. The majority of grain crushing and breaking happens in the final part of the millstones where the distance between the stones is the very small.
With the help of micro-indentation and micro-scratch tests have been measured the micro-scale friction forces have been, and with a friction force sensor, with which, was the indenter equipped was measured lateral forces. The tests provide friction results from the interface between the lower millstone and the flour particle, respectively between the flour particle and upper millstone. Also, was measured the friction between a small section of material of the lower millstone and the upper one. Then, to create a scenario of more complex testing was translated over the substrate section from the material of lower millstone with impregnated flour particles.
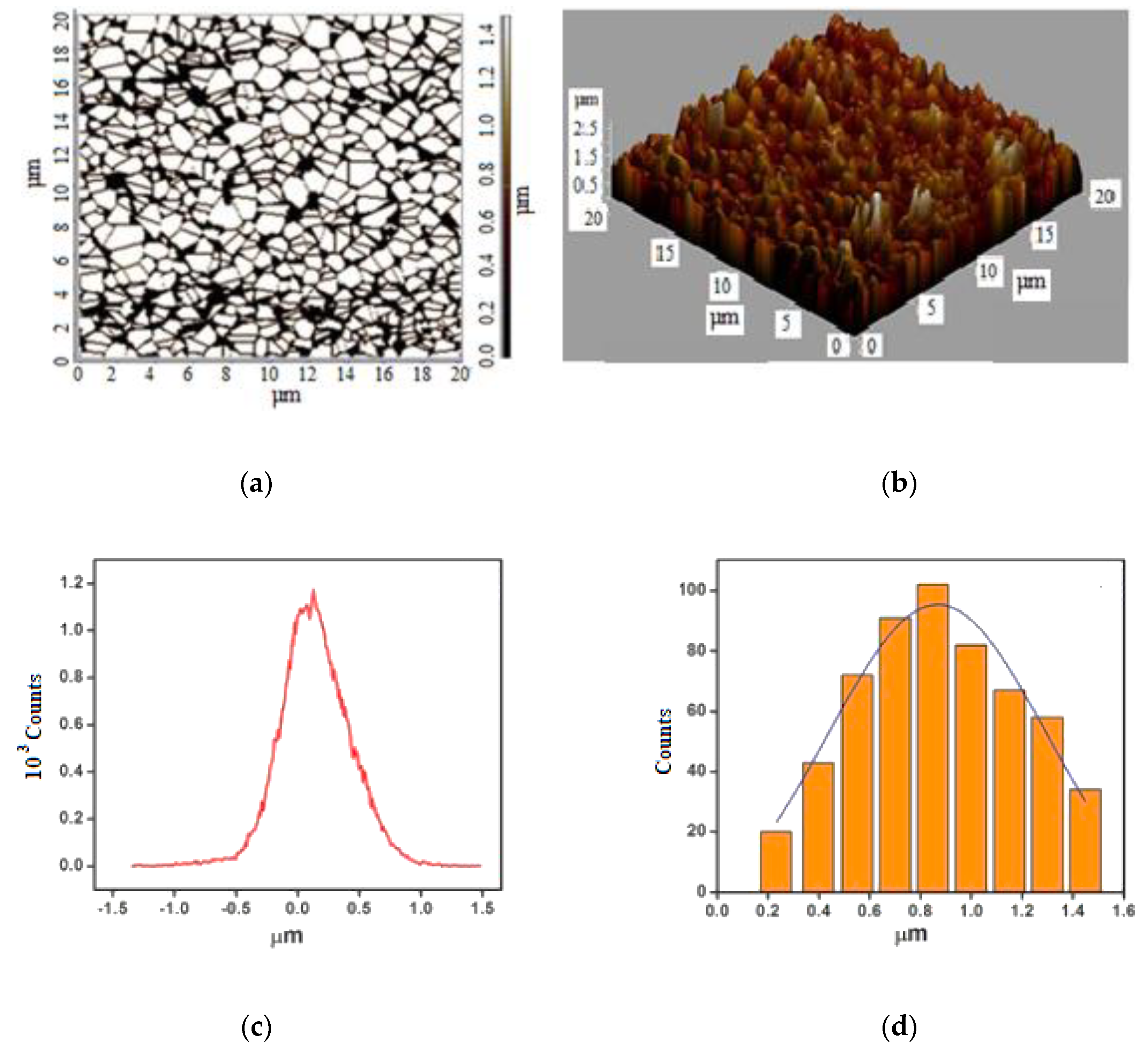
The frictional forces can be affected by the individual flour particles at contact with the asperities of the lower millstone and of the upper one. The Atomic Force Microscope (AFM) was used to measure the material’s asperities. The lower millstone structure is very porous, around 200 μm.
With the help of AFM was captured the regions between the opened pores, were to be able to measure the asperities of these regions at the micro-scale. Figure 6 shows specific AFM images with data (Figure 6a,b), along with the asperity histogram (Figure 6c) and the distribution curve of the grinding stone ceramics grains size (Figure 6d).
Examining the AFM images of ceramic from which the millstone is made, Figure 4a shows the surface morphology of grains and grain boundary in a two-dimensional image of ceramic. It is noted that the AFM image of ceramic exhibits a compact structure with granular morphology, buffer layer, and flat grains with clear boundaries. A three-dimensional AFM image of the ceramic surface is presented in Figure 5b shows, which exhibits the maximum peak height of the grain asperities of 2.52 µm within the scan area 20 µm × 20 µm, and Figure 5c shows the three-dimensional surface roughness of grinding stone ceramic. The average and root mean square roughness were found to be 0.225 µm and 0.290 µm, respectively. The AFM analysis revealed the presence of the seeds with a wider size distribution in the ceramics material of the grinding stone taken into analysis. The average grain size estimated by the two-dimensional AFM image was found to be 0.620 µm out of 630 contacts as shown in the histogram of Figure 5d.
To perform the friction measurements, it was used the pin/disc tribometer, on whose disc are fixed samples of a lower millstone, and on the articulated arm, the upper millstone samples are fixed. At the same time, the arm is provided with load sensors, and the friction is measured in simulated conditions of the grinding process by applying a normal load on the arm, to maintain in contact the lower and upper millstone samples.
This type of tribometer was used because it is the most suitable for measuring the frictional forces at the interface between the grinding stones and the cereal grains and then between these and the flour particles. The flour particles were obtained by fixing cereal grains between the circular pin with a diameter of 10 mm and the plate with a diameter of 80 mm, rotated at 60 rpm, which in the friction process will crumble until the flour powder is obtained. At the same time, the arm is provided with load sensors, and the friction is measured in simulated conditions of the grinding process by applying a normal load on the arm, to maintain the contact the lower and upper millstone samples and cereal grains particles.
Additionally, the friction work process is similar to the work process of a mill with grinding stones, and the samples are made of the material of the grinding stones with the same structure and morphology of the surface of the millstones (corundum ceramic). The distinction from the actual grinding process consists in the absence of the possibility of using a large number of cereal grains, just grain by grain, and their flour for measuring the frictional forces from the surface, forces that may differ relatively little from the real ones. The difference is due to the fact that first the grains are transformed into coarse flour particles and then into finer ones. Also, the contact area between the grinding stone samples used on the pin/disk tribometer differs from the actual contact area in the friction grinding mill, being much smaller. Precisely, this is proven by simulation and analytical modeling.
The difference is due to the fact that first the grains are transformed into coarse flour particles and then finer and finer, similar to those of grinding process in stone mill. Also, the contact area between the grinding stone samples used on the pin/disk tribometer differs from the actual contact area in the friction grinding mill, being much smaller.
In added, the effect of grinding on the flow ability of flour can be evaluated using flow indicators, as: frictional coefficient (in this paper), bulk density, and angle of repose, cohesive index, caking strength, and flour flow stability. Both, flow indicators and powder flow analysis showed that the flours from stone mill are cohesive. Based on the friction forces measured on the pin/disc tribometer, the friction coefficient was determined (with the help of the Amontons-Coulomb law), because it is one of the flow indicators by which the effect of grinding on the flour flow ability can be evaluated.
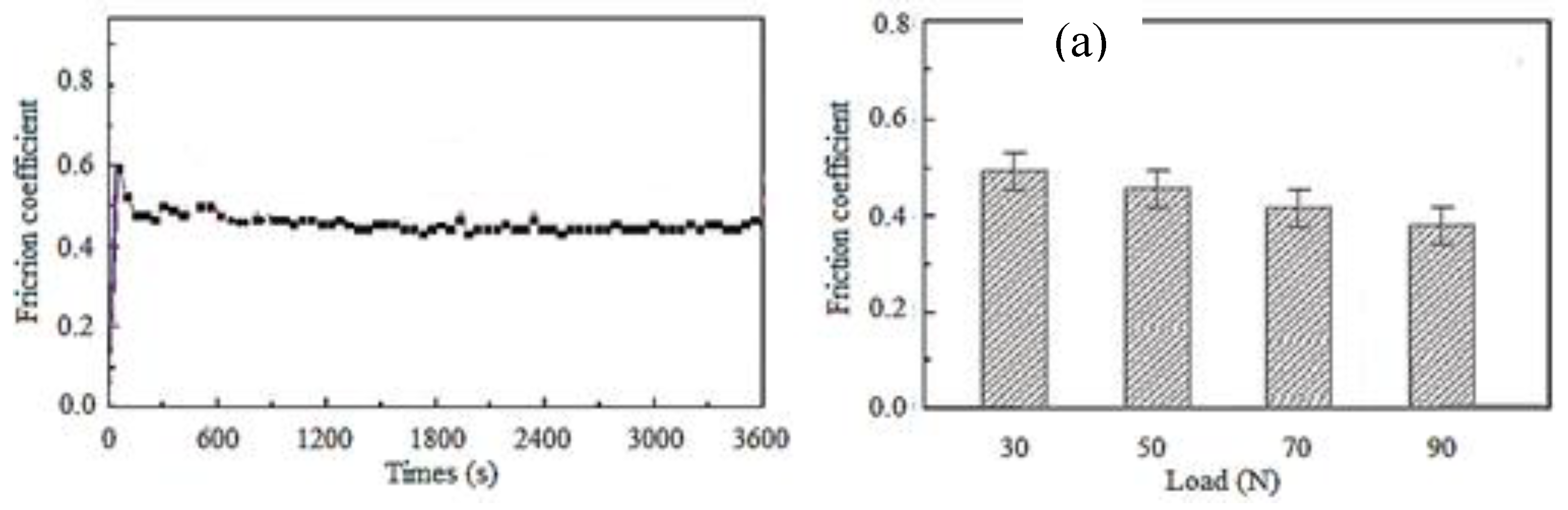
Thus, the variation of the friction coefficient over time and with the load at the sliding speed of 0.016 m/s is shown in Figure 7.
It can be seen from Figure 7a that the friction coefficient at sliding increases initially then slightly decreases until stabilizes relatively around a value, which apparently indicates that the friction pairs go through an essential friction running-in/accommodation process. This is because the flour film on the surface has not formed well at the beginning of the test, which could lead to relatively high friction coefficient, for a very short time. After the formation of the flour film, friction tends to decrease and friction coefficient stabilize (see Figure 7a), while this decreases as the load increased (as average values, see Figure 7b).
Therefore, the model for determining the friction force can explain the experimental phenomena through the obtained results. For example, for a normal contact force, F of 30 N (made by the weights placed on the arm of the pin/disc tribometer), a friction force, Ff ≈ 14.8 N, was experimentally obtained, while by using the analytical model based on the relationship/ equation (1) obtained Ff ≈ 14.6 N, and by the two-factor model (given by the relation/equation (2)), the friction force was Ff ≈ 15.2 N. So, it is found, a correlation good of the experimental results with those determined analytically (very close), which justifies the validation of the modeling, without identifying significant deficiencies in order to improve the model.
Instead, to develop a contact model was used the resulting asperities geometry was by measuring the asperities replicas of lower millstone using a profilometer. Also, the virtual micro-tribometer was used to simulate the contact under loads on the basis of the contact pressure prediction on asperity. All this was aimed the identifying areas, where the contact pressure caused grain material shear and delamination, in a well-controlled manner. At the same time, the modeling technique significantly influences flour quality, dough rheological properties, and bread characteristics. In added, it leads to ease of use and the system simplicity; higher concentrations of macro elements, micro elements, and polyphenols in flour; increased volume of the finished flour products and popularity with consumers. Precisely, these things are proven by simulation and analytical modeling of experimental results.

4. Conclusions

For friction phenomenon understanding and interpretation in the grinding process, this has been modeled by simulation and experimentation.
A model was developed for the analytical determination of the total friction force together with its components, in the work process and validated by simulation and experiment.
Frictional forces are periodically distributed across the contact surfaces of the millstones due to the small flour particles are anchored and distributed symmetrically on each surface and of the constant relative velocity.
At the same time, the forces microscopic forces of contact are affected by the individual flour particles at contact with the asperities of the millstones, and AFM data and images were needed to analyze their distribution and measure the asperities on the grinding stones surfaces, at micro-scale.
Experimentally, it was possible to relatively measure the total friction force at the interface in the working process, using the pin/disc tribometer.
Friction measurements in the grinding process helped in the identification of the interactions between the millstones, seeds, and flour, respectively surface topography because these evolve and are exposed during the grind.
Moreover, to better understand the grinding process and to improve its endpoint monitoring (obtained flour), was needed a contact model based on asperities geometry by measuring asperities replicas of lower millstone using the profilometer, respectively simulated with a virtual micro-tribometer, based on the load on an asperity.
It was observed by simulation, experimentation, and modeling analytically that the frictional forces is influenced by individual flour particles in contact with the grinding stones’ surface asperities.
The simulation and experiment methods used highlighted the interactions among grains, the grinding stones, and flours during the grinding process in order to understand and interpret the friction phenomena at the micro-scale, thereby establishing a basis for optimizing grinding performance.
The results obtained in the grinding process by friction have practical utility in the stone mills, through the research benefits: it allows the development of quality, reliability, and flexible grinding; the quality control of the flours and uniformity degree (fineness/shredding) of them.
Subsequent research will consider the expansion of these tests in much more comprehensive conditions and the making of the grinding process for different combinations, identifying those conditions effective for an adequate grind.

Author Contributions

Conceptualization, F.I.; methodology, F.I., C.D.C., A-F.H.; software, C.D.C.; validation, F.I., C.D.C., A-F.H.; formal analysis, C.D.C., A-F.H.; investigation, F.I. C.D.C., A-F.H.; resources, F.I., C.D.C., A-F.H.; data curation, F.I. C.D.C., A-F.H.; writing—original draft preparation, F.I.; writing—review and editing, F.I.; visualization, C.D.C., A-F.H.; supervision, F.I., C.D.C., A-F.H.; project administration, F.I.; funding acquisition, F.I. C.D.C., A-F.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Li, A., Han Y., Jia F., Zhang J., Meng X., Chen P., Xiao Y., Zhao H., Examination milling non-uniformity in friction rice mills using by discrete element method and experiment. Biosystems Engineering 2021, 211, 247–259. [CrossRef]
  2. Jung, H., Youn Ju Lee Y.J., Yoon W.B. Effect of Moisture Content on the Grinding Process and Powder Properties in Food: A Review. Processes 2018, 6, 69. [CrossRef]
  3. Zeng Y., Jia F., Meng X., Han Y., Xiao Y., The effects of friction characteristic of particle on milling process in a horizontal rice mill. Advanced Powder Technology 2018, 29, 1280–1291. [CrossRef]
  4. Li A., Jia F., Zhang J., Han Y., Meng X., Chen P., Wang Y., Zhao H., The effects of filling level on the milling accuracy of rice in the friction rice mill. Powder Technology 2022, 398, 117052. [CrossRef]
  5. Almessiere M.A., Algarou N.A., Slimani Y., Sadaqat A., Baykal A., Manikandan A., Trukhanov S.V., Trukhanov A.V., Ercan I. Investigation of exchange coupling and microwave properties of hard/soft (SrNi0.02Zr0.01Fe11.96O19)/(CoFe2O4)x nanocomposites. Mater. Today Nano 2022, 18, 100186. [CrossRef]
  6. Kaliniewicz Z., Jadwisieńczak K., Żuk Z., Konopka S., Frączyk A., Krzysiak Z., Effects of Friction Plate Hardness and Surface Orientation on the Frictional Properties of Cereal Grain. International Journal of Food Science 2020, 6639233. [CrossRef]
  7. Khozyaev I., Savenkov D., Kirischiev O., Kirischieva Y, Tupolskikh T., Study of the dynamics of the coefficient of external friction of seeds crops with shell. E3S Web of Conferences 2021, INTERAGROMASH 2021, 273, 01032. [CrossRef]
  8. Savenkov, D., Kirischiev O., Kirischieva Y, Tupolskikh T., Tatiana Maltseva T., Magomedov M., Chistyakov A. Study of the nature of the dynamic coefficient of internal friction of grain materials. E3S Web of Conferences 2019. [CrossRef]
  9. Kozlovskiy, A.L., Zdorovets M. V. Study of hydrogenation processes in radiation-resistant nitride ceramics. J. Mater. Sci.: Mater. Electron 2020, 31, 11227–11237. [CrossRef]
  10. Available online: https://www.twi-global.com/ (accessed on 10 August 2023).
  11. Available online: https://www.laboratuar.com/ro/ (accessed on 10 August 2023).
  12. Popok V.N., Vučković S., Campbell E.E.B., Jensen J., Samela J., Nordlund, Energetic Cluster-urface Interactions, Conference: Ion-Surface Interactions K., Proceedings of XIX International Conference 2009, 1, 49-54, Zvenigorod, Russia.
  13. Sweatman M., Afify N., Ferreiro-Rangel C., Jorge M., Sefcik J., Molecular Dynamics Investigation of Clustering in Aqueous Glycine Solutions. J. Phys. Chem. B 2022, 126, 4711−4722. [CrossRef]
  14. Afify N., Ferreiro-Rangel C., Sweatman M., Molecular Dynamics Investigation of Giant Clustering in Small-Molecule Solutions: The Case of Aqueous PEHA. J. Phys. Chem. B 2022, 126, 8882–8891. [CrossRef] [PubMed]
  15. Ilie F., Movement, and collision of nanoparticles in the process of chemical mechanical polishing (CMP). INMATEH – Agricultural Engineering 2013, 39, 85–90.
  16. Ilie F., Ipate G., Chemical-Mechanical Impact of Nanoparticles and pH Effect of the Slurry on the CMP of the Selective Layer Surfaces, Lubricants 2017, 5, Article Number 15. [CrossRef]
  17. Xia J., Yu J., Lu S., Huang Q., Xie C., Wang Z., Surface Morphology Evolution during Chemical Mechanical Polishing Based on Microscale Material Removal Modeling for Monocrystalline Silicon. Materials 2022, 15, 5641. [CrossRef] [PubMed]
  18. Salerno E., Casotti D. , Paolicelli G., Gualtieri E., Ballestrazzi A., Gazzadi G.C., Bolelli G., Lusvarghi L., Valeri S., Rota A., Friction and wear of DLC films deposited on additive manufactured AlSi10Mg: the role of surface finishing. Surface and Coatings Technology 2023, 463, 129531. [CrossRef]
  19. Albahrani S.M.B, Alves J.T, Duval A., Chaise T., De Vaujany J-P., and Michèle Guingand M., Modelling of elastoplastic, multi-scale and multi-contact problems: application to worm gears. Mechanics & Industry 2022, 23, 6. [CrossRef]
  20. Boning D., Xie X., Sorooshian J., Philipossian A., Stein D., Hetherington D., Relationship between patterned wafer topography evolution and STI CMP motor current endpoint signals. In Proceedings of the 9th International CMP-MIC Conference; 2004; Volume 341.
Preprints 86821 g001
Figure 1. Micro-scale asperities between the upper millstone (above) and lower millstone (down), upper millstone and seeds, and seeds and lower millstone.
Figure 1. Micro-scale asperities between the upper millstone (above) and lower millstone (down), upper millstone and seeds, and seeds and lower millstone.
Preprints 86821 g001
Preprints 86821 g002
Figure 2. Block scheme of grinding system.
Figure 2. Block scheme of grinding system.
Preprints 86821 g002
Preprints 86821 g003
Figure 3. Highlighting of friction force, Ff between lower millstone and upper millstone.
Figure 3. Highlighting of friction force, Ff between lower millstone and upper millstone.
Preprints 86821 g003
Preprints 86821 g004
Figure 4. View of grooving in the millstones and the direction of movement of seeds during grinding (blue arrows): a) seed movement on the stone that wheels (lower), b) seed movement on the stone that remains fixed (upper).
Figure 4. View of grooving in the millstones and the direction of movement of seeds during grinding (blue arrows): a) seed movement on the stone that wheels (lower), b) seed movement on the stone that remains fixed (upper).
Preprints 86821 g004
Preprints 86821 g005
Figure 5. Section through the stone mill: a) input of seeds, b) action of stones on the seeds during the movement of lower millstone.
Figure 5. Section through the stone mill: a) input of seeds, b) action of stones on the seeds during the movement of lower millstone.
Preprints 86821 g005
Preprints 86821 g006
Figure 6. AFM images of the grinding stone surface from ceramic: (a) two-dimensional image showing grains and grain boundaries; (b) three-dimensional image; (c) histogram of surface three-dimensional grains asperity and (d) of the grains size distribution curve.
Figure 6. AFM images of the grinding stone surface from ceramic: (a) two-dimensional image showing grains and grain boundaries; (b) three-dimensional image; (c) histogram of surface three-dimensional grains asperity and (d) of the grains size distribution curve.
Preprints 86821 g006
Preprints 86821 g007
Figure 7. Variation of the friction coefficient over time (a) and with the load (b).
Figure 7. Variation of the friction coefficient over time (a) and with the load (b).
Preprints 86821 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated