Prerpints.org logo
Preprint
Article

Comparative Study of Novel Non-Fluorine Polymers as Electron Transport Layer for Perovskite Solar Cell

Altmetrics

Downloads

165

Views

88

Comments

0

Submitted:

05 October 2023

Posted:

06 October 2023

You are already at the latest version

Alerts
Abstract
Perovskite solar cells have shown significant progress, but their commercialization remains hindered by lead-based toxicity. Many nontoxic perovskite-based solar cells have demonstrated potential such as Cs2AgBi0.75Sb0.25Br6, but their power-conversion efficiency is inadequate. To address this issue, some researchers are focusing on emerging acceptor-donor-acceptor'-donor-acceptor (A-DA'D-A) type non-fullerene acceptors (NFAs) for Cs2AgBi0.75Sb0.25Br6 to find effective electron transport layers for high-performance photovoltaic responses with low voltage drops. In this comparative study, four novel A-DA'D-A types NFAs such as BT-LIC, BT-BIC, BT-L4F, and were used as an electron transport layer (ETL) for the proposed devices, FTO/PEDOT: PSS/ Cs2AgBi0.75Sb0.25Br6/ETL/Au. Comprehensive simulations were conducted to optimize the devices. The simulations showed that all optimized devices exhibit photovoltaic responses, with the BT-BIC device having the highest power conversion efficiency (13.2%) and the BT-LIC device having the lowest (6.8%). The BT-BIC as ETL provides fewer interfacial traps and better band alignment, enabling greater open-circuit voltage for efficient photovoltaic responses.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Hybrid perovskite materials have demonstrated excellent performance over the past several years in the field of solar devices and as a result their power conversion efficiency increased from a few percent to 27% in a very short period of time [1,2,3]. To further improve the performance of perovskite solar cells, substantial research efforts are being made to address several outstanding problems. Due to these efforts, perovskite solar cells are more advantageous than other types of solar cells in a number of aspects, including cost, weight, flexibility, portability, wide-area application, and low-temperature production [4,5]. Even though perovskite solar cells have made great advances in the laboratory environment, there are still a number of barriers to their general commercialization [6,7].
It is commonly known that the lead-based toxicity, power-conversion efficiency, stability, and degradation of perovskite solar cells are the most significant unsolved challenges [8,9]. A highly stable double perovskite class of Cs2AgBiBr6 absorber layer has recently been reported as a viable substitute for Pb-based perovskite. As a result, Cs2AgBi0.75Sb0.25Br6 is favored for this study due to its several benefits, including being lead-free, non-toxic, extremely stable, and compatible with a variety of transport layers as reported in the literature [10,11,12].
Despite the perovskite absorber layer, the design architectures, material properties of the charge transport layer, and other design limitations also have serious impacts on the abovementioned problems. Two design architectures —(i) standard n-i-p and (ii) inverted p-i-n are frequently used for the fabrication of perovskite solar cells, depending on the front electron-transport layer or hole-transport layer facing the photons for solar cell applications. In both architectures, the perovskite absorber layer is sandwiched between the electron transport layer and the hole transport layer. Additionally, each architecture has unique benefits and drawbacks. Currently, the traditional n-i-p design is used to create the highest-performing photovoltaic devices [13,14,15]. Therefore, the proposed devices use n-i-p architecture for this study.
The electron transport layer is one of the most significant functional layers in perovskite solar cells due to its crucial role in enhancing stability, power-conversion efficiency, cost, and consequently overall performance [15,16,17]. The vital electronic parameters of the electron transport layer that are fundamentally necessary for fine-tuning the effective photovoltaic response such as (i) energy bandgap, (ii) electron affinity (LUMO), (iii) ionization energy (HOMO), (iv) molecular packaging, (v) carrier mobilities, (vi) reorganization energy, etc. The great majority of polymer and perovskite solar cells used for photovoltaic applications include an electron transport layer composed of fullerene materials as PC60BM ([6,6]-phenyl C61-butyric acid methyl ester) and/or PC70BM ([6,6]-phenyl-C71-butyric acid methyl ester) [18,19,20]. The fullerene-based electron transport layer, unfortunately, has several drawbacks, such as (i) poor optical absorption, especially in the near-infrared and visible range; (ii) thermal instability; (iii) photochemical instability; (iv) restricted tuneability; etc. [21,22].
Designing a non-fullerene-based (NFA) electron transport layer might potentially overcome the drawbacks of the fullerene-based electron transport layer. The stability, tuneability, and optical absorption can all be improved by easily adjusting the chemical molecular structure, highest-occupied molecular orbital (HOMO), and lowest unoccupied molecular orbital (LUMO) of a non-fullerene-based electron transport layer over a reasonably wide range [23,24,25]. The design of NFAs that are reported often falls into one of the two categories. One choice is the acceptor-donor-acceptor (A-D-A) type molecule, which has a simple manufacturing process and an energy level that is easily adjusted. The other A-DA'D-A type molecule, on the other hand, was supported by a greater short-circuit current density (JSC) and wider absorption thanks to its bigger conjugated plane and enhanced intramolecular charge transfer (ICT). It is quite interesting to design organic/polymer electron transport materials, notably with the help of A-DA'D-A type NFA and their variants [26,27,28,29,30,31,32,33,34,35]. All these designing parameters can be greatly tuned for an effective electron transport layer in a perovskite solar cell by making use of various physiochemical methodologies [36,37,38,39]. On the basis of these physiochemical methodologies, four novel A-DA’D-A types of NFA as electron-transport layers have recently been reported, which are the end-group derivatives of Y5 and Y6 materials and named linear as BT-LIC, bent as BT-BIC, BT-L4F, and BT-BO-L4F [40,41,42,43], as shown in Figure 1. All these (i) BT-LIC, (ii) BT-BIC, (iii) BT-L4F, and (iv) BT-BO-L4F are highly novel materials for the electron-transport layer, with very little and nearly negligible information available in the reported literature.
In most cases, it may be difficult to dope polymers for electron/hole transport layers (ETLs) at higher concentrations. This problem is caused by many variables, including (i) solubility and compatibility, (ii) aggregation and phase separation, (iii) doping-induced defects, and (iv) doping process restrictions. It is crucial to note that although high doping concentrations in polymer transport layers might be difficult, they are not always required. The maximum doping of the electron/hole transport layer is still reported in the literature at a value of 1020cm-3. For this reason, in our simulation of the suggested solar cell, we employ a maximum doping density of up to 1020 cm-3 for both electron and hole transport layers [44,45].
In this study, conventional n-i-p type perovskite solar cells were chosen as they demonstrate relatively higher efficiency and ease of fabrication, as discussed above [46,47,48,49,50]. Similarly, PEDOT: PSS (poly(3,4-ethylenedioxythiophene) polystyrene sulfonate) as the hole transport layer, and Cs2AgBi0.75Sb0.25Br6 was selected for the perovskite layer due to many advantages such as being lead-free, highly stable, compatible with both transport layers, etc. [51,52]. Figure 2 shows the design architecture of the four proposed devices with their energy band diagrams, namely (i) FTO/PEDOT: PSS/ Cs2AgBi0.75Sb0.25Br6/BT-LIC/Au (Device BT-LIC), (ii) FTO/PEDOT: PSS/ Cs2AgBi0.75Sb0.25Br6/BT-BIC/Au (Device BT-BIC), (iii) FTO/PEDOT: PSS/ Cs2AgBi0.75Sb0.25Br6/BT-L4F/Au (Device BT-L4F), and (iv) FTO/PEDOT: PSS/ Cs2AgBi0.75Sb0.25Br6/ BT-BO-L4F /Au, (Device BT-BO-L4F) respectively. The main goal of this study is to comprehensively investigate, optimize, and compare the devices as a function of above hole-transport layer to determine the different design parameters that can offer the maximum power conversion efficiency.

2. Device Models for Simulation

Software for modeling solar cells typically solves a set of coupled differential equations for semiconductor devices using conventional mathematical techniques. The general photovoltaic responses of solar cells, such as short-circuit current, open-circuit voltage, fill factor, and power conversion efficiency, will be identified using the solution of these equations. The solar model differential equations can be classified into the following groups [53,54,55,56]:

2.1. Poisson’s Equation

The electric field and potential (φ) produced by this excess charge (hole (p(x)), electron (n(x)), donor (ND), acceptor (NA), trapped hole (ρp,), trapped electron (ρn) densities) as well as their relationship to the charge distribution inside the various solar cell layers as a function of the thickness (x), is described by Poisson's equation. Mathematically, Poisson's equation can be defined as
d 2 ϕ x d x 2 = e ϵ o ϵ r p x − n x + N D − N A + ρ p − ρ n
In this case, the absolute and relative dielectric constants of the semiconducting material in each layer are " ϵ 0 " and “ ϵ r   " respectively, and " e ” represents the electric charge (1.602 x 10-19 C).

2.2. Continuity Equation

An equation that explains the life cycle (generation (G), recombination ( R)) of electrons and holes in terms of electron current density (Jn) and hole current density (Jp) separately is known as a continuity equation or in some literature known as a transport equation.
d J n d x = G − R
d J p d x = G − R

2.3. Charge Transport Model

The proposed devices FTO/PEDOT: PSS/ Cs2AgBi0.75Sb0.25Br6/ETL/Au are simply p-i-n diodes. The semiconductor p-i-n junction diode is the basic building block of any solar cell. Therefore, to simulate the photovoltaic response, any charge transport models that are appropriate to p-i-n junction diodes may be utilized and one of the most common of them is listed below. The diode charge transport model states that each current density also represents the overall responses of the drift and diffusion currents, respectively, and that the total current is the sum of the current densities of both electrons and holes.
J = J n + J p
  J n = D n d n d x + μ n n d ϕ d x
J p = − D p d p d x + μ p p d ϕ d x

2.4. Photons Absorption Model

From a variety of optical absorption models offered by SCAPS-1D, the conventional model for optical absorption is selected for this study and it is given below as Equation (7). According to this conventional model, the optical absorption coefficient " α " is defined as " α ( λ ) " and is dependent on the optical wavelength " λ " with energy " h ν ". Equation (7) states that in this model, A and B are both arbitrary constants, and " E g " stands for the energy bandgap of the relevant thin-film layer and all these variables are interrelated as [57].
α   ( λ ) = A + B h ν h ν − E g

3. Simulation Software

A solar cell's photovoltaic response may be estimated using the mathematical equations mentioned above, which are the foundation of any photovoltaic modeling software. In theory, simulation software is a tool that allows users to foretell the output response of solar devices without doing actual testing in a variety of settings. Simulation software can reasonably predict the experimental results of a solar cell [58,59]. The conditions must be met by modeling software to accurately forecast the output of photovoltaic responses accurately. Numerous researchers assert that SCAPS 1D is extremely trustworthy software that satisfies many of the criteria listed in the reference [60,61,62,63] and may be used to simulate a wide range of photovoltaic processes. SCAPS 1D has thus been selected for this investigation.

4. Simulation Steps:

In general, the SCAPS-1D simulation steps are a list of feasible actions that must be executed. The following is a list of the simulation processes necessary applied to the suggested devices in order to obtain the highest power conversion efficiency.
  • Step 1, Start of Simulation: Define the environment, geometry, and physical parameters of all the device’s layers.
  • Step 2, Extraction of Simulation Parameters: Extract the input physical and material characteristics for the perovskite absorber layer, the hole-transport layer (HTL), and the electron-transport layer (ETL) using the literature [62,63,64,65,66,67,68,69,70] as a guide.
  • Step 3, Estimation of Ranges for Different Parameters: Propose the range of thickness and doping density for each layer of the devices (i) Device BT-LIC, (ii) Device BT-BIC, (iii) Device BT-L4F, and (iv) Device BT-BO-L4F from the literature.
  • Step 4, Thickness Optimization of HTL: Determine the optimal thickness of PEDOT:PSS for each device as a hole transport layer through a series of simulations, which gives the maximum power-conversion efficiency and quantum efficiency (QE). After that, update with the optimal thickness of PEDOT:PSS for further simulations.
  • Step 5, Determination of PV Parameters as a Function of HTL Thickness: Determine the photovoltaic parameters such as open-circuit voltage, short-circuit current, fill factor, and power conversion efficiency of each device as a function of PEDOT:PSS thickness. But for simplicity, only the photovoltaic parameters of a highly efficient device are shown and discussed.
  • Step 6, Thickness Optimization of ETL: Determine the optimal thickness of ETL ( (i) BT-LIC, (ii) BT-BIC, (iii) BT-L4F, and (iv) BT-BO-L4F) for each device as an electron transport layer through a series of simulations, which gives the maximum power-conversion efficiency and quantum efficiency. After that, update with the optimal thickness of ETL for further simulations.
  • Step 7, Determination of PV Parameters as a Function of Optimized ETL Thickness: Determine the photovoltaic parameters such as open-circuit voltage, short-circuit current, fill factor, and power conversion efficiency of each device as a function of electron-transfer layer thickness. But for simplicity, only the photovoltaic parameters of a highly efficient device are shown and discussed.
  • Step 8, Thickness Optimization of Perovskite Absorber Layer: Determine the optimal thickness of the perovskite absorber layer Cs2AgBi0.75Sb0.25Br6) for each device as an absorber layer through a series of simulations, which gives the maximum power-conversion efficiency and quantum efficiency. Then, update with the optimal thickness of the absorber for further simulations.
  • Step 9, Determination of PV Parameters as a Function of Perovskite Thickness: Determine the photovoltaic parameters such as open-circuit voltage, short-circuit current, fill factor, and power conversion efficiency of each device as a function of absorber thickness. But for simplicity, only the photovoltaic parameters of a highly efficient device are shown and discussed.
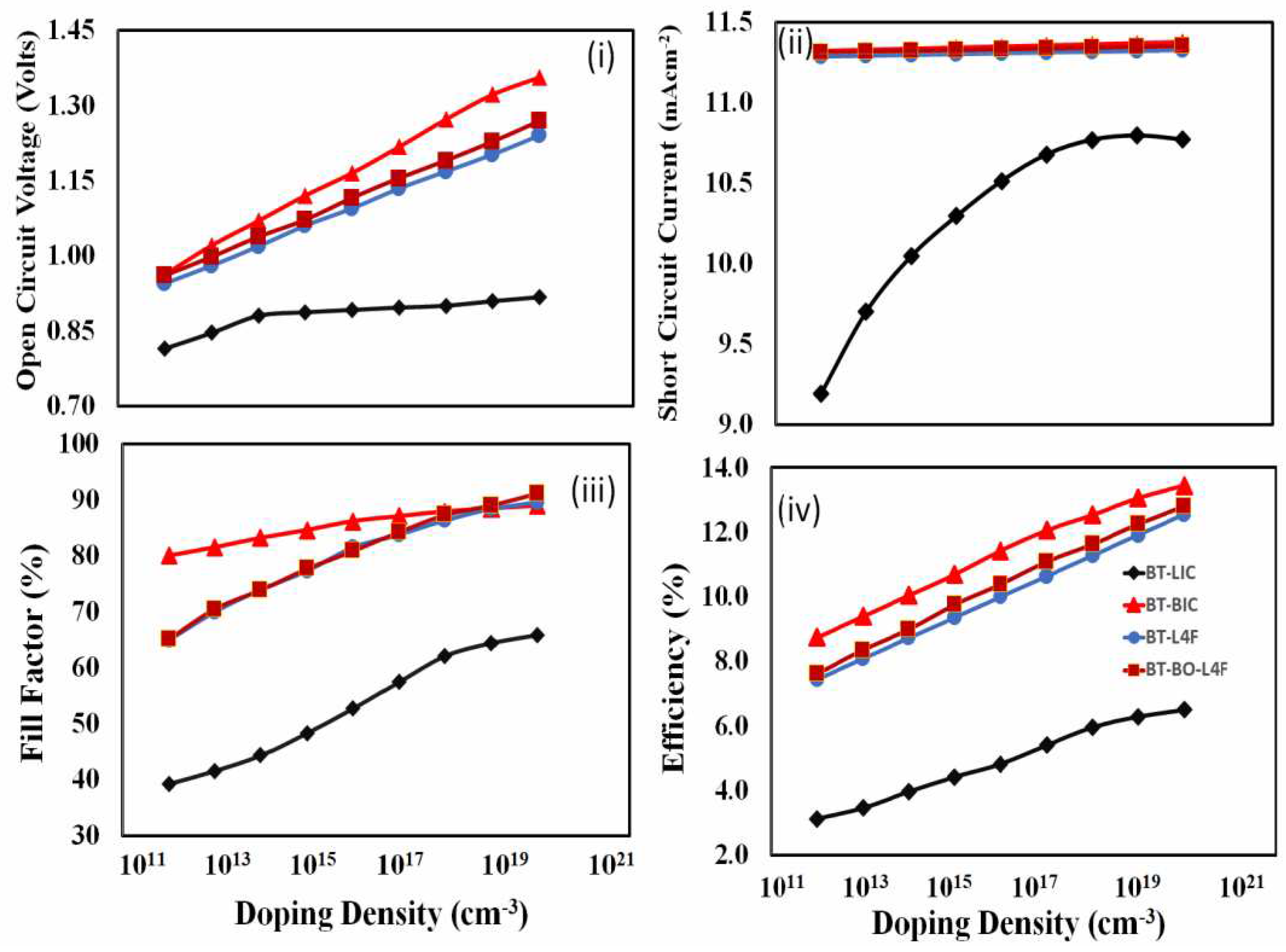
  • Step 10, Determination of PV parameters as a function of ETL Doping: Determine the photovoltaic parameters such as open-circuit voltage, short-circuit current, fill factor, and power conversion efficiency of each device as a function of ETL doping density.
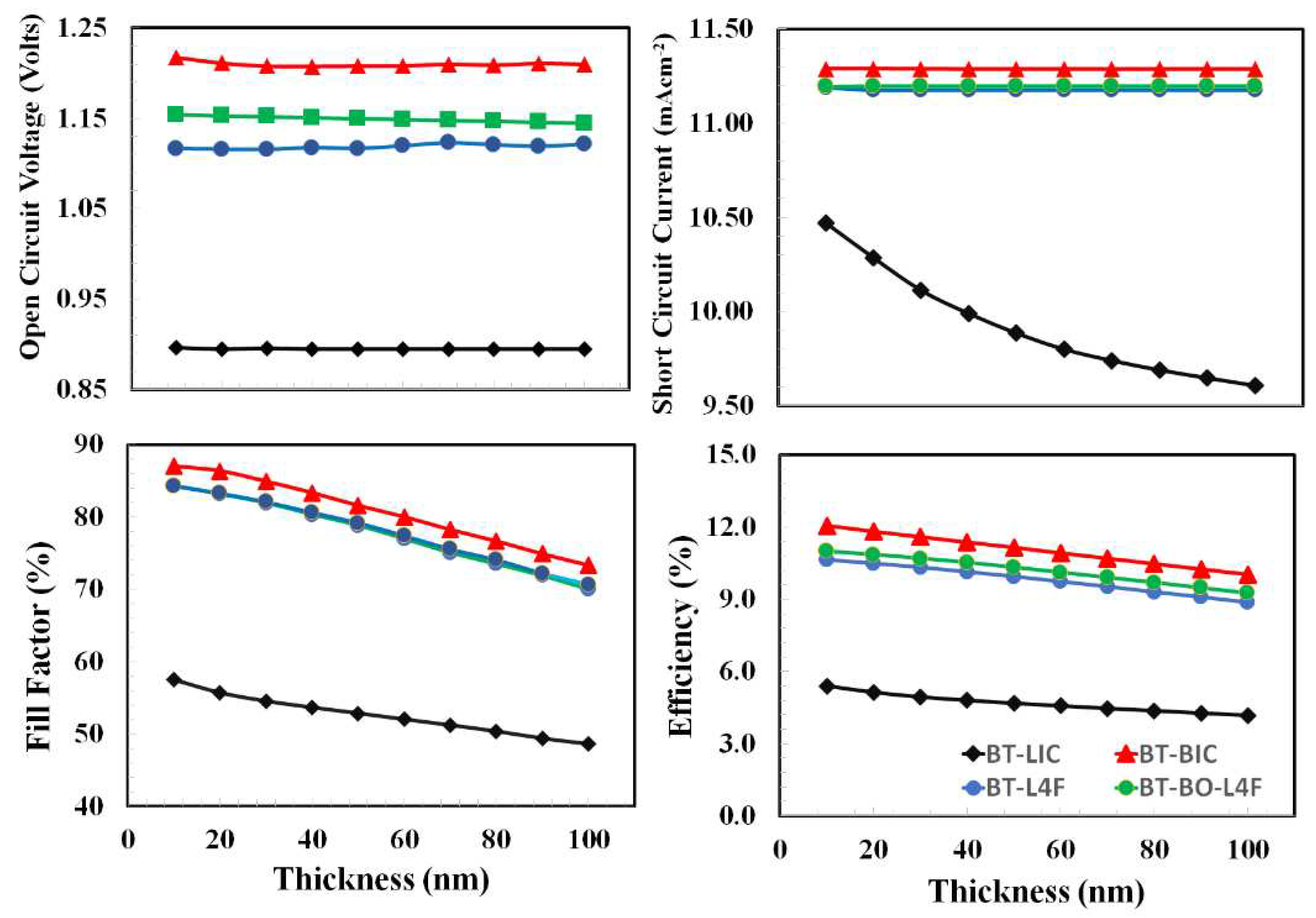
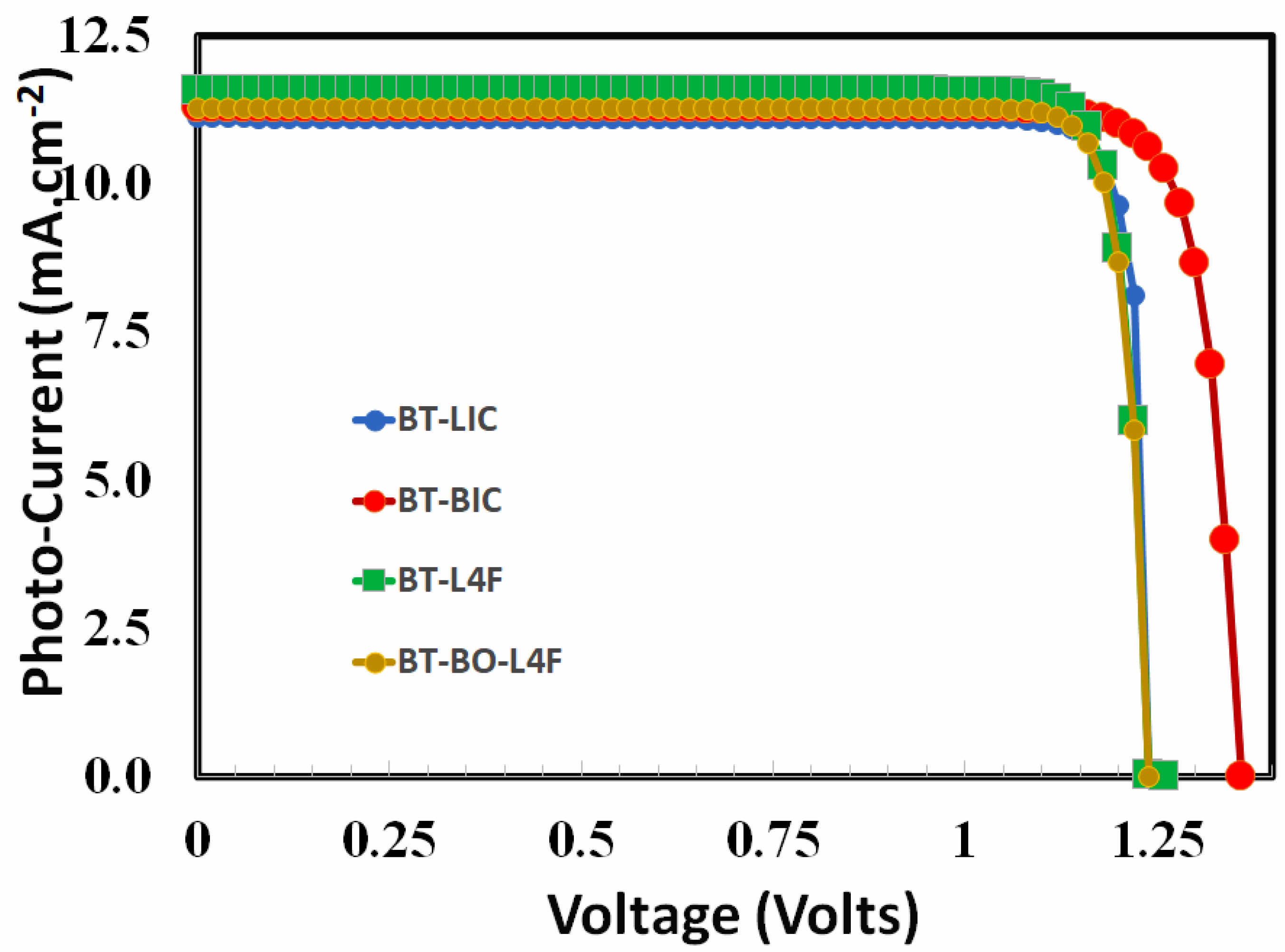
  • Step 11, Determination of PV Response and Parameters of the Optimized Devices: Determine the photovoltaic current-voltage response and other photovoltaic parameters of all the optimized devices. such as open-circuit voltage, short-circuit current, fill factor, and power conversion efficiency of each device as a function of ETL doping density.
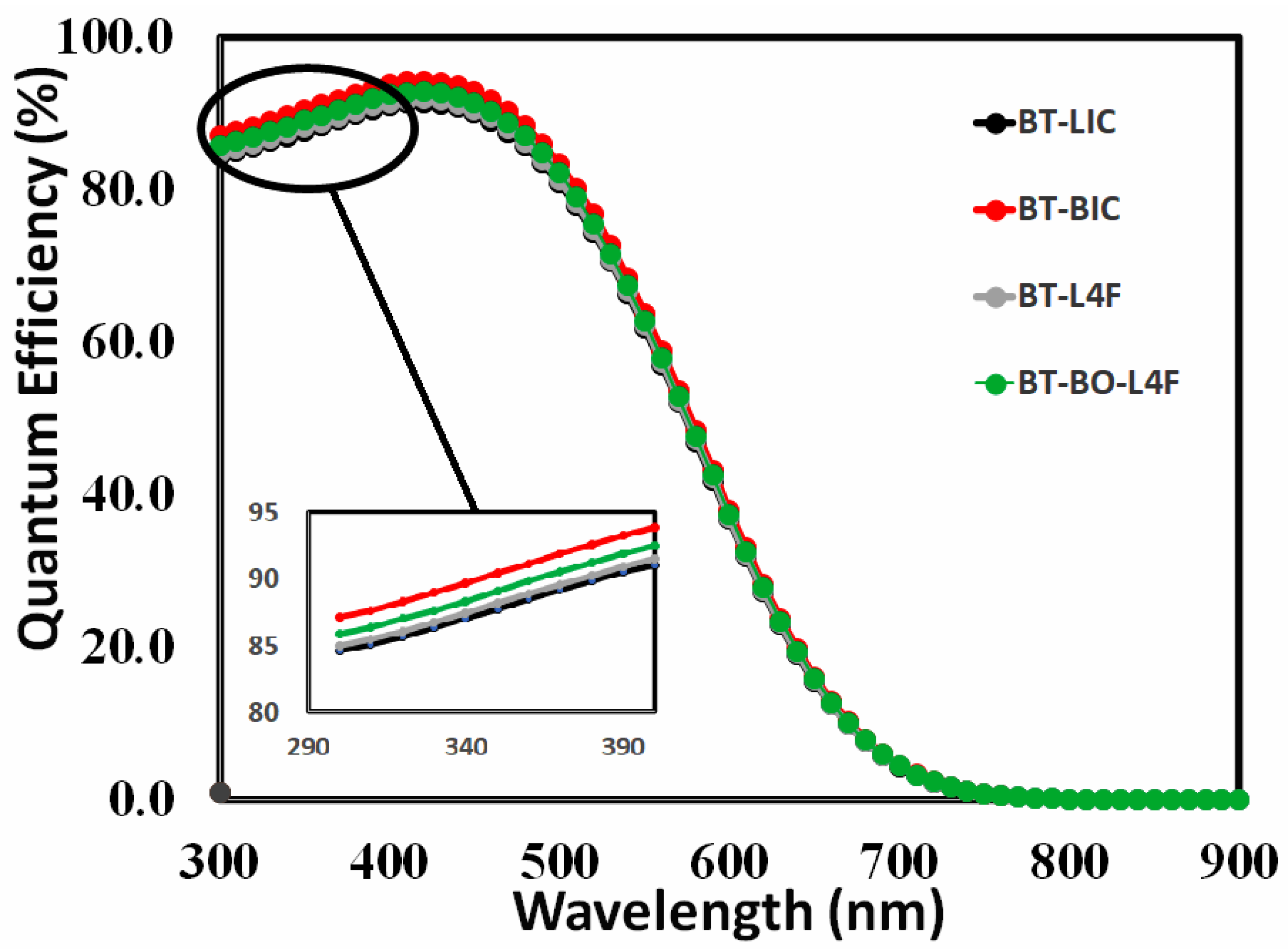
  • Step 12, Determination of QE Response of the Optimized Devices: Determine the quantum efficiency of all the optimized devices.
  • Step 13, End of Simulation.

5. Simulation Material Parameters

For the optimization of each layer of a perovskite solar cell as well as for the prediction of reliable photovoltaic behavior of the proposed devices, the proper selection of material parameters for each layer is essential. For this reason, great care was taken when choosing the simulation material parameters for this study. As electron transport materials (i) BT-LIC, (ii) BT-BIC, (iii) BT-L4F, and (iv) BT-BO-L4F are novel, the extensive amount of related literature is reviewed to extract the simulation parameters, while for PEDOT: PSS and Cs2AgBi0.75Sb0.25Br6 materials, the parameters are selected from highly reliable references as listed in Table 1.
Both the proposed perovskite absorber and the polymer-based transport layer offer an inherently high density of defects. In most cases, these electronic defects are grown during the crystal growth or fabrication process due to uncontrolled impurities, inconsistencies in polymerization or crystal growth, thin film deposition processes, and other environmental parameters [73,74,75,76]. Therefore, a defect density of 1014 cm2 is introduced into the bulk region of the absorber, hole-transport layer, and electron transport layer, as indicated in Table 1.

6. Results and Discussion

6.1. Thickness Optimization of the Hole-Transport Layer

Generally, for any type of solar cell, the thickness of the hole transport layer (HTL) plays a crucial role in improving the overall performance of the solar cell. The effectiveness of the charge transfer process between the perovskite absorber layer and the electrode can be considerably impacted by the thickness of the hole transport layer. To obtain the highest possible efficiency in solar cells, it is essential to optimize the thickness of the hole transport layer.
Therefore, determining the optimized thickness of the hole transport layer is a design challenge for perovskite solar cells. In order to determine the optimal thickness of hole transport layer thickness, each of these four devices is simulated as a function of hole transport layer thickness, and a nearly very similar photovoltaic response is observed, here for simplicity randomly elected Device D ( BT-LIC) responses are shown for in Figure 3. The photo current-voltage response may be used to estimate the thickness of the hole transport layer for perovskite solar cells with the maximum feasible efficiency. Therefore, the photovoltaic responses of Device D are depicted in Figure 3 as functions of the thickness of the hole transport layer, which ranges from 10 nm to 90 nm, respectively. Based on Figure 3, it can be seen that Device D exhibits respectable photovoltaic behavior. However, when thickness increases, the photovoltaic responsiveness suffers as they are severely degraded.
The photovoltaic parameters are calculated, and the results are shown in Figure 4 as a function of PEDOT: PSS thickness. Therefore, the photovoltaics parameters such as (i) open-circuit voltage, short-circuit current (Figure 4a), (ii) fill factor, and power-conversion efficiency (Figure 4b) follow more or less very similar trends, where all these parameters are severely degraded. According to a previous report, PEDOT: PSS like many other organic/polymer semiconductors inherently has a large number of traps that serve as recombination centers. The density of traps exponentially rises as PEDOT: PSS thickness increases, and photovoltaic characteristics rapidly deteriorate [77,78,79]. As power-conversion efficiency is a decisive parameter and it is maximum at 10 nm for each device (here only Device D is shown), it can be justified that 10 nm is the optimum thickness of the hole transport layer for each device. Because the optimal PEDOT:PSS doping density for each proposed device is obtained at 1020 cm-3 through simulation, which is quite comparable to our previous results [7,60,61,67,68,69], simulation data are not shown here for simplicity.
For a perovskite-type solar cell, the optimal thickness of the hole transport layer can also be estimated using external quantum efficiency (EQE). The external quantum efficiency depends on the wavelength of the incident light and is often stated in terms of percentage. Figure 5 shows the external quantum efficiency of Device D (BT-BO-L4F) as a function of the thickness of PEDOT: PSS. It also confirms that as thickness increases then, the area under the QE curve also decreases. It clearly demonstrates that the total charges collected at the respective electrodes also decrease and hence it can be inferred that more and more recombination will take place at the higher thickness of PEDOT:PSS. Both power-conversion efficiency and external quantum efficiency are decisive factors in the selection of the thickness of PEDOT:PSS for efficient photovoltaic response and maximum power conversion efficiency and quantum efficiency is observed at 10 nm of PEDOT:PSS, so it can be justified that 10 nm is the most optimum thickness of PEDOT:PSS for the proposed devices.

6.2. Thickness Optimization of the Absorber Layer

To increase the photo-conversion efficiency of perovskite solar cells, the thickness of the absorber layer of Cs2AgBi0.75Sb0.25Br6 must be optimized. The ideal thickness of the perovskite absorber layer depends on a number of parameters, including the composition of the perovskite material, the design of the photovoltaic device, and the thin-film deposition process. While thick perovskite absorber layers can boost photon absorption, and on the other side thin perovskite absorber layers can decrease recombination losses and lead to improved power conversion efficiency [80,81]. In the literature, both experimental methods and device simulation modeling can be used to determine the optimal thickness of the perovskite absorber layer.
As discussed above the optimization of perovskite layer thickness is a critical parameter in determining the performance of a solar cell. In order to achieve a suitable balance between light absorption and charge carrier extraction, it is often necessary to optimize the thickness of the active layer. Increased thickness of the active layer facilitates enhanced light absorption due to the greater availability of material for photon interaction. However, a thick active layer increases the carrier recombination. In thicker active layers, the distance that charge carriers need to travel to reach the electrodes increases. Conversely, when the active layer is very thin, it may lead to inadequate light absorption, thus leading to less production of photocurrent. Similarly, a thin active layer may also limit the ability to extract charge carriers efficiently, leading to poor charge collection and reduced overall performance.
Here, the optimal thickness of the perovskite absorber Cs2AgBi0.75Sb0.25Br6 layer was estimated using simulation techniques. The photovoltaic response of device D is depicted in Figure 6 as a function of absorber layer thickness from 10 nm to 100 nm. According to the device's photovoltaic response, unlike the thickness of the hole transport layer, the photovoltaic response is degraded at lower absorber layer thicknesses, increases up to the absorber layer reaches its maximum photovoltaic response, and then again gradually decreases, the above discuss responses are more clearly observed in Figure 7.
Figure 7a,b illustrate the photovoltaic parameters of each device as a function of absorber layer thickness, including open-circuit voltage, short-circuit current, fill factor, and power conversion efficiency. Complex photovoltaic parameter patterns are observed, where the open-circuit voltage and fill factor climb suddenly, peak, and then rapidly deteriorate. While short-circuit current and power-conversion efficiency behavior are different for a device as a function of absorber layer thickness, both of these photovoltaic parameters increase gradually, and the power conversion efficiency in particular reaches its maximum at 70 nm thickness of absorber layer before beginning to slowly decline.
Figure 8 illustrates the quantum efficiency response of the proposed perovskite solar cell for devices where the thickness of the absorber layer (Cs2AgBi0.75Sb0.25Br6) is varied from 10 nm to 100 nm and the thickness of the PEDOT: PSS is optimized at 10 nm. It is not clearly observed from the figure which thickness of the absorber layer gives the maximum area under the quantum efficiency curve. However with the help of software calculations, it is found that at the thickness of 70 nm absorber layer, the device gives the maximum quantum efficiency, which further supports the finding that 70 nm is the optimum thickness of the absorber layer.
The thickness of the hole transport layer can directly or indirectly affect the performance of quantum efficiency. Under normal conditions, the hole transport layer PEDOT:PSS demonstrates a high degree of transparency with little optical absorption enabling the efficient passage of light to the perovskite layer as shown in Figure 2. Therefore, the quantum efficiency of a perovskite solar cell is not directly affected by the thickness of the hole transport layer owing to its optical transparency. However, the influence of the thickness of the hole transport layer on the quantum efficiency may be indirect in nature. The quantum efficiency can be defined as the fraction of electron-hole pairs generated in the external circuit for a particular wavelength of incoming photon. It depends on several parameters, such as charge extraction, recombination, transport, and energy-level alignment. The use of PEDOT:PSS as a hole transport layer exhibits dispersive charge transport, whereby the efficiency of both charge transport and recombination decreases considerably with an increase in the thickness of the hole transport layer. Hence, it can be shown from Figure 5 that a thickness of 70 nm for the PEDOT:PSS layer demonstrates the most favorable thickness for the hole transport layer.

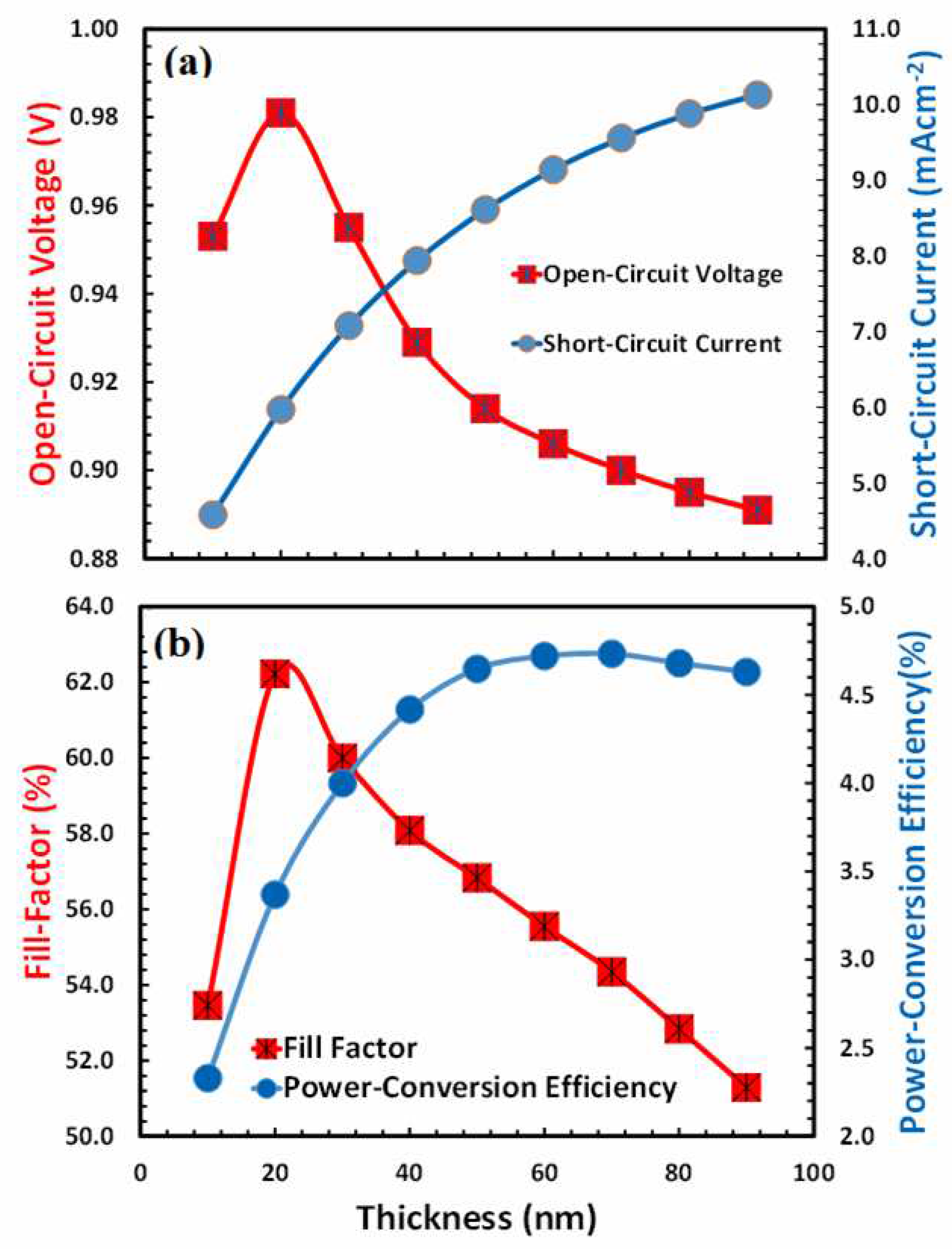
6.3. Thickness Optimization of Electron Transport Layer

Another critical design factor for producing highly efficient perovskite solar cells is the thickness optimization of the electron transport layer. Thickness optimization, particularly for polymer-based electron layers, is very important because it affects several physical, material, and photovoltaic parameters.
(a)
Device architecture: The optimal electron transport layer thickness may vary according to the specific device architecture, such as whether the solar cell has a planar or mesoporous structure.
(b)
Material characteristics: The ideal thickness for effective charge transfer and extraction can be influenced by the electron transport layer's material characteristics, such as (i) electron transport, (ii) series resistance, (iii) shunt resistance, (iv) carrier lifetime, (v) electron mobility, (vi) electron density, (vii) recombination losses, (viii) charge extraction efficiency, (ix) optical absorption, and (x) interface energy level alignment, among others.
(c)
Thin film deposition method: There are several thin-film deposition methods that may be used to manage the electron transport layer's thickness, and each has advantages and limitations of its own. Spin-coating, for instance, is a very cheap and simple method.
(d)
Post-deposition method: By modifying the thickness of the electron transport layer using post-deposition techniques like solvent or annealing, the morphology and interface properties of the electron transport layer may be altered.
(e)
Photovoltaic performance matrices: Depending on the device's individual performance metrics, such as power conversion efficiency, short circuit current, and fill factor, the ideal electron transport layer thickness may vary. These metrics may all be influenced by the electron transport layer's thickness.
(f)
Trade-offs: When determining the ideal electron transport layer thickness, it is frequently necessary to compromise between several device characteristics, such as reducing leakage currents while increasing charge transfer efficiency.
(g)
Interaction with other layers: The electron transport layer's thickness can have an impact on how the electrode, absorber layer, and hole transport layer interact with other layers in the device. This might make the optimization procedure more challenging.
Overall, the complicated interactions between these variables make optimizing the electron transport layer thickness a difficult iterative process that frequently calls for simulation methods.
The photovoltaic parameters (a) open-circuit voltage, (ii) short-circuit current, (iii) fill-factor, and (d) power-conversion efficiency are shown in Figure 9 as functions of the thickness of the electron transport layer for the devices (i) A (BT-LIC), (ii) B (BT-BIC), (iii) C (BT-L4F), and (iv) D (BT-BO-L4F), respectively. Figure 9 demonstrates that although the open-circuit voltage varies for each device, it does not change relatively as the thickness of the electron transport layer increases. Because the open-circuit voltage is generally determined by the energy bandgap offset, and its value is generally unaffected by the thickness of the electron transport layer [82,83], as observed in Figure 9. In addition, Figure 9 shows the relative short-circuit responses for the devices as functions of the thickness of the electron transport layer. The figure demonstrates that all devices behave in a consistent manner, with short-circuit current reducing as the thickness of the electron layer grows. Device A's behavior stands out, whereas other devices' rates of decrease are very insignificant. Similarly, when the thickness of the electron transport layer increases, the fill-factor behavior of all devices likewise deteriorates. It could be because devices experience increasing series resistance and recombination losses as the thickness of the electron layer rises. The power-conversion efficiency responses, which are the resultant behavior of open-circuit voltage, short-circuit current, and fill-factor responses, also behave in a very similar way. Where power-conversion efficiency deteriorates as a function of electron-transport layer thickness. The figure clearly demonstrates that device A (BT-LIC) is sharply degraded, while device B (BT-BIC) shows excellent power conversion efficiency response as a function of electron-transport layer thickness. Power conversion efficiency is the most important parameter, and all devices show maximum power conversion efficiency at 25 nm. So, it can be inferred that 25 nm is the most optimal thickness of the corresponding electron-transport layer for each device.

6.4. Doping Density Optimization of the Electron Transport Layer

The electron transport layer's doping density can have a big influence on the electrical conductivity of solar cells, charge carrier mobility, and overall power conversion efficiency. Usually, organic, or polymeric compounds with strong electron-withdrawing groups and significant electron affinities are used as dopants to dope polymer-based electron-transport layers [84,85]. High doping of the electron transport layer (ETL) can improve the power conversion efficiency of a perovskite solar cell by lowering the series resistance and electrode-transport layer interface losses, but on the other hand, excessive doping can increase charge carrier recombination and degrade the device's overall efficiency. Therefore, doping optimization of the electron transport layer is crucial for the efficient design of the proposed perovskite solar cells.
Therefore, the photovoltaic parameters (a) open-circuit voltage, (ii) short-circuit current, (iii) fill-factor, and (d) power-conversion efficiency were estimated through simulation and the results are shown in Figure 10 as functions of the doping density of the electron transport layer for the devices (a) A (BT-LIC), (b) B (BT-BIC), (c) C (BT-L4F), and (d) D (BT-BO-L4F), respectively. The figure shows that all photovoltaic parameters open-circuit voltage, short-circuit current, fill factor, and power-conversion efficiency are improving as the doping density is increased in the corresponding electron transport layer. The thickness of the electron-transport layer is already optimized, it can be assumed that the electron transport layer offers very little recombination losses, therefore reduction of resistivity as a function of increasing doping density is the dominating factor for each device. As power-conversion efficiency is a decisive parameter and it is maximum at 1020 cm-3 for each device, it can be justified that 1020 cm-3 is the optimum doping of the electron transport layer for each device.

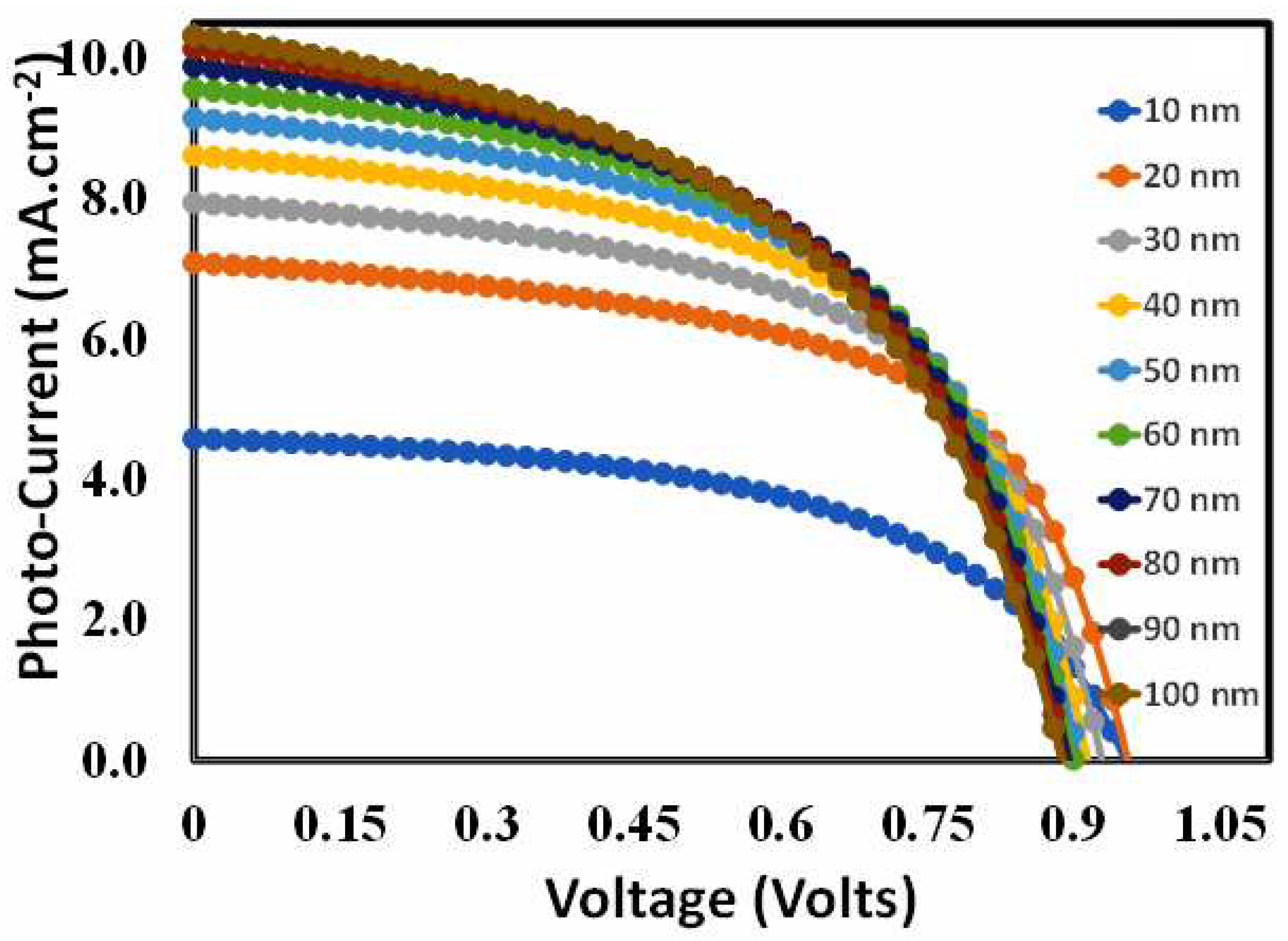
6.5. Photo Current-Voltage Response of the Optimized Devices

The influence of the electron-transport layer on the overall performance of perovskite solar cells may be further investigated by using the photo current-voltage responses of the optimized perovskite solar cells. In Figure 11, the typical photo current-voltage responses of the perovskite solar cells are observed. The figure offers important information about its photovoltaic performance parameters such as open-circuit voltage, short-circuit current, fill factor, and power-conversion efficiency, respectively. Table 2 displays all these photovoltaic parameters as estimated from Figure 11 for each device. The figure and Table 2 clearly reveal that all devices perform differently, while device B (BT-BIC) has the best photovoltaic response (power-conversion efficiency ~13.2% ), and device A (BT-LIC) has the worst photovoltaic response (power-conversion efficiency ~6.8% ). It is also observed that the improvement in open-circuit voltage as well as Fill-Factor are relatively higher for device B. This clearly demonstrates that the photovoltaic device B fabricated with BT-BIC as an electron transport layer may manage high build-in potential and excellent interface quality which in turn improve the overall charge collection, charge transport and to suppress recombination losses [86,87,88], compared to the other electron transport layers for devices A, C and D respectively.

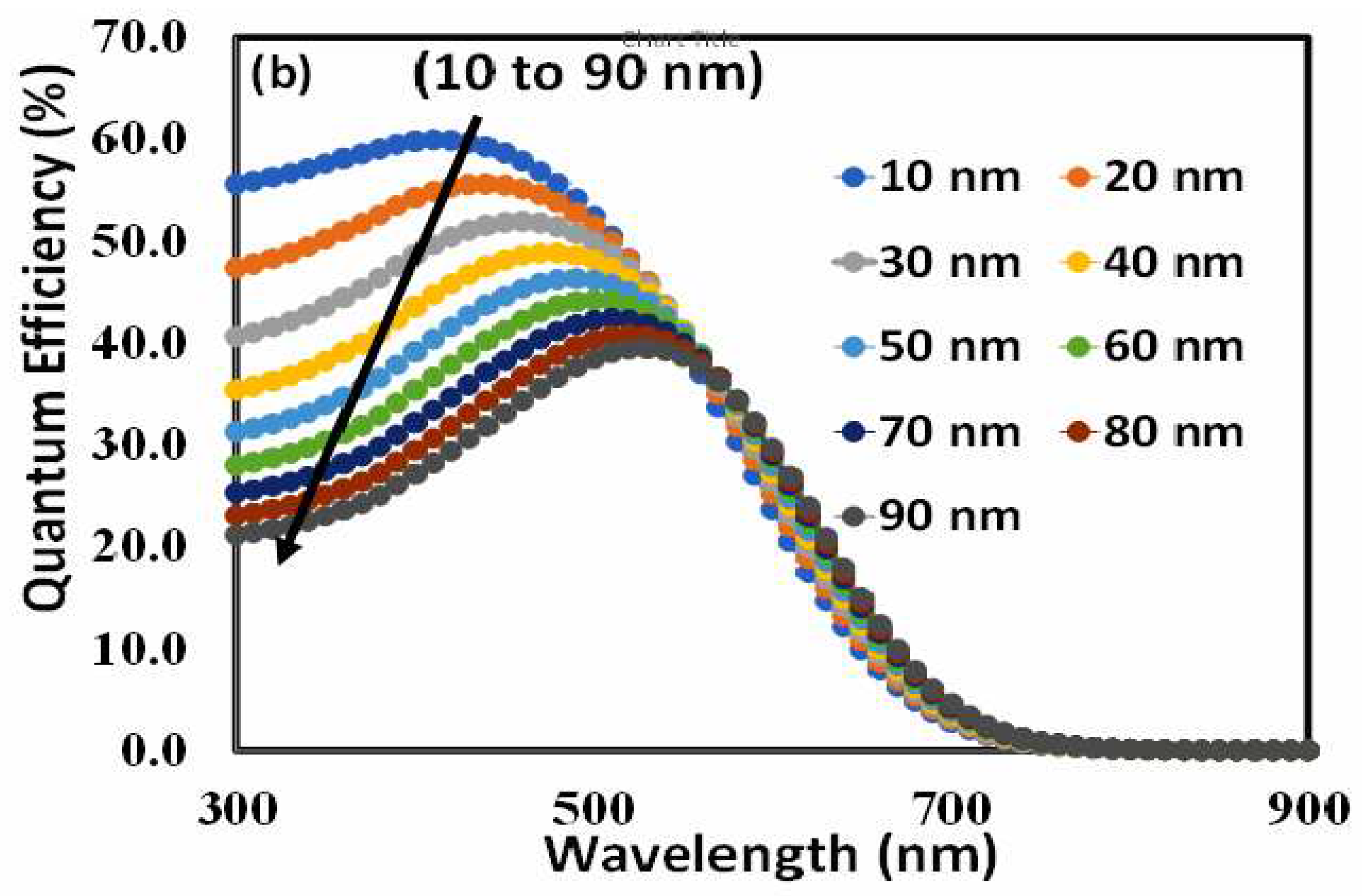
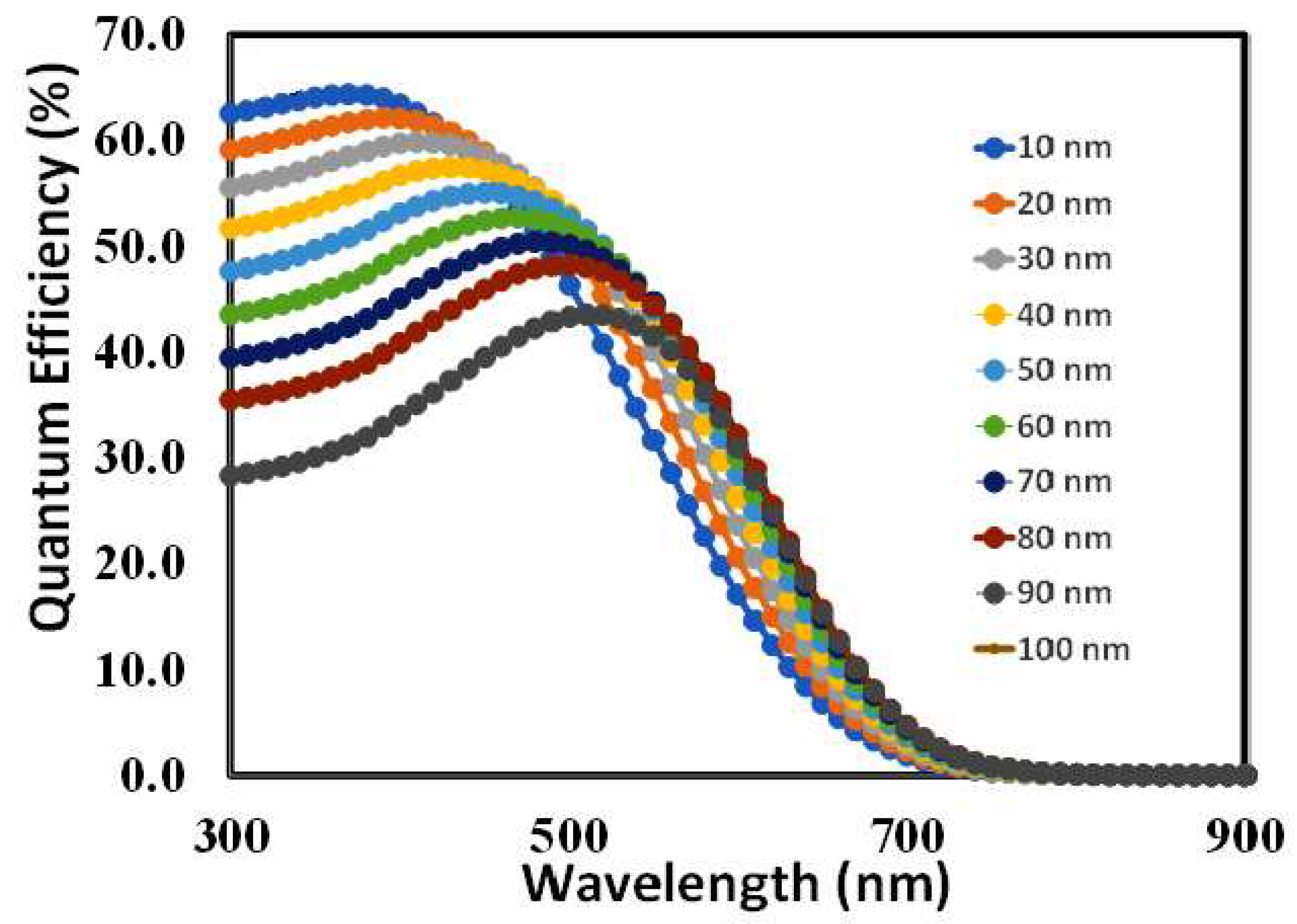
6.6. External Quantum Efficiency Response of the Optimized Devices

The external quantum efficiency responses of the fully optimized devices may be used to further examine the impact of the electron-transport layer on the overall performance of perovskite solar cells. The external quantum efficiency can be defined as the fraction of the total number of collected charge carriers at the electrodes to the total number of incident photons [89]. Mathematically, external quantum efficiency (QE) can be defined as a function of either energy (E) or wavelength (λ) and therefore the relation between quantum efficiency and short-circuit current (Jsc) can be expressed as:
J S C =   q   ∫ ∅ λ   Q E λ d λ
where φ(λ) is the incident flux of photons per unit wavelength. Figure 12 shows the external quantum efficiency responses of the devices (i) A (BT-LIC), (ii) B (BT-BIC), (iii) C (BT-L4F), and (iv) D (BT-BO-L4F) as a function of incident photon wavelength from 300 to 900 nm, more or less very similar responses are observed for all devices. It can be spotted from the figure that for all devices the quantum efficiency raises from photons wavelengths greater than 300 nm; while the highest QE is achieved about 480-485 nm range of photons wavelengths for all devices, and then the QE of devices are gradually decreased, the relative magnified of quantum efficiency responses for all devices are shown in the inset of Figure 12. This clearly reveals that Device B, which uses BT-BIC as its electron transport layer, exhibits relatively improved quantum efficiency, and it also confirms the earlier simulation results that were already discussed.
In addition, Figure 12 shows that the quantum efficiency of the BT-BIC device reaches its optimum value, even though the short-circuit current does not. As shown in Figure 11, the device BT-L4F displays the maximum short-circuit current. While there is a correlation between short-circuit current and quantum efficiency, it is essential to recognize that recombination losses can lead to such discrepancies. Quantum efficiency refers to the measurement of the effectiveness of photon absorption and subsequent transformation into charge carriers. In contrast, the short-circuit current density includes other variables, such as recombination losses, resistive losses, and other internal variables. Consequently, the presence of these losses may cause a slight decrease in the short-circuit current relative to the theoretical quantum efficiency. Given the comparative nature of this study, it can be argued that while the BT-LIC device has a slightly lower short circuit current than the BT-L4F device, it has superior electrical and optical properties. Figure 11 depicts the enhanced photovoltaic response as evidence.

5. Conclusions

In this comparative study, four non-fullerene acceptors (NFA) such as (i) BT-LIC, (ii) BT-BIC, (iii) BT-L4F, and (iv) BT-BO-L4F were used as electron transport layers for novel proposed solar devices i.e., FTO/PEDOT: PSS/ Cs2AgBi0.75Sb0.25Br6 /ETL/Au respectively. All these devices were comprehensively investigated through simulation to determine the most efficient electron transport layer for the proposed devices. For this purpose, comprehensive simulations were carried out to optimize each layer with respect to film-thickness and doping density and then the photovoltaic responses of all the optimized devices were simulated as a function of the electron transport layer, and determined open-circuit voltage, short-circuit current, fill factor, and power-conversion efficiency. It is observed that all devices show reasonable photovoltaic responses and the device containing BT-BIC as an electron transport layer shows the highest power conversion efficiency of ~ 13.2%, (open-circuit voltage = ~1.36 V, short-circuit current = ~12.1 mA/cm2, and fill factor = ~80%). While the BT-LIC device shows the lowest power conversion efficiency of approximately ~6.8% (open-circuit voltage = ~1.23 V, short-circuit current = ~11.2 mA/cm2, and fill factor = ~50%). It is also observed that the improvement in open-circuit voltage and as well as fill factor are relatively higher for Device B. This clearly demonstrates that the photovoltaic Device B fabricated with BT-BIC as an electron transport layer may manage high build-in potential and excellent interface quality which in turn improve the overall charge collection, charge transport, and suppress recombination losses, compared to the other electron transport layers BT-LIC, BT-L4F, and BT-BO-L4F respectively.

Author Contributions

Equal contributions were made to the idea, methodology, validation, formal analysis, and writing of the paper by SAM, MSA, and ANMA. The published version of the work has been reviewed and approved by all authors.

Funding

This research was funded by THE DEPUTYSHIP FOR RESEARCH & INNOVATION, MINISTRY OF EDUCATION IN SAUDI ARABIA, GRANT NUMBER IFP22UQU4330024DSR208.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Available on request.

Acknowledgments

The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number: IFP22UQU4330024DSR208.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Liu, S.; Biju, V. P.; Qi, Y.; Chen, W.; Liu, Z. Recent Progress in the Development of High-Efficiency Inverted Perovskite Solar Cells. NPG Asia Mater 2023, 15, 27. [Google Scholar] [CrossRef]
  2. Shao, M.; Bie, T.; Yang, L.; Gao, Y.; Jin, X.; He, F.; Zheng, N.; Yu, Y.; Zhang, X. Over 21% Efficiency Stable 2D Perovskite Solar Cells. Advanced Materials 2022, 34. [Google Scholar] [CrossRef]
  3. Rong, Y.; Hu, Y.; Mei, A.; Tan, H.; Saidaminov, M. I.; Seok, S. Il; McGehee, M. D.; Sargent, E. H.; Han, H. Challenges for Commercializing Perovskite Solar Cells. Science. 2018. [CrossRef] [PubMed]
  4. Liu, J.; Aydin, E.; Yin, J.; De Bastiani, M.; Isikgor, F. H.; Rehman, A. U.; Yengel, E.; Ugur, E.; Harrison, G. T.; Wang, M.; Gao, Y.; Khan, J. I.; Babics, M.; Allen, T. G.; Subbiah, A. S.; Zhu, K.; Zheng, X.; Yan, W.; Xu, F.; Salvador, M. F.; Bakr, O. M.; Anthopoulos, T. D.; Lanza, M.; Mohammed, O. F.; Laquai, F.; De Wolf, S. 28.2%-Efficient, Outdoor-Stable Perovskite/Silicon Tandem Solar Cell. Joule 2021, 5. [Google Scholar] [CrossRef]
  5. Babayigit, A.; Ethirajan, A.; Muller, M.; Conings, B. Toxicity of Organometal Halide Perovskite Solar Cells. Nature Materials. 2016. [CrossRef] [PubMed]
  6. Ding, G.; Zheng, Y.; Xiao, X.; Cheng, H.; Zhang, G.; Shi, Y.; Shao, Y. Sustainable Development of Perovskite Solar Cells: Keeping a Balance between Toxicity and Efficiency. Journal of Materials Chemistry A. 2022. [CrossRef]
  7. Moiz, S. A.; Alahmadi, A. N. M.; Alshaikh, M. S. Lead-Free FACsSnI3 Based Perovskite Solar Cell: Designing Hole and Electron Transport Layer. Nanomaterials 2023, 13. [Google Scholar] [CrossRef]
  8. Xu, F.; Zhang, M.; Li, Z.; Yang, X.; Zhu, R. Challenges and Perspectives toward Future Wide-Bandgap Mixed-Halide Perovskite Photovoltaics. Adv Energy Mater 2023, 13. [Google Scholar] [CrossRef]
  9. Bello, O. O.; Emetere, M. E. Progress and Limitation of Lead-Free Inorganic Perovskites for Solar Cell Application. Solar Energy. 2022. [CrossRef]
  10. Yu, W.; Zou, Y.; Wang, H.; Qu, B.; Chen, Z.; Xiao, L. Expanding the Absorption of Double Perovskite Cs2AgBiBr6 to NIR Region. J Phys Chem Lett 2023, 14, 5310–5317. [Google Scholar] [CrossRef]
  11. Zhai, M.; Chen, C.; Cheng, M. Advancing Lead-Free Cs2AgBiBr6 Perovskite Solar Cells: Challenges and Strategies. Solar Energy. 2023. [CrossRef]
  12. Igbari, F.; Xu, F. F.; Shao, J. Y.; Ud-Din, F.; Siffalovic, P.; Zhong, Y. W. Stacking Interactions and Photovoltaic Performance of Cs2AgBiBr6 Perovskite. Solar RRL. 2023. [CrossRef]
  13. Momblona, C.; Gil-Escrig, L.; Bandiello, E.; Hutter, E. M.; Sessolo, M.; Lederer, K.; Blochwitz-Nimoth, J.; Bolink, H. J. Efficient Vacuum Deposited P-i-n and n-i-p Perovskite Solar Cells Employing Doped Charge Transport Layers. Energy Environ Sci 2016, 9, 3456–3463. [Google Scholar] [CrossRef]
  14. Correa-Baena, J. P.; Saliba, M.; Buonassisi, T.; Grätzel, M.; Abate, A.; Tress, W.; Hagfeldt, A. Promises and Challenges of Perovskite Solar Cells. Science. 2017. [CrossRef] [PubMed]
  15. Foo, S.; Thambidurai, M.; Senthil Kumar, P.; Yuvakkumar, R.; Huang, Y.; Dang, C. Recent Review on Electron Transport Layers in Perovskite Solar Cells. International Journal of Energy Research. 2022. [CrossRef]
  16. Mohamad Noh, M. F.; Teh, C. H.; Daik, R.; Lim, E. L.; Yap, C. C.; Ibrahim, M. A.; Ahmad Ludin, N.; Mohd Yusoff, A. R. Bin; Jang, J.; Mat Teridi, M. A. The Architecture of the Electron Transport Layer for a Perovskite Solar Cell. Journal of Materials Chemistry C. 2018. [CrossRef]
  17. Mihailetchi, V. D.; Van Duren, J. K. J.; Blom, P. W. M.; Hummelen, J. C.; Janssen, R. A. J.; Kroon, J. M.; Rispens, M. T.; Verhees, W. J. H.; Wienk, M. M. Electron Transport in a Methanofullerene. Adv Funct Mater 2003, 13. [Google Scholar] [CrossRef]
  18. Yang, D.; Zhang, X.; Wang, K.; Wu, C.; Yang, R.; Hou, Y.; Jiang, Y.; Liu, S.; Priya, S. Stable Efficiency Exceeding 20.6% for Inverted Perovskite Solar Cells through Polymer-Optimized PCBM Electron-Transport Layers. Nano Lett 2019, 19. [Google Scholar] [CrossRef]
  19. Karuppuswamy, P.; Hanmandlu, C.; Moorthy Boopathi, K.; Perumal, P.; Liu, C.; Chen, Y.-F.; Chang, Y.-C.; Wang, P.-C.; Lai, C.-S.; Chu, C.-W. Solution-Processable Electron Transport Layer for Efficient Hybrid Perovskite Solar Cells beyond Fullerenes. Solar Energy Materials and Solar Cells 2017, 169, 78–85. [Google Scholar] [CrossRef]
  20. Saki, Z.; Aitola, K.; Sveinbjörnsson, K.; Yang, W.; Svanström, S.; Cappel, U. B.; Rensmo, H.; Johansson, E. M. J.; Taghavinia, N.; Boschloo, G. The Synergistic Effect of Dimethyl Sulfoxide Vapor Treatment and C60 Electron Transporting Layer towards Enhancing Current Collection in Mixed-Ion Inverted Perovskite Solar Cells. J Power Sources 2018, 405, 70–79. [Google Scholar] [CrossRef]
  21. Etxebarria, I.; Ajuria, J.; Pacios, R. Polymer:Fullerene Solar Cells: Materials, Processing Issues, and Cell Layouts to Reach Power Conversion Efficiency over 10%, a Review. J Photonics Energy 2015, 5, 57214. [Google Scholar] [CrossRef]
  22. Wang, D.; Ye, T.; Zhang, Y. Recent Advances of Non-Fullerene Organic Electron Transport Materials in Perovskite Solar Cells. J Mater Chem A Mater 2020, 8. [Google Scholar] [CrossRef]
  23. Heo, J. H.; Lee, S.-C.; Jung, S.-K.; Kwon, O.-P.; Im, S. H. Efficient and Thermally Stable Inverted Perovskite Solar Cells by Introduction of Non-Fullerene Electron Transporting Materials. J Mater Chem A Mater 2017, 5, 20615–20622. [Google Scholar] [CrossRef]
  24. Padula, D.; Landi, A.; Prampolini, G. Assessing Alkyl Side Chain Effects on Electron Transport Properties of Y6-Derived Non-Fullerene Acceptors. Energy Advances 2023. [Google Scholar] [CrossRef]
  25. Cao, X.; Li, P.; Zhu, X.; Li, H.; Xu, R.; Li, J.; Ma, L.; Dong, H.; Wu, Z. Nonfullerene Agent Enables Efficient and Stable Tin-Based Perovskite Solar Cells. Solar RRL 2023, 7, 2300268. [Google Scholar] [CrossRef]
  26. Lin, Y.; Wang, J.; Zhang, Z. G.; Bai, H.; Li, Y.; Zhu, D.; Zhan, X. An Electron Acceptor Challenging Fullerenes for Efficient Polymer Solar Cells. Advanced Materials 2015, 27. [Google Scholar] [CrossRef] [PubMed]
  27. Zhou, D.; Wang, J.; Xu, Z.; Xu, H.; Quan, J.; Deng, J.; Li, Y.; Tong, Y.; Hu, B.; Chen, L. Recent Advances of Nonfullerene Acceptors in Organic Solar Cells. Nano Energy. 2022. [CrossRef]
  28. Wei, Q.; Liu, W.; Leclerc, M.; Yuan, J.; Chen, H.; Zou, Y. A-DA′D-A Non-Fullerene Acceptors for High-Performance Organic Solar Cells. Sci China Chem 2020, 63, 1352–1366. [Google Scholar] [CrossRef]
  29. Yuan, J.; Zhang, Y.; Zhou, L.; Zhang, G.; Yip, H.-L.; Lau, T.-K.; Lu, X.; Zhu, C.; Peng, H.; Johnson, P. A.; Leclerc, M.; Cao, Y.; Ulanski, J.; Li, Y.; Zou, Y. Single-Junction Organic Solar Cell with over 15% Efficiency Using Fused-Ring Acceptor with Electron-Deficient Core. Joule 2019, 3, 1140–1151. [Google Scholar] [CrossRef]
  30. Cui, Y.; Yao, H.; Zhang, J.; Xian, K.; Zhang, T.; Hong, L.; Wang, Y.; Xu, Y.; Ma, K.; An, C.; He, C.; Wei, Z.; Gao, F.; Hou, J. Single-Junction Organic Photovoltaic Cells with Approaching 18% Efficiency. Advanced Materials 2020, 32. [Google Scholar] [CrossRef]
  31. Zhu, C.; Yuan, J.; Cai, F.; Meng, L.; Zhang, H.; Chen, H.; Li, J.; Qiu, B.; Peng, H.; Chen, S.; Hu, Y.; Yang, C.; Gao, F.; Zou, Y.; Li, Y. Tuning the Electron-Deficient Core of a Non-Fullerene Acceptor to Achieve over 17% Efficiency in a Single-Junction Organic Solar Cell. Energy Environ Sci 2020, 13, 2459–2466. [Google Scholar] [CrossRef]
  32. Cai, Y.; Li, Y.; Wang, R.; Wu, H.; Chen, Z.; Zhang, J.; Ma, Z.; Hao, X.; Zhao, Y.; Zhang, C.; Huang, F.; Sun, Y. A Well-Mixed Phase Formed by Two Compatible Non-Fullerene Acceptors Enables Ternary Organic Solar Cells with Efficiency over 18.6%. Advanced Materials 2021, 33, 2101733. [Google Scholar] [CrossRef] [PubMed]
  33. Liu, Q.; Jiang, Y.; Jin, K.; Qin, J.; Xu, J.; Li, W.; Xiong, J.; Liu, J.; Xiao, Z.; Sun, K.; Yang, S.; Zhang, X.; Ding, L. 18% Efficiency Organic Solar Cells. Sci Bull (Beijing) 2020, 65. [Google Scholar] [CrossRef] [PubMed]
  34. Jin, K.; Xiao, Z.; Ding, L. 18.69% PCE from Organic Solar Cells. Journal of Semiconductors. 2021. [CrossRef]
  35. Li, S.; Ye, L.; Zhao, W.; Zhang, S.; Mukherjee, S.; Ade, H.; Hou, J. Energy-Level Modulation of Small-Molecule Electron Acceptors to Achieve over 12% Efficiency in Polymer Solar Cells. Advanced Materials 2016, 28. [Google Scholar] [CrossRef] [PubMed]
  36. Lin, Y.; He, Q.; Zhao, F.; Huo, L.; Mai, J.; Lu, X.; Su, C. J.; Li, T.; Wang, J.; Zhu, J.; Sun, Y.; Wang, C.; Zhan, X. A Facile Planar Fused-Ring Electron Acceptor for As-Cast Polymer Solar Cells with 8.71% Efficiency. J Am Chem Soc 2016, 138. [Google Scholar] [CrossRef] [PubMed]
  37. Pan, H.; Zhao, X.; Gong, X.; Li, H.; Ladi, N. H.; Zhang, X. L.; Huang, W.; Ahmad, S.; Ding, L.; Shen, Y.; Wang, M.; Fu, Y. Advances in Design Engineering and Merits of Electron Transporting Layers in Perovskite Solar Cells. Mater Horiz 2020, 7. [Google Scholar] [CrossRef]
  38. Mahmood, K.; Sarwar, S.; Mehran, M. T. Current Status of Electron Transport Layers in Perovskite Solar Cells: Materials and Properties. RSC Advances. 2017. [CrossRef]
  39. Saif, O. M.; Elogail, Y.; Abdolkader, T. M.; Shaker, A.; Zekry, A.; Abouelatta, M.; Salem, M. S.; Fedawy, M. Comprehensive Review on Thin Film Homojunction Solar Cells: Technologies, Progress and Challenges. Energies (Basel) 2023, 16. [Google Scholar] [CrossRef]
  40. Bagade, S. S.; Barik, S. B.; Malik, M. M.; Patel, P. K. Impact of Band Alignment at Interfaces in Perovskite-Based Solar Cell Devices. Mater Today Proc 2023. [Google Scholar] [CrossRef]
  41. Ma, L.; Zhang, S.; Hou, J. Crystal Structures in State-of-the-Art Non-Fullerene Electron Acceptors. Journal of Materials Chemistry A. 2022. [CrossRef]
  42. Li, G.; Zhang, X.; Jones, L. O.; Alzola, J. M.; Mukherjee, S.; Feng, L. W.; Zhu, W.; Stern, C. L.; Huang, W.; Yu, J.; Sangwan, V. K.; Delongchamp, D. M.; Kohlstedt, K. L.; Wasielewski, M. R.; Hersam, M. C.; Schatz, G. C.; Facchetti, A.; Marks, T. J. Systematic Merging of Nonfullerene Acceptor π-Extension and Tetrafluorination Strategies Affords Polymer Solar Cells with >16% Efficiency. J Am Chem Soc 2021, 143. [Google Scholar] [CrossRef] [PubMed]
  43. Xin, J.; Li, W.; Zhang, Y.; Liang, Q.; Song, C.; Zhao, Y.; He, Z.; Liu, J.; Ma, W. A Review of Nonfullerene Solar Cells: Insight into the Correlation among Molecular Structure, Morphology, and Device Performance. Battery Energy 2023, 2. [Google Scholar] [CrossRef]
  44. Liang, C.; Xing, G. Doping Electron Transporting Layer: An Effective Method to Enhance JSC of All-Inorganic Perovskite Solar Cells. ENERGY & ENVIRONMENTAL MATERIALS 2021, 4, 500–501. [Google Scholar] [CrossRef]
  45. Lee, S.; Paine, D. C.; Gleason, K. K. Heavily Doped Poly(3,4-Ethylenedioxythiophene) Thin Films with High Carrier Mobility Deposited Using Oxidative CVD: Conductivity Stability and Carrier Transport. Adv Funct Mater 2014, 24, 7187–7196. [Google Scholar] [CrossRef]
  46. Xu, Z.; Li, N.; Niu, X.; Liu, H.; Liu, G.; Chen, Q.; Zhou, H. Balancing Energy-Level Difference for Efficient n-i-p Perovskite Solar Cells with Cu Electrode. Energy Material Advances 2022, 2022. [Google Scholar] [CrossRef]
  47. Wu, X.; Li, B.; Zhu, Z.; Chueh, C. C.; Jen, A. K. Y. Designs from Single Junctions, Heterojunctions to Multijunctions for High-Performance Perovskite Solar Cells. Chemical Society Reviews. 2021. [CrossRef]
  48. Zhang, S.; Liu, Z.; Zhang, W.; Jiang, Z.; Chen, W.; Chen, R.; Huang, Y.; Yang, Z.; Zhang, Y.; Han, L.; Chen, W. Barrier Designs in Perovskite Solar Cells for Long-Term Stability. Advanced Energy Materials. 2020. [CrossRef]
  49. Fan, R.; Huang, Y.; Wang, L.; Li, L.; Zheng, G.; Zhou, H. The Progress of Interface Design in Perovskite-Based Solar Cells. Adv Energy Mater 2016, 6. [Google Scholar] [CrossRef]
  50. Hossain, M. K.; Samajdar, D. P.; Das, R. C.; Arnab, A. A.; Rahman, M. F.; Rubel, M. H. K.; Islam, M. R.; Bencherif, H.; Pandey, R.; Madan, J.; Mohammed, M. K. A. Design and Simulation of Cs2BiAgI6 Double Perovskite Solar Cells with Different Electron Transport Layers for Efficiency Enhancement. Energy and Fuels 2023, 37. [Google Scholar] [CrossRef]
  51. Mali, S. S.; Hong, C. K. P-i-n/n-i-p Type Planar Hybrid Structure of Highly Efficient Perovskite Solar Cells towards Improved Air Stability: Synthetic Strategies and the Role of p-Type Hole Transport Layer (HTL) and n-Type Electron Transport Layer (ETL) Metal Oxides. Nanoscale 2016, 8, 10528–10540. [Google Scholar] [CrossRef]
  52. Wu, S.; Liu, M.; Jen, A. K. Y. Prospects and Challenges for Perovskite-Organic Tandem Solar Cells. Joule. 2023. [CrossRef]
  53. Sun, K.; Zhang, S.; Li, P.; Xia, Y.; Zhang, X.; Du, D.; Isikgor, F. H.; Ouyang, J. Review on Application of PEDOTs and PEDOT:PSS in Energy Conversion and Storage Devices. Journal of Materials Science: Materials in Electronics 2015, 26, 4438–4462. [Google Scholar] [CrossRef]
  54. Liu, F.; Zhu, J.; Wei, J.; Li, Y.; Lv, M.; Yang, S.; Zhang, B.; Yao, J.; Dai, S. Numerical Simulation: Toward the Design of High-Efficiency Planar Perovskite Solar Cells. Appl Phys Lett 2014, 104. [Google Scholar] [CrossRef]
  55. Neukom, M. T.; Schiller, A.; Züfle, S.; Knapp, E.; Ávila, J.; Pérez-del-Rey, D.; Dreessen, C.; Zanoni, K. P. S.; Sessolo, M.; Bolink, H. J.; Ruhstaller, B. Consistent Device Simulation Model Describing Perovskite Solar Cells in Steady-State, Transient, and Frequency Domain. ACS Appl Mater Interfaces 2019, 11, 23320–23328. [Google Scholar] [CrossRef] [PubMed]
  56. Gummel, H. K. A Self-Consistent Iterative Scheme for One-Dimensional Steady State Transistor Calculations. IEEE Trans Electron Devices 1964, 11. [Google Scholar] [CrossRef]
  57. Gwyn, C. W.; Scharfetter, D. L.; Wirth, J. L. The Analysis of Radiation Effects in Semiconductor Junction Devices. IEEE Trans Nucl Sci 1967, NS-14. [Google Scholar] [CrossRef]
  58. Burgelman, M.; Nollet, P.; Degrave, S. Modelling Polycrystalline Semiconductor Solar Cells. Thin Solid Films 2000, 361. [Google Scholar] [CrossRef]
  59. Liu, Y.; Sun, Y.; Rockett, A. A New Simulation Software of Solar Cells - WxAMPS. Solar Energy Materials and Solar Cells 2012, 98. [Google Scholar] [CrossRef]
  60. Moiz, S. A. Optimization of Hole and Electron Transport Layer for Highly Efficient Lead-Free Cs2TiBr6-Based Perovskite Solar Cell. Photonics 2022, 9. [Google Scholar] [CrossRef]
  61. Moiz, S. A.; Alahmadi, A. N. M. Design of Dopant and Lead-Free Novel Perovskite Solar Cell for 16.85% Efficiency. Polymers (Basel) 2021, 13. [Google Scholar] [CrossRef]
  62. Burgelman, M.; Decock, K.; Khelifi, S.; Abass, A. Advanced Electrical Simulation of Thin Film Solar Cells. In Thin Solid Films; 2013; Vol. 535. [CrossRef]
  63. Burgelman, M.; Verschraegen, J.; Degrave, S.; Nollet, P. Modeling Thin-Film PV Devices. Progress in Photovoltaics: Research and Applications 2004, 12, (2–3). [Google Scholar] [CrossRef]
  64. Verschraegen, J.; Burgelman, M. Numerical Modeling of Intra-Band Tunneling for Heterojunction Solar Cells in Scaps. Thin Solid Films 2007, 515. [Google Scholar] [CrossRef]
  65. He, Y.; Xu, L.; Yang, C.; Guo, X.; Li, S. Design and Numerical Investigation of a Lead-Free Inorganic Layered Double Perovskite Cs4cusb2cl12 Nanocrystal Solar Cell by Scaps-1d. Nanomaterials 2021, 11. [Google Scholar] [CrossRef] [PubMed]
  66. Chowdhury, M. S.; Shahahmadi, S. A.; Chelvanathan, P.; Tiong, S. K.; Amin, N.; Techato, K.; Nuthammachot, N.; Chowdhury, T.; Suklueng, M. Effect of Deep-Level Defect Density of the Absorber Layer and n/i Interface in Perovskite Solar Cells by SCAPS-1D. Results in Physics. 2020. [CrossRef]
  67. Moiz, S. A.; Albadwani, S. A.; Alshaikh, M. S. Towards Highly Efficient Cesium Titanium Halide Based Lead-Free Double Perovskites Solar Cell by Optimizing the Interface Layers. Nanomaterials 2022, 12. [Google Scholar] [CrossRef]
  68. Moiz, S. A.; Alzahrani, M. S.; Alahmadi, A. N. M. Electron Transport Layer Optimization for Efficient PTB7:PC70BM Bulk-Heterojunction Solar Cells. Polymers (Basel) 2022, 14. [Google Scholar] [CrossRef]
  69. Moiz, S. A.; Alahmadi, A. N. M.; Aljohani, A. J. Design of a Novel Lead-Free Perovskite Solar Cell for 17.83% Efficiency. IEEE Access 2021, 9. [Google Scholar] [CrossRef]
  70. McClure, E. T.; Ball, M. R.; Windl, W.; Woodward, P. M. Cs2AgBiX6 (X = Br, Cl): New Visible Light Absorbing, Lead-Free Halide Perovskite Semiconductors. Chemistry of Materials 2016, 28. [Google Scholar] [CrossRef]
  71. Amri, K.; Belghouthi, R.; Aillerie, M.; Gharbi, R. Device Optimization of a Lead-Free Perovskite/Silicon Tandem Solar Cell with 24.4% Power Conversion Efficiency. Energies (Basel) 2021, 14. [Google Scholar] [CrossRef]
  72. Zhang, G.; Lin, F. R.; Qi, F.; Heumüller, T.; Distler, A.; Egelhaaf, H. J.; Li, N.; Chow, P. C. Y.; Brabec, C. J.; Jen, A. K. Y.; Yip, H. L. Renewed Prospects for Organic Photovoltaics. Chemical Reviews. 2022. [CrossRef] [PubMed]
  73. Liu, H.; Dai, T.; Zhou, J.; Wang, H.; Guo, Q.; Guo, Q.; Zhou, E. The Development of A-DA’D-A Type Nonfullerene Acceptors Containing Non-Halogenated End Groups. Nano Res 2023. [Google Scholar] [CrossRef]
  74. Perdigón-Toro, L.; Zhang, H.; Markina, A.; Yuan, J.; Hosseini, S. M.; Wolff, C. M.; Zuo, G.; Stolterfoht, M.; Zou, Y.; Gao, F.; Andrienko, D.; Shoaee, S.; Neher, D. Barrierless Free Charge Generation in the High-Performance PM6:Y6 Bulk Heterojunction Non-Fullerene Solar Cell. Advanced Materials 2020, 32. [Google Scholar] [CrossRef] [PubMed]
  75. Shi, T.; Zhang, H. S.; Meng, W.; Teng, Q.; Liu, M.; Yang, X.; Yan, Y.; Yip, H. L.; Zhao, Y. J. Effects of Organic Cations on the Defect Physics of Tin Halide Perovskites. J Mater Chem A Mater 2017, 5. [Google Scholar] [CrossRef]
  76. Cao, W.; Hu, Z.; Lin, Z.; Guo, X.; Su, J.; Chang, J.; Hao, Y. Defects and Doping Engineering towards High Performance Lead-Free or Lead-Less Perovskite Solar Cells. Journal of Energy Chemistry. 2022. [CrossRef]
  77. Friedel, B.; Keivanidis, P. E.; Brenner, T. J. K.; Abrusci, A.; McNeill, C. R.; Friend, R. H.; Greenham, N. C. Effects of Layer Thickness and Annealing of PEDOT:PSS Layers in Organic Photodetectors. Macromolecules 2009, 42, 6741–6747. [Google Scholar] [CrossRef]
  78. Moiz, S. A.; Khan, I. A.; Younis, W. A.; Masud, M. I.; Ismail, Y.; Khawaja, Y. M. Solvent Induced Charge Transport Mechanism for Conducting Polymer at Higher Temperature. Mater Res Express 2020, 7. [Google Scholar] [CrossRef]
  79. Karimov, Kh. S.; Ahmed, M. M.; Moiz, S. A.; Babadzhanov, P.; Marupov, R.; Turaeva, M. A. Electrical Properties of Organic Semiconductor Orange Nitrogen Dye Thin Films Deposited from Solution at High Gravity. Eurasian Chemico-Technological Journal 2007, 5. [Google Scholar] [CrossRef]
  80. Sherkar, T. S.; Momblona, C.; Gil-Escrig, L.; Ávila, J.; Sessolo, M.; Bolink, H. J.; Koster, L. J. A. Recombination in Perovskite Solar Cells: Significance of Grain Boundaries, Interface Traps, and Defect Ions. ACS Energy Lett 2017, 2. [Google Scholar] [CrossRef] [PubMed]
  81. Moiz, S. A.; Alahmadi, A. N. M.; Aljohani, A. J. Design of Silicon Nanowire Array for PEDOT:PSS-Silicon Nanowire-Based Hybrid Solar Cell. Energies (Basel) 2020, 13. [Google Scholar] [CrossRef]
  82. Della Gaspera, E.; Peng, Y.; Hou, Q.; Spiccia, L.; Bach, U.; Jasieniak, J. J.; Cheng, Y. B. Ultra-Thin High Efficiency Semitransparent Perovskite Solar Cells. Nano Energy 2015, 13. [Google Scholar] [CrossRef]
  83. Brendel, R.; Queisser, H. J. On the Thickness Dependence of Open Circuit Voltages of P-n Junction Solar Cells. Solar Energy Materials and Solar Cells 1993, 29, 397–401. [Google Scholar] [CrossRef]
  84. Zhang, C.; Zhu, X. N-Type Quinoidal Oligothiophene-Based Semiconductors for Thin-Film Transistors and Thermoelectrics. Advanced Functional Materials. 2020. [CrossRef]
  85. Naab, B. D.; Gu, X.; Kurosawa, T.; To, J. W. F.; Salleo, A.; Bao, Z. Role of Polymer Structure on the Conductivity of N-Doped Polymers. Adv Electron Mater 2016, 2. [Google Scholar] [CrossRef]
  86. Moiz, S. A.; Alahmadi, A. N. M.; Karimov, K. S. Improved Organic Solar Cell by Incorporating Silver Nanoparticles Embedded Polyaniline as Buffer Layer. Solid State Electron 2020, 163. [Google Scholar] [CrossRef]
  87. Guo, Z.; Jena, A. K.; Kim, G. M.; Miyasaka, T. The High Open-Circuit Voltage of Perovskite Solar Cells: A Review. Energy Environ. Sci. 2022, 15, 3171–3222. [Google Scholar] [CrossRef]
  88. Shao, Y.; Yuan, Y.; Huang, J. Correlation of Energy Disorder and Open-Circuit Voltage in Hybrid Perovskite Solar Cells. Nat Energy 2016, 1. [Google Scholar] [CrossRef]
  89. Shaheen, S. E.; Brabec, C. J.; Sariciftci, N. S.; Padinger, F.; Fromherz, T.; Hummelen, J. C. 2.5% Efficient Organic Plastic Solar Cells. Appl Phys Lett 2001, 78, 841–843. [Google Scholar] [CrossRef]
Preprints 87029 g001
Figure 1. The molecular structure of (a) BT-LIC, (b) BT-BIC, (c) BT-L4F, and (d) BT-BO-L4F is used as a non-fluorine electron transport layer.
Figure 1. The molecular structure of (a) BT-LIC, (b) BT-BIC, (c) BT-L4F, and (d) BT-BO-L4F is used as a non-fluorine electron transport layer.
Preprints 87029 g001
Preprints 87029 g002
Figure 2. Design architecture of the proposed perovskite solar cell with their energy band diagram: (a) FTO/PEDOT:PSS/ Cs2AgBi0.75Sb0.25Br6/BT-LIC/Au (Device BT-LIC), (b) FTO/PEDOT:PSS/ Cs2AgBi0.75Sb0.25Br6/BT-BIC/Au (Device BT-BIC), (c) FTO/PEDOT:PSS/ Cs2AgBi0.75Sb0.25Br6/BT-L4F/Au (Device BT-L4F), and (d) FTO/PEDOT:PSS/ Cs2AgBi0.75Sb0.25Br6/ BT-BO-L4F /Au, (Device BT-BO-L4F) respectively.
Figure 2. Design architecture of the proposed perovskite solar cell with their energy band diagram: (a) FTO/PEDOT:PSS/ Cs2AgBi0.75Sb0.25Br6/BT-LIC/Au (Device BT-LIC), (b) FTO/PEDOT:PSS/ Cs2AgBi0.75Sb0.25Br6/BT-BIC/Au (Device BT-BIC), (c) FTO/PEDOT:PSS/ Cs2AgBi0.75Sb0.25Br6/BT-L4F/Au (Device BT-L4F), and (d) FTO/PEDOT:PSS/ Cs2AgBi0.75Sb0.25Br6/ BT-BO-L4F /Au, (Device BT-BO-L4F) respectively.
Preprints 87029 g002
Preprints 87029 g003
Figure 3. The photo current-voltage responses of the proposed perovskite solar cell for devices where absorber and ETL (Device D) thickness are randomly selected (optimization will be performed in a later stage), but the thickness of PEDOT:PSS is varied from 10 nm to 90 nm respectively.
Figure 3. The photo current-voltage responses of the proposed perovskite solar cell for devices where absorber and ETL (Device D) thickness are randomly selected (optimization will be performed in a later stage), but the thickness of PEDOT:PSS is varied from 10 nm to 90 nm respectively.
Preprints 87029 g003
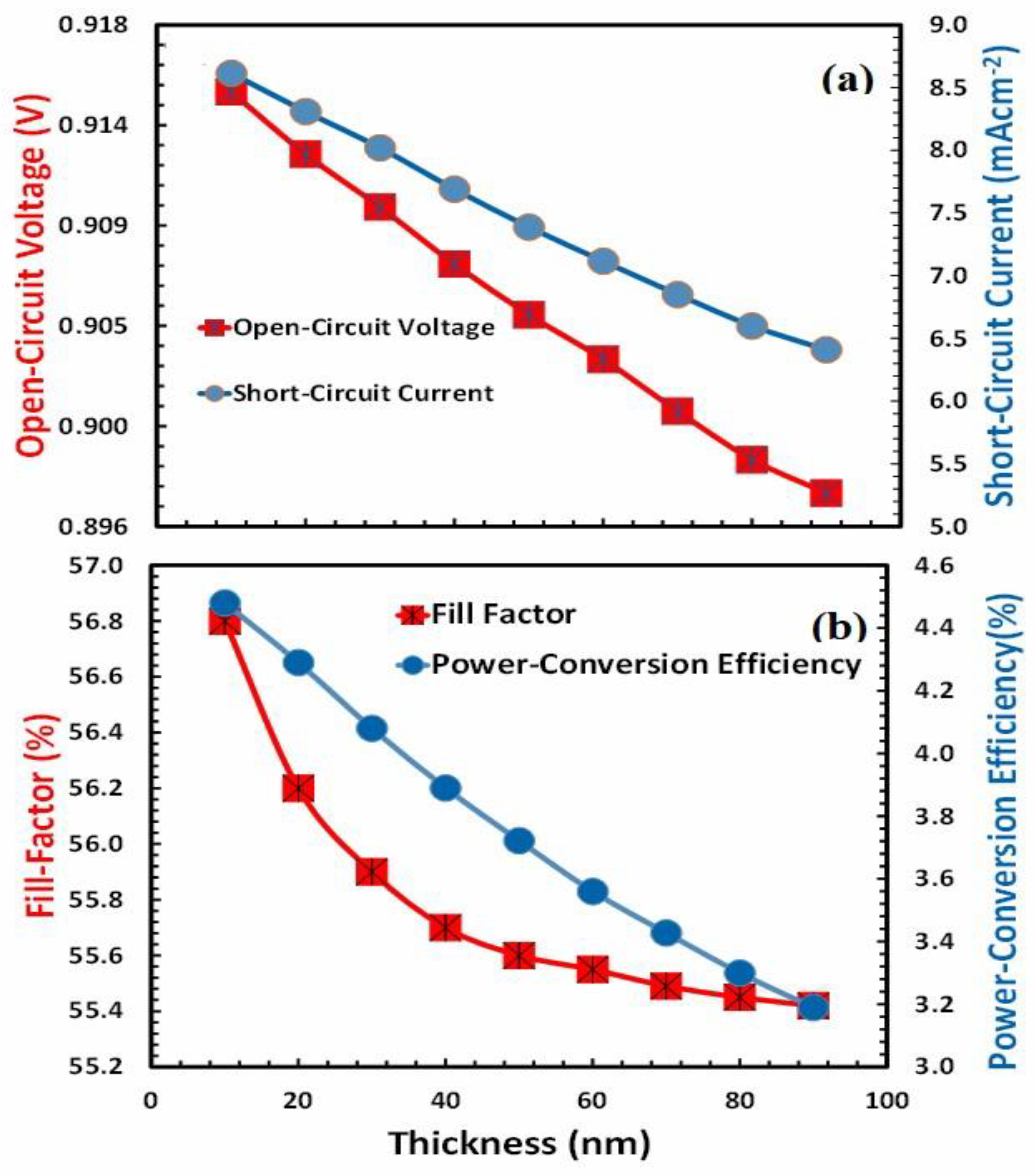
Preprints 87029 g004
Figure 4. Shows the photovoltaic parameters (a) open-circuit voltage (Preprints 87029 i001), short-circuit current (Preprints 87029 i002), (b) fill factor (Preprints 87029 i003), and power-conversion efficiency (Preprints 87029 i004) of Device D as a function of the thickness of the PEDOT:PSS as hole-transport layer.
Figure 4. Shows the photovoltaic parameters (a) open-circuit voltage (Preprints 87029 i001), short-circuit current (Preprints 87029 i002), (b) fill factor (Preprints 87029 i003), and power-conversion efficiency (Preprints 87029 i004) of Device D as a function of the thickness of the PEDOT:PSS as hole-transport layer.
Preprints 87029 g004
Preprints 87029 g005
Figure 5. The external quantum efficiency responses of the proposed perovskite solar Device D (BT-BO-L4F) as a function of incident photons wavelength from 300 to 900 nm as a function of PEDOT:PSS thickness from 10 to 90 nm respectively.
Figure 5. The external quantum efficiency responses of the proposed perovskite solar Device D (BT-BO-L4F) as a function of incident photons wavelength from 300 to 900 nm as a function of PEDOT:PSS thickness from 10 to 90 nm respectively.
Preprints 87029 g005
Preprints 87029 g006
Figure 6. The photo current-voltage responses of the proposed perovskite solar cell for device D, while the thickness of the absorber layer (Cs2AgBi0.75Sb0.25Br6 ) is varied from 10 nm to 100 nm respectively.
Figure 6. The photo current-voltage responses of the proposed perovskite solar cell for device D, while the thickness of the absorber layer (Cs2AgBi0.75Sb0.25Br6 ) is varied from 10 nm to 100 nm respectively.
Preprints 87029 g006
Preprints 87029 g007
Figure 7. Shows the photovoltaic parameters (a) open-circuit voltage, short-circuit current, (b) fill factor, and power-conversion efficiency responses of the proposed perovskite solar cell for device D, while the thickness of the absorber layer (Cs2AgBi0.75Sb0.25Br6 ) is varied from 10 nm to 100 nm respectively.
Figure 7. Shows the photovoltaic parameters (a) open-circuit voltage, short-circuit current, (b) fill factor, and power-conversion efficiency responses of the proposed perovskite solar cell for device D, while the thickness of the absorber layer (Cs2AgBi0.75Sb0.25Br6 ) is varied from 10 nm to 100 nm respectively.
Preprints 87029 g007
Preprints 87029 g008
Figure 8. Shows the quantum efficiency responses of the proposed perovskite solar cell for device D, where the thickness of the absorber layer (Cs2AgBi0.75Sb0.25Br6 ) is varied from 10 nm to 100 nm respectively.
Figure 8. Shows the quantum efficiency responses of the proposed perovskite solar cell for device D, where the thickness of the absorber layer (Cs2AgBi0.75Sb0.25Br6 ) is varied from 10 nm to 100 nm respectively.
Preprints 87029 g008
Preprints 87029 g009
Figure 9. Shows the photovoltaic parameters (i) open-circuit voltage, (ii) short-circuit current, (iii) fill factor, and (iv) power-conversion efficiency of all devices (a) Device BT-LIC, (b) Device BT-BIC, (c) Device BT-L4F, and (d) Device BT-BO-L4F as a function of the thickness of the electron-transport layer.
Figure 9. Shows the photovoltaic parameters (i) open-circuit voltage, (ii) short-circuit current, (iii) fill factor, and (iv) power-conversion efficiency of all devices (a) Device BT-LIC, (b) Device BT-BIC, (c) Device BT-L4F, and (d) Device BT-BO-L4F as a function of the thickness of the electron-transport layer.
Preprints 87029 g009
Preprints 87029 g010
Figure 10. Shows the photovoltaic parameters such as (i) open-circuit voltage, (ii) short-circuit current, (iii) fill factor, and (iv) power-conversion efficiency of the proposed devices (a) Device BT-LIC, (b) Device BT-BIC, (c) Device BT-L4F, and (d) Device BT-BO-L4F respectively as a function of the doping density of the electron-transport layer.
Figure 10. Shows the photovoltaic parameters such as (i) open-circuit voltage, (ii) short-circuit current, (iii) fill factor, and (iv) power-conversion efficiency of the proposed devices (a) Device BT-LIC, (b) Device BT-BIC, (c) Device BT-L4F, and (d) Device BT-BO-L4F respectively as a function of the doping density of the electron-transport layer.
Preprints 87029 g010
Preprints 87029 g011
Figure 11. The photo current-voltage responses of the proposed perovskite solar cells for (i) Device A (Device BT-LIC), (ii) Device B (Device BT-BIC), (iii) Device C (Device BT-L4F), and (iv) Device D (Device BT-BO-L4F) respectively.
Figure 11. The photo current-voltage responses of the proposed perovskite solar cells for (i) Device A (Device BT-LIC), (ii) Device B (Device BT-BIC), (iii) Device C (Device BT-L4F), and (iv) Device D (Device BT-BO-L4F) respectively.
Preprints 87029 g011
Preprints 87029 g012
Figure 12. The external quantum efficiency responses of the proposed perovskite solar cells for (i) Device A (Device BT-LIC), (ii) Device B (Device BT-BIC), (iii) Device C (Device BT-L4F), and (iv) Device D (Device BT-BO-L4F) as a function of incident photons wavelength from 300 to 900 nm. The inset of the figure shows the magnified responses of all the devices for the incident photons' wavelength range from 300 to 390 nm.
Figure 12. The external quantum efficiency responses of the proposed perovskite solar cells for (i) Device A (Device BT-LIC), (ii) Device B (Device BT-BIC), (iii) Device C (Device BT-L4F), and (iv) Device D (Device BT-BO-L4F) as a function of incident photons wavelength from 300 to 900 nm. The inset of the figure shows the magnified responses of all the devices for the incident photons' wavelength range from 300 to 390 nm.
Preprints 87029 g012
Table 1. The random simulation parameters such as thickness and doping are used for the novel non-fluorine polymer acceptor-transport layer, while other simulation parameters for given materials are taken from the given references.
Table 1. The random simulation parameters such as thickness and doping are used for the novel non-fluorine polymer acceptor-transport layer, while other simulation parameters for given materials are taken from the given references.
Photovoltaic Parameters PEDOT: PSS Perovskite
Cs2AgBi0.75Sb0.25Br6 		BT- LIC BT- BIC BT- L4F BT- BO-L4F
Thickness (nm) 50 500 100 100 100 100
Energy Band Gap (Eg, eV) 2.2 1.8 1.57 1.73 1.58 1.6
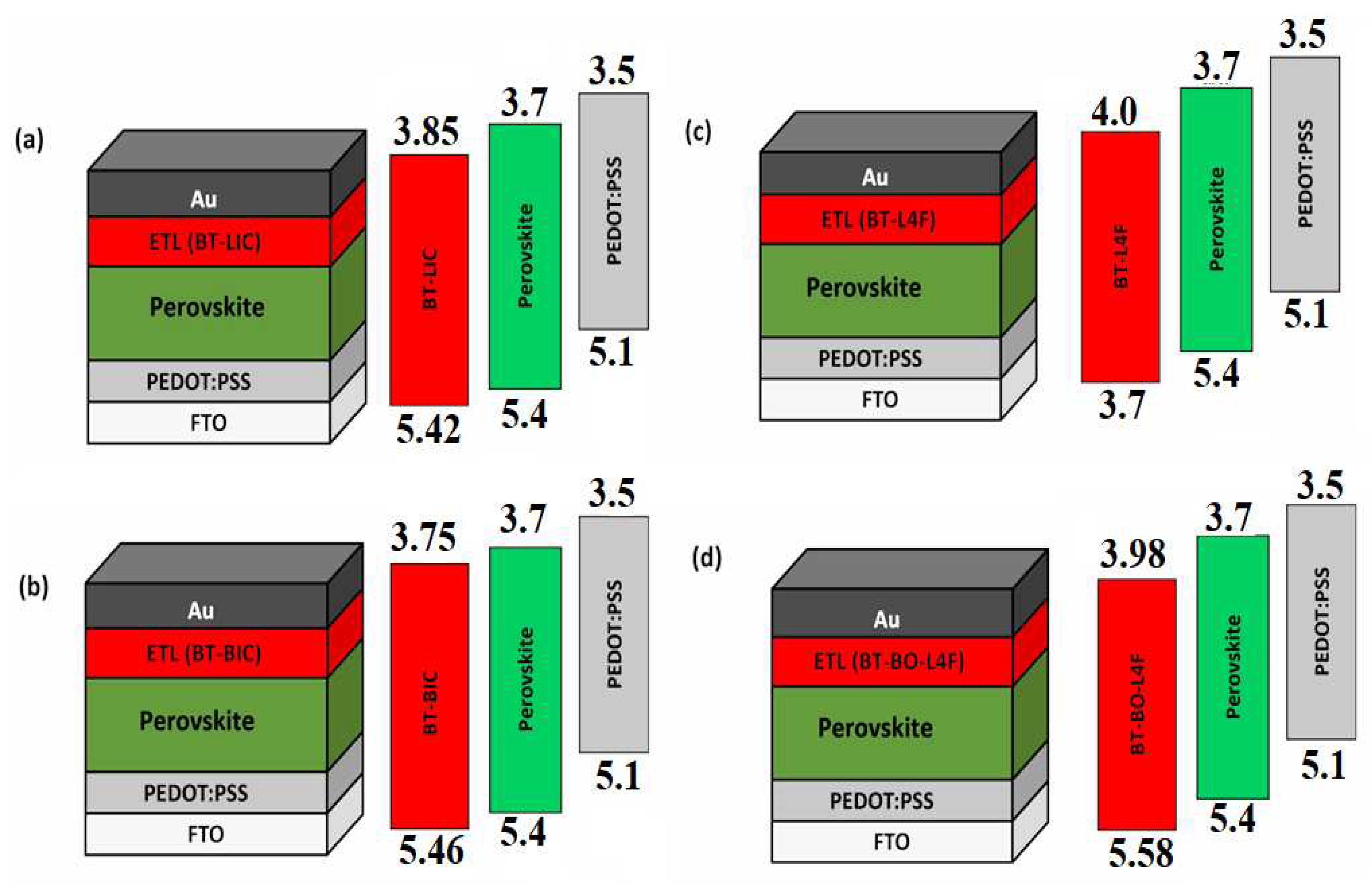
Electron Affinity (X, eV) 2.9 3.58 3.85 3.73 4 3.98
Dielectric Permittivity ( ϵ r ) 3.0 6.5 3.5 3.5 3.5 3.5
Effective Density of States at Conduction Band (Nc , cm-3 ) 2.2x1015 2.2x1018 1x1020 1x1020 1x1020 1x1020
Effective Density of States at Valence Band (Nv , cm-3 ) 1.8 x 1018 1.8 x 1019 1x1020 1x1020 1 x1020 1x1020
Hole Thermal Velocity (Vh, cm/s) 1x107 1x107 1x107 1x107 1x107 1x107
Electron Thermal Velocity (Ve, cm/s) 1x107 1x107 1x107 1x107 1x107 1x107
Electron Mobility ( μ e , cm-2/V.s) 10 2 1x10-4 1x10-4 1x10-4 1x10-4
Hole Mobility ( μ h , cm-2/V.s) 10 2 4x10-4 1x10-4 1x10-4 1x10-4
Uniform Shallow Donor Doping (Nd,,cm-3) - - 1x1016 1x1016 1x1016 1x1016
Uniform Shallow Acceptor Doping (Na, cm-3 ) 1015 - 1x1016 - - -
Defect Density (Nt, cm-3 ) 1014 1014 1014 1014 1014 1014
Reference [64,65,66,67,68] [69,70,71] [72,73]
Table 2. Optimized photovoltaic responses (i) open-circuit voltage, (ii) short-circuit current, (iii) fill-factor, and (iv) power-conversion efficiency of the proposed (i) device A (Device BT-LIC), (ii) Device B (Device BT-BIC), (iii) device C (Device BT-L4F), and (iv) device D (Device BT-BO-L4F) respectively.
Table 2. Optimized photovoltaic responses (i) open-circuit voltage, (ii) short-circuit current, (iii) fill-factor, and (iv) power-conversion efficiency of the proposed (i) device A (Device BT-LIC), (ii) Device B (Device BT-BIC), (iii) device C (Device BT-L4F), and (iv) device D (Device BT-BO-L4F) respectively.
Device Open-Circuit Voltage
(Volts)		 Short-Circuit Current (mA.cm-2 ) Fill-Factor (%) Power-Conversion Efficiency (%)
Devise A (BT-LIC) 1.23 11.2 50 6.8
Devise B (BT-LIC) 1.36 12.1 80 13.2
Devise C (BT-L4F) 1.26 12.01 71 10.7
Devise D (BT-BO-L4F) 1.24 12.5 78 12.09
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated