Image Processing for the Detection and Analysis of Microcracks Caused by Fatigue in Steel

This article presents a method that uses a semi-automatic algorithm for the detection and analysis of microcracks in steel test specimens using binarized image analysis. It obtains the length along the crack path in contrast to previous methods that have obtained linear length, thereby achieving a closer approximation to its actual value. Additionally, this method automatically calculates the COD and COA parameters with measurement deviations in micrometres, thus providing greater precision than previous methods proposed to date.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

The continuous evolution of technology demands a shift toward processing automation due to the higher economic costs and time associated with manual execution. In a previous work [1], a comparison was made between manual crack detection and image processing methods, highlighting the advantages of the latter, which provided higher image resolution and reduced system uncertainty compared to manual methods.

Building upon this approach, in [2,3], the classification of images containing fatigue is proposed by categorizing them into three groups: (1) fractured surface imaging, (2) damaged surface imaging, and (3) deformed surface imaging. Each category corresponds to different acquisition and processing methods. The acquisition methods involve electron microscopy, optical microscopy, or laser scanning, while the processing methods include directional filtering via Fourier transform with Haralick’s segmentation process, conventional matrix processing, and shape classification. The objectives of each category are summarised as follows: (1) determining the overall orientation and average spacing between striations, (2) measuring surface density while assessing the orientation and spacing of slip bands (micro-plastic deformations in ductile materials), and (3) extracting high-frequency deformation information (HFD) and measuring material deformation.

Image processing for crack detection has been extensively studied in both 2D and 3D images, including computed tomography (CT) as a non-destructive method that can detect and monitor crack growth under increasing loads [4]. In Ref. [5], tomography is used to determine the 3D volume correlation, extract crack geometry, obtain displacement discontinuity, model the crack, and estimate stress intensity factors in cast iron. For carbon fibre-reinforced plastic (CFRP) materials, the fatigue damage can be quantified through the image analysis of X-ray-computed tomography (CT) scan images [6].

In recent years, numerous crack detection methods based on image analysis have been developed. For example, Ref. [7] uses a method to locate crack point configurations that are identified using thinned images to generate a skeleton integrated into the crack point distance field, which is then calculated using the Distance Transform. This approach automatically analyses structures after earthquakes. Similarly, Ref. [8] proposes an automatic crack detection technique that is focused on concrete surfaces using pattern recognition with artificial neural networks to calculate crack properties such as width, length, orientation, and pattern. In [9], a method for analysing microcracks in rocks employs 2D imaging analysis involving binarization and filtering to detect cracks in the image and extract their properties. Digital image correlation (DIC) has been extensively applied to determine the geometric characteristics of fatigue cracks [10], even for glass-reinforced polymer composites [11]. The measurement of the strain field at the fatigue crack tip based on sub-image stitching and matching with DIC has been developed with CT specimens [12]. Also, Digital image correlation (DIC) and convolutional neural networks have been combined to detect fatigue crack paths [13]. In this review [14] and based on transfer learning-based algorithms for the detection of fatigue crack initiation sites, several recent works of research can be followed.

The development of such methods has gained significant importance in recent years, leading to the implementation of algorithms for crack detection in pavements based on multiscale image fusion [15,16], as seen in [17] with the FOSA algorithm, and is capable of identifying the crack start and end points; [18,19] introduced an automatic crack detection method named Crack-Tree, which involves shadow removal, crack probability map construction, and crack identification based on seed cracks generated by the probability map. Furthermore, crack detection and analysis are crucial not only for structural purposes but also in fields such as heat transfer [20] to detect the fatigue crack growth rate in heat-resistant steel, other fields, such as medicine [21], for bone fracture detection even in the biscuit industry [22].

The choice of analysis method, algorithm, and parameters varies depending on the material under study, as crack growth in concrete differs from that in steel, for instance. For metallic materials with cracks, one commonly used criterion is the “Crack-tip-opening angle or displacement (CTOA/CTOD) fracture criterion”, which is discussed in detail in [23], outlining its advantages, issues, and limitations.

In this article, a new method is presented for the automatic detection and identification of cracks and microcracks in steel specimens. One of the main differences in relation to previous publications is the micrometre’s precision compared to the millimetre one.

This article is organised as follows: Section 2 provides a detailed description of the materials and the developed method. Section 3 presents the most relevant results obtained from applying our method, and offers a comprehensive discussion of the experimental results, and finally, Section4 concludes this article with our findings.

2. Materials and Methods

2.1. Materials

The material we worked with is low-carbon steel EN 10025 S 355 J2G3, which is commonly used in general metal constructions. The test specimens made from this material, where various axial and torsional loads would be applied, were hollow tubular structures. The geometry of these test specimens is depicted in Figure 1.

Figure 1. Geometry of the steel test specimens used in the experiments. Dimensions in mm.

The experiments were conducted using an MTS 809 biaxial testing machine equipped with two control signals: one for the axial channel and another for the torsional channel. The input variables for the machine were the strain (ε) for the axial channel and the angular strain (Θ) for the torsional channel. Data were collected during the test using a biaxial extensometer with a gauge length of 25 mm alongside measurement ranges for axial and angular deformations of ±10% and ±2°, respectively. Additionally, to ensure proper lighting for valid experiments, two Jansjö lamps and an ACE I SCHOOTT light source were employed. For image acquisition, a Pike F-505 ALLIED camera with 5 megapixels was utilised, coupled with the QUESTAR QM100 microscope objective, providing a resolution of 1 µm and a focal distance range of 12–40 cm.

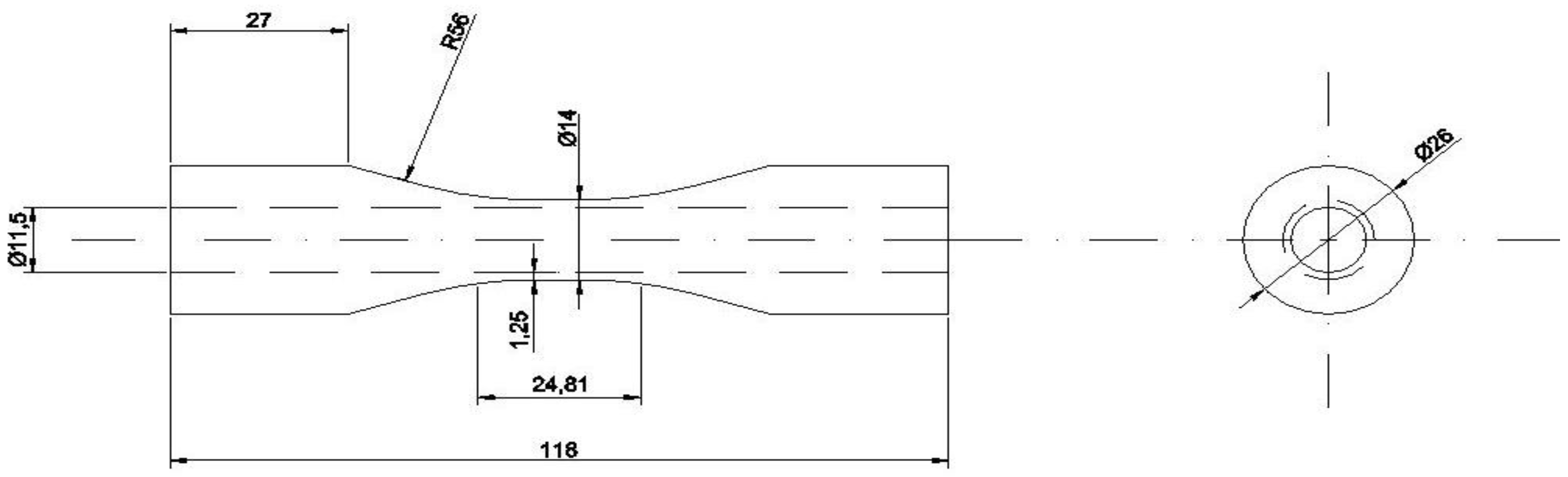
2.2. Methods

2.2.1. Image Acquisition

The images were captured using VIC-Snap software at an acquisition rate of 20 images per second, saving 100 images every 25 cycles. This enabled us to capture and store the entire crack development process from its initiation until it reached its maximum growth, which was the plastic limit at the crack tip. This process can be observed in Figure 2.

Figure 2. Images showing the progression of crack growth.

2.2.2. Images Processing

For image processing, similar to the rest of the program’s implementation, MATLAB software was used. Once the image was loaded into the program, it underwent a binarization process to detect the crack. From this point, we worked with the binarized image. After the initial step of detecting cracks on the right and left, the program located the origin and tip of both cracks, as well as calculated their length and the COD (Crack Opening Displacement) and COA (Crack Opening Angle) parameters of the crack. At the crack tip, these parameters were denoted as CTOD (Crack Tip Opening Displacement) and CTOA (Crack Tip Opening Angle), respectively, with their values corresponding to zero if the deformation at that point was purely elastic [12]. Figure 3 illustrates the flowchart of the implemented algorithm.

Figure 3. Flowchart of the crack detection algorithm.

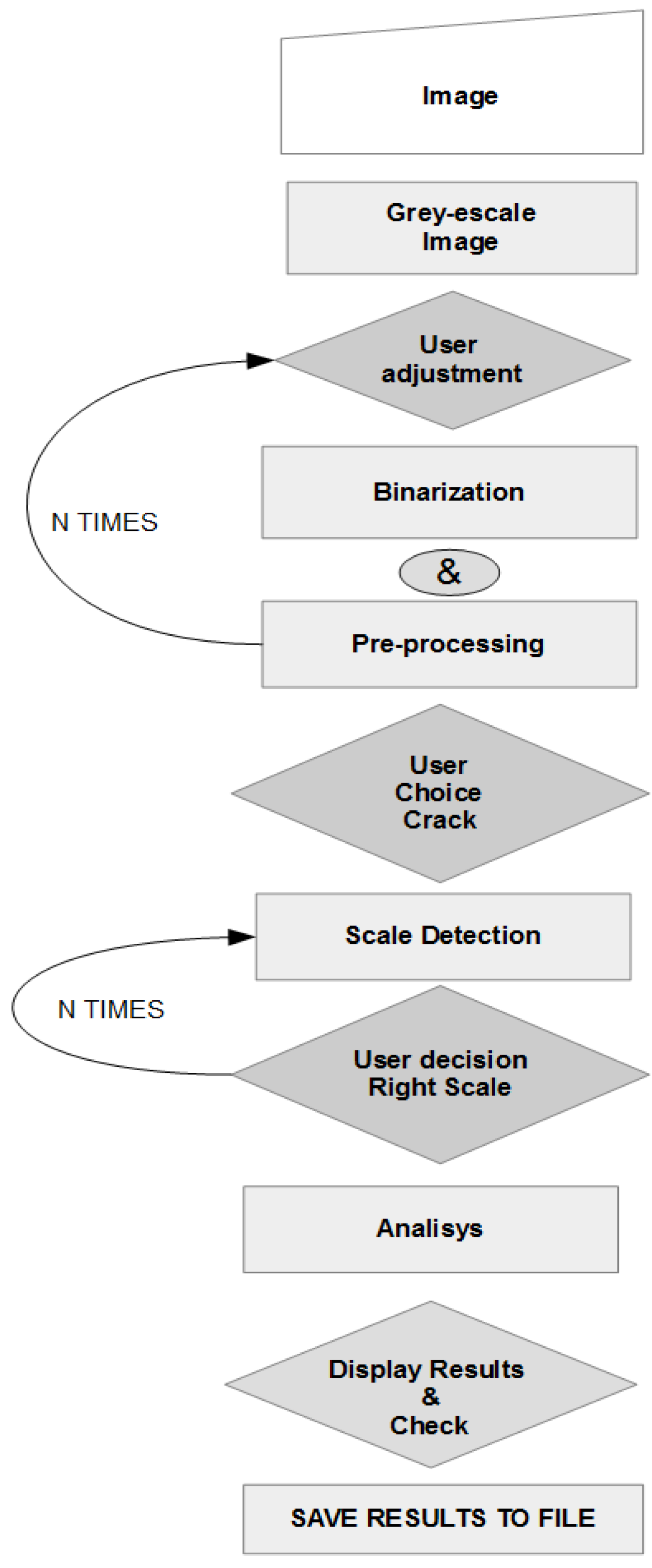
Binarizing and Pre-Processing

The first step was to convert the image to grayscale. Since the experiments were conducted with good lighting, the surface of the specimen was represented by light shades of grey, while the cracks were represented by darker tones. To ensure that this image was optimal in grayscale, the threshold or adjustment level had to be set correctly. In each test, the images had different lighting and, therefore, different tonalities. This is why the threshold could not be the same for all images. Hence, the user needs to participate in this process. The program starts with a base threshold, and the user should adjust it using the keyboard to increase or decrease the contrast until the desired image is achieved. Once this image is obtained, a binarization process can be applied.

Since the threshold depends on the lighting, there are cases where the adjustment level may not be ideal for analysing both cracks. For this reason, it was decided to study the cracks separately. To conduct this, the user can specify the threshold using the method described earlier and define a window using two points that frame the right crack. Then, the same process can be performed for the left crack unless the user decides to use the same threshold for both cracks. In that case, they only need to define the window where the crack is located.

If the grayscale image has a light tone, it appears white in the binarized image, while if it is dark, it appears black. In this way, both the right and left cracks can be detected with a higher degree of accuracy. Figure 4 illustrates the different processes that the image undertakes.

Figure 4. Image processing (a) Original image; (b) Image with magnification thanks to the Binary image; (c) Edge image.

Analysis

This stage of the developed algorithm is where the crack is detected. The user must specify which crack they want to analyse, either the right or left one, and mark a point on it in the image. The closer the marked point is to the crack’s origin, the better the algorithm detects the crack’s contour. With this input parameter, the algorithm can locate the origin, the centreline along the entire crack, and the chosen crack’s tip and calculate its length, including both its linear and actual length. The length obtained is in pixels; therefore, it is necessary to determine the scale factor of the image with respect to reality. The algorithm determines this factor using circle detection. Similarly, it calculates the COD of the selected crack. Figure 5 provides a graphical representation of these parameters, where the length of the crack is denoted as 2c, and Equation (1) shows how COD can be analytically calculated.

Figure 5. Crack Opening Displacement for a central crack in an infinite elastic shell.

The parameter ‘c’ represented in Figure 6 is what the program refers to as the linear length of the crack.

Figure 6. Crack Opening Displacement over the real crack.

Figure 7 presents a comparison between the COD results obtained through the algorithm and the results obtained manually from a fatigue test. It also offers the option to obtain data for the other crack by repeating the same previous process, except for determining the scale, as it remains the same for both cracks.

C O D = {2 u}_{y} = \frac{4 σ}{E} \sqrt{c^{2} - x^{2}}; {C O D}_{m á x} = \frac{4 σ c}{E}

(1)

Figure 7. COD calculated over the real right crack.

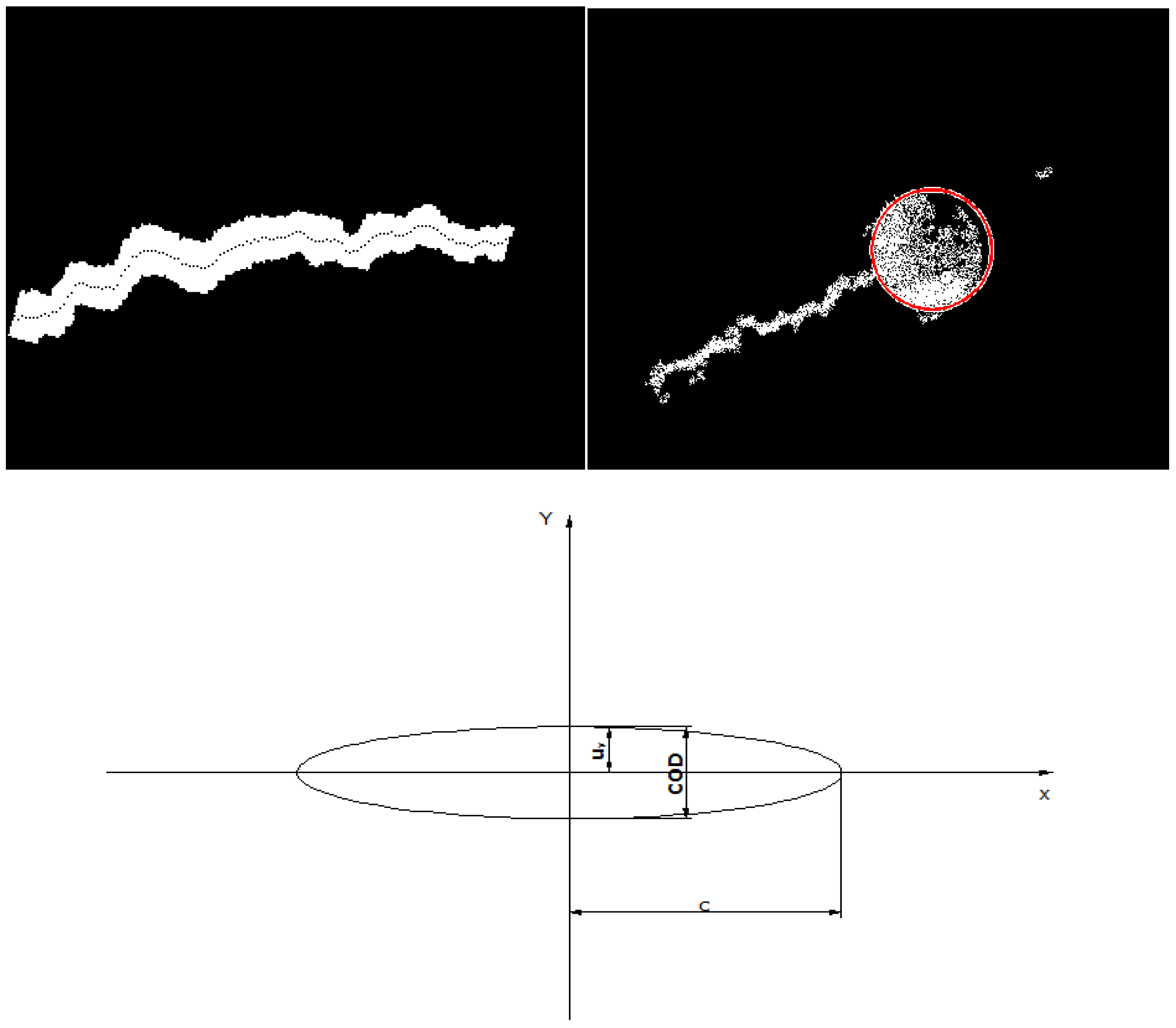
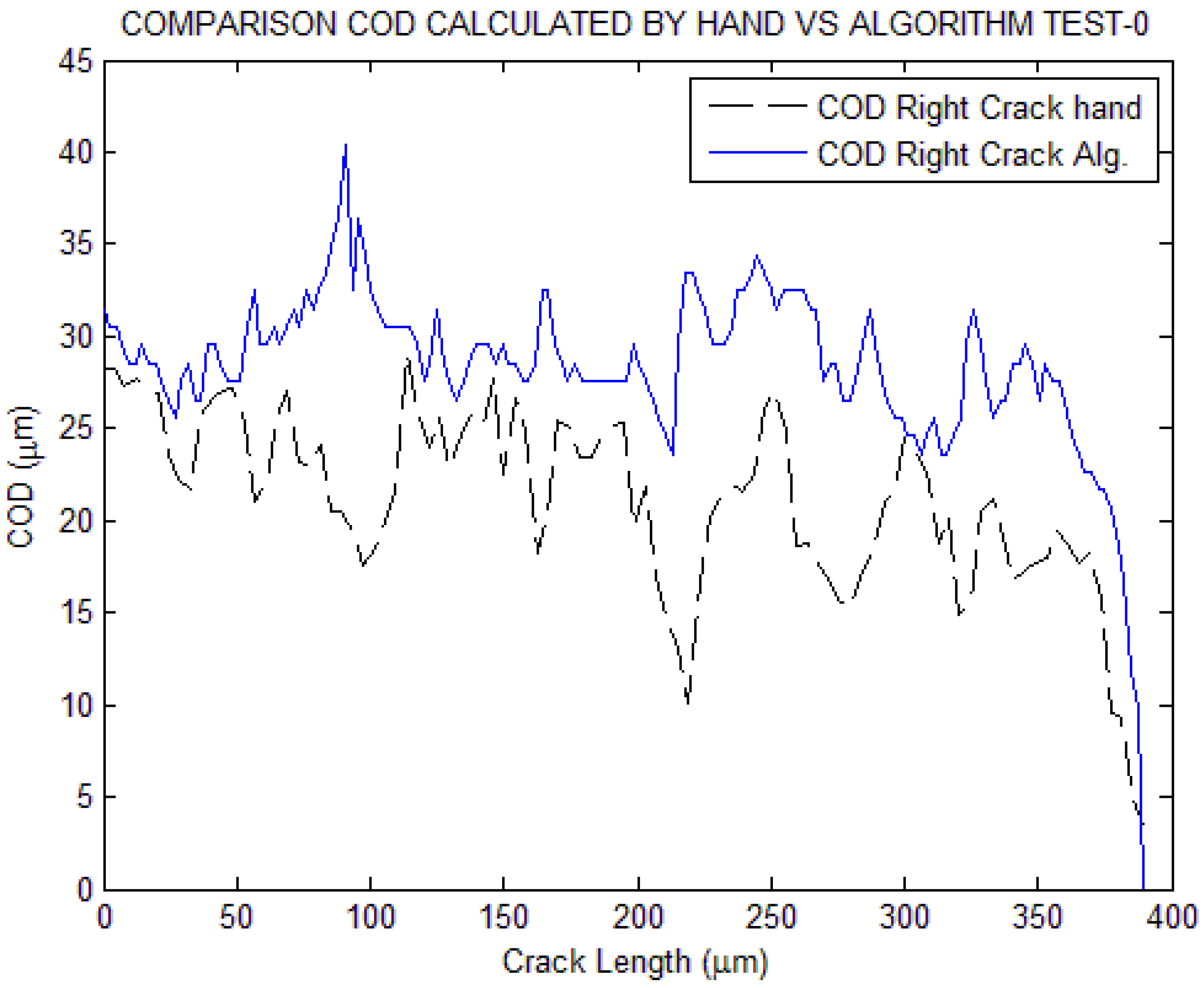
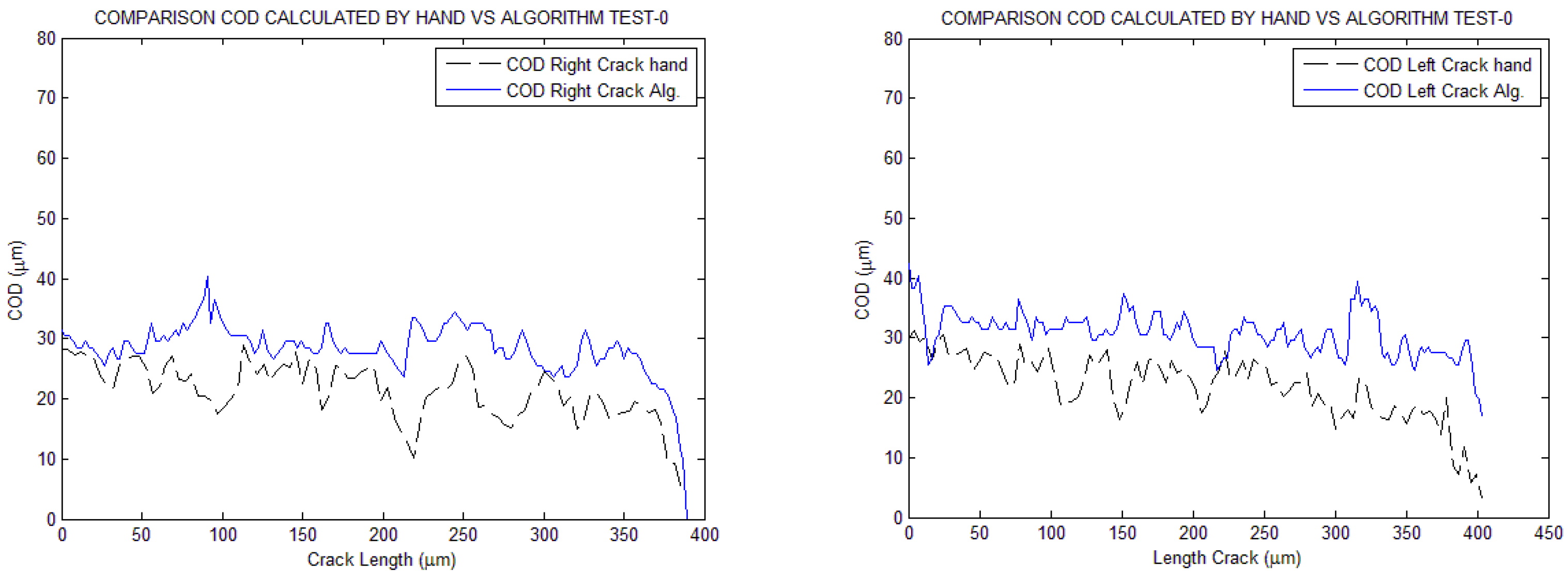
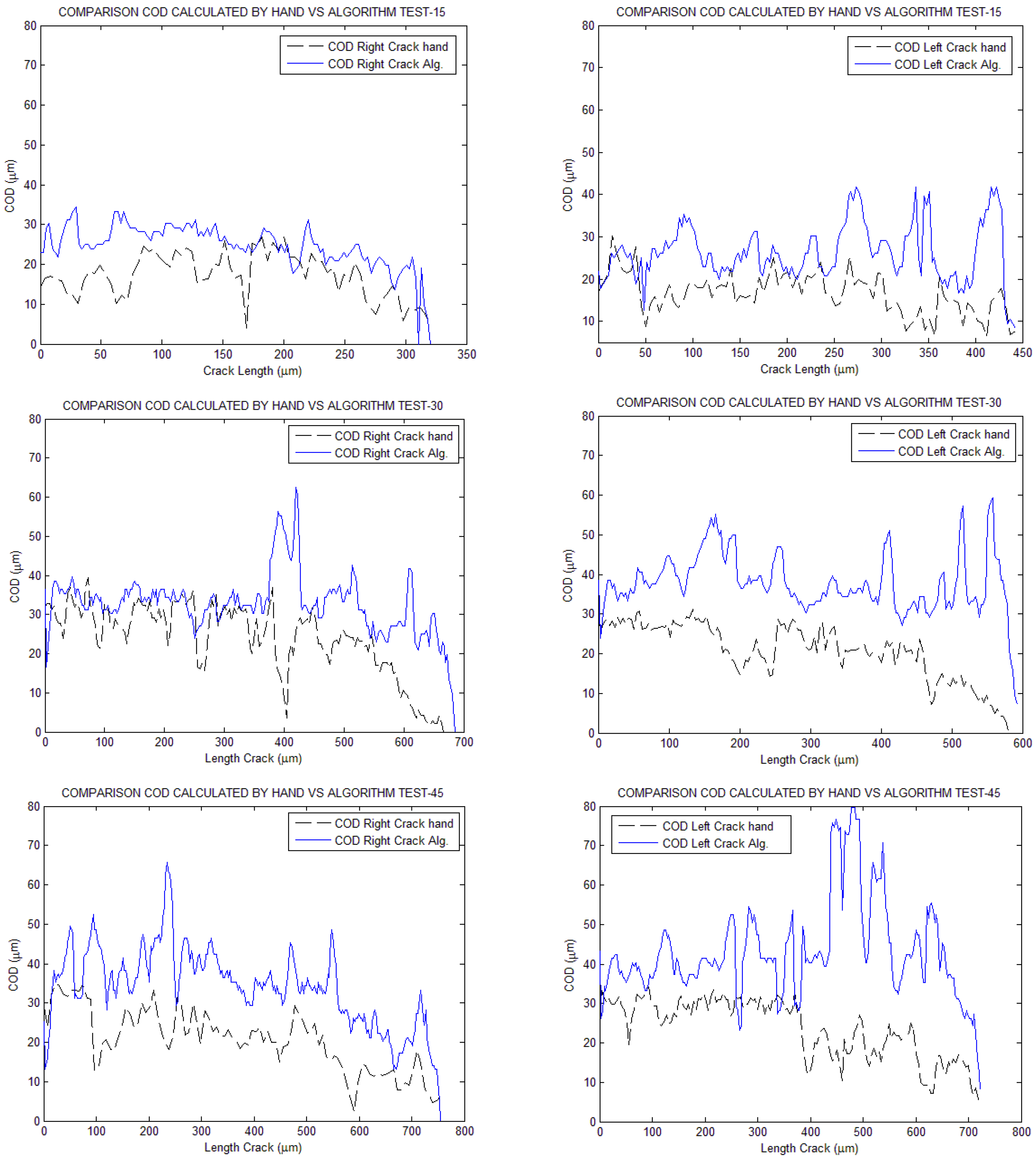
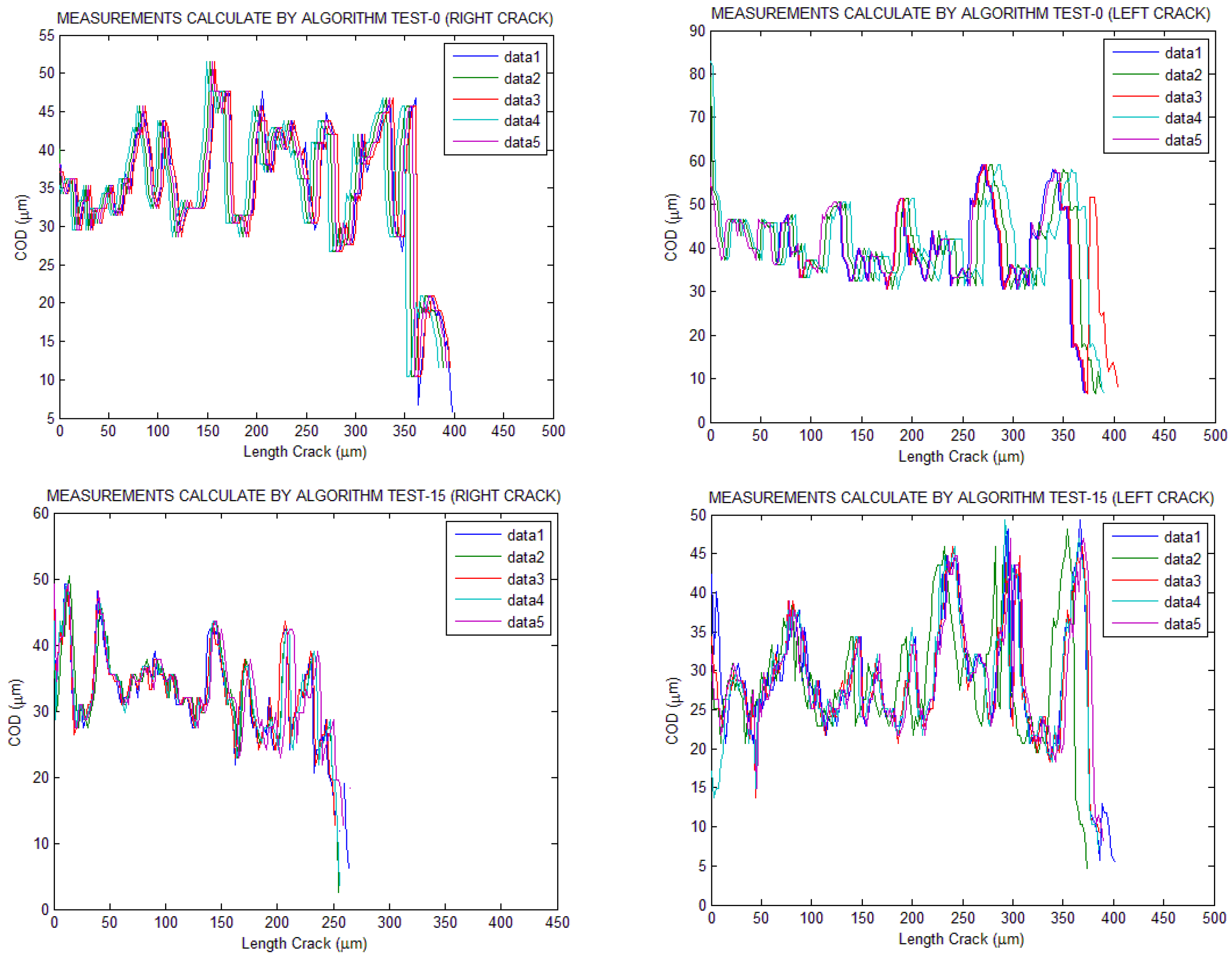
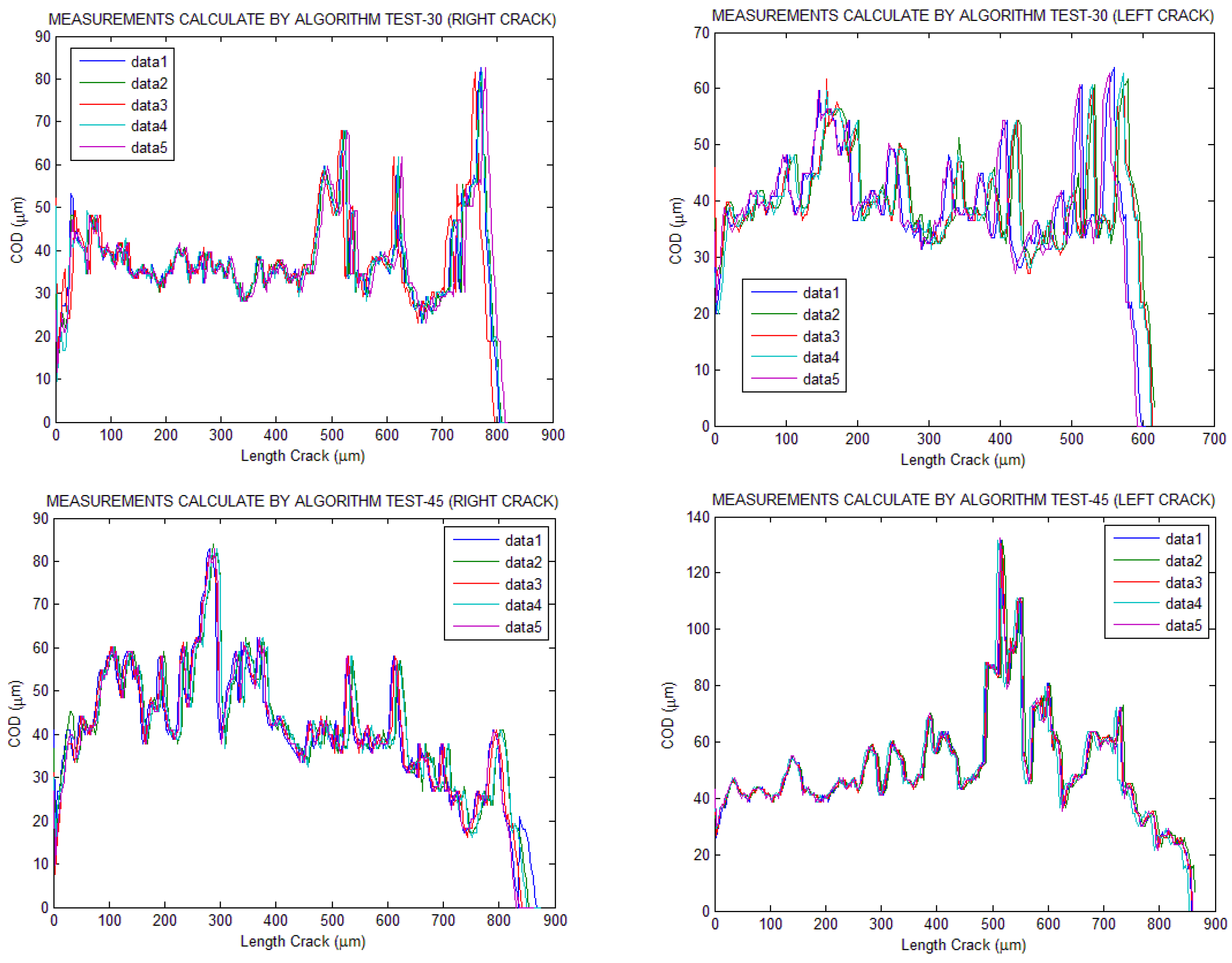
3. Results Discussion

The algorithm’s validity was verified by measuring the lengths of the cracks, both to the right and left. Five different measurements were taken for each of the tests where the load was applied to the specimen at different angles: 0°, 15°, 30°, and 45°.

The lengths of the cracks and the calculated COD values using the algorithm were recorded. Like [1], these data were compared with measurements obtained manually from the same tests. In this way, Figure 8 provides a graphical comparison of both methods.

The graphs in Figure 8 show how the measurements taken by both methods followed a similar linear progression. However, the line of COD values obtained along the crack by this algorithm was generally higher than that obtained manually, except for some exceptions in one or two points of the crack. This could be due to several factors.

Firstly, the measurement of COD must be perpendicular to the direction of the crack at the point where the measurement is taken. Since both methods used the same measurement criterion, considering the predominant angle of the crack, we could rule this out as the reason behind the measurement differences. Additionally, image processing during the algorithm’s preprocessing also contributed to increasing the differences between the measurements obtained by both methods, both in terms of length and COD. This is because the illumination of this image is essential for both the human eye and the computer. Thus, a shadow or stain in the image may be considered part of the crack by the human eye, while the computer considers it noise, and vice versa.

The following tables present the numerical results of the different measurements taken when analysing the tests. In Table 1, the medians of the measurements obtained using the algorithm for both cracks in each of the tests available are presented, as well as the conversion factor calculated by the program. Table 2 shows the manually obtained length for the same cases and the conversion factors obtained. In the case of this algorithm, the conversion factors were found using ellipse detection, while in the manual calculation process, a circle was placed over the distorted image of the hole.

Table 1. Medians of the measurements calculated using the algorithm.

	Right crack		Left crack		Cycle	Factor
	Lineal length (µm)	Real length (µm)	Lineal length (µm)	Real length (µm)	Cycle	Factor
Test-0°	346.3178	453.4994	329.8621	453.38	825	0.9533
Test-15°	258.062	404.2203	317.3452	492.2306	875	1.1463
Test-30°	563.0178	812.8901	437.127	612.7134	1400	1.0461
Test-45°	657.1362	869.9099	562.0036	859.2285	1975	1.0774

Table 2. Measurements calculated by hand.

	Right crack	Left crack	Factor
	Length (µm) (by Hand)	Length (µm) (by Hand)	Factor
Test-0°	425.5912	438.2894	1.1292
Test-15°	408.8691	565.7139	1.1559
Test-30°	795.8696	559.5837	1.1853
Test-45°	594.5870	599.7877	0.9016

Figure 8. Graphical comparison of both methods: hand vs. algorithm.

Table 3 and Table 4 show the variance and standard deviation of the crack lengths obtained for each of the tests. As you can see in these tables, the values obtained are sufficiently small to consider the system quite robust. For example, in the case of the standard deviation, we worked with a deviation range of [0.56–12.56] µm, where it is worth noting that, in most cases, this occurs on the order of 2 µm. When comparing the results obtained using our method with those developed by (1), we determined a significant improvement. The standard deviation of the length obtained with (1)’s method fell in the range of [0.006–0.031] mm, whereas, with ours, it was in the range [0.565–12.569]·10⁻³ mm.

Table 3. Standard deviation of length measurements using the algorithm.

	Standard deviation
	Right crack		Left crack
	Lineal length (µm)	Real length (µm)	Lineal length (µm)	Real length (µm)
Test-0°	2.994009675	2.50368766	2.186817385	7.298339817
Test-15°	2.065488871	5.238372848	2.226731313	8.001147359
Test-30°	1.392092394	9.684152475	2.961942653	6.554759513
Test-45°	3.235506587	5.826145377	0.565502651	3.667433013

Table 4. Variance of length measurements using the algorithm.

	Variance
	Right crack		Left crack
	Lineal length (µm)	Real length (µm)	Lineal length (µm)	Real length (µm)
Test-0°	7.171275146	5.014761518	3.825736222	42.61261127
Test-15°	3.412995422	21.95244007	3.966665874	51.21468724
Test-30°	1.550336986	75.02624732	7.018483422	34.37189782
Test-45°	8.374802298	27.15517597	0.255834598	10.76005192

In Table 5, the calculated mean values for each type of test conducted are shown, and Table 6 contains the mean standard deviations. As can be seen, the deviation did not exceed 4 µm.

Table 5. Mean of COD measurements using the algorithm.

	Mean
	Right crack	Left crack
	COD	COD
Test-0°	30.4514	34.1000
Test-15°	20.8312	22.8107
Test-30°	37.4639	39.5683
Test-45°	40.5614	50.7675

Table 6. Standard deviation of COD measurements using the algorithm.

	Standard deviation
	Right crack	Left crack
	COD (µm)	COD (µm)
Test-0°	2.3069	2.7625
Test-15°	1.1773	2.0918
Test-30°	2.6022	3.2553
Test-45°	2.3468	1.2570

Figure 9 depicts the graphs of the COD values obtained by the algorithm for the different tests and their corresponding studies. Once these graphs were examined, it became evident that the algorithm was not only robust in calculating the length but also in calculating the COD and, consequently, the crack angles.

Figure 9. Different COD measurements calculated in each test using the algorithm.

Finally, to demonstrate the validity of our method, as undertaken in [8], the relationship between the values obtained by both methods, the algorithm and manual, was established using the Relative Difference (RD), as defined by the following Equation (2):

R D = \frac{|w_{n e w} \times w_{c o n}|}{w_{c o n}}

(2)

where w_new is the measured variable (length, angle, COD) calculated using the proposed algorithm, and w_con is the measurement obtained using the optical or manual method.

Thus, in Table 7 and Table 8, a comparison of the values obtained using both methods for the lengths of the right and left cracks, respectively, is shown, along with the resulting RD. We considered comparing the COD obtained by both methods and their corresponding RD coefficient, but due to the fact that the manually obtained values were not the same quantity and were not obtained at the same points as those obtained by the algorithm, these results would not be valid.

Table 7. Comparison between measurements performed by hand and the algorithm for the right crack.

	Right crack
	Length (µm) (Hand)	Length (µm) ALG.	RD (%)
Test-0°	425.5912	453.4994	6.153973167
Test-15°	408.8691	404.2203	1.150067136
Test-30°	795.8696	812.8901	2.093828079
Test-45°	594.5870	869.9099	31.64958808

The user’s involvement in preprocessing was conducted to enhance the analysis, as it was considered necessary to obtain the correct binarization threshold for each crack, which could not be achieved automatically. Reference [9] supports user interaction to achieve better analysis when using their algorithm.

Table 8. Comparison between measurements performed by hand and the algorithm for the left crack.

	Left crack
	Length (µm) (Hand)	Length (µm) ALG.	RD (%)
Test-0°	438.2894	453.38	3.443064456
Test-15°	565.7139	492.2306	12.98948066
Test-30°	559.5837	612.7134	9.494509636
Test-45°	599.7877	859.2285	43.25543855

4. Conclusions

This article presents a method for detecting and analysing microcracks in steel specimens using grayscale image analysis. Compared to the methods used so far, we believe it has the following advantages:

It calculates the crack’s length along its path, or neutral line, instead of calculating it as a linear distance from the origin to the tip, as in traditional methods. This provides a better approximation of its actual length. It also calculates the linear distance as an interesting data point.
It calculates both the total slope of the crack, from origin to tip, and the point-to-point slope along the centreline. This allows for a better approximation of COD at each point along the crack by applying it perpendicularly.
It allows for separate analysis of cracks, treating them as different images. This enables the application of different preprocessing and binarization treatments to each one for accurate analysis. This is primarily due to differences in illumination in different parts of the image.

The resolution of the images and variations in lighting, causing shadows, can lead to measurement errors in both manual and algorithm-developed analysis methods. Thus, it is common to observe discrepancies between the measurements made by these methods.

Author Contributions

Conceptualization A.G.-G and P.L.-C. Methodology A.G.-G and A.S.C., Software, C.C.-E and A.S.C. Data curation, C.C.-E and A.S.C. Writing—original draft, C.C.-E Supervision, A.G.-G and P.L.-C. All authors have read and agreed to the published version of the manuscript.

Funding

Not applicable.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Raw data of this article are available upon request from the authors.

Conflicts of Interest

The authors declare no conflict of interest.

References

Lyngbye, J.; Brincker, R. Aalborg Universitet Crack Detection by Digital Image Processing; Department of Building Technology and Structural Engineering, Aalborg University: Aalborg, Denmark, 1990. [Google Scholar]
Savary, G.; Cans, M.; Luiz Bastian, F. Characterization of optical, electronic and topographic images in fatigue research. Image Vis. Comput. 1995, 13, 609–622. [Google Scholar] [CrossRef]
Lauschmann, H.; Nedbal, I. Applications of Image Analysis in Fractography of Fatigue Failures. Mater. Sci. 2013. [Google Scholar]
Krause, M.; Hausherr, J.M.; Krenkel, W. (Micro)-Crack detection using local Radon transform. Mater. Sci. Eng. A 2010, 527, 7126–7131. [Google Scholar] [CrossRef]
Rannou, J.; Limodin, N.; Réthoré, J.; Gravouil, A.; Ludwig, W.; Baïetto-Dubourg, M.C.; Buffiere, J.-Y.; Combescure, A.; Hild, F.; Roux, S. Three dimensional experimental and numerical multiscale analysis of a fatigue crack. Comput. Methods Appl. Mech. Eng. 2010, 199, 1307–1325. [Google Scholar] [CrossRef]
John, M.; Prakash, R.V. Quantification of Fatigue Damage in Carbon Fiber Composite Laminates through Image Processing. Materials Today: Proceedings. Volume 5. 2018. Available online: www.sciencedirect.comwww.materialstoday.com/proceedings2214-7853 (accessed on).
Zhu, Z.; German, S.; Brilakis, I. Visual retrieval of concrete crack properties for automated post-earthquake structural safety evaluation. Autom. Constr. 2011, 20, 874–883. [Google Scholar] [CrossRef]
Lee, B.Y.; Kim, Y.Y.; Yi, S.T.; Kim, J.K. Automated image processing technique for detecting and analysing concrete surface cracks. Struct. Infrastruct. Eng. 2013, 9, 567–577. [Google Scholar] [CrossRef]
Arena, A.; Delle Piane, C.; Sarout, J. A new computational approach to cracks quantification from 2D image analysis: Application to micro-cracks description in rocks. Comput. Geosci. 2014, 66, 106–120. [Google Scholar] [CrossRef]
Bazaron, S.A.; Damdinova, T.T.; Bochektueva, E.B. Determination of the geometric characteristics of fatigue cracks by digital image processing method. In IOP Conference Series: Materials Science and Engineering; IOP Publishing Ltd.: Bristol, UK, 2019. [Google Scholar]
Gonabadi, H.; Oila, A.; Yadav, A.; Bull, S. Fatigue damage analysis of GFRP composites using digital image correlation. J. Ocean. Eng. Mar. Energy. 2021, 7, 25–40. [Google Scholar] [CrossRef]
Lin, Z.; Shang, H.; Gao, H.; Huang, X. In Situ Measurement of the Strain Field at the Fatigue Crack Tip Based on Sub-Image Stitching and Matching DIC. Materials 2022, 15, 5150. [Google Scholar] [CrossRef] [PubMed]
Strohmann, T.; Starostin-Penner, D.; Breitbarth, E.; Requena, G. Automatic detection of fatigue crack paths using digital image correlation and convolutional neural networks. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 1336–1348. [Google Scholar] [CrossRef]
Wang, S.Y.; Guo, T. Transfer Learning-Based Algorithms for the Detection of Fatigue Crack Initiation Sites: A Comparative Study. Front. Mater. 2021, 8, 756798. [Google Scholar] [CrossRef]
Li, C.; Wen, Y.; Shi, Q.; Yang, F.; Ma, H.; Tian, X. A Pavement Crack Detection Method Based on Multiscale Attention and HFS. Comput. Intell. Neurosci. 2022, 2022, 1822585. [Google Scholar] [CrossRef] [PubMed]
Li, H.; Song, D.; Liu, Y.; Li, B. Automatic Pavement Crack Detection by Multi-Scale Image Fusion. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2025–2036. [Google Scholar] [CrossRef]
Li, Q.; Zou, Q.; Zhang, D.; Mao, Q. FoSA: F* Seed-growing Approach for crack-line detection from pavement images. Image Vis. Comput. 2011, 29, 861–872. [Google Scholar] [CrossRef]
Zou, Q.; Cao, Y.; Li, Q.; Mao, Q.; Wang, S. CrackTree: Automatic crack detection from pavement images. Pattern Recognit. Lett. 2012, 33, 227–238. [Google Scholar] [CrossRef]
Matarneh, S.; Elghaish, F.; Al-Ghraibah, A.; Abdellatef, E.; Edwards, D.J. An automatic image processing based on Hough transform algorithm for pavement crack detection and classification. Smart Sustain. Built Environ. 2023. ahead-of-print. [Google Scholar] [CrossRef]
Maruschak, P.; Vorobel, R.; Student, O.; Ivasenko, I.; Krechkovska, H.; Berehulyak, O.; Mandziy, T.; Svirska, L.; Prentkovskis, O. Estimation of Fatigue Crack Growth Rate in Heat-Resistant Steel by Processing of Digital Images of Fracture Surfaces. Metals 2021, 11, 1776. [Google Scholar] [CrossRef]
Linda, C.H.; Jiji, G.W. Crack detection in X-ray images using fuzzy index measure. Appl. Soft Comput. 2011, 11, 3571–3579. [Google Scholar] [CrossRef]
Nashat, S.; Abdullah, A.; Abdullah, M.Z. Machine vision for crack inspection of biscuits featuring pyramid detection scheme. J. Food Eng. 2014, 120, 233–247. [Google Scholar] [CrossRef]
Newman, J.C.; James, M.A.; Zerbst, U. A review of the CTOA/CTOD fracture criterion. Eng. Fract. Mech. 2003, 70, 371–385. Available online: www.elsevier.com/locate/engfracmech (accessed on). [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Image Processing for the Detection and Analysis of Microcracks Caused by Fatigue in Steel

Abstract

1. Introduction

2. Materials and Methods

2.1. Materials

2.2. Methods

2.2.1. Image Acquisition

2.2.2. Images Processing

Binarizing and Pre-Processing

Analysis

3. Results Discussion

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe