Prerpints.org logo
Preprint
Article

An Integrated Photoelasticity Based Approach for Reconstruction of Stress Profiles and Optical Anisotropy of GRIN Lenses

Altmetrics

Downloads

88

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 October 2023

Posted:

10 October 2023

You are already at the latest version

Alerts
Abstract
The paper shows that it is possible to obtain reliable information on the dependence of radial distribution of longitudinal birefringence in glass cylindrical elements with radial distribution of refractive index (GRIN lenses) on the basis of transverse polarization tomography data of residual stresses. This does not require complicated procedures of sample preparation, as is necessary in the case of longitudinal translucency measurements. The approach developed was verified in the experiments with a set of different GRIN lenses formed with ion exchange technique, and the closeness of the data obtained from transversal and conventional longitudinal transmission measurements was demonstrated.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Gradient-index rods with radial distribution of refractive index n(r) (GRIN lenses) are widely used in image translators in copiers and medical devices, as collimating and focusing lenses in fiber-optic passive and active connectors. In addition, GRIN lenses in combination with, for example, diffraction gratings are used in light flow splitters, optical switches, multiplexers, demultiplexers, etc. [1,2,3]. The most common technology for obtaining a given radial refractive index (RI) distribution in GRIN lenses is high-temperature ion exchange (IE) of alkaline cations in the glass-salt melt system. IE synthesis of such GRINs is carried out at glass viscosities of 108–1010 Pa·s with possible use of isothermal annealing outside the melt at various temperatures [4,5,6]. Due to diffusion, a gradient of the refractive index is formed across the cross section of the GRIN lens, corresponding to the substitution of alkali ions (e.g., Li (glass) ⇔ Na (salt melt)). When cooling GRIN lenses from the ion exchange temperature corresponding to the viscoelastic state of the material, residual stresses (RS) σij(r) arise due to radial gradients of the temperature coefficient of linear expansion and glass transition temperature Tg. Because of the kinetic nature of the glass transition, the distribution of RS significantly depends on the temperature and duration of the sample cooling. RS hinder the creation of a given RI distribution in gradient rods, and can lead to their bending due to the loss of stability and, ultimately, to destruction.
One of the most important manifestations of the residual stress in the GRIN lenses is radial birefringence, a consequence of elastic-optical effects. Radial birefringence causes polarization aberrations that, for example, degrade image quality in endoscopes. In fiber-optic sensors of stress, strain or pressure, which use the modulation of optical signal directly by GRIN lenses, RS change the polarization of light, thereby limiting the sensitivity of the sensor to deformation [7,8,9]. The negative influence of RS can also be noted in GRIN lenses of large diameter used in macro-optics, and in axisymmetric acoustic lenses with a gradient radial distribution of elastic properties [10,11,12]. It has recently been shown [13,14,15] that the combination of polarization characteristics of GRIN lenses (i.e., radial birefringence) and their focusing properties turned out to be very effective for the generation of optical vortex beams [16,17,18]. In this respect, it is noted [13,14,15] that it is relevant to increase low level of optical anisotropy of GRIN lenses, that is their birefringence. Besides, the use of GRIN lenses with high birefringence has also enabled significant progress in polarization imaging of biological tissue structure, which is potentially a powerful tool for clinical diagnostics [19,20].
Thus, the development of gradient optical elements with both minimal and significant birefringence is of essential interest. In this regard, the issues of characterization RS in GRIN lenses, determining the optimal modes of ion exchange and heat treatment of the glass rods to obtain the required characteristics are relevant.
The method of integrated photoelasticity [21,22] is widely used to study the RS distribution in transparent gradient-free objects. Inverse (A) and direct (B) problems can be considered: A - reconstruction of RS distributions on the basis of measurements of the parameters of polarized light that passed through the object under study; B - determination of the birefringence distribution from known RS (e.g., obtained from the results of A, or by modeling).
The mathematical apparatus of the integrated photoelasticity method is well developed only for rectilinear propagation of probing beams. However, in GRIN lenses, rays deviate significantly from straight-line propagation due to the gradient of refractive index (in high-aperture GRIN lenses, refractive index change can reach up to Δn ∼ 0.14).
This raises the problem of generalizing method of the integrated photoelasticity to the case of cylindrical rods with radial RI distribution, that should allow to adjust the parameters of technological processes to ensure given distributions of RS and optical anisotropy.
Such a generalization of the relations in the inverse and direct problems of integral photoelasticity for the cases of transverse, longitudinal, and sagittal translucency GRIN lenses, taking into account the curvature of the trajectories of the rays propagating in them, was made in [23,24]. The analysis for the first two cases was also published in [25].
Both in these works and below, it is also assumed that in the considered weakly anisotropic gradient objects, the waves retain the transverse structure (quasi-isotropic approximation of geometrical optics for inhomogeneous media [26]) and the ray trajectories with mutually perpendicular polarization can be considered geometrically identical and corresponding to the initial axisymmetric RI distribution.
In this paper, new relations are obtained for:
1) reconstruction of the radial rather than the axial component of the RS from the data of transverse translucencе of GRIN lenses (inverse problem), which excludes from differentiation of experimental dependences under the sign of the integral increasing the errors (as it takes place at reconstruction of the axial component of the RS);
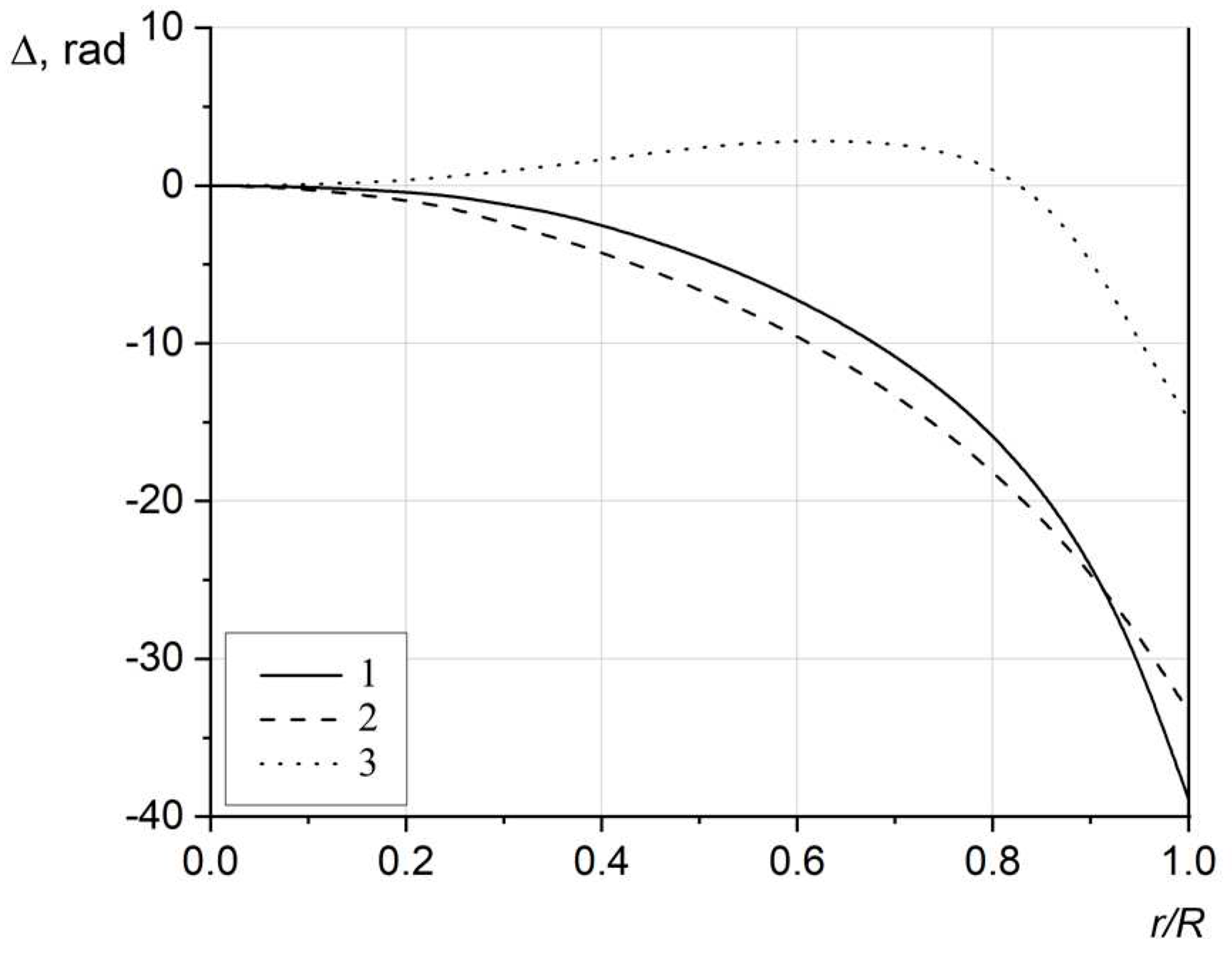
2) longitudinal birefringence (integral phase difference) calculations – direct problem from RS reconstruction data, based on the results of 1) for GRIN lens segments.
Using computational algorithms developed on the basis of relations 1) and 2)we obtained RS distributions for a number of GRIN lenses (inverse problem of transversal translucency). Using these data as input for calculations (the direct problem in longitudinal incidence), the radial distributions of integral phase difference (birefringence) are determined for the case of meridional rays propagation in these GRIN lenses.
Examples of reconstruction of radial RS distributions and optical anisotropy profiles for glass GRIN lens produced by high-temperature ion exchange are presented.

2. Methods

Entering a stressed medium, a polarized ray splits into two rays having mutually perpendicular polarizations. For these rays, due to the stress-induced optical anisotropy, the refractive index distributions are different, which causes phase difference Δ after passing the rays through the medium. The relations connecting integral phase difference Δ (IPD) and the differences of quasi-principal RI values (nn, nl) or the differences of quasi-principal components (σn, σl) of the stress tensor in the plane perpendicular to the light ray (Wertheim's integral law [27]) have the form:
Δ = 2 π λ ∫ ( l ) ( n n − n l ) d l = C 0 ∫ ( l ) ( σ n − σ l ) d l .
where C0 is the optical stress coefficient, λ – is the wavelength. The integrals are taken over the ray path l.
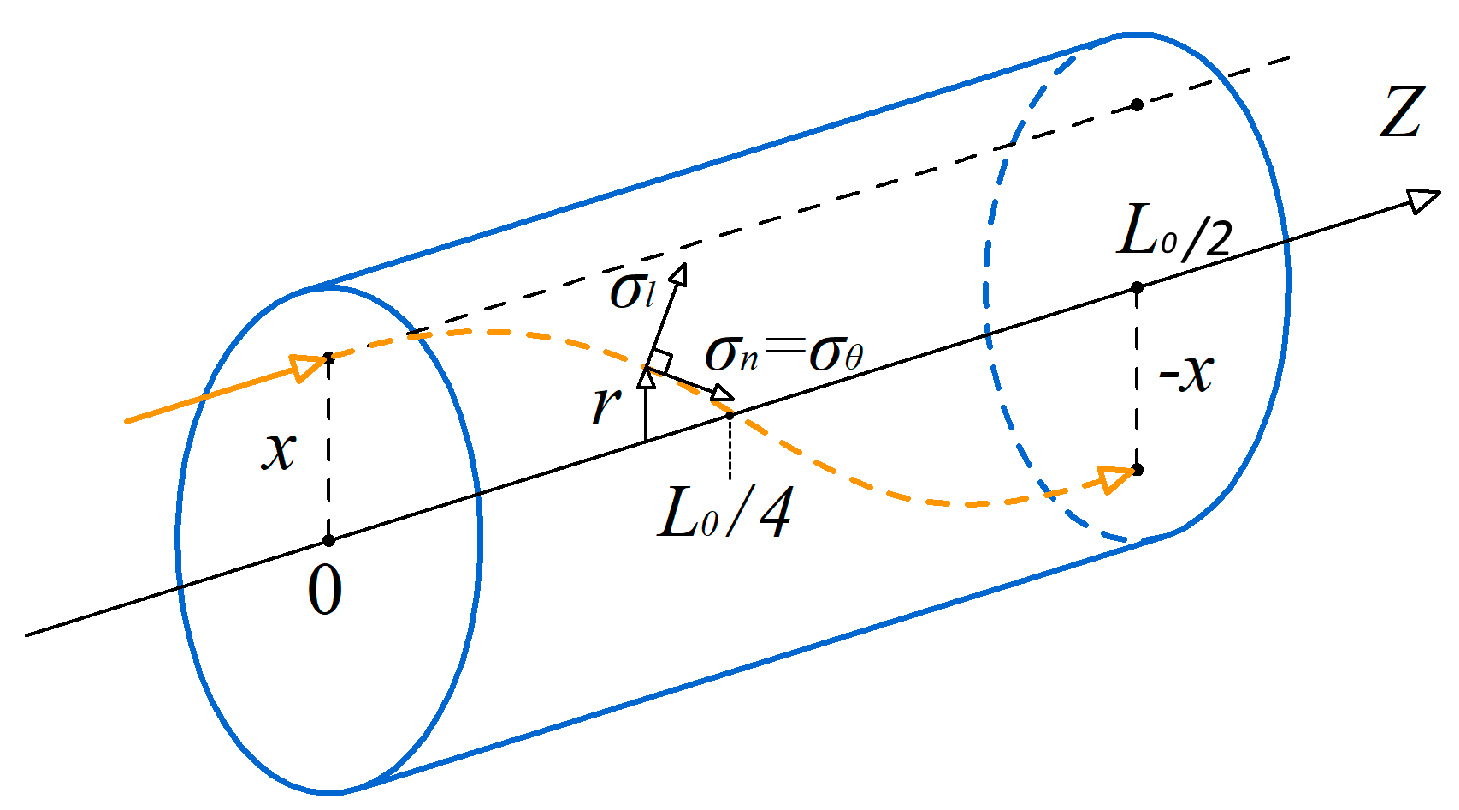
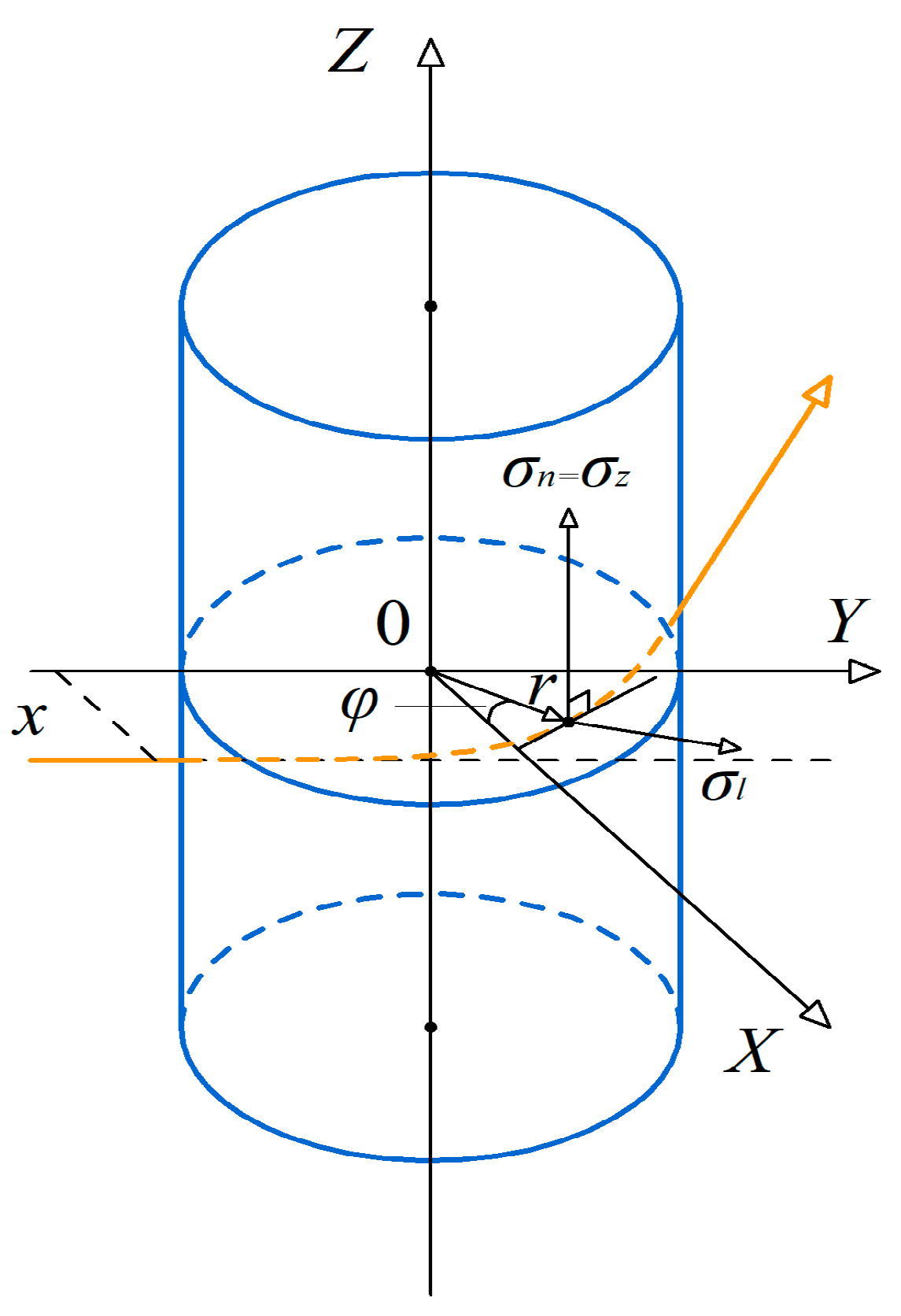
Since a long rod, L > 2R (L and R are the length and radius of the cylinder, respectively), with radial RI distribution usually has no stress gradient along its axis (z coordinate), shear stresses σzr(r) in cylindrical coordinates are absent, and the stress state is characterized by 3 principal stress components: axial σzz(r), radial σrr(r), and tangential σθθ (r), depending only on the radial coordinate r [28,29]). Reconstructing the local distribution of principal stress components from translucency and Δ(x) measurements for different distances x from the optical axis is an incorrected (i.e., unstable with respect to input data errors) inverse problem of integral photoelasticity. The geometry of the longitudinal and transversal translucency is shown in Figure 1 and Figure 2.
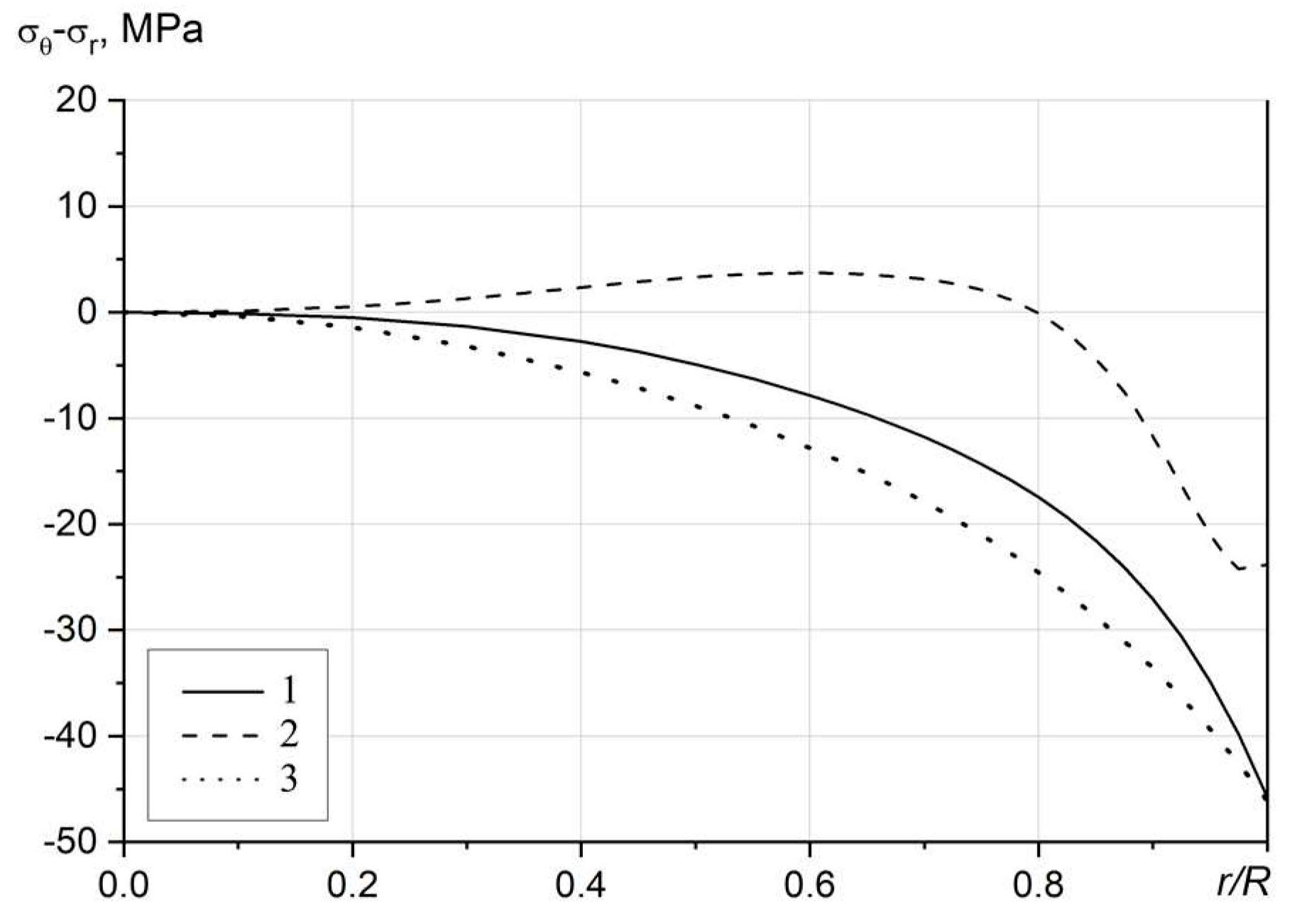
As shown in [23,24,25], in the case of weakly and moderately gradient axisymmetric objects, polarization of a probing beam is influenced by axial stresses σz(r) in transverse translucence, and by the difference of tangential and radial stresses Δσ(r) = Δσθr(r) = σθ(r) - σr(r) in longitudinal translucence. RS difference distributions Δσθr(r) can be used to solve the direct problem of longitudinal translucence, that is, finding the radial distribution of the IPD and birefringence for GRIN segments of various lengths.
The derivation of a novel algorithm for solving the direct problem for longitudinal ray propagation in GRIN lenses and relations for the reconstruction of RS in their transverse translucency are presented in Section 2.1 and Section 2.2.

2.1. An Algorithm for Calculations of Longitudinal IPD (Direct Problem)

At the preliminary stage of development of optimal modes of synthesis of GRIN lenses, it is usually limited to the search for conditions under which the parabolic (2) or paraxial refractive index profile is realized. To analyze IPD for longitudinal ray propagation in a GRIN lens (within the framework of a direct problem), it is more convenient to use the expression for the hypersecant refractive index profile (3).
n 2 r = n 0 2 1 − g 2 r 2 ,
n 2 r = n 0 2 sec h 2 g r ,
where n0 = n(0) – RI on the axis of the rod, g is power constant. When the input face of the GRIN lens at z = 0 is perpendicular to its axis and the rays fall at the input face parallel to the axis, the analytical expression of the trajectory equation at hypersecant RI distribution (3) is [30]:
r z = 1 g arcsh sh g r 0 cos ⁡ g z
and at parabolic RI (2):
r z = r 0 cos ⁡ g 1 − g 2 r 0 2 .
That is, the length of the periodicity L0 depends on the   g R constant:
L 0 = 2 π g 1 − g 2 r 0 2 .
Calculations of the relative differences in periodicity lengths depending on the ray entrance position x into the GRIN lens for gR ≤ 0.3 show that the difference in ray propagation in GRIN lenses with parabolic and hypersecant index profiles is insignificant.
In the case of longitudinal translucency GRIN lens (0.25 pitch), the relation (1) for the IPD ΔL can be written as:
Δ L = Δ 0 L + Δ 1 L ,   Δ 0 L = ∫ 0 L C 0 σ θ − σ r n b d z ,   Δ 1 L = ∫ 0 L C 0 σ r − σ z 1 − b 2 n 2 n b d z .
For the direct problem, we also take into account the contribution to the IPD from the component Δ 1 L , which was neglected when considering the inverse problem for longitudinal translucency (i.e., the reconstruction of the RS from the corresponding experiments) [23,24,25].
As can be seen from expressions (7), it is required to perform integration along the GRIN lens axis, for which it is necessary to transform the input distributions (σ(r), n(r), C0 (r)) into functions of z coordinate. In the case of hypersecant distribution of RI, this problem is solved easily, since the explicit form of the trajectory equation r(z) (4) is known.
Let us denote the integrand in (7) as:
f 0 r = C 0 σ θ − σ r n r n x   ,     f 1 r = C 0 σ r − σ z n r n x − n x n r   .
If the initial stress values are given as an array of values for some points 0 = r1 < r2 < … < rn = R, it is quite simple to express the function f0 from the coordinate z, namely at the points ri, where i = 1, 2, ..., n, the values f0j (j = n – i + 1) are calculated and their corresponding values z are found:
z j = 1 g arc cos ⁡ sh ( g r i ) sh ( g x )   .
The integrand expressions in (7) are then approximated by splines with knots 0 = z1 < z2 < … < zn = L0/4, and the spline function can be integrated analytically:
∫ 0 L s z d z = ∑ i = 1 m − 1 I z i ; z i + 1 + I z m , L , I z i , z i + 1 = ∫ z i z i + 1 s z d z ,   f ( z ) ≈ s ( z ) = a i + b i ( z − z i ) + c i ( z − z i ) 2 + d i ( z − z i ) 3 .
In this case 0 < L < L0/4, zm < L < zm+1.
The program based on this algorithm allows one to calculate Δ0 and Δ1 for lengths L ≤ L0/4. For other lengths, one should take advantage of the fact that the ray propagates along a periodic trajectory and calculate Δ as follows:
Δ 0,1 = k ∫ 0 L 0 4 f 0,1 z d z + ∫ 0 L − k L 0 4 f 0,1 z d z , k − is   even ,   Δ 0,1 = ( k + 1 ) ∫ 0 L 0 / 4 f 0,1 ( z ) d z − ∫ 0 L − k L 0 4 f 0,1 ( z ) d z , k − is   odd .  
Here k represents the number of quarters of a period on the trajectory.

2.2. Reconstruction of the Residual Stresses in Transversal Translucency (Inverse Problem)

When determining the stresses with this method, it is common to perform translucency of separate cross-sections of the object. As shown in [23,24], the integral equation for the phase difference (1) is reduced to the Abel integral equation for the case of transverse translucency of GRIN lenses with g R ≤ 0.3:
Δ T ( a ) = 2 ∫ a u R C 0 σ z d r d u n d u u 2 − a 2 ,
which gives:
σ z ( r ) = − ( π C 0 ) − 1 d u d r ∫ u ( r ) u R d Δ T d a d a a 2 − u 2 ,
where ΔT(x) is the IPD of 2 plane-polarized oscillations in transverse translucence of the GRIN lens, a = xnR, u = rn(r), nR ≡ n (R) is RI on the surface of the lens.
The stress components σθ(r), σr(r) can be found by using the so-called "sum rule" (14) [31]. which is valid in the absence of an axial OH gradient, and the equilibrium condition for the cylinder (15) [28]:
σ z r = σ θ r + σ r r ,
σ θ = d ( r σ r ) / d r .
Expression (13) includes a singular convergent integral; dΔT/da = 0 for a = 0 due to symmetry; dΔT/da = ∞ for a = uR (as a result, ΔT(x) cannot be measured precisely when x→ R). Taking these into account, a regularized algorithm based on the spline approximation of Δ(x) and optimization of boundary conditions for ensuring the stability of the solution near the boundaries of the interval (0, R) was developed in [23,24,25].
It is important to note that in the integral in (13) contains the derivative of the measured function, which leads to the enhancement of errors present in the experimental data.
In [32], it was shown how to avoid this in the case of a uniform (RI constant) glass cylinder with quenching stresses, which is used, in particular, in [33] for the reconstruction of RS in optical fiber preforms.
Let us find an analogous expression for the case of a cylindrical rod with RI gradient. From the relation (14), taking into account (15), we obtain:
σ z ( r ) = 1 r d d r r 2 σ r
Substituting (16) into (12) and assuming that C0(r)n(r) ~ C0nR, we obtain the Abel equation, the inversion of which gives:
σ r ( r ) = − 1 π C 0 n R 1 r 2 ∫ u ( r ) u R a Δ T ( a ) d a a 2 − u 2 .
The components σθ(r), σz(r) can be found by using (14) and (15).
In the limiting case of no RI gradient, (17) converges to the relation, obtained in [32].
Thus, we eliminate the differentiation of the experimental function in the case of RS reconstruction for a cylinder with a RI gradient. Further, we use the algorithm based on relation (17) to reconstruct the RS in GRIN lenses from transverse translucency data.

2.3. Measurements

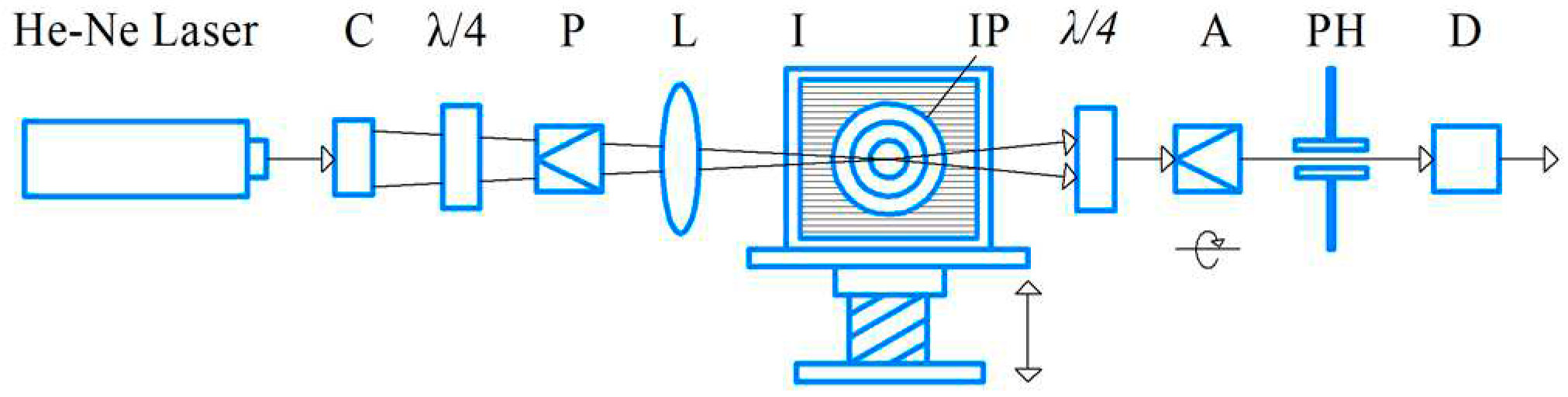
A polarization-optical setup with a He-Ne laser and a Senarmon compensator were used for the measurements (Figure 3).
The rotation angles of the polarizer, the λ/4 plate, and the analyzer were measured with an accuracy better than ± 1°, i.e., the difference of the path between the radially and tangentially polarized beams could be measured with an accuracy of ± 3,5 10-6 mm (λ= 0,633 µm). With a specimen length of 20 mm, this corresponds to a measurement accuracy of
δ Δ n r θ = ±   2 · 1 0 − 5 .
The specimen under study is immersed in cuvette with an index matching fluid to eliminate the refraction of light at the specimen surface. Compensation angles ψi = Δi(xi) were recorded during the measurements for a given translucency parameter xi, which was varied by precise moving the cuvette stage.
To estimate the reconstruction error δσz from transverse translucency data of cylindrical lenses, we use the expression obtained for the gradient-free case [34]:
δ σ Z = λ / 2 π π C δ x δ Δ δ x / r ln ⁡ 2 r / δ x ,
where δx and δΔ are errors in the translucency parameter x and phase difference Δ. For used polarimetric unit it amounted to δΔ~10' (3⋅10-3 rad). The uncertainty of the parameter x is determined by the radius of the beam waist; Δx~40 µm. Thus, at С0=3.5 Br, r= 0.1 mm the error is δσz~0.06 kg/mm2; at r=1mm it is δσz~0.03 kg/mm2 (0.6 and 0.3 MPa, respectively). These calculations do not account uncertainties in the determination of RS, refractive index and the influence of the gradient, but nevertheless allow us to conclude that the reconstruction technique used provides results with satisfactory accuracy.

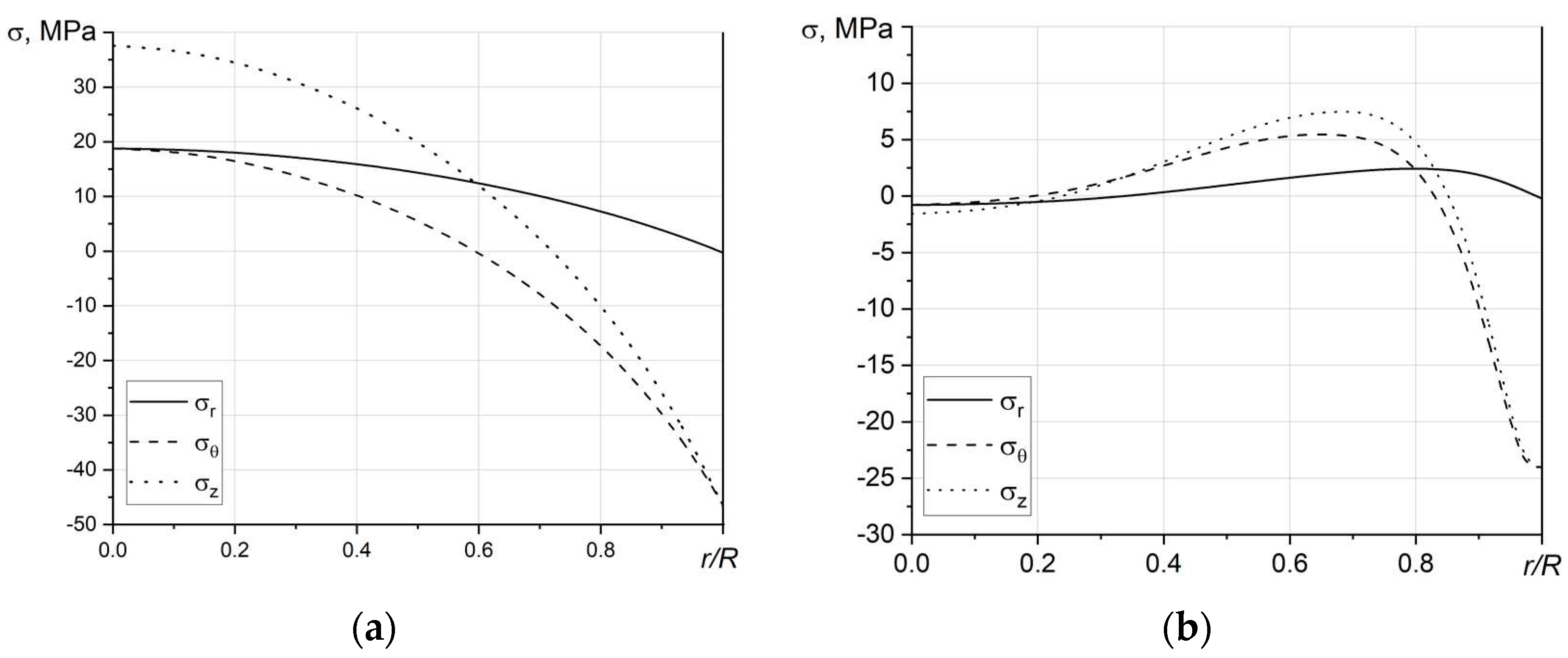
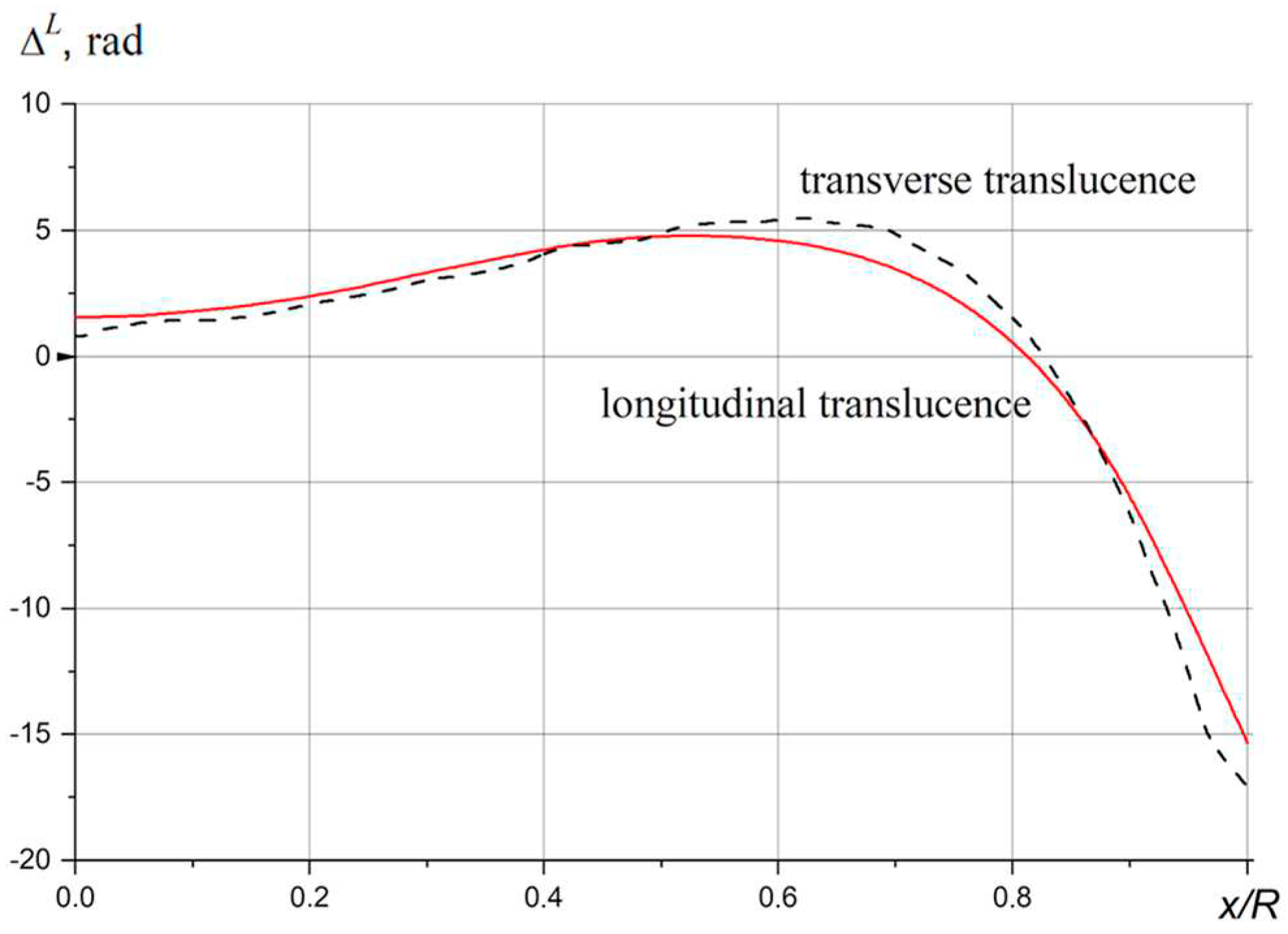
2.4. Samples under Study

To illustrate and verify the approach developed we have studied GRIN lenses of lithium zirconosilicate glass OPS [35,36] and alumosilicate glass TSM-412 [37] subjected to lithium-sodium ion exchange, elaborated and provided by S. I. Vavilov State Optical Institute Scientific Production Association and St. Petersburg Technological University of Plant Polymers. Characteristics of the investigated GRIN lenses are given in Table 1.
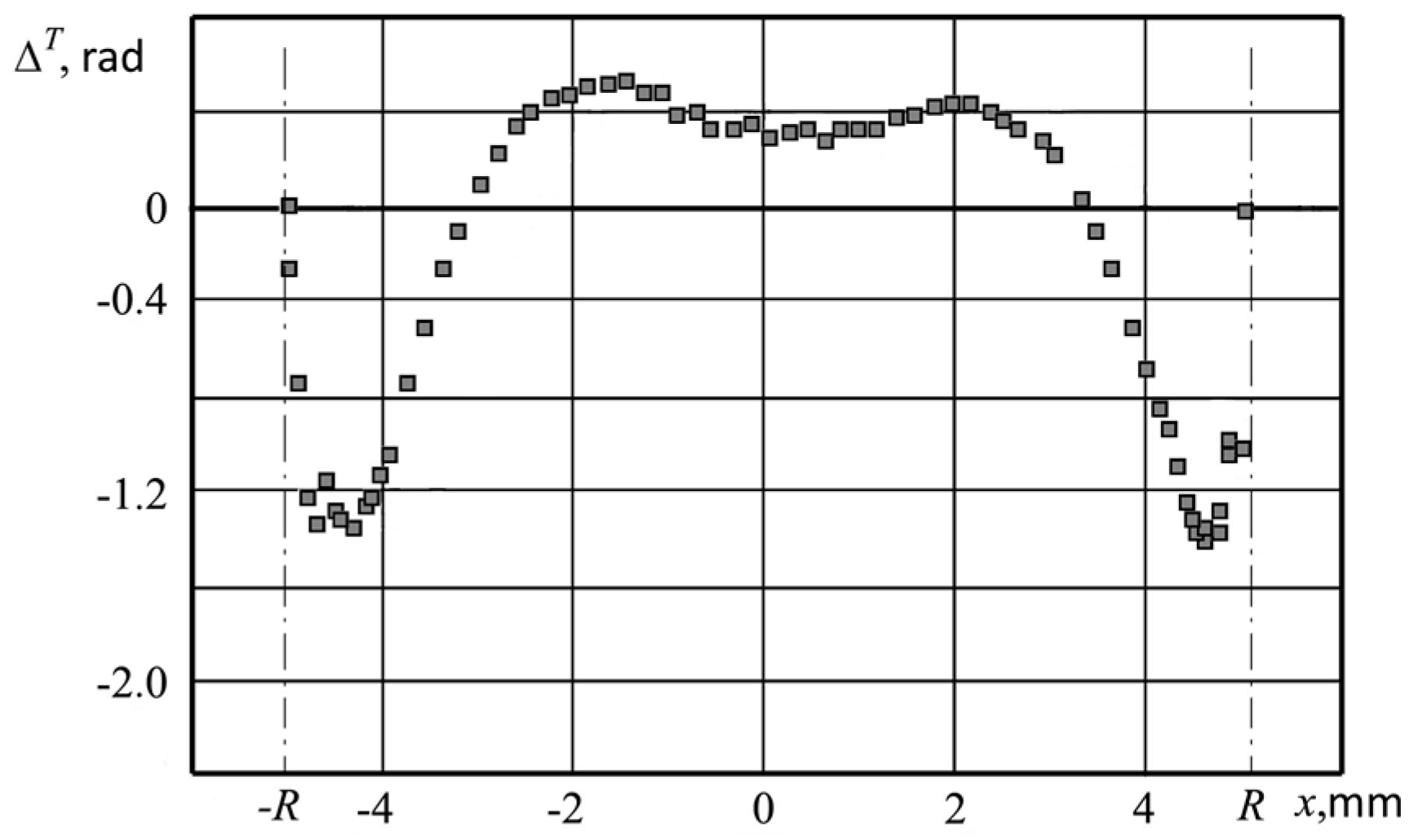
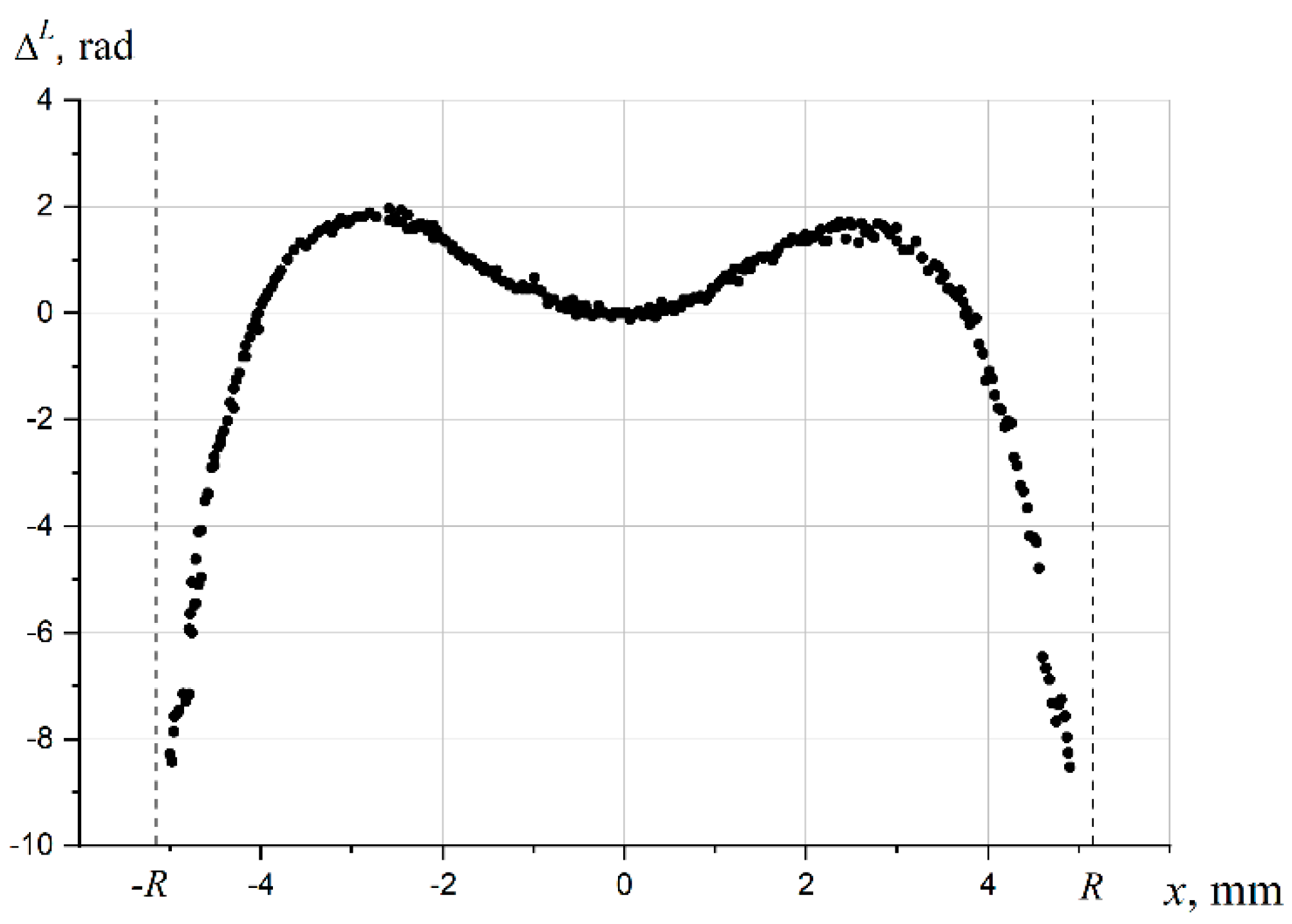
In the present study samples 1 and 2 were investigated by transverse translucency only and sample 3 by both transverse and longitudinal translucency. Two types of characterization were used, i.e. by a wide beam with scanning by a pinhole in the image plane of the object – longitudinal translucency (∆L(x) and scanning of the object itself by a focused beam ~ 40 µm in diameter – transverse translucency (∆T(x)). RS distributions σ(r) were reconstructed using a spline approximation Δ(x).

3. Results and Discussion

3.1. Residual Stresses

Figure 4 shows deduced from the measurements of the phase difference dependence on the transverse translucency parameter x for specimen 3.
In the RS reconstruction code, the experimental data were smoothed by splines.
Figure 5 shows reconstructed residual stress distribution σ(r) for all RS components for specimens 1 and 3. Radial distribution of differences in tangential and radial components Δσθr in specimens 1, 2 and 3 are shown in Figure 6.
As mentioned, positive σz(r) correspond to tensile stresses, while negative correspond to compressive ones.

3.2. Integral Phase Difference

For GRIN lenses 1, 2 and 3, using the obtained RS distributions as input, the IPD was calculated for the hypersecant RI distribution using the "direct problem" solution algorithm (see Section 2.1). The results are presented in Figure 7.
Using specimen 3 we studied the longitudinal translucency, which is presented in Figure 8.
As in the case of the transverse translucency, the averaged experimental data were smoothed by splines.
Thus, the results show that all investigated GRIN-lenses are characterized by sufficiently strong compressive stresses in the near-surface layers, which provides them with increased mechanical strength. A related effect is the large values of tangential and radial stress differences and, as a consequence, significant optical anisotropy in these GRIN lenses.
An example of comparison of the IPD deduced from the transverse translucency data with experimental data on longitudinal translucency is shown in Figure 9 for specimen 3.
As can be seen, the calculated phase differences are quite close to the experimental ones, which confirms the applicability and accuracy of the developed algorithms.

4. Conclusions

Finally, in this paper for the first time we present an algorithm allowing to reconstruct the distribution of residual stresses and longitudinal optical anisotropy of GRIN lenses on the base of transversal transmission measurements. Measurements of this kind, contrary to longitudinal transmission measurements, do not require precise segmentation of GRIN lenses, which essentially simplifies the lenses characterization and, respectively, experimental studies aimed to the design of new gradient structures. The approach developed was verified in the experiments with a set of different GRIN lenses formed with ion exchange technique, and the closeness of the data obtained from transversal and conventional longitudinal transmission measurements was demonstrated. The approach is also prospective for using in design GRIN structures for generation of optical vortex beams and for polarization imaging of biological tissue structure.

Author Contributions

Conceptualization, A.A.L.; methodology, V.V.Z and D.D.K.; validation, A.S.K. and V.V.L.; formal analysis, N.T.S. and V.M.K.; investigation, D.I.D. and E.A.N.; data curation, D.D.K.; writing—original draft preparation, D.D.K. and D.I.D.; writing—review and editing, V.M.K. and D.D.K.; supervision, V.V.L. and D.D.K.; project administration, V.V.L. All authors have read and agreed to the published version of the manuscript.

Funding

The research is funded by the Ministry of Science and Higher Education of the Russian Federation as part of World-class Research Center program: Advanced Digital Technologies (contract No. 075-15-2022-311 dated 20.04.2022).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lipovskiĭ, A.A.; Rusan, V.V.; Tagantsev, D.K. Rapid technique for the determination of the refractive index of experimental glasses for graded-index optics. J. Opt. Technol., 2021; Volume 88, № 3, pp. 151–157. [CrossRef]
  2. Gordova, M.R. et al. Prototype of hybrid diffractive/graded-index splitter for fiber optics. Opt. Eng., 2001; Volume 40, № 8, pp. 1507–1512.
  3. Huland, D.M. et al. In vivo imaging of unstained tissues using long gradient index lens multiphoton endoscopic systems. Biomedical Opt. Express, 2012; Volume 3, № 5, pp. 1077–1085. [CrossRef]
  4. Il'in, V.G.; Karapetyan, G.O.; Remizov, N.V.; Petrovsky, G.T.; Polyansky, M.N. Optics of Gradient-Index materials. Usp. Nauchn. Fotogr, 1985; Volume 23, pp. 106–121.
  5. Tagantsev, D.K.; Lipovskii, A.A.; Tatarintsev, B.V.; Zhurikhina, V.V.; Schultz, P.C. Silver-phosphate glasses for grin lenses with high numerical aperture. Proceedings of International Congress on Glass (Strasbourg, France. July 1-6, 2007): 2007, paper L17.
  6. Tagantsev D. K.; Lipovskii, A.A.; Schultz, P.C.; Tatarintsev, B.V. Phosphate glasses for GRIN structures by ion exchange. J. Non-Cryst. Solids, 2008; Volume 354, № 12-13, pp. 1142–1145. [CrossRef]
  7. Abdulhalim, I.; Pannell, C.N. Photoelastically induced light modulation in gradient-index lenses. Opt. Lett., 1993; Volume 18, № 15, pp. 1274–1276. [CrossRef]
  8. Wang, A.; He, S.; Fang, X.; Jin, X.; Lin J. Optical fiber pressure sensor based on photoelasticity and its application. J. Lightwave Technol., 1992; Volume 10, № 10, pp. 466–472. [CrossRef]
  9. Wang, A.; Wu, B.; He, S.; Lin, J.X. Theoretical and experimental study of modal noise for non-function fiber sensors. Opt. Commun. Technol. (Chinese), 1988; Volume 12, № 1, pp. 27–31.
  10. Visconti, A.; Bentley, J. Fabrication of large diameter radial gradient-index lenses by ion exchange of Na+ for Li+ in titania silicate glass. Opt. Eng, 2013; Volume 52, № 11, pp. 112103–112103. [CrossRef]
  11. Mermillod-Blondin, A.; McLeod, E.; Arnold, C. B. High-speed varifocal imaging with a tunable acoustic gradient index of refraction lens. Opt. Lett., 2008; Volume 33, № 18, pp. 2146–2148. [CrossRef]
  12. Abramovich, A.А. Acoustic studies of gradient glasses. Acoust. J., 2009; Volume 55, № 3, pp. 350-355. [CrossRef]
  13. He, C. et al. GRIN lens: a new element for complex vectorial beam modulation. Proc. SPIE, 2020; Volume 11297, pp. 98–104.
  14. He, C. et al. Complex vectorial optics through gradient index lens cascades. Nature Comm., 2019; Volume 10, № 1, pp. 4264. [CrossRef]
  15. Forbes, A. Common elements for uncommon light: vector beams with GRIN lenses. Light Sci. Appl., 2019, № 8, paper 111. [CrossRef]
  16. Willner, A.E. et al. Optical communications using orbital angular momentum beams. Adv. Opt. and Photon., 2015; Volume 7, № 1, pp. 66–106. [CrossRef]
  17. Shen, Y.J. et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl, 2019; Volume 8, paper. 90. [CrossRef]
  18. Khonina, S.N.; Striletz, A.S.; Kovalev, A.A.; Kotlyar, V.V. Propagation of laser vortex beams in a parabolic optical fiber. Proc. SPIE, 2010; Volume 7523, pp. 82–93.
  19. Chang, J. et al. Optimization of GRIN lens Stokes polarimeter. Appl. Opt., 2015; Volume 54, № 24, pp. 7424–7432. [CrossRef]
  20. Chang, J. et al. Removing the polarization artifacts in Mueller matrix images recorded with a birefringent gradient-index lens. J. Biomed. Opt., 2014; Volume 19, № 9, pp. 095001–095001. [CrossRef]
  21. Aben, H. K. Integrated Photoelasticity. McGraw-Hill International Book Company, 1979.
  22. Aben, H.; Ainola, L.; Anton, J. Integrated photoelasticity for nondestructive residual stress measurements in glass. Opt. and Lasers in Eng., 2000; Volume 33, № 1, pp. 49–64. [CrossRef]
  23. Karov, D.D. et al. Photoelastic Express Diagnostics of the Surface Stresses in Rod Elements with Radial Refractive Index Gradient. IEEE (EExPolytech), 2020; pp. 196–200.
  24. Karov, D.; Puro, A.; Kuzmina, A. Polarization-optical tomography of mechanical stresses in dielectric cylindrical structures of hexagonal single crystal. AIP Conference Proceedings, 2020; Volume 2308, № 1.
  25. Karov, D.; Puro, A.; Fadeev, A.; Kuzmina, A. Optical tomography of residual stresses in GRIN rod lenses with transverse and longitudinal translucence. 2019. J. Phys.: Conf. Ser. Volume 1236, paper 012038. [CrossRef]
  26. Fuki, A.A; Kravtsov, Y.A.; Naida, O.N. Geometrical Optics of Weakly Anisotropic Media. Amsterdam: Gordon and Breach Science Publishers, 1998.
  27. Ainola, L.; Aben, H. On the generalized Wertheim law in integrated photoelasticity. J. Opt. Soc. Am. A, 2008; Volume 25, № 8, pp. 1843–1849. [CrossRef]
  28. Timoshenko, S.P.; Goodier, J. N. Theory of Elasticity. Third ed., McGraw-Hill, New York, 1970.
  29. Boley, B.A.; Weiner, J.H. Theory of Thermal Stresses. Wiley, New York, 1960.
  30. Marchand, E.W. (1973). Progress in Optics. Volume 11. VII Gradient Index Lenses, pp, 305–337. [CrossRef]
  31. O'Rourke, R.C. Three-dimensional photoelasticity. J. Appl. Phys., 1951; Volume 22, № 7, pp. 872–878.
  32. Saenz, A.W. Determination of residual stresses of quenching origin in solid and concentric hollow cylinders from interferometric observations. J. Appl. Phys., 1950; Volume 21, № 10, pp. 962–965. [CrossRef]
  33. Calligaro, R.B., Payne, D.N., Anderssen, R.S., Ellem, B.A. Determination of stress profiles in optical-fibre preforms. Elect. Lett., 1982; Volume 18, № 11, рp. 474–475. [CrossRef]
  34. Chu, P.L. Non-destructive measurement of index profile of an optical-fibre prerform. Elect. Lett., 1977; Volume 13, № 24, pp. 786–788. [CrossRef]
  35. Livshits, V.Ya. Composition, structure and properties of glasses for ion exchange in a salt melt. Phys. and Chem. Glasses, 1993; Volume 19, № 3, pp. 521–535.
  36. Livshits, V.Ya.; Shchavelev, O.S.; Goldenfang, B.G.; Nakhapetyan, R.A. Change of optical refractive index of alkali-silicate glasses containing zirconium oxide during ion exchange from salt melt. Phys. and Chem. Glasses, 1987; Volume 13, № 6, pp. 921–923.
  37. Livshits, V.Ya.; Kozyrev, V.K.; Karapetyan, G.O.; Viktorova Y.N. Gradient glass in the Li2O-Na2O-Al2O3-SiO2 system in the composition region [R2O/Al2O3]=1. Phys. and Chem. Glasses, 1982; Volume 8, Issue 2, pp. 212–215.
Preprints 87130 g001
Figure 1. Longitudinal translucence of a GRIN lens.
Figure 1. Longitudinal translucence of a GRIN lens.
Preprints 87130 g001
Preprints 87130 g002
Figure 2. Transverse translucence of a GRIN lens.
Figure 2. Transverse translucence of a GRIN lens.
Preprints 87130 g002
Preprints 87130 g003
Figure 3. Experimental setup for determining stress profiles in GRIN lenses. C – chopper, λ/4 – quarter-wave plate, P – polarizer, L – lens, I - ditch with immersion liquid, IP – investigated preform, A – analyzer, PH – pin hole, D – detector.
Figure 3. Experimental setup for determining stress profiles in GRIN lenses. C – chopper, λ/4 – quarter-wave plate, P – polarizer, L – lens, I - ditch with immersion liquid, IP – investigated preform, A – analyzer, PH – pin hole, D – detector.
Preprints 87130 g003
Preprints 87130 g004
Figure 4. Phase difference vs. transverse translucency parameter for specimen 3.
Figure 4. Phase difference vs. transverse translucency parameter for specimen 3.
Preprints 87130 g004
Preprints 87130 g005
Figure 5. Radial distribution of all RS components in specimens 1 (a) and 3 (b).
Figure 5. Radial distribution of all RS components in specimens 1 (a) and 3 (b).
Preprints 87130 g005
Preprints 87130 g006
Figure 6. Radial distribution of differences in tangential and radial components σθ(r) - σr(r) in specimens 1, 2 and 3.
Figure 6. Radial distribution of differences in tangential and radial components σθ(r) - σr(r) in specimens 1, 2 and 3.
Preprints 87130 g006
Preprints 87130 g007
Figure 7. IPD ΔL dependences for GRIN lenses 1, 2 and 3.
Figure 7. IPD ΔL dependences for GRIN lenses 1, 2 and 3.
Preprints 87130 g007
Preprints 87130 g008
Figure 8. Dependences of IPD on the longitudinal translucency parameter for specimen 3 (L = L0/4).
Figure 8. Dependences of IPD on the longitudinal translucency parameter for specimen 3 (L = L0/4).
Preprints 87130 g008
Preprints 87130 g009
Figure 9. Dependences of IPD on the longitudinal translucency parameter for sample 3 (L = L0/2): solid line – experiment on longitudinal translucency; dashed line – calculation, direct problem (from radial distributions of RS according to transverse translucency data).
Figure 9. Dependences of IPD on the longitudinal translucency parameter for sample 3 (L = L0/2): solid line – experiment on longitudinal translucency; dashed line – calculation, direct problem (from radial distributions of RS according to transverse translucency data).
Preprints 87130 g009
Table 1. Characteristics of the investigated GRINs.
Table 1. Characteristics of the investigated GRINs.
Specimen № Glass RI original
nD 		Сo,
Br		 Δn Rod diameter,
mm		 Temp.
IE,
°C		 IE duration,
h		 Content of alkali oxides, mol. %
Li2O
Na2O
1 ОPS-83 1.61 2.8 0.0108 15 630 57 13
13
-
2 ОPS-83 1.66 2.8 0.0134 16 630 60 13
13
-
3 TSM-412 1.524 2.7 0.008 9.9 660 24 11
10
-
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated