Prerpints.org logo
Preprint
Article

An Infinite Slope Model Considering unloading joints for Spatial Evaluation of Coseismic Landslide Hazard: A Case Study of the 2013 Lushan Earthquake

Altmetrics

Downloads

131

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 September 2023

Posted:

11 October 2023

You are already at the latest version

Alerts
Abstract
Coseismic landslides pose significant threats, causing widespread destruction of buildings, roads, pipelines, and leading to numerous casualties. In recent years, the frequency of earthquakes has increased, prompting a growing interest in regional-scale assessment techniques for coseismic landslides. The infinite slope model proposed by Newmark is widely used to evaluate coseismic landslide hazard. However, the infinite slope model fails to reflect the impact of rock mass structure on the stability of slopes. This paper proposes a novel approach for mapping the hazards of coseismic landslides by considering the roughness of the potential slide surfaces in the inner slope. The proposed method is validated using data from the 2013 Lushan earthquake. The datasets, including geological units, peak ground acceleration (PGA), and high-resolution digital elevation models of topography, are rasterized at a grid spacing of 30 meters. They are then combined within an infinite slope model based on Newmark permanent-deformation analysis, enabling the estimation of coseismic landslide displacement in each grid area resulting from the Lushan earthquake. The modeled displacements are compared with the inventory of landslides triggered by the Lushan earthquake, allowing the derivation of a confidence level function that relates predicted displacement to the spatial variation of coseismic landslides. Ultimately, a hazard map of coseismic landslides is generated based on the established confidence level function. This map serves as a valuable tool for predicting the hazard zone of seismic regions and offers essential insights for decision-making related to infrastructure development and post-earthquake construction.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geography

1. Introduction

Earthquakes are one of the primary triggers for landslides, often resulting in widespread coseismic landslides within specific regions [1]. In recent years, there has been a rise in strong earthquakes globally, leading to frequent coseismic landslide hazards and causing significant loss of life and property damage. Consequently, the evaluation of regional coseismic landslide hazards holds paramount importance for pre-earthquake urban planning and post-earthquake reconstruction efforts.
Early attempts to assess the coseismic stability of slopes utilized the pseudo-static analysis method introduced by Terzaghi [2] and the finite-element modeling technique pioneered by Clough and Chopra [3]. Additionally, Newmark [4] introduced a straightforward and practical method, which is still widely employed today, to estimate the coseismic permanent displacements of slopes [5]. Franklin and Chang [6] conducted permanent displacement calculations on earth and rock dam slopes using the Newmark method, incorporating 179 actual strong motion records and 10 artificially fitted accelerograms. This extensive dataset greatly expanded upon the information presented in Newmark's 1965 report, significantly bolstering the credibility of the finite sliding displacement methodology. To enhance the accuracy of estimating earthquake-induced permanent displacement, decoupled analysis was introduced by Makdisi and Seed [7]. The decoupled analysis accounts for the deformation of the sliding block during the sliding process. In the decoupled method, the block's deformation is calculated independently, without considering sliding. Subsequently, this deformation is treated as a new acceleration history to be applied to the sliding system. Bray and Rathje [8] introduced a streamlined seismic displacement method by utilizing a fully nonlinear decoupled one-dimensional dynamic analysis technique in conjunction with Newmark's rigid-plastic sliding block analysis. Building upon this work, Bary and Travasarou [9] proposed a simplified approach to predict earthquake-induced permanent displacement. Their method, based on a nonlinear fully coupled sliding block model, incorporates critical acceleration, dominant sliding block period, and seismic spectral acceleration, providing a more efficient and accurate framework for seismic displacement prediction. Rathje and Bray [10,11] introduced the coupled analysis that incorporate the deformation of the sliding block during the sliding process. In the coupled method, deformation and displacement are considered simultaneously, offering a more realistic portrayal of slope response under seismic forces.
Jibson et al. [12,13] conducted an extensive investigation concerning the Northridge earthquake of 1994, which struck in close proximity to Los Angeles, California. Their research focused on the Oak Mountain region, situated to the north of the earthquake's epicenter. In a systematic manner, they elucidated the computational process of the Newmark method for the regional assessment of seismic landslide susceptibility. Additionally, they presented a comprehensive seismic landslide susceptibility zoning map for the study area. This pioneering work significantly advanced the utilization and refinement of the Newmark method within the realm of regional seismic landslide susceptibility analysis. Subsequently, numerous scholars have adopted and applied the Newmark method in their assessments of regional seismic landslide susceptibility. Yuan et al. [14] applied the basic methodology outlined by Jibson [12,13] to derive the Newmark displacement of landslides based on strong ground-motion recordings during the 2013 Lushan Ms 7.0 earthquake. Different empirical equations with new fitting coefficients for estimating Newmark displacement are developed for comparative analysis. Zhang et al. [15] have introduced a novel model for evaluating seismic slope stability, building upon the foundation established by Jibson [16] in the Newmark model. In this enhanced model, the influence of velocity pulse seismic motion on permanent slope displacement was meticulously considered. The study meticulously incorporates the effects of near-fault pulse characteristics, thereby presenting an advanced framework for assessing seismic slope stability under the specific influence of these pulses. Zhang et al. [17] delved into the nuanced topic of force direction applied to the sliding block within the framework of the Newmark model. Their study advocates for the adoption of a pragmatic approach by suggesting a more realistic horizontal base direction for the force exerted on the sliding block.
Natural slopes often develop a series of shallow unloading joints parallel to the surface due to valley incisions [18,19]. Research indicates that during strong earthquakes, rock slopes exhibit collapsing and sliding failures along these shallow unloading joints, with approximately 90% of coseismic landslides being shallow falls and slides [20,21,22,23]. Unstable rock blocks are frequently fragmented and mobilized along these joints [24]. However, prior studies have not sufficiently considered the shear strength of these rock joints in the assessment of coseismic landslides. In addressing this gap, Zang et al. [25] introduced the Barton model [26] into the Newmark analysis to enhance the estimation of slopes' dynamic stability. This method was initially employed to assess the hazards posed by coseismic landslides, utilizing data from the 2014 Ludian earthquake in Yunnan Province, southwestern China. The seismogenic fault associated with the 2014 Ludian earthquake is identified as the Baogunao-Xiaohe fault, characterized by left-lateral strike-slip movement [27]. In this study, we critically review the initial methodology and refine it through recalibration, utilizing the coseismic landslide dataset from the 2013 Lushan earthquake. The Lushan earthquake is categorized as a blind reverse-fault events [28].

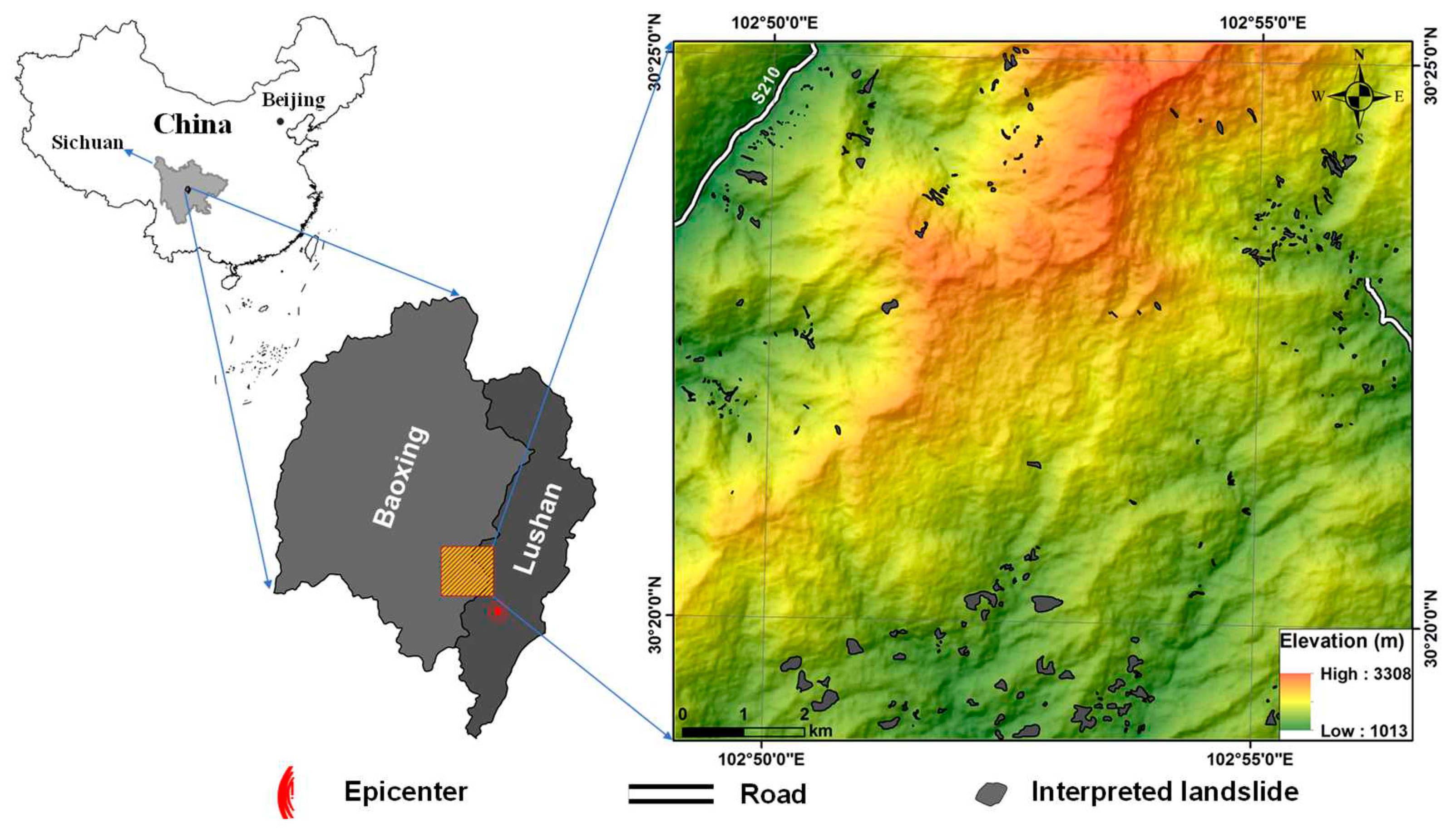
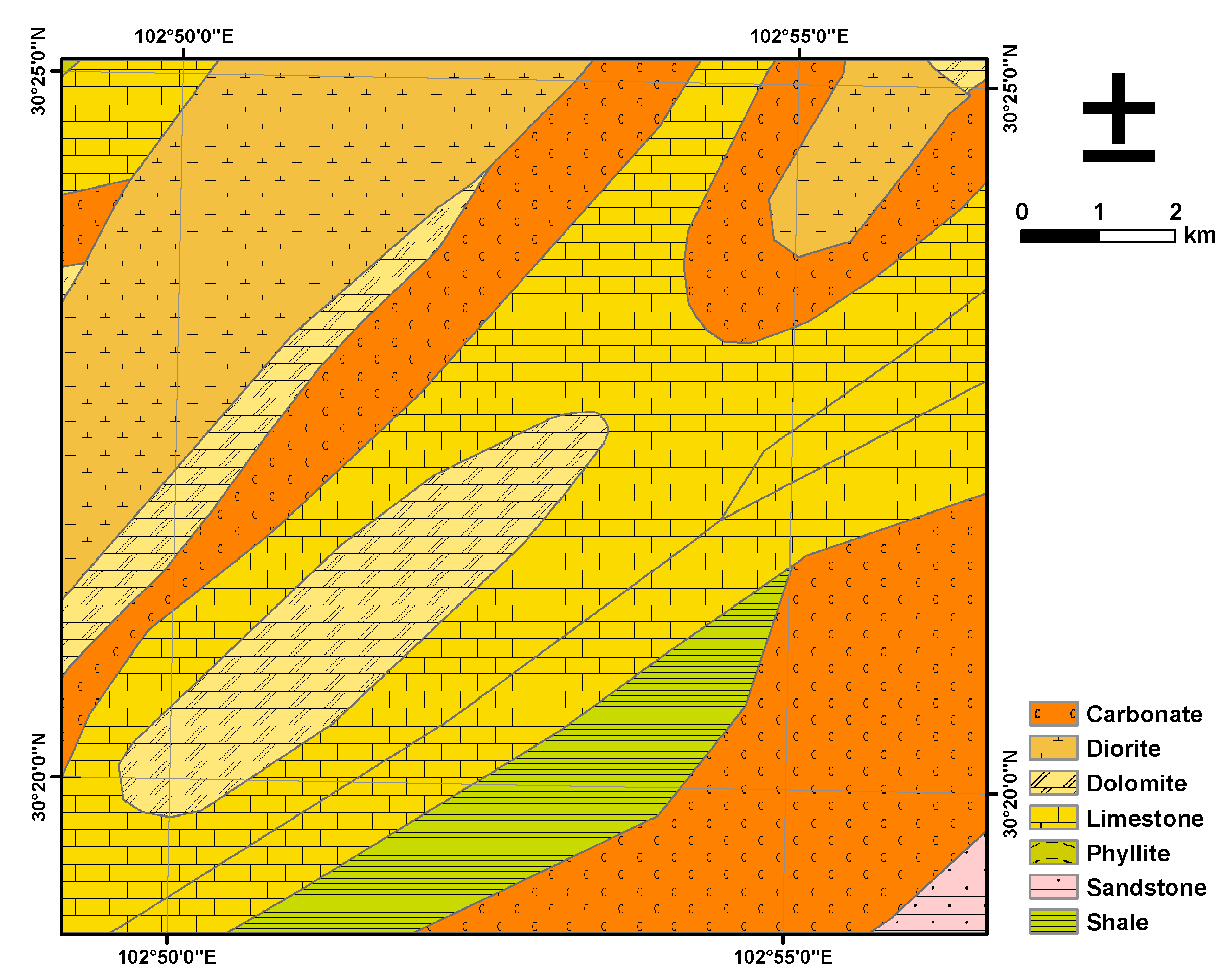
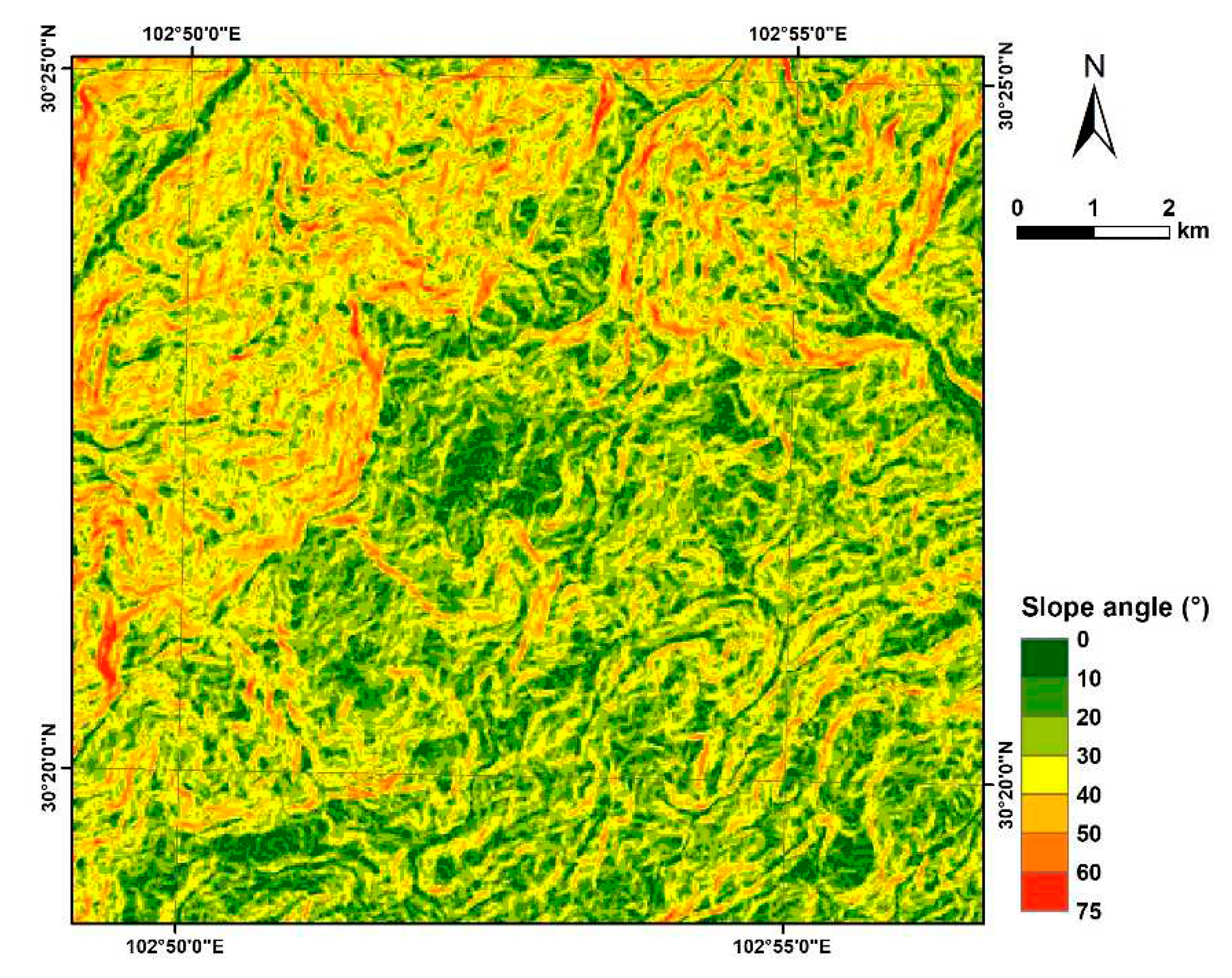
2. Study Area

The epicenter of the 2013 M w 6.6 Lushan earthquake is located at the southern segment of the Longmenshan fault zone, on the eastern margin of the Tibetan Plateau [29,30]. A rectangular containing dense concentrations of earthquake-induced landslides was chosen as the study area (Figure 1). The area is located about 12 km northwest of the epicenter and lies on the border of two earthquake-hit counties, i.e., Baoxing county and Lushan county in Sichuan Province, China, covering 138 km2 (Figure 1). The study area is characterized by deeply incised valleys and high mountains, with an elevation ranged from 1013 to 3308 m above sea level (Figure 1). Exposures of the geological units have an age that varies from the Sinian to the Triassic, including carbonate, diorite, dolomite, limestone, phyllite, sandstone and shale (Figure 2).
There have been 17 earthquakes with magnitudes ≥ 4.7 in the history in the Lushan earthquake zone [31]. Strong tectonic activity provides favorable conditions that prone to landslides. The Lushan earthquake has triggered thousands of landslides [32]. An inventory of 308 coseismic landslides was compiled by comparisons between pre-earthquake satellite images and post-earthquake aerial photographs in the study area. The total area of these interpreted landslides is 5 km2. A majority of landslides developed along the deeply incised river valleys.

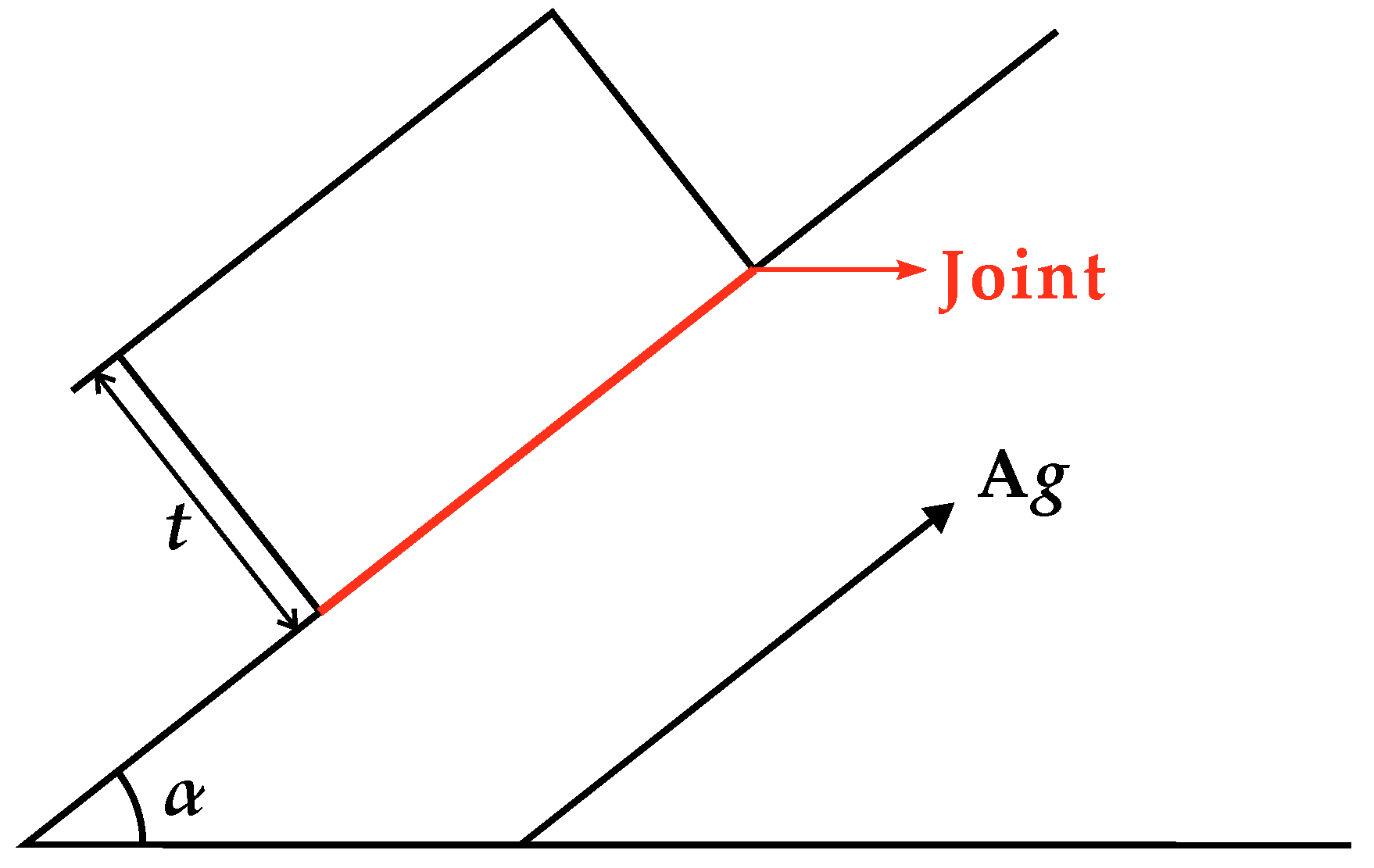
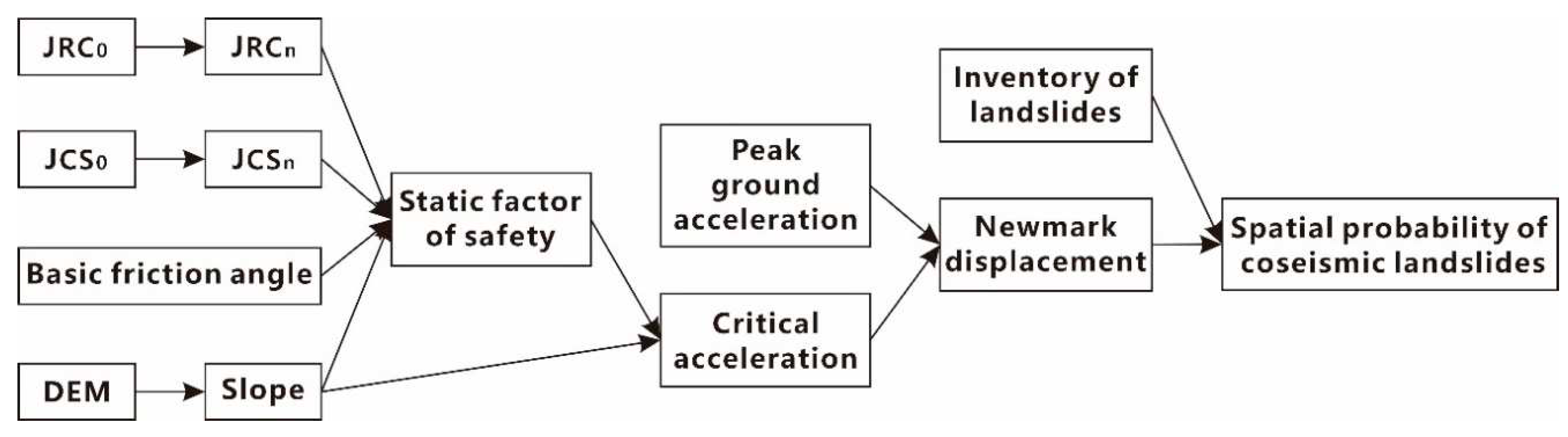
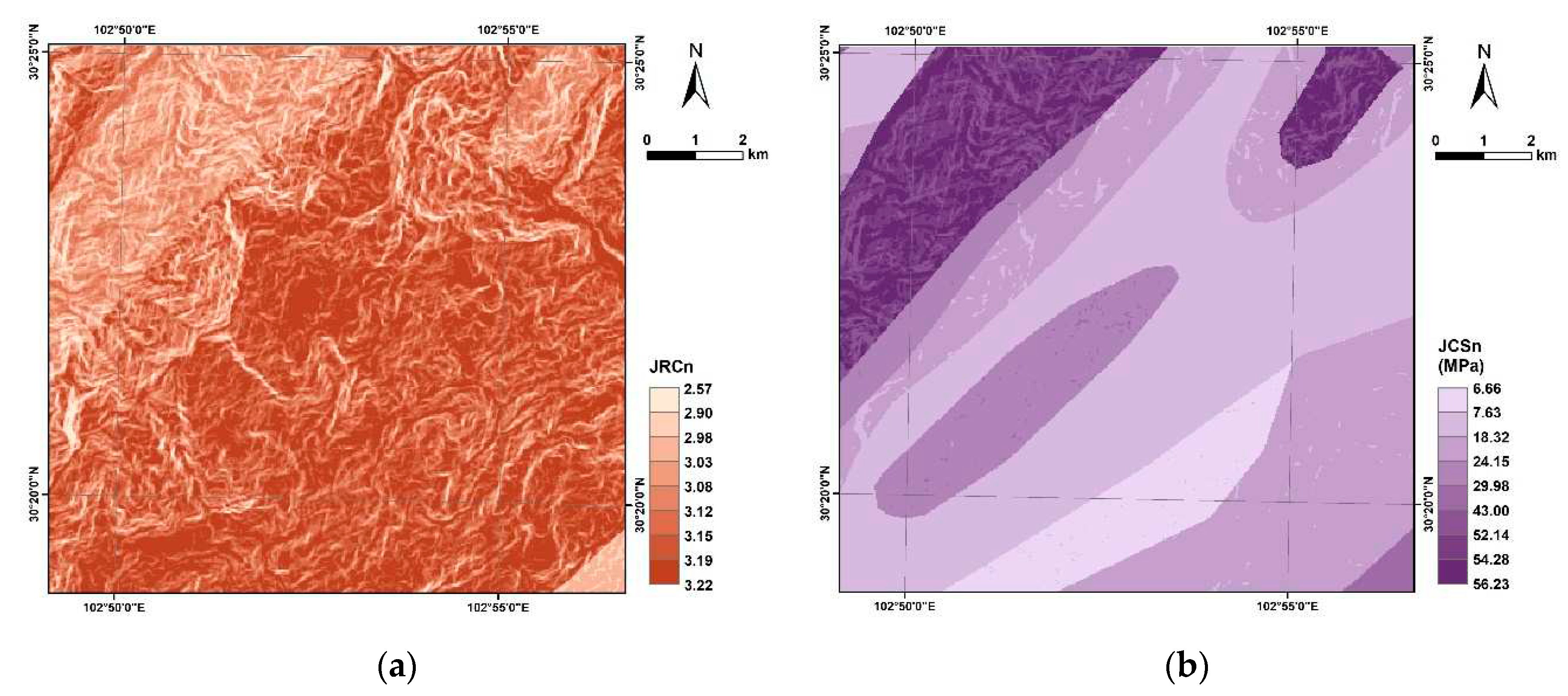
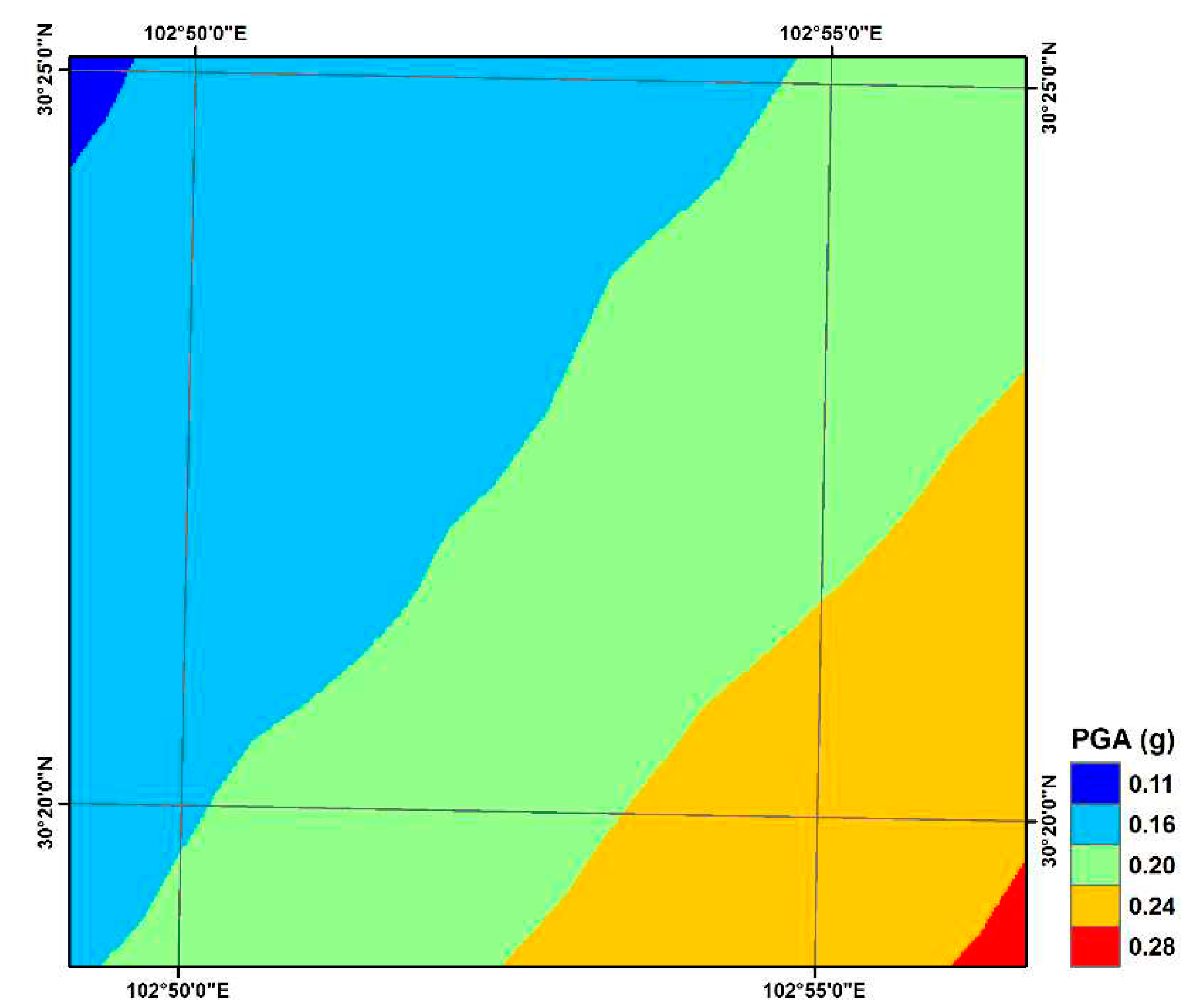
3. Methodology

Newmark in 1965 [33] proposed an infinite slope model for the analysis of the dynamic stability of slopes. Newmark’s method [33] simulates a landslide as a rigid plastic friction block lying on an inclined plane with a known critical acceleration (Figure 3). It calculates the cumulative permanent displacement of the block relative to its base as it is subjected to the effects of an earthquake acceleration-time history [12,13]. The Newmark displacement is a valuable index for evaluating the dynamic performance of slopes.
Once an acceleration-time history has been selected, those portions of the record that exceed the critical acceleration (Figure 4a) are integrated once to derive a velocity profile (Figure 4b); the velocity-time history is then integrated a second time to obtain the cumulative displacement of the block (Figure 4c) [12,13,34].
From Figure 4, we can see that the critical acceleration provides a base for predicting the cumulative permanent displacement of a slope. Newmark [33] showed that the critical acceleration of a potential landslide block can be expressed as a simple function of the static factor of safety and the geometry of the slope [12,13]:
a c = F S − 1 g s i n α ,
where a c is the critical acceleration in terms of g, F S is the static factor of safety, and α is the angle from the horizontal at which the center of the slide block moves when displacement first occurs [12,13]. For a planar slip surface parallel to the slope, this angle generally approximates to the angle of the slope [34].
Natural rock slopes are often cut by a group of shallow unloading joints due to valley incisions, forming a unloading zone on the surface of slopes [18,19]. Slopes behave as collapsing and sliding failures of shallow unloading joints under strong earthquakes [34], and 90% of coseismic landslides are shallow falls and slides [20,22,23,35]. Unstable rock blocks are often activated along the rock joints during seismic shaking (Figure 3). Therefore, the static factor of safety is related to the shear strength of these rock joints [34].
Zang et al. [34] derived the static factor of safety of a slope based on the Barton [26] shear strength criterion for rock joints in another research:
F S = R e s i s t i n g f o r c e D r i v i n g f o r c e = τ γ t s i n α = σ n t a n ⁡ [ J R C n log 10 ⁡ J C S n σ n + ϕ b ] γ t s i n α = γ t c o s α t a n ⁡ [ J R C n log 10 ⁡ J C S n γ t c o s α + ϕ b ] γ t s i n α = t a n ⁡ [ J R C n log 10 ⁡ J C S n γ t c o s α + ϕ b ] t a n α ,
where τ is the peak shear strength of the rock joint, γ is the unit weight of the rock mass, t is the thickness of the failure rock block, σ n is the effective normal stress, J R C n is the joint roughness coefficient in the in-situ scale, J C S n is the joint wall compressive strength in the in-situ scale, and ϕ b is the basic friction angle.
Considering the impact of joint size, the J R C n and J C S n can be defined as [36]:
J R C n = J R C 0 L n L 0 − 0.02 J R C 0 ,
J C S n = J C S 0 L n L 0 − 0.03 J R C 0 ,
where the nomenclature adopted incorporates (0) and (n) for values of the laboratory scale and the in-situ scale, respectively.
It is impractical to conduct a rigorous Newmark’ method during the regional analysis. Therefore, researchers have proposed different empirical regressions to estimate Newmark displacement as a function of the critical acceleration and ground motion parameters [16,37,38,39,40,41]. In this study, we chose a vector model that developed according to more than 2000 strong motion records [40]:
l n D = 4.89 − 4.85 a c P G A − 19.64 a c P G A 2 + 42.49 a c P G A 3 − 29.06 a c P G A 4 + 0.72 l n ⁡ ( P G A ) + 0.89 M w − 6 ,
where D is the predicted Newmark displacement, P G A is the peak ground acceleration, and M w is the moment magnitude. D is in centimeters, and a c and P G A are in units of g.
Figure 5 is a flowchart showing the sequential steps of the spatial evaluation of coseismic landslides. After calculating the Newmark displacement, the predicted displacement were then compared with an inventory of landslides triggered by the Lushan earthquake to map the spatial variation of coseismic landslide hazards with the help of the certainty factor model [42]. The certainty factor model (CFM) is a model of inexact reasoning that created by Shortliffe and Buchanan [42] and improved by Heckerman [43], to explore the relationship between the predicted displacement and the occurrence of landslides. In the CFM, the certainty factor (CF) represents the net confidence in a hypothesis H based on the evidence E [43], ranging from -1 to 1. A value of -1 means a total lack of confidence, whereas a value of 1 means total confidence. Values greater than zero favor the hypothesis while those less than zero favor its negation. The probabilistic interpretation of CF can be expressed as follows [43]:
C F = p H E − p H p H E 1 − p H ,     p H E > p H p H E − p H p H 1 − p H E ,     p H E < p H ,
where CF is the certainty factor, p H E is the posterior probability that denotes the conditional probability for a posterior hypothesis that relies on evidence, and p H is the prior probability without any evidence. For the spatial evaluation of coseismic landslides, p H E was defined as the proportion of the area of the landslide within a specific displacement area, and p H was defined as the proportion of the landslide area within the entire study area [34]. In this way, values of CF represented the confidence level for occurrences of coseismic landslides. Positive values corresponded to an increase in the confidence level in slope failure while negative quantities corresponded to its negation [34].

4. Mapping of Coseismic Landside Hazard

In this section, each step involved in the mapping of coseismic landslide hazard is discussed in detail.

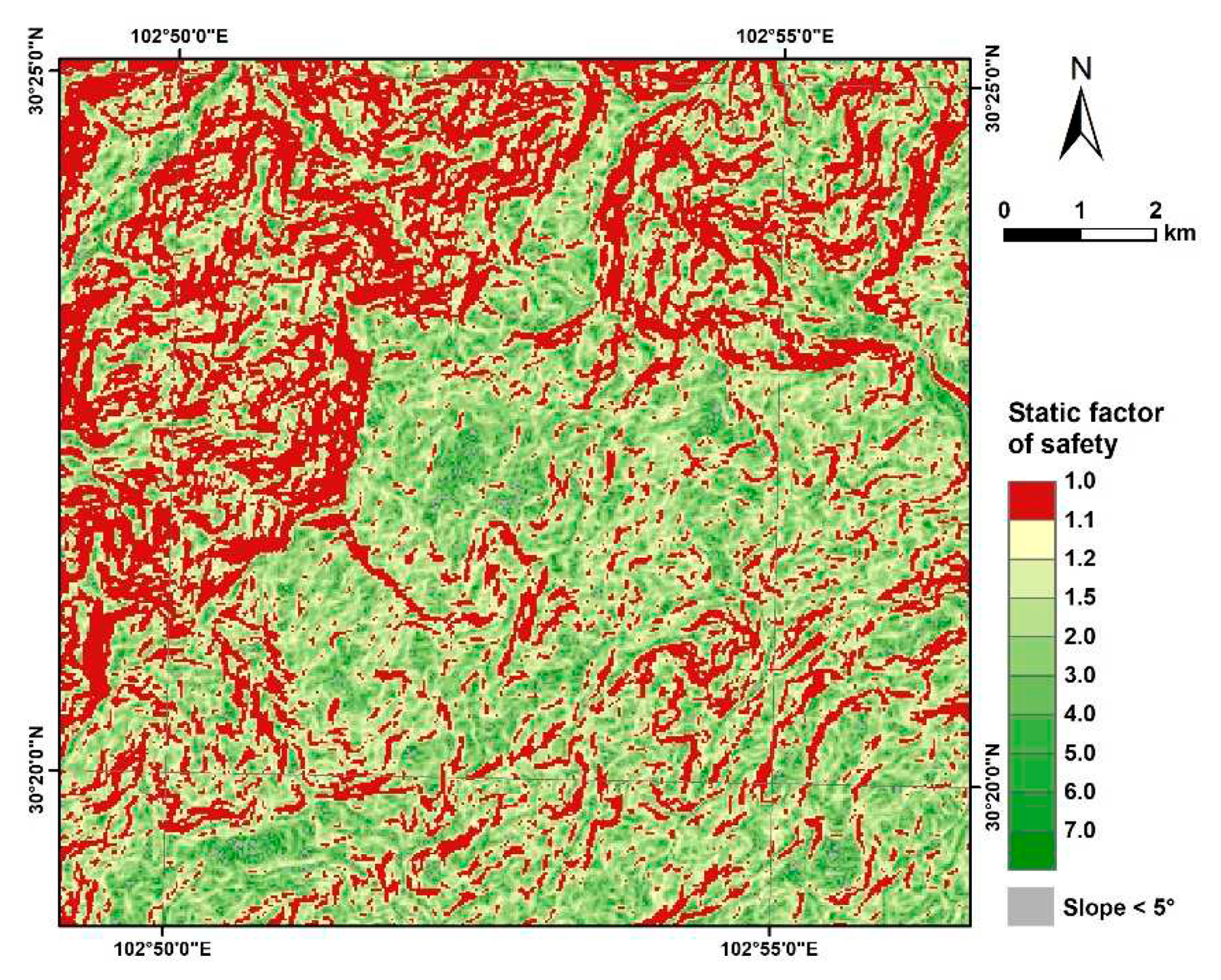
4.1. Static Factor of Safety Map

We selected a 30 m digital elevation model (DEM) to produce a slope map (Figure 6) by applying a basic slope algorithm, where the slop was identified as the steepest downhill descent among adjacent cells [44]. The derived slopes ranged from 0° to 75°. The northwestern and northeastern portions of the study area are high mountains and deeply incised valleys with slopes greater than 50°, and the central and southeastern parts of the area are relatively flat (Figure 6).
We assigned physical and mechanical parameters to the rock types using a digital geological map (Figure 2). The map was rasterized at 30 m grid spacing for following calculation after the parameter assignment. Studies have shown that J R C 0 and J C S 0 strongly depend on lithology [45,46,47,48,49,50,51,52,53,54,55]. Values of J R C 0 and J C S 0 assigned to each rock types were estimated based on test data from the references listed in Table 1. These values were obtained from laboratory tests with a sample length of L 0 =100 mm. As we used a projected coordinate system for regional analysis and the grid spacing was 30 m, the engineering dimension, L n , in a grid cell was equal to 30 m/ cos α . We can calculate J R C n and J C S n by substituting J R C 0 , J C S 0 , L 0 and L n into Equations (3) and (4), respectively. And the spatial distribution of J R C n and J C S n are shown in Figure 7a,b, respectively. Other parameters such as γ and ϕ b are listed in Table 1.
For the sake of simplicity, the thickness of the failure rock block (Figure 3) t was set to 3 m according to the filed investigation on typical slope failures of the Lushan earthquake. We produced the map of static factor of safety by combing the data layer of α , J R C n , J C S n , γ and ϕ b in Equation (2). The calculated static factors of safety ranged from 0.2 to 133.8. Grid cells with static factors of safety less than 1 indicated that the slopes were statically unstable, but this did not necessarily mean that they were sliding under seismic shaking [34]. However, according to Equation (1), to avoid a negative value of the critical acceleration, we assigned a minimal static factor of safety of 1.01 for these cells. Keefer [56] showed that the minimum slope angle for earthquake-induced landslides was 5°. In addition, the calculated static factors of safety for the cells with a slope angle less than 5° were very high, and these cells did not produce a statistically significant sample in the analysis [34]. Therefore, slopes gentler than 5° were not analyzed. The adjusted static factors of safety range from 1 to 10.4, as shown in Figure 9. Statically unstable slopes with a static factor of safety less than 1.2 are mainly distributed in the northwestern, northeastern, and southeastern parts of the study area (Figure 8).

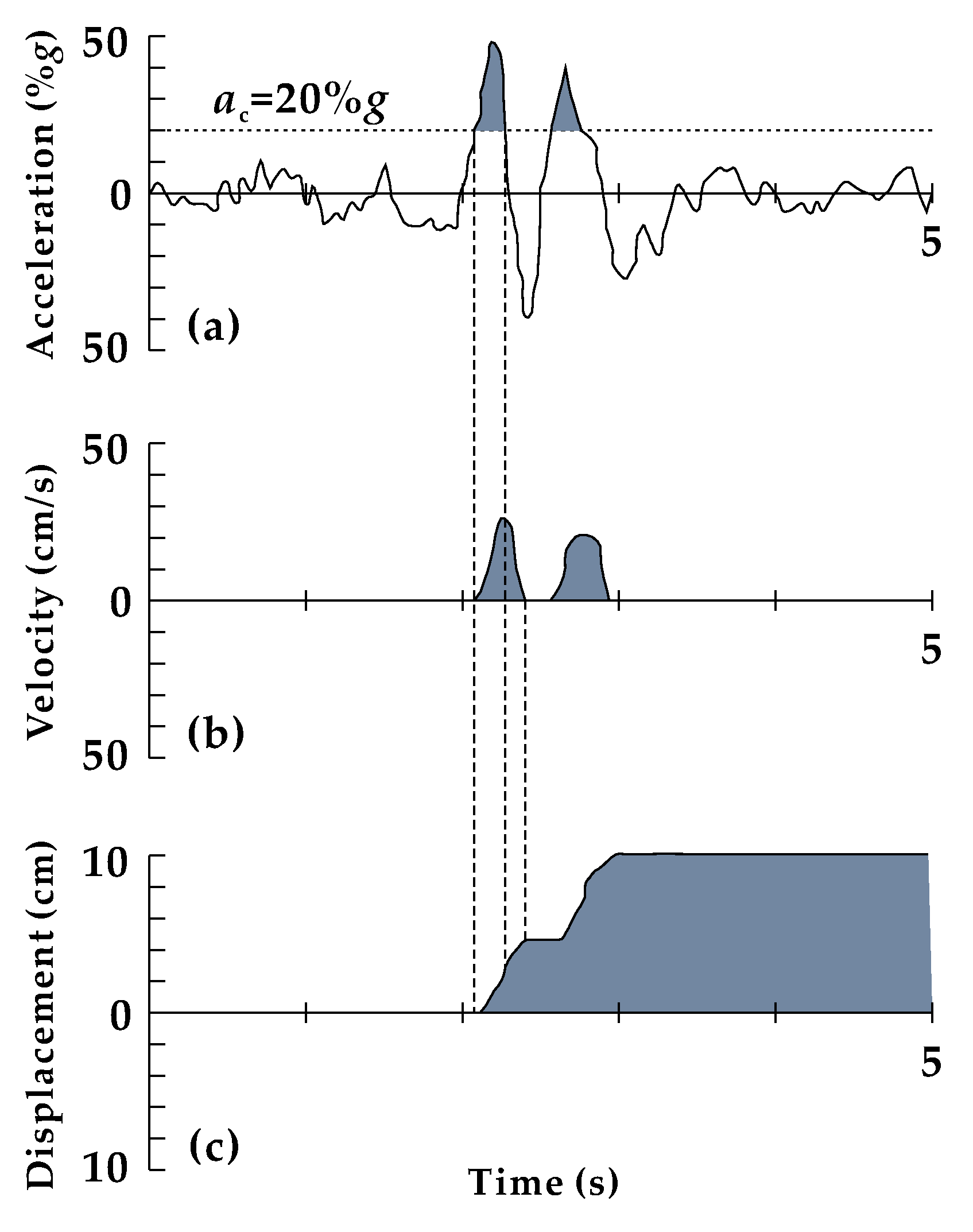
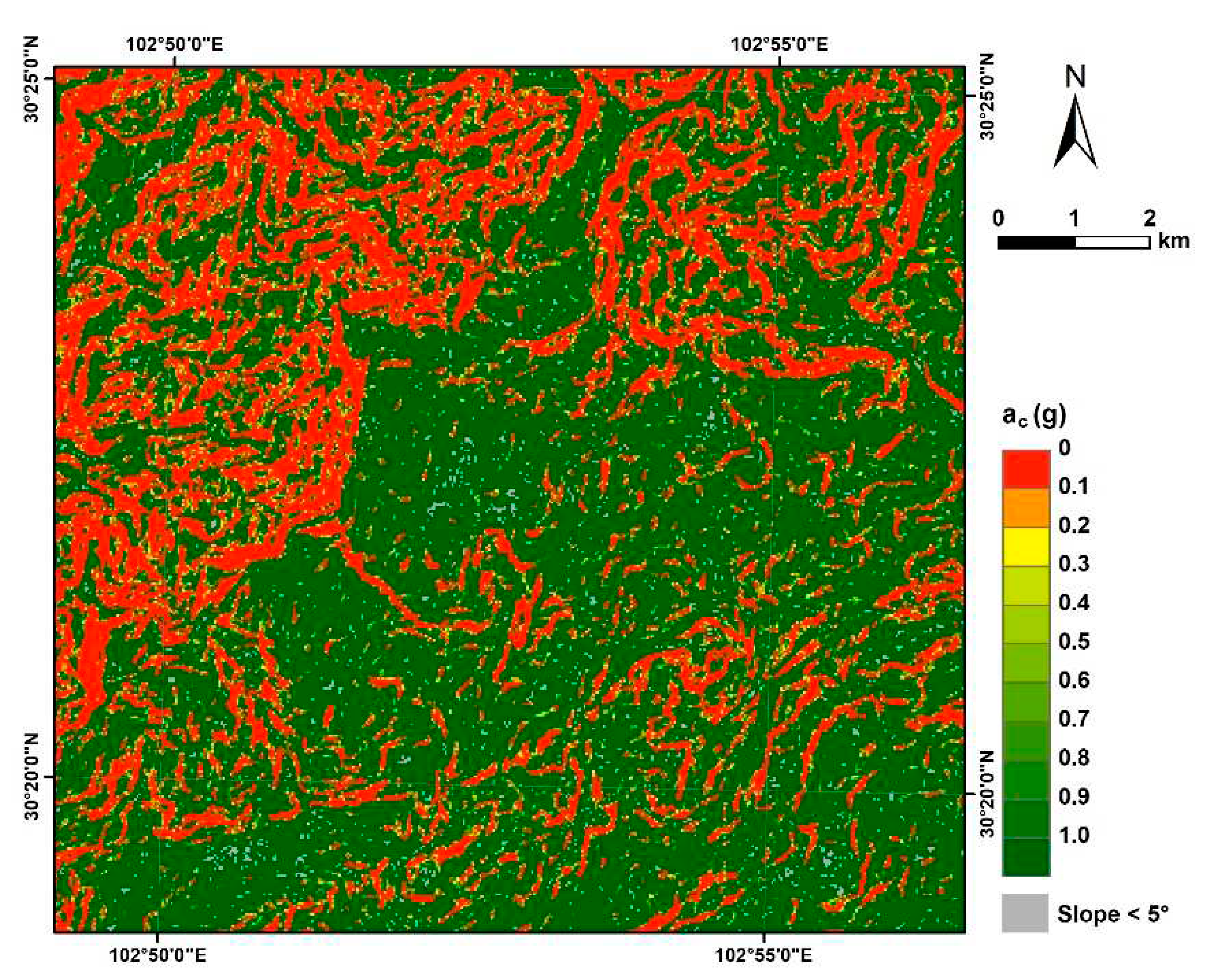
4.2. Critical Acceleration Map

After the adjustment of static factors of safety, we produced the map of critical acceleration using Equation (1) to combine the slope angle with the static factors of safety (Figure 9). The critical acceleration represents the intrinsic properties of slopes independent of any shaking scenario; thus, the critical acceleration map indicates the susceptibility of coseismic landslides [12,13]. A smaller value of critical acceleration denotes a lower intensity of shaking needed to overcome the stability of slope. Therefore, coseismic sliding is more likely to develop on the slope. From Figure 9, dynamically unstable slopes with a critical acceleration less than 0.3 g are mainly distributed in the northwestern part of the study area, and only a small portion is present in the southern part of the study area.

4.3. Predicted Dispalcement Map

We downloaded the contour map of peak ground acceleration (PGA) of the study area (Figure 10) from the United States Geological Survey. The Newmark displacement of each cell was calculated by employing Equation (5) to combine corresponding grid values of critical acceleration, PGA, and moment magnitude. The predicted displacements range from 0 to 76 cm (Figure 11). Slopes with a predicted displacement ranging between 0 cm and 4 cm are distributed in the northwestern portion of the study area, slopes with a predicted displacement ranging between 4 cm and 6 cm are distributed in the middle portion of the study area, slopes with a predicted displacement ranging between 6 cm and 15 cm are scattered in the area with a displacement between 4 cm and 6 cm, and slopes with a predicted displacement greater than 15 cm are only distributed in the southeastern portion of the study area. According to the statistical sizes of the areas, displacements less than 4 cm occupy 90.5 % of the study area, displacements between 4 cm and 6 cm occupy 5.5 % of the study area, and displacements between 6 cm and 15 cm occupy 3.6 % of the study area. Displacements greater than 15 cm occupy a very small area.

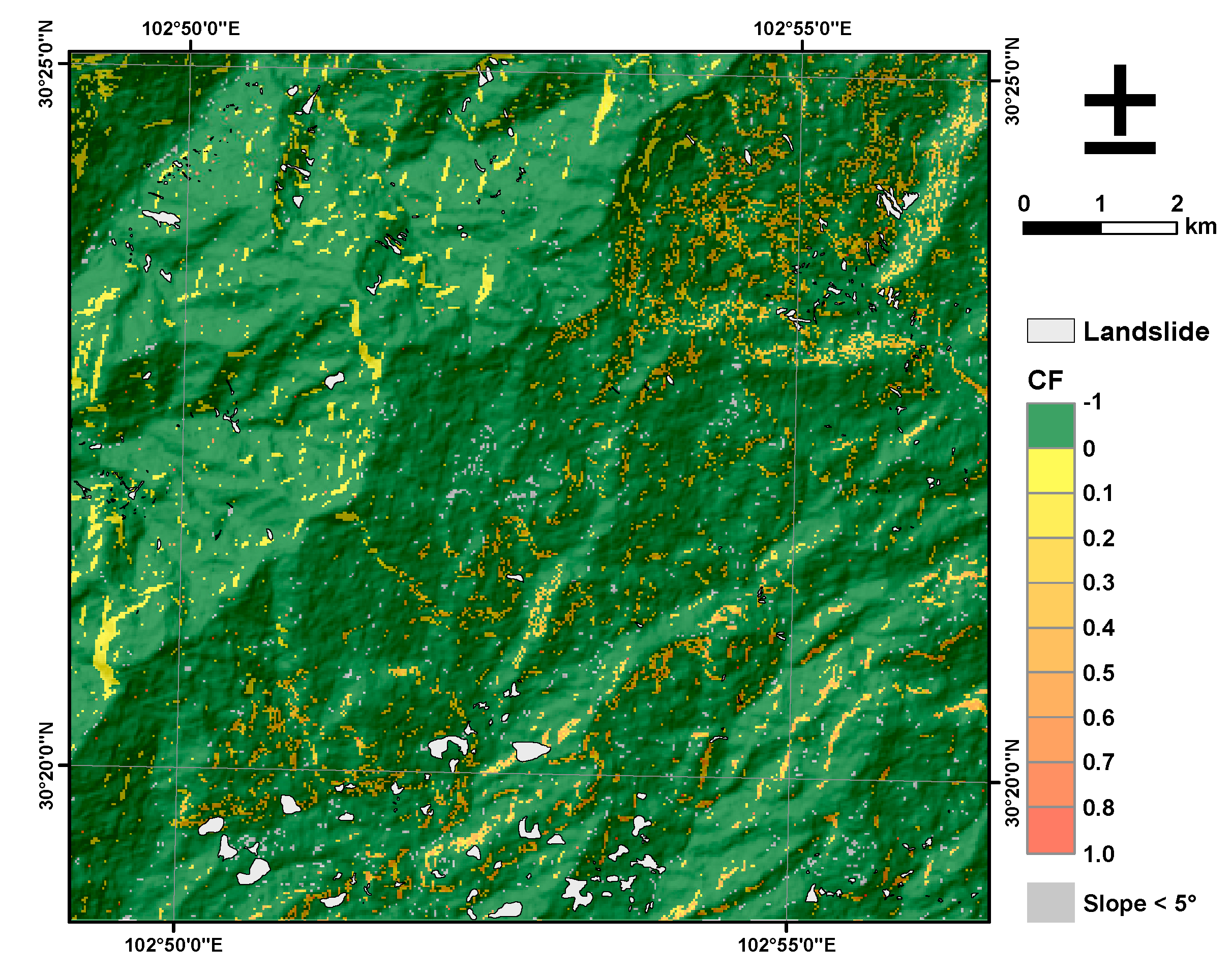
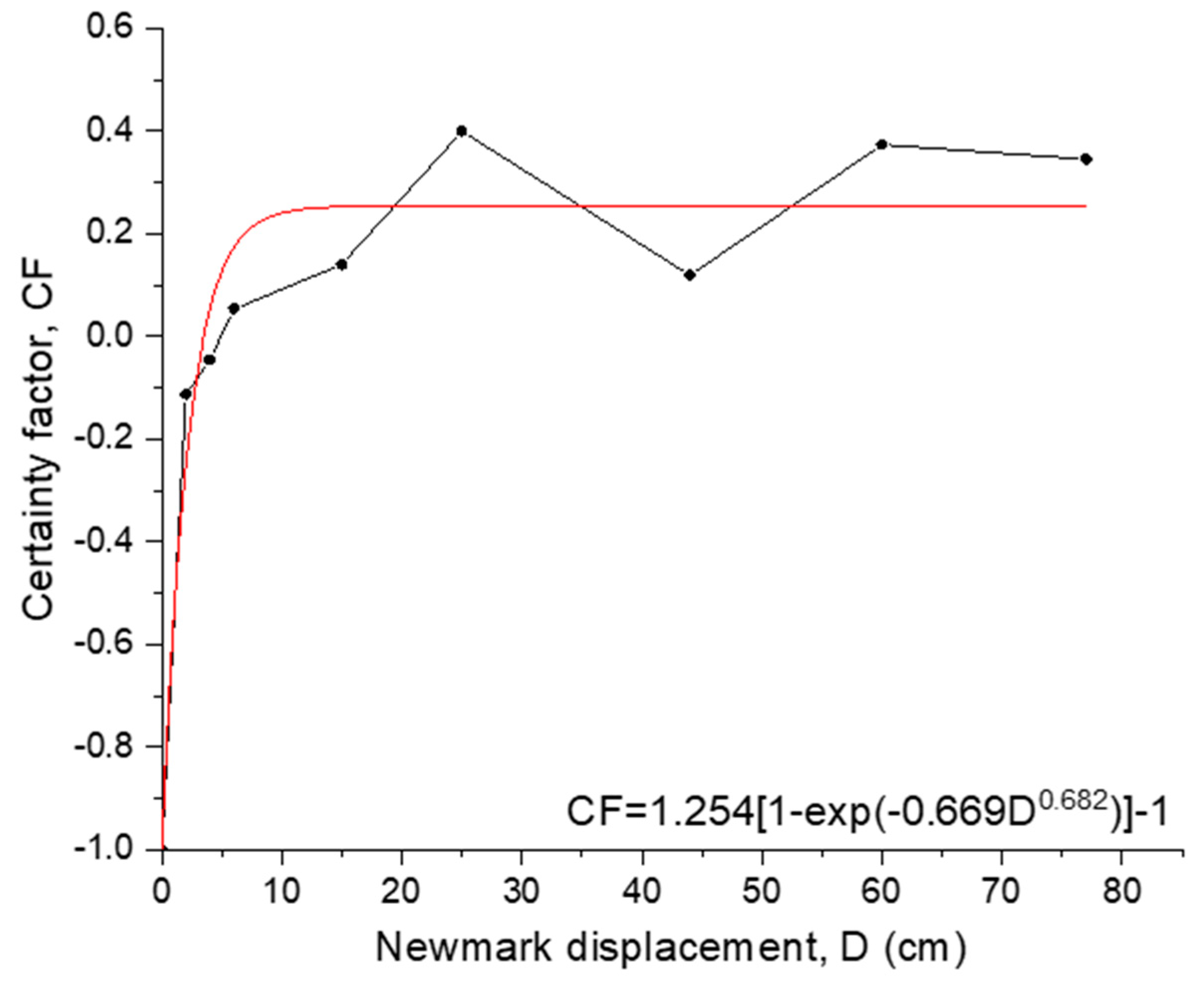
4.4. Coseismic Landslides Hazard Map

Jibson et al. [12,13] showed that Newmark displacements provide an index of the seismic performance of slopes but do not correspond directly to measurable slope movements in the field. Therefore, predicted displacements needed to be compared with an inventory of landslides triggered by earthquakes to be used in a predictive scenario of coseismic landslide hazards. We employed Equation (6) to produce a coseismic landslide hazard map in terms of certainty factors.
The Newmark displacement cells every 1 cm were grouped into bins, such that all cells with displacements between 0 cm and 1 cm were grouped into the first bin; those with displacements between 1 cm and 2 cm were grouped into the second bin, and so on [12,13,34]. The predicted displacements were grouped into 75 bins. For each bin, the proportion of cells occupied by landslide areas was calculated. This proportion represents the posterior probability of the bin according to Equation (6). The proportion of the entire landslide area within the entire study area was calculated to obtain the prior probability, which was same in each bin. We used Equation (6) to compute values of CF by combing the corresponding values of the posterior and prior probabilities. The calculated certainty factors ranged from −1 to 0.99. The CFM provides a necessary linkage between the Newmark displacements and confidence levels of coseismic landslide occurrence in the study area. We produced the coseismic landslide hazard map for the ground shaking scenario of the Lushan earthquake based on the values of CF, as shown in Figure 12. The landslides triggered by the Lushan earthquake were shown to demonstrate the goodness of fit for the predicted confidence levels of coseismic landslides.

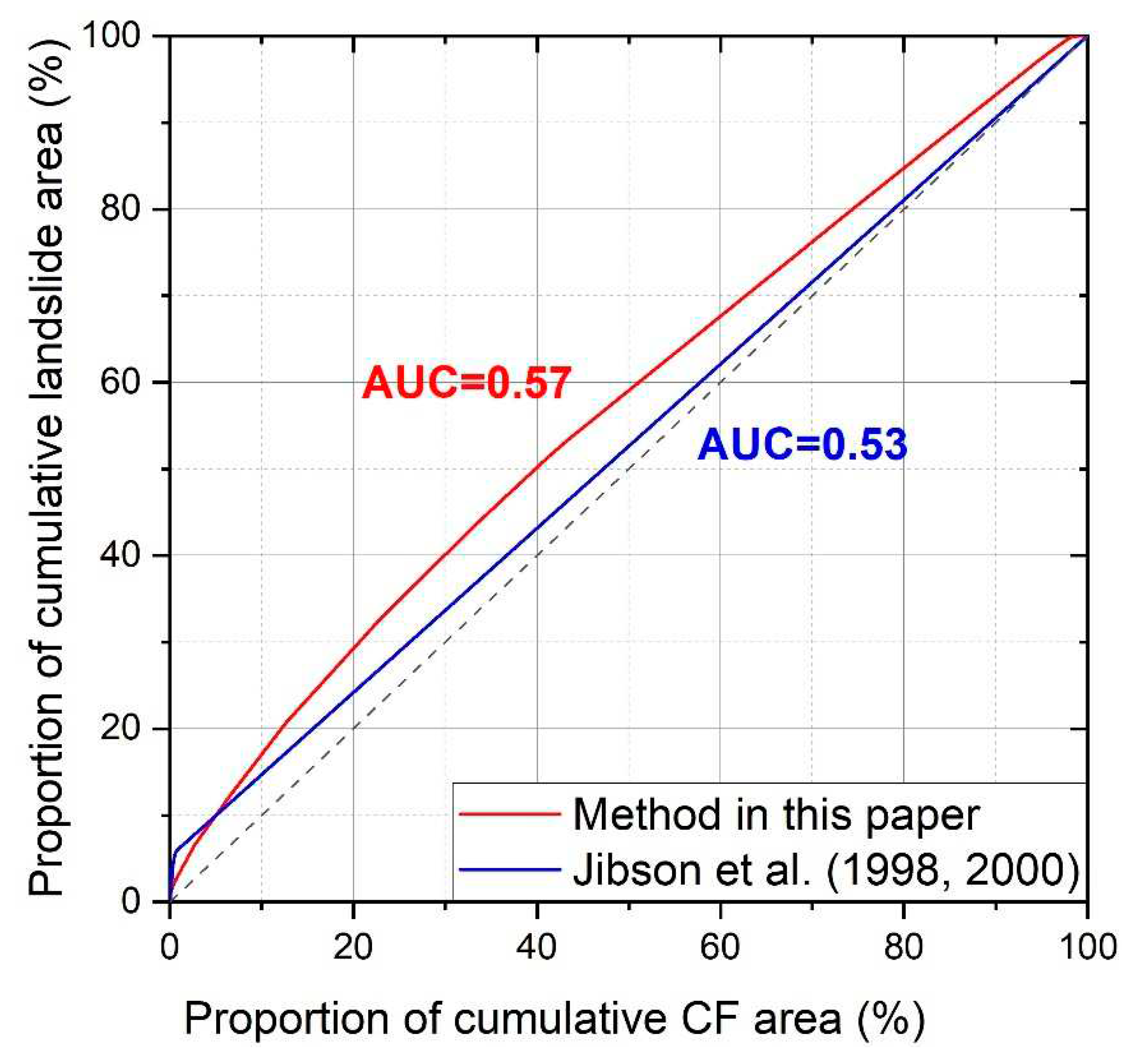
5. Discussion

The predicted displacement is the cumulative sliding displacement of slopes for a given history of acceleration. As depicted in Figure 11, the predicted displacements range from 0 to 76 cm. Analysis of the statistical size of each displacement area indicates that 90.5% of the study area experiences displacements less than 4 cm, while 99.6% of the study area experiences displacements less than 15 cm. Displacements greater than 15 cm are observed in a very small area. Jibson et al. suggested that shallow, disrupted rock falls and rock slides in relatively brittle, poorly cemented sediments tend to collapse at small displacements [12,13]. Thus, the study area is more susceptible to shallow falls and slides. According to high-resolution aerial photographs and field investigations, most of the landslides triggered by the Lushan earthquake were rock falls and relatively shallow, disrupted slides, typically 1–5 m in depth [23,32,57]. Therefore, the proposed model is particularly useful for predicting the spatial distribution of the typical coseismic landslides in the study area.
Predicted displacements do not accurately reflect the actual slope movement in the field. Instead, modeled displacements serve as an indicator that can be correlated with field performance [12,13]. By using a function that incorporates Newmark displacement and CF, confidence levels of slope failure in the field can be estimated, and the spatial variation in coseismic landslides can be predicted under any set of ground-shaking conditions [12,13,34]. The number of Newmark displacement cells per 1 cm was uneven, so the predicted displacement cells were grouped into bins based on quantile statistics to obtain a more rational regression curve relating the predicted displacement and CF. The breakpoints were set at 0, 2, 4, 6, 15, 25, 44, 60, and 76, with an equal number of cells in each bin. For each bin, the proportion of cells in landslide areas was calculated, and the CF value of Newmark displacement was plotted as a dot. To fit the data, a modified Weibull [58] curve proposed by Zang et al. [8] was employed, with the following functional form:
C F = m 1 − exp ⁡ − a D b − 1 ,
where CF is the certainty factor, ( m − 1 ) is the maximum CF value, D is the predicted displacement, and a and b are the regression constants. The regression curve based on the Lushan data is:
C F = 1.254 1 − exp ⁡ − 0.669 D 0.682 − 1 .
The data fits the curve well with an R-squared value of 92%. The CF value can be used to directly predict the confidence level of slope failure as a function of Newmark displacement. Figure 13 shows, the CF value increases monotonically with increasing Newmark displacement. The CF value increases rapidly in the first 10 cm of Newmark displacement and then levels off abruptly after 15 cm range at a CF value of about 0.25.
Equation (8) takes the same forms as our previously published equation [34]. But the equation proposed in this study has different regression constants owing to a different data. Once calibrated, the curve and corresponding equation can be used in any set of ground-shaking conditions to predict the confidence level of slope failure as a function of predicted Newmark displacement [12,13]. However, a problem exposed by the earlier study should be noted. The maximum CF value is equal to ( m − 1 ) not m / 2 as indicated by Zang et al. [34]. The values of m , a , and b in Equation (8) may vary in other regions if the lithology, topography, and ground motion conditions significantly differ from those observed in the study area. Additionally, in regions where the predominant type of slope failure differs, the shape of the fitting curve in Figure 13 would probably exhibit some variations [12,13]. If rock falls and rock slides in more brittle materials were predominant, the fitting curve would likely be more steep and might flatten out at a smaller maximum displacement value [12,13,34].
Figure 9 shows the distribution of critical acceleration in the study area. The critical acceleration describes seismic susceptibility of a slope. Newmark [33] showed that the critical acceleration is a function of static factor of safety and slope angle (Equation (1)). Compare Figure 6 with Figure 8 and Figure 9, respectively, we found that the modeling procedure is heavily slope-driven, which is consistent with the findings from Jibson et al. [12,13]. However, compared Figure 11 with Figure 10, we observed that the distribution pattern of Newmark displacements bears a resemblance to that of PGA. Areas with displacements between 2–4 cm, 4–6 cm, and 6–15 cm are distributed in bands in the study area, indicating the dominant role of seismic ground motion in triggering coseismic landslides during the Lushan earthquake.
In Section 3, it was mentioned that during seismic activity, unstable rock blocks tend to slide along shallow un-loading joints. The static factor of safety is closely related to the shear strength of these rock joints. The conventional Newmark analysis traditionally describes the shear strength of rocks using Coulomb's constants, such as friction angle and cohesion, but these values vary significantly between laboratory conditions with high normal stress and field conditions with low normal stress [26]. Additionally, these values are also dependent on the scale of the analysis[46]. To address these challenges, we introduced the Barton model into the Newmark analysis. This model enables us to predict the shear strength of rock joints and reduce the variability associated with Coulomb's constants. Furthermore, we considered the impact of scale effects by incorporating Equation (3) and Equation (4) to prevent overestimation of the shear strength of geological units in regional analysis. We also conducted a conventional Newmark analysis using assigned strengths, such as friction angle and cohesion, as shown in Table 1. The predicted displacements obtained through the conventional Newmark's method ranged from 0 to 78 cm, whereas the proposed method yielded values ranging from 0 to 76 cm. Subsequently, the calculation of the CF using the conventional Newmark analysis produced a range of -1 to 0.74, while the proposed method resulted in a range of -1 to 0.99. To evaluate the performance of the two methods, we utilized the area under the curve (AUC) analysis. The AUC plot illustrates the cumulative area of CFs within each interval of calculated values, representing the proportion of the total study area (x-axis), and the proportion of cumulative landslides falling within those CFs (y-axis) [59]. An AUC value of 0.5 suggests performance no better than random guessing, while a value of 1 indicates perfect performance [59]. Figure 14 depicts the results of the AUC analysis for both methods, with a calculated value of 0.57 for the proposed method and 0.53 for the conventional Newmark's method. Therefore, the introduced method yields improved results compared to the conventional Newmark analysis.
However, it is noteworthy that both methods yield relatively not large AUC values. This outcome can be attributed to the seismic landslide interpretation data employed in the analysis. As is well-known, landslides can be categorized into three distinct areas: the source area, the transport area, and the deposition area. The interpretation data utilized for the calculations encompasses all three areas. The initiation of landslides occurs in the source area, while the deposition area is where the landslide material comes to rest. The source area is typically characterized by steep slopes, leading to relatively large Newmark displacements that align with the model's predictions. Conversely, the deposition area tends to exhibit flatter terrain with smaller slopes, resulting in relatively smaller Newmark displacements. Nevertheless, following the occurrence of a landslide, a substantial amount of material accumulates in the deposition area. Consequently, a significant portion of the landslide area in the interpretation data falls within regions associated with smaller Newmark displacements. This leads to deviations in the predictive outcomes of the model. To achieve more accurate results, it is crucial to precisely delineate the source area of seismic landslides and employ it as the primary input for hazard assessment. This aspect warrants considerable attention in future assessments of seismic landslide hazards.

6. Conclusions

This study presents a pioneering method to assess the coseismic landslide hazards triggered by the 2013 Lushan earthquake, incorporating the roughness of potential sliding surfaces in the inner slope. The primary findings are outlined below:
(1) The process of mapping data from the 2013 Lushan earthquake demonstrates the viability of integrating Newmark analysis with Barton’s shear strength criterion. This approach holds practical utility in evaluating regional seismic hazards.
(2) By associating Newmark displacements with the certainty factor model, the effectiveness of Newmark’s method in predicting the hazard posed by coseismic landslides was enhanced.
(3) The outcomes of the AUC analysis demonstrate the higher reliability of the proposed method compared to the conventional Newmark approach.

Author Contributions

Conceptualization, M.Z. and S.Q.; methodology, G.L. and M.Z.; validation, T.L.; formal analysis, G.L., M.Z., and T.L.; investigation, M.Z.; resources, M.Z.; data curation, M.Z.; writing—original draft preparation, G.L. and M.Z.; writing—review and editing, M.Z., S.Q., and G.Y.; project administration, S.Q. and J.B.; funding acquisition, M.Z. and S.Q. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (grant nos. 41825018 and 42207215).

Data Availability Statement

Data will be made available on request.

Acknowledgments

The authors thank the National Natural Science Foundation of China (grant nos. 41825018 and 42207215). We appreciate the insightful comments from the reviewing experts and academic editor, which significantly enhanced the quality of this manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Keefer, D.K. Landslides Caused by Earthquakes. Geol Soc Am Bull GSA Bull. 1984, 95, 406–421. [Google Scholar] [CrossRef]
  2. Terzaghi, K. Mechanism of Landslides. In Application of Geology to Engineering Practice; Paige, S., Ed.; Geological Society of America: New York, N. Y, 1950; pp. 83–123. ISBN 0-8137-4301-X. [Google Scholar] [CrossRef]
  3. Clough, R.W.; Chopra, A.K. Earthquake Stress Analysis in Earth Dams. J. Eng. Mech. Div. 1966, 92, 197–212. [Google Scholar] [CrossRef]
  4. Newmark, N.M. Effects of Earthquakes on Dams and Embankments. Géotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
  5. Jibson, R.W. Methods for Assessing the Stability of Slopes during Earthquakes—A Retrospective. Eng. Geol. 2011, 122, 43–50. [Google Scholar] [CrossRef]
  6. Franklin, A.G.; Chang, F.K. Earthquake Resistance of Earth and Rock-Fill Dams: Report 5, Permanent Displacements of Earth Embankments by Newmark Sliding Block Analysis; Department of Defense, Department of the Army, Corps of Engineers, Waterways Experiment Station, Soils and Pavements Laboratory, 1977. [Google Scholar]
  7. Makdisi, F.I.; Seed, H.B. Simplified Procedure for Estimating Dam and Embankment Earthquake-Induced Deformations. J. Geotech. Eng. Div. 1978, 104, 849–867. [Google Scholar] [CrossRef]
  8. Bray, J.D.; Rathje, E.M. Earthquake-Induced Displacements of Solid-Waste Landfills. J. Geotech. Geoenvironmental Eng. 1998, 124, 242–253. [Google Scholar] [CrossRef]
  9. Bray, J.D.; Travasarou, T. Simplified Procedure for Estimating Earthquake-Induced Deviatoric Slope Displacements. J. Geotech. Geoenvironmental Eng. 2007, 133, 381–392. [Google Scholar] [CrossRef]
  10. Rathje, E.M.; Bray, J.D. An Examination of Simplified Earthquake-Induced Displacement Procedures for Earth Structures. Can. Geotech. J. 1999, 36, 72–87. [Google Scholar] [CrossRef]
  11. Rathje, E.M.; Bray, J.D. Nonlinear Coupled Seismic Sliding Analysis of Earth Structures. J. Geotech. Geoenvironmental Eng. 2000, 126, 1002–1014. [Google Scholar] [CrossRef]
  12. Jibson, R.W.; Harp, E.L.; Michael, J.A. A Method for Producing Digital Probabilistic Seismic Landslide Hazard Maps; an Example from the Los Angeles, California, Area. Open-File Rep. 1998. [Google Scholar] [CrossRef]
  13. Jibson, R.W.; Harp, E.L.; Michael, J.A. A Method for Producing Digital Probabilistic Seismic Landslide Hazard Maps. Eng. Geol. 2000, 58, 271–289. [Google Scholar] [CrossRef]
  14. Yuan, R.; Deng, Q.; Cunningham, D.; Han, Z.; Zhang, D.; Zhang, B. Newmark Displacement Model for Landslides Induced by the 2013 Ms 7.0 Lushan Earthquake, China. Front. Earth Sci. 2016, 10, 740–750. [Google Scholar] [CrossRef]
  15. Zhang, Y.; Xiang, C.; Chen, Y.; Cheng, Q.; Xiao, L.; Yu, P.; Chang, Z. Permanent Displacement Models of Earthquake-Induced Landslides Considering near-Fault Pulse-like Ground Motions. J. Mt. Sci. 2019, 16, 1244–1257. [Google Scholar] [CrossRef]
  16. Jibson, R.W. Regression Models for Estimating Coseismic Landslide Displacement. Eng. Geol. 2007, 91, 209–218. [Google Scholar] [CrossRef]
  17. Zhang, Y.; Xiang, C.; Yu, P.; Zhao, L.; Zhao, J.X.; Fu, H. Investigation of Permanent Displacements of Near-Fault Seismic Slopes by a General Sliding Block Model. Landslides 2022, 19, 187–197. [Google Scholar] [CrossRef]
  18. Gu, D. Engineering Geomechanics of Rock Mass; Science Press: Beijing, 1979. [Google Scholar]
  19. Hoek, E.; Bray, J.D. Rock Slope Engineering; 3rd editon.; Taylor & Francis: Abingdon, 1981. [Google Scholar]
  20. Harp, E.L.; Jibson, R.W. Landslides Triggered by the 1994 Northridge, California, Earthquake. Bull. Seismol. Soc. Am. 1996, 86, S319–S332. [Google Scholar] [CrossRef]
  21. Khazai, B.; Sitar, N. Evaluation of Factors Controlling Earthquake-Induced Landslides Caused by Chi-Chi Earthquake and Comparison with the Northridge and Loma Prieta Events. Eng. Geol. 2004, 71, 79–95. [Google Scholar] [CrossRef]
  22. Dai, F.C.; Xu, C.; Yao, X.; Xu, L.; Tu, X.B.; Gong, Q.M. Spatial Distribution of Landslides Triggered by the 2008 Ms 8.0 Wenchuan Earthquake, China. J. Asian Earth Sci. 2011, 40, 883–895. [Google Scholar] [CrossRef]
  23. Tang, C.; Ma, G.; Chang, M.; Li, W.; Zhang, D.; Jia, T.; Zhou, Z. Landslides Triggered by the 20 April 2013 Lushan Earthquake, Sichuan Province, China. Eng. Geol. 2015, 187, 45–55. [Google Scholar] [CrossRef]
  24. Qi, S.; Yan, C.; Liu, C. Two Typical Types of Earthquake Triggered Landslides and Their Mechanisms.; Banff, Canada, June 3 2012; pp. 1819–1823.
  25. Zang, M.; Qi, S.; Zou, Y.; Sheng, Z.; Zamora, B.S. An Improved Method of Newmark Analysis for Mapping Hazards of Coseismic Landslides. Nat. Hazards Earth Syst. Sci. 2020, 20, 713–726. [Google Scholar] [CrossRef]
  26. Barton, N. Review of a New Shear-Strength Criterion for Rock Joints. Eng. Geol. 1973, 7, 287–332. [Google Scholar] [CrossRef]
  27. Xu, X.-W.; Jiang, G.-Y.; Yu, G.-H.; Wu, X.-Y.; Zhang, J.-G.; Li, X. Discussion on Seismogenic Fault of the Ludian Ms6.5 Earthquake and Its Tectonic Attribution. Chin. J. Geophys. 2014, 57, 3060–3068. [Google Scholar]
  28. Xu, X.; Wen, X.; Han, Z.; Chen, G.; Li, C.; Zheng, W.; Zhnag, S.; Ren, Z.; Xu, C.; Tan, X.; et al. Lushan MS7.0 Earthquake: A Blind Reserve-Fault Event. Chin. Sci. Bull. 2013, 58, 3437–3443. [Google Scholar] [CrossRef]
  29. Han, Z.; Ren, Z.; Wang, H.; Wang, M. The Surface Rupture Signs of the Lushan “4.20” Ms 7.0 Earthquake at Longmen Township, Lushan County and Its Discussion. Seismol. Geol. 2013, 35, 388–397. [Google Scholar]
  30. Chen, X.L.; Yu, L.; Wang, M.M.; Lin, C.X.; Liu, C.G.; Li, J.Y. Brief Communication: Landslides Triggered by the Ms = 7.0 Lushan Earthquake, China. Nat. Hazards Earth Syst. Sci. 2014, 14, 1257–1267. [Google Scholar] [CrossRef]
  31. Xu, C.; Xu, X.; Zheng, W.; Wei, Z.; Tan, X.; Han, Z.; Li, C.; Liang, M.; Li, Z.; Wang, H.; et al. Landslides Triggered by the April 20, 2013 Lushan, Sichuan Province Ms 7.0 Strong Earthquake of China. Seismol. Geol. 2013, 35, 641–660. [Google Scholar]
  32. Xu, C.; Xu, X.; Shyu, J.B.H. Database and Spatial Distribution of Landslides Triggered by the Lushan, China Mw 6.6 Earthquake of 20 April 2013. Geomorphology 2015, 248, 77–92. [Google Scholar] [CrossRef]
  33. Newmark, N.M. Effects of Earthquakes on Dams and Embankments. Géotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
  34. Zang, M.; Qi, S.; Zou, Y.; Sheng, Z.; Zamora, B.S. An Improved Method of Newmark Analysis for Mapping Hazards of Coseismic Landslides. Nat. Hazards Earth Syst. Sci. 2020, 20, 713–726. [Google Scholar] [CrossRef]
  35. Khazai, B.; Sitar, N. Evaluation of Factors Controlling Earthquake-Induced Landslides Caused by Chi-Chi Earthquake and Comparison with the Northridge and Loma Prieta Events. Eng. Geol. 2004, 71, 79–95. [Google Scholar] [CrossRef]
  36. Barton, N.; Bandis, S. Effects of Block Size on the Shear Behavior of Jointed Rock; Berkeley: California, USA, 1982; pp. 739–760. [Google Scholar]
  37. Ambraseys, N.N.; Menu, J.M. Earthquake-Induced Ground Displacements. Earthq. Eng. Struct. Dyn. 1988, 16, 985–1006. [Google Scholar] [CrossRef]
  38. Bray, J.D.; Travasarou, T. Simplified Procedure for Estimating Earthquake-Induced Deviatoric Slope Displacements. J. Geotech. Geoenvironmental Eng. 2007, 133, 381–392. [Google Scholar] [CrossRef]
  39. Saygili, G.; Rathje, E.M. Empirical Predictive Models for Earthquake-Induced Sliding Displacements of Slopes. J. Geotech. Geoenvironmental Eng. 2008, 134, 790–803. [Google Scholar] [CrossRef]
  40. Rathje, E.M.; Saygili, G. Probabilistic Assessment of Earthquake-Induced Sliding Displacements of Natural Slopes. Bull. N. Z. Soc. Earthq. Eng. 2009, 42, 18–27. [Google Scholar] [CrossRef]
  41. Hsieh, S.-Y.; Lee, C.-T. Empirical Estimation of the Newmark Displacement from the Arias Intensity and Critical Acceleration. Eng. Geol. 2011, 122, 34–42. [Google Scholar] [CrossRef]
  42. Shortliffe, E.H.; Buchanan, B.G. A Model of Inexact Reasoning in Medicine. Math. Biosci. 1975, 23, 351–379. [Google Scholar] [CrossRef]
  43. Heckerman, D. Probabilistic Interpretations for Mycin’s Certainty Factors* *This Work Was Supported in Part by the Josiah Macy, Jr. Foundation, the Henry J. Kaiser Family Foundation, and the Ford Aerospace Corporation. Computing Facilities Were Provided by the SUMEX-AIM Resource under NIH Grant RR-00785. In Machine Intelligence and Pattern Recognition : Uncertainty in Artificial Intelligence; KANAL, L.N., LEMMER, J.F., Eds.; North-Holland, 1986; Vol. 4, pp. 167–196. ISBN 0923-0459. [Google Scholar]
  44. Burrough, P.A.; McDonnell, R.A. Principles of Geographical Information Systems, 2nd ed.; Oxford University Press: Oxford, 1998; ISBN 0198322663. [Google Scholar]
  45. Coulson, J.H. Shear Strength of Flat Surfaces in Rock.; Cording, E.J., Ed.; American Society of Civil Engineers: Urbana, Illinois, United States, 1972; pp. 77–105. [Google Scholar]
  46. Barton, N.; Choubey, V. The Shear Strength of Rock Joints in Theory and Practice. Rock Mech. Felsmech. Mcanique Roches 1977, 10, 1–54. [Google Scholar] [CrossRef]
  47. Bandis, S.C.; Lumsden, A.C.; Barton, N.R. Fundamentals of Rock Joint Deformation. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 249–268. [Google Scholar] [CrossRef]
  48. Bilgin, H.A.; Pasamehmetoğlu, A.G. Shear Behaviour of Shale Joints under Heat in Direct Shear.; Barton, N., Stephansson, O., Eds.; CRC Press: Loen, Norway, 1990; pp. 179–183. [Google Scholar]
  49. Priest, S.D. Discontinuity Analysis for Rock Engineering; Springer Science & Business Media, 1993; ISBN 978-94-010-4656-5. [Google Scholar]
  50. Singh, T.N.; Kainthola, A.; Venkatesh, A. Correlation Between Point Load Index and Uniaxial Compressive Strength for Different Rock Types. Rock Mech. Rock Eng. 2012, 45, 259–264. [Google Scholar] [CrossRef]
  51. Rock Engineering and Rock Mechanics: Structures in and on Rock Masses; Alejano, R.; Perucho, Á.; Olalla, C.; Jiménez, R. (Eds.) CRC Press: Vigo, Spain, 2014. [Google Scholar]
  52. Giusepone, F.; Da Silva, L.A.A. Hoek & Brown and Barton & Bandis Criteria Applied to a Planar Sliding at a Dolomite Mine in Gandarela Synclinal.; International Society for Rock Mechanics and Rock Engineering: Goiania, Brazil, 2014. [Google Scholar]
  53. Photogrammetric Calculation of JRC for Rock Slope Support Design; Sirkiä, J.; Kallio, P.; Iakovlev, D.; Uotinen, L. (Eds.) 14 September 2016. [Google Scholar]
  54. Yong, R.; Ye, J.; Liang, Q.-F.; Huang, M.; Du, S.-G. Estimation of the Joint Roughness Coefficient (JRC) of Rock Joints by Vector Similarity Measures. Bull. Eng. Geol. Environ. 2018, 77, 735–749. [Google Scholar] [CrossRef]
  55. Bao, H.; Zhang, G.; Lan, H.; Yan, C.; Xu, J.; Xu, W. Geometrical Heterogeneity of the Joint Roughness Coefficient Revealed by 3D Laser Scanning. Eng. Geol. 2020, 265, 105415. [Google Scholar] [CrossRef]
  56. Keefer, D.K. Landslides Caused by Earthquakes. GSA Bull. 1984, 95, 406–421. [Google Scholar] [CrossRef]
  57. Xu, C.; Xu, X.; Shyu, J.B.H.; Gao, M.; Tan, X.; Ran, Y.; Zheng, W. Landslides Triggered by the 20 April 2013 Lushan, China, Mw 6.6 Earthquake from Field Investigations and Preliminary Analyses. Landslides 2015, 12, 365–385. [Google Scholar] [CrossRef]
  58. Weibull, W. A Statistical Theory of the Strength of Materials; Generalstabens litografiska anstalts förlag: Stockholm, 1939. [Google Scholar]
  59. Miles, S.B.; Keefer, D.K. Evaluation of CAMEL — Comprehensive Areal Model of Earthquake-Induced Landslides. Eng. Geol. 2009, 104, 1–15. [Google Scholar] [CrossRef]
Preprints 86585 g001
Figure 1. Location of the study area and the interpreted landslides.
Figure 1. Location of the study area and the interpreted landslides.
Preprints 86585 g001
Preprints 86585 g002
Figure 2. Geological map of the study area.
Figure 2. Geological map of the study area.
Preprints 86585 g002
Preprints 86585 g003
Figure 3. Conceptual sliding-block model of Newmark analysis (adapted from Newmark 1965; Zang et al., 2020). α is the angle of the slope, t is the thickness of the failure rock block, A is a constant, and g is the acceleration due to the Earth’s gravity.
Figure 3. Conceptual sliding-block model of Newmark analysis (adapted from Newmark 1965; Zang et al., 2020). α is the angle of the slope, t is the thickness of the failure rock block, A is a constant, and g is the acceleration due to the Earth’s gravity.
Preprints 86585 g003
Preprints 86585 g004
Figure 4. Demonstration of the Newmark analysis algorithm (adapted from Wilson and Keefer, 1983; Jibson et al., 1998, 2000). a c is the critical acceleration in terms of g.
Figure 4. Demonstration of the Newmark analysis algorithm (adapted from Wilson and Keefer, 1983; Jibson et al., 1998, 2000). a c is the critical acceleration in terms of g.
Preprints 86585 g004
Preprints 86585 g005
Figure 5. Flow chart showing sequential steps of the hazard mapping procedure.
Figure 5. Flow chart showing sequential steps of the hazard mapping procedure.
Preprints 86585 g005
Preprints 86585 g006
Figure 6. Slope map derived from the DEM of the study area.
Figure 6. Slope map derived from the DEM of the study area.
Preprints 86585 g006
Preprints 86585 g007
Figure 7. Map showing shear strength components assigned to geological formations in the study area. (a) JRCn component of shear strength; (b) JCSn component of shear strength.
Figure 7. Map showing shear strength components assigned to geological formations in the study area. (a) JRCn component of shear strength; (b) JCSn component of shear strength.
Preprints 86585 g007
Preprints 86585 g008
Figure 8. Static factor-of-safety map of the study area.
Figure 8. Static factor-of-safety map of the study area.
Preprints 86585 g008
Preprints 86585 g009
Figure 9. Map showing critical accelerations in the study area.
Figure 9. Map showing critical accelerations in the study area.
Preprints 86585 g009
Preprints 86585 g010
Figure 10. Contour map of peak ground acceleration (PGA). PGA values shown are in g.
Figure 10. Contour map of peak ground acceleration (PGA). PGA values shown are in g.
Preprints 86585 g010
Preprints 86585 g011
Figure 11. Map showing predicted displacements in the study area.
Figure 11. Map showing predicted displacements in the study area.
Preprints 86585 g011
Preprints 86585 g012
Figure 12. Map showing confidence levels of coseismic landslides using the proposed method. Confidence levels are portrayed in terms of values of CF.
Figure 12. Map showing confidence levels of coseismic landslides using the proposed method. Confidence levels are portrayed in terms of values of CF.
Preprints 86585 g012
Preprints 86585 g013
Figure 13. CF as a function of Newmark displacement. A dot shows the CF value of a Newmark displacement bin; the red line is the fitting curve of the data using a modified Weibull function.
Figure 13. CF as a function of Newmark displacement. A dot shows the CF value of a Newmark displacement bin; the red line is the fitting curve of the data using a modified Weibull function.
Preprints 86585 g013
Preprints 86585 g014
Figure 14. Plots of area under the curve comparing the proposed method with the conventional Newmark’s method.
Figure 14. Plots of area under the curve comparing the proposed method with the conventional Newmark’s method.
Preprints 86585 g014
Table 1. Shear strengths assigned to rock types in the study area.
Table 1. Shear strengths assigned to rock types in the study area.
Rock type γ 1 ( kN / m 3 ) ϕ b J C S 0   ( MPa ) J R C 0 φ 1 c 1 ( kPa ) References
Carbonate 23.7 35° 150 9.3 44° 33 Bandis et al. (1983)
Singh et al. (2012)
Alejano et al. (2014)
Giusepone and da Silva (2014)
Yong et al. (2018)
Diorite 26.9 30° 200 6.8 50° 40 Sirkiä, et al. (2016)
Bao et al. (2020)
Dolomite 25.9 32° 140 9.5 43° 35 Singh et al. (2012)
Alejano et al. (2014)
Giusepone and da Silva (2014)
Limestone 21.5 37° 160 9 45° 30 Bandis et al. (1983)
Singh et al. (2012)
Yong et al. (2018)
Phyllite 28 28° 130 6 40° 20 Andrade and Saraiva (2008)
Sandstone 23.5 35° 100 6 42° 24 Coulson (1972)
Bandis et al. (1983)
Priest (1993)
Shale 24.9 27° 75 8 27° 16 Barton and Choubey (1977)
Bilgin and Pasamehmetoglu (1990)
1 Friction angle (φ), cohesion (c), and unit weight (γ) were derived from the Geological Engineering Handbook (Geological Engineering Handbook Editorial Committee, 2018).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated