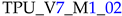Extrusion-Based Additive Manufacturing Driven Design and Testing of the Snapping Interlocking Metasurface Mechanism ShroomLock

Preprint

Article

Extrusion-Based Additive Manufacturing Driven Design and Testing of the Snapping Interlocking Metasurface Mechanism ShroomLock

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Philip Gloyer^‡,Lucca Nikita Schek^‡,

Hans Lennart Flöttmann,Paul Wüst,

Christina Völlmecke^*

Philip Gloyer^‡,Lucca Nikita Schek^‡,

Hans Lennart Flöttmann,Paul Wüst,

Christina Völlmecke^*

^‡ These authors contributed equally to this work.

This version is not peer-reviewed

Submitted:

10 October 2023

Posted:

11 October 2023

You are already at the latest version

Alerts

Abstract

This study presents the manufacturing process driven development of an interlocking metasurface mechanism (ILM) for Fused Filament Fabrication (FFF) with a focus on open-source accessibility. The presented ILM is designed to enable strong contact between to planar surfaces. The mechanism consists of spring elements and locking pins which snap together when forced into contact. The mechanism is designed to optimize mechanical properties, functionality and printability with common FFF printers. The mechanisms is printed from thermoplastic polyurethane (TPU) filament which was selected for its flexibility, crucial for spring element performance and tolerances of the fabrication method. To characterize the designed mechanism a tensile test is carried out to assess the holding force of the ILM. The force-displacement profiles are analyzed and categorized into distinct phases, highlighting the interplay between spring deformation, sliding, and disengagement. The results show variations in holding forces attributed to geometric and material-related factors. The testing results are compared and discussed to a numerical simulation carried out with a frictionless approach with a nonlinear Neo–Hookean material law. The study underscores the importance of meticulous parameter control in 3D printing for consistent and reliable performance of interlocking metasurface mechanisms. The investigation leads to a scalable model of a ILM element pair with a distinct three-phase snapping characteristics ensuring reliable holding capabilities.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Extrusion based additive manufacturing (AM), is one of the most used AM method and commonly referred to as 3D printing [1,2,3]. Complex designs, which can be challenging or even impossible to manufacture using conventional methods, can be fabricated using extrusion based approaches, e. g., FFF [4,5,6]. However, owing to the layer-wise deposition of material it also requires certain design constraints to be printable and lasting and foremost functional [3,6,7]. This might not be an issue for larger or less complex objects but may be challenging for more individual designs with smaller or more fragile components, or when considering reduction of filament consumption per printed specimen. Thus, a manufacturing process driven design appears to be essential for efficient and reliable production using material extrusion manufacturing such as fused filament fabrication (FFF) [8].

Interlocking metasurfaces (ILM), which are a type of architectured locking surfaces, can serve as an example of this shape complexity. Here, naturally non-occurring structured surface pairs are designed that can be temporarily connected or permanently joined to open up new mounting possibilities between surfaces. These pairs can be constructed with similarly shaped (androgynous) or with topologically different features (e. g., tongue and groove) [9]. The properties of parts manufactured by fused filament fabrication (FFF) can differ, for example, from components manufactured by injection molding [6,10].

Accordingly, there is also an increasing academic interest in investigating basic properties of 3D printed parts to analyze an appropriate handling of the limitations and errors of different extrusion based AM [11].

ILMs have already been investigated by several research groups. A thorough overview and an introduction into the topic of ILMs may be found in [9]. Furthermore, in [12] experiments and simulations on T-slot sliding mechanisms and their implementation in aerospace technology were conducted. Topology optimized ILMs with sliding characteristics have also been investigated in [13]. Additionally, a study on modeling and testing interlocking structures fabricated with additive layer manufacturing processes (ALM) was published in [14].

In this work a similar approach to the aforementioned studies was adopted and a printable ILM was designed and investigated. However, in contrast to the aforementioned studies, the mechanism under investigation in this study does not possess sliding properties. Instead, it employs a behavior known as snapping. Snapping mechanisms entail substantial deformation during assembly and disassembly, with only minor deformation occurring during loading when the components are locked together. These mechanisms can be identified by their distinctive clicking behavior. Consequently, the locking characteristics significantly differ from those of sliding mechanisms, where deformation is not the driving force behind interlocking; rather, it results solely from the rigid geometry. The snapping interlocking mechanism developed within the scope of this work, named ShroomLock, consists of pin and spring elements which lock together. The pin elements securely snap into the spring elements, establishing a reversible connection between the two components. Once locked together, these elements can withstand forces up to a specific threshold, beyond which the unsnapping phase initiates. This capability enables the temporary fastening of two bodies to each other. To establish a connection between these two bodies, both elements have to be distributed over the contacting surfaces, thereby creating two corresponding metasurfaces. Due to the element wise nature of this ILM, the mechanical features of the surface connection can be traced back to a single representative cell. This drastically simplifies the study of this ILM.

In this manuscript, the design of ShroomLock is explained and evaluated. For this, the testable representative cell is 3D printed using the FFF printing method. Experimental and numerical testing is carried out. To achieve an elastic snapping connection, a flexible filament material is used for fabrication. Thermoplastic polyurethane (TPU) is characterized by its higher elongation at break and elasticity compared to polylactide (PLA) based filaments. This behavior can be advantageous for the necessary deformation during assembly of the mechanism [15].

The manufactured parts are tested for their holding force in the closing direction in tensile tests on a Zwick/Roell zwickiLine z2.5 kN testing machine (ZwickRoell GmbH & Co. KG, Ulm, Germany). This allows a characterization of a force-displacement curve and a possible maximum holding force of a representative element of the mechanism can be determined.

The design and fabrication processes are discussed in Section 2 and Section 3 respectively. The conduction of the experimental investigation is documented in Section 4 and its evaluation is carried out in Section 5. Numerical simulations of the mechanism using the open source library FEniCSx [16,17] are introduced in Section 6 and finally in Section 7 possibilities, prospective applications and limitations for the designed ILM are discussed. All measured data, design files as well as the code for numerical testing is available in a public repository which is linked in the data availability statement.

2. Additive manufacturing method driven design

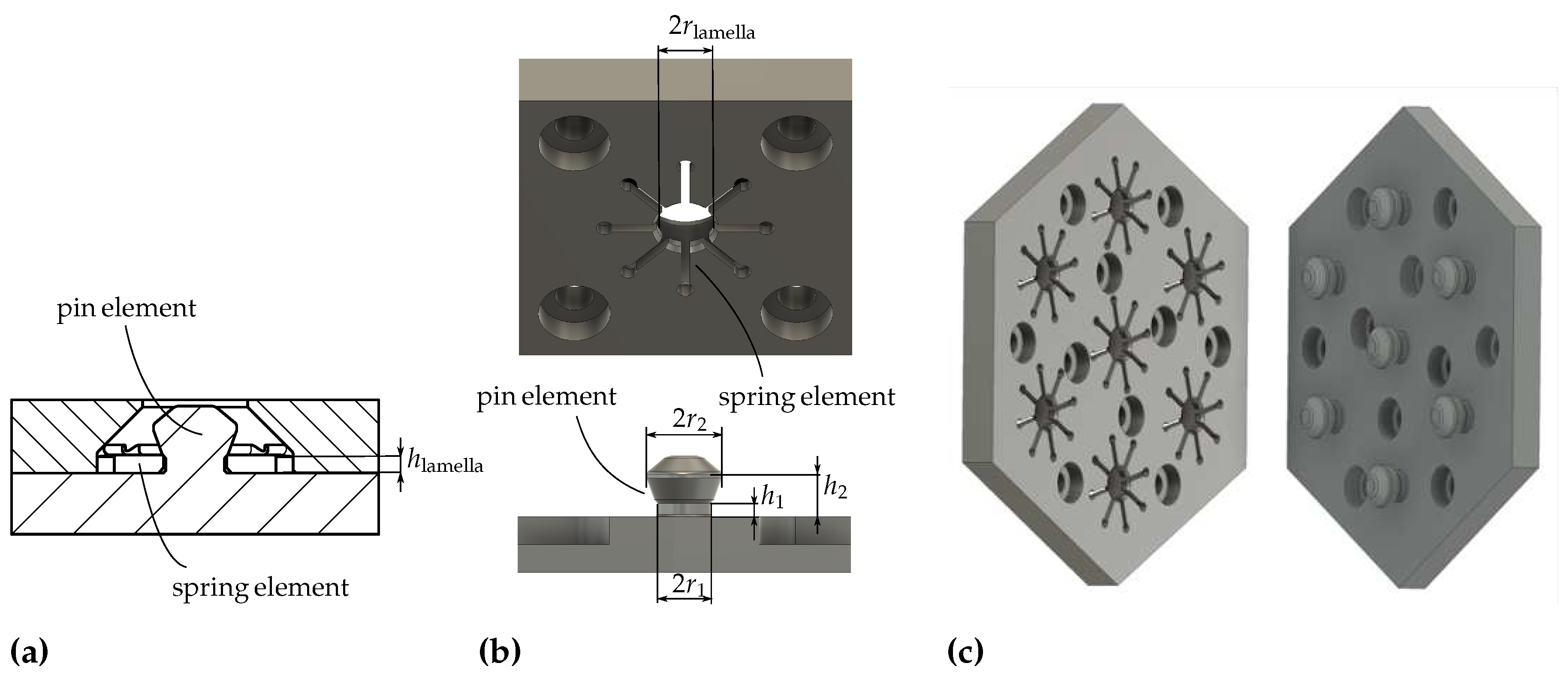
To obtain the optimal shape of the pin and spring elements (see Figure 1a) the possibilities of the printing methods have to be taken into account. The design goal is to achieve a high strength, i. e. large holding force, and a reliable snapping behavior. However, the shape which allows great snapping performance as well as the best holding power may not be printable at all. The design of the interlocking metasurface is therefore mostly driven by the choice of the manufacturing process, and the elements have to be optimized for strength and snapping under the restrictions given by the manufacturing method. As the intended mechanism is aimed to be an open source project and printable for the majority of users, e. g. in the 3D printing community, the FFF or FDM method is used, since it is one of the most commonly used 3D printing method.

The ILM elements are designed to be reasonably small, i. e. height and width are smaller than 10 mm, to maximize adaptability to specific applications. Here the strength of the pin element has to be considered w.r.t. its size. A smaller pin will result in a smaller holding force, however a smaller pin will also allow for a higher distribution density on the targeted surface which results in a higher holding force over the surface. Smaller pins will also distribute the loading more evenly over the contacting surfaces. The choice to design the smallest possible pin was therefore made, where the minimal pin size was restricted by the available printer’s characteristics. Aspects such as the line width when printing had to be considered for the minimum pin diameter, these key values which the pin dimensions are tied to are listed in Table 1.

The ILM was traced back to a representative individual mechanism cell for the design process and further studies. The individual mechanism comprises two components. On one side, there are radially arranged spring elements with an undercut feature between each lamella (see Figure 1a and Figure 1b). These spring elements can be printed flat (horizontally), ensuring higher strength and consistency among the lamellae since the printing path of each element will be similar and fragile parallel filament tracks are avoided. For the functionality of the spring elements, elastic material properties as found with TPU are mandatory. On the other side, there is a pin specifically designed to interact with the spring elements. When the pin is inserted, it pushes the spring elements aside and guides them to the locking position. To maintain the desired locking performance over multiple cycles of engagement and disengagement, a proper fit between the pin element and the upper and lower faces of the spring element is necessary. On the one hand, this is ensured by the relation between

h_{1}

and

h_{lamella}

from Table 1. Here, to compensate the tolerances in 3D printing and circumvent play between the two elements in the snapped state,

h_{1}

is chosen to be smaller than

h_{lamella}

in the design files, see Figure 1a. After printing, this results in the snapping condition being fulfilled and both heights being roughly equal. This results from the fact that the first layers of the lamellae are also the first layers on the print bed, resulting in a thinner profile. To ensure the relation between both heights, proper bed alignment is inevitable. On the other hand, chamfers and tapers have to be added to the contacting edges to ensure a proper fit and prevent wear. A taper is added to the lower part of the pin element’s neck to compensate over extrusion, this has to be matched with a chamfer on the lower face of the spring element to avoid contact between the two elements. On the upper part of the pin element’s neck, a taper is added to ease the transition from neck to pin. No matching chamfer is added to the spring element to ensure a snug fit of the lamellae between the bottom surface contact and the upper surface’s edge resting on the upper pin taper. With this, over-extrusion in the initial layer can be compensated and an undercut on the pin side can be avoided. The pin side of the representative mechanism is also printed parallel to its connecting surface. Although this may not be the ideal printing orientation, it is necessary to avoid support structures and, thus, enhance the printing quality. To strengthen layer adhesion, the pin itself is meant to be manufactured solidly. Preliminary tests at various pull speeds showed no visual impairments. A demonstrator was designed to show how the individual mechanisms could be arranged to work as an ILM, as shown in Figure 1c. For applying the ShroomLock geometry to more complicated objects, the printability has to be evaluated for each specific object shape.

Table 2. Characteristic dimensions of developed ILM.

Parameter	Value
$r_{lamella}$	$2.6$
$h_{lamella}$	$1.5$
$r_{1}$	$2.4$
$r_{2}$	$3.4$
$h_{1}$	$1.2$
$h_{2}$	$3.5$

3. Materials and Methods

In initial approaches, the mechanism was printed with two different materials, PLA for the pin element and TPU for the spring element. The quality of the pins printed with PLA is significantly higher than extruded with TPU, the latter requires specific adjustment of print parameters and can be susceptible to imperfections and stringing in the extrusion printing process. However, one of the aims is to implement a workflow without changing filaments, and thus recalibration of the printer and changing printer settings. Consequently, this leads to the choice of the flexible filament. Furthermore, the authors expected possible damage to the pin parts if printed with less flexible materials in case as the matching surface elements are not aligned perfectly, due to the user or printing discrepancies. Using TPU can allow for a greater tolerance regarding the range of the pin-movement and thus decrease the possibility for damage to the parts. Though, printing with TPU can cause issues during the creation of the print profile since flexible material requires a different approach than stiffer materials i. e. retraction and flow rate, since the filament bends whilst retraction and compresses while being extruded outwards.

For the following investigation, a total of 8 pairs of the individual ILM cells were printed with an Anycubic Vyper FFF printer (Anycubic, Shenzhen, Guangdong, China). The FFF printer is equipped with a standard

0.4 mm

nozzle. Due to its high elongation at break of 490% and relatively easy processability, the filament FLEX HARD (

1.75 mm

) from extrudr (Extrudr | FD3D GmbH, Lauterach, Austria) was chosen as the printing material. FLEX HARD (

1.75 mm

) is a hard TPU with a shore hardness of D58, which to put the material into perspective is harder than skateboard wheels. Ultimaker Cura (Ultimaker B.V., Geldermalsen, The Netherlands) was selected as the slicing software. For the manufacturing of the ILM mechanisms, an optimized TPU printing profile was created. The key printing parameters are summarized in Table 3. The complete printing profile can be found in the provided repository, see the data availability statement below. The layer height is set to 0.1 mm, ensuring fine details and smoother surfaces. To prevent under extrusion due to TPU’s flexibility, the flow rate is increased to 103 %, guaranteeing consistent material deposition. Enhancing strength and durability, the wall thickness is set to

2.4 mm

, providing full material in the pins. To avoid potential issues with snapping, random z seam alignment is employed, reducing the risk of consistent vertical z seams. Aligning the top/bottom thickness with the height

h_{lamella}

of the spring elements at

1.5 mm

ensures maximum strength. To maintain precise print quality, the combing mode is set to “All”, keeping the nozzle inside the printed object to minimize stringing. Print cooling is enabled to further enhance print quality by optimizing layer adhesion and reducing stringing during the printing process.

4. Experimental Tensile Test Series

The pairs of measurements, pin and spring element, are examined for their holding force in the direction of joining, i. e. orthogonal to the surface. The goal is to create a characteristic curve of the holding force over the displacement, as well as to determine a maximum holding force. To minimize potential changes in material properties resulting from storage and environmental factors, the individual components are 3D printed from the same TPU roll, and the time interval between printing and testing is kept equally for both test sets. The experimental examination was conducted in two sessions, with four mechanisms tested during each session.

The tensile tests are performed on a Zwick/Roell testing machine (ZwickRoell GmbH & Co. KG, Ulm, Germany) of the zwickiLine z2.5 TN series with a linear measuring range of

2.5

kN. Further specifications are documented in Table 4.

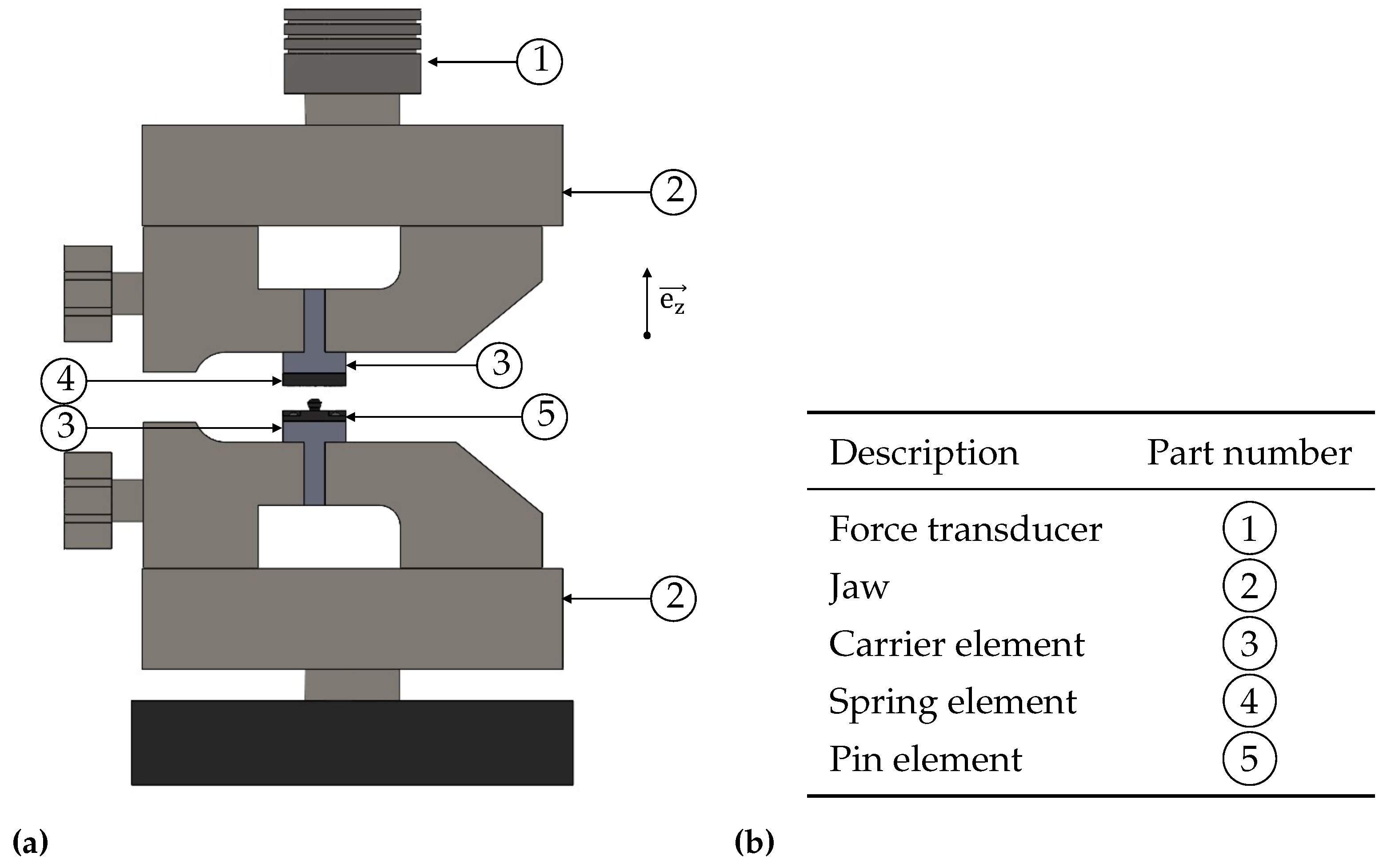
Figure 2a shows the experimental setup of the test series. The components to be tested, pin ④ and spring element ⑤, are fastened to the carrier elements ③ using threaded screws, which are clamped in the jaws of the testing machine ②. The carrier elements are 3D printed from PLA and equipped with insert nuts. The use of the carrier elements prevents possible influences of the jaws on the test objects, e. g. due to possible deformation when the measurement pairs are directly attached to the machine, and increases repeatability due to its assembly guides. The upper jaw is connected to the traverse for vertical displacement via the force transducer ①.

The test objects are screwed to the carriers and then connected for the first time using the snap mechanism. Initially, the assembled mechanism is clamped in the lower jaw, and the upper part of the testing machine is moved to the desired position, i. e., at the height of the carrier of the spring element. The system is tared before clamping the upper part. Eight mechanisms are investigated with four tensile tests each. Each tensile test consists of a full loading cycle up to the unsnapping of the pin from the spring element.

The pairs of elements are named consecutively with the printing material (TPU), the model version of the CAD model (VX), the pair of measurements (MY, 1 to 8), and the tensile test number (ZZ, 01 to 04). For example, the naming of the first pair of measurements of the seventh model version (V7)(M1) with the second tensile test (02) is shown:

5. Evaluation and Discussion

The focus of the evaluation will be first on the results of a case study of one of the printed mechanism pairs. This includes presenting all four measurements of that mechanism pair along with the mean calculation and the respective 95% confidence interval between different measurements of the unsnapping. Then the results for different mechanism pairs are compared with each other to evaluate and discuss the repeatability of the production of the ILM mechanism. Finally, an average of all means over the different printed mechanisms along with the confidence interval is calculated, and a correlation between the force profile and geometry is established.

5.1. Individual Results and Comparison

For each mechanism, a diagram with the force-displacement curves from the 4 tests is created, as shown in Figure 3a, representatively for the third test pair. What is immediately noticeable is that the first measurement - and with that the very first snap the mechanisms endured - has a significantly higher unlocking force. The same behavior is also shown by all other printed pairs. This systematic behavior suggests that after the first load cycle, which consists of the first snap to bring the elements together and then the first unsnap to separate them again, the elastic shakedown is reached [18]. For all further loading cycles no continued accumulation of plastic strain occurs as the unchanging force curves for the remaining measurements suggests. The material undergoes at first a slight plastic deformation where a higher force is needed, but then settles in an elastic response after the shakedown has been reached where a lower force is needed to reach the same displacement. To examine the mechanical features of the locking mechanism in its working range, only the measured data for the loading cycles after the elastic shakedown has been reached, is considered. Measurements preceding the elastic shakedown were excluded for all further analyses.

The three remaining curves of each test pair are averaged (full-colored curve) and presented including the standard deviation within a

95 %

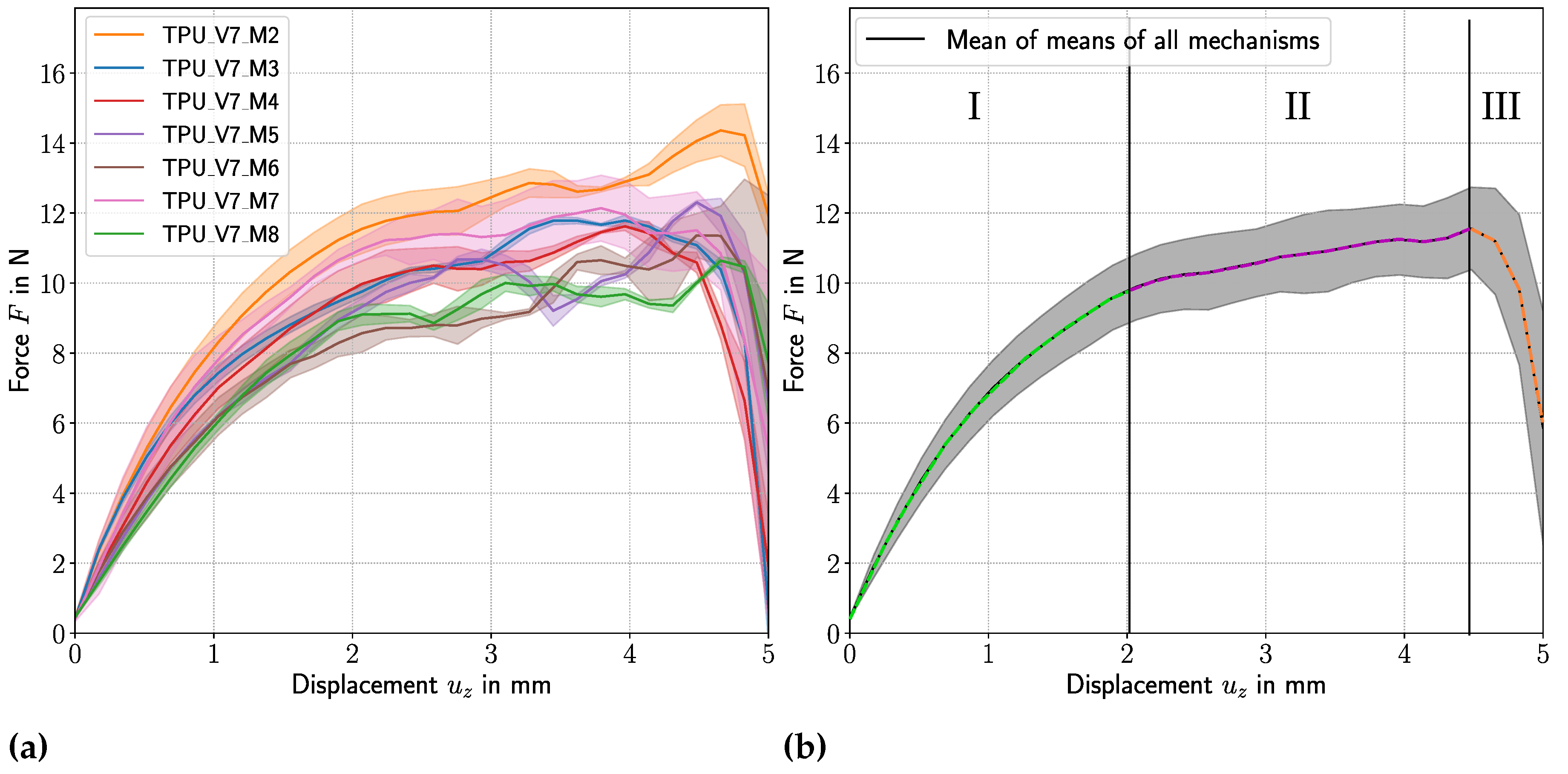
confidence interval (shaded areas), as illustrated in Figure 3b, representatively for the third mechanism. In this case, a nearly imperceptibly low standard deviation is evident in the range of 0 mm to 5 mm. Similar behavior with relatively small standard deviations can be observed across all test series. For comparison, the individual means and SD of the respective test mechanisms are displayed in one diagram in Figure 4a. It is apparent here that the measurements of TPU_V7_M2 especially between 4 mm to 5 mm significantly stand out compared to the other mechanisms. Possible explanations include microscopic deviations in the shape of the elements due to their different locations on the printing bed during manufacturing. Additionally, these differences may lead to slight positioning variations of the mechanism on the testing machine. This, in turn, can result in the lamella element not being perfectly aligned with the pin element during the tensile tests, leading to a higher maximum holding force when pulled apart.

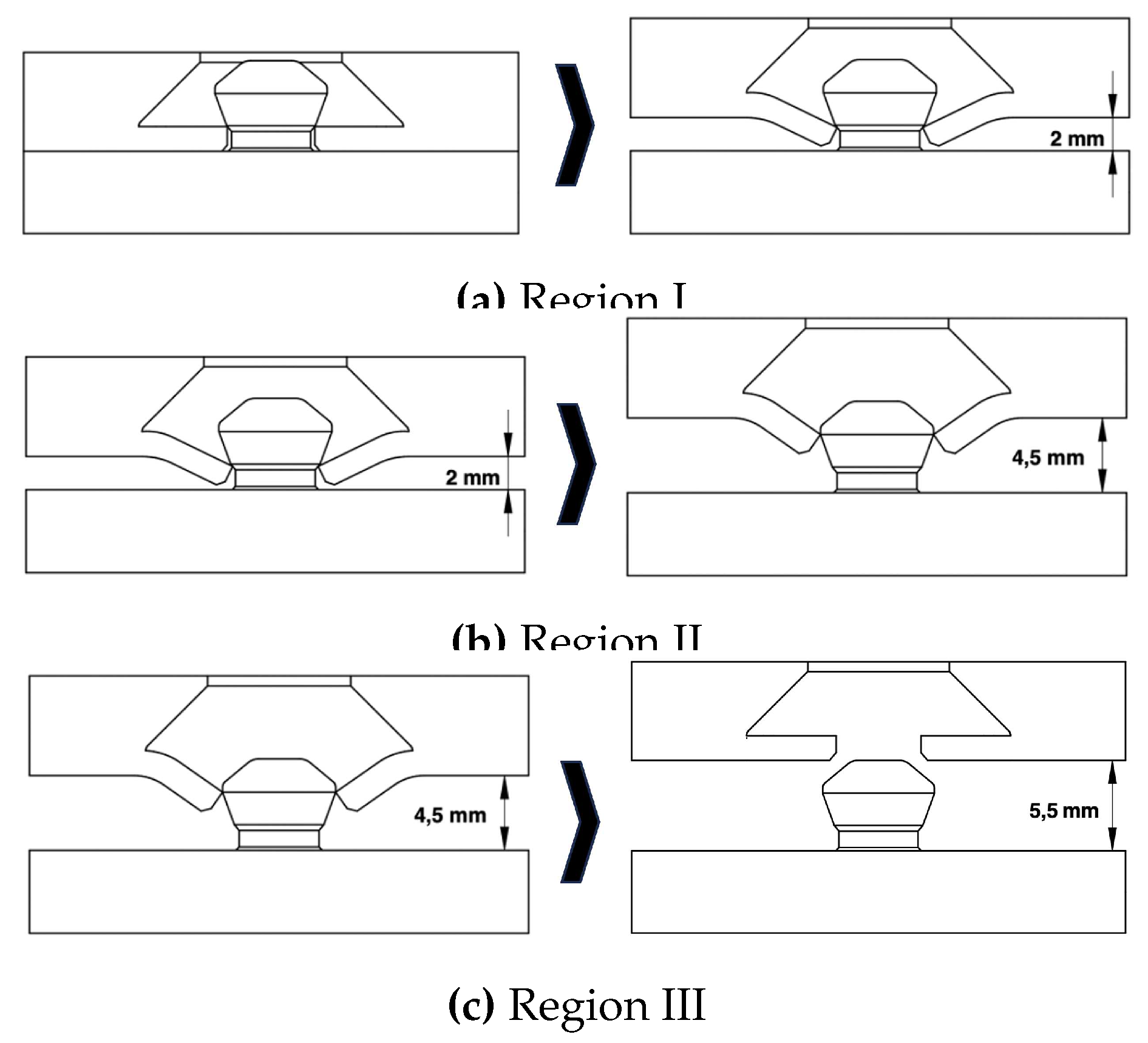
5.2. Geometry Force-Profile Relationship

Averaging all the individual means of all tensile tests results in a force-displacement curve as shown in Figure 4b. In this figure, the force profile is segmented into three distinct regions, enabling a correlation between the force profile and the geometry of the representative mechanisms.

In region I, the lamellae adhere to the bevel of the pin, causing a deformation which establishes a spring force in the z-direction (see Figure 5a). Here, no relative displacement between the pin and the spring element occurs.

In region II, the deformation of the lamellae increases further, such that the spring force is large enough to move the spring element over the pin element’s bevel. The sliding of the lamellae along the pin, results in a frictional force opposing the direction of motion, which decreases the curve’s slope. Additionally, the lamellae continue to deform as the pin widens upwards, leading to a reaction force in the radial direction and a reaction force in the z-direction (see Figure 5b).

In region III, the mechanism disengages, the holding force reduces to zero, and the lamellae return to their initial position (see Figure 5c).

This distinct phase separation allows for a reliable characterization of the ILM. The holding force for the mechanisms is assigned to region I. Considering the standard deviation within the 95% confidence interval, an average maximum holding force for this region was measured of roughly

10

\pm

0.4 N to 0.8 N. Because of a significant maximum deviation of roughly 8 %, it is advisable to account for a safety margin. Consequently, a maximum overall holding force of

8.5

N is determined for a representative element of the presented type of ILM. In region II, the mechanism starts to lock out, and in region III, the mechanism is completely locked out. It can be observed that the overall curve runs smoothly, yet the mean profile of the individual mechanisms exhibit occasional slight force fluctuations in region II. In Figure 6, it becomes apparent that the precision of the pin varies. Especially in the area where the lamellae slide over the pin and the force curve settles into region II, some grooves are noticeable. This behavior is explained by the fact that individual lamellae jump into the grooves of the imperfections of the pin, leading to a brief relaxation and a slight reduction in the spring force in the z-direction.

5.3. Error Analysis

As stated, there are some artifacts and imperfections in the appearance of the test objects, noticeably on the pin-side. This could result from the choice of material, paired with the fabrication method, and lead to different behavior of the holding mechanisms between several prints. This is demonstrated by the partially erratic curve in region II of the individual test pieces. In any case, the FFF printing method – especially with printers that may not meet the manufacturing quality of an industrial-grade device – and filament material each can involve differences e. g. between each print, material batch or by changing environmental influences. Thus, material and printer influences might be investigated to narrow down the causes. While all mechanisms showed similar curve characteristics, variations in holding forces were measured. These differences can be attributed to discrepancies in alignment and centering during the tensile test series, as well as printing imperfections. For the investigation of the first set (TPU_V7_M1-4_XX), the curves of the first mechanism (TPU_V7_M1_XX) exhibited profiles significantly higher compared to the subsequent measurements. This discrepancy can be attributed to misalignment, resulting in the exclusion of results from the first mechanism as outliers. For comprehensive documentation, all data related to the tensile tests have been archived in the repository.

6. Numerical modeling of the mechanism

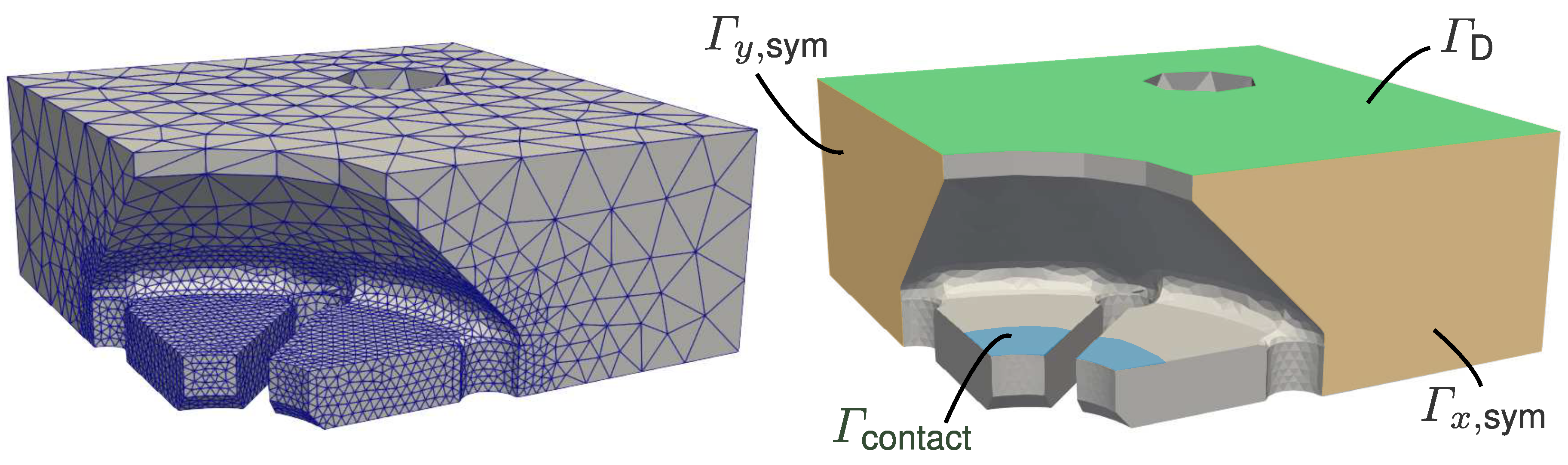
To assess the force and strain paths in the mechanism, as well as to help with future geometry optimization, a numerical analysis is carried out. The analysis may also be used to evaluate the mechanisms holding force. A corresponding boundary value problem (BVP) is formulated for the spring element ④. Its domain is discretized as

Ω

. The BVP is expressed as a minimization problem, seeking the displacement field

u : Ω \to R^{3}

that minimizes the total potential energy

Π

. The spring element is modeled as a hyperelastic medium where the total potential energy is obtained as the sum of elastic stored energy

Ψ

, the work of body- and traction-forces,

b

and

t

respectively

Π = \int_{Ω} Ψ (u) d V - \int_{Ω} b \cdot u d V - \int_{\partial Ω} t \cdot u d A .

(1)

The material is modeled by a nonlinear Neo–Hooke material law [19]

Ψ = \frac{μ}{2} (tr (C) - 3) - μ ln (J) + \frac{λ}{2} ln {(J)}^{2}

(2)

with the deformation gradient

F

, the right Cauchy–Green tensor

C

, the volume ratio J and the Lamé parameters

λ

and

μ

which in terms of the Young’s modulus E and Poisson ratio

ν

are given as [20]

λ = \frac{E}{(1 + ν) (1 - 2 ν)}, μ = \frac{E}{2 (1 + ν)} .

(3)

A variation of (1) yields in the weak equilibrium formulation (

δ Π = 0

) of the BVP for which in the numerical analysis, a piecewise solution

u

for varying

δ u

in a specific function space defined on the discretized domain is sought after. Two open-source software packages, GMSH [21] for meshing the domain and FEniCSx [16,17] for carrying out the numerical analysis, are used. Taking advantage of the symmetry of the spring element, the domain is reduced to a quarter of the actual component. This drastically reduces computation time. The corresponding mesh as well as the different boundary regions are depicted in Figure 7.

In the following, the BVP for modeling the unlocking of the mechanism is set up. The pin element ⑤ is assumed to be rigid and the contact during unlocking between it and the hyperelastic spring element is modeled. The setup is explained in Section 6.1, in Section 6.2 remarks on the modeling method are given and a comparison to the experimental testing from Section 5 is discussed.

6.1. Modeling the contact between two solids with FEniCSx

For modeling the proper contact between the rigid pin element and the hyperelastic spring element, a frictionless approach is realized similarly as has been explained for the classical Hertzian contact in [22]. Speaking in analogy to the classical Hertzian problem, the pin element may be referred to as the indenter, as it is pulled out of the spring element similar to an indentation where the indenter is pushed into an elastic medium. The surface is approximately1 parameterized in the z-direction by a linear function and the gap between it and the spring element in dependence of the prescribed distance during unlocking is denoted as

h (r) = - u_{pull} + \frac{h_{2} - h_{1}}{r_{2} - r_{1}} (r - r_{1}), for r \leq r_{2} .

(4)

This allows the formulation of the actual gap between the two components taking into account the z-displacement of the hyperelastic spring element

g (r) = h (r) - u_{z} (r) .

(5)

In the contact area

Γ_{contact}

the Signorini (see [22]) condition is formulated

\{\begin{matrix} p = 0, & g > 0 \\ p > 0, & g = 0 \end{matrix} \Rightarrow g p = 0 .

(6)

If there is no contact between the components the gap is nonzero and since the contact area is not loaded the pressure must be zero. If on the other hand the gap is zero, the contact area is loaded under the contact pressure which is in turn nonzero. This condition can be worked into the weak form by employing a large penalty parameter

k_{pen}

and the Mackauley bracket

{〈 \cdot 〉}_{+}

giving the positive part of the gap

\int_{Ω} \frac{\partial Ψ (u)}{\partial F} \cdot \cdot grad (δ u) d V = \int_{Ω} b \cdot δ u d V + \int_{\partial Ω} t \cdot δ u d A + k_{pen} \int_{Γ_{contact}} {〈 u_{z} - h 〉}_{+} d A .

(7)

Due to the nonlinearity of the problem in the contact formulation as well as in the Neo–Hookean material law, the weak form (7) is solved incrementally and

u_{pull}

is updated in small steps. The full BVP including the realization of the symmetry conditions reads as

\{\begin{matrix} u = 0, & in Γ_{D} \\ u \cdot e_{x} = 0, t \cdot e_{y} = 0, t \cdot e_{z} = 0, & in Γ_{x, sym} \\ u \cdot e_{y} = 0, t \cdot e_{x} = 0, t \cdot e_{z} = 0, & in Γ_{y, sym} \\ k_{pen} 〈 u_{z} - h (u_{pull}) 〉 = 0, & in Γ_{contact} \\ t = 0, & in \partial Ω ∖ {Γ_{D}, Γ_{contact}, Γ_{x, sym}, Γ_{y, sym}} . \end{matrix}

(8)

The penalty parameter

k_{pen}

, the z-displacement

u_{pull}

are chosen and the elasticity constants are provided by the filament manufacturer as

k_{pen} = 1 \times 10^{14}, u_{pull} = 4 mm, E = 40 MPa, ν = 0.45

(9)

and

u_{pull}

is updated in 200 time steps. Results are shown in Figure 8.

6.2. Examining the numerical results

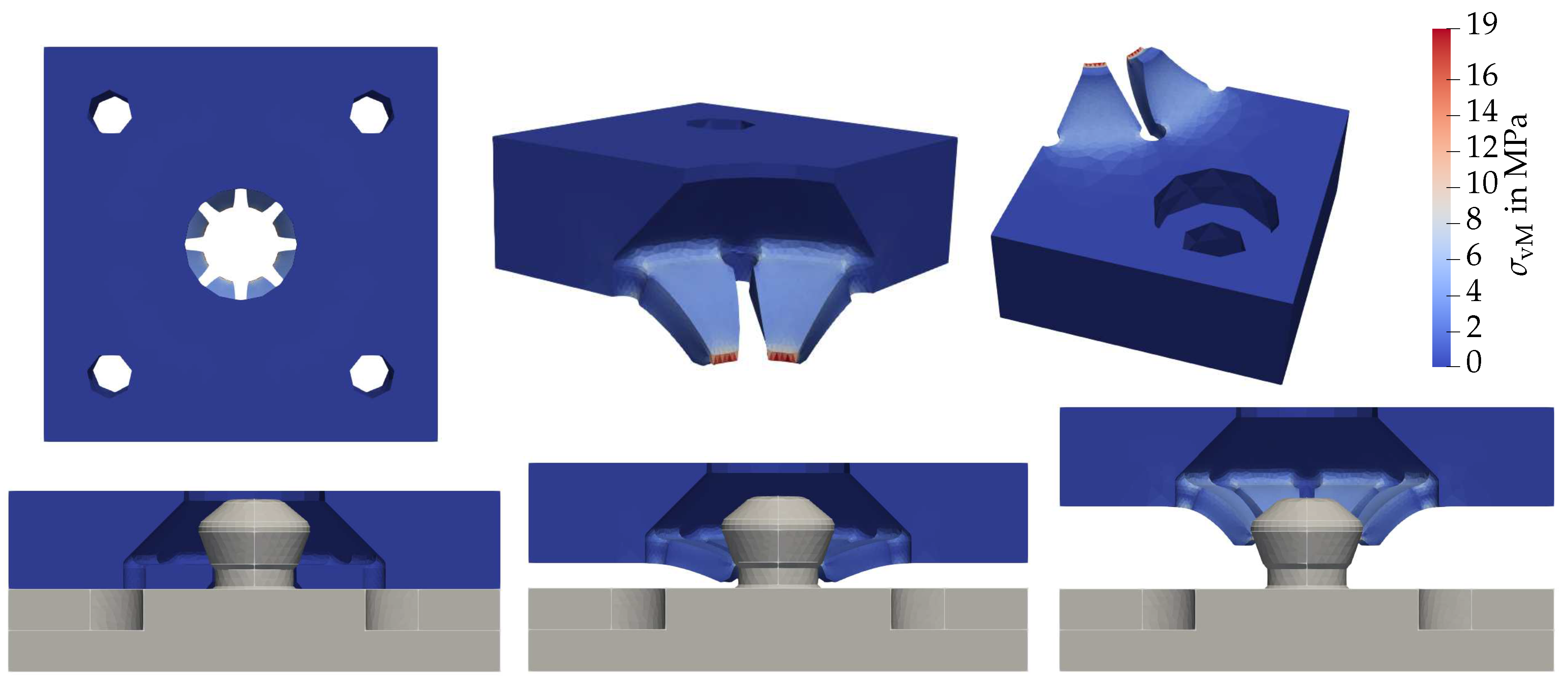
Examining the resulting displacement field, a good fit is noticeable. However, the strong limitations of this approach also become clear. As the contact area

Γ_{contact}

is assumed to be equal to the maximum radius of the pin element, a highly concentrated stress appears in

Γ_{contact}

. Compared to the actual loading which the spring element endures, this is rather unrealistic and the stress should be concentrated over a larger area. This limitation may easily be overcome by incrementally changing the contact area as the load increases. In that case, the reference position should always be set to the last resulting deformed mesh. This would then have an effect on the gap calculated between the pin and spring elements. Another aspect that should be mentioned is the choice of the penalty parameter. In this work it is chosen as a constant, however as it should directly correspond to the contact pressure a variable formulation where the solution is not only sought for the varying field

δ u

but also a varying pressure field

δ p

is worth looking into.

The force necessary to unsnap the components is found to be roughly

22

N, this differs significantly from the force measured in the experimental section of this work. The discrepancy is, however, easily explained by considering the origin of the material parameters. Manufacturers of 3D printing filaments give out the elasticity parameters for a normed and injection molded part. These parameters are helpful for comparing different filaments as they give relative information between two or more different filaments – if one material is stiffer than the other the provided elasticity parameters will certainly tell. The parameters however do not directly correspond to the actual parameters of the printed parts. On the one hand, the mismatch between the filament parameters and the parameters of the printed part is due to the difference in manufacturing. The normed, injection molded part undergoes different environmental influences compared to the 3D printed part. On the other hand, and probably more important to explain the mismatch, the difference in density of the part resulting from the different manufacturing methods is substantial. See e. g. [23] for a treatment of this in the context of PLA printing.

The same should also be considered when assessing the maximum von Mises stress found in the numerical analysis, observing Figure 8 stresses with up to

19

MPa are found. This value however should not directly be compared to the TPU’s yield strength as the failing mode of the printed part should not directly correspond to the failure of the pure material but a delayering of the printed layers. The distribution of the stress in the part however still provides accurate information. Here the numerical analysis helps to optimize shapes where large changes in stress occur which result in a higher wear in these areas. This may be used when working on further changes of the mechanism.

To give some concluding remarks on the numerical modeling, it should be mentioned that the modeling presented in this section does not claim to fully represent the actual contact. Shortcomings of the used approach were discussed and suggestions for a more involved model were made. The code developed for this work is firstly intended to serve as the starting point for a rigorous modeling of the contact. The simplified model did however result in good estimates in terms of the distribution of the maximum stresses. Regarding the estimation of the maximum load, for an accurate estimation, effective material parameters are still required as discussed above. The code for the further development of the contact modeling can be found in the linked GitHub repository. Of special interest in further work is the adjustment of the contact pressure represented by the penalty parameter and a more suitable approximation of the contact surface.

7. Summary and prospective applications

In this work, the design and developing process of the interlocking metasurface mechanism, which was named ShroomLock, was presented. The primary objective was to develop a surface mechanism that exhibits significant deformation during assembly and disassembly, yet experiences only minor deformation when locked together, a behavior which was characterized as snapping. The concept was successfully realized in a printable mechanism made of TPU.

The developed mechanism boasts several outstanding features, including scalability over almost arbitrarily shaped surfaces, ease of use and reliable snapping behavior. As the entire surface mechanism can be traced back to a single snapping element, it becomes easily testable. Through experimental testing, consistent force-displacement characteristics were obtained and three distinct displacement or force ranges were found. This three-phase snapping characteristic ensures the mechanism’s ability to securely mount objects.

Looking ahead, the potential applications of this mechanism are diverse. For instance, it can be arranged as a surface and serve as a versatile tool wall or function as a reliable wall or ceiling mount for various devices, such as projectors. Improvements on the mechanisms can also be introduced to achieve a more uniform holding force across multiple mechanisms, one potential avenue is fabricating the pins from different materials, thereby increasing the printing accuracy. The mechanism may also be extended to work with screws instead of printed pin elements. This would help to overcome surface effects due to the rough printing results on the pin elements, which was discussed in Section 5. For further research, the developed mechanism offers many areas that warrant further exploration. On the one hand, there is the numerical modeling of the snapping mechanisms. An open-source based FEM code with a contact formulation was established. The model shows a good approximation of the contact, but many hard assumptions were made, suggestions for a more rigorous model were made and further development of the code was motivated. On the other hand, when it comes to testing the developed mechanisms, only the unlocking behavior was tested. Additional aspects that were not extensively tested, such as sustained loads on the closed mechanism or repeated snapping and unsnapping cycles, which are critical for ensuring the mechanism’s long-term performance are yet to be tested. Expanding the tests and investigating how the mechanism behaves after a certain number of interactions and identify the number of interactions that lead to any significant changes, as well as determining if the holding force diminishes over time in a sustained loading test. Furthermore, exploring the scalability of the mechanism is of great interest. Understanding how the mechanism behaves if distributed over a surface would also offer valuable insight for various applications. Here, the stiffness of the pin surface will greatly affect whether the holding force scales linearly as more pins are added to a surface.

To help with future research, a GitHub repository 2 was set up. It includes the code for numerical testing, all measured data from the experiments as well as the design and printing files.

Author Contributions

Conceptualization, L.N.S, P.G., H.F., P.W. and C.V.; methodology, L.N.S. and P.G.; software, L.N.S and P.W.; validation, P.G. and L.N.S.; formal analysis, P.G. and L.N.S.; investigation, H.F., L.N.S., P.W. and P.G; resources, C.V. and P.W.; data curation, L.N.S. and P.G.; writing—original draft preparation,L.N.S, P.G., H.F., P.W.; writing—review and editing, P.G., L.N.S. and C.V.; visualization, L.N.S., P.G., P.W.; supervision, C.V.; project administration, C.V.; funding acquisition, C.V. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

All measured data, design files for printing the locking mechanisms and code for numerical testing is available in the linked GitHub repository https://github.com/lschek/ShroomLock.git.

Acknowledgments

The authors would like to thank Arion Juritza (TU Berlin) for assisting in conducting the experimental test series.

Conflicts of Interest

The authors declare no conflict of interest.

Notes

1	The lower lip is neglected as a very fine mesh would be needed to correctly model the shape.
2	https://github.com/lschek/ShroomLock.git

References

Sun, X.; Mazur, M.; Cheng, C.T. A review of void reduction strategies in material extrusion-based additive manufacturing. Additive Manufacturing 2023, 67, 103463. [Google Scholar] [CrossRef]
Dönitz, A.; Köllner, A.; Richter, T.; Löschke, O.; Auhl, D.; Völlmecke, C. Additive Manufacturing of Biodegradable Hemp-Reinforced Polybutylene Succinate (PBS) and Its Mechanical Characterization. Polymers 2023, 15. [Google Scholar] [CrossRef] [PubMed]
Gordelier, T.J.; Thies, P.R.; Turner, L.; Johanning, L. Optimising the FDM additive manufacturing process to achieve maximum tensile strength: a state-of-the-art review. Rapid Prototyping Journal 2019, 25, 953–971. [Google Scholar] [CrossRef]
Dilberoglu, U.M.; Gharehpapagh, B.; Yaman, U.; Dolen, M. The Role of Additive Manufacturing in the Era of Industry 4.0. Procedia Manufacturing 2017, 11, 545–554, 27th International Conference on Flexible Automation and Intelligent Manufacturing, FAIM2017, 27-30 June 2017, Modena, Italy. [Google Scholar] [CrossRef]
Pérez, M.; Carou, D.; Rubio, E.M.; Teti, R. Current advances in additive manufacturing. Procedia CIRP 2020, 88, 439–444, 13th CIRP Conference on Intelligent Computation in Manufacturing Engineering, 17-19 July 2019, Gulf of Naples, Italy. [Google Scholar] [CrossRef]
Özen, A.; Auhl, D.; Völlmecke, C.; Kiendl, J.; Abali, B.E. Optimization of Manufacturing Parameters and Tensile Specimen Geometry for Fused Deposition Modeling (FDM) 3D-Printed PETG. Materials 2021, 14. [Google Scholar] [CrossRef] [PubMed]
Patterson, A.E.; Chadha, C.; Jasiuk, I.M. Identification and Mapping of Manufacturability Constraints for Extrusion-Based Additive Manufacturing. Journal of Manufacturing and Materials Processing 2021, 5. [Google Scholar] [CrossRef]
Patterson, A. Meso-Scale FDM Material Layout Design Strategies Under Manufacturability Constraints and Fracture Conditions. PhD thesis, University of Illinois at Urbana-Champaign, 2021.
Bolmin, O.; Young, B.; Leathe, N.; Noell, P.J.; Boyce, B.L. Interlocking metasurfaces. J. Mater. Sci. 2023, 58, 411–419. [Google Scholar] [CrossRef]
Lay, M.; Thajudin, N.L.N.; Hamid, Z.A.A.; Rusli, A.; Abdullah, M.K.; Shuib, R.K. Comparison of physical and mechanical properties of PLA, ABS and nylon 6 fabricated using fused deposition modeling and injection molding. Composites Part B: Engineering 2019, 176, 107341. [Google Scholar] [CrossRef]
Bai, W.; Fang, H.; Wang, Y.; Zeng, Q.; Hu, G.; Bao, G.; Wan, Y. Academic Insights and Perspectives in 3D Printing: A Bibliometric Review. Applied Sciences 2021, 11. [Google Scholar] [CrossRef]
Young, B.; Bolmin, O.; Boyce, B.; Noell, P. Synergistic strengthening in interlocking metasurfaces. Materials & Design 2023, 227, 111798. [Google Scholar] [CrossRef]
Brown, N.K.; Young, B.; Clark, B.; Bolmin, O.; Boyce, B.L.; Noell, P.J. Optimized design of interlocking metasurfaces. Materials and Design 2023, 233, 112272. [Google Scholar] [CrossRef]
Peralta Marino, G.; De la Pierre, S.; Salvo, M.; Díaz Lantada, A.; Ferraris, M. Modelling, additive layer manufacturing and testing of interlocking structures for joined components. Scientific Reports 2022, 12, 1–11. [Google Scholar] [CrossRef] [PubMed]
Technisches Datenblatt TPU Flex Hard, 2022.
Scroggs, M.W.; Dokken, J.S.; Richardson, C.N.; Wells, G.N. Construction of arbitrary order finite element degree-of-freedom maps on polygonal and polyhedral cell meshes. ACM Transactions on Mathematical Software 2022, 48, 18:1–18:23. [Google Scholar] [CrossRef]
Logg, A.; Mardal, K.; Wells, G.N. others. Automated Solution of Differential Equations by the Finite Element Method; Springer, 2012. [CrossRef]
Suresh, S. Fatigue of materials, 2nd ed.; Cambridge University Press: Cambridge, 1998. [Google Scholar]
Holzapfel, G.A. Nonlinear solid mechanics: A continuum approach for engineering,, repr ed.; Wiley: Chichester and Weinheim, 2010. [Google Scholar]
Bertram, A.; Glüge, R. Solid Mechanics; Springer International Publishing: Cham, 2015. [Google Scholar] [CrossRef]
Geuzaine, C.; Remacle. , J.F. Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. International Journal for Numerical Methods in Engineering 2009. [Google Scholar] [CrossRef]
Bleyer, J. Numerical Tours of Computational Mechanics with FEniCS, 2018. [CrossRef]
Tognana, S.; Montecinos, S.; Gastien, R.; Salgueiro, W. Influence of fabrication parameters on the elastic modulus and characteristic stresses in 3D printed PLA samples produced via fused deposition modelling technique. Journal of Polymer Engineering 2021, 41, 490–498. [Google Scholar] [CrossRef]

Figure 1. Design of the developed ILM: (a) Sectional view of individual ILM cell in snapped state (b) Individual ILM mechanism cell in unsnapped state (c) ILM demonstrator over a hexagonal surface in unsnapped state.

Figure 2. Setup for experimental testing of the ILM cell. (a) Front view of experimental setup with the locking elements loaded into the testing machine. (b) List of the components in the experimental setup.

Figure 3. (a) Experimental results of the testing of part 3. The curve describes the relation between the pulling force and the corresponding shift of the pin element during unsnapping. The part underwent no snapping before the testing, and the elastic shakedown is clearly visible for the first measurement. (b) Measurements 2-4 of part 3 averaged and plotted alongside the standard deviation.

Figure 4. (a) Averaged curves of mechanisms 1 to 8. Each mean curve is a result of the second up to the fourth snap of the respective mechanism. (b) Average curve of the average curves of mechanisms 1 to 8. The division of the average curve into three regions (I, II and III) as well as the coloring (green, pink and orange respectively) refers to the different snapping phases.

Figure 5. Three snapping phases visualized.

Figure 6. Picture of TPU_V7_M8.

Figure 7. Discretized domain for the numerical analysis and designation of the boundaries. Symmetry conditions are applied on

Γ_{x, sym}

and

Γ_{y, sym}

. The radius of

Γ_{contact}

corresponds to the maximum radius of the carrier element

r_{2}

Figure 7. Discretized domain for the numerical analysis and designation of the boundaries. Symmetry conditions are applied on

Γ_{x, sym}

and

Γ_{y, sym}

. The radius of

Γ_{contact}

corresponds to the maximum radius of the carrier element

r_{2}

Figure 8. Results for the contact formulation. The full spring element can be assembled by exploiting the symmetry conditions and simply reflecting the obtained result. In the bottom, three time steps of the incremental load procedure are shown. For each, the von Mises stress is colored. The pin element is not part of the numerical study and is only visualized to give a reference.

Table 1. Technical requirements of the ILM mechanism.

Category	Requirement
Connection properties	Detachable connection Restriction of all degrees of freedom between the surfaces Snapping mechanism (deformation until form lock) Force transmission based on form lock
Snapping conditions	$r_{2} > r_{lamella}$ $h_{1} \approx h_{lamella}$ Spring elements made of flexible material
Design guidelines	Overhangs up to $50^{\circ}$ Consideration of anisotropic material properties (build orientation) Minimum diameter of vertical pins greater than 8 times the line width Chamfer on the bottom edge to compensate over-extrusion in the initial layer
Production process	Fused filament fabrication (FFF), $0.4$ mm Nozzle
Material	Thermoplastic polyurethane (TPU)

Table 3. Used printing parameters for printing the ILM on the Vyper 3D printer from Anycubic.

Parameter	Value/Setting
Layer Height	$0.1$
Wall Thickness	$2.4$
Top/Bottom Thickness	$1.5$
Z Seam Alignment	Random
Flow	103%
Combing Mode	All
Enable Print Cooling	On
Print Sequence	One at a time

Table 4. Machine parameters of the used Zwick/Roell testing machine.

Parameter	Value/Unit
Linear measuring range	$2.5$ $k$ $N$
Sensor accuracy Class 0.5	$0.5$ %
Sensor resolution (ADC)	19 bit
Sampling rate	100 $Hz$
Traverse speed	2 mm/min

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Extrusion-Based Additive Manufacturing Driven Design and Testing of the Snapping Interlocking Metasurface Mechanism ShroomLock

Abstract

1. Introduction

2. Additive manufacturing method driven design

3. Materials and Methods

4. Experimental Tensile Test Series

5. Evaluation and Discussion

5.1. Individual Results and Comparison

5.2. Geometry Force-Profile Relationship

5.3. Error Analysis

6. Numerical modeling of the mechanism

6.1. Modeling the contact between two solids with FEniCSx

6.2. Examining the numerical results

7. Summary and prospective applications

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Notes

References

MDPI Initiatives

Important Links

Subscribe