Prerpints.org logo
Preprint
Article

A Compact Particle Detector for Space-Based Applications: Development of the Low Energy Module (LEM) for the NUSES Space Mission

Altmetrics

Downloads

92

Views

22

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

15 October 2023

Posted:

16 October 2023

You are already at the latest version

Alerts
Abstract
NUSES is a planned space mission aiming to test innovative observational and technological approaches related to the study of low-energy cosmic rays, gamma rays and high-energy astrophysical neutrinos. Two scientific payloads will be hosted onboard the NUSES space mission: Terzina and Zirè. Terzina will be an optical telescope readout by SiPM arrays, for the detection and study of Cerenkov light emitted by Extensive Air Showers generated by high-energy cosmic rays and neutrinos in the atmosphere. Zirè will focus on the detection of protons and electrons up to a few hundred MeV and to 0.1-10 MeV photons and will include the Low Energy Module (LEM). The LEM will be a particle spectrometer devoted to the observation of fluxes of low-energy electrons in the 0.1-7 MeV range and protons in the 3-50 MeV range along the Low Earth Orbit (LEO) followed by the hosting platform. The detection of Particle Bursts (PBs) in this Physics channel of interest could give new insight into the understanding of complex phenomena such as eventual correlations between seismic events or volcanic activity with the collective motion of particles in the plasma populating van Allen belts. With its compact sizes and limited acceptance, the LEM will allow the exploration of hostile environments such as the South Atlantic Anomaly (SAA) and the inner van Allen belt, in which are expected electron fluxes of the order of 106−7 cm−2 sr−1 s−1. Concerning the vast literature of space-based particle spectrometers, the innovative aspect of the LEM resides in its compactness, within 10x10x10 cm3, and in its “active collimation” approach dealing with the problem of multiple scattering at these very low energies. In this work, the geometry of the detector, its detection concept, its operation modes and the hardware adopted will be presented. Some preliminary results from the Monte Carlo simulation (Geant4) will be shown.
Keywords: 
Subject: Physical Sciences  -   Space Science

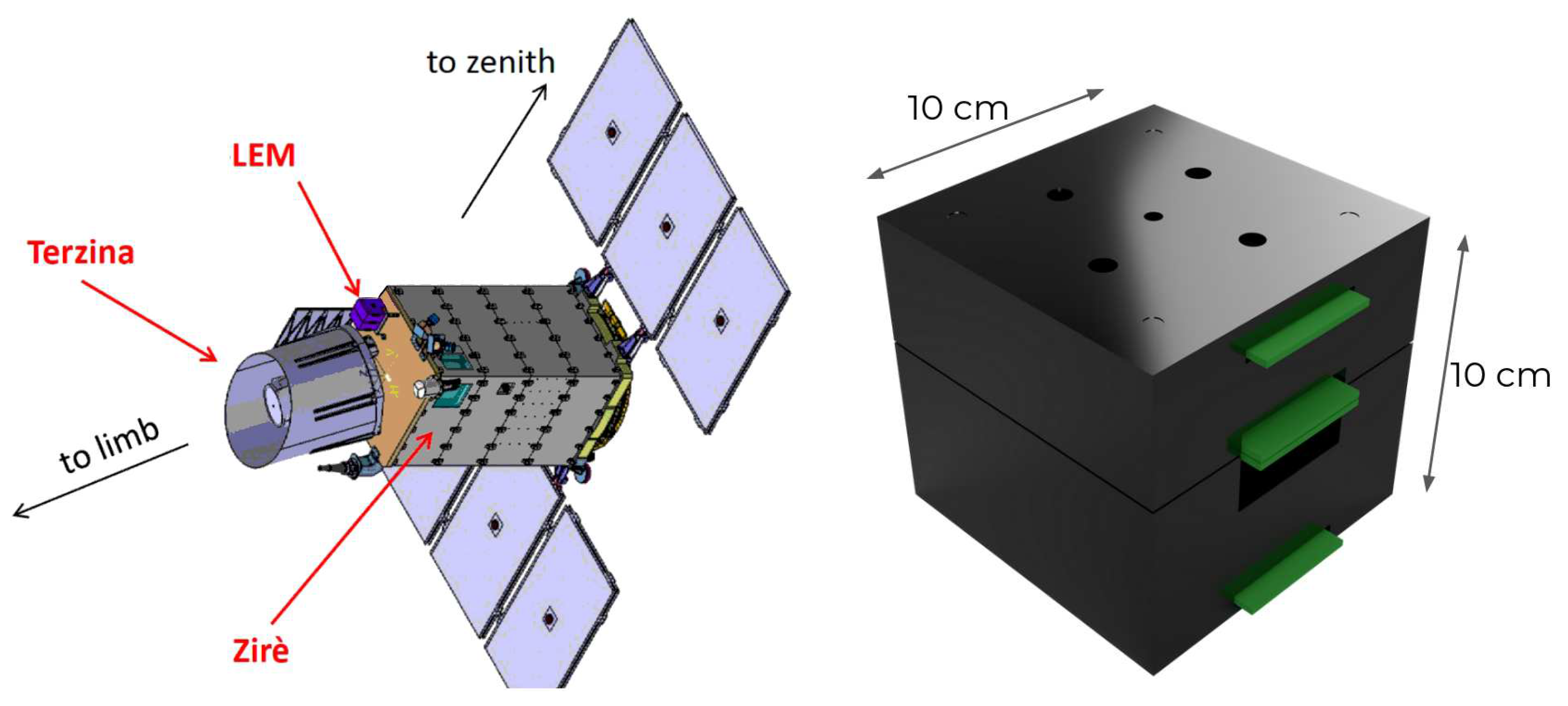
1. Introduction: The NUSES space mission

NUSES is a planned space mission aiming to test innovative observational and technological approaches related to the study of low-energy cosmic rays, gamma rays and high-energy astrophysical neutrinos. The satellite will host two payloads, named Terzina [1,2] and Zirè [3,4,5,6,7]. Terzina will be a pathfinder for future missions devoted to observing Ultra High Energy Cosmic Rays (UHECRs) and neutrino astronomy using space-based instruments[8,9,10,11].
Zirè is a particle detector measuring electron, proton and light nuclei fluxes from a few up to hundreds MeV, also testing new tools for the detection of γ -rays. The main purpose of the detector is to measure the counting rates of the trapped particles precipitating from the Van Allen Belts (VABs), looking for eventual anomalies occurring in the proximity of catastrophic events such as earthquakes or volcanic activities involving the lithosphere. Another essential science objective of ZIRÈ is to monitor solar activity and its periodical cycle characterised by a duration of about 11 years. In particular, it is useful to monitor the occurrence of events such as Solar Flares (SFs) or Coronal Mass Ejections (CMEs) during solar maxima[12]. The investigation of energetic particles in the magnetosphere will improve the understanding of the acceleration mechanisms involved during those events with the possibility of space weather broadcasts. The other science objective is to detect photons with energies up to tens of MeV. This allows the study of some of the most violent and energetic events in astrophysics which are the so-called Gamma Ray Bursts (GRBs) [13,14], rapid and intense pulses of gamma rays coming from very far sources.
Zirè will be equipped with an additional sub-detector: the Zirè-Low Energy Module (LEM). The LEM will be attached to the external structure of the NUSES satellite (see Figure 1). It will fit within a volume of 10x10x10cm3 and it will be able to perform event-based Particle Identification (PID) for low-energy charged particles, such as electrons and protons.

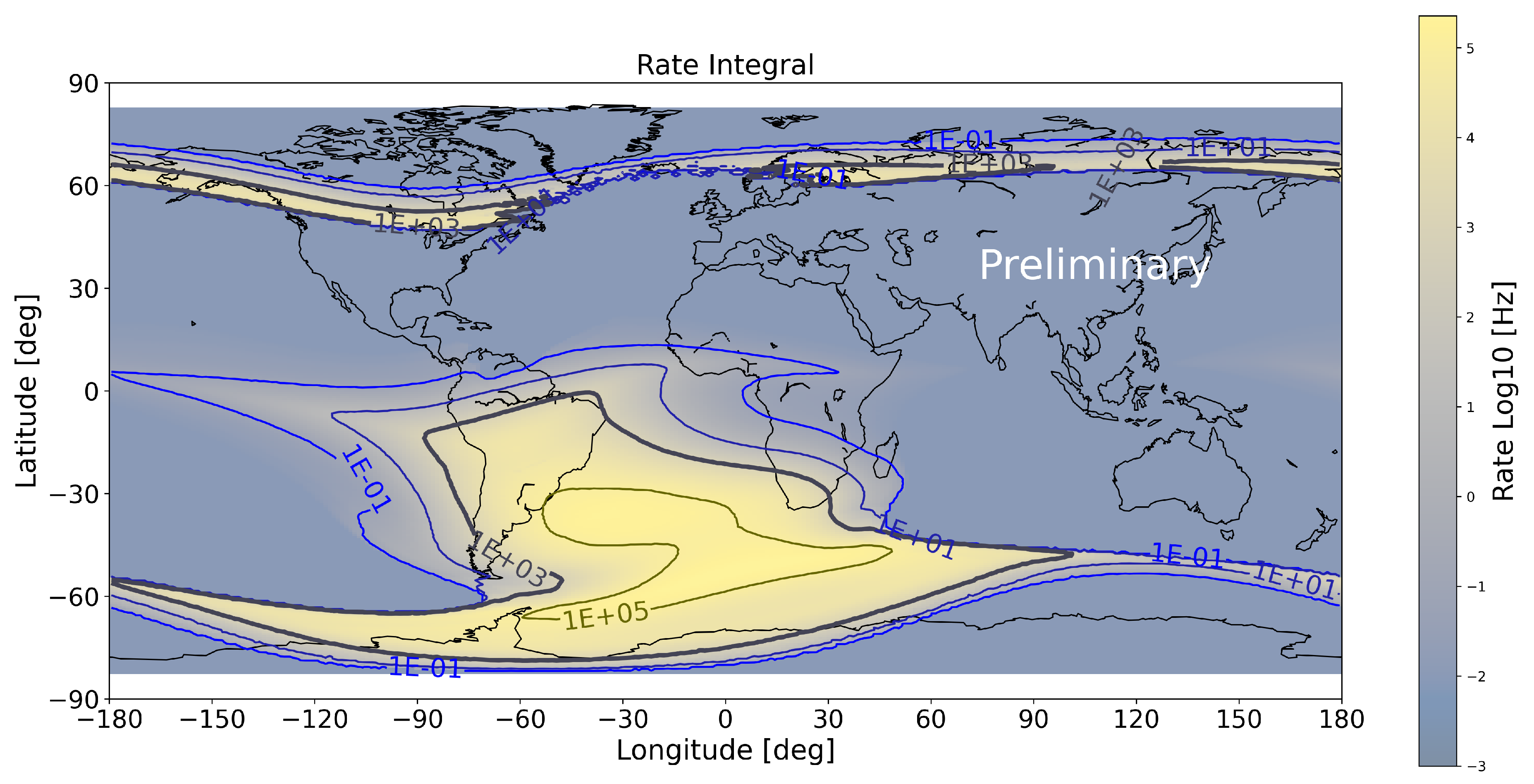
2. The need for a Low Energy Module

As mentioned before, one of the NUSES mission goals is the monitoring of particle precipitations from Van Allen Belts (VABs) investigating for possible correlations with earthquakes and validating Lithopsphere-Atmosphere-Ionosphere-Magnetosphere coupling models. Several processes can cause a precipitation of the trapped charged particles from the radiation belts. These processes are not fully understood yet, but the primary cause is thought to be electromagnetic fluctuations in the radiation belt. These electromagnetic fluctuations can be produced through solar-magnetic storms, lightning storms, man-made electromagnetic emissions and seismic activity. It is known that the measurement of the fluxes of trapped charged particles can improve the models of the coupling between the lithosphere, atmosphere, ionosphere, and magnetosphere [15]. In particular, statistical evidence of a temporal correlation between particle precipitations from Van Allen Belts and strong seismic events has been pointed out [16]. These observations, motivate the interest in further, detailed, measurements of electron fluxes in the energy window 0 . 1 − 7 MeV that could be a promising channel to identify hypothetical seismic precursors.
Therefore, with the aim to extend the measurements to lower energies, a Zirè Low Energy Module (LEM), has been introduced in the design of the NUSES satellite. The Low Energy Module will be a compact spectrometer, fitting within a volume of 10x10x10cm3 (right panel of Figure 1 for the volume envelope of the LEM), able to perform an event-based measurement of energy, direction and composition of low energy charged particles, in particular down to 0.1 MeV for electrons. The main goal of this detector is the monitoring of the magnetosphere and ionosphere environment. Other goals of the LEM detector will be the study of Space Weather, monitoring the flux of low energy protons, and the investigation of the particle composition within the harsh environment of the South Atlantic Anomaly (SAA), measuring the isotopic abundances of H, He and eventually the fraction of heavier nuclei.

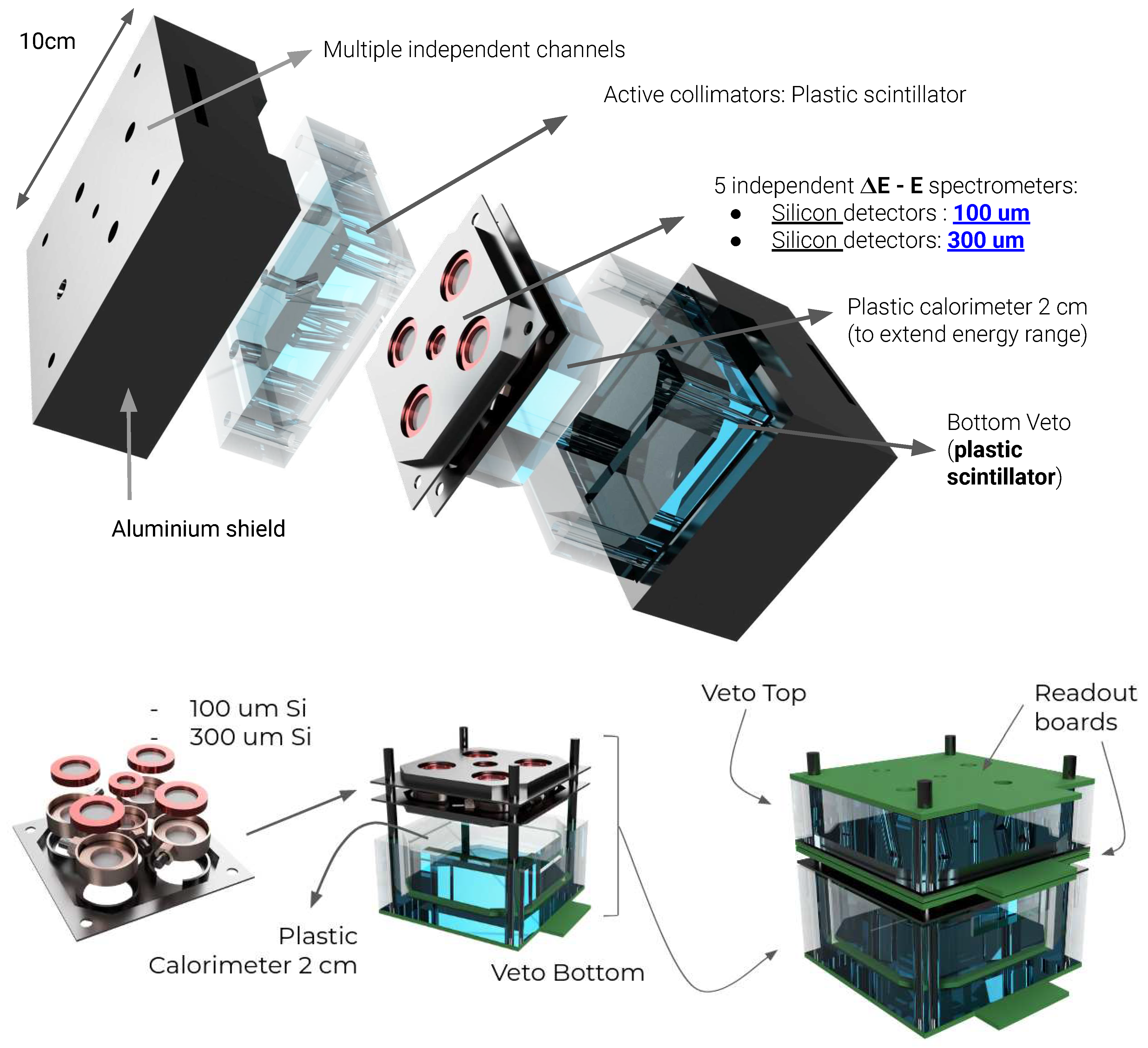
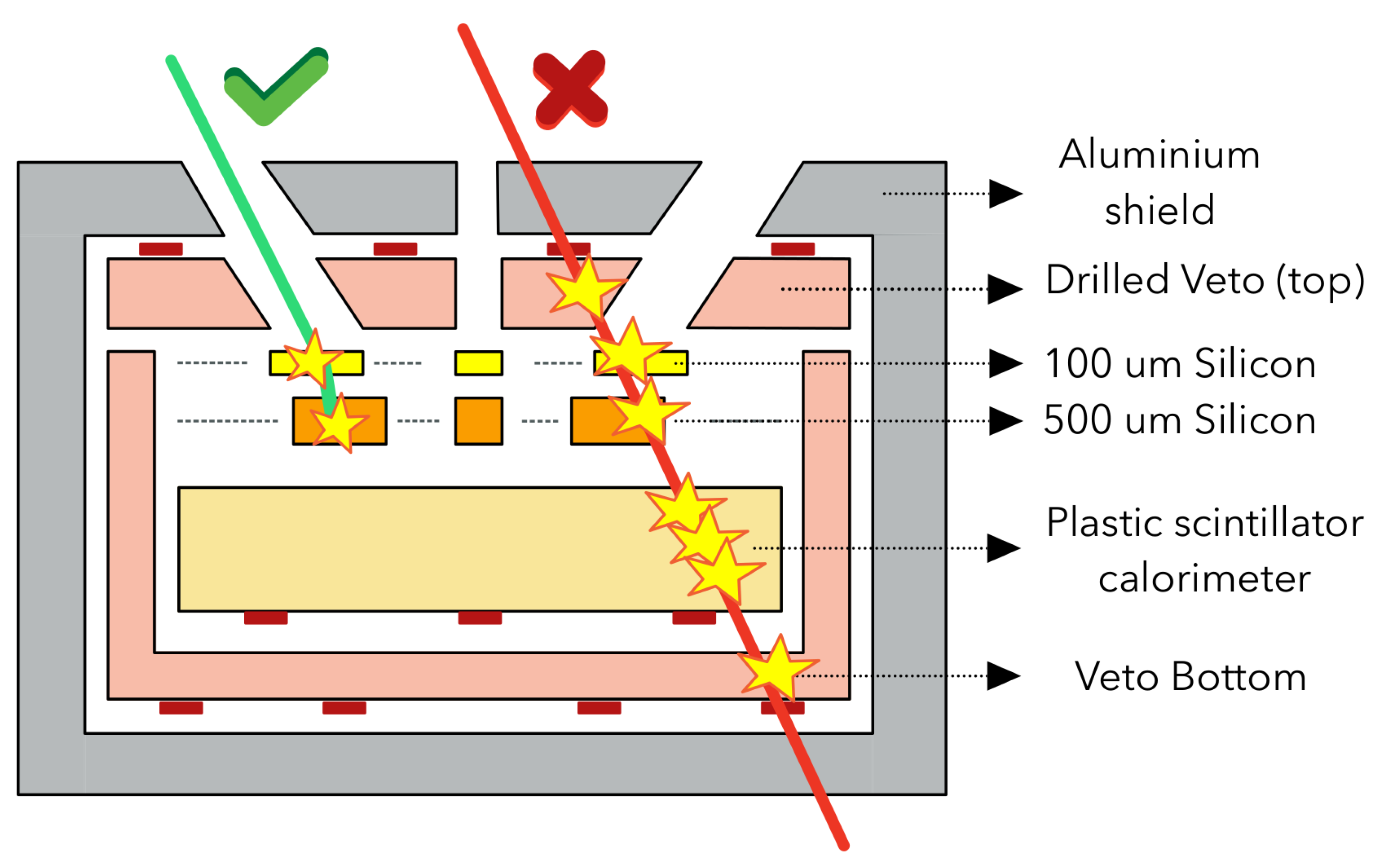
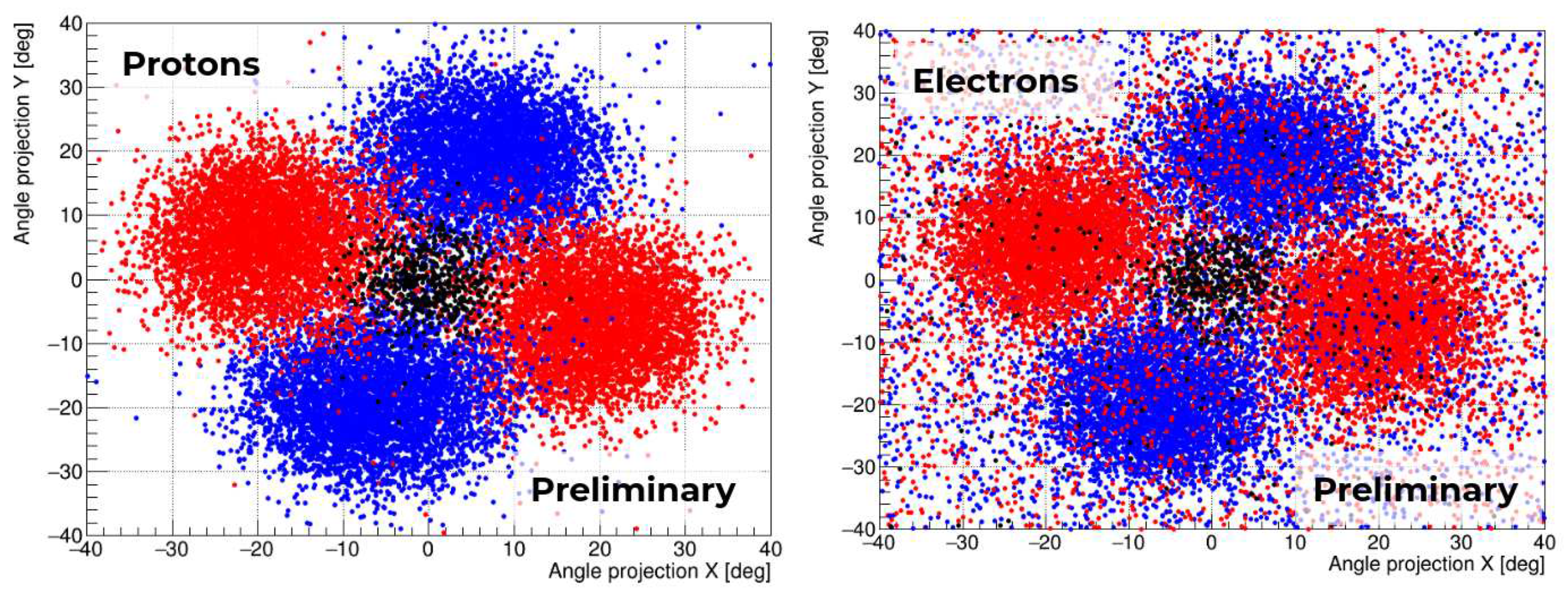
3. Geometry and detection concept of the LEM

In a particle spectrometer (like e.g. Zirè) the measurement of the particle direction is usually performed by tracking technique; however, for low energetic particles, the standard tracking approach fails due to large multiple Coulomb scattering within the first detector layer. For the measurement of the arrival direction of low energy particles, a collimation technique must be adopted [17]. In the collimation technique, a shaped passive shield must be thick enough to stop energetic particles from “unknown”/random directions. The passive collimator allows the detection of particles arriving from the "known" directions. To avoid bulky and heavy passive shields, the technique of “active collimation” is developed for the LEM spectrometer. This technique relies on the use of shaped plastic scintillators as a veto, tagging the particles that are crossing only a relatively light passive shield. To limit the occupancy of the veto detectors in the SAA and in the lower Van Allen belt near the poles, permitting a reliable measurement of the particle composition there, a 0.8 cm thick aluminium shield is considered for the LEM. The particle identification capability of the LEM relies on the consolidated Δ E-E spectrometric technique [18,19,20], performed by five pairs of thin Passivated Implanted Planar Silicon (PIPS) detectors placed in a telescopic configuration. The typical resolution of the PIPS detector is ≃10 keV.
In Figure 2 an exploded view of the detector shows the components and a preliminary assembly of the detector. On the other hand, in Figure 3, a schematic representation of the instruments explains its adopted detection scheme. Coming from the zenith, a particle can enter inside the LEM through the holes drilled in the top shield avoiding being tagged by the drilled top veto. Depending on the particle direction, the nature of the charged particle is identified by one of the five Δ E-E spectrometers. Each spectrometer is composed of a 100 μ m thin silicon detector superimposed to a 300 μ m thick silicon detector. To extend the energy range capability for the LEM particle identification, a lower calorimeter is placed below the PIPS. A lower calorimeter made by a 2 cm thick plastic scintillator allows a flux measurement of up to 10 MeV for electrons, thus a reasonable overlap is expected with the Zirè flux measurements [21]. Finally, a bottom veto is identifying particles of relatively large energy, that are not contained by the lower calorimeter. A good particle identification capability is expected for contained particles that are crossing one of the 100 μ m top PIPS.
Assuming a low energy non-relativistic charged particle passing through the thin PIPS detector, both the energy deposited, Δ E ∝ Z 2 β 2 , and the total kinetic energy, E k ≈ 1 2 m ( β c ) 2 , are velocity dependent. Combining these quantities, a particle classifier can be defined: PID = log 10 Δ E · E k ≈ log 10 Z 2 m + c o n s t . , that is mainly dependent on the particle mass, m, and charge, Z, but is almost energy independent.
For the characterisation of the detector’s performances, a GEANT4 Monte Carlo simulation [22] was appositely developed. For the simulation of the geometry reported in Figure 2, developed with a parametric computer-aided design (CAD) software, we adopted the Geometry Description Markup Language (GDML) [23]. We generated the GDML file (compatible with the GEANT4 toolkit) using the GDML Workbench [24] for FreeCAD 0.20.
The PID classifier is shown in the left plot of Figure 4. The non-relativistic approximation is not valid for electrons, however they are identified thanks to the very low mass. The poor energy resolution expected by the plastic scintillator calorimeter is responsible for the PID performance degradation at relatively large energy where the particles are crossing the thick PIPS stopping in the plastic calorimeter.
To estimate the particle identification efficiency, it is possible to define some specific intervals for the PID for each particle: [-3, 0] for electrons, [0.7, 1.4] for protons, and [1.6, 2.5] for alpha particles. In the right panel of Figure 4, the particle identification tagging efficiencies, for the three families of particle, is higher than 90 % in the three respective PID proxy intervals. In particular, we observed that for accepted electrons, protons, and alpha particles, respectively the 99 % , 94 % , and 96 % were correctly tagged.
In Figure 5, the characterisation of the LEM Field of View (FoV) and angular resolution for protons and electrons is shown. The scatter plot shows the incoming direction of the particle (at the Monte Carlo truth level) projected on the plane. Here, the zenith direction is assumed to be encoded by the origin of the plot. The colour identifies which Δ E-E channel has been triggered. The overall LEM FoV is ≈ 45°. The obtained angular RMS is ≈ 6° for proton and α particles while a worse resolution (≈ 12°) is expected for electrons due to interactions with the inner fringes of the LEM aperture.
The overall LEM geometrical factor1 is ≈ 0.2-0.3 cm2sr. It is approximately constant for electrons in the range 0.2-5 MeV, for protons in the range 3-50 MeV and for α particles in the range 20-200 MeV. In Figure 6, the geometric factor estimated for electrons, protons, and alpha particles is shown.
Knowing the orbit parameters of the NUSES mission (Sun-synchronous, 97 degrees, LEO 550km), a preliminary map of the expected rates of the LEM can be evaluated using the model International Radiation Environment Near Earth AE9/AP9 (IRENE-AE9/AP9) [26]. In the LEO environment, the most impacting populations of charged particles are trapped protons and electrons. With IRENE-AE9/AP9 we could estimate the differential omnidirectional/isotropic fluxes of those particles.
In Figure 7 it is shown that the LEM will experience a high acquisition rate (≈ 50 kHz) in the SAA, thus a twofold data transmission approach is in preparation (“event-based” for rates below 1kHz and “histogram based” for larger rates) to fulfil the data bandwidth assigned to LEM in the NUSES mission.

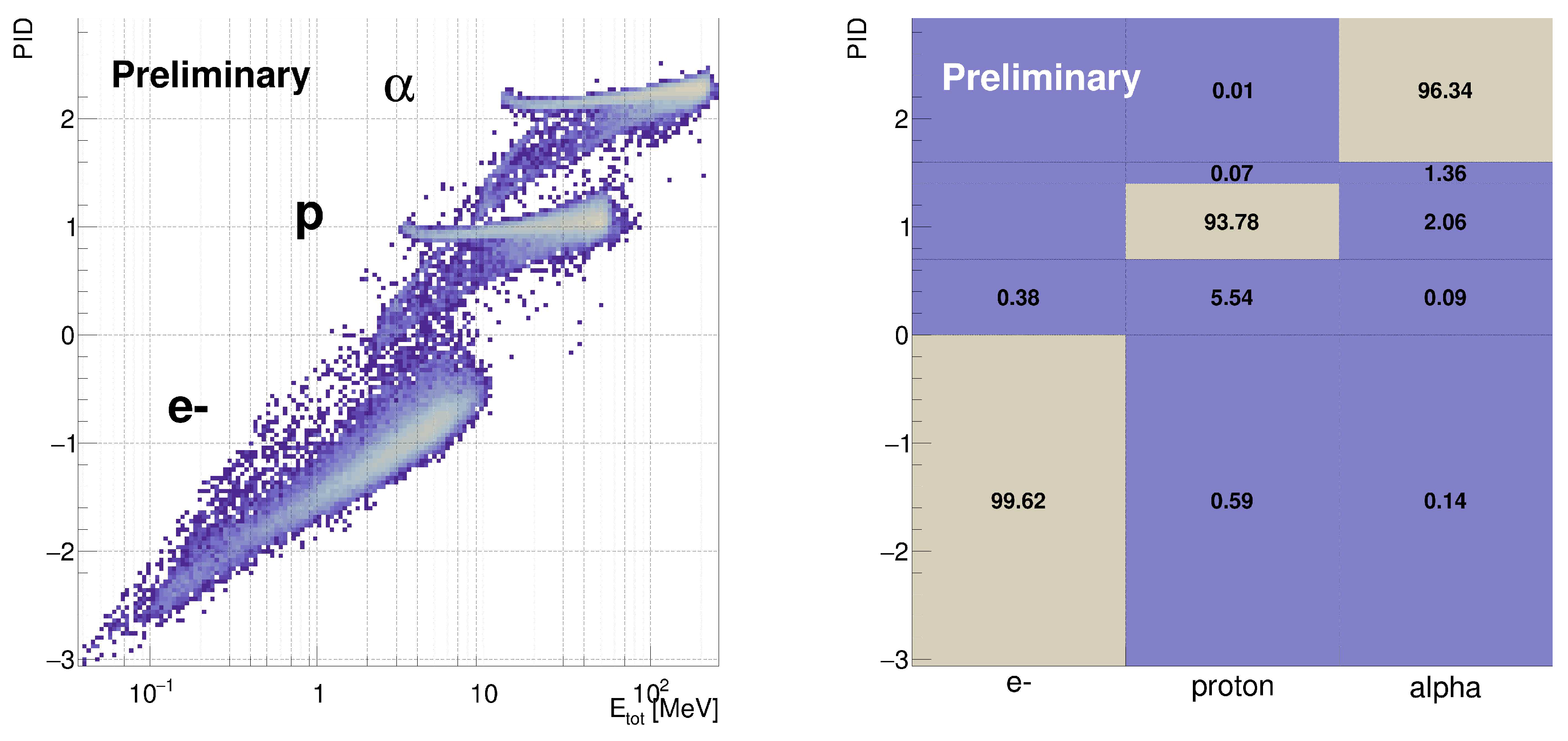
4. Preliminary test on PIPS sensors.

The heart of the LEM detector is composed of the PIPS spectrometer. The spectrometer will use four circular PIPS with an area of 150 mm2 surrounding a central one with an area of 55 mm2 (see Figure 8). The central PIPS diameter is smaller to equalize the geometrical acceptance among the five channels. The five top sensors, with thickness 100 μ m, will be the R-series (ruggedized) PIPS manufactured by ORTEC/AMETEK [27].
The two sides of the 100 μ m PIPS are covered by an aluminium and a gold layer with a thickness of ≈50 μ g/cm2 and ≈40 μ g/cm2, respectively. These layers ensure that the PIPS detectors are light-tight and “ruggedized”. The five bottom sensors, with thickness 300 μ m, will be manufactured by Canberra/MIRION [28]. The two sides of the 300 μ m PIPS are covered by aluminium with a thickness of ≈70 μ g/cm2 and ≈250 μ g/cm2, respectively, to ensure the detector is light tight.
A preliminary set-up for the measurement of the performances of a PIPS detector was tested in the INFN-TIFPA laboratory. The depletion voltage of the PIPS sensor was 60V and the preliminary measurement of the power budget of the used charge amplifier is below 100mW/ch. The sensor was tested acquiring atmospheric muons in telescopic configuration, γ -rays from 176Lu source and α -particles and γ -rays from 241Am source. Excellent linearity of the energy scale was obtained. Moreover, the PIPS response to particles with very different specific ionization (muons, recoiling electrons and α ) has been found to be compatible within a few per cent, as expected.
Two key requirements for the LEM project are guaranteeing a low energy threshold and a relatively fast response. The acquired measures verify the feasibility of the 40 keV energy threshold adopted in the LEM simulations as well as the 10 keV energy resolution.
Another important factor for the LEM is the measurement of the signal decay time; this is related to the detector occupancy which could be an issue in the harsh environment of the SAA. The ≈ 200 ns measured signal decay time prevents the possible pile-up of overlapping signals from different particles in the SAA.

5. Conclusion

The project of a compact (10x10x10cm3) particle spectrometer, the Low Energy Module (LEM) as part of the Zirè instrument on board the NUSES space mission is in the construction and testing phase. Prototypes of PIPS detector readout have been tested in the INFN-TIFPA laboratory, confirming ≈ 10 keV energy resolution and ≈ 100 ns signal decay time. The LEM will be able to perform measurements of energy, direction, and composition of low-energy charged particles down to 0.1 MeV kinetic energy, studying the coupling between the lithosphere and magnetosphere, measuring the particle fluxes in the SAA and monitoring the Space Weather.

Full NUSES Author List

R. Aloisio 1,2, C. Altomare 3, F. C. T. Barbato 1,2, R. Battiston 4,5, M. Bertaina 6,7, E. Bissaldi 3,8, D. Boncioli 2,9, L. Burmistrov 10, I. Cagnoli 1,2, M. Casolino 11,12, A.L. Cummings 13, N. D’Ambrosio 2, I. De Mitri 1,2, G. De Robertis 3, C. De Santis 11, A. Di Giovanni 1,2, A. Di Salvo 7, M. Di Santo 1,2, L. Di Venere 3, J. Eser 14, M. Fernandez Alonso 1,2, G. Fontanella 1,2, P. Fusco 3,8, S. Garbolino 7, F. Gargano 3, R. A. Giampaolo 1,7, M. Giliberti 3,8, F. Guarino 15,16, M. Heller 10, R. Iuppa 4,5, J. F. Krizmanic 17,18, A. Lega 4,5, F. Licciulli 3, F. Loparco 3,8, L. Lorusso 3,8, M. Mariotti 19,20, M. N. Mazziotta 3, M. Mese 15,16, H. Miyamoto 1,7, T. Montaruli 10, A. Nagai 10, R. Nicolaidis 4,5, F. Nozzoli 4,5, A. V. Olinto 14, D. Orlandi 2, G. Osteria 15, P. A. Palmieri 6,7, B. Panico 15,16, G. Panzarini 3,8, A. Parenti 1,2, L. Perrone 21,22, P. Picozza 12,11, R. Pillera 3,8, R. Rando 19,20, M. Rinaldi 11, A. Rivetti 7, V. Rizi 2,9, F. Salamida 2,9, E. Santero Mormile 6, V. Scherini 21,22, V. Scotti 15,16, D. Serini 3, I. Siddique 1,2, L. Silveri 1,2, A. Smirnov 1,2, R. Sparvoli 11, S. Tedesco 7,23, C. Trimarelli 10, L. Wu 1,2,†, P. Zuccon 4,5, S. C. Zugravel 7,23.
1 Gran Sasso Science Institute (GSSI), Via Iacobucci 2, I-67100 L’Aquila, Italy
2 Istituto Nazionale di Fisica Nucleare (INFN) - Laboratori Nazionali del Gran Sasso, I-67100 Assergi, L’Aquila, Italy
3 Istituto Nazionale di Fisica Nucleare, Sezione di Bari, via Orabona 4, I-70126 Bari, Italy
4 Dipartimento di Fisica, Università di Trento, via Sommarive 14 I-38123 Trento, Italy
5 Istituto Nazionale di Fisica Nucleare (INFN) - TIFPA, via Sommarive 14 I-38123 Trento, Italy
6 Dipartimento di Fisica, Università di Torino, Via P. Giuria, 1 I-10125 Torino, Italy
7 Istituto Nazionale di Fisica Nucleare (INFN) - Sezione di Torino, I-10125 Torino, Italy
8 Dipartimento di Fisica M. Merlin, dell’Università e del Politecnico di Bari, via Amendola 173, I-70126 Bari, Italy
9 Dipartimento di Scienze Fisiche e Chimiche, Università degli Studi di L’Aquila, I-67100 L’Aquila, Italy
10 Département de Physique Nuclèaire et Corpusculaire, Université de Genève, 1205 Genève, Switzerland
11 INFN Roma Tor Vergata, Dipartimento di Fisica, Universitá di Roma Tor Vergata, Roma, Italy
12 RIKEN, 2-1 Hirosawa, Wako, Saitama, Japan
13 Departments of Physics and Astronomy & Astrophysics, Institute for Gravitation and the Cosmos, Pennsylvania State University, University Park, PA 16802, USA
14 Department of Astrophysics & Astronomy, The University of Chicago, Chicago, IL 60637, USA
15 Istituto Nazionale di Fisica Nucleare, Sezione di Napoli, via Cintia, I-80126 Napoli, Italy
16 Dipartimento di Fisica E. Pancini dell’Università di Napoli Federico II, via Cintia, I-80126 Napoli, Italy
17 CRESST/NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
18 University of Maryland, Baltimore County, Baltimore, MD 21250, USA
19 Università di Padova, I-35122 Padova, Italy
20 Istituto Nazionale di Fisica Nucleare (INFN) - Sezione di Padova, I-35131 Padova, Italy
21 Dipartimento di Matematica e Fisica “E. De Giorgi", Università del Salento, Via per Arnesano, I-73100 Lecce, Italy
22 Istituto Nazionale di Fisica Nucleare - INFN - Sezione di Lecce, Via per Arnesano, I-73100 Lecce, Italy
23 Department of Electrical, Electronics and Communications Engineering, Politecnico di Torino, Corso Duca degli Abruzzi 24, I-10129 Torino, Italy
† Now at Institute of Deep Space Sciences, Deep Space Exploration Laboratory, Hefei 230026, China

Author Contributions

Conceptualization, F.N., R.N.; methodology, F.N., R.N.; software, R.N.; validation, F.N. and R.N.; formal analysis, R.N.; investigation, F.N., R.N.; resources, F.N., R.N., G.P. and NuSES coll.; data curation, R.N. and F.N.; writing—original draft preparation, R.N. and F.N.; writing—review and editing, R.N., F.N., G.P. and NuSES coll.; visualization, R.N., F.N., G.P.; supervision, F.N., G.P.; project administration, F.N., G.P. and NuSES coll.; and funding acquisition, F.N, G.P. and NuSES coll. All of the authors have read and agreed to the published version of the manuscript.

Funding

NUSES is funded by the Italian Government (CIPE n. 20/2019), by the Italian Minister of Economic Development (MISE reg. CC n. 769/2020), by the Italian Space Agency (CDA ASI n. 15/2022), by the Swiss National Foundation (SNF grant n. 178918) and by the European Union - NextGenerationEU under the MUR National Innovation Ecosystem grant ECS00000041 - VITALITY - CUP D13C21000430001.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ACD Anti-coincidence detector
CSA Charge sensitive amplifier
FOV Field Of View
GDML Geometry Description Markup Language
GEANT Geometrty and tracking
GRB Gamma-ray burst
IRENE International Radiation Environment Near Earth
LAIM Lithosphere atmosphere ionosphere magnetosphere
LEM Low-energy module
LEO Low earth orbit
LYSO Lutetium–yttrium oxyorthoSilicate
MILC Magnetosphere ionosphere lithosphere coupling
MIP Minimum ionising particle
MPV Most probable value
PID Particle identification
PIPS Passivated implanted planar silicon
SAA South Atlantic Anomaly
TGF Terrestrial gamma-ray flash
VAB Van Allen Belt

References

  1. Burmistrov, L. Terzina on board NUSES: a pathfinder for EAS Cherenkov Light Detection from space. arXiv 2023, arXiv:2304.11992. [Google Scholar]
  2. Aloisio, R.; Burmistrov, L.; Di Giovanni, A.; Heller, M.; Montaruli, T.; Trimarelli, C. The Terzina instrument onboard the NUSES space mission. arXiv preprint 2023, arXiv:2308.15342. [Google Scholar]
  3. De Mitri, I.; Di Santo, M.; collaboration, N.; others. The NUSES space mission. Journal of Physics: Conference Series. IOP Publishing, 2023, Vol. 2429, p. 012007.
  4. Di Giovanni, A.; Di Santo, M. The NUSES space mission 2022.
  5. Di Santo, M.; Di Giovanni, A. The NUSES space mission 2022.
  6. Mazziotta, M.N.; Altomare, C.; Bissaldi, E.; De Gaetano, S.; De Robertis, G.; Dipinto, P.; Di Venere, L.; Franco, M.; Fusco, P.; Gargano, F.; et al. A light tracker based on scintillating fibers with SiPM readout. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 2022, 1039, 167040. [Google Scholar]
  7. Mazziotta, M.N.; Pillera, R. The light tracker based on scintillating fibers with SiPM readout of the Zire instrument on board the NUSES space mission. Proceedings of 38th International Cosmic Ray Conference — PoS(ICRC2023) 2023.
  8. Olinto, A.V.; Krizmanic, J.; Adams, J.; Aloisio, R.; Anchordoqui, L.; Anzalone, A.; Bagheri, M.; Barghini, D.; Battisti, M.; Bergman, D.; et al. The POEMMA (probe of extreme multi-messenger astrophysics) observatory. Journal of Cosmology and Astroparticle Physics 2021, 2021, 007. [Google Scholar]
  9. Olinto, A.V.; Adams, J.H.; Aloisio, R.; Anchordoqui, L.A.; Bergman, D.R.; Bertaina, M.E.; Bertone, P.; Bustamante, M.; Christl, M.J.; Csorna, S.E.; et al. POEMMA: probe of extreme multi-messenger astrophysics. arXiv 2017, arXiv:1708.07599. [Google Scholar]
  10. Denton, P.B.; Kini, Y. Ultrahigh-energy tau neutrino cross sections with GRAND and POEMMA. Physical Review D 2020, 102, 123019. [Google Scholar]
  11. Krizmanic, J. POEMMA: Probe of extreme multi-messenger astrophysics. EPJ Web of Conferences. EDP Sciences, 2019, Vol. 210, p. 06008.
  12. Kahler, S. Solar flares and coronal mass ejections. Annual review of astronomy and astrophysics 1992, 30, 113–141. [Google Scholar]
  13. Fishman, G.J.; Meegan, C.A. Gamma-ray bursts. Annual Review of Astronomy and Astrophysics 1995, 33, 415–458. [Google Scholar]
  14. Piran, T. The physics of gamma-ray bursts. Reviews of Modern Physics 2005, 76, 1143. [Google Scholar]
  15. D’Angelo, G.; Piersanti, M.; Battiston, R.; Bertello, I.; Carbone, V.; Cicone, A.; Diego, P.; Papini, E.; Parmentier, A.; Picozza, P.; et al. Haiti Earthquake (Mw 7.2): Magnetospheric–Ionospheric–Lithospheric Coupling during and after the Main Shock on 14 August 2021. Remote Sensing 2022, 14, 5340. [Google Scholar]
  16. Battiston, R.; Vitale, V. First evidence for correlations between electron fluxes measured by NOAA-POES satellites and large seismic events. Nuclear Physics B-Proceedings Supplements 2013, 243, 249–257. [Google Scholar]
  17. Li, X.; Xu, Y.; An, Z.; Liang, X.; Wang, P.; Zhao, X.; Wang, H.; Lu, H.; Ma, Y.; Shen, X.; et al. The high-energy particle package onboard CSES. Radiation Detection Technology and Methods 2019, 3, 1–11. [Google Scholar]
  18. Scarduelli, V.; Gasques, L.; Chamon, L.; Lépine-Szily, A. A method to optimize mass discrimination of particles identified in ΔE-E silicon surface barrier detector systems. The European Physical Journal A 2020, 56, 1–7. [Google Scholar]
  19. Evensen, L.; Westgaard, T.; Avdeichikov, V.; Carlen, L.; Jakobsson, B.; Murin, Y.; Martensson, J.; Oskarsson, A.; Siwek, A.; Whitlow, H.; et al. Thin detectors for the CHICSi/spl Delta/EE telescope. IEEE Transactions on Nuclear Science 1997, 44, 629–634. [Google Scholar]
  20. Carboni, S.; Barlini, S.; Bardelli, L.; Le Neindre, N.; Bini, M.; Borderie, B.; Bougault, R.; Casini, G.; Edelbruck, P.; Olmi, A.; et al. Particle identification using the ΔE–E technique and pulse shape discrimination with the silicon detectors of the FAZIA project. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 2012, 664, 251–263. [Google Scholar]
  21. Alonso, M.F.; Mitri, I.D. The Zire experiment on board the NUSES space mission. Proceedings of 38th International Cosmic Ray Conference — PoS(ICRC2023) 2023.
  22. Agostinelli, S.; Allison, J.; Amako, K.a.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—a simulation toolkit. Nuclear instruments and methods in physics research section A: Accelerators, Spectrometers, Detectors and Associated Equipment 2003, 506, 250–303. [Google Scholar]
  23. Chytracek, R.; McCormick, J.; Pokorski, W.; Santin, G. Geometry description markup language for physics simulation and analysis applications. IEEE Transactions on Nuclear Science 2006, 53, 2892–2896. [Google Scholar]
  24. Sloan, K.; Hindi, M.; luzpaz.; lambdam94.; Lei, Z.; JakubDmochowski. KeithSloan/GDML: New Release for FreeCAD 0.20, 2022. [CrossRef]
  25. Sullivan, J. Geometric factor and directional response of single and multi-element particle telescopes. Nuclear Instruments and methods 1971, 95, 5–11. [Google Scholar]
  26. PI, G.G.; Guild, S.H.T.; Su, Y.J.; Roth, C.; Charron, J.; Quinn, R.; Starks, M.; Whelan, P.; Friedel, R.; Lindstrom, C.; others. The IRENE (International Radiation Environment Near Earth):(AE9/AP9/SPM) model was developed by the Air Force Research Laboratory in partnership with MIT Lincoln Laboratory, Aerospace Corporation, Atmospheric and Environmental Research, Incorporated, Los Alamos National Laboratory and Boston College Institute for Scientific Research. IRENE (AE9/AP9/SPM) development team: Wm. Robert Johnston1 (PI), T. Paul O’Brien2 (PI).
  27. ORTEC/AMETEK. Si Charged Particle Radiation Detectors for Research Applications. https://www.ortec-online.com/products/radiation-detectors/silicon-charged-particle-radiation-detectors/si-charged-particle-radiation-detectors-for-research-applications.
  28. Technologies, M. PIPS detectors. https://www.mirion.com/products/technologies/spectroscopy-scientific-analysis/research-education-and-industrial-solutions/.
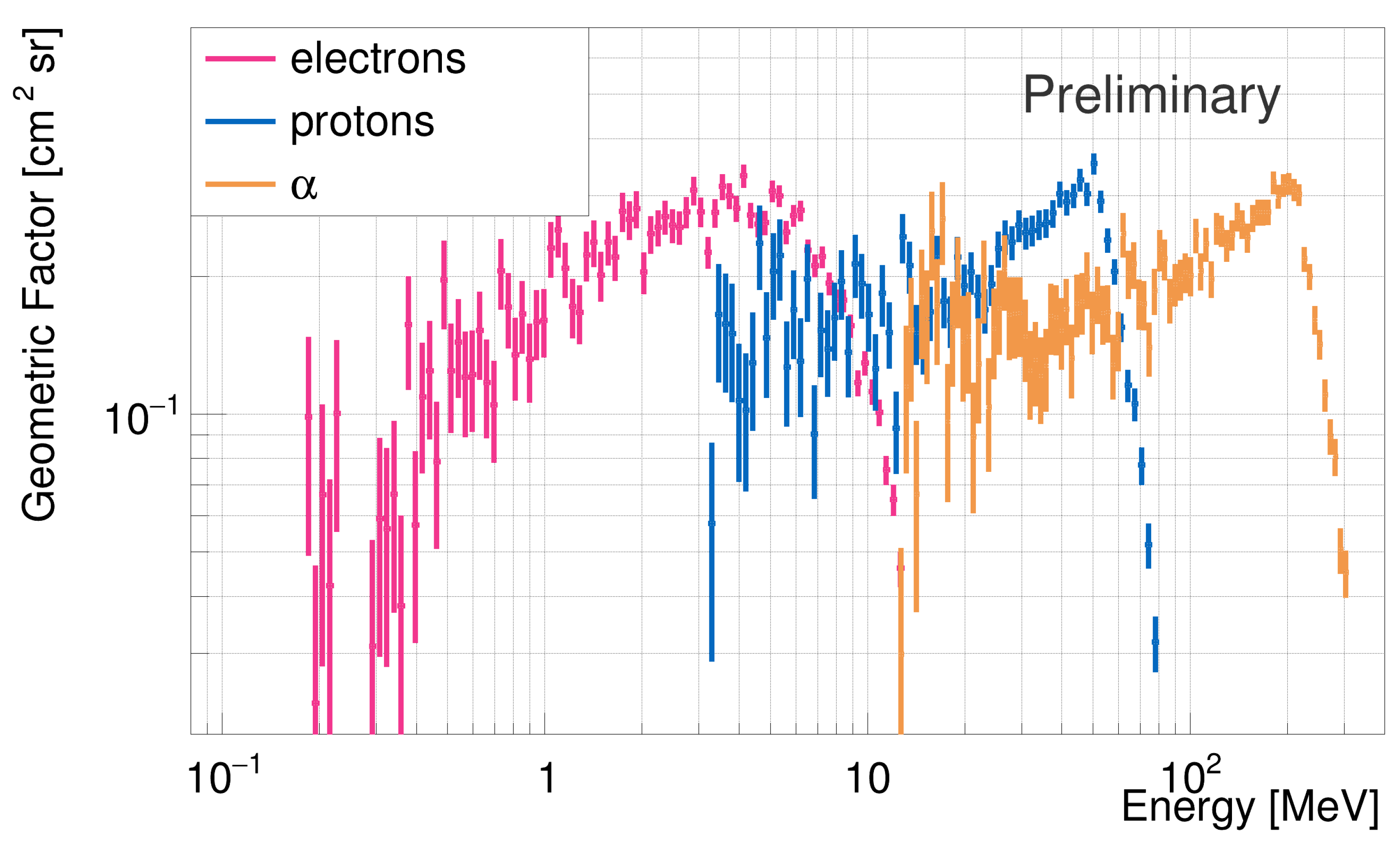
1
The estimation of the geometric factor was carried out assuming the definitions and methods described in [25].
Preprints 87845 g001
Figure 1. [Left panel] Schematic view of the NUSES mission satellite. The Terzina optical telescope will observe the night side of the Earth limb, the Zirè detector will measure charged particles and γ -rays, and the LEM spectrometer will measure low energy charged particles arriving from the zenith. [Right panel] The LEM detector inside the passive aluminium shield. The flux of charged particles crossing the five top holes is measured.
Figure 1. [Left panel] Schematic view of the NUSES mission satellite. The Terzina optical telescope will observe the night side of the Earth limb, the Zirè detector will measure charged particles and γ -rays, and the LEM spectrometer will measure low energy charged particles arriving from the zenith. [Right panel] The LEM detector inside the passive aluminium shield. The flux of charged particles crossing the five top holes is measured.
Preprints 87845 g001
Preprints 87845 g002
Figure 2. (Upper Panel) Exploded view of the LEM detector. (Lower Panel) These images describe the assembling and the geometry of the Low Energy Module (LEM) detector.
Figure 2. (Upper Panel) Exploded view of the LEM detector. (Lower Panel) These images describe the assembling and the geometry of the Low Energy Module (LEM) detector.
Preprints 87845 g002
Preprints 87845 g003
Figure 3. Schematics of the LEM detection approach; the green line is an example of accepted events, and the red line represents an example of an event to be rejected.
Figure 3. Schematics of the LEM detection approach; the green line is an example of accepted events, and the red line represents an example of an event to be rejected.
Preprints 87845 g003
Preprints 87845 g004
Figure 4. (Left panel) Particle identification capability for events crossing the top 100 μ m PIPS and contained in the LEM. (Right panel) Particle tagging efficiency for the three families of particles: electrons, protons, and alpha particles. For each particle family (Monte Carlo truth) reported on the horizontal axis, the tagging efficiency is reported on each bin of the histogram.
Figure 4. (Left panel) Particle identification capability for events crossing the top 100 μ m PIPS and contained in the LEM. (Right panel) Particle tagging efficiency for the three families of particles: electrons, protons, and alpha particles. For each particle family (Monte Carlo truth) reported on the horizontal axis, the tagging efficiency is reported on each bin of the histogram.
Preprints 87845 g004
Preprints 87845 g005
Figure 5. Field of view and angular resolution of the LEM detector for protons (left panel) and electrons (right panel), the different colours are encoding which pair in the Δ E-E spectrometer detects the particle.
Figure 5. Field of view and angular resolution of the LEM detector for protons (left panel) and electrons (right panel), the different colours are encoding which pair in the Δ E-E spectrometer detects the particle.
Preprints 87845 g005
Preprints 87845 g006
Figure 6. Geometric factor estimation for the LEM.
Figure 6. Geometric factor estimation for the LEM.
Preprints 87845 g006
Preprints 87845 g007
Figure 7. Expected rate map considering the satellite polar orbit and the ≃ 0.2 cm2sr acceptance. The thicker contour in the map represents the region inside of which the LEM will operate in the histogram-based mode.
Figure 7. Expected rate map considering the satellite polar orbit and the ≃ 0.2 cm2sr acceptance. The thicker contour in the map represents the region inside of which the LEM will operate in the histogram-based mode.
Preprints 87845 g007
Preprints 87845 g008
Figure 8. (Left panel) Mounting arrangement of the PIPS in the LEM spectrometer. (Right panel) A picture of the 100 μ m thin PIPS manufactured by ORTEC/AMETEK.
Figure 8. (Left panel) Mounting arrangement of the PIPS in the LEM spectrometer. (Right panel) A picture of the 100 μ m thin PIPS manufactured by ORTEC/AMETEK.
Preprints 87845 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated