Submitted:
06 November 2023
Posted:
07 November 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Integration and Excitation of Plasmonic Structures
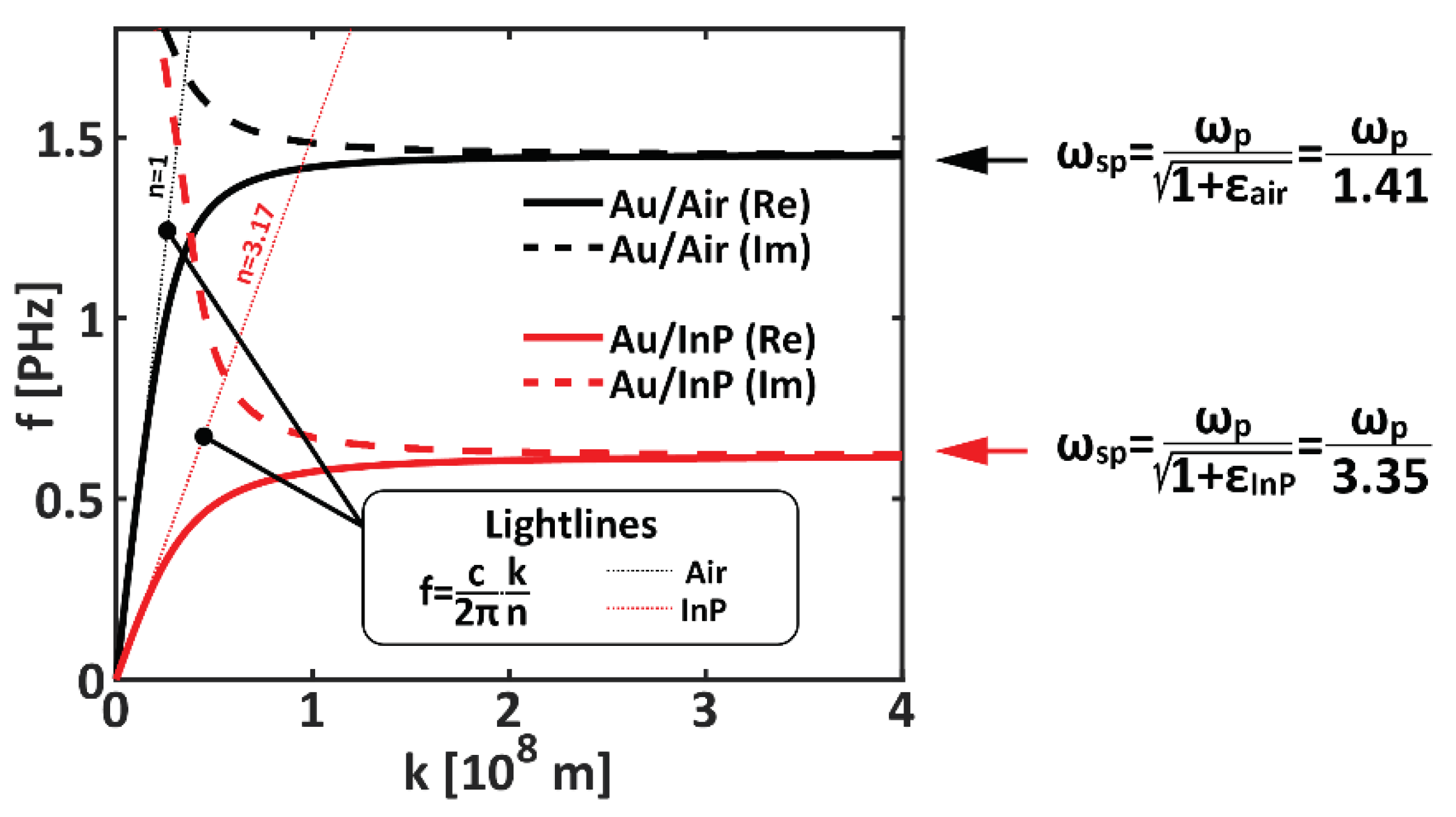
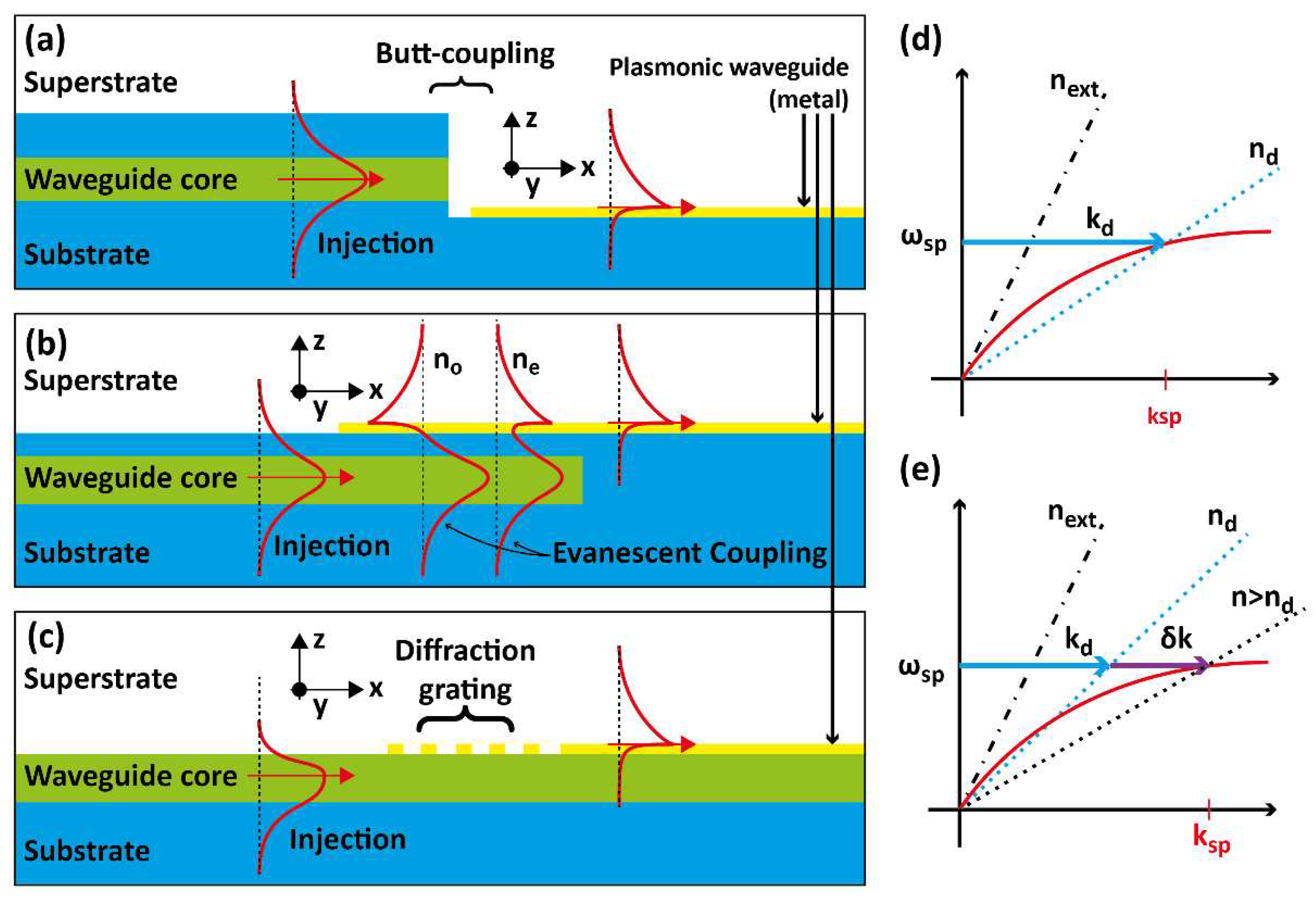
2.1. Propagative Surface Plasmon
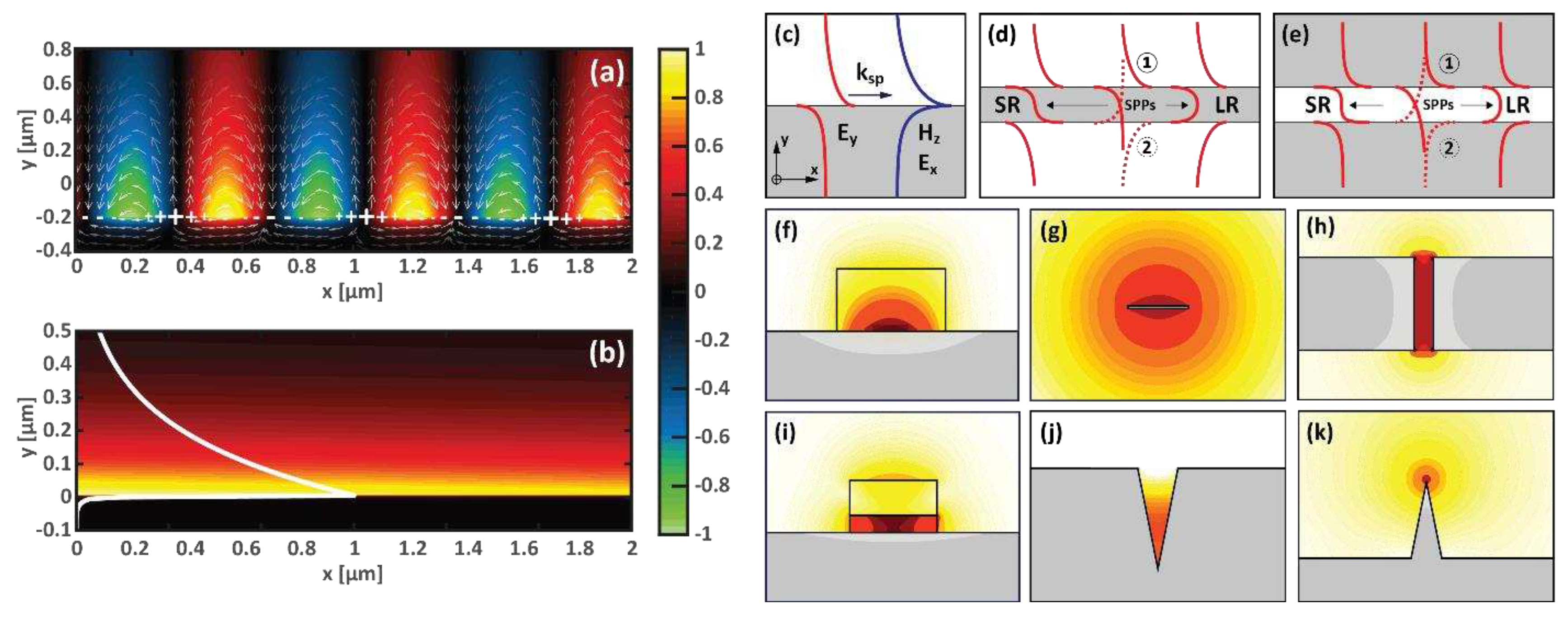
2.2. Localized Surface Plasmon
- Coupling efficiency:
- Strong coupling:
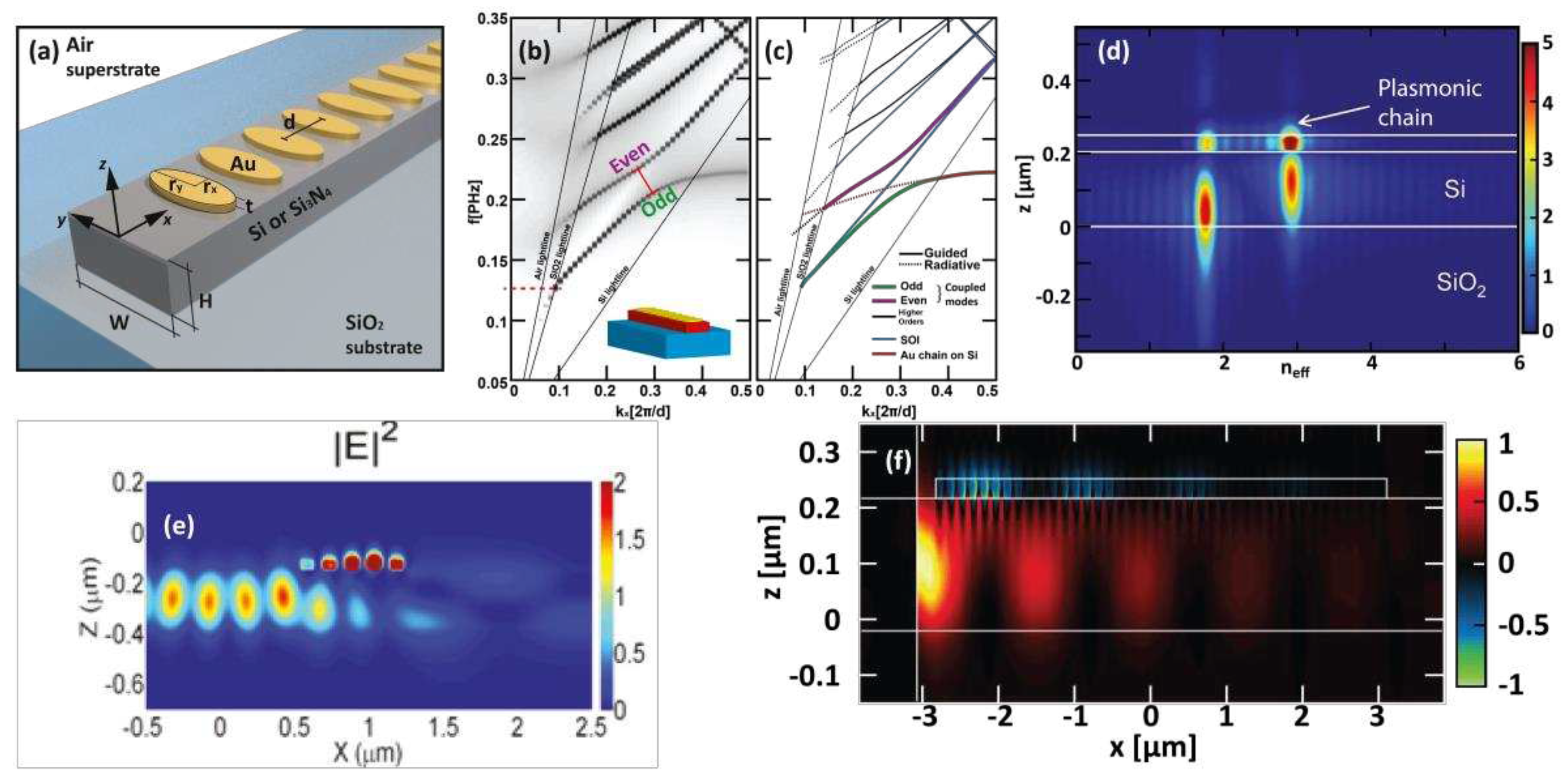
3. Surface Plasmons in Photonic Integrated Circuits
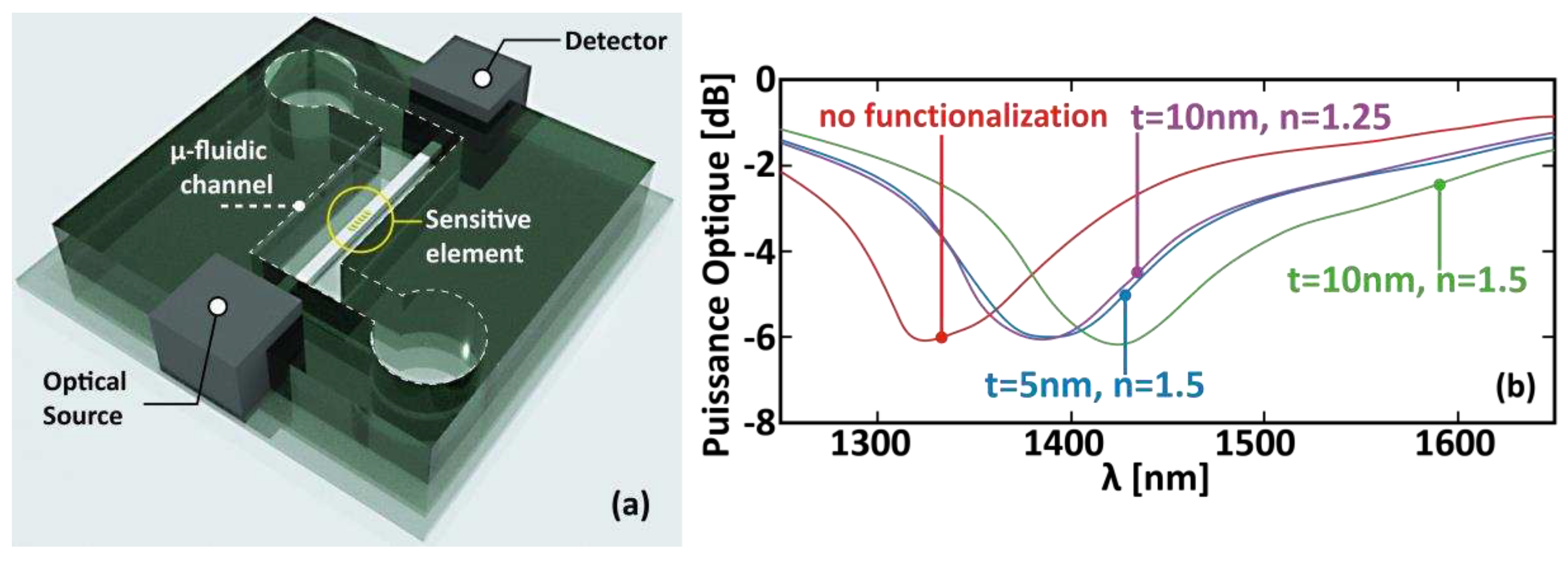
3.1. LSPR for Molecules Biosensing
- -
- the excitation electromagnetic energy can be fully transferred in the LSP, like in the case of a 5 MNP chain [88], leading to an improved sensitivity,
- -
- parallel or series sensing areas can be implemented on the chip, with the same optical source: the global analysis capacity is considerably enhanced.
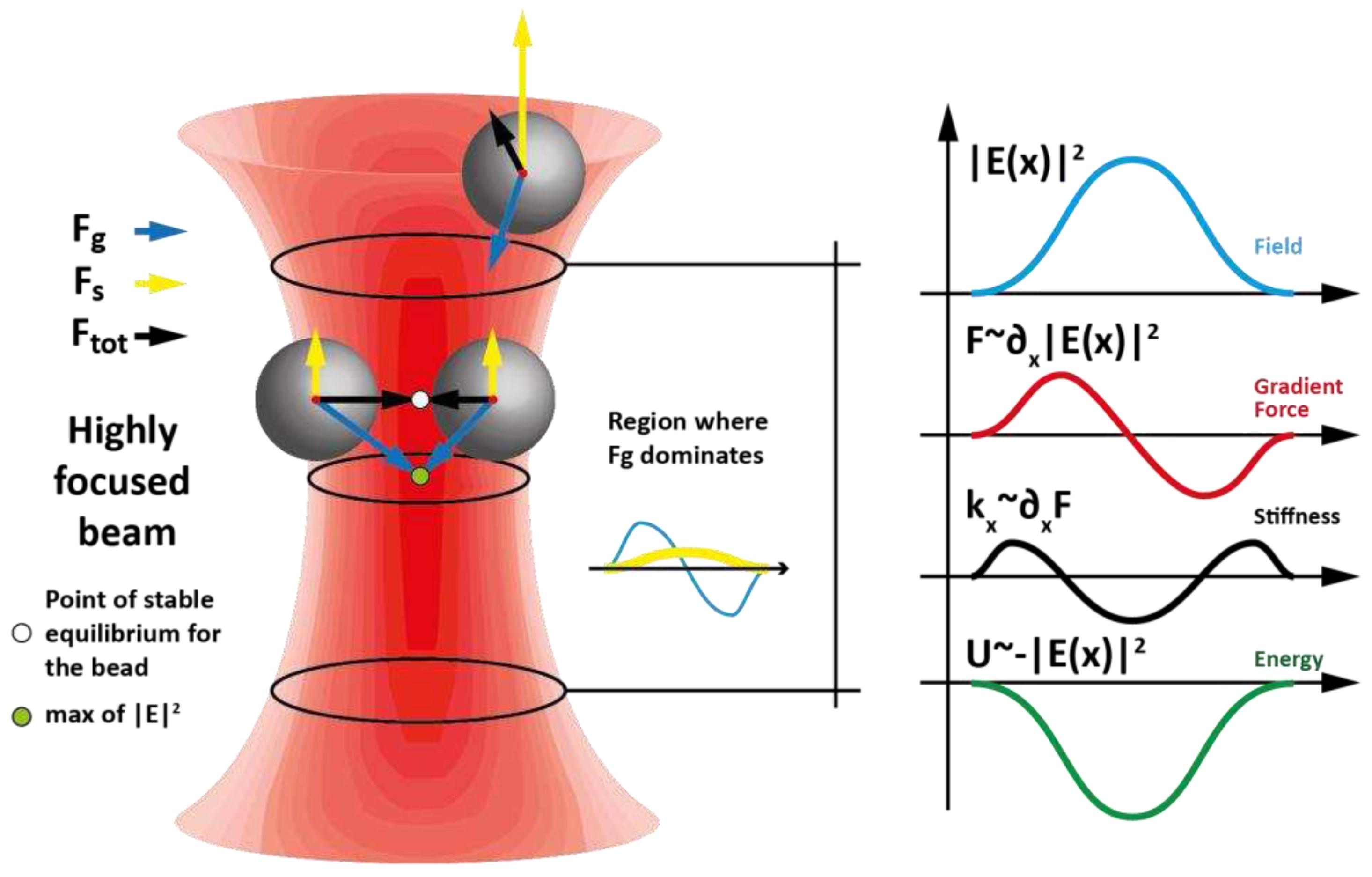
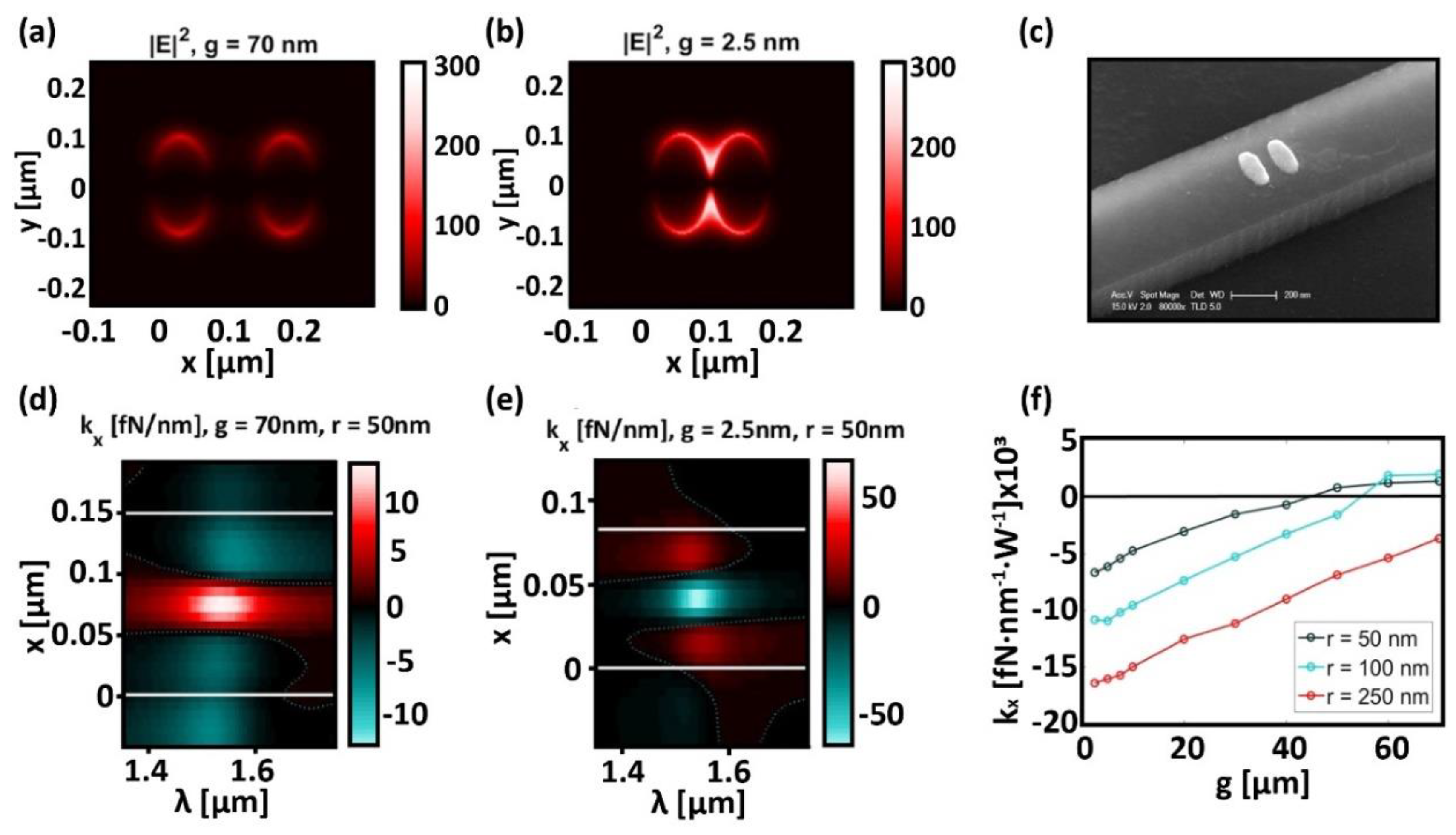
3.2. Plasmonic Nano-Tweezers and Nano-Manipulators
- Basis on optical tweezers
- -
- If the trapped object doesn’t modify the local electromagnetic field, the optical density map is calculated first, and then the trap characteristics are deduced from Fg et Fs calculation for different object positions.
- -
- if the presence of the object induces a non-negligible perturbation, the optical field must be calculated, and the Maxwell stress tensor must be fully integrated for all the possible positions of the object.
- Plasmonic tweezers
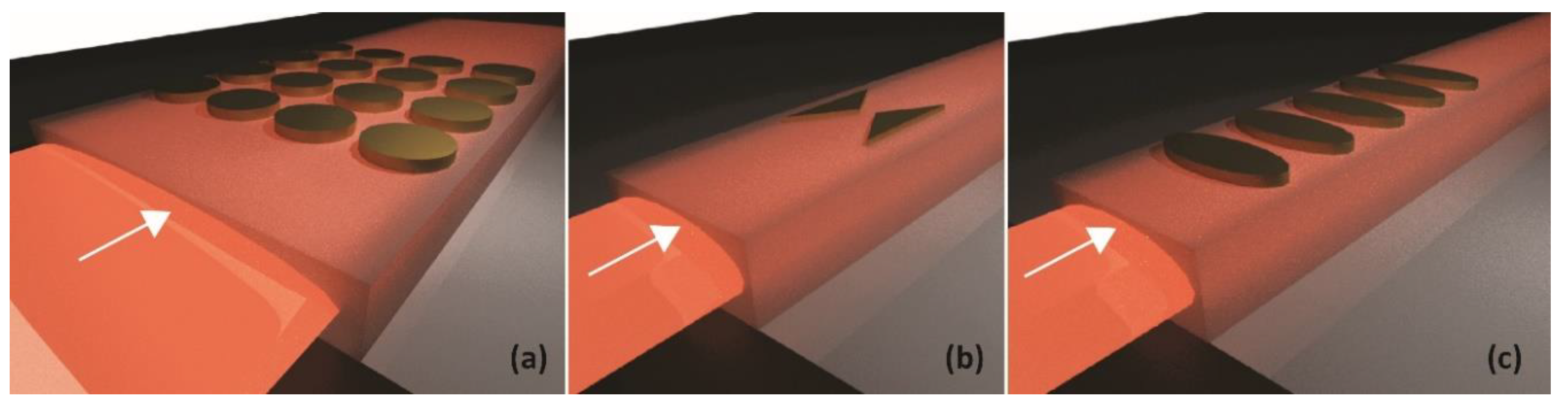
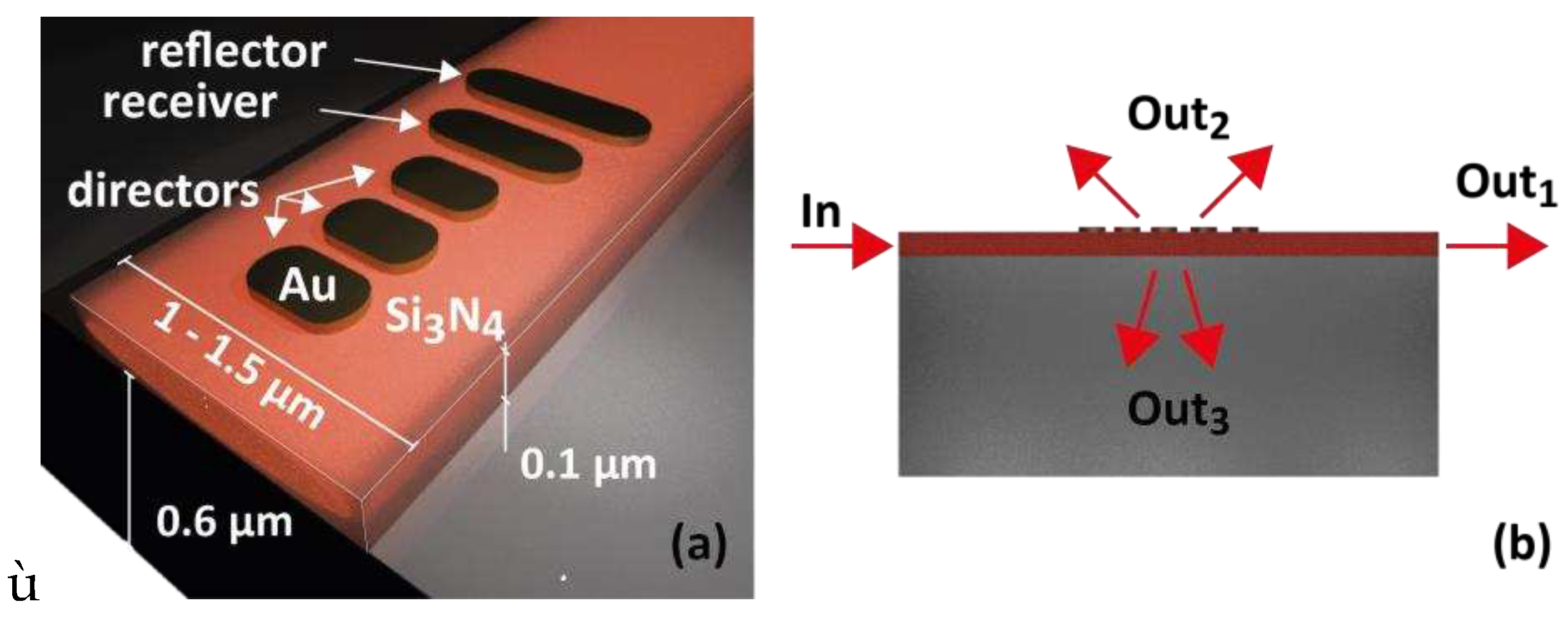
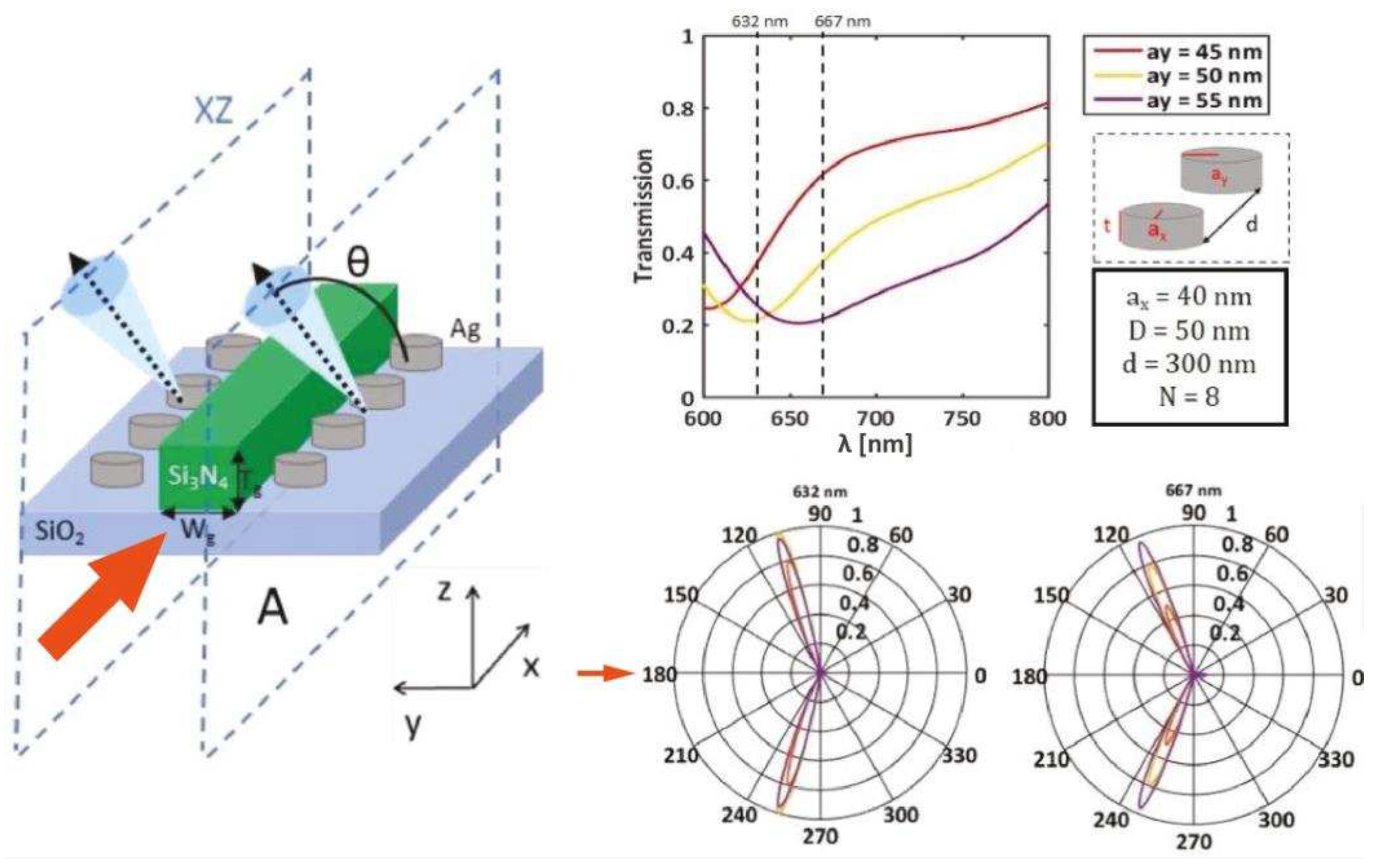
3.3. Plasmonic Antennas
- -
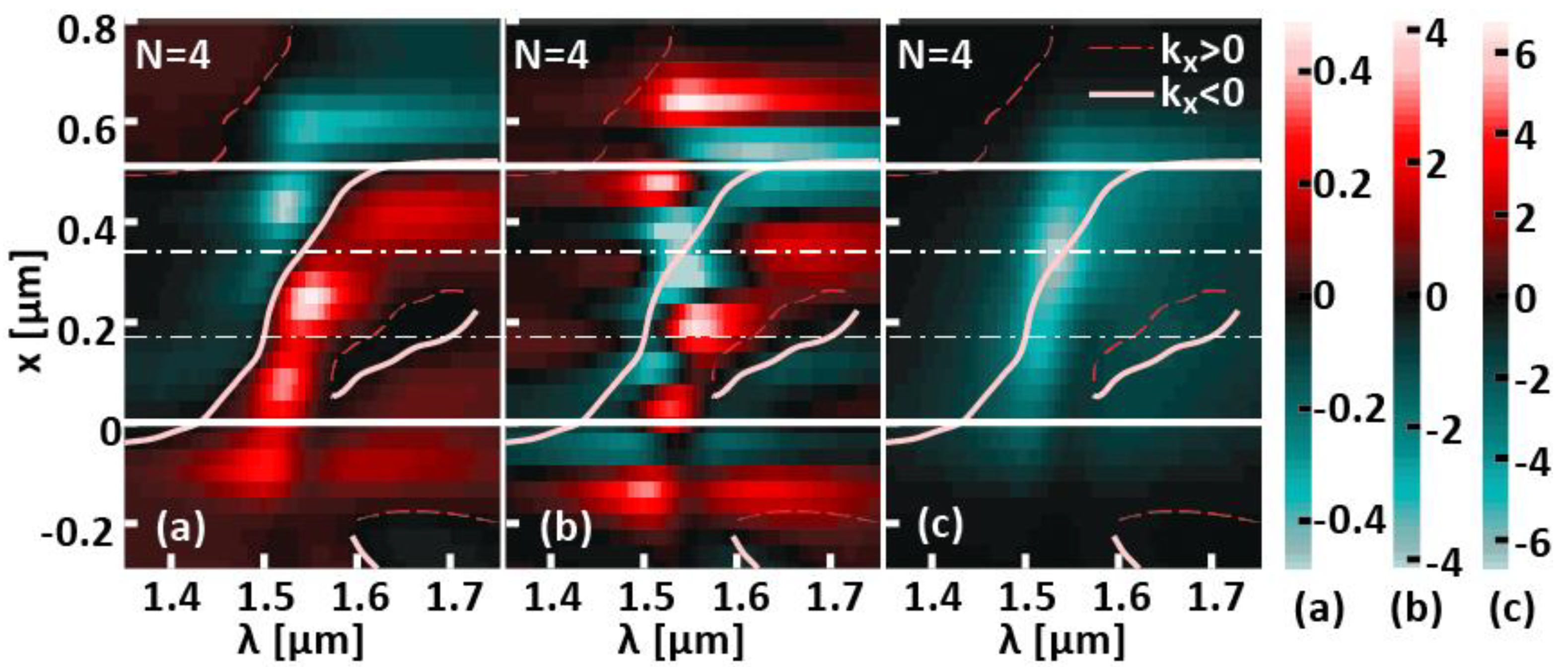
- The chain resonance modifies the coupling efficiency independently of the emission angle and directivity control: the MNP size is chosen to have resonant or resonant-shifted chain.
- -
- The chain can be positioned freely around the waveguide, without diffraction efficiency modification as long as the chain and waveguide modes overlap remains similar.
- -
- The chain period determines the emission angle, independently of the coupling efficiency.
- -
- Several chains can be simultaneously excited, for example to shape the radiation diagram: two chains on both sides of the waveguide generate radiation similar to Young’s slits interferences.
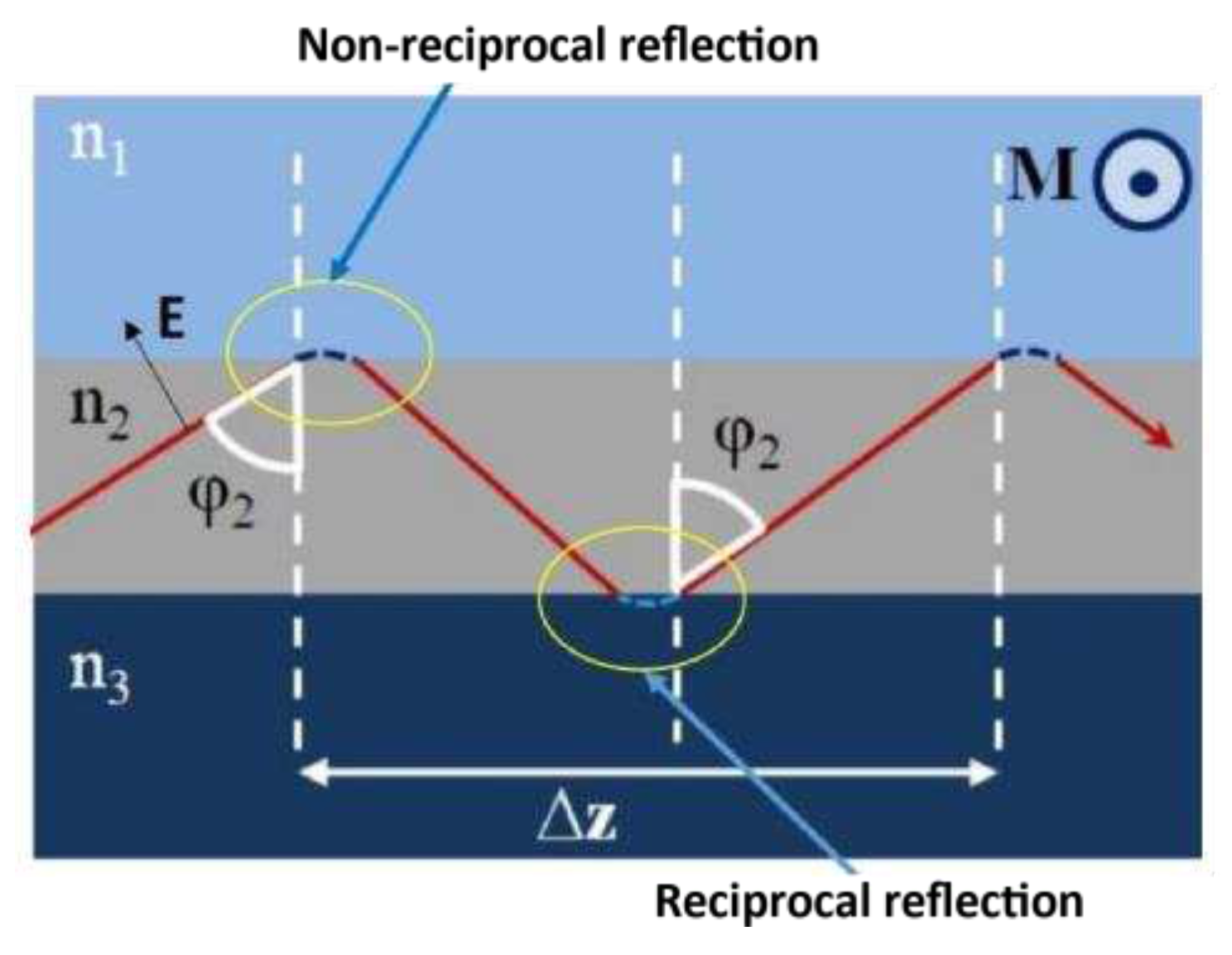
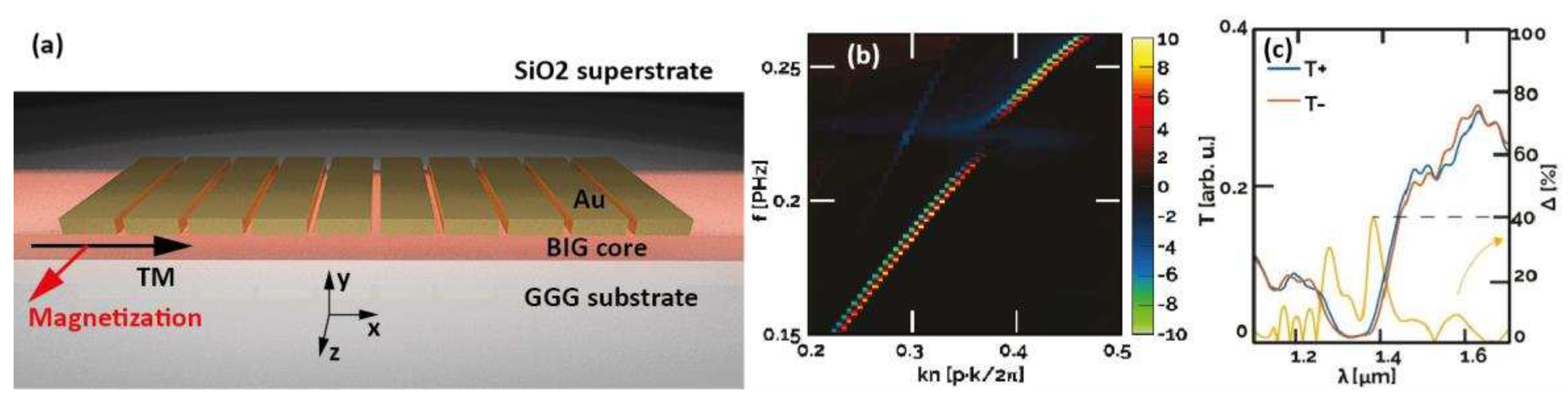
3.4. Integrated Magnetoplasmonics
| Structure | Mechanism | Coupling efficiency | λ [µm] | Coupling length Lc (Footprint) | ref | year | |
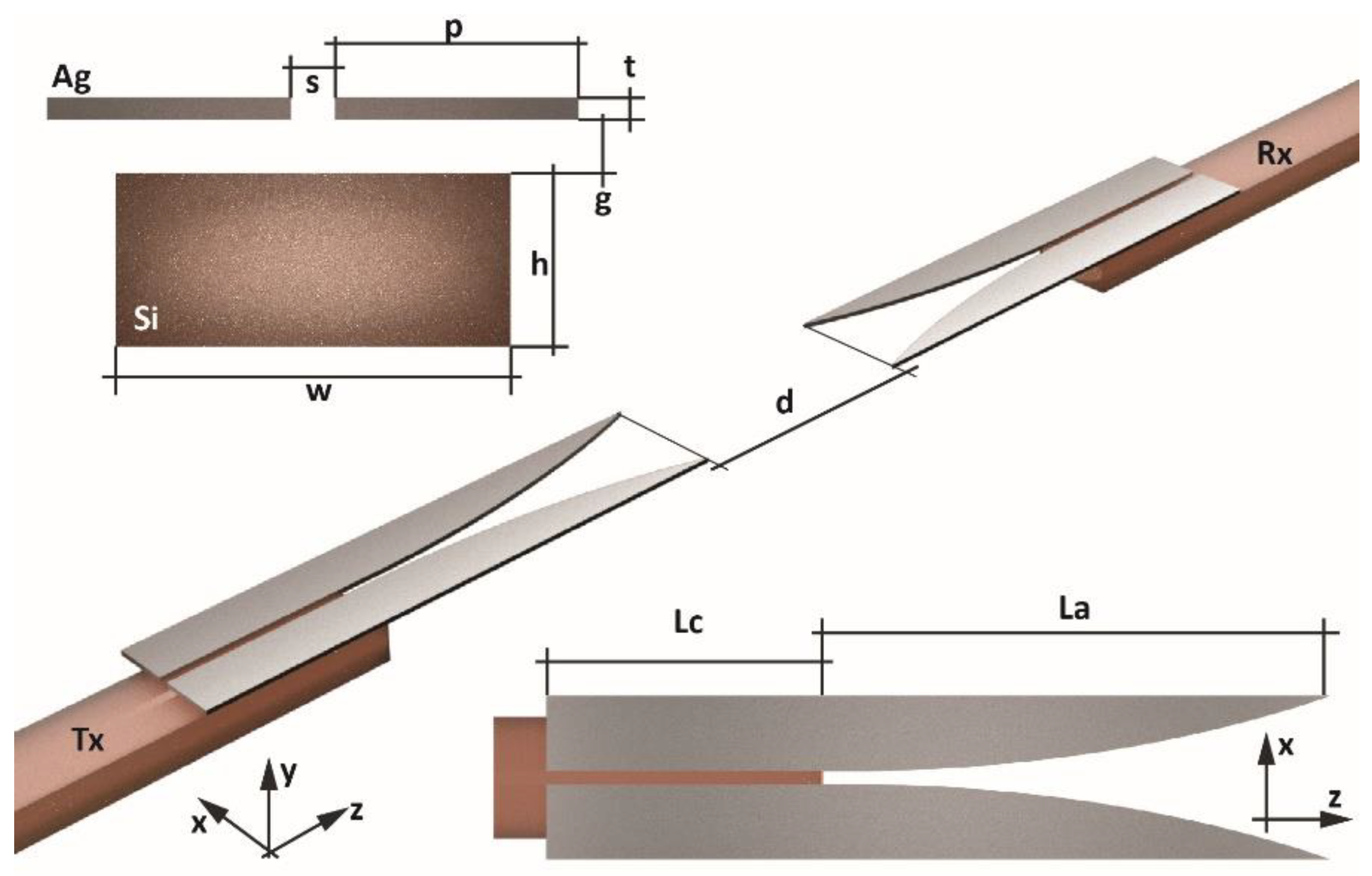
| SPP waveguide | Cu slot waveguide/SOI waveguide | Evanescent coupling | 70% (LRSPP) | 1.55 | 0.9 µm | [20] | 2010 |
| ‘buried plasmonic waveguide’/SU8 waveguide/glass | Evanescent coupling | 88% (LRSPP) | 0.633 | 5.3 µm | [57] | 2012 | |
| Si waveguide/buried plasmonic waveguide/glass | Evanescent coupling | 95.5% (LRSPP) | 1.55 | 2.85 µm | [133] | 2013 | |
| Gold film/semiconductor waveguide | Grating based coupling | 24% | 1.3 | 5.5 µm | [59] | 2011 | |
| SOI waveguide/plasmonic slot waveguide | Butt-coupling/end-fire coupling | 61% numerical/43% measured | 1.55 | (>10 µm) | [134] | 2010 | |
| InP membrane waveguide/plasmonic slot waveguide | Butt-coupling/end-fire coupling | ~55% numerical/~13% measured | 1.55 | (~5µm) | [56] |
2020 | |
| LSP, LSP chain waveguide | 1 single NP/Si3N4 waveguide | Evanescent excitation | 9.7 % | 0.850µm | NP width (<100nm) | [75] | 2013 |
| LSP subwavelength chain/SOI waveguide | Evanescent coupling | 99% | 1.55 | 0.6 µm | [76] | 2012 | |
| LSP subwavelength chain/Si3N4 waveguide /SiO2 | Evanescent coupling | / | 1.4 | 1.635 µm | [78] | 2017 | |
| Antenna on waveguide | Vivaldi antenna /SOI waveguide | Evanescent coupling | 91% (numerical) | 1.55 | 1.63 µm | [108] | 2017 |
| Yagi-Uda antenna/SOI waveguide | Evanescent excitation | 20% in-coupling | 0.85 | (~1 µm) | [109] | 2012 | |
| LSP nanoantenna/silicon | Evanescent excitation | ~4% | 1.55 | (400 nm) | [110] | 2017 | |
| LSP gratings (antenna) aside Si3N4 waveguide | Evanescent coupling | Tunable, from 10% to 50% | 0.633 | ~0.8 µm | [113] | 2018 |
4. Conclusions
Author Contributions
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lelit, M.; Słowikowski, M.; Filipiak, M.; Juchniewicz, M.; Stonio, B.; Michalak, B.; Pavłov, K.; Myśliwiec, M.; Wiśniewski, P.; Kaźmierczak, A.; et al. Passive Photonic Integrated Circuits Elements Fabricated on a Silicon Nitride Platform. Materials (Basel). 2022, 15. [Google Scholar] [CrossRef] [PubMed]
- Albiero, R.; Pentangelo, C.; Gardina, M.; Atzeni, S.; Ceccarelli, F.; Osellame, R. Toward Higher Integration Density in Femtosecond-Laser-Written Programmable Photonic Circuits. Micromachines 2022, 13. [Google Scholar] [CrossRef]
- Korthorst, T.; Bogaerts, W.; Boning, D.; Heins, M.; Bergman, B. Photonic Integrated Circuit Design Methods and Tools. In Integrated Photonics for Data Communication Applications; Glick, M., Liao, L., Schmidtke, K.B.T.-I.P. for D.C.A., Eds.; Elsevier, 2023; pp. 335–367. ISBN 978-0-323-91224-2. [Google Scholar]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface Plasmon Subwavelength Optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Maier, S. Plasmonics: Fundamentals and Applications; Springer, 2007; ISBN 0387331506. [Google Scholar]
- Raether, H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings; Springer-Verlag: Berlin, 1998. [Google Scholar]
- Cheng, C.-W.; Gwo, S. Fundamentals of Plasmonic Materials. In Plasmonic Materials and Metastructures; Gwo, S., Alù, A., Li, X., Shih, C.-K.B.T.-P.M. and M., Eds.; Elsevier: 2024; pp. 3–33. ISBN 978-0-323-85379-8.
- Ebbesen, T.W.; Genet, C.; Bozhevolnyi, S.I. Surface-Plasmon Circuitry. Phys. Today 2008, 61, 44–50. [Google Scholar] [CrossRef]
- Luo, Y.; Chamanzar, M.; Apuzzo, A.; Salas-Montiel, R.; Nguyen, K.N.; Blaize, S.; Adibi, A. On-Chip Hybrid Photonic–Plasmonic Light Concentrator for Nanofocusing in an Integrated Silicon Photonics Platform. Nano Lett. 2015, 15, 849–856. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Zheng, Q.; Wen, L.; Cumming, D.R.S.; Chen, Q. Miniaturized Spectroscopy with Tunable and Sensitive Plasmonic Structures. Opt. Lett. 2021, 46, 4264–4267. [Google Scholar] [CrossRef] [PubMed]
- Rasolian Lafmejani, S.; Khatir, M. Miniaturized Plasmonic Magneto-Optic Mach-Zehnder Isolator Using Graphene and Optical Gain Medium. Optik (Stuttg). 2021, 228, 166200. [Google Scholar] [CrossRef]
- Tuniz, A.; Bickerton, O.; Diaz, F.J.; Käsebier, T.; Kley, E.-B.; Kroker, S.; Palomba, S.; de Sterke, C.M. Modular Nonlinear Hybrid Plasmonic Circuit. Nat. Commun. 2020, 11, 2413. [Google Scholar] [CrossRef]
- Tuniz, A. Nanoscale Nonlinear Plasmonics in Photonic Waveguides and Circuits. La Riv. del Nuovo Cim. 2021, 44, 193–249. [Google Scholar] [CrossRef]
- Huttunen, M.J.; Dolgaleva, K.; Törmä, P.; Boyd, R.W. Ultra-Strong Polarization Dependence of Surface Lattice Resonances with out-of-Plane Plasmon Oscillations. Opt. Express 2016, 24, 28279–28289. [Google Scholar] [CrossRef]
- Baffou, G.; Cichos, F.; Quidant, R. Applications and Challenges of Thermoplasmonics. Nat. Mater. 2020, 19, 946–958. [Google Scholar] [CrossRef] [PubMed]
- Ciraulo, B.; Garcia-Guirado, J.; de Miguel, I.; Ortega Arroyo, J.; Quidant, R. Long-Range Optofluidic Control with Plasmon Heating. Nat. Commun. 2021, 12, 2001. [Google Scholar] [CrossRef]
- Rudé, M.; Simpson, R.E.; Quidant, R.; Pruneri, V.; Renger, J. Active Control of Surface Plasmon Waveguides with a Phase Change Material. ACS Photonics 2015, 2, 669–674. [Google Scholar] [CrossRef]
- Kats, M.A.; Blanchard, R.; Genevet, P.; Yang, Z.; Qazilbash, M.M.; Basov, D.N.; Ramanathan, S.; Capasso, F. Thermal Tuning of Mid-Infrared Plasmonic Antenna Arrays Using a Phase Change Material. Opt. Lett. 2013, 38, 368–370. [Google Scholar] [CrossRef]
- Kabashin, A. V.; Evans, P.; Pastkovsky, S.; Hendren, W.; Wurtz, G.A.; Atkinson, R.; Pollard, R.; Podolskiy, V.A.; Zayats, A. V. Plasmonic Nanorod Metamaterials for Biosensing. Nat. Mater. 2009, 8, 867–871. [Google Scholar] [CrossRef]
- Delacour, C.; Blaize, S.; Grosse, P.; Fedeli, J.M.; Bruyant, A.; Salas-Montiel, R.; Lerondel, G.; Chelnokov, A. Efficient Directional Coupling between Silicon and Copper Plasmonic Nanoslot Waveguides: Toward Metal-Oxide-Silicon Nanophotonics. Nano Lett. 2010, 10, 2922–2926. [Google Scholar] [CrossRef]
- Wang, J.; Ning, N.; Wang, Z.; Li, G.; Xu, J.; Lu, Y. Compact General Interference Hybrid-Plasmonic Multimode Interferometers Used for Optical Hybrid. Appl. Opt. 2019, 58, 5320–5327. [Google Scholar] [CrossRef]
- Celebrano, M. Plasmonics: The Future Is Ultrafast and Ultrasmall. Front. Photonics 2022, 3. [Google Scholar] [CrossRef]
- Schirato, A.; Crotti, G.; Gonçalves Silva, M.; Teles-Ferreira, D.C.; Manzoni, C.; Proietti Zaccaria, R.; Laporta, P.; de Paula, A.M.; Cerullo, G.; Della Valle, G. Ultrafast Plasmonics Beyond the Perturbative Regime: Breaking the Electronic-Optical Dynamics Correspondence. Nano Lett. 2022, 22, 2748–2754. [Google Scholar] [CrossRef] [PubMed]
- Ono, M.; Taniyama, H.; Xu, H.; Tsunekawa, M.; Kuramochi, E.; Nozaki, K.; Notomi, M. Deep-Subwavelength Plasmonic Mode Converter with Large Size Reduction for Si-Wire Waveguide. Optica 2016, 3, 999–1005. [Google Scholar] [CrossRef]
- Hung, Y.-T.; Huang, C.-B.; Huang, J.-S. Plasmonic Mode Converter for Controlling Optical Impedance and Nanoscale Light-Matter Interaction. Opt. Express 2012, 20, 20342–20355. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Z.; Zhang, Z.; Sun, X.; Tsang, H.K. Fabrication-Tolerant and Low-Loss Hybrid Plasmonic Slot Waveguide Mode Converter. J. Light. Technol. 2021, 39, 2106–2112. [Google Scholar] [CrossRef]
- Melikyan, A.; Alloatti, L.; Muslija, A.; Hillerkuss, D.; Schindler, P.C.; Li, J.; Palmer, R.; Korn, D.; Muehlbrandt, S.; Van Thourhout, D.; et al. High-Speed Plasmonic Phase Modulators. Nat. Photonics 2014, 8, 229–233. [Google Scholar] [CrossRef]
- Hoessbacher, C.; Josten, A.; Baeuerle, B.; Fedoryshyn, Y.; Hettrich, H.; Salamin, Y.; Heni, W.; Haffner, C.; Kaiser, C.; Schmid, R.; et al. Plasmonic Modulator with >170 GHz Bandwidth Demonstrated at 100 GBd NRZ. Opt. Express 2017, 25, 1762–1768. [Google Scholar] [CrossRef] [PubMed]
- Ansell, D.; Radko, I.P.; Han, Z.; Rodriguez, F.J.; Bozhevolnyi, S.I.; Grigorenko, A.N. Hybrid Graphene Plasmonic Waveguide Modulators. Nat. Commun. 2015, 6, 8846. [Google Scholar] [CrossRef]
- Emboras, A.; Hoessbacher, C.; Haffner, C.; Heni, W.; Koch, U.; Ma, P.; Fedoryshyn, Y.; Niegemann, J.; Hafner, C.; Leuthold, J. Electrically Controlled Plasmonic Switches and Modulators. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 276–283. [Google Scholar] [CrossRef]
- Zhan, G.; Liang, R.; Liang, H.; Luo, J.; Zhao, R. Asymmetric Band-Pass Plasmonic Nanodisk Filter with Mode Inhibition and Spectrally Splitting Capabilities. Opt. Express 2014, 22, 9912–9919. [Google Scholar] [CrossRef]
- Abadía, N.; Samani, A.; Boulbar, E.D. Le; Hayes, D.; Smowton, P.M. Plasmonic Integrated Multimode Filter. In Proceedings of the 2019 21st International Conference on Transparent Optical Networks (ICTON); 2019; pp. 1–3. [Google Scholar]
- Khani, S.; Danaie, M.; Rezaei, P. Realization of Single-Mode Plasmonic Bandpass Filters Using Improved Nanodisk Resonators. Opt. Commun. 2018, 420, 147–156. [Google Scholar] [CrossRef]
- Wang, M.; Sun, S.; Ma, H.F.; Cui, T.J. Supercompact and Ultrawideband Surface Plasmonic Bandpass Filter. IEEE Trans. Microw. Theory Tech. 2020, 68, 732–740. [Google Scholar] [CrossRef]
- Emboras, A.; Niegemann, J.; Ma, P.; Haffner, C.; Pedersen, A.; Luisier, M.; Hafner, C.; Schimmel, T.; Leuthold, J. Atomic Scale Plasmonic Switch. Nano Lett. 2016, 16, 709–714. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Zhang, X.; Xiao, J.; Gong, Q. Submicron Bidirectional All-Optical Plasmonic Switches. Sci. Rep. 2013, 3, 1451. [Google Scholar] [CrossRef]
- Ghosh, R.R.; Dhawan, A. Integrated Non-Volatile Plasmonic Switches Based on Phase-Change-Materials and Their Application to Plasmonic Logic Circuits. Sci. Rep. 2021, 11, 18811. [Google Scholar] [CrossRef]
- Ono, M.; Hata, M.; Tsunekawa, M.; Nozaki, K.; Sumikura, H.; Chiba, H.; Notomi, M. Ultrafast and Energy-Efficient All-Optical Switching with Graphene-Loaded Deep-Subwavelength Plasmonic Waveguides. Nat. Photonics 2020, 14, 37–43. [Google Scholar] [CrossRef]
- Azzam, S.I.; Kildishev, A. V; Ma, R.-M.; Ning, C.-Z.; Oulton, R.; Shalaev, V.M.; Stockman, M.I.; Xu, J.-L.; Zhang, X. Ten Years of Spasers and Plasmonic Nanolasers. Light Sci. Appl. 2020, 9, 90. [Google Scholar] [CrossRef]
- Sarkar, D.; Cho, S.; Yan, H.; Martino, N.; Dannenberg, P.H.; Yun, S.H. Ultrasmall InGa(As)P Dielectric and Plasmonic Nanolasers. ACS Nano 2023, 17, 16048–16055. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Li, C.; Huang, Y.-Z.; Zhang, Q. Plasmonic Nanolasers in On-Chip Light Sources: Prospects and Challenges. ACS Nano 2020, 14, 14375–14390. [Google Scholar] [CrossRef]
- Sun, J.-Y.; Nguyen, D.H.; Liu, J.-M.; Lo, C.-Y.; Ma, Y.-R.; Chen, Y.-J.; Yi, J.-Y.; Huang, J.-Z.; Giap, H.; Nguyen, H.Y.T.; et al. On-Chip Monolithically Integrated Ultraviolet Low-Threshold Plasmonic Metal‒Semiconductor Heterojunction Nanolasers. Adv. Sci. 2023, 10, 2301493. [Google Scholar] [CrossRef]
- Gonçalves, P.A.D.; Christensen, T.; Rivera, N.; Jauho, A.-P.; Mortensen, N.A.; Soljačić, M. Plasmon–Emitter Interactions at the Nanoscale. Nat. Commun. 2020, 11, 366. [Google Scholar] [CrossRef] [PubMed]
- Ge, D.; Issa, A.; Jradi, S.; Couteau, C.; Marguet, S.; Bachelot, R. Advanced Hybrid Plasmonic Nano-Emitters Using Smart Photopolymer. Photonics Res. 2022, 10, 1552–1566. [Google Scholar] [CrossRef]
- Ge, D.; Marguet, S.; Issa, A.; Jradi, S.; Nguyen, T.H.; Nahra, M.; Béal, J.; Deturche, R.; Chen, H.; Blaize, S.; et al. Hybrid Plasmonic Nano-Emitters with Controlled Single Quantum Emitter Positioning on the Local Excitation Field. Nat. Commun. 2020, 11, 3414. [Google Scholar] [CrossRef]
- Siampour, H.; Kumar, S.; Bozhevolnyi, S.I. Nanofabrication of Plasmonic Circuits Containing Single Photon Sources. ACS Photonics 2017, 4, 1879–1884. [Google Scholar] [CrossRef]
- Tame, M.S.; McEnery, K.R.; Özdemir, Ş.K.; Lee, J.; Maier, S.A.; Kim, M.S. Quantum Plasmonics. Nat. Phys. 2013, 9, 329–340. [Google Scholar] [CrossRef]
- Leon, N.P. de; Lukin, M.D.; Park, H. Quantum Plasmonic Circuits. IEEE J. Sel. Top. Quantum Electron. 2012, 18, 1781–1791. [Google Scholar] [CrossRef]
- Hong, F.Y.; Xiong, S.J. Quantum Interfaces Using Nanoscale Surface Plasmons. Eur. Phys. J. D 2008, 50, 325–329. [Google Scholar] [CrossRef]
- Heeres, R.W.; Kouwenhoven, L.P.; Zwiller, V. Quantum Interference in Plasmonic Circuits. Nat. Nanotechnol. 2013, 8, 719–722. [Google Scholar] [CrossRef]
- Sun, P.; Xu, P.; Zhu, K.; Zhou, Z. Silicon-Based Optoelectronics Enhanced by Hybrid Plasmon Polaritons: Bridging Dielectric Photonics and Nanoplasmonics. Photonics 2021, 8. [Google Scholar] [CrossRef]
- Joannopoulos, J.; Johnson, S.; Winn, J.; Meade, R. Photonic Crystals: Molding the Flow of Light; 2011; ISBN 9780691124568. [Google Scholar]
- Palik, E.D.; Ghosh, G. Handbook of Optical Constants of Solids II; Academic Press: Orlando, 1998; ISBN 0125444206 (alk. paper). [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, 1998. [Google Scholar]
- Berini, P.; De Leon, I. Surface Plasmon-Polariton Amplifiers and Lasers. Nat. Photonics 2012, 6, 16–24. [Google Scholar] [CrossRef]
- Van Der Tol, J.J.G.M.; Jiao, Y.; Van Engelen, J.P.; Pogoretskiy, V.; Kashi, A.A.; Williams, K. InP Membrane on Silicon (IMOS) Photonics. IEEE J. Quantum Electron. 2020, 56, 1–7. [Google Scholar] [CrossRef]
- Magno, G.; Grande, M.; Petruzzelli, V.; D’Orazio, A. High-Efficient Ultra-Short Vertical Long-Range Plasmonic Couplers. J. Nanophotonics 2012, 6, 061609. [Google Scholar] [CrossRef]
- Magno, G.; Grande, M.; Petruzzelli, V.; D’Orazio, A. Numerical Analysis of the Coupling Mechanism in Long-Range Plasmonic Couplers at 155 Μm. Opt. Lett. 2013, 38, 46. [Google Scholar] [CrossRef]
- Tetienne, J.P.; Bousseksou, A.; Costantini, D.; De Wilde, Y.; Colombelli, R. Design of an Integrated Coupler for the Electrical Generation of Surface Plasmon Polaritons. Opt. Express 2011, 19, 18155–18163. [Google Scholar] [CrossRef]
- Kelly, K.L.; Coronado, E.; Zhao, L.L.; Schatz, G.C. The Optical Properties of Metal Nanoparticles: The Influence of Size, Shape, and Dielectric Environment. ChemInform 2003, 34, 668–677. [Google Scholar] [CrossRef]
- Maier, S.A.; Brongersma, M.L.; Kik, P.G.; Atwater, H.A. Observation of Near-Field Coupling in Metal Nanoparticle Chains Using Far-Field Polarization Spectroscopy. Phys. Rev. B 2002, 65, 193408. [Google Scholar] [CrossRef]
- Koenderink, A.F.; Polman, A. Complex Response and Polariton-like Dispersion Splitting in Periodic Metal Nanoparticle Chains. Phys. Rev. B - Condens. Matter Mater. Phys. 2006, 74. [Google Scholar] [CrossRef]
- Moritake, Y.; Ono, M.; Notomi, M. Far-Field Optical Imaging of Topological Edge States in Zigzag Plasmonic Chains. 2022, 11, 2183–2189. [CrossRef]
- Buendía, Á.; Sánchez-Gil, J.A.; Giannini, V. Exploiting Oriented Field Projectors to Open Topological Gaps in Plasmonic Nanoparticle Arrays. ACS Photonics 2023, 10, 464–474. [Google Scholar] [CrossRef]
- Yan, Q.; Cao, E.; Sun, Q.; Ao, Y.; Hu, X.; Shi, X.; Gong, Q.; Misawa, H. Near-Field Imaging and Time-Domain Dynamics of Photonic Topological Edge States in Plasmonic Nanochains. Nano Lett. 2021, 21, 9270–9278. [Google Scholar] [CrossRef]
- He, Z.; Bobylev, D.A.; Smirnova, D.A.; Zhirihin, D. V; Gorlach, M.A.; Tuz, V.R. Reconfigurable Topological States in Arrays of Bianisotropic Particles. ACS Photonics 2022, 9, 2322–2326. [Google Scholar] [CrossRef]
- Sinev, I.S.; Mukhin, I.S.; Slobozhanyuk, A.P.; Poddubny, A.N.; Miroshnichenko, A.E.; Samusev, A.K.; Kivshar, Y.S. Mapping Plasmonic Topological States at the Nanoscale. Nanoscale 2015, 7, 11904–11908. [Google Scholar] [CrossRef] [PubMed]
- Gong, M.; Hu, P.; Song, Q.; Xiang, H.; Han, D. Bound States in the Continuum from a Symmetric Mode with a Dominant Toroidal Dipole Resonance. Phys. Rev. A 2022, 105, 33504. [Google Scholar] [CrossRef]
- Song, Q.; Yi, Z.; Xiang, H.; Han, D. Dynamics and Asymmetric Behavior of Loss-Induced Bound States in the Continuum in Momentum Space. Phys. Rev. B 2023, 107, 165142. [Google Scholar] [CrossRef]
- Jin, Y.; Wu, K.; Sheng, B.; Ma, W.; Chen, Z.; Li, X. Plasmonic Bound States in the Continuum to Tailor Exciton Emission of MoTe2. Nanomaterials 2023, 13. [Google Scholar] [CrossRef]
- Magno, G.; Leroy, B.; Barat, D.; Pradere, L.; Dagens, B. Numerical Demonstration of Surface Lattice Resonance Excitation in Integrated Localized Surface Plasmon Waveguides. Opt. Express 2022, 30, 5835–5847. [Google Scholar] [CrossRef]
- Utyushev, A.D.; Zakomirnyi, V.I.; Rasskazov, I.L. Collective Lattice Resonances: Plasmonics and Beyond. Rev. Phys. 2021, 6, 100051. [Google Scholar] [CrossRef]
- Kravets, V.G.; Schedin, F.; Grigorenko, A.N. Extremely Narrow Plasmon Resonances Based on Diffraction Coupling of Localized Plasmons in Arrays of Metallic Nanoparticles. Phys. Rev. Lett. 2008, 101, 87403. [Google Scholar] [CrossRef]
- Pikalov, A.M.; Dorofeenko, A. V; Lozovik, Y.E. Dispersion Relations for Plasmons in Complex-Shaped Nanoparticle Chains. Phys. Rev. B 2018, 98, 85134. [Google Scholar] [CrossRef]
- Chamanzar, M.; Xia, Z.; Yegnanarayanan, S.; Adibi, A. Hybrid Integrated Plasmonic-Photonic Waveguides for on-Chip Localized Surface Plasmon Resonance (LSPR) Sensing and Spectroscopy. Opt. Express 2013, 21, 32086. [Google Scholar] [CrossRef]
- Février, M.; Gogol, P.; Aassime, A.; Mégy, R.; Delacour, C.; Chelnokov, A.; Apuzzo, A.; Blaize, S.; Lourtioz, J.M.; Dagens, B. Giant Coupling Effect between Metal Nanoparticle Chain and Optical Waveguide. Nano Lett. 2012, 12, 1032–1037. [Google Scholar] [CrossRef]
- Novotny, L. Strong Coupling, Energy Splitting, and Level Crossings: A Classical Perspective. Am. J. Phys. 2010, 78, 1199–1202. [Google Scholar] [CrossRef]
- Magno, G.; Fevrier, M.; Gogol, P.; Aassime, A.; Bondi, A.; Mégy, R.; Dagens, B. Strong Coupling and Vortexes Assisted Slow Light in Plasmonic Chain-SOI Waveguide Systems. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Dagens, B.; Février, M.; Gogol, P.; Blaize, S.; Apuzzo, A.; Magno, G.; Mégy, R.; Lerondel, G. Direct Observation of Optical Field Phase Carving in the Vicinity of Plasmonic Metasurfaces. Nano Lett. 2016, 16. [Google Scholar] [CrossRef]
- Li, Z.; Kim, M.-H.; Wang, C.; Han, Z.; Shrestha, S.; Overvig, A.C.; Lu, M.; Stein, A.; Agarwal, A.M.; Lončar, M.; et al. Controlling Propagation and Coupling of Waveguide Modes Using Phase-Gradient Metasurfaces. Nat. Nanotechnol. 2017, 12, 675–683. [Google Scholar] [CrossRef] [PubMed]
- Divya, J.; Selvendran, S.; Raja, A.S.; Sivasubramanian, A. Surface Plasmon Based Plasmonic Sensors: A Review on Their Past, Present and Future. Biosens. Bioelectron. X 2022, 11, 100175. [Google Scholar] [CrossRef]
- Shrivastav, A.M.; Cvelbar, U.; Abdulhalim, I. A Comprehensive Review on Plasmonic-Based Biosensors Used in Viral Diagnostics. Commun. Biol. 2021, 4, 70. [Google Scholar] [CrossRef] [PubMed]
- Hamza, M.E.; Othman, M.A.; Swillam, M.A. Plasmonic Biosensors: Review. Biology (Basel). 2022, 11. [Google Scholar] [CrossRef] [PubMed]
- Duan, Q.; Liu, Y.; Chang, S.; Chen, H.; Chen, J. Surface Plasmonic Sensors: Sensing Mechanism and Recent Applications. Sensors 2021, 21. [Google Scholar] [CrossRef]
- Steglich, P.; Schasfoort, R.B.M. Surface Plasmon Resonance Imaging (SPRi) and Photonic Integrated Circuits (PIC) for COVID-19 Severity Monitoring. COVID 2022, 2, 389–397. [Google Scholar] [CrossRef]
- Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; Van Duyne, R.P. Biosensing with Plasmonic Nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef]
- Kretschmann, E.; Raether, H. Radiative Decay of Nonradiative Surface Plasmons Excited by Light. Zeitschrift Für Naturforsch. Sect. A A J. Phys. Sci. 1968, 23, 2135. [Google Scholar] [CrossRef]
- Février, M.; Gogol, P.; Barbillon, G.; Aassime, A.; Mégy, R.; Bartenlian, B.; Lourtioz, J.-M.; Dagens, B. Integration of Short Gold Nanoparticles Chain on SOI Waveguide toward Compact Integrated Bio-Sensors. Opt. Express 2012, 20, 17402. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a Single-Beam Gradient Force Optical Trap for Dielectric Particles. Opt. Angular Momentum 2016, 11, 196–198. [Google Scholar] [CrossRef]
- Falconi, M.C.; Magno, G.; Colosimo, S.; Yam, V.; Dagens, B.; Prudenzano, F. Design of a Half-Ring Plasmonic Tweezers for Environmental Monitoring. Opt. Mater. X 2022, 13, 100141. [Google Scholar] [CrossRef]
- Wong, H.M.K.; Righini, M.; Gates, J.C.; Smith, P.G.R.; Pruneri, V.; Quidant, R. On-a-Chip Surface Plasmon Tweezers. Appl. Phys. Lett. 2011, 99, 061107–061107. [Google Scholar] [CrossRef]
- Ecarnot, A.; Magno, G.; Yam, V.; Dagens, B. Ultra-Efficient Nanoparticle Trapping by Integrated Plasmonic Dimers. Opt. Lett. 2018, 43, 455. [Google Scholar] [CrossRef]
- Magno, G.; Ecarnot, A.; Pin, C.; Yam, V.; Gogol, P.; Mégy, R.; Cluzel, B.; Dagens, B. Integrated Plasmonic Nanotweezers for Nanoparticle Manipulation. Opt. Lett. 2016, 41, 3679. [Google Scholar] [CrossRef]
- Wang, G.; Ying, Z.; Ho, H.; Huang, Y.; Zou, N.; Zhang, X. Nano-Optical Conveyor Belt with Waveguide-Coupled Excitation. Opt. Lett. 2016, 41, 528. [Google Scholar] [CrossRef]
- Pin, C.; Magno, G.; Ecarnot, A.; Picard, E.; Hadji, E.; Yam, V.; de Fornel, F.; Dagens, B.; Cluzel, B. Seven at One Blow: Particle Cluster Stability in a Single Plasmonic Trap on a Silicon Waveguide. ACS Photonics 2020, 7, 1942–1949. [Google Scholar] [CrossRef]
- Coward, J.F.; Chalfant, C.H.; Chang, P.H. A Photonic Integrated-Optic RF Phase Shifter for Phased Array Antenna Beam-Forming Applications. J. Light. Technol. 1993, 11, 2201–2205. [Google Scholar] [CrossRef]
- Sattari, H.; Graziosi, T.; Kiss, M.; Seok, T.J.; Han, S.; Wu, M.C.; Quack, N. Silicon Photonic MEMS Phase-Shifter. Opt. Express 2019, 27, 18959–18969. [Google Scholar] [CrossRef] [PubMed]
- Edinger, P.; Takabayashi, A.Y.; Errando-Herranz, C.; Khan, U.; Sattari, H.; Verheyen, P.; Bogaerts, W.; Quack, N.; Gylfason, K.B. Silicon Photonic Microelectromechanical Phase Shifters for Scalable Programmable Photonics. Opt. Lett. 2021, 46, 5671–5674. [Google Scholar] [CrossRef]
- Firby, C.J.; Elezzabi, A.Y. High-Speed Nonreciprocal Magnetoplasmonic Waveguide Phase Shifter. Optica 2015, 2, 598–606. [Google Scholar] [CrossRef]
- Bonjour, R.; Burla, M.; Abrecht, F.C.; Welschen, S.; Hoessbacher, C.; Heni, W.; Gebrewold, S.A.; Baeuerle, B.; Josten, A.; Salamin, Y.; et al. Plasmonic Phased Array Feeder Enabling Ultra-Fast Beam Steering at Millimeter Waves. Opt. Express 2016, 24, 25608–25618. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, L.; Bock, K. Current Development in the Field of Optical Short-Range Interconnects BT - Optical Polymer Waveguides: From the Design to the Final 3D-Opto Mechatronic Integrated Device. Franke, J., Overmeyer, L., Lindlein, N., Bock, K., Kaierle, S., Suttmann, O., Wolter, K.-J., Eds.; Springer International Publishing: Cham, 2022; pp. 1–13. ISBN 978-3-030-92854-4. [Google Scholar]
- Zhang, H.C.; Zhang, L.P.; He, P.H.; Xu, J.; Qian, C.; Garcia-Vidal, F.J.; Cui, T.J. A Plasmonic Route for the Integrated Wireless Communication of Subdiffraction-Limited Signals. Light Sci. Appl. 2020, 9, 113. [Google Scholar] [CrossRef] [PubMed]
- Gupta, T. Copper Interconnect Technology; Springer New York: New York, NY, 2009; ISBN 978-1-4419-0075-3. [Google Scholar]
- Croes, K.; Adelmann, C.; Wilson, C.J.; Zahedmanesh, H.; Pedreira, O. V; Wu, C.; Leśniewska, A.; Oprins, H.; Beyne, S.; Ciofi, I.; et al. Interconnect Metals beyond Copper: Reliability Challenges and Opportunities. In Proceedings of the 2018 IEEE International Electron Devices Meeting (IEDM); 2018; pp. 5.3.1–5.3.4. [Google Scholar]
- Merlo, J.M.; Nesbitt, N.T.; Calm, Y.M.; Rose, A.H.; D’Imperio, L.; Yang, C.; Naughton, J.R.; Burns, M.J.; Kempa, K.; Naughton, M.J. Wireless Communication System via Nanoscale Plasmonic Antennas. Sci. Rep. 2016, 6, 31710. [Google Scholar] [CrossRef] [PubMed]
- Calò, G.; Bellanca, G.; Alam, B.; Kaplan, A.E.; Bassi, P.; Petruzzelli, V. Array of Plasmonic Vivaldi Antennas Coupled to Silicon Waveguides for Wireless Networks through On-Chip Optical Technology - WiNOT. Opt. Express 2018, 26, 30267. [Google Scholar] [CrossRef] [PubMed]
- Fuschini, F.; Barbiroli, M.; Zoli, M.; Bellanca, G.; Calò, G.; Bassi, P.; Petruzzelli, V. Ray Tracing Modeling of Electromagnetic Propagation for On-Chip Wireless Optical Communications. J. Low Power Electron. Appl. 2018, 8. [Google Scholar] [CrossRef]
- Bellanca, G.; Calò, G.; Kaplan, A.E.; Bassi, P.; Petruzzelli, V. Integrated Vivaldi Plasmonic Antenna for Wireless On-Chip Optical Communications. Opt. Express 2017, 25, 16214. [Google Scholar] [CrossRef]
- Bernal Arango, F.; Kwadrin, A.; Koenderink, A.F. Plasmonic Antennas Hybridized with Dielectric Waveguides. ACS Nano 2012, 6, 10156–10167. [Google Scholar] [CrossRef]
- Guo, R.; Decker, M.; Setzpfandt, F.; Gai, X.; Choi, D.-Y.; Kiselev, R.; Chipouline, A.; Staude, I.; Pertsch, T.; Neshev, D.N.; et al. High–Bit Rate Ultra-Compact Light Routing with Mode-Selective on-Chip Nanoantennas. Sci. Adv. 2023, 3, e1700007. [Google Scholar] [CrossRef]
- Fevrier, M.; Gogol, P.; Aassime, A.; Megy, R.; Bouville, D.; Lourtioz, J.M.; Dagens, B. Localized Surface Plasmon Bragg Grating on SOI Waveguide at Telecom Wavelengths. Appl. Phys. A Mater. Sci. Process. 2012, 109, 935–942. [Google Scholar] [CrossRef]
- Février, M.; Gogol, P.; Lourtioz, J.-M.; Dagens, B. Metallic Nanoparticle Chains on Dielectric Waveguides: Coupled and Uncoupled Situations Compared. Opt. Express 2013, 21, 24504. [Google Scholar] [CrossRef]
- Leroy, B.; Magno, G.; Barat, D.; Pradere, L.; Dagens, B. Integrated Nanoantenna Gratings for Planar Holographic Signalisation System. In Proceedings of the Asia Communications and Photonics Conference, ACP; 2018. Vol. 2018-Octob. [Google Scholar]
- Maccaferri, N.; Gabbani, A.; Pineider, F.; Kaihara, T.; Tapani, T.; Vavassori, P. Magnetoplasmonics in Confined Geometries: Current Challenges and Future Opportunities. Appl. Phys. Lett. 2023, 122, 120502. [Google Scholar] [CrossRef]
- Armelles, G.; Cebollada, A.; García-Martín, A.; García-Martín, J.M.; González, M.U.; González-Díaz, J.B.; Ferreiro-Vila, E.; Torrado, J.F. Magnetoplasmonic Nanostructures: Systems Supporting Both Plasmonic and Magnetic Properties. J. Opt. A Pure Appl. Opt. 2009, 11, 114023. [Google Scholar] [CrossRef]
- González-Díaz, J.B.; García-Martín, A.; Armelles, G.; Navas, D.; Vázquez, M.; Nielsch, K.; Wehrspohn, R.B.; Gösele, U. Enhanced Magneto-Optics and Size Effects in Ferromagnetic Nanowire Arrays. Adv. Mater. 2007, 19, 2643–2647. [Google Scholar] [CrossRef]
- González-Díaz, J.B.; García-Martín, A.; Reig, G.A. Unusual Magneto-Optical Behavior Induced by Local Dielectric Variations under Localized Surface Plasmon Excitations. Nanoscale Res. Lett. 2011, 6, 408. [Google Scholar] [CrossRef]
- Díaz-Valencia, B.F.; Porras-Montenegro, N.; Oliveira, O.N.J.; Mejía-Salazar, J.R. Nanostructured Hyperbolic Metamaterials for Magnetoplasmonic Sensors. ACS Appl. Nano Mater. 2022, 5, 1740–1744. [Google Scholar] [CrossRef]
- Maccaferri, N.; Berger, A.; Bonetti, S.; Bonanni, V.; Kataja, M.; Qin, Q.H.; van Dijken, S.; Pirzadeh, Z.; Dmitriev, A.; Nogués, J.; et al. Tuning the Magneto-Optical Response of Nanosize Ferromagnetic Ni Disks Using the Phase of Localized Plasmons. Phys. Rev. Lett. 2013, 111, 167401. [Google Scholar] [CrossRef]
- Damasceno, G.H.B.; Carvalho, W.O.F.; Cerqueira Sodré, A.J.; Oliveira, O.N.J.; Mejía-Salazar, J.R. Magnetoplasmonic Nanoantennas for On-Chip Reconfigurable Optical Wireless Communications. ACS Appl. Mater. Interfaces 2023, 15, 8617–8623. [Google Scholar] [CrossRef]
- Royer, F.; Varghese, B.; Gamet, E.; Neveu, S.; Jourlin, Y.; Jamon, D. Enhancement of Both Faraday and Kerr Effects with an All-Dielectric Grating Based on a Magneto-Optical Nanocomposite Material. ACS Omega 2020, 5, 2886–2892. [Google Scholar] [CrossRef]
- Belotelov, V.I.; Kreilkamp, L.E.; Akimov, I.A.; Kalish, A.N.; Bykov, D.A.; Kasture, S.; Yallapragada, V.J.; Venu Gopal, A.; Grishin, A.M.; Khartsev, S.I.; et al. Plasmon-Mediated Magneto-Optical Transparency. Nat. Commun. 2013, 4, 2128. [Google Scholar] [CrossRef]
- Singh, R.S.; Sarswat, P.K. From Fundamentals to Applications: The Development of Magnetoplasmonics for next-Generation Technologies. Mater. Today Electron. 2023, 4, 100033. [Google Scholar] [CrossRef]
- Firby, C.J.; Elezzabi, A.Y. Magnetoplasmonic Isolators Utilizing the Nonreciprocal Phase Shift. Opt. Lett. 2016, 41, 563. [Google Scholar] [CrossRef]
- Zvezdin, A.K.; Kotov, V.A. Modern Magnetooptics and Magnetooptical Materials. Mod. Magnetooptics Magnetooptical Mater. 1997. [Google Scholar] [CrossRef]
- Shimizu, H.; Nakano, Y. Fabrication and Characterization of an InGaAsp/InP Active Waveguide Optical Isolator with 14.7 DB/Mm TE Mode Nonreciprocal Attenuation. J. Light. Technol. 2006, 24, 38–43. [Google Scholar] [CrossRef]
- Van Parys, W.; Moeyersoon, B.; Van Thourhout, D.; Baets, R.; Vanwolleghem, M.; Dagens, B.; Decobert, J.; Le Gouezigou, O.; Make, D.; Vanheertum, R.; et al. Transverse Magnetic Mode Nonreciprocal Propagation in an Amplifying AlGaInAs/InP Optical Waveguide Isolator. Appl. Phys. Lett. 2006, 88, 71115. [Google Scholar] [CrossRef]
- Yokoi, H.; Mizumoto, T.; Shoji, Y. Optical Nonreciprocal Devices with a Silicon Guiding Layer Fabricated by Wafer Bonding. Appl. Opt. 2003, 42, 6605. [Google Scholar] [CrossRef]
- Tien, M.-C.; Mizumoto, T.; Pintus, P.; Kromer, H.; Bowers, J.E. Silicon Ring Isolators with Bonded Nonreciprocal Magneto-Optic Garnets. Opt. Express 2011, 19, 11740. [Google Scholar] [CrossRef]
- Magno, G.; Yam, V.; Dagens, B. Integrated Magneto-Plasmonics for Non-Reciprocal Optical Devices. In Proceedings of the ECIO, Session M2: Advanced Materials, Eindhoven, Nederlands; 2017. [Google Scholar]
- Abadian, S.; Magno, G.; Yam, V.; Dagens, B. Integrated Magneto-Plasmonic Isolation Enhancement Based on Coupled Resonances in Subwavelength Gold Grating. Opt. Commun. 2021, 483, 126633. [Google Scholar] [CrossRef]
- Belotelov, V.I.; Akimov, I.A.; Pohl, M.; Kotov, V.A.; Kasture, S.; Vengurlekar, A.S.; Gopal, A.V.; Yakovlev, D.R.; Zvezdin, A.K.; Bayer, M. Enhanced Magneto-Optical Effects in Magnetoplasmonic Crystals. Nat. Nanotechnol. 2011, 6, 370–376. [Google Scholar] [CrossRef]
- Magno, G.; Grande, M.; Petruzzelli, V.; D’Orazio, A. Numerical Analysis of the Coupling Mechanism in Long-Range Plasmonic Couplers at 1.55 Μm. Opt. Lett. 2013, 38, 46–48. [Google Scholar] [CrossRef]
- Yang, R.; Wahsheh, R.A.; Lu, Z.; Abushagur, M.A.G. Efficient Light Coupling between Dielectric Slot Waveguide and Plasmonic Slot Waveguide. Opt. Lett. 2010, 35, 649–651. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





