4.1. Details of the procedure and variants
Since the aim of the paper is the analysis of the Four Quadrant operating characteristics (Q11, n11, M11), with the idea of determination of legality that exist.It is known that in pump mode and turbine mode of the operating curves (Q11, n11, M11) are stable and the data for those regimes have been studied in more detail in the literature than for the complete Four Quadrant characteristic curves.
The authors of this paper are in the Matlab program based on the data of 11 Suter curves for 11 pump turbine models and based on the data of 1 Suter curve for 1 pump model from the paper - Thorley, R. D. & A. Chaudry, A. (1996) -
Pump characteristics for transient flow analysis [
5], and based on 1 Suter curve for 1 pump model from the book - Stepanoff, A. J. (1959).
Radial und Axialpumpen. Springer-Verlag Berlin Heidelberg GmbH [
2], developed a numerical model using the polynomial regression procedure, to obtain Universal equations for
Wh and
Wm characteristics, to analyze the existence of a more general legality in the form of the obtained curves depending on the specific speed -
nq. The process of developing a numerical model to obtain the Universal Equation for
Wh and
Wm characteristics consists of the following steps that were carried out:
In the first step, for all thirteen Suter curves (for each curve separately for both the
Wh characteristic and the
Wm characteristic) for 11 pump-turbine models and 2 pump models in the theta range from 0° to 360°, is passed through each of thirteen Suter curves the Fourier function of 2 orders, which is clearly shown in the
Figure 4,
Figure 5 and
Figure 6 (for
Wh characteristic) and in the Figures 13–15 (for
Wm characteristic), in this paper, not all diagrams for all thirteen Suter curves through which the Fourier function of 2 orders is passed are shown, in order not to overload this paper with a large number of diagrams, have already shown diagrams for six Suter curves with the following
nq (
nq=24.34,
nq=24.8,
nq=25,
nq=28.6,
nq=38,
nq=41.6), for
Wh and
Wm characteristics.
In the second step, the coefficients (
ao,
a1, a2, b1, b2, w) were taken from thirteen Fourier functions of 2 orders, which passed through each of thirteen Suter curves (11 pump-turbine models and 2 pump models), for each curve separately for both the
Wh characteristic and the
Wm characteristic. And then the authors of this paper separately (on separate diagrams) grouped the values for each of these coefficients from thirteen Fourier functions of 2 orders which passed through each of thirteen Suter curves (11 pump turbine models and 2 pump models), for each curve separately and for the
Wh characteristic and for the
Wm characteristic. On each of these diagrams, which are shown in
Figure 7,
Figure 8 and
Figure 9 for the
Wh characteristic and in Figures 16–18 for the
Wm characteristic, the values of these coefficients from the Fourier functions of 2 orders are shown depending on the specific speed -
nq. And on each of these diagrams, a polynomial of 9 orders is passed through the values of the coefficients listed on these diagrams, which are taken from thirteen Fourier functions of 2 orders which passed through each of thirteen Suter curves (11 pump-turbine models and 2 pump models), and each of these polynomials of 9 orders has the role of showing the dependence of these coefficients on the specific speed -
nq.
In the third step, by polynomial regression (polynomial of 9 orders) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (ao, a1, a2, b1, b2, w) and specific speed – nq (11 pump turbine models and 2 pump models) was determined.
In the fourth step, based on the afore mentioned steps in the developed numerical model in the Matlab program, the Universal equation for the Wh characteristic and the Universal equation for the Wm characteristic were obtained depending on the specific speed. The Universal equation for Wh and Wm characteristics is expressed in the developed numerical model in the Matlab program with the Fourier equation of 2 orders depending on the specific speed.
In the fifth step, based on the developed numerical model in the Matlab program, from the Universal equations for
Wh and
Wm characteristics, the authors of this paper obtained values for
Wh and
Wm characteristics for 13 Suter curves with different specific speed -
nq and compared those values with the values for
Wh and
Wm characteristics for 13 Suter curves obtained by recalculation of model curves with different specific sped -
nq (11 pump-turbine models and 2 pump models).The authors of this paper compared Suter curves for
Wh and
Wm characteristics which were obtained by recalculation from model curves, with Suter curves for
Wh and
Wm characteristics which were obtained from the developed Universal equations for
Wh and
Wm characteristics, in order not to overload this paper with a large number of diagrams, diagrams for six Suter curves are presented, as shown in
Figure 10,
Figure 11 and
Figure 12 (for
Wh characteristic for six Suter curves -
nq=24.34,
nq=24.8,
nq=25,
nq=28.6,
nq=41.6,
nq=64.04) and in the Figures 19–21 (for
Wm characteristic for six Suter curves -
nq=24.34,
nq=24.8,
nq=25,
nq=27,
nq=28.6,
nq=64.04). Figure 22 shows Suter curves for
Wh characteristics obtained by recalculation model curves and Suter curves for
Wh characteristics obtained from the Universal equation for
Wh characteristics (11 pump turbine-models and 2 pump models) and
Figure 23 shows the Suter curves for
Wm characteristics obtained by recalculation model curves and the Suter curves for
Wm characteristics obtained from the Universal equation for
Wm characteristics (11 pump-turbine models and 2 pump models).
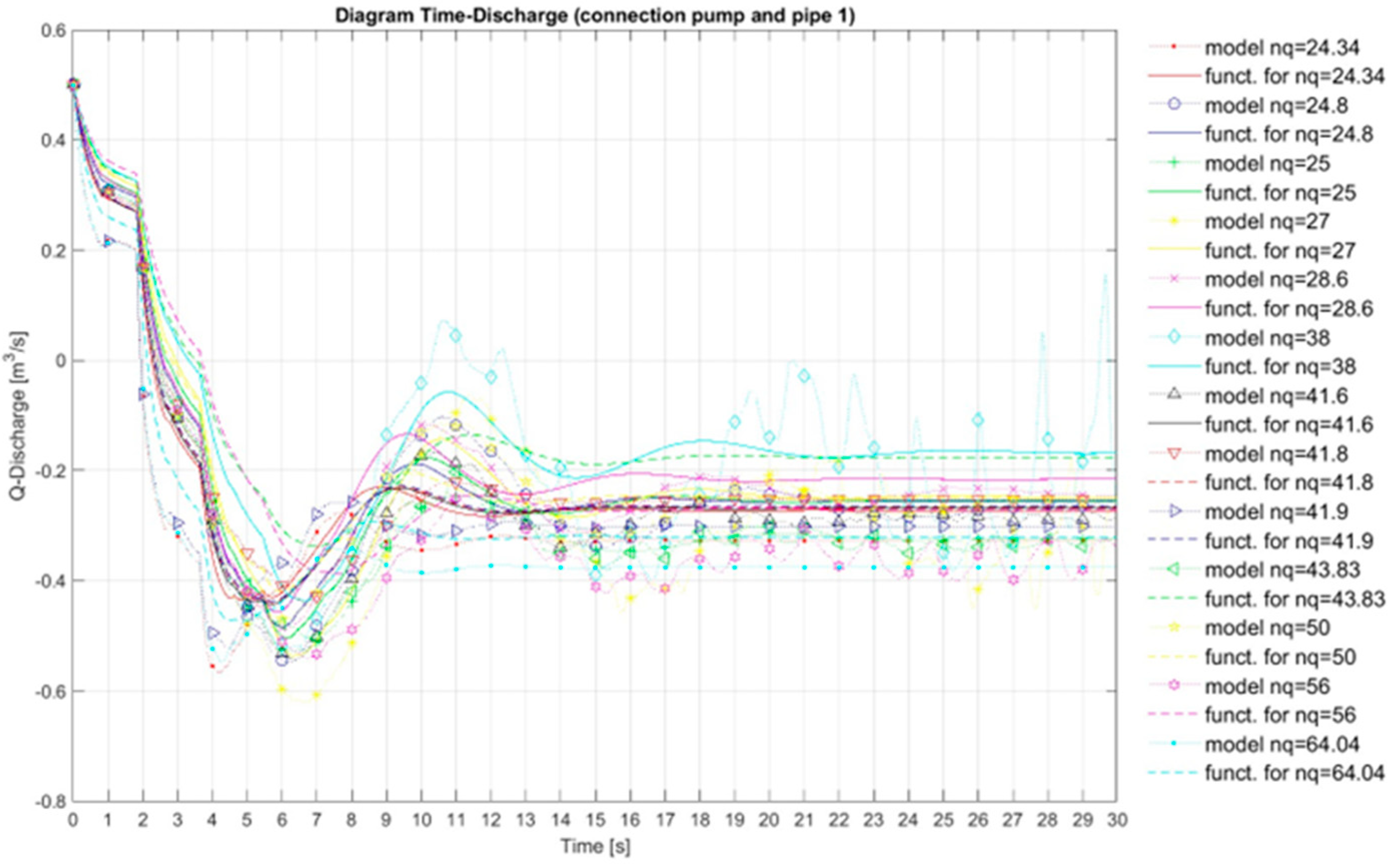
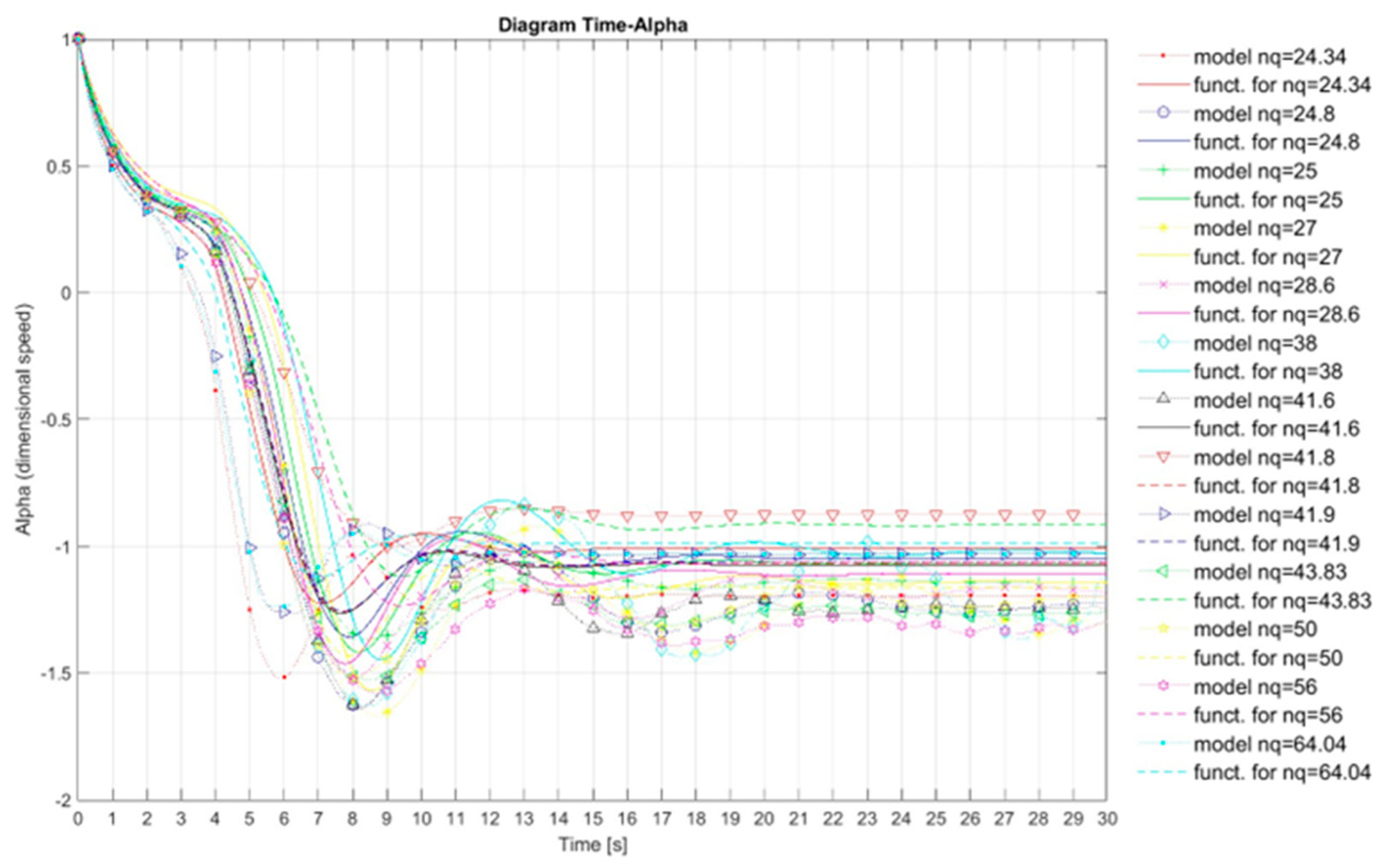
The Matlab program has been developed with the numerical model for calculating the transient processes in a pumping plant where two pumps are installed (the method of characteristics - MOC was used to develop this numerical model), and as input data in this numerical model, the authors of this paper used the Suter curve for Wh and Wm characteristics, which were obtained by recalculation the model curves Q11, n11, M11 for different values of specific speed, also as input data in this numerical model, the authors of this paper used Suter curves for Wh and Wm characteristics obtained from Universal equations for Wh and Wm characteristics for various values of specific speed, more about the previously mentioned will be mentioned in the next chapter of this paper.
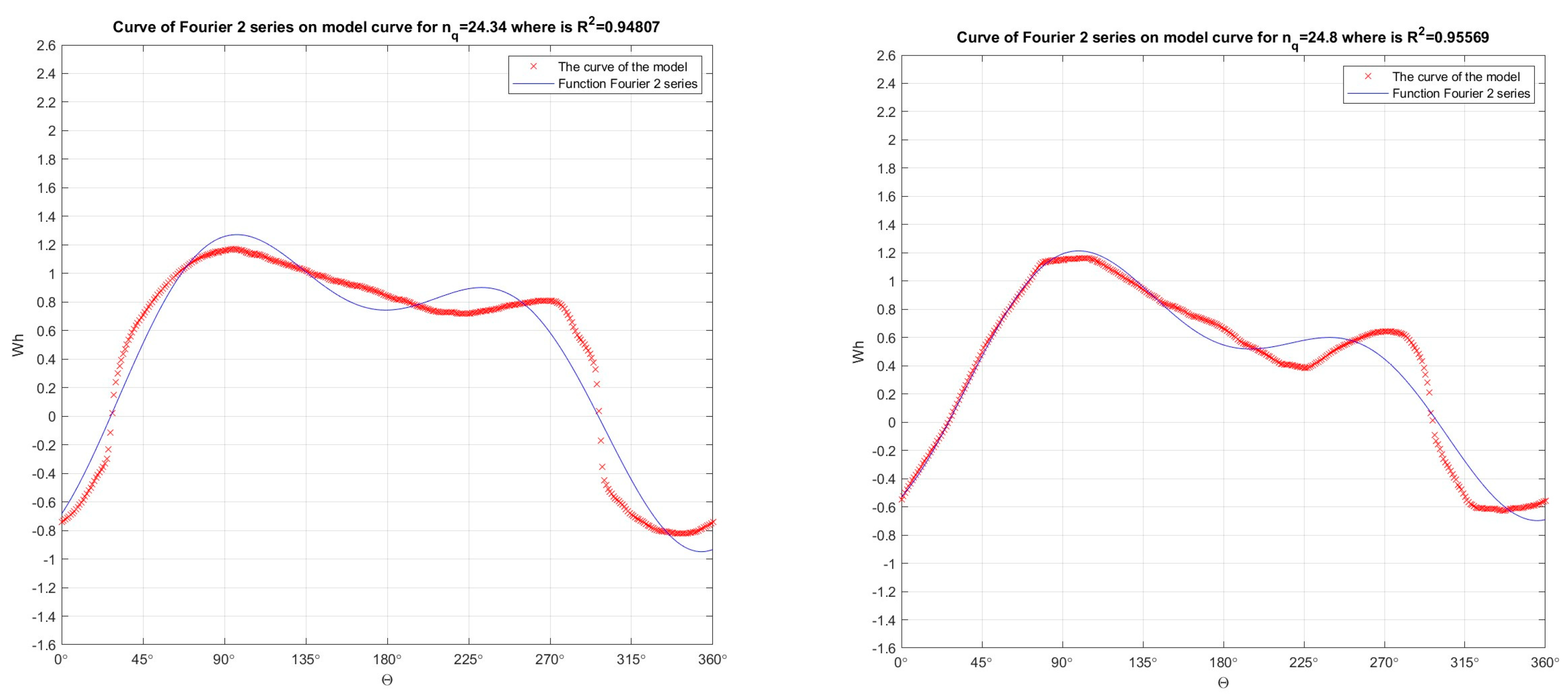
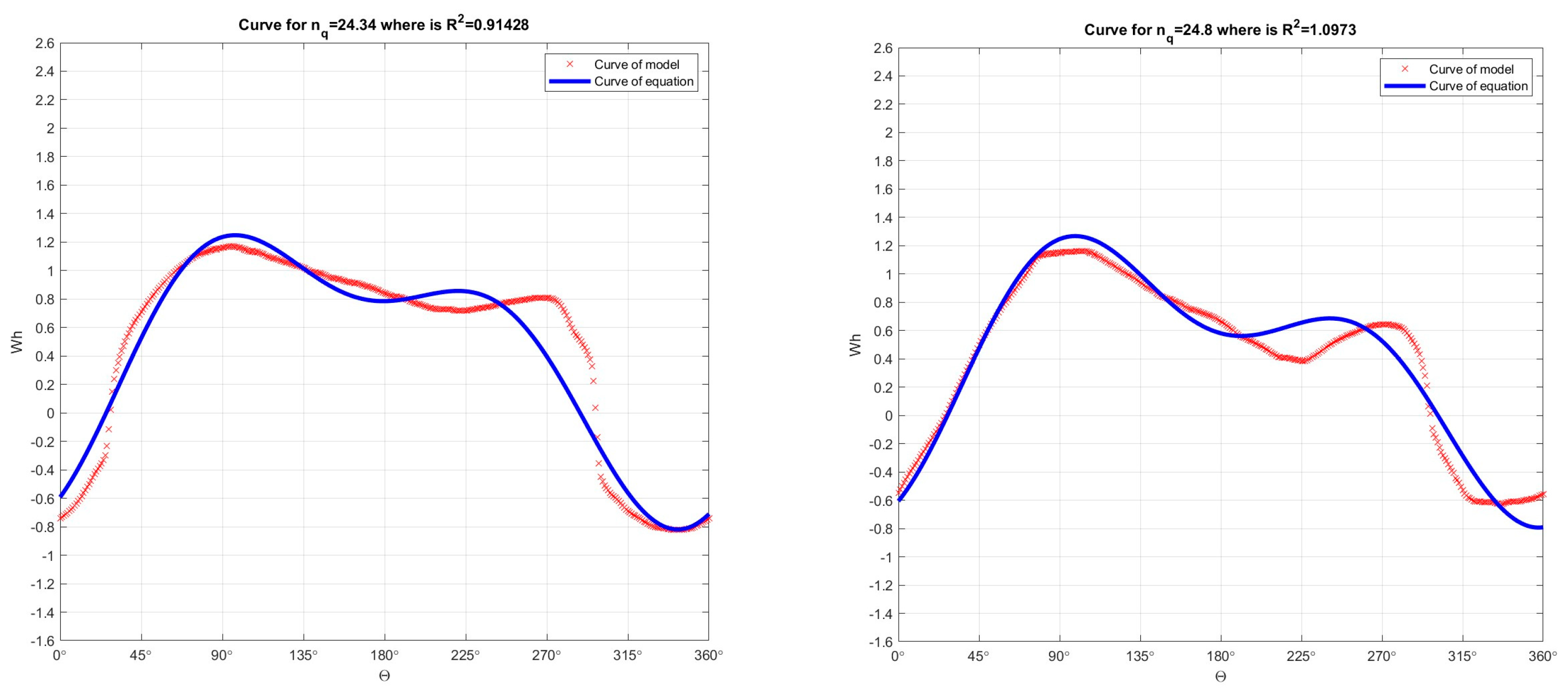
Figure 4.
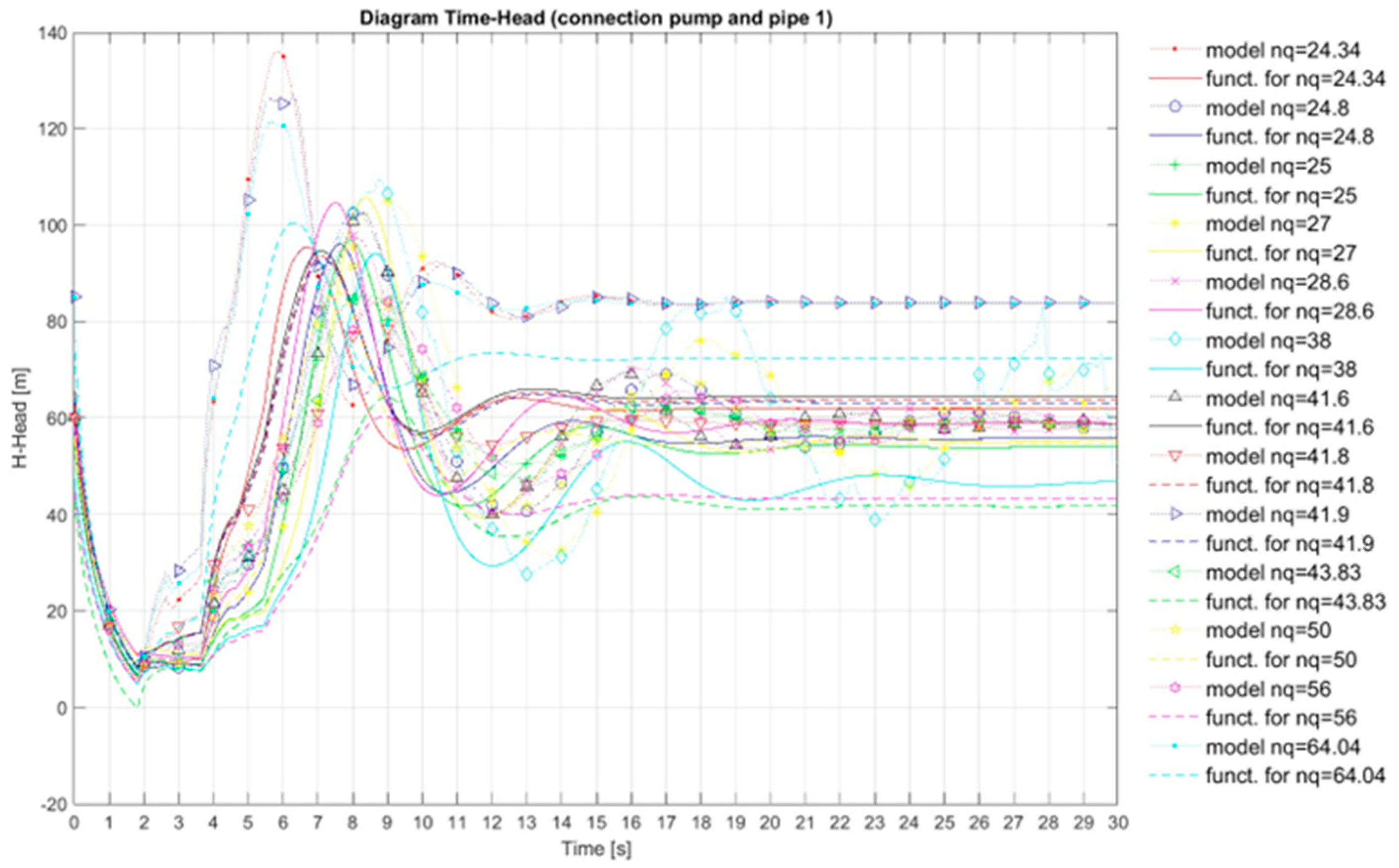
In the developed numerical model in the Matlab program, the Fourier function of 2 orders was passed through the Suter curves (which were obtained by recalculation the model curves Q11, n11, M11) for nq=24.34 (R2=0.94807) and for nq=24.8 (R2=0.95569), for Wh characteristics.
Figure 4.
In the developed numerical model in the Matlab program, the Fourier function of 2 orders was passed through the Suter curves (which were obtained by recalculation the model curves Q11, n11, M11) for nq=24.34 (R2=0.94807) and for nq=24.8 (R2=0.95569), for Wh characteristics.
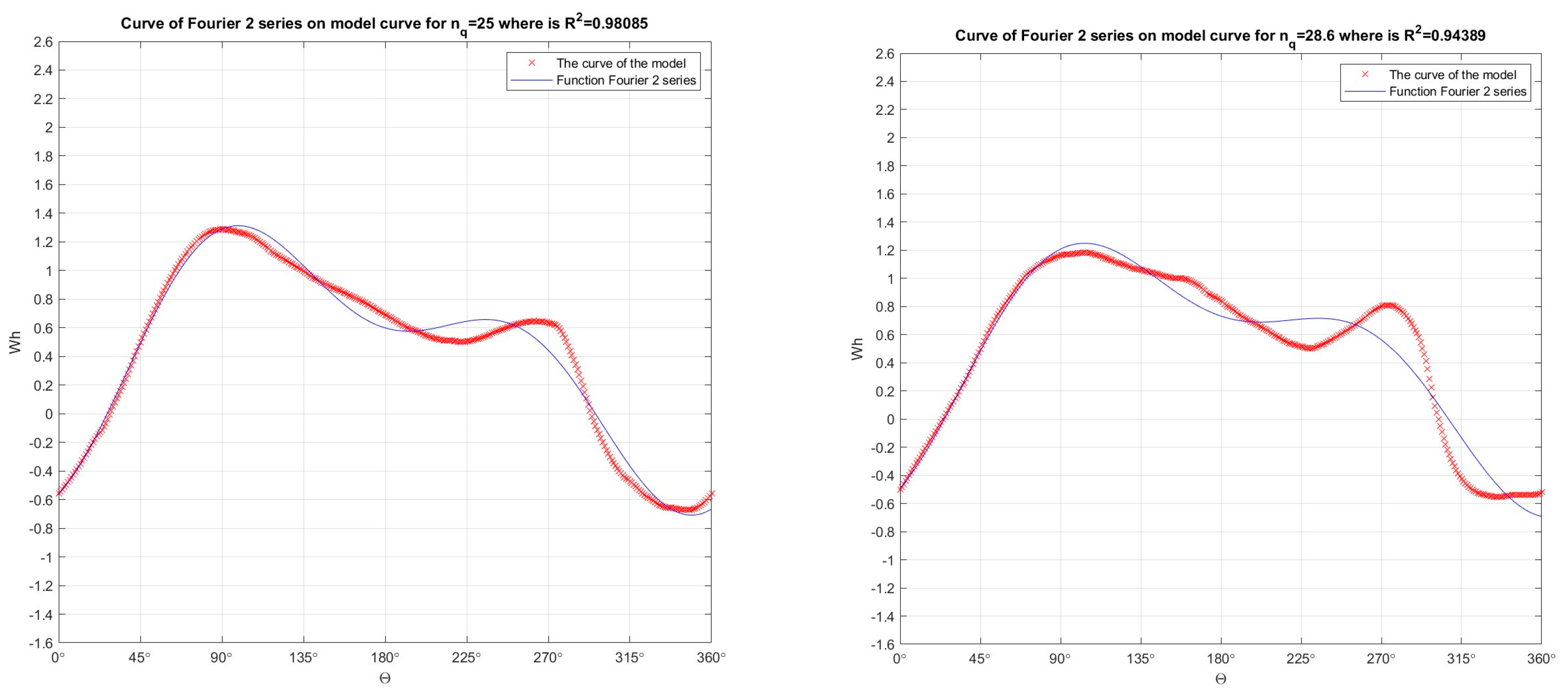
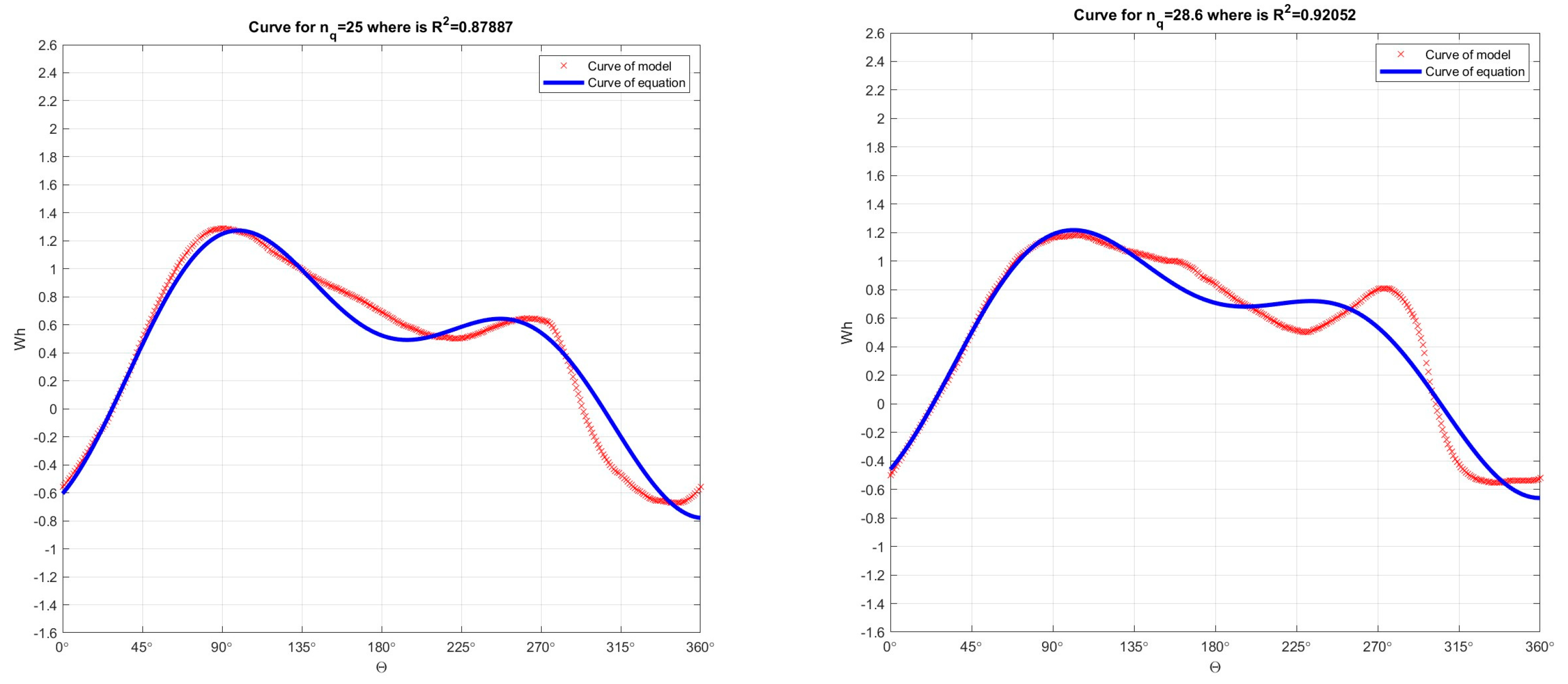
Figure 5.
In the developed numerical model in the Matlab program, the Fourier function of 2 orders was passed through the Suter curves (which were obtained by recalculation the model curves Q11, n11, M11) for nq=25 (R2=0.98085) and for nq=28.6 (R2=0.94389), for Wh characteristics.
Figure 5.
In the developed numerical model in the Matlab program, the Fourier function of 2 orders was passed through the Suter curves (which were obtained by recalculation the model curves Q11, n11, M11) for nq=25 (R2=0.98085) and for nq=28.6 (R2=0.94389), for Wh characteristics.
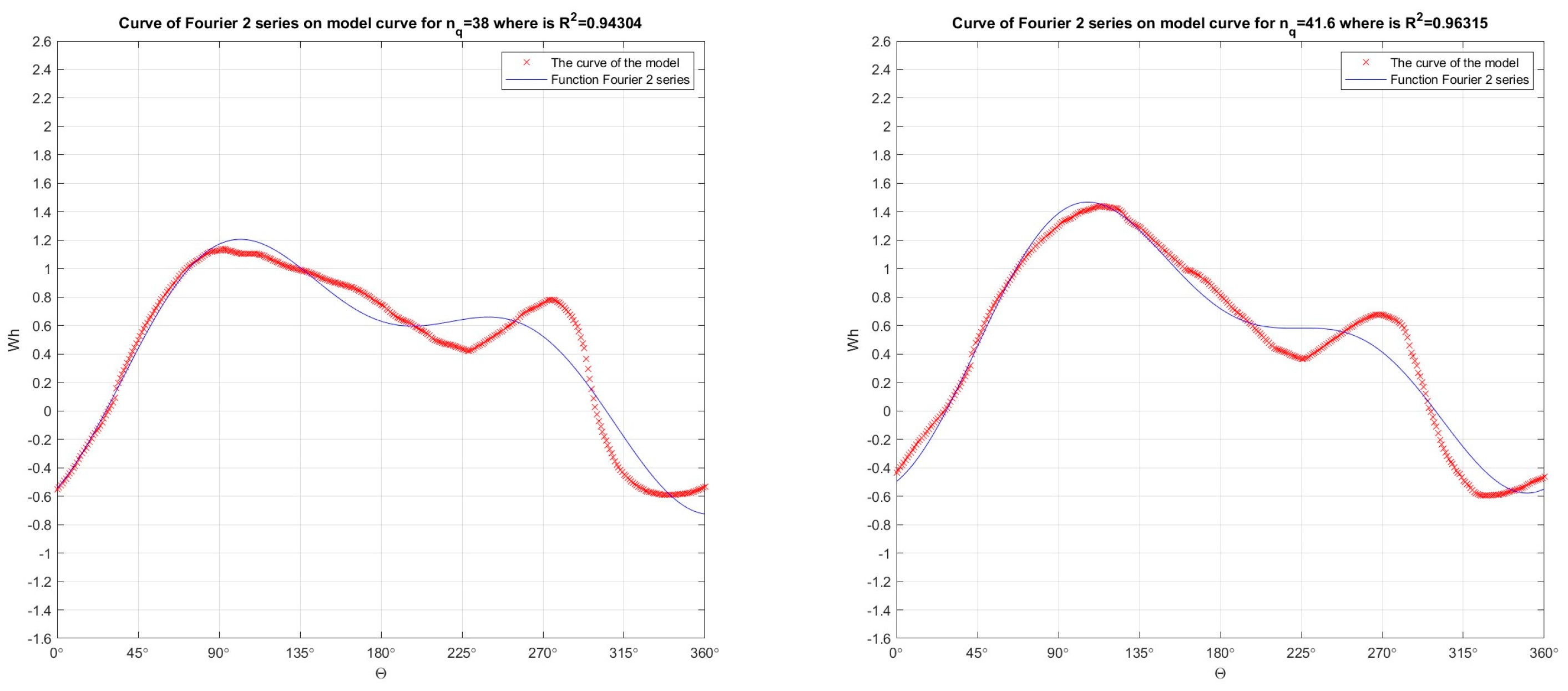
Figure 6.
In the developed numerical model in the Matlab program, the Fourier function of 2 orders was passed through the Suter curves (which were obtained by recalculation the model curves Q11, n11, M11) for nq=38 (R2=0.94304) and for nq=41.6 (R2=0.96315), for Wh characteristics.
Figure 6.
In the developed numerical model in the Matlab program, the Fourier function of 2 orders was passed through the Suter curves (which were obtained by recalculation the model curves Q11, n11, M11) for nq=38 (R2=0.94304) and for nq=41.6 (R2=0.96315), for Wh characteristics.
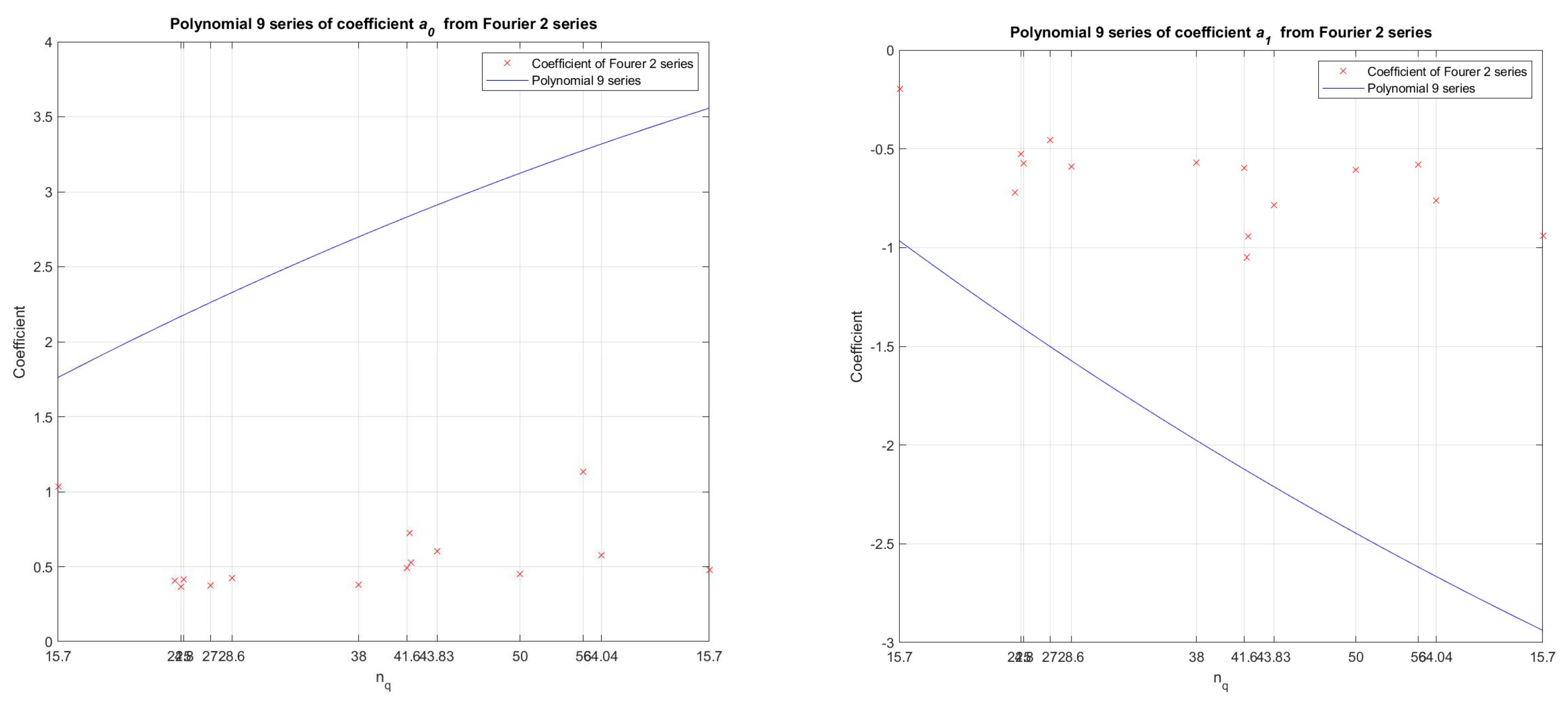
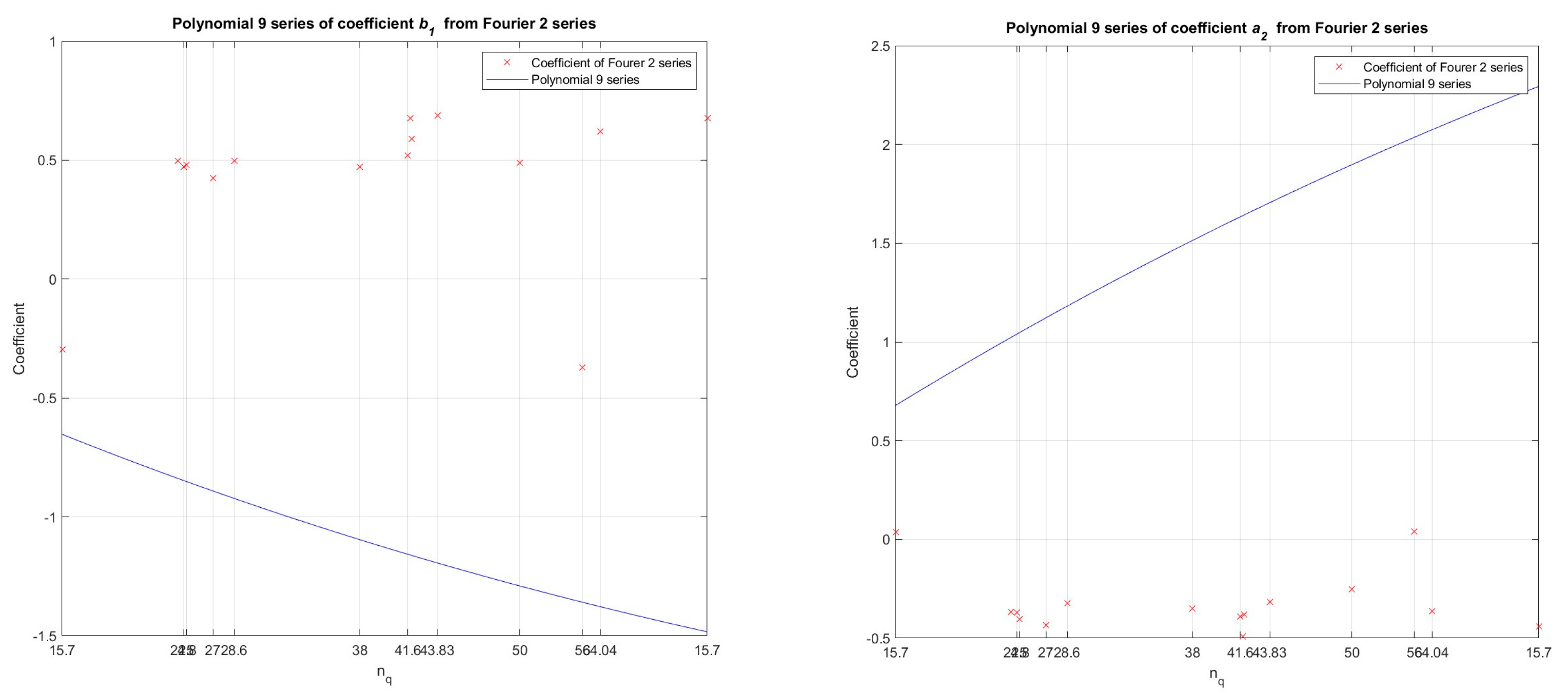
Figure 7.
By polynomial regression (polynomial of the 9 order) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (ao, a1 - from the Fourier function of 2 order) and specific speed - nq (11 pump-turbine models and 2 pump models) was determined, for Wh characteristics.
Figure 7.
By polynomial regression (polynomial of the 9 order) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (ao, a1 - from the Fourier function of 2 order) and specific speed - nq (11 pump-turbine models and 2 pump models) was determined, for Wh characteristics.
Figure 8.
By polynomial regression (polynomial of the 9 order) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (b1, a2 - from the Fourier function of 2 order) and specific speed - nq (11 pump-turbine models and 2 pump models) was determined, for Wh characteristics.
Figure 8.
By polynomial regression (polynomial of the 9 order) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (b1, a2 - from the Fourier function of 2 order) and specific speed - nq (11 pump-turbine models and 2 pump models) was determined, for Wh characteristics.
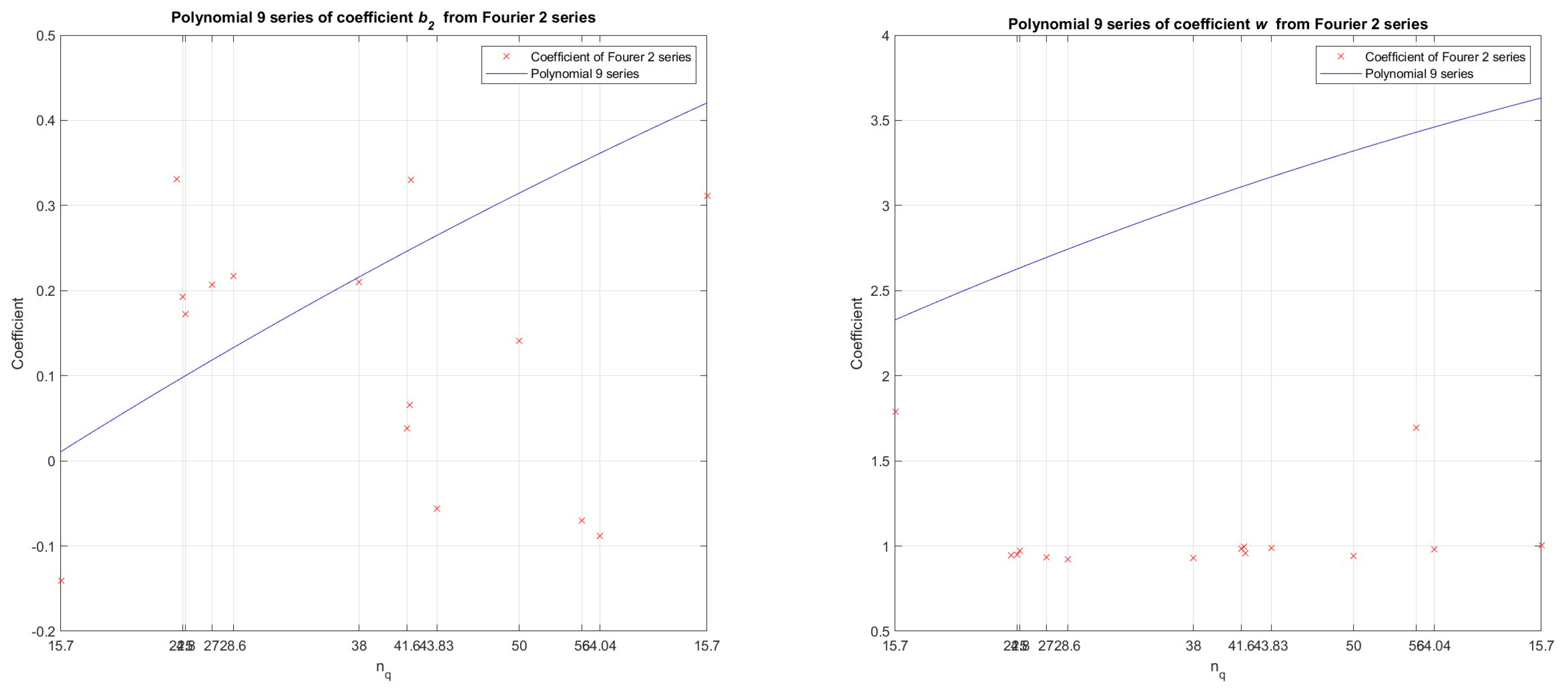
Figure 9.
By polynomial regression (polynomial of the 9 order) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (b2, w - from the Fourier function of 2 order) and specific speed - nq (11 pump-turbine models and 2 pump models) was determined, for Wh characteristics.
Figure 9.
By polynomial regression (polynomial of the 9 order) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (b2, w - from the Fourier function of 2 order) and specific speed - nq (11 pump-turbine models and 2 pump models) was determined, for Wh characteristics.
Figure 10.
Comparison of Suter curves for Wh characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wh characteristics which were obtained from the Universal equation for Wh characteristics, for nq=24.34 and for nq=24.8.
Figure 10.
Comparison of Suter curves for Wh characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wh characteristics which were obtained from the Universal equation for Wh characteristics, for nq=24.34 and for nq=24.8.
Figure 11.
Comparison of Suter curves for Wh characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wh characteristics which were obtained from the Universal equation for Wh characteristics, for nq=25 and for nq=28.6.
Figure 11.
Comparison of Suter curves for Wh characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wh characteristics which were obtained from the Universal equation for Wh characteristics, for nq=25 and for nq=28.6.
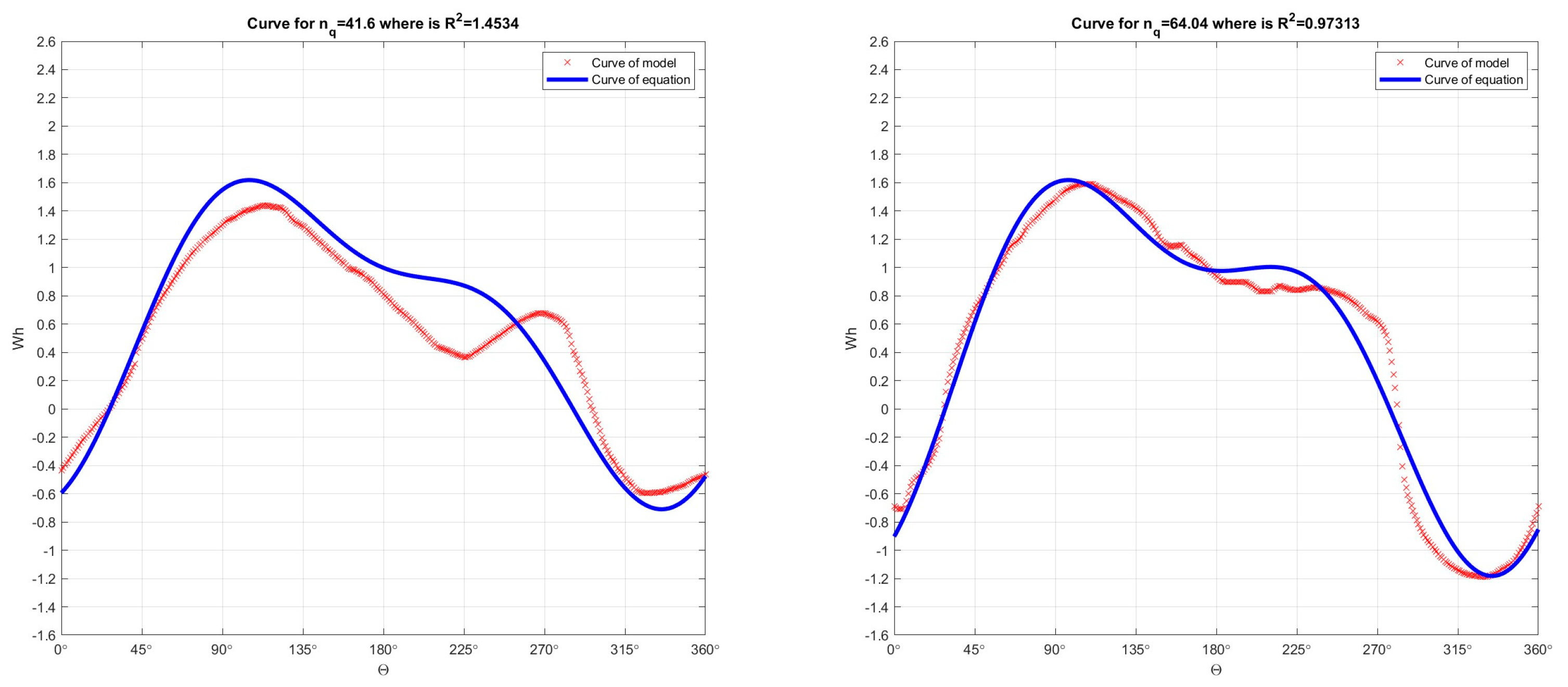
Figure 12.
Comparison of Suter curves for Wh characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wh characteristics which were obtained from the Universal equation for Wh characteristics, for nq=41.6 and for nq=64.04.
Figure 12.
Comparison of Suter curves for Wh characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wh characteristics which were obtained from the Universal equation for Wh characteristics, for nq=41.6 and for nq=64.04.
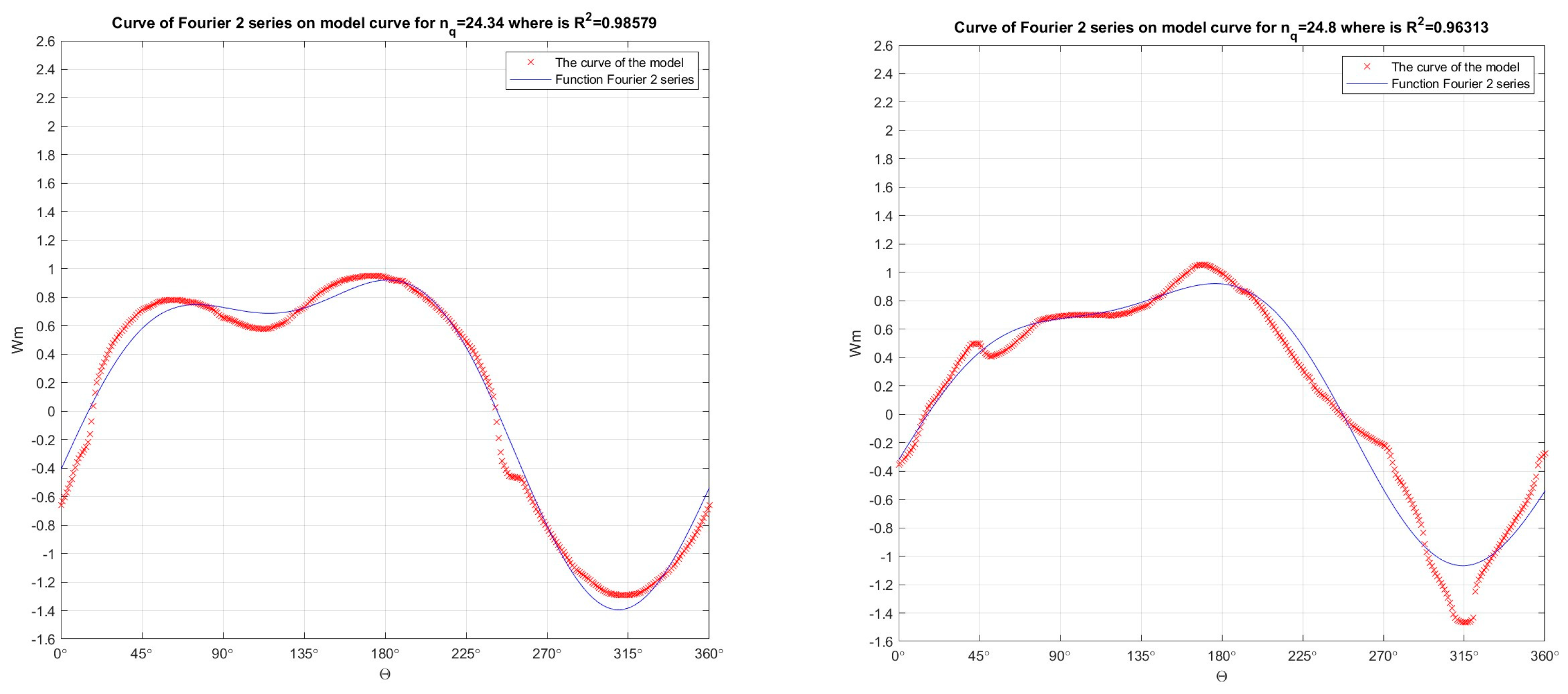
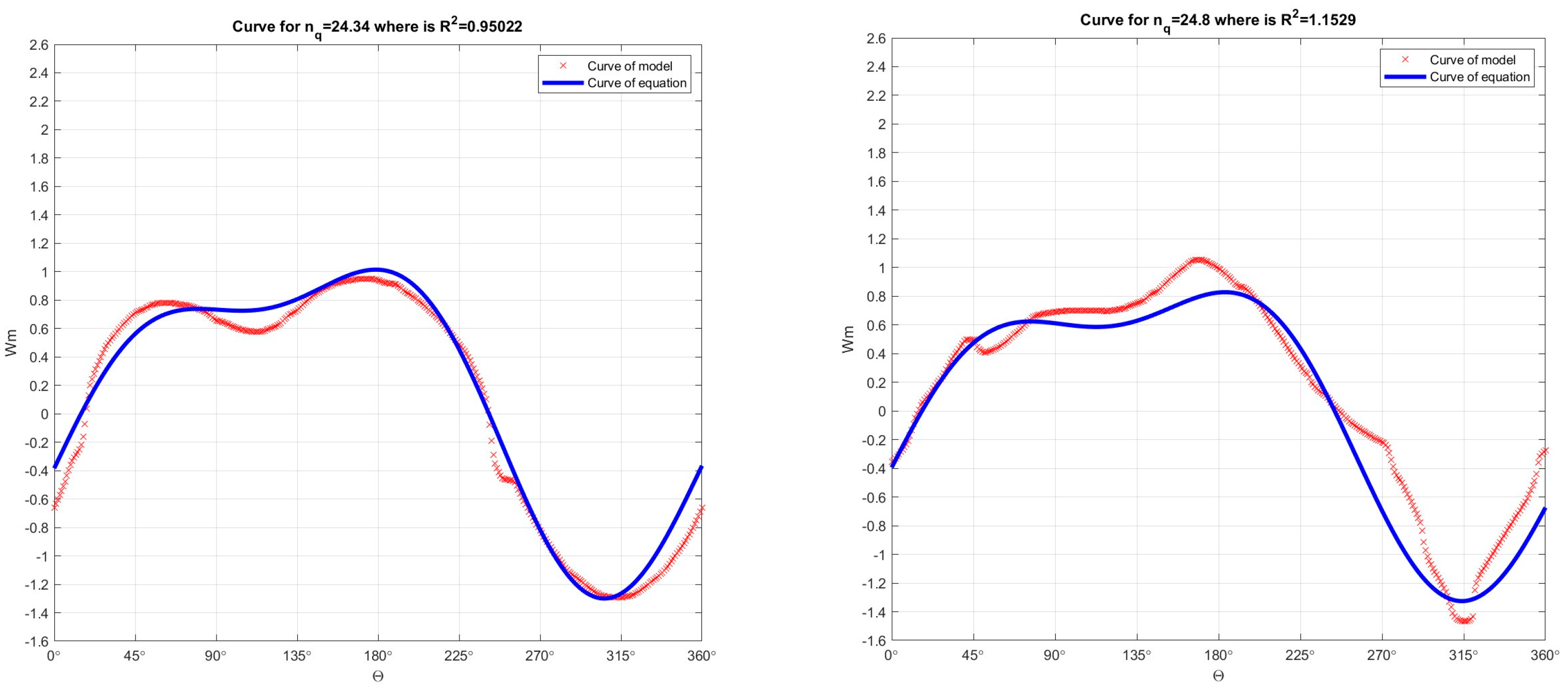
Figure 13.
In the developed numerical model in the Matlab program, the Fourier function of 2 orders was passed through the Suter curves (which were obtained by recalculation the model curves Q11, n11, M11) for nq=24.34 (R2=0.98579) and for nq=24.8 (R2=0.96313), for Wm characteristics.
Figure 13.
In the developed numerical model in the Matlab program, the Fourier function of 2 orders was passed through the Suter curves (which were obtained by recalculation the model curves Q11, n11, M11) for nq=24.34 (R2=0.98579) and for nq=24.8 (R2=0.96313), for Wm characteristics.
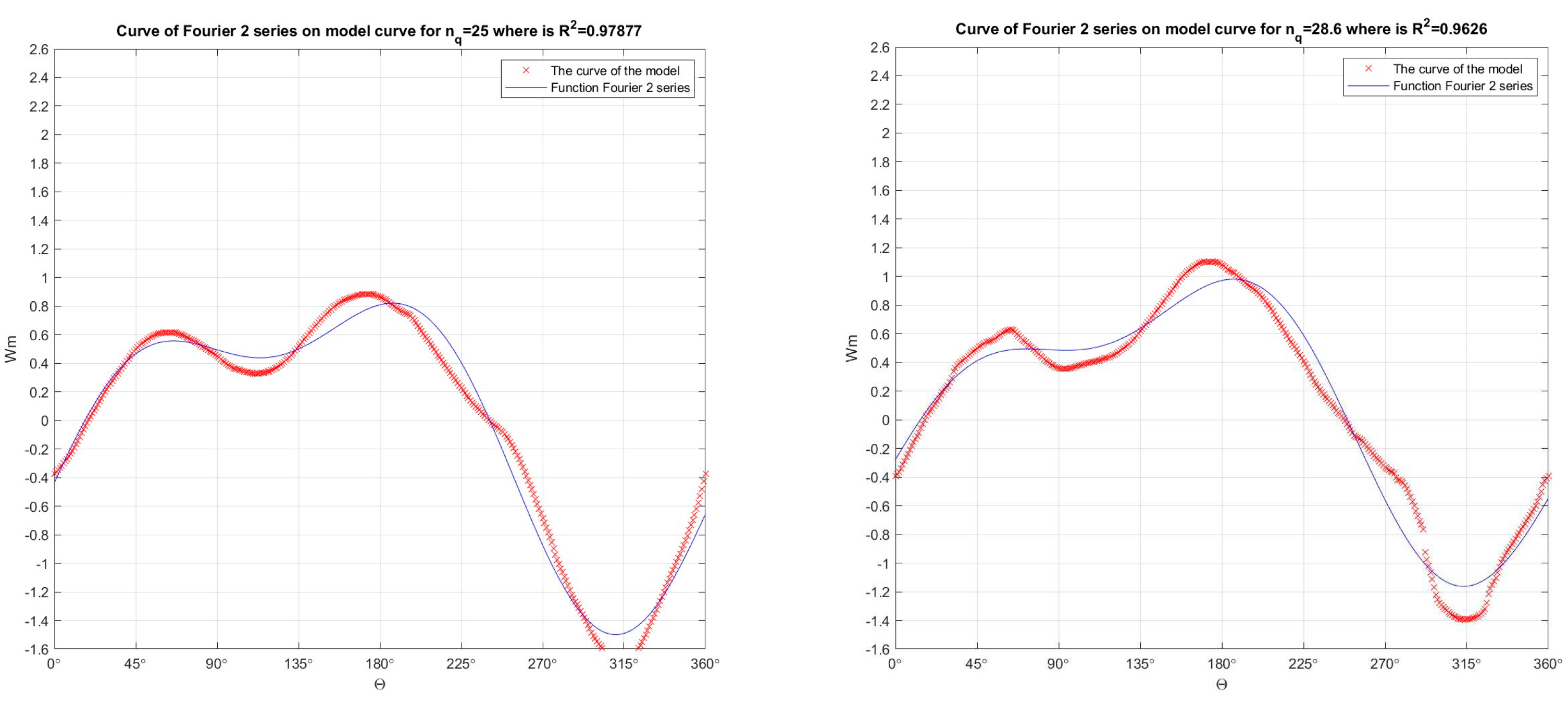
Figure 14.
In the developed numerical model in the Matlab program, the Fourier function of 2 orders was passed through the Suter curves (which were obtained by recalculation the model curves Q11, n11, M11) for nq=25 (R2=0.97877) and for nq=28.6 (R2=0.9626), for Wm characteristics.
Figure 14.
In the developed numerical model in the Matlab program, the Fourier function of 2 orders was passed through the Suter curves (which were obtained by recalculation the model curves Q11, n11, M11) for nq=25 (R2=0.97877) and for nq=28.6 (R2=0.9626), for Wm characteristics.
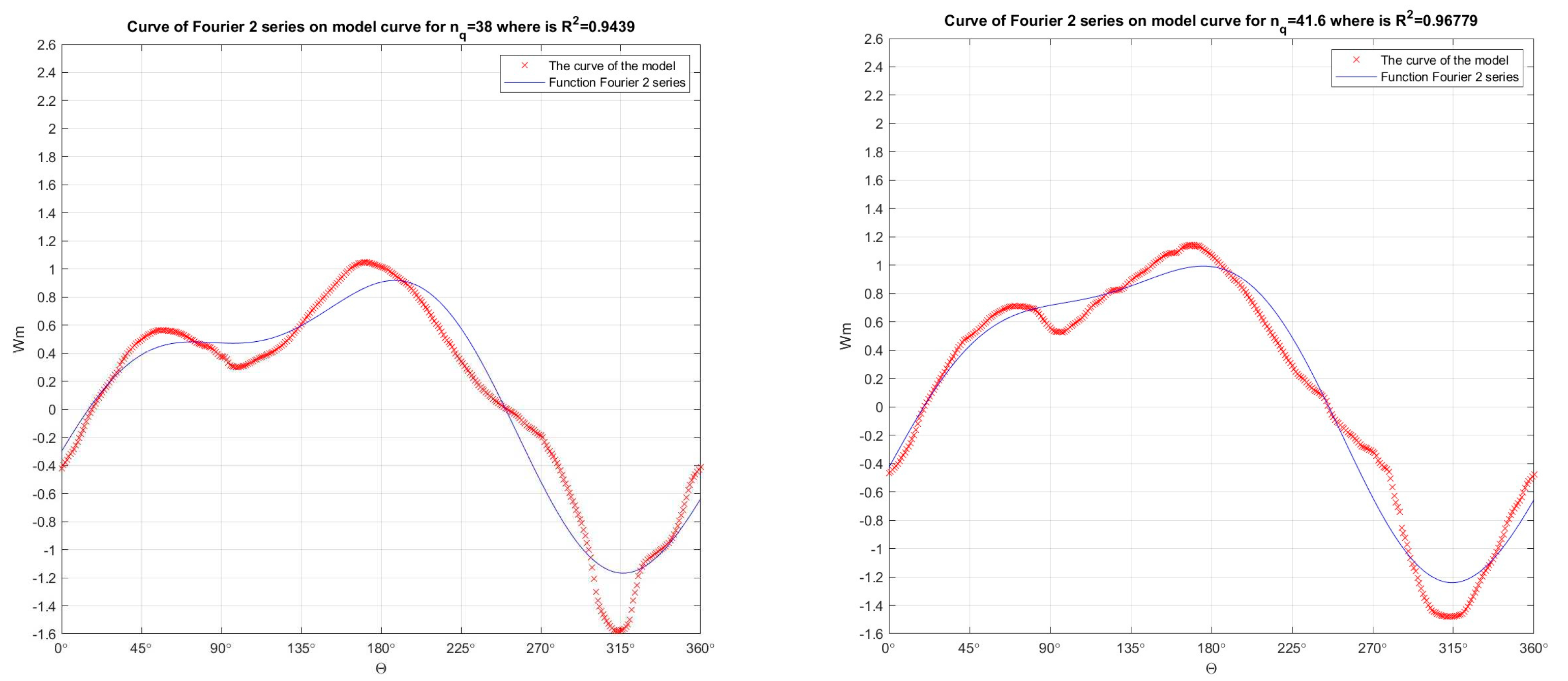
Figure 15.
In the developed numerical model in the Matlab program, the Fourier function of 2 orders was passed through the Suter curves (which were obtained by recalculation the model curves Q11, n11, M11) for nq=38 (R2=0.9439) and for nq=41.6 (R2=0.96779), for Wm characteristics.
Figure 15.
In the developed numerical model in the Matlab program, the Fourier function of 2 orders was passed through the Suter curves (which were obtained by recalculation the model curves Q11, n11, M11) for nq=38 (R2=0.9439) and for nq=41.6 (R2=0.96779), for Wm characteristics.
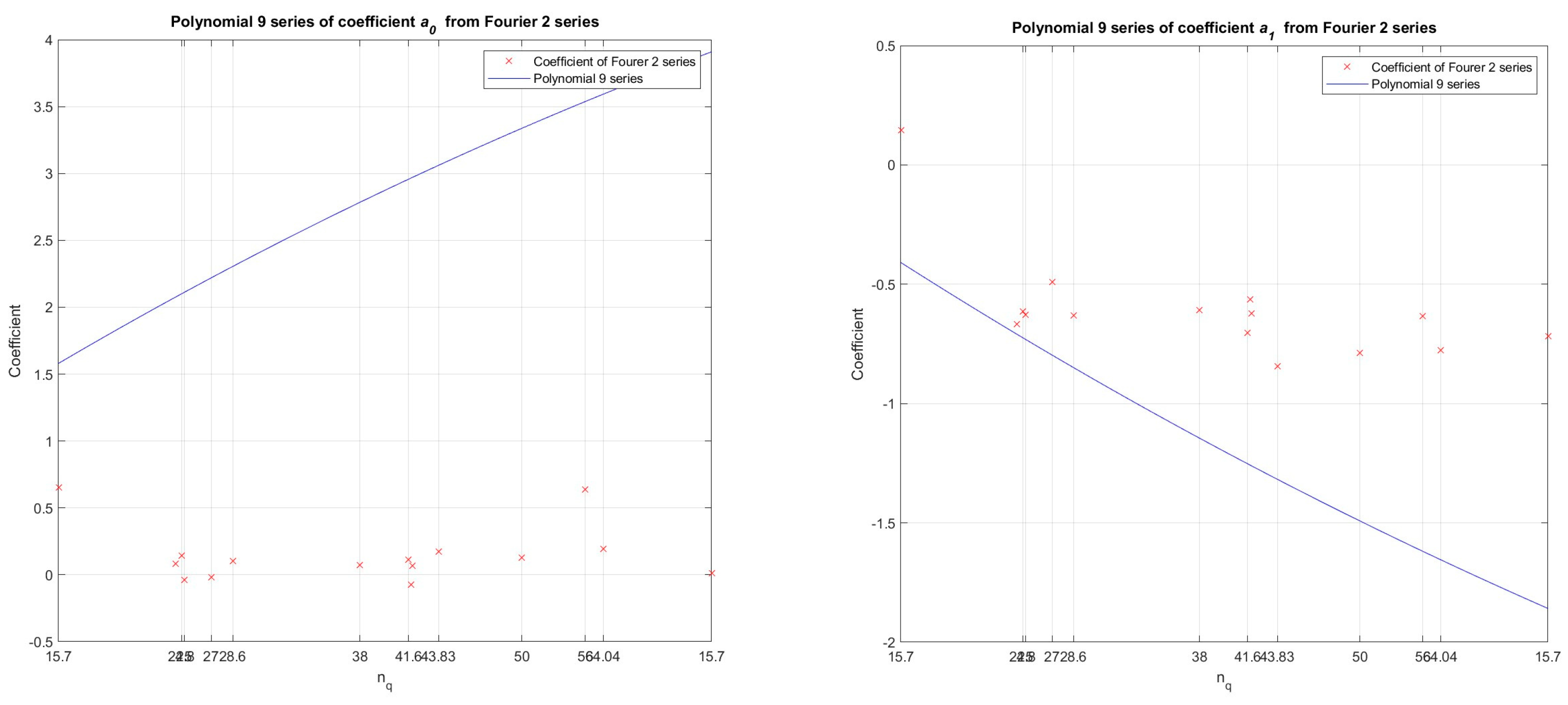
Figure 16.
By polynomial regression (polynomial of the 9 order) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (ao, a1 - from the Fourier function of 2 order) and specific speed - nq (11 pump-turbine models and 2 pump models) was determined, for Wm characteristics.
Figure 16.
By polynomial regression (polynomial of the 9 order) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (ao, a1 - from the Fourier function of 2 order) and specific speed - nq (11 pump-turbine models and 2 pump models) was determined, for Wm characteristics.
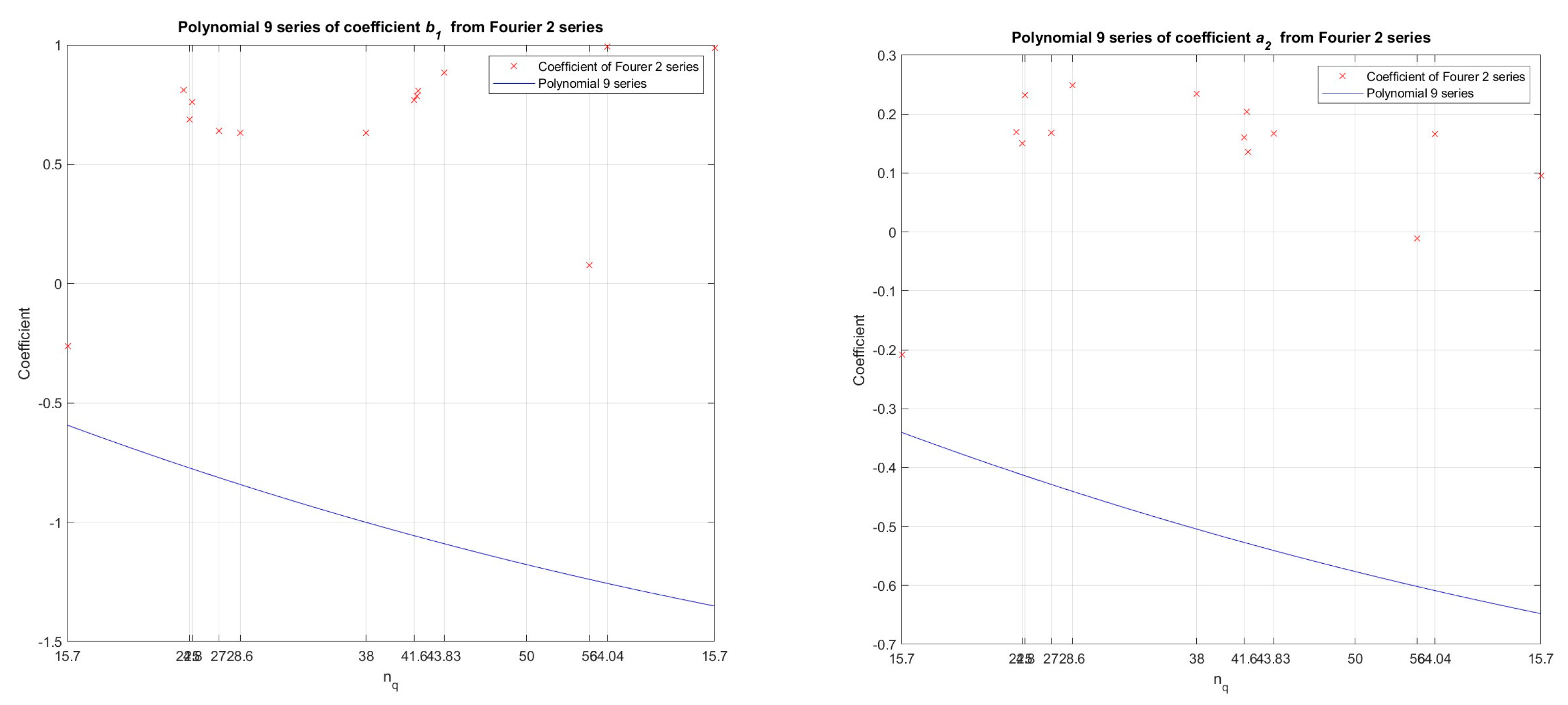
Figure 17.
By polynomial regression (polynomial of the 9 order) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (b1, a2 - from the Fourier function of 2 order) and specific speed - nq (11 pump-turbine models and 2 pump models) was determined, for Wm characteristics.
Figure 17.
By polynomial regression (polynomial of the 9 order) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (b1, a2 - from the Fourier function of 2 order) and specific speed - nq (11 pump-turbine models and 2 pump models) was determined, for Wm characteristics.
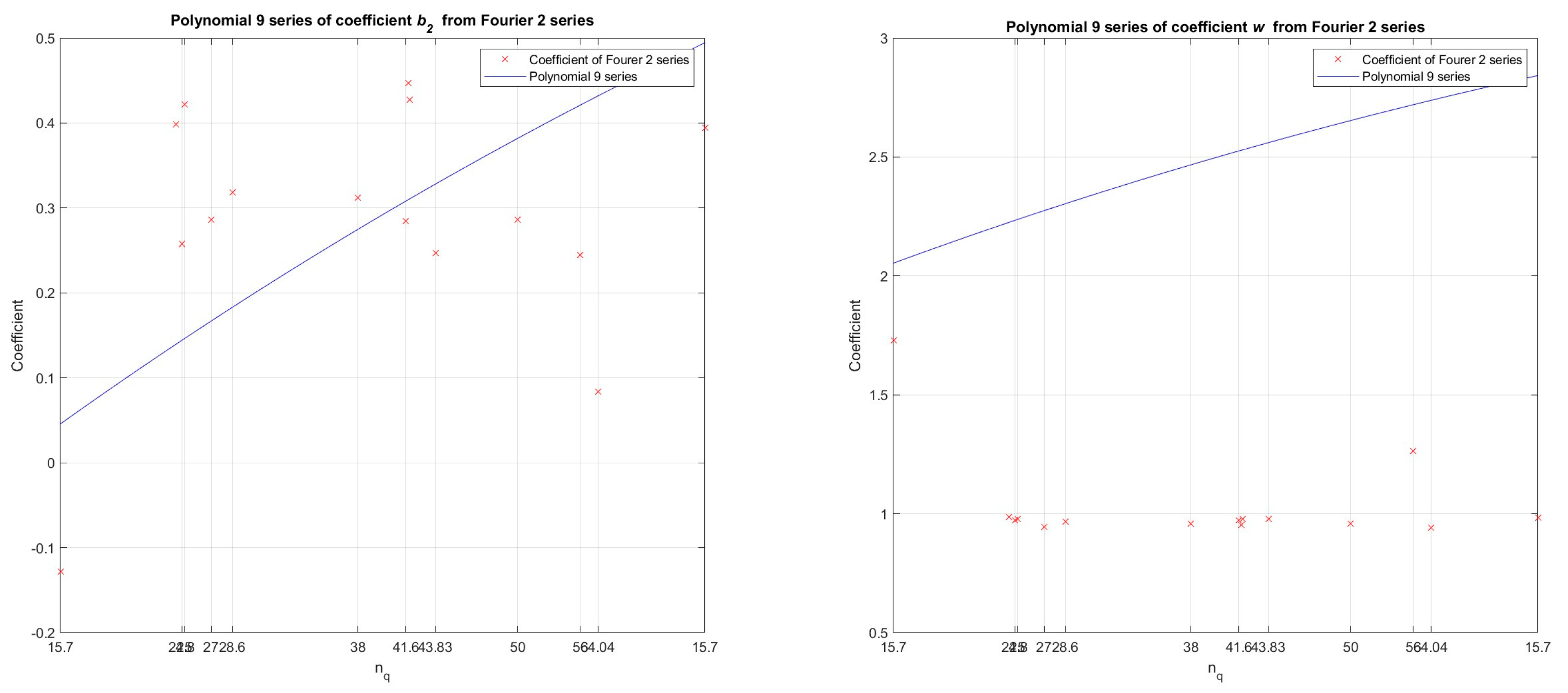
Figure 18.
By polynomial regression (polynomial of the 9 order) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (b2, w- from the Fourier function of 2 order) and specific speed - nq (11 pump-turbine models and 2 pump models) was determined, for Wm characteristics.
Figure 18.
By polynomial regression (polynomial of the 9 order) in the developed numerical model in the Matlab program, the dependence between the values of the coefficients (b2, w- from the Fourier function of 2 order) and specific speed - nq (11 pump-turbine models and 2 pump models) was determined, for Wm characteristics.
Figure 19.
Comparison of Suter curves for Wm characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wm characteristics which were obtained from the Universal equation for Wm characteristics, for nq=24.34 and for nq=24.8.
Figure 19.
Comparison of Suter curves for Wm characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wm characteristics which were obtained from the Universal equation for Wm characteristics, for nq=24.34 and for nq=24.8.
Figure 20.
Comparison of Suter curves for Wm characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wm characteristics which were obtained from the Universal equation for Wm characteristics, for nq=25 and for nq=27.
Figure 20.
Comparison of Suter curves for Wm characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wm characteristics which were obtained from the Universal equation for Wm characteristics, for nq=25 and for nq=27.
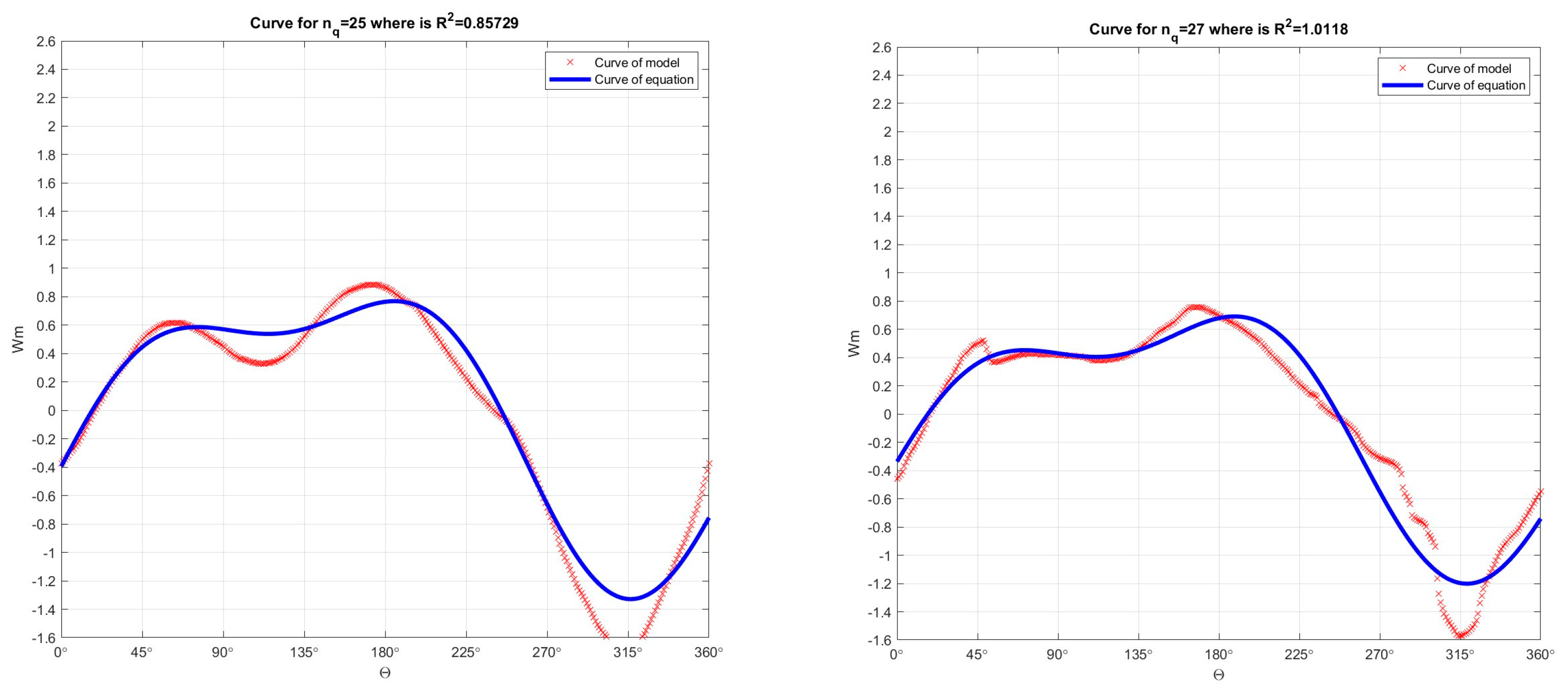
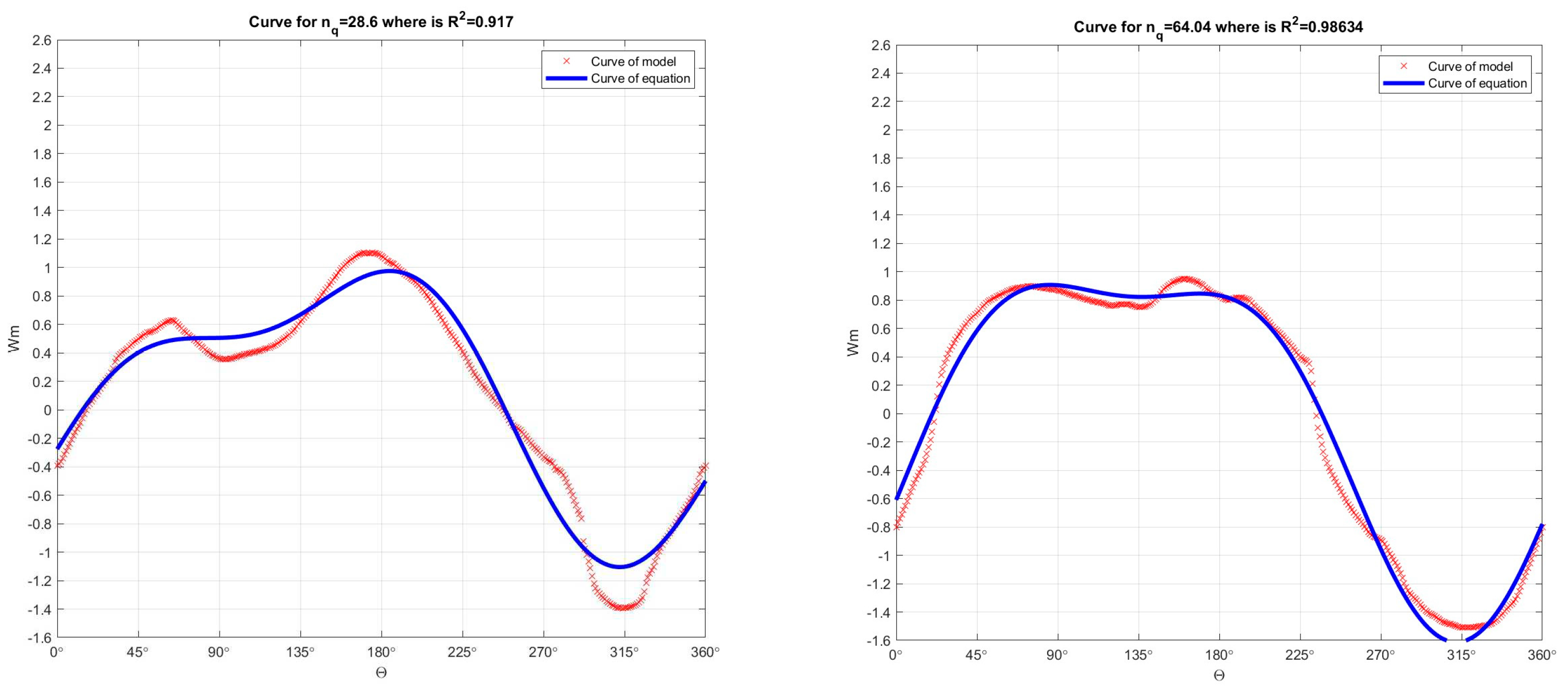
Figure 21.
Comparison of Suter curves for Wm characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wm characteristics which were obtained from the Universal equation for Wm characteristics, for nq=28.6 and for nq=64.04.
Figure 21.
Comparison of Suter curves for Wm characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wm characteristics which were obtained from the Universal equation for Wm characteristics, for nq=28.6 and for nq=64.04.
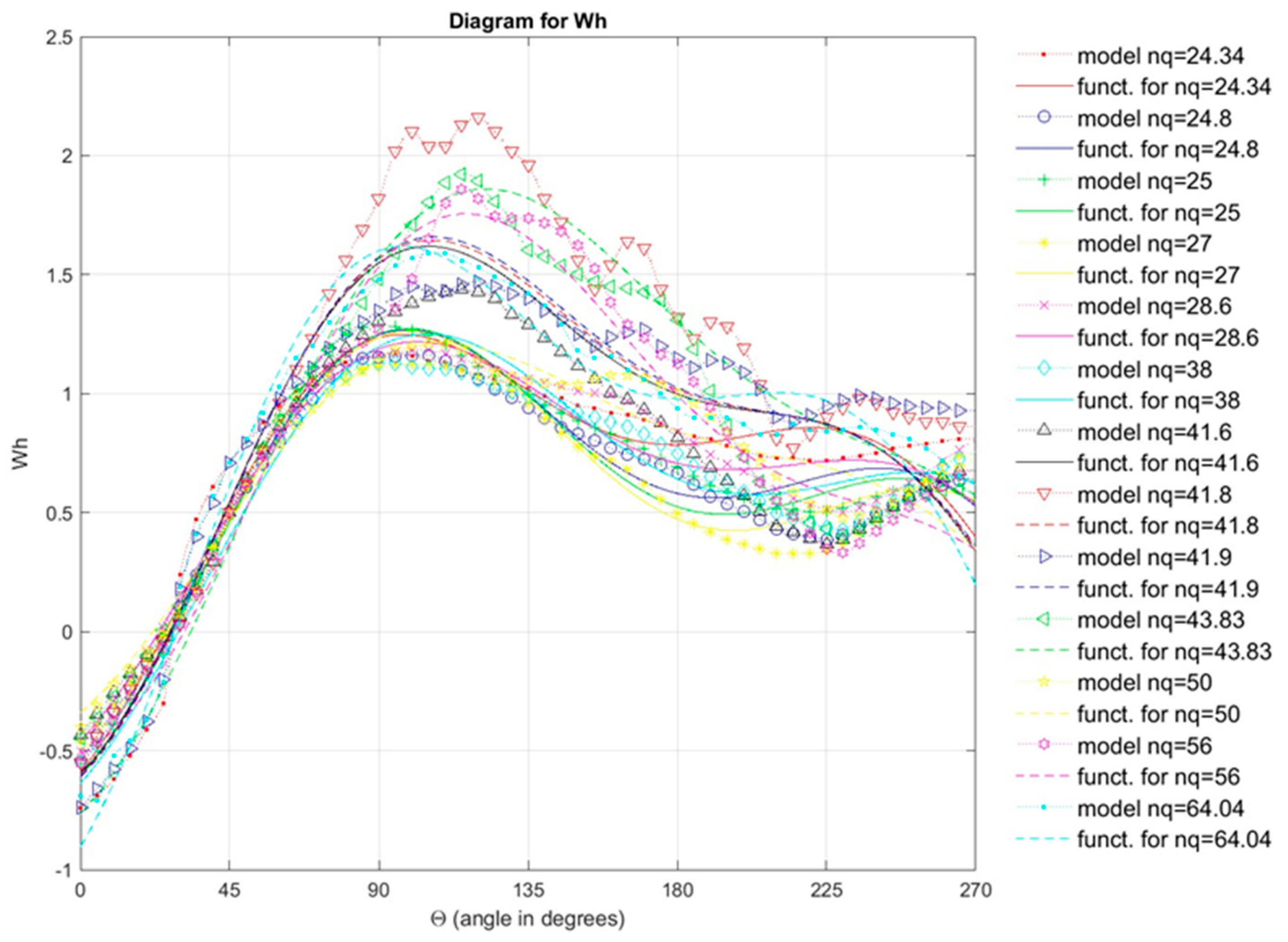
Figure 22.
Comparison of Suter curves for Wh characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wh characteristics which were obtained from the Universal equation for Wh characteristics (11 models of pump-turbine and 2 models of pump).
Figure 22.
Comparison of Suter curves for Wh characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wh characteristics which were obtained from the Universal equation for Wh characteristics (11 models of pump-turbine and 2 models of pump).
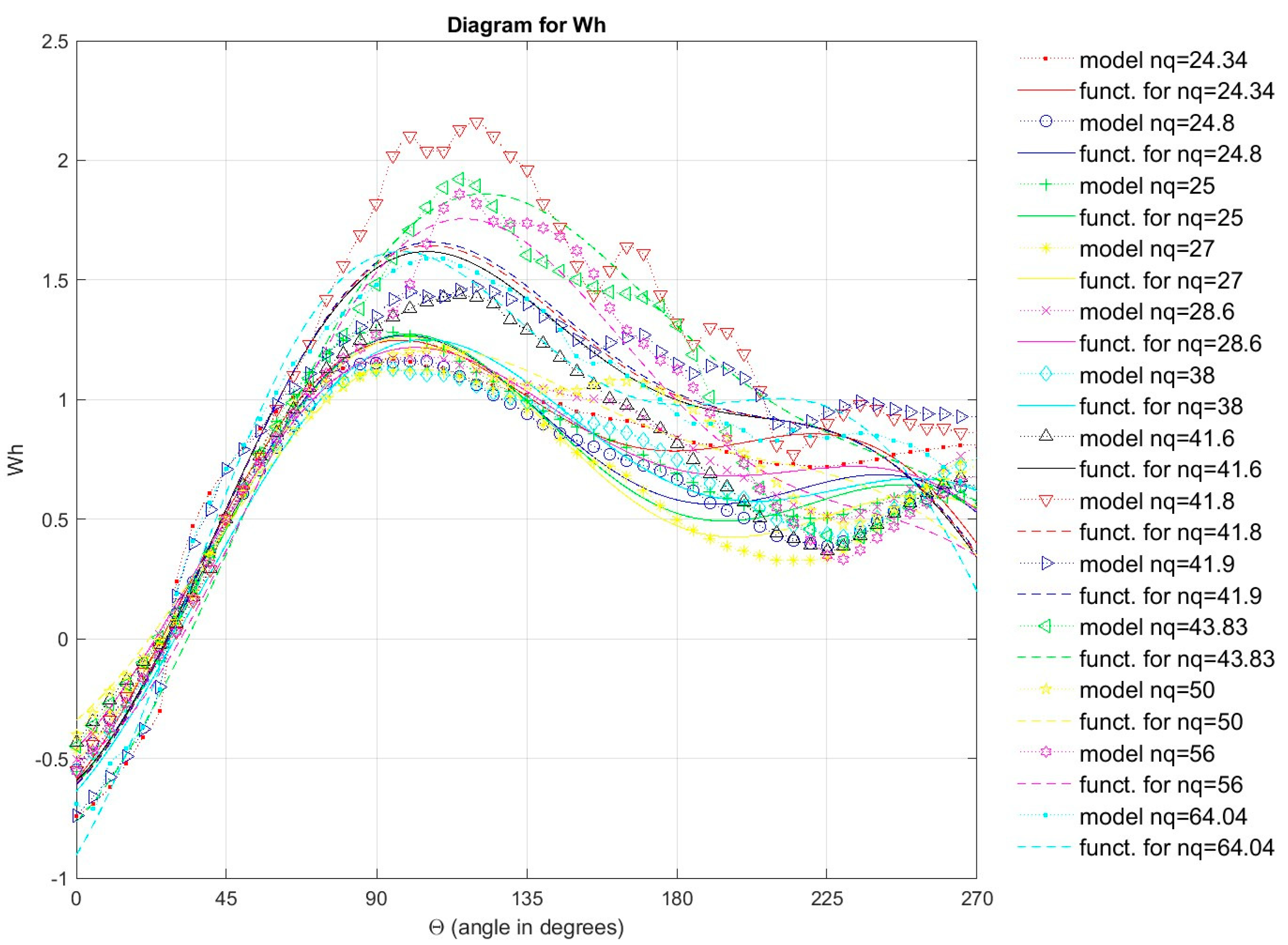
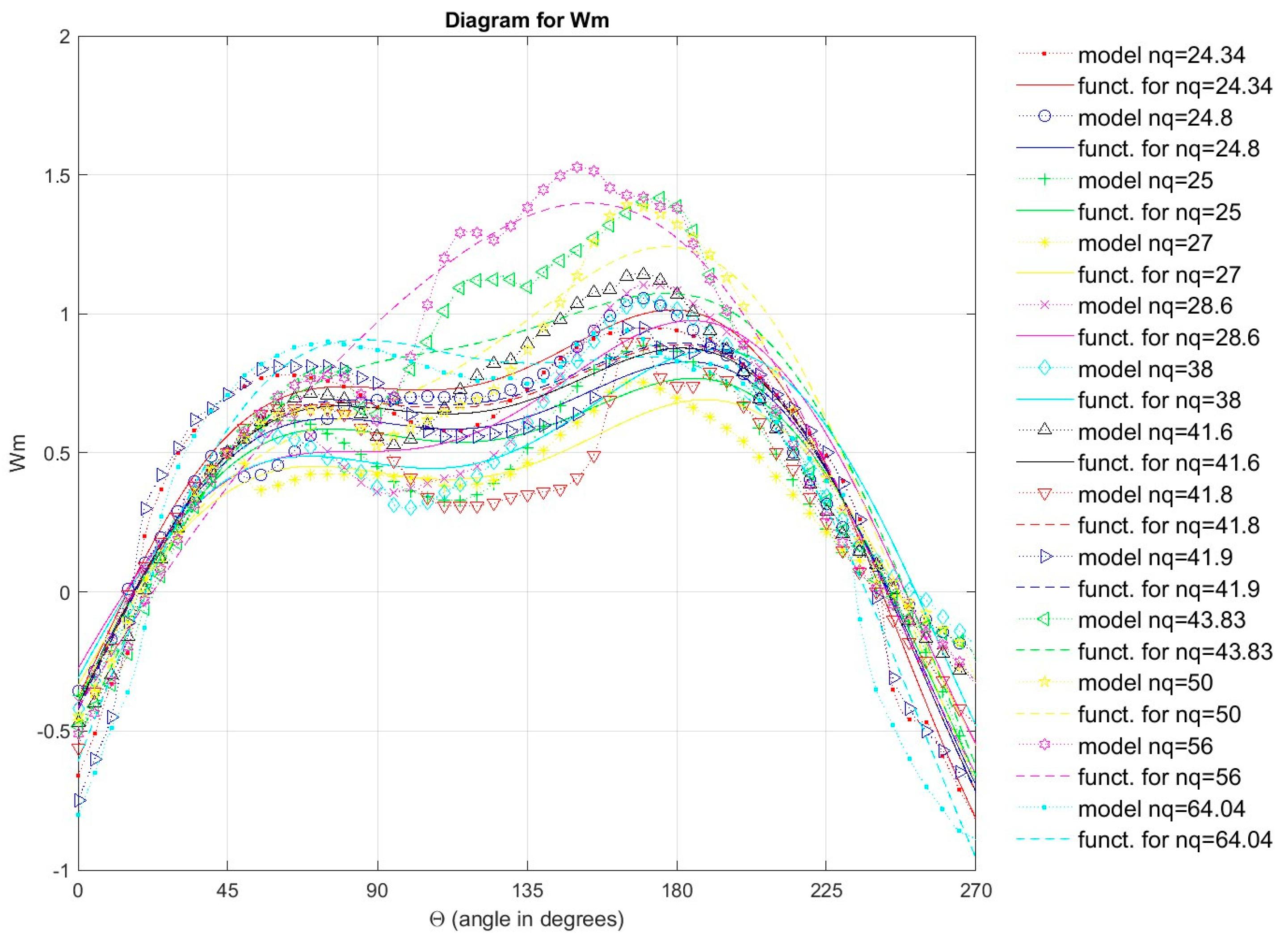
Figure 23.
Comparison of Suter curves for Wm characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wm characteristics which were obtained from the Universal equation for Wm characteristics (11 models of pump-turbine and 2 models of pump).
Figure 23.
Comparison of Suter curves for Wm characteristics which were obtained by recalculation the model curves Q11, n11, M11 with Suter curves for Wm characteristics which were obtained from the Universal equation for Wm characteristics (11 models of pump-turbine and 2 models of pump).