Prerpints.org logo
Preprint
Article

Acoustic Monitoring in Underwater Wireless Sensor Networks using Energy-efficient Artificial Fish Swarm-based Clustering Protocol (EAFSCP)

This is a preprint, it has not been peer-reviewed.

Submitted:

19 October 2023

Posted:

23 October 2023

You are already at the latest version

Abstract
Underwater wireless sensor networks (UWSNs) represent a specialized category of WSNs with versatile applications including acoustic monitoring, oil and gas exploration, and military surveillance. UWSNs face formidable challenges such as limited energy resources, extended propagation delays, and harsh conditions. Existing clustering and multi-hop routing protocols often unevenly distribute nodes geographically, causing network fragmentation and disproportionately draining the battery life of nodes near the sink due to higher data transmission demands. In this paper, we introduce an Energy-efficient Artificial Fish Swarm-based Clustering Protocol (EAFSCP), inspired by the collective behavior of fish swarms. EAFSCP is a decentralized clustering algorithm designed for acoustic monitoring in UWSNs. Its decentralized nature makes it particularly well-suited for large-scale UWSNs, where centralized algorithms may not be feasible. Through comprehensive comparisons with existing cluster-based routing protocols, our findings indicate that EAFSCP consistently outperforms them across multiple key performance metrics, including network lifetime, energy consumption, packet delivery ratio, packet loss rate, and throughput. According to the results, EAFSCP represents an effective clustering algorithm that enhances network performance, prolongs network lifespan by reducing energy consumption, promotes scalability, and provides valuable guidance for emergency response efforts.
Keywords: 
  -  

1. Introduction

The growing demand for instantaneous data acquisition, remote surveillance, and autonomous functionality in submerged settings has catalyzed the evolution of Underwater Wireless Sensor Networks (UWSNs) [1]. Given the challenges presented by the marine environment, conventional electromagnetic radio waves are impractical for underwater applications. Consequently, acoustic waves have emerged as the preferred medium, renowned for their exceptional effectiveness in enabling underwater communication [2]. UWSNs represent intricate, self-organizing networks comprising acoustic sensor nodes that operate beneath the water's surface [3]. These networks have many applications across various domains such as navigation assistance, disaster prevention (through earthquake and tsunami warnings), environmental monitoring (covering sea currents, wind patterns, and fish tracking), exploratory missions (encompassing oil, mineral, and fish detection), and tactical surveillance [4].
Over the past years, there have been significant strides in the progress of routing algorithms designed for terrestrial Wireless Sensor Networks (WSNs) [5,6,7,8,9,10]. However, the aquatic environment presents a markedly different set of challenges for routing protocols in underwater settings. These challenges include restricted data transmission rates, scarcity of channel bandwidth, significant signal attenuation, substantial delays, elevated bit error rates, increased energy consumption, and dynamic topology changes. As a result, traditional routing protocols are unsuitable for direct use in UWSNs. Acoustic signals in UWSNs operate at considerably lower energy levels than their radio counterparts, leading to prolonged end-to-end delays and heightened bit error rates for transmitted data packets. To effectively tackle the distinct challenges posed by underwater environments, it becomes imperative to develop underwater-specific routing protocols to ensure energy-efficient communication while meeting the unique performance requirements demanded by UWSNs [11].
While numerous routing strategies have been developed to alleviate the strain on energy resources in UWSNs, the persistent hotspot problem continues to challenge these networks, leading to premature sensor failure. To address this issue [12,13,14], clustering approaches stand out as a superior solution. Cluster-based routing protocols are designed to optimize network performance by organizing sensor nodes into clusters. In this arrangement, each cluster is typically managed by a cluster head (CH) tasked with the aggregation and transmission of data to a base station (i.e., sink) [13]. Using the process of data aggregation, clustering technology reduces the volume of packets traversing the network, channeling data through CHs. The decrease in both the quantity of active nodes and the collective energy consumption among these nodes plays a vital role in extending the overall lifespan of the network [15].
To overcome the aforementioned challenges and bridge the existing gaps in research, we present an Energy-efficient Artificial Fish Swarm-based Clustering Protocol (named EAFSCP). This protocol is specifically designed for acoustic monitoring within UWSNs, addressing critical issues and advancing the field. Our contribution in introducing the EAFSCP protocol holds significant importance for the following reasons:
  • The EAFSCP addresses the challenges of the existing cluster-based protocols stemming from the dynamic nature of underwater environments, limited communication ranges, and high energy demands.
  • EAFSCP employs a metaheuristic-driven solution method rooted in the Artificial Fish Swarm algorithm (AFSA) to attain an equitable distribution of CHs ensuring a balanced coverage of CHs while concurrently minimizing the network's collective energy consumption.
  • EAFSCP operates in a decentralized manner, making it suitable for acoustic UWSNs, where centralized control is absent, and nodes must operate autonomously.
  • Comprehensive simulations are conducted to assess the performance of EAFSCP, comparing it to state-of-the-art classical and metaheuristic-driven clustering techniques including LEACH, CMSE2R, ChoA-HGS, and MOR. The outcomes reveal that EAFSCP surpasses current approaches in aspects related to network longevity, energy efficiency, and coverage metrics.
The structure of this paper unfolds as follows: In Section 2, we embark on an exhaustive exploration of the current routing protocols employed in UWSNs. Section 3 provides a thorough exposition of the proposed EAFSCP. Moving to Section 4, we present the outcomes derived from our experiments, encompassing an in-depth analysis of the results alongside comparisons with established methodologies. Finally, in Section 5, we provide our conclusions by and delineating prospective avenues for future research endeavors.

2. Literature Review

Typically, UWSNs are intentionally self-organizing and self-healing, with sensors intercommunicating with each other to optimize data collection and transmission. Ongoing research and development efforts are focused on improving the capabilities of UWSNs, including increased communication range, improved energy efficiency, and higher data transmission rates. These meliorations will further enhance the potential for underwater wireless sensors to overturn underwater data collection and monitoring. Acoustic UWSNs comprise underwater environments where collaborative monitoring tasks are undertaken through the deployment of acoustic sensor nodes and underwater unmanned submarine vehicles, specifically tailored for such aquatic settings [2,3,16]. The connectivity of a typical UWSN is shown in Figure 1.
Many routing strategies have been developed to lessen the load on UWSNs' energy resources and increase their operational lifetime [13]. For dealing with a small-scale UWSN, the scheduling technique may be used effectively; however, due to the significant latency in acoustic connections, this approach is not viable when dealing with a large-scale UWSN [17]. Because of this, clustering techniques have been developed, whereby the nodes closest to the cluster's center form subgroups [15], and the other nodes eventually merge into these larger groups. In the following, the existing clustering techniques used for UWSNs are reviewed.
In the original LEACH method [18], the choice of CHs relies solely on a predetermined threshold function, without considering other factors affecting network longevity. To address this issue, I-LEACH [19] introduced enhancements by selecting CHs based on residual energy, node location, and neighboring node counts. Meanwhile, LEACH-C [20] offers a centralized LEACH-based approach that optimizes CH selection considering the remaining energy of nodes. LEACH-C addresses the inefficiencies of traditional LEACH by selecting the most qualified CHs from a pool of candidates. During the initial stage, nodes communicate their locations and remaining energy to the sink, enabling the sink to choose CHs with higher energy reserves. This approach improves network efficiency, with the remaining nodes operating as standard sensors, functioning much like in the traditional LEACH protocol.
Cluster-based Ant Colony Optimization NETwork (CACONET) [21] considers the average length of clusters and the number of CHs to figure out how well the network works. It clusters sensor nodes by orchestrating them into groups optimized for robust and high-performing connections. The study encompassed various parameters, including network grid sizes, node transmission ranges, and node quantities, to comprehensively assess CACONET's efficacy. Leveraging aspects such as node transmission range, directionality, and node mobility, CACONET aimed to maximize the advantages of clustering.
Distributed Underwater Clustering Method (DUCS) [22] is a clustering protocol for UWSNs. It employs a distributed algorithm to create clusters, with nodes forming themselves into hierarchical clusters. EBECRP (Energy-efficient and Balanced Energy Consumption Cluster-based Routing Protocol) [17] employs node clustering to diminish both the need for multi-hop selections and energy usage. Within this framework, mobile sinks ensure a uniform node workload, while clustering serves to minimize both multi-hop selections and energy expenditure.
Cluster-based Energy-Efficient Routing (CBE2R) [23] is another approach that consumes the least energy while still allowing for the most significant level of productivity. According to this paradigm, the ocean may be thought of as having seven different layers. These layers have added significant nodes working their way down from the top to enhance the nodes' battery life. The information collected by the sensor nodes is sent to the hub by the transport nodes (i.e., CHs) which often have access to more energy and memory resources. In order to form a cluster, courier nodes communicate with their surroundings by sending a "join" message.
Cluster-based Multipath Shortest-distance Energy-Efficient Routing (CMSE2R) [24] presents a four-stage approach to clustering in UWSNs. These stages include network configuration, cluster formation, intra-cluster connections, and data exchange. It establishes multiple connections within the same cluster and optimizes data exchange. Notably, the protocol enhances connection quality by utilizing static carrier nodes and implementing multipath routing, making it an effective solution for energy-efficient data transmission in UWSNs.
Adaptive Clustering Underwater Network (ACUN) [25] takes into account node residual energy and route energy loss to choose CHs. This algorithm employs a multi-level adaptive clustering strategy to organize sensor nodes efficiently. It dynamically adjusts cluster formation based on the network's energy levels. By adaptively managing CHs and data transmission routes, ACUN enhances the network's energy efficiency and prolongs its operational lifetime. However, distance is not a component considered in the existing research.
Cluster-based UWSN (CUWSN) [26] delves into the process of choosing Cluster Heads (CHs) by taking into account the remaining energy level of nodes and employs multi-hop routing to convey data packets to the target node. Through extensive simulations and performance comparisons, the paper offers valuable insights into protocol selection to optimize energy consumption and network longevity in underwater environments. Even though the CUWSN can potentially increase network performance and lower energy consumption, the distance and multi-hop pathways still need to be improved.
The AMDC routing protocol was introduced by Junfeng et al. [27], which was specifically designed for UWSNs, considering challenging fading channel conditions acoustic applications. The protocol accounts for the asymmetrical nature of underwater noise and the attenuated nature of the noise in the underwater propagation environment. It focuses on a multi-path division approach, where the transmission path to the sink node is divided into multiple channels of varying quality. They investigated the benefits of leveraging these asymmetric paths to improve the reliability and efficiency of data transmission.
Coutinho et al. [28] combined the geographic routing principles with opportunistic routing strategies into a protocol, named GEDAR, to optimize data transmission in UWSNs. They addressed the challenges of underwater routing including high attenuation and dynamic network topology by leveraging location information and opportunistic data forwarding. This protocol improves the energy efficiency of the network by transitioning away from the conventional approach of using control messages for discovering and sustaining routes across empty regions. Instead, it adopted a recovery mode process reliant on topology control using adjustments in the depth of the void nodes.
Quality of service Evolutionary Routing Protocol (QERP) [29] is another cluster-based protocol that focuses on optimizing data transmission in UWSNs while ensuring Quality of Service (QoS). It incorporates an evolutionary algorithm to adapt to the unique challenges of underwater environments, such as variable link quality and energy constraints. This protocol enhances the rate of successful packet delivery, reduces the average end-to-end delay, mitigates energy consumption, and fulfills QoS criteria.
Our review of the literature revealed that researchers have employed diverse clustering protocols in terrestrial WSNs, while relatively fewer techniques have been explored for UWSNs. A comprehensive comparison of the reviewed techniques is presented in Table 1 and Table 2. Drawing from the insights gained through this literature review, we can identify specific gaps and areas for enhancement in our work within the realm of cluster-based routing protocols for UWSNs. These challenges and improvement opportunities include acoustic channel modeling, energy efficiency, adaptation to changes in the network conditions (including node failures, dynamic topology changes, and varying energy levels), scalability to large-scale UWSNs, and cross-layer optimization.

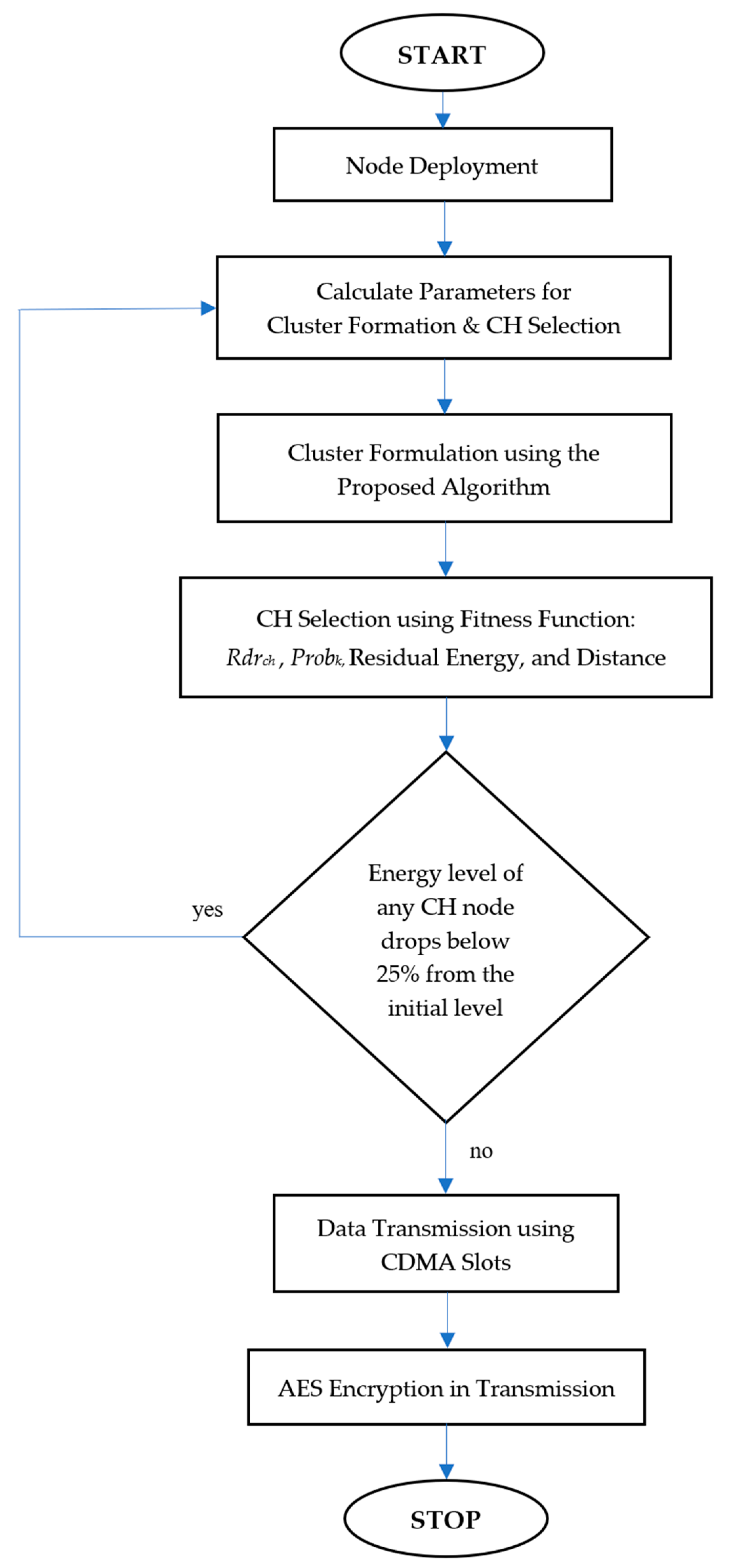
3. Proposed EAFSCP Model

In the proposed model, all mobile nodes are capable of bidirectional communication, fostering interconnectivity among nodes. This model takes into account both mobility and energy efficiency within the UWSN structure to ensure network scalability and an extended operational lifetime. Within the cluster-based network model, sensor nodes are systematically organized into clusters, each governed by a dedicated CH serving as the local coordinator. This approach streamlines network management, as configuration details are confined to clusters, reducing routing table complexities and overhead. The CH selection process identifies the most qualified nodes to act as CHs, considering their ability to sustain network connectivity with other nodes for extended periods.
The comprehensive schematic of the proposed clustering-based EAFSCP protocol is depicted in Figure 2. The EAFSCP protocol operates under the following assumptions:
  • Sensor nodes have non-removable batteries with uniform initial charge levels, ceasing operation when the battery is depleted.
  • Nodes remain stationary in their original deployment locations.
  • Each node is equipped with GPS, battery life awareness, and a unique identifier.
  • Collaborative resource pooling among nodes within a cluster enables data collection from multiple sources.
  • Sensor nodes possess their processing and storage capabilities, allowing them to perform various tasks, such as data delineation and aggregation.

3.1. Energy Model

Excessive CH re-election and interface refreshing are both triggered by mobility, resulting in the detriment of cluster stability. To address this issue, we propose leveraging mobility data to establish consistent connections among nodes that exhibit less frequent movement. By doing so, we can alleviate the burden of control maintenance within the network [14]. While constructing effective pathways between nodes is important, a fundamental goal of any routing protocol is to ensure the network's continuous and reliable operation. In this regard, the max-min routing strategy selects the path with the highest remaining energy in bottleneck nodes [15]. In contrast, the maximum efficiency routing approach prioritizes paths with the lowest overall energy consumption for packet transmission. Energy consumption can be calculated according to the change in energy over a specified period, as follows:
E C O N S ( t , Δ t ) = E R E S   ( t ) − E R E S   ( t + Δ t )
where ECONS represents the energy consumption between two time points, t (start time) and t + Δt (finish time). Moreover, ERES (t) and ERES (t+Δt) are the residual energy at time t and t + Δt, respectively.

3.2. Clustering Model

The importance of a node to be selected as a CH is measured in part by its degree and in part by the volume of data passing through it. Mobility information and energy levels are used to establish a starting point for determining the system's cluster and CH. The increased mobility-induced frequency with which interfaces must be refreshed and CHs selected inevitably results in less stable clusters [30]. The CH commences the cluster creation process by transmitting a broadcast request packet to all sensor nodes within its radio range [31]. While using a single node, communication with the CH is clear; when using a multibounce, all sensor nodes communicate with the CH via their nearest neighbor.

3.2.1. CH Selection

In addition to granting its members access to radio infrastructure, a Cluster Head (CH) assumes a pivotal role in orchestrating communications among nodes residing in distinct clusters [32]. The primary criterion for selecting CH nodes revolves around the count of neighboring sensor nodes. Each sensor node's neighborhood encompasses all other sensor nodes situated within a specified radius. The neighborhood radius ca be expressed as:
R d r C H = A r × A r / π × q
where R d r C H   is the neighborhood radius for a CH node, Ar is the approximate radius of the network where wireless sensor nodes are dispersed, and q is a constant parameter determining the distribution (density) of sensor nodes in the specified region.
Starting with a random chance, each node chooses to be a CH for that round. Accordingly, the predicted number of CHs in the current round can be calculated as:
X = ∑ k = 1 N ( P r o b k t / R d r C H )
where N represents the total number of network’s nodes, k is the index of sensor nodes, and Probk (t) is the probability of node k for becoming a CH in the current round (t) which can be expressed as:
P r o b k t = E x p N u m C H s E x p N u m N o n C H s P r e
where E x p N u m C H s is the expected number of CHs, and E x p N u m N o n C H s P r e is the expected number of nodes that are not selected as CHs in the previous rounds.
It is guaranteed that in N X rounds, each node will be used exactly once. There is an equal likelihood that each given node in a cluster will be designated as CH [33]. This guarantees that the energy at each node remains roughly constant during the whole game. Clustering is more likely to occur at higher-energy nodes than at lower-energy anodes [15]. The energy consumption for a CH node in the network can be calculated as follows:
E n e r g y   C H = N − X × r   m o d N X × A v g R e s E n × N X − ( X × m o d N X r )
where AvgResEn denotes the mean remaining energy of all nodes in the network, and r represents the current round of simulations.

3.2.2. Cluster Formation

We propose the utilization of an AFSA-driven clustering algorithm aimed at optimizing the performance of CHs in UWSN. The attainment of cluster stability in UWSN is a vital prerequisite. It's crucial to underscore that in networks where data traverses from source to destination through CHs, the mere selection of highly qualified nodes as CHs does not guarantee the efficiency of clustering.
The AFSA serves as a means to enhance the exploration capacity within the search space by acting as a localized optimizer. In the natural world, fish locate richer feeding areas through individual exploration or by trailing other fish; typically, areas with a greater concentration of fish are more abundant in nourishment. AFSA is an effective, stochastic, and parallel searching technique, first introduced by Li in 2002 [34]. This approach employs the local exploration tendencies of individual fish to ultimately achieve the global optimal solution by mimicking fish behaviors like hunting, grouping, and shadowing.
In AFSA, each artificial fish (AF) symbolizes a potential solution to the optimization problem, aiming to pinpoint the optimum point within the fish swarm with the highest food concentration. Initially, AFs' are randomly generated, and the position with the highest quality is noted on the bulletin board. AFs improve their positions by performing behaviors including swarm, follow, foraging, and random movement. Based on these behaviors' outcomes, they decide whether to relocate, and the bulletin board updates with the best AF position. Over iterations, AFs gradually fine-tune their locations, ultimately converging to the optimal solution recorded on the bulletin board.
In the search for a target position with a superior food concentration, each AF engages in swarming, following, and foraging behaviors. When the predefined criteria for any of these behaviors are met, they are carried out successfully, resulting in the discovery of a fresh position. However, if none of the behaviors of swarm, follow, or foraging, can be executed successfully, the AF resorts to random behavior, adopting the resultant position as its new location. In cases where one or more of the swarm, follow, and foraging behaviors prove effective, the AF chooses the new position with the highest food concentration as its updated location. Details regarding these behaviors are elaborated upon in the following section.
  • Swarm behavior
Denoting UC as the center of positions for all agents within the partnership (neighborhood area) of AF i within its visual range, the swarm behavior is initiated if UC exhibits a higher food concentration, and the vicinity of UC remains uncrowded. Subsequently, AF i takes a random step towards UC, leading to the determination of its new position, denoted as U i   ( t + 1 ) , which can be expressed as follows:
U i    ( t + 1 ) = U i ( t ) + U C − U i t | U C − U i t |   . S T E P . R N D
where U i ( t ) is the current position of the AF i at the current time period t, U i   ( t + 1 ) is the updated position of the same AF at the next time period, STEP is a parameter that signifies the largest possible step size that an organism can move in one time period, and RND represents a random value generated between 0 and 1. Moreover, ||Uj – Ui|| is the Euclidean distance between the AFs i and j.
  • Follow behavior
Every AF seeks out the optimal position, denoted as UBST , characterized by the highest food concentration within its visual range. When UBST boasts a superior food concentration, and the immediate vicinity of UBST remains uncongested, the follow behavior is executed effectively. Under the follow behavior, AF i randomly takes a step towards UBST, acquiring a fresh position as outlined below:
U i    ( t + 1 ) = U i ( t ) + U B S T − U i t | U B S T − U i t |   . S T E P . R N D
  • Foraging behavior
According to the foraging behavior, the AF i may collect the states of the other fishes and randomly select a state Uj that falls inside its detection range. Then, updating of AF i can be expressed as follows:
U i    ( t + 1 ) = U i ( t ) + U j − U i t | U j − U i t |   . S T E P . R N D
  • Random behavior
If none of the swarm, follow, or foraging behaviors are executed successfully, the algorithm resorts to a random movement. This random behavior serves as an effective mechanism to avoid getting trapped in local optimums. Under this approach, AF i takes a random step from its current position, resulting in its new location as described below:
U i    ( t + 1 ) = U i ( t ) + S t e p . ( 2 * R N D − 1 )
  • Fitness evaluation
Depending on the application, a different fitness measure can be used to determine the effectiveness of each particle. Our proposed fitness function for this strategy aims to do two things: (1) Make CHs more durable, and (2) Limit the intra-cluster distance between nodes and their CHs. It can be formulated as:
Fitness =   A v g I n t e r D i s t A v g I n t r a D i s t × A v g E n C H s
where AvgEnCHs is the average energy of the selected CHs. Moreover, AvgInterDist and AvgIntraDist are the average inter-cluster distance and average intra-cluster distance, which can be calculated as:
A v g I n t e r D i s t = 1 M × ( M − 1 ) × ∑ i = 1 M ∑ j = 1 j ≠ i M d ( C i , C j )
A v g I n t r a D i s t = 1 N × ∑ k = 1 N d ( k , C H k )
where M is the number of selected CHs, Ci represents the position of i-th CH within the network, k is the node number, CHk is the CH of node k, and d(x,y) is the Euclidean distance between nodes x and y.

3.3. Transmission Phase

In the transmission stage, the CH nodes aggregate the data collected from their respective members. This consolidation of data yields substantial savings in terms of additional data transmission costs, particularly when sensor nodes are situated in close proximity to each other, share substantial sensor data overlap, and receive similar environmental data [35]. Following this data gathering, CH nodes then forward this compiled information to the sink. Nonetheless, within the network, there might be sensor nodes that are closer to the sink than any of the CH nodes. In such instances, these sensor nodes are configured to transmit their data directly to the sink, bypassing the CH nodes responsible for Code Division Multiple Access (CDMA), thus avoiding signal interference. This configuration minimizes the incentive for CH nodes located far from the sink to migrate closer in order to connect to the network [36,37,38]. Subsequently, the transmitted data in the CDMA slot undergoes encryption using Advanced Encryption Standard (AES) encryption algorithms [39]. By implementing this approach, we can reduce unnecessary data transfers while reaping the benefits of the hierarchical algorithm's utilization of planar algorithms.

4. Experimental Results

In this subsection, we present the cluster-based routing protocols that have been selected as reference benchmarks for the validation of our proposed EAFSCP. These reference protocols include LEACH [18], CMSE2R [24], ChoA-HGS [40], and MOR [3]. To assess the resilience of the network, we evaluated key metrics such as the average duration of network operation, energy consumption, and the percentage of lost packets. These rigorous trials were carried out using MATLAB R2022b, employing the network parameters as detailed in Table 3.

4.1. Packet Delivery

Packet delivery ratio (PDR) holds significant importance as a performance metric in UWSNs. It signifies the percentage of packets that are effectively transmitted from the source node to the destination node, free from errors or losses. The scrutiny of PDR in UWSNs plays a critical role in comprehending network performance and uncovering potential issues that could impact data transmission quality. In Figure 3 and Table 4, we conducted a comprehensive comparison of our EAFSCP protocol against state-of-the-art techniques, taking into account variations in the number of nodes and simulation rounds. Notably, the EAFSCP consistently outperforms the other algorithms.

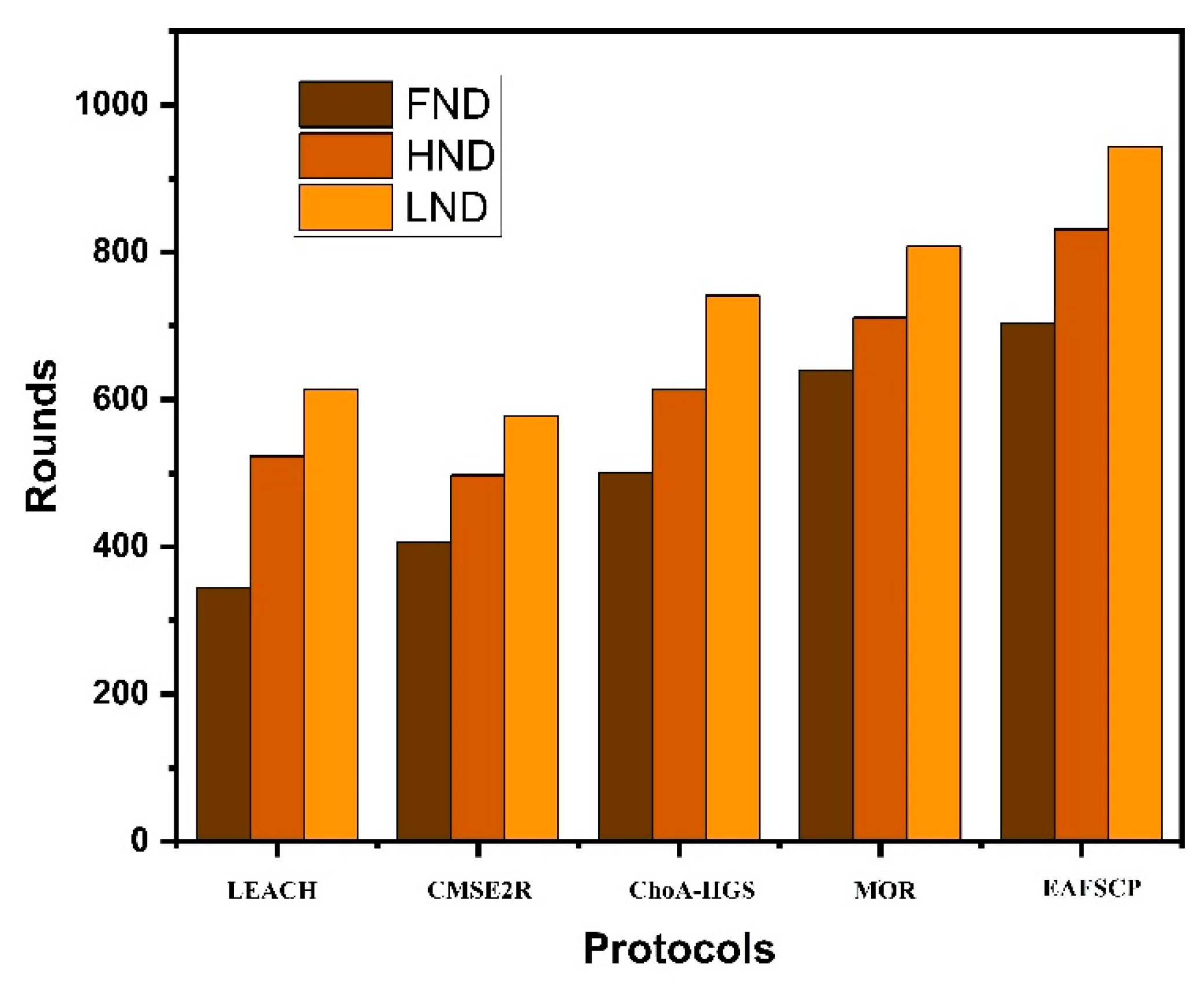
4.2. Network Lifetime

In the realm of UWSNs, the network lifetime represents the duration for which the network can operate using its allocated resources, such as battery power, without the need for recharging or replacement. The lifespan of a UWSN hinges on various factors, including the energy consumption of individual sensors, the deployment strategy, the communication protocols employed, and the data processing techniques utilized. Maximizing network lifetime is of paramount importance in many applications, particularly because underwater environments pose challenges when it comes to access, and replacing or recharging sensors can be both daunting and costly. In this section, we delve into an examination of five protocols, comparing them based on the number of nodes that remain active at First Node Dead (FND), Half Nodes Dead (HND), and Last Node Dead (LND). As depicted in Figure 4 and detailed in Table 5, it's evident that with the passage of rounds, the percentage of nodes that are still operational diminishes across all protocols. However, our suggested EAFSCP maintains a higher percentage of surviving nodes in comparison to the alternative protocols.

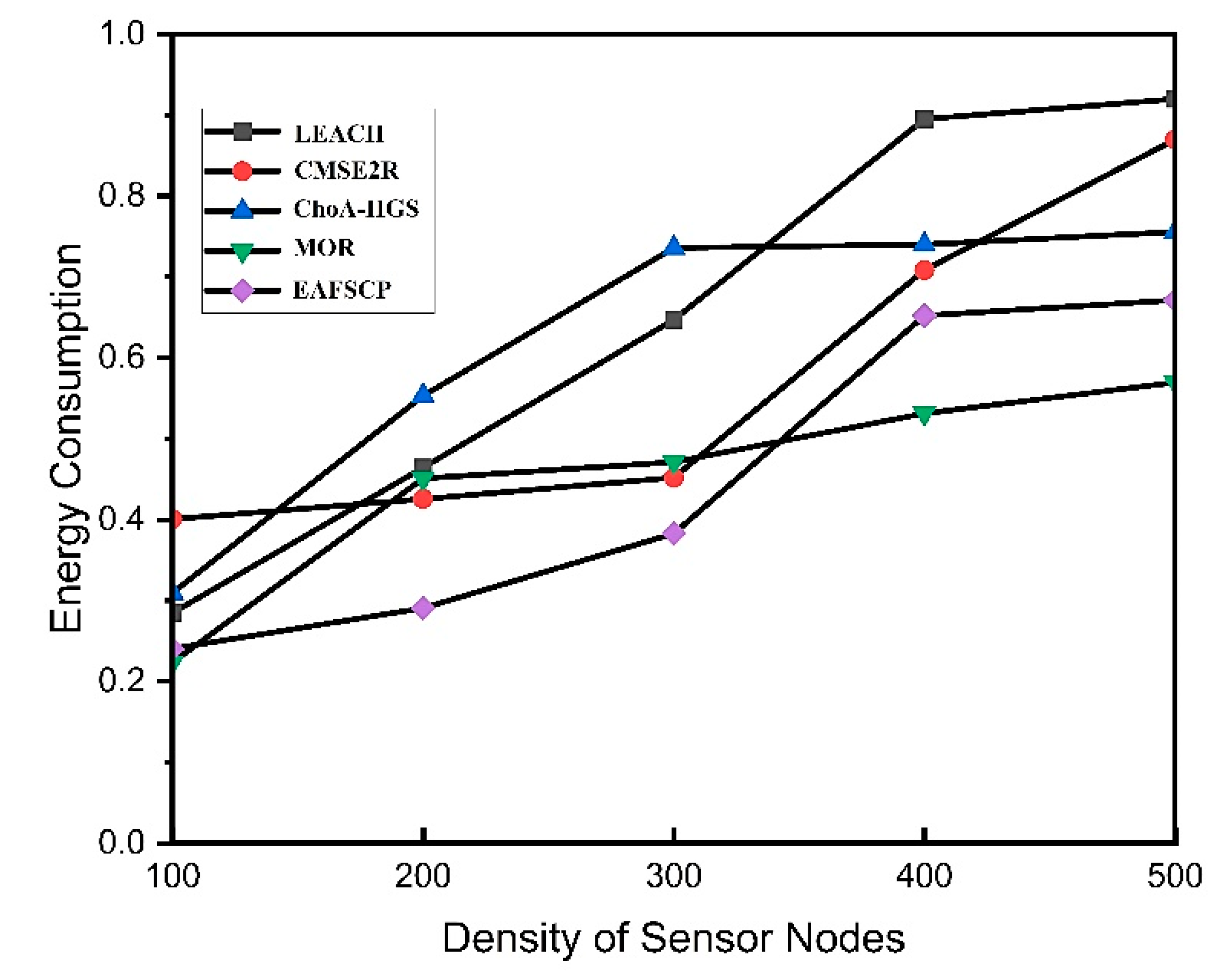
4.3. Energy Consumption

Energy consumption holds immense significance in the context of UWSNs because these sensors are typically reliant on battery power and have constrained energy reservoirs. Consequently, the minimization of energy consumption becomes a pivotal objective, as it directly contributes to the extension of network lifetime while concurrently reducing the necessity for frequent maintenance and battery replacements. In this section, we scrutinize the energy utilization of the different techniques in Table 6 and Figure 5. While EAFSCP consumes more energy than its counterparts, it emerges as the top performer in terms of energy efficiency. Specifically, the improvements of the proposed EAFSCP range from 32.8% when compared to LEACH, to 24.5% versus CMSE2R, 30.2% when measured against ChoA-HGS, and 4.8% when contrasted with MOR.

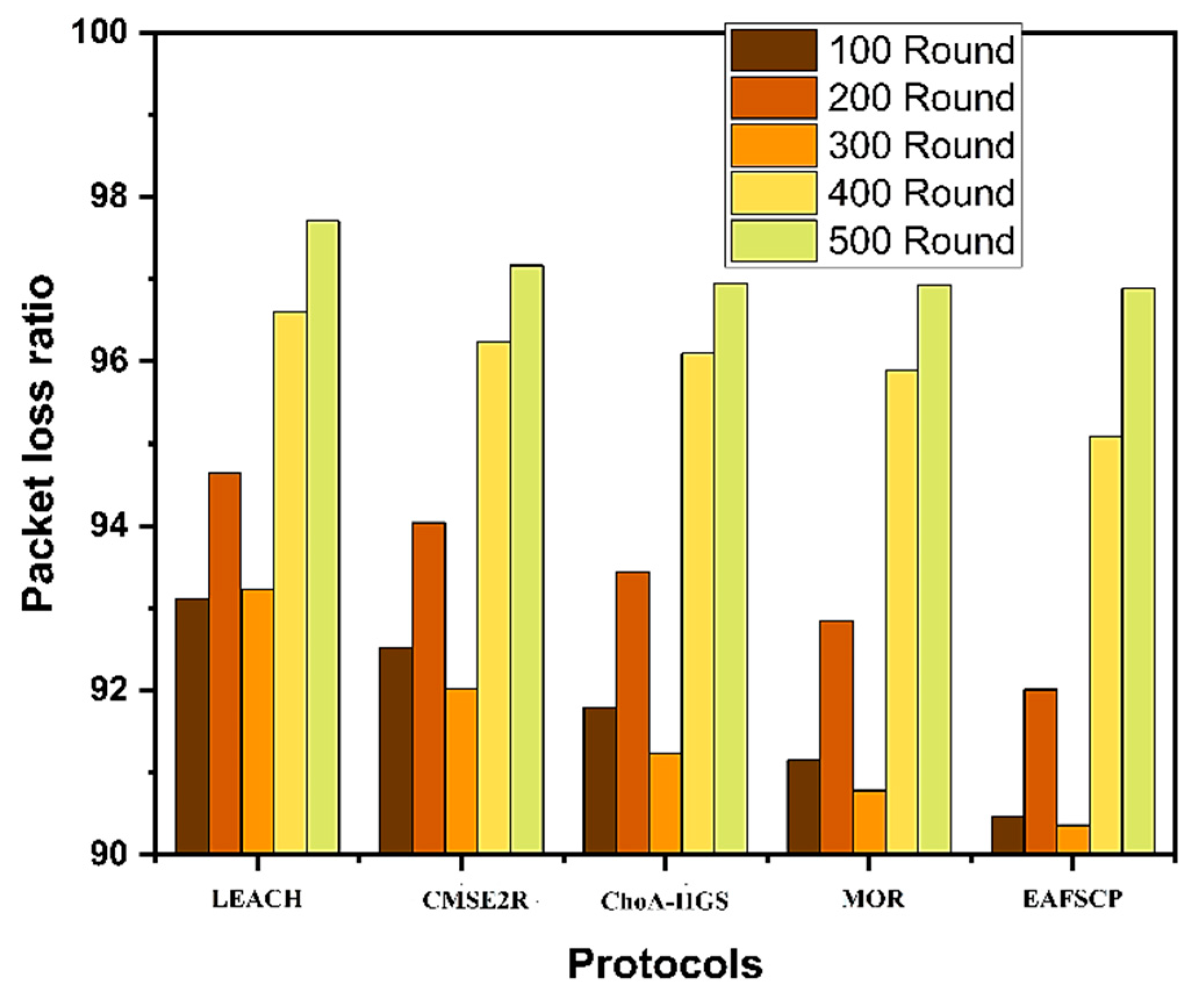
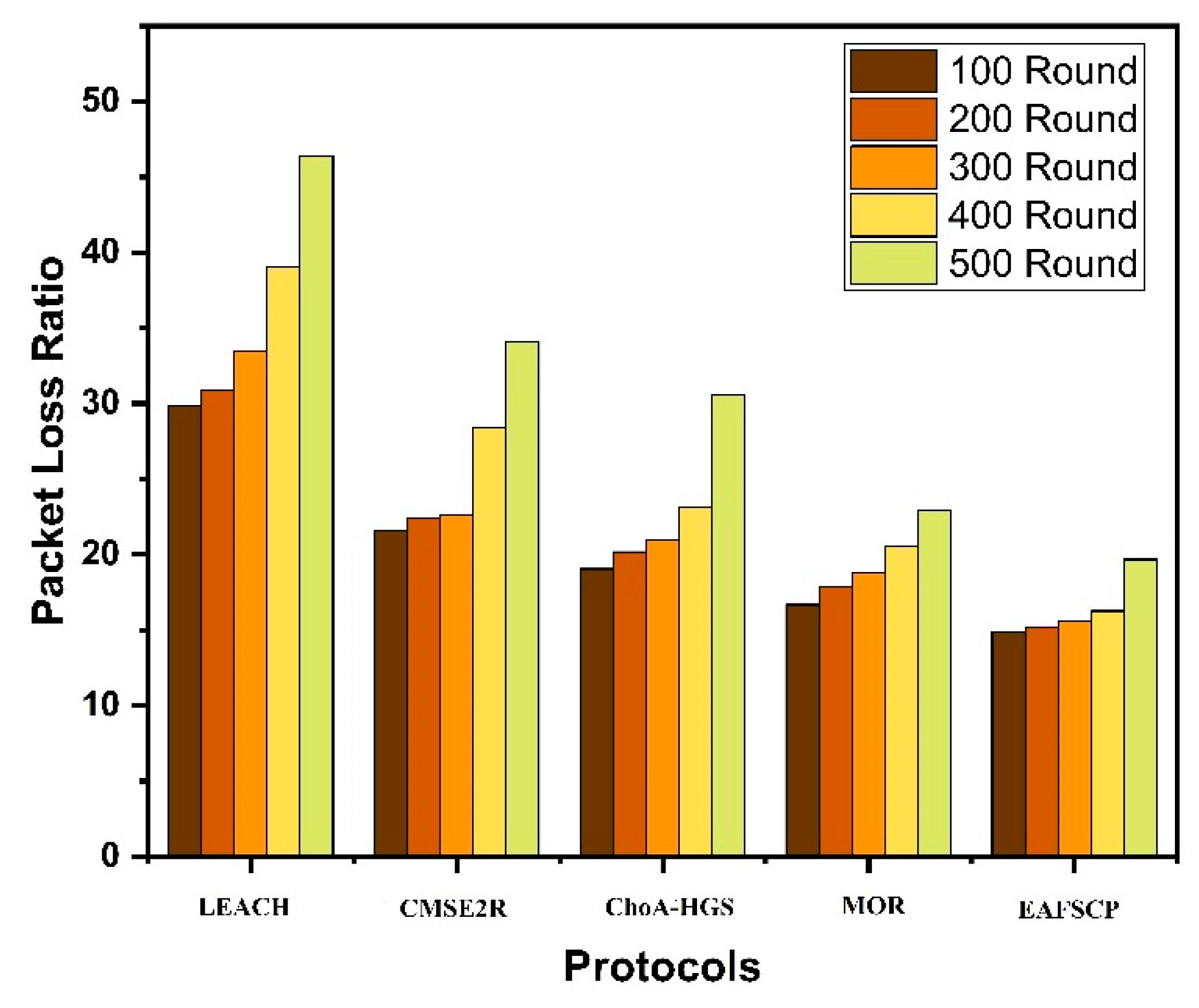
4.4. Packet Loss

Packet loss rate pertains to the percentage of packets transmitted by sensors that fail to reach their intended destination due to various factors, including signal attenuation, noise, interference, or collisions. Elevated packet loss rates can result in data inconsistencies, heightened energy consumption, and a diminished network lifespan. In Table 7 and Figure 6, we conduct a comparative analysis of the five protocols with regard to their packet loss rates, spanning multiple rounds of simulation. Observing a linear correlation between the network load and packet loss rate in all techniques, it becomes apparent that the packet loss rate increases in tandem with heightened network demands. In contrast, our proposed algorithm consistently maintains the lowest packet loss ratio among all protocols. This highlights the robustness of our algorithm in maintaining data integrity and network reliability, even under increased load conditions.

4.5. Throughput

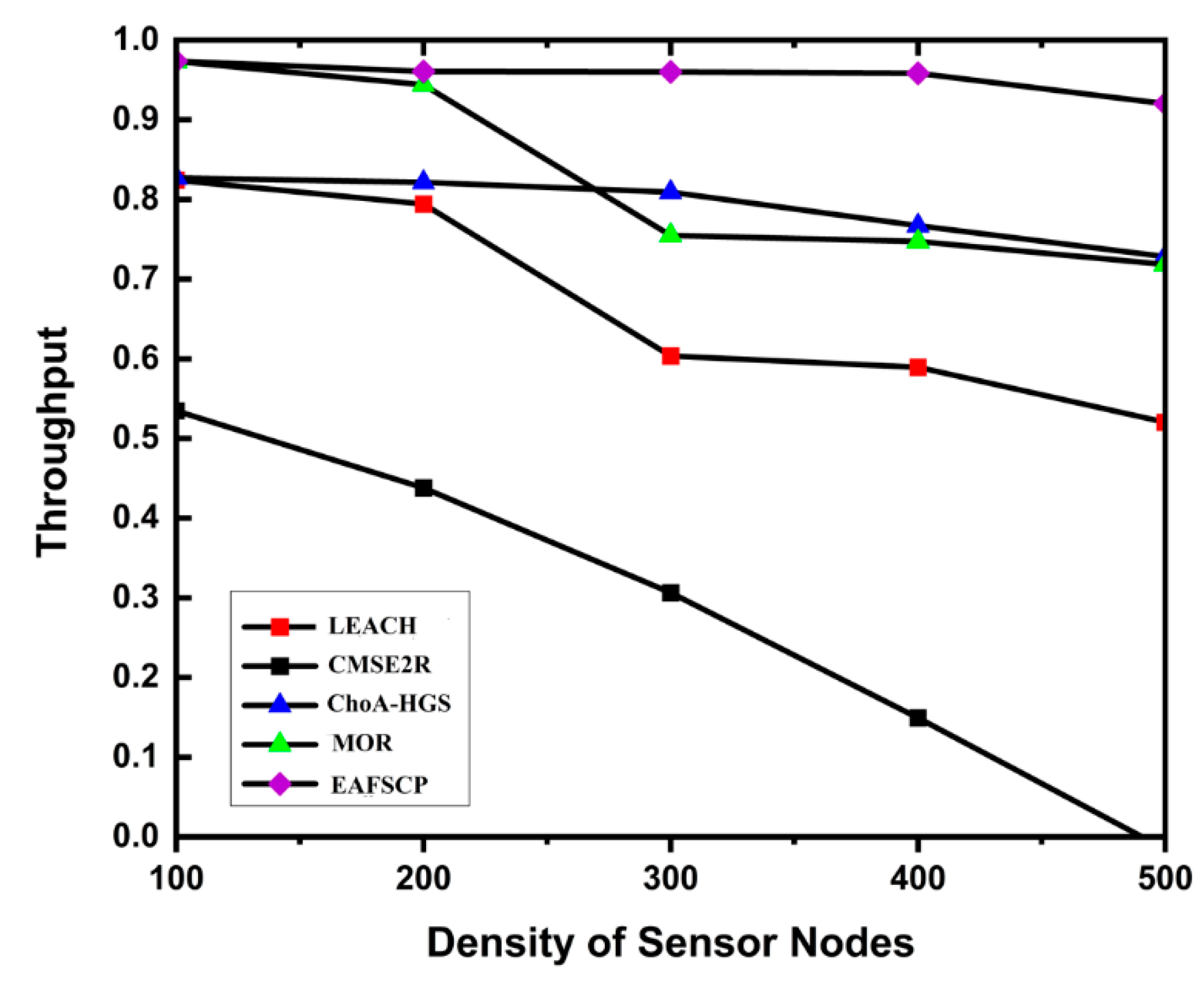
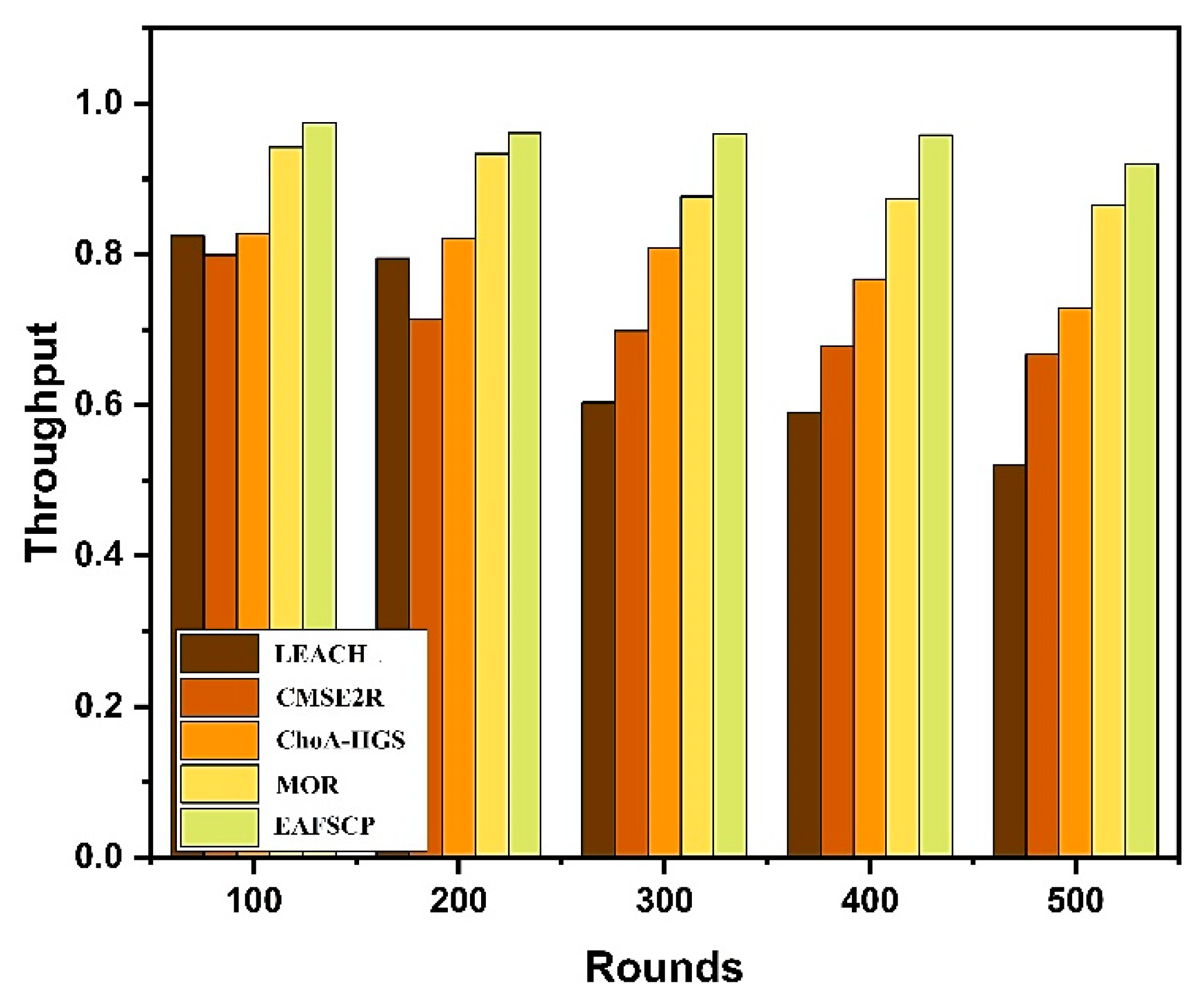
Throughput is a vital execution metric for UWSN, addressing the quantity of data that can be transmitted effectively over a given period. The obtained results in Table 8 and Figure 7 and Figure 8 demonstrate that the proposed EAFSCP seems to perform better than LEACH, CMSE2R, MOR, and ChoA-HGS techniques in grounded of throughput.

5. Conclusion

In this study, an energy-efficient artificial fish swarm-based clustering protocol (named EAFSCP) has been introduced as a solution to the unique challenges faced by UWSNs, with a particular focus on acoustic monitoring applications. EAFSCP, inspired by the collective behavior of fish swarms, addresses these issues through a decentralized clustering algorithm tailored for UWSNs. Our comparative analysis against existing classical and metaheuristic-driven clustering protocols underscores the superior performance of EAFSCP across key metrics such as energy consumption, network lifetime, packet delivery ratio, packet loss rate, and throughput. EAFSCP demonstrates its proficiency in enhancing network performance, prolonging network lifespan, promoting scalability, and providing valuable support for emergency response efforts.
Looking ahead, several promising avenues for future research emerge. Firstly, efforts to bolster the protocol's resilience against noisy data and topology changes are crucial for real-world deployment. Furthermore, optimization studies can explore the influence of diverse network factors such as node density, transmission range, and communication channels on EAFSCP's performance. Finally, field trials in underwater environments are essential to validate the protocol's efficacy and viability in practical scenarios. In essence, the introduction of EAFSCP and the direction outlined for future research hold substantial promise in advancing the field of UWSNs, particularly in the context of acoustic monitoring.

Author Contributions

Conceptualization, Puneet Kaur, Kiranbir Kaur, Kuldeep Singh, and Salil Bharany; Data curation, Kiranbir Kaur, Puneet Kaur and Salil Bharany; Formal analysis, Kuldeep Singh, Guojiang Xiong, Ali Mohamed and Frank Werner; Funding acquisition, Abdulaziz S. Almazyad; Investigation, Kiranbir Kaur, Puneet Kaur, Kuldeep Singh, Salil Bharany and Frank Werner; Methodology, Kiranbir Kaur, Puneet Kaur, Ali Mohamed, Mohammad Shokouhifar and Frank Werner; Resources, Kiranbir Kaur, Puneet Kaur and Salil Bharany; Software, Kiranbir Kaur, Puneet Kaur, Kuldeep Singh and Salil Bharany; Supervision, Abdulaziz S. Almazyad, Ali Mohamed, Mohammad Shokouhifar and Frank Werner; Validation, Guojiang Xiong and Mohammad Shokouhifar; Writing – original draft, Kiranbir Kaur, Puneet Kaur, Kuldeep Singh and Salil Bharany; Writing – review & editing, Abdulaziz S. Almazyad, Ali Mohamed, Mohammad Shokouhifar and Frank Werner.

Funding

This research is funded by Researchers Supporting Program at King Saud University (RSPD2023R809).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used in the study is available with the authors and can be shared upon reasonable requests.

Acknowledgments

The authors would like to express their gratitude to King Saud University for generously supporting the publication of this research through the Researchers Supporting Program, King Saud University, Riyadh, Saudi Arabia.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Han, X.; Yin, J.; Tian, Y.; Sheng, X. Underwater acoustic communication to an unmanned underwater vehicle with a compact vector sensor array. Ocean Eng. 2019, 184, 85–90. [Google Scholar] [CrossRef]
  2. Alamu, O.; Olwal, T.O.; Djouani, K. Energy harvesting techniques for sustainable underwater wireless communication networks: A review. e-Prime 2023, 5. [Google Scholar] [CrossRef]
  3. Sun, Y.; Zheng, M.; Han, X.; Ge, W.; Yin, J. MOR: Multi-objective routing for underwater acoustic wireless sensor networks. AEU - Int. J. Electron. Commun. 2023, 158. [Google Scholar] [CrossRef]
  4. Bhaskarwar, R.V.; Pete, D.J. Energy efficient clustering with compressive sensing for underwater wireless sensor networks. Peer-to-Peer Netw. Appl. 2022, 15, 2289–2306. [Google Scholar] [CrossRef]
  5. Shokouhifar, M.; Jalali, A. Optimized sugeno fuzzy clustering algorithm for wireless sensor networks. Eng. Appl. Artif. Intell. 2017, 60, 16–25. [Google Scholar] [CrossRef]
  6. Toor, A.S.; Jain, A. Energy Aware Cluster Based Multi-hop Energy Efficient Routing Protocol using Multiple Mobile Nodes (MEACBM) in Wireless Sensor Networks. AEU - Int. J. Electron. Commun. 2019, 102, 41–53. [Google Scholar] [CrossRef]
  7. Singh, M.K.; Amin, S.I.; Choudhary, A. Genetic algorithm based sink mobility for energy efficient data routing in wireless sensor networks. AEU - Int. J. Electron. Commun. 2021, 131, 153605. [Google Scholar] [CrossRef]
  8. Esmaeili, H.; Hakami, V.; Bidgoli, B.M.; Shokouhifar, M. Application-specific clustering in wireless sensor networks using combined fuzzy firefly algorithm and random forest. Expert Syst. Appl. 2022, 210. [Google Scholar] [CrossRef]
  9. Aryai, P.; Khademzadeh, A.; Jassbi, S.J.; Hosseinzadeh, M.; Hashemzadeh, O.; Shokouhifar, M. Real-time health monitoring in WBANs using hybrid Metaheuristic-Driven Machine Learning Routing Protocol (MDML-RP). AEU - Int. J. Electron. Commun. 2023, 168. [Google Scholar] [CrossRef]
  10. Fanian, F.; Rafsanjani, M.K. CFMCRS: Calibration fuzzy- metaheuristic clustering routing scheme simultaneous in on-demand WRSNs for sustainable smart city. Expert Syst. Appl. 2023, 211. [Google Scholar] [CrossRef]
  11. Yadav, S.; Kumar, V. Hybrid compressive sensing enabled energy efficient transmission of multi-hop clustered UWSNs. AEU - Int. J. Electron. Commun. 2019, 110. [Google Scholar] [CrossRef]
  12. Khan, M.F.; Aadil, F.; Maqsood, M.; Bukhari SH, R.; Hussain, M.; Nam, Y. Moth flame clustering algorithm for internet of vehicle (MFCA-IoV). IEEE Access 2018, 7, 11613–11629. [Google Scholar] [CrossRef]
  13. Bharany, S.; Badotra, S.; Sharma, S.; Rani, S.; Alazab, M.; Jhaveri, R.H.; Gadekallu, T.R. Energy efficient fault tolerance techniques in green cloud computing: A systematic survey and taxonomy. Sustain. Energy Technol. Assessments 2022, 53. [Google Scholar] [CrossRef]
  14. Gupta, D.; Khanna, A.; Sk, L.; Shankar, K.; Furtado, V.; Rodrigues, J.J.P.C. Efficient artificial fish swarm based clustering approach on mobility aware energy-efficient for MANET. Trans. Emerg. Telecommun. Technol. 2018, 30. [Google Scholar] [CrossRef]
  15. Bharany, S.; Sharma, S.; Badotra, S.; Khalaf, O.I.; Alotaibi, Y.; Alghamdi, S.; Alassery, F. Energy-Efficient Clustering Scheme for Flying Ad-Hoc Networks Using an Optimized LEACH Protocol. Energies 2021, 14, 6016. [Google Scholar] [CrossRef]
  16. Bharany, S.; Sharma, S.; Badotra, S.; Khalaf, O.I.; Alotaibi, Y.; Alghamdi, S.; Alassery, F. Energy-Efficient Clustering Scheme for Flying Ad-Hoc Networks Using an Optimized LEACH Protocol. Energies 2021, 14, 6016. [Google Scholar] [CrossRef]
  17. Majid, A.; Azam, I.; Waheed, A.; Zain-Ul-Abidin, M.; Hafeez, T.; Khan, Z.A.; Qasim, U.; Javaid, N. An Energy Efficient and Balanced Energy Consumption Cluster Based Routing Protocol for Underwater Wireless Sensor Networks. 2016 IEEE 30th International Conference on Advanced Information Networking and Applications (AINA). LOCATION OF CONFERENCE, SwitzerlandDATE OF CONFERENCE; pp. 324–333. [CrossRef]
  18. Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. (2000, January). Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the 33rd annual Hawaii international conference on system sciences (pp. 10-pp). IEEE. [CrossRef]
  19. Beiranvand, Z.; Patooghy, A.; Fazeli, M. I-LEACH: An efficient routing algorithm to improve performance & to reduce energy consumption in Wireless Sensor Networks. 2013 5th Conference on Information and Knowledge Technology (IKT). pp. 13–18. [CrossRef]
  20. Heinzelman, W.; Chandrakasan, A.; Balakrishnan, H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
  21. Aadil, F.; Bajwa, K.B.; Khan, S.; Chaudary, N.M.; Akram, A. CACONET: Ant Colony Optimization (ACO) Based Clustering Algorithm for VANET. PLOS ONE 2016, 11, e0154080–e0154080. [Google Scholar] [CrossRef]
  22. Khan, M.F.; Yau, K.-L.A.; Noor, R.M.; Imran, M.A. Routing Schemes in FANETs: A Survey. Sensors 2019, 20, 38. [Google Scholar] [CrossRef]
  23. Ahmed, M.; Salleh, M.; Channa, M. CBE2R: clustered-based energy efficient routing protocol for underwater wireless sensor network. Int. J. Electron. 2018, 105, 1916–1930. [Google Scholar] [CrossRef]
  24. Ahmed, M.; Soomro, M.A.; Parveen, S.; Akhtar, J.; Naeem, N. CMSE2R: Clustered-based Multipath Shortest-distance Energy Efficient Routing Protocol for Underwater Wireless Sensor Network. Indian J. Sci. Technol. 2019, 12, 1–7. [Google Scholar] [CrossRef]
  25. Wan, Z.; Liu, S.; Ni, W.; Xu, Z. An energy-efficient multi-level adaptive clustering routing algorithm for underwater wireless sensor networks. Clust. Comput. 2018, 22, 14651–14660. [Google Scholar] [CrossRef]
  26. Bhattacharjya, K.; Alam, S.; De, D. CUWSN: energy efficient routing protocol selection for cluster based underwater wireless sensor network. Microsyst. Technol. 2019, 28, 543–559. [Google Scholar] [CrossRef]
  27. Xu, J.; Li, K.; Min, G. Asymmetric multi-path division communications in underwater acoustic networks with fading channels. J. Comput. Syst. Sci. 2013, 79, 269–278. [Google Scholar] [CrossRef]
  28. Coutinho, R.W.L.; Boukerche, A.; Vieira, L.F.M.; Loureiro, A.A.F. Geographic and Opportunistic Routing for Underwater Sensor Networks. IEEE Trans. Comput. 2016, 65, 548–561. [Google Scholar] [CrossRef]
  29. Faheem, M.; Tuna, G.; Gungor, V.C. QERP: Quality-of-Service (QoS) Aware Evolutionary Routing Protocol for Underwater Wireless Sensor Networks. IEEE Syst. J. 2017, 12, 2066–2073. [Google Scholar] [CrossRef]
  30. Bharany, S.; Kaur, K.; Badotra, S.; Rani, S.; Kavita; Wozniak, M.; Shafi, J.; Ijaz, M.F. Efficient Middleware for the Portability of PaaS Services Consuming Applications among Heterogeneous Clouds. Sensors 2022, 22, 5013. [Google Scholar] [CrossRef]
  31. Das, U.C.; Islam, M.Z.; Malaker, T. Directional vector forward focused beam routing protocol for underwater sensor network. International Journal of Engineering, Science and Mathematics 2019, 8, 114–125. [Google Scholar]
  32. Li, X., Wang, Y., & Zhou, J. (2012, December). An energy-efficient clustering algorithm for underwater acoustic sensor networks. In 2012 International conference on control engineering and communication technology (pp. 711-714). IEEE. [CrossRef]
  33. Alhazmi, A.S.; Moustafa, A.I.; AlDosari, F.M. Energy Aware Approach For Underwater Wireless Sensor Networks Scheduling: UMOD_LEACH. 2018 21st Saudi Computer Society National Computer Conference (NCC). LOCATION OF CONFERENCE, Saudi ArabiaDATE OF CONFERENCE; pp. 1–5. [CrossRef]
  34. Li, X.L. An optimizing method based on autonomous animats: fish-swarm algorithm. Systems engineering-theory & practice 2002, 22, 32–38. [Google Scholar]
  35. Yang, G.; Dai, L.; Si, G.; Wang, S.; Wang, S. Challenges and Security Issues in Underwater Wireless Sensor Networks. Procedia Comput. Sci. 2019, 147, 210–216. [Google Scholar] [CrossRef]
  36. Moharamkhani, E.; Zadmehr, B.; Memarian, S.; Saber, M.J.; Shokouhifar, M. Multiobjective fuzzy knowledge-based bacterial foraging optimization for congestion control in clustered wireless sensor networks. Int. J. Commun. Syst. 2021, 34, e4949. [Google Scholar] [CrossRef]
  37. Fanian, F.; Rafsanjani, M.K.; Saeid, A.B. Fuzzy multi-hop clustering protocol: Selection fuzzy input parameters and rule tuning for WSNs. Appl. Soft Comput. 2020, 99, 106923. [Google Scholar] [CrossRef]
  38. Bharany, S.; Sharma, S.; Bhatia, S.; Rahmani, M.K.I.; Shuaib, M.; Lashari, S.A. Energy Efficient Clustering Protocol for FANETS Using Moth Flame Optimization. Sustainability 2022, 14, 6159. [Google Scholar] [CrossRef]
  39. Lalle, Y.; Fourati, M.; Fourati, L.C.; Barraca, J.P. Communication technologies for Smart Water Grid applications: Overview, opportunities, and research directions. Comput. Networks 2021, 190, 107940. [Google Scholar] [CrossRef]
  40. Yang, Y.; Wu, Y.; Yuan, H.; Khishe, M.; Mohammadi, M. Nodes clustering and multi-hop routing protocol optimization using hybrid chimp optimization and hunger games search algorithms for sustainable energy efficient underwater wireless sensor networks. Sustain. Comput. Informatics Syst. 2022, 35, 100731. [Google Scholar] [CrossRef]
Preprints 88260 g001
Figure 1. UWSN connectivity.
Figure 1. UWSN connectivity.
Preprints 88260 g001
Preprints 88260 g002
Figure 2. Overall flowchart of the proposed method.
Figure 2. Overall flowchart of the proposed method.
Preprints 88260 g002
Preprints 88260 g003
Figure 3. Packet delivery ratio.
Figure 3. Packet delivery ratio.
Preprints 88260 g003
Preprints 88260 g004
Figure 4. Network lifetime analysis.
Figure 4. Network lifetime analysis.
Preprints 88260 g004
Preprints 88260 g005
Figure 5. Energy consumption.
Figure 5. Energy consumption.
Preprints 88260 g005
Preprints 88260 g006
Figure 6. Packet loss ratio.
Figure 6. Packet loss ratio.
Preprints 88260 g006
Preprints 88260 g007
Figure 7. Throughput.
Figure 7. Throughput.
Preprints 88260 g007
Preprints 88260 g008
Figure 8. Throughput graph comparison.
Figure 8. Throughput graph comparison.
Preprints 88260 g008
Table 1. Qualitative comparison of the existing clustering techniques.
Table 1. Qualitative comparison of the existing clustering techniques.
Protocol Energy
Efficiency		 Scalability Fault
Tolerance		 Reliability Network
Longevity		 Delays Clustering Overhead Load
Balancing
LEACH [18] + 0 - + - + + 0
I-LEACH [19] + + 0 + + 0 + +
LEACH-C [20] - - + - - + 0 +
CACONET [21] 0 + - 0 + - + 0
EBECRP [17] 0 0 - - + + + +
CBE2R [23] - + 0 - - 0 0 -
CMSE2R [24] + - + 0 0 + + +
ACUN [25] 0 0 + - - - - -
CUWSN [26] + - - + - 0 0 -
AMDC [27] - - - 0 + - - 0
GEDAR [28] + 0 + + - + 0 0
QERP [29] 0 + - - - - + -
* - : Low, 0 : Medium, + : High.
Table 2. Advantages and deficiencies of the existing clustering techniques.
Table 2. Advantages and deficiencies of the existing clustering techniques.
Protocol Advantages Deficiencies
LEACH [18]
  • Reduce energy consumption
  • Can handle a large number of nodes
  • Distributed manner
  • Unequal clustering
  • Limited data aggregation
I-LEACH [19]
  • High Energy consumption
  • Probabilistic algorithm
  • Limited scalability
  • Limited load balancing
LEACH-C [20]
  • Deterministic algorithm to select CHs
  • LEACH-C reduces energy consumption
  • Balances the workload
  • Limited scalability
  • Complex algorithm
CACONET [21]
  • Robust communication
  • Packet routing cost is minimized
  • Number of nodes are not dynamic
  • Complex system
EBECRP [17]
  • Avoid depth base routing
  • Good balance of load
  • Reduce communication overhead
  • Number of transmissions
  • Lifetime is not independent
CBE2R [23]
  • High energy consumption
  • Considering propagation delay
  • Transmission loss is reduced
  • All is dependent on setup phase
  • Re-clustering
CMSE2R [24]
  • Improves the link quality
  • Reduce the average energy consumption.
  • Multipath route development is complex
ACUN [25]
  • Uses a multi-level hierarchical network
  • Excessive energy burdens reduced
  • Energy balance
  • No fault tolerance mechanism
CUWSN [26]
  • High average path loss
  • High throughput
  • Fixed and short communication scale
  • Area coverage
  • Security
AMDC [27]
  • High energy efficiency
  • Better total Packet Error Rate (PER)
  • Complexity and difficulty to scale directly
GEDAR [28]
  • Improves the network performance
  • Balance network traffic loads
  • Topology dependable
  • Lifetime of the network is dependable
QERP [29]
  • Low energy consumption
  • High packet delivery ratio
  • Low network delay
  • High network traffic and node density
  • High the probability of collisions
Table 3. Network parameters.
Table 3. Network parameters.
Parameter Value
Network size 5 km × 5 km × 2 km
Number of nodes 300, 400, 500
Sink coordinate (2000, 2000, 0)
Data packet size 1024 bits
Receiving power 50 μW
Transmission rate 1024 bps
Table 4. Packet delivery ratio tabular comparison.
Table 4. Packet delivery ratio tabular comparison.
Density of Sensor Nodes LEACH CMSE2R ChoA-HGS MOR EAFSCP
100 93.12 94.64 93.23 96.61 97.71
200 92.52 94.04 92.02 96.24 97.17
300 91.79 93.44 91.24 96.10 96.95
400 91.15 92.85 90.78 95.89 96.93
500 90.47 92.01 90.36 95.09 96.89
Table 5. Network lifetime tabular comparison.
Table 5. Network lifetime tabular comparison.
Protocol FND HND LND
LEACH 345 523 613
CMSE2R 407 497 577
ChoA-HGS 501 613 741
MOR 640 711 808
EAFSCP 703 831 943
Table 6. Energy consumption tabular comparison.
Table 6. Energy consumption tabular comparison.
Density of Sensor Nodes LEACH CMSE2R ChoA-HGS MOR EAFSCP
100 0.2848 0.4007 0.3095 0.2333 0.2408
200 0.4643 0.4257 0.5531 0.4511 0.2806
300 0.6470 0.4519 0.7358 0.4711 0.3730
400 0.8950 0.7084 0.7400 0.5415 0.6221
500 0.9199 0.8700 0.7557 0.5695 0.6415
Average 0.6422 0.5713 0.6188 0.4533 0.4316
Table 7. Packet loss rate tabular comparison.
Table 7. Packet loss rate tabular comparison.
Protocol/Rounds 100 200 300 400 500
LEACH 29.85 30.87 33.48 39.06 46.41
CMSE2R 21.59 22.44 22.65 28.39 34.09
ChoA-HGS 19.04 20.17 20.94 23.16 30.56
MOR 16.67 17.88 18.78 20.57 22.95
EAFSCP 14.89 15.19 15.55 16.25 19.67
Table 8. Throughput tabular comparison.
Table 8. Throughput tabular comparison.
Density of Sensor Nodes LEACH CMSE2R ChoA-HGS MOR EAFSCP
100 0.8243 0.7988 0.8271 0.9420 0.9737
200 0.7944 0.7143 0.8214 0.9332 0.9608
300 0.6036 0.6985 0.8092 0.8765 0.9601
400 0.5894 0.6781 0.7672 0.8742 0.9585
500 0.5204 0.6677 0.7284 0.8655 0.9201
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated