Prerpints.org logo
Preprint
Article

Formulation of an Efficiency Model Valid for High Vacuum Flat Plate Collectors

Altmetrics

Downloads

75

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

20 October 2023

Posted:

24 October 2023

You are already at the latest version

Alerts
Abstract
High Vacuum Flat Plate Collectors (HVFPCs) are the only type of Flat Plate Thermal Collectors capable of producing thermal energy for middle-temperature applications (until 180 °C). As the trend of research plans to develop new Selective Solar Absorbers to extend the range of HVFPC application until 250 °C, it is necessary to correctly evaluate the collector efficiency up to such temperature to predict the energy production accurately. We propose an efficiency model for these collectors based on the selective absorber optical properties. The proposed efficiency model explicitly includes the radiative heat exchange with the ambient, which is the main source of thermal losses for evacuated collectors at high temperatures. It also decouples the radiative losses that depend on the optical properties of the absorber adopted from the other thermal losses due to HVFPC architecture. The model has been validated by applying it to MT-Power HVFPC manufactured by TVP-Solar, and it has been used to predict the efficiency and energy production of HVFPC equipped with new, optimized selective solar absorbers developed in recent years.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

According to the International Energy Agency [1], industrial heat makes up two-thirds of industrial energy demand and almost one-fifth of global energy consumption. Since the majority of industrial heat is produced by fossil fuel combustion, it creates a substantial stream of CO2 emitted every year [2]. Decarbonizing the heat production field requires a significant shift in generating industrial heat, especially in the high and medium-temperature heating sectors [3]. Solar collectors’ technology is constantly evolving, enabling the spread of their use to an increasing number of utilizations [4]. The trend of the annual global change in renewable heat consumption by source in 2022 [5] shows that the more significant portion of the 150 PJ of extra energy produced by solar thermal technology in the former year was used to satisfy the building sector energy demand and just a small amount the industrial heat demand. Solar thermal energy systems can be classified into three categories regarding operating temperature: Low-temperature systems (<150 °C) include Conventional Flat Plate Collectors, Evacuated Tube Collectors, and Compound Parabolic Collectors; Medium temperature systems (from 150 to 400 °C) are Parabolic Trough Collectors, Linear Fresnel Collectors and High Vacuum Flat Plate Collectors (HVFPCs) while as High-Temperature systems (>400 °C) can be classified Large Parabolic Trough Collectors and Linear Fresnel Collectors [6]. Flat Plate (FP) systems are the most fundamental and studied technology for solar-powered domestic hot water systems. The overall idea behind this technology is simple. They can collect diffuse and direct rays without solar tracking, being cheaper than concentrating collectors [7]. However, Conventional Flat Plates are mostly used in applications requiring temperatures lower than 100 °C since they experience high thermal losses caused by conduction, convection, and radiation. The conduction heat losses occur from the sides and the back of the collector plate, the convection heat losses take place from the absorber plate to the glazing cover, and the radiation losses occur from the absorber plate to the envelop [8]. To minimize conduction loss, it should be used use materials with low thermal conductivity, whereas a drastic reduction of convective losses to a negligible value can be obtained by evacuating the space around the absorber plate [9]. A high vacuum-insulated collector means that the pressure inside the collector is maintained below 10-4 mbar [10]. High vacuum insulation technology allowed the development of highly efficient solar collectors in the sector of solar thermal, with High Vacuum Flat Plate Collectors HVFPCs, like SRB [11] and TVP-Solar MT-Power collectors [12], or even for hybrid photovoltaic thermal systems, like virtu collector manufactured by Naked Energy.
For their features, HVFPCs, compared with conventional thermal collectors, exhibit a reduction in heat loss coefficient, resulting in a noticeable increase in efficiency [13,14] and executable thermal performance in industrial applications. They also achieve better solar conversion efficiency than the concentrating collectors particularly in the regions with a high proportion of diffuse solar irradiance [15,16]. High vacuum insulation in a panel with a flat structure can combine the high fill factor and the ease of building integration with low heat losses. Consequently, evacuated collectors can cover a larger range of applications that require thermal heat. Despite the noticeable advantages, few manufacturers produce an industrial version of flat collectors under high vacuum because dealing with vacuum requires great attention in the collector architecture design. In an HVFPC, the flat absorber is contained within an evacuated enclosure with a glass cover on top supported against atmospheric pressure loading. Even if high-vacuum insulation suppresses convection, the radiative heat exchange is still present and represents the main heat exchange mechanism in a vacuum environment. It becomes more significant with the rise of the operating collector temperature. The importance of the radiative behavior of an HVFPC makes the adoption of a Selective Solar Absorber (SSA) necessary to guarantee high absorptance in the solar irradiation spectrum (λ = 0.3-2.5 μm) and low emissivity in the infrared (IR) region (λ>2.5 μm), factors that reduce the drop of the absorber efficiency at high temperatures [17,18]. The low thermal emittance of the selective absorber also reduces the radiative losses, resulting in a very high thermal efficiency, which is the most significant parameter to express the performance of a thermal solar collector [19]. Its most general expression is the ratio between the useful thermal power Pu transferred to the heat transfer fluid (HTF) and the incident solar irradiation G on the collector aperture surface Ac [20]:
η t h = P u G ∗ A c
At present, the most common expression (eq. (2)) to describe the flat plate collector efficiency approximates thermal losses to a second order dependence from the difference between the average of the working fluid temperatures at the inlet and the outlet of the collector (Tm) and the ambient temperature (Tamb ) [21]. This expression is also the most used in solar keymark certification and, in this manuscript, will be indicated as standard efficiency and expressed as eq. (2):
η t h s t = η 0 I A M θ − c 1 T m − T a m b G + c 2 T m − T a m b 2 G
where η 0 is the zero-loss efficiency (when the fluid temperature is identical to the ambient temperature Tamb). The factors c1 and c2 are the first and second-order heat loss coefficients, respectively. The incidence angle modifier (IAMθ) function describes the optical efficiency for a certain radiation incidence angle θ normalized by optical efficiency evaluated at perpendicular irradiation conditions [22]. All the coefficients in the standard formula are obtained through a test whose methodology is prescribed by EN 12975 [23]. The efficiency values for operating temperatures higher than the maximum tested temperature cannot be evaluated with standard efficiency curve extrapolation since the radiative losses are not taken explicitly into account by the standard formula (eq. (2)). The error made with standard efficiency curve extrapolation at high temperatures is evident if we observe at Figure 1 in which are represented, with a red solid line, the standard efficiency curve of MT-Power HVFPC manufactured by TVP-Solar and its mathematical extrapolation with the dashed line. The efficiency in Figure (1) is expressed as function of the average collector temperature Tm assuming a fixed Tamb of 20 °C. The standard test for this particular collector was conducted in a controlled environment at Tamb=20 °C, with the maximum temperature (Tm) reaching 180 °C.
The MT-Power certification, along with the standard efficiency curve, indicates also the stagnation temperature value of the collector (equilibrium temperature of the generated and lost power, where η=0 ) when Tamb=20°C, which is equal to 302 °C.
It can be seen that in correspondence with the certified stagnation temperature, the mathematical extrapolation of the standard curve overestimates the thermal efficiency to a value of 0.1, indicating that the extrapolation overestimates the efficiency and cannot be used to predict the collector behavior at higher temperatures. Nowadays, HVFPCs are used to produce heat up to 180 °C but the improvements of this technology, like the development of new optimized SSA coatings [24,25] and glass cover [26,27], will bring in the short term to cover applications up to 250 °C [28]. A reliable method for evaluating the annual energy production of an HVFPC equipped with a new SSA would allow for estimations regarding the potential economic advantages of adopting the new absorber. Such method is missing in literature, and it would be essential to provides insights into how much to invest in adopting this innovation. This paper fill this gap and presents a novel efficiency model for the performance characterization of HVFPCs; it overcomes the limits of the standard efficiency formula, allowing the efficiency calculation up to the stagnation temperature. The proposed formula decouples the losses that depend on collector architecture from the optical and radiative losses of the SSA. It will allow us to predict the HVFPC performances at temperatures higher than the certified temperature and to accurately estimate the efficiency of HVFPCs equipped with new SSAs with different properties.

2. Methods

This paragraph describes the efficiency model developed for the energetic characterization of High Vacuum Flat Plate Collectors (HVFPCs). The proposed model is applicable to various HVFPCs and is derived from an energy balance analysis of the thermal system known as the "High Vacuum Flat Plate Solar Collector.

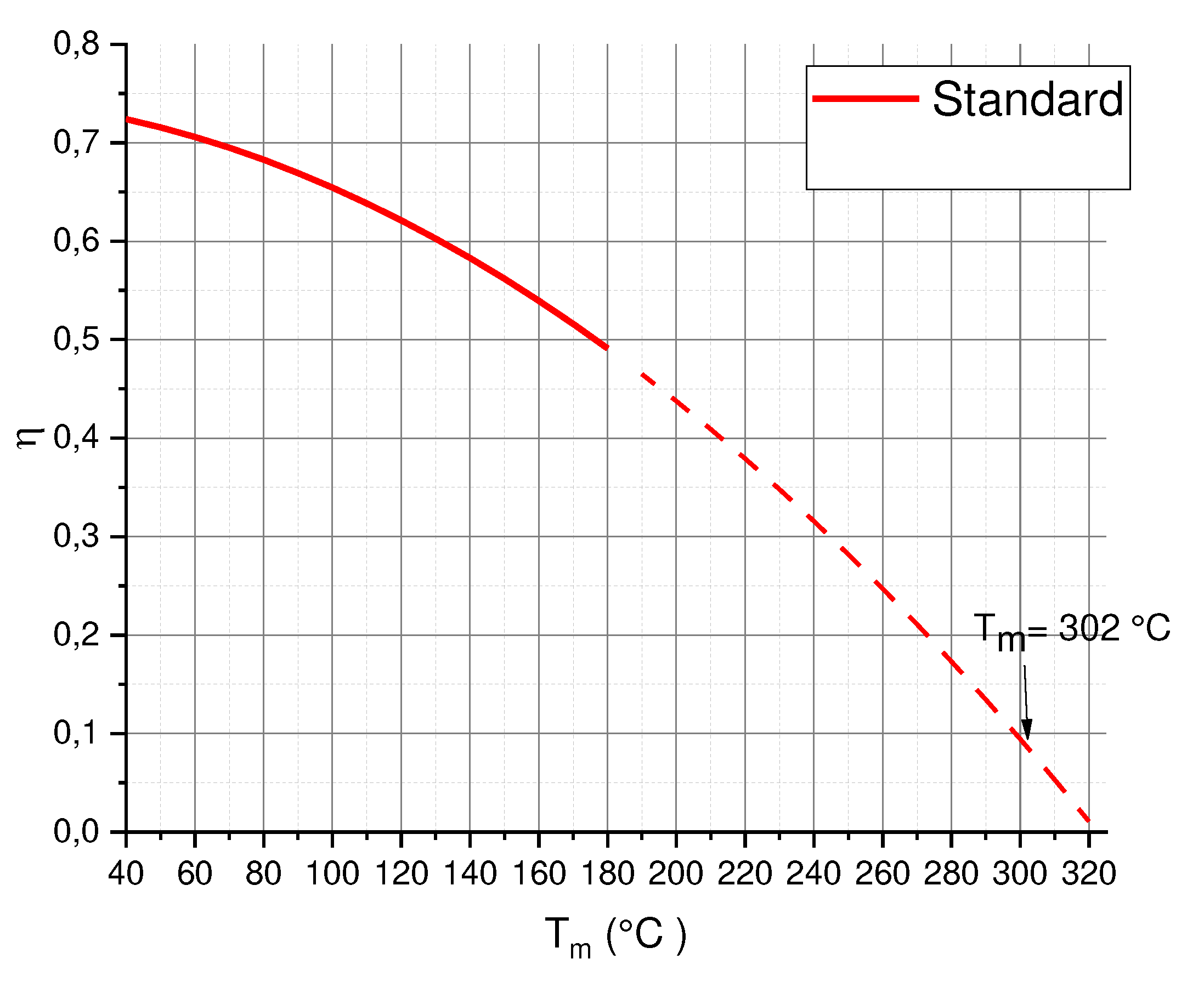
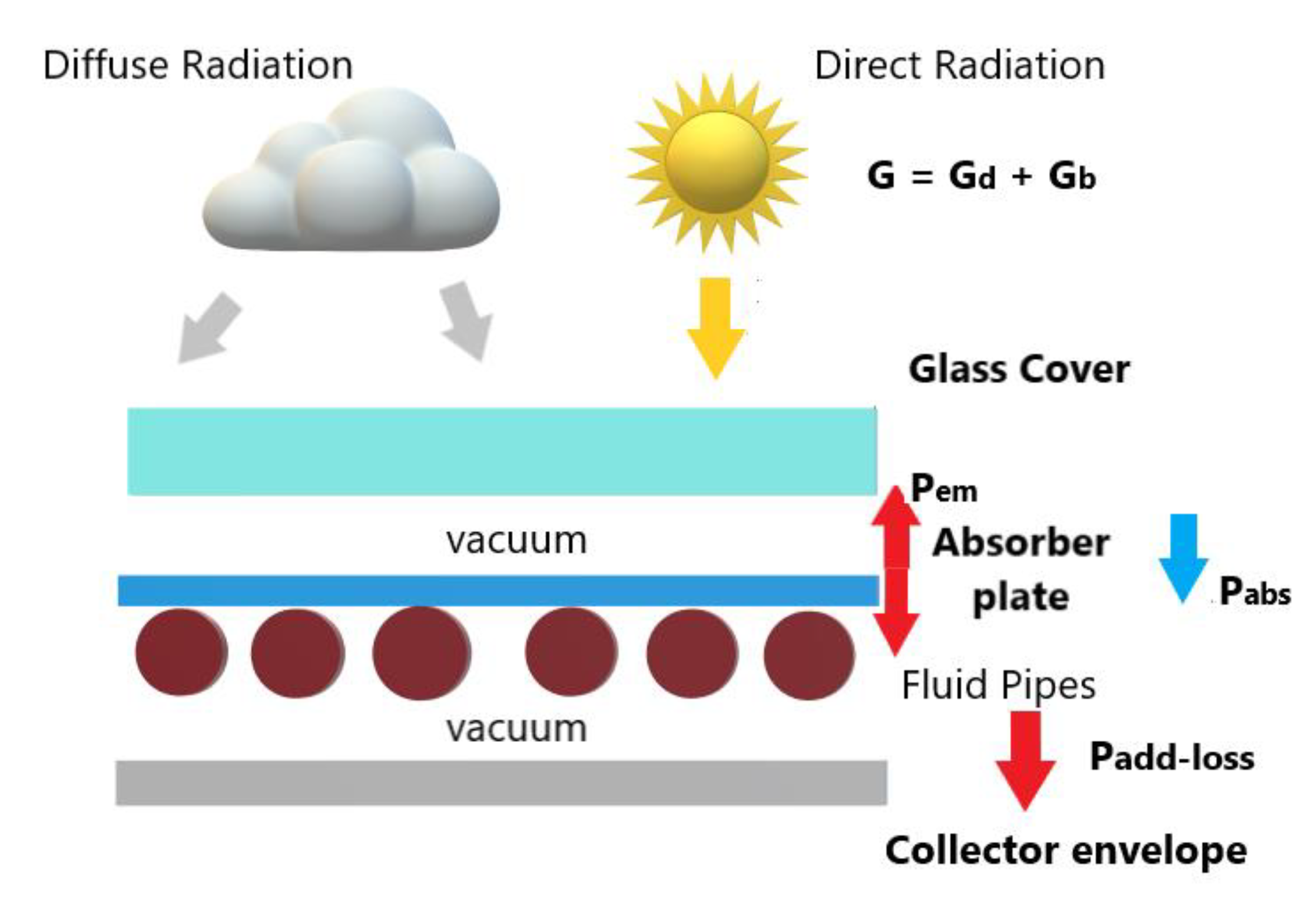
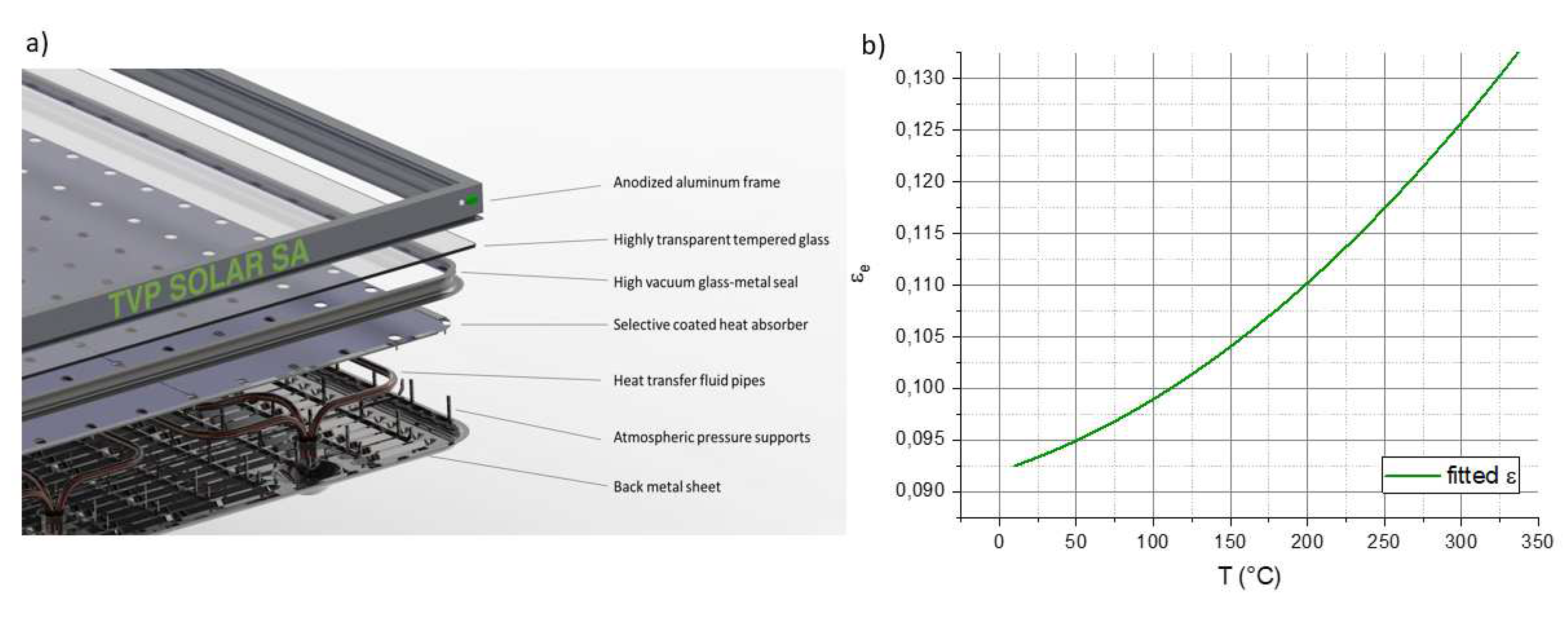
2.1. Efficiency Model for HVFPCs

A thermal solar collector can be defined as a device that converts solar power into useful heat, increasing the internal energy, i.e., the temperature, of an HTF that will be used for the end-user application. The energy transfer from solar radiation to the HTF will occur through different heat exchange mechanisms, as shown in Figure 2.
The main losses in HVFPCs are the radiative losses, which depend on the absorber radiative properties (absorptance and emittance) and the glass cover transmittance, and additional thermal losses, mostly conductive, due to the thermal contact with the supporting structure; therefore, Pu can be expressed as:
P u = P a b s − P e m + P a d d − l o s s
where 𝑃𝑎𝑏𝑠 represents the amount of power transmitted by the glass, absorbed by the SSA plate, and converted into HTF internal energy increment. It can be expressed as the product of the collector zero-loss efficiency η 0 and the Incident Angle Modifier IAMθ :
P a b s = η 0 ∗ I A M θ
𝑃𝑒𝑚 is the absorber emitted power due to the radiative heat exchange between the absorber and the surrounding elements:
P e m = A a b s ∗ ( ε   e a b s T m σ ( T m + 273.15 ) 4 − ( T g + 273.15 ) 4 + ε   e s u b T σ ( T m + 273.15 ) 4 − ( T v + 273.15 ) 4 )
In eq. (5), Tm is the average absorber temperature, which will be considered approximately equal to the average HTF temperature. Eq. (5) considers the effective thermal emittance of the two sides. The first (εeabs) refers to the absorbing side facing the glass at Tg, and the second (εesub) refers to the substrate side facing the stainless-steel vessel at temperature Tv.
For the surfaces of the components of a flat collector, the model of infinite parallel plates [29] can be used to calculate the effective emittances 𝜀e that govern the radiative exchange between them, so 𝜀eabs and 𝜀esub can be written as:
ε e a b s = 1 1 ε a b s + 1 ε g l a s s − 1
ε e s u b = 1 1 ε s u b + 1 ε v e s s e l − 1
Experimental measurements showed that the difference between Tg, Tv, and Tamb never exceeds 10 °C, impacting less than 1% on the radiated power; for this reason, we can safely assume Tg= Tv = Tamb, and eq. (5) becomes:
P e m     = ε e ( T m ) σ A a b s   ( T m + 273.15 ) 4 − ( T a m b + 273.15 ) 4
where 𝜀𝑒 is the sum of 𝜀eabs and 𝜀𝑒sub and is the total effective emittance of the absorber. In the term 𝑃𝑎𝑑𝑑−𝑙𝑜𝑠s of eq. (3) included all the HVFPC losses due to the panel architecture.
P a d d − l o s s = k T m − T a m b z
where k is the conductive heat losses coefficient while the exponent z determines the type of the additional heat losses, and it is expected to be equal to one (mostly conductive heat losses).
Explicating all the terms, eq. (1) becomes eq. (10):
    η t h , n e w = η 0 ∗ I A M θ − ε e T m ∗ σ   ( T m + 273.15 ) 4 − ( T a m b + 273.15 ) 4 G ∗ A a b s A c +   k ( T m − T a m b ) z G
Equation (10) is the expression of the proposed efficiency model valid for HVFPCs. The novelty of the eq. (10) is that decouples the absorber radiative losses from the losses due to HVFPC architecture (with the variation of parameter k , specific for a given HVFPC design). A particular mention deserves its adaptability to different absorber coatings if considering the panel architecture unchanged: by changing the absorber radiative properties in eq. (10), it is possible to quantify the change in the collector thermal efficiency and correctly estimate the energy production.

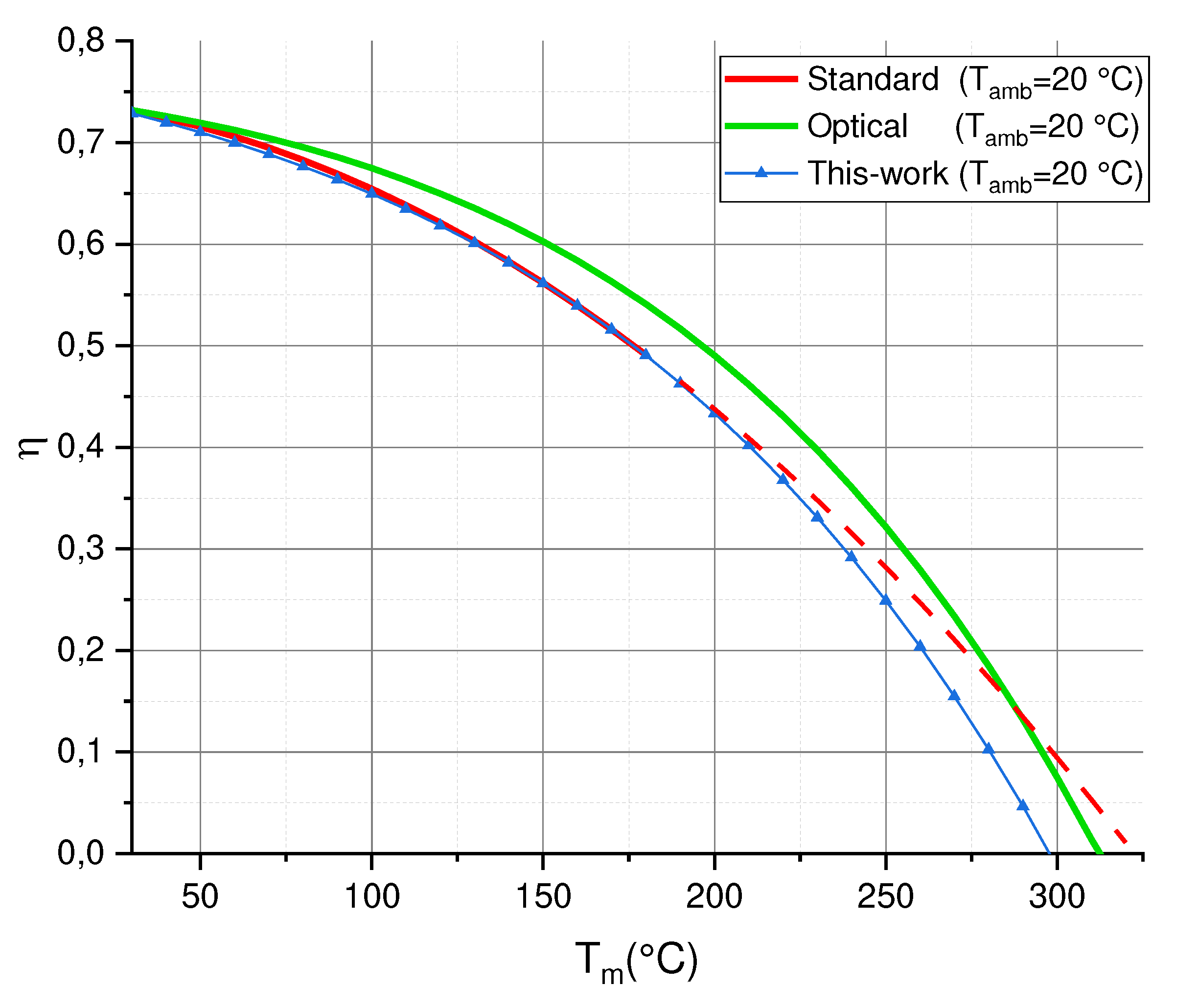
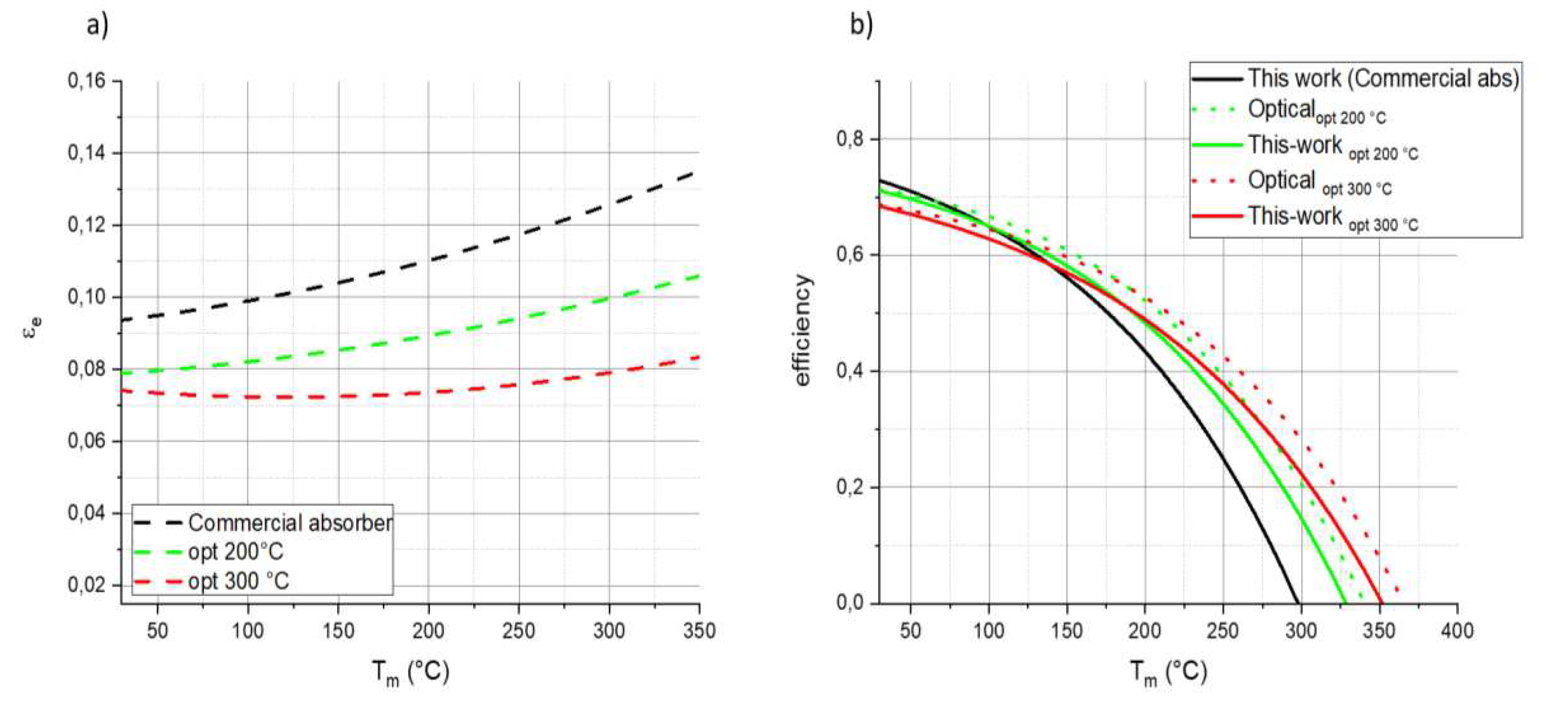
3. Results and Discussion

In the following section, this efficiency model will be applied to a commercially available HVFPC and various realizable versions of this collector, equipped with optimized selective solar absorbers having improved optical properties.

3.1. Application of Proposed HVFPCs Efficiency Model to MT-Power TVP-Solar Collector

In this work, the proposed efficiency model devised for HVFPCs will be validated by its application to the MT-Power collector produced by TVP- Solar company. The architecture of MT-Power and the thermal emittance curve of the selective absorber mounted in it are shown in Figure 3a) and 3b), respectively.
The curve was experimentally obtained by averaging the thermal emittance measured with a calorimetric approach [30,31] .To withstand the pressure loading, the glass is supported by pillars that pass through holes in the absorber. The enclosure follows a ‘tray’ style design, employing a stainless-steel tray with a single cover glass on the front. Approximately 3% of the absorber area is occupied by the through holes, leaving 97% of the ‘absorber area’ to absorb heat. The MT-Power operates at a maximum temperature of 180 °C and employs a commercial absorber with a multi-layer structure consisting of an aluminum substrate coated with an absorption layer and an anti-reflection layer. When deriving the thermal efficiency formula of MT-Power, the optical properties of the SSA, such as absorptance α and effective emittance ε𝑒(𝑇), were obtained through calorimetric measurements following the procedure described in [31]. The spectrally averaged absorptivity (𝛼) remains constant at 0.95 regardless of the absorber average temperature (𝑇𝑚). However, the ε𝑒(𝑇m) exhibits a quadradic dependence on absorber plate temperature, as shown in Figure 3 b). Given the known SSA optical properties, the unknown terms in equation (10) are the additional losses coefficient (k) and the exponent (z). To determine the value of k and z, equation (10) can be fitted to the certified efficiency data obtained using the standard efficiency formula of the collector. The standard efficiency coefficients to design the standard efficiency curve are obtained from a performance test performed indoors at controlled conditions (G= 950 W/m2, IAMθ = 1 and Tamb= 20 °C) where the maximum operating temperature Tm was equal to 180 °C.
The standard efficiency curve is certified in the range between the minimum and the maximum tested temperature. The proposed efficiency model equation (eq. (10)) should accurately replicate the standard formula (eq. (2)) until Tm = 180 °C. Through the fitting procedure, it was determined that the exponent (z) of the additional losses function that reproduce the certified efficiency is 0.93 (+/- 0.08) with a χ2 value of 2.8E-05. This value confirms that dissipative effects other than radiation losses have a linear dependence on (Tm-Tamb), suggesting that they are due to thermal conduction. Since the fit result is compatible with the exponent 1 of the conductive loss, we fix the value of z at 1 to compute the coefficient of additional losses, k. The best fit was obtained for a k value equal to 0.258, and it returned a χ2 value of 2.8E-05, and R 2 = 0.999 identical to the previous ones. The low value of the additional losses’ coefficient is not surprising due to the presence of a high vacuum in the panel and to the advanced architecture of MT-Power, specially designed to minimize conductive losses.
The efficiency formula of the MT-power collector obtained from the best fit of the solar key mark data is reported here:
η t h = η 0 ∗ I A M θ − ε e T m ∗ σ T m 4 − T a m b 4 G ∗ A a b s A c + 0.275   T m − T a m b G
Figure 4 shows three curves: the standard efficiency curve (red line) extended up to the stagnation temperature (red dashed line), the optical efficiency curve (yellow line) representing radiative losses only, and the curve generated by Eq. 11 (blue line with dots). All curves are plotted for normal irradiance at an angle of incidence of θ=0. The x-axis of Figure 4 represents the average temperature Tm because the optical efficiency curve and Eq. (11) depend on the fourth power of the ambient temperature Tamb and the absorber temperature Tm separately. To plot a single efficiency curve, Tamb must be fixed. In this case, Figure 4 uses the value at which the standard test was performed (indoor measurements), i.e., Tamb = 20 °C.
It's important to highlight that, unlike the standard curve extrapolation (Figure 1), Eq. (11) reaches zero efficiency at Tm = 302°C, which corresponds to the collector's stagnation temperature stated in the Solar Keymark certification. Our proposed efficiency formula, Eq. (11), corrects the absence of the quartic temperature dependence in the standard thermal efficiency formula. Using the standard formula, the power available at 250°C amounts to 525 W, while employing our proposed efficiency formula yields 464 W, resulting in a difference of 61 W. This discrepancy increases notably with higher operating temperatures T m . Furthermore, the same fitting procedure for Eq. (10) can be applied to HVFPCs with different architectures, given that we know the absorber optical properties and the standard efficiency coefficients from the Solar Keymark certification. The fitting process will provide the additional losses coefficient 'k' and the efficiency equation that can be used to extrapolate the collector performance up to stagnation.
The stagnation temperature in the certification is a vital information to obtain the new efficiency equation. The fact that the obtained equation passes through this specific point serves as a significant validation of the efficiency extrapolation outside the temperature range explored by the certification.
3.2. Application of Proposed HVFPCs Efficiency Model to Collectors with New Optimized Solar Absorbers
The proposed model allows us to predict the efficiency of an HVFPC equipped with a new SSA with different optical properties. This feature is crucial because absorber properties can change over time due to aging. Additionally, there are ongoing developments of new types of selective solar absorbers that enable efficient operation at temperatures higher than 180 °C.
In this section, we apply the newly developed efficiency model to an MT-Power HVFPC architecture equipped with multi-layered SSA optimized for operating temperatures of 200 °C and 300 °C [28]. To achieve maximum efficiency at the selected operating temperatures, the thickness of each layer was determined using a genetic algorithm [28]. The optimized absorbers exhibit optical properties suitable to HVFPCs, ensuring a significantly low emittance at high temperature.
As illustrated in Figure 5a), the optimization led to a significant reduction in thermal emittance, which is the primary source of heat loss for HVFPCs at elevated temperatures [24]. However, this reduction came with a slight trade-off in absorptance, with values of αcomm=0.95, αopt200 =0.925, αopt300 =0.890.
In Figure 5b), the curves labelled "this work" depict the MT-Power with commercial absorber (black continuous line) and the HVFPCs with the same structural characteristics as the MT-Power but equipped with SSAs optimized for 200 °C (green continuous line) and 300 °C (red continuous line). Due to the different value of α, HVFPCs equipped with the optimized SSAs exhibit zero-loss efficiencies (η0) different from those of the HVFPCs equipped with commercial absorbers. The efficiency of the optimized SSA is consistently higher than that of the commercial absorber at temperature higher than 120°C since the last was not optimized to work in high vacuum. The optical efficiencies of the optimized cases [28] are also reported in Figure 5b) as dashed line to underscore the importance of accounting for conductive losses, especially at elevated temperatures.

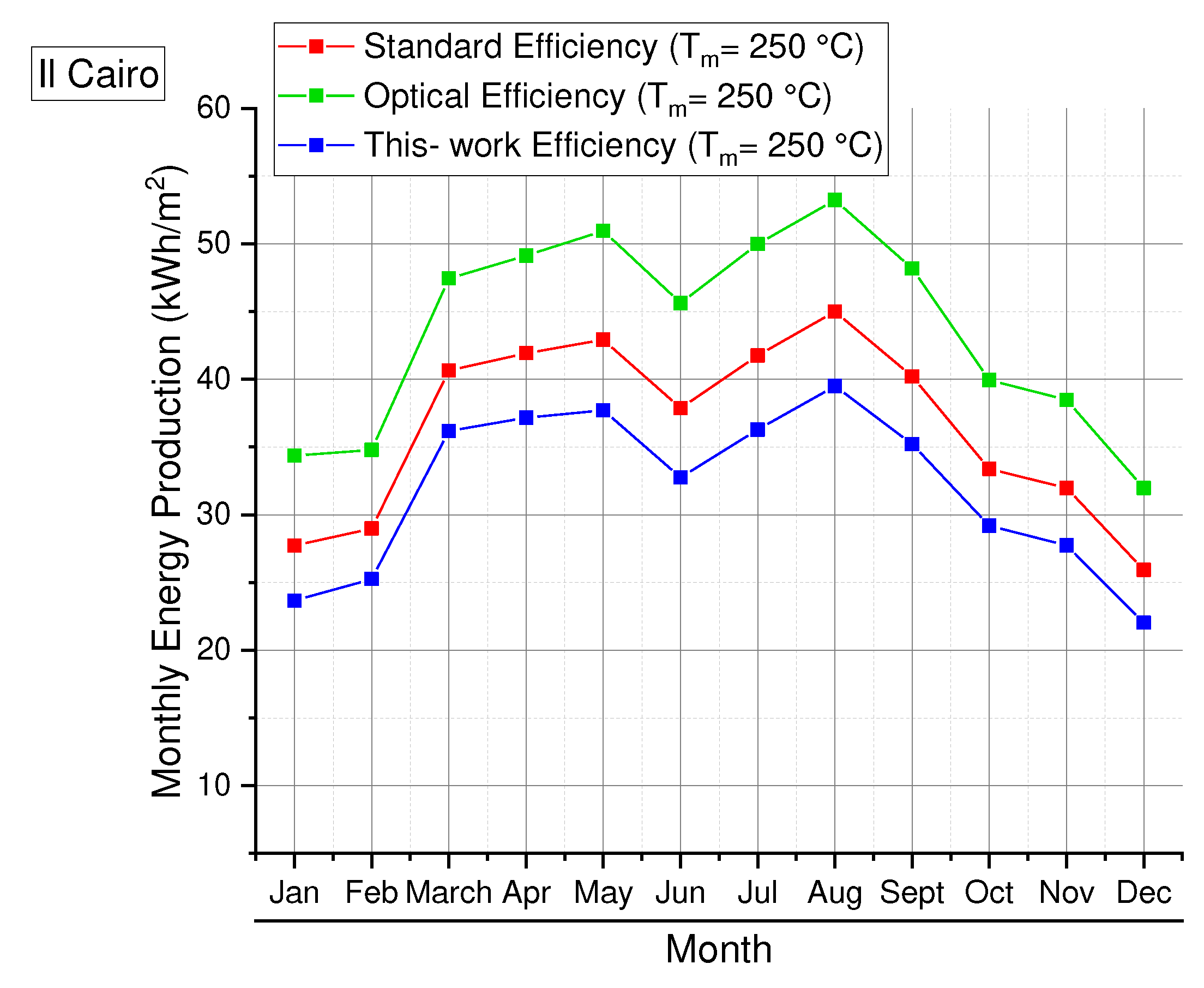
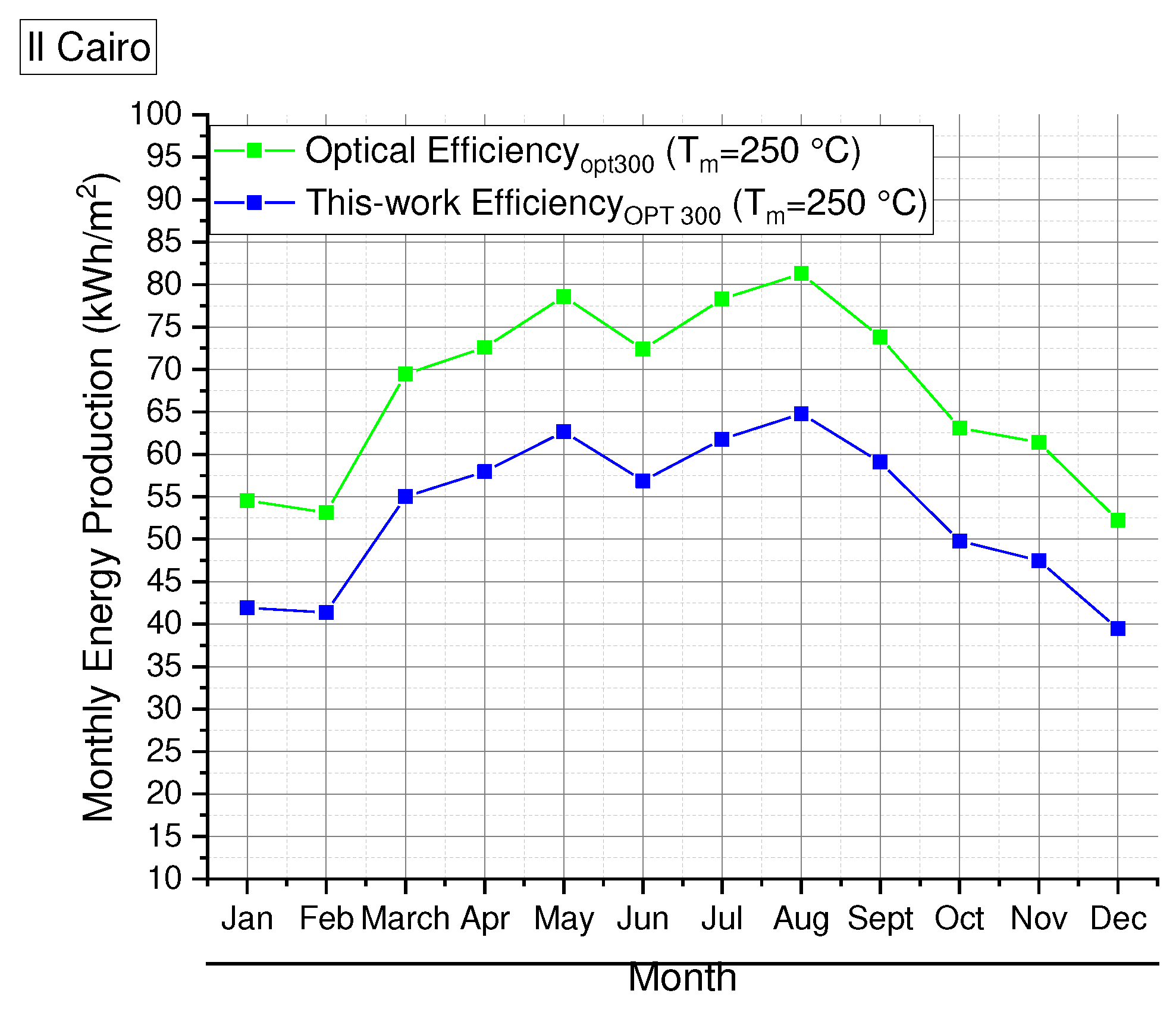
3.3. HVFPCs Annual Energy Producibility Calculation

The thermal efficiency of a solar thermal collector is the crucial parameter for energy predictions and estimating the collector's production under specific climatic conditions.
Failing to account for radiative losses in the efficiency equation can led to inaccurancies in estimating the collector's performance especially at high operating temperatures. Figure 6 presents the monthly energy production of the MT-Power at Tm=250 °C, calculated using 2019 irradiation data from the specific location (Il Cairo). The calculation considers the energy converted by a collector that is oriented to the south and tilted at 35 °.
Three distinct efficiency formulas were employed: Optical (illustrated by green line squares), This-Work (represented by blue line squares), and Standard (depicted by red line squares). It's apparent that relying on the Standard efficiency formula results in an overestimation of energy production. To be specific, for the year 2019, an annual energy production of 438 kWh/m2 would be projected In contrast, using the This-Work efficiency formula indicates a more conservative estimate of 383 kWh/m2, leading to a difference of roughly 13%.
Drawing from the MT-Power example, Figure 7 underscores the importance of accounting for additional conductive losses in the efficiency calculations of HVFPCs. The figure highlights the variance in monthly energy production of an HVFPC fitted with a new absorber (optimized at 300°C) set at an operating temperature of 250°C.
The comparisons are drawn between results obtained using the optical efficiency and those derived from the proposed This-Work efficiency model. The estimated annual energy production, as per the optical efficiency formula, stands at 811 kWh/m2. In contrast, the This-Work efficiency formula suggests a value of 638 kWh/m2. These calculations, too, were based on the 2019 irradiation data from Il Cairo.

4. Conclusions

This manuscript introduces a thermal efficiency model tailored to predict the performance of High Vacuum Flat Plate Collectors (HVFPCs). Unlike traditional models, the proposed framework gives explicit attention to radiative losses, the predominant energy loss mechanism in high vacuum collectors. These losses are inherently linked to the optical properties of the absorber that can be measured independently. The efficiency model equation (eq. (10)) includes the absorber optical properties and an additional heat conductive loss coefficient k, which can be determined using the standard efficiency coefficients (η0, c1, c2) specific to the HVFPC being analyzed. To validate the proposed efficiency model, it was applied to the TVP-Solar MT-Power HVFPC and its precision was confirmed when the zero-efficiency point for the MT-Power matched with the collector's certified stagnation temperature (302°C). Therefore, it's evident that the presented thermal efficiency model for HVFPCs is capable of computing thermal efficiency across the full spectrum of operating temperatures, extending to the collector's stagnation temperature, provided the optical properties of the absorber are known.
Moreover, the model was employed to predict the efficiency of HVFPCs, potentially equipped with different Selective Solar Absorbers (SSAs) optimized to meet heat demand at 200 °C and 300 °C.
This predictive capability it is not present in the efficiency formula that do not include the radiative term. This predictive aptitude paves the way for more accurate estimations of annual energy output of these optimized HVFPCs, as illustrated in figures 6 and 7.
In conclusion, the proposed efficiency model for HVFPCs is flexible and can provide valuable insights for designing and optimizing SSA for HVFP collectors taking in to account their annual energy production.

Acknowledgment

The Ph.D. grant of E.G is funded by the CNR-Confindustria “Dottorati di Ricerca Industriali” program XXXVI ciclo. This study was partially supported by the Eurostar Program powered by EUREKA and the European Community (Project ESSTEAM reference E! 115642 CUP B69J21036070005).

Nomenclature

Aabs Absorber Surface (m2) DHW Domestic Hot Water
Ac Collector Aperture Surface (m2) HTF Heat Transfer Fluid
c1 First Order Heat Loss Coefficient HVFPC High Vacuum Flat Plate Collector
c2 Second Order Heat Loss Coefficient IAM Incident Angle Modifier
cp Specific Heat at constant pressure (kJ/kg K) SSA Selective Solar Absorber
G Solar Irradiation (W/m2) sub Substrate
m ˙ Mass flow rate (kg/s) th thermal
Pabs Absorbed Power (W) IR InfraRed
Padd-loss Lost Power due to conductive losses (W) Symbols
Pem Emitted Power (W) α Spectrally averaged absorptivity
Pu Useful Power (W) ε Spectrally averaged emissivity
Tm Average Temperature (°C) η Efficiency
Tamb Ambient Temperature (°C) η 0 Zero-Loss efficiency
Tg Glass Temperature (°C) σ Stefan-Boltzmann constant (W/m2K4)
Tv Vessel Temperature (°C) λ Wavelength
Abbreviations k Conductive Heat losses coefficient (W /m2K)
abs Absorber
comm Commercial

References

  1. «United States Environmental Protection Agency».
  2. «Our world in Data website https://ourworldindata.org/co2-emissions».
  3. G. P. Thiel e A. K. Stark, «To decarbonize industry, we must decarbonize heat», Joule, vol. 5, fasc. 3, pp. 531–550, mar. 2021. [CrossRef]
  4. L. Kumar, M. L. Kumar, M. Hasanuzzaman, e N. A. Rahim, «Global advancement of solar thermal energy technologies for industrial process heat and its future prospects: A review», Energy Conversion and Management, vol. 195, pp. 885–908, set. 2019. [CrossRef]
  5. «IEA (2020), World Energy Statistics and Balances 2020 (database)».
  6. S. K. Verma, N. K. S. K. Verma, N. K. Gupta, e D. Rakshit, «A comprehensive analysis on advances in application of solar collectors considering design, process and working fluid parameters for solar to thermal conversion», Solar Energy, vol. 208, pp. 1114–1150, set. 2020. [CrossRef]
  7. S. C. Bhatia, A c. di, Advanced Renewable Energy Systems, (Part 1 and 2), 0 ed. WPI Publishing, 2014. [CrossRef]
  8. R. Eismann, «Accurate analytical modeling of flat plate solar collectors: Extended correlation for convective heat loss across the air gap between absorber and cover plate», Solar Energy, vol. 122, pp. 1214–1224, dic. 2015. [CrossRef]
  9. H. Herwig, «What Exactly is the Nusselt Number in Convective Heat Transfer Problems and are There Alternatives?», Entropy, vol. 18, fasc. 5, p. 198, mag. 2016. [CrossRef]
  10. D. Gao, J. D. Gao, J. Li, X. Ren, T. Hu, e G. Pei, «A novel direct steam generation system based on the high-vacuum insulated flat plate solar collector», Renewable Energy, vol. 197, pp. 966–977, set. 2022. [CrossRef]
  11. C. Benvenuti, «The SRB solar thermal panel», Europhysics News, vol. 44, fasc. 3, pp. 16–18, mag. 2013. [CrossRef]
  12. «TVP Solar, MT-30 datasheet <http://www.tvpsolar.com/files/pagine/1464011780_MTPower%20Datasheet%20(v4.2x)(ver5).pdf>».
  13. et al. , «Roadmap for the next-generation of hybrid photovoltaic-thermal solar energy collectors», Solar Energy, vol. 174, pp. 386–398, nov. 2018. [CrossRef]
  14. R. W. Moss, P. R. W. Moss, P. Henshall, F. Arya, G. S. F. Shire, T. Hyde, e P. C. Eames, «Performance and operational effectiveness of evacuated flat plate solar collectors compared with conventional thermal, PVT and PV panels», Applied Energy, vol. 216, pp. 588–601, apr. 2018. [CrossRef]
  15. C. B. Eaton e H. A. Blum, «The use of moderate vacuum environments as a means of increasing the collection efficiencies and operating temperatures of flat-plate solar collectors», Solar Energy, vol. 17, fasc. 3, pp. 151–158, lug. 1975. [CrossRef]
  16. H. Zheng, J. H. Zheng, J. Xiong, Y. Su, e H. Zhang, «Influence of the receiver’s back surface radiative characteristics on the performance of a heat-pipe evacuated-tube solar collector», Applied Energy, vol. 116, pp. 159–166, mar. 2014. [CrossRef]
  17. D. De Maio et al., «A Selective Solar Absorber for Unconcentrated Solar Thermal Panels», Energies, vol. 14, fasc. 4, p. 900, feb. 2021. [CrossRef]
  18. D. Gao et al., «Experimental and numerical analysis of an efficiently optimized evacuated flat plate solar collector under medium temperature», Applied Energy, vol. 269, p. 115129, lug. 2020. [CrossRef]
  19. M. A. Rosen, «Energy efficiency and sustainable development», IEEE Technol. Soc. Mag., vol. 15, fasc. 4, pp. 21–26, 1996. [CrossRef]
  20. D. E. Prapas, B. D. E. Prapas, B. Norton, e S. D. Probert, «Optics of parabolic-trough, solar-energy collectors, possessing small concentration ratios», Solar Energy, vol. 39, fasc. 6, pp. 541–550, 1987. [CrossRef]
  21. S. A. Kalogirou, «Solar thermal collectors and applications», Progress in Energy and Combustion Science, vol. 30, fasc. 3, pp. 231–295, 2004. [CrossRef]
  22. W. J. Platzer, D. W. J. Platzer, D. Mills, e W. Gardner, «Linear Fresnel Collector (LFC) solar thermal technology», in Concentrating Solar Power Technology, Elsevier, 2021, pp. 165–217. [CrossRef]
  23. S. Fischer e H. Drück, «Standards and Certification Schemes for Solar Thermal Collectors, Stores and Systems — An Overview about the Latest Developments», Energy Procedia, vol. 57, pp. 2867–2871, 2014. [CrossRef]
  24. F. Cao, K. F. Cao, K. McEnaney, G. Chen, e Z. Ren, «A review of cermet-based spectrally selective solar absorbers», Energy Environ. Sci., vol. 7, fasc. 5, p. 1615, 2014. [CrossRef]
  25. D. De Maio et al., «Multilayers for efficient thermal energy conversion in high vacuum flat solar thermal panels», Thin Solid Films, vol. 735, p. 138869, ott. 2021. [CrossRef]
  26. C. D’Alessandro et al., «Performance analysis of evacuated solar thermal panels with an infrared mirror», Applied Energy, vol. 288, p. 116603, apr. 2021. [CrossRef]
  27. D. De Luca, D. D. De Luca, D. Kortge, E. Di Gennaro, R. Russo, e P. Bermel, «Ultra-thin sputter-deposited infrared rugate mirror for enhancing solar-to-thermal energy conversion», Opt. Lett., vol. 47, fasc. 2, p. 230, gen. 2022. [CrossRef]
  28. D. De Maio, C. D. De Maio, C. D’Alessandro, A. Caldarelli, M. Musto, e R. Russo, «Solar selective coatings for evacuated flat plate collectors: Optimisation and efficiency robustness analysis», Solar Energy Materials and Solar Cells, vol. 242, p. 111749, ago. 2022. [CrossRef]
  29. J. R. Howell, M. P. J. R. Howell, M. P. Mengüç, K. Daun, e R. Siegel, Thermal Radiation Heat Transfer, 7a ed. Seventh edition. | Boca Raton : CRC Press, 2021. | Revised edition of: Thermal radiation heat transfer / John R. Howell, M. Pinar Mengüç, Robert Siegel. Sixth edition. 2015.: CRC Press, 2020. [CrossRef]
  30. C. D’ Alessandro et al., «Low Cost High Intensity LED Illumination Device for High Uniformity Laboratory Purposes», ENGINEERING, preprint, giu. 2020. [CrossRef]
  31. C. D’Alessandro et al., «Calorimetric testing of solar thermal absorbers for high vacuum flat panels», Solar Energy, vol. 243, pp. 81–90, set. 2022. [CrossRef]
Preprints 88327 g001
Figure 1. MT-Powerstandard efficiency curve and its mathematical extrapolation dashed line). In the figure is also indicated with the black arrow the point at which the efficiency should be equal to zero for MT-Power (Tm=302 °C).
Figure 1. MT-Powerstandard efficiency curve and its mathematical extrapolation dashed line). In the figure is also indicated with the black arrow the point at which the efficiency should be equal to zero for MT-Power (Tm=302 °C).
Preprints 88327 g001
Preprints 88327 g002
Figure 2. Simplified Scheme of an HVFPC.
Figure 2. Simplified Scheme of an HVFPC.
Preprints 88327 g002
Preprints 88327 g003
Figure 3. a) scheme of the components that form the structure of TVP-Solar HVFPC MT-Power; b) Fitted emissivity curve of the Selective coated commercial heat absorber mounted.
Figure 3. a) scheme of the components that form the structure of TVP-Solar HVFPC MT-Power; b) Fitted emissivity curve of the Selective coated commercial heat absorber mounted.
Preprints 88327 g003
Preprints 88327 g004
Figure 4. Standard (red), optical (yellow), and this work (blue) TVP-Solar MT-Power HVFPC efficiency curves: the optical efficiency is obtained considering only the thermal losses caused by radiative heat transfer while this work efficiency curve by considering the additional losses term obtained by fitting the proposed efficiency model.
Figure 4. Standard (red), optical (yellow), and this work (blue) TVP-Solar MT-Power HVFPC efficiency curves: the optical efficiency is obtained considering only the thermal losses caused by radiative heat transfer while this work efficiency curve by considering the additional losses term obtained by fitting the proposed efficiency model.
Preprints 88327 g004
Preprints 88327 g005
Figure 5. a): fitted thermal emittance of the commercial absorber mounted on TVP-solar HVFPCs (black dashed line) and thermal emittance of SSAs optimized to work at different operating temperatures: 200 °C (green dashed line) and 300 °C (red dashed line); b) : Thermal efficiency curves of TVP-solar HVFPC equipped with Commercial (black line ) and optimized SSAs obtained with the proposed efficiency model. For the optimized coatings are also reported the optical efficiency curves (dot line).
Figure 5. a): fitted thermal emittance of the commercial absorber mounted on TVP-solar HVFPCs (black dashed line) and thermal emittance of SSAs optimized to work at different operating temperatures: 200 °C (green dashed line) and 300 °C (red dashed line); b) : Thermal efficiency curves of TVP-solar HVFPC equipped with Commercial (black line ) and optimized SSAs obtained with the proposed efficiency model. For the optimized coatings are also reported the optical efficiency curves (dot line).
Preprints 88327 g005
Preprints 88327 g006
Figure 6. Comparison of monthly energy production (year 2019) of MT-power working at Tm =250 °C and installed at Il Cairo computed using optical (green), standard (red) and this-work (blue) efficiency formulas.
Figure 6. Comparison of monthly energy production (year 2019) of MT-power working at Tm =250 °C and installed at Il Cairo computed using optical (green), standard (red) and this-work (blue) efficiency formulas.
Preprints 88327 g006
Preprints 88327 g007
Figure 7. Comparison of monthly energy production (year 2019) of HVFPC equipped with coating optimized to work at Tm=300 °C considering an operating temperature of Tm =250 °C and installed at Il Cairo computed using optical (green), and this-work (blue) efficiency formulas.
Figure 7. Comparison of monthly energy production (year 2019) of HVFPC equipped with coating optimized to work at Tm=300 °C considering an operating temperature of Tm =250 °C and installed at Il Cairo computed using optical (green), and this-work (blue) efficiency formulas.
Preprints 88327 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated